A Downscaling Intercomparison Study: The Representation of Slope- and Ridge-Scale Processes in Models of Different Complexity

Spatially distributed meteorological information at the slope scale is relevant for many processes in complex terrain, yet information at this sub-km spatial resolution is difficult to obtain. While downscaling to kilometer resolutions is well described in literature, moving beyond the kilometer scale is not. In this work, we present a methodical comparison of three downscaling methods of varying complexity, that are used to downscale data from the Numerical Weather Prediction model COSMO-1 at 1.1 km horizontal resolution to 250 and 50 m over a domain of highly complex terrain in the Swiss Alps. We compare WRF, a dynamical atmospheric model; ICAR, a model of intermediate complexity; and TopoSCALE, an efficient topography-based downscaling scheme. Point-scale comparisons show similar results amongst all three models w.r.t. mean-error statistics, but underlying dynamics are different. Ridge-flow interactions show reasonable agreement between WRF and ICAR at 250 m model resolution. However, at 50 m resolution WRF is able to simulate complex flow patterns that ICAR cannot. Validation against Lidar data suggests that only WRF is able to capture preferential deposition of snow. Based on these findings and the significant reduction in computational costs, ICAR is a cost efficient alternative to WRF at the 250 m resolution. TopoScale performs very well in point-scale comparisons, but it is unclear if this can be attributed to the model itself or to the forcing data and the observations assimilated therein. Further study is required to quantify this effect.

1 Introduction

Interactions between the atmosphere and orography in alpine environments can threaten downstream communities with avalanching, flooding, or mass movement events (Petley, 2012), or support their livelihood with water resources (Sturm et al., 2017). Recent mass movement events on Piz Cengalo in Switzerland and in Chamoli (Shugar et al., 2021), India exemplify the humanitarian and economic cost of such events. Understanding how the frequency and distribution of these processes will change in the future is thus an area of focused research (Gariano and Guzzetti, 2016). These processes involve complex interactions between meteorological variables and terrain properties such as permafrost degradation (Seneviratne et al., 2012; Phillips et al., 2017), freeze-thaw action on rock fractures (Crozier, 2010), or precipitation infiltration into the subsurface pore space (Selby, 1988). Indeed, extreme precipitation has been found to coincide with mass movement events (Kirschbaum et al., 2012). Forecasting meteorological conditions in complex terrain, and precipitation in particular, remains challenging due to the interplay between local terrain-induced flows, microphysics, and atmospheric state (Mott et al., 2014; Gerber et al., 2017; Gerber et al., 2018). Orographic enhancement of precipitation (Houze, 2012), preferential deposition of snow (Lehning et al., 2008; Mott et al., 2018), and cold air pooling and thermal inversions are a few examples of processes that give rise to strongly heterogeneous spatial patterns (Zhong et al., 2001). Properly resolving such processes requires high spatial and temporal resolutions (Hearman and Hinz, 2007; Coulthard and Skinner, 2016). Prior studies have shown that running atmospheric models at spatial resolutions as high as 1.3 km (Garvert et al., 2007), 50 m (Gerber et al., 2019), 25 m (Raderschall et al., 2008) or 20 m (Mott et al., 2019) may be required to resolve the dynamics which give rise to these specific phenomena.

The temporal and spatial variability of snow accumulation can be associated with wind-driven processes ranging from orographic precipitation at large scale to preferential deposition of snowfall and wind-induced redistribution of snow at smaller scales (Mott et al., 2018). Following Mott et al. (2018) it is useful to distinguish between the mountain ridge scale (hundred to thousands of meters, or O (10²–10³ m) and the slope scale (several to hundreds of meters, or O (1–10² m). Gerber et al. (2019) recently demonstrated that the effect of terrain-flow-precipitation interactions may increase snow accumulation on the leeward side of the mountain ridge by about 30% with respect to the windward side. Wang and Huang (2017) showed how the deposition maxima shift from the windward side of a mountain under weak advection, to the leeward side with stronger winds. The ability of models to capture the change in snow accumulation due to terrain-induced wind effects was shown by multiple studies to be strongly dependent on the representation of the terrain-induced flow field (Vionnet et al., 2017; Gerber, 2018; Roth et al., 2018; Gerber et al., 2019). Furthermore, a model study performed by Comola et al. (2019) applying Large eddy simulations showed that ridge-scale deposition patterns strongly depend on the governing processes inertia, flow advection and gravity.

The technique of running physically based models to downscale coarser model output, referred to as dynamic downscaling, can be computationally costly over large domains or long time periods. As an alternative, downscaling of coarse model output using empirical relationships and existing spatial patterns is often done through a process known as statistical downscaling (Fowler et al., 2007; Schomburg et al., 2012). The major drawbacks of using such statistical downscaling approaches are their decreased accuracy and agreement when predicting extreme events. Importantly, these extreme events often trigger the dynamic land-atmosphere processes mentioned above (Caine, 1980). Furthermore, statistical methods are generally unable to account for dynamical inter-variable dependencies (Themeßl et al., 2012; Gutiérrez et al., 2013; Sunyer et al., 2015), although methods exist to include statistical inter-variable dependencies (Li and Babovic, 2019).

It is difficult to evaluate the accuracy of downscaling schemes at resolving spatial patterns of variables at high resolutions, since distributed observations at these resolutions are rare or non-existent. Thus, evaluations of dynamic and statistical downscaling focus on point-scale comparisons, comparison with spatially-interpolated point observations, or qualitative comparisons between dynamic and statistical downscaling schemes. As discussed in Flaounas et al. (2013), comparison with spatially-interpolated point observations introduces biases due to the interpolation technique used, and point-based evaluations may favor statistical techniques that train on data from the same locations used in evaluation, even if separate training and evaluation time periods are used. In light of this, in this study we will not rely on spatially interpolated products. Results from intercomparison studies rarely observe identical spatial patterns between statistical and dynamic downscaling in general (Flaounas et al., 2013; Gutmann et al., 2016; Tang et al., 2016). Other studies have noted both strong seasonality to the predictive accuracy of dynamic and statistical downscaling schemes, with higher predictive skill in winter than summer, and overall higher predictive skill for precipitation frequency than extremes (Haylock et al., 2006; Schmidli et al., 2007). Schmidli et al. (2007) noted that despite this seasonal variability, dynamic downscaling schemes had more agreement among themselves than statistical downscaling schemes over all seasons. Due to the aforementioned dearth of spatially extensive direct observations, it is challenging to judge which approach will yield a more “correct” pattern. Still, the discrepancy in observed spatial patterns can sometimes be attributed to physical properties captured by dynamic downscaling schemes (Gutmann et al., 2012). Due to this, conclusions of these intercomparison studies often focus on the agreement between ensembles of downscaling schemes, particularly concerning future trends or large-scale spatial patterns. For a more thorough review of the literature on statistical and dynamic downscaling schemes, the reader is referred to Vaittinada Ayar et al. (2016).

Intercomparison studies of downscaling techniques often focus on scale lengths greater than the sub-kilometer scale, meaning that they have not yet evaluated model accuracy within the context of slope scale processes. Advances in atmospheric modeling over the past decades have recently allowed atmospheric models to rival the predictive skill of high-resolution statistical interpolation techniques used to validate them (Lundquist et al., 2019). This advance is particularly useful when forecasting extreme events, as atmospheric models rely on physical principles for prediction instead of empirical relationships dependent on prior observations of extreme events. Similar to this, statistical downscaling techniques that propagate prior patterns into a future climate may incorrectly assume that spatial patterns are invariant to changes in the climate (Vrac et al., 2007; Gutmann et al., 2012). In addition to improvements in the accuracy of atmospheric models, the development of more computationally efficient algorithms (Fuhrer et al., 2014) and investments in research computing resources have allowed these models to be run at high spatial resolutions down to 50 m over single basins (Gerber et al., 2019) or 1 km over a mountain range (Pontoppidan et al., 2017), and in experimental settings, even the globe (Fuhrer et al., 2018). At these scales the topographic heterogeneity of complex terrain and the resulting meteorological heterogeneity can be better resolved.

With a variety of options for downscaling meteorological variables in complex terrain, each downscaling approach should be examined for its representation of physical processes and the horizontal and temporal resolution that can be simulated given available computational resources. This tradeoff between model resolution, computational efficiency, and physical accuracy is the focus of this intercomparison study. Here, the ability of three downscaling schemes to downscale meteorological variables to high resolution grids ($<=250$ m) in complex terrain is examined. This scale regime is chosen based on the studies discussed above, which showed such resolutions are necessary to resolve spatial heterogeneity of precipitation and winds (Raderschall et al., 2008; Gerber et al., 2019). An important goal of this work is to provide an overview of the strengths and weaknesses of these models, not only in terms of absolute performance but also in relation to their computational costs. This will inform future users on the right downscaling tool for their purposes, as downscaling e.g. an ensemble of climate change projections will require a different approach than the downscaling of a single meteorological event. We therefore analyzed computational costs of the models and their limitations regarding model domains and time frames.

The models featured in this comparison are the Weather Research and Forecasting (WRF) model (Skamarock et al., 2008a), the Intermediate Complexity Atmospheric Research (ICAR) model (Gutmann et al., 2016), and TopoSCALE (Fiddes and Gruber, 2014), a computationally efficient topography-based downscaling scheme. These models are further described in Section 2. In Section 3.1, modeled variables are compared to observations from a network of meteorological sensors. In Section 3.2, spatial patterns of precipitation are then compared between the models, and modeled spatial patterns of snow deposition for particular storm events are compared to LiDAR observations of snow depth. The computational demands of these individual downscaling schemes are then contrasted in Section 3.3, followed by a discussion of their strengths and weaknesses in Section 4. To improve readability, in this text, resolution will refer to horizontal spatial resolution unless otherwise indicated.

2 Methodology

This study comprises one efficient topography based approach (TopoSCALE) and two dynamic meteorological models of different complexity (WRF, ICAR). As these approaches differ with regards to forcing data, downscaling methodology and computational costs, we will quantitatively and qualitatively compare the strengths and limitations of the models and their performance at different spatial and temporal resolutions with a particular focus on the very high resolutions (slope scale, i.e. hundreds of meters and below). The time periods, model domains and spatial and temporal resolutions that the models were run for, are specified in Table 1. In order to run each model in its optimal configuration we allow the models to use different physical schemes based on model requirements (see details below). However, to be able to have a direct comparison of the atmospheric models with respect to precipitation patterns and the influence of the boundary layer flow on the ridge-scale precipitation patterns the same microphysical scheme is used by ICAR and WRF. All models are driven by COSMO-1 analysis. For all models (both forcing and downscaling), the output consists of hourly instantaneous values. As we are particularly interested in downscaling meteorological fields to very high spatial resolutions, all models are run for a target model domain at 250 m spatial resolution (Figure 1, D1), that covers the region of Davos and Prättigau (Figure 1), with a size of 37.5 and 45 km in west-east and north-south direction, respectively. We introduce a smaller target domain (D2) for 50 m resolution runs to allow us to highlight the benefits of fully dynamical models and models resolving non-linear effects such as WRF. This is a dedicated test for model runs focused on intense precipitation events. All models are run at 50 m resolution for target area D2 (Figure 1) to reflect the impact of ultra-high resolution terrain on the downscaling of meteorological variables. We include two considerable storm events on our analysis, which occurred in spring 2017 and winter 2019 (Table 1). All models are tested in their ability to reproduce the spatial and temporal variability of slope-scale processes during strong precipitation events. For model evaluation at the point scale, we use the root-mean-square error (RMSE) and mean bias error (MBE) defined as

$RMSE=\sqrt{\frac{{\sum }_{t=1}^T{\left(y_{mod}-y_{obs}\right)}^2}{T}}andMBE=\frac{1}{T}\sum _{t=1}^T\left(y_{mod}-y_{obs}\right)(1)$

where t = 1, … , T are individual observations, y_mod is the modeled parameter, and y_obs the observed parameter.

TABLE 1

TABLE 1. Overview of model runs.

FIGURE 1

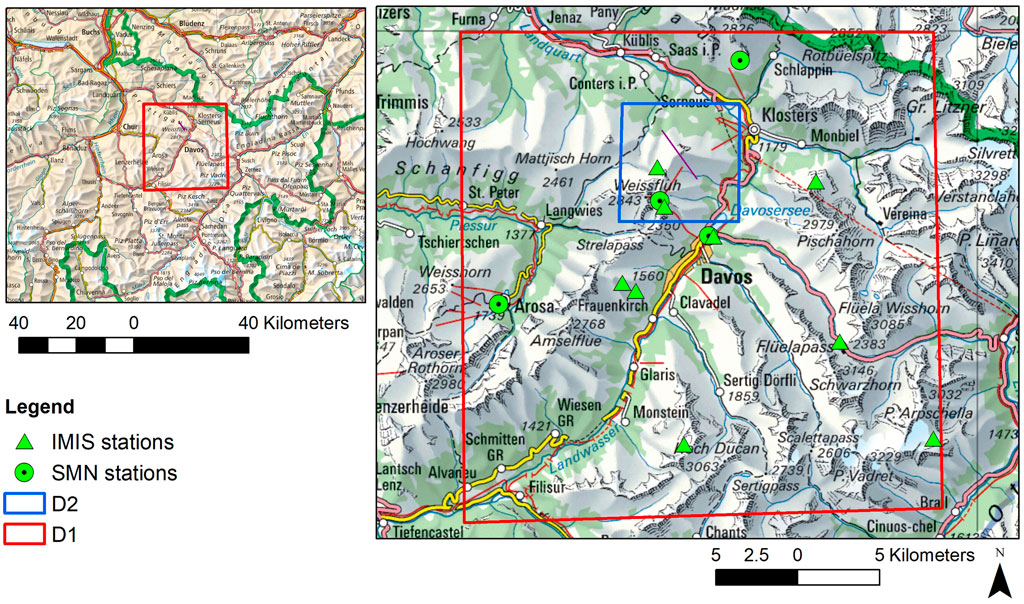
FIGURE 1. Domains D1 and D2. IMIS and SMN stations are shown. The purple NW-SE line in the center of D2 indicates the transect for the cross section shown in Figures 8, 9. Map data from Swisstopo, copyright Bundesbehörden der Schweizerischen Eidgenossenschaft.

ICAR and TopoSCALE are additionally analyzed for season-long simulations. For this purpose, these two models are run for two 8 months-long periods from October through May (run4 and run5, see Table 1 for details). Due to the very high computational costs of WRF, the analysis of WRF is restricted to the shorter simulations of run1, run2 and run3.

2.1 Forcing Data: COSMO-1

All downscaling models are driven by analysis data from the COSMO-1 model¹, operated by the Swiss weather service MeteoSwiss². This analysis dataset consists of the first 3 h of each operational run, which is initialized 8 times per day. The model uses a sophisticated data assimilation scheme described in Schraff et al. (2016). Some of the meteorological stations used for the validation of the downscaling methods are included in this assimilation scheme, which is discussed in Section 2.3. The COSMO-1 model has a spatial resolution of 0.01°, which roughly equates to 1.1 km. The COSMO-1 model is driven by boundary conditions from the IFS ENS global ensemble system, and uses a rotated grid to minimize numerical errors. It has 80 vertical levels with thickness ranging from 23 m at the surface to 800 m at the model top, which is around 22 km above sea level. The model uses the Smooth LEvel VErtical (SLEVE) coordinate (Schär et al., 2002; Leuenberger et al., 2010), a vertical coordinate scheme specifically developed for the complex terrain of the Alps, that is aimed at minimizing numerical errors due to vertical grid distortion.

2.2 Model Description and Settings

2.2.1 TopoSCALE

TopoSCALE (Fiddes and Gruber, 2014) can be described as an efficient physically-based downscaling scheme which formulates physical principles to account for the effect of a high-resolution topography on boundary layer meteorology. Its main purpose is to generate high resolution output that account for the main consequences of surface variability and enable efficient simulations up to large (regional) scales. TopoSCALE performs a 3D interpolation of atmospheric fields available on pressure levels to account for time varying lapse rates and a topographic correction of radiative fluxes. These include a cosine correction of incident direct shortwave radiation on a slope, adjustment of diffuse shortwave and longwave by the sky view factor and elevation correction of both longwave and direct shortwave. These radiation correction schemes have recently been shown to have limited accuracy (von Rütte et al., 2021) but are computationally efficient and consistent with the general complexity of TopoSCALE. Additionally, a simple lapse rate is implemented to allow orographic enhancement of precipitation to be considered (Liston and Elder, 2006). In practice, variability in snow accumulation and depletion is controlled mainly by the energy balance (wind redistribution is not considered). TopoSCALE is coupled to the snow model FSM (Essery, 2015) to simulate snow parameters and surface temperature. It has been well tested in various geographical regions and applications, e.g., Permafrost in the European Alps (Fiddes et al., 2015), Northern hemisphere permafrost (Westermann et al., 2015), Antarctic permafrost (Obu et al., 2020), Arctic snow-cover (Aalstad et al., 2018), Alpine snow cover (Fiddes et al., 2019). Typically, TopoSCALE has been driven by reanalysis from ECMWF (ERA-Interim, ERA5). In this study the scheme is adapted for a COSMO-1 forcing, with topography based on the SRTM30 dataset³, resampled to 50 and 250 m. For more details on TopoSCALE the reader is referred to Fiddes and Gruber (2014).

2.2.2 ICAR

ICAR (Gutmann et al., 2016) is a simplified three-dimensional atmospheric model. The input requirements for ICAR are the same as those of a regional climate model (RCM): three-dimensional time-varying temperature, pressure, humidity, and wind fields. However, unlike a traditional RCM, ICAR uses the three-dimensional fields of pressure and wind from the driving low-resolution model throughout the domain, while temperature and humidity are only applied at the boundaries of the model as in a traditional RCM. ICAR advects heat and moisture based on a transient three-dimensional wind field. This wind field is calculated from the forcing dataset and interpolated onto the high-resolution topography. This forms the primary simplification in ICAR; it permits ICAR to avoid directly solving the Navier–Stokes equations of motion, which form the numerical core of a traditional atmospheric model. ICAR uses microphysics scheme(s) similar to other atmospheric models to calculate precipitation and other hydrometeorological and thermodynamic tendencies.

Low-resolution fields are linearly interpolated to the ICAR high-resolution grid, and pressure is adjusted for the change in elevation between the interpolated input grid and the ICAR grid. The model version used for the work described here makes use of a Smooth Level Vertical (SLEVE) coordinate as described in Schär et al. (2002); Leuenberger et al. (2010), where different decay rates for small scale and large scale topography can be set. This allows for better advection and smaller numerical errors. The boundary layer scheme is a simple local scheme based on Hong and Pan (1996). The microphysics scheme used is described in Thompson and Eidhammer (2014). The surface scheme is the Noah scheme described in Chen and Dudhia (2001). Radiation is dealt with by a simple scheme based on Finch and Best (2004). No convection parameterization is used and the advection is handled by the simple scheme as described in Gutmann et al. (2016) (Eq. 10), with the exception that density is not taken into account in the advection equation. The model’s internal time step is adaptive, and is calculated each forcing time step based on the maximum wind speed and spatial resolution. ICAR simulations are run at a horizontal resolution of 250 and 50 m, with 60 vertical layers that increase in thickness from 9.7 m at the bottom to 975 m at the model top, which is at 10.200 m above the surface. ICAR’s vertical coordinate is height-based but under standard atmospheric pressure the model top would roughly equate to 250 hPa. The domain corresponds to D1 in Figure 1 with an additional km around the borders.

Topography and land use information are based on the Aster 1 s digital elevation model (DAAC, 2019) and the Coordination of Information on the Environment (Corine) dataset (European Environmental Agency, 2006), respectively. The static data are prepared using WRF’s preprocessing scheme as described in (Gerber and Sharma, 2018). To avoid pressure gradient errors caused by steep slopes (de Wekker, 2002), the 1-2-1 smoothing option of WRF (Gerber and Sharma, 2018) is applied to keep all slopes in domain D1 and D2 below 45°.

The most notable changes in ICAR with regards to the description in Gutmann et al. (2016) are: 1) The addition of a SLEVE vertical coordinate (Schär et al., 2002; Leuenberger et al., 2010) described earlier in this section; and 2) We do not use linear mountain wave theory to calculate the disturbances to the windfield. Given the high spatial resolution and the complexity of the topography, it highly debatable whether the atmosphere can be assumed to be in a steady state—a crucial assumption for mountain wave theory to apply. Therefore, a new wind solver has been developed, whose working can be summarized as follows: First, the grid-relative vertical velocity is calculated using the direct-differencing method to balance out any existing divergence in the horizontal wind field. This step follows the same procedure that is in the original ICAR model (Gutmann et al., 2016). Testing showed that this method can produce large vertical velocities near the model top. To remedy this, the grid-relative vertical velocity at the model top is subtracted from the vertical profile of grid-relative vertical velocity, weighted by height above ground:

$w_{adj}=w-w_{top}\frac{z}{z_{top}}(2)$

where z is the elevation above ground, z_top is the height of the model top, w_top is the grid-relative vertical velocity at the model top for a given column, and w is the grid-relative vertical velocity obtained from the direct-differencing step. This step introduces divergence into the 3D wind field by unbalancing the horizontal and vertical velocities. To re-balance the 3D wind field while maintaining the new grid-relative vertical velocity, the divergence reduction approach outlined in Goodin et al. (1980) is used to adjust the horizontal vectors to balance the prescribed grid-relative vertical velocity profile.

These new features are featured as optional settings in version 2 (v2) of the model linked to in Section 6.

2.2.3 WRF

The non-hydrostatic and fully compressible Weather Research and Forecasting (WRF) model (Skamarock et al., 2008b) is one of the most widely used atmospheric models. In this study, we use version 4.1.5. Simulations for run1 and run 2 are run with a nested approach with 2 domains. The parent domain D0 covers a domain of about 184 km in west-east direction and 221 km in south-north direction with a horizontal resolution of 1.25 km centered over the region of Davos (not shown in Figure 1). Domain D1 is nested into this domain with a resolution of 250 m, and is shown in Figure 1. Both simulation domains are run with 60 vertical levels, with the model top at 150 hPa. The simulation timesteps are 5 and 1 s for domains D0 and D1, respectively. Simulation run3 is run with an additional nest (domain D2) with a horizontal resolution of 50 m and 90 vertical levels. The simulation setup is similar to the setup by Gerber et al. (2018), with some adaptations. The boundary layer is parameterized using the Shin-Hong scale–aware scheme (Shin and Hong, 2015). Mixing terms are evaluated in physical space and the subgrid scale turbulence is solved by the horizontal Smagorinsky first order closure while the vertical diffusion is taken care of by the boundary layer scheme (Shin and Hong, 2015).

To be able to better asses how the dynamics affect results, in both ICAR and WRF microphysics are parameterized by the Thompson and Eidhammer scheme (Thompson and Eidhammer, 2014). The land surface is taken care of by the Noah land surface model with multiparameterization options (Niu et al., 2011; Yang et al., 2011), which is not available in ICAR. The link between the surface and the atmosphere is parameterized by the Monin-Obukhov surface layer parameterization (Dyer and Hicks, 1970; Paulson, 1970; Webb, 1970; Zhang and Anthes, 1982; Beljaars, 1995). Noah-MP is run in default mode, except from the partitioning of rain and snow, which is snowfall if T_air < T_frz + 2.2^oK (Niu et al., 2011). The long- and shortwave RRTMG radiation schemes (Iacono et al., 2008) are called every 5 min. Table 2 lists the main differences in model set-ups and parameterizations.

TABLE 2

TABLE 2. Overview of main components/modules for the downscaling models.

Topography and land use information are based on the Aster 1 s digital elevation model (DAAC, 2019) and the Coordination of Information on the Environment (Corine) dataset (European Environmental Agency, 2006), respectively. The static data was prepared as WRF input based on Gerber and Sharma (2018). To avoid pressure gradient errors caused by steep slopes (de Wekker, 2002), one smoothing cycle using the 1-2-1 smoothing option of WRF (Gerber and Sharma, 2018) is applied to keep all slopes in domain D1 below 45° in simulations run1 and run2. Four smoothing cycles were applied to keep all slopes in domain D2 below 45° in simulation run3. For consistency between the domains within one simulation run the same smoothing is applied for all domains. Additionally, the roughness length of snow is set to 0.2 m to take missing roughness elements into account (Gerber et al., 2018). These procedures are the same for the WRF and ICAR simulations.

2.3 Validation Data

2.3.1 Station Data: IMIS and SMN Station Data

For the point validation 4 SMN (SwissMetNet) and 10 IMIS (Intercantonal Measurement and Information System) stations located in domain D1 are used. The recorded time series of hourly and daily wind speeds, air temperature and snow depths are used to compare the models’ output to. The IMIS network (Lehning et al., 1999) was developed to assist in avalanche warning, and therefore has stations predominantly located in the mountainous area of the country. IMIS stations are located at either exposed or sheltered locations, and are classified as such. This allows us to asses the performance of the models in both types of terrain. For wind speed and direction, we therefor only use the IMIS stations, so that we can separately assess model performance in exposed vs. sheltered locations.

The SMN network was developed to aid in weather forecasting, and has more stations at middle and low elevations compared to the IMIS network. There are various differences w.r.t. instrumentation between the stations from these two networks, the most relevant for the current study are discussed here briefly. Temperature sensors at the SMN stations are ventilated, which minimizes the effects of radiation on the temperature measurements. The IMIS stations do not have ventilated temperature measurements (Huwald et al., 2009). IMIS station measure the snow depth by means of SR50 sonic ranger, whereas SMN stations only measure precipitation. This is however done with heated precipitation gauges. Although some IMIS stations also feature simple precipitation gauges, since these are not heated or shielded the errors are significant (Yang et al., 1999) and we therefor exclude them in this study. Wind measurements at IMIS stations are conducted at 6.8 m above the (snow free) surface by means of Young wind sensors, whereas SMN stations measure wind speed at 10 m above the (snow free) surface. For both station types, wind speeds, wind direction, 2 m temperature and humidity are hourly averaged values, whereas snow height shows an instantaneous (current) value, and precipitation is the hourly sum.

2.3.2 Snow Depth Distribution

Snow depth data from Airborne Laser Scanning (ALS) is used for a subset of domain D1. Data was acquired on 3 days during 2017 (20 March, 31 March and 17 May) providing important information of snow accumulation and ablation patterns. The snow-off flight was conducted on August 29, 2017 to yield the summer digital elevation model. The measurement setup included a Riegl Q -1560 ALS scanning at a 800 kHz pulse rate with a 60° scan angle (Mazzotti et al., 2019). The ALS-derived data set from 20 March in 1 m resolution was validated against data from snow probing within the forest. This resulted in a RMSE of 13 cm and a bias of −5 cm (Helbig et al., 2021). The ALS data set used in this study covers an area of about 260 km² in 3 m resolution. The high-resolution snow depth data is aggregated to 50 m resolution and 250 m resolution grids. The time period between 20 and 31 March was mainly governed by snow ablation. Contrary, snow depth changes between March and May suggest a strong influence of preferential deposition of precipitation during this time period of 7 weeks covering several precipitation events. The data set is therefore used to test model performances in reproducing solid precipitation amounts per elevation bands and in capturing leeward slope loading by preferential deposition of snowfall.

3 Results

3.1 Model Performance at the Point Scale

Figures 2, 3 show the error statistics of modeled wind, air temperature, relative humidity and precipitation at the IMIS and SMN stations. In order to characterize the effect of topographic exposure to wind, the IMIS stations are grouped by sheltered and exposed locations according to IMIS standards. For the point-scale comparison Root-Mean-Square error (RMSE) and Mean Bias Error (MBE) statistics are calculated over the hourly values of run1 and run2 (Figure 2), and of run4 and run5 (Figure 3). The number and type of stations that the statistics are calculated over are indicated in the plot. It is worth reiterating that data from the SMN stations are assimilated into the COSMO-1 model. This will reduce the error for the COSMO-1 model. Neither of the downscaling methods assimilates any observational data, which allows them to deviate from the forcing in varying degrees: For ICAR and WRF most forcing is only applied at the domain boundaries, although interpolated forcing for wind and pressure are applied throughout the domain for ICAR. TopoSCALE has less freedom to deviate from the forcing data as it operates on 1D samples of the forcing data.

FIGURE 2

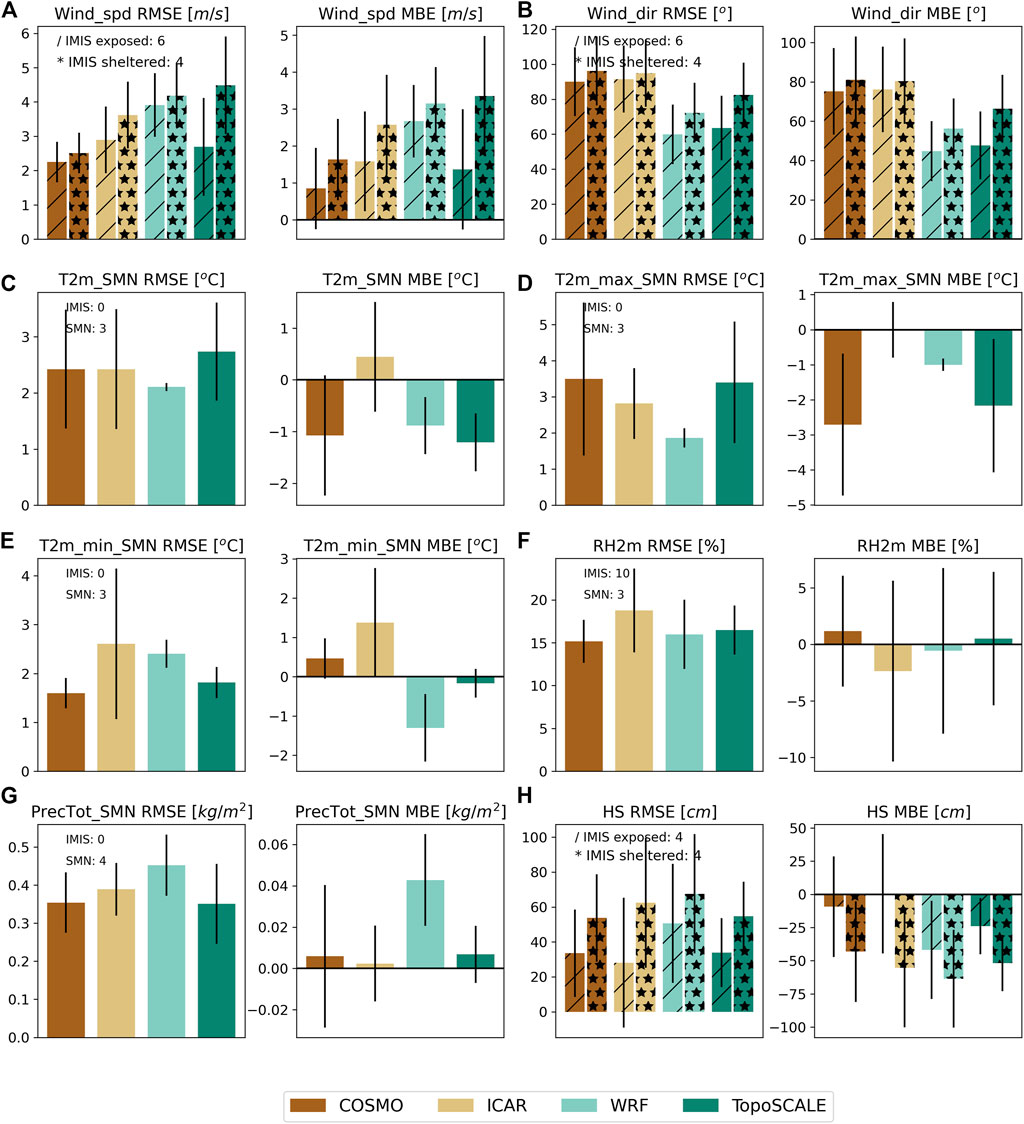
FIGURE 2. Panel pairs of average Root-Mean-Square (RMSE) and Mean Bias Errors (MBE) for point-scale comparison of (A) wind speed (Wind_spd), (B) Wind direction (Wind_dir), (C) 2 m air temperature (T2m), (D) daily maximum 2 m air temperature (T2m_max), (E) daily minimum 2 m air temperature (T2m_min), (F) relative 2 m humidity (RH2m), (G) total precipitation (PrecTot) and (H) snow depth (HS). These results are based on run1 and run2, and are averaged over the stations used for each parameter’s analysis. Annotated in each panel pair is the number of stations from each network that the calculations are based on. Error bars indicate standard deviations.

FIGURE 3

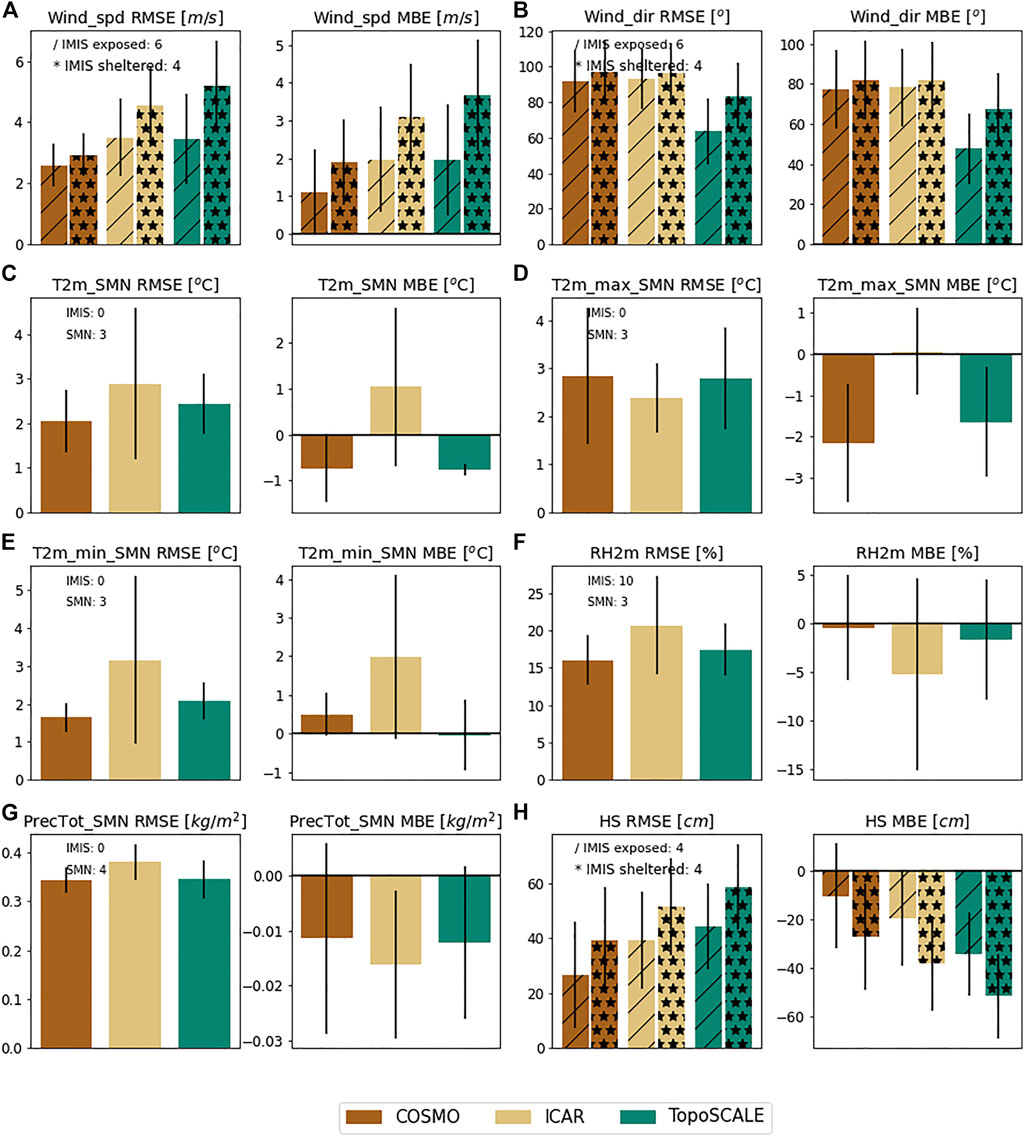
FIGURE 3. Panel pairs of average Root-Mean-Square (RMSE) and Mean Bias Errors (MBE) for point-scale comparison of (A) wind speed (Wind_spd), (B) Wind direction (Wind_dir), (C) 2 m air temperature (T2m), (D) daily maximum 2 m air temperature (T2m_max), (E) daily minimum 2 m air temperature (T2m_min), (F) relative 2 m humidity (RH2m), (G) total precipitation (PrecTot) and (H) snow depth (HS). These results are based on run4 and run5 (i.e., 2 full winter seasons), and are averaged over the stations used for each parameter’s analysis. This number of stations is annotated in each panel pair specified per network and type. Error bars indicate standard deviations.

3.1.1 Wind

Figure 2A Shows the average root-mean-square error and average mean bias error of modeled wind velocity at the first grid level compared to the IMIS stations in the domain. For this parameter, we choose to distinguish between the exposed and sheltered IMIS locations, and exclude the SMN stations, because the SMN stations cannot be easily categorized as exposed or sheltered, and it is insightful to look at these to categories separately.

All four models, including COSMO-1, tend to overestimate wind velocities, as can be seen from the positive bias ranging between 1 m/s (COSMO) and 3 m/s (WRF). The performance of the models is very similar for the event-based simulations (runs 1 and 2, Figure 2) and the seasonal simulations (Runs 4 and 5, Figure 3). Comparing the downscaling methods, the performance of wind speed is slightly better for ICAR. All models tend to particularly overestimate wind speeds at sheltered locations, indicating that the 250 m model resolution is still not capable of resolving sheltered locations in mountainous terrain. This finding is in agreement with Gerber et al. (2018), who showed that locally sheltered locations of meteorological stations are not well represented in models, even at a scale of hundreds of meters. TopoSCALE performs similar to ICAR for the exposed locations (Figure 3), or even slightly better (Figure 2), whereas its performance in sheltered locations is the poorest of all 3 downscaling methods. The overall high biases in wind speed for all models might be explained by two reasons. First, a considerable positive bias is already present in the forcing data (COSMO-1). With increasing model resolutions ICAR and WRF predict terrain-induced flow acceleration at high elevations, which might explain the increase in the positive bias shown by the higher resolution models. The wind stations in domain D1 are all located at mid to high elevations, where such terrain-induced speed up effects are to be expected. A domain featuring more low-elevation stations might therefore display a lower bias. We can plot the bias against the station elevations (Figure 4) to confirm this hypothesis. For COSMO-1, ICAR and TopoSCALE, there is virtually no bias below 2000 m.a.s.l. Above this elevation, bias (and spread) increase, especially for sheltered IMIS stations (indicated with a “+” in Figure 4). We can also see that WRF’s positive bias occurs over all elevations. This is in line with several studies noting a positive bias in WRF’s wind speeds (Gómez-Navarro et al., 2015; Gerber et al., 2018). Secondly, the strong positive bias is to some degree a result of the difference between model level and actual measurement height [mean height of lowest mass level: 4.7 m (ICAR), 22.5 m (WRF), and 9.5 m (COSMO-1)]. We have chosen not to use a log law to correct for height due to strong uncertainties associated with the choice of the roughness length (for further discussion see Section 4). Since ICAR has smaller model layers close to the surface than WRF or COSMO-1, the difference between measurement height and first model level is smallest for ICAR and might thus affect the results.

FIGURE 4

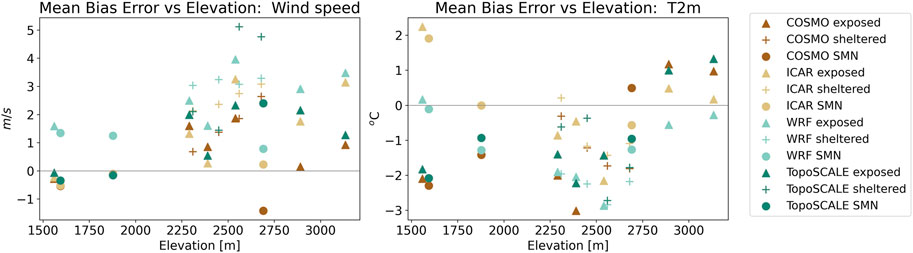
FIGURE 4. Mean Bias Error (MBE) vs. station elevation, for hourly temperature (left) and wind speed (right) measurements. Included are all IMIS stations [classified as exposed (triangle) or sheltered (plus)] and the SMN stations (dot), which is more than the analysis in Figure 2. Plot is based on the event simulations in run1 and run2.

The comparison of modeled and measured wind directions (Figure 2B) looks somewhat different than for wind speed. Both the downscaling methods as well as the forcing data show significant deviations in wind direction with biases ranging between 40 and 80°. For the downscaling methods, ICAR shows the largest errors, both in absolute (RMSE) and bias terms. ICAR exhibits the same bias as COSMO-1, since no deflection or directional modification of the wind field is done in the model. WRF and Toposcale perform slightly better. Similar to wind speed, the bias in wind direction is larger for sheltered locations as these topographic features are not well represented in the models. For the full winter season simulations (Figures 3A,B), the results look very similar, albeit the magnitude of the RMSE is slightly larger.

3.1.2 Air Temperature and Relative Humidity

Figure 2C shows the RMSE and MBE of modeled air temperature compared to three SMN stations for the event-based simulations. The same statistics are shown for the seasonal scale in Figure 3C. The analysis was limited to the SMN stations, as these are the only ones with ventilated temperature sensors, which means they are not affected by heating due to radiation. COSMO, WRF and TopoSCALE all under-predict air temperatures at the SMN stations. For both the event- (Figure 2) and seasonal simulations (Figure 3), the forcing data (COSMO) already shows a negative bias of approx. 1°C at these 3 stations. ICAR converts this to a positive bias in both the event-based (0.3°C) and season-long simulations (1°C), whereas WRF and TopoScale maintain a negative bias with the same magnitude as the forcing data. If we look closer to how these errors relate to the station’s elevation (left panel of Figure 4), we can see that COSMO-1 and TopoSCALE have negative biases at lower ($<$ 2000 m) elevations, that tend to 0 or slightly positive with increasing elevation. ICAR on the other hand has a significant positive bias at low elevations, that however tends to 0 with increasing elevation. WRF has an overall negative bias, that is most pronounced in the 2,000–2,700 m.a.s.l. range, which is where all models show the strongest negative bias. However, the IMIS stations in this plot are not ventilated, which means that on clear days with low wind speeds a negative model bias is to be expected due to the radiative heating of the sensors. When basing the same analysis solely on the ventilated SMN stations, the conclusions are the same, although the low number of measurement points (3) does not yield high confidence.

We also compare the models’ abilities to simulate the daily maximum and minimum temperatures at 2 m above the surface (Figures 2D, 3D and Figures 2E, 3E, respectively), which reflects the ability of the models to capture diurnal dynamics. This analysis shows that except for ICAR, all models underestimate the daily temperature maximum, with WRF displaying the lowest RMSE. The temperature minima are overestimated by ICAR, whereas WRF underestimates the daily minima. TopoSCALE performs the best in downscaling daily minimum temperatures, with a bias close to 0. These results emphasize the tendency of WRF to show strong diurnal cycles of air temperatures. Contrarily, ICAR tends to increase the overall air temperatures with rather small diurnal cycles.

Figures 2F, 3F show the comparison of relative humidity for the stations. Results for all three models are very similar with ICAR showing slightly higher errors and negative bias. This could be a result of the slight temperature overestimation (positive bias) in subplots C through E, since higher temperatures result in a lower relative humidity given the same water vapor concentration.

If we compare the findings for the event-based (Figures 2C–F) to the seasonal simulations (Figures 3C–F) we see very similar trends both in terms of air temperature and relative humidity biases.

3.1.3 Temperature Inversions

Figure 5 shows the air temperature time series at a valley station (DAV, 1594 m.a.s.l., top plot), a nearby mountain station (WFJ, 2691 m.a.s.l., middle plot) as well as the lapse rate between these two stations (bottom plot). Both stations feature ventilated temperature sensors and are part of the SMN network. Shown are 6 days during run2 where a temperature inversion could be observed in the measurement data. This inversion is the result of a strong diurnal cycle of daytime warming and nighttime cooling at the valley station DAV, whereas the higher station WFJ registers very little to no diurnal cycle. As a result the lapse rate becomes positive during the nighttime/early morning. We can see that none of the models are able to capture the strong atmospheric stability reflected by the two stations. The driving model COSMO-1 only shows a weak diurnal cycle of air temperature but still shows a negative lapse rate during night time, not capturing the temperature inversions. This can probably be explained by the inadequate representation of the valley floor in the coarser resolution COSMO-1 model, which results in a smaller difference in elevation between the two stations. WRF is able to capture the dynamics of the diurnal cycle at the valley (DAV) better than any other model. However, WRF also overestimates the diurnal cycle at the mountain station and as a result simulates no temperature inversion. ICAR severely overestimates the temperature in the valley, although it performs rather well at high elevation. As a result no inversion is simulated. TopoSCALE follows COSMO’s forcing data very closely in the valley, where it shows a weak diurnal cycle. At the mountain station TopoSCALE’s temperature is slighly higher, which results in a weak inversion on two of the four inversion days.

FIGURE 5

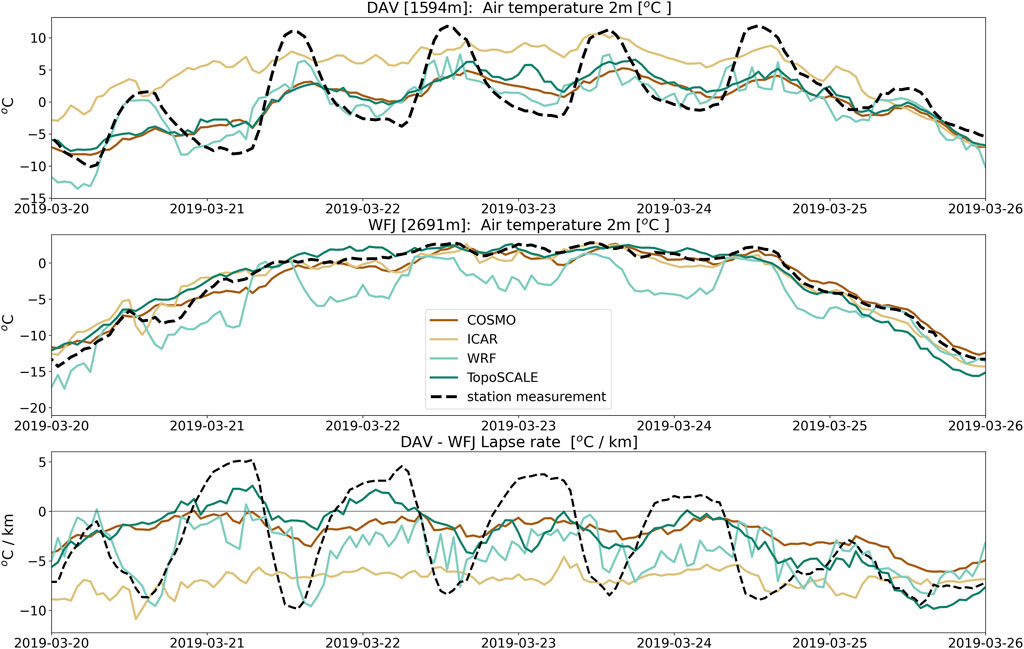
FIGURE 5. Temperature time series (top two plots) and resulting lapse rate between the valley station DAV, and mountain station WFJ. Positive lapse rate values during night indicate situations with temperature inversions.

3.1.4 Solid and Liquid Precipitation

Precipitation comparisons with the SMN stations are shown in Figure 2G, and Figure 3G. COSMO, ICAR and TopoSCALE show very similar point-scale predictions of total precipitation. The bias for point-scale precipitation is smallest for ICAR over the event-based simulations in Figure 2G, whereas over the season-long simulations ICAR shows a stronger negative bias (Figure 3G). WRF shows a tendency to overestimate total precipitation amounts. It should be noted that during the short winter simulations in Figure 2G, very little liquid precipitation was recorded.

Figures 2H, 3H show the average root-mean-square error and average mean bias error of modeled daily snow depth compared to IMIS stations. All models show a similar negative bias w.r.t. modeled snow depth for sheltered locations. Over the event-based simulations, ICAR shows almost no bias for exposed locations, something that is not upheld in the season-long simulations however. This underestimation might be partly explained by the very sheltered location of IMIS snow stations and tendency of those stations to measure above-average snow amounts (Grünewald et al., 2014), which is also reflected by a significantly smaller RMSE and bias for exposed locations. Overall, ICAR has slightly smaller bias and lower RMSE compared to WRF, although the difference is small. It should be further noted that since snow depth, rather than snowfall amounts are measured at the stations, effects of settling and snow melt have a significant impact on the modeled snow depth. Ideally we would validate against snow water equivalent (SWE) measurements as this would remove uncertainty due to simple densification and settling schemes in the snow models. More sophisticated snow cover models, such as available in CRYOWRF (Sharma et al., 2021) would improve the model representation of snow depth. The aforementioned warm bias in ICAR leads to increased melt rates, which contribute to the error and negative bias in snow depth. To illustrate this behavior, snow depth is plotted for the IMIS station SLFPAR in Figure 6. Both ICAR and TopoSCALE miss the precipitation event in November (potentially due to a higher 0° limit; higher elevation stations do capture this event). During the entire season the decline in snow height after each snowfall is steeper for ICAR than the other models or measurements. This behavior is observed consistently throughout all the individual stations’ time series (not depicted here for brevity’s sake).

FIGURE 6

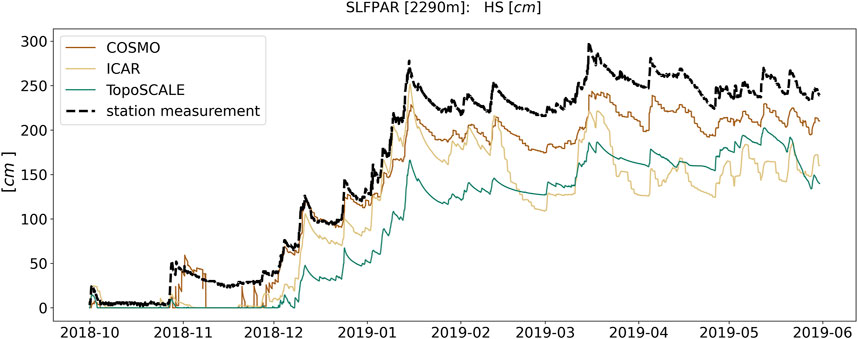
FIGURE 6. Time series of snow depth for the IMIS station SLFPAR. The effect of the positive temperature bias in ICAR on the snow depth can clearly be seen, and is representative of the behavior observed at other stations. COSMO-1 is nudged to spatially interpolated snow depth observations every 24 h.

Comparing the downscaling methods to the forcing data in the season-long simulations, one might be tempted to conclude these models perform worse than the lower resolution forcing model. It is therefore important to note that the snow height in COSMO-1 is calibrated once per day based on (interpolated) point measurements and satellite data⁴. This observational nudging produces a snow cover simulation that cannot deviate far from the observed snow cover. All downscaling methods calculate snow depths from precipitation data, and use no nudging. This allows these downscaling models more freedom to deviate from observation.

3.2 Model Performance at the Spatial Scale: Evaluation of Near-Surface Terrain-Flow-Precipitation Interaction

In this section we will analyze the interaction between flow field and precipitation, in particular the ability of models to capture preferential deposition of snowfall. An important question is whether better representation of small-scale terrain can improve model simulations of small-scale processes such as preferential deposition of snowfall.

3.2.1 The Spatial Distribution of Precipitation at Larger Scale

Here we compare the spatial precipitation patterns from the different models in a qualitative manner and discuss their differences. Figure 7 shows the total precipitation (liquid and solid) for run1 and run2. WRF shows more precipitation overall compared to both COSMO-1 and the other two downscaling models. This holds especially true for the 2017 event (run1), and to a smaller degree for the 2019 event (run2). Based on the 4 point-scale comparisons within the domain (Figure 2G), we can cautiously conclude that WRF overestimates precipitation amounts.

FIGURE 7

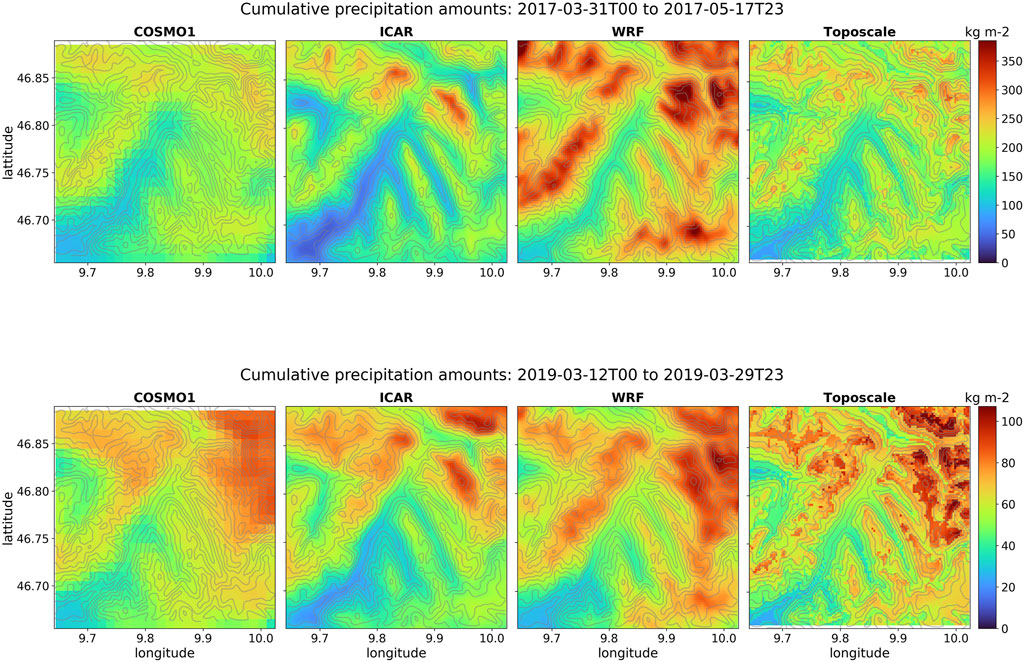
FIGURE 7. Comparison of modeled precipitation at 250 m resolution for run1 (2017 event, top) and run2 (2019 event, bottom).

We can see that ICAR produces slightly less precipitation than the other models at lower (1,400–1,900 m.a.s.l.) elevations, but from 2,000 m.a.s.l. and upward, COSMO, TopoSCALE and ICAR produce similar precipitation. For 2019 these effects are less pronounced. The slightly dryer interior of the ICAR domain also is of lower elevation. Based on Figure 2 in Section 3.1 we concluded that ICAR has a positive temperature bias, that is more pronounced at lower elevations (Figure 5). However, ICAR also has a first order advection scheme, whereas both other dynamical models (COSMO, WRF) have more sophisticated advection schemes that may behave better over the steep gradients in this domain. The drier interior domain may therefore be explained by either the higher air temperature (and consequent increased ability of the air to contain moisture). But it may also be that ICAR’s advection scheme plays a role here.

TopoSCALE shows distinctly sharper gradients in its precipitation patterns than all the other models, which can be explained by the model working on 1D samples. This does not allow for lateral dynamical effects, such as the influence of upwind orography, to be incorporated on the smaller scale.

3.2.2 The Ridge-Scale Flow and Associated Snow Deposition Fields

In this section we analyze the representation of ridge-scale flow patterns and their effect on snow deposition patterns. Terrain-induced flow features include speed-up effects at the ridge crest, flow deceleration at leeward slopes, leeward recirculation zones and flow blocking on leeward slopes. We analyze the representation of those flow features by different models and the changes following an increase in model resolution from 250 to 50 m. In the analysis of three-dimensional flow dynamics we only compare the model outputs from COSMO-1, ICAR and WRF as TOPOSCALE does not provide three-dimensional information of the flow field. In Figure 8 a cross section of wind velocity and wind vectors crossing the Casanna ridge (Davos region) are shown for a north-westerly situation. Flow fields are shown for two different situations (2019-03-13 23:00 and 2019-03-14 01:00) characterized by prevailing north-westerly winds of different strengths. We choose to depict the fallen snow rather than the snow depth, in order to minimize the effect of the different land cover schemes through densification of the snowpack and snow melt on the results. The strong difference in the representation of the topography between the coarser resolution model COSMO-1 and the higher-resolution models WRF and ICAR is striking. While in the 250 m the Casanna peak becomes much more pronounced, the 50 m representation of the topography shows a pronounced ridge with a secondary ridge in 500 m distance. Contrary, COSMO’s coarser topography shows a stretched hill, which obviously has a significantly smaller effect on the flow field dynamics. As a result, COSMO-1 predicts a smooth flow field at the ridge area with an increase in wind velocity with height. Wind velocities strongly increase at approximately 2,600 m and do not show any clear signature of the topography, such as speed-up effects or significant up- and downdrafts. On the other hand, for ICAR and especially for WRF, the topography has a pronounced impact on the near-surface flow field.

FIGURE 8

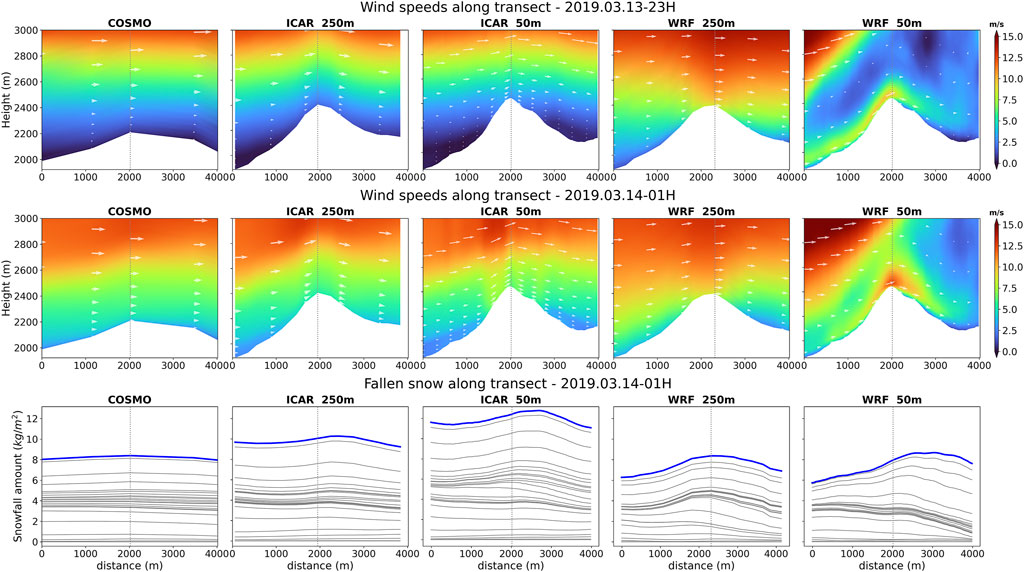
FIGURE 8. A cross section displaying the wind field along a ridge for ICAR and WRF simulations at 250 and 50 m horizontal resolutions. The bottom row shows the accumulated snowfall through time since the beginning of the simulation at 2019-03-13 00:00. WRF is spun up starting at 2019-03-12 00:00, this spin up period is not depicted. Arrows in the wind plot are not representative of grid spacing, but for illustrational purposes only.

When downscaling COSMO-1 data to 250 m, ICAR shows lower wind velocities in the valley than COSMO-1 and a slight speed-up of the flow on the windward slopes of the ridge crest accompanied with an updraft area. On the leeward slope, a downdraft zone with slightly smaller wind velocities is visible but without a significant flow deceleration. Thus, the modification of the flow by the terrain is minor. Those effects become more pronounced when downscaling the flow field to a resolution of 50 m. As ICAR uses a simple interpolation scheme of wind to the local topography, the change in topography has a direct effect on the magnitude of wind speed in the ridge crest area. Changes in wind speed affect the up- and downdrafts in ICAR, as these are calculated from the flow divergence. Comparing ICAR to WRF highlights the differences in the calculation of flow field dynamics. While ICAR does not develop any turbulence due to its linear dynamics, WRF clearly shows nonlinear effects on the leeward side of the ridge, in particular when increasing the model resolution. WRF shows much stronger dynamics in the flow field, reflecting the ability of the model to better resolve turbulent structures and thus the modification of the near-surface flow by the terrain. Contrary to ICAR, WRF shows strong differences in the flow dynamics for the two different resolutions. At 250 m, WRF predicts much higher wind speeds in ridge crest areas compared to COSMO-1 and ICAR as well as downdrafts on the leeward slopes. The downscaled flow field at 50 m shows much more spatial dynamics of near-surface flow patterns at the ridge crest areas. The flow field close to the ridge crest is characterized by a strong speed-up in the first 100 m above the surface and a decrease in wind velocities aloft. On the leeward slope a shallow air layer with a flow deceleration is visible with a strong downdraft of the flow at layers above. These results show that horizontal grid spacing of 50 m is required to resolve flow patterns such as flow separation on the leeward slopes. These changes in flow behavior when changing the model resolution from 250 to 50 m also strongly affect the snow deposition patterns along the ridge crest area. At 250 m resolution, peak snow deposition is close to the ridge crest with stronger snow accumulation at the leeward slopes induced by the up- and downdrafts and stronger horizontal advection of snow particles in downwind direction of the ridge crest. At 50 m resolution, the more pronounced speed up effect at the ridge crest induces a stronger depletion of falling snow particles at the upwind area. Flow separation on the leeward zone and associated flow deceleration result in enhanced snow deposition on the leeward slope. We can thus clearly see the increase in preferential deposition with the non-linear dynamics of the WRF model. However, a model resolution of 50 m is required to adequately resolve lee-side flow separation, and thereby preferential deposition. These findings are in agreement with finding from Gerber et al. (2019).

A more complex initial situation is reflected in Figure 9. COSMO-1 predicts a large-scale northerly flow at higher atmospheric levels and a near-surface southerly flow up to a height of 200 m above ground. The two flow systems appear to be disconnected. In both WRF and ICAR, the two flow systems start to interact with eddies developing at the southerly exposed slopes of Casanna ridge. WRF predicts a flow separation at the southerly exposed slopes and a pronounced downdraft flow over the northerly exposed slopes. Contrary, ICAR simulates a very strong updraft at the northerly Casanna slopes.

FIGURE 9

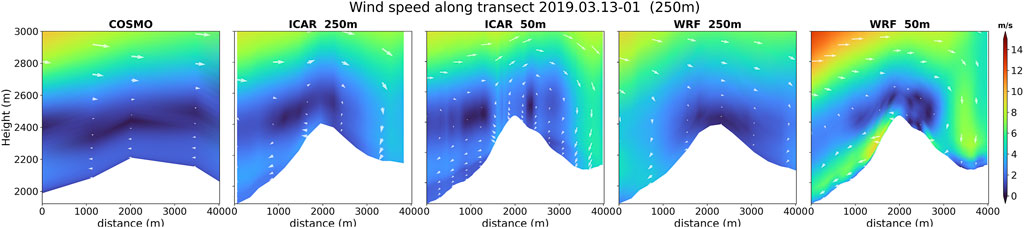
FIGURE 9. A cross section displaying the wind speeds along a ridge for ICAR and WRF simulations at 250 and 50 m horizontal resolution.

3.2.3 Validation of the Spatial Distribution of Solid Precipitation at the Ridge Scale

Figure 10 shows measured snow depths at March 31, 2017 and May 17, 2017 as well as the snow depth changes for this period (run1). The bottom plot of Figure 10 further displays the measured and modeled change in snow depth grouped per elevation band. Since model runs are started in the middle of the snow season, both WRF and ICAR are initialized with snow depth from the COSMO-1 model. The coarser resolution of this model does not allow for narrow valleys to be resolved. Since these narrow valleys are accurately resolved during the simulation, the difference over the simulation shows some artefacts; e.g., that in both models the main valley is snow free at March 31 (not shown), whereas in the lidar data shows there is still snow (Figure 10). These constraints due to the initialization do not allow for a proper comparison at low elevations.

FIGURE 10

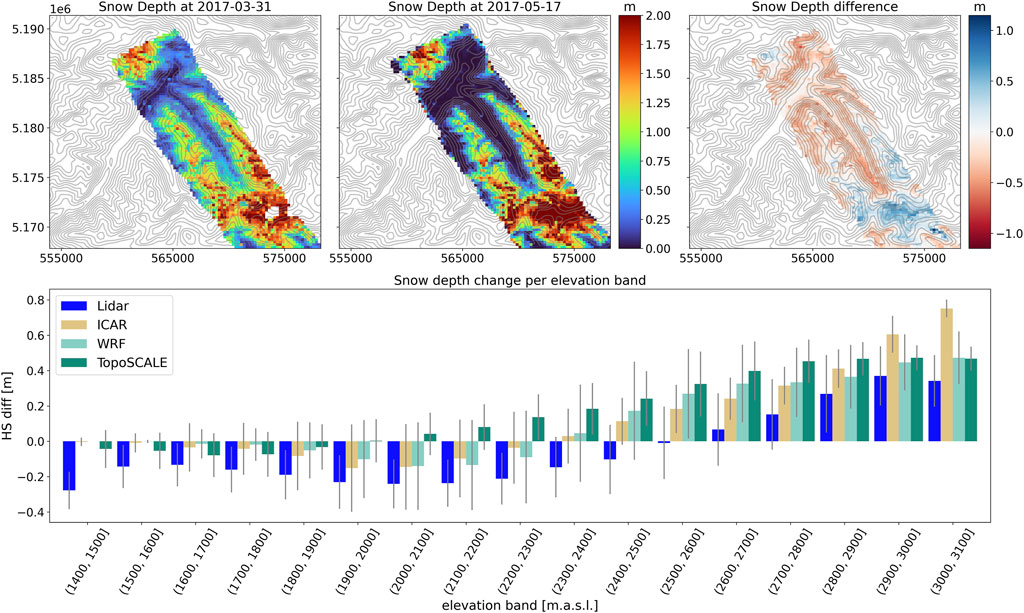
FIGURE 10. Lidar snow depth measurements on the 31 March 2017 and 17 May 2017 (top left and middle, respectively). (top right) Measured snow depth differences between the 17 May 2017 and 31 March 2017. (bottom) Mean measured and modeled changes in snow depth over the 2017 (run1) period per 100m elevation band for Lidar measurements (blue), ICAR (brown) WRF (mint) and TopoSCALE (green). Error bars indicate standard deviations.

WRF and ICAR simulate a similar snow line after the precipitation event, which is reflected by the elevation band of zero-accumulation during the respective period (2,300–2,400 m.a.s.l.). The snow line is a result of the snowfall line during the different precipitation events and snow melt. The snow line is approx. 200 m lower than observed by the LiDAR data. Contrarily, TopoSCALE predicts an even lower snowfall line at 1,900–2,000 m.a.s.l., which is approx. 600 m below the measured snow line. Furthermore, all models tend to overestimate the increase in snow depth at higher elevations, with TopoSCALE showing the largest overestimation up to an elevation of 2,900 m. The overestimation at the mid to high elevation ranges (2,300–2,700 m.a.s.l.) might partly be an effect of weaker settling rates in the models. ICAR strongly overestimates snow depths at the ridge crest area (i.e., above 2,800 m.a.s.l.). At those high elevations WRF captures snow accumulation very well. TopoSCALE shows snow depths similar to WRF. At lower elevations, where measurements show snow depletion, both dynamic models behave very similarly. At mid-elevations (2,300–1,700 m.a.s.l.), the decrease in snow depth is rather well captured by both dynamic models. Contrary, TopoSCALE shows snow accumulation above 2000 m.a.s.l. and too little snow depletion at elevations below. The elevations below 1700 m.a.s.l. were already snow free at the start of the simulations, which does not allow for an accurate simulation of snow melt.

In order to analyze the ability of the models to capture spatial snow accumulation patterns at the slope scale, Figure 11 shows snow depths and snow depth changes for the mountain ridge area which was mainly dominated by snow accumulation throughout the period. The dominant wind direction during the precipitation event was from the south, and we can see that the difference in snow depth (right column) shows preferential deposition on the north side of the ridge in the Lidar data. ICAR is not able to replicate this pattern very well and mainly shows snow accumulation at the ridge tops. This indicates that the flow field and advection scheme in ICAR do not allow for sufficient advection of snow particles towards the leeward slopes. In absence of any advection calculations TopoSCALE predicts precipitation with strong elevation gradients. WRF on the other hand does show stronger snow accumulation on the leeward slopes (Figure 11I). This significant difference in snow accumulation representation by the models can be explained by the near-surface flow field adaptation to the local terrain. In WRF the local flow field shows more pronounced near-ridge speed-up effects, allowing stronger advection across the ridge crests and deposition on the leeward slopes (see Section 3.2.2).

FIGURE 11

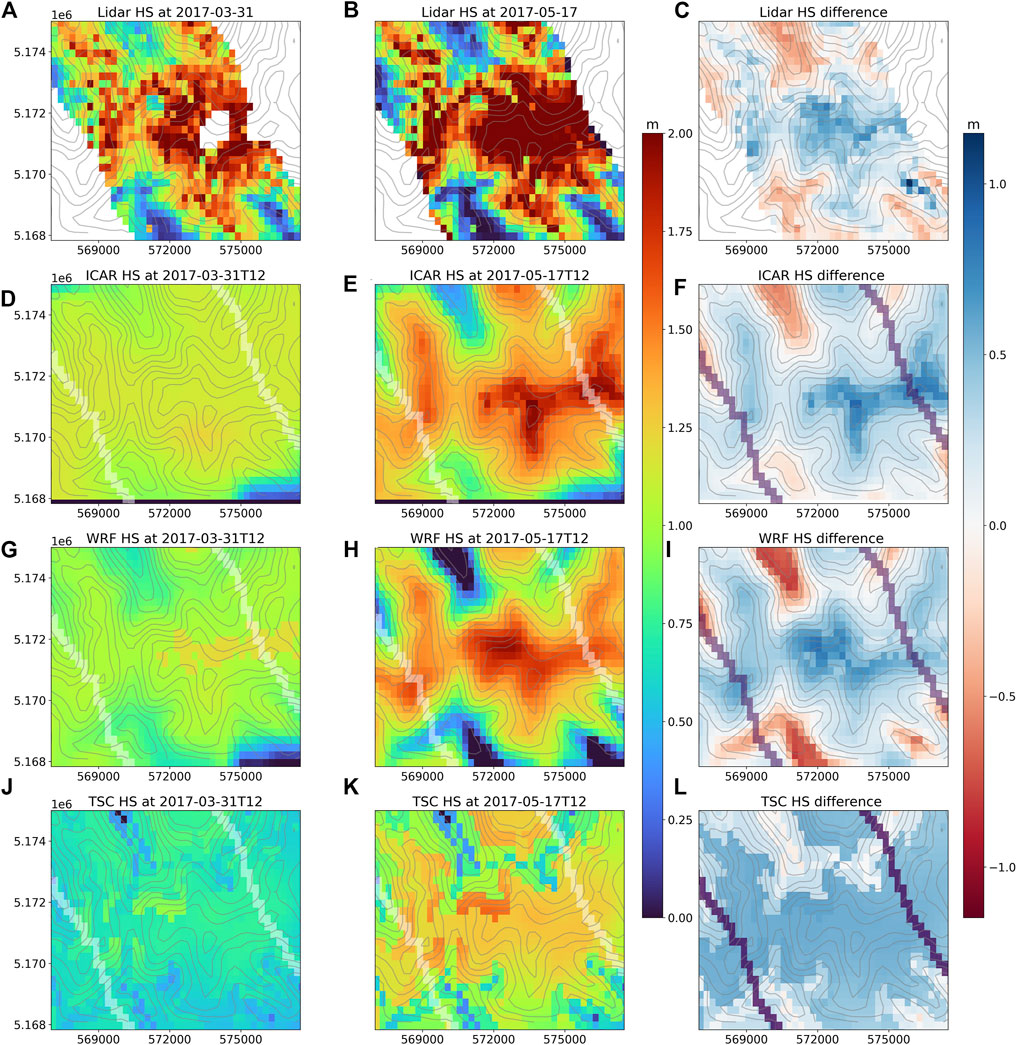
FIGURE 11. The snow depth distribution at 31 March 2017 (A), 17 May 2017 (B) and difference (C) for Lidar measurement (A–C), ICAR (D–F), WRF (G–I) and TopoSCALE (J–L). All model output is at 250 m resolution. The white and purple lines in the model plots (F,I,L) indicate the borders of the lidar measurement.

3.3 Computational Demands

Table 3 shows the computational demands for the different models and simulations. WRF and ICAR were run on the CSCS supercomputer piz Daint. WRF has roughly 26 to 60 times the computational requirements of ICAR for a similar domain. It should be emphasized however that WRF was run with an additional domain at 1 km resolution to allow for turbulence and hydrometeors to develop properly. It is our hypothesis that with further tuning and improvements of the coupling to the forcing data, this additional domain could possibly be excluded. However, this exclusion will reduce computational demands by 15% for the 250 m domain and significantly less for the 50 m domain (based on a back-of-the-envelope calculation of grid points and time steps). Thus, even in the case we were to exclude the additional domain in WRF, the difference in computational demands would be in the order of a factor 20 to 50.

TABLE 3

TABLE 3. Overview of computational demands. ICAR and WRF simulations were performed on the CSCS supercomputer piz Daint, with ICAR running on 8 (run1, run2), 16 (run3) or 12 nodes (run4, run5) with 36 cpus each, and WRF running on 24 nodes with 36 cpus each. Toposcale was run on the WSL cluster Hyperion using 8 cpus in all simulations.

TopoSCALE was run on the WSL cluster Hyperion using 8 cores in all simulations and at a cost of 0.11–0.16 cpu hours per simulated day, depending on resolution. There is thus no debate as to which model is computationally more efficient, as TopoSCALE wins this comparison by a very large margin.

4 Discussion

In this study we present a comparison of various downscaling methods of different numeric complexity. The ways of comparing are not unambiguous, and certain choices are made that affect the results. Furthermore, the models are generally not applied to the settings they were developed for. In this section we will discuss the most significant choices in the model settings, the reasons behind them, as well as limitations of the study.

2ptThis study is undertaken for the complex terrain of the Swiss Alps, for which there is high resolution forcing data available from a fully dynamical model that was developed specifically for this complex alpine domain. This model, COSMO-1, due to its high resolution and specific application, already captures many dynamical effects specific to complex mountainous terrain (Schär et al., 2002; Leuenberger et al., 2010; Leutert et al., 2015; Goger et al., 2016; Kruyt et al., 2018) and is nudged to observations via an advanced data assimilation scheme (Schraff et al., 2016). Where many downscaling techniques, including TopoSCALE and ICAR, have been developed to downscale forcing data from the 20–100 km scale to kilometer-scale resolutions, we have chosen to apply these techniques to forcing data with a 1.1 km horizontal resolution. In doing so, we are the first to undertake a systematic comparison of downscaling techniques of varying complexity at very high resolutions in alpine terrain. It remains to be seen if a comparison with significantly coarser forcing data would yield similar results: Many dynamical effects at the kilometer scale, such as convection or turbulence (Weusthoff et al., 2010; Ban, 2015; Chow et al., 2019), require dynamical models to be accurately represented, and thus one can argue that the scales, which the downscaling techniques aim to bridge, are relevant for the choice of the downscaling model. For dynamical modes, it is known that certain numerical artefacts may be produced when running at resolutions in the so-called “grey zone”, which according to Chow et al. (2019) is “the range of grid resolutions where particular features are neither subgrid nor fully resolved, but rather are partially resolved. The definition of a gray zone depends strongly on the feature being represented and its relationship to the model resolution.” On the other hand, non-dynamical models may lack inter-variable dependence and are unable to capture non-linear effects or terrain induced dynamics.

It is especially important when interpreting the results of this work to keep in mind that the forcing data from the COSMO-1 model are nudged to observations through a data-assimilation scheme based on interpolated data from measurement stations, soundings, and satellite data (Schraff et al., 2016). This has several effects. For one, it may appear that the downscaling schemes are unable to improve significantly upon the forcing (Figures 2, 3). It should however be considered that models that are only forced at the boundaries (WRF, ICAR) have far greater freedom to deviate from these observations than COSMO-1. The goal of this study is therefore not to assess the improvement these models are able to make upon the forcing data, but to assess their individual differences. Secondly, since TopoSCALE is not forced at the domain boundaries like WRF and ICAR, but at each grid point, TopoSCALE has far less freedom to deviate from the forcing, and thus from the observations the forcing is nudged to. This will have a non-trivial effect on the results, and should be considered in their interpretation, although the effect is hard to quantify. Future comparisons, where forcing data without assimilated observations is downscaled, will provide more insight into this. Given the goals (high resolution) and consequent limitations (COSMO-1 being the available forcing) this shortcoming was unavoidable in our study’s design. However, these results also highlight the necessity of data assimilation for downscaling schemes in case the forcing data contains nudged observations. This is particularly important for state variables such as snow depth, which can strongly deviate over a full season.

When comparing models, a few choices have to be made. Wind speeds are measured at a height of 6.8 m (IMIS) and 10 m (SMN) above the (snow free) surface. The lowest model levels in our 250 m simulations have respective mass heights of 4.7 m (ICAR), 22.5 m (WRF), and 9.5 m (COSMO) when averaged over domain D1. Due to the different dynamics of each model, the effect of roughness lengths varies. In ICAR, the lowest model level is unaffected by the roughness length and only the diagnostic 10 m wind speeds include a correction based on surface roughness. The COSMO-1 forcing data resolves some surface effects however. WRF on the other hand, given its full dynamic solution, will experience drag from the surface. TopoSCALE outputs wind speed at pixel elevation and does not include additional surface effects apart from what is present in the parent model forcing. One way to compare the wind speeds at station height is to use a log law to correct for elevation. However, it has been mentioned by Cattin et al. (2002); Draxl and Mayr (2009) that in complex terrain, the vertical wind profile does not behave like a logarithmic one, in absence of an upwind fetch. Thus, correcting wind speeds via a log law may not be very accurate. Yet at the same time, it is clear that the comparison is not fair as it is now. A definitive solution to this problem remains to be found. For now, given that all downscaling methods—without a log-law correction—lead to similar results for wind speed, we leave it as is, and conclude that these methods produce very close results. This may in part be attributed to the very good performance of the forcing model for this variable. Furthermore, the comparison of instantaneous model output to hourly averaged wind speed and direction introduces a source of error. This could in future work be mitigated by modifying the model codes to output hourly averaged fields, akin to WRF’s time series option. Modifying the various model codes was outside the scope of this study however. When comparing snow depths over the shorter event-based simulations (run1 and run2), there are some things to consider: For TopoSCALE, the data from run1 and run2 is a subset from the seasonal runs 4 and 5. On the other hand, WRF and ICAR are initalized with COSMO-1 snow heights at the beginning of run 1 and 2 (i.e., at mid-winter, when there is a considerable amount of snow on the ground). Given COSMO’s lower resolution, narrow valleys are not resolved properly, and there may be an over- or underestimation of snow depth in such valleys (either due to reduced air temperatures or reduced terrain shading). This has an effect on the statistics in Figure 2, as the starting snow-heights are not the same for all models. TopoSCALE’s snow heights for run 1 and run 2 can develop at 250 m resolution from the snow-free start of winter. Therefore the terrain and resulting snow height are accurately resolved over the entire snow season, and depending on station location (valley vs. ridge) may yield better performance. Hence, when comparing snow depths between (COSMO) ICAR and TopoSCALE, Figure 3 is more appropriate, since all models start this simulation with a snow free surface.

Generally, when downscaling with dynamical models, care should be taken to address physics in a consistent matter across domains and scales. Here, we disregard any fundamental differences in the microphysics between the forcing model COSMO-1, and the dynamical downscaling methods WRF and ICAR. It could very well be that using one of the many other microphysics schemes in WRF would yield better results, since it treats hydrometeors in a manner similar to COSMO-1. However, due to the limited availability of microphysics schemes in ICAR, we choose to preserve consistency between WRF and ICAR, which is why we opt to run WRF only with the Thompson and Eidhammer microphysics scheme (Thompson and Eidhammer, 2014).

5 Conclusion

In this study, we compare three downscaling methods of varying complexity. TopoSCALE: A very efficient topography-based model, ICAR: an atmospheric model of intermediate complexity, and WRF: a fully dynamical atmospheric model, widely used in the scientific community. Simulations driven by the COSMO-1 model are compared both at the point scale and in terms of spatial patterns (precipitation). Finally, for high-resolution ridge-scale flow processes, a qualitative comparison of the 3D flow field and resulting precipitation effects is conducted for the models ICAR and WRF, as the TopoSCALE model only produces surface (i.e., 2D) output.

Point-scale comparison against various meteorological stations with different sensor set-ups reveal the following: All models produce very comparable results in terms of wind speed. Somewhat surprisingly, none of the downscaling methods are able to improve significantly upon COSMO’s wind speed predictions at the point scale (although WRF and TopoSCALE improve the forecasted direction somewhat). All models overestimate wind speeds, where the overestimation increases with elevation. This is in part due to the presence of sheltered measurement stations at elevation, where the error is larger. It can be concluded that at 250 m resolution, the sheltered nature of these stations cannot be resolved by any of the models.

With regards to hourly temperature, as well as daily minima and maxima, mean model performance is also relatively close amongst the downscaling methods. There are however, significant differences when we look more closely. ICAR has the tendency to overestimate temperatures in the valley, at elevations below ca 1700 m.a.s.l., whereas COSMO-1 and TopoSCALE both have a significant negative biases at these low elevations. At higher elevations biases are reduced. WRF has an overall negative bias w.r.t. temperature.

Temperature inversions are not captured accurately by any of the models, due to various reasons. WRF is most capable of simulating a diurnal cycle, but also simulates a daily cycle at higher elevations, where none was observed. TopoSCALE does at times produce the positive lapse rate observed over stations, but it is unclear if this is a product of its negative bias at low elevations or not. The warm bias in ICAR has an effect on the accuracy of predicted snow heights, where increased melt rates contribute to the model’s error. Nevertheless, it still performs slightly better than the other models, especially when compared to TopoSCALE in simulations over entire snow seasons. Similarly, the negative bias in ICAR’s relative humidity assessment could also stem from its temperature bias.

A comparison of 2 full winter (hydrological) seasons (October through May) of the models ICAR and TopoSCALE shows very similar results to the point-scale comparison of shorter simulations (Figures 3 vs. Figure 2), indicating that shorter comparisons are indeed representative. The only exception is snow depth, where errors accumulate over a season, and initializing a model half way through the snow-season can contaminate results.

TopoSCALE performs surprisingly well at the point scale and 250 m spatial resolution in light of its computational efficiency. However, in this study we use forcing data that already contains many dynamic effects that happen at the km scale. It remains to be seen if forcing data of a significantly lower resolution would lead to similar results. It could well be that the dynamical nature of WRF and ICAR can make a stronger impact when downscaling data from 20 to 100 km resolution to the sub-km scale, because dynamic processes at these scales cannot be simulated by TopoSCALE. Further comparison of downscaling methods over various scales is required to support such claims, but it could very well be that the added benefits of fully dynamical models are less relevant at certain scales, while at other crucial scale steps, a dynamical approach is essential. It may also be that scales where dynamical models struggle, such as the so-called “Grey Zone” (Chow et al., 2019), form an opportunity for simpler downscaling techniques. Based on the current work, we can only conclude that when downscaling forcing data with an already high resolution to the 250 m scale, the differences between dynamical and more static downscaling techniques—based on point validations—are very small. Most importantly however, where WRF and (to a lesser degree) ICAR only take COSMO’s forcing data at the domain’s lateral boundaries, TopoSCALE works on the 1D column of forcing data. In doing so, it can benefit from the observational nudging in the forcing that is lost to the other downscaling schemes, and as a result TopoSCALE has less freedom to deviate from observations. This is a result of the choice of forcing data rather than a model trait, and in the case of forecasts and climate studies, this benefit would be lost.

Qualitative comparison of wind fields and snowfall patterns at increasing resolutions shows changes due to the improved representation of the topography when downscaling to 250 m resolution. Although noticeable, the difference between WRF and ICAR is relatively small at this resolution. At the next scale step however, when increasing the horizontal resolution to 50 m, differences are more pronounced. WRF’s non-linear dynamics allow for complex re-circulation patterns to appear in the simulation, where ICAR’s linear dynamics, although showing some signs of these complex structures, show distinctly less of such effects. This is in agreement with Gerber et al. (2018), Gerber et al. (2019), who showed that leeward loading/preferential deposition require(s) horizontal model resolution of 50 m or less to be represented.

To summarize, taking into account the vast computational differences, we conclude that:

• ICAR is an efficient alternative for WRF when downscaling to 250 m resolution, as the computational demands are reduced by a factor 20–50. Although this factor is less than reported by Gutmann et al. (2016), this is still a significant step, and part of the difference may be due to differences in I/O routines. Simulations from ICAR and WRF at the 250 m resolution are in close agreement, both at the point and spatial scale, although it should be noted ICAR tends to overestimate temperatures at lower (1,500–2,000 m.a.s.l.) elevations.

• TopoSCALE provides very similar results to the more complex models when compared to point-based observations, but it is unclear how much of this performance can be attributed to the chosen forcing data. This forcing data 1) due to its high resolution already resolves many dynamical processes that non-dynamical models like TopoSCALE cannot simulate, and 2) has extensive observational nudging, which TopoSCALE can benefit from, whereas WRF and ICAR cannot. However, the computational efficiency of TopoSCALE is orders of magnitude above that of ICAR and especially WRF, which is a strong benefit when doing large simulations, or when computationally restricted.

• At very high resolutions of 50 m, the non-linear dynamics of WRF allow for the representation of complex flow structures, and their effects on leeward snowfall that less sophisticated models like TopoSCALE and ICAR cannot. Thus, processes like preferential deposition can only be captured by such non-linear models.

This study shows that ICAR is not suited to capture high-resolution terrain-induced flow precipitation interactions in complex terrain. In order to better account for terrain-induced flows in complex terrain a new version of ICAR is currently under development. This version aims to represent terrain-induced flow features such as speed-up, flow deceleration, flow separation and flow blocking. Future work will show how this improved model version compares to WRF in its ability to simulate such complex flow features, and at what computational cost. To extend the conclusions of the current work, it would be interesting to compare downscaling methods across scales: i.e., downscaling forcing data of various resolutions to different target resolutions, to investigate if there are specific “scale steps” at which more complex models provide significant benefits. Conducting such a work without observational nudging will allow for a better comparison of model capabilities.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

BK ran ICAR simulations, and was responsible for the intercomparison analysis, the main graphics and text. RM was responsible for the study design, and provided the main input to the qualitative model comparison in Section 3.2.2. JF ran the TopoSCALE simulations and provided input to the document. FG and VS conducted the WRF simulations and provided input to the document. DR contributed to the literature study and introduction, and assisted with ICAR simulations.

Funding

This work was funded by the Swiss National Science foundation under project 200 020_179130. We would furthermore like to express our gratitude to the Swiss National Supercomputing Centre CSCS⁵, where simulations carried out under projects s873, s938 and s999 contributed to this paper. Also, a warm thanks to MeteoSwiss for the use of the COSMO-1 analysis data. Tobias Jonas provided lidar data used in Section 3.2.3, for which we are grateful. Ethan Gutmann provided invaluable support for the ICAR model. This work was partially funded through the Climate Change and Mass Movements (CCAMM) program at the Swiss Federal Institute for Forest, Snow and Landscape Research WSL⁶.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Model documentation available at www.cosmo-model.org

²https://www.meteoswiss.admin.ch/home/measurement-and-forecasting-systems/warning-and-forecasting-systems/cosmo-forecasting-system.html

³icesat.gsfc.nasa.gov/icesat/tools/SRTM30_Documentation.html.

⁴Source: Personal communication with MeteoSwiss.

⁵www.cscs.ch

⁶ccamm.slf.ch

References

Aalstad, K., Westermann, S., Schuler, T. V., Boike, J., and Bertino, L. (2018). Ensemble-based Assimilation of Fractional Snow-Covered Area Satellite Retrievals to Estimate the Snow Distribution at Arctic Sites. The Cryosphere 12, 247–270. doi:10.5194/tc-12-247-2018

CrossRef Full Text | Google Scholar

Ban, N. (2015). Convection-Resolving Climate Simulations For the Greater Alpine Region : Development , Evaluation And Climate Projections. Ph.D. thesis. Zurich: ETHZ.

Google Scholar

Beljaars, A. C. M. (1995). The Parametrization of Surface Fluxes in Large-Scale Models under Free Convection. Q.J R. Met. Soc. 121, 255–270. doi:10.1002/qj.49712152203

CrossRef Full Text | Google Scholar

Caine, N. (1980). The Rainfall Intensity: Duration Control of Shallow Landslides and Debris Flows. Geografiska Annaler. Ser. A, Phys. Geogr. 62, 23. doi:10.2307/520449

CrossRef Full Text | Google Scholar

Cattin, R., Schaffner, B., Buzzi, M., and Kunz, S. (2002). Wind Modeling in Mountainous Terrain: Validation by Sodar, 4–7.

Google Scholar

Chen, F., and Dudhia, J. (2001). Coupling an Advanced Land Surface-Hydrology Model with the Penn State-NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Wea. Rev. 129, 569–585. doi:10.1175/1520-0493(2001)129<0569:caalsh>2.0.co;2

CrossRef Full Text | Google Scholar

Chow, F., Schär, C., Ban, N., Lundquist, K., Schlemmer, L., and Shi, X. (2019). Crossing Multiple gray Zones in the Transition from Mesoscale to Microscale Simulation over Complex Terrain. Atmosphere 10, 274. doi:10.3390/atmos10050274

CrossRef Full Text | Google Scholar

Comola, F., Giometto, M. G., Salesky, S. T., Parlange, M. B., and Lehning, M. (2019). Preferential Deposition of Snow and Dust over Hills: Governing Processes and Relevant Scales. J. Geophys. Res. Atmos. 124, 7951–7974. doi:10.1029/2018JD029614

CrossRef Full Text | Google Scholar

Coulthard, T. J., and Skinner, C. J. (2016). The Sensitivity of Landscape Evolution Models to Spatial and Temporal Rainfall Resolution. Earth Surf. Dynam. 4, 757–771. doi:10.5194/esurf-4-757-2016

CrossRef Full Text | Google Scholar

Crozier, M. J. (2010). Deciphering the Effect of Climate Change on Landslide Activity: A Review. Geomorphology 124, 260–267. doi:10.1016/j.geomorph.2010.04.009

CrossRef Full Text | Google Scholar

Daac, N. E. L. P. (2019). ASTER Global Digital Elevation Model V003. 10.5067.

Google Scholar

de Wekker, S. F. J. (2002). Structure and Morphology of the Convective Boundary Layer in Mountainous Terrain.

Google Scholar

Draxl, C., and Mayr, G. J. (2009). Meteorological Wind Energy Potential in the Alps Using ERA40 and Wind Measurement Sites in the Tyrolean Alps. Wind Energy 14, 471–489. doi:10.1002/we.436

CrossRef Full Text | Google Scholar

Dyer, A. J., and Hicks, B. B. (1970). Flux-gradient Relationships in the Constant Flux Layer. Q.J R. Met. Soc. 96, 715–721. doi:10.1002/qj.49709641012

CrossRef Full Text | Google Scholar

Essery, R. (2015). A Factorial Snowpack Model (FSM 1.0). Geosci. Model. Dev. 8, 3867–3876. doi:10.5194/gmd-8-3867-2015

CrossRef Full Text | Google Scholar

European Environmental Agency (2006). CORINE Land Cover (CLC) 2006 Raster Data. Version 13.

Google Scholar

Fiddes, J., Aalstad, K., and Westermann, S. (2019). Hyper-resolution Ensemble-Based Snow Reanalysis in Mountain Regions Using Clustering. Hydrol. Earth Syst. Sci. 23, 4717–4736. doi:10.5194/hess-23-4717-2019

CrossRef Full Text | Google Scholar

Fiddes, J., Endrizzi, S., and Gruber, S. (2015). Large-area Land Surface Simulations in Heterogeneous Terrain Driven by Global Data Sets: Application to Mountain Permafrost. The Cryosphere 9, 411–426. doi:10.5194/tc-9-411-2015

CrossRef Full Text | Google Scholar

Fiddes, J., and Gruber, S. (2014). TopoSCALE v.1.0: Downscaling Gridded Climate Data in Complex Terrain. Geosci. Model. Dev. 7, 387–405. doi:10.5194/gmd-7-387-2014

CrossRef Full Text | Google Scholar

Finch, J. W., and Best, M. J. (2004). The Accuracy of Downward Short- and Long-Wave Radiation at the Earth’s Surface Calculated Using Simple Models. Meteorol. Appl. 11, 33–39. doi:10.1017/S1350482703001154

CrossRef Full Text | Google Scholar

Flaounas, E., Drobinski, P., Vrac, M., Bastin, S., Lebeaupin-Brossier, C., Stéfanon, M., et al. (2013). Precipitation and Temperature Space-Time Variability and Extremes in the Mediterranean Region: Evaluation of Dynamical and Statistical Downscaling Methods. Clim. Dyn. 40, 2687–2705. doi:10.1007/s00382-012-1558-y

CrossRef Full Text | Google Scholar

Fowler, H. J., Blenkinsop, S., and Tebaldi, C. (2007). Linking Climate Change Modelling to Impacts Studies: Recent Advances in Downscaling Techniques for Hydrological Modelling. Int. J. Climatol. 27, 1547–1578. doi:10.1002/joc.1556

CrossRef Full Text | Google Scholar

Fuhrer, O., Chadha, T., Hoefler, T., Kwasniewski, G., Lapillonne, X., Leutwyler, D., et al. (2018). Near-global Climate Simulation at 1 Km Resolution: Establishing a Performance Baseline on 4888 GPUs with COSMO 5.0. Geosci. Model. Dev. 11, 1665–1681. doi:10.5194/gmd-11-1665-2018

CrossRef Full Text | Google Scholar

Fuhrer, O., Osuna, C., Lapillonne, X., Gysi, T., Cumming, B., Bianco, M., et al. (2014). Towards a Performance Portable, Architecture Agnostic Implementation Strategy for Weather and Climate Models. Jsfi 1. doi:10.14529/jsfi140103

CrossRef Full Text | Google Scholar

Gariano, S. L., and Guzzetti, F. (2016). Landslides in a Changing Climate. Earth-Science Rev. 162, 227–252. doi:10.1016/j.earscirev.2016.08.011

CrossRef Full Text | Google Scholar

Garvert, M. F., Smull, B., and Mass, C. (2007). Multiscale Mountain Waves Influencing a Major Orographic Precipitation Event. J. Atmos. Sci. 64, 711–737. doi:10.1175/JAS3876.1

CrossRef Full Text | Google Scholar

Gerber, F., Besic, N., Sharma, V., Mott, R., Daniels, M., Gabella, M., et al. (2018). Spatial Variability of Snow Precipitation and Accumulation in COSMO-WRF Simulations and Radar Estimations over Complex Terrain. Cryosphere Discuss., 1–30. doi:10.5194/tc-2018-50

CrossRef Full Text | Google Scholar

Gerber, F. (2018). From the Clouds to the Ground Effects of Flow-Precipitation Interactions on Snow Distribution in Complex alpine Terrain. Ph.D. thesis.

Google Scholar

Gerber, F., Lehning, M., Hoch, S. W., and Mott, R. (2017). A Close-ridge Small-Scale Atmospheric Flow Field and its Influence on Snow Accumulation. J. Geophys. Res. Atmos. 122, 7737–7754. doi:10.1002/2016JD026258

CrossRef Full Text | Google Scholar

Gerber, F., Mott, R., and Lehning, M. (2019). The Importance of Near-Surface winter Precipitation Processes in Complex alpine Terrain. J. Hydrometeorology 20, 177–196. doi:10.1175/JHM-D-18-0055.1

CrossRef Full Text | Google Scholar

Gerber, F., and Sharma, V. (2018). Running COSMO – WRF on Very High Resolution over Complex Terrain, 1–20.

Google Scholar

Goger, B., Rotach, M. W., Gohm, A., Stiperski, I., and Fuhrer, O. (2016). Current Challenges for Numerical Weather Prediction in Complex Terrain: Topography Representation and Parameterizations. 2016 International Conference on High Performance Computing and Simulation, HPCS 2016 , 890–894. doi:10.1109/HPCSim.2016.7568428

CrossRef Full Text | Google Scholar

Gómez-Navarro, J. J., Raible, C. C., and Dierer, S. (2015). Sensitivity of the WRF Model to PBL Parametrisations and Nesting Techniques: Evaluation of Wind Storms over Complex Terrain. Geosci. Model. Dev. 8, 3349–3363. doi:10.5194/gmd-8-3349-2015

CrossRef Full Text | Google Scholar

Goodin, W. R., McRae, G. J., and Seinfeld, J. H. (1980). An Objective Analysis Technique for Constructing Three-Dimensional Urban-Scale Wind Fields. J. Appl. Meteorol. 19, 98–108. doi:10.1175/1520-0450(1980)019<0098:aoatfc>2.0.co;2

CrossRef Full Text | Google Scholar

Grünewald, T., Bühler, Y., and Lehning, M. (2014). Elevation Dependency of Mountain Snow Depth. The Cryosphere 8, 2381–2394. doi:10.5194/tc-8-2381-2014

CrossRef Full Text | Google Scholar

Gutiérrez, J. M., San-Martín, D., Brands, S., Manzanas, R., and Herrera, S. (2013). Reassessing Statistical Downscaling Techniques for Their Robust Application under Climate Change Conditions. J. Clim. 26, 171–188. doi:10.1175/JCLI-D-11-00687.1

CrossRef Full Text | Google Scholar

Gutmann, E., Barstad, I., Clark, M., Arnold, J., and Rasmussen, R. (2016). The Intermediate Complexity Atmospheric Research Model (ICAR). J. Hydrometeorology 17, 957–973. doi:10.1175/JHM-D-15-0155.1

CrossRef Full Text | Google Scholar

Gutmann, E. D., Rasmussen, R. M., Liu, C., Ikeda, K., Gochis, D. J., Clark, M. P., et al. (2012). A Comparison of Statistical and Dynamical Downscaling of winter Precipitation over Complex Terrain. J. Clim. 25, 262–281. doi:10.1175/2011JCLI4109.1

CrossRef Full Text | Google Scholar

Haylock, M. R., Cawley, G. C., Harpham, C., Wilby, R. L., and Goodess, C. M. (2006). Downscaling Heavy Precipitation over the United Kingdom: A Comparison of Dynamical and Statistical Methods and Their Future Scenarios. Int. J. Climatol. 26, 1397–1415. doi:10.1002/joc.1318

CrossRef Full Text | Google Scholar

Hearman, A. J., and Hinz, C. (2007). Sensitivity of point Scale Surface Runoff Predictions to Rainfall Resolution. Hydrol. Earth Syst. Sci. 11, 965–982. doi:10.5194/hess-11-965-2007

CrossRef Full Text | Google Scholar

Helbig, N., Schirmer, M., Magnusson, J., Mäder, F., van Herwijnen, A., Quéno, L., et al. (2021). A Seasonal Algorithm of the Snow-Covered Area Fraction for Mountainous Terrain. Cryosphere Discuss. 2021, 1–28. doi:10.5194/tc-2020-377

CrossRef Full Text | Google Scholar

Hong, S. Y., and Pan, H. L. (1996). Nonlocal Boundary Layer Vertical Diffusion in a Medium-Range Forecast Model. doi:10.1175/1520-0493(1996)124<2322:nblvdi>2.0.co;2

CrossRef Full Text | Google Scholar

Houze, R. A. (2012). Orographic Effects on Precipitating Clouds. Rev. Geophys. 50, 1–47. doi:10.1029/2011RG000365

CrossRef Full Text | Google Scholar

Huwald, H., Higgins, C. W., Boldi, M.-O., Bou-Zeid, E., Lehning, M., and Parlange, M. B. (2009). Albedo Effect on Radiative Errors in Air Temperature Measurements. Water Resour. Res. 45, 1–13. doi:10.1029/2008WR007600

CrossRef Full Text | Google Scholar

Iacono, M. J., Delamere, J. S., Mlawer, E. J., Shephard, M. W., Clough, S. A., and Collins, W. D. (2008). Radiative Forcing by Long-Lived Greenhouse Gases: Calculations with the AER Radiative Transfer Models. J. Geophys. Res. 113. doi:10.1029/2008JD009944

CrossRef Full Text | Google Scholar

Idso, S. B., and Jackson, R. D. (1969). Thermal Radiation from the Atmosphere. J. Geophys. Res. 74, 5397–5403. doi:10.1029/JC074i023p05397

CrossRef Full Text | Google Scholar

Kirschbaum, D., Adler, R., Adler, D., Peters-Lidard, C., and Huffman, G. (2012). Global Distribution of Extreme Precipitation and High-Impact Landslides in 2010 Relative to Previous Years. J. Hydrometeorology 13, 1536–1551. doi:10.1175/JHM-D-12-02.1

CrossRef Full Text | Google Scholar

Kruyt, B., Dujardin, J., and Lehning, M. (2018). Improvement of Wind Power Assessment in Complex Terrain: The Case of COSMO-1 in the Swiss Alps. Front. Energ. Res. 6, 102. doi:10.3389/fenrg.2018.00102

CrossRef Full Text | Google Scholar

Lehning, M., Bartelt, P., Brown, B., Russi, T., Stöckli, U., and Zimmerli, M. (1999). SNOWPACK Model Calculations for Avalanche Warning Based upon a New Network of Weather and Snow Stations. Cold Regions Sci. Technology 30, 145–157. doi:10.1016/S0165-232X(99)00022-1

CrossRef Full Text | Google Scholar

Lehning, M., Löwe, H., Ryser, M., and Raderschall, N. (2008). Inhomogeneous Precipitation Distribution and Snow Transport in Steep Terrain. Water Resour. Res. 44, 1–19. doi:10.1029/2007WR006545

CrossRef Full Text | Google Scholar

Leuenberger, D., Koller, M., Fuhrer, O., and Schär, C. (2010). A Generalization of the SLEVE Vertical Coordinate. Monthly Weather Rev. 138, 3683–3689. doi:10.1175/2010MWR3307.1

CrossRef Full Text | Google Scholar

Leutert, T., Leuenberger, D., and Schubiger, F. (2015). Neighborhood Verification of Convection in the Swiss COSMO Models with Radar and Satellite Measurements 1 Introduction 2 Veri Cation Approach 3 Observational Data 4 Model Data 5 Veri Cation of the 12th June 2014 Case. COSMO Newsl. 5, 40–51.

Google Scholar

Li, X., and Babovic, V. (2019). Multi-site Multivariate Downscaling of Global Climate Model Outputs: an Integrated Framework Combining Quantile Mapping, Stochastic Weather Generator and Empirical Copula Approaches. Clim. Dyn. 52, 5775–5799. doi:10.1007/s00382-018-4480-0

CrossRef Full Text | Google Scholar

Liston, G. E., and Elder, K. (2006). A Meteorological Distribution System for High-Resolution Terrestrial Modeling (MicroMet). J. Hydrometeorol. 7, 217–234. doi:10.1175/jhm486.1

CrossRef Full Text | Google Scholar

Lundquist, J., Hughes, M., Gutmann, E., and Kapnick, S. (2019). Our Skill in Modeling Mountain Rain and Snow Is Bypassing the Skill of Our Observational Networks. Bull. Am. Meteorol. Soc. 100, 2473–2490. doi:10.1175/BAMS-D-19-0001.1

CrossRef Full Text | Google Scholar

Mazzotti, G., Currier, W. R., Deems, J. S., Pflug, J. M., Lundquist, J. D., and Jonas, T. (2019). Revisiting Snow Cover Variability and Canopy Structure within Forest Stands: Insights from Airborne Lidar Data. Water Resour. Res. 55, 6198–6216. doi:10.1029/2019WR024898

CrossRef Full Text | Google Scholar

Mazzotti, G., and Jonas, T. (2019). ALS-based Snow Depth and Canopy Height Maps from Flights in 2017. Grisons: CH and Grand Mesa, CO. doi:10.16904/envidat.126

CrossRef Full Text | Google Scholar

Mott, R., Scipión, D., Schneebeli, M., Dawes, N., Berne, A., and Lehning, M. (2014). Orographic Effects on Snow Deposition Patterns in Mountainous Terrain. J. Geophys. Res. Atmos. 119, 1419–1439. doi:10.1002/2013JD019880

CrossRef Full Text | Google Scholar

Mott, R., Vionnet, V., and Grünewald, T. (2018). The Seasonal Snow Cover Dynamics: Review on Wind-Driven Coupling Processes. Front. Earth Sci. 6. doi:10.3389/feart.2018.00197

CrossRef Full Text | Google Scholar

Mott, R., Wolf, A., Kehl, M., Kunstmann, H., Warscher, M., and Grünewald, T. (2019). Avalanches and Micrometeorology Driving Mass and Energy Balance of the Lowest Perennial Ice Field of the Alps: a Case Study. The Cryosphere 13, 1247–1265. doi:10.5194/tc-13-1247-2019

CrossRef Full Text | Google Scholar

Niu, G.-Y., Yang, Z.-L., Mitchell, K. E., Chen, F., Ek, M. B., Barlage, M., et al. (2011). The Community Noah Land Surface Model with Multiparameterization Options (Noah-MP): 1. Model Description and Evaluation with Local-Scale Measurements. J. Geophys. Res. 116, 1–19. doi:10.1029/2010JD015139

CrossRef Full Text | Google Scholar

Obu, J., Westermann, S., Vieira, G., Abramov, A., Balks, M. R., Bartsch, A., et al. (2020). Pan-Antarctic Map of Near-Surface Permafrost Temperatures at 1 Km2 Scale. The Cryosphere 14, 497–519. doi:10.5194/tc-14-497-2020

CrossRef Full Text | Google Scholar

Paulson, C. A. (1970). The Mathematical Representation of Wind Speed and Temperature Profiles in the Unstable Atmospheric Surface Layer. J. Appl. Meteorol. 9, 857–861. doi:10.1175/1520-0450(1970)009<0857:tmrows>2.0.co;2

CrossRef Full Text | Google Scholar

Petley, D. (2012). Global Patterns of Loss of Life from Landslides. Geology 40, 927–930. doi:10.1130/G33217.1

CrossRef Full Text | Google Scholar

Phillips, M., Wolter, A., Lüthi, R., Amann, F., Kenner, R., and Bühler, Y. (2017). Rock Slope Failure in a Recently Deglaciated Permafrost Rock wall at Piz Kesch (Eastern Swiss Alps), February 2014. Earth Surf. Process. Landforms 42, 426–438. doi:10.1002/esp.3992

CrossRef Full Text | Google Scholar

Pontoppidan, M., Reuder, J., Mayer, S., and Kolstad, E. W. (2017). Downscaling an Intense Precipitation Event in Complex Terrain: the Importance of High Grid Resolution. Tellus A: Dynamic Meteorology and Oceanography 69, 1271561. doi:10.1080/16000870.2016.1271561

CrossRef Full Text | Google Scholar

Raderschall, N., Lehning, M., and Schär, C. (2008). Fine-scale Modeling of the Boundary Layer Wind Field over Steep Topography. Water Resour. Res. 44, 1–18. doi:10.1029/2007WR006544

CrossRef Full Text | Google Scholar

Reiff, J., Blaauboer, D., de Bruin, H. A. R., van Ulden, A. P., and Cats, G. (1984). An Air Mass Transformation Model for Short-Range Weather Forecasting. Mon. Wea. Rev. 112, 393–412. doi:10.1175/1520-0493(1984)112<0393:aamtmf>2.0.co;2

CrossRef Full Text | Google Scholar

Roth, A., Hock, R., Schuler, T. V., Bieniek, P. A., Pelto, M., and Aschwanden, A. (2018). Modeling Winter Precipitation over the Juneau Icefield, Alaska, Using a Linear Model of Orographic Precipitation. Front. Earth Sci. 6, 1–19. doi:10.3389/feart.2018.00020

CrossRef Full Text | Google Scholar

Rütte, F., Kahl, A., Rohrer, J., and Lehning, M. (2021). How Forward‐Scattering Snow and Terrain Change the Alpine Radiation Balance with Application to Solar Panels. Geophys. Res. Atmos. 126. doi:10.1029/2020JD034333

CrossRef Full Text | Google Scholar

Schär, C., Leuenberger, D., Fuhrer, O., Lüthi, D., and Girard, C. (2002). A New Terrain-Following Vertical Coordinate Formulation for Atmospheric Prediction Models. Mon. Wea. Rev. 130, 2459–2480. doi:10.1175/1520-0493(2002)130<2459:antfvc>2.0.co;2

CrossRef Full Text | Google Scholar

Schmidli, J., Goodess, C. M., Frei, C., Haylock, M. R., Hundecha, Y., Ribalaygua, J., et al. (2007). Statistical and Dynamical Downscaling of Precipitation: An Evaluation and Comparison of Scenarios for the European Alps. J. Geophys. Res. 112, 1–20. doi:10.1029/2005JD007026

CrossRef Full Text | Google Scholar

Schomburg, A., Venema, V., Ament, F., and Simmer, C. (2012). Disaggregation of Screen-Level Variables in a Numerical Weather Prediction Model with an Explicit Simulation of Subgrid-Scale Land-Surface Heterogeneity. Meteorol. Atmos. Phys. 116, 81–94. doi:10.1007/s00703-012-0183-y

CrossRef Full Text | Google Scholar

Schraff, C., Reich, H., Rhodin, A., Schomburg, A., Stephan, K., Periáñez, A., et al. (2016). Kilometre‐scale Ensemble Data Assimilation for the COSMO Model (KENDA). Q.J.R. Meteorol. Soc. 142, 1453–1472. doi:10.1002/qj.2748

CrossRef Full Text | Google Scholar

Selby, M. J. (1988). Landslides: Causes, Consequences and Environment. J. R. Soc. New Zealand 18, 343. doi:10.1080/03036758.1988.10429158

CrossRef Full Text | Google Scholar

Seneviratne, S. I., Nicholls, N., Easterling, D., Goodess, C. M., Kanae, S., Kossin, J., et al. (2012). “Changes in Climate Extremes and Their Impacts on the Natural Physical Environment,” in Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change. doi:10.1017/CBO9781139177245.006

CrossRef Full Text | Google Scholar

Sharma, V., Gerber, F., and Lehning, M. (2021). Introducing CRYOWRF v1.0: Multiscale Atmospheric Flow Simulations with Advanced Snow Cover Modelling. Geoscientific Model. Development Discuss. 2021, 1–46. doi:10.5194/gmd-2021-231

CrossRef Full Text | Google Scholar

Shin, H. H., and Hong, S.-Y. (2015). Representation of the Subgrid-Scale Turbulent Transport in Convective Boundary Layers at Gray-Zone Resolutions. Monthly Weather Rev. 143, 250–271. doi:10.1175/MWR-D-14-00116.1

CrossRef Full Text | Google Scholar

Shugar, D. H., Jacquemart, M., Shean, D., Bhushan, S., Upadhyay, K., Sattar, A., et al. (2021). A Massive Rock and Ice Avalanche Caused the 2021 Disaster at Chamoli, Indian Himalaya. Science 373, 300–306. doi:10.1126/science.abh4455

PubMed Abstract | CrossRef Full Text | Google Scholar

Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, D., Duda, M. G., et al. (2008b). A Description of the Advanced Research WRF Version 3. Natl. Cent. Atmos. Res. Boulder, Colo. doi:10.5065/D68S4MVH

CrossRef Full Text | Google Scholar

Skamarock, W., Klemp, J., Dudhi, J., Gill, D., Barker, D., Duda, M., et al. (2008a). A Description of the Advanced Research WRF Version 3. Tech. Rep. 113. doi:10.5065/D6DZ069T

CrossRef Full Text | Google Scholar

Sturm, M., Goldstein, M. A., and Parr, C. (2017). Water and Life from Snow: A Trillion Dollar Science Question. Water Resour. Res. 53, 3534–3544. doi:10.1002/2017WR020840

CrossRef Full Text | Google Scholar

Sunyer, M. A., Hundecha, Y., Lawrence, D., Madsen, H., Willems, P., Martinkova, M., et al. (2015). Inter-comparison of Statistical Downscaling Methods for Projection of Extreme Precipitation in Europe. Hydrol. Earth Syst. Sci. 19, 1827–1847. doi:10.5194/hess-19-1827-2015

CrossRef Full Text | Google Scholar

Tang, J., Niu, X., Wang, S., Gao, H., Wang, X., and Wu, J. (2016). Statistical Downscaling and Dynamical Downscaling of Regional Climate in China: Present Climate Evaluations and Future Climate Projections. J. Geophys. Res. Atmos. 121, 2110–2129. doi:10.1002/2015JD023977

CrossRef Full Text | Google Scholar

Themeßl, M. J., Gobiet, A., and Heinrich, G. (2012). Empirical-statistical Downscaling and Error Correction of Regional Climate Models and its Impact on the Climate Change Signal. Climatic Change 112, 449–468. doi:10.1007/s10584-011-0224-4

CrossRef Full Text | Google Scholar

Thompson, G., and Eidhammer, T. (2014). A Study of Aerosol Impacts on Clouds and Precipitation Development in a Large winter Cyclone. J. Atmos. Sci. 71, 3636–3658. doi:10.1175/JAS-D-13-0305.1

CrossRef Full Text | Google Scholar

Vaittinada Ayar, P., Vrac, M., Bastin, S., Carreau, J., Déqué, M., and Gallardo, C. (2016). Intercomparison of Statistical and Dynamical Downscaling Models under the EURO- and MED-CORDEX Initiative Framework: Present Climate Evaluations. Clim. Dyn. 46, 1301–1329. doi:10.1007/s00382-015-2647-5

CrossRef Full Text | Google Scholar

Vionnet, V., Martin, E., Masson, V., Lac, C., Naaim Bouvet, F., and Guyomarc'h, G. (2017). High-Resolution Large Eddy Simulation of Snow Accumulation in Alpine Terrain. J. Geophys. Res. Atmos. 122, 005–011. doi:10.1002/2017JD026947

CrossRef Full Text | Google Scholar

Vrac, M., Stein, M. L., Hayhoe, K., and Liang, X.-Z. (2007). A General Method for Validating Statistical Downscaling Methods under Future Climate Change. Geophys. Res. Lett. 34. doi:10.1029/2007GL030295

CrossRef Full Text | Google Scholar

Wang, Z., and Huang, N. (2017). Numerical Simulation of the Falling Snow Deposition over Complex Terrain. J. Geophys. Res. Atmos. 122, 980–1000. doi:10.1002/2016JD025316

CrossRef Full Text | Google Scholar

Webb, E. K. (1970). Profile Relationships: The Log-Linear Range, and Extension to strong Stability. Q.J R. Met. Soc. 96, 67–90. doi:10.1002/qj.49709640708

CrossRef Full Text | Google Scholar

Westermann, S., Østby, T. I., Gisnås, K., Schuler, T. V., and Etzelmüller, B. (2015). A Ground Temperature Map of the North Atlantic Permafrost Region Based on Remote Sensing and Reanalysis Data. The Cryosphere 9, 1303–1319. doi:10.5194/tc-9-1303-2015

CrossRef Full Text | Google Scholar

Weusthoff, T., Ament, F., Arpagaus, M., and Rotach, M. W. (2010). Assessing the Benefits of Convection-Permitting Models by Neighborhood Verification: Examples from MAP D-PHASE. Monthly Weather Rev. 138, 3418–3433. 10.1175/2010MWR3380.1.

CrossRef Full Text | Google Scholar

Yang, D., Goodison, B. E., Metcalfe, J. R., Louie, P., Leavesley, G., Emerson, D., et al. (1999). Quantification of Precipitation Measurement Discontinuity Induced by Wind Shields on National Gauges. Water Resour. Res. 35, 491–508. doi:10.1029/1998WR900042

CrossRef Full Text | Google Scholar

Yang, Z.-L., Niu, G.-Y., Mitchell, K. E., Chen, F., Ek, M. B., Barlage, M., et al. (2011). The Community Noah Land Surface Model with Multiparameterization Options (Noah-MP): 2. Evaluation over Global River Basins. J. Geophys. Res. 116, 1–16. doi:10.1029/2010JD015140

CrossRef Full Text | Google Scholar

Zhang, D., and Anthes, R. A. (1982). A High-Resolution Model of the Planetary Boundary Layer-Sensitivity Tests and Comparisons with SESAME-79 Data. J. Appl. Meteorol. 21, 1594–1609. doi:10.1175/1520-0450(1982)021<1594:ahrmot>2.0.co;2

CrossRef Full Text | Google Scholar

Zhong, S., Whiteman, C. D., Bian, X., Shaw, W. J., and Hubbe, J. M. (2001). Meteorological Processes Affecting the Evolution of a Wintertime Cold Air Pool in the Columbia basin. Monthly Weather Rev. doi:10.1175/1520-0493(2001)129<2600:mpateo>2.0.co;2

CrossRef Full Text | Google Scholar