Research on lethal levels of buildings based on historical seismic data

Due to the influences of buildings, geographical and geomorphological environments, road conditions, etc., the probabilities and numbers of casualties in different areas after an earthquake are different. Accordingly, we propose the concept of the lethal level, which attains different grades representing the mortality rate of differing intensities. Different regions have unique lethal levels, and regional lethal levels are affected mainly by the proportion of each building type and the corresponding lethal level, as different types of buildings also have unique lethal levels. Based on data of 52 historical earthquake disasters, we constructed a lethal level calculation model and obtained the lethal level of each building type. The results reveal that the lethal level ranges of different building types are fixed and unequal; moreover, the ranges of different building types overlap each other. The lethal level range of adobe structures is 0.85–1, that of civil structures is 0.75–0.95, that of brick-wood structures is 0.6–0.9, that of brick-concrete structures is 0.33–0.6, that of wood structures is 0.2–0.35, and that of reinforced concrete structures is 0.1–0.25. Based on the lethal levels of these building types, the overall level of a region can be quantified and graded, and this classification does not depend on the geographical location or administrative boundaries. In pre-earthquake evaluation efforts, the lethal level of an area can be derived through field research. After an earthquake, the number of casualties can be quickly assessed based on the mortality rate corresponding to the intensity of the area. This approach can further provide scientific support for risk zoning and risk assessment research.

Introduction

Earthquakes are geological disasters that occur abruptly and often result in casualties, property damage, the destruction of resources and the environment, and detrimental impacts on social and economic functions (Fu, 1993). The lethality of an earthquake is affected by many factors, mainly the earthquake parameters, regional environmental factors, and building properties, among others (Feng et al., 2013). The parameters of earthquakes mainly include the magnitude, intensity, occurrence time, and focal depth, while regional environmental factors predominantly include the earthquake location, population density, percentage of personnel present, economic level, and topography of the earthquake area, and building factors include the building structure type, proportions of building types, construction year, and building style; in addition, other factors include the types of seismic fortification, earthquake prediction, secondary disasters, the efficiency of earthquake emergency rescue efforts, the ability of personnel to help each other, and traffic and road factors. Moreover, these influencing factors have different effects on the number of deaths. Nevertheless, it is not earthquakes that result in deaths but the collapse and destruction of buildings caused by the earthquake (Zhu and Yang, 1998). Hence, the number of people killed during an earthquake is related to the number of buildings that collapse and are destroyed (Ma and Zhao, 2008; Spence et al., 2008; So, 2011). Therefore, research on methods to evaluate the number of casualties based on influencing factors such as the earthquake magnitude, intensity, and building vulnerability is an important research direction.

At present, assessment methods are divided into two main categories: evaluation methods are based on seismic parameters and building vulnerability, while methods based on seismic parameters are used primarily to obtain empirical functions and models based on the earthquake magnitude, intensity, and focal depth and the number of deaths through statistical fitting and to assess the number of possible casualties induced by an earthquake (Samardjieva and Oike, 1992; Ma and Xie, 2000). For example, the death evaluation model is based on impact factors such as the magnitude and population density (Christoskov and Samardjieva, 1984; Samardjieva, 2002; Badal and Samardjieva, 2003; Badal et al., 2005). Nonetheless, although the influencing factors in these models may be the same, the final fitted models are not completely identical due to regional differences and variations in the selected historical earthquake cases (Oike, 1991; Wang et al., 2011; Ceferino et al., 2018a; Zhang et al., 2018). As another example, the empirical function method uses only the seismic parameters of historical earthquakes (Jaiswal et al., 2015); since this method considers only the impacts of the earthquake magnitude, intensity and other factors on the number of deaths, the need for basic data is small, and thus, this approach can be used to rapidly assess the number of casualties after an earthquake. However, historical seismic data are limited and are not available in all regions, especially historical data of casualties. Therefore, the current models obtained based on historical seismic data are not generally applicable, the regional application of such methods is restricted by certain limitations, and the accuracy of the evaluation results is low.

Evaluation methods based on building vulnerability rely predominantly on statistical fitting relationships between the building vulnerability and mortality rate to build a model to evaluate the resulting casualties. At present, the most commonly used casualty assessment approach is based on historical seismic data through regression fitting to obtain the building vulnerability function (Miyakoshi et al., 1998; Goncharov and Frolova, 2011; Alel and Pahang, 2013). Scholars have also carried out research on various alternative methods (Miyakoshi et al., 1998; Alexander, 2011), including research on the relationship between building damage and casualties (Okada and Takai. 1999; Ferreira et al., 2011), new classification methods of building damage (Spence et al., 2011), new methods for assessing the vulnerability of various types of buildings (Pomonis et al., 2011), and methods based on the population size, intensity, building type, proportions of building types and level of damage. (Zhize and He, 1996; So and Spence, 2013). However, the existing research methods on the vulnerability of buildings have an excessively high demand on the requirement for basic data, and there are many research methods to choose from, which also introduces certain limitations in the evaluation methods.

At the same time, various other casualty assessment methods are available, such as the casualty assessment model based on performance-based earthquake engineering (PBEE) (Ceferino et al., 2018b; Pang et al., 2020), which has achieved good success in various applications, such as the proposed model adopting the FEMA P-58 framework for risk assessment.

Furthermore, because different methods require different types of basic data, the accuracy of the results also varies. Assessment methods based on the vulnerability of buildings fully consider the impact of the destruction of the building on the number of deaths, which greatly improves the accuracy of the evaluation results. However, the actual numbers of casualties caused by the 2014 Ludian (3 August 2014, Ludian County, Zhaotong City, Yunnan Province, Mw6.5, the focal depth is 12 km) and Jinggu (7 October 2014, Jinggu Dai and Yi Autonomous County, Pu’er City, Yunnan Province, Mw6.6, the focal depth is 5 km) earthquakes differed enormously (617 versus 1, respectively), even though the magnitudes of the two earthquakes, the population densities, and the geomorphological environments were all similar. Table 1 describes the proportions of various types of buildings in these two earthquake areas. Both of the affected areas contain relatively equal proportions of reinforced concrete structures and brick-concrete structures, but the Ludian earthquake area is dominated by civil structures (characterized by the use of bamboo strips instead of steel bars and clay instead of concrete for the walls of houses; some walls are mixed with straw with wood being used as beams and tile or hay employed as the cover), while the Jinggu earthquake area is dominated by wood structures. The vulnerability matrices of various types of buildings are almost identical, and the proportions of damaged buildings are the same, but there was a considerable difference in the number of deaths.

TABLE 1

TABLE 1. Building types and proportion data in Ludian earthquake and Jinggu earthquake area.

The above example reveals that the probability of death is different after the collapse and severe damage of different types of buildings. Accordingly, we hypothesized that we can quantify the difference in the possibility of death caused by such buildings to obtain the correlation between building destruction and the probability of death. By investigating this relationship, we can carry out research on a method to evaluate the deaths caused by earthquakes.

Data

The data sources for this study are the 1996–2000 and 2001–2005 versions of the Assessment and Compilation of Earthquake Disaster Loss in Mainland China, the 2006–2010, 2011, 2012, 2013, and 2014 versions of the Earthquake Disaster Assessment Report published by the China Earthquake Administration. At the same time, we referenced some scholars’ relevant literature on the statistics of earthquake casualties and obtained the proportions of various types of buildings during 52 historical earthquakes. The data mainly include the numbers of casualties and injuries and the proportions of destroyed buildings. Damage to buildings is divided into five main classifications: basically intact, minor damage, moderate damage, severe damage and destruction, as shown in Table 2. We mainly use data on the proportions of destroyed buildings for each earthquake to conduct a comparative analysis of the mortality rate, where the extent of the studied region refers mainly to the intensity zone delineated for each earthquake. At the same time, we also collected the proportion data of various types of buildings in each earthquake area. The results are shown in Table 4.

TABLE 2

TABLE 2. 52 historical earthquake data selected in this paper.

As shown in Figure 1, the proportions of buildings destroyed in historical earthquakes are generally concentrated in less than 30% of the affected area. The distribution characteristics of the proportions of buildings destroyed during earthquakes in different regions with different magnitudes are obviously similar. Similarly, the distribution of the mortality rate is relatively fixed and generally concentrated in the range below 0.001. In general, the distributions of the mortality rate and proportion of destroyed buildings correspond to each other. However, there is no one-to-one positive correlation between the proportion of destroyed buildings and the mortality rate. Hence, if a death assessment model is constructed based only on data of the proportion of destroyed buildings, large errors are inevitable. Based on an analysis of historical earthquakes, it was found that the destruction of buildings is not the only factor responsible for deaths; secondary geological disasters and various other factors are also responsible, and among them, building collapse is the dominant cause of casualties during earthquakes (Jaiswal et al., 2011). Thus, to comprehensively express the number of deaths caused by these factors, we introduced the concept of the lethal level (LL) (Nie et al., 2020; Xia et al., 2020; Nie et al., 2021), which represents the comprehensive possibility or level of various factors that cause death after a building is destroyed and other reason. It is expressed by the predominant mortality rate at a certain level under various intensities.

FIGURE 1

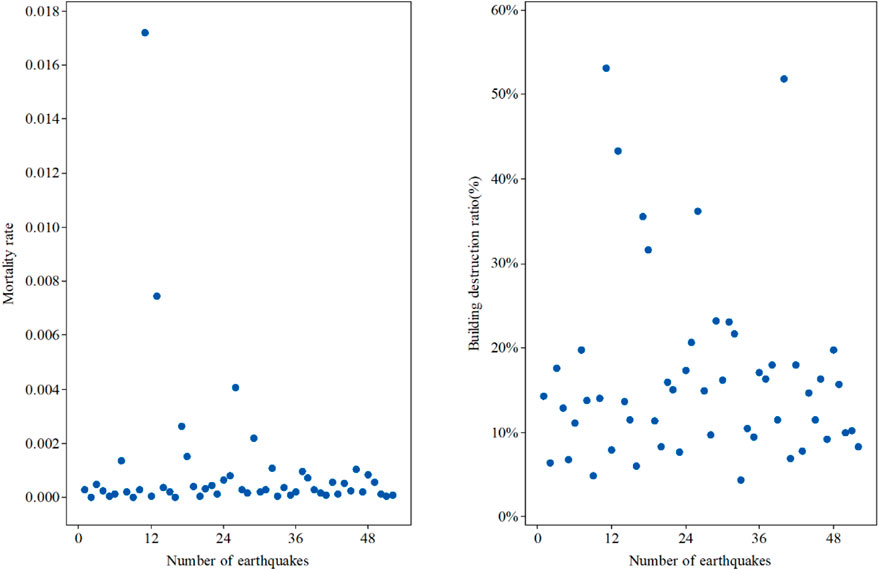
FIGURE 1. Distribution of the mortality rate and the proportion of building destruction of 52 earthquakes.

After an earthquake, the factors resulting in the death of people are very complicated; these factors include building damage, collapsing walls, collapsing gatehouses, falling wall hangings, rolling stones, landslides, fires, and inadequate treatment, etc. Therefore, to comprehensively describe the possible extent and number of deaths caused by earthquakes in various disaster areas, a novel concept needs to be introduced, that is, the regional LL, the weight of each factor varies among different disaster areas; for example, in plain areas, it is directly related to the possibility of death after the destruction of a building, whereas in mountainous areas, it may include the possibility of death after building damage and the possibility of death from rolling stones and post seismic landslides. The casualties induced by landslides and rockfalls exceed the casualties caused by building destruction, and the number of deaths in areas with inconvenient traffic conditions and complex distributions of buildings can even increase due to transportation interruptions and inadequate treatment.

The best indicator of the LL is the mortality rate caused by an earthquake, and the effects of the various lethal factors of an earthquake are comprehensively reflected in the mortality rate of the disaster area. In other words, after an earthquake, if an area is in a different intensity range, then its corresponding death rate is different, or the same area (county or township) may be in a different intensity range, so the corresponding death rate of the same area is also different, different LLs correspond to mortality rates of differing intensity. Thus, it is crucial to quantify the mortality rate within a region. Then, after an earthquake, regardless of the intensity range within an area, given the level of that area, a mortality rate must correspond to the intensity. Therefore, one of the main purposes of this article is to develop a method to quantify the LL of an area.

Materials and methods

The analysis of historical earthquake data reveals that data can be obtained on the mortality rate and the proportion of buildings destroyed in the historical earthquake area. Thus, we can construct a model to obtain the regional LL which based on various types of data, such as the proportion of damaged buildings, the mortality rate etc. The overall seismic capacity of a region are affected mainly by the types and proportions of buildings (as different types of buildings have different seismic capacities due to variations in building materials), construction methods and building quality. In other words, different types of buildings have different capacities to cause death after being damaged, therefore, we can obtain the LL of each building type according to the overall level of each historical earthquake area and the proportion data of each type of building.

Lethal level model

For historical earthquakes, many factors comprehensively account for the causes of death, the destruction of buildings is the main factor; other factors include the occurrence time of the earthquake and the population density. This article presents an evaluation model of casualties based on the proportion of damaged buildings proposed by Yin Zhiqian (Yin, 1991), we selected the influencing factors such as the percentage of personnel present, the population density etc. To constructed the model, as shown in Eq. 1:

$\mathit{log}\mathit{R}\mathit{D}=\mathit{12.479}\times {\left({\mathit{P}}_t\times \rho \times \mathit{R}\mathit{A}\times \alpha \right)}^{\mathit{0.1}}-\mathit{13.3}(1)$

where RD is the mortality rate of the earthquake (the ratio of the number of casualties to the total population), RA is the proportion of collapsed and destroyed buildings in the earthquake area, α is the overall LL in the earthquake area, ρ is the population density in the earthquake area, and P_t is the average occupancy rate of personnel (i.e., the average proportion of personnel in buildings during the earthquake). Among them, the average occupancy rate mainly refers to the research of relevant scholars: during the daytime, the average occupancy rate is 0.75, whereas at night, the occupancy rate is set as 1 (Xu et al., 2008; Wei et al., 2017).

Lethal levels of different types of buildings

For a historical earthquake, the regional LL is affected mainly by the proportions of various types of buildings in the region and their unique LLs. Therefore, based on the proportion of each type of building, a method for calculating the LL of each building is established, as shown in Eq. 2:

$\mathit{\alpha }={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{i}\mathit{max}}\left({\mathit{\beta }}_{\mathit{i}}\times {\mathit{\lambda }}_{\mathit{i}}\right)(2)$

where α refers to the overall LL of the historical earthquake area,β_i refers to the proportion of the i-th type building in the earthquake area,λ_i refers to the LL of the i-th type of building in the earthquake area, and i_max is determined mainly based on the actual number of types of buildings in the earthquake area.

The above formula is a multivariate linear equation, the regional LL (y₁-y_n which refer to the α) and the proportions of various types of buildings (a₁-a_q which refer to theβ) are known quantities in this equation, the calculation of the LL of each building type is actually the process of solving the multivariate linear equation based on each earthquake area:

$\begin{array}{l}{a}_{\mathrm{1}}{x}_{\mathrm{11}}+\cdot \cdot \cdot +a_j{x}_{\mathrm{1}j}+\cdot \cdot \cdot +a_q{x}_{\mathrm{1}q}=y_{\mathrm{1}},\\ a_{\mathrm{1}}{x}_{\mathrm{21}}+\cdot \cdot \cdot +a_j{x}_{\mathrm{2}j}+\cdot \cdot \cdot +a_q{x}_{\mathrm{2}q}=y_{\mathrm{2}},\\ ⋮\\ a_{\mathrm{1}}{x}_{i\mathrm{1}}+\cdot \cdot \cdot +a_j{x}_{ij}+\cdot \cdot \cdot +a_q{x}_{iq}=y_i,\\ ⋮\\ a_{\mathrm{1}}{x}_{n\mathrm{1}}+\cdot \cdot \cdot +a_j{x}_{nj}+\cdot \cdot \cdot +a_q{x}_{nq}=y_n,\end{array}(3)$

where a₁-a_q denote the proportions of different types of buildings in different earthquake areas, x₁₁-x_nq denote the LLs of those different types of buildings in different earthquake areas, and y₁-y_n denote the overall LLs in different earthquake areas. Among them, since a₁-a_q represents the proportional data of various types of buildings, it is obtained based on the actual collection results, the specific results are shown in Table 4.

In fact, if there are 4 building types in the area, then a quaternary linear equation is constructed, in theory, four historical earthquake data can be used to solve the equation system, which will inevitably lead to abnormal results. In order to avoid this situation, we arrange and combine the historical seismic data with the same building type, so as to obtain as many calculations results as possible, and to some extent avoid the result error caused by single data.

Results

The number of building types varies among different earthquake regions, therefore, we use the number of building types as a grouping standard, if different regions have the same building type, it will into one group, in this way, according to the number of building types, different multivariate linear equations can be constructed, in this study, 52 historical earthquakes are first grouped according to the building type, as shown in Table 3, the first group includes 6 earthquakes (2 in Gansu, 2 in Xinjiang, and 2 in Yunnan), the location distribution is mainly in the northwest region of China and the building types are adobe, civil, brick-wood and brick-concrete structures, there are 4 types of buildings, then quadratic linear equations can be constructed, and since the number of historical earthquakes is 6, a total of 15 quadratic linear equations are obtained, and each equation system can be calculated, the results of these 4 types of buildings, which may be a discrete result or a centralized distribution result, corresponding, the second group includes 6 earthquakes (3 in Sichuan, 1 in Xinjiang, 1 in Yunnan, and 1 in Gansu), and the building types include civil, brick-wood, brick-concrete, reinforced concrete and wood structures, a total of 6 fourth-order linear equations are obtained, the third group includes 12 earthquakes (divided into 2 regional groups: 6 earthquakes in Xinjiang, Gansu, Sichuan and Chongqing in the west and 6 earthquakes in Hebei, Heilongjiang and Guangxi in the east), and the building types include civil, brick-wood and brick-concrete structures, altogether, the two earthquakes groups yield 40 third-order linear equations, the fourth group includes a total of 28 earthquakes divided into 4 groups according to their spatial distribution (each group has 7 earthquakes; three groups include earthquakes mainly in Yunnan Province, while the other group includes earthquakes in Sichuan, Xizang, Xinjiang, Neimenggu, and Jiangxi), and the building types include civil, brick-wood, brick-concrete, and reinforced concrete structures, these four groups yield 140 quadratic linear equations. Solve different multivariate linear equations separately, and the result obtained is the lethality level of different building types.

TABLE 3

TABLE 3. 52 historical earthquake data grouping and the number of equations.

As shown in Table 4, an analysis of the calculation results reveals that the LLs among the earthquake areas are significantly different even if the proportion of destroyed buildings and the mortality rate are similar, for instance, even if the proportion of destroyed buildings is high, the corresponding LL is not necessarily high, in other words, for different areas, the overall proportion of destroyed buildings may be the same, but the LLs in different areas may differ greatly.

TABLE 4

TABLE 4. 52 historical earthquake building destruction proportion, mortality rate, lethal level and proportion of each type of building.

As shown in Figure 2, the distribution characteristics of the LL are obvious with values mainly within 0.5–0.9, in particular, there are 20 earthquake areas with 0.7–0.8, and these areas are distributed mainly in 3 regions: Yunnan Province, Sichuan Province and Gansu Province, considering the geographical distribution in the 52 historical earthquake areas, the distribution does not depend on the spatial distribution of historical earthquakes, the regional LL of historical earthquakes in the same Province may be different, but in different Provinces may be similar.

FIGURE 2

FIGURE 2. The frequency distribution of the regional lethal level of 52 historical earthquakes.

Furthermore, Figure 3 shows the distributions of the proportion of destroyed buildings, mortality rate and LL in each of the 52 historical earthquake areas, the main distribution interval of the proportion of destroyed buildings is concentrated within 0.1–0.3, the larger the proportion of destroyed buildings is, the higher the mortality rate, but this relationship is not absolute. In fact, there is a situation where the proportion of destroyed buildings is large but the mortality rate is relatively small, nevertheless, the mortality rate is positively correlated with the LL.

FIGURE 3

FIGURE 3. Comparative analysis of building destruction ratio, lethal level and mortality rate.

A comparative analysis of the correlations between these three parameters demonstrates that the proportions of destroyed buildings are similar between the two earthquakes, but due to the obvious difference in the regional LL, the mortality rates of the two earthquakes vary, the proportions of destroyed buildings in the two earthquake areas also differ considerably, but due to the large difference in the LL between the two areas, the overall mortality rates of the two earthquakes may be the same, this finding confirms that the it is one of the main influencing factors of the mortality rate, and it can reflect the comprehensive level of an earthquake area.

Generally, for the same earthquake area, although the impact fields of earthquakes at different times are not completely the same, since earthquakes at different times are basically within the scope of an administrative area, the basic physiology (such as the geography and geological landforms) in an area will not change substantially, and thus, there should be no major differences in the LL in the same area at different times, however, we found a significant difference in the same area, for example, among the 6 earthquakes that occurred in Jiashi, Xinjiang, from 1996 to 2003, the LLs were 0.8422, 0.5691, 0.5978, 0.7839, 0.6897, and 0.8182; thus, the difference in the same area at different times reached 0.2731, similarly, for the earthquakes that occurred in Lijiang, Yunnan, on 3 February 1996, 2 July 1996, and 25 September 1996, the LLs were 0.7583, 0.8428, and 0.8514, respectively, and the difference reached 0.0931, for the earthquakes that struck Minxian, Gansu Province, on 13 November 2003, and 7 September 2004, it were 0.7074 and 0.716, respectively, and the difference reached 0.0086, for the earthquakes that occurred in Wen County, Gansu Province, on 15 April 1999, and 21 June 2006, it were 0.7118 and 0.8197, respectively, with a difference of 0.1079, for the earthquakes that occurred in Yibin, Sichuan, on 28 February 1996, and 17 June 2004, it were 0.7051 and 0.4321, respectively, and the difference reached 0.273. We postulate that such different in the same areas may be due to the different types and proportions of buildings in those areas because the types and proportions of buildings in an area may change with economic development over time, but the geography and landforms in the same area will not undergo remarkable change.

As shown in Figure 4, the results of the 6 building types show relatively obvious distribution interval characteristics, although the distribution intervals of adobe and wood structures are less obvious due to the relatively small number of these buildings, nevertheless, the calculated LLs of adobe structures are concentrated above 0.85, those of wood structures are distributed between 0.15 and 0.35, those of civil structures are between 0.5 and 1, those of brick-wood structures are between 0.3 and 0.9, those of brick-concrete structures have a scattered distribution ranging from 0 to 1, and those of reinforced concrete structures are between 0 and 0.4, in other words, even for earthquakes with different occurrence times, regional environments, and magnitudes, the LLs of the same type of buildings are relatively similar, consequently, there are no significant differences in the LL of the same building type among the different areas.

FIGURE 4

FIGURE 4. Calculation results of lethal level of different types of buildings.

As shown in Figure 5, the distributions of the LLs of various types of buildings are relatively concentrated within certain ranges, according to the average values of the LL of various types of buildings, adobe structures have the highest LLs, followed by civil structures and brick-wood structure, the distribution of the brick-concrete structures is more scattered, and the concentration distribution interval is relatively insignificant, reinforced concentrate structures exhibit have the lowest, and the distribution intervals are relatively concentrated, moreover, the number of wood structures is relatively small, but the overall distribution interval is relatively concentrated between those of brick-concrete structures and reinforced concentrate structures.

FIGURE 5

FIGURE 5. Different types of buildings lethal level distribution characteristics.

As shown in Figure 6, from the calculation results of 95% confidence intervals of the LLs of the 6 building types reveals the following: the average LL of adobe structures is 0.9175, and the standard deviation is 0.04063; the civil structures is 0.8491, and the standard deviation is 0.08855; the brick-wood structures is 0.7469, and the standard deviation is 0.133; the brick-concrete structures is 0.4585, and the standard deviation is 0.2673; the reinforced concrete structures is 0.1692, and the standard deviation is 0.101; and the wood structures is 0.2724, and the standard deviation is 0.04963, in addition, the distributions of the average values are relatively concentrated, the average LLs of adobe and wood structures are relatively less abundant, but they can still reflect the distribution trends of these two types of buildings, that is, the calculation results based on the 95% confidence interval can better reflect the concentrated partial range of the LL of each type of building.

FIGURE 6

FIGURE 6. 95% confidence interval distribution of lethal level of different types of buildings.

As shown in Table 5, according to the calculated results of each building type, we obtained the sample mean, standard deviation, sampling average error and allowable error of each building type, based on the mean and allowable error, the lower and upper confidence limits of each building type were obtained, we define these lower and upper confidence limits as the upper and lower limits of the LL interval of each building type, the interval range of the LLs of adobe structures is within 0.85–1, that of civil structures is within 0.75–0.95, that of brick-wood structures is within 0.6–0.9, that of brick-concrete structures is within 0.33–0.6, that of wood structures is within 0.2–0.35, and that of reinforced concrete structures is within 0.1–0.25, these distribution interval ranges can further represent the main concentrated distribution areas of various types of buildings, however, the distributions of the building typologies are regionally dependent (Pavic et al., 2019; Pavic et al., 2020a; Pavic et al., 2020b), and it should be noted that the LL range corresponding to each type of building obtained in this article is just a theoretically calculated range of values based on each type, moreover, the same building types even have different structure and properties among different regions/cities/municipalities; therefore, to determine the actual LLs of buildings in earthquake areas, it is still necessary to construct a corresponding model for calculations based on this interval.

TABLE 5

TABLE 5. 95% confidence interval index parameters of building lethal level.

As shown in Table 6, we determined the range of LLs for each type of building, at the same time, based on a large amount of field investigation experience, we found that each type of building has different factors affecting its LL, including the construction style, building materials, building age, construction measures, building height, building use, cement type, foundation type, etc., in other words, for each type of building, the different details of its construction are responsible for the differences in the LL, but the actual values of various buildings should be within the ranges corresponding to the above types of structures.

TABLE 6

TABLE 6. Lethal level range and influencing factors of various types of buildings.

Discussion

Based on an analysis of historical earthquakes, the magnitude, population density, geographical and geomorphological environment, and proportion of damaged buildings are similar between the two earthquakes, but there is a considerable difference in the number of casualties, earthquake-induced deaths are affected not only by the proportion of damaged buildings but also by the combined effects of regional geological features, road traffic, and incidental factors, we constructed a matrix of mortality rates based on the LL and intensity (Xia et al., 2020); in fact, it represents different intensities, and the corresponding mortality rate is different, so for different regions, different LLs correspond to personnel mortality rates with intensities of VI-XI, its different to the casualty assessment method by the United States Geological Survey (USGS) which has only one component of the mortality rate by intensity for a country, if we can obtain the LL of an area prior to an earthquake, then after the earthquake, we can select the corresponding mortality rate for evaluation and calculation, this also provides another possibility for rapidly assessing earthquake casualties.

The LL of an area is affected by many influencing factors, of which buildings are dominant, which means that different types of buildings have unique LLs, it is an extension of the vulnerability level, which is concerned mainly with the probability that different buildings will cause different damage states after an earthquake, and different damage levels correspond to the mortality rate, however, for different buildings, even is the proportion of damaged buildings is the same, the mortality rate still varies, therefore, this article employs historical earthquake data to quantitatively calculate the LLs of various types of buildings.

The LLs of different historical earthquake areas far from one another may be similar, but those of areas adjacent to each other may be quite different; hence, the LL does not depend on the geographical location, theoretically, for different earthquakes located in the same area, even at different times, the geological and geomorphological conditions within the area will not change significantly, furthermore, the population size and density will not vary considerably, thus, without a large difference in the earthquake magnitude, the main mechanism responsible for the differences in the LL in the same area may be the impacts of buildings in the area, an analysis of the building types and their proportions in each earthquake area reveals that the main cause of changes in the regional LL is the differences between the building types and their proportions.

The earthquakes that occur in different time periods in the same area, building types undergo certain changes after their restoration and reconstruction, inevitably leading to differences in regional LLs, for example, for the Jiashi earthquake in Xinjiang on 19 March 1996, the buildings in the earthquake area were predominantly adobe structures (composing 93.19% of all structures), whereas brick-concrete structures accounted for only 5%, and the LL was 0.8422, the buildings in the same earthquake area on 21 January 1997, were likewise dominated by adobe and brick-concrete structures, but their proportions were 45.84% and 38.01%, respectively; the proportion of the latter was relatively large, which caused the LL of the area to change significantly (0.5691), in other words, the influences of building types and proportions in an area are the main reason for the differences in the LL; therefore, the unique LL of a region can be comprehensively reflected by the building types, the proportions of buildings, the LLs of the various types of buildings.

Moreover, for a given building type, differences in the building materials, construction methods, and building quality cause the LL to differ, in other words, the actual LLs of buildings of the same type in different areas may be greatly different; nevertheless, regardless of this difference, the range of change should be within (should not exceed) the range corresponding to that type of building, the type of building, construction materials, construction time, etc., all affect the value, and the weights of these impacts are vary, based on these weights, the actual LL of a building can be quantitatively calculated.

The LLs of different building types have unique concentrated distribution interval ranges that are not equal, some buildings have small ranges, such as civil structures, whereas others have large ranges, such as brick-concrete structures, in addition, the LL ranges of different building types overlap, for example, the range of wood structures is 0.2–0.35, and that of brick-concrete structures is 0.33–0.6, generally, the wood structures is higher than that of a brick-concrete structure, but the lower limit of the interval range of brick-concrete structures is lower than the upper limit of wooden structures, which is also consistent with the actual survey situation, for example, the LL of a high-quality brick-concrete structure with a complete building structure may be lower than that of a wood structure of poor quality that is older in age, therefore, the actual LL of each type of building in each area needs to be determined according to its actual situation.

Conclusion

This paper proposed the concept of the LL and constructs a calculation model for determining the regional LL, based on data of 52 historical earthquakes, the LLs of the types of buildings in different regions were obtained, based on theoretical calculations and field survey experience, we obtained the ranges of LLs for various types of buildings, thereby providing a theoretical basis for the field investigation and quantitative calculation for buildings in different areas.

Based on historical earthquakes, the LL of each building type is within an interval range; that is, even among the same type of buildings, due to differences in the building structure, quality, and age, etc., their actual LLs diverge, in addition, the interval ranges of different types of buildings are not equivalent, and these ranges overlap with each other, hence, the LL of one type of building is not necessarily lower than that of another type of building, these quantitative results can also reduce errors caused by classifications based solely on building types.

By calculating and determining the LLs of buildings, it is possible to quantitatively calculate the LL of a region, the quantitative result of this calculation reflects the probability of casualties for the whole region, different LLs represent a group of dominant mortality rates of various intensities, based on the different LLs of regions, it is possible to achieve the zonation of regions, and these zones is not limited to simple administrative divisions or geographic boundaries, instead, it is a quantitative metric of the overall capacity of an area, which reduces the need to acquire detailed building data, it can intuitively reflect the overall earthquake resistance of an area and can also provide support for the risk assessment of casualties.

This paper used mainly historical seismic data to determine the LLs of buildings and obtained the ranges of different types of buildings, these findings provide insight into and a method for quantitatively calculating the seismic capacity of buildings, subsequent studies will need to introduce methods to determine the LLs of various other types of buildings.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XC, LH, ZJ, YR, and ZX directed and performed field experiments, processed data and produced some figures. FX processed data and produced some figures. NG oversaw the complete project and provided guidelines. XC prepared the first draft manuscript. All authors were involved in the final manuscript preparation. All authors read and approved the final manuscript.

Funding

This work was jointly supported by the National Nonprofit Fundamental Research Grant of China, Institute of Geology, China Earthquake Administration (Grant No. IGCEA2106) and the National Natural Science Foundation of China (Grant No. 42071337) and the National Natural Science Foundation of China (Grant No. 41907397).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alel, M. N. A. (2013). “Estimation of life casualties for seismic vulnerability assessment in Bukit Tinggi,” in Geocon 2013 Proceedings, 30 Jun 2014 (Johor Bahru: GEOCON2013).

Google Scholar

Alexander, D. E. (2011).“Mortality and morbidity risk in the L’aquila, Italy earthquake of 6 April 2009 and lessons to be learned,” in Human casualties in earthquakes. Editors R. Spence, E. So, and C. Scawthorn. (Dordrecht: Springer), 29. doi:10.1007/978-90-481-9455-1_13

CrossRef Full Text | Google Scholar

Badal, J., and Samardjieva, E. (2003). Prognostic estimations of casualties caused by strong seismic impacts. Nice, France: EGS-AGU-EUG Joint Assembly.

Google Scholar

Badal, J., Zquez-Prada, M. V., and Gonz-lez, R. (2005). Preliminary quantitative assessment of earthquake casualties and damages. Nat. Hazards (Dordr). 34 (3), 353–374. doi:10.1007/s11069-004-3656-6

CrossRef Full Text | Google Scholar

Ceferino, L., Kiremidjian, A., and Deierlein, G. (2018a). Regional multiseverity casualty estimation due to building damage following a Mw 8.8 earthquake scenario in Lima, Peru. Earthq. Spectra 34 (4), 1739–1761. doi:10.1193/080617eqs154m

CrossRef Full Text | Google Scholar

Ceferino, L., Kiremidjian, A., and Deierlein, G. (2018b). Probabilistic model for regional multiseverity casualty estimation due to building damage following an earthquake. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 4 (3), 04018023. doi:10.1061/ajrua6.0000972

CrossRef Full Text | Google Scholar

Christoskov, L., and Samardjieva, E. (1984). An approach for estimation of the possible number of casualties during strong earthquakes [J]. Bulg. Geophys J. 4, 94–106.

Google Scholar

Feng, T., Hong, Z., Wu, H., Fu, Q., Wang, C., Jiang, C., et al. (2013). Estimation of earthquake casualties using high-resolution remote sensing: A case study of dujiangyan city in the may 2008 wenchuan earthquake. Nat. Hazards (Dordr). 69 (3), 1577–1595. doi:10.1007/s11069-013-0764-1

CrossRef Full Text | Google Scholar

Ferreira, M., Oliveira, C., and Sá, F. (2011). “Estimating human losses earthquake models: A discussion [M], human casualties in earthquakes,” in Advances in natural and technological hazards research. Dordrecht: Springer.

Google Scholar

Fu, Z. (1993). A preliminary study on establishment of probabilistic vulnerability matrix of life from earthquakes [J]. Earthq. Res. china 3, 205–210.

Google Scholar

Goncharov, S., and Frolova, N. (2011). Casualty estimation due to earthquakes: Injury structure and dynamics. Dordrecht: Springer.

Google Scholar

Jaiswal, K., Wald, D., and D'Ayala, D. (2011). Developing empirical collapse fragility functions for global building types. Earthq. spectra 27 (3), 775–795. doi:10.1193/1.3606398

CrossRef Full Text | Google Scholar

Jaiswal, K., Bausch, D., Chen, R., Bouabid, J., and Seligson, H. (2015). Estimating annualized earthquake losses for the conterminous United States. Earthq. Spectra 31 (1), S221–S243. doi:10.1193/010915EQS005M

CrossRef Full Text | Google Scholar

Ma, Y., and Xie, L. (2000). Research on the estimation method of earthquake casualties[J]. Earthq. Eng. Eng. Vib. 20 (4), 140–147. doi:10.3969/j.issn.1004-4574.2000.03.013

CrossRef Full Text | Google Scholar

Ma, Y., and Zhao, G. (2008). Earthquake disaster risk analysis and management. Beijing: Science Press.

Google Scholar

Miyakoshi, J., Hayashi, Y., and Tamura, K. (1998). “Damage ratio functions of building using damage data of the 1995 hyogo-ken nanbu earthquake,” in 7th International Conference on Structural Safety and Reliability (ICOSSAR ‘97), Kyoto, Japan, November 24–28, 1997. 1, 349–354.

Google Scholar

Nie, G., Xia, C., and Fan, X. (2020). Classification of anti-lethal level based on historical earthquake death data[J]. Chin. J. Geol. 55 (4), 1298–1314. doi:10.12017/dzkx.2020.078

CrossRef Full Text | Google Scholar

Nie, G., Xia, C., Fan, X., and Li, H. (2021). Research on the lethal level of buildings based on historical seismic data[J]. Chin. J. Geol. 56 (4), 1250–1266. doi:10.12017/dzkx.2021.068

CrossRef Full Text | Google Scholar

Oike, K. (1991). “A discussion on the relation between the magnitude and the number of the dead by earthquakes [M],” in Proc of the International Seminar on Earthquake (Tsukuba: Prediction and Hazard Mitigation Technology), 333–341.

Google Scholar

Okada, S., and Takai, N. (1999). Classifications of structural types and damage patterns of buildings for earthquake field investigation [J]. Nihon. Kenchiku. Gakkai. Kozokei. Ronbunshu. 64 (524), 65–72. doi:10.3130/aijs.64.65_5

CrossRef Full Text | Google Scholar

Pang, W., Majdalaweyh, S., Safiey, A., Rokneddin, K., Prabhu, S., Javanbarg, M., et al. (2020). A probabilistic casualty model to include injury severity levels in seismic risk assessment. Report.

Google Scholar

Pavić, G., Bulajić, B., and Hadzima-Nyarko, M. (2019). The vulnerability of buildings from the osijek database [J]. Front. Built Environ. 5 (66), 1–14. doi:10.3389/fbuil.2019.00066

PubMed Abstract | CrossRef Full Text | Google Scholar

Pavić, G., Hadzima-Nyarko, M., and Bulajić, B. (2020a). A contribution to a UHS-based seismic risk assessment in Croatia—a case study for the city of osijek. Sustainability 12 (5), 1796–1824. doi:10.3390/su12051796

CrossRef Full Text | Google Scholar

Pavić, G., Hadzima-Nyarko, M., Bulajić, B., and Jurković, Ž. (2020b). Development of seismic vulnerability and exposure models – a case study of Croatia. Sustainability 12 (3), 973–1024. doi:10.3390/su12030973

CrossRef Full Text | Google Scholar

Pomonis, A., Kappos, A., and Karababa, F. (2011). “Seismic vulnerability and collapse probability assessment of buildings in Greece [M],” in S. R., S. E., S. C., Human Casualties in Earthquakes, 08 December 2010 (Dordrecht: Advances in Natural and Technological Hazards Research), 153–170.

CrossRef Full Text | Google Scholar

Samardjieva, E. (2002). Estimation of the expected number of casualties caused by strong earthquakes. Bull. Seismol. Soc. Am. 92 (6), 2310–2322. doi:10.1785/0120010112

CrossRef Full Text | Google Scholar

Samardjieva, E., and Oike, K. (1992). Modelling the number of casualties from earthquakes [J]. J. Nat. disaster Sci. 14 (1), 17–28.

Google Scholar

So, E. (2011). Challenges in collating earthquake casualty field data. Dordrecht: Springer.

Google Scholar

So, E., and Spence, R. (2013). Estimating shaking-induced casualties and building damage for global earthquake events: A proposed modelling approach. Bull. Earthq. Eng. 11 (1), 347–363. doi:10.1007/s10518-012-9373-8

CrossRef Full Text | Google Scholar

Spence, R., So, E., and Cultrera, G. (2008). “Earthquake loss estimation and mitigation in europe: A review and comparison of alternative approaches [C],” in The 14th World Conference on Earthquake Engineering, 12/10/2008-18/10/2008 (Beijing, China: World Conference on Earthquake Engineering).

Google Scholar

Spence, R., So, E., Jenkins, S., Coburn, A., and Ruffle, S. (2011). “A global earthquake building damage and casualty database,” in Human casualties in earthquakes, Editor Spence, R., So, E., and Scawthorn, C.(Dordrecht: Springer), 29. doi:10.1007/978-90-481-9455-1_5

CrossRef Full Text | Google Scholar

Wang, H. X., Niu, J. X., and Wu, J. F. (2011). ANN model for the estimation of life casualties in earthquake engineering. Syst. Eng. Procedia 1, 55–60. doi:10.1016/j.sepro.2011.08.010

CrossRef Full Text | Google Scholar

Wei, B., Nie, G., Su, G., Sun, L., Bai, X., and Qi, W. (2017). Risk assessment of people trapped in earthquake based on km grid: A case study of the 2014 ludian earthquake, China. Geomat. Nat. Hazards Risk 8 (2), 1289–1305. doi:10.1080/19475705.2017.1318795

CrossRef Full Text | Google Scholar

Xia, C., Gaozhong, N., Xiwei, Z., and Junxue, P. (2020). Research on the rapid assessment of earthquake casualties based on the anti-lethal levels of buildings. Geomat. Nat. Hazards Risk 11 (1), 377–398. doi:10.1080/19475705.2019.1710581

CrossRef Full Text | Google Scholar

Xu, J., Fuquan, W., and Zhang, L. (2008). Preliminary study on evaluating the number of casualties and trapped victims by an earthquake - a case study of Zhangzhou City, Fujian Province [J]. J. Seismol. Res. 31 (4), 382–387. doi:10.3969/j.issn.1000-0666.2008.04.014

CrossRef Full Text | Google Scholar

Yin, Z. (1991). Research on earthquake disaster loss prediction [J]. Earthq. Eng. Eng. Vib. 4, 89–98.

Google Scholar

Zhang, Y., Lin, Q., Liu, Y., and Wang, Y. (2018). The quick assessment model of casualties for asia based on the vulnerability of earthquake [J]. Nat. Hazards Earth Syst. Sci. Discuss. 1–22. doi:10.5194/nhess-2018-21

CrossRef Full Text | Google Scholar

Zhize, F., and He, J. (1996). Earthquake casualty prediction research: —taking lunan area as an example [J]. J. Seismol. 000 (1), 58–62.

Google Scholar

Zhu, J., and Yang, M. (1998). Prediction and facts about the casualties caused by the earthquake: The relationship between house destruction and the number of deaths[J]. Seismol. Sci. Technol. Inf. 000 (004), 32–37.

Google Scholar