Tidal Modulation of Ice Streams: Effect of Periodic Sliding Velocity on Ice Friction and Healing

Basal slip along glaciers and ice streams can be significantly modified by external time-dependent forcing, although it is not clear why some systems are more sensitive to tidal stresses. We have conducted a series of laboratory experiments to explore the effect of time varying load point velocity on ice-on-rock friction. Varying the load point velocity induces shear stress forcing, making this an analogous simulation of aspects of ice stream tidal modulation. Ambient pressure, double-direct shear experiments were conducted in a cryogenic servo-controlled biaxial deformation apparatus at temperatures between −2°C and −16°C. In addition to a background, median velocity (1 and 10 μm/s), a sinusoidal velocity was applied to the central sliding sample over a range of periods and amplitudes. Normal stress was held constant over each run (0.1, 0.5 or 1 MPa) and the shear stress was measured. Over the range of parameters studied, the full spectrum of slip behavior from creeping to slow-slip to stick-slip was observed, similar to the diversity of sliding styles observed in Antarctic and Greenland ice streams. Under conditions in which the amplitude of oscillation is equal to the median velocity, significant healing occurs as velocity approaches zero, causing a high-amplitude change in friction. The amplitude of the event increases with increasing period (i.e. hold time). At high normal stress, velocity oscillations force an otherwise stable system to behave unstably, with consistently-timed events during every cycle. Rate-state friction parameters determined from velocity steps show that the ice-rock interface is velocity strengthening. A companion paper describes a method of analyzing the oscillatory data directly. Forward modeling of a sinusoidally-driven slider block, using rate-and-state dependent friction formulation and experimentally derived parameters, successfully predicts the experimental output in all but a few cases.

Introduction

Ice streams represent a significant portion of the Antarctic ice mass balance (Bamber et al., 2000). Much of the dynamics that control ice stream flow rates are not well constrained, particularly sliding at the base. Modeling efforts often consider local variation and evolution of basal resistance as a control on flow rates (Clarke, 2005). However, our knowledge of the base is limited to but a few locations. Meanwhile, a growing body of literature documents the sensitivity of ice stream flow to tidal forcing (Riedel et al., 1999; Doake et al., 2002; Bindschadler et al., 2002; 2003; Gudmundsson, 2007; Wuite et al., 2009; Brunt et al., 2010; Rosier et al., 2014; 2017), with modulation measured up to 100 km upstream from the grounding line (Anandakrishnan and Alley, 1997). Ice stream tidal modulation displays great variations in the type and periodicity of modulation. For instance, Mercer and Bindschlader Ice Streams display smooth, diurnal modulation (Brunt and MacAyeal, 2014; Anandakrishnan et al., 2003) whereas Rutford Ice Stream’s smooth modulation is semi-diurnal and more closely tuned to the spring-neap cycle (Murray et al., 2007; Minchew et al., 2017). Long period modulation provides changes in horizontal flow velocities in the range of 5–20% of the mean velocity, whereas the short period modulations have given rise to ∼300% the mean velocity, in some cases causing periodic reversal in flow direction (Makinson et al., 2012). Whillans Ice Stream is a noteworthy example in which the tidal modulation is in the form of stick-slip, captured by both GPS and seismic records (Weins et al., 2008; Winberry et al., 2009; Winberry et al., 2011; Winberry et al., 2014; Pratt et al., 2014; Barcheck et al., 2021) in which bursts of motion are followed by long periods of near stagnation. The twice-daily 30 min events occur just before low tide and just after high tide (Wiens et al., 2008). The relationship between displacement during an event and recurrence interval suggests a time-dependent strengthening, or healing, at the basal interface between events (Winberry et al., 2014). Variations in modulation style and tuning from location to location raise the possibility of using glacier response to relatively well-known tidal signals to infer basal properties.

The effects of periodic perturbations on frictional stability has been studied in laboratory experiments on both solid and granular materials, with oscillations in shear forcing (Lockner and Beeler, 1995; Savage and Marone, 2007; 2008), oscillations in normal stress forcing (Richardson and Marone, 1999; Boettcher and Marone, 2004; Hong and Marone, 2005), and oscillations in principal stresses (Beeler and Lockner, 2003). The effects of periodic perturbations have additionally been reviewed in theoretical treatments (Tworzydlo and Hamzeh, 1997; Voisin, 2001, 2002; Perfettini and Schmittbuhl, 2001; Perfettini et al., 2003). These studies have provided insight into frictional modulation and dynamic triggering of stick-slip, including the frequency- and amplitude-dependences of rock and gouge systems.

The theory of basal sliding has historically been based on viscous deformation and regelation processes (Weertman, 1957; Schoof, 2005; Gagliardini et al., 2007). However, stick-slip, rate-weakening, and healing are processes observed in natural glaciers that do not fit into the Weertman-style sliding laws because they represent a departure from purely viscous behavior. Traditional models that neglect elastic behavior and brittle failure may not be capturing the full dynamic range of processes occurring at ice streams (Tsai et al., 2008; Gimbert et al., 2021). Theoretical considerations are beginning to include stick-slip events into quantitative descriptions of glacier sliding in the form of rate- and state-dependent frictional models (Sergienko et al., 2009; Zoet et al., 2013; Goldberg et al., 2014; Lipovsky and Dunham, 2016; Lipovsky et al., 2019; Minchew and Meyer, 2020). Zoet et al., 2020 showed that rate- and state-dependent friction from laboratory experiments were directly applicable to glacier seismology by generating stick-slips in the lab with a de-stiffened rig. Seismology plays a major part in the understanding of stick-slip motion because, like earthquakes on tectonically loaded faults, stick-slick motion of glaciers emits seismic energy (Winberry et al., 2009; Zoet et al., 2012; Winberry et al., 2014; Helmstetter et al., 2015; Podolskiy and Walter, 2016). Additionally, many ice streams are thought to be at the pressure melting temperature at the bed. Water pressures can vary considerably in both time and space (Kamb et al., 1985). Although oscillating water pressure has been suggested as the control on glacial velocities, borehole observations of maximum sliding velocity while pressure is still rising contradict this. Rather, a stick-slip mechanism is needed to reconcile those observations (Bahr and Rundel, 1996).

In an attempt to provide physical mechanisms responsible for differing sliding behaviors and aid in prediction of future flow rates, we run a series of cyclically forced friction experiments to explore the onset of stick-slip and slow slip in a simple ice-on-rock system. We explore the effects of temperature, period, amplitude, normal stress, and velocity on the frictional strength and stability. We apply the mathematical framework of rate-and-state friction with an analysis of velocity steps to describe the laboratory results and forward model the behavior with a simple one degree of freedom slider block model to determine if the observed behavior is consistent with existing theory.

Materials and Methods

Rectangular samples of polycrystalline ice were fabricated using a modified version of the “standard ice” protocol (Cole, 1979; McCarthy et al., 2017), which used seed ice that was shaved, sieved (between 250 and 106 μm), and packed into a rectangular mold. The mold was placed in an ice bath (T = 0°C) for ∼30 min, under vacuum. Upon temperature equilibration, the mold was flooded with degassed deionized water and then placed on a cold copper plate (T = −5°C) within a chest freezer, insulated on all sides, to allow directional solidification from the bottom up. The resulting samples were nearly pore-free (<1%) with uniform grain size of approximately 1 mm (due to subsequent grain growth at the relatively warm −5°C). Samples were made intentionally oversized; after removal from the mold, they were cut down to precise dimensions (50 × 50 × 100 mm) with a microtome located in a cold room (T = −17°C). The ice sliding surfaces were roughened with 100 grit sandpaper just before loading into the apparatus.

Experiments were conducted in a double-direct shear configuration (Figure 1 inset) using an ambient pressure, servo-controlled biaxial apparatus (McCarthy et al., 2016). Experiments were conducted over a range of temperatures that were controlled via a circulating fluid cryostat (−2 < T(°C) < −16). In the experiments, the central polycrystalline ice block (50 × 50 × 100 mm) was slid between two stationary blocks of Barre granite (50 × 50 × 30 mm) such that the nominal area of contact (50 × 50 on each of two sliding faces) was constant during sliding. The Barre granite stationary blocks had a grain size of 1–5 mm and the surfaces were polished with a surface grinder to surface roughness (Ra) of 2.8 ± 2 μm, as determined by a profilometer. The roughened central ice block surfaces were Ra = 7 ± 1. A horizontal piston pushing against a screw stop applied constant normal stress that was maintained using force feedback servo control. Shear stress was induced by a vertical ram that was servo-controlled in displacement feedback using a computer-controlled driving program. The force applied and the displacement travelled in each direction were measured by load cells and displacement transducers, respectively, mounted outside the cryostat. The stiffness of the apparatus and sample assembly K was determined in situ by two methods. The first was the conventional method of fitting a line to the plot of shear stress vs. displacement during the initial moments of the experiment. This run-in or ramp stiffness was measured for eleven of the twelve experiments and is provided in Table 1 as K_ramp, with the average value as 0.47 ± 0.23 kPa/μm. Stiffness was also determined later in the experiment using a velocity step and solving for K (rather than assuming a constant). Such values are called K* and are provided in Table 2. The two types of measurements are compared in Figure 7H.

FIGURE 1

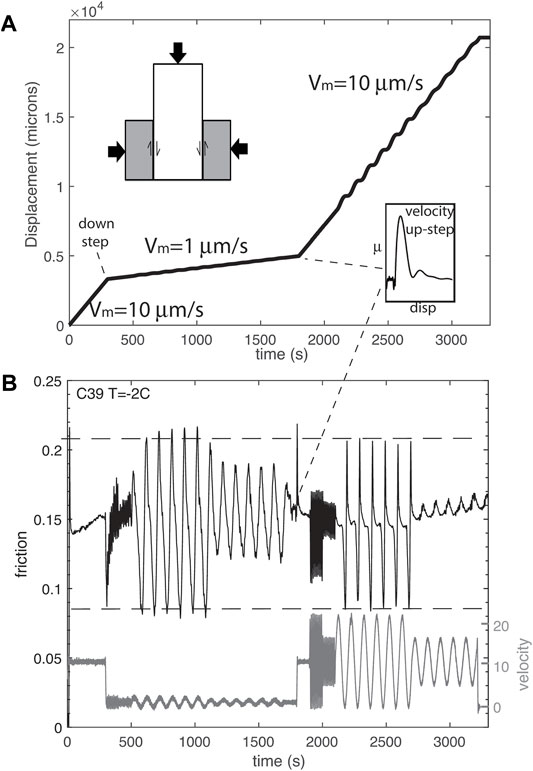
FIGURE 1. (A) Displacement vs. time showing the driving control program. (B) Driving velocity in gray and measured friction (black) for a single run (C39) of ice sliding on rock in double direct shear (upper inset) at −2°C.

TABLE 1

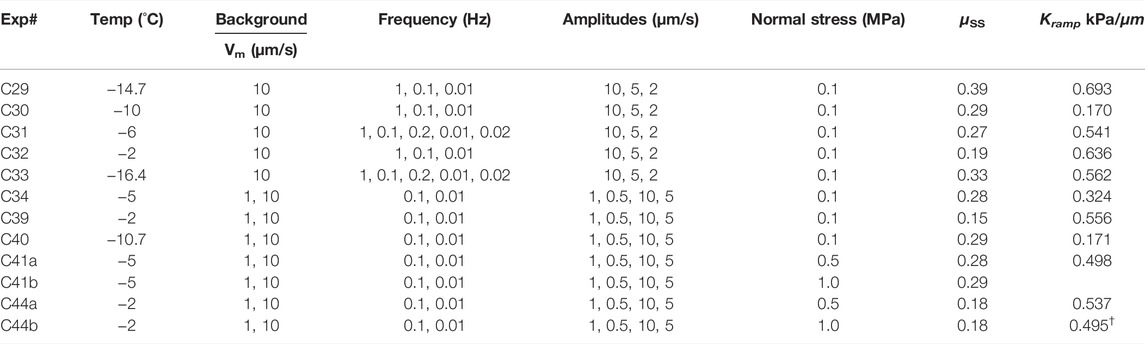
TABLE 1. List of experiments, intended driving conditions*, steady-state friction measured at the end of the loading ramp, prior to oscillations, and run-in stiffness, K_ramp(determined from slope of the ramp). The a and b runs for samples C41 and C44 represent runs at two different normal stresses on the sample, all other conditions were the same. ^†K_ramp at 41b could not be measured because the system was not fully unloaded before the b run was initiated. *Fitted velocities were 1.1 and 11.1 μm/s.

TABLE 2

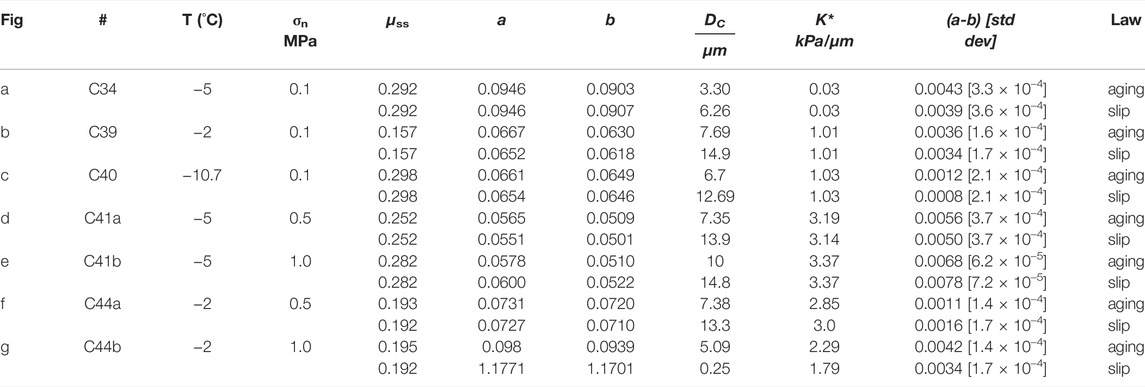
TABLE 2. Fitted rate-state parameters to velocity up steps in Figure 7.

We combined a constant load point velocity with sinusoidal oscillations (Figure 1A). In every experiment, a constant velocity was first applied for approximately 3 mm of displacement to precondition the sample such that steady-state friction was reached. After that, multiple amplitudes and periods were applied in succession (from short to long) to study the frictional response (Table 1). The load point was moving at V(t), which we describe as a function of forcing period P and amplitude A as:

$V\left(t\right)={\mathit{V}}_m+A\cos \left(\frac{\text{2}\pi t}{P}\right).(1)$

Specifically, two different driving protocols were used. Experiments C28 to C33 used a single median driving velocity (V_m = 10 μm/s) and cycled through three periods (1, 10, and 100 s) with three amplitudes each (10, 5, and 2 μm/s, which are 100, 50, and 20% of V_m), such that at the highest amplitude velocities slowed to zero once per cycle, but the sample never moved backward. Experiments C31 and C33 further explored 5 and 50 s periods. Experiments C34 to C44 tested only two periods (10 and 100 s) and two amplitudes (100 and 50% of V_m) but employed two median driving velocities (1 and 10 μm/s) such that a full set of oscillations were conducted at 1 μm/s, the velocity was increased to 10 μm/s, and another full set of oscillations were repeated (Figure 1). The transition between the two rates represents a velocity upstep (Figure 1A inset), which was used to measure rate-state parameters described in Eqs 2–4. During most experiments, a constant normal stress of ∼0.1 MPa was applied, with the exception of C41 and C44, during which we first ran the two-velocity cycling program under 0.5 MPa normal stress and then repeated the program under 1 MPa normal stress. In total, 10 samples were tested with runs covering 107 different combinations of V_m, T, P, and A conditions. Some conditions were additionally repeated to confirm reproducibility, as discussed in Reproducibility Section and in the Supplementary Material.

Temperature during an experiment was held constant with a circulating fluid-controlled cryostat described in McCarthy et al., 2016; 2017. However, several improvements were incorporated into the temperature control and monitoring system since those previous works. A resistance temperature detector (RTD) embedded in the rock monitored temperature at the sliding interface between ice and rock. The RTD has an error of ±0.1°C, which was a significant improvement over the previously used thermocouples. Additionally, here the bottom plate of the cryostat was made of insulating material (polycarbonate) so that external heating did not transfer to the stationary steel blocks holding the rock samples. Finally, we pre-chilled all rock and metal in the cryostat overnight at the desired testing temperature before each experiment. These three changes created a system that achieved and held a desired temperature more efficiently than our previous cryostat. An example of the temperature control throughout the experiment is provided in the supplemental material (Supplementary Figure S2B).

Inversion for Rate and State Friction Parameters and Forward Modeling

The empirically derived rate-and-state friction (RSF) formulation has successfully been used to characterize frictional slip on faults and has been the common methodology for describing earthquake physics for the last 40 years (Dieterich, 1979, 1981; Ruina, 1983). For more recent treatments of RSF, one can turn to works by Marone (1998) and Scholz (2019) and the numerous references therein. Use of RSF has previously been used to describe ice friction experimental studies (Fortt and Schulson, 2009; Zoet et al., 2013; McCarthy et al., 2017; Zoet and Iverson, 2018). The observation of basal seismicity caused by stick-slip, which requires rate-weakening behavior, provides the license for application of RSF formulation in the field of glaciology as well and it has recently been employed to describe sliding behavior in Antarctic Ice Streams [e.g. Zoet et al., 2013; Lipovsky and Dunham, 2017; Lipovsky et al., 2019]. Therefore, variations between smooth (stable) sliding and stick-slip (unstable) sliding in cyclically forced ice friction experiments described here are analyzed using rate-and-state friction, which describes frictional strength as a function of both sliding velocity V (the relative slip rate across a contact interface) and state θ (which at steady state is the lifetime of asperity contact). In the formulation, the evolution of friction is controlled by two coupled equations, the first of which is:

$\mu \left(\mathit{V,}\theta \right)=\frac{\tau }{{\sigma }_n}={\mu }_0+a\ln \frac{V}{V_0}+b\ln \frac{V_0\theta }{D_C},(2)$

in which τ and σ_n are shear and normal stresses, respectively, a is the “direct effect” accounting for variations in frictional strength due to changes in slip rate from a reference velocity, b is the “evolution effect” that determines the change in friction due to evolution of state from a reference steady state, and D_C is the critical slip distance that is needed for the system to evolve from one steady-state to another (Dieterich, 1979; Marone, 1998). Parameters a, b, and D_C are determined from experimental velocity step data (Figure 1 inset) and µ₀ and V₀, are reference values such that µ₀ is the reference friction at reference velocity V₀. The two forms of the time evolution of state are:

$\theta =1-\frac{V\theta }{D_C},(3)$

the Aging Law (Dieterich, 1978)

and

$\theta =-\frac{V\theta }{D_C}\text{I}\text{n}\frac{V\theta }{D_C},(4)$

the Slip Law (Ruina, 1983).

The Aging law and Slip Law are similar in that at steady-state sliding, both are Vθ/D_C = 1. They differ in that the Aging law describes state evolution during stationary contact while the Slip Law describes state changing only during slip. Hooke’s law applied to a single-degree-of -freedom spring slider is used to approximate the elastic response of the apparatus (and sample), which, combined with the rate-and-state friction equations, allows experimental data to be analyzed (e.g. Marone, 1998). In terms of velocity and the friction coefficient, the relation is:

$\frac{\partial \mu }{\partial t}=k\left(V_L-V\right)(5)$

where V_L is the load point velocity, inertia is negligible, and the frictional surface is assumed to be rigid so that all elastic deformation is included in k, the spring constant of the loading environment, expressed as the apparatus stiffness (herein K_ramp or K*) normalized by normal stress σ_n and thus having units of 1/length.

Previous experimental studies introduced a critical forcing period of the oscillating velocity, which determines the stability transition of the system. There are two timescales that have been proposed to govern the response of sliding to a given frequency. One is the natural period of the spring-slider system. There have not been enough experiments run at different conditions (e.g. stable sliding vs. stick-slip) to solve for all of the constants in this relationship, but several papers which we reference have shown that the critical period must be proportional to the critical slip distance D_C and load point velocity V as (Rice and Ruina, 1983; Boettcher and Marone, 2004; Savage and Marone, 2007; van der Elst and Savage, 2015):

$P_C\alpha \frac{D_C}{V}.(6)$

When examining the dynamic response of a system to periodic or transient triggering, the nucleation timescale has been identified as (Dieterich, 1994; Beeler and Lockner, 2003; van der Elst and Savage, 2015):

$P_n=\frac{a{\sigma }_n}{\tau }(7)$

where stressing rate τ is the load point velocity multiplied by the system or apparatus stiffness K, which includes the stiffness of the apparatus and the sample. In a series of experiments with faults subjected to load oscillations, Beeler and Lockner (2003) found that when P_n was shorter than the forcing period, maximum seismicity rate correlated with maximum stressing rate but when P_n was longer than forcing period, maximum seismicity correlated with peak stress amplitude.

An additional timescale of consideration in a periodically forced system is the forcing period relative to the natural oscillation period, which will determine whether it may oscillate harmonically or be damped. Natural oscillation period is controlled in part by critical stiffness K_C, which is defined as:

$K_C=\frac{{\sigma }_n\left(b-a\right)}{D_C}(8)$

such that steady, stable sliding occurs when the system stiffness exceeds critical stiffness K > K_c (Rice and Ruina, 1983; Gu et al., 1984; Scholz, 1998; Gomberg et al., 2001). This critical stiffness relationship was more recently explored and confirmed in a laboratory study of debris-laden ice sliding over rock (Zoet et al., 2020).

The relative values of a and b from Eq. 2 determine the stability of a system. Determined from a step up in velocity (Figure 1A inset) a shows the response after a velocity change, from the steady state friction value to the peak. Term b represents the change in friction from peak to the new steady state at the new velocity. When (a-b ≥ 0), this is termed rate-strengthening friction and corresponds to stable sliding or smoothly sliding. However, when a velocity up step results in a lower steady-state friction, (a-b < 0) the system is rate-weakening and conditionally unstable. This is the necessary condition for stick-slip behavior (e.g., Scholz, 1998). Stress decreases during a slipping event, and thus healing is also needed to facilitate strength recovery for repeated slip events (e.g., Carpenter et al., 2011).

Velocity up-steps from raw data were analyzed with a nonlinear least squares fitting routine to a spring slider with spring constant k. In the fitting GUI (RSFit3000), slider velocity, friction coefficient (Eq. 2), both Eq. 3 (Aging) and 4 (Slip) descriptions of state, and Eq. 5 are cast as coupled ordinary differential equations (ODEs) (Skarbek and Savage, 2019). Although recent studies have shown that the Slip law does a better job of describing experimental data (Bhattacharya et al., 2015; 2017), we provide fits for both for comparison. A single state variable was used and the fitting program minimizes the difference between the data for steady-state friction, a, b, and D_C user inputs for initial guesses. The standard deviation of the (a-b) combined parameter in the GUI is computed using the covariance between a and b (Skarbek and Savage, 2019; their Eq. 7). Since recent studies demonstrate evolution of RSF parameters with displacement and slip velocity (Ikari and Saffer, 2011; Ikari et al., 2013), we additionally solved for k (provided in Table 2 as K*, such that K* = kσ_n). For more discussion of this and for additional details about the RSFit3000 fitting GUI, see Skarbek and Savage, 2019. Finally, a weighting function was included to ensure that the weight vector takes on values greater than unity at the velocity step and decays exponentially with load point displacement (Reinen and Weeks, 1993; Blanpied et al., 1998).

A forward model was created that uses a single degree of freedom elastic slider block (Eq. 5) and Eqs. 2, 8 with sinusoidal load point velocity of Eq. 1 and the individual fitted parameters provided in Table 2 to predict the frictional response of the system at desired periods and amplitudes. Inertia is ignored in the model, such that the slider block is considered rigid. The forward model can employ either the Aging or Slip forms of state, but here we use Slip. The governing equations for state variable, friction coefficient, and slip velocity are cast as coupled ODEs.

Results

The results from these periodic forcing experiments, the first conducted in our apparatus, demonstrate first and foremost that by simply changing the frequency and amplitude of forcing, the full range of frictional behavior can be observed within a single experiment (Figure 2). At small forcing amplitudes (20% of V_m) at longest and shortest periods, we see no discernible modulation of the friction coefficient (Figure 2A) and erratic oscillation that cannot keep up with the forcing (Figure 3A), respectively. For many conditions, particularly at long period, the response to a sinusoidal driving velocity is an in-phase sinusoid in friction (left side of Figure 2D). At the longest period (100 s) a high amplitude event during each cycle is observed in the frictional response (Figure 2D). For this event and the transitional stage in Figure 2C, the maxima are not exactly in phase with the forcing. Rather, the minima occur just after the low velocity and the maxima just before the high velocity, so the response is always within the increasing velocity leg of the cycle. A similar observation of peak friction prior to peak velocity was observed in a modeling study that used a field-derived diurnal velocity signal (Zoet et al., 2021). Starting from the median point in velocity and continuing with decreasing velocity (Figure 2C), friction begins to relax. Just after velocity increases above zero (t1), friction responds rapidly to a peak value (at t2) then rapidly evolves back to the background oscillation value. This slow slip event thus resembles a slide-hold-slide superimposed on a sinusoid (to be discussed further in Amplitude and Period effects Section and the discussion). At some conditions slipping events occur twice per cycle (Figure 2E) and at yet other conditions (high amplitude, high normal stress), audible stick-slips occur with significant stress drops, sometimes skipping cycles (period doubling; Figure 2F). Herein we quantify specific effects related to systematically changing temperature, amplitude, normal stress, and median forcing velocity.

FIGURE 2

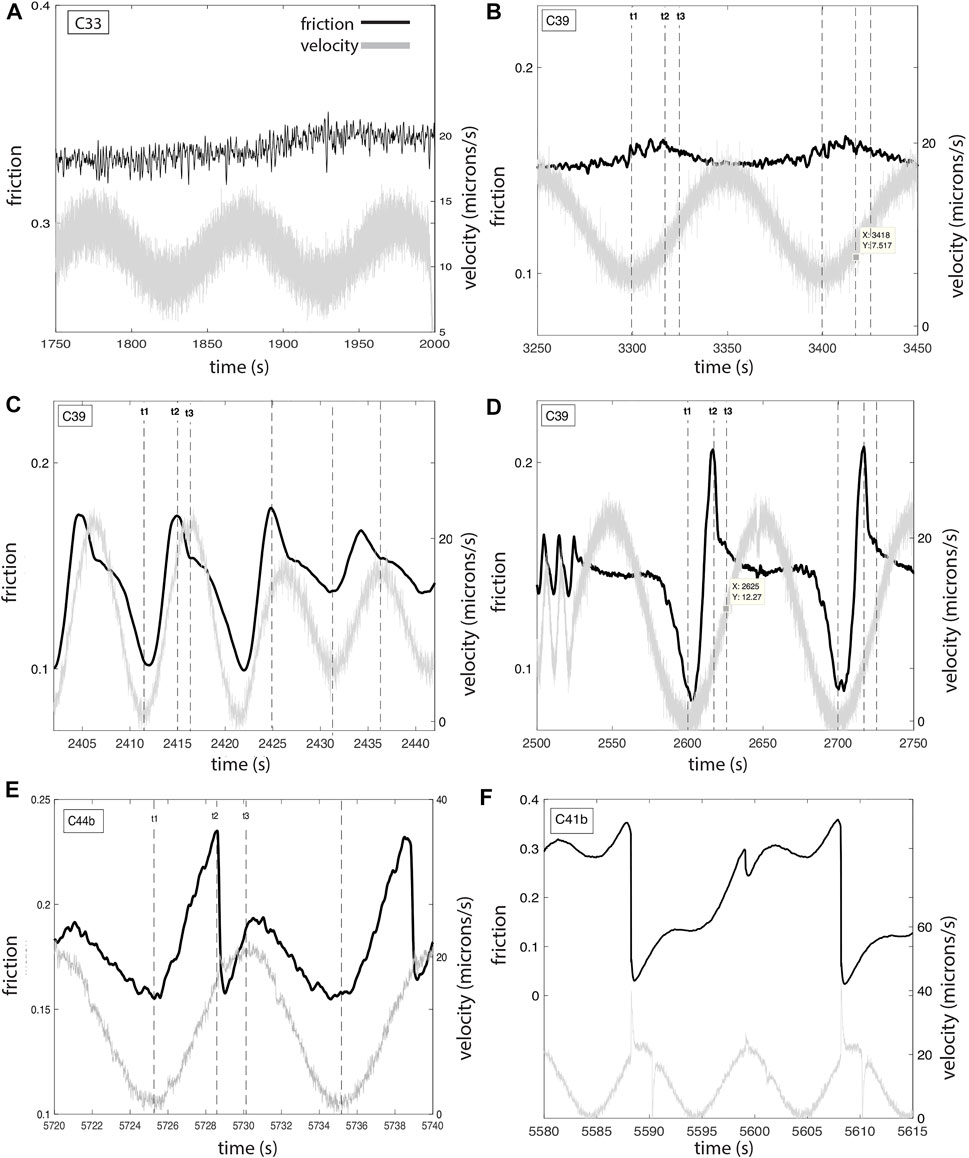
FIGURE 2. Examples and magnification of different responses observed in the experiments: (A) at long period and small amplitude (20% of Vm) there is no modulation (C33); (B) at long period at 50% of Vm response is slight, with small uptick in friction occurring between the low velocity point (t1) and peak acceleration (t3) (C39); (C) at shorter period (10s) both 100% Vm and 50% Vm are modulated, but not with a simple sine wave (C39); (D) a high amplitude event or slow slip event, which resembles a relaxation hold superimposed on a sine wave (C39); (E) a double event (one fast, one slow) within a single cycle (C44b); (F) pronounced stick-slip events, with almost total stress drop, occurring every other cycle (period doubling) at 1 sec before maximum velocity (C41b).

FIGURE 3

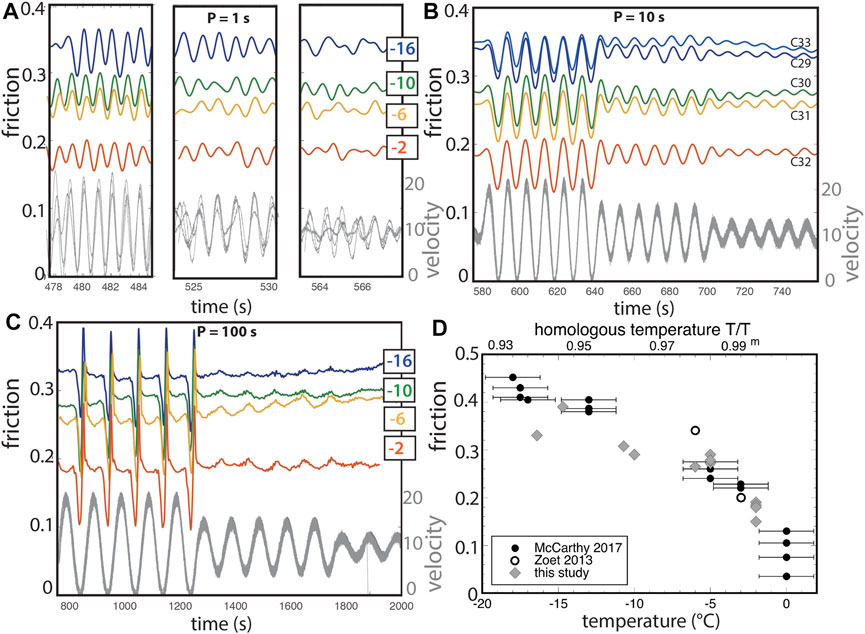
FIGURE 3. Frictional response to periodic load point velocity (gray) as a function of temperature between −16.4°C and −2°C, from samples C29 − C33 at, respectively, at (A) 1 s periods; (B) 10 s periods; and (C) 100 s periods. (D) Temperature directly affects the average friction, consistent with steady-state friction coefficients from previous studies (Zoet et al.,2013; McCarthy et al., 2017).

Temperature Effects

Under the range of conditions explored here, in which homologous temperatures T/T_m were quite high, the primary effect of temperature was a general decrease in the friction value. The average friction values of these data, which are determined from the average of values prior to and after oscillations, are consistent with steady-state friction reported in a previous study (McCarthy et al., 2017), in which samples were prepared identically, but were tested under constant load point velocities instead of oscillations. In the McCarthy et al., 2017 study, a linear fit to the data described an inverse relationship of friction on temperature of −0.0182/°C. Based on other studies of ice-on-ice friction, we do not anticipate this linearity to continue indefinitely (Beeman et al., 1988; Schulson and Fortt, 2012). At approximately 0.75 T/T_m (−70°C) friction of ice flattens to between μ = 0.6–0.9 without strong temperature dependence at homologous temperatures lower than that. The one exception to consistency here is the lowest temperature measured in this study, which deviates from the previous linear temperature dependence. It is not clear if this discrepancy in Figure 3D at T = −16.4°C is a reduction of friction due to oscillations or is just due to uncertainty in measuring temperature in our previous study (which used thermocouples).

Apart from this control on average friction, temperature effects on the style or amplitude of the frictional response are negligible at low normal stress over this temperature range (Figure 3). There is no temperature dependence on the amplitude of shear stress oscillations (Figures 3B,C) and, as shown in Amplitude and Period effects and Velocity effects Sections, no discernable temperature dependence of healing or rate dependence (a-b) behavior, respectively. There is also no discernable effect of temperature on individual rate-state parameters (Table 2) within this admittedly narrow range of temperatures.

Amplitude and Period Effects

Due to the similarity in form to slide-hold-slides, we measured the mid-to-peak amplitude of those oscillatory friction data that approach and reach zero velocity (Figure 4 inset). Although the peak level of friction upon reloading is more rounded than in typical slide-hold-slides, we use the maximum value during the cycle. The midpoint is determined by drawing a straight line from the steady state friction values before and after the oscillations. As shown in Figure 4, the mid-to-peak amplitude of the oscillatory response is clearly a function of the period of forcing. The response resembles, in both magnitude and in slope, frictional strengthening determined from slide-hold-slide experiments in a previous study (McCarthy et al., 2017). A plot of amplitude vs. temperature provided in the Supplementary Material demonstrates no clear temperature dependence on the amplitude of the frictional response.

FIGURE 4

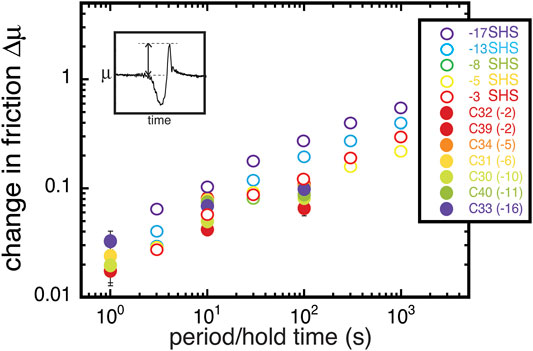
FIGURE 4. Frictional amplitude (inset) vs. period of forcing from this study (closed symbols) for those cycles that approach and reach zero velocity compared to change in friction and log hold time from previous slide-hold-slide experiments (open symbols) (McCarthy et al., 2017).

Normal Stress Effects

In Figures 5, 6 we document sliding behavior over a range of normal stresses (0.1–1 MPa) at T = −2°C (Figure 5) and −5°C (Figure 6). Shear stress increases linearly with normal stress at both of these temperatures (insets), consistent with Coulomb behavior. At lowest normal stress (0.1 MPa) for both temperatures, smooth sliding is observed under most forcings, similar to the data in Figure 3. However, at elevated normal stresses of 0.5 and 1 MPa the data show sudden stress drops that were accompanied by audible pops during the experiment. In Figure 6B, the response at σ_n = 1 MPa demonstrates an event every other cycle (i.e. period doubling), with almost complete stress release during each event. These are stick-slips that occur ∼1 s before peak velocity (Figure 2F). The events cause the piston and sample to jolt forward at almost 40 μm/s (double the programmed rate). Both the 0.5 and 1 MPa normal stress datasets also show a smaller event at the low velocity point. Stick-slip instabilities in the lab, that are accompanied by audible high velocity events, are analogous to crustal earthquakes (Brace and Byerlee, 1966; Tullis, 1988; Wong and Zhao, 1990) or stick slip events in glaciers (Helmstetter et al., 2015; Podolskiy and Walter, 2016).

FIGURE 5

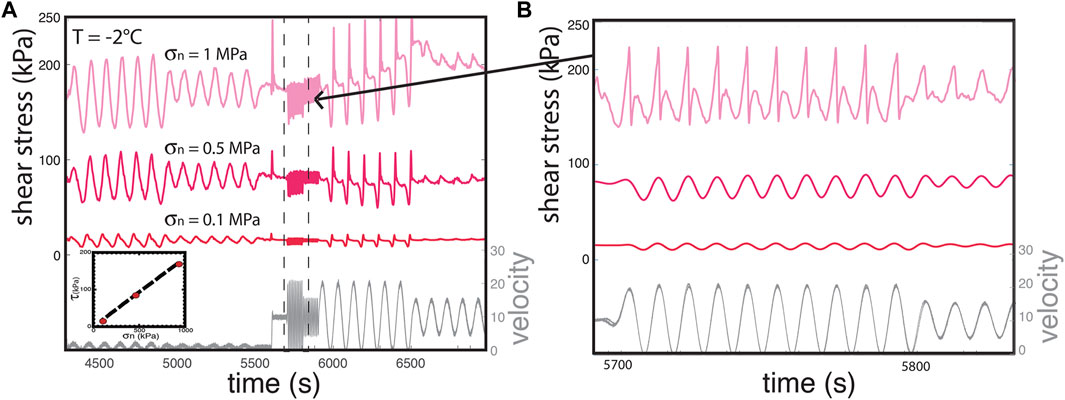
FIGURE 5. (A) Shear stress response to periodic velocity as a function of normal stress, at T = −2°C. Data at 1.0 MPa is sample C32. Data at 0.5 and 1.0 MPa are from sample C44a and C44b, respectively. A plot of shear stress vs. normal stress (inset) demonstrates Coulomb behavior with no cohesion. (B) A magnification of the 10 s period data shows that at increasing normal stress, stick-slips are observed in the 1.0 MPa data.

FIGURE 6

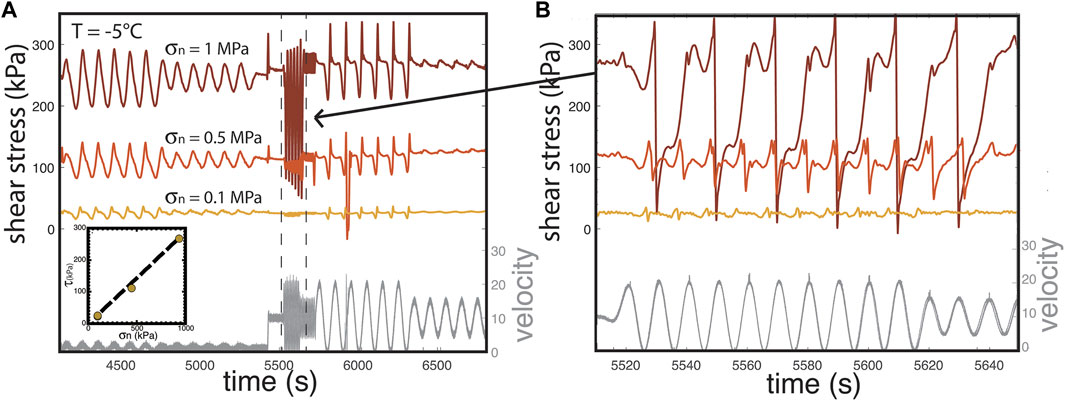
FIGURE 6. (A) Shear stress response to periodic velocity as a function of normal stress, at T = −5°C. Data at 0.1 MPa is sample C34. Data at 0.5 and 1.0 MPa are from sample C41a and C41b, respectively. A plot of shear stress vs. normal stress (inset) demonstrates Coulomb behavior with no cohesion. (B) A magnification of the 10 s period data shows that at increasing normal stress, stick-slips and period doubling are observed.

Velocity Effects

During experiments C34—C44, we employed a positive step in load point velocity from 1 μm/s to 10 μm/s at approximately the halfway point of the experiment (Figure 1 inset). Using a least-squares inversion (Skarbek and Savage, 2019), we fit Eq. 2 and both the Aging (Eq. 3) and Slip (Eq. 4) forms of state evolution to the velocity steps (Figure 7). Since filtering has the effect of smoothing out spikes and lowering peak amplitudes, we here use raw data (black). Curve fits are shown in green (the Aging Law) and red (the Slip Law). The parameters so determined are provided in Table 2. As shown in Figure 7, both laws do a good job of fitting the steady-state friction (the y-intercept), the stiffness (the upslope of the peak), and a and b. The only apparent difference is that the Slip law consistently provides a larger D_C value than the Aging law (Figure 7H). There is no significant dependence of D_C on temperature or normal stress. Values for stiffness K (kPa/μm) as measured from the slope of initial ramps K_ramp (gray circles; Table 1) and fit from the velocity step program K* (black squares, Table 2) are shown in Figure 7I. The fit values (measured at the up step during the middle of the experiment) are consistently stiffer than the ramp in values. The difference is likely due to a difference in maturity of the sliding interface from the beginning of the experiment to that reached during steady state (Skarbek et al., 2022). No apparent temperature dependence was observed in either measurement of K. A plot of (a-b) vs. temperature is shown in Figure 8; at all temperatures and normal stresses from the study, the velocity step analysis shows (a-b) values that are velocity-strengthening.

FIGURE 7

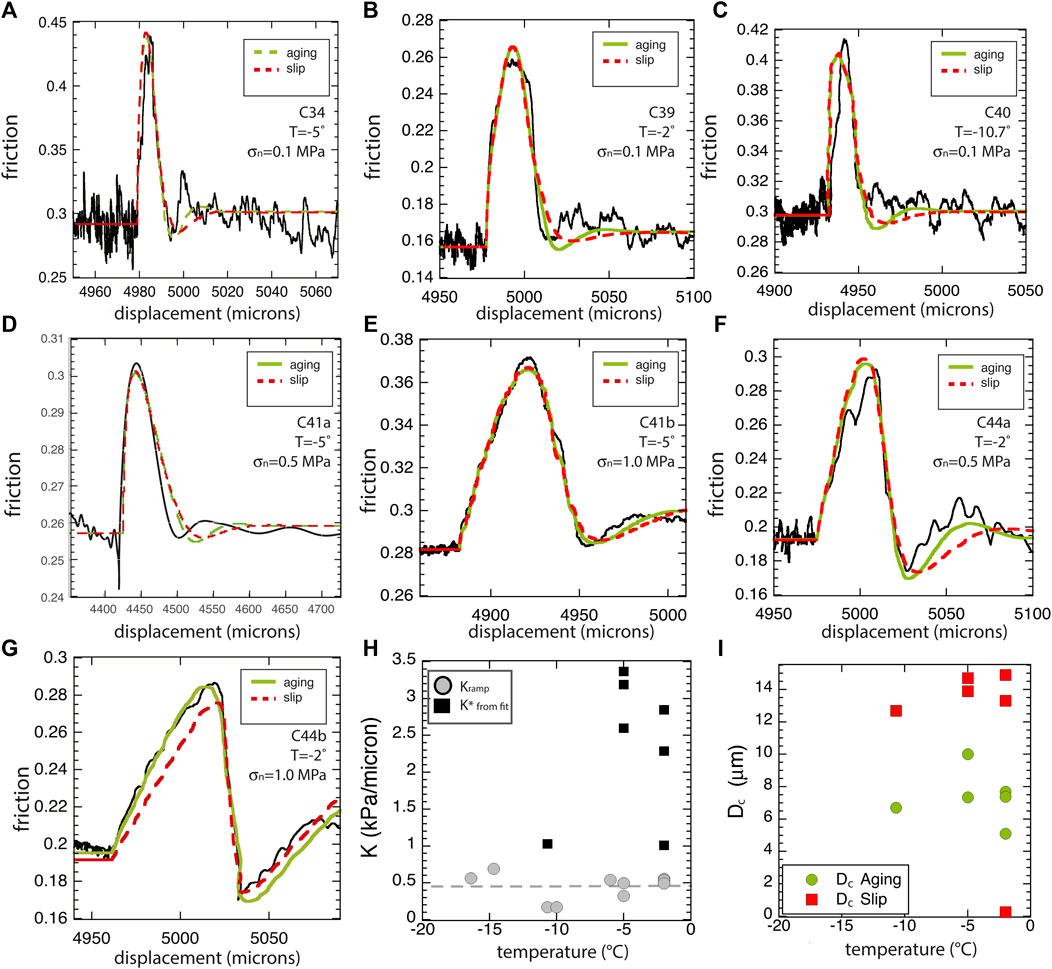
FIGURE 7. (A–G) Velocity up steps from 1 to 10 microns/s from experiments C34-44 with curve fits (of both Aging and Slip laws) overlain. (H) fitted values of K from velocity steps and from the loading ramp as a function of temperature (at 0.1 MPa normal stress) and (I) D_C (from Aging and Slip fits) as a function of temperature.

FIGURE 8

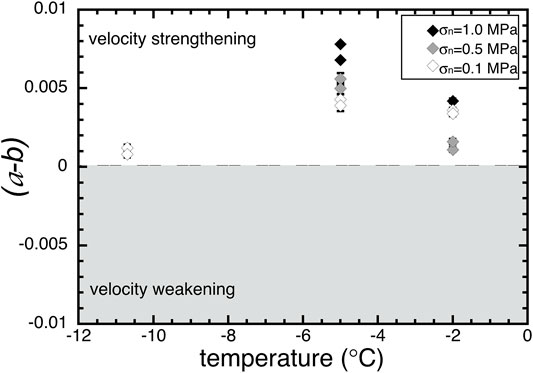
FIGURE 8. Rate dependence of friction, a-b, vs. temperature, from experiments C34-44 each measured from a velocity step from 1 μm/s to 10 μm/s using the GUI described in Skarbek and Savage, 2019. Where error bars cannot be seen, they are smaller than the symbol size. Analysis of velocity steps indicates only velocity strengthening behavior over this temperature/velocity range.

Reproducibility

Although not every set of conditions was reproduced, select temperatures and runs were performed in duplicate to test the reproducibility of the response. An example and discussion of this are provided in the Supplementary Material.

Forward Model Results

In Figure 9, we show forward modeling results of a slider block with measured RSF parameters (Table 2) with a sinusoidal load point velocity (Eq. 1) at applicable periods and amplitudes, compared to the measured experimental response from three runs, which were selected for their variations in temperature and normal stress. The values used in the forward model were those determined from Slip fits to velocity steps (Table 2). In all three pairs of figures, we see that the model predicts, with only small differences, the variations in frictional response. One significant deviation occurs in the far left of each figure. Just prior to the high frequency oscillations was a down step in median velocity from the 10 μm/s ramp to 1 μm/s branch of the run (Figure 1). The overall experimental response to the down velocity step is a direct drop and gradual evolution to new background state, with the oscillations superimposed. These down step conditions were not incorporated into the forward model. The predictions are striking in their ability to capture both form and amplitude. Since the model does not include inertia, it does not predict the large high frequency stick-slips, with stress drops (Figure 9C). In order to predict such behavior, a model with inertia must be included (Im et al., 2007).

FIGURE 9

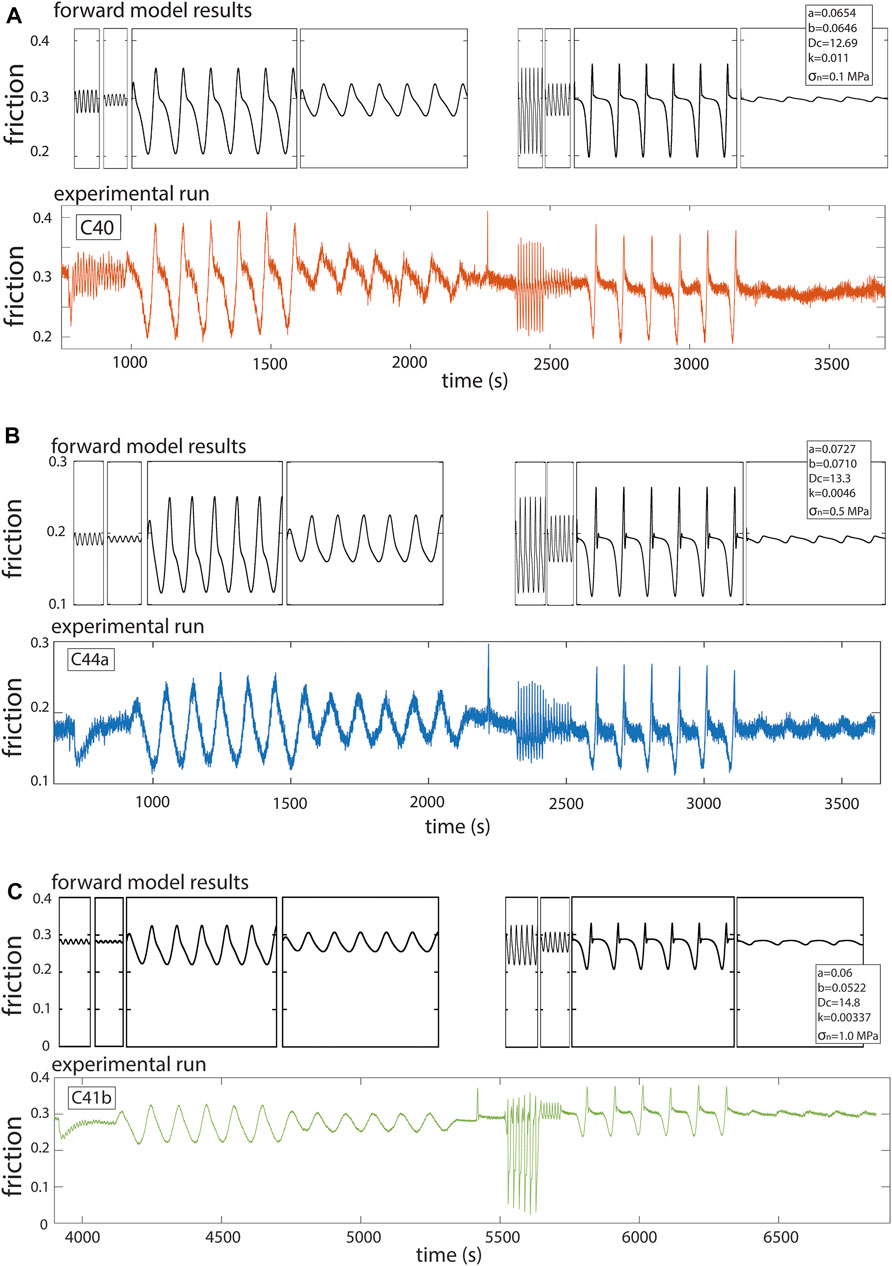
FIGURE 9. Forward model results compared to three selected experimental runs. Values for models are those listed, which are determined from the velocity step analysis (Table 2) using the Slip form of state (A) at normal stress = 0.1 MPa; (B) at a mid-range of normal stress = 0.5 MPa; and (C) at highest normal stress = 1.0 MPa.

Discussion

In these experiments, we see that oscillatory modulation of frictional sliding depends on a combination of amplitude and frequency of the load velocity, normal stress, and stiffness of the system. Temperature and median velocity play only minor roles. We categorize the responses into four groups: no modulation, smooth modulation, slow-slip events (which are ostensibly relaxation holds superimposed on a sine wave), and stick-slips. No measurable change in frictional sliding is found for conditions of low normal stress (100 kPa) with low amplitude (less than 50% of V_m) and long period (100 s). We interpret this to mean that the stressing rate is slow enough throughout the modulation to not perturb the average friction. At higher normal stresses and smaller amplitudes, we see smooth modulation. At longer periods and high amplitudes, healing is activated and slow-slip events occur. As indicated by the dashed lines in Figure 1B, the amplitude of the frictional response at V_m = 1 μm/s and V_m = 10 μm/s are nearly the same (∆μ ∼ 0.125) when the amplitude of the forcing velocity is 100% of V_m. This demonstrates that the amplitude of the frictional response is not proportional to the oscillation amplitude of the driving velocity, but rather the ratio of the oscillation amplitude to the median driving velocity and in particular is sensitive to whether the velocity approached or equaled zero, as is the case during a hold.

We emphasize that a full spectrum of slip responses, from steady sliding to stick-slip, can be generated by small changes in our driving conditions. However, fitting to the velocity steps in our experiments show that the frictional rate parameters are velocity strengthening for all conditions tested here. Although we did not test a wide range of conditions, previous work has shown that ice friction analyzed in this way is generally velocity strengthening at a wide range of velocities at temperature above −12°C (McCarthy et al., 2017; Zoet et al., 2013). In a companion paper, however, fitting to the oscillations directly produced dominantly velocity-weakening behavior (Skarbek et al, 2022).

Although a-b values are slightly positive and within a range commonly seen in friction experiments, the absolute values of a and b are large compared to most studies of rock at lower homologous temperature. These high values may be in part due to high healing. In our previous study (McCarthy et al., 2017), we demonstrated through slide-hold-slide experiments that ice exhibits strong healing during holds. Healing is typically described in the rock mechanics literature as β = ∆μ/log (time). The measured healing (β) of ice on rock from our previous study was at least an order of magnitude greater than that of rocks despite showing comparable steady-state friction values. Similar high healing was observed in other ice on rock and ice on till friction studies (Zoet et al., 2013; Zoet and Iverson, 2018). Due to the high homologous temperature of ice at these conditions (which are consistent with terrestrial glaciers and ice streams) healing has been attributed to changes in real area of contact accomplished by high temperature viscous deformation (Kennedy et al., 2000; Schulson and Fort, 2012; McCarthy et al., 2017) and pressure-enhanced melting at asperities (Zoet and Iverson, 2018).

Although laboratory healing rates for ice are much higher than for rock, fault sliding behavior may be similarly dictated by healing rates. Faults have been shown to be sensitive to oscillating stresses at a variety of frequencies, such as seismic waves, tidal stresses, and seasonal loading due to snowpack, groundwater and surface water fluctuations (Hill et al., 1993; Gomberg et al., 2001; Heki, 2003; Saar and Manga, 2003; Cochran et al., 2004; Brodsky and Prejean, 2005; Johnson et al., 2017). Faults like the San Andreas have shown that low-frequency earthquakes and tremor are sensitive to tides in its creeping section (Thomas et al., 2009; van der Elst et al., 2016). These events are mostly located below 20 km and might be enhanced by higher healing rates at relatively higher homologous temperatures than more shallow portions of the fault. We suggest that more experiments at high homologous temperatures for common fault rocks might further demonstrate the influence that enhanced fault healing at high temperatures might have on fault slip style towards the brittle/ductile transition and below.

We postulate that the frictional response of ice can be thought of as a competition between stressing rate and healing rate. When stressing rate is modest compared to healing rate, little healing occurs, and the sliding follows the forcing oscillation. When stressing rate is low, for instance at longer periods during the approach to zero velocity, frictional healing has more time to be effective, and healing-induced slow slip events occur. Only at the highest stressing rates do we see true stick-slip events. As shown in Figure 2, these occur when the normal stress is high and when velocity is increasing at higher rate (i.e. where the peak acceleration is high, not peak velocity, which is the same for almost all experiments: ∼20 μm/s), which is why stick-slip events are seen in the 10 s periods but rarely in the 100 s periods. Additionally if one compares the frictional amplitude in Figure 1B, the response to a velocity amplitude of 1 μm/s is the same if not larger than that at 10 μm/s. So we posit that it is peak acceleration relative to the background velocity that is also important. This represents a slight modification of the definition of stressing rate provided in Eq. 7, where instead of = K*V, here we instead employ a loading rate equal to K*V⋅/V_m. Figure 10 is a response “phase diagram” which qualitatively maps out the style of sliding (for the four types defined at the beginning of this section) in stress vs. frictional forcing. More specifically we plot the change in friction Δμ normalized by steady-state friction µ_SS (to remove temperature dependence) multiplied by normal stress (therefore “normalized shear stress amplitude”) versus peak frictional forcing, σ_n/(D_CK*V⋅/V_m). The clustering of open squares on the figure shows that the large stick-slip events can occur over a variety of conditions and periods when stressing rate is high relative to the average velocity.

FIGURE 10

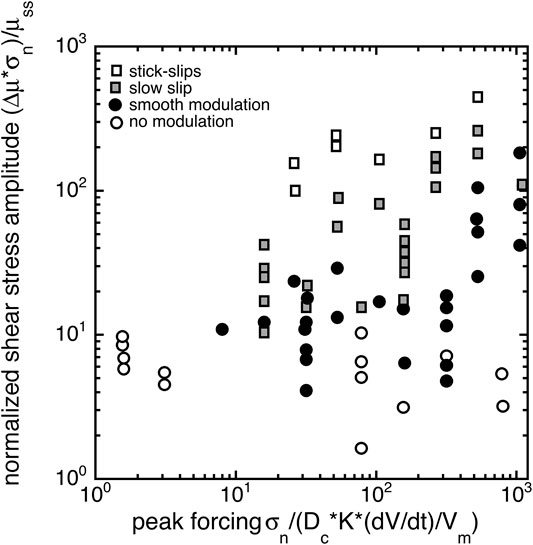
FIGURE 10. Simple response phase diagram demonstrating the effect of forcing rate on the frictional response style and amplitude (normalized delta friction multiplied by normal stress).

At almost all conditions, forward modeling with a simple 1D slider, a periodic forcing velocity, and rate-state parameters determined from velocity steps can predict the frictional response. However, the high stressing rate experiments, which cause stick-slips and large stress drops, cannot be predicted by the simple model. In a companion paper, Skarbek et al., 2022, we determine the rate-state parameters directly from oscillatory data, instead of velocity steps. In such analysis, velocity-weakening parameters were measured from these same experiments. Previous studies have demonstrated that rate dependence can depend on velocity (Ikari and Saffer, 2011), so it should come as no surprise that a system with ever changing velocity may have different frictional properties than those measured at steady state. The new method of determining parameters from oscillatory data not only allows for significantly more information to be pulled from an experiment such as ours, it also provides a means of determining rate-state parameters from naturally oscillating systems.

Implications for Ice Sheets and Glaciers

Sliding under ice sheets and glaciers should be controlled by a similar competition between healing and strain rate. Depending on overburden conditions and whether temperature is near the pressure melting point, glaciers can exhibit a variety of normal stresses at the base. It is often assumed that melt present under ice streams results in low effective normal stress on order of 100 kPa (the stress at which the majority of experiments here were conducted). We posit that variations in frictional sliding behavior emerge from a difference in velocity induced by the tides. Taking the assumptions provided by Winberry et al, 2009, the water height can be described as a resistive force to constant upstream force, such that the net force is sinusoidal. When the tide is high, the resistance is high and velocity slows; when tide is low, resistance is low and velocity increases. GPS Field observations have confirmed along-flow variations in displacement relative to the mean that correspond to the tides, with decreasing amplitude and increasing phase lag observed the farther up stream from the grounding line (Minchew et al., 2017). The amplitudes in downstream motion thus depend on local conditions. In places with a low median sliding rate compared to tidally-forced amplitude, our experimental results suggest that these locations would be likely to experience significant healing during their cycle. In places additionally having localized high normal stress, we would expect unsteady sliding, as seen at Whillans Ice Stream. Although there are length and time scaling differences between our lab experiments and nature, we achieve similar normal stress, temperature, and median sliding rate conditions. Estimates of stress accumulation over recurrence time for Whillans yield a healing rate of 0.029/log(s) (Winberry et al., 2009, 2014). At temperatures greater than −5°C, this is in line with our lab estimates of healing at 100 kPa normal stress. The similarities in healing rate are somewhat surprising, as our sample configuration of ice on rock is quite simplistic compared to the ice-till-bedrock interface beneath glaciers. That the timing of events in our experiments (just before peak velocity and just after low velocity) corresponds to events timed just before low tide and just after high tide is additionally intriguing.

One important difference between our laboratory conditions and natural conditions is that the period of our forcing signal (1–100 s) is orders of magnitude shorter than the period of the diurnal tide experienced by many ice sheets (∼104 s). Other differences include roughness of the sliding interfaces and D_C, which here are on order of microns, but in the field are possibly much greater, although there is much uncertainty (Lipovsky and Dunham, 2017, and references therein). The base of ice sheets should also contain a much wider range in asperity sizes. It is difficult to ascertain at this stage how these results directly scale to the field setting. Additional experimental and observational studies are needed to understand the relative importance and scaling of the multiple factors that control ice stream flow and stability. Here we have explored specifically the concepts of periodic velocity variations on frictional response and found that the effects can be modeled well using a forward model that includes rate- and state- dependent friction, elasticity, and a sinusoidal driving velocity. Future work will include more in depth applications of the model to tidally modulated ice stream and glacier slip.

Conclusion

The results from this study show that rate- and state- dependent friction formulations can describe oscillatory frictional behavior in ice. The Aging and Slip forms of state appear to be equally suitable to describing the velocity steps in this study. The ability of small variations in velocity to create large variations in the frictional response is likely due to high healing at the ice-rock interfaces, which at this high homologous temperature, is orders of magnitude greater than healing values measured in low temperature studies of rocks. Both the experimental work of ice on rock here (which replicates most of the conditions of ice streams) and natural ice streams are more influenced by the tides than their land-based, rocky brethren (Vidale et al., 1998). Although analysis of velocity steps shows velocity-strengthening behavior at all conditions tested here, distinct repeatable stick-slips were observed at some conditions. A companion paper (Skarbek et al., 2022) provides a way of analyzing oscillatory data directly, and in so doing, determined velocity-weakening behavior.

Data Availability Statement

The datasets generated by this study can be downloaded from USAP-DC at https://doi.org/10.15784/601497.

Author Contributions

CM ran experiments, analysed the data, and initiated publication. RS wrote the programs for determining rate-state parameters from velocity steps and the forward modelling routine and assisted with writing and interpretation of results. HS advised on experimental methods, interpretation of results, and writing of publication.

Funding

The study was funded by NSF under award numbers 1245871 and 1854629.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors wish to thank L. Zoet and two reviewers for constructive feedback that improved the manuscript. The authors thank M. A. Nielson and T. Koczynski for critical assistance in the laboratory.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.719074/full#supplementary-material

References

Anandakrishnan, S., and Alley, R. B. (1997). Tidal Forcing of Basal Seismicity of Ice Stream C, West Antarctica, Observed Far Inland. J. Geophys. Res. 102 (15), 183–215. doi:10.1029/97jb01073

CrossRef Full Text | Google Scholar

Anandakrishnan, S., Voigt, D. E., Alley, R. B., and King, M. A. (2003). Ice Stream D Flow Speed Is Strongly Modulated by the Tide beneath the Ross Ice Shelf. Geophys. Res. Lett. 30 (7), 1361. doi:10.1029/2002gl016329

CrossRef Full Text | Google Scholar

Bahr, D. B., and Rundle, J. B. (1996). Stick‐slip Statistical Mechanics at the Bed of a Glacier. Geophys. Res. Lett. 23 (16), 2073–2076. doi:10.1029/96gl02069

CrossRef Full Text | Google Scholar

Bamber, J. L., Vaughan, D. G., and Joughin, I. (2000). Widespread Complex Flow in the Interior of the Antarctic Ice Sheet. Science 287 (5456), 1248–1250. doi:10.1126/science.287.5456.1248

PubMed Abstract | CrossRef Full Text | Google Scholar

Barcheck, G., Brodsky, E. E., Fulton, P. M., King, M. A., Siegfried, M. R., and Tulaczyk, S. (2021). Migratory Earthquake Precursors Are Dominant on an Ice Stream Fault. Sci. Adv. 7 (6), eabd0105. doi:10.1126/sciadv.abd0105

PubMed Abstract | CrossRef Full Text | Google Scholar

Beeler, N. M., and Lockner, D. A. (2003). Why Earthquakes Correlate Weakly with the Solid Earth Tides: Effects of Periodic Stress on the Rate and Probability of Earthquake Occurrence. J. Geophys. Res. 108 (B8), 2391. doi:10.1029/2001jb001518

CrossRef Full Text | Google Scholar

Beeman, M., Durham, W. B., and Kirby, S. H. (1988). Friction of Ice. J. Geophys. Res. 93 (B7), 7625–7633. doi:10.1029/JP093iB0762510.1029/jb093ib07p07625

CrossRef Full Text | Google Scholar

Bhattacharya, P., Rubin, A. M., Bayart, E., Savage, H. M., and Marone, C. (2015). Critical Evaluation of State Evolution Laws in Rate and State Friction: Fitting Large Velocity Steps in Simulated Fault Gouge with Time‐, Slip‐, and Stress‐dependent Constitutive Laws. J. Geophys. Res. Solid Earth 120 (9), 6365–6385. doi:10.1002/2015jb012437

CrossRef Full Text | Google Scholar

Bhattacharya, P., Rubin, A. M., and Beeler, N. M. (2017). Does Fault Strengthening in Laboratory Rock Friction Experiments Really Depend Primarily upon Time and Not Slip? J. Geophys. Res. Solid Earth 122, 6389–6430. doi:10.1002/2017jb013936

CrossRef Full Text | Google Scholar

Bindschadler, R. A., King, M. A., Alley, R. B., Anandakrishnan, S., and Padman, L. (2003). Tidally Controlled Stick-Slip Discharge of a West Antarctic Ice. Science 301, 1087–1089. doi:10.1126/science.1087231

PubMed Abstract | CrossRef Full Text | Google Scholar

Bindschadler, R., Vornberger, P., King, M., and Padman, L. (2002). Tidally-driven Stick-Slip Motion in the Mouth of Whillans Ice Stream, Antarctica. Ann. Glaciology 36 (1), 263–272. doi:10.3189/172756403781816284

CrossRef Full Text | Google Scholar

Blanpied, M. L., Tullis, T. E., and Weeks, J. D. (1998). Effects of Slip, Slip Rate, and Shear Heating on the Friction of Granite. J. Geophys. Res. 103 (B1), 489–511. doi:10.1029/97jb02480

CrossRef Full Text | Google Scholar

Boettcher, M. S., and Marone, C. (2004). Effects of normal Stress Variation on the Strength and Stability of Creeping Faults. J. Geophys. Res. 109 (B03406), 2824. doi:10.1029/2003jb002824

CrossRef Full Text | Google Scholar

Brace, W. F., and Byerlee, J. D. (1966). Stick-Slip as a Mechanism for Earthquakes. Science 153 (3739), 990–992. doi:10.1126/science.153.3739.990

PubMed Abstract | CrossRef Full Text | Google Scholar

Brodsky, E. E., and Prejean, S. G. (2005). New Constraints on Mechanisms of Remotely Triggered Seismicity at Long Valley Caldera. J. Geophys. Res. Solid Earth 110 (B4). doi:10.1029/2004jb003211

CrossRef Full Text | Google Scholar

Brunt, K. M., King, M. A., Fricker, H. A., and MacAyeal, D. R. (2010). Flow of the Ross Ice Shelf, Antarctica, Is Modulated by the Ocean Tide. J. Glaciol. 56 (195), 157–161. doi:10.3189/002214310791190875

CrossRef Full Text | Google Scholar

Brunt, K. M., and MacAyeal, D. R. (2014). Tidal Modulation of Ice-Shelf Flow: a Viscous Model of the Ross Ice Shelf. J. Glaciol. 60 (221), 500–508. doi:10.3189/2014jog13j203

CrossRef Full Text | Google Scholar

Carpenter, B. M., Marone, C., and Saffer, D. M. (2011). Weakness of the San Andreas Fault Revealed by Samples from the Active Fault Zone. Nat. Geosci 4, 251–254. doi:10.1038/ngeo1089

CrossRef Full Text | Google Scholar

Clarke, G. K. C. (2005). Subglacial Processes. Annu. Rev. Earth Planet. Sci. 33, 247–276. doi:10.1146/annurev.earth.33.092203.122621

CrossRef Full Text | Google Scholar

Cochran, E. S., Vidale, J. E., and Tanaka, S. (2004). Earth Tides Can Trigger Shallow Thrust Fault Earthquakes. Science 306 (5699), 1164–1166. doi:10.1126/science.1103961

PubMed Abstract | CrossRef Full Text | Google Scholar

Cole, D. M. (1979). Preparation of Polycrystalline Ice Specimens for Laboratory Experiments. Cold Regions Sci. Tech. 1, 153–159. doi:10.1016/0165-232x(79)90007-7

CrossRef Full Text | Google Scholar

Dieterich, J. H. (1994). A Constitutive Law for Rate of Earthquake Production and its Application to Earthquake Clustering. J. Geophys. Res. 89 (B6), 4196–4202. doi:10.1029/93jb02581

CrossRef Full Text | Google Scholar

Dieterich, J. H. (1981). Constitutive Properties of Faults with Simulated Gouge. Mech. Behav. Crustal Rocks, Geophys. Monogr. Ser. Vol. 24, 103–120. doi:10.1029/GM024p0103

CrossRef Full Text | Google Scholar

Dieterich, J. H. (1979). Modeling of Rock Friction: 1. Experimental Results and Constitutive Equations. J. Geophys. Res. 84, 2161–2168. doi:10.1029/jb084ib05p02161

CrossRef Full Text | Google Scholar

Dieterich, J. H. (1978). Time-dependent Friction and the Mechanics of Stick-Slip. Pageoph 116, 790–806. doi:10.1007/bf00876539

CrossRef Full Text | Google Scholar

Doake, C. S. M., Corr, H. F. J., Nicholls, K. W., Gaffikin, A., Jenkins, A., Bertiger, W. I., et al. (2002). Tide-induced Lateral Movement of Brunt Ice Shelf. Antarctica Geophys. Res. Lett. 28, 1226. doi:10.1029/2001GL014606

CrossRef Full Text | Google Scholar

Fortt, A. L., and Schulson, E. M. (2009). Velocity-dependent Friction on Coulombic Shear Faults in Ice. Acta Materialia 57 (15), 4382–4390. doi:10.1016/j.actamat.2009.06.001

CrossRef Full Text | Google Scholar

Gagliardini, O., Cohen, D., Råback, P., and Zwinger, T. (2007). Finite-element Modeling of Subglacial Cavities and Related Friction Law. J. Geophys. Res. 112 (F2), F02027. doi:10.1029/2006jf000576

CrossRef Full Text | Google Scholar

Gimbert, F., Gilbert, A., Gagliardini, O., Vincent, C., and Moreau, L. (2021). Do Existing Theories Explain Seasonal to Multi-Decadal Changes in Glacier Basal Sliding Speed? Geophys. Res. Lett. 48 (15), e2021GL092858. doi:10.1029/2021gl092858

CrossRef Full Text | Google Scholar

Goldberg, D. N., Schoof, C., and Sergienko, O. V. (2014). Stick-slip Motion of an Antarctic Ice Stream: The Effects of Viscoelasticity. J. Geophys. Res. Earth Surf. 119, 1564–1580. doi:10.1002/2014jf003132

CrossRef Full Text | Google Scholar

Gomberg, J., Reasenberg, P. A., Bodin, P., and Harris, R. A. (2001). Earthquake Triggering by Seismic Waves Following the Landers and Hector Mine Earthquakes. Nature 411 (6836), 462–466. doi:10.1038/35078053

PubMed Abstract | CrossRef Full Text | Google Scholar

Gu, J.-C., Rice, J. R., Ruina, A. L., and Tse, S. T. (1984). Slip Motion and Stability of a Single Degree of freedom Elastic System with Rate and State Dependent Friction. J. Mech. Phys. Sol. 32 (3), 167–196. doi:10.1016/0022-5096(84)90007-3

CrossRef Full Text | Google Scholar

Gudmundsson, G. H. (2007). Tides and the Flow of Rutford Ice Stream, West Antarctica. J. Geophys. Res. 112 (F4), F04007. doi:10.1029/2006jf000731

CrossRef Full Text | Google Scholar

Heki, K. (2003). Snow Load and Seasonal Variation of Earthquake Occurrence in Japan. Earth Planet. Sci. Lett. 207 (1-4), 159–164. doi:10.1016/s0012-821x(02)01148-2

CrossRef Full Text | Google Scholar

Helmstetter, A., Nicolas, B., Comon, P., and Gay, M. (2015). Basal Icequakes Recorded beneath an Alpine Glacier (Glacier d'Argentière, Mont Blanc, France): Evidence for Stick-Slip Motion? J. Geophys. Res. Earth Surf. 120 (3), 379–401. doi:10.1002/2014jf003288

CrossRef Full Text | Google Scholar

Hill, D. P., Reasenberg, P. A., Michael, A., Arabaz, W. J., Beroza, G., Brumbaugh, D., et al. (1993). Seismicity Remotely Triggered by the Magnitude 7.3 Landers, California, Earthquake. Science 260 (5114), 1617–1623. doi:10.1126/science.260.5114.1617

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, T., and Marone, C. (2005). Effects of normal Stress Perturbations on the Frictional Properties of Simulated Faults. Geochem. Geophys. Geosyst. 6, Q03012. doi:10.1029/2004gc000821

CrossRef Full Text | Google Scholar

Ikari, M. J., Marone, C., Saffer, D. M., and Kopf, A. J. (2013). Slip Weakening as a Mechanism for Slow Earthquakes. Nat. Geosci. 6 (6), 468–472.

CrossRef Full Text | Google Scholar

Ikari, M. J., and Saffer, D. M. (2011). Comparison of Frictional Strength and Velocity Dependence between Fault Zones in the Nankai Accretionary Complex. Geochem. Geophys. Geosystems 12, 4. doi:10.1029/2010gc003442

CrossRef Full Text | Google Scholar

Im, K., Elsworth, D., Marone, C., and Leeman, J. (2007). The Impact of Frictional Healing on Stic-Slip Recurrence Interval and Stress Drop; Implications for Earthquake Scaling. J. Geophys. Res. Solid Earth 122 (10), 102117. doi:10.1002/2017JB014476

CrossRef Full Text | Google Scholar

Johnson, C. W., Fu, Y., and Bürgmann, R. (2017). Seasonal Water Storage, Stress Modulation, and California Seismicity. Science 356 (6343), 1161–1164. doi:10.1126/science.aak9547

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamb, B., Raymond, C. F., Harrison, W. D., Engelhardt, H., Echelmeyer, K. A., Humphrey, N., et al. (1985). Glacier Surge Mechanism: 1982-1983 Surge of Variegated Glacier, Alaska. Science 227 (4686), 469–479. doi:10.1126/science.227.4686.469

PubMed Abstract | CrossRef Full Text | Google Scholar

Kennedy, F. E., Schulson, E. M., and Jones, D. E. (2000). The Friction of Ice on Ice at Low Sliding Velocities. Philosophical Mag. A 80, 1093–1110. doi:10.1080/01418610008212103

CrossRef Full Text | Google Scholar

Lipovsky, B. P., and Dunham, E. M. (2017). Slow‐slip Events on the Whillans Ice Plain, Antarctica, Described Using Rate‐and‐state Friction as an Ice Stream Sliding Law. J. Geophys. Res. Earth Surf. 122, 973–1003. doi:10.1002/2016jf004183

CrossRef Full Text | Google Scholar

Lipovsky, B. P., and Dunham, E. M. (2016). Tremor during Ice-Stream Stick Slip. The Cryosphere 10, 385–399. doi:10.5194/tc-10-385-2016

CrossRef Full Text | Google Scholar

Lipovsky, B. P., Meyer, C. R., Zoet, L. K., McCarthy, C., Hansen, D. D., Rempel, A. W., et al. (2019). Glacier Sliding, Seismicity and Sediment Entrainment. Ann. Glaciol. 60 (79), 182–192. doi:10.1017/aog.2019.24

CrossRef Full Text | Google Scholar

Lockner, D. A., and Beeler, N. M. (1995). Premonitory Slip and Tidal Triggering of Earthquakes. J. Geophys. Res. 104 (B920), 133151.

Google Scholar

Makinson, K., King, M. A., Nicholls, K. W., and Gudmundsson, G. H. (2012). Diurnal and Semidiurnal Tide-Induced Lateral Movement of Ronne Ice Shelf, Antarctica. Geophys. Res. Lett. 39, L10501. doi:10.1029/2012gl051636

CrossRef Full Text | Google Scholar

Marone, C. (1998). Laboratory-derived Friction Laws and Their Application to Seismic Faulting. Annu. Rev. Earth Planet. Sci. 26, 643–696. doi:10.1146/annurev.earth.26.1.643

CrossRef Full Text | Google Scholar

McCarthy, C., Savage, H. M., Koczynski, T., and Nielson, M. A. (2016). An Apparatus to Measure Frictional, Anelastic, and Viscous Behavior in Ice at Temperate and Planetary Conditions. Rev. Scientific Instr. 87, 055112. doi:10.1063/1.4950782

CrossRef Full Text | Google Scholar

McCarthy, C., Savage, H., and Nettles, M. (2017). Temperature Dependence of Ice-On-Rock Friction at Realistic Glacier Conditions. Phil. Trans. R. Soc. A. 375, 20150348. doi:10.1098/rsta.2015.0348

PubMed Abstract | CrossRef Full Text | Google Scholar

Minchew, B. M., Simons, M., Riel, B., and Milillo, P. (2017). Tidally Induced Variations in Vertical and Horizontal Motion on Rutford Ice Stream, West Antarctica, Inferred from Remotely Sensed Observations. J. Geophys. Res. Earth Surf. 122, 167–190. doi:10.1002/2016jf003971

CrossRef Full Text | Google Scholar

Minchew, B. M., and Meyer, C. R. (2020). Dilation of Subglacial Sediment Governs Incipient Surge Motion in Glaciers with Deformable Beds. Proc. R. Soc. A. 476, 20200033. doi:10.1098/rspa.2020.0033

PubMed Abstract | CrossRef Full Text | Google Scholar

Murray, T., Smith, A. M., King, M. A., and Weedon, G. P. (2007). Ice Flow Modulated by Tides at up to Annual Periods at Rutford Ice Stream, West Antarctica. Geophys. Res. Lett. 34 (18), L18503. doi:10.1029/2007gl031207

CrossRef Full Text | Google Scholar

Perfettini, H., Schmittbuhl, J., and Cochard, A. (2003). Shear and normal Load Perturbations on a Two-Dimensional Continuous Fault: 1. Static Triggering. J. Geophys. Res. 108 (B9), 2409. doi:10.1029/2002jb001804

CrossRef Full Text | Google Scholar

Perfettini, H., and Schmittbuhl, J. (2001). Periodic Loading on a Creeping Fault: Implications for Tides. Geophys. Res. Lett. 28 (3), 435–438. doi:10.1029/2000gl011686

CrossRef Full Text | Google Scholar

Podolskiy, E. A., and Walter, F. (2016). Cryoseismology. Rev. Geophys. 54 (4), 708–758. doi:10.1002/2016rg000526

CrossRef Full Text | Google Scholar

Pratt, M. J., Winberry, J. P., Wiens, D. A., Anandakrishnan, S., and Alley, R. B. (2014). Seismic and Geodetic Evidence for Grounding-Line Control of Whillans Ice Stream Stick-Slip Events. J. Geophys. Res. Earth Surf. 119 (2), 333–348. doi:10.1002/2013jf002842

CrossRef Full Text | Google Scholar

Reinan, L. A., and Weeks, J. D. (1993). Determination of Rock Friction Constitutive Parameters Using an Iterative Least-Squares Inversion Method. J. Geophys. Res. 98 (15), 937950–938015.

Google Scholar

Rice, J. R., and Ruina, A. L. (1983). Stability of Steady Frictional Slipping. J. Appl. Mech. 50 (2), 343–349. doi:10.1115/1.3167042

CrossRef Full Text | Google Scholar

Richardson, E., and Marone, C. (1999). Effects of normal Stress Vibrations on Frictional Healing. J. Geophys. Res. 104 (B12), 859878–859928. doi:10.1029/1999jb900320

CrossRef Full Text | Google Scholar

Riedel, B., Nixdorf, U., Heinert, M., Eckstaller, A., and Mayer, C. (1999). The Response of the Ekströmisen (Antarctica) Grounding Zone to Tidal Forcing. Ann. Glaciol. 29, 239–242. doi:10.3189/172756499781821247

CrossRef Full Text | Google Scholar

Rosier, S. H. R., Gudmundsson, G. H., and Green, J. A. M. (2014). Insights into Ice Stream Dynamics through Modelling Their Response to Tidal Forcing. The Cryosphere 8, 1763–1775. doi:10.5194/tc-8-1763-2014

CrossRef Full Text | Google Scholar

Rosier, S. H. R., Gudmundsson, G. H., King, M. A., Nicholls, K. W., Makinson, K., and Corr, H. F. J. (2017). Strong Tidal Variations in Ice Flow Observed across the Entire Ronne Ice Shelf and Adjoining Ice Streams. Earth Syst. Sci. Data 9, 849–860. doi:10.5194/essd-9-849-2017

CrossRef Full Text | Google Scholar

Ruina, A. (1983). Slip Instability and State Variable Friction Laws. J. Geophys. Res. 88, 359370. doi:10.1029/jb088ib12p10359

CrossRef Full Text | Google Scholar

Saar, M. O., and Manga, M. (2003). Seismicity Induced by Seasonal Groundwater Recharge at Mt. Hood, Oregon. Earth Planet. Sci. Lett. 214 (3-4), 605–618. doi:10.1016/s0012-821x(03)00418-7

CrossRef Full Text | Google Scholar

Savage, H. M., and Marone, C. (2007). Effects of Shear Velocity Oscillations on Stick-Slip Behavior in Laboratory Experiments. J. Geophys. Res. 112, B02301. doi:10.1029/2005jb004238

CrossRef Full Text | Google Scholar

Savage, H. M., and Marone, C. (2008). Potential for Earthquake Triggering from Transient Deformations. J. Geophys. Res. 113, B05302. doi:10.1029/2007JB005277

CrossRef Full Text | Google Scholar

Scholz, C. H. (2019). The Mechanics of Earthquakes and Faulting 3rd edition. New York, NY: Cambridge University Press.

Google Scholar

Scholz, C. H. (1998). Earthquakes and Friction Laws. Nature 391 (6662), 37–42. doi:10.1038/34097

CrossRef Full Text | Google Scholar

Schoof, C. (2005). The Effect of Cavitation on Glacier Sliding. Proc. R. Soc. A. 461, 609–627. doi:10.1098/rspa.2004.1350

CrossRef Full Text | Google Scholar

Schulson, E. M., and Fortt, A. L. (2012). Friction of Ice on Ice. J. Geophys. Res. 117, B12204. doi:10.1029/2012jb009219

CrossRef Full Text | Google Scholar

Sergienko, O. V., Macayeal, D. R., and Bindschadler, R. A. (2009). Stick-slip Behavior of Ice Streams: Modeling Investigations. Ann. Glaciol. 50 (52), 87–94. doi:10.3189/172756409789624274

CrossRef Full Text | Google Scholar

Skarbek, R. M., McCarthy, C., and Savage, H. M. (2022). Oscillatory Loading Can Alter the Velocity Rate Dependence of Ice-On-Rock Friction. Geochem. Geophys. Geosystems 23 (2), e2021GC009954. doi:10.1029/2021GC009954

CrossRef Full Text | Google Scholar

Skarbek, R. M., and Savage, H. M. (2019). RSFit3000: A MATLAB GUI-Based Program for Determining Rate and State Frictional Parameters from Experimental Data. Geosphere 15 (5), 1665–1676. doi:10.1130/ges02122.1

CrossRef Full Text | Google Scholar

Thomas, A. M., Nadeau, R. M., and Bürgmann, R. (2009). Tremor-tide Correlations and Near-Lithostatic Pore Pressure on the Deep San Andreas Fault. Nature 462 (7276), 1048–1051. doi:10.1038/nature08654

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, V. C., Rice, J. R., and Fahnestock, M. (2008). Possible Mechanisms for Glacial Earthquakes. J. Geophys. Res. 113, F03014. doi:10.1029/2007jf000944

CrossRef Full Text | Google Scholar

Tullis, T. E. (1988). Rock Friction Constitutive Behavior from Laboratory Experiments and its Implications for an Earthquake Prediction Field Monitoring Program. Pageoph. 126, 555–588. doi:10.1007/bf00879010

CrossRef Full Text | Google Scholar

Tworzydlo, W. W., and Hamzeh, O. N. (1997). On the Importance of normal Vibrations in Modeling of Stick-Slip in Rock Sliding. J. Geophys. Res. Solid Earth 102, 103–115. doi:10.1029/97jb01167

CrossRef Full Text | Google Scholar

van der Elst, N. J., Delorey, A. A., Shelly, D. R., and Johnson, P. A. (2016). Fortnightly Modulation of San Andreas Tremor and Low-Frequency Earthquakes. Proc. Natl. Acad. Sci. USA 113 (31), 8601–8605. doi:10.1073/pnas.1524316113

CrossRef Full Text | Google Scholar

van der Elst, N. J., and Savage, H. M. (2015). Frequency Dependence of Delayed and Instantaneous Triggering on Laboratory and Simulated Faults Governed by Rate-State Friction. J. Geophys. Res. Solid Earth 120 (5), 3406–3429. doi:10.1002/2014jb011611

CrossRef Full Text | Google Scholar

Vidale, J. E., Agnew, D. C., Johnston, M. J. S., and Oppenheimer, D. H. (1998). Absence of Earthquake Correlation with Earth Tides: An Indication of High Preseismic Fault Stress Rate. Journal Of Geophysical Research. Solid Earth 103 (B1024), 567572–567624. doi:10.1029/98jb00594

CrossRef Full Text | Google Scholar

Voisin, C. (2001). Dynamic Triggering of Earthquakes: The Linear Slip-dependent Friction Case. Geophys. Res. Lett. 28, 3357–3360. doi:10.1029/2001gl013101

CrossRef Full Text | Google Scholar

Voisin, C. (2002). Dynamic Triggering of Earthquakes: The Nonlinear Slip-dependent Friction Case. J. Geophys. Res. 107 (B12), 10–11. doi:10.1029/2001jb001121

CrossRef Full Text | Google Scholar

Weertman, J. (1957). On the Sliding of Glaciers. J. Glaciol. 3 (21), 33–38. doi:10.1017/s0022143000024709

CrossRef Full Text | Google Scholar

Wiens, D. A., Anandakrishnan, S., Winberry, J. P., and King, M. A. (2008). Simultaneous Teleseismic and Geodetic Observations of the Stick-Slip Motion of an Antarctic Ice Stream. Nature 453, 770–774. doi:10.1038/nature06990

PubMed Abstract | CrossRef Full Text | Google Scholar

Winberry, J. P., Anandakrishnan, S., Alley, R. B., Bindschadler, R. A., and King, M. A. (2009). Basal Mechanics of Ice Streams: Insights from the Stick-Slip Motion of Whillans Ice Stream, West Antarctica. J. Geophys. Res. 114, F01016. doi:10.1029/2008jf001035

CrossRef Full Text | Google Scholar

Winberry, J. P., Anandakrishnan, S., Alley, R. B., Wiens, D. A., and Pratt, M. J. (2014). Tidal Pacing, Skipped Slips and the Slowdown of Whillans Ice Stream, Antarctica. J. Glaciol. 60, 795–807. doi:10.3189/2014jog14j038

CrossRef Full Text | Google Scholar

Winberry, J. P., Anandakrishnan, S., Wiens, D. A., Alley, R. B., and Christianson, K. (2011). Dynamics of Stick-Slip Motion, Whillans Ice Stream, Antarctica. Earth Planet. Sci. Lett. 305, 283–289. doi:10.1016/j.epsl.2011.02.052

CrossRef Full Text | Google Scholar

Wong, T. F., and Zhao, Y. (1990). Effects of Load point Velocity on Frictional Instability Behavior. Tectonophysics 175, 177–195.

Google Scholar

Wuite, J., Jezek, K. C., Wu, X., Farness, K., and Carande, R. (2009). The Velocity Field and Flow Regime of David Glacier and Dryglaski Ice Tongue, Antarctica. Polar. Geogr. 32 (3-4), 111–127. doi:10.1080/10889370902815499

CrossRef Full Text | Google Scholar

Zoet, L. K., Anandakrishnan, S., Alley, R. B., Nyblade, A. A., and Wiens, D. A. (2012). Motion of an Antarctic Glacier by Repeated Tidally Modulated Earthquakes. Nat. Geosci. 5 (9), 623–626. doi:10.1038/ngeo1555

CrossRef Full Text | Google Scholar

Zoet, L. K., Carpenter, B., Scuderi, M., Alley, R. B., Anandakrishnan, S., Marone, C., et al. (2013). The Effects of Entrained Debris on the Basal Sliding Stability of a Glacier. J. Geophys. Res. Earth Surf. 118, 656–666. doi:10.1002/jgrf.20052

CrossRef Full Text | Google Scholar

Zoet, L. K., Ikari, M. J., Alley, R. B., Marone, C., Anandakrishnan, S., Carpenter, B. M., et al. (2020). Application of Constitutive Friction Laws to Glacier Seismicity. Geophys. Res. Lett. 47, e2020GL088964. doi:10.1029/2020gl088964

CrossRef Full Text | Google Scholar

Zoet, L. K., and Iverson, N. R. (2018). A Healing Mechanism for Stick-Slip of Glaciers. Geology 46 (9), 807–810. doi:10.1130/g45099.1

CrossRef Full Text | Google Scholar

Zoet, L. K., Iverson, N. R., Andrews, L., and Helanow, C. (2021). Transient Evolution of Basal Drag during Glacier Slip. J. Glaciol., 1–10. doi:10.1017/jog.2021.131

CrossRef Full Text | Google Scholar