Similar ratio experiment and characteristic analysis of quasi-sandstone

The stability control of surrounding rock in deep roadway is becoming more and more difficult, and grouting reinforcement support has become the mainstream of roadway control. In order to obtain the ratio of quasi-sandstone material corresponding to the grouting body, this paper uses river sand as aggregate, cement and gypsum as cementing agent, retarder and defoamer as additives, and carries out orthogonal proportioning tests with three influencing factors: water-binder ratio (ratio of water to mass of cementing agent), gypsum-cement ratio (ratio of gypsum to mass of cement) and binder-aggregate ratio (ratio of cementing agent to aggregate mass), and compares and analyzes the sensitivity of each factor on the density, compressive strength, tensile strength, elastic modulus, Poisson’s ratio, longitudinal wave velocity, elasticity index and brittleness index of quasi-sandstone material. The results show that 1) the Water-binder ratio has the greatest effect on the sensitivity of material compressive strength, tensile strength, elastic modulus, Poisson’s ratio and longitudinal wave velocity; the gypsum-cement ratio has the greatest effect on the sensitivity of material deformation index and brittleness index; the binder-aggregate ratio has the greatest effect on the sensitivity of material density. 2) Reducing the Water-binder ratio can improve the density, compressive strength and tensile strength of the material; reducing the paste ratio can improve the modulus of elasticity, Poisson’s ratio and longitudinal wave speed of the material; as the gypsum-cement ratio increases, the deformation index first decreases and then increases and then decreases; as the binder-aggregate ratio increases, the brittleness index first increases and then decreases and then increases. 3) The empirical equations between physical and mechanical properties of sandstone-like materials and Water-binder ratio, gypsum-cement ratio and binder-aggregate ratio were established based on multiple linear regression analysis, and more reasonable material ratios were quickly obtained by physical and mechanical parameters of materials. The results of the study provide theoretical references for similar material simulation tests for quasi-sandstone grouting.

1 Introduction

With Chinese coal resources into deep mining, deep roadway surrounding rock in high stress, strong mining of the mutual superposition of the role of deep roadway surrounding rock stability control increasingly difficult, surrounding rock grouting reinforcement support has become the mainstream of roadway control (He 2021; Jia et al., 2022a; Jia et al., 2022b; Jing et al., 2022; Li et al., 2022; Wang et al., 2022; Zhang and Yin, 2022). In recent years, physical model tests have been widely used in the field of underground engineering because of the advantages of easy fabrication, controllable size and variables, and low price, so carrying out the raw rock similar material proportioning experiments to prepare raw rock and obtain the similar material proportioning of quasi-sandstone corresponding to the grouted body provides an experimental basis for further research on the slurry seepage diffusion law and grouting reinforcement effect in quasi-sandstone under true triaxial stress environment, which is of deep The seepage flow grouting support of the tunnel surround rock has important practical significance (Lu et al., 2022; Liu et al., 2017; Kang et al., 2020; Zhang et al., 2020).

Rich results have been achieved in the proportioning of similar materials for quasi-sandstone materials, (Wang et al., 2006; Zhang et al., 2008; Zhang et al., 2019; Deng et al., 2020; Bai et al., 2021; Liu et al., 2022; Qin et al., 2022; Zhai et al., 2022), by using the similarity theory, similar specimens of the original rock were prepared using similar materials, and the physical and mechanical properties and damage laws were investigated. Optimized the ratio of rock-like materials prepared by 3D printing technology (Wu et al., 2020). Quasi-Sandstone similar materials were prepared using cement, gypsum, sand and coal dust, and it was concluded that gypsum and cement were the main controlling factors for deformation and strength of similar materials, respectively (Chen et al., 2019). Using hardener (CA), epoxy resin (ER) and rosin saturated solution (RSS) as proportional materials, the observability of this type of rock material after fracture generation was demonstrated based on physical and mechanical properties experiments (Ge et al., 2019). The quartz sand was selected as aggregate, and high-strength gypsum powder and talcum powder were used as cementing materials to prepare rock-like materials. The effects of sand-to-gel ratio, water curing, molding pressure and molding time on elastic modulus, compressive strength and permeability were investigated (Hou et al., 2022). Artificial sandstone was prepared using quartz sand as aggregate, montmorillonite and illite as clay, and epoxy resin as binder, and the effect law of clay ratio on the permeability of artificial sandstone was explored (Zhang et al., 2018). A four-factor, three-level orthogonal test was designed using ceramic sand, cement, gypsum and water as raw materials to simulate similar materials of red sandstone, and the test results of physical and mechanical properties of similar materials were subjected to extreme difference analysis and multiple linear regression analysis to obtain the degree of influence of each influencing factor on physical and mechanical properties of similar materials and empirical equations for the proportioning of similar materials of red sandstone (Hu et al., 2020). Mortar-like rock materials were prepared, and (E/ ${\sigma }_c$) was introduced as the deformation index and (${\sigma }_c$/ ${\sigma }_t$)as the brittleness index, and rock-like ratios meeting the deformation index and brittleness index were selected (Song et al., 2020). In summary, previous authors have prepared quasi-sandstone similar material specimens in different ratios using different similar materials and studied the basic physical and mechanical properties with fruitful results. However, most of the current studies are limited to the selection of similar materials with quartz sand and baryte powder as the main aggregates, which are expensive and limited in wide application.

In this paper, river sand, cement and gypsum are used as raw materials, retarder and defoamer are used as additives. Density, longitudinal wave velocity, compressive strength, tensile strength, elastic modulus, Poisson’s ratio, brittleness index (${\sigma }_c$/ ${\sigma }_t$) and deformation index (E/ ${\sigma }_c$) are selected as the characteristic indexes of similar materials. Through the orthogonal ratio test, the ratio of water to cementitious material quality (water-binder ratio), the ratio of cement to gypsum quality (gypsum-cement ratio), and the ratio of cementitious material to aggregate quality (binder-aggregate ratio) are used as the influencing factors of the test. The sensitivity analysis of each index is carried out by using the range analysis method, and the sensitivity of each factor to the physical and mechanical indexes of sandstone-like similar materials is obtained. Then, through multiple non-linear regression, the empirical equation of the influencing factors of the characteristics of quasi-sandstone similar materials is obtained. Finally, the optimal ratio scheme is determined according to the physical and mechanical parameters.

2 Raw material selection

According to previous studies, appropriate sandstone similar materials should be selected for conducting physical model tests, and the following three principles need to be followed (Li et al., 2017). 1) The physical and mechanical properties of sandstone analogues are similar to those of sandstone. 2) The raw materials of similar materials are widely available, inexpensive, non-toxic and non-hazardous, and stable in physical and mechanical properties. 3) The physical and mechanical properties of sandstone analogues can be adjusted to a larger extent by changing the proportioning scheme.

A well-prepared sandstone similar specimen must have a certain compressive strength. Ordinary silicate cement is a cementing material widely used to regulate the strength of specimens at present, and the compressive strength of sandstone similar material is mainly related to the amount of cement content. Gypsum as a cementing agent has obvious brittle characteristics, which can regulate the range of compressive strength and modulus of elasticity, and the specimens with gypsum added mainly undergo brittle deformation, and its brittle characteristics are mainly determined by the amount of gypsum content. River sand is one of the most common materials similar to sandstone, so this test used Huaihe River sand as aggregate with an average particle size of 0.125 mm–0.25 mm to reduce the effect of particle size gradation on the strength of the specimens.

In this paper, Renlou coal mine perimeter rock (sandstone mainly) is used as the research object, and ordinary silicate cement P.O 42.5 and gypsum are selected as cementing materials, which not only ensure the sandstone similar materials to better simulate the influence of gravity field under real environment, but also meet the mechanical properties of the materials. Because gypsum is added to the similar material as cemented river sand (0.125 mm–0.225 mm) as aggregate and retarder and defoamer as added materials, thus a certain proportion of retarder borax was needed to slow down the setting rate of gypsum and facilitate the fabrication of specimens.

3 Experiment

3.1 Experimental scheme

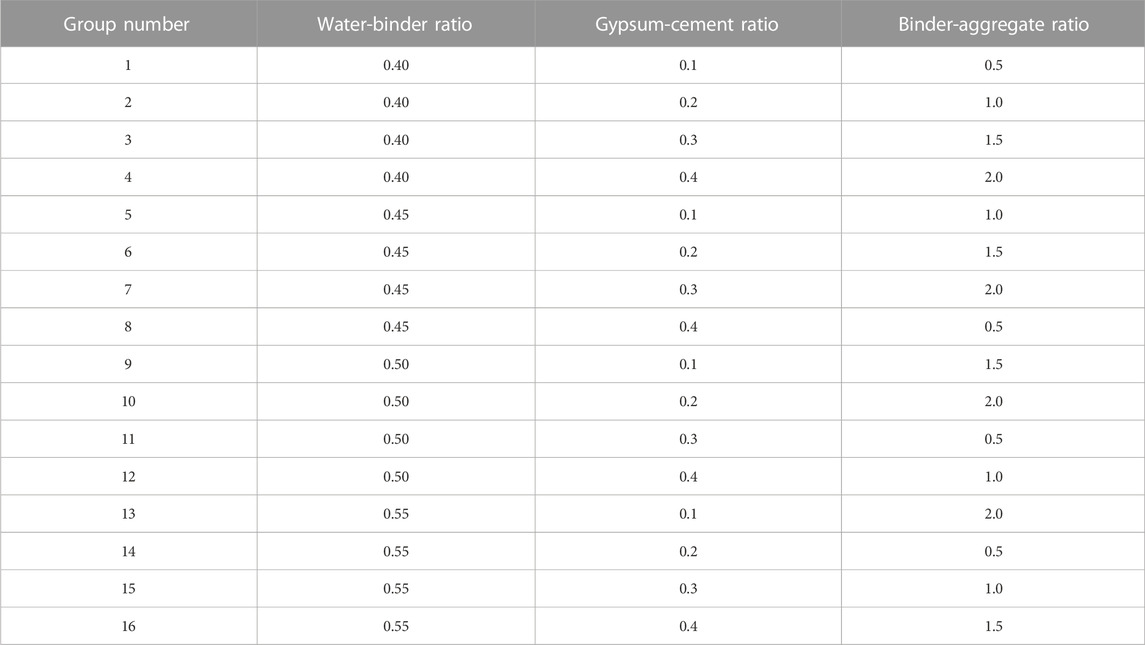
Three factors, water-cement ratio, gypsum-cement ratio and binder-aggregate ratio, are selected as the influencing factors of the test, and four levels of each factor are selected. In order to simplify the analysis process, ignoring the interaction between the factors. The specific factor level settings were determined after pre-experimental blending as shown in Table 1. When designing an orthogonal table for the experiment, it is necessary to select an orthogonal table with the same number of levels and not less than the number of columns than the number of factors as a reference, so this experiment chose a 3-factor 4-level orthogonal design scheme L16 (43). The specific combination of each group is shown in Table 2.

TABLE 1

TABLE 1. Horizontal setting of orthogonal test factors for class 1 sandstone materials.

TABLE 2

TABLE 2. Orthogonal design combination of class 2 sandstone materials.

Note: The effect of defoamer and water-reducing agent on the test was not explored in the test. The amount of defoamer is 0.1% of the mass of binder, and the amount of water-reducing agent is 1% of the mass of binder.

3.2 Sample preparation

According to the orthogonal design combination table in Table 2, quasi-sandstone similar material samples are made, as shown in Figure 1. Weigh the quality of various raw materials using an electronic balance, the use of cement mixer raw materials will be evenly stirred into the slurry, the slurry will be poured into the 150 mm × 150 mm × 150 mm cube mold, and vibration on the shaking Table 1 ∼ 3 min, the use of shaking table to eliminate bubbles inside the specimen, improve the homogeneity of the specimen. The molds are placed in the constant temperature and humidity chamber for 2 days by standard maintenance. During the period, the temperature in the curing box was kept at 201°C and the relative humidity was more than 99%, and the mold was removed after the specimen is formed and continued to be placed in the constant temperature and humidity box for 28 days. The well-cared cubic specimens were cored, cut and polished into two standard cylindrical specimens: 50 mm × 25 mm for Brazilian splitting test and 50 mm × 100 mm for uniaxial compression test according to the recommended sample preparation requirements of the International Society of Rock Mechanics (ISRM) Recommended Methods for Rock Mechanics Testing (1982) (Zhai et al., 2022).

FIGURE 1

FIGURE 1. Sample making process.

3.3 Physical parameters of sample

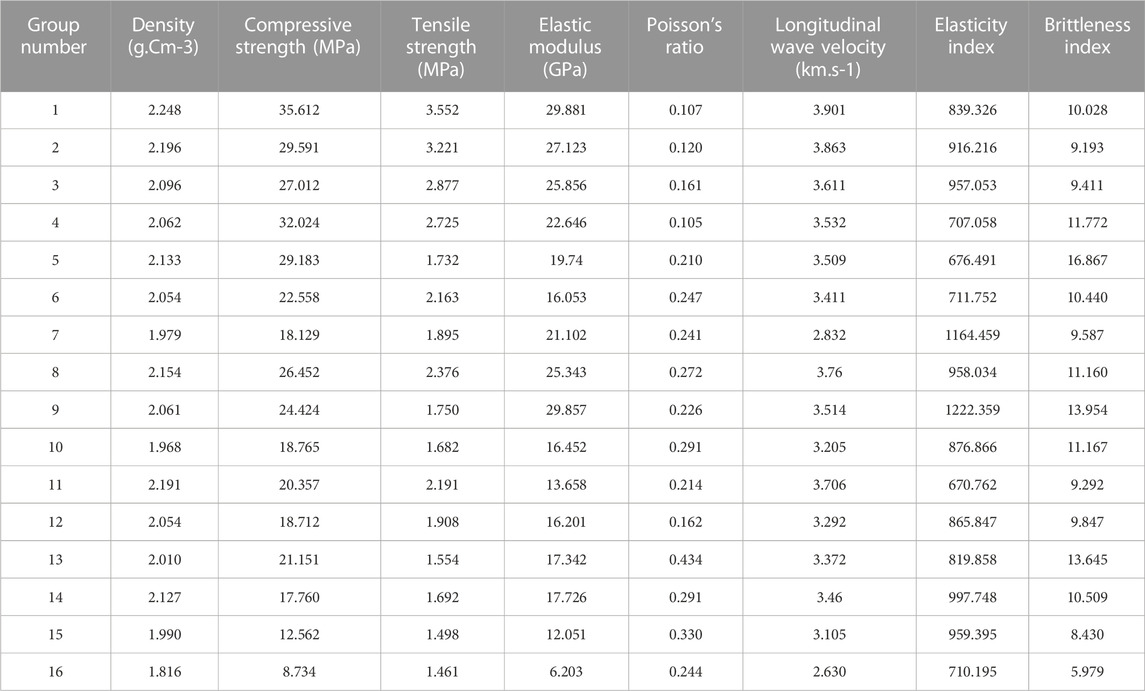
The basic physical test, ultrasonic longitudinal wave velocity test, Brazilian splitting test and uniaxial compression test are performed on the orthogonal test group, and the natural density ${\rho }_0$ , uniaxial compressive strength ${\sigma }_c$, tensile strength ${\sigma }_{\mathrm{t}}$, modulus of elasticity $E$, longitudinal wave velocity $v$ and Poisson’s ratio $u$ of the specimens is measured as shown in Table 3. The instrument used in the longitudinal wave velocity test is HC-U81 concrete ultrasonic detector, as shown in Figure 2, with a measurement range of 0–99999s and a repeatability error of 0.1s; the instruments used in the Brazilian splitting test and uniaxial compression test are both RMT rock mechanics testing machines, as shown in Figure 3, and the test process is carried out by displacement loading with a loading rate of 0.02 mm/s.

TABLE 3

TABLE 3. Measurement results of physical and mechanical parameters.

FIGURE 2

FIGURE 2. Test system.

FIGURE 3

FIGURE 3. Density sensitivity analysis.

4 Sensitivity analysis of test results

The range analysis method commonly used in orthogonal experimental design is a more intuitive data analysis method, which usually obtains the optimal level combination under an index. Since the indexes of rock similar materials designed in this experiment are all interval values, the criterion selected is the index closest to the median value of the index range when selecting the optimal level combination. Sensitivity analysis is the analysis of the problem by calculating the average range for each factor, that is, by subtracting the minimum value from the maximum average of the test results for each influencing factor. The specific calculation methods are shown in Formula 1 and Formula 2.

$I_i=X_1+X_2{+\dots X}_i)/i(1)$

$R=I_{\mathit{max}}-I_{\mathit{min}}(2)$

In the formula: $I_i$ is the average value of the test results of any influencing factors; $X_i$ is the test result of any influencing factor; $I$ is the $i$ test results of any influencing factor; $R$ is range; $I_{\mathit{max}}$ is the maximum value of any influencing factor test results; $I_{\mathit{min}}$ is the minimum value of the test results for any influencing factor.

4.1 Density sensitivity analysis

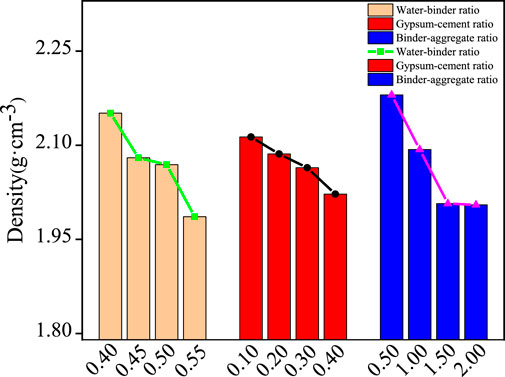
Through the orthogonal proportional test results, the specimen density is analyzed by using the polar difference analysis method, and the polar difference and influence law of each influencing factor are shown in Table 4 and Figure 3. The binder-aggregate ratio has the greatest effect on the density, with the extreme difference of 0.175 g cm⁻³, indicating that the ratio of cement to the total mass of aggregate had the highest effect on the density of the material, and the gypsum-cement ratio has the least effect on the density, with the extreme difference of 0.027 g cm⁻³, indicating that the ratio of gypsum to cement in the cement has the lowest effect on the density of the material. The extreme differences of binder-aggregate ratio, water-binder ratio and gypsum-cement ratio decreased in order, and the degree of influence of each factor is binder-aggregate ratio > water-binder ratio > gypsum-cement ratio The density of the specimens is approximately negatively correlated with the water-binder ratio, negatively correlated with the gypsum-cement ratio, and negatively correlated with the gypsum-cement ratio.

TABLE 4

TABLE 4. Density range analysis (g.cm⁻³).

4.2 Sensitivity analysis of compressive strength

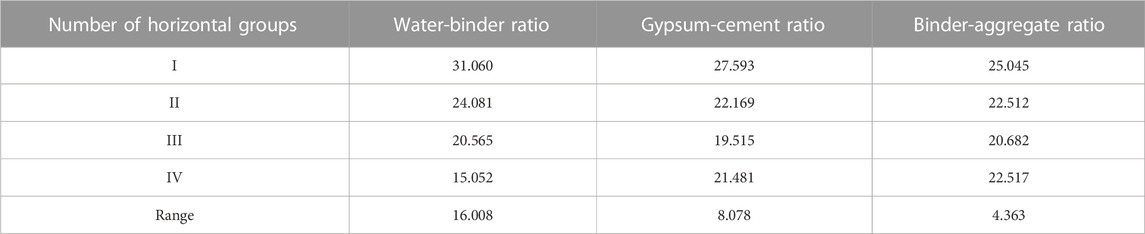
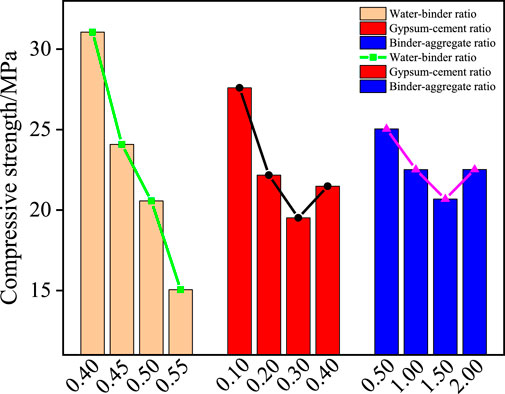
Through the orthogonal proportional test results, the specimen compressive strength is analyzed by using the polar difference analysis method, and the polar difference and influence law of each influencing factor are shown in Table 5 and Figure 4. The water-binder ratio has the greatest effect on the compressive strength, with the extreme difference of 16.008 MPa, indicating that the proportion of water consumption and cementing agent had the highest degree of influence on the compressive strength of the material, and the binder-aggregate ratio has the least effect on the tensile strength, with the extreme difference of 4.363 MPa, indicating that the proportion of cementing agent and aggregate had the lowest degree of influence on the compressive strength of the material. The extreme differences of water-binder ratio, gypsum-cement ratio and binder-aggregate ratio decreases in turn, and the degree of influence of each factor is water-binder ratio > gypsum-cement ratio > binder-aggregate ratio. The compressive strength of the specimens is approximately negatively correlated with the water-binder ratio, and the compressive strength of the specimens can be increased by decreasing the water-binder ratio and then increasing it, and the compressive strength reachs the minimum value of 19.515 MPa when the water-binder ratio is 0.3, and decreased and then increased with the increase of the binder-aggregate ratio, and the compressive strength reached the minimum value of 20.682 MPa when the binder-aggregate ratio is 1.5.

TABLE 5

TABLE 5. Compressive strength range analysis (MPa).

FIGURE 4

FIGURE 4. Sensitivity analysis of compressive strength.

4.3 Tensile strength sensitivity analysis

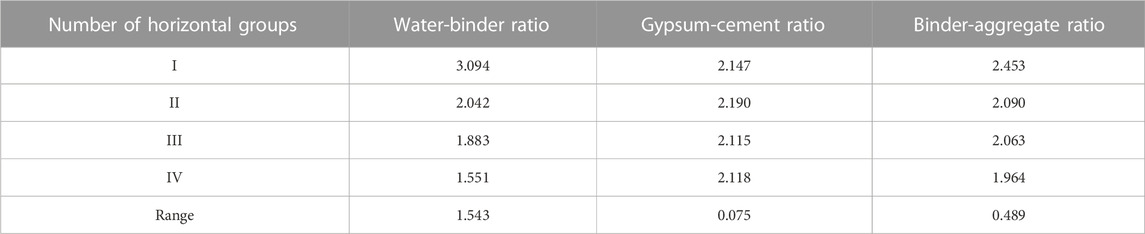
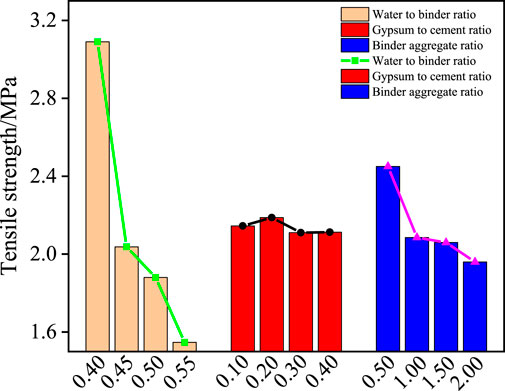
Through the orthogonal proportional test results, the specimen tensile strength is analyzed by using the polar difference analysis method, and the polar difference and influence law of each influencing factor are shown in Table 6 and Figure 5. The water-binder ratio has the greatest influence on the tensile strength, with the extreme difference of 1.543 MPa, indicating that the proportion of water consumption and cementing agent has the highest influence on the tensile strength of the material, and the gypsum-cement ratio has the least influence on the tensile strength, with the extreme difference of 0.075 MPa, indicating that the proportion of gypsum and cement in the cementing agent has the lowest influence on the tensile strength of the material. The extreme differences of water-cement ratio, binder-aggregate ratio and gypsum-cement ratio. Decreased in order, and the degree of influence of each factor is water-cement ratio > binder-aggregate ratio > gypsum-cement ratio. The tensile strength of the sample is approximately negatively correlated with the water-binder ratio. Reducing the water-binder ratio can increase the tensile strength of the sample, has no significant correlation with the gypsum-cement ratio, and is approximately negatively correlated with the binder-aggregate ratio.

TABLE 6

TABLE 6. Analysis of extreme differences in tensile strength (unit: MPa).

FIGURE 5

FIGURE 5. Sensitivity analysis of tensile strength.

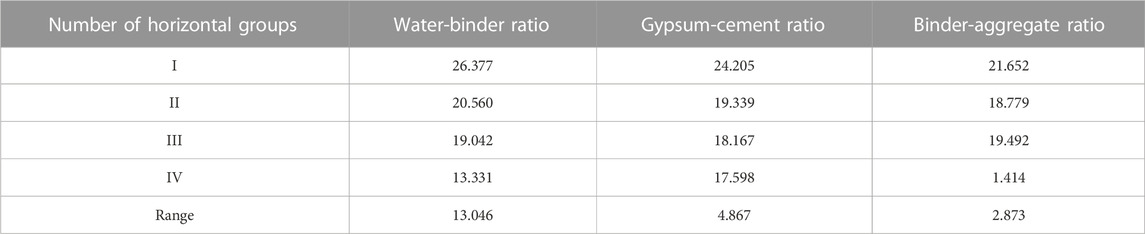
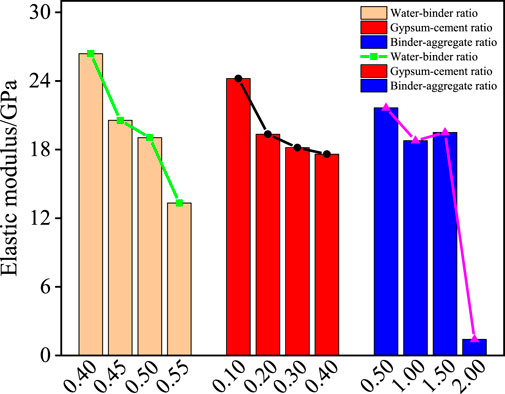
4.4 Elastic modulus sensitivity analysis

Through the orthogonal proportional test results, the specimen elastic modulus is analyzed by using the polar difference analysis method, and the polar difference and influence law of each influencing factor are shown in Table 7 and Figure 6. The water-binder ratio has the greatest effect on the elastic modulus with a polar difference of 13.046 GPa, indicating that the proportion of water used to the cementing agent has the highest degree of influence on the elastic modulus of the material, and the binder-aggregate ratio has the least effect on the elastic modulus with a polar difference of 2.873 GPa, indicating that the proportion of cementing agent to the aggregate has the lowest effect on the elastic modulus of the specimen. The extreme differences of water-binder ratio, gypsum-cement ratio and binder-aggregate ratio decrease in order, and the degree of influence of each factor is water-binder ratio > gypsum-cement ratio > binder-aggregate ratio. The modulus of elasticity of the specimen and the water-binder ratio is approximately negatively correlated, lowering the water-binder ratio can improve the modulus of elasticity of the specimen, and the gypsum-cement ratio is approximately negatively correlated, with the increase of the binder-aggregate ratio first decreases and then increases and then decreases.

TABLE 7

TABLE 7. Range analysis of elastic modulus.

FIGURE 6

FIGURE 6. Elastic modulus sensitivity analysis.

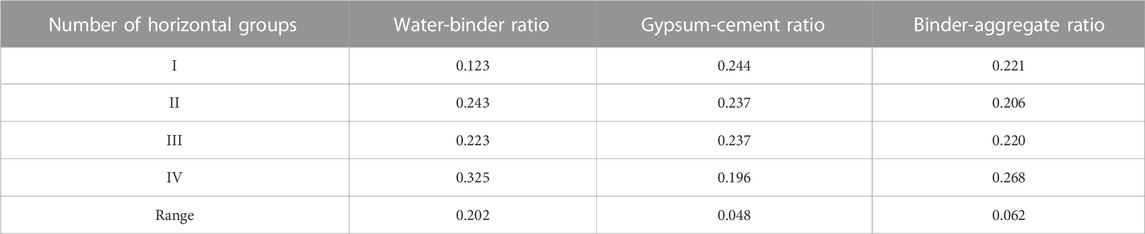
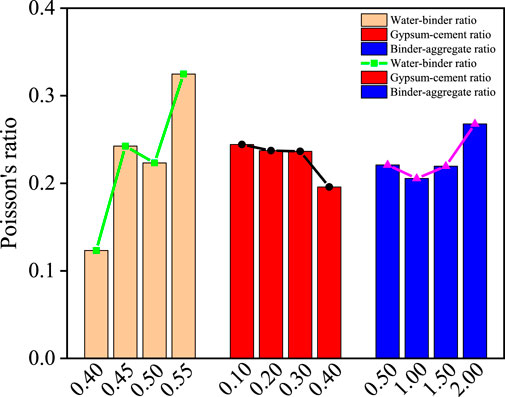
4.5 Poisson’s ratio sensitivity analysis

Through the orthogonal proportional test results, the specimen Poisson’s ratio is analyzed by using the polar difference analysis method, and the polar difference and influence law of each influencing factor are shown in Table 8 and Figure 7. The water-binder ratio has the greatest influence on Poisson’s ratio, with a polar difference of 0.202, which indicates that the water consumption and the proportion of cement have the highest influence on Poisson’s ratio, and the gypsum-cement ratio has the least influence on Poisson’s ratio, with a polar difference of 0.048, which indicates that the proportion of gypsum and cement in the cement has the lowest influence on Poisson’s ratio. The extreme differences of water-binder ratio, binder-aggregate ratio and gypsum-cement ratio decrease in order, and the degree of influence of each factor is water-binder ratio > binder-aggregate ratio > gypsum-cement ratio. The Poisson’s ratio of the specimens is approximately positively correlated with the water-binder ratio and negatively correlated with the gypsum-cement ratio, which decreased first and then increased with the increase of the binder-aggregate ratio, and reached the minimum value when the binder-aggregate ratio is 1.0.

TABLE 8

TABLE 8. Range analysis of Poisson’s ratio.

FIGURE 7

FIGURE 7. Sensitivity analysis of Poisson’s ratio.

4.6 Longitudinal wave speed sensitivity analysis

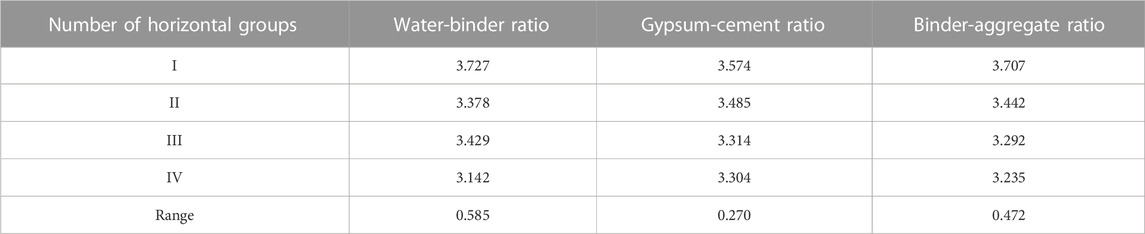
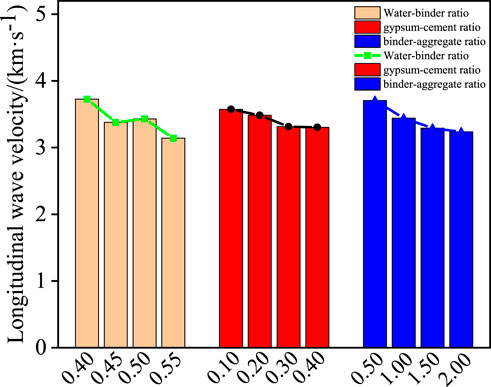
Through the orthogonal proportional test results, the specimen longitudinal wave speed is analyzed by using the polar difference analysis method, and the polar difference and influence law of each influencing factor are shown in Table 9 and Figure 8. The water-binder ratio has the greatest influence on the longitudinal wave speed, with the extreme difference of 0.585 km/s, which indicates that the proportion of water consumption and cement has the highest influence on the longitudinal wave speed of the material, and the gypsum-cement ratio has the least influence on the longitudinal wave speed, with the extreme difference of 0.270 km/s, which indicates that the proportion of gypsum and cement in the cement has the lowest influence on the longitudinal wave speed of the material. The extreme differences of water-binder ratio, gypsum-cement ratio and binder-aggregate ratio decrease in order, and the degree of influence of each factor is water-binder ratio > gypsum-cement ratio > binder-aggregate ratio. The longitudinal wave velocity of the specimen is approximately negatively correlated with the water-binder ratio, and is approximately negatively correlated with the gypsum-cement ratio, that is, it is approximately negatively correlated with the binder-aggregate ratio.

TABLE 9

TABLE 9. Range analysis of longitudinal wave velocity (km/s).

FIGURE 8

FIGURE 8. Sensitivity analysis of longitudinal wave velocity.

4.7 Sensitivity analysis of deformation index

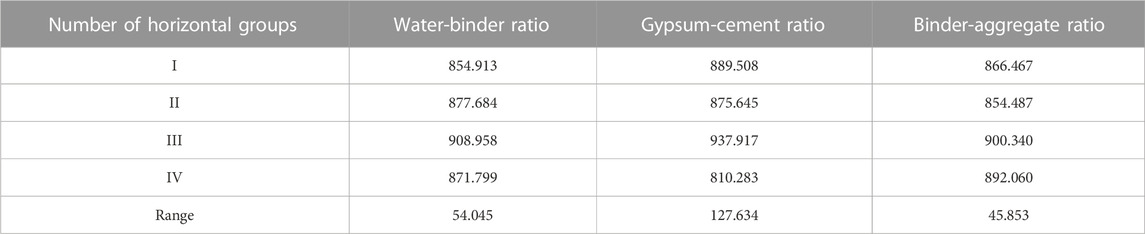
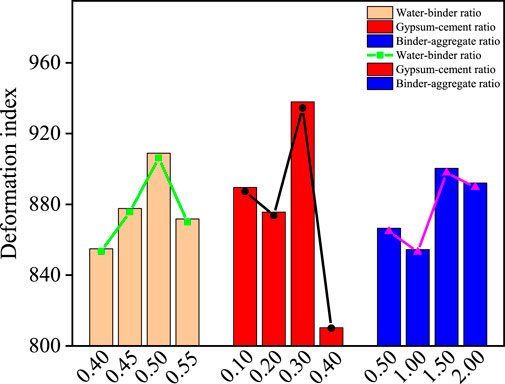
Through the orthogonal proportional test results, the specimen deformation index is analyzed by using the polar difference analysis method, and the polar difference and influence law of each influencing factor are shown in Table 10 and Figure 9. The gypsum-cement ratio has the greatest effect on the deformation index with an extreme difference of 127.634, indicating that the ratio of gypsum to cement in the cementing agent has the highest degree of influence on the deformation index of the material. The binder-aggregate ratio has the least effect on the deformation index with an extreme difference of 45.853, indicating that the ratio of cement to aggregate has the lowest effect on the elastic modulus of the specimen. The extreme differences of the gypsum-cement ratio, water-binder ratio and binder-aggregate ratio decreased in order, and the degree of influence of each factor is gypsum-cement ratio > water-binder ratio > binder-aggregate ratio. With the increase of water-binder ratio, the deformation index first increases and then decreases, when the water-binder ratio is 0.50, the deformation index reaches the maximum; with the increase of gypsum-cement ratio, the deformation index first decreases and then increases and then decreases, with the increase of binder-aggregate ratio, the deformation index first decreases and then increases and then decreases.

TABLE 10

TABLE 10. Range analysis of deformation index.

FIGURE 9

FIGURE 9. Sensitivity analysis of deformation index.

4.8 Sensitivity analysis of brittleness index

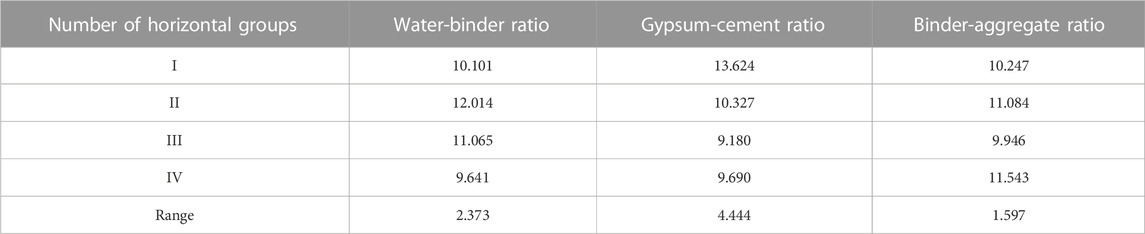
Through the orthogonal proportional test results, the specimen brittleness index is analyzed by using the polar difference analysis method, and the polar difference and influence law of each influencing factor are shown in Table 11 and Figure 10.

TABLE 11

TABLE 11. Range analysis of brittleness index.

FIGURE 10

FIGURE 10. The gypsum-cement ratio has the greatest effect on the brittleness index with an extreme difference of 4.444, indicating that the ratio of gypsum to cement in the cementing agent has the highest degree of influence on the material deformation index.

The binder-aggregate ratio has the least effect on the brittleness index with an extreme difference of 1.597, indicating that the ratio of cement to aggregate has the lowest degree of influence on the material brittleness index. The extreme differences of the gypsum-cement ratio, water-binder ratio and binder-aggregate ratio decrease in order, and the degree of influence of each factor is gypsum-cement ratio > water-binder ratio > binder-aggregate ratio. As the water-binder ratio increases, the brittleness index first increases and then decreases, and the brittleness index reaches the maximum value when the water-binder ratio is 0.45. As the gypsum-cement ratio increases, the brittleness index first decreases and then increases, and the brittleness index reaches the minimum value when the gypsum-cement ratio is 0.3. As the binder-aggregate ratio increases, the index first increases and then decreases and then increases.

5 Multiple linear regression analysis

According to the results of quasi-sandstone similar material ratio test and the sensitivity analysis of each factor, it can be seen that except for the change of deformation index and brittleness index, each factor has obvious linear relationship with the properties of quasi-sandstone similar materials. In order to improve the efficiency of quasi-sandstone similar material ratio test, it is necessary to find the quantitative relationship between each factor and each parameter. Therefore, multiple linear regression analysis is carried out on the test results.

Assuming that $\mathrm{Y}$ is the dependent variable and $X$ is the independent variable, the multiple linear regression model can be expressed as (Li and Hu, 2010):

$\mathrm{Y}=\left[\begin{array}{ccccc}{a}_{11}& a_{12}& a_{13}& \cdots & a_{1m}\\ a_{21}& a_{22}& a_{23}& \cdots & a_{2m}\\ a_{31}& a_{32}& a_{33}& \cdots & a_{3m}\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_{n1}& a_{n2}& a_{n3}& \cdots & a_{nm}\end{array}\right]X+P(3)$

Where: $a_{11}$, $a_{12}$, …, $a_{nm}$ are partial regression coefficients; $p$ are constants.

According to the analysis of the results of quasi-sandstone similar material proportioning tests and the sensitivity of each factor, it can be seen that, except for the insignificant changes of deformation index and brittleness index, each factor has an obvious linear relationship with the properties of quasi-sandstone similar materials. In order to improve the efficiency of quasi-sandstone similar proportioning tests, it is necessary to find the quantitative relationship between each factor and each parameter, so multiple linear regression analysis was performed on the test results.

$\mathrm{Y}=\left[\begin{array}{ccc}-1.012& -0.297& -0.122\\ -103.080& -20.989& -1.883\\ -9.573& -0.163& -0.299\\ -81.311& -20.992& -1.217\\ 1.166& -0.146& 0.031\\ -3.408& -0.983& -0.313\end{array}\right]\mathrm{X}+\left[\begin{array}{c}2.779\\ 79.253\\ 7.103\\ 65.219\\ -0.329\\ 5.675\end{array}\right];R=\left[\begin{array}{c}0.917\\ 0.915\\ 0.913\\ 0.801\\ 0.821\\ 0.832\end{array}\right](4)$

For ease of description, let $X={\left[x_1{x}_2{x}_3\right]}^{\mathrm{T}}$, Where $x_1$ is the Water-binder ratio, $x_2$ is the gypsum-cement ratio, $x_3$ is the binder-aggregate ratio, let $\mathrm{Y}={\left[y\right.}_1{y}_2{y}_3{y}_4{y}_5{y}_6$], Among them, $\mathrm{Y}$ is the density, compressive strength, tensile strength, elastic modulus, Poisson’s ratio and longitudinal wave velocity of quasi-sandstone r materials, respectively. Using the analysis module of SPSS software, the optimal coefficients $a_1$, $a_2$ and constant term $b$ are obtained. The results are shown in formula 4, where $R$ the linear correlation coefficient is obtained.

According to the analysis of the results of quasi-sandstone similar material proportioning tests and the sensitivity of each factor, it can be seen that, except for the insignificant changes of deformation index and brittleness index, each factor has an obvious linear relationship with the properties of quasi-sandstone similar materials. In order to improve the efficiency of quasi-sandstone similar proportioning tests, it is necessary to find the quantitative relationship between each factor and each parameter, so multiple linear regression analysis is performed on the test results Figure 11.

FIGURE 11

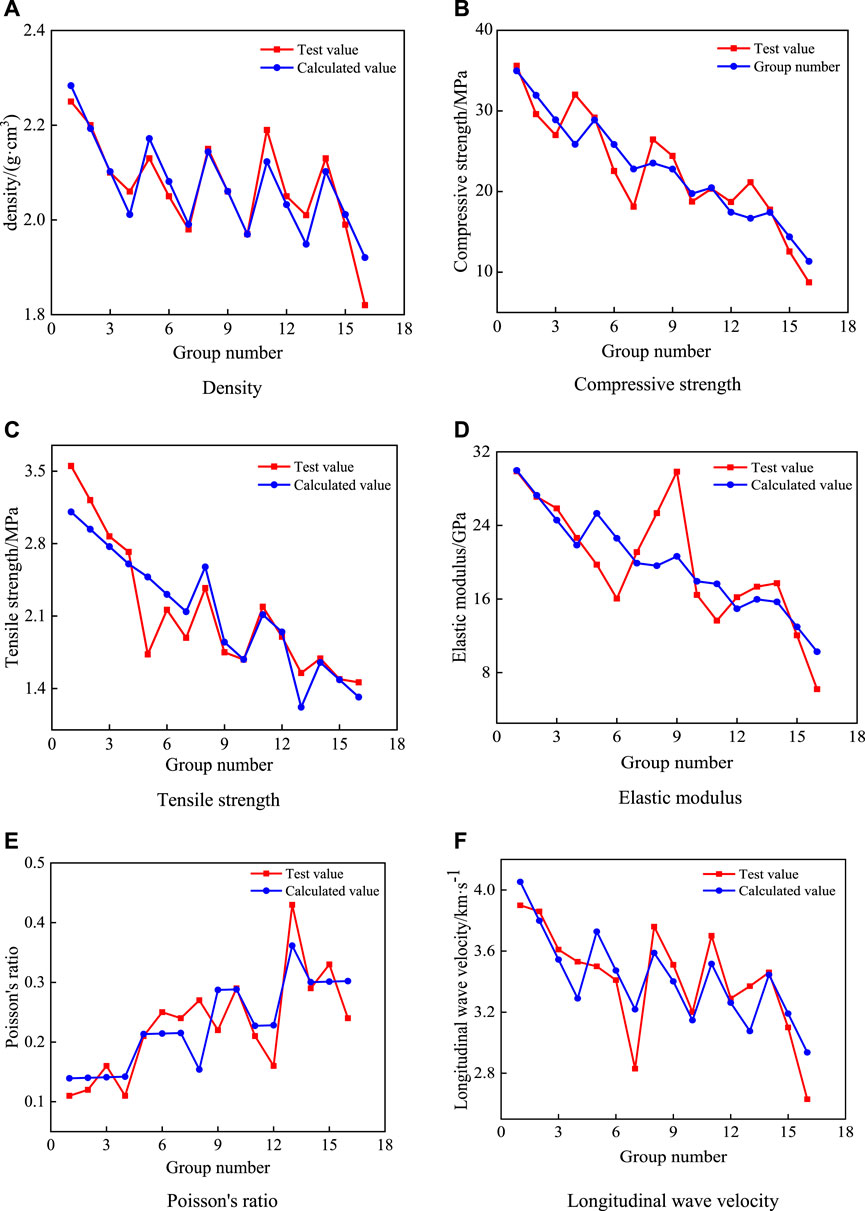
FIGURE 11. Comparison between test results and calculation results of various parameters. (A) Density (B) Compressive strength (C) Tensile strength (D) Elastic modulus (E) Poisson's ratio (F) Longitudinal wave velocity.

6 Discussion

The method described in this paper is used to prepare similar quasi-sandstone materials corresponding to the grouting body. The relationship between the physical and mechanical properties of similar materials and the three factors of water-binder ratio, gypsum-cement ratio and binder-aggregate ratio is mainly explored. Based on multiple linear regression analysis, the empirical formula of the three factors and physical and mechanical properties is obtained, which overcomes the blindness of the previous preparation of quasi-sandstone materials. The introduction of deformation index and brittleness index increases the mechanical properties of similar materials and reduces the error caused by the difference between the properties of similar materials and the original sandstone in the indoor test of replacing rock. To a certain extent, it ensures that the prepared quasi-sandstone material has a certain similarity with the natural original sandstone, and can better carry out the test of slurry seepage diffusion law and grouting reinforcement effect of rock and rock mass under true triaxial stress environment.

However, in some indoor tests, it is sometimes necessary to select appropriate physical and mechanical parameters. Therefore, it is necessary to quickly find the corresponding material ratio based on the empirical formula and then reversely adjust the three factors to change their properties. It can be seen from Figure 12A that the density, compressive strength and tensile strength of the material are approximately negatively correlated with the water-binder ratio, and the density, compressive strength and tensile strength of the material can be improved by reducing the water-binder ratio. It can be seen from Figure 12B that with the increase of gypsum-cement ratio, the elastic modulus, Poisson’s ratio and longitudinal wave velocity of the material gradually decrease. The elastic modulus, Poisson‘s ratio and longitudinal wave velocity of the material can be improved by reducing the paste-mud ratio. It can be seen from Figure 12C that with the increase of the binder-aggregate ratio, the deformation index decreases first, then increases and then decreases. With the increase of the binder-aggregate ratio, the brittleness index increases first and then decreases.

FIGURE 12

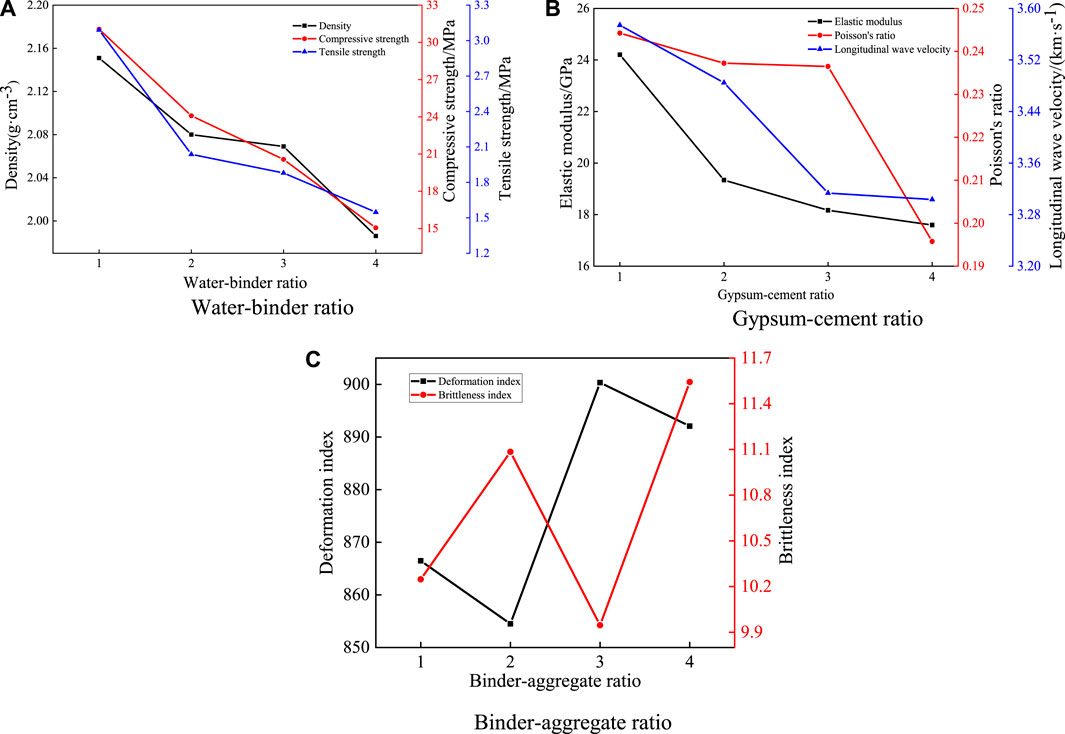
FIGURE 12. Comparative analysis of three factors and physical mechanical properties. (A) Water-binder ratio (B) Gypsum-cement ratio (C) Binder-aggregate ratio.

7 Conclusion

In this paper, using the method of orthogonal test, three factors of water-binder ratio, gypsum-cement ratio and binder-aggregate ratio are used as the influencing factors of the test, and the sensitivity analysis of each index is carried out by using the method of extreme difference analysis, and the influence of the sensitivity degree of each factor on the physical and mechanical indexes of similar materials of quasi-sandstone is obtained, based on the multiple linear regression analysis method, the empirical equation of the influencing factors of similar material properties of quasi-sandstone is obtained, and the physical and mechanical parameters of sandstone can be indicators to determine the optimal proportioning scheme of sandstone-like material corresponding to the grouted body. The main conclusions are as follows:

1) Using river sand as aggregate, cement and gypsum as cementing agent, we can prepare a density of 1.816–2.248g/cm⁻³, compressive strength of 8.734–35.642 MPa, modulus of elasticity of 6.203 GPa–29.881GPa, Poisson’s ratio of 0.161–0.434, longitudinal wave speed of 2.630 km/s∼3.901 km/s, deformation index of 670.762–1222.359, and brittleness index of 5.979–16.867.

2) Based on the range analysis method, the effects of water-binder ratio, gypsum-cement ratio and binder-aggregate ratio on the physical and mechanical properties of sandstone-like similar materials were analyzed by orthogonal similarity ratio test. The water-binder ratio had the greatest influence on the compressive strength, tensile strength, elastic modulus, Poisson’s ratio and longitudinal wave velocity sensitivity of the material. The gypsum-cement ratio has the greatest influence on the sensitivity of material deformation index and brittleness index. The binder-aggregate ratio has the greatest influence on the density sensitivity of the material.

3) Reducing the water-binder ratio can improve the density, compressive strength and tensile strength of the material; reducing the gypsum-cement ratio can improve the elastic modulus, Poisson‘s ratio and longitudinal wave velocity of the material; with the increase of Binder-aggregate ratio, the deformation index decreases first, then increases and then decreases. With the increase of binder-aggregate ratio, the brittleness index increases first, then decreases and then increases.

4) The multiple linear regression analysis of the test data is carried out by using SPSS analysis software. The empirical formula between the physical and mechanical properties of quasi-sandstone materials and water-binder ratio, gypsum-cement ratio and binder-aggregate ratio is obtained. The feasibility and reliability of the empirical formula are verified by the linear correlation coefficient R, which can provide a theoretical reference for the simulation test of quasi-sandstone grouting similar materials.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LY: Conceptualization, Methodology, Software, Data curation, Validation, Writing-original draft, Funding acquisition. JC: Data curation, Writing-review and editing, Funding acquisition. LQ: Supervision, Writing-review and editing, Funding acquisition. WS: Writing review and editing, Funding acquisition. TW: Funding acquisition, Writing-review and editing. DP: Writing-review and editing. YL: Writing-review and editing. YG: Writing-review and editing.

Funding

This work was supported by National natural science foundation of China (52174105), Key R & D project of Anhui province (202004a07020045), Collaborative Innovation Project of Anhui Universities (GXXT-2019-0294).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, H., Du, W., Shou, Y. D., Chen, L. C., and Berto, F. (2021). Experimental investigation of cracking behaviors of ductile and brittle rock-like materials. Fract. Struct. Integr. Int. J. Italian Group Fract. 15 (56), 16–45. doi:10.3221/IGF-ESIS.56.02

CrossRef Full Text | Google Scholar

Chen, J. Z., Li, X. B., and Cao, H. (2019). Experimental investigation of coal–like materials for hydraulic fracturing based on fluid–solid interaction. J. Nat. Gas Sci. Eng. 69, 102928. doi:10.1016/j.jngse.2019.102928

CrossRef Full Text | Google Scholar

Deng, H. W., Tian, G. L., Yu, S. T., Jiang, Z., Zhong, Z. M., and Zhang, Y. N. (2020). Research on strength prediction model of sand-like material based on nuclear magnetic resonance and fractal theory. Appl. SCIENCES-BASEL 10 (18), 6601. doi:10.3390/app10186601

CrossRef Full Text | Google Scholar

Ge, J. J., Xu, Y., and Candido, F. P. (2019). A method for making transparent hard rock-like material and its application. Adv. Mater. Sci. Eng. 2019 (2), 1–14. doi:10.1155/2019/1274171

CrossRef Full Text | Google Scholar

He, M. C. (2021). Research progress of deep shaft construction mechanics. J. China Coal Soc. 46 (03), 726–746. doi:10.13225/j.cnki.jccs.YT21.0124

CrossRef Full Text | Google Scholar

Hou, X. W., Zhou, X. Z., and Pan, J. N. (2022). Similar material proportioning and preparation of ductile surrounding rocks for simulating in situ coalbed methane production from tectonically deformed coals. Rock Mech. Rock Eng. 55 (9), 5377–5392. doi:10.1007/S00603-022-02951-3

CrossRef Full Text | Google Scholar

Hu, M., Yang, X. M., and Luo, X. D. (2020). Study on mixture ratio scheme of similar materials of red sandstone based on orthogonal experiment. J. Hefei Univ. Technol. Nat. Sci. 43 (06), 736–740. doi:10.3969/j.issn.1003-5060.2020.06.004

CrossRef Full Text | Google Scholar

Jia, B. X., Wan, W. Y., Ma, C. Y., Liu, F. P., and Zhang, J. J. (2022a). Ratio test and characteristic analysis of similar materials in white sand rock. Chin. J. Undergr. space Eng. 18 (02), 503–512. doi:10.3969/j.issn.1673-0836.2022.2.dxkj202202018

CrossRef Full Text | Google Scholar

Jia, S. P., Yang, J. W., Gao, M., Jia, L. F., Wen, C. X., and Wu, G. J. (2022b). Experimental and numerical analysis of deformation and failure behaviour for deep roadways in soft rocks. Bull. Eng. Geol. Environ. 81 (11), 466. doi:10.1007/S10064-022-02959-7

CrossRef Full Text | Google Scholar

Jing, W., Liu, S. X., Yang, R. S., Jing, L. W., and Xue, W. P. (2022). Mechanism of aging deformation zoning of surrounding rock in deep high stress soft rock roadway based on rock creep characteristics. J. Appl. Geophys. 202, 104632. doi:10.1016/j.jappgeo.2022.104632

CrossRef Full Text | Google Scholar

Kang, H. P., Jiang, P. F., Huang, B. X., Guang, X. M., Wang, Z. G., Wu, Y. Z., et al. (2020). Roadway strata control technology by means of bolting-modification-destressing in synergy in 1000 m. J. China Coal Soc. 45 (03), 845–864. doi:10.13225/j.cnki.jccs.SJ20.0204

CrossRef Full Text | Google Scholar

Li, G. C., Yu, S., Sun, Y. T., Xie, J. W., and Li, J. H. (2022). Research progress of roadway surrounding strata rock control technologies under complex. Coal Sci. Technol. 50 (06), 29–45. doi:10.13199/j.cnki.cst.2022-0304

CrossRef Full Text | Google Scholar

Li, S. G., Bie, C. F., Zhao, P. X., Li, L., and Lin, H. F. (2017). Study on influence factors of new solid-gas coupling simulation. material J. Min. Saf. Eng. 34 (05), 981–986. doi:10.13545/j.cnki.jmse.2017.05.023

CrossRef Full Text | Google Scholar

Li, Y. Y., and Hu, C. R. (2010). Experiment design and data processing. Beijing: Chemical Industry Press, 82–127.

Google Scholar

Liu, L. S., Yang, Y., Chai, Y. G., Zhong, S. L., Chen, H., Xia, S. M., et al. (2022). A study of the dynamic damage characteristics of Rock-Like materials with different connectivity of concealed structural surfaces. Theor. Appl. Fract. Mech. 121, 103497. doi:10.1016/J.TAFMEC.2022.103497

CrossRef Full Text | Google Scholar

Liu, Q. S., Lei, G. F., Lu, C. B., Peng, X. X., Zhang, J., and Wang, J. T. (2017). Experimental study of grouting reinforcement influence on mechanical properties of rock fracture. Chin. J. Rock Mech. Eng. 36 (1), 3140–3147. doi:10.13722/j.cnki.jrme.2016.0459

CrossRef Full Text | Google Scholar

Lu, H. F., Zhang, K., Yi, J. L., and Wei, A. C. (2022). A study on the optimal selection of similar materials for the physical simulation experiment based on rock mineral components. Eng. Fail. Anal. 140, 106607. doi:10.1016/J.ENGFAILANAL.2022.106607

CrossRef Full Text | Google Scholar

Qin, Y., Xu, N. X., Guo, Y. X., Li, J. Y., and Han, W. B. (2022). Physical simulation of the influence of the original rock strength on the compaction characteristics of caving rock in longwall goaf. R. Soc. Open Sci. 9 (9), 220558. doi:10.1098/RSOS.220558

PubMed Abstract | CrossRef Full Text | Google Scholar

Song, Y., Liu, B. G., Liu, H., Sun, J. L., Yu, M. Y., and Ren, D. R. (2020). Orthogonal test method for determination of the proportion of rock-like material based on properties of deformation and brittleness. Rock Soil Mech. 41 (08), 2675–2684. doi:10.16285/j.rsm.2019.1711

CrossRef Full Text | Google Scholar

Wang, H. P., Li, S. C., Zhang, Q. Y., Li, Y., and Guo, X. H. (2006). Development of a new geomechanical similar material. Chin. J. Rock Mech. Eng. 25 (09), 1842–1847. doi:10.3321/j.issn:1000-6915.2006.09.016

CrossRef Full Text | Google Scholar

Wang, X. F., Zhang, Y. Y., Zhang, Q., Wei, Y. Y., Liu, W. G., and Jiang, T. (2022). Space-time evolution characteristics of deformation and failure of surrounding rock in deep soft rock roadway. Sustainability 14 (19), 12587. doi:10.3390/su141912587

CrossRef Full Text | Google Scholar

Wu, T. T., Zhao, H., Xu, Q., and Zhao, Y. X. (2020). Optimal analysis of material ratio for artificial rock by 3D printing technique. Geomechanics Geoengin. 17 (1), 260–268. doi:10.1080/17486025.2020.1739752

CrossRef Full Text | Google Scholar

Zhai, C., Zheng, Y. F., Yu, X., Xu, J. Z., Sun, Y., Cong, Y. Z., et al. (2022). Experimental study on the mechanical properties of coal-like materials for hydraulic fracturing simulation. Coal Geol. Explor. 50 (08), 16–22. doi:10.12363/issn.1001-1986.22.04.0272

CrossRef Full Text | Google Scholar

Zhang, Q. Y., Li, S. C., Guo, X. H., Li, Y., and Wang, H. P. (2008). Research and development of new typed cementitious geotechnical similar material for iron crystal sand and its application. Rock Soil Mech. 29 (08), 2126–2130. doi:10.16285/j.rsm.2008.08.002

CrossRef Full Text | Google Scholar

Zhang, S. K., and Yin, S. D. (2022). Analytical approach based on full-space synergy technology to optimization support design of deep mining roadway. Minerals 12 (6), 746. doi:10.3390/min12060746

CrossRef Full Text | Google Scholar

Zhang, Y. L., Wu, Y. P., and Xie, P. S. (2019). Orthogonal testing on ratio of physical simulation material similar to sandstone. IOP Conf. Ser. Mater. Sci. Eng. 688 (3), 033007. doi:10.1088/1757-899X/688/3/033007

CrossRef Full Text | Google Scholar

Zhang, Y., Zhou, H. W., Zhong, J. C., and Wang, R. (2018). An experimental study on artificial sandstone-clay proportioning on permeation behavior. Chin. J. Rock Mech. Eng. 37 (S1), 3253–3262. doi:10.13722/j.cnki.jrme.2016.1540

CrossRef Full Text | Google Scholar

Zhang, Z. F., Kang, H. P., Jiang, Z. Y., Li, W. Z., Jiang, P. F., Cai, R. C., et al. (2020). Study and application of high-pressure splitting grouting modification technology in coalmine with depth more than 1 000 m. J. China Coal Soc. 45 (03), 972–981. doi:10.13225/j.cnki.jccs.SJ19.1545

CrossRef Full Text | Google Scholar