- 1International Center for Climate and Environment Sciences (ICCES), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China
- 2College of Earth and Planetary Science, University of Chinese Academy of Sciences, Beijing, China
- 3Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters (CIC-FEMD), Nanjing University of Information Science and Technology, Nanjing, China
Centennial drought characteristics in Equatorial East Africa (EEA) is investigated using the Standardized Precipitation Evapotranspiration Index (SPEI) derived from the Climatic Research Unit (CRU) dataset. The spatial pattern of drought distribution, as well as drought duration, intensity and frequency, are analyzed for SPEI at a 3-month timescale for March-April-May (MAM) season. Rotated Empirical Orthogonal Function (REOF), Mann-Kendall method (MK), and wavelet analyses are used to study drought’s spatial pattern, trend, and periodicity. The result of the principal component analysis returned six homogenous drought sub-regions. A low drought frequency characterizes EEA (<20%). The drought in the MAM season lasts between 2.2 and 2.8 months. Overall, the result showed a weak long-term drying trend for most parts of EEA that were significant in some sub-regions and insignificant in others. An increase in drought areal extent after the 1980s could be ascribed to the increase in potential evapotranspiration (PET) and is consistent with the negative trend in SPEI value over the six sub-regions. The apparent increase is mainly attributed to the increase in moderate and severe droughts area rather than extreme drought areas. The spectral analysis further reveals that inter-annual drought variability with periodicities less than 8 years dominates in all sub-regions of Equatorial East Africa, which is associated with the critical role of El-Niño in driving the drought variations in EEA.
1 Introduction
Drought is an extreme event characterized by a protracted period of insufficient water supply emanating from erratic and irregular rainfall distribution, high evapotranspiration and higher demand for water than supply (Bhuiyan, 2009). Unlike other meteorological disasters, drought developed slowly and is only recognized once its effect on the environment and population is felt. It places an immense burden on agricultural production, water resource, energy production and causes damage to the ecological environment (Iglesius et al., 2001; Winslow et al., 2011). Droughts may emanate from a combination of drivers of climate variability and anthropogenic forcing and, as such, cannot be blamed on one driver alone. Beyond the drought itself, the extent of the impact depends on the vulnerability and exposure of societies. Poor land management practices can also worsen the drought and lead to soil degradation (Cook et al., 2009). Dai (2013) suggested that the warming trend since the 1980s has led to the expansion of global drought areas by about 8%. Many studies reported more frequent and severe droughts in different regions in the 21st century as the global mean surface temperature continues to rise (Sheffield et al., 2012; Cook et al., 2015; Schwalm et al., 2017; Trenberth et al., 2013).
Equatorial East Africa (hereafter, EEA) is among the drought-sensitive regions owing to the large interannual rainfall variability. The observed variability has been characterized by the region’s increased frequency and intensity of extreme events (Nicholson, 2014). In addition, as much as 69% of East Africa may be classified as arid and semi-arid, with annual rainfall less than 50% of the mean annual potential evapotranspiration (UNDP/UNSO, 1997). The demand for water resources is increasingly under pressure owing to population growth and the region’s larger interannual rainfall variability. Severe drought has occurred in East Africa in recent decades, and the events have direly impacted socio-economic activities in the region. Funk et al. (2014) reported that East Africa experienced drought for 8 years between the 1990s and 2000s. The economic impact of drought has been significant. For instance, Mogaka et al. (2006) estimated the 1998–2000 drought episode over East Africa caused agricultural losses estimated to be worth USD 370M. On the other hand, the 2008–2011 dry conditions affected over 13 million people in the region and led to a severe shortage of water, food and pasture, leading to loss of life and livelihood (AghaKouchak, 2015; Uhe et al., 2017). These losses and the impact of earlier severe droughts, such as 1983/84, highlight the region’s susceptibility to drought.
East Africa has shown a neutral to slight decline in rainfall (Lyon and Dewitt, 2012; Yang et al., 2014; Tierney et al., 2015). Nicholson (2014) reported that the first decade of the 21st century experienced an increased frequency of below-average rainfall that lasted over a longer time in the Greater Horn of Africa (GHA) region. The reduction in rainfall, coupled with the increase in regional temperature, has increased the frequency and intensity of drought over the region. For example, Mpelasoka et al. (2018) linked the region’s drought-like crises to rainfall reduction. Several studies have attempted to explain the causal mechanisms of these droughts and the observed rainfall variability. For instance, it is a well-established fact that La-Niña suppresses rainfall over East Africa (Ogallo, 1989). Lyon (2014) reported that the post-1998 decline in rainfall is strongly driven by natural multi-decadal variability in the tropical Pacific Ocean rather than anthropogenic climate change. Hastenrath et al. (2005, 2010) reported that the surface equatorial westerlies were fast during the 2005 and 2008 droughts. Consequently, they linked the 2005 and 2008 droughts to the fast-moving westerlies, often accompanied by anomalously cold waters in the northwestern and warm anomalies in the southeastern Indian Ocean. Lyon (2014) further found that sea surface temperature (SST) anomalies in the tropical Pacific and Indian Oceans shows a strong association with October-November-December (OND) season drought, especially in locations that have a bimodal rainfall pattern. The study also reported that this influence depended on the ability of ENSO to affect SSTs outside the Pacific. Wainright et al. (2019) reported that the decrease in rainfall results from the late onset and early withdrawal of rainbands over East Africa. Williams and Funk (2011) link the reduction in rainfall to the enhanced warming of Indian Ocean sea surface temperature (SST), which they argue is driven by anthropogenic emissions.
Defining drought is complicated due to its complex nature. Among the indices developed to monitor and characterize drought, the Standard Precipitation Index (SPI; McKee et al., 1993), the Standardized Precipitation Evapotranspiration Index (SPEI; Vicente-Serrano et al., 2010) and the Palmer drought severity index (PDSI; Palmer, 1965) are the popular and the commonly used. However, PDSI has limitations such as having a fixed time scale, limited spatial comparability, and dependent on data calibration (Wells et al., 2004; Andreadis et al., 2005). On the other hand, SPI boasts simple calculations but is solely based on rainfall. Indeed, Ntale and Gan (2003) recommended using SPI over East Africa owing to its ability to produce more consistent spectral patterns, modest data requirements and adaptability to the local climate. However, while changes in rainfall patterns broadly define drought, processes such as temperature and wind speed determine water availability by controlling the evapotranspiration rate, thus affecting the drought. Given this, the SPEI drought index is adopted in the current study, which incorporates a water balance making it suited to quantify drought much better (Beguería et al., 2013).
Studies that give spatial and temporal variability of drought in the region are limited. Most studies focus on explaining the drivers responsible for a drought event or declining rainfall in the region. In addition, most of the earlier studies are confined to watersheds scale or larger areas (e.g. GHA) but with different climate zones. Despite the increasing drought risk, the intrinsic characteristics of East Africa climate zones have been given little or no attention in past drought studies. For instance, Mpelasoka et al. (2018) found regional differences in the probability of occurrence of drought year over the GHA region, while Gebremeskel et al. (2020) reported differences in drought trends for individual East Africa countries. This shows that while a large-scale forcing may drive the regional drought, the local response may lead to variation in drought intensity. However, studies on the entire region or country level led to a loss of information on the uniqueness of climate regime-specific responses. Consequently, to address this, the current study classifies East Africa into homogenous sub-regions using principal component analysis and varimax rotation and proposes the drought characteristics for each zone.
In addition, studies show that successive seasons are uncorrelated over East Africa; thus, drought development in one season does not guarantee its persistence to the next season (Nicholson et al., 2014; Lyon, 2014). Given this, the current study focuses on the spring season (March-April-May, MAM) drought characteristics over East Africa using the centennial drought dataset since 1901. The season locally referred to as Masika, corresponds to the primary planting season for major food crops across East Africa when moisture availability is critical for the plant’s growth (Supplementary Figure S1).
Specifically, the study aims to analyze the spatio-temporal characteristics of drought events over EEA-during 1901–2020 using the SPEI index at regional and sub-regional scales and further delineate the possible relationship between SPEI and key regional climatic indices. The paper is organized as follows. Section 2 describes the data and analysis methods, while Section 3 discusses the region’s characteristics and dynamics of droughts. Finally, Section 4 gives a summary and concludes the research findings.
2 Study area, data and methodology
2.1 Study domain
The current study defines Equatorial East Africa (EEA) as the area bounded by Kenya, Uganda, Tanzania, Rwanda, and Burundi (28.5oE-42oE, 12oS-5.5oN) as shown in Figure 1. Rainfall in most of EEA shows a bimodal seasonal distribution pattern influenced by the seasonal movement of the Inter-Tropical Convergence Zone (ITCZ; Mutai and Ward 2000; Camberlin and Philippon 2002). This movement of ITCZ is accompanied by a change in wind direction that brings in moisture from the adjacent Indian Ocean. The rainfall peaks occur in March-May and October-December seasons and are separated by short dry periods in June and July and January and February. The mean annual precipitation varies from about 400 mm in the eastern and northern parts of Kenya to more than 2800 mm over the Lake Victoria basin. The region is dotted with lakes, key among them L. Victoria which drives a local land/lake breeze that controls the convective activities around the lake basin (Anyah et al., 2006; Onyango et al., 2020). On the other hand, the Kenyan highland deflects the cross-equatorial flow strengthening it during boreal summer (Peagle and Geisler, 1986; Chakraborty et al., 2009).
2.2 Data
While in situ rainfall data remains the most accurate, the gauge network density in EA is sparse, thus inadequate to describe drought’s spatial distribution accurately. In addition, the limited length and inconsistency in the observational data (Schreck and Semazzi, 2004; Shilenje and Ongoma, 2016) limit our ability to assess the long-time observed drought changes over the region. In this study, the monthly rainfall and potential evapotranspiration data from CRU TS 4.05 (Harris et al., 2014) were used to calculate the drought index.
One of the reasons for using CRU data is because it includes all the climate variables that allow for the SPEI index computation. Secondly, all grid points have complete data over a 120-year long period during 1900–2020 with relatively higher resolution of 0.5° x 0.5°. Meanwhile, the PET data from CRU uses the FAO-recommended Penman-Monteith method that incorporates daily temperature, radiation, humidity and wind speed. Moreover, the CRU dataset performs relatively well in hydrometeorological studies over East Africa. Ongoma and Chen (2017) found that CRU data outperforms the GPCC dataset in reproducing the East Africa rainfall cycle. The CRU dataset has also been widely used for climate variability studies over East Africa, including the rainfall decadal variation and the model performance evaluation (e.g., Yang et al., 2014; Ayugi et al.,2020; Mbigi et al., 2022). It is noted that, the spring season in this study refers to March, April and May (MAM). Monthly Nino3.4 and PDO indices data were obtained from the NOAA Climate Prediction Center (https://psl.noaa.gov/gcos_wgsp/Timeseries/).
2.3 Method
2.3.1 Definition of drought index
The study used SPEI to define drought during the MAM season. The index was estimated using the monthly rainfall and the potential evapotranspiration (PET) for 1901–2020. SPEI is based on a water balance approach and uses the difference between rainfall and potential evapotranspiration (PET) to analyze the dry and wet spells over multiple timescales (Vicente-Serrano et al., 2010). The index is computed by subtracting potential evapotranspiration from corresponding rainfall and summing up the result with a moving window of width equivalent to the user-specified timescale known as the accumulation period. The accumulated monthly values are then fitted to a parametric statistical distribution where non-exceedance probabilities are transformed into a standard normal distribution (McKee et al., 1993; Guttmann, 1998). The parameter of the Log-logistic distribution function is adopted here to fit cumulative probability distribution aggregated over 3-month rainfall time series. SPEI values were computed using the R package developed by Vicente-Serrano et al. (2010).
To obtain the drought classification, the SPEI drought index was firstly calculated from CRU hydrometeorological observations, then the drought category was further classified based on the predefined threshold on the SPEI index value as defined by Vicente-Serrano et al. (2010), and was shown in Table 1. We adopted the run model (Yevjevich, 1967) to define the drought-related characteristics for our study period. Here, drought is considered anytime the SPEI value equals or less than −1 and ends when the value is above this threshold. Once a drought event is detected, it is assigned drought characteristics. These are drought duration, the number of consecutive months in which the SPEI value remains below the threshold value. At the same time, the area under the curve represents the magnitude of drought severity. The ratio of drought severity to its duration gives the drought intensity. SPEI3 values from May 1901–2020 were used to analyze drought in this study.
2.3.2 Rotated empirical orthogonal function analysis
Due to the high dimensionality and non-linearity of hydrometeorological data (Hannachi et al., 2007), the Empirical Orthogonal Function (EOF) is commonly used to systematically decompose data into a smaller set of variables that explain most of the original variance. However, EOF often exhibits subdomain instability, domain shape dependence, and sampling problems that may hamper their utility in isolating individual modes of variation (Richman, 1986). Consequently, the Rotated Empirical Orthogonal Function (REOF) methodology has been applied to the SPEI dataset in this study to identify the regions with similar drought features. REOF is computed by the rotation of eigenvectors obtained in the EOF analysis to achieve a more stable localized pattern that retains its orthogonality. The number of EOF retained for rotation is decided based on the rule of thumb (North et al., 1982) and the cumulative proportion of variance explained by the principal components.
2.3.3 Wavelet analysis
In general, the variation of SPEI can be analyzed using Fourier transform. However, owing to the intricacy of factors from which the drought arises, its time series may exhibit non-stationary properties (Abdourahamane, 2018). The time series of REOF is analyzed in a time-frequency domain using continuous wavelet transform (CWT) to identify the periodicity. CWT transforms the temporal drought variability pattern onto a time-frequency plane where their duration and dominant periodicities can be easily identified.
Further, the study investigated the relationship between the Niño3.4 index, a leading mode of regional interannual variability, and SPEI using wavelet coherence (WCO; Torrence and Compo, 1998; Grinsted et al., 2004). WCO measures the time and scale of interaction between two processes as a function of frequency and may be taken as a decomposition of the correlation coefficient across multiple timescales (Casagrande et al., 2015). We adopt the Morlet wavelet function due to its ability to balance time and frequency. The analysis was tested for significance using Monte Carlo techniques at a 95% confidence level. The WCO values range from zero to one, and a closer value to one shows a higher correlation.
2.3.4 Trend analysis
The long-term wetting and drying trend were estimated at each grid point over EEA for the study period 1901–2020 using the non-parametric Mann-Kendall test (MK; Mann 1945; Kendall 1975). The MK test is a non-parametric test that applies to all types of distribution. Due to its low sensitivity, MK does not require samples to conform to any particular distribution. It is also less sensitive to the missing values making it appropriate for studying hydrometeorological variables. The mathematical description of the MK method can be found in Gao et al. (2020).
3 Results
3.1 Regionalization of spring drought characteristics over EA
In order to clarify the sub-regional difference in drought characteristics over EEA, this study adopted the maximum loading rule (Vincent Serrano, 2006) to identify the sub-regional boundaries for drought analysis. Figure 2 presents the spatial pattern of the top six dominant REOF modes that were well-demarcated and shows clear spatially disjunctive patterns that did not overlap when a loading threshold of ±0.05 was applied. The six modes explained approximately 77.9% of the total variance in the original SPEI series. The leading mode of variability explains 18.5% of the total variance and has a maximum magnitude in northeastern Kenya. The second mode represents the south of Lake Victoria basin, central and western Tanzania and explains 18.3% of the total variance. The third mode represents Kenya and Tanzania’s coastal strip and explains 12.9% of the total variance. The fourth mode explains 10.1% of the total variance and has its center in western Kenya, Central and northern Uganda. The fifth mode has its maximum magnitude in southern Tanzania and explains 9.9% of the total variance. Lastly, the sixth mode has the largest magnitude in south Uganda, Rwanda and Burundi.
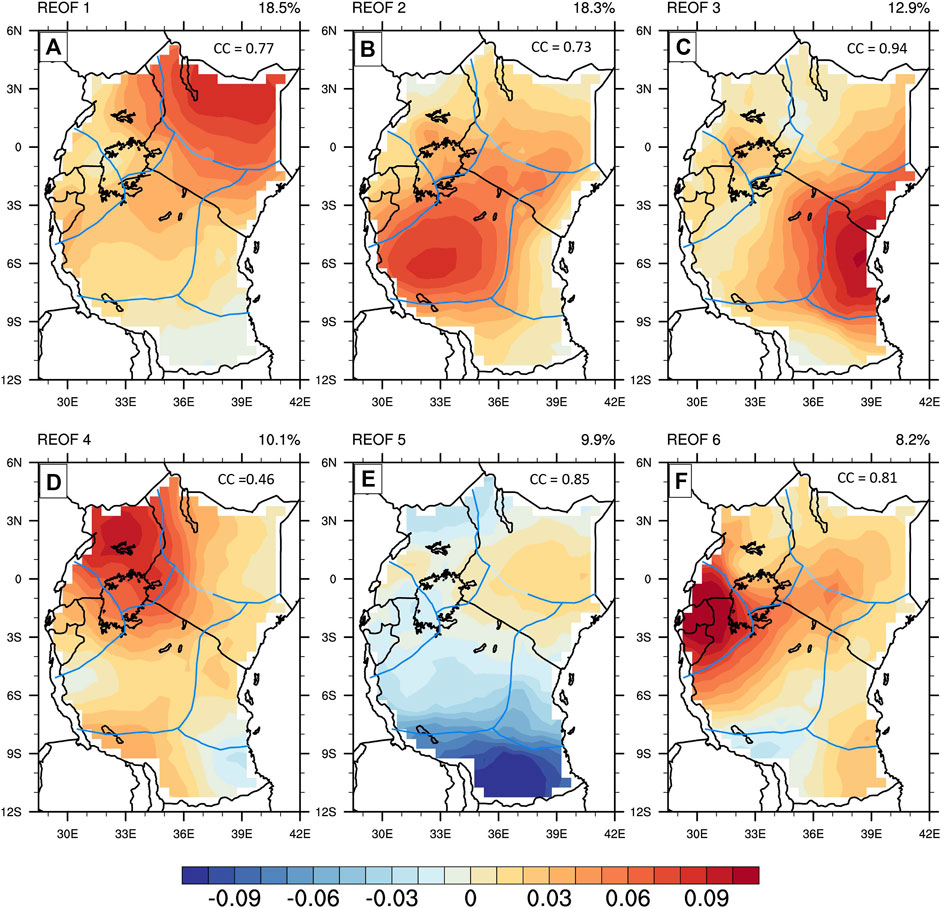
FIGURE 2. Spatial patterns of the six leading Rotated Empirical Orthogonal Function (REOF) modes of SPEI3 over equatorial East Africa. (A) is the leading mode representing NK, (B) the second mode representing CR, (C) the third mode representing CS, (D) the fourth mode representing NU, (E) the fifth mode representing ST and (F) the sixth mode representing WS. The solid blue line indicates the boundary of sub-regions based on the spatial pattern of the leading REOFs. CC gives the temporal correlation coefficients between the rotated principal component and the corresponding averaged SPEI values over the sub-region.
For brevity, the zones were named as follows; Northern Kenya (NK; REOF1), Central Region (CR; REOF2), Coastal Strip (CS; REOF3), Northern Uganda (NU; REOF4), Southern Tanzania (ST; REOF5) and Western Sector (WS; REOF6). We further performed a Spearman correlation between the rotated principal component (RPC) for each dominant REOF mode and the averaged SPEI values corresponding to each region. The correlation coefficients were generally higher than 0.70, except for the NU Region, with a coefficient value of 0.46. The high correlation coefficients between any two corresponding regions imply that the demarcation is appropriate for studying regionally homogeneous drought characteristics.
3.2 Spatial pattern of drought characteristics
The estimated SPEI values were used to characterize drought based on frequency, intensity and duration for the analysis period. The spatial distribution of drought characteristics over EA is shown in Figure 3, with lower drought frequency (<20%) found over the region. More specifically, the frequency is relatively lower in the WS sub-region, with a value below 14%. Conversely, CR, NU, ST, and NK sub-regions have a relatively higher frequency (15–20%) of drought occurrence (Figure 3A). The frequency has a maximum magnitude of ∼20% in the CR region at the border of Kenya and Tanzania. On the other hand, Figure 3B reveals that drought in the MAM season lasts between 2.2 and 2.8 months. Drought rarely occurs in all months of the season as it coincides with the long rainfall season when the region receives its maximum rainfall. Higher drought duration occurs mostly in NU, with a large portion of the sub-region having an average duration of 2.7 months. Parts of the western CR and southern WS sub-regions also experience a high average drought duration of 2.6 months. The CS region shows the lowest drought frequency relative to the other sub-region, with the highest duration of approximately 2.2 months. Figure 3C shows that CR and NK sub-regions exhibit relatively lower drought intensity (∼1.44/month) than the rest of EEA, while the WS shows the largest intensity (1.6/month). Generally, the higher frequency and lower intensity of drought in the CR and NK sub-regions indicates that the zones experience more droughts that are less intense, probably due to the reduced rainfall received in the season. In contrast, the NU sub-region showed higher frequency that lasted a relatively longer duration hence the large drought intensity over the region during the MAM season.
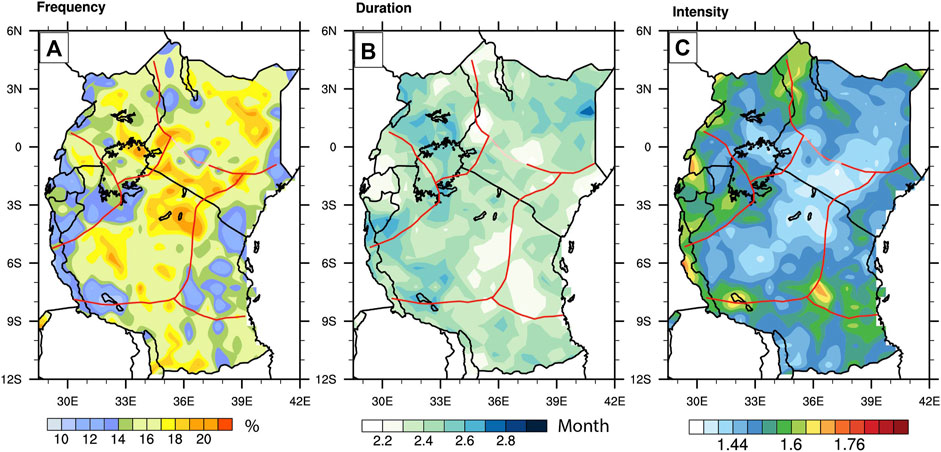
FIGURE 3. Spatial patterns of MAM seasonal mean (A) drought frequency (B) Drought duration and (C) drought intensity over Equatorial East Africa during the 1901–2020 period. The solid red line indicates the boundary for various sub-region.
3.3 Spatial distribution of drought trends
The spatial distributions of the drought trend for the entire study period are mapped in Figure 4. The linear trend of MAM SPEI3 majorly returned drying over EA. The trend is insignificant at a 95% confidence level in most parts of EA except southwestern Tanzania, northern Tanzania and parts of northern Kenya and Uganda, where the magnitude is about −0.008/yr (Figure 4B). The result shows that most regions had a mild to moderate increase in drought. Conversely, a small region north of Lake Victoria Basin and southeastern Tanzania shows a weak wetting trend of about 0.002 years−1. Lake Victoria is known to control the diurnal variation of rainfall in the surrounding area, making the basin wetter than the surrounding. Skliris et al. (2016) found that the Lake makes its basin wetter relative to other regions through the “amplification of the water cycle” that occurs at a slower rate due to global warming. Figure 4B reveals a mixture of an increasing and a decreasing trend in drought duration that is largely insignificant over EA. CS sub-region mainly shows an increase in drought duration with an annual trend reaching 0.008/yr for some areas that exhibit a significant trend. Similarly, the NK sub-region shows a positive trend in most parts but appears insignificant, with an annual trend value of about 0.004/yr. Figure 4C shows that drought intensity also shows a combination of both downward and upward trends. The reduction in intensity is mainly located in northwestern Kenya (∼0.006/yr) and parts of western CR sub-regions (∼0.003/yr), where the trend is significant. The decreasing trend is mainly located in WS and western parts of NU sub-regions, where the trend is as high as 0.007/yr.
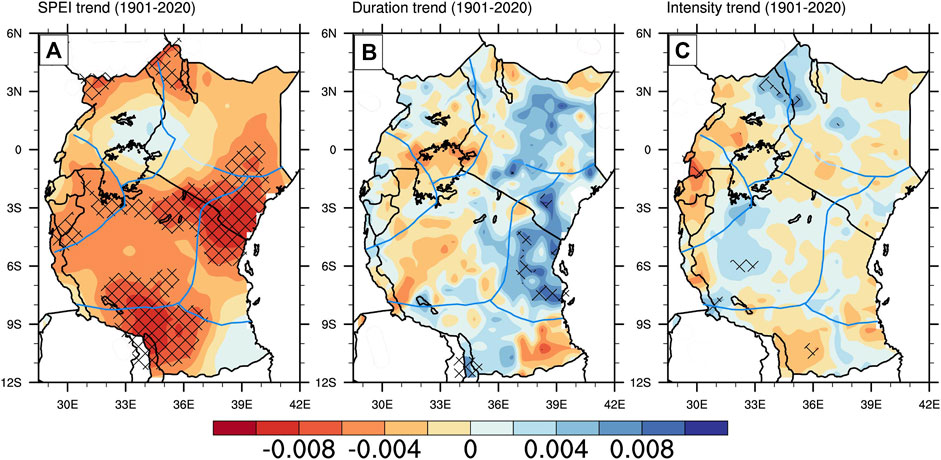
FIGURE 4. Spatial pattern of Mann-Kendall (MK) trend for (A) SPEI, (B) Drought duration and (C) Drought Intensity over equatorial East Africa during the 1901–2020 period. Cross-hatching shows regions where trends are significant at a 95% confidence level.
3.4 Temporal variation of drought indices over EA
The time series of SPEI in different sub-regions may help understand the temporal evolution of drought indices at a sub-domain scale and their regional differences. Figure 5 gives the temporal evolution of SPEI over the six sub-regions. The linear trend line and the local regression (LOESS) curves with 11 years are fitted to the SPEI time series to represent the linear and non-linear patterns of SPEI. From Figure 5, we can find that the SPEI3 drought index shows considerable inter-annual variation between wet and dry years. Meanwhile, the 11-year loess curve reveals that negative SPEI3 values have dominated the SPEI evolution since the 1980s in all sub-regions. This indicates that a large portion of EEA is gradually becoming drier in recent decades. The evolution of the SPEI drought index reveals the widespread drought events over EA in 1902, 1921, 1924/25, 1933, 1943, 1949, 1953, 1955, 1961, 1969, 1971/73, 1976, 1983/84, 1992/93, 2000/01, 2004/05, 2007/09, 2011/2012, 2014, and 2017. The drought events identified in the second half of the 20th century correspond well with the findings of previous studies (e.g., Nicholson, 2014; Agutu et al., 2017).
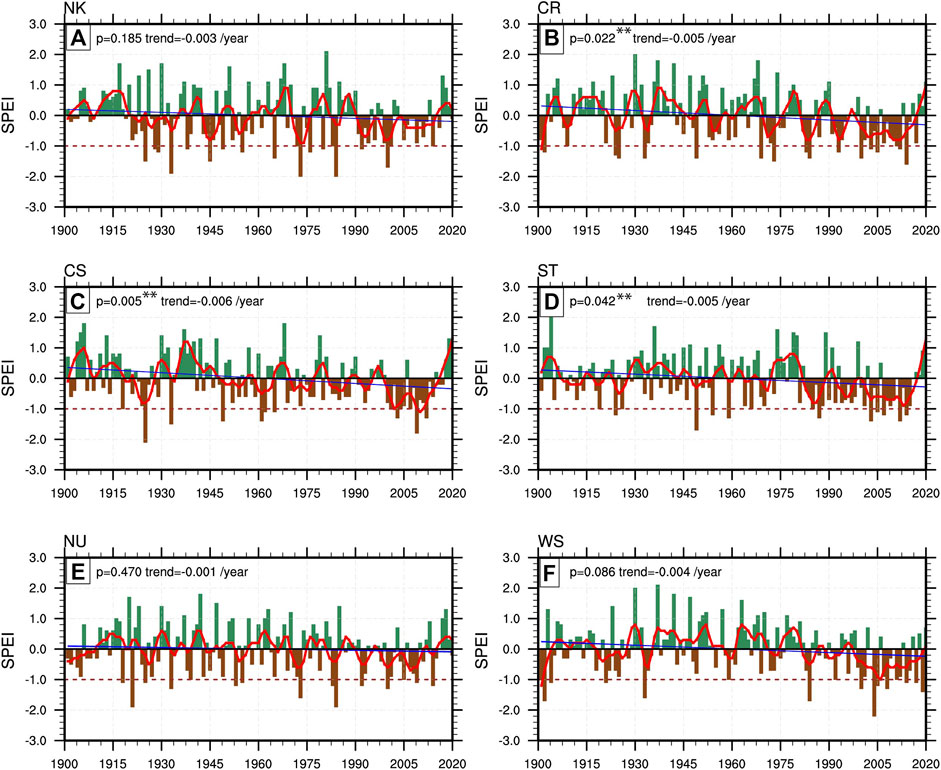
FIGURE 5. Temporal evolution of SPEI3 over six sub-regions of equatorial East Africa (A) NK, (B) CR, (C) CS, (D) ST, (E) NU and (F) WS. The red line shows an 11-year smoothed LOESS line, and the trend (blue) shows the rate of change of SPEI based on the Mann-Kendall trend test. p values with an asterisk (**) show statistically significant trends at a 95% confidence level.
Regarding the regional differences, even more, drought years were identified in different years. For instance, the NK sub-region had drought events in 1928/29, 1938,1945,1976,1980, and 1999 (Figure 5A); CR had droughts in 1909 and 1993 (Figure 5B); CS had droughts in 1961 and 1962 (Figure 5C). For ST, more drought can be found in 1919, 1954, 1957, 1964, 1970, and 1988 (Figure 5D); for NU in 1905, 1939, 1943, and 1953 (Figure 5E) and WS in 1901, 1904, and 2020 (Figure 5F). Generally, many years identified as having sub-regional droughts had negative SPEI values in some of the sub-regions that did not satisfy our drought threshold. This indicates that while there would be a large-scale driver of drought in a particular year, each zone’s distinct interaction with the local physical mechanism may suppress or enhance the dry condition. The time evolution of SPEI shows a weak negative trend in all the sub-regions. The trend is significant in CR (0.005/yr.), CS (0.006/yr.), and ST (0.005/yr.) and insignificant in NK (0.003/yr.), NU (0.001/yr.) and WS (0.004/yr.).
3.5 Temporal variation of the drought area
The areal drought extent was computed as a ratio of grid points with SPEI values less than −1 to the total number of all the grid points in that sub-region. Figure 6 shows the time series of percentage drought areas for the six sub-regions of EEA, we can find that the area affected by drought fluctuated significantly year by year, with magnitude ranging between 0% and 95% for the six sub-regions during the study period. Meanwhile, increasing trend of drought affected areas can also be found for all six sub-regions.
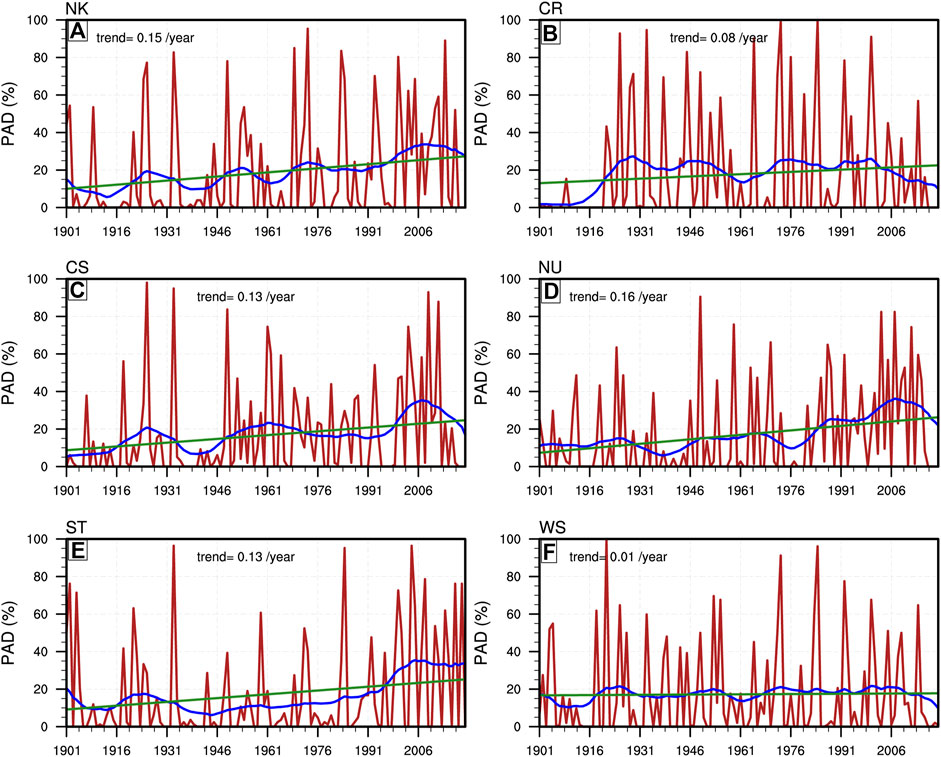
FIGURE 6. Temporal Evolution of percentage area under drought (PAD) for (A) NK, (B) CR, (C) CS, (D) ST, (E) NU and (F) WS sub-regions of the equatorial East Africa. The blue line denotes the reconstructed area under drought using the leading SSA principal component, while the black curve is the trend in the percentage drought area.
The variability of the drought area suggests that the positive linear trend observed may not be monotonous during the entire study period. Moreover, the high percentages of drought areas experienced in the later stages of the study period are likely to affect changes in the slope of the linear fitting. Consequently, we performed a non-linear trend analysis using singular value decomposition (SSA) for each sub-region separately. We chose a window frame of 11 years and reconstructed the time series using the dominant mode to represent the time evolution of the series better. Figure 6 reveals a gradual rise in the area under drought for NK, CS, ST, and NU sub-regions, while the CR and WS show a flat curve, with relatively smaller increasing trends.
The percentage drought areas can further be categorized into four classes, i.e., moderate, severe and extreme drought area. For each category, the percentage area is obtained by comparing the total number of grids under that specific category to the total number of grids in each year. The result revealed that the total increase of percentage drought area is dominated by an increase in the area under moderate and severe droughts, rather than that under extreme drought (Supplementary Figure S2).
In most regions with larger increasing trend of percentage drought area extent, large spatial extension of drought can be also found after the 1980s. Previous study suggested that the decadal variation of rainfall anomalies in East Africa could be linked to the Pacific decadal oscillation (PDO; Bahaga et al., 2018). To understand the potential linkage between drought variation in EEA and PDO, the time series of the PDO index and 11-year running mean SPEI3 drought index over EEA region during 1900–2020 is presented (Supplementary Figure S3). It is found that the correlation between PDO index and SPEI drought index is weak during the whole study period, with temporal correlation coefficient of only 0.17. However, the correlation increase to around 0.88 after 1980. These suggest that the PDO signal can enhance the drought extension after 1980s, but this relationship is not significant over the whole time period.
3.6 Contribution of PET and rainfall to the drought
Based on the SPEI definition, the driving factors considered were rainfall and PET and, thus, their contribution to the total drought area. However, the influence of PET and rainfall on SPEI depend on their independence from one another (Cook et al., 2014). To quantify the contribution of rainfall and PET on SPEI-based drought changes, we adopted the detrending method described by Hamlet and Lettenmaier (2007), which references the SPEI by incorporating changes in either variable. To isolate the impact of rainfall, we calculated the SPEI index using the original data that retained the transient changes in rainfall and detrended PET and named it SPEI-PRE. Similarly, to isolate the impact of PET, SPEI was calculated using detrended rainfall and the original values of PET and referred result as SPEI-PET.
As shown in Figure 9, the combined effects of rainfall and PET on drought either reinforced the area under drought (mid-20th century) or acted in opposition (beginning and end of the 20th century) to mitigate the effect of each other for most regions in EEA. Additionally. Figure 7 also reveals that in the first half of the 20th century, the percentage of drought area computed using detrended rainfall (PET) was higher (lower) than the observed conditions in all six regions. Consequently, the findings suggest that lower PET values reduced drought intensity. However, the result reverses in the post-1975 period, where the increase in PET had a positive effect on drought, indicated by the rise in drought area calculated using varPre. Therefore, the apparent increase in areal drought extent in the post-1980s may be attributed to the high evaporative demands that exert greater stress on an already declining rainfall, thus exacerbating the drought severity. The impact of PET was pronounced in CR, NK, WS, and NU regions (Figure 7).
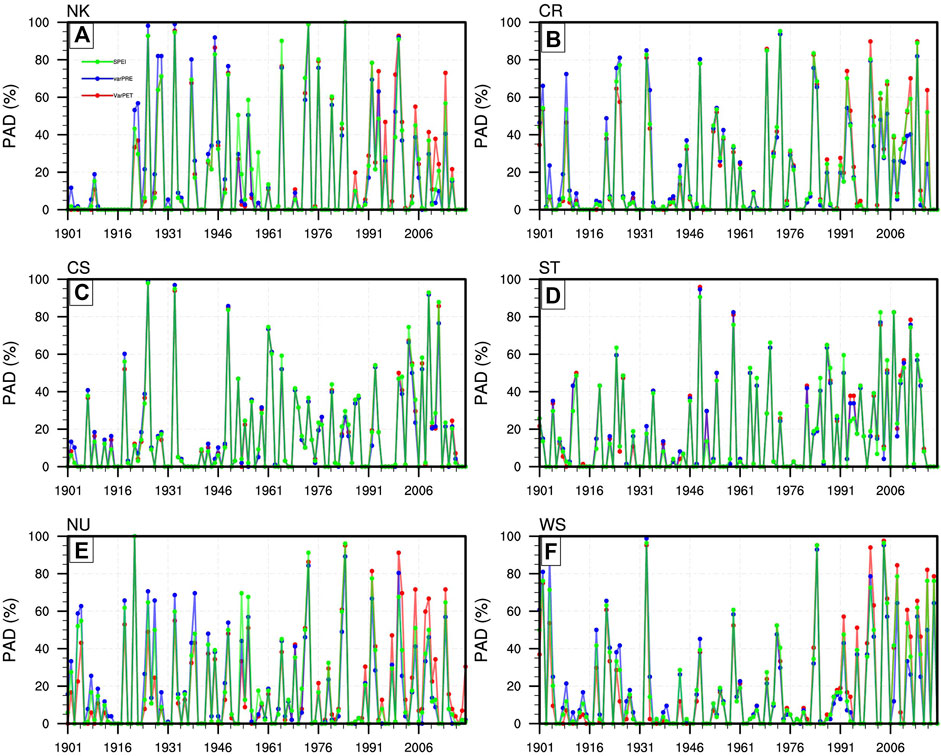
FIGURE 7. Temporal evolution of the percentage area under drought conditions computed for (A) NK, (B) CR, (C) CS, (D) ST, (E) NU and (F) WS sub-regions of Equatorial East Africa. The green time series represent the original SPEI, blue computed by varying rainfall and red computed by varying PET.
To explore the impact of PET on areal drought extent further, we compared the area under drought computed using SPEI to that SPI index (Supplementary Figure S4). The result shows divergent evolution of the percentage of land area affected by drought defined by the two indices. Furthermore, the result indicates that since the 1950s, the SPEI index has progressively identified more drought extent, thus pointing to the role of PET in the increase of drought coverage in all the sub-regions. Therefore, the apparent growth in drought areal extent in the post-1980s may be attributed to the high evaporative demands that exerted significant stress on an already declining rainfall, thus exacerbating the drought severity.
3.7 Variability of spring drought and its relationship with climate indices
REOF helps identify drought variability patterns but fails to provide information on the periodicities of the observed variabilities. Consequently, we apply the wavelet analysis to isolate dominant periodicity in the drought records and identify the coherence between drought and teleconnection indices. Figure 8 shows the result of the wavelet power spectrum of spatially averaged SPEI3 over the six sub-regions. The thick black line encloses values that have passed the red noise test at a 95% confidence level as determined by the Monte Carlo process (Jevrejeva et al., 2003). However, the Cone of Influence (COI) gives the region potentially influenced by the edge effect of data during wavelet transformation, and the area inside it provides an accurate time-frequency representation of the data. In contrast, the area outside it suffers from edge effects, thus unreliable.
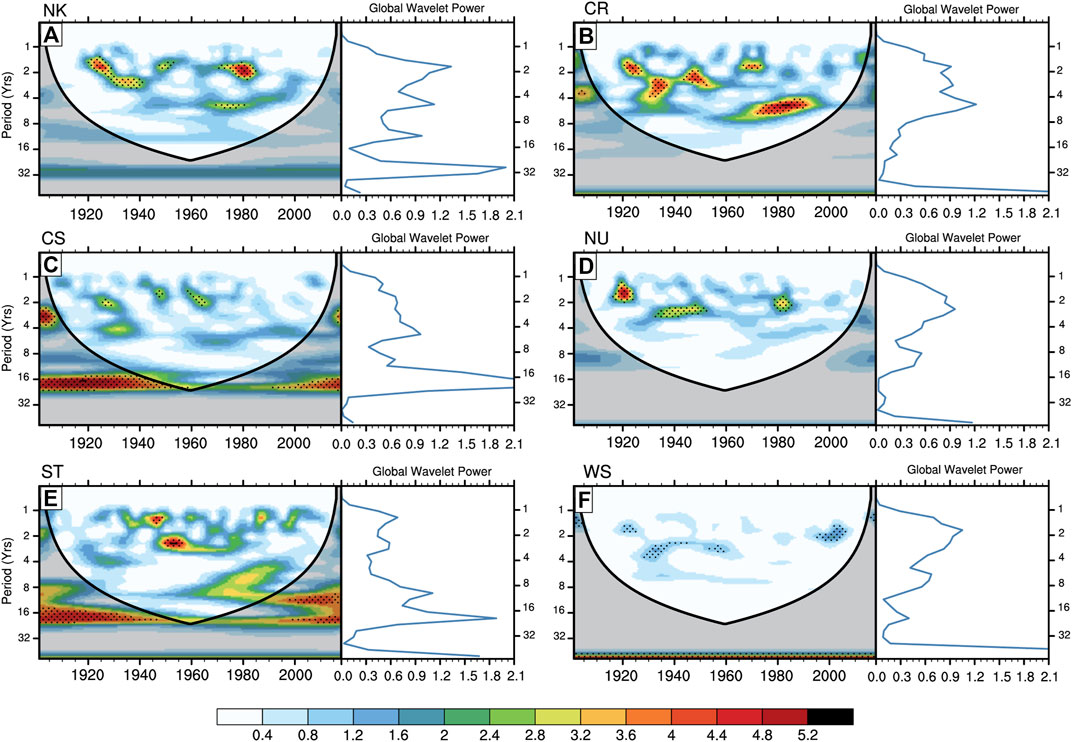
FIGURE 8. Wavelet power spectra of averaged SPEI time series over (A) NK, (B) CR, (C) CS, (D) ST, (E) NU and (F) WS sub-regions of equatorial East Africa. The solid dark contour denotes the 95% confidence level against the red noise. The cone of influence (COI) is shown as a semi-circle with a dark shade.
For the NK sub-region (Figure 8A), a significant power region exists in the 3 years band in the 1920s, increasing to a periodicity of 6 years in the 1940s before decreasing and decaying by 1955. In addition, there is a strong amplitude between the 1970s and 1985 in the 4 years band and a weak amplitude in the 8 years band between 1940 and 2000s. Figure 8B shows that for the CR sub-region, significant power regions are distributed in the 3–6 years band between 1920 and 1950 and a 9–14 years band between the 1960s and 1990s. Figure 8C shows intermittent wave spectra between 1901 and 1980 in the CS sub-region. A weak 8–12 years band exists between 1960 and 2010, as well as a strong band outside the cone of influence in the 30–48 years band. Figure 8D shows the local wavelet spectra in the 2–7 years band for the NU sub-region. The result appears weak throughout the study period except in 1920, 1930–1950, and 1980–1985. For the ST sub-region, the local wavelet spectra are in the 2–6 years band and 8–30 years band between 1950 and 2000 (Figure 8E). The inter-annual periodicity decreases from the 6 years to 2 years band from the 1980s. The sub-region also has a significant wavelet power in the 30–48 years band outside the cone of influence. In contrast, Figure 8F shows that WS has the weakest periodicity of all the sub-regions throughout the study period, with a reduced level of activities in pre-1920 and post-2000. In general, the regular periodicity is relatively stable at 2–6 years, indicating a large inter-annual variability within the period 1920–1980, while a decadal (8–16 years) variability also exists in some sub-regions. This suggests that inter-annual periodicities (<6years) dominate drought variability across EA. Overall, CR, CS, and ST sub-regions revealed the strongest interannual variations with maximum yellow regions.
Over EEA region, the dominant inter-annual (2–6 years) oscillations observed in the periodicity are mainly modulated by the El-Niño southern oscillation (ENSO; Ogallo, 1989; Kiladis and Diaz, 1989; Nicholson and Kim, 1997; Indeje et al., 2000). Consequently, we explore the interdependency between SPEI3 and the Niño3.4 index using cross-wavelet transformations. In case of any association between the two indices, a slowly varying phase lag is expected, and the phenomenon would be phase-locked, i.e., the phase arrows point only in one direction for a given wavelength (Grinsted et al., 2004). The use of arrows expresses the relationship between the two factors. The arrows pointing east reflect the in-phase relationship, whereas the arrow pointing west indicates an out-of-phase relationship. Conversely, arrows pointing upward (downward) indicate drought lag (lead) the index by a quarter cycle and reveals a non-linear relationship. Higher wavelength transforms coefficients correspond to a stronger correlation between drought and the Niño3.4 index.
Figure 9 shows the result of cross wavelet transformation between Niño3.4 and SPEI with high wavelet coherence larger than 0.6 shown with arrows. As shown in Figure 9A, NK showed high energies between SPEI and Niño3.4 in the 8–12 years frequency band in 1920–1960 years; and 4–6 years in the 1930s. The observed coherence between Niño3.4 and SPEI was in-phase during the periods as arrows points to the east. However, from 1970 to 1990, the two indices were out of phase within the 3–5 years period band. Nevertheless, the coherence in the later period failed the significance test. In the CR sub-region, a significant correlation between the indices appeared intermittently from the 1920s to 1990s in the 2–6 years band (Figure 9B). In the beginning, the two indices were in-phase, followed by Niño3.4 leading SPEI and later an antiphase relationship. Figure 9C shows that the CS sub-region exhibited a statistically significant relationship between SPEI and Niño3.4 between 1940 and 1970; however, the former index led the latter by about 3–4 months. The anti-phase association infers no or weak influence on drought by the ENSO. Another high power appears in the 16–24 years band where the relationship is in-phase. NU sub-region shows a scattered high coherence between the two indices within a 2–6 years band with in-phase coherence between 1920–1940 and Niño3.4 leading SPEI by 3–4 months in the 1950s and 1980s (Figure 9D). Figure 9E reveals that SPEI were out of phase with Niño3.4 in the 1920s over the ST sub-region with high energies lasting 2–6 years. Another statistically significant high power is evident in the 1970s and 1980s, where SPEI lags Niño3.4 by 3–4 months lasting between 9 and 15 years. Over the WS sub-region, significant high power was concentrated in the 2–6 years band and was in-phase between 1920–1940, while the variability of SPEI lagged that of Niño3.4 in 1960 (Figure 9F).
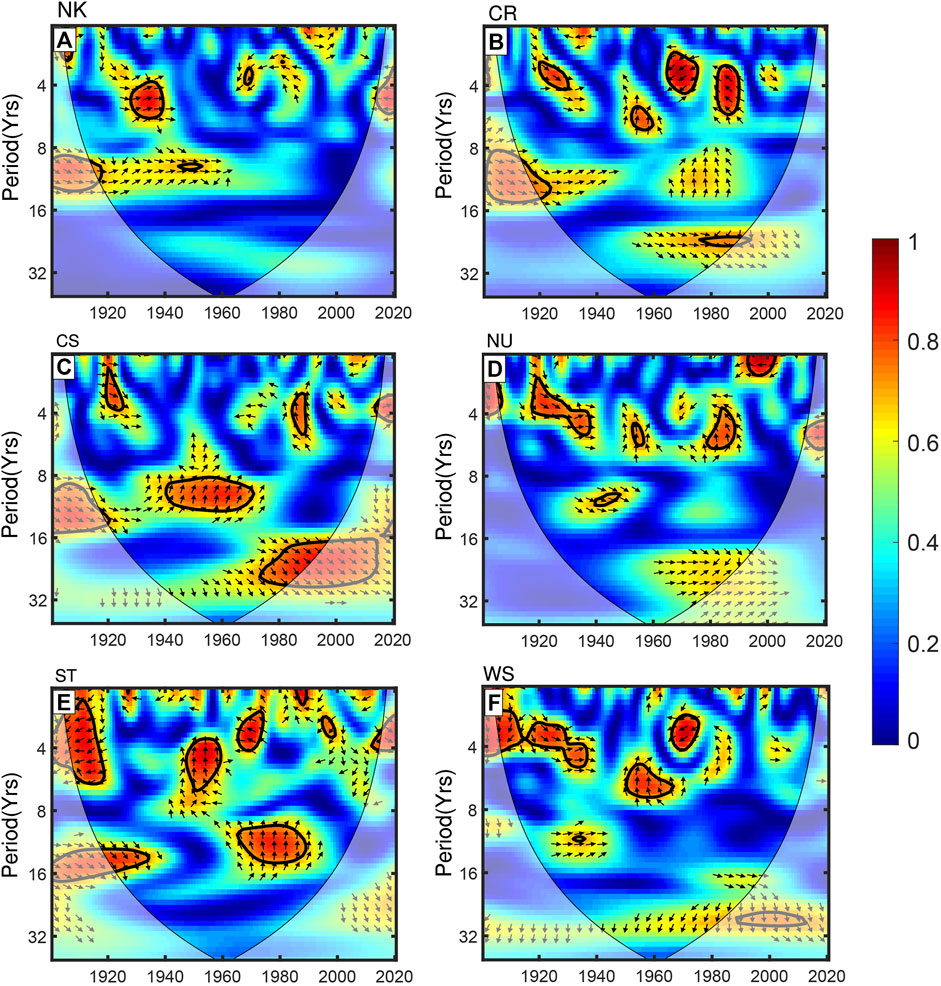
FIGURE 9. Squared wavelet coherence between the spatially averaged SPEI for (A) NK, (B) CR, (C) CS, (D) ST, (E) NU and (F) WS sub-regions and MAM Niño3.4. The colour increment from blue to red denotes the increasing coherency between the two indices. Phase arrows pointing right indicate signals are in phase, whereas left-pointing arrows indicate an antiphase relationship. Arrows pointing upward (downward) shows lead (lag) relationships between the two signals. The black contour designates the 95% confidence level against red noise, and the cone of influence (COI) is shown as a black semi-circle with a lighter shade.
In general, the 2–6 years oscillation is more robust, suggesting a strong inter-annual coherence between drought and ENSO, and this is consistent with findings by previous studies (Rodhe and Virji, 1976; Nicholson and Entekhabi, 1986). It is suggested that ENSO can produce anomalous diabatic heating/cooling over the western Pacific Ocean, creating a dynamically forced anomalous ascent/descent in the region, thus modifying the walker-type zonal circulation in the equatorial Indian Ocean (Goddard and Graham 1999; Mutai and Ward, 2000). Pohl and Camberlin (2011) also reported that the interannual variability of rainfall in all season except the boreal summer over EEA are strongly controlled by zonal wind shear between 850 mb and 150 mb level over the equatorial Indian Ocean, which was closely correlated to ENSO in all seasons.
4 Discussion and conclusion
The current study gives a simple but complete picture of meteorological drought characteristics over EEA during the MAM season based on SPEI3 using a long-term CRU dataset. MAM was chosen because it corresponds to the primary planting season for major food and because the season is the best candidate for investigating the observed rainfall decline’s impact on drought characteristics. SPEI index is relatively easier to characterize but provides subtle information on drought behavior vital to drought mitigation and water resource management. The Meteorological drought discussed herein is the precursor for other types of drought. Therefore, the knowledge of its temporal variability may reveal the susceptibility of an area to different drought types. The evolution of SPEI during the period of study points toward an increase in spatial coverage of drought areal extent. Most of this increase was observed in moderate and severe drought, while extreme drought remained stable during the observation period. The result of REOF identified six distinct spatial patterns that partly resemble the MAM daily rainfall homogeneous sub-regions identified by Indeje et al. (2000). The observed variation may be attributed to the SPEI calculation, which uses PET that is influenced by other climatic factors. The sub-regions identified may be helpful in regional drought risk assessment and management. SPEI3 used was able to capture the major drought events documented over EEA. For the study period, the notable droughts occurred in 1902, 1921, 1924/25, 1933, 1943, 1949, 1953, 1955, 1961, 1969, 1971/73, 1976, 1983/84, 1992/93, 2000/01, 2004/05, 2007/09, 2011/2012, 2014, and 2017.
Although there is no apparent pattern in the occurrence of these events, the first 2 decades at the beginning of the 20th century are marked by a persistent period of positive SPEI values. The opposite has been true from the late 20th century to recent decades, signaling the increase in drought events in the region. The recent increase in drought has been linked to warming in the western Pacific Ocean that is associated with the cold PDO phase (Williams and Funk, 2011; Funk et al., 2014).
The warming extends the warm pool into the eastern Indian Ocean, creating an anticyclonic flow that disrupts the moisture flow to EA by enhancing subsidence over EEA. A similar decline in rainfall has also been reported in Africa’s monsoon region (Han et al., 2019). Non-etheless, Bahaga et al. (2018) found that the Greater Horn of Africa (a larger part of eastern Africa) receives above (below) normal rain during warm (cold) PDO phases. However, the correlation coefficient between PDO and drought variation is pretty weak, when only Equatorial East Africa region is considered. Consequently, this points to a complicated relationship between decadal pacific variability and drought over Equatorial East Africa in MAM season, and care should be taken when analyzing such a relationship.
EEA region generally experienced increased drought frequency between 1981 and 2020, with the drought-afflicted area remaining at an average above 30% for most of the sub-regions. Such an increase in areal extent increases the community’s vulnerability through reduced portable water and food production. Additionally, the strength and direction of the SPEI trend seemed to change depending on the period chosen. However, the trend magnitude weakened considerably when the entire study period was considered. We further analyzed how changes in rainfall and PET influence SPEI. The contribution of rainfall was dominant over the contribution of PET on SPEI variation; however, the latter has contributed positively to the increase in drought areas in the post-1980 era. The implicit assumption from the above result is that factors that drive droughts, such as temperature, have changed over the decades. Indeed, the comparison between the percentage of land affected by drought using SPI and SPEI indices showed a progressive divergent evolution. The difference between the two indices shows the percentage of land area affected by drought should the phenomenon be defined using the water balance rather than rainfall alone. The result suggests that before the 1970s, changes in drought were primarily related to the rainfall variability over the region. Besides the decline in rainfall during the MAM season, evapotranspiration has exacerbated the spread of drought. These findings are coherent with rainfall and temperature evolution over EEA, where studies have reported general temperature increases and reductions in rainfall (Ongoma and Chen, 2017). While the SPEI value shows a decreasing trend, it lacks clear evidence of substantial significant changes. This result agrees with the findings of Mpelasoka et al. (2018), who reported a lack of significant changes in the long-term probability of the annual occurrence of drought over the larger greater horn of Africa.
The result of spectral analysis of the cyclic behavior of MAM drought reveals that 2–6 years cycles are frequent in almost all sub-regions suggesting that inter-annual periodicities (<6 years) dominate drought variability across EA. The periodicity nature of drought signifies good news for policymakers as this implies ease of predicting the drought phenomenon. Analyses of drought using wavelets show a significant relationship with Niño3.4 at a periodicity of 2–6 years that occurs intermittently throughout the study period. The strength of influence of Niño3.4 varies from one period to another and from one sub-region to another. Onyutha and Willems (2017) reported that although the large-scale mechanism responsible for drought may be the same, its characteristics may be influenced by the local land-atmosphere feedback response determined by topography and the presence of water bodies (Funk et al., 2015; Wainwright et al., 2019).
Data availability statement
All the CRU TS 4.05 data used in this study are available at https://crudata.uea.ac.uk/cru/data/hrg/index.htm#current. Nino 3.4 and PDO indices are available in NOAA Climate Prediction Center website at https://psl.noaa.gov/gcos_wgsp/Timeseries/
Author contributions
ZL: conceptualized, supervised, reviewed and edited the manuscript while the AO curated the data, did formal analysis and drafted the original manuscript. Both authors have read and agreed to the published version of the manuscript.
Funding
This study is jointly supported by the Chinese Academy of Sciences Strategic Priority Research Program (Grant No. XDA19030403), the National Natural Science Foundation of China (Grant Nos. 42075166 and 41975119), and NSFC Research Fund for International Young Scientists (Grant No. 42150410394).
Acknowledgments
The authors are grateful to the University of East Anglia Climate Research Program for the CRU dataset and NOAA Climate Prediction Center for the Nino3.4 and PDO data used. OA acknowledges the support of the CAS-TWAS President Fellowship and the CAS-TWAS Center of Excellence for Climate and Environment Sciences for the infrastructure to conduct the study. We also thank the anonymous reviewers for their helpful comments and suggestions.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.1064940/full#supplementary-material
SUPPLEMENTARY FIGURE S1 | Major planting season for various food crops in EA. Adopted from FAO GIEWS - Global Information and Early Warning System (Accessed 28 March 2022).
SUPPLEMENTARY FIGURE S2 | Evolution of percentage area under drought for NK (A–D), different sub-regions for moderate drought (left column), severe drought (mid column) and extreme (right column). Figures CR (E–H), CS (I–L), ST (M–P), NU (Q–T) and WS (U–X) The blue denotes the reconstructed area under drought using the leading SSA principal component, while the black curve is the trend in the percentage drought area.
SUPPLEMENTARY FIGURE S3 | Time series of PDO (red) and Equatorial East Africa spatially averaged SPEI (green) for MAM. An 11-year moving average has was applied to both series. R denotes the correlation coefficient between the PDO and SPEI time series.
SUPPLEMENTARY FIGURE S4 | Difference in percent area under drought calculated as the difference between MAM SPEI and SPI for (A) NK, (B) CR, (C) CS, (D) ST, (E) NU and (F) WS sub-regions of the equatorial East Africa.
References
Abdourahaman, E. Z. S., and Acar, R. (2018). Analysis of meteorological drought variability in Niger and its connections with climate indices. Hydrol. Sci. J., v. 63, n. 8, p. 1203–1218, doi:10.1080/02626667.2018.1489542
AghaKouchak, A. (2015). A multivariate approach for persistence-based drought prediction: Application to the 2010–2011 East Africa drought. J. Hydrol. X. 526, 127–135. doi:10.1016/j.jhydrol.2014.09.063
Agutu, N., Awange, J., Zerihun, A., Ndehedehe, C., Kuhn, M., and Fukuda, Y. (2017). Assessing multi-satellite remote sensing, reanalysis, and land surface models' products in characterizing agricultural drought in East Africa. Remote Sens. Environ. 194 (0), 287–302. doi:10.1016/j.rse.2017.03.041
Andreadis, K. M., Clark, E. A., Wood, A. W., Hamlet, A. F., and Lettenmaier, D. P. (2005). Twentieth-century drought in the conterminous United States. J. Hydrometeorol. 6 (6), 985–1001. doi:10.1175/jhm450.1
Anyah, R. O., Semazzi, F. H., and Xie, L. (2006). Simulated physical mechanisms associated with climate variability over Lake Victoria basin in East Africa. Mon. Weather Rev. 134 (12), 3588–3609. doi:10.1175/mwr3266.1
Ayugi, B., Tan, G., Gnitou, G. T., Ojara, M., and Ongoma, V. (2020). Historical evaluations and simulations of precipitation over East Africa from Rossby centre regional climate model. Atmos. Res. 232, 104705. doi:10.1016/j.atmosres.2019.104705
Bahaga, T. K., Fink, A. H., and Knippertz, P. (2018). Revisiting inter-annual to decadal teleconnections influencing seasonal rainfall in the Greater Horn of Africa during the 20th century. Int. J. Climatol. 39, 2765–2785. doi:10.1002/joc.5986
Beguería, S., Vicente-Serrano, S. M., Reig, F., and Latorre, B. (2013). Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 34 (10), 3001–3023. doi:10.1002/joc.3887
Bhuiyan, C., Flügel, W. A., and Singh, R. P. (2009). Modelling of ground water recharge-potential in the hard-rock aravalli terrain, India: A GIS approach. Environ. Earth Sci. 59 (4), 929–938. doi:10.1007/s12665-009-0087-4
Camberlin, P., and Philippon, N. (2002). The East african march–may rainy season: Associated atmospheric dynamics and predictability over the 1968–97 period. J. Clim. 15, 1002–1019. doi:10.1175/1520-0442(2002)015<1002:teammr>2.0.co;2
Casagrande, E., Mueller, B., Miralles, G., Entekhab, i. D., and Molini, A. (2015). Wavelet correlations to reveal multiscale coupling in geophysical systems. J. Geophys. Res. Atmos. 120, 7555–7572. doi:10.1002/2015jd023265
Chakraborty, A., Nanjundiah, R. S., and Srinivasan, J. (2009). Impact of African orography and the Indian summer monsoon on the low-level Somali jet. Int. J. Climatol. 29 (7), 983–992. doi:10.1002/joc.1720
Cook, B. I., Miller, R. L., and Seager, R. (2009). “Amplification of the North American Dust Bowl drought through human-induced land degradation,” in Proceedings of the National Academy of Sciences. doi_10.1073.pnas.0810200106.New York, NY.
Cook, B. I., Seager, R., and Smerdon, J. E. (2014). The worst north American drought year of the last millennium: 1934. Geophys. Res. Lett. 41 (20), 7298–7305. doi:10.1002/2014GL061661
Cook, B. I., Smerdon, J. E., Seager, R., and Coats, S. (2015). Global warming and 21st century drying. Clim. Dyn. 43, 2607–2627. doi:10.1007/s00382-014-2075-y
Dai, A. (2013). Increasing drought under global warming in observations and models. Nat. Clim. Chang. 3, 52–58. doi:10.1038/nclimate1633
Funk, C., Hoell, A., Shukla, S., Bladé, I., Liebmann, B., Roberts, J. B., et al. (2014). Predicting East African spring droughts using Pacific and Indian Ocean sea surface temperature indices. Hydrol. Earth Syst. Sci. 18 (12), 4965–4978. doi:10.5194/hess-18-4965-2014
Funk, C., Nicholson, S. E., Landsfeld, M., Klotter, D., Peterson, P., and Harrison, L. (2015). The centennial trends Greater Horn of Africa precipitation dataset. Sci. Data 2, 150050. doi:10.1038/sdata.2015.50
Gao, F., Wang, Y., Chen, X., and Yang, W. (2020). Trend analysis of rainfall time series in Shanxi Province, Northern China (1957–2019). Water 12 (9), 2335. doi:10.3390/w12092335
Gebremeskel Haile, G., Tang, Q., Leng, G., Jia, G., Wang, J., Cai, D., et al. (2020). Long-term spatiotemporal variation of drought patterns over the Greater Horn of Africa. Sci. Total Environ. 704, 135299. doi:10.1016/J.SCITOTENV.2019.135299
Goddard, L., and Graham, N. E. (1999). Importance of the Indian Ocean for simulating rainfall anomalies over eastern and southern Africa. J. Geophys. Res. 104, 19099–19116. doi:10.1029/1999jd900326
Grinsted, A., Moore, J. C., and Jevrejeva, S. (2004). Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear process. geophys. 11, 561–566. doi:10.5194/npg-11-561-2004
Guttman, N. (1998). Comparing the palmer drought index and the standardized precipitation index. J. Am. Water Resour. Assoc. 34, 113–121. doi:10.1111/j.1752-1688.1998.tb05964.x
Hamlet, A. F., and Lettenmaier, D. P. (2007). Effects of 20th century warming and climate variability on flood risk in the Western US. Water Resour. Res. 43, W06427. doi:10.1029/2006WR005099
Han, Z., Su, T., Huang, B., Feng, T., Qu, S., and Feng, G. (2019). Changes in global monsoon precipitation and the related dynamic and thermodynamic mechanisms in recent decades. Int. J. Climatol. 39 (3), 1490–1503. doi:10.1002/joc.5896
Hannachi, A. (2007). Pattern hunting in climate: A new method for finding trends in gridded climate data. Int. J. Climatol. 27, 1–15. doi:10.1002/joc.1375
Harris, I., Jones, P. D., Osborn, T. J., and Lister, D. H. (2014). Updated high-resolution grids of monthly climatic observations –the CRU TS3.10 Dataset. Int. J. Climatol. 34, 623–642. doi:10.1002/joc.3711
Hastenrath, S., Polzin, D., and Mutai, C. (2005). Diagnosing the 2005 drought in Equatorial East Africa. J. Clim. 20, 4628–4637. doi:10.1175/jcli4238.1
Hastenrath, S., Polzin, D., and Mutai, C. (2010). Diagnosing the droughts and floods in Equatorial East Africa during boreal autumn 2005-08. J. Clim. 23, 813–817. doi:10.1175/2009JCLI3094.1
Iglesius, A., Yang, X. B., Epstein, P., Chivian, E., and Rosenzweig, C. (2001). Climate change and extreme weather events-implications for food production, plant diseases, and pests. Glob. Chang. Hum. Heal. 2, 90–104. doi:10.1023/A:1015086831467
Indeje, M., Semazzi, F. H. M., and Ogallo, L. J. (2000). ENSO signals in East African rainfall seasons. Int. J. Climatol. 20 (1), 19–46. doi:10.1002/(sici)1097-0088(200001)20:1<19::aid-joc449>3.0.co;2-0
Jevrejeva, S., Moore, J. C., and Grinsted, A. (2003). Influence of the Arctic oscillation and El Niño-Southern oscillation (ENSO) on ice conditions in the Baltic Sea: The wavelet approach. J. Geophys. Res. 108 (D21), 4677. doi:10.1029/2003JD003417
Lyon, B., and Dewitt, D. G. (2012). A recent and abrupt decline in the East African long rains. Geophys. Res. Lett. 39 (2), L02702. doi:10.1029/2011GL050337
Lyon, B. (2014). Seasonal drought in the greater horn of Africa and its recent increase during the march–may long rains. J. Clim. 27, 7953–7975. doi:10.1175/jcli-d-13-00459.1
Mann, H. B., Mbigi, D., Onyango, A. O., Mtewele, Z. F., Kiprotich, P., and Xiao, Z. (1945). Non-parametric tests against trend. Econometrica 13Coupled model intercomparison project phase 6 simulations of the spatial structure of rainfall variability over East Africa: Evaluation and projection. Int. J. Climatol. 1, 245–259. – 21. doi:10.1002/joc.7868
McKee, T. B., Doeskin, N. J., and Kleist, J. (1993). “The relationship of drought frequency and duration to time scales,” in Proceedings of the 8th Conference on Applied Climatology(Boston, MA: American Meteorological Society), 179–184.
Mogaka, H., Gichere, S., Davis, R., and Hirji, R. (2006). World Bank Working Paper No. 69. Washington, DC: World Bank (Accessed July 11, 2019).Climate variability and water resources degradation in Kenya: Improving water resources development and management
Mpelasoka, F., Awange, J. L., and Zerihun, A. (2018). Influence of coupled ocean–atmosphere phenomena on the Greater Horn of Africa droughts and their implications. Sci. Total Environ. 610–611, 691–702. doi:10.1016/j.scitotenv.2017.08.109
Mutai, C. C., and Ward, M. N. (2000). East African rainfall and the tropical circulation/convection on intraseasonal to interannual timescales. J. Clim. 13, 3915–3939. doi:10.1175/1520-0442(2000)013<3915:earatt>2.0.co;2
Nicholson, S. E. (2014). A detailed look at the recent drought situation in the Greater Horn of Africa. J. Arid. Environ. 103, 71–79. doi:10.1016/j.jaridenv.2013.12.003
Nicholson, S. E., and Entekhabi, D. (1986). The quasi-periodic behavior of rainfall variability in Africa and its relationship to the Southern Oscillation. Arch. Mater. Geoph. Biocl. A 34, 311–348. doi:10.1007/bf02257765
Nicholson, S. E., and Kim, J. (1997). The relationship of the el-niño-southern oscillation to african rainfall. Int. J. Climatol., 17, 117–135. doi:10.1002/(SICI)1097-0088
North, G., Bell, T., Cahalan, R., and Moeng, F. (1982). Sampling errors in the estimation of empirical orthogonal functions. Mon. Wea. Rev. 110, 699–706. doi:10.1175/1520-0493(1982)110<0699:seiteo>2.0.co;2
Ntale, H. K., and Gan, T. Y. (2003). Drought indices and their application to East Africa. Int. J. Climatol. 3, 1335–1357. doi:10.1002/joc.931
Ogallo, L. J. (1989). The spatial and temporal patterns of the East African seasonal rainfall derived from principal component analysis. Int. J. Climatol. 9, 145–167. doi:10.1002/joc.3370090204
Ongoma, V., and Chen, H. (2017). Temporal and spatial variability of temperature and precipitation over East Africa from 1951 to 2010. Meteorol. Atmos. Phys. 129 (2), 131–144. doi:10.1007/s00703-016-0462-0
Onyango, A. O., Xu, H. M., and Lin, Z. H. (2020). Diurnal cycle of rainfall over Lake Victoria Basin during the long-rain season based on TRMM satellite estimate. Int. J. Climatol., 40, 4622–4637, doi:10.1002/joc.6479
Onyutha, C., and Willems, P. (2017). Influence of spatial and temporal scales on statistical analyses of rainfall variability in the River Nile basin. Dyn. Atmos. Oceans 77, 26–42. doi:10.1016/j.dynatmoce.2016.10.008
Peagle, J., and Geisler, J. E. (1986). The effect of East African topography on flow driven by zonally symmetric forcing. J. Atmos. Sci. 43 (17), 1862–1872. doi:10.1175/1520-0469(1986)043<1862:teoeat>2.0.co;2
Pohl, B., and Camberlin, P. (2011). Intraseasonal and interannual zonal circulations over the equatorial Indian Ocean. Theor. Appl. Climatol. 104, 175–191. doi:10.1007/s00704-010-0336-1
Richman, M. B. (1986). Rotation of principal components. J. Climatol. 6, 293–335. doi:10.1002/joc.3370060305
Rodhe, H., and Virji, H. (1976). Trends and periodicities in East African rainfall data. Mon. Weather Rev. 104, 307–315. doi:10.1175/1520-0493
Schreck, C. J., and Semazzi, F. H. M. (2004). Variability of the recent climate of eastern Africa. Int. J. Climatol. 24, 681–701. doi:10.1002/joc.1019
Schwalm, C., Anderegg, W., Michalak, A., Fisher, J. B., Biondi, F., Koch, G., et al. (2017). Global patterns of drought recovery. Nature 548, 202–205. doi:10.1038/nature23021
Sheffield, J., Wood, E. F., and Roderick, M. L. (2012). Little change in global drought over the past 60 years. Nature 491, 435–438. doi:10.1038/nature11575
Shilenje, Z., and Ongoma, V. (2016). The effectiveness of agrometeorological information in the realization of Kenya's vision 2030; lessons learned from China. Ital. J. Agrometeorol. 21 (1), 67–72.
Skliris, N., Zika, J. D., Nurser, G., Josey, S. A., and Marsh, R. (2016). Global water cycle amplifying at less than the Clausius-Clapeyron rate. Sci. Rep. 6, 38752. doi:10.1038/srep38752
Tierney, J. E., Ummenhofer, C. C., and De-Menocal, P. B. (2015). Past and future rainfall in the horn of Africa. Sci. Adv. 1 (9), e1500682. doi:10.1126/sciadv.1500682
Torrence, C., and Compo, G. P. (1998). A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78. doi:10.1175/1520-0477(1998)079<0061:apgtwa>2.0.co;2
Uhe, P., Philip, S., Kew, S., Shah, K., Kimutai, J., Mwangi, E., et al. (2017). Attributing drivers of the 2016 Kenyan drought. Int. J. Climatol. 38 (51), e554–e568. doi:10.1002/joc.5389
Undp/, U. N. S. O. (1997). New York: UNDP Office to Combat Desertification and Drought UNSO.Aridity zones and dryland populations: An assessment of population levels in the world's drylands with particular reference to Africa
Vicente-Serrano, S. M., Beguería, S., and López-Moreno, J. I. (2010). A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 23 (7), 1696–1718. doi:10.1175/2009jcli2909.1
Wainwright, C. M., Marsham, J. H., Keane, R. J., Rowell, D. P., Finney, D. L., Black, E., et al. (2019). Eastern African Paradox' rainfall decline due to shorter not less intense Long Rains. npj Clim. Atmos. Sci. 2, 34. doi:10.1038/s41612-019-0091-7
Wells, N., Goddard, S., and Hayes, M. J. (2004). A self-calibrating palmer drought severity index. J. Clim. 17, 2335–2351. doi:10.1175/1520-0442(2004)017<2335:aspdsi>2.0.co;2
Winslow, M. D., Vogt, J. V., Thomas, R. J., Sommer, S., Martius, C., and Akhtar-Schuster, M. (2011). Science for improving the monitoring and assessment of dryland degradation. Land Degrad. Dev. 22 (2), 145–149. doi:10.1002/ldr.1044
Yang, W., Seager, R., Cane, M. A., and Lyon, B. (2014). The East African long rains in observations and models. J. Clim. 27, 7185–7202. doi:10.1175/JCLI-D-13-00447.1
Keywords: drought trend, drought variability, SPEI, equatorial East Africa, rotated empirical orthogonal function (REOF)
Citation: Omondi OA and Lin Z (2023) Trend and spatial-temporal variation of drought characteristics over equatorial East Africa during the last 120 years. Front. Earth Sci. 10:1064940. doi: 10.3389/feart.2022.1064940
Received: 08 October 2022; Accepted: 25 November 2022;
Published: 11 January 2023.
Edited by:
Bo Sun, Nanjing University of Information Science and Technology, ChinaReviewed by:
Anning Huang, Nanjing University, ChinaGang Zeng, Nanjing University of Information Science and Technology, China
Copyright © 2023 Omondi and Lin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhaohui Lin, bHpoQG1haWwuaWFwLmFjLmNu
 Onyango Augustine Omondi
Onyango Augustine Omondi Zhaohui Lin
Zhaohui Lin