Assessing the apparent viscosity of decane-water emulsion in underground porous media based on the lattice Boltzmann method

The groundwater system is one of the most important subsurface resources on Earth, which offers many important services to humankind, such as irrigated agriculture, household use, and manufacturing. However, the safety of groundwater resources is seriously threatened by contamination from human activities. The emulsion has been proposed as a potential solution for the removal of contaminants due to its high apparent viscosity. Here we reveal the pore-scale mechanism for the viscosity increase in decane-water emulsions by lattice Boltzmann simulations. We assess the effect of phase saturation, interfacial tension, and contact angle, on the apparent viscosity of decane-water emulsions in porous media. Our results show that the apparent viscosity of the emulsion reaches its maximum value when the decane saturation is around 20%. We also find that this maximum viscosity increases with interfacial tension, and it is larger in decane-wet or water-wet systems than it is in intermedia-wet media.

Introduction

As a crucial component in the hydrosphere, groundwater plays an important role in water balance, widely affecting many water systems such as urban domestic water (Kuroda, K., and Fukushi, 2008), industrial water (Foster, and Chilton, 2003), agricultural irrigation water (Garduño, and Foster, S., 2010). However, groundwater pollution caused by contaminants migration (Postigo, et al., 2018), percolation of liquid sprayed over land (Beckett, 1993), or inter-aquifer leakage (Nyer, 1992), has become a serious threat to the safety of groundwater systems. Some of the contaminants may be trapped in small pores and become a long-term source of groundwater pollution (Illangasekare, T. H., 1998). As the pollution process is slow and the subsurface geological structure is complex, groundwater pollution is difficult to be treated (Foster, S., et al., 2002).

The foam/emulsion system has been proposed as one of the most promising ways to reduce groundwater pollution (Osei-Bonsu, et al., 2018). With a favorable mobility ratio due to its high apparent viscosity, the foam/emulsion system can suppress uneven displacements (Mauray, A., et al., 2020) and enhance displacement efficiency (Xie, C., et al., 2018a). As a result, the pollution trapped in small pores is more likely to be displaced by foam/emulsion (Jeong, S. W., and Corapcioglu, M. Y., 2003).

Many studies have focused on the viscosity of foam/emulsion systems. Theoretically, (Hirasaki and Lawson, 1985) established a mathematical model showing that the foam’s apparent viscosity grows proportionally with the bubble density and decreases with the velocity. (Yan, W., et al., 2006) developed a set of mathematical models for foam flow in uniform cracks, and the effect of gas flow rate on apparent viscosity was investigated. (Valko, P. and Economides, M. J., 1992) developed a constitutive equation for foamed polymer solutions, which showed that the apparent viscosity increases with the foam quality. These theoretical works are based on many idealized assumptions, which limits their practical applications. Experimentally, (Zhang, et al., 2012) measured the average apparent foam viscosity and found that it was significantly higher than the viscosity of gas or water. (Mauray, et al., 2020) studied foam flow in a porous medium, and found that the relationship between the apparent viscosity and the capillary number follows a decreasing power-law function. (Shojaei, et al., 2019) illustrated that the roughness of the fracture wall strongly increases the foam’s apparent viscosity and shear rate. These experiments have presented solid evidence for the foam’s high apparent viscosity, yet they are difficult to reveal its mechanisms at the pore scale. Numerically, (Omirbekov, S., et al., 2020) performed Darcy-scale simulations and showed the impact of foam quality on its apparent viscosity at a fixed flow rate. (Abbaszadeh, M., et al., 2014) constructed an empirical foam model in a commercial reservoir simulator, and successfully predicted the apparent foam viscosity compared with experimental data. (Sun, J., et al., 2021) simulated the two-phase flow of Newtonian oil and non-Newtonian foam in a straight channel by the Volume of Fluid (VOF) method, and they found an optimum oil/foam flow rate ratio for the best oil transportation.

The lattice Boltzmann method (LBM) has become one of the most powerful numerical tools for investigating the pore-scale mechanisms of many subsurface flow problems, due to its advantages in easy boundary treatment and efficient parallel computing (Lin, X., et al., 2021; Liu, H., et al., 2016; Guo. Y and Wang. M, 2015; Xie, C., et al., 2017; Chen, Y., et al., 2019; Xie, C., et al., 2020; Xie, C., et al., 2021; Xie, C., et al., 2022; Zhang, T. and Sun, S. 2019; Zhang, T., et al., 2020). Mobarak, M., et al. (2022) evaluated the permeability of different foam structures by lattice Boltzmann simulations. (Radhakrishnan, A., et al., 2022) investigated how the roughness of fractured carbonates affects the foam stability, and found that the foam’s apparent viscosity increases with the decrease in cracks of the rough surface. Although the aforementioned studies have investigated structure effects on the foam properties, the effects and pore-scale mechanisms of key fluid properties such as fluid saturation, phase distribution, interfacial tension, and contact angle on the apparent viscosity of foam/emulsion system remain to be studied.

In this paper, the flow of decane-water emulsion system in porous media is comprehensively investigated by a series of LBM simulations, with a special focus on the apparent viscosity. The numerical scheme is primarily verified against theoretical solutions. Then the effects of fluids’ saturation, interfacial tension, and contact angle on the apparent viscosity of decane-water emulsion system are discussed.

Methodology

Lattice Boltzmann method

In this work, the Rothman- Keller (RK) type LB model (Leclaire, S., et al., 2017; Xie et al., 2018b) is selected as the basic multiphase flow solver, and the D2Q9 model (Qian, Y.H., et al., 1992) is chosen to discrete the velocity space, which is defined as:

${\mathit{c}}_i=\left[c_{ix},c_{iy}\right]=\{\begin{array}{l}\left[\mathrm{0,0}\right],i=0\\ \left\{\mathit{cos}\left[\frac{\pi }{2}\left(i-1\right)\right],\mathit{sin}\left[\frac{\pi }{2}\left(i-1\right)\right]\right\}c,i=\mathrm{1,2,3,4}\\ \left\{\mathit{cos}\left[\frac{\pi }{4}+\frac{\pi }{2}\left(i-5\right)\right],\mathit{sin}\left[\frac{\pi }{4}+\frac{\pi }{2}\left(i-5\right)\right]\right\}\sqrt{2}c,i=\mathrm{5,6,7,8}\end{array}(1)$

with the weight parameters $W_i$ being:

$W_i=\{\begin{array}{l}4/9,i=0\\ 1/9,i=\mathrm{1,2,3,4}\\ 1/36,i=\mathrm{5,6,7,8}\end{array}(2)$

In the model, each lattice Boltzmann equation for fluid k is defined as:

$f_i^k\left(\mathit{x}+{\mathit{c}}_i∆t,t+∆t\right)-f_i^k\left(\mathit{x},t\right)={\mathrm{\Omega }}_i^k\left[f_i^k\left(\mathit{x},t\right)\right]+{\mathrm{\Gamma }}_i\left(\frac{{\rho }^k}{\rho }\mathit{F}\left(\mathit{x},t\right)\right)(3)$

where $f_i^k$ is the distribution function, the subscript $i$ denotes the direction of the discrete velocity space; $\mathit{x}$ represents the lattice position, and $\Delta t$ is the time step; ${\Omega }_i^k$ and ${\Gamma }_i$ are the collision term and the modified forcing term (Guo, Z., et al., 2002), respectively.

The fluid density and the flow velocity are calculated as follows:

${\rho }^k={\displaystyle \sum }_i{f}_i^k={\displaystyle \sum }_i{f}_i^{k,eq}(4)$

$\rho ={\displaystyle \sum }_k{\rho }^k,\mathit{u}=\left(\mathit{F}/2+{\displaystyle \sum }_i{\displaystyle \sum }_k{f}_i^k{\mathit{c}}_i\right)/\rho (5)$

where ${\rho }^k$ represents the macroscopic phase density, $\rho$ is the total density, and $\mathit{u}$ denotes the flow velocity.

The equilibrium distribution function $f_i^{k,eq}$ can be given by

$f_i^{k,eq}\left({\rho }^k,u,{\alpha }^k\right)={\rho }^k\left({\varphi }_i^k+W_i\left(\frac{3c_i\cdot u}{c^2}+\frac{9{\left(c_i\cdot u\right)}^2}{2c^4}-\frac{3u^2}{2c^2}\right)\right)+{\mathrm{\Phi }}_i^k(6)$

where

${\varphi }_i^k=\{\begin{array}{l}{\alpha }^k,i=0\\ \left(1-{\alpha }^k\right)/5,i=\mathrm{1,2,3,4}\\ \left(1-{\alpha }^k\right)/20,i=\mathrm{5,6,7,8}\end{array}(7)$

where ${\alpha }^k\left(0<{\alpha }^k<1\right)$ is a parameter related to the density ratio between fluids

$\frac{1-{\alpha }^l}{1-{\alpha }^k}=\frac{{\rho }^{k,0}}{{\rho }^{l,0}}(8)$

where superscript 0 represents the initial value of density.

To obtain the right momentum for different density ratios, the ${\Phi }_i^k$ in Eq. 6 is set as (Leclaire, S. et al., 2013a):

${\mathrm{\Phi }}_i^k=\{\begin{array}{l}-3{\nu }_{eff}\left(u\cdot \nabla {\rho }^k\right)/c^2,i=9\\ 4{\nu }_{eff}\left({\mathit{D}}^k:c_i\otimes c_i\right)/c^4,i=\mathrm{1,2,3,4}\\ {\nu }_{eff}\left({\mathit{D}}^k:c_i\otimes c_i\right)/c^4,i=\mathrm{5,6,7,8},\end{array}(9)$

with ${\mathit{D}}^k=\left[\left(\mathit{u}\otimes \nabla {\rho }^k\right)+{\left(\mathit{u}\otimes \nabla {\rho }^k\right)}^T\right]/8$.

The collision term ${\Omega }_i^k$ in Eq. 3 is combined by three sub operators as:

${\Omega }_i^k={\left({\Omega }_i^k\right)}^M\left[{\left({\Omega }_i^k\right)}^S+{\left({\Omega }_i^k\right)}^I\right],(10)$

where ${\left({\Omega }_i^k\right)}^S$ is the single-phase operator, ${\left({\Omega }_i^k\right)}^I$ is the perturbation operator and ${\left({\Omega }_i^k\right)}^M$ is the recoloring operator.

The perturbation operator related to the interfacial effect of multiphase flow is written as:

${\left({\mathrm{\Omega }}_i^k\right)}^I=f_i^k+{\displaystyle \sum }_{l\left(l\ne k\right)}\frac{A^{kl}{C}^{kl}}{2}\left|{\mathit{G}}^{kl}\right|\left(W_i\frac{{\left({\mathit{c}}_i\cdot {\mathit{G}}^{kl}\right)}^2}{{\left|{\mathit{c}}_i\right|}^2{\left|{\mathit{G}}^{kl}\right|}^2}-B_i\right)∆x,(11)$

where

$B_i=\{\begin{array}{l}-4/27,i=0\\ 2/27,i=\mathrm{1,2,3,4}\\ 5/108,i=\mathrm{5,6,7,8}\end{array}(12)$

and ${\mathit{G}}^{kl}$ is the “color” gradient perpendicular to the interface between the phases $k$ and $l$:

${\mathit{G}}^{kl}\left(\mathit{x},t\right)=\frac{{\rho }^l}{\rho }\nabla \left(\frac{{\rho }^k}{\rho }\right)-\frac{{\rho }^k}{\rho }\nabla \left(\frac{{\rho }^l}{\rho }\right)(13)$

A concentration factor that limits the range of interfacial action (Leclaire, S., et al., 2013b) is defined as:

$C^{kl}=\mathit{min}\left\{{10}^6\frac{{\rho }^k{\rho }^l}{{\rho }^{k,0}{\rho }^{l,0}},1\right\}(14)$

and $A^{kl}$ is related to interfacial tension ${\gamma }^{kl}$:

$A^{kl}=A^{lk}=\frac{9}{2}\frac{{\gamma }^{kl}}{{\tau }_{eff}{c}^2\Delta x}(15)$

The recoloring operator, which ensures that each phase satisfies the conservation of mass perfectly, is written as

${\left({\mathrm{\Omega }}_i^k\right)}^M=\frac{{\rho }^k}{\rho }{\displaystyle \sum }_k{f}_i^k+{\displaystyle \sum }_{l\left(l\ne k\right)}\left[{\beta }^{kl}\frac{{\rho }^k{\rho }^l}{{\rho }^2}\mathit{cos}\left({\phi }_i^{kl}\right)\times {\displaystyle \sum }_k{f}_i^{k,eq}\left({\rho }^k,0,{\alpha }^k\right)\right](16)$

where the parameter ${\beta }^{kl}$ controls the interface thickness of phases $k$ and $l$, and the ${\phi }_i^{kl}$ is the angle between ${\mathit{c}}_i$ and ${\mathit{G}}^{kl}$.

Apparent viscosity

To obtain the apparent viscosity of decane-water emulsion, we also simulate the single-phase flow of water as a reference. Based on the comparison between the single- and two-phase flow, the apparent viscosity can be calculated as (Xie and Balhoff, 2021):

${\mu }_{app}={\mu }_s\frac{F_t/Q_t}{F_s/Q_s}(17)$

where the subscripts $t$ and $s$ denote the two-phase and single-phase flow states, respectively, ${\mu }_s$ is the dynamic viscosity of the single-phase reference fluid, $F$ and $Q$ represent the body force and flow rate, respectively.

In our simulations, we apply a body force of the same magnitude for both single- and two-phase flows. Therefore, the above equation to obtain the apparent viscosity is simplified as:

${\mu }_{app}={\mu }_s\frac{Q_s}{Q_t}(18)$

Workflow

The workflow of this work is shown in Figure 1. Primarily, we verify our LB model for the simulation of a co-current two-phase flow problem with theoretical solutions. Then the structure of a model porous medium is constructed to investigate the flow of decane-water emulsion through porous media.

FIGURE 1

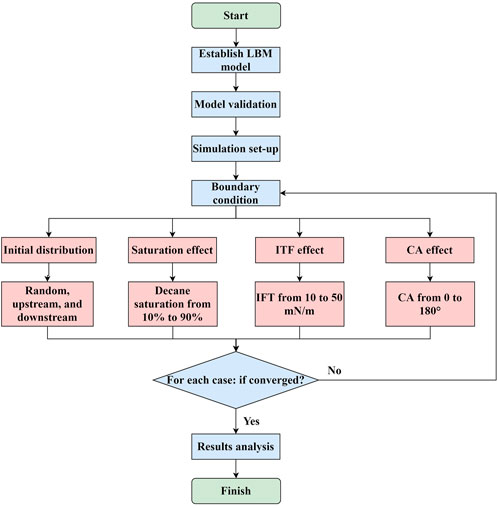
FIGURE 1. Workflow to study the impact of different factors on the apparent viscosity of the decane-water emulsion.

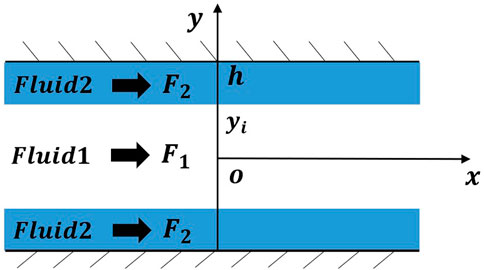
Model verification

We consider a two-phase co-current flow problem as sketched in Figure 2 to verify our LB model. Fluid 1 (density of 60 $\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$, kinematic viscosity of 0.0167 $m^2/s$) in the center and Fluid 2 (density of 980 $kg/m^3$, kinematic viscosity of 0.0167 $m^2/s$) on two sides of a straight channel are driven by the body force $F_1$ =16 $Pa/m$ and $F_2$ =0 $Pa/m$, respectively. The simulation domain is a rectangle with a length of 400 mm and a width of 200 mm. Periodic boundary conditions are applied at the inlet and outlet, the upper and lower boundaries are wall boundaries. The cross-sectional theoretical velocity profile of the problem can be found in (Xie. C., et al., 2016).

FIGURE 2

FIGURE 2. The sketch of a two-phase co-current flow.

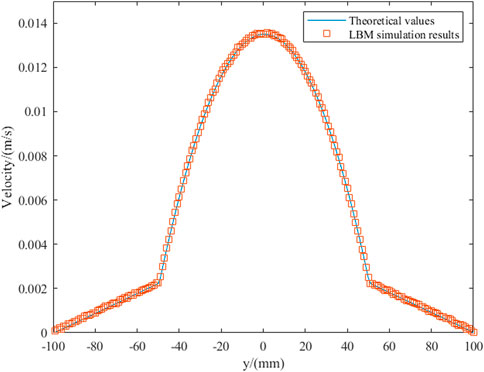
The comparison between the simulation results obtained by our LB model and the theoretical values is shown in Figure 3, which shows good agreement. These results verify the LB model for the dynamic two-phase flow simulations.

FIGURE 3

FIGURE 3. Comparison results of two-phase co-current flow.

Results and discussion

Simulation domain and parameters

The computation domain is a homogeneous porous media with a total length of 14 mm and a width of 9.5 mm, containing evenly distributed round solid grains, as shown in Figure 4. The diameter of the solid grain is 2.8 mm. The periodic boundary condition is applied in the horizontal direction, and the fluids are driven by a horizontal body force from left to right. For the two-phase flow simulations, the fluids are water and decane, while for the single-phase flow simulation, the fluid is water. Their physical properties and other key parameters in the LBM simulation are listed in Table 1.

FIGURE 4

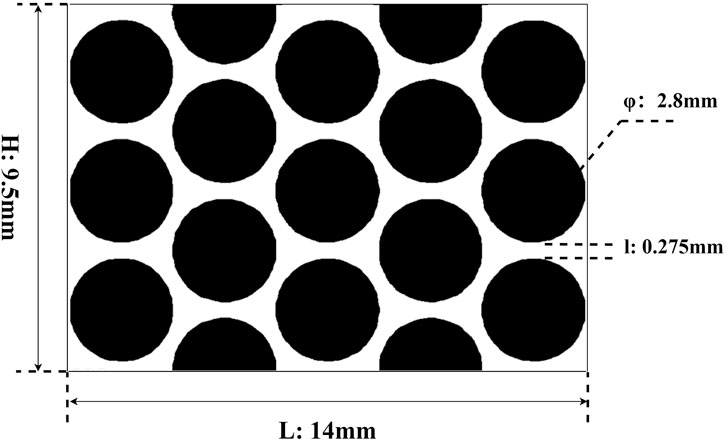
FIGURE 4. Simulation domain: the black represents the solid grain, and the white represents the porous space.

TABLE 1

TABLE 1. Fluid properties and LBM simulation parameters.

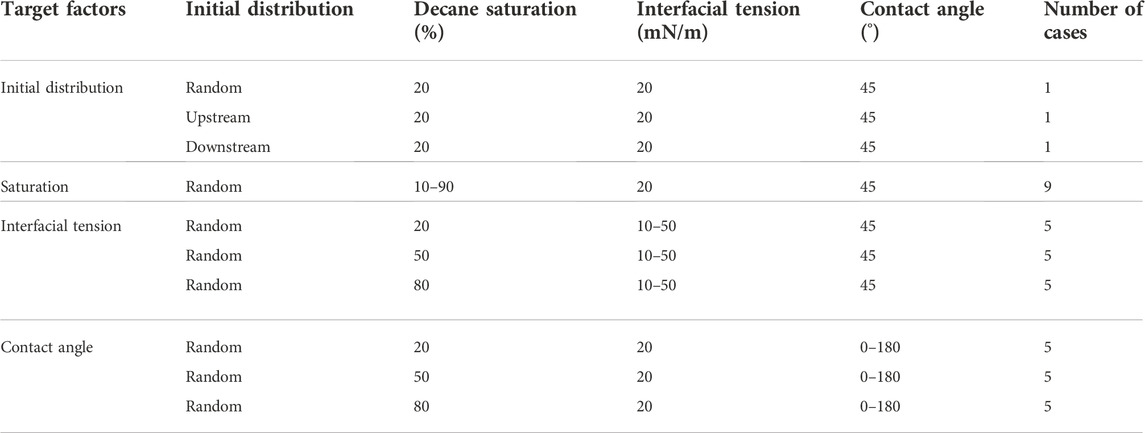
42 simulation cases in total are prepared to discuss the effect of initial distribution, saturation, interfacial tension (IFT), and contact angle (CA) on the apparent viscosity of the decane-water emulsion in porous media. We compare three types of initial fluid distributions, including the upstream-decane distribution, the downstream-decane distribution, and the random distribution. The saturation, interfacial tension, and contact angle are varied from 10% to 90%, 10 mN/m to 50 mN/m, and 0–180°, respectively. In the default case, the decane saturation is 20%, initially randomly distributed in the porous media with a contact angle of 45°, and the interfacial tension between the decane and water is 20 mN/m. A summary of parameters discussed in all simulation cases is given in Table 2.

TABLE 2

TABLE 2. The summary of parameters discussed in all simulation cases.

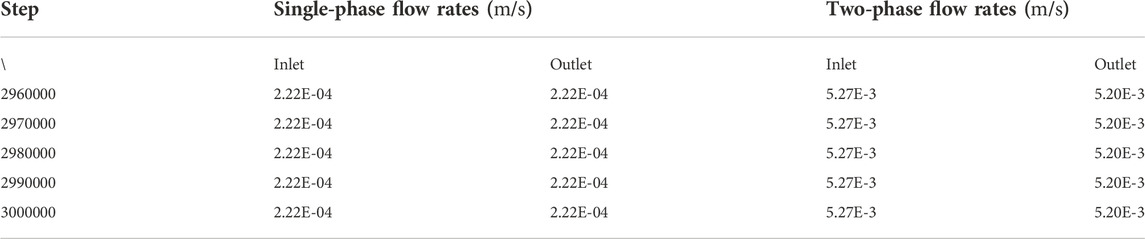
For each case, the simulation is terminated once the flow stabilizes and the fluid distribution does not change. The inlet and outlet flow rates of the single-phase case and the default two-phase flow case in the last 40000 steps (the gap is 10000 steps) are shown in Table 3. In both cases, the inlet flow rates are approximately equal to the outlet flow rates, and the gaps between the inlet and outlet rates stabilize in the last 40000 steps, which illustrates that the total time step we set is adequate for the flow stabilization.

TABLE 3

TABLE 3. The inlet and outlet flow rates of the single-phase and the default two-phase flow case.

The effect of initial phase distribution

We discuss three kinds of initial fluid distributions, which include the random distribution, upstream distribution, and downstream distribution as shown in Figures 5A,C,E. The simulation results at the last steps are also shown in Figures 5B,D,F. The results show that the different initial states lead to different distributions at the last time step. However, all of the last-time distributions are qualitatively random, no matter how the fluids are distributed at the initial time step. This result indicates that the impact of initial phase distribution on the apparent viscosity is weak.

FIGURE 5

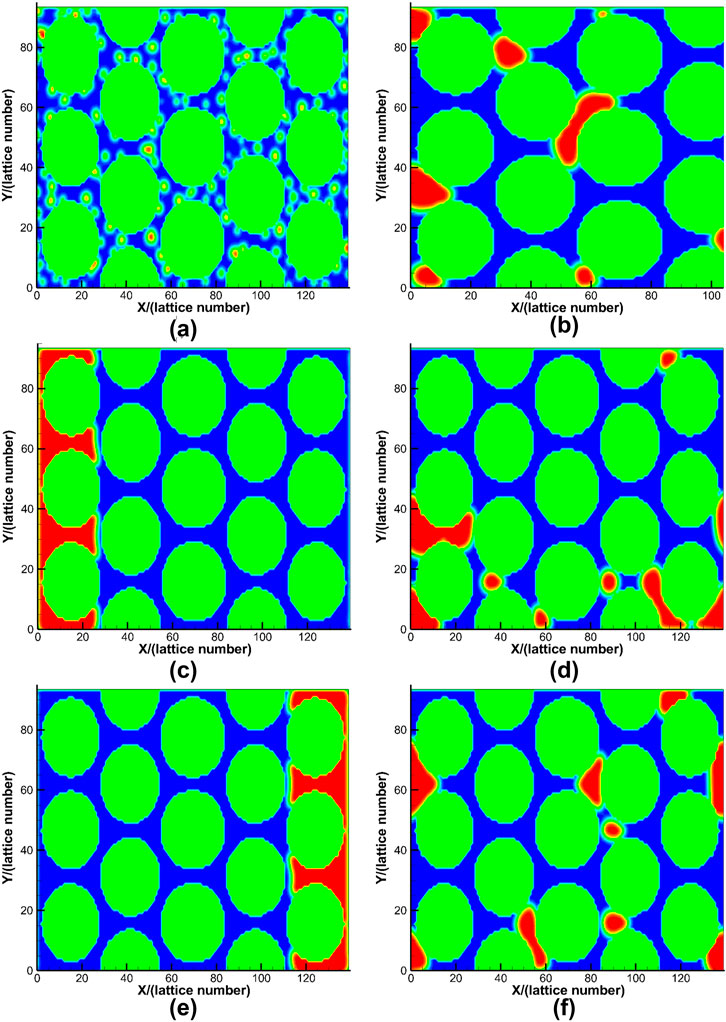
FIGURE 5. The simulation results of three initial distributions (red for decane, and blue for water): (A) The random distribution at the initial time step. (B) The random distribution at the last time step. (C) The upstream distribution at the initial time step. (D) The upstream distribution at the last time step. (E) The downstream distribution at the initial time step. (F) The downstream distribution at the last time step.

The effect of saturation

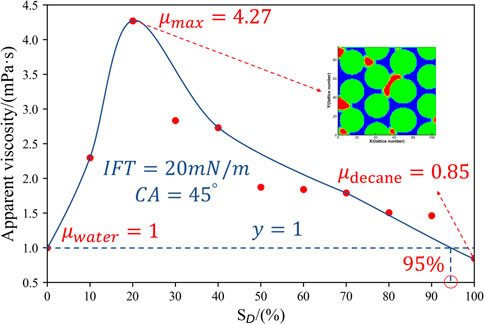
The effect of decane saturation on the apparent viscosity of the emulsion system is shown in Figure 6. When the decane saturation is 0, the apparent viscosity is the water dynamic viscosity of 1 mPa s. While the decane is added to form the decane-water emulsion, the apparent viscosity increases. This is because the original single-phase flow state becomes the two-phase flow state, and the interfacial interaction between water and decane occurs and the capillary trapping force arises, leading to the increase in the apparent viscosity, even though the dynamic viscosity of decane is lower than that of water. The apparent viscosity of the decane-water reaches its maximum value of 4.27 mPa s when the decane saturation is 20%, after which, the apparent viscosity gradually decreases with the increase in the decane saturation. The emulsion’s apparent viscosity decreases to the water viscosity of 1 mPa s when the decane saturation reaches around 95%. It is worth mentioning that this value may vary in a small range if different fitting functions are applied. If the decane saturation is higher than 95%, the emulsion’s apparent viscosity is lower than 1 mPa s, and finally reaches its minimum value, that is the dynamic viscosity of decane (0.85 mPa s).

FIGURE 6

FIGURE 6. The effect of saturation on apparent viscosity: $S_D$ is the decane saturation.

The effect of interfacial tension

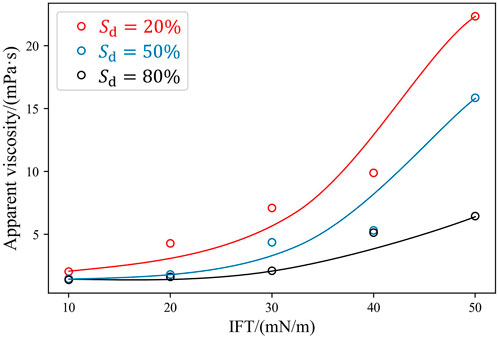
Figure 7 shows the effect of interfacial tension between the water and decane on the emulsion’s apparent viscosity. Here we also change the decane saturation from 20% to 80%. We find that the emulsion’s apparent viscosity increases with the increase in interfacial tension for all satuations. This is because the capillary dragging force increases with interfacial tension. Therefore, the increase in interfacial tension decreases the effective flow rates, which leads to higher apparent viscosities of the emulsion. The maximum value of apparent viscosity is 22.3 mPa s, which is about 20 times greater than the dynamic viscosity of water. The minimum of that is 1.37 mPa s, also greater than the dynamic viscosity of water.

FIGURE 7

FIGURE 7. The effect of interfacial tension on apparent viscosity: IFT is the interfacial tension.

The effect of contact angle

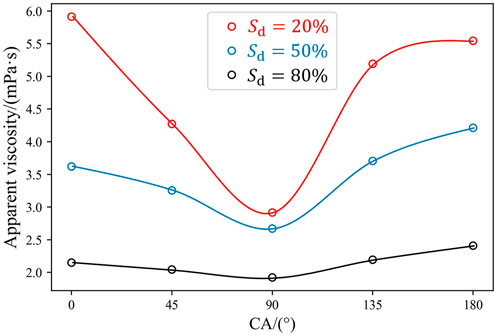
Figure 8 shows the change in the emulsion’s apparent viscosity with contact angles. Here we also consider the change in the decane saturation from 20% to 80%. As is seen, for all satuations, higher apparent viscosities are found in decane-wet and water-wet systems, and the apparent viscosity reaches the lowest value in intermediate-wet porous media. This is because the decane-wet and water-wet porous geometry have stronger adsorption capacities for decane and water, respectively, than that of intermediate-wet media, and the stronger adsorption capacity leads to the higher apparent viscosity.

FIGURE 8

FIGURE 8. The effect of contact angle (CA) on apparent viscosity.

Conclusion

In this paper, we investigate the apparent viscosity of decane aqueous solution in porous media by LBM simulation. To verify the established LBM model, a two-phase co-current flow simulation is performed primarily. Then the effects of four factors, including the initial phase distribution, phase saturation, interfacial tension, and contact angle, on the apparent viscosity of the decane-water emulsion are discussed. We find that the apparent viscosity of the decane-water emulsion increases first and then decreases as the decane saturation increases. The emulsion’s apparent viscosity reaches the highest value when the decane saturation is around 20%. In addition, the apparent viscosity of decane aqueous solution increases with the interfacial tension. We also find that the apparent viscosity of decane aqueous solution in decane-wet or water-wet systems is greater than it is in intermedia-wet porous media.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LS: Write original draft, investigation, data curation, visualization. PL: Methodology, investigation, supervision. JZ: Validation, discussion. YZ: Investigation. CX: Conceptualization, methodology, reviewing and editing, supervision.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

${\alpha }^k$, parameter related to the density ratio between fluids; ${\beta }^{\mathrm{k}\mathrm{l}}$, parameter controls the interface thickness of phases $\mathrm{k}$ and $\mathrm{l}$; ${\gamma }^{\mathrm{k}\mathrm{l}}$, interfacial tension; ${\rho }^{\mathrm{k}}$, macroscopic phase density; $\rho$, total density; ${\phi }_{\mathrm{i}}^{\mathrm{k}\mathrm{l}}$, angle between ${\mathrm{c}}_{\mathrm{i}}$ and ${\mathrm{G}}^{\mathrm{k}\mathrm{l}}$; ${\mu }_{\mathrm{s}}$, dynamic viscosity of the single-phase reference fluid; ${\mu }_{\mathrm{a}\mathrm{p}\mathrm{p}}$, apparent viscosity; ${\Omega }_{\mathrm{i}}^{\mathrm{k}}$, collision term; ${\left({\Omega }_{\mathrm{i}}^{\mathrm{k}}\right)}^{\mathrm{S}}$, single-phase operator; ${\left({\Omega }_{\mathrm{i}}^{\mathrm{k}}\right)}^{\mathrm{I}}$, perturbation operator; ${\left({\Omega }_{\mathrm{i}}^{\mathrm{k}}\right)}^{\mathrm{M}}$, recoloring operator; ${\Gamma }_{\mathrm{i}}$, modified forcing term; ${\mathrm{A}}^{\mathrm{k}\mathrm{l}}$, parameter related to interfacial tension; ${\mathrm{c}}_{\mathrm{i}}$, velocity space; ${\mathrm{f}}_{\mathrm{i}}^{\mathrm{k}}$, distribution function; ${\mathrm{f}}_{\mathrm{i}}^{\mathrm{k},\mathrm{e}\mathrm{q}}$, equilibrium distribution function; $\mathrm{F}$, body force; ${\mathrm{G}}^{\mathrm{k}\mathrm{l}}$, “color” gradient perpendicular to the interface between the phases $\mathrm{k}$ and $\mathrm{l}$; $\mathrm{i}$, direction of the discrete velocity space; $\mathrm{Q}$, flow rate; $\mathrm{s}$, single-phase flow state; $\mathrm{t}$, two-phase flow state; $\Delta \mathrm{t}$, time step; $\mathrm{u}$, flow velocity; ${\mathrm{W}}_{\mathrm{i}}$, weight parameters; $\mathrm{x}$, lattice position.

References

Abbaszadeh, M., Nia Korrani, A. K., Lopez-Salinas, J. L., Rodriguez-de La Garza, F., Villavicencio Pino, A., and Hirasaki, G. (2014). Experimentally-based empirical foam modeling. In proceedings of the SPE improved oil recovery symposium. OnePetro, Tulsa, OK, USA.

CrossRef Full Text | Google Scholar

Beckett, M. J. (1993). Land contamination, contaminated land, problems and solution. Edited by Tom Cairney. CRC Press, Boca Raton, Florida.

Google Scholar

Chen, Y., Valocchi, A. J., Kang, Q., and Viswanathan, H. S. (2019). Inertial effects during the process of supercritical CO2 displacing brine in a sandstone: Lattice Boltzmann simulations based on the continuum-surface-force and geometrical wetting models. Water Resour. Res. 55 (12), 11144–11165. doi:10.1029/2019wr025746

CrossRef Full Text | Google Scholar

Foster, S., Hirata, R., Gomes, D., D'Elia, M., and Paris, M. (2002). Groundwater quality protection: A guide for water utilities, municipal authorities, and environment agencies. Washington, DC: World Bank.

Google Scholar

Foster, S. S. D., and Chilton, P. J. (2003). Groundwater: The processes and global significance of aquifer degradation. Phil. Trans. R. Soc. Lond. B 358 (1440), 1957–1972. doi:10.1098/rstb.2003.1380

PubMed Abstract | CrossRef Full Text | Google Scholar

Garduño, H., and Foster, S. (2010). Sustainable groundwater irrigation. San Francisco.: Wiley.

Google Scholar

Guo, Y., and Wang, M. (2015). Phonon hydrodynamics and its applications in nanoscale heat transport. Phys. Rep. 595, 1–44. doi:10.1016/j.physrep.2015.07.003

CrossRef Full Text | Google Scholar

Guo, Z., Zheng, C., and Shi, B. (2002). Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 65 (4), 046308. doi:10.1103/physreve.65.046308

PubMed Abstract | CrossRef Full Text | Google Scholar

Hirasaki, G. J., and Lawson, J. B. (1985). Mechanisms of foam flow in porous media: Apparent viscosity in smooth capillaries. Soc. Petroleum Eng. J. 25 (02), 176–190. doi:10.2118/12129-pa

CrossRef Full Text | Google Scholar

Illangasekare, T. H. (1998). “Flow and entrapment of nonaqueous phase liquids in heterogenous soil formations,” in Physical nonequilibrium in soils modeling and application (Boca Raton, Florida: CRC Press), 417–435.

Google Scholar

Jeong, S. W., and Corapcioglu, M. Y. (2003). A micromodel analysis of factors influencing NAPL removal by surfactant foam flooding. J. Contam. hydrology 60 (1-2), 77–96. doi:10.1016/s0169-7722(02)00054-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuroda, K., and Fukushi, T. (2008). “Groundwater contamination in urban areas,” in Groundwater management in Asian cities (Tokyo: Springer), 125–149.

Google Scholar

Leclaire, S., Parmigiani, A., Malaspinas, O., Chopard, B., and Latt, J. (2017). Generalized three-dimensional lattice Boltzmann color-gradient method for immiscible two-phase pore-scale imbibition and drainage in porous media. Phys. Rev. E 95 (3), 033306. doi:10.1103/physreve.95.033306

PubMed Abstract | CrossRef Full Text | Google Scholar

Leclaire, S., Pellerin, N., Reggio, M., and Trépanier, J. Y. (2013a). Enhanced equilibrium distribution functions for simulating immiscible multiphase flows with variable density ratios in a class of lattice Boltzmann models. Int. J. Multiph. Flow 57, 159–168. doi:10.1016/j.ijmultiphaseflow.2013.07.001

CrossRef Full Text | Google Scholar

Leclaire, S., Reggio, M., and Trépanier, J. Y. (2013b). Progress and investigation on lattice Boltzmann modeling of multiple immiscible fluids or components with variable density and viscosity ratios. J. Comput. Phys. 246, 318–342. doi:10.1016/j.jcp.2013.03.039

CrossRef Full Text | Google Scholar

Lin, X., Xu, W. J., Lv, K., and Li, Y. J. (2022). Multiple-relaxation-time lattice Boltzmann method for three dimensional free-surface flows with multi-bubble model. Comput. Fluids 233, 105247. doi:10.1016/j.compfluid.2021.105247

CrossRef Full Text | Google Scholar

Liu, H., Kang, Q., Leonardi, C. R., Schmieschek, S., Narváez, A., Jones, B. D., et al. (2016). Multiphase lattice Boltzmann simulations for porous media applications. Comput. Geosci. 20 (4), 777–805. doi:10.1007/s10596-015-9542-3

CrossRef Full Text | Google Scholar

Mauray, A., Chabert, M., and Bodiguel, H. (2020). Yield stress fluid behavior of foam in porous media. Phys. Rev. Fluids 5 (9), 094004. doi:10.1103/physrevfluids.5.094004

CrossRef Full Text | Google Scholar

Mobarak, M., Gatternig, B., Delgado, A., Bernstein, T., McHardy, C., and Rauh, C. (2022). Foam drainage parametric study using the lattice Boltzmann method considering the non-Newtonian behavior. Chem. Eng. Technol. 45 (8), 1371–1379. doi:10.1002/ceat.202200067

CrossRef Full Text | Google Scholar

Nyer, E. K. (1992). Groundwater treatment technology. Hoboken, New Jersey: John Wiley & Sons.

Google Scholar

Omirbekov, S., Davarzani, H., Colombano, S., and Ahmadi-Senichault, A. (2020). Experimental and numerical upscaling of foam flow in highly permeable porous media. Adv. Water Resour. 146, 103761. doi:10.1016/j.advwatres.2020.103761

CrossRef Full Text | Google Scholar

Osei-Bonsu, K., Grassia, P., and Shokri, N. (2018). Effects of pore geometry on flowing foam dynamics in 3D-printed porous media. Transp. Porous Media 124 (3), 903–917. doi:10.1007/s11242-018-1103-5

CrossRef Full Text | Google Scholar

Postigo, C., Martinez, D. E., Grondona, S., and Miglioranza, K. S. B. (2018). Groundwater pollution: Sources, mechanisms, and prevention. Berlin: ResearchGate. doi:10.1016/B978-0-12-409548-9.09880-8

CrossRef Full Text | Google Scholar

Qian, Y. H., d'Humières, D., and Lallemand, P. (1992). Lattice BGK models for Navier-Stokes equation. Europhys. Lett. 17 (6), 479–484. doi:10.1209/0295-5075/17/6/001

CrossRef Full Text | Google Scholar

Radhakrishnan, A., Gigliotti, A., Johnston, K. P., DiCarlo, D., and Prodanovic, M. (2022). Understanding foam flow in rough carbonate fractures. In Proceedings of the SPE Improved Oil Recovery Conference. OnePetro, Tulsa USA.doi:10.2118/209410-MS

CrossRef Full Text | Google Scholar

Shojaei, M. J., De Castro, A. R., Méheust, Y., and Shokri, N. (2019). Dynamics of foam flow in a rock fracture: Effects of aperture variation on apparent shear viscosity and bubble morphology. J. colloid interface Sci. 552, 464–475. doi:10.1016/j.jcis.2019.05.068

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, J., Guo, L., Jing, J., Duan, L., Lu, Y., Ullmann, A., et al. (2021). A comparison of numerical simulations with experimental and theoretical investigations of highly-viscous oil-aqueous foam horizontal flow. J. Petroleum Sci. Eng. 201, 108507. doi:10.1016/j.petrol.2021.108507

CrossRef Full Text | Google Scholar

Valko, P., and Economides, M. J. (1992). Volume equalized constitutive equations for foamed polymer solutions. J. Rheology 36 (6), 1033–1055. doi:10.1122/1.550300

CrossRef Full Text | Google Scholar

Xie, C., and Balhoff, M. T. (2021). Lattice Boltzmann modeling of the apparent viscosity of thinning–elastic fluids in porous media. Transp. Porous Media 137 (1), 63–86. doi:10.1007/s11242-021-01544-y

CrossRef Full Text | Google Scholar

Xie, C., Lei, W., Balhoff, M. T., Wang, M., and Chen, S. (2021). Self-adaptive preferential flow control using displacing fluid with dispersed polymers in heterogeneous porous media. J. Fluid Mech. 906, A10. doi:10.1017/jfm.2020.763

CrossRef Full Text | Google Scholar

Xie, C., Lei, W., and Wang, M. (2018b). Lattice Boltzmann model for three-phase viscoelastic fluid flow. Phys. Rev. E 97 (2), 023312. doi:10.1103/physreve.97.023312

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, C., Lv, W., and Wang, M. (2018a). Shear-thinning or shear-thickening fluid for better EOR?—a direct pore-scale study. J. Petroleum Sci. Eng. 161, 683–691. doi:10.1016/j.petrol.2017.11.049

CrossRef Full Text | Google Scholar

Xie, C., Raeini, A. Q., Wang, Y., Blunt, M. J., and Wang, M. (2017). An improved pore-network model including viscous coupling effects using direct simulation by the lattice Boltzmann method. Adv. water Resour. 100, 26–34. doi:10.1016/j.advwatres.2016.11.017

CrossRef Full Text | Google Scholar

Xie, C., Xu, K., Mohanty, K., Wang, M., and Balhoff, M. T. (2020). Nonwetting droplet oscillation and displacement by viscoelastic fluids. Phys. Rev. Fluids 5 (6), 063301. doi:10.1103/physrevfluids.5.063301

CrossRef Full Text | Google Scholar

Xie, C., Xu, K., Qi, P., Xu, J., and Balhoff, M. T. (2022). A new mechanism of viscoelastic fluid for enhanced oil recovery: Viscoelastic oscillation. Adv. Geo-Energy Res. 6 (3), 267–268. doi:10.46690/ager.2022.03.10

CrossRef Full Text | Google Scholar

Xie, C., Zhang, J., Bertola, V., and Wang, M. (2016). Lattice Boltzmann modeling for multiphase viscoplastic fluid flow. J. Newt. Fluid Mech. 234, 118–128. doi:10.1016/j.jnnfm.2016.05.003

CrossRef Full Text | Google Scholar

Yan, W., Miller, C. A., and Hirasaki, G. J. (2006). Foam sweep in fractures for enhanced oil recovery. Colloids Surfaces A Physicochem. Eng. Aspects 282, 348–359. doi:10.1016/j.colsurfa.2006.02.067

CrossRef Full Text | Google Scholar

Zhang, T., Li, Y., Cai, J., Meng, Q., Sun, S., and Li, C. (2020). A digital twin for unconventional reservoirs: A multiscale modeling and algorithm to investigate complex mechanisms. Geofluids 2020. doi:10.1155/2020/8876153

CrossRef Full Text | Google Scholar

Zhang, T., and Sun, S. (2019). A coupled Lattice Boltzmann approach to simulate gas flow and transport in shale reservoirs with dynamic sorption. Fuel 246, 196–203. doi:10.1016/j.fuel.2019.02.117

CrossRef Full Text | Google Scholar

Zhang, Z. F., Zhong, L., White, M. D., and Szecsody, J. E. (2012). Experimental investigation of the effective foam viscosity in unsaturated porous media. Vadose zone J. 11 (4), vzj2011–0190. doi:10.2136/vzj2011.0190

CrossRef Full Text | Google Scholar