Tropical cyclone rapid intensification and the excitation of inertia-gravity waves on the edges of an evolving potential vorticity structure

The problem of tropical cyclone rapid intensification is reduced to a potential vorticity (PV) equation and a second order, inhomogeneous, partial differential equation for the azimuthal wind. The latter equation has the form of a Klein-Gordon equation, the right-hand side of which involves the radial derivative of the evolving PV field. When the PV field evolves rapidly, inertia-gravity waves are excited at the edges of the evolving PV structure. In contrast, when the PV field evolves slowly, the second order time derivative term in the Klein-Gordon equation is negligible, inertia-gravity waves are not excited, and the equation reduces to an invertibility principle for the PV. The above concepts are presented in the context of an axisymmetric shallow water model, in both its linear and nonlinear forms. The nonlinear results show a remarkable sensitivity of vortex intensification to the percentage of mass that is diabatically removed from the region inside a given absolute angular momentum surface.

1 Introduction

While modern numerical weather prediction has produced significant skill in forecasting tropical cyclone tracks, the forecasting of rapid intensification remains an important challenge (DeMaria et al., 2014). The status of present observational, theoretical, and numerical modeling efforts to improve intensity forecasting can be found in the special collection of thirty articles that have appeared recently in five of the journals published by the American Meteorological Society (see the Doyle and Ferek, 2017, reference for the website that describes this special collection associated with the Tropical Cyclone Intensity Experiment). A concise and excellent review of much of this previous work can be found in Martinez et al. (2019). The present paper explores some of the theoretical aspects of the rapid intensification problem. In particular, this paper discusses how the problem of tropical cyclone intensification can be reduced to the solution of a coupled pair of partial differential equations—a first order equation for the time evolution of the potential vorticity (PV) field, and a second order, Klein-Gordon equation for the evolution of the rotational wind field. In many interesting cases the potential vorticity equation can be solved analytically and the result used as a forcing term in the Klein-Gordon equation. Examples of this approach, in the case when the Klein-Gordon equation reduces to an elliptic invertibility principle, are given in Schubert and Alworth (1987) and Möller and Smith (1994).

The forcing term in the Klein-Gordon equation can be especially large at the edges of an evolving PV structure. When this forcing effect varies slowly in time, the second order time derivative term in the Klein-Gordon equation can be neglected, which converts this hyperbolic equation into an elliptic, PV invertibility principle. When the forcing does not vary slowly in time, the second order time derivative term must be retained and the Klein-Gordon equation maintains its hyperbolic character, thereby describing both the balanced flow and the generation and propagation of inertia-gravity waves. These basic concepts are presented in the simple context of the axisymmetric shallow water model (Section 2), where curvature effects and gradient balance come into play. In the linear case (Section 3), the primary results are the PV solution, given in Eq. 8, and the linear Klein-Gordon equation for v (r, t), given in the middle entry of Eq. 11, or the linear invertibility principle for v_b (r, t), given by the middle entry of Eq. 12. These linear results are generalized to the nonlinear case through the use of a Lagrangian description of the flow (Section 4). In the nonlinear case, the primary results are the PV solution, given in Eq. 21, and the nonlinear Klein-Gordon equation for V (R, τ), given by Eq. 24, or the nonlinear invertibility principle for V_b(R, τ), given by Eq. 26. Solutions of the nonlinear problem illustrate how rapid intensification can occur when a large percentage of the original lower tropospheric mass inside a given absolute angular momentum surface is diabatically removed via eyewall convection.

2 Shallow water model

Consider the inviscid, axisymmetric, nonlinear shallow water equations

$\frac{Du}{Dt}-\left(f+\frac{v}{r}\right)v+g\frac{\partial h}{\partial r}=0,\frac{Dv}{Dt}+\left(f+\frac{v}{r}\right)u=0,\frac{Dh}{Dt}+h\frac{\partial \left(ru\right)}{r\partial r}=-hS,(1)$

where u (r, t) is the radial velocity component, v (r, t) the azimuthal velocity component, h (r, t) the fluid depth, g the acceleration of gravity, f the constant Coriolis parameter, (D/Dt) = (∂/∂t) + u (∂/∂r) the material derivative, and S (r, t) the specified mass sink. The potential vorticity principle associated with Eq. 1 is

$\frac{DP}{Dt}=PS\text{where}P=\frac{\left(f+\zeta \right)\bar{h}}{h}\text{and}\zeta =\frac{\partial \left(rv\right)}{r\partial r},(2)$

with the constant $\bar{h}$ denoting the far-field fluid depth. Our goal in Section 4 is to solve Eq. 1 as a forced, nonlinear, transient, gradient adjustment problem. The approach is to solve analytically for P and then use this solution as a forcing in the second order partial differential equation for v. However, the derivation of a single nonlinear partial differential equation for v is not a straightforward task. For example, one approach might be as follows. First, take (∂/∂r) of $hP=\bar{h}(f+\zeta )$, and use the result to eliminate (∂h/∂r) from the radial momentum equation. Then, write the azimuthal momentum equation in an angular momentum form. The momentum equations then take the form

$\frac{Du}{Dt}-\left(f+\frac{v}{r}\right)v+\frac{g\bar{h}}{P}\frac{\partial }{\partial r}\left(\frac{\partial \left(rv\right)}{r\partial r}\right)=\frac{gh}{P}\frac{\partial P}{\partial r}\text{and}\frac{1}{r}\frac{D\left(rv\right)}{Dt}+fu=0,(3)$

which we can regard as a coupled pair of equations for u (r, t) and v (r, t) if P (r, t) is regarded as known from the solution of the PV principle (Eq. 2). Taking D/Dt of the second entry in Eq. 3 and using the result to eliminate Du/Dt from the first entry, we obtain

$\begin{array}{cc}\hfill \frac{\partial }{\partial r}\left(\frac{\partial \left(rv\right)}{r\partial r}\right)& -\frac{{\widehat{f}}^2}{gh}v-\frac{P}{fg\bar{h}}\frac{D}{Dt}\left(\frac{1}{r}\frac{D\left(rv\right)}{Dt}\right)=\frac{h}{\bar{h}}\frac{\partial P}{\partial r},\hfill \\ \hfill & \text{where}\frac{{\widehat{f}}^2}{gh}=\frac{1}{gh}\left(f+\frac{v}{r}\right)\left(f+\frac{\partial \left(rv\right)}{r\partial r}\right)=\frac{1}{g\bar{h}}\left(f+\frac{v}{r}\right)P.\hfill \end{array}(4)$

It is tempting to regard Eq. 4 as a nonlinear Klein-Gordon equation for the single variable v (r, t), with a time dependent forcing term that is proportional to the radial derivative of the potential vorticity. However, it is important to note that the variables u (r, t) and h (r, t) have not been completely eliminated from Eq. 4, with u (r, t) appearing in the D/Dt operator. In Section 4 we discuss the transformation of Eqs 2–4 to a Lagrangian coordinate, which simplifies the material derivative D/Dt to a local derivative. This not only simplifies the (D/Dt)-terms in Eqs 2–4, but also allows for time integration of the potential vorticity equation (Eq. 2), thereby making the forcing term in Eq. 4 a known function. If the forcing term varies slowly enough in time, the term in Eq. 4 involving D/Dt becomes negligible, so that the diagnostic equation for the gradient balanced wind v_b (r, t) is

$\begin{array}{cc}\hfill \frac{\partial }{\partial r}\left(\frac{\partial \left(r{v}_b\right)}{r\partial r}\right)& -\frac{{\widehat{f}}_b^2}{gh}{v}_b=\frac{h}{\bar{h}}\frac{\partial P}{\partial r},\hfill \\ \hfill & \text{where}\frac{{\widehat{f}}_b^2}{gh}=\frac{1}{gh}\left(f+\frac{v_b}{r}\right)\left(f+\frac{\partial \left(r{v}_b\right)}{r\partial r}\right)\hfill \end{array}(5)$

which is the shallow water version of the nonlinear invertibility relation discussed by Hoskins et al. (1985). However, before discussing the nonlinear problem, we consider in Section 3 the linearized version of the shallow water dynamics (Eq. 1). Although it is limited to weak vortices, the linear analysis of Section 3 provides a useful guide to the nonlinear analysis of Section 4.

Although the analysis presented here is in the context of the shallow water equations, a more general interpretation is that these equations approximately describe the dynamics of an atmospheric layer confined between two isentropic surfaces. The analogy is as follows. When there is a mass sink in the shallow water continuity equation, the two isentropic surfaces bounding the layer should be regarded as lower tropospheric surfaces (e.g., with the layer defined by 320 ≤ θ ≤ 325K). In contrast, when there is a mass source, the two isentropic surfaces should be regarded as upper tropospheric surfaces (e.g., with the layer defined by 355 ≤ θ ≤ 360K). This interpretation is justified by noting that the shallow water continuity equation in the independent variables (r, t) and the continuity equation for a stratified hydrostatic model in the independent variables (r, θ, t) can respectively be written as

$\frac{\partial h}{\partial t}+\frac{\partial \left(ruh\right)}{r\partial r}=-hS\text{and}\frac{\partial \sigma }{\partial t}+\frac{\partial \left(ru\sigma \right)}{r\partial r}=-\sigma \left(\frac{\partial \left(\sigma \dot{\theta }\right)}{\sigma \partial \theta }\right),(6)$

where σ = −(1/g) (∂p/∂θ) is the pseudodensity, p is the pressure, θ is the potential temperature, and $\sigma \dot{\theta }$ is the diabatic mass flux. Because of the close correspondence of the two equations in Eq. 6, we can make the following analogies: h ⇔ σ and $S\iff [\partial (\sigma \dot{\theta })/\sigma \partial \theta ]$. Note that in regions where the fractional variation of σ with respect to θ is much less than the fractional variation of $\dot{\theta }$ with respect to θ, this analogy simplifies to $S\iff (\partial \dot{\theta }/\partial \theta )$. In the lower tropospheric core region of a tropical cyclone, $[\partial (\sigma \dot{\theta })/\sigma \partial \theta ]>0$, so there should be an analogous mass sink in the shallow water equations to simulate a lower tropospheric layer. In the upper tropospheric core region of a tropical cyclone, $[\partial (\sigma \dot{\theta })/\sigma \partial \theta ]<0$, so there should be an analogous mass source in the shallow water equations to simulate an upper tropospheric layer. In Section 4 and Supplementary Appendix C we develop an alternative analogy based on potential vorticity dynamics rather than simply the mass conservation principles in Eq. 6. Although these analogies help interpret the shallow water model results in terms of the dynamics of a continuously stratified fluid, the analysis of the detailed vertical structure of tropical cyclones requires a complete θ-coordinate model, in which case the Klein-Gordon equations and the invertibility principles discussed in Section 3 and Section 4 would include terms that involve second order partial derivatives in θ.

3 Linear dynamics

As a guide to the nonlinear analysis of Section 4, let us first linearize the system Eq. 1 about a state of rest with constant mean depth $\bar{h}$. The linear equations are

$\frac{\partial u}{\partial t}-fv+g\frac{\partial h^{\prime }}{\partial r}=0,\frac{\partial v}{\partial t}+fu=0,\frac{\partial h^{\prime }}{\partial t}+\bar{h}\frac{\partial \left(ru\right)}{r\partial r}=-\bar{h}S,(7)$

where $h^{\prime }(r,t)=h(r,t)-\bar{h}$ is the deviation depth. As initial conditions for Eq. 7 we assume there is no flow and no anomaly in the fluid depth, i.e., u (r, 0) = 0, v (r, 0) = 0, and h′(r, 0) = 0. With these assumptions, any flow that develops is due to the mass sink S (r, t). The equation for the potential vorticity anomaly P′(r, t), derived from the second and third entries in Eq. 7, and its solution are given by

$\frac{\partial P^{\prime }}{\partial t}=fS\text{where}{P}^{\prime }=P-f=\frac{\partial \left(rv\right)}{r\partial r}-\frac{f}{\bar{h}}{h}^{\prime }\Rightarrow P^{\prime }\left(r,t\right)=f{\int }_0^{t}S\left(r,t^{\prime }\right)d{t}^{\prime }.(8)$

In order to better understand the stationary and oscillatory solutions of the unforced version of Eq. 7, assume the solutions are separable in r and t, with the time dependent part given by e^iωt, where ω is the frequency of oscillation. It can then be shown that the radially dependent part of h′ satisfies an order zero Bessel equation and the radially dependent parts of u and v satisfy order one Bessel equations (for further discussion, see Schubert et al., 1980). In other words, we can simply begin with the assumed separable forms $u(r,t)=c\widehat{u}{J}_1(kr)e^{i\omega t}$, $v(r,t)=c\widehat{v}{J}_1(kr)e^{i\omega t}$, and $h^{\prime }(r,t)=(c^2/g)\widehat{h}{J}_0(kr)e^{i\omega t}$, where $\widehat{u},\widehat{v},\widehat{h}$ are dimensionless complex constants, k is the radial wavenumber, J₀ and J₁ are Bessel functions of order zero and order one respectively, and $c={(g\bar{h})}^{1/2}$ is the pure gravity wave speed. Substituting these assumed solutions into the unforced version of Eq. 7 and using the Bessel function derivative relations dJ₀ (kr)/dr = −kJ₁ (kr) and d [rJ₁ (kr)]/rdr = kJ₀ (kr), we obtain

$\begin{array}{ll}\hfill \left(\begin{array}{ccc}\hfill i\omega \hfill & \hfill -f\hfill & \hfill -ck\hfill \\ \hfill f\hfill & \hfill i\omega \hfill & \hfill 0\hfill \\ \hfill ck\hfill & \hfill 0\hfill & \hfill i\omega \hfill \end{array}\right)\left(\begin{array}{c}\hfill \widehat{u}\hfill \\ \hfill \widehat{v}\hfill \\ \hfill \widehat{h}\hfill \end{array}\right)& =0\Rightarrow \omega \left({\omega }^2-f^2-c^2{k}^2\right)=0\hfill \\ \hfill & \Rightarrow \omega =\left\{\begin{array}{c}{\omega }_0=0\hfill \\ {\omega }_1={\left(f^2+c^2{k}^2\right)}^{1/2}\hfill \\ {\omega }_2=-{\left(f^2+c^2{k}^2\right)}^{1/2}.\hfill \end{array}\right.\hfill \end{array}(9)$

The three eigenvectors corresponding to the three eigenvalues ω₀, ω₁, ω₂ are

${\left(\begin{array}{c}\hfill \widehat{u}\hfill \\ \hfill \widehat{v}\hfill \\ \hfill \widehat{h}\hfill \end{array}\right)}_0=A\left(\begin{array}{c}\hfill 0\hfill \\ \hfill ck\hfill \\ \hfill -f\hfill \end{array}\right),\hspace{0.17em}{\left(\begin{array}{c}\hfill \widehat{u}\hfill \\ \hfill \widehat{v}\hfill \\ \hfill \widehat{h}\hfill \end{array}\right)}_1=\frac{A}{\sqrt{2}}\left(\begin{array}{c}\hfill -i{\omega }_1\hfill \\ \hfill f\hfill \\ \hfill ck\hfill \end{array}\right),{\left(\begin{array}{c}\hfill \widehat{u}\hfill \\ \hfill \widehat{v}\hfill \\ \hfill \widehat{h}\hfill \end{array}\right)}_2=\frac{A}{\sqrt{2}}\left(\begin{array}{c}\hfill -i{\omega }_2\hfill \\ \hfill f\hfill \\ \hfill ck\hfill \end{array}\right),(10)$

where $A={\left(f^2+c^2{k}^2\right)}^{-1/2}$ is the normalization constant. Using the assumed form of solution and the derivative relation for rJ₁ (kr), the potential vorticity anomaly can be written as $P^{\prime }=(ck\widehat{v}-f\widehat{h})J_0(kr)e^{i\omega t}$. For the eigenvector corresponding to the eigenvalue ω₀, the potential vorticity anomaly is $P^{\prime }={\left(f^2+c^2{k}^2\right)}^{1/2}{J}_0(kr)$. In contrast, since the factor $ck\widehat{v}-f\widehat{h}$ vanishes for both the eigenvector corresponding to the eigenvalue ω₁ and the eigenvector corresponding to the eigenvalue ω₂, both of these inertia-gravity modes have P′ = 0. In other words, although the inertia-gravity waves contribute to the u (r, t), v (r, t), and h′(r, t) fields, these waves are invisible in the P′(r, t) field. The remainder of this section is devoted to understanding how inertia-gravity waves can be excited on the edge of a rapidly intensifying PV disk or the edges of a rapidly intensifying PV annulus.

Single, independent, second order partial differential equations for u (r, t), v (r, t), and h′(r, t) can be found. The easiest to derive is the equation for the divergent component u (r, t), which can be found by taking ∂/∂t of the radial momentum equation and then using the other two equations to eliminate ∂v/∂t and ∂h′/∂t. Then, including boundary and initial conditions, the complete linear problem for the radial flow is given in the first entry of Eq. 11. Since the rotational wind component v (r, t) plays such a central role in tropical cyclone dynamics, the single partial differential equation for v (r, t) is of particular interest. This equation can be obtained by taking (∂/∂t) of the v-equation in Eq. 7, then using the u-equation to eliminate (∂u/∂t), and finally using the second entry in Eq. 8 to eliminate h′. Then, including boundary and initial conditions, the complete linear problem for the azimuthal flow is given in the second entry of Eq. 11. Similarly, and again making use of the second entry in Eq. 8, we can derive the single partial differential equation for h′(r, t), which is given in the third entry of Eq. 11. To summarize, the linear primitive equation problems for u (r, t), v (r, t), and h′(r, t) as independent equations are as follows:

$\begin{array}{c}\hfill \underline{\mathbf{\text{Linear Klein}}-\mathbf{\text{Gordon Equations for}}u\left(r,t\right),v\left(r,t\right),h^{\prime }\left(r,t\right)}\hfill \\ \hfill \begin{array}{cc}\hfill \frac{\partial }{\partial r}\left(\frac{\partial \left(ru\right)}{r\partial r}\right)-\frac{1}{c^2}\left(f^2+\frac{{\partial }^2}{\partial t^2}\right)u& =-\frac{\partial S}{\partial r}\hfill \\ \hfill \text{with}& \left.\left\{\begin{array}{cc}\text{BCs:}\hfill & u=0\text{at}r=0,ru\to 0\text{as}r\to \infty \hfill \\ \text{ICs:}\hfill & u=0\text{and}{u}_t=0\text{at}t=0\hfill \end{array}\right.\right\},\hfill \\ \hfill \frac{\partial }{\partial r}\left(\frac{\partial \left(rv\right)}{r\partial r}\right)-\frac{1}{c^2}\left(f^2+\frac{{\partial }^2}{\partial t^2}\right)v& =\frac{\partial P^{\prime }}{\partial r}\hfill \\ \hfill \text{with}& \left.\left\{\begin{array}{cc}\text{BCs:}\hfill & v=0\text{at}r=0,rv\to 0\text{as}r\to \infty \hfill \\ \text{ICs:}\hfill & v=0\text{and}{v}_t=0\text{at}t=0\hfill \end{array}\right.\right\},\hfill \\ \hfill \frac{\partial }{r\partial r}\left(r\frac{\partial h^{\prime }}{\partial r}\right)-\frac{1}{c^2}\left(f^2+\frac{{\partial }^2}{\partial t^2}\right)h^{\prime }& =\frac{f}{g}{P}^{\prime }+\frac{1}{g}\frac{\partial S}{\partial t}\hfill \\ \hfill \text{with}& \left.\left\{\begin{array}{cc}\text{BCs:}\hfill & \frac{\partial h^{\prime }}{\partial r}=0\text{at}r=0,r{h}^{\prime }\to 0\text{as}r\to \infty \hfill \\ \text{ICs:}\hfill & h^{\prime }=0\text{and}{h}_t^{\prime }=-\bar{h}S\text{at}t=0\hfill \end{array}\right.\right\}.\hfill \end{array}\hfill \end{array}(11)$

Equations of the type Eq. 11 are often referred to as linear, inhomogeneous, Klein-Gordon equations (Whitham, 1974), or, in the context of electromagnetic theory, as equations of telegraphy (see Cahn Jr, 1945, and sections 4.10 and 5.6 of Copson, 1975). See Supplementary Appendix A for historical notes on the Klein-Gordon equation. The initial conditions listed in Eq. 11 guarantee that the evolving flow results entirely from the forcing S (r, t). Note that the three equations in Eq. 11 contain time-dependent inhomogeneities that depend on the forcing. For the idealized forcing given below in the first entry of Eq. 13, P′(r, t) grows as shown in the second entry of Eq. 13, so that |∂P′/∂r| at the PV edge increases with time and inertia-gravity waves can be excited there. Thus, more generally, the inner and outer edges of a PV annulus can be regions for the generation of inertia-gravity waves. Since the three Klein-Gordon equations in Eq. 11 are linear, they can be solved by transform methods, e.g., Laplace transforms in time or Hankel transforms in radius. The Hankel transform solution of the Klein-Gordon equation for v (r, t) is discussed in Supplementary Appendix B.

When the forcing is slow enough, the pressure field and the azimuthal wind field remain close to a state of balance, so that the radial wind equation could be discarded and replaced by $v_b=(g/f)(\partial h_b^{\prime }/\partial r)$. This is equivalent to saying that the (∂²/∂t²) terms in Eq. 11 all become negligible. Also, when the forcing is slow enough, the time derivative of the forcing becomes small and can be neglected. Thus, in this slow forcing case, each of the equations in Eq. 11 simplifies to a diagnostic equation, with the first equation in Eq. 11 reducing to a diagnostic equation for the slowly evolving divergent flow u_b (r, t), the second equation in Eq. 11 reducing to an invertibility principle for the balanced rotational flow v_b (r, t), and the third equation in Eq. 11 reducing to an invertibility principle for the balanced mass field $h_b^{\prime }(r,t)$. The only initial condition required is on P′(r, t), so that the hyperbolic problems in Eq. 11 reduce to

$\begin{array}{c}\hfill \underline{\mathbf{\text{Linear Balanced Problems for}}{u}_b\left(r,t\right),v_b\left(r,t\right),h_b^{\prime }\left(r,t\right)}\hfill \\ \hfill \begin{array}{cccc}\hfill \frac{\partial }{\partial r}\left(\frac{\partial \left(r{u}_b\right)}{r\partial r}\right)-{\mu }^2{u}_b& =-\frac{\partial S}{\partial r}\hfill & \hfill & \text{with\hspace{0.17em}BCs:}{u}_b=0\text{at}r=0,r{u}_b\to 0\text{as}r\to \infty ,\hfill \\ \hfill \frac{\partial }{\partial r}\left(\frac{\partial \left(r{v}_b\right)}{r\partial r}\right)-{\mu }^2{v}_b& =\frac{\partial P^{\prime }}{\partial r}\hfill & \hfill & \text{with\hspace{0.17em}BCs:}{v}_b=0\text{at}r=0,r{v}_b\to 0\text{as}r\to \infty ,\hfill \\ \hfill \frac{\partial }{r\partial r}\left(r\frac{\partial h_b^{\prime }}{\partial r}\right)-{\mu }^2{h}_b^{\prime }& =\frac{f}{g}{P}^{\prime }\hfill & \hfill & \text{with\hspace{0.17em}BCs:}\frac{\partial h_b^{\prime }}{\partial r}=0\text{at}r=0,r{h}_b^{\prime }\to 0\text{as}r\to \infty ,\hfill \end{array}\hfill \end{array}(12)$

where μ = f/c is the inverse of the Rossby length.

In order to provide examples of the solutions of the linear balanced flow problems (Eq. 12), we now assume that the mass sink S (r, t) vanishes for r > r₀ and is horizontally uniform for r ≤ r₀, where r₀ is a specified constant. The time dependence of the mass sink is assumed to be $(t/t_s^2)e^{-t/t_s}$, where the specified constant t_s is the time at which the mass sink is a maximum. Small values of t_s correspond to rapid forcing and large values of t_s to slow forcing, but the total forcing is independent of t_s since ${\int }_0^{\infty }(t/t_s^2)e^{-t/t_s}dt=1$. This forcing S (r, t) and the result of using it in Eq. 8 are given by

$\begin{array}{ll}\hfill S\left(r,t\right)& =\frac{\mathcal{V}}{\pi r_0^2\bar{h}}\left\{\begin{array}{cc}\left(t/t_s^2\right)e^{-t/t_s}\hfill & 0\le r\le r_0\hfill \\ 0\hfill & r_0<r<\infty \hfill \end{array}\right.\hfill \\ \hfill & \Rightarrow P^{\prime }\left(r,t\right)=\frac{f\mathcal{V}}{\pi r_0^2\bar{h}}\left\{\begin{array}{cc}1-\left(1+t/t_s\right)e^{-t/t_s}\hfill & 0\le r\le r_0\hfill \\ 0\hfill & r_0<r<\infty ,\hfill \end{array}\right.\hfill \end{array}(13)$

where $\mathcal{V}$ is a specified constant. Thus, the P′ field is a disk of fixed radius r₀, with the value of P′ in its interior increasing in time. The ultimate value of P′ in the disk is independent of the specified constant t_s since $P^{\prime }(r,t)\to f(\mathcal{V}/\pi r_0^2\bar{h})$ as t → ∞ for r ≤ r₀. With this particular forcing S (r, t), integration of the linearized continuity equation over all r and all t yields $2\pi {\int }_0^{\infty }[\bar{h}-h(r,\infty )]rdr=\mathcal{V}$, so the constant $\mathcal{V}$ can be interpreted as the total volume of fluid removed by the mass sink over its life cycle. We now assume that $\mathcal{V}=\pi r_0^2\bar{h}$, i.e., the mass sink removes all the fluid initially inside r = r₀. Because the linear dynamics have the limitation that |P′| < f, this value of $\mathcal{V}$ is essentially the maximum allowable value, since, according to the second entry in Eq. 13, it allows the magnitude of the growing PV jump at r = r₀ to maximize at the value f. The time dependence of the mass sink S (r, t) for r ≤ r₀ is shown in Figure 1A for the three choices t_s = 3, 6, 12 h. The time dependence of P′(r, t)/f for r ≤ r₀, as given by the second entry in Eq. 13, is shown in Figure 1B. Thus, without restating the boundary conditions, the linear balanced problems (Eq. 12) with this forcing (Eq. 13) take the forms

$\begin{array}{c}\hfill \underline{\mathbf{\text{Linear Balanced Problems for the Specified Forcing}}\left(\text{13}\right)}\hfill \\ \hfill \begin{array}{cc}\hfill r^2\frac{{\partial }^2{u}_b}{\partial r^2}+r\frac{\partial u_b}{\partial r}& -\left({\mu }^2{r}^2+1\right)u_b=0\text{for}r\ne r_0\hfill \\ \hfill & \text{with}{\left[u_b\right]}_{r_0-}^{r_0+}=0\text{and}{\left[\frac{\partial \left(r{u}_b\right)}{r\partial r}\right]}_{r_0-}^{r_0+}=\left(t/t_s^2\right)e^{-t/t_s},\hfill \\ \hfill r^2\frac{{\partial }^2{v}_b}{\partial r^2}+r\frac{\partial v_b}{\partial r}& -\left({\mu }^2{r}^2+1\right)v_b=0\text{for}r\ne r_0\hfill \\ \hfill & \text{with}{\left[v_b\right]}_{r_0-}^{r_0+}=0\text{and}{\left[\frac{\partial \left(r{v}_b\right)}{r\partial r}\right]}_{r_0-}^{r_0+}=-f\left[1-\left(1+t/t_s\right)e^{-t/t_s}\right],\hfill \\ \hfill r^2\frac{{\partial }^2{h}_b^{\prime }}{\partial r^2}+r\frac{\partial h_b^{\prime }}{\partial r}& -{\mu }^2{r}^2{h}_b^{\prime }=\frac{f^2{r}^2}{g}\left\{\begin{array}{cc}1-\left(1+t/t_s\right)e^{-t/t_s}\hfill & \text{if}0\le r<r_0\hfill \\ 0\hfill & \text{if}{r}_0<r<\infty ,\hfill \end{array}\right.\hfill \\ \hfill & \text{with}{\left[h_b^{\prime }\right]}_{r_0-}^{r_0+}=0\text{and}{\left[\frac{\partial h_b^{\prime }}{\partial r}\right]}_{r_0-}^{r_0+}=0.\hfill \end{array}\hfill \end{array}(14)$

FIGURE 1

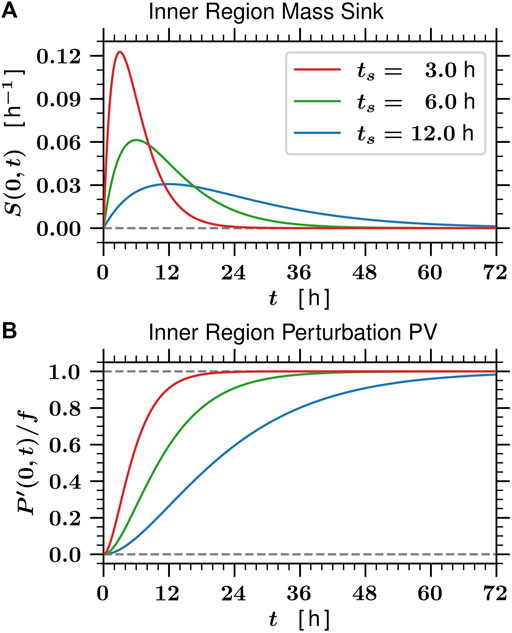
FIGURE 1. Panel (A) shows the time dependence of the mass sink S (r, t) for r ≤ r₀, as given by the first entry in Eq. 13, with $\mathcal{V}=\pi r_0^2\bar{h}$, for the three choices t_s =3,6,12 h, where the specified constant t_s is the time at which the mass sink is a maximum. Since the areas under the three curves are identical, the total mass removed by the mass sink is independent of t_s. Panel (B) shows the corresponding time dependence of P′(r, t)/f for r ≤ r₀, as given by the second entry in Eq.13, again for the three choices t_s =3,6,12 h. Although the rate of increase of P′(r, t) depends on t_s, the ultimate value of the P′(r, t) is independent of t_s, with P′(r, t)→ f as t →∞ for r ≤ r₀.

Note that the relations Eq. 13 for S (r, t) and P′(r, t) result in Dirac delta functions on the right-hand sides of the u_b and v_b equations in Eq. 12. In Eq. 14, these become jump conditions on the radial derivatives of ru_b and rv_b. The equations governing u_b (r, t) and v_b (r, t) for r ≠ r₀ are homogeneous modified Bessel equations of order one, while the equation governing $h_b^{\prime }(r,t)$ is an inhomogeneous modified Bessel equation of order zero. This difference in orders arises from the difference in the radial derivative operators in Eq. 12. The jump conditions on the radial derivatives of ru_b and rv_b can be derived via integration of the first two equations in Eq. 12 over a narrow radial interval surrounding r = r₀.

As can be checked by direct substitution, the solutions of Eq. 14, along with the associated formula for the relative vorticity, are

$\begin{array}{c}\hfill \underline{\mathbf{\text{Solutions of the Linear Balanced Problems}}\left(\text{14}\right)}\hfill \\ \hfill \begin{array}{cc}\hfill u_b\left(r,t\right)& =-r_0\left(t/t_s^2\right)e^{-t/t_s}\left\{\begin{array}{cc}{I}_1\left(\mu r\right)K_1\left(\mu r_0\right)\hfill & \text{if}0\le r\le r_0\hfill \\ I_1\left(\mu r_0\right)K_1\left(\mu r\right)\hfill & \text{if}{r}_0\le r<\infty ,\hfill \end{array}\right.\hfill \\ \hfill v_b\left(r,t\right)& =r_{0}f\left[1-\left(1+t/t_s\right)e^{-t/t_s}\right]\left\{\begin{array}{cc}{I}_1\left(\mu r\right)K_1\left(\mu r_0\right)\hfill & \text{if}0\le r\le r_0\hfill \\ I_1\left(\mu r_0\right)K_1\left(\mu r\right)\hfill & \text{if}{r}_0\le r<\infty ,\hfill \end{array}\right.\hfill \\ \hfill h_b^{\prime }\left(r,t\right)& =-\bar{h}\left[1-\left(1+t/t_s\right)e^{-t/t_s}\right]\left\{\begin{array}{cc}1-\mu r_0{I}_0\left(\mu r\right)K_1\left(\mu r_0\right)\hfill & \text{if}0\le r\le r_0\hfill \\ \mu r_0{I}_1\left(\mu r_0\right)K_0\left(\mu r\right)\hfill & \text{if}{r}_0\le r<\infty ,\hfill \end{array}\right.\hfill \\ \hfill {\zeta }_b\left(r,t\right)& =f\left[1-\left(1+t/t_s\right)e^{-t/t_s}\right]\left\{\begin{array}{cc}\mu r_0{I}_0\left(\mu r\right)K_1\left(\mu r_0\right)\hfill & \text{if}0\le r\le r_0\hfill \\ -\mu r_0{I}_1\left(\mu r_0\right)K_0\left(\mu r\right)\hfill & \text{if}{r}_0<r<\infty ,\hfill \end{array}\right.\hfill \end{array}\hfill \end{array}(15)$

where I₀ and K₀ are the zero order modified Bessel functions, and I₁ and K₁ are the first order modified Bessel functions. All four of the solution fields in Eq. 15 are continuous across r = r₀ except ζ_b (r, t). The fact that the solutions u_b (r, t) and v_b (r, t) given in Eq. 15 satisfy the jump conditions can be checked by using the derivative relations d [rI₁ (μr)]/rdr = μI₀ (μr) and d [rK₁ (μr)]/rdr = −μK₀ (μr), and the Wronskian I₀ (μr₀)K₁ (μr₀) + K₀ (μr₀)I₁ (μr₀) = 1/(μr₀). Using this Wronskian, it is easily seen that the jump in ζ_b across r = r₀ is the same as the jump in P′. The maximum inflow occurs at r = r₀ when t = t_s, while the maximum azimuthal flow occurs at r = r₀ as t → ∞ and the minimum fluid depth anomaly occurs at r = 0 as t → ∞.

We now examine actual solutions of the linear balanced model and the linear primitive equation model, using the parameters specified in Table 1 and the three forcing cases shown in Figure 1. The solutions of the linear primitive equation model (Eq. 7) are obtained numerically using a second-order, centered finite differencing scheme radially, a fourth-order Runge-Kutta scheme temporally, an outer radial boundary set at r = 5000 km, a 100 m radial resolution, and a 1 s temporal resolution. Select properties of the linear balanced solutions, specifically the values of u_b (r₀, t_s), v_b (r₀, ∞), and $h_b^{\prime }(0,\infty )$, are given in Table 2. For the rapid forcing case t_s = 3 h, the linear balanced solutions $u_b(r,t),v_b(r,t),h_b^{\prime }(r,t)$ and the linear primitive equation solutions u (r, t), v (r, t), h′(r, t) are respectively plotted in the left and right columns of Figure 2. Similarly, Figure 3 shows linear balanced (left column) and linear primitive equation (right column) results for parameter settings identical to those in Figure 2, except that the time scale t_s has been increased from 3 h to 6 h. Note from Figures 2, 3 that the differences between the balanced and primitive equation results become smaller as the forcing time scale t_s increases from 3 h to 6 h. In fact, we have chosen not to show the t_s = 12 h case because the balanced solutions and the primitive equation solutions are so similar for this case. To better understand the nature of the inertia-gravity wave motion excited in the primitive equation model, Figure 4 shows the time behavior of the u, v, h′ fields at r = 200, 400, 600, 800, 1000 km for the t_s = 3 h case (left column) and for the t_s = 6 h case (right column). The h′(r, t) field most clearly shows the outward-propagating inertia-gravity wave packet. For the t_s = 3 h case, that wave packet causes the negative depth anomaly to overshoot before returning to an equilibrium value that is the same as that given by the balanced solution $h_b^{\prime }(r,\infty )$. Although individual inertia-gravity wave components can have shorter time scales, the superposition of these individual components into an inertia-gravity wave packet results in an outward-propagating wave pattern that has a time scale (period) of approximately 11 h.

TABLE 1

TABLE 1. Parameters used for the linear balanced and linear primitive equation solutions.

TABLE 2

TABLE 2. The maximum radial inflow, maximum azimuthal wind, and final central depth anomaly for the three forcing cases t_s =3,6,12 h, as computed from the linear balanced solutions (Eq. 15) using the specified and computed constants listed in Table 1. The maximum radial inflow is proportional to 1/t_s, but the weaker inflows last progressively longer. Since the same volume of fluid is removed in each case, the final values v_b (r₀,∞) and $h_b^{\prime }(0,\infty )$ are the same. Even though all the original mass inside r = r₀ has been removed by the mass sink, almost all of this mass has been replaced by the time-integrated inflow at r = r₀, so that the final central depth anomaly is only −11.43 m. Detailed plots of the t_s =3 h and t_s =6 h cases are presented in Figures 2, 3. The t_s =12 h case is not shown since the balanced solutions and the primitive equation solutions are so similar.

FIGURE 2

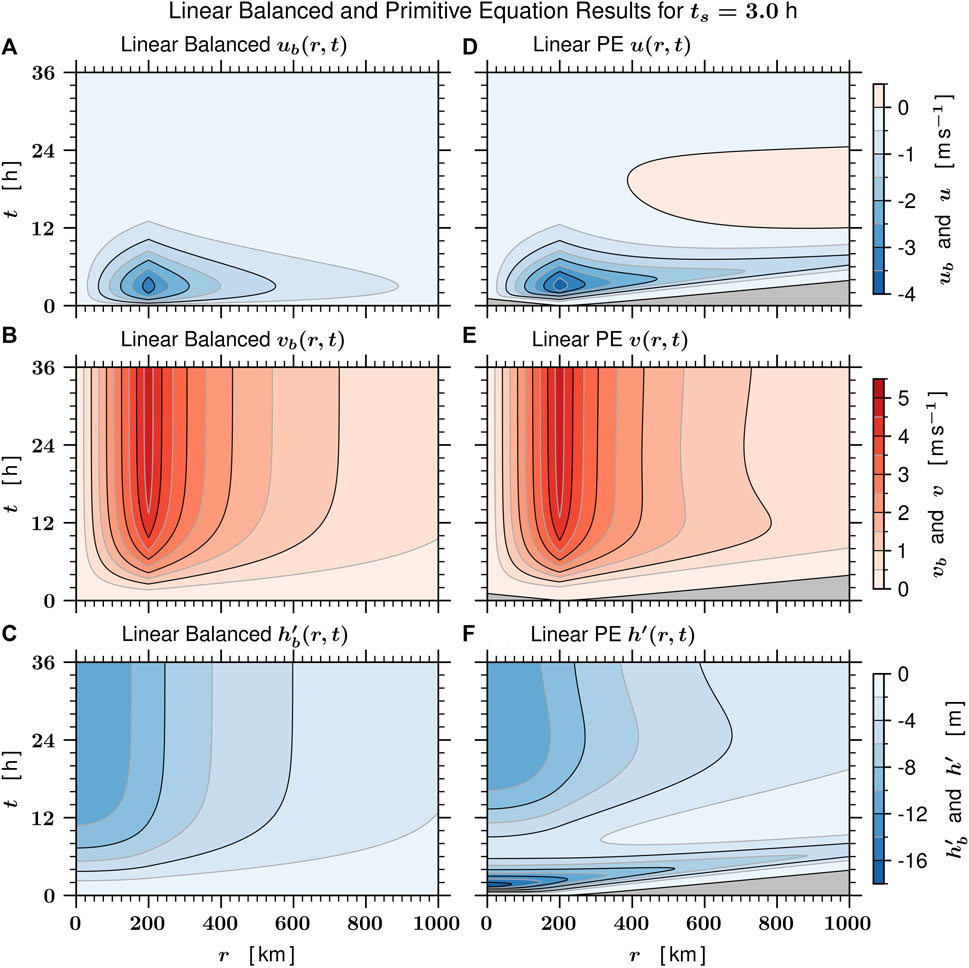
FIGURE 2. Panels (A-C) show the linear balanced solutions $u_b(r,t),v_b(r,t),h_b^{\prime }(r,t)$ obtained from Eq. 15, while panels (D-F) show the corresponding linear primitive equation (PE) solutions u (r, t), v (r, t), h′(r, t) obtained from Eq. 7 or equivalently from Eq. 11, all for the rapid forcing case t_s =3 h. The isoline intervals are 0.5 m s⁻¹ for the radial and azimuthal flow and 2.0 m for the perturbation depth, and the gray regions indicate initial regions where the plotted field is zero. The peak radial inflow is −3.3 m s⁻¹ for the balanced case and −3.8 m s⁻¹ for the primitive equation case, which has a slight overshoot. As t →∞, both v_b (r₀, t) and v (r₀, t) approach 4.8 m s⁻¹, while both $h_b^{\prime }(0,t)$ and h′(0, t) approach −11.4 m. Note that in the outer region 800< r <1000 km, the balanced model response to the inner core forcing is instantaneous (action at a distance), while in the primitive equation model there is a 4–5 h delay as the inertia-gravity wave packet propagates outward at 50 m s⁻¹. The pink area in the u (r, t) panel is weak outward radial velocity and is associated with inertia-gravity waves having very small radial wavenumber k, so that the relevant frequency ${(f^2+c^2{k}^2)}^{1/2}$ is close to the inertia frequency ω ≈ f (i.e., a period of approximately 34.9 h).

FIGURE 3

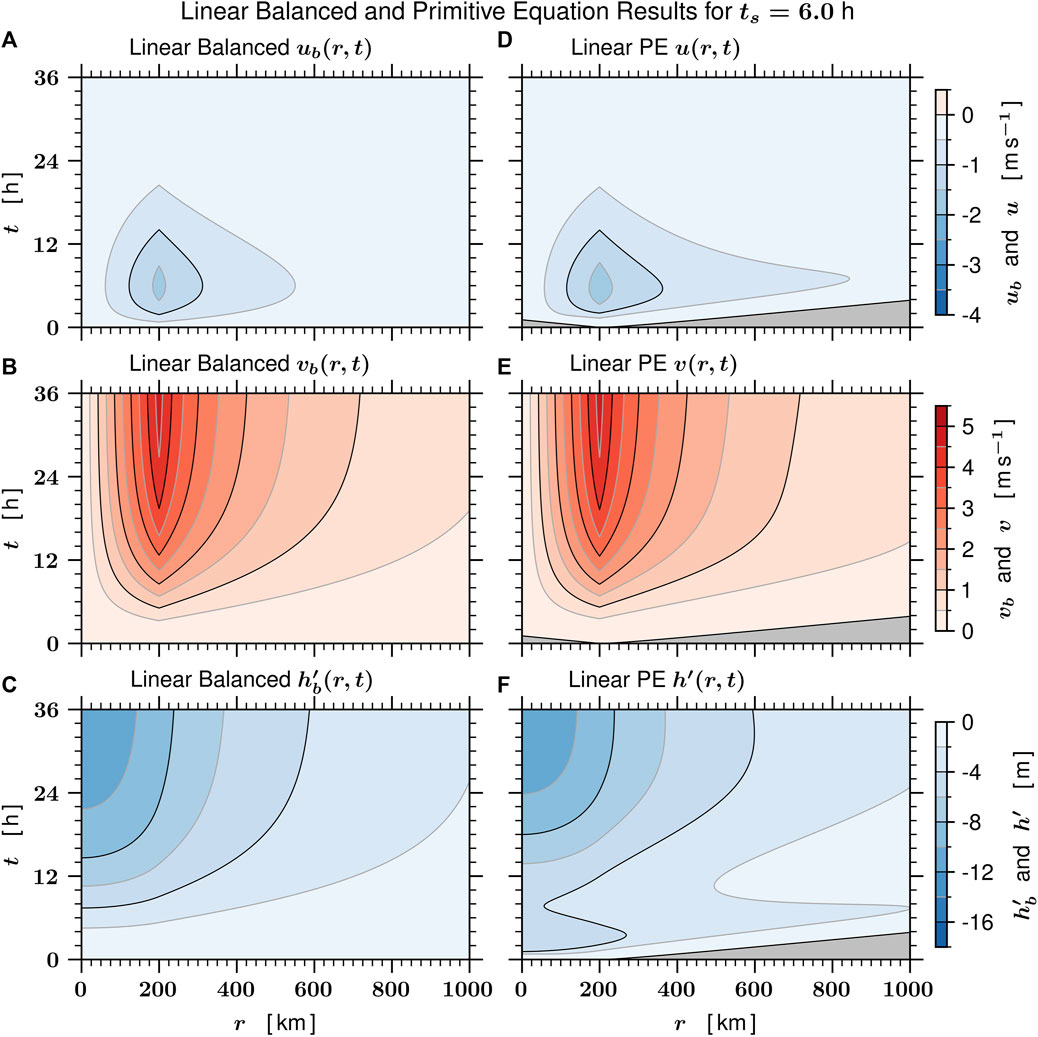
FIGURE 3. As in Figure 2, panels (A-C) show the linear balanced solutions $u_b(r,t),v_b(r,t),h_b^{\prime }(r,t)$ while panels (D-F) show the corresponding linear primitive equation solutions u (r, t), v (r, t), h′(r, t). All parameter settings used in this figure are identical to those used in Figure 2, except that t_s has been changed, i.e., Figure 2 corresponds to the rapid forcing case t_s =3 h, while the present figure corresponds to the less rapid forcing t_s =6 h. Note that, with less rapid forcing, the differences between the balanced and primitive equation solutions are smaller.

FIGURE 4

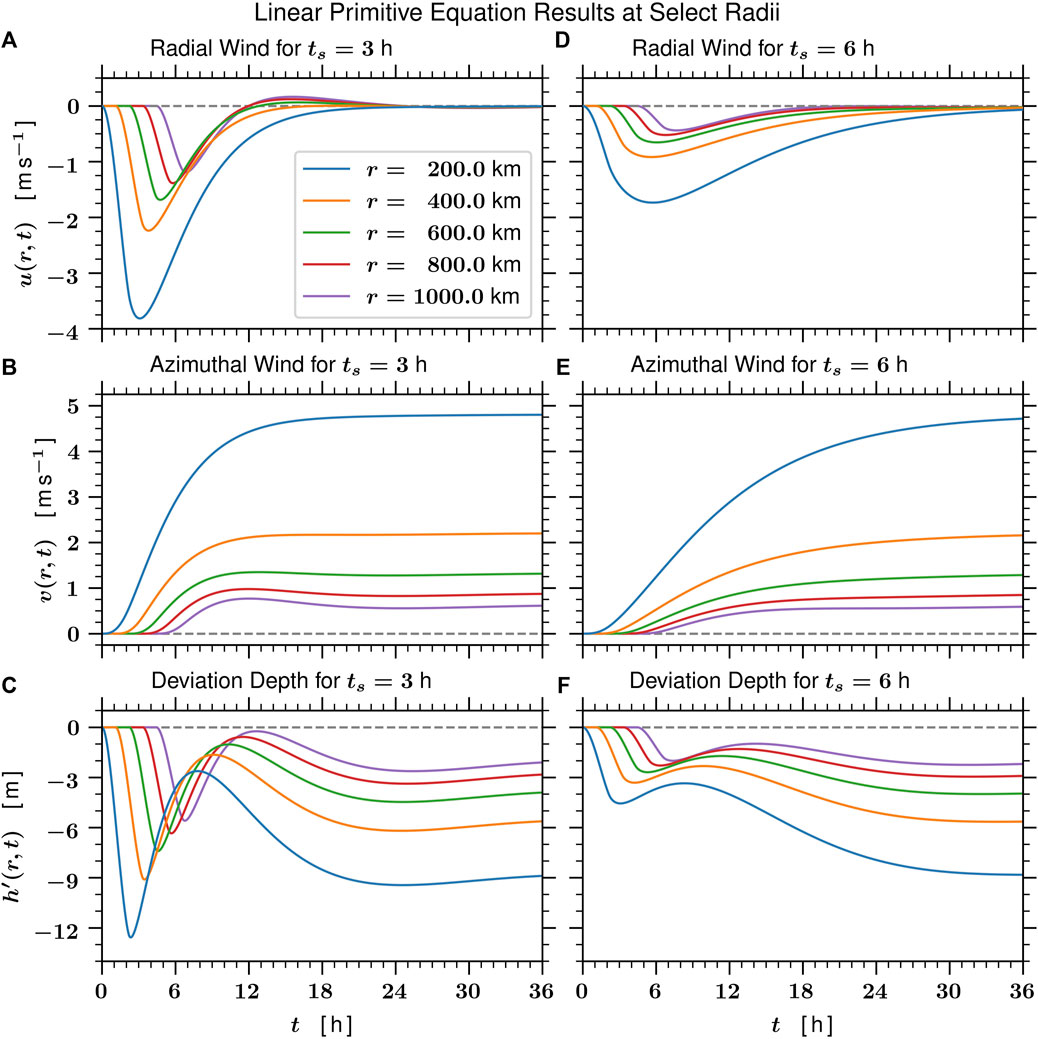
FIGURE 4. This figure shows the time dependence of the linear primitive equation solutions for the radial flow u (r, t), the azimuthal flow v (r, t), and the deviation depth h′(r, t) at the selected radii r =200,400,600,800,1000 km for the rapid forcing case t_s =3 h (A-C) and for the less rapid forcing case t_s =6 h (D-F). Note that these curves are simply vertical cross sections from Figures 2, 3. The outward propagating inertia-gravity wave packet is most readily apparent in the h′(r, t)-field, where it is immediately seen at r =200 km, and is seen, for example, with an approximately 4.5 h delay at r =1000 km. At each radius for the rapid forcing case (t_s =3 h) these linear primitive equation solutions for h′(r, t) overshoot before coming into adjustment at a value that equals $h_b^{\prime }(r,\infty )$. The less rapid forcing case (t_s =6 h) generates a weaker inertia-gravity wave packet that does not result in such an overshoot in the h′(r, t) solutions.

The fundamental difference between the radial and azimuthal wind fields plotted in Figures 2, 3 can be understood as follows. The Dirac delta function on the right-hand side of the Klein-Gordon equation for u (r, t) and on the right-hand side of the diagnostic equation for u_b (r, t) is characterized by a single pulse in time, so that both u (r, t) and u_b (r, t) go to zero as t → ∞, similar to S (r, t). In contrast, the Dirac delta function on the right-hand side of the Klein-Gordon equation for v (r, t) and on the right-hand side of the invertibility principle for v_b (r, t) is characterized by the same time behavior as the PV, so that both $v\left(r,17\right.$ and v_b (r, t) approach nonzero values as t → ∞.

The solution of the invertibility problem for v_b (r, t) or the solution of the invertibility problem for $h_b^{\prime }(r,t)$ can be viewed as essentially converting the radial distribution of P′ into the radial distributions of ζ_b and $h_b^{\prime }$. This is a nonlocal process since it involves the solution of a second order differential equation. Since $P^{\prime }=\zeta -(f/\bar{h})h^{\prime }$ and since P′ = 0 for r > r₀, we obtain ${\zeta }_b=(f/\bar{h})h_b^{\prime }<0$ for r > r₀. The situation is quite different in the region r ≤ r₀, where P′ > 0. In this region, ζ_b > 0 and $h_b^{\prime }<0$, so both the wind field and the mass field contribute to the positive PV anomaly. To better understand how the partitioning between ζ_b and $h_b^{\prime }$ in the core (r ≤ r₀) depends on vortex size, note that the average vorticity in the core is given by 2v_b (r₀, t)/r₀, which allows us to write

$\begin{array}{ll}\hfill \frac{\text{Average\hspace{0.17em}Core\hspace{0.17em}Vorticity}}{\text{Core\hspace{0.17em}PV\hspace{0.17em}Anomaly}}& =\frac{2v_b\left(r_0,t\right)/r_0}{P^{\prime }\left(0,t\right)}=2I_1\left(\mu r_0\right)K_1\left(\mu r_0\right)\hfill \\ \hfill & =\left(0.960,0.891,0.817,0.746,0.680\right)\hfill \\ \hfill & \text{for}\mu r_0=\left(0.2,0.4,0.6,0.8,1.0\right),\hfill \end{array}(16)$

where the second equality follows from the cancellation of the time dependence of v_b (r₀, t) with the time dependence of P′(0, t). Thus, as long as the radius of the vortex core is less than a Rossby length (i.e., μr₀ < 1), most of the PV anomaly in the core is partitioned to the vorticity field rather than to the mass field.

Since P′(r, t) grows as shown in Eq. 8, then |∂P′/∂r| at the PV edge increases with time and inertia-gravity waves can be excited there. Thus, the outer edge of a PV tower can be a region for the spontaneous generation of inertia-gravity waves. The inertia-gravity wave packets initiated at r = 200 km propagate inward and outward at $c={(g\bar{h})}^{1/2}=50$ m s⁻¹ = 180 km h⁻¹, so that at r = 920 km the radial flow u, the azimuthal flow v, and the free surface height anomaly h′ remain zero for the first 4 hours, immediately after which the height anomaly quickly becomes negative, the radial flow quickly becomes inward, and the azimuthal flow becomes cyclonic. Although the inertia-gravity wave packets are visible in the u (r, t), v (r, t), and h′(r, t) fields, they are invisible in the P′(r, t) field. Even though the balanced solutions $u_b(r,t),v_b(r,t),h_b^{\prime }(r,t)$ filter inertia-gravity waves, they are useful approximations of the primitive equation solutions u (r, t), v (r, t), h′(r, t) even when the time scale of the mass sink is as short as t_s = 3 h. Since the balanced dynamics have an elliptic rather than a hyperbolic character, the response at large radius to a mass sink at small radius is immediate, i.e., it can be described as “action at a distance.” In this regard, the following analogy is useful: The balanced model is to the primitive equation model as Newton’s gravitational theory is to general relativity, i.e., in the shallow water primitive equations information cannot radially propagate faster than $c={(g\bar{h})}^{1/2}$, while in general relativity information cannot propagate faster than the speed of light.

We may use the results of this section as the basis for the following physical picture. Each pulse of eyewall convective mass transport from the lower to the upper troposphere is accompanied by a corresponding pulse in the divergent circulation, which ratchets up the rotational circulation and ratchets down the fluid depth. According to the balanced model, the time dependence of the divergent circulation is in lock-step with the forcing S (r, t); this behavior is due to the mathematically elliptic character of the balanced divergent flow (i.e., action at a distance). Convection in the hurricane eyewall can fluctuate on a variety of time scales, so the secondary circulation is expected to fluctuate in a roughly similar fashion. If the convective fluctuations have a vertical structure similar to the first internal mode of the troposphere, the associated gravity wave speed is approximately 50 m s⁻¹ (180 km h⁻¹), so the information from eyewall convective fluctuations will propagate outward to 1000 km in approximately 4.5 h. For eyewall convective fluctuations having time scales larger than 6 h, the amplitude of the associated inertia-gravity wave packet is small, but for eyewall convective fluctuations with time scales less than 3 h, the amplitude of the associated wave packets may be considerably larger. In a continuously stratified fluid the inertia-gravity wave packets also propagate vertically, an important aspect that is further discussed in Section 5.

Although the linear analysis presented in this section provides a helpful guide to the nonlinear analysis of Section 4, the linearization used in Eq. 7 means that we are not analyzing true gradient adjustment and are restricting applications of the analytical results to situations where ζ < f, whereas real tropical cyclones involve situations in which ζ ∼ 100f. In Section 4 we examine the full nonlinear case.

4 Nonlinear dynamics in the Lagrangian coordinate

We now return to the nonlinear shallow water equations of Section 2, and perform numerical integrations using two types of forcing. The first type uses the mass sink defined by Eq. 13, i.e., the mass sink is confined within a disk of fixed radius (0 ≤ r ≤ r₀). The second type, defined below in Eq. 27, uses a mass sink that is confined within the disk 0 ≤ R ≤ R₀, where R is a Lagrangian coordinate that collapses as the vortex intensifies. As we shall see, there are some remarkable differences in the vortices that can be produced by these two types of forcing.

Figure 5 compares the nonlinear (left panels) and linear (right panels) numerical integrations using the identical parameter settings and forcing used to obtain the results shown in the right column of Figure 2. A major difference between the linear and nonlinear cases is the inward shift of the radius of maximum wind in the nonlinear case. In the linear case the azimuthal equation is (∂v/∂t) = −fu, so the radial distributions of (∂v/∂t) and − u are identical. In the nonlinear case the azimuthal equation is (∂v/∂t) = −(f + ζ)u, so the radial distribution of (∂v/∂t) is shifted inward when compared to the radial distribution of − u. During the first 24 h, the radius of maximum azimuthal wind shifts inward from 200 km to about 150 km and the maximum azimuthal wind approaches 5.3 m s⁻¹. Thus, for 24 ≤ t ≤ 48 h, the average relative vorticity inside r = 150 km is approximately 1.4f, somewhat outside the range of validity for linear theory.

FIGURE 5

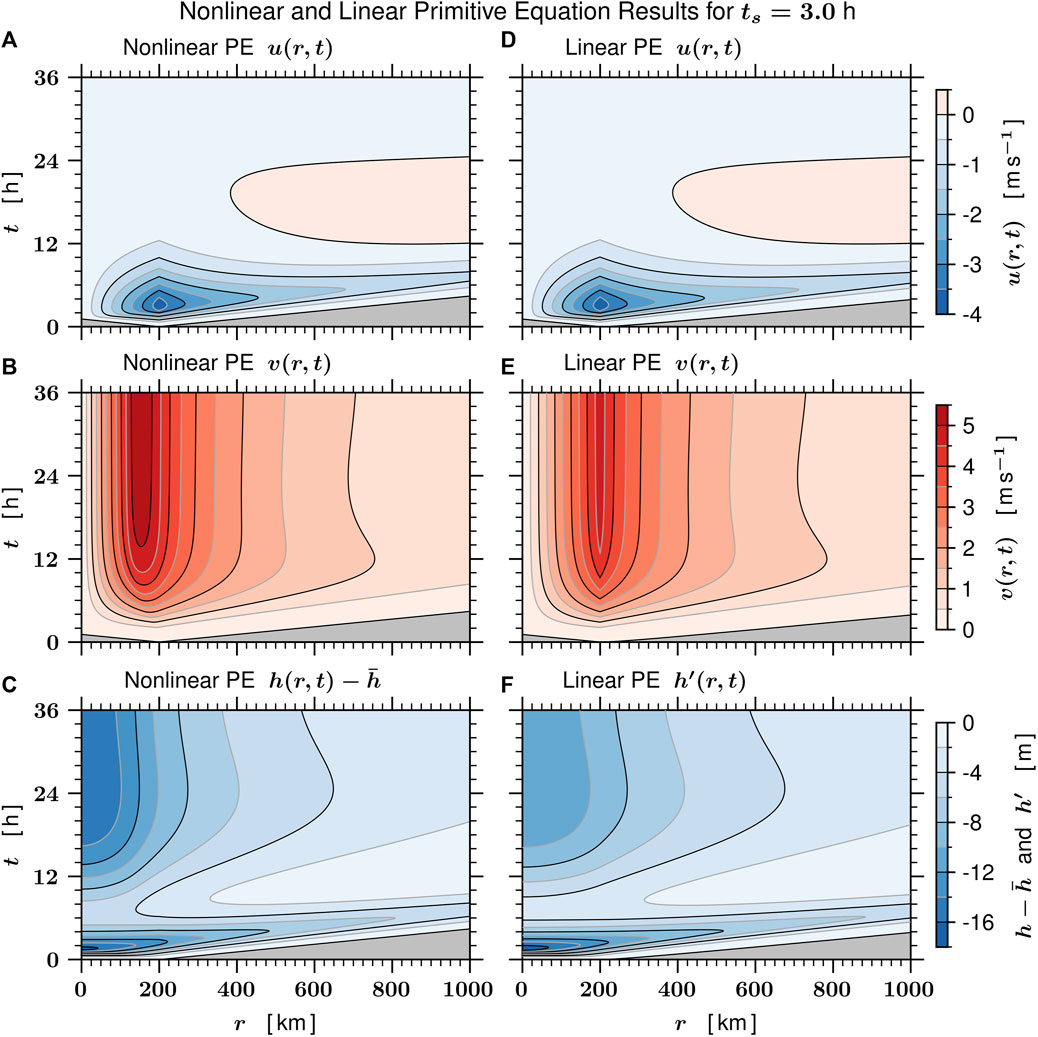
FIGURE 5. Panels (D-F) show the linear primitive equation solutions u (r, t), v (r, t), h′(r, t) for the rapid forcing case t_s =3 h as shown previously in the right panels of Figure 2. Panels (A-C) show the nonlinear primitive equation solutions $u(r,t),v(r,t),h(r,t)-\bar{h}$ obtained from Eq. 1 for the rapid forcing case t_s =3 h obtained using the same parameters and forcing as those used for the linear results. The isoline intervals are identical to those used in the linear case (Figure 2), i.e., 0.5 m s⁻¹ for the radial and azimuthal flow and 2.0 m for the perturbation depth, and the gray regions again indicate initial regions where the plotted field is zero. For the nonlinear results, the peak radial inflow is −3.8 m s⁻¹ and occurs at r =200 km, the central depth anomaly $h(0,t)-\bar{h}$ approaches −15.4 m as t →∞, and the maximum azimuthal flow approaches 5.3 m s⁻¹ at about r =150 km. It follows that, for 24≤ t ≤48 h, the average relative vorticity inside r =150 km is approximately 1.47 f. A major difference between the linear and nonlinear cases is the inward shift of the radius of maximum wind in the nonlinear case. Further discussion of this effect is given in Hack and Schubert (1986).

Before discussing results of the second type of forcing, we note that insight into nonlinear model results can be obtained by transforming from the original independent variables (r, t) to the new independent variables (R, τ), where τ = t and R is defined by $\frac{1}{2}f{R}^2=\frac{1}{2}f{r}^2+rv=\frac{1}{2}f{r}^2+RV$, with V = (r/R)v denoting the new dependent variable. Note that in general (∂/∂τ) ≠ (∂/∂t) since (∂/∂τ) implies fixed R while (∂/∂t) implies fixed r. We can think of R as an absolute angular momentum coordinate with the unit of length, or equivalently, as the potential radius, i. e., the radius to which a fluid particle must be moved, conserving its absolute angular momentum, in order for its azimuthal wind to vanish. Finally, in the present context of inviscid flow, R can also be viewed as a Lagrangian coordinate, i. e., as a fluid particle label. Noting that

$\left(1+\frac{2v}{fr}\right)\left(1-\frac{2V}{fR}\right)=1,(17)$

we can easily confirm that transformations between r, v and R, V can be written in the form

$\left\{\begin{array}{cc}\hfill R& ={\left(1+\frac{2v}{fr}\right)}^{1/2}r\hfill \\ \hfill V& ={\left(1+\frac{2v}{fr}\right)}^{-1/2}v\hfill \end{array}\right\}\iff \left\{\begin{array}{cc}\hfill r& ={\left(1-\frac{2V}{fR}\right)}^{1/2}R\hfill \\ \hfill v& ={\left(1-\frac{2V}{fR}\right)}^{-1/2}V\hfill \end{array}\right\}.(18)$

Since the relative circulation 2πrv divided by the area πr² is 2v/r, the factor (1 + 2v/fr) can be interpreted as the absolute circulation per unit area, measured in units of f, or equivalently, as the dimensionless average absolute vorticity inside the radius r. In the core of a hurricane we typically find (1 + 2v/fr) ∼ 100 and (1 − 2V/fR) ∼ (1/100), so that r ∼ (1/10) R and v ∼ 10 V. Because of the conservation of absolute angular momentum, the material derivative is (D/Dt) = (∂/∂t) + u (∂/∂r) = (∂/∂τ). As discussed below, this simplification of the material derivative will allow the PV equation to be directly integrated in time, so that the PV part of the dynamics can be treated analytically. The fact that (D/Dt) = (∂/∂τ) means that the radial advective effects u (∂u/∂r), u (∂v/∂r), u (∂h/∂r), and u (∂P/∂r) become implicit in the coordinate transformation r → R. If the solutions of the nonlinear shallow water equations are obtained in R-space, the effects of the radial advection terms do not appear until the final step of transforming the results back to r-space. Many of the characteristics of rapid intensification appear in this transformation R → r.

To further understand the transformation between v(r) and V(R), it is useful to consider the special case of a Rankine vortex. This example is simple because if V has a Rankine structure in R, then v has a Rankine structure in r, i. e.,

$V\left(R\right)=V_0\left\{\begin{array}{cc}R/R_0\hfill & \text{if}0\le R\le R_0\hfill \\ R_0/R\hfill & \text{if}{R}_0\le R<\infty \hfill \end{array}\right.\iff v\left(r\right)=v_0\left\{\begin{array}{cc}r/r_0\hfill & \text{if}0\le r\le r_0\hfill \\ r_0/r\hfill & \text{if}{r}_0\le r<\infty ,\hfill \end{array}\right.(19)$

where r₀, v₀ are related to R₀, V₀ by

$r_0={\left(1-\frac{2V_0}{f{R}_0}\right)}^{1/2}{R}_0\text{and}{v}_0={\left(1-\frac{2V_0}{f{R}_0}\right)}^{-1/2}{V}_0.(20)$

Thus, if we specify R₀ and V₀, then compute r₀ and v₀ from Eq. 20, we can plot V(R) and v(r) using Eq. 19. Figure 6 shows a family of Rankine vortices with R₀ = 300 km and 0 ≤ v₀ ≤ 65 m s⁻¹ where isolines of the physical azimuthal wind v in the (r, v₀)-plane are shown in the top panel and isolines of the transformed azimuthal wind V in the (R, v₀)-plane are shown in the bottom panel. For a particular value of v₀, the associated horizontal cross section from the top panel gives v(r) for that particular Rankine vortex and the same horizontal cross section from the bottom panel gives the corresponding V(R) for that same Rankine vortex. Since all the effects of radial advection are implicit in the R-coordinate, these often striking radial advective effects appear in the transformation back from R to r, i.e., in going from the bottom panel to the top panel in Figure 6. Some of the information in Figure 6 can also be presented in tabular form, as shown in Table 3. In constructing Table 3 we have chosen R₀ = 300 km and a convenient set of values for v₀, and then used Eq. 20 to determine r₀ and V₀. The determination of r₀ is easily accomplished by noting that the two equations in Eq. 20 can be combined into $r_0=[{({\alpha }^2+1)}^{1/2}-\alpha ]R_0$, where α = v₀/(fR₀). Once r₀ is thereby found, V₀ can be computed from V₀ = (r₀/R₀)v₀. Table 3 shows properties for a sequence of Rankine vortices with R₀ = 300 km, running from tropical depression (TD), to tropical storm (TS), and on upward to category five hurricane strength.

FIGURE 6

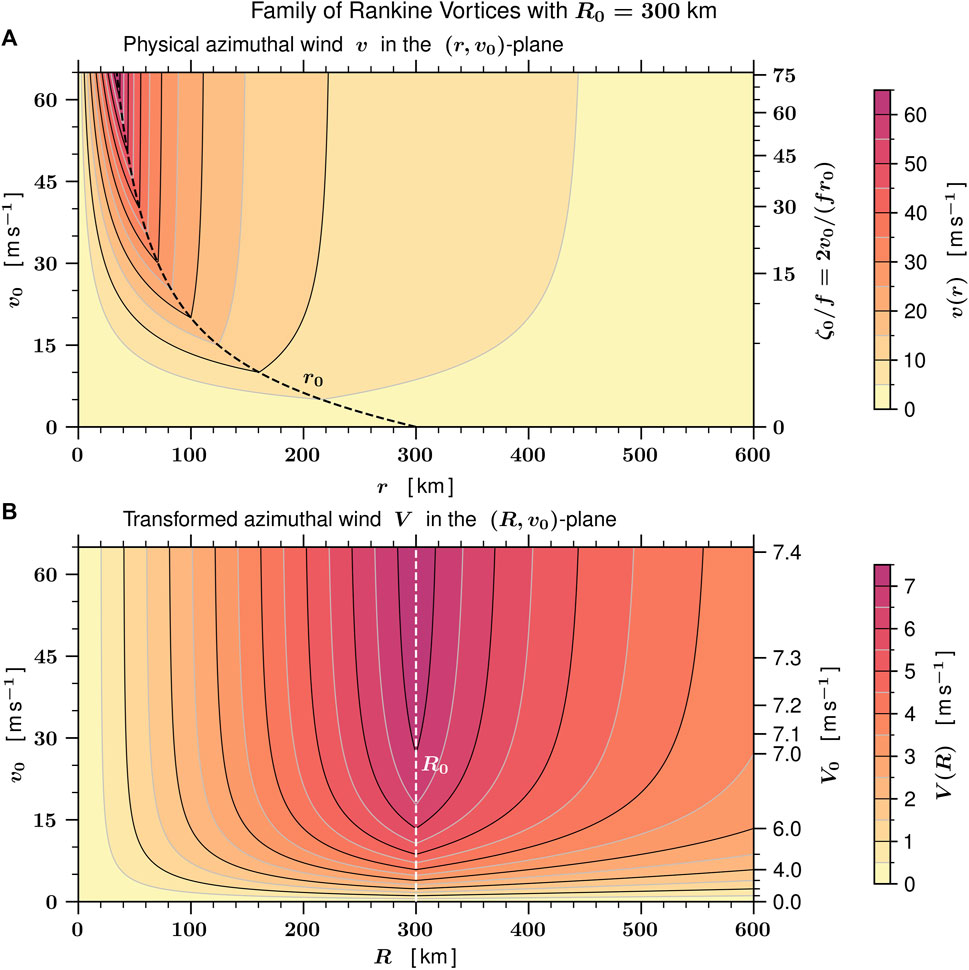
FIGURE 6. An illustration of the transformation relations Eq. 18 for the special case of a family of Rankine vortices, as defined in Eqs. 19, 20, with R₀=300 km and f =5×10^–5 s⁻¹, so that $\frac{1}{2}f{R}_0=7.5$ m s⁻¹. Panel (A) shows isolines of the physical azimuthal wind v in the (r, v₀)-plane with an isoline interval of 5 m s⁻¹, and panel (B) shows isolines of the transformed azimuthal wind V in the (R, v₀)-plane with an isoline interval of 0.5 m s⁻¹. In both (A,B) the range on the left ordinate is 0≤ v₀≤65 m s⁻¹. This corresponds to the range 0≤ V₀≤7.403 m s⁻¹, as shown on the right ordinate of panel (B), and to the range 0≤ ζ₀/f ≤76.10, as shown on the right ordinate of panel (A), where ζ₀/f =2v₀/(fr₀) is the dimensionless core vorticity. Note the striking difference in the behavior of V(R) and v(r). As V (R₀) increases from rest to 7.403 m s⁻¹, v (r₀) increases from rest to 65 m s⁻¹ and the radius of maximum wind decreases from r₀=300 km to r₀=34.17 km.

TABLE 3

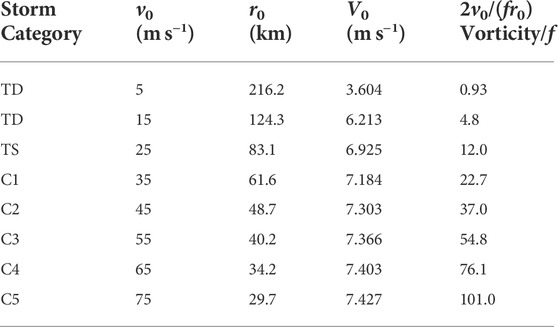
TABLE 3. Rankine vortex properties for a variety of storm categories, ranging from tropical depression (TD), to tropical storm (TS), to the five hurricane categories (C1–C5), and computed using Eq. 20 with R₀=300 km and f =5×10^–5 s⁻¹. A range of values of the maximum physical azimuthal wind v₀ is specified in the second column followed by computed values in the next three columns of the radius of maximum wind r₀, the maximum transformed azimuthal wind V₀, and the quantity 2v₀/(fr₀), which can be interpreted as the core’s relative vorticity, measured in units of f. Since the validity of the linearized dynamics discussed in Section 3 requires that 2v₀/(fr₀)<1, seven of the eight storm categories shown here fall outside the scope of linear theory.

Because of the conservation of absolute angular momentum, the material derivative is (D/Dt) = (∂/∂t) + u (∂/∂r) = (∂/∂τ). This allows the potential vorticity equation (Eq. 2) and its solution to be written as

$\frac{\partial P}{\partial \tau }=PS\Rightarrow \left\{\begin{array}{c}P\left(R,\tau \right)=f\exp \left({\int }_0^{\tau }S\left(R,{\tau }^{\prime }\right)d{\tau }^{\prime }\right)\hfill \\ \text{and}\hfill \\ h^{\ast }\left(R,\tau \right)=\bar{h}\exp \left(-{\int }_0^{\tau }S\left(R,{\tau }^{\prime }\right)d{\tau }^{\prime }\right),\hfill \end{array}\right.(21)$

where the potential depth h* is related to the potential vorticity by $P{h}^{\ast }=f\bar{h}$. Comparing the second entry in Eq. 21 with the linear version (Eq. 8), note that the appearance of the exponential function in Eq. 21 will lead to much faster growth of the P field in the nonlinear case. In fact, it is the appearance of this exponential function that is the crux of the rapid intensification process. In order to make practical use of this and related theoretical results, Hendricks et al. (2021) have introduced and tested a minimal, axisymmetric, shallow water modeling system (SWAMI) as an aid to forecasting short-term tropical cyclone intensity and wind structure changes.

Now consider the transformation of the nonlinear equations (Eq. 3). Using Eqs. 17, 18, and the definitions for R and V, the following useful relationships can be derived

$\begin{array}{cc}\hfill \frac{\partial }{r\partial r}& =\left(\frac{f+\zeta }{f}\right)\frac{\partial }{R\partial R},\left(f+\frac{\partial \left(rv\right)}{r\partial r}\right)\left(f-\frac{\partial \left(RV\right)}{R\partial R}\right)=f^2=\left(f+\frac{2v}{r}\right)\left(f-\frac{2V}{R}\right),\hfill \\ \hfill r^2\left(f+\frac{v}{r}\right)& =R^2\left(f-\frac{V}{R}\right),\text{and}\frac{\partial }{r\partial r}\left(\frac{\partial \left(rv\right)}{r\partial r}\right)={\left(\frac{f+\zeta }{f}\right)}^3\frac{\partial }{R\partial R}\left(\frac{\partial \left(RV\right)}{R\partial R}\right).\hfill \end{array}(22)$

Using Eq. 22 and the definitions for P and h*, the nonlinear equations (Eq. 3) become

$\begin{array}{ll}\hfill \frac{\partial u}{\partial \tau }-{\left(\frac{R}{r}\right)}^3\left(f-\frac{V}{R}\right)V& +\frac{gh}{f}\left(\frac{h^{2}r}{h^{\ast 2}R}\right)\frac{\partial }{\partial R}\left(\frac{\partial \left(RV\right)}{R\partial R}\right)=-g\left(\frac{h^{2}r}{h^{\ast 2}R}\right)\frac{\partial h^{\ast }}{\partial R}\hfill \\ \hfill & \text{and}\frac{R}{r}\frac{\partial V}{\partial \tau }+fu=0.\hfill \end{array}(23)$

The single, nonlinear partial differential equation for V (R, τ) can now be obtained by eliminating u from the system in Eq. 23. Taking (r/R) (∂/∂τ) of the V-equation in Eq. 23, and then making use of the u-equation, we obtain

$\begin{array}{c}\hfill \underline{\mathbf{\text{Nonlinear Klein}}-\text{Gordon Equation for}V\left(R,\tau \right)}\hfill \\ \hfill \begin{array}{cc}\hfill \frac{\partial }{\partial R}\left(\frac{\partial \left(RV\right)}{R\partial R}\right)& -\frac{1}{gh}{\left(\frac{h^{\ast }R}{hr}\right)}^2\left\{f{\left(\frac{R}{r}\right)}^2\left(f-\frac{V}{R}\right)V+r\frac{\partial }{\partial \tau }\left(\frac{1}{r}\frac{\partial V}{\partial \tau }\right)\right\}=-\frac{f}{h}\frac{\partial h^{\ast }}{\partial R}\hfill \\ \hfill & \text{with}\left.\left\{\begin{array}{cc}\text{BCs:}\hfill & V\left(0,\tau \right)=0,RV\left(R,\tau \right)\to 0\text{as}R\to \infty \hfill \\ \text{ICs:}\hfill & V\left(R,0\right)=0,V_{\tau }\left(R,0\right)=0\hfill \end{array}\right.\right\},\hfill \end{array}\hfill \end{array}(24)$

which is the nonlinear generalization of the middle entry in Eq. 11. The initial conditions and boundary conditions in Eq. 24 result from the assumption that the evolving flow is due entirely to a localized forcing S (R, τ). The factors r and h appearing in Eq. 24 can be expressed in terms of V by

$r=R{\left(1-\frac{2V}{fR}\right)}^{1/2}\text{and}h=h^{\ast }f{\left(f-\frac{\partial \left(RV\right)}{R\partial R}\right)}^{-1}.(25)$

When the forcing term on the right-hand side of Eq. 24 is slow enough, the azimuthal flow remains close to gradient balance. Then, the r (∂/∂τ)[(1/r) (∂V/∂τ)] term becomes negligible and Eq. 24 simplifies to the following invertibility principle for the balanced transformed azimuthal wind V_b(R, τ):

$\begin{array}{c}\hfill \underline{\mathbf{\text{Nonlinear Invertibility Problem for}}{V}_b\left(R,\tau \right)}\hfill \\ \hfill \begin{array}{cc}\hfill R^2\frac{{\partial }^2{V}_b}{\partial R^2}+R\frac{\partial V_b}{\partial R}& -\left({\mu }_b^2{R}^2+1\right)V_b=-\frac{f{R}^2}{h}\frac{\partial h^{\ast }}{\partial R}\hfill \\ \hfill & \text{with\hspace{0.17em}BCs:}{V}_b\left(0,\tau \right)=0,R{V}_b\left(R,\tau \right)\to 0\text{as}R\to \infty \hfill \\ \hfill & \text{where}{\mu }_b\left(R,\tau \right)={\left[\frac{f}{gh}\left(f-\frac{V_b}{R}\right)\right]}^{1/2}{\left(f-\frac{2V_b}{R}\right)}^{-1}\left(f-\frac{\partial \left(R{V}_b\right)}{R\partial R}\right).\hfill \end{array}\hfill \end{array}(26)$

Once again the h appearing in Eq. 26 can be expressed in terms of V by using Eq. 25.

In analogy with the argument given in Section 3 for the linear case, we now assume that the mass sink S (R, τ) vanishes for R > R₀ and is horizontally uniform for R ≤ R₀, where R₀ is a specified constant. The time dependence of S (R, τ) is again assumed to be $(\tau /{\tau }_s^2)e^{-\tau /{\tau }_s}$, where τ_s is a specified constant. Again, small values of τ_s correspond to fast forcing and large values of τ_s to slow forcing. This forcing S (R, τ) and the result of using it in Eq. 21 are given by

$S\left(R,\tau \right)=-\ln \left(1-ϵ\right)\left\{\begin{array}{cc}\left(\tau /{\tau }_s^2\right)e^{-\tau /{\tau }_s}\hfill & \text{if}0\le R\le R_0\hfill \\ 0\hfill & \text{if}{R}_0<R<\infty ,\hfill \end{array}\right.(27)$

and

$h^{\ast }\left(R,\tau \right)=\bar{h}\left\{\begin{array}{cc}{\left(1-ϵ\right)}^{1-\left(1+\tau /{\tau }_s\right)e^{-\tau /{\tau }_s}}\hfill & \text{if}0\le R\le R_0\hfill \\ 1\hfill & \text{if}{R}_0<R<\infty ,\hfill \end{array}\right.(28)$

where $ϵ=\mathcal{V}/(\pi R_0^2\bar{h})$ and, as confirmed below, the specified constant $\mathcal{V}$ is the total volume of fluid removed by the mass sink. Note that ϵ is the percentage of the initial fluid volume inside the potential radius R₀ that is removed by the mass sink and that − ln (1 − ϵ) ≈ ϵ for ϵ ≪ 1, in which case the forcing for the nonlinear case (Eq. 27) is essentially the same as the forcing for the linear case (Eq. 13). The h* field is a disk of potential radius R₀, with values of h* in its interior decreasing with time. To confirm that the constant $\mathcal{V}$ is the total volume of fluid removed, integrate the mass continuity equation over the entire spatial domain to obtain

$\begin{array}{ll}\hfill \frac{\partial }{\partial t}\left\{2\pi {\int }_0^{\infty }\left[\bar{h}-h\left(r,t\right)\right]rdr\right\}& =2\pi {\int }_0^{\infty }Shrdr\hfill \\ \hfill & =2\pi {\int }_0^{R_0}S{h}^{\ast }RdR=-\pi R_0^2\frac{\partial h^{\ast }\left(0,\tau \right)}{\partial \tau },\hfill \end{array}(29)$

where we have made use of hr dr = h*R dR, the assumption that S = 0 for R > R₀, and the assumption that S (R, τ) and h*(R, τ) are independent of R for R ≤ R₀. The last equality in Eq. 29 results from writing the first entry of Eq. 21 in the form (∂h*/∂τ) = −Sh*. The total volume of fluid removed is now obtained by integrating Eq. 29 over time, giving

$2\pi {\int }_0^{\infty }\left[\bar{h}-h\left(r,\infty \right)\right]rdr=\pi R_0^2\left[\bar{h}-h^{\ast }\left(0,\infty \right)\right]=\pi R_0^2\bar{h}ϵ=\mathcal{V},(30)$

where the second to last equality in Eq. 30 results from the use of Eq. 28 to show that $h^{\ast }(0,\infty )=(1-ϵ)\bar{h}$. This confirms that $\mathcal{V}$ is the total volume of fluid removed by the mass sink over its life cycle. In other words, for a fixed value of $\mathcal{V}$ in Eq. 27, the total volume of fluid removed by the mass sink is independent of the choice of the constants τ_s and R₀, although the choice of R₀ should satisfy $\pi R_0^2\bar{h}>\mathcal{V}$ so that 1 − ϵ > 0. Note that since R is a Lagrangian coordinate, fluid does not flow across R surfaces, so ϵ is constrained to be less than unity. As we shall now discuss, a crucial aspect of the forcing (Eq. 27) is its confinement to R ≤ R₀, i.e., in physical space the forcing collapses as the angular momentum surface R₀ collapses. This confines the forcing to the high PV region (Musgrave et al., 2012) and leads to rapid increases in the core PV.

Since $P/f=\bar{h}/h^{\ast }$, the solution in Eq. 28 can also be expressed in the potential vorticity form

$\begin{array}{cc}\hfill P\left(R,\tau \right)& =f\left\{\begin{array}{cc}{\left(1-ϵ\right)}^{\left(1+\tau /{\tau }_s\right)e^{-\tau /{\tau }_s}-1}\hfill & \text{if}0\le R\le R_0\hfill \\ 1\hfill & \text{if}{R}_0<R<\infty ,\hfill \end{array}\right.\hfill \\ \hfill & \Rightarrow P\left(0,\infty \right)=\frac{f}{1-ϵ}=f{\left(1-\frac{\mathcal{V}}{\pi R_0^2\bar{h}}\right)}^{-1},\hfill \end{array}(31)$

A plot of P (0, ∞)/f as a function of $\mathcal{V}/(\pi R_0^2\bar{h})$ is given in Figure 7. As discussed in Supplementary Appendix D, the solution Eq. 31 can be used to obtain a simple upper bound on the rotational flow v (r, t). If we regard R₀ as fixed, the abscissa of Figure 7 can be interpreted as a measure of the total volume of fluid removed by the mass sink. If the total volume of fluid removed is $\mathcal{V}=0.5(\pi R_0^2\bar{h})$, then P (0, ∞) = 2f. If the total volume of fluid removed is $\mathcal{V}=0.90(\pi R_0^2\bar{h})$, then P (0, ∞) = 10f. In the extreme case when the total volume of fluid removed is $\mathcal{V}=0.99(\pi R_0^2\bar{h})$, then P (0, ∞) = 100f. In other words, it is the removal of the last vestiges of the original mass inside R₀ that spins up the PV to such large values. This effect can also be seen in Figure 8, which shows plots of P (0, τ)/f, as given by Eq. 31, for the time range 0 ≤ τ ≤ 72 h and for the fixed volume parameter $\mathcal{V}=3.174\times 10^{13}$ m³. The nine curves correspond to combinations of the three choices τ_s = 3, 6, 12 h and the three choices R₀ = 200, 300, 400 km, the latter of which give ϵ = 0.990, 0.440, 0.248. The nine curves illustrate the sensitivity of the core PV to the value of R₀ for fixed $\mathcal{V}$. They also illustrate the concepts of long incubation times and vortex preconditioning (see section 15 of Ooyama, 1969). For example, although all nine cases in Figure 8 have the same value of $\mathcal{V}$, the R₀ = 400 km case has the mass sink spread over the largest area, so the vortex experiences a long period of incubation, with the PV increasing to only $\sim 1.3f$ by the end of the mass sink. The R₀ = 300 km case also experiences long incubation, with the PV increasing to $\sim 1.7f$ by the end of the mass sink. In contrast, the PV in the R₀ = 200 km case increases to $\sim 100f$ in 72 h when developing from a resting initial state. However, if the R₀ = 200 km case were initialized with P (0, 0) = 5f, it could reach a core PV of $\sim 100f$ in less than 24 h. Such a vortex might be said to be preconditioned for rapid development. The most detailed observations and analyses of a rapidly intensifying hurricane are those of Hurricane Patricia, which occurred in the northeast Pacific in October 2015. The potential vorticity analysis of Martinez et al. (2019) indicates that Hurricane Patricia could be roughly interpreted as the preconditioned R₀ = 200 km case, although any detailed comparison would involve the important roles of frictional boundary layer pumping and moist physical processes.

FIGURE 7

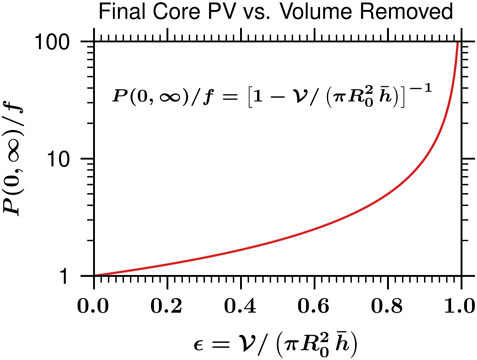
FIGURE 7. The final, dimensionless core potential vorticity P (0,∞)/f as a function of $ϵ=\mathcal{V}/(\pi R_0^2\bar{h})$, as given by Eq. 31 and shown by the displayed formula. Note that the scale on the ordinate is logarithmic. If we regard R₀ as given, the abscissa is a measure of the total volume of fluid removed by the mass sink. This graph implies that it is the removal of the last 10% of the initial volume of fluid inside R₀ that can rapidly spin up the PV from 10f to more than 100f. Since $P=(f+\zeta )(\bar{h}/h)$, large values of P are associated with large values of the absolute vorticity (f + ζ) and small values of the fluid depth h.

FIGURE 8

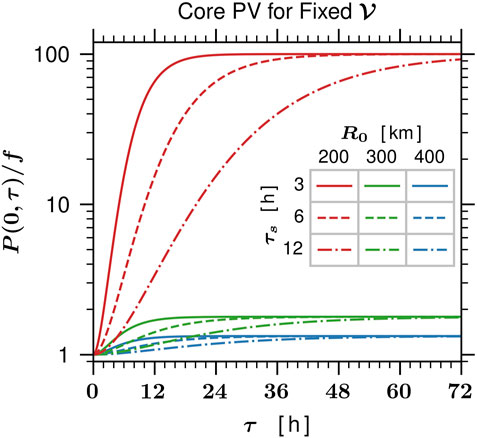
FIGURE 8. Plots of P (0, τ)/f, as given by Eq. 31 for the three choices τ_s =3,6,12 h, and for the three choices R₀=200,300,400 km. The time evolution of P (0, τ)/f is plotted for 0≤ τ ≤72 h, and the volume parameter is chosen to be $\mathcal{V}=3.174\times 10^{13}$ m³. This specified value of $\mathcal{V}$ is 99.0% of the initial volume inside the potential radius R₀=200 km, 44.0% of the initial volume inside the potential radius R₀=300 km, and 24.8% of the initial volume inside the potential radius R₀=400 km.

As a final illustration of the remarkable intensification that can result with the second type of forcing, Figure 9 shows the results of two nonlinear primitive equation model integrations using the forcing in Eq. 27 with t_s = 3 h. The right three panels show the time evolution of u (r, t), v (r, t), and $h(r,t)-\bar{h}$ for the parameter settings R₀ = 300 km and ϵ = 0.44, while the left three panels show the corresponding results for R₀ = 200 km and ϵ = 0.99. Since $\mathcal{V}=\pi R_0^2\bar{h}ϵ$, the same total volume of fluid is removed in each case. However, the vortex intensification is quite different in the two cases, with the ϵ = 0.99 case intensifying to hurricane strength and the ϵ = 0.44 case intensifying to only about 4 m s⁻¹. This is consistent with the sensitivity of PV evolution illustrated in Figures 7, 8.

FIGURE 9

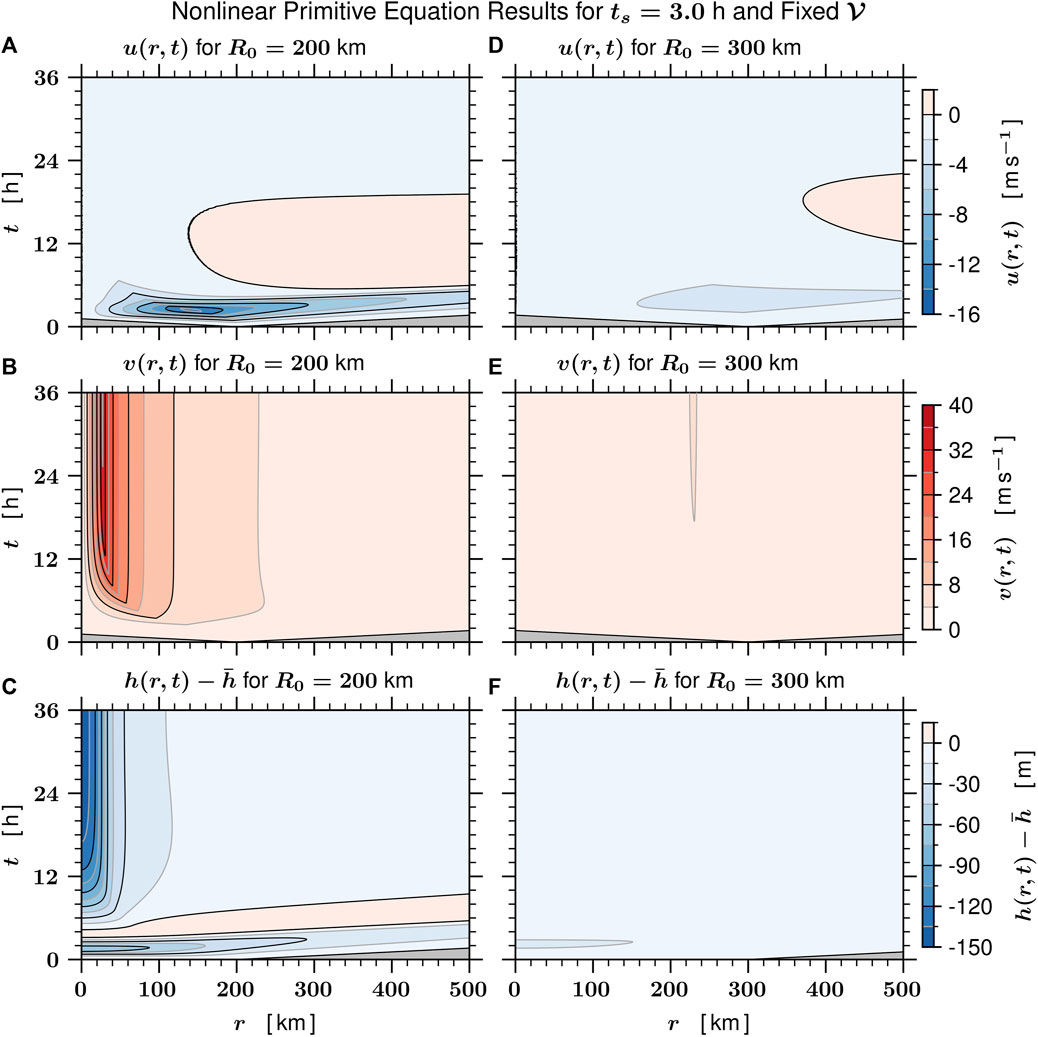
FIGURE 9. Panels (A–F) show the nonlinear primitive equation solutions obtained from Eq. 1 for the radial flow u (r, t), the azimuthal flow v (r, t), and the deviation depth $h(r,t)-\bar{h}$ for the forcing in Eq. 27 with t_s =3 h. Panels (A-C) use the parameters R₀=200 km and ϵ =0.99, while panels (D-F) use R₀=300 km and ϵ =0.44. Since $\mathcal{V}=\pi R_0^2\bar{h}ϵ$, the same volume of fluid is removed in each case. For the ϵ =0.44 case shown in (D-F), the maximum azimuthal winds are only about 4 m s⁻¹, while for the ϵ =0.99 case shown in (A-C), the maximum azimuthal winds increase to hurricane strength. The gray regions indicate initial regions where the plotted field is zero.

5 Concluding remarks

It is important to note that the simple axisymmetric shallow water model framework of this work does not include environmental effects and the frictional boundary layer, both of which certainly play a role in the rapid intensification process. Nevertheless, the nonlinear results presented here provide what we believe is an important part of the puzzle and are consistent with the notion that intensity forecasting is a difficult problem. For example, suppose (quite hypothetically) that we have a tropical cyclone with its core diabatic forcing (convection) confined by the absolute angular momentum surface R = R₀. As can be see from Figures 7–9, if that diabatic forcing is able to remove 99% of the original mass inside that R₀ surface over the next 24 h, then that tropical cyclone will undergo rapid intensification, but if the forcing only removes 50% of the original mass, then it will only slightly intensify. This does not mean that larger storms, i.e., storms with larger R₀ values, cannot undergo rapid intensification, just that such a larger storm may require a longer incubation period before rapid intensification can occur.

Concerning the frictional boundary layer, consider a region bounded by two R-surfaces and two lower tropospheric θ-surfaces just above the boundary layer, i.e., an (R, θ)-pseudovolume. The removal of mass from such a pseudovolume involves both diabatic processes and boundary layer pumping. Boundary layer pumping may play a dual role, helping to keep the diabatic heating radially confined so that it collapses with the R-surfaces, but also limiting the percentage of mass that can be removed from that (R, θ)-pseudovolume. We might conclude that accurate determination of the location and magnitude of both frictional and diabatic mass fluxes is necessary for forecasting rapid intensification. The inclusion of environmental effects, such as vertical shear, would require fully three-dimensional arguments and thus a more detailed PV analysis or a generalized omega equation analysis (DeMaria, 1996; Wang and Zhang, 2003), which is an important topic for future research. While the present paper certainly does not solve the rapid intensification problem, perhaps it better defines the nature of the problem.

In closing we note that it can be argued that inertia-gravity waves generated by tropical cyclones are simply “the zero-PV icing on the cake” of what is fundamentally a balanced, potential vorticity phenomenon. Although there is merit to this argument, the observational monitoring of inertia-gravity waves as they propagate upward into the stratosphere and mesosphere can reveal information about eyewall convection. Some of this information might be of practical use in the prediction of rapid intensification. Inertia-gravity waves excited by inner core tropical cyclone convection can sometimes be observed at mesosphere levels by airglow observations from the Earth’s surface or from low Earth orbit (Miller et al., 2012, 2015). For example, Suzuki et al. (2013) described inertia-gravity wave patterns in the mesopause region caused by tropospheric convection in Typhoon Pongsona on 10 December 2002. Concentric rings of inertia-gravity waves in the OH airglow were observed simultaneously by all-sky imagers in a Japanese network of surface stations located between 31.0N and 43.5N. Such ground-based optical measurements require clear-sky conditions, so must be obtained at some distance from the tropical cyclone core in order to avoid persistent cirrus overcast. Such concentric mesospheric airglow waves can also be observed from space (Yue et al., 2014). As a recent example, Figure 10 shows a nocturnal Suomi-NPP VIIRS Day/Night Band image that captured concentric mesospheric airglow waves propagating upward from Super Typhoon Surigae near the time of its peak intensity on 17 April 2021. Concerning evidence from data at stratospheric levels, signatures of stratospheric inertia-gravity waves that have large vertical wavelengths can be found in Atmospheric Infrared Sounder (AIRS) radiance measurements in the 4.3 μm CO₂ waveband. Such measurements detect the wave-induced perturbations in stratospheric temperature at levels between 30 and 40 km. Using such data, Hoffmann et al. (2018) searched for an association of stratospheric inertia-gravity waves with the intensification of tropical cyclones. They found a statistical correlation between stratospheric inertia-gravity wave activity and tropical cyclone intensification, lending support to the idea that variability in inertia-gravity wave signatures as a result of changing storm behavior may constitute a useful diagnostic tool for rapid intensification. This interesting possibility led Tratt et al. (2018) to propose a satellite mission concept for monitoring stratospheric inertia-gravity waves from geostationary orbit, which would open up the possibility of continuous monitoring. Although the theoretical results presented here are limited to shallow water dynamics, they do highlight some of the subtleties that are involved in linking inertia-gravity wave activity to rapid intensification. Thus, as research on this topic evolves with the use of full physics numerical models, it would not be surprising to encounter subtleties in the relationship of stratospheric inertia-gravity wave activity to rapid intensification.

FIGURE 10

FIGURE 10. A nocturnal (several hours before sunrise) Suomi-NPP VIIRS Day/Night Band image (0.7 μm) showing concentric mesospheric airglow waves that have propagated upward from the convective core of Super Typhoon Surigae near the time of its peak intensity on 17 April 2021, when it was just east of the Philippines. From Bachmeier (2021).

An important result presented here is the nonlinear, inhomogeneous, Klein-Gordon equation (Eq. 24), which describes essential aspects of the rapid intensification of the potential vorticity and azimuthal wind fields in a tropical cyclone. Although this equation has an unfamiliar form, it may be of interest to note a relevant point made by Weinberg (1977, page 131) concerning results derived from sound physical and mathematical principles: “This is often the way it is in physics—our mistake is not that we take our theories too seriously, but that we do not take them seriously enough. It is always hard to realize that these numbers and equations we play with at our desks have something to do with the real world.”

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author contributions

WS researched and derived the scientific aspects of this work and wrote the majority of this paper. RT developed and ran the numerical models, created all of the figures, and provided editing and LaTeX support.

Funding

Our research has been supported by the National Science Foundation under grant AGS-1841326.

Acknowledgments

We thank Chris Slocum and Mark DeMaria for their helpful comments and Eric Hendricks, Jonathan Vigh, and Chris Rozoff for sharing with us their ideas on how PV concepts associated with a forced, balanced, axisymmetric shallow water model can be used for understanding short-term tropical cyclone intensification and wind structure changes. We would also like to thank the two reviewers for their useful comments and suggestions.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.1038351/full#supplementary-material

References

Bachmeier, S. (2021). Rapid intensification of super Typhoon Surigae. Wisconsin: University of Wisconsin. CIMSS Satellite Blog. Available at: https://cimss.ssec.wisc.edu/satellite-blog/archives/date/2021/04/16 (Accessed 04 25, 2022).

Google Scholar

Cahn, A. (1945). An investigation of the free oscillations of a simple current system. J. Meteor. 2, 113–119. doi:10.1175/1520-0469(1945)002<0113:AIOTFO>2.0.CO;2

CrossRef Full Text | Google Scholar

Copson, E. T. (1975). Partial differential equations. Cambridge: Cambridge University Press, 280.

Google Scholar

DeMaria, M., Sampson, C. R., Knaff, J. A., and Musgrave, K. D. (2014). Is tropical cyclone intensity guidance improving? Bull. Am. Meteorol. Soc. 95, 387–398. doi:10.1175/BAMS-D-12-00240.1

CrossRef Full Text | Google Scholar

DeMaria, M. (1996). The effect of vertical shear on tropical cyclone intensity change. J. Atmos. Sci. 53, 2076–2088. doi:10.1175/1520-0469(1996)053<2076:TEOVSO>2.0.CO;2

CrossRef Full Text | Google Scholar

Doyle, J. D., and Ferek, R. (2017). Tropical cyclone intensity experiment (TCI). AMS Special Collection. Boston: American Meteorological Society. Available at: https://journals.ametsoc.org/collection/TCI (Accessed 10 07, 2022).

Google Scholar

Hack, J. J., and Schubert, W. H. (1986). Nonlinear response of atmospheric vortices to heating by organized cumulus convection. J. Atmos. Sci. 43, 1559–1573. doi:10.1175/1520-0469(1986)043<1559:NROAVT>2.0.CO;2

CrossRef Full Text | Google Scholar

Hendricks, E. A., Vigh, J. L., and Rozoff, C. M. (2021). Forced, balanced, axisymmetric shallow water model for understanding short-term tropical cyclone intensity and wind structure changes. Atmosphere 12, 1308. doi:10.3390/atmos12101308

CrossRef Full Text | Google Scholar

Hoffmann, L., Wu, X., and Alexander, M. J. (2018). Satellite observations of stratospheric gravity waves associated with the intensification of tropical cyclones. Geophys. Res. Lett. 45, 1692–1700. doi:10.1002/2017GL076123

CrossRef Full Text | Google Scholar

Hoskins, B. J., McIntyre, M. E., and Robertson, A. W. (1985). On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 111, 877–946. doi:10.1002/qj.49711147002

CrossRef Full Text | Google Scholar

Martinez, J., Bell, M. M., Rogers, R. F., and Doyle, J. D. (2019). Axisymmetric potential vorticity evolution of Hurricane Patricia (2015). J. Atmos. Sci. 76, 2043–2063. doi:10.1175/JAS-D-18-0373.1

CrossRef Full Text | Google Scholar

Miller, S. D., Mills, S. P., Elvidge, C. D., Lindsey, D. T., Lee, T. F., and Hawkins, J. D. (2012). Suomi satellite brings to light a unique frontier of nighttime environmental sensing capabilities. Proc. Natl. Acad. Sci. U. S. A. 109, 15706–15711. doi:10.1073/pnas.1207034109

PubMed Abstract | CrossRef Full Text | Google Scholar

Miller, S. D., Straka, W. C., Yue, J., Smith, S. M., Alexander, M. J., Hoffmann, L., et al. (2015). Upper atmospheric gravity wave details revealed in nightglow satellite imagery. Proc. Natl. Acad. Sci. U. S. A. 112, E6728–E6735. doi:10.1073/pnas.1508084112

PubMed Abstract | CrossRef Full Text | Google Scholar

Möller, J. D., and Smith, R. K. (1994). The development of potential vorticity in a hurricane-like vortex. Q. J. R. Meteorol. Soc. 120, 1255–1265. doi:10.1002/qj.49712051907

CrossRef Full Text | Google Scholar

Musgrave, K. D., Taft, R. K., Vigh, J. L., McNoldy, B. D., and Schubert, W. H. (2012). Time evolution of the intensity and size of tropical cyclones. J. Adv. Model. Earth Syst. 4, 15. doi:10.1029/2011MS000104

CrossRef Full Text | Google Scholar

Ooyama, K. (1969). Numerical simulation of the life cycle of tropical cyclones. J. Atmos. Sci. 26, 32–40. doi:10.1175/1520-0469(1969)026<0003:NSOTLC>2.0

CrossRef Full Text | Google Scholar

Schubert, W. H., and Alworth, B. T. (1987). Evolution of potential vorticity in tropical cyclones. Q. J. R. Meteorol. Soc. 113, 147–162. doi:10.1002/qj.49711347509

CrossRef Full Text | Google Scholar

Schubert, W. H., Hack, J. J., Silva Dias, P. L., and Fulton, S. R. (1980). Geostrophic adjustment in an axisymmetric vortex. J. Atmos. Sci. 37, 1464–1484. doi:10.1175/1520-0469(1980)037<1464:GAIAAV>2.0.CO;2

CrossRef Full Text | Google Scholar

Suzuki, S., Vadas, S. L., Shiokawa, K., Otsuka, Y., Kawamura, S., and Murayama, Y. (2013). Typhoon-induced concentric airglow structures in the mesopause region. Geophys. Res. Lett. 40, 5983–5987. doi:10.1002/2013GL058087

CrossRef Full Text | Google Scholar

Tratt, D. M., Hackwell, J. A., Valant-Spaight, B. L., Walterscheid, R. L., Gelinas, L. J., Hecht, J. H., et al. (2018). Ghost: A satellite mission concept for persistent monitoring of stratospheric gravity waves induced by severe storms. Bull. Am. Meteorol. Soc. 99, 1813–1828. doi:10.1175/BAMS-D-17-0064.1

CrossRef Full Text | Google Scholar

Wang, X., and Zhang, D.-L. (2003). Potential vorticity diagnosis of a simulated hurricane. Part I: Formulation and quasi-balanced flow. J. Atmos. Sci. 60, 1593–1607. doi:10.1175/2999.1

CrossRef Full Text | Google Scholar

Weinberg, S. (1977). The first three minutes: A modern view of the origin of the universe. New York: Basic Books, 188.

Google Scholar

Whitham, G. B. (1974). Linear and nonlinear waves. New York: John Wiley & Sons, 636.

Google Scholar

Yue, J., Miller, S. D., Hoffmann, L., and Straka, W. C. (2014). Stratospheric and mesospheric concentric gravity waves over tropical cyclone Mahasen: Joint AIRS and VIIRS satellite observations. J. Atmos. Sol. Terr. Phys. 119, 83–90. doi:10.1016/j.jastp.2014.07.003

CrossRef Full Text | Google Scholar