The influences of seismic load on dynamic deformation properties of rock material under different confining pressures

Long-term geological storage of carbon dioxide in underground engineering is the most economically viable option for reducing emissions of this greenhouse gas to the atmosphere. Underground engineering projects are often subjected to earthquakes during their lives, thus it is essential to investigate the deformation characteristics of surrounding rock of those underground engineering works subjected to seismic load under different confining pressures. To date, however, there have been notably few studies on the characteristics of rock materials under seismic load and the influences of seismic load on dynamic deformation properties of rock material under different confining pressures remain unclear. Therefore, a numerical study of the dynamic mechanical properties of a rock material (T_2y6 marble) under Kobe seismic load with four different maximum stresses and four different confining pressures was conducted. The results show cyclic behavior, strain rate effect and damage are found in the stress-strain curves of the rock under simulated Kobe seismic load. Confining pressure can significantly limit the increases in lateral strain and volumetric strain, thus dilation can occur in the rock when the maximum stress of seismic load is large, and the confining pressure is small. Seismic load with small maximum stress cannot cause severe damage to the rock, but the influence is larger than that of static load. The maximum stress can be treated as a main factor affecting the damage to rock under seismic loads, while the effect of confining pressure thereon is smaller than that of the maximum stress. Furthermore, the relationships between deformation characteristics of the rock under these seismic loads, such as maximum strain, residual strain, plastic internal variable, deformation modulus, and maximum stress are different from that between the deformation characteristics and confining pressure.

Introduction

Since the 21st century, global carbon emissions have grown rapidly, and global carbon dioxide emissions were increased by 40% from 2000 to 2019. According to the statistics of the World Energy Statistical Yearbook (70th Edition) released by BP, in 2019, global carbon emissions reached 34.36 billion tons, a record high. As the most economically viable option for reducing emissions of carbon dioxide to the atmosphere, the long-term safety of underground engineering for the long-term geological storage of the greenhouse gas is extremely important (Al-Ameri et al., 2016; Lu et al., 2019; Xu et al., 2021), however, these underground engineering works are likely to be subjected to earthquakes during their service lives (Liu et al., 2018). Similar problems will be encountered for rock slopes (Aydan 2016; Huang et al., 2018; Huang et al., 2020; Chang et al., 2022; Du et al., 2022; Fu et al., 2022). Thus, it is crucial to characterize the mechanical behavior of the rock surrounding such works under seismic loads.

Due to the amplitude of a seismic load varying with time, seismic loads are generally simplified to common cyclic loading events for convenience. In recent decades, experimental investigations on the mechanical properties of rock materials subjected to cyclic loading have been conducted. Bagde and Petros (2005) and Fuenkajorn and Phueakphum (2010) performed uniaxial cyclic loading tests on sandstone and rock salt. Results from the tests indicate that the compressive strength of rocks decreases with increasing number of loading cycles. Amplitude, loading frequency, maximum stress, and waveform of cyclic loading are usually deemed significant in terms of their effects on the mechanical properties of rock. Heap and Fuenkajorn (2008) conducted increasing-amplitude cyclic loading experiments and constant-amplitude cyclic loading experiments to quantify the contribution of microcracking to the static elastic response of Westerly granite. Tests results imply that increasing-amplitude stress cycling causes 11% decrease in Young’s modulus measured at a constant stress. Liu et al. (2012) found that frequency has a strong influence on the deformation, stiffness, and failure mode of sandstone. The higher the frequency, the larger the strength of sandstone and granite (Peng et al., 2020; Vaneghi et al., 2020). From the results of cyclic loading tests of rock salt, it was found that with the increase in maximum stress of cyclic loading, the damage evolution of rock salt becomes more evident (Liu et al., 2014). Sinusoidal, ramp, and square waveforms were applied by Bagde and Petros (2005) to assess the effect on the fatigue properties of sandstone, and results show that the loading waveform affects the accumulation of damage to the rock. Furthermore, triaxial cyclic loading tests have been conducted to study the influence of confining pressure on the mechanical properties of rock materials (Yang et al., 2020; Jiang et al., 2021; Yang et al., 2021). Chen et al. (2021) applied five different confining pressures in triaxial cyclic loading tests on intact sandstone to expound the damage evolution and failure behavior. Experimental results show that the confining pressure can stop the formation and propagation of fractures in rock samples and reduces damage thereto. Similarly, triaxial cyclic loading tests under five confining pressures were conducted to investigate the variation of energy evolution and distribution characteristics with confining pressure: the confining pressure can limit the energy dissipation and release due to fracture or failure of the rocks (Meng et al., 2021). However, surrounding rock is generally in a true triaxial state of stress. Gao and Feng (2019), Feng et al. (2020), Gao and Wang (2021), and Duan et al. (2021) measured the mechanical and damage characteristics of rocks under true triaxial cyclic loading. Results show that the variation of damage in the intermediate principal stress direction is different from that in the maximum and minimum principal stress directions, while the variation of damage in the latter two directions is similar.

The literature shows that studying the mechanical responses of rock materials subjected to cyclic loading remains the focus of research, while the applying loads of research are limited to common cyclic loading. To date, metallic and reinforced concrete materials (Faisal et al., 2013; Li et al., 2014) were applied to explore their mechanical properties under random cyclic loading. However, the mechanical response of rocks under seismic load has never been studied (Liu et al., 2018), furthermore, the influences of seismic load on dynamic deformation properties of rock material under different confining pressures remain far from being understood, hence the need for the present work. The rest of this manuscript is organized as follows: firstly, a dynamic constitutive model for rock materials under seismic load is presented. Secondly, a triaxial numerical test loading scheme on a hard rock specimen (T_2y6 marble) is introduced. Thirdly, the dynamic responses of the rock samples are evaluated. Fourthly, the relationship between dynamic deformation properties of rock material and maximum stress is studied. Then, the influence of confining pressure on the deformation properties of rock materials is analyzed. Finally, the conclusions are drawn.

The dynamic constitutive model under seismic load

Hashiguchi (2005) and Tsutsumi and Hashiguchi (2005) built models using sub-loading surface theory, proving it can reflect the deformation characteristics of materials under cyclic loading. Thus, Zhou et al. (2020a, 2020b) applied the theory to rock materials, and established a constitutive model for rock materials subjected to triaxial cyclic loading based on the Drucker-Prager criterion. Numerical results almost matched the experimental results of different rocks under cyclic loading. Furthermore, to simulate the strain rate effect on rock under dynamic load and the coupling effect of strain rate effect and damage effect under dynamic cyclic loading, Zhou et al. (2022) constructed a dynamic constitutive model for rock materials suited to a medium and low-strain-rate dynamic cyclic loading regimes. Similarly, the dynamic constitutive model also demonstrates good performance compared with the experimental results under dynamic cyclic loading. In general, seismic load can be treated as a medium and low-strain-rate dynamic cyclic loading. Thus, the dynamic constitutive model is also suited to seismic load, and the yield function on the normal-yield surface of the dynamic constitutive model is written as:

$f\left(\sigma ,\dot{\epsilon },\kappa \right)=\sqrt{J_2}+\beta \left(\kappa \right)I_1=Q\left(\dot{\epsilon },\kappa \right),(1)$

$\beta \left(\kappa \right)=\frac{2\sin \varphi \left(\kappa \right)}{\sqrt{3}\left(3-\sin \varphi \left(\kappa \right)\right)},(2)$

$Q\left(\dot{\epsilon },\kappa \right)=\frac{6c\left(\dot{\epsilon },\kappa \right)\cos \varphi \left(\kappa \right)}{\sqrt{3}\left(3-\sin \varphi \left(\kappa \right)\right)},(3)$

$\varphi \left(\kappa \right)=\{\begin{array}{cc}1,& \left(\kappa \le {\kappa }_{{\varphi }_0}\right),\\ 1+\frac{{\kappa }_{{\varphi }_0}-\kappa }{{\kappa }_{{\varphi }_0}-{\kappa }_{{\varphi }_1}}\left(\frac{{\varphi }_r}{{\varphi }_0}-1\right),& \left({\kappa }_{{\varphi }_0}<\kappa <{\kappa }_{{\varphi }_1}\right),\\ \frac{{\varphi }_r}{{\varphi }_0},& \left(\kappa >{\kappa }_{{\varphi }_1}\right)\end{array}(4)$

$c\left(\dot{\epsilon },\kappa \right)=\{\begin{array}{cc}{c}_0\left(d\mathrm{l}\mathrm{g}\left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_s}\right)+1\right),& \left(\kappa \le {\kappa }_{c_0}\right),\\ c_0\left(d\mathrm{l}\mathrm{g}\left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_s}\right)+1\right)\left(\frac{c_r}{c_0}+\frac{{\kappa }_{c_1}-\kappa }{{\kappa }_{c_1}-{\kappa }_{c_0}}\left(1-\frac{c_r}{c_0}\right)\right),& \left({\kappa }_{c_0}<\kappa <{\kappa }_{c_1}\right),\\ c_r\left(d\mathrm{l}\mathrm{g}\left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_s}\right)+1\right),& \left(\kappa >{\kappa }_{c_1}\right),\end{array}(5)$

$\kappa =\int d\kappa =\int G\sqrt{\frac{2}{3}\left(d{\epsilon }^p-\frac{1}{3}tr\left(d{\epsilon }^p\right)\right)\left(d{\epsilon }^p-\frac{1}{3}tr\left(d{\epsilon }^p\right)\right)},(6)$

where$\dot{\epsilon }$is the strain rate, $I_1$ represents the first invariant and $J_2$ is second invariant of the deviatoric stress, f is a yield surface function, R denotes a similarity ratio, $c$and $\varphi$ refer to the cohesion and internal friction angle of the rock, respectively; ${\varphi }_0$ and ${\varphi }_r$represent the initial and residual internal friction angles; $\kappa$ is a plastic internal variable, ${\kappa }_{{\varphi }_0}$ and ${\kappa }_{{\varphi }_1}$are the thresholds at which the internal friction angle starts to change and reaches its residual value, respectively. $G$ is a function which considers the dependence of plastic deformation on the confining pressure, and $d{\epsilon }^p$represents the increment of plastic strain. $c_0$and $c_r$are the initial and residual cohesions; ${\kappa }_{c_0}$and ${\kappa }_{c_1}$denote the thresholds at which the cohesion starts to change and reach its residual value, respectively. ${\dot{\epsilon }}_s$ is the static strain rate (set to 1 × 10^–5 s⁻¹), and $d$ is a material constant.

The dynamic constitutive model is established based on the sub-loading surface theory, thus the yield function on sub-loading surface is

$f\left(\overline{\sigma },\dot{\epsilon },\kappa \right)=\sqrt{{\overline{J}}_2}+\beta \left(\kappa \right){\overline{I}}_1=Q\left(\dot{\epsilon },\kappa \right),(7)$

$\overline{\sigma }=\sigma -R\alpha +s\left(R-1\right),(8)$

where s is the similarity-center, $\alpha$denotes the geometric center of the normal-yield surface, $\overline{\sigma }$ represents the current stress considering the geometric center of the sub-loading surface, ${\overline{I}}_1$ is the first invariant of the current stress tensor, ${\overline{J}}_2$ represents second invariant of the current deviatoric stress, and R denotes a similarity ratio.

Meanwhile, like the variation of strength, the Young’s modulus of rock materials is also a function of strain rate and damage under dynamic cyclic loading. Thus, the Young’s modulus of rock materials under seismic load was also established by Zhou et al. (2022) as given by

$E\left(\dot{\epsilon },\kappa \right)=\{\begin{array}{cc}{E}_s\left(a_0{\left(\mathrm{l}\mathrm{g}\left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_s}\right)\right)}^b+1\right),& \kappa =0,\\ E_s\left(a_0{\left(\mathrm{l}\mathrm{g}\left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_s}\right)\right)}^b+1\right)\left(1-\left(1-\frac{E_E}{E_s}\right)\frac{\kappa }{{\kappa }_E}\right),& 0<\kappa \le {\kappa }_E,\\ \left(a_0{\left(\mathrm{l}\mathrm{g}\left(\frac{\dot{\epsilon }}{{\dot{\epsilon }}_s}\right)\right)}^b+1\right)E_E& \kappa >{\kappa }_E,\end{array}(9)$

where ${\kappa }_E$is the threshold at which the Young’s modulus reaches its residual value under static strain conditions, $E_s$and$E_E$ represent the initial and residual Young’s modulus under static strain conditions, and $a_0$ and $b$are material parameters.

Numerical test loading scheme

Zhou et al. (2020b, 2022) elucidated the physical meaning and determined the parameters of the dynamic constitutive model in detail. To study the effects of seismic loads with different maximum stresses on the deformation properties of rock material under different confining pressures, triaxial tests were performed and the dynamic constitutive model was applied to simulate the response of a rock specimen. The rock specimen is a T_2y6 marble which comes from a hydropower station in China (Zhang et al., 2010), and each specimen is a cube with a side-length of 100 mm. The seismic loads are applied at the top of the rock specimen and a vertical constraint is applied at the bottom of the calculation model; the confining pressure is applied around the specimen. The parameters of T_2y6 marble are listed in Table 1. It should be noted that the initial and final Young’s moduli are the same under different confining pressure conditions.

TABLE 1

TABLE 1. Parameters for T_2y6 marble.

The Kobe Earthquake refers to an earthquake disaster with a magnitude of 7.3 that occurred in the Kansai region of Japan at 5:46:52 (Japanese Standard Time) on 17 January 1995. The Kobe wave is chosen for the present analysis and its velocity-time history curve is shown in Figure 1A. The loading diagram of Kobe seismic load with four maximum stresses (i.e., 30 MPa, 60 MPa, 70 MPa, and 80 MPa) is shown in Figure 1B and is obtained from the velocity-time history curve. To ensure that the applied loads induce compressive stresses, a maximum static load is applied before applying seismic load as listed in Table 2. Furthermore, the triaxial tests are performed at the four following confining pressures: 0, 5, 10, and 15 MPa. Firstly, the rock is subjected to a static load at a strain rate of 1 × 10^–5 s⁻¹ in the three principal directions of the rock sample, and the static load is linearly increased with time. Then, the load is held constant in the two lateral directions when the load reaches the confining pressure. Finally, the seismic load is applied when the static load reaches the maximum value in the axial direction.

FIGURE 1

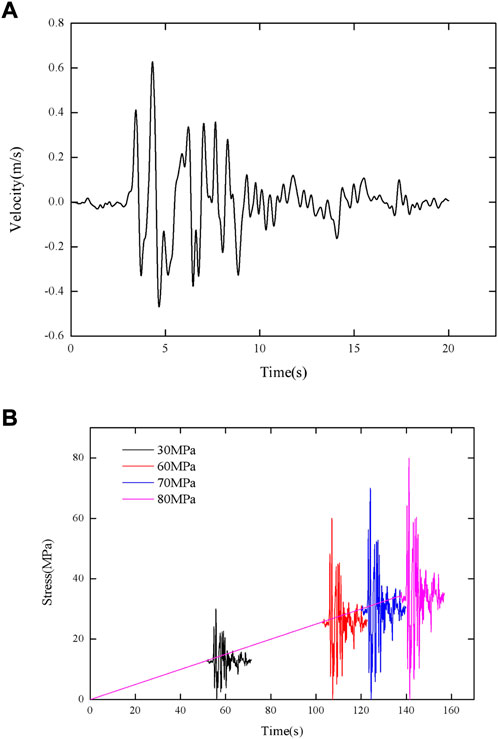
FIGURE 1. The velocity time history and load time history of Kobe seismic load with different maximum stresses: (A) Velocity time history; (B) Load time history.

TABLE 2

TABLE 2. Test plan.

The software used for numerical simulation is developed using C++ language and is a seismic dynamic analysis software for rock engineering based on the continuum method. It mainly includes three major blocks: basic mathematical calculation module, data management module, and finite element kernel module. The software used for the numerical simulation is a self-programming finite element method software.

The numerical results

The stress-strain curves and volumetric strain-axial strain curves

The stress-strain curves of the rock under Kobe seismic load with different confining pressures are illustrated in Figure 2. The stress-strain curves of the rock under seismic load with different confining pressures are shown to be similar, and the stress-strain curve displays the cyclic behavior of rock materials, such as hysteresis and cumulative plastic strain. Meanwhile, the deformation modulus of the rock becomes larger when the seismic load is applied. This implies that the seismic load is not only cyclic loading, but also is dynamic load. However, the size and range of loading and unloading in each cycle are different. This is because seismic load is different from the common cyclic loading for its the amplitude being time-variant. Furthermore, the axial strain is larger than the lateral strain. With the increase of the confining pressure, the size of hysteresis loop and cumulative plastic strain are decreasing, as shown in Figure 2A: the same phenomenon can be seen in Figure 2B at a maximum stress of 80 MPa. Upon the increase of the maximum stress of seismic load, the size of the hysteresis loop and cumulative plastic strain increase. Figure 3 shows the stress-strain curves of the rock under Kobe seismic load with different maximum stresses in uniaxial loading test and triaxial loading test at a confining pressure of 15 MPa. The confining pressure can significantly limit the increase in lateral strain.

FIGURE 2

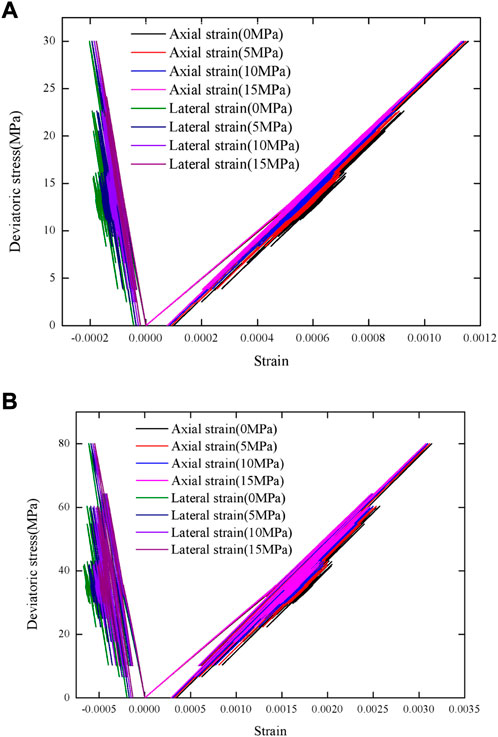
FIGURE 2. The stress-strain curves of the rock under Kobe seismic load with different confining pressures: (A) Maximum stress of 30 MPa; (B) Maximum stress of 80 MPa.

FIGURE 3

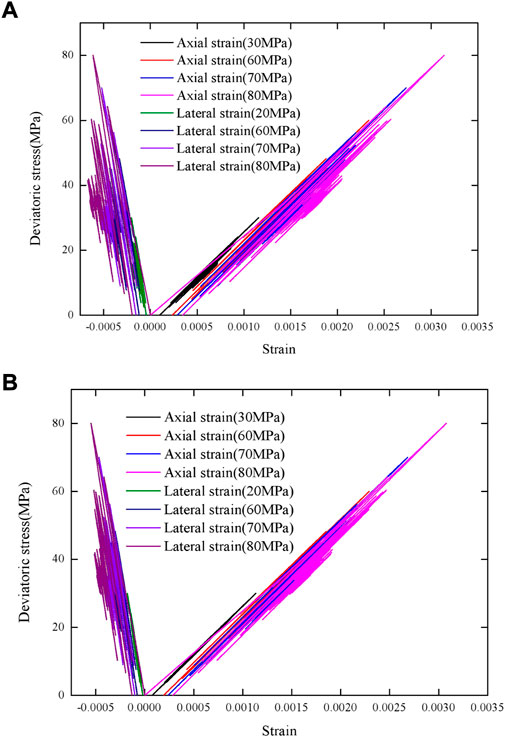
FIGURE 3. The stress-strain curves of the rock under Kobe seismic load with different maximum stresses: (A) Uniaxial loading; (B) Triaxial loading with confining pressure of 15 MPa.

Figure 4 depicts the volumetric strain-axial strain curves of the rock under Kobe seismic load with different confining pressures: the volumetric strain and axial strain are quasi-linearly related. As the axial strain increases, the volumetric strain decreases, and the volumetric strain is positive when the maximum stress is 30 MPa, as shown in Figure 4A. This shows that the rock has been in a state of shrinkage under seismic load when the maximum stress is 30 MPa on the condition of four different confining pressures. However, though the volumetric strain in most instances is positive when the maximum stress is 80 MPa, as shown in Figure 4B, dilation occurs when the confining pressures are less than 10 MPa. This suggests that rock materials can be in the state of dilation when the maximum stress of seismic load is large, and the confining pressure is small. The similar phenomenon is also observed in Figure 5. Dilation occurs in the rock regardless of the maximum stress of the seismic load in the case of uniaxial loading, as shown in Figure 5A. While, the rock is always in the state of shrinkage in the case of triaxial loading with the confining pressure of 15 MPa, as shown in Figure 5A. Furthermore, the larger the confining pressure and the smaller the maximum stress, the greater the volumetric strain is under the same axial strain.

FIGURE 4

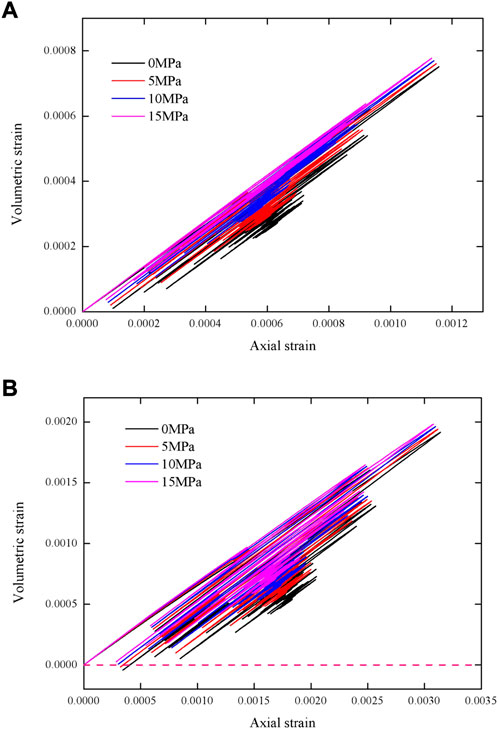
FIGURE 4. The volumetric strain-axial strain curves of the rock under Kobe seismic load with different confining pressures: (A) Maximum stress of 30 MPa; (B) Maximum stress of 80 MPa.

FIGURE 5

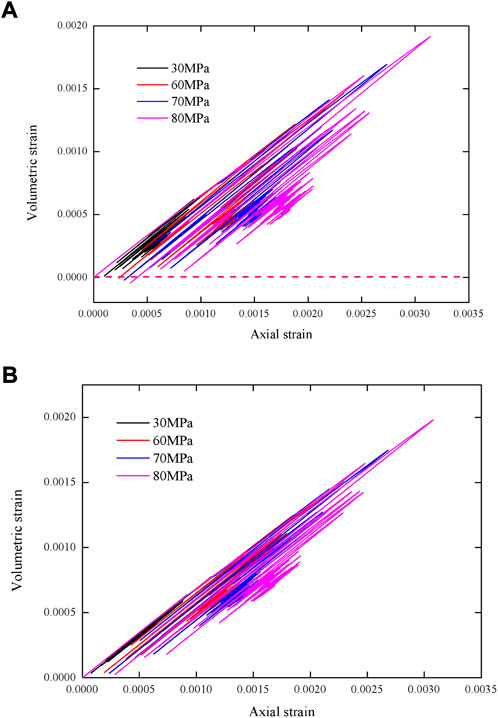
FIGURE 5. The volumetric strain-axial strain curves of the rock under Kobe seismic load with different maximum stresses: (A) Uniaxial loading; (B) Triaxial loading with confining pressure of 15 MPa.

The variation of deformation properties

Though the plastic internal variable is the function of the plastic strain, it can reflect the damage of rock under loads based on formulae (5) and 9. The variations in plastic internal variable of the rock with time under Kobe seismic load with different confining pressures are shown in Figure 6. The shape of the variation in plastic internal variable of the rock with time is similar under seismic load with different confining pressures. The larger the confining pressure, the smaller the plastic internal variable and its rate of change. The plastic internal variable increases slowly under static load, while it increases more rapidly when applying a simulated seismic load. When the maximum stress of seismic load is 30 MPa, the maximum plastic internal variable is less than 0.02, suggesting that seismic load with a small maximum stress cannot cause severe damage to the rock, but the influence is larger than that of static load. A similar phenomenon can also be seen in Figure 6B when the maximum stress of seismic load is 80 MPa. While, the maximum plastic internal variable is significantly larger than that when the maximum stress of seismic load is 30 MPa, suggesting that the maximum stress is the main factor affecting the plastic internal variable of, even damage to, rock materials. The variations in plastic internal variable of the rock with time under Kobe seismic load with different maximum stresses are shown in Figure 7. Compared with results under the conditions of confining pressures of 5 MPa and 15 MPa, the difference of plastic internal variable in these two cases is found to be small, suggesting that the effect of confining pressure on damage of rock materials under seismic loads is smaller than that of the maximum stress.

FIGURE 6

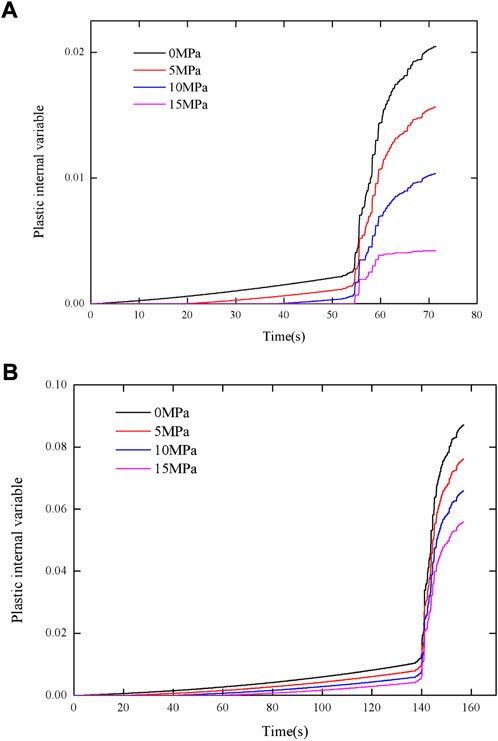
FIGURE 6. The variation in plastic internal variable of the rock under Kobe seismic load with different confining pressures: (A) Maximum stress of 30 MPa; (B) Maximum stress of 80 MPa.

FIGURE 7

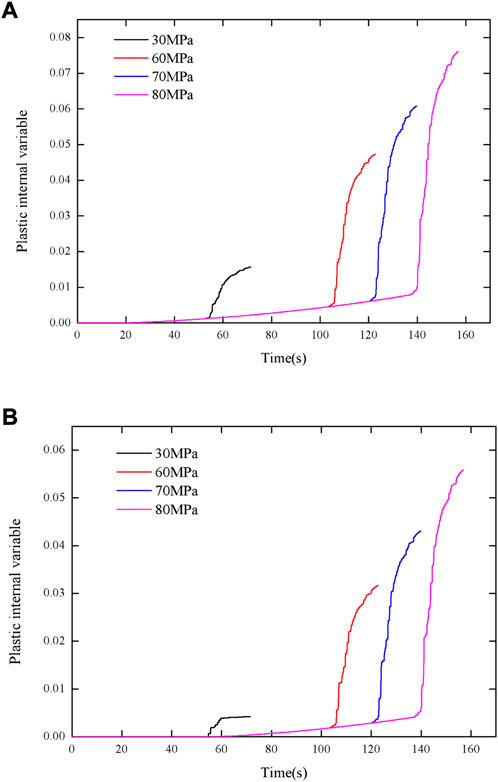
FIGURE 7. The variation in plastic internal variable of the rock under Kobe seismic load with different maximum stresses: (A) Triaxial loading with confining pressure of 5 MPa; (B) Triaxial loading with confining pressure of 15 MPa.

The variations in the deformation modulus of the rock with time under Kobe seismic load with different confining pressures are shown in Figure 8: the variations in the deformation modulus under different confining pressures are almost the same, and the difference can be negligible. This is because the initial and final Young’s moduli are the same under different confining pressures. The deformation modulus depends on the plastic internal variable and strain rate based on formula (9), and the strain rate is the same under different confining pressures, thus, the difference in the deformation modulus mainly reflect in the difference of the plastic internal variable. In general, there are three stages in the variation of the deformation modulus of the rock under seismic load: remaining constant, rapidly increasing, and decreasing slowly. This suggests that seismic load can increase the deformation modulus due to the strain rate effect. A similar phenomenon can also be seen in Figure 9 where it can also be seen that the difference of the deformation modulus under different maximum stresses is also not large. The reason is that the maximum strain rates of different maximum stresses are similar and the effect of strain rate on deformation modulus is mainly reflected through a logarithmic relationship based on formula (9).

FIGURE 8

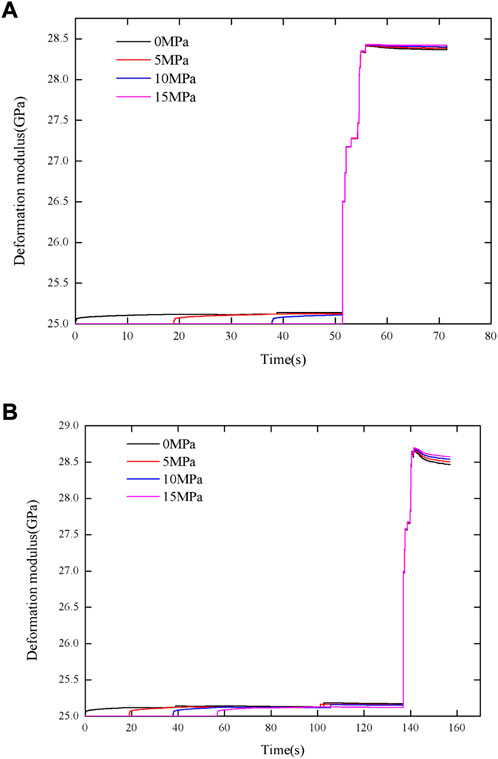
FIGURE 8. The variation in deformation modulus of the rock under Kobe seismic load with different confining pressures: (A) Maximum stress of 30 MPa; (B) Maximum stress of 80 MPa.

FIGURE 9

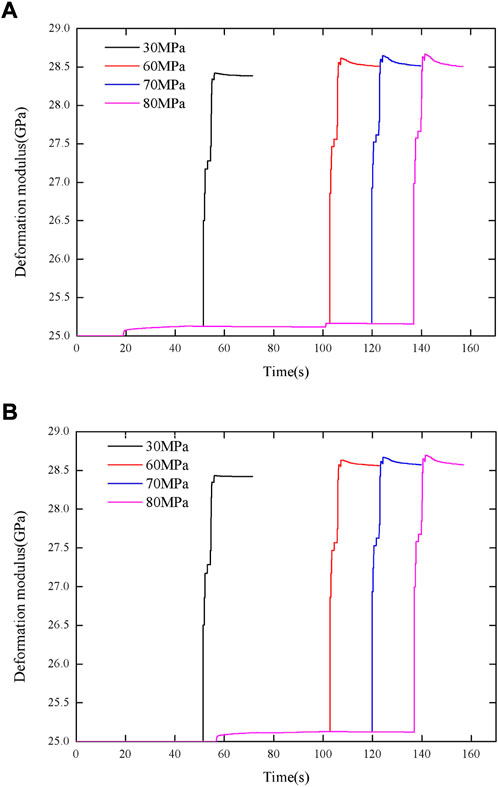
FIGURE 9. The variation in deformation modulus of the rock under Kobe seismic load with maximum stresses: (A) Triaxial loading with confining pressure of 5 MPa; (B) Triaxial loading with confining pressure of 15 MPa.

The relationship between the dynamic deformation properties and maximum stress

The relationship between the dynamic deformation properties of the rock and maximum stress under Kobe seismic load with different confining pressures is shown in Figure 10. It can be found that the maximum axial strain and residual axial strain increase quasi-linearly with maximum stress under different confining pressures, as illustrated in Figure 10A. Al though the maximum axial strain and residual axial strain decrease as confining pressure increases, the difference in the maximum axial strain and residual axial strain under different confining pressures is small, whereas the maximum lateral strain, residual lateral strain and maximum stress have a negative linear relationship, as shown in Figure 10B. As well, the difference of the maximum lateral strain and residual lateral strain under different confining pressures is small, but the difference between maximum lateral strain and residual lateral strain is not more than 0.0001. Based on the axial strain and lateral strain, the relationship between the volumetric strain and maximum stress under different confining pressures is demonstrated in Figure 10C. Like the axial strain, the maximum volumetric strain, residual volumetric strain, and maximum stress show a linear relationship. As the maximum stress increases, the difference between maximum volumetric strain and residual volumetric strain under different confining pressures increases. The variations in the maximum plastic internal variable with maximum stress under different confining pressures are shown in Figure 10D; the maximum plastic internal variable and its rate of change increase with the increase of the maximum stress under different confining pressures. As the confining pressures increases, the maximum plastic internal variable becomes smaller at the same maximum stress. Figure 10E illustrates the relationship between the maximum stress and the maximum deformation modulus, residual deformation modulus of rock under different confining pressures; the maximum deformation modulus increases as the maximum stress increases under different confining pressures, and its rate of change decreases gradually. When the residual deformation modulus increases in the stage of maximum stress from 30 MPa to 60 MPa, then remaining almost unchanged as the maximum stress increases under different confining pressures. This is because the damage in the initial loading stage is small, the deformation modulus mainly depends on the maximum strain rate, however, the damage increases owing to the influence of seismic load, thus the deformation modulus not only depends on the maximum strain rate, but also the plastic internal variable.

FIGURE 10

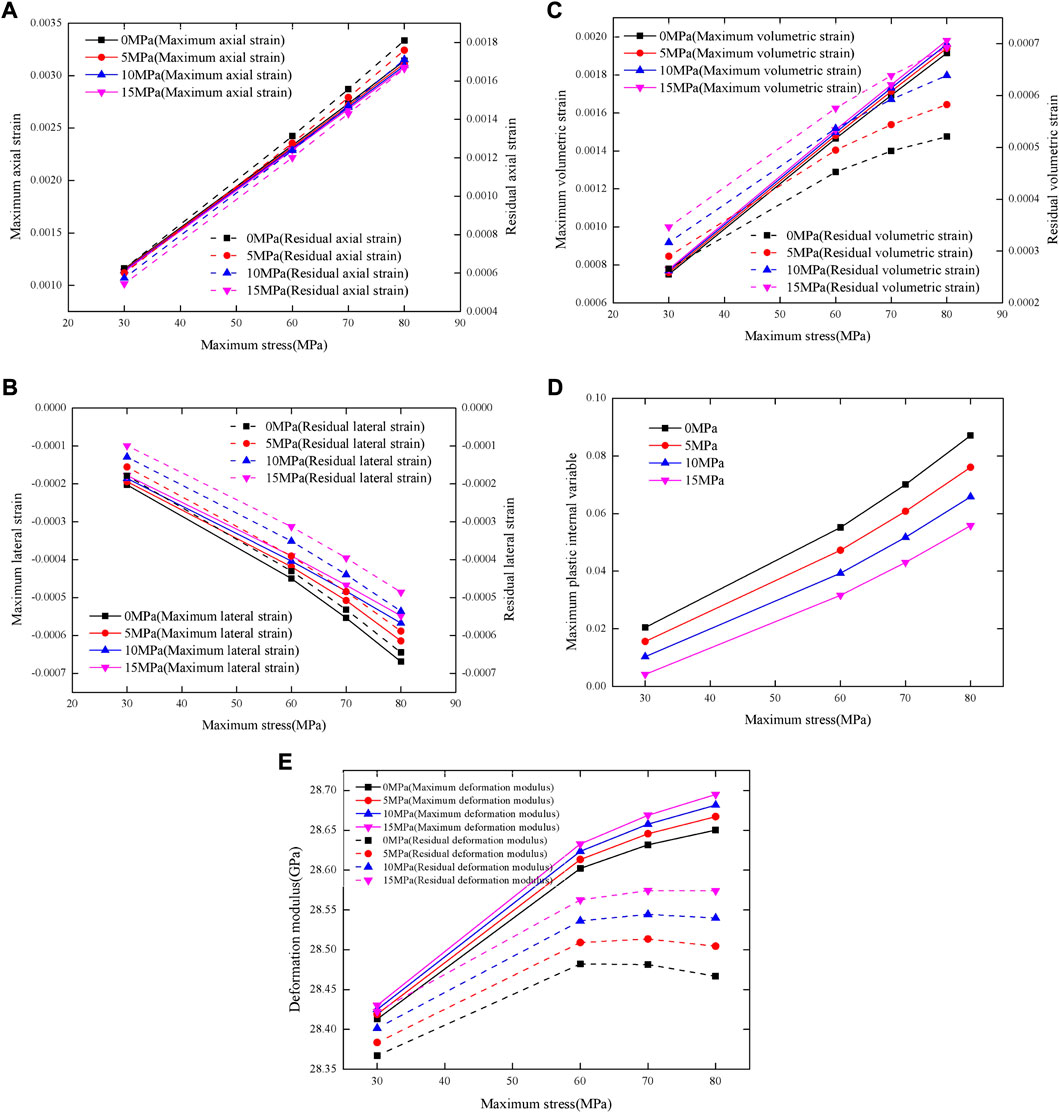
FIGURE 10. The variation in deformation properties of the rock with maximum stress under Kobe seismic load with different confining pressures: (A) Axial strain; (B) Lateral strain; (C) Volumetric strain; (D) Maximum plastic internal variable; (E) Deformation modulus.

The relationship between the dynamic deformation properties and confining pressure

Figure 11 depicts the relationship between the dynamic deformation properties of the rock and confining pressure under Kobe seismic load with different maximum stresses. The maximum axial strain and residual axial strain show a negative quasi-linear relationship with confining pressure under different maximum stresses, as illustrated in Figure 11A; the difference between the maximum axial strain and residual axial strain under different maximum stresses is less than 0.0002. While, the maximum lateral strain, residual lateral strain and confining pressure have a linear relationship, as shown in Figure 11B, and the linear correlation between the residual lateral strain and confining pressure is stronger than that between the maximum lateral strain and confining pressure. The relationship between the volumetric strain and confining pressure under different maximum stresses is demonstrated in Figure 11C. As the confining pressure increases, the maximum volumetric strain and residual volumetric strain increase linearly, albeit slowly. Unlike the relationship between the maximum plastic internal variable and maximum stress, it shows a negative quasi-linear relationship between the maximum plastic internal variable and confining pressure under different maximum stresses, as shown in Figure 11D. The variations in the maximum deformation modulus and residual deformation modulus of rock with confining pressure under different maximum stresses are shown in Figure 11E; this also differs from that with maximum stress. There is a linear relationship between the maximum deformation modulus, residual deformation modulus of rock and confining pressure. The reason is that the maximum strain rate under different confining pressures at the same maximum stress is the same, thus the plastic internal variable becomes the main factor for determining the deformation modulus based on formula (9). The plastic internal variable in the initial loading stage is small, while it increases because of the influence of seismic load, therefore, according to the variation of the maximum plastic internal variable with confining pressure as shown in Figure 11D, the increasing rate of the residual deformation modulus with the increase of confining pressure is greater than that of the maximum deformation modulus.

FIGURE 11

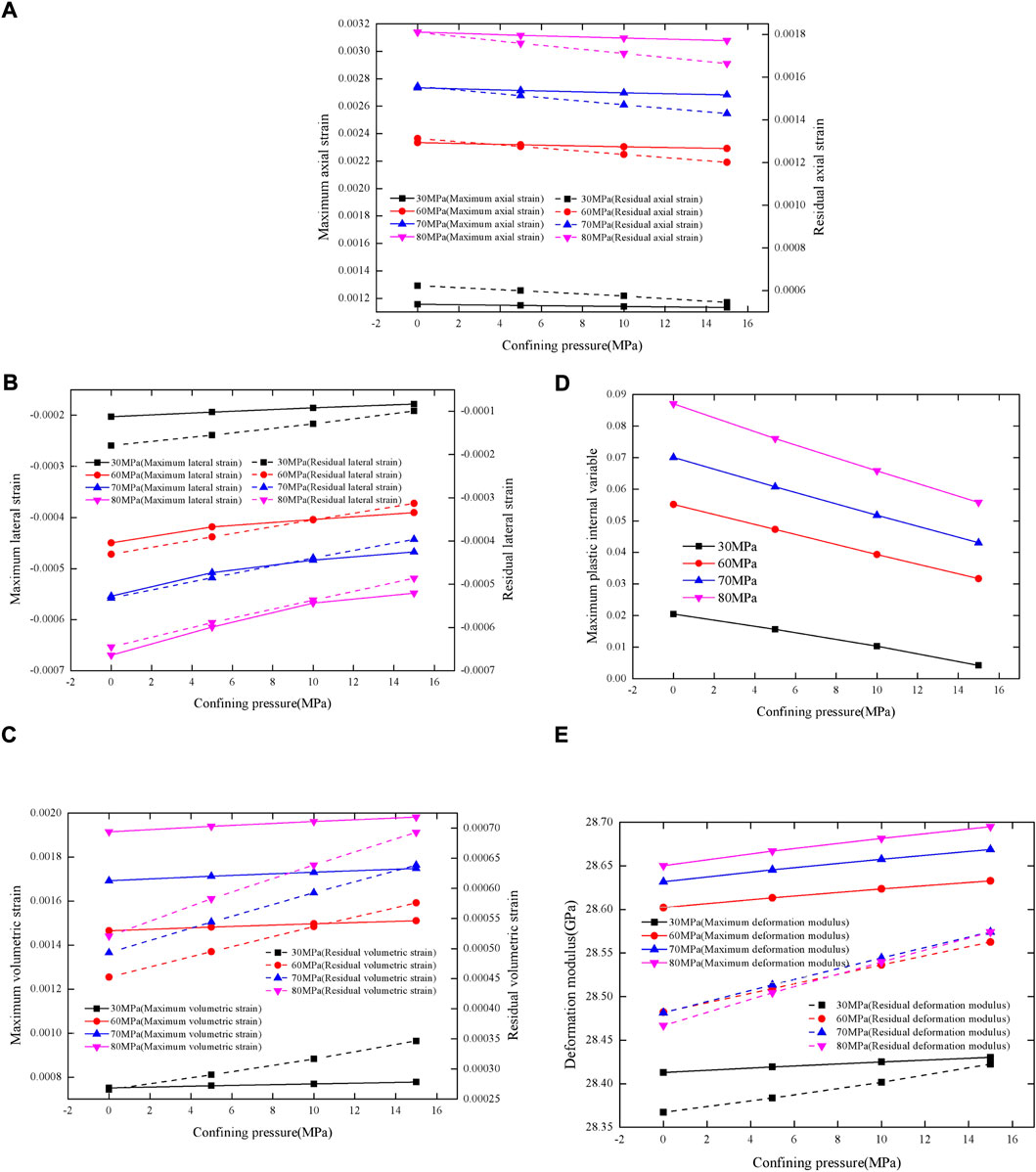
FIGURE 11. The variation in deformation properties of the rock with confining pressure under Kobe seismic load with different maximum stresses: (A) Axial strain; (B) Lateral strain; (C) Volumetric strain; (D) Maximum plastic internal variable; (E) Deformation modulus.

Conclusion

The influences of confining pressures on the dynamic deformation properties of T_2y6 marble under Kobe seismic load with four different maximum stresses were studied through numerical simulation. The main conclusions are as follows:

1) Hysteresis loops, cumulative plastic strain, strain rate effect, and damage are found in the stress-strain curves of the rock under Kobe seismic load, while the size and range of loading and unloading in each cycle are different.

2) The volumetric strain and axial strain are quasi-linearly related, and the rock tends to shrink under seismic load, whereas dilation occurs in the rock when the maximum stress of seismic load is large and the confining pressure is small.

3) Seismic load with small maximum stress cannot induce significant damage in the rock, but the influence thereof is greater than that of a static load. The maximum stress is the main factor affecting the damage to rock materials under seismic loads, while the effect of confining pressure on damage is smaller than that of maximum stress.

4) The maximum axial strain, residual axial strain, maximum volumetric strain, residual volumetric strain, and maximum plastic internal variable almost linearly increase with maximum stress under different confining pressures; the maximum lateral strain, residual lateral strain, and maximum stress have a negative linear relationship. The maximum deformation modulus and final deformation modulus show a non-linear relationship with maximum stress.

5) The maximum axial strain, residual axial strain, and maximum plastic internal variable demonstrate a negative quasi-linear relationship with confining pressure under different maximum stresses. While, the maximum lateral strain, residual lateral strain, maximum volumetric strain, residual volumetric strain, maximum deformation modulus, residual deformation modulus, and confining pressure have a linear relationship.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Ethics statement

Written informed consent was obtained from the [individual(s) AND/OR minor(s)’ legal guardian/next of kin] for the publication of any potentially identifiable images or data included in this article.’

Author contributions

YZ and JH were involved in the final development of the project and manuscript preparation. YZ, SD and JH wrote the manuscript draft. WY, SC and JH analyzed the data. All authors: corrections, modifications, and final acceptation.

Funding

The work reported in this paper is financially supported by the Key Laboratory of Roads and Railway Safety Control (Shijiazhuang Tiedao University), Ministry of Education (STDTKF202103), National Natural Science Foundation of China (No. U21A20159; No. 52179117), the Youth Innovation Promotion Association CAS (No.2021325). The authors are thankful for their support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Ameri, W. A., Abdulraheem, A., and Mahmoud, M. (2016). Long-Term effects of CO2 sequestration on rock mechanical properties. J. Energy Resour. Technol. 138 (1), 012201. doi:10.1115/1.4032011

CrossRef Full Text | Google Scholar

Aydan, O, (2016). Large rock slope failures induced by recent earthquakes. Rock Mech. Rock Eng. 49 (6), 2503–2524. doi:10.1007/s00603-016-0975-3

CrossRef Full Text | Google Scholar

Bagde, M. N., and Petros, V. (2005). Fatigue properties of intact sandstone samples subjected to dynamic uniaxial cyclical loading. Int. J. Rock Mech. Min. Sci. 42 (2), 237–250. doi:10.1016/j.ijrmms.2004.08.008

CrossRef Full Text | Google Scholar

Chang, Z. L., Catani, F., Huang, F. M., Liu, G. Z., Meena, S. R., Huang, J. S., et al. (2022). Landslide susceptibility prediction using slope unit-based machine learning models considering the heterogeneity of conditioning factors. J. Rock Mech. Geotechnical Eng. 21. doi:10.1016/j.jrmge.2022.07.009

CrossRef Full Text | Google Scholar

Chen, X., Tang, M., and Tang, C. (2021). Effect of confining pressure on the damage evolution and failure behaviors of intact sandstone samples during cyclic disturbance. Rock Mech. Rock Eng. 55, 19–33. doi:10.1007/s00603-021-02672-z

CrossRef Full Text | Google Scholar

Du, W. J., Sheng, Q., Fu, X. D., Chen, J., and Zhou, Y. Q. (2022). A TPDP-MPM-based approach to understanding the evolution mechanism of landslide-induced disaster chain. J. Rock Mech. Geotechnical Eng. 14 (4), 1200–1209. doi:10.1016/j.jrmge.2022.03.004

CrossRef Full Text | Google Scholar

Duan, M., Jiang, C., Yin, W., Yang, K., Li, J., and Liu, Q. (2021). Experimental study on mechanical and damage characteristics of coal under true triaxial cyclic disturbance. Eng. Geol. 295, 106445. doi:10.1016/j.enggeo.2021.106445

CrossRef Full Text | Google Scholar

Feng, X. T., Gao, Y., Zhang, X., Wang, Z., and Han, Q. (2020). Evolution of the mechanical and strength parameters of hard rocks in the true triaxial cyclic loading and unloading tests. Int. J. Rock Mech. Min. Sci. 131 (6), 104349. doi:10.1016/j.ijrmms.2020.104349

CrossRef Full Text | Google Scholar

Fu, X. D., Ding, H. F., Sheng, Q., Zhang, Z. P., Yin, D. W., and Chen, F. (2022). Fractal analysis of particle distribution and scale effect in a soil-rock mixture. Fractal Fract. 6 (2), 120. doi:10.3390/fractalfract6020120

CrossRef Full Text | Google Scholar

Fuenkajorn, K., and Phueakphum, D. (2010). Effects of cyclic loading on mechanical properties of Maha Sarakham salt. Eng. Geol. 112, 43–52, doi:10.1016/j.enggeo.2010.01.002

CrossRef Full Text | Google Scholar

Gao, Y., and Feng, X. T. (2019). Study on damage evolution of intact and jointed marble subjected to cyclic true triaxial loading. Eng. Fract. Mech. 215, 224–234. doi:10.1016/j.engfracmech.2019.05.011

CrossRef Full Text | Google Scholar

Gao, Y., and Wang, Z. (2021). Experimental study on the damage process of marble under true triaxial pre-peak unloading conditions. Int. J. Damage Mech. 30, 1542–1557. doi:10.1177/10567895211020799

CrossRef Full Text | Google Scholar

Hashiguchi, K. (2005). Generalized plastic flow rule. Int. J. Plasticity 21, 321–351. doi:10.1016/j.ijplas.2003.12.003

CrossRef Full Text | Google Scholar

Heap, M. J., and Faulkner, D. R. (2008). Quantifying the evolution of static elastic properties as crystalline rock approaches failure. Int. J. Rock Mech. Min. Sci. 45 (4), 564–573. doi:10.1016/j.ijrmms.2007.07.018

CrossRef Full Text | Google Scholar

Huang, F. M., Zhang, J., Zhou, C. B., Wang, Y. H., Huang, J. S., and Li, Z. (2020). A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 17 (01), 217–229. doi:10.1007/s10346-019-01274-9

CrossRef Full Text | Google Scholar

Huang, J.Q., , Zhao, M., , Xu, C.S., , Du, X.L., , Jin, L., , and Zhao, X., (2018). Seismic stability of jointed rock slopes under obliquely incident earthquake waves. Earthq. Eng. Eng. Vib. 17 (3), 527–539. doi:10.1007/s11803-018-0460-y

CrossRef Full Text | Google Scholar

Jiang, C., Li, Z., Wang, W., Wen, Z., Duan, M., and Geng, W. (2021). Experimental investigation of the mechanical characteristics and energy dissipation of gas-containing coal under incremental tiered cyclic loading. Geomech. Geophys. Geo. Energy. Ge. Resour. 75 (7). doi:10.1007/s40948-021-00274-1

CrossRef Full Text | Google Scholar

Liu, E., Huang, R., and He, S. (2012). Effects of frequency on the dynamic properties of intact rock samples subjected to cyclic loading under confining pressure conditions. Rock Mech. Rock Eng. 45, 89–102. doi:10.1007/s00603-011-0185-y

CrossRef Full Text | Google Scholar

Liu, J., Xie, H., Hou, Z., Yang, C., and Liang, C. (2014). Damage evolution of rock salt under cyclic loading in unixial tests. Acta Geotech. 9 (1), 153–160. doi:10.1007/s11440-013-0236-5

CrossRef Full Text | Google Scholar

Lu, J., Yin, G., Deng, B., Zhang, W., Li, M., Chai, X., et al. (2019). Permeability characteristics of layered composite coal-rock under true triaxial stress conditions. J. Nat. Gas Sci. Eng. 66, 60–76. doi:10.1016/j.jngse.2019.03.023

CrossRef Full Text | Google Scholar

Meng, Q. B., Liu, J. F., Huang, B. X., Pu, H., Wu, J. Y., and Zhang, Z. Z. (2021). Effects of confining pressure and temperature on the energy evolution of rocks under triaxial cyclic loading and unloading conditions. Rock Mech. Rock Eng. 55, 773–798. doi:10.1007/s00603-021-02690-x

CrossRef Full Text | Google Scholar

Peng, K., Zhou, J., Zou, Q., and Song, X. (2020). Effect of loading frequency on the deformation behaviours of sandstones subjected to cyclic loads and its underlying mechanism. Int. J. Fatigue 131 (2), 105349. doi:10.1016/j.ijfatigue.2019.105349

CrossRef Full Text | Google Scholar

Tsutsumi, S., and Hashiguchi, K. (2005). General non-proportional loading behavior of soils. Int. J. Plasticity 21, 1941–1969. doi:10.1016/j.ijplas.2005.01.001

CrossRef Full Text | Google Scholar

Vaneghi, R. G., Thoeni, K., Dyskin, A. V., Sharifzadeh, M., and Sarmadivaleh, M. (2020). Fatigue damage response of typical crystalline and granular rocks to uniaxial cyclic compression. Int. J. Fatigue 138, 105667. doi:10.1016/j.ijfatigue.2020.105667

CrossRef Full Text | Google Scholar

Xu, L., Li, Q., Mathias, S. A., Tan, Y., and Fan, C. (2021). Strain characteristics and permeability evolution of faults under stress disturbance monitoring by fibre Bragg grating sensing and pressure pulses. Geomech. Geophys. Geo. Energy. Ge. Resour. 7, 93. doi:10.1007/s40948-021-00289-8

CrossRef Full Text | Google Scholar

Yang, S. Q., Yang, J., and Xu, P. (2020). Analysis on pre-peak deformation and energy dissipation characteristics of sandstone under triaxial cyclic loading. Geomech. Geophys. Geo. Energy. Ge. Resour. 6 (1), 24. doi:10.1007/s40948-020-00146-0

CrossRef Full Text | Google Scholar

Yang, Y., Jiang, C., Guo, X., Peng, S., and Yan, F. (2021). Experimental investigation on the permeability and damage characteristics of raw coal under tiered cyclic unloading and loading confining pressure. Powder Technol. 389, 416–429. doi:10.1016/j.powtec.2021.05.062

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, H., Feng, X. T., Shao, J. F., Yang, Y. S., and Zhang, Y. G. (2010). Experimental research on elastoplastic coupling character of marble. Rock Soil Mech. 31 (8), 2425–2434.

Google Scholar

Zhou, Y., Sheng, Q., Li, N., Fu, X., and Zhang, Z. (2022). A dynamic constitutive model for rock materials subjected to medium- and low-strain-rate dynamic cyclic loading. J. Eng. Mech. doi:10.1061/(ASCE)EM.1943-7889.0002055

CrossRef Full Text | Google Scholar

Zhou, Y., Sheng, Q., Li, N., Fu, X., Zhang, Z., and Gao, L. (2020b). A constitutive model for rock materials subjected to triaxial cyclic compression. Mech. Mat. 144, 103341. doi:10.1016/j.mechmat.2020.103341

CrossRef Full Text | Google Scholar

Zhou, Y., Sheng, Q., Li, N., and Fu, X. (2020a). Numerical analysis of the mechanical properties of rock materials under tiered and multi-level cyclic load regimes. Soil Dyn. Earthq. Eng. 135. 106186. doi:10.1016/j.soildyn.2020.106186

CrossRef Full Text | Google Scholar