
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 11 January 2023
Sec. Environmental Informatics and Remote Sensing
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.1023883
This article is part of the Research Topic Advances and Applications of Non-Explosive Rock Fracturing in Exploitation of Geological Resources View all 5 articles
 Biao Zhang1*
Biao Zhang1* Quanli Sun2
Quanli Sun2Considering the intermediate principal stress effect of soils, the unified strength theory was applied to correct the shear strength index of soils. Based on a mechanical model of the anti-seismic stability of slopes, the analytical formula of the stability coefficient was deduced by the upper bound method and the quasi-static method. Then the optimal solution of the stability coefficient was figured out via the Matlab software. The result shows that, if the intermediate principal stress is ignored, the shear strength of soils would obviously be underestimated; this is also the case with the slope stability coefficient, the relative error of which could reach 39.87%. The horizontal and vertical seismic forces significantly affect slope stability. When the horizontal seismic force is considered, the slope stability coefficient Ns is reduced by 79.82%. Similarly, if the seismic effect is not neglected, the stability of the slope would be seriously overestimated. Slope cutting can significantly improve slope stability. When the slope angle is reduced from 90° to 50°, the stability factor increases by 279.82%. The suitable design angle of the slope is between 50° and 60° without taking into account additional elements like groundwater level and stratum structure.
Earthquakes not only demolish surface structures, but also cause serious disasters like landslides which threaten human existence and the safety of property. For instance, the 5.12 Wenchuan earthquake in 2008 caused a large-scale landslide that left 20,000 people who died or disappeared. In the “4·14 Yushu earthquake in 2010,” landslides and debris flows directly hit residential areas and killed more than 3,000 people. In 2015, a 7.8 magnitude earthquake hit Afghanistan, which caused a landslide that killed about 180 people. A 7 magnitude earthquake occurred in Luzon Island, Philippines in 2022 and triggered landslides that killed four people and wounded 60. As can be seen, the influence of earthquakes on slope stability cannot be overlooked in earthquake-prone locations. Therefore, the study of slope seismic stability has significant engineering value and research significance.
Nowadays there are numerous ways to study the seismic stability of slopes, including theoretical analysis, simulation test, and numerical analysis. Qin and Chian (2020) assessed the seismic stability of a reinforced slope using the quasi-dynamic approach. The seismic stability of an underwater slope was assessed by Yang et al. (2021) using a modified version of the Newmark technique. Srilatha et al. (2013) conducted a comparative study of unreinforced and reinforced soil slopes by a shaking table test. With the development of computer technology, numerical analysis has become increasingly significant in the seismic stability of slopes. Zhang Z. L. et al. (2017) tested the dynamic behavior and failure mechanism of a slope during an earthquake using the FLAC 2D numerical simulation program. However, the above method requires a significant amount of labor and a lengthy time period, which is not conducive to its application in engineering. Since Terzaghi first applied the quasi-static method to the geotechnical engineering field, the method has been widely used in engineering and has been incorporated into corresponding codes and guidance manuals. Therefore, using the quasi-static method is reliable for analysis and calculation. Michalowski and Martel (2011) introduced the seismic force simplified by the quasi-static method into the calculation of the slope, and obtained the upper limit solution of the stability factor. Nian et al. (2016) analyzed the seismic stability of a slope reinforced with row piles via the quasi-static method. The analytical expression of the stability factor was derived based on the combination of limit analysis and strength reduction. Moreover, the influence of the horizontal seismic coefficient on the horizontal stability force and optimal pile position in a seismic area was studied. Su et al. (2018) utilized the upper bound method of limit analysis and analyzed the seismic stability of a slope considering the influence of bolts. Wang et al. (2019) analyzed the seismic stability of unsaturated soil slopes using a semi-analytical method. Zhang et al. (2021a) introduced the quasi-static method into the calculation of slope stability, calculated the optimal solution of the stability factor of a saturated soft soil slope based on the upper limit method of limit analysis, and analyzed the stability factor of the saturated soft clay slope affected by the horizontal and vertical seismic forces. Xu and Yang (2018) analyzed the seismic stability of heterogeneous slopes using the quasi-static method, and studied the effects of reinforcement, slope angle, seismic force, and soil properties on slope stability.
The aforementioned scholars studied slope stability under seismic activity in great detail, but the majority of the strength criteria they employed were based on the M-C criterion, which is only considered for major stress and minor principal stress, and ignores the impact of intermediate principal stress on the soil. Yu et al. (1983) proposed the theory of twin shear stress strength based on the twin shear stress yield criterion. Although the theory considered the influence of intermediate principal stress, it is applicable to a single material. Based on this, Yu (2002) proposed the unified strength theory based on the unified yield criterion, which not only takes the influence of large and small principal stresses into account, but also considers the influence of intermediate principal stresses on the soil. It includes the M-C strength theory, weighted twin shear strength theory, maximum tensile strain strength theory, and other strength theories, which can be basically applied to all kinds of geotechnical materials. Thus, it is recognized by scholars in the geotechnical engineering field. Deng et al. (2019) studied the influence of unified strength theory on the failure characteristics and bearing capacity of strip foundations, and determined the appropriate intermediate principal stress influence parameters via model tests and numerical simulations. Zhao et al. (2016) obtained the unified solution of Rankine Earth pressure based on the twin shear unified strength theory by considering the intermediate principal stress, which proved that the potential strength of soil could be better used with consideration of the intermediate principal stress effect.
In fact, the shear strength of soil will be underestimated without considering the Mohr-Coulomb strength of the intermediate principal stress effect, and the stability of a slope cannot be correctly evaluated. Based on the former study, this work takes the intermediate principal stress effect on slope stability under seismic forces into account, and the unified strength theory is introduced into the slope seismic stability analysis. The seismic stability coefficient is obtained using the upper limit method of plastic theoretical limit analysis and the quasi-static method, and the intermediate principal stress influences on parameter b, slope angle, and seismic stability coefficient are sufficiently studied. Therefore, using unified strength theory in slope stability analysis may fully use the potential of soil shear strength, properly evaluate the stability of rock and soil slopes, and provide a reference for engineering practice.
The unified strength theory is based on the twin shear theory which includes many strength theories. The unified strength theory parameter b is between 0 and 1, which is the convex theory. Parameter b also reflects the degree of influence of intermediate principal stress on material failure, so it is also known as the influence parameter of intermediate principal stress. The unified strength theory expressed by the initial cohesion of soil and the initial angle of internal friction is as follows (Yu, 2011):
When
When
The intermediate principal stress for soil entering the plastic is stated as
where c0, φ0 is the initial cohesion and internal friction angle of the soil; b is the value range: (−1, 1); and σ1, σ2, σ3 are the major, intermediate, and minor principal stress, respectively.
The limit equilibrium condition in the soil may be calculated via the ultimate Mohr circle and shear strength envelope as follows:
Under the intermediate principal stress effect, the unified cohesion c and the internal friction angle φ of the soil can be described as (Tang et al., 2022)
The upper bound limit analysis method is an effective method to study geotechnical structure stability (Zhang B. et al., 2020; Zhang J. H. et al., 2020). It points out that the external power equals the internal loss power, and the obtained load is not less than the real failure load, as seen below:
where Ti is the surface force acting on the boundary and surface of the object; Fi is the volume force acting on the object, respectively;
The current common method for quantifying seismic effects is the quasi-static method (Zhang D. B. et al., 2021), which is adopted by engineers due to its clear mechanics concept and easy calculation.
The quasi-static method regards instantaneous seismic action as static action on the center of gravity of the structure. The expressions for the vertical static force and the horizontal static force are as follows:
where the horizontal acceleration coefficients kh under earthquakes are generally 0, 0.1, 0.2, 0.3; kv is equal to ζ kh; the value of the proportion coefficients of vertical seismic acceleration ζ are −1, −0.5, 0, 0.5, 1 (Zhang B. et al., 2021b; Zhang J. H. et al., 2022); and G is the gravity value of the structure.
Different from the failure characteristics of rock mass, the failure of soils generally has a curved shape (Wu et al., 2021; Wang et al., 2022). The research shows that when a soil slope is damaged, the actual failure surface approximates the logarithmic spiral curve (Michalowski and Drescher 2009; Utili 2013). According to the results of academic research, a slope calculation model is constructed. In Figure 1, the sliding mechanism rotates clockwise around the point O with an angular velocity ω, and the angle between the velocity and the discontinuities AC is φ, where φ is the friction angle of the soil, and the failure surface AC is the logarithmic spiral curve. The slope top is level, the slope height is H, the slope angle is β, OA=r0, AB=L, θ0, θh are the angles between OA, OC, and the horizontal plane, and θ is the angle between any diameter of O origin and the horizontal datum line.
The expression for AC is
Therefore, the length of OC is
It is derivable from the geometric relationship:
When the anti-seismic stability of slopes is assessed with the upper bound method, the following presumptions must be satisfied (Wu et al., 2019; Zhang D. B. et al., 2019): 1) the soil is an ideal plastic material, and obeys the associated flow law; 2) seismic action does not cause the effect of soil liquefaction; 3) the soil yield surface is convex in the stress space.
The external power of a slope under seismic activity is divided into two sections. One is the power exerted by the weight force of the sliding body, the other is the power exerted by the seismic force. For the convenience of calculation, the external power produced by the ABC sliding body is regarded as the power produced by the ACO block minus the power produced by the ABO and BCO blocks.
An area element in the logarithmic spiral ACO region was taken, and the external power generated in this region was obtained as
The external power generated by the block ABO is
The external power generated by the block BCO is
Therefore, the external power made by the sliding body ACB is
where
The total power generated by the horizontal and vertical seismic forces is
in which kh is the horizontal acceleration coefficient under the earthquake, and kv is the vertical seismic acceleration coefficient under the earthquake.
The total external power is shown as follows:
where
The internal energy loss rate Ps along the sliding plane is
According to the energy conservation theorem,
The critical height of slopes can be expressed as
Then the stability factor can be written as
From Figures 2A,B and Table 1, as the influence parameter b of the intermediate principal stress increases, the internal friction angle φ and the cohesion c show an increasing trend. This is when the intermediate principal stress (b=0) is ignored, that is, the soil obeys the M-C strength criterion. At this point, the soil cohesion c and the internal friction angle φ are the initial cohesion c0 and the initial internal friction angle φ0. When the intermediate principal stress (b=0.25, 0.5, 0.75, 1) was considered, a set of initial soil shear strength indicators (c0=20 kPa, φ0=20°) were taken. When b=0.25, the cohesion force c=21.62 kPa, and the internal friction angle φ=21.48°, the relative error reached 7.49% and 6.87%, respectively. When b=0.5, the cohesion force c=22.86 kPa, and the internal friction angle φ=22.59°, the relative error reached 12.52% and 11.47%, respectively. When b=0.75, the cohesive force c=23.85 kPa, and the internal friction angle φ=23.46°, the relative error reached 16.15% and 14.76%, respectively. When b=1, the cohesive force c=24.65 kPa, and the internal friction angle φ=24.16°, the relative error reached 18.88% and 17.23%, respectively. Therefore, the shear strength of soil will obviously be underestimated and underutilized if the intermediate principal stress is ignored.
As the initial internal friction angle φ0 of the soil increases from 10° to 20°, the internal friction angle φ increases from 12.64° to 24.16°; when the intermediate principal stress is considered (b=1), the relative error decreases from 20.90% to 17.23%. As the initial cohesion c0 of the soil increases from 15 kPa to 25 kPa (φ0=25°), the cohesion c increases from 18.27 kPa to 30.45 kPa; when the principal stress is considered (b=1), the relative error remains unchanged at 15.53%. When the influence of intermediate principle stress is considered, with the increase of initial internal friction angle φ0, the relative error of internal friction angle φ decreases gradually. However, when the initial internal friction angle is constant, the relative error of cohesion c remains unchanged with the increase of initial cohesion c0.
In order to more intuitively reflect the influence of the change of the intermediate principal stress influence parameter b on the soil shear strength index, three different soils were selected for comparative analysis (Jiang et al., 2022). In Figures 3A,B, the change curve of the friction angle φ in the three soils is relatively steep, while the change curve of the soil cohesion c is relatively gentle. Therefore, the intermediate principal stress has a greater notable effect on the internal friction angle of the soil. Likewise, among the three types of soil, the intermediate principal stress influence on parameter b has the most obvious influence on the shear strength index of strongly weathered mudstone, followed by silty clay, and the effect on the mixed fill is slight.
As shown in Figures 4A,B; Table 2, with the increase of the influence parameter b of intermediate principal stress, the stability factor Ns increases linearly. When the initial internal friction angle φ0 increases, the variation curve slope of the stability factor Ns increases, while the slope angle β increases and the variation curve slope of the stability factor Ns decreases. When the intermediate principal stress is ignored (b=0, ζ=0.5, kh=0.2, φ0=30°, β=50°), the stability factor Ns of the slope is 12.33, and while other conditions remain unchanged, the intermediate principal stress is considered. When b=0.25 and the stability factor Ns is 13.49, the relative error reached 8.06%, while when b=0.5 and the stability factor Ns is 14.49, the relative error reaches 14.86%. When b=0.75 and the stability factor Ns is 15.33, the relative error reaches 19.56%, while b=1 and the stability factor Ns is 16.10, the relative error reaches 23.41%. Consequently, the slope stability will obviously be underestimated if the intermediate principal stress is ignored.
The initial internal friction angle φ0 is 15°, 20°, 25°, and 30° when the influence of the intermediate principal stress (b=0.5, β=40°) is considered. The stability factor Ns is 8.57, 11.55, 16.42, and 26.08, which increases by 30.50%, 58.08%, 149.92%, and 296.94%, respectively, compared with φ0=10°. According to the aforementioned analysis results, slope stability is greatly sensitive to changes in the initial internal friction angle φ0. Thus, increasing the initial internal friction angle φ0 of the soil can significantly improve the slope stability.
As shown in Figures 5A,C, as the slope angle decreases, the slope stability factor Ns increases nonlinearly, and the curve of stability coefficient Ns has an obvious inflection point at the slope angle β=50°. Combining with Table 3, the stability factor Ns is 6.69 when β=90° (kh=0, ζ=0, φ0=30°). By cutting the slope, when the slope angle β decreases from 90° to 40°, the stability factor Ns is 58.27, which increases by 771%. When β decreases from 90° to 50°, the stability factor Ns is 15.41, which increases 279.92%. As β decreases from 90° to 60°, the stability factor Ns is 16.04, an increase of 139.76%. As β decreases from 90° to 70°, the stability factor Ns is 11.49, an increase of 71.74%. As β decreases from 90° to 80°, the stability factor Ns is 8.68, with an increase of 29.74%. Consequently, slope cutting is beneficial to slope stability, and the slope angle reduced to 40°–60° can significantly improve slope stability. The computation outcomes are substantially influenced by the change in slope angle, which is very sensitive to the slope sliding stability.
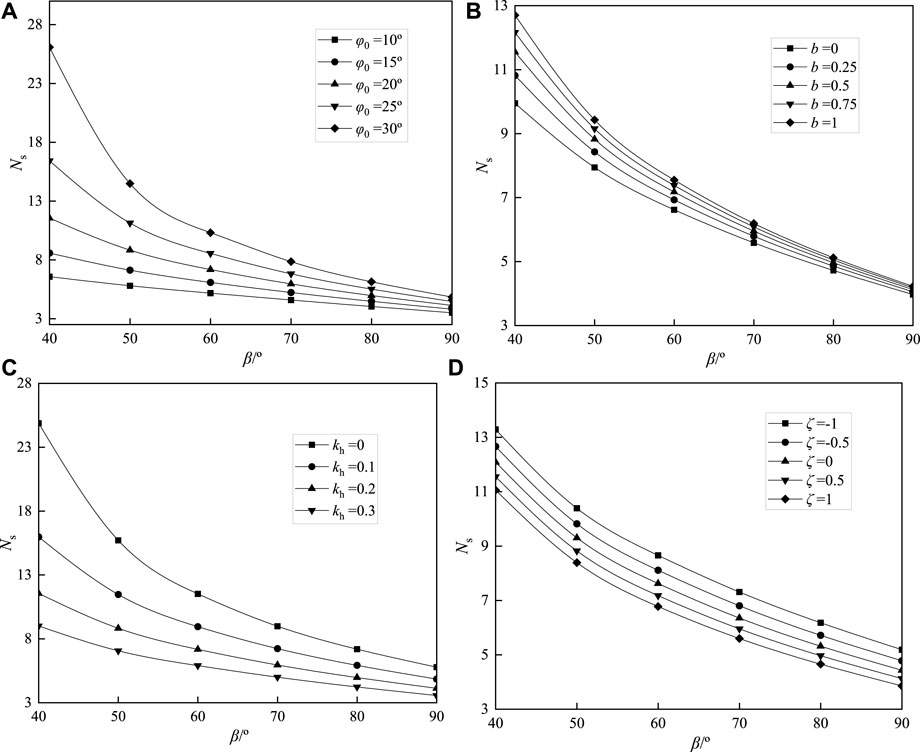
FIGURE 5. Effect of slope angle on stability factor: (A) kh=0.2, b=0.5, ζ=0.5; (B) kh=0.2, φ0=20°, ζ=0.5; (C) φ0=20°, b=0.5, ζ=0.5; (D) φ0=20°, b=0.5, kh=0.2.
From Figure 5B, when kh=0.2, φ0=20° and ζ=0.5 and the slope angle β=90°, the stability factor Ns is about 4.2, which is slightly affected by the intermediate principal stress parameter b. In Figure 5D, under the conditions of φ0=20°, b=0.5, and kh=0.2, with the slope angle β decreasing, the variation law of the stability factor Ns curve under different vertical seismic force acceleration proportional coefficient ζ is almost the same.
From Figures 6A,C, the slope stability factor Ns shows a decreasing trend as the horizontal seismic force acceleration coefficient kh increases. In Tables 4, 5, under the conditions of φ0=20°, β=70°, b=0.5, ζ=0.2, when the horizontal seismic force (kh=0) is overlooked, the stability factor Ns is 8.98. While the horizontal seismic force (kh=0.1, 0.2, 0.3) is considered, the stability factor Ns is 7.23, 5.95, and 5.00, respectively. Compared with overlooking the horizontal seismic force (kh=0), the stability factor Ns is reduced by 24.22%, 50.90%, and 79.82%, respectively. Therefore, the slope stability is significantly impacted by the horizontal seismic force. If the horizontal seismic force is disregarded, the slope stability will be seriously overestimated, resulting in a potential landslide risk.
From Figures 6B,D, with the vertical seismic force acceleration proportional coefficient ζ (kh≠0) increasing, the slope stability factor Ns decreases linearly. In Tables 4, 5, under the conditions of φ0=20°, β=70°, and b=0.5, when just the horizontal seismic force (kh=0.2, ζ=0) is taken into account, the stability factor Ns is 6.35. While both horizontal and vertical seismic forces (kh=0.2, ζ=1) are considered, the stability factor Ns is 5.60, which is reduced by 13.39%, compared to just considering the horizontal seismic force. Thus, the influence of the vertical seismic force on slope stability cannot be ignored. If the vertical seismic force is disregarded, the slope stability will be overestimated to some extent.
1) If the intermediate principal stress of soils is ignored, the shear strength of soils would obviously be reduced, which resulted in a serious underestimation of slope stability. Compared with considering the effect of intermediate principal stress (b = 1), when the effect of intermediate principal stress is not considered (b = 0). relative difference of the cohesion c and the internal friction angle φ reaches 21.39% and 20.90% respectively (φ0 = 10°, c0 = 20 kPa). Similarly, the relative difference of stability factor Ns of slopes reaches 23.41% with the conditions of φ0 = 30°, β = 50°, kh = 0.2 and ζ = 0.5. Accordingly, a suitable strength theory should be used to properly take into account the impact of the intermediate principal stress for the stability analyses of different soil slopes.
2) Slope cutting is an effective way to strengthen slope stability. When the slope angle decreases from 90° to 60°, 50°, and 40°, the stability factor Ns increases by 139.76%, 279.92%, and 771%, respectively. For slope stability, the sensitivity of physical parameters from large to small is as follows: slope angle β, initial internal friction angle φ0, horizontal seismic force parameter kh, medium principal stress influence parameter b, and vertical seismic force parameter ζ. The value of slope angle beta has the greatest influence on the calculation results. Without taking into account additional elements like groundwater level and stratum structure, the design slope angle is between 50° and 60°, which balances economy and safety.
3) The slope stability would be seriously overstated if the seismic force was disregarded. When the horizontal seismic force acceleration coefficient kh increases from 0 to 0.3 (φ0=20°, β=70°, b =0.5, and ζ=0.5), the stability factor Ns reduces by 79.82%. While the vertical seismic force acceleration proportional coefficient ζ increases from 0 to 1 (φ0=20°, β=70°, b=05, and kh=0.2), the stability factor Ns decreases by 13.39%. It is clear that the slope stability would be obviously exaggerated if the horizontal seismic force and the vertical seismic force were ignored. Besides, the effect of vertical seismic force on the stability of slopes is not as great as the effect of horizontal seismic force. However, neglecting these two effects will greatly increase the risk of slope landslide.
4) There is a certain inaccuracy with the actual scenario since the slope is treated as a two-dimensional plane for analysis in this work, which ignores the influence of slope width and boundary conditions. As a result, future research work could focus on the three-dimensional influence and boundary conditions of a slope.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
This study's goals and ideas are offered by BZ. BZ derived the formula, analyzed the original data, and wrote the first manuscript. QS revised and polished the manuscript. All of the listed authors contributed substantially to the research and gave approval for the paper’s publication.
This study was supported by the National Natural Science Foundation of China (52004088) and the Science Foundation of Hunan University of Science and Technology (E52076).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Deng, L.-S., Fan, W., Yin, Y.-P., and W, Y. (2019). Parametric study of the unified strength theory for a loess foundation supporting a strip footing. Environ. Earth Sci. 78, 344. doi:10.1007/s12665-019-8338-5
Jiang, W., Ouyang, Y., Yan, J.-Z., Wang, Z.-J., and Liu, L.-P. (2022). Inversion iterative correction method for estimating shear strength of rock and soil mass in slope engineering. Rock Soil Mech. 43 (8), 2287–2295. doi:10.16285/j.rsm.2021.1578
Michalowski, R. L., and Drescher, A. (2009). Three-dimensional stability of slopes and excavations. Géotechnique 59 (10), 839–850. doi:10.1680/geot.8.P.136
Michalowski, R. L., and Martel, T. (2011). Stability charts for 3D failures of steep slopes subjected to seismic excitation. J. Geotech. Geoenviron. Eng. 137 (2), 183–189. doi:10.1061/(ASCE)GT.1943-5606.0000412
Nian, T.-K., Jiang, J.-C., Wang, F.-W., Yang, Q., and Luan, M.-T. (2016). Seismic stability analysis of slope reinforced with a row of piles. Soil Dyn. Earthq. Eng. 84, 83–93. doi:10.1016/j.soildyn.2016.01.023
Qin, C.-B., and Chian, S.-C. (2020). Discretization-based kinematic analysis method to seismic stability of geosynthetic-reinforced slopes involving differing earthquake approaches. Int. J. Geomech. 20 (7), 060200. doi:10.1061/(asce)gm.1943-5622.0001660
Srilatha, N., Latha, G. M., and Puttappa, C. G. (2013). Effect of frequency on seismic response of reinforced soil slopes in shaking table tests. Geotext. Geomembranes 36, 27–32. doi:10.1016/j.geotexmem.2012.10.004
Su, L.-J., Sun, C.-N., Yu, F.-W., and Ali, S. (2018). Seismic stability analysis of slopes with pre-existing slip surfaces. J. Mt. Sci. 15 (6), 1331–1341. doi:10.1007/s11629-017-4759-3
Tang, R.-H., Mao, F., Chen, C.-F., and Lei, M. (2022). Upper bound solution for active thrust of nonhomogeneous cohesive soil considering effects of intermediate principal stress. J. Cent. South Univ. 29 (2), 582–595. doi:10.1007/s11771-022-4902-3
Utili, S. (2013). Investigation by limit analysis on the stability of slopes with cracks. Geotechnique 63 (2), 140–154. doi:10.1680/geot.11.P.068
Wang, L., Sun, D., Chen, B., and Li, J. (2019). Three-dimensional seismic stability of unsaturated soil slopes using a semi-analytical method. Comput. Geotechnics 110, 296–307. doi:10.1016/j.compgeo.2019.02.008
Wang, S.-F., Sun, L.-C., Li, X.-B., Zhou, J., Du, K., Wang, S.-Y., et al. (2022). Experimental investigation and theoretical analysis of indentations on cuboid hard rock using a conical pick under uniaxial lateral stress. Geomech. Geophys. Geo. Energy. Ge. Resour. 8, 34. doi:10.1007/s40948-022-00345-x
Wu, Q.-H., Li, X.-B., Weng, L., Li, Q.-F., Zhu, Y.-J., and Luo, R. (2019). Experimental investigation of the dynamic response of prestressed rockbolt by using an SHPB-based rockbolt test system. Tunn. Undergr. Space Technol. 93, 103088. doi:10.1016/j.tust.2019.103088
Wu, Q.-H., Weng, L., Zhao, Y.-L., and Feng, Fan. (2021). Influence of infilling stiffness on mechanical and fracturing responses of hollow cylindrical sandstone under uniaxial compression tests. J. Cent. South Univ. 28 (8), 2485–2498. doi:10.1007/s11771-021-4781-z
Xu, J.-S., and Yang, X.-L. (2018). Seismic and static stability analysis for 3D reinforced slope in nonhomogeneous and anisotropic soils. Int. J. Geomech. 18 (7), 04018065. doi:10.1061/(ASCE)GM.1943-5622.0001177
Yang, Q., Zhu, B., and Hiraishi, T. (2021). Probabilistic evaluation of the seismic stability of infinite submarine slopes integrating the enhanced Newmark method and random field. Bull. Eng. Geol. Environ. 80 (3), 2025–2043. doi:10.1007/s10064-020-02058-5
Yu, M.-H. (2002). Advances in strength theories for materials under complex stress state in the 20th century. Appl. Mech. Rev. 55, 169–218. doi:10.1115/1.1472455
Yu, M.-H., H, L. N., and S, L. Y. (1983). Twin shear stress theory and its generalization. Sci. China, Ser. A 11, 1174
Zhang, B., Jiang, J., Zhang, D.-B., and Liu, Z. (2021b). Upper bound solution of collapse pressure and permanent displacement of 3D tunnel faces using the pseudo-dynamic method and the kinematic approach. Geomechanics Eng. 25 (6), 521–533. doi:10.12989/gae.2021.25.6.521
Zhang, B., Jiang, Y., Cheng, H., and Liu, Z. (2021a). Upper bound analysis of the stability of 3D slopes in the saturated soft clay subjected to seismic effect. Front. Earth Sci. (Lausanne). 9, 795854. doi:10.3389/feart.2021.795854
Zhang, D.-B., Sun, W.-C., Wang, C.-Y., and Yu, Biao. (2021). Reliability analysis of seismic stability of shield tunnel face under multiple correlated failure modes. KSCE J. Civ. Eng. 25 (8), 3172–3185. doi:10.1007/S12205-021-2174-3
Zhang, J.-H., Peng, Xu., Sun, W.-C., and Li, Bo. (2022). Seismic reliability analysis of shield tunnel faces under multiple failure modes by pseudo-dynamic method and response surface method. J. Cent. South Univ. 29 (5), 1553–1564. doi:10.1007/s11771-022-5067-9
Zhang, B., Ma, Z.-Y., Wang, X., Zhang, J.-S., and Peng, W.-Q. (2020). Stability analysis of the pressurized 3D tunnel face in anisotropic and nonhomogeneous soils. Int. J. Geomech. 20 (1), 43–54. doi:10.1061/(ASCE)GM.1943-5622.0001635
Zhang, D.-B., Ma, Z.-Y., Yu, B., and Yin, H.-D. (2019). Upper bound solution of surrounding rock pressure of shallow tunnel under nonlinear failure criterion. J. Cent. South Univ. 26 (7), 1696–1705. doi:10.1007/s11771-019-4126-3
Zhang, J.-H., Zhang, L.-Y., Wang, W.-J., Zhang, D.-B., and Zhang, B. (2020). Probabilistic analysis of three-dimensional tunnel face stability in soft rock masses using Hoek-Brown failure criterion. Int. J. Numer. Anal. Methods Geomech. 44 (11), 1601–1616. doi:10.1002/nag.3085
Zhang, Z.-L., Wang, T., Wu, S.-R., Tang, H.-M., and Liang, C.-Y. (2017). Seismic performance of loess-mudstone slope in Tianshui-Centrifuge model tests and numerical analysis. Eng. Geol. 222, 225–235. doi:10.1016/j.enggeo.2017.04.006
Keywords: unified strength theory, intermediate principal stress, upper bound analysis, seismic force, stability coefficient
Citation: Zhang B and Sun Q (2023) Upper bound analysis of the anti-seismic stability of slopes considering the effect of the intermediate principal stress. Front. Earth Sci. 10:1023883. doi: 10.3389/feart.2022.1023883
Received: 20 August 2022; Accepted: 21 September 2022;
Published: 11 January 2023.
Edited by:
Shaofeng Wang, Central South University, ChinaReviewed by:
Dianchun Du, Southeast University, ChinaCopyright © 2023 Zhang and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Biao Zhang, MTAyMDE3NkBobnVzdC5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.