- 1Department of Civil Engineering, University of Bristol, Bristol, United Kingdom
- 2Hydrodynamic Technology Research Center, National Research and Innovation Agency (BRIN), Surabaya, Indonesia
- 3Department of Earth Sciences, Western University, London, ON, Canada
- 4Department of Statistical and Actuarial Sciences, Western University, London, ON, Canada
- 5Disaster Prevention Research Institute, Kyoto University, Kyoto, Japan
Integrated disaster resilience approaches are paramount for enhancing risk management of coastal communities in subduction zones under climate-geological risks. Cascading compounding climate-geological risks are dynamic, interact, and evolve with time. Also, classical convolution of hazard, vulnerability, and exposure does not allow easy implementation of causalities and dependencies that are critical in modelling impact chains due to cascading compounding multi-hazards. A new dynamic multi-hazard catastrophe modelling framework is proposed to fill important research gaps in the temporal evolution of climate-geological risks. Systemic modelling is a key tool where time-dependent and interacting risks are explicitly modelled, and multiple risk metrics can be computed. Furthermore, a possible new entropy-based approach for harmonising risk metrics is presented. Such a harmonisation can facilitate the decision-making process for disaster risk reduction. Finally, a way forward for future implementation of the proposed methodologies is discussed with a focus on the need for the development of new numerical and analytical tools.
Introduction
A globally agreed definition of risk does not exist yet (Aven and Renn, 2009). However, it is commonly accepted that risk analyses must account for uncertainties and produce expected consequences described probabilistically for all possible adverse hazardous events affecting a specific regional context (Aven et al., 2018). For example, natural disaster risks can be related to hazardous events of geologic nature (e.g., earthquake, tsunami, landslide, liquefaction, and subsidence) and climate-change phenomena (e.g., extreme weather, polar cap melting, and sea-level rise). These two typologies of risks are currently characterised and managed separately; however, they are not independent (Gallina et al., 2016), and impact chains must be modelled. An impact chain is a high-level representation of how a specific stressor/perturbance (e.g., climatic and geologic) propagates through a system (e.g., natural and built environment), considering possible impacts and system dependencies. Therefore, impact chains should be studied to jointly account for cascading compounding hazards and avoid neglecting possible cause-effect events in a multi-hazard framework (Zebisch et al., 2022). For instance, it has been demonstrated that a 50-cm sea-level rise might double the inundation area of future tsunami events (Li et al., 2018). Moreover, subduction earthquakes may also trigger coastal subsidence (Wang et al., 2013), simultaneously worsening tsunami effects and storm surges already affected by climate change (Hallegatte et al., 2011). The last example demonstrates how coastal communities in subduction zones are particularly susceptible to such chains of events triggered by climatic and geological hazards. Coastal communities are the focus of this paper.
In more general terms, from a mathematical point of view, risk is an operator (functional) transforming hazard, vulnerability, and exposure into quantifiable risk metrics, such as economic losses and casualties (Pflug and Pichler, 2014). Such an operator is dynamic as hazards, exposure, and vulnerability are time-dependent. Analogously to a dynamic system, the risk may be stable (or known) or may present bifurcation leading to instability (or unknown) and can be stationary or non-ergodic (Der Kiureghian 2005). For example, climate risks have slow onset (months to years), while geological risks linked to earthquakes and tsunamis are rapid (seconds to minutes). Climatic projections have a time horizon spanning from a couple of decades (near-term, Kirtman et al., 2013) to a century (long-term, Collins et al., 2013). Such slow-developing catastrophic risks are associated with gradual, imperceptible changes in the baseline that are unheeded until they lead to irreversible and devastating changes (IRGC 2013). Earthquakes and tsunamis may have projections spanning hundreds to thousands of years (mainshocks, Cornell 1968) to a few days (aftershocks, Yeo and Cornell, 2009). In contrast with climate change, seismic phenomena can be modelled as a discrete series of events rather than a continuous process. Vulnerability and exposure modules are also time-dependent. Vulnerability can increase because of ageing phenomena or can decrease because of adaptation measures. Also, current guidelines, building codes, and policy decisions will affect future situations (Galasso et al., 2021). It is essential to underline that this paper does not address all possible components of an impact chain potentially affecting a specific coastal community. The scope is to present an example considering risk components that are identified as relevant for coastal communities in subduction zones. Also, it is essential to clarify that the short- and long-term mentioned above depend on the risk components under assessment and the considered phenomena that will be modelled.
Importantly, risk is systemic and multi-component because interconnectivity between systems is one of the features of modern society (IRCG 2018). When consequences are assessed and quantified, in addition to the heterogeneous nature of the cascading hazards, multiple heterogeneous risk metrics are produced, e.g., economic losses, loss of lives, and environmental damage (Chakraborty et al., 2021; Cremen et al., 2022). Such metrics represent the critical input to policy development. Furthermore, risk metrics should also integrate local socioeconomic facets as future mitigation actions must accommodate a mechanism to achieve more equitable risk allocations among stakeholders considering gender, cultural, socioeconomic, and demographic balance (Peacock et al., 2014; Howell and Elliott, 2018). Harmonising existing quantifiable risk metrics and defining new ones, accounting for different responses/attitudes to risk, is still an outstanding task. Also, risk acceptability limits (e.g., limits of the as low as reasonably practicable or ALARP region) have not been defined yet. This becomes even more important when impact chains are directly modelled.
Several studies have defined general multi-risk frameworks (e.g., Marzocchi et al., 2012; Selva 2013; Mignan et al., 2014; Liu et al., 2015; Ming et al., 2015), and the multi-risk assessment due to cascading hazards presents several challenges (Schmidt et al., 2011; Kappes et al., 2012; Gill and Malamud, 2016). For example, De Risi and Goda (2016) and Goda and De Risi (2018) demonstrated how to treat the case of earthquake-tsunami hazards and risks by adapting the performance-based earthquake engineering approach to the multi-hazard case. Cremen et al. (2022) recently presented a detailed review of existing methodologies to model and quantify future risk from natural hazards. They also mention a general approach for the way forward to the application. Also, Dunant et al. (2021) presented a novel approach based on graph theory where the multi-risk problem is transformed into and visualised as a network where the nodes are the hazard sources and the components of the built environment, and the links are the impact-related correlation between the nodes. Building upon the literature and considering the shortcomings identified previously, it is evident that future research on risk assessment for coastal communities in subduction zones should focus on:
• Modelling the risk dynamically considering the time-dependence of the impact-chains facets;
• Modelling the risk under cascading compounding climate-geological hazards systemically; and
• Aggregating heterogeneous risk metrics with single risk/resilience indicators to facilitate risk management and implement future mitigation actions.
In this perspective paper, a discussion of these three aspects and some suggestions for possible implementations of these research topics are provided. Specifically, the authors’ opinion is provided on these topics as there are no broadly accepted methodologies to approach them. First, the dynamic nature of risk is presented with emphasis on the time dependence of the risk components. The implementation of a stress-test framework for risk management is discussed, where a stress test is a simulation intended to establish the ability of a system (e.g., communities facing subduction zones) to deal with crises (e.g., multiple cascading hazards) considering available resources both in the short- and long-term. Then, a new systemic approach for risk modelling is proposed. Finally, a potential homogenisation technique of risk metrics is presented.
Dynamic risks for coastal communities
In assessing the risk, particular emphasis should be devoted to the temporal aspect because cascading events depend on the time scale. The equation below incorporates such time dependency.
Multi-hazards and compound effects on coastal communities are challenging to model and forecast. Probabilistic methodologies exist (Behrens et al., 2021). However, developing a holistic time-dependent model capable of accounting for multiple hazard sequences and time-dependent exposure-vulnerability remains outstanding. Ultimately, the dynamic nature of the risk and its components is of paramount importance for long-term planning and risk management. Figure 1A depicts a schematic representation of the problem for coastal communities in subduction zones.
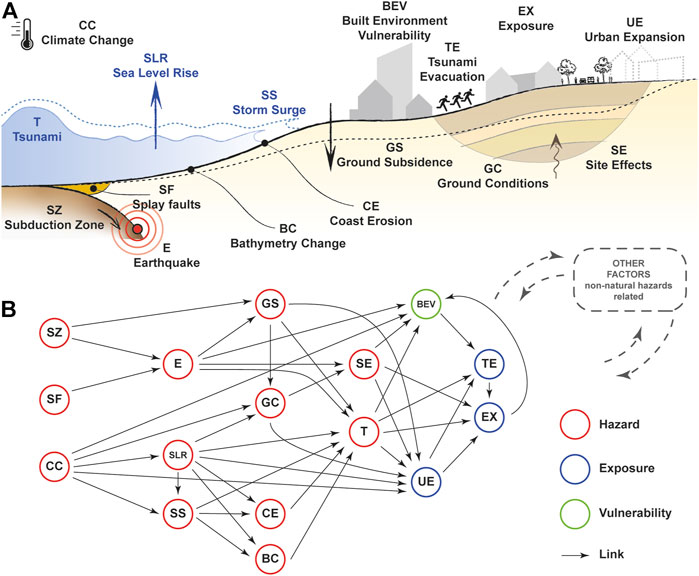
FIGURE 1. (A) Cascading compounding climate-geological hazards and effects. (B) Network-based schematisation of the dynamic risk for coastal communities in subduction zones.
Regarding the hazard assessment, it has been demonstrated that climate change can affect the risk for coastal communities (McInnes et al., 2003; Kato and Afifuddin, 2021). Therefore, the time dependence involves at least two aspects: 1) sea-level rise and 2) seismic sequences. Sea-level rise projections are built on historical data (Church and White, 2011) and simulation-based climate projections. The simulation-based climate projections (following the Intergovernmental Panel on Climate Change IPCC, Allan et al., 2021) are mainly focused on assessing the melting of glaciers due to the temperature rise; the glacier melting, in turn, changes the mean sea level on a monthly to annual scale. Climate change can also affect tropical cyclones and extra-tropical cyclones (Roberts et al., 2020; Ninomiya et al., 2021) as well as storm surges (Mori et al., 2019, 2021), making their size and intensity stronger and making their track and forward velocity even more unpredictable (Knutson et al., 2020). Sea level rise and storm surges can modify the bathymetry and accelerate coastal erosion. Also, for very low-probability cases, tsunamis may arrive on top of high astronomical tides and peaks of storm surges or in succession with short intervals, producing even more catastrophic effects. Time dependence on the seismic models requires a different level of sophistication, spanning from simple probabilistic renewal processes to fault rupture scenarios based on paleoseismicity (Abaimov et al., 2008; Field et al., 2015; Goda, 2019). The seismic issue is even more complicated when splay faults are considered because they affect both the tsunami generation and the time dependency of the problem (Moore et al., 2007). The interaction of seismic and tsunami hazards with climate change is not trivial for small to medium size tsunamis. Alhamid et al. (2022) presented an innovative framework where nonstationary sea-level rise due to climate change based on a non-Poisson stochastic renewal process is considered prior to the tsunami assessment. The multi-hazard problem becomes even more complex when ground conditions are considered dependent on climate change and sea-level rise (e.g., Ishii and Mori, 2020).
The exposure component is time-dependent (Calderón and Silva, 2021). Exposure to multiple hazards in active subduction zones is growing because more population migrates to and lives in coastal regions for economic reasons. Such long-term exposure has steadily increased over the last decades and will continue to evolve due to adaptation to climate change. Expansion of cities and towns occurs with urbanisation; such long-term dynamic behaviour can be computed with several methods, such as SLEUTH (Mesta et al., 2022). Urbanisation may be rapid and unplanned in some parts of the world (De Risi et al., 2018), leading to inequalities in coping with hazards and climate change (González-Dueñas and Padgett, 2022). In the case of tsunamis, the exposure in terms of human life also has a short-term variation due to the evacuation triggered by early-warning systems (Muhammad et al., 2021).
Several models exist in the literature regarding the vulnerability component, and they must adapt and change with time (Cremen et al., 2022). For example, in the case of tsunami fragility models (De Risi et al., 2017a; 2017b), existing models do not account for 1) time-dependent ageing (i.e., long-term effect) and 2) compounding effects due to cascading hazards (i.e., short-term effect); therefore, advancements are still needed for portfolio of structures (Attary et al., 2021). Also, vulnerability is strongly affected by codified designs and guidelines; today’s policy decisions will affect tomorrow’s situation (Galasso et al., 2021). Moreover, built environment components may change in the future due to climate change adaptation.
Finally, regarding the resilience dimension of the problem, together with the risk assessment discussed above, there is also a need to model and monitor how human activities recover after a shock (Eyre et al., 2020). This aspect introduces an additional temporal dimension to the problem as the system struck by a catastrophe must also be followed up in the months and years after the shock (Sharma et al., 2018; Doorn et al., 2019).
In summary, to perform a sound risk assessment considering the dynamic nature of the problem, it is necessary to:
• Account for the cascading compounding effects due to the multi-hazard context by constructing a rational description of the impact chain.
• Describe the temporal renewal process for each hazard, independently and jointly, considering the dependencies identified in the description of the impact chain.
• Describe the interface among natural, built, and human-societal environments.
• Identify the system at risk (ISO 13824, 2020), i.e., the exposure and characterisation of the time-evolution of the exposure components.
• Identify the vulnerability components and their long-term and short-term variability due to ageing and hazard sequences and interactions.
• Describe the time dimension of the recovery after a single shock or a sequence of shocks to feed resiliency models.
A practical and versatile way to implement these aspects is to use simulation-based probabilistic procedures after implementing the problem with a systemic representation. Such an implementation will also allow running simulations (e.g., stress tests) on possible implications associated with specific new disaster risk reduction policies that may have a long-term effect on the exposure and vulnerability of the components of the built environment. Stress tests are a perfect tool to assess how coastal communities can cope with severe future hazardous scenarios and ensure that there are enough resources to withstand extreme shocks, thereby facilitating the implementation of workable solutions in socially acceptable and equitable ways.
Systemic implementation for coastal communities
The idea proposed herein builds upon the work of Gill and Malamud (2016) and Dunant et al. (2021). The suggested underlying analytical framework consists of a probabilistic graph/network-based simulator of multi-hazard risks accounting for long-term and short-term variability by treating temporally evolving hazards, exposures, and vulnerabilities as nodes connected with causality and dependency links. Eventually, all causality and dependency must be characterised and mapped against simulated outputs consisting of quantifiable risk measures (Figure 1B). It is essential to underline that in this paper, almost all the risk components are mainly related to natural hazards and climate change; however, if other non-natural hazard-related phenomena must be accounted for, this is still possible due to the modularity of the proposed implementation (see the dashed lines in Figure 1B). Also, the systemic implementation using network-based tools is the natural approach for modelling the network of networks schematisation if built-human-societal interactions are going to be implemented explicitly (Dueñas-Osorio et al., 2007).
In general, fault and logic trees are convenient tools accounting for all possible circumstances and consequences in an impact chain framework. However, these tools may not be sufficient for the simulation-based procedure because the structure of any decision tree is designed to represent the order of the events and not necessarily their occurrence time (Cabasino et al., 2013). Bayesian Networks (BNs), Dynamic Bayesian Networks (DBNs), and Petri Nets (PNs) allow for overcoming such a problem (Kabir and Papadopoulos, 2019). BNs and DBNs have a flexible structure that enables easy uncertainty propagation and allow leveraging expert knowledge and problem characteristics; however, there are no clear semantic guidelines for developing BNs. DBNs are an extension of BNs, allowing the implementation of the time dimension, and have been used to model time-varying factors and cascading effects in coastal regions (Gonzalez-Duenas and Padgett, 2021), as well as the resilience of systems (Kammouh, Gardoni, and Cimellaro 2020). PNs are well suited for modelling complex, distributed, and concurrent systems (Peterson, 1981) and come with solid semantic development guidelines allowing more coherent models (Kabir and Papadopoulos, 2019). Therefore, PNs, although potentially more computationally expensive than BNs, may be the way forward for the dynamic quantification of risk due to cascading compounding climate-geological hazards.
A PN, also known as place/transition net, is commonly used to describe discrete events in a dynamic system. Such a schematisation is a bipartite graph composed of two node typologies: places and transitions. Places can be connected only to transitions, and transitions can be connected only to places. Arrows/arcs/edges represent the flow of information between transitions and conditions, i.e., the relationships between places are characterised via transitions. Also, inhibition arcs exist. Usually depicted with circles, places represent the components of the system. The status of each component is described by tokens (usually depicted with black dots within places) representing the measure of activities of a given system entity. Such tokens represent intermediate results and can be binary or have numerical values attached to them (i.e., coloured PN). The transitions, conventionally represented with bars or boxes, are operations ruling the progression of the simulation downstream of the network. Tokens travel across the net as transitions are experienced. The transition is conditioned by the status of the states connected to it, by the nature of the arcs, and can be governed by time (i.e., timed PN). Tokens travelling in the network will activate a specific state status and/or will bring some numerical values with them. Therefore, transition nodes can account for cascading events containing the temporal properties described in the “Dynamic risks for coastal communities” section and simplify the assessment of compound consequences. Ultimately, PNs allow the schematisation of the order and occurrence of the events, which are defined deterministically, and both places and transitions can be modelled probabilistically. The network, at any given time, is a single scenario. Running the network many times will allow to create a stochastic catalog of multi-hazard events that can be post-processed probabilistically.
To improve the understanding of the potential modelling, the impact chain for the tsunami risk is described with reference to Figure 1. The subduction zone (SZ) and the splay fault (SF) can generate an earthquake (E), potentially leading to a tsunami (T). Both short-term and long-term earthquake occurrences should be properly modelled and implemented. Strong subduction earthquakes can trigger ground subsidence (GS) that can affect the tsunami assessment as it changes the topography of the site of interest, changing the inundation consequently. At the same time, climate change (CC) can affect sea level rise (SLR) and storm surges (SS). These two phenomena, on one hand, accelerate coastal erosion (CE) and change the bathymetry (BC), affecting the propagation of the waves; on the other hand, SLR and SS can be concurrent or close in time to tsunami events, making the impact even worse. CC can also directly impact the built environment with two competing effects, either 1) accelerating ageing phenomena and deteriorating the strength characteristics of the physical elements of the built environment, or 2) reducing the vulnerability through mitigation actions. Also, CC can affect the ground conditions (GC) that, in turn, modify the seismic site response (SR) under the built environment. The seismic actions (E) and site effects (SE) can reduce the strength of the built environment that can also be affected by a tsunami (T). The risk assessment should be conducted on the exposure (EX) that should account for long-term (urban expansion UE) and short-term (tsunami evacuation TE) variations. EX and UE are also affected by T as preferential urban expansion schemes and potential relocation policies may be needed. This brief presentation of the impact chains shows the challenge of recognising possible scenarios and comprehensively accounting for possible links. This example is not exhaustive, further hazards and dependency links can be added, e.g., earthquake-induced landslides potentially blocking evacuation routes.
Risk metrics homogenisation
The systemic simulation-based implementation of the dynamic risk framework presented above will simplify the convolution of the different system components to assess economic losses, loss of lives, and even CO2 emissions due to the need to repair and rebuild the built environment. The aspect of human life is always a delicate topic; a broadly accepted approach consists of adopting the Life Quality Index, LQI, with regard to natural, anthropogenic, and technological risks (Rackwitz, 2002; Goda and Hong, 2006). A key aspect associated with the multi-dimensionality of such quantifiable risk metrics/indices is the need for homogenisation. A broadly acceptable principle to harmonise all risk metrics is not yet available. This makes difficult for risk managers to decide which metric to prioritise and which one to use in designing disaster policies.
It is, therefore, evident that a new quantifiable risk/resilience metric/index addressing local needs is required by accounting for multiple aspects and different responses/attitudes to risks and socioeconomic characteristics (necessary to simplify equitable risk appraisal and resource allocation). Ultimately, such indexes must make disaster policies straightforward through risk-informed early actions, proposing viable risk mitigation options, and making use of generalised cost-benefit tools.
A way of harmonising multiple risk metrics can be acquired from the entropy-based approach for multi-criteria problems (Hwang and Yoon, 1981). The entropy-based approach is conventionally adopted when multiple alternatives are available, and each alternative is assessed against a plethora of criteria. Adapting the entropy-based methodology to the framework presented in this paper consists of substituting the alternatives with values obtained with the simulation-based approach. Specifically, let L be a matrix with m rows (equal to the number of simulations) and n columns (equal to the number of risk metrics); therefore, the generic term lij of the matrix L is the loss for the simulation i corresponding to the risk metric j. Being lij computed from the dynamic framework presented above, these values will account already for the time dimension. The different columns of L cannot be represented on the same plot as they have heterogeneous units (e.g., dollars, casualties, and kgCO2e). However, the columns can be combined with a weighted sum where the weights can be computed with the entropy-based approach.
First, the terms of L must be normalised as follows:
Second, the entropy for each jth risk metric can be computed as follows:
Third, the weights can be calculated for each risk metric using the following relationship:
Such weights can account for subjectivity by introducing further weights (Guo et al., 2017). Finally, the dimensionless values
Pathway to future research development
In this paper, a perspective on future research on dynamic risk assessment under cascading compounding climate-geological hazards is presented. Three main aspects are discussed: 1) the dynamic nature of risk, 2) the systemic modelling needed to account for impact chains due to cascading and compounding multi-hazards, and 3) the outline of a procedure on how to harmonise risk metrics. Although a real case study or application is not provided, this paper paves the way for potential future research by defining a theoretical background. Therefore, future efforts are needed to develop tools to implement such an approach and demonstrate the viability and replicability of the procedure in multiple regions. The proposed methodologies may have a broader impact as they overcome the classical risk integration and can be adapted to other multi-hazard contexts.
Author contributions
The authors contributed equally to this perspective paper.
Funding
RDR acknowledges the COST Action CA18109 AGITHAR, supported by COST (European Cooperation in Science and Technology). KG is funded by the Canada Research Chair program (950-232015) and the NSERC Discovery Grant (RGPIN-2019-05898). NM is funded by JSPS Grant-in-Aid for Scientific Research (A) 19H00782, SENTAN Program (JPMXD0722678534) supported by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, and DPRI Research funds.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abaimov, S. G., Turcotte, D. L., Shcherbakov, R., Rundle, J. B., Yakovlev, G., Goltz, C., et al. (2008). Earthquakes: Recurrence and interoccurrence times. Pure Appl. Geophys. 165 (3), 777–795. doi:10.1007/s00024-008-0331-y
Alhamid, A. K., Akiyama, M., Aoki, K., Koshimura, S., and Frangopol, D. M. (2022). Stochastic renewal process model of time-variant tsunami hazard assessment under nonstationary effects of sea-level rise due to climate change. Struct. Saf. 99, 102263. doi:10.1016/j.strusafe.2022.102263
Allan, R. P., Hawkins, E., Bellouin, N., Collins, B., Masson-Delmotte, V., Zhai, P., et al. (2021). “IPCC, 2021: Summary for policymakers,” in Climate change 2021: The physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental Panel on climate change. Editors O. Yelekçi, R. Yu, and B. Zhou (Cambridge, UK: Cambridge University Press).
Attary, N., Van De Lindt, J. W., Barbosa, A. R., Cox, D. T., and Unnikrishnan, V. U. (2021). Performance-based tsunami engineering for risk assessment of structures subjected to multi-hazards: Tsunami following earthquake. J. Earthq. Eng. 25 (10), 2065–2084.
Aven, T., Ben-Haim, Y., Boje Andersen, H., Cox, T., Droguett, E. L., Greenberg, M., et al. (2018). Society for risk analysis glossary. Available at: https://www.sra.org/wp-content/uploads/2020/04/SRA-Glossary-FINAL.pdf. Last access: 25/07/2022..
Aven, T., and Renn, O. (2009). On risk defined as an event where the outcome is uncertain. J. Risk Res. 12 (1), 1–11. doi:10.1080/13669870802488883
Behrens, J., Løvholt, F., Jalayer, F., Lorito, S., Salgado-Gálvez, M. A., Sørensen, M., et al. (2021). Probabilistic tsunami hazard and risk analysis: A review of research gaps. Front. Earth Sci. (Lausanne). 9, 114. doi:10.3389/feart.2021.628772
Cabasino, M. P., Giua, A., and Seatzu, C. (2013). “Introduction to Petri nets,” in Control of discrete-event systems (London: Springer), 191–211.
Calderón, A., and Silva, V. (2021). Exposure forecasting for seismic risk estimation: Application to Costa Rica. Earthq. Spectra 37 (3), 1806–1826. doi:10.1177/8755293021989333
Chakraborty, L., Thistlethwaite, J., Minano, A., Henstra, D., and Scott, D. (2021). Leveraging hazard, exposure, and social vulnerability data to assess flood risk to indigenous communities in Canada. Int. J. Disaster Risk Sci. 12 (6), 821–838. doi:10.1007/s13753-021-00383-1
Church, J. A., and White, N. J. (2011). Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 32 (4), 585–602. doi:10.1007/s10712-011-9119-1
Collins, M., Knutti, R., Arblaster, J., Dufresne, J. L., Fichefet, T., Friedlingstein, P., ..., , and Booth, B. B. (2013). “Long-term climate change: Projections, commitments and irreversibility,” in Climate change 2013-the physical science basis: Contribution of working group I to the fifth assessment report of the intergovernmental Panel on climate change (Cambridge, UK: Cambridge University Press), 1029–1136.
Cornell, C. A. (1968). Engineering seismic risk analysis. Bull. Seismol. Soc. Am. 58 (5), 1583–1606. doi:10.1785/bssa0580051583
Cremen, G., Galasso, C., and McCloskey, J. (2022). Modelling and quantifying tomorrow's risks from natural hazards. Sci. Total Environ. 817, 152552. doi:10.1016/j.scitotenv.2021.152552
De Risi, R., Goda, K., Mori, N., and Yasuda, T. (2017a). Bayesian tsunami fragility modeling considering input data uncertainty. Stoch. Environ. Res. Risk Assess. 31 (5), 1253–1269. doi:10.1007/s00477-016-1230-x
De Risi, R., and Goda, K. (2016). Probabilistic earthquake–tsunami multi-hazard analysis: Application to the tohoku region, Japan. Front. Built Environ. 2, 25. doi:10.3389/fbuil.2016.00025
De Risi, R., Goda, K., Yasuda, T., and Mori, N. (2017b). Is flow velocity important in tsunami empirical fragility modeling? Earth-Science Rev. 166, 64–82. doi:10.1016/j.earscirev.2016.12.015
Der Kiureghian, A. (2005). Non‐ergodicity and PEER's framework formula. Earthq. Eng. Struct. Dyn. 34 (13), 1643–1652. doi:10.1002/eqe.504
Doorn, N., Gardoni, P., and Murphy, C. (2019). A multidisciplinary definition and evaluation of resilience: The role of social justice in defining resilience. Sustain. Resilient Infrastructure 4 (3), 112–123. doi:10.1080/23789689.2018.1428162
Dueñas-Osorio, L., Craig, J. I., Goodno, B. J., and Bostrom, A. (2007). Interdependent response of networked systems. J. Infrastruct. Syst. 13 (3), 185–194. doi:10.1061/(asce)1076-0342(2007)13:3(185)
Dunant, A., Bebbington, M., and Davies, T. (2021). Probabilistic cascading multi-hazard risk assessment methodology using graph theory, a New Zealand trial. Int. J. Disaster Risk Reduct. 54, 102018. doi:10.1016/j.ijdrr.2020.102018
Eyre, R., De Luca, F., and Simini, F. (2020). Social media usage reveals recovery of small businesses after natural hazard events. Nat. Commun. 11 (1), 1629–1710. doi:10.1038/s41467-020-15405-7
Field, E. H., Biasi, G. P., Bird, P., Dawson, T. E., Felzer, K. R., Jackson, D. D., et al. (2015). Long‐term time‐dependent probabilities for the third Uniform California Earthquake Rupture Forecast (UCERF3). Bull. Seismol. Soc. Am. 105 (2A), 511–543. doi:10.1785/0120140093
Galasso, C., McCloskey, J., Pelling, M., Hope, M., Bean, C., Cremen, G., et al. (2021). Editorial. Risk-Based, pro-poor urban design and planning for tomorrow's cities. Int. J. Disaster Risk Reduct. 58, 102158. doi:10.1016/j.ijdrr.2021.102158
Gallina, V., Torresan, S., Critto, A., Sperotto, A., Glade, T., and Marcomini, A. (2016). A review of multi-risk methodologies for natural hazards: Consequences and challenges for a climate change impact assessment. J. Environ. Manag. 168, 123–132. doi:10.1016/j.jenvman.2015.11.011
Gill, J. C., and Malamud, B. D. (2016). Hazard interactions and interaction networks (cascades) within multi-hazard methodologies. Earth Syst. Dyn. 7 (3), 659–679. doi:10.5194/esd-7-659-2016
Goda, K., and De Risi, R. (2018). Multi-hazard loss estimation for shaking and tsunami using stochastic rupture sources. Int. J. Disaster Risk Reduct. 28, 539–554. doi:10.1016/j.ijdrr.2018.01.002
Goda, K., and Hong, H. P. (2006). Optimal seismic design considering risk attitude, societal tolerable risk level, and life quality criterion. J. Struct. Eng. (N. Y. N. Y). 132 (12), 2027–2035. doi:10.1061/(asce)0733-9445(2006)132:12(2027)
Goda, K. (2019). Time-dependent probabilistic tsunami hazard analysis using stochastic rupture sources. Stoch. Environ. Res. Risk Assess. 33 (2), 341–358. doi:10.1007/s00477-018-1634-x
González-Dueñas, C., and Padgett, J. E. (2022). Considering time-varying factors and social vulnerabilities in performance-based assessment of coastal communities exposed to hurricanes. J. Struct. Eng. (N. Y. N. Y). 148 (8), 04022107. doi:10.1061/(asce)st.1943-541x.0003400
Guo, A., Liu, Z., Li, S., and Li, H. (2017). Seismic performance assessment of highway bridge networks considering post-disaster traffic demand of a transportation system in emergency conditions. Struct. Infrastructure Eng. 13 (12), 1523–1537. doi:10.1080/15732479.2017.1299770
Hallegatte, S., Ranger, N., Mestre, O., Dumas, P., Corfee-Morlot, J., Herweijer, C., et al. (2011). Assessing climate change impacts, sea level rise and storm surge risk in port cities: A case study on copenhagen. Clim. Change 104 (1), 113–137. doi:10.1007/s10584-010-9978-3
Howell, J., and Elliott, J. R. (2018). As disaster costs rise, so does inequality. Socius. 4, 2378023118816795. doi:10.1177/2378023118816795
Hwang, C. L., and Yoon, K. (1981). “Methods for multiple attribute decision making,” in Multiple attribute decision making (Berlin, Heidelberg: Springer), 58–191.
Irgc, (2018). Guidelines for the governance of systemic risks. Lausanne: International risk governance center (IRGC). Available from: www.//irgc.org/irgc.epfl.ch. Last access: 25/07/2022. doi:10.5075/epfl-irgc-257279
Irgc, (2013). Preparing for future catastrophe. Governance principles for slow-developing risk that may have potentially catastrophic consequences. Lausanne: International Risk Governance Center (IRGC). Available from: https://irgc.org/risk-governance/preparing-for-future-catastrophes/. Last access: 25/07/2022.
Ishii, M., and Mori, N. (2020). d4PDF: large-ensemble and high-resolution climate simulations for global warming risk assessment. Prog. Earth Planet. Sci. 7, 58. Article number 58. doi:10.1186/s40645-020-00367-7
ISO 13824, (2020). Bases for design of structures — general principles on risk assessment of systems involving structures. International Standards. Second edition.
Kabir, S., and Papadopoulos, Y. (2019). Applications of bayesian networks and Petri nets in safety, reliability, and risk assessments: A review. Saf. Sci. 115, 154–175. doi:10.1016/j.ssci.2019.02.009
Kammouh, O., Gardoni, P., and Cimellaro, G. P. (2020). Probabilistic framework to evaluate the resilience of engineering systems using Bayesian and dynamic Bayesian networks. Reliab. Eng. Syst. Saf. 198, 106813. doi:10.1016/j.ress.2020.106813
Kappes, M. S., Keiler, M., von Elverfeldt, K., and Glade, T. (2012). Challenges of analyzing multi-hazard risk: A review. Nat. Hazards (Dordr). 64 (2), 1925–1958. doi:10.1007/s11069-012-0294-2
Kato, S., and Afifuddin, M. (2021). Coupling sea-level rise with tsunamis: Projected adverse impact of future tsunamis on Banda Aceh city, Indonesia. Int. J. Disaster Risk Reduct. 55, 102084 doi:10.1016/j.ijdrr.2021.102084
Kirtman, B., Power, S. B., Adedoyin, A. J., Boer, G. J., Bojariu, R., Camilloni, I., ..., , and Wang, H. J. (2013). Near-term climate change: Projections and predictability. Climate change 2013: The physical science basis. IPCC Work. Group I Contribution AR5, 953–1028.
Knutson, T., Camargo, S. J., Chan, J. C., Emanuel, K., Ho, C. H., Kossin, J., et al. (2020). Tropical cyclones and climate change assessment: Part II: Projected response to anthropogenic warming. Bull. Am. Meteorological Soc. 101 (3), E303–E322. doi:10.1175/bams-d-18-0194.1
Li, L., Switzer, A. D., Wang, Y., Chan, C. H., Qiu, Q., and Weiss, R. (2018). A modest 0.5-m rise in sea level will double the tsunami hazard in Macau. Sci. Adv. 4 (8), eaat1180. doi:10.1126/sciadv.aat1180doi:eaat1180
Liu, Z., Nadim, F., Garcia-Aristizabal, A., Mignan, A., Fleming, K., and Luna, B. Q. (2015). A three-level framework for multi-risk assessment. Georisk Assess. Manag. risk Eng. Syst. geohazards 9 (2), 59–74. doi:10.1080/17499518.2015.1041989
Marzocchi, W., Garcia-Aristizabal, A., Gasparini, P., Mastellone, M. L., and Di Ruocco, A. (2012). Basic principles of multi-risk assessment: A case study in Italy. Nat. Hazards (Dordr). 62 (2), 551–573. doi:10.1007/s11069-012-0092-x
McInnes, K. L., Walsh, K. J. E., Hubbert, G. D., and Beer, T. (2003). Impact of sea-level rise and storm surges on a coastal community. Nat. Hazards 30 (2), 187–207. doi:10.1023/a:1026118417752
Mesta, C., Cremen, G., and Galasso, C. (2022). Urban growth modelling and social vulnerability assessment for a hazardous Kathmandu Valley. Sci. Rep. 12 (1), 6152. doi:10.1038/s41598-022-09347-x
Mignan, A., Wiemer, S., and Giardini, D. (2014). The quantification of low-probability–high-consequences events: Part I. A generic multi-risk approach. Nat. Hazards (Dordr). 73 (3), 1999–2022. doi:10.1007/s11069-014-1178-4
Ming, X., Xu, W., Li, Y., Du, J., Liu, B., and Shi, P. (2015). Quantitative multi-hazard risk assessment with vulnerability surface and hazard joint return period. Stoch. Environ. Res. Risk Assess. 29 (1), 35–44. doi:10.1007/s00477-014-0935-y
Moore, G. F., Bangs, N. L., Taira, A., Kuramoto, S., Pangborn, E., and Tobin, H. J. (2007). Three-dimensional splay fault geometry and implications for tsunami generation. Science 318 (5853), 1128–1131. doi:10.1126/science.1147195
Mori, N., Ariyoshi, N., Shimura, T., Miyashita, T., and Ninomiya, J. (2021). Future projection of maximum potential storm surge height at three major bays in Japan using the maximum potential intensity of a tropical cyclone, Clim. Change, 164, 25. doi:10.1007/s10584-021-02980-x
Mori, N., Shimura, T., Yoshida, K., Mizuta, R., Okada, Y., Fujita, M., et al. (2019). Future changes in extreme storm surges based on mega-ensemble projection using 60-km resolution atmospheric global circulation model. Coast. Eng. J. 61, 295–307.
Morim, J., Vitousek, S., Hemer, M., Reguero, B., Erikson, L., Casas-Prat, M., et al. (2021). Global-scale changes to extreme ocean wave events due to anthropogenic warming. Environ. Res. Lett. 16, 074056. doi:10.1088/1748-9326/ac1013
Muhammad, A., De Risi, R., De Luca, F., Mori, N., Yasuda, T., and Goda, K. (2021). Are current tsunami evacuation approaches safe enough? Stoch. Environ. Res. Risk Assess. 35 (4), 759–779. doi:10.1007/s00477-021-02000-5
Ninomiya, J., Taka, Y., and Mori, N. (2021). Projecting changes in explosive cyclones and high waves around Japan using a mega-ensemble projection. Ocean. Eng. 237 (1), 109634. doi:10.1016/j.oceaneng.2021.109634
Peacock, W. G., Van Zandt, S., Zhang, Y., and Highfield, W. E. (2014). Inequities in long-term housing recovery after disasters. J. Am. Plan. Assoc. 80 (4), 356–371. doi:10.1080/01944363.2014.980440
Pflug, G. Ch., and Pichler, A. (2014). “Multistage stochastic optimization,” in Springer series in operations research and financial engineering (Switzerland: Springer International Publishing Switzerland). doi:10.1007/978-3-319-08843-3
Rackwitz, R. (2002). Optimization and risk acceptability based on the life quality index. Struct. Saf. 24 (2-4), 297–331. doi:10.1016/s0167-4730(02)00029-2
Roberts, M. J., Camp, J., Seddon, J., Vidale, P. L., Hodges, K., Vanniere, B., et al. (2020). Projected future changes in tropical cyclones using the CMIP6 HighResMIP multimodel ensemble. Geophys. Res. Lett. 47 (14), e2020GL088662. doi:10.1029/2020gl088662
Schmidt, J., Matcham, I., Reese, S., King, A., Bell, R., Henderson, R., et al. (2011). Quantitative multi-risk analysis for natural hazards: A framework for multi-risk modelling. Nat. Hazards (Dordr). 58 (3), 1169–1192. doi:10.1007/s11069-011-9721-z
Selva, J. (2013). Long-term multi-risk assessment: Statistical treatment of interaction among risks. Nat. Hazards (Dordr). 67 (2), 701–722. doi:10.1007/s11069-013-0599-9
Sharma, N., Tabandeh, A., and Gardoni, P. (2018). Resilience analysis: A mathematical formulation to model resilience of engineering systems. Sustain. Resilient Infrastructure 3 (2), 49–67. doi:10.1080/23789689.2017.1345257
Wang, P. L., Engelhart, S. E., Wang, K., Hawkes, A. D., Horton, B. P., Nelson, A. R., et al. (2013). Heterogeneous rupture in the great Cascadia earthquake of 1700 inferred from coastal subsidence estimates. J. Geophys. Res. Solid Earth 118 (5), 2460–2473. doi:10.1002/jgrb.50101
Yeo, G. L., and Cornell, C. A. (2009). A probabilistic framework for quantification of aftershock ground‐motion hazard in California: Methodology and parametric study. Earthq. Eng. Struct. Dyn. 38 (1), 45–60. doi:10.1002/eqe.840
Keywords: climate change, tsunami and earthquake disaster assessment, resilience, network model, homogenisation approach
Citation: De Risi R, Muhammad A, De Luca F, Goda K and Mori N (2022) Dynamic risk framework for cascading compounding climate-geological hazards: A perspective on coastal communities in subduction zones. Front. Earth Sci. 10:1023018. doi: 10.3389/feart.2022.1023018
Received: 19 August 2022; Accepted: 20 September 2022;
Published: 07 October 2022.
Edited by:
Carmine Galasso, University College London, United KingdomReviewed by:
Gemma Cremen, University College London, United KingdomMarco Baiguera, University of Southampton, United Kingdom
Catalina Gonzalez Duenas, Rice University, United States
Copyright © 2022 De Risi, Muhammad, De Luca, Goda and Mori. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Raffaele De Risi, cmFmZmFlbGUuZGVyaXNpQGJyaXN0b2wuYWMudWs=
 Raffaele De Risi
Raffaele De Risi Ario Muhammad
Ario Muhammad Flavia De Luca
Flavia De Luca Katsuichiro Goda
Katsuichiro Goda Nobuhito Mori
Nobuhito Mori