
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 26 September 2022
Sec. Geohazards and Georisks
Volume 10 - 2022 | https://doi.org/10.3389/feart.2022.1010710
This article is part of the Research TopicSediment Dynamics and Geohazards in Estuaries and DeltasView all 14 articles
The rheological properties of natural mud are closely related to nautical depth estimation, wave propagation, and morphology evolution of muddy coast. In this study, the rheological properties of the natural mud collected from Luxi Island and Zhoushan Island in China were investigated. Shear stresses in steady state or oscillatory state were imposed on mud samples directly to obtain the yielding process under tidal currents or waves. The results showed that both apparent viscosity and complex viscosity experienced two sharp declines with increasing shear stress, indicating a two-step yielding nature of natural mud. Two yield stresses, namely, static yield stress and fluidic yield stress correspond to the yielding processes of elasticity and viscosity breakdown, respectively. The static yield stress in the oscillatory shear stress tests was lower than that in the steady shear stress tests, and the fluidic yield stress of natural mud in oscillatory shear stress tests was higher than that in the steady shear stress tests. The above phenomenon was explained by the viscoelastic-oscillation theory. Furthermore, the experimental results indicated that the initial storage modulus had a closer connection to both yield stresses in comparison with mud density. This study not only provided a guideline for having a better understanding of the two-step yielding process of natural mud, but will also provide scientific support for the assessment of fluid-mud formation, sediment transport and morphology evolution, the interaction between waves or tidal currents and muddy seabed, and protection of seafloor infrastructures.
Muddy coasts are widespread in estuaries, regressive deltaic coasts, and open coast tidal flats, such as the Amazon Estuary, the Yellow River Estuary, and the Gulf of Mexico (Almashan and Dalrymple, 2015; Vanlede et al., 2019), and a quarter of China’s coasts are muddy coasts (Pang et al., 2020). Natural mud compositions, such as clay minerals, saline water, organic contents, and some amounts of sand form the complex internal microstructures. The microstructures can be destroyed and reformed under large shear loads such as waves and tidal currents, causing mud fluidization and forming a fluid-mud layer at the seabed surface (Green and Coco, 2014; McAnally et al., 2016). The fluid mud is a high-concentration aqueous non-Newtonian fluid within a density range of 1,030–1,300 kg/m3 and has high potential mobility, which can flow down slopes as a mudflow and accumulate at the bottom, reducing the nautical depth and impeding navigation (McAnally et al., 2007). In addition, the fluid mud can absorb a large amount of wave energy for its high viscosity when waves propagate over the muddy seabed, resulting in significant wave attenuation (Sheremet, 2003; Safak et al., 2017), which has been especially concerning for a long time; on the other hand, the fluid mud can reduce the vertical eddy viscosity and bottom drag coefficient in the bottom boundary layer (Xia and Zhu, 2010), which may have a significant effect on tidal dynamics and change the tidal characteristics such as tidal current amplitudes and phases (Wang, 2002; Wang et al., 2005). Moreover, the mudflow is not only an important sediment transport process in the ocean environment with a significant effect on the morphology evolution, but also poses a threat to seafloor infrastructures such as pipelines (Mehta et al., 2014; McAnally et al., 2016; Kirichek et al., 2020; Kameda and Yohei, 2021). Furthermore, the transport of polluted mud is a highly controversial issue in coastal environmental studies (McAnally et al., 2007; Song et al., 2018; Mirlean et al., 2020). Therefore, accurate knowledge of mud rheological behaviors plays a crucial role in coastal dynamics and is of great significance to engineering design and coastal hazards.
During past decades, numerous experimental results show that natural mud exhibits complex rheological behaviors (e.g., Jiang and Mehta, 1990; Van Kessel and Blom, 1998; Huang and Huhe, 2009; Yang et al., 2014; Xu and Huhe, 2016; Nie et al., 2018; Shakeel et al., 2020a), among which the yield stress, marking the transition from solid to fluidic behavior, is a critical parameter to estimate the incipient motion of cohesive sediments (McAnally et al., 2016; Wang and Sturm, 2016; Zhang and Yu, 2017; Kirichek et al., 2020). Yield stress can be determined indirectly and directly (Nguyen and Boger, 1992). In indirect methods, the yield stress is usually determined by extrapolating the measured flow curve to zero shear rate with the help of a rheological model. The commonly used rheological models are the Herschel–Bulkley model (Kameda and Yohei, 2021), the Bingham model (O’Brien and Julien, 1988; Bai et al., 2002), the dual Bingham model (Huang and Huhe, 2009), the dual Herschel–Bulkley model (Xu and Huhe, 2016), and the Casson model (Wang et al., 2022). Since the extrapolation of the measured flow curve is highly dependent on the selected rheological model, the great scatter of the yield stress determined from different rheological models can always be observed (Huang and Huhe, 2009; Messaoudi et al., 2018; Wang et al., 2022). The direct methods generally rely on some independent assessment of the critical shear stress at which the mud starts to flow according to the experimental data. For example, the yield stress can be determined from the sharp variation of apparent viscosity in shear stress sweep tests (Shakeel et al., 2020a). Therefore, direct methods may be a better choice to determine the yield stress of the natural mud.
The direct methods to determine the yield stress are usually conducted under steady and oscillatory shear loads, which are similar to shear loads such as tidal currents and waves imposed to the natural mud. In a coastal environment, natural mud is usually disturbed by tidal currents and waves, forced by these two different shear loads, and the yielding process of the natural mud may be different. In the past decades, a rich literature has been built up on the yielding process and rheological properties of natural mud under steady shear loads (Coussot and Piau, 1994; Bai et al., 2002; Messaoudi et al., 2018; Fonseca et al., 2019), while the natural mud in coastal areas is usually disturbed by oscillatory shear loads such as waves. The knowledge about the yield process of the natural mud under the oscillatory shear loads is still insufficient. Furthermore, the exterior shear loads imposed on the natural mud are usually assumed as shear stress rather than shear rate or shear strain, especially when researchers estimate incipient motion and the transportation of the natural mud and establish the numerical model (Zhang et al., 2017; Emami et al., 2020; Orseau et al., 2020). Additionally, attributing to the improvement of rheometer accuracy, the rheological behaviors of the natural mud in very low shear rate regions have been investigated; contrary to the single yielding behavior, a two-step yielding process for natural mud was observed by researchers (Nie et al., 2020; Shakeel et al., 2021). This two-step yielding phenomenon also has been reported for other soft materials in the previous literature (Koumakis and Petekidis, 2011; Ahuja et al., 2020a; Minami et al., 2020), which was attributed to the two different length levels of internal structures of materials. In addition, the two-step yielding feature relates to the two critical shear stresses when natural mud transits its state from solid to solid-fluidic state and from the solid-fluid state to the fluidic state. Based on the long-term average values of the shear stress from waves or currents in a muddy coast and the two yield stresses mentioned above, the state of natural mud can be determined and then the influence of the natural mud on wave attenuation and tidal dynamics can be estimated. Therefore, it is important to figure out the two-step yielding process of the natural mud when it was forced to shear stress directly and investigate the similarities and differences of the yielding process under steady and oscillatory shear stress.
In this study, the rheological properties of the natural mud collected from Luxi Island and Zhoushan Island in China are analyzed based on the experimental results. This study aims to deepen our understanding of the yielding process of the natural mud under steady and oscillatory shear stress and identify the similarities and differences between the yielding process under these two types of shear stress.
The natural mud samples used in this study were from Zhejiang Province in China, three of them were collected from Luxi Island where the source of fine sediment is influenced by the Oujiang Estuary, and the other one from Zhoushan Island (Figure 1) where the source of fine sediment is influenced by the Yangtze Estuary and Hangzhou Bay. A gravity-based grab sampler was adopted in this study, which can be inserted into the seabed to collect the natural mud sample; after the collection, the mud samples were packed in different sealed containers to avoid evaporation of water.
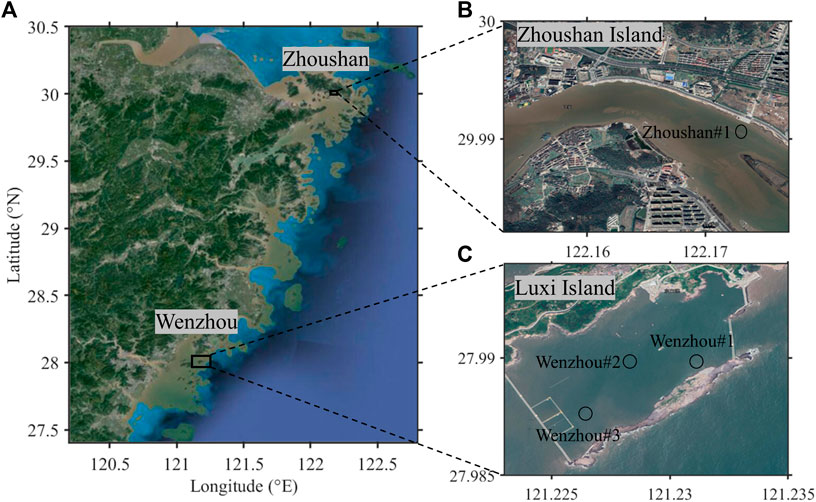
FIGURE 1. (A) Geographical location of Luxi Island and Zhoushan Island; (B) and (C) depict the selected location in Zhoushan Island and Luxi Island for collecting natural mud samples.
Particle size distributions of the natural mud samples were determined using static light scattering methods (Malvern MasterSizer 3000), and the results are given in Figure 2. To determine the density of the mud samples, small amounts of each mud sample were dried at 105°C for 24 h in a drying box, and the corresponding water content of each mud sample was determined by calculating the weight difference between the mud sample before and after drying. The dry density of the mud samples was assumed to be 2,650 kg/m3, based on the water content of each mud sample, and the bulk density of the mud samples was obtained. The characters of the four mud samples are summarized in Table 1.
The rotational rheometer DHR-I (TA Instruments, United States) equipped with a cone and plate geometry was adopted in this study to investigate the rheological response under steady and oscillatory shear stress, as this geometry can produce more constant shear loads on the natural mud samples and has successful application in previous studies (Huang and Huhe, 2009; Shakeel et al., 2020b; Knappe et al., 2020). The cone and plate geometry has a diameter of 40 mm with a 2° cone angle and a 0.048-mm gap between the cone and plate. The rheometer is characterized by high precision and accuracy, and its minimum torque in steady and oscillatory shear tests is 10 and 20 nNm, respectively. The temperature was maintained at 20°C during all the experiments using a Peltier controller system.
The experimental procedures in this study are organized as follows. First, each natural sample was homogenized by mild hand stirring before experiments to ensure the repeatability of the experiments. Second, the preliminary oscillatory amplitude sweep tests were performed to estimate the linear viscoelastic region of each natural mud sample, and the oscillatory shear stress logarithmically increased from 1 to 200 Pa at a constant frequency of 1 Hz. Based on the evolution of the storage modulus versus the oscillatory shear stress, the linear viscoelastic region can be determined (Figure 5). Third, the measurements of the rheological response of the natural mud under steady and oscillatory shear stress were performed. After attaining the measurement position, a waiting time was given to eliminate the disturbance created by the insertion of the bob; meanwhile, an oscillatory time sweep test in a linear viscoelastic regime was conducted to monitor the evolution of the storage modulus and the oscillatory shear stress was set to 1 Pa for all natural mud samples. When the increase of the storage modulus as a function of time was slight, the shear stress sweep tests and the oscillating amplitude sweep tests were performed.
In the shear stress sweep tests, the applied shear stress logarithmically increased from 1 to 300 Pa, and the corresponding motor displacement was recorded; thus, the shear rate and apparent viscosity can be determined. In the oscillatory amplitude sweep tests, the natural mud was applied to sinusoidal shear stress which increases logarithmically from 1 to 200 Pa at a constant frequency of 1 Hz, and the rheological parameters such as storage modulus (G′) and loss modulus (G″) are obtained. To obtain adequate experimental data for analysis, twenty measuring points were set in each decade with a measuring time of 15 s for each point for both steady and oscillatory shear stress tests. The technology flow of the experiments is given in Figure 3.
Figure 4 depicts the apparent viscosity and shear rate evolution with increasing shear stress of the Wenzhou#1 natural mud sample. It is noted that with increasing shear stress, the apparent viscosity experienced two sharp declines (Figure 4A), indicating that the yielding process of natural mud is not a single behavior as observed in previous studies (e.g., Coussot and Piau, 1994; Van Kessel and Blom, 1998; Bai et al., 2002; Kameda and Hirauchi, 2018) but a two-step yielding process which exists a transition state between solid state and fluidic state.
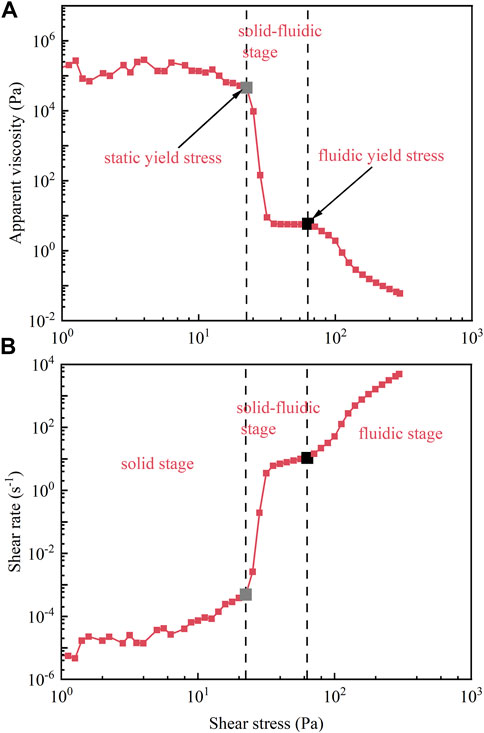
FIGURE 4. The apparent viscosity (A) and shear rate (B) evolution with increasing shear stress of the Wenzhou#1 mud sample. In the figure, the grey point and the black point represent the first yielding point and second yielding point of the Wenzhou#1 natural mud sample, respectively.
The yielding process of the Wenzhou#1 mud sample can be divided into three stages. In the initial stage, the apparent viscosity shows a slight variation with increasing shear stress until the imposed shear stress exceeds a critical value where the mud samples yield for the first time. In this stage, the natural mud behaves like a solid material for its large apparent viscosity. Subsequently, the apparent viscosity experienced a sharp decline with increasing shear stress where the apparent viscosity is reduced by five orders of magnitude in a very narrow range of shear stress, and meanwhile, the shear rate suddenly increases from 10−3 to 10 s−1. After this sharp decline, the apparent viscosity reaches a plateau, and the shear rate experienced slow growth. In this stage, the natural mud exhibits both characteristics of solid and fluid. As the shear stress continues to increase, the apparent viscosity departed from the plateau and decreased again, and the apparent viscosity reduced from 5 to 0.05, indicating the natural mud yield again.
The two-step yielding process has been reported in glassy systems, colloidal gels, electro and magnetorheological fluids, and commercial formulations, indicating the presence of two characteristic forces between the interacting particles or two varying representative length scales (Altieri et al., 2018; Ahuja et al., 2020b; Minami et al., 2020; Moghimi and Petekidis, 2020). This two-step yielding behavior is consistent with the previous study conducted by Shakeel et al. (2020a), who investigated the rheological properties of the natural mud from the Port of Hamburg.
Corresponding to the two-step yielding process, there are two yield stresses, namely, static yield stress (τs) and fluidic yield stress (τf) put forward by previous studies (Ahuja et al., 2020a; Shakeel et al., 2020b; Nie et al., 2020). These two yield stresses are critical stresses when the natural mud transitions from solid to solid-fluidic state and from the solid-fluid state to the fluidic state, which can be determined directly from the apparent viscosity curve based on two sharp declines. In Figure 4, the static yield stress and the fluidic yield stress of the Wenzhou#1 natural mud sample are marked as a grey point and a black point, respectively.
The results of oscillatory amplitude sweep tests for the Wenzhou#1 natural mud sample are given in Figures 5, 6. From Figure 5, it is noted that both storage modulus G′ and loss modulus G″ experience two sharp declines with the increasing oscillatory stress, which is familiar to the evolution of the apparent viscosity shown in Figure 4. The yielding process of natural mud under oscillatory shear stress can also be divided into three stages as steady shear stress tests. In the first stage, the storage modulus is one order magnitude larger than the loss modulus and their values are almost constant, indicating the solid nature of the mud sample and meaning that the internal microstructures of the mud sample are not destroyed by oscillatory shear stress in this time. Correspondingly, the complex viscosity shows behavior similar to that of the storage modulus (Figure 6); its value remains unchanged in this region, and the small phase angle shown in Figure 5 also indicates the solid nature of the mud sample. At this time, the mud sample behaves as a linearly elastic solid (Yang and Yu, 2018; Shakeel et al., 2020a; Nie et al., 2020).
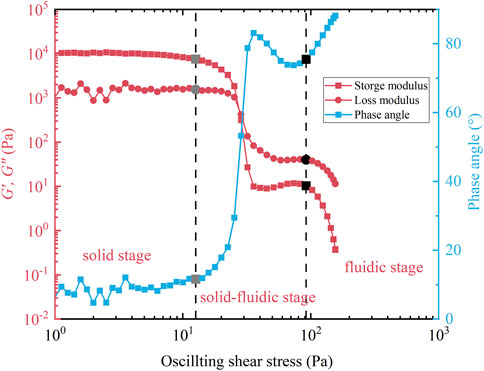
FIGURE 5. Results of amplitude sweep tests for Wenzhou#1 mud samples, the storage modulus G′, the loss modulus G″, and phase angle evolution with increasing oscillatory shear stress. In the figure, the grey point and the black point represent the first yielding point and the second yielding point of the Wenzhou#1 natural mud sample, respectively.
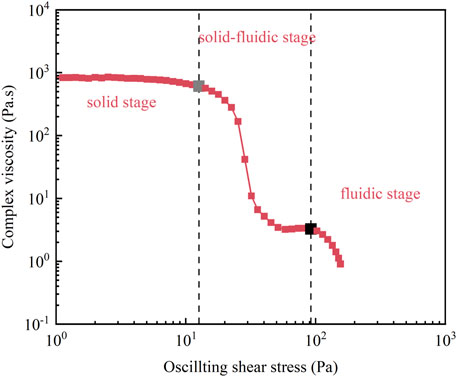
FIGURE 6. Results of amplitude sweep tests for Wenzhou#1 mud samples: the complex viscosity evolution with increasing oscillatory shear stress. In the figure, the grey point and the black point represent the first yielding point and the second yielding point of the Wenzhou#1 natural mud sample, respectively.
In the second stage, the storage modulus G′, the loss modulus G″, and the complex viscosity experienced a sharp decline and subsequently reached a new state of equilibrium. During this time, the storage modulus decreases faster than the loss modulus and is lower than the loss modulus eventually (Figure 5), indicating that the elastic effect is weakened and the viscous effect dominates in this stage. In the meanwhile, the phase angle given in Figure 5 increases with the oscillatory shear stress and reached around 90° quickly; furthermore, the complex viscosity shown in Figure 6 decreased three orders in its magnitudes, indicating that the internal microstructures of the natural mud sample are gradually destroyed by the imposed oscillatory shear stress, meaning the natural mud yields for the first time and the mud samples experienced the transition from the solid state to the solid-fluidic state.
In the final stage, the natural mud yields again. After a transient equilibrium state, the storage modulus and the loss modulus declined again, and the decrease rate of the storage modulus was still larger than that of the loss modulus (Figure 5), meaning that the internal microstructures of the mud samples are destroyed more thoroughly. In addition, the increasing phase angle (Figure 5) and the decreasing complex viscosity (Figure 6) also implied the destroyed internal microstructures of the mud samples; at the end of the experiments, the mud sample behaves like fluids.
Compared to Figure 4, it can be seen that under the oscillatory shear stress, the mud samples also show the “two-step” yielding feature, indicating that the two-step yielding process is the instinctive feature of the mud sample and irrelevant to the manner of the exposed loads. The “two-step” yielding feature closely relates to the variation of microstructures of the natural mud sample under external shear stress, and the linkages between the particles are gradually destroyed by the imposed loads, indicating the presence of two characteristic forces between the interacting particles or two varying representative length scales of the natural mud, which is similar to other materials in previous studies (Ahuja et al., 2020b; Moghimi and Petekidis, 2020).
Figure 7 depicts the evolution of the flow curve and the apparent viscosity of the natural mud samples; it can be seen that all the mud samples show the two-step yielding feature, despite their different density and particle size distribution. In addition, it is worth noting that though the apparent viscosity of the natural mud samples is different from each other in the first stage, they nearly reached the same value in a plateau after the first yielding process. The yielding process of the natural mud is influenced by both density and particle size distribution. From Figure 7, it can be seen that the Zhoushan#1 mud sample (ρ=1619 kg/m3) has the highest apparent viscosity and yield stress compared to other mud samples, which can be attributed to its relatively large density. However, the particle size distribution also affects the yielding process of the natural mud. For instance, the densities of Wenzhou#1 (ρ=1,484 kg/m3) and Wenzhou#3 (ρ=1,474 kg/m3) are almost equal, but the yield stress of Wenzhou#3 is obviously higher than that of Wenzhou#1, which may be attributed to the finer grained particles distribution of the Wenzhou#3, as the finer particles are more likely to form the internal bonds and destroying it requires higher shear stress.
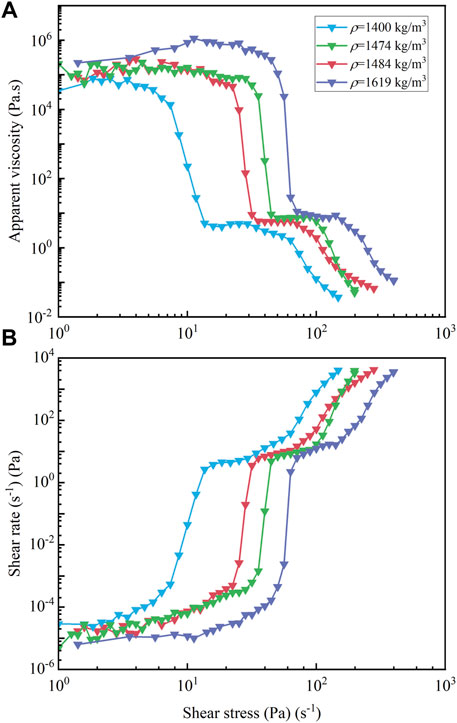
FIGURE 7. The apparent viscosity (A) and shear rate (B) evolution with increasing shear stress of the different mud samples.
The results of oscillatory shear stress sweep tests with different mud samples are shown in Figures 8, 9, indicating that all the mud samples show the similar “two-step” yielding feature independent of their density and particle size distribution. According to the picture, it can be seen that the Zhoushan#1 mud sample (ρ=1,619 kg/m3) shows the maximum storage modulus and complex viscosity, which may be attributed to the maximum density in these mud samples; correspondingly, the Wenzhou#2 (ρ=1,400 kg/m3) displays the minimum storage modulus and complex viscosity. By comparing the Wenzhou#1 (ρ=1,484 kg/m3) and Wenzhou#3 (ρ=1,474 kg/m3), it can be seen that despite the slightly higher density of the Wenzhou#1 mud sample, the Wenzhou#3 mud sample shows the higher storage modulus and complex viscosity and the higher static yield stress. The results of the Wenzhou#2 mud sample show a slight difference from the other mud samples: it shows the minimum storage modulus and complex viscosity. From the aforementioned, both density and particle size distribution can affect the rheology of the mud samples; in the final analysis, all of them can have a significant effect on the internal structure of the mud samples.
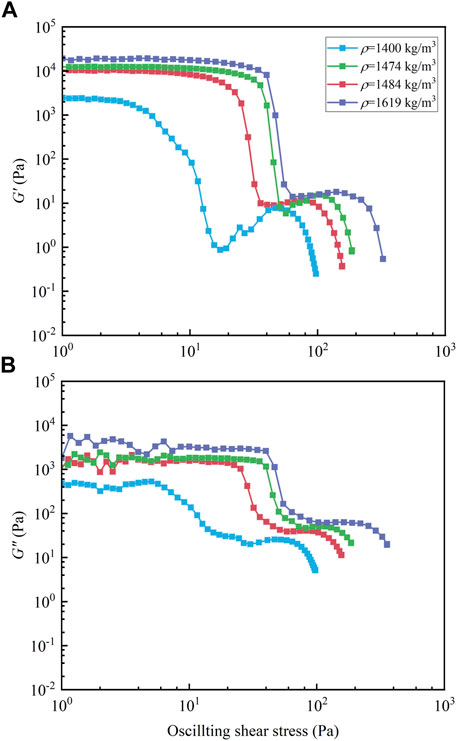
FIGURE 8. Results of oscillatory stress sweep tests for different mud samples: (A) the storage modulus G′ and (B) the loss modulus G″.
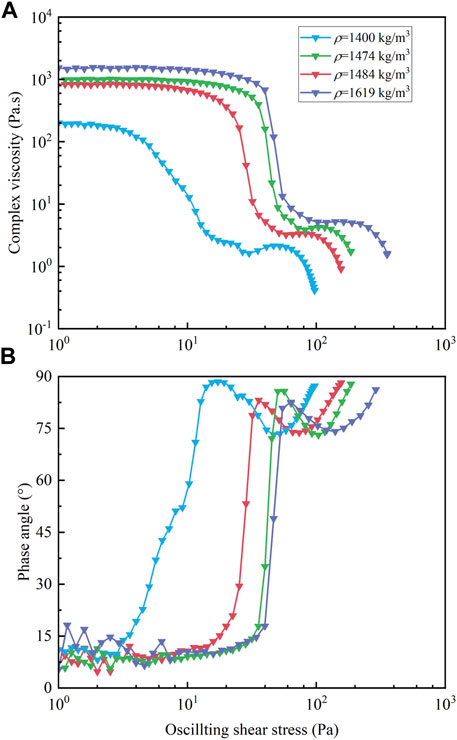
FIGURE 9. Results of oscillatory stress sweep tests for different mud samples: (A) the complex viscosity and (B) the phase angle evolution versus imposed oscillatory shear stress.
The density affects the particle amounts per unit volume of the natural mud, and the linkages between different particles determine the state of the natural mud; if these linkages are undamaged, the natural mud behaves as a solid state; furthermore, if these linkages are partially destroyed, the natural mud presents a transition state, which shows the solid-fluidic character; ultimately, if all linkages are destroyed, the natural mud shows a fluid behavior. The more the amount of particles per unit volume of the natural mud, the larger the exposed loads needed to destroy the linkage between the particles; therefore, the Zhoushan#1 mud sample shows the largest storage modulus and the complex viscosity in Figure 8, and the Wenzhou#2 mud sample shows the lowest storage modulus and the complex viscosity. Similar to the density, the particle size distribution of the natural mud has a significant effect on the amounts per unit volume of the natural mud; when the density of the natural mud is determined, the smaller particle size means the more the amount of particles per unit volume of the natural mud, the more the linkages between these particles, so the transition from the solid state to the solid-fluid state needs the higher oscillatory stress of Wenzhou#3 compared to that of Wenzhou#1 shown in Figures 8, 9, despite the slightly higher density of the Wenzhou#1 mud sample.
In this study, the natural mud was imposed on the shear stress in the experiments as the natural mud was subjected to the shear stress from exterior loads directly (Shakeel et al., 2020a); thus, the yield stress can be determined directly from the results without extra extrapolation. The experimental results presented show the “two-step” yielding feature of the mud samples; correspondingly, there are two yielding stresses that existed, consistent with the two-step yielding process. The first yielding stress, namely, static yield stress (τs), is the critical stress when the mud samples transform from the solid state to the solid-fluidic state. Similarly, the second yield stress, namely, fluidic yield stress (τf), is the critical stress when the mud samples transform from the solid-fluid state to the fluidic state.
The density is a crucial parameter which has been adopted to predict the yield stress of natural mud in previous studies (e.g., Huang and Huhe, 2009; Mehta et al., 2014; Xu and Huhe, 2016); however, the other parameters such as temperature, pH, compositions, and particle size distribution also affect the value of the yield stress. Therefore, it is necessary to adopt a more suitable parameter to predict the yield stress. The value of yield stress reflects the ability to resist to flow of the natural mud, which usually relates to the internal microstructures of the natural mud. The initial storage modulus before shearing is an appropriate parameter to assess the structural level (Shakeel et al., 2020c), which may be a better choice to predict the yield stress of natural mud.
Figure 10 shows the static yield stress and the fluidic yield stress of the different mud samples versus density (Figure 10A) and initial modulus (Figure 10B); the initial storage modulus of each natural mud sample is obtained through the oscillatory time sweep within the linear viscoelastic regions before the steady and oscillatory shear stress tests. It is noted that both static yield stress and fluidic yield stress increase with initial storage modulus (Figure 10B), while the correlation between these two yield stresses and densities is not monotonous, indicating the initial storage modulus is a better choice to predict the yield stress of natural mud.
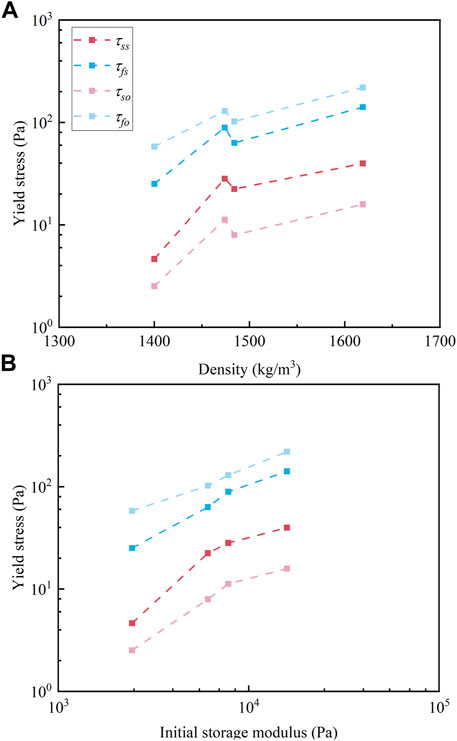
FIGURE 10. Plots of yield stress versus (A) density and (B) initial storage modulus. The first letter of subscript “s” and “f” of τ denote static and fluidic, respectively, and the second letter of subscript “s” and “o” represent steady and oscillatory, respectively.
The exposed manner of exterior loads has a significant effect on the static yield stress and fluidic yield stress. Figure 10 presents the comparison of static yield stress and fluidic yield stress between two exposed exterior loads. For the static yield stress, it is noted that the results of the steady shear stress sweep tests are higher than those of the oscillatory shear stress sweep tests for all the mud samples, which indicates that the mud samples need higher loads to transform from solid to the solid-fluidic state when it is imposed to the static loads. On the contrary, for the static yield stress, the comparison shows that the steady shear stress sweep tests are lower than the oscillatory shear stress sweep tests for all the mud samples, which means that mud samples require higher shear stress to transform their state from the solid-fluidic state to the fluidic state when it is imposed to the oscillatory loads.
As a viscoelastic material, under the exterior loads, the shear force F of natural mud satisfies the following equation:
where m is the mass of the natural mud,
For the oscillatory shear test, as shown in Figure 5, the elastic force is dominant at this moment and the viscous force can be omitted; thus, Eq. 1 can be rewritten as
As a simple harmonic motion, Eq. 3 can be rewritten as
where superscript ^ means the amplitude; thus
Equation 5 explains why static yield stress in steady shear tests is larger compared to that of oscillatory shear tests. Similarly, when the natural mud yields the second time, viscous force is dominant; for the steady shear tests, Eq. 1 can be rewritten as
For the oscillatory shear test, as shown in Figure 5, viscous force is dominant at the moment, and Eq. 1 can be rewritten as
As a simple harmonic motion, Eq. 7 can be rewritten as
Using the complex variable method, Eq. 8 can be rewritten as
Equation 9 explains why the fluidic yield stress in oscillatory shear tests is larger compared to that of steady shear tests.
Figures 11A,Bgive the apparent viscosity and the complex viscosity at the first and the second yielding point, respectively. Under steady shear stress, the apparent viscosity at the first yielding point increases with the initial storage modulus, whereas the variation of the apparent viscosity in the second yielding point is slight with the initial storage modulus. Furthermore, the apparent viscosity in the first yielding point is nearly three orders of magnitude higher than it is in the second yielding point. For the oscillatory shear stress test, the complex viscosity in these two yielding points are increasing with initial storage modulus, and the complex viscosity in the first yielding point is two orders of magnitude higher than it is in the second yielding point.
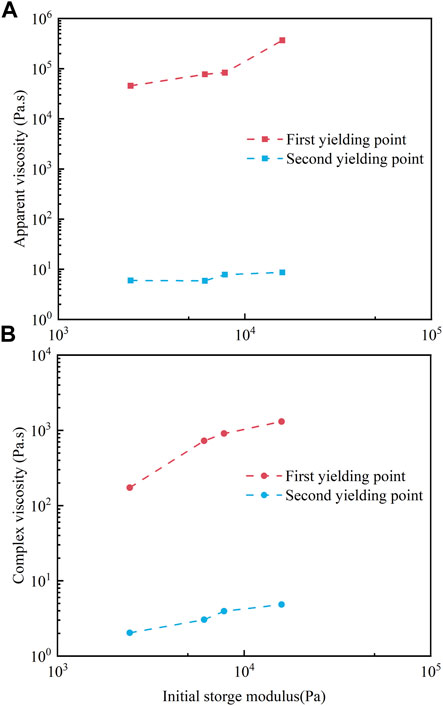
FIGURE 11. Variations of apparent viscosity (A) and complex viscosity (B) as functions of initial storage modulus.
The natural soft mud on the coastal areas is usually disturbed by various exterior loads, such as currents, waves, tides, and storms. As aforementioned, the natural mud needs higher exterior loads to fluidize when it is imposed on the oscillatory loads, meaning that currents, instead of waves, make the natural mud easier to be fluidic, and the mud needs higher exterior loads to fluidize when it is forced to the waves. The fluidization of natural mud is closely related to the fluid-mud formation; besides, the fluidic yield stress is found to be exponentially proportional to the critical Shields parameter of cohesive sediments (Wang and Sturm, 2016; Zhang and Yu, 2017). Due to the difference of yield stress of natural mud when it is imposed to waves or tidal currents, it is of great importance to consider the dominant hydrodynamic condition of a specific muddy coast when estimating the fluid-mud formation and the incipient motion of cohesive sediment.
In this study, the yielding process of four different natural mud samples collected from Zhejiang Province in China was investigated through a DHR-I rheometer with a cone-plate geometry. Both steady and oscillatory shear stresses were imposed on the natural mud samples directly, and a two-step yielding feature of the natural mud was observed. Based on the analysis of the experimental data, the main findings are summarized as follows:
1) The yielding process of natural mud is a two-step yielding behavior. Both results of steady and oscillatory shear stress tests show that the viscosity (apparent viscosity and complex viscosity) experienced two sharp declines, meaning the “two-step” yielding feature is the intrinsic character of the natural soft mud; consequently, the two-step yielding process of natural mud can be divided into three stages. In the solid stage, the elastic effect dominates and the natural mud behaves as a linearly elastic solid; with increasing shear stress, the elastic effect is weakened, and the viscous effect gradually dominates in the solid-fluidic stage and the fluidic stage, and natural mud behaves like fluids.
2) The initial storage modulus is a better parameter to predict the yield stress than the density of the natural mud. Compared to density, the initial storage modulus reflects the internal microstructures before steady and oscillatory shear stress tests. The experimental results show that both static yield stress and fluidic yield stress monotonically increase with initial storage modulus.
3) Both static yield stress and fluidic yield stress are susceptive to the imposed manner of the exterior loads. The static yield stress in the oscillatory shear tests is lower than that in the steady shear tests (τso<τss), and the fluidic yield stress of natural mud in oscillatory shear tests is higher than that in the steady shear tests (τfo>τfs), which can be explained by introducing the viscoelastic-oscillation theory.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.
SW, HG, and YX conceived and designed the framework of this study. SW performed experiments, analyzed the experimental data, and drafted the original manuscript. ZH reviewed the manuscript and with constructive discussions. HG helped conduct the experiments and process data. YX reviewed the manuscript and funded this study.
The study was financially supported by the National Natural Science Foundation of China (42076177), the National Key Research and Development Program of China (2020YFD0900803), and the Talent Program of Zhejiang Province (2021R52049).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ahuja, A., Pappas, I., and Potanin, A. (2020a). Relation between structure and stability of toothpaste with two-step yielding. Rheol. Acta 59, 133–145. doi:10.1007/s00397-019-01183-7
Ahuja, A., Potanin, A., and Joshi, Y. M. (2020b). Two step yielding in soft materials. Adv. Colloid Interface Sci. 282, 102179. doi:10.1016/j.cis.2020.102179
Almashan, N., and Dalrymple, R. A. (2015). Damping of waves propagating over a muddy bottom in deep water: Experiment and theory. Coast. Eng. 105, 36–46. doi:10.1016/j.coastaleng.2015.08.008
Altieri, A., Urbani, P., and Zamponi, F. (2018). Microscopic theory of two-step yielding in attractive colloids. Phys. Rev. Lett. 121, 185503. doi:10.1103/PhysRevLett.121.185503
Bai, Y., Ng, C., Shen, H., and Wang, S. (2002). Rheological properties and incipient motion of cohesive sediment in the haihe estuary of China. China Ocean. Eng. 16, 483–498. doi:10.3321/j.issn:0890-5487.2002.04.005
Coussot, P., and Piau, J. M. (1994). On the behavior of fine mud suspensions. Rheol. Acta 33, 175–184. doi:10.1007/bf00437302
Emami, S., Mousavi, S., Hosseini, K., Fouladfar, H., and Mohammadian, M. (2020). Comparison of different turbulence models in predicting cohesive fluid mud gravity current propagation. Int. J. Sediment Res. 35, 504–515. doi:10.1016/j.ijsrc.2020.03.010
Fonseca, D. L., Marroig, P. C., Carneiro, J. C., Gallo, M. N., and Vinzón, S. B. (2019). Assessing rheological properties of fluid mud samples through tuning fork data. Ocean. Dyn. 69, 51–57. doi:10.1007/s10236-018-1226-9
Green, M. O., and Coco, G. (2014). Review of wave-driven sediment resuspension and transport in estuaries. Rev. Geophys. 52, 77–117. doi:10.1002/2013RG000437
Huang, Z., and Huhe, A. (2009). A laboratory study of rheological properties of mudflows in Hangzhou Bay, China. Int. J. Sediment Res. 24, 410–424. doi:10.1016/S1001-6279(10)60014-5
Jiang, F., and Mehta, A. J. (1990). Mudbanks of the southwest coast of India iv: Mud viscoelastic properties. J. Coast. Res. 11, 918–926.
Kameda, J., and Hirauchi, K. (2018). Rheological properties of composite serpentine-brucite suspensions: Implications for mudflow behavior on forearc seamounts. Mar. Geol. 403, 191–196. doi:10.1016/j.margeo.2018.06.004
Kameda, J., and Yohei, H. (2021). Influence of biopolymers on the rheological properties of seafloor sediments and the runout behavior of submarine debris flows. Sci. Rep. 11, 1493. doi:10.1038/s41598-021-81186-8
Kirichek, A., Shakeel, A., and Chassagne, C. (2020). Using in situ density and strength measurements for sediment maintenance in ports and waterways. J. Soils Sediments 20, 2546–2552. doi:10.1007/s11368-020-02581-8
Knappe, E., Manga, M., and Le Friant, A. (2020). Rheology of natural sediments and its influence on the settling of dropstones in hemipelagic marine sediment. Earth Space Sci. 7, e2019E–e2876E. doi:10.1029/2019EA000876
Koumakis, N., and Petekidis, G. (2011). Two step yielding in attractive colloids: Transition from gels to attractive glasses. Soft Matter 7, 2456. doi:10.1039/c0sm00957a
McAnally, W. H., Friedrichs, C., Hamilton, D., Hayter, E., Shrestha, P., Rodriguez, H., et al. (2007). Management of fluid mud in estuaries, bays, and lakes. I: Present state of understanding on character and behavior. J. Hydraul. Eng. 133, 9–22. doi:10.1061/(asce)0733-9429(2007)133:1(9)
McAnally, W. H., Kirby, R., Hodge, S. H., Welp, T. L., Greiser, N., Shrestha, P., et al. (2016). Nautical depth for U.S. Navigable waterways: A review. J. Waterw. Port. Coast. Ocean. Eng. 142, 4015014. doi:10.1061/(ASCE)WW.1943-5460.0000301
Mehta, A. J., Samsami, F., Khare, Y. P., and Sahin, C. (2014). Fluid mud properties in nautical depth estimation. J. Waterw. Port. Coast. Ocean. Eng. 140, 210–222. doi:10.1061/(ASCE)WW.1943-5460.0000228
Messaoudi, A., Bouzit, M., and Boualla, N. (2018). Physical and rheological properties of the chorfa dam mud: Dependency on solids concentration. Appl. Water Sci. 8, 178. doi:10.1007/s13201-018-0805-8
Minami, S., Watanabe, T., Sasaki, Y., Minato, H., Yamamoto, A., Suzuki, D., et al. (2020). Two-step yielding behavior of densely packed microgel mixtures with chemically dissimilar surfaces and largely different sizes. Soft Matter 16, 7400–7413. doi:10.1039/D0SM00366B
Mirlean, N., Calliari, L., and Johannesson, K. (2020). Dredging in an estuary causes contamination by fluid mud on a tourist ocean beach. Evidence via ree ratios. Mar. Pollut. Bull. 159, 111495. doi:10.1016/j.marpolbul.2020.111495
Moghimi, E., and Petekidis, G. (2020). Mechanisms of two-step yielding in attractive colloidal glasses. J. Rheology 64, 1209–1225. doi:10.1122/8.0000057
Nguyen, Q. D., and Boger, D. V. (1992). Measuring the flow properties of yield stress fluids. Annu. Rev. Fluid Mech. 24, 47–88. doi:10.1146/annurev.fl.24.010192.000403
Nie, S., Jiang, Q., Cui, L., and Zhang, C. (2020). Investigation on solid-liquid transition of soft mud under steady and oscillatory shear loads. Sediment. Geol. 397, 105570. doi:10.1016/j.sedgeo.2019.105570
Nie, S., Jiang, Q., Wang, L., Zhang, J., and Liu, P. (2018). A laboratory study of rheological properties of soft mud using a dynamic shear-controlled oscillatory viscometer. J. Coast. Res. 85, 1226–1230. doi:10.2112/SI85-246.1
O'Brien, J. S., and Julien, P. Y. (1988). Laboratory analysis of mudflow properties. J. Hydraulic Eng. 114114, 8778–8887. doi:10.1061/(ASCE)0733-9429
Orseau, S., Huybrechts, N., Tassi, P., Pham Van Bang, D., and Klein, F. (2020). Two-dimensional modeling of fine sediment transport with mixed sediment and consolidation: Application to the gironde estuary, France. Int. J. Sediment Res. 36, 736–746. doi:10.1016/j.ijsrc.2019.12.005
Pang, Q., Zhang, R., and Wen, C. (2020). Fluid mud induced by super typhoon and fluvial flood in a deep-dredged waterway of xiamen, China. J. Waterw. Port. Coast. Ocean. Eng. 146, 4020004. doi:10.1061/(ASCE)WW.1943-5460.0000567
Safak, I., Sheremet, A., Davis, J., and Kaihatu, J. M. (2017). Nonlinear wave dynamics in the presence of mud-induced dissipation on atchafalaya shelf, Louisiana, USA. Coast. Eng. 130, 52–64. doi:10.1016/j.coastaleng.2017.09.014
Shakeel, A., Kirichek, A., and Chassagne, C. (2020c). Effect of pre-shearing on the steady and dynamic rheological properties of mud sediments. Mar. Petroleum Geol. 116, 104338. doi:10.1016/j.marpetgeo.2020.104338
Shakeel, A., Kirichek, A., and Chassagne, C. (2020a). Rheological analysis of mud from Port of Hamburg, Germany. J. Soils Sediments 20, 2553–2562. doi:10.1007/s11368-019-02448-7
Shakeel, A., Kirichek, A., and Chassagne, C. (2020b). Yield stress measurements of mud sediments using different rheological methods and geometries: An evidence of two-step yielding. Mar. Geol. 427, 106247. doi:10.1016/j.margeo.2020.106247
Shakeel, A., MacIver, M. R., van Kan, P. J. M., Kirichek, A., and Chassagne, C. (2021). A rheological and microstructural study of two-step yielding in mud samples from a Port area. Colloids Surfaces A Physicochem. Eng. Aspects 624, 126827. doi:10.1016/j.colsurfa.2021.126827
Sheremet, A. (2003). Observations of nearshore wave dissipation over muddy sea beds. J. Geophys. Res. 108, 3357. doi:10.1029/2003JC001885
Song, J., Qu, B., Li, X., Yuan, H., Li, N., and Duan, L. (2018). Carbon sinks/sources in the Yellow and East China seas—air-sea interface exchange, dissolution in seawater, and burial in sediments. Sci. China Earth Sci. 61, 1583–1593. doi:10.1007/s11430-017-9213-6
Van Kessel, T., and Blom, C. (1998). Rheology of cohesive sediments: Comparison between a natural and an artificial mud. J. Hydraulic Res. 36, 591–612. doi:10.1080/00221689809498611
Vanlede, J., Dujardin, A., Fettweis, M., Van Hoestenberghe, T., and Martens, C. (2019). Mud dynamics in the Port of zeebrugge. Ocean. Dyn. 69, 1085–1099. doi:10.1007/s10236-019-01273-3
Wang, H., Zentar, R., and Wang, D. (2022). Rheological characterization of fine-grained sediments under steady and dynamic conditions. Int. J. Geomech. 22, 4021260. doi:10.1061/(ASCE)GM.1943-5622.0002243
Wang, X. H. (2002). Tide-induced sediment resuspension and the bottom boundary layer in an idealized estuary with a muddy bed. J. Phys. Oceanogr. 32, 3113–3131. doi:10.1175/1520-0485(2002)032<3113:TISRAT>2.0.CO;2
Wang, X. H., Byun, D. S., Wang, X. L., and Cho, Y. K. (2005). Modelling tidal currents in a sediment stratified idealized estuary. Cont. Shelf Res. 25, 655–665. doi:10.1016/j.csr.2004.10.013
Wang, Y., and Sturm, T. W. (2016). Effects of physical properties on erosional and yield strengths of fine-grained sediments. J. Hydraul. Eng. 142, 4016049. doi:10.1061/(ASCE)HY.1943-7900.0001193
Xia, Y., and Zhu, K. (2010). A study of wave attenuation over a maxwell model of a muddy bottom. Wave Motion 47, 601–615. doi:10.1016/j.wavemoti.2010.05.001
Xu, J., and Huhe, A. (2016). Rheological study of mudflows at lianyungang in China. Int. J. Sediment Res. 31, 71–78. doi:10.1016/j.ijsrc.2014.06.002
Yang, W., and Yu, G. (2018). Rheological response of natural soft coastal mud under oscillatory shear loadings. J. Waterw. Port. Coast. Ocean. Eng. 144, 5018005. doi:10.1061/(ASCE)WW.1943-5460.0000461
Yang, W., Yu, G., Tan, S. K., and Wang, H. (2014). Rheological properties of dense natural cohesive sediments subject to shear loadings. Int. J. Sediment Res. 29, 454–470. doi:10.1016/S1001-6279(14)60059-7
Zhang, M., and Yu, G. (2017). Critical conditions of incipient motion of cohesive sediments. Water Resour. Res. 53, 7798–7815. doi:10.1002/2017WR021066
Keywords: natural mud, rheological properties, yield stress, two-step yielding, storage modulus
Citation: Wang S, He Z, Gu H and Xia Y (2022) The “two-step” yielding process of the natural mud under steady and oscillatory shear stress. Front. Earth Sci. 10:1010710. doi: 10.3389/feart.2022.1010710
Received: 03 August 2022; Accepted: 06 September 2022;
Published: 26 September 2022.
Edited by:
Ya Ping Wang, East China Normal University, ChinaReviewed by:
Chao Chen, Zhejiang Ocean University, ChinaCopyright © 2022 Wang, He, Gu and Xia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhiguo He, aGV6aGlndW9Aemp1LmVkdS5jbg==; Yuezhang Xia, eXp4aWFAemp1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.