Effect of Thermoelastic Properties of the Pyrope-Almandine Solid Solutions on the Entrapment Pressure of Garnet-Related Elastic Geobarometer

The pyrope (Prp)–almandine (Alm) solid solutions are the most fundamental garnet components on the Earth, and both the quartz inclusions in garnet (QuiG) barometry and the garnet inclusions in diamond barometry need to be constrained by the thermoelastic parameters of Prp-Alm solid solution garnets. Here, we report the thermoelastic properties of a series of synthetic Prp-Alm solid solutions based on the high-pressure and high-temperature (HP–HT) in situ synchrotron single-crystal x-ray diffraction (SCXRD) experiments up to ∼20 GPa and 700 K, using diamond anvil cell (DAC). Fitting the SCXRD data by the Birch-Murnaghan equation of state (BM-EoS) and the thermal-pressure EoS, we obtain the thermoelastic parameters of Prp-Alm solid solution garnets, including bulk modulus (K₀), its pressure derivative (K′₀), and the thermal expansion coefficient (${\alpha }_0$). The K₀ along the Prp-Alm solid solution changes linearly with Prp content within their uncertainties and can be expressed by K₀ (GPa) = 181.0(8) – 0.11(1) X_prp (R² = 0.91, X_prp is the Prp mole fraction and K′₀ fixed at 4). Our result indicates that the compressibility of the Prp-Alm solid solution increases with the increasing Prp content. However, the thermal expansion coefficient of Prp-Alm solid solution at ambient pressure shows a non-linear trend with Prp content and can be expressed by α₀ (10⁻⁵ K⁻¹) = 2.7 (1) + 3.0 (5) X_Prp − 3.2 (4) X²_Prp (R² = 0.985). It shows that the Prp-Alm solid solution with intermediate composition has a larger thermal expansion coefficient than those close to the endmembers at ambient conditions. Furthermore, we also evaluated the influence of thermoelastic properties of the Prp-Alm solid solution on the entrapment pressure (P_e) estimation for two types of elastic geobarometers. Our results indicate that the garnet component may significantly influence entrapment pressure, and among the thermoelastic parameters of garnet, the thermal expansion coefficient has the main effect on the estimation of P_e.

Introduction

Diamond is the only direct sample obtained from inaccessible portions of Earth (Nestola et al., 2019) and the subduction zone metamorphism controls many global geochemical cycles and the lithosphere (Ashley et al., 2016). Estimating the pressure and temperature of these minerals or rocks provides fundamental data for studying many such geological processes, but their determination remains extremely controversial (Bebout, 2007; Tajčmanová et al., 2021). To date, various methods have been developed to address the geological history of rocks. Previous studies have used mineral–mineral equilibrium based on Gibbs free energy minimization or partitioning major or trace elements between phases to recover these geological processes (De Capitani and Petrakakis, 2010; Holland and Powell, 2011). Despite advances in analytical techniques, geothermobarometers still suffer from problems due to alteration processes, such as the erasure of peak metamorphic mineral assemblages (e.g., Korsakov et al., 2009; Jamtveit et al., 2016), chemical re-equilibration, diffusion, and kinetic limitations (e.g., Anzolini et al., 2019; Gonzalez et al., 2019). Additionally, part of the difficulty in determining the pressure of rocks is the lack of typical pressure-dependent mineral equilibria, especially for the diamond-inclusion system (Ashley et al., 2016; Nestola et al., 2017).

Ideally, geobarometers should yield accurate pressure estimates using only commonly found minerals and not be susceptible to significant resetting during exhumation. Recently, an alternative method based on the mechanical equilibrium between entrapped mineral inclusions (e.g., quartz and garnet) and host mineral (e.g., garnet and diamond) has received significant attention and could vastly expand the range of barometers available to petrologists (e.g., Enami et al., 2007; Kohn, 2014; Milani et al., 2015; Cisneros et al., 2020). Inclusions encapsulated in host minerals such as garnet or diamond have different elastic properties; they produce a residual pressure (P_inc) following exhumation, thereby allowing us to determine the entrapment pressure (Rosenfeld and Chase, 1961; Zhang, 1998). The P_inc and the equations of state (EoS) of the host-inclusion system can be used to calculate unique P–T curves (called isomekes) along which the pressure of the host and the inclusion are equal despite the changes in P–T conditions. Detailed discussions of this application are given by Angel et al. (2015) and Gonzalez et al. (2019).

Much of the previous work has focused on the factors affecting the calculation accuracy of the elastic geobarometer, such as the viscosity/plasticity relaxation properties of the inclusions (Zhong et al., 2020), the elastic anisotropy of minerals (Murri et al., 2018; Mazzucchelli et al., 2019), and the non-ideal geometry of inclusions (Mazzucchelli et al., 2018). Moreover, precisely determining the P_inc in inclusions has attracted many studies, as measured by x-ray diffractometry (Angel et al., 2014b) or Raman spectroscopy (Enami et al., 2007; Korsakov et al., 2009; Ashley et al., 2016; Murri et al., 2018; Bonazzi et al., 2019). However, researchers rarely explored the effect of thermoelastic parameters of minerals in entrapment pressure (P_e) calculations, which is crucial to improving elastic geobarometry precision (Angel et al., 2015; Moulas et al., 2020). Only Angel et al. (2015) considered the influence of thermoelastic parameters of diamond in determining the pressure of formation of diamond-inclusion systems. Moreover, as garnet rarely has a homogeneous composition, Moulas et al. (2020) considered the possible propagation of errors caused by the uncertainty of garnet composition in entrapment pressure (P_e) calculations. Therefore, in this study, we evaluated the influence of the thermoelastic parameters of the concerned minerals on the calculated results of the two types of elastic geobarometers, garnet (inclusion)–diamond (host) system and quartz (inclusion)–garnet (host) system (QuiG). The garnet–diamond system is very appropriate for estimating the formation pressure of diamond because the garnet is the most abundant occurring inclusion mineral in the diamond (Milani et al., 2015). Similarly, QuiG is also suitable for geobarometers because quartz is highly compressible relative to garnet, and the garnet host can maintain a large stress difference caused by changes in P–T conditions (Ashley et al., 2016). In these two types of elastic geobarometers, diamond and quartz are generally virtually pure endmember, and their thermoelastic parameters have been accurately determined (Angel et al., 2015; Angel et al., 2017a). However, the effect of composition of garnet on its thermoelastic parameters is still not very clear (Fan et al., 2017; Fan et al., 2018; Xu et al., 2019).

Garnet has cubic symmetry with Ia $\overline{3}$ d. The structure of garnet ${\mathrm{X}}_3^{2+}{\mathrm{Y}}_2^{3+}\mathrm{S}{\mathrm{i}}_3{\mathrm{O}}_{12}$ consists of a mixed framework of corner-sharing SiO₄ tetrahedra and YO₆ octahedra, with XO₈ triangular dodecahedron lying in between (Geiger, 2013) (Supplementary Figure S1). Garnet is flexible in accommodating a variety of cations with different ionic radii. Generally, divalent cations (e.g., Mg²⁺, Fe²⁺, Ca²⁺, Mn²⁺) occupy the X-site while trivalent cations (e.g., Al³⁺, Fe³⁺, Cr³⁺) occupy the Y-site. Natural garnet usually does not exist as pure endmember components but form solid solutions through element partitioning (Fan et al., 2015). Summary and analysis of garnet compositions from the global major ultra-high-pressure metamorphic (UHPM) rocks and kimberlites indicate that garnet is mainly composed of pyrope (Prp, Mg₃Al₂Si₃O₁₂), almandine (Alm, Fe₃Al₂Si₃O₁₂), and grossular (Grs, Ca₃Al₂Si₃O₁₂) with some other endmember components like spessartine (Sps, Mn₃Al₂Si₃O₁₂) and andradite (Adr, Ca₃ $\mathrm{F}{\mathrm{e}}_2^{3+}$ Si₃O₁₂) (Zhang et al., 2010; Kosman et al., 2016; Riches et al., 2016; Broadwell et al., 2019; Cruciani et al., 2019; Xu et al., 2019; Liu et al., 2020). In addition, the modal abundance of Prp and Alm can reach ∼70% and become higher with the increasing of the metamorphic pressure.

Understanding the thermoelastic properties of garnet, especially the Prp-Alm solid solution, is not only important to model the structure of the subducted slab but also a primary step in quantifying the P–T conditions of subduction and exhumation (Bass et al., 2008; Ashley et al., 2014). There are already extensive studies about the thermoelastic properties of Prp and Alm endmember component (Zhang L. et al., 1998; Gwanmesia et al., 2006; Fan et al., 2009; Li et al., 2011; Zou et al., 2012; Arimoto et al., 2015; Chantel et al., 2016; Hu et al., 2016; Fan et al., 2019b; Hartwig and Galkin, 2021). However, there is still a lack of tight constraints on the variation behavior of thermoelastic parameters developed when Prp-Alm solid solution is varying with composition (Takahashi and Liu, 1970; Huang and Chen, 2014; Milani et al., 2015). It is known that, for different mineral compositions, a variety of different cations incorporated in the garnets will affect their thermoelastic properties (Zhang et al., 1999; Kuang et al., 2019). In the 1970s, Takahashi and Liu (1970) conducted the pressure–volume (P–V) EoS study on four garnet samples with different compositions (Prp₁₀₀, Prp₆₀Alm₃₁, Prp₂₂Alm₇₂, and Alm₁₀₀) up to 32.8 GPa using single-crystal x-ray diffraction (SCXRD) and diamond anvil cell (DAC). They inferred that the bulk modulus (K₀) of the Prp-Alm solid solution decreases with the increasing Alm content. However, the conclusion from Takahashi and Liu (1970) needs to be further verified because they did not use any gasket in their high-pressure SCXRD experiments, which may significantly influence their experimental results. Similarly, Huang and Chen (2014) also performed the P–V EoS study on three synthetic Prp-Alm solid solutions (Prp₈₃Alm₁₇, Prp₅₄Alm₄₆, and Prp₃₀Alm₇₀) up to ∼21 GPa using in situ XRD combined with DAC, but obtained the opposite conclusion from Takahashi and Liu (1970), that is, the K₀ increases with the increasing Alm content. Furthermore, Huang and Chen (2014) also obtained the relationship between the K₀ of the Prp-Alm solid solutions and Alm content: K₀ = 170.5 (2.6) + 0.12 (4) X_Alm (X_Alm is the mole fraction of Alm). Subsequently, Milani et al. (2015) studied the P–V EoS on three synthetic Prp-Alm solid solutions (Prp₁₀₀, Prp₆₀Alm₄₀, and Alm₁₀₀) and obtained the same conclusion as that of Huang and Chen (2014). Nevertheless, to date, the thermoelastic properties of the Prp-Alm solid solutions at simultaneous high-pressure and high-temperature (HP–HT) conditions are still not entirely well constrained.

In this study, we selected eight synthetic Prp-Alm solid solution samples (Prp₉Alm₉₁, Prp₂₃Alm₇₆, Prp₃₁Alm₆₈, Prp₄₈Alm₅₂, Prp₅₇Alm₄₃, Prp₆₇Alm₃₂, Prp₇₈Alm₂₂, and Prp₈₇Alm₁₂) for the synchrotron SCXRD measurements up to ∼20 GPa and four Prp-Alm solid solution samples (Prp₁₄Alm₈₆, Prp₃₁Alm₆₈, Prp₄₈Alm₅₂, and Prp₆₇Alm₃₂) for the synchrotron SCXRD measurements up to ∼20 GPa and 700 K. Based on the obtained thermoelastic parameters of the systematic Prp-Alm solid solutions, we discussed the effects of composition (Mg²⁺-Fe²⁺ substitution) on the thermoelastic parameters of Prp-Alm solid solutions. Finally, we used these results to calculate the P_e in two host-inclusion systems and discussed the effects of the thermoelastic parameters of Prp-Alm-rich garnet on the results of P_e calculations.

Samples and Experimental Methods

The single crystals of Prp-Alm solid solutions (Prp₉Alm₉₁, Prp₁₄Alm₈₆, Prp₂₃Alm₇₆, Prp₃₁Alm₆₈, Prp₄₈Alm₅₂, Prp₅₇Alm₄₃, Prp₆₇Alm₃₂, Prp₇₈Alm₂₂, and Prp₈₇Alm₁₂) used in this study were synthesized at HP–HT conditions using a multi-anvil pressure apparatus (YJ-3000t) at the Institute of Geochemistry, Chinese Academy of Sciences, Guiyang, China. The detailed information about the garnet sample synthesis and subsequent compositional and structural analysis are described by Kuang et al. (2019). In general, with the increasing Alm content, the typical size of granular Prp-Alm crystals increases from ∼60 μm to more than 100 μm. The Prp-Alm solid solutions with good euhedral crystals, high quality, and without inclusions were selected for the SCXRD experiments. We successively double-side polished our sample pieces to ∼20–30 μm thickness, using the 3M diamond lapping films with grain size from coarse to a final 1 μm. The polished platelets were then cleaved into several square pieces of the desired size (∼40–60 μm) for SCXRD experiments.

High pressure and room temperature (HP–RT) SCXRD experiments were conducted on eight Prp-Alm solid solution samples using three short symmetrical DACs (cell-1: Prp₉Alm₉₁, Prp₃₁Alm₆₈, Prp₄₈Alm₅₂; cell-2: Prp₅₇Alm₄₃, Prp₆₇Alm₃₂, Prp₇₈Alm₂₂, and Prp₈₇Alm₁₂, and cell-3: Prp₂₃Alm₇₆). Rhenium (Re) gaskets of ∼250 μm thickness were pre-indented to ∼65 μm thickness using a pair of 500-μm culet size diamond anvils. Subsequently, a ∼300-μm-diameter cylindrical hole was drilled in the pre-indented area as the sample chamber. The selected single-crystal platelets with diameters of ∼40–60 μm were then placed into the sample chamber together with gold powder, which served as the pressure standard (Fei et al., 2007). The diffraction patterns of gold were collected before and after sample data collection for each pressure, and the average pressure values were used for the EoS fitting. A small ruby sphere of ∼10 μm was also loaded into each DAC sample chamber and used as the pressure indicator during the neon gas-loading. The neon pressure medium was loaded into the sample chamber using the gas-loading system at GeoSoilEnviroCARS (GSECARS) (Rivers et al., 2008). After the neon gas loading, the diameter of the sample chamber was ∼220 μm.

HP–HT SCXRD experiments were carried out using an externally heated DAC (EHDAC) equipped with an alumina ceramic heater coiled with two Pt wires of 200 μm in diameter and 48 cm length (Kantor et al., 2012; Fan et al., 2019a). A rhenium foil was used as the gasket material and pre-indented to ∼60 μm thickness using a pair of diamond anvils with 500-μm culet size and then a 300-μm-diameter sample chamber was drilled at the center of pre-indentation. The selected single-crystal platelets (Prp₁₄Alm₈₆, Prp₃₁Alm₆₈, Prp₄₈Alm₅₂, and Prp₆₇Alm₃₂) with a diameter of ∼40 μm were loaded into the sample chamber together with gold powder, which served as the pressure standard at HP–HT conditions. For each P–T point, the diffraction patterns of gold were collected before and after sample data collection, and the average pressure values were used. Likewise, a small ruby sphere of ∼10 μm was loaded as the pressure indicator for the gas-loading with neon as the pressure transmitting medium using the GSECARS gas-loading system. Heating was carried out by a resistance-heating system (Fan et al., 2010). A Pt₉₀Rh₁₀-Pt₁₀₀ thermocouple was attached to one of the diamond surfaces, approximately 500 μm away from its culet, and clad with a ceramic adhesive (Resbond 920) for temperature measurements (Kantor et al., 2012). To minimize temperature instability for each heating run, we first heated the sample chamber to an expected temperature and then kept it at this temperature for 15 min. The temperatures of the sample chamber were actively stabilized within ±1 K using the temperature-power feedback program with a remotely controlled Tektronix Keithley DC power supply during the experiments (Sinogeikin et al., 2006).

Both of the HP–RT and HP–HT synchrotron SCXRD experiments were conducted at the 13-BMD beamline of the GeoSoilEnviroConsortium for Advanced Radiation Sources (GSECARS) of Advanced Photon Source (APS), Argonne National Laboratory (ANL). An incident x-ray beam of 0.3344 Å wavelength focused on a 3 × 7 μm² area was used to determine the unit-cell volume of Prp-Alm solid solution samples in the DACs. Diffraction images were acquired on a stationary Perkin-Elmer area detector. Tilting and rotation of the detector and the sample-to-detector distance were calibrated using ambient LaB₆ as the diffraction standard. Wide and stepped φ-rotation exposure were collected for the single-crystal samples at each loading run, with an exposure time of 2 s/deg. The φ-rotation (the opening angle of the DAC is ±15°) axis was horizontal and perpendicular to the incident x-ray direction. The diffraction images collected at each P–T point were analyzed using the GSE_ADA/RSV software (Dera et al., 2013).

Results

Equations of State of Prp-Alm Solid Solutions at High Pressure and Room Temperature

The unit-cell volumes change with pressure at room temperature for eight Prp-Alm solid solution garnets and are presented in Supplementary Table S1 and Figure 1, showing that the unit-cell volumes of Prp-Alm solid solution with increasing pressure garnets decrease systematically. Using the console program EosFit7c (Angel et al., 2014a; Gonzalez-Platas et al., 2016), the EoS parameters, including the room P–T volume, the isothermal bulk modulus, and its pressure derivative of these Prp-Alm solid solutions, were refined by fitting their P–V data using two different EoSs (Birch-Murnaghan EoS and Vinet EoS).

FIGURE 1

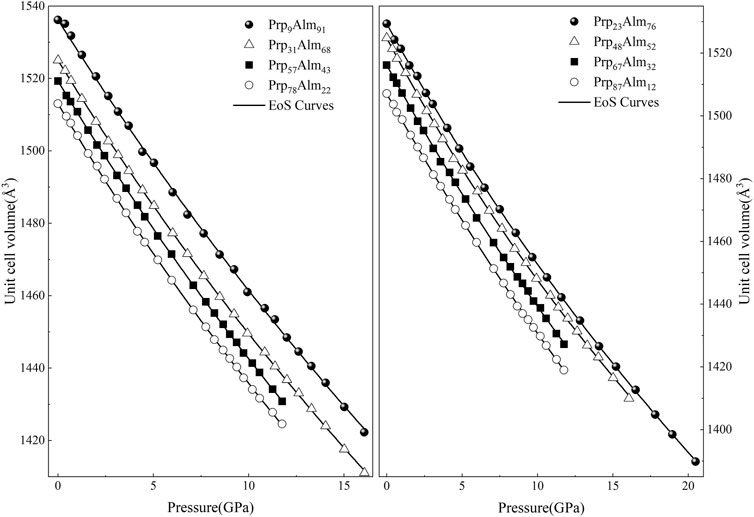
FIGURE 1. Unit-cell volume compression of pyrope-almandine solid solution garnets at high pressure and room temperature in this study. The error bars of the data points are smaller than the symbols.

Birch-Murnaghan equation of state. The P–V relations of these Prp-Alm solid solutions have been determined by fitting their HP–RT data to the third-order Birch-Murnaghan EoS, which is given in the following form:

$\mathrm{P}=\left(3/2\right)K_0\left[{\left(\frac{V_0}{V}\right)}^{7/3}-{\left(\frac{V_0}{V}\right)}^{5/3}\right]\times \left[1+\left(\frac{3}{4}\right)\left(K_0^{\prime }-4\right)\left[{\left(\frac{V_0}{V}\right)}^{2/3}-1\right]\right],(1)$

where V₀, K₀, and K′₀ are the unit-cell volume, isothermal bulk modulus, and its pressure derivative at ambient conditions, respectively. We obtained the V₀, K₀, and K′₀ of Prp-Alm solid solutions, as shown in Table 1. The refined value of V₀ was within 1σ or so of the measured V₀ by XRD at ambient conditions, indicating the accuracy of the refined results (Angel, 2000). It can be found that the bulk moduli of Prp-Alm solid solutions gradually increase with increasing Alm content, especially when K′₀ was fixed at 4 (Table 1). Furthermore, this trend is also in agreement with the conclusion of Huang and Chen (2014) and Milani et al. (2015).

TABLE 1

TABLE 1. Bulk moduli and their first pressure derivative of garnets along the Prp-Alm join.

Vinet equation of state. We also analyzed the P–V data using the Vinet EoS (Vinet et al., 1986), which is derived from a “universal equation” for solids and is represented as follows:

$P\left(V\right)=3K_0{y}^{-2}\left(1-y\right)exp\left[{\eta }_0\left(1-y\right)\right],(2)$

where y = x^1/3, x = V/V₀, and ƞ₀ = (3/2) (K′ 0-1). Analyses of Equation 2 yielded V₀, K_0, and K′₀ for the Prp-Alm solid solutions (Table 1), which are reasonably consistent with those derived by fitting to the Birch-Murnaghan EoS.

Supplementary Table S2 summarizes the bulk moduli and their pressure derivatives for Prp and Alm endmembers and their solid solutions determined with various experimental techniques. As shown in Supplementary Table S2, the K₀ values of Prp endmember from the literature range from 163.7 (17) to 175 (2) GPa. Among them, Milani et al. (2015) reported the least value (163.7 GPa) due to their largest K′₀ value (6.4) than those of other studies (4.3–4.6). There is a trade-off between the bulk modulus and its pressure derivative, which negatively correlates (Gatta et al., 2011). So, we obtained the confidence ellipses of K₀ and K′₀ for pyrope from previous XRD studies, as shown in Figure 2. From Figure 2, we can see that the previous XRD results of pyrope all fall within the 68.3% (1σ) confidence interval, with mean values of 171 (8) GPa and 4 (2) for K₀ and K′₀, respectively. Meanwhile, the obtained K₀ of pyrope [170.0 (2)–175 (2) GPa] by using Brillouin light spectroscopy (BLS) and ultrasonic interferometry (UI) methods are also consistent with the results from the XRD method (Supplementary Table S2 and Figure 2). For the Alm endmember, the K₀ value [172.6 (15) GPa] obtained by Milani et al. (2015) was also smaller than other XRD results [179 (3)–185 (3) GPa]. The main reason remains that the K′₀ value (5.6) obtained by Milani et al. (2015) is higher than those of other studies (4–4.2). Moreover, Arimoto et al. (2015) reported that the K₀ value [174.2 (12) GPa] of Alm endmember using the UI method is slightly smaller than the result [179 (3) GPa] using the XRD method.

FIGURE 2

FIGURE 2. Confidence ellipses of K₀ and K′ for pyrope from previous studies.

As a comparison, until now, the previous EoS studies on the Prp-Alm solid solutions are relatively limited. Huang and Chen (2014) measured three synthetic Prp-Alm solid solutions (Prp₈₃Alm₁₇, Prp₅₄Alm₄₆, and Prp₃₀Alm₇₀) by the XRD method up to 7, 21, and 19 GPa, respectively. With fixed K′₀ at 4.3, the K₀ obtained for these three samples were 172 (4), 174 (2), and 183 (2) GPa, respectively. Subsequently, Milani et al. (2015) reported a significantly smaller value [167.2 (17) GPa], also using the XRD method for synthetic Prp₆₀Alm₄₀. As a consequence, the previous experimental studies indicated that the K₀ range along the Prp-Alm solid solutions from Prp to Alm endmembers is expected to be 163.7 (1)–185 (3) GPa (Supplementary Table S2). Our results show that the bulk moduli of our eight Prp-Alm solid solutions (Table 1) are within this range. Because the bulk modulus and its pressure derivative have a negative correlation of bulk modulus and its pressure derivative, the K′₀ is permanently fixed at 4 for the following discussion of the relationship between the bulk moduli of Prp-Alm solid solutions and their compositions. Figure 3 shows the bulk moduli of Prp-Alm solid solutions as a function of composition, and we can observe that the compressibilities of Prp-Alm solid solutions increase with increasing Prp concentrations. Furthermore, by linear fitting of the results in this study, the bulk moduli of the Prp-Alm solid solutions as a function of Prp content can be expressed by K₀ (GPa) = 181.0 (8)–0.11(1) X_prp (R² = 0.91, K′₀ fixed at 4). It is worth noting that the K₀ of most previous studies are in harmony with our fitting line, except for Milani et al. (2015) (Figure 3). It may be attributed to the higher K′₀ [5.6 (5)–6.4 (4)] of Milani et al. (2015) than those of others [3.9 (3)–4.61 (14)] (Supplementary Table S2).

FIGURE 3

FIGURE 3. Bulk moduli of pyrope-almandine solid solution garnets as a function of pyrope content.

Equations of State of Prp-Alm Solid Solutions at High Pressure and High Temperature

The unit-cell volumes of Prp₁₄Alm₈₆, Prp₃₁Alm₆₈, Prp₄₈Alm₅₂, and Prp₆₇Alm₃₂ at HP–HT conditions up to ∼19.67 GPa and 700 K are shown in Supplementary Table S3. Figure 4 also shows the pressure–volume–temperature (P–V–T) data of these Prp-Alm solid solution samples. In this study, we applied the thermal-pressure model EoS to describe the P–V–T behavior of Prp-Alm solid solutions. There are two ways to calculate the P–V–T properties of a mineral (as shown in Figure 1 of Milani et al., 2017). One way to characterize the P–V–T behavior of minerals is to describe how the V_T0, K_T0, and K'_T0 vary with temperature (at room pressure) and then use these parameters to calculate the isothermal compressibility at the high temperature (as shown by the rough path in Figure 1 of Milani et al., 2017). A potential weakness of this method is that the variation of K'_T0 with temperature has rarely been measured, where K'_T0 should increase slightly with increasing temperature, rather than not change with temperature, as the common assumption. Additionally, this assumption, coupled with the approximation that dK_T0/dT is a constant, has often given rise to a non-physical negative coefficient of thermal expansion for many materials at reasonably moderate pressures (Helffrich and Connolly, 2009).

FIGURE 4

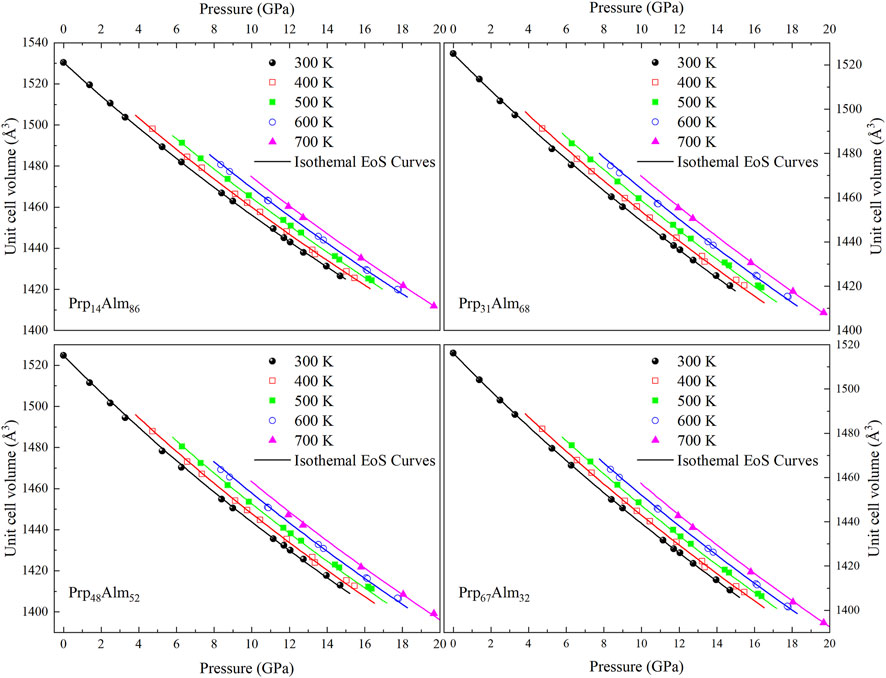
FIGURE 4. The unit-cell volume of pyrope-almandine solid solution garnet as a function of pressure and temperature. The lines represent the isothermal compression curve from fitting HTBM EoS at 300, 400, 500, 600, and 700 K. The error bars of the data points are smaller than the symbols.

Furthermore, the maximum experimental temperature of only 700 K in this study and the relatively limited number of high-temperature data points make the fitting of the thermal expansion coefficient at high temperatures more inaccurate. Therefore, we employ the concept of thermal pressure (Anderson, 1995) to describe the P–V–T behavior of Prp-Alm solid solutions. Then, as shown by the thin path in Figure 1 of Milani et al., 2017, the P at a given V and T can be expressed as the sum of two terms:

$P\left(V,T\right)=P\left(V,T_{ref}\right)+P_{th}\left(T\right),(3)$

The P(V, T_ref) is the isothermal EoS for minerals at the reference temperature, up to the volume at P and T_ref. The thermal-pressure Pth(T) is the pressure generated by raising the temperature from T_ref to T at a constant volume, which is the isochor of the mineral passing through the final P–T point. Details of the employment of a thermal-pressure EoS and any necessity assumptions have been reviewed by Milani et al. (2017). In this study, we used the Birch-Murnaghan isothermal EoS in combination with the Holland and Powell (2011) model of thermal-pressure EoS to determine the thermoelastic parameters of four Prp-Alm solid solutions, as shown in Table 2. All described in this study have been performed with the EosFit7c program (Angel et al., 2014a; Gonzalez-Platas et al., 2016). The Einstein temperature, θ_E, of Prp-Alm solid solutions in this study are calculated from the values of the pyrope (320 K) and almandine (400 K) and according to the ideal solution model (Milani et al., 2015). The V₀ and K_T0 derived from HP–HT data were roughly consistent with that from P–V data at room temperature, especially as the K'_T0 was fixed at 4 (Table 1 and Table 2).

TABLE 2

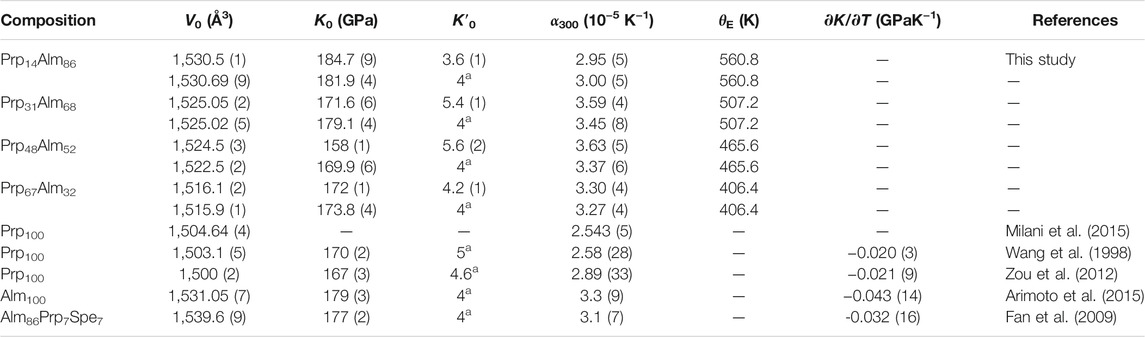
TABLE 2. Thermoelastic parameters of garnets along the Prp-Alm join, as compared with previous studies.

Figure 5 shows the thermal expansion coefficient at ambient conditions (α₀) of four Prp-Alm solid solutions in this study, combined with the results from previous studies. As shown in Figure 5, there is a non-linear correlation between α₀ and the Prp content of the Prp-Alm solid solution. The α₀ of Prp-Alm solid solution varies with the composition getting a parabola. At ambient conditions, Prp-Alm solid solution with intermediate composition demonstrates a larger α₀ than the composition close to endmember, the maximum variation in the α₀ from Prp₁₄Alm₈₆ to Prp₄₈Alm₅₂ is about 23%. The α₀ of the Prp-Alm solid solutions as a function of Prp content can be expressed by α₀ (10⁻⁵K⁻¹) = 2.7 (1) + 3.0 (5) X_Prp − 3.2 (4) X²_Prp (R² = 0.985).

FIGURE 5

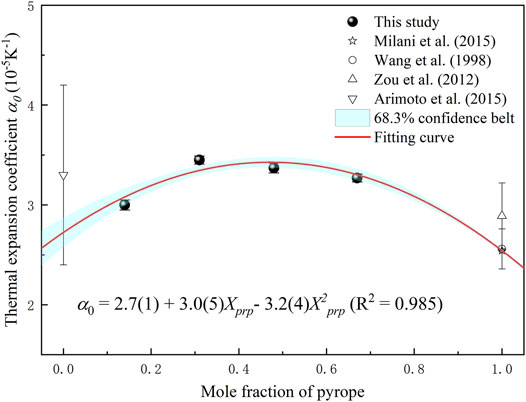
FIGURE 5. The thermal expansion coefficient of pyrope-almandine solid solution garnet at 300 K as a function of pyrope content.

Discussion

Mg²⁺-Fe²⁺ Substitution Effect on Bulk Moduli of Prp-Alm Solid Solutions

Among previous studies about the compositional effect on bulk modulus of different mineral groups, minerals with Mg²⁺-Fe²⁺ solid solutions have been extensively investigated because of their importance in understanding the composition and dynamic property of the Earth’s interior (Takahashi and Liu, 1970; Zhang J. et al., 1998; Zhang et al., 1999; Speziale et al., 2004; Huang and Chen, 2014). The Fe and Mg component dependence of bulk modulus in mantle minerals is interesting for modeling the mineralogical composition of the mantle and mineral crystal chemistry. Anderson and Anderson (1970) proposed a simple bulk modulus (K₀)–volume (V₀) systematics, where K₀V₀ = constant. However, for most of the ferromagnesian silicates and carbonates that have been studied so far, the bulk modulus appears to increase with increasing Fe content, such as garnet (Huang and Chen, 2014), olivine (Speziale et al., 2004), and siderite (Zhang J. et al., 1998), which is inconsistent with bulk modulus–volume systematics. To sum up, it is necessary to understand the Mg²⁺-Fe²⁺ substitution effect on the bulk modulus of garnet.

Figure 3 shows the bulk moduli of Prp-Alm solid solutions as functions of compositions in this study and compared with those of previous studies. Mg²⁺-Fe²⁺ substitution results in a nearly linear decrease of the bulk modulus. The reduction of bulk moduli from Prp₉Alm₉₁ to Prp₈₇Alm₁₂ is ∼3%, mainly consistent with the ∼6% decrease from Prp₃₀Alm₇₀ to Prp₈₃Alm₁₇ reported by Huang and Chen (2014).

The bulk moduli of minerals are mainly controlled by their constituent polyhedral compressibilities, primarily determined by the mean cation–oxygen bond length in the polyhedral (Hazen et al., 1994). Many previous high-pressure studies have shown that the SiO₄ tetrahedrons of silicate minerals are essentially rigid units (Robinson et al., 1971; Zhang et al., 1997; Xu et al., 2017). The selected bond distances of Prp-Alm solid solutions at the ambient condition (data from Kuang et al., 2019) as functions of composition are shown in Figure 6. Inspection of Figure 6 demonstrates that the d_<M-O> (M is the divalent cations in X-site) decreases significantly with the increasing Prp content, mainly due to the smaller effective ionic radius of Mg²⁺ (0.89 Å) in eightfold coordination than that of Fe²⁺(0.92 Å) (Shannon, 1976). In contrast, the average d_<Si-O> of the SiO₄ tetrahedron and d_<Al-O> of the AlO₆ octahedron change negligibly with increasing Prp mol%. These results imply that the compressibility of the MO₈ dodecahedron mainly controls the bulk modulus of the Prp-Alm solid solution. However, other factors, such as the compressibilities of the SiO₄ tetrahedron and the AlO₆ octahedron, may be secondary important to the bulk modulus of Prp-Alm solid solution.

FIGURE 6

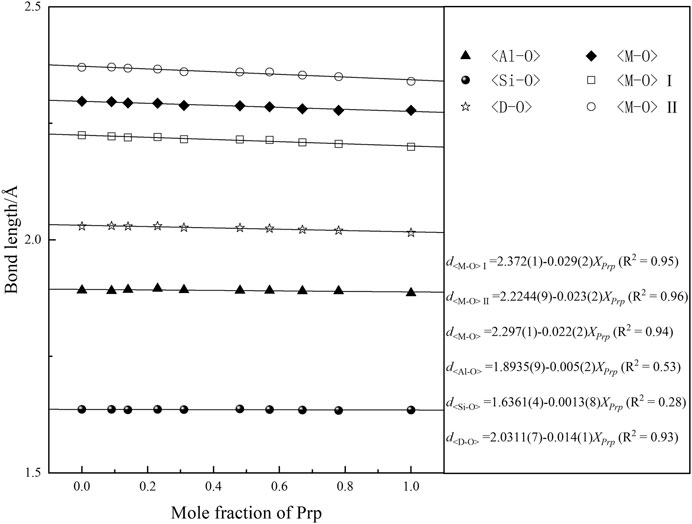
FIGURE 6. The bond length of the pyrope-almandine solid solution garnet at ambient conditions as a function of pyrope content.

Besides, this study shows that FeO₈ dodecahedron is less compressible than MgO₈ dodecahedron. Similar conclusions were also obtained about the structures with sixfold coordinated Mg²⁺ and Fe²⁺ cations (Zhang et al., 1997), implying that the bonding character plays an essential role in such anomalous compression, whereas structure type and polyhedral coordination may be less critical. Furthermore, the electronegativity of the element, which describes the ability of an atom to attract electrons, may be an essential factor for the bonding character. The electronegativity of Mg (1.31) is distinctly smaller than that of Fe (1.83) (Allred, 1961), resulting in the less compressible FeO₈ dodecahedron than MgO₈ dodecahedron.

Moreover, Hazen et al. (1994) suggested that the SiO₄ octahedra and AlO₆ tetrahedra framework may also dictate the bulk modulus of garnet. Subsequently, Zhang L. et al. (1998) showed that the kinking degree of the Si-O-Al angle decreased continuously with increasing pressure, and the Si-O-Al angle in Alm is less kinked than that in Prp over the same pressure range (Zhang et al., 1999). Furthermore, the Raman spectroscopy results of Kuang et al. (2019) show that both the stretching motions of Si-O and the rotation motions of SiO₄ decreased linearly with increasing Alm content. Thus, the degree of distortion and rotation of SiO₄ may also affect the bulk moduli of the Prp-Alm solid solutions.

To sum up, the bulk moduli of Prp-Alm solid solutions are primarily governed by the compressibility of MO₈ dodecahedra. The difference in the compressibilities of MO₈ can be attributed to the different effective ionic radius and electronegativities of the Mg and Fe atoms. Also, the kinking degree of the Si-O-Al angle and the distortion and rotation of SiO₄ may affect the bulk moduli of Prp-Alm solid solutions.

Mg²⁺-Fe²⁺ Substitution Effect on Thermal Expansion Coefficient of Prp-Alm Solid Solutions

Contrary to the effect of Mg²⁺-Fe²⁺ substitution on the bulk modulus of Prp-Alm solid solutions, the α₀ of Prp-Alm solid solutions varies with the composition forming a parabola. As shown in Figure 5, at ambient temperatures, the composition of the Prp-Alm solid solution near the intermediate composition displays a larger thermal expansion coefficient than the composition near the endmember. While the causes of this result are yet to be revealed, we think that the most likely reason is the local arrangement of Mg²⁺and Fe²⁺. For the garnet, the different-sized divalent cations substitution on the dodecahedral site can make its thermodynamic properties (e.g., volume, enthalpy, entropy, free energy, etc.) deviate from the ideal mixing results (Bosenick et al., 2001; Vinograd et al., 2004; Dachs et al., 2014; Du et al., 2016). Besides, the magnitude of the non-ideal mixing is correlated with the size difference between the substituting cations on the dodecahedral site (Geiger and Rossman, 1994). The study on the local structure of the pyrope-grossular garnet solid solution shows that the Mg/Ca substitution can produce significant amounts of short-range order rather than long-range order in garnets (Bosenick et al., 2000). Furthermore, the compositions near Prp₅₀Grs₅₀ depart most strongly from random mixing, and all the compositions tend to random disorder at high temperatures. Although the size difference between Mg²⁺ (0.89Å) and Fe²⁺ (0.92Å) is smaller than that between Mg²⁺and Ca²⁺ (1.12 Å) (Shannon, 1976), the influence on the local arrangement by the Mg/Fe substitution cannot be overlooked. It is speculated that local disorder caused by the Mg/Fe substitution is the main reason for a non-linear relationship between thermal expansion coefficient and the composition of the Prp-Alm solid solution.

Implications for Elastic Geobarometer

It is ordinary to use host-inclusion systems to infer the geological history of a mineral or a rock (Guiraud and Powell, 2006). The history of study on elastic geobarometers can be traced back to the 1980s. Roedder and Bodnar (1980) made the first estimation for the formation pressure of minerals from the fluid inclusions in them. The basic principle is that when the host mineral captures the fluid, it experiences a different P–T path than the host mineral because its volume is limited by the space inside the mineral and is subjected to the pressure exerted on it by the host mineral during subsequent changes in temperature and pressure conditions. In turn, this difference and its associated physicochemical properties can be used to estimate the P–T conditions experienced by the host mineral. This principle is not only applicable to fluid/melt inclusions but also to other solid mineral inclusions within the mineral that differ from its thermoelastic properties. This method underwent significant developments in the past decade and is gradually gaining the interest of geologists (e.g., Murri et al., 2018; Alvaro et al., 2019; Anzolini et al., 2019; Bonazzi et al., 2019; Gonzalez et al., 2019; Mazzucchelli et al., 2019; Moulas et al., 2020).

The pressure estimation by an elastic geobarometer has some prerequisite assumptions (Bonazzi et al., 2019): (1) The inclusions are in the same pressure environment as the host mineral at the time of capture, and the inclusions fill the vacancies entirely within the host mineral. (2) The host mineral and the inclusions are always reversibly and elastically deformed after capture. In this way, the captured pressure can be estimated by measuring the residual pressure of the inclusions due to the difference in elastic properties between the two minerals under normal temperature and pressure conditions and by combining the equation of the state of the two minerals. In this study, the method for estimating the pressure is based on entrapment isomekes proposed by Angel et al. (2017b). Entrapment isomekes is a single P–T path along which the fractional volume change in host and inclusion are equal (Gonzalez et al., 2019). The calculation of P_e was performed with EosFit-Pinc, and the details of this method were described in Angel et al. (2017b).

As mentioned in the introduction section of this study, much of the previous work has focused on the factors affecting the calculation accuracy of the elastic geobarometer except the influence of the thermoelastic parameters of minerals. So, we selected two garnet-related host-inclusion pairs to evaluate the influence of the thermoelastic parameters of the concerned minerals on the calculated results of elastic geobarometers. Quartz is generally a virtually pure endmember, and it is stable over a wide range of metamorphic conditions (Korsakov et al., 2009). Garnet has also served as a central focus of metamorphic studies to discern P–T paths because it can store the entire history of metamorphism by its inclusion suites such as quartz, graphite, and rutile (Ague and Carlson, 2013; Baxter et al., 2013; Caddick and Kohn, 2013). Hence, QuiG is considered a particularly useful geobarometer and has been widely used to infer the geological history of the rock from the collisional orogenic belts (Wolfe and Spear, 2018), the subduction complex (Bayet et al., 2018; Alvaro et al., 2019), and ultrahigh-pressure metamorphic complex (Korsakov et al., 2009; Gonzalez et al., 2019; Zhong et al., 2019; Moulas et al., 2020). Similarly, as the primeval samples from inaccessible regions of Earth, diamonds and their inclusions provide direct information of deep Earth’s evolution. This information is precious if it can be combined with depth estimates (Anzolini et al., 2019). An estimate of their formative pressure (depth of provenance) can be used to constrain and understand the environment in which they formed. Therefore, the thermoelastic parameters of the minerals play a crucial role in determining the accuracy of the pressure calculation. The garnet, a widespread mineral solid solution in nature, can have varying elastic properties depending on its composition (Du et al., 2015; Fan et al., 2017; Fan et al., 2018; Xu et al., 2019). In most cases, however, the thermoelastic properties used for calculation are the results of the endmember garnet (Milani et al., 2015; Gonzalez et al., 2019; Zhong et al., 2019), or assumed that the solid solution is isotropic and ideal (Johnson et al., 2021). Based on the results of this study, the thermoelastic properties of the Prp-Alm solid solutions may not follow the ideal mode (e.g., Figure 5). Therefore, the thermoelastic properties of garnet estimated from the endmember components may cause divergence. It is necessary to discuss the influence of garnet composition on the accuracy of these two elastic geobarometers.

These calculations utilized the thermoelastic coefficients of quartz with a curved α-β transition (Angel et al., 2017a) and the thermoelastic coefficients of the diamond from Angel et al. (2015). The shear modulus and its P and T derivative of Prp-Alm garnet were calculated by combining the results of the endmembers pyrope and almandine in proportion to their measured abundances, assumed as an ideal solid solution (Arimoto et al., 2015; Fan et al., 2019b). The final full set of thermoelastic coefficients for the P_e estimation are shown in Table 3.

TABLE 3

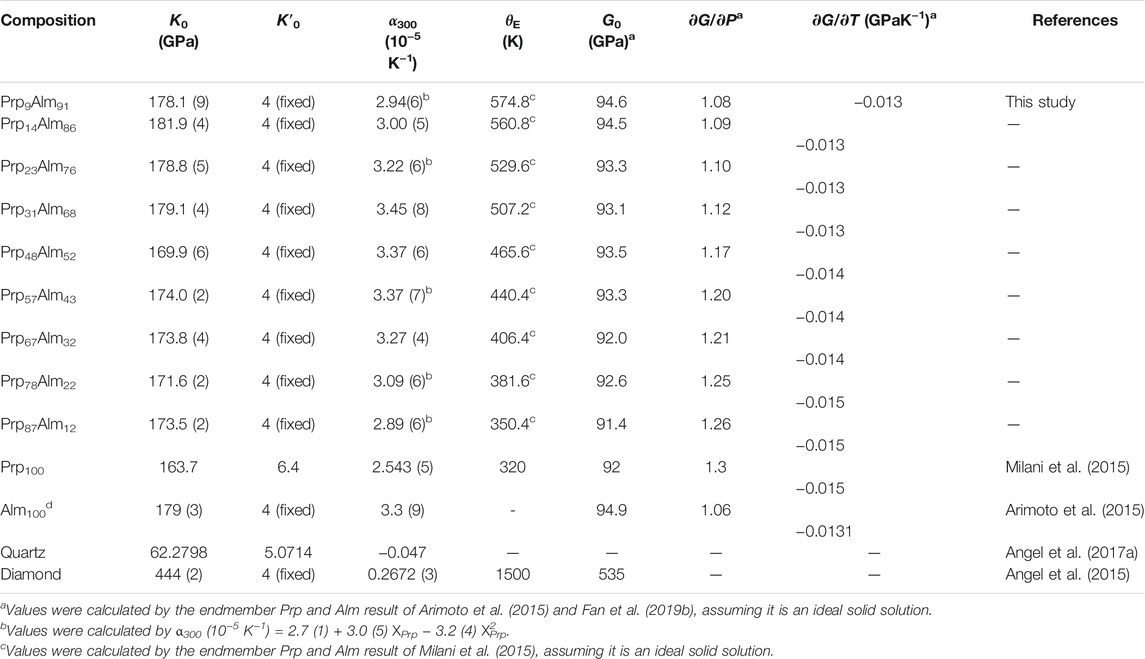
TABLE 3. Room pressure–temperature EoS coefficients for selected minerals ( Prp-Alm garnets, diamond and quartz).

Firstly, the uncertainties of the thermoelastic properties of garnets in the QuiG application should be considered. Here, we take the Prp₁₄Alm₈₆ garnet to demonstrate the effect of the uncertainties in thermoelastic properties. We chose 0.65 GPa as the P_inc obtained by laser Raman spectroscopy for quartz inclusions in garnet from eclogite for our P_e estimation (Zhong et al., 2019). Supplementary Table S4 lists the calculated P_e for Prp₁₄Alm₈₆ considering the uncertainties of the thermoelastic properties. Compared to the bulk modulus, the thermal expansion coefficient in this study has the most considerable effect in calculated P_e (Figure 7A). A 1.7% uncertainty in the value of α₀ of garnet changes the P_e by ∼0.007 GPa at 500 K, and with the temperature rising, it makes the P_e change ∼0.016 GPa at 1300 K. The accuracy of bulk modulus obtained in this study has almost no effect on the P_e estimation. A 0.22% uncertainty in the value of K₀ of garnet changes the P_e by only 0.001 GPa. In conclusion, the maximal error caused by the thermoelastic properties of garnet on P_e estimation is less than 0.02 GPa (Figure 7A). Besides, as shown in Figure 7A, we have calculated the P_e of the other two garnets with different components (Prp₄₈Alm₅₂ and Prp₈₇Alm₁₂), and the results obtained are consistent with the Prp₁₄Alm₈₆.

FIGURE 7

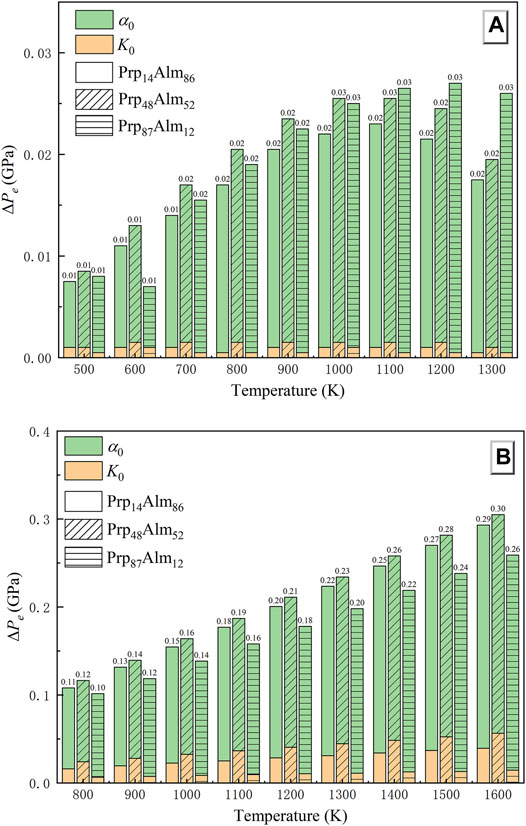
FIGURE 7. The total uncertainty of the thermal equation of state parameters on the results of P_e. (A): Garnet-quartz elastic barometer; (B): Diamond-garnet elastic barometer.

For the P_e calculations of the diamond–garnet pair, we assume a residual pressure P_inc on the garnet inclusion of 0.2 (1) GPa, and we use the thermoelastic properties given in Table 3. Supplementary Table S5 lists the calculated P_e for Prp₁₄Alm₈₆. The conclusions drawn from Supplementary Table S5 and Figure 7B are that a 0.22% uncertainty of K₀ may contribute an error of ∼0.03 GPa to the calculated P_e. Same as in QuiG, the thermal expansion coefficient in this study has the most considerable effect in the calculated P_e of the diamond–garnet system (Figure 7B). A 1.7% uncertainty in the value of α₀ of garnet changes the P_e by ∼0.092 GPa at 800 K, and with the temperature rising, it makes the P_e change ∼0.254 GPa at 1600 K. The maximal error caused by the thermoelastic properties of garnet in the diamond–garnet system is ∼0.3 GPa at 1,600 K (Figure 7B). It can be found that for the same garnet composition, the P_e change caused by the uncertainties of its thermoelastic properties is unequal in the two types of elastic geobarometers. The P_e change in the diamond–garnet pair is almost ten times as large as it is in QuiG.

Here, the Pyp-Alm garnets of different compositions (Table 3) are used to calculate the P_e, and the results of two elastic geobarometers are shown in Figures 8A,B. The effect of garnet composition on the predicted entrapment pressure is relatively large, especially for the diamond–garnet system (Figure 8B). At 1,400 K, the different compositions of garnet can cause a variation of P_e up to 4.5 GPa in the diamond–garnet system. In the QuiG, the difference of inferred entrapment pressure may reach ca. 0.35 GPa at 1,060 K. As mentioned above, this is mainly due to the distinct thermal expansion coefficient among them.

FIGURE 8

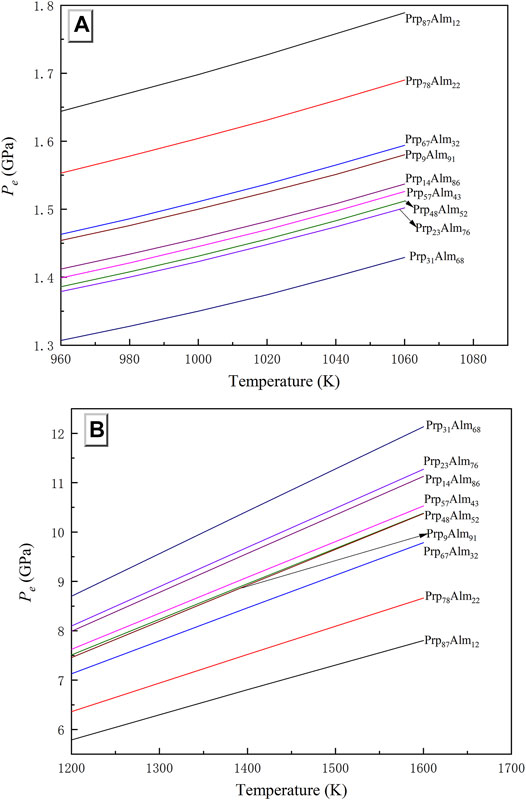
FIGURE 8. P_e results for different garnet components in (A) Garnet-quartz elastic barometer and (B) Diamond-garnet elastic barometer.

To sum up, even though the procedure of applying an elastic barometer to host-inclusion mineral systems requires several steps that involve various assumptions (Angel et al., 2015), and there are lots of possible factors that could influence the precision and accuracy of calculated P_e value as mentioned above, its advantages could not be ignored. Much previous work suggested that QuiG, and diamond–garnet elastic barometer, may preserve different aspects of garnet history in complex terranes (Wolfe and Spear, 2018; Alvaro et al., 2019; Spear and Wolfe, 2020; Johnson et al., 2021). The advantages of QuiG or other inclusion-based methods are relatively easy to apply and require far less data acquisition than conventional methods. Our results suggest that the entrapment pressure may be significantly influenced by the thermoelastic parameters of garnet, which is selected to have a different component from the research sample, while the thermal expansion coefficient is the main influencing factor for the elastic barometer to P_e estimation, compared with other thermoelastic parameters. Therefore, the effect of the composition of garnet on the P_e estimation could not be ignored. Furthermore, one factor that must not be overlooked is the effect of viscous relaxation, which occurs very rapidly at temperatures >110 K (Moulas et al., 2020) and the preserved P_e may then be a reflection of re-equilibration (Zhong et al., 2020). In the future application of elastic barometer, as the most common garnet component in the Earth, the thermoelastic parameters (especially the thermal expansion coefficient) of the pyrope-almandine-grossular ternary solid solutions must also be considered.

Conclusion

In summary, the thermoelastic parameters of systematic Prp-Alm solid solutions were obtained by fitting the P–V–T or P–V data to the EoS and compared with previous studies. The relationship between the bulk moduli of the Prp-Alm solid solutions and Prp content can be expressed as K₀ (GPa) = 181.0 (8) − 0.11 (1) X_prp (R² = 0.91, K′₀ fixed at 4). Our results demonstrate that the Prp content will decrease the incompressibilities of Prp-Alm solid solutions, which is inconsistent with bulk modulus–volume systematics: K₀V₀ = constant. The possible reasons for this difference may be multiple and complicated. In our view, the most likely reason is the larger compressibility of MgO₈ than that of FeO₈. Also, the kinking degree of the Si-O-Al angle and the degree of distortion and rotation of SiO₄ may affect the compressibilities of the Prp-Alm solid solutions. The thermal expansion coefficient with the component of Prp-Alm solid solution also has a relational expression, α₀ (10⁻⁵K⁻¹) = 2.7 (1) + 3.0 (5) X_Prp − 3.2 (4) X²_Prp (R² = 0.985), where the Prp-Alm solid solutions with intermediate composition show a larger coefficient than the endmembers at ambient condition. Furthermore, for two types of elastic geobarometers, we evaluate the correlation of the uncertainties of thermoelastic properties with P_e estimation accuracy. Compared with bulk modulus, the thermal expansion coefficient has the main effect on the estimation of P_e. The P_e change caused by the uncertainties of thermoelastic properties of garnets in the diamond–garnet pair is almost 10 times larger than it is in QuiG. Besides, by calculating P_e with different garnet components, the result suggests that the garnet component may significantly influence entrapment pressure, especially in the diamond–garnet system and the pyrope-almandine-grossular ternary solid solutions EoS must also be considered in the future study.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

Conceptualization and methodology, DF and WZ; investigation, BL, JX, ST, and VP; sample source, BL and WZ; experimental analysis, BL, JX, DF, and WZ; writing—original draft preparation, BL; writing—review and editing, DF, WZ, JJ, JX, BL, ZY, SH, WG, and YZ; plotting, BL; software, BL and JX. All authors have read and agreed to the published version of the manuscript.

Funding

This project was supported by the National Natural Science Foundation of China (Grant Nos. 41802043, U2032118, and 42172048), the Youth Innovation Promotion Association CAS (DF, 2018434), the Chinese Academy of Sciences “Light of West China” Program (2019), the Science and Technology Foundation of Guizhou Province (QKHJC-ZK (2021) ZD042), and the Innovation and Entrepreneurship Funding of High-Level Overseas Talents of Guizhou Province (DF, (2019) 10).

Conflict of Interest

BL, WG, and YZ were employed by PetroChina.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge Wei Chen and Yunqian Kuang for the High P–T experiments assistance. The experimental works were conducted at the GeoSoilEnviroCARS (Sector 13), Advanced Photon Source (APS), and Argonne National Laboratory.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.833405/full#supplementary-material

References

Ague, J. J., and Carlson, W. D. (2013). Metamorphism as Garnet Sees it: The Kinetics of Nucleation and Growth, Equilibration, and Diffusional Relaxation. Elements 9, 439–445. doi:10.2113/gselements.9.6.439

CrossRef Full Text | Google Scholar

Allred, A. L. (1961). Electronegativity Values from Thermochemical Data. J. Inorg. Nucl. Chem. 17, 215–221. doi:10.1016/0022-1902(61)80142-5

CrossRef Full Text | Google Scholar

Alvaro, M., Mazzucchelli, M. L., Angel, R. J., Murri, M., Campomenosi, N., Scambelluri, M., et al. (2019). Fossil Subduction Recorded by Quartz from the Coesite Stability Field. Geology 48, 24–28. doi:10.1130/g46617.1

CrossRef Full Text | Google Scholar

Anderson, D. L., and Anderson, O. L. (1970). Brief Report: The Bulk Modulus-Volume Relationship for Oxides. J. Geophys. Res. 75, 3494–3500. doi:10.1029/JB075i017p03494

CrossRef Full Text | Google Scholar

Anderson, O. L. (1995). Equations of State of Solids for Geophysics and Ceramic Science. New York: Oxford University Press on Demand.

Google Scholar

Angel, R. J., Alvaro, M., and Gonzalez-Platas, J. (2014a). EosFit7c and a Fortran Module (Library) for Equation of State Calculations. Z. Kristallogr Cryst. Mater. 229, 405–419. doi:10.1515/zkri-2013-1711

CrossRef Full Text | Google Scholar

Angel, R. J., Alvaro, M., Miletich, R., and Nestola, F. (2017a). A Simple and Generalised P-T-V EoS for Continuous Phase Transitions, Implemented in EosFit and Applied to Quartz. Contrib. Mineral. Petrol. 172, 29. doi:10.1007/s00410-017-1349-x

CrossRef Full Text | Google Scholar

Angel, R. J., Alvaro, M., Nestola, F., and Mazzucchelli, M. L. (2015). Diamond Thermoelastic Properties and Implications for Determining the Pressure of Formation of Diamond-Inclusion Systems. Russ. Geol. Geophys. 56, 211–220. doi:10.1016/j.rgg.2015.01.014

CrossRef Full Text | Google Scholar

Angel, R. J. (2000). Equations of State. Rev. Mineralogy Geochem. 41, 35–59. doi:10.2138/rmg.2000.41.2

CrossRef Full Text | Google Scholar

Angel, R. J., Mazzucchelli, M. L., Alvaro, M., and Nestola, F. (2017b). EosFit-Pinc: A Simple GUI for Host-Inclusion Elastic Thermobarometry. Am. Mineral. 102, 1957–1960. doi:10.2138/am-2017-6190

CrossRef Full Text | Google Scholar

Angel, R. J., Mazzucchelli, M. L., Alvaro, M., Nimis, P., and Nestola, F. (2014b). Geobarometry from Host-Inclusion Systems: The Role of Elastic Relaxation. Am. Mineral. 99, 2146–2149. doi:10.2138/am-2014-5047

CrossRef Full Text | Google Scholar

Anzolini, C., Nestola, F., Mazzucchelli, M. L., Alvaro, M., Nimis, P., Gianese, A., et al. (2019). Depth of Diamond Formation Obtained from Single Periclase Inclusions. Geology 47, 219–222. doi:10.1130/g45605.1

CrossRef Full Text | Google Scholar

Arimoto, T., Gréaux, S., Irifune, T., Zhou, C., and Higo, Y. (2015). Sound Velocities of Fe3Al2Si3O12 Almandine up to 19 GPa and 1700 K. Phys. Earth Planet. Interiors 246, 1–8. doi:10.1016/j.pepi.2015.06.004

CrossRef Full Text | Google Scholar

Ashley, K. T., Caddick, M. J., Steele-Macinnis, M. J., Bodnar, R. J., and Dragovic, B. (2014). Geothermobarometric History of Subduction Recorded by Quartz Inclusions in Garnet. Geochem. Geophys. Geosyst. 15, 350–360. doi:10.1002/2013gc005106

CrossRef Full Text | Google Scholar

Ashley, K. T., Steele-Macinnis, M., Bodnar, R. J., and Darling, R. S. (2016). Quartz-in-garnet Inclusion Barometry under Fire: Reducing Uncertainty from Model Estimates. Geology 44, 699–702. doi:10.1130/g38211.1

CrossRef Full Text | Google Scholar

Bass, J. D., Sinogeikin, S. V., and Li, B. (2008). Elastic Properties of Minerals: A Key for Understanding the Composition and Temperature of Earth's Interior. Elements 4, 165–170. doi:10.2113/gselements.4.3.165

CrossRef Full Text | Google Scholar

Baxter, E. F., Caddick, M. J., and Ague, J. J. (2013). Garnet: Common Mineral, Uncommonly Useful. Elements 9, 415–419. doi:10.2113/gselements.9.6.415

CrossRef Full Text | Google Scholar

Bayet, L., John, T., Agard, P., Gao, J., and Li, J.-L. (2018). Massive Sediment Accretion at ∼80 Km Depth along the Subduction Interface: Evidence from the Southern Chinese Tianshan. Geology 46, 495–498. doi:10.1130/g40201.1

CrossRef Full Text | Google Scholar

Bebout, G. E. (2007). Metamorphic Chemical Geodynamics of Subduction Zones. Earth Planet. Sci. Lett. 260, 373–393. doi:10.1016/j.epsl.2007.05.050

CrossRef Full Text | Google Scholar

Bonazzi, M., Tumiati, S., Thomas, J. B., Angel, R. J., and Alvaro, M. (2019). Assessment of the Reliability of Elastic Geobarometry with Quartz Inclusions. Lithos 350-351, 105201. doi:10.1016/j.lithos.2019.105201

CrossRef Full Text | Google Scholar

Bosenick, A., Dove, M. T., and Geiger, C. A. (2000). Simulation Studies on the Pyrope-Grossular Garnet Solid Solution. Phys. Chem. Minerals 27, 398–418. doi:10.1007/s002690000088

CrossRef Full Text | Google Scholar

Bosenick, A., Dove, M. T., Heine, V., and Geiger, C. A. (2001). Scaling of Thermodynamic Mixing Properties in Garnet Solid Solutions. Phys. Chem. Minerals 28, 177–187. doi:10.1007/s002690000141

CrossRef Full Text | Google Scholar

Broadwell, K. S., Locatelli, M., Verlaguet, A., Agard, P., and Caddick, M. J. (2019). Transient and Periodic Brittle Deformation of Eclogites during Intermediate-Depth Subduction. Earth Planet. Sci. Lett. 521, 91–102. doi:10.1016/j.epsl.2019.06.008

CrossRef Full Text | Google Scholar

Caddick, M. J., and Kohn, M. J. (2013). Garnet: Witness to the Evolution of Destructive Plate Boundaries. Elements 9, 427–432. doi:10.2113/gselements.9.6.427

CrossRef Full Text | Google Scholar

Chantel, J., Manthilake, G. M., Frost, D. J., Beyer, C., Ballaran, T. B., Jing, Z., et al. (2016). Elastic Wave Velocities in Polycrystalline Mg3Al2Si3O12-Pyrope Garnet to 24 GPa and 1300 K. Am. Mineral. 101, 991–997. doi:10.2138/am-2016-5335

CrossRef Full Text | Google Scholar

Cisneros, M., Ashley, K. T., and Bodnar, R. J. (2020). Evaluation and Application of the Quartz-Inclusions-In-Epidote Mineral Barometer. Am. Mineral. 105, 1140–1151. doi:10.2138/am-2020-7379

CrossRef Full Text | Google Scholar

Cruciani, G., Franceschelli, M., Scodina, M., and Puxeddu, M. (2019). Garnet Zoning in Kyanite-Bearing Eclogite from Golfo Aranci: New Data on the Early progradeP-Tevolution in NE Sardinia, Italy. Geol. J. 54, 190–205. doi:10.1002/gj.3169

CrossRef Full Text | Google Scholar

Dachs, E., Geiger, C. A., and Benisek, A. (2014). Thermodynamic Mixing Properties and Behavior of Grossular-Spessartine, (Ca Mn1−)3Al2Si3O12, Solid Solutions. Geochimica et Cosmochimica Acta 141, 294–302. doi:10.1016/j.gca.2014.06.034

CrossRef Full Text | Google Scholar

De Capitani, C., and Petrakakis, K. (2010). The Computation of Equilibrium Assemblage Diagrams with Theriak/Domino Software. Am. Mineral. 95, 1006–1016. doi:10.2138/am.2010.3354

CrossRef Full Text | Google Scholar

Dera, P., Zhuravlev, K., Prakapenka, V., Rivers, M. L., Finkelstein, G. J., Grubor-Urosevic, O., et al. (2013). High Pressure Single-Crystal Micro X-Ray Diffraction Analysis with GSE_ADA/RSV Software. High Press. Res. 33, 466–484. doi:10.1080/08957959.2013.806504

CrossRef Full Text | Google Scholar

Du, W., Clark, S. M., and Walker, D. (2016). Excess Mixing Volume, Microstrain, and Stability of Pyrope-Grossular Garnets. Am. Mineral. 101, 193–204. doi:10.2138/am-2016-5128

CrossRef Full Text | Google Scholar

Du, W., Clark, S. M., and Walker, D. (2015). Thermo-Compression of Pyrope-Grossular Garnet Solid Solutions: Non-Linear Compositional Dependence. Am. Mineral. 100, 215–222. doi:10.2138/am-2015-4752

CrossRef Full Text | Google Scholar

Enami, M., Nishiyama, T., and Mouri, T. (2007). Laser Raman Microspectrometry of Metamorphic Quartz: A Simple Method for Comparison of Metamorphic Pressures. Am. Mineral. 92, 1303–1315. doi:10.2138/am.2007.2438

CrossRef Full Text | Google Scholar

Fan, D., Fu, S., Yang, J., Tkachev, S. N., Prakapenka, V. B., and Lin, J.-F. (2019a). Elasticity of Single-Crystal Periclase at High Pressure and Temperature: The Effect of Iron on the Elasticity and Seismic Parameters of Ferropericlase in the Lower Mantle. Am. Mineral. 104, 262–275. doi:10.2138/am-2019-6656

CrossRef Full Text | Google Scholar

Fan, D., Kuang, Y., Xu, J., Li, B., Zhou, W., and Xie, H. (2017). Thermoelastic Properties of Grossular-Andradite Solid Solution at High Pressures and Temperatures. Phys. Chem. Minerals 44, 137–147. doi:10.1007/s00269-016-0843-4

CrossRef Full Text | Google Scholar

Fan, D., Li, B., Chen, W., Xu, J., Kuang, Y., Ye, Z., et al. (2018). Research Progress of the Equation of State for Garnet Minerals. Chin. J. High Press Phys. 32, 1–13. doi:10.11858/gywlxb.20170597

CrossRef Full Text | Google Scholar

Fan, D. W., G. Zhou, W., Liu, C. Q., Liu, Y. G., Wan, F., Xing, Y. S., et al. (2009). The Thermal Equation of State of (Fe0.86Mg0.07Mn0.07)3Al2Si3O12 Almandine. Mineral. Mag. 73, 95–102. doi:10.1180/minmag.2009.073.1.95

CrossRef Full Text | Google Scholar

Fan, D., Xu, J., Lu, C., Tkachev, S. N., Li, B., Ye, Z., et al. (2019b). Elasticity of Single-crystal Low Water Content Hydrous Pyrope at High-Pressure and High-Temperature Conditions. Am. Mineral. 104, 1022–1031. doi:10.2138/am-2019-6897

CrossRef Full Text | Google Scholar

Fan, D., Xu, J., Ma, M., Liu, J., and Xie, H. (2015). P-V-T Equation of State of Spessartine-Almandine Solid Solution Measured Using a Diamond Anvil Cell and In Situ Synchrotron X-ray Diffraction. Phys. Chem. Minerals 42, 63–72. doi:10.1007/s00269-014-0700-2

CrossRef Full Text | Google Scholar

Fan, D., Zhou, W., Wei, S., Liu, Y., Ma, M., and Xie, H. (2010). A Simple External Resistance Heating Diamond Anvil Cell and its Application for Synchrotron Radiation X-ray Diffraction. Rev. Scientific Instr. 81, 053903. doi:10.1063/1.3430069

PubMed Abstract | CrossRef Full Text | Google Scholar

Fei, Y., Ricolleau, A., Frank, M., Mibe, K., Shen, G., and Prakapenka, V. (2007). Toward an Internally Consistent Pressure Scale. Proc. Natl. Acad. Sci. 104, 9182–9186. doi:10.1073/pnas.0609013104

PubMed Abstract | CrossRef Full Text | Google Scholar

Gatta, G. D., Merlini, M., Lee, Y., and Poli, S. (2011). Behavior of Epidote at High Pressure and High Temperature: a Powder Diffraction Study up to 10 GPa and 1,200 K. Phys. Chem. Minerals 38, 419–428. doi:10.1007/s00269-010-0415-y

CrossRef Full Text | Google Scholar

Geiger, C. A. (2013). Garnet: A Key Phase in Nature, the Laboratory, and Technology. Elements 9, 447–452. doi:10.2113/gselements.9.6.447

CrossRef Full Text | Google Scholar

Geiger, C., and Rossman, G. (1994). Crystal Field Stabilization Energies of Almandine-Pyrope and Almandine-Spessartine Garnets Determined by FTIR Near Infrared Measurements. Phys. Chem. Minerals 21, 516–525. doi:10.1007/BF00203926

CrossRef Full Text | Google Scholar

Gonzalez, J. P., Thomas, J. B., Baldwin, S. L., and Alvaro, M. (2019). Quartz‐in‐Garnet and Ti‐in‐Quartz Thermobarometry: Methodology and First Application to a Quartzofeldspathic Gneiss from Eastern Papua New Guinea. J. Metamorph. Geol. 37, 1193–1208. doi:10.1111/jmg.12508

CrossRef Full Text | Google Scholar

Gonzalez-Platas, J., Alvaro, M., Nestola, F., and Angel, R. (2016). EosFit7-GUI: A New Graphical User Interface for Equation of State Calculations, Analyses and Teaching. J. Appl. Cryst. 49, 1377–1382. doi:10.1107/S1600576716008050

CrossRef Full Text | Google Scholar

Guiraud, M., and Powell, R. (2006). P-V-T Relationships and Mineral Equilibria in Inclusions in Minerals. Earth Planet. Sci. Lett. 244, 683–694. doi:10.1016/j.epsl.2006.02.021

CrossRef Full Text | Google Scholar

Gwanmesia, G. D., Zhang, J., Darling, K., Kung, J., Li, B., Wang, L., et al. (2006). Elasticity of Polycrystalline Pyrope (Mg3Al2Si3O12) to 9GPa and 1000°C. Phys. Earth Planet. Interiors 155, 179–190. doi:10.1016/j.pepi.2005.10.008

CrossRef Full Text | Google Scholar

Hartwig, J., and Galkin, V. (2021). Heat Capacity, Thermal Expansion, and Elastic Parameters of Pyrope. J. Therm. Anal. Calorim. 144, 71–79. doi:10.1007/s10973-020-09396-2

CrossRef Full Text | Google Scholar

Hazen, R. M., Downs, R. T., Conrad, P. G., Finger, L. W., and Gasparik, T. (1994). Comparative Compressibilities of Majorite-Type Garnets. Phys. Chem. Minerals 21, 344–349. doi:10.1007/BF00202099

CrossRef Full Text | Google Scholar

Helffrich, G., and Connolly, J. A. D. (2009). Physical Contradictions and Remedies Using Simple Polythermal Equations of State. Am. Mineral. 94, 1616–1619. doi:10.2138/am.2009.3262

CrossRef Full Text | Google Scholar

Holland, T. J. B., and Powell, R. (2011). An Improved and Extended Internally Consistent Thermodynamic Dataset for Phases of Petrological Interest, Involving a New Equation of State for Solids. J. Metamorph. Geol. 29, 333–383. doi:10.1111/j.1525-1314.2010.00923.x

CrossRef Full Text | Google Scholar

Hu, Y., Wu, Z., Dera, P. K., and Bina, C. R. (2016). Thermodynamic and Elastic Properties of Pyrope at High Pressure and High Temperature by First-Principles Calculations. J. Geophys. Res. Solid Earth 121, 6462–6476. doi:10.1002/2016JB013026

CrossRef Full Text | Google Scholar

Huang, S., and Chen, J. (2014). Equation of State of Pyrope-Almandine Solid Solution Measured Using a Diamond Anvil Cell and In Situ Synchrotron X-ray Diffraction. Phys. Earth Planet. Interiors 228, 88–91. doi:10.1016/j.pepi.2014.01.014

CrossRef Full Text | Google Scholar

Jamtveit, B., Austrheim, H., and Putnis, A. (2016). Disequilibrium Metamorphism of Stressed Lithosphere. Earth-Science Rev. 154, 1–13. doi:10.1016/j.earscirev.2015.12.002

CrossRef Full Text | Google Scholar

Johnson, T. A., Cottle, J. M., and Larson, K. P. (2021). Delineation of Multiple Metamorphic Events in the Himalayan Kathmandu Complex, Central Nepal. J. Metamorph. Geol. 39 (4), 443–472. doi:10.1111/jmg.12583

CrossRef Full Text | Google Scholar

Kantor, I., Prakapenka, V., Kantor, A., Dera, P., Kurnosov, A., Sinogeikin, S., et al. (2012). BX90: A New Diamond Anvil Cell Design for X-ray Diffraction and Optical Measurements. Rev. Scientific Instr. 83, 125102. doi:10.1063/1.4768541

PubMed Abstract | CrossRef Full Text | Google Scholar

Kohn, M. J. (2014). "Thermoba-Raman-try": Calibration of Spectroscopic Barometers and Thermometers for mineral Inclusions. Earth Planet. Sci. Lett. 388, 187–196. doi:10.1016/j.epsl.2013.11.054

CrossRef Full Text | Google Scholar

Korsakov, A. V., Perraki, M., Zhukov, V. P., De Gussem, K., Vandenabeele, P., and Tomilenko, A. A. (2009). Is Quartz a Potential Indicator of Ultrahigh-Pressure Metamorphism? Laser Raman Spectroscopy of Quartz Inclusions in Ultrahigh-Pressure Garnets. Eur. J. Mineral. 21, 1313–1323. doi:10.1127/0935-1221/2009/0021-2006

CrossRef Full Text | Google Scholar

Kosman, C. W., Kopylova, M. G., Stern, R. A., Hagadorn, J. W., and Hurlbut, J. F. (2016). Cretaceous Mantle of the Congo Craton: Evidence from Mineral and Fluid Inclusions in Kasai Alluvial Diamonds. Lithos 265, 42–56. doi:10.1016/j.lithos.2016.07.004

CrossRef Full Text | Google Scholar

Kuang, Y., Xu, J., Li, B., Ye, Z., Huang, S., Chen, W., et al. (2019). Crystal-Chemical Properties of Synthetic Almandine-Pyrope Solid Solution by X-Ray Single-Crystal Diffraction and Raman Spectroscopy. Crystals 9, 541. doi:10.3390/cryst9100541

CrossRef Full Text | Google Scholar

Li, L., Weidner, D. J., Brodholt, J., Alfè, D., and Price, G. D. (2011). Ab Initio Molecular Dynamic Simulation on the Elasticity of Mg3Al2Si3O12 Pyrope. J. Earth Sci. 22, 169–175. doi:10.1007/s12583-011-0169-6

CrossRef Full Text | Google Scholar

Liu, Q., Hermann, J., Zheng, S., and Zhang, J. (2020). Evidence for UHP Anatexis in the Shuanghe UHP Paragneiss from Inclusions in Clinozoisite, Garnet, and Zircon. J. Metamorph. Geol. 38, 129–155. doi:10.1111/jmg.12515

CrossRef Full Text | Google Scholar

Mazzucchelli, M. L., Burnley, P., Angel, R. J., Morganti, S., Domeneghetti, M. C., Nestola, F., et al. (2018). Elastic Geothermobarometry: Corrections for the Geometry of the Host-Inclusion System. Geology 46, 231–234. doi:10.1130/G39807.1

CrossRef Full Text | Google Scholar

Mazzucchelli, M. L., Reali, A., Morganti, S., Angel, R. J., and Alvaro, M. (2019). Elastic Geobarometry for Anisotropic Inclusions in Cubic Hosts. Lithos 350-351, 105218. doi:10.1016/j.lithos.2019.105218

CrossRef Full Text | Google Scholar

Milani, S., Angel, R. J., Scandolo, L., Mazzucchelli, M. L., Ballaran, T. B., Klemme, S., et al. (2017). Thermo-Elastic Behavior of Grossular Garnet at High Pressures and Temperatures. Am. Mineral. 102, 851–859. doi:10.2138/am-2017-5855

CrossRef Full Text | Google Scholar

Milani, S., Nestola, F., Alvaro, M., Pasqual, D., Mazzucchelli, M. L., Domeneghetti, M. C., et al. (2015). Diamond-garnet Geobarometry: The Role of Garnet Compressibility and Expansivity. Lithos 227, 140–147. doi:10.1016/j.lithos.2015.03.017

CrossRef Full Text | Google Scholar

Moulas, E., Kostopoulos, D., Podladchikov, Y., Chatzitheodoridis, E., Schenker, F. L., Zingerman, K. M., et al. (2020). Calculating Pressure with Elastic Geobarometry: A Comparison of Different Elastic Solutions with Application to a Calc-Silicate Gneiss from the Rhodope Metamorphic Province. Lithos 378-379, 105803. doi:10.1016/j.lithos.2020.105803

CrossRef Full Text | Google Scholar

Murri, M., Mazzucchelli, M. L., Campomenosi, N., Korsakov, A. V., Prencipe, M., Mihailova, B. D., et al. (2018). Raman Elastic Geobarometry for Anisotropic Mineral Inclusions. Am. Mineral. 103, 1869–1872. doi:10.2138/am-2018-6625CCBY

CrossRef Full Text | Google Scholar

Nestola, F., Jung, H., and Taylor, L. A. (2017). Mineral Inclusions in Diamonds May Be Synchronous but Not Syngenetic. Nat. Commun. 8, 14168. doi:10.1038/ncomms14168

PubMed Abstract | CrossRef Full Text | Google Scholar

Nestola, F., Zaffiro, G., Mazzucchelli, M. L., Nimis, P., Andreozzi, G. B., Periotto, B., et al. (2019). Diamond-Inclusion System Recording Old Deep Lithosphere Conditions at Udachnaya (Siberia). Sci. Rep. 9, 1–8. doi:10.1038/s41598-019-48778-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Riches, A. J. V., Ickert, R. B., Pearson, D. G., Stern, R. A., Jackson, S. E., Ishikawa, A., et al. (2016). In Situ Oxygen-Isotope, Major-, and Trace-Element Constraints on the Metasomatic Modification and Crustal Origin of a Diamondiferous Eclogite from Roberts Victor, Kaapvaal Craton. Geochimica et Cosmochimica Acta 174, 345–359. doi:10.1016/j.gca.2015.11.028

CrossRef Full Text | Google Scholar

Rivers, M., Prakapenka, V., Kubo, A., Pullins, C., Holl, C., and Jacobsen, S. (2008). The COMPRES/GSECARS Gas-Loading System for Diamond Anvil Cells at the Advanced Photon Source. High Press. Res. 28, 273–292. doi:10.1080/08957950802333593

CrossRef Full Text | Google Scholar

Robinson, K., Gibbs, G. V., and Ribbe, P. H. (1971). Quadratic Elongation: A Quantitative Measure of Distortion in Coordination Polyhedra. Science 172, 567–570. doi:10.1126/science.172.3983.567

PubMed Abstract | CrossRef Full Text | Google Scholar

Roedder, E., and Bodnar, R. J. (1980). Geologic Pressure Determinations from Fluid Inclusion Studies. Annu. Rev. Earth Planet. Sci. 8, 263–301. doi:10.1146/annurev.ea.08.050180.001403

CrossRef Full Text | Google Scholar

Rosenfeld, J. L., and Chase, A. B. (1961). Pressure and Temperature of Crystallization from Elastic Effects Around Solid Inclusions in Minerals? Am. J. Sci. 259, 519–541. doi:10.2475/ajs.259.7.519

CrossRef Full Text | Google Scholar

Shannon, R. D. (1976). Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. Sect A. 32, 751–767. doi:10.1107/s0567739476001551

CrossRef Full Text | Google Scholar

Sinogeikin, S., Bass, J., Prakapenka, V., Lakshtanov, D., Shen, G., Sanchez-Valle, C., et al. (2006). Brillouin Spectrometer Interfaced with Synchrotron Radiation for Simultaneous X-ray Density and Acoustic Velocity Measurements. Rev. Scientific Instr. 77, 103905. doi:10.1063/1.2360884

CrossRef Full Text | Google Scholar

Spear, F. S., and Wolfe, O. M. (2020). Revaluation of "Equilibrium" P-T Paths from Zoned Garnet in Light of Quartz Inclusion in Garnet (QuiG) Barometry. Lithos 372-373, 105650. doi:10.1016/j.lithos.2020.105650

CrossRef Full Text | Google Scholar

Speziale, S., Duffy, T. S., and Angel, R. J. (2004). Single-Crystal Elasticity of Fayalite to 12 GPa. J. Geophys. Res. 109, 1–15. doi:10.1029/2004jb003162

CrossRef Full Text | Google Scholar

Tajčmanová, L., Manzotti, P., and Alvaro, M. (2021). Under Pressure: High-Pressure Metamorphism in the Alps. Elements 17, 17–22. doi:10.2138/gselements.17.1.17

CrossRef Full Text | Google Scholar

Takahashi, T., and Liu, L.-G. (1970). Compression of Ferromagnesian Garnets and the Effect of Solid Solutions on the Bulk Modulus. J. Geophys. Res. 75, 5757–5766. doi:10.1029/JB075i029p05757

CrossRef Full Text | Google Scholar

Vinet, P., Ferrante, J., Smith, J. R., and Rose, J. H. (1986). A Universal Equation of State for Solids. J. Phys. C: Solid State. Phys. 19, L467–L473. doi:10.1088/0022-3719/19/20/001

CrossRef Full Text | Google Scholar

Vinograd, V. L., Sluiter, M. H. F., Winkler, B., Putnis, A., Hålenius, U., D. Gale, J., et al. (2004). Thermodynamics of Mixing and Ordering in Pyrope - Grossular Solid Solution. Mineral. Mag. 68, 101–121. doi:10.1180/0026461046810174

CrossRef Full Text | Google Scholar

Wang, Y. B., Weidner, D. J., Zhang, J. Z., Gwanrnesia, G. D., and Liebermann, R. C. (1998). Thermal equation of state of garnets along the pyrope-majorite join. Phys. Earth Planet. Interiors 105, 59–71. doi:10.1016/S0031-9201(97)00072-1

CrossRef Full Text | Google Scholar

Wolfe, O. M., and Spear, F. S. (2018). Determining the Amount of Overstepping Required to Nucleate Garnet during Barrovian Regional Metamorphism, Connecticut Valley Synclinorium. J. Metamorph. Geol. 36, 79–94. doi:10.1111/jmg.12284

CrossRef Full Text | Google Scholar

Xu, J., Zhang, D., Dera, P., Zhang, B., and Fan, D. (2017). Experimental Evidence for the Survival of Augite to Transition Zone Depths, and Implications for Subduction Zone Dynamics. Am. Mineral. 102, 1516–1524. doi:10.2138/am-2017-5959

CrossRef Full Text | Google Scholar

Xu, J., Zhang, D., Fan, D., Dera, P. K., Shi, F., and Zhou, W. (2019). Thermoelastic Properties of Eclogitic Garnets and Omphacites: Implications for Deep Subduction of Oceanic Crust and Density Anomalies in the Upper Mantle. Geophys. Res. Lett. 46, 179–188. doi:10.1029/2018gl081170

CrossRef Full Text | Google Scholar

Zhang, H.-F., Zhou, M.-F., Sun, M., and Zhou, X.-H. (2010). The Origin of Mengyin and Fuxian Diamondiferous Kimberlites from the North China Craton: Implication for Palaeozoic Subducted Oceanic Slab-Mantle Interaction. J. Asian Earth Sci. 37, 425–437. doi:10.1016/j.jseaes.2009.10.006

CrossRef Full Text | Google Scholar

Zhang, J., Martinez, I., Guyot, F., and Reeder, R. J. (1998a). Effects of Mg-Fe (Super 2+) Substitution in Calcite-Structure Carbonates; Thermoelastic Properties. Am. Mineral. 83, 280–287. doi:10.2138/am-1998-3-411

CrossRef Full Text | Google Scholar

Zhang, L., Ahsbahs, H., Hafner, S. S., and Kutoglu, A. (1997). Single-Crystal Compression and Crystal Structure of Clinopyroxene up to 10 GPa. Am. Mineral. 82, 245–258. doi:10.2138/am-1997-3-402

CrossRef Full Text | Google Scholar

Zhang, L., Ahsbahs, H., Kutoglu, A., and Geiger, C. A. (1999). Single-Crystal Hydrostatic Compression of Synthetic Pyrope, Almandine, Spessartine, Grossular and Andradite Garnets at High Pressures. Phys. Chem. Minerals 27, 52–58. doi:10.1007/s002690050240

CrossRef Full Text | Google Scholar

Zhang, L., Ahsbahs, H., and Kutoglu, A. (1998b). Hydrostatic Compression and Crystal Structure of Pyrope to 33 GPa. Phys. Chem. Minerals 25, 301–307. doi:10.1007/s002690050118

CrossRef Full Text | Google Scholar

Zhang, Y. (1998). Mechanical and Phase Equilibria in Inclusion–Host Systems. Earth Planet. Sci. Lett. 157 (3-4), 209–222. doi:10.1016/S0012-821X(98)00036-3

CrossRef Full Text | Google Scholar

Zhong, X., Andersen, N. H., Dabrowski, M., and Jamtveit, B. (2019). Zircon and Quartz Inclusions in Garnet Used for Complementary Raman Thermobarometry: Application to the Holsnøy Eclogite, Bergen Arcs, Western Norway. Contrib. Mineral. Petrol. 174, 1–17. doi:10.1007/s00410-019-1584-4

CrossRef Full Text | Google Scholar

Zhong, X., Moulas, E., and Tajčmanová, L. (2020). Post-Entrapment Modification of Residual Inclusion Pressure and its Implications for Raman Elastic Thermobarometry. Solid Earth 11, 223–240. doi:10.5194/se-11-223-2020

CrossRef Full Text | Google Scholar

Zou, Y., Gréaux, S., Irifune, T., Whitaker, M. L., Shinmei, T., and Higo, Y. (2012). Thermal Equation of State of Mg3Al2Si3O12 Pyrope Garnet up to 19 GPa and 1,700 K. Phys. Chem. Minerals 39, 589–598. doi:10.1007/s00269-012-0514-z

CrossRef Full Text | Google Scholar