Stability Satisfied Design and Construction of Excavated Soil Dumps in a Soft Soil Region in China

Dumping is the main disposal method of the excavated soil from underground engineering in China; however, due to a lack of construction experiences and technical standards, landslide disasters often occurred during rapid dumping of excavated soil in soft soil regions. In this paper, geotechnical tests were conducted on the excavated soil from a foundation engineering site in Hangzhou, where the excavated soil would be used to construct a piled mountain. On this basis, a numerical study was carried out to investigate the effects of the design parameters (heap height, slope gradient) and construction parameters (layer thickness, heap speed) on the dump stability and failure mode. The results show that the safety factor of the excavated soil dump decreases with increasing heap height, slope gradient, layer thickness, and heap speed. The potential slide surfaces are toe circle, and compared to layer thickness and heap speed, the heap height and slope gradient have more remarkable influence on the depth and area of potential slide mass. The heap height limit increases with a decrease in slope gradient, and the heap speed limit decreases with an increase in layer thickness. Under the premise of ensuring the slope stability, the optimal design and construction parameters were obtained, i.e., heap height 28 m, slope gradient 1:2.75, layer thickness 1.0 m, and heap speed 0.50 m/day. Compared to the original design scheme, the storage capacity increases by 20.01%, and the construction duration decreases by 30.25% in the optimal design.

1 Introduction

With the rapid development of China’s urbanization, a great amount of construction and demolition waste, including excavated soil, engineering mud, construction residue, demolition waste, and decoration garbage, are produced (Shang et al., 2013; Kataguiri et al., 2019; Sun, 2020). The excavated soil, which accounts for the highest proportion in the five types of wastes, is mainly generated during the excavation of building foundations, metro tunnels, etc. In China, approximately 2 billion tons of excavated soil was generated in 2017 (Zhan et al., 2019). Currently, the main disposal method for excavated soil in China is dumping, which includes the traditional manner of landfilling and the newly developing way of mountain piling. However, due to a lack of construction experiences and technical standards, landslide disasters often occurred during rapid dumping of excavated soil in soft soil regions of China. In 2015, a worldwide concerned disaster occurred in the excavated soil landfill of Guangming New District in Shenzhen, China. During this event, approximately 2.51 × 10⁶ m³ of excavated soil slid out of the landfill site affecting approximately 0.38 km², destroyed 33 buildings, and killed 77 people (Yin et al., 2016; Zhan et al., 2019). In 2009, an artificial mountain piled with excavated soil in Wuxi, China, collapsed when heaping to the height of 44.7 m and resulted in a horizontal displacement of 3.6 m for the mountain toe (Gu et al., 2011). Therefore, appropriate guidelines that satisfied the slope stability are sorely needed for the design and construction of excavated soil dump site.

The design parameters (e.g., heap height, slope gradient) and construction parameters (e.g., layer thickness, heap speed) significantly affect the slope stability of a soft soil dump (Zhang, 2019; Li, 2020). Many researchers found that higher heap height and/or steeper slope gradient resulted in lower safety factor of soft soil slopes (Kjærnsli and Simons, 1962; Lim et al., 2015; Zhang, 2019; Guo et al., 2020). By using the response surface method and the finite element-based software (Plaxis 2D), respectively, Kostić et al. (2016) and Shiferaw (2021) found the stability of clay slopes improved with decreasing heap height and/or slope gradient. Similarly, the stability of peat and clayey deposits on river dykes is significantly affected by the heap height and slope gradient (Rupke et al., 2007). Rapid heap speed can also result in slope failure during construction, such as an open pit mine in Indonesia and the catastrophic landslide in Shenzhen in China in 2015 (Ladd, 1991; Wang and Griffiths, 2019; Zhan et al., 2021). Additionally, layer thickness during dumping stages is an important factor influencing the stability of soft soil dumps, which was associated with the dissipation of pore water pressure (Ladd, 1991; Liu and Zhao, 2009). To the authors’ knowledge, the studies are limited on comprehensively investigating the effects of design and construction parameters on the slope stability of soft soil dumps and then putting forward the stability satisfied design and construction implications.

In this paper, excavated soil was sampled from a foundation engineering site in Hangzhou, China, and was tested for geotechnical properties. On this basis, a numerical model was built to simulate the planned piled mountain by using Plaxis 2D; the effects of design parameters (heap height, slope gradient) and construction parameters (layer thickness, heap speed) on the stability and failure mode of soil slopes were analyzed, and the heap height limit under different slope gradients and the heap speed limit under different layer thicknesses were investigated. Finally, the optimal design parameters to maximize storage capacity and the optimal construction parameters to minimize construction duration were discussed, under the premise of ensuring the slope stability.

2 Materials and Methods

2.1 Geotechnical Properties of Excavated Soil

The excavated soil samples were taken from a foundation engineering site in Hangzhou, a city located in a soft soil region of China. The soil excavated from this foundation engineering would be used to construct a piled mountain in a park in Hangzhou. The geotechnical properties of the soil samples were tested, including water content, natural density, specific density, liquid-plastic limit, particle size distribution, permeability coefficient, consolidation characteristic, and shear strength. All the above tests were conducted according to Chinese standard for geotechnical testing method (MHURD-PRC, 2019).

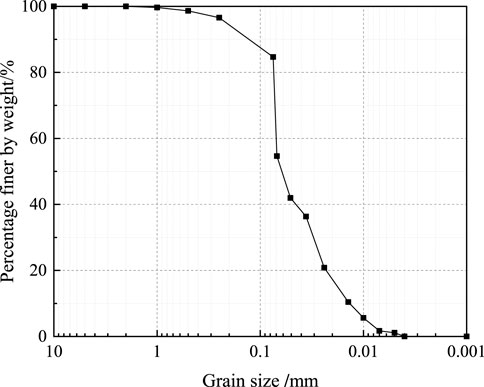
The geotechnical properties of the soil sample are given in Table 1, and the grain size distribution curve is presented in Figure 1. The constrained diameter (d₆₀), median diameter (d₅₀), and effective diameter (d₁₀) of the excavated soil are 0.064, 0.031, and 0.014, respectively, and hence the non-uniformity coefficient and curvature coefficient can be obtained as 4.57 and 1.07. Therefore, this soil belongs to fine-grained soil with poor gradation according to the Chinese specification of soil test (MWR-PRC, 1999). Besides, the liquid limit and plastic limit are 41.80% and 22.72%, respectively, and the corresponding liquidity index and plasticity index are 0.65 and 19.08. Thus, the excavated soil is low liquid limit clay in plastic state according to the Chinese specification of soil test (MWR-PRC, 1999).

TABLE 1

TABLE 1. Geotechnical properties of the excavated soil sample.

FIGURE 1

FIGURE 1. Grain size distribution.

2.2 Numerical Method of the Piled Mountain by Using the Excavated Soil

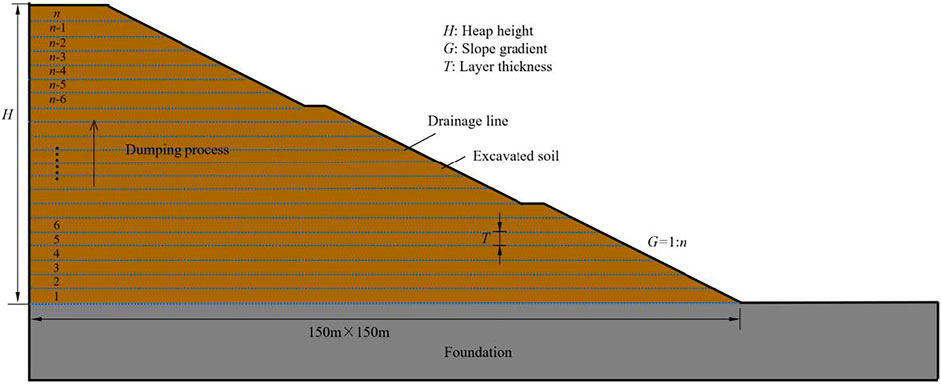
As mentioned above, a pile mountain was planned to be constructed in a park in Hangzhou, China. The maximum permissible length and width at the bottom of the dumpsite were both approximately 300 m, and the originally designed heap height and slope gradient were 20.0 m and 1:3.00, respectively. The original construction parameters were designed as follows: the layer thickness was 1.0 m, and the heap speed was 0.20 m/day. To optimize the original design scheme and therefore to dump more excavated soil and shorten construction duration, the numerical simulation work is carried out.

The finite element program, Plaxis 2D, is used in the numerical simulation in the present study. Plaxis 2D has advanced constitutive models for the simulation of the nonlinear, time-dependent, and anisotropic behavior of soils. Such higher-order elements as quadratic 6-node and 4th-order 15-node triangular element are suitable to model the deformations and stresses in the soils (Wu et al., 2014). Plaxis 2D uses Biot consolidation theory, and the formulae are described in Eqs 1, 2 (Wang and Zheng, 2010; Sun et al., 2015). When undertaking the “consolidation calculation,” the Biot consolidation theory accurately reflects the relationship between pore pressure dissipate and soil skeleton and realizes the coupling in real significance (Wang and Zheng, 2010). Plaxis 2D uses the shear strength reduction technique and the formulae are described in Eqs 3, 4 (Matsui and San, 1992). When undertaking the “safety calculation,” the shear strength reduction technique reduces cohesion and friction angle gradually. The slope instability criterion is generalized plastic strain, or equivalent plastic strain propagates throughout from the toe to the top of the slope (Matsui and San, 1992; Sauffisseau and Ahangar-Asr, 2018).

$\{\begin{array}{l}-G{\nabla }^2{w}_x-\frac{G}{1-2v}\frac{\partial }{\partial x}\left(\frac{\partial w_x}{\partial x}+\frac{\partial w_y}{\partial y}+\frac{\partial w_z}{\partial z}\right)+\frac{\partial u_w}{\partial x}=0\\ -G{\nabla }^2{w}_y-\frac{G}{1-2v}\frac{\partial }{\partial y}\left(\frac{\partial w_x}{\partial x}+\frac{\partial w_y}{\partial y}+\frac{\partial w_z}{\partial z}\right)+\frac{\partial u_w}{\partial y}=0\\ -G{\nabla }^2{w}_z-\frac{G}{1-2v}\frac{\partial }{\partial z}\left(\frac{\partial w_x}{\partial x}+\frac{\partial w_y}{\partial y}+\frac{\partial w_z}{\partial z}\right)+\frac{\partial u_w}{\partial z}=-\gamma \end{array}(1)$

$\frac{\partial }{\partial t}\left(\frac{\partial w_x}{\partial x}+\frac{\partial w_y}{\partial y}+\frac{\partial w_z}{\partial z}\right)-\frac{1}{{\gamma }_w}\left[\frac{\partial }{\partial x}\left(k_x\frac{\partial u_w}{\partial x}\right)+\frac{\partial }{\partial y}\left(k_y\frac{\partial u_w}{\partial y}\right)+\frac{\partial }{\partial z}\left(k_z\left(\frac{\partial u_w}{\partial z}+{\gamma }_w\right)\right)\right]=0,(2)$

where G is the shear modulus; v is the Poisson's ratio; γ is the soil bulk density; u_w is the pore water pressure; w_x, w_y, and w_z are the displacement components in x, y, and z axes, respectively; k_x, k_y, and k_z are the permeability coefficients in x, y, and z axes, respectively; γ_w is the water bulk density.

$c_r=\frac{c}{F_r}(3)$

${\phi }_r=\arctan \frac{\tan \phi }{F_r},(4)$

where c is the cohesion; c_r is the reduced cohesion; F_r is the shear strength reduction ratio; φ is the friction angle; φ_r is the reduced friction angle. The shear strength reduction ratio is equal to the safety factor of the slope reaching instability state.

The numerical model of the piled mountain profile is shown in Figure 2. The geotechnical parameters of the foundation soil were referenced from Yu et al. (2021). The excavated soil was modeled using an elastic-plastic constitutive model with Mohr–Coulomb yield criterion and the non-associated flow rule. The failure surface of the Mohr–Coulomb yield criterion can be described in Eqs 5, 6 (Lee and Bobet, 2014; Li et al., 2005). All of the analyses were performed using meshes made up of 4th order 15-node triangles within each rectangle. The base length and width of slope were both fixed as 150 m in the simulation, being half of the designed values of the dumpsite on account of the model symmetry. The deformation of bottom boundary was fixed, while the deformation of the top boundary was allowed to move freely in both horizontal and vertical directions. In addition, the deformation of the two side boundaries was fixed in the horizontal direction but was allowed to move freely in the vertical direction (Gao et al., 2020). The flow of the left side boundary was closed; however, the flows of the bottom boundary and the top and right side boundaries were open.

$f=\frac{I_1}{3}\sin \phi +\sqrt{J_2}\left[\cos \theta -\frac{1}{\sqrt{3}}\sin \theta \sin \phi \right]-c\cos \phi (5)$

$\theta =\frac{1}{3}{\sin }^{-1}\left[\frac{3\sqrt{3}{J}_3}{2J_2^{3/2}}\right],(6)$

where I₁ = σ_ii is the first stress invariant of the stress tensor σ_ij; J₂ = s_ijs_ji/2 is the second invariant of the deviatoric stress tensor s_ij=(σ_ij−δ_ijσ_kk/3); J₃ = s_ijs_jks_ki/3 is the third invariant of the deviatoric stress tensor s_ij=(σ_ij−δ_ijσ_kk/3); θ is the stress Lode angle.

FIGURE 2

FIGURE 2. Numerical model of the piled mountain profile.

It is stipulated in the Chinese standard for waste dump design of nonferrous metal mines (MHURD-PRC, 2018) that the allowable value of bench height is 10–15 m, and the bench width should not be smaller than 4 m. Therefore, the bench height and the bench width in the numerical model were chosen as 10 m and 4 m, respectively. The designed cases in the present numerical analysis are shown in Table 2. Case 1 was conducted by varying the heap height and slope gradient to investigate the effect of heap height and slope gradient on the soil dump stability and failure mode. In Case 2, the influences of layer thickness and heap speed on the soil dump stability and failure mode were analyzed.

TABLE 2

TABLE 2. Designed cases in the finite-element simulations.

3 Results and Analysis

3.1 Effects of Heap Height and Slope Gradient on Soil Dump Stability

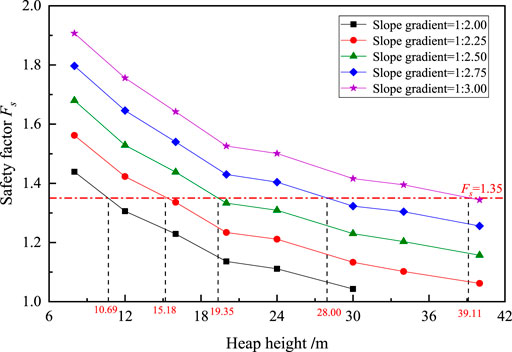
The variation of safety factor (F_s) with heap height (H) under different slope gradients (G) is shown in Figure 3. It is noted that the F_s are lower than 1.00 under the conditions that H ≥ 34 m and G = 1:2.00, which are not included in the analysis of this paper. It can be found that the F_s decreases with an increase in heap height under a given slope gradient. For example, the F_s decreases from 1.439 to 1.043 with heap height increasing from 8 to 30 m when the slope gradient is fixed at 1:2.00. This result is probably associated with the build-up of excess pore-water pressure in the lower soil layer occurring with the increase of heap height, and the excess pore-water pressure is difficult to dissipate, especially for the cohesive soil with high water content. Under this condition, along with the increase of heap height, the shear stress of the lower soil layer increases continuously, while its effective stress and shear strength hardly or slightly increase, resulting in a weakening of slope stability (Zhan et al., 2019). It can be also found that the F_s increases with the slope gradient decreasing under a given heap height. For example, the F_s increases from 1.043 to 1.416 with the slope gradient decreasing from 1:2.00 to 1:3.00 when the heap height is fixed at 30 m. This is because the larger the slope gradient, the greater the sliding force caused by self-weight stress and the smaller the anti-sliding force, which results in a smaller safety factor (Wang and Xu, 2021).

FIGURE 3

FIGURE 3. Variation of safety factor with heap height under different slope gradients.

The potential slide surfaces of the soil dump with different heap heights at a fixed slope gradient of 1:2.50 are shown in Figure 4A. The potential slide surface is determined by connecting the mutation points of the displacement in the slope (Fan et al., 2015), and the results are presented with dotted lines. It is seen that all the simulation cases indicate a typical circular arc failure mode of the soil dump. This potential slide surface is known as toe circle, which often occurs in the clayey and sandy clay soil slopes (Shiferaw, 2021). Taylor (1937) proposed a term, n_d, which is the ratio between the depth from the slope top to the stiff stratum and the depth from the slope top to the slope bottom, to identify the failure mode of the soil dump. When n_d is smaller than 4 and the slope angle is lower than 58°, it is possible to have the failure mode of toe circle (Petterson, 1955; Steward et al., 2011; Salmasi et al., 2019). In addition, the results indicate that the heap height has significant influence on the potential slide surface of soil dump. The circle center of potential slide surface moves up vertically with an increase in heap height, as presented in Figure 4A. The parameters, maximum depth (D) and area (S) of the slide mass, are often used to assess the scale of a potential landslide (Jiang and Yamagami, 2006; Jiang and Yamagami, 2008; Lin and Cao, 2011; Zhang et al., 2015). The parameter, D, is defined as the maximum vertical depth of potential slide mass below slope surface, as shown in Figure 4A. The variations of maximum depth (D) and area (S) of the potential slide mass with heap height (H) at a fixed slope gradient of 1:2.50 are shown in Figure 5. It is found that both D and S increase almost linearly with an increase in heap height, and the fitted lines are D = 0.2955H + 2.4028(H ≥ 8) and S = 34.3060H-280.58(H ≥ 8), respectively. Similar results are also reported in Jiang and Yamagami (2006). It can be also found that the area is positively related to the maximum depth. Therefore, here comes a conclusion: for an excavated soil dump, the higher the heap height, the larger area of the potential slide mass, which means a greater destructive catastrophe.

FIGURE 4

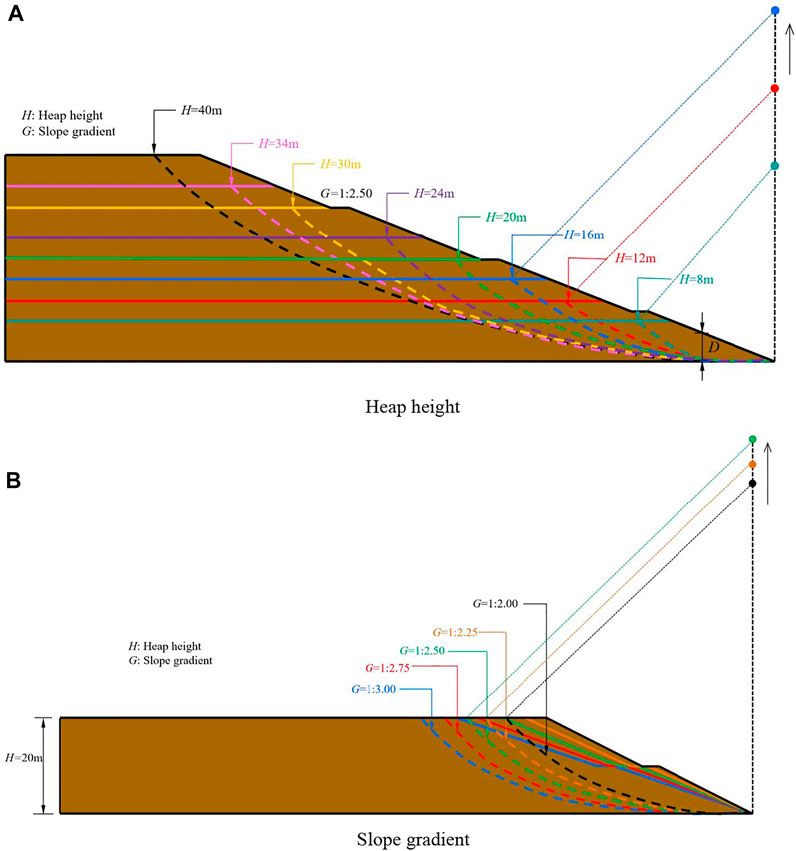
FIGURE 4. Effect of design parameters on the location of potential slide surface. (A) Heap height, (B) slope gradient.

FIGURE 5

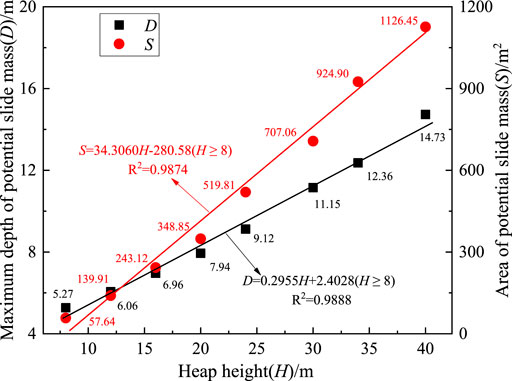
FIGURE 5. Variations of maximum depth and area of potential slide mass with heap height at G = 1:2.50.

The potential slide surfaces of the soil dump with different slope gradients at a fixed heap height of 20 m are shown in Figure 4B. Similar to Figure 4A, the potential slide surface is also toe circle, and the circle center moves up vertically with a decrease in slope gradient, as presented in Figure 4B. To describe the scale of the potential slide mass, a dimensionless parameter, relative maximum depth D/H₀, is adopted, where H₀ is the vertical distance between two end points of the potential sliding surface. The variations of relative maximum depth (D/H₀) and area (S) of the potential slide mass with slope gradient (G) at a fixed heap height of 20 m are shown in Figure 6. It is found that both D/H₀ and S increase almost linearly with decreasing slope gradient, and the fitted lines are D/H₀ = −0.3818G + 0.55 (G ≤ 1:2.00) and S = −733.61G + 647.36 (G ≤ 1:2.00), respectively. Similar results are also reported in Gao W et al. (2016). It can be also found that S is positively related to D/H₀. Therefore, for an excavated soil dump, the steeper the slope gradient, the smaller area of the potential slide mass, which means a smaller destructive catastrophe.

FIGURE 6

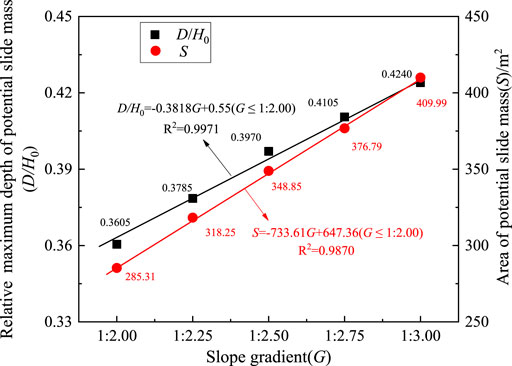
FIGURE 6. Variations of relative maximum depth and area of potential slide mass with slope gradient at H = 20 m.

3.2 Effects of Layer Thickness and Heap Speed on Slope Stability

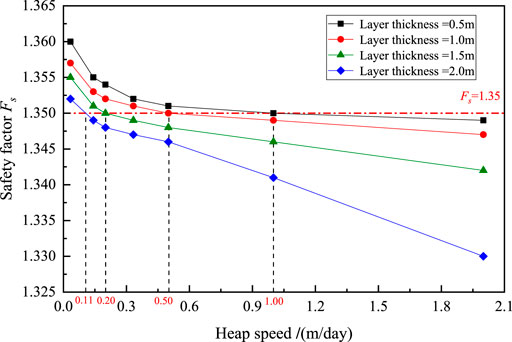
The variation of safety factor (F_s) with heap speed (E) under different layer thicknesses (T) is shown in Figure 7. It is seen that F_s decreases with an increase in heap speed under a given layer thickness. For example, the F_s decreases from 1.352 to 1.330 with heap speed increasing from 0.03 to 2.00 m/day when the layer thickness is 2.0 m. This result might be explained by the increase of consolidation duration due to a decrease in heap speed, and therefore the shear strength slightly increases (Suzuki and Yasuhara, 2007; Park et al., 2014). In addition, it is observed that F_s increases with a decrease in layer thickness under a given heap speed. For example, F_s increases from 1.341 to 1.350 with the layer thickness decreasing from 2.0 to 0.5 m when the heap speed is 1.00 m/day. This result might be related to the drainage path of excavated soil. The drainage distance increases due to an increase in layer thickness, and therefore the consolidation process becomes slower (Zhou et al., 2021). Compared with heap height and slope gradient, the impact of layer thickness and heap speed on safety factor is smaller.

FIGURE 7

FIGURE 7. Variation of safety factor with heap speed under different layer thicknesses.

The potential slide surfaces of the soil dump with different heap speeds at a fixed layer thickness of 2.0 m are shown in Figure 8A. The numerical results indicate that the influence of heap speed on the potential slide surface of soil dump is smaller than that of heap height and slope gradient. Again, the potential slide surface is toe circle, and the circle center slightly moves up with decreasing heap speed. The variations of relative maximum depth (D/H₀) and area (S) of the potential slide mass with heap speed (E) at a fixed layer thickness of 2.0 m are shown in Figure 9. It can be found that D/H₀ decreases logarithmically and S decreases almost linearly with increasing heap speed, and the fitted lines are D/H₀ = −0.03ln(E) + 0.443 (E ≥ 0.033) and S = −38.861E + 747.59 (E ≥ 0.033), respectively. As stated above, the c increases due to a decrease in heap speed, and the D/H₀ increases (Gao Y et al., 2016). It can be also found that S is positively related to D/H₀. Therefore, for an excavated soil dump, the quicker the heap speed, the smaller area of the potential slide mass, which means a smaller destructive catastrophe.

FIGURE 8

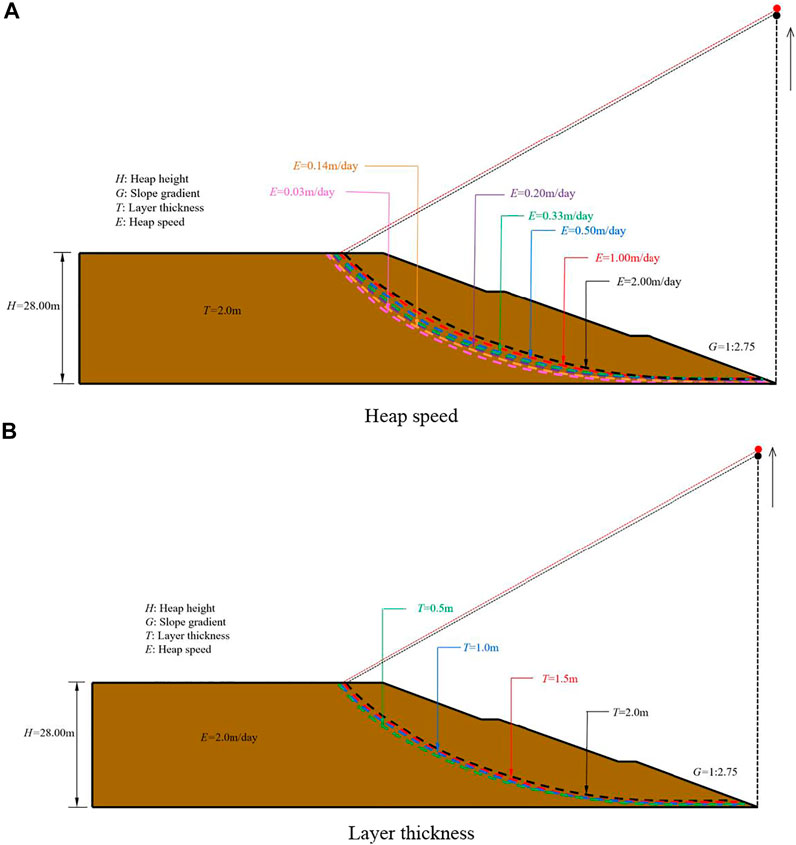
FIGURE 8. Effect of construction parameters on the location of potential slide surface. (A) Heap speed, (B) layer thickness.

FIGURE 9

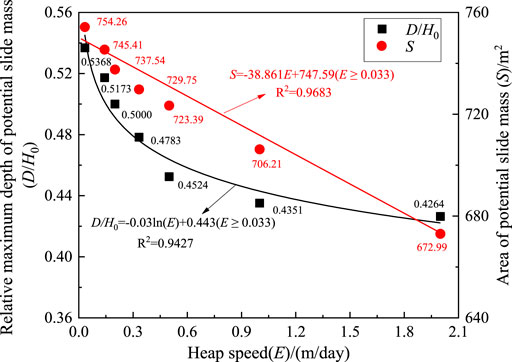
FIGURE 9. Variations of relative maximum depth and area of potential slide mass with heap speed at T = 2.0 m.

The potential slide surfaces of the soil dump with different layer thicknesses at a fixed heap speed of 2.0 m/day are shown in Figure 8B. The numerical results indicate that the influence of layer thickness on the potential slide surface of soil dump is smaller than that of heap height and slope gradient and is similar to that of heap speed. As shown in Figure 8B, the circle center of potential slide surface moves up tardily with decreasing layer thickness. The variations of relative maximum depth (D/H₀) and area (S) of the potential slide mass with layer thickness (T) at a fixed heap speed of 2.0 m/day are shown in Figure 10. It can be found that both D/H₀ and S decrease almost linearly with increasing layer thickness, and the fitted lines are D/H₀ = −0.0409T + 0.5068 (T ≥ 0.5) and S = −20.15T + 713.63 (T ≥ 0.5). The drainage distance decreases due to a decrease in layer thickness, and the c increases as well as the D/H₀ (Gao W et al., 2016; Zhou et al., 2021). Similar to Figure 9, it can be found that S is positively related to D/H₀. Therefore, for an excavated soil dump, the thicker the layer thickness, the smaller area of the potential slide mass, which means a smaller destructive catastrophe.

FIGURE 10

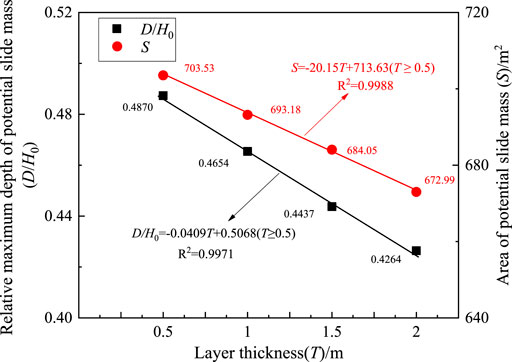
FIGURE 10. Variations of relative maximum depth and area of potential slide mass with layer thickness at E = 2.0 m/day.

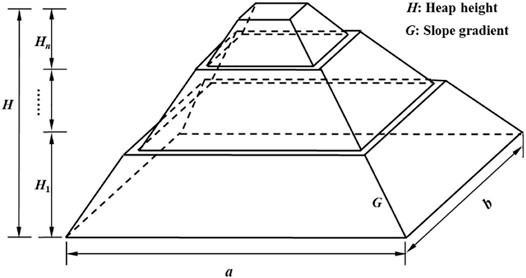
4 Stability Satisfied Design and Construction of the Excavated Soil Dump

For the sake of simplification to illustrate the spatiality of the piled mountain process, the mountain with a square flat bottom surface is generally utilized for dumping, as shown in Figure 11. The storage capacity of the piled mountain can be calculated by Eq. 7. As mentioned in section 2.2, the originally designed heap height and slope gradient are 20.0 m and 1:3.00, respectively. Therefore, the storage capacity of excavated soil can be calculated as 1,143.04 × 103 m³. The originally designed layer thickness and heap speed are 1.0 and 0.20 m/day, respectively. Therefore, the total construction duration of piled mountain is 119 days, under the assumption that the construction time of each drainage line is 1.0 day.

$V={\displaystyle \sum _{j=1}^n\frac{1}{3}}{H}_j\left(S_j+S_{j+1}+\sqrt{S_j{S}_{j+1}}\right),(7)$

where n is the number of the bench; H_j is the height with regard to the nth bench; S_j and S_j+1 are the lower and upper areas of the nth bench, respectively.

FIGURE 11

FIGURE 11. Calculation model of storage capacity of piled mountain.

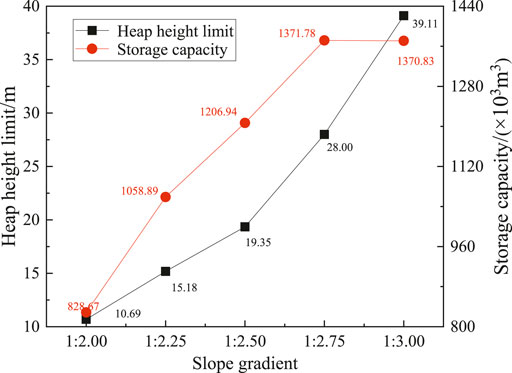
According to the Chinese technical code for building slope engineering (MHURD-PRC, 2013), the F_s of slope stability in this planned piled mountain project should not be smaller than 1.35. On this account, the heap height limit (H_s) of the soil dump can be determined from Figure 3 when F_s reaches 1.35. Figure 12 shows the H_s of the soil dump under different slope gradients (G), together with the slope stability satisfied capacity storage calculated by Eq. 8. It can be seen that the H_s are 10.69, 15.18, 19.35, 28.00, and 39.11 m when slope gradients are 1:2.00, 1:2.25, 1:2.50, 1:2.75, and 1:3.00, respectively. The results show that the H_s increases with a decrease in slope gradient. Similar results were also reported in Zhan et al. (2021) in the completely decomposed granite dump with an initial water content of 23%, and the H_s is 13.73 m when the slope gradient is 1:2.00. It is noted that the H_s of that completely decomposed granite dump is larger than that of the present excavated soil dump at a given slope gradient, which might be attributed to the greater cohesion and friction angle of the completely decomposed granite. For the storage capacity, it increases at first and then slightly decreases with the decreasing slope gradient. And the maximum value of storage capacity is achieved as 1,371.78 × 103 m³ when H_s = 28.00 m and G = 1:2.75. It is common knowledge that the storage capacity increases with the increase of heap height or/and slope gradient. However, under the premise of ensuring the slope stability, increasing the slope gradient will cause a decrease in the heap height limit, resulting in an increase or decrease of storage capacity. Hence, there exists a maximum value of storage capacity, which corresponds to the optimal design of heap height and slope gradient. Compared to the original design scheme, the storage capacity of optimal design scheme increases by 20.01%.

FIGURE 12

FIGURE 12. Variations of heap height limit and storage capacity with slope gradient.

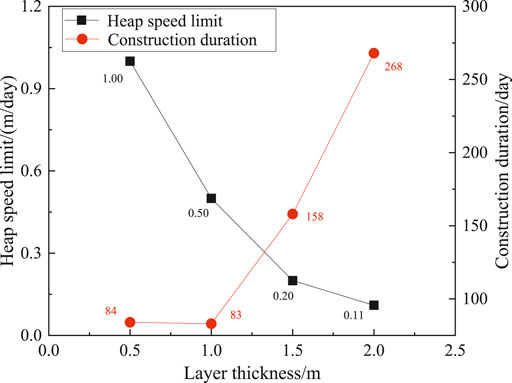
Under the optimal design of heap height and slope gradient, the heap speed limit (E_s) under different layer thicknesses (T) is determined from Figure 7 when F_s of the soil dump reaches 1.35, and the corresponding construction duration can be obtained, as shown in Figure 13. It is observed that the E_s are 1.00, 0.50, 0.20, and 0.11 m/day when the layer thicknesses are 0.5, 1.0, 1.5, and 2.0 m, respectively. The results show that E_s decreases with an increase in layer thickness. It is also observed that the construction duration decreases slightly at first and then increases with the increasing layer thickness. And the minimum value of construction duration is 83 days under the conditions of T = 1.00 m and E_s = 0.50 m/day. It is known that the construction duration decreases with the increase of layer thickness or/and heap speed. However, under the premise of ensuring the slope stability, increasing the layer thickness will cause a decrease in the heap speed limit, resulting in an increase or decrease of construction duration. Hence, there exists a minimum value of construction duration, which corresponds to the optimal construction of layer thickness and heap speed. Compared to the original construction scheme, the construction duration of the optimal construction scheme decreases by 30.25%.

FIGURE 13

FIGURE 13. Variations of heap speed limit and construction duration with layer thickness.

5 Conclusion

This paper conducted numerical analyses on the effects of the design parameters (e.g., heap height, slope gradient) and construction parameters (e.g., layer thickness, heap speed) on the stability and failure mode of excavated soil dumps. The heap height limit under different slope gradients and the heap speed limit under different layer thicknesses in the excavated soil dump were investigated. The optimal design parameters to maximize storage capacity and the optimal construction parameters to minimize construction duration were discussed, under the premise of ensuring the slope stability. The following conclusions and suggestions are drawn:

(1) The safety factor of the excavated soil dump decreases with increasing heap height and slope gradient, and it also decreases with increases in the layer thickness and heap speed.

(2) The potential slide surface of the excavated soil dump is typical toe circle, and its shape is significantly influenced by the heap height and slope gradient. The area of the potential slide mass increases approximately linearly with increasing heap height and with decreasing slope gradient, heap speed, and layer thickness.

(3) The heap height limit increases from 10.69 to 39.11 m when the slope gradient decreases from 1:2.00 to 1:3.00. The heap speed limit decreases from 1.00 to 0.11 m/day when the layer thickness increases from 0.5 to 2.0 m.

(4) Under the premise of ensuring the slope stability, the optimal design and construction parameters of the soil dump is obtained as heap height 28.00 m, slope gradient 1:2.75, layer thickness 1.00 m, and heap speed 0.50 m/day. In the optimal design, the storage capacity increases by 20.01%, and the construction duration decreases by 30.25%, when compared to the original design scheme.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

Writing and analysis: J-NW, S-ZL, and L-NW; review and editing: HX and L-TZ. All authors have read and agreed to the published version of the manuscript.

Funding

This work has been supported by the National Natural Science Foundation of China (Grant No. 42172309), the Natural Science Foundation of Zhejiang Province (Grant No. LY21E08002), and the Science Technology Department of Zhejiang Province (Grant No. 2019C03107).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Fan, W., Cao, P., Zhang, K., Li, K., and Chen, C. (2015). Stability Assessment and Optimization Design of lakeside Open-Pit Slope Considering Fluid-Solid Coupling Effect. Math. Probl. Eng. 2015, 1–11. doi:10.1155/2015/691826

CrossRef Full Text | Google Scholar

Gao, J. J., Xu, H., Qian, J. W., Gong, Y. F., Zhan, L. T., and Chen, P. (2020). Settlement Behavior of Soft Subgrade Reinforced by Geogrid-Encased Stone Column and Geocell-Embedded Sand Cushion: A Numerical Analysis. Adv. Civil Eng. 2020, 1–11. doi:10.1155/2020/8874520

CrossRef Full Text | Google Scholar

Gao, W., Wang, X., Dai, S., and Chen, D. (2016). Numerical Study on Stability of Rock Slope Based on Energy Method. Adv. Mater. Sci. Eng. 2016 (20), 1–10. doi:10.1155/2016/2030238

CrossRef Full Text | Google Scholar

Gao, Y. F., Wu, D., Zhang, F., Qin, H. Y., and Zhu, D. S. (2016). Effects of Nonlinear Strength Parameters on Stability of 3D Soil Slopes. J. Cent. South. Univ. 23 (9), 2354–2363. doi:10.1007/s11771-016-3294-7

CrossRef Full Text | Google Scholar

Gu, F. X., Yan, C. H., Wang, B., Xu, B. T., and Yan, H. R. (2011). Mechanism Analysis of Heap hill Collapse in Urban Area of Southern Jiangsu. J. Eng. Geology. 19 (5), 697–702. (in Chinese).

Google Scholar

Guo, S., Li, N., Liu, W., Ma, Z., Liu, N., and Lv, G. (2020). Influence of Both Soil Properties and Geometric Parameters on Failure Mechanisms and Stability of Two-Layer Undrained Slopes. Adv. Mater. Sci. Eng. 2020 (3), 1–13. doi:10.1155/2020/4253026

CrossRef Full Text | Google Scholar

Jiang, J. C., and Yamagami, T. (2008). A New Back Analysis of Strength Parameters from Single Slips. Comput. Geotechnics 35 (2), 286–291. doi:10.1016/j.compgeo.2007.09.004

CrossRef Full Text | Google Scholar

Jiang, J. C., and Yamagami, T. (2006). Charts for Estimating Strength Parameters from Slips in Homogeneous Slopes. Comput. Geotech. 33 (6-7), 294–304. doi:10.1016/j.compgeo.2006.07.005

CrossRef Full Text | Google Scholar

Kataguiri, K., Boscov, M. E. G., Teixeira, C. E., and Angulo, S. C. (2019). Characterization Flowchart for Assessing the Potential Reuse of Excavation Soils in Sao Paulo City. J. Clean. Prod. 240, 118–215. doi:10.1016/j.jclepro.2019.118215

CrossRef Full Text | Google Scholar

Kjærnsli, B., and Simons, N. (1962). Stability Investigations of the north Bank of the Drammen River. Geotechnique 12 (2), 147–167.

Google Scholar

Kostić, S., Vasović, N., and Jevremović, D. (2016). Stability of Earth Slopes under the Effect of Main Environmental Properties of Weathered clay–marl Deposits in Belgrade (Serbia). Environ. Earth Sci. 75 (6), 1–10 doi:10.1007/s12665-016-5339-5

CrossRef Full Text | Google Scholar

Ladd, C. C. (1991). Stability Evaluation during Staged Construction. J. Geotechnical Eng. 117 (4), 540–615. doi:10.1061/(asce)0733-9410(1991)117:4(540)

CrossRef Full Text | Google Scholar

Lee, Y.-K., and Bobet, A. (2014). Instantaneous Friction Angle and Cohesion of 2-D and 3-D Hoek-Brown Rock Failure Criteria in Terms of Stress Invariants. Rock Mech. Rock Eng. 47 (2), 371–385. doi:10.1007/s00603-013-0423-6

CrossRef Full Text | Google Scholar

Li, W. (2020). Centrifuge Modeling of Pore Pressure Generation and Dissipation in the Rapidly-Filled Waste Soils. Hangzhou, Zhejiang, China: Zhejiang University. (in Chinese).

Google Scholar

Li, Y. C., Ling, D. S., and Chen, Y. M. (2005). Mohr–Coulomb Yield Criterion for Cosserat Continua and its Applications. J. Zhejiang Univ. (Engineering Science) 39 (2), 253–258.

Google Scholar

Lim, K., Li, A. J., and Lyamin, A. V. (2015). Three-dimensional Slope Stability Assessment of Two-Layered Undrained clay. Comput. Geotechnics 70, 1–17. doi:10.1016/j.compgeo.2015.07.011

CrossRef Full Text | Google Scholar

Lin, H., and Cao, P. (2011). Potential Slip Surfaces of Slope with Strength Parameters. Amr 243-249, 3315–3318. doi:10.4028/www.scientific.net/amr.243-249.3315

CrossRef Full Text | Google Scholar

Liu, H., Xiang, T., and Zhao, R. (2009). Research on Non-linear Structural Behaviors of Prestressed concrete Beams Made of High Strength and Steel Fiber Reinforced Concretes. Construction Building Mater. 23, 85–95. (in Chinese). doi:10.1016/j.conbuildmat.2008.01.016

CrossRef Full Text | Google Scholar

Matsui, T., and San, K.-C. (1992). Finite Element Slope Stability Analysis by Shear Strength Reduction Technique. Soils and Foundations 32 (1), 59–70. doi:10.3208/sandf1972.32.59

CrossRef Full Text | Google Scholar

Ministry of Housing and Urban Rural Development of the People′s Republic of China (MHURD-PRC) (2019). “Chinese Standard for Geotechnical Testing Method (GB/T 50123-2019)”. Beijing, China: China Planning Press.

Google Scholar

Ministry of Housing and Urban Rural Development of the People′s Republic of China (MHURD-PRC) (2018). “Chinese Standard for Waste Dump Design of Nonferrous Metal Mines (GB 50421-2018)”. Beijing, China: China Planning Press.

Google Scholar

Ministry of Housing and Urban Rural Development of the People′s Republic of China (MHURD-PRC) (2013). “Chinese Technical Code for Building Slope Engineering (GB 50330-2013)”. Beijing, China: China Architecture & Building Press.

Google Scholar

Ministry of Water Resources of the People's Republic of China (MWR-PRC) (1999). “Chinese Specification of Soil Test (SL 237-1999)”. Beijing, China: China Water & Power Press.

Google Scholar

Park, Y. M., Um, I. J., Miura, N., and Baek, S. C. (2014). A Change of Undrain Shear Strength of Soft Ground during Consolidation Process. Amm 513-517, 269–272. doi:10.4028/www.scientific.net/amm.513-517.269

CrossRef Full Text | Google Scholar

Petterson, K. E. (1955). The Early History of Circular Sliding Surfaces. Géotechnique 5 (4), 275–296. doi:10.1680/geot.1955.5.4.275

CrossRef Full Text | Google Scholar

Rupke, J., Huisman, M., and Kruse, H. M. G. (2007). Stability of Man-Made Slopes. Eng. Geology. 91 (1), 16–24. doi:10.1016/j.enggeo.2006.12.009

CrossRef Full Text | Google Scholar

Salmasi, F., Pradhan, B., and Nourani, B. (2019). Prediction of the Sliding Type and Critical Factor of Safety in Homogeneous Finite Slopes. Appl. Water Sci. 9 (7), 1–11. doi:10.1007/s13201-019-1038-1

CrossRef Full Text | Google Scholar

Sauffisseau, R., and Ahangar-Asr, A. (2018). Stratified Slopes, Numerical and Empirical Stability Analysis. Proc. Inst. Civil Eng. - Eng. Comput. Mech. 171 (4), 174–185. doi:10.1680/jencm.18.00017

CrossRef Full Text | Google Scholar

Shang, C., Zhu, Y., and Zhang, Z. (2013). A Glance at the World. Waste Manage 33, 489–492.

Google Scholar

Shiferaw, H. M. (2021). Study on the Influence of Slope Height and Angle on the Factor of Safety and Shape of Failure of Slopes Based on Strength Reduction Method of Analysis. Beni-suef Univ. J. Basic Appl. Sci. 10 (1), 1–11. doi:10.1186/s43088-021-00115-w

CrossRef Full Text | Google Scholar

Steward, T., Sivakugan, N., Shukla, S. K., and Das, B. M. (2011). Taylor's Slope Stability Charts Revisited. Int. J. Geomech. 11 (4), 348–352. doi:10.1061/(asce)gm.1943-5622.0000093

CrossRef Full Text | Google Scholar

Sun, M. Q., Wang, Q., Niu, C. C., Yan, H., Dong, J. Q., Xiao, G. P., et al. (2015). Rheological Consolidation Theory of Soft Soils with Secondary Consolidation Effect. J. Eng. Geology. 23 (04), 675–680. doi:10.13544/j.cnki.jeg.2015.04.013 (in Chinese).

CrossRef Full Text | Google Scholar

Sun, Q. Q. (2020). Estimation of Undrained Shear Strength of High Water Content Waste Soils during Rapid Landfilling and Stability Analysis. Hangzhou, Zhejiang, China: Zhejiang University. (in Chinese).

Google Scholar

Suzuki, K., and Yasuhara, K. (2007). Increase in Undrained Shear Strength of clay with Respect to Rate of Consolidation. Soils and Foundations 47 (2), 303–318. doi:10.3208/sandf.47.303

CrossRef Full Text | Google Scholar

Taylor, D. W. (1937). Stability of Earth Slopes. J. Boston Soc. Civil Eng. 24, 197–246.

Google Scholar

Wang, J. N., and Xu, H. (2021). Study on the Comprehensive Performance Evaluation of the Capillary Barrier Soil Cover System in Humid Climate Zone Built with Construction Wastes. J. Zhejiang Sci-Tech Univ. 45 (1), 136–148. (in Chinese). doi:10.3696/j.issn.1673-3851(n).2021.01.017

CrossRef Full Text | Google Scholar

Wang, S. F., and Zheng, M. X. (2010). Application of Biot Consolidation Theory to Analyze Land Subsidence. Amr 168-170, 2615–2618. doi:10.4028/www.scientific.net/amr.168-170.2615

CrossRef Full Text | Google Scholar

Wang, W., and Griffiths, D. V. (2019). Case Study of Slope Failure during Construction of an Open Pit Mine in Indonesia. Can. Geotech. J. 56 (5), 636–648. doi:10.1139/cgj-2017-0662

CrossRef Full Text | Google Scholar

Wu, J.-j., Cheng, Q.-g., Liang, X., and Cao, J.-L. (2014). Stability Analysis of a High Loess Slope Reinforced by the Combination System of Soil Nails and Stabilization Piles. Front. Struct. Civ. Eng. 8 (3), 252–259. doi:10.1007/s11709-014-0260-z

CrossRef Full Text | Google Scholar

Yin, Y., Li, B., Wang, W., Zhan, L., Xue, Q., Gao, Y., et al. (2016). Mechanism of the December 2015 Catastrophic Landslide at the Shenzhen Landfill and Controlling Geotechnical Risks of Urbanization. Engineering 2 (2), 230–249. doi:10.1016/j.eng.2016.02.005

CrossRef Full Text | Google Scholar

Yu, J. l., Zhou, J. J., Gong, X. N., Xu, R. Q., Li, J. Y., and Xu, S. D. (2021). Centrifuge Study on Behavior of Rigid Pile Composite Foundation under Embankment in Soft Soil. Acta Geotech. 16 (6), 1909–1921. doi:10.1007/s11440-020-01109-1

CrossRef Full Text | Google Scholar

Zhan, L. T., Guo, X. G., Sun, Q. Q., Chen, Y. M., and Chen, Z. Y. (2021). The 2015 Shenzhen Catastrophic Landslide in a Construction Waste Dump: Analyses of Undrained Strength and Slope Stability. Acta Geotech. 16 (4), 1247–1263. doi:10.1007/s11440-020-01083-8

CrossRef Full Text | Google Scholar

Zhan, L. T., Zhang, Z., Chen, Y., Chen, R., Zhang, S., Liu, J., et al. (2019). The 2015 Shenzhen Catastrophic Landslide in a Construction Waste Dump: Reconstitution of Dump Structure and Failure Mechanisms via Geotechnical Investigations. Eng. Geol. 238, 15–26. doi:10.1016/j.enggeo.2018.02.019

CrossRef Full Text | Google Scholar

Zhang, F., Chen, D. D., and Shen, G. J. (2015). The Numerical Simulation of Settlement and Stability of Slope of Surcharged Deep-Soft Soil. Sci. Tech. Innovation Herald 12 (31), 60–64+66. (in Chinese).

Google Scholar

Zhang, S. H. (2019). Stability Monitoring and Analysis of Artificial Filling Mountain. Zhenjiang, Jiangsu, China: Jiangsu University. (in Chinese).

Google Scholar

Zhou, C. Y., Yu, L., Huang, Z. R., Liu, Z., and Zhang, L. H. (2021). Analysis of Microstructure and Spatially Dependent Permeability of Soft Soil during Consolidation Deformation. Soils Found. 61 (3), 708–733. doi:10.1016/j.sandf.2021.02.004

CrossRef Full Text | Google Scholar