Disturbance and Control of National Strategic Gas Storage Induced by Adjacent Tunnel Blasting

Underground gas storage are often subject to external dynamic loads, blast vibrations, and seismic disturbances, since they function as backup areas for the strategic national energy reserve, supply and demand dispatch, and gas and energy storage. Currently, the research on dynamic response characteristics, dynamic stability, and disturbance control of underground gas storages under dynamic loads is still incomplete and of great practical importance to ensure national strategic security. Therefore, this paper takes the blasting project of the Sansheng tunnel, which passes through the national strategic gas storage reservoir, as the engineering background. Based on the geological conditions and rock characteristics, the dynamic response characteristics of the rock surrounding the tunnel and gas storage are studied using the finite element method. The peak vibration velocity distribution of the surrounding rocks at different blasting source distances is analyzed and compared with the theoretical formula. Subsequently, an asymmetric uncoupled blasting vibration control technique is proposed and used for field blasting. The results show that the numerical results are consistent with the theoretical formula. The blasting vibration velocity decreases exponentially with an increase in the blasting source distance. Overall, the proposed technique significantly decreases the average peak vibration velocity by 22.64% compared to the original vibration velocity.

Introduction

The current international situation is complex and volatile since the primary energy-producing regions are being affected by external disturbances and internal instability. Their energy production via fossil fuels such as oil and natural gas has been greatly restricted, causing a significant rise in international crude oil prices and natural gas prices. Some of the major energy-demanding countries, including China, rely mainly on imports for their energy supply. Therefore, there is great uncertainty surrounding the energy security situation of energy-demanding countries due to the impact of the above-mentioned changes in the energy pattern. In response to this situation, several countries are also actively developing strategic energy reserves (Lee and Lim, 2010; Liu et al., 2015). Because of their excellent confinement safety, cost-effectiveness, and stability, underground gas storages (Xiong et al., 2021) have received widespread attention as national energy reserves that can be used for nuclear waste disposal (Li et al., 2014; Mahlia et al., 2014). currently, there are three main types of underground energy reservoirs: 1) underground salt cavern gas reservoirs (Deyi et al., 2016; Fan et al., 2019; Fan et al., 2020; Peng et al., 2020; Li et al., 2021) with crystalline structures (Jiang et al., 2021), high denseness (Kang et al., 2021), high ductility (strain can reach almost 30–40%) (Liu et al., 2020a), low permeability (<10⁻²⁰m²) (Liu et al., 2020b), ultra-low porosity (<1%) and self-healing characteristics (Urai et al., 1986), which comprise salt rock as the constitutive medium; 2) depleted oil and gas reservoirs formed by the transformation of non-operational wells (Wang et al., 2021); 3) underground water-sealed gas/oil reservoirs wherein oil and liquid gas are sealed in large underground caverns that have been excavated (Chung et al., 2009; Lee and Lim, 2010).

The strategic value of underground gas storages is self-evident; therefore, their stability, tightness, ability to resist external loads, and operational reliability are topical issues requiring attention for the current strategic security of the country and the needs of the community. In particular, there is a need to investigate the impact of other power construction projects around the gas storages, such as tunnels, underground chambers, slopes, pits, tunnels, and underground pipelines (Liu et al., 2020; Leng et al., 2021; Liu et al., 2021; Yiwei et al., 2021). These projects are constructed by drilling and blasting methods, and blasting vibration waves will inevitably be generated during the drilling and blasting construction process, and the unstable loading and unloading effect of blast vibration waves will also greatly weaken the stability and reliability of underground gas storages (Fan et al., 2021). Many scholars have conducted detailed studies on the effects of blast vibration on adjacent existing structures, and analyzed the disturbance response characteristics of structures under the excitation of external dynamic loads (Verma et al., 2017; Zhang et al., 2017; Wu et al., 2019; Dai et al., 2020) and internal blast loads (Lu et al., 2011; Song et al., 2019; Huang et al., 2020). Meanwhile, the basic theories of the finite element approach, discrete element method and blast impact dynamics mechanisms have also been used to systematically investigated the factors (Qiu et al., 2020) affecting blast vibration velocity and vibration principal frequency distribution, such as blast source location, blast source distance, burial depth, surrounding rocks characteristics and in-situ stress level (Chen et al., 2016; Li et al., 2018a; Xia et al., 2018; Zhao et al., 2020). Certain scholars have analyzed the blasting capacity and seismic design of different structures (Zhao et al., 2016; Yang et al., 2018; Ma et al., 2021). Among them, Li et al. (2018b) studied the blasting cracking mechanism associated with the lining structure of a gas-bearing tunnel and evaluated the cracking degree of the lining structure. Mandal et al. (2020) focused on analyzing the blasting response modes and blasting limit capacity of tunnels with three different cross-section shapes. Sadique et al. (2021) compared the acceleration, pressure, strain energy, lining axial force, deformation and damage patterns of the overall tunnel structure after blasting, and subsequently explored the blasting resistance of three rock types.

Thus far, researches have generally elucidated the dynamic response of underground energy storage structures by using the finite element method, blast stress wave theory, maximum tensile strength theory, impact dynamics and blasting safety specifications to analyze the peak vibration velocity distribution and primary frequency distribution of the disturbed structure, and focusing on blast vibration control and safety protection. To evaluate the reservoir stability, Aliyuda and Lingzhong (2021) used data-driven technology to establish a dynamic evaluation model that can reflect the pressure changes of underground oil and gas reservoirs in real-time to understand the pore pressure changes during the gas injection and extraction processes. Zhuang et al. (2017) combined the micro-seismic method and engineering geological analysis to study the influence mechanism of unloading disturbance on the energy release law and determine the stability of groundwater sealed oil storage caverns.

In summary, most existing studies have focused on the dynamic blasting behavior of tunnels, mine tunnels and their internal lining structures. However, there have been insufficient reports on the dynamic response of existing underground gas storage reservoirs under adjacent blasting loads, and corresponding studies have concentrated on the analysis of salt cavern gas storage reservoirs and underground water-sealed gas storage reservoirs. Furthermore, existing research on gas storage reservoirs has focused more on the structure stability evaluation and static characteristics of the surrounding rock masses. Meanwhile, little research has been conducted on the dynamic vibration characteristics associated with the surrounding rock of gas storage reservoirs. In this paper, the Sansheng tunnel, which passes through the national strategic gas storage reservoir, as the engineering research background. The propagation law of explosive-induced blast vibration waves at the tunnel palm surface is calculated using ANSYS/LS-DYNA software, and the three-dimensional (3D) vibration velocity distribution characteristics and vibration attenuation law of the surrounding rock mass between the tunnel and the gas storage are analyzed. The vibration velocity at each point is compared with the theoretical calculated value and field measured data. In addition, to effectively ensure the safe operation of the gas storage and prevent gas leakage, this study proposes an asymmetric uncoupled charging technology, which reduces the vibration intensity of the rock near the wellbore of the gas storage reservoir by decreasing the blasting input energy of the rock mass.

Finite Element Modelling of the Tunnel-Gas Storage Reservoir

Overview of Sansheng Tunnel Project

Sansheng tunnel is a part of the expressway project from Changshou to Hechuan in Chongqing, with a design speed of 80 km/h. The tunnel is 3,802 m and 3,830 m long from the left and right entrance, respectively, with a maximum burial depth of approximately 425 m and design elevation of 432–442 m. The tunnel passes through the Longwangdong anticline and is located on the eastern part of the Huaying Mountain Range, where the topography and geological structure are closely related to the surrounding rock lithology. The comprehensive grades of the surrounding rock in the tunnel site area are III, IV, and V, and the surrounding rock lithology is mainly sandstone, shale and sandstone sandwich shale.

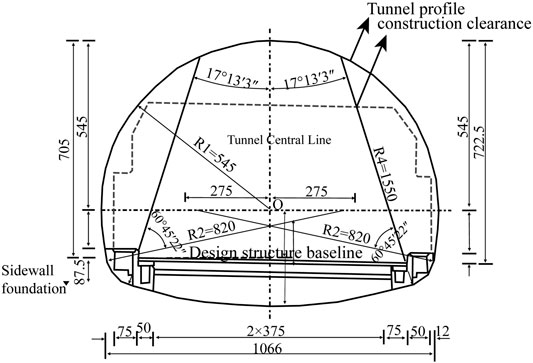
The inner profile of the main tunnel lining is determined according to the requirements of the tunnel construction limits and the space required for cable ditches, drainage ditches, tunnel ventilation, electromechanical facilities, etc. The inner profile of the tunnel is a tri-centric circular curved sidewall structure with an arch height of 7.05 m and an upper semicircle radius of 5.45 m; it has a headroom of 64.28 m² and a perimeter of 31.17 m. The inner profile of the main tunnel lining is shown in Figure 1.

FIGURE 1

FIGURE 1. Outline of the main tunnel.

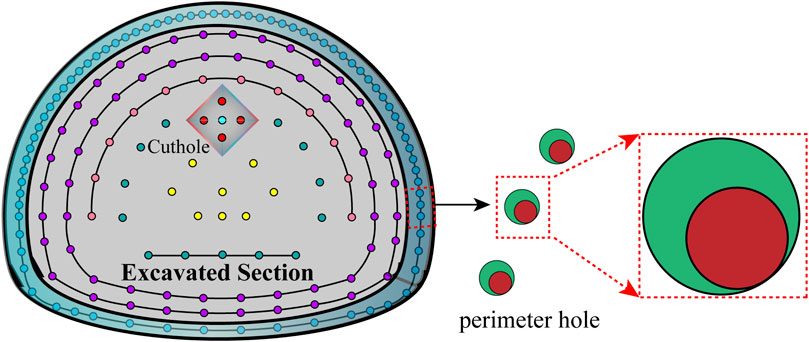
During tunnel blasting construction, the footage and charge must be controlled in accordance with the standards to reduce over-/under-excavation and control the damage caused to the surrounding rock, while blast vibrations should be minimized. For complete section blasting, multiple millisecond detonators are sequentially loaded in the order of detonation. The design of the blasting parameters is shown in Table 1.

TABLE 1

TABLE 1. Upper excavation blasting parameters.

Overview of Xiangguosi Gas Reservoir

Xiangguosi gas reservoir in the Yubei District of Chongqing is the first gas storage in Southwest China. Xiangguosi gas reservoir has a unique structure since it is located on the narrow backslope at the southeast side of the Huayingshan prominent anticline (also known as Longwangdong anticline). Xiangguosi reservoir is made of carboniferous breccia dolomite sourced from a depleted oil and gas reservoir. Its reservoir structure and tectonic zone shape are shown in Figure 2. The reservoir is buried at 2000–3,000 m, and the scale of reservoir construction is approximately 4 billion cubic meters. The designed operating pressure of the reservoir is 13.2–28 MPa. The maximum injection pressure at the surface is 30 MPa, the minimum extraction pressure at the wellhead is 7 MPa, and the working gas volume is 22.8 × 108 m³; the maximum and the minimum single-day injection volume is 1380 × 104 m³ and 750 × 104 m³, respectively.

FIGURE 2

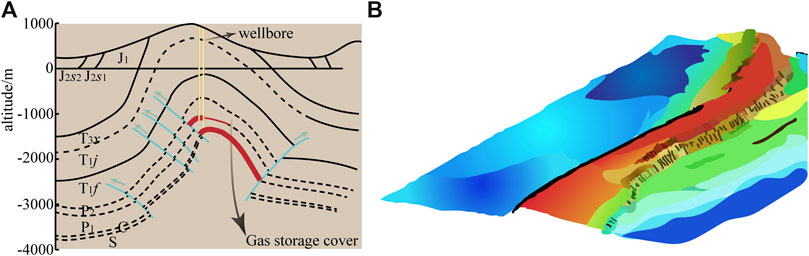
FIGURE 2. Xiangguosi reservoir and tectonic structure. (A) schematic diagram of the tectonic section of Xiangguosi; (B) reservoir map of Xiangguosi gas storage.

Spatial Relationship Between Gas Storage and Sansheng Tunnel

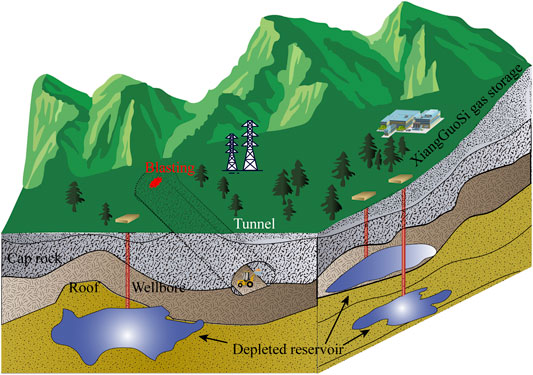
Xiangguosi gas reservoir is a deep storage reservoir that uses surface injection and extraction wells to compress natural gas into rock formations in order to meet a part of the demand of seasonal peak shaving. The Sansheng tunnel is a newly planned line that crosses the Xiangguosi reservoir section. Reservoir injection wells 19 and 22 are located near the Sansheng tunnel, and well 19 intersects the tunnel and well 22 does not; therefore, this paper aims to elucidate the impact of blasting on well 19 at the exit section of the Sansheng tunnel. The spatial locations of the tunnel and gas storage are shown in Figure 3.

FIGURE 3

FIGURE 3. Diagram of the spatial locations of the tunnel and gas storage.

Laboratory Mechanical Tests

Before simulating tunnel blasting, mechanical properties of the surrounding rock mass between the tunnel and gas storage must be clarified for establishing an accurate blasting model. To this end, this paper first drills and cores the rock masses after tunnel blasting out of the slag. Subsequently, cylindrical specimens (φ50 mm*100 mm) were prepared in accordance with the rock mechanics experimental specimens were ground and polished to ground and polished to ensure that the flatness of the specimen ends was within 0.05 mm. After the rock specimens were prepared, multiple sets of uniaxial compression tests were performed by using equipment such as the AGI250 Electronic Tensile Compression Material Experiment Machine from the State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University.

The full stress-strain curve or rock compression was extracted, and the results of the stress-strain curve revealed that the surrounding rock is a typical brittle rock whose mechanical behavior obeys four characteristics: initial compaction, linear elasticity, unstable rupture, and peak failure. The detailed mechanical parameters of the surrounding rock are shown in Table 2.

TABLE 2

TABLE 2. Conventional mechanical parameters of surrounding rock.

Model Establishment

Based on the spatial distribution of the Sansheng tunnel and the gas storage reservoir, a 3D finite element model was established in conjunction with the site blasting construction plan. The overall size of the model is 2800 m*2800 m*20 m, and the tunnel is modelled according to the actual size of the three-center arch. The gas reservoir model includes a wellbore and a cover layer buried at a depth of 2000–4000 m, and the top of the reservoir is 1500 m away from the tunnel. The shaft extends from the top of the caprock to the surface, and its horizontal distance from the tunnel is 902 m. The perimeter and bottom surface of the model are set as non-reflection boundaries to eliminate the interference of reflected waves at the interface, and the upper surface of the model is set as the free boundary. The detailed model and grid are shown in Figure 4. Moreover, gravity constraints were applied to the model to reflect the effects of vertical and horizontal stresses on stress wave propagation and the stress conditions in the surrounding rock mass.

FIGURE 4

FIGURE 4. Models and grids.

Construction of Material Model and Equation of State

The material model includes rock, explosive and gas models. The details of the material model and state equation are as follows:

(1) Rock model

The surrounding rock is brittle, with low strength and elastic modulus. To better describe the strain rate effect of the surrounding rock under impact loading, the plastic follow-hardening model (*MAT_Plastic_Kinematic) is used in this study, and the parameters are shown in Table 4.

The plastic follow-hardening model considers failure in terms of strain (Chen and Hao, 2013; Zhao and Qian, 2019), while depicting specific failure behavior through the hardening parameter β; that is, β = 0 for follow-hardening and β = 1 for isotropic hardening. The yield strength of the surrounding rock after it has been subjected to a low to medium strain rate load can be expressed using Equation 1.

${\sigma }_Y=\left[1+{\left(\frac{\dot{\epsilon }}{c}\right)}^{\frac{1}{P}}\right]\left({\sigma }_0+\beta E_P{\epsilon }_P^{eff}\right)(1)$

Where σ₀ is the initial yield stress, $\dot{\epsilon }$ is the strain rate, c and P are the Cowper Symonds strain rate parameters, and E_P is the plastic hardening modulus:

$E_P=\frac{E_{\tan }E}{E-E_{\tan }}(2)$

Where E_tan is the tangential modulus and E is the modulus of elasticity. The calculated parameters for the rock are shown in Table 3.

(2) Explosive material model and state equation

TABLE 3

TABLE 3. Rock parameters.

The main parameters involved in the explosive model include explosive density, detonation velocity, detonation pressure and other essential parameters. The Jones-Wilkins-Lee (JWL) equation generally describes the explosion characteristics of explosives (Wang et al., 2012; Yan et al., 2020):

$P_e=A\left(1-\frac{\omega }{R_{2}V}\right)e^{-R_{1}V}+B\left(1-\frac{\omega }{R_{2}V}\right)e^{-R_{2}V}+\frac{\omega E_0}{V}(3)$

Where Pe is the blast product pressure from the equation of state; V is the relative volume; e is the internal energy density per unit volume; A, B, R₁, R₂, and ω are the input parameters. According to the field blasting scheme, this study chooses emulsified explosives to perform the simulation. Table 4 shows the explosive blasting parameters.

(3) Air material model and its equation of state

TABLE 4

TABLE 4. Explosive blasting parameters.

The air equation of state is described via LINEAR_POLYNOMIAL and the linear polynomial equation of state (Ding et al., 2019; Ouellet et al., 2019) is:

$P_a=C_0+C_1\mu +C_2{\mu }^2+C_3{\mu }^3+\left(C_4+C_5\mu +C_6{\mu }^2\right)E_a(4)$

$\mu =\frac{\rho }{{\rho }_0}-1=\frac{1}{\raisebox{1ex}{$v$}\!\left/ \!\raisebox{-1ex}{$v_0$}\right.}-1=\frac{1}{v_r}-1(5)$

Where P_a is the burst pressure. E_a is the internal energy. ρ/ρ₀ is the ratio of the relative density. v is the relative volume, and v₀ is the initial volume. C₀ = C₁ = C₂ = C₃ = C₆ = 0 and C₄ = C₅ = γ₀-1, where γ₀ is the adiabatic index and generally assumes a value of 3.

Analysis of Original Blast Vibration Results

The stress cloud diagram of the tunnel surrounding the rock body was determined using numerical simulation methods (Figure 5). After the detonation of each section of explosives, stress waves are generated in the internal surrounding rock body of the palm face. The stress waves begin to propagate outward in the radial direction after experiencing initial radial propagation and superposition. During this propagation process, the destructive effect of the strong shock wave on the surrounding rock body can be seen, and the internal stress of the surrounding rock body changes dramatically, which is accompanied by the occurrence of considerable deformation and large strain. When the stress wave propagates from the near blasting area to the far blasting area, its peak intensity, energy, vibration intensity, dominant frequency, and vibration velocity begin to decay, while the attenuation range becomes wide. With a continuous increase in the propagation distance, the stress wave does not tend to cause damage to the surrounding rock due to attenuation and will continue to propagate in the form of a seismic wave.

FIGURE 5

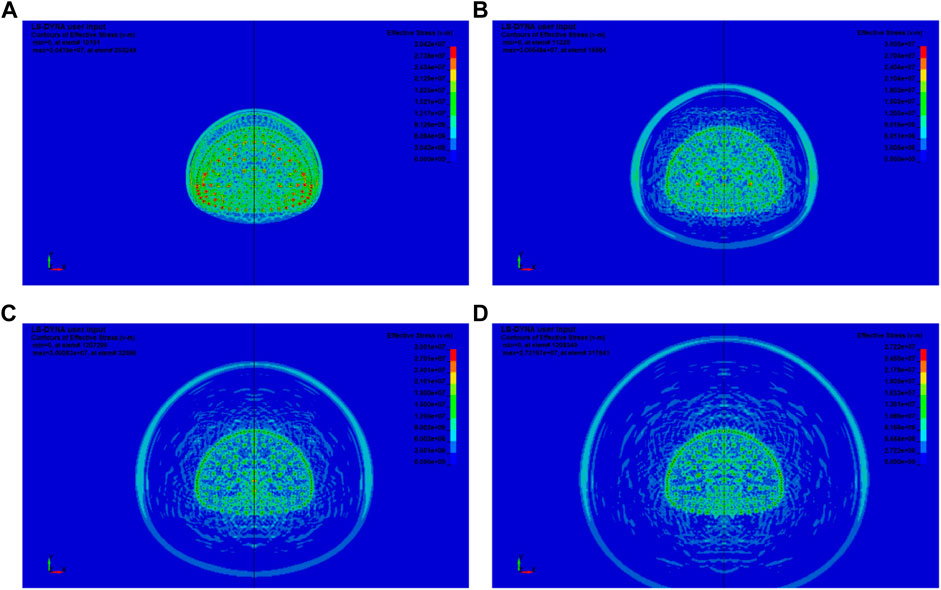
FIGURE 5. Stress wave propagation and attenuation. (A) detonate each section of explosive; (B) the stress wave propagates outward in the radial direction; (C) the stress wave begins to decay; (D) the stress wave attenuates continuously until it becomes a seismic wave.

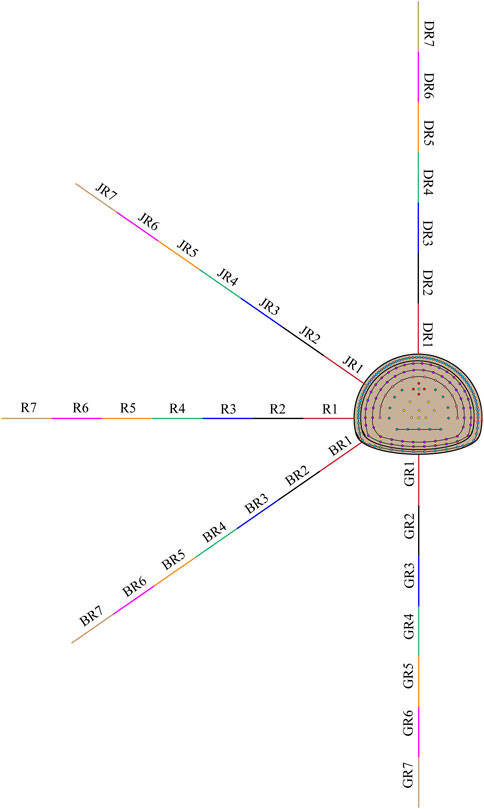
As there is a special positional relationship between well 19 and the tunnel with regard to the plane intersections, well 19 can increase the damage range caused by excavation disturbance. To elucidate the effect of tunnel blasting on the confinement of injection and extraction wells, several monitoring measurement points were set up along the direction of wave propagation; the measurement points were numbered from DR1 to DR7, JR1-JR7, R1-R7, BR1-BR7, GR1-GR7. These points were distributed using an equal gradient of 5 m (Figure 6). By extracting the vibration velocity values in the X, Y, and Z directions at each monitoring point after blasting, blasting vibration distribution characteristics of the surrounding rock between the tunnel and gas storage reservoir were obtained (Figure 7).

FIGURE 6

FIGURE 6. Distribution of measuring points.

FIGURE 7

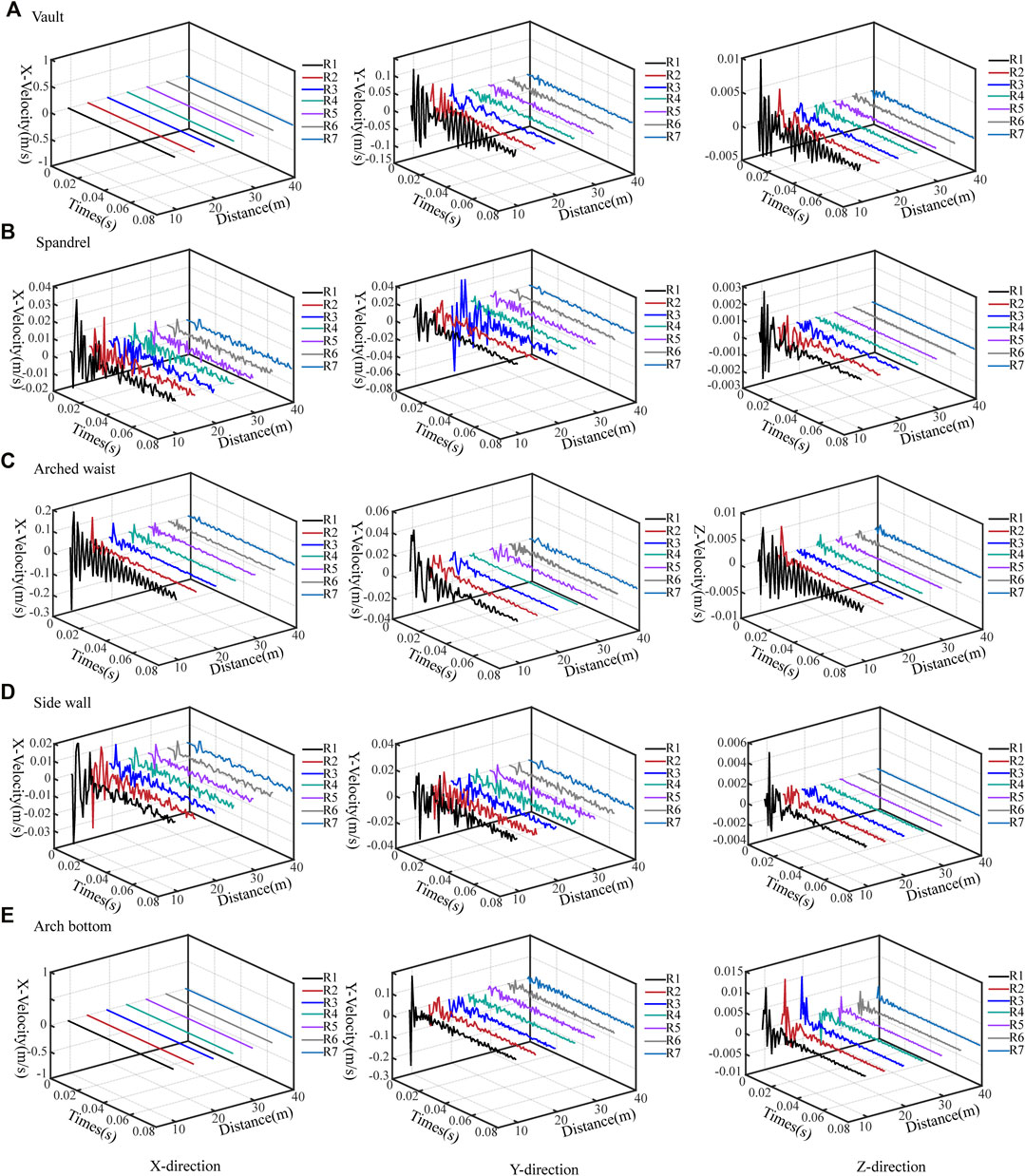
FIGURE 7. Vibration velocity distribution in the X, Y, and Z directions. (A) Vault; (B) Spandrel; (C) Arched waist; (D) Side wall; (E) Arch bottom.

Figure 7 reflects the characteristics of the three-way vibration velocity distribution of the measurement points at different distances. It can be seen that the three-dimensional vibration velocity peaks at each position of the tunnel show typical nonlinear attenuation characteristics with the increase of propagation distance. In order to save space, this paper only analyzes the vibration velocity of the measuring points at the arch waist position. At the waist of the arch, the X-directional vibration velocity shows an apparent monotonic decreasing trend with increasing distance, while exhibiting the maximum and minimum vibration velocity at R1 (28.64 cm/s) and R7 (1.7 cm/s), respectively. The attenuation characteristic of the Y-direction vibration velocity is the most evident between the R1 and R2. It decreases from 4 cm/s to 1.4 cm/s (65% decrease), while exhibiting stability after R2. The Y-directional velocity decayed the fastest between R2 and R3 (from 0.5 cm/s to 0.07 cm/s, which is a drop of 86% decrease). By comparing the one-way velocity change at each measurement point, the overall velocity at each measurement point is found to be negatively correlated with the distance. Meanwhile, the velocity decay rate and decay characteristics in different directions are not consistent; the slowest decline is shown by the longitudinal wave velocity, and the velocities in the other two directions decrease rapidly.

The variation curve of the maximum vibration velocity at each measurement point with increasing distance is plotted (Figure 8A). The maximum vibration velocity decays as an exponential function with increasing distance. To verify the reliability of numerical simulation results, this study uses Sadovsky empirical theory (Eq. 6) to calculate the vibration speed at different blast source distances (Zeng et al., 2018; Matidza et al., 2020); the K and α values are based on the uniaxial compressive strength of the surrounding rock, which is less than 60 MPa this in case. By calculating and fitting the vibration velocity values of each point, the variation law of vibration velocity is obtained (Figures 8B). The variation trend of vibration velocity obtained using theoretical calculations obeys the exponential function.

$v=K{\left(\frac{Q^{1/2}}{R}\right)}^{\alpha }(6)$

Where K and α are the rock parameters, with values of 168.5 and 18, respectively. R is the distance; and Q is the maximum single-section explosive quantity.

FIGURE 8

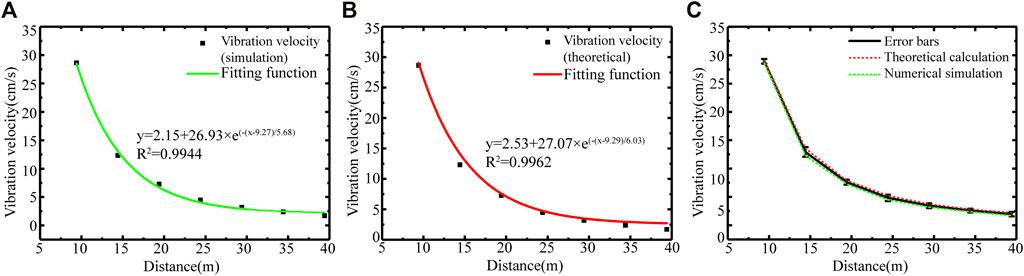
FIGURE 8. Comparison of blasting vibration velocities. (A) numerical simulation; (B) theoretical calculation; (C) comparison of results.

The variation patterns of numerical simulation results and theoretical calculation results (Figure 8C) are basically the same, thereby revealing the correctness of the model and calculation method and indicating that numerical simulation results can provide some guidance for blasting excavation of tunnels passing through structures. After validating the numerical simulation results, the vibration velocity of the rock near the wellbore has been determined, and the results show that the vibration velocity values are stable (0.086 cm/s) at each measurement point. According to the relevant requirements for blasting vibration velocity in Xiangguosi gas reservoir, the safe vibration velocity at well 19 and injection well 11 in Xiangguosi gas reservoir should be within 0.087 cm/s. Under the original blasting scheme, the vibration velocity of the surrounding rock near the wellbore is in compliance with the regulations and will not affect the normal operation of the gas storage reservoir. However, given that the measured vibration velocity is close to the critical vibration velocity, further control of blasting vibration is required to ensure the safety and stability of the Xiangguosi Gas Storage Facility.

Blasting Vibration Control

Tunnel blasting vibration will inevitably affect the stability of gas storages and even lead to extreme situations such as structural instability and gas leakage. To solve this problem, existing tunnel blasting techniques employ measures such as weak blasting techniques and the addition of damping trenches/damping strips. However, weak blast may affect the blasting effect at the palm face of the tunnel; the damping trenches may exacerbate the damage to the surrounding rock and increase the construction cost, while not being conducive to tunnel boring. Therefore, this study proposes an asymmetric uncoupled refined blasting technique, which improves the explosive loading of the tunnel perimeter holes by adjusting the position of the explosives, thereby reducing the blasting disturbance to the surrounding rock and structures.

The charge structure diagram associated with asymmetric charge blasting is shown in Figure 9. The location of the explosive in the asymmetric charge structure changes with a variation in hole position and drilling angle. With an increase in the explosive offset distance, the energy of incident waves entering the surrounding rock tends to decrease. Accordingly, amplitude of the blasting vibration wave and vibration velocity of the surrounding rock will continue to decrease. The asymmetric uncoupled charge is coupled into the calculation model to determine the vibration velocity at points R1 to R7 (Figure 10).

FIGURE 9

FIGURE 9. Asymmetric charge structure.

FIGURE 10

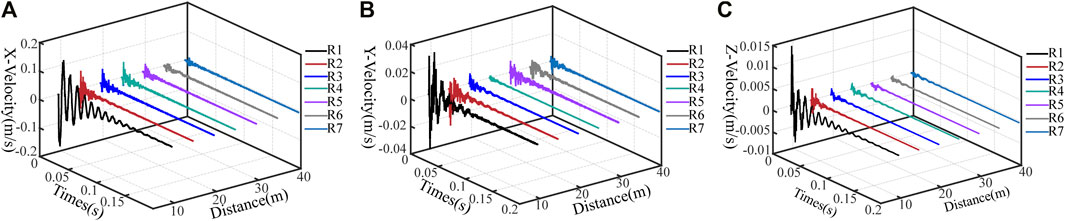
FIGURE 10. Variation trend of vibration velocity under asymmetric blasting. (A) X-directional velocity; (B) Y-directional velocity; (C) Z-directional velocity.

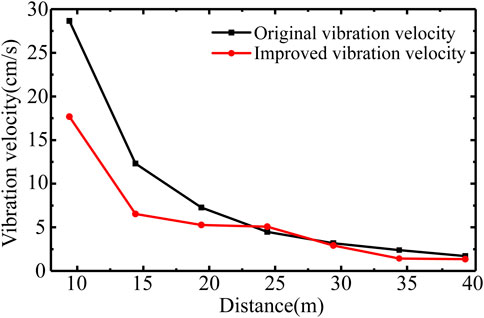
Figure 11 shows the asymmetric blasting results, which reveal that the three-dimensional vibration velocity at each measuring point is greatly attenuated. The maximum vibration velocities in the X, Y, and Z directions at R1 are 17.68 cm/s, 3.9 cm/s and 1.3 cm/s, respectively. Compared with the original blasting vibration, the attenuation rates associated with vibration velocities in the X, Y, and Z directions under asymmetric blasting are 38%, 2.5% and −53.8%, respectively; the attenuation rate of resultant velocity is 38.6%. The maximum X, Y and Z velocities at R7 are 1.36 cm/s, 0.77 cm/s and 0.05 cm/s, respectively; these values respectively represent 20%, −45%, and 54% change in the velocities in X, Y, and Z directions and a 19.4% change in combined velocity when compared to the original blast. Based on the variation in the vibration velocities at R1 and R7 above, it can be concluded that asymmetric blasting can be used to reduce the blast vibration velocities in both near and far areas. Figure 11 shows that the vibration velocity suddenly increases at point R4 (distance of 24.409 m). At point R4 the drop in vibration velocity associated with asymmetric blast was higher than that associated with the original blast scheme, and the drop in vibration velocity was relatively greater at distances smaller than 24.409 m. In summary, the combined velocity reduction rates from R1 to R7 were 38.6, 44.7, 23.9%, −13.4, 10.1, 35.2, and 19.4%, respectively, with an average reduction rate of 22.64%; this result shows that the blast vibration velocity can be reduced by using asymmetric blasting. However, the blast vibration velocity approximately shows a step-down trend. That is, in the first step (distance less than 25 m) the blasting vibration is clearly reduced; however, while at the second stage (distance greater than 25 m), the vibration attenuation trends associated with asymmetric and original blasts are similar, and the reduction in vibration velocity is smaller.

FIGURE 11

FIGURE 11. Comparison of blast vibration speeds.

Conclusion

In this study, the impact of the drilling and blasting methods process of the Sansheng tunnel on the wellbores of the national strategic gas storage reservoir was analyzed using field investigations, indoor tests and numerical simulation. By monitoring the variation of vibration velocity in the surrounding rock near the tunnel-gas storage reservoir, the real-time variation law associated with vibration velocity at different distances is obtained, and the variation law is compared and verified with the theoretical calculation results. To further control the blasting vibration velocity of surrounding rock near the tunnel and gas storage, an asymmetric charge blasting vibration reduction technique has been proposed; this approach allows the position of the explosives in the hole to be adjusted according to the safety level of the structure, vibration velocity requirements, and surrounding rock endowment conditions, thereby controlling the incident wave energy of the surrounding rock mass and achieving the purpose of vibration energy attenuation. This study can be summarized as follows.

(1) According to the field investigation, the spatial location and plane interactions of tunnel and gas storage are determined. The physical and mechanical parameters of surrounding rock are obtained through laboratory tests. Based on the on-site blasting construction of the tunnel, the dynamic finite element model of tunnel gas storage (caprock-wellbore system) is established.

(2) After each cycle of explosive blasting, the stress wave begins to propagate outwards in the radial direction and decays with increasing distance until it transforms into a seismic wave. The three-way velocities associated with blasting in the surrounding rocks near the tunnel and the gas storage reservoir show an exponential decay with increasing propagation distances, and and the x-directional vibration velocity (longitudinal wave velocity) decays the slowest. The vibration velocity of the rocks near the gas storage reservoir is less variable and stable at 0.086 cm/s, which is in line with the requirement for the blasting vibration velocity affecting gas storage.

(3) The blasting vibration velocity and its variation trend calculated by numerical simulation are consistent with the theoretical calculation results, which implies that the numerical simulation can accurately and effectively reflect the dynamic response behavior of the surrounding rock near the tunnel and gas storage shaft.

(4) This study presents an asymmetric uncoupled charging method that controls the incident wave energy of the rock to be retained and the vibration velocity of the structure by adjusting the eccentric distance of the explosive. The results of applying this method to perimeter hole blasting in tunnels show that the change in vibration velocity of the surrounding rock under asymmetric blasting conditions follows a “two-step” decay trend, with the first step showing a rapid decay in vibration velocity and the second stage showing a slow decline in vibration velocity. Overall, the asymmetric blasting vibration velocity is lower than associated with original blasting, and the average vibration reduction rate is 22.64%.

The objective of this study is to provide an effective seismic mitigation measure for tunnels passing through underground gas storage reservoirs, while offering a preliminary feasibility assessment associated with the safety of the reservoir structure. Future research should also consider the effects of other blast design parameters on the blast vibration response, while analyzing the main frequency characteristics associated with the gas storage reservoir shaft and cap layer. Furthermore, machine learning, data fusion and intelligent identification methods should be combined to build a 3D visualization platform for intelligent early warning of blast vibrations (Lu et al., 2011; Chen et al., 2016; Zhao et al., 2016; Verma et al., 2017; Zhang et al., 2017; Li et al., 2018a; Xia et al., 2018; Yang et al., 2018; Song et al., 2019; Wu et al., 2019; Qiu et al., 2020; Zhao et al., 2020; Dai et al., 2020; Huang et al., 2020; Ma et al., 2021).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding authors.

Author Contributions

RL and PL designed numerical experiments. LM, FL, GX and LC conducted experiments. LM and RL wrote analysed experimental data; LM wrote the main manuscript and prepared figures. All authors reviewed the manuscript.

Funding

This study was supported by the Fundamental Research Funds for the National Natural Foundation of China (NSFC, grant numbers 51834003, 51904039, 51774057 and 52074048), Chongqing Postdoctoral Science Foundation (cstc2019jcyjbshX0084) and the Special Key Project of Chongqing Technology Innovation and Application Development (cstc2019jscx-tjsbX0015).

Conflict of Interest

Authors FL and GX were employed by the company China Coal Technology Engineering Group Huaibei Blasting Technology Research Institute Limited Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, A., and Guo, L. (2021). Data-driven Based Investigation of Pressure Dynamics in Underground Hydrocarbon Reservoirs. Energ. Rep. 7, 104–110. doi:10.1016/j.egyr.2021.02.036

CrossRef Full Text | Google Scholar

Chen, M., Lu, W. B., Yan, P., and Hu, Y. G. (2016). Blasting Excavation Induced Damage of Surrounding Rock Masses in Deep-Buried Tunnels. KSCE J. Civ Eng. 20 (2), 933–942. doi:10.1007/s12205-015-0480-3

CrossRef Full Text | Google Scholar

Chen, W., and Hao, H. (2013). NUMERICAL STUDY OF BLAST-RESISTANT SANDWICH PANELS WITH ROTATIONAL FRICTION DAMPERS. Int. J. Struct. Stab. Dyn. 13 (6), 1350014. doi:10.1142/s0219455413500144

CrossRef Full Text | Google Scholar

Chung, I. M., Kim, T., Lee, K.-K., and Han, I. Y. (2009). Efficient Method for Estimating Groundwater Head in the Vicinity of the Underground Gas Storage Caverns in Fractured Media. J. Hydrol. Eng. 14 (3), 261–270. doi:10.1061/(asce)1084-0699(2009)14:3(261)

CrossRef Full Text | Google Scholar

Dai, C., Sui, H., and Ma, C. (2020). Study on the Vibration Effect of Short Footage Blasting Load on Surrounding Rock-Support Structure of Tunnel. Shock and Vibration 2020, 1–15. doi:10.1155/2020/8829349

CrossRef Full Text | Google Scholar

Deyi, J., Jinyang, F., Chen, J., Li, L., and Cui, Y. (2016). A Mechanism of Fatigue in Salt under Discontinuous Cycle Loading. Int. J. Rock Mech. Mining Sci. 86, 255–260. doi:10.1016/j.ijrmms.2016.05.004

CrossRef Full Text | Google Scholar

Ding, Y., Lu, Y., Lu, Q., Luo, M., and Dai, Z. (2019). Coupled Dynamic Analysis of Liquid Storage Tanks under Implosion-Generated Overpressure. Int. J. Str. Stab. Dyn. 19 (11), 1950128. doi:10.1142/s0219455419501281

CrossRef Full Text | Google Scholar

Fan, J., Jiang, D., Liu, W., Wu, F., Chen, J., and Daemen, J. (2019). Discontinuous Fatigue of Salt Rock with Low-Stress Intervals. Int. J. Rock Mech. Mining Sci. 115, 77–86. doi:10.1016/j.ijrmms.2019.01.013

CrossRef Full Text | Google Scholar

Fan, J., Liu, W., Jiang, D., Chen, J., Tiedeu, W. N., and Daemen, J. J. K. (2020). Time Interval Effect in Triaxial Discontinuous Cyclic Compression Tests and Simulations for the Residual Stress in Rock Salt. Rock Mech. Rock Eng. 53 (9), 4061–4076. doi:10.1007/s00603-020-02150-y

CrossRef Full Text | Google Scholar

Fan, Y., Cui, X., Leng, Z., Zheng, J., Wang, F., and Xu, X. (2021). Rockburst Prediction from the Perspective of Energy Release: A Case Study of a Diversion Tunnel at Jinping II Hydropower Station. Front. Earth Sci. 9 (624), 711706. doi:10.3389/feart.2021.711706

CrossRef Full Text | Google Scholar

Huang, J., Luo, Y., Zhang, G., Zheng, B., Li, X., Xu, M., et al. (2020). Numerical Analysis on Rock Blasting Damage in Xiluodu Underground Powerhouse Using an Improved Constitutive Model. Eur. J. Environ. Civil Eng., 1–18. doi:10.1080/19648189.2020.1780475

CrossRef Full Text | Google Scholar

Jiang, D., Li, Z., Liu, W., Ban, F., Chen, J., Wang, Y., et al. (2021). Construction Simulating and Controlling of the two-well-Vertical(TWV) Salt Caverns with Gas Blanket. J. Nat. Gas Sci. Eng. 96, 104291. doi:10.1016/j.jngse.2021.104291

CrossRef Full Text | Google Scholar

Kang, Y., Fan, J., Jiang, D., and Li, Z. (2021). Influence of Geological and Environmental Factors on the Reconsolidation Behavior of Fine Granular Salt. Nat. Resour. Res. 30 (1), 805–826. doi:10.1007/s11053-020-09732-1

CrossRef Full Text | Google Scholar

Lee, J.-Y., and Lim, H. S. (2010). Identification and Characterization of the Encrusting Materials in a Coastal Liquefied Petroleum Gas Storage Cavern. Environ. Earth Sci. 61 (6), 1165–1177. doi:10.1007/s12665-009-0439-0

CrossRef Full Text | Google Scholar

Leng, X., Wang, C., Sheng, Q., Chen, J., and Li, H. (2021). An Enhanced Ubiquitous-Joint Model for a Rock Mass with Conjugate Joints and its Application on Excavation Simulation of Large Underground Caverns. Front. Earth Sci. 9 (765). doi:10.3389/feart.2021.744900

CrossRef Full Text | Google Scholar

Li, D., Liu, W., Jiang, D., Chen, J., Fan, J., and Qiao, W. (2021). Quantitative Investigation on the Stability of Salt Cavity Gas Storage with Multiple Interlayers above the Cavity Roof. J. Energ. Storage 44, 103298. doi:10.1016/j.est.2021.103298

CrossRef Full Text | Google Scholar

Li, X., Li, C., Cao, W., and Tao, M. (2018a). Dynamic Stress Concentration and Energy Evolution of Deep-Buried Tunnels under Blasting Loads. Int. J. Rock Mech. Mining Sci. 104, 131–146. doi:10.1016/j.ijrmms.2018.02.018

CrossRef Full Text | Google Scholar

Li, Y., Liu, W., Yang, C., and Daemen, J. J. K. (2014). Experimental Investigation of Mechanical Behavior of Bedded Rock Salt Containing Inclined Interlayer. Int. J. Rock Mech. Mining Sci. 69, 39–49. doi:10.1016/j.ijrmms.2014.03.006

CrossRef Full Text | Google Scholar

Li, Z., Wu, S., Cheng, Z., and Jiang, Y. (2018b). Numerical Investigation of the Dynamic Responses and Damage of Linings Subjected to Violent Gas Explosions inside Highway Tunnels. Shock and Vibration 2018, 1–20. doi:10.1155/2018/2792043

CrossRef Full Text | Google Scholar

Liu, P., Fan, J., Jiang, D., and Li, J. (2021). Evaluation of Underground Coal Gas Drainage Performance: Mine Site Measurements and Parametric Sensitivity Analysis. Process Saf. Environ. Prot. 148, 711–723. doi:10.1016/j.psep.2021.01.054

CrossRef Full Text | Google Scholar

Liu, R., He, Y., Zhao, Y., Jiang, X., and Ren, S. (2020). Tunnel Construction Ventilation Frequency-Control Based on Radial Basis Function Neural Network. Automation in Construction 118, 103293. doi:10.1016/j.autcon.2020.103293

CrossRef Full Text | Google Scholar

Liu, W., Zhang, X., Fan, J., Zuo, J., Zhang, Z., and Chen, J. (2020a). Study on the Mechanical Properties of Man-Made Salt Rock Samples with Impurities. J. Nat. Gas Sci. Eng. 84, 103683. doi:10.1016/j.jngse.2020.103683

CrossRef Full Text | Google Scholar

Liu, W., Zhang, Z., Fan, J., Jiang, D., Li, Z., and Chen, J. (2020b). Research on Gas Leakage and Collapse in the Cavern Roof of Underground Natural Gas Storage in Thinly Bedded Salt Rocks. J. Energ. Storage 31, 101669. doi:10.1016/j.est.2020.101669

CrossRef Full Text | Google Scholar

Liu, Y., Li, H., Li, J., Liu, B., and Xia, X. (2015). In Situ Stress Determination for Liquefied Petroleum Gas Storage Caverns by Hydraulic Tests on Pre-existing Fractures. Rock Mech. Rock Eng. 48 (3), 1313–1319. doi:10.1007/s00603-014-0616-7

CrossRef Full Text | Google Scholar

Lu, W., Yang, J., Chen, M., and Zhou, C. (2011). An Equivalent Method for Blasting Vibration Simulation. Simulation Model. Pract. Theor. 19 (9), 2050–2062. doi:10.1016/j.simpat.2011.05.012

CrossRef Full Text | Google Scholar

Ma, L. H., Jiang, X., Chen, J., Zhao, Y. F., Liu, R., and Ren, S. (2021). Analysis of Damages in Layered Surrounding Rocks Induced by Blasting during Tunnel Construction. Int. J. Str. Stab. Dyn. 21 (07), 2150089. doi:10.1142/s0219455421500899

CrossRef Full Text | Google Scholar

Mahlia, T. M. I., Saktisahdan, T. J., Jannifar, A., Hasan, M. H., and Matseelar, H. S. C. (2014). A Review of Available Methods and Development on Energy Storage; Technology Update. Renew. Sust. Energ. Rev. 33, 532–545. doi:10.1016/j.rser.2014.01.068

CrossRef Full Text | Google Scholar

Mandal, J., Agarwal, A. K., and Goel, M. D. (2020). Numerical Modeling of Shallow Buried Tunnel Subject to Surface Blast Loading. J. Perform. Constructed Facil. 34 (6), 04020106. doi:10.1061/(asce)cf.1943-5509.0001518

CrossRef Full Text | Google Scholar

Matidza, M. I., Jianhua, Z., Gang, H., and Mwangi, A. D. (2020). Assessment of Blast-Induced Ground Vibration at Jinduicheng Molybdenum Open Pit Mine. Nat. Resour. Res. 29 (2), 831–841. doi:10.1007/s11053-020-09623-5

CrossRef Full Text | Google Scholar

Ouellet, F., Park, C., Rollin, B., Haftka, R. T., and Balachandar, S. (2019). A Kriging Surrogate Model for Computing Gas Mixture Equations of State. J. Fluids Engineering-Transactions Asme 141 (9), 091301. doi:10.1115/1.4042890

CrossRef Full Text | Google Scholar

Peng, H., Fan, J., Zhang, X., Chen, J., Li, Z., Jiang, D., et al. (2020). Computed Tomography Analysis on Cyclic Fatigue and Damage Properties of Rock Salt under Gas Pressure. Int. J. Fatigue 134, 105523. doi:10.1016/j.ijfatigue.2020.105523

CrossRef Full Text | Google Scholar

Qiu, J., Li, D., Li, X., and Zhu, Q. (2020). Numerical Investigation on the Stress Evolution and Failure Behavior for Deep Roadway under Blasting Disturbance. Soil Dyn. Earthquake Eng. 137, 106278. doi:10.1016/j.soildyn.2020.106278

CrossRef Full Text | Google Scholar

Sadique, M. R., Zaid, M., and Alam, M. M. (2021). Rock Tunnel Performance under Blast Loading through Finite Element Analysis. Geotech Geol. Eng. doi:10.1007/s10706-021-01879-9

CrossRef Full Text | Google Scholar

Song, S., Li, S., Li, L., Shi, S., Zhou, Z., Liu, Z., et al. (2019). Model Test Study on Vibration Blasting of Large Cross-Section Tunnel with Small Clearance in Horizontal Stratified Surrounding Rock. Tunnelling Underground Space Tech. 92, 103013. doi:10.1016/j.tust.2019.103013

CrossRef Full Text | Google Scholar

Urai, J. L., Spiers, C. J., Zwart, H. J., and Lister, G. S. (1986). Weakening of Rock Salt by Water during Long-Term Creep. Nature 324 (6097), 554–557. doi:10.1038/324554a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Verma, A. K., Jha, M. K., Mantrala, S., and Sitharam, T. G. (2017). Numerical Simulation of Explosion in Twin Tunnel System. Geotech Geol. Eng. 35 (5), 1953–1966. doi:10.1007/s10706-017-0219-7

CrossRef Full Text | Google Scholar

Wang, H., Zha, X., and Ye, J. (2012). Dynamic Response of Metallic sandwich Panels under Blast Loadings. Int. J. Str. Stab. Dyn. 12 (3), 1250017. doi:10.1142/s0219455412500174

CrossRef Full Text | Google Scholar

Wang, J., Tan, X., Wang, J., Zhang, H., Zhang, Y., Guo, D., et al. (2021). Characteristics and Genetic Mechanisms of Normal-Pressure Fractured Shale Reservoirs: A Case Study from the Wufeng-Longmaxi Formation in Southeastern Chongqing, China. Front. Earth Sci. 9 (258). doi:10.3389/feart.2021.661706

CrossRef Full Text | Google Scholar

Wu, P., Yang, T., and Jia, W. (2019). Reliability Analysis and Prediction on Tunnel Roof under Blasting Disturbance. KSCE J. Civ Eng. 23 (9), 4036–4046. doi:10.1007/s12205-019-1887-z

CrossRef Full Text | Google Scholar

Xia, X., Li, H., Liu, Y., and Yu, C. (2018). A Case Study on the Cavity Effect of a Water Tunnel on the Ground Vibrations Induced by Excavating Blasts. Tunnelling Underground Space Tech. 71, 292–297. doi:10.1016/j.tust.2017.08.026

CrossRef Full Text | Google Scholar

Xiong, Z. A., Wei, L. A., Dj, A., Wq, B., El, C., Nan, Z. D., et al. (2021). Investigation on the Influences of Interlayer Contents on Stability and Usability of Energy Storage Caverns in Bedded Rock Salt. Energy 231, 120968. doi:10.1016/j.energy.2021.120968

CrossRef Full Text | Google Scholar

Yan, Q., Liu, C., Wu, J., Wu, J., and Zhuang, T. (2020). Experimental and Numerical Investigation of Reinforced Concrete Pile Subjected to Near-Field Non-contact Underwater Explosion. Int. J. Str. Stab. Dyn. 20 (6), 2040003. doi:10.1142/s0219455420400039

CrossRef Full Text | Google Scholar

Yang, J., Lu, W., Li, P., and Yan, P. (2018). Evaluation of Rock Vibration Generated in Blasting Excavation of Deep-Buried Tunnels. KSCE J. Civ Eng. 22 (7), 2593–2608. doi:10.1007/s12205-017-0240-7

CrossRef Full Text | Google Scholar

Yiwei, R., Yuan, Q., Jiang, D., JFan, , Liu, W., Wei, L., et al. (2021). A Non-darcy Gas Flow Model for Coalbed Methane in Mine Gobs. Phys. Fluids 33, 129901. doi:10.1063/5.0065252

CrossRef Full Text | Google Scholar

Zeng, Y., Li, H., Xia, X., Liu, B., Zuo, H., and Jiang, J. (2018). Blast-induced Rock Damage Control in Fangchenggang Nuclear Power Station, China. J. Rock Mech. Geotechnical Eng. 10 (5), 914–923. doi:10.1016/j.jrmge.2018.04.010

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, Y., Tan, Y., and Feng, J. (2017). Effect of Underground Stress Waves with Varied Wavelengths on Dynamic Responses of Tunnels. Geotech Geol. Eng. 35 (5), 2371–2380. doi:10.1007/s10706-017-0252-6

CrossRef Full Text | Google Scholar

Zhao, H.-b., Long, Y., Li, X.-h., and Lu, L. (2016). Experimental and Numerical Investigation of the Effect of Blast-Induced Vibration from Adjacent Tunnel on Existing Tunnel. KSCE J. Civ Eng. 20 (1), 431–439. doi:10.1007/s12205-015-0130-9

CrossRef Full Text | Google Scholar

Zhao, W., and Qian, J. (2019). Dynamic Response and Shear Demand of Reinforced concrete Beams Subjected to Impact Loading. Int. J. Str. Stab. Dyn. 19 (8), 1950091. doi:10.1142/s0219455419500913

CrossRef Full Text | Google Scholar

Zhao, X., Sun, K., Xu, W., Tang, L., Wang, H., and Hong, Y. (2020). Safety Analysis of Lining Structure Influenced by Blasting of Tunnel with Extralarge Section and Small Space. Shock and Vibration 2020, 1–14. doi:10.1155/2020/8852702

CrossRef Full Text | Google Scholar

Zhuang, D. Y., Tang, C. A., Liang, Z. Z., Ma, K., Wang, S. Y., and Liang, J. Z. (2017). Effects of Excavation Unloading on the Energy-Release Patterns and Stability of Underground Water-Sealed Oil Storage Caverns. Tunnelling Underground Space Tech. 61, 122–133. doi:10.1016/j.tust.2016.09.011

CrossRef Full Text | Google Scholar