Rainfall Infiltration Process of a Rock Slope with Considering the Heterogeneity of Saturated Hydraulic Conductivity

In order to analyze the effects of rainfall events on the stability of an open-pit rock slope, with considering the spatial variability of saturated hydraulic conductivity, based on the unsaturated seepage theory and the random filed theory, modified functions of the unit saturation, the hydraulic conductivity (k), and the shear strength parameters are established for unsaturated slope, by using FISH and the non-intrusive stochastic method. A saturated-unsaturated seepage random field model is proposed. And then the impacts of the rainfall intensity, the rainfall duration, and the spatial variability of saturated hydraulic conductivity (k_s) on the infiltration process and stability of the unsaturated rock slope are analyzed. The results show that the proposed model can estimate rainfall infiltration of rock slope accurately. Rainfall mainly affects the seepage field in the shallow layer of the slope, where a transient saturated zone can be formed. With the development of the rainfall duration, the weight of the rock mass increased, the matric suction reduced, the negative pore pressure, the degree of saturation, and the infiltration depth of the rock slope increased, and the water in the slope root connects with the initial water table gradually, the unsaturated zone shrinks, which causes the safety factor of the model decreases, but the trend of change slows down gradually. As the rainfall intensity strengthened, the infiltration depth increased and the safety factor of the slope reduced, while the changing rate increases first and then decreases. Increasing the correlation length of k can reduces the infiltration depth and safety factor of the slope. Increasing the variation coefficient of k will increase the infiltration depth, while the safety factor of the slope decreases. The infiltration depth and safety factor of the slope are most affected by rainfall duration, but its sensitivity to the variability coefficient of k will be strengthened when the rainfall intensity exceeds the infiltration capacity. This conclusion can provide reference significance for the risk estimation of slope geological hazards, which are induced by the rainfall infiltration.

Introduction

The impact of water on the safety and stability of slope is not ignorable, the rock mass of a slope generally contains a large amount of groundwater, and, what is more, it is eroded by seasonal rainfall. In recent years, the global climate anomalies, for example, extreme rainfall, may lead to frequent occurrence of various geological disasters on slope. Rainfall events affect the seepage of a slope differently, short-term rainfall can form a transient saturation zone in the shallow layer of a slope, and a continuous rainfall can even raise the groundwater level. Rainfall infiltration is a continuous and dynamic process, and the physical composition, sedimentary feature, and complex geological processes on the rock and soil mass have significant differences. It is necessary to comprehensively analyze the effect of rainfall infiltration on the seepage field and stability of rock slope with considering its natural spatial variability.

Many scholars, both foreign and domestic, expended significant research on the infiltration of water into soil; some of them take into account the natural spatial heterogeneity of hydraulic soil properties, from the late 1970s. Horton (1939) defined the infiltration capacity (IC) of soil as a hyetograph separation rate, and put forward that if the rainfall intensity exceeds the IC, a portion of the rainfall will runoff the soil surface. Santoso et al. (2011) analyzed the probability of slope failure induced by rainfall with considering the spatial variability of hydraulic conductivity. Based on the limit equilibrium method and finite element method, Collins and Znidarcic (2004) studied the mechanism of rainfall-induced landslides, and then analyzed the slope stability under multiple rainfall conditions. Chu-Agor et al. (2008), Huang and Jia (2007), and Oh and Vanapalli (2010) analyzed the influence of rainfall infiltration on the shear strength and stability of a slope. Considering the shear strength changes with the matric suction, Cho and Lee (2001) carried out a two-dimensional flow-deformation coupled model to analyze the stability of a soil slope under rainfall infiltration. Morbidelli et al. (2018) reviewed the research on infiltration models, such as models established by Green, Ampt, Horton, Philip, Brutsaert, Parlange, etc., and put forward that the natural spatial variability of soil hydraulic characteristics and that of rainfall make the estimate of infiltration has further challenges. Cai et al. (2020) developed a coupled hydro mechanical model of unsaturated soil considering the effect of the microscopic pore structure, and analyzed the effects of rainfall intensity and rainfall duration on the pore pressure, fluid velocity, and displacement of the unsaturated soil slope. Some scholars adopt the saturated-unsaturated seepage theory to analyze the rainfall infiltration process of rock slope (Qin et al., 2003; Rong et al., 2005; Liu and Xu 2017; Pan et al., 2020; Zhang et al., 2021). Huang and Qi (2002) discussed the effect of unsaturated soil’s suction on slope stability, suggested a modified model and applied it to an open pit mine slope, and analyzed some basic laws of suction on slope stability. Based on the unsaturated soil theory, Xu et al. (2005) analyzed the stability of unsaturated soil slope under rainfall infiltration. Introducing a fluid-mechanical interaction model based on continuous porous media theory and mixture theory, Xie et al. (2019) applying FISH language to program, studied the saturated-unsaturated seepage with FLAC3D. Jiang et al. (2014) studied the unsaturated seepage module and seepage calculation algorithm used in FLAC3D platform, based on that analyzed the unsaturated seepage of slope under rainfall condition. Fu et al. (2014) carried out the numerical simulation on the safety factor variation on an embankment slope of Six River highway in Guangxi, and analyzed the slope stability during continuous rainfall. Li et al. (2012) proposed a modified adjusting element permeability method to correct the permeability of unsaturated zone strictly, after calculation, an exact continuous smooth seepage surface and saturated-unsaturated seepage of a slope are obtained. Hu et al. (2017) investigated the effect of spatial variability of the shear strength parameters on the stability of completely decomposed granite slopes under intense rainfall infiltration. Based on the Monte Carlo method, Qin et al. (2017) established a reliability analysis model of bedrock laminar slope with considering the variability of k_s of slope soil, analyzed the failure probability of Zhang jia wan landslide under different variation coefficients of k_s and different rainfall intensities. Jiang et al. (2014) developed a modified Green-Ampt model to determine the distribution of moisture content of soils and the wetting front depth within the slope under different rainfall durations, and investigated the failure mechanism of the infinite slope considering the interaction of the spatial variability of multiple soil parameters and the rainfall infiltration. And some scholars considered the randomness of the geotechnical properties of rock and soil when studying the rainfall infiltration process and slope landslides induced by rainfall (Wang et al., 2019; Chen et al., 2020; Hamrouni et al., 2020; Han et al., 2020; Liu and Wang, 2021).

The above references mostly considered the rainfall infiltration process of soil slopes and/or the effects of the spatial variability of slope soil parameters on slope stability. While the surface of an open-pit mine rock slope is mainly composed of a mixture of soil and rock, coupled with the seasonal rainfall effect and the natural spatial variability of the slope rock and soil, which greatly increases the risk of geological disasters, even if the open-pit mine ceased operation, the risks are still greatly. Based on the above researches, the non-intrusive stochastic method was realized in this paper by using FISH and MATLAB, which can be used to simulating the unsaturated seepage stochastic filed, and the numerical realization of a saturated-unsaturated seepage random field was carried out by adopting the seepage coupling function module in FLAC3D. Then, the seepage field and stability of a rock slope under different rainfall intensity and rainfall duration was analyzed, with considering the variability of k of rock slope. The result can provide technical support for further study on the risk assessment of geological disasters of open-pit mines slope that induced by extreme rainfall.

Saturated-Unsaturated Seepage Random Field

Saturated-Unsaturated Seepage Theory

The upper-layer of a rock slope, which is above the water table, is unsaturated. Water entry into the shallow layer of a slope during the rainfall process changes the initial water content of the slope, and the matric suction changes with it too. The matric suction is one of the important parameters reflecting unsaturated soil mechanics. Between the degree of saturation or the value of k of the unsaturated seepage zone and the matric suction, there exists a functional relation (Guo et al., 2005). According to the soil water characteristic curve (SWCC), many scholars are committed to fitting the empirical formula, such as Liakopoulos, Alonso, Van Genuchten (1980), and so on. Alonso et al. (1995) put forward the relationship between liquid permeability and matric suction, and then the hydraulic conductivity can be obtained as a function of matric suction.

$\{\begin{array}{c}s={\mathrm{s}}_{\mathrm{r}}+\frac{\left(1-{\mathrm{s}}_{\mathrm{r}}\right)a_s}{{\mathrm{a}}_{\mathrm{s}}+{\left({\mathrm{b}}_{\mathrm{s}}{p}_c\right)}^{\mathrm{n}}}\\ k_w=\frac{a_k{\mathrm{k}}_{\mathrm{s}}}{{\mathrm{a}}_{\mathrm{k}}+{\left({\mathrm{b}}_{\mathrm{k}}{p}_c\right)}^{\mathrm{c}}}\end{array}(1)$

where ${\text{s}}_{\text{r}}$ is the residual degree of saturation, which is dimensionless, and $p_c$ is the matric suction, the unit is kPa. Parameters a_s, b_s, a_k, b_k, and c are the model parameters. ${\text{k}}_{\text{s}}$ is the hydraulic conductivity of saturated soil (the unit is cm/s).

Therefore, according to (1), the unit saturation and k of unsaturated soil can be determined by user-defined functions in FLAC3D. In the unsaturated zone, the value of saturation and pore water pressure at the zone gridpoint changes with the development of rainfall duration; what is more, the value at the unit changes with it. Therefore, it is necessary to correct the degree of saturation and the value of k at the unit at each time step in calculation. In addition, it is necessary to modify the strength criterion to analyze the slope stability. Bishop proposed the shear strength of unsaturated rock mass in 1960, and Fredlund and Rahardio (1997) put forward the revised formula in 1978.

${\tau }_f={\text{c}}^{\prime }+\left(\sigma -u_a\right)\tan {\text{φ}}^{\prime }+\left({\mathit{u}}_a-{\mathit{u}}_w\right)tan{\text{φ}}^{\text{b}}(2)$

$c^{\ast }={\text{c}}^{\prime }+\left({\mathit{u}}_a-{\mathit{u}}_w\right)tan{\text{φ}}^{\text{b}}(3)$

where ${\mathit{u}}_a-{\mathit{u}}_w$ is the matric suction of the potential failure surface (the unit is kPa), ${\mathit{u}}_a$ is the pore-air pressure, and ${\mathit{u}}_w$ is the pore-water pressure (the unit is kPa). ${\text{c}}^{\prime }$, ${\text{φ}}^{\prime }$, are the effective cohesion and friction angle, and ${\text{φ}}^{\text{b}}$ is an angle defining the increase in shear strength for an increase in matric suction. The cohesion can be corrected according to (3), when calculating the safety factor via FLAC3D.

Verification of Saturated-Unsaturated Seepage Filed Model

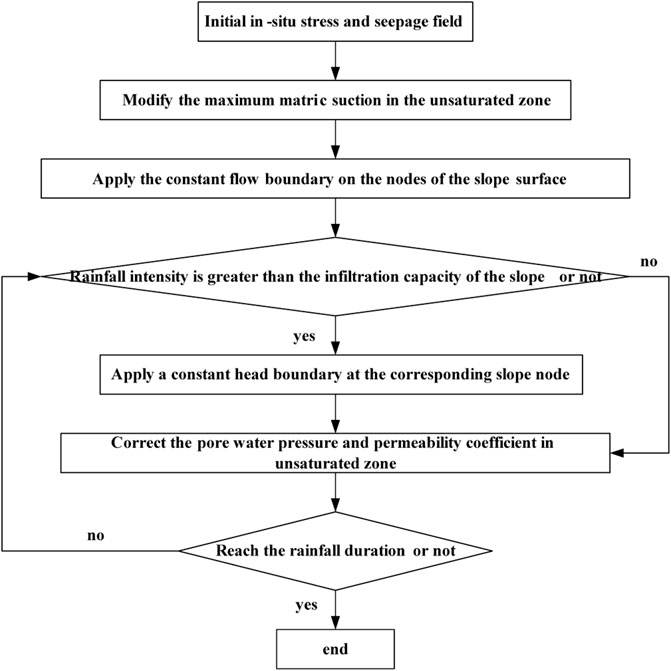
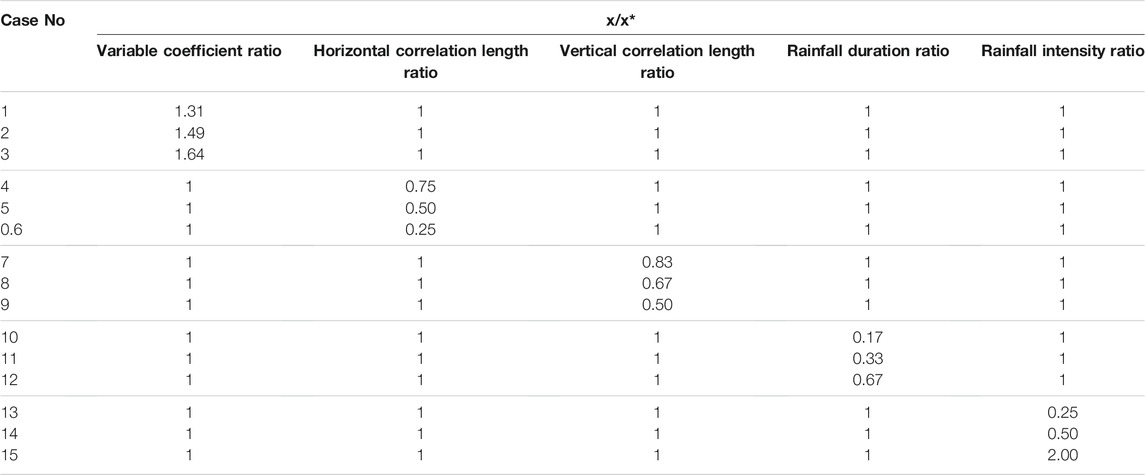
Figure 1 shows the schematic diagram for developing the saturated-unsaturated seepage procedure. In order to verify the accuracy of the development program of the modified algorithm for the seepage field in FLAC3D, the results in this paper were compared with that of the reference (Xie et al., 2019) and the results were obtained using the SEEP/W module of GEO-Studio. Figure 2A shows the simple model for a homogeneous rock slope, the height of the model is 40 m and the length is 100 m, the height of the slope is 20 m, and the angle is 45°. The initial water level is horizontal and below the ground, so the water table is at the height of 20 m, and a zero flux condition is imposed at the bottom, the front, and back of the model. The left and right boundaries of the model represent a constant head boundary below the water table. The surface of the model is free. In addition, the water pressure on the slope surface is not considered, so the zero pressure head boundary is applied when the slope surface exhibits transient saturation. And the softening effect on the rock mass under rainfall is ignored. The initial groundwater level of the slope is at h = 20 m, and the value of k_s is set to 5.56 × 10⁻⁶ m/s. The maximum value of the matric suction in the unsaturated zone is 50 kPa. The rainfall intensity is 5 × 10⁻⁵ m/s, the rainfall durations selected is 84 h, and the mechanical parameters of the rock slope are consistent with the reference (Xie et al., 2019). The simulation results shown in Figure 2 are basically consistent with the results get in reference (Xie et al., 2019) and the laws obtained by GEO-Studio, which indicate the correctness of the development program. It can be seen from Figure 2, at the end of 84 h continuous rainfall events, the wetting front depth increased, and the pore water pressure at the slope surface rises to a stable value of zero, and the rock mass in the up-layer of the slope exhibits a transient saturation. As the rainfall continues, the transient saturated zone formed in the shallow layer of the slope expands gradually, and the range of the unsaturated zone decreases.

FIGURE 1

FIGURE 1. Schematic diagram of saturated-unsaturated seepage procedure.

FIGURE 2

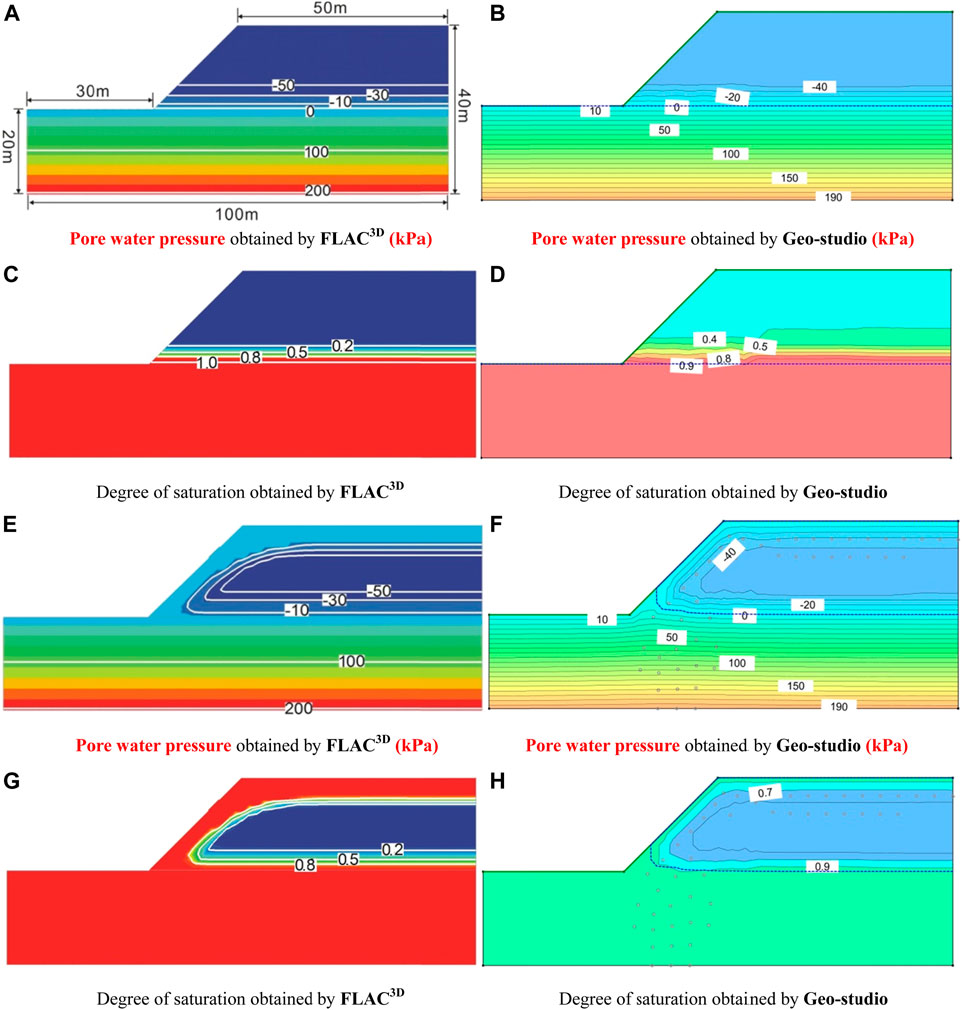
FIGURE 2. Distributions of pore water pressure and saturation under different conditions obtained by using FLAC3D and Geo-studio: (A) Pore water pressure before raining, (B) Pore water pressure before raining, (C) Degree of saturation before raining obtained, (D) Degree of saturation before raining, (E) Pore water pressure after rainfall last 84 h, (F) Pore water pressure after rainfall last 84 h, (G) Degree of saturation after rainfall last 84 h, (H) Degree of saturation after rainfall last 84 h.

Random Field for Hydraulic Conductivity of the Rock Slope

The Non-invasive Stochastic Method for Random Field

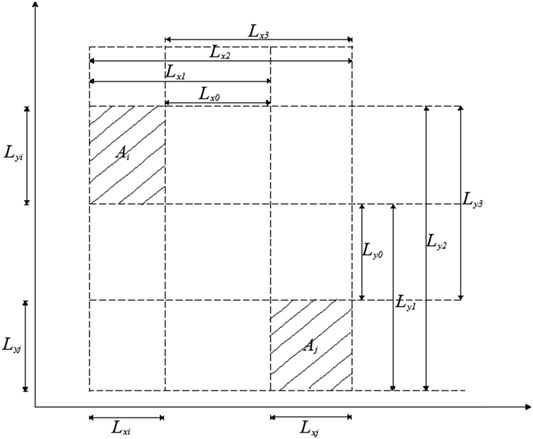
Many scholars have adopted the random field theory in geotechnical engineering to characterize the natural spatial variability of k_s (Cho 2014; Yang et al., 2018; Nguyen and Likitlersuang 2019; Jiang et al., 2020; Zhang et al., 2021). In addition, the non-intrusive stochastic method is more simple and easier to implement than the traditional stochastic finite elements method (such as perturbed stochastic finite element method PSFEM, Neumann stochastic finite element method NSFEM and spectral stochastic finite element method SSFEM) (Wang and Xu, 2014; Zhang et al., 2020). Discretizing the random field and determining the covariance matrix are the core issue of a random field realization. Methods to discretize the random field include the center of discrete method, local average method, interpolation function method, weighted integral method, and random field orthogonal expansion method. The local average method is relatively simple and widely used, and Figure 3 detailed the mathematical method that can be used to discretize the random field. The random field is divided into units through mesh generation, and then the statistical characteristics of these units can be described approximately by the mean, variance, and covariance of stochastic variables (Vanmarcke, 2010).

FIGURE 3

FIGURE 3. Local average random fields.

The elements of the covariance matrix can be got according to Eq. 4, and then the elements of the correlation coefficient matrix M can be obtained according to $\rho \left(E_i,E_j\right)=\frac{Cov\left(E_i,E_j\right)}{\sqrt{D\left(E_i\right)D\left(E_j\right)}}$.

$\begin{array}{l}Cov(E_i,E_j)=\frac{{\sigma }^2}{4A_i{A}_j}{\displaystyle \sum _{k=0}^3{\displaystyle \sum _{l=0}^3{\left(-1\right)}^{k+l}{\left(L_{xk}{L}_{yl}\right)}^2\mathit{\Gamma }\left(L_{xk}{L}_{yl}\right)}}\\ =\frac{{\sigma }^2}{4A_i{A}_j}{\displaystyle \sum _{k=0}^3{\displaystyle \sum _{l=0}^3{\left(-1\right)}^{k+l}{\left(L_{xk}{L}_{yl}\right)}^2\mathit{\Gamma }\left(L_{xk}\right)\mathit{\Gamma }\left(L_{yl}\right)}}\end{array}(4)$

where, $E_i$, $E_j$ mean the ith and jth unit in the random field. $D\left(E_i\right)$, $D\left(E_j\right)$ are the variance of the random variable. $A_i$, $A_j$ represent the area of a rectangular unit at different positions in the x and y-direction of the local average units; the edges of the unit are parallel to the coordinate axis. $L_{xk}$, $L_{yl}(k=\mathrm{0,1,2,3};l=\mathrm{0,1,2,3})$ indicate the distance between the edge of different rectangular units in the x and y-direction, respectively. For example, the distances from the left side of $A_i$ to the left and right sides of $A_j$ are denoted as $L_{x1}$ and $L_{x2}$, respectively; the distances from the right side of $A_i$ to the left and right sides of $A_j$ are denoted as $L_{x0}$ and $L_{x3}$, respectively; and the distances from the upper and lower sides of $A_i$ to the sides of $A_j$ are detailed in Figure 3. $\mathit{\Gamma }\left(L_{xk}\right)$ is the variation reduction function, which can be expressed as the attenuation of the variance of random variable in the local average process of the random field, that is, the relationship between the changing of the local average range and the degree of variation reduction. The variation reduction function can be established by the correlation function which is shown in Eq. 5 as a triangular form.

$\mathit{\Gamma }\left(T\right)=\{\begin{array}{cc}1-\frac{T}{3\theta }& T\le \theta \\ \frac{\theta }{T}\left(1-\frac{T}{3\theta }\right)& T>\theta \end{array}(5)$

where $\theta =\delta$, $\delta$ is the correlation length, the unit is m.

According to Eqs 4, 6, mathematical transformation for the random variable k can be carried out via using Matlab, and then a random field model can be obtained, which has same units with the numerical model.

$\overline{Y}=\mu +\sigma L_{1}Y{L}_2(6)$

where $\overline{Y}$, $\mu$, and $\sigma$ represent the column vector of the random field, the mean value, and the standard deviation of k, respectively. $L_1$ is the conjugate transpose form of the triangular matrix obtained by the Cholesky decomposition of the autocorrelation coefficient matrix. $Y$ is the column vector of the random variable k. $L_2$ is the upper triangular matrix obtained by the Cholesky decomposition of the cross-correlation matrix.

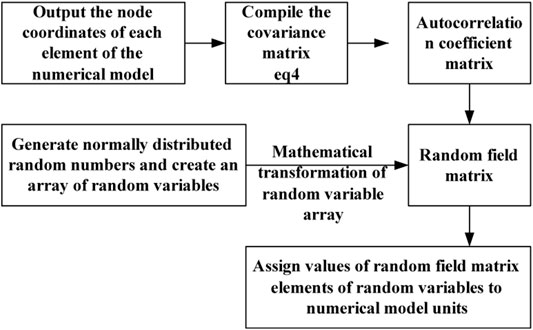
In order to analyze the impact of the variability of k on the seepage characteristic of a rock slope, this paper refers to the non-intrusive stochastic method proposed by Dou et al., 2016, and Figure 4 details the development flow chart of the method. The value of k of the rock slope is smaller than that of the soil, referring to the locale data of an open-pit mine coal rock slope, and the k_s of the rock slope is set to 1 × 10⁻⁴ cm/s. According to the flow chart shown in Figure 4, a k_s random field of the model can be obtained firstly, and then update the value of k in the unsaturated zone according to Figure 3. In addition, considering the weathering effect on the slope surface, which caused a significantly increases in the value of k, take the layer within 2 m from the slope surface as the weathered layer, in which the value of k is magnified by 10 times.

FIGURE 4

FIGURE 4. Schematic diagram of program development for non-intrusive stochastic method.

Simplified Model

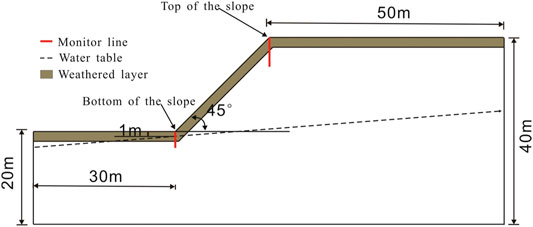
To analyze the seepage and stability of the slope under rainfall infiltration, it is necessary to form a simplified steady-state seepage field as the initial condition for the transient seepage calculation. Figure 5 shows the numerical model. A saturated hydraulic conductivity random field can be generated, when the value of random variable k is assigned to each unit of the model. The displacements of the bottom boundary and the normal displacements of the left and right boundaries of the model are fixed. In addition, the other boundaries are free. And then the initial water table is set, the water table on the left side is at h = 18 m, and that on the right is at h = 25 m. Firstly, carrying out the balance calculation of the initial in situ stress field and the saturated-unsaturated seepage field, and then modifying the unsaturated seepage field, the steady seepage field can be obtained. Secondly, apply constant rainfall intensity on the slope surface.

FIGURE 5

FIGURE 5. Slope geometry and boundary conditions.

The pore water pressure at the model node changed constantly when the rainfall boundary is applied, which means the matric suction of the model is changed. According to Eq. 1, the saturation is a function of pore water pressure, and the value of saturation at the model node can be obtained. In addition, the value of the unit saturation can be calculated. What is more, the pore water pressure at the unit should be modified with its changing value at the model node, and then the value of k at the unit can be acquired according to Eq. 1. So the value of k and saturation should be modified at each time step in calculation. While the rainfall intensity is greater than the infiltration capacity of the slope, the boundary on the slope surface becomes a constant head condition. Finally, according to Eq. 3, the unit cohesion of the model is corrected, and the safety factor of the rock slope under rainfall infiltration can be got by using the strength reduction method. The initial safety factor of the slope is 3.24, indicating that the rock slope is safety. The mechanical parameters E, μ, c^’、 ${\phi }^{\text{'}}$, ${\sigma }_t$, $\rho$ and k_s are determined from the laboratory test results of rock slope in an open-pit mine in China, which has ceased excavating. Other parameters are determined combing previous studies (Xie et al., 2019). The mechanical parameters of rock mass are detailed in Table 1.

TABLE 1

TABLE 1. Mechanics parameters of the model.

Initial Conditions

Based on the non-invasive method and the simplified model, the realization of the random field is shown in Figure 6A, the variation coefficient of k_s is set to 0.45, the horizontal correlation length is 60 m, and the vertical is 6 m. The maximum value of the matric suction is 50 kPa. Different colors in Figure 6A represent different values of k, the darker the color, the smaller the value of k. The value of k distributed randomly ranges from 1.0689 × 10⁻¹² to 1.127 × 10⁻⁹ m²/Pa^.s (it is necessary to convert the unit of k from m/s to m²/Pa^.s for calculation) (Liu et al., 2020). There is a nonlinear relationship between the value of k and the matric suction of unit in the unsaturated zone: the larger the matric suction, the smaller the value of k. The value of k of the unit in unsaturated zone is corrected according to Eq. 1. The value of k decreases rapidly with the increase of matric suction, so the value in the unsaturated zone is obviously smaller than that in the saturated zone (except for the superficial weathered layer). Figures 6B–D show the initial density, the pore water pressure, and the saturation distribution of the rock slope, respectively. Density, pore water pressure, and saturation have undergone major changes above and below the water table. The zero pore water pressure line is defined as the water table. The rock below the groundwater level is saturated, and the density and saturation of the rock mass are large, and the pore water pressure is positive. But, the rock above the groundwater level is unsaturated, where the density, the saturation, and the negative pore water pressure all transition to a minimum value rapidly.

FIGURE 6

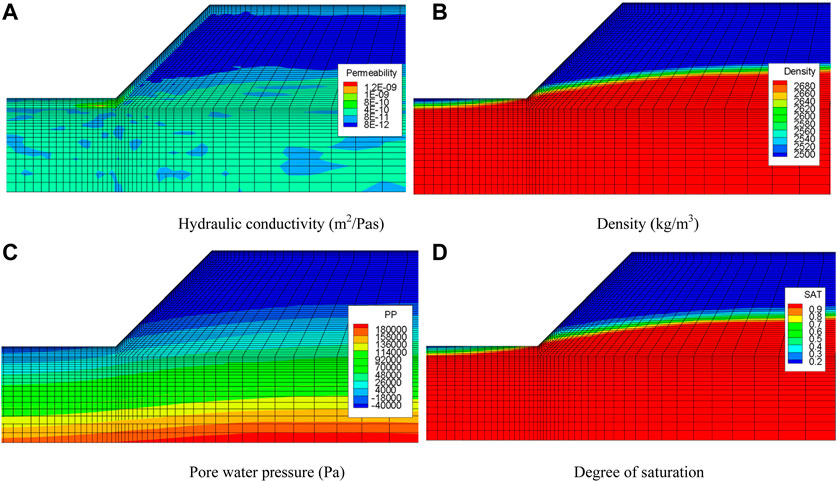
FIGURE 6. Initial state of seepage random field of rock slope: (A) Hydraulic conductivity, (B) Density, (C) Pore water pressure, (D) Degree of saturation.

Rainfall Infiltration Characteristics and Stability of the Rock Slope

Influence of Rainfall Duration

Figures 7A–D show the pore water pressure inside the rock slope with the rainfall last different times, 12, 24, 48 and 72 h, when the rainfall intensity is 7.2 mm/h. Figures 7E–H show the degree of saturation. It can be seen from Figure 7 that rainfall events have an important impact on the unsaturated zone of the slope. The negative pore water pressure in the unsaturated zone changes greatly with the development of rainfall duration. With the extension of the rainfall, the more water penetrates into the slope, the greater the impact on the negative pore water pressure. As the rainfall intensity exceeds the infiltration capacity of the soil, only a portion of it can infiltrate while the remaining quantity runoff the slope surface at the beginning of the rainfall, and the surface of the slope enters a transient saturation rapidly. Under the action of gravity and hydraulic gradient, rainwater moves continuously from the slope surface to the inside of the slope, and the infiltration depth will first increase rapidly and then slowly, and the range of transient saturation expands continuously. The transient saturation connects with the water table at the bottom of the slope, and then raises the water level. The unsaturated zone, between the top of the slope and the water table, shrinks gradually, and the negative pore water pressure of the rock mass in the unsaturated zone increase continuously, while the matric suction decreases. Figures 7E–H show that the changes of saturation is basically consistent with that of pore water pressure of the rock slope suffering continuous rainfall.

FIGURE 7

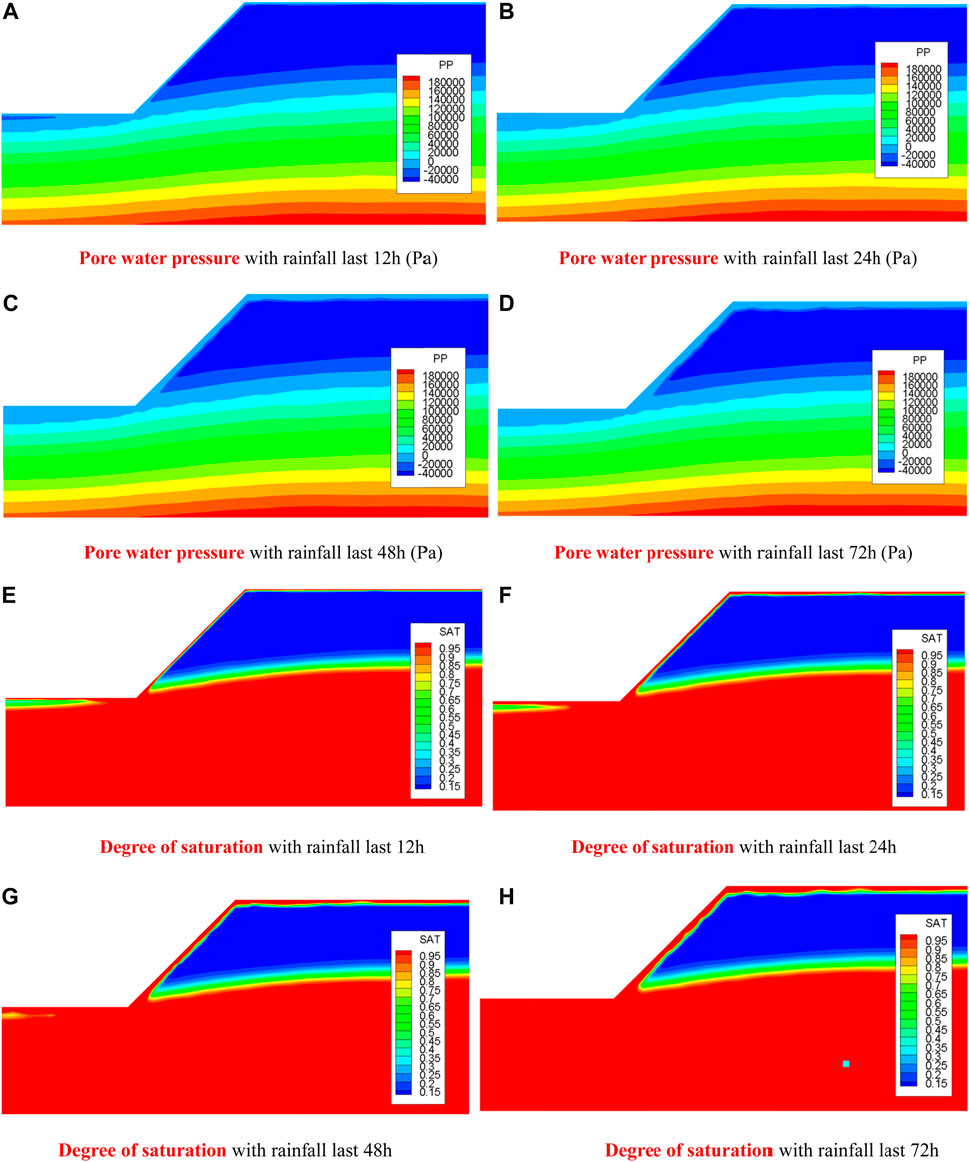
FIGURE 7. Pore water pressure and saturation under different rainfall duration: (A) Pore water pressure with rainfall last 12h (Pa), (B) Pore water pressure with rainfall last 24 h (Pa), (C) Pore water pressure with rainfall last 48 h (Pa), (D) Pore water pressure with rainfall last 72 h (Pa), (E) Degree of saturation with rainfall last 12 h, (F) Degree of saturation with rainfall last 24 h, (G) Degree of saturation with rainfall last 48 h, (H) Degree of saturation with rainfall last 72 h.

In order to analyze the rainfall infiltration in the shallow layer of the slope, monitoring points within 10 and 5 m away from the slope surface at the top and bottom of the slope are selected, and the location is detailed in Figure 5 and the negative pore water pressure and the degree of saturation at the monitoring points are compared. Figures 8A–D show the curves of pore water pressure and saturation within different distances to the slope surface at the top and bottom of the slope at the end of different continuous rainfall events. With the distance away from the slope surface, the rainfall effect on the slope decreases gradually until there is no change. With the development of rainfall duration, negative pore water pressure and saturation have similar changes in time and spatial. The negative pore water pressure increases gradually from −50 kPa to approximately 0 kPa, and the saturation changes from 0.08 to approximately 1, which is a dynamic process. The negative pore water pressure on the slope surface and the points near the surface rises sharply and reaches the peak value 0 kPa earliest. But with the distance away from the slope surface, the rising trend slows down gradually. The rainfall infiltration has a certain hysteresis. The vertical distance from the surface at the slope root to the water table is only 1 m, and considering the impact of rainfall infiltration and surface runoff, the transient saturation zone at the slope root connected with the groundwater soon after the rainfall begins, and the groundwater level raises quickly. The transient saturation zone of the upper layer expanded gradually with the continuous rainfall, and the infiltration depth at the end of 24, 48, and 72 h rainfall duration are 1.15, 1.64, and 2.24 m in sequence, and the relationship between the infiltration depth and the rainfall duration is shown in Figure 8E.

FIGURE 8

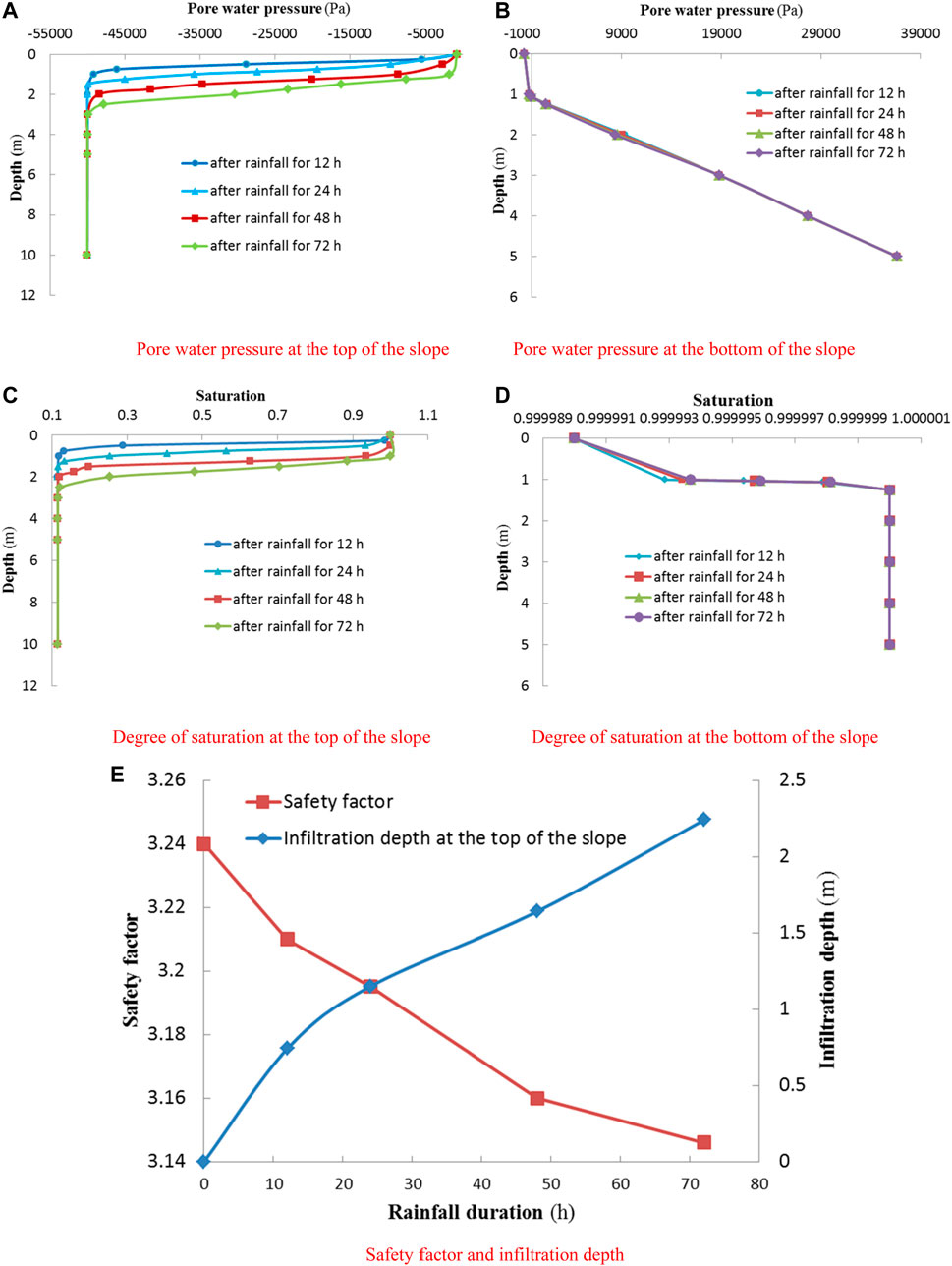
FIGURE 8. The seepage and stability of the slope with the development of rainfall duration: (A) Pore water pressure at the top of the slope, (B) Pore water pressure at the bottom of the slope, (C) Degree of saturation at the top of the slope, (D) Degree of saturation at the bottom of the slope, (E) Safety factor and infiltration depth.

The transient saturation caused by rainfall events has an important impact on the safety and stability of the slope. The safety factor is an important parameter for evaluating the stability of a slope: the greater the safety factor, the more safety the slope (Zhang et al., 2021). The safety factor of the slope changes with the development of rainfall duration, and the changing rules are detailed in Figure 8E. It can be seen from the figure that the safety factor at the initial stage of rainfall is relatively large, and it decreases linearly as the rainfall continues. The safety factors are 3.195, 3.160, and 3.146 at the end of 24, 48, and 72 h rainfall duration, respectively. As the rainwater infiltrates into the slope, the internal water content of the slope changes, and a transient saturation zone appears at the shallow layer of the slope, which increases the weight of the rock mass, reduces the matric suction, and deteriorates the shear strength of the slope. Eventually, the anti-sliding ability of the slope is reduced, and its safety factor is reduced.

Influence of Rainfall Intensity

Based on the same seepage random field conditions, the impact of rainfall intensity on the rainfall infiltration process of the slope is calculated. Considering four different rainfall intensities, with the rainfall last 3 days, the pore water pressure and the degree of saturation of the unsaturated zone and the slope stability are analyzed. Referring to the rainfall classification standards issued by the National Meteorological department, the rainfall intensities considered for analysis are 1.8 mm/h (heavy rain), 3.6 mm/h (torrential rain), 7.2 mm/h (downpour), and 14.4 mm/h (heavy downpour).

Figures 9A–D show the negative pore water pressure of the rock slope at the end of 72 h continuous rainfall under different rainfall intensities, 1.8, 3.6, 7.2, and 14.4 mm/h. Figures 9E–H show the saturation. It can be seen from Figure 9 that, at the end of 72 h continuous rainfall under different rainfall intensities, a transient saturated zone can be formed in the shallow layer of the slope, and it will be connected with the initial groundwater at the slope root, and then raising the groundwater level. The pore water pressure and saturation in the transient saturation zone change greatly with the rainfall intensity. The greater the rainfall intensity, the more water penetrates into the slope, and the seepage field of the slope is affected more significantly. With the rainfall intensity increases, the range of the transient saturated zone enlarged, and the depth of infiltration becomes deeper, which means the range of the unsaturated zone decreased.

FIGURE 9

FIGURE 9. Pore water pressure and saturation under different rainfall intensity: (A) Pore water pressure, (B) Pore water pressure, (C) Pore water pressure, (D) Pore water pressure, (E) Degree of saturation, (F) Degree of saturation, (G) Degree of saturation, (H) Degree of saturation.

Figures 10A–D show the pore water pressure and saturation at the top and bottom of the slope under different rainfall intensities. The impact of rainfall intensity on the seepage field weakened gradually with the distance away from the slope surface, and the infiltration depth was within 1.31–2.6 m. As the rainfall intensity changes, the negative pore water pressure and saturation exhibits similar characteristic in spatial. The negative pore water pressure and saturation at the slope surface and the points close to the surface increased sharply, and are closer to the peak value. But its rate of increase decrease gradually. Increasing the rainfall intensity will increase the negative pore water pressure and saturation at one point, while the rainfall intensity reaches the downpour level, the change extend will decrease because of the limitation of infiltration capacity. At the end of 72 h continuous rainfall, under different rainfall intensities, heavy rain, torrential rain, downpour, and heavy downpour, the maximum infiltration depth is 1.31, 1.66, 2.31, and 2.6 m, respectively.

FIGURE 10

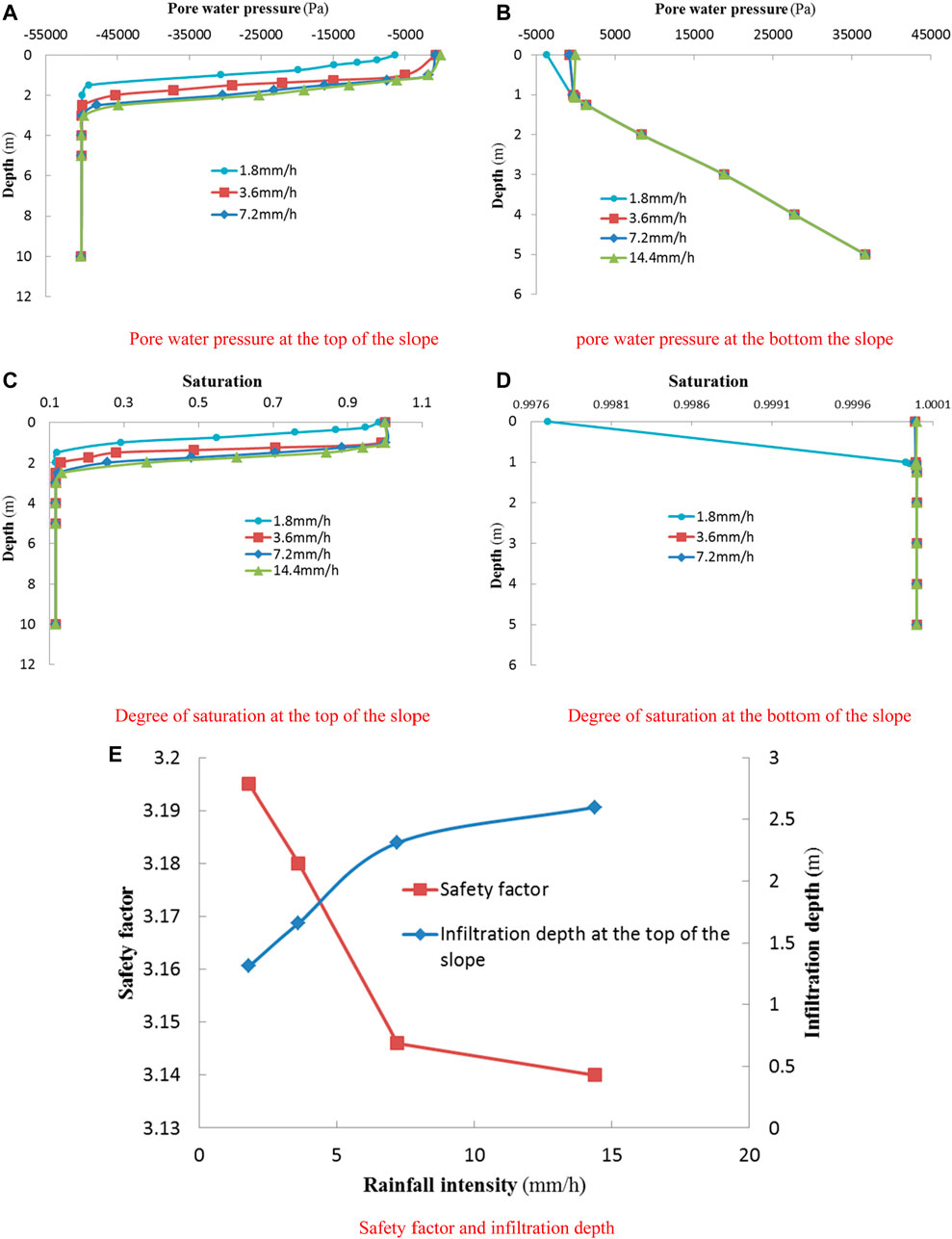
FIGURE 10. Distribution of pore water pressure and degree of saturation under different rainfall intensities: (A) Pore water pressure at the top of the slope, (B) Pore water pressure at the bottom of the slope, (C) Degree of saturation at the top of the slope, (D) Degree of saturation at the bottom of the slope, (E) Safety factor and infiltration depth.

Figure 10E shows the relationship between the slope safety factor and the rainfall intensity. It can be seen from Figure 10E that when the rainfall intensity is heavy rain, the safety factor is relatively large. When the rainfall intensity is heavy rain, torrential rain, downpour, and heavy downpour, the safety factors of the slope are 3.195, 3.180, 3.146, and 3.140, respectively. With the increases of rainfall intensity, the volume of water infiltrates into the slope increased. Then, the weight of the transient saturation zone becomes larger, and the impact on the matric suction of the rock and soil becomes greater. The infiltration depth is rapidly increased, so the safety factor of the slope is rapidly reduced. While the rainfall intensity reaches the torrential level or above, that is, it overcomes the infiltration capacity of the slope, the rainwater cannot fully penetrates into the slope, and part of the water will runoff the slope surface. Therefore, the rising rate of the infiltration depth and the rate of decline of the safety factor will slow down.

Influence of the Variability of Hydraulic Conductivity

The physical and mechanical properties of rock and soil of the rock slope has obvious natural spatial variability, and the sensitivity analysis method (Jiang et al., 2014) can be used to study the influence of variability of rock parameters on the seepage and stability of the slope. Jiang et al., 2020 proposed that although the mechanical parameters of soil exhibit variability, there also exist certain correlations between different points of the model. For example, the horizontal correlation length and the vertical represent the fluctuation range of the correlation of rock mass in the horizontal and vertical directions, respectively. The main parameters reflecting the variability of k include the variation coefficient, the horizontal correlation length, and the vertical. The single factor sensitivity analysis method is used to deal with the above factors. A base case is established, where the rainfall intensity is set to 7.2 mm/h, rainfall duration is 72 h, and the variation coefficient and the horizontal and the vertical correlation length of k is 0.45, 60, and 6 m, respectively. In addition, in accordance with the statistics on the variability and the autocorrelation length of geotechnical parameters at China and abroad, the horizontal correlation length ranges from 10 to 75 m, while the vertical is significantly smaller and ranges from 0.1 to 8 m (Jiang et al., 2014). So comparison cases are established, and the calculation conditions are detailed in Table 2, where x represents the value of the rainfall intensity, rainfall duration, variation coefficient of k, and horizontal or vertical correlation length in a comparison case, and x* represents the value of parameters in the base case; a total of 15 numerical simulations are carried out. According to the numerical results of different cases, the relationship between impact factors and infiltration depth or safety factor can be obtained, which are shown in Figure 11. Taking x/x* as the X-axis, and taking F/F* as the Y-axis, F represents the infiltration depth or safety factor of a comparison case, and F* represents the corresponding results of the base case. The absolute value of the curve slope is defined as the sensitivity coefficient, which reflects the influence degree of various factors on the seepage of the model (Wu et al., 2010). The larger the sensitivity coefficient is, the greater the impact of the factor on the seepage of the slope.

TABLE 2

TABLE 2. Ratios setting in different calculation conditions.

FIGURE 11

FIGURE 11. Sensitivity comparison of different impact factors: (A) Infiltration depth, (B) Safety factor.

It can be seen from Figure 11 that the effects of various factors on the slope seepage and stability are significantly different. The increase in rainfall intensity, rainfall duration, and variation coefficient can lead to an increase in the infiltration depth, while an increase in horizontal and/or vertical length will result in a reduction in the infiltration depth. The impact of various factors on the safety factor of the slope exhibit a same trend, and increasing the value of the influence factor will cause decrease of the safety factor. When the rainfall intensity is smaller than the infiltration capacity of the rock and soil, the slope of the curve referring to the rainfall intensity and rainfall duration is larger than that of the variability of k_s, that is, the infiltration process of the rock slope is more sensitive to the rainfall intensity and/or duration. While the rainfall intensity reaches the downpour level or above, the impact degree of rainfall events on the infiltration depth and safety factor is slowed down, even lower than the impact of the variability of k. This is mainly due to the high rainfall intensity, which results in the water forms runoff on the slope surface, and then the impact of rainfall intensity on the seepage and stability of the slope is alleviated. Considering the variability of k, the slope is most affected by the variation coefficient of k, followed by the vertical correlation distance, while the least sensitive to the horizontal correlation length, which is mainly related to the geological sedimentation history of the rock layer. Figure 12 shows the sensitivity of the slope to various factors, and the order of the sensitivity is: rainfall duration, variation coefficient of k, rainfall intensity, vertical correlation length of k, and horizontal correlation length.

FIGURE 12

FIGURE 12. Sensitivity coefficient of infiltration depth and safety factor to different parameters.

Conclusion

1) Based on the unsaturated theory, a program for the saturated-unsaturated seepage of a rock slope under rainfall infiltration is established. Comparing the results of this paper with previous research and results obtained via Geo-studio, the correctness of the development program is verified.

2) The spatial variability of saturated hydraulic conductivity (k_s) has great impact on rainfall infiltration process. According to the local average random field theory, the spatial variability of k_s can be described with parameters such as variation coefficient and correlation length. The variance reduction function is used to obtain the connection between the variability of points and space. The non-invasive realization of the random field k_s of rock mass is carried out by adopting MATLAB; on this basis, the numerical simulation of the seepage random field of the slope suffering rainfall is carried out. The dynamic seepage characteristic is obtained with considering both the variability of k_s and the rainfall infiltration.

3) Rainfall infiltration has a great impact on the shallow layer of the rock slope, and the infiltration process leads to an increase in the value of pore water pressure and the degree of saturation in the unsaturated zone of the slope. A transient saturated zone appears in the upper layer of the slope, and it connects with the initial groundwater level at the slope root firstly. With the increasing of rainfall duration and/or rainfall intensity, both the negative pore water pressure and the degree of saturation in the transient saturation zone all increased. The infiltration depth is positively associated with the rainfall too; while the rainfall intensity reaches the downpour level, the increase rate of the infiltration depth slows down.

4) Rainfall infiltration is a dynamic process from surface to inside of the slope, from shallow to deep. Water penetrates into the slope gradually with the continuous of the rainfall. This process increases the weight of the shallow layer of the slope and causes the reduction of the matric suction, which makes the shear strength of the slope reduced. Then the safety factor of the slope decreases with the increase of rainfall duration, rainfall intensity, variation coefficient, and/or relative length. When the rainfall intensity reaches the downpour level, the deceleration rate slows down.

5) Considering the variability of the k_s, the seepage of the slope is most sensitive to the variation coefficient, followed by the vertical correlation length, while it is least sensitive to the horizontal length. Compared with the variability of the k_s, the seepage field is more sensitive to rainfall duration and rainfall intensity. However, when the rainfall intensity reaches the downpour level, the impact of the variation coefficient of k_s is greater than the rainfall intensity. For practical engineering, it is necessary to consider both the spatial variability of saturated hydraulic conductivity and the unsaturated seepage characteristics of rock slopes.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

QZ contributed significantly to analysis and manuscript preparation; LW helped perform the analysis with constructive discussions; HZ performed the data analyses and wrote the manuscript.

Funding

This study was supported by the National Key R&D Program of China (grant no. 2017YFC1503102), National Natural Science Foundation of China (grant no. 51504124), and Scientific Research Project of Education Department of Liaoning Province (grant no. LJKZ0335).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alonso, E., Gens, A., Lloret, A., and Delahaye, C. (1995). “Effect of Rain Infiltration on the Stability of Slopes,” in Proceedings of the International Conference on Unsaturated Soils, Paris, 241–249.

Google Scholar

Cai, G., Li, M., Han, B., Di, K., Liu, Q., and Li, J. (2020). Numerical Analysis of Unsaturated Soil Slopes Under Rainfall Infiltration Based on the Modified Glasgow Coupled Model. Adv. Civil Eng. 2020, 1–13. doi:10.1155/2020/8865179

CrossRef Full Text | Google Scholar

Chen, J., Liu, P., Xu, Q., and Li, J. (2020). Seismic Analysis of Hardfill Dams Considering Spatial Variability of Material Parameters. Eng. Structures 211, 110439. doi:10.1016/j.engstruct.2020.110439

CrossRef Full Text | Google Scholar

Cho, S. E., and Lee, S. R. (2001). Instability of Unsaturated Soil Slopes Due to Infiltration. Comput. Geotechnics 28 (3), 185–208. doi:10.1016/s0266-352x(00)00027-6

CrossRef Full Text | Google Scholar

Cho, S. E. (2014). Probabilistic Stability Analysis of Rainfall-Induced Landslides Considering Spatial Variability of Permeability. Eng. Geology. 171, 11–20. doi:10.1016/j.enggeo.2013.12.015

CrossRef Full Text | Google Scholar

Chu-Agor, M. L., Fox, G. A., Cancienne, R. M., and Wilson, G. V. (2008). Seepage Caused Tension Failures and Erosion Undercutting of Hill Slopes. J. Hydrol. 359 (3-4), 247–259. doi:10.1016/j.jhydrol.2008.07.005

CrossRef Full Text | Google Scholar

Collins, B. D., and Znidarcic, D. (2004). Stability Analyses of Rainfall Induced Landslides. J. Geotech. Geoenviron. Eng. 130 (4), 362–372. doi:10.1061/(asce)1090-0241(2004)130:4(362)

CrossRef Full Text | Google Scholar

Dou, H-Q., Han, T-C., and Gong, X-N. (2016). Reliability Analysis of Slope Stability Considering Variability of Soil Saturated Hydraulic Conductivity under Rainfall Infiltration. Rock Soil Mech. 37 (4), 1144–1152. doi:10.16285/j.rsm.2016.04.029

CrossRef Full Text | Google Scholar

Fredlund, D. G., and Rahardio, H. (19971997). Mechanics of Unsaturated Soils [M]. Translated by Chen Zhongyi. Beijing: China Construction Industry Press.

Google Scholar

Fu, H-Y., Wu, Y., He, Z-M., and Shi, Z-N. (2014). Embankment Slope Stability Safety Factor Variation of Coarse Grained Soil under Continuous Rainfall. J. Changsha Univ. Sci. Technol. (Natural Science) (2), 48–53. doi:10.3969/j.issn.1672-9331.2014.02.009

CrossRef Full Text | Google Scholar

Guo, X., Zhao, C., and Yu, W. (2005). Stability Analysis of Unsaturated Soil Slope and its Progress. China Saf. Sci. J. 15 (1), 14–18. doi:10.3969/j.issn.1003-3033.2005.01.004

CrossRef Full Text | Google Scholar

Hamrouni, A., Dias, D., and Sbartai, B. (2020). Soil Spatial Variability Impact on the Behavior of a Reinforced Earth Wall. Front. Struct. Civil Eng. 14, 518–531. doi:10.1007/s11709-020-0611-x

CrossRef Full Text | Google Scholar

Han, T., Liu, L., and Li, G. (2020). The Influence of Horizontal Variability of Hydraulic Conductivity on Slope Stability Under Heavy Rainfall. Water 12 (9), 2567. doi:10.3390/w12092567

CrossRef Full Text | Google Scholar

Horton, R. E. (1939). Analysis of Runoff-Plat Experiments with Varying Infiltration-Capacity. Trans. AGU 20 (4), 693. doi:10.1029/tr020i004p00693

CrossRef Full Text | Google Scholar

Hu, J., Zhang, J., Chen, H., Wang, H., and Zheng, W. (2017). Stability of Completely Decomposed Granite Slopes under Intense Rainfall Infiltration Based on the Random Field Theory. South. Energ. Construction 4 (03), 107–114. doi:10.16516/j.gedi.issn2095-8676.2017.03.020

CrossRef Full Text | Google Scholar

Huang, M., and Jia, C. Q. (2007). Strength Reduction FEM in Stability Analysis of Soil Slopes Subjected to Transient Unsaturated Seepage. Chin. J. Rock Mech. Eng. 36 (1-2), 93–101. doi:10.1016/j.compgeo.2008.03.006

CrossRef Full Text | Google Scholar

Huang, R., and Qi, G. (2002). The Effect of Unsaturated Soil Suction on Slope Stability. J. Eng. Geology. 10 (4), 343–348. doi:10.3969/j.issn.1004-9665.2002.04.002

CrossRef Full Text | Google Scholar

Jiang, S., Li, D., and Zhou, C. (2014). Slope Reliability Analysis Considering Effect of Autocorrelation Functions. China Saf. Sci. J. 36 (03), 508–518. doi:10.11779/CJGE201403014

CrossRef Full Text | Google Scholar

Jiang, S.-H., Liu, X., and Huang, J. (2020). Non-intrusive Reliability Analysis of Unsaturated Embankment Slopes Accounting for Spatial Variabilities of Soil Hydraulic and Shear Strength Parameters. Eng. Comput. doi:10.1007/s00366-020-01108-6

CrossRef Full Text | Google Scholar

Jiang, Z., Zeng, L., Fu, H., and Xiong, X. (2014). Dynamic Stability Analysis of Soft Rock Slope Due to Extremely Prolonged Rainfall[J]. China J. Highw. Transport 27 (2), 27–34. doi:10.3969/j.issn.1001-7372.2014.02.004

CrossRef Full Text | Google Scholar

Jiang, Z-M., Xiao-hu, X., and Zeng, L. (2014). Unsaturated Seepage Analysis of Slope Under Rainfall Condition Based on FLAC3D. Rock Soil Mech. 35 (03), 855–861. doi:10.16285/j.rsm.2014.03.016

CrossRef Full Text | Google Scholar

Li, Y., Wu, J., and Kun, L. (2012). Saturated-unsaturated Seepage Analysis Based on FLAC3D. Rock Soil Mech. 33 (02), 617–622. doi:10.16285/j.rsm.2012.02.001

CrossRef Full Text | Google Scholar

Liu, W., Zhang, Z., Fan, J., Jiang, D., Li, Z., and Chen, J. (2020). Research on Gas Leakage and Collapse in the Cavern Roof of Underground Natural Gas Storage in Thinly Bedded Salt Rocks. J. Energ. Storage 31, 101669. doi:10.1016/j.est.2020.101669

CrossRef Full Text | Google Scholar

Liu, X., and Wang, Y. (2021). Probabilistic Simulation of Entire Process of Rainfall-Induced Landslides Using Random Finite Element and Material Point Methods with Hydro-Mechanical Coupling. Comput. Geotechnics 132, 103989. doi:10.1016/j.compgeo.2020.103989

CrossRef Full Text | Google Scholar

Liu, X., and Xu, M. (2017). The Unsaturated Hydromechanical Coupling Model of Rock Slope Considering Rainfall Infiltration Using DDA. Geofluids 2017, 1–15. doi:10.1155/2017/1513421

CrossRef Full Text | Google Scholar

Morbidelli, R., Corradini, C., Saltalippi, C., Flammini, A., Dari, J., and Govindaraju, R. (2018). Rainfall Infiltration Modeling: A Review. Water 10 (12), 1873. doi:10.3390/w10121873

CrossRef Full Text | Google Scholar

Nguyen, T. S., and Likitlersuang, S. (2019). Reliability Analysis of Unsaturated Soil Slope Stability Under Infiltration Considering Hydraulic and Shear Strength Parameters. Bull. Eng. Geology. Environ. 78, 5727–5743. doi:10.1007/s10064-019-01513-2

CrossRef Full Text | Google Scholar

Oh, W. T., and Vanapalli, S. K. (2010). Influence of Rain Infiltration on the Stability of Compacted Soil Slopes. Comput. Geotechnics 37 (5), 649–657. doi:10.1016/j.compgeo.2010.04.003

CrossRef Full Text | Google Scholar

Pan, Y., Wu, G., Zhao, Z., and He, L. (2020). Analysis of Rock Slope Stability Under Rainfall Conditions Considering the Water-Induced Weakening of Rock. Comput. Geotechnics 128, 103806. doi:10.1016/j.compgeo.2020.103806

CrossRef Full Text | Google Scholar

Qin, G., Huang, R., Su, B., Hu, Y., and Zhan, M. (2003). Numeric Simulation on Rainfall Infiltration on Rock Slope. Chin. J. Rock Mech. Eng. 22 (4), 625–629. doi:10.3321/j.issn.1000-6915.2003.04.023

CrossRef Full Text | Google Scholar

Qin, X., Liu, D., Song, Q., Wu, Y., Zhang, Y., and Ye, Y. (2017). Reliability Analysis of Bedrock Laminar Slope Stability Considering Variability of Saturated Hydraulic Conductivity of Soil Under Heavy Rainfall. Chin. J. Geotechnical Eng. 39 (6), 1065–1073. doi:10.11779/CJGE201706012

CrossRef Full Text | Google Scholar

Rong, G., Zhang, W., and Zhou, C-B. (2005). Numerical Analysis of Saturated-Unsaturated Seepage Problem of Rock Slope Under Rainfall Infiltration. Rock Soil Mech. 26 (10), 1545–1550. doi:10.16285/j.rsm.2005.10.005

CrossRef Full Text | Google Scholar

Santoso, A. M., Phoon, K. K., and Quek, S. T. (2011). Effects of Soil Spatial Variability on Rainfall-Induced Landslides. Comput. Structures 89 (11-12), 893–900. doi:10.1016/j.compstruc.2011.02.016

CrossRef Full Text | Google Scholar

Van Genuchten, M. T. (1980). A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. America J. 44 (5), 892–898. doi:10.2136/sssaj1980.03615995004400050002x

CrossRef Full Text | Google Scholar

Vanmarcke, E. H. (2010). Random Fields: Analysis and Synthesis (Revised and Expanded). New Edn. Singapore: World Scientific Publishing Co. Pte. Ltd.

Google Scholar

Wang, L., and Xu, Q. (2014). Analysis of Three Dimensional Random Seepage Field Based on Monte Carlo Stochastic Finite Element Method. Rock Soil Mech. 35 (01), 287–292. doi:10.16285/j.rsm.2014.01.002

CrossRef Full Text | Google Scholar

Wang, L., Wu, C., Li, Y., Liu, H., Zhang, W., and Chen, X. (2019). Probabilistic Risk Assessment of Unsaturated Slope Failure Considering Spatial Variability of Hydraulic Parameters. KSCE J. Civ Eng. 23 (12), 5032–5040. doi:10.1007/s12205-019-0884-6

CrossRef Full Text | Google Scholar

Wu, Z., Wang, S., Tang, H., and Ge, X. (2010). A New Sensitivity Analysis Approach for Slope Stability-Reliability Analysis Method. Chin. J. Rock Mech. Eng. 29 (10), 2050–2055.

Google Scholar

Xie, Q., Tian, D-L., Jin-hui, L., Jian-hua, Z., and Zhi-bin, Z. (2019). Simulation of Seepage Flow on Soil Slope and Special Stress-Correction Technique. Rock Soil Mech. 40 (03), 879–892. doi:10.16285/j.rsm.2017.1827

CrossRef Full Text | Google Scholar

Xiong, Z. A., Wei, L., Jiang, D., Qiao, W., Liu, E., Zhang, F., et al. (2020). Investigation on the Influences of Interlayer Contents on Stability and Usability of Energy Storage Caverns in Bedded Rock Salt. Energy 231, 120968. doi:10.1016/j.energy.2021.120968

CrossRef Full Text | Google Scholar

Xu, H., Zhu, Y., Cai, Y., and Zhu, F. (2005). Stability Analysis of Unsaturated Soil Slopes Under Rainfall Infiltration. Rock Soil Mech. 26 (12), 1957–1962. doi:10.3969/j.issn.1000-7598.2005.12.019

CrossRef Full Text | Google Scholar

Yang, H.-Q., Zhang, L., Xue, J., Zhang, J., and Li, X. (2018). Unsaturated Soil Slope Characterization with Karhunen–Loève and Polynomial Chaos via Bayesian Approach. Eng. Comput. 35, 337–350. doi:10.1007/s00366-018-0610-x

CrossRef Full Text | Google Scholar

Zhang, G., Lu, G., Xia, C., Wu, L., Xu, Z., Bai, Y., et al. (2021). A Sensitivity Analysis of the Anisotropy of Hydraulic Conductivity to the Seepage, Deformation and Stability of Anti-dipping Layered Rock Slopes: A Case Study of the Pulang Area in Southwestern China. Geotechnical Geol. Eng. doi:10.1007/s10706-021-01910-z

CrossRef Full Text | Google Scholar

Zhang, Q., Wang, L., Zhang, H., Ran, L., and Guo, z. (2020). Non-intrusive Random Analysis on Reliability of Weak Layers Bench Slope. J. Saf. Sci. Technol. 16 (11), 33–39. doi:10.11731/j.issn.1673-193x.2020.11.005

CrossRef Full Text | Google Scholar

Zhang, W.-G., Meng, F.-S., Chen, F.-Y., and Liu, H.-L. (2021). Effects of Spatial Variability of Weak Layer and Seismic Randomness on Rock Slope Stability and Reliability Analysis. Soil Dyn. Earthquake Eng. 146 (2021), 106735. doi:10.1016/j.soildyn.2021.106735

CrossRef Full Text | Google Scholar