- 1School of Civil Engineering, Southeast University, Nanjing, China
- 2Department of Civil Engineering, Monash University, Clayton, VIC, Australia
- 3China Construction Eighth Engineering Division Corp., LTD, Shanghai, China
The size effect on mechanical behaviors of rock materials has been a challenging topic. The previous research is mainly to study the relationship between known large-scale models and representative element volumes. However, only limited scale models can be obtained in situ or laboratory in many cases, so tests or simulations of mechanical response behaviors of large-scale models cannot be carried out. In order to obtain large-scale models, this paper proposes a multi-scale enlarged digital modeling method to synthesize granite models based on texture self-similarity. The representational ability of synthetic granite is analyzed by using mathematical statistics and finite-difference numerical method. The results show that synthetic granite can characterize the natural rock well in terms of texture morphology, geometric characteristics, and mechanical behaviors. Then, the size effect on mechanical behaviors of intact granite is performed based on an enlarged digital model. The results show that the uniaxial compressive strength of intact granite increases with the increase of model size. In addition, the relationship between heterogeneity and homogeneity is established at different unit scales by using the synthetic digital granite model. The enlarged digital rock model has great potential in studying size effects with rock heterogeneity.
1 Introduction
Rock is a kind of natural geological mass after long-term geological movement and weathering. Rock engineering, such as tunnel engineering and slope engineering, usually has a large-scale, so the in-situ test is expensive and difficult to carry out. The rock mechanics test in the laboratory is at the scale of cm-level, which can obtain many basic theories of rock mechanics. However, these theories are difficult to generalize to rock engineering because the physical properties of rocks have a strong size effect. Therefore, it is of great significance to study the influence of rock size on applying laboratory theories in the engineering field.
Heterogeneity and end friction effect are two main factors leading to the size effect of rocks (Li et al., 2020). Rock heterogeneity includes structural and material heterogeneity. In terms of structural heterogeneity, rock structure mainly includes pore-fracture defects and grain boundaries at various scales, which greatly influence the size effect of rocks. Generally, these defects and boundaries were described and expressed by fracture criteria or constitutive equations (Shang et al., 2018; Li et al., 2021; Pan et al., 2021).
The formation of rock material heterogeneity is mainly due to the random distribution of mineral grains with different physical properties. Material heterogeneity results in a strong size effect of rock materials. Shirole et al. (2020) analyzed the heterogeneous mechanical responses of sandstone and granite under different mineral grain sizes by using 2D digital image correlation. Kang and Li (2021) studied the cracking mechanism of granite with different grain sizes under different temperature loads. The research on the heterogeneity of rock materials mainly used the numerical simulation method (Chen et al., 2004; Mahabadi et al., 2012; Tan et al., 2016; Li et al., 2018; Yu et al., 2018). However, numerical models in the numerical simulation are mainly random models which have low representational ability.
Numerical models can grasp some characteristics of rock structure to analyze the size effect on mechanical behaviors of heterogeneous rock, but the model has a low representational ability to describe natural rocks (Peng et al., 2017; Wang and Cai, 2019). Because the numerical model mainly keeps the statistic law (such as the proportion of different mineral grains), it has a weak description of grain morphology and Mosaic relationship (an arrangement mode that is no overlaps and gaps between grains) of natural rocks.
The size effect under heterogeneous conditions for a single sample is studied by using the representative element volume. The representative element volume method is usually based on the known large-scale model, and its partial small-scale model is used to analyze the mechanical behaviors. Due to the opacity of rock, only the small-scale rock model can be obtained using CT, but the whole large-scale model of rock is difficult to obtain. Therefore, the relationship between representative element volume and full-scale rock cannot be established. In this case, if the large-scale information can be deduced from the limited sample, the light calculation methods from full-scale to small-scale and the refinement models from small-scale to large-scale can be constructed. It will be more enlightening to study the size effect.
For digital rock modeling, Xiao et al. (2021b) used the texture synthesis method to generate multiple heterogeneous digital rock samples from a single sample to analyze the mechanical and deformation properties. The texture synthesis method can also be referred to in the literature (Wei and Levoy, 2000; Efros and Freeman, 2001; Kwatra et al., 2005). Xiao et al. (2021a) deduced three-dimensional samples from two-dimensional rock samples, which can be well verified in texture color, geometric characteristics, and permeability behaviors. However, the digital rock model has not been verified to analyze the size effect on mechanical behaviors of rocks.
In this paper, synthetic enlarged digital rock is innovatively used to study the size effect of rock materials. This paper includes the modeling method, the geometric characteristic, the mechanical behavior and the size effect analysis of the synthetic enlarged digital rock.
2 Materials and Methods
2.1 Materials
This paper used sesame gray granite to study the size effect of heterogeneous rocks because this kind of rock has large and multiple mineral grains. Sesame gray granite mainly contains quartz in transparent gray, feldspar in off-white, and mica in black, in which colors can easily distinguish from each other. The three minerals are closely coupled to make up the rock that has self-similarity in texture. In this paper, the granite is assumed to be an intact rock without considering the defective structures of pores and fractures. As shown in Figure 1, the side length of the granite is 10 cm long and corresponds to 400 pixels, each pixel representing 0.25 mm × 0.25 mm.
2.2 Methods
2.2.1 The Enlarged Digital Modeling Method
Since sesame gray granite has strong texture self-similarity, any two texture blocks should have similarities and random differences. The previous research (Wei and Levoy, 2000; Efros and Freeman, 2001) has shown that the model with random self-similarity texture can be reproduced by the Markov random field method (Xiao et al., 2021b). The pixel block is taken as the basic element to duplicate and reproduce in new models, as shown in Figure 2. Then, the enlarged digital model can be synthesized. For a detailed description of the method, please refer to the literature (Wei and Levoy, 2000; Efros and Freeman, 2001; Kwatra et al., 2005; Xiao et al., 2021b).
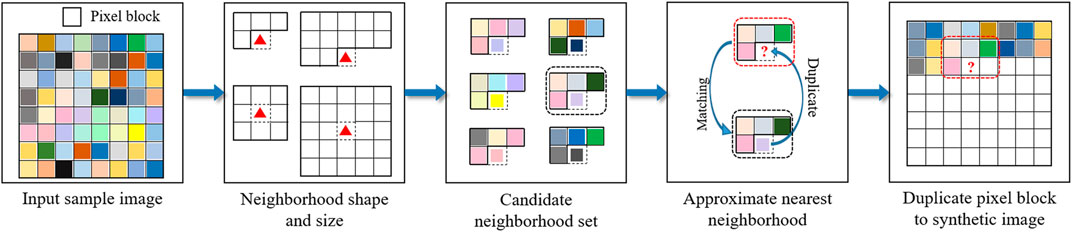
FIGURE 2. Digital modeling method based on pixel block (revised from Xiao et al., 2021b).
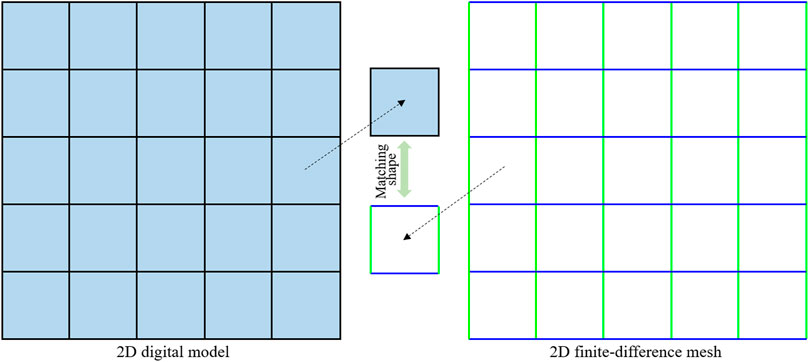
2.2.2 Mapping Method Between the 2D Digital Model and Numerical Model
The digital model of granite can be synthesized based on the Markov random field method. In order to study the mechanical properties of synthetic digital granite, the digital model needs to be transformed into a numerical model that can be used for numerical simulation. The digital model is made up of lattice pixels. This paper establishes a numerical model based on the finite-difference mesh to map the lattice attribute into the numerical model accurately. As shown in Figure 3, the lattice of the digital model and the finite-difference grid have exactly matching shapes. Therefore, the geometric and physical attributes of the digital model can be accurately transformed into the finite-difference mesh model. The specific steps are as follows. Firstly, the feldspar, quartz and mica in granite are segmented by using the image processing method. Then, the coordinates of the same kind of minerals are placed in the same group. Finally, the mineral grain type and coordinate are imported by groups into the numerical model.
2.2.3 The Calculation Method of Heterogeneity
The heterogeneity and homogeneity of rock materials are closely related to rock size. When studying the mechanical properties of rock samples in the laboratory, rock materials are considered to be heterogeneous. When studying the mechanical properties of rock mass in engineering sites, rock materials are considered to be homogeneous. In order to describe the heterogeneity of rock materials quantitatively, the Euclidean distance between heterogeneous and homogeneous rock models is used to describe.
The Euclidean distance between the original heterogeneous model and the homogeneous model is
where D (IO, IA) is the Euclidean distance between heterogeneous and homogeneous digital model; IO is the original heterogeneous digital model; IA is the corresponding homogeneous model; i, j is the coordinate of a pixel.
In order to eliminate the influence of the number of pixels on the heterogeneous results, the distance between images is normalized by the number of pixels, and the average distance is
where, S is the average distance between the original heterogeneous model and homogeneous model; m is the pixel number of the width side; n is the pixel number of the length side.
In order to eliminate the influence of gray pixel values on the heterogeneous results, the mean distance is homogenized
The heterogeneity value obtained by formula (Eq. 3) is between 0 and 1, and the larger the value is, the stronger the heterogeneity is.
3 Results
This section will first verify the representational ability of synthetic granite models of equal and enlarged sizes to natural granite models. Then, the size effect of the enlarged granite model is analyzed. Finally, the relationship between rock heterogeneity and homogeneity is discussed.
3.1 Equal-Size Synthetic Digital Granite Models
3.1.1 Geometric Characteristics
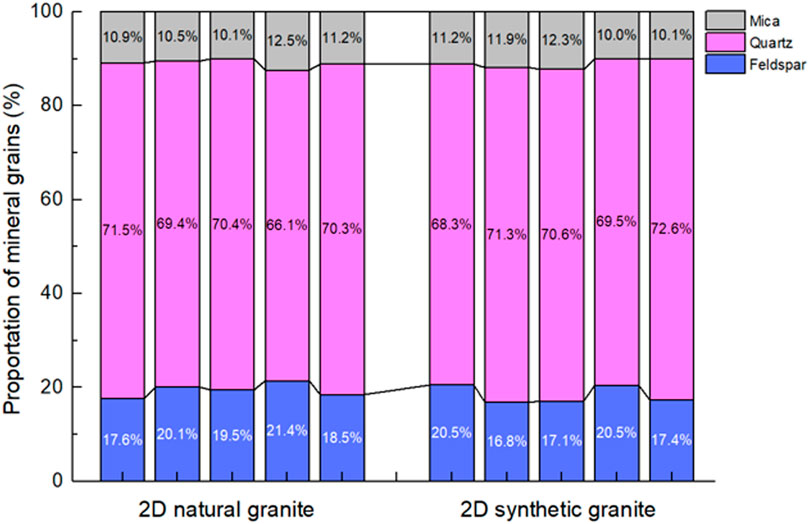
The mechanical properties of different rock samples have random discreteness. In order to reduce the influence of discreteness on the evaluation of the characterization ability of synthetic digital granite models, the natural rock model is cut to provide more control samples of natural rock. As shown in Figure 4, the original rock sample with a side length of 10 cm is divided into five samples with a side length of 5 cm. Sample 5 is the master mask for synthesizing the digital granite model. Five equal-size digital granite models are synthesized based on sample 5 by the Markov random field method.
In order to evaluate the characterization ability of the synthetic granite model to natural granite, the geometric characteristics of the synthetic model will be analyzed first. From the perspective of rock texture, the synthetic granite model remains the complex Mosaic relationship between the mineral grains of the natural rock, and it is difficult to distinguish the synthetic model and natural model visually. Therefore, the synthetic rock model is very similar to the natural rock in texture. As shown in Figure 5, the proportion of the quartz grain in natural rocks and synthetic rocks is the highest, ranging from 66.1 to 71.5% and 68.3 to 72.6%, respectively. The proportion of the mica grain in these two kinds of models is the lowest, ranging from 10.1 to 12.5% and 10.0 to 12.3%, respectively. The proportion of the feldspar grain in these two kinds of models ranges from 17.6 to 21.4% and from 16.8 to 20.5%, respectively. The proportions of mineral grain in these two kinds of models coincide extremely well.
3.1.2 Mechanical Behaviors
In order to verify the mechanical behaviors of synthetic granite models, the finite-difference method is used to calculate and analyze the mechanical behaviors of five synthetic granite models and five natural granite models. The finite-difference model is built based on the digital model by using the mapping method in Section 2.2.2. The constitutive model is the Mohr-Coulomb model, and the physical parameters of mineral grains are derived from the literature (Chen et al., 2004), as shown in Table 1. The physical parameters of the homogeneous model are weighted according to the proportion of mineral grains. The boundary condition is that the upper and lower boundaries are velocity loads, which are 1.9 × 10–9 m/step, and the other boundaries are free.

TABLE 1. Physical parameters of different minerals (revised from Chen et al., 2004).
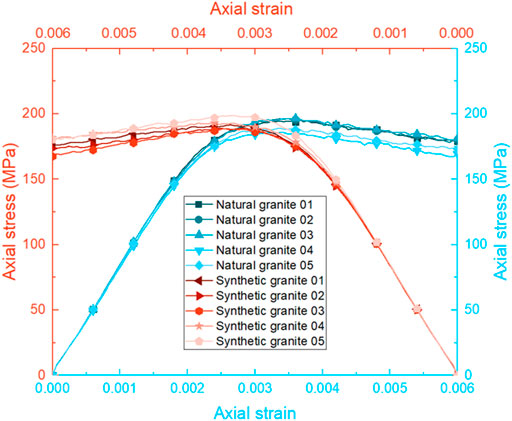
The stress-strain curves of synthetic granite and natural granite are analyzed based on the above computational models and parameters. In order to distinguish the stress-strain law of these two kinds of granite models clearly, the change on strain curves of these two kinds of granite models is set in opposite directions. As shown in Figure 6, the stress-strain curves of these two kinds of models show high mirror symmetry. Specifically, the stress increases linearly with the increase of strain, and both rock models are in an elastic stage. When the strain reaches around 0.002, the relationship between stress and strain enters a nonlinear plastic stage. With the increase in the number of plastic elements, the stress reaches the peak value. When the plastic element is formed to fracture, the stress tends to decrease with the increase of strain. The elastic-plastic variation of the numerical element in the whole loading cycle has been discussed in detail in the literature (Xiao et al., 2021b). The uniaxial compressive strength (UCS) of five natural granites are 195.41, 196.42, 196.61, 185.79, and 189.07 MPa, respectively, and the UCS of five synthetic granite are 191.54, 188.84, 188.73, 193.03, and 198.81 MPa, respectively. The average UCS of these two kinds of granite is 192.66 and 192.19 MPa, and the corresponding standard deviation is 4.41 and 3.69, respectively. The USC and fluctuation keep a very high consistency between natural granite and synthetic granite. Therefore, the synthetic equal-size rock model can be highly consistent with natural rock in terms of stress-strain curves and UCS during the uniaxial compressive tests.
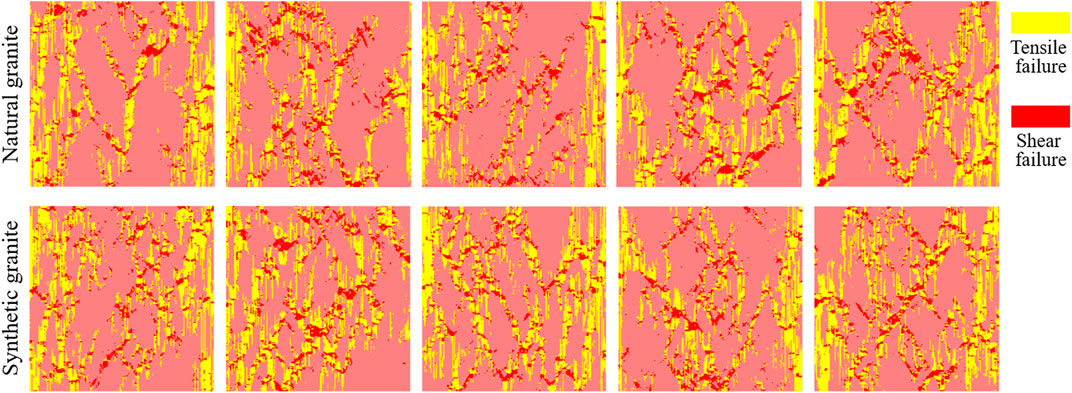
In order to analyze the influence of rock heterogeneity on rock damage, the damage morphology of the numerical rock model is selected when the strain is 0.006. As shown in Figure 7, the five images in the upper area are the damage and failure modes of natural rocks. The left and right outer edges of the model are dominated by tensile failure, and the interior is formed by tensile failure and shear failure together. However, the final failure patterns are quite different due to the heterogeneity caused by the different distribution of mineral grains in rock models. Similarly, the five synthetic rocks in the bottom area show similar tensile and shear failure modes and different final failure patterns as natural rocks.
3.2 Enlarged Synthetic Digital Granite Models
Geometric characteristics and mechanical behaviors of equal-size synthetic granite models are analyzed and verified in Section 3.1. In this section, the enlarged synthetic granite model will be further verified and analyzed to lay a solid foundation for analyzing the size effect. The five kinds of size of enlarged models are synthesized based on natural rock 5 (Figure 4), and each kind has five samples. The side lengths of the models are 6.25, 7.50, 8.75, and 10.00 cm, respectively, and the corresponding pixel lengths are 250, 300, 350, and 400 pixels, respectively. The side length of the control group is 6.25, 7.50, 8.75 and 10.00 cm, respectively, in the middle area of natural rocks, as shown in Figure 8.
3.2.1 Geometric Characteristics
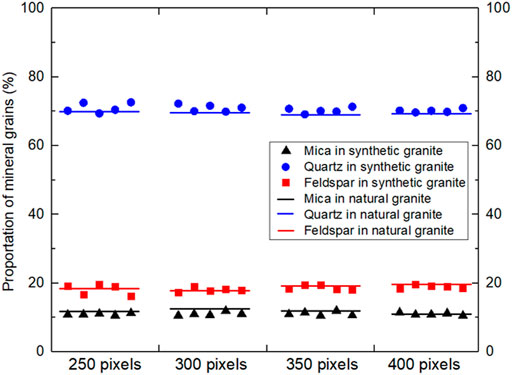
From the distribution characteristics of mineral grains, the enlarged synthetic granite model keeps a similar complex Mosaic relationship with the natural granite, as shown in Figure 9. In addition, from a quantitative point of view, as shown in Figure 10, the proportions of mineral grains of the synthetic granite model at different scales are all very similar to that of the natural granite model. For the mica grain, the fourth model with a side length of 7.50 cm (300 pixels) has the largest difference from natural granite, with an error of 9.77%. For the quartz grain, the largest difference between synthetic and natural granite minerals is the third model with a side length of 6.25 cm (250 pixels), with an error of 2.41%. For the feldspar grain, the largest difference between synthetic and natural granite is the second model with a side length of 6.25 cm (250 pixels), with an error of 9.44%. In the above 25 synthetic models of different scales, the maximum error of the proportion of mineral grain is less than 10%, indicating that the enlarged synthetic granite model can well characterize the texture and mineral composition of natural granite.
3.2.2 Mechanical Behaviors
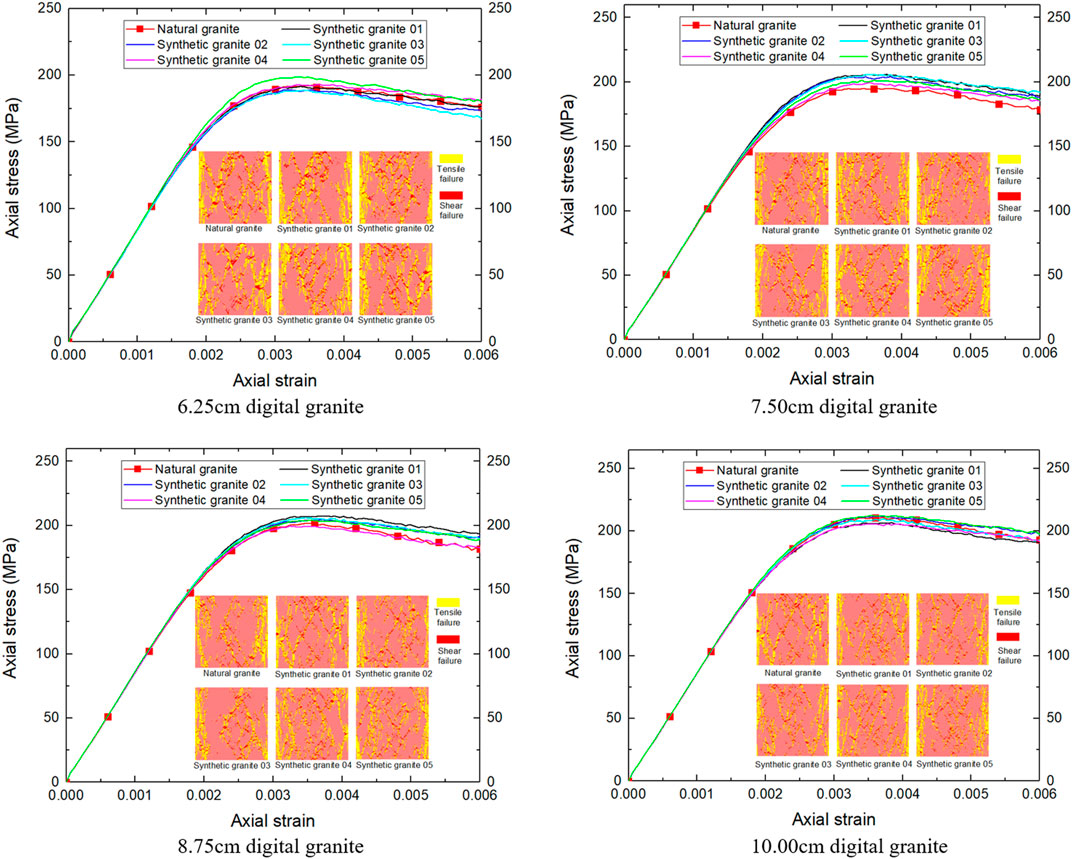
In order to verify the ability of the enlarged synthetic granite model to represent natural granite, the finite-difference method is used to analyze the mechanical behaviors of the enlarged rock model. The constitutive model, physical parameters and boundary conditions are the same as those in Section 3.1.2. The stress-strain law of synthetic granite is basically consistent with that of natural granite at multi-scale, as shown in Figure 11. The UCS of natural granite with a side length of 6.25, 7.50, 8.75, and 10.00 cm is 192.50, 194.93, 201.78, and 211.08 MPa. The average UCS of synthetic granite with a side length of 6.25, 7.50, 8.75, and 10.00 cm is 192.19, 203.38, 204.31, and 209.39 MPa. The corresponding error is 0.16, 4.33, 1.25, and 0.80%. In addition, from the perspective of the final failure pattern, they all show the tensile and shear failure modes. Moreover, due to the heterogeneity, the final failure mode has a random difference, which is consistent with the different failure modes among natural rocks. Overall, the enlarged synthetic granite model can characterize natural granite in terms of stress-strain law, UCS, and failure patterns.
3.3 Size Effect on Mechanical Behaviors of Heterogeneous Granite
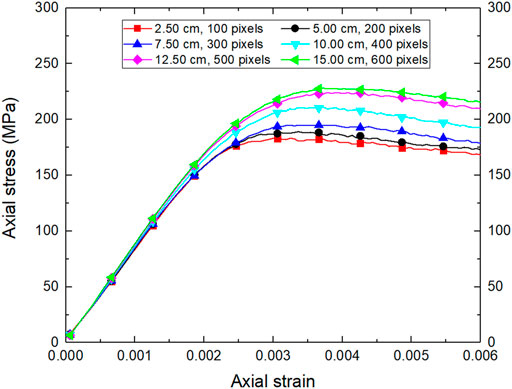
The enlarged digital rock model can well represent the geometric characteristics and mechanical behaviors of natural rock. The model can provide materials for studying the size effect of heterogeneous rock. This section analyzes the stress and strain laws of digital granite models with side lengths of 2.50, 5.00, 7.50, 10.00, 12.50, and 15.00 cm. The constitutive model, physical parameters and boundary conditions are the same as those in Section 3.1. As shown in Figure 12, in the elastic stage, the stress-strain curves of granite models of all scales almost coincide because they have similar elastic modulus. As the loading continues, the smaller the sample size, the earlier it enters the plastic stage. The UCS of the digital granite model with side lengths of 2.50, 5.00, 7.50, 10.00, 12.50, and 15.00 cm is 183.11, 189.07, 194.93, 211.08, 224.13, and 228.05 MPa.
Finite-difference elements represent different mineral grains types with different physical properties. As shown in Figures 13A–F, the progressive failure process of these models with different sizes has the following in common. Firstly, the mica grains with weak mechanical properties reach the shear yield state in the early stage. Secondly, with the increase of axial strain, the partial feldspar grains reach the shear yield state, and the area between mica grains reaches the tensile yield state. Thirdly, as the number of yield elements increases, the axial stress gradually reaches its peak and the yield elements are gradually connected. Fourthly, the intact granite reaches yield with a large area under the condition of high strain. In addition, because the number of mineral grains in small-scale granite is less than that in large-scale granite, the connected fracture is easy to penetrate the whole sample with the increase of the yield elements. Therefore, the smaller the size of intact granite is, the smaller the uniaxial compressive strength is.

FIGURE 13. The progressive failure process of digital granite with different sizes. (A) 2.50 cm, (B) 5.00 cm, (C) 7.50 cm, (D) 10.00 cm, (E) 12.50 cm, and (F) 15.00 cm.
3.4 The Relationship Between Heterogeneity and Homogeneity
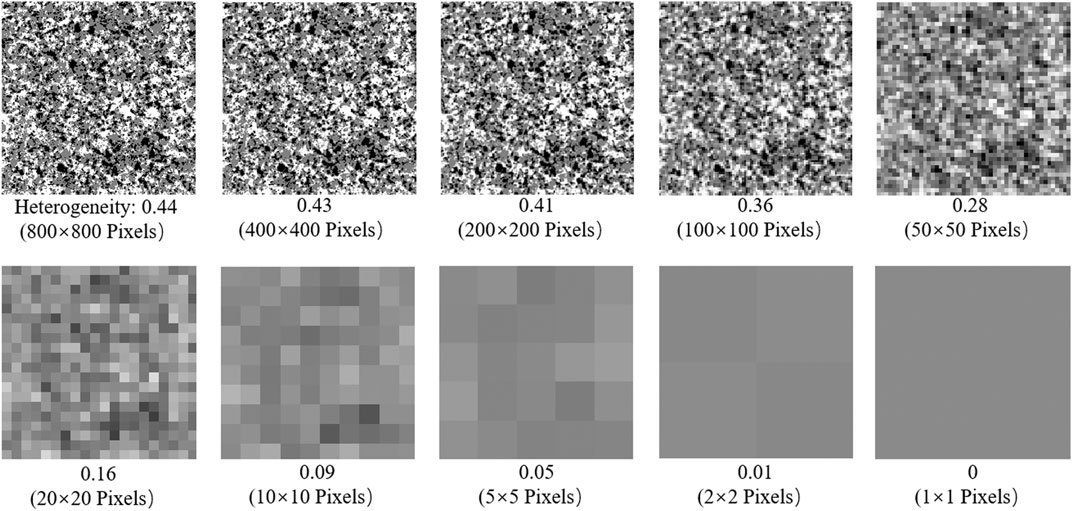
Heterogeneity is an important factor affecting the rock scale effect. The heterogeneity effect of rocks variance at different scales. Establishing the relationship between rock heterogeneity and homogeneity will provide references for studying scale effects. When numerical model elements are used to describe heterogeneous digital models, the size represented by numerical elements will affect the heterogeneous effect of rocks. If the physical properties of rock mineral grains are assumed to be homogeneous when each numerical unit represents a small size, rock mineral particles may be composed of many numerical units, and it is easy to use numerical units to describe heterogeneous models. When the size of the study is large, a numerical unit requires to represent multiple mineral particle models, and the physical properties of each numerical unit are the average of several mineral particles. The calculation of heterogeneity in this section is based on the method described in Section 2.3. For instance, as shown in Figure 14, when the numerical element is far smaller than the mineral grains, heterogeneity degree will be large; along with the increase of the representatives of the unit size difference between the physical parameters of the unit is increasingly small, and gradually tend to be homogenization. When each unit on behalf of 1 cm, only 0.09 heterogeneity degree, basically rock can be regarded as a homogeneous rock. Therefore, the heterogeneity or homogeneity of rocks is closely related to the study of rock size.
4 Discussion
In this paper, the synthetic enlarged high-fidelity granite can be used to study the mechanical behaviors of rock on a large scale, which makes up for the shortcomings of analyzing large-scale problems with representative units of downsampling. The synthetic multi-scale digital rock has a strong ability to characterize the natural rock through the analysis of texture characteristics, mineral distribution, mechanical behaviors. Compared with the traditional numerical model generated by random method, the synthetic digital rock model can accurately describe the natural mineral morphology and Mosaic relationship. In addition, the representative element volume is used to represent the known large model. In this paper, the enlarged model is reverse deduced the local information on a large scale, which can provide a reference for the complex rock structures.
The research has some limitations. Firstly, the cost of computation is very high due to the numerical model based on numerous pixels. In addition, only the material heterogeneity is considered to analyze the size effect on the mechanical behavior of rocks, while the influence of structural heterogeneity, such as grain boundary and defective structures of pores and fractures, is not considered. In further research, a lightweight numerical model needs to be built. Moreover, the grain boundary and defective structures of pore and fractures need to be considered to study the influence of heterogeneity on the size effect.
5 Conclusion
In this paper, the enlarged digital rock models that are synthesized by the Markov random field method are innovatively proposed to study the size effect. The geometric characteristics, mechanical behaviors of synthetic models are also verified and analyzed. Firstly, the texture and proportion of synthetic and natural rocks are very similar, with a maximum error of 9.77%. Secondly, for the stress and strain law and uniaxial compression strength, the synthetic rock also shows good characterization ability, and the maximum error of uniaxial compression strength is 4.33%. In the failure mode, synthetic rocks show random differences, which is similar to the failure laws of natural rocks. Finally, the uniaxial compressive strength of rock increases with increasing size under considering material heterogeneity rather than defect structure (pores or fractures) heterogeneity. Therefore, the synthetic equal and enlarged digital rock models can provide a large number of samples for mechanical analysis and provide a new idea for studying the size effect of rock materials and establishing a bridge between homogeneity and heterogeneity.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
HX: methodology, software, analysis, and writing-original draft preparation; LH: Conceptualization, supervision, and writing-review and editing; RS: software, and writing-original draft preparation; JS: Data curation; YT: Visualization; QZ: writing-review and editing.
Funding
This work was supported by the research projects of China Construction Eighth Engineering Division Corp., LTD. (No. H202120511) and China Railway 16th Bureau Group Co., LTD. (No. H202120303).
Conflict of Interest
Author PS was employed by company China Construction Eighth Engineering Division Corp., LTD.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Chen, S., Yue, Z. Q., and Tham, L. G. (2004). Digital Image-Based Numerical Modeling Method for Prediction of Inhomogeneous Rock Failure. Int. J. Rock Mech. Mining Sci. 41 (6), 939–957. doi:10.1016/J.IJRMMS.2004.03.002
Efros, A. A., and Freeman, W. T. (2001). “Image Quilting for Texture Synthesis and Transfer,” in Proceedings of the 28th annual conference on Computer graphics and interactive techniques, New York, NY, August 2001, 341–346. doi:10.1145/383259.383296
Kang, F., Li, Y., and Tang, C. a. (2021). Grain Size Heterogeneity Controls Strengthening to Weakening of Granite over High-Temperature Treatment. Int. J. Rock Mech. Mining Sci. 145, 104848. doi:10.1016/j.ijrmms.2021.104848
Kwatra, V., Essa, I., Bobick, A., and Kwatra, N. (2005). Texture Optimization for Example-Based Synthesis. ACM Trans. Graph. 24 (3), 795–802. doi:10.1145/1073204.1073263
Li, K., Cheng, Y., and Fan, X. (2018). Roles of model size and particle size distribution on macro-mechanical properties of Lac du Bonnet granite using flat-joint model. Comput. Geotechnics 103, 43–60. doi:10.1016/j.compgeo.2018.07.007
Li, S., Chen, J., Wang, H., Nie, X., Zhao, J., and Yao, H. (2020). A Study on the Origin of Scale Effect of Rock Strength Based on Multi-Scale Shale Brazilian Splitting Test. Mech. Enigineering (In Chinese) 42 (1), 35–41. doi:10.6052/1000-0879-19-300
Li, X. F., Li, H. B., and Zhao, J. (2021). Transgranular Fracturing of Crystalline Rocks and its Influence on Rock Strengths: Insights from a Grain-Scale Continuum-Discontinuum Approach. Comput. Methods Appl. Mech. Eng. 373, 113462. doi:10.1016/j.cma.2020.113462
Mahabadi, O. K., Randall, N. X., Zong, Z., and Grasselli, G. (2012). A Novel Approach for Micro-scale Characterization and Modeling of Geomaterials Incorporating Actual Material Heterogeneity. Geophys. Res. Lett. 39 (1), a–n. doi:10.1029/2011GL050411
Pan, C., Li, X., He, L., and Li, J. (2021). Study on the Effect of Micro-geometric Heterogeneity on Mechanical Properties of Brittle Rock Using a Grain-Based Discrete Element Method Coupling with the Cohesive Zone Model. Int. J. Rock Mech. Mining Sci. 140, 104680. doi:10.1016/j.ijrmms.2021.104680
Peng, J., Wong, L. N. Y., and Teh, C. I. (2017). Influence of Grain Size Heterogeneity on Strength and Microcracking Behavior of Crystalline Rocks. J. Geophys. Res. Solid Earth 122 (2), 1054–1073. doi:10.1002/2016JB013469
Shang, J., Zhao, Z., Hu, J., and Handley, K. (2018). 3D Particle-Based DEM Investigation into the Shear Behaviour of Incipient Rock Joints with Various Geometries of Rock Bridges. Rock Mech. Rock Eng. 51 (11), 3563–3584. doi:10.1007/s00603-018-1531-0
Shirole, D., Walton, G., and Hedayat, A. (2020). Experimental Investigation of Multi-Scale Strain-Field Heterogeneity in Rocks. Int. J. Rock Mech. Mining Sci. 127, 104212. doi:10.1016/j.ijrmms.2020.104212
Tan, X., Konietzky, H., and Chen, W. (2016). Numerical Simulation of Heterogeneous Rock Using Discrete Element Model Based on Digital Image Processing. Rock Mech. Rock Eng. 49 (12), 4957–4964. doi:10.1007/s00603-016-1030-0
Wang, X., and Cai, M. (2019). A Comprehensive Parametric Study of Grain-Based Models for Rock Failure Process Simulation. Int. J. Rock Mech. Mining Sci. 115, 60–76. doi:10.1016/j.ijrmms.2019.01.008
Wei, L.-Y., and Levoy, M. (2000). “Fast Texture Synthesis Using Tree-Structured Vector Quantization,” in Proceedings of the 27th annual conference on Computer graphics and interactive techniques, New York, NY, July 2000, 479–488. doi:10.1145/344779.345009
Xiao, H., He, L., Li, J., Zou, C., and Shao, C. (2021a). Permeability Prediction for Porous sandstone Using Digital Twin Modeling Technology and Lattice Boltzmann Method. Int. J. Rock Mech. Mining Sci. 142, 104695. doi:10.1016/j.ijrmms.2021.104695
Xiao, H., He, L., Li, X., Zhang, Q., and Li, W. (2021b). Texture Synthesis: a Novel Method for Generating Digital Models with Heterogeneous Diversity of Rock Materials and its CGM Verification. Comput. Geotechnics 130, 103895. doi:10.1016/j.compgeo.2020.103895
Keywords: digital rock, heterogeneity, size effect, enlarged model, numerical simulation
Citation: Xiao H, He L, Shi R, Song J, Tang Y, Zhang Q and Shi P (2021) Size Effect on Mechanical Behaviors of Intact Rocks Based on Enlarged Digital Models. Front. Earth Sci. 9:803406. doi: 10.3389/feart.2021.803406
Received: 27 October 2021; Accepted: 11 November 2021;
Published: 20 December 2021.
Edited by:
Junlong Shang, University of Glasgow, United KingdomReviewed by:
Jingjing Meng, Luleå University of Technology, SwedenQibin Lin, Central South University, China
Copyright © 2021 Xiao, He, Shi, Song, Tang, Zhang and Shi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lei He, aGVsZWlfY2l2aWxAc2V1LmVkdS5jbg==
 Huaiguang Xiao
Huaiguang Xiao Lei He1*
Lei He1* Yudi Tang
Yudi Tang