Statistical Relationship Between the Decrease of Major Seismicity and Drought in Southern California Since 1900

Bragato, Pier Luigi

doi:10.3389/feart.2021.790412

ORIGINAL RESEARCH article

Front. Earth Sci., 11 November 2021

Sec. Geohazards and Georisks

Volume 9 - 2021 | https://doi.org/10.3389/feart.2021.790412

Statistical Relationship Between the Decrease of Major Seismicity and Drought in Southern California Since 1900

Pier Luigi Bragato*

National Institute of Oceanography and Applied Geophysics—OGS, Udine, Italy

The seismicity in Southern California significantly decreased over the last decades. The decrease went in parallel with the reduction of meteoric groundwater recharge, which is a well-known factor capable of affecting seismicity. In this work the existence of a systematic statistical relationship was investigated by comparing the time density of Mw ≥ 5.7 earthquakes since 1900 with the time series of the Palmer Drought Severity Index (PDSI), an indicator of soil moisture roughly correlated with groundwater recharge. Given the non-stationarity of the two signals, the formal comparison was performed using both binomial logistic regression and cointegration testing. The analysis showed a significant statistical relationship, with peaks of seismicity 8 years behind those of PDSI. This finding suggests the hypothesis that groundwater recharge might affect earthquakes at a multi-year time scale. Proving this theory requires accurate measures and hydrogeological modeling, which is behind the scope of this work. Nonetheless, according to previous studies, the observed time lag might be explained by the slow propagation of pore pressure from the surface to the seismogenic volume. The ongoing trend towards an arid climate, made more evident by the recent severe droughts, might have contributed to the earthquake reduction of the last decades. The connection is particularly evident in the Salton Trough, with possible implications for the interpretation of its paleoseismicity.

Introduction

Seismic activity is caused for the largest part by the tectonic movements, with consequent accumulation of stress in the crust and its release through faulting. Previous studies recognized or at least postulated other phenomena that can marginally affect seismicity by altering the cycle of accumulation and release of energy, leading to the time clustering of earthquakes or fluctuations of their rate of occurrence. Some of the proposed effects are internal to the seismic phenomena, with earthquakes triggering other earthquakes, for example by stress diffusion (Hough, 2005) or viscoelastic relaxation (Mantovani et al., 2010). Others involve an external forcing, like for example, tidal and astronomic effects (Tolstoy et al., 2002; Scafetta and Mazzarella, 2015), impulses in the Earth’s rate of rotation and interaction of adjacent seismic regions (Liritzis et al., 1995). Special attention was paid to the external forcing possibly driven by the climate, with a series of works summarized by Scafetta and Mazzarella (2015): snow and glacier load changes, typhoons, rain, sea-level changes as well as variations in air pressure (Neuberg, 2000). They work at different time scales, ranging from days (Scafetta and Mazzarella, 2018) to seasons (Saar and Manga, 2003; Bettinelli et al., 2008; Panda et al., 2018), years (Huang et al., 1979) up to millennia (Luttrell and Sandwell, 2010). It has also been postulated that astronomical processes could drive both the climate and seismicity (Mazzarella and Palumbo, 1989; Scafetta and Mazzarella, 2015). Often the support to these hypotheses is observational and the conclusions controversial, given the difficulty of developing valid physical models and proving them with actual measurements. Many studies concern earthquakes triggered by accumulation or depletion of water both on the surface and underground (Saar and Manga, 2003 and references therein). Part of the research was stimulated by the need to explain earthquakes triggered by human activities, like the creation artificial water reservoirs (many cases around the world reported by Gupta, 2002) or the disposal of wastewater underground (Ellsworth, 2013). Raleigh et al. (1976) theorized the possibility to exploit artificial groundwater recharge in order to control the frequency and magnitude of earthquakes, by alternately injecting and recovering water from wells penetrating a seismic zone. The works of greatest interest here are those concerning the earthquakes possibly triggered by the natural groundwater recharge caused by meteoric precipitation. Cases have been studied in Greece (Liritzis and Petropoulos, 1992, 1994), in the United States (Saar and Manga, 2003), along the Alps in Germany (Kraft et al., 2006), Switzerland (Husen et al., 2007) and Italy (Pintori et al., 2021), in the Italian Apennines (D’Agostino et al., 2018; De Luca et al., 2018), and in the Himalaya (Bettinelli et al., 2008; Panda et al., 2018). Bragato and Holzhauser (2019) observed that the strong seismicity of the last millennium in Italy was modulated according to the phases of the Little Ice Age in Europe, characterized by lower temperature and increased precipitation, both phenomena affecting positively groundwater recharge. The triggering effect of groundwater is explained by the combination of two mechanisms (poroelastic models) widely described and modeled in the literature (see e.g., Ellswort, 2013 for an short introduction). The first effect is that of the groundwater load, which increases the elastic stress in the crust, and in particular on faults, promoting their slipping. The second effect is that of fluid pore pressure propagation: the pulse of pore pressure generated by the increase of water in the crust reaches the fault internally, reducing its frictional strength. This mechanism requires hydraulic continuity from the surface to the seismogenic fault. According to the cases observed by Talwani et al. (2007) the pulse of fluid pressure can transmit even at long distances (up to 30 km) within years, travelling through fractures and joints having high permeability.

The relationship between water and earthquakes was also studied in Southern California. Various authors investigated the long quiescence of the Southern San Andreas Fault (about 300 years since the last large earthquake) and its possible connection with the drying up of Lake Cahuilla in the Salton Trough. In their studies they have tried to assess the significance and the nature of the relationship by combining paleoseismic estimations of strong earthquakes, reconstructions of the lake level and geophysical modeling (Luttrel et al., 2007; Brothers et al., 2011; Rockwell et al., 2018; Hill et al., 2020). Concerning the connection between precipitation and strong earthquakes in the entire Southern California, it is worth mentioning the pioneering work by Huang et al. (1979). They recognized a recurrent time pattern opened by a period of 4–6 years with scarce rainfall, followed by 1–3 years of intense precipitation, and closed by a strong earthquake 4–24 months after the peak of precipitation. The finding is of particular interest because the last strong earthquake that occurred in Southern California (the Ridgecrest earthquake of July 6, 2019, Mw 7.1, red star in Figure 1) took place in similar circumstances, after one of the worst historical droughts in California. Huang et al. (1979) tentatively explained the observed regularity as an effect of earthquake triggering by pore-pressure propagation, where even the initial dry period may contribute to creating physical conditions that are more favorable for faulting.

FIGURE 1

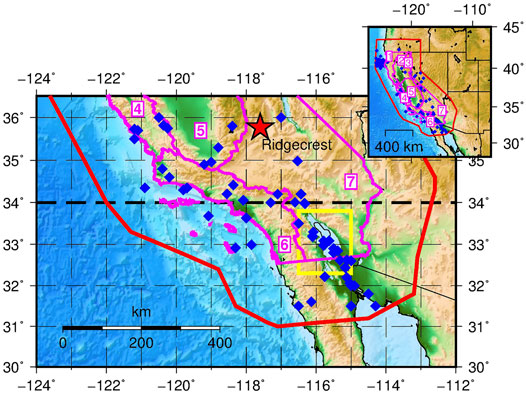
FIGURE 1. Epicenters of the mainshocks with Mw ≥ 5.7 occurred in Southern California and the surrounding area between 1900 and 2020 (blue diamonds, the red star represents the epicenter of the Ridgecrest earthquake of July 6, 2019, Mw 7.1). In red the border of the area covered by the earthquake catalog; in magenta the borders of the climatic divisions of California enumerated from 1 to 7; in yellow the Salton Trough area.

The present work further investigated the connection between precipitation, groundwater recharge and seismicity in Southern California with a statistical analysis of the relationship between the time distribution of the Mw ≥ 5.7 earthquakes occurred since 1900 and the evolution at the regional scale of the Palmer Drought Severity Index (PDSI), a standardized measure of soil moisture (Palmer, 1965). The PDSI at a given time is calculated taking into account the previous history of precipitation and surface temperature combined with a simplified model of water evaporation and plant transpiration. It is intended for agricultural applications, in order to provide an indication of the water that is available for plants in the shallow soil. The working hypothesis adopted here was that PDSI could act as a proxy for the quantity of groundwater, supposing that what happens in depth reflects what observed on the surface. This assumption is supported by the findings by Dai (2011), who showed that PDSI correlates over most land areas with the water storage changes estimated from GRACE (Gravity Recovery and Climate Experiment) satellite observations. It is also to note that the values of PDSI here considered are those averaged over the entire study area and not directly above each epicenter. The aim was to check if a coarse, large-scale groundwater indicator (which is also easily available and continuously updated) could be sufficient to evidence interesting characteristics of the groundwater/earthquake interaction. PDSI was used for a similar comparison in northeastern Italy (Bragato, 2021), where a systematic enhancement of seismicity following the peaks of PDSI was found. As any statistical investigation, that proposed in this study does not demonstrate the existence of a physical connection between groundwater recharge and seismicity. Rather, through the assessment of the significance levels and robustness checking, it tries to show that any similarity of the trends has low probability of occurring by chance and deserves further investigation.

This paper is organized as follows: a presentation of the available data and their selection criteria; a description of the methods of analysis and their application; an assessment of the robustness of the results in respect to various parameters (among these, slight different choices of the study area and lower magnitude thresholds available for recent time periods); a focus section on the Salton Trough area; a final discussion summarizing the main findings, also in connection with previous studies in Southern California and worldwide. In the analysis of the relationship between seismicity and PDSI, particular attention was paid to the possible bias induced by the long-term trends that are present in the time series, coupling binomial logistic regression (which is possibly affected by the trends) with cointegration testing (Engle and Granger, 1987).

Data Selection

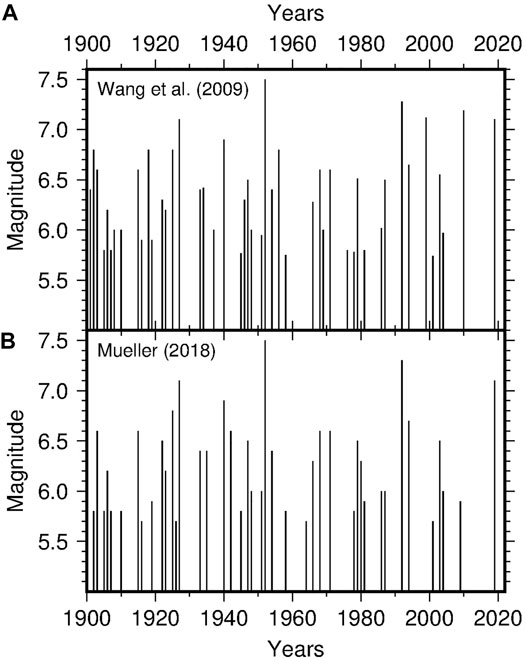
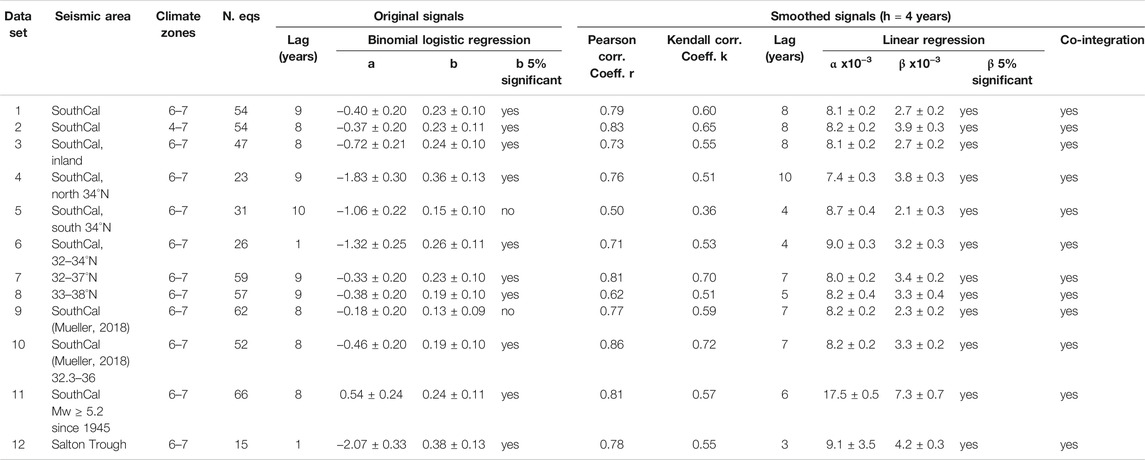
Earthquake data were drawn from the catalog of California by Wang et al. (2009) covering the time period 1900–2007. The catalog was integrated up to the end of 2020 with data from the online catalog of the USGS National Earthquake Information Service (see Data Availability Statement). The selected data set includes 54 mainshocks (diamonds in Figure 1) with epicenter located south of 36°N and moment magnitude Mw ≥ 5.7, a threshold that should guarantee the completeness of the catalog (Bragato and Sugan, 2014). The catalog by Wang et al. (2009) has no explicit separation between mainshocks and aftershocks. To each earthquake it is attributed a probability of independence, that is, the probability of not being triggered by previous earthquakes estimated using the epidemic-type aftershock sequence (ETAS) model (Zhuang et al., 2002). The sub-catalog here considered includes the earthquakes with probability of independence p ≥ 0.8. Their magnitude/time distribution is shown in Figure 2A. As discussed in the following sections, the robustness of the results was checked taking into account the uncertainties on the estimation of Mw and of the epicentral coordinates. These are time dependent and, in general, have a decreasing trend. The reported uncertainty on Mw goes from 0.4 in the earliest part of the catalog, based on macroseismic observations, to less than 0.1 in recent years. The location errors range from 30 km to less than 1 km.

FIGURE 2

FIGURE 2. Magnitude/time distribution of the earthquakes considered in this work.

As an alternative, some analysis was performed using the declustered catalog of the western United States by Mueller (2018, 2019) cut for the same area. It spans a longer time period (till the end 2016) with a revised set of earthquakes, locations, and magnitude values. It includes only mainshocks recognized using the distance- and time-windowing declustering scheme of Gardner and Knopoff (1974). The present analysis was carried out for 63 mainshocks having the magnitude/time distribution shown in Figure 2B. The two data sets of Figure 2 agree on 43 earthquakes, with the largest part of the difference depending on the definition of mainshock. In particular, according to the independence criteria of Wang et al. (2009), the most independent event of a sequence is not necessary the strongest one and sometimes it is under the magnitude threshold 5.7, which may lead to discard also the following stronger earthquake. The purpose of this paper was not to discuss the best choice for declustering, but to check if the results of the analysis persist under the two alternatives. Further checking took in consideration different choices of the investigated area and of the magnitude threshold (after 1945, when the catalogue became complete for lower magnitudes). Figure 1 shows a few earthquakes located offshore. At a first consideration they should be excluded from the analysis because not directly affected by groundwater load. On the other hand, it cannot be excluded that the corresponding faults have hydraulic continuity with the inland and are affected by pulses of pore pressure originated from there. This is because it has been shown (Talwani et al., 2007) that a triggering pulse can transmit at tens of km from its source. To avoid any possible bias and limitation, the analysis was carried out for both the entire data set and the subset of earthquakes located inland.

The Palmer Drought Severity Index (PDSI) is an indicator for the accumulation of precipitation water in the soil based on rainfall data and surface temperature, which in turn determines evaporation and plant transpiration (Palmer, 1965). The PDSI ranges from about -10, denoting very dry conditions, to +10, denoting very wet conditions. The present study adopted the time series with monthly step available at the National Oceanic and Atmospheric Administration/National Climatic Data Center (NOAA/NCDC) (Vose et al., 2014). They are computed for a series of climate divisions in United States, seven of which covering the state of California (borders and number in magenta in Figure 1). The procedure used for the computation at NOAA/NCDC is that original by Palmer (1965) adapted according to Heddinghaus and Sabol (1991). It is quite complex and involves a series of variables and empirical relations that are specific of soil hydrology. Basically, the procedure takes as input the monthly time series of temperature and precipitation, the latitude of the location of interest (to calculate the average monthly solar insolation), and the Available Water Capacity (AWC) of a reference soil. These elements are used to estimate the water balance of each month according to a simplified physical model, which in turn enters in the computation of PDSI. The main formula is

X_{i} = 0.897 X_{i - 1} + \frac{Z_{i}}{3}, (1)

where X_i is the PDSI at the ith month and Z_i is a function of the water balance during the same month. A detailed explanation of the index is given by Alley (1984) and Heim (2002). The FORTRAN code used at NOAA/NCDC is available at ftp://ftp.ncdc.noaa.gov/pub/software/palmer/pdi.f, while (Jacoby et al., 2013) have developed a re-implementation in MATLAB with an accurate description of the computation and of the parameters that are involved. The main use of PDSI is for operative purposes, in order to apply drought response actions of different nature, from management of water resources to economical. According to the US Drought Monitor (https://droughtmonitor.unl.edu) their weekly drought reports (based on PDSI and other indexes) are used by various authorities in United States for disaster declaration and consequent emission of low-interest loans, tax deferral or forage supply. More in general, PDSI is used for studies on drought hazard, especially on its evolution in connection with the ongoing climate change (e.g., Burke et al., 2006). For the comparison with the seismicity in Southern California the time series of PDSI was averaged over the climate divisions 6 and 7, containing the majority of the epicenters. The values of PDSI are published without indication of the estimation error, which prevent a sensitivity analysis similar to that performed for earthquake magnitude and location errors. Alternatively, the robustness of the relationship was assessed by repeating the analysis for the PDSI averaged over the four zones 4–7 (see the following section). Furthermore, the reliability of the climate signal summarized by PDSI was checked by comparison with the level of snow in the Sierra Nevada. The two PDSI curves averaged over the climate divisions 6–7 and 4–7 are compared in Figure 3 (thin lines): they are very similar, with Pearson correlation coefficient r = 0.94. More evident in the smoothed curves (thick lines in Figure 3), the two PDSI signals have a decreasing trend with superimposed a few large oscillations. They testify the general tendency towards a warm/dry climate although with the interposition of multi-year phases characterized by cold/wet conditions, when an increase of the groundwater volume is expected. The reliability of such a climate trend was confirmed by comparison with the snow coverage of the Sierra Nevada quantified by the 1 April Snow Water Equivalent (SWE) available till the year 2015 (Belmecheri et al., 2016). Similarly to PDSI, increases of the SWE are favored by cold/wet conditions. Figure 4 shows an analogous trend, quantified by Pearson correlation coefficient r = 0.67 for SWE and PDSI averaged over the climate zones 6–7. The coefficient increases to 0.77 considering PDSI averaged over climate zones 4–7. In particular, the curves share major peaks around 1910, 1940 and 1980, as well as a minor peak around 1995.

FIGURE 3

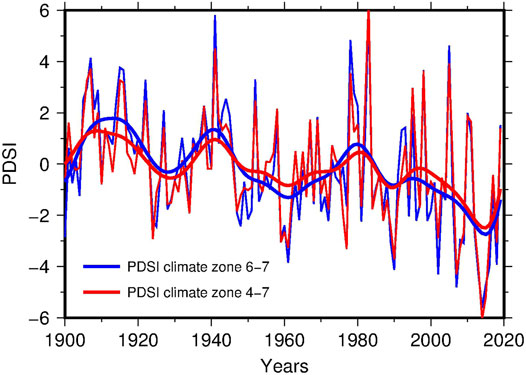
FIGURE 3. PDSI averaged over the climate zones 6–7 (thin blue line) and 4–7 (thin red line). The thick lines are the corresponding smoothed curves obtained by Gaussian kernel smoothing with bandwidth parameter h = 4 years.

FIGURE 4

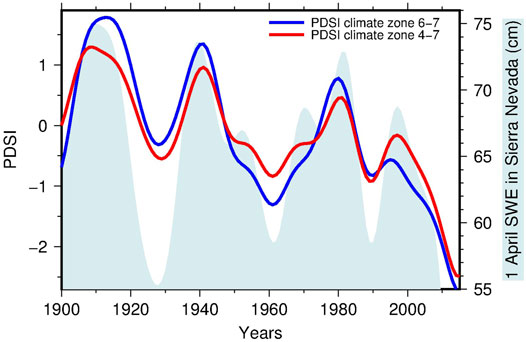
FIGURE 4. PDSI averaged over the climate zones 6–7 (blue line) and 4–7 (red line) compared with the trend of the 1 April Snow Water Equivalent (SWE) in Sierra Nevada (light blue area). All the curves were smoothed by Gaussian kernel smoothing with bandwidth parameter h = 4 years.

Analysis

The analysis carried out for this work faced two problems. Firstly, the comparison concerned data of different numerical nature: a point process (a sparse set of earthquake origin times) and a time series with values sampled regularly each year (PDSI). Secondarily, PDSI has a decreasing trend and, as formally checked in the following, is nonstationary. This latter condition can lead to spurious results using correlation and regression methods (Johansen, 2012). The limitation applies in particular to Poisson and logistic regression, often used for similar comparisons, like earthquakes vs El Niño–Southern Oscillation (Guillas et al., 2010). The solution here adopted was to test the correlation between PDSI and earthquakes by binomial logistic regression (Venables and Ripley, 2002) and counter-checking the result by cointegration testing (Engle and Granger, 1987), a technique dealing with nonstationary time series. To apply the latter method, the series of earthquake origin times was replaced by their smoothed time density sampled each year, introducing a dependence on the smoothing parameter discussed in the following.

Binomial logistic regression allows a direct comparison of a point process with a time series. In the case here considered it was estimated the probability of occurrence of an earthquake at year i as a function of the PDSI observed di years before (year i-di), trying different values of di in order to obtain the best-fitting model according to the Akaike Information Criterion (AIC). For a given di, it was considered the set of observations ${x_{i - d i}, y_{i}}$ , where $x_{i - d i}$ is the PDSI value of the year i-di, and $y_{i}$ takes the values one in case of occurrence of an earthquake on year i, 0 otherwise (the rare years with more than one earthquake were represented by multiple identical couples ${x, 1}$ in the set of observations). Binomial logistic regression assumes that the observations $y_{i}$ are drawn from a set of independent Bernoulli random variables $Y_{i}$ . Each $Y_{i}$ takes the value 1 with probability $p_{i}$ and 0 with probability $1 - p_{i}$ . In turn, the values of $p_{i}$ depends on $x_{i - d i}$ through the logit transformation $l o g i t (p_{i}) = a + b x_{i - d i}$ , where $l o g i t (p_{i}) = l n [p_{i} / (1 - p_{i})]$ . By regression it is possible to estimate the parameters a and b as well as the corresponding uncertainties. The value of b and its significance level give an indication of the degree of correlation between the two covariates. Regression was performed using the function ‘‘glm’’ of the package MASS (Venables and Ripley, 2002) implemented in the R software system (R Core Team, 2012). The best model was obtained for earthquakes following PDSI by 9 years (di = 9 years) and b = 0.23 ± 0.10, statistically significant at the 5% level (see the results for the data set 1 in Table 1).

TABLE 1

TABLE 1. Results of binomial logistic regression and cointegration analysis for various data sets.

Cointegration testing applies to two equally sampled time series. To the purpose, the earthquake point process was transformed in a yearly sampled time series by considering its time density estimated by Gaussian kernel smoothing (Bowman and Azzalini, 1997) using the smoothing parameter h = 4 years (red line in Figure 5A). The value of h was chosen nearly equal to two times the average inter-arrival time of the earthquakes, judged sufficient for a robust estimation of the time density. The choice of h is critical and may influence the result of the analysis, so that alternative values of the parameter were considered (more details in the following section). For homogeneity, the time series of PDSI was also smoothed by Gaussian kernel regression (Bowman and Azzalini, 1997) with the same smoothing parameter h = 4 years (blue line in Figure 5). A preliminary visual inspection of the two curves revealed a general good agreement with a series of fluctuations over a decreasing trend, with seismicity delayed in respect to PDSI. The time lag was quantified using the correlation function r(τ). The best matching was obtained anticipating the earthquake data of 8 years (red line in Figure 5B), obtaining Pearson correlation coefficient r = 0.79 (see the results for the data set 1 in Table 1). In Table 1 the degree of association between the two variables is also quantified by the Kendall rank correlation coefficient k, which is significantly positive (p-value < 0.001) although lower than r (0.60 vs 0.79). As discussed before, this high correlation deserves further checking. In fact, both signals are characterized by decreasing trend and, checked with the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test (Kwiatkowski et al., 1992), the null hypothesis of stationarity is rejected at a significance level of 5%. This condition suggests the use of cointegration testing (Engle and Granger, 1987). In this approach a time series X(t_i) is defined to be integrated of the order 1, or I(1), if its differential time series ∆X(t_i) = X(t_i)-X(t_i-1) is stationary, or I(0). Two non-stationary time series are cointegrated if they are both I(1) and a linear combination of them exists which is I(0), that is

\begin{array}{l} e (t_{i}) = Y (t_{i}) - [α X (t_{i}) + β], \\ e (t_{i}) is stationary . \end{array} (2)

FIGURE 5

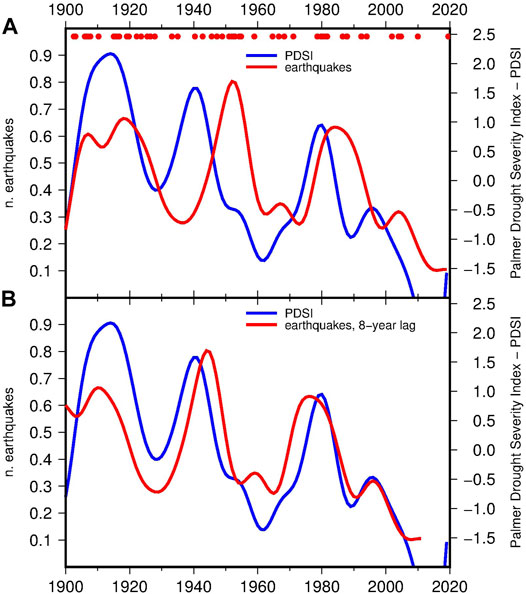
FIGURE 5. Time density of Mw ≥ 5.7 earthquakes in Southern California (red lines) and PDSI averaged over the climate zones 6–7 (blue lines). (A) curves obtained by Gaussian kernel smoothing with bandwidth parameter h = 4 years; (B) the same curves with the earthquake time density anticipated by 8 years in order to maximize the correlation with PDSI (see the results for the data set 1 in Table 1). The dots indicate the time of occurrence of the earthquakes.

Cointegration means that Y(t_i) and αX(t_i)+β cannot drift too far apart: their distance e(t_i), being stationary, oscillates around a constant mean, with finite constant variance and no trend. Here cointegration was checked taking the time density of earthquakes as Y(t_i) and PDSI as X(t_i), also using the KPSS test of stationarity (5% significance level) and ordinary least square regression for the estimation of the linear model in Equation 2. Tested in this way, the null hypothesis of cointegration between seismicity and PDSI was not rejected at a significance level of 5% (Table 1, data set number 1).

Robustness Checking

The reliability of the results was tested taking into account the uncertainty of the data and some variants parameters chosen for the analysis. The first check concerned the variability of the smoothed time series and its consequences for cointegration analysis. Confidence intervals for the smoothed time series were computed using the bootstrap method suggested by Bowman and Azzalini (1997). The available data were resampled to obtain 1,000 alternative time series on which kernel estimation was carried out. The results are shown in Figure 6 for both PDSI and earthquake time density: the gray lines are the 1,000 kernel estimations of the smoothed time series, while the continuous and dashed color lines represent the mean of the estimations in each year and the 68% confidence interval. Even considering the confidence interval, the general structure common to earthquakes and PDSI is maintained. Repeated for the mean curves (blue and red continuous lines in Figure 6) cointegration testing confirms a significant cointegration at a 5% level. In this case the best matching was obtained for seismicity 7 years behind PDSI with Pearson correlation coefficient r = 0.78, compared to 8 years and r = 0.79, respectively, for the two original data sets.

FIGURE 6

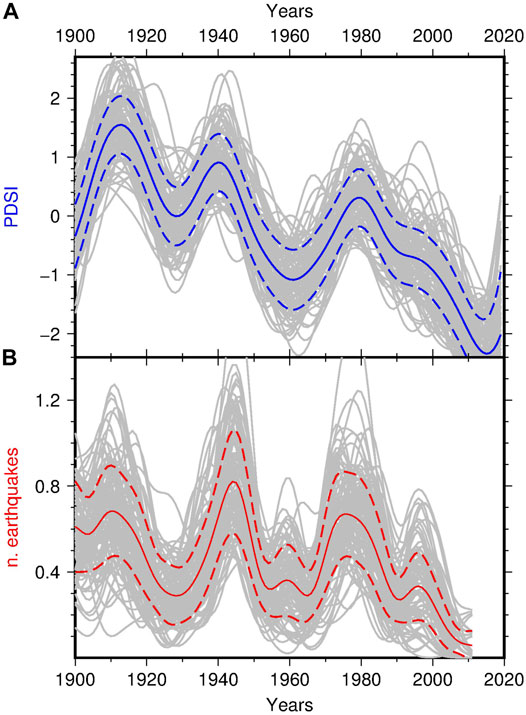
FIGURE 6. Bootstrap confidence intervals for the kernel regression of PDSI averaged over the climate zones 6 and 7 (A) and the time density of earthquakes located in Southern California (B). The gray lines are the 1,000 smoothed curves estimated with the resampled data. The colored lines indicate the mean value in each year (continuous) and the 68% confidence interval (dashed).

A further critical point for the cointegration testing is its possible dependence on the level of smoothing adopted. This aspect was taken into consideration by repeating the analysis with the smoothing parameter h taking the values 1, 2 and 3 years for both earthquakes and PDSI (Figure 7). Even in those cases the cointegration of the time series was confirmed.

FIGURE 7

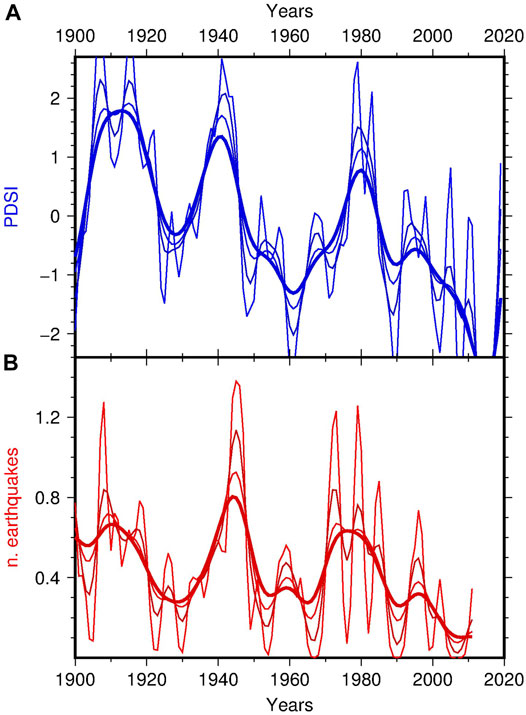
FIGURE 7. Curves obtained for different choices of the smoothing parameter h (from 1 to 4 years). (A) kernel regression of PDSI averaged over the climate zones 6 and 7; (B) kernel estimation of the time density of earthquakes in Southern California.

The uncertainties on magnitude and location affect the selection of the earthquakes by magnitude threshold and epicentral area. The consequences on the time distribution of the earthquakes and on its relationship with PDSI were assessed using a randomization of the entire seismic catalog by (Wang et al., 2019). The magnitude and the epicentral coordinates of each earthquake were perturbed with a random value drawn from a zero-mean normal distribution with standard deviation equal to the error reported in the catalog. Then, the earthquakes were selected by magnitude threshold and epicentral area similarly to the original data set. The process was repeated to obtain 1,000 perturbed catalog. For each them it was performed logistic regression with PDSI (time lag 8 years) to obtain 1,000 estimations of the b parameter, used to assess its sample distribution and its statistical significance. The analysis lead to estimate b = 0.22 ± 0.05, which is significant at the 5% level, in agreement with what obtained for the original data set (b = 0.23 ± 0.10, data set 1 in Table 1). The result confirms the strength of the association with PDSI against magnitude and location uncertainties.

In the robustness analysis it was also checked if slight changes of the selected climate and seismic areas affect the results in a significant way. A series of alternative data sets were taken into account for binomial logistic regression and cointegration analysis, with the results reported in Table 1. For the choice of the climate zones, the analysis was repeated using the average of PDSI over the four zones 4–7 instead of 6–7 (curves in Figure 3). Even including two more zones and, potentially, larger climate variability, the strength of the relationship between PDSI and earthquakes was confirmed for both logistic regression and cointegration analysis (data set 2 in Table 1). The same considering only earthquakes located inland (data set 3 in Table 1 with 47 out of 54 earthquakes). A further test concerned the internal persistence of the relationship, assessed for two disjoint subsets of earthquakes obtained by splitting the study area at latitude 34°. Apart from the geographical separation, the two sectors differ for the spatial distribution of seismicity (Figure 1), more scattered in northern sector and aligned in NW/SE direction along the Salton Through and the Colorado River Delta in the southern sector. According to the results reported in Table 1 (data sets 4 and 5) the relationship between PDSI and earthquakes holds in the northern sector but appears weaker in the southern sector. There the b parameter estimated by logistic regression is not significant at the 5% level and the Pearson correlation coefficients for the smoothed curves drops to 0.50. The loss of similarity is mainly caused by the earthquakes located in the southernmost portion of the area, in Mexico along the Pacific and the Gulf of California coasts. The significance of the logistic b parameter and high correlation between the smoothed curves (r = 0.71) are restored after moving the southern border to 32°N and discarding five earthquakes (data set 6 in Table 1). To note that the northern and southern sectors have different time lags compared to PDSI (10 and 4 years respectively for the smoothed curves, Figure 8).

FIGURE 8

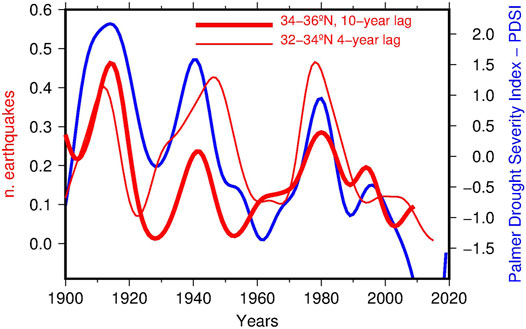
FIGURE 8. Time density of earthquakes for a north/south partitioning of the territory (red lines) compared with the trend of PDSI averaged over the climate zones 6 and 7 (all the curves obtained by Gaussian kernel smoothing using a bandwidth smoothing parameter h = 4 years). The earthquake time densities were anticipated by 10 years (northern sector, thick red line) and 4 years (southern sector, thin red line) in order to maximize the correlation with PDSI (see also the results for the data sets 4 and 6 in Table 1).

The stability of the relationship was also checked by shifting the seismic area to the north, in the sectors 32–37°N and 33–38°N (data sets 7 and 8 compared to the original data set 1 in Table 1). Graphically (Figure 9) they agree on the clustering of seismic activity in the first part of the 20th century and around 1980, while the common peak around 1950 progressively diminishes its amplitude by moving to north. In any case the relationship with PDSI remains statistically significant (see the results for the data sets 7 and 8 in Table 1).

FIGURE 9

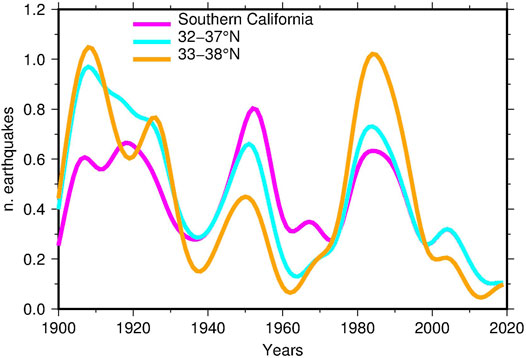
FIGURE 9. Smoothed time densities of earthquakes obtained for the original data set (magenta) and moving the study area to the north by one degree of latitude (cyan) and two degrees of latitude (orange).

It was checked if the statistical results described so far were robust against the overall set of changes introduced by the alternative catalog by Mueller (2018, 2019) described before. For the study area, this catalog includes 63 mainshocks with Mw ≥ 5.7 (data set 9 in Table 1). Their time distribution is compared with the trend of PDSI in Figure 10 (lines in magenta and blue, respectively) with and without the correction for the 7-years time lag estimated by correlation analysis. The agreement on the peaks near to 1910 and 1940 is still evident. Differences emerge between 1960 and 2000, when the seismic activity appears distributed around three minor peaks, compared to the single prominent peak of PDSI around 1980. This dissimilarity has consequences for logistic regression, leading to a not-significant b parameter (data set 9 in Table 1). The largest part of the alteration is imputable to numerous earthquakes located in Mexico, not present in the catalog by Wang et al. (2009). The similarity with PDSI is restored after removing these earthquakes, by placing the southern limit of the study area at 32.3°N (data set 10 in Table 1 and orange curve in Figure 10).

FIGURE 10

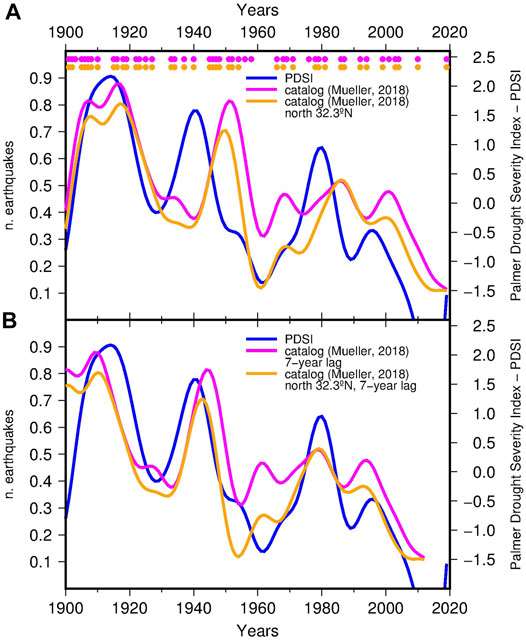
FIGURE 10. PDSI averaged over the climate zone 6–7 (blue lines) compared with the time density of Mw ≥ 5.7 earthquakes in Southern California computed for the declustered seismic catalog by Mueller (2018), Mueller (2019) (lines in magenta) and for the same catalog with the southern limit moved to 32.3°N (lines in orange). (A) original data; (B) earthquake time densities anticipated by 7 years in order to maximize the correlation with PDSI (see also the results for the data sets 9 and 10 in Table 1). The dots indicate the time of occurrence of the earthquakes.

Reducing the observation period to post 1945, thanks to the improvement of the seismic networks, the magnitude of completeness of the catalog by Wang et al. (2009) reduces to 5.0. This reduction gives the possibility of checking if the observed trend persists at lower magnitudes. In Figure 11A the time behavior of seismicity for Mw ≥ 5.7 after 1945 is compared with that of the independent data set obtained for Mw between 5.2 and 5.7 (curves in orange and magenta, respectively): the bimodality of seismicity (similar to that of PDSI) persists for the lower magnitude range, albeit with a time shift of the two maxima. Looking at the cumulative curves (those for Mw ≥ 5.7 and Mw ≥ 5.2 in Figure 11B), apart from the overall number of earthquakes, the difference is negligible and the statistical significance of the relationship with PDSI is preserved (data set 11 in Table 1). Figure 11A also shows the time distributions for Mw between 5 and 5.2 (curve in cyan). Although the number of earthquakes is low, the available data indicate a time distribution that is complementary to that of the stronger earthquakes (lines in orange and magenta), with the exchange of highs and lows. A hypothesis is that what observed may be an effect of over-declustering, with independent earthquakes belonging to background seismicity mistaken for aftershocks and removed in greater percentage during periods of increased strong earthquakes. Independently on its interpretation, the effect is symptomatic of the difficulty of extending this same analysis to lower magnitudes. Similar conclusions for the magnitude-dependent analysis were reached using the catalog by Mueller (2018).

FIGURE 11

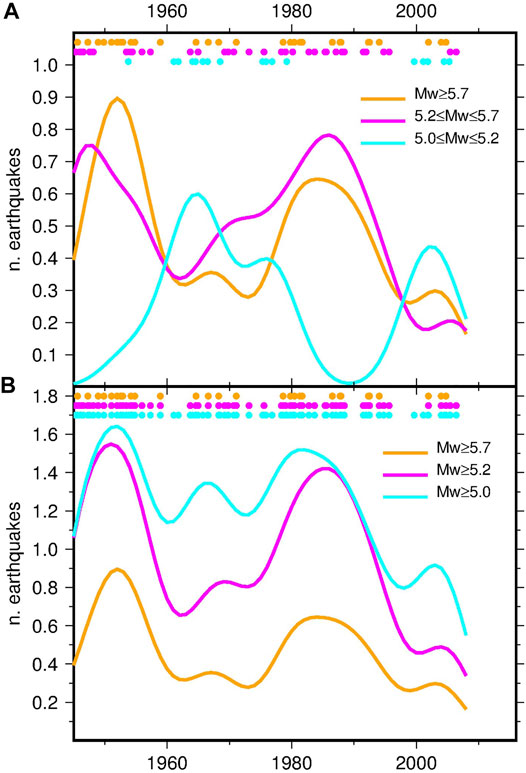
FIGURE 11. Smoothed time densities of earthquakes in Southern California since 1945 computed for various magnitude ranges. The dots indicate the time of occurrence of the earthquakes.

Focus on the Salton Trough Area

The available data allowed looking in more detail at what happened by the Salton Trough in modern times and drawing some hints for the interpretation of paleoseismicity in this crucial region. A simple preliminary analysis was performed using the subset of 15 earthquakes located in the area investigated by (Luttrel et al., 2007), that is latitude between 32.3° and 33.8°N and longitude between −116.5°E and −115°E (yellow rectangle in Figure 1). In Figure 12 the earthquake time density is compared with PDSI: with a few exceptions (including the last earthquake of 2009), the seismicity of the Salton Trough is modulated similarly to the PDSI, with three major clusters of earthquakes and a delay respect to PDSI estimated between 1 year with logistic regression and 3 years by correlation analysis (data set 12 in Table 1), compared to 9 and 8 years respectively for the complete data set (data set 1 in Table 1). Although there are a few earthquakes, this visual inspection suggests that seismicity in this area may be extremely sensitive to the regional groundwater load, with a relatively rapid reaction time. Figure 12 also reports the water level of the Salton Sea (Imperial Irrigation District, 2010), the modern successor of the much larger Lake Cahuilla investigated by Luttrel et al. (2007). The Salton Sea is a man-made lake formed between 1905 and 1907 as a consequence of the bad management of the irrigation system feeding the Imperial Valley coupled with a series of large floods on the Colorado River in winter and spring 1905 (Oglesby, 2005). According to Figure 12, after its initial filling the lake dried naturally by evaporation till about 1920, roughly following the trend of PDSI. Later the level of the lake was artificially regulated and gradually increased up to 1995, when it started its current drainage. Looking at the initial period 1900–1920 one could attribute the earthquake triggering to the filling of the lake, but the later behaviour clarifies that seismicity is statistically related to PDSI while it is independent on the lake level.

FIGURE 12

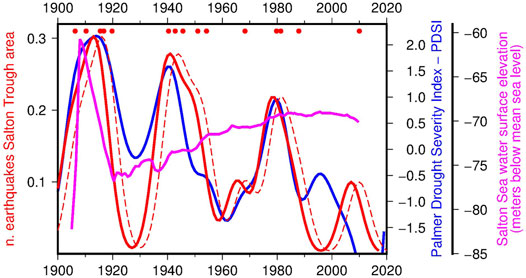
FIGURE 12. Time density of Mw ≥ 5.7 earthquakes in the Salton Trough area compared with the smoothed curve of PDSI averaged over the climate zones 6 and 7 and the water surface elevation of the Salton Sea (meters below mean sea level). For the earthquakes they are reported both the original density curve (red dashed line) and the same curve anticipated by 3 years (red continuous line) in order to maximizes the correlation with PDSI (see the results for the data set 12 in Table 1). The dots indicate the time of occurrence of the 15 earthquakes.

Discussion and Conclusion

According to this study, seismicity and PDSI in Southern California are statistically significantly related. In general, there are fewer earthquakes in drought periods, an effect that is particularly evident in the last decades. On the other hand, major clusters of strong earthquakes occurred around 1910, 1950 and 1980 preceded by corresponding wet periods (Figure 5). The robustness of the association was checked by performing different types of analysis (logistic regression and cointegration testing), taking into account errors in magnitude and earthquake location, and considering an alternative catalog using a different declustering approach. In absence of an estimation error for PDSI, the reliability of the drought index was successfully assessed by varying the area of definition and by comparison with the trend of snow coverage in the Sierra Nevada. The comparison after 1945 indicates that the relationship is valid also for magnitude Mw down to 5.2, while it tends to vanish for lower magnitude. This effect is possibly due to over-declustering, with normal background seismicity taken for aftershocks. By varying the seismic area of analysis, it was shown that the association of earthquakes with PDSI is stable towards north and in the Salton Trough, while it deteriorates near and beyond the border with Mexico. The effect is particularly evident for the catalog by Mueller (2018), which loses the connection with PDSI after 1945.

In general terms, the results outlined here agree with those concerning paleoseismicity by the Salton Trough (Luttrel et al., 2007; Hill, 2020) and the strong earthquakes in the entire Southern California between 1917 and 1979 (Huang et al., 1979). Altogether these works suggest the hypothesis of a physical connection, with groundwater recharge possibly enhancing major seismicity in a significant way. The validation of this hypothesis requires in-depth physical investigation and modeling, which were not attempted in the present study. Nonetheless, it is possible to observe that the multi-year delay of seismicity in respect to groundwater recharge is compatible with a triggering effect by pore pressure propagation. Based on the analysis of a large number of real cases, Talwani et al. (2007) concluded that, in order to trigger seismicity, the fluid pressure wave should travel along pre-existing narrow drained paths (fractures and joints) characterized by higher permeability than the confining mediums, having hydraulic diffusivity in a limited range (0.1–10 m²s⁻¹). Modeling the effect of a loading/unloading cycle for a hydraulic diffusivity of 0.1 m²s⁻¹, it has been shown (Mulargia and Bizzarri, 2014) that in 8 years the peak of pressure transmits at about 12 km from the source. This distance is comparable with the depth of the seismogenic layer estimated for the area (mainly between 13.9 and 16.2 km according to Nazareth and Hauksson, 2004), and with the average depth of the earthquakes considered in this study (10.3 ± 5.8 km for the mainshocks occurred since 1980, when depth estimation became more reliable). By the Salton Trough a hydraulic diffusivity slightly higher than 0.1 m²s⁻¹ could justify the reduction of the water/seismic delay to about 3 years. Furthermore, the fact that in this area the seismicity follows the groundwater recharge independently on the Salton Sea level suggests an alternative hypothesis also for paleoseismicity: it is possible that the rising of the Lake Cahuilla considered in previous studies was not the direct cause of the increase of seismicity, but rather an indicator of a large-scale climate change towards wet conditions, with consequent huge groundwater accumulation at the regional level and earthquake triggering. In this alternative view Lake Cahuilla worked just as a small tip signaling a large iceberg (a large groundwater volume).

The earthquake reduction of the last decades is not specific of Southern California. It is common to the entire Northern Hemisphere and its main tectonic sub-regions, where the rate of M ≥ 7 earthquakes reduced by about 40% in 114 years (Bragato and Sugan, 2014). The northern one is the hemisphere with the largest percentage of emerged land, which make it potentially more vulnerable to the seismic effect of precipitation. This observation is far from being explicative of the earthquake reduction and must be considered as a hint for further investigation. The tendency of strong seismicity to synchronize worldwide was analyzed in a number of previous studies. Among the most recent, Bendick and Bilham (2017) discussed how even a global weak stress forcing is sufficient to obtain the synchronization. They envisage as the possible sources of additive stress the seismicity itself, with stress transfer at teleseismic distances, or other sources of lithospheric loading such as Earth’s variable rotation. Using a similar data set (M ≥ 7 earthquakes occurred worldwide since 1900), Scafetta and Mazzarella (2015) showed the spectral coherence between climate oscillations and variations of the global seismic rate. They suggest that large earthquakes are mutually triggered by crust deformations related to astronomical forcing through climatic and oceanic oscillations. In Italy, thanks the availability of a reliable seismic catalog covering the last millennium, it was possible to see the current decreasing trend in a long-term perspective (Bragato and Holzhauser, 2019). For Italy the decrease is placed at the end of a seismic transient originated around 1300 AD and characterized by high average seismic rate with large fluctuations almost coincident with the most severe phases of the Little Ice Age. These phases were characterized in Europe by increased precipitation and lower evaporation, made evident by the augment of ice and snow. Seen from this point of view, the behavior observed in Southern California might be a further evidence of the global geological consequences of the ongoing climate change.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: earthquake catalogs from the cited papers; earthquake data for the time period 2007–2019 https://www.usgs.gov/natural-hazards/earthquake-hazards/earthquakes; PDSI data for the climate divisions of California https://www7.ncdc.noaa.gov/CDO/CDODivisionalSelect.jsp; time series of SWE in Sierra Nevada https://www1.ncdc.noaa.gov/pub/data/paleo/treering/reconstructions/california/sierra2015swe.txt.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This study was carried out with contributions from Regione Friuli Venezia Giulia and Regione Veneto.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Russell S. Vose kindly provided the borders of the 7 climate divisions in Figure 1. The statistical analysis was carried out with the R software system (R Core Team, 2012). All the figures were produced using the Generic Mapping Tools (Wessel et al., 2019).

References

Alley, W. M. (1984). The Palmer Drought Severity Index: Limitations and Assumptions. J. Clim. Appl. Meteorol. 23, 1100–1109. doi:10.1175/1520-0450(1984)023<1100:TPDSIL>2.0.CO;2