Imaging Complex Subsurface Structures for Geothermal Exploration at Pirouette Mountain and Eleven-Mile Canyon in Nevada

Accurate imaging of subsurface complex structures with faults is crucial for geothermal exploration because faults are generally the primary conduit of hydrothermal flow. It is very challenging to image geothermal exploration areas because of complex geologic structures with various faults and noisy surface seismic data with strong and coherent ground-roll noise. In addition, fracture zones and most geologic formations behave as anisotropic media for seismic-wave propagation. Properly suppressing ground-roll noise and accounting for subsurface anisotropic properties are essential for high-resolution imaging of subsurface structures and faults for geothermal exploration. We develop a novel wavenumber-adaptive bandpass filter to suppress the ground-roll noise without affecting useful seismic signals. This filter adaptively exploits both characteristics of the lower frequency and the smaller velocity of the ground-roll noise than those of the signals. Consequently, this filter can effectively differentiate the ground-roll noise from the signal. We use our novel filter to attenuate the ground-roll noise in seismic data along five survey lines acquired by the U.S. Navy Geothermal Program Office at Pirouette Mountain and Eleven-Mile Canyon in Nevada, United States. We then apply our novel anisotropic least-squares reverse-time migration algorithm to the resulting data for imaging subsurface structures at the Pirouette Mountain and Eleven-Mile Canyon geothermal exploration areas. The migration method employs an efficient implicit wavefield-separation scheme to reduce image artifacts and improve the image quality. Our results demonstrate that our wavenumber-adaptive bandpass filtering method successfully suppresses the strong and coherent ground-roll noise in the land seismic data, and our anisotropic least-squares reverse-time migration produces high-resolution subsurface images of Pirouette Mountain and Eleven-Mile Canyon, facilitating accurate fault interpretation for geothermal exploration.

Introduction

The geothermal exploration areas at Pirouette Mountain and Eleven-Mile Canyon are located near the margins of Dixie Valley in Nevada, United States. Eleven-Mile Canyon lies next to the surface rupture terminations of 1954 Fairview Peak—Dixie Valley earthquake sequence (Caskey et al., 1996). The area contains a complex network of steeply-dipping faults and fractures, which creates the highly permeable fractures for the potential production zone at 2–3 km in depth (Unruh et al., 2016). It is crucial to accurately image and delineate subsurface fracture/fault zones for geothermal exploration and optimizing well placement, because faults/fracture zones provide paths for hydrothermal flow, but they may also be effective barriers to geothermal flow in some situations (Ba et al., 2015). It is particularly challenging to accurately image the subsurface structures at Pirouette Mountain and Eleven-Mile Canyon because of complex heterogeneities and possible anisotropies in both fracture zones and geologic formations.

In 2013, the U.S. Navy Geothermal Program Office carried out a seismic reflection survey (Alm et al., 2016) along five lines to evaluate the geothermal potential at Pirouette Mountain and Eleven-Mile Canyon, NV. Lines 1, 2, 3, and 4 were aligned west-east to cross the valley, while Line 5 was placed along a north-south trend to intersect Lines 1–3 (Figure 1). Lines 1, 2, 3, and 5 are located at Pirouette Mountain, and Line 4 is at Eleven-Mile Canyon. Such a geometry of the survey aimed to allow enhanced horizon and fault interpretations.

FIGURE 1

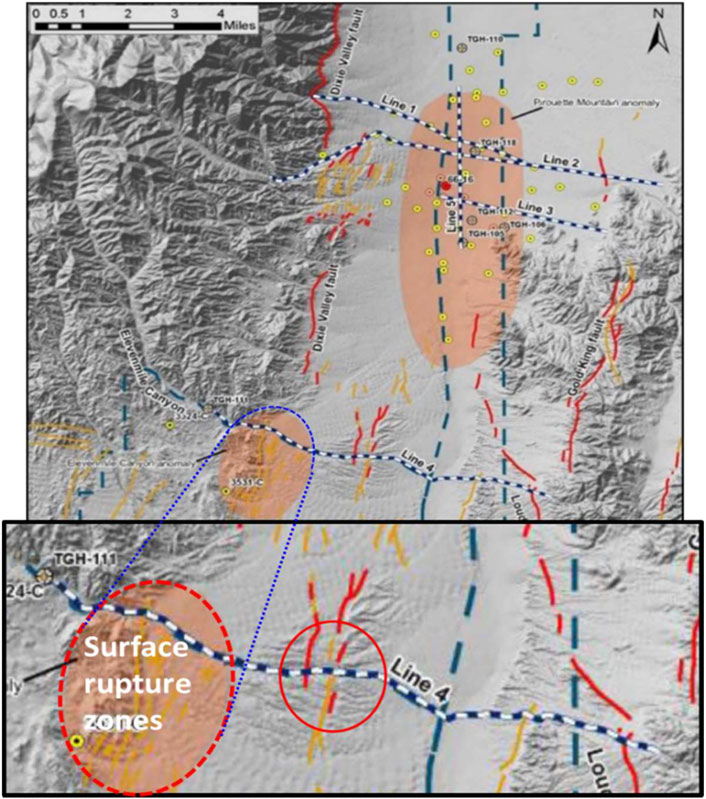
FIGURE 1. Location map of the geothermal exploration areas at Pirouette Mountain and Eleven-Mile Canyon in southern Dixie Valley, Nevada, with five lines of seismic survey depicted in rails. The faults shown are from the U.S. Geological Survey Quaternary fault and fold database. Surface rupture zones correspond to the 1954 earthquake sequence (Unruh et al., 2016). The northern shaded region is at Pirouette Mountain, and the southern shaded region is at Eleven-Mile Canyon.

For imaging complex subsurface structures at Pirouette Mountain and Eleven-Mile Canyon, we first need to properly suppressing ground-roll noise in the acquired seismic data.

Ground-roll noise refers to high-amplitude and coherent surface waves (Sheriff, 2002), which not only provide little information regarding deeper reflectors of interest, but also contaminate subsequent geophysical imaging, particularly for waveform inversion and least-squares reverse-time migration that are based on waveform fitting. Although Rayleigh waves dominate ground-roll noise, the latter may also include Love waves, reverberated refractions, and waves scattered by near-surface heterogeneities. Ground-roll noise often masks shallow reflections at near offsets and deep reflections at far offsets. This problem is acute for land surface seismic data acquired at Pirouette Mountain and Eleven-Mile Canyon for geothermal exploration.

Because of near-surface layers and unconsolidated weathering zones, ground-roll noise propagates more slowly and exhibits lower frequency than do seismic reflections. A simple method to reduce ground-roll noise is therefore to apply a low-cut filter. Unfortunately, this method also eliminates the low-frequency part of seismic reflection data, which is critical to waveform inversion and least-squares reverse-time migration.

Several methods were developed to suppress the ground-roll noise over the past several decades. A common motivation is to express the signal and the noise in a certain transform domain that helps separate the signal from the noise. A number of filtering methods were designed (Shieh and Herrmann, 1990), but the reflection data within the frequency bands overlapping with those of the noise could be filtered out (Coruh and Costain, 1983). One of techniques in the transform domain uses f-k filtering (Embree et al., 1963; Treitel et al., 1967; Yilmaz, 2001). Radon, or τ-p, transform was also applied to ground-roll noise suppression (Brysk and McCowan, 1986; Henley, 2003). Sparse Radon transforms (Trad et al., 2003) produce sparse representations of the signal and noise in the transform domain, thereby facilitating signal and noise separation. Challenges exist, however, when the moveout of seismic signals in a common-shot gather is irregular because of irregularities in the surface topography and weathering zones. Other techniques for suppressing the ground-roll noise include interferometry (Halliday, 2011), Karhunen–Loève (K–L) transform (Liu, 1999), singular value decomposition (SVD) (Jin and Ronen, 2005), wavelet transform (Deighan and Watts, 1997), and Wiener filtering (Karsli and Bayrak, 2008).

We develop a novel method to suppress the ground-roll noise without affecting reflection data. To distinguish the ground-roll noise from the signal, we exploit the information of the frequency content, wavenumber, and the relative offset in seismic data. Ground-roll noise exhibits dispersion, resulting in shingled events. The dip of each individual event lies opposite to those of reflections. This observation allows us to design a bandpass filter that is adaptive to wavenumber to fulfill our aim of ground-roll noise suppression.

After suppressing ground-roll noise in the seismic data acquired at Pirouette Mountain and Eleven-Mile Canyon using our novel wavenumber-adaptive bandpass filter, we can use the data to image subsurface structures and faults for geothermal exploration.

Reverse-time migration (RTM) is a powerful tool for imaging complex subsurface structures. In essence, RTM relocates the wave energy in seismic data to subsurface reflectors where the seismic waves are reflected before reaching seismic receivers at the surface for a surface seismic survey. Such a relocation of seismic-wave energy relies on numerical simulations of seismic-wave forward and backward propagation. When the subsurface media are anisotropic, as are typical in complex geothermal exploration fields (Gao and Huang, 2015), it is crucial to properly account for the subsurface anisotropic properties to allow accurate simulations of seismic wavefields. Anisotropic RTM can account for anisotropy for high-resolution subsurface imaging of complex structures with faults.

While RTM performs wave-energy relocation non-iteratively, an extension of RTM is termed least-squares RTM (LSRTM) (Nemeth et al., 1999), which iteratively adjusts the subsurface reflectors so that synthetic seismic data would maximally resemble (in the sense of least-squares residue) real seismic data. Because of ambiguity in the velocity model and limited numbers of sources and receivers, the non-iterative RTM suffers from migration artifacts. By contrast, because of the feedback control mechanism in the iterative LSRTM, the discrepancy between the imaged reflectors and the physical reflectors is restrained.

We apply our anisotropic least-squares reverse-time migration algorithm to the seismic data acquired at the Pirouette Mountain and Eleven-Mile Canyon geothermal exploration areas for reliable imaging of the complex subsurface structures with faults. First, we use our wavenumber-adaptive bandpass filter to suppress the ground-roll noise of the five 2D lines of surface seismic data acquired at Pirouette Mountain and Eleven-Mile Canyon. Then we apply our anisotropic LSRTM to the resulting data to obtain high-resolution subsurface images, and compare the images with industrial images and those obtained using anisotropic RTM.

We organize our paper as follows. We first introduce the methodology of our wavenumber-adaptive bandpass filter and anisotropic least-squares reverse-time migration, present results of ground-roll suppression using our wavenumber-adaptive bandpass filter, give anisotropic LSRTM images with comparison with industrial images and those obtained using anisotropic RTM images, and draw our findings in the Conclusion section.

Methodology

We present the methodology of our novel wavenumber-adaptive bandpass filter for suppressing the ground-roll noise, and our anisotropic least-squares reverse-time migration below.

Wavenumber-Adaptive Bandpass Filter

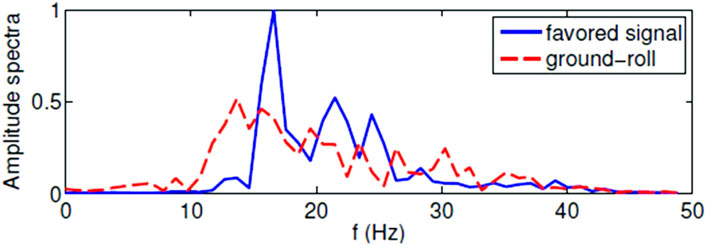
In a typical common-shot gather of surface seismic data, the ground-roll noise appears to be coherent and energetic (Figure 2). Figure 3 shows spectra of two temporal slices of the reflection signals (blue line in Figure 2) and the ground-roll noise (red dashed line in Figure 2). Although the ground-roll noise is of lower frequency compared with the signal, it is evident that there is much overlap between the frequency bands of the signal and the noise. Note that the slice for the ground-roll noise (red dashed line in Figure 2) may also contain signals. This explains the existence of the high-frequency component (above 15 Hz) in the red dashed curve in Figure 3. In the low-frequency band, the signal spectrum (blue curve) encroaches on the spectrum of the ground-roll noise. Therefore, a simple low-cut filtering to suppress the ground-roll noise would also filter out some low-frequency component of the signal, while low-frequency data are crucial for full-waveform inversion.

FIGURE 2

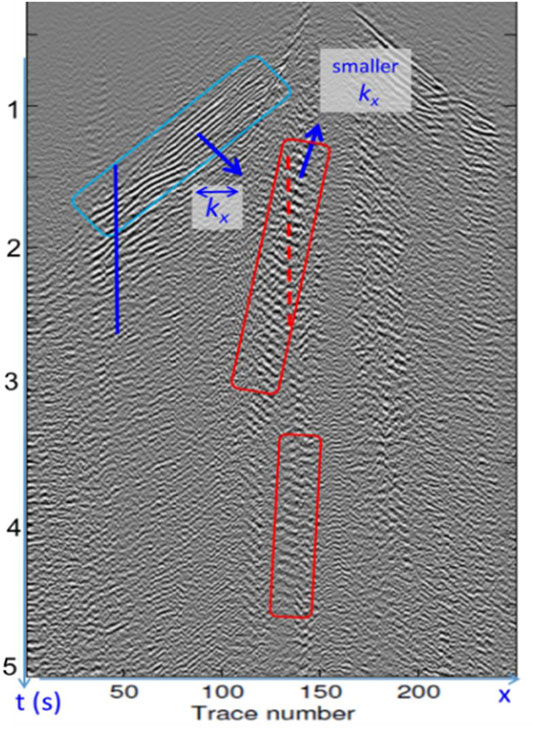
FIGURE 2. A representative common-shot gather of surface seismic data. Red rectangles enclose the ground-roll noise. The cyan rectangle encloses reflection signals. The vertical red dashed line and blue solid line stride across the ground-roll noise and reflection signals, respectively. The single-barbed arrows indicate the wavenumber directions.

FIGURE 3

FIGURE 3. The spectra of the ground-roll noise (red) and the reflection signal (blue).

If an input trace is the signal (e.g., of the blue spectral profile in Figure 3), we would enforce a wide bandpass filter, e.g., of the blue filtering profile in Figure 4. This filter is wide because the low cut-off frequency $f_2$ is small. On the other hand, if an input trace is the ground-roll noise, we would enforce a narrow bandpass filter, e.g., of the red filtering profile in Figure 3. This filter is narrow because the low cut-off frequency $f_1$ is large. In reality, however, we do not know whether an input trace is signal or ground-roll noise a priori. Fortunately, the wavenumbers in common-shot gathers can indicate the likelihood whether an input trace is the ground-roll noise.

FIGURE 4

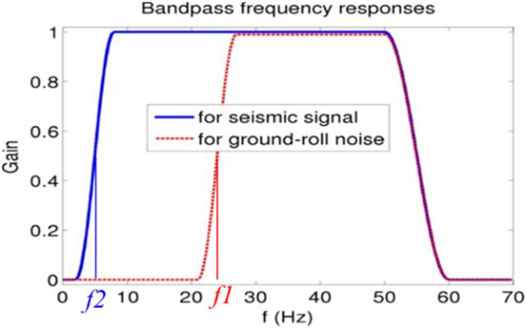
FIGURE 4. If the input data are likely seismic signals, a bandpass filter with low cut-off frequency $f_2$ is preferable. Otherwise, a bandpass filter with a relatively high cut-off frequency $f_1$ is used to reject the ground-roll noise, of which the spectrum lies below $f_1$.

Figure 2 shows that the wavenumber-magnitude $\left|k_x\right|$ of the ground-roll noise is smaller than that of the reflection signal, because the apparent horizontal wavelength ${\lambda }_x$ of the ground-roll noise is larger than that of the reflection signal. Furthermore, the dipping angles of the narrow ‘wavefronts’ of the ground-roll noise within the red rectangles are opposite to those of the signal within the cyan rectangle. One can infer whether an input is the ground-roll noise using this wavenumber information. We use this information to design an f-k filter as shown in Figure 5 for suppressing the ground-roll noise.

FIGURE 5

FIGURE 5. Illustration of the new wavenumber-adaptive bandpass filter for seismic traces on the left side of the shot in a common-shot gather. The vertical slices along the blue and red lines yield the bandpass profiles in Figure 4. The cut-off frequencies $f_1$ and $f_2$ take the same values as in Figure 4.

For seismic traces on the left side of the shot in a common-shot gather, any vertical cross-section of Figure 5 is a bandpass filter, similar to the profiles in Figure 4. When $k_x$ is large, the input should be signal, and therefore, the bandpass filter would have a small low-cut frequency $f_2$ value. On the other hand, when signed $k_x$ is small, the input should be the ground-roll noise, and therefore, the bandpass filter would have a large low-cut frequency $f_1$. The $k_1$ and $k_2$ values in Figure 5 define a transition zone between those two bandpass filters. Since the bandpass filter’s parameterization changes with respect to wavenumber $k_x$, we name our filter “the wavenumber-adaptive bandpass filter.” For seismic traces on the right side of a shot in a common-shot gather, Figure 5 is mirror-reflected with respect to the k_x axis.

We use the following procedure to determine parameters of the wavenumber-adaptive bandpass filter:

1) Pick f₂, e.g., 5 Hz, and f₁, e.g., 24 Hz (Figure 4).

2) Work on a few common-shot gathers. Enclose regions of ground-roll (G) and reflections (R), e.g., Figure 2. Let the objective function J = e(R) - e(G), where e is average energy.

3) Pick initial values of k₁ = 0, k₂ = 2π/λ₂ where λ₂ = 578 m. Update k₁ and k₂ by maximizing J (Figure 5).

4) Construct the F-K filter (Figure 5).

Then we use the following procedure to attenuate the ground-roll noise:

1) For a common-shot gather (CSG) with shot s_x, pick the left part where traces g_x < s_x + margin.

2) Apply the F-K filter (Figure 5) on this left part, to yield AGN1.

3) For this same CSG, pick the right part where traces g_x > s_x – margin.

4) Mirror-reflect the F-K filter in Figure 5; namely k_x ← -k_x.

5) Apply this mirror-reflected F-K on the right part, to yield AGN2.

6) Merge AGN1 and AGN2; use a cosine interpolation weight in their overlapping regions.

Anisotropic Least-Squares Reverse-Time Migration

Least-squares reverse-time migration (LSRTM) seeks to improve a reflectivity model $\mathit{m}$ over iterations, by minimizing a least-squares data residue $\mathit{J}$ defined as

$J=\frac{1}{2}\parallel \mathbf{d}-\mathbf{Lm}{\parallel }_2^2,(1)$

where d represents observed seismic data, and operator L is the Born modeling operator. The Born modeling operator is based on the full-wavefield propagator. For 2D tilted transversely isotropic (TTI) media, we adopt a decoupled qP-wave equation to describe the qP-wave propagation (Zhan et al., 2012):

$\frac{1}{V_{p0}^2}\frac{{\partial }^{2}P}{\partial t^2}={\nabla }_{\mathrm{aniso}}^{2}P,(2)$

where the spatial Laplacian ${\nabla }_{aniso}^2$ for acoustic TTI media is

${\nabla }_{\mathrm{aniso}}^2=-\left\{\begin{array}{l}{k}_x^2+k_z^2\\ +\left(2\epsilon {\cos }^4\theta +2\delta {\sin }^2\theta {\cos }^2\theta \right)\frac{k_x^4}{k_x^2+k_z^2}+\left(2\epsilon {\sin }^4\theta +2\delta {\sin }^2\theta {\cos }^2\theta \right)\frac{k_z^4}{k_x^2+k_z^2}\\ +\left(-4\epsilon \sin 2\theta {\cos }^2\theta +\delta \sin 4\theta \right)\frac{k_x^3{k}_z}{k_x^2+k_z^2}+\left(3\epsilon {\sin }^{2}2\theta -\delta {\sin }^{2}2\theta +2\delta {\cos }^{2}2\theta \right)\frac{k_x^2{k}_z^2}{k_x^2+k_z^2}\end{array}\right\}(3)$

where $V_{p0}$ is the qP-wave velocity along the TTI symmetry axis; $k_x$ and $k_z$ are the spatial wavenumbers in the $x$ and $z$ directions, respectively; $\epsilon$ and $\delta$ are the Thomsen parameters (Thomsen, 1986), where $\epsilon$ describes the difference between the qP-wave velocities perpendicular to and parallel with the TTI symmetry axis (i.e., the long offset effect), $\delta$ describes the near-symmetry-axis qP-wave velocity variation (i.e., the short offset effect), and $\theta$ is the tilt angle of the TTI symmetry axis.

To minimize the misfit functional J, m is updated iteratively through

$\begin{array}{c}{\mathbf{m}}^{\left(k+1\right)}={\mathbf{m}}^{\left(k\right)}-{\alpha }^{\left(k\right)}{\nabla }_{\mathbf{m}}J\\ ={\mathbf{m}}^{\left(k\right)}+{\alpha }^{\left(k\right)}{\mathbf{L}}^{\text{T}}\left(\mathbf{d}-{\mathbf{Lm}}^{\left(k\right)}\right),\end{array}(4)$

where the superscripts $\left(k\right)$ and $(k+1)$ denote the $k$^th and $(k+1)$^th iteration, respectively, and ${\alpha }^{\left(k\right)}$denotes the step length at the $k$^th iteration. Note that when $m^{\left(k\right)}=0$ at the second line of Eq. (4), the line is proportional to$\mathit{ }{L}^{\text{T}}d$, which is considered as the image of RTM. Therefore, RTM is merely the first iteration of LSRTM when starting from$m^{\left(0\right)}=0$.

The gradient term ${\mathbf{L}}^{\text{T}}\left(\mathbf{d}-{\mathbf{Lm}}^{}\right)$ is equivalent to computing an imaging condition as in reverse-time migration by migrating the data residue$\left(\mathbf{d}-{\mathbf{Lm}}^{}\right)$. To more accurately form this imaging condition free of low-wavenumber artifacts, we implement this step as below:

$\begin{array}{l}{G}_{\mathrm{pp},\mathrm{down}}\left(\mathbf{x}\right)={\displaystyle \sum _{N_s,N_r}{\displaystyle \underset{0}{\overset{T}{\int }}\left[P_s{P}_r-H_z\left(P_s\right)H_z\left(P_r\right)-P_s{H}_z\left(H_t\left(P_r\right)\right)-H_z\left(P_s\right)H_t\left(P_r\right)\right]}}dt,\\ G_{\mathrm{pp},\mathrm{left}}\left(\mathbf{x}\right)={\displaystyle \sum _{N_s,N_r}{\displaystyle \underset{0}{\overset{T}{\int }}\left[P_s{P}_r-H_x\left(P_s\right)H_x\left(P_r\right)+P_s{H}_x\left(H_t\left(P_r\right)\right)+H_x\left(P_s\right)H_t\left(P_r\right)\right]}}dt,\\ G_{\mathrm{pp},\mathrm{right}}\left(\mathbf{x}\right)={\displaystyle \sum _{N_s,N_r}{\displaystyle \underset{0}{\overset{T}{\int }}\left[P_s{P}_r-H_x\left(P_s\right)H_x\left(P_r\right)-P_s{H}_x\left(H_t\left(P_r\right)\right)-H_x\left(P_s\right)H_t\left(P_r\right)\right]}}dt,\end{array}(5)$

where $G_{pp,•}$’s are gradients associated with the directional PP images; $P$ is the pure qP-wavefield, and subscripts $s$and $r$ represent the source and receiver, respectively; and $H_x$, $H_z$ and $H_t$ represent the Hilbert transforms in the horizontal direction, vertical direction, and time domain, respectively.

To produce more reliable and high-resolution images when the observed data are noisy, irregular, and sparse, we employ a modified total-variation regularization scheme (Gao et al., 2015; Lin and Huang, 2015) to improve the convergence and imaging fidelity. The misfit function in Eq. (1) becomes

$J\left(\mathbf{m},\mathbf{u}\right)=\underset{\mathbf{m}}{\min }\left\{\underset{\mathbf{u}}{\min }\left\{\frac{1}{2}{\Vert \mathbf{d}-\mathbf{Lm}\Vert }_2^2+{\mathit{\lambda }}_1{\Vert \mathbf{m}-\mathbf{u}\Vert }_2^2+{\mathit{\lambda }}_2{\Vert \mathbf{u}\Vert }_1^1\right\}\right\},(6)$

where λ₁ and λ₂ are regularization parameters. We solve this regularized minimization problem using an alternating-direction minimization scheme (Lin and Huang, 2015).

Suppressing the Ground-Roll Noise of Land Surface Seismic Data From Pirouette Mountain and Eleven-Mile Canyon

We apply our novel wavenumber-adaptive bandpass filter to five lines of 2-D seismic data acquired at Pirouette Mountain and Eleven-Mile Canyon for geothermal exploration (Figure 1) to suppress the ground-roll noise. As an example of ground-roll noise suppression for the seismic data on Line 1, we depict the results of three common-shot gathers in Figure 6. Comparing the second and third columns in Figure 6, we find that the ground-roll noise is mostly suppressed in the third column. The signals within the blue ellipses preserve the low-frequency component.

FIGURE 6

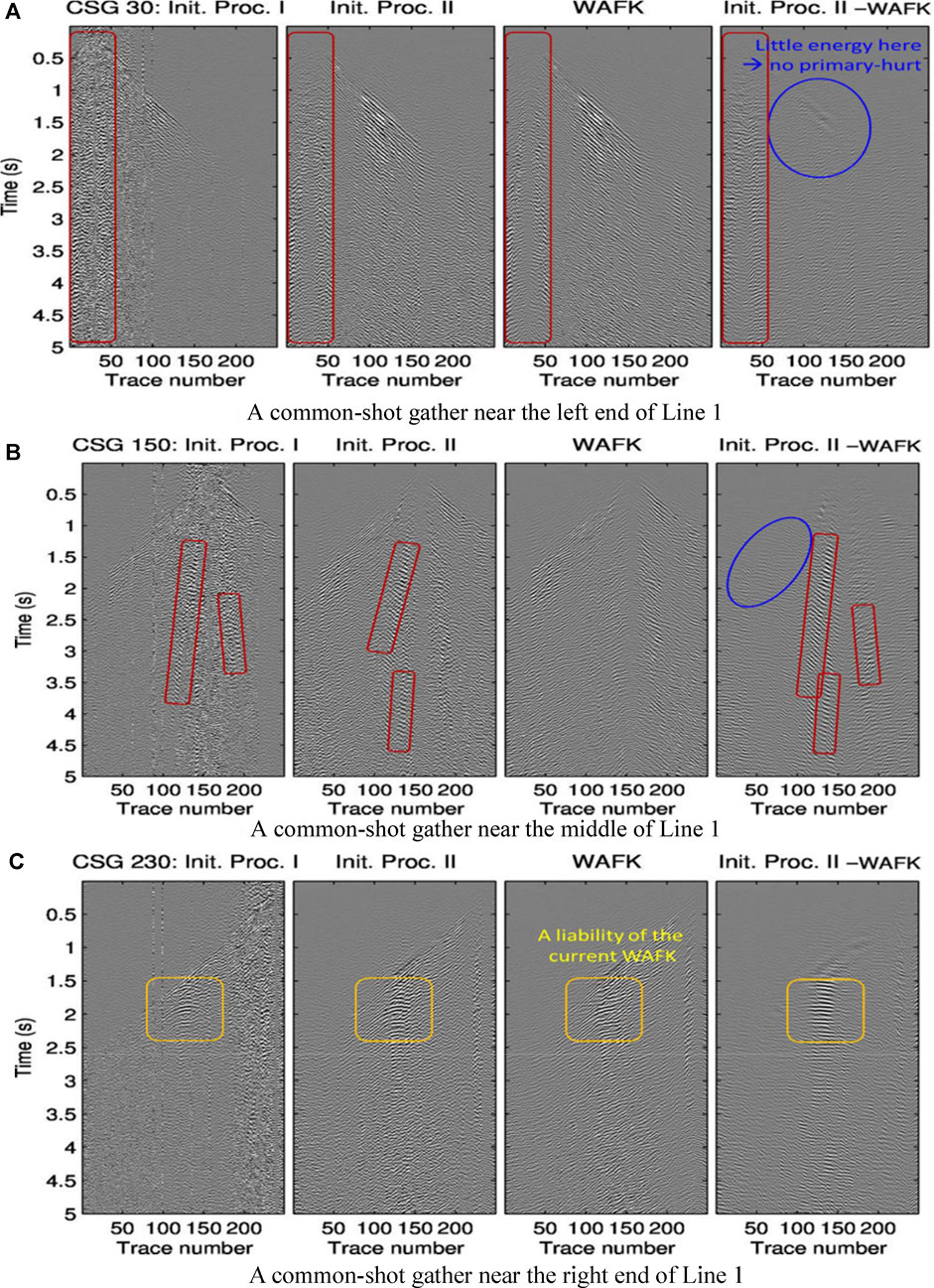
FIGURE 6. Three common-shot gathers (CSGs 30, 150, and 230) corresponding to the three shots along Line 1: (A) CSG near the left end, (B) CSG around the middle, and (C) CSG near the right end of Line 1. The leftmost column shows an industry-processed data. The column titled “Init. Proc. II” presents the other industry-processed data. Our wavenumber-adaptive F-K filter (WAFK) operates upon this column, yielding results shown in column “WAFK.” The rightmost column shows the difference between the inputs and outputs of WAFK. (A) A common-shot gather near the left end of Line 1. (B) A common-shot gather near the middle of Line 1. (C) A common-shot gather near the right end of Line 1.

Figure 7 shows a common-shot gather before and after wavenumber-adaptive bandpass filtering. Some coherent subsurface reflections can be identified on the processed common-shot gather displayed on the right panel of Figure 7.

FIGURE 7

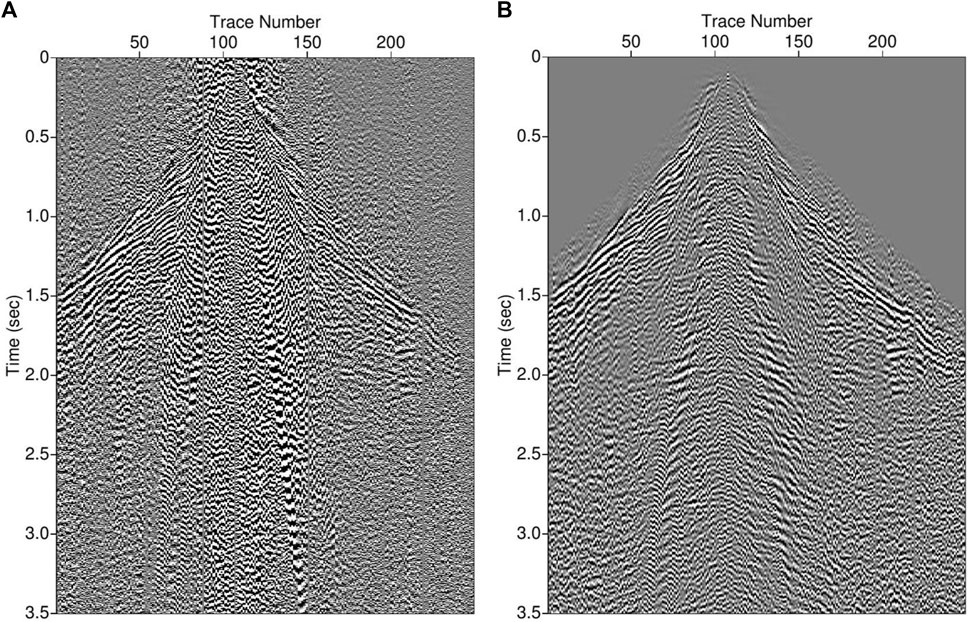
FIGURE 7. Another example of a common-shot gather from Pirouette Mountain and Eleven-Mile Canyon before (A) and after (B) wavenumber-adaptive bandpass filtering. Waveforms before first arrivals in the right panel are muted with a cosine taper near the first arrivals. Coherent subsurface reflections become visible after filtering.

Note that the wavenumber-adaptive bandpass filters used are the same for all common-shot gathers. However, in case the nature of common-shot gathers differs a lot, then it is necessary to determine different values for parameters f₁, f₂, and k₂.

We use the processed data with the ground-roll noise removed to produce subsurface complex structural images using anisotropic RTM and anisotropic LSRTM.

Anisotropic Least-Squares Reverse-Time Migration of Seismic Data From Pirouette Mountain and Eleven-Mile Canyon

After suppressing the ground-roll noise in the surface seismic data along five 2D lines (Figure 8) acquired at Pirouette Mountain and Eleven-Mile Canyon, we apply anisotropic LSRTM to the resulting data, and compare our imaging results with industrial Kirchhoff migration images and those of anisotropic RTM. We carry out necessary preprocessing steps, such as converting the phase of the seismic data from 3D to 2D because we perform migration imaging in 2D, in addition to the ground-roll noise removal. For anisotropic RTM and anisotropic LSRTM, we first obtain a velocity model and anisotropic parameters $(V_{P0},\epsilon ,\delta ,\theta )$ using multi-scale anisotropic full-waveform inversion with total generalized p-variation regularization (Gao and Huang 2019). Our full-waveform inversion starts from a low-frequency band and an initial velocity model obtained using refraction traveltime tomography to produce reliable models of anisotropic parameters. Figure 9 shows the initial velocity V_p models along the five seismic survey lines at Pirouette Mountain and Eleven-Mile Canyon obtained using refraction tomography, and our anisotropic waveform inversion results of V_p0.

FIGURE 8

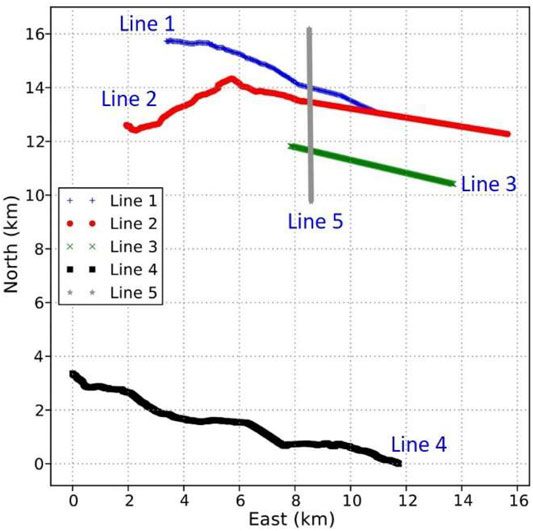
FIGURE 8. Five 2D seismic survey lines at Pirouette Mountain and Eleven-Mile Canyon, Nevada, United States.

FIGURE 9

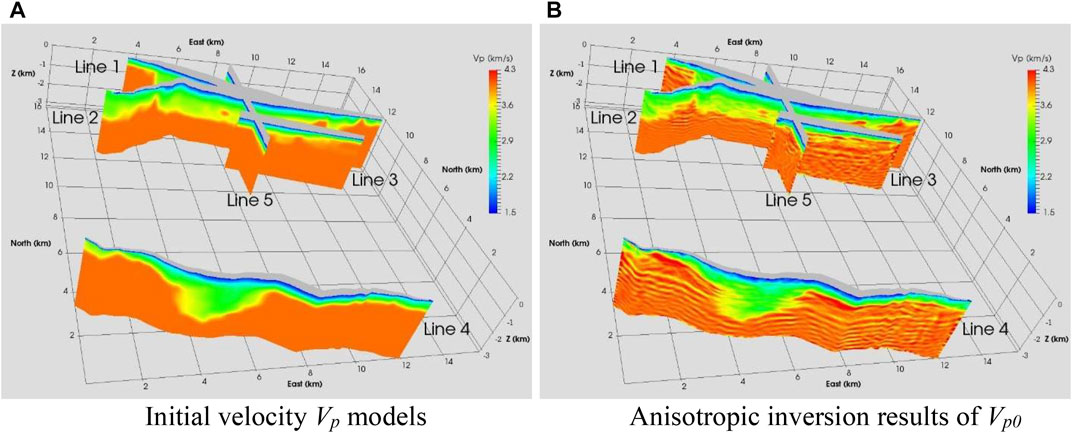
FIGURE 9. Initial velocity models V_p and anisotropic waveform inversion results of V_p0 along five 2D lines at Pirouette Mountain and Eleven-Mile Canyon. (A) Initial velocity V_p models. (B) Anisotropic waveform inversion results of V_p0.

Figures 10–14 show images of the industrial Kirchnoff migration, anisotropic RTM, and anisotropic LSRTM, for seismic survey Lines 1–5. Both anisotropic RTM and anisotropic LSRTM images outperform the industrial images, and anisotropic LSRTM outperforms anisotropic RTM. Kirchhoff migration generates poor images, and particularly in the deep regions. Anisotropic LSRTM produces images with higher resolution, particularly in the deep region and the regions near both end of each line, than anisotropic RTM.

FIGURE 10

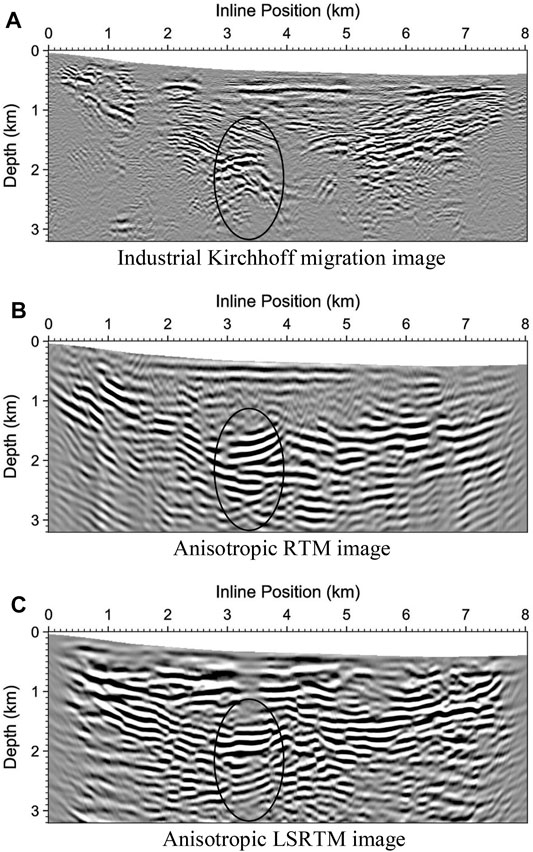
FIGURE 10. Subsurface migration images of Line 1 at Pirouette Mountain produced using various migration methods: (A) Industrial Kirchhoff migration, (B) Anisotropic RTM, (C) Anisotropic LSRTM. Two nearly-vertical faults can be clearly identified within the ellipse region in (C).

FIGURE 11

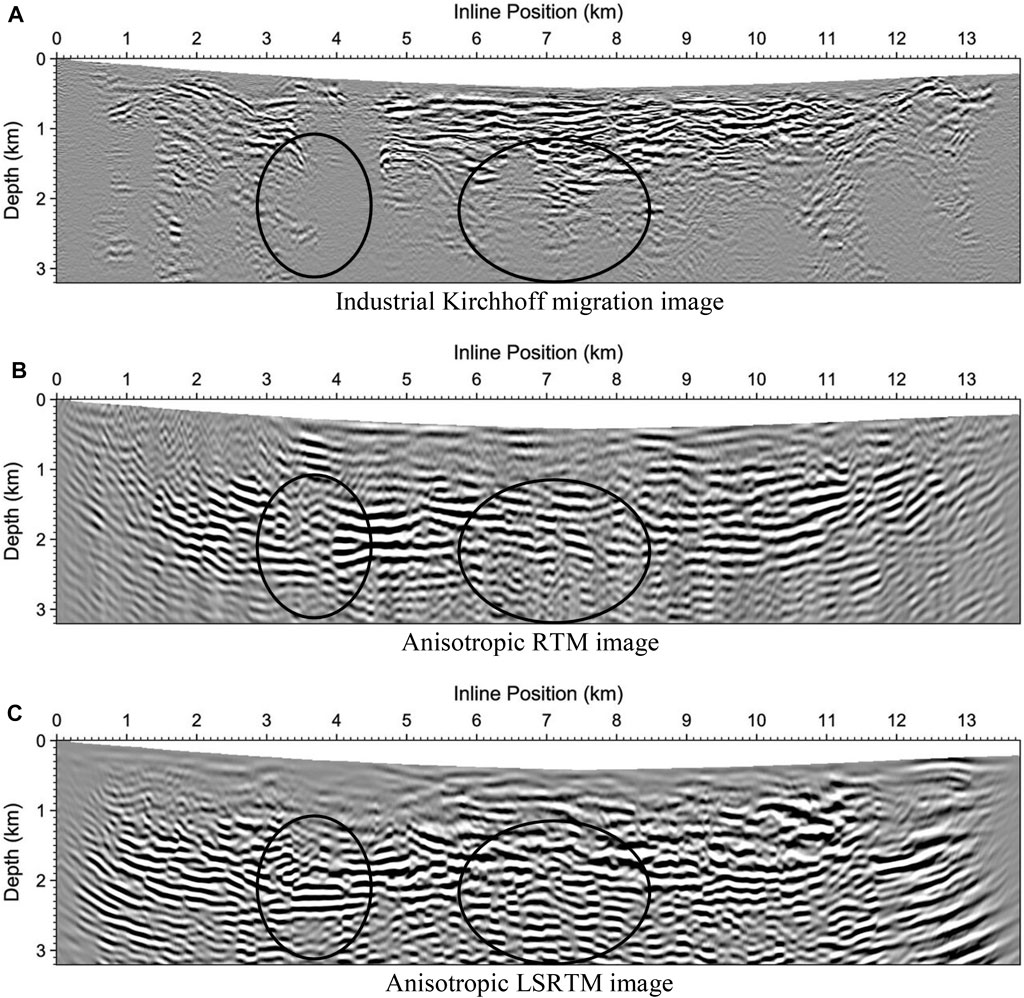
FIGURE 11. Subsurface migration images of Line 2 at Pirouette Mountain produced using various migration methods: (A) Industrial Kirchhoff migration, (B) Anisotropic RTM, (C) Anisotropic LSRTM. The images within the ellipse regions in (C) are much better than those in (B), and are not imaged in (A).

FIGURE 12

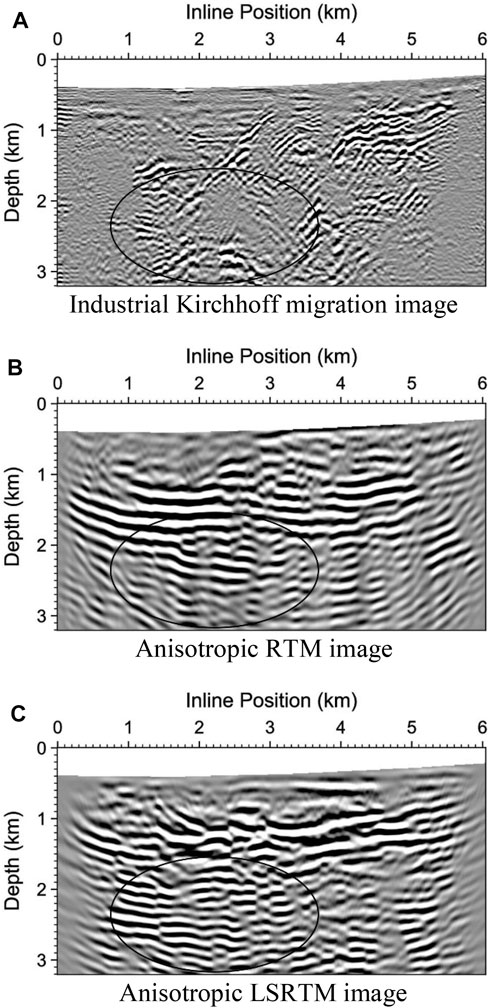
FIGURE 12. Subsurface migration images of Line 3 at Pirouette Mountain produced using various migration methods: (A) Industrial Kirchhoff migration, (B) Anisotropic RTM, (C) Anisotropic LSRTM. The image within the ellipse region in (C) has higher resolution than that in (B), and is imaged very poorly in (A).

FIGURE 13

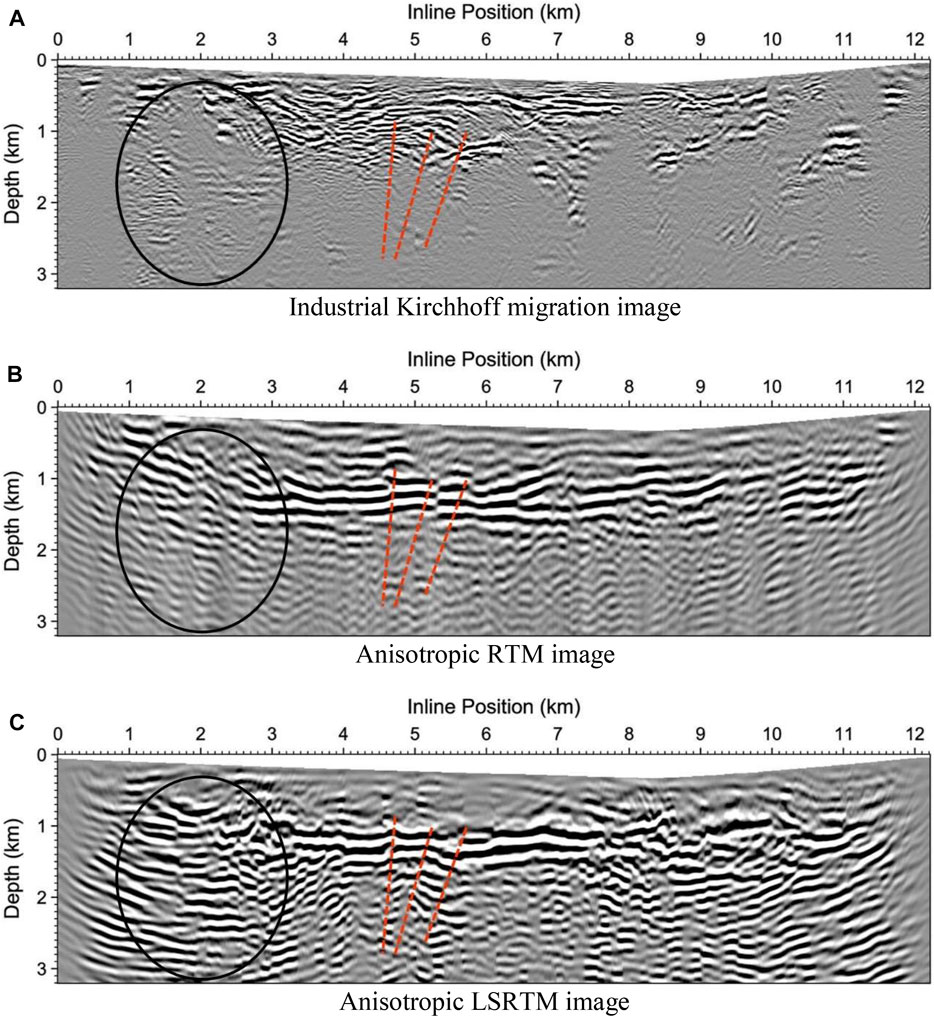
FIGURE 13. Subsurface migration images of Line 4 at Eleven-Mile Canyon produced using various migration methods: (A) Industrial Kirchhoff migration, (B) Anisotropic RTM, (C) Anisotropic LSRTM. The image within the ellipse region in (C) corresponds to the rupture region as shown in Figure 1. The image in this region has higher resolution than that in (B), and is almost invisible in (A). The delineated faults in (C) may correspond to the faults identified in the U.S. Geological Survey Quaternary fault and fold database as shown in Figure 1.

FIGURE 14

FIGURE 14. Subsurface migration images of Line 5 at Pirouette Mountain produced using various migration methods: (A) Industrial Kirchhoff migration, (B) Anisotropic RTM, (C) Anisotropic LSRTM. The image within the ellipse region in (C) shows high-resolution structures in the deep region that are not well imaged in (B) and (A).

As shown within the ellipse regions in Figure 10 for Line 1, two steeply-dipping faults can be clearly identified on the anisotropic LSRTM image, which cannot be easily recognized on the anisotropic RTM image, and are invisible on the Kirchhoff migration image.

Figure 11 shows that anisotropic LSRTM reveals more structures in the deep region along Line 2. For example, the images within the ellipse regions in the anisotropic LSRTM image depicted in Figure 11C are much better than those of anisotropic RTM in Figure 11B, and are not imaged by Kirchhoff migration in Figure 11A.

Along Line 3 as shown in Figure 12, the image within the ellipse region of the anisotropic LSRTM result in Figure 12C has higher resolution than that of anisotropic RTM in Figure 12B, and is imaged very poorly by Kirchhoff migration in Figure 12A.

The image within the ellipse region in Figure 13C along Line 4 obtained using anisotropic LSRTM corresponds to the rupture region as shown in Figure 1. The image in this region has higher resolution than that of anisotropic RTM in Figure 13B, and is almost invisible in the industrial Kirchhoff migration image in Figure 13A. The delineated faults in Figure 13C may correspond to the faults identified in the U.S. Geological Survey Quaternary fault and fold database as shown in Figure 1.

Line 5 cuts through Lines 1-3 along the North-South direction. The image within the ellipse region of the anisotropic LSRTM image in Figure 14C shows high-resolution structures in the deep region that are not well imaged in the other two methods shown in Figures 14A,B.

Figure 15 displays a comparison between 3D views of industrial Kirchhoff migration (left) and our anisotropic LSRTM migration (right) for the five seismic survey lines at Pirouette Mountain and Eleven-Mile Canyon. Anisotropic LSRTM reveals high-resolution subsurface images along five seismic survey lines that can be used to identify faults for geothermal exploration.

FIGURE 15

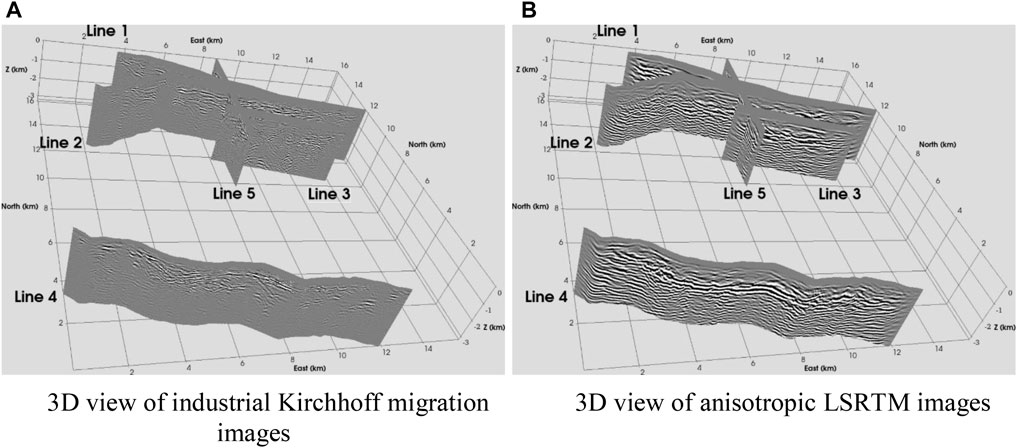
FIGURE 15. Comparison between 3D views of industrial Kirchhoff migration (left) and our anisotropic LSRTM migration (right). Anisotropic LSRTM reveals high-resolution subsurface images along five seismic survey lines at Pirouette Mountain and Eleven-Mile Canyon that can be used to identify faults for geothermal exploration. (A) 3D view of industrial Kirchhoff migration images. (B) 3D view of anisotropic LSRTM images.

The final data misfit of anisotropic LSRTM reduces to approximately 50–60% of the initial data misfit after eight iterations. Anisotropic RTM is the first iteration of anisotropic LSRTM. Therefore, our anisotropic LSRTM images are more reliable than those of anisotropic RTM for geothermal exploration.

Conclusion

We have developed a novel wavenumber-adaptive bandpass filtering method for suppressing the ground-roll noise in land seismic data without filtering out seismic signals. This method employs the fact that the frequency-wavenumber information of the ground-roll noise differs from that of the signal. We have applied our new method to five 2D lines of seismic data acquired at Pirouette Mountain and Eleven-Mile Canyon in Nevada for geothermal exploration, and have successfully suppressed the strong and coherent ground-roll noise. We have applied our anisotropic least-squares reverse-time migration method to the processed seismic data and produced high-resolution subsurface images. Compared with both industrial Kirchhoff migration and anisotropic reverse-time migration, our anisotropic least-squares reverse-time migration improves the subsurface images significantly, both in image resolution and image quality, particularly in the deep region. Our images reveal faults more clearly, some of which are invisible on the other images. This improvement is particularly evidenced by the subsurface images of Line 4, where our image manifests faults consistent with the geology. These results demonstrate that anisotropic least-squares reverse-time migration is an advantageous addition to the state-of-the-art anisotropic reverse-time migration for imaging complex subsurface structures with various faults. Our high-resolution subsurface images at Pirouette Mountain and Eleven-Mile Canyon facilitate accurate fault interpretation for reliable geothermal exploration.

Data Availability Statement

The data analyzed in this study are subject to the following licenses/restrictions: Data are available through the US Navy Geothermal Program Office by contacting co-author AS. Requests to access these datasets should be directed to AS.

Author Contributions

YH performed ground-roll suppression and imaging. MZ performed data analyses and anisotropic waveform inversion. KG developed the inversion and imaging codes. AS provided the field seismic data, and performed geologic interpretation. LH was the principal investigator of the research project, obtained funding, provided the research ideas, wrote the paper.

Funding

This work was supported by the Geothermal Technologies Office of the U.S. Department of Energy (DOE) through the Los Alamos National Laboratory (LANL), which is operated by Triad National Security, LLC, for the National Nuclear Security Administration (NNSA) of U.S. DOE under Contract No. 89233218CNA000001. This research used resources provided by the LANL Institutional Computing Program, which is supported by the U.S. DOE NNSA under Contract No. 89233218CNA000001.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank reviewers YL and BH for their valuable comments.

References

Alm, S., Walker, J. D., and Blake, K. (2016). Structural Complexity of the Pirouette Mountain and Elevenmile Canyon Geothermal Systems. Trans. Geothermal Resour. Counc. 40, 433–438.

Google Scholar

Ba, J., Du, Q., Carcione, J. M., Zhang, H., and Muller, T. M. (2015). Seismic Exploration of Hydrocarbons in Heterogeneous Reservoirs. Amsterdam, Netherlands: Elsevier.

Google Scholar

Brysk, H., and McCowan, D. W. (1986). A Slant‐stack Procedure for point‐source Data. Geophysics 51 (7), 1370–1386. doi:10.1190/1.1442187

CrossRef Full Text | Google Scholar

Caskey, S. J., Wesnousky, S. G., Zhang, P., and Slemmons, D. B. (1996). Surface Faulting of the 1954 Fairview Peak (MS 7.2) and Dixie Valley (MS 6.8) Earthquakes, Central Nevada. Bull. Seismological Soc. America 86, 761–787. doi:10.1785/BSSA0860030761

CrossRef Full Text | Google Scholar

Coruh, C., and Costain, J. K. (1983). Noise Attenuation by Vibroseis Whitening (VSW) Processing. Geophysics 48 (5), 543–554. doi:10.1190/1.1441485

CrossRef Full Text | Google Scholar

Deighan, A. J., and Watts, D. R. (1997). Ground‐roll Suppression Using the Wavelet Transform. Geophysics 62 (6), 1896–1903. doi:10.1190/1.1444290

CrossRef Full Text | Google Scholar

Embree, P., Burg, J. P., and Backus, M. M. (1963). Wide‐band Velocity Filtering-The Pie‐slice Process. Geophysics 28 (6), 948–974. doi:10.1190/1.1439310

CrossRef Full Text | Google Scholar

Gao, K., and Huang, L. (2019). Acoustic- and Elastic-Waveform Inversion with Total Generalized P-Variation Regularization. Geophys. J. Int. 218, 933–957. doi:10.1093/gji/ggz203

CrossRef Full Text | Google Scholar

Gao, K., and Huang, L. (2015). Anisotropic Elastic-Waveform Modeling for Fracture Characterization in EGS Reservoirs. Proceedings of the 40th Workshop on Geothermal Reservoir Engineering, CA (United States), 26-28 Jan 2015. Stanford, CA: Stanford University. doi:10.2172/1168705

CrossRef Full Text | Google Scholar

Halliday, D. (2011). Adaptive Interferometry for Ground-Roll Suppression. The Leading Edge 30 (5), 532–537. doi:10.1190/1.3589110

CrossRef Full Text | Google Scholar

Henley, D. C. (2003). Coherent Noise Attenuation in the Radial Trace Domain. Geophysics 68 (4), 1408–1416. doi:10.1190/1.1598134

CrossRef Full Text | Google Scholar

Jin, S., and Ronen, S. (2005). Ground Roll Detection and Attenuation by 3C Polarization Analysis. Proceedings of the 67th Annual Conference and Exhibition, Madrid, Spain, Jun 2005. Extended Abstracts (Houten, The Netherlands: European Association of Geoscientists & Engineers). doi:10.3997/2214-4609-pdb.1.b020

CrossRef Full Text | Google Scholar

Karsli, H., and Bayrak, Y. (2008). Ground-Roll Attenuation Based on Wiener Filtering and Benefits of Time-Frequency Imaging. The Leading Edge 27 (2), 206–209. doi:10.1190/1.2840368

CrossRef Full Text | Google Scholar

Lin, Y., and Huang, L. (2015). Acoustic- and Elastic-Waveform Inversion Using a Modified Total-Variation Regularization Scheme. Geophys. J. Int. 200, 489–502. doi:10.1093/gji/ggu393

CrossRef Full Text | Google Scholar

Liu, X. (1999). Ground Roll Supression Using the Karhunen‐Loeve Transform. Geophysics 64 (2), 564–566. doi:10.1190/1.1444562

CrossRef Full Text | Google Scholar

Nemeth, T., Wu, C., and Schuster, G. T. (1999). Least‐squares Migration of Incomplete Reflection Data. Geophysics 64, 208–221. doi:10.1190/1.1444517

CrossRef Full Text | Google Scholar

Sheriff, R. E. (2002). Encyclopedic Dictionary of Applied Geophysics. Soc. exploration geophysicists, 442. doi:10.1190/1.9781560802969

CrossRef Full Text | Google Scholar

Shieh, C. F., and Herrmann, R. B. (1990). Ground Roll: Rejection Using Polarization Filters. Geophysics 55 (9), 1216–1222. doi:10.1190/1.1442937

CrossRef Full Text | Google Scholar

Thomsen, L. (1986). Weak Elastic Anisotropy. Geophysics 51, 1954–1966. doi:10.1190/1.1442051

CrossRef Full Text | Google Scholar

Trad, D., Ulrych, T., and Sacchi, M. (2003). Latest Views of the Sparse Radon Transform. Geophysics 68 (1), 386–399. doi:10.1190/1.1543224

CrossRef Full Text | Google Scholar

Treitel, S., Shanks, J. L., and Frasier, C. W. (1967). Some Aspects of Fan Filtering. Geophysics 32 (5), 789–800. doi:10.1190/1.1439889

CrossRef Full Text | Google Scholar

Unruh, J., Gray, B., Christopherson, K., Pullammanappallil, S., Alm, S., and Blake, K. (2016). Seismic Reflection and Magnetotelluric Imaging of Southwestern Dixie Valley Basin, Nevada. Trans. Geothermal Resour. Counc. 40, 455–461.

Google Scholar

Yilmaz, Ö. (2001). Seismic Data Analysis: Processing, Inversion, and Interpretation of Seismic Data. Soc. exploration geophysicists 10, 837–1000. doi:10.1190/1.9781560801580

CrossRef Full Text | Google Scholar

Zhan, G., Pestana, R. C., and Stoffa, P. L. (2012). Decoupled Equations for Reverse Time Migration in Tilted Transversely Isotropic media. Geophysics 77, T37–T45. doi:10.1190/geo2011-0175.1

CrossRef Full Text | Google Scholar