Microscopic Mechanism Angle of Repose in Friable Loess and Its Relationship With Slope Angle

The angle of repose in soil particles plays a key role in slope stability. There was a need for the investigation on the association between the angle of repose in loess particles and the angle of slopes. The fixed funnel methods with different particle sizes were carried out. The pressure of particle gravity weight was obtained based on the vibration stacking test. Four contact structures in loess particles were put forward including the triangular pyramid contact structure (TS), rectangular pyramid contact structure (RS), pentagonal pyramid contact structure (PS), and hexagon contact structure (HS). The particles transformed successively in four kinds of contact structures. The transformation of entropy value of the particles in different accumulation areas was discussed during the process of accumulation. The relationship between the natural angle of repose and the evolution of the contact structures was established. Combined with the existing experimental conclusion that loess particles transform in four stable states, in turn, the reason that the friction angle of uniform sand particles proposed by Shields in 1936 is 33° was explained. The formation theory of the loess angle of repose was well extended to speculate the formation process of the loess slope system. It is verified that loess slopes were mainly distributed under 30°.

Introduction

Loess, as a special sedimentary product of the Quaternary, has a very wide distribution. As shown in Figure 1. In the northern and northwestern regions of China, the loess deposits cover an area of 6.24 × 10⁵ km² (Xu et al., 2017). According to the survey, about 100 million people live on the loess land. However, the loess has the characteristics of vertical joint development, porous and strong water collapsibility. Those features lead to the instability and failure of loess slopes easily. As a result, the loess slopes which exist nearby the human living areas threaten people’s life and property safety momentarily. So the stability problem of loess slopes has always been an urgent research problem for national geologists. For example, Wang et al. (2018) took a loess mountain airport as the research object and conducted a large number of research studies on the failure mechanism of slope deformation. Huntley et al. (2019) took the slow-moving landslide which is near Ashcroft, British Columbia, Canada, as the research object. The failure mechanism of the slow-moving landslide was investigated by using the multidimensional electrical dispersion tomography datasets.

FIGURE 1

FIGURE 1. Local loess distribution of China and cases sites.

In general, the inducing factors of loess landslide can be summarized as vibration (Xu et al., 2020a; Xu et al., 2000b; Zhang et al., 2021), rainfall (Ma et al., 2019; Wang et al., 2019a), and the coupling effect of vibration and rainfall (Wang et al., 2021). Just like engineering problems in Figure 2. It is worth noting that inducible factors such as external factors still act on the internal particles ultimately. The movement direction of the internal particles is the real reason that controls the deformation mode of macroscopic objects (Duran, 2001). According to the hypothesis of the eolian origin for loess, the birth of loess landform is still based on deposition and accumulation. As a large accumulation body, the stability of the loess slope is closely related to the accumulation stability of granular particles, that is, the controlling factors that maintain the stability of the loess slope are similar to those that maintain the stability of granular particles (Evesque and Rajchenbach, 1989; Pahtz et al., 2021).

FIGURE 2

FIGURE 2. New geological hazards induced by vibration, rainfall, or the coupling effect. (A) Landslide in the Yonghua section of the Beijing–Guangzhou Railway. (B) Typical landslides along a heavy-load railway in Shanxi. (C) Landslide along the Yang-Da Railway (Wang et al., 2021). (D) Landslides along the section close to Strasbourg at the France and Germany border as TGV (Train À Grande Vitesse) is approaching (https://www.sohu.com/a/377989394_100016456). (E) Landslides along the railway near Ashcroft, Canada (Huntley et al., 2019).

After years of research, it has been found that the accumulation stability of granular particles is related to the accumulation threshold angle. Once the accumulation angle exceeds this threshold angle, granular particles will show their characteristic of flow. Therefore, only below this threshold angle, the accumulation body will show its characteristic of stability. But this angle is not a fixed value. Just as the example, the stable stacking angle of large particles is smaller than those minimal particles (Holsappl. 2013; Li et al., 2020). This average threshold angle under unconstrained conditions at the time of stacking without collapsing is called the angle of repose (Muller et al., 2021).

As for the angle of repose, there are related studies in different disciplines. In the field of agronomy, Karimi et al. (2009) studied the effects of moisture content of wheat grain and bottom roughness of valley mound on the angle of repose. In the field of biology, Bacherikov et al. (2021) took Pinus sylvestris L. seeds as the research object and used different measurement methods to determine the angle of repose in order to solve the problem of reasonable discrete feeding of seeds. In the field of geotechnical engineering, Lajeunesse et al. (2004) used the fixed funnel method to research the effects of particle size, substrate roughness, substrate stiffness, and granular particle mass on the angle of repose. Atwood–Stone and McEwen (2013) studied the variation of granular particles’ angle of repose under low-gravity conditions. Chou et al. (2013) used image processing technology and particle tracking technology to explore the relationship between fluid viscosity, particle density, and the angle of repose. Soltanbeigi (2021) proposed several methods to represent the shape of the accumulation body through the angle of repose and direct shear tests. In addition, the angle of repose has been used in many fields such as hydrodynamics, sedimentology, particle technology, and material science.

However, few scholars have associated the angle of repose with the stability of the loess slope. In fact, as the threshold angle for the accumulation body to maintain its stability, the angle of repose also has a controlling effect on the loess slope which is considered as large deposition. In order to explore the relationship between the angle of repose and the stability of the loess slope, four different contact models are proposed in this article. The fixed funnel method and vibration stacking test are used to prove the rationality of the contact models directly and describe the contact transformation of granular particles during the accumulation process. Furthermore, the formation mechanism of accumulation body’s angle of repose is explained from the perspective of particles. And it is extended to the loess slope. Based on the principle that controlling the maximum accumulation angle of granular particles is the angle of repose, the allowable variation range of loess slope angle under the condition of maintaining its stability is deduced. Then the theoretical relationship between the angle of repose and slope stability is established.

Structures and Methods

Contact Structures

The accumulation body is not the superposition of multiple particles simply but the chimera of particles and accumulation body. In most cases, the sedimentary particles will be embedded into the accumulation body and form a new contact structure together with it. For the loess accumulation body, this chimeric structure is the structure of the soil accumulation body. Therefore, it is the foundation for the study of the soil structure to explore the contact structure of particles. That is also the problem of how particles embed with each other and form the basic contact models. The contact structure of loess is very complex. However, the first step to studying any complex problem is to discuss and understand the characteristics of the most important relevant properties of this problem under ideal conditions. In order to facilitate the study and discussion of the contact structure between loess particles, the contact models established in this article are all proposed under some special assumptions. That is to say, the deposited loess particles are spherical, rigid, and equal in size and have complete homogeneity. The loess accumulation body only contains the pores caused by the contact models themselves. The pores caused by other factors will not be discussed temporarily. Therefore, the deformation of particles, sedimentation rotation caused by occlusion, and the dominant subsidence channels generated by particles in the process of sedimentation compression are not considered in the test. The test time of this experiment is transitory. The spatial position and temperature fluctuation of the test are also very small. Therefore, the air humidity will also not have a great fluctuation, and the air humidity will not affect the microscopic effect between particles.

According to the conditions of assumptions, the deposited loess particles are spherical, rigid, and equal in size and have complete homogeneity. One of the spherical particles is taken as the object of observation, and other particles are inserted around the spherical particles. The center points of spherical particles contacting each other are connected to determine the shape of the contact model and name it accordingly. The structure of the accumulation body is a three-dimensional spatial concept, so the contact model reflecting its structure must be a three-dimensional structural model. A single or even three spherical particles cannot satisfy the basic concept which is a three-dimensional structural model. The three-dimensional structure is not constructed successfully until the fourth spherical particle is considered. That is, the other three spherical particles at the bottom around the spherical particle at the top together form a triangular pyramid structure, called the triangular pyramid contact structure (TS). As the top particle moves down, the space at the bottom gradually expands until the fourth spherical particle at the bottom can be embedded. Four spherical particles at the bottom around the top spherical particle together form a rectangular pyramid structure. It is known as the rectangular pyramid contact structure (RS). In the same way, it can be known that there is a pentagonal pyramid contact structure (PS) and hexagon contact structure (HS). As shown in Figure 3. Strictly speaking, HS is a two-dimensional structural model. It is contrary to the basic concept which is the three-dimensional structural model. In addition, when there are particles embedded in the upper layer of HS stably, the HS and TS express the same contact form. But the HS is a special contact form of TS. It can more clearly express the particles’ contact form at continuous but distinct interfaces. For example, when particles are stacked on a flat interface, the contact structure of the particles is a typical HS. Moreover, the process from the TS to HS is a continuous transformation. It is of great significance in understanding and studying the transformative process of particles’ contact structure in the stacking process. Therefore, the HS can be and needs to be listed separately to form a special contact model.

FIGURE 3

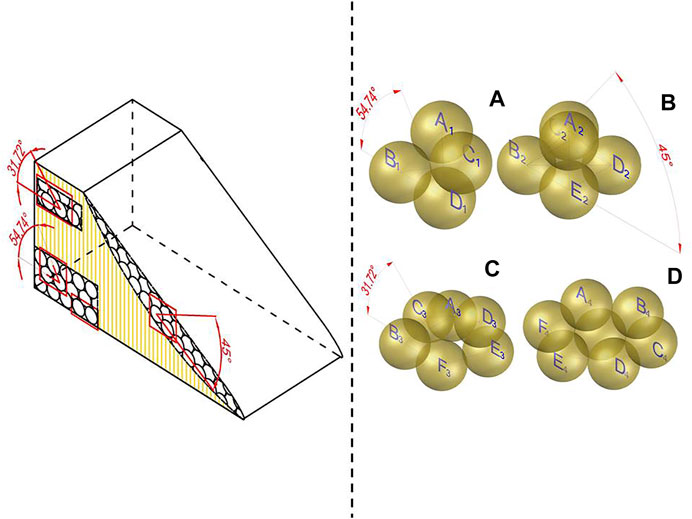
FIGURE 3. Four different contact models. (A) Triangular pyramid contact structure; (B) rectangular pyramid contact structure; (C) pentagonal pyramid contact structure; (D) hexagon contact structure.

Fixed Funnel Method Test

According to relevant studies, when the particle size is less than 50 μm, cohesion plays a major role in the connection between particles (Lumay et al., 2012). However, the main content of this study is to explore the influence of the particle structure on the stability of the accumulation body. Hence, the uniform particle size of the accumulated particles is required to be greater than 50 μm. As shown in Figure 4. In order to prove the influence of the structure of loess particles on the stability of the accumulation body more directly, three kinds of particles with different particle sizes are screened through the screening method in this fixed funnel method test: a) angular gravel whose particle size exceeds 2.000 mm and particle content accounts for the size is more than 50% of the total mass; b) coarse sand whose particle size exceeds 0.500 mm and particle content accounts for the size is more than 50% of the total mass; and c) sand loess whose particle size exceeds 0.075 mm and particle content accounts for the size is more than 50% of the total mass. These three kinds of particle sizes are used for experiments.

FIGURE 4

FIGURE 4. Screening results of particles with three sizes. (A) Angular gravel with a diameter of 1.000–2.000 mm. (B) Coarse sand with a diameter of 0.500–1.000 mm. (C) Sand loess with a diameter of 0.075–0.500 mm.

The main purpose of this test is to simulate the transformation of particles’ contact structure under the conditions of deposition and accumulation and to measure the angle of repose of the accumulation body. In order to simulate the real situation of particles with certain kinetic energy during deposition and accumulation accurately, the fixed funnel method is used in the stacking test. According to the provisions of 2.582 in the FEM standard, the ratio between the diameter and the particle size of the accumulation body should be more than 20. However, on the basis of the study of Rackl et al. (2017), the ratio between the diameter and the particle size should be more than 40. Judging by the requirements of particle size in this fixed funnel method test, the maximum particle size is 0.500 mm. Therefore, the diameter of the accumulation body in this accumulation test is required to exceed 200 mm uniformly.

Based on the research results of Liu (2011), the funnel lifting speed can be divided into two ways: low speed (2∼3 cm/s) and high speed (7∼8 cm/s). The process of loess particle deposition and accumulation simulated in this research is a natural process. The huge disturbance caused by humans or unpredictable earthquakes is not taken into account. Therefore, the fixed funnel method test should not be lifted up too fast. The test adopts the way of low-speed lifting. The angle of repose of the accumulation body is also affected by the roughness of the basement. The rougher the basement is, the larger the particles’ angle of repose will be. Therefore, the emery paper with stronger roughness is uniformly used in this accumulation test to control the diffusion range of the first layer of particles. When the diffusion range of the first layer of particles can be controlled, most of the particles will accumulate and have contact. Then, the contact structure in the accumulation body will be observed more easily because only the contact structure on the surface of the accumulation body can be observed through the fixed funnel method. The method cannot reflect the transformation of particle contact structure inside the accumulation body well. So the test is improved according to the fixed funnel method. A transparent separator is erected beside the sand outlet at the bottom of the funnel. Relative to the accumulation body, the transparent separator can be considered as the boundless side limit in this direction. But for the other directions, the transparent separator has no influence. After the completion of the fixed funnel method test, the experimenter can observe the transformation of particle contact structure inside the accumulation body through the transparent separator. Since the transparent separator only restricts the orientation of the partition and has no effect on the other directions, when the accumulation body is in a critical state that can be accumulated without collapsing, the angle of accumulation body observed through the transparent separator is the angle of repose that needs to be measured. As shown in Figure 5.

FIGURE 5

FIGURE 5. (A) Fixed funnel method principle. (B) Frontal projection of laser measurement. (C) Fixed funnel method. (D) Measure the angle with laser. (E) Vibration table (F) Cross laser penetrating the accumulation body.

So far, the measurement of the angle of repose in the fixed funnel method test is mainly divided into two kinds. The first one is measured by the protractor directly. But this approach has an obvious flaw that the measurement accuracy is not enough. The other way is to adopt the overlapping multi-sphere clump method in the discrete element method (DEM) to simulate accumulation body effectively. Then, the size of the angle of repose is calculated (Zheng and Hryciw. 2016; Zhou et al., 2018; Hua and Shultis. 2021). But this simulating method cannot completely simulate the irregularity and diversity of angular particles, and the calculation of the angle of repose is not accurate enough. To solve this problem, the test also made some improvements in data measurement. The horizontal cross laser is fired by using the horizontal laser instrument. Because the cross laser cannot penetrate the accumulation body, the cross focus cannot be found on the ruler of the transparent partition board. At the time, the cross focus can be found on the ruler of the transparent partition board; it means that the cross laser just passes the top of the accumulation body. At this time, the height of the cross laser’s focus on the ruler H is the height of accumulation body. Similarly, the points on both sides of the bottom of the accumulation body can be found, and the diameter L of the accumulation body can be measured. According to formula 1, the angle of repose of α can be calculated as follows:

$\alpha ={\tan }^{-1}\frac{2H}{L},(1)$

The angle of repose based on this calculative method is the base angle of an idealized cone which is formed by connecting the top and bottom accumulation points of the accumulation body. As shown in Figure 6. The generatrix of the idealized cone is a straight line which is against the fact. The fact is that the generatrix of the accumulation body is irregular. After multiple fixed funnel method tests, it is found that the accumulation body presents a convex shape locally. Just like the slope of Zaoling landslide in Shanxi Province, the pre-slide slope, on the upper part, is steep with 53°and the pre-slide slope on the lower part is 37° (Cui et al., 2020). Therefore, the method used by Penkavova et al. (2021) is adopted by determining the angle of repose. A Canon SD126601 camera is used to photograph the frontal projection of the accumulation body. And then CAD is used to depict and measure the angle of repose θ of the accumulation body directly. Several groups of repose angles are obtained by multiple measurements. The average value of laser repose angle ${\overline{\alpha }}_1$, as in formula 2, can be calculated for the first fixed funnel method test.

${\overline{\alpha }}_1=\frac{\frac{{{\displaystyle \sum }}_1^n{\alpha }_n}{n}+\theta }{2},(2)$

FIGURE 6

FIGURE 6. Accumulation body and measured surface.

After many fixed funnel method tests, the final mean value of laser measured angle of repose $\overline{\alpha }$ was calculated as formula 3.

$\overline{\text{α}}=\frac{{{\displaystyle \sum }}_1^n{\overline{\alpha }}_n}{n},(3)$

Vibration Stacking Test

A stacking test can show contact structures of particles intuitively. But for a small laboratory test, the gravity pressure of friable deposits is not enough to make particles move and even not enough to promote the contact models to transform from each other. Even if the giant particles deposit with enough gravity pressure, it really needs a long time to consolidate due to its gravity pressure. Decades of years may appear very tiny changes. To strengthen the particle rolling effect under gravity pressure and to promote the transformation of each contact model, the vertical vibration load is added on the basis of the stacking test. As shown in Figure 7. The downward momentum of particles keeps converting into gravitational potential energy by adopting the vertical vibration whose frequency is 20 Hz and strength is 15%. This way can promote the transformation of contact models under the gravity pressure. The vibration frequency and strength can be controlled by using a VT 700 vibration table.

FIGURE 7

FIGURE 7. Surface of stacking test results with different particle sizes [(A–C) is before vibration. (D–F) is after vibration. A and D is the angular gravel. (B, E) is coarse sand. (C, F) is sand loess from left to right successively].

Results and Discussion

Microscopic Mechanism of Angle of Repose

As for the accumulation body, during the process of deposition and accumulation, particles on both sides will continue to roll down, while the interior of the accumulation body will gradually compact and the overall height will decrease. Individual particles will first roll down from the dominant channel before compaction. Therefore, it should be mentioned that the change in the contact structure between particles is carried out after compaction. The results of the accumulation test are shown in Figures 8, 9. The main distribution ranges of the angle of repose of the three particle sizes are slightly different. The main distribution range of the angle of repose of the angular gravel deposit is 32°–34°. The main distribution range of the coarse sand deposit is 34°–36°. And the main distribution range of the angle of repose of the sandy loess deposit is 36°–38°. Even in the vibration stacking test, the main distribution range of the angle of repose of angular gravel deposit body is less than 20°. The main distribution range of the angle of repose of coarse sand deposit body is 21°–24°, and the main distribution range of the angle of repose of sandy loess deposit body is 27°–30°. The accumulation body before and after vibration has the same change trend. Based on all those data, the angle of repose of the accumulation body is inversely proportional to the particle size. And the reason is closely related to the accumulation process. In the process of accumulation which is under the vibration load test, for example, the particles of gravity stress are enough to change the contact structure. The first layer of particles flats out in the basement initially and spreads around constantly. Because the basement has certain roughness, the kinetic energy of particles has been dissipated as the accumulation of particles spreads. As a result, the accumulation body cannot spread indefinitely. If the particles have a smaller diffusion range, the higher the height at which the accumulation can be maintained without collapsing under the same accumulation mass and the greater the angle of repose will be. It also suggests that the roughness of the basement for particles has a certain control effect. If the basement is rougher, the dissipation of the kinetic energy will be faster. And the smaller the particle diffusion range is, the greater the angle of repose will be. When the diffusion range of particles is defined, the tiled particles of the first layer gradually contacted each other with the increase in the accumulated particles. The HS is formed. The form of HS also means that the bottom layer of TS has been formed. Since the particles in the upper accumulation body are tiny and the gravity weight of the particles is small, the stability of the contact structure can be maintained when the top particles are rolled into the middle of the three particles at the bottom. At this point, the TS is formed. The deposit weight of upper particles is larger and larger along with the increase in the accumulated particle number. The particles at the top of TS are subjected to the gradually increasing gravity weight pressure at the upside. And then the particles at the bottom are constantly pressed down. According to Metcalf (1966), the motion of particles is basically in the form of rolling. And only under certain special circumstances can sliding occur between particles. The upper part of the particles’ gravity weight pressure is not distributed uniformly in the process of accumulation. So it is supposed that the particles at the top side, in the process of accumulation, are in a state of rolling down in this study. The excess kinetic energy is transferred to the bottom, causing the bottom particles to spread around. And the diffusion range of the bottom particles of the accumulation body becomes larger and redefined. Until the bottom particles of TS are expanded enough for the insertion of the fourth particle, and RS is formed. Similarly, when the space required by the fifth particle is squeezed out due to the increasing gravity weight pressure, PS is formed immediately. And the HS is formed again until the top of PS is squeezed to the bottom. As the particle size is inversely proportional to the kinetic energy dissipation rate (Li et al., 2017), the smaller the particle size dissipation rate is, the more excess kinetic energy is dissipated by the base, and the larger the range of the bottom particles to be redefined, the smaller the angle of repose will be. Therefore, the angle of repose of the accumulation body is inversely proportional to the particle size.

FIGURE 8

FIGURE 8. Stacking test results and angle of repose distribution without vibration.

FIGURE 9

FIGURE 9. Stacking test results and angle of repose distribution under vibration.

As shown in Figure 10. The transformation process of the contact models, just like samsara, is very interesting. It seems to show that the samsara itself is the most essential change law in nature. In fact, in the whole process of transformation, the closer you get to a certain stable state during the transition of the contact models, the more difficult it is to achieve. Although the tensile strength of soil is far less than the compressive strength and shear strength of soil (Wang et al., 2019b), the soil is rarely subjected to the action of tension. In most cases, the load form of soil is compressive load. And the shear strength of soil is also relatively smaller than the compressive strength of soil. So when the contact structure between the particles is suitable for resistance to shearing action, the soil will show more stability. In particle contact models, the transformation process from TS to PS is the compaction process of soil under compressive stress. When the top particle moves horizontally relative to the entire contact model causing the contact model to be damaged, it is the process of shear damage of the soil. The process of diffusion decomposition of the contact model is the process of destruction caused by tension, as shown in Figure 11. If particles at the bottom act the same force on the top particles in the whole process of contact models transformation, the shear strength φ which resists granular horizontal sliding force will gradually be strengthened as the angle of its connection between the contact points of the spherical particles and the center of the contact model decreases. And the relative forces f between the particles decreases. This means that at the later stage of the transformation of the contact models, the top particles need more force to make the bottom particles move. It also indicates that the transformation process of the contact models from TS to PS is a gradual stabilization process.

FIGURE 10

FIGURE 10. Model transformation process under gravity weight pressure.

FIGURE 11

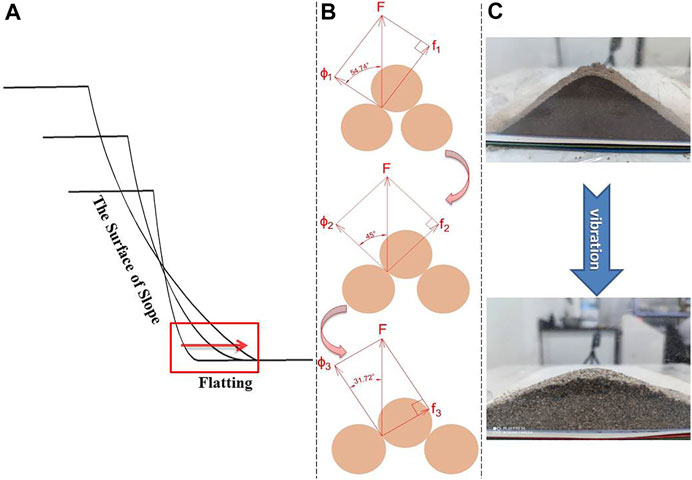
FIGURE 11. (A) Slope changes caused by vibration. (B) Vibration induced contact model changes in slopes. (C) The change of accumulation body caused by vibration.

According to existing studies, the angle of repose of the accumulation body is related to the angle of internal friction linearly. And the size of the angle of repose is basically close to the size of the angle of internal friction. Even under ideal conditions, the tangent of the angle of repose of the accumulation body is the static friction coefficient of particles (Metcalf. 1966; Ghazavi et al., 2008; Liu, 2011; Al-Hashemi and Al-Amoudi, 2018). Although the contact model can be viewed as the smallest accumulation body, the angle of connection between the bottom particles and the top particles in different contact models is different. Those different connections cause that the shear strength φ required to break through for particle movement is different. Furthermore, the internal friction angle of the accumulation body is different from the angle of repose of the accumulation body. The stability of the contact models reflects the stability of the deposit essentially. Under ideal conditions, that is, the particle size is exactly the same, and the bottom of the contact model is parallel to the basement of the accumulation body, the contact model’s angle that the connection between the top particle and the bottom particle center of the model with the horizontal plane is equal to its angle of repose. Combined with the stacking test, the angle of sandy soil under various particle sizes distribute in the range of 32°–38°. That may prove that the vast majority of particles, at the beginning of the accumulation, are in the transition of the RS to PS contact structure in the complex particle contact structures. It is enough to make the particle contact structure stay in a stable state temporarily under the static state. But in the later accumulation which is during the period of consolidation, the particles in the transition contact state from RS to PS will transform to PS under the gravity weight pressure until most of the particles are in PS in order to maintain absolute stability. The angle which is the connection between the spherical center of the top particles and the bottom particles with the horizontal plane is 31.72°. It is close to the 32° measured in the fixed funnel method test. It also conforms to the conclusion that the friction angle of uniform sand particles is 33°proposed by Shields in 1936.

In order to explain the evolution process of the angle of repose during the accumulation process better, the concept of entropy in the second law of thermodynamics is introduced to explain the cause of the angle of repose from the indicator of order and chaos. Entropy was first proposed by Rudolf Julius Emanuel Clausius, a German mathematician, to solve thermodynamic problems. Later, it was gradually extended to the field of physics. Since then, the concept of entropy gradually became clear. That is, the essence of entropy is to reflect the level of chaos inside a system. The stack arrangement of TS which is also the HS is very simple. And even multiple TS can be completely repeated and extremely ordered, so its entropy value is pretty low. In the transformation process from TS to PS, the arrangement of multiple contact models gradually becomes complicated and disordered, so its entropy value is relatively higher. According to the law of entropy increase, if there is no addition of external energy, the isolated system will always develop toward the direction of entropy increase and become a chaotic and disordered stable body. Therefore, TS will gradually transform to PS even without the addition of energy. That also can be considered as the consolidation process of soil. New particles are constantly added to the surface of the accumulation body in the process of accumulation of friable particles. The upper part of the deposit gravity pressure is very small, so the particles form TS initially. For this reason, the surface of the accumulation body tends to be a relatively regular and orderly unstable state first. That state also means the entropy caused by external energy. Under the action of gravity pressure, particles on the surface of the deposit slip. It transforms from an unstable structure to a relatively stable structure gradually. While the bottom particle gradually becomes stable due to the gravity weight pressure of the upper particle and gradually transitions from TS to PS. It is the process of entropy increase. As the top particles are undergoing the same transformation process of the bottom particles, the accumulation body system contains both entropy increase and entropy decrease. But on the whole, the accumulation body is in a state of entropy decrease and reaches some disordered structure finally. This structure is in a stable state.

The Relationship With Slope Angle

The German geographer F. Richthofen put forward the hypothesis of the eolian origin for loess in 1877. He believed that loess originated from the desert and Gobi. The particles from the desert or Gobi become the atmospheric dust through the wind transport and gradually deposited and accumulated with the weakening of wind. Therefore, the loess landform itself is a huge accumulation body. The loess slopes are not an exception. The accumulative body produced by using the indoor stacking test is equivalent to a miniature version of the loess slope. The angle of repose as a threshold angle shows that particles are stacking without collapsing is the slope angle relative to the loess slope. The natural loess slope is in a state of stability or in a critical state, so the natural deposit slope angle is less than or equal to the angle of repose. Once its size exceeds the angle of repose, the surface of the slope will produce the phenomenon of particles rolling off. Just like the surface of the accumulation body in a stacking test, so as to maintain the stability of the whole slope. Therefore, the slope angle also has a controlling effect on the slope stability. Since the gravity weight of particles has a great influence on the angle of repose of the accumulation body (Kleinhans et al., 2011), the gravity weight pressure of particles should also be taken into account for the slope. So the stacking test under vibration will be more in line with the actual situation of the loess slope. According to the results of the vibration stacking test, the main distribution range of the angle of repose of the angular gravel deposit body is less than 20°. The main distribution range of the angle of repose of the coarse sand deposit body is 21°–24°, and the main distribution range of angle of repose of sandy loess deposit body is 27°–30°. Therefore, it is speculated that under long-term gravity weight pressure, the critical slope angle of loess slope is no more than 30°. And not all slopes are in a critical state. Because of the external factors of non-gravity pressure, the slope angle concentration range of most slopes is usually less than 30°. In order to verify this conclusion, this article uses the research results of scholar (Hu et al., 2018) to verify the measurement results of 2,443 slopes selected from 6,627 slopes randomly. Among the 2,443 slopes, only 39 slope angles are greater than 30°, and 2404 slope angles are all less than 30°. And the concentration range of slope angles is 10°–20°, which is less than 30° under the critical condition. The actual investigation results are in full agreement with the speculative conclusion.

In fact, a large number of phenomena can prove this hypothesis indirectly. In the process of natural deposition, slope surface particles rolled off and adjusted the slope angle which promoted the slope body to maintain its overall stability. As shown in Figure 12, there are a large number of accumulation bodies at the foot of the slope along the line from Dingxi to Tianshui in Gansu Province. This kind of accumulation body can even stretch several kilometers, but its height is greatly different from the overall slope. The accumulation volume is small, and the slope is significantly reduced. There is no obvious disturbance around the slope because the slope is accumulated in the process of natural sedimentation regulation. And the reality is that the loess has cohesive force. The instantaneous change will cause severe geological disasters. In Jixian Jichang town of Shanxi Province, there was a large area of loess slope with the collapse of natural geological disasters. Twenty-two people were buried. There were no rains, vibrations, or other factors before the natural disasters. Experts called it a typical loess slope collapse. This shows that the slope angle is too large due to long-term sedimentation. And in order to adjust its stability, the slope can produce landslides and other major geological disasters.

FIGURE 12

FIGURE 12. Areas of particle rolling down and slide accumulation in the slope.

Conclusion

In this article, a principle about the accumulation of friable deposits until the generation of their angle of repose is proposed from the perspective of particles. The principle is extended to the loess slope, and the relationship between the stability of microscopic particle structure and the stability of macroscopic slope is established from a new point of view. This method can help readers understand the formation process of the accumulation body from the perspective of particles. And it can also connect the accumulation body with the slope which is two objects with large variability of their scales. It will help readers to understand that the slope is only a large accumulation body and the stability of slope is controlled by the base angle just like the small accumulation body. The conclusions of this article are as follows:

1) According to the gravity pressure of static particles in different positions is different, four kinds of contact models which are triangular pyramid contact structure (TS), rectangular pyramid contact structure (RS), pentagonal pyramid contact structure (PS), and hexagon contact structure (HS) are set up and the transformation principle of those four contact models is put forward. The stability of four contact models is compared with the view of mechanics. It is proved that the process from TS to HS is a gradually stable process.

2) The modified fixed funnel method is conducted to test the particles with different sizes. It reveals that four contact structures exist between particles in the process of accumulation and proves the universality of the contact models under different particle sizes conditions directly. According to the test results, the distribution range of sand repose angle is 32°–38°. It explains Shields’ conclusion that the friction angle of uniform sand particles is 33°.

3) It is more corresponding to the real situation that vertical vibration load is applied to the stacking test to strengthen the effect of particle gravity pressure for the slope. Thus, the relationship between the repose angle of accumulation body and slope angle is established. Therefore, it is speculated that the distribution range of the slope angle is less than 30°. Combined with field investigation data, the rationality of this relationship is proved. The reliability of the hypothesis is verified by two engineering cases which are the line from Dingxi to Tianshui in Gansu Province and the slope in Jixian Jichang town of Shanxi Province.

The contact models will be improved later. In order to get closer to the real characteristics of loess particles and the contact models can be extended to all other loess particles, it is not only considered the friction between particles but also put the cohesive force between particles, the shape, and the size of particles into the calculation scope of contact models. In addition, the real loess slope is subject to many disturbance factors, such as precipitation, vibration, and other single factors as well as various coupling effects. Therefore, these are also one of the problems to be solved urgently in the future.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

The main content of this article is written by HD. The theme of the article is guided by JW and the details of the experiment are guided by DZ. The pictures are modified by YX. Finally, the content language is modified by ZL.

Funding

This research was supported by the National Science Foundation of China (Grant Nos. 42027806 and 41630639) and National Key Research and Development Program (Grant No. 2018YFC1504703).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Al-Hashemi, F. M. B., and Al-Amoudi, O. S. B. (2018). A Review on the Angle of Repose of Granular Materials, Powder Tech., 330, 397–417. doi:10.1016/j.powtec.2018.02.003

CrossRef Full Text | Google Scholar

Atwood-Stone, C., and McEwen, A. S. (2013). “Measuring Dynamic Angle of Repose in Low Gravity Enviornments Using Martian Sand Dunes”, in 44th Lunar and Planetary Science Conference, March 18–22, 2013, Woodlands, Texas, 3, 1175–1177.

Google Scholar

Bacherikov, I., Novikov, A., and Petrishchev, E. (2021). Discrete Seed Feeder Designing for Mobile Apparatus: Early Results for Pinus Sylvestris L. Species. Inventions 6 (1), 14–21. doi:10.3390/inventions6010014

CrossRef Full Text | Google Scholar

Chou, H. T., Chou, S. H., and Hsiau, S. S. (2014). The Effects of Particle Density and Interstitial Fluid Viscosity on the Dynamic Properties of Granular Slurries in a Rotating Drum. Powder Tech. 252, 42–50. doi:10.1016/j.powtec.2013.10.034

CrossRef Full Text | Google Scholar

Cui, Y., Xu, C., Xu, S., Chai, S., Fu, G., and Bao, P. (2020). Small-scale Catastrophic Landslides in Loess Areas of China: An Example of the March 15, 2019, Zaoling Landslide in Shanxi Province. Landslides 17 (3), 669–676. doi:10.1007/s10346-019-01322-4

CrossRef Full Text | Google Scholar

Duran, J. (2001). Sand, Powders and Grains; An Introduction to the Physics of Granular Materials, Spring-Verlag. Butsuri 56 (1), 52–53. doi:10.11316/butsuri1946.56.1.52_2

CrossRef Full Text | Google Scholar

Evesque, P., and Rajchenbach, J. (1989). Instability in a Sand Heap. Phys. Rev. Lett. 62 (1), 44–46. doi:10.1103/PhysRevLett.62.44

PubMed Abstract | CrossRef Full Text | Google Scholar

Ghazavi, M., Hosseini, M., and Mollanouri, M. (2008). “A Comparison between Angle of Repose and Friction Angle of Sand,” in The 12th International Conference of International Association for Computer Methods and Advances in Geomechanics (IACMAG), Goa, India, 1272–1275.

Google Scholar

Holsapple, K. A. (2013). Modeling Granular Material Flows: The Angle of Repose, Fluidization and the Cliff Collapse Problem. Planet. Space Sci. 82-83, 11–26. doi:10.1016/j.pss.2013.03.001

CrossRef Full Text | Google Scholar

Hu, S., Qiu, H., Wang, X., Gao, Y., Wang, N., Wu, J., et al. (2018). Acquiring High-Resolution Topography and Performing Spatial Analysis of Loess Landslides by Using Low-Cost UAVs. Landslides 15 (3), 593–612. doi:10.1007/s10346-017-0922-8

CrossRef Full Text | Google Scholar

Hua, X., and Shultis, K. (2021). Kinematics of Cohesive and Elongated Particulate Materials in a Vertical axis Mixer. Powder Tech. 386 (prepublish), 540–546. doi:10.1016/j.powtec.2021.03.030

CrossRef Full Text | Google Scholar

Huntley, D., Bobrowsky, P., Hendry, M., Macciotta, R., Elwood, D., Sattler, K., et al. (2019). Application of Multi-Dimensional Electrical Resistivity Tomography Datasets to Investigate a Very Slow-Moving Landslide Near Ashcroft, British Columbia, Canada. Landslides 16, 1033–1042. doi:10.1007/s10346-019-01147-1

CrossRef Full Text | Google Scholar

Karimi, M., Kheiralipo, K., Tabatabaee, A., Khoubakht, G. M., Naderi, M., and Heidarbeig, K. (2008). The Effect of Moisture Content on Physical Properties of Wheat. Pakistan J. Nutr. 8 (1), 90–95. doi:10.3923/pjn.2009.90.95

CrossRef Full Text | Google Scholar

Kleinhans, M. G., Markies, H., de Vet, S. J., in 't Veld, A. C., and Postema, F. N. (2011). Static and Dynamic Angles of Repose in Loose Granular Materials under Reduced Gravity. J. Geophys. Res. 116 (E11), 1–13. doi:10.1029/2011JE003865

CrossRef Full Text | Google Scholar

Lajeunesse, E., Mangeney-Castelnau, A., and Vilotte, J. P. (2004). Spreading of a Granular Mass on a Horizontal Plane. Phys. Fluids 16 (7), 2371–2381. doi:10.1063/1.1736611

CrossRef Full Text | Google Scholar

Li, C., Honeyands, T., O'Dea, D., and Moreno-Atanasio, R., (2017). The Angle of Repose and Size Segregation of Iron Ore Granules: DEM Analysis and Experimental Investigation. Powder Tech. 320, 257–272. doi:10.1016/j.powtec.2017.07.045

CrossRef Full Text | Google Scholar

Li, W., Yue, D., Colombera, L., Mountney, N. P., and Wu, S. (2020). A Novel Method for Estimating Sandbody Compaction in Fluvial Successions. Sediment. Geology. 404, 105675. doi:10.1016/j.sedgeo.2020.105675

CrossRef Full Text | Google Scholar

Liu, Z. C. (2011). Measuring the Angle of Repose of Granular Systems Using Hollow Cylinders. Available at: http://d-scholarship.pitt.edu/6401/(Acessed 11 22, 2011).

Google Scholar

Lumay, G., Boschini, F., Traina, K., Bontempi, S., Remy, J.-C., Cloots, R., et al. (2012). Measuring the Flowing Properties of Powders and Grains. Powder Tech. 224, 19–27. doi:10.1016/j.powtec.2012.02.015

CrossRef Full Text | Google Scholar

Ma, P. H., Peng, J. B., Wang, Q. Y., Zhuang, J. Q., and Zhang, F. Y. (2019). The Mechanisms of a Loess Landslide Triggered by Diversion-Based Irrigation: A Case Study of the South Jingyang Platform, China. Bull. Eng. Geol. Environ. 78 (7), 4945–4963. doi:10.1007/s10064-019-01467-5

CrossRef Full Text | Google Scholar

Metcalf, J. R. (1966). Angle of Repose and Internal Friction. Int. J. Rock Mech. Mining Sci. Geomech. Abstr. 3 (2), 155–161. doi:10.1016/0148-9062(66)90005-2

CrossRef Full Text | Google Scholar

Müller, D., Fimbinger, E., and Brand, C. (2021). Algorithm for the Determination of the Angle of Repose in Bulk Material Analysis. Powder Tech. 383, 598–605. doi:10.1016/j.powtec.2021.01.010

CrossRef Full Text | Google Scholar

Pähtz, T., Liu, Y., Xia, Y., Hu, P., He, Z., and Tholen, K. (2021). Unified Model of Sediment Transport Threshold and Rate Across Weak and Intense Subaqueous Bedload, Windblown Sand, and Windblown Snow. J. Geophys. Res. Earth Surf. 126 (4), 1–36. doi:10.1029/2020JF005859

CrossRef Full Text | Google Scholar

Penkavova, V., Kulaviak, L., Ruzicka, M. C., and Puncochar, M. (2021). Anisometric Granular Materials: Compression and Shear Properties. Granular Matter 23 (2), 29–46. doi:10.1007/s10035-020-01082-2

CrossRef Full Text | Google Scholar

Rackl, M., Grötsch, F. E., Rusch, M., and Fottner, J. (2017). Qualitative and Quantitative Assessment of 3D-Scanned Bulk Solid Heap Data. Powder Tech. 321, 105–118. doi:10.1016/j.powtec.2017.08.009

CrossRef Full Text | Google Scholar

Soltanbeigi, B., Podlozhnyuk, A., Kloss, C., Pirker, S., Ooi, J. Y., and Papanicolopulos, S.-A. (2021). Influence of Various DEM Shape Representation Methods on Packing and Shearing of Granular Assemblies. Granular Matter 23 (2), 25–41. doi:10.1007/s10035-020-01078-y

CrossRef Full Text | Google Scholar

Wang, J., Xu, Y., Ma, Y., Qiao, S., and Feng, K. (2018a). Study on the Deformation and Failure Modes of Filling Slope in Loess Filling Engineering: A Case Study at a Loess Mountain Airport. Landslides 15 (12), 2423–2435. doi:10.1007/s10346-018-1046-5

CrossRef Full Text | Google Scholar

Wang, J., Zhang, D., Wang, N., and Gu, T. (2019a). Mechanisms of Wetting-Induced Loess Slope Failures. Landslides 16 (5), 937–953. doi:10.1007/s10346-019-01144-4

CrossRef Full Text | Google Scholar

Wang, J., Li, P., Gu, Q., Xu, Y., and Gu, T. (2019b). Changes in Tensile Strength and Microstructure of Loess Due to Vibration. J. Asian Earth Sci. 169, 298–307. doi:10.1016/j.jseaes.2018.10.011

CrossRef Full Text | Google Scholar

Wang, J., Xu, Y., Zhang, D., and Gu, T. (2021). Vibration-induced Acceleration of Infiltration in Loess. Sci. China Earth Sci. 64 (04), 611–630. doi:10.1007/s11430-020-9741-x

CrossRef Full Text | Google Scholar

Xu, X.-Z., Guo, W.-Z., Liu, Y.-K., Ma, J.-Z., Wang, W.-L., Zhang, H.-W., et al. (2017). Landslides on the Loess Plateau of china: A Latest Statistics Together with a Close Look. Nat. Hazards 86 (3), 1393–1403. doi:10.1007/s11069-016-2738-6

CrossRef Full Text | Google Scholar

Xu, Y., Allen, M. B., Zhang, W., Li, W., and He, H. (2020a). Landslide Characteristics in the Loess Plateau, Northern China. Geomorphology 359, 107150. doi:10.1016/j.geomorph.2020.107150

CrossRef Full Text | Google Scholar

Xu, Y., Liu-Zeng, J., Allen, M. B., Allen, M. B., Zhang, W., and Du, P. (2020b). Landslides of the 1920 Haiyuan Earthquake, Northern China. Landslides 18 (3), 935–953. doi:10.1007/s10346-020-01512-5

CrossRef Full Text | Google Scholar

Zhang, F. Y., Peng, J. B., Huang, X. W., and Lan, H. X. (2021). Hazard Assessment and Mitigation of Non-seismically Fatal Landslides in China. Nat. Hazards 106 (prepublish), 785–804. doi:10.1007/s11069-020-04491-x

CrossRef Full Text | Google Scholar

Zheng, J., and Hryciw, R. D. (2016). A Corner Preserving Algorithm for Realistic DEM Soil Particle Generation. Granular Matter 18 (4), 83–101. doi:10.1007/s10035-016-0679-0

CrossRef Full Text | Google Scholar

Zhou, Y., Wang, H. B., Zhou, B., and Li, J. M. (2018). DEM-aided Direct Shear Testing of Granular Sands Incorporating Realistic Particle Shape. Granular Matter 20 (3), 54–66. doi:10.1007/s10035-018-0828-8

CrossRef Full Text | Google Scholar