Influence of Rainfall Conditions on Stability of Slope Reinforced by Polymer Anti-slide Pile

Traditional reinforced concrete piles have high strength and low cost in slope engineering, but the slow forming and long maintenance period make it difficult to meet the needs of emergency and disaster relief tasks, such as landslides caused by rainfall. In this paper, the influence of a new type of polymer anti-slide pile on slope stability under rainfall conditions is studied. With the advantages of fast forming, high strength, simple construction technology, and small disturbance to slope, the new type of anti-slide pile can meet the requirements of emergency and disaster relief tasks. The influence of different rainfall duration, rainfall form, location, and spacing of pile laying on the stability of rainfall slope is explored with fluid-solid coupling analysis. The results show that the slope stability gradually deteriorates with the increase of the peak duration of rainfall intensity. Without rainfall conditions, the reinforcement effect is optimal when the position of pile cloth is 1/2–3/4 L away from the foot of the slope (L is the horizontal length of the slope); with rainfall conditions, when the position of pile cloth is 1/4–1/2 L away from the foot of the slope, the reinforcement effect is optimal. Without rainfall conditions, the reduction of pile spacing can improve the reinforcement effect; with rainfall conditions, the reduction of pile spacing will affect the flow and discharge of seepage rainwater and reduce the reinforcement effect.

Introduction

Landslide is a sliding geological phenomenon of slope rock mass along the through shear failure surface. The mechanism of a landslide is that the shear stress on a sliding surface exceeds the shear strength of that surface. In 2019, 6,181 geological disasters occurred in China, including 4,220 landslides, causing hundreds of deaths and direct economic losses of more than 2 billion yuan. At present, most of the ways to prevent landslide disasters in engineering are by setting slope retaining materials, such as an anti-slide retaining wall, anchor rod, anti-slide pile, and micro anti-slide pile, etc. Among them, anti-sliding piles and micro-anti-sliding piles are widely used in slope reinforcement engineering because of their simple structure, strong anti-sliding ability, and mature construction technology.

In recent years there has been a large amount of research and analysis of the stability of slope reinforcement and anti-slide piles. (Cai et al., 1998; Cai and Ugai, 2000; Wei and Cheng, 2009; Gao et al., 2015; Tan et al., 2018) studied the stability of slope reinforced by anti-sliding piles, using the finite element strength reduction method. Chen and Martin (2002) used finite element analysis software to explore the influence of soil arching effect on the stability of anti-sliding piles. Li et al. (2019), Mao et al. (2019) found that the deformation patterns of adjacent piles in pile groups are different, resulting in different degrees of axial forces and bending moments. Piles in the shear zone will separate and pile groups will be destroyed with the increase of fault displacement. Tang et al. (2014) found that the maximum soil pressure exerted by anti-sliding piles occurs in the middle and upper part of the sliding mass. The distribution of soil pressure has complex changing rules during deformation.

Even though the above scholars studied design optimization and other aspects of anti-slide piles to a significant extent, they did not consider the influence of rainfall. A large number of landslide accidents indicate that rainfall is an important factor in causing a landslide as major landslide accidents often occur after rainstorms. It is therefore very important to study the influence of rainfall on slope stability. Studies by Bogaard and Greco (2016), Sidle and Bogaard (2016), Morbidelli et al. (2018), Fan et al. (2019), Gidon and Sahoo (2020) have explored the influence of rainfall on slope stability and Luo et al. (2021) explore the influence of rainfall on highway slopes. Chatra et al. (2019) separately analyzed the influence of rainfall on the stability of soil slope with different densities. Wang et al. (2020) studied the influence of rainfall on the stability of multi-layer unsaturated soil slopes. Tang et al., (2017) proposed a method to incorporate the initial conditions of pore water pressure distribution into slope stability analysis based on rainfall data in the Three Gorges reservoir area. Moreover, Wu et al. (2017) have carried out tests on the dynamic characteristics of loess slopes under artificial rainfall conditions, and explored the influence of rainfall intensity and duration on stability. He et al. (2021) analyzed the characteristics of soil slope saturated zones and the influence of water body characteristic parameters on slope stability, and put forward a landslide prediction model based on the critical curve of the shallow saturated zone and one-dimensional model. Cai and Ugai (2000), Cai and Ugai (2004), Yao et al. (2021) have studied the influence of rainfall intensity and the hydraulic characteristics on slope stability by strength reduction method and finite element seepage analysis. However, they only consider the influence of rainfall on hydraulic characteristics and stability of the natural slope, and the influence caused by the existence of anti-slide piles is neglected. Li et al. (2018), Li et al. (2020) have undertaken stability analysis of slopes reinforced by anti-slide piles under rainfall conditions, but this study only analyzed the effect of one form of rainfall and ignored how the change of the form of rainfall would affect the slope stability.

The above studies are based on anti-slide piles made of concrete and gravel concrete. Traditional concrete materials have the characteristics of low price, high strength, and are easily sourced. They also have the disadvantages of long maintenance periods and long construction periods. For the dangerous landslide rescue task, these shortcomings may cause more casualties and more economic losses. The polyurethane polymer material is a new engineering material developed in recent years. It has the characteristics of early forcing, fast formation, high strength, simple construction technology, and causes minimal disturbance to the slope, etc. (Liu et al., 2018; Lin et al., 2020). It can be adopted to the needs of rescue and disaster relief tasks. Wang et al.(Wang et al., 2019; Wang et al., 2021a; Wang et al., 2021b) have explored the shear behavior between polymer material and concrete through the interfacial shear test. Using a model test and numerical analysis, they concluded that the effect of polyurethane polymer gravel piles on reinforcing the soft soil subgrade of the expressway is better than that of traditional piles (Wang et al., 2018). Shi et al.(Shi et al., 2014) explored the influence of length, diameter, and density of polyurethane polymer anchor rod on bond strength through bond performance test between polyurethane polymer anchor rod and silt. The author has previously studied the optimum design scheme for side slope reinforcement with high polymer micro anti-slide piles. However, the influence of rainfall on slope reinforcement by micro-piles was not considered.

Existing numerical analysis software can only realize the fluid-solid coupling analysis of rainfall slope and the safety factor analysis of slope without rainfall conditions. It cannot analyze the stability of slope strengthened by anti-slide pile with rainfall conditions. In this paper, a flow-solid coupling calculation model considering the characteristic curve of permeability coefficient and the soil-water characteristic curve is established, and rainfall infiltration analysis of the slope was carried out. The data of hole pressure, saturation, stress, and strain of slope reinforced by high polymer anti-slide piles during rainfall were obtained. Finally, combined with the characteristics of high polymer material, through the development of a numerical analysis software subroutine, the safety factor of the slope after rainfall was obtained by the strength reduction method.

Soil Hydraulic Characteristics and Seepage Pattern

Characteristic Curve of Hydraulic Permeability Coefficient and Soil-Water Characteristic Curve

The biggest mechanical difference between unsaturated soil and saturated soil is the existence of suction, which has a great influence on the deformation and strength of unsaturated soil. In unsaturated soils, water conductivity decreases due to partial aeration in the soil pores. As soil water first discharges from the macropore under suction, water flow can only flow in the micropore with the increase of suction. Therefore, from saturated to unsaturated soil, its permeability will decrease dramatically. However, the permeability coefficient of unsaturated soils cannot be assumed to be constant and is strongly influenced by the change of matrix suction and saturation of soils.

In the analysis of this paper, the permeability coefficient of water in soil refers to the calculation Eq. 1 proposed by Alonso E (Alonso et al., 1995), which defines the relationship between permeability coefficient and matrix suction:

$\frac{k_{\text{w}}=a_{\text{w}}{k}_{\text{ws}}}{\left(a_{\text{w}}+{\left\{b_{\text{w}}\left(u_{\text{a}}-u_{\text{w}}\right)\right\}}^{c_{\text{w}}}\right)},(1)$

k_w is the permeability coefficient and k_ws is the saturated permeability coefficient of soil, a_w, b_w, c_w are constant parameters, a_w, b_w, c_w are taken as 1,000, 0.01, and 1.7 respectively.

In this paper, the relationship between matrix suction and saturation is defined using the calculation formula of Equation 2 (Alonso et al., 1995) for the characteristic curve of water and soil in the model.

$\frac{S_{\text{r}}=S_{\text{i}}+\left(S_{\text{n}}-S_{\text{i}}\right)a_{\text{s}}}{\left(a_{\text{s}}+{\left\{b_{\text{s}}\left(u_{\text{a}}-u_{\text{w}}\right)\right\}}^{c_{\text{s}}}\right)}.(2)$

S_r is saturated; S_i is residual saturation, 0.08 is taken in this paper. S_n is the maximum saturation and 1 is chosen in this paper, a_s, b_s, c_s are constant parameters. The values of a_s, b_s, c_s are 1 and 5 × 10^–5, 3.5.

Infiltration and Runoff Modes

The rainfall infiltration mode of an unsaturated soil slope exists in various forms and the infiltration process is very complex. Mein and Larson (Mein and Larson, 1973) describe the process and behavior of rainfall infiltration by comparing three parameters: rainfall intensity q, permissible infiltration capacity f_p of soil, and saturated permeability coefficient k_ws of soil.

1) q < k_ws: At this time, surface runoff will not occur and all rainfall will infiltrate, while the infiltration capacity of water remains unchanged.

2) f_p > q > k_ws: All rainwater infiltrates, f_p decreases with the increase of infiltration depth, but the rainfall intensity has not reached the permissible infiltration capacity of soil at this time, so the infiltration capacity will not decrease and the infiltration capacity is very high.

3) q > f_p: At this time, the infiltration process is complicated, and rainwater cannot infiltrate completely. Runoff forms on the surface of the slope body and the infiltration capacity change constantly. This situation is not considered in this paper.

Soil Failure Criteria

The failure readiness of saturated soils is mostly Mohr-Coulomb criterion. However, due to the presence of matrix suction in unsaturated soils, the Mohr-Coulomb criterion does not apply to unsaturated soils. In the 1960s, Bishop (Bishop and Blight, 1963) proposed an expression for the strength of unsaturated soils:

${\tau }_{\text{f}}=c^{\prime }+\left({\sigma }_{\text{n}}-u_{\text{a}}\right)\tan {\phi }^{\prime }+\chi \left(u_{\text{a}}-u_{\text{w}}\right)\tan {\phi }^{\prime },(3)$

u_a is pore pressure because it is connected to the atmosphere, u_a takes 0. u_w is pore water pressure. c’ and φ′ are effective internal friction angle and effective cohesion respectively. However, because $\chi$ is an empirical coefficient and is related to saturation, it is difficult to determine the value, so it is not widely used.

Fredlund (Fredlund et al., 1978) proposed another formula for shear strength:

${\tau }_{\text{f}}=c^{\prime }+\left({\sigma }_{\text{n}}-u_{\text{a}}\right)\tan {\phi }^{\prime }+\left(u_{\text{a}}-u_{\text{w}}\right)\tan {\phi }_{\text{b}},(4)$

φ_b is an angle defining the increase in shear strength for an increase in matric suction. Fredlund’s formula indicates that the shear strength of unsaturated soils is not only related to cohesion and friction angle but also matrix suction and internal friction angle changing with suction.

During the rainfall process, the matrix suction and saturation of the slope will change with the infiltration of rainwater, which will change the physical properties of the soil and affect the overall stability of the slope. The foot of the slope will slide and the top of the slope will sink. Although the overall sliding tendency is very small, its influence on the stability of the slope cannot be ignored.

In this paper, the fluid-solid coupling analysis of the slope model reinforced by high polymer anti-slide piles under different schemes was carried out to obtain the saturation and pore pressure of the rainfall slope at different times. Through secondary development of numerical analysis software, the stress and strain on the slope caused by long-term rainfall and gravity are applied to slope stability analysis.

Establishment and Analysis of Numerical Model

In slope engineering with anti-slide pile reinforcement, considering rainfall conditions, the influence of slope saturation and pore pressure variation on the mechanical characteristics of unsaturated soil is mainly analyzed. Rainfall form, intensity, duration, spacing of anti-slide piles, and different pile positions will affect seepage field and stress field changes of the entire slope, and then affect the overall stability of the slope.

Geometric Models and Material Parameters

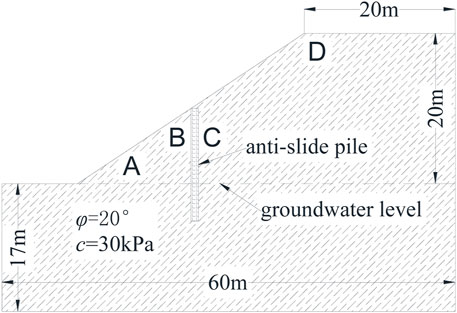
A typical example of slope reinforcement with an anti-slide pile was selected. The slope height is 20 m, the foundation depth is 17 m, the groundwater level is below ground, the total horizontal length of the model is 60 m, and the slope gradient is 1:1.5. We then set up four monitoring units A, B, C, and D. Point A is set at the foot of the slope, point B and C are at the same height, point B is in front of the pile, point C is behind the pile and point D is at the top of the slope. The pile body forming material of the anti-slide pile is polyurethane high polymer, the diameter of the pile is D = 1 m, and the slope soil material is unsaturated soil. The sketch of the slope model is shown in Figure 1.

FIGURE 1

FIGURE 1. Sketch of the slope model.

In the numerical analysis software, the bottom of the model was set as the origin of the coordinate axis. For the subsurface boundary of the model, the pore pressure boundary condition is set, which is expressed in analytical form 10* (17-Y). The pore pressure boundary condition of the model ground is set to 0. The pore pressure boundary condition of the pile body is also set at 0 because the polymer material has the function of water plugging and has no permeability and the permeability coefficient is 0. At the same time, displacement constraints are set at the bottom of the model, X-direction displacement constraints are set at the left and right, and Z-direction displacement constraints are set at the front and rear. The rainfall intensity perpendicular to the slope is set at 0.0166 m/h and 0.02 m/h perpendicular to the ground. Rainfall forms are single-peak and double-peak, with a duration of 72, 96, and 120H respectively. An anti-sliding pile is considered the ideal elastomer. The contact interaction between pile and soil is adopted and the coefficient of friction between pile and soil is 0.46. With the increase in the length of the anti-slide pile, the construction difficulty and cost of the project will increase. Therefore, according to the height of the slope, the pile length is assumed to be 15 m. The mechanical parameters of soil and pile are shown in Table 1 (Liu et al., 2018; Lin et al., 2020). Soil hydraulic parameters are shown in Table 2.

TABLE 1

TABLE 1. Mechanical parameters of soil and pile.

TABLE 2

TABLE 2. Hydraulic parameters of soil.

Without Rainfall Conditions

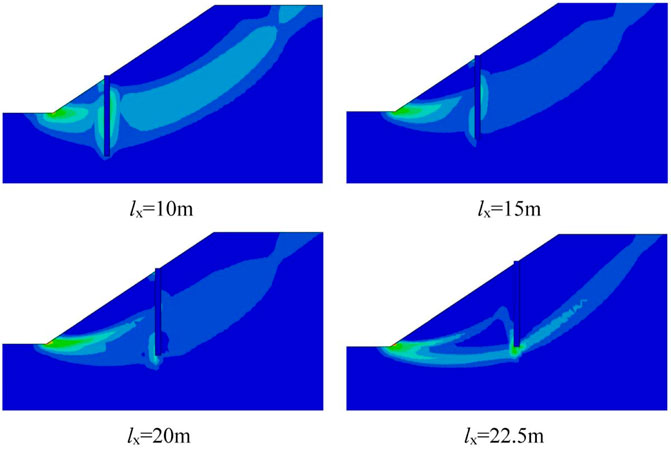
Influence of Pile Laying Position on Reinforcement Effect

Assuming the spacing of piles is 3D, the stability of slope reinforced by anti-sliding piles under different positions of pile laying is analyzed respectively. Figure 2 illustrates the equivalent plastic strain diagram of a slope at different pile locations. Figure 3 illustrates the safety factors of slope at different pile locations and pile spacing under, without rainfall conditions. It can be seen from Figure 3A that when the pile position is l_x = 20 m away from the foot of the slope, the safety factor of the slope is the largest and the reinforcement effect is the best under without rainfall conditions (l_x stands for the distance from the foot of the slope). As can be seen in Figure 2, when l_x = 22.5 m, the pile is close to the top of the slope, the sliding zone appears at the lower part of the pile, which results in the anti-sliding pile being unable to fully play its anti-sliding role. As can be seen in Figure 2 and Figure 3A, if the pile position changes from l_x = 20 m to l_x = 7.5 m, the reinforcement effect will gradually become worse and with the change of pile position, the plastic slip zone of the slope also shows an upward trend. Therefore, it can be inferred that if the pile is located at the foot of the slope, the sliding zone of the slope may be located above the pile, and the anti-sliding pile cannot play a role in anti-sliding. When the pile is located at the middle and upper part, the safety factor of the slope is relatively large and the anti-sliding effect of the anti-sliding pile is the best. Because the anti-sliding force provided by the anti-sliding pile and the anti-sliding force provided by the soil in front of the pile can be fully used to resist the sliding force produced by the soil after the pile and maintain the stability of the slope. When the pile body is close to the top of the slope, although the sliding force of the soil slope behind the pile is small, the whole soil slope will generate a plastic penetration area under the pile body, which will lead to slope instability. When the pile body is close to the foot of the slope, the soil in front of the pile cannot give fully provide anti-sliding force, the safety factor of the slope is too small, and the reinforcement effect is poor.

FIGURE 2

FIGURE 2. Plastic strain diagram at different pile positions.

FIGURE 3

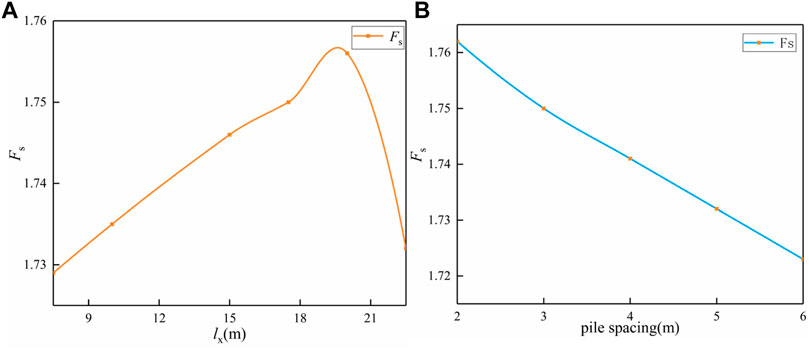
FIGURE 3. Slope safety factor under different pile positions and different pile spacing without rain.

Influence of Pile Spacing on Reinforcement Effect

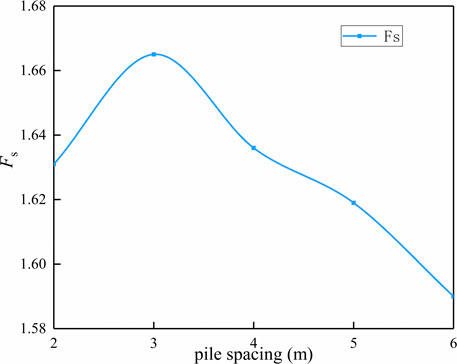
Assuming that the length of piles is l = 15 m and the location of piles is l_x = 17.5 m, the stability of slope reinforced by anti-slide piles with different spacing between piles under without rainfall conditions is analyzed respectively. Figure 3B illustrates the slope safety factors after reinforcement with different pile spacing. From Figure 3B, it can be seen that when the spacing between piles is 6D, the safety factor of the slope after reinforcement is 1.723, and when the spacing between piles is 2D, the safety factor of the slope after reinforcement is 1.762. As the spacing between piles decreases, the pile group effect of anti-sliding piles is more easily brought into play, which makes the reinforcement effect of anti-sliding piles better and the safety factor increases constantly. However, if the spacing between piles is reduced continuously, the reinforcing cost will be increased, and the reinforcing effect will exceed the reinforcing demand, resulting in waste. Therefore, it is necessary to choose the spacing between piles reasonably according to the reinforcing demand.

Impact of Rainfall on Stability of Slope After Reinforcement

Rainfall infiltration is one of the important factors affecting the stability of a slope. Rainfall infiltration will change the overall seepage flow field of a slope, which will cause the mechanical characteristics of the soil to attenuate to a certain extent and the stability of the slope to decrease. Because of the existence of anti-slide piles, the seepage field inside the slope strengthened with anti-slide piles will be different from that inside the natural slope. The length of rainfall, the form of rainfall, the position of the anti-slide pile, and the distance between piles will affect the seepage field inside the slope and also the stability of the slope to some extent. It can be seen from the results of slope reinforcement by anti-slide piles when there is no rainfall the sliding zone of the slope has already occurred under the pile body when the pile position l_x > 22.5 m. When l_x < 7.5 m, the reinforcement effect of the anti-slide pile is poor. Therefore, the stability analysis of slope rainfall when l_x < 7.5 m and l_x > 22.5 m is no longer carried out. In this section, the effects of rainfall form, duration, position, and spacing of piles on slope stability under rainfall conditions are explored respectively, and the optimum pile position and spacing of anti-slide piles for slope reinforcement under rainfall are analyzed.

Influence of Rainfall Form and Duration on Slope Stability

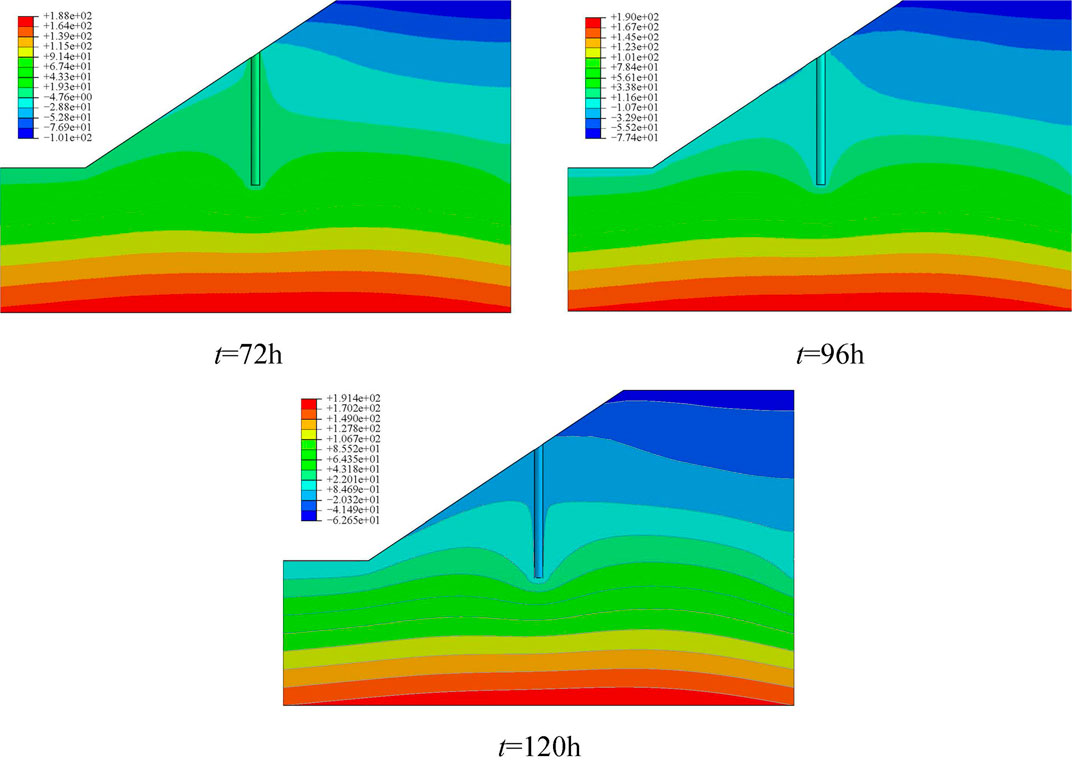
Assuming that the precipitation is single-peak precipitation and the location of pile arrangement is l_x = 20m, Figure 4 depicts a cloud chart of pore pressure distribution on a slope as rainfall intensity begins to decrease at different rainfall durations. Figure 5 depicts a cloud chart of pore pressure distribution on a slope at the end of rainfall. The matrix suction loss at the top of the slope is the largest, so the matrix suction change at the top of the slope is selected as one of the evaluation criteria. As can be seen in Figure 4, when the duration of rainfall is 72, 96, and 120H, matrix suction losses at the top of the slope are 200 kPa–37.9 kPa, 200 kPa–33.7 kPa, and 200 kPa–29.78 kPa, respectively. Although the difference of maximum suction loss of the slope soil matrix is small, the same degree of loss occurs in the overall mechanical characteristics of the slope, which reduces the overall stability of the slope. As it can be seen in Figure 5, at the end of rainfall, the matrix suction at the top of the slope recovered from 37.9 kPa, 33.7 kPa, 29.78 kPa–101 kPa, 77.4 kPa, and 62.65 kPa, respectively. Therefore, with the increase of rainfall time, the recovery ability of mechanical characteristics of slope soil gradually decreases. Although the suction of the soil before pile and in the shallow soil mass of the slope has little change, the saturation has changed a lot, and the mechanical properties of the soil have also been attenuated to a certain extent, which makes it easier for plastic failure to occur. The matrix suction of the soil body behind the pile and the soil above the slope decreases greatly, but it still has better mechanical characteristics compared with the soil before the pile and in the shallow soil mass of the slope.

FIGURE 4

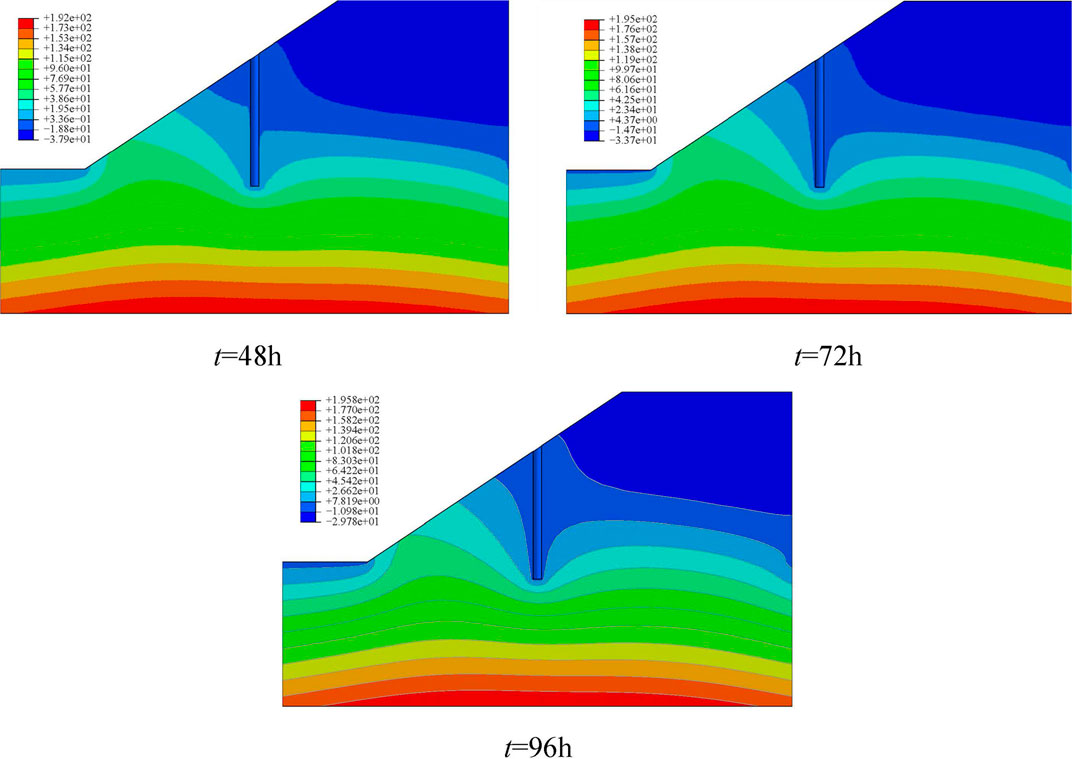
FIGURE 4. Distribution of pore pressure at peak rainfall intensity for different rainfall durations.

FIGURE 5

FIGURE 5. Pore pressure distribution map of the slope after rain in different rainfall duration.

Figure 6 illustrates the pore pressure distribution of the side slope at four different times with l_x = 20 m of pile location and double-peak rainfall in the form of rainfall, the total duration of rainfall is 120 h. From Figure 6, it can be seen that the pore pressure of soil mass is relatively small at 30 and 90 h. Because the rainfall intensity reaches the first and second peak respectively at 30 and 90 h, the matrix suction of soil mass decreases greatly and the strength of soil mass decreases. Because the pile body is formed by non-permeable polyurethane polymer and the internal pore water pressure is 0, the pore pressure distribution of the soil around the anti-slide pile is slightly different from that of the adjacent soil. It can also be seen from Figure 6 that matrix suction recovers to a large extent at 60H and 120 h but does not return to its original state as the rainfall intensity gradually decreases to 0. When the duration of precipitation is from 0 to 30 h and then to 60 h, the intensity of precipitation decreases from 0 to peak and then to 0, the matrix suction at the top of slope decreases from 200 kPa to 44 kPa and then recovers to 133 kPa. During the second rainfall process, the matrix suction at the top of the slope decreases from 133 kPa to 40.5 kPa and then recovers to 118 kPa. During the whole rainfall process, the matrix suction of the soil is restored twice, and the mechanical properties of the soil and the stability of the slope are improved.

FIGURE 6

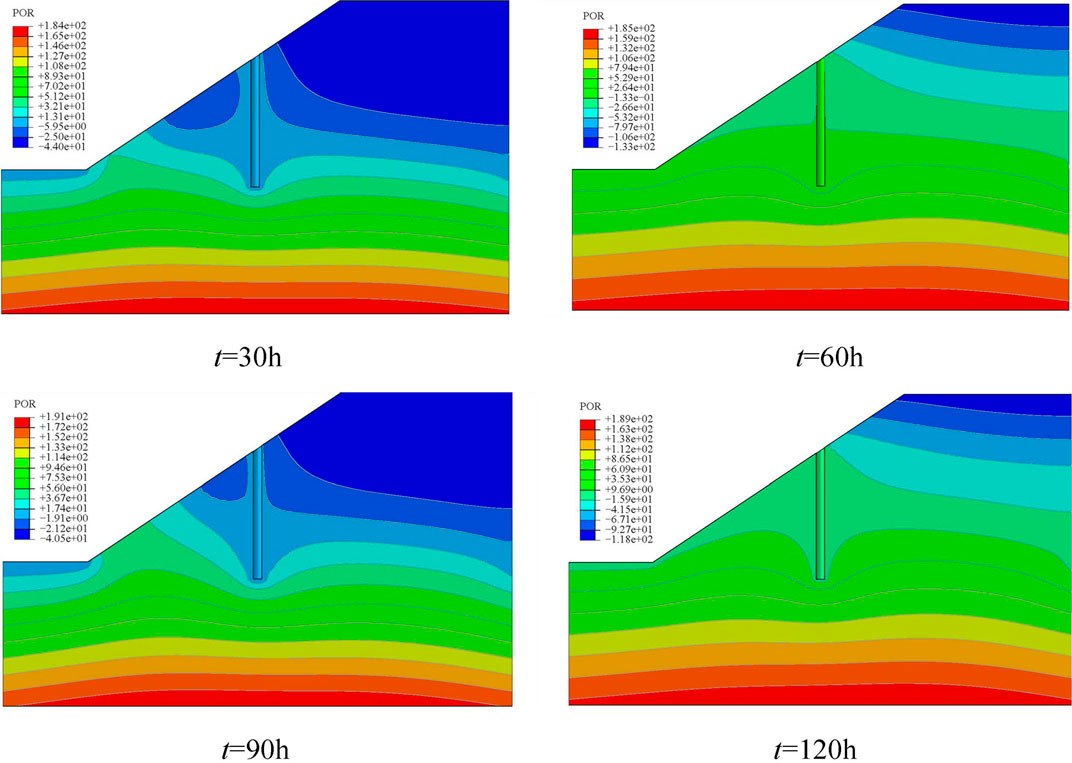
FIGURE 6. Distribution of pore water pressure of the slope at different times in the form of double peak.

Figure 7 illustrates the pore pressure distribution of a slope at two different rainfall moments with single-peak rainfall. Although the duration of single-peak precipitation is the same as that of double-peak precipitation, the process of single-peak precipitation reaching its peak is longer which belongs to long-term strong precipitation, the process of double-peak precipitation reaching its peak is shorter which belongs to short-term strong precipitation. The time at t = 96 h and t = 120 h mean that the rainfall intensity begins to decrease and the rainfall ends. From Figure 7, it can be seen that at t = 96 h, the matrix suction of the slope top is reduced from 200 kPa to 29.78 kPa; when t = 120 h, the matrix suction at the top of the slope recovered from 29.78 to 62.65 kPa. During the whole process of rainfall, the mechanical properties of soil decrease, and the slope stability and mechanical properties of soil cannot be improved and restored in time. When the rainfall form is double peak rainfall, the mechanical properties of slope soil can be restored in time during the whole rainfall process; when the rainfall form is single peak rainfall, in the whole rainfall process, the recovery ability of slope soil mechanical properties is poor, and the risk of slope instability increases.

FIGURE 7

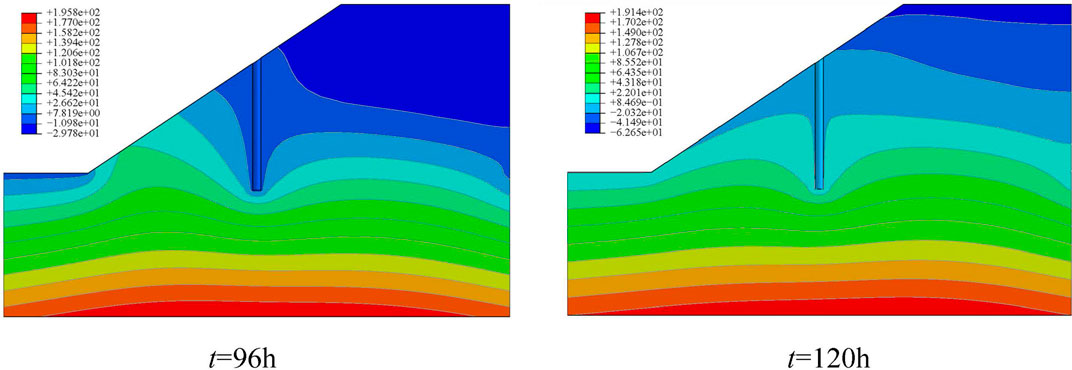
FIGURE 7. Distribution of pore water pressure of the slope at different times in the form of a single peak.

Influence of Different Pile Locations on Slope Stability Under Rainfall Conditions

The selection of pile position of the anti-slide pile will affect the change of seepage field inside the slope under rainfall conditions. It is assumed that the spacing between piles is 3D and the duration of rainfall is 120H. Figure 8 describes the matrix suction and saturation changes at the top monitoring unit D in different pile locations. In the absence of piles, the suction of the matrix near the top of the slope before rainfall should be 190–200 kPa in theory, but it can be seen from Figure 8A that the distribution of the suction of the whole foundation of the slope is affected by the existence of anti-slide piles. When the pile location is selected near the top of the slope, the suction of the soil matrix on the upper part of the slope will be greatly affected and the suction of the matrix will be reduced. When the position of pile arrangement is located in the middle and lower part of the slope, the suction of the soil matrix on the upper part of the slope is less affected. Under different pile laying conditions, the suction of the soil matrix near the top of the slope decreases rapidly as the rainfall intensity increases from 0 to the peak value. Within 3–4 h after the rainfall intensity reaches its peak value, the suction of the soil matrix near the top of the slope continues to decrease, and then the suction of the soil matrix near the top of the slope changes slightly over time. The soil matrix suction near the top of the slope shows a trend of recovery after 6–7 h of rainfall intensity reduction. When the position of pile arrangement is close to the middle and lower part of the slope, the recovery speed is relatively fast. It can be seen from Figure 8B that the saturation of the soil near the top of the slope first increases and then decreases during the rainfall process. Soil saturation increases continuously from residual saturation 0.08 before rainfall intensity begins to decay. When the rainfall intensity begins to decay, the infiltrated rainwater begins to drain, the soil saturation decreases rapidly, and the matrix suction of soil appears a trend of recovery at this moment. The changes of Figure 8A and Figure 8B mean that when the pile position is arranged close to the middle and lower part during the rainfall, the mechanical characteristics of the soil mass on the upper part of the slope decay first and then recover to a certain extent, and the stability of the upper part of the slope decreases first and then recovers to a certain extent.

FIGURE 8

FIGURE 8. Matrix suction and saturation at monitoring Unit D under different pile positions.

Figure 9 illustrates the safety factors of a slope at different pile locations after rainfall. Due to the influence of rainfall, the mechanical properties of soils are attenuated, and the soils in front of piles cannot provide enough anti-sliding force, at the same time, the slope as a whole is subject to varying degrees of strain. Therefore, the safety coefficient of slopes under different positions of pile arrangement has changed compared with that without rainfall. From Figure 9, it can be seen that the anti-slide pile can play a better anti-slide effect when the pile position is close to the middle and lower part of the slope.

FIGURE 9

FIGURE 9. Slope safety factors at different pile locations after rain.

Therefore, in the process of rainfall, when the position of pile arrangement is close to the middle and lower part of the slope, the matrix suction of the upper and lower part of the slope is relatively large and the mechanical characteristics are relatively good. After rainfall, the soil matrix suction recovers relatively quickly and the slope stability is relatively good.

Influence of Different Pile Spacing on Slope Stability Under Rainfall Conditions

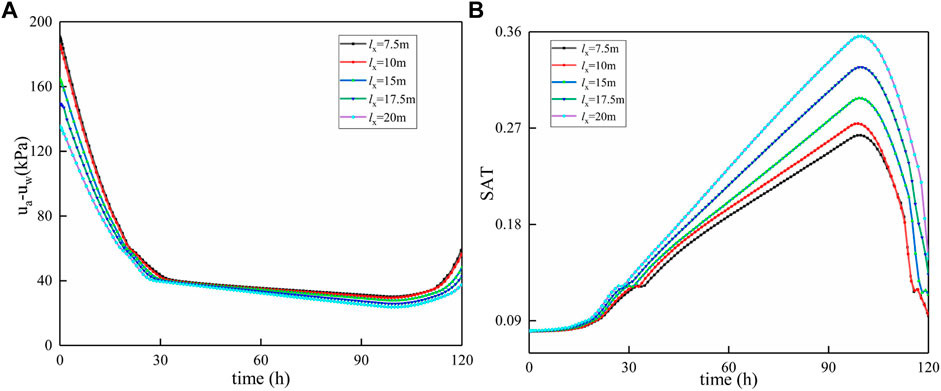
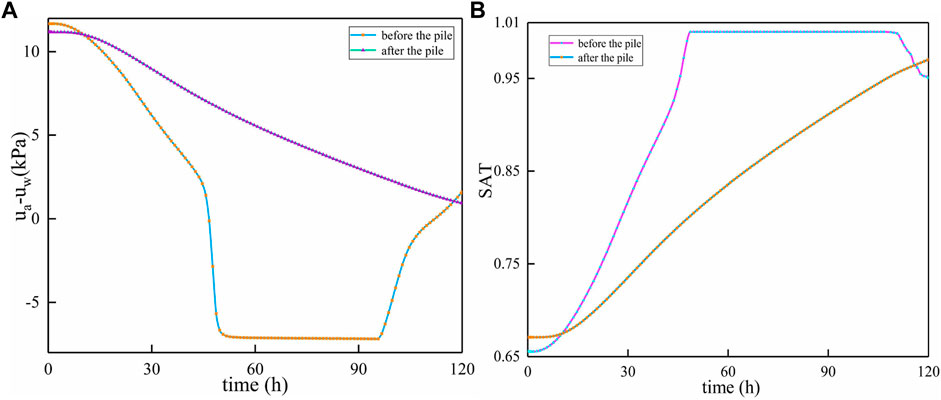
Due to the existence of anti-slide piles, the suction and saturation of the foundation before and after the piles are quite different. When the spacing between piles is changed, the area before and after the piles is the most affected. Generally, the total amount of rainwater infiltration in front of the pile is less than that in the back of the pile, so pore pressure differences may occur during the process of rainwater infiltration. The rainwater infiltrated in front of the pile will flow back to the pile. At this time, the existence of the pile will hinder the flow of seepage rainwater, and the spacing between the piles will affect the ability to hinder. It is assumed that the location of pile laying is l_x = 15 m and the precipitation is single-peak precipitation with the duration of 120H. Figure 10 illustrates the change of suction and saturation of the foundation before and after the pile when the spacing between the piles is 2D. As can be seen from Figure 10A, the suction of the soil matrix in front of the pile decreases relatively quickly. As rainfall progresses, matrix suction of soil decreases, and saturation increases. When the saturation reaches 1, the value of matrix suction becomes the value of maximum pore water pressure. Pore water pressure begins to decrease rapidly within 8–9 h after rainfall intensity begins to decrease. When the saturation degree begins to be less than 1, the suction of the soil matrix before the pile starts to recover, the pore water pressure disappears and the mechanical properties of the soil are restored. The change rule of matrix suction of soil after the pile is quite different from that of the soil before the pile. The matrix suction of soil after the pile shows a trend of continuous decrease and the saturation shows a trend of continuous increase. With the change of location of the monitoring unit, the specific value may change, but the change rule of suction and saturation of foundation before and after pile will not change.

FIGURE 10

FIGURE 10. Matrix suction and saturation of soil around the pile.

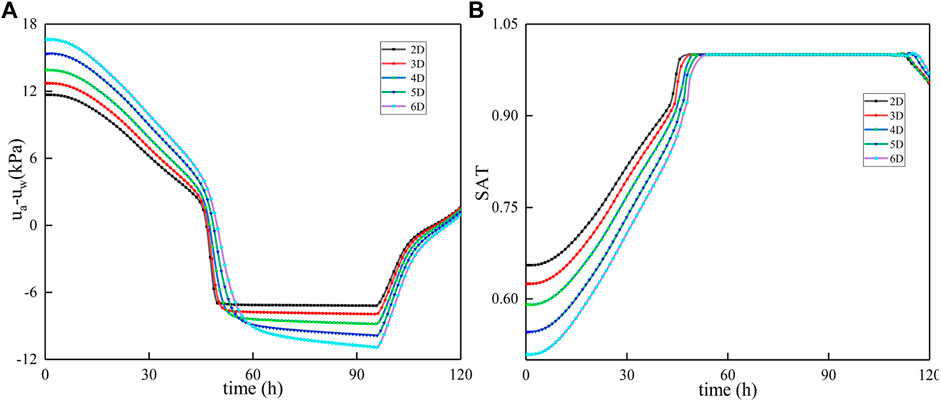
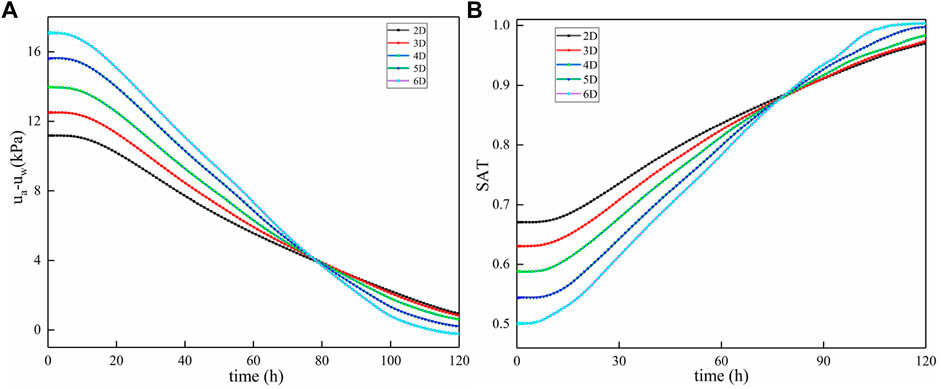
Figure 11 describes the change of suction and saturation of matrix at monitoring unit B at different pile spacing. It can be seen from Figure 11A that in the early and middle stages of the precipitation process, the soil mass in front of piles has better mechanical characteristics by choosing a larger spacing between piles. When the rainfall is over, choosing a large spacing between piles can accelerate the recovery rate of soil mechanical properties in front of the piles. It can be seen from Figure 11B that when the spacing between piles decreases, it is not conducive to drainage and the flow of seepage rainwater, and the soil in front of piles needs less time to reach saturation, which will lead to more plastic failure of soil in front of piles. At the same time, the soil mass in front of the pile will lose the matrix suction faster, which will reduce the resistance of the soil in front of the pile and reduce the overall stability of the slope.

FIGURE 11

FIGURE 11. Matrix suction and saturation at monitoring Unit B with different pile spacings.

Matrix suction and saturation changes at monitoring unit C at different pile spacings are described in Figure 12. As can be seen from Figure 12A, the suction of the soil matrix tends to decay continuously with different pile spacings. Selecting a large spacing between piles can make the soil behind the piles have a greater matrix suction in the early and middle stages of the rainfall process and provide a relatively larger anti-sliding force for the soil behind the piles. From Figure 12B, it can be seen that the soil saturation after piles shows a continuous growth trend with different spacing between piles. The regularity of suction and saturation of soil matrix at monitoring unit C under different pile spacings is due to the difference of pore pressure between soil body in front of piles and soil body behind piles and the difference of saturation between soil body before the pile and soil body behind the pile, which results in rainwater infiltrating before pile flowing to behind pile. The larger the spacing between the piles, the more infiltrated rainwater flows behind the piles, resulting in a larger change rate of suction and saturation of soil matrix behind the piles. However, in general, the increase of the spacing between piles is conducive to the flow and discharge of infiltrated rainwater, which can improve the mechanical characteristics of soil mass in front of piles to a certain extent and, as can be seen from Figure 13, a proper reduction of pile spacing can increase the stability of the slope.

FIGURE 12

FIGURE 12. Matrix suction and saturation at monitoring Unit C with different pile spacings.

FIGURE 13

FIGURE 13. Slope safety factors with different pile spacings.

Conclusion

In this paper, the anti-slide pile and slope are considered as a whole. In the rainfall infiltration analysis, a calculation model considering the flow-solid coupling of permeability coefficient characteristic curve and soil-water characteristic curve is established. On this basis, the fluid-solid coupling analysis of unsaturated soil slope with different rainfall duration, different rainfall forms, different pile positions, and different pile spacing are carried out respectively, and the stability of slope after rainfall is analyzed by strength reduction method. The main conclusions are as follows:

1) With the increase of rainfall duration, the suction of the soil matrix decreases, and the recovery rate of suction of the soil matrix decreases gradually. During rainfall, the saturation of soil in front of the pile and shallow soil of slope changes greatly, which makes plastic damage more likely. The matrix suction of the soil behind the pile and the soil above the slope decreases greatly, but it still has better mechanical characteristics than the soil in front of the pile and shallow soil.

2) Compared with the two-peak rainfall, the single-peak rainfall has a greater influence on the mechanical characteristics of soil, more serious loss of suction of soil mass matrix, and worse recovery ability after rainfall. This means that the duration of peak rainfall intensity has a key influence on the recovery ability of slope soil mass. When the rainfall intensity reaches its peak value, the recovery ability of mechanical characteristics of slope soil gradually decreases as the rainfall process continues.

3) Without rainfall conditions, the soil resistance in front of the pile can be better combined with the resistance of the pile body in the middle and upper part of the slope to give play to the anti-slide effect of the anti-slide pile. The best pile location is 1/2L-3/4L. With rainfall conditions, when the position of piles is located in the middle and lower part of the slope, the matrix suction of the soil body is relatively large, and the suction recovery ability of the soil body is strong after rainfall. The reinforced slope has a large safety factor and the overall slope has better stability. The best pile location is 1/4L-1/2L.

4) Without rainfall conditions, the smaller the spacing between piles, the easier the pile group effect of anti-sliding piles can be brought into play, the better the anti-sliding effect is, but at the same time, the economic cost will be increased. With rainfall conditions, the spacing between piles decreases, which is not conducive to the drainage and flow of seepage rainwater. Soil body in front of piles is more likely to reach saturation state, which reduces the resistance of soil in front of piles, resulting in plastic damage of the soil body in front of piles and reducing overall stability of the slope.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

YW: Conceptualization, Methodology, Investigation. MH: Data curation, Writing—original draft. XL: Methodology, Data curation. DL: Provide data support. HY: Provide data support. LZ: Provide data support.

Funding

The work present in this paper was supported by the National Natural Science Foundation of China (Grant No. 52178369; 52109140); Key Projects of High Schools of Henan province (20A560021); Natural Science Foundation of Henan Province (202300410424); Youth Talent Promotion Project of Henan Province (2021HYTP016); Key Specialized Research and Development Breakthrough in Henan Province (212102310977); and China Postdoctoral Science Foundation (2019M662533).

Conflict of Interest

Authors DL, HY and LZ were employed by CCCC Nanjing Traffic Engineering Management Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer (HW) declared a shared affiliation, with the authors (YW, MH) to the handling editor at the time of the review.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alonso, E., Gens, A., and Lloret, A. (1995). “Effect of Rain In Filtration on the Stability of Slopes,” in Proceedings of the International Conference on Unsaturated Soils, Paris, September 8, 1995.

Google Scholar

Bishop, A. W., and Blight, G. E. (1963). Some Aspects of Effective Stress in Saturated and Partly Saturated Soils. Géotechnique 13 (3), 177–197. doi:10.1680/geot.1963.13.3.177

CrossRef Full Text | Google Scholar

Bogaard, T. A., and Greco, R. (2016). Landslide Hydrology: From Hydrology to Pore Pressure. WIREs Water 3 (3), 439–459. doi:10.1002/wat2.1126

CrossRef Full Text | Google Scholar

Cai, F., and Ugai, K. (2004). Numerical Analysis of Rainfall Effects on Slope Stability. Int. J. Geomech. 4 (2), 69–78. doi:10.1061/(asce)1532-3641(2004)4:2(69)

CrossRef Full Text | Google Scholar

Cai, F., and Ugai, K. (2000). Numerical Analysis of the Stability of a Slope Reinforced with Piles. Soils and Foundations 40 (1), 73–84. doi:10.3208/sandf.40.73

CrossRef Full Text | Google Scholar

Cai, F., Ugai, K., Wakai, A., and Li, Q. (1998). Effects of Horizontal Drains on Slope Stability under Rainfall by Three-Dimensional Finite Element Analysis. Comput. Geotechnics 23 (4), 255–275. doi:10.1016/s0266-352x(98)00021-4

CrossRef Full Text | Google Scholar

Chatra, A. S., Dodagoudar, G. R., and Maji, V. B. (2019). Numerical Modelling of Rainfall Effects on the Stability of Soil Slopes. Int. J. Geotechnical Eng. 13 (5), 425–437. doi:10.1080/19386362.2017.1359912

CrossRef Full Text | Google Scholar

Chen, C.-Y., and Martin, G. R. (2002). Soil-Structure Interaction for Landslide Stabilizing Piles. Comput. Geotechnics 29 (5), 363–386. doi:10.1016/s0266-352x(01)00035-0

CrossRef Full Text | Google Scholar

Fan, X., Scaringi, G., Korup, O., West, A. J., Westen, C. J., Tanyas, H., et al. (2019). Earthquake‐Induced Chains of Geologic Hazards: Patterns, Mechanisms, and Impacts. Rev. Geophys. 57 (2), 421–503. doi:10.1029/2018rg000626

CrossRef Full Text | Google Scholar

Fredlund, D. G., Morgenstern, N. R., and Widger, R. A. (1978). The Shear Strength of Unsaturated Soils. Can. Geotech. J. 15 (3), 313–321. doi:10.1139/t78-029

CrossRef Full Text | Google Scholar

Gao, Y.-f., Ye, M., and Zhang, F. (2015). Three-Dimensional Analysis of Slopes Reinforced with Piles. J. Cent. South. Univ. 22 (6), 2322–2327. doi:10.1007/s11771-015-2757-6

CrossRef Full Text | Google Scholar

Gidon, J. S., and Sahoo, S. (2020). Rainfall-Induced Slope Failures and Use of Bamboo as a Remedial Measure: A Review. Indian Geotech J. 50 (5), 766–783. doi:10.1007/s40098-020-00409-3

CrossRef Full Text | Google Scholar

He, J., Wang, S., Liu, H., Nguyen, V., and Han, W. (2021). The Critical Curve for Shallow Saturated Zone in Soil Slope under Rainfall and its Prediction for Landslide Characteristics. Bull. Eng. Geol. Environ. 80 (3), 1927–1945. doi:10.1007/s10064-020-02016-1

CrossRef Full Text | Google Scholar

Li, C.-H., Lin, M.-L., and Huang, W.-C. (2019). Interaction between Pile Groups and Thrust Faults in a Physical Sandbox and Numerical Analysis. Eng. Geology. 252, 65–77. doi:10.1016/j.enggeo.2019.02.023

CrossRef Full Text | Google Scholar

Li, N., Hao, J. W., Xu, J. C., and Zhang, L. W. (2020). Numerical Analysis on Stability of Anti-Slide Pile Slope under Rainfall Condition. Water Resour. Hydropower Eng. 51 (4), 1–9. (in Chinese). doi:10.13928/j.cnki.wrahe.2020.04.001

CrossRef Full Text | Google Scholar

Li, N., Liu, G. L., Xu, J. C., Zhang, L. W., Li, Y. C., and Wang, X. (2018). 3D Numerical Analysis of the Stability of a Slope Reinforced with Piles under Rainfall Conditions. Chin. J. Geol. Hazard Control. 29 (3), 38–46. (in Chinese). doi:10.16031/j.cnki.issn.1003-8035.2018.03.06

CrossRef Full Text | Google Scholar

Lin, Z., Guo, C., Cao, D., Ni, P., and Wang, F. (2020). An Experimental Study on the Cutting Failure of Polymer Grouting. Construction Building Mater. 258, 119582. doi:10.1016/j.conbuildmat.2020.119582

CrossRef Full Text | Google Scholar

Liu, H., Wang, F., Shi, M., and Tian, W. (2018). Mechanical Behavior of Polyurethane Polymer Materials under Triaxial Cyclic Loading: A Particle Flow Code Approach. J. Wuhan Univ. Technol.-Mat. Sci. Edit. 33 (4), 980–986. doi:10.1007/s11595-018-1922-9

CrossRef Full Text | Google Scholar

Luo, X., Yuan, J., and Gu, T. (2021). Study on the Stability of Slopes on Both Sides of Highway in Rock Area under Rainfall. Arabian J. Geosciences 14 (6), 1–6. doi:10.1007/s12517-021-06857-2

CrossRef Full Text | Google Scholar

Mao, W., Liu, B., Rasouli, R., Aoyama, S., and Towhata, I. (2019). Performance of Piles with Different Configurations Subjected to Slope Deformation Induced by Seismic Liquefaction. Eng. Geology. 263, 105355. doi:10.1016/j.enggeo.2019.105355

CrossRef Full Text | Google Scholar

Mein, R. G., and Larson, C. L. (1973). Modeling Infiltration during a Steady Rain. Water Resour. Res. 9 (2), 384–394. doi:10.1029/wr009i002p00384

CrossRef Full Text | Google Scholar

Morbidelli, R., Saltalippi, C., Flammini, A., and Govindaraju, R. S. (2018). Role of Slope on Infiltration: A Review. J. Hydrol. 557, 878–886. doi:10.1016/j.jhydrol.2018.01.019

CrossRef Full Text | Google Scholar

Shi, M. S., Xia, W. Y., Wang, F. M., Liu, H., and Pan, Y. H. (2014). Experimental Study on Bond Performance between Polymer Anchorage Body and silt. Chin. J. Geotechnical Eng. 36 (4), 724–730. (in Chinese). doi:10.11779/CJGE201404017

CrossRef Full Text | Google Scholar

Sidle, R. C., and Bogaard, T. A. (2016). Dynamic Earth System and Ecological Controls of Rainfall-Initiated Landslides. Earth-Science Rev. 159, 275–291. doi:10.1016/j.earscirev.2016.05.013

CrossRef Full Text | Google Scholar

Tan, Q., Tang, H., Huang, L., Li, C., and Kou, T. (2018). LSP Methodology for Determining the Optimal Stabilizing Pile Location for Step-Shaped Soil Sliding. Eng. Geology. 232, 56–67. doi:10.1016/j.enggeo.2017.11.005

CrossRef Full Text | Google Scholar

Tang, D., Li, D.-Q., and Cao, Z.-J. (2017). Slope Stability Analysis in the Three Gorges Reservoir Area Considering Effect of Antecedent Rainfall. Georisk: Assess. Manage. Risk Engineered Syst. Geohazards 11 (2), 161–172. doi:10.1080/17499518.2016.1193205

CrossRef Full Text | Google Scholar

Tang, H., Hu, X., Xu, C., Li, C., Yong, R., and Wang, L. (2014). A Novel Approach for Determining Landslide Pushing Force Based on Landslide-Pile Interactions. Eng. Geology. 182, 15–24. doi:10.1016/j.enggeo.2014.07.024

CrossRef Full Text | Google Scholar

Wang, F. M., Fang, H. Y., Cao, K., and Ma, S. C. (2018). Model Tests and Numerical Analyses of Polymer Gravel Piles. Chin. J. Geotechnical Eng. 40 (S2), 1–5. (in Chinese). doi:10.11779/CJGE2018S2001

CrossRef Full Text | Google Scholar

Wang, Y., Chai, J., Cao, J., Qin, Y., Xu, Z., and Zhang, X. (2020). Effects of Seepage on a Three-Layered Slope and its Stability Analysis under Rainfall Conditions. Nat. Hazards 102 (3), 1269–1278. doi:10.1007/s11069-020-03966-1

CrossRef Full Text | Google Scholar

Wang, Y., Gao, Y., Li, B., Guo, L., Cai, Y., and Mahfouz, A. H. (2019). Influence of Initial State and Intermediate Principal Stress on Undrained Behavior of Soft clay during Pure Principal Stress Rotation. Acta Geotech. 14 (5), 1379–1401. doi:10.1007/s11440-018-0735-5

CrossRef Full Text | Google Scholar

Wang, Y., Han, M., Cao, T., Yu, X., and Song, Y. (2021a). Cyclic Interface Behavior of Non-Water Reactive Polymer and concrete during Dam Restoration. Structures 34, 748–757. doi:10.1016/j.istruc.2021.08.020

CrossRef Full Text | Google Scholar

Wang, Y., Wan, Y., Guo, C., Zeng, C., Shao, J., and Wang, F. (2021b). Experimental Investigation on the Monotonic, Cyclic and post Cyclic Interfacial Behavior of Non-Water Reacted Polymer and concrete. Construction Building Mater. 292, 123323. doi:10.1016/j.conbuildmat.2021.123323

CrossRef Full Text | Google Scholar

Wei, W. B., and Cheng, Y. M. (2009). Strength Reduction Analysis for Slope Reinforced with One Row of Piles. Comput. Geotechnics 36 (7), 1176–1185. doi:10.1016/j.compgeo.2009.05.004

CrossRef Full Text | Google Scholar

Wu, L. Z., Zhou, Y., Sun, P., Shi, J. S., Liu, G. G., and Bai, L. Y. (2017). Laboratory Characterization of Rainfall-Induced Loess Slope Failure. Catena 150, 1–8. doi:10.1016/j.catena.2016.11.002

CrossRef Full Text | Google Scholar

Yao, Y., Ni, J., and Li, J. (2021). Stress-Dependent Water Retention of Granite Residual Soil and its Implications for Ground Settlement. Comput. Geotechnics 129, 103835. doi:10.1016/j.compgeo.2020.103835

CrossRef Full Text | Google Scholar