Analysis of Flexural Toppling Failure in Rock Slopes Using Discrete Element Method

Flexural toppling failure is a common failure mode of natural and artificial rock slopes, which has caused serious damage to human life and property. In this work, an advanced numerical method called the Universal Distinct Element Code (UDEC) was used to study the mechanism of flexural toppling failure. In total, more than twenty slope models were built and analyzed. Two new parameters (displacement discontinuity and transition coefficient of failure surface) were introduced to present a further understanding of flexural toppling. The results show the failure zone of rock slopes subjected to flexural toppling includes two parts: the first-order instability part (FOIP) and the independent toppling zone (ITZ). The FOIP can be further divided into two subzones: the sliding zone (SZ) and the superimposed toppling zone (STZ). The occurrence of surface deformation discontinuities is the precursor to flexural toppling failure. The first displacement discontinuity occurs on the boundary between the FOIP and the ITZ. The angle, spacing, and angle of the joints, the angle of the slope has a significant influence on the stability of anti-dip bedding rock slopes. However, they do not affect the deformation and failure pattern of the slope.

Introduction

Flexural toppling failure often occurs in artificial and natural slopes with anticlinal bedding structures (called anti-dip bedding rock slopes, as shown in Figure 1), which has been recognized and studied for several decades. Anti-dip bedding rock slopes are a very common type of slope in nature, accounting for 33% of all landslides (Huang and Li, 2011). Ashby (1971) proposed the concept of “toppling”, and De Freitras and Watters (1973) verified the phenomenon through field observations. Then, toppling failure has been considered as an important failure type as sliding. To better analyze it, Goodman and Bray (1976) proposed an exclusive classification for toppling instabilities, and flexural toppling is one of them.

FIGURE 1

FIGURE 1. An anti-dip bedding rock slope facing Bohai Sea in China modified from Zhao et al. (2020).

In a two-dimensional model, rock layers in such failure behave like cantilever beams, which bend and deform under the combined action of gravity and external loads. Aydan and Kawamoto (1992) used the solid mechanics of cantilever beams to analyze this type of failure and proved it by base friction tests. Centrifugal tests and physical model tests under excavation at the toe area of the slope were also employed by many researchers (Adhikary et al., 1997; Zheng et al., 2019; Zheng et al., 2018a; Zhu et al., 2020). Based on these experimental results, they made some improvements for the analytical method and gave suggestions for the reinforcement of the slope. Meanwhile, Ning et al. (2019) and Li et al. (2019) used shaking tables to simulate this type of failure under seismic load. The shaking table was also utilized by Fan et al. (2016) to discuss the effect of the weak intercalation on the failure patterns of anti-dip bedding rock slopes. In addition to seismic load, Ning et al. (2021) and Gu and Huang (2016) suggested that the river downcutting should also be considered as an incentive of flexural toppling failure.

Numerical tools are also often employed by scholars and engineers to discuss and analyze flexural toppling failure, especially when the geological conditions of the slope were very complex. A finite element method was undertaken by Adhikary and Dyskin (2007) to analyze their physical model tests. Based on the distinct lattice spring model, Lian et al. (2018) analyzed flexural toppling failure by incorporating the gravity increase method. Zhang et al. (2020) tried to take the discontinuous deformation analysis (DDA) to simulate the tensile failure of blocks in toppling mode, but this method needs to add contacts at the failure surface in advance. As a commercial software commonly used in geotechnical engineering, the universal distinct element code (UDEC) was also utilized by a lot of researchers. For example, Alzo’ubi et al. (2010) used it to analyze the effect of tensile strength on the stability of slopes. Zheng et al. (2019a) used it to investigate the influence of rock bolts on the failure patterns. Weng et al. (2020) implemented a new failure criterion into this software to predict this failure.

As outlined above, many scholars have studied the mechanism of flexural toppling failure through theoretical analysis, model tests, and numerical simulation since its recognition as an important failure mode. However, the whole process of initiation, development, and penetration of the failure surface of the slope subjected to flexural toppling is still unclear. Compared to model tests, numerical simulations are less expensive and allow easy access to parameters that cannot be measured in model tests (Zhang et al., 2019; Wang et al., 2020; Yang et al., 2020; Meng et al., 2021; Yan et al., 2021). UDEC is ideal in modelling jointed rock masses since it can simulate both the behavior of the intact rock and the joints (Itasca, 2004). Furthermore, UDEC can simulate large deformations, such as tensile cracks between rock layers, which are a key feature of toppling failure. In this work, UDEC is thus used to investigate flexural toppling failure in rock slopes with various geometric and mechanical parameters. Two new parameters (displacement discontinuity and transition coefficient of failure surface) are introduced to present a further understanding of this type of failure. Moreover, based on the results of systematic numerical simulations, the whole evolution process of flexural toppling failure is discussed.

Universal Distinct Element Code Model

Model Configuration and Boundary Conditions

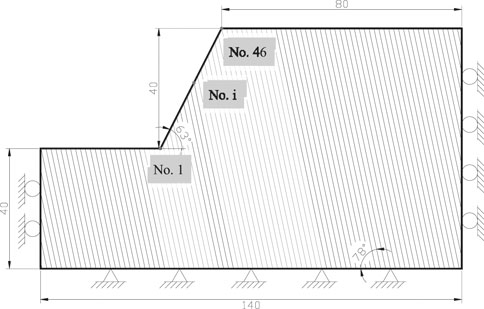
In order to understand the fundamental mechanism of flexural toppling in rock slopes, the basic calculation model used in this work is an ideal anti-dip bedding rock slope (Figure 2). The slope height and angle are 40 m and 63°, respectively, and the joint spacing and angle are 1.6 m and 78°, respectively. The geometric and mechanical parameters of the model are shown in Table 1.

FIGURE 2

FIGURE 2. Geometry and boundary conditions of the basic model used in this work (Length unit: m).

TABLE 1

TABLE 1. Slope parameters used in the numerical simulations.

Displacement constraints were used in the numerical simulation. Specifically, horizontal and vertical displacements at the base of the model were constrained while only the horizontal displacement was restricted at the lateral boundaries. A series of monitoring points (1 m apart) were laid out on the surface of the slope to monitor the horizontal and vertical displacement. The number of the measuring points is assigned as No.1 to No.46 starting from the toe of the slope to the top of the slope, as illustrated in Figure 2.

Constitutive Model and Model Parameters

The deformation and failure of anti-dip bedding rock slopes involve both intact rock and joints. In this work, two commonly used constitutive models, namely the Mohr-Coulomb model and the Coulomb slip model, were employed to describe the mechanical behavior of the intact rock and the joints, respectively.

Toppling failure mostly occurs in slopes with lithology or lithological combination of thin layered slate, schist, slate, sandstone, and muddy limestone (Tu et al., 2007; Amini et al., 2018; Zheng et al., 2018a; Huang et al., 2018; Zhang et al., 2018; García-Moya et al., 2019; Ning et al., 2021). This work relies on an actual limestone slope facing the Jingzhu Road in Southern China (Zheng et al., 2018a). Therefore, the lithology modelled in this work is limestone with low strength. The parameters used in the calculations are summarized in Table 1.

Influencing Factors Studied in the Simulation

In order to have a comprehensive understanding of the flexural toppling mechanism, four factors were studied in the simulations: angle of the joints, spacing of the joints, strength of the joints, and angle of the slope. Each factor includes 6 to 11 scenarios, and there are 26 models in total. It is important to note that a univariate analysis is used, i.e., when analyzing the influence of one parameter on the flexural toppling, the other parameters keep constant.

Results Analysis

In this section, distribution characteristics of the surface displacement and the plastic zone were studied to access the whole process of formation of the failure surface of the slope, and thus reveal the mechanism of flexural toppling failure. Moreover, the factors that play a controlling role in flexural toppling can be also found. Whether the surface displacement is perpendicular to the joints is a preliminary indication of flexural toppling. If it is perpendicular to the joints, the slope is likely to experience flexural toppling failure, otherwise the slope is experiencing sliding failure.

Effect of the Joint Angle

The prerequisite to the occurrence of toppling failure is that rock layers are misaligned with each other (Goodman and Bray, 1976). In the shallow part of the slope, the direction of the maximum principal stress is approximately parallel to the surface of the slope, as shown in Figure 3.

FIGURE 3

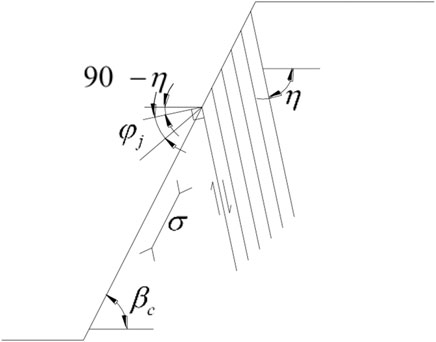
FIGURE 3. Toppling stability analysis in an anti-dip bedding rock slope (Goodman and Bray, 1976).

Only when the angle between the maximum principal stress and the normal to the joints is greater than the friction angle of the joints (ignoring the joint cohesion), mutual misalignment between adjacent rock layers is possible. It can be written as (Goodman and Bray, 1976):

$\left({90}^0-{\beta }_c\right)+{\phi }_j<\eta (1)$

where ${\beta }_c$and $\eta$ are the angle of the slope and the angle of the joints, respectively, and ${\phi }_j$ is the friction angle of the joints.

The stability of rock slopes in six cases of $\eta$ = 40°, 50°, 60°, 70°, 78°, and 90° were studied in the numerical simulations. Figure 4 shows the distribution of horizontal displacement (xdis), vertical displacement (ydis), and ydis/xdis for each measuring point for different joint angles. The vertical black dashed line indicates the position of the crest of the slope and the vertical red solid line indicates the position where the first displacement discontinuity (FDD) occurs. The horizontal solid line indicates the value of $\tan \beta$(the angle of the normal to the joints), which is used to determine the direction of the displacement. ydis/xdis = $\tan \beta$ means that the direction of the displacement is perpendicular to the joints, which is an important feature of toppling deformation.

FIGURE 4

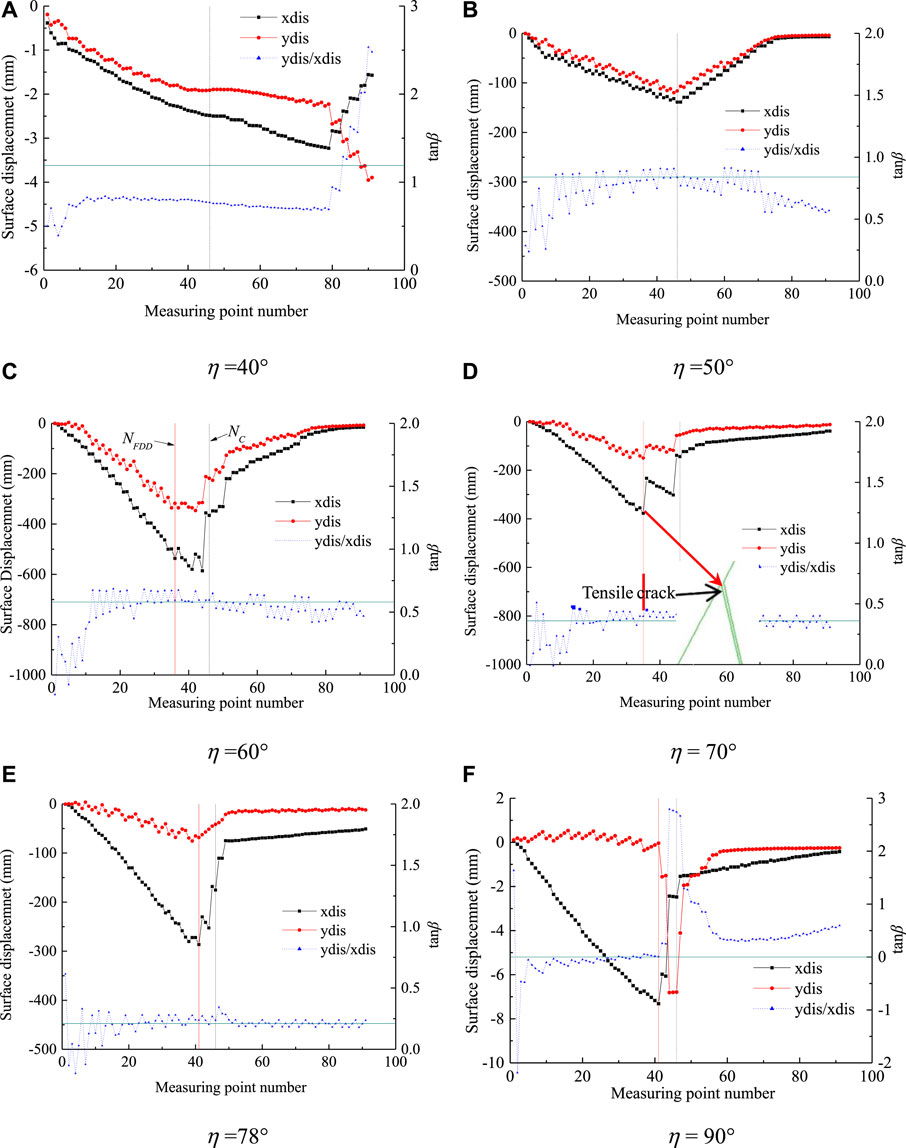
FIGURE 4. Surface displacement distribution of slope for different joint angles ($\eta$). $N_C$ and $N_{FDD}$: Measuring points corresponding to the slope crest and first displacement discontinuity, respectively.

From Figure 4, we can find that, as the value of $\eta$ increases, the slope displacement tends to increase first and then decrease. The measuring point with the largest displacement is not necessarily located at the crest of the slope. When there are displacement discontinuities, the largest displacement tends to occur at the position where the first displacement discontinuity occurs, as shown in Figure 4D, Figure 3F. When $\eta$ = 40°, the value of ydis/xdis at most measuring points is less than $\tan \beta$, which means that the direction of the displacement is not perpendicular to the joints. In other words, insignificant toppling deformation of the slope occurs. However, as the value of $\eta$ exceeds 50°, the displacement direction below the crest of the slope is approximately perpendicular to the joints, except for the points near the toe of the slope. That is, the slope exhibits typical characteristics of toppling failure. As the value of $\eta$ increases to 90°, the displacement direction after the crest of the slope is no longer perpendicular to the joints and the toppling deformation becomes unremarkable.

Figure 3 indicates that no displacement discontinuities are found at $\eta$ = 40° and 50°. However, the situation changes immediately when the value of $\eta$ exceeds 50°. Displacement discontinuity means that a tensile crack appears at the corresponding position along the joint, as shown in Figure 4D. The first tensile crack above the toe of the slope forms the trailing boundary of the first-order instability part (FOIP) and controls its range. Thus, the location of the first displacement discontinuity is a key factor in the analysis of toppling failure. To analyze this factor quantitatively, a new parameter named transition coefficient of failure surface (${\lambda }_t$) is introduced:

${\lambda }_t=\frac{m_d}{m_c}(2)$

where $m_d$ and $m_c$ are the measuring point numbers at the first displacement discontinuity and the crest of the slope, respectively.

The variation in the value of transition coefficient of failure surface (${\lambda }_t$) as a function of joint angle ($\eta$) is plotted in Figure 5A. It is seen that the value of ${\lambda }_t$ tends to increase overall as the value of $\eta$ increases, which indicates that the trailing boundary of the FOIP gradually moves upwards.

FIGURE 5

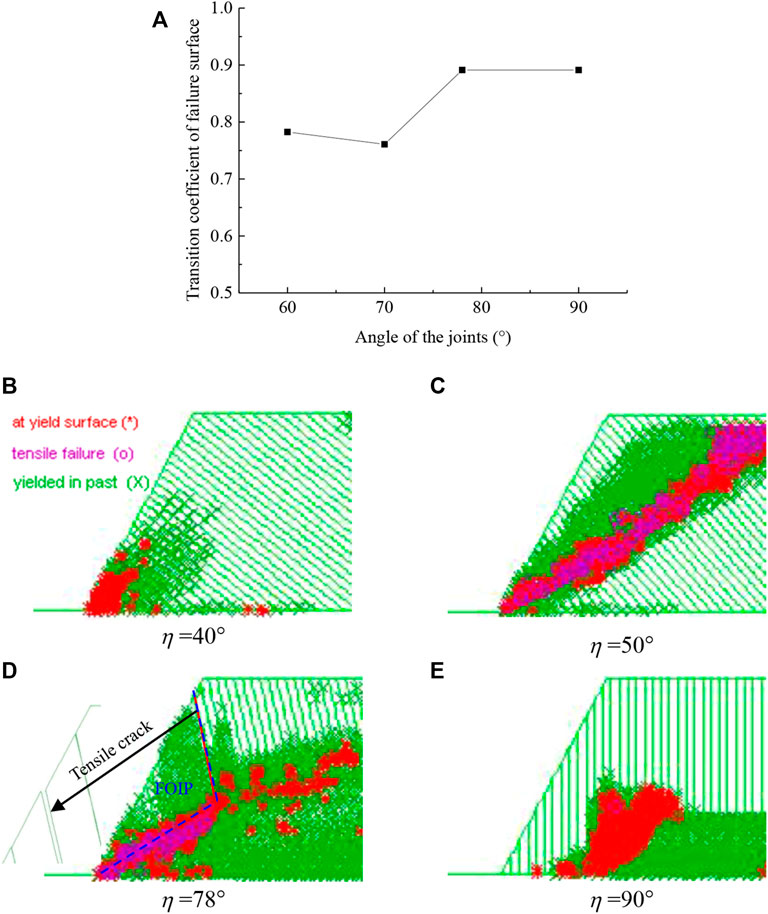
FIGURE 5. Failure distribution of the slope for different joint angles ($\eta$). (A): Relationship between the transition coefficient of failure surface and the joint angle; (B–E): Plots show the simulated plastic zone for different joint angles.

Figures 4B–E show the simulated plastic zone obtained using UDEC for different joint angles ($\eta$). Due to the similarity in the distribution of plastic zone at $\eta$ = 60°, 70°, and 78°, only a representative one $\eta$ = 78° is shown here. It can be found that the plastic zone only appears around the toe of the slope at $\eta$ = 40°. The corresponding displacement distribution indicates that no tensile cracks occur along the joints (Figure 4D). The slope is therefore stable when $\eta$ = 40°, which is consistent with the result obtained from the criteria (Eq. 1) proposed by Goodman and Bray (1976). When the value of $\eta$ increases to 50°, a through plastic zone is formed from the toe to the top of the slope, which indicates that the slope undergoes a complex shearing–flexural toppling failure (Figure 5C). Although there is no through plastic zone within the slope at $\eta$ = 78°, conditions for the formation of a landslide are met: the plastic zone forms the sliding surface, and the tensile crack forms the rear boundary of the sliding body (Figure 5D). Under the action of gravity, rock mass above the plastic zone moves towards the toe of the slope, thus forming the FOIP. After this, due to a large space available, the rock layer adjacent to the free surface undergoes a significant toppling deformation until instability occurs (Figure 6). In this case, the rock layer works as a cantilever beam and the forces acting on both the left and right sides can are zero. Similar deformation and failure occur in other layers above until the length of the cantilevered section is less than the corresponding self-stabilizing height (Zheng et al., 2018a).

FIGURE 6

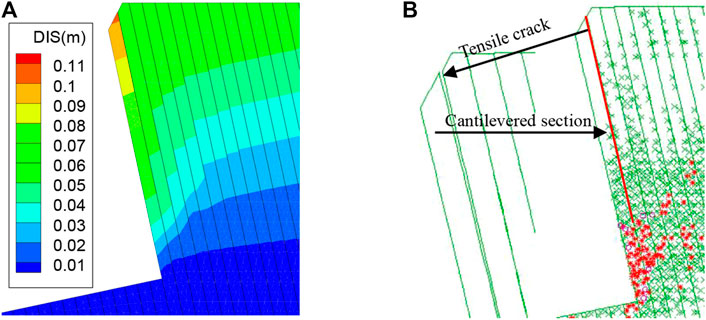
FIGURE 6. Displacement and plastic zone distribution of the upper rock layers after the formation of the FOIP. (A): Displacement distribution; (B) Plastic zone distribution.

Effect of the Joint Spacing

Joint spacing ($t$) has been found to be an important factor affecting the stability of anti-dip bedding rock slopes (Adhikary et al., 1997; Adhikary and Dyskin, 2007; Zheng et al., 2020a). Here, six cases of $t$= 0.5, 1.0, 1.6, 2.0, 2.5, and 3.0 m were simulated to further investigate the effect of joint spacing on the deformation and failure patterns of this kind of slope. Figure 7 shows the distribution of horizontal displacement (xdis), vertical displacement (ydis) and ydis/xdis at each measuring point for different joint spacing. Figure 8 shows the failure distribution of the slope for different joint spacing ($t$).

FIGURE 7

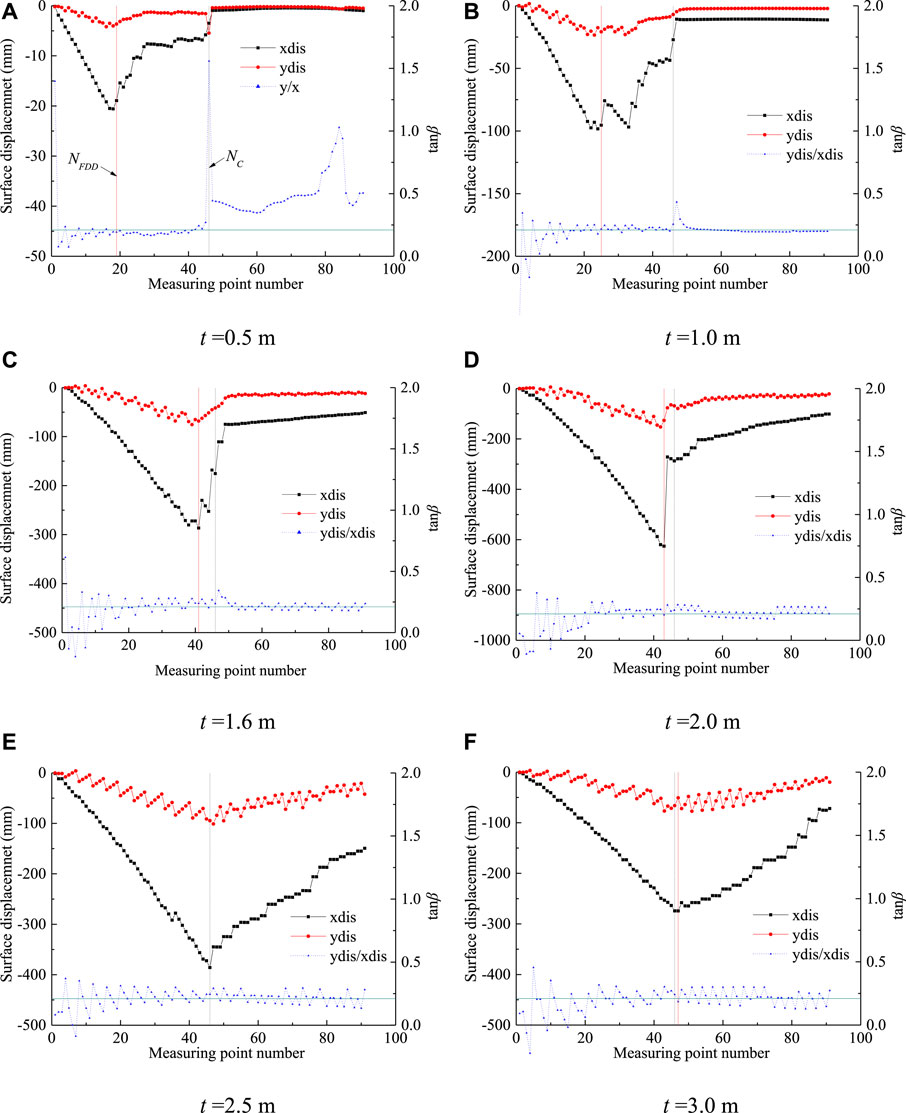
FIGURE 7. Surface displacement distribution of slope for different joint spacing ($t$). $N_C$ and $N_{FDD}$: Measuring points corresponding to the slope crest and first displacement discontinuity, respectively.

FIGURE 8

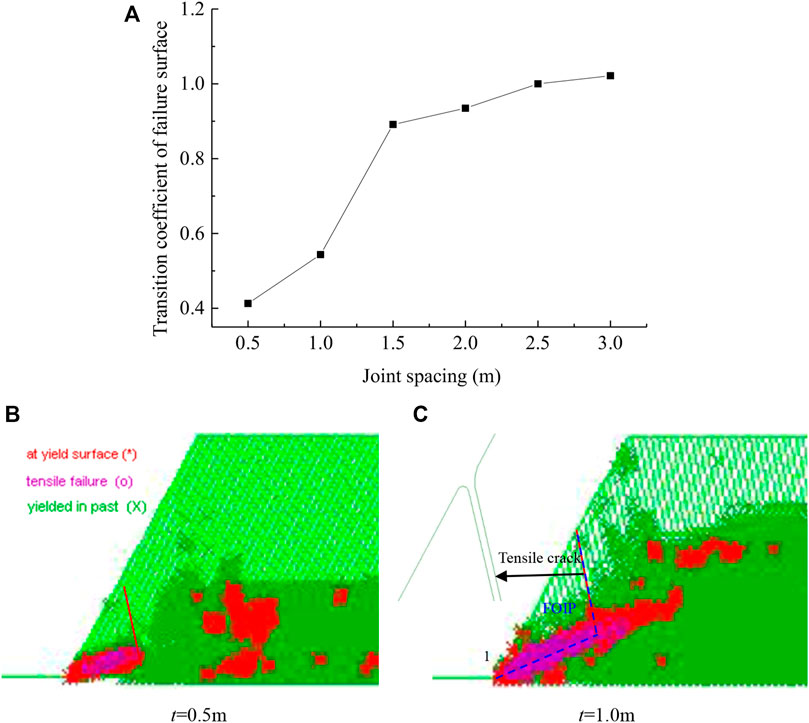
FIGURE 8. Failure distribution of the slope for different joint spacing ($t$). (A): Relationship between the transition coefficient of failure surface and the joint spacing; (B,C): The simulated plastic zone obtained using UDEC for different joint spacing.

It can be seen from Figure 7 that the surface displacement tends to increase and then decrease as the joint spacing increases and the maximum value occurs at the first displacement discontinuity. Except for the measuring points after the crest of the slope at $t$= 0.5 m, the direction of the surface displacement is basically the same for different joint spacing. They all show that the displacement at most points is perpendicular to the joints, except for a few points near the toe area of the slope. In other words, the deformation of the slope is dominated by toppling in all cases. These imply that joint spacing has an insignificant effect on the deformation pattern of this kind of slope. Displacement discontinuities (tensile cracks) occur in all cases. From Figure 8A, it can be seen that the first displacement discontinuity moves upwards as the value of $t$ increases. The first displacement discontinuity is located below the crest of the slope when $t$ < 2.5 m, and above the crest after reaching 2.5 m.

Figures 7B,C shows the simulated plastic zone obtained using UDEC for different joint spacing ($t$). It should be noted that the distribution of the plastic zone within the slope is similar for different joint spacing, so only the results for $t$ = 0.5 and 1.0 m are shown here. It can be seen that several rock layers at the toe area undergo shear failure while those above undergo complex tensile-shear failure. The range of the FOIP for $t$ = 0.5 m is less than that for $t$ = 1.0 m. This is because the smaller the joint spacing, the lower the bending resistance of the rock layer, and the smaller the corresponding range of self-stabilizing rock layers at the toe area of the slope (Zheng et al., 2018b; 2019b).

Effect of the Joint Strength

According to Eq. (1), to prevent the slope from toppling failure, the friction angle of the joints (${\phi }_j$) needs to be greater than a critical value, ${\phi }_{jcr}=\eta +{\beta }_c-{90}^{\text{o}}$. Taking $\eta$ = 78° and ${\beta }_c$ = 63° into the equation gives ${\phi }_{jcr}$ = 51° for the basic model. In this work, the deformation and failure mechanism of slopes were analyzed for eleven cases: ${\phi }_j$= 0°, 6°, 12°, 18°, 24°, 30°, 36°, 42°, 48°, 54°, and 60°. Figure 9 shows the distribution of horizontal displacement (xdis), vertical displacement (ydis) and ydis/xdis at each measuring point for different joint friction angles. It should be noted that, for the sake of simplicity, only representative graphics are shown. Figure 10 shows the failure distribution of the slope for different joint friction angles (${\phi }_j$)

FIGURE 9

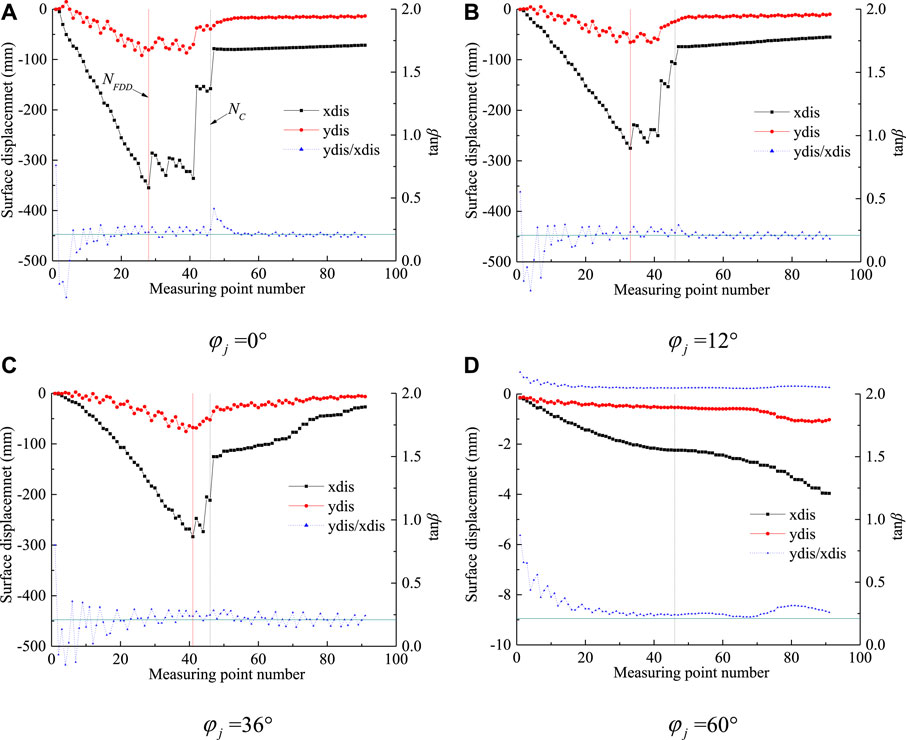
FIGURE 9. Surface displacement distribution of slope for different joint friction angles (${\phi }_j$).$N_C$ and $N_{FDD}$: Measuring points corresponding to the slope crest and first displacement discontinuity, respectively.

FIGURE 10

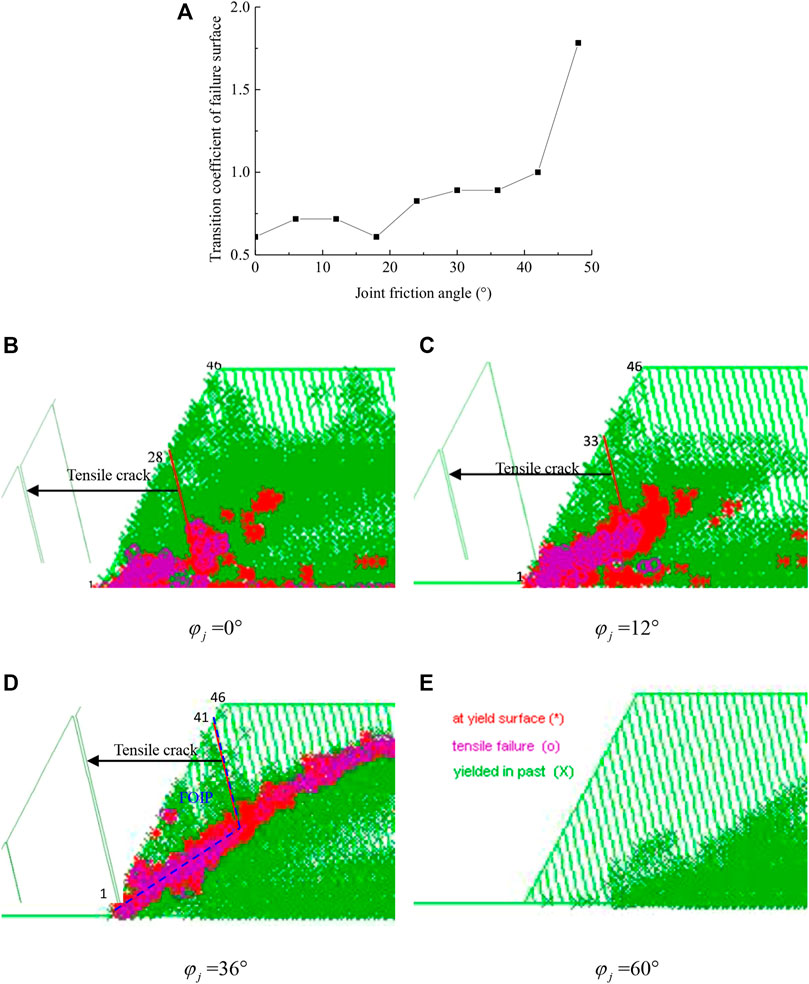
FIGURE 10. Failure distribution of the slope for different joint friction angles (${\phi }_j$). (A): Relationship between the transition coefficient of failure surface and the joint friction angles; (B–E): The simulated plastic zone for different joint friction angles.

It can be seen that, when ${\phi }_j$ = 0°, 12°, and 36°, the surface displacements do not differ much, and the maximum values are all located at the first displacement discontinuity. However, after ${\phi }_j$ reaches the value of 60°, the surface displacements decrease sharply. Moreover, the first three cases all show discontinuities in surface displacement (i.e., tensile cracks) whereas when ${\phi }_j$ = 60°, it is continuous. The position of the first displacement discontinuity (trailing boundary of the FOIP) generally moves upwards as the value of ${\phi }_j$ increases (Figure 10A).

Figures 9B–E show the simulated plastic zone obtained using UDEC for different joint friction angles (${\phi }_j$). It can be seen that, for ${\phi }_j$ = 0°, 12°, and 36°, the FOIP is formed within each slope, which means that the corresponding slope has failed. However, no plastic zone occurs within the slope for ${\phi }_j$ = 60° and it is in a stable state. The simulated results demonstrate that it is feasible to estimate the critical friction angle using the equation of ${\phi }_{jcr}=\eta +{\beta }_c-{90}^{\text{o}}$.

Effect of the Cut Slope Angle

The angle of the slope (${\beta }_c$) is a key parameter in slope design. The toppling stability of an anti-dip bedding rock slope is also closely related to the value of ${\beta }_c$(Eq. 1). Here, six cases of ${\beta }_c$= 30, 43, 53, 63, 73, and 83° were studied using UDEC. Figure 11 shows the distribution of horizontal displacement (xdis), vertical displacement (ydis) and ydis/xdis at each measuring point for different joint friction angles (only representative graphics are shown). Figure 12 shows the failure distribution of the slope for different slope angles (${\beta }_c$).

FIGURE 11

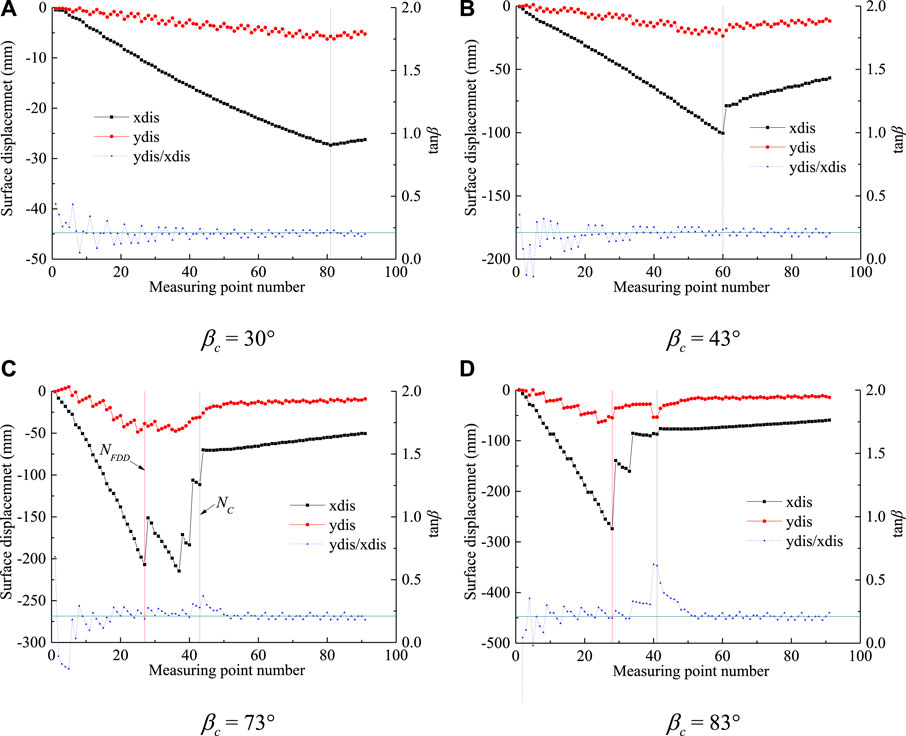
FIGURE 11. Surface displacement distribution of slope for different slope angles (${\beta }_c$).$N_C$ and $N_{FDD}$: Measuring points corresponding to the slope crest and first displacement discontinuity, respectively.

FIGURE 12

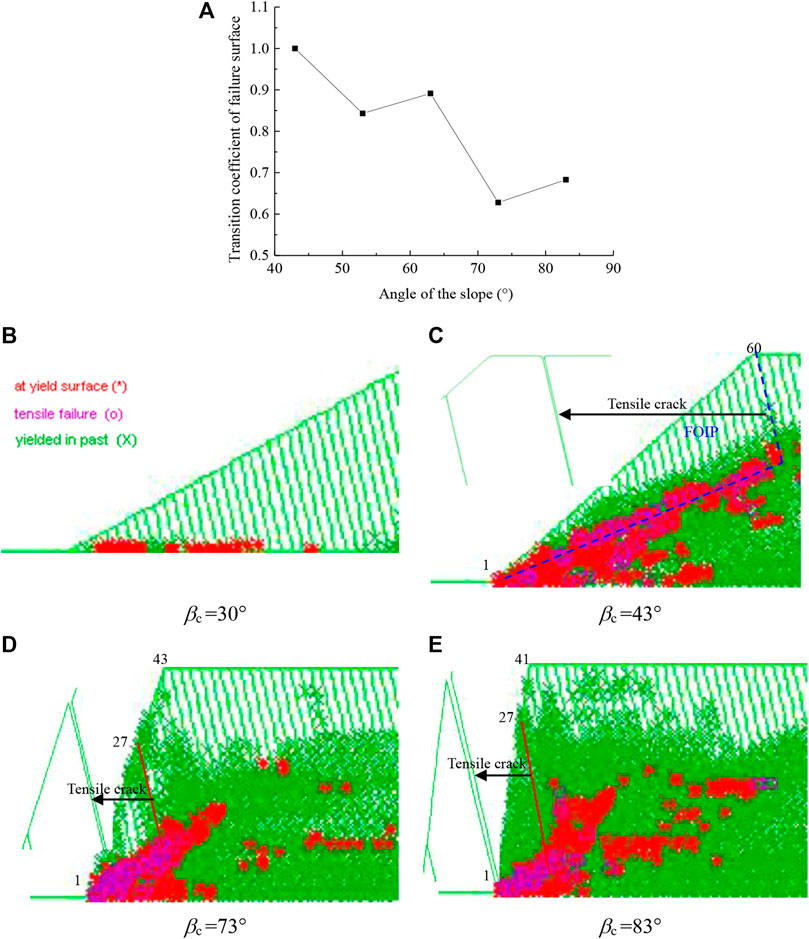
FIGURE 12. Failure distribution of the slope for different slope angles (${\beta }_c$). (A): Relationship between the transition coefficient of failure surface and the slope angle; (B–E): The simulated plastic zone obtained using UDEC for different slope angles.

From Figure 11, it can be found that the surface displacement increase as the slope angle increases and the position of the maximum displacement point varies with ${\beta }_c$. The larger the value of ${\beta }_c$, the closer the maximum displacement point is to the toe of the slope. The displacement direction is insensitive to the change of the angle of the slope. Except for a few points near the toe of the slope, the displacement vector of each point is basically perpendicular to the joints (xdis/ydis≈$\tan \beta$), regardless of the slope angle taken, and all slopes present typical characteristics of toppling deformation.

Figure 11 also shows that when ${\beta }_c$ = 30°, no displacement discontinuities occur on the surface of the slope. However, the situation changes immediately as the value of ${\beta }_c$ exceeds 30°, which implies that the occurrence of slope instability. As the value of ${\beta }_c$ increases, the overall trend of ${\lambda }_t$ deceases (Figure 12A), indicating that the larger the value of ${\beta }_c$, the closer the first displacement discontinuity (tensile crack) is to the toe of the slope. The reason for this is that the larger the angle of the slope, the less stable the rock layer is, and thus the smaller the range of the self-stabilizing section of the rock layers.

Figures 11B–E shows plots of the simulated plastic zone obtained using UDEC for different slope angles (${\beta }_c$). When ${\beta }_c$ = 30°, the absence of a through plastic zone within the slope means that the slope is in a stable state. However, the distribution of plastic zones in other cases differs considerably from it. The plastic zone and the tensile crack form the bottom slip surface and the trailing boundary of the sliding body, respectively, which means that the slope is unstable (Figure 12c–12E). The results show that whether a slope undergoes flexural toppling failure or not is closely related to the angle of the slope.

Discussion

Based on the results of the above numerical simulation, we can find that flexural toppling failure starts at the toe of the slope (Figure 13). Under the combined action of gravity and pushing forces from the upper rock layers, the layers at the toe area of the slope are the first to lose stability. The instability mode of each rock layer is controlled by the relative magnitude of its resistance to bending and shearing. If the bending resistance of a rock layer is greater than its shearing resistance, the layer undergoes shearing failure; otherwise, it undergoes flexural toppling failure (Zheng et al., 2018a; 2018b).

FIGURE 13

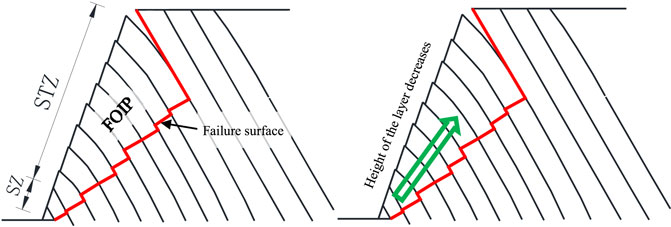
FIGURE 13. The failure zones of an anti-dip bedding rock slope. SZ: sliding zone; STZ: superimposed toppling zone; FOIP: first-order instability part.

Due to the small ratio of height to width of the rock layers around the toe of the slope, they have strong bending resistance and are therefore less prone to toppling failure. Under the combined action of gravity and pushing forces from the upper rock layers, the layers at the toe area often undergo shearing failure, forming the sliding zone (SZ). However, as the distance from the toe of the slope increases, the bending resistance of rock layers decreases due to the increase of the layer height. Then, the failure mode of rock layers gradually changes from shearing to flexural toppling, forming the superimposed toppling zone (STZ). Flexural toppling failure extends to the first displacement discontinuity (tensile crack), at which point a through plastic zone appears within the slope (Figure 5D). The through plastic zone referred to here is a penetration to the tensile crack rather than the surface of the slope, forming the boundaries of the first-order instability part (FOIP) together. After the occurrence of FOIP, the upper rock layers then have enough space for deformation that they undergo flexural toppling failure under the action of gravity, forming the independent toppling zone (ITZ), as shown in Figure 14.

FIGURE 14

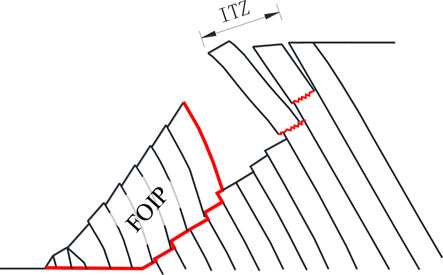
FIGURE 14. The failure process after the formation of the first-order instability part (FOIP). ITZ: independent toppling zone.

The failure surface of an anti-dip bedding rock slope is a complex stepped surface rather than a simple plane (Figure 13). Thus, finding the failure surface is a hard issue in carrying out stability assessment of this kind of slope. Limit equilibrium methods combined with optimization algorithms such as Genetic Algorithm and Bi-directional Evolutionary Structural Optimization (BESO) method have proved to be effective means of solving this problem (Zheng et al., 2020a, 2020b, 2021; Liu et al., 2021). Taking the first displacement discontinuity as the boundary, the lower rock layers are in close contact with each other despite the occurrence of interlayer slip, and the overall deformation is characterized as ‘superimposed cantilever beams’. However, for the upper rock layers, tensile cracks appear between adjacent layers, and the side forces is approximately zero. Each rock layer can be considered as an ‘independent cantilever beam’ (Figure 14). Thus, separate mechanical models need to be developed for these two parts of the rock layers (Zheng et al., 2018a).

Conclusion

In this work, the mechanism of flexural toppling failure in anti-dip bedding rock slopes is systematically studied using numerical simulation, and the main conclusions obtained are as follows:

1) The failure zone of rock slopes subjected to flexural toppling includes two parts: the first-order instability part (FOIP) and the independent toppling zone (ITZ). The FOIP can be further divided into two subzones: the sliding zone (SZ) and the superimposed toppling zone (STZ).

2) The mechanical behaviors of rock layers in the FOIP and ITZ are different. In the FOIP, rock layers are in close contact with each other and behave as “superimposed cantilever beams”. However, the layers in the ITZ behave as “superimposed cantilever beams” and can deform freely.

3) The occurrence of surface deformation discontinuities can be considered to be a precursor to flexural toppling failure and the first displacement discontinuity is the boundary between the FOIP and the ITZ.

4) The angle of the joints, spacing of the joints, strength of the joints, and angle of the slope have significant influences on the stability of anti-dip bedding rock slopes. However, their variations do not change the deformation and failure pattern of the slope.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Ethics Statement

Written informed consent was obtained from the (individual(s) AND/OR minor(s)’ legal guardian/next of kin) for the publication of any potentially identifiable images or data included in this article’.

Author Contributions

YZ: Conceptualization, Methodology, Writing—original draft. RW: Writing—review and editing. CC: Supervision. FM: Writing—review and editing.

Funding

The research was financially supported by National Natural Science Foundation of China (Grant Nos. 12072358 and 12102315) and the Open Research Fund of the State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences (Grant No. Z018009).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge the reviewers and the editors for their comments and suggestions.

References

Adhikary, D. P., and Dyskin, A. V. (2007). Modelling of Progressive and Instantaneous Failures of Foliated Rock Slopes. Rock Mech. Rock Engng. 40 (4), 349–362. doi:10.1007/s00603-006-0085-8

CrossRef Full Text | Google Scholar

Adhikary, D. P., Dyskin, A. V., Jewell, R. J., and Stewart, D. P. (1997). A Study of the Mechanism of Flexural Toppling Failure of Rock Slopes. Rock Mech. Rock Engng. 30 (2), 75–93. doi:10.1007/bf01020126

CrossRef Full Text | Google Scholar

Alzo’ubi, A. K., Martin, C. D., and Cruden, D. M. (2010). Influence of Tensile Strength on Toppling Failure in Centrifuge Tests. Int. J. Rock Mech. Mining Sci. 47 (6), 974–982. doi:10.1016/j.ijrmms.2010.05.011

CrossRef Full Text | Google Scholar

Amini, M., Sarfaraz, H., and Esmaeili, K. (2018). Stability Analysis of Slopes with a Potential of Slide-Head-Toppling Failure. Int. J. Rock Mech. Mining Sci. 112, 108–121. doi:10.1016/j.ijrmms.2018.09.008

CrossRef Full Text | Google Scholar

Ashby, J. (1971). Sliding and Toppling Modes of Failure in Model and Jointed Rock Slopes. Dissertation of Master Degree. London: Royal School of Mines.

Google Scholar

Aydan, O., and Kawamoto, T. (1992). The Stability of Slopes and Underground Openings against Flexural Toppling and Their Stabilisation. Rock Mech. Rock Engng. 25 (3), 143–165. doi:10.1007/bf01019709

CrossRef Full Text | Google Scholar

De Freitas, M. H., and Watters, R. J. (1973). Some Field Examples of Toppling Failure. Géotechnique 23 (4), 495–513. doi:10.1680/geot.1973.23.4.495

CrossRef Full Text | Google Scholar

Fan, G., Zhang, J., Wu, J., and Yan, K. (2016). Dynamic Response and Dynamic Failure Mode of a Weak Intercalated Rock Slope Using a Shaking Table. Rock Mech. Rock Eng. 49 (8), 3243–3256. doi:10.1007/s00603-016-0971-7

CrossRef Full Text | Google Scholar

García-Moya, S. A., González-Galindo, J., and Olalla, C. (2019). Underdip Toppling Failure Mechanism: Case Study Retrospective Analysis and its Most Determinant Parameters. Int. J. Geomech. 19 (6), 1–13. doi:10.1061/(asce)gm.1943-5622.0001408

CrossRef Full Text | Google Scholar

Goodman, R. E., and Bray, J. W. (1976). “Toppling of Rock Slopes,” in Rock Engineering for Foundations & Slopes (New York: ASCE), 201–234.

Google Scholar

Gu, D., and Huang, D. (2016). A Complex Rock Topple-Rock Slide Failure of an Anaclinal Rock Slope in the Wu Gorge, Yangtze River, China. Eng. Geol. 208, 165–180. doi:10.1016/j.enggeo.2016.04.037

CrossRef Full Text | Google Scholar

Huang, R., and Li, W. (2011). Formation, Distribution and Risk Control of Landslides in China. J. Rock Mech. Geotech. Eng. 3 (2), 97–116. doi:10.3724/sp.j.1235.2011.00097

CrossRef Full Text | Google Scholar

Huang, D., Gu, D. M., Song, Y. X., Cen, D. F., and Zeng, B. (2018). Towards a Complete Understanding of the Triggering Mechanism of a Large Reactivated Landslide in the Three Gorges Reservoir. Eng. Geol. 238, 36–51. doi:10.1016/j.enggeo.2018.03.008

CrossRef Full Text | Google Scholar

Itasca (2004). UDEC Version 4.0 User’s Manual. Minneapolis: Itasca Consulting Group Inc.

Google Scholar

Li, L.-q., Ju, N.-p., Zhang, S., and Deng, X.-x. (2019). Shaking Table Test to Assess Seismic Response Differences between Steep Bedding and Toppling Rock Slopes. Bull. Eng. Geol. Environ. 78, 519–531. doi:10.1007/s10064-017-1186-1

CrossRef Full Text | Google Scholar

Lian, J.-J., Li, Q., Deng, X.-F., Zhao, G.-F., and Chen, Z.-Y. (2018). A Numerical Study on Toppling Failure of a Jointed Rock Slope by Using the Distinct Lattice spring Model. Rock Mech. Rock Eng. 51 (2), 513–530. doi:10.1007/s00603-017-1323-y

CrossRef Full Text | Google Scholar

Liu, T., Ding, L., Meng, F., Li, X., and Zheng, Y. (2021). Stability Analysis of Anti-dip Bedding Rock Slopes Using a Limit Equilibrium Model Combined with Bi-directional Evolutionary Structural Optimization (Beso) Method. Comput. Geotechn. 134 (4), 104116. doi:10.1016/j.compgeo.2021.104116

CrossRef Full Text | Google Scholar

Meng, F., Song, J., Wong, L. N. Y., Wang, Z., and Zhang, C. (2021). Characterization of Roughness and Shear Behavior of Thermally Treated Granite Fractures. Eng. Geol. 293, 106287. doi:10.1016/j.enggeo.2021.106287

CrossRef Full Text | Google Scholar

Ning, Y., Zhang, G., Tang, H., Shen, W., and Shen, P. (2019). Process Analysis of Toppling Failure on Anti-dip Rock Slopes under Seismic Load in Southwest China. Rock Mech. Rock. Eng. 52 (11), 4439–4455. doi:10.1007/s00603-019-01855-z

CrossRef Full Text | Google Scholar

Ning, Y., Tang, H., Zhang, G., Smith, J. V., Zhang, B., Shen, P., et al. (2021). A Complex Rockslide Developed from a Deep-Seated Toppling Failure in the Upper Lancang River, Southwest China. Eng. Geol. 293, 106329. doi:10.1016/j.enggeo.2021.106329

CrossRef Full Text | Google Scholar

Tu, X. B., Dai, F. C., Lu, X. J., and Zhong, H. Y. (2007). Toppling and Stabilization of the Intake Slope for the Fengtan Hydropower Station Enlargement Project, Mid-south china. Eng. Geol. 91 (2-4), 152–167. doi:10.1016/j.enggeo.2007.01.009

CrossRef Full Text | Google Scholar

Wang, Z.-F., Shen, S.-L., Modoni, G., and Zhou, A. (2020). Excess Pore Water Pressure Caused by the Installation of Jet Grouting Columns in clay. Comput. Geotechn. 125, 103667. doi:10.1016/j.compgeo.2020.103667

CrossRef Full Text | Google Scholar

Weng, M.-C., Chang, C.-Y., Jeng, F.-S., and Li, H.-H. (2020). Evaluating the Stability of Anti-dip Slate Slope Using an Innovative Failure Criterion for Foliation. Eng. Geol. 275, 105737. doi:10.1016/j.enggeo.2020.105737

CrossRef Full Text | Google Scholar

Yan, C., Zheng, Y., Huang, D., and Wang, G. (2021). A Coupled Contact Heat Transfer and thermal Cracking Model for Discontinuous and Granular media. Comput. Methods Appl. Mech. Eng. 375, 113587. doi:10.1016/j.cma.2020.113587

CrossRef Full Text | Google Scholar

Yang, Y., Xu, D., Liu, F., and Zheng, H. (2020). Modeling the Entire Progressive Failure Process of Rock Slopes Using a Strength-Based Criterion. Comput. Geotechn. 126, 103726. doi:10.1016/j.compgeo.2020.103726

CrossRef Full Text | Google Scholar

Zhang, G., Wang, F., Zhang, H., Tang, H., Li, X., and Zhong, Y. (2018). New Stability Calculation Method for Rock Slopes Subject to Flexural Toppling Failure. Int. J. Rock Mech. Mining Sci. 106, 319–328. doi:10.1016/j.ijrmms.2018.04.016

CrossRef Full Text | Google Scholar

Zhang, C., Pu, C., Cao, R., Jiang, T., and Huang, G. (2019). The Stability and Roof-Support Optimization of Roadways Passing through Unfavorable Geological Bodies Using Advanced Detection and Monitoring Methods, Among Others, in the Sanmenxia Bauxite Mine in China's Henan Province. Bull. Eng. Geol. Environ. 78 (7), 5087–5099. doi:10.1007/s10064-018-01439-1

CrossRef Full Text | Google Scholar

Zhang, Y., Wang, J., Zhao, J. X., Chen, G., Yu, P., and Yang, T. (2020). Multi-spring Edge-To-Edge Contact Model for Discontinuous Deformation Analysis and its Application to the Tensile Failure Behavior of Rock Joints. Rock Mech. Rock Eng. 53, 1243–1257. doi:10.1007/s00603-019-01973-8

CrossRef Full Text | Google Scholar

Zhao, W., Wang, R., and Nian, T. (2020). Stability Analysis of Anti-dip Rock Slopes with Flexural Toppling Failure Based on Deformation Compatibility. Rock Mech. Rock Eng. 53, 3207–3221. doi:10.1007/s00603-020-02098-z

CrossRef Full Text | Google Scholar

Zheng, D., Wang, Q. Y., Mao, F., and Su, H. (2019). Centrifuge Model Test Study on Key hazard-inducing Factors of Deep Toppling Deformation and Disaster Patterns of Counter-tilt Layered Rock Slopes. Chin. J. Rock Mech. Eng. 38 (10), 1954–1963. (in Chinese). doi:10.13722/j.cnki.jrme.2018.1484

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, C., Liu, T., Xia, K., and Liu, X. (2018a). Stability Analysis of Rock Slopes against Sliding or Flexural-Toppling Failure. Bull. Eng. Geol. Environ. 77 (4), 1383–1403. doi:10.1007/s10064-017-1062-z

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, C., Liu, T., Zhang, H., Xia, K., and Liu, F. (2018b). Study on the Mechanisms of Flexural Toppling Failure in Anti-inclined Rock Slopes Using Numerical and Limit Equilibrium Models. Eng. Geol. 237, 116–128. doi:10.1016/j.enggeo.2018.02.006

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, C., Liu, T., Song, D., and Meng, F. (2019a). Stability Analysis of Anti-dip Bedding Rock Slopes Locally Reinforced by Rock Bolts. Eng. Geol. 251, 228–240. doi:10.1016/j.enggeo.2019.02.002

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, C., Liu, T., Zhang, H., and Sun, C. (2019b). Theoretical and Numerical Study on the Block-Flexure Toppling Failure of Rock Slopes. Eng. Geol. 263, 105309. doi:10.1016/j.enggeo.2019.105309

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, C., Meng, F., Liu, T., and Xia, K. (2020a). Assessing the Stability of Rock Slopes with Respect to Flexural Toppling Failure Using a Limit Equilibrium Model and Genetic Algorithm. Comput. Geotechn. 124, 103619. doi:10.1016/j.compgeo.2020.103619

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, C., Meng, F., Zhang, H., Xia, K., and Chen, X. (2020b). Assessing the Stability of Rock Slopes with Respect to Block-Flexure Toppling Failure Using a Force-Transfer Model and Genetic Algorithm. Rock Mech. Rock Eng. 53, 3433–3445. doi:10.1007/s00603-020-02122-2

CrossRef Full Text | Google Scholar

Zheng, Y., Chen, C., Liu, T., and Ren, Z. (2021). A New Method of Assessing the Stability of Anti-dip Bedding Rock Slopes Subjected to Earthquake. Bull. Eng. Geology. Environ. 80 (4), 1–18. doi:10.1007/s10064-021-02188-4

CrossRef Full Text | Google Scholar

Zhu, C., He, M., Karakus, M., Cui, X., and Tao, Z. (2020). Investigating Toppling Failure Mechanism of Anti-dip Layered Slope Due to Excavation by Physical Modelling. Rock Mech. Rock Eng. 53 (11), 5029–5050. doi:10.1007/s00603-020-02207-y

CrossRef Full Text | Google Scholar

Glossary

List of Symbols

${\beta }_c$ Angle of the slope

$\beta$ Angle of the normal to the joints

$\eta$ Angle of the joints

$c$, $c_j$ Cohesion of the intact rock and joints, respectively

$E$ Elastic modulus of the intact rock

FOIP First-order instability part of the slope

$\upsilon$ Poisson’s ratio

$\phi$, ${\phi }_j$ Friction angle of the intact rock and joints, respectively${\sigma }_t$Tensile strength of the intact rock

$k_n$, $k_s$ Normal and shear stiffness of the joints, respectively

$N_C$, $N_{FDD}$ Measuring points corresponding to the slope crest and first displacement discontinuity, respectively

$t$ Spacing of the joints

$\rho$ Density of the intact rock

${\lambda }_t$ Transition coefficient of the failure surface