Applications of an Innovative Strength Parameter Estimation Method of the SoilRock Mixture in Evaluating the Deposit Slope Stability Under Rainfall

Deposit landslides are one of the most representative geological hazards around the world, and the poor understanding of the mechanical characteristics of the soilrock mixture (S-RM) increases the difficulties in evaluating the stability of the deposit slope subjected to rainfall. This study attempted to propose an innovative strength parameter estimation method of the S-RM based on the concept and format of the generalized HoekBrown criterion. The system of “rock blocks–soil–contact surface” was considered the main source providing resistance to the external force, and the effect of the soil matrix, rock blocks, and the contact surface between them was taken into account. The verification of the estimation method was proved based on the abundant test data. A typical deposit slope located in the Taoyuan region of Yunnan Province, China, was selected as a case study, and the estimation method was applied to provide the shear parameters of the S-RM. The slope stability subjected to different types of rainfall was analyzed considering the parameter deteriorations, and the results show that the deposit landslide is more prone to the wave-type rainfall, which shows a deeper response depth of pore water pressure and a smaller safety factor. The present study suggests a simple estimation method for the shear parameters of the S-RM using a few parameters for the engineers and provides an understanding of the deposit slope stability during the rainfall process.

Introduction

Worldwide, a large number of deep and loose deposits such as moraine, alluvial, and fluviallacustrine sediments are formed under dynamic actions such as tectonic uplift, river erosion, earthquake, and glaciation. Under the disturbance of the natural and artificial processes, it is commonly found that the occurrence of the deposit slope hazard with the characteristics of huge scale and quantity, such as collapse, landslide, and debris flow (Fu et al., 2020a; Zheng et al., 2021). The deposit slope hazard has been intensely studied in the last two decades due to its high risk and serious damage, and the results indicate that rainfall is a great threat to the deposit slopes in the mountainous region and even leads to deposit landslide and debris flow (Cascini et al., 2010; Fiorillo et al., 2013; Fu et al., 2020b; Pantaleone et al., 2018; Shang et al., 2003; Xiao et al., 2020; Wang et al., 2015). Many deposit slope hazards induced by rainfall have been reported in recent years, which have posed a serious threat to the safety and property of the local human and infrastructure constructions. Therefore, the stability of the deposit slope in the mountainous area is an important research subject.

The soilrock mixture (S-RM) is the main component of the deposit slope. As a typical multi-phase geomaterial, it possesses the characteristics of anisotropy, discontinuity, and scale effect. Compared with soil and rock, the research on the mechanical properties of the S-RM is not comprehensive enough. So far, studies on the mechanical properties of the S-RM are in progress, employing mechanical tests predominantly, and the large-scale apparatuses are more preferred to avoid the constraints on the motions of rock fragments inside because of the equipment boundary. The numerical simulation methods on the S-RM could be divided into continuous and discontinuous medium simulations (Ding et al., 2010; Fu et al., 2017; Fu et al., 2019; Liu et al., 2020; Liu et al., 2021; Meng et al., 2018; Qi et al., 2021; Yang et al., 2020; Zou et al., 2011). The test and simulation results show that the mechanical properties are affected by several influencing factors such as rock block proportion, water content, compactness, and granulometric composition, and the rock block proportion plays an important role in the mechanical properties (Afifipour and Moarefvand, 2014; Monkul and Ozden, 2007; Xu et al., 2011; Yang Y. et al., 2016; Chang and Phantachang, 2016; Xu et al., 2019). Several test results show that the strength parameters of the S-RM present a complex variation law as the rock block proportion increases, and the turning points of the parameters could be observed in a relatively low and high rock block proportion, which presents considerable challenges in the determination of the shear parameters of the natural S-RM. These results provide important inspiration for the discussion of the relationship between the strength characteristics of the natural S-RM and the rock block proportion. The determination methods of the shear parameters widely used make attempts to treat the S-RM as the coarse-grained soil or completely strongly weathered rock equivalently, which lacks the discussions about the strength of the contact surfaces and the roles rock blocks and soil matrix play in the overall strength (He et al., 2018; Lü et al., 2019; Miščević and Vlastelica, 2014; Wörman, 1993; Zhang et al., 2019). Furthermore, the influence of water content on the mechanical properties of S-RM also deserves careful study. The strength parameters are fragile to water and show obvious deteriorations as water content increases, which is responsible for the failure of the deposit slope during rainfall (Duong et al., 2013; Deng, 2016; Huang, 2016; Qi, 2016; Zhou et al., 2016; Wei et al., 2019). However, the variabilities in the mechanical characteristics of the S-RM in different regions and the limitations of the simulation software result that the shear parameter deteriorations are difficult to take into account in the deposit slope assessments.

This study aims to investigate the strength characteristics of the natural S-RM and propose an innovative strength parameter estimation method to obtain the strength parameters. Given the similarities between the natural S-RM and rock masses, the relative concepts and variables in the generalized H-B criterion are taken as references for the determination and calculation of the strength parameters of the S-RM. The rock block proportion and strength of contact surface between rock blocks and soil matrix were chosen as key influence factors of the overall strength based on the test data. The nonlinear strength criterion to estimate strength was proposed, and the verification of the estimated method was performed based on a series of test data. The strength deterioration due to the effect of water was also taken into consideration. A typical deposit slope near the site of the Taoyuan Jinsha River suspension bridge in Yunnan Province, China, was selected as the case study. The slope stability was evaluated considering the shear parameter deteriorations subjected to different types of rainfall.

Expressions of the Nonlinear Strength Criterion

The HoekBrown Criterion

In the past decades, as one of the most famous and commonly used nonlinear strength criteria, the HoekBrown (H-B) criterion proposed by Hoek and Brown (1980), has been applied successfully in describing rock failure mechanisms, and the accuracy has been improved in rock engineering and rock mechanics. The original H-B criterion is a nonlinear strength criterion, which is based on several conventional rock laboratory and in situ test data, and the expression is as follows:

${\sigma }_1={\sigma }_3+{\sigma }_c{\left(m\frac{{\sigma }_3}{{\sigma }_c}+s\right)}^{0.5},(1)$

where σ₁ and σ₃ are the maximum and minimum principal stresses, respectively; σ_c is the unconfined compressive strength of the rock; m is a dimensionless empirical parameter of the rock, which is utilized to describe the degree of hardness of the rock; s is a dimensionless empirical parameter reflecting the degree of integrity of the rock mass, for intact rock s = 1.

The criterion was modified later by Hoek et al. (1992) to the generalized version as follows:

${\sigma }_1={\sigma }_3+{\sigma }_c{\left(m_b\frac{{\sigma }_3}{{\sigma }_c}+s\right)}^a(2)$

where parameter a can be estimated from the geological strength index (GSI) as follows:

$a=0.5+\frac{1}{6}\left[\exp \left(-GSI/15\right)-\exp \left(-20/3\right)\right].(3)$

The parameters m_b and s could be obtained based on GSI, which characterizes the quality of the rock masses. The GSI depends on the structure of the rock sample and the surface condition of the joints. The parameters m_b and s are defined by Hoek et al. (1992) as follows:

$m_b=m_i\exp \left(\frac{GSI-100}{28-14D}\right),(4)$

$s=\exp \left(\frac{GSI-100}{9-3D}\right),(5)$

where D is proposed as a disturbance coefficient, which varies from 0.0 for the undisturbed in situ rock masses to 1.0 for very disturbed rock masses; m_b is the value for m for intact rock and can be obtained from experiments. Considering the case without available test data, Hoek et al. (2002) and Marinos and Hoek (2001) also provided an approximate value range of m_i for different types of rock as reference.

In the practical engineering construction, to estimate the safety of the deposit slope, the MohrCoulomb (M-C) criterion strength parameters, cohesion and friction angle, of geomaterials are commonly used. Therefore, many attempts have been made to derive the equivalent M-C parameters from the nonlinear strength criterion. Hoek and Brown (1997) proposed a nonlinear shear strength relationship based on the generalized H-B criterion and a series of test values, and the equation is defined as follows:

$\tau =A{\sigma }_c{\left(\frac{{\sigma }_n}{{\sigma }_c}-T\right)}^B,(6)$

where τ and σ_n are the shear and normal stresses, respectively; A and B are materials constants, and the parameter T is defined as follows:

$T=\left(m_b-\sqrt{m_b^2+4s}/2\right),(7)$

where the meaning of parameters m_b and s are shown above, and the calculation equation of the parameters are Eqs 4, 5.

Strength Characteristics of the Natural SoilRock Mixture

Natural S-RM is composed of the soil matrix with different sizes of rock blocks mixed up. There are huge differences in the mechanical properties of the individual components, which thus leads to the complex strength characteristics of the geomaterial. Figure 1 shows the features and transformation of the structure of the S-RM with different rock block proportions. The results show that the spatial feature of the rock blocks inside changes from floating in the soil matrix to a dense state and finally in a skeleton state as the rock block proportion increases. During the process, the main source of the overall S-RM strength also changes from the soil-matrix to rock blocks-soil-contact surface and rock blocks. The effect of the contact surface between the soil matrix and rock blocks is crucial for the resistance of S-RM to the external force, as well as the individual components.

FIGURE 1

FIGURE 1. Sketch map of the structural transformation of the soilrock mixture.

The Nonlinear Strength Criterion for the SoilRock Mixture

In fact, the components of the natural S-RM are similar to the strongly weathered rock, and both are formed by the rock fragments with various sizes, fine-grained soil, and pores. The structure and surface conditions are chosen as the important factors for the strength of the rock in the H-B criterion. Similarly, the structure and strength of the contact surface between rock blocks and soil matrix (short as “contact surface”) also play the dominant role in the strength of the S-RM. Thus, the concept and format of the nonlinear shear strength criterion proposed by Hoek and Brown (1997) could be used as the reference, and the format of the nonlinear strength criterion for the S-RM is defined as follows:

$\tau =f\left({\sigma }_n,{\sigma }_{c-SRM},T_s,n\dots \right).(8)$

Based on the expression of the nonlinear shear strength criterion shown in Eq. 6 and the influence factors as shown in Eq. 8, a power-law nonlinear strength criterion of the S-RM is proposed and is defined as follows:

$\tau =A_s{\sigma }_{c-SRM}\left(\frac{{\sigma }_n}{{\sigma }_{c-SRM}}-T_s\right){,}^n(9)$

where σ_c-SRM is the unconfined compressive strength of the S-RM, which is utilized to describe the strength of the contact surface; A_s is a nonlinear strength constant of the power-law criterion, and n is the nonlinearity coefficient; parameter T_s is a material constant, which is related to the rock block proportion, and strength of fine-grained soil and rock blocks.

Innovative Strength Parameter Estimation Method of the SoilRock Mixture

Shear Parameter Estimation Method of the SoilRock Mixture

The unconfined confined strength (UCS) σ_c-SRM is used in the power-law criterion to describe the strength of the contact surface inside the S-RM. Several studies have shown that the value of UCS decreases compared with the soil sample as the rock block proportion increases (Afifipour and Moarefvand, 2014; Hu, 2014; Zhang et al., 2020). There is a lot of evidence that the emergence of the contact surface with low strength is responsible for the decreasing trend. Thus, the UCS of the S-RM is chosen to describe the strength of the contact surface indirectly, and the expression proposed by Kalender et al. (2014) for the value is utilized as follows:

$\raisebox{1ex}{${\sigma }_{c-SRM}$}\!\left/ \!\raisebox{-1ex}{${\sigma }_c$}\right.=\frac{A-A^{\eta }}{A-1},(10)$

where σ_c is the UCS value of the soil matrix; characteristic parameter A is a strength constant, which represents the contact strength between the soil and rock blocks, and it could be determined based on the value diagram using σ_c and the internal friction angle or the roughness of the rock blocks; η is the volume ratio of the rock blocks.

In order to obtain the required constant parameters in the nonlinear strength criterion, more than 140 groups of direct shear test data were collected as the shear parameter database of the natural S-RM (Avşar et al., 2015; Chang and Cheng, 2014; Chang and Phantachang, 2016; Deng, 2016; Deng et al., 2013; Deng, 2014; Liu et al., 2017; Ma et al., 2019; Monkul and Ozden, 2007; Qi, 2016; Rahardjo et al., 2008; Sun et al., 2014; Tang et al., 2018; Wang et al., 2016; Wang, 2011; Wang et al., 2013; Wei et al., 2008; Wu, 2015; Wu et al., 2017; Xu et al., 2019; Xu et al., 2011; Xue et al., 2014; Yang JH. et al., 2016; Yang et al., 2010; Zhang et al., 2016). Considering the limitations of the test data and the object of the study, the scope of application of the estimation method in this study must meet three conditions.

1) Based on the rock block proportion threshold in the previous literature, a range of rock block proportion was set as 30–90%.

2) The particle diameter range of the rock block of the geomaterial for the nonlinear strength criterion should be also set to no more than 60 mm.

3) The normal stress range of 0–1200 kPa was set as the applicable range

With the guide of the expressions in the nonlinear shear strength criterion, the quantitative expressions of the constant parameters are proposed based on test data after a lot of trials and nonlinear fitting.

The expression of T_s is similar to the equation of the parameter T of the H-B criterion as shown in Eq. 7 and is presented as follows:

$T=\left(m_s-\sqrt{m_s+4s_R}/2\right),(11)$

where m_s is a dimensionless constant that is related to the rock block proportion and the strength of the contact surface. The expression of m_s is defined as follows:

$m_s=m_{Ri}\frac{100}{G}\left(\exp \left(26.21{\gamma }^3-49.83{\gamma }^2+32.48\gamma -8.81\right)\right)0.3\le \gamma \le 0.9,(12)$

where γ is the mass ratio of the rock block in the S-RM; the parameter m_Ri is a dimensionless constant which is utilized to describe the fragment degree of the geomaterial, and the expression is defined as follows:

$m_{Ri}=25\exp \left(0.25-\gamma \right)0.3\le \gamma \le 0.9,(13)$

As the rock block proportion increases, the S-RM turns from the fine-grained soil matrix into the mixture of rock blocks and soil in a dense state and finally converts into the heavily broken masses with the void structure as shown in Figure 1, where the RBP is the abbreviation of rock block proportion. Compared to the soil matrix, the fragment degree of the geomaterial increases as the rock block proportion increases, and the value of the parameter m_Ri keeps decrease.

The parameter G in Eq. 12 is defined as the geological parameter of the S-RM with the guide of GSI in the generalized H-B criterion, and the value is related to the friction effect provided by the contact surface inside the geomaterials. The strength of the contact surface could be divided into the cohesive and internal friction effects. The former one is mainly controlled by the strength of the soil matrix and the roughness of the rock blocks, which has been considered by introducing the parameter σ_c-SRM and characteristic parameter A into the criterion. The latter one is mainly controlled by the number of contact surfaces and the roughness of the rock blocks. Figure 1 shows that the larger the rock block proportion is, the more the contact surface is and the more obvious the internal friction effect provided by the contact surface is. Thus, based on the test data, the expression of G is shown as follows:

$G=30.45\ln \left(100\gamma \right)-44.190.3\le \gamma \le 0.9,(14)$

The undetermined parameters A_s and n in the strength criterion of the S-RM could be obtained based on the test data using the nonlinear fitting. To improve the engineering applicability and extend the scope of the application for the estimation of the shear parameters, the relationships between A_s or n and rock block proportion were also proposed based on the database, respectively, and the expressions are defined as follows:

$A_s=\{\begin{array}{cc}\left(-3.315\gamma +3.305\right)\gamma & 0.3\le \gamma \le 0.6\\ \left(-3.353{\gamma }^2+4.156\gamma +0.104\gamma \right)\gamma & 0.6<\gamma \le 0.9\end{array},(15)$

$n=\{\begin{array}{cc}-8.291{\gamma }^2+7.046\gamma -0.594& 0.3\le \gamma \le 0.6\\ -5.2{\gamma }^2+8.367\gamma -2.478& 0.6<\gamma \le 0.9\end{array}.(16)$

To bring the nonlinear strength criterion into evaluating the stability of the deposit slope, the tangential method was applied to calculate the equivalent M-C parameters for the S-RM with the nonlinear strength envelope. As illustrated in Figure 2, a tangent line could be made through one-point P on the nonlinear strength envelope, and the tangent line could replace the nonlinear relationship with the form of the equivalent M-C strength parameters. Taking the stress status at point P as an example, the expression of the tangent line could be represented as follows:

$\tau =c_{i-SRM}+{\sigma }_n\tan {\phi }_{i-SRM},(17)$

where the parameters c_i-SRM and φ_i-SRM are the equivalent M-C shear parameters. According to Figure 2, the gradient of the tangent line at the point P could be derived from Eq. 9 as Eq. 18 shown. The equivalent cohesion could be obtained with the combination of Eqs 18 and Eq. 19. The expressions of the equivalent M-C shear parameters based on the nonlinear strength criterion are as follows:

${\phi }_{i-SRM}=\arctan \left[A_{s}n{\sigma }_{i-SRM}{\left(\frac{{\sigma }_n}{{\sigma }_{i-SRM}}-T_s\right)}^{n-1}\right],(18)$

$c_{i-SRM}=\tau -{\sigma }_n\tan {\phi }_{i-SRM}(19)$

FIGURE 2

FIGURE 2. Nonlinear strength envelope and the tangent line.

The Shear Parameters Estimation Method Considering the Effect of Water

Many researchers have employed mechanical experiments to focus on the mechanical properties of the natural S-RM subjected to various water contents, and results show that the shear parameters are sensitive to water, which should be focused on in the evaluation of the deposit slope (Al-Shayea, 2001; Al Aqtash and Bandini, 2015; Malizia and Shakoor, 2018; Zhou et al., 2020). Several types of fitting curves between the shear parameters and the water content have been proposed to represent the deterioration trends of the mechanical properties based on the test data, such as the exponential, power, linear, and parabola function. However, this type of fitting function barely describes the deterioration trend based on the test data and is only suitable for the material from one region, which could not be utilized widely as a reference.

In this study, the empirical approaches proposed by Zhang et al. (2021) are used to estimate the shear parameters considering water softening, which were proposed by test data to describe a more general deterioration feature. The expressions are as follows:

$c=c_0{a}^{-0.089\left(a^2-5.93a+12.56\right)},(20)$

$\phi ={\phi }_0\left[\sqrt{e^{\left(1-\gamma \right)\left(a-1\right)/a}}-0.49{\log }_{10}a\right],(21)$

where a is the water content variation ratio, c₀ is the reference cohesion, and φ₀ is the reference friction angle of the S-RM sample with natural water content.

Verification of the Strength Estimation Method Based on Test Data

To verify the accuracy of the proposed nonlinear strength criterion of the S-RM, the large-scale direct test data in the database were utilized as the standard values, and the comparisons between the standard and the estimated values of shear strength calculated by the nonlinear strength criterion were made as shown in Figure 3. The results show that the estimated and test shear strength values are concentrated on both sides of the line of y = x, and the relationship between the estimated and test values is y = 0.9515x, with the coefficient of determination as 0.9082. The data points located under the y = x are more than the ones above the blue line. The area of error range ±50 kPa and ±100 kPa is marked as the dark and light blue areas, respectively. Most of the estimated values are distributed in the dark blue area, which means the absolute error of the estimated values is around ±50 kPa. A few estimated values located outside the blue area are ±100 kPa larger than the measured values. Although the estimated values are overall smaller than the test values, the error between the estimated and test values is acceptable. The results prove that the nonlinear strength criterion of the S-RM proposed in this study could be utilized for the shear parameter estimations.

FIGURE 3

FIGURE 3. Comparison between the estimated and test shear strength values.

Background and Modeling of a Case

Background

The engineering application of the nonlinear strength criterion of the S-RM was performed using a typical deposit slope in the following. The slope is located near the Taoyuan Jinsha River suspension bridge site in Yunnan Province, China (Figure 4A). The Taoyuan Jinsha River suspension bridge is located in the K76 along the Dali-Yongsheng expressway, which spans the reservoir area 21 km upstream of Ludila hydropower station. The rock of the North Bank of the suspension bridge (Yongsheng bank) is mainly moderately weathered limestone with good rock mass stability. However, at the South Bank of the suspension bridge (Dali bank), in the long-term geological evolution process, including strong crustal movement, river undercutting erosion, and historical landslide, deep and loose deposits were formed. The suspension bridge adopts the gravity anchor foundation as the bearing structure. The anchor foundation construction needs large-scale excavation, with an excavation area of more than 3000 m².

FIGURE 4

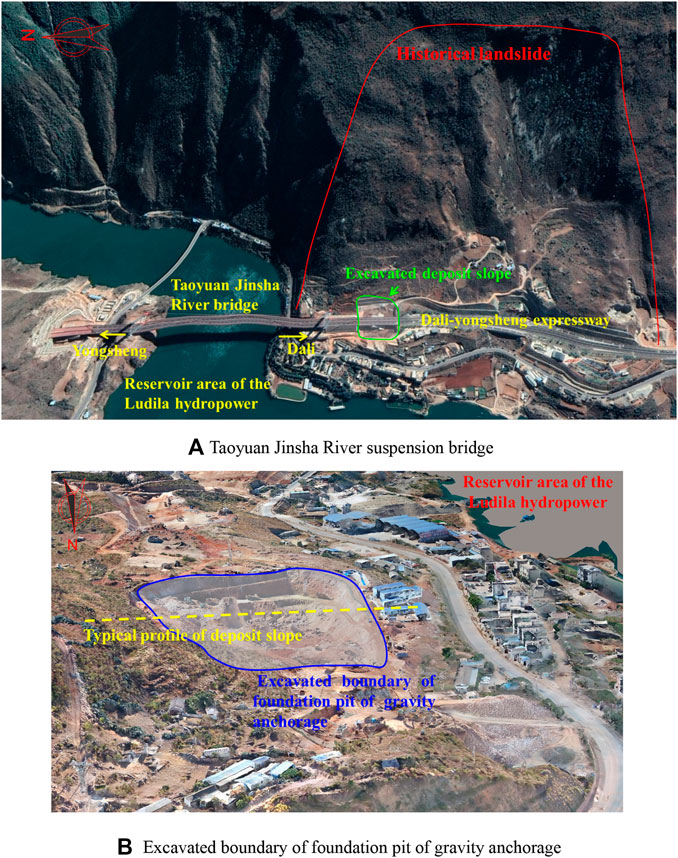
FIGURE 4. Site investigation of the case. (A) Taoyuan Jinsha River suspension bridge. (B) Excavated boundary of foundation pit of gravity anchorage.

The 3D model based on tilt photography using an unmanned aerial vehicle shows the excavated boundary of the foundation pit of gravity anchorage (Figure 4B). During the construction of the gravity anchorage, the disturbance shows a negative impact on the stability of the east slope. In addition, the climatic condition of the Taoyuan region is complex, and the annual rainfall is about 750 mm. The stability of the excavation slope subjected to different types of rainfall is important for anchorage construction. Therefore, the deposit slope was selected as a case study as the application of the nonlinear strength criterion, and the stability assessment of the slope considering parameter deterioration was performed to better understand the influence of rainfall on the slope failure.

Geological and Numerical Model

As shown in Figure 4B, a typical profile of deposit slope is selected, and the geological and numerical models are shown in Figure 5. The slope included about five parts according to the survey data: the first one was the S-RM with small size gravels in a slightly dense state, the second one was the S-RM with large size gravels in the dense state, the third one was the dense silt-semi-rock layer, the fourth layer was the dense silt soil, and the fifth one was comprised of the moderately weathered limestone. The height of the model was about 235 m, and the width was set to 360 m. In the numerical model, the number of the grid points was 11,439, and the number of the triangle-quadrilateral zone was 11,384.

FIGURE 5

FIGURE 5. Geological and numerical model of the deposit slope.

Determination of the Shear Parameters of the S-RM

As shown in Figure 5, the emergence stratum consists of the Quaternary Holocene colluvium layer, the Quaternary Pleistocene alluvial layer, and the Devonian stratum. Among these, the Quaternary Holocene colluvium and Pleistocene alluvial layer consist of clay, silt, and limestone fragments of various sizes, which could be classified as the typical S-RM. The field investigation shows that the maximum particle diameter of the gravels in the shallow region is about 60 mm due to the weathering effect, while the maximum diameter of the gravel in the deeper layers lies in the range of 60–90 mm. Therefore, the colluvial type S-RM in the shallow region is suitable for the nonlinear strength criterion, and the shear parameters of the material are determined as follows:

1) Determination of the rock block proportion. Several groups of the natural S-RM samples were collected from the deposit slope, and the particle size test was performed. The cumulative curve of the particle size of the S-RM sample from the east slope is shown in Figure 6. The soil-rock threshold was set as 2 mm, and the rock block proportion of the S-RM on the east slope is 62%.

2) Determination of the parameter of the nonlinear strength criterion. The UCS value of the soil matrix is obtained as 812.67 kPa based on the uniaxial compressive test. Geological data show that the gravels in the S-RM commonly assume in the angularsubangular shape. The characteristic parameter A was determined as 0.5 utilizing the value chart proposed by Kalender et al. (2014) taking the UCS value of the soil matrix and the roughness of the gravel into account.

3) Determination of the shear parameters of the S-RM. On the basis of the rock block proportion and UCS value of the S-RM, the nonlinear strength envelope of the S-RM with 68% rock block proportion was drawn as shown in Figure 7. The cohesion and friction angle of the geomaterial could be obtained using the tangential method, and the shear parameters have the following values: c = 89.85 kPa, φ = 23.33°.

FIGURE 6

FIGURE 6. Cumulative curve of the particle diameter of the soilrock mixture.

FIGURE 7

FIGURE 7. Strength envelope of the soilrock mixture of the case.

Material Parameter of the Deposit Slope

The mechanical parameters of the S-RM located in the shallow region of the deposit slope have been obtained based on the nonlinear strength criterion. The mechanical parameters of the geomaterial in other strata were determined according to the prospecting data and experience reduction. The physical and mechanical parameters of geomaterials are listed in Table 1.

TABLE 1

TABLE 1. Physical and mechanical parameters of the geomaterials.

The assessment of the deposit slope under different types of rainfall was performed using the SEEP/W module of Geo-studio software. The module takes full advantage of the saturatedunsaturated seepage calculation in the rainfall numerical simulation, which fully considers the influence of the negative pore-water pressure (matrix suction) on the slope stability. In the unsaturated seepage process, the water content and permeability coefficient of the geomaterial are not fixed values, which are related to the change of the matrix suction. Therefore, the hydraulic curves of the S-RM in the slightly dense and dense state were set as shown in Figure 8.

FIGURE 8

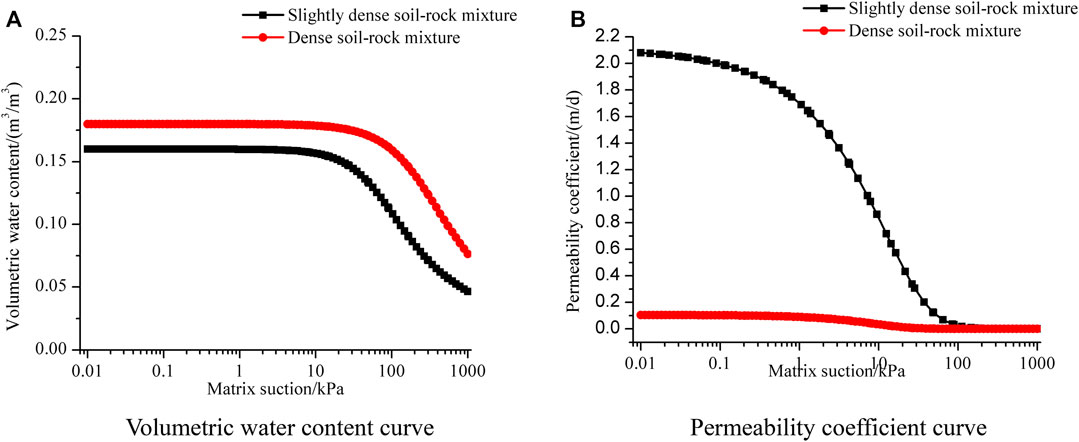
FIGURE 8. Curves of hydraulic parameters with pore water pressure of the material in the layer of deposit. (A) Volumetric water content curve. (B) Permeability coefficient curve.

Stability Assessments of the Deposit Slope Under Excavation and Rainfall

Simulation Schemes

The numerical scheme of the stability evaluation of the deposit slope is divided into two parts: first, the deposit slope was excavated in four steps according to the design plan for the construction, and then, two types of rainfall were performed on the excavation slope to analyze the stability considering parameter deteriorations. The SIGMA module in the Geo-studio software was adopted to present the excavation process, and the SEEP/W module was utilized for the seepage analyses during the rainfall. Then, the SLOPE module was embedded used to obtain the potential sliding surfaces along with their safety factors based on the limit equilibrium theory of the deposit slope under rainfall.

The rainfall in the Taoyuan region is concentrated from June to September, and the total rainfall is relatively small. The rainfall types of the rainfall events in the Taoyuan region could be divided into two types: increasing and wave type. The total rainfall for the numerical model was set as 280mm, and the rainfall duration for the two types was the same as 7 days. The daily rainfall of two rainfall types was shown in Figure 9.

FIGURE 9

FIGURE 9. Distributions of two types of rainfall intensities.

Stability Evaluations

Figure 10A shows that the potential sliding surface of the slope before excavation is located nearly the top of the slope, and the bottom of the surface has reached the dense S-RM layer. The safety factor of the potential surface is 2.842, which is within the corresponding range of the stable slope.

FIGURE 10

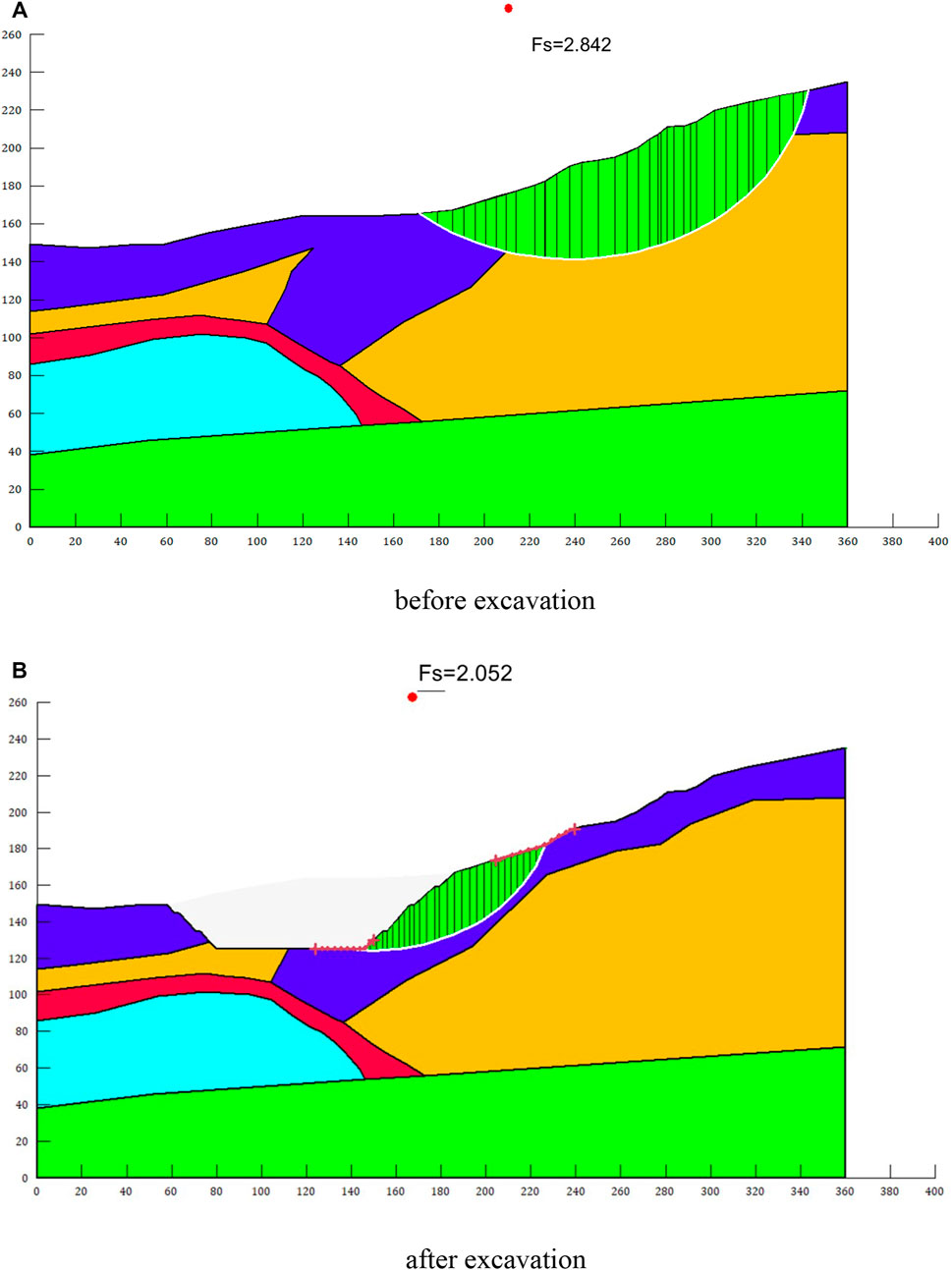
FIGURE 10. Safety factors and potential sliding surface of the deposit slope. (A) before excavation. (B) after excavation.

Figure 10B shows the location of the potential sliding surface along with its safety factor after excavation. Compared with the location of the potential sliding surface before excavation, the potential sliding surface changed from the top to the nearby excavation area, which indicates that the stability of the slope has been controlled by the stress status due to excavation disturbance. The safety factor of the potential sliding surface was decreased from 2.842 to 2.052, and the slope was still in a stable state. There was no obvious local destroy observed in the excavation slope based on the field survey, which is consistent with the numerical result.

To analyze the influence of rainfall type on the seepage and stability of the deposit slope, the increasing and wave types of rainfall were performed under the same rainfall and rainfall duration considering the parameter deterioration. As shown in Figure 5, to quantitatively describe the variations of the hydraulic parameters due to rainfall infiltration, seven monitor points were set in the layer of the slightly dense S-RM. Figure 11 shows the variations of the pore water pressure in different depths during the rainfall. The pore water pressure of #1 point near the surface responded immediately since the rainfall started, and the pore pressure water increased from −541.58 kPa to −423.18 kPa and −359.97 kPa under the effect of the increasing (Figure 11A) and wave-type (Figure 11B) rainfall, respectively. According to the rainfall intensity variations (Figure 9), the intensity of the wave type is larger than the increasing type in the first five days of rainfall. The pore water pressure of #1 under the wave-type rainfall has reached −133.68 kPa after five days of rainfall while the value is still less than −150 kPa under the increasing type. The pore water pressure of #5 with the height of 144 m has shown an increase after five wave-type rainy days, which indicates that the deepest pore-water pressure response depth of the wave-type rainfall in Figure 11B has reached 20 m below the surface. Under the same rainfall duration, the rainfall influence depth is much shallower subjected to the increasing type of rainfall, and the pore water pressure #4 has just shown an increasing trend after five rainy days. The rainfall intensity of the wave-type rainfall starts to decrease after the fifth day, which also leads to the decrease of pore water pressure of points #1 and 2# in the last two days of rainfall. In contrast, the intensity of the increasing type increases monotonically, and the pore water pressure in the shallow region keeps increasing in the whole rainfall process. Under the same total rainfall and rainfall duration, the deepest response depth of pore water pressure of the increasing type is still under 25 m, while the obvious increase of the pore water pressure at the same depth under the wave-type rainfall has been observed at the end of rainfall.

FIGURE 11

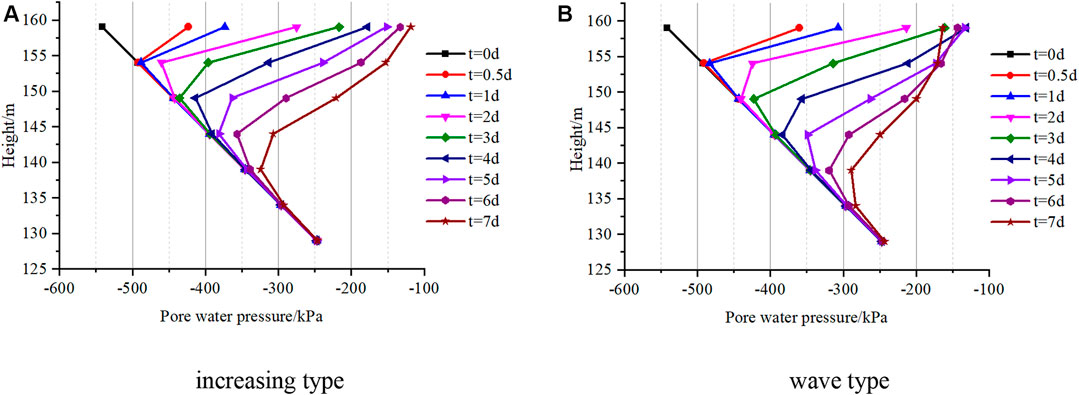
FIGURE 11. Pore water pressure of monitor points under different rainfall conditions. (A) increasing type. (B) wave type.

As shown in Figures 12A,B, a similar phenomenon also appeared in the variation of the water content of the monitor points. The values of the points located near the surface are more sensitive to the variation of rainfall intensity; the water content of the #1 and #2 decreases after the fifth rainy day in Figure 12B, which is attributed to the reduction of rainfall intensity in the wave-type rainfall. The water content of point #7 has shown an increasing trend compared to the initial state, which means the rainfall infiltration has reached that depth and supply. In summary, the wave-type rainfall has a deeper infiltration depth and a larger influence area on the pore water pressure and water content than the increasing type rainfall, which could be seen as the dangerous rainfall type for slope stability.

FIGURE 12

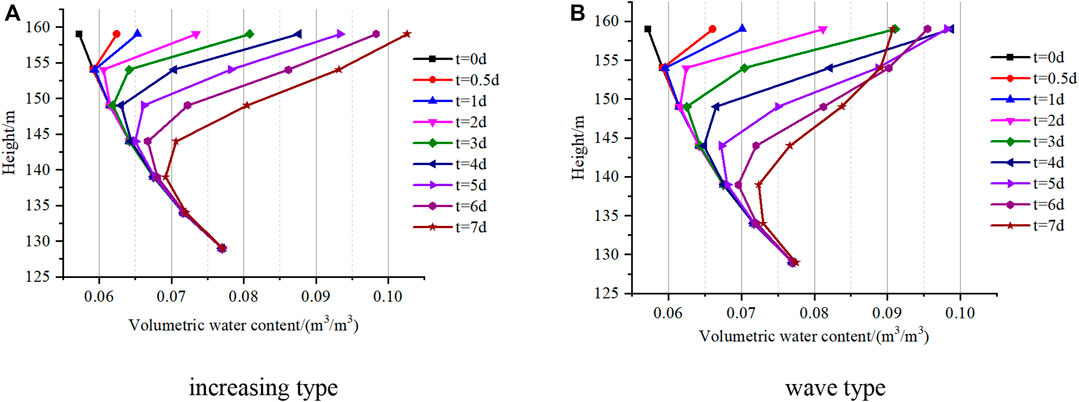
FIGURE 12. Water content of monitor points under different rainfall conditions. (A) increasing type. (B) wave type.

The stabilities of the deposit slope subjected to two types of rainfall considered parameter deterioration were carried out. Figure 13 presents the variations of the safety factor of the potential sliding surfaces during the two different types of rainfall. The results show that the safety factor of the potential sliding surface is closely related to the rainfall intensity. During the first five days of the rainfall, the intensity of the wave type is much larger than that of the increasing type, which leads to a faster decrease in the safety factor after the same rainfall duration. During the last two days of rainfall, the intensity of the increasing type rainfall has been greater than the wave type, and the decrease of the safety factor of the deposit slope is also larger than that under the wave type, the former about 0.068, from 1.789 to 1.721, while the latter one is only 0.048. The largest intensity of the two types of rainfall appears at the fifth and the end day of rainfall, respectively, and an obvious decrease could be observed after the peak rainfall intensity, which is attributed to the hysteresis due to rainfall infiltration. After the same rainfall duration, the safety factor of the wave type is smaller than the increasing type.

FIGURE 13

FIGURE 13. Safety factors of the deposit slope under different rainfall conditions.

Figure 14 shows the locations of the potential sliding surfaces of the deposit slope after the increasing and wave type of rainfall. Compared to the simulation result before excavation in Figure 10B, the location of the potential sliding surface is much shallower. The parameter deterioration was considered in the calculation of the safety factor, which is related to the increase of pore water pressure. Therefore, the location of the potential sliding surface is controlled by the variable region of the pore water pressure is near the surface, which shows very good agreement with the common shallow retrogressive landslides due to rainfall.

FIGURE 14

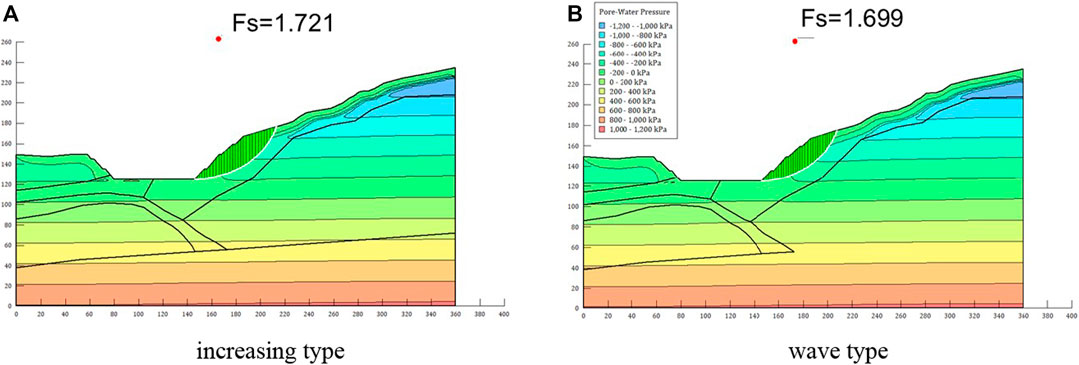
FIGURE 14. Safety factors and potential sliding surface of the deposit slope after different rainfall conditions. (A) increasing type. (B) wave type.

Conclusion

S-RM is one of the most common geological materials and presents considerable challenges due to its complex mechanical characteristics and compositions. An innovative shear parameter estimation method was proposed in this study, and its application for the deposit slope with the parameter deterioration was discussed subjected to different types of rainfall. The following conclusions and recommendations could be derived:

1) The empirical nonlinear strength criterion of the S-RM and the shear parameter estimation method were proposed. Based on the similarities between the natural S-RM and the rock masses, the generalized H-B was utilized as the reference format of the expression of the nonlinear strength criterion, and the rock block proportion and the strength of the contact surface were chosen as the vital influence factors. The scope of the estimation method was given considering the test conditions, and the influence of water on the shear parameters was also discussed.

2) A series of large-scale direct test data were collected to build the database of the natural S-RM, which was utilized as the reference for the verification of the nonlinear strength criterion. In addition, the natural S-RM located in the deposit slope in Taoyuan, Yunnan Province, China, was selected as the research object, and its mechanical parameters were determined using the estimation method proposed in this study.

3) The numerical case study was performed to study the influence of rainfall type on the seepage field and stability considering the parameter deterioration. The results from the numerical study indicate that the pore water pressure and water content are related to the rainfall intensity, and the wave-type rainfall presents a larger infiltration area. The same situation was also observed in the variation of the safety factor, and the wave-type rainfall shows a more serious impact on the slope stability.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

Written informed consent was obtained from relevant individuals for the publication of any potentially identifiable images or data included in this article.

Author Contributions

ZZ and QS were involved in the final development of the project and manuscript preparation. XF wrote the manuscript draft. YZ and JH analyzed the data. ZW and ML carried out the field investigation. All authors: corrections, modifications, and final acceptance.

Funding

The work reported in this paper was financially supported by the Youth Innovation Promotion Association CAS (No.2021325), the National Natural Science Foundation of China (No. 51779250), and the International Partnership Program of Chinese Academy of Sciences (Grant No. 131551KYSB20180042).

Conflict of Interest

ZW and ML are employed by China State Construction International Holdings Limited and China State Construction International Investments (Hubei) Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to acknowledge the reviewers and the editors for their comments and suggestions.

References

Afifipour, M., and Moarefvand, P. (2014). Mechanical Behavior of Bimrocks Having High Rock Block Proportion. Int. J. Rock Mech. Mining Sci. 65, 40–48. doi:10.1016/j.ijrmms.2013.11.008

CrossRef Full Text | Google Scholar

Al Aqtash, U., and Bandini, P. (2015). Prediction of Unsaturated Shear Strength of an Adobe Soil from the Soil-Water Characteristic Curve. Construction Building Mater. 98, 892–899. doi:10.1016/j.conbuildmat.2015.07.188

CrossRef Full Text | Google Scholar

Al-Shayea, N. A. (2001). The Combined Effect of clay and Moisture Content on the Behavior of Remolded Unsaturated Soils. Eng. Geology. 62 (4), 319–342. doi:10.1016/s0013-7952(01)00032-1

CrossRef Full Text | Google Scholar

Avşar, E., Ulusay, R., and Mutlutürk, M. (2015). An Experimental Investigation of the Mechanical Behavior and Microstructural Features of a Volcanic Soil (Isparta, Turkey) and Stability of Cut Slopes in This Soil. Eng. Geology. 189, 68–83.

Google Scholar

Cascini, L., Cuomo, S., Pastor, M., and Sorbino, G. (2010). Modeling of Rainfall-Induced Shallow Landslides of the Flow-type. J. Geotech. Geoenviron. Eng. 136 (1), 85–98. doi:10.1061/(asce)gt.1943-5606.0000182

CrossRef Full Text | Google Scholar

Chang, K.-T., and Cheng, M.-C. (2014). Estimation of the Shear Strength of Gravel Deposits Based on Field Investigated Geological Factors. Eng. Geology. 171, 70–80. doi:10.1016/j.enggeo.2013.12.014

CrossRef Full Text | Google Scholar

Chang, W.-J., and Phantachang, T. (2016). Effects of Gravel Content on Shear Resistance of Gravelly Soils. Eng. Geology. 207, 78–90. doi:10.1016/j.enggeo.2016.04.015

CrossRef Full Text | Google Scholar

Deng, H. F. (2016). “Test Research on the Shear Strength Characteristics of Rock-Soil Aggregate Mixture,” (Fuzhou: East China University of Technology). M.Sc.

Google Scholar

Deng, H. F., Yuan, X. F., Li, J. L., Li, J. L., Luo, Q., and Zhu, M. (2013). Research on Failure Characteristics and Determination Method for Shear Strength of Earth-Rock Aggregate in Direct Shear Tests. Chin. J. Rock Mech. Eng. 32 (S2), 4065–4072. doi:10.3969/j.issn.1000-6915.2013.z2.133

CrossRef Full Text | Google Scholar

Deng, X. C. (2014). “The Tunnel Excavation and its Slope Stability in the Accumulation Body,” (Chongqing: Chongqing Jiaotong University). M.Sc.

Google Scholar

Ding, X. L., Li, Y. X., and Wang, X. (2010). Particle Flow Modeling Mechanical Properties of Soil and Rock Mixtures Based on Digital Image. Chin. J. Rock Mech. Eng. 29 (3), 477–484. doi:10.1360/972008-2552

CrossRef Full Text | Google Scholar

Duong, T. V., Tang, A. M., Cui, Y.-J., Trinh, V. N., Dupla, J.-C., Calon, N., et al. (2013). Effects of Fines and Water Contents on the Mechanical Behavior of Interlayer Soil in Ancient Railway Sub-structure. Soils and Foundations 53 (6), 868–878. doi:10.1016/j.sandf.2013.10.006

CrossRef Full Text | Google Scholar

Fiorillo, F., Esposito, L., Grelle, G., Revellino, P., and Guadagno, F. M. (2013). Further Hydrological Analyses on Landslide Initiation in the Sarno Area (Italy). Ital. J. Geosciences 132, 341–349. doi:10.3301/ijg.2012.43

CrossRef Full Text | Google Scholar

Fu, X. D., Sheng, Q., Du, W. J., Mei, H. R., Chen, H., and Du, Y. X. (2020a). Evaluation of dynamic stability and analysis of reinforcement measures of a landslide under seismic action: a case study on the Yanyangcun landslide. Bulletin of Engineering Geology and the Environment. 79, 2847–2862.

CrossRef Full Text | Google Scholar

Fu, X. D., Sheng, Q., Zhang, Y. H., Chen, J., Zhang, S. K., and Zhang, Z. P. (2017). Computation of the safety factor for slope stability using discontinuous deformation analysis and the vector sum method. Computers and Geotechnics 92, 68–76.

CrossRef Full Text | Google Scholar

Fu, X. D., Sheng, Q., Tang, H., Chen, J., Du, Y. X., Zhang, Z. P., and Mei, H. R. (2019). Seismic stability analysis of a rock block using the block theory and Newmark method. International Journal for Numerical and Analytical Methods in Geomechanics 43(7), 1392–1409.

CrossRef Full Text | Google Scholar

Fu, X. D., Sheng, Q., Li, G., Zang, Z. P., Zhou, Y. Q., and Du, Y. X. (2020b). Analysis of landslide stability under seismic action and subsequent rainfall: a case study on the Ganjiazhai giant landslide along the Zhaotong-Qiaojia road during the 2014 Ludian earthquake, Yunnan, China. Bulletin of Engineering Geology and the Environment. 79, 5229–5248.

CrossRef Full Text | Google Scholar

He, Z.-M., Tang, H.-l., and Deng, X. (2018). Effect of Seepage Force on Stability of High Embankment with Coarse-Grained Soil during Rainfall. J. Highw. Transp. Res. Dev. (English Ed.) 12 (1), 44–52. doi:10.1061/jhtrcq.0000609

CrossRef Full Text | Google Scholar

Hoek, E., Carranza-Torres, C., and Corkum, B. (2002). “Hoek-Brown Failure Criterion-2002 Edition,” in Proc. NARMS-TAC Conference, Volume 1: Toronto, 267–273.

Google Scholar

Hoek, E., Wood, D., and Shah, S. (1992). “A Modified Hoek–Brown Failure Criterion for Jointed Rock Masses,” in Proceedings Rock Characterization: ISRM Symposium, Eurock'92, Chester, UK, 14–17 September 1992 (Thomas Telford Publishing), 209–214.

Google Scholar

Hoek, E., and Brown, E. T. (1980). Empirical Strength Criterion for Rock Masses. J. Geotech. Engrg. Div. 106 (9), 1013–1035. doi:10.1061/ajgeb6.0001029

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (1997). Practical Estimates of Rock Mass Strength. Int. J. Rock Mech. Mining Sci. 34 (8), 1165–1186. doi:10.1016/s1365-1609(97)80069-x

CrossRef Full Text | Google Scholar

Hu, W. (2014). “Experimental Study on Shear Strength of Soil-Rock Mixture in Xiluodu Reservior,” (Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences). Ph.D.

Google Scholar

Huang, J. H. (2016). “Study on the Strength Characteristics of Glacial deposit Body in Taoping, Li County, Sichuan Province,” (Chengdu: Chengdu University of Technology). M.Sc.

Google Scholar

Kalender, A., Sonmez, H., Medley, E., Tunusluoglu, C., and Kasapoglu, K. E. (2014). An Approach to Predicting the Overall Strengths of Unwelded Bimrocks and Bimsoils. Eng. Geology. 183, 65–79. doi:10.1016/j.enggeo.2014.10.007

CrossRef Full Text | Google Scholar

Liu, X. R., Tu, Y. L., Wang, P., Zhong, Z-L., Tang, W. B., and Du, L. B. (2017). Particle Breakage of Soil-Rock Aggregate Based on Large-Scale Direct Shear Tests. Chin. J. Geotechnical Eng. 39 (08), 1425–1434. doi:10.11779/CJGE201708009

CrossRef Full Text | Google Scholar

Liu, Z. Y., Su, L. J., Zhang, C. L., Iqbal, J., Hu, B. L., and Dong, Z. B. (2020). Investigation of the dynamic process of the Xinmo landslide using the discrete element method. Computers and Geotechnics 123, 103561.

CrossRef Full Text | Google Scholar

Lü, Q., Chen, P., Kim, B., Zheng, J., and Ji, J. (2019). Probabilistic Assessment of Seismic Stability of a Rock Slope by Combining the Simulation of Stochastic Ground Motion with Permanent Displacement Analysis. Eng. Geology. 260, 105210. doi:10.1016/j.enggeo.2019.105210

CrossRef Full Text | Google Scholar

Ma, C., Zhan, H., Zhang, T., and Yao, W. (2019). Investigation on Shear Behavior of Soft Interlayers by Ring Shear Tests. Eng. Geology. 254, 34–42. doi:10.1016/j.enggeo.2019.04.002

CrossRef Full Text | Google Scholar

Malizia, J. P., and Shakoor, A. (2018). Effect of Water Content and Density on Strength and Deformation Behavior of clay Soils. Eng. Geology. 244, 125–131. doi:10.1016/j.enggeo.2018.07.028

CrossRef Full Text | Google Scholar

Marinos, P., and Hoek, E. (2001). Estimating the Geotechnical Properties of Heterogeneous Rock Masses Such as Flysch. Bull. Eng. Geology. Environ. 60 (2), 85–92. doi:10.1007/s100640000090

CrossRef Full Text | Google Scholar

Meng, Y. W., Wang, Y., Shao, Y. Z., Yan, Z., and Chen, F. (2018). “Numerical Analysis of Excavation Stability of Loose deposit on Highway High Slope,” in APCIM & ICTTE 2018: Proceedings of the Asia-Pacific Conference on Intelligent Medical 2018 & International Conference on Transportation and Traffic Engineering 2018, December 2018, in Beijing, China, 59–62. doi:10.1145/3321619.3321648

CrossRef Full Text | Google Scholar

Miščević, P., and Vlastelica, G. (2014). Impact of Weathering on Slope Stability in Soft Rock Mass. J. Rock Mech. Geotechnical Eng. 6 (3), 240–250. doi:10.1016/j.jrmge.2014.03.006

CrossRef Full Text | Google Scholar

Monkul, M. M., and Ozden, G. (2007). Compressional Behavior of Clayey Sand and Transition Fines Content. Eng. Geology. 89 (3), 195–205. doi:10.1016/j.enggeo.2006.10.001

CrossRef Full Text | Google Scholar

Pantaleone, D. V., Francesco, F., Rita, T., and Delia, C. (2018). Seasonal and Event-Based Hydrological and Slope Stability Modeling of Pyroclastic Fall Deposits Covering Slopes in Campania (Southern Italy). Water 10 (9), 1140. doi:10.3390/w10091140

CrossRef Full Text | Google Scholar

Qi, C., Li, L., Li, R., Gan, F., Zhang, W., and Han, H. (2021). Stability Mechanism Recognition and Failure Risk Assessment on a High Slope by Synthesizing Different Analysis Methods. Nat. Hazards 108 (2), 1569–1584. doi:10.1007/s11069-021-04745-2

CrossRef Full Text | Google Scholar

Qi, D. (2016). “Experimental Study on the Mechanical Properties of Soil-Rock Mixture,” (Zhengzhou: North China University of Water Resources and Electric power). M.Sc.

Google Scholar

Rahardjo, H., Indrawan, I. G. B., Leong, E. C., and Yong, W. K. (2008). Effects of Coarse-Grained Material on Hydraulic Properties and Shear Strength of Top Soil. Eng. Geology. 101 (3), 165–173. doi:10.1016/j.enggeo.2008.05.001

CrossRef Full Text | Google Scholar

Shang, Y. J., Yang, Z. F., Li, L. H., Liua, D., Liaoa, Q., and Wang, Y. (2003). A Super-large Landslide in Tibet in 2000: Background, Occurrence, Disaster, and Origin. Geomorphology 54 (3), 225–243. doi:10.1016/s0169-555x(02)00358-6

CrossRef Full Text | Google Scholar

Sun, S. R., Peng Lei, X., Ji Min, W., Wengan, F., Jin, L. J., and Kanungo, D. P. (2014). Strength Parameter Identification and Application of Soil–Rock Mixture for Steep-Walled Talus Slopes in Southwestern China. Bull. Eng. Geology. Environ. 73 (1), 123–140. doi:10.1007/s10064-013-0524-1

CrossRef Full Text | Google Scholar

Tang, J., Xu, D., and Liu, H. (2018). Effect of Gravel Content on Shear Behavior of Sand-Gravel Mixture. Rock Soil Mech. 39 (01), 93–102. doi:10.16285/j.rsm.2017.1527

CrossRef Full Text | Google Scholar

Wang, C. D., Shen, Q., Wu, R., Wu, R., Fu, M., and Yang, C. G. (2016). Experimental Study on Effect of Stone Content on Engineering Performance of Crushed Stone Soil. Railway Eng. 02, 97–101. doi:10.36012/etr.v2i10.2804

CrossRef Full Text | Google Scholar

Wang, J. C. (2011). “Experimental Research on Shear Parameter of High Cut Slope Gravel Soil in Badong and its Engineering Application,” (Yichang: China Three Gorges University). M.Sc.

Google Scholar

Wang, X., Pedrycz, W., and Niu, R. (2015). Spatio-temporal Analysis of Quaternary deposit Landslides in the Three Gorges. Nat. Hazards 75 (3), 2793–2813. doi:10.1007/s11069-014-1462-3

CrossRef Full Text | Google Scholar

Wang, Z. G., Hu, R. L., Zhang, R., and Xu, W. (2013). Study of Geotechnical Mechanical Characteristics of a Large Soil-Rock Mixture in a Hydropower Project. Chin. J. Rock Mech. Eng. 32 (S2), 3836–3843. doi:10.21656/1000-0887.400225

CrossRef Full Text | Google Scholar

Wei, H. Z., Wang, R., Hu, M. J., and Zhao, H.-Y. (2008). Strength Behaviour of Gravelly Soil with Different Coarse-Grained Contents in Jiangjiagou Ravine. Rock Soil Mech. 01, 48–51+57. doi:10.12677/hjce.2020.911127

CrossRef Full Text | Google Scholar

Wei, Y., Wu, X., Xia, J., Miller, G. A., Cai, C., Guo, Z., et al. (2019). The Effect of Water Content on the Shear Strength Characteristics of Granitic Soils in South China. Soil Tillage Res. 187, 50–59. doi:10.1016/j.still.2018.11.013

CrossRef Full Text | Google Scholar

Wörman, A. (1993). Seepage‐Induced Mass Wasting in Coarse Soil Slopes. J. Hydraulic Eng. 119 (10), 1155–1168. doi:10.1061/(asce)0733-9429(1993)119:10(1155)

CrossRef Full Text | Google Scholar

Wu, R. (2015). “Study on the Strength experiment of Gravel Soil in the Slope of Daqianshiling Tunnel,” (Wuhan: China university of Geosciences). Ms.c.

Google Scholar

Wu, R. A., Zhang, Y. S., Wang, X. L., Yao, X. L., Yang, Z. H., Du, G. L., et al. (2017). In Situ direct Shearing Test on Landslide Accumulation Body Intensity of Wenchuan Earthquake Region. J. Geomechanics 23 (01), 105–114. doi:10.5194/nhess-2016-193-rc1

CrossRef Full Text | Google Scholar

Xiao, S. Y., Su, L. J., Jiang, Y. J., Qu, X., Xu, M., Hu, X. B., et al. (2020). Experimental investigation on the impact force of the dry granular flow against a flexible barrier. Landslides 17, 1465–1483.

Google Scholar

Xu, D.-S., Tang, J.-Y., Zou, Y., Rui, R., and Liu, H.-B. (2019). Macro and Micro Investigation of Gravel Content on Simple Shear Behavior of Sand-Gravel Mixture. Construction Building Mater. 221, 730–744. doi:10.1016/j.conbuildmat.2019.06.091

CrossRef Full Text | Google Scholar

Xu, W. J., Xu, Q., and Hu, R. L. (2011). Study on the Shear Strength of Soil–Rock Mixture by Large Scale Direct Shear Test. Int. J. Rock Mech. Mining Sci. 48 (8), 1235–1247. doi:10.1016/j.ijrmms.2011.09.018

CrossRef Full Text | Google Scholar

Xue, Y. D., Liu, Z. Q., and Wu, J. (2014). Direct Shear Tests and PFC2D Numerical Simulation of Colluvial Mixture. Rock Soil Mech. 35 (S2), 587–592. doi:10.1007/978-94-015-9285-7_25

CrossRef Full Text | Google Scholar

Yang, J. H., Dong, J. Y., Huang, Z. Q., Zheng, H. G., Qi, D., et al. (2016a). Large-scale Direct Shear Tests on Accumulation Body with Different Stone Contents. Chin. J. Geotechnical Eng. 38 (S2), 161–166. doi:10.18400/tekderg.606816

CrossRef Full Text | Google Scholar

Yang, J. H., Dong, J. Y., Liu, H. D., Huang, Z. Q., Jiang, T., et al. (2010). In Situ direct Shear Tests of the Large-Scale Accumulation Body and Three-Dimensional Stability Analysis of the Slope. J. China Coal Soc. 35 (03), 392–396. doi:10.4028/www.scientific.net/amm.170-173.1124

CrossRef Full Text | Google Scholar

Yang, Y., Sun, G., Zheng, H., and Fu, X. (2016b). A Four-Node Quadrilateral Element Fitted to Numerical Manifold Method with Continuous Nodal Stress for Crack Analysis. Comput. Structures 177, 69–82. doi:10.1016/j.compstruc.2016.08.008

CrossRef Full Text | Google Scholar

Yang, Y. T., Xu, D. D., Liu, F., and Zheng, H. (2020). Modeling the entire progressive failure process of rock slopes using a strength-based criterion. Computers and Geotechnics 126, 103726.

CrossRef Full Text | Google Scholar

Zhang, Z.-L., Xu, W.-J., Xia, W., and Zhang, H.-Y. (2016). Large-scale In-Situ Test for Mechanical Characterization of Soil-Rock Mixture Used in an Embankment Dam. Int. J. Rock Mech. Mining Sci. 86, 317–322. doi:10.1016/j.ijrmms.2015.04.001

CrossRef Full Text | Google Scholar

Zhang, Z. P., Fu, X. D., Sheng, Q., and Du, Y. (2021). Stability of Cracking Deposit Slope Considering Parameter Deterioration Subjected to Rainfall. Int. J. Geomechanics 21 (7), 05021001. doi:10.1061/(asce)gm.1943-5622.0002045

CrossRef Full Text | Google Scholar

Zhang, Z. P., Sheng, Q., Fu, X. D., and Du, Y. X. (2019). An approach to predicting the shear strength of soil-rock mixture based on rock block proportion. Bulletin of Engineering Geology and the Environment 79(1), 2423–2437.

CrossRef Full Text | Google Scholar

Zhang, Z., Sheng, Q., Fu, X., Zhou, Y., Huang, J., and Du, Y. (2020). An Approach to Predicting the Shear Strength of Soil-Rock Mixture Based on Rock Block Proportion. Bull. Eng. Geol. Environ. 79 (5), 2423–2437. doi:10.1007/s10064-019-01658-0

CrossRef Full Text | Google Scholar

Zheng, Y., Wang, R. Q., Chen, C. X., Sun, C. Y., Ren, Z. H., and Zhang, W. (2021). Dynamic analysis of anti-dip bedding rock slopes reinforced by pre-stressed cables using discrete element method. Engineering Analysis with Boundary Elements 130(4), 79–93.

CrossRef Full Text | Google Scholar

Zhou, J. W., Cui, P., and Yang, X. G. (2016). Effects of Material Composition and Water Content on the Mechanical Properties of Landslide Deposits Triggered by the Wenchuan Earthquake. Acta Geologica Sinica (English Edition) 90 (1), 242–257. doi:10.1111/acgs.2016.90.issue-5

CrossRef Full Text | Google Scholar

Zhou, Z., Liu, Z.-z., Yang, H., Gao, W.-y., and Zhang, C.-c. (2020). Freeze-thaw Damage Mechanism of Elastic Modulus of Soil-Rock Mixtures at Different Confining Pressures. J. Cent. South. Univ. 27 (2), 554–565. doi:10.1007/s11771-020-4316-z

CrossRef Full Text | Google Scholar

Zou, L. F., Xu, W. Y., and Shi, C. (2011). Three Dimensional Numerical Analysis of Deformation and Stability of Zone II of Xiazanri Slope deposit. Appl. Mech. Mater. 90-93, 2372–2379. doi:10.4028/www.scientific.net/amm.90-93.2372

CrossRef Full Text | Google Scholar