Shallow Compaction Modeling and Upscaling: A One-Dimensional Analytical Solution and Upscaling

Natural depositional processes frequently give rise to the heterogeneous multilayer system, which is often overlooked but essential for the simulation of a geological process. The sediments undergo the large-strain process in shallow depth and the small-strain process in deep depth. With the transform matrix and Laplace transformation, a new method of solving multilayer small-strain (Terzaghi) and large-strain (Gibson) consolidations is proposed. The results from this work match the numerical results and other analytical solutions well. According to the method of transform matrix which can consider the integral properties of multilayer consolidation, a relevant upscaling method is developed. This method is more effective than the normally used weighted average method. Correspondingly, the upscaling results indicate that the upscaled properties of a multilayer system vary in the consolidation process.

Introduction

Sediment compaction involves the process of reduction in pore volume of the sediment accompanied by an increase in density (Bjørlykke et al., 2009). The physical characteristics of the sediment change after deposition due to stress from overburden (gravitational), biological, or chemical reactions. To explain the major processes for the sediment compaction and help visualize the relationship of porosity loss with depth, various models were developed over the years to better capture the compaction process.

Athy’s (1930a, 1930b) compaction model illustrates that the decrease in porosity with depth is as a result of expulsion of the interstitial fluid within the pores. Hence, porosity reduction and density increase are directly proportional to the increase of overburden and tectonic stresses. Hedberg (1936) classified the process of sediment compaction into four stages: 1) mechanical rearrangement and dewatering of sediments as porosity reduces from 90 to 75%; 2) loss of adsorbed water as porosity reduces from 75 to 35%; 3) mechanical deformation as the sediment resists further compaction, leading to grain recrystallization with porosity from 35 to 10% to even below 10%; and 4) chemical readjustment stage. Athy’s, Hedberg’s, and Terzaghi’s data were adopted for Weller’s model (1959) which states that clay particles occupy the void spaces as the non-clay particles deform and share mutual contact. In addition, Power’s (1967) compaction model is based on changes in clay mineralogy with burial depth and explains clay transformation and changes in the adsorbed water content at different depths.

Teodorovich and Chernov (1968) in their model explained that compaction occurs in three stages: 1) fast expulsion of a large volume of fluid takes place with initial porosity loss, from 66 to 40% for clays and sandstones, and from 56 to 40% for siltstones; 2) porosity falls sharply to approximately 20%; and 3) porosity plunges to about 7–8% for shale and sandstones, at 1,400–6,000 m burial depth. Burst’s (1969) compaction model resembles the previous models of clay transformation and dehydration, and states that the amount of water in movement should constitute 10–15% of the compacted bulk volume. However, this model has not been substantiated by experimental investigation. Interestingly, Beall’s model (1970) is based on his study on core data from offshore Louisiana and from high-pressure experiments on marine muds. Beall’s model involves the expulsion of fluid during initial stages of sediment burial with a pore throat angle at approximately six around a depth of 1,006 m. Here, the porosity decreases at a slower rate during the third stage of compaction where the angle is > 1 Å. In Overton and Zanier’s (1970) model, the compaction of sediments in four stages resembles Beall’s model. This model states that in the Gulf Coast, sands and shales are difficult to distinguish on self-potential electric log at depths less than 3,000 ft due to similarities of water in them. Consequently, Overton and Zanier’s model focused on the different water types in four stages at different depths.

Natural deposition processes frequently give rise to layered soil deposits with alternating or random layers, which are characterized by varying properties such as permeability, compressibility, and thickness. The deposited sediments undergo a large-strain process at shallow depth and a small-strain process in deeper locations. The existence of these processes has been recognized in geology/geotechnical engineering to influence compaction. Small-strain mechanical compaction typically involves minimal deformation of compacted grains due to vertical load and captures the behavior of sediments buried deeply in a basin, whereas large-strain compaction involves large deformation of compacted grains due to its interaction with varying loads at shallow depths. These heterogeneous fine-grained sediments at shallow burial (<1000 m) below the seafloor experience not only large strain but also variable degrees of overpressure in their pore space as a result of disequilibrium dissipation of pore fluid (Mondol et al., 2007). Consequently, the shallow overpressure poses a significant risk to the economics and safety of hydration production and may impact hydrocarbon generation deep in a basin and hydrocarbon migration to traps during basin evolution. In fine-grained sediments, deformations related to mechanical processes are dominant in the very first kilometers of depth (Hedberg, 1936; Maltman, 1994). At greater depths and temperatures, chemically modified consolidation becomes an important porosity-reducing process (Schmid and Mcdonald, 1979; Bjørlykke et al., 1989; Bjørlykke, 1998; Bjørlykke, 1999).

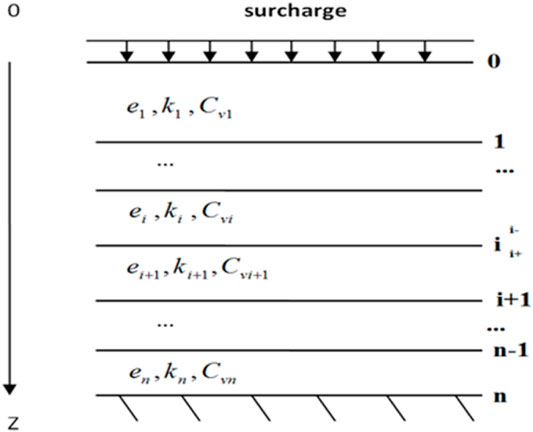
A sketch map for a one-dimensional consolidation model is shown in Figure 1 (left). The surcharge, which is an additional load in the form of a concentrated force or distributed load that acts on a ground surface or inside the soil body, is applied on the top of the sediment with an infinite horizontal width and is surmounted by a certain depth of water on the top of the sediment. The sediment undergoes consolidation processes, in which water flows out from the top and/or bottom boundaries as the sediment height decreases. The top (T) and bottom (B) boundaries may be permeable (P) or impermeable (I) and, hence, can be marked as PTIB (permeable top and impermeable bottom) and PTPB (permeable top and permeable bottom). Figure 1B shows a typical consolidation curve, depicting the consolidation degree versus the time. The consolidation degree is the ratio of the settlement at time t to the final settlement. Hence, the consolidation curve captures the sediment’s consolidation characteristics.

FIGURE 1

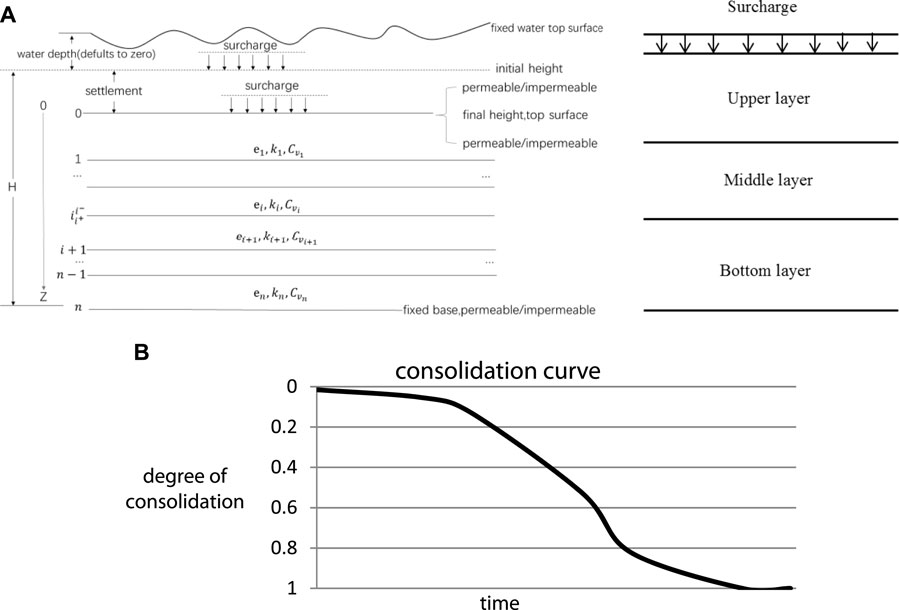
FIGURE 1. (A) Consolidation model sketch map (left), simplified sketch map of three layers with different properties (right). (B) Consolidation curve.

Some geotechnical engineering studies such as basin modeling require the research object to be discretized into blocks, with sizes in kilometers laterally and hundreds of meters vertically. Each block is then assumed to behave according to a single (homogeneous) compaction and flow relationship, even though the material is typically heterogeneous to variable degrees. The basin modeling ignores the heterogeneity of the sediment, large-strain deformation, and fluid flow conditions that occur at smaller length- and/or time-scales than those at basin scales. This can lead to incorrect predication of shallow compaction and overpressure, and subsequently basin evolution (refer to general software in the basin simulation field, such as PetroMod). Therefore, the effects of intra-block heterogeneity must be taken into account by upscaling, which then substitutes the heterogeneous property region consisting of fine grid cells with an equivalent homogeneous region of a single coarse-grid cell having an effective property value (Jingchen 2015).

Theories have been developed by researchers to describe the large-strain and small-strain consolidation processes. However, the widely adopted theories are the Terzaghi theory (Terzaghi, 1943) for small-strain and the Gibson theory (Gibson et al., 1967) for large-strain consolidations. The Terzaghi consolidation theory is widely adopted for small-strain consolidation due to its convenience and its improved methods which are still widely adopted in geotechnical engineering and other fields (Terzaghi, 1943; ArminKauerauf, 2009). As for the large-strain consolidation, the Gibson consolidation theory is more effective (Gibson et al., 1967; Gibson et al., 1981; Gibson et al., 1982), and the equation solutions are primarily based on numerical solution. However, some analytical solutions have been provided under certain conditions (Xie and Leo, 2004; Morris and Dux, 2010).

As for the multilayer system, analytical solutions such as state space (Ai et al., 2008a), three-dimensional transfer matrix solution (Ai et al., 2008b), and differential quadrature method (Chen et al., 2005) have been developed, and numerical finite difference is also widely adopted. In addition, a great deal of research has been done on multilayer consolidation, considering small-strain and large-strain processes (Schiffman and Stein, 1970; Lee et al., 1992; Xie et al., 1999; Xie et al., 2002; Chen, 2004; Chen et al., 2005; Abbasi et al., 2007; Cai et al., 2007; Ai et al., 2008b; Geng, 2008; Ai et al., 2011). However, there are two main drawbacks associated with the previous research studies. The first is that the solutions are under restricted (some parameters such as permeability, compressibility, and height are the same for different layers), and second, none of those researches focused on upscaling and supplying integral property for the multilayer consolidation system. Our work therefore focuses on overcoming these drawbacks.

As earlier mentioned, the effects of intra-block heterogeneity must be taken into account by upscaling. Since the weighted average method commonly adopted in geological engineering for multilayer systems is presently not supported by theoretical derivation, we then implemented the transform matrix and Laplace transformation to solve the multilayer small-strain (Terzaghi) and large-strain (Gibson) consolidations. According to the method of transform matrix which considers the properties of multilayer consolidation, an upscaling method is developed. Results obtained accurately match the numerical and other analytical solutions. Hence, this method is more effective than the common weighted average method. The upscaling results indicate that the properties of multilayer systems change during the consolidation processes.

Analytical Solution and Upscaling for Multilayer Terzaghi Consolidation

Governing Equations of Solution and Upscaling for Multilayer Terzaghi Consolidation

The Terzaghi theory for one-dimensional consolidation states that all quantifiable changes in the stress of a soil (compression, deformation, and shear resistance) are a direct result of changes in effective stress. The effective stress $\sigma \prime$ is related to total stress $\sigma$ and the pore pressure $p$ by the following relationship:

$\sigma =\sigma \prime +p(1)$

The overpressure dissipation is described by the following equation:

$C_{\text{v}}\frac{{\partial }^{2}u}{\partial z^2}=\frac{\partial u}{\partial t},(2)$

$C_{\text{v}}=\frac{k{E}_s}{{\gamma }_w},(3)$

where $C_{\text{v}}$ is the coefficient of consolidation, $E_s$ is the modulus of compressibility, $k$ is the hydraulic conductivity, ${\gamma }_w$ is the unit weight of water, and $u$ is the excess pore pressure.

In addition, Terzaghi’s consolidation theory (Terzaghi, 1929; Terzaghi, 1943) was put forward under the following assumptions:

(1) The soil is homogeneous.

(2) The soil is fully saturated.

(3) The solid particles and water are incompressible.

(4) Soil compression and flow are one-dimensional.

(5) Strains in the soil are relatively small.

(6) Darcy’s law is valid for all hydraulic gradients.

(7) The coefficient of permeability and the coefficient of volume compressibility remain constant throughout the process.

(8) There is a unique relationship, independent of time, between the void ratio and the effective stress.

It is therefore necessary to point out that according to the principle of effective stress, total stress increment is produced by the load applied on the multilayer systems. Resultantly, the effective stress increases with excess pore pressure decrease as time goes on.

$\sigma \prime =\sigma -P(4)$

According to Eq. 4, the following equation with the variable of effective stress increment can be obtained, which will benefit our solution.

$C_{\text{v}}\frac{{\partial }^2\sigma \prime }{\partial z^2}=\frac{\partial \sigma \prime }{\partial t}(5)$

The common weighted average method generates a $C_{\text{v}}$ for the whole multilayer system according to

$C_v=\frac{{\displaystyle \sum _{i=1}^n{h}_i\times C_{v_i}}}{{\displaystyle \sum _{i=1}^n{h}_i}}.(6)$

The Laplace transform is a widely used integral transform with many applications in physics and engineering. Hence, Stehfest numerical inversion of Laplace transforms is adopted (Stehfest, 1960) for our study, and we utilize the transformation matrix to connect parts within the multilayer system. According to the integral multilayer transformation matrix and transformation matrix between different layers, the distribution of effective stress increments and excess pore pressure can be obtained. Moreover, results are verified with an implicit finite difference numerical solution. Figure 2 shows a schematic plot of the multilayer Terzaghi consolidation.

FIGURE 2

FIGURE 2. Schematics of multilayer Terzaghi consolidation (positive axis from 0 to z).

Consequently, the Laplace transform of Eq. 5 can be expanded to

$C_v\frac{{\partial }^2\tilde{\sigma }\prime \left(z,s\right)}{\partial z^2}=s\tilde{\sigma }\prime \left(z,s\right)- \sigma \prime \left(z,0\right),(7)$

where $\tilde{\sigma }\prime \left(z,s\right)$ is the Laplace transform of $\sigma \prime \left(z,t\right)$.

At the beginning of consolidation, according to the effective stress principle, pore pressure is equal to overburden stress, which is zero initial effective stress; thus Eq. 7 can be obtained.

$C_v\frac{{\partial }^2\tilde{\sigma }\prime \left(z,s\right)}{\partial z^2}=s\tilde{\sigma }\prime \left(z,s\right).(\mathrm{7a})$

Then, the general solution of the ordinary differential equation for Eq. 7 is as follows:

$\tilde{\sigma }\prime \left(z,s\right)= c_1\exp \left(\beta z\right)+c_2\exp \left(-\beta z\right),(8)$

where $c_1$ and $c_2$ are constants, $\beta =\sqrt{\frac{s}{c_v}}$ .

Combining Eq 9 错误!未找到引用源。 and its partial derivative about z, the following expression can be derived:

$\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(z,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z,s\right)}{\partial z}\end{array}\right]=\left[\begin{array}{cc}\exp \left(\beta z\right)& \exp \left(-\beta z\right)\\ \beta \exp \left(\beta z\right)& -\beta \exp \left(-\beta z\right)\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right].(9)$

When $\mathbf{z}=0$:

$\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(0,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(0,s\right)}{\partial z}\end{array}\right]=\left[\begin{array}{cc}1& 1\\ \beta & -\beta \end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right].(\mathrm{9a})$

Combining Eq 10 and Eq 11 yields Eq. 12:

$\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(0,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(0,s\right)}{\partial z}\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\left[\exp \left(-\beta z\right)+\exp \left(\beta z\right)\right]& \frac{1}{2\beta }\left[\exp \left(-\beta z\right)-\exp \left(\beta z\right)\right]\\ \frac{\beta }{2}\left[\exp \left(-\beta z\right)-\exp \left(\beta z\right)\right]& \frac{1}{2}\left[\exp \left(-\beta z\right)+\exp \left(\beta z\right)\right]\end{array}\right]\left[\begin{array}{c}\stackrel{\sim }{\sigma }\prime \left(z,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z,s\right)}{\partial z}\end{array}\right].(10)$

And when $z_i$ is not zero:

$\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(z_i,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z_i,s\right)}{\partial z}\end{array}\right]=\left[\begin{array}{cc}1& 1\\ \beta & -\beta \end{array}\right]\left[\begin{array}{cc}\exp \left(\beta z_i\right)& 0\\ 0& \exp \left(-\beta z_i\right)\end{array}\right]\left[\begin{array}{cc}\frac{\beta }{2\beta \exp \left(\beta z\right)}& \frac{1}{2\beta \exp \left(\beta z\right)}\\ \frac{\beta }{2\beta \exp \left(-\beta z\right)}& \frac{-1}{2\beta \exp \left(-\beta z\right)}\end{array}\right]\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(z,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z,s\right)}{\partial z}\end{array}\right].(11)$

Then the relationship between the top surface stress and the bottom stress can be derived. When considering the equation of continuous stress, and flow conservation, between two layers, the relationship between different layers can be derived.

$k_i\frac{\partial \stackrel{\sim }{{\sigma }^{\prime }}\left(z_i^{-},s\right)}{\partial z}=k_{i+1}\frac{\partial \stackrel{\sim }{{\sigma }^{\prime }}\left(z_i^{+},s\right)}{\partial z},(12)$

$\stackrel{\sim }{{\sigma }^{\prime }}\left(z_i^{-},s\right)=\stackrel{\sim }{{\sigma }^{\prime }}\left(z_i^{+},s\right).(13)$

Combining Eq 12 and Eq 13 yields Eq. 16:

$\left[\begin{array}{c}\stackrel{\sim }{{\sigma }^{\prime }}\left(z_i^{-},s\right)\\ \frac{\partial \stackrel{\sim }{{\sigma }^{\prime }}\left(z_i^{-},s\right)}{\partial z}\end{array}\right]=\left[\begin{array}{cc}1& \\ & \frac{k_{i+1}}{k_i}\end{array}\right]\left[\begin{array}{c}\stackrel{\sim }{{\sigma }^{\prime }}\left(z_i^{+},s\right)\\ \frac{\partial \stackrel{\sim }{{\sigma }^{\prime }}\left(z_i^{+},s\right)}{\partial z}\end{array}\right].(14)$

Stress distribution in the same layer and in the interface can be derived, respectively, by using Eq. 11 and Eq. 14. With the equation of each layer combined together, a transform matrix T can be obtained to express the relationship between $z=0$ and $z=z_n$.

$\left[\begin{array}{c}\stackrel{\sim }{{\sigma }^{\prime }}\left(0,s\right)\\ \frac{\stackrel{\sim }{\partial {\sigma }^{\prime }}\left(0,s\right)}{\partial z}\end{array}\right]=T\left[\begin{array}{c}\stackrel{\sim }{{\sigma }^{\prime }}\left(z_n,s\right)\\ \frac{\stackrel{\sim }{\partial {\sigma }^{\prime }}\left(z_n,s\right)}{\partial z}\end{array}\right](15)$

Here, this article only considers the situation of the pervious top surface and impervious bottom PTIB for illustration.

The following boundary conditions are implemented:

$\text{z}=\text{0,u}\left(\text{z,t}\right){=\text{0; z}=\text{z}}_{\text{n}}\text{ , }\frac{\partial \text{u}\left(z,t\right)}{\partial z}=0.(16)$

The corresponding Laplace transformation:

$z=0,\stackrel{\sim }{{\sigma }^{\prime }}\left(0,s\right)=\frac{\sigma }{s};z=z_n,\frac{\stackrel{\sim }{\partial {\sigma }^{\prime }}\left(z_n,s\right)}{\partial z}=0(17)$

Hence

$\stackrel{\sim }{{\sigma }^{\prime }}\left(z_n,s\right)=\frac{\sigma }{T_{11}S},(18)$

where σ is the pressure on the surface and T₁₁ is the value of the first column and the first row of T.

With $\stackrel{\sim }{\sigma \prime }\left(z_n,s\right)$, the stress at each upper point $\stackrel{\sim }{\sigma \prime }\left(z,s\right)$ can be obtained by the transformation matrix. Moreover, the real stress distribution can be derived by the inverse of Laplace transformation.

As for an n-layer consolidation system, the multilayer consolidation transform matrix is

$\begin{array}{l}{T}_1=\left[\begin{array}{cc}\frac{1}{2}\left[\exp \left(-{\beta }_1{h}_1\right)+\exp \left({\beta }_1{h}_1\right)\right]& \frac{k_2}{k_1}\frac{1}{2{\beta }_1}\left[\exp \left(-{\beta }_1{h}_1\right)-\exp \left({\beta }_1{h}_1\right)\right]\\ \frac{{\beta }_1}{2}\left[\exp \left(-{\beta }_1{h}_1\right)-\exp \left({\beta }_1{h}_1\right)\right]& \frac{k_2}{k_1}\frac{1}{2}\left[\exp \left(-{\beta }_1{h}_1\right)+\exp \left({\beta }_1{h}_1\right)\right]\end{array}\right]\\ T_i=\left[\begin{array}{cc}\frac{1}{2}\left[\exp \left(-{\beta }_i{h}_i\right)+\exp \left({\beta }_i{h}_i\right)\right]& \frac{k_{i+1}}{k_i}\frac{1}{2{\beta }_i}\left[\exp \left(-{\beta }_i{h}_i\right)-\exp \left({\beta }_i{h}_i\right)\right]\\ \frac{{\beta }_i}{2}\left[\exp \left(-{\beta }_i{h}_i\right)-\exp \left({\beta }_i{h}_i\right)\right]& \frac{k_{i+1}}{k_i}\frac{1}{2}\left[\exp \left(-{\beta }_i{h}_i\right)+\exp \left({\beta }_i{h}_i\right)\right]\end{array}\right]\\ T_n=\left[\begin{array}{cc}\frac{1}{2}\left[\exp \left(-{\beta }_n{h}_n\right)+\exp \left({\beta }_n{h}_n\right)\right]& \frac{1}{2{\beta }_n}\left[\exp \left(-{\beta }_n{h}_n\right)-\exp \left({\beta }_n{h}_n\right)\right]\\ \frac{{\beta }_n}{2}\left[\exp \left(-{\beta }_n{h}_n\right)-\exp \left({\beta }_n{h}_n\right)\right]& \frac{1}{2}\left[\exp \left(-{\beta }_n{h}_n\right)+\exp \left({\beta }_n{h}_n\right)\right]\end{array}\right]\\ \left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(0,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(0,s\right)}{\partial z}\end{array}\right]=T_1\cdot \cdot T_i\cdot \cdot T_n.\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(z_n,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z_n,s\right)}{\partial z}\end{array}\right],i=2,3.......n-1\end{array}(19)$

The common weighted average method will lead to the following weighted average method transform matrix:

$\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(0,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(0,s\right)}{\partial z}\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\left[\exp \left(-\beta z_n\right)+\exp \left(\beta z_n\right)\right]& \frac{1}{2\beta }\left[\exp \left(-\beta z_n\right)-\exp \left(\beta z_n\right)\right]\\ \frac{\beta }{2}\left[\exp \left(-\beta z_n\right)-\exp \left(\beta z_n\right)\right]& \frac{1}{2}\left[\exp \left(-\beta z_n\right)+\exp \left(\beta z_n\right)\right]\end{array}\right]\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(z_n,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z_n,s\right)}{\partial z}\end{array}\right].(20)$

When $t\to \infty ,s\to 0,\beta \to 0$, by applying the following Taylor expansion we obtain

$e^x={\displaystyle \sum _{n=0}^{\infty }\frac{x^n}{n!}}.(21)$

As for a multilayer transform matrix, Eq. 18 will develop into

$\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(0,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(0,s\right)}{\partial z}\end{array}\right]=\left[\begin{array}{cc}1& -\left(h_n+{\displaystyle \sum _{i=1}^{n-1}\frac{k_n}{k_i}{h}_i}\right)\\ 0& \frac{k_n}{k_1}\end{array}\right]\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(z_n,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z_n,s\right)}{\partial z}\end{array}\right].(22)$

Then, the weighted average method transform matrix given in Eq. 20 will develop into

$\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(0,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(0,s\right)}{\partial z}\end{array}\right]=\left[\begin{array}{cc}1& -z\\ 0& 1\end{array}\right]\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(z,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z,s\right)}{\partial z}\end{array}\right].(23)$

It can therefore be concluded that when conductivities in different layers are nearly the same, the weighted average method can be adopted for the whole multilayer system, which is the situation of homogenous.

Verification

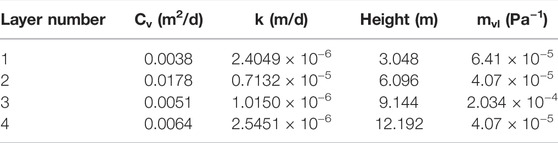
This analytical solution is verified against the results of Lee et al. (1992), as shown in Figure 3. The parameters used in Lee’s model are shown in Table 1, and the model sketch map follows the illustration in Figure 1 (right), showing a simplified sketch map of four layers with a PTIB and without overlaying water.

FIGURE 3

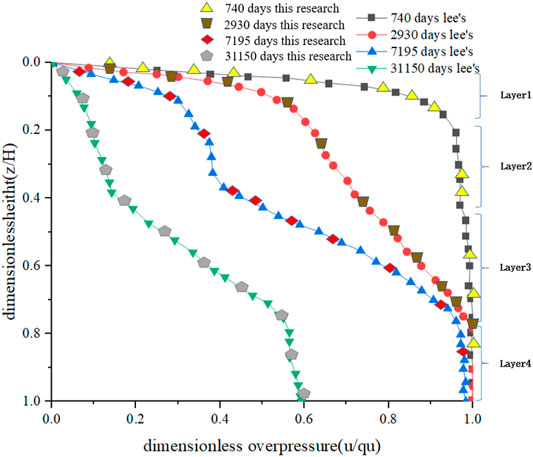
FIGURE 3. Verification with Lee—excess pore water pressure isochrones and PTIB ($q_u$ is the surcharge on the surface and $H$ is the height of the multilayer system).

TABLE 1

TABLE 1. Parameters of Lee’s model $\left(m_{vl}=1/E_s\right).$

To compare different upscaling methods, an implicit finite-difference numerical model is developed. This study utilizes a numerical model as a benchmark model and is verifiable with both laboratory tests and a basin model (Jingchen Zhang., 2015). Analytical results are also compared with implicit finite difference numerical solution for verification. The parameters of the three different layers are shown in Table 2. Comparison of the results is then shown in Figure 4. Hence, a conclusion can be reached that this method can be applied to multilayer Terzaghi consolidation compaction. It should be noted that the values of $m_{vl}$ and surcharge ensure the small strain, and correspondingly nearly no settlement can be seen in Figure 4. Resultantly, the small changes in height are shown in Figure 5.

TABLE 2

TABLE 2. Model parameters $\left(m_{vl}=1/E_s\right).$

FIGURE 4

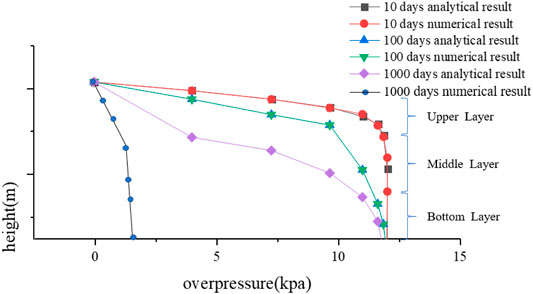
FIGURE 4. Comparison of overpressure evolution of three layers with different properties between analytical and numerical results for 10, 100, 1,000 days.

FIGURE 5

FIGURE 5. Graph of height evolution with respect to time.

Comparisons of Different Upscaling Methods

Here, $T$ represents the properties of the multilayer system; then a new consolidation coefficient $C_{\text{v}}$ is needed to represent the whole multilayer system. With the new $C_{\text{v}}$, a new transform matrix for the multilayer consolidation $T\prime$ can be obtained. The new $C_{\text{v}}$ should be the one that makes the minimum of Eq. 24, to numerically match $T$ and $T\prime$.

$\sqrt{{\left(T\prime \left(\mathrm{1,1}\right)-T\left(\mathrm{1,1}\right)\right)}^2+{\left(T\prime \left(\mathrm{1,2}\right)-T\left(\mathrm{1,2}\right)\right)}^2+{\left(T\prime \left(\mathrm{2,1}\right)-T\left(\mathrm{2,1}\right)\right)}^2+{\left(T\prime \left(\mathrm{2,2}\right)-T\left(\mathrm{2,2}\right)\right)}^2}(24)$

Under the condition of PTIB, it can be found that $\frac{\stackrel{\sim }{\partial \sigma \prime }\left(z_n,s\right)}{\partial z}=0$, so $\stackrel{\sim }{\sigma }\left(0,s\right)=T\left(\mathrm{1,1}\right)\times \stackrel{\sim }{\sigma \prime }\left(z_n,s\right)\prime$. This provides a thought of using a homogeneous layer $T\left(\mathrm{1,1}\right)$ to represent multilayer nonhomogeneous consolidation. A new $\beta$ is required to fit the value of $T\left(\mathrm{1,1}\right)$. The example of the afore-mentioned three layers with different properties is adopted for this illustration. The new $C_{\text{v}}$ can be derived from

$\frac{1}{2}\left[e^{-\beta z}+e^{\beta z}\right]=T\left(\mathrm{1,1}\right).(25)$

$C_{\text{v}}$ changes with time according to Eq. 25, as shown in Figure 6.

FIGURE 6

FIGURE 6. Plot of consolidation coefficient $c_v$ versus time.

In light of the long-time consolidation, $C_{\text{v}}$ is set to be 1.4 × 10⁻⁸ (m²/s). A homogeneous layer with the new upscaling $C_{\text{v}}$ can then be compared with the three-layer system. Specifically, the transform matrix for a three-layer system is

$\begin{array}{l}{T}_1=\left[\begin{array}{cc}\frac{1}{2}\left[e^{-{\beta }_1{h}_1}+e^{{\beta }_1{h}_1}\right]& \frac{k_2}{k_1}\frac{1}{2{\beta }_1}\left[e^{-{\beta }_1{h}_1}-e^{{\beta }_1{h}_1}\right]\\ \frac{{\beta }_1}{2}\left[e^{-{\beta }_1{h}_1}-e^{{\beta }_1{h}_1}\right]& \frac{k_2}{k_1}\frac{1}{2}\left[e^{-{\beta }_1{h}_1}+e^{{\beta }_1{h}_1}\right]\end{array}\right]\\ T_2=\left[\begin{array}{cc}\frac{1}{2}\left[e^{-{\beta }_2{h}_2}+e^{{\beta }_2{h}_2}\right]& \frac{k_3}{k_2}\frac{1}{2{\beta }_2}\left[e^{-{\beta }_2{h}_2}-e^{{\beta }_2{h}_2}\right]\\ \frac{{\beta }_2}{2}\left[e^{-{\beta }_2{h}_2}-e^{{\beta }_2{h}_2}\right]& \frac{k_3}{k_2}\frac{1}{2}\left[e^{-{\beta }_2{h}_2}+e^{{\beta }_2{h}_2}\right]\end{array}\right].\\ T_3=\left[\begin{array}{cc}\frac{1}{2}\left[e^{-{\beta }_3{h}_3}+e^{{\beta }_3{h}_3}\right]& \frac{1}{2{\beta }_3}\left[e^{-{\beta }_3{h}_3}-e^{{\beta }_3{h}_3}\right]\\ \frac{{\beta }_3}{2}\left[e^{-{\beta }_3{h}_3}-e^{{\beta }_3{h}_3}\right]& \frac{1}{2}\left[e^{-{\beta }_3{h}_3}+e^{{\beta }_3{h}_3}\right]\end{array}\right]\\ \left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(0,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(0,s\right)}{\partial z}\end{array}\right]=T_1{T}_2{T}_3.\left[\begin{array}{c}\stackrel{\sim }{\sigma \prime }\left(z_3,s\right)\\ \frac{\stackrel{\sim }{\partial \sigma \prime }\left(z_3,s\right)}{\partial z}\end{array}\right].\end{array}(26)$

Meanwhile, the common weighted average method will lead to another $C_{\text{v}}$. Here, C_v = 3.0093 × 10⁻⁸ (m²/s) in the weighted average method is used. With this $C_{\text{v}}$, a new $\beta$ and a weighted average transform matrix can be derived. Comparisons between the three methods are shown in Figure 7.

$R=\frac{{\displaystyle \sum _{i=1}^n\left|u_i^{\prime }-u_i\right|/u_i}}{n}(27)$

FIGURE 7

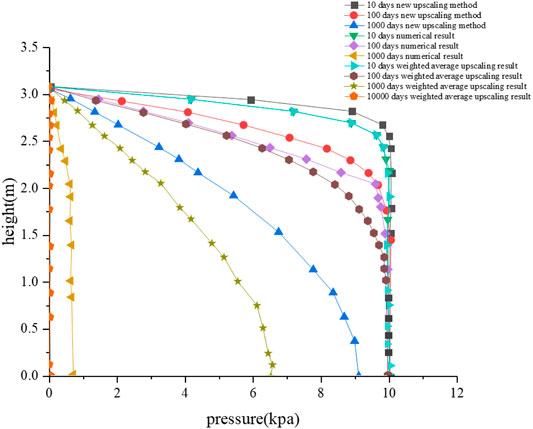
FIGURE 7. Overpressure evolution comparison between the two upscaling methods (weighted average and the new method) and numerical results for 10, 100, 1,000, and 10,000 days.

According to Eq. 27, the relative error between the weighted average method or the new upscaling method and the three-layer numerical results can be obtained, as shown in Figure 8.

FIGURE 8

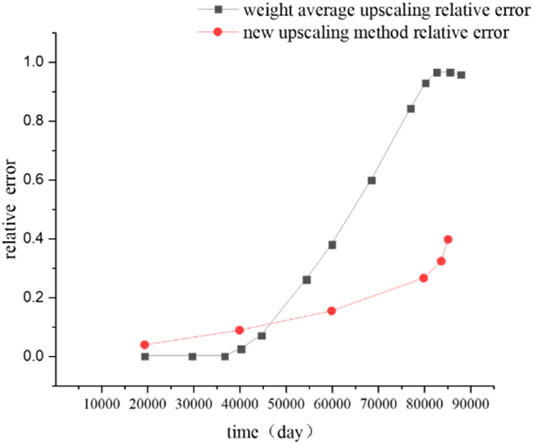
FIGURE 8. Plot of relative error change with time for weighted average upscaling and the new upscaling method.

When it comes to 20,000 days, there is nearly no overpressure; hence, the multilayer system’s characteristics are studied within 20,000 days. As can be seen from Figure 9, in the first 100 days, the weighted average method is more efficient than the upscaling method. As fluid flows out through the top surface, the whole system is determined by the properties of the first layer before pressure reduction reaches the second layer. Overpressure distributions of one homogeneous layer (same properties with the upper layer) and three nonhomogeneous layers’ consolidation are the same. This can explain why the results of changing $C_{\text{v}}$ and the weighted average method compact faster than the real situation. The possible explanation is that bigger $C_{\text{v}}$ of the upper layer is applied to the whole layers with small $C_{\text{v}}$ characteristics. The multilayer consolidation will show the integral properties more accurately after the stimulation reaches the bottom.

FIGURE 9

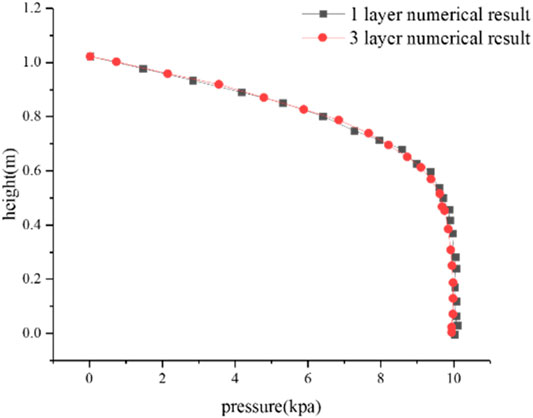
FIGURE 9. Result of one homogeneous layer and three layers’ consolidation before the stimulation reaches the second layer, overpressure distribution at 10 days.

Analytical Solution and Upscaling for Multilayer Gibson Consolidation

Governing Equations of Solution and Upscaling for Multilayer Gibson Consolidation

Gibson et al. (1967) developed a large-strain consolidation theory with more general basic assumptions than the small-strain theory in (3), (5), and (7) of Terzaghi’s assumptions. The limitation of small strains was not imposed, and the soil compressibility and permeability are allowed to vary with the void ratio during consolidation. These assumptions are closer to the actual scenario. Furthermore, Darcy’s law is assumed to be valid, but it is recasted in a form in which it is the relative velocity of the soil skeleton and the pore fluid. The fluid velocity is related to the excess pore pressure gradient.

$-\frac{1}{1+e_0}\frac{\partial e}{\partial t}+\left(\frac{{\gamma }_{\text{s}}}{{\gamma }_{\text{w}}}-1\right)\frac{d}{de}\left[\frac{k}{1+e}\right]\frac{\partial e}{\partial z}+\frac{\partial }{\partial z}\left[-\frac{k\left(1+e_0\right)}{{\gamma }_{\text{w}}\left(1+e\right)}\frac{d\sigma \prime }{de}\frac{\partial e}{\partial z}\right]=0,(28)$

where $e$ is the void ratio; $e_0$ is the initial void ratio; $k$ is the conductivity; ${\gamma }_w$ and ${\gamma }_s$ are the unit weight of water and soil, respectively;$z$ is the solid coordinate; and $\sigma \prime$ is the effective stress.

To apply the transfer matrix method to large-strain consolidation, the simplification of Xie et al. is adopted to simplify Gibson’s equation (Xie and Leo, 2004). The influence and theoretical analysis of this simplification can be found in his research.

The coefficient of volume compressibility of the soil skeleton for a large strain is defined as

$-\frac{1}{1+e}\frac{de}{d\sigma \prime }=m_{vl}.(29)$

Then Gibson’s equation can be changed to

$\frac{1}{{\gamma }_w}\frac{\partial }{\partial z}\left[\frac{k\left(1+e_0\right)}{\left(1+e\right)}\frac{\partial u}{\partial z}\right]=m_{vl}\frac{1+e}{1+e_0}\left(\frac{\partial u}{\partial t}-\frac{\partial q_u}{\partial t}\right),(30)$

where $q_u$ is the surcharge and $m_{vl}$ is constant during consolidation.

The relationship between conductivity $k$ and void ratio is

$\frac{k}{k_o}={\left(\frac{1+e}{1+e_0}\right)}^2,(31)$

where $k_o$ is the initial conductivity at time t = 0, $k$ is often found empirically to be a logarithmic function of the void ratio, and e₀ is the initial void ratio.

A load $q_u$ is applied suddenly at t = 0 on the top surface of the model and remains constant thereafter. According to the effective stress principle and Xie’s assumption (Xie, K. & Leo, C., 2004), the relationship between the void ratio and the excess pore water pressure can be deduced as follows.

$\frac{1+e}{1+e_0}=\exp \left(-m_{vl}\left(q_u-u\right)\right)(32)$

With Eq. 29, Eq. 30 and Eq. 32 can now be changed to the following one, which determines excess pore evolution in Lagrangian coordinates:

$c_{vo}\left[\frac{{\partial }^{2}u}{\partial z^2}+m_{vl}{\left(\frac{\partial u}{\partial z}\right)}^2\right]=\frac{\partial u}{\partial t},(33)$

where $c_{vo}$ is the initial coefficient of consolidation at time t = 0 given by

$c_{vo}=\frac{k_o}{m_{vl}{r}_w}.(34)$

The solution to the large consolidation theory is facilitated by the following transformation.

$\omega =\omega \left(z,t\right)=\exp \left(m_{vl}u\right)(35)$

In consideration of the permeable top impermeable base (PTIB) boundary condition, with Eq. 35 and Eq. 33, the equation of the Terzaghi form will be obtained as follows:

$\begin{array}{l}{c}_v\frac{{\partial }^2\omega }{\partial z^2}=\frac{\partial \omega }{\partial t}\\ \omega \left(0,t\right)=1\\ \frac{\partial \omega }{\partial z}\left(H,t\right)=0\\ \omega \left(H,0\right)=\exp \left(m_{vl}{q}_u\right).\end{array}(36)$

Then the transfer matrix can be adopted for the solution and upscaling of multilayer Gibson consolidation. To use the transfer matrix method, $\omega$ should be continuous; hence, different layers share the same $m_{vl}$. Then according to Eq. 34, what upscaled is actually $k_o$, i.e., conductivity upscaling.

Verification

Analytical solution is compared with the developed implicit finite difference numerical code for verification. The model sketch map follows Figure 1 错误!未找到引用源。 (right), PTIB, and no overlying water. A three-layer model is adopted for comparison, with the surcharge 1 × 105 Pa, γ_s = 26.950 kN/m³, and γ_w = 10.045 kN/m³. For each layer, m_vl = 4 × 10⁻⁶ Pa⁻¹ and thickness = 5 m. The $k_o$ of the surface, middle, and bottom layers are 1.00 × 10⁻⁹ m/s, 1.16 × 10⁻¹⁰ m/s, and 1.04 × 10⁻⁹ m/s. The $e_0$ of the surface, middle, and bottom layers are 3, 4, and 5. Figure 10 shows the comparison results, which are consistent and proves the effectiveness of this method in solving large-strain multilayer consolidation.

FIGURE 10

FIGURE 10. Overpressure evolution comparison of numerical and analytical results for the three layers with different properties for 1, 10, 100, and 1,000 years.

Comparisons of Different Upscaling Methods

To evaluate this upscaling method, comparison with the weighted average method is carried out here, utilizing the same three-layer model in Verification. When it comes to 1,000 years, there are nearly no excess pore pressures according to the weighted average method; hence, we focus within 1,000 years.

Upscaling $k_{vo}$ changes with time as shown in Figure 11. In consideration of the long geology process, the $k_o$ value is set to be 2.8356 × 10⁻¹⁰ (m/s), and $C_{\text{v}}$ is 7.2337 × 10⁻⁹ (m²/s). While for the weighted average method, $k_o$ is 7.1867 × 10⁻¹⁰ (m/s) and $C_{\text{v}}$ is 1.8333 × 10⁻⁹ (m²/s). The comparisons of the two upscaling methods and numerical solution are shown in Figure 12.

FIGURE 11

FIGURE 11. lot of upscaled permeability k_o changes with respect to time.

FIGURE 12

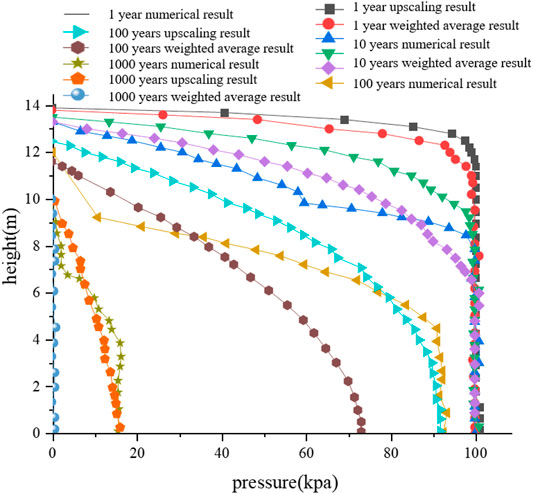
FIGURE 12. Overpressure evolution comparison between the two upscaling methods (weighted average and the new method) and numerical results for 1, 10, 100, and 1,000 years.

The whole model only shows properties of the first layer before the pressure reduction reaches the second layer. Also, the weighted average $k_o$ is closer to the first layer’s $k_o$ than the upscaled $k_o$. Hence, within the first 10 years, the results obtained through the weighted average method are closer to the numerical results than those obtained through the upscaling method. However, as a whole, the upscaling method is more effective than the weighted average method.

The multilayer system only shows properties of the place affected by the stimulation, and the integral properties will change with the increase in the affected region. This can partly explain the result of a changing upscaled $k_o$. Consequently, this upscaling method is more accurate than the common weighted average method as a whole for multilayer large-strain consolidation.

Conclusion

This work studies the modeling and upscaling of a shallow compaction using a one-dimensional analytical solution approach. The basic law of one-dimensional basin sedimentary simulation is revealed considering the effects of intra-block heterogeneity for both small-strain (deep compaction in the basin) and large-strain (shallow compaction in the basin) consolidations. And the following conclusions are made:

1. Multilayer small-strain (Terzaghi) and large-strain (Gibson) consolidations are solved with the transform matrix and Laplace transformation. The transfer matrix can upscale the heterogeneous multilayer system into one homogenous layer; therefore, it is more convenient and effective in both physical significance and the numerical form than the common weighted average method.

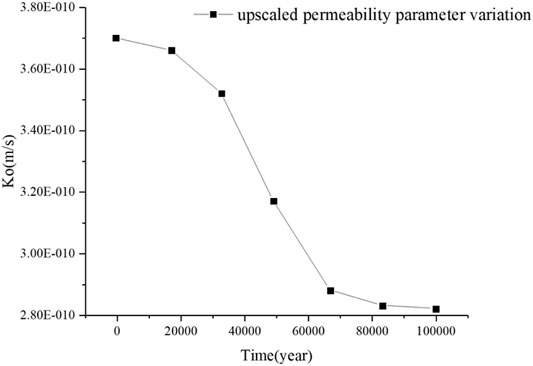
2. The upscaling properties of the whole multilayer system are dynamic, and the multilayer systems only show integral properties of the place affected by the stimulation. The integral properties vary with the increase in the affected region for both small-strain and large-strain consolidations.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

JZ is the key contributor. JM plays a guiding role. GDC: research supervision and obtaining fund.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The research content reported here is part of the first author's PhD research at Heriot-Watt University, Edinburgh, United Kingdom, under CAPROCKS consortium of United Kingdom universities, Newcastle University, Cardiff University, Heriot-Watt University, and University of Leeds. This study was funded by the following companies: Anadarko, BG, BHP Billiton, BP, Chevron, ConocoPhillips, ENI, ExxonMobil, Petrobras, Shell, StatoilHydro, Total, and Unocal.

References

Abbasi, N., Rahimi, H., Javadi, A. A., and Fakher, A. (2007). Finite Difference Approach for Consolidation with Variable Compressibility and Permeability. Comput. Geotechnics 34, 41–52. doi:10.1016/j.compgeo.2006.09.003

CrossRef Full Text | Google Scholar

Ai, Z. Y., Cheng, Y. C., and Zeng, W. Z. (2011). Analytical Layer-Element Solution to Axisymmetric Consolidation of Multilayered Soils. Comput. Geotechnics 38, 227–232. doi:10.1016/j.compgeo.2010.11.011

CrossRef Full Text | Google Scholar

Ai, Z. Y., Cheng, Z. Y., and Han, J. (2008a). State Space Solution to Three-Dimensional Consolidation of Multi-Layered Soils. Int. J. Eng. Sci. 46, 486–498. doi:10.1016/j.ijengsci.2007.12.003

CrossRef Full Text | Google Scholar

Ai, Z. Y., Wu, C., and Han, J. (2008b). Transfer Matrix Solutions for Three-Dimensional Consolidation of a Multi-Layered Soil with Compressible Constituents. Int. J. Eng. Sci. 46, 1111–1119. doi:10.1016/j.ijengsci.2008.04.005

CrossRef Full Text | Google Scholar

ArminKauerauf, I. T. H. (2009). Fundamentals of Basin and Petroleum Systems Modeling.

Google Scholar

Athy, L. F. (1930b). Compaction and Oil Migration. AAPG Bull. 14, 25–35. doi:10.1306/3d93289f-16b1-11d7-8645000102c1865d

CrossRef Full Text | Google Scholar

Athy, L. F. (1930a). Density, Porosity, and Compaction of Sedimentary Rocks. AAPG Bull. 14 (1), 1–24. doi:10.1306/3d93289e-16b1-11d7-8645000102c1865d

CrossRef Full Text | Google Scholar

Beall, A. O., and Fisher, A. G. (1969). “Sedimentology”. Editors (Washington, D.C: US. Govt. Printing Office), 1, 672. doi:10.2973/dsdp.proc.1.124.1969Initial Reports of the Deep-Sea Drilling Project

CrossRef Full Text | Google Scholar

Bjørlykke, K. (1998). Clay Mineral Diagenesis in Sedimentary Basins - a Key to the Prediction of Rock Properties. Examples from the North Sea Basin. Clay Minerals 33, 15–34.

Google Scholar

Bjørlykke, K., Jahren, J., Mondol, N. H., Marcussen, O., Croize, D., Christer, P., et al. (2009). “Sediment Compaction and Rock Properties,” in AAPG International Conference and Exhibition.

Google Scholar

Bjørlykke, K. (1999). Muds and Mudstones: Physical and Fluid Flow Properties. London, United Kingdom: The Geological Society (London) Special Publications, 73–78.Principal Aspects of Compaction and Fluid Flow in Mudstones

Google Scholar

Bjørlykke, K., Ramm, M., and Saigal, G. C. (1989). Sandstone Diagenesis and Porosity Modification during Basin Evolution. Geologische Rundschau 78, 243–268.

Google Scholar

Burst, J. F. (1969). Diagenesis of Gulf Coast Clayey Sediments and its Possible Relation to Petroleum Migration. AAPG Bull. 53, 73–93. doi:10.1306/5d25c595-16c1-11d7-8645000102c1865d

CrossRef Full Text | Google Scholar

Cai, Y.-Q., Geng, X.-Y., and Xu, C.-J. (2007). Solution of One-Dimensional Finite-Strain Consolidation of Soil with Variable Compressibility under Cyclic Loadings. Comput. Geotechnics 34, 31–40. doi:10.1016/j.compgeo.2006.08.008

CrossRef Full Text | Google Scholar

Chen, G. J. (2004). Consolidation of Multilayered Half Space with Anisotropic Permeability and Compressible Constituents. Int. J. Sol. Structures 41, 4567–4586. doi:10.1016/j.ijsolstr.2004.03.019

CrossRef Full Text | Google Scholar

Chen, R. P., Zhou, W. H., Wang, H. Z., and Chen, Y. M. (2005). One-Dimensional Nonlinear Consolidation of Multi-Layered Soil by Differential Quadrature Method. Comput. Geotechnics 32, 358–369. doi:10.1016/j.compgeo.2005.05.003

CrossRef Full Text | Google Scholar

Geng, X. (2008). Proceedings of the 2008 International Conference on Advanced Computer Theory and Engineering. IEEE Computer Society, 773–777. doi:10.1109/icacte.2008.219Multi-Dimensional Consolidation Theory for Cyclic Loadings

CrossRef Full Text | Google Scholar

Gibson, R. E., England, G. L., and Hussey, M. J. L. (1967). The Theory of One-Dimensional Consolidation of Saturated Clays. Géotechnique 17, 261–273. doi:10.1680/geot.1967.17.3.261

CrossRef Full Text | Google Scholar

Gibson, R. E., Schiffman, R. L., and Cargill, K. W. (1982). The Theory of One-Dimensional Consolidation of Saturated Clays: Reply. Can. Geotech. J. 19, 116. doi:10.1139/t82-013

CrossRef Full Text | Google Scholar

Gibson, R. E., Schiffman, R. L., and Cargill, K. W. (1981). The Theory of One-Dimensional Consolidation of Saturated Clays. Ii. Finite Nonlinear Consolidation of Thick Homogeneous Layers. Can. Geotech. J. 18, 280–293. doi:10.1139/t81-030

CrossRef Full Text | Google Scholar

Hedberg, H. D. (1936). Gravitational Compaction of Clays and Shales. Am. J. Sci. s5-31, 241–287. doi:10.2475/ajs.s5-31.184.241

CrossRef Full Text | Google Scholar

Jingchen, Zhang. (2015). Modelling and Upscaling of Shallow Compaction in Basins. PHD thesis: Heriot-watt university.

Google Scholar

Lee, P. K. K., Xie, K. H., and Cheung, Y. K. (1992). A Study on One-Dimensional Consolidation of Layered Systems. Int. J. Numer. Anal. Methods Geomech. 16, 815–831. doi:10.1002/nag.1610161104

CrossRef Full Text | Google Scholar

Maltman, A. (1994). The Geological Deformation of Sediments. London: Chapman & Hall, 1–35. doi:10.1007/978-94-011-0731-0_1Introduction and Overview

CrossRef Full Text | Google Scholar

Mondol, N. H., Bjørlykke, K., Jahren, J., and Høeg, K. (2007). Experimental Mechanical Compaction of clay mineral Aggregates-Changes in Physical Properties of Mudstones during Burial. Mar. Pet. Geology. 24 (5), 289–311. doi:10.1016/j.marpetgeo.2007.03.006

CrossRef Full Text | Google Scholar

Morris, P. H., and Dux, P. F. (2010). Analytical Solutions for Bleeding of Concrete Due to Consolidation. Cement Concrete Res. 40, 1531–1540. doi:10.1016/j.cemconres.2010.06.007

CrossRef Full Text | Google Scholar

Overton, H. L., and Zanier, A. M. (1970). Hydratable Shales and the Salinity High enigma, 2989. Houston, TX, Pap: Fall Meeting of the Society of Petroleum Engineers of AIMESociety of Petroleum Engineers, 9.

Google Scholar

Powers, M. C. (1967). Fluid-release Mechanism in Compacting marine Mud-Rocks and Their Importance in Oil Exploration. AAPG Bull. 51, 1240–1245. doi:10.1306/5d25c137-16c1-11d7-8645000102c1865d

CrossRef Full Text | Google Scholar

Schiffman, R. L., and Stein, J. R. (1970). One-Dimensional Consolidation of Layered Systems. J. Soil Mech. Found. Div. 96 (4), 1499–1504. doi:10.1061/jsfeaq.0001453

CrossRef Full Text | Google Scholar

Schmidt, V., and Mcdonald, D. A. (1979). “The Role of Secondary Porosity in the Course of Sandstone Diagenesis,”. Editors P. A. SchoUe, and P. R. Schluger (Tulsa, Oklahoma: SEPM Spec. Pub), 26, 175–207. doi:10.2110/pec.79.26.0175The Role of Secondary Porosity in the Course of Sandstone Diagenesis. Aspects Of Diagenesis

CrossRef Full Text | Google Scholar

Stehfest, H. (1960). Numerical Inverse of Laplace Transform. Commun. ACM 3 (3), 171–173.

Google Scholar

Teodorovich, G. I., and Chernov, A. A. (1968). Character of Changes with Depth in Productive Deposits of Apsheron Oil-Gas-Bearing Region. Soviet Geol. 4, 83–93.

Google Scholar

Terzaghi, K. V. (1929). Settlement Analysis - the Backbone of Foundation Research. Tokyo): Word Engineering Congress, 8.

Google Scholar

Terzaghi, K. V. (1943). Theoretical Soil Mechanics. New York: John Wiley & Sons.

Google Scholar

Weller, E. A. (1959). Compaction of Sediments. AAPG Bull. 43, 273–310. doi:10.1306/0bda5c9f-16bd-11d7-8645000102c1865d

CrossRef Full Text | Google Scholar

Xie, K.-H., Xie, X.-Y., and Gao, X. (1999). Theory of One Dimensional Consolidation of Two-Layered Soil with Partially Drained Boundaries. Comput. Geotechnics 24, 265–278. doi:10.1016/s0266-352x(99)00012-9

CrossRef Full Text | Google Scholar

Xie, K.-H., Xie, X.-Y., and Jiang, W. (2002). A Study on One-Dimensional Nonlinear Consolidation of Double-Layered Soil. Comput. Geotechnics 29, 151–168. doi:10.1016/s0266-352x(01)00017-9

CrossRef Full Text | Google Scholar

Xie, K. H., and Leo, C. J. (2004). Analytical Solutions of One-Dimensional Large Strain Consolidation of Saturated and Homogeneous Clays. Comput. Geotechnics 31, 301–314. doi:10.1016/j.compgeo.2004.02.006

CrossRef Full Text | Google Scholar