- Planetary Structural Geology and Tectonics Group, Department of Geosciences, Mississippi State University, Mississippi State, MS, United States
Thrust fault-related landforms, smooth plains units, and impact craters and basins have all been observed on the surface of Mercury. While tectonic landforms point to a long-lived history of global cooling and contraction, smooth plains units have been inferred to represent more punctuated periods of effusive volcanism. The timings of these processes are inferred through impact cratering records to have overlapped, yet the stress regimes implied by the processes are contradictory. Effusive volcanism on Mercury is believed to have produced flood basalts through dikes, the propagation of which is dependent on being able to open and fill vertical tensile cracks when horizontal stresses are small. On the contrary, thrust faults propagate when at least one horizontal stress is very large relative to the vertical compressive stress. We made sense of conflicting stress regimes through modeling with frictional faulting theory and Earth analogue work. Frictional faulting theory equations predict that the minimum and maximum principal stresses have a predictable relationship when thrust faulting is observed. The Griffith Criterion and Kirsch equations similarly predict a relationship between these stresses when tensile fractures are observed. Together, both sets of equations limit the range of stresses possible when dikes and thrusts are observed and permitted us to calculate deviatoric stresses for regions of Earth and Mercury. Deviatoric stress was applied to test a physical model for dike propagation distance in the horizontally compressive stress regime of the Columbia River Flood Basalt Province, an Earth analogue for Borealis Planitia, the northern smooth plains, of Mercury. By confirming that dike propagation distances from sources observed in the province can be generated with the physical model, we confidently apply the model to confirm that dikes on Mercury can propagate in a horizontally compressive stress regime and calculate the depth to the source for the plains materials. Results imply that dikes could travel from ∼89 km depth to bring material from deep within the lithosphere to the surface, and that Mercury’s lithosphere is mechanically layered, with only the uppermost layer being weak.
1 Introduction
The geologic history of Mercury has been dominated by global contraction—a reduction in the volume of the planet due to cooling (Solomon, 1977). This process, along with possible others like tidal despinning, polar reorientation, and changes in orbital characteristics, have resulted in a global population of thrust faults inferred from thousands of observations of thrust fault-related landforms (Watters and Nimmo, 2010; Watters et al., 2015). These landforms deform Mercury’s entire surface including smooth plains units (Byrne et al., 2014; Crane and Klimczak, 2019a). Smooth plains units are inferred to be of flood volcanic origins and likely emplaced through diking (Strom et al., 1975; Head et al., 2011; Denevi et al., 2013); however, no vents or exposed dikes have been observed. Volcanic plains cover 40% of Mercury’s surface (Denevi et al., 2009). The density of thrust fault-related landforms is lower in the smooth plains compared to the rest of the planet’s surface (Watters et al., 2015; Crane and Klimczak, 2019a). Still, many studies observe linear to arcuate, high topography landforms occasionally bounded by surface breaking faults cross cutting smooth plains units (e.g., Byrne et al., 2014). Impact craters and basins are observed cutting and crosscut by thrust fault-related landforms and plains deposits (Freed et al., 2012; Klimczak et al., 2012), highlighting the longest-lived process effecting the terrestrial planet’s surface—impact cratering.
Stratigraphic relationships of thrust fault-related landforms and Smooth Plains deposits indicate that global contraction both preceded and continued after the effusive volcanism that produced the plains (Klimczak et al., 2012; Banks et al., 2015; Galluzzi et al., 2019). The oldest thrust fault-related landforms are crosscut by impact craters estimated to have formed during the Tolstojan Period [∼3.9–3.7 Ga, Marchi et al. (2009)]. Thus, faults must have begun propagating and global contraction operating prior to this time (Crane and Klimczak, 2017). The youngest thrust-fault related landforms are estimated to be less than 50 Ma due to their small sizes and crisp morphologies (Watters et al., 2016). Based on the stratigraphic relationships of thrust fault-related landforms and aged impact craters, global contraction was most active during and before the Calorian period (3.9–3.25 Ga or 3.7–1.7 Ga); (Spudis and Guest, 1988; Marchi et al., 2009; Crane and Klimczak, 2017). The magnitude of estimated strain rates due to global contraction for these periods depends on the length of the time period used in the calculation; however, estimates of the absolute age limits for time periods vary (Spudis and Guest, 1988; Banks et al., 2017). Applying the time systems from Spudis and Guest (1988), the Calorian ended ∼3.25 Ga, and a quieter period of global contraction began. Unlike the long history of global contraction, the Smooth Plains have been estimated to be emplaced in <100 Ma, between 3.1 and 3.9 Ga (Ostrach et al., 2015; Byrne et al., 2016).
Although the periods of strongest global contraction and volcanism overlap, the stress regimes implied by these processes are contradictory (Figure 1). The causal stresses associated with both processes can be broken down simplistically into three perpendicular, principal compressive stresses: two horizontal stresses (SH and Sh where SH > Sh) and one vertical stress (Sv).
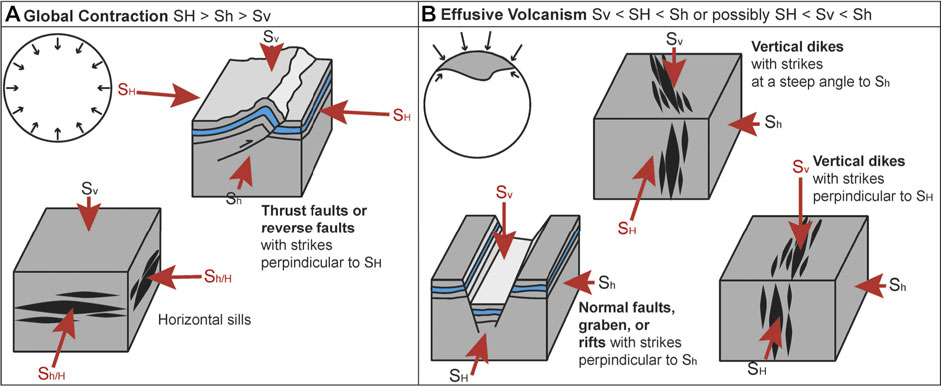
FIGURE 1. This figure illustrates the expected landforms from stress regimes associated with global contraction and effusive volcanism. (A) A globally contracting lithosphere is expected to produce maximum horizontal stresses and minimum vertical stresses that promote the formation of thrust faults and horizontal sills (Anderson, 1905). (B) Effusive volcanism is facilitated by minimum horizontal stresses (Anderson, 1951), which when combined with maximum vertical stresses, also produce normal faults and graben (Anderson, 1905).
Stresses expected to produce a global population of thrust faults must be strongly horizontally compressive (Solomon, 1978). Even when considered in the context of other geologic processes, global contraction is considered to have been pervasive and intense enough to produce and influence the formation of thrust faults (Klimczak, 2015). The observation of these thrust faults (or geomorphology associated with blind, non-surface breaking thrusts) implies that SH > Sh > Sv where Sv must be the least compressive principal stress (Anderson, 1905; Zoback, 2010). A small Sv allows for the development of positive topography which is observed and characterizes thrust fault-related landforms (Crane, 2020). Volcanic sills (filled, horizontal, tensile cracks) may also form in this stress regime and will open perpendicular to the least principal stress (Gretener, 1969). However, strong horizontally compressive stresses should limit dike (filled, vertical, tensile cracks) propagation, effectively closing off pathways for magma to rise to the surface (Solomon, 1977).
In some settings, effusive volcanic deposits have been attributed to sill complexes and sill-fed dikes. For example, flood basalts in the Ferrar Large Igneous Province (LIP) were at least partially emplaced by sill-fed dikes at shallow depths (Muirhead et al., 2014; Elliot and Fleming, 2018); however, these studies note that sills are most likely to contribute to volcanism when extensional stresses are negligible and in sedimentary basin settings. The Warakurna LIP of Western Australia is an exception in which igneous sills intruded through crystalline bedrock (Magee et al., 2019a). Dikes and sills are certainly related to each other and regional stresses during the upward migration of magmas (Magee et al., 2019b), but understanding the roles that each play in bringing igneous material to the surface relies on studies of surface exposures, seismic data, or topographic signatures of uplift associated with sill emplacement (Magee et al., 2019a). A lack of erosion and limited data resolution has left the surface of Mercury with no visually resolvable, exposed outcrops of sill and dike complexes, and obviously no seismic data are available. The only resolvable topographic high, the Northern Rise, is magnitudes larger than observed forced folds associated with sill intrusion (Magee et al., 2017), and has a genetic connection to a magnetic signature from the core-mantle boundary (Plattner and Johnson, 2021), suggesting a deeper influence on this topography. It may be possible that sills contribute to the emplacement of smooth plains units on Mercury, but until more information can be gained through future missions, emplacement through dikes can allow for end member models of plains emplacement to be investigated.
In such models, effusive volcanism is a process attributed to sub-vertical to vertical dikes bringing magma to the surface (Anderson, 1951; Rubin, 1995; Rivalta et al., 2015). Vertical dikes should result from minimum horizontal compressive stresses such that two stress regimes are possible when dikes are observed: Sv > SH > Sh or SH > Sv > Sh (Anderson, 1951). If paired with a maximum vertical compressive stress (Sv > SH > Sh), minimum horizontal compressive stresses should also result in normal faulting or graben formation (Anderson, 1905). Normal faults may also be used as pathways for magma to migrate upwards. However, normal faults are not observed on Mercury outside of impact craters and basins (Watters and Nimmo, 2010). Strong vertically compressive stresses would have also prevented or limited the formation of thrust faults, and therefore this stress scenario is unlikely. If Sv was an intermediate stress (SH > Sv > Sh), vertical dikes could still form perpendicular to Sh and would be expected to propagate laterally in the direction of SH. This regime would not be expected to form normal faults or thrust faults, although strike-slip faulting could be possible (Anderson, 1905).
From observations of thrust fault-related landforms and plains deposits, two stress regimes are then possible: SH > Sh > Sv and SH > Sv > Sh—with the first regime limiting the ability for magma to be transported to the surface and the second preventing the formation of thrust faults. In this paper, we make sense of these conflicting stress regimes using frictional faulting theory and deduce that diking must have happened in a horizontally compressive stress regime. We then use Earth analogues to 1) confirm that such a scenario is possible on a large scale to produce a massive flood basalt province and 2) derive depths for potential sources for the flood basalts that produced Mercury’s Smooth Plains.
2 Methods
A three-step methodology allowed us to address dike propagation in the horizontally compressive stress setting of a globally contracting Mercury. First, we queried frictional faulting theory to determine the stress state of the planet and the possibility that diking could occur in a horizontally compressive regime. We then test the viability of dike propagation by applying an equation for the distance that dikes propagate in a compressed, physical analogue model to an Earth analogue setting. Finally, with confidence, we apply this model to Mercury to calculate the propagation distance for dikes that produced the smooth plains units.
2.1 Dike Propagation in a Compressive Stress Regime
Frictional faulting theory is a set of equations that relate the three principal compressive stresses and that when satisfied, indicate if and what type of faults can form (Zoback, 2010). The equations are derived from the Coulomb failure envelope and Mohr circle (Anderson, 1905; Jaeger et al., 2007) and are therefore also dependent on the friction coefficient and pore pressure. The theory has been graphically illustrated in Zoback (2010) as a polygon with edges defined by the equations where points along the edges of the polygon define stress combinations associated with normal, strike-slip, and reverse or thrust faulting (Figure 2A). Reverse and thrust faulting are represented along the upper edge, which (neglecting pore pressure) is defined as
where
when
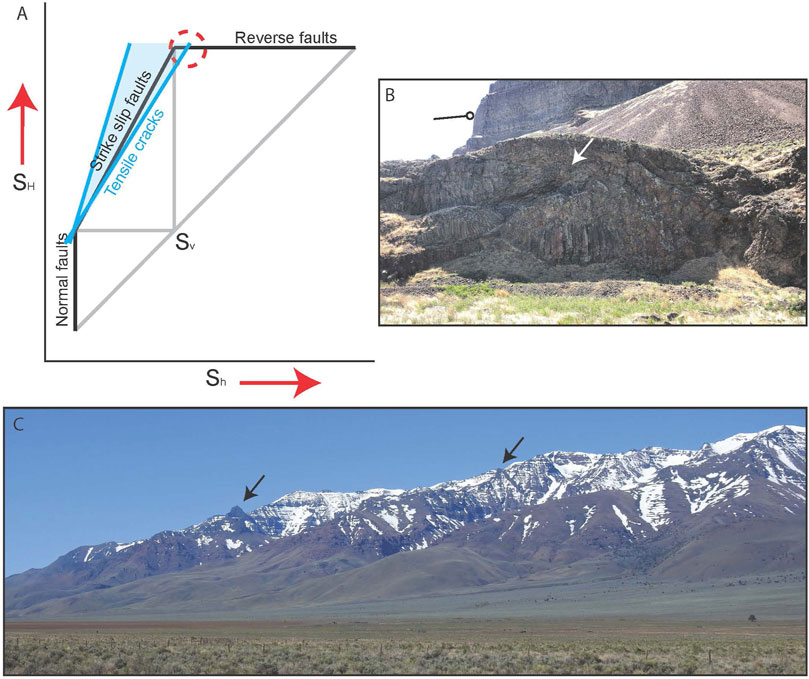
FIGURE 2. A graphical representation of frictional faulting theory (adapted from Zoback, 2010) illustrates the stress relationships that must be satisfied when normal, strike-slip, or reverse faults are observed along the black lines of the polygon (A). The combinations of Sh and SH along the outer, black edges of the polygon are defined by the relationship between these values that must be observed when a Mohr circle defined by these stresses and Sv is tangential to a Mohr Coulomb failure envelope with a given coefficient of internal friction. Points along the lower vertical edge, sloping edge, and upper horizontal edge represent stress combinations that would produce normal, strike-slip, and reverse faulting, respectively, and points below these edges represent stresses not capable of producing faulting. The blue window conveys the relative Sh and SH stresses that are expected when tensile cracks are observed or inferred either through borehole imaging or outcrop exposures. The steep edge of this window is defined by the Griffith Criterion while the shallower edge is defined by the Kirsch equations. Gray lines simply show the relationship between Sv and other stresses. The representations of equations governing the stress relationships between SV and SH when reverse faults are observed and SH and Sh when tensile cracks are observed do intersect, and for this narrow window of stresses (red dashed circle), both dikes and thrust faults could propagate. (B) Evidence of such syn-volcanic tectonism is observed in the Yakima fold province where flows thin or show onlapping (white arrow) in the direction of dip (tadpole) for large scale thrust fault-related landforms. (C) Large, vertical dikes observed near the surface are inferred to be feeder dikes. Here, we show an example of Steens dikes (black arrows) exposed at the surface and photographed during our fieldwork in Fields, OR.
Tensile cracks can form in compression, parallel to the greatest principal stress (Schultz, 2019). The Griffith Criterion, which defines the stresses necessary for crack formation, allows for the relation of the maximum and minimum principal stress when cracks are opening (Hoek and Martin, 2014). Hoek (1965) found that as opening mode cracks lengthen compared to wingtip cracks, a maximum to minimum principal stress ratio of 5.88 is approached, limiting the maximum principal stress (steep blue line, Figure 2). For rocks with lower friction angles, this ratio may be even less (Hoek and Martin, 2014). An equation for the relationship between Sh and SH when tensile cracks are observed is also derived from the Kirsch equations, which are most often used for predicting borehole stresses during drilling (Zoback, 2010, shallow blue line, Figure 2). Although the tensile fractures for which the Kirsch equations are applied are specifically produced during drilling, the stresses that produce the fractures directly at the borehole wall are often reflections of the far field stresses. The application of this second equation also narrows the window of possible stress relationships. This equation,
When neglecting pore pressure (Pp), closely follows the frictional faulting equation (and edge in the Zoback polygon) for strike-slip faults. Note that by increasing the slope of this line to 5.88, one can show the relationship between stresses for the Griffith Criterion. The window, or range of stresses between the Kirsch equation and the Griffith Criterion overlaps the polygon. This window is visualized as the light blue zone overlapping the polygon in Figure 2. Most of this window overlaps with the strike-slip portion of the polygon indicating that tensile cracks can propagate in transpressive stress settings. However, some portion of this window intersects the upper edge of the polygon describing stresses associated with reverse and thrust faulting. This treatment of tensile crack propagation does not address stresses under which cracks can open in extensional stress domains.
It follows that in theory, the stress relationships described by the intersection of these two equations must closely reflect the relative stresses associated with global contraction and effusive volcanism: SH >> Sh ≥ Sv. Dikes must be able to propagate in a compressive stress regime when the vertical stress is minimum but similar in magnitude to the minimum horizontal stress.
2.1.1 Numerical and Physical Models of Dike Propagation
Numerical models of dike propagation have shown the prediction of propagation direction to be influenced by many factors over the last 2 decades (Dahm, 2000; Kuhn and Dahm, 2004; Maccaferri et al., 2011). After simulating fluid-filled fracture growth through numerical modeling, Dahm (2000) found that the direction of propagation is controlled by tectonic stress, apparent buoyancy, and fracture length. Propagation paths of mid-ocean ridge dikes have been found to be affected by mantle rock flow, which builds dynamic pressure, increases deviatoric stresses, and increases the buoyancy force (Kuhn and Dahm, 2004). A dike-dike interaction has also been found to affect dike propagation paths with dikes converging to areas with evenly spaced, high dike density in mid-ocean ridge settings (Kuhn and Dahm, 2008). Maccaferri and others (2011) also studied dikes as systems, finding that volcanic system dike propagation paths can be affected by differences in tensile strength of rock layers, topographic loads, buoyancy of magma, and inhomogeneity of layers. Roman and Jaupart (2014) also found that topographic loads from volcanic structures affect dike propagation paths.
Maccaferri et al. (2011) specifically address criterion that promote dike eruption. They determine that buoyant magma migrating upwards into weaker materials and beneath topographic loads increases the chances for dike eruption. Without the ability to image below the surface of Mercury, we cannot address the influence of magma chambers, mantle flow, and volcanic systems. Similarly, unexposed dikes prevent an analysis of the influence of dike density and dike-dike interactions. However, we are able to observe that smooth plains materials must have imposed a load upon previously excavated terrain (via impact cratering), and assume that weaker, more fractured strata superpose stronger, more intact volcanic materials on Mercury. We therefore impose load stresses from the plains in determining deviatoric stresses and turn to physical models to learn about the affects that rock strength and these deviatoric stresses have on dike propagation.
Physical models have shown that dikes can propagate in compressive stress regimes (Menand et al., 2010). Hardened gelatin has been shown to accurately represent the lithosphere, and fluids like air, water, or oils have been injected to study the path of dikes through the subsurface (Rivalta et al., 2015). Menand et al. (2010) modeled the path of dike propagation in a horizontally compressive stress regime by injecting gelatin with air while the gelatin was horizontally compressed in one direction and the other was held constant. Modeled dikes were observed to propagate upward a certain distance, d, before rotating into a sill, the orientation expected for the stress regime.
The vertical propagation distance, d, was found to be a function of the tensile strength of the host rock (Ts), density difference between the magma and the host rock (∆ρ), gravity (g), and the deviatoric or differential stress
This equation was derived from laboratory experiments, and we were unable to locate studies in which it was directly tested against observations of volcanic systems. The experiments neglected the driving force for vertical propagation that may come from the overpressure of the dikes’ source (Menand et al., 2010). Despite this, the result that dikes can propagate vertically in horizontally compressive stress settings before becoming sills is supported by other experiments on dike rotation that model propagation through vertical stress gradients (Dahm, 2000; Watanabe et al., 2002). Observations of convergent margins on Earth also indicate that magmas must be able to propagate to the surface in compressive stress settings. Stratovolcanoes within the Andes, basalt flows and cinder cones within the Mojave Desert, and Aragats stratovolcano in Armenia are all examples of volcanism produced in horizontally compressive stress settings where thrust and reverse faults were active during emplacement (Tibaldi et al., 2010).
Based on the frictional faulting equation for reverse faults and the modified Kirsch equation, we can estimate a minimum differential stress to be the difference between SH and Sv. If SH is 3.1 Sv, then the difference in stress must be 2.1 Sv for locations on Mercury’s surface where thrusts and dikes were simultaneously active. Before applying this equation to Mercury to derive potential distances for smooth plains dikes, we must determine if this is applicable to Earth. We therefore investigate if the equation could accurately reproduce the estimated necessary depths for sources of large-scale flood basalt provinces on Earth.
2.2 Earth Analogue Diking and Faulting
Dikes must be able to propagate from depth and produce enough magma to be a viable source for a large volcanic province. While Menand et al. (2010) were able to mathematically show that their equation would scale for an Earth-scale effusive event, we aimed to test if the physically derived equation for dike propagation would hold for a well-known Earth analogue site to the Smooth Plains: the Columbia River Flood Basalt and Yakima Fold Provinces (Plescia and Golombek, 1986; Watters, 1992; Crane, 2020).
The smooth plains of Mercury, and Borealis Planitia, the northern smooth plains, in particular, share important similarities with the Columbia River Basalt and Yakima Fold Provinces. The smooth plains are volcanically emplaced units with mafic, presumed basaltic, composition covering a laterally extensive region (5.59 × 106 km2) in ∼0–2 km of volcanic material (Head et al., 2011; Denevi et al., 2013; Ostrach et al., 2015). These units were emplaced through multiple episodes of effusive volcanism over ∼100 Ma (Ostrach et al., 2015), a short span compared to the long-lived processes of impact cratering and thrust faulting. Northern plains deposits cover 6–7% of Mercury’s surface (Head et al., 2011) and cover the northern hemisphere in what have been inferred to be low magnesium basalts (Stockstill-Cahill et al., 2012; Weider et al., 2012; Weider et al., 2015). Thrust fault-related landforms propagate through the plain units representing post- or syn-depositional tectonics (Figure 3A). Fault propagation depths are estimated to be ∼2.5 km in Suisei Planitia, a terrain within the northern plains (Crane, 2020); however, other fault models that do not consider the effects of folding derive much greater depths (>15 km and >30 km, Peterson et al., 2020 and Egea-González et al., 2012, respectively). Comparing the emplacement time estimates for the smooth plains with the strain rate estimates for various periods in Mercury’s geologic history, we infer that emplacement occurred during the most intense periods of global contraction—the Calorian and Tolstojan periods (before 3.25 Ga, Spudis and Guest (1988)). After these periods, stratigraphic relationships with craters show that large scale volcanism ceased, and tectonism slowed substantially (Crane and Klimczak, 2017).
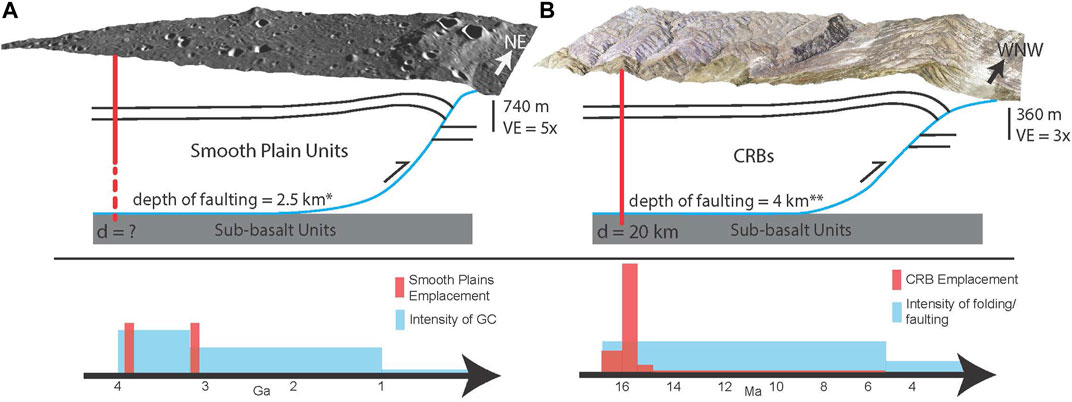
FIGURE 3. This figure compares the geomorphology, subsurface structural interpretation, and timing of formation for thrust fault-related landforms in Mercury’s smooth plains units (A) and faults and folds of the Yakima Fold Province (B). Both sets of structures have been modeled with listric thrusts that root into sub-basalt units and both likely formed topographic expressions during volcanism (Crane and Klimczak, 2019b; Crane, 2020). Imagery and digital elevation models for (A) and (B) are MDIS Global Monochrome Mosaic and DLR DEM for Mercury and NAIP imagery and USGS DEM for Earth. Timing of deformation and volcanism for Mercury (Ostrach et al., 2015; Crane and Klimczak, 2017) and Earth (Reidel, 1984; Reidel et al., 2013a; Kelsey et al., 2017) are shown on billion-year and million-year scales, respectively.
The Columbia River Flood Basalt Province is an extensive flood basalt province often tied to crustal extension and melting due to the mantle plume also associated with the Snake River Plain Hot Spot Track (Camp et al., 2013). However, the northern section of the basalt province is deformed through thrusting and folding of its sub-basalt, basalt, and intra-volcanic strata (Reidel et al., 2013a). Multiple effusive events covered ∼210,000 km2 of Washington, Oregon, and Idaho in relatively thick (∼4 km) volcanics of largely basaltic composition (Reidel et al., 2013b). The basalts were emplaced over a geologically short period of time in multiple events between 16.8 and 5 Ma, with dikes exposed in multiple locations (Figure 2C; Camp et al., 2017). Most importantly for this study, the basalts were deforming contemporaneously with deposition in the Yakima Fold Province, a structural region of southern Washington contained within the boundaries of the Columbia River Flood Basalt Province (Figure 3B; Reidel, 1984; Kelsey et al., 2017). Faults that cut the basalts here extend to 4 km depth (Casale and Pratt, 2015; Crane and Klimczak, 2019b). In this region, uplifted, folded basalts show thinning of deposited units toward topographically elevated fold hinges (Figure 2B) and thickening in synclines and structural lows, indicating syn-volcanic thrusting and deformation (personal observations during fieldwork). Estimations of uplift from aged terraces and structural models indicate that uplift and volcanism were largely coeval, and that the intensity of both processes decreased with time (Bender et al., 2016; Staisch et al., 2018).
The Columbia River Flood Basalt Province is also a superb analogue because of the abundance of mapped dikes associated with basalt emplacement. Three main dike swarms have been described: the oldest, Steens Mountain dikes which sourced the southernmost flows, the younger, Monument dikes to the northwest of Steens Mountain, and the youngest and largest Chief Joseph dikes to the north (Barry et al., 2013). The Chief Joseph dike swarm covers northeastern Oregon and eastern Washington and was responsible for multiple basalt flows that cover the Yakima Fold Province and are deformed by its thrusts (Morriss et al., 2020). The depths to sources for the dikes are largely constrained to mid- to lower crustal sources. Davenport et al. (2017) observed a high velocity region at ∼20 km depth below a small section of the Chief Joseph dike swarm in their geophysical study of the Western Idaho Shear Zone that could be inferred to be a source. Morriss et al. (2020) estimate depths between 15 and 30 km, but state that these depths are simply the half and full thickness of the crust in the study region. Other geophysical studies constrain sources to similar depths (Hales et al., 2005; Wolff et al., 2008).
A new digitized dataset compiled from the fieldnotes of Columbia River Basalt researcher Dr. W. H. Taubeneck contains the location and description of many identified dikes. Combined with other vectorized Columbia River Basalt dikes from other dike swarms, Morriss et al. (2020) have produced a digital dataset that we used to test the physical dike propagation model of Menand et al. (2010).
We utilized a Geographic Information System and ESRI’s ArcMap to perform analyses on the dike data. All dikes and dike swarms from the dataset were combined into a single shapefile in ArcMap for analysis. The Data Management Toolbox was then used to divide each dike into 500 m long separate segments. Each segment was assigned a unique identification number and row in the new shapefile. Dividing dikes, especially very long dikes (>100 km), into segments allowed us to reflect the changing geologic conditions that might lead to varying propagation distance estimates along the length of a single dike.
Parameters were then added to this shapefile. The physically modeled equation for propagation distance relies on estimates for density of the dike magma and tensile strength and density of the dikes’ host rocks. Dike composition (usually basaltic but sometimes andesitic basalt) was recorded in the Morriss et al. combined dataset, and 2.7 g/cm3, an average density for flood basalt lavas was used (Hartley and Maclennan, 2018). Accepted values for the density of basaltic and andesitic-basaltic lavas were added to the shapefile attribute table for the dike segments. The statewide, vectorized geologic maps for Washington, Oregon, and Idaho were also imported into the GIS.
The geologic maps were used to identify the rock type through which the dikes propagated. We divided the rock mass through which the dikes propagated into a basement and bedrock layered stratigraphy. Seismic and well data for the Yakima fold Province suggest bedrock-basement contacts near 8 km (Casale and Pratt, 2015; Crane and Klimczak, 2019b). Because studies estimate crustal thicknesses between 20 and 39 km for the region (Catchings and Saltus, 1994; Das and Nolet, 1998; Davenport et al., 2017), we repeated calculations for propagation depth with three model stratigraphies to reflect maximum and minimum stratigraphic arrangements. These model stratigraphies assume that over the total distance propagated, one-tenth, one quarter, and one half of the strata are bedrock and nine-tenths, three quarters, and one half are underlying basement, respectively. We only assumed relative thicknesses for each. The equation for dike propagation distance was modified to reflect these two layers by scaling the contribution of each layer to the distance, similar to the calculation of a weighted sum.
Basement composition was assumed to be gabbro west of the Hite fault and granite east of the Hite fault, the boundary between accreted ocean crust and the North American craton (Reidel et al., 2013a). Above the gabbro or granite basement, we defined the bedrock composition as that which was recorded in the geologic map. When shallow surficial deposits were recorded as the geologic unit (i.e., alluvium or till), we instead used the host rock data recorded in the Morriss et al. (2020) dataset. The values for tensile strength and density for each of these rock types were taken from engineering sources described in Supplementary Table S1 in the Supplementary Materials. When the geologic map units were generic, we used values for rocks which most closely aligned with these descriptions. For example, values for parameters associated with shale were used when the geology was defined as “offshore marine sedimentary rock”. Tensile strength and density values for the bedrock and basement were added to the shapefile attribute table in the GIS. Once these attributes had been added, the shapefile was exported as a spreadsheet.
Dike propagation distance, d, was calculated for each dike segment. In order to calculate d, we first needed to estimate the vertical stress Sv, associated with thrust fault propagation. Based on previous estimates, thrust faults were believed to propagate upward from ∼4 km or deeper (Casale and Pratt, 2015; Kelsey et al., 2017; Crane and Klimczak, 2019b). At any depth, vertical stress can be estimated using the following formula for lithostatic stress:
where ρ is bulk density of the overlying rock, g is gravity, and z is depth (Jaeger et al., 2007). Although Sv can deviate from this value and principal stresses can rotate due to local heterogeneities such as magma chambers, some previous studies have not observed these features in the seismic data for the province and others only observe them locally (Wolff et al., 2008; Crane and Klimczak, 2019b). We therefore use the equation above to estimate Sv. For the Yakima Fold Province, ρ = 2,700 kg/m3, g = 9.81 m/s2, z = 4,000 m, provide an estimate of Sv of 106 MPa. Because we know from frictional faulting theory that differential stress is estimated to be 2.1 Sv, we could predict that the differential stress at depth at the time of fault propagation in the Yakima Fold Province was 222 MPa. With the calculation of differential stress, an estimate for d could be provided for each dike segment.
The d value was added to the shapefile so that dike segments could be color coded by their propagation distance. The distances and trends in distances for dikes in the Columbia River Basalt Province were compared to previously established estimates. Similarities (discussed in section 3 Results) supported the application of the equation for propagation distance to Mercury’s Smooth Plains.
2.3 Estimating Dike Propagation Distance for Mercury
Dike propagation distance was calculated for Mercury’s smooth plains using the equation for d. Gravity on Mercury was taken to be 3.71 m/s2. Tensile strength for the presumed basaltic surface composition was taken to be 14.9 MPa (Van Noort et al., 2017), although we acknowledge that depending on the degree of fracturing due to impact cratering, this value could be as low as 2 MPa (Schultz, 1993). The range in tensile strengths contribute to upper and lower bounds in our calculation of dike propagation distance.
The vertical and horizontal stresses at depth for Mercury were derived from our knowledge of frictional faulting theory and stresses associated with the topographic load of smooth plains emplacement. Topographic load was considered as this factor would have increased the vertical stresses for thrust faults to overcome and has been shown to affect the magnitude and orientation of principal stresses (Hooper et al., 2011; Roman and Jaupart, 2014). Vertical, horizontal, and shear load stresses associated with a uniform smooth plains deposit 50 km-wide and 4 km deep were calculated (Figure 4; Davis and Selvadurai, 1996; Dahm, 2000). The vertical stresses associated with this load were superimposed on the vertical lithostatic stress, and together, these stresses determined the magnitude of the maximum horizontal stress needed to overcome the yield strength of the rock mass. Some horizontal stress was also induced through loading, but the remainder was accommodated through tectonic stresses. Although we discuss global contraction as the cause for this stress, many other processes could have also produced horizontal stresses. The source of this stress is less important than its magnitude, for which a lower bound can be determined as 3.1 times the vertical stress.
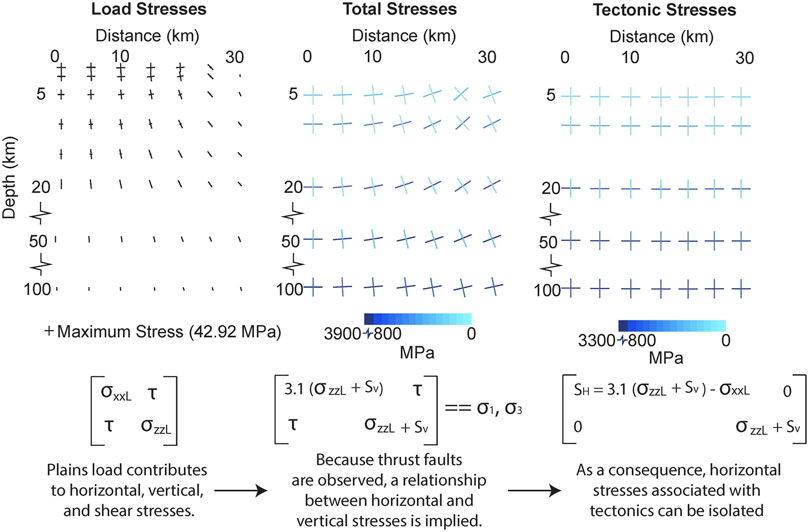
FIGURE 4. These graphs depict the maximum and minimum principal stresses associated with the (left) load of a 50 km-wide, 4 km-deep section of thick northern smooth plains deposits, (center) superimposed tectonic and load stresses, and (right) tectonic stresses necessary to produce thrust faults in the stress context of the smooth plains. Only the right half of the affected space is shown. Stress tensors associated with each scenario are also provided where σxxL, σzzL, and
The vertical stress at the depth of thrust fault initiation (2.5 km) due to a rock mass with a bulk basalt density of 2,850 kg/m3 is ∼64 MPa, and horizontal stresses associated with loading and tectonic activity were estimated to be ∼39 and ∼160 MPa, respectively. Differential stress was therefore calculated to be ∼135 MPa. Magma density was assumed to be 2,800 kg/m3 based on estimates for Earth analogue lavas and lunar basalt melts (Delano, 1990; Greeley et al., 1998). This higher density is more appropriate for Mercury, as it is believed that the surface composition of Mercury may be closer to a komatiite composition (Head et al., 2011). Applying the given parameters, upper and lower bounds for propagation distance were calculated.
3 Results
3.1 Earth Analogue Results
Model results approximate current estimates for dike propagation distances in the Columbia River Basalts. Mid-crustal estimates from Davenport et al. (2017) and Morriss et al. (2020) range from 15 to ∼20 km while lar2gest d values in this study are ∼33 km, with most d values between 10 and 25 km. The largest values are associated with dikes that propagated through gabbro basement and meta-volcanic bedrock. Most large values (20–25 km) are generally instead associated with granite basement rock.
Trends in d values show a shallowing to the north (Figure 5). Propagation distances between 20 and 30 km were more commonly observed in the Steens and Monument dike swarms while values in the Chief Joseph dike swarm were closer to 7–10 km. Outside of the extent of the Columbia River Basalt Province, dike propagation depth variability increases with few trends in dike depth associated with direction.
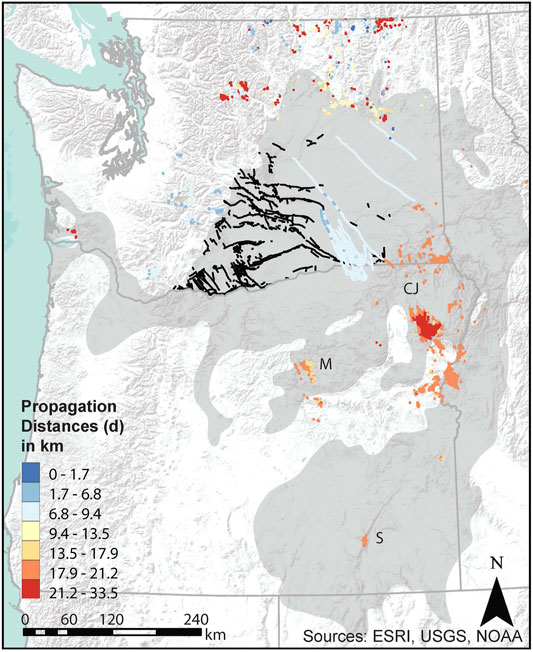
FIGURE 5. This map shows the spatial relationships of the faults within the Yakima Fold Province (black lines), Columbia River Basalt Province (gray region; Camp and Ross, 2004), and dikes which have been color coded by their propagation distances. Warmer hues indicate deeper depths from which the dikes have propagated, and cooler hues indicate shallower propagation depths. Color coding is based on the Jenks method of classification which groups lengths in a way that maximizes across group differences. State boundaries are shown in gray. CJ = Chief Joseph Dike Swarm, M = Monument Dike Swarm, S = Steens Dikes.
3.2 Mercury Smooth Plains Results
Dike propagation distances for Mercury’s smooth plains were variable depending on the tensile strength for basalt used in the calculation. For intact basalt with a tensile strength of 14.9 MPa, d values ranged from 81.3 to 88.7 km. For heavily impacted basalt with a reduced tensile strength of 2 MPa, d values ranged from 10.8 to 10.9 km.
4 Discussion
4.1 Earth Analogue
The application of an Earth analogue to this research confirmed that theoretical and physical models of dike propagation could be applied to Mercury. Dike propagation distance estimates for the Columbia River Basalt Province suggest a lower to mid-crustal source for the basalts consistent with geophysical evidence (Hales et al., 2005; Wolff et al., 2008; Davenport et al., 2017). We also observed a trend in source depths shallowing to the northern region of the province. The northward progression of decreasing source depth reflects the observed age progression of dikes younging to the north (Barry et al., 2013). These observations are consistent with the prevailing hypotheses for the origin of the basalts.
Evidence that such a large volume of basalt erupted in a short period of time and in a setting with low rates of back arc extension supports a plume origin for the basalts. A plume hypothesis holds that as the North American craton moved southwest over a mantle plume, the head and tail of the plume separated. While the tail of the plume moved along the Snake River Plain hot spot track, the head of the plume promoted melting and formation of the flood basalts (Camp and Ross, 2004). Plume models can include a delamination of the upper mantle and lower crust. The convecting plume head migrated northward and surfaceward, producing shallower crustal melt sources for the basalts over time. Segments of delaminated lower crust could have been entrained and melted within the plume head consistent with compositional data from the basalts (Camp and Hanan, 2008). Alternatively, a plume fed magma chamber with crustal contamination of craton material could produce similar compositions (Wolff et al., 2008). In either case, the high magnesium, high silica compositions of all but one flow unit imply a melted, mafic crustal source. Advancing plume heads in these models have also been connected to the development of shortening structures in front of the head (Camp and Hanan, 2008).
Other hypotheses for the flood basalt origins also align with the younging and shallowing northward pattern in the dikes. Liu and Stegman (2012) propose a model with an opening slap tear (tearing to the north) contributing to the production and northward migration of basalt. Others contend that the passive, northward propagating back-arc extension associated with the subduction of the Farallon slab would have promoted the volcanism (Carlson and Hart, 1987).
Despite an overall northward propagation pattern, the dikes indicative of the deepest source are not located near the Steens flows. Instead, they are located farther north, in the southern region of the Chief Joseph dike swarm (red points, Northeastern Oregon, Figure 5). The high d values calculated for this region are located within the Wallowa Mountains. While some studies conclude that this particular area represents the location of a plume fed and crustally contaminated magma chamber (Wolff et al., 2008), others contend that this area, characterized by at least 2 km of uplift, represents the relative zone of interaction between a plume and the granitic root of the Wallowa Mountains (Hales et al., 2005). These authors hypothesize that a plume triggered a gravitational instability, encouraging the delamination of the plutonic mountains and their subsequent uplift. In either case, these studies imply that this region may be a center of dike propagation, and so it follows that it should be characterized by the deepest source.
Our results likely reflect these important spatial patterns due to the compositions of the basement rocks and the surface rocks which formed as a consequence of these processes. If the depths had been strictly divided based on basement rock, then we would expect to only see two general dike propagation distances. Instead, the variability to the north outside of the extent of the basalt province and the deep propagation depths near the Wallowa Mountains indicate that bedrock composition also plays a role in determining the dike patterns. Smaller d values are associated with sedimentary bedrock or andesite volcanic bedrock over gabbro basement rock, due to the smaller tensile strength of sedimentary rocks and large density difference between andesite and gabbro.
4.2 Mercury
Dike propagation depths for Mercury have consequences for understanding potential sources for the effusive deposits and the geologic history of the planet as a whole. When tied to compositional data, they allow us to speculate on the sources and causes of melting. Our upper bound estimates of ∼81–89 km likely correspond to some depth within Mercury’s upper mantle early in the planet’s history (Figure 6). Mantle melts would be expected to be higher in magnesium than is observed, at least in the northern plains deposits (Weider et al., 2012; Weider et al., 2015) where lower magnesium and an inferred majority plagioclase composition are observed (Namur and Charlier, 2017). This implies that for the northern plains either a thicker crust had already developed, or by analogy to the Columbia River Basalt generation, some kind of delamination had occurred to melt crustal material at mantle depths.
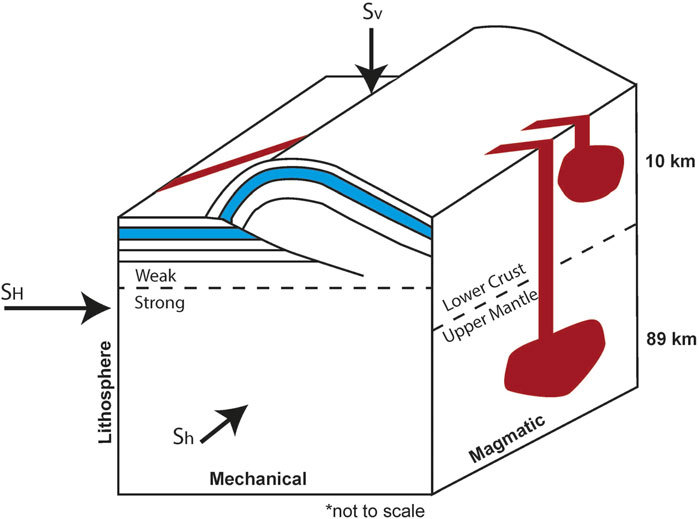
FIGURE 6. This conceptual diagram (not to scale) shows dikes and thrust faults propagating simultaneously in a horizontally compressive stress regime where propagation distances range between 10 and 89 km, and the lithosphere through which dike propagation occurs is mechanically layered.
These depths are also consistent with depths estimated by Wilson and Head (2008). These authors considered dike propagation as function of density, crustal thickness, and the distance a dike would have to travel through the mantle before reaching the crust. They consider the stress the dike material must exert in order to keep the crack open. However, Wilson and Head present a range of solutions because this stress was unconstrained. They calculate possible dike propagation paths over a reasonable parameter space.
Our work constrains this space by calculating a narrower range of deviatoric stresses through which the dikes propagated. Our source of variability arises largely from the host rock tensile strengths. We can however learn something about mechanical stratigraphy of the lithosphere as a consequence. The lower bounds for d values (∼10 km) are not consistent with a reasonable range proposed by Wilson and Head (2008). It seems unlikely that in Mercury’s thick shell enough melt could be produced at 10 km depth to cover 40% of the planet or the vast expanse of Borealis Planitia. We take this to mean that the tensile strength of impacted basalt (2 MPa) is not indicative of a significant portion of the lithosphere. This supports the conclusions of Byrne et al. (2016) who observe nonporous (stronger) target rock and porous (weaker) target rock parameters to produce better fitting crater chronologies for larger and smaller craters, respectively. This implies that larger craters deform deeper (but still relatively shallow), stronger rock.
Global contraction is often cited as the reason that volcanism slowed (e.g., Solomon, 1978); however, finding that both processes can operate together opens up new possibilities for causal mechanisms. It is important to notice that the most intense periods of global contraction and volcanism overlap and that both processes slow contemporaneously. This implies that the shrinking lithosphere may not have been the cause for the waning volcanism. Instead, global cooling may have decreased the ability for magmagenesis and melting while simultaneously prompting contraction. The slowed rate of impact cratering would have also brought less heat to the planet, decreasing the likelihood of melting.
Viewing thrust faulting and volcanism as connected processes from a compressional stress perspective paves the way for future work studying the cessation of global contraction. Because global contraction would have peaked during the earlier periods- the time coincident with volcanism-we can assume that horizontal compressive stresses only decreased with time. Thus, by studying faults that represent a spectrum of ages postdating the smooth plains emplacement and estimating fault propagation depth, one could track the relative relaxation of stresses by calculating the deviatoric stresses associated with each fault population. It may also be possible to study pre-plains fault populations and calculate minimum deviatoric and horizontal compressive stresses for older thrusts and early periods of global contraction on Mercury.
The depths of older faults outside of the plains, but that propagated around the same time, also provide some insight into the character of diking at depth. Geometric models of faults ∼4.0 Ga place their lower tips near 30–40 km, with the elastic lithosphere extending to the same depths (Watters et al., 2002; Egea-González et al., 2012). More recent models show the present-day brittle-ductile transition (BDT) between ∼75 and 125 km (Klimczak et al., 2019). Thus, during the diking associated with smooth plains emplacement, the BDT must have ranged between these values, but closer to 40 km depth. If the maximum estimate for dike propagation distance (81–89 km) is accurate, then much of dike propagation was through the ductile regions of the lithosphere. Dikes can still propagate upward through this region, as observed in the Scandinavian Caledonides (Kjøll et al., 2019). Dikes propagating through ductile regimes have undulating contacts with host rocks, rounded shapes, and pinch and swell structures due to viscoelastic fingering and fracturing (Bertelsen et al., 2018; Kjøll et al., 2019), but importantly, dikes still migrate upwards as long as tectonic strain rates are much slower than dike propagation rates (Rivalta et al., 2015).
Because thrust fault-related landforms- and thrust faults by association-have been shown to have preferred orientations within Borealis Planitia (Crane and Klimczak, 2019a), it may be possible to map stress orientations and magnitudes through time within these plains. These stresses and their orientations and magnitudes could be linked to causes other than global contraction to explore tidal despinning and changes in orbital parameters with absolute stress values.
The methodology described here could furthermore be used to differentiate magma sources for different plains units. The differential stress value used in the source depths calculation presented in this study was derived from the fault observations in Borealis Planitia. This unit has a distinct composition from other plains units (Weider et al., 2015). At least three compositions have been inferred from spectral data (Denevi et al., 2013) and at least one of these units could represent higher degrees of partial melting and a komatiite composition- possibly implying a deeper source (Head et al., 2011). If faults in these regions are modeled, then their derived depths could be used for differential stress and d value calculations.
5 Conclusion
Global contraction and effusive volcanism are often presented as conflicting processes. While there is no doubt that strong, horizontal compressive stresses do not encourage volcanism, these stresses also do not necessarily prevent magma from reaching the surface.
We examined the possibility of coincident dike (tensile crack) and thrust fault propagation. We applied frictional faulting theory and a window of possible stresses for tensile crack propagation produced from the Griffith Criterion and Kirsch equations to limit the estimations of maximum and minimum horizontal stresses. The frictional faulting theory equation for reverse faulting overlaps with the window of stresses capable of producing tensile cracks. This allows us to recognize that there must be a limited range of stress scenarios where diking and thrust faulting can be coincident. It is possible that dikes propagated vertically on Mercury while thrust faults were deforming the planet’s lithosphere.
We then applied our working knowledge of the depth of faulting on Earth and Mercury, to calculate a range for horizontal and vertical stresses during tectonic and volcanic activity on Mercury and at an Earth analogue site in the Columbia River Basalt Province. These stresses permitted the calculation of the deviatoric stress and the testing of an application of a physically derived equation for dike propagation depth at the Earth analogue site. Many studies had already proposed a narrow window of magma source depths for this site, and dikes had been well mapped and characterized.
Upon validation on a large scale of the model, we calculated dike propagation depths for Mercury’s smooth plains units. We conclude that 1) global contraction did not preclude effusive volcanism and 2) the dikes that produced the plains could have been sourced from ∼89 km depth. Importantly, this result explains a possible deep source for the massive expanses of volcanic plains that cover 40% of Mercury’s surface. Now that this method has been tested, it can be applied to further advance our understanding of global contraction, Mercury’s paleostress regimes, and melt sources within Mercury’s crust and upper mantle. In particular, the broad distribution of plains materials and thrust faulting may allow for a deeper understanding of the depths to melt sources across the planet.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Crane conceived of the idea for the study and lead the student (AB) through the research process. AB lead the GIS analysis of dike data. Crane wrote the manuscript with significant help from AB.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Dr. Jeannette Luna and attendees at the MEXAG 2021 meeting for their feedback. We also acknowledge the minor contributions in early stages of preliminary work of an additional graduate student, Kevin Branigan. We thank the Department of Geosciences at Mississippi State University for funding the open access fee for this submission.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.752864/full#supplementary-material
References
Anderson, E. M. (1905). The Dynamics of Faulting. Trans. Edinb. Geol. Soc. 8, 387–402. doi:10.1144/transed.8.3.387
Anderson, E. M. (1951). The Dynamics of Faulting and Dyke Formation with Applications to Brittan. Edinburgh: Oliver & Boyd.
Banks, M. E., Xiao, Z., Watters, T. R., Strom, R. G., Braden, S. E., Chapman, C. R., et al. (2015). Duration of Activity on Lobate-Scarp Thrust Faults on Mercury. J. Geophys. Res. Planets 120, 1751–1762. doi:10.1002/2015JE004828
Banks, M. E., Xiao, Z., Braden, S. E., Barlow, N. G., Chapman, C. R., Fassett, C. I., et al. (2017). Revised Constraints on Absolute Age Limits for Mercury's Kuiperian and Mansurian Stratigraphic Systems. J. Geophys. Res. Planets 122, 1010–1020. doi:10.1002/2016JE005254
Barry, T. L., Kelley, S. P., Reidel, S. P., Camp, V. E., Self, S., Jarboe, N. A., et al. (2013). Eruption Chronology of the Columbia River Basalt Group. Geol. S. Am. S. 497, 45–66. doi:10.1130/2013.2497(2)
Bender, A. M., Amos, C. B., Bierman, P., Rood, D. H., Staisch, L., Kelsey, H., et al. (2016). Differential Uplift and Incision of the Yakima River Terraces, central Washington State. J. Geophys. Res. Solid Earth 121, 365–384. doi:10.1002/2015JB012303
Bertelsen, H. S., Rogers, B. D., Galland, O., Dumazer, G., and Abbana Benanni, A. (2018). Laboratory Modeling of Coeval Brittle and Ductile Deformation during Magma Emplacement into Viscoelastic Rocks. Front. Earth Sci. 6, 199. doi:10.3389/feart.2018.00199
Byerlee, J. D. (1968). Brittle-ductile Transition in Rocks. J. Geophys. Res. 73, 4741–4750. doi:10.1029/JB073i014p04741
Byrne, P. K., Klimczak, C., Celâl Şengör, A. M., Solomon, S. C., Watters, T. R., and Hauck, S. A. (2014). Mercury's Global Contraction Much Greater Than Earlier Estimates. Nat. Geosci. 7, 301–307. doi:10.1038/ngeo2097
Byrne, P. K., Ostrach, L. R., Fassett, C. I., Chapman, C. R., Denevi, B. W., Evans, A. J., et al. (2016). Widespread Effusive Volcanism on Mercury Likely Ended by about 3.5 Ga. Geophys. Res. Lett. 43, 7408–7416. doi:10.1002/2016GL069412
Camp, V. E., and Hanan, B. B. (2008). A Plume-Triggered Delamination Origin for the Columbia River Basalt Group. Geosphere 4, 480–495. doi:10.1130/GES00175.1
Camp, V. E., and Ross, M. E. (2004). Mantle Dynamics and Genesis of Mafic Magmatism in the Intermontane Pacific Northwest. J. Geophys. Res. 109, 1–14. doi:10.1029/2003JB002838
Camp, V. E., Reidel, S. P., Ross, M. E., Wolff, J. A., Martin, B. S., Tolan, T. L., et al. (2013). Origin of Columbia River Basalt: Passive Rise of Shallow Mantle, or Active Upwelling of a Deep-Mantle Plume. Geol. S. Am. S. 497, 181–199. doi:10.1130/2013.2497(07)
Camp, V. E., Reidel, S. P., Ross, M. E., Brown, R. J., and Self, S. (2017). Field-trip Guide to the Vents, Dikes, Stratigraphy, and Structure of the Columbia River Basalt Group, Eastern Oregon and southeastern Washington. Reston, VA: US Geological Survey, 1–88. No. 2017-5022-N. doi:10.3133/sir20175022N
Carlson, R. W., and Hart, W. K. (1987). Crustal Genesis on the Oregon Plateau. J. Geophys. Res. 92, 6191–6206. doi:10.1029/JB092iB07p06191
Casale, G., and Pratt, T. L. (2015). Thin‐ or Thick‐Skinned Faulting in the Yakima Fold and Thrust Belt (WA)? Constraints from Kinematic Modeling of the Saddle Mountains Anticline. Bull. Seismol. Soc. Am. 105, 745–752. doi:10.1785/0120140050
Catchings, R. D., and Saltus, R. W. (1994). Upper-crustal Structure beneath the Columbia River Basalt Group, Washington: Gravity Interpretation Controlled by Borehole and Seismic Studies: Discussion and Reply. Geol. Soc. Am. Bull. 106, 1096–1101. doi:10.1130/0016-7606(1994)106<1096:ucsbtc>2.3.co;2
Crane, K. T., and Klimczak, C. (2017). Timing and Rate of Global Contraction on Mercury. Geophys. Res. Lett. 44, 3082–3089. doi:10.1002/2017GL072711
Crane, K. T., and Klimczak, C. (2019a). Tectonic Patterns of Shortening Landforms in Mercury's Northern Smooth plains. Icarus 317, 66–80. doi:10.1016/j.icarus.2018.05.034
Crane, K. T., and Klimczak, C. (2019b). A 3-D Structural Model of the Saddle Mountains, Yakima Fold Province, Washington, USA: Implications for Late Tertiary Tectonic Evolution of the Columbia River Flood Basalt Province. Tectonophysics 766, 1–13. doi:10.1016/j.tecto.2019.05.015
Crane, K. (2020). Structural Interpretation of Thrust Fault-Related Landforms on Mercury Using Earth Analogue Fault Models. Geomorphology 369, 107366. doi:10.1016/j.geomorph.2020.107366
Dahm, T. (2000). Numerical Simulations of the Propagation Path and the Arrest of Fluid-Filled Fractures in the Earth. Geophys. J. Int. 141, 623–638. doi:10.1046/j.1365-246x.2000.00102.x
Das, T., and Nolet, G. (1998). Crustal Thickness Map of the Western United States by Partitioned Waveform Inversion. J. Geophys. Res. 103, 30021–30038. doi:10.1029/98JB01119
Davenport, K. K., Hole, J. A., Tikoff, B., Russo, R. M., and Harder, S. H. (2017). A strong Contrast in Crustal Architecture from Accreted Terranes to Craton, Constrained by Controlled-Source Seismic Data in Idaho and Eastern Oregon. Lithosphere 9, 325–340. doi:10.1130/L553.1
Davis, R. O., and Selvadurai, A. P. S. (1996). Elasticity and Geomechanics. Cambridge, UK: Cambridge University Press.
Delano, J. W. (1990). Buoyancy-driven Melt Segregation in the Earth's Moon. I-Numerical Results. Lunar Planet. Sci. Conf. Proc. 20, 3–12.
Denevi, B. W., Robinson, M. S., Solomon, S. C., Murchie, S. L., Blewett, D. T., Domingue, D. L., et al. (2009). The Evolution of Mercury's Crust: A Global Perspective from MESSENGER. Science 324, 613–618. doi:10.1126/science.1172226
Denevi, B. W., Ernst, C. M., Meyer, H. M., Robinson, M. S., Murchie, S. L., Whitten, J. L., et al. (2013). The Distribution and Origin of Smooth plains on Mercury. J. Geophys. Res. Planets 118, 891–907. doi:10.1002/jgre.20075
Egea-González, I., Ruiz, J., Fernández, C., Williams, J.-P., Márquez, Á., and Lara, L. M. (2012). Depth of Faulting and Ancient Heat Flows in the Kuiper Region of Mercury from Lobate Scarp Topography. Planet. Space Sci. 60, 193–198. doi:10.1016/j.pss.2011.08.003
Elliot, D. H., and Fleming, T. H. (2018). “The Ferrar Large Igneous Province: Field and Geochemical Constraints on Supra-crustal (High-level) Emplacement of the Magmatic System,” in Large Igneous Provinces from Gondwana and Adjacent Regions. Editors S. Sensarma, and B. C. Storey (London, United kingdom: Geologyical Society, London, Special Publications), 463, 41–58. doi:10.1144/SP463.1
Freed, A. M., Blair, D. M., Watters, T. R., Klimczak, C., Byrne, P. K., Solomon, S. C., et al. (2012). On the Origin of Graben and Ridges within and Near Volcanically Buried Craters and Basins in Mercury's Northern plains. J. Geophys. Res. 117, 1–15. doi:10.1029/2012JE004119
Galluzzi, V., Ferranti, L., Massironi, M., Giacomini, L., Guzzetta, L., and Palumbo, P. (2019). Structural Analysis of the Victoria Quadrangle Fault Systems on Mercury: Timing, Geometries, Kinematics, and Relationship with the High‐Mg Region. J. Geophys. Res. Planets 124, 2543–2562. doi:10.1029/2019JE005953
Greeley, R., Fagents, S. A., Harris, R. S., Kadel, S. D., Williams, D. A., and Guest, J. E. (1998). Erosion by Flowing Lava: Field Evidence. J. Geophys. Res. 103, 27325–27345. doi:10.1029/97JB03543
Gretener, P. E. (1969). On the Mechanics of the Intrusion of Sills. Can. J. Earth Sci. 6, 1415–1419. doi:10.1139/e69-143
Hales, T. C., Abt, D. L., Humphreys, E. D., and Roering, J. J. (2005). A Lithospheric Instability Origin for Columbia River Flood Basalts and Wallowa Mountains Uplift in Northeast Oregon. Nature 438, 842–845. doi:10.1038/nature04313
Hartley, M., and Maclennan, J. (2018). Magmatic Densities Control Erupted Volumes in Icelandic Volcanic Systems. Front. Earth Sci. 6, 29. doi:10.3389/feart.2018.00029
Head, J. W., Chapman, C. R., Strom, R. G., Fassett, C. I., Denevi, B. W., Blewett, D. T., et al. (2011). Flood Volcanism in the Northern High Latitudes of Mercury Revealed by MESSENGER. Science 333, 1853–1856. doi:10.1126/science.1211997
Hoek, E., and Martin, C. D. (2014). Fracture Initiation and Propagation in Intact Rock - A Review. J. Rock Mech. Geotechn. Eng. 6 (4), 287–300. doi:10.1016/j.jrmge.2014.06.001
Hoek, E. (1965). Rock Fracture under Static Stress Conditions. South Africa: National Mechanical Engineering Research Institute Council for Scientific and Industrial Research.
Hooper, A., Ófeigsson, B., Sigmundsson, F., Lund, B., Einarsson, P., Geirsson, H., et al. (2011). Increased Capture of Magma in the Crust Promoted by Ice-Cap Retreat in Iceland. Nat. Geosci. 4, 783–786. doi:10.1038/ngeo1269
Jaeger, J. C., Cook, N. G. W., and Zimmerman, R. (2007). Fundamentals of Rock Mechanics. 4th Ed. Malden, MA: Blackwell Publishing.
Kavanagh, J. L., Menand, T., and Sparks, R. S. J. (2006). An Experimental Investigation of Sill Formation and Propagation in Layered Elastic media. Earth Planet. Sci. Lett. 245, 799–813. doi:10.1016/j.epsl.2006.03.025
Kelsey, H. M., Ladinsky, T. C., Staisch, L., Sherrod, B. L., Blakely, R. J., Pratt, T. L., et al. (2017). The Story of a Yakima Fold and How it Informs Late Neogene and Quaternary Backarc Deformation in the Cascadia Subduction Zone, Manastash Anticline, Washington, USA. Tectonics 36, 2085–2107. doi:10.1002/2017TC004558
Kjøll, H. J., Galland, O., Labrousse, L., and Andersen, T. B. (2019). Emplacement Mechanisms of a Dyke Swarm across the Brittle-Ductile Transition and the Geodynamic Implications for Magma-Rich Margins. Earth Planet. Sci. Lett. 518, 223–235. doi:10.1016/j.epsl.2019.04.016
Klimczak, C., Watters, T. R., Ernst, C. M., Freed, A. M., Byrne, P. K., Solomon, S. C., et al. (2012). Deformation Associated with Ghost Craters and Basins in Volcanic Smooth plains on Mercury: Strain Analysis and Implications for plains Evolution. J. Geophys. Res. 117, 1–15. doi:10.1029/2012JE004100
Klimczak, C., Byrne, P. K., Şengör, A. M. C., and Solomon, S. C. (2019). Principles of Structural Geology on Rocky Planets. Can. J. Earth Sci. 56, 1437–1457. doi:10.1139/cjes-2019-0065
Klimczak, C. (2015). Limits on the Brittle Strength of Planetary Lithospheres Undergoing Global Contraction. J. Geophys. Res. Planets 120, 2135–2151. doi:10.1002/2015JE004851
Kuhn, D., and Dahm, T. (2004). Simulation of Magma Ascent by Dykes in the Mantle beneath Mid-ocean Ridges. J. Geodynamics 38, 147–159. doi:10.1016/j.jog.2004.06.002
Kuhn, D., and Dahm, T. (2008). Numerical Modelling of Dyke Interaction and its Influence on Oceanic Crust Formation. Tectonophysics 447, 53–65. doi:10.1016/j.tecto.2006.09.018
Lister, J. R. (1991). Steady Solutions for Feeder Dykes in a Density-Stratified Lithosphere. Earth Planet. Sci. Lett. 107, 233–242. doi:10.1016/0012-821X(91)90073-Q
Liu, L., and Stegman, D. R. (2012). Origin of Columbia River Flood basalt Controlled by Propagating Rupture of the Farallon Slab. Nature 482, 386–389. doi:10.1038/nature10749
Maccaferri, F., Bonafede, M., and Rivalta, E. (2011). A Quantitative Study of the Mechanisms Governing dike Propagation, dike Arrest and Sill Formation. J. Volcanol. Geothermal Res. 208, 39–50. doi:10.1016/j.jvolgeores.2011.09.001
Magee, C., Jackson, C. A.-L., Hardman, J. P., and Reeve, M. T. (2017). Decoding Sill Emplacement and Forced Fold Growth in the Exmouth Sub-basin, Offshore Northwest Australia: Implications for Hydrocarbon Exploration. Interpretation 5 (3), SK11–SK22. doi:10.1190/INT-2016-0133.1
Magee, C., Ernst, R. E., Muirhead, J., Phillips, T., and Jackson, C. A.-L. (2019a). “Magma Transport Pathways in Large Igneous Provinces: Lessons from Combining Field Observations and Seismic Reflection Data,” in Dyke Swarms of the World: A Modern Perspective. Editors R. Srivastava, R. Ernst, and P. Peng (Singapore: Springer), 45–85. doi:10.1007/978-981-13-1666-1_2
Magee, C., Muirhead, J., Schofield, N., Walker, R. J., Galland, O., Holford, S., et al. (2019b). Structural Signatures of Igneous Sheet Intrusion Propagation. J. Struct. Geol. 125, 148–154. doi:10.1016/j.jsg.2018.07.010
Marchi, S., Mottola, S., Cremonese, G., Massironi, M., and Martellato, E. (2009). A New Chronology for the Moon and Mercury. Astronomical J. 137, 4936–4948. doi:10.1088/0004-6256/137/6/4936
Menand, T., Daniels, K. A., and Benghiat, P. (2010). Dyke Propagation and Sill Formation in a Compressive Tectonic Environment. J. Geophys. Res. 115 (B8), 1–12. doi:10.1029/2009JB006791
Morriss, M. C., Karlstrom, L., Nasholds, M. W. M., and Wolff, J. A. (2020). The Chief Joseph dike Swarm of the Columbia River Flood Basalts, and the Legacy Data Set of William H. Taubeneck. William H. Taubeneck. Geosphere. 16, 1082–1106. doi:10.1130/GES02173.1
Muirhead, J. D., Airoldi, G., White, J. D. L., and Rowland, J. V. (2014). Cracking the Lid: Sill-Fed Dikes Are the Likely Feeders of Flood basalt Eruptions. Earth Planet. Sci. Lett. 406, 187–197. doi:10.1016/j.epsl.2014.08.036
Namur, O., and Charlier, B. (2017). Silicate Mineralogy at the Surface of Mercury. Nat. Geosci 10, 9–13. doi:10.1038/ngeo2860
Ostrach, L. R., Robinson, M. S., Whitten, J. L., Fassett, C. I., Strom, R. G., Head, J. W., et al. (2015). Extent, Age, and Resurfacing History of the Northern Smooth plains on Mercury from MESSENGER Observations. Icarus 250, 602–622. doi:10.1016/j.icarus.2014.11.010
Peterson, G. A., Johnson, C. L., Byrne, P. K., and Phillips, R. J. (2020). Fault Structure and Origin of Compressional Tectonic Features within the Smooth Plains on Mercury. J. Geophys. Res. Planets 125, e2019E006183. doi:10.1029/2019JE006183
Plattner, A. M., and Johnson, C. L. (2021). Mercury's Northern Rise Core‐Field Magnetic Anomaly. Geophys. Res. Lett. 48, e2021GL094695. doi:10.1029/2021GL094695
Plescia, J. B., and Golombek, M. P. (1986). Origin of Planetary Wrinkle Ridges Based on the Study of Terrestrial Analogs. Geol. Soc. Am. Bull. 97, 1289–1299. doi:10.1130/0016-7606(1986)97<1289:oopwrb>2.0.co;2
Reidel, S. P., Camp, V. E., Tolan, T. L., Kauffman, J. D., and Garwood, D. L. (2013a). Tectonic Evolution of the Columbia River Flood basalt Province. Geol. S. Am. S. 497, 293–324. doi:10.1130/2013.2497(12)
Reidel, S. P., Camp, V. E., Tolan, T. L., Martin, B. S., Ross, M. E., Wolff, J. A., et al. (2013b). The Columbia River Flood basalt Province: Stratigraphy, Areal Extent, Volume, and Physical Volcanology. Geol. S. Am. 497, 1–43. doi:10.1130/2013.2497(01)
Reidel, S. P. (1984). The Saddle Mountains; the Evolution of an Anticline in the Yakima Fold belt. Am. J. Sci. 284, 942–978. doi:10.2475/ajs.284.8.942
Rivalta, E., Taisne, B., Bunger, A. P., and Katz, R. F. (2015). A Review of Mechanical Models of dike Propagation: Schools of Thought, Results and Future Directions. Tectonophysics 638, 1–42. doi:10.1016/j.tecto.2014.10.003
Roman, A., and Jaupart, C. (2014). The Impact of a Volcanic Edifice on Intrusive and Eruptive Activity. Earth Planet. Sci. Lett. 408, 1–8. doi:10.1016/j/epsl.2014.09.01610.1016/j.epsl.2014.09.016
Rubin, A. M. (1995). Propagation of Magma-Filled Cracks. Annu. Rev. Earth Planet. Sci. 23, 287–336. doi:10.1146/annurev.ea.23.050195.001443
Schultz, R. A. (1993). Brittle Strength of Basaltic Rock Masses with Applications to Venus. J. Geophys. Res. 98, 10883–10895. doi:10.1029/93JE00691
Schultz, R. A. (2019). Geologic Fracture Mechanics. Cambridge, United Kingdom: Cambridge University Press. doi:10.1017/9781316996737
Solomon, S. C. (1977). The Relationship between Crustal Tectonics and Internal Evolution in the Moon and Mercury. Phys. Earth Planet. Interiors 15, 135–145. doi:10.1016/0031-9201(77)90026-7
Solomon, S. C. (1978). On Volcanism and thermal Tectonics on One-Plate Planets. Geophys. Res. Lett. 5, 461–464. doi:10.1029/GL005i006p00461
Spudis, P. D., and Guest, J. E. (1988). “Stratigraphy and Geologic History of Mercury,” in Mercury. Editors F. Vilas, C. R. Chapman, and M. S. Matthews (Tuscon, AZ: University of Arizona Press), 118–164.
Staisch, L., Blakely, R., Kelsey, H., Styron, R., and Sherrod, B. (2018). Crustal Structure and Quaternary Acceleration of Deformation Rates in central Washington Revealed by Stream Profile Inversion, Potential Field Geophysics, and Structural Geology of the Yakima Folds. Tectonics 37, 1750–1770. doi:10.1029/2017TC004916
Stockstill-Cahill, K. R., McCoy, T. J., Nittler, L. R., Weider, S. Z., and Hauck, S. A. (2012). Magnesium-rich Crustal Compositions on Mercury: Implications for Magmatism from Petrologic Modeling. J. Geophys. Res. 117, 1–13. doi:10.1029/2012JE004140
Strom, R. G., Trask, N. J., and Guest, J. E. (1975). Tectonism and Volcanism on Mercury. J. Geophys. Res. 80, 2478–2507. doi:10.1029/JB080i017p02478
Tibaldi, A., Pasquarè, F., and Tormey, D. (2010). “Volcanism in Reverse and Strike-Slip Fault Settings,” in New Frontiers in Integrated Solid Earth Sciences. Editors S. Cloetingh, and J. Negendank (Dordrecht, Heidelberg, London, New York: Springer Science and Business Media), 315–348. doi:10.1007/978-90-481-2737-5_9
Van Noort, R., Wolterbeek, T., Drury, M., Kandianis, M., and Spiers, C. (2017). The Force of Crystallization and Fracture Propagation during In-Situ Carbonation of Peridotite. Minerals 7, 190. doi:10.3390/min7100190
Watanabe, T., Masuyama, T., Nagaoka, K., and Tahara, T. (2002). Analog Experiments on Magma-Filled Cracks: Competition between External Stresses and Internal Pressure. Earth Planet. Sp 54 (12), e1247–e1261. doi:10.1186/bf03352453
Watters, T. R., and Nimmo, F. (2010). “The Tectonics of Mercury,” in Planetary Tectonics. Editors T. R. Watters, and R. A. Schultz (Cambridge, UK: Cambridge University Press), 15–80.
Watters, T. R., Schultz, R. A., Robinson, M. S., and Cook, A. C. (2002). The Mechanical and thermal Structure of Mercury's Early Lithosphere. Geophys. Res. Lett. 29, 37–1374. doi:10.1029/2001GL014308
Watters, T. R., Selvans, M. M., Banks, M. E., Hauck, S. A., Becker, K. J., and Robinson, M. S. (2015). Distribution of Large‐scale Contractional Tectonic Landforms on Mercury: Implications for the Origin of Global Stresses. Geophys. Res. Lett. 42, 3755–3763. doi:10.1002/2015GL063570
Watters, T. R., Daud, K., Banks, M. E., Selvans, M. M., Chapman, C. R., and Ernst, C. M. (2016). Recent Tectonic Activity on Mercury Revealed by Small Thrust Fault Scarps. Nat. Geosci. 9, 743–747. doi:10.1038/ngeo2814
Watters, T. R. (1992). System of Tectonic Features Common to Earth, Mars, and Venus. Geol 20, 609–612. doi:10.1130/0091-7613(1992)020<0609:sotfct>2.3.co;2
Weider, S. Z., Nittler, L. R., Starr, R. D., McCoy, T. J., Stockstill-Cahill, K. R., Byrne, P. K., et al. (2012). Chemical Heterogeneity on Mercury's Surface Revealed by the MESSENGER X-Ray Spectrometer. J. Geophys. Res. 117, 1–15. doi:10.1029/2012JE004153
Weider, S. Z., Nittler, L. R., Starr, R. D., Crapster-Pregont, E. J., Peplowski, P. N., Denevi, B. W., et al. (2015). Evidence for Geochemical Terranes on Mercury: Global Mapping of Major Elements with MESSENGER's X-Ray Spectrometer. Earth Planet. Sci. Lett. 416, 109–120. doi:10.1016/j.epsl.2015.01.023
Wilson, L., and Head, J. W. (2008). Volcanism on Mercury: A New Model for the History of Magma Ascent and Eruption. Geophys. Res. Lett. 35, L23205. doi:10.1029/2008GL035620
Wolff, J. A., Ramos, F. C., Hart, G. L., Patterson, J. D., and Brandon, A. D. (2008). Columbia River Flood Basalts from a Centralized Crustal Magmatic System. Nat. Geosci. 1, 177–180. doi:10.1038/ngeo124
Keywords: Mercury, fault (fracture) section, structural geology, tectonics, dike, Earth analogs
Citation: Crane K and Bohanon A (2021) Dike Propagation During Global Contraction: Making Sense of Conflicting Stress Histories on Mercury. Front. Earth Sci. 9:752864. doi: 10.3389/feart.2021.752864
Received: 03 August 2021; Accepted: 30 November 2021;
Published: 23 December 2021.
Edited by:
Matteo Massironi, University of Padua, ItalyReviewed by:
Valentina Galluzzi, Institute for Space Astrophysics and Planetology (INAF), ItalyValerio Acocella, Roma Tre University, Italy
Copyright © 2021 Crane and Bohanon. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kelsey Crane, a2Vsc2V5Y3JhbmVAZ2Vvc2NpLm1zc3RhdGUuZWR1
 Kelsey Crane
Kelsey Crane Allison Bohanon
Allison Bohanon