Minimum Detectable Mass and Volume Fluxes During Magmatic Recharge at High Prominence Volcanoes: An Application to Erciyes Dağ Volcano (Turkey)

Magma reservoir recharge is widely recognised as a precursor of eruptive activity. However, the causative relationships between reservoir rejuvenation and surface observables such as gravitational potential field changes and ground deformation are still poorly understood. At intermediate and silicic intra-plate volcanoes where crustal mechanical heterogeneity combined with high-prominence are expected to fundamentally affect the crustal stress and strain relationship, protracted period of repose and absence of monitoring data raise questions about the detectability of magma recharge. Here we report results from integrated geodetic forward modelling of ground displacements and gravity changes from reservoir recharge at Erciyes Dağ, a large prominence (∼2,800 m), yet poorly studied, stratovolcano of the Central Anatolian Volcanic Province in Turkey. The most recent eruption at ∼7000 BC, close proximity to the Kayseri Metropolitan Area and absence of dedicated volcano monitoring set a precedent to explore stealth magmatic processes at the volcano. Using finite element analysis we systematically explore the influence of subsurface mechanical heterogeneities and topography on surface deformation and gravity changes from magmatic recharge of Erciyes Dağ’s reservoir. We show that whilst crustal heterogeneity amplifies ground displacements and gravity variations, the volcano’s substantial prominence has the opposite effect. For generic reservoir pressure and density changes of 10 MPa and 10 kg m⁻³ predicted vertical displacements vary by a factor of 5 while residual gravity changes vary by a factor of 12 between models ignoring topography or mechanical heterogeneity and those that do not. We deduce reservoir volume and mass changes of order 10^–3 km³ and 10¹⁰ kg, respectively, at the detectability limit of conventional surveying techniques at the volcano. Though dependent on model assumptions, all results indicate that magma recharge at Erciyes Dağ may go undetected at fluxes 1) sufficient to maintain an active reservoir containing eruptable magma and 2) similar to those reported for intermediate/silicic volcanoes with repose times of 100–1,000s of years (e.g., Parinacota) and persistently active mafic volcanoes such as Mt. Etna and Stromboli. Our findings may be utilised to inform integrated geodetic and gravimetric monitoring at Erciyes Dağ and other large prominence silicic volcanoes and could provide early insights into reservoir rejuvenation with implications for the development of disaster risk reduction initiatives.

1 Introduction

Joint ground deformation and microgravity observations are important methods for assessing subsurface processes at active volcanoes including during unrest and the lead-up to eruptive activity (Rymer and Brown, 1989; Carbone et al., 2007; Battaglia et al., 2008; Currenti, 2014; Carbone et al., 2017; Fernández et al., 2017; Gottsmann et al., 2020). Coupled with data modelling using both analytical and numerical approaches, these techniques allow the delineation of spatio-temporal variations in density and mass in sub-volcanic plumbing systems. Most analytical geodetic models rely on the concept of a causative source embedded within an isotropic, homogeneous, elastic half-space beneath a flat free surface (Mogi, 1958; Hagiwara, 1977). However, it has been acknowledged that such simplifications may lead to biased results on source parameters because volcanic regions have 1) substantial topographical relief, with some volcanic edifices showing significant >2,000 m topographic prominence (Cayol and Cornet, 1998; Williams and Wadge, 1998) and 2) are characterised by complex crustal heterogeneities due to the nature of geodynamic and eruptive processes underpinning volcanism (Gudmundsson and Brenner, 2004). Currenti et al. (2007) highlight a negative correlation between topographic prominence and detectable ground displacements and residual gravity variations. Medium heterogeneity fundamentally affects the subsurface stress vs. strain relationship and thus the resultant deformation measured at the surface (Bonaccorso et al., 2005; Hickey et al., 2016). The magnitude of surface displacement and thus gravity variations may be amplified, or muted, by mechanically soft and stiff lithologies, respectively, with amplification effects intensified at shallower depths where crustal layers are typically softer (Geyer and Gottsmann, 2010). Topographic and mechanical complexities necessitate the use of numerical approaches which come at substantial computational costs and are hence often ignored in favour of analytical approaches. This stands in contrast to observations, particularly at steep-sided stratovolcanoes, which show a significant number of eruptions that occur with no prior surface deformation (Biggs et al., 2014). Here we focus on Erciyes Dağ in Central Anatolia, Turkey, an active and large prominence volcano that lacks dedicated volcano monitoring. Hence little to nothing is known about subsurface processes currently operating at the volcano and their relation with surface observables. Exploring both analytical and numerical modelling, this study aims to determine reservoir mass and volume changes at Erciyes Dağ from minimum resolvable surface deformation and gravity changes. The hypothesis underpinning this work is that magma reservoir rejuvenation at Erciyes Dağ may occur at below the detectability limit of spatio-temporal geodetic and gravimetric anomalies.

2 Geodynamic and Geological Background

2.1 Central Anatolian Volcanic Province

A series of Miocene-to-recent calderas, stratovolcanoes and monogenetic fields that constitute the Central Anatolian Volcanic Province (CAVP) (Innocenti et al., 1982) are situated within the Central Anatolian Fault Zone (CAFZ) (Koçyiğit and Beyhan, 1998) (Figure 1). The CAFZ represents a 730 km intracontinental transform fault zone, with ensuing ENE-WSW extension resulting in the regional intra-plate volcanism of the CAVP (Koçyiğit and Beyhan, 1998; Sen et al., 2004). Within the CAFZ, the Erciyes pull-apart basin (EPB) is formed by a S-shaped horst and graben structure creating an extensional depression in which Erciyes Dağ is located (Koçyiğit and Beyhan, 1998).

FIGURE 1

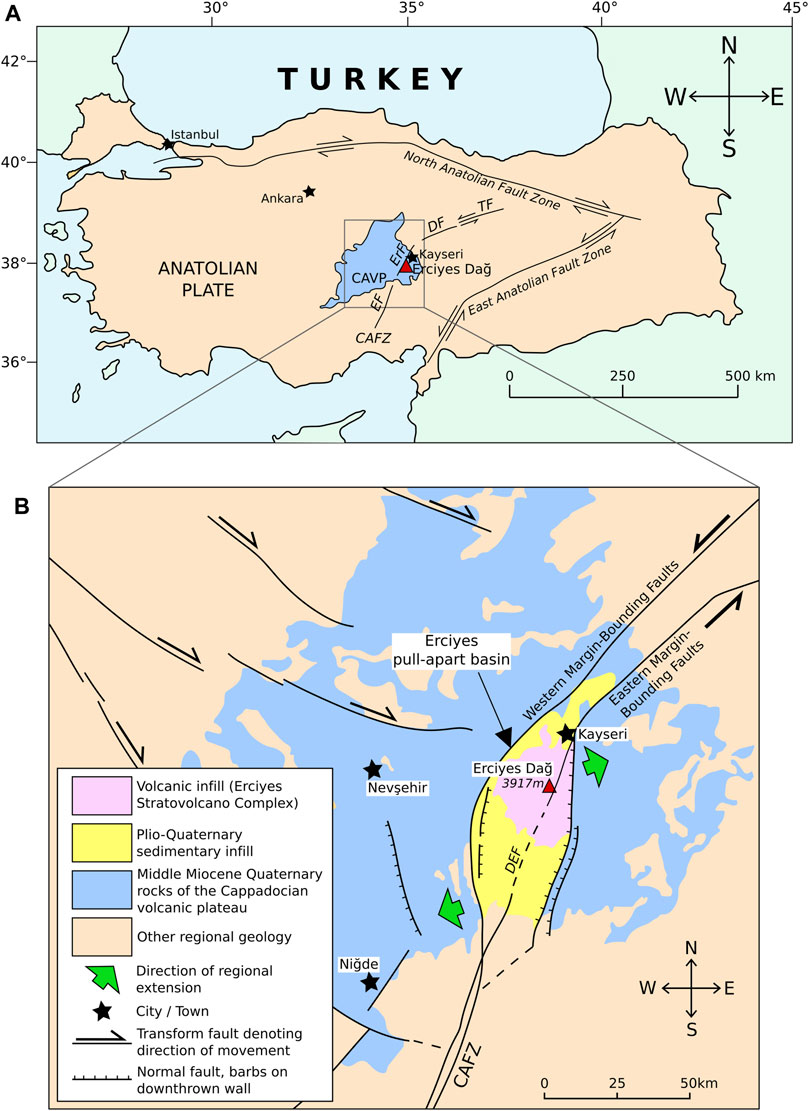
FIGURE 1. Location of Erciyes Dağ within the Central Anatolian Volcanic Province (CAVP). (A) Tectonic overview map of Central Anatolia and Turkey after Dogan et al. (2013). The Anatolian plate is bounded by the Northern and Eastern Fault Zones between the colliding Eurasian and Arabian plates. (B) Regional volcano-tectonic map of Erciyes Dağ after Koçyiğit and Erol (2001). The volcano is located 25 km south of the city centre of Kayseri and within the Erciyes pull-apart basin (EPB). Note: CAFZ = Central Anatolian Fault Zone, TF = Tecer Fault, DF = Deliler Fault, ErF = Erciyes Fault, EF = Ecemis Fault, DEF = Dundarli-Erciyes Fault segment.

2.2 Erciyes Dağ

Erciyes Dağ is an active Pliocene-Quaternary age stratovolcano, with its last known eruption in 6880 BC (Kürkcüoglu et al., 2004). With a summit height of 3,917 m a.s.l., it has a prominence over the surrounding topographic plateau of ∼2,800 m (Gazioğlu et al., 2004). Located ca 25 km south of Kayseri city centre and in the centre of a 14 km by 18 km wide Pleistocene caldera, the volcano towers above the Metropolitan Municipality of Kayseri. With a population of ∼1 million, the southern municipal boundaries reach within a few km of the volcano’s edifice. The Dundarli-Erciyes fault segment of the larger Ecemis fault zone intersects Erciyes’ edifice and the locations of the most recently formed domes along the fault segment are suggestive of magma-tectonic interactions (Koçyiğit and Erol, 2001; Sen et al., 2004). Koçyiğit and Erol (2001) proposed the coeval formation of the EPB alongside Erciyes Dağ’s edifice, with associated crustal thinning encouraging the migration of magma. Seismic data of the crustal architecture of Central Anatolia indicate an overall increase in compressive and shear wave velocities with depth (Salah et al., 2014).

Erciyes Dağ evolved over two principal stages: the initial andesitic-basaltic Koç Dağ stage, and the most recent andesitic-dacitic Erciyes stage (Şen et al., 2003). At the end of the Erciyes stage rhyodacitic domes were extruded along the Dundarli-Erciyes fault segment (Dikkartin Dağ and Perikatin Dağ). Wider geodynamic studies of magmatic sources within Central Anatolia advocate a connection to the ongoing collision of the Eurasian and Arabian tectonic plates (Pasquare et al., 1988) and trace element contributions in magmas from Erciyes Dağ are ascribed to lithospheric assimilation from past subductive periods (Kürkçüoglu et al., 1998). Petrological studies (Dogan et al., 2011, 2013) indicate the presence of two interacting magma reservoirs which fuel eruptions at the volcano: 1) an upper-crustal reservoir at depths of 4–10 km and 2) a deeper-seated (>15 km depth) reservoir that feeds magma to the shallower reservoir (Dogan et al., 2011). The currently preferred petrogenic model for Erciyes describes the flux of parental basaltic melts into the mid to lower crust, at which point they evolve in composition, enriching in silica via processes of crustal assimilation and differentiation (Dogan et al., 2013). These more evolved melts then rise to shallower crustal depths of 4–10 km, at which point they mix with existing entrained crystals and melts within the shallow reservoir (Dogan et al., 2013). This petrogenic model concurs with the concept of transcrustal magma systems occupied by crystal mush and mobile magma (Cashman et al., 2017).

3 Methods

3.1 Potential Field and Ground Deformation Analysis

Subsurface mass redistribution and deformation modify the crustal density distribution Δρ(x, y, z). As a result the gravitational potential ϕ_g changes and we quantify this in our models by solving the following differential equation (Cai and Wang, 2005):

${\nabla }^2{\varphi }_g=-4\pi G\mathrm{\Delta }\rho \left(x,y,z\right)(1)$

where G is the universal gravitational constant. The problem is mathematically closed by imposing Dirichlet boundary conditions of zero at infinity.

Here we are concerned with the variations in the vertical component of gravity that is typically measured in volcano gravimetric surveying such that:

$\mathrm{\Delta }g\left(x,y,z\right)=\left(-\frac{\delta {\varphi }_g}{\delta z}\right).(2)$

Three source terms (Figure 2) quantify the different contributions to the redistribution of subsurface density (Bonafede and Mazzanti, 1998; Zhang et al., 2004; Currenti et al., 2007):

$\mathrm{\Delta }\rho \left(x,y,z\right)=-\mathbf{u}\cdot \nabla {\rho }_0+\mathrm{\Delta }{\rho }_i-{\rho }_0\nabla \cdot \mathbf{u}.(3)$

where u represents the displacement field, ρ₀ denotes the density of the embedding medium, and Δρ_i is the density change from magma injection into the source.

FIGURE 2

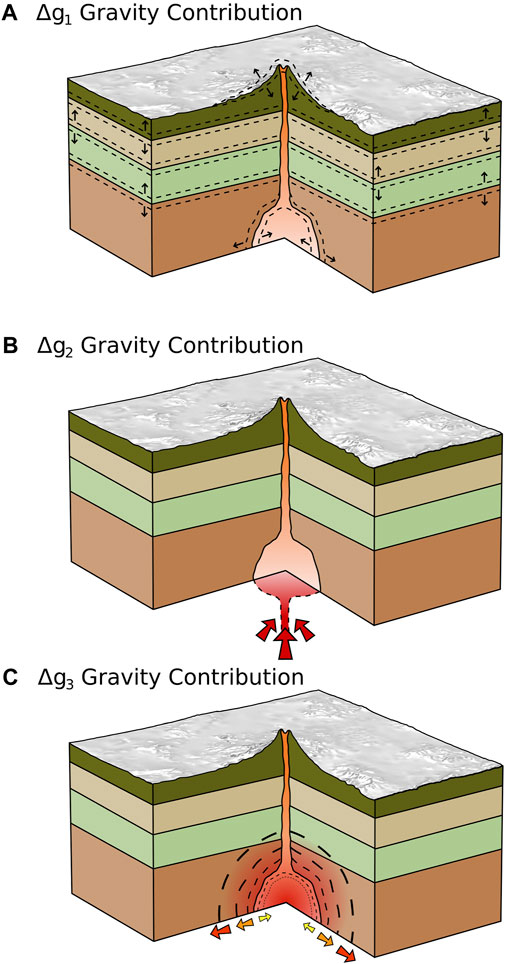
FIGURE 2. Schematics of the principal contributions to gravity changes measured at volcanoes from changes in the subsurface density distribution produced by: (A) the displacement of density boundaries (including the free surface, the source walls, and crustal density boundaries), (B) the source mass change, and (C) the volume change of the reservoir itself modulated by crustal compressibility (after Bonafede and Mazzanti (1998) and Currenti et al. (2007)).

The first term (denoted Δg₁ hereafter) arises from the shifting of density boundaries within the crust. The second term (Δg₂) quantifies density variations due to the change in mass in the source volume and is composed of two components: 1) the density change resulting from the input of new mass into the reservoir at constant volume V and the compression of resident magma and 2) the density change accompanying the volume expansion ΔV of the reservoir. The first component is dependent on reservoir compressibility β_r = β_c+1/ρ × Δρ/ΔP, where β_c is the compressibility of the encasing host rock, while the second component is dependent on the density change induced by the deforming reservoir and the replacement of mass surrounding the reservoir. The third term (Δg₃) reflects modulation of the changes in source volume by host-rock compressibility (Bonafede and Mazzanti, 1998).

To obtain residual changes in the vertical component of gravity (Δg_r), one needs to also account for the “Free-Air” gravity change Δg₀ that accompanies vertical surface deformation:

$\mathrm{\Delta }{g}_0=\gamma w(4)$

where γ is the Free-Air gradient (−308.6 µGal m⁻¹; 1 µGal = 10^–8 m s⁻²) and w is the vertical change in the position of the observation point.

All four terms contribute to the residual gravity variation:

$\mathrm{\Delta }{g}_r=\mathrm{\Delta }{g}_0+\mathrm{\Delta }{g}_1+\mathrm{\Delta }{g}_2+\mathrm{\Delta }{g}_3(5)$

In this study we only consider elastic deformation in the form of Hooke’s law which relates stress σ and strain ϵ via:

$\sigma =2\mu ϵ+\lambda \mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}\left(ϵ\right)I(6)$

$ϵ=0.5\left(\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^T\right)(7)$

where μ and γ are the Lamé parameters and I is the identity matrix.

Eastward, northward and vertical displacement vectors u, v and w, respectively, are derived directly from the model from which total displacements are calculated.

Ground displacement and gravity change data must be modelled jointly and simultaneously to quantify the different contributions to changes in the gravitational potential from subsurface processes.

3.2 Model Development and Parameterisation

We solve the above equations numerically using Finite Element Analysis in COMSOL Multiphysics v5.4 for a suite of 2D axisymmetric and 3D forward models to study the effect of crustal mechanical heterogeneity and topography on measured ground displacements and gravity changes from rejuvenation of Erciyes Dağ’s magmatic reservoir. Model parameters and symbols utilised throughout this study may be found in Table 1.

TABLE 1

TABLE 1. Model parameters, symbols and abbreviations used in this study.

3.2.1 Subsurface Mechanics

Geophysical data on the subsurface architecture of Erciyes Dağ are largely absent. Seismic tomography data by Salah et al. (2014) provide low resolution 1D p-wave velocities (V_p) and p-wave/s-wave velocity ratios (V_p/V_s) across Central Anatolia for depths of 4, 12, 25 and 40 km which we use to parameterise subsurface mechanical heterogeneity (Figure 3). Owing to the absence of seismic data for the uppermost (<4 km depth) Central Anatolian crust, we use seismic data from the Cascades around Mt. St. Helens (Kiser et al., 2016) as a geologically plausible alternative due to similar seismic velocity distribution at depth >4 km (e.g., at 4 km depth V_p and V_p/V_s data in Central Anatolia are only <1.5% larger than in the Cascades). We use the seismic data to derive elastic properties following empirical equations presented in Brocher (2005):

$\rho =1.6612V_p-0.4721{V_p}^2+0.0671{V_p}^3-0.0043{V_p}^4+0.000106{V_p}^5(8)$

FIGURE 3

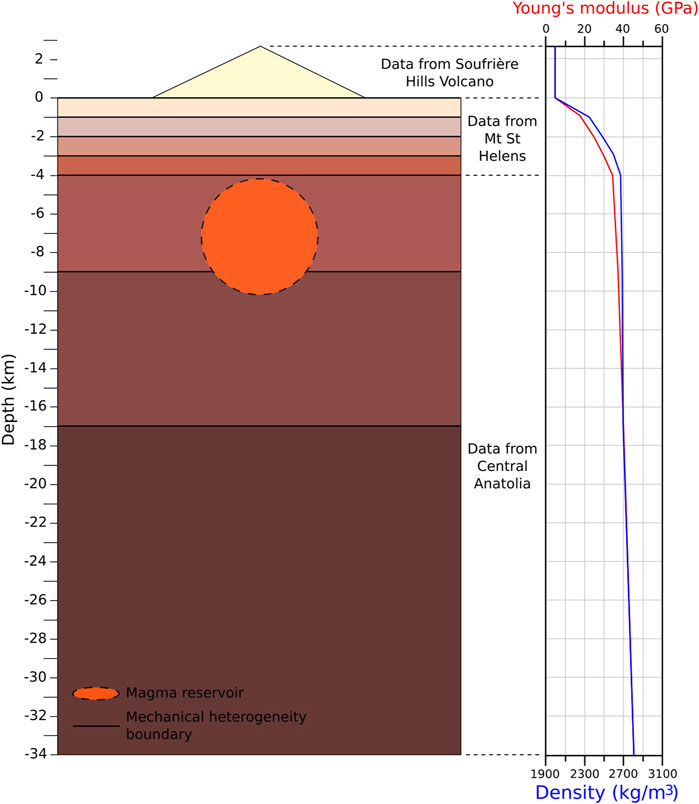
FIGURE 3. Schematic of subsurface material properties (crustal density ρ_c and crustal static Young’s modulus E_s) of the layered TOPO model (LTM) derived from 1D seismic tomography data of central Anatolia (Salah et al., 2014) using Eqs 8–10. In the absence of shallow crustal data for the volcano and surrounding areas, we use seismic data from the Cascades around Mt St Helens (Kiser et al., 2016). Edifice properties are taken from Soufrière Hills Volcano (Young and Gottsmann, 2015). An idealised topographic relief of Erciyes Dağ is shown for simplicity rising ∼3 km from the surrounding plateau (z = 0). Digital elevation data is used to parameterise the topographic surface in the Finite Element models. The magma reservoir is represented by a sphere with its centroid located directly beneath the summit of the volcano at a depth of z = −7 km.

Depth dependent Poisson’s ratios (ν) were determined from V_p/V_s ratios:

$\nu =\left({\left[V_p/V_s\right]}^2-2\right)/\left({\left[V_p/V_s\right]}^2-1\right)(9)$

to derive the dynamic Young’s modulus E_d from:

$E_d=\left(V_p^2\nu \left(1+\nu \right)\left(1-2\nu \right)\right)/\left(1-\nu \right)(10)$

We convert E_d to static Young’s moduli E_s for appropriate pressures and temperatures following Eissa and Kazi (1988) such that E_s = 0.5E_d. Parameters are computed for each depth segment of the crust shown in Figure 3, for 0 > z > -34 km (the depth of the Moho), with values reported in Table 2. Note that in all models, depth is expressed by negative values of z. For clarity, in the text we refer to depth by positive values. Median average values of subsurface mechanics used in generic models are shown in Table 3. Elastic properties for Erciyes Dağ’s edifice were taken from Montserrat (Young and Gottsmann, 2015) due to broadly similar eruptive products of dome-building andesite volcanism at both volcanoes. In all derivations, effects of temperature variations in the subsurface on elastic properties are neglected.

TABLE 2

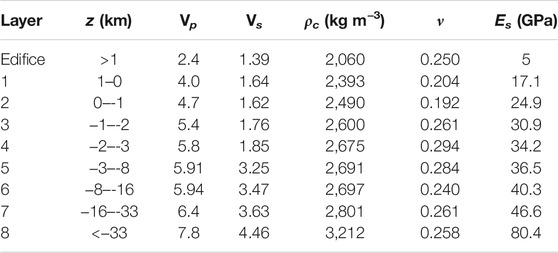
TABLE 2. Mechanical properties assigned to subdomains in layered models based on seismic velocities (V_p V_s). In the absence of local seismic data for the edifice and uppermost portions of the crust, data from Soufrière Hills volcano Young and Gottsmann (2015) are used for z > 1 km and from the Cascades Kiser et al. (2016) for 1 ≥ z ≥ −3 km. Values for z < -3 km are derived from data presented in Salah et al. (2014). The plateau surrounding Erciyes Dağ is at z = 0 km in the model, thus the edifice extends to a height of 2,917 m. See Eq. 8 and Table 1 for further information on the derivation of the values.

TABLE 3

TABLE 3. Median values of mechanical properties (for 0 > z > −33 km reported in Table 2) and source parameter changes assigned to generic models.

3.2.2 Magma Reservoir

In the absence of any geophysical constraints, we use petrological data in combination with calculations of the magma chamber volume to estimate source parameters such as depth and geometry. Dogan et al. (2013) used amphibole geobarometry to define an upper crustal magma reservoir located at 4–10 km depth beneath Erciyes Dağ within a homogeneous crust. We recalculated the barometric data to derive reservoir depth account for the subsurface density distribution. This provided a centroid depth of the reservoir of z = −7 km beneath the surface. The total volume of a magma reservoir (V_m) with magma compressibility (β_m), located in country rock with in-situ tensile strength (T₀) and average compressibility (β_c), is related to the volume of ejected material (V_e) for a given eruptive phase (Browning et al., 2015) via:

$V_m=\frac{V_e}{T_0\left({\beta }_m+{\beta }_c\right)}(11)$

We calculate an average value of β_c = $\frac{3(1-2\nu )}{E_s}$ = 1.78 × 10^–11 Pa⁻¹ for the reservoir depth range and set β_m = 7.6 × 10^–10 Pa⁻¹ to account for the explosive nature of Erciyes’ dome-forming eruptions (Voight et al., 2010). A dense rock equivalent (DRE) V_e = 0.958 km³ for Erciyes’ most recent dome-forming eruption at Dikkartin Dağ (Şen et al., 2002) gives V_m = 123.5 km³. In the absence of any information that would indicate otherwise, a spherical reservoir of radius α = 3.1 km is the most plausible representation of the reservoir given the volumetric and petrological constraints. In all models the surface projection of the centroid is at 38°31′54″N and 35°26′48″E.

3.3 Model Suite

Sets of different 2D axisymmetric and 3D models are developed to systematically explore the influence of crustal heterogeneity and topography on source parameter changes (generic models) and minimum detectable mass and volume fluxes (minimum detectability models). Models with a flat free surface are labelled “FLAT,” while models implementing a topography are labelled “TOPO”: 1) Base models (BM) including FLAT models (FM) and Layered FLAT models (LFM), and 2) TOPO models (TM) including layered TOPO models (LTM) and non-layered TOPO models (NLTM). 2D models are covered in the Supplementary Material. Here we focus on the development and analysis of 3D models with model characteristics summarised in Table 4.

TABLE 4

TABLE 4. Details of 3D mechanically homogeneous (Ho) and heterogeneous (He) models developed in this study and results for generic input parameters listed in Table 3. Δg₁, Δg₂, and Δg₃ are the maximum magnitudes of the three different contributions of gravity variations to residual gravity changes Δg_r (all rounded to the nearest μGal). u, v and w are maximum eastward, northward and vertical displacements (in m), respectively. See also Figures 5, 6 for full spatial coverage of model results.

3.3.1 3D Base Models

An initial 3D FM is created to benchmark against a 2D axisymmetric FM. An 80 km * 80 km * 68 km computational domain is created in order to prevent artefacts within the numerical solution inflicted by boundary effects. The base of the model is set at z = −34 km, representing the Moho depth, with the free surface, representing the volcanic plateau, set at z = 0 km. Median average values for mechanical properties reported in Table 3 are applied to invoke subsurface mechanics. Dirichlet boundary conditions are set to zero on the outer faces, a fixed base is added, and roller conditions are applied to the lateral faces of the domain for z < 0 km. Coefficient form Partial Differential Equations (PDE) representing the Δg₁, Δg₂ and Δg₃ terms are solved for the edifice, crust and source to calculate gravitational potential variations at the surface. The Δg₀ term is accounted for during post-processing. A 3D LFM is then compared to a 3D FM to resolve the effect of subsurface density variations within the crust. The LFM incorporates eight layers with material properties defined in Table 2.

3.3.2 3D Layered TOPO Models

Building on the LFM we implement a 3D topography using 90 m SRTM data to generate a digital elevation model (DEM) of the surface to obtain an LTM. The DEM is imported and introduced as a parametric surface with a relative tolerance of 0.001 and a maximum number of 150 knots to optimise resolution of the surface whilst precluding excessive computational cost. The source is implemented at the coordinates as in the BM and sits directly beneath the edifice at a centroid depth of 7 km beneath the plateau. Parametric surfaces representing Erciyes’ subsurface layers are employed, along with a cylinder of radius 10 km extending to a depth of 1 km around the volcanic edifice for meshing purposes (Figure 4). The PDEs are solved to each subsurface layer individually. Meshing follows a structured approach whereby mesh refinement is applied to the cylindrical domain encompassing the edifice and the source (Hickey et al., 2015). Through a computational cost-benefit analysis, it was determined that higher resolution, low-cost models may be obtained by adding a point to the topographic surface at the centre of the edifice and creating a custom mesh around it. Maximum and minimum element sizes of 20 and 5 m, respectively, are defined with a maximum element growth rate of 1.1 and a curvature factor of 0.4. The effect of topography in integrated geodetic modelling is evaluated by comparing results from the LTM against those from the LFM. Additionally, the LTM results are contrasted with those from the TM to assess the effect of subsurface layering.

FIGURE 4

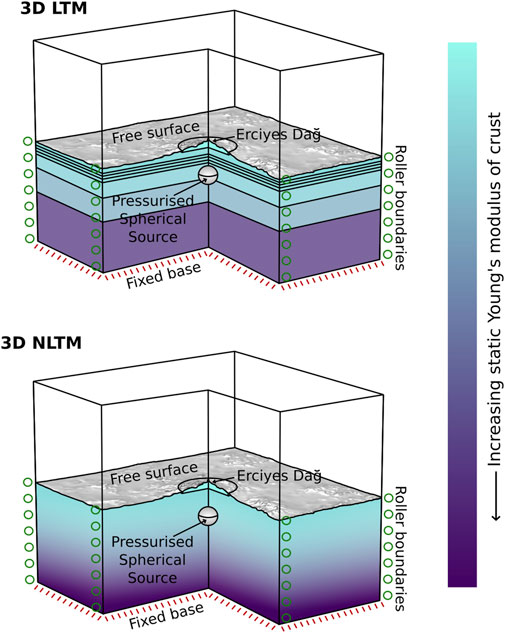
FIGURE 4. Schematics of 3D model setups for the heterogeneous layered and non-layered TOPO models (LTM and NLTM) including applied domain boundary conditions. Whilst the subsurface of the layered model contains discrete mechanical layers throughout the crust, the non-layered model comprises gradually varying mechanical properties. The two models denote end-member implementations of a heterogeneous mechanical crustal structure beneath Erciyes Dağ.

3.3.3 3D Non-Layered TOPO Models

Whilst the mesh refinement technique described above prevents high computational cost, the expense is still large. To further reduce cost, 3D NLTMs are produced, decreasing the required quantity of mesh elements due to fewer subsurface layers. Polynomial fits to ρ_c, E_s, and ν data presented in Table 2 are used to parameterise the NLTM (Figure 2. The model domain geometry is set up as before minus the parametric surfaces defining the layers (Figure 4). The cylindrical domain of radius 10 km remains around Erciyes’ edifice due to the greater disparity between the edifice and subsurface crustal properties, as do the material properties assigned to the edifice and source. Model physics and a structured mesh as described above are added to the domain, and Δg₁, Δg₂ and Δg₃ terms are solved for the edifice, crust and source. Results are compared to those of the LTM to determine the effect of discrete vs. gradual subsurface layering on gravity variations and surface deformation. The NLTMs provide insight on the gravity change contributions from shifting density boundaries in a layered versus non-layered crust. Moreover, depending on acceptable uncertainties within the results, the penalty in terms of accuracy between models may be determined given that the crust is neither fully density layered, nor does subsurface density gradually vary throughout. The LTM solves for ∼5.5 million degrees of freedom, whereas the NLTM solves for ∼2.3 million degrees of freedom and solves ∼50% faster.

3.4 Mass and Volume Fluxes at the Detectability Limit

We determine mass and volume changes upon reservoir recharge for given source pressurisation (ΔP) and source density change (Δρ) at the detectability limits of joint gravimetric and geodetic field surveys. We set the limits to 0.01 m for vertical surface displacements and 0 ± 5 μGal (1μ = 10^–8 m s⁻²) for residual gravity changes based on the typical sensitivity of field instrumentation and survey protocols as well as constraints from remote sensing of volcanoes in the CAVP (Biggs et al., 2021). The minimum detectable volume flux into the reservoir is given by McTigue (1987):

$\mathrm{\Delta }V=\frac{\alpha \pi }{\mu }\mathrm{\Delta }P(12)$

where α is the source radius and μ is the shear modulus. The associated reservoir minimum mass change is calculated from

$\mathrm{\Delta }M=\mathrm{\Delta }V{\rho }_m(13)$

using the relationship between mass change, density and volume change.

4 Results

4.1 Generic Models

All results from generic models are reported in Table 4. Here we focus on presenting the differences in results by comparing different modelling approaches as a function of increasing complexity.

4.1.1 FM Versus TM

The addition of topography triggers an overall halving of magnitudes of surface displacement and gravity changes. The TM yields maximum total surface displacement and w values 53% less than the FLAT model. Values of u and v decrease by 45 and 46%, respectively, between the FM and TM. The Δg₁ maximum value decreases by 40%, whilst the minimum value decreases by 42% in the TM compared to the FM. The Δg₂ contribution value reduces by 54% in the TM compared to the FLAT model, and Δg₃ decreases by 41%. These disparities result in a decrease of the Δg_r value by 45% in the TM compared to the FM.

4.1.2 TM Versus LTM

Subsurface mechanical layering increases magnitudes of all model outputs compared to those from implementing homogeneous mechanics. Total displacement and w increase 2.8 fold between the TM and the LTM, with u and v increasing 2.9 and 3 times, respectively (Figure 5). The maximum magnitude of Δg₁ increases by a factor of 2.7 in the LTM whereas the minimum Δg₁ value increases 2.3 fold. The Δg₂ term is increased 8.6 times and the Δg₃ contribution is increased by a factor of 3.3 in the LTM compared to the TM. The resulting Δg_r value increases 13.3 fold in the LTM (Figure 6).

FIGURE 5

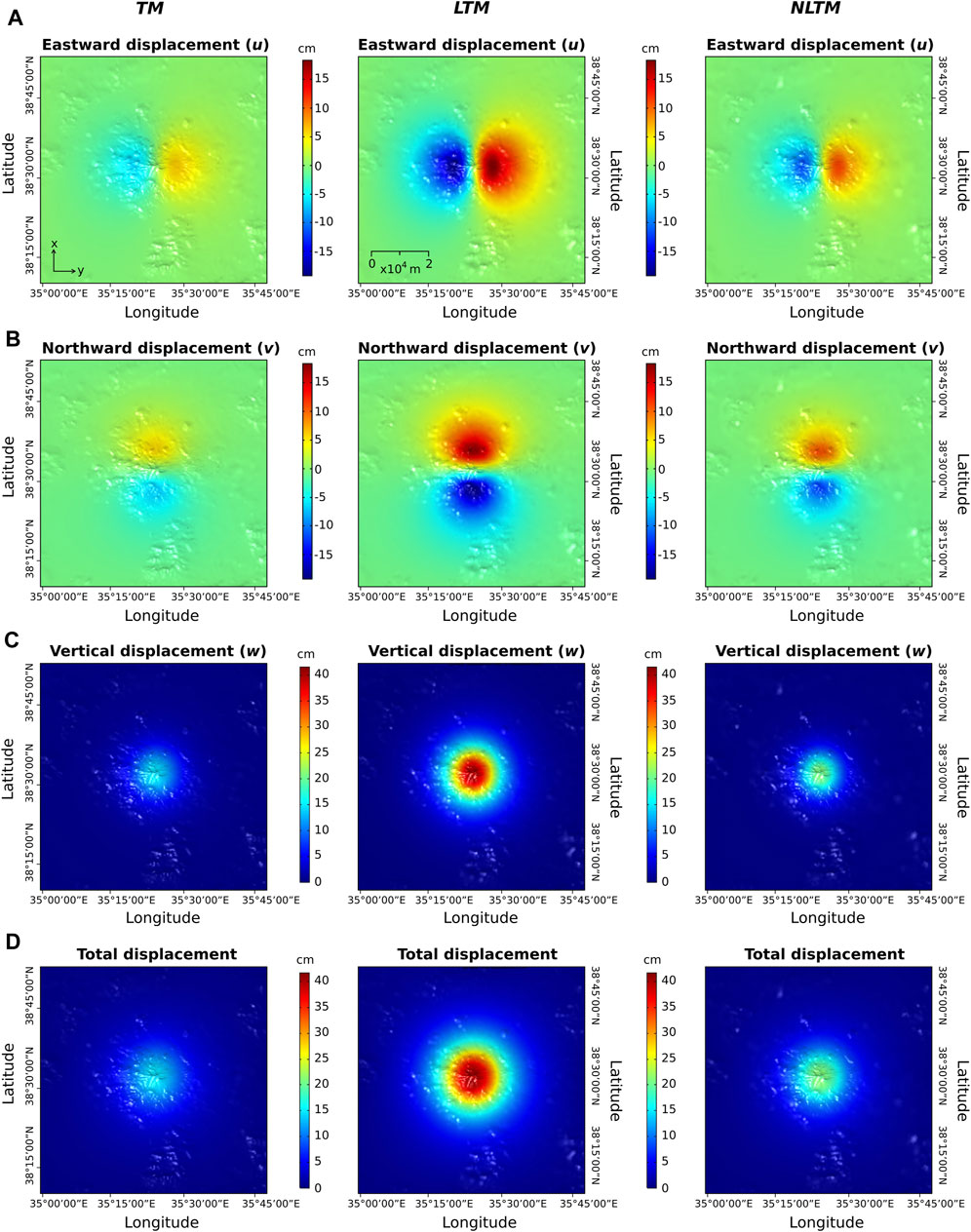
FIGURE 5. Surface displacements at Erciyes Dağ from generic TM, LTM and NLTM simulations using parameters reported in Table 3. (A–D) show horizotal eastwards (u), horizontal northwards (v), vertical (w) and total displacements, respectively. The color bars depict the same range in values for each deformation component, facilitating comparison of variations in displacement magnitudes across different models.

FIGURE 6

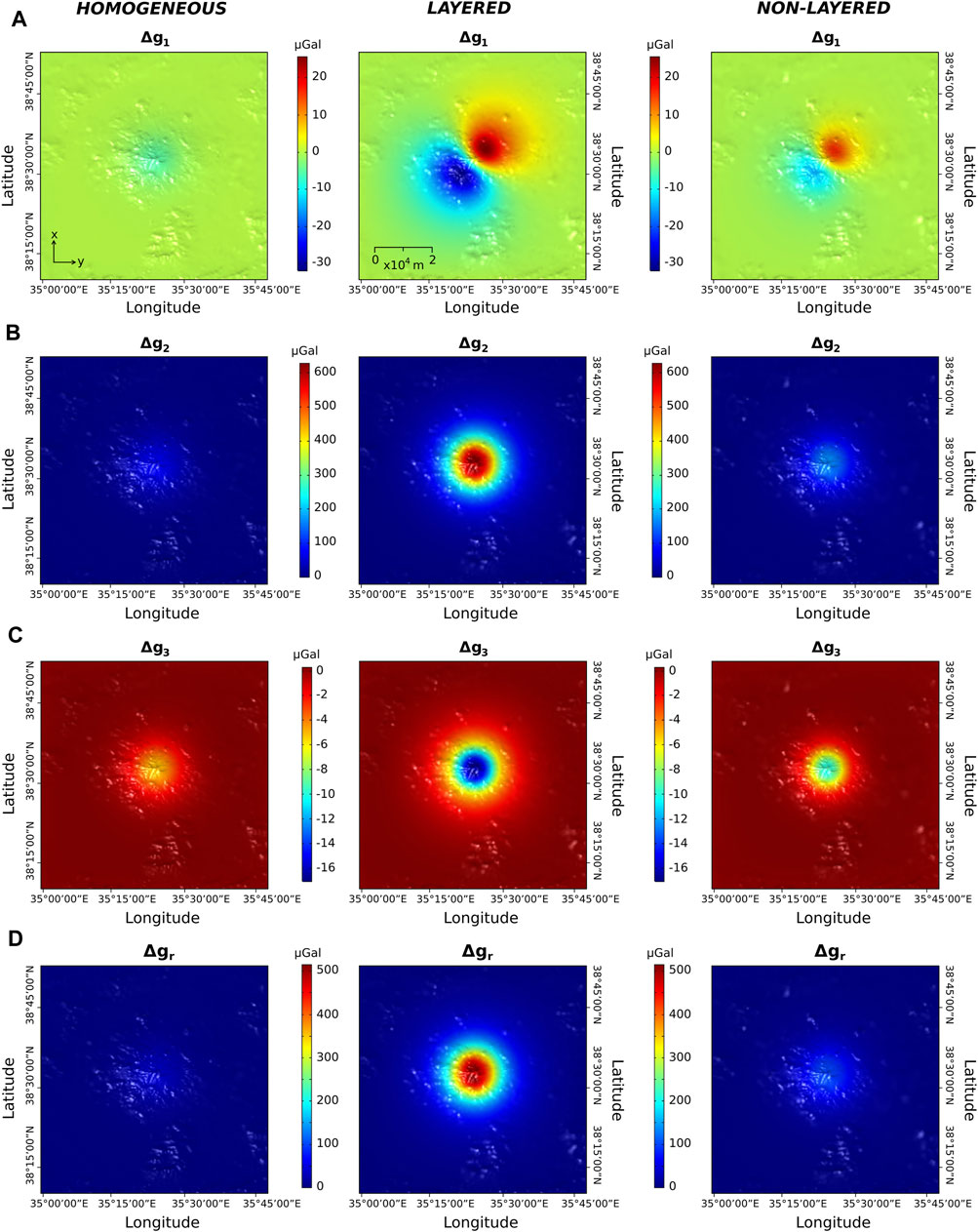
FIGURE 6. Gravity variations at Erciyes Dağ from generic TM, LTM and NLTM simulations using parameters reported in Table 3. (A–C) show contributions from gravity terms Δg₁, Δg₂ and Δg₃, respectively (Eqs 2, 3). (D) shows the resultant residual gravity changes Δg_r (see Eq. 5). The color bars depict the same range in values for each gravity change component, facilitating comparison of variations in magnitudes of gravity changes across different models.

4.1.3 LTM Versus NLTM

Approximating subsurface mechanical heterogeneity by gradual changes in properties mutes the magnitudes of all results compared to models implementing discrete changes in subsurface mechanics. Maximum magnitudes of u and v are decreased by 39 and 38%, respectively, in the NLTM, with total and w displacements decreased by 48% between the LTM and NLTM (Figure 5). The NLTM predicts maximum values of Δg₁ that are 36% smaller than the LTM and minimum values that are 54% smaller. The Δg₂ contribution is reduced by 74% in the NLTM, with the Δg₃ contribution reduced by 41%. These changes result in a reduction of the Δg_r values by 81% in the NLTM compared to the LTM (Figure 6).

4.2 Minimum Detectability Models

Value pairs of ΔP and Δρ that produce mass and volume changes upon magma reservoir recharge at the minimum detectability limit of surface uplift (0.01 m) and residual gravity changes (±5 µGal) are reported in Table 5. To illustrate, for the assumptions underpining the LTM we derive a pressure change of 0.25 MPa and concurrent density change of ±0.067 kg m⁻³ at the detectability limit.

TABLE 5

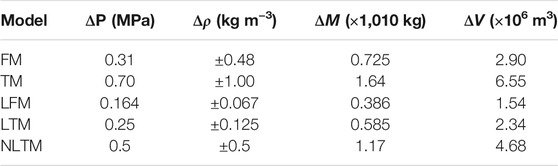
TABLE 5. Source pressure ΔP and density changes Δρ and associated mass and volume changes (ΔM and ΔV, respectively) for minimum resolvable surface residual gravity changes and uplift obtained from the 3D models.

The LFM predicts the smallest ΔP values with the TM predicting the highest. Δρ values vary between ±0.067 kg m⁻³ in the LFM and ±1 kg m⁻³ in the TM. The LFM and TM bracket the range in values at the lower and upper end, respectively. The deduced reservoir mass and volume changes vary accordingly across the different models. The NLTM predicts >50% larger mass and volume changes at the detectability compared to the LTM. Results for the “simplest” model (i.e., a FM) fall between the values predicted for the most complex models (i.e., LTM and NLTM). Figure 7 shows the contrast in resolvable source changes in the TM, LTM and NLTM with respect to those derived from the FM.

FIGURE 7

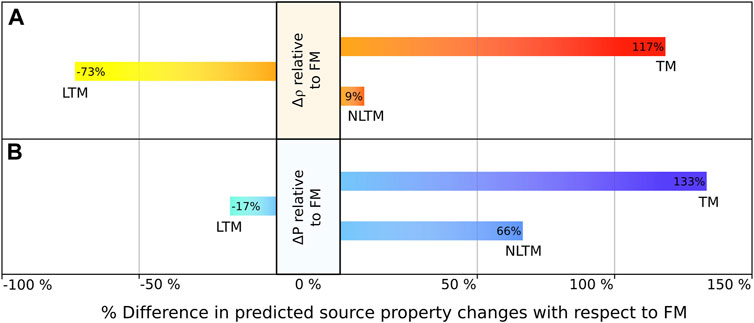
FIGURE 7. Percentage difference in reservoir parameter changes from TM, LTM and NLTM with respect to the FM to produce minimum detectable mass and volume changes upon magma recharge (see also Table 5). (A) displays the % changes in the predicted Δρ values, whilst (B) gives the % changes in the predicted ΔP values.

5 Discussion

At long-quiescent volcanoes with no monitoring data, the analysis and interpretation of synthetic results produced by models such as those developed in this study is challenging. Results are highly sensitive to assumptions underpinning modelling approaches (Tables 4, 5). To better understand the impact of topography and mechanical heterogeneity on deduced mass flux and volume changes due to magma recharge at Erciyes Dağ, we disentangle the individual contributions to surface gravity variations and displacements from our models.

5.1 Application of Analytical Models

Our study shows the limited applicability of traditional homogeneous elastic half-space models to inform processes at Erciyes Dağ. Though usually preferred in volcano geodetic modelling, the elastic homogeneous half-space Mogi model (Mogi, 1958) only provides accurate solutions for source depth: source radius ratios of >5. At Erciyes Dağ a maximum source radius for Erciyes Dağ of 1.4 km would be permissible for a source depth of 7 km derived from petrological data (Dogan et al., 2013). Consequently, the 3.1 km source radius calculated from previous eruption volumes is more than twice larger than the maximum permissible value, causing the Mogi solution to underpredict both vertical and horizontal deformation at the surface for given source pressurisation. This agrees with our original hypotheses and matches the results of previous studies (e.g., Battaglia and Segall, 2004), providing support to prioritise numerical models over analytical models to study ground deformation and gravity variations at Erciyes Dağ under the assumption that the reservoir source depth: source radius ratio is ≪5.

5.2 The Effect of Subsurface Heterogeneities

Subsurface heterogeneities fundamentally modulate the stress vs. strain relationship, affecting surface displacements (Gudmundsson and Brenner, 2004; Geyer and Gottsmann, 2010; Gottsmann et al., 2020) and gravity variations by either muting or amplifying strain depending on the subsurface distribution of mechanically stiff and weak lithologies. The impact of subsurface heterogeneities on changes in gravity is that they modulate the subsurface density distribution expressed by the u and ∇u terms of Eq. 2. This effect is demonstrated by the >100% increase in w, Δg₁ and Δg₃ components and the >700% increase in Δg₂ in the LFM compared to the FM. The extraordinary change in the magnitude of Δg₂ between homogeneous and heterogeneous models is attributed to the more pronounced expansion of a reservoir embedded in mechanically weaker rocks and the associated shifting of density boundaries permitting the influx of additional mass into the reservoir volume. Most notably, the resultant residual gravity change is 14 times greater in the LFM compared to the FM.

In our models, the combination of a mechanically weak volcanic edifice and upper-crustal mechanical weaknesses exert the greatest modulation of surface strain and the gravity field from upper-crustal reservoir pressurisation (Figures 5, 6). It thus follows that the magnitudes of the Δg₁ and Δg₃ terms correlate with higher degrees of mechanical complexities; e.g., the number of abrupt changes in the subsurface density distribution.

In comparing predicted residual gravity changes from FM with those from LTM and NLTM for the set of generic model parameterisations (Table 3), their magnitude is greatly increased primarily by amplified Δg₂ contributions. Currenti et al. (2007) analysed the effects of subsurface heterogeneities using 2D axisymmetric models for a smaller source radius (1 km) and larger pressure changes (100 MPa). Whilst their observations are analogous to ours in relation to the amplification of gravity changes and displacements, their calculated magnitudes are smaller owing to a diminished Δg₂ term due to the mass addition to a smaller source with a greater overburden producing smaller crustal strain.

The displacement of density boundaries between the source and host rock, along with the free-air effect, permit significant reservoir mass changes at net source density changes of ∼0 kg m⁻³. This signifies the importance of considering contributions to gravity changes from a heterogeneous subsurface in volcanic areas. Modelling approaches relying on the assumption of a mechanically homogeneous subsurface would need to attribute residual gravity changes almost exclusively to source density changes with major implications for the interpretation of causative subsurface processes amid volcano uplift. Judging from the Δρ values reported in Table 5 for a FM compared to a LFM, around one order of magnitude larger reservoir density changes would be deduced under the assumption of medium homogeneity.

Implementing a gradual change in mechanical properties instead of discrete changes in the form of layers has a number of implications for modelling approaches and the interpretation of results. First, non-layered models solve for <50% of the degrees of freedom of layered models at a much reduced computational cost. This cost efficiency could be compensated, for example, by the inclusion of a greater number of complexities, such as a higher resolution topographic surface. Second, in our study generic non-layered models produce vertical and total displacements that are ∼50% of the magnitude of layered models due to the amplification of surface strain by low rigidity discrete layers in the upper crust (Geyer and Gottsmann, 2010; Ronchin et al., 2015). Third, whilst reducing computational cost, non-layered models predict significantly different magnitudes of gravity changes compared to layered models. The large diminution of the Δg₂ contribution in non-layered models results in a residual gravity change over 5 times smaller than in layered models. Because the crust is neither composed solely of discrete density layers, nor is it best described by a single density gradient (Zhu et al., 2019), the layered and non-layered models represent end-member scenarios of the crustal architecture. Source property changes deduced from the evaluation of gravity changes and surface displacements using either mechanically heterogeneous layered or non-layered models likely map the uncertainties behind data interpretations.

5.3 The Effect of Topography

The inclusion of topography in models to study subsurface processes at high-prominence volcanoes results in decreased magnitudes of surface displacements compared to models ignoring topography for given source changes. In general we find that edifice prominence and magnitudes of ground displacement are negatively correlated. This is in agreement with previous studies (e.g., Cayol and Cornet, 1998; Williams and Wadge, 1998; Ronchin et al., 2015), and is due to the addition of a crustal mechanical domain that influences the subsurface stress and strain relationship. The effect of displacement modulation decreases with increasing source depth, particularly with respect to vertical displacement, and hence has a major influence on gravity source terms 1 and 3 given the 53% reduction in w in a FM compared to a TM (Table 4).

Muting the effect of crustal straining by source pressurisation, coupled with the mass-related gravitational attraction being chiefly determined by the distance between the computational surface and the source (Charco et al., 2009), volcano prominence has a major influence on deduced source mass and volume changes from monitoring observables. Whilst subsurface heterogeneities influence the magnitude of modeled anomalies, topography modifies both the magnitude and the spatial pattern of surface displacements and gravity changes. Prominence contributes to a flattening of the peak magnitude of both observables, with the largest impact at Erciyes Dağ noted directly over the summit where the slope angle is greatest (Figures 5, 6). These findings broadly corroborate results from axisymmetric models presented in Cayol and Cornet (1998) and Charco et al. (2007) and attest to the importance of considering topography for interpreting data from large-prominence volcanoes.

5.4 Minimum Detectable Mass Intrusions and Volume Changes at Erciyes Dağ

A significant mass addition of between 10⁹ and 10¹⁰ kg to the reservoir feeding Erciyes Dağ is possible without detection at the surface. The range of deduced values is model dependent with mechanically homogeneous models requiring larger source changes than layered models at the detectability limits. These disparities are explained by the inclusion of subsurface layers which result in an increase in gravity changes and surface displacements for given source changes (Currenti et al., 2007). This amplification reduces the minimum detectable reservoir mass change as a smaller mass input is required to achieve surface changes at the detection limit.

5.4.1 Simple Vs. Complex Models

Whilst the minimum detectable ΔP and Δρ values in models employing both a flat surface and a homogeneous subsurface (i.e., a FM) are distinct from the results of more complex models, associated mass and volume changes for the FM fall between results for the most complex models (LTM and NLTM). One could be tempted to argue that the simplest model yields results that do not differ too much from the ones obtained by the more complex models (LTM and NLTM). In our study the simplest model (FM) already implements Median subsurface mechanical parameters derived from seismic studies, and does not utilise generic values that are often applied in analytical geodetic modelling. We would expect differences in results between more complex models and simpler models to become larger with increasing simplifications of the “true” subsurface mechanics. Source parameters from inverse models implementing a 3D mechanical architecture are significantly different to those from isotropic, homogeneous and elastic half-space models (Hickey et al., 2016). The marked differences between results from FMs compared to more complex models become evident for plausible (yet generic) changes in source parameters for surface observables significantly above the detectability thresholds (Figures 5, 6) where predicted ground upift varies by a factor of ∼5 and residual gravity changes differ by more than one order of magnitude for the same source processes.

The principal disparities between the layered and non-layered models are the increases of magnitudes in Δg₁ and Δg₂ terms. Since the Δg₁ term relates to the shifting of subsurface density boundaries, the minimum detectable mass influx upon magma recharge is greater in non-layered models as a result of the removal of discrete boundary layers. It thus follows that the Δg₂ term related to the introduction of new mass increases in non-layered models as a greater mass influx may occur before detection thresholds are reached.

5.4.2 Magma Reservoir Dynamics

The influx of magma at Erciyes Dağ’s reservoir is likely modulated by a highly compressible magma mush given the explosive nature of its most recent dome-forming eruptions. Magma reservoirs feeding stratovolcanoes have characteristically high magma compressibilities and distinctively higher rates of eruptions that are not preceded by measurable surface deformation (Biggs et al., 2014) due to a combination of crustal mechanics, local stress fields and high H₂O-contents (Mastin et al., 2008; Ebmeier et al., 2013).

Notwithstanding the influence of magma compressibility on the detectability limits of ground displacements and gravity changes, the shallow depth and large size of the reservoir modelled in this study create larger displacements and gravity field variations than a similar-sized reservoir at greater depth. This implies that the deduced mass and volume fluxes represent the lower-bound estimates of plausible, yet, undetectable magma rejuvenation.

Minimum magma volume fluxes of between 5 × 10^–3 and 10^–2 km³ yr⁻¹ are required to sustain large volumes of mobile magma and prevent their solidification (Annen, 2009; Gelman et al., 2013). Whilst these magma fluxes provide a useful reference for the magma fluxes required for caldera-forming eruptions, Erciyes Dağ’s most recent eruptions suggest that dome-forming eruptions are more likely to occur in the future. Annen et al. (2015) determined that to prevent complete crystallisation of a volcanic storage region, a time-averaged magma flux exceeding 10⁻⁴–10⁻³ km³/yr is required. This emplacement rate would permit the development of a storage region into a potentially active magma reservoir.

These findings relate to the significant source volume increase of 2–5 × 10^–3 km³ upon magma recharge at Erciyes Dağ without observable surface displacement or residual gravity variations. Under the reasonable assumption that magma reservoir replenishment at Erciyes Dağ occurs below the detection limit of surface uplift velocities of 0.01 m yr⁻¹ (Biggs et al., 2021), the reservoir may currently sustain eruptable magma if deduced mass changes are taken as annual fluxes. This “stealth” magma flow into the reservoir matches and exceeds reported magma fluxes at several intermediate and silicic stratovolcanoes with repose times of 100–1000s of years (e.g., Parinacota, Soufrière Hills volcano and Mt. Pelée) as well as persistently active mafic volcanoes such as Mt. Etna and Stromboli (Figure 8). This likely attests to fundamentally different geometries and dynamics of magmatic plumbing systems at persistently active mafic volcanoes with high-level magma storage compared to non-mafic volcanoes with mid-to lower crustal magma reservoirs and protracted repose times. It is therefore distinctly possible that Erciyes Dağ has an active magma reservoir fed by magma intrusions that are accommodated by crustal elasticity and high magma compressibility. The presence of eruptable magma may imply that future eruptions may occur at short notice and within a matter of days or weeks (White and McCausland, 2019).

FIGURE 8

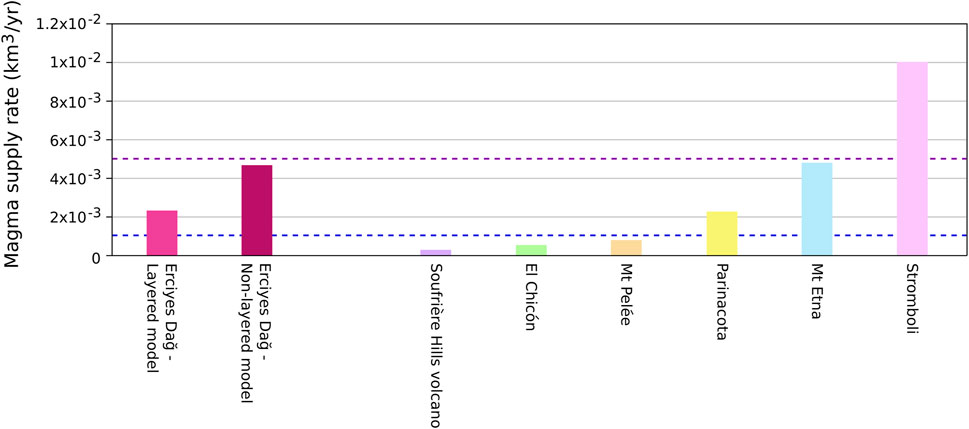
FIGURE 8. Bar chart of volume fluxes from this study with reported values from six other stratovolcanoes: Soufrière Hills volcano (Le Friant et al., 2004), El Chicón (Layer et al., 2009), Mt Pelée (Germa et al., 2015), Parinacota (Clavero et al., 2004), Mt. Etna (Branca and Ferrara, 2013), and Stromboli (Allard et al., 1994). The blue dashed line represents the minimum volume flux that is required to retain mobile and eruptable magma within the reservoir (Annen et al., 2015). The purple dashed line represents the minimum volume flux required to produce caldera-forming super-eruptions (Gelman et al., 2013). Minimum detectable magma fluxes for Erciyes Dağ are representative of the two end-member models (LTM and NLTM).

5.5 Model Limitations

We have used available multi-parametric data for Erciyes Dağ to constrain reservoir shape and location as well as crustal mechanical heterogeneity to the best of our knowledge. Implementing a 1D heterogeneity profile based on low-resolution seismic tomography data of Central Anatolia augmented by shallow crustal data from Mt. St. Helens and Soufrière Hills Volcano likely affect the accuracy of the results. However, with broadly similar near-surface geologies, upper-crustal and edifice mechanical characteristics of the three volcanoes, we do not consider our results to be fundamentally flawed. A much greater bias of model results are expected from the assumption of source sphericity and crustal elasticity in response to magma rejuvenation. Thermomechanical effects (Hickey et al., 2015; Morales Rivera et al., 2019; Gottsmann et al., 2020) are expected to affect results with the implication that inelastic accommodation of magma would render the derived mass and volume changes lower-bound estimates. The reservoir dimensions are such that they satisfy both available petrological, volumetric and volcanological constraints, rendering a spherical geometry as the most plausible. An alternative geometric representation of the reservoir is a vertically extensive spheroid (e.g., a prolate ellipsoid). Such a reservoir geometry yields smaller vertical displacements, resulting in a more nuanced free-air effect and smaller magnitudes of Δg₁ and Δg₃ contributions. As a result, larger source volume changes and larger mass changes compared to those derived for a spherical reservoir are required to be detectable. However, a reservoir of prolate ellipsoidal geometry matching the volume estimate of 124 km³ would need to extend to depths well beyond those constrained by petrological evidence. Hence, a prolate geometry would also imply a smaller reservoir volume. To simultaneously address the potential overestimation of reservoir volume and a non-spherical reservoir geometry, we developed a NLTM for a prolate reservoir of major-semi axis = 3.1 km and semi-minor axes of 2.2 km (matching a reservoir volume of ∼62 km³, i.e., ∼50% of the derived volume in Eq. 1). This model requires a ∼50% larger source volume change and a ∼45% higher source density change at the detectability limit compared to the NLTM for a spherical source of 124 km³. This indicates that, given the data currently available for Erciyes Dağ, model results are less sensitive to reservoir geometry.

Our models ignore potential volcano-tectonic linkages (Figure 9). The Dundarli-Erciyes fault segment which intersects Erciyes’ edifice and caldera boundary faults may 1) encourage the migration of magma from the source to the surface along the fault systems and 2) permit volcano-tectonic stress interactions. The location of the most recently formed domes along the fault segment and its intersections with the caldera boundary fault (Şen et al., 2003) matches observations of faults providing pathways for fluid and magma migration (Miller et al., 2017). In all our models, the volcanic reservoir is located directly beneath the edifice. Whilst informed by petrological data, the lack of geophysical data preclude further constraining of the location of the reservoir. A reservoir positioned further from the edifice would be expected to require smaller mass and volume changes at the detectability limit due to the reduced influence of topography. To test this we developed a NLTM with the reservoir’s centroid located 5 km south of the edifice as shown in Figure 9. The predicted residual gravity changes and total displacements for generic source change parameters reported in Table 3 were up to 124 and 117% larger, respectively, compared to the results from the centroid’s position directly beneath the edifice. This implies mass and volume changes at the detectability limit that are a factor of ∼2 smaller than derived from models with a reservoir centered beneath the summit.

FIGURE 9

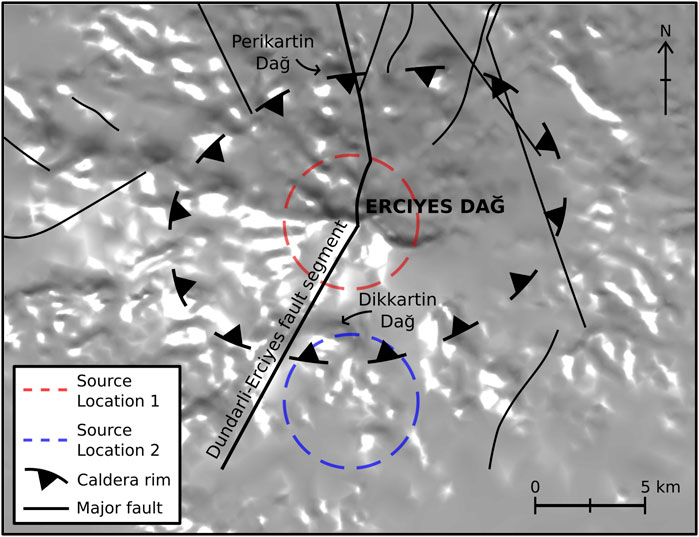
FIGURE 9. Volcano-tectonic map of Erciyes Dağ and surface projections of explored magma reservoirs (to scale). Dikkartin Dağ and Perikartin Dağ, the two most recent eruptive centres of the volcanic complex are located along the Dundarli-Erciyes fault segment and near the segment’s intersections with the southern and northern caldera rim and caldera boundary faults. Source location 1 marks the surface projection of the model reservoir directly beneath the summit, whereas source location 2 marks a reservoir 5 km to the south of the summit. Data presented in Şen et al. (2003) was utilised to determine the locations of the caldera rim and major faults.

6 Conclusion and Implications

Reservoir volume and mass changes of orders 10^–3 km³ and 10¹⁰ kg, respectively, derived for Erciyes Dağ at the detectability limit of integrated geodetic surveys support the hypothesis that magma recharge within a mechanically heterogeneous crust beneath high-prominence volcanoes may go undetected using conventional geodetic and gravimetric monitoring techniques. Ignoring subsurface heterogeneity and topography in models biases the interpretation of gravitational potential field changes and surface displacements. First, Erciyes Dağ’s high prominence significantly decreases the magnitude and alters the spatial pattern of surface displacement and gravity variations. Second, mechanically compliant lithologies in the upper crust and edifice amplify ground displacements and gravity changes.

Our findings demonstrate that geodetic and gravity time series data must be jointly modelled and interpreted. This permits the quantification of subsurface mass and volume fluxes upon reservoir recharge which is particularly important at stratovolcanoes where a significant proportion of eruptions occur with no prior ground deformation due to high magma compressibility (Biggs et al., 2014). The deduced amplitude of reservoir replenishment at Erciyes Dağ commensurate with the geodetic detection limit of 0.01 m yr⁻¹ of uplift is potentially sufficient to maintain an active magma reservoir containing eruptable magma. Based on our findings we recommend the implementation of routine joint geodetic and gravimetric monitoring of Erciyes Dağ for disaster risk prevention owing to the volcano’s proximity to the densely populated Kayseri Metropolitan Area.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: Zenodo repository (https://doi.org/10.5281/zenodo.5142185).

Author Contributions

JG conceived and coordinated the research study underpinning this paper. KM developed the models, analysis and initial interpretation as part of an undergraduate project and thesis at the University of Bristol under the supervision of JG. Both authors drafted, read and approved the final manuscript.

Funding

The authors acknowledge support from the Newton Fund TurkVolc project, NE/P008437/1 and NERC grant NE/S008845/1.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

JG expresses his gratitude to TurkVolc project team members Gökhan Atıcı and Mehmet Çobankaya for stimulating discussions that inspired the study. We thank two reviewers and handling editor AC for their constructive comments.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.750063/full#supplementary-material

References

Allard, P., Carbonnelle, J., Métrich, N., Loyer, H., and Zettwoog, P. (1994). Sulphur Output and Magma Degassing Budget of Stromboli Volcano. Nature 368, 326–330. doi:10.1038/368326a0

CrossRef Full Text | Google Scholar

Annen, C., Blundy, J. D., Leuthold, J., and Sparks, R. S. J. (2015). Construction and Evolution of Igneous Bodies: Towards an Integrated Perspective of Crustal Magmatism. Lithos 230, 206–221. doi:10.1016/j.lithos.2015.05.008

CrossRef Full Text | Google Scholar

Annen, C. (2009). From Plutons to Magma chambers: Thermal Constraints on the Accumulation of Eruptible Silicic Magma in the Upper Crust. Earth Planet. Sci. Lett. 284, 409–416. doi:10.1016/j.epsl.2009.05.006

CrossRef Full Text | Google Scholar

Battaglia, M., Gottsmann, J., Carbone, D., and Fernández, J. (2008). 4d Volcano Gravimetry. Geophysics 73. doi:10.1190/1.2977792

CrossRef Full Text | Google Scholar

Battaglia, M., and Segall, P. (2004). “The Interpretation of Gravity Changes and Crustal Deformation in Active Volcanic Areas,” in The Interpretation of Gravity Changes and Crustal Deformation in Active Volcanic Areas (Springer), 1453–1467. doi:10.1007/978-3-0348-7897-5_10

CrossRef Full Text | Google Scholar

Biggs, J., Ebmeier, S. K., Aspinall, W. P., Lu, Z., Pritchard, M. E., Sparks, R. S., et al. (2014). Global Link between Deformation and Volcanic Eruption Quantified by Satellite Imagery. Nat. Commun. 5, 3471–3477. doi:10.1038/ncomms4471

PubMed Abstract | CrossRef Full Text | Google Scholar

Biggs, J., Dogru, F., Dagliyar, A., Albino, F., Yip, S., Brown, S., et al. (2021). Baseline Monitoring of Volcanic Regions with Little Recent Activity: Application of sentinel-1 Insar to Turkish Volcanoes. J. Appl. Volcanology 10, 1–14. doi:10.1186/s13617-021-00102-x

CrossRef Full Text | Google Scholar

Bonaccorso, A., Cianetti, S., Giunchi, C., Trasatti, E., Bonafede, M., and Boschi, E. (2005). Analytical and 3-d Numerical Modelling of Mt. etna (italy) Volcano Inflation. Geophys. J. Int. 163, 852–862. doi:10.1111/j.1365-246x.2005.02777.x

CrossRef Full Text | Google Scholar

Bonafede, M., and Mazzanti, M. (1998). Modelling Gravity Variations Consistent with Ground Deformation in the Campi Flegrei Caldera (italy). J. Volcanology Geothermal Res. 81, 137–157. doi:10.1016/s0377-0273(97)00071-1

CrossRef Full Text | Google Scholar

Branca, S., and Ferrara, V. (2013). The Morphostructural Setting of Mount etna Sedimentary Basement (italy): Implications for the Geometry and Volume of the Volcano and its Flank Instability. Tectonophysics 586, 46–64. doi:10.1016/j.tecto.2012.11.011

CrossRef Full Text | Google Scholar

Brocher, T. M. (2005). Empirical Relations between Elastic Wavespeeds and Density in the Earth's Crust. Bull. seismological Soc. America 95, 2081–2092. doi:10.1785/0120050077

CrossRef Full Text | Google Scholar

Browning, J., Drymoni, K., and Gudmundsson, A. (2015). Forecasting Magma-Chamber Rupture at Santorini Volcano, greece. Sci. Rep. 5, 15785–15788. doi:10.1038/srep15785

PubMed Abstract | CrossRef Full Text | Google Scholar

Cai, Y., and Wang, C.-y. (2005). Fast Finite-Element Calculation of Gravity Anomaly in Complex Geological Regions. Geophys. J. Int. 162, 696–708. doi:10.1111/j.1365-246x.2005.02711.x

CrossRef Full Text | Google Scholar

Carbone, D., Currenti, G., and Del Negro, C. (2007). Elastic Model for the Gravity and Elevation Changes before the 2001 Eruption of etna Volcano. Bull. Volcanol 69, 553–562. doi:10.1007/s00445-006-0090-5

CrossRef Full Text | Google Scholar

Carbone, D., Poland, M. P., Diament, M., and Greco, F. (2017). The Added Value of Time-Variable Microgravimetry to the Understanding of How Volcanoes Work. Earth-Science Rev. 169, 146–179. doi:10.1016/j.earscirev.2017.04.014

CrossRef Full Text | Google Scholar

Cashman, K. V., Sparks, R. S., and Blundy, J. D. (2017). Vertically Extensive and Unstable Magmatic Systems: a Unified View of Igneous Processes. Science 355, eaag3055. doi:10.1126/science.aag3055

PubMed Abstract | CrossRef Full Text | Google Scholar

Cayol, V., and Cornet, F. H. (1998). Effects of Topography on the Interpretation of the Deformation Field of Prominent Volcanoes-Application to Etna. Geophys. Res. Lett. 25, 1979–1982. doi:10.1029/98gl51512

CrossRef Full Text | Google Scholar

Charco, M., Camacho, A. G., Tiampo, K. F., and Fernández, J. (2009). Spatiotemporal Gravity Changes on Volcanoes: Assessing the Importance of Topography. Geophys. Res. Lett. 36. doi:10.1029/2009gl037160

CrossRef Full Text | Google Scholar

Charco, M., Fernández, J., Luzón, F., Tiampo, K. F., and Rundle, J. B. (2007). Some Insights into Topographic, Elastic and Self-Gravitation Interaction in Modelling Ground Deformation and Gravity Changes in Active Volcanic Areas. Pure Appl. Geophys. 164, 865–878. doi:10.1007/s00024-004-0190-y

CrossRef Full Text | Google Scholar

Clavero, R. J. E., Sparks, S. J., Polanco, E., and Pringle, M. S. (2004). Evolution of Parinacota Volcano, central andes, Northern chile. Revista geológica de Chile 31, 317–347. doi:10.4067/s0716-02082004000200009

CrossRef Full Text | Google Scholar

Currenti, G., Del Negro, C., and Ganci, G. (2007). Modelling of Ground Deformation and Gravity fields Using Finite Element Method: an Application to etna Volcano. Geophys. J. Int. 169, 775–786. doi:10.1111/j.1365-246x.2007.03380.x

CrossRef Full Text | Google Scholar

Currenti, G. (2014). Numerical Evidence Enabling Reconciliation Gravity and Height Changes in Volcanic Areas. Geophys. J. Int. 197, 164–173. doi:10.1093/gji/ggt507

CrossRef Full Text | Google Scholar

Dogan, A. U., Dogan, M., Peate, D. W., and Dogruel, Z. (2011). Textural and Mineralogical Diversity of Compositionally Homogeneous Dacites from the summit of Mt. Erciyes, central Anatolia, turkey. Lithos 127, 387–400. doi:10.1016/j.lithos.2011.09.003

CrossRef Full Text | Google Scholar

Dogan, A. U., Peate, D. W., Dogan, M., Yesilyurt-Yenice, F. I., and Unsal, O. (2013). Petrogenesis of Mafic-Silicic Lavas at Mt. Erciyes, central Anatolia, Turkey. J. volcanology geothermal Res. 256, 16–28. doi:10.1016/j.jvolgeores.2013.01.020

CrossRef Full Text | Google Scholar

Ebmeier, S. K., Biggs, J., Mather, T. A., and Amelung, F. (2013). On the Lack of Insar Observations of Magmatic Deformation at central American Volcanoes. J. Geophys. Res. Solid Earth 118, 2571–2585. doi:10.1002/jgrb.50195

CrossRef Full Text | Google Scholar

Eissa, E., and Kazi, A. (1988). Relation between Static and Dynamic Young’s Moduli of Rocks. Int. J. Rock Mech. Mining Geomechanics Abstr. 25, 479–482. doi:10.1016/0148-9062(88)90987-4

CrossRef Full Text | Google Scholar

Fernández, J., Pepe, A., Poland, M. P., and Sigmundsson, F. (2017). Volcano Geodesy: Recent Developments and Future Challenges. J. Volcanology Geothermal Res. 344, 1–12. doi:10.1016/j.jvolgeores.2017.08.006

CrossRef Full Text | Google Scholar

Gazioğlu, C., Yücel, Z., Kaya, H., and Doğan, E. (2004). “Geomorphological Features of Mt. Erciyes Using by Dtm and Remote Sensing Technologies,” in XXth International Society for Photogrammetry and Remote Sensing conference proceedings Istanbul: International archives of the photogrammetry, remote sensing and spatial information sciences.

Google Scholar

Gelman, S. E., Gutiérrez, F. J., and Bachmann, O. (2013). On the Longevity of Large Upper Crustal Silicic Magma Reservoirs. Geology 41, 759–762. doi:10.1130/g34241.1

CrossRef Full Text | Google Scholar

Germa, A., Lahitte, P., and Quidelleur, X. (2015). Construction and Destruction of Mont Pelée Volcano: Volumes and Rates Constrained from a Geomorphological Model of Evolution. J. Geophys. Res. Earth Surf. 120, 1206–1226. doi:10.1002/2014jf003355

CrossRef Full Text | Google Scholar

Geyer, A., and Gottsmann, J. (2010). The Influence of Mechanical Stiffness on Caldera Deformation and Implications for the 1971-1984 Rabaul Uplift (Papua New Guinea). Tectonophysics 483, 399–412. doi:10.1016/j.tecto.2009.10.029

CrossRef Full Text | Google Scholar

Gottsmann, J., Biggs, J., Lloyd, R., Biranhu, Y., and Lewi, E. (2020). Ductility and Compressibility Accommodate High Magma Flux beneath a Silicic continental Rift Caldera: Insights from Corbetti Caldera (ethiopia). Geochem. Geophys. Geosystems 21. doi:10.1029/2020gc008952

CrossRef Full Text | Google Scholar

Gudmundsson, A., and Brenner, S. L. (2004). How Mechanical Layering Affects Local Stresses, Unrests, and Eruptions of Volcanoes. Geophys. Res. Lett. 31, L16606. doi:10.1029/2004GL020083

CrossRef Full Text | Google Scholar

Hagiwara, Y. (1977). The Mogi Model as a Possible Cause of the Crustal Uplift in the Eastern Part of Izu peninsula and the Related Gravity Change. Bull. Earthq. Res. Inst. 52, 301–309.

Google Scholar

Hickey, J., Gottsmann, J., and Mothes, P. (2015). Estimating Volcanic Deformation Source Parameters with a Finite Element Inversion: The 2001-2002 Unrest at Cotopaxi Volcano, Ecuador. J. Geophys. Res. Solid Earth 120, 1473–1486. doi:10.1002/2014jb011731

CrossRef Full Text | Google Scholar

Hickey, J., Gottsmann, J., Nakamichi, H., and Iguchi, M. (2016). Thermomechanical Controls on Magma Supply and Volcanic Deformation: Application to Aira Caldera, japan. Sci. Rep. 6, 32691. doi:10.1038/srep32691

PubMed Abstract | CrossRef Full Text | Google Scholar

Innocenti, F., Manetti, P., Mazzuoli, R., Pasquare, G., and Villari, L. (1982). “Anatolia and north-western iran,” in Andesites: Orogenic Andesites and Related Rocks. Editors R. S. Thorpe (New York: Wiley), 327–349.

Google Scholar

Kiser, E., Palomeras, I., Levander, A., Zelt, C., Harder, S., Schmandt, B., et al. (2016). Magma Reservoirs from the Upper Crust to the Moho Inferred from High-Resolution Vp and vs Models beneath Mount St. Helens, washington State, usa. Geology 44, 411–414. doi:10.1130/g37591.1

CrossRef Full Text | Google Scholar

Koçyigit, A., and Erol, O. (2001). A Tectonic Escape Structure: Erciyes Pull-Apart basin, Kayseri, central Anatolia, turkey. Geodinamica Acta 14, 133–145. doi:10.1016/s0985-3111(00)01055-x

CrossRef Full Text | Google Scholar

Koçyiğit, A., and Beyhan, A. (1998). A New Intracontinental Transcurrent Structure: the central Anatolian Fault Zone, turkey. Tectonophysics 284, 317–336.

Google Scholar

Kürkcüoglu, B., Sen, E., Temel, A., Aydar, E., and Gourgaud, A. (2004). Interaction of Asthenospheric and Lithospheric Mantle: the Genesis of Calc-Alkaline Volcanism at Erciyes Volcano, central Anatolia, turkey. Int. Geology. Rev. 46, 243–258. doi:10.2747/0020-6814.46.3.243

CrossRef Full Text | Google Scholar

Kürkçüoglu, B., Sen, E., Aydar, E., Gourgaud, A., and Gündogdu, N. (1998). Geochemical Approach to Magmatic Evolution of Mt. Erciyes Stratovolcano central Anatolia, turkey. J. Volcanology Geothermal Res. 85, 473–494. doi:10.1016/s0377-0273(98)00067-5

CrossRef Full Text | Google Scholar

Layer, P., García-Palomo, A., Jones, D., Macías, J., Arce, J., and Mora, J. (2009). El Chichón Volcanic Complex, Chiapas, México: Stages of Evolution Based on Field Mapping and 40ar/39ar Geochronology. Geofísica internacional 48, 33–54. doi:10.22201/igeof.00167169p.2009.48.1.98

CrossRef Full Text | Google Scholar

Le Friant, A., Harford, C. L., Deplus, C., Boudon, G., Sparks, R. S. J., Herd, R. A., et al. (2004). Geomorphological Evolution of montserrat (West Indies): Importance of Flank Collapse and Erosional Processes. J. Geol. Soc. 161, 147–160. doi:10.1144/0016-764903-017

CrossRef Full Text | Google Scholar

Mastin, L. G., Roeloffs, E., Beeler, N. M., and Quick, J. E. (2008). Constraints on the Size, Overpressure, and Volatile Content of the Mount St. Helens Magma System from Geodetic and Dome-Growth Measurements during the 2004-2006+ Eruption. US Geol. Surv. Prof. Pap. 1750, 461–488. doi:10.3133/pp175022

CrossRef Full Text | Google Scholar

McTigue, D. F. (1987). Elastic Stress and Deformation Near a Finite Spherical Magma Body: Resolution of the point Source Paradox. J. Geophys. Res. 92, 12931–12940. doi:10.1029/jb092ib12p12931

CrossRef Full Text | Google Scholar

Miller, C. A., Le Mével, H., Currenti, G., Williams-Jones, G., and Tikoff, B. (2017). Microgravity changes at the laguna del maule volcanic field: Magma-induced stress changes facilitate mass addition. J. Geophys. Res. Solid Earth 122, 3179–3196. doi:10.1002/2017jb014048

CrossRef Full Text | Google Scholar

Mogi, K. (1958). Relations between the Eruptions of Various Volcanoes and the Deformation of the Ground Surfaces Around Them. Bull. Earthquake Res. Inst. 36.

Google Scholar

Morales Rivera, A. M., Amelung, F., Albino, F., and Gregg, P. M. (2019). Impact of Crustal Rheology on Temperature‐Dependent Viscoelastic Models of Volcano Deformation: Application to Taal Volcano, Philippines. J. Geophys. Res. Solid Earth 124, 978–994. doi:10.1029/2018jb016054

CrossRef Full Text | Google Scholar

Pasquarè, G., Poli, S., Vezzoli, L., and Zanchi, A. (1988). Continental Arc Volcanism and Tectonic Setting in central Anatolia, turkey. Tectonophysics 146, 217–230. doi:10.1016/0040-1951(88)90092-3

CrossRef Full Text | Google Scholar

Ronchin, E., Geyer, A., and Martí, J. (2015). Evaluating Topographic Effects on Ground Deformation: Insights from Finite Element Modeling. Surv. Geophys. 36, 513–548. doi:10.1007/s10712-015-9325-3

CrossRef Full Text | Google Scholar

Rymer, H., and Brown, G. (1989). Gravity Changes as a Precursor to Volcanic Eruption at Poás Volcano, Costa Rica. Nature 342, 902–905. doi:10.1038/342902a0

CrossRef Full Text | Google Scholar

Salah, M. K., Şahin, Ş., and Topatan, U. (2014). Crustal Velocity and Vp/Vs Structures beneath central Anatolia from Local Seismic Tomography. Arab J. Geosci. 7, 4101–4118. doi:10.1007/s12517-013-1038-7

CrossRef Full Text | Google Scholar

Şen, E., Aydar, E., Gourgaud, A., and Kurkcuoglu, B. (2002). Initial Explosive Phases during Extrusion of Volcanic Lava Domes: Example from Rhyodacitic Dome of Dikkartin Dag, Erciyes Stratovolcano, central Anatolia, Turkey. Comptes Rendus Geosci. 334 (1), 27–33. doi:10.1016/s1631-0713(02)01698-x

CrossRef Full Text | Google Scholar

Şen, E., Kürkcüoğlu, B., Aydar, E., Gourgaud, A., and Vincent, P. M. (2003). Volcanological Evolution of Mount Erciyes Stratovolcano and Origin of the Valibaba Tepe Ignimbrite (central Anatolia, turkey). J. Volcanology Geothermal Res. 125, 225–246. doi:10.1016/S0377-0273(03)00110-0

CrossRef Full Text | Google Scholar

Sen, P. A., Temel, A., and Gourgaud, A. (2004). Petrogenetic Modelling of Quaternary post-collisional Volcanism: a Case Study of central and Eastern Anatolia. Geol. Mag. 141, 81–98. doi:10.1017/S0016756803008550

CrossRef Full Text | Google Scholar

Voight, B., Widiwijayanti, C., Mattioli, G., Elsworth, D., Hidayat, D., and Strutt, M. (2010). Magma-sponge Hypothesis and Stratovolcanoes: Case for a Compressible Reservoir and Quasi-Steady Deep Influx at Soufrière hills Volcano, montserrat. Geophys. Res. Lett. 37. doi:10.1029/2009gl041732

CrossRef Full Text | Google Scholar

White, R. A., and McCausland, W. A. (2019). A Process-Based Model of Pre-eruption Seismicity Patterns and its Use for Eruption Forecasting at Dormant Stratovolcanoes. J. Volcanology Geothermal Res. 382, 267–297. doi:10.1016/j.jvolgeores.2019.03.004

CrossRef Full Text | Google Scholar

Williams, C. A., and Wadge, G. (1998). The Effects of Topography on Magma Chamber Deformation Models: Application to Mt. etna and Radar Interferometry. Geophys. Res. Lett. 25, 1549–1552. doi:10.1029/98gl01136

CrossRef Full Text | Google Scholar

Young, N. K., and Gottsmann, J. (2015). Shallow Crustal Mechanics from Volumetric Strain Data: Insights from Soufrière Hills Volcano, Montserrat. J. Geophys. Res. Solid Earth 120, 1559–1571. doi:10.1002/2014jb011551

CrossRef Full Text | Google Scholar

Zhang, J., Wang, C. Y., Shi, Y., Cai, Y., Chi, W. C., Dreger, D., et al. (2004). Three‐dimensional Crustal Structure in central Taiwan from Gravity Inversion with a Parallel Genetic Algorithm. Geophysics 69, 917–924. doi:10.1190/1.1778235

CrossRef Full Text | Google Scholar

Zhu, H., Tian, Y., Zhao, D., Li, H., and Liu, C. (2019). Seismic Structure of the Changbai Intraplate Volcano in Ne china from Joint Inversion of Ambient Noise and Receiver Functions. J. Geophys. Res. Solid Earth 124, 4984–5002. doi:10.1029/2018jb016600

CrossRef Full Text | Google Scholar

NE/P008437/1 NE/S008845/1