Influence of Saline Fluids on the Electrical Conductivity of Olivine Aggregates at High Temperature and High Pressure and Its Geological Implications

The electrical conductivities of hydrous olivine (Ol) aggregates and Ol–H₂O, Ol–NaCl–H₂O (salinity: 1–21 wt%; fluid fraction: 5.1–20.7 vol%), Ol–KCl–H₂O (salinity: 5 wt%; fluid fraction: 10.9–14.0 vol%) and Ol–CaCl₂–H₂O systems (salinity: 5 wt%; fluid fraction: 10.7–13.7 vol%) were measured at 2.0–3.0 GPa and 773–1073 K using a multi-anvil apparatus. The electrical conductivity of saline fluid-bearing olivine aggregates slightly increases with increasing pressure and temperature, and the electrical conductivities of both hydrous and saline fluid-bearing samples are well described by an Arrhenius relation. The dihedral angle of the saline fluids is approximately 50° in the Ol–NaCl–H₂O system with 5 wt% NaCl and 5.1 vol% fluids, which implies that the fluids were interconnected along grain boundaries under the test conditions. The electrical conductivities of the Ol–NaCl–H₂O system with 5 wt% NaCl and 5.1 vol% fluids are ∼two to four orders of magnitude higher than those of hydrous olivine aggregates. The salinity and fluid fraction moderately enhance the sample electrical conductivities owing to the interconnectivity of the saline fluids. The activation enthalpies of the electrical conductivities for the Ol–NaCl–H₂O systems range from 0.07 to 0.36 eV, and Na⁺, Cl⁻, H⁺, OH⁻, and soluble ions from olivine are proposed to be the main charge carriers. For a fixed salinity and fluid fraction, the electrical conductivities of the Ol–NaCl–H₂O system resemble the Ol–KCl–H₂O system but are slightly higher than that of the Ol–CaCl₂–H₂O system. The Ol–NaCl–H₂O system with a salinity of ∼5 wt% NaCl and fluid fraction larger than 1.8 vol% can be employed to reasonably explain the origin of the high-conductivity anomalies observed in mantle wedges.

Introduction

Electrical conductivities of geological materials at high temperatures and pressures in combination with magnetotelluric data can be used to infer the material compositions and thermodynamic conditions of the Earth’s interior (Vallianatos, 1996; Heise et al., 2019). Previous field magnetotelluric results confirmed that high-conductivity layers (HCLs), as the special weak zones, are widely distributed in the Earth’s interior (McGary et al., 2014; Selway, 2015; Hata et al., 2017). Typically, the HCLs have a characteristic of abnormally low velocity on the basis of seismic sounding data (Selway and O’Donnell, 2019; Manthilake et al., 2021a). The electrical conductivities of geological samples at high temperatures and high pressures are required to invert the MT profiles. Numerous studies have therefore investigated the conductivity of the dominant geological materials in the Earth’s interior (Reynard et al., 2011; Saltas et al., 2013, 2020; Manthilake et al., 2015, 2016; Dai and Karato, 2020). Dehydration, metasomatism, and magmatism processes are considerably more active in subduction zones than in the stable continental lithosphere. The dehydration products of hydrous minerals (e.g., amphibole, lawsonite etc.) have been proposed to be the main origin of the high-conductivity anomalies in subduction zones (Manthilake et al., 2015; Hu et al., 2018). However, the dehydration products of typical hydrous minerals are present throughout the subduction tunnel and therefore widely distributed between the transitional interface of the subducted slab and mantle wedge. The aqueous fluid dehydration products migrate upward to the mantle wedge, as do silicate and carbonate melts from subduction zone magmatism (Wang et al., 2020). Aqueous fluids and melts have thus been inferred to be plausible candidates for the origin of the high-conductivity and low-velocity anomalies in mantle wedge regions (Pommier and Evans, 2017; Vargas et al., 2019; Manthilake et al., 2021c). Silicate/carbonate melts with or without aqueous fluids form and converge in regions at sufficiently high temperature; however, aqueous fluids as an independent fluid phase can be stable in regions with temperatures below the rock matrix solidus. The high-conductivity anomalies have been shown to occur in relatively cold subduction zones, which might be caused by the presence of aqueous fluids (Pommier and Evans, 2017). Previous studies of fluid inclusions in deep Earth rocks and high-temperature and high-pressure experiments have demonstrated that aqueous fluids with some form of volatile and salt species are abundant in subduction zones (Carter et al., 2015; Huang et al., 2019; Lacovino et al., 2020). NaCl-bearing aqueous fluids have been proposed to be the most significant saline fluid in subduction environments because Na⁺ and Cl⁻ are the most dominant ions in most saline fluid inclusions (Morikawa et al., 2016). Free water, as the solvent of saline fluids, dominantly forms by the dehydration of hydrous minerals in subduction slabs (Manthilake et al., 2015; Hu et al., 2018). Saline ions (Na⁺ and Cl⁻) in aqueous fluids are released from subduction slabs during dehydration and metasomatism (Reynard, 2016; Förster et al., 2019; Manthilake et al., 2021b). Numerous studies have attributed the origin of the high-conductivity anomalies in the mid-lower crust and some subduction zones to the distribution of NaCl-bearing aqueous fluids along the grain boundaries of silicate minerals (Shimojuku et al., 2012, 2014; Guo et al., 2015; Sinmyo and Keppler, 2017; Li et al., 2018; Sun et al., 2020). However, the effect of saline fluids on the electrical conductivity of silicate minerals in mantle wedge regions remains poorly constrained.

Olivine (Ol) is the dominant rock-forming mineral of the Earth’s upper mantle with a volume percentage of ∼63% (Ringwood, 1982; Lin et al., 2013). The Ol–NaCl–H₂O system is therefore a relevant representation of the composition of wet regions in the uppermost mantle, e.g., mantle wedges of subduction zones. Although numerous studies have reported the high-pressure electrical conductivity of olivine single crystals and polycrystalline aggregates (Dai et al., 2010; Dai and Karato, 2014a; Dai and Karato, 2014b; Dai and Karato, 2014c; Dai and Karato, 2014d; Dai and Karato, 2020), the detailed Ol–NaCl–H₂O system has not been previously reported under high-temperature and high-pressure conditions. In addition to the effects of pressure and oxygen fugacity, the molar percentages of magnesium and iron in synthetic olivine also exert a significant effect on the electrical conductivity of anhydrous samples at high temperatures and pressures (Dai and Karato, 2014b). Water is another crucial factor that can enhance the electrical conductivity of olivine and its high-pressure polymorphs at high temperatures and pressures by several orders of magnitude (Dai and Karato, 2009; Dai and Karato, 2014b). Previous geophysical field observations of the electrical conductivity in the asthenosphere, including the high and highly anisotropic conductivity regions, have been attributed to the high water contents, which is consistent with geochemical models based of the reported electrical conductivity values of anisotropic hydrous single-crystal olivine (Dai and Karato, 2014a). The olivine in geologically active regions is hydrous owing to the existence of aqueous fluids from the dehydration of hydrous minerals. Hydrogen-related point defects can significantly enhance the conductivity of olivine; thus hydrous olivine is a possible candidate for the origin for the high-conductivity anomalies in the upper mantle (Dai and Karato, 2014a). However, the electrical conductivity of hydrous olivine at its maximum probable water content (∼1,000 ppm) in the mantle wedge region is approximately 10^–1 S/m (Dai and Karato, 2014b), whereas the center of the semi-ellipsoidal HCL shapes in mantle wedges show maximum conductivities of ∼1 S/m, which gradually decrease to approximately 10^–2 S/m at the edges (McGary et al., 2014; Hata et al., 2017). The presence of hydrous olivine may therefore generate conductivities in the range of ∼10⁻²–10⁻¹ S/m (Dai and Karato, 2014b), but cannot be employed to interpret conductivities in the range of ∼10⁻¹–1 S/m. It is possible that interconnected saline fluids can be employed to interpret the high conductivities of ∼10⁻¹–1 S/m in some HCLs of mantle wedges, in which interconnected saline fluid-bearing peridotite is surrounded by hydrous peridotite with or without disconnected saline fluids. Huang et al. (2019) recently demonstrated that NaCl-bearing aqueous fluids might be interconnected in mantle wedges. The electrical conductivities of clinopyroxene (Cpx)–NaCl–H₂O, plagioclase (Pl)–NaCl–H₂O, albite (Ab)–NaCl–H₂O and pure NaCl-bearing saline fluid systems have been previously investigated (Guo et al., 2015; Li et al., 2018; Guo and Keppler, 2019; Sun et al., 2020), but the electrical conductivity of saline fluid-bearing olivine aggregates has not been reported. Although saline fluids exert a dominant control over the conductivities of saline fluid-bearing mineral aggregates, the mineral species still play a significant role in the system conductivity as a whole (Guo et al., 2015; Li et al., 2018; Sun et al., 2020). The conductivities of saline fluids in mineral–NaCl–H₂O systems calculated using theoretical models (e.g., Hashin–Shtrikman upper model (HS⁺) and cube model) were reported to be substantially lower than those of pure NaCl-bearing aqueous fluids (Sinmyo and Keppler, 2017; Li et al., 2018; Guo and Keppler, 2019; Sun et al., 2020). This implies that the dissolution of silicate minerals into saline fluids significantly affects the conductivities of the aqueous fluids, and the distribution characteristics and channel morphology of the aqueous fluids on the mineral boundaries might influence the conductivity of saline fluid-bearing mineral aggregates to some extent. An accurate determination of the electrical conductivity of saline fluid-bearing olivine aggregates is therefore difficult to precisely estimate using the HS⁺ and cube theoretical models based on the conductivity of hydrous olivine aggregates and pure saline fluids. In-situ measurements of the electrical conductivity of saline fluid-bearing polycrystalline olivine are therefore required to interpret the origin of the high-conductivity anomalies in mantle wedges.

In the present study, the electrical conductivity of olivine aggregates mixed with saline fluids (solute: NaCl, KCl and CaCl₂) was measured in-situ over a pressure range of 2.0–3.0 GPa and temperature range of 773–1073 K. The effects of temperature, pressure, salinity, fluid fraction, and ionic species on electrical conductivity were explored in detail. Three representative saline fluid-bearing systems (Ol–NaCl–H₂O, Ol–KCl–H₂O, and Ol–CaCl₂–H₂O) were comprehensively compared over the investigated pressure and temperature range. The results are applied to discuss the possible geological implications of the electrical conductivities of saline fluid-bearing olivine aggregates at high temperature and pressure.

Experimental Methods

Sample Preparation

The natural, fresh and pure olivine with a gem-grade single crystal grain was collected from Damaping village, Wanquan County, Zhangjiakou City, Hebei Province, China. The chemical compositions of the olivine were tested using an electron probe microanalyzer (EPMA) at the State Key Laboratory of Ore Deposit Geochemistry, Chinese Academy of Science (CAS), Guiyang, China. The molar Fe/(Fe + Mg) ratio was 9.3%, which is very similar to that for San Carlos olivine (10%) (Supplementary Table S1). As described in supplementary material in detail, the samples of hydrous olivine aggregates, Ol–H₂O and Ol–NaCl/KCl/CaCl₂–H₂O systems were precisely prepared. For the saline fluid-bearing olivine aggregates, the salinity and fluid fraction ranges were 0–21 wt% and 5.1–20.7 vol%, respectively. The detailed salinity and fluid fraction values of the saline fluid-bearing olivine aggregates are listed in Table 1. High-temperature-resistant quartz glass sleeves (SiO₂ content: ∼100 wt%) with a 3-mm inner diameter, 6-mm outer diameter and 4-mm height were employed as the sample capsules. Although the reaction of quartz and olivine can take place at high temperatures and pressures and produce a very thin pyroxene-bearing layer, the contribution to the bulk conductivity could be negligible because the conductivity of pyroxene is much lower than that of interconnected fluid phases (Huang et al., 2021). Two Au stoppers were applied to seal the top and bottom of the sample capsule using a small amount of silver colloid.

TABLE 1

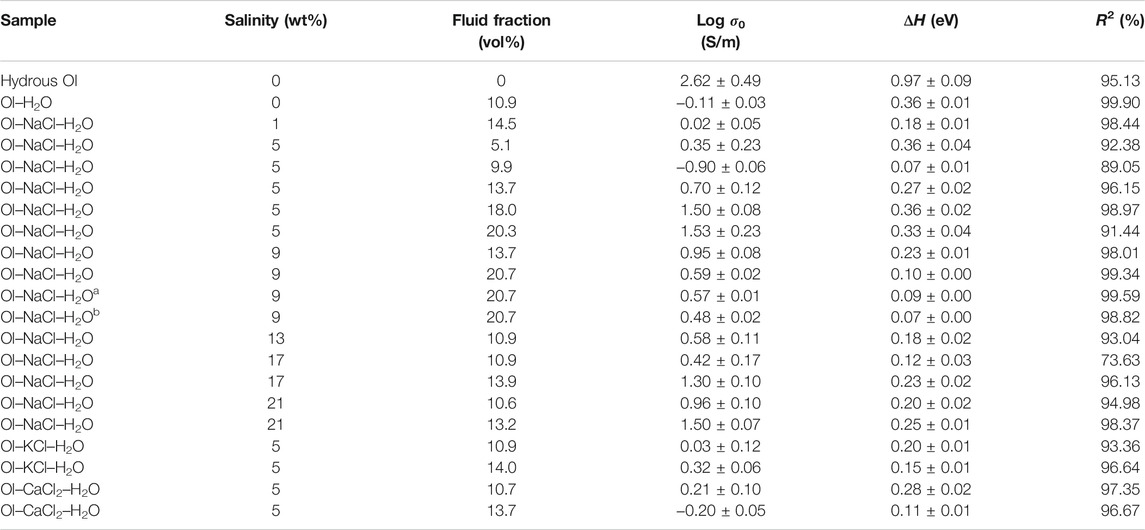
TABLE 1. Thermodynamic parameters for the electrical conductivities of hydrous olivine aggregates, the Ol–H₂O system, and saline fluid-bearing olivine aggregates with various salinities and fluid fractions at 2.0 GPa and 773–1073 K, except for runs a and b, which were conducted at 2.5 and 3.0 GPa, respectively.

Impedance Spectra Measurements

Sample assembly for the in-situ measurement of electrical conductivity was displayed in Supplementary Figure S1. The high-temperature and high-pressure conditions were provided using a YJ–3000t cubic multi-anvil apparatus at the Key Laboratory of High-Temperature and High-Pressure Study of the Earth’s Interior, Institute of Geochemistry, CAS, Guiyang, China. The target pressure was achieved using a slow compression rate of 0.5 GPa/h to avoid damaging the quartz sleeve. Once reaching the target pressure, the temperature was rapidly increased to 1073 K. Our measurement results have shown that the resistance of saline fluid-bearing polycrystalline olivine dramatically increases with time to values greater than 1 MΩ at 1073 K when the quartz sleeve sample capsule is damaged. However, the quartz sleeves remained undamaged in the successful runs and the low resistance values of the saline fluid-bearing systems only slightly increased with time. This is because saline fluids might weakly diffuse to the exterior of the sample capsule when the aqueous fluids and olivine grains have approximately equilibrated. At a given pressure, the impedance spectra were firstly collected continuously at the highest temperature of 1073 K, and the spectra gradually reached stable after ∼30 min. It reflected that the saline fluids gradually diffused along olivine grain boundaries, and finally it reached a uniform distribution of fluid in the sample. Meanwhile, a very small amount of olivine is dissolved into the saline fluids with time. At a fixed temperature, pressure and volume fraction, the electrical conductivities of olivine–NaCl–H₂O systems slightly decreased due to the loss of saline fluids. In order to avoid the inevitable influence of the loss of saline fluids, at the highest measurement point of 1073 K, the olivine–NaCl–H₂O system was kept a relatively longer time in order to reach an equilibrium state by continuously checking the variation of impedance spectroscopy of sample. After that, a decreasing temperature cycle from 1073 to 773 K was chosen to quickly measure the electrical conductivity of sample at the temperature interval of 50 K. Due to the small solubility of olivine in the saline fluids, the change of the geometry of the olivine grain boundaries was feeble (Macris et al., 2003). We proposed that the distribution of saline fluids was dominated by the salinities and volume fractions of fluids, and the grain sizes and geometries of olivine grains. And thus, the textures of the olivine–NaCl–H₂O systems were almost stable, and the very slight change of texture due to the dissolution of olivine in the saline fluids cannot affect the conductivities of the olivine–NaCl–H₂O systems. The fluid fraction of the aqueous fluid-bearing system remained mostly stable during the impedance spectra measurements, with less than 10% error of the fluid fraction in the aqueous fluid-bearing system, and the salinity remained unchanged during the experiments. The impedance spectra of the aqueous fluid-bearing system were continuously collected twice at a given temperature, and the two measured resistances were similar. This supports that the impedance spectra of the aqueous fluid-bearing system were collected during a relatively stable state. It is worthily mentioned that the reaction of quartz and olivine can take place at high temperatures and pressures, and a very thin pyroxene-bearing layer might be produced. However, the contribution of the thin pyroxene-bearing layer to the bulk conductivity could be negligible because the conductivity of pyroxene is much lower than that of interconnected fluid phases (Huang et al., 2021). Stable impedance spectra of hydrous polycrystalline olivine were collected using a similar process to that for the aqueous fluid-bearing system. The detailed thermodynamic conditions of the runs are listed in Table 1. The errors of the experimental pressures and temperatures were ±0.2 GPa and ±10 K, respectively.

Post-Experiment Sample Analysis

The chemical compositions of the recovered olivine for the olivine–NaCl–H₂O system with 5 wt% salinity and 20.3 vol% volume fraction were measured by EPMA. The chemical compositions of olivine were similar before and after the electrical conductivity measurements, as shown in Supplementary Table S1. The internal structures of the recovered samples were also observed using a scanning electron microscope (SEM) at the Center for Lunar and Planetary Sciences, Institute of Geochemistry, CAS, Guiyang, China. The SEM images show that the boundaries of the large olivine grains were curved and smooth, and small ellipsoidal olivine grains were distributed in the triangular spaces between the large olivine grains. A corrosion border is clearly visible on the olivine grains and numerous small circular holes are observed in the grain interiors (Figure 1). These phenomena reflect the strong dissolution and corrosion of olivine by the saline fluids at high temperature and pressure. Furthermore, the median dihedral angle of the saline fluids in of the Ol–NaCl–H₂O system with 5 wt% NaCl and 5.1 vol% fluids was found to be 50° (Supplementary Figure S2). The detail relevant analysis process was described in the supplementary material.

FIGURE 1

FIGURE 1. Scanning electron microscope images of the recovered samples of saline fluid-bearing olivine aggregates after electrical conductivity measurements. (A) and (B) show the Ol–NaCl–H₂O system with a salinity of 5 wt% and fluid fraction of 13.7 vol%, (C) and (D) show the Ol–CaCl₂–H₂O system with a salinity of 5 wt% and fluid fraction of 10.7 vol%, and (E) and (F) show the Ol–NaCl–H₂O system with a salinity of 5 wt% and fluid fraction of 18.0 vol%. The saline fluids are uniformly distributed on the olivine grain boundaries, and the cross-sections of pores occupied by saline fluids contain triangular, elliptical, and irregular shapes. Fluid channels formed in the shattered zones among the large olivine grains.

Results

The representative impedance spectra of the Ol–H₂O and Ol–NaCl–H₂O systems comprise two parts: an approximate semicircle in the high-frequency region (10⁶–10³ Hz), and an additional tail in the low-frequency region (10³–10⁻¹ Hz) (Figure 2). Previous relevant studies have shown that the high-frequency semicircle reflects the conduction process of the bulk sample (Guo et al., 2015; Sinmyo and Keppler, 2017), and the low-frequency tail might correspond to an electrode effect (Tyburczy and Roberts, 1990). A comparison of the impedance spectra of the Cpx–NaCl–H₂O system suggests that inductive reactance did not appear for all of the saline fluid-bearing systems (Sun et al., 2020). For all of the hydrous olivine, Ol–H₂O system and Ol–NaCl–H₂O system samples, the bulk resistances were obtained by fitting the impedance spectra. The equivalent circuit of the impedance spectra comprises a series connection of R_S–CPE_S and R_E–CPE_E, where R_S and CPE_S represent the sample resistance and sample constant–phase element, respectively, and R_E and CPE_E indicate the resistance and constant–phase element for the interaction of the charge carrier with the electrode. The R_S errors were caused by the weak diffusion of aqueous fluids and fitting errors of the impedance spectra. Our evaluation indicates that the sample resistance errors were less than 10%. The calculation formula for the electrical conductivity (σ) is given as:

$\sigma =\mathit{G}/\mathit{R}(1)$

where G is the sample geometric constant calculated based on L/S, in which L is the sample height (m) and S is the cross-sectional area of the electrodes (m²), and R is the fitting resistance (Ω) of the sample.

FIGURE 2

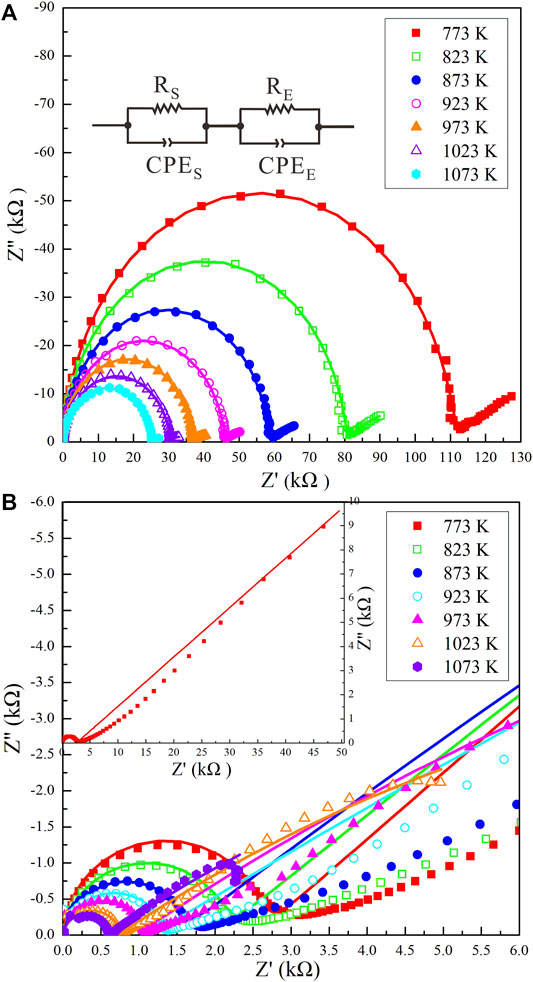
FIGURE 2. Representative complex impedance spectra for (A) the Ol–H₂O system with a fluid fraction of 10.9 vol% and (B) the Ol–NaCl–H₂O system with a salinity of 5 wt% and fluid fraction of 17.8 vol% at 2.0 GPa and 773–1073 K. The equivalent circuit for the impedance spectra of the Ol–H₂O and Ol–NaCl–H₂O systems comprises a series connection of R_S–CPE_S and R_E–CPE_E, where R_S and CPE_S represent the sample resistance and sample constant–phase element, respectively, and R_E and CPE_E indicate the resistance and constant–phase element for the interaction of the charge carrier with the electrode.

The results show that the conductivity of the Ol–NaCl–H₂O system with 9 wt% salinity and 20.7 vol% volume fraction slightly increases with increasing pressure (Figure 3). This indicates that pressure has a weakly positive effect on the conductivity of saline fluid-bearing olivine aggregates. A comparison of the relationship between temperature and electrical conductivity of hydrous olivine aggregates shows that the positive temperature effect is substantially weaker on the conductivities of the Ol–H₂O and Ol–NaCl–H₂O systems, as shown in Figure 4. In comparison with the thermodynamic conditions (T and P), the salinity and fluid fraction have a much more significant effect on the olivine aggregate conductivities. The electrical conductivity of the Ol–NaCl–H₂O system moderately increases with increasing salinity and fluid fraction (Figures 4, 5).

FIGURE 3

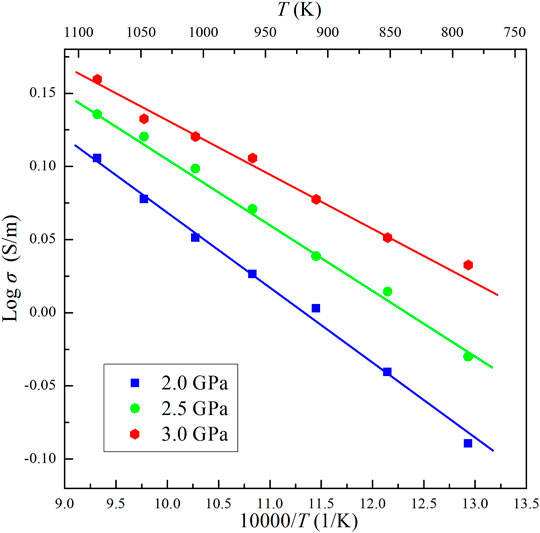
FIGURE 3. Electrical conductivities of the Ol–NaCl–H₂O system with a salinity of 9 wt% and fluid fraction of 20.7 vol% at 2.0–3.0 GPa and 773–1073 K.

FIGURE 4

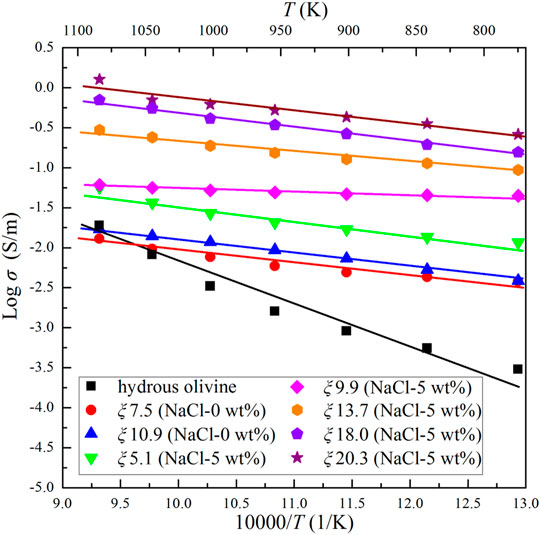
FIGURE 4. Electrical conductivities of hydrous olivine aggregates and the Ol–NaCl–H₂O system with a salinity of 0–5 wt% and fluid fraction of 5.1–20.3 vol% at 2.0 GPa and 773–1073 K.

FIGURE 5

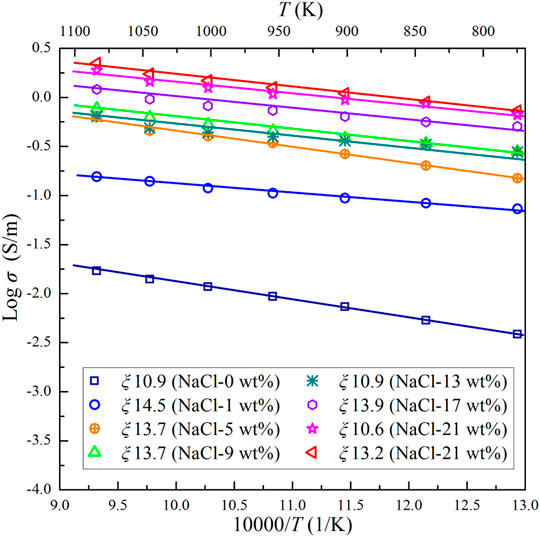
FIGURE 5. Electrical conductivities of the Ol–NaCl–H₂O system with a salinity of 0–21 wt% and fluid fraction of 10.9–14.5 vol% at 2.0 GPa and 773–1073 K.

The median dihedral angle (50°) for the Ol–NaCl–H2O system with 5 wt% NaCl, and 5.1 vol% saline fluids is less than 60°, which indicates that the saline fluids were interconnected in the systems where fluid fractions were substantially higher than 5.1 vol% (Bulau, 1982; Holness, 1995). The conductivities of the olivine aggregates with interconnected saline fluids do not regularly increase with increasing salinity and fluid fraction (Figures 4, 5). The conductivity of the Ol–NaCl–H₂O system is similar to that of the Ol–KCl–H₂O system under similar salinity and fluid fraction conditions, but slightly higher than that of the Ol–CaCl₂–H₂O system (Figure 6). The activation enthalpy of the electrical conductivity of the saline fluid-bearing olivine aggregates provides a crucial thermodynamic parameter that reveals the difficulty level for potential charge carriers to migrate in the samples. At a given pressure, the logarithmic electrical conductivities of the samples and reciprocal temperatures conform to approximate linear relations (Figures 4–6). The activation enthalpies of the conductivities of saline fluid-bearing olivine aggregates can thus be obtained by the following modified Arrhenius relation:

$\mathrm{Log\sigma }=\mathrm{Log}{\mathrm{\sigma }}_{\mathrm{0}}+\frac{-\Delta \mathit{H}}{\mathrm{Log}\mathit{e}\mathit{k}}\frac{1}{\mathit{T}}(2)$

where σ (S/m) denotes the sample conductivity, σ₀ is a fitting constant, k is the Boltzmann constant, T is temperature (K) and ΔH is the activation enthalpy for the sample conductivity. We calculated the activation enthalpies of the hydrous olivine aggregates, Ol–H₂O and Ol–NaCl/KCl/CaCl₂–H₂O systems based on Eq. 2 and the slopes of the linear fitting relation for the logarithmic conductivities and reciprocal temperatures (details given in Table 1). The activation enthalpy of hydrous olivine aggregates (0.97 eV) is substantially higher than those for the Ol–H₂O and Ol–NaCl/KCl/CaCl₂–H₂O systems (0.07–0.36 eV) owing to the different conduction mechanisms that operate at high temperatures and pressures.

FIGURE 6

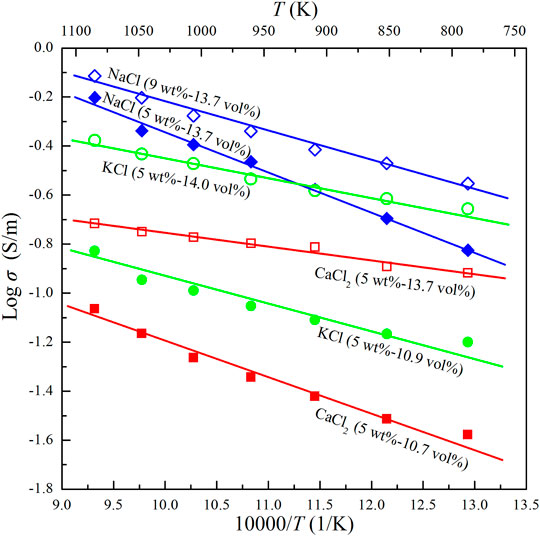
FIGURE 6. Electrical conductivities of the Ol–NaCl–H₂O, Ol–KCl–H₂O and Ol–CaCl₂–H₂O systems with various salinity and fluid fraction conditions at 2.0 GPa and 773–1073 K.

Disscussion

Effect of Temperature and Pressure on Conductivity

Temperature and pressure, which are crucial thermodynamic conditions of the Earth’s interior, affect the electrical conductivity of most minerals, rocks, melts and aqueous fluids to varying degrees. Temperature and pressure fundamentally constrain the species, molar concentration and mobility of thermally activated charge carriers in materials and further influence the bulk conductivity. The conductivity of hydrous olivine aggregate is highly sensitive to temperature and increases by approximately two orders of magnitude upon increasing the temperature from 773 to 1073 K at 2 GPa (Figure 4). The effect of temperature on the conductivities is closely related to the activation enthalpy, which is directly constrained by the conduction mechanism in the samples. The conductivities and temperatures of hydrous olivine aggregates conform to an Arrhenius relation under the conditions of 2.0 GPa and 773–1073 K. The activation enthalpy for the conductivity of hydrous olivine aggregates is 0.97 eV and hydrogen-related point defects are proposed to be the dominant charge carriers (Dai and Karato, 2014a, 2020). This value is substantially lower than that from the model of Karato (1990) (1.50 eV), but similar to that from Dai and Karato, 2014b (0.82 eV). Huang et al. (2005) proposed that the electrical conductivity of hydrous olivine is related to the migration of free protons produced by an ionization reaction:

${\left(2\mathrm{H}\right)}_{\text{M}}^{\times }\rightleftharpoons {\text{H}}_{\text{M}}^{\text{−}}+{\text{H}}^{•}(3)$

where ${\left(2\text{H}\right)}_{\text{M}}^{\times }$ represents two hydrogen ions at an M-site, ${\text{H}}_{\text{M}}^{\text{'}}$ is a proton trapped at the M-site vacancy, and ${\text{H}}^{•}$ is a free proton. For hydrous olivine with a fixed water content, the molar concentration and migration rate of the free proton might increase with increasing temperature. The temperature effect on the conductivity of hydrous olivine is also substantially weaker than that for dry olivine, where small polaron is the dominant charge carrier, owing to the different conduction mechanisms (Dai and Karato, 2014b). For the Ol–NaCl/KCl/CaCl₂–H₂O systems, the conductivities slightly increase with increasing temperature and conform to an Arrhenius relation. The effect of temperature on the conductivities of the Ol–NaCl/KCl/CaCl₂–H₂O systems is considerably weaker than that for hydrous olivine aggregates at 2.0 GPa and 773–1073 K (Figures 4–6). This is because of the lower activation enthalpies (0.07–0.36 eV) for the dominant charge carriers of the Ol–NaCl/KCl/CaCl₂–H₂O systems. The electrical conductivity of olivine aggregates with interconnected aqueous fluids is dominantly constrained by the conductivities of the aqueous fluids. Free ions of Na⁺/K⁺/Ca²⁺, Cl⁻, H⁺, and OH⁻ have been proposed to be the dominant charge carriers for olivine aggregates with interconnected saline fluids. According to the previous studies, the dissociation ratios of NaCl in the fluid phase of Ol–NaCl–H₂O systems were estimated to be ∼95–100% under the conditions of 2.0–3.0 GPa and 773–1073 K (Manning, 2013). It was implied that the dissociation ratios of NaCl were very high, and thus the Na⁺ and Cl⁻ might be the most dominant charge carriers in the Ol–NaCl–H₂O systems. In addition, Macris et al. (2003) reported that the solubility of olivine in the saline aqueous fluid is much higher than that of pure water, and decreases the dihedral angle simultaneously. As shown in Figure 1, corrosion borders are widely distributed on the olivine grains of the recovered samples. The conductivities of saline fluid-bearing olivine aggregates were measured from the highest temperature (1073 K) to the lowest temperature (773 K); thus, the olivine content dissolved in the aqueous fluids was approximately the same over the full temperature region in each experiment. The ionic groups from the reaction of olivine and saline fluids at high temperatures and pressures participate in the conduction process to some extent. The effect of pressure on the conductivity of dry and hydrous olivine has been previously reported to have a slightly negative correlation (Dai et al., 2010; Dai and Karato, 2014d). In this study, the electrical conductivity of saline fluid-bearing olivine aggregates is found to slightly increase with increasing pressure. As shown in Figure 3, the electrical conductivity of the Ol–NaCl–H₂O system with a salinity of 9 wt% and fluid fraction of 20.7 vol% increased by 0.05–0.15 orders of magnitude with increasing pressure from 2 to 3 GPa. According to previous studies, the conductivity of NaCl-bearing aqueous fluids weakly increases with pressure between 1 and 4 GPa and 773–1073 K (Guo and Keppler, 2019). The weak positive pressure effect on the conductivity of the Ol–NaCl–H₂O system is thus due to the presence of interconnected saline fluids. At a certain temperature, the saline fluids on the boundary of olivine particles become more interconnected with increasing pressure. The pressure might also increase the rate of salt decomposition in the aqueous fluids, and the molar concentration of the charge carriers in the fluids thus increase correspondingly. These might be the primary causes for the positive effect of pressure on the conductivity of the Ol–NaCl–H₂O system.

Effect of Salinity and Fluid Fraction on Conductivity

Salinity directly affects the conductivity of saline fluids, and the fluid fraction significantly influences the interconnectivity of the fluids in the matrix. The salinity and fluid fraction are thus closely related to the conductivity of saline fluid-bearing olivine aggregates. The median dihedral angle for the saline fluids of the Ol–NaCl–H₂O system with a salinity of 5 wt% and fluid fraction of 5.1 vol% is 50°, which indicates that the saline fluids were interconnected on the polycrystalline olivine boundaries (Supplementary Figure S2). The dihedral angles of the Ol–(NaCl)–H₂O system are found to be higher than those of the Pl–NaCl–H₂O and Cpx–NaCl–H₂O systems and dehydration products of lawsonite (Supplementary Figure S3). This might imply that aqueous fluids in the uppermost mantle are more difficult to interconnect than those in the mid-to lower crust and interfaces of subduction slabs. It’s should be noted that pressure and temperature affect the dihedral angles for the aqueous fluids in the polycrystalline silicate minerals to some extent (Yoshino et al., 2007), but the dihedral angles for the aqueous fluids-bearing systems might be dominated by the mineral constituent and the salinity and fluid fraction of the saline fluids. As shown in Figure 5, the conductivities of the Ol–NaCl–H₂O system with a salinity of 1 wt% and fluid fraction of 14.5 vol% are ∼1–1.5 orders magnitudes higher than those of the Ol–H₂O system with the fluid fraction of 10.9 vol%. However, the conductivities of the Ol–NaCl–H₂O system with a salinity of 5 wt% and fluid fraction of 13.7 vol% are only ∼0.2–0.5 orders magnitudes higher than those of the Ol–H₂O system with a salinity of 1 wt% and fluid fraction of 14.5 vol%. This implies that a small quantity of salt can dramatically enhance the conductivity of the Ol–H₂O system owing to the sharp increase of charge carrier concentrations in the aqueous fluids. The molar concentration of Na⁺ and Cl⁻ increases with increasing salinity and accordingly enhances the conductivity of the Ol–NaCl–H₂O system. However, the decomposition ratio of the solute might decrease with increasing salinity at a certain temperature and pressure; thus the conductivity of saline fluid-bearing olivine aggregates does not proportionately increase with increasing salinity (0–21 wt%). Supplementary Figure S4 shows the logarithmic conductivity values versus salinity for the Ol–NaCl–H₂O system with similar fluid fractions (10.9–14.5 vol%). The conductivity of the Ol–NaCl–H₂O system dramatically increases with increasing salinity in the lower salinity range (< 17 wt%), but remains nearly unchanged in the higher salinity range (17–21 wt%). It should be noted that the conductivity of the Ol–NaCl–H₂O system with a salinity of 13 wt% and fluid fraction of 10.9 vol% is slightly lower than that of the Ol–NaCl–H₂O system with a salinity of 9 wt% and fluid fraction of 13.7 vol% at 2 GPa and 873–1073 K. We propose that the degree to which the fluid fraction influences the conductivity of saline fluid-bearing olivine aggregates is more significant than that of salinity when salinities are sufficiently high (>9 wt%). Salinity might also influence the solubility of olivine in saline fluids, which would explain the different activation enthalpies of the various saline fluid-bearing olivine aggregates (Table 1). Previous studies have shown that the solubility of quartz and albite in NaCl–H₂O fluids decreases with increasing salinity, whereas the solubility of diopside in NaCl–H₂O fluids positively relates to salinity (Newton and Manning, 2000; Shmulovich et al., 2001). According to the research of Macris et al. (2003), the solubility of olivine in the saline aqueous fluid is much higher than that of pure water, which increases the concentration of dissolved component and decreases the dihedral angle simultaneously. We propose that the dissolution of olivine in saline fluids might play an important role in the conductivity of the Ol–NaCl–H₂O system. The logarithmic conductivity of the Ol–NaCl–H₂O system with a salinity of 5 wt% linearly relates to the logarithmic fluid fractions (Supplementary Figure S5). The bulk conductivity and fluid fraction thus conform to Archie’s law (Archie, 1942):

${\sigma }_{\text{bulk}}=\text{c}{\mathit{\Phi }}^{\text{n}}{\sigma }_f(4)$

where σ_bulk and σ_f are the conductivities of the Ol–NaCl–H₂O systems and saline fluids, respectively, Φ is the fluid fraction, and as well as c and n are constants, respectively. Upon increasing the temperature from 773 to 1073 K, n increases from 2.34 to 4.12. This reflects that the conductivity of the Ol–NaCl–H₂O system significantly increases with increasing fluid fraction, and the fluid fraction has a more significant influence on conductivity at higher temperatures. The electrical conductivity of aqueous fluids (σ_f) distributed in the interspaces of the olivine aggregates remains unclear and is difficult to directly measure in the Ol–NaCl–H₂O system. The conductivity of interconnected aqueous fluids distributed in the solid matrix can be calculated based on the HS⁺ model and cube model (Hashin and Shtrikman, 1962; Waff, 1974). According to the HS⁺ model, the electrical conductivity of the aqueous fluids in the Ol–NaCl–H₂O system is calculated by:

${\sigma }_{\text{b}}={\sigma }_{\text{f}}+\frac{1-\mathit{\Phi }}{\frac{1}{{\sigma }_{\text{s}}-{\text{σ}}_{\text{f}}}-\frac{\mathit{\Phi }}{3{\sigma }_{\text{f}}}}(5)$

where σ_b, σ_s and σ_f are the conductivities of the Ol–NaCl–H₂O system, hydrous olivine aggregates and saline fluids, respectively. The mathematical formula for the cube model is expressed as:

${\sigma }_{\text{b}}=\left(1-{\left(1-\mathit{\Phi }\right)}^{2/3}\right){\sigma }_{\text{f}}(6)$

We apply our experimental data to calculate the conductivity of aqueous fluids using Eq. 5, Eq. 6. As shown in Table 2, the conductivities of NaCl–H₂O fluids calculated from the HS⁺ and cube models are substantially lower than experimental data reported by Sinmyo and Keppler (2017) and Guo and Keppler (2019). A similar phenomenon was reported by Guo et al. (2015), Li et al. (2018) and Sun et al. (2020). This discrepancy might be mainly caused by the compositional differences between the pure NaCl–H₂O fluids and aqueous fluids in the Ol–NaCl–H₂O system. For aqueous fluids in the Ol–NaCl–H₂O system, Na⁺ and Cl⁻ have been proposed to be the dominant charge carriers and a small quantity of H⁺, OH⁻ and soluble ions from olivine slightly enhance the conductivity, whereas tiny particles of silicate minerals in the aqueous fluids might dramatically impede charge carrier migration. The degree of NaCl dissociation might decrease owing to the presence of olivine aggregates. Furthermore, the true distribution of aqueous fluids in the systems possibly differs from those for the ideal HS⁺ and cube models. Aqueous fluids are distributed in a variety of pathways, such as on mineral surfaces, spherical holes, triple junctions and local channels. Although the hydrodynamic pressure of the fluids is relatively homogeneous, the geometric shapes of the local aggregation fluids are constrained by the sizes and shapes of the olivine grains. In addition, the olivine has faceted interfaces due to its anisotropy, which could affect the fluid connectivity even with a low dihedral angle (Price et al., 2006), resulting in a more tortuous network of fluid. Notably, it is inevitable that a slow fluid movement from the temperature gradient of sample capsule is also of the possible effect on the measured conductivity results of the NaCl–H₂O and Ol–NaCl–H₂O systems.

TABLE 2

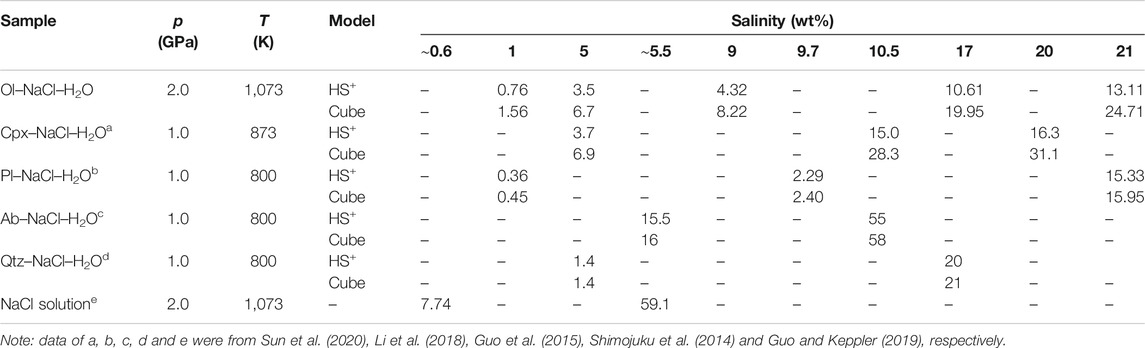
TABLE 2. Electrical conductivities (S/m) of saline fluids with various NaCl contents in the Ol–NaCl–H₂O, Cpx–NaCl–H₂O, Pl–NaCl–H₂O, Ab–NaCl–H₂O, and Qtz–NaCl–H₂O systems, and NaCl solutions calculated on the basis of the HS⁺ and cube models at high temperatures and pressures.

Comparison With Previous Studies

The electrical conductivity of hydrous olivine aggregates determined in this study (∼10^–3.5–10^−1.25) is similar to that reported by Dai and Karato, 2014b, and the iron contents of the two hydrous olivine aggregates are very similar (Figure 7). This supports that the water content in our olivine is similar to that in the olivine from Dai and Karato, 2014b (130 ppm). The presence of pure water dramatically enhances the conductivity of olivine aggregates at lower temperature, but the conductivity of the Ol–H₂O system is similar to those of hydrous olivine aggregates with increasing temperature. The effect of saline fluids on the conductivity of olivine aggregates is substantially more significant than that of pure water (Figure 7). As shown in Figure 7, we compared the electrical conductivities of iron-free forsterite–fluid system from Huang et al. (2021) and the conductivities of iron-bearing olivine–fluid system from the present study. It was shown that the conductivity of iron-free forsterite–fluid system was moderately higher than that of iron-bearing olivine–fluid system at the same salinity and similar fluid fractions. And thus, the existence of iron in the olivine might be obstructive to the interconnectivity of saline fluids. The influence of aqueous fluids on the various silicate mineral aggregates also differs to some extent. The conductivity of olivine aggregates with interconnected pure water (10.9 vol%) is approximately one order of magnitude lower than that of clinopyroxene aggregates with 25 vol% pure water. In comparison with the electrical conductivity of Cpx–NaCl–H₂O system with a salinity of 10 wt% and fluid fraction of 20 vol%, the conductivity of Ol–NaCl–H₂O system with a salinity of 9 wt% and fluid fraction of 20.7 vol% is slightly lower. Under similar salinity and fluid fraction conditions, the conductivity of the Ol–NaCl–H₂O system is slightly lower than that of the Pl–NaCl–H₂O system, but dramatically lower than that of the Ab–NaCl–H₂O system (Figure 7). For example, the conductivity of the Ol–NaCl–H₂O system with a salinity of 5 wt% and fluid fraction of 9.9 vol% is slightly lower than that of the Pl–NaCl–H₂O system with a salinity of 3.3 wt% and fluid fraction of 8.3 vol%, but approximately 1.5 orders of magnitude lower than that of the Ab–NaCl–H₂O system with a salinity of 3.4 wt% and fluid fraction of 8.9 vol% (Guo et al., 2015; Li et al., 2018). The interconnected saline fluids thus dominantly constrain the conductivity of saline fluid-bearing silicate mineral aggregates, but the silicate minerals still play a significant role in the electrical properties of the systems. This is because the conductivities of various silicate minerals, (e.g., olivine, clinopyroxene, plagioclase and albite) differ under a given temperature and pressure condition. The various dissolution mechanisms and solubilities of different silicate minerals in saline fluids might therefore significantly affect the species and migration speed of the charge carriers in the fluids. Furthermore, the distribution characteristics of saline fluids in the interspaces of the solid matrix might be closely related to the grain size and shape, viscosity, defect concentration, and solubility of the minerals in the saline fluids-bearing systems. The electrical conductivity of the Ol–NaCl–H₂O system slightly increases with increasing pressure. A similar effect of pressure on the conductivity of the NaCl–H₂O system was reported by Guo and Keppler (2019). Salinity significantly affects the conductivity of the NaCl–H₂O system at high temperatures and pressures (Sinmyo and Keppler, 2017; Guo and Keppler, 2019), and further influences the conductivity of saline fluid-bearing rocks. The electrical conductivity of the Ol–NaCl–H₂O system with a salinity of 9 wt% and fluid fraction of 20.7 vol% is similar to that of the NaCl–H₂O system with a molar concentration of 0.01 mol/L (salinity: ∼0.059 wt%), and approximately one order of magnitude lower than that of the NaCl–H₂O system with a molar concentration of 0.1 mol/L (salinity: ∼0.58 wt%). Furthermore, the conductivity of the NaCl–H₂O system with a molar concentration of 1 mol/L (salinity: ∼5.5 wt%) is substantially higher than that of the silicate mineral–NaCl–H₂O system with higher salinities (>5.7 wt%) (Figure 7). We propose that the dissolution of silicate minerals into the saline fluids might affect the conductivities of the aqueous fluids to some extent, and the hydrological regime in the silicate rocks dramatically affects the conductivities of fluid–rock systems. The measured conductivities of pure saline fluids are therefore significantly different from the calculated conductivities of saline fluids in silicate mineral–NaCl–H₂O systems based on the HS⁺ and cube models.

FIGURE 7

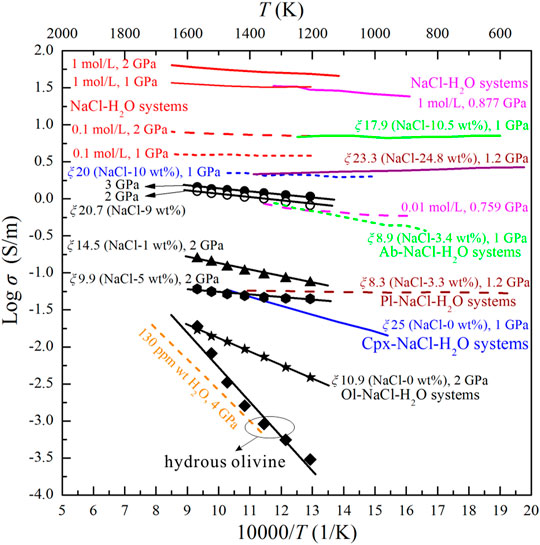
FIGURE 7. Electrical conductivities of hydrous olivine aggregates and the Ol–H₂O and Ol–NaCl–H₂O systems in this study and relevant systems from previous studies. The dashed orange line indicates the conductivities of the hydrous olivine aggregates (Dai and Karato, 2014b). The purple five-pointed star indicates the conductivity of saline fluids-bearing forsterite aggregates (Huang et al., 2021). The solid and dashed blue lines indicate the conductivities of the Cpx–H₂O and Cpx–NaCl–H₂O systems (Sun et al., 2020), respectively. The dashed and solid brown lines indicate the conductivities of the Pl–NaCl–H₂O systems (Li et al., 2018). The dashed and solid green lines indicate the conductivities of the Ab–NaCl–H₂O systems (Guo et al., 2015). The red and pink lines indicate the conductivities of NaCl–H₂O systems (Sinmyo and Keppler, 2017; Guo and Keppler, 2019). The relationships between the logarithmic conductivities of the various hydrous olivine aggregates and saline fluid-bearing systems and reciprocal temperature are distinguished in different colors.

Electrical conductivities of the Ol–NaCl–H₂O systems were the latest measuring results at the various thermodynamic conditions of 2.0–3.0 GPa and 773–1073 K. Effects of temperature and pressure on the conductivities of the Ol–NaCl–H₂O systems were very slight, but salinity and fluid fraction are important influence factors on the conductivities. Electrical conductivities of the Ol–NaCl–H₂O systems were compared with the conductivities of the Ol–KCl–H₂O and Ol–CaCl₂–H₂O systems with a certain salinity and fluid fraction. It was shown that the conductivities of the Ol–NaCl–H₂O systems were close to those of the Ol–KCl–H₂O systems, but moderately higher than the Ol–CaCl₂–H₂O systems at the similar salinities and fluid fractions. Although the formation mechanism and evolution low for the saline fluids in the mantle wedges have not been researched in detail, the previous studies have proposed that NaCl is the dominant salt in the saline fluids based on the material compositions of the inclusion fluids in the mantle xenoliths (Kawamoto et al., 2013; Morikawa et al., 2016; Huang et al., 2019). And thus, the presence of NaCl fluids might be the origin of the high-conductivity anomalies in the mantle wedges. It’s important to constrain the volume fractions of the saline fluids in the high-conductivity layers of the mantle wedges.

Geophysical Implications

Subduction zones are the most active geological environments on Earth, where various geological processes lead to complex material compositions and structural characteristics. Magnetotelluric profiles indicate that high-conductivity geological bodies are widely distributed in the mantle wedges of subduction zones. Various hypotheses regarding the origin for the high-conductivity anomalies have been proposed based on field geological investigations and high-temperature and high-pressure experiments (Dai and Karato, 2014a; Manthilake et al., 2015; Guo et al., 2017; Hu et al., 2018; Li et al., 2018). In subduction zones, the dehydration products of hydrous minerals, which contain residual minerals and aqueous fluids, are located along the interface between the subduction slab and mantle wedge. Owing to the wide distribution of aqueous fluids in mantle wedges (Peslier et al., 2017), hydrogen-related defects are likely to exist in nominally anhydrous minerals (Karato, 1990), causing a significant increase of the electrical conductivity in relevant regions (Dai and Karato, 2014b). According to the magnetotelluric profiles, the unusually high electrical conductivities of the high-conductivity layers in the mantle wedges were ∼10⁻²–1 S/m (Yamaguchi et al., 2009; Burd et al., 2013; McGary et al., 2014; Hata et al., 2017). The largest conductivity of hydrous San Carlos olivine with 0.1 wt% H₂O (close to the solubility of water in olivine) is approximately 10^–1 S/m under the uppermost mantle conditions (Dai and Karato, 2014b), and thus the unusually high electrical conductivities of ∼10⁻²–10⁻¹ S/m in the high-conductivity layers of the mantle wedges can be interpreted by the conductivities of hydrous peridotite. However, the unusually high conductivities of 10⁻¹–1 S/m in the mantle wedges were higher than the largest conductivity of hydrous peridotite (10^–1 S/m), indicating that the conductivities of hydrous peridotite cannot interpret the unusually high electrical conductivities of 10⁻¹–1 S/m in the mantle wedges. Therefore, it’s possible that the interconnected saline fluids cause the high-conductivity anomalies with the conductivities of ∼10⁻¹–1 S/m in the mantle wedges.

Hydrous minerals (e.g., chlorite, epidote, serpentine, phengite) in subducting plates are transported into the Earth’s deep interior, and subsequent dehydration reactions are triggered under the dehydration thermodynamic conditions of high temperatures and pressures (Zheng, 2019). A large proportion of free water released from hydrous minerals migrates upwards to a certain depth within the mantle wedges. A certain amount of solutes dissolve into the free water during the compositional differentiation of free water and residual minerals. The presence of NaCl-bearing aqueous fluids has been determined to be a significant cause of the high-conductivity anomalies in the middle to lower crust of subduction zones (Guo et al., 2015; Sinmyo and Keppler, 2017; Li et al., 2018; Guo and Keppler, 2019; Sun et al., 2020). The question of whether or not saline fluids are present and interconnected in the mantle wedges of subduction zones has been long debated. Huang et al. (2019) recently demonstrated that interconnected NaCl-bearing aqueous fluids are present in mantle wedges based on high-temperature and high-pressure experiments. This was an important discovery, which implies that NaCl-bearing aqueous fluids might cause the high-conductivity anomalies in the mantle wedges. Fluid fraction and salinity are significant factors that influence the conductivities of HCLs that might be caused by saline fluids. To quantitatively constrain the origin of the high-conductivity anomalies related to NaCl-bearing aqueous fluids in mantle wedges, we compare the conductivities of the HCLs in mantle wedges and NaCl-bearing aqueous fluids with various salinities and fluid fractions. Magnetotelluric profiles indicate that the highest conductivities of the HCLs in most mantle wedges are close to 1 S/m (Yamaguchi et al., 2009; Burd et al., 2013; McGary et al., 2014; Hata et al., 2017). The conductivities of ellipsoidal HCLs gradually decrease from core to edge. In regions with aqueous fluids, the lattice water in nominally anhydrous minerals should be saturated. The presence of hydrous olivine can be employed to interpret the origin of HCLs with conductivities on the order of 10⁻²–10⁻¹ S/m (Dai and Karato, 2014b), but regions with conductivities of 10⁻¹–1 S/m are possibly related to saline fluids. The conductivities of the Ol–NaCl–H₂O system with various fluid fractions (0.1–100 vol%) and salinities (1–21 wt%) were calculated based on the HS⁺ and cube models, as shown in Figure 8. The effects of temperature and pressure on the conductivities of the interconnected saline fluid-bearing olivine aggregates are very limited; thus the calculated conductivities are obtained based on the experimental data at 2.0 GPa and 1073 K. In the conductivity range of 10⁻¹–1 S/m, the conductivities of the Ol–NaCl–H₂O system estimated from the HS⁺ and cube models at a certain salinity and fluid fraction differ slightly. This discrepancy might be caused by differences of the fluid distribution in the ideal cube and HS⁺ models and real Ol–NaCl–H₂O system. For the Ol–NaCl–H₂O system with a certain salinity and electrical conductivity, the real fluid fractions are close to the average fluid fractions obtained from the HS⁺ and cube models. The fluid fractions in the HCLs can be approximated by combining the electrical conductivities of HCLs in mantle wedges and those of the Ol–NaCl–H₂O system at a certain salinity. For the lower bound of conductivity (10^–1 S/m) in the HCLs, the fluid fractions of the Ol–NaCl–H₂O system with a salinity of 1, 5, 9, 17 and 21 wt% are 9.0, 1.8, 1.5, 0.7 and 0.5 vol%, respectively. For the upper bound of conductivity (1 S/m) in the HCLs, the fluid fractions of the Ol–NaCl–H₂O system with a salinity of 5, 9, 17 and 21 wt% are 21.9, 17.9, 6.9 and 5.9 vol%, respectively. For the Ol–NaCl–H₂O system with a salinity of 1 wt%, the fluid fraction employed to interpret the upper bound for the high conductivities (1 S/m) is close to 100 vol%. The presence of the Ol–NaCl–H₂O system with a salinity of ∼1 wt% can therefore not be the origin of the HCLs in mantle wedges. The original salinities of the aqueous fluids from the dehydration of subduction slabs are proposed to be 0.5–2.0 wt% NaCl (Li and Hermann, 2015). However, the salinity of the saline fluids measured in a peridotite xenolith from a mantle wedge was reported to be 5.1 ± 1.0 wt% NaCl (Kawamoto et al., 2013). In addition, the NaCl contents in slab-derived aqueous fluids that upwell up to forearc regions are close to 6.6 wt% (Morikawa et al., 2016). The higher salinities might be caused by the chromatographic fractionation during the hydration reaction of the mantle wedge after the fluid is released from the subduction slab (Huang et al., 2019). According to all of these above-mentioned evidences, it makes clear that the salinities of most stable aqueous fluids in the mantle wedges are close to 5.0 wt%. The Ol–NaCl–H₂O systems with the salinity of ∼5.0 wt% and fluid fractions larger than 1.8 vol% might thus be the origin of the HCLs in mantle wedges.

FIGURE 8

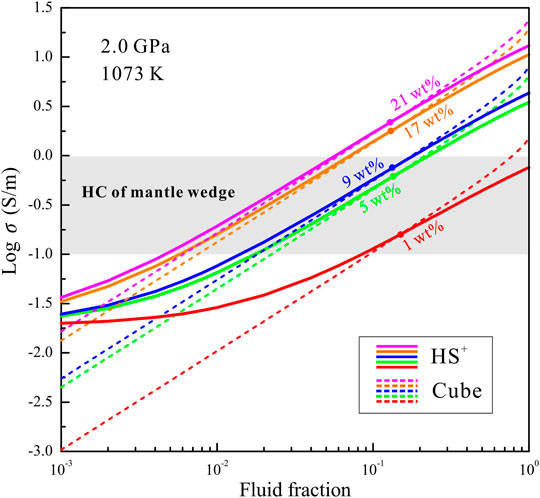
FIGURE 8. Electrical conductivities of the Ol–NaCl–H₂O systems with constant salinity (1, 5, 9, 17, and 21 wt%) and various fluid fractions (0.1–100 vol%) based on the HS⁺ and cube models at 2.0 GPa and 1073 K. The electrical-conductivity region (0.1–1 S/m) of the high-conductivity layers in the mantle wedges of subduction zones is indicated by a gray rectangle (Yamaguchi et al., 2009; Burd et al., 2013; McGary et al., 2014; Hata et al., 2017). The solid and dashed color curves represent the conductivities from the HS⁺ and cube models, respectively.

Conclusion

Pressure and temperature play a relatively minor role on the electrical conductivity of olivine aggregates with interconnected saline fluids. The conductivity of saline fluid-bearing olivine aggregates slightly increases with the rise of temperature and pressure. The salinity and fluid fraction significantly affect the conductivity of saline fluid-bearing olivine aggregates at 2.0 GPa and 773–1073 K. At a fixed salinity and fluid fraction condition, the conductivity of the Ol–NaCl–H₂O system is similar to that of the Ol–KCl–H₂O system, but slightly higher than that of the Ol–CaCl₂–H₂O system. The electrical conductivity of the Ol–NaCl–H₂O system with interconnected saline fluids is constrained by the conductivity of NaCl-bearing saline fluids. For the Ol–NaCl–H₂O system, the dominant charge carriers are proposed to be Na⁺, Cl⁻, H⁺, OH⁻, and soluble ions from olivine. The activation enthalpies of charge carriers in the Ol–NaCl–H₂O systems are 0.07–0.36 eV, which are substantially lower than that of hydrous olivine aggregates (0.97 eV). Under a similar salinity and fluid fraction condition, our presently obtained electrical conductivity of the Ol–NaCl–H₂O system is slightly lower than those of other previous saline fluid-bearing systems (Cpx–NaCl–H₂O, Pl–NaCl–H₂O, and Al–NaCl–H₂O). The conductivities of saline fluids in the Ol–NaCl–H₂O system and other systems calculated using theoretical models (HS⁺ and cube) differ to some extent and are substantially lower than the measured conductivities of saline fluids. The dissolution of olivine and other silicate minerals is proposed to dramatically reduce the conductivity of saline fluids distributed on the boundaries of silicate mineral aggregates. The distribution characteristics of saline fluids in olivine or other silicate mineral aggregates significantly influence the conductivities of saline fluid-bearing mineral aggregates. The salinity of stable saline fluids in mantle wedges is close to 5 wt% NaCl, and fluid fractions larger than 1.8 vol% can be employed to interpret the high-conductivity anomalies in mantle wedges based on the magnetotelluric result and calculated conductivities of the Ol–NaCl–H₂O system.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.

Author Contributions

LD designed the project. WS and LD wrote the initial draft of the work and the final paper. LD, HH and WS contributed in interpreting the results. WS, JJ, MW, ZH, CJ performed and interpreted the high-pressure electrical conductivity experiments and scanning electron microscope images.

Funding

This research was financially supported by the NSF of China (42072055, 41774099, 41772042, and 42002043), Youth Innovation Promotion Association of CAS (Grant No. 2019390), Special Fund of the West Light Foundation of CAS, the Foundation of the Key Laboratory of Earthquake Forecasting and United Laboratory of High-Pressure Physics and Earthquake Science, the Institute of Earthquake Forecasting, Chinese Earthquake Administration and as well as Special Fund from Shandong Provincial Key Laboratory of Water and Soil Conservation and Environmental Protection.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.749896/full#supplementary-material

References

Archie, G. E. (1942). The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. Am. Inst. Min. Metall. Pet. Eng. Inc. 146, 54–62. doi:10.2118/942054-G

CrossRef Full Text | Google Scholar

Bulau, J. R. (1982). Intergranular Fluid Distribution in Olivine–Liquid basalt Systems. PhD dissertation. New Haven, Connecticut: Yale University.

Google Scholar

Burd, A. I., Booker, J. R., Mackie, R., Pomposiello, C., and Favetto, A. (2013). Electrical Conductivity of the Pampean Shallow Subduction Region of Argentina Near 33 S: Evidence for a Slab Window. Geochem. Geophys. Geosyst. 14, 3192–3209. doi:10.1002/ggge.20213

CrossRef Full Text | Google Scholar

Carter, M. J., Zimmerman, M. E., and Teyssier, C. (2015). The Fate of Fluid Inclusions during High-Temperature Experimental Deformation of Olivine Aggregates. J. Geophys. Res. Solid Earth 120, 3077–3095. doi:10.1002/2014JB011782

CrossRef Full Text | Google Scholar

Dai, L., and Karato, S.-i. (2009). Electrical Conductivity of Wadsleyite at High Temperatures and High Pressures. Earth Planet. Sci. Lett. 287, 277–283. doi:10.1016/j.epsl.2009.08.012

CrossRef Full Text | Google Scholar

Dai, L., and Karato, S.-i. (2014a). High and Highly Anisotropic Electrical Conductivity of the Asthenosphere Due to Hydrogen Diffusion in Olivine. Earth Planet. Sci. Lett. 408, 79–86. doi:10.1016/j.epsl.2014.10.003

CrossRef Full Text | Google Scholar

Dai, L., and Karato, S.-i. (2014b). Influence of FeO and H on the Electrical Conductivity of Olivine. Phys. Earth Planet. Interiors 237, 73–79. doi:10.1016/j.pepi.2014.10.006

CrossRef Full Text | Google Scholar

Dai, L., and Karato, S.-i. (2014d). Influence of Oxygen Fugacity on the Electrical Conductivity of Hydrous Olivine: Implications for the Mechanism of Conduction. Phys. Earth Planet. Interiors 232, 57–60. doi:10.1016/j.pepi.2014.04.003

CrossRef Full Text | Google Scholar

Dai, L., and Karato, S.-i. (2014c). The Effect of Pressure on the Electrical Conductivity of Olivine under the Hydrogen-Rich Conditions. Phys. Earth Planet. Interiors 232, 51–56. doi:10.1016/j.pepi.2014.03.010

CrossRef Full Text | Google Scholar

Dai, L., and Karato, S. i. (2020). Electrical Conductivity of Ti‐Bearing Hydrous Olivine Aggregates at High Temperature and High Pressure. J. Geophys. Res. Solid Earth 125, e2020JB020309. doi:10.1029/2020JB020309

CrossRef Full Text | Google Scholar

Dai, L., Li, H., Li, C., Hu, H., and Shan, S. (2010). The Electrical Conductivity of Dry Polycrystalline Olivine Compacts at High Temperatures and Pressures. Mineral. Mag. 74, 849–857. doi:10.1180/minmag.2010.074.5.849

CrossRef Full Text | Google Scholar

Förster, M. W., Foley, S. F., Marschall, H. R., Alard, O., and Buhre, S. (2019). Melting of Sediments in the Deep Mantle Produces saline Fluid Inclusions in Diamonds. Sci. Adv. 5, eaau2620. doi:10.1126/sciadv.aau2620

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, H., and Keppler, H. (2019). Electrical Conductivity of NaCl‐Bearing Aqueous Fluids to 900 °C and 5 GPa. J. Geophys. Res. Solid Earth 124, 1397–1411. doi:10.1029/2018JB016658

CrossRef Full Text | Google Scholar

Guo, X., Li, B., and Ni, H. W. (2017). Electrical Conductivity of Hydrous Andesitic Melts Pertinent to Subduction Zones. J. Geophys. Res. Solid Earth 122, 1777–1788. doi:10.1002/2016JB013524

CrossRef Full Text | Google Scholar

Guo, X. Z., Yoshino, T., and Shimojuku, A. (2015). Electrical Conductivity of Albite–(quartz)–Water and Albite–Water–NaCl Systems and its Implication to the High Conductivity Anomalies in the continental Crust. Earth Planet. Sci. Lett. 412, 1–9. doi:10.1016/j.epsl.2014.12.021

CrossRef Full Text | Google Scholar

Hashin, Z., and Shtrikman, S. (1962). A Variational Approach to the Theory of the Effective Magnetic Permeability of Multiphase Materials. J. Appl. Phys. 33, 3125–3131. doi:10.1063/1.1728579

CrossRef Full Text | Google Scholar

Hata, M., Uyeshima, M., Handa, S., Shimoizumi, M., Tanaka, Y., Hashimoto, T., et al. (2017). 3-D Electrical Resistivity Structure Based on Geomagnetic Transfer Functions Exploring the Features of Arc Magmatism beneath Kyushu, Southwest Japan Arc. J. Geophys. Res. Solid Earth 122, 172–190. doi:10.1002/2016JB013179

CrossRef Full Text | Google Scholar

Heise, W., Ogawa, Y., Bertrand, E. A., Caldwell, T. G., Yoshinura, R., Ichihara, H., et al. (2019). Electrical Resistivity Imaging of the Inter-plate Coupling Transition at the Hikurangi Subduction Margin, New Zealand. Earth Planet. Sci. Lett. 524, 115710. doi:10.1016/j.epsl.2019.115710

CrossRef Full Text | Google Scholar

Holness, M. B. (1995). The Effect of Feldspar on quartz–H₂O–CO₂ Dihedral Angles at 4 Kbar, with Consequences for the Behaviour of Aqueous Fluids in Migmatites. Contrib. Mineral. Petrol. 118, 356–364. doi:10.1007/s004100050020

CrossRef Full Text | Google Scholar

Hu, H. Y., Dai, L. D., Li, H. P., Sun, W. Q., and Li, B. S. (2018). Effect of Dehydrogenation on the Electrical Conductivity of Fe-Bearing Amphibole: Implications for High Conductivity Anomalies in Subduction Zones and continental Crust. Earth Planet. Sci. Lett. 498, 27–37. doi:10.1016/j.epsl.2018.06.003

CrossRef Full Text | Google Scholar

Huang, X. G., Xu, Y. S., and Karato, S. I. (2005). Water Content of the Mantle Transition Zone from the Electrical Conductivity of Wadsleyite and Ringwoodite. Nature 434, 746–749. doi:10.1038/nature03426

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Y. S., Guo, H. H., Nakatani, T., Uesugi, K., Nakamura, M., and Keppler, H. (2021). Electrical Conductivity in Texturally Equilibrated Fluid-Bearing Forsterite Aggregates at 800^oC and 1 GPa: Implications for the High Electrical Conductivity Anomalies in Mantle Wedges. J. Geophys. Res. Solid Earth 126, e2020JB021343. doi:10.1029/2020JB021343

CrossRef Full Text | Google Scholar

Huang, Y. S., Nakatani, T., Nakamura, M., and McCammon, C. (2019). Saline Aqueous Fluid Circulation in Mantle Wedge Inferred from Olivine Wetting Properties. Nat. Commun. 10, 5557. doi:10.1038/s41467-019-13513-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Karato, S. I. (1990). The Role of Hydrogen in the Electrical Conductivity of the Upper Mantle. Nature 347, 272–273. doi:10.1038/347272a0

CrossRef Full Text | Google Scholar

Kawamoto, T., Yoshikawa, M., Kumagai, Y., Mirabueno, M. H. T., Okuno, M., and Kobayashi, T. (2013). Mantle Wedge Infiltrated with saline Fluids from Dehydration and Decarbonation of Subducting Slab. Proc. Natl. Acad. Sci. USA 110, 9663–9668. doi:10.1073/pnas.1302040110

PubMed Abstract | CrossRef Full Text | Google Scholar

Lacovino, K., Guild, M. R., and Till, C. B. (2020). Aqueous Fluids Are Effective Oxidizing Agents of the Mantle in Subduction Zones. Contrib. Mineral. Petrol. 175, 36. doi:10.1007/s00410-020-1673-4

CrossRef Full Text | Google Scholar

Li, H., and Hermann, J. (2015). Apatite as an Indicator of Fluid Salinity: an Experimental Study of Chlorine and Fluorine Partitioning in Subducted Sediments. Geochim. Cosmochim. Acta 166, 267–297. doi:10.1016/j.gca.2015.06.029

CrossRef Full Text | Google Scholar

Li, P., Guo, X. Z., Chen, S. B., Wang, C., Yang, J. L., and Zhou, X. F. (2018). Electrical Conductivity of the Plagioclase–NaCl–Water System and its Implication for the High Conductivity Anomalies in the Mid-lower Crust of Tibet Plateau. Contrib. Mineral. Petrol. 173, 1–12. doi:10.1007/s00410-018-1442-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, J. F., Speziale, S., Mao, Z., and Marquardt, H. (2013). Effects of the Electronic Spin Transitions of Iron in Lower Mantle Minerals: Implications for Deep Mantle Geophysics and Geochemistry. Rev. Geophys. 51, 244–275. doi:10.1002/rog.20010

CrossRef Full Text | Google Scholar

Macris, C. A., Newton, R. C., Wykes, J., Pan, R. G., and Manning, C. E. (2003). Diopside, Enstatite and Forsterite Solubilities in H₂O and H₂O-NaCl Solutions at Lower Crustal and Upper Mantle Conditions. Geochim. Cosmochim. Acta 279, 119–142. doi:10.1016/j.gca.2020.03.035

CrossRef Full Text | Google Scholar

Manning, C. E. (2013). Thermodynamic Modeling of Fluid-Rock Interaction at Mid-crustal to Upper-Mantle Conditions. Rev. Mineral. Geochem. 76, 135–164. doi:10.2138/rmg.2013.76.5

CrossRef Full Text | Google Scholar

Manthilake, G., Bolfan-Casanova, N., Novella, D., Mookherjee, M., and Andrault, D. (2016). Dehydration of Chlorite Explains Anomalously High Electrical Conductivity in the Mantle Wedges. Sci. Adv. 2, e1501631. doi:10.1126/sciadv.1501631

PubMed Abstract | CrossRef Full Text | Google Scholar

Manthilake, G., Chantel, J., Guignot, N., and King, A. (2021a). The Anomalous Seismic Behavior of Aqueous Fluids Released during Dehydration of Chlorite in Subduction Zones. Minerals 11, 70. doi:10.3390/min11010070

CrossRef Full Text | Google Scholar

Manthilake, G., Koga, K. T., Peng, Y., and Mookherjee, M. (2021b). Halogen Bearing Amphiboles , Aqueous Fluids , and Melts in Subduction Zones : Insights on Halogen Cycle from Electrical Conductivity. J. Geophys. Res. Solid Earth 126, e2020JB021339. doi:10.1029/2020JB021339

CrossRef Full Text | Google Scholar

Manthilake, G., Mookherjee, M., Bolfan-Casanova, N., and Andrault, D. (2015). Electrical Conductivity of Lawsonite and Dehydrating Fluids at High Pressures and Temperatures. Geophys. Res. Lett. 42, 7398–7405. doi:10.1002/2015GL064804

CrossRef Full Text | Google Scholar

Manthilake, G., Mookherjee, M., and Miyajima, N. (2021c). Insights on the Deep Carbon Cycle from the Electrical Conductivity of Carbon-Bearing Aqueous Fluids. Sci. Rep. 11, 3745. doi:10.1038/s41598-021-82174-8

PubMed Abstract | CrossRef Full Text | Google Scholar

McGary, R. S., Evans, R. L., Wannamaker, P. E., Elsenbeck, J., and Rondenay, S. (2014). Pathway from Subducting Slab to Surface for Melt and Fluids beneath Mount Rainier. Nature 511, 338–340. doi:10.1038/nature13493

PubMed Abstract | CrossRef Full Text | Google Scholar

Morikawa, N., Kazahaya, K., Takahashi, M., Inamura, A., Takahashi, H. A., Yasuhara, M., et al. (2016). Widespread Distribution of Ascending Fluids Transporting Mantle Helium in the Fore-Arc Region and Their Upwelling Processes: Noble Gas and Major Element Composition of Deep Groundwater in the Kii Peninsula, Southwest Japan. Geochim. Cosmochim. Acta 182, 173–196. doi:10.1016/j.gca.2016.03.017

CrossRef Full Text | Google Scholar

Newton, R. C., and Manning, C. E. (2000). Quartz Solubility in H₂O–NaCl and H₂O–CO₂ Solutions at Deep Crust–Upper Mantle Pressures and Temperatures: 2–15 Kbar and 500–900^oC. Geochim. Cosmochim. Acta 64, 2993–3005. doi:10.1016/S0016-7037(00)00402-6

CrossRef Full Text | Google Scholar

Peslier, A. H., Schönbächler, M., Busemann, H., and Karato, S. I. (2017). Water in the Earth’s interior: Distribution and Origin. Space Sci. Rev. 212, 743–810. doi:10.1007/s11214-017-0387-z

CrossRef Full Text | Google Scholar

Pommier, A., and Evans, R. L. (2017). Constraints on Fluids in Subduction Zones from Electromagnetic Data. Geosphere 13, 1026–1041. doi:10.1130/GES01473.1

CrossRef Full Text | Google Scholar

Price, J. D., Wark, D. A., Watson, E. B., and Smith, A. M. (2006). Grain-scale Permeabilities of Faceted Polycrystalline Aggregates. Geofluids 6, 302–318. doi:10.1111/j.1468-8123.2006.00149.x

CrossRef Full Text | Google Scholar

Reynard, B. (2016). Mantle Hydration and Cl-Rich Fluids in the Subduction Forearc. Prog. Earth Planet. Sci. 3, 9. doi:10.1186/s40645-016-0090-9

CrossRef Full Text | Google Scholar

Reynard, B., Mibe, K., and de Moortèle, B. Van. (2011). Electrical Conductivity of the Serpentinised Mantle and Fluid Flow in Subduction Zones. Earth Planet. Sci. Lett. 307, 387–394. doi:10.1016/j.epsl.2011.05.013

CrossRef Full Text | Google Scholar

Ringwood, A. E. (1982). Phase Transformations and Differentiation in Subducted Lithosphere: Implications for Mantle Dynamics, basalt Petrogenesis and Crustal Evolution. J. Geol. 90, 611–643. doi:10.1086/628721

CrossRef Full Text | Google Scholar

Saltas, V., Chatzistamou, V., Pentari, D., Paris, E., Triantis, D., Fitilis, I., et al. (2013). Complex Electrical Conductivity Measurements of a KTB Amphibolite Sample at Elevated Temperatures. Mater. Chem. Phys. 139, 169–175. doi:10.1016/j.matchemphys.2013.01.016

CrossRef Full Text | Google Scholar

Saltas, V., Pentari, D., and Vallianatos, F. (2020). Complex Electrical Conductivity of Biotite and Muscovite Micas at Elevated Temperatures: A Comparative Study. Minerals 13, 3513. doi:10.3390/ma13163513

PubMed Abstract | CrossRef Full Text | Google Scholar

Selway, K. (2015). Negligible Effect of Hydrogen Content on Plate Strength in East Africa. Nat. Commun. 8, 543–546. doi:10.1038/NGEO2453

CrossRef Full Text | Google Scholar

Selway, K., and O’Donnell, J. P. (2019). A Small, Unextractable Melt Fraction as the Cause for the Low Velocity Zone. Earth Planet. Sci. Lett. 517, 117–124. doi:10.1016/j.epsl.2019.04.012

CrossRef Full Text | Google Scholar

Shimojuku, A., Yoshino, T., and Yamazaki, D. (2014). Electrical Conductivity of Brine-Bearing Quartzite at 1 GPa: Implications for Fluid Content and Salinity of the Crust. Earth Planets Space 66, 2. doi:10.1186/1880-5981-66-2

CrossRef Full Text | Google Scholar

Shimojuku, A., Yoshino, T., Yamazaki, D., and Okudaira, T. (2012). Electrical Conductivity of Fluid-Bearing Quartzite under Lower Crustal Conditions. Phys. Earth Planet. Inter. 198–199, 1–8. doi:10.1016/j.pepi.2012.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Shmulovich, K., Graham, C., and Yardley, B. (2001). Quartz, Albite and Diopside Solubilities in H₂O–NaCl and H₂O–CO₂ Fluids at 0.5–0.9 GPa. Contrib. Mineral. Petrol. 141, 95–108. doi:10.1007/s004100000224

CrossRef Full Text | Google Scholar

Sinmyo, R., and Keppler, H. (2017). Electrical Conductivity of NaCl-Bearing Aqueous Fluids to 600^oC and 1 GPa. Contrib. Mineral. Petrol. 172, 4. doi:10.1007/s00410-016-1323-z

CrossRef Full Text | Google Scholar

Sun, W. Q., Dai, L. D., Li, H. P., Hu, H. Y., Jiang, J. J., and Wang, M. Q. (2020). Electrical Conductivity of Clinopyroxene–NaCl–H₂o System at High Temperatures and Pressures: Implications for High-Conductivity Anomalies in the Deep Crust and Subduction Zone. J. Geophys. Res. Solid Earth 125, e2019JB019093. doi:10.1029/2019JB019093

CrossRef Full Text | Google Scholar

Tyburczy, J. A., and Roberts, J. J. (1990). Low Frequency Electrical Response of Polycrystalline Olivine Compacts: Grain Boundary Transport. Geophys. Res. Lett. 17, 1985–1988. doi:10.1029/GL017i011p01985

CrossRef Full Text | Google Scholar

Vallianatos, F. (1996). Magnetotelluric Response of a Randomly Layered Earth. Geophys. J. Int. 125, 577–583. doi:10.1111/j.1365-246X.1996.tb00020.x

CrossRef Full Text | Google Scholar

Vargas, J. A., Meqbel, N. M., Ritter, O., Brasse, H., Weckmann, U., Yáñez, G., et al. (2019). Fluid Distribution in the central Andes Subduction Zone Imaged with Magnetotellurics. J. Geophys. Res. Solid Earth 124, 4017–4034. doi:10.1029/2018JB016933

CrossRef Full Text | Google Scholar

Waff, H. S. (1974). Theoretical Considerations of Electrical Conductivity in a Partially Molten Mantle and Implications for Geothermometry. J. Geophys. Res. Solid Earth Planets 79, 4003–4010. doi:10.1029/JB079i026p04003

CrossRef Full Text | Google Scholar

Wang, J. T., Takahashi, E., Xiong, X. L., Chen, L. L., Li, L., Suzuki, T., et al. (2020). The Water-Saturated Solidus and Second Critical Endpoind of Peridotite: Implications for Magma Genesis within the Mantle Wedge. J. Geophys. Res. Solid Earth 125, e2020JB019452. doi:10.1029/2020JB019452

CrossRef Full Text | Google Scholar

Yamaguchi, S., Uyeshima, M., Murakami, H., Sutoh, S., Tanigawa, D., Ogawa, T., et al. (2009). Modification of the Network-MT Method and its First Application in Imaging the Deep Conductivity Structure beneath the Kii Peninsula, Southwestern Japan. Earth Planet. Sci. Lett. 61, 957–971. doi:10.1186/BF03352946

CrossRef Full Text | Google Scholar

Yoshino, T., Nishihara, Y., and Karato, S. (2007). Complete Wetting of Olivine Grain Boundaries by a Hydrous Melt Near the Mantle Transition Zone. Earth Planet. Sci. Lett. 256, 466–472. doi:10.1016/j.epsl.2007.02.002

CrossRef Full Text | Google Scholar

Zheng, Y. F. (2019). Subduction Zone Geochemistry. Geosci. Front. 10, 1223–1254. doi:10.1016/j.gsf.2019.02.003

CrossRef Full Text | Google Scholar