Current- and Wave-Generated Bedforms on Mixed Sand–Clay Intertidal Flats: A New Bedform Phase Diagram and Implications for Bed Roughness and Preservation Potential

The effect of bedforms on frictional roughness felt by the overlying flow is crucial to the regional modelling of estuaries and coastal seas. Bedforms are also a key marker of palaeoenvironments. Experiments have shown that even modest biotic and abiotic cohesion in sand inhibits bedform formation, modifies bedform size, and slows bedform development, but this has rarely been tested in nature. The present study used a comprehensive dataset recorded over a complete spring–neap cycle on an intertidal flat to investigate bedform dynamics controlled by a wide range of wave and current conditions, including the effects of wave–current angle and bed cohesion. A detailed picture of different bedform types and their relationship to the flow, be they equilibrium, non-equilibrium, or relict, was produced, and captured in a phase diagram that integrates wave-dominated, current-dominated, and combined wave–current bedforms. This bedform phase diagram incorporates a substantially wider range of flow conditions than previous phase diagrams, including bedforms related to near-orthogonal wave–current angles, such as ladderback ripples. Comparison with laboratory-derived bedform phase diagrams indicates that washed-out ripples, lunate interference ripples and upper-stage plane beds replace the subaqueous dune field; such bedform distributions may be a key characteristic of intertidal flats. The field data also provide a means of predicting the dimensions of these bedforms, which can be transferred to other areas and grain sizes. We show that an equation for the prediction of equilibrium bedform size is sufficient to predict the roughness, even though the bedforms are highly variable in character and only in equilibrium with the flow for approximately half the time. Whilst the effect of cohesive clay is limited under more active spring conditions, clay does play a role in reducing the bedform dimensions under more quiescent neap conditions. We also investigated which combinations of waves, currents, and bed clay contents in the intertidal zone have the highest potential for bedform preservation in the geological record. This shows that combined wave–current bedforms have the lowest preservation potential and equilibrium current ripples have the highest preservation potential, even in the presence of moderate and storm waves. Hence, the absence of wave ripples and combined-flow bedforms and their primary stratification in sedimentary successions cannot be taken as evidence that waves were absent at the time of deposition.

Introduction

Bedforms are amongst the most common and important sedimentary structures in modern and ancient marine depositional environments. They characterise the roughness of the modern seabed, cause flow modification and energy dissipation, and enhance sediment suspension (e.g., Allen, 1984; Soulsby and Whitehouse, 2005; Soulsby et al., 2012). Currents, waves, and combined flows generate different types of bedform, which are used routinely as a proxy for reconstructing depositional environments and near-bed hydrodynamic processes in the sedimentary record (e.g., Allen 1984; Clifton and Dingler, 1984; Van den Berg and Van Gelder, 1993; Baas et al., 2016; Parsons et al., 2016; Collinson and Mountney, 2019). The development of accurate models for tidal and wave energy dissipation, sediment transport, flooding, and acoustic reflectivity of the seabed relies on correct predictions of bedform dimensions, shape, and plan morphology, and the parameterization of bed roughness (e.g., Soulsby et al., 2012; Aldridge et al., 2015). Existing bedform predictors, encompassing bedform stability diagrams and empirical equations based on laboratory flume and field studies, focus on specific bedform types, such as wave ripples, current ripples, and dunes (Allen, 1984; Van Rijn, 1984; Southard and Boguchwal, 1990; Van den Berg and Van Gelder, 1993; Soulsby, 1997; Kleinhans, 2005; Soulsby and Whitehouse, 2005; Camenen, 2009; Pedocchi and García, 2009a, 2009b; Nelson et al., 2013). In contrast to stability diagrams for current- and wave-generated bedforms, stability diagrams for combined-flow bedforms of the basic form shown in Figure 1 (e.g., Arnott and Southard, 1990; Dumas et al., 2005; Kleinhans, 2005; Perillo et al., 2014) cover such a small fraction of the parameter space that their application is challenging. This is because laboratory flume investigations typically do not allow for the evaluation of more than two or three variables, and field studies of more complex combined-flow bedform dynamics are poorly integrated into these stability diagrams (Amos et al., 1988, 1999; Gallagher et al., 1998; Li and Amos, 1998; Gallagher, 2003; Hay and Mudge, 2005; Smyth and Li, 2005; Larsen et al., 2015; Wengrove et al., 2018, 2019; Wu and Parsons, 2019; Cuadrado, 2020). For example, despite being the most comprehensive flume study available in the literature, the experimental dataset of Perillo et al. (2014) is limited to co-linear waves and currents, a single sand size, and three closely spaced wave periods. In geological outcrops, the comparison of observed combined-flow bedforms with existing predictors for these bedforms is often cursory (e.g., Myrow and Southard, 1991; Myrow et al., 2002; Harazim and McIlroy, 2015; Wang et al., 2015; Taral and Chakraborty, 2017; Bádenas et al., 2018; Isla et al., 2018), possibly because the existing stability diagrams for combined-flow bedforms use different bedform terminologies and do not include all the bedform types recognised in nature (e.g., ladderback ripples; Klein, 1970).

FIGURE 1

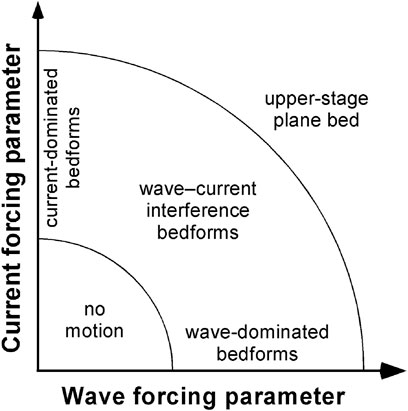
FIGURE 1. Basic form of phase diagrams for combined-flow bedforms used in literature and in the present study. The wave and current forcing parameters can be wave velocity amplitude and depth-averaged current velocity or dimensional or non-dimensional wave and current bed shear stresses. Here, bed shear stress is preferred, because it describes near-bed bedform dynamics better than velocity. It should be noted that specific bedform types and phase boundaries may vary with sediment size and wave–current angle.

A better understanding of the hydrodynamic conditions required to form current-dominated, wave-dominated, and combined-flow bedforms requires field measurements that integrate methods to record hydrodynamics, sediment dynamics, biogenic effects, and bedform development. To cover a parameter space that flume experiments cannot mimic, such measurements should include time-series of all variables that are known to affect the shape, size, and plan morphology of bedforms, i.e., sediment size, physical and biological cohesion, flow depth, bed shear stress, angle between wave and current, suspended sediment concentration, bedform migration rate, and adaptation time of bedforms in waning and waxing flow.

From a geological perspective, the shape and size of bedforms, and their primary stratification patterns, are essential for interpreting the relative importance of waves and currents in the depositional environment. Up to now, this has focussed mainly on hydrodynamic conditions that result in the formation of hummocky cross-stratification (e.g., Duke, 1985; Dumas and Arnott, 2006; Tinterri, 2011), but published research in laboratories and modern environments suggest that a wider range of bedform types exists in combined flows, such as ladderback ripples and different kinds of ripple-sized and dune-sized, symmetric and asymmetric, and two-dimensional and three-dimensional bedforms (Klein, 1970; Arnott and Southard, 1990; Dumas et al., 2005; Perillo et al., 2014). Process interpretations from geological outcrops and cores require that combined-flow bedforms are preserved after their formation. Given that mixed wave–current forcing is highly variable temporally, especially in tidal environments, we hypothesise that preservation potential varies with bedform type, because some types are more common than others and because the preservation potential depends on the hydrodynamic and sediment dynamic conditions after the formation of each bedform type. Conditions expected to promote preservation are rapidly waning flows, rapid deposition of sediment on top of the bedforms, and bed stabilisation by cohesive clay and biological polymers.

The present paper uses field data from a mixed sand–mud intertidal flat in the Dee estuary (NW England, United Kingdom) collected with state–of–the–art instrumentation (Figure 2) and incorporates an unprecedented combination of the above controls on bedform dynamics, including variations in bed cohesion, current, wave, and combined-flow bed shear stresses, water depth, and wave–current angle. This dataset has allowed us to link equilibrium bedform size, shape, and plan morphology to flow dynamics, but also distinguish between equilibrium, relict, and non-equilibrium bedforms, based on evolutionary trends in bed morphology. The specific aims of this study were to:

1) Classify equilibrium bedform type as a function of wave, current, and combined-flow forcing, and bed material properties using a bedform phase diagram;

2) Establish the relative importance of non-equilibrium, relict, and equilibrium bedforms in a full spring–neap tidal cycle with and without wave forcing;

3) Determine the residence time and preservation potential of various wave-dominated, current-dominated, and combined-flow bedforms;

4) Make recommendation for sediment transport rate predictions and preservation potential of intertidal bedforms in modern environments and the geological record.

FIGURE 2

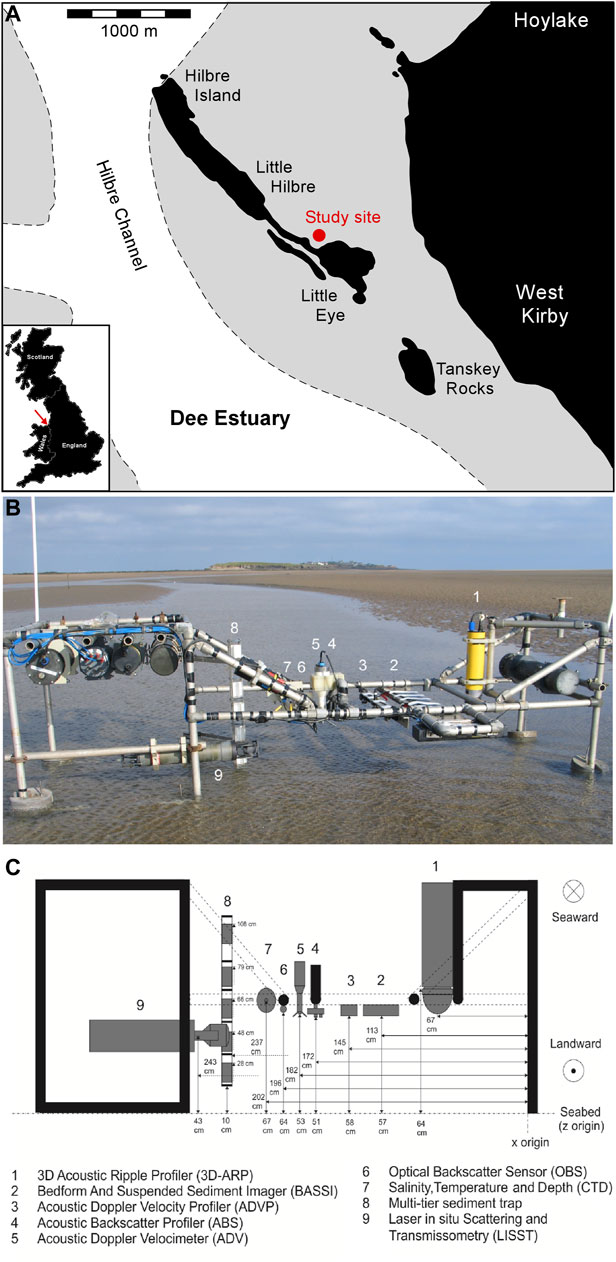
FIGURE 2. Schematic map of the Dee Estuary around Hilbre Island (A), with the main tidal channel in white and the study area located on the grey-coloured intertidal flat to the north-west of Little Eye. The four islands are defined by the area above the mean highwater mark and by any area of bedrock exposed at low water immediately below this mark. SEDbed instrument frame. looking seaward towards Little Hilbre and Hilbre Island (B), and diagram of instruments on frame (C). Vertical and horizontal distances in centimetres are above the sediment bed and relative to the edge of the frame, respectively.

Materials and Methods

The hydrodynamic and sediment dynamic data used in this study were acquired on a mixed sand–mud intertidal flat in the Dee Estuary near Hilbre Island, United Kingdom (Figure 2). The Dee Estuary is connected to Liverpool Bay, and it is funnel-shaped and macrotidal, with a mean spring tidal range of 7–8 m at Hilbre Island. Hilbre Island separates Hilbre Channel from intertidal flats west of the town of West Kirby (Figure 2). These tidal flats are flood-dominated and rich in fine-grained sediment (Moore et al., 2009), especially towards the landward limit of the estuary (Halcrow, 2013). Waves are mainly generated locally within Liverpool Bay; north-westerly waves have the strongest influence on the sedimentary processes in the Dee Estuary (Brown and Wolf, 2009; Villaret et al., 2011). The intertidal flats to the north-west of Little Eye (Figure 2) are ideal for studying bedform dynamics in mixed sand–mud, owing to the large variation in sand–mud ratio, ranging from pure sand to sandy mud, and the variable hydrodynamic forcing by currents and waves (Way, 2013; Lichtman et al., 2018; Baas et al., 2019). Three sites were studied over a spring–neap tidal cycle from neap to neap between May 21st and June 3rd, 2013, to record a time-series of bedform evolution controlled by tides, waves, and sediment dynamics. These sites were located in or near a shallow intertidal gully within 140 m of each other, differing in bed elevation by 0.19 m.

Sediment samples taken at regular intervals during the field deployment revealed a seabed dominated by medium sand with a median size of 0.227 mm. The cohesive clay fraction in this sediment ranged from 0.6 to 5.4 volume %, and the fraction of cohesive extracellular polymeric substances (EPS) was between 0.02 and 0.30 weight %, with the lowest bed clay and EPS fractions between May 21st and 29th and gradually increasing bed clay and EPS contents between May 29th and June 3rd (Lichtman et al., 2018: their Figure 4).

A suite of instruments on the SEDbed frame of the National Oceanography Centre was deployed at each site. The present study used water velocity data collected with an Acoustic Doppler Velocimeter (ADV; located at 0.53 m height in Figure 2; Supplementary Table S1) and measuring at 0.37 m above the sediment surface. These data were acquired at a frequency of 8 Hz, and tidal currents were extracted by applying a 5-min running mean. The ADV time-series were used to compute the equivalent linear current-only, wave-only and non-linear combined-flow bed shear stresses associated with skin friction, using the two-layer logarithmic model of Malarkey and Davies (2012) and the PUV method of Gordon and Lohrmann (2001), as elaborated by Lichtman et al. (2018). In flows where both currents and waves are present, the combined bed shear stress is affected by the angle between the wave and current directions. For a vector addition of the wave-only and current-only stresses, the maximum linear combined bed shear stress during the wave cycle, τ_max, is:

Eq. 1, maximum linear combined bed shear stress:

${\tau }_{\max }={\left({\tau }_c^{ 2}+{\tau }_w^{ 2}+2{\tau }_c{\tau }_w\cos \phi \right)}^{0.5}(1)$

where τ_c is the current-only shear stress, τ_w is the wave-only shear stress, and φ is the angle between the wave and the current (0 ≤ φ ≤ 90°). In the present paper, only these linear skin-friction stresses are considered and referred to as simply the wave, current and combined stresses. For combined flows, the threshold for cohesionless sediment movement corresponds to τ_max = τ₀, where τ₀ is the critical shear stress for movement, with τ₀ = 0.18 Nm⁻² for 0.227 mm sand (Appendix Equation A1). In the two wave–current directional extremes of co-linear (φ = 0°) and orthogonal (φ = 90°), τ₀ can thus be expressed as:

Eq. 2, critical shear stresses for sediment movement for co-linear and orthogonal waves and currents:

${\tau }_{\max }={\tau }_0=\{\begin{array}{ll}{\tau }_c+{\tau }_w,\hfill & \phi =0°,\hfill \\ {\left({\tau }_c^{ 2}+{\tau }_w^{ 2}\right)}^{0.5},\hfill & \phi =90°\hfill \end{array}(2)$

or for a particular current shear stress, τ_c = τ₀‒τ_w, for φ = 0°, and τ_c = (τ₀²‒τ_w²)^0.5, for φ = 90°. Thus, τ₀ requires a larger current shear stress for orthogonal than for co-linear waves and currents. All other intermediate angles (0 < φ < 90°) lie between these two directional extremes.

The ADV also measured water pressure at 0.53 m above the seabed, which, in combination with pressure data from a Conductivity, Temperature, and Depth (CTD) system (Figure 2; Supplementary Table S1) and after correction for air pressure, were converted to water depth, following the procedure described in Lichtman et al. (2018). A 3D Acoustic Ripple Profiler (3D–ARP; Figure 2; Supplementary Table S1) provided seabed topography data. The 3D–ARP is a dual-axis, mechanically rotated, pencil beam scanning sonar operating at 1.1 MHz (Thorne and Hanes, 2002; Marine Electronics, 2009; Krämer and Winter 2016; Thorne et al., 2018). It measured a 12 m² area of the bed every 30 min, from which a central region of c. 1.4 m² was selected for analysis over the entire field deployment (Supplementary Video S1). The initial step in the analysis of the 3D–ARP data was to remove the large-scale bed morphology from the scans using a linear fit. The 3D–ARP scans were then corrected for the bedform orientation. Lichtman et al. (2018) found that the bedform migration was closely associated with the maximum stress in the wave cycle. Thus, the default bedform orientation was aligned with the maximum stress direction. This was a reasonable assumption for the vast majority of the bedforms in the 3D–ARP scans. However, there were exceptions. If the bedforms were relict, i.e. the maximum shear stress was below τ₀, the last above-threshold orientation was used. These orientations were determined by eye in cases where two types of bedform with different orientations were superimposed on one another. The orientations were not necessarily orthogonal to one another or aligned with the wave or current stresses, because the 3D–ARP scanning process takes longer to complete than some rapid changes in bedform orientation. Once the orientation had been decided, the bedform dimensions were determined along three fixed transects, and subsequently averaged together. The dimensions were calculated by the zero-crossing method (Van der Mark et al., 2008; Krämer and Winter 2016) once outliers greater than four standard deviations from the mean were removed. The zero-crossing method was used to locate the position of the crests and troughs, but these were also checked by eye for consistency and to ensure that the dominant dimensions were being faithfully represented. The asymmetry of the bedforms was quantified by the longer crest to trough distance divided by the total bedform length along each transect. The method applied herein to determine bedform heights, lengths and asymmetries was distinct from that of Lichtman et al. (2018), because it allowed for the measurement of separate heights and lengths for the wave-induced and current-induced parts of combined-flow bedforms.

The bedforms on the seabed were also visualised using a Bedform And Suspended Sediment Imager (BASSI; Figure 2; Supplementary Table S1). The BASSI produces an acoustic curtain over a 2D vertical slice of the near-bed water column, with centimetric resolution over intrawave and turbulence timescales (Moate et al., 2016; Thorne et al., 2018). The BASSI can thus be used to trace trains of moving bedforms and suspended sediment above these bedforms at higher temporal resolution than the 3D–ARP. In the present study, the BASSI was set to record vertical cells of 3.3 mm length. The rate of recording was 12.5 Hz, the burst length was 10 min, and the burst interval was 30 min. The analysis of the BASSI data focussed on the bedforms, to obtain an independent check of the bedform dimensions obtained with the 3D–ARP as well as a record of high-frequency changes in bed morphology.

During the field deployment, the tidal flats experienced a wide range of current, wave and combined flow conditions (Figures 3A,B). Maximum current stresses were largest during the spring tide, 0.7 Nm⁻², and up to one order of magnitude smaller during the neap tides. From May 21st to 24th, when neap tide progressed towards spring tide, waves had a strong influence on the hydrodynamics and the bedform evolution, caused by wind ranging from a moderate breeze to gale force (Beaufort scale 4–8: 5.8–17.6 ms⁻¹). Moderate waves were present at around noon on May 27th (spring tide) and after midnight on May 30th (spring tide progressing towards neap tide). On the other days, waves had little to no influence on the hydrodynamic forcing of the bedforms on the seabed. Wave period ranged from 2 to 10 s and wave height was up to 0.5 m (Lichtman et al., 2018).

FIGURE 3

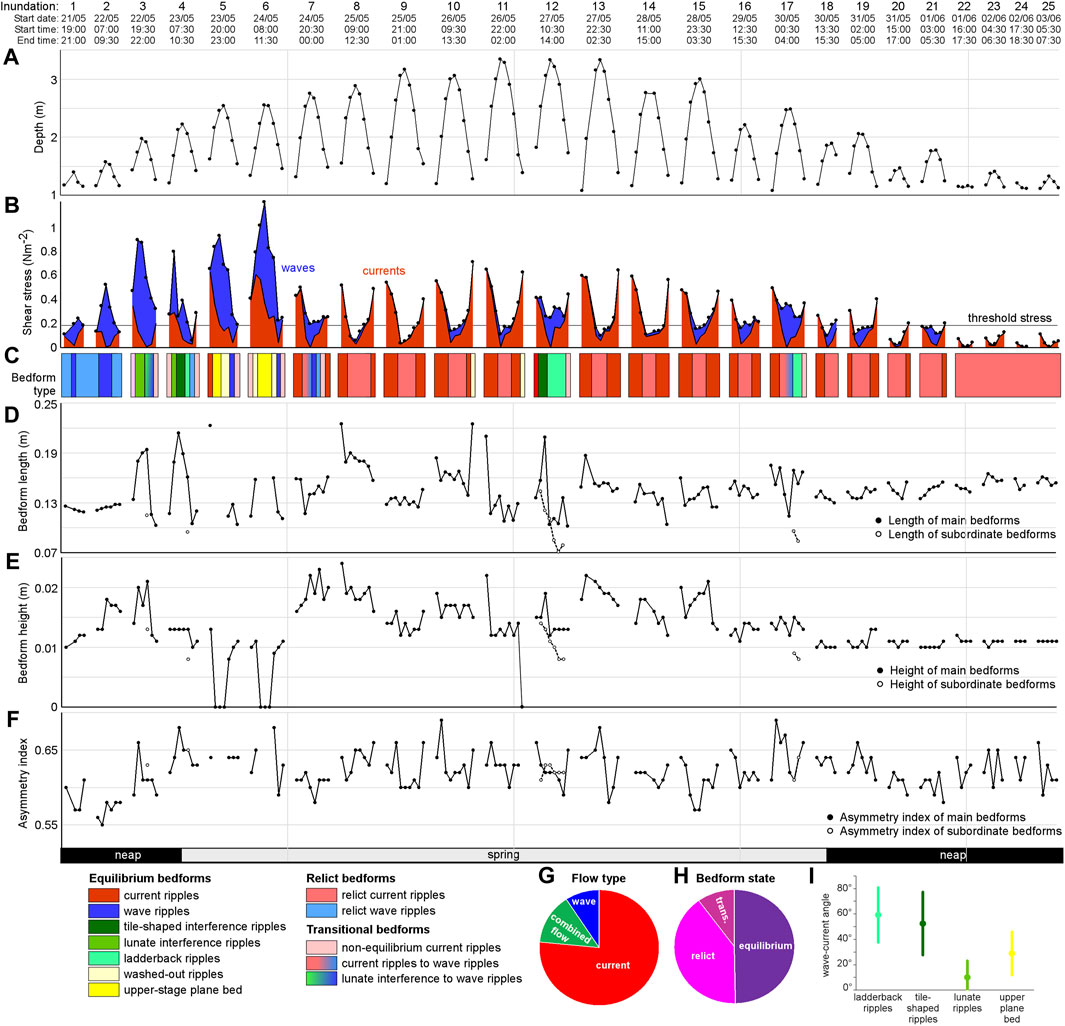
FIGURE 3. Summary of observations during the spring–neap cycle. The dates and times for each tidal inundation shown at the top are for time-series of: (A) water depth; (B) maximum combined stress showing wave and current stress contributions; (C) bedform types; (D) bedform length; (E) bedform height; and (F) asymmetry index. The graphs at the bottom right denote: (G) distribution of flow types; (H) distribution of equilibrium, relict, and transitional bedform states, given in shades of purple; and (I) mean and standard deviation of wave–current angles for three types of combined-flow ripples and upper-stage plane bed. Colour legend for bedform types in (C,I) is shown on bottom left. (B,C,G,I) Wave stress and wave ripples are given in shades of blue, current stress and current ripples in shades of red, and combined-flow bedforms in shades of green. The transitional bedforms include non-equilibrium current ripples, which in turn comprise incipient and straight-crested current ripples sensu Baas (1994). Clay and EPS content gradually increased from 2 to 5% and 0.05 to 0.08%, respectively, from inundation 16 onwards (Lichtman et al., 2018).

Linking Bedforms to Hydrodynamic Data: Observations and Process Interpretations

General

Figures 3–10, Table 1, Supplementary Table S2, and Supplementary Video S1 provide a detailed summary of all the field data collected on the tidal flat during the spring–neap cycle between May 21st and June 3rd, 2013. Figure 3 presents time-series of water depth (Figure 3A), wave and current stresses (Figure 3B), bedform types (Figure 3C), bedform length (Figure 3D), bedform height (Figure 3E), and asymmetry index (Figure 3F). The relative importance of currents, waves, and combined flow for the generation of these bedforms is shown in Figures 3G,H shows the percentage equilibrium, relict, and transitional bedform states. The wave–current angles for ladderback ripples, tile-shaped interference ripples, lunate interference ripples, and upper-stage plane beds are plotted in Figure 3I. Figures 4–8 show characteristic 3D–ARP and BASSI data for selected tidal inundations, and Figure 9 displays the main geometric properties of the equilibrium, relict, and transitional bedform types present, as well as the characteristic hydrodynamic conditions at which these bedforms formed. The phase diagram in Figure 10A shows how the various bedform types are related to the wave and current stresses, and Figure 10B shows the equivalent for the wave velocity amplitude, U₀, and depth-averaged current velocity, ū, as used by Perillo et al. (2014). Whilst both the stresses and velocities are dimensional, the stresses in Figure 10A can more readily be made non-dimensional, e.g., by using Shields parameters (Kleinhans, 2005), since the median size of the sand particles on the bed was constant in the study area.

FIGURE 4

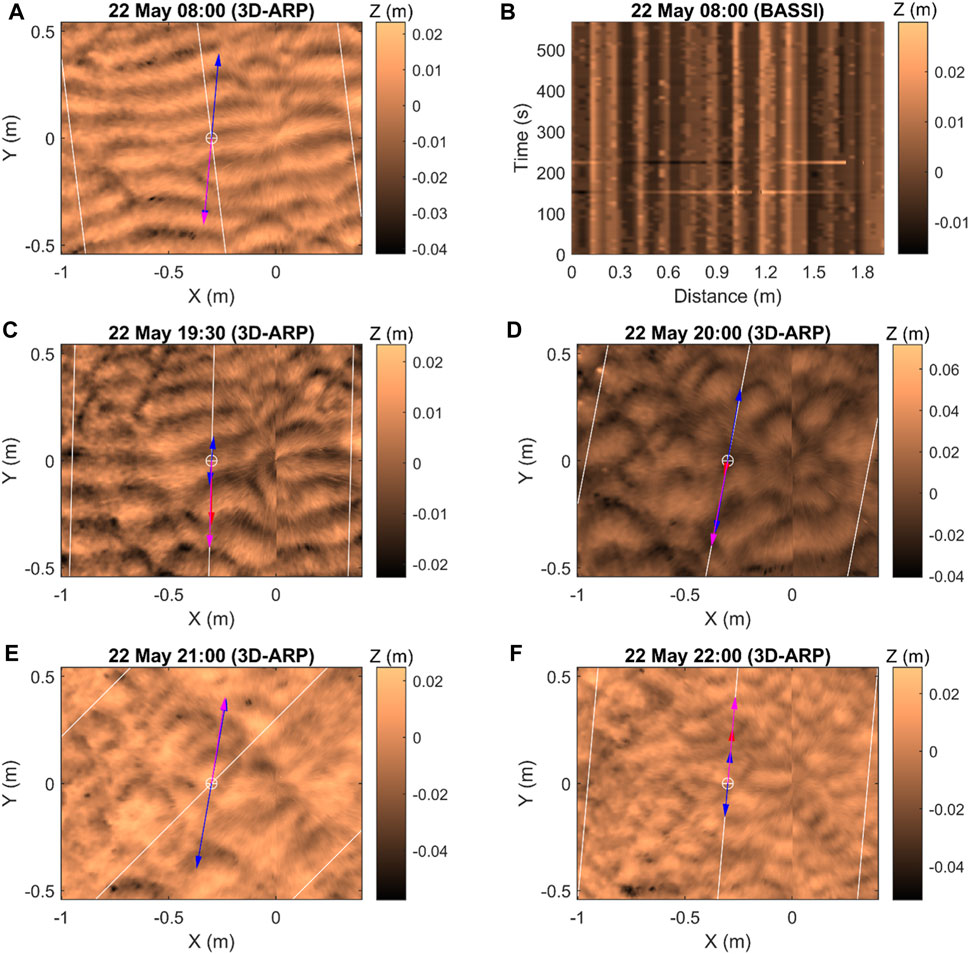
FIGURE 4. Equilibrium wave ripples recorded by the (A) 3D ARP and (B) BASSI at high slack water in tidal inundation 2 (May 22nd, am). (C–F) Bedforms generated during tidal inundation 3: (C) Wave ripples evolving into lunate interference ripples during flood; (D) Lunate interference ripples during flood; (E) Lunate interference ripples evolving into wave ripples at high slack water; (F) Small incipient current ripples during ebb. Red, blue and magenta arrows indicate current, wave, and combined flow directions, respectively. The length of the arrows is a qualitative measure of the relative shear stress magnitude. White lines indicate cross-sections along which ripple heights and lengths were measured. The discontinuities in C,D,F relate to morphological changes that took place during the 30-min radial scanning time.

FIGURE 5

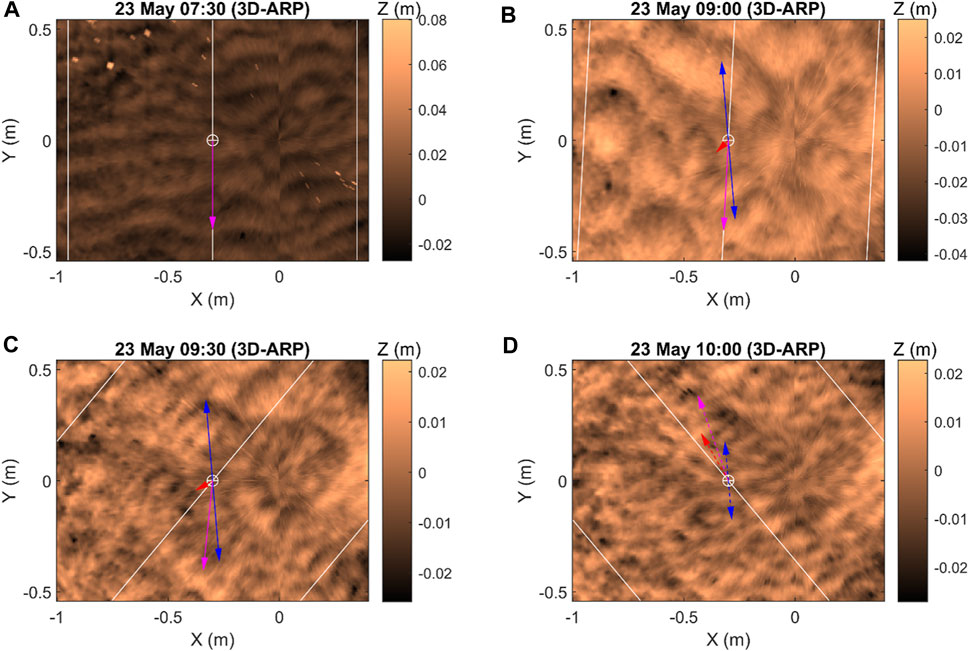
FIGURE 5. Bedforms generated during tidal inundation 4. (A) Straight-crested current ripples during flood; (B) Relict tile-shaped interference ripples at the end of flood; (C) Ladderback ripples during high slack water; (D) Relict wave ripples with straight but discontinuous crestlines near the end of high slack water. See Figure 4 for explanation of line colours. Dashed arrows in (D) denote stresses below threshold of motion.

FIGURE 6

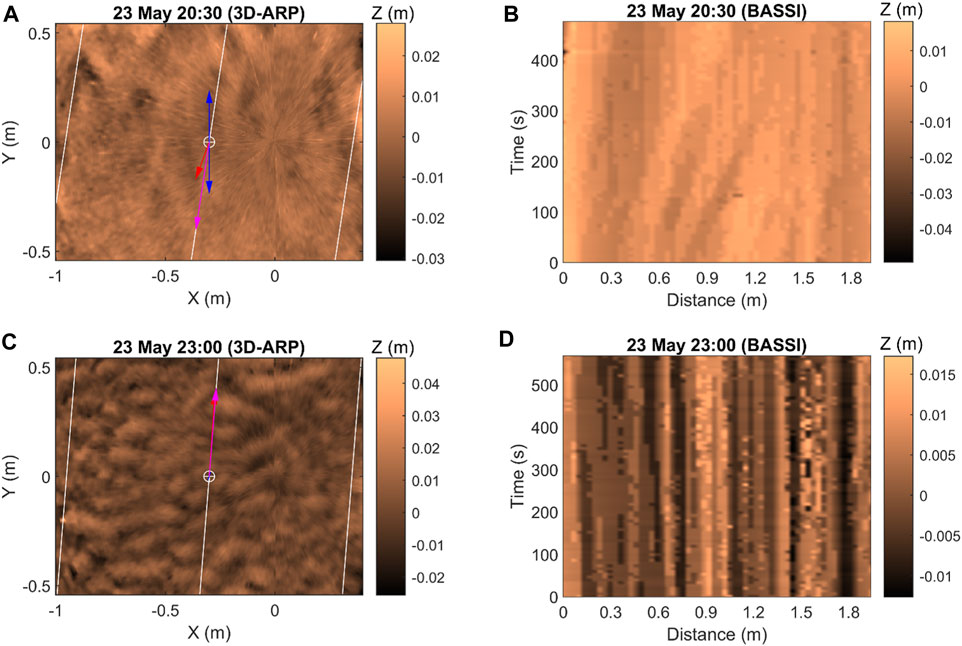
FIGURE 6. Bedforms generated during tidal inundation 5. Upper-stage plane bed recorded by the (A) 3D–ARP and (B) BASSI during flood. The 3D–ARP image shows wave-parallel longitudinal ribbons. Slowly migrating wave ripples in the process of transforming into straight-crested current ripples, recorded by the (C) 3D–ARP and (D) BASSI during ebb. See Figure 4 for explanation of line colours.

FIGURE 7

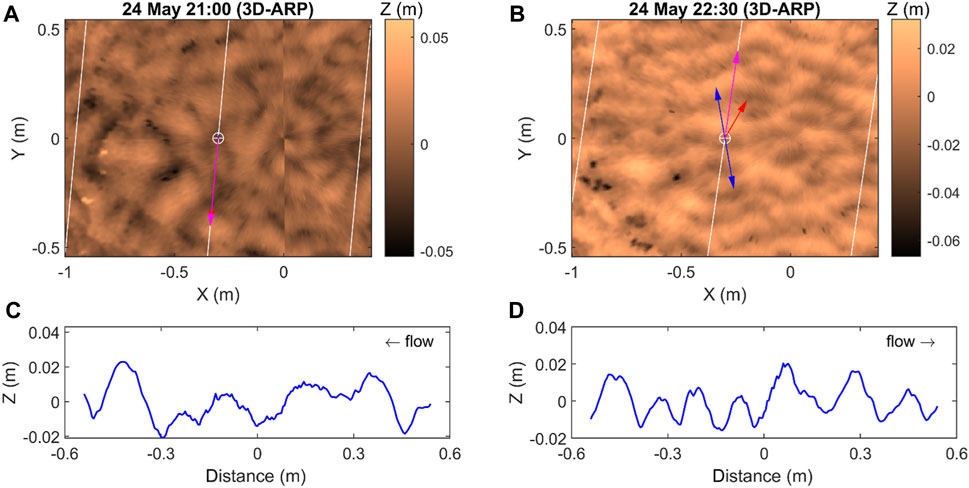
FIGURE 7. Plan and cross-sectional views (central transect) of bedforms generated during tidal inundation 7. (A,C) Equilibrium linguoid current ripples during flood; (B,D) Equilibrium wave ripples during high slack water. See Figure 4 for explanation of line colours.

FIGURE 8

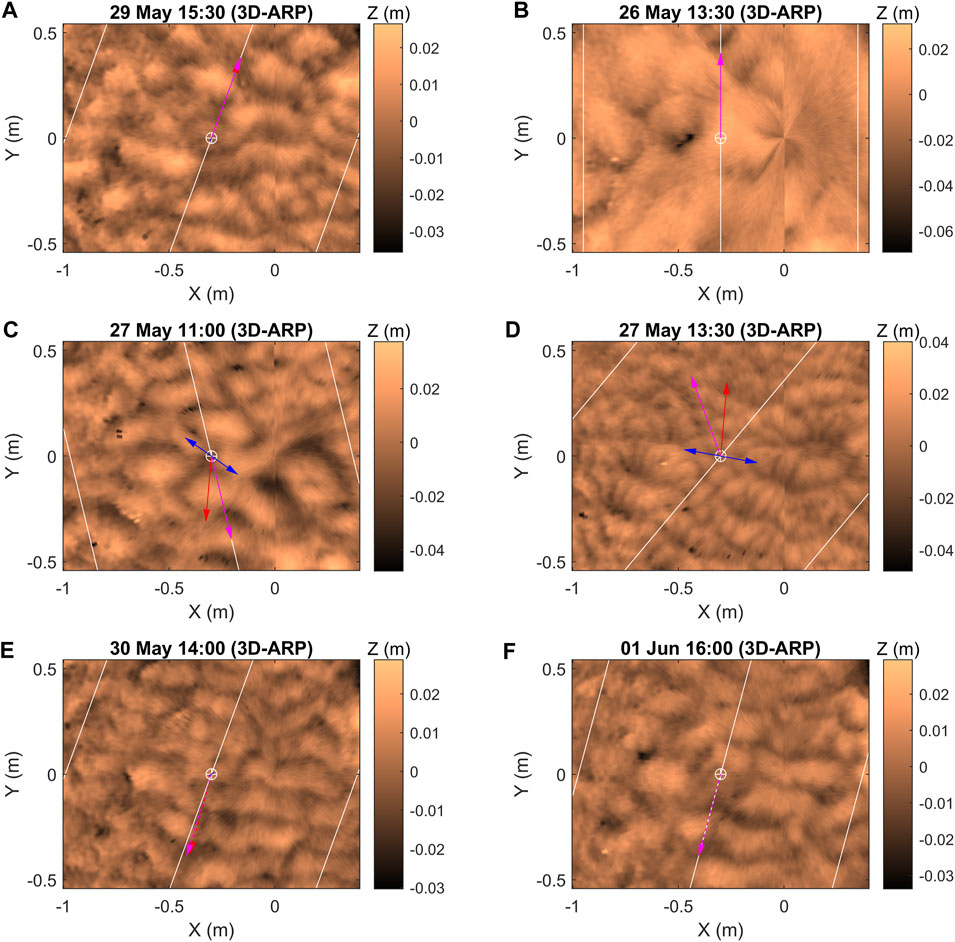
FIGURE 8. (A) Equilibrium linguoid current ripples formed during ebb in tidal inundation 16; (B) Washed-out ripples formed during ebb in inundation 10; (C) Tile-shaped interference ripples formed during ebb in inundation 12; (D) Ladderback ripples formed during ebb in inundation 12. (E–F) Current ripples in plan form during the neap tide: (E) Migrating equilibrium linguoid current ripples formed during ebb in tidal inundation 18; (F) Stationary, relict linguoid current ripples at high slack water in tidal inundation 22. See Figure 4 for explanation of line colours.

FIGURE 9

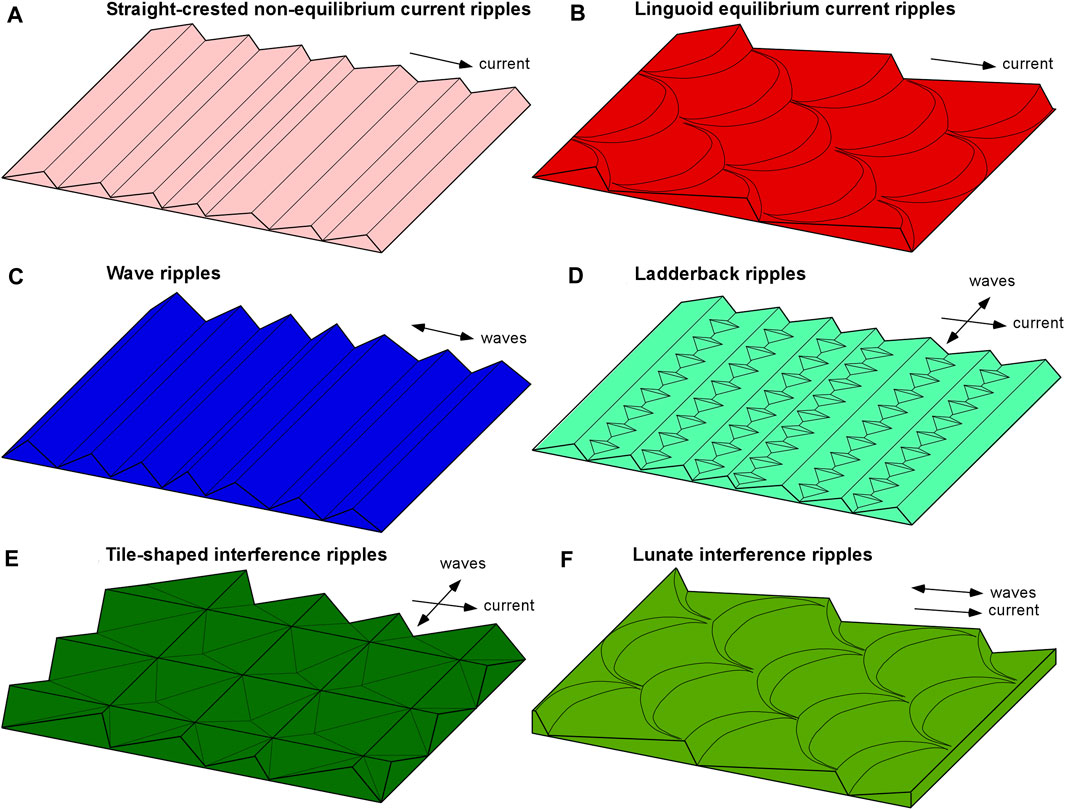
FIGURE 9. Schematic drawings of (A) straight-crested non-equilibrium current ripples, (B) linguoid equilibrium current ripples, (C) wave ripples, (D) ladderback ripples, (E) tile-shaped interference ripples, (F) lunate interference ripples. Not to scale.

FIGURE 10

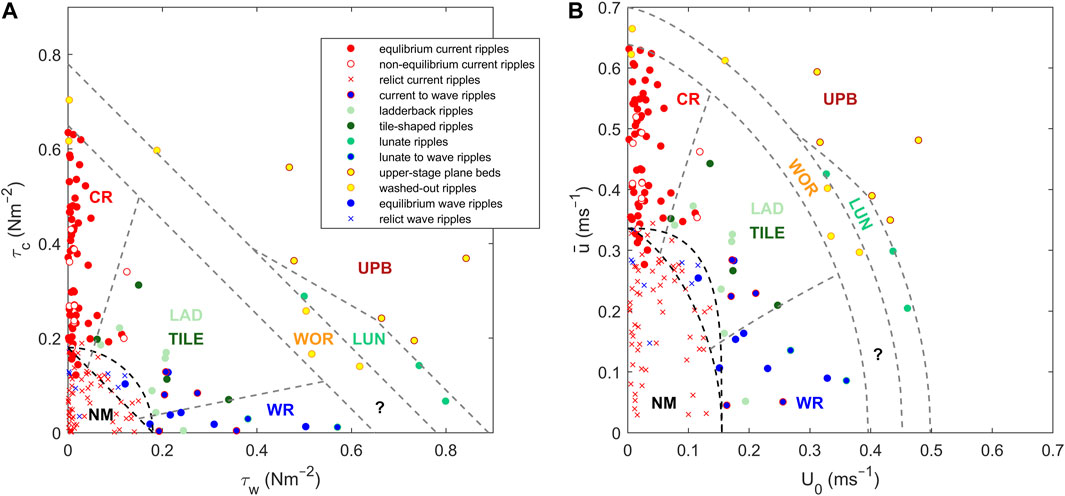
FIGURE 10. (A) Wave stress, τ_w, against current stress, τ_c, for all bedform types. (B) Equivalent phase diagram for the wave velocity amplitude, U₀, against depth-averaged current velocity, ū, based on approximate parameterisations that are specific to this dataset applied to (A) (τ_w = 2.313U₀^1.37 and τ_c = 1.593ū²); symbols are the same as in (A). Black dashed curves indicate maximum combined stresses for critical limit of sediment motion (based on orthogonal and co-linear wave–current end members). Grey dashed curves separate the stability regimes of different bedform types. NM = no motion; CR = current ripples; WR = wave ripples; LAD = ladderback ripples; TILE = tile-shaped interference ripples; WOR = washed-out ripples; LUN = lunate interference ripples; UPB = upper-stage plane bed. The question mark denotes a field in which washed-out ripples may not form, since lunate interference ripples were found to change into wave ripples without going through a washed-out phase in inundation 3 (Figure 3A).

TABLE 1

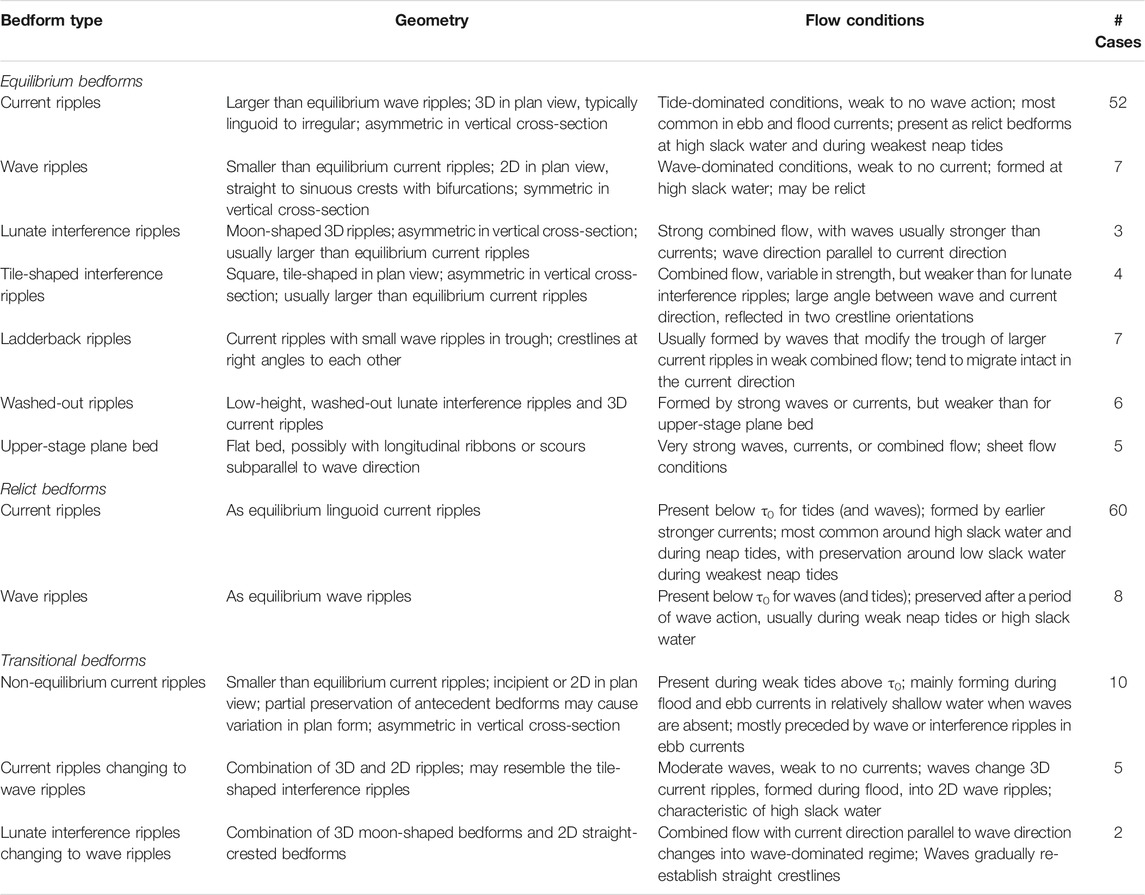
TABLE 1. Main properties and characteristic flow conditions for all equilibrium, relict, and transitional bedform types.

Tidal Inundations 1 and 2

In tidal inundations 1 (May 21st, pm) and 2 (May 22nd, am), the current stresses were below τ₀ at all times, whereas the wave stresses exceeded τ₀ around high slack water (Figures 3A,B). In both inundations, the currents and waves were co-linear. The 3D–ARP shows small, straight-crested, near-symmetric ripples with bifurcation patterns that are typical of wave ripples (Figures 4A, 9C, 10; Table 1; Allen, 1984; Perron et al., 2018). Since the wave stress was close to zero at the start of inundation 1, these wave ripples are interpreted as relict bedforms generated by waves in an earlier inundation. During flood and ebb, when current stresses reached 0.09–0.18 Nm⁻², the wave ripples migrated slowly in the downstream direction (slightly inclined vertical lines in BASSI data in Figure 4B), possibly because these weak currents helped the combined stresses to exceed τ₀ (Figure 3B). Relatively high, equilibrium wave ripples were present around high slack water on May 22nd, when the wave stress reached 0.5 Nm⁻² (Figures 3B,C,E), which signifies the precursor of the storm that started to affect the field site later that day. The length of the wave ripples in tidal inundations 1 and 2 was 124 mm (Figures 3C,D), whereas the height of these bedforms increased from 10 to 16 mm, reaching a temporary maximum of 18 mm during the period of large wave stresses in tidal inundation 2 (Figures 3B,C,E).

Tidal Inundation 3

Tidal inundation 3 (May 22nd, pm) experienced a peak current stress of 0.34 Nm⁻² during flood and a peak wave stress of 0.8 Nm⁻² immediately before high slack water (Figures 3A,B), and the currents and waves remained co-linear. Strong combined currents and waves during the flood (τ_max < 0.88 Nm⁻²; Figure 3B) caused the two-dimensional wave ripples of inundation 2 to evolve into larger, more asymmetric bedforms with a moon-shaped plan morphology, classified as lunate interference ripples (Figures 3A–F, 4C,D, 9F, 10; Table 1). Figure 4C shows that this process included an initial period in which both bedform types were present on the sediment bed. The lunate interference ripples were particularly high and long for c. 1 h around high slack water (Figures 3C–E, 4D), Thereafter, when the current stress was small and the wave stress decreased, the lunate interference ripples changed back gradually to smaller wave ripples (Figures 3B–E, 4E). During the ebb, these transitional bedforms formed the nucleus for the formation of incipient current ripples (Baas, 1994; Table 1), which were about half the size of the lunate interference ripples (Figures 3A,C–E, 4F). The current stress was larger than the wave stress at the end of inundation 3 (Figure 3B), which supports the presence of these non-equilibrium current ripples.

Tidal Inundation 4

Tidal inundation 4 (May 23rd, am) reveals complex and rapidly changing hydrodynamics, which caused rapidly changing bed morphology. The wave stress was 0–0.50 Nm⁻² during the flood, it decreased around high slack water, and waves were absent during the ebb (Figures 3A,B). The tidal currents rotated clockwise from south-southeast to north-west and the wave direction varied between east and south-east. The 3D–ARP recordings start with small, asymmetric, two-dimensional bedforms formed by the flood current (Figures 3A–F, 5A). These bedforms resemble straight-crested current ripples (Figures 9A, 10; Table 1), which probably evolved around low slack water from the incipient current ripples in inundation 3. The bed then changed to lunate interference ripples, similar to those in inundation 3 under large co-linear wave and current stresses. Thereafter, the wave stresses fluctuated between 0.06 Nm⁻² and 0.34 Nm⁻² (Figure 3B), the tidal current waned, and the wave–current angle increased to 65°. This resulted in the formation of tile-shaped bedforms that were clearly asymmetric in cross-section on the 3D–ARP and BASSI profiles, with two crest-line orientations that corresponded to the current and wave directions (Figures 5B, 9E; Table 1). These tile-shaped interference ripples became relict towards the end of the flood (Figures 3A–C), but waves continued to reshape the bed during high slack water by forming small wave ripples in the troughs of the tile-shaped interference ripples, classified as ladderback ripples (Figures 5C, 9D, 10; Table 1; Klein, 1970). Near the end of high slack water, the ladderback ripples had evolved into wave ripples. Local remnants of the tile-shaped interference ripples caused the wave ripples to have straight but discontinuous crestlines (Figure 5D) and possibly also an uncharacteristically large asymmetry (Figures 3C,F). The ebb current, in the absence of waves, was strong enough to form small, quickly migrating, incipient to locally straight-crested current ripples (Figures 3A–E).

Tidal Inundations 5 and 6

A storm passed the field site during tidal inundations 5 (May 23rd, pm) and 6 (May 24th, am). The current stresses were generally close to or well above τ₀, with a peak stress of c. 0.6 Nm⁻² during flood, more than twice the peak stress in inundation 4 (Figure 3B). The wave stresses were also larger than in inundation 4, particularly around high slack water (Figures 3A,B). Upper-stage plane beds (Figures 6A,B, 10; Table 1) prevailed during most of the flood tide when the combined stress was in the sheet flow regime (Figures 3A–C). The 3D–ARP recorded ribbon-like features (McLean, 1981), oriented parallel to the wave direction (Figure 6A), on these plane beds. In inundation 5, the upper-stage plane bed was preceded during the flood tide by a bed covered in asymmetric, equilibrium linguoid current ripples (cf., Baas, 1994; Figures 9B, 10; Table 1), formed when strong currents acted in the same direction as weak waves in relatively shallow water. In inundation 6, however, the plane beds were preceded by washed-out, lunate interference ripples (Table 1) during somewhat weaker combined flow. The 3D–ARP recorded smaller straight-crested to slightly three-dimensional current ripples, when the hydrodynamics were current-dominated, half an hour before the bed was covered with the washed-out ripples (Figures 3B,C). After the flood in both inundations, when the current stresses were small, but the wave stresses caused τ_max >> τ₀, washed-out ripples (Table 1) and then more pronounced ripples with straight but discontinuous crestlines appeared on the flat bed. Based on the dominance of wave action and the large wave–current angle, these bedforms are interpreted as wave ripples in which the weak tidal current disrupted the two-dimensional plan morphology. The wave-free ebb current (Figures 3A,B) may have been just powerful enough to move the wave ripples in a downstream direction (Figure 6C), given their low migration rate (Figure 6D), and initiate a change to current ripples at the end of the inundation.

Tidal Inundation 7

At the start of tidal inundation 7 (May 24th, pm), the storm had peaked and the tide was midway between neap and spring. The current stresses dominated the combined stresses during the flood and ebb, reaching 0.48 Nm⁻² and 0.25 Nm⁻², respectively, and the wave stresses pushed the combined stresses above τ₀ around high slack water (Figures 3A,B). Current ripples and wave ripples dominated this inundation. Downstream-migrating equilibrium linguoid current ripples (Baas, 1994) formed during the flood (Figures 3A–C, 7A,C). At high slack water, moderate waves slowly modified these current ripples into wave ripples by slightly decreasing the asymmetry and forming more continuous crestlines. Upon the decrease in wave stress during ebb, these wave ripples became relict and then changed gradually to more asymmetric equilibrium linguoid current ripples (Figures 3A–C,F, 7B,D).

Tidal Inundations 8 to 16

Except for tidal inundation 12 (May 27th, am), the wave stresses were small or absent in tidal inundation 8 (May 25th, am) to inundation 16 (May 29th, pm) (Figure 3B). Current-generated bedforms therefore dominated these inundations. Equilibrium linguoid current ripples formed during the flood and ebb tides (Figures 3A–C, 8A). These bedforms were stationary and thus relict during high slack water, even when the bed was exposed to weak waves in inundations 10, 11, 15, and 16. The BASSI data show that the migration rate of these ripples increased, as the current stresses increased (cf., Lichtman et al., 2018). Spring tidal current stresses peaked at 0.6–0.7 Nm⁻² in the final recording of the ebb in inundations 10 and 11 (Figures 3A,B), resulting in the formation of washed-out ripples (Figures 3C, 8B). On either side of these peak spring inundations, the ebb current formed merely linguoid current ripples.

Spring tide inundation 12 was different in that it captured large maximum current stresses in combination with moderate wave stresses during high slack water that caused the combined stresses to be above τ₀ throughout the inundation (Figures 3A,B). These conditions led to a dominance of two types of combined-flow bedforms, both of which formed at large wave–current angles of between 40° and 85°. Tile-shaped interference ripples were recorded during the last hour of the flood tide (Figures 3A–C, 8C). These bedforms replaced equilibrium linguoid current ripples that formed earlier, when the current stress was at its peak and waves were absent. The second type of combined-flow bedforms were ladderback ripples (Figure 8D). These bedforms formed during high slack water and the ebb, mostly when the wave stresses were larger than the current stresses, and they were roughly 50% lower and shorter than the tile-shaped interference ripples (Figures 3A–E). The height and length of the subordinate bedforms in the trough of the ladderback ripples gradually decreased in time in parallel with a gradual change from wave-dominated to current-dominated flow. The final recording during the ebb, when the flow depth had reduced to 1.72 m and waves were absent, revealed asymmetric, non-equilibrium current ripples that were partly straight-crested and in the process of replacing the ladderback ripples (Figures 3A–C).

Tidal Inundation 17

The wave stress had a significant influence on the bedform dynamics during tidal inundation 17 (May 30th, am). Wave stress dominated the combined stress around high slack water, whereas the current stress was dominant during the flood and ebb (Figures 3A,B). Consequently, the 3D–ARP data show a bed occupied by equilibrium linguoid current ripples during most of the flood. The waves gradually changed these current ripples into wave ripples over high slack water and then into ladderback ripples at the start of the ebb. The final recording shows bedforms in which the wave-generated “steps” of the ladderback patterns had almost disappeared and the current-generated crests had become more pronounced; these bedforms thus started to resemble non-equilibrium straight-crested current ripples. All the bedforms in inundation 17 migrated in the direction of the flood and ebb current, helped by the waves when the current stress was small. The current ripples were more asymmetric than the wave ripples and the ladderback ripples (Figures 3C,F).

Tidal Inundations 18 to 25

Tidal inundations 18 (May 30th, pm) to 21 (June 1st, am) experienced small wave stresses and peak current stresses that progressively decreased, in line with the change from spring to neap tide, but were above τ₀ (Figures 3A,B). This current dominance resulted in the formation of asymmetric equilibrium current ripples (Figures 3C, 8E) that were stationary, and therefore classified as relict, when the current stress was below c. 0.18 Nm⁻². These current ripples migrated during part of the flood in inundation 18, but this swapped to migration during the ebb in inundations 20 and 21. In the intermediate inundation 19, the current ripples migrated during both the flood and ebb tides (Figure 3A). The bed morphologies can be followed across the low slack water between the tidal inundations, as the current ripples migrated over a short distance without radically changing their plan morphology. When waves were present, the wave stress was largest during high slack water, but this did not significantly modify the current ripples.

During the neap tide inundations 22–25, the linguoid current ripples that were actively migrating earlier became stationary and therefore relict (Figure 8F). Waves were entirely absent, and all flood and ebb current stresses were below 0.12 Nm⁻² and thus too weak to move the current ripples (Figures 3A,B), even at shallow depths around low slack water.

Linking Bedforms to Hydrodynamic Data: Synthesis

Bedform Phase Diagram for Combined-Flow Bedforms

As expected, equilibrium current ripples (Figure 9B) formed when the combined stress was above τ₀ = 0.18 Nm⁻² for 0.227 mm sand and current-dominated (Figure 10A). The equilibrium current ripples formed at stresses below c. 0.65 Nm⁻². Likewise, equilibrium wave ripples (Figure 9C) formed at wave-dominant combined stresses between 0.18 Nm⁻² and 0.65 Nm⁻². The grey dashed lines near to the axes in Figure 10A delimit the stability regimes of equilibrium wave ripples and equilibrium current ripples, based, on the following equations:

Eq. 3, regime boundaries for equilibrium wave ripples:

${\tau }_c<0.2 {\tau }_w,0.18<\left({\tau }_c+{\tau }_w\right)<0.65(3)$

Eq. 4, regime boundaries for equilibrium current ripples:

${\tau }_c>3.3 {\tau }_w,0.18<\left({\tau }_c+{\tau }_w\right)<0.65(4)$

Using Eq. 2 to calculate τ₀ for single and combined currents and waves, the black dashed quarter circle in Figure 10A, based on φ = 90°, accurately delimits a no-motion regime with stationary, and therefore relict current ripples and wave ripples. The black dashed straight line, based on φ = 0°, is shown for comparison. Non-equilibrium, incipient and straight-crested current ripples (Figure 9A) plot mostly within the current ripple stability regime, but these bedforms are characterised by combined stresses between 0.18 Nm⁻² and 0.44 Nm⁻² (Figure 10A). Such small current stresses explain the transitional state of these bedforms, as non-equilibrium current ripples need more time to reach linguoid equilibrium morphology as the current stress is reduced (Baas, 1994, 1999; Oost and Baas, 1994) and therefore are more likely to be recorded at small than at large current stresses. For a similar reason, bedforms that were transitional from current ripples to wave ripples plot at small, combined stresses, where the wave stresses dominate (Figure 10A).

With few exceptions, the combined-flow bedforms plot well outside the stability regimes for current ripples, wave ripples, and no motion in Figure 10. Lunate interference ripples (Figure 9F) have combined wave–current stresses between 0.8 Nm⁻² and 0.9 Nm⁻², when the wave direction was almost parallel to the current direction (Figure 3I) and the wave stresses were larger than the current stresses (Figure 10A). The lunate interference ripples may correspond to the lunate megaripples and the oriented hummocks in the combined-flow phase diagram of Kleinhans (2005). The ladderback ripples (Figure 9D) and tile-shaped interference ripples (Figure 9E) were stable at smaller combined stresses than the lunate interference ripples. The ladderback ripples formed at combined stresses of 0.26 ± 0.04 Nm⁻². The tile-shaped interference ripples formed at a slightly larger combined stress of 0.33 ± 0.08 Nm⁻², but there is a substantial overlap in the combined stresses for these two bedform types. The angles between the wave and current directions for the ladderback and tile-shaped interference ripples were mostly above 45° (Figure 3I). The ladderback and tile-shaped interference ripples may correspond to the mixed wave–current ripples and the three-dimensional asymmetrical ripples in the combined-flow phase diagrams of Kleinhans (2005) and Perillo et al. (2014), respectively. These phase diagrams also include symmetric and asymmetric dunes between ripples and upper-stage plane beds for a similar grain size, but these large bedforms were not present at the study site. This may be because the flow conditions changed too quickly for dunes to develop, causing wave ripples and current ripples to change directly to and from washed-out ripples and upper-stage plane bed.

Washed-out ripples formed mainly at large shear stresses in current-dominant and wave-dominated flow, averaging 0.69 Nm⁻² (Figure 10A). In contrast, upper-stage plane beds mostly required strong combined stresses between 0.81 Nm⁻² and 1.20 Nm⁻². The formation of upper-stage plane beds appears independent of the wave–current angle, because it covers a wide range of angles from 0° to 70° (Figure 3I) whereas the lunate interference ripples are confined to angles less than 25°. Combined stresses of 0.78 Nm⁻² and 0.89 Nm⁻² can be used to separate the stability regime of the lunate interference ripples from that of washed-out ripples and upper-stage plane bed under strong wave-dominated conditions (Figure 10). Lunate interference ripples do not appear to form under current-dominated conditions, approximated by a gradual tapering of the phase boundary between lunate interference ripples and upper-stage plane bed in Figure 10A, according to the following equation:

Eq. 5, regime boundaries for lunate interference ripples:

${\tau }_c<-0.593{\tau }_w+0.621,0.39<{\tau }_w<0.66(5)$

Comparing the field-based bedform phase diagrams in Figure 10 with laboratory-based phase diagrams (e.g., Arnott and Southard, 1990; Yokokawa et al., 1995; Dumas et al., 2005; Kleinhans, 2005; Tinterri, 2011; Perillo et al., 2014) is complicated by the large number of physical variables that bedform dynamics are controlled by under natural wave–current conditions. Phase diagrams of the principal form presented in Figure 1 do not incorporate the effects of, for example, grain diameter, water depth, wave–current angle, wave period, bed clay content, and tide-induced shear-stress variations. Although Dumas et al. (2005) and Perillo et al. (2014) proposed phase diagrams for different wave periods and grain diameters, no diagram covers a full range of controlling parameters yet. Another difference is that the field data were collected in an intertidal environment, where the hydrodynamic forcing changed on the scale of tens of minutes, whereas the laboratory-based phase diagrams used constant wave and current forcing, thus essentially simulating subtidal conditions in which bedforms are more likely to be in equilibrium with the hydrodynamic forcing and water depth plays a smaller role than in intertidal environments. For example, storm waves were found to have only a small effect on bedform dynamics during shallow water at the field site.

Despite these complications, some of the bedforms found at the field site can be matched to those recognised in experimental flumes. The linguoid current ripples and wave ripples in Figure 10 correspond to the 3D current ripples and 2D/3D symmetric ripples of Perillo et al. (2014), respectively. These bedforms also appear in the phase diagrams of Arnott and Southard (1990), Yokokawa et al. (1995), and Dumas et al. (2005), but a comparison of forcing parameters is hampered by the small current velocities simulated in these experiments. The stability regime of the tile-shaped interference ripples overlaps with the 3D quasi-asymmetrical and asymmetrical ripples of Perillo et al. (2014), although the plan morphology of the tile-shaped interference ripples in this study is more regular. This difference might be explained by the fact that the tile-shaped interference ripples were formed at large wave–current angles and Perillo et al. (2014)’s 3D quasi-asymmetric and asymmetric ripples were associated with co-linear waves and currents. Subaqueous dunes were not found at the field site. Instead, the stability fields of 3D symmetric and asymmetric dunes and current dunes of Perillo et al. (2014) are occupied by washed-out ripples, lunate interference ripples, and upper-stage plane beds in Figure 10. This may be a key characteristic of intertidal environments, where water depths are generally shallow and rapidly changing, thus hindering the development of dunes, which need greater water depths and more time to form than ripple-sized bedforms. Dunes were seen on intertidal flats adjacent to the field site, but these dunes were poorly defined, with large form indices—the ratio between length and height. The 3D-ARP data did not show any hummocks, which have been considered to form in combined flow (Duke, 1985; Arnott and Southard, 1990; Dumas et al., 2005; Dumas and Arnott, 2006; Tinterri, 2011). The washed-out ripples at the field site are probably nearest to small-scale hummocks (Tinterri, 2011), because these share a similar size and large form index, but their shape is closer to flattened current ripples and lunate interferences ripples. The lack of conventional hummocks at the field site agrees with the facts that: 1) hummocks have not been described in estuarine sedimentary sequences (Tinterri, 2011, his Table 2); 2) hummocky cross-stratification serves “as a useful indicator of deposition in unrestricted, open-water conditions” (Dumas et al., 2005) instead of semi-enclosed esturaries, and; 3) hummocks form by wave-dominated combined flows with wave periods of 8–10 s (Dumas et al., 2005), whereas the measured wave periods at the field site were c. 6–8 s for the lunate interference ripples, washed-out ripples, and upper-stage plane beds and c. 3–6 s for the wave ripples. Hence, a dominance of ladderback ripples and tile-shaped and lunate interference ripples over hummocks and dunes might be diagnostic in sedimentary successions of estuarine mixed sand–mud tidal flats.

Temporal Distribution of Bedforms

The time-series in Figures 3A–F reveal that equilibrium current ripples dominated the flood and ebb during spring tides; these bedforms were relict for a short period around high slack water. Some of the highest-energy ebb currents during the spring tide, at current stresses of 0.6 Nm⁻² – 0.7 Nm⁻² (inundations 10 and 11), were able to form washed-out ripples from these equilibrium current ripples. The flood currents during spring tide did not form washed-out ripples within the measurement period, even though the shear stress was occasionally as large as in the ebb currents (e.g., tidal inundation 11). The relict current ripples became progressively less frequent in the runup to spring tide and more frequent during the transition from spring to neap tide. Around neap tide, the current ripples stopped moving altogether and near-identical bed morphologies could be traced across areal exposure in tidal inundations 22–25 (Figures 8E,F).

Water surface waves modified or replaced the current-generated bedforms during nine tidal inundations. The wave stresses were largest just before and at high slack water, suggesting that during ebb and most of the flood, when water depths were up to 3 m lower than during high slack water, waves largely dissipated before reaching the study site. This resulted in 23% of the bedforms showing wave-dominance or combined-flow properties (Figure 3G). The storm waves between May 22nd and 24th (inundations 3–6) had the largest influence on the bed morphology. The relict wave ripples at the start of inundation 2 evolved into equilibrium wave ripples when the waves were strong enough to move sediment around high slack water. Combined flow was dominant at the peak of storm intensity, resulting in the development of tile-shaped interference ripples and ladderback ripples at relatively weak current stresses, and lunate interference ripples, washed-out ripples and upper-stage plane beds at relatively large current stresses. The bedform evolution closely followed temporal changes in wave stress, best exemplified in inundations 4 and 6. In inundation 4, non-equilibrium current ripples existed when waves were absent. These current ripples then rapidly evolved into lunate interference ripples as the wave stress quickly increased, followed by tile-shaped interference ripples, ladderback ripples and wave ripples during decreasing current and wave stresses, and ending with non-equilibrium current ripples in the wave-free ebb current. Inundation 6 also started and ended with non-equilibrium current ripples. In between these, washed-out ripples followed by upper-stage plane beds formed around peak wave stress. Eventually, wave ripples and then current ripples formed during decreasing wave stress and small current stresses. The wave stress during tidal inundation 7 was just large enough to form wave ripples from relict current ripples during high slack water. These wave ripples became relict and then evolved into current ripples during the ebb. In inundation 17, ladderback ripples formed as an intermediate stage between the wave ripples and the current ripples. Finally, relatively weak waves affected the bed during the spring tide of inundation 12, forming a temporal sequence of tile-shaped interference ripples to ladderback ripples over high slack water and the ensuing ebb tide.

In summary, the field data show that strong waves lead to the formation of predominately lunate interference ripples, washed-out ripples and upper-stage plane beds, whereas weaker waves generate merely tile-shaped interference and ladderback ripples. Spring tides promote the development of upper-stage plane beds. In this dynamic environment, only 50% of the bedforms were found to be in equilibrium with the flow conditions (Figure 3H).

Comparison of Bedform Dimensions and Geometric Properties

Figures 3D,E show that the bedforms found in the study area are remarkably similar in height and length, even though the sediment bed was exposed to substantial variations in current stresses during the neap–spring cycle and to several periods of large wave and combined stresses. Except for the upper-stage plane beds, bedform height and length ranged from 11 to 17 mm (average: 14 ± 2 mm) and from 122 to 192 mm (average: 149 ± 23 mm), respectively. However, within this small range of bedform dimensions, which will be covered in more detail in the following sections, distinct differences in the asymmetry index and form index were distinguished, when grouped based on bedform type (Figure 11).

FIGURE 11

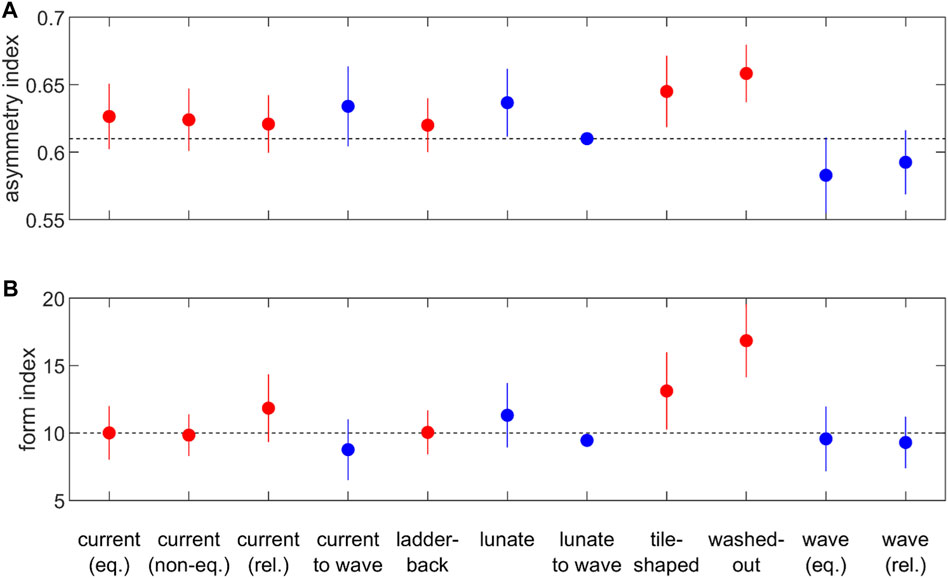
FIGURE 11. (A) Mean asymmetries and (B) form indices, including standard deviation of the mean, for all bedform types observed in the field campaign and separated into wave-dominated (blue) and current-dominated (red).

Although fully symmetric ripples, i.e., with an asymmetry index of 0.5, did not form, the wave ripples were more symmetric than the current ripples and the interference ripples, with the lunate interference ripples, tile-shaped interference ripples, and washed-out ripples showing the highest asymmetry (Figure 11). Based on their phase space positions in Figure 10, a set of wave-dominated bedforms can be grouped together, including the transitional current–to–wave, lunate interference, transitional lunate–to–wave, and wave ripples. The ladderback and tile-shaped interference ripples are wave-influenced, but these bedforms are grouped with the remaining current-dominated ripples, because the near orthogonal waves and currents resulted in two distinct sets of bedforms where those associated with the waves were subordinate. Except for the transitional current–to–wave and lunate interference ripples, the asymmetry index for the wave-dominated bedforms was below 0.61, the significance of which will be explained in the next section, and this provides a way of distinguishing wave- and current-dominated bedforms. The wave ripples had the lowest form index of all the bedform types encountered at the study site, and indeed a form index of below 10 distinguishes all but the lunate interference ripples in the wave-dominated set. The tile-shaped interference ripples had relatively high asymmetry and form indices whereas the ladderback ripples had indices much more in keeping with current ripples. Although being considerably smaller, the subordinate bedforms in the trough of the ladderback ripples had similar form and asymmetry indices to the main bedforms. As expected, the washed-out ripples had the highest form and asymmetry indices (Baas and De Koning, 1995; Figure 11). The size and shape of the transitional lunate–to–wave and current–to–wave ripples were in between their end members. For the transitional current–to–wave ripples, the form index already represented that of the wave ripples, but the asymmetry was still closer to that of the current ripples (Figure 11).

Predicting the Size of Bedforms Affected by Waves

The bedforms that were affected by waves in the field area include equilibrium and relict wave ripples, ladderback ripples, tile-shaped and lunate interference ripples, and transitional current–to–wave and lunate–to–wave ripples. The widely used wave bedform size predictor of Wiberg and Harris (1994) is chosen to verify if it is sufficiently accurate to generalise the relationships between wave-generated and combined-flow bedform size, and flow and sediment parameters found in this study. The non-iterative version of Wiberg and Harris’ (1994) predictor (Malarkey and Davies, 2003; Appendix Equation A2) depends only on the ratio of the wave orbital diameter, d₀, (= TU₀/π, where T is the wave period and U₀ is the wave velocity amplitude; Lichtman et al., 2018) and the median grain diameter, D₅₀. The predictor distinguishes between orbital ripples (d₀/D₅₀ < 1754), where the bedform dimensions depend on the orbital diameter, anorbital ripples (d₀/D₅₀ > 5,587), where the bedform dimensions depend on the grain diameter, and suborbital ripples (1754 < d₀/D₅₀ < 5,587) where the bedform dimensions depend on both the orbital and grain diameters. Soulsby and Whitehouse (2005) produced a similar wave ripple predictor, whereas some researchers have done away with the intermediate suborbital range (e.g., Traykovski, 2007). The presence of a small current is accounted for with an enhanced orbital diameter, d_wc, following the approach of Lacy et al. (2007):

Eq. 6, Enhanced orbital diameter:

$d_{wc}=\sqrt{d_0^2+0.25{\left(T{u}_{\delta }\right)}^2+d_{0}T{u}_{\delta }\cos \phi }(6)$

where u_δ = 0.65ū is the current velocity at c. 20 mm above the bed in terms of ū, the depth-averaged current velocity. In the absence of a current, ū = 0, the enhanced orbital diameter returns to its wave-only value, d_wc = d₀. As in the wave-only case, Eq. 6 determines the distance a particle is advected in half a wave cycle. This definition is only meaningful if the magnitude of the freestream velocity has two minima in the wave cycle, corresponding to (u_δ/U₀)cosφ < 1. Therefore, Eq. 6 was applied only when this condition was met. The comparison for the measured bedform heights and lengths is shown in Figures 12A,B.

FIGURE 12

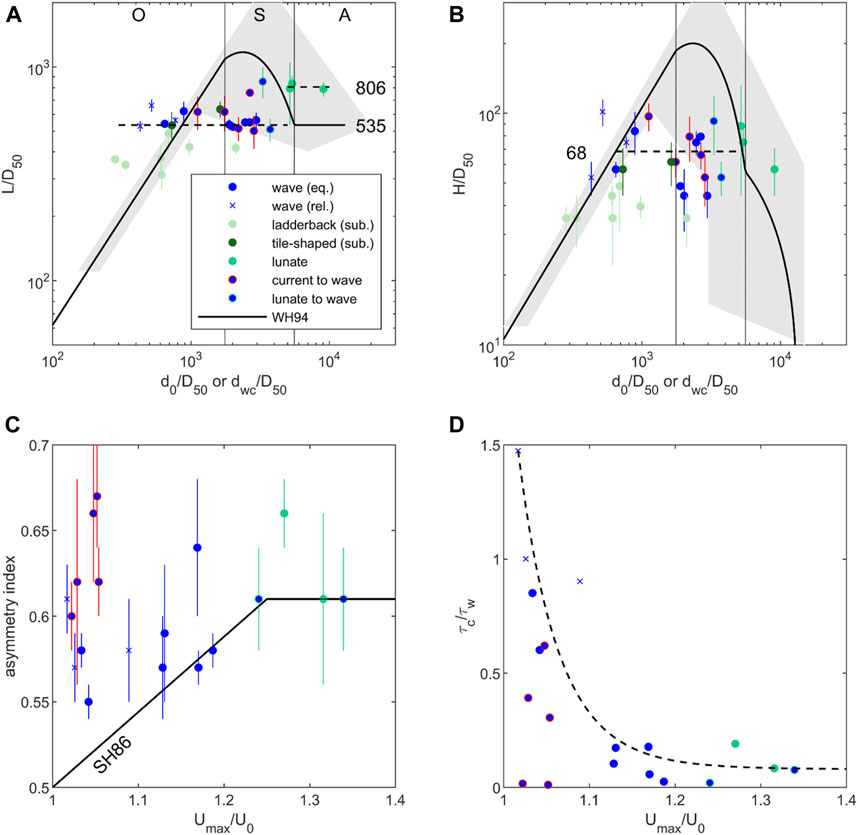
FIGURE 12. (A) Length and (B) height for equilibrium wave ripples and relict, above-threshold (based on $\phi =0°$ in Eq. 2) wave ripples, lunate interference ripples and transitional current–to–wave and lunate–to–wave ripples, using d_wc (Eq. 6), and for the subordinate bedforms in ladderback and tile-shaped interference ripples, using d₀ (Appendix Equation A2), compared to the Wiberg and Harris (1994) predictor (WH94). (C) Asymmetry index and Sato and Horikawa’s (1986) asymmetry prediction (SH86) against freestream wave velocity asymmetry from Stokes second order theory, U_max/U₀. (D) Relative current shear stress against wave asymmetry. Symbols in (B,C,D) are the same as in (A), with vertical lines denoting error bars (one standard deviation); grey shading reflects the spread of the original data; O = orbital, S = suborbital, A = anorbital, and dashed lines in (A) correspond to 535D₅₀ and 806D₅₀ and in (B) correspond to 68D₅₀. (C,D) do not show the lunate interference ripples with the largest d_wc/D₅₀ values from (A,B) with an asymmetry index of 0.64 and relative current shear stress of 0.58, because of an unrealistically large wave asymmetry. The dashed line in (D) is an inverse trend line.

The subordinate bedforms in the ladderback and tile-shaped interference ripples are of interest here, since the crest of these bedforms tend to be oriented perpendicular to the wave propagation direction. It is therefore anticipated that these subordinate bedforms are dependent on the wave-only orbital diameter d₀, rather than d_wc. The subordinate dimensions of the ladderback and tile-shaped interference ripples tend to be lower than the dimensions of the wave ripples. Their lengths are in the orbital range, but their heights are lower than expected for orbital ripples (Figures 12A,B). This may be because the subordinate bedforms are topographically constrained by their superimposition on the main bedforms in the ladderback and tile-shaped interference ripples.

Figure 12A shows that the relict wave ripples fall to the left of the grey shading associated with the original experimental scatter of Wiberg and Harris’ (1994) predictor, because the orbital diameters of the waves were too weak to influence the bedforms. Moreover, most equilibrium wave ripples and transitional current–to–wave ripples fall within the original laboratory and field data scatter and have lengths that are close to Wiberg and Harris’ (1994) anorbital value of 535D₅₀. Most of these ripple types can be considered as suborbital, but their dimensions correspond to anorbital ripples. This agrees with a laboratory study by Lacy et al. (2007), who found that wave-dominated ripples in combined wave–current flow fall in a similar suborbital region of the Wiberg and Harris (1994) plot. Anorbital ripples are analogous to current ripples in that their size depends only on the grain diameter. This may explain why there were only modest changes in the ripple dimensions during the field campaign when evolving from wave-dominated to current-dominated conditions. Indeed, since several wave ripples developed from current ripples at the beginning of the flood and weak currents commonly accompanied the wave ripples (Figures 3A–C), we infer that these currents may have forced the wave ripples towards becoming anorbital.

Because of their formation under wave-dominated conditions (Figure 10), it is reasonable to test the lunate interference ripples against the Wiberg and Harris (1994) predictor. These bedforms tend towards the anorbital range, but their length is larger than the predicted value for anorbital bedforms. Various researchers have found that the dimensions of anorbital ripples can have wave-period dependence (Mogridge et al., 1994; O’Donoghue et al., 2006), which is reflected in the scatter in the original Wiberg and Harris (1994) data in Figure 12A. This wave-period dependence may thus also apply to the lunate interference ripples.

For practical purposes, the length of the equilibrium and relict wave ripples and the transitional current–to–wave ripples can be considered constant, hence independent of the orbital diameter, at Wiberg and Harris’ (1994) anorbital value of 535D₅₀. However, the length of the lunate interference ripples, which is distinct from the wave ripples, is better described by 806D₅₀. Hence, L = 535D₅₀, for d_wc/D₅₀ < 5,320 and L = 806D₅₀, for d_wc/D₅₀ ≥ 5,320 (Figure 12A). Assuming that the bedform height can also be represented by a constant value, the mean of all the heights, other than for the lunate interference ripples, gives H = 68D₅₀ (Figure 12B). Since the lunate interference ripples represent wave-dominated bedforms with the highest combined stress before upper-stage plane beds develop and are well described by Wiberg and Harris’ (1994) predicted heights for anorbital ripples, a better predictor in this case would be H = 68D₅₀ for d_wc/D₅₀ < 5,320 and H = H_WH, for d_wc/D₅₀ ≥ 5,320, where H_WH is the height from the Wiberg and Harris (1994) predictor. This yields a representative form index of c. 7.7 for the wave ripples and transitional current–to–wave ripples and 12.5 for the lunate interference ripples. These predicted form indices are close to those shown in Figure 11B.

Since it is anticipated that wave ripples are more symmetric than current ripples and perhaps combined-flow bedforms, it is worth comparing the asymmetry indices of the wave ripples, lunate interference ripples and transitional current–to–wave ripples with the asymmetry indices found in literature. Sato and Horikawa (1986) determined that the asymmetry of wave ripples formed in the laboratory has an upper limit of 0.61, based on the steepest part of the upstream slope reaching the angle of repose. The ripple asymmetry increased up to this limit with increasing wave asymmetry (skewness), as determined by U_max/U₀, where U_max is the maximum near-bed velocity in the wave cycle, U_max/U₀ is calculated by Stokes 2^nd order (U_max/U₀ = 1+3kH/8sinh³kh, where H and k are the surface wave height and number and h is the water depth, Soulsby, 1997), and U_max/U₀ = 1 corresponds to a symmetric wave. Sato and Horikawa’s (1986) prediction is shown in Figure 12C together with all the bedforms shown in Figures 12A,B. The accompanying Figure 12D shows τ_c/τ_w versus U_max/U₀. Figure 12C reveals that the asymmetry is generally in the correct range for the wave ripples and the transitional lunate–to–wave ripples, even though Sato and Horikawa’s (1986) expression tends to underpredict the ripple asymmetry as a function of wave asymmetry. Figure 12D shows that there is an inverse relationship between the relative current stress and the wave asymmetry, and Figure 12C shows that the weaker the wave asymmetry is the more substantial the ripple asymmetry underprediction, thus strongly suggesting that the presence of the current causes additional ripple asymmetry. This is valid in particular for the transitional current–to–wave ripples, which have ripple asymmetries that are completely independent of wave asymmetry and generally greater than 0.61. The lunate interference ripples, although fitting the general predicted trend in wave asymmetry (Figures 12C,D), show a slightly larger asymmetry (Figure 11A), possibly because their larger form index (Figure 11B) means they are not constrained by Sato and Horikawa’s (1986) angle-of-repose limit.

Predicting the Size of Current-Dominated Bedforms

Most of the bedforms in the field area were either wholly or partially influenced by currents. These include the equilibrium, non-equilibrium, and relict current ripples; the dominant bedforms in the ladderback ripples and tile-shaped interference ripples; washed-out ripples; and upper-stage plane beds. These bedforms can be used to test the accuracy of the Soulsby and Whitehouse (2005) equilibrium current ripple predictor (Appendix Equation A3) and possibly extend its use to combined wave–current flows under natural conditions. Appendix Equation A3 has a grain size dependence but also predicts a linear decrease in ripple height with increasing stress for washed-out ripples, with the height becoming zero for sheet flows on upper-stage plane beds. Because waves and currents were both present at the field site, it is the maximum shear stress, τ_max, rather than the current stress, that controls the ripple height. Also, we optimised the Soulsby and Whitehouse (2005) descriptor for this dataset by forcing H_max = 67D₅₀ and L = 655D₅₀, based on the mean height and length of the equilibrium current ripples, and τ_wo = 0.65 Nm⁻² and τ_sf = 0.78 Nm⁻², based on the lower and upper boundaries of washed-out ripples in Figure 10A (according to Appendix Equation A3, H_max = 84D₅₀ and L = 674D₅₀, τ_wo = 0.76 Nm⁻² and τ_sf = 1.08 Nm⁻²).

The heights and lengths of all the current-dominated ripples are plotted against τ_max in Figures 13A,B, respectively. These figures also show the predicted values according to Soulsby and Whitehouse (2005). The range in the dimensions of the current ripples appears to increase, as the maximum stress increases, with the largest mean heights and lengths at τ_max > 0.5 Nm⁻². This increase in current ripple size agrees with the presence of relatively large ripples at high shear stresses in laboratory experiments with 0.238 mm sand, interpreted as bedforms transitional to subaqueous dunes (Baas, 1999).

FIGURE 13

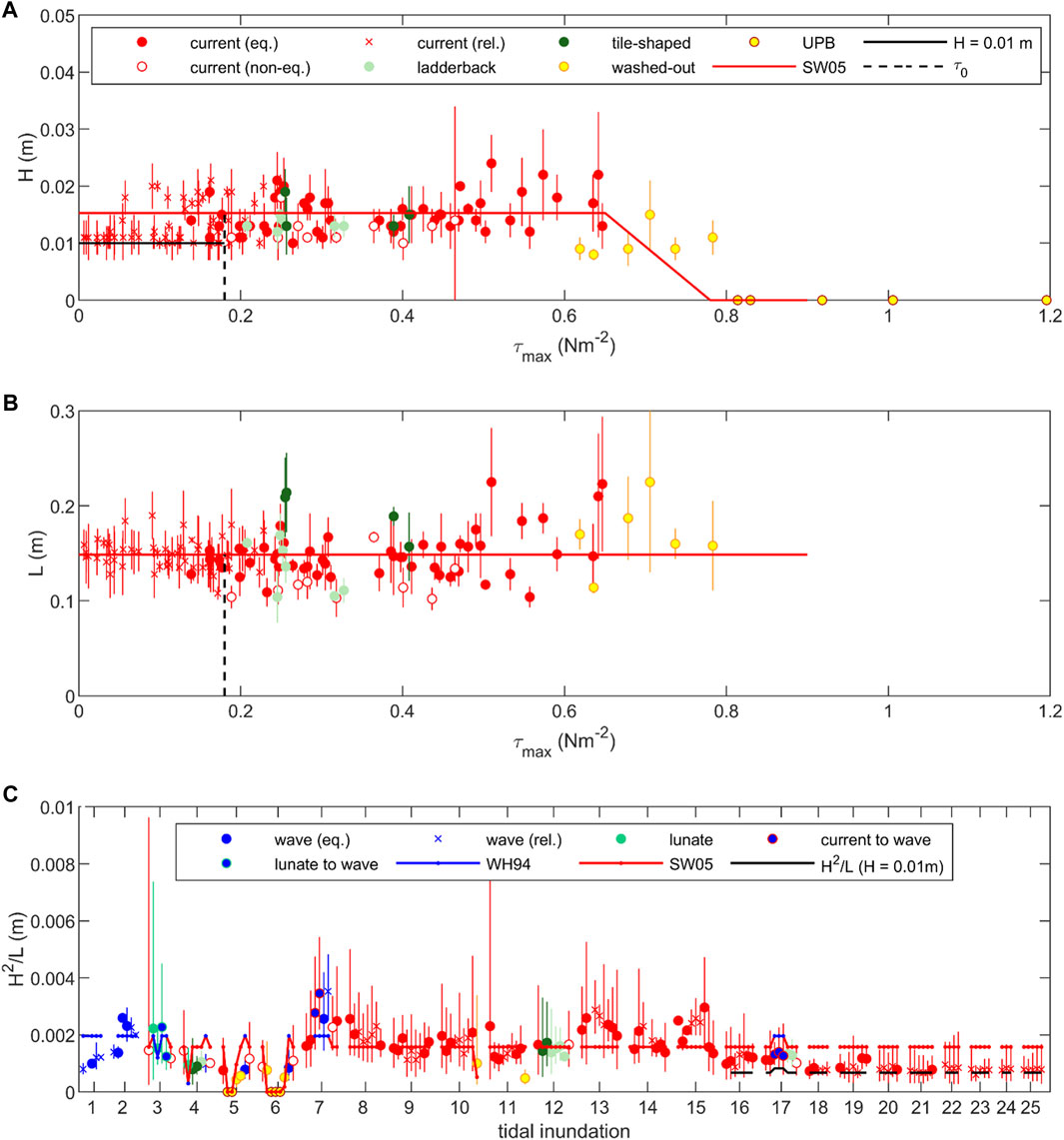
FIGURE 13. (A) Ripple height and (B) length against the maximum shear stress for all current-dominated bedforms, i.e., equilibrium, non-equilibrium, and relict current ripples, ladderback and tile-shaped interference ripples, washed-out ripples and upper-stage plane beds, compared to Soulsby and Whitehouse’s (2005) equilibrium current ripple predictor (SW05). (C) Bed roughness over the measurement campaign for all bedforms, including wave-dominated ripples, compared to bed roughness calculations based on the SW05 predictor and the modified Wiberg and Harris (1994) predictor (WH94) (cf., Figures 12A,B).

The dominant bedforms in the ladderback and tile-shaped interference ripples are also well described by the Soulsby and Whitehouse (2005) predictor. However, the non-equilibrium current ripples have lower heights and lengths, and some relict current ripples have lower heights (c. 10 mm instead of 15 mm), but not lower lengths, than predicted. The non-equilibrium current ripples were clearly not fully developed, and therefore plot below the equilibrium heights and lengths predicted by Soulsby and Whitehouse (2005) in Figures 13A,B. Moreover, these non-equilibrium ripples were most common during ebb, near the end or directly after periods of declining wave stress. The low-amplitude relict current ripples were present during neap tides with increased bed clay and EPS content (inundations 16–24). The greater reduction in height than in length of these relict ripples is consistent with increased bed clay and EPS content in the experiments of Baas et al. (2013) and Malarkey et al. (2015), respectively. The gradual reduction in ripple height during inundations 15, 16, and 17 is inferred to relate to the increase in bed clay and EPS content measured by Lichtman et al. (2018, their Figure 4) by drawing cohesive clay into the bed through hyporheic processes (Dallmann et al., 2020; Wu et al., 2021).

Discussion and Implications: Roughness Prediction

Determining turbulence and hence sediment transport rates is crucially dependent on the bed roughness. When bedforms are present, the main contribution to the roughness is through the form drag associated with their dimensions, as defined by the quantity H²/L (for example, k_s’’ = 20H²/L in the Chézy coefficient definition of Van Rijn (2006; 2011), where k_s’’ is the form roughness height of Nikuradse). In certain field settings, waves and currents each have their own roughness, e.g., combined strong waves and weak orthogonal currents over two-dimensional bedforms (Guerrero et al., 2021). However, it is reasonable to assume that there is a common wave–current roughness based on the main bedform heights and lengths in the study area, because of the varied wave–current angle, varied relative strengths of the waves and the currents, and the general three-dimensionality of the bedforms. The H²/L values, based on the measured bedform heights and lengths for all the different types of bedform, are shown in Figure 13C together with the H²/L values determined from the equilibrium current ripple and wave ripple predictors described in the previous sections. Figure 13C shows that the uncertainty in roughness is almost always larger than the variation over a tidal inundation, such that there is a limit to how well the roughness can be defined. However, Figure 13C also reveals that, with the exception of the 10-mm high relict current ripples in inundations 16–24, where the black dashed line is the roughness calculated with H = 10 mm, the predicted roughness agrees reasonably well with the measured roughness. This includes the non-equilibrium current ripples, despite the fact that these bedforms had smaller heights and lengths than their equilibrium and relict counterparts.

However, this independence of bed roughness on current ripple development stage may be particular to the study site. In other field studies, the need to adjust bedforms towards equilibrium may therefore require a more involved hysteresis-type calculation. Another aspect of the roughness predictions at the study site is that the wave ripple predictor makes only a modest difference to the roughness calculations. The current ripple predictor alone could therefore be considered sufficient to do the roughness calculations for most of the bedforms encountered at the study site. However, there are notable exceptions. The low roughness of the current ripples affected by high bed clay and EPS content in tidal inundations 16–24 indicates that cohesive forces can significantly reduce the bed roughness, and can start to do this at bed clay contents of 2%, corresponding to inundation 16 at the study site (Lichtman et al., 2018). This lower boundary of 2% clay corresponds reasonably well with the 3% clay proposed by Baas et al. (2019) as the lower boundary for the onset of bed stabilisation by cohesive forces. Moreover, the most substantial reductions to the bed roughness relate to the low-relief washed-out ripples and the upper-stage plane beds (Figure 13C). These bedform types were relatively rare at the study site, but their effect could be greater in areas that are exposed to larger waves and longer periods of wave forcing during ebb–flood tidal cycles.

Discussion and Implications: Preservation Potential of Intertidal Bedforms

Conditions for Preservation of Bedforms

The large variety of sedimentary bedforms in the study area underlines the complex interactions between hydrodynamics and sediment dynamics on intertidal flats (e.g., Deloffre et al., 2007; Gao, 2009). However, this large variety does not necessarily mean that each bedform type has a preservation potential in sedimentary successions of intertidal flats that matches its frequency of occurrence on modern intertidal flats. The present study shows that bedform type is often related in a predictable way to tidal phase and bed shear stress, the presence or absence of waves, and large (near orthogonal) or small (near co-linear) wave–current angles (Table 1). Since previous studies have shown at which conditions intertidal sediment is most likely to be preserved (e.g., Deloffre et al., 2007; Gao, 2009), it should also be possible to predict which intertidal bedform types have the highest preservation potential in the sedimentary record.

Using a combination of numerical modelling and field validation, Gao (2009) found that supratidal, high intertidal, and subtidal environments have a higher preservation potential than low intertidal environments, such as the study area. This reflects the notion that salt marshes and tidal channels usually have more space to accommodate net sediment accumulation than intertidal flats. Intertidal flat sediment can be preserved when the rate of bed aggradation is higher than the rate of bed erosion, but such aggradation rates are often too low to preserve entire bedforms, as exemplified by a comparative study of three estuaries by Deloffre et al. (2007). Even in the highly dynamic Seine estuary, NW France, the aggradation rates did not exceed 6 mm per semi-diurnal tidal cycle (Deloffre et al., 2007). Specific conditions are therefore required to preserve diagnostic sets of cross-stratification or entire bedform profiles in vertical cross-section. These include: 1) rapid aggradation after a sudden large influx of sediment by decelerating current-dominated or combined flow; 2) deposition of a protective layer of cohesive, ‘sticky’ clay during high slack water; 3) formation of a biofilm, i.e. a protective surface layer of extracellular polymeric substances (EPS) produced by benthic micro-organisms, during low slack water (Hope et al., 2020); and 4) a prolonged period of small stress and absence of strong bed erosion after these events, most likely around neap tide after the largest spring tides (Deloffre et al., 2007), and in the absence of strong waves over periods of at least weeks to months. Examples of large influxes of sediment are river floods, strong flood tides combined with strong onshore wind, and upstream breaching of, for example, the cut bank of a meandering tidal channel (e.g., Van den Berg et al., 2002). The formation of a protective layer of cohesive clay is most effective during long high slack water periods, i.e. at spring tide, in the estuarine turbidity maximum and in estuaries with strong ebb–flood asymmetry (Deloffre et al., 2007; Friedrichs, 2011; Kirwan and Guntenspergen, 2012; Lichtman et al., 2018). Protection from erosion by biofilm growth is most common during spring and summer, when storm events are less frequent along most coastlines, and during neap tides, when the period of bed strengthening by drying owing to atmospheric exposure is longest (Amos et al., 1988; Lichtman et al., 2018).

Preservation of Bedforms in the Absence of Waves

Although the sediment bed in the Dee estuary was not exposed to significant periods of deposition or erosion during the field study, the above-mentioned conditions for bedform preservation can be used to predict the preservation potential of the various types of bedform in the sedimentary record (Figure 3). In the absence of wave stresses, the tidal stresses almost exclusively formed current ripples. Upper-stage plane beds and washed-out ripples were found only for maximum ebb stresses during spring tides, although their generation during flood tides at depths below the minimum measurement depth of the instruments on the SEDbed frame cannot be ruled out. The upper-stage plane beds and the washed-out ripples have a low preservation potential, because these bedforms transform rapidly into current ripples, as the flow decelerates to slack water. Their preservation is probably limited to periods of rapid bed aggradation, thus forming sequences of plane-parallel lamination or climbing washed-out ripples. Migrating equilibrium current ripples were most common during flood and ebb in between neap and spring, whereas relict equilibrium current ripples were characteristic of high, and possibly also low, slack water periods and neap tides in the study area. In the absence of waves, these equilibrium ripples have a high preservation potential, not only because of their abundance, but also because these bedforms are stationary under the small current stresses around neap and become covered by increasing amounts of cohesive clay and EPS in the transition from spring to neap (Lichtman et al., 2018). The preservation potential of current ripples is expected to be even higher under weaker hydrodynamic forcing than at the study site, e.g. towards salt marshes or in estuaries with a lower tidal range, where the stresses are weaker and bed strengthening by cohesive clay and EPS is enhanced. However, such conditions are more likely to lead to the preservation of non-equilibrium than equilibrium current ripples, because the bedform development rate decreases exponentially with decreasing current stress (Baas, 1993, 1999). Even though upper-stage plane beds and washed-out ripples will be more common under stronger hydrodynamic forcing than at the study site, e.g. towards tidal channels, where tidal stresses are larger and cohesive clay and EPS are less abundant, the sediment bed is still subjected to rapid current ripple development when entering the current ripple stability regime during flow deceleration. An exception is fast runoff on steep local slopes during late ebb by sheet flow, which is prone to preserving upper stage plane beds (e.g., Collinson and Mountney, 2019). Hence, equilibrium current ripples are expected to remain the dominant bedform type in sedimentary successions of such dynamic intertidal environments, provided that τ_w << τ_c.

Effect of Weak and Moderate Waves on Preservation

Weak waves (τ_w < τ₀) had little effect on the bedforms in the study area, even for large combined stresses. Moderate waves (τ_w > τ₀), such as in inundations 2, 7, 12, and 17, were able to modify the currents and thus change the bedform type. During neap tides, equilibrium wave ripples formed around high slack water and these bedforms became relict during the flood and ebb. This suggests that wave ripples can replace current ripples and persist as relict bedforms on the bed during neap tides, when currents are not strong enough to move bed sediment, as exemplified by tidal inundation 1. However, moderate waves are unlikely to be accompanied by a large influx of sediment during neap when τ_c < τ₀. Hence, the high aggradation rates required to preserve wave ripples in this way are inferred to be rare. This leaves the potential to preserve wave ripples by the bed strengthening effect of clay and EPS, as discussed above. The clay would be preserved as a drape over the wave ripples in the sedimentary record.

During spring tides and the transitions between spring and neap, moderate waves modified the flow field to form tile-shaped interference ripples, wave ripples, and ladderback ripples at the study site. The ladderback ripples evolved rapidly from wave ripples or tile-shaped interference ripples around high slack water and then into current ripples in late ebb (e.g., tidal inundations 12 and 17). Because of these rapid changes in bed morphology, we anticipate the tile-shaped interference ripples, wave ripples, and ladderback ripples to be preserved only in exceptional circumstances, also because the formation of the tile-shaped interference ripples and ladderback ripples requires large wave–current angles, and the moderate waves prevent the tide from reaching zero stress at high slack water (e.g., tidal inundation 12 in Figures 3A,B) needed for bed strengthening by clay deposition. This leaves rapid sediment delivery and bed aggradation—here, during a period of up to 3 h (tidal inundation 12; Figure 3C)—combined with rapid waning of the waves, as the only scenario at which the tile-shaped interference ripples and ladderback ripples might be preserved. This rapid aggradation without clay deposition would be reflected in the sedimentary record as co-sets of climbing bedforms, but the lack of descriptions of such co-sets in the geological literature might be indicative of their scarcity. Instead of exhibiting a clay drape, the tops of these rare co-sets may be reworked into current ripples and cross-lamination, since τ_w < τ₀ in the late ebb, presumably because the moderate waves are dissipated before reaching the study site. In fact, these non-equilibrium and equilibrium current ripples have a higher preservation potential than the tile-shaped interference ripples, wave ripples, and ladderback ripples, because they may be stabilised by EPS and clay around low slack water (Lichtman et al., 2018; Hope et al., 2020). In contrast, the equilibrium current ripples formed in the early flood (Figures 3A–C) have a low preservation potential, because these bedforms are rapidly replaced by wave ripples or tile-shaped interference ripples during late flood.

Although it is reasonable to assume that the preservation potential of wave ripples and combined-flow ripples increases as moderate waves recur more often, it is more difficult to predict their preservation potential under conditions of weaker and stronger current stresses than at the study site. Smaller current stresses during neap may lead to an increased preservation potential of wave ripples (cf., inundation 2; Figures 3A–C). Larger current stresses during neap may cause tile-shaped interference ripples and ladderback ripples to become more common, with their preservation potential requiring the same specific conditions as those mentioned above. Smaller current stresses during spring may induce a shift in preservation from tile-shaped interference ripples and ladderback ripples to wave ripples (cf., inundation 7; Figures 3A–C), whereas larger current stresses during spring may cause a change to washed-out ripples, upper-stage plane beds, and possibly lunate interference ripples. However, it should be mentioned that the present dataset lacks a clear picture of stable bedform types at moderate wave stresses and large current stresses (Figure 10A).

Effect of Storm Waves on Preservation

During the transition from neap to spring in tidal inundations 3–6, storm waves (τ_w >> τ₀), with wave stresses up to 0.84 N m⁻², formed upper-stage plane beds, washed-out ripples, lunate interference ripples, tile-shaped interference ripples, and ladderback ripples under the rapidly changing contributions of waves and currents to the combined stresses. For reasons similar to those discussed for moderate waves above, we anticipate these bedforms to be preserved only in exceptional circumstances, limiting the preservation to sets of plane-parallel lamination and co-sets of climbing current ripples without clay drapes, but possibly with the tops reworked into non-climbing current ripples during the late ebb. Again, these current ripples have a higher preservation potential than the storm-wave induced bedforms, because the current ripples may be stabilised by EPS and clay around low slack water (Hope et al., 2020), if the storm wanes rapidly. The relatively high preservation potential of these late-ebb current ripples is remarkable because it may conceal evidence of waves, including storm waves, in the sedimentary record.

No recordings of storm waves during neap, spring, and the transition from spring to neap are available from the study site. Predicting bedform types and their preservation potential is therefore more challenging. Storm waves affecting the bed during neap are hypothesised to induce a dominance of wave ripples and wave-induced upper-stage plane beds around high slack water. The upper-stage plane beds are unlikely to be preserved because they change into wave ripples as water levels drop during the ebb, and rapid bed aggradation and clay drape formation are unlikely to take place during large wave stresses combined with small current stresses. The wave ripples may be larger than those formed by moderate waves during neap, discussed earlier, but their preservation potential is similar. Storm waves occurring during spring (τ_max >> τ₀) are expected to promote the formation of bedforms typical of large combined stresses, i.e., upper-stage plane beds, washed-out ripples and lunate interference ripples (Figure 10A). Upper-stage plane beds and washed-out ripples may also dominate shallow-water flood and ebb tides, when the wave stresses are small and the current stresses are in or just below the sheet flow regime. The preservation potential of these bedforms is probably similar to that of the bedforms formed by storm waves during the transition from neap to spring and by tidal currents in the absence of waves during spring at the field site, as discussed earlier. However, the highly dynamic conditions induced by storm waves during spring tides may cause bed scouring that removes bedforms preserved in earlier tidal inundations. Finally, it seems reasonable to assume that bedforms forming in the transition from spring to neap are similar to those forming in the transition from neap to spring. However, their preservation potential may be somewhat higher because current stresses progressively decrease from spring to neap, thus the potential for bed reworking also decreases.

Summary: Bedform Preservation

Figure 14 summarises the preservation potential of bedforms on intertidal flats using a relative scale, as quantification of the preservation potential is not possible yet. The schematic drawings of sedimentary deposits in Figure 14 are based on the most likely scenarios at which each bedform type can be preserved. Current ripples generated under wave-free conditions have the highest preservation potential, as individual ripple trains or climbing ripple co-sets covered by clay drapes and further stabilised by EPS. Wave ripples formed by moderate or strong oscillatory flow combined with relatively weak currents, for example during neap, have a moderate preservation potential, as individual wave ripple trains stabilised by clay and EPS, but not as climbing ripple co-sets. These deposits comprised of current ripples or wave ripples resemble flaser and lenticular bedding (Reineck and Singh, 1980). In contrast, combined-flow ripples, upper-stage plane beds, and washed-out ripples have a low to very low preservation potential, limited to conditions of rapid aggradation. These bedforms are unlikely to form part of flaser and lenticular bedding, but the plane-parallel laminated sets and climbing-ripple co-sets they generate may be covered by current ripples and their cross-lamination that form during ebb and around low slack water. So even under storm conditions, current ripples are more likely to be preserved than upper-stage plane beds, wave ripples and combined-flow ripples. Figure 14 is primarily based on the synthesis of the data collected in the Dee Estuary, so further work is needed to test the concepts presented. This should include combined hydrodynamic and sediment dynamic data acquisition on microtidal, mesotidal, and other macrotidal sand and mixed sand–mud flats in different wave climates, as well as targeted studies of bedforms and primary current lamination in sedimentary successions of intertidal flats.

FIGURE 14

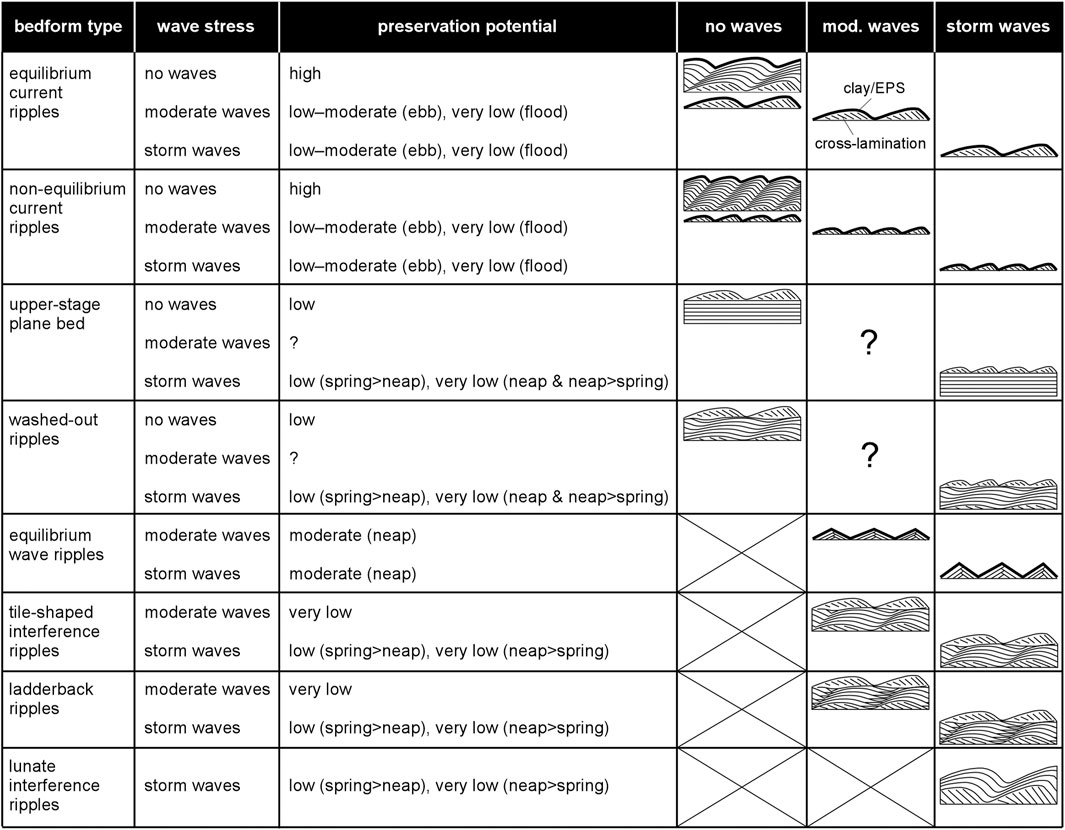
FIGURE 14. Summary of preservation potential of bedforms on intertidal flats without wave influence and with moderate and storm waves. No data are available for upper-stage plane beds and washed-out ripples under moderate waves.

Conclusion

Our comprehensive 2-week times-series of bedform dynamics on a mixed sand–mud flat in the Dee Estuary, United Kingdom, allowed us to propose a new bedform phase diagram in which the stability regimes of different types of bedform are delineated using the relative contributions of the current stress and wave stress to the maximum combined stress. As expected, non-equilibrium and equilibrium current ripples form in current-dominated flows without significant wave influence, and wave ripples form in wave-dominated flows without significant current influence. Relict current ripples and wave ripples are stable bedform phases below the critical combined flow shear stress of 0.18 Nm⁻², and ladderback ripples and tile-shaped interference ripples form when the maximum combined stress is between 0.18 and c. 0.65 Nm⁻², and both the wave and current stress make a significant contribution to the maximum combined stress. For maximum combined stresses above 0.65 Nm⁻², the bedform type changes from washed-out ripples (0.65–0.78 Nm⁻²) via lunate interference ripples (0.78–0.89 Nm⁻²) to upper-stage plane bed (>0.89 Nm⁻²). The lunate interference ripples were only observed in flows where the wave stress has the largest contribution to the maximum combined stress. The subaqueous dune field in laboratory-derived bedform phase diagrams was found to be occupied by washed-out ripples, lunate interference ripples and upper stage plane beds; this absence of dunes may be a key characteristic of intertidal flats.

The dataset also reveals that current ripples are the dominant bedform type on tidal flats, with actively migrating equilibrium current ripples dominating spring tides, stationary relict current ripples dominating neap tides, and non-equilibrium and equilibrium current ripples dominating early flood and late ebb tides, even under conditions of moderate or strong wave forcing. Wave ripples and combined-flow ripples form around high slack water when surface water waves are present. These bedforms change to washed-out ripples and upper-plane stage beds under storm waves. Around half of the bedforms were in equilibrium with the flow conditions, the remainder being either relict or in a transitional state between two bedform types. This confirms that the lack of a one–to–one relationship between flow forcing and bedform size might be a source of error in sediment transport rate predictions. However, most of the bedforms at the study site can be described by a single roughness value of H²/L = 1.6 mm, even the non-equilibrium current ripples, thus potentially simplifying sediment transport rate predictions. Exceptions are washed-out ripples and upper-stage plane beds, as controlled by the maximum combined stress, and current ripples in sand with at least 2% clay, which all have a significantly lower roughness.

Based on an assessment of the frequency of the various bedform types, their probability of being modified in flood–ebb and neap–spring tidal cycles as a function of bed aggradation rate and bed strengthening by clay drapes and biofilms, and extrapolation to tidal flats with weaker and stronger wave and current forcing, current ripples are inferred to have the highest preservation potential. Wave ripples have moderate preservation potential, and combined flow bedforms, such as ladderback and tile-shaped interference ripples, have the lowest preservation potential in sedimentary successions of intertidal flats. Since current ripples were the stable bedform phase near the end of the ebb in almost all the tidal inundations, even in the presence of moderate waves and storm waves, the waves and combined flows may rarely leave a permanent imprint on the sediment bed in intertidal environments. Therefore, the absence of wave ripples and combined-flow bedforms and their primary stratification in sedimentary successions cannot be taken as evidence that waves were absent at the time of deposition.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the United Kingdom’s Natural Environment Research Council (NERC) under Grant NE/I027223/1 (COHBED). JM, Julie Hope, and Daniel Parsons were partially funded by a Horizon 2020 European Research Council Consolidator Award (GEOSTICK, Grant 725955). The GEOSTICK project also kindly contributed the article processing fees. Andrew Manning’s contribution toward this research was partly supported by the National Science Foundation grants OCE-1924532 and OCE-1736668, TKI-MUSA project 11204950-000-ZKS-0002, and the HR Wallingford company research project FineScale (Grant Nos. ACK3013_62). DP received funding from the MASTS pooling initiative (The Marine Alliance for Science and Technology for Scotland) and their support is gratefully acknowledged. MASTS is funded by the Scottish Funding Council (Grant reference HR09011) and contributing institutions.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors are grateful to Roberto Tinterri and Kurt Eric Sundell, who made valuable suggestions for improvement of an earlier version of this paper. We are grateful to the NOC Ocean Technology and Engineering group and the field technicians of the School of Ocean Sciences of Bangor University for instrument set up and deployment.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.747567/full#supplementary-material

Appendix A: Threshold of Motion and Ripple Predictors

According to Soulsby (1997), the threshold Shields parameter is:

Eq. A1, Shields parameter for threshold of motion:

${\theta }_0=\frac{0.3}{1+1.2D_{\ast }}+0.055\left(1-e^{-0.02D_{\ast }}\right)(\mathrm{A1})$

where θ₀ = τ₀/(ρ_s‒ρ)gD₅₀, ρ is the density of sea water, ρ_s is the density of sediment, g is the acceleration due to gravity (= 9.81 ms⁻²), D_* = D₅₀ [(ρ_s‒ρ)g/ρν²]^1/3 and ν is the kinematic viscosity. For the non-iterative Wiberg and Harris (1994) ripple predictor (Malarkey and Davies, 2003), the equilibrium length and height are:

Eq. A2, equilibrium bedform length and height according to Wiberg and Harris (1994):

$\begin{array}{c}\frac{L}{D_{50}}=\{\begin{array}{ll}0.62\Delta ,\hfill & \Delta \le 1754,\hfill \\ 535\exp \left[f\left(\Delta \right)\right],\hfill & 1754<\Delta \le 5587,\hfill \\ 535,\hfill & \Delta >5587,\hfill \end{array}\\ \frac{H}{D_{50}}=\Delta \exp \left\{{\left[B_3-B_1\ln \left(\Delta D_{50}/L\right)\right]}^{\mathrm{½}}-B_2\right\}\end{array}(\mathrm{A2})$

where Δ = d₀/D₅₀, f (Δ) = ‒ln (0.62x)[Q‒(B₃‒B₃lnx)^½], x = Δ/535, Q = ln (0.01)+B₃, B₁ = 1/0.095, B₂ = 0.721B₁, and B₃ = B₂²‒2.28B₁. For the Soulsby and Whitehouse (2005) equilibrium current ripple predictor the equilibrium height and length are:

Eq. A3, equilibrium bedform height and length according to Soulsby and Whitehouse (2005):

$\frac{H_{\max }}{D_{50}}=202D_{\ast }^{-0.554},\frac{L}{D_{50}}=500+1881D_{\ast }^{-1.5}(\mathrm{A3})$

where H is controlled by θ_c, the Shields parameter associated with the current stress [ = τ_c/(ρ_s‒ρ)gD₅₀], H = H_max for θ_c ≤ θ_wo, H = H_max (θ_sf‒θ_c)/(θ_sf‒θ_wo) for θ_wo < θ_c ≤ θ_sf, H = 0 for θ_c > θ_sf and θ_wo and θ_sf are the wash-out and sheet-flow Shields parameters, given by θ_wo = 1.66D_*^−1.3 or 0.916 and θ_sf = 2.26D_*^−1.3 or 1.25, for D_* > 1.58 or D_* ≤ 1.58, respectively [θ_wo = τ_wo/(ρ_s‒ρ)gD₅₀ and θ_sf = τ_sf/(ρ_s‒ρ)gD₅₀].

References

Aldridge, J. N., Parker, E. R., Bricheno, L. M., Green, S. L., and Van der Molen, J. (2015). Assessment of the Physical Disturbance of the Northern European Continental Shelf Seabed by Waves and Currents. Continental Shelf Res. 108, 121–140. doi:10.1016/j.csr.2015.03.004

CrossRef Full Text | Google Scholar

Allen, J. R. L. (1984). Sedimentary Structures: Their Character and Physical Basis. Amsterdam: Elsevier.

Google Scholar

Amos, C. L., Bowen, A. J., Huntley, D. A., Judge, J. T., and Li, M. Z. (1999). Ripple Migration and Sand Transport under Quasi-Orthogonal Combined Flows on the Scotian Shelf. J. Coastal Res. 15, 1–14.

Google Scholar

Amos, C. L., Van Wagoner, N. A., and Daborn, G. R. (1988). The Influence of Subaerial Exposure on the Bulk Properties of fine-grained Intertidal Sediment from Minas Basin, Bay of Fundy. Estuarine, Coastal Shelf Sci. 27, 1–13. doi:10.1016/0272-7714(88)90028-5

CrossRef Full Text | Google Scholar

Arnott, R. W., and Southard, J. B. (1990). Exploratory Flow-Duct Experiments on Combined-Flow Bed Configurations, and Some Implications for Interpreting Storm-Event Stratification. J. Sediment. Petrol. 60, 211–219. doi:10.1306/212f9156-2b24-11d7-8648000102c1865d

CrossRef Full Text | Google Scholar

Baas, J. H. (1994). A Flume Study on the Development and Equilibrium Morphology of Current Ripples in Very fine Sand. Sedimentology 41, 185–209. doi:10.1111/j.1365-3091.1994.tb01400.x

CrossRef Full Text | Google Scholar

Baas, J. H. (1999). An Empirical Model for the Development and Equilibrium Morphology of Current Ripples in fine Sand. Sedimentology 46, 123–138. doi:10.1046/j.1365-3091.1999.00206.x

CrossRef Full Text | Google Scholar

Baas, J. H., Baker, M. L., Malarkey, J., Bass, S. J., Manning, A. J., Hope, J. A., et al. (2019). Integrating Field and Laboratory Approaches for Ripple Development in Mixed sand-clay-EPS. Sedimentology 66, 2749–2768. doi:10.1111/sed.12611

PubMed Abstract | CrossRef Full Text | Google Scholar

Baas, J. H., Best, J. L., and Peakall, J. (2016). Predicting Bedforms and Primary Current Stratification in Cohesive Mixtures of Mud and Sand. J. Geol. Soc. 173, 12–45. doi:10.1144/jgs2015-024

CrossRef Full Text | Google Scholar

Baas, J. H., Davies, A. G., and Malarkey, J. (2013). Bedform Development in Mixed Sand-Mud: The Contrasting Role of Cohesive Forces in Flow and Bed. Geomorphology 182, 19–32. doi:10.1016/j.geomorph.2012.10.025

CrossRef Full Text | Google Scholar

Baas, J. H., and De Koning, H. (1995). Washed-out Ripples; Their Equilibrium Dimensions, Migration Rate, and Relation to Suspended-Sediment Concentration in Very fine Sand. J. Sediment. Res. A65, 431–435. doi:10.1306/d42680e5-2b26-11d7-8648000102c1865d

CrossRef Full Text | Google Scholar

Baas, J. H. (1993). Dimensional Analysis of Current Ripples in Recent and Ancient Depositional Environments. Geologica Ultraiectina 106, 199.

Google Scholar

Bádenas, B., Aurell, M., and Gasca, J. M. (2018). Facies Model of a Mixed Clastic-Carbonate, Wave‐dominated Open‐coast Tidal Flat (Tithonian-Berriasian, north‐east Spain). Sedimentology 65, 1631–1666. doi:10.1111/sed.12441

CrossRef Full Text | Google Scholar

Brown, J. M., and Wolf, J. (2009). Coupled Wave and Surge Modelling for the Eastern Irish Sea and Implications for Model Wind-Stress. Continental Shelf Res. 29, 1329–1342. doi:10.1016/j.csr.2009.03.004

CrossRef Full Text | Google Scholar

Camenen, B. (2009). Estimation of the Wave-Related Ripple Characteristics and Induced Bed Shear Stress. Estuarine, Coastal Shelf Sci. 84, 553–564. doi:10.1016/j.ecss.2009.07.022

CrossRef Full Text | Google Scholar

Clifton, H. E., and Dingler, J. R. (1984). Wave-formed Structures and Paleoenvironmental Reconstruction. Mar. Geology. 60, 165–198. doi:10.1016/0025-3227(84)90149-x

CrossRef Full Text | Google Scholar

Collinson, J., and Mountney, N. (2019). Sedimentary Structures. 4th Edition. Edinburgh: Dunedin Academic Press, 320.

Google Scholar

Cuadrado, D. G. (2020). Geobiological Model of Ripple Genesis and Preservation in a Heterolithic Sedimentary Sequence for a Supratidal Area. Sedimentology 67, 2747–2763. doi:10.1111/sed.12718

CrossRef Full Text | Google Scholar

Dallmann, J., Phillips, C. B., Teitelbaum, Y., Sund, N., Schumer, R., Arnon, S., et al. (2020). Impacts of Suspended Clay Particle Deposition on Sand‐Bed Morphodynamics. Water Resour. Res. 56, e2019WR027010. doi:10.1029/2019WR027010

CrossRef Full Text | Google Scholar

Deloffre, J., Verney, R., Lafite, R., Lesueur, P., Lesourd, S., and Cundy, A. B. (2007). Sedimentation on Intertidal Mudflats in the Lower Part of Macrotidal Estuaries: Sedimentation Rhythms and Their Preservation. Mar. Geology. 241, 19–32. doi:10.1016/j.margeo.2007.02.011

CrossRef Full Text | Google Scholar

Duke, W. L. (1985). Hummocky Cross-Stratification, Tropical Hurricanes, and Intense winter Storms. Sedimentology 32, 167–194. doi:10.1111/j.1365-3091.1985.tb00502.x

CrossRef Full Text | Google Scholar

Dumas, S., and Arnott, R. W. C. (2006). Origin of Hummocky and Swaley Cross-Stratification- the Controlling Influence of Unidirectional Current Strength and Aggradation Rate. Geol 34, 1073–1076. doi:10.1130/g22930a.1

CrossRef Full Text | Google Scholar

Dumas, S., Arnott, R. W. C., and Southard, J. B. (2005). Experiments on Oscillatory-Flow and Combined-Flow Bed Forms: Implications for Interpreting Parts of the Shallow-marine Sedimentary Record. J. Sediment. Res. 75, 500–513. doi:10.2110/jsr.2005.039

CrossRef Full Text | Google Scholar

Friedrichs, C. T. (2011). “Tidal Flat Morphodynamics,” in Treatise on Estuarine and Coastal Science. Editors E. Wolanski, and D. McLusky (Waltham: Academic Press), 137–170. doi:10.1016/b978-0-12-374711-2.00307-7

CrossRef Full Text | Google Scholar

Gallagher, E. L. (2003). A Note on Megaripples in the Surf Zone: Evidence for Their Relation to Steady Flow Dunes. Mar. Geology. 193, 171–176. doi:10.1016/s0025-3227(02)00662-x

CrossRef Full Text | Google Scholar

Gallagher, E. L., Elgar, S., and Thornton, E. B. (1998). Megaripple Migration in a Natural Surf Zone. Nature 394, 165–168. doi:10.1038/28139

CrossRef Full Text | Google Scholar

Gao, S. (2009). Modeling the Preservation Potential of Tidal Flat Sedimentary Records, Jiangsu Coast, Eastern Chinaflat Sedimentary Records, Jiangsu Coast, Eastern China. Continental Shelf Res. 29, 1927–1936. doi:10.1016/j.csr.2008.12.010

CrossRef Full Text | Google Scholar

Gordon, L., and Lohrmann, A. (2001). “Near-shore Doppler Current Meter Wave Spectra,” in Ocean Wave Measurement and Analysis: Proceedings of ASCE Waves 2001 conference (Reston, VA: ASCE).

Google Scholar

Guerrero, Q., Williams, M. E., Guillén, J., Lichtman, I. D., Thorne, P. D., and Amoudry, L. O. (2021). Small-scale Bedforms and Associated Sediment Transport in a Macro-Tidal Lower Shoreface. Continental Shelf Res. 225, 104483. doi:10.1016/j.csr.2021.104483

CrossRef Full Text | Google Scholar

Halcrow (2013). North West Estuaries Processes Reports: Dee Estuary. Merseyside: Sefton Council.

Google Scholar

Harazim, D., and McIlroy, D. (2015). Mud-rich Density-Driven Flows along an Early Ordovician Storm-Dominated Shoreline: Implications for Shallow-marine Facies Models. J. Sediment. Res. 85, 509–528. doi:10.2110/jsr.2015.38

CrossRef Full Text | Google Scholar

Hay, A. E., and Mudge, T. (2005). Principal Bed States during SandyDuck97: Occurrence, Spectral Anisotropy, and the Bed State Storm Cycle. J. Geophys. Res. 110, C03013. doi:10.1029/2004JC002451

CrossRef Full Text | Google Scholar

Hope, J. A., Malarkey, J., Baas, J. H., Peakall, J., Parsons, D. R., Manning, A. J., et al. (2020). Interactions between Sediment Microbial Ecology and Physical Dynamics Drive Heterogeneity in Contextually Similar Depositional Systems. Limnol Oceanogr 65, 2403–2419. doi:10.1002/lno.11461

CrossRef Full Text | Google Scholar

Isla, M. F., Schwarz, E., and Veiga, G. D. (2018). Bedset Characterization within a Wave-Dominated Shallow-marine Succession: an Evolutionary Model Related to Sediment Imbalances. Sediment. Geology. 374, 36–52. doi:10.1016/j.sedgeo.2018.07.003

CrossRef Full Text | Google Scholar

Kirwan, M. L., and Guntenspergen, G. R. (2012). Feedbacks between Inundation, Root Production, and Shoot Growth in a Rapidly Submerging Brackish Marsh. J. Ecol. 100, 764–770. doi:10.1111/j.1365-2745.2012.01957.x

CrossRef Full Text | Google Scholar

Klein, G. D. V. (1970). Depositional and Dispersal Mechanics of Intertidal Sand Bars. J. Sediment. Petrol. 40, 1095–1127.

Google Scholar

Kleinhans, M. G. (2005). Phase Diagrams of Bed States in Steady, Unsteady, Oscillatory and Mixed Flows. SANDPIT Rep., 16.

Google Scholar

Krämer, K., and Winter, C. (2016). Predicted Ripple Dimensions in Relation to the Precision of In Situ Measurements in the Southern North Sea. Ocean Sci. 12, 1221–1235. doi:10.5194/os-12-1221-2016

CrossRef Full Text | Google Scholar

Lacy, J. R., Rubin, D. M., Ikeda, H., Mokudai, K., and Hanes, D. M. (2007). Bed Forms Created by Simulated Waves and Currents in a Large Flume. J. Geophys. Res. 112, C10018. doi:10.1029/2006JC003942

CrossRef Full Text | Google Scholar

Larsen, S. M., Greenwood, B., and Aagaard, T. (2015). Observations of Megaripples in the Surf Zone. Mar. Geology. 364, 1–11. doi:10.1016/j.margeo.2015.03.003

CrossRef Full Text | Google Scholar

Li, M. Z., and Amos, C. L. (1998). Predicting Ripple Geometry and Bed Roughness under Combined Waves and Currents in a continental Shelf Environment. Continental Shelf Res. 18, 941–970. doi:10.1016/s0278-4343(98)00034-x

CrossRef Full Text | Google Scholar

Lichtman, I. D., Baas, J. H., Amoudry, L. O., Thorne, P. D., Malarkey, J., Hope, J. A., et al. (2018). Bedform Migration in a Mixed Sand and Cohesive clay Intertidal Environment and Implications for Bed Material Transport Predictions. Geomorphology 315, 17–32. doi:10.1016/j.geomorph.2018.04.016

CrossRef Full Text | Google Scholar

Malarkey, J., Baas, J. H., Hope, J. A., Aspden, R. J., Parsons, D. R., Peakall, J., et al. (2015). The Pervasive Role of Biological Cohesion in Bedform Development. Nat. Commun. 6, 6257. doi:10.1038/ncomms7257

PubMed Abstract | CrossRef Full Text | Google Scholar

Malarkey, J., and Davies, A. G. (2003). A Non-iterative Procedure for the Wiberg and Harris (1994) Oscillatory Sand Ripple Predictor. J. Coastal Res. 19, 738–739.

Google Scholar

Malarkey, J., and Davies, A. G. (2012). A Simple Procedure for Calculating the Mean and Maximum Bed Stress under Wave and Current Conditions for Rough Turbulent Flow Based on Method. Comput. Geosciences 43, 101–107. doi:10.1016/j.cageo.2012.02.020

CrossRef Full Text | Google Scholar

Marine Electronics (2009). User Manual for the 3D Sand Ripple Profiling Logging Sonar, Issue 1.1. Vale, Channel Islands, U.K.: Marine Electronics Ltd.

Google Scholar

McLean, S. R. (1981). The Role of Non-uniform Roughness in the Formation of Sand Ribbons. Mar. Geology. 42, 49–74. doi:10.1016/0025-3227(81)90158-4

CrossRef Full Text | Google Scholar

Moate, B. D., Thorne, P. D., and Cooke, R. D. (2016). Field Deployment and Evaluation of a Prototype Autonomous Two Dimensional Acoustic Backscatter Instrument: The Bedform and Suspended Sediment Imager (BASSI). Continental Shelf Res. 112, 78–91. doi:10.1016/j.csr.2015.10.017

CrossRef Full Text | Google Scholar

Mogridge, G. R., Davies, M. H., and Willis, D. H. (1994). Geometry Prediction for Wave-Generated Bedforms. Coastal Eng. 22, 255–286. doi:10.1016/0378-3839(94)90039-6

CrossRef Full Text | Google Scholar

Moore, R. D., Wolf, J., Souza, A. J., and Flint, S. S. (2009). Morphological Evolution of the Dee Estuary, Eastern Irish Sea, UK: A Tidal Asymmetry Approach. Geomorphology 103, 588–596. doi:10.1016/j.geomorph.2008.08.003

CrossRef Full Text | Google Scholar

Myrow, P. M., Fischer, W., and Goodge, J. W. (2002). Wave-modified Turbidites: Combined-Flow Shoreline and Shelf Deposits, Cambrian, Antarctica. J. Sediment. Res. 72, 641–656. doi:10.1306/022102720641

CrossRef Full Text | Google Scholar

Myrow, P. M., and Southard, J. B. (1991). Combined-flow Model for Vertical Stratification Sequences in Shallow marine Storm-Deposited Beds. J. Sediment. Res. 61, 202–210. doi:10.1306/d42676d1-2b26-11d7-8648000102c1865d

CrossRef Full Text | Google Scholar

Nelson, T. R., Voulgaris, G., and Traykovski, P. (2013). Predicting Wave-Induced Ripple Equilibrium Geometry. J. Geophys. Res. 97 (C8), 17245–12761. doi:10.1002/jgrc.20241

CrossRef Full Text | Google Scholar

O'Donoghue, T., Doucette, J. S., van der Werf, J. J., and Ribberink, J. S. (2006). The Dimensions of Sand Ripples in Full-Scale Oscillatory Flows. Coastal Eng. 53, 997–1012. doi:10.1016/j.coastaleng.2006.06.008

CrossRef Full Text | Google Scholar

Oost, A. P., and Baas, J. H. (1994). The Development of Small Scale Bedforms in Tidal Environments: an Empirical Model for Unsteady Flow and its Applications. Sedimentology 41, 883–903. doi:10.1111/j.1365-3091.1994.tb01430.x

CrossRef Full Text | Google Scholar

Parsons, D. R., Schindler, R. J., Hope, J. A., Malarkey, J., Baas, J. H., Peakall, J., et al. (2016). The Role of Biophysical Cohesion on Subaqueous Bed Form Size. Geophys. Res. Lett. 43, 1566–1573. doi:10.1002/2016gl067667

PubMed Abstract | CrossRef Full Text | Google Scholar

Pedocchi, F., and García, M. H. (2009a). Ripple Morphology under Oscillatory Flow: 1. Prediction. J. Geophys. Res. 114, C12014. doi:10.1029/2009JC005354

CrossRef Full Text | Google Scholar

Pedocchi, F., and García, M. H. (2009b). Ripple Morphology under Oscillatory Flow: 2. Experiments. J. Geophys. Res. 114, C12015. doi:10.1029/2009JC005356

CrossRef Full Text | Google Scholar

Perillo, M. M., Best, J. L., and Garcia, M. H. (2014). A New Phase Diagram for Combined-Flow Bedforms. J. Sediment. Res. 84, 301–313. doi:10.2110/jsr.2014.25

CrossRef Full Text | Google Scholar

Perron, J. T., Myrow, P. M., Huppert, K. L., Koss, A. R., and Wickert, A. D. (2018). Ancient Record of Changing Flows from Wave Ripple Defects. Geology 46, 875–878. doi:10.1130/g45463.1

CrossRef Full Text | Google Scholar

Reineck, H. E., and Singh, I. B. (1980). Depositional Sedimentary Environments: With Reference to Terrigenous Clastics. Berlin: Springer, 551.

Google Scholar

Sato, S., and Horikawa, K. (1986). “Laboratory Study on Sand Transport over Ripples Due to Asymmetric Oscillatory Flows,” in Proceedings of 20th International Conference on Coastal Engineering (New York: ASCE), 1481–1495. doi:10.9753/icce.v20.109

CrossRef Full Text | Google Scholar

Smyth, C. E., and Li, M. Z. (2005). Wave-current Bedform Scales, Orientation, and Migration on Sable Island Bank. J. Geophys. Res. 110, C02023. doi:10.1029/2004JC002569

CrossRef Full Text | Google Scholar

Soulsby, R. (1997). Dynamics of Marine Sands: A Manual for Practical Applications. London: Thomas Telford.

Google Scholar

Soulsby, R. L., Whitehouse, R. J. S., and Marten, K. V. (2012). Prediction of Time-Evolving Sand Ripples in Shelf Seas. Continental Shelf Res. 38, 47–62. doi:10.1016/j.csr.2012.02.016

CrossRef Full Text | Google Scholar

Soulsby, R. L., and Whitehouse, R. J. S. (2005). Prediction of Ripple Properties in Shelf Seas; Mark 2 Predictor for Time Evolution. Rep. TR 154¸ Release 2.0, HR Wallingford, 99.

Google Scholar

Southard, J. B., and Boguchwal, L. A. (1990). Bed Configuration in Steady Unidirectional Water Flows; Part 2, Synthesis of Flume Data. J. Sediment. Res. 60, 658–679. doi:10.1306/212f9241-2b24-11d7-8648000102c1865d

CrossRef Full Text | Google Scholar

Taral, S., and Chakraborty, T. (2017). Deltaic Coastline of the Siwalik (Neogene) Foreland basin: Evidences from the Gish River Section, Darjeeling Himalaya. Geol. J. 53, 203–229. doi:10.1002/gj.2886

CrossRef Full Text | Google Scholar

Thorne, P. D., and Hanes, D. M. (2002). A Review of Acoustic Measurement of Small-Scale Sediment Processes. Continental Shelf Res. 22, 603–632. doi:10.1016/s0278-4343(01)00101-7

CrossRef Full Text | Google Scholar

Thorne, P. D., Hurther, D., Cooke, R. D., Caceres, I., Barraud, P. A., and Sánchez-Arcilla, A. (2018). Developments in Acoustics for Studying Wave-Driven Boundary Layer Flow and Sediment Dynamics over Rippled Sand-Beds. Continental Shelf Res. 166, 119–137. doi:10.1016/j.csr.2018.07.008

CrossRef Full Text | Google Scholar

Tinterri, R. (2011). Combined Flow Sedimentary Structures and the Genetic Link between Sigmoidal and Hummocky-Cross Stratification. Geologica Acta 10, 43–85.

Google Scholar

Traykovski, P. (2007). Observations of Wave Orbital Scale Ripples and a Nonequilibrium Time-dependent Model. J. Geophys. Res. 112, C06026. doi:10.1029/2006JC003811

CrossRef Full Text | Google Scholar

Van den Berg, J. H., and Van Gelder, A. (1993). “A New Bedform Stability Diagram, with Emphasis on the Transition of Ripples to Plane Bed in Flows over fine Sand and silt,” in Alluvial Sedimentation. International Association of Sedimentologists Special Publication 17. Editors M. Marzo, and C. Puigdefábregas (Oxford, UK: Blackwell Publishing Ltd.), 11–21.

Google Scholar

Van den Berg, J. H., Van Gelder, A., and Mastbergen, D. R. (2002). The Importance of Breaching as a Mechanism of Subaqueous Slope Failure in fine Sandfine Sand. Sedimentology 49, 81–95. doi:10.1111/j.1525-139x.2006.00168.x-i1

CrossRef Full Text | Google Scholar

Van der Mark, C. F., Blom, A., and Hulscher, S. J. M. H. (2008). Quantification of Variability in Bedform Geometry. J. Geophys. Res. 113, F03020. doi:10.1029/2007JF000940

CrossRef Full Text | Google Scholar

Van Rijn, L. C. (2006). Bed Form Tracking, Manual Sediment Transport Measurements in Rivers Estuaries and Coastal Seas, Sub-section 5.5.2. Delft, Netherlands: Delft Hydraulics Laboratory.

Google Scholar

Van Rijn, L. C. (2011). Principles of Fluid Flow and Surface Waves in Rivers, Estuaries, Seas and Oceans. Amsterdam: Aqua Publications, 900.

Google Scholar

Van Rijn, L. C. (1984). Sediment Transport, Part III: Bed Forms and Alluvial Roughness. J. Hydraul. Eng. 110, 1733–1754. doi:10.1061/(asce)0733-9429(1984)110:12(1733)

CrossRef Full Text | Google Scholar

Villaret, C., Huybrechts, N., Davies, A. G., and Way, O. (2011). “Effect of Bed Roughness Prediction on Morphodynamic Modelling: Application to the Dee Estuary (UK) and to the Gironde Estuary (France),” in Proceedings of 34th IAHR World Congress, 26 June-1 July 2011, Brisbane, Australia. International Association for Hydro-Environment Engineering and Research (IAHR), 1149–1156.

Google Scholar

Wang, J., Jiang, Z., and Zhang, Y. (2015). Subsurface Lacustrine Storm-Seiche Depositional Model in the Eocene Lijin Sag of the Bohai Bay Basin, East China. Sediment. Geology. 328, 55–72. doi:10.1016/j.sedgeo.2015.07.014

CrossRef Full Text | Google Scholar

Way, O. (2013). “The Migration of Large Scale Bed Forms in the Dee Estuary,” (Wales, U. K.: Bangor University), 398. PhD Thesis.

Google Scholar

Wengrove, M. E., Foster, D. L., Lippmann, T. C., de Schipper, M. A., and Calantoni, J. (2018). Observations of Time‐Dependent Bedform Transformation in Combined Wave‐Current Flowsflows. J. Geophys. Res. Oceans 123, 7581–7598. doi:10.1029/2018jc014357

CrossRef Full Text | Google Scholar

Wengrove, M. E., Foster, D. L., Lippmann, T. C., de Schipper, M. A., and Calantoni, J. (2019). Observations of Bedform Migration and Bedload Sediment Transport in Combined Wave‐Current Flows. J. Geophys. Res. Oceans 124, 4572–4590. doi:10.1029/2018jc014555

CrossRef Full Text | Google Scholar

Wiberg, P. L., and Harris, C. K. (1994). Ripple Geometry in Wave-Dominated Environments. J. Geophys. Res. 99 (C1), 775–789. doi:10.1029/93jc02726

CrossRef Full Text | Google Scholar

Wu, X., Fernández, R., Baas, J., Malarkey, J., and Parsons, D. (2021). Discontinuity in Equilibrium Wave-Current Ripple Size and Shape Caused by a Winnowing Threshold in Cohesive Sand-clay Beds. EarthArxiv. doi:10.31223/X5HC98

CrossRef Full Text | Google Scholar

Wu, X., and Parsons, D. R. (2019). Field Investigation of Bedform Morphodynamics under Combined Flow. Geomorphology 339, 19–30. doi:10.1016/j.geomorph.2019.04.028

CrossRef Full Text | Google Scholar

Yokokawa, M., Masuda, F., and Endo, N. (1995). Sand Particle Movement on Migrating Combined-Flow Ripples. J. Sediment. Res. A65, 40–44.

Google Scholar