An Enhanced Ubiquitous-Joint Model for a Rock Mass With Conjugate Joints and Its Application on Excavation Simulation of Large Underground Caverns

A conjugate jointed rock mass (CJRM) is a rock mass with two sets of intersecting joints formed from intact rock under shear. Its mechanical properties and excavation-induced hazards of large underground caverns are different from those of common rock masses because of the unique geological origin thereof. To demonstrate numerically the excavation responses of CJRM, the ubiquitous-joint model is enhanced by consideration of the specific mechanical behaviors of the rock mass. In the enhanced model, CJRM is considered as the composite of columns of rock and two sets of weak planes of joints. The local coordinates, failure modes, and failure sequences of the rock columns and joints are redefined based on the composite characteristics of CJRM, and the failure criteria and plastic potential functions are accordingly modified. The enhanced model is verified numerically by triaxial compression tests and then employed to simulate the excavation of large underground caverns of a pumped storage power station in China. Results show that the modification of the local coordinate system, failure modes, and failure sequences made in the enhanced model is suited to the simulation of the mechanical behaviors of CJRM. Compared with the original ubiquitous-joint model, the enhanced model allows better predictions of the distribution of plastic zones and magnitudes of deformations in simulating underground excavations in CJRM and helps to assess the excavation-triggered hazards more accurately.

Introduction

Joints are often found in rock masses around underground caverns and usually occur in one or more sets in different directions, cutting the rock mass into blocky structures (Bandis et al., 1983; Jaeger et al., 2007; Wu et al., 2018). Jointed rock masses can be divided into several categories based on the number of joint sets, such as layered (or bedded) jointed rock masses with only one dominant set of joints, conjugate jointed rock masses (CJRM) with two dominant sets of joints, and other jointed rock masses with three or more sets of joints (Jaeger et al., 2007). Each set of joints affects the mechanical properties of the rock mass (Hoek and Brown, 1997); therefore, suitable descriptions of the constitutive relationships thereof are necessary for numerical stability analysis and hazard assessment of underground excavations (Agharazi et al., 2012; Ding et al., 2019).

Many studies have been conducted to assess the strength and deformation characteristics as well as the excavation responses of jointed rock masses. Theoretical investigations mainly focused on the prediction of the mechanical parameters of jointed rock masses based on superposition theory (Goodman et al., 1968; Jaeger et al., 2007), elasto-plastic damage theory (Chen et al., 2010; Yang et al., 2019), or displacement discontinuity method (Shen et al., 2016; Do and Wu, 2020). In experimental investigations, researchers obtained stress-strain relationships by conducting triaxial compression tests and validated the theoretical predictions through comparative analysis with the experimental results (Nova, 1980; Tien and Kuo, 2001; Singh et al., 2002; Tien et al., 2006; Chen et al., 2012; Chang et al., 2019). Numerical-analysis-based researches investigated the effects of the distribution properties (such as the orientation and spacing) and mechanical parameters of layered joints on the failure mode, plastic zones, and deformation of the surrounding rock masses (Adhikary and Dyskin, 1997; Park and Adachi, 2002; Wang and Huang, 2014; Zhou et al., 2016; Sainsbury and Sainsbury, 2017; Zhou et al., 2019; Yang et al., 2019; Zhou et al., 2021) as well as the internal forces and failure modes of the reinforcements (Hatzor et al., 2015; Gao et al., 2019) of underground caverns. Furthermore, many researchers proposed or modified constitutive models for layered jointed rock masses. For example, Jaeger (1960) proposed a theory based on the action of a single weak plane to predict the strength properties; Nova (1980)(Nova and Zaninetti, 1990) used the traditional Mohr–Coulomb (M–C) strength criterion to analyze the directional failures and this method has been used in the development of the ubiquitous-joint (U-J) model in Flac^3D (Itasca Consulting Group, 2011). Other researchers (Adhikary and Dyskin, 1998; Sitharam et al., 2001; Wang and Huang, 2009; Sainsbury and Sainsbury, 2017; Zhou et al., 2017; Das et al., 2019) further improved the constitutive equations of U-J model based on equivalent continuum methods.

These studies indicate that layered jointed rock masses have significant anisotropy of strength and deformation, are prone to shear and tensile failures on the weak planes of joints, and are prone to bending, shear, and tensile failures of the intact rock layers (Chen et al., 2012; Shen et al., 2016; Chang et al., 2019; Do and Wu, 2020). In addition, other investigations have proved that many engineering failure events triggered by underground excavation occur in such jointed rock masses (Chen et al., 2013; Ding et al., 2019; Do and Wu, 2020), and with increasing complexity of the joint sets, the excavation-induced disaster is usually greater (Jiang et al., 2014; Hatzor et al., 2015; Zhao et al., 2020). However, although the mechanical behaviors of layered jointed rock masses have been widely studied, little attention has been paid to CJRM which has more complexity of joint sets and few corresponding engineering case studies have been reported.

CJRM is usually shaped into rock columns (intact columnar rocks) by conjugate joints. Geological research indicates that the conjugate joints are formed when two sets of in situ shear stress act, and since the direction of shear stress does not change significantly within a local area, the joints in the same set are roughly parallel (Deng et al., 2009; Ning et al., 2009; Wang et al., 2020). Besides, there are no weak interlayers in the joints due to the shear stress-induced formation process thereof, so conjugated joints can be regarded as two sets of parallel weak planes instead of weak interlayers. Thus, CJRM can be considered as the composite of columns of rock and two sets of weak planes of joints (Nova and Zaninetti, 1990; Wang and Huang, 2014).

The rock columns and weak planes of joints have different failure modes in the surrounding rock masses during underground excavations (Jia and Tang, 2008; Wang et al., 2014). Chinese researchers (Jiang et al., 2014; Fan et al., 2017; Li et al., 2018; Jiang et al., 2019; Zhao et al., 2020) investigated the excavation-induced failure of the columnar jointed basalt of Baihetan hydropower station and ascertained the effects of joints on the spatially inhomogeneous distribution of damage zones, but the failure modes of the rock columns and joints are scarcely understood. Wang and Huang (2009; 2014) extended U-J model to include the failure mode and deformation performance for blocky rock masses with multiple sets of joints; however, their model did not consider the specific mechanical behaviors of the two sets of joints and the rock columns of CJRM, such as the bending failure of the rock columns and the effect of the angle between the two sets of joints.

This study improves U-J model for such specific mechanical behaviors of CJRM and uses the enhanced model to analyze the stability of underground caverns during excavation. In the enhanced model, the local coordinate system is redefined and the related failure modes, failure sequences, failure criteria, and plastic potential functions are accordingly modified on the basis of U-J model in Flac^3D. The enhanced model is verified by numerical triaxial compression tests and used to investigate the excavation-induced deformation and plastic zones of the rock mass surrounding the underground caverns of a pumped storage power station in China. By comparing the simulation results arising from use of the enhanced model with those by the similar constitutive models, including the Mohr–Coulomb (M–C) model and U-J model, results show that the enhanced model provides a better prediction of the distribution of plastic zones and magnitudes of deformation when used to simulate underground excavations in CJRM.

Preparation for the Enhanced Model

Assumption of the Failure Process

CJRM (Figure 1A) contains two sets of joints (joint sets 1 and 2), which cut the rock mass into columns. The mechanical behaviors of such rock mass are determined by the joints and rock columns (Wang and Huang, 2014; Chang et al., 2019; Do and Wu, 2020). In the enhanced model, the assumed failures of CJRM include three categories: 1) the shear and tensile failures on the weak planes of joints, 2) shear and tensile failures of the rock columns, and 3) bending failure along the rock column axes. In addition, the assumed failure sequences between the weak planes and rock columns are such that 4) the weak planes fail before the rock columns, and 5) the weak plane at the greater distance from the stress state point to the corresponding strength envelope fails first if both weak planes fail in the same iteration process.

FIGURE 1

FIGURE 1. Method for establishing the local coordinate system of CJRM.

The reasons for making such assumptions are as follows: firstly, in the cross-section plane of the rock columns (Figure 1B), the rock mass is blocky so that the strength and deformability are mainly controlled by the joints (Singh et al., 2002; Singh and Rao, 2005). Assumption 1) ensures that material failures in such plane occur only on the weak planes of joints and that plastic deformation in the cross-section plane is mainly controlled by sliding deformation on the weak planes and tensile deformation perpendicular thereto. Secondly, in the axial direction of rock columns, the failures of the rock mass mainly occur in the rock columns. The failure modes include shear and tensile failures of the rock columns and bending failure (Adhikary and Guo, 2002; Neff et al., 2008) along the rock columns, as per assumptions 2) and 3), respectively. Thirdly, studies (Jiang et al., 2006; Hatzor et al., 2015) have shown that jointed rock masses usually fail on the joints first, followed by failure of the intact rocks, so assumption 4) guarantees a reasonable sequence of failure events between joints and rock columns.

Definition of the Local Coordinate System

Similar to the principle of U-J model, the enhanced model is a completely equivalent continuum model (Mühlhaus, 1993; Adhikary and Dyskin, 1998; Sitharam et al., 2001) that the influence of the joints is smeared into the continuum description of the rock mass, so the distributions (such as the spacing and length) of the joints, except the orientation, are not necessarily defined explicitly (Agharazi et al., 2012; Wang and Huang, 2014; Zhou et al., 2021). In the enhanced model, the local coordinate system is redefined based on the orientations of the two sets of joints the better to describe the mechanical properties of CJRM.

One of the rock columns is taken as an example to illustrate the method for establishing the local coordinate system (Figures 1B,C). First, the axial direction of the rock column is defined as the $z^{\prime }$-axis; second, the direction perpendicular to $z^{\prime }$-axis and in the plane of joint set 1 is defined as the $x^{\prime }$-axis, and the direction perpendicular to $z^{\prime }$-axis and in the plane of joint set 2 is defined as the $y^{\prime }$-axis. Since the orientations of the two joint sets are not necessarily perpendicular, the angle between the $x^{\prime }$-axis and $y^{\prime }$-axis is between 0 and 180° on the cross-section of the rock column (Figure 1D). The directions of the local coordinates $x^{\prime }$-, $y^{\prime }$-, and $z^{\prime }$-axes are determined as described below.

Vectors ${\mathit{J}}_1$ and ${\mathit{J}}_2$ are defined as direction vectors normal to the weak planes of joint sets 1 and 2, respectively, and vectors ${\mathit{x}}^{\prime }$, ${\mathit{y}}^{\prime }$, and ${\mathit{z}}^{\prime }$ are defined as the positive direction vectors of the local coordinate $x^{\prime }$-, $y^{\prime }$-, and $z^{\prime }$-axes, respectively. Based on the perpendicularity relationships between the five vectors, the directions of the local coordinate axes are given by

$\begin{array}{ccc}{\mathit{z}}^{\prime }:& {\mathit{J}}_1\cdot {\mathit{z}}^{\prime }=0& \begin{array}{cc}{\mathit{J}}_2\cdot {\mathit{z}}^{\prime }=0& \left|{\mathit{z}}^{\prime }\right|=1\end{array},\\ {\mathit{x}}^{\prime }:& {\mathit{J}}_1\cdot {\mathit{x}}^{\prime }=0& \begin{array}{cc}{\mathit{z}}^{\prime }\cdot {\mathit{x}}^{\prime }=0& \left|{\mathit{x}}^{\prime }\right|=1\end{array},\\ {\mathit{y}}^{\prime }:& {\mathit{J}}_2\cdot {\mathit{y}}^{\prime }=0& \begin{array}{cc}{\mathit{z}}^{\prime }\cdot {\mathit{y}}^{\prime }=0& \left|{\mathit{y}}^{\prime }\right|=1\end{array},\end{array}(1)$

where ${\mathit{J}}_1$ and ${\mathit{J}}_2$ are calculated from the dip angles ($Di{p}_1$ and $Di{p}_2$) and dip directions ($D{D}_1$ and $D{D}_2$) of joint sets 1 and 2, respectively.

$\begin{array}{c}{\mathit{J}}_1=\left(\text{sin}D{D}_1,\text{cos}D{D}_1,\text{cot}Di{p}_1\right),\\ {\mathit{J}}_2=\left(\text{sin}D{D}_2,\text{cos}D{D}_2,\text{cot}Di{p}_2\right).\end{array}(2)$

Matrix $\left[C\right]$ is defined as the rotation tensor between the local and the global coordinate systems, and then the transformation of stress components between the two coordinate systems (Itasca Consulting Group, 2011) is given by

${\left[\sigma \right]}^{\prime }={\left[C\right]}^T\left[\sigma \right]\left[C\right]\left[\sigma \right]=\left[C\right]\left[\sigma \right]\prime {\left[C\right]}^T,(3)$

where $\left[C\right]$ is

$\left[C\right]=\left[\begin{array}{ccc}\text{cos}(x^{\prime },x)& \text{cos}(x^{\prime },y)& \text{cos}(x^{\prime },z)\\ \text{cos}(y^{\prime },x)& \text{cos}(y^{\prime },y)& \text{cos}(y^{\prime },z)\\ \text{cos}(z^{\prime },x)& \text{cos}(z^{\prime },y)& \text{cos}(z^{\prime },z)\end{array}\right].(4)$

Generalized Stress and Strain Components

Weak planes of joints in the enhanced model are ubiquitous in the rock mass based on the theory of the equivalent continuum model (Mühlhaus, 1993; Adhikary and Dyskin, 1998; Sitharam et al., 2001). The stress and strain components at any point in the rock mass can be expressed as shown in Figure 2 without consideration of the spacing and length of the joints in the local coordinate system. On the weak planes of joint set 1, shear stress ${\tau }_{1^{\prime }}$ and shear strain ${\gamma }_{1^{\prime }}$ have the following forms:

$\begin{array}{l}{\tau }_{1^{\prime }}=\sqrt{{\sigma }_{2\prime 1\prime }^2+{\sigma }_{3\prime 1\prime }^2},\\ {\gamma }_{1^{\prime }}=\sqrt{{\mathit{ϵ}}_{2\prime 1\prime }^2+{\mathit{ϵ}}_{3\prime 1\prime }^2}.\end{array}(5)$

FIGURE 2

FIGURE 2. Stress (A) and strain (B) components of CJRM in the local coordinate system.

The equivalent forms are readily obtained for joint set 2:

$\begin{array}{l}{\tau }_{2^{\prime }}=\sqrt{{\sigma }_{1^{\prime }{2}^{\prime }}^2+{\sigma }_{3^{\prime }{2}^{\prime }}^2},\\ {\gamma }_{2^{\prime }}=\sqrt{{\mathit{ϵ}}_{1^{\prime }{2}^{\prime }}^2+{\mathit{ϵ}}_{3^{\prime }{2}^{\prime }}^2}.\end{array}(6)$

On the cross-sections of the rock columns, the similar forms are

$\begin{array}{l}{\tau }_{3^{\prime }}=\sqrt{{\sigma }_{1^{\prime }{3}^{\prime }}^2+{\sigma }_{2^{\prime }{3}^{\prime }}^2},\\ {\gamma }_{3^{\prime }}=\sqrt{{\mathit{ϵ}}_{1^{\prime }{3}^{\prime }}^2+{\mathit{ϵ}}_{2^{\prime }{3}^{\prime }}^2}.\end{array}(7)$

In what follows, the failures of rock mass are detected by the six components of the generalized stress vector: ${\sigma }_{1^{\prime }{1}^{\prime }}$, ${\sigma }_{2^{\prime }{2}^{\prime }}$, ${\sigma }_{3^{\prime }{3}^{\prime }}$, ${\tau }_{1^{\prime }}$, ${\tau }_{2^{\prime }}$, and ${\tau }_{3^{\prime }}$ whose components of the corresponding generalized strain vector are ${\mathit{ϵ}}_{1^{\prime }{1}^{\prime }}$, ${\mathit{ϵ}}_{2^{\prime }{2}^{\prime }}$, ${\mathit{ϵ}}_{3^{\prime }{3}^{\prime }}$, ${\gamma }_{1^{\prime }}$, ${\gamma }_{2^{\prime }}$, and ${\gamma }_{3^{\prime }}$.

Enhancement of U-J Model for Conjugate Jointed Rock Mass

On the basis of U-J model, the enhanced model for CJRM is proposed using the redefined local coordinate system and the generalized stress and strain components. The mechanical behaviors of CJRM, such as the number of joint sets as well as the failure modes and failure sequences of the joints and rock columns, are considered in the enhanced model and then implemented as a plug-in dynamic link library (.DLL) file into the finite difference code FLAC^3D using the user-defined constitutive models function.

Description of the Joints

The failure criterion for the weak planes of joints used in the enhanced model is a composite M–C criterion with a tension cut-off expressed in terms of ${\sigma }_{i^{\prime }{i}^{\prime }}$ and ${\tau }_{i^{\prime }}$ (where $i=1, 2, 3$), as illustrated in Figure 3.

FIGURE 3

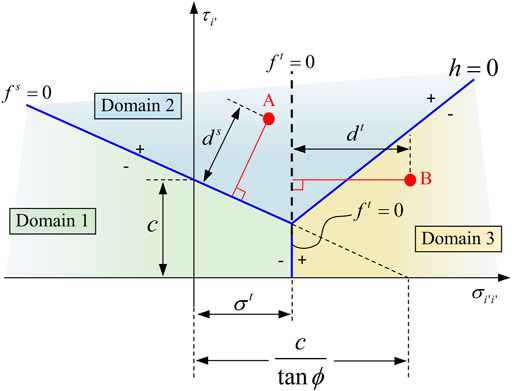
FIGURE 3. Failure criterion in M–C constitutive model (Itasca Consulting Group, 2011) and judgment of the failure sequence of joints.

When shear failures occur on the weak planes of joints, the stress states calculated using the initial elastic estimate are located in Domain 2 (Itasca Consulting Group, 2011). The corresponding failure criteria meet the following conditions:

For joint set 1,

$\begin{array}{l}{f}_{J1}^s={\tau }_{1^{\prime }}+{\sigma }_{1^{\prime }{1}^{\prime }}\text{tan}{\varphi }_{J1}-c_{J1}>0,\\ h_{J1}=\tau -{\tau }_{J1}^P-a_{J1}^P\left({\sigma }_{1^{\prime }{1}^{\prime }}-{\sigma }_{J1}^t\right)>0.\end{array}(8)$

For joint set 2,

$\begin{array}{l}{f}_{J2}^s={\tau }_{2^{\prime }}+{\sigma }_{2^{\prime }{2}^{\prime }}\text{tan}{\varphi }_{J2}-c_{J2}>0,\\ h_{J2}=\tau -{\tau }_{J2}^P-a_{J2}^P\left({\sigma }_{2^{\prime }{2}^{\prime }}-{\sigma }_{J2}^t\right)>0,\end{array}(9)$

and

$\begin{array}{l}{\tau }_{J1}^P=c_{J1}-{\sigma }_{J1}^t\text{tan}{\varphi }_{J1},\\ a_{J1}^P=\sqrt{1+\text{tan}{\varphi }_{J1}^2}-\text{tan}{\varphi }_{J1},\\ {\tau }_{J2}^P=c_{J2}-{\sigma }_{J2}^t\text{tan}{\varphi }_{J2},\\ a_{J2}^P=\sqrt{1+\text{tan}{\varphi }_{J2}^2}-\text{tan}{\varphi }_{J2},\end{array}(10)$

where $c_{J1}$, $c_{J2}$, ${\varphi }_{J1}$, ${\varphi }_{J2}$, ${\sigma }_{J1}^t$, and ${\sigma }_{J2}^t$ are the cohesion, angle of internal friction, and tensile strength of the weak planes of joints, respectively. For weak planes with non-zero internal friction angles, the maximum values of the tensile strengths are given by

${\sigma }_{J1}^t\le \frac{c_{J1}}{\text{tan}{\varphi }_{J1}}{\sigma }_{J2}^t\le \frac{c_{J2}}{\text{tan}{\varphi }_{J2}}.(11)$

The potential functions $g_{J1}^s$ and $g_{J2}^s$ corresponding to a non-associated flow rule have the following forms:

For joint set 1,

$g_{J1}^s=\tau +{\sigma }_{1^{\prime }{1}^{\prime }}tan{\psi }_{J1}.(12)$

For joint set 2,

$g_{J2}^s=\tau +{\sigma }_{2^{\prime }{2}^{\prime }}tan{\psi }_{J2},(13)$

where ${\psi }_{J1}$ and ${\psi }_{J2}$ are the angles of dilation of the weak planes.

When tensile failures occur on the weak planes of joints, the stress states calculated from the elastic estimate are located in Domain 3. The corresponding failure criteria meet the following conditions:

For joint set 1,

$\begin{array}{l}{f}_{J1}^t={\sigma }_{1^{\prime }{1}^{\prime }}-{\sigma }_{J1}^t>0,\\ h_{J1}=\tau -{\tau }_{J1}^P-a_{J1}^P\left({\sigma }_{1^{\prime }{1}^{\prime }}-{\sigma }_{J1}^t\right)\le 0.\end{array}(14)$

For joint set 2,

$\begin{array}{l}{f}_{J2}^t={\sigma }_{2^{\prime }{2}^{\prime }}-{\sigma }_{J2}^t>0,\\ h_{J2}=\tau -{\tau }_{J2}^P-a_{J2}^P\left({\sigma }_{2^{\prime }{2}^{\prime }}-{\sigma }_{J2}^t\right)\le 0.\end{array}(15)$

The potential functions $g_{J1}^t$ and $g_{J2}^t$ corresponding to an associated flow rule have the following forms:

For joint set 1,

$g_{J1}^t={\sigma }_{1^{\prime }{1}^{\prime }}.(16)$

For joint set 2,

$g_{J2}^t={\sigma }_{2^{\prime }{2}^{\prime }}.(17)$

When no failures occur on the weak planes of joints, the stress states calculated using the elastic estimate are located in Domain 1 and are considered as the final incremental stress without any correction by way of potential functions. The corresponding failure criteria meet the following conditions:

For joint set 1,

$\begin{array}{l}{f}_{J1}^s={\tau }_{1^{\prime }}+{\sigma }_{1^{\prime }{1}^{\prime }}\text{tan}{\varphi }_{J1}-c_{J1}\le 0,\\ f_{J1}^t={\sigma }_{1^{\prime }{1}^{\prime }}-{\sigma }_{J1}^t\le 0.\end{array}(18)$

For joint set 2,

$\begin{array}{l}{f}_{J2}^s={\tau }_{2^{\prime }}+{\sigma }_{2^{\prime }{2}^{\prime }}\text{tan}{\varphi }_{J2}-c_{J2}\le 0,\\ f_{J2}^t={\sigma }_{2^{\prime }{2}^{\prime }}-{\sigma }_{J2}^t\le 0.\end{array}(19)$

In addition, it should be noted that both of the weak planes may fail in the same iteration process under a certain stress state in the rock mass. The choice of potential functions for stress correction is determined by the failure sequence and affects the corrected stress state. In the enhanced model, the failure sequence is judged by the distances, $d_{Ji}^s$ and $d_{Ji}^t$, from stress state points A and B to the corresponding envelopes, $f_{Ji}^s$ and $f_{Ji}^t$, as illustrated in Figure 3. The greater the distance (either $d_{Ji}^s$ or $d_{Ji}^t$), the greater the amount by which the stress calculated by the elastic estimate exceeds the corresponding failure envelope; so, the weak plane with the greater value of $d_{Ji}^s$ or $d_{Ji}^t$ is more prone to failure than the other and it fails first. The distance functions have the forms:

$\begin{array}{l}{d}_{Ji}^s=\frac{f_{Ji}^s}{\sqrt{1+ta{n}^2{\varphi }_{Ji}}},\\ d_{Ji}^t=f_{Ji}^t.\end{array}(20)$

Description of the Rock Columns

The failure mode of the rock columns involve shear and tensile failures of the columns and bending failure along the columns as assumed (Adhikary and Guo, 2002; Neff et al., 2008). When shear and tensile failures occur, a similar procedure to that used in M–C constitutive model (Itasca Consulting Group, 2011) can be used to calculate the incremental stress and strain. This section mainly discusses the bending failure of the rock columns.

Figure 4 illustrates the bending failure of a rock column in the local coordinate system. When a bending moment acts on the rock column, as shown in Figure 4, the rock column is subjected to compressive stress on the upper side and tensile stress on its lower side. With increasing bending moment, the tensile stress on the lower side increases until it exceeds the tensile strength, resulting in a bending failure on the lower side (Agharazi et al., 2012; Sainsbury and Sainsbury, 2017). However, the tensile stress is difficult to calculate accurately, as joints are smeared into the continuum description of the rock mass by an equivalent continuum method and have no boundaries and thickness (Agharazi et al., 2012; Wang and Huang, 2014; Zhou et al., 2021). Thus, the normal stress on the column cross-section ${{\sigma }^{\prime }}_{3^{\prime }{3}^{\prime }}$ is used as an approximate replacement for the tensile stress. The bending failure criterion has the form:

$f^b={\sigma }_{3^{\prime }{3}^{\prime }}^{\prime }-{\sigma }_0^b\ge 0,(21)$

where ${\sigma }_0^b$ is the bending strength of rock columns. Generally, the bending strength is less than the tensile strength although it has similar forms of failure criterion in the $z^{\prime }$-direction. The potential function $g^b$ corresponding to an associated flow rule has the form:

$g^b={{\sigma }^{\prime }}_{3^{\prime }{3}^{\prime }}.(22)$

FIGURE 4

FIGURE 4. Bending failure of a rock column.

Verification of the Enhanced Model

Verification Settings

Numerical triaxial compression tests were conducted to verify the enhanced model. The samples used in the tests were cylinders with a diameter of 1 m and a height of 2 m. The compressive strength, plastic zones, and deformation of the samples were analyzed: contrasting simulations were conducted using the enhanced model and U-J model. The material parameters used in these simulations are listed in Table 1. The confining pressure used in all such simulated tests is 1 MPa.

TABLE 1

TABLE 1. Material parameters for the triaxial compression tests.

The difference of the triaxial compression test samples between use of U-J model and the enhanced model mainly lies in the consideration of the number of joint sets and local coordinate system. For the sample simulated using U-J model, only one set of joints is considered at a time (Figure 5A); the three local coordinate axes are mutually orthogonal and meet the right-handed spiral criterion. By contrast, two sets of joints are considered at a time for the sample simulated using the enhanced model (Figure 5B); the included angle of the local coordinate axes $x^{\prime }$ and $y^{\prime }$ is determined by the occurrence of joints, which ranges from 90° to 270°, and the coordinate axis $z^{\prime }$ is perpendicular to the plane formed by axes $x^{\prime }$ and $y^{\prime }$.

FIGURE 5

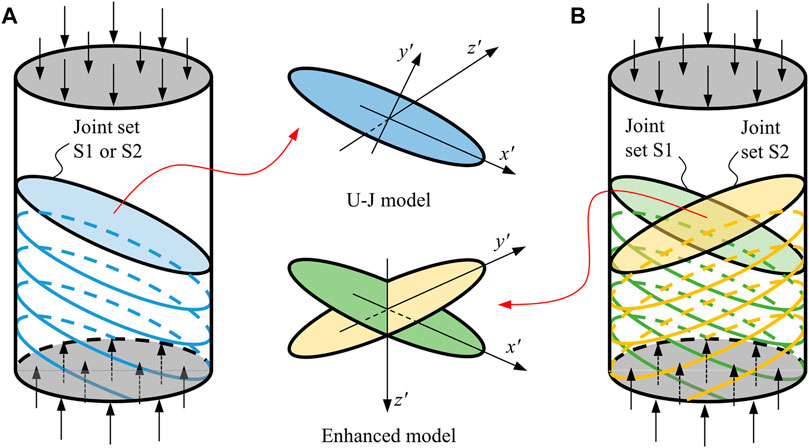
FIGURE 5. Schematic diagram of difference in triaxial compression tests between the use of U-J model (A) and the enhanced model (B).

During the numerical simulations, the compression stress and confining pressure acting on the samples are initially 0.1 MPa and gradually increased with an increment of 0.1 MPa. The confining pressure stops increasing when it reaches the target value of 1 MPa and then stays the same. The compression stress keeps increasing until the calculation no longer converges. The total compression stress of the final converged solution is taken as the compressive strength of the samples (Neff et al., 2008; Chang et al., 2019).

Results and Discussion

Strength

Figure 6A shows the compressive strength of the samples simulated using the enhanced model and U-J model, considering different joint sets with varying dip angles. As shown in the figure, there is a significant difference between the compressive strength calculated using the U-J model and that calculated using the enhanced model. When U-J model is used to consider one of the joint sets, the relationship between the triaxial compressive strength and the dip angles of joints is a typically U-shaped curve, where the dip angles are the acute angles between the normal direction of the joints and the axis direction of the samples. The compressive strength is at a minimum when the dip angle of the joints is close to ($\text{π}/4+{\varphi }_j/2$) where ${\varphi }_j$ is the friction angle of the weak planes of joints (Jaeger et al., 2007). However, when the enhanced model is used to consider the two joint sets, the compressive strength is the lower value of those calculated by U-J model, considering one of the two joint sets, and the relationship may no longer be U-shaped curve.

FIGURE 6

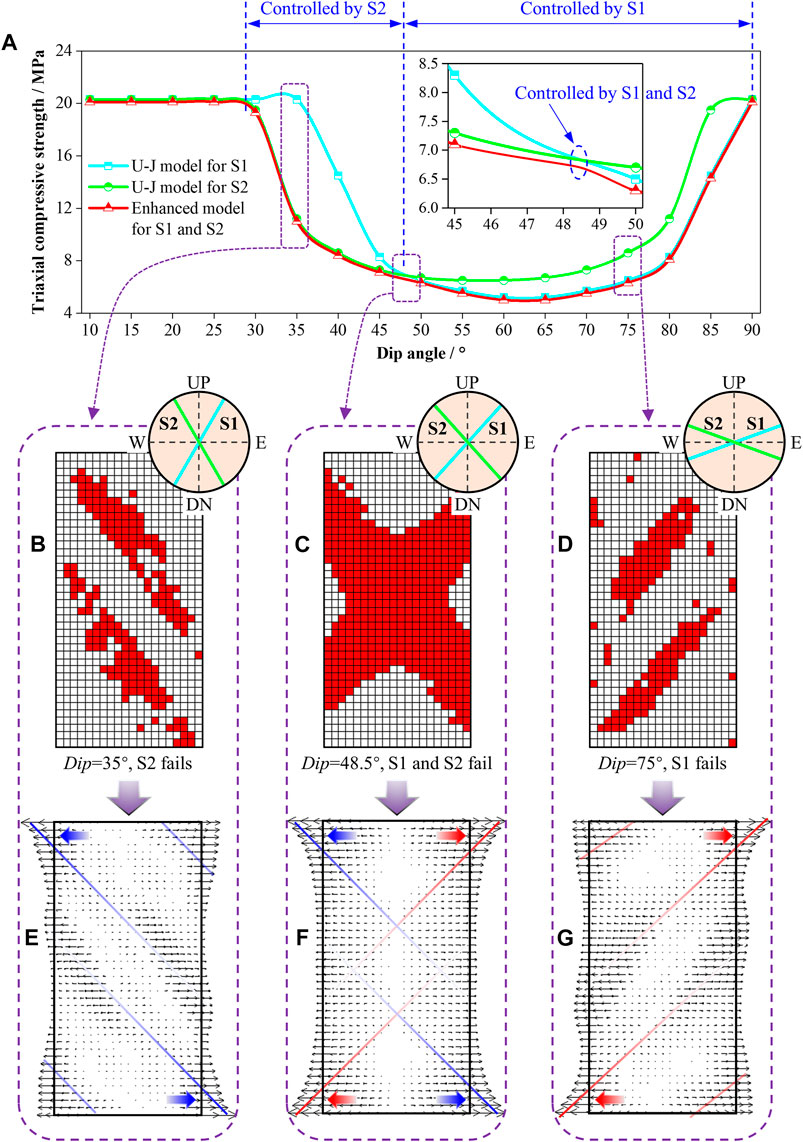
FIGURE 6. Results of the verification simulation: (A) relations between the triaxial compressive strength and the dip angles of joints; (B–D) failures of the joints; (E,F) horizontal components of the total deformations.

It also can be seen from Figure 6A that the strength of the samples of CJRM in Table 1 is mainly controlled by one of the two sets of joints with dip angles ranging from 30° to 90°. The strength is controlled by joint set S2 when the dip angles range from 30° to 48.5°, by joint set S1 when the dip angles range from 48.5° to 90°, and by both of S1 and S2 when the dip angles are about 48.5°. The strength of CJRM behaves consistently with the theoretical prediction (superposition theory) of multiple sets of joints proposed by Jaeger (Jaeger et al., 2007), which indicates that the enhanced model is implemented correctly and suitable for strength simulation of CJRM.

Plastic Zones

Figures 6B–D show the performance of the enhanced model in terms of the simulation of plastic zones. The samples with dip angles of 35°, 48.5°, and 75°, respectively, are taken to study the failure modes of CJRM based on the behavior in compressive strength. As shown in the figures, the plastic zones mainly occur in the strike direction of joint set S2 (Figure 6B) when the dip angles of the two sets of joints are 35°, in the strike direction of joint set S1 (Figure 6D) when the dip angles are 75°, and in the strike directions of both the joint sets S1 and S2 (Figure 6C) when the dip angles are about 48.5°. This phenomenon shows that with the change of the dip angle of the two sets of joints, the failures of the samples occur on different sets of joints. In general, the failure modes of the samples coincide with the compressive strength, indicating that the enhanced model can reasonably reflect the failure modes of CJRM.

Deformation

The deformations of the samples of CJRM with dip angles of 35°, 48.5°, and 75°, respectively, were calculated using the enhanced model. The horizontal components of the total deformations are presented to illustrate the contribution of joints to the total deformations (Figures 6E–G). As shown in Figure 6E, the horizontal deformation of the sample is at a maximum in the strike direction of joint set S2 when the dip angles of joints are 35°. Similar results can be obtained when the dip angles of joints are 48.5° (Figure 6F) and 75° (Figure 6G), respectively, showing that the deformations of the samples increase in the strike directions of the joints controlling the strength and plastic zone distribution of the samples. Comparing the distribution of plastic zones of the samples, it can be inferred that the increased deformation in the strike direction of the joints is derived from the plastic flows of the plastic zones occurring on the weak planes of joints. In conclusion, the joints in CJRM exert an important influence on the deformation, which is consistent with our previous assumptions.

Simulation of Underground Excavation Responses Using the Enhanced Model

Background of the Engineering Case

The case study involves the underground excavation simulation of a pumped storage power station in China. The underground caverns are located in a medium-coarse-grained granite (Figure 7A). Two conjugate sets of joints, J1 and J2, occur therein (Figure 7B). The axial directions of the powerhouse and transformer chamber are parallel and lie along the north-south direction (Figure 7C). The in situ stresses in the rock mass are such that 1) the horizontal major principal stress ${\sigma }_1$ ranges from 12 to 18 MPa with the east-west direction; 2) the horizontal minor principal stress ${\sigma }_3$ ranges from 7 to 11 MPa with the north-south direction; and 3) the vertical principal stress ranges from 6.6 to 9.3 MPa. The dimensions and excavation sequence of the underground caverns are shown in Figure 7D. The main support measures include 1) mortar anchors with lengths of 6 or 9 m at 1.5 m × 1.5 m grid spacings, 2) prestressed anchor cables with a length of 25 m at 4.5 m × 4.5 m spacings, and 3) steel fibreconcrete liners with a thickness of 150 mm sprayed onto the surface of the cavern walls. The mechanical properties of the rock mass are listed in Table 2 and those of the support structures are listed in Table 3.

FIGURE 7

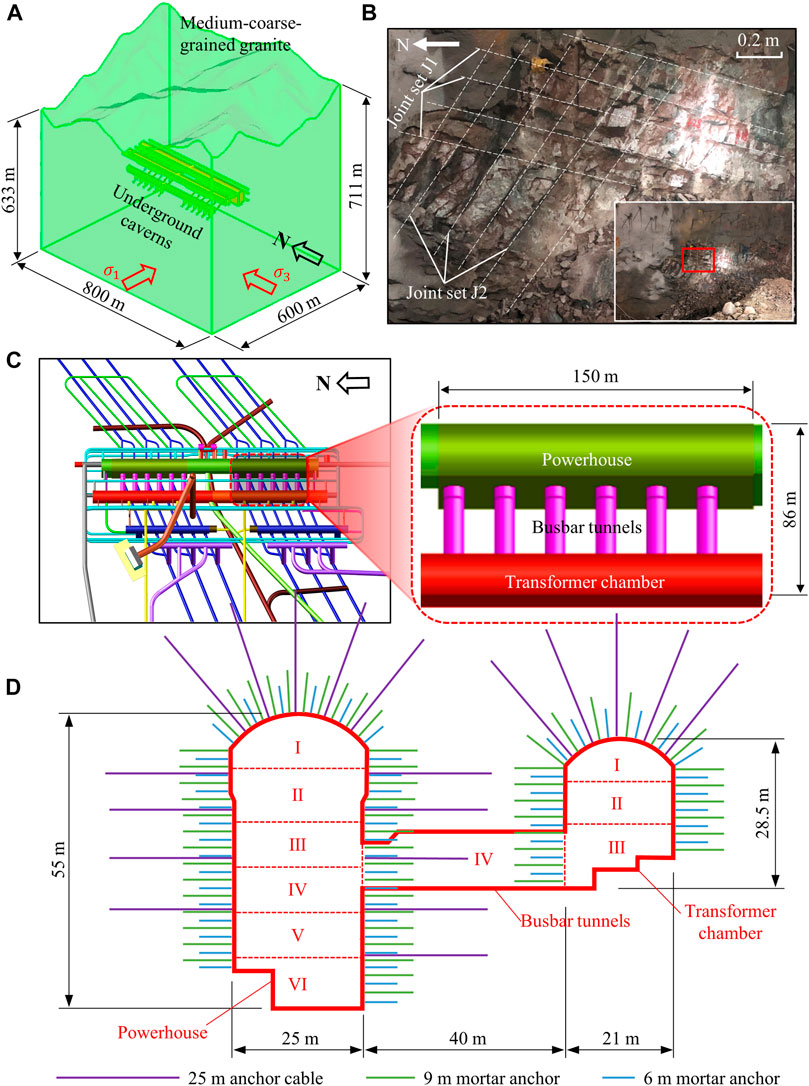
FIGURE 7. Geological conditions (A,B), dimensions (C), and support measures (D) of the underground caverns.

TABLE 2

TABLE 2. Mechanical parameters of the rock mass.

TABLE 3

TABLE 3. Parameters of the support structures.

The main engineering problems encountered in the underground caverns during the excavation are as follows: 1) with the downward excavation of the powerhouse and transformer chamber, the stress field of the surrounding rock mass evolves, resulting in joint slippage and cracking of the liners (Figure 8A); 2) after the excavation of IV step is finished, the total deformation of the surrounding rock mass with a maximum value of 100 mm is much greater than the designed value of 50–60 mm. The monitored total deformations on some main cross-sections of the powerhouse are shown in Figure 8B. Compared with other underground engineering with similar lithology, in situ stress, size of excavation, and other conditions (Zhu et al., 2008; Zhu et al., 2010), the most prominent geological feature of the present engineering is that the conjugate joints in the rock mass are relatively well-developed. Therefore, it can be inferred that one of the possible factors inducing the aforementioned engineering problems is the strength reduction of the rock mass due to the conjugate joints, making it necessary to use the enhanced model to study the plastic zones and deformation characteristics of the surrounding rock mass.

FIGURE 8

FIGURE 8. Cracked liner (A) and monitored deformation (B) of the powerhouse.

Preparation for the Simulation

In the excavation simulation of the underground caverns, the excavation sequence is I through VI, as shown in Figure 7D. The anchors and cables are simulated by cable elements and the liners are simulated by shell elements (Itasca Consulting Group, 2011). The parameter settings of the anchors, cables, and liners are consistent with those listed in Table 3. The enhanced model, as well as M–C model and U-J model used as contrasting models, are each used to calculate the distribution of plastic zones and deformation of the surrounding rock mass. The rock mass properties used in the simulation are those listed in Table 2.

M–C model and U-J model are selected as contrasting models for the enhanced model due to both the similarities and differences between them. The similarities lie in the failure criteria and the potential functions for joints and intact rocks, i.e., they are all derived from M–C yield criterion. The differences lie in the consideration of the numbers of joint sets and the enhancements in the local coordinate system, failure modes, and failure sequences of the enhanced model. In terms of the numbers of joint sets, neither joint set J1 nor J2 can be considered in M–C model, either J1 or J2 can be considered in U-J model, but both J1 and J2 can be considered in the enhanced model. Thus, by comparing the results calculated using the three models, the effects of joints on strength and deformation behaviors of the surrounding rock mass and the responses of the enhanced model in underground excavation simulations can be determined.

Distribution of Plastic Zones

The distributions of plastic zones calculated by the three models are presented in Figure 9: when U-J model is used to simulate either joint set J1 or J2, the distributions of plastic zones are mainly concentrated on the upper left and lower right corners of the powerhouse (when considering J1) or on the lower left and upper right corners (when considering J2). By contrast, when the enhanced model is used to simulate both joint sets J1 and J2, the plastic zones are distributed all around the powerhouse. The notable difference in the distributions of plastic zones indicates that the plastic zones are significantly affected by the joints and it is necessary to fully consider the effects of the two sets of joints in the simulation of excavation-induced failure in CJRM.

FIGURE 9

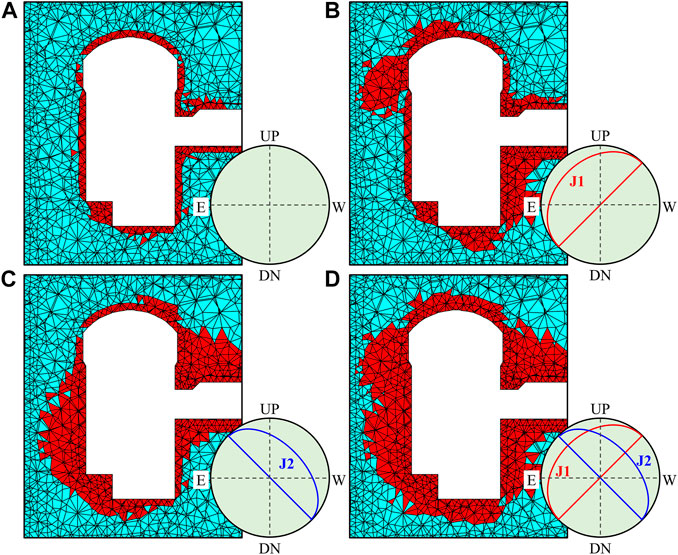
FIGURE 9. Comparison of the plastic zones calculated by the (A) M–C model, (B,C) U-J model, and (D) enhanced model.

The volumes of plastic zones calculated using the enhanced model are significantly larger than those calculated using the U-J model (Figure 9): the difference in the volumes is quantified by comparing the normalized volumes calculated using the three models (Figures 10A,B). Compared with the plastic zone volumes calculated using M–C model considering no joints, those calculated using U-J model considering either joint set J1 or J2 are almost 1.8 times greater, and those calculated using the enhanced model considering both joint sets J1 and J2 are 2.5 times greater (Figure 10A). As the excavation proceeds, the growth rates of plastic zone volumes calculated using each of the three models become significantly different (Figure 10B). From the first excavation step to the final excavation step, the plastic zone volumes increase 1–2.6 times when using M–C model, 1.8–5 times when using U–J model, and as many as 2.2–7 times when using the enhanced model.

FIGURE 10

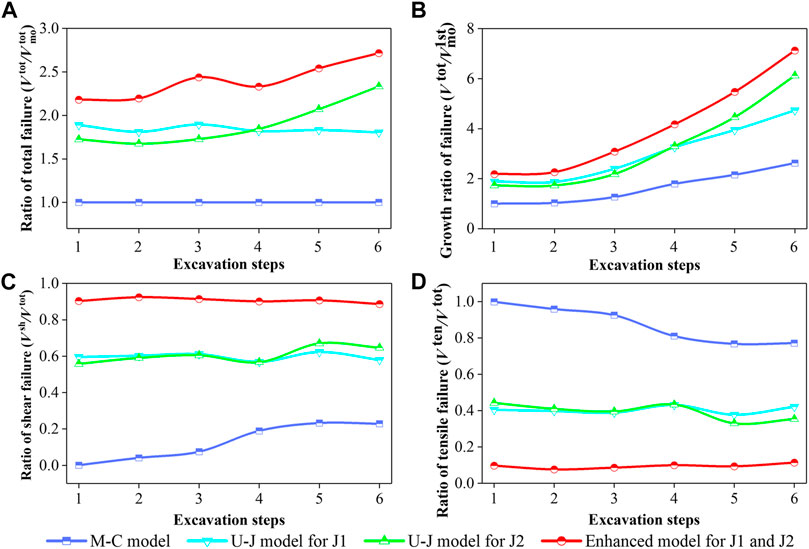
FIGURE 10. Comparison of (A) the volume ratios of total plastic zones ($V^{\text{tot}}/V_{\text{mo}}^{\text{tot}}$), (B) the growth ratios of plastic zone volumes ($V^{\text{tot}}/V_{\text{mo}}^{1\text{st}}$), (C) the volume ratios of shear failures ($V^{\text{sh}}/V^{\text{tot}}$), and (D) the volume ratios of tensile failures ($V^{\text{ten}}/V^{\text{tot}}$) at each excavation step. $V^{\text{tot}}$ is the total failure volume (including volumes of shear and tensile failures); $V_{\text{mo}}^{\text{tot}}$ is the total failure volume calculated using M–C model; $V_{\text{mo}}^{1\text{st}}$ is the failure volume calculated using M–C model at the first excavation step; $V^{\text{sh}}$ is the shear failure volume; $V^{\text{ten}}$ denotes the tensile failure volume.

The proportional occurrence of the failure types of the rock mass is different when using different models. As shown in Figures 10C,D, when M–C model is used, the failure of the rock mass is mainly tensile, and the proportions of shear failure and tensile failure are 20 and 80%, respectively. On the contrary, when the U-J model or the enhanced model is used, the rock mass is mainly subjected to shear failure. The proportions of shear failure and tensile failure calculated using U-J model are 60 and 40%, respectively, while the proportions calculated using the enhanced model are 90 and 10%, respectively.

Displacement Characteristics

The displacement contours (Figure 11) calculated using each of the three models are similar in terms of the deformation mode: the deformation of the surrounding rock mass develops towards the opening and the largest deformation occurs on the sidewalls of the powerhouse upon completion of the excavation. The deformation characteristics are consistent with those reported elsewhere (Jia and Tang, 2008; Hatzor et al., 2015), indicating the correctness of the enhanced model in terms of the deformation response. However, there are some differences among the deformation magnitudes calculated using the three models. Compared with the displacement magnitude contour calculated using M–C model (Figure 11A), those calculated using U-J model (Figures 11B,C) are increased on the sidewalls (especially where the arrows indicate in the figures) and the magnitude calculated using the enhanced model (Figure 11D) is increased on almost all of the sidewalls (especially where also found to have been increased when using U-J model, as the arrows indicate in the figure).

FIGURE 11

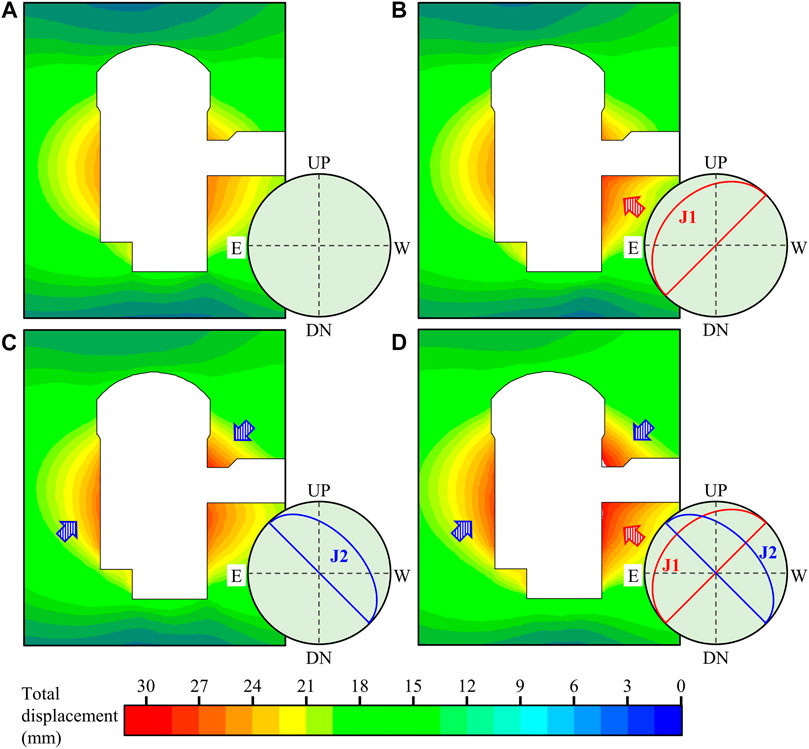
FIGURE 11. Total displacement contours calculated using the (A) M–C model, (B,C) U-J model, and (D) enhanced model.

For further study, the magnitudes of the total displacements calculated using the three models at each excavation step are compared (Figure 12). The total displacements calculated using the three models contain both of the elastic and plastic components. The elastic components are almost the same since they are calculated under the same stress condition, but the plastic components are different since they are derived from plastic flows of different plastic zones. As shown in Figure 12, the displacement magnitudes of the monitored points calculated using the enhanced model are generally similar to, but slightly larger than, those calculated using M–C model and U-J model. This indicates that the total displacements are mainly controlled by the elastic components and the plastic components which are derived from plastic flows of plastic zones entailing only minor corrections to the total displacements.

FIGURE 12

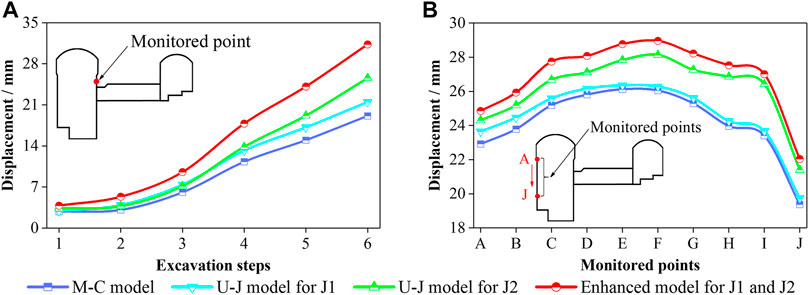
FIGURE 12. Total displacement of (A) the monitored point as the excavation proceeds and (B) the monitored points upon completion of the excavation.

Discussion

Previous work has assessed the use of various constitutive models for layered jointed rock masses (Adhikary and Dyskin, 1998; Sitharam et al., 2001; Sainsbury and Sainsbury, 2017; Zhou et al., 2017) and their strength and deformation performance in the simulation of underground excavations (Jiang et al., 2006; Jia and Tang, 2008; Das et al., 2019; Ding et al., 2019). These studies were mainly focused on rock masses with a set of joints, while little attention has been paid to the mechanical characteristics of CJRM and their excavation responses in underground engineering. In fact, CJRM or similar rock masses often appear in engineering practice. For example, conjugate sets of joints can be found among the multiple sets of joints in the rock mass at Baihetan hydropower station (Jiang et al., 2014; Fan et al., 2017; Li et al., 2018; Jiang et al., 2019; Zhao et al., 2020). In this study, U-J model was enhanced by considering the specific mechanical behaviors of CJRM based on the equivalent continuum method (Mühlhaus, 1993; Adhikary and Dyskin, 1998; Sitharam et al., 2001). The enhanced model was verified by numerical triaxial compression tests and used to simulate the excavation responses of the underground caverns of a pumped storage power station in China.

The comparison of results calculated using the M–C model, U-J model, and enhanced model shows that the mechanical behaviors of jointed rock masses are greatly affected by the number of joint sets. In the triaxial compression tests, the strength of the samples of CJRM is the lower one of the two strengths of the corresponding layered jointed rock masses. These findings are consistent with the superposition theory of multiple sets of joints proposed by Jaeger et al. (2007). In addition, because of the modification of the local coordinate system, failure modes and failure sequences based on the characteristics of CJRM, the enhanced model shows a significant difference from M–C model and U-J model in the simulated excavation of underground caverns in CJRM. The mechanical responses, such as the distribution of plastic zones and displacement of the surrounding rock mass, are significantly underestimated by the M–C model or U-J model but are reasonably estimated by the enhanced model, suggesting that the enhanced model can be used to simulate the mechanical behavior of underground excavations in CJRM.

The prediction of the excavation-induced plastic zones (also considered as excavation-disturbed zones, EDZ) of the surrounding rock mass is of great significance to the design of support measures and the assessment of related hazards of underground caverns (Parise and Lollino, 2011; Chen et al., 2013; Zhao et al., 2020). For the present engineering case, the plastic zone volumes calculated using the enhanced model are 2.5 and 1.4 times greater than those, respectively, calculated using the M–C model and U-J model. Moreover, the failure modes of the surrounding rock mass calculated using each of the three models are quite different. The failure mode predicted using M–C model involved mainly tensile failure, which accounted for 80% of all failures; however, the failure modes predicted using the U-J model and the enhanced model involved mainly shear failure, accounting for 60 and 90% of all failures, respectively. Comparing the failure modes and failure scales predicted using the three models with the practical engineering problems, including joint slippage and cracking of the liners (Figure 8A), it can be found that the enhanced model provides more accurate predictions than M–C model and U-J model in the simulation of underground excavations in CJRM.

The total deformations of surrounding rock masses are composed of elastic and plastic parts (Chen et al., 2013; Wang and Huang, 2014). For the three models used in the present engineering case, there is no difference in the calculation of elastic deformations, but a significant difference in those of the plastic deformations. Compared with the M–C model, the enhanced model and U-J model add deformation corrections of the joints to the total deformations, i.e., the U-J model considers one of the two sets of joints and the enhanced model considers both sets of joints. The results showed that the deformation patterns and magnitudes calculated using the three models differed (albeit not to any significant extent), indicating that the total deformations are mainly controlled by the elastic deformations and the plastic deformations made only minor corrections thereto. Comparing the calculated deformations with those measured in situ, the deformation calculated using the enhanced model is closer to those monitored, even if there remained certain differences between them. In future work, the prediction of the deformation of CJRM can be further modified by considering the stiffness of joints, thus improving such simulations (Wang and Huang, 2009; Chen et al., 2012).

Conclusion

CJRM or the similar rock masses often appear in engineering practice, but their specific mechanical performance is much less explored in numerical simulation (Wang and Huang, 2014; Yang et al., 2019; Zhao et al., 2020). This study enhanced U-J model by consideration of the particular mechanical behaviors of CJRM based on an equivalent continuum method and used the enhanced model to study the excavation responses of the large underground caverns in CJRM. It is obtained from the study that

1) The modification of the local coordinate system, failure modes, and failure sequences based on the structural and mechanical characteristics of CJRM is suitable for the simulation of the strength, deformation, and distribution of plastic zones of the rock mass. The presence of the conjugate joints greatly affects the performance of CJRM, and the effect of each set of joints on the mechanical behaviors is consistent with the superposition theory of general jointed rock masses.

2) The underground excavation in CJRM causes a much larger scale of plastic zones of the surrounding rock mass compared with those in unjointed or layered jointed rock masses. The failure modes of the underground caverns in CJRM involve mainly shear failure of the joints, which accounts for about 90% of all failures and is manifested as the joint slippage and cracking of the liners in the practical engineering.

3) The deformation of the underground excavations in CJRM is larger than those in unjointed or layered jointed rock masses. This is partly reflected in the plastic flow generated by the larger scale of the plastic zones in the calculation using the enhanced model; however, the deformation component derived from joint slippage is not considered, so the calculated deformation is smaller than that in practice. This weakness of the enhanced model can be improved in future work by considering the stiffness reduction of CJRM.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

XL designed the research. CW processed the corresponding data. XL and CW wrote the first draft of the manuscript. QS and HL helped to organize the manuscript. JC revised and edited the final version.

Funding

This work was supported by the National Natural Science Foundation of China (No. 52079135), the International Partnership Program of the International Cooperation Bureau of Chinese Academy of Sciences (No. 131551KYSB20180042), and the National Key Research and Development Program (No. 2017YFF0108706).

Conflict of Interest

Author HL was employed by the company PowerChina Beijing Engineering Corporation Limited.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adhikary, D., and Dyskin, A. (1998). A Continuum Model of Layered Rock Masses with Non‐associative Joint Plasticity. Int. J. Numer. Anal. Meth. Geomech. 22, 245–261. doi:10.1002/(SICI)1096-9853(199804)22:4<245::AID-NAG916>3.0.CO;2-R

CrossRef Full Text | Google Scholar

Adhikary, D. P., and Dyskin, A. V. (1997). Modelling the Deformation of Underground Excavations in Layered Rock Masses. Int. J. Rock Mech. Min Sci. 34 (3), 5.e1–5.e12. doi:10.1016/s1365-1609(97)00201-3

CrossRef Full Text | Google Scholar

Adhikary, D. P., and Guo, H. (2002). An Orthotropic Cosserat Elasto-Plastic Model for Layered Rocks. Rock Mech. Rock Eng. 35, 161–170. doi:10.1007/s00603-001-0020-y

CrossRef Full Text | Google Scholar

Agharazi, A., Martin, C. D., and Tannant, D. D. (2012). A Three-Dimensional Equivalent Continuum Constitutive Model for Jointed Rock Masses Containing up to Three Random Joint Sets. Geomech. Geoengin. 7 (8), 227–238. doi:10.1080/17486025.2012.714476

CrossRef Full Text | Google Scholar

Bandis, S. C., Lumsden, A. C., and Barton, N. R. (1983). Fundamentals of Rock Joint Deformation. Int. J. Rock Mech. Mining Sci. Geomech. Abstr. 20 (6), 249–268. doi:10.1016/0148-9062(83)90595-8

CrossRef Full Text | Google Scholar

Chang, L., Konietzky, H., and Frühwirt, T. (2019). Strength Anisotropy of Rock with Crossing Joints: Results of Physical and Numerical Modeling with Gypsum Models. Rock Mech. Rock Eng. 52, 2293–2317. doi:10.1007/s00603-018-1714-8

CrossRef Full Text | Google Scholar

Chen, G. Q., Li, T. B., Gao, M. B., Chen, Z. Q., and Xiang, T. B. (2013). Deformation Warning and Dynamic Control of Dangerous Disaster for Large Underground Caverns. Disaster Adv. 6 (1), 422–430.

Google Scholar

Chen, L., Shao, J. F., and Huang, H. W. (2010). Coupled Elastoplastic Damage Modeling of Anisotropic Rocks. Comput. Geotech. 37, 187–194. doi:10.1016/j.compgeo.2009.09.001

CrossRef Full Text | Google Scholar

Chen, X., Liao, Z., and Peng, X. (2012). Deformability Characteristics of Jointed Rock Masses under Uniaxial Compression. Int. J. Mining Sci. Techn. 22, 213–221. doi:10.1016/j.ijmst.2011.08.012

CrossRef Full Text | Google Scholar

Das, A. J., Mandal, P. K., Paul, P. S., Sinha, R. K., and Tewari, S. (2019). Assessment of the Strength of Inclined Coal Pillars through Numerical Modelling Based on the Ubiquitous Joint Model. Rock Mech. Rock Eng. 52, 3691–3717. doi:10.1007/s00603-019-01826-4

CrossRef Full Text | Google Scholar

Deng, B., Liu, S., Yang, S., Zhang, Z., and Song, G. (2009). Structural Characteristics of Joints and its' Implication in the Lingtanchang Anticline. J. Mineral. Petrol. 29, 83–90. doi:10.1049/el:19730006

CrossRef Full Text | Google Scholar

Ding, X., Niu, X., Pei, Q., Huang, S., Zhang, Y., and Zhang, C. (2019). Stability of Large Underground Caverns Excavated in Layered Rock Masses with Steep Dip Angles: a Case Study. Bull. Eng. Geol. Environ. 78, 5101–5133. doi:10.1007/s10064-018-01440-8

CrossRef Full Text | Google Scholar

Do, T. N., and Wu, J.-H. (2020). Simulation of the Inclined Jointed Rock Mass Behaviors in a Mountain Tunnel Excavation Using DDA. Comput. Geotech. 117, 103249. doi:10.1016/j.compgeo.2019.103249

CrossRef Full Text | Google Scholar

Fan, Q., Feng, X., Weng, W., Fan, Y., and Jiang, Q. (2017). Unloading Performances and Stabilizing Practices for Columnar Jointed basalt: A Case Study of Baihetan Hydropower Station. J. Rock Mech. Geotech. Eng. 9, 1041–1053. doi:10.1016/j.jrmge.2017.07.003

CrossRef Full Text | Google Scholar

Gao, M., Liang, Z., Jia, S., Li, Y., and Yang, X. (2019). An Equivalent Anchoring Method for Anisotropic Rock Masses in Underground Tunnelling. Tunn. Undergr. Space Technol. 85, 294–306. doi:10.1016/j.tust.2018.12.017

CrossRef Full Text | Google Scholar

Goodman, R. E., Taylor, R. L., and Brekke, T. L. (1968). A Model for the Mechanics of Jointed Rock. J. Soil Mech. Found. Div. 94 (3), 637–659. doi:10.1061/JSFEAQ.000800310.1061/jsfeaq.0001133

CrossRef Full Text | Google Scholar

Hatzor, Y. H., Feng, X.-T., Li, S., Yagoda-Biran, G., Jiang, Q., and Hu, L. (2015). Tunnel Reinforcement in Columnar Jointed Basalts: The Role of Rock Mass Anisotropy. Tunn. Undergr. Space Techn. 46, 1–11. doi:10.1016/j.tust.2014.10.008

CrossRef Full Text | Google Scholar

Hoek, E., and Brown, E. T. (1997). Practical Estimates of Rock Mass Strength. Int. J. Rock Mech. Mining Sci. 34, 1165–1186. doi:10.1016/S1365-1609(97)80069-X

CrossRef Full Text | Google Scholar

Itasca Consulting Group (2011). Itasca Flac3D V5.0, Fast Lagrangian Analysis of Continua in 3 Dimensions, User’s Guide. Minneapolis, Minnesota: Itasca Consulting Group Inc.

Jaeger, J. C., Cook, N. G., and Zimmerman, R. (2007). Fundamentals of Rock Mechanics. Oxford, United Kingdom: John Wiley & Sons: Blackwell Publishers.

Jaeger, J. C. (1960). Shear Failure of Anistropic Rocks. Geol. Mag. 97, 65–72. doi:10.1017/S0016756800061100

CrossRef Full Text | Google Scholar

Jia, P., and Tang, C. A. (2008). Numerical Study on Failure Mechanism of Tunnel in Jointed Rock Mass. Tunn. Undergr. Space Technol. 23, 500–507. doi:10.1016/j.tust.2007.09.001

CrossRef Full Text | Google Scholar

Jiang, Q., Feng, X.-t., Hatzor, Y. H., Hao, X.-j., and Li, S.-j. (2014). Mechanical Anisotropy of Columnar Jointed Basalts: An Example from the Baihetan Hydropower Station, China. Eng. Geol. 175, 35–45. doi:10.1016/j.enggeo.2014.03.019

CrossRef Full Text | Google Scholar

Jiang, Q., Wang, B., Feng, X.-T., Fan, Q.-X., Wang, Z., Pei, S., et al. (2019). In Situ failure Investigation and Time-dependent Damage Test for Columnar Jointed basalt at the Baihetan Left Dam Foundation. Bull. Eng. Geol. Environ. 78, 3875–3890. doi:10.1007/s10064-018-1399-y

CrossRef Full Text | Google Scholar

Jiang, Y., Tanabashi, Y., Li, B., and Xiao, J. (2006). Influence of Geometrical Distribution of Rock Joints on Deformational Behavior of Underground Opening. Tunn. Undergr. Space Techn. 21 (5), 485–491. doi:10.1016/j.tust.2005.10.004

CrossRef Full Text | Google Scholar

Li, T., Xu, N., Dai, F., Li, T., Fan, Y., and Li, B. (2018). Stability Analysis of Left Bank Abutment Slope at Baihetan Hydropower Station Subjected to Excavation. Rock Soil Mech. 39, 665–674. doi:10.16285/j.rsm.2016.0387

CrossRef Full Text | Google Scholar

Mühlhaus, H.-B. (1993). Continuum Models for Layered and Blocky Rock. Compreh Rock Eng. 2, 209–230. doi:10.1016/b978-0-08-040615-2.50014-9

CrossRef Full Text | Google Scholar

Neff, P., Chełmiński, K., Müller, W., Wieners, C., and Bathe, K. (2007). A Numerical Solution Method for an Infinitesimal Elasto-Plastic Cosserat Model. Math. Models Methods Appl. Sci. 17, 1211–1239. doi:10.1142/S021820250700225X

CrossRef Full Text | Google Scholar

Ning, F., Tang, L., Wang, P., and Meng, T. (2009). Growing Characteristics of Joints in Qiannan Depression (Southern Guizhou) and its Implication to Tectonic Stress Field Switch. J. China Univ. Pet. Edition Natrual Sci. 33, 22–26.

Google Scholar

Nova, R. (1980). The Failure of Transversely Isotropic Rocks in Triaxial Compression. Int. J. Rock Mech. Mining Sci. Geomech. Abstr. 17, 325–332. doi:10.1016/0148-9062(80)90515-X

CrossRef Full Text | Google Scholar

Nova, R., and Zaninetti, A. (1990). An Investigation into the Tensile Behaviour of a Schistose Rock. Int. J. Rock Mech. Mining Sci. Geomech. Abstr. 27, 231–242. doi:10.1016/0148-9062(90)90526-8

CrossRef Full Text | Google Scholar

Parise, M., and Lollino, P. (2011). A Preliminary Analysis of Failure Mechanisms in Karst and Man-Made Underground Caves in Southern Italy. Geomorphology 134, 132–143. doi:10.1016/j.geomorph.2011.06.008

CrossRef Full Text | Google Scholar

Park, S.-H., and Adachi, T. (2002). Laboratory Model Tests and FE Analyses on Tunneling in the Unconsolidated Ground with Inclined Layers. Tunn. Undergr. Space Techn. 17, 181–193. doi:10.1016/S0886-7798(02)00003-2

CrossRef Full Text | Google Scholar

Sainsbury, B. L., and Sainsbury, D. P. (2017). Practical Use of the Ubiquitous-Joint Constitutive Model for the Simulation of Anisotropic Rock Masses. Rock Mech. Rock Eng. 50, 1507–1528. doi:10.1007/s00603-017-1177-3

CrossRef Full Text | Google Scholar

Shen, B., Shi, J., Rinne, M., Siren, T., Suikkanen, J., Kwon, S., et al. (2016). Two-dimensional Displacement Discontinuity Method for Transversely Isotropic Materials. Int. J. Rock Mech. Mining Sci. 83, 218–230. doi:10.1016/j.ijrmms.2016.01.012

CrossRef Full Text | Google Scholar

Singh, M., Rao, K. S., and Ramamurthy, T. (2002). Strength and Deformational Behaviour of a Jointed Rock Mass. Rock Mech. Rock Eng. 35, 45–64. doi:10.1007/s006030200008

CrossRef Full Text | Google Scholar

Singh, M., and Seshagiri Rao, K. (2005). Empirical Methods to Estimate the Strength of Jointed Rock Masses. Eng. Geol. 77, 127–137. doi:10.1016/j.enggeo.2004.09.001

CrossRef Full Text | Google Scholar

Sitharam, T. G., Sridevi, J., and Shimizu, N. (2001). Practical Equivalent Continuum Characterization of Jointed Rock Masses. Int. J. Rock Mech. Mining Sci. 38, 437–448. doi:10.1016/S1365-1609(01)00010-7

CrossRef Full Text | Google Scholar

Tien, Y. M., and Kuo, M. C. (2001). A Failure Criterion for Transversely Isotropic Rocks. Int. J. Rock Mech. Mining Sci. 38, 399–412. doi:10.1016/S1365-1609(01)00007-7

CrossRef Full Text | Google Scholar

Tien, Y. M., Kuo, M. C., and Juang, C. H. (2006). An Experimental Investigation of the Failure Mechanism of Simulated Transversely Isotropic Rocks. Int. J. Rock Mech. Mining Sci. 43, 1163–1181. doi:10.1016/j.ijrmms.2006.03.011

CrossRef Full Text | Google Scholar

Wang, K., Cao, T., Wei, H., Xiao, A., and Zhou, L. (2020). The Palaeo Uplift of Late Cretaceous and Tectonic Stress Field Reconstruction of the Eastern Kuqa Depression. Acta Geol. Sin. 94, 1716–1726. doi:10.19762/j.cnki.dizhixuebao.2020090

CrossRef Full Text | Google Scholar

Wang, T.-T., and Huang, T.-H. (2009). A Constitutive Model for the Deformation of a Rock Mass Containing Sets of Ubiquitous Joints. Int. J. Rock Mech. Mining Sci. 46, 521–530. doi:10.1016/j.ijrmms.2008.09.011

CrossRef Full Text | Google Scholar

Wang, T.-T., and Huang, T.-H. (2014). Anisotropic Deformation of a Circular Tunnel Excavated in a Rock Mass Containing Sets of Ubiquitous Joints: Theory Analysis and Numerical Modeling. Rock Mech. Rock Eng. 47, 643–657. doi:10.1007/s00603-013-0405-8

CrossRef Full Text | Google Scholar

Wang, Z., Qiao, C., Song, C., and Xu, J. (2014). Upper Bound Limit Analysis of Support Pressures of Shallow Tunnels in Layered Jointed Rock Strata. Tunn. Undergr. Space Techn. 43, 171–183. doi:10.1016/j.tust.2014.05.010

CrossRef Full Text | Google Scholar

Wu, W., Zhu, H., Lin, J.-S., Zhuang, X., and Ma, G. (2018). Tunnel Stability Assessment by 3D DDA-Key Block Analysis. Tunn. Undergr. Space Techn. 71, 210–214. doi:10.1016/j.tust.2017.07.015

CrossRef Full Text | Google Scholar

Yang, W., Zhang, Q., Ranjith, P. G., Yu, R., Luo, G., Huang, C., et al. (2019). A Damage Mechanical Model Applied to Analysis of Mechanical Properties of Jointed Rock Masses. Tunn. Undergr. Space Techn. 84, 113–128. doi:10.1016/j.tust.2018.11.004

CrossRef Full Text | Google Scholar

Zhao, Z., Guo, T., Li, S., Wu, W., Yang, Q., and Chen, S. (2020). Effects of Joint Surface Roughness and Orientational Anisotropy on Characteristics of Excavation Damage Zone in Jointed Rocks. Int. J. Rock Mech. Mining Sci. 128, 104265. doi:10.1016/j.ijrmms.2020.104265

CrossRef Full Text | Google Scholar

Zhou, Y.-Y., Feng, X.-T., Xu, D.-P., and Fan, Q.-X. (2017). An Enhanced Equivalent Continuum Model for Layered Rock Mass Incorporating Bedding Structure and Stress Dependence. Int. J. Rock Mech. Mining Sci. 97, 75–98. doi:10.1016/j.ijrmms.2017.06.006

CrossRef Full Text | Google Scholar

Zhou, Y.-Y., Feng, X.-T., Xu, D.-P., and Fan, Q.-X. (2016). Experimental Investigation of the Mechanical Behavior of Bedded Rocks and its Implication for High Sidewall Caverns. Rock Mech. Rock Eng. 49 (9), 3643–3669. doi:10.1007/s00603-016-1018-9

CrossRef Full Text | Google Scholar

Zhou, Y.-Y., Xu, D.-P., Gu, G.-K., Liu, K., Wan, L.-P., Wang, T.-L., et al. (2019). The Failure Mechanism and Construction Practice of Large Underground Caverns in Steeply Dipping Layered Rock Masses. Eng. Geol. 250, 45–64. doi:10.1016/j.enggeo.2019.01.006

CrossRef Full Text | Google Scholar

Zhou, Y.-Y., Xu, D.-P., Liu, K., and Chen, D.-F. (2021). Understanding the Failure Mechanism of a Large Underground Cavern in Steeply Dipping Layered Rock Mass Using an Enhanced Ubiquitous-Joint Model. Bull. Eng. Geol. Environ. 80, 4621–4638. doi:10.1007/s10064-021-02213-6

CrossRef Full Text | Google Scholar

Zhu, W. S., Li, X. J., Zhang, Q. B., Zheng, W. H., Xin, X. L., Sun, A. H., et al. (2010). A Study on Sidewall Displacement Prediction and Stability Evaluations for Large Underground Power Station Caverns. Int. J. Rock Mech. Mining Sci. 47, 1055–1062. doi:10.1016/j.ijrmms.2010.07.008

CrossRef Full Text | Google Scholar

Zhu, W. S., Sui, B., Li, X. J., Li, S. C., and Wang, W. T. (2008). A Methodology for Studying the High wall Displacement of Large Scale Underground Cavern Complexes and It's Applications. Tunn. Undergr. Space Techn. 23, 651–664. doi:10.1016/j.tust.2007.12.009

CrossRef Full Text | Google Scholar