Quantitative Assessment of Temporal Changes in Subaqueous Hydrothermal Activity in Active Crater Lakes During Unrest Based on a Time-Series of Lake Water Chemistry

Regular sampling of lake water has been performed at many volcanoes to assess the state of volcanic activity. However, it is not clear whether the absolute concentrations or, instead, rate of changes in concentrations are more suitable for such assessments. In this study, we show that temporal changes in concentrations of an element in lake water are described by a simple differential equation, assuming changes in lake volume and chemical processes are negligible. The time constants (63% response time for changes in the chemical concentration in lake water) have a wide range varying between 20 and 1,000 days for the studied volcanoes in Japan, meaning it takes a long time to assess volcanic activity based on the absolute concentration of an element. In order to assess the volcanic activity in a shorter time period, based on a time-series of lake element concentration data, we developed a numerical model to calculate temporal changes in the steady-state concentration, which is proportional to the elemental concentrations of the bulk hydrothermal fluid injected from subaqueous fumaroles and hot springs. We applied our method to Yugama crater lake at Kusatsu–Shirane volcano, Japan, and quantitatively evaluated temporal changes in the hydrothermal input from 1964 to 2020. As a result, we detected changes in the Cl concentrations of the bulk hydrothermal input that were associated with unrest including the phreatic eruption in 1976 and earthquake swarms in 1989–1992 and 2014–2020. The future concentration in the lake water can be predicted from the most recent steady-state concentrations. Comparing the predicted concentration curve with the concentration obtained from lake water samples, it is possible to quickly assess whether the concentration of the bulk hydrothermal input has increased/decreased or remained constant.

1 Introduction

Volcanic lakes can cause a variety of hazards, such as phreatic eruptions, mud eruptions, tsunamis, base surges, and lahars (Morrissey et al., 2010; Manville, 2015; Edwards et al., 2017). These can be hazards near the volcanic lake, and also near rivers that drain the lake. Therefore, assessing activity of a volcanic lake is a critical issue for society. In addition, volcanic lakes can act as condensers of heat and materials released from hydrothermal systems. To understand material circulation in hydrothermal systems, measurements of lake water levels, temperatures, and concentrations of elements have been undertaken at crater lakes worldwide (e.g., Pasternack and Varekamp, 1997).

Prior to an eruption, increases/decreases in lake volume have occurred (Barberi et al., 1992; Werner et al., 2008; Fournier et al., 2009, 2011; Christenson et al., 2017), which have been interpreted to reflect changes in the mass flux and enthalpy of fluid emitted from the lake bottom (Terada and Hashimoto, 2017). Monitoring the surface water temperature of volcanic lakes, which is a simple remote measurement by infrared thermometry, is a key observation for monitoring volcanic activity (Oppenheimer, 1997; Lewicki et al., 2016; Cigolini et al., 2018; Candela-Becerra et al., 2020). In addition, regular sampling of lake water has been performed at many volcanoes, including Ruapehu (Giggenbach and Glover, 1975; Hurst et al., 1991; Christenson, 2000), Kusatsu–Shirane (Ohba et al., 1994, 2008), Poás (Rowe et al., 1992; Martínez et al., 2000; Rouwet et al., 2017), Kawah Ijen (van Hinsberg et al., 2017), Copahue (Agusto et al., 2017), and crater lakes in Mexico (Armienta et al., 2000; Rouwet et al., 2008; Peiffer and Taran, 2013; Peiffer et al., 2015).

Yugama crater lake of Kusatsu–Shirane volcano has repeatedly experienced gradual increases/decreases in concentrations of chemical components, although water temperatures and levels have not changed significantly (Ohba et al., 2008). Such changes in concentrations are accompanied by earthquake swarms, ground deformation, and thermal demagnetization beneath the crater lake (Takahashi and Fujii, 2014), corresponding to a volcano with slow unrest (Stix, 2018).

Although phreatic eruptions have occurred repeatedly at Yugama crater lake since the 1880s, the lake is a popular tourist attraction. In the assessment of volcanic activity at Kusatsu–Shirane volcano, the Japan Meteorological Agency (JMA) considers changes in concentrations of elements to be a key parameter, in addition to geophysical observations. However, it is unclear whether the absolute concentrations or rate of changes in concentrations are more suitable for such assessments. Concentrations of lake water are adjusted according to the mass balance of the lake system (Pasternack and Varekamp, 1997; Rouwet and Tassi, 2011). Furthermore, the absolute lake concentration depends on the history of the lake concentration because the current concentration is a result of integrating the past inputs and outputs of the element. The rate of changes in concentrations can occur slowly in large-volume crater lakes (Varekamp, 2002, 2015; Rouwet et al., 2014), and thus it takes a long time to assess changes in volcanic activity based on absolute concentrations. To assess changes in volcanic activity, monitoring changes in the concentration of the hydrothermal fluid injected from the lake bottom is more suitable rather than tracking element concentrations in lake water.

In this study, we developed a simple numerical model to calculate temporal changes in concentrations of the bulk hydrothermal fluid injected from the lake bottom, by assuming the water volume remains largely constant during each analytical period. If pH of lake water is not extremely low (pH > 0), this model can be applied to elements such as chloride (Cl) for which chemical reactions and evaporation from the lake surface are negligible (Rouwet and Ohba 2015; Capaccioni et al., 2017). In addition, we propose a method for predicting future lake concentrations based on a time-series of recent concentrations of water samples taken from crater lakes. Our model is applied to active crater lakes in Japan, particularly Yugama crater lake at Kusatsu–Shirane volcano, in order to test the validity of our assessment of volcanic activity.

2 Modeling

Volcanic lakes, particularly active hot crater lakes, exhibit variable chemical characteristics from lake to lake (e.g., Rouwet et al., 2014). Such lakes with diameters greater than several tens of meters in Japan are Yugama crater lake at Kusatsu–Shirane volcano (Kusakabe et al., 2000; Ohba et al., 2008), Yudamari cater lake at Aso volcano (Terada et al., 2012), Oyunuma crater lake at Noboribetsu volcano (Murozumi et al., 1966; Fukutomi et al., 1968; Inoue and Aoki, 2000), and Okama crater lake at Zao volcano (Anzai, 1961; Miura et al., 2012) (Figure 1). In such crater lakes, the annual water level is largely maintained throughout periods of volcanic quiescence, although there are seasonal fluctuations due to meteorological factors. Our model does not take into account chemical reactions.

FIGURE 1

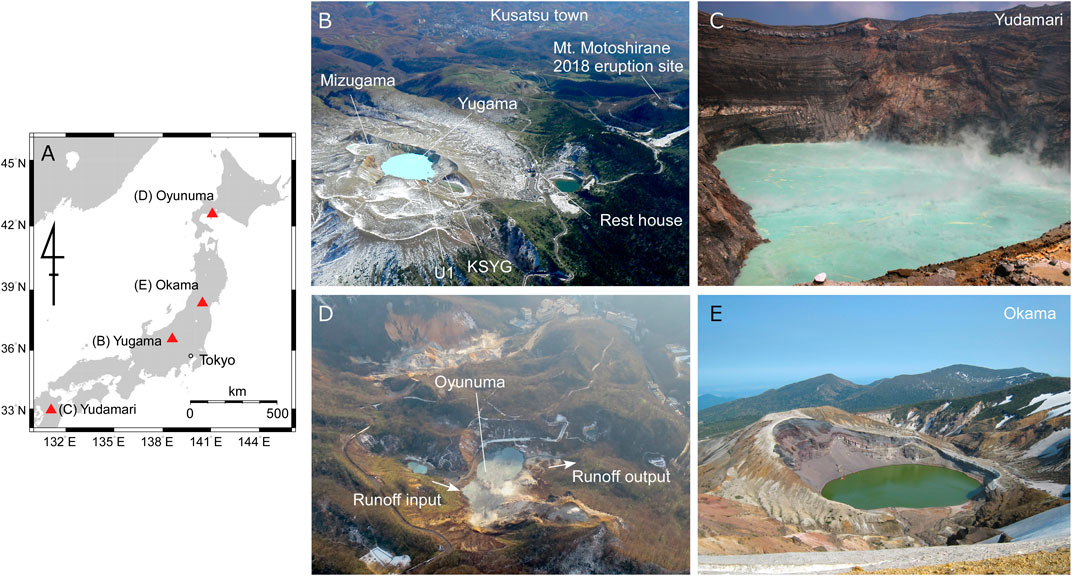
FIGURE 1. (A) Location map of active crater lakes in Japan. Photographs of (B) Yugama crater lake at Kusatsu–Shirane volcano taken on November 6, 2017, (C) Yudamari crater lake at Aso volcano taken by Shin Yoshikawa on July 27, 2007, (D) Oyunuma crater lake at Noboribetsu volcano taken by Hiroshi Aoyama on December 7, 2020 with the cooperation of the Hokkaido Regional Development Bureau, and (E) Okama crater lake at Zao volcano taken by Mare Yamamoto on May 29, 2017.

2.1 General Mass Balance of a Chemical Component of Interest

We assumed that fumaroles and hot-water fountains exist on the bottom of the crater lakes. All mass injected from the lake bottom is absorbed by the lake water. For simplicity, it was assumed that the lake water is well mixed, and thus the element concentration in the lake water is homogeneous. We considered a closed lake without surface runoff outlets and inlets, which is the case for Yugama, Yudamari, and Okama crater lakes (Figures 1A–C). Oyunuma crater lake (Figure 1D) is affected by surface runoff inlets and outlets, and is discussed further in Notes on the Analysis.

The lake water is supplied by fluid injected from the hydrothermal system beneath the lake bottom ($m_{in}$ in kg/s) and by precipitation (rainfall) inflow ($m_{pr}$ in kg/s). Lake water is lost by evaporation from the lake surface ($m_{ev}$ in kg/s) and seepage through the lake bottom ($m_{sp}$ in kg/s) (e.g., Hurst et al., 1991; Rowe et al., 1992; Pasternack and Varekamp, 1997). If $V\left(t\right)$ (in m³) is the lake volume as a function of time ($t$ in s) and the density of lake water ($\rho$ in 1,000 kg/ m³) (Table 1), the mass conservation for an element in the lake water (Taran and Rouwet, 2008; Rouwet and Tassi, 2011) is:

$\rho \frac{d}{dt}\left[V\left(t\right)C\left(t\right)\right]=m_{in}{C}_{in}-m_{sp}C\left(t\right) + m_{pr}{C}_{pr}-m_{ev}{C}_{ev}(1)$

where $C\left(t\right)$ is the concentration of the element (mg/kg) as a function of $t$. Parameters $C_{in}$, $C_{pr}$, and $C_{ev}$ are the concentrations of the bulk hydrothermal fluid injected from the lake bottom, rain water, and evaporated water, respectively.

TABLE 1

TABLE 1. Definitions of abbreviations.

2.2 Steady-State Condition

We assumed that evaporation loss of elements from the lake surface is negligible. This assumption can be applied to elements such as Cl (Simonson and Palmer, 1993) as long as pH of lake water is not extremely low to evaporate HCl (Rouwet and Ohba 2015; Capaccioni et al., 2017). Assuming conservative elements such as Cl or Mg as the chemical tracers in our model, $C_{pr}$ and $C_{ev}$ are negligible compared to $C\left(t\right)$ and $C_{in}$. Eq. 1 is rewritten

$\rho \frac{d}{dt}\left[V\left(t\right)C\left(t\right)\right]=m_{in}{C}_{in}-m_{sp}C\left(t\right)(2)$

If $V\left(t\right)$ and $C\left(t\right)$ are approximately maintained, i.e., the mass equilibrium of the lake system is achieved, the steady-state concentration of the element, $C_{eq}$ mg/kg, is defined as

$C_{eq}=\frac{m_{in}}{m_{sp}}{C}_{in}(3)$

Equation 3 corresponds to the expression for the steady-state lake by Varekamp (2002). In the lake system represented by Eq. 1, $C_{eq}$ is not equal to $C_{in}$ in the steady-state because the water mass is balanced between $m_{pr}$ and $m_{ev}$, which do not contain the element of interest, as well as $m_{in}$ and $m_{sp}$.

2.3 Non-steady State Conditions

In a lake system where a fluid with a constant concentration of an element enters at a constant rate and the lake water leaves at a constant rate, the temporal change in the concentration can be represented by a response of a first-order system (Albarède, 1995; Varekamp, 2002, 2015). In this section, we represent the time constant of the system, assuming the water volume is constant.

If the temporal change in water volume is negligible, Eq. 3 can be rewritten with $C_{eq}$ as:

$\frac{dC\left(t\right)}{dt}=\frac{m_{sp}}{\rho V}(C_{eq}-C\left(t\right))(4)$

A nearly constant water volume suggests that temporal changes in $m_{in}$ and $m_{sp}$ are negligible. Assuming constant $m_{in}$ and $m_{sp}$, the change in $C\left(t\right)$ in response to the constant $C_{in}$ is obtained by integrating Eq. 4:

$C\left(t\right)=C_{eq}+\left(C_0-C_{eq}\right)e^{-\frac{t}{a}}(5)$

where $C_0$ is the concentration of the element in lake water at $t$ = 0. Here, $a$ is a time constant, corresponding to the residence time (Taran and Rouwet, 2008):

$a=\frac{\rho V}{m_{sp}}(6)$

The time constant $a$ increases with increasing $V$, whereas it decreases with increasing $m_{sp}$. Figure 2 shows calculations for the dimensionless concentration $\left(C\left(\tau \right)/C_0\right)$ as a function of dimensionless time $\tau =t/a$. For a given $C_0$ and $a$, which are proportional to $V/m_{sp}$, the rate of change in concentration $C\left(t\right)$ increases with $C_{eq}$, which is proportional to $C_{in}$. Response times at 63, 90, and 98% were calculated to be $2a$, $2.2a$, and $3.8a$, respectively.

FIGURE 2

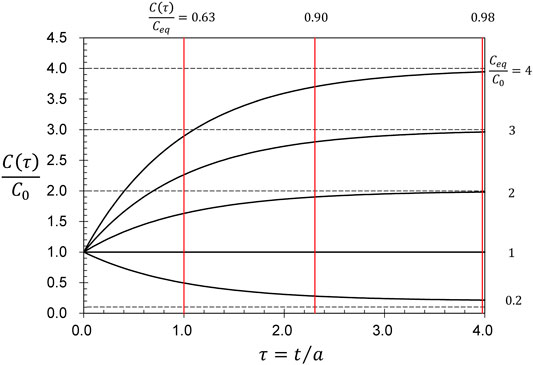
FIGURE 2. The dimensionless concentration $C\left(\tau \right)/C_0$ as a function of dimensionless time $\tau =t/a$, assuming $C_{eq}/C_0$ = 0.2, 1.0, 2.0, 3.0, and 4.0. Red bars show the 63, 90, and 98% response for $C\left(\tau \right)/C_0$.

2.4 Estimations of the Time Constant

The seepage flux $\left(m_{sp}\right)$ is required to estimate the time constant $a$. For Yugama crater lake (Figure 1B), daily seepage flux ($m_{sp}\times \mathrm{86,400}$) is estimated to be $V/1000$, based on temporal changes in ¹³⁴Cs and ¹³⁶Cs activity (Hirayama et al., 2021). Therefore, the time constant $a$ was estimated to be 8.6 × 10⁷ s (1,000 days) from Eq. 6 (Table 2).

TABLE 2

TABLE 2. Summary of the seepage flux $m_{sp}$, water volume $V$, and time constant $a$ for each volcano. Numbers refer to the following references: [1] Hirayama et al. (2020), [2] Terada et al. (2012), [3] Kato (1960), and [4] Fukutomi et al. (1968).

In the case of Yudamari crater lake (Figure 1C), $V$ and $m_{sp}$ during calm periods (2006/10/21–12/21, 2007/9/20–11/7, and 2008/3/12–5/31) were estimated by Terada et al. (2012) using a numerical model, which takes into account mass and energy balance and meteorological conditions. Therefore, the time constant $a$ was estimated to be 2.0–2.2 × 10⁷ s (230–250 days) (Table 2).

For Okama crater lake (Figure 1D), the $m_{sp}$ has not yet been estimated. In such a situation, the empirical relationship $m_{sp}= 0.2 \times V_e^{0.39}$ $(V_e$ is the equivalent water volume of the lake, which is the product of lake area and mean depth; Figure 6 in Terada et al., 2012) can be applied. Using a surface area of 8.3 × 10⁴ m² and mean depth of 18.1 m (Kato, 1960), $m_{sp}$ is calculated to be 48 kg/ s and, therefore, the time constant was estimated to be 3.1 × 10⁷ s (360 days) (Table 2).

3 Evaluation of Changes in the Steady State Concentration

In this section, we calculate temporal changes in $C_{eq}$ (steady-state concentration of an element of interest in the lake water) based on two or three analyses of the lake composition. If $m_{in}/m_{sp}$ (mass flux ratio of the bottom input fluid to seepage through the lake bottom) is known, temporal changes in the concentration of the bulk hydrothermal fluid injected from the subaqueous fumaroles and hot springs C_in can be estimated from Eq. 3.

3.1 Estimation of the Temporal Changes in the Steady-State Concentration $C_{eq}$

We define $C^i$ as the concentration of an element in the lake water at time $t^i$. The time interval between $t^i$ and $t^{i-1}$ is referred to as $\Delta t_i$. During each analytical period ($t^{i-1}<t<t^i$), we assumed the concentration of the bulk hydrothermal input $C_{in}^i$ and time constant $a^i$ were constant. In such a case, the relationship between $C^i$ and $C^{i-1}$ in each period is expressed using Eq. 5 as follows:

$C^{i-1}=C_{eq}^i+\left(C^i-C_{eq}^i\right)\cdot e^{\frac{\Delta t^i}{a^i}}(7)$

Here we define $F^i$ as:

$F^i\equiv e^{-\frac{\Delta t^i}{a^i}}(8)$

Combining Eqs 7, 8, the lake concentration $C^i$ at time $t_i$ can be rewritten as:

$C^i=\left(1-F^i\right)C_{eq}^i+F^i{C}^{i-1}(9)$

This equation corresponds to the form of a recursive filter (Smith, 1997; Robert et al., 2014). The time-series of $C_{eq}^i$ at time $t_i$ was calculated sequentially by Eq. 9 using data, $C^{i-1}$ and $C^i$, as a two data calculation:

$C_{eq}^i=\frac{C^i-F^i{C}^{i-1}}{1-F^i}(10)$

The concentration of the lake water can fluctuate due to meteorological factors and analytical uncertainties. To reduce the effects of such fluctuations, we used $C^{i-2}$ in addition to $C^{i-1}$ and $C^i$. We define $G^i$ as:

$G^i\equiv e^{-\frac{\Delta t^{i-1}}{a^{i-1}}}(11)$

where $\Delta t_{i-1}=t_{i-1}-t_{i-2}$. Like Eq. 9, $C^i$ is expressed by the following equation:

$C^i=\left(1-F^i{G}^i\right)C_{eq}^i+F^i{G}^i{C}^{i-2}(12)$

Summing Eqs 9, 12, $C_{eq}^i$ at a time $t_i$ can be calculated by the following equation as a three data calculation:

$C_{eq}^i=\frac{2C^i-F^i{C}^{i-1}-F^i{G}^i{C}^{i-2}}{2-F^i-F^i{G}^i}(13)$

Assuming $C_{eq}^i$ does not change during each period of $t^{i-2}< t < t^i$, we sequentially calculated temporal changes in $C_{eq}^i$. If $C_{in}$ and $m_{in}$/$m_{sp}$ do not change during each period, then temporal changes in $C_{in}^i$ were calculated by Eq. 3 with an assumed ${\left(m_{in}/m_{sp}\right)}_{in}^i$.

3.2 Computational Test of ${\mathit{C}}_{\mathit{eq}}^{\mathit{i}}$

Figure 3 shows the time-series computational test for the $C_{eq}^i$ estimations described in Estimation of the Temporal Changes in the Steady-State Concentration $C_{eq}$. The time-series of the test $C_i$ data in response to step-like changes in $C_{eq}^{set}$ (2,300, 11,500, 23,000, 2,300, and 17,000 mg/ kg) were calculated using Eq. 5 at intervals of 30 days, assuming $a$ = 8.6 × 10⁷ s (1,000 days), which corresponds to Yugama crater lake (Table 2). Here the chemical concentration of the lake water at t = 0, $C_0$, was set to 2,300 mg/ kg (Figure 3A). The results for $C_{eq}^i$ calculated with the two data calculation (Figure 3B) are in good agreement with the temporal changes in $C_{eq}^{set}$. For the results of the three data calculation (Figure 3C), transitional responses in calculated $C_{eq}^i$ occur when $C_{eq}^{set}$ has step-like changes.

FIGURE 3

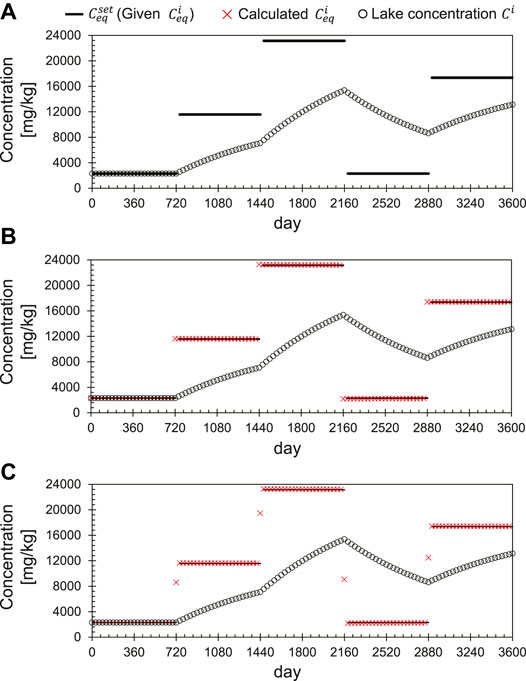
FIGURE 3. Time-series computational test of the $C_{eq}^i$ estimation described in Estimation of the Temporal Changes in the Steady-State Concentration $C_{eq}$, assuming $a$ = 1,000 days, corresponds to the case of Yugama crater lake (Table 2). (A) Time-series of $C^i$ (at intervals of 30 days) in response to step-like changes in $C_{eq}$ defined as $C_{eq}^{set}$ = 2,300, 11,500, 23,000, 2,300, and 17,000 mg/ kg, as calculated by Eq. 5. (B) Two data (Eq. 10) and (C) three data (Eq. 13) calculation of $C_{eq}^i$ from $C^i$.

4 Analysis of Yugama Crater Lake at Kusatsu–Shirane Volcano

In this section we apply the model introduced in Evaluation of Changes in the Steady State Concentration to Kusatsu-Shirane volcano, as a representative case for which long-term time series of lake element concentration data have been obtained. Kusatsu–Shirane volcano has a hot crater lake, called Yugama, with a pH ∼ 1.0. Phreatic eruptions have occurred repeatedly at the volcano, including from the Mizugama Crater in 1976 (Ossaka et al., 1980) (Figure 1B) and from the Yugama Crater in 1982–1983 (Ohba et al., 2008) and 1989 (Ida et al., 1989). In 2018, a phreatic eruption occurred at the Motoshirane pyroclastic cone group, which is located 1.2 km south of Yugama crater lake (Kametani et al., 2021; Terada et al., 2021; Yamada et al., 2021). In 1989–1993 and 2014–2020, earthquake swarms were observed around Yugama crater lake. In this section, we analyze temporal changes in Cl concentrations. We assumed a time constant $a^i$ of 8.6 × 10⁷ s (1,000 days) (Table 2) throughout the analysis, because the lake water volume has not been recorded accurately but the lake level has remained largely unchanged over the long term as seen in photographs.

4.1 Chloride Concentrations of Yugama Crater Lake

The earliest Cl concentration data are from 1949 (Minami et al., 1952). After 1967, regular sampling of the lake water has been carried out at site U1 located on its southern shore (Figure 1B) (Ohba et al., 2008). We used the data of Ossaka et al. (1997) from 1967/7/4–1985/7/26 and Ohba et al. (2008) from 1985/10/22–2005/10/3. Lake waters sampled by us from 2005/11/4 to 2005/11/4 were analyzed by ion chromatography at the Meteorological Research Institute, JMA (Yaguchi et al., 2021).

Figure 4A shows the temporal changes in Cl concentrations. Sampling prior to 1984 was undertaken once a year in summer and, since April 1985, monthly sampling has been carried out except in winter. Snow cover hinders fieldwork during winter, but from 1990 to the early 2000s, helicopters allowed sampling at site U1. Apart from the period prior to 1984 and 2010–2014, the mean sampling interval was 44 days. We labeled the periods (a)‒(d), based on the trend of temporal changes in Cl concentrations. Figure 4B shows the monthly numbers of earthquakes around Yugama crater lake. Earthquake swarms in periods (b) and (d) were accompanied by an increase in Cl concentrations (arrows in Figure 4A). During a series of phreatic eruptions in 1982–1983 (Figure 4A) earthquake swarms occurred, but Cl concentrations remained unchanged (Ohba et al., 2008). The annual precipitation (Figure 4C) observed at Kusatsu town, which is located 6 km east of the Yugama Crater, is almost constant at ∼1,700 mm and does not affect the temporal changes in Cl concentrations over the long term.

FIGURE 4

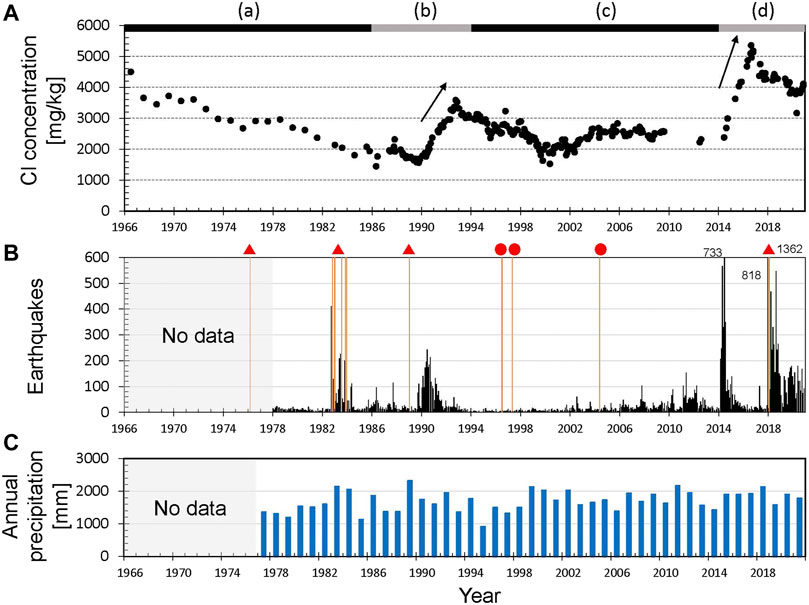
FIGURE 4. (A) Cl concentrations of Yugama crater lake. (a–d) represent the periods defined in estimations of $C_{eq}^i$. (B) Monthly numbers of earthquakes with maximum amplitudes of >0.05 μm and S–P times of <2 s measured by the UD component at a seismic station that is 1 km northeast of Yugama crater lake. Triangles indicate the eruption at Kusatsu–Shirane volcano, and circles show lake water turbulence at Yugama crater lake, such as the appearance of a water dome. (C) Annual rainfall at Kusatsu town, which is 6 km east of Yugama crater lake. The data in (B) and (C) were provided by the JMA.

4.2 Estimations of $C_{eq}^i$

A moving average of ±60 days at intervals of 60 days was applied to smooth the raw data (Figure 4A), because Cl concentrations can fluctuate due to atmospheric conditions, such as heavy rain, snow melt, and drought, leading to changes in lake water volume. The moving average also reduces uncertainties related to the analyses and potential concentration heterogeneities around the sampling site.

Computational results for $C_{eq}^i$ (steady-state concentration of an element of interest in the lake water for each period $i$) are shown in Figures 5A,B using the two and three data calculations, respectively. The results of the three data calculation show less fluctuation than those of the two data calculation throughout the entire period. Both moving averages of $C_{eq}^i$ are similar, and thus we discuss the results from the three data calculation for each period.

FIGURE 5

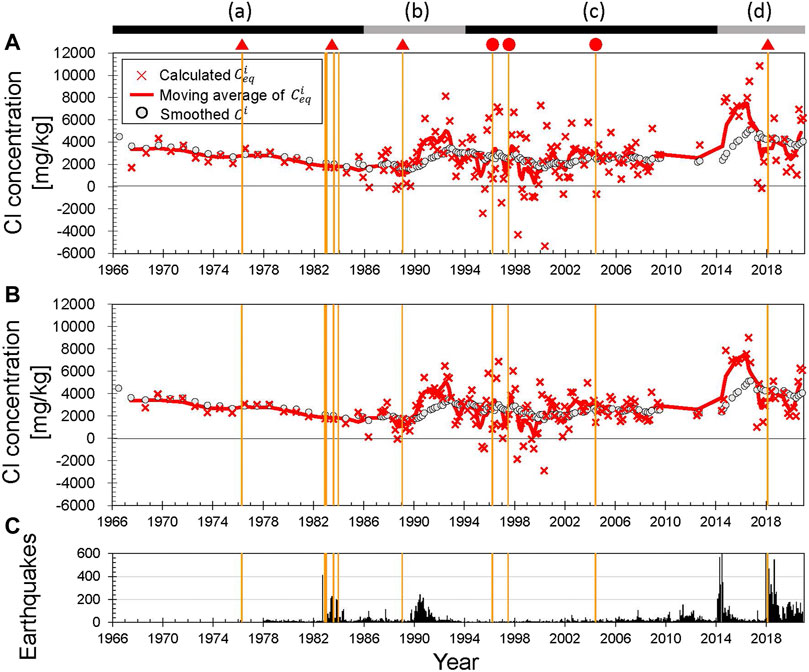
FIGURE 5. Computational results for $C_{eq}^i$ using (A) the two and (B) the three data calculation (red crosses) of Yugama crater lake at Kusatsu-Shirane volcano. Smoothed Cl concentrations are shown as gray circles. (a–d) represent the periods defined in estimations of $C_{eq}^i$. (C) Monthly numbers of earthquakes, which is the same as Figure 4B.

4.2.1 Period (a), 1966–1986

Prior to the eruptions in 1982–1983, calculated $C_{eq}^i$ values gradually decreased from 3,500 to 2,000 mg/ kg at a rate of 70 mg kg⁻¹ yr⁻¹ (Figure 6A). Although water level fluctuated annually by 1‒2 m before the start of the eruptions in 1982–1983, there was no long-term increase/decrease in lake water level, suggesting no long-term changes in $m_{in}$ (mass flux of the bottom input fluid) during the period (a) (Terada and Hashimoto, 2017). Therefore, our results indicate that the Cl concentrations of the bulk hydrothermal input decreased gradually preceding the eruptions.

FIGURE 6

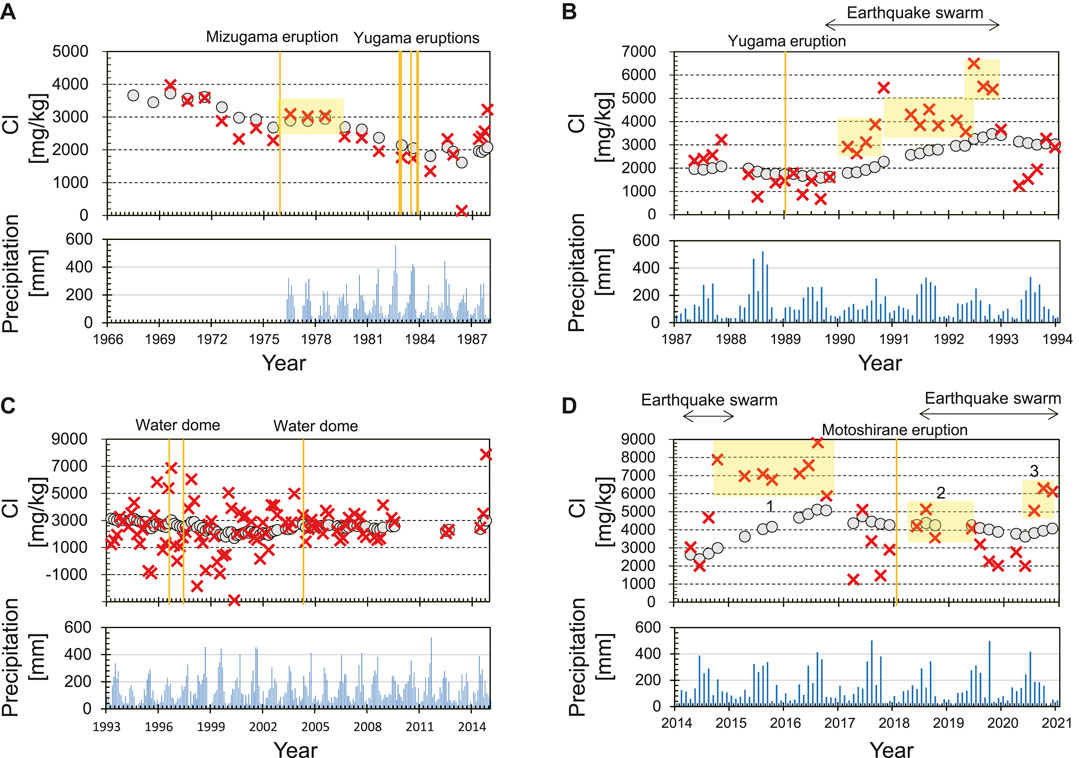
FIGURE 6. Smoothed $C^i$ values (gray circles) and computational results for $C_{eq}^i$ (red crosses) using the three data calculation (Eq. 13) and monthly precipitation at Kusatsu town, which is 6 km east of Yugama crater lake, as measured by the JMA for each time period. The yellow vertical lines represent eruptions at Kusatsu–Shirane volcano or unusual turbulence events on the surface of Yugama crater lake. (A) Period a, 1966–1986, (B) period b, 1987–1993, (C) period c, 1994–2013 and (D) period d, 2014–2020.

However, calculated $C_{eq}$ values were temporarily constant at 3,500 mg/kg in 1976–78 (A yellow hatch in Figure 6A). The hiatus in the decrease in $C_{eq}$ values was probably caused by a transient increase in subaqueous hydrothermal activity, which may have been associated with the phreatic eruption that occurred at the Mizugama Crater (Figure 1B) in 1976.

During the series of eruptions in 1982–1983, Cl concentrations of the lake water showed no eruption-related changes, resulting in no eruption-related changes in $C_{eq}$ values. After the eruptions, calculated $C_{eq}$ values fluctuated around 1,900 mg/kg.

Our calculation results show that the concentration of the bulk hydrothermal input gradually decreased over the long term, except for 1976–1978 after the Mizugama eruption. The lowest value of $C_{eq}$ (130 mg/kg), in spring in 1986, was probably caused by localized, temporary dilution around the sampling site U1 due to enhanced snow melting in spring.

4.2.2 Period (b), 1987–1993

This period includes unrest in terms of an earthquake swarm and increase in Cl concentrations from 1989 to 1992. After the temporary increase in $C_{eq}$ values in 1987, $C_{eq}$ values fluctuated around 1,400 mg/ kg (Figure 6B). The small eruption at Yugama crater lake (Ida et al., 1989) occurred at a time when $C_{eq}$ values were low. From 1990, $C_{eq}$ values increased markedly (3,000–6,000 mg/kg, yellow hatches in Figure 6B), which was accompanied by the earthquake swarm (Figure 5C) and thermal demagnetization around the Yugama Crater (Takahashi and Fujii, 2014). In 1993, the $C_{eq}$ values decreased to values of 1,000–2,000 mg/ kg, which correspond to concentrations prior to the earthquake swarm.

After the earthquake swarm from 1989 to 1992, the annual mean water temperature increased by 5°C (Ohba et al., 2008), suggesting that evaporative loss from the lake surface increased. The water level did not decrease at this time, which means that the mass flux of the hydrothermal fluid injected from the subaqueous fumaroles and hot springs ($m_{in}$) increased after the earthquake swarms (Terada and Hashimoto, 2017).

Our calculations reveal that the small eruption in 1989 occurred when $C_{eq}$ fluctuated at a relatively low value. The marked increase in $C_{eq}$ values corresponds to an increase in magmatic fluid supply suggested by geophysical observations. At the end of the earthquake swarm period, our calculation results indicate that the increase in $C_{in}$ stopped before the Cl concentration achieved a steady-state condition.

4.2.3 Period (c), 1994–2013

Chloride concentrations decreased slowly, albeit with large fluctuations, from 1993 to 2000, and increased slowly in the early 2000s (Figure 6C). This period is characterized by significant short-term fluctuations in calculated $C_{eq}$ values, especially in the 1990s. It is notable that water domes and jetting, which may be related to the earthquake swarm and thermal demagnetization in 1989–1992, were observed on the lake surface during the short-term fluctuations. Since 2005, these significant short-term fluctuations have subsided.

Such significant short-term fluctuations in $C_{eq}$ can be caused by an unstable $C_{in}$ (the concentration of the bulk hydrothermal input), however, the significant short-term fluctuations in $C_{eq}$ can also be attributed to an unstable $m_{in}$ (mass flux of the bottom input fluid) causing temporary changes in water volume $V$.

It is difficult to identify the reason for the significant short-term fluctuations in $C_{eq}$ during this period. If non-negligible changes in $m_{in}$ (mass flux of the bottom input fluid) occurred, changes in the values of $C_{eq}$ would not represent actual changes in $C_{in}$ (the concentration of the bulk hydrothermal input). Furthermore, snowmelt and heavy rains may have caused local and temporary dilution around sampling site U1, resulting in extremely low and negative $C_{eq}$ values. Water level needs to be monitored in order to evaluate the possible changes in $m_{in}$ (mass flux of the bottom input fluid), and to correct for the effects of meteoric factors based on an accurate time constant value $a$ calculated by the lake volume $V$.

4.2.4 Period (d), 2014–2020

This period corresponds to a phase of unrest and unusual volcanic activity. A marked increase in Cl concentrations from 2014 to 2016 (Figure 6D) was followed by a slight decrease in Cl concentrations from 2017 to 2020 while calculated $C_{eq}$ values indicate three events of an increase in the Cl concentrations of the bulk hydrothermal input occurred in 2014–2016, 2018, and 2020.

During the first event in 2014–2016, calculated $C_{eq}$ values were constant at ∼7,000 mg/ kg (A yellow hatch 1 in Figure 6D), which was three times higher than the value before the onset of the earthquake swarm. A high CO₂ concentration in nearby subaerial fumaroles was observed in 2014 (Ohba et al., 2019). From 2014 to 2016, a tiltmeter network revealed that volume inflation of 1.2 × 10⁵ m³ at a depth of 1,000 m beneath Yugama crater lake was observed from 2014 to 2016 (Terada et al., 2021). Moreover, Munekane (2021) also detected a significant increase in pressure at 6.4 km beneath the volcano. These geodetic studies suggest an increase in the supply of magmatic fluid from depth to the hydrothermal reservoir, which is consistent with the increase in $C_{eq}$.

Since 2017, Cl concentrations of Yugama crater lake have decreased slowly, but fluctuated. In 2017, calculated $C_{eq}$ values fluctuated around 2,300 mg/kg, similar to the values prior to the earthquake swarm. No earthquake swarm and ground deformation were observed in 2017, indicating that the supply of magmatic fluid from depth has not increased. The marked decrease in $C_{eq}$ values in the spring of 2017 were probably caused by a localized, temporary dilution of the lake water around the sampling site U1 due to melting of snow.

In 2018, during the second event, calculated $C_{eq}$ values increased to 4,000 mg/kg (A yellow hatch 2 in Figure 6D) and this was accompanied by a re-activated earthquake swarm and ground deformation (Munekane, 2021). Prior to the second event, a phreatic eruption occurred at Mt. Motoshirane (Figure 1B). In 2019, calculated $C_{eq}$ values decreased, similar as observed in 2017. However, ground deformation and an earthquake swarm became more intense in the latter half of 2019 preceding the third event in 2020 (A yellow hatch 3 in Figure 6D). The calculated $C_{eq}$ value increased markedly from 2,300 to 6,000 mg/kg in 2020. Moderate ground deformation and an earthquake swarm continued throughout 2020, indicating repeated increases in the supply of magmatic fluid from depth to the hydrothermal reservoir.

During this period, we have detected changes in $C_{eq}$ values which are consistent with geophysical observations and changes in gas composition nearby subaerial fumaroles. Since the water temperature and level did not change significantly, the changes in $C_{eq}$ values can be attributed to the changes in $C_{in}$ (the concentration of the bulk hydrothermal input) as changes in magmatic fluid supply altered chemical composition of the hydrothermal reservoir. The phreatic eruption in 2018 occurred when $C_{eq}$ fluctuated at a relatively low value, similar to the small eruption in 1989 (Period (b), 1987–1993). Therefore, we consider that $C_{eq}$ is a good indicator to evaluate subaqueous hydrothermal activity.

5 Discussion

In order to assess changes in volcanic activity, based on a time-series of concentrations of an element in lake water, such as Cl, we developed a numerical model to calculate temporal changes in $C_{eq}$ (steady-state concentration of an element of interest in the lake water, which changes depending on the concentration of the bulk hydrothermal input $C_{in}$). Our assumption can be applied during unrest or quiescent periods if there are no significant changes in water level and temperature, meaning that $m_{in}$ (mass flux of the bottom input fluid) remains constant. In the case of Yugama crater lake, temporal changes in Cl concentrations can occur over a long time (e.g., >1,000 days; Table 2), whereas our model uses two or three recent concentration measurements to estimate changes in $C_{eq}$. In our analysis for Yugama crater lake during the unrest in 2014–2020 (Figure 6D), by the end of 2014, the gradual increase in Cl concentration from June 2014 could be identified as a step-like increase in $C_{eq}$, without the need for gradual increase in $C_{in}$. Our calculation results for Yugama crater lake suggest that $C_{eq}$ is a good indicator to evaluate subaqueous hydrothermal activity of a volcanic lake. In this section, we consider different situations where the model is appropriate or needs adjustment to account for various conditions. Prediction of temporal changes in the lake concentration will also be discussed.

5.1 Estimation of the Concentration of the Bulk Hydrothermal Input ${\mathit{C}}_{\mathit{in}}$

For some volcanic lakes, $m_{in}$ (mass flux of the bottom input fluid) and $m_{sp}$ (seepage flux through the lake bottom) have been estimated using a box model. If ${\left(m_{sp}/m_{in}\right)}^i$ is known, we can calculate a time-series for $C_{in}^i$ based on the estimated $C_{eq}^i$.

For Yugama crater lake of Kusatsu-Shirane volcano, $m_{in}$ and $m_{sp}$ were calculated by Ohba et al. (1994) for 1988–1993. In the period of the earthquake swarm from 1990 to 1993 (Figure 5), the average $m_{in}$ and $m_{sp}$ were 22 and 30 kg/ s, respectively, meaning that $m_{sp}/m_{in}$ = 1.4. In this period, $C_{eq}^i$ varied between 3,000 and 4,500 mg/kg (Figure 6B). Assuming ${\left(m_{sp}/m_{in}\right)}^i$ = 1.4, $C_{in}^i$ can be calculated to be 4,100–6,100 mg/ kg (Table 3). This value is almost the same as the average of 6,600 mg/ kg estimated for the same period (1990–1993) by a box model (Ohba et al., 1994). On the other hand, $m_{sp}$ for 2012–2014 was estimated to be 6.8 kg/ s (Hirayama et al., 2021), which is one-third of the estimate for 1990–1993 by Ohba et al. (1994). To estimate the recent $C_{in}$ value of Yugama crater lake, it is necessary to examine the recent mass balance of the lake.

TABLE 3

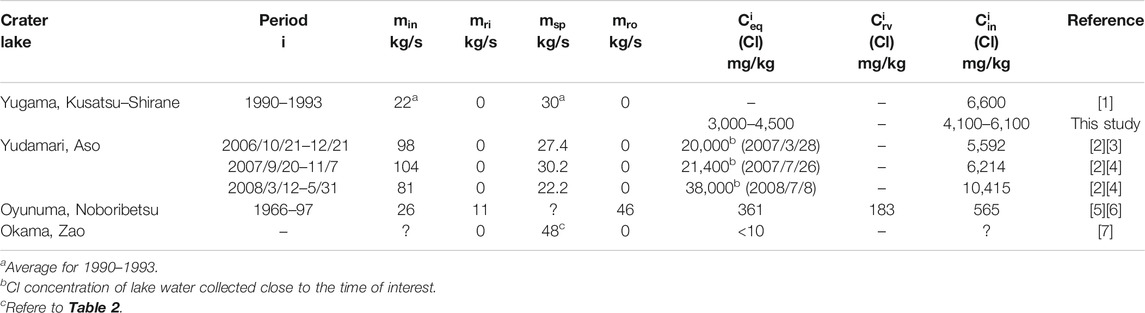
TABLE 3. Summary of the Cl concentrations of the bulk hydrothermal fluid injected from subaqueous fumaroles and hot springs $C_{in}^i$ in the period of interest $i$. In the cases of Yugama and Yudamari crater lakes, $C_{in}^i$ were calculated from Eq. 3, based on $m_{in}$, $m_{sp}$, and $C_{eq}^i$. For Oyunuma crater lake, $C_{in}^i$ was calculated from Eq. 16, using  $m_{rv}$ and $C_{rv}^i$, in addition to $m_{in}$, $m_{sp}$, and $C_{eq}^i$. The $C_{eq}^i$ for Yugama crater lake was obtained from this study. $C_{eq}^i$ for Yudamari and Oyunuma crater lakes are the Cl concentrations of the lake water assuming steady-state conditions. Numbers refer to the following references: [1] Ohba et al. (1994), [2] Terada et al. (2012), [3] Miyabuchi and Terada (2009), [4] Shinohara et al. (2015), [5] Murozumi et al. (1966), [6] Fukutomi et al. (1968), and [7] Kato (1960).

At Yudamari crater lake of Aso volcano, regular water samplings have not been performed due to steep topography, but a few water samples have revealed that the Cl concentrations of Yudamari crater lake during quiescent period were 20,000–38,000 mg/ kg (Miyabuchi and Terada, 2009; Shinohara et al., 2015). During this period, $m_{sp}/m_{in}$ has been estimated to be ∼0.3, without significant changes in lake volume (Terada et al., 2012). Assuming that the Cl concentrations of the lake water correspond to $C_{eq}$ (i.e., a steady-state condition was achieved, $C\left(t\right)$ = $C_{eq}$, the Cl concentrations of the bulk hydrothermal input $C_{in}$ can be calculated to be 5,600–10,000 mg/kg, which correspond to the values during the recent unrest from 2014 to 2020 at Yugama crater lake of Kusatsu-Shirane volcano (Table 3). It should be noted that pH of Yudamari crater lake was less than 0.4 (Shinohara et al., 2015). Considering HCl degassing from the lake surface, the calculated $C_{in}$ of 5,600–10,000 mg/ kg is a minimum estimate.

5.2 Effects of Surface Runoff Input and Output

If the surface runoff output and input contain the element of interest, the mass balance in Eq. 2 is modified as follows:

$\rho \frac{d}{dt}\left[V\left(t\right)C\left(t\right)\right]=m_{in}{C}_{in}+m_{ri}{C}_{ri}-\left(m_{sp}+m_{ro}\right)C\left(t\right)(14)$

where $m_{ri}$ and $C_{ri}$ are the mass flux (kg/s) and concentration (mg/kg) of the element of interest of the runoff input, respectively. We define $m_{ro}$ as the surface runoff output (kg/s). Assuming that the lake volume $V$ is approximately constant, Eq. 14 can be rewritten as:

$\frac{dC\left(t\right)}{dt}=\frac{m_{sp}+m_{ro}}{\rho V}\left(C_{eq}^{\prime }-C\left(t\right)\right)(15)$

where $C{\prime }_{eq}$ is the concentration at the steady-state. $C\left(t\right)$ = $C{\prime }_{eq}$ can be expressed by the following equation:

$C_{eq}^{\prime }=\frac{m_{in}{C}_{in}+m_{rv}{C}_{rv}}{m_{sp}+m_{ro}}(16)$

Oyunuma crater lake at Noboribetsu volcano has both surface runoff inputs and outputs relevant to the element of interest (Murozumi et al., 1966; Fukutomi et al., 1968; Inoue and Aoki, 2000) (Figure 1D). The seepage through the lake bottom is unconstrained, and thus we assumed the surface runoff output is dominant compared with the seepage through the lake bottom ($m_{sp}\ll m_{ro}$).

In this case, $a$ is estimated to be 2.0 × 10⁶ s (23 days) from Eq. 6, based $m_{ro}$ instead of $m_{sp}$ (Table 2). Table 3 lists $m_{in}$, $m_{rv}$, and $m_{ro}$ values, which are averages for 1966–1967 estimated by Fukutomi et al. (1968). The Cl concentration of the surface runoff input $C_{rv}$ in 1964 was 361 mg/ kg (Murozumi et al., 1966). Assuming that the Cl concentrations correspond to $C_{eq}$ (i.e., steady-state conditions), $C_{in}$ is estimated to be 565 mg/ kg from Eq. 16 (Table 3).

5.3 Notes on the Analysis

Our model is based on a simple mass balance model represented in Eq. 2. This model has been applied to other volcanoes including El Chichón in Mexico (Taran and Rouwet, 2008) and Maly Semyachik in Kamchatka (Taran et al., 2021). This model can be applied to non-reactive elements (e.g. Cl and Mg) in various volcanic lakes if the evaporation losses of the elements from the lake surface are negligible. However, in the case of extremely low pH crater lakes (less than ∼0) (Rouwet and Ohba 2015; Capaccioni et al., 2017) such as Poás during eruption period (Martínez et al., 2000), Kawah Ijen (van Hinsberg et al., 2017), White Island (Christenson et al., 2017) and Yudamari crater lake at Aso volcano (Shinohara et al., 2015), the application of this model requires the evaluation of evaporation loss of HCl.

One of the factors that create uncertainty in $C_{eq}$ estimation is the analytical error of the elements. The error of the chemical analysis used in this study is 0.15% for Cl (Yaguchi et al., 2021). In the case of two data calculation (Eq. (10)), assuming Kusatsu-Shirane [time constant $a$ = 1,000 days, time interval of samplings Δt = 60 days, and Cl concentration of 3,000 mg/ kg), the error of calculated $C_{eq}$ is estimated to be 110 mg/ kg, based on the law of propagation of errors (63 mg/ kg error for three data calculation, Eq. 13)]. The analytical error is small enough to discuss the changes in $C_{eq}$ associated with changes in volcanic activity.

Our model yields a time-series for $C_{eq}$ values, by assuming that changes in the water volume $V$ are negligible during each analysis period $i$ [$t^{i-1}< t < t^i$ or $t^{i-2}< t < t^i$, Eqs 10, 13]. However, $V$ would vary due to changes in $m_{in}$ (mass flux of the bottom input fluid), $m_{sp}$ (seepage flux through the lake bottom) and meteorological factors such as snow melting, heavy rainfalls and drought. In such cases, calculated $C_{eq}$ not always represents actual changes in $C_{in}$. In the case where the water volume changes with time, the time constant $a^i$ must be specified for each analysis period ($\Delta t^i$). Therefore, monitoring of the water level or volume using photographs is essential for a hyper-acidic hot crater lake (Rouwet, 2011; Terada et al., 2008). If temporal changes in $m_{in}$ are not negligible, as suggested by changes in lake volume and temperature (Terada and Hashimoto, 2017), it is necessary to evaluate changes in $\left(m_{sp}/m_{in}\right)$ using the box model (e.g., Pasternack and Varekamp, 1997) to calculate changes in $C_{in}$.

An element concentration in lake water can fluctuate due to meteorological factors and local heterogeneity around the water sampling site. In such a situation, a low-path filter including the moving average is effective in smoothing out the short-term fluctuations. When a moving average of ±60 days at intervals of 60 days was applied to the time-series of Cl concentrations in Yugama crater lake, temporal changes in $C_{eq}$ are detected (Figure 6), whereas short-term changes in $C_{eq}$ can be obscured. The moving average parameters should be selected on a case-by-case basis for each crater lake. Moreover, Inoue and Aoki (2000) identified spatial heterogeneity in element concentrations in Oyunuma crater lake at Noboribetsu volcano. In this case, use of the spatial mean concentration is desirable to estimate $C_{eq}$.

The time constant ($a$) is a critical parameter for calculating $C_{eq}$; however, it is difficult to estimate $m_{sp}$ without precise field surveys and a box model. We applied the empirical relationship presented in Estimations of the Time Constant (Table 2), while Varekamp (2015) proposed that both $C_{eq}$ and $a$ can be obtained simultaneously by fitting to a time-series of concentration data using the following equation:

$\log \left[C\left(t\right)-C_{eq}\right]=-\frac{t}{a}\log \left[C_0-C_{eq}\right](17)$

This equation is obtained by taking the logarithm of Eq. 5. Although the time range for fitting Eq. 17 to the data is somewhat arbitrary, time constant $a$ estimated from Eq. 17 can be used to calculate $m_{sp}$ from Eq. 6. This allows $m_{sp}$ to be estimated when Cl concentrations change gradually and the water volume is broadly constant.

5.4 Prediction and Monitoring of Lake Water

Provided $V$ (lake volume) and $m_{sp}$ (mass flux of seepage through the lake bottom) do not change significantly during the period of interest, the future concentration in the lake water can be predicted from Eq. 5, based on the latest $C_{eq}^i$ value calculated from two or three analyses of the recent chemical concentration $C_i$ values. By comparing the predicted and observed concentration, it is possible to assess whether the concentration of the bulk hydrothermal input has increased/decreased or remained constant.

In this section, we predict temporal changes in Cl concentration of Yugama crater lake at Kusatsu-Shirane volcano, as a representative case for which a long-term time series has been obtained. We believe that the crystallizing magma, surrounded with a self-sealing zone (Fournier, 1999), is underlain in a shallow depth beneath Yugama crater lake (Ohba et al., 2008; Tseng et al., 2020; Yaguchi et al., 2021). When the overpressure of the crystallizing magma causes fractures in the self-sealing zone, the supply of magma fluid such as HCl from within the self-sealing zone is expected to increase. Therefore, measurements of temporal changes in Cl concentration are essential to monitor the volcanic activity of Kusatsu-Shirane volcano.

Figure 7A shows the predicted Cl concentrations of Yugama crater lake after June 2014, as a representative period when the concentration increased steadily. Here, the initial concentration $C_0$ was set to 2,380 mg/ kg, corresponding to the smoothed measured concentration in the lake water in June 2014 (average observed concentration over ±60 days). We used $C_{eq}$ = 7,200 mg/ kg estimated from Figure 6D.

FIGURE 7

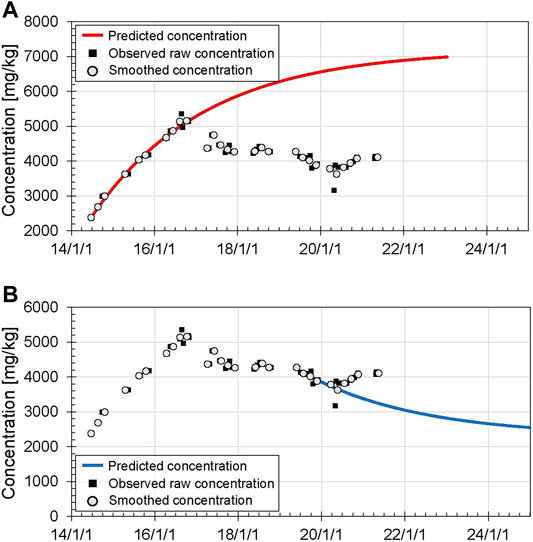
FIGURE 7. Predicted Cl concentrations of Yugama crater lake calculated with Eq. 5, assuming $V$ and $m_{sp}$ do not change during the period of interest. Black squares and gray circles represent raw and smoothed $C^i$ values, respectively. (A) Predicted concentration curve after June 2014. The initial concentration $C_0$ was set to 2,380 mg/ kg. This is the smoothed Cl concentration of the lake on June 22, 2014, which was the average observed concentration over ± 60 days. $C_{eq}$ was set to 7,200 mg/ kg as estimated by Figure 5B. (B) Predicted concentration curve after September 2019. The initial concentration $C_0$ was set to 4,020 mg/kg. This is the smoothed Cl concentration of the lake on September 24, 2019, which was the average observed concentration over ±60 days. $C_{eq}$ was set to 2,300 mg/ kg as estimated by Figure 5B.

The predicted Cl concentration increases with time because $C_0 < C_{eq}$. The curve of the predicted Cl concentration is in good agreement with the observed concentrations obtained until 2016, meaning that the gradual increase from 2014 to 2016 was caused by an initial change in $C_{eq}$, without the need for further increase in the concentration of the bulk hydrothermal input. Since 2017, the observed Cl concentrations have deviated significantly from the predicted curve. The water level and temperature did not change significantly, suggesting $m_{in}$ (the hydrothermal input from the lake bottom) is not expected to decrease (Terada and Hashimoto, 2017). Therefore, the deviation from the predicted curve in 2017 is interpreted as a decrease in the Cl concentrations of the bulk hydrothermal input in 2017 as compared with 2014–2016, although Cl concentrations in the lake water remained high values of >4,000 mg/ kg.

Figure 7B shows the predicted Cl concentrations after September 2019, as a representative period when the concentration decreased steadily. Here, the initial concentration $C_0$ was set to 4,020 mg/ kg, corresponding to the smoothed measured concentration in the lake water in September 2019 (average observed concentration over ± 60 days). We use $C_{eq}$ = 2,300 mg/ kg calculated from the smoothed $C^i$ values (27 May, 26 July, and September 24, 2019) obtained from Eq. 13 (Figure 6D). The predicted Cl concentration curve shows decrease in the concentration with time because $C_0 > C_{eq}$, which is in good agreement with the observed concentrations until May 2020. Therefore, in 2019, we can see that $C_{in}$ (the concentrations of the bulk hydrothermal input) returned to the value observed before the start of the earthquake swarm in 2014.

The curve predicts that chloride concentrations of the lake water will decrease from 4,020 mg/ kg in September 2019 to 2,470 mg/ kg in January 2026 as the 90% response, or 2,335 mg/ kg in May 2030 as the 98% response. Thus, it takes a long time if absolute concentrations are to be used as the basis for assessing the end of unrest. However, by the end of 2019, our model indicates the decreases in the Cl concentrations of the bulk hydrothermal input using the three recent concentration data. Furthermore, the predicted curve also clearly reveals an increase Cl concentration in the bulk hydrothermal input ($C_{in}$) in the latter half of 2020. For Kusatsu-Shirane volcano, our model using time-series of lake concentration for the past 6 months can be used to quickly assess the state of volcanic activity.

6 Conclusions

Temporal changes in the concentrations in the lake can take a long time to be evident (e.g., >1,000 days). In order to assess volcanic activity based on a time-series of concentrations of an element in crater lake waters, we developed a numerical model to calculate temporal changes in the steady-state concentration $C_{eq}$, assuming the water volume in the lake $V$ is almost constant. The $C_{eq}$ values are proportional to the values of $C_{in}$ (the concentrations of the bulk hydrothermal fluid injected from subaqueous fumaroles and hot springs) and, therefore, can be used to assess volcanic activity. Our analyses for Yugama crater lake suggest that $C_{eq}$ is a good indicator to evaluate subaqueous hydrothermal activity. Future concentrations in the lake water at a given time can be predicted based on the recent steady state concentration $C_{eq}$. The values of $C_{eq}$ can be easily calculated using time series of lake water concentrations, time interval of water samplings and lake water volume. Temporal changes in the concentrations of the bulk hydrothermal input $C_{in}$ were calculated based on $C_{eq}$ when the ratio of seepage flux to fluid emitted from the lake bottom ($m_{sp}/m_{in}$) remains constant. Therefore, we conclude that steady-state concentration $C_{eq}$ is the key parameter in assessing volcanic activity. For Kusatsu-Shirane volcano, our model using time-series of Cl concentration for the past 6 months can be used to quickly assess the state of volcanic activity.

Data Availability Statement

Chemical concentration data for Yugama crater lake were published in Ossaka et al. (1997), Ohba et al. (2008), and Yaguchi et al. (2021).

Author Contributions

AT constructed the numerical model, analyzed the time-series of the lake data, and drafted the manuscript. MY and TO analyzed the water chemistry and helped interpret the data. All authors read and approved the final manuscript.

Funding

This research was supported by the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan through its Second Earthquake and Volcano Hazards Observation and Research Program (Earthquake and Volcano Hazard Reduction Research) and Integrated Program for Next Generation Volcano Research and Human Resource Development.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Officials of Kusatsu town and the Ministry of Agriculture, Forestry, and Fisheries provided approval for our research observations. We also thank Jun’ichi Hirabayashi and the staff at the Volcanic Fluid Research Center, School of Science, Tokyo Institute of Technology, for their valuable comments. Hiroshi Aoyama, Mare Yamamoto, and Shin Yoshikawa kindly allowed us to use their photographs. The Japan Meteorological Agency provided the number of earthquakes at Kusatsu–Shirane volcano. We used Generic Mapping Tools (Wessel and Smith, 1998) to generate the maps. We thank Dmitri Rouwet and the reviewers for their constructive revision.

References

Agusto, M. R., Caselli, A., Daga, R., Varekamp, J., Trinelli, A., Dos Santos Afonso, M., et al. (2016). The Crater Lake of Copahue Volcano (Argentina): Geochemical and Thermal Changes between 1995 and 2015. Geol. Soc. Lond. Spec. Publications 437, 107–130. doi:10.1144/SP437.16

CrossRef Full Text | Google Scholar

Albarède, F. (1995). Introduction to Geochemical Modeling. Cambridge: Cambridge University Press. doi:10.1017/CBO9780511622960

CrossRef Full Text | Google Scholar

Anzai, T. (1961). The Mysterious Crater Lake Okama, Zao Volcano. Yamagata, Japan: Yamagata Geological Institute, 224 p.

Google Scholar

Armienta, M. A., De la Cruz-Reyna, S., and Macías, J. L. (2000). Chemical Characteristics of the Crater Lakes of Popocatetetl, El Chichon, and Nevado de Toluca Volcanoes, Mexico. J. Volcanol. Geotherm. Res. 97, 105–125. doi:10.1016/S0377-0273(99)00157-2

CrossRef Full Text | Google Scholar

Barberi, F., Bertagnini, A., Landi, P., and Principe, C. (1992). A Review on Phreatic Eruptions and Their Precursors. J. Volcanol. Geotherm. Res. 52, 231–246. doi:10.1016/0377-0273(92)90046-G

CrossRef Full Text | Google Scholar

Candela-Becerra, L. J., Toyos, G., Suárez-Herrera, C. A., Castro-Godoy, S., and Agusto, M. (2020). Thermal Evolution of the Crater Lake of Copahue Volcano with ASTER during the Last Quiescence Period between 2000 and 2012 Eruptions. J. Volcanol. Geotherm. Res. 392, 106752. doi:10.1016/j.jvolgeores.2019.106752

CrossRef Full Text | Google Scholar

Capaccioni, B., Rouwet, D., and Tassi, F. (2017). HCl Degassing from Extremely Acidic Crater Lakes: Preliminary Results from Experimental Determinations and Implications for Geochemical Monitoring. Geol. Soc. Lond. Spec. Publications 437, 97–106. doi:10.1144/SP437.12

CrossRef Full Text | Google Scholar

Christenson, B. W. (2000). Geochemistry of Fluids Associated with the 1995-1996 Eruption of Mt. Ruapehu, New Zealand: Signatures and Processes in the Magmatic-Hydrothermal System. J. Volcanol. Geotherm. Res. 97, 1–30. doi:10.1016/S0377-0273(99)00167-5

CrossRef Full Text | Google Scholar

Christenson, B. W., White, S., Britten, K., and Scott, B. J. (2017). Hydrological Evolution and Chemical Structure of a Hyper-Acidic spring-Lake System on Whakaari/White Island, NZ. J. Volcanol. Geotherm. Res. 346, 180–211. doi:10.1016/j.jvolgeores.2017.06.017

CrossRef Full Text | Google Scholar

Cigolini, C., Coppola, D., Yokoo, A., and Laiolo, M. (2018). The Thermal Signature of Aso Volcano during Unrest Episodes Detected from Space and Ground-Based Measurements. Earth Planets Space 70, 67. doi:10.1186/s40623-018-0831-7

CrossRef Full Text | Google Scholar

Edwards, M. J., Kennedy, B. M., Jolly, A. D., Scheu, B., and Jousset, P. (2017). Evolution of a Small Hydrothermal Eruption Episode through a Mud Pool of Varying Depth and Rheology, White Island, NZ. Bull. Volcanol. 79, 16. doi:10.1007/s00445-017-1100-5

CrossRef Full Text | Google Scholar

Fournier, N., Moreau, M., and Robertson, R. (2011). Disappearance of a Crater Lake: Implications for Potential Explosivity at Soufrière Volcano, St Vincent, Lesser Antilles. Bull. Volcanol. 73, 543–555. doi:10.1007/s00445-010-0422-3

CrossRef Full Text | Google Scholar

Fournier, N., Witham, F., Moreau-Fournier, M., and Bardou, L. (2009). Boiling Lake of Dominica, West Indies: High-Temperature Volcanic Crater Lake Dynamics. J. Geophys. Res. 114, B02203. doi:10.1029/2008jb005773

CrossRef Full Text | Google Scholar

Fournier, R. O. (1999). Hydrothermal Processes Related to Movement of Fluid from Plastic into Brittle Rock in the Magmatic-Epithermal Environment. Econ. Geol. 94, 1193–1211. doi:10.2113/gsecongeo.94.8.1193

CrossRef Full Text | Google Scholar

Fukutomi, T., Nakao, K., Miyoshi, H., and Tanoue, R. (1968). Studies of Water Balance and Heat Budget at Ōyunuma Hot Lake in Noboribetsu, Hokkaido. Geophys. Bull. Hokkaido Univ. 19, 1–19. doi:10.14943/gbhu.19.1

CrossRef Full Text | Google Scholar

Giggenbach, W. F., and Glover, R. B. (1975). The Use of Chemical Indicators in the Surveillance of Volcanic Activity Affecting the Crater Lake on Mt Ruapehu, New Zealand. Bull. Volcanol. 39, 70–81. doi:10.1007/BF02596947

CrossRef Full Text | Google Scholar

Hirayama, Y., Okawa, A., Nakamachi, K., Aoyama, T., Okada, Y., Oi, T., et al. (2020). Estimation of Water Seepage Rate in the Active Crater Lake System of Kusatsu-Shirane Volcano, Japan, Using FDNPP-Derived Radioactive Cesium as a Hydrological Tracer. J. Environ. Radioactivity 218, 106257. doi:10.1016/j.jenvrad.2020.106257

PubMed Abstract | CrossRef Full Text | Google Scholar

Hurst, A. W., Bibby, H. M., Scott, B. J., and McGuinness, M. J. (1991). The Heat Source of Ruapehu Crater Lake; Deductions from the Energy and Mass Balances. J. Volcanol. Geotherm. Res. 46, 1–20. doi:10.1016/0377-0273(91)90072-8

CrossRef Full Text | Google Scholar

Ida, Y., Osada, N., Sawada, M., Koyama, E., and Kagiyama, T. (1989). Seismological Study Based on Recently Installed Permanent Stations and a Small Eruptive Event on January 6, 1989 at Kusatsu-Shirane Volcano. Bull. Earth. Res. Ins. 64, 325–345. (in Japanese with English abstract). doi:10.15083/0000032805

CrossRef Full Text | Google Scholar

Inoue, A., and Aoki, M. (2000). Mineralogy of Ohyunuma Explosion Crater Lake, Hokkaido, Japan Part 1: Geochemistry, Hydrology, and Bulk Mineralogy. Clay Sci. 11, 147–168. doi:10.11362/jcssjclayscience1960.11.147

CrossRef Full Text | Google Scholar

Kametani, N., Ishizaki, Y., Yoshimoto, M., Maeno, F., Terada, A., Furukawa, R., et al. (2021). Total Mass Estimate of the January 23, 2018 Phreatic Eruption of the Kusatsu-Shirane Volcano, Central Japan. Earth Planets Space 73, 141. doi:10.1186/s40623-021-01468-3

CrossRef Full Text | Google Scholar

Kato, T. (1960). Some Limnological Remarks on the Crater Lake, “Okama”. Jpn. J. Limnol. 21, 141–150. doi:10.3739/rikusui.21.141

CrossRef Full Text | Google Scholar

Kusakabe, M., Komoda, Y., Takano, B., and Abiko, T. (2000). Sulfur Isotopic Effects in the Disproportionation Reaction of Sulfur Dioxide in Hydrothermal Fluids: Implications for the δ34S Variations of Dissolved Bisulfate and Elemental Sulfur from Active Crater Lakes. J. Volcanol. Geotherm. Res. 97, 287–307. doi:10.1016/S0377-0273(99)00161-4

CrossRef Full Text | Google Scholar

Lewicki, J. L., Caudron, C., van Hinsberg, V. J., and Hilley, G. E. (2016). High Spatio-Temporal Resolution Observations of Crater Lake Temperatures at Kawah Ijen Volcano, East Java, Indonesia. Bull. Volcanol. 78, 53. doi:10.1007/s00445-016-1049-9

CrossRef Full Text | Google Scholar

Manville, V. (2015). “Volcano-Hydrologic Hazards from Volcanic Lakes,” in Volcanic Lakes. Advances in Volcanology. Editors D. Rouwet, B. Christenson, F. Tassi, and J. Vandemeulebrouck (Berlin, Heidelberg: Springer), 21–71. doi:10.1007/978-3-642-36833-2_2

CrossRef Full Text | Google Scholar

Martínez, M., Fernández, E., Valdés, J., Barboza, V., Van der Laat, R., Duarte, E., et al. (2000). Chemical Evolution and Volcanic Activity of the Active Crater Lake of Poás Volcano, Costa Rica, 1993–1997. J. Volcanol. Geotherm. Res. 97, 127–141. doi:10.1016/S0377-0273(99)00165-1

CrossRef Full Text | Google Scholar

Minami, E., Yamagata, N., Shima, M., and Saijô, Y. (1952). Crater Lake "Yugama" of Volcano Kusatsu-Shirane. I. Jpn. J. Limnol. 16, 1–5. (in Japanese). doi:10.3739/rikusui.16.1

CrossRef Full Text | Google Scholar

Miura, K., Ban, M., Ohba, T., and Fujinawa, A. (2012). Sequence of the 1895 Eruption of the Zao Volcano, Tohoku Japan. J. Volcanol. Geotherm. Res. 247-248, 139–157. doi:10.1016/j.jvolgeores.2012.08.005

CrossRef Full Text | Google Scholar

Miyabuchi, Y., and Terada, A. (2009). Subaqueous Geothermal Activity Revealed by Lacustrine Sediments of the Acidic Nakadake Crater Lake, Aso Volcano, Japan. J. Volcanol. Geotherm. Res. 187, 140–145. doi:10.1016/j.jvolgeores.2009.08.001

CrossRef Full Text | Google Scholar

Morrissey, M., Gisler, G., Weaver, R., and Gittings, M. (2010). Numerical Model of Crater Lake Eruptions. Bull. Volcanol. 72, 1169–1178. doi:10.1007/s00445-010-0392-5

CrossRef Full Text | Google Scholar

Munekane, H. (2021). Modeling Long-Term Volcanic Deformations at the Kusatsu-Shirane and Asama Volcanoes, Japan Using the GNSS Coordinate Time Series. Earth Planets Space 73, 192. doi:10.1186/s40623-021-01512-2

CrossRef Full Text | Google Scholar

Murozumi, M., Abiko, T., and Nakamura, S. (1966). Geochemical Investigation of the Noboribetsu Oyunuma Explosion Crater Lake. J. Volcanol. Soc. Jpn. 11, 1–16. doi:10.18940/kazanc.11.1_1

CrossRef Full Text | Google Scholar

Ohba, T., Hirabayashi, J., and Nogami, K. (2008). Temporal Changes in the Chemistry of Lake Water within Yugama Crater, Kusatsu-Shirane Volcano, Japan: Implications for the Evolution of the Magmatic Hydrothermal System. J. Volcanol. Geotherm. Res. 178, 131–144. doi:10.1016/j.jvolgeores.2008.06.015

CrossRef Full Text | Google Scholar

Ohba, T., Hirabayashi, J., and Nogami, K. (1994). Water, Heat and Chloride Budgets of the Crater Lake, Yugama at Kusatsu-Shirane Volcano, Japan. Geochem. J. 28, 217–231. doi:10.2343/geochemj.28.217

CrossRef Full Text | Google Scholar

Ohba, T., Yaguchi, M., Nishino, K., Numanami, N., Tsunogai, U., Ito, M., et al. (2019). Time Variation in the Chemical and Isotopic Composition of Fumarolic Gasses at Kusatsu-Shirane Volcano, Japan. Front. Earth Sci. 7, 249. doi:10.3389/feart.2019.00249

CrossRef Full Text | Google Scholar

Oppenheimer, C. (1997). Ramifications of the Skin Effect for Crater Lake Heat Budget Analysis. J. Volcanol. Geotherm. Res. 75, 159–165. doi:10.1016/S0377-0273(96)00037-6

CrossRef Full Text | Google Scholar

Ossaka, J., Ossaka, T., Oi, T., Kikawada, K., Yamano, M., Hukuhara, H., et al. (1997). Volcanic Activity of Kusatsu-Shirane Volcano, Gunma, and Secular Change in Water Quality of Crater Lake, Yugama. Chikyukagaku 31, 119–128. (in Japanese).

Google Scholar

Ossaka, J., Ozawa, T., Nomara, T., Ossaka, T., Hirabayashi, J., Takaesu, A., et al. (1980). Variation of Chemical Compositions in Volcanic Gases and Water at Kusatsu-Shirane Volcano and its Activity in 1976. Bull. Volcanol. 43, 207–216. doi:10.1007/BF02597622

CrossRef Full Text | Google Scholar

Pasternack, G. B., and Varekamp, J. C. (1997). Volcanic Lake Systematics I. Physical Constraints. Bull. Volcanol. 58, 528–538. doi:10.1007/s004450050160

CrossRef Full Text | Google Scholar

Peiffer, L., Rouwet, D., and Taran, Y. (2015). “Fluid Geochemistry of El Chichón Volcano-Hydrothermal System,” in Active Volcanoes of Chiapas (Mexico): El Chichón and Tacaná. Active Volcanoes of the World. Editors T. Scolamacchia, and J. Macías (Berlin, Heidelberg: Springer), 77–95. doi:10.1007/978-3-642-25890-9_4

CrossRef Full Text | Google Scholar

Peiffer, L., and Taran, Y. (2013). Heat and Mass Fluxes Monitoring of El Chichon Crater Lake. Rev. Mex. Cienc. Geol. 30, 500–511.

Google Scholar

Roberts, T. J., Saffell, J. R., Oppenheimer, C., and Lurton, T. (2014). Electrochemical Sensors Applied to Pollution Monitoring: Measurement Error and Gas Ratio Bias - A Volcano Plume Case Study. J. Volcanol. Geotherm. Res. 281, 85–96. doi:10.1016/j.jvolgeores.2014.02.023

CrossRef Full Text | Google Scholar

Rouwet, D. (2011). A Photographic Method for Detailing the Morphology of the Floor of a Dynamic Crater Lake: the El Chichón Case (Chiapas, Mexico). Limnology 12, 225–233. doi:10.1007/s10201-011-0343-7

CrossRef Full Text | Google Scholar

Rouwet, D., Mora-Amador, R., Ramírez-Umaña, C. J., González, G., and Inguaggiato, S. (2017). Dynamic Fluid Recycling at Laguna Caliente (Poás, Costa Rica) before and during the 2006-ongoing Phreatic Eruption Cycle (2005-10). Geol. Soc. Lond. Spec. Publications 437, 73–96. doi:10.1144/SP437.11

CrossRef Full Text | Google Scholar

Rouwet, D., and Ohba, T. (2015). “Isotope Fractionation and HCl Partitioning during Evaporative Degassing from Active Crater Lakes,” in Volcanic Lakes. Advances in Volcanology. Editors D. Rouwet, B. Christenson, F. Tassi, and J. Vandemeulebrouck (Berlin, Heidelberg: Springer), 179–200. doi:10.1007/978-3-642-36833-2_7

CrossRef Full Text | Google Scholar

Rouwet, D., Taran, Y., Inguaggiato, S., Varley, N., and Santiago Santiago, J. A. (2008). Hydrochemical Dynamics of the “Lake-spring” System in the Crater of El Chichón Volcano (Chiapas, Mexico). J. Volcanol. Geotherm. Res. 178, 237–248. doi:10.1016/j.jvolgeores.2008.06.026

CrossRef Full Text | Google Scholar

Rouwet, D., and Tassi, F. (2011). Geochemical Monitoring of Volcanic Lakes. A Generalized Box Model for Active Crater Lakes. Annal. Geophys. 54. doi:10.4401/ag-50310.4401/ag-5035

CrossRef Full Text | Google Scholar

Rouwet, D., Tassi, F., Mora-Amador Sandri, R. L., Sandri, L., and Chiarini, V. (2014). Past, Present and Future of Volcanic Lake Monitoring. J. Volcanol. Geotherm. Res. 272, 78–97. doi:10.1016/j.jvolgeores.2013.12.009

CrossRef Full Text | Google Scholar

Rowe, G. L., Brantley, S. L., Fernandez, M., Fernandez, J. F., Borgia, A., and Barquero, J. (1992). Fluid-volcano Interaction in an Active Stratovolcano: the Crater Lake System of Poás Volcano, Costa Rica. J. Volcanol. Geotherm. Res. 49, 23–51. doi:10.1016/0377-0273(92)90003-V

CrossRef Full Text | Google Scholar

Shinohara, H., Yoshikawa, S., and Miyabuchi, Y. (2015). “Degassing Activity of a Volcanic Crater Lake: Volcanic Plume Measurements at the Yudamari Crater Lake, Aso Volcano, Japan,” in Volcanic Lakes. Advances in Volcanology. Editors D. Rouwet, B. Christenson, F. Tassi, and J. Vandemeulebrouck (Berlin, Heidelberg: Springer), 201–217. doi:10.1007/978-3-642-36833-2_8

CrossRef Full Text | Google Scholar

Simonson, J. M., and Palmer, D. A. (1993). Liquid-vapor Partitioning of HCl(aq) to 350°C. Geochimica et Cosmochimica Acta 57, 1–7. doi:10.1016/0016-7037(93)90462-6

CrossRef Full Text | Google Scholar

Smith, S. W. (1997). The Scientist and Engineer's Guide to Digital Signal Processing. San Diego, California, USA: California Technical Publishing, 626. Chapter 19.

Google Scholar

Stix, J. (2018). Understanding Fast and Slow Unrest at Volcanoes and Implications for Eruption Forecasting. Front. Earth Sci. 6, 56. doi:10.3389/feart.2018.00056

CrossRef Full Text | Google Scholar

Takahashi, K., and Fujii, I. (2014). Long-term Thermal Activity Revealed by Magnetic Measurements at Kusatsu-Shirane Volcano, Japan. J. Volcanol. Geotherm. Res. 285, 180–194. doi:10.1016/j.jvolgeores.2014.08.014

CrossRef Full Text | Google Scholar

Taran, Y., Kalacheva, E., Dvigalo, V., Melnikov, D., and Voloshina, E. (2021). Evolution of the Crater Lake of Maly Semyachik Volcano, Kamchatka (1965-2020). J. Volcanol. Geotherm. Res. 418, 107351. doi:10.1016/j.jvolgeores.2021.107351

CrossRef Full Text | Google Scholar

Taran, Y., and Rouwet, D. (2008). Estimating Thermal Inflow to El Chichón Crater Lake Using the Energy-Budget, Chemical and Isotope Balance Approaches. J. Volcanol. Geotherm. Res. 175, 472–481. doi:10.1016/j.jvolgeores.2008.02.019

CrossRef Full Text | Google Scholar

Terada, A., Hashimoto, T., and Kagiyama, T. (2012). A Water Flow Model of the Active Crater Lake at Aso Volcano, Japan: Fluctuations of Magmatic Gas and Groundwater Fluxes from the Underlying Hydrothermal System. Bull. Volcanol. 74, 641–655. doi:10.1007/s00445-011-0550-4

CrossRef Full Text | Google Scholar

Terada, A., Hashimoto, T., Kagiyama, T., and Sasaki, H. (2008). Precise Remote-Monitoring Technique of Water Volume and Temperature of a Crater Lake in Aso Volcano, Japan: Implications for a Sensitive Window of a Volcanic Hydrothermal System. Earth Planet. Space 60, 705–710. doi:10.1186/BF03353134

CrossRef Full Text | Google Scholar

Terada, A., and Hashimoto, T. (2017). Variety and Sustainability of Volcanic Lakes: Response to Subaqueous Thermal Activity Predicted by a Numerical Model. J. Geophys. Res. Solid Earth 122, 6108–6130. doi:10.1002/2017JB014387

CrossRef Full Text | Google Scholar

Terada, A., Kanda, W., Ogawa, Y., Yamada, T., Yamamoto, M., Ohkura, T., et al. (2021). The 2018 Phreatic Eruption at Mt. Motoshirane of Kusatsu–Shirane Volcano, Japan: Eruption and Intrusion of Hydrothermal Fluid Observed by a Borehole Tiltmeter Network. Earth Planets Space 73, 157. doi:10.1186/s40623-021-01475-4

CrossRef Full Text | Google Scholar

Tseng, K. H., Ogawa, Y., Nurhasan, , , Tank, S. B., Ujihara, N., Honkura, Y., et al. (2020). Anatomy of Active Volcanic Edifice at the Kusatsu-Shirane Volcano, Japan, by Magnetotellurics: Hydrothermal Implications for Volcanic Unrests. Earth Planets Space 72, 161. doi:10.1186/s40623-020-01283-2

CrossRef Full Text | Google Scholar

van Hinsberg, V., Vigouroux, N., Palmer, S., Berlo, K., Mauri, G., Williams-Jones, A., et al. (2017). Element Flux to the Environment of the Passively Degassing Crater Lake-hosting Kawah Ijen Volcano, Indonesia, and Implications for Estimates of the Global Volcanic Flux. Geol. Soc. Lond. Spec. Publications 437, 9–34. doi:10.1144/SP437.2

CrossRef Full Text | Google Scholar

Varekamp, J. C. (2002). Lake Contamination Models for Evolution towards Steady State. J. Limnol. 62, 67–72. doi:10.4081/jlimnol.2003.s1.67

CrossRef Full Text | Google Scholar

Varekamp, J. C. (2015). “The Chemical Composition and Evolution of Volcanic Lakes,” in Volcanic Lakes. Advances in Volcanology. Editors D. Rouwet, B. Christenson, F. Tassi, and J. Vandemeulebrouck (Berlin, Heidelberg: Springer), 93–123. doi:10.1007/978-3-642-36833-2_4

CrossRef Full Text | Google Scholar

Werner, C., Hurst, T., Scott, B., Sherburn, S., Christenson, B. W., Britten, K., et al. (2008). Variability of Passive Gas Emissions, Seismicity, and Deformation during Crater Lake Growth at White Island Volcano, New Zealand, 2002-2006. J. Geophys. Res. 113, B01204. doi:10.1029/2007JB005094

CrossRef Full Text | Google Scholar

Wessel, P., and Smith, W. H. F. (1998). New, Improved Version of Generic Mapping Tools Released. EOS Trans. AGU 79, 579. doi:10.1029/98EO00426

CrossRef Full Text | Google Scholar

Yaguchi, M., Ohba, T., and Terada, A. (2021). Groundwater Interacting at Depth with Hot Plastic Magma Triggers Phreatic Eruptions at Yugama Crater Lake of Kusatsu-Shirane Volcano (Japan). Front. Earth Sci. 9, 741742. doi:10.3389/feart.2021.741742

CrossRef Full Text | Google Scholar

Yamada, T., Kurokawa, A. K., Terada, A., Kanda, W., Ueda, H., Aoyama, H., et al. (2021). Locating Hydrothermal Fluid Injection of the 2018 Phreatic Eruption at Kusatsu-Shirane Volcano with Volcanic Tremor Amplitude. Earth Planets Space 73, 14. doi:10.1186/s40623-020-01349-1

CrossRef Full Text | Google Scholar