Mass Exchange of Water and Soil on the Soil Surface in the Rainfall Splash Erosion

This research aims to unfold the mass exchange mechanism of water and soil on the soil surface in the rainfall splash erosion process. We regard the rainfall splash erosion process as a collision process between the raindrop and the soil particle on the soil interface. This recognition allows us to incorporate research approaches from the spring vibrator model, which has been developed for simulating the impact of liquid drops on solid surface. We further argue that because a same set of factors determine the splash amount and infiltration amount and it is relatively simpler to observe the infiltration amount, an investigation into the relationship between the splash amount and infiltration amount would be able to provide a new channel for quantifying the splash erosion. This recognition leads us to examining the relationship between single raindrop, rainfall kinetic energy and splash erosion from both theoretical and empirical angles, with an emphasis on the relationship between the infiltration amount and the splash erosion. Such an investigation would add value to the collective effort to establish mass exchange law in water-soil interface during rainfall splash erosion. It is found that during the rainfall splash process, the splash erosion is proportional to the rainfall kinetic energy; and has a linear relation to the infiltration amount, with the rainfall intensity as one of important parameters and the slope depending on the unit conversation of the infiltration amount and the splash erosion. If the units of two items are same, the slope is the ratio of the soil and water density, and the splash erosion velocity of the rainfall is half of the rainfall terminal velocity. The single raindrop kinetic energy and the splash erosion have a quadratic parabola relation, and the splash velocity is about 1/3 of single raindrop terminal velocity.

Introduction

Rainfall splash is mainly composed of rainfall, infiltration and splash factors. There has been a better understanding of the relationship between rainfall and infiltration than that between rainfall and splash in the literature (Li et al., 2011; Wang et al., 2015). One of the current research trends on the latter relationship is to establish the statistical relationship between splash erosion rate or amount and the characteristics of rainfall and earth surface. Publications in this stream of research use statistical regression and dimension analysis to deal with the experiment data, and some of them apply the force analysis and the momentum theorem without considering the momentum loss (Li et al., 2011). The studies on the relationship between the infiltration amount and the splash erosion are confined into experimental analysis. However, the regression results of such experimental analysis vary with experiment conditions. In addition, the theoretical analysis model of the relation has not yet been established (Sun, 1997; Wang et al., 2015). There is an urgent need to advance both theoretical and empirical researches about the relationship across the splash erosion, rainfall and infiltration amount, as well as the mechanism of splash erosion mechanics.

It is widely recognized that the splash erosion mainly depends on the characteristics of earth surface and rainfall. The former includes slope, canopy vegetation and soil layer formation, and the latter includes rainfall, rain intensity, rainfall energy, raindrop’s diameter, raindrop’s velocity and rainfall duration, etc., (Sun, 1997; Wang et al., 2015).

A large number of experimental tests have been done to quantify the relationship between characteristics of earth surface and splash erosion, including studies on the effect of different diameter of aggregate on the loessal soil splash erosion velocity (Hu, 2015); the relationship among the soil initial moisture content, the red earth splash erosion and the moisture content of early stage corresponding to the raindrop splash amount with constant soil bulk density 1.2g/cm3 (Zhao et al., 2003; Ma et al., 2014); the influence of the changing grain size of red earth aggregate on the splash (Ma et al., 2013); the influence of purple soil, loess and chernozen soil crust on the splash, and the time history of the splash erosion (Bu et al., 2014); and the influence of bulk density, porosity, angle of internal friction, cohesion, and the soil particle size distribution on splash erosion rate after mixing different quality of silty clay, sand clay and sand (Wei et al., 2015). In the case of calcareous soil surface, compared with the influences caused by shear strength (SS), mean weight diameter (MWD), organic matter (OM), calcium carbonate, clay content, silt and sand fraction estimation, Saedi et al. (2016)argue that SS, MWD are the key indicators of the splash erosion. Based on the monitoring data of natural rainfall splash erosion across different soil types in NE Spain, Angulo et al. (2012)find that the splash erosion has little difference across different soil types.

Similarly, there also a large body of empirical researches to assess the influence of rainfall characteristics on the splash erosion. For example, based on indoor artificial rainfall experiments, Yin et al. (2011) regress the raindrop splash erosion on distance, the surface layer thickness, and raindrop kinetic energy and find that the kinetic energy increases with the splash erosion amount; Zheng et al. (2016) established statistical relationships between disturbance water-course thickness and sediment splash erosion under the condition of single and multiple raindrop splash with different soil types such as soil, loess and chernozen soil. Based on outdoor artificial rainfall experiments, Cheng et al. (2015) showed that the fine sand with the grain diameter 0.05–0.2 mm was most vulnerable to splash erosion, while the small size with the grain diameter less than 0.002 mm and the large size with the grain diameter larger than 0.2 mm were not easy to be splashed. They drawed conclusion that the splash erosion amount had an exponential relationship with the rainfall intensity and a linear relationship with the rainfall kinetic energy; and the splash rate had an exponential relationship with the duration of rainfall and a negative exponential relationship with the distance of the splash erosion. Qin et al. (2014) carried out splash tests with the raindrops generator and their experiment results show that, if the raindrop kinetic energy is less than 0.0674 × 10⁻³ J, there is no splash erosion being produced, and that the splash erosion grows linearly with the raindrop kinetic energy within a certain range of raindrop diameter. The results of the indoor artificial rainfall experiments reported in Hu et al. (2016) indicate that the critical energy of the splash erosion is 3∼ 6Jm⁻²mm⁻¹;each of the uphill, downhill, net, total splash erosion amounts has a power function relation with the rainfall energy, respectively, whereas the side-slope splash erosion has a quadratic polynomial relation with the rainfall energy. Majid et al. (2016) conducted outdoor runoff plot experiment to investigate the plausible relationship between the splash erosion and the runoff erosion under different rainfall intensities and slopes.

In this paper, we will analyze the mass exchange mechanism on the soil surface based on the concept of energy balance and with the assistance of the spring damping model (Zhou et al., 2012). We regard the rainfall splash erosion process as a collision process between the raindrop and the soil particle on the soil interface. This recognition allows us to incorporate research approaches from the spring model, which has been developed for analyzing collision process between solid and solid objects, and between liquid and solid objects; from the spring vibrator model, which has been developed for explaining the process of the droplets impacting the super-hydrophobic surface (Miao et al., 2012; Yang et al., 2010); and the mass-spring model, which has been developed for simulating the impact of liquid drops on solid surface (Zang et al., 2015). In addition, because a same set of factors determine the splash amount and infiltration amount, and it is relatively simpler to observe the infiltration amount, an investigation into the relationship between the splash amount and infiltration amount would be able to provide a new channel for quantifying the splash erosion. This recognition leads us to examining the relationship between single raindrop, rainfall kinetic energy and splash erosion from both theoretical and empirical angles, with an emphasis on the relationship between the infiltration amount and the splash erosion. Such an investigation would add value to the collective effort to establish mass exchange law in water-soil interface during rainfall splash erosion.

Raindrop Kinetic Energy Model

Equivalent Spring Damping Model Based on Energy Balance

Spring damping method treats the collision process as a continuous dynamics problem, and thus regarding the contact force being equivalent to a spring damping model. Based on the Hunt’s assumption, energy is dissipated during the collision. The hysteretic damping coefficient and the relationship between the two speeds before and after the collision are determined by the energy balance relationship. With the assistance of Newton recovery coefficient e, the kinetic energy loss is calculated according to Eq. 1 (Zhang et al., 2013; Lin et al., 2016):

$\Delta E=\frac{1}{2}\frac{m_1{m}_2}{m_1+m_2}{\left(v_1-v_{20}\right)}^2\left(1-e^2\right)(1)$

Where ΔE is kinetic energy loss(J), m₁,v₁ are the mass (kg) and the terminal velocity (m/s) of the raindrops, respectively, m₂, v₂₀ are the mass (kg) and the splash speed (m/s)of the soil particles, respectively; e is newton’s coefficient of restitution(unitless).

The Relationship Between Single Raindrop Kinetic Energy and Splash Erosion Amount

In general, the collision process is composed of compaction and recover phases. In the compaction phase, raindrops generate deformation along the normal line of the contact surface, until the relative speed decreases to zero, when the relative deformation reaches maximum. Subsequently parts of raindrops adhere to the soil particle, other raindrops separate from the soil particle, and at this moment, the collision process finishes. The following section will analyze the scenario under which the soil surface slope is zero.

Since the soil particle is hydrophilic, the Newton recovery coefficient equals to zero, therefore the kinetic energy loss of the rainfall splash erosion system is shown during the collision process as follow:

$\Delta E=\frac{1}{2}\frac{m_1{m}_2}{m_1+m_2}{\left(v_1-v_{20}\right)}^2(2)$

Assuming that there is no rebounding after the raindrops collide with the soil particle, meaning that v₂₀ (m/s) equals to 0. For convenience of analysis, the kinetic energy of the raindrops is taken as E(J), the mass of the soil particle after splash erosion is M₂ (kg), which includes the mass of the attached water, and the splash speed is v2 (m/s). Combining kinetic energy theorem with Eq. 1, we have

$\frac{1}{2}\frac{m_1{M}_2}{m_1+M_2}{v}_1^2=\frac{1}{2}{m}_1{v}_1^2-\frac{1}{2}{M}_2{v}_2^2(3)$

$M_{2}E=\left(E-\frac{1}{2}{M}_2{v}_2^2\right)\left(m_1+M_2\right)$

$E=\frac{1}{2}{M}_2{v}_2^2+\frac{1}{2}\frac{M_2^2}{m_1}{v}_2^2(4)$

Eq. 4 demonstrates that the relationship between the kinetic energy of single raindrop and splash erosion is quadratic parabola, the coefficient depends on the splash speed and the rainfall capacity.

Results and Discussion

The Relationship Between the Single Raindrops Terminal Velocity and the Soil Particle Splash Speed

There is little literature on the relationship between the raindrops speed and the soil particle splash speed during the collision process. When the single raindrop collides with the liquid wall surface with certain depth, the speeds of single raindrop before and after the collision present a linear relation according to (Song et al., 2013). Thus the quantitative relation between the speeds of a raindrop and the soil particle is v₁ = kv_2.

Table 1 demonstrates that the raindrops terminal speed and the coefficient with different diameter, if v₁ = 3v₂, the coefficient of M₂² in Eq. 4 is about 120.0～240.0, which coincide with the value 146.4–250.8 (Angulo et al., 2012).

TABLE 1

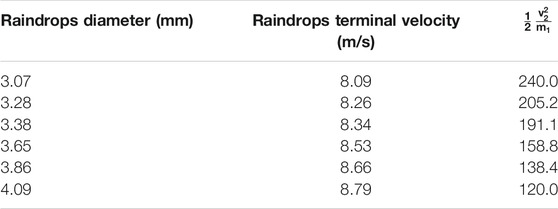
TABLE 1. Comparison of the single raindrops terminal velocity and the coefficient with different raindrops diameter.

Collision Model of Rainfall Flow on Slope

Because of the diversity of the size distribution of the raindrops and of the landing speed of the raindrops group, it is highly necessary to analyze the relationship between the splash erosion, the kinetic energy of the raindrops and the infiltration. In addition, it is of great importance to understand the splash erosion generated by the rainfall. Now, take the rainfall raindrops as a whole, the kinetic physical model of the rainfall can be constructed based on the concept of the rainfall flow proposed by Wang (Wang et al., 2005), to verify the feasibility of Eq. 3.

The Relationship Between the Rainfall Flow Mean Kinetic Energy and the Splash Erosion

According to the physical model presented by Wang (Wang et al., 2005), the average terminal velocity of the rainfall flow is expressed by

$v_d=\frac{I}{k_1\left(C_1+C_{2}I\right)}(5)$

Where k₁ is the unit conversion factor, k₁ = 60,000; I represents the rainfall intensity(mm/min).

The mass of the rainfall flow (m₁, with the unit kg/m³) is

$m_1=\frac{{\rho }_w}{C_1+C_{2}I}(6)$

Where ρ_w is the density of water (kg/m³); C₁ represents the volume ratio of the rainfall critical raindrops group (mm³/mm³); C₂ is the coefficient of rainfall intensity effect, which stands for the volume ratio increment of the rainfall raindrops group caused by adding one unit rainfall intensity (min/mm). If 15 times test rainfall intensity is 0.492–3.694 mm/min, the average terminal velocity of the rainfall is 5.276–5.766 m/s, C₁ and C₂ are determined as 1.52519 × 10⁻⁷, 2.84913 × 10⁻⁶ by experiment, respectively.

Combined with the rainfall intensity presented by Cheng (Cheng et al., 2015), the second item 1/m₁ in the right of equation is 10⁻³—10⁻⁴kg⁻¹, which is 10^−3–10⁻⁴ times of the first item, therefore, the second item can be ignored, simplify Eq. 4:

$E=\frac{1}{2}{M}_2{v}_2^2(7)$

We can deem that it is linear proportional between the splash erosion and the kinetic energy of the rainfall, which tally with the literatures (Liu et al., 2011; Cheng et al., 2015; Zheng et al., 2016; Kinnell, 2019; Nives et al., 2021).

The Relationship Between Mean Terminal Velocity of Rainfall Flow and the Soil Particles Splash Speed

The terminal velocity of single raindrops with the diameter 1.8 mm is 6.09 m/s, which is larger than the average terminal velocity of the rainfall flow, 5.276–5.766 m/s. Therefore, it is necessary to verify the relationship between the average terminal velocity of rainfall flow and the soil particles splash speed. In order to compare with test data, convert Eq. 7 into:

$M_2=\frac{2}{v_2^2}E(8)$

Table 2 shows the comparison of the coefficient of Eq. 8 by calculating the average terminal velocity with the test rain intensity presented by Cheng (Cheng et al., 2015). Take the interplay between raindrops into consideration, there is v_d = 2v₂.

TABLE 2

TABLE 2. Comparison of calculation and test results.

The rain splash erosion experiment selected 31.4, 67.2, 95.3 mm/h rainfall intensity, nine duration rainfalls (3, 6, 10, 15, 20, 25, 30, 40, 50 min), and the test slope was determined as 5. The splash erosion plate is made of steel plate, with the inner diameter 100 cm, outer diameter 220 cm, which is applied to measure the splash erosion quantity. The datum of the up, down, left, right slope four azimuths splash erosion quantity and the rainfall kinetic energy was analyzed with regression analysis. As a result, the linear fitting results are best shown in Table 3.

TABLE 3

TABLE 3. The fitting function between the splash erosion and the rainfall kinetic energy of four azimuths.

Compare the coefficient term of E in Table 3 with that of Table 2, it can be seen that the average terminal velocity of the rainfall is approximately twice of the speed of the splash particle. Although there regresses different slopes, the coefficient of the three rainfall intensities 31.4, 67.2 and 95.3 mm/h are 302.4, 274.1and 267.2, respectively, which is near to the coefficient of the E item in Table 3, while there exists some difference with the situation of the up and down slope, this may cause by the influence of the position potential energy.

Relational Model of the Splash Erosion and Infiltration Amount

Theoretical Relation Model

Because the relationship, which is of the splash erosion and the average kinetic energy of single raindrop and of rainfall, accords with the experiment, it is of rational to describe the splash erosion process with the equivalent spring damping model based on the energy balance. Now it would be right time to apply the proposed model to analyze the relationship between the splash erosion and the infiltration amount.

Assumed that the rainfall was deducted the infiltration, the rest raindrops and the soil particle were splashed together. Suppose the mass of the splashed water is m_1-f, according to the energy conservation, the kinetic energy loss is the difference of the kinetic energy of splash erosion born before and after the splash.

$\frac{1}{2}\frac{m_1\left(m_2+m_1-f\right)}{2m_1+m_2-f}{v}_1^2=\frac{1}{2}{m}_1{v}_1^2-\frac{1}{2}\left(m_2+m_1-f\right)v_2^2(9)$

Simply Eq. 9, there is

$v_2^2{f}^2-\left(3m_1{v}_2^2+2m_2{v}_2^2\right)f=-m_2^2{v}_2^2-3m_1{m}_2{v}_2^2+m_1^2{v}_1^2-2m_1^2$

Further finishing:

$v_2^2{\left(f-m_2\right)}^2-3m_1{v}_2^2\left(f-m_2\right)+m_1^2\left(v_1^2-2\right)=0$

$f-m_2=\frac{3}{2}{m}_1+\frac{1}{2v_2}{m}_1\sqrt{9v_2^2-4v_1^2+8}(10)$

Eq. 10 demonstrates that the relationship between the splash erosion m₂ and the infiltration amount f is linearly proportional.

There are several important points by analyzing Eq. 10:

1) The slope of the linear ration of the former two items is determined by the unit conversion relation. Additionally, Eq. 10 provides a new method for identifying the splash erosion amount.

2) The line intercept depends on the rainfall, raindrop terminal velocity and the soil splash erosion velocity. While the intercept is ultimately determined by the rainfall intensity according to Eq. 5 and Eq. 6.

3) If $\frac{3}{2}{m}_1$>$\frac{1}{2v_2}{m}_1\sqrt{9v_2^2-4v_1^2+8}$ there is f > m₂ and the average terminal velocity of the rainfall v₂>$\sqrt{2}$, which shows that the infiltration amount is larger than the splash erosion. Based on Eq. 5 and Eq. 6, the corresponding rainfall intensity is 0.017 mm/min. However, when the rainfall intensity is greater than 0.017 mm/min, the infiltration amount is larger than the splash erosion.

4) In the process of the individual rainfall splash, it can increase the difference of the infiltration amount and the splash erosion by decreasing the value v₂, which is one of the major measures to increase the surface roughness in practical.

5) In the rainfall process, there exists the mass exchange between the infiltration and the splash erosion on the soil surface.

6) If the practical energy of the raindrop splash erosion is less than the critical energy (Qin et al., 2014; Hu et al., 2016), there will not generate the splash erosion, that is v₂ = 0, Eq. 10 and the above conclusions can be false.

Model Validation

The experiment soil is the loess soil collected from the Loess Hilly and gully region, the northwest water Ansaichafang Experiment Station mountain range. The rainfall area is 2 m × 3 m, the rainfall intensity is 0.822, 1.090,1.468,1.757, 2.037 mm/min, the slope is 10°, 15°, 20°, 25°, 30°. The soil equipment is a wooden box with 40 cm width, 35 cm height and 100 cm projected length. The wall tops of the box are made into wedge-shaped, the bottom of the box is drilled with many micropores with the diameter 2.5mm, these micropores are designed in quincunx-shape in order to simulate the natural channel. The other side of the box are installed to observe the splash erosion (Wu et al., 1992).

Figure 1 shows the relationship between the infiltration amount and the rainfall splash erosion.

FIGURE 1

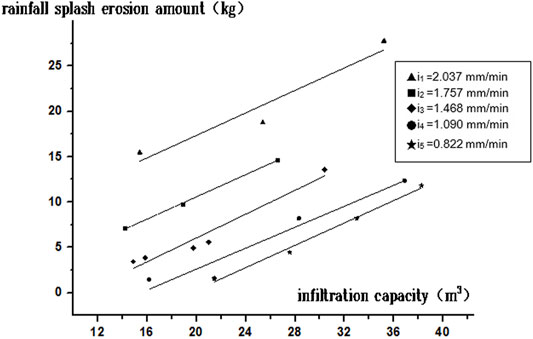
FIGURE 1. Experimental results of the relationship between rainfall splash erosion amount and infiltration volume.

The results manifest that the relationship presents a cluster of li nes, different rainfall intensities correspond to different intercepts, and the relationship mainly depends on the rainfall intensity, which tally with Eq. 10, further verify that the rest raindrops and the soil particles adhere each other and are splashed together.

The slopes of the five lines are 0.577–0.657, which can be approximately as the reciprocal of the loessal soil density 1,500–1700 kg/m³. If convert the ordinate and abscissa, i.e. the infiltration amount is the ordinate, the line slope just is the soil density, which manifest that the slope is determined by the unit conversion relationship. This conclusion also agrees with Eq. 10.

Conclusion

In summary, this paper clearly verified the relationships of single raindrop, the average kinetic energy of the rainfall and the splash erosion with the equivalent spring damper model based on some relevant experiments datum, it comes out several major conclusions as follow:

Basically reasonable the rainfall kinetic energy and the splash erosion by the equivalent spring damping model in the process of rainfall splash erosion, there exist the mass exchange of infiltration and splash erosion on the soil surface, which provides a new approach to identify the splash erosion. The equivalent spring damping model is usefull to describe the relationship between spatter amount and infiltration amount, rainfall (flow) kinetic energy and spatter amount.

Under the condition of the rainfall splash erosion, it is a linear relation between the splash erosion amount and the infiltration amount, which slope is determined by the unit conversion of two former items. If select the same units, the slope is the ratio of the soil density and the water density. The ratio is identified by rainfall mass, terminal velocity and the splash erosion of soil particle, while these three parameters are determined by the rain intensity in the end, and there have different intercepts corresponding with different rain intensities.

In the case of rainfall splash erosion, the kinetic energy of rainfall is linearly proportional to the amount of splash erosion, the rainfall terminal velocity is two times of the soil erosionrate. If consider the single raindrop, the kinetic energy and the splash erosion amount are quadric parabolic relation, and the raindrop terminal velocity is three times of the soil erosion rate.

These proposed results are summarized without considering the influence of the position potential energy, however which has little effect on the results, when dealing with the practical problems, it can be considered specially.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author/s.

Author Contributions

ZY and LP Mainly engaged in testing and analysis work.

Funding

This work was supported by the National Key R& D Program of China (2018YFE0206200) and the National Natural Science Foundation of China (51869009).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We also appreciate the helpful data from authors of paper and suggestions from the reviewers.

References

Angulo-Martínez, M., Beguería, S., Navas, A., and Machín, J. (2012). Splash Erosion under Natural Rainfall on Three Soil Types in NE Spain. Geomorphology 175-176, 38–44. doi:10.1016/j.geomorph.2012.06.016

CrossRef Full Text | Google Scholar

Bu, C.-f., Wu, S.-f., and Yang, K.-b. (2014). Effects of Physical Soil Crusts on Infiltration and Splash Erosion in Three Typical Chinese Soils. Int. J. Sediment Res. 29, 491–501. doi:10.1016/s1001-6279(14)60062-7

CrossRef Full Text | Google Scholar

Cheng, J. H., Qin, Y., Zhang, H. J., Cong, Y., Yang, F., and Yan, Y. Q. (2015). Splash Erosion under Artificial Rainfall in Rocky Mountain Area of Northern China. Trans. Chin. Soc. Agric. Machinery 46, 153–161. doi:10.6041/j.issn.1000-1298.2015.02

CrossRef Full Text | Google Scholar

Hu, W., Zheng, F. L., and Bian, F. (2016). Effects of Raindrop Kinetic Energy on Splash Erosion in Typical Black Soil Region of Northeast China. Acta Ecol. Sinica 36, 4708–4717 10. doi:10.5846/stxb201412312613

CrossRef Full Text | Google Scholar

Hu, X. (2015). Effect of Granular Structure on Soil Splash Erosion Rate and Soil Crust Development of Loessial Soil. Chin. Agric. Sci. Bull. 31, 229–235.

Google Scholar

Kinnell, P. I. A. (2019). Comment on “Evaluating and modelling splash detachment capacity based on laboratory experiments” by Wu et al. (2019). Catena 176, 189–196. Catena 183, 104189. doi:10.1016/j.catena.2019.104189

CrossRef Full Text | Google Scholar

Li, W. J., Li, D. X., and Wang, X. K. (2011). Study on Raindrop Splash Detachment Model. J. Basic Sci. Eng. 19, 689–699.

Google Scholar

Lin, J., Lin, Y., and Qian, J. (2016). Adhesive Contact Mechanics: from Deterministic to Stochastic Description. Chin. Sci. Bull. 61, 701–706. doi:10.1360/n972015-00736

CrossRef Full Text | Google Scholar

Liu, H. P., Fu, S. H., Wang, X. Y., Xu, L., Fang, N., Liu, B. Y., et al. (2011). Effects of Slope Gradient on Raindrop Splash Erosion. Acta Pedologica Sinica 48, 479–486.

Google Scholar

Ma, R. M., Cai, C. F., Li, Z. X., Wang, J. G., Feng, J. Y., Wu, X. G., et al. (2014). Effect of Antecedent Soil Moisture on Aggregate Stability and Splash Erosion of Krasnozem. Trans. Chin. Soc. Agric. Eng. 30, 95–103.10.3969/j.issn.1002-6819.2014.03.013.

Google Scholar

Ma, R. M., Wang, J. G., Li, Z. X., Cai, C. F., and Wang, S. (2013). Effects of Dynamic Distribution of Aggregate Size on Splash Erosion under Rainfall in Red Soils. Resour. Environ. Yangtze Basin 22, 779–784.

Google Scholar

Mahmoodabadi, M., and Sajjadi, S. A. (2016). Effects of Rain Intensity, Slope Gradient and Particle Size Distribution on the Relative Contributions of Splash and Wash Loads to Rain-Induced Erosion. Geomorphology 253, 159–167. doi:10.1016/j.geomorph.2015.10.010

CrossRef Full Text | Google Scholar

Miao, S. G., Dou, J. X., Chen, F., Li, J., and Li, A. G. (2012). Analysis of Observations on the Urban Surface Energy Balance in Beijing. Sci. China:earth Sci. 42, 1394–1402. doi:10.1007/s11430-012-4411-6

CrossRef Full Text | Google Scholar

Qin, Y., Cheng, J. H., Zhang, H. J., and Li, Z. (2014). A Study of the Raindrop Impact to Splash Erosion. J. Soil Water Conservation 28, 74–78. doi:10.13870/j.cnki.stbcxb.2014.02.014

CrossRef Full Text | Google Scholar

Saedi, T., Shorafa, M., Gorji, M., and Khalili Moghadam, B. (2016). Indirect and Direct Effects of Soil Properties on Soil Splash Erosion Rate in Calcareous Soils of the central Zagross, Iran: A Laboratory Study. Geoderma 271, 1–9. doi:10.1016/j.geoderma.2016.02.008

CrossRef Full Text | Google Scholar

Song, Y. C., Ning, Z., Sun, C. H., Lv, M., Yan, K., and Fu, J. (2013). Movement and Splashing of a Droplet Impacting on a Wet Wall. Chin. J. Theor. Appl. Mech. 45, 833–842. doi:10.6052/0459-1879-13-053

CrossRef Full Text | Google Scholar

Sun, S. X. (1997). Study on Relationship between Rainfall Splash Erosion and Infiltration on Loess Slopeland. J. Soil Water Conservation 3, 92–94.

Google Scholar

Wang, B., Ma, J. M., Cheng, J. H., Yu, X. Y., Dai, Q. J., Lv, P. Y., et al. (2015). Effects of Gravel Coverage on Splash Erosion in the Mountainous Region of Northern China. Sci. Soil Water Conservation 13, 93–98. doi:10.16843/j.sswc.2015.05.016

CrossRef Full Text | Google Scholar

Wang, Z. L., Sun, Q. M., Zheng, F. L., and Niu, Z. H. (2005). Physically-Based Model of Rain Fall Flow Kinetic Energy. J. Hydraulic Eng. 36, 1280–1285.

Google Scholar

Wei, Y. J., Wu, X. L., and Cai, C. F. (2015). Splash Erosion of Clay-Sand Mixtures and its Relationship with Soil Physical Properties: The Effects of Particle Size Distribution on Soil Structure. CATENA 135, 254–262. doi:10.1016/j.catena.2015.08.003

CrossRef Full Text | Google Scholar

Wu, P. T., and Zhou, P. H. (1992). The Action of Rain Drop Splash on Sheet Flow Erosion. Bull. Soil Water Concervation 12, 19–47. doi:10.13961/j.cnki.stbctb.1992.04.003

CrossRef Full Text | Google Scholar

Yang, J., Zhang, Y., Liu, D., and Wei, X. (2010). CFD-DEM Simulation of Three-Dimensional Aeolian Sand Movement. Sci. China Phys. Mech. Astron. 53, 1306–1318. doi:10.1007/s11433-010-4038-6

CrossRef Full Text | Google Scholar

Yin, W. J., Wang, J., and Liu, D. D. (2011). Effect of Surface Water Thickness on the Amount of Splash Erosion. J. Irrigation Drainage 30, 115–117. doi:10.13522/j.cnki.ggps.2011.04.011

CrossRef Full Text | Google Scholar

Zambon, N., Johannsen, L. L., Strauss, P., Dostal, T., Zumr, D., Cochrane, T. A., et al. (2021). Splash Erosion Affected by Initial Soil Moisture and Surface Conditions under Simulated Rainfall. Catena 196, 104827. doi:10.1016/j.catena.2020.104827

CrossRef Full Text | Google Scholar

Zang, D., Li, Y., Chen, Z., Li, J., Geng, X. G., and Cheng, X. P. (2015). Shape Evolution of Free Falling Deformed Droplets. Chin. Sci. Bull. 60, 917–921.

CrossRef Full Text | Google Scholar

Zhang, R., Zhu, W., and Zheng, X. J. (2013). Investigation into the Three-Dimensional Sand Particle-Bed Collision Process. J. Lanzhou Univ. Nat. Sci. 49, 861–869. doi:10.13885/j.issn.0455-2059.2013.06.013

CrossRef Full Text | Google Scholar

Zhao, X. G., and Shi, H. (2003). Prescription of Soil Anti-erosion Capability under Water Erosion. Arid Land Geogr. 26, 12–16. doi:10.13826/j.cnki.cn65-1103/x.2003.01.003

CrossRef Full Text | Google Scholar

Zheng, T. H., Xing, Y. Y., He, K. X., Teng, F., and Li, G. L. (2016). Rain Splash and Sheet Flow Mixed Sediment Transport Mechanism. J. Northwest A F Univ. Nat. Sci. Edition 44, 211–218. doi:10.13207/j.cnki.jnwafu.2016.03.029

CrossRef Full Text | Google Scholar

Zhou, Z. C., Wu, X. Y., Zhang, W. Q., and Xie, Z. W. (2012). Study on Contact Dynamics Based Springy Damper Model. J. Hubei Univ. Technology 27, 125–128.

Google Scholar