Review of Electrical Resistivity Measurements and Calculations of Fe and Fe-Alloys Relating to Planetary Cores

There is a considerable amount of literature on the electrical resistivity of iron at Earth’s core conditions, while only few studies have considered iron and iron-alloys at other planetary core conditions. Much of the total work has been carried out in the past decade and a review to collect data is timely. High pressures and temperatures can be achieved with direct measurements using a diamond-anvil cell, a multi-anvil press or shock compression methods. The results of direct measurements can be used in combination with first-principle calculations to extrapolate from laboratory temperature and pressure to the relevant planetary conditions. This review points out some discrepancies in the electrical resistivity values between theoretical and experimental studies, while highlighting the negligible differences arising from the selection of pressure and temperature values at planetary core conditions. Also, conversions of the reported electrical resistivity values to thermal conductivity via the Wiedemann-Franz law do not seem to vary significantly even when the Sommerfeld value of the Lorenz number is used in the conversion. A comparison of the rich literature of electrical resistivity values of pure Fe at Earth’s core-mantle boundary and inner-core boundary conditions with alloys of Fe and light elements (Si, S, O) does not reveal dramatic differences. The scarce literature on the electrical resistivity at the lunar core suggests the effect of P on a wt% basis is negligible when compared to that of Si and S. On the contrary, studies at Mercury’s core conditions suggest two distinct groups of electrical resistivity values but only a few studies apply to the inner-core boundary. The electrical resistivity values at the Martian core-mantle boundary conditions suggest a negligible contribution of Si, S and O. In contrast, Fe-S compositions at Ganymede’s core-mantle boundary conditions result in large deviations in electrical resistivity values compared to pure Fe. Contour maps of the reported values illustrate ρ(P, T) for pure Fe and its alloys with Ni, O and Si/S and allow for estimates of electrical resistivity at the core-mantle boundary and inner-core boundary conditions for the cores of terrestrial-like planetary bodies.

Introduction

The current interest in direct measurements and modelling of electrical resistivity (ρ) originates mainly from an interest in heat flow modelling of planetary cores. For terrestrial-like planetary bodies that contain predominantly Fe cores, the applications are thermal evolution of the core, which includes freezing of an inner core and sustenance of a dynamo. To model core thermal evolution, the adiabatic heat flow is needed and is normally calculated via the thermal conductivity (k). Although ρ and k of metals are directly related through electron transfer of charge and energy, respectively, the following quote indicates the tolerance for variation in each of these properties in relation to our understanding of core processes. “A factor of two or so uncertainty in ρ does not appear critical to dynamo theory but it has a strong impact on calculations of the thermal regime of the core.” (Stacey and Anderson, 2001). The literature on ρ of pure Fe is rich and the values are scattered while the reported data on Fe-alloys is more scarce but less dispersed. The inconsistencies in measurements and modelling may be the result of different techniques in addition to the range of pressures and temperatures attributed to planetary cores. Much of the total work has been carried out in the past decade and Figure 1 shows the cumulative number of papers published on ρ of pure Fe and Fe-alloys during the past half-century. At the time of writing this article, the four studies labelled on Figure 1 combined for more than 1,000 citations and are viewed as responsible for the increased rate of activity following their publication. This review attempts to summarize both older and recent results to identify a range of reliable and representative values for ρ of the cores of terrestrial-like planetary bodies composed of pure Fe or Fe-alloys.

FIGURE 1

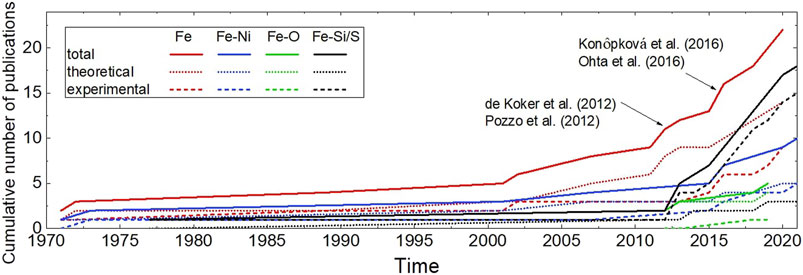
FIGURE 1. Cumulative number of publications on theoretical and experimental methods of estimating ρ of Fe, Fe-Ni, Fe-O and Fe-Si and S alloys at the core conditions of Earth, Moon, Mercury, Mars, and Ganymede.

A general formulation of the core adiabatic heat flow is described as:

${\mathit{q}}_{\mathit{ad}}=-{\mathit{k}}_{\mathit{c}}\frac{\mathit{\alpha gT}}{{\mathit{C}}_{\mathit{p}}}(1)$

where k_c is k of the core, $\alpha$ is thermal expansion coefficient, $g$ is gravitational acceleration, T is temperature at the top of the core, and $C_p$ is heat capacity at constant pressure (P). Direct measurements of k are difficult to make at core-relevant P and T. In contrast, direct measurements of electrical conductivity (σ), which is inversely proportional to ρ, are achievable with relatively high accuracy. The two variables may be related through the electronic component of k (k_e) with the Wiedemann-Franz Law (WFL), where L is the Lorenz number:

${\mathit{k}}_{\mathit{e}}=\mathit{LT\sigma }=\mathit{LT}/\mathit{\rho }(2)$

Thermal conductivity is controlled by electrons and phonons, but the phonon contribution is negligible in metals and metallic alloys (Klemens and Williams, 1986). The appropriate values of the Lorenz number for specific compositions at relevant T are not well constrained. The theoretical value, the Sommerfeld value ($L_0$ = 2.44·10⁻⁸ W·Ω·K⁻²), has been shown to account for more than 99% of k_e for Fe, suggesting that its use at high T and P < 6 GPa is reasonable (Secco, 2017). While L > L₀ for Fe-Si alloys at high T and low P (Secco, 2017), calculations at Earth core P, T conditions have shown that L < L₀ (de Koker et al., 2012; Xu et al., 2018). The following relationship was developed from measurements of the Seebeck coefficient of Fe up to 6 GPa and 2,100 K (Secco, 2017):

${\left[\frac{\mathit{dL}}{\mathit{dP}}\right]}_{\mathit{melt boundary},\mathit{ }<5\mathit{ GPa}}=\frac{\mathit{\rho }{\mathit{k}}_{\mathit{e}}}{{\mathit{K}}_{\mathit{T}}\mathit{T}}\left\{\frac{1}{3}-\frac{{\mathit{K}}_{\mathit{T}}}{\mathit{T}}{\left(\frac{\mathit{dT}}{\mathit{dP}}\right)}_{\mathit{melt boundary},\mathit{ }<5\mathit{ GPa}}\right\}\mathit{ }=\mathit{ }-3.98\cdot {10}^{-10}\frac{\mathit{W}\mathbf{\Omega }}{{\mathit{K}}^2\mathit{GPa}}(3)$

where K_T is isothermal bulk modulus. For metals in general, ρ is governed by the scattering rate of conduction electrons. Similarly, the Lorenz number has been shown to be both lower and higher than L₀ depending on the state and composition of the system (Pozzo et al., 2012; Pozzo et al., 2013; Pozzo et al., 2014; Pozzo and Alfè, 2016a; Pozzo and Alfè, 2016b; Pourovskii et al., 2020). The scattering rate of conduction electrons is affected by electron-phonon, electron-magnon, and electron-electron interactions. Electrical resistivity is proportional to the inverse of the electron mean free path (d), which is proportional to the amplitudes of atomic vibrations (A) and thus proportional to T:

$\mathit{\rho }\propto \mathit{ }\frac{1}{\mathit{d}}\propto {\mathit{A}}^2\propto \mathit{ T}(4)$

Electron-phonon interactions are electron scattering caused by lattice vibrations and are relatively negligible at low T. At high T, the occupation of phonon density of states shifts toward higher energy states which increases the frequency of collisions with conduction electrons. Electron-magnon interactions, or spin-disorder scattering, is only relevant in ferromagnetic metals such as Fe and their ferromagnetic alloys. This interaction increases scattering as a function of T² up to the Curie T (T_c) and dominates ρ up to approximately 300 K. In Fe-alloys, the interaction of electron-lattice defects (including impurities) also affects the scattering rate of conduction electrons. The increased lattice defects cause electron structure perturbations and shorter electron mean free paths, which results in a larger ρ. The interactions between electrons and lattice defects dominate over the electron-phonon, electron-magnon and electron-electron interactions at low T. Overall, the net effect of T is to increase ρ, while ρ decreases with P as the decreased amplitude of lattice vibrations increases the electron mean free path. The Ioffe-Regel criterion argues that the growth of resistivity is reduced with T increase, i.e. saturates, as the electron mean free path approaches the interatomic distance (Mooij, 1973; Wiesmann et al., 1977; Gurvitch, 1981). Bohnenkamp et al. (2002) estimated a saturation value of 1.68 μΩm for Fe at 1 atm and up to 1,663 K, while there are variations in the saturation value of Fe-Si alloys at high P (Kiarasi and Secco, 2015; Gomi et al., 2016). Gomi et al. (2013) were the first to propose the idea of resistivity saturation for Fe at Earth core conditions however recent work (Zhang et al., 2020) provides contradictory results and suggests resistivity saturation behavior was an experimental artifact.

Methods of Electrical Resistivity Determination

Theory: First-Principles Calculations

Initially meant to describe the diffusion of gases in the atmosphere, Boltzmann (1894) developed the following equation that considers the electronic band structure, phonon dispersion and electron-phonon interactions:

$\mathit{\rho }=\frac{\mathit{\pi }\mathbf{\Omega }{\mathit{k}}_{\mathit{B}}\mathit{T}}{\mathit{N}\left({\mathit{\epsilon }}_{\mathit{F}}\right){\mathit{V}}_{\mathit{F}}^2\mathit{ }}{\mathit{\lambda }}_{\mathit{tr}}(5)$

where $N\left({\epsilon }_F\right)$ is the electronic density of states per atom per spin at the Fermi energy (ε_F) level, $k_B$ is the Boltzmann constant, $\text{Ω}$ is the unit cell volume, $V_F$ is the Fermi velocity, and ${\lambda }_{tr}$ is the transport coefficient. This work was followed by the introduction of the Free Electron model by Sommerfeld (1928), based on the classical Drude model of electrical conduction (Drude, 1900a; Drude, 1900b) and Fermi-Dirac statistics describing the distribution of particles over energy states. The model predicts σ from the electron density, the mean free time (time between collisions), and the electron charge. The model includes many relations, including the Wiedemann-Franz law, the Seebeck coefficient of the thermoelectric effect and the shape of the electronic density of states function. In their analysis of Earth’s magnetic field variations, Elsasser (1946) estimated the ρ of a pure Fe core from the theory of electronic conductivity, which states that σ is inversely proportional to the absolute T and directly proportional to the square of the Debye temperature ($\text{Θ}$_D).

$\mathit{\rho }\propto \mathit{ }{\mathbf{\Theta }}_{\mathit{D}}^{-2}\mathit{ }(6)$

The Debye temperature is proportional to the sound velocity and the acoustic phonon cut-off frequency and inversely proportional to volume (Kittel, 2005). Ziman (1960) later described the Nearly-Free Electron model, which is based on the behavior of electrons, ions, and holes. In the Free Electron model, all energy states from 0 to $\infty$ are allowed, whereas the Nearly-Free Electron model allows for weak perturbations of electrons by periodic potential ions. Following this idea, Ziman (1961) developed a theory for the behavior of liquid metals. This model was modified by Evans et al. (1971) to include a transition matrix term, introducing a more complex method of calculating ρ of a metallic liquid for metals that have empty d-band states in to which s-conduction electrons may jump (s-d transitions):

$\mathit{\rho }=\frac{3\mathit{\pi }{\mathbf{\Omega }}_0}{{\mathit{e}}^2\hslash {\mathit{V}}_{\mathit{F}}^2}\underset{0}{\overset{1}{{\displaystyle \int }}}\mathit{d}\left(\frac{\mathit{q}}{2{\mathit{K}}_{\mathit{F}}}\right)\mathit{*}4\left(\frac{\mathit{q}}{2{\mathit{K}}_{\mathit{F}}}\right)\mathit{*a}\left(\mathit{q}\right)\mathit{*}{\left|\mathit{t}\left(\frac{\mathit{q}}{2{\mathit{K}}_{\mathit{F}}}\right)\right|}^2(7)$

where e is the electron charge, $K_F$ is the radius of the Fermi surface, $q=K-K\text{'}$ relates to the scattering angle of the Fermi surface, ${\text{Ω}}_0$ is the atomic volume of the liquid, $a\left(q\right)$ is the structure factor, $\hslash$ is the modified Planck constant, and $t(K, K^{\text{'}})$ is the transition matrix that describes the scattering cross-section related to s-electron to d-band (s-d) scattering. While this formulation focuses on the liquid state of a metal, Mott (1972) and Mott (1980) derived a relationship for the solid state of a metal. Mott’s theory considers the thermal and impurity contributions, as well as a magnetic contribution in ferromagnetic metals. The theory describes the relationship between ρ and the area of the Fermi surface (S_F). The relationship can be written as follows:

$\mathit{\rho }=\frac{12{\mathit{\pi }}^3\hslash }{{\mathit{S}}_{\mathit{F}}{\mathit{e}}^2\mathit{d}}(8)$

The more complex, and commonly used, Kubo-Greenwood formula (Kubo, 1957; Greenwood, 1958) describes the frequency dependent electron conductivity and yields the linear contribution to the current response. The T dependence of ρ, which is related to electron-phonon interactions, is described by the Bloch–Grüneisen equation. Combined with the Bloch–Grüneisen equation for ρ as a function of volume (V) and T, the Kubo–Greenwood equation can be written as follows:

$\mathit{\rho }(\mathit{V},\mathit{T})\mathit{ }=\mathit{ }{\mathit{\rho }}_{0\mathit{R}}{\left[\frac{\mathit{V}}{{\mathit{V}}_{\mathit{R}}}\right]}^{\mathit{a}}+{\mathit{\rho }}_{1\mathit{R}}{\left[\frac{\mathit{V}}{{\mathit{V}}_{\mathit{R}}}\right]}^{\mathit{b}}\frac{\mathit{T}}{{\mathit{T}}_{\mathit{R}}}(9)$

where a and b are constants relating to the volume dependence of the vibrational frequencies, the subscript R refers to the reference state, and ${\rho }_{0R}$ and ${\rho }_{1R}$ are composition-dependent model parameters (de Koker et al., 2012). The electronic structure of a system can be investigated via Density-Functional Theory (DFT), which mainly describes the potential energies of a system. The DFT approach investigates an approximate solution to the Schrödinger equation in 3D based on the electron density, which results in solutions for ion-electron, ion-ion, and electron-electron potential energies (Argaman and Makov, 2000). Often used in combination with DFT, the dynamical mean field theory (DMFT) is a powerful numerical approximation of the potential of a many-particle system, such as electrons in solids. The complex many-particle system is studied by reducing it to a simpler single-particle system with an external mean field. The external field essentially accounts for the other particles in addition to the interactions and local quantum fluctuations that would occur in the many-particle system (Vollhardt et al., 2012). Drchal et al. (2019) and Korell et al. (2019) investigated the effects of magnetism on the electronic properties of metals via the Kubo-Greenwood equation along with DFT and the Tight-Binding Linear Muffin-Tin Orbital method (a method of calculating short-range transitions between electrons in s-, d- and f- orbitals), respectively. Korell et al. (2019) suggested that spin polarization must be accounted for in order to reconcile the first-principle calculations of ρ with measurements. In addition to drawing a similar conclusion, Drchal et al. (2019) suggested that the contributions of the various scattering mechanisms (caused by electron-phonon interactions, electron-magnon interactions, electron-electron interactions, and electron-lattice defects) are comparable but not additive. Through these first-principle calculations which require values of the thermal properties at a reference P and T, theoretical studies are able to estimate ρ of any metal or metal-alloys.

Experiments

Static: Multi-Anvil Press

Static experiments are typically carried out in a multi-anvil press. A typical multi-anvil press uses hydraulic pumps to drive uniaxially a hydraulic ram to compress a pressure cell located at the center of an arrangement of tungsten carbide (WC) anvils. In the 3000-ton press at the University of Western Ontario for example, there are three steel wedges on the bottom and three wedges on the top part of the pressure module. The wedges provide a nest for eight truncated WC cubes that house and converge on an octahedral pressure cell assembly. The octahedral cell may vary in size depending on the truncation edge length (TEL) of the WC cubes. The TEL may vary from 3 to 25 mm, and the smallest sizes are used to reach higher P, albeit on smaller sample volumes. The octahedral pressure cells are usually composed of Magnesium Oxide (MgO) which provides a balance between machinability, low k and hardness that allows for efficient conversion of applied force to the sample inside. With compression, the octahedral cell extrudes out between the WC cubes creating gaskets. Similarly, other multiple anvil apparatus designs such as the cubic anvil press, which consists of six WC anvils that compress a cubic pressure cell assembly made typically of the mineral pyrophyllite, creates gaskets as the cell extrudes out between the anvils. The insulating material, furnace, sample, and electrodes are placed inside the cell, and arranged co-axially in a hole connecting two opposite faces. Elevated temperatures are generated by Joule heating of an electrically resistant furnace, typically made of graphite, lanthanum chromite or rhenium foil, surrounding the sample. The electrical resistance (R) of the sample is measured with a four-wire method, where a pair of thermocouple wires is placed at each end of the sample. Each pair acts as a temperature sensor, while opposite pairs are assigned as potential and current leads in a switchable circuit configuration. The electrical resistivity is then calculated using the following equation which combines Ohm’s law and Pouillet’s law:

$\mathit{\rho }=\frac{\Delta \mathit{E}}{\mathit{I}}\cdot \frac{\mathit{A}}{\mathit{l}}(10)$

where ΔE is the voltage drop across the sample, I is the input current, $A$ is the cross-sectional area of a wire-shaped sample and $l$ the length of the sample. The general experimental methods for multi-anvil apparatuses are described in more detail by Liebermann (2011) and Ito (2015).

Static: Diamond-Anvil Cell Experiments

A Diamond-Anvil Cell (DAC) consists of two opposing gem-quality diamonds that enable the compression of small (∼10⁻⁴ mm³ scale) samples placed between the two diamond culets. Applying moderate force generates high pressures due to the small diameter, typically 50–250 µm, of the culet. Considering that P is applied uniaxially, a metal gasket with a hole drilled to form the sample chamber provides lateral support. A pressure-transmitting medium such as a gas (Ne, Ar, He, N₂) in the sample chamber must be added to obtain hydrostatic pressure but for high T experiments a solid medium (SiO₂, KCl, Al₂O₃, KBr, NaCl) is often used. The system is therefore translucent and allows for the use of XRD to determine the crystallographic structure of the sample. The two main pressure scales are the equation of state of a reference material and the shift in ruby fluorescence lines, although the latter is less reliable at high T. The equation of state describes the relationship between P, T, and V. Measurements of changes in V are compared with a known V-P relation in order to determine the experimental P. The second pressure scale relies on the P-dependent shift in fluorescence wavelength of an irradiated ruby included in the sample chamber. The sample is insulated from the gasket by adding a layer of insulating material, such as Al₂O₃. High temperatures can be achieved with single or double-sided laser heating or by internal resistive heating of a metal element, which may be the sample itself. Resistive heating allows for the precise measurement of T with thermocouples but is limited by the oxidization of diamond in air at approximately 973 K. Laser heating can achieve much higher T (up to 7000 K), although large T gradients can exist and care is needed to locate the sample measurements in a relatively uniform T-field. A common method for measuring the sample resistance in DAC experiments is the Van der Pauw method. This method is used for samples of arbitrary shape, as long as the sample is approximately two-dimensional such as a sheet or foil. Four electrodes are connected to the perimeter of the sample. Two opposite electrodes serve as potential leads, which can be machined within the same foil as the sample or carefully connected manually and fixed by applying pressure. The ρ of the sample at a particular P can be calculated as follows:

$\mathit{\rho }={\mathit{\rho }}_0{\left(\frac{\mathit{V}}{{\mathit{V}}_0}\right)}^{\frac{1}{3}}\frac{\mathit{R}}{{\mathit{R}}_0}(11)$

where the subscript zero refers to the ambient conditions. The experimental methods for DAC are described in more detail by Mao and Mao (2007) and Anzellini and Boccato (2020).

Dynamic: Shock Compression Experiments

Shock compression is a dynamic method of generating high pressures which can be used in conjunction with an experimental configuration that allows determination of the physical properties of a sample, usually conducted in a vacuum. This apparatus consists of using compressed gas and/or gunpowder to launch a metallic projectile onto a stationary sample. The collision generates a strong shock wave that results in simultaneous high P and high T across the sample. The projectile, typically referred to as a flyer plate and made of W or Fe, accelerates to the desired velocities on the order of a few km/s (Bi et al., 2002). A high P, T conductivity zone propagates through the sample under shock compression. The σ of the sample can be measured by contact or contactless methods. The contactless method requires the remote probing of the sample by optical and electromagnetic field sources, which results in values of the impact velocity of the flyer and shock velocity. The arrival of the shock waves generates two electromotive forces that relate to the product of σ and thickness of sample (Gilev, 2011). The contact method requires typically four electrodes placed in contact with the sample. Two electrodes provide the voltage measurements while the other two are used to input constant current. The interface temperatures are usually measured with an optical pyrometer (Gilev, 2011). The most fundamental shock wave characteristic of the sample is its principal Hugoniot curve, which is formed by the locus of shock states along a compression path from initial P, T, and density. The P, T and density properties at the final state are obtained using a standard impedance matching method (Bi et al., 2002). In both methods, σ can be calculated from:

${\mathit{\sigma }}_{\mathit{F}}=\mathit{ }\left(\Delta {\mathit{E}}_0/\Delta {\mathit{E}}_{\mathit{F}}\right)\left({\mathit{V}}_0/{\mathit{V}}_{\mathit{F}}\right){\mathit{\sigma }}_0(12)$

where the subscripts 0 and F refer to the initial and final states, respectively, and $V$ is the specific volume. The experimental methods for shock compression experiments are described in more detail by Ahrens (2007) and Asimow (2015).

Electrical Resistivity of the Cores of Terrestrial-Type Bodies

Earth

It is widely accepted that the Earth’s core composition must be composed of Fe, Ni and some light elements in order to satisfy the core density (Birch, 1961; Birch, 1964; Jeanloz, 1979; Mao et al., 1990). Approximately 10 wt% of light elements is expected in the outer core (Poirier, 1994; Litasov and Shatskiy, 2016). In the inner core, approximately 3–8 wt% of light elements has been suggested (Alfè et al., 2007; Badro et al., 2007; Mao et al., 2012). In addition to approximately 5–10 wt% Ni in the core, light elements include C, H, Si, O and S (Poirier, 1994; Stixrude et al., 1997; Li and Fei, 2003; Alfè et al., 2007). Accordingly, the ρ of multiple Fe binary, ternary and even quaternary alloys must be investigated.

Gardiner and Stacey (1971) used available ρ measurements of liquid Fe from the literature to investigate the effects of T, P, and composition. They reported ρ of 0.25 µΩm at 2,500 K and 3,000 km, which corresponds to the Core-Mantle Boundary (CMB). Similarly, they reported 0.69 µΩm at 5,500 K and 5,000 km, which corresponds to the Inner-Core boundary (ICB). These extrapolations were achieved by applying a P-dependence of ρ of solid Fe (Bridgman, 1957) to measurements of liquid Fe at 1 atm (Baum et al., 1967), as shown below:

${\mathit{\rho }}_{\mathit{P}}\left(\mathit{T}\right)=\mathit{ }{\mathit{\rho }}_0\left(\mathit{T}\right){\left(\frac{{\mathbf{\Theta }}_{{\mathit{D}}_0}}{{\mathbf{\Theta }}_{{\mathit{D}}_{\mathit{P}}}}\right)}^2\frac{{\mathit{D}}_{\mathit{P}}}{{\mathit{D}}_0}(13)$

where the subscript P refers to the final pressure, the subscript 0 refers to zero pressure, and D is density. Shock wave experiments by Keeler and Royce (1971) reported a similar value of 0.67 µΩm at 140 GPa, which corresponds to CMB conditions. However, it has been suggested by Bi et al. (2002) that the previous shock compression experiments above 50 GPa underestimated ρ due to the shunting effect of epoxy, which is used to fill gaps between the sample and insulator. Bi et al. (2002) conducted shock compression measurements of σ of Fe up to 208 GPa, corrected for the shunting effect, and suggested a value for ρ of 0.69 µΩm at conditions near the CMB (2,010 K, 101 GPa) and 1.31 µΩm for conditions near the ICB (5,220 K, 208 GPa). Although these values represent a correction to previously underestimated values, they remain lower than the values reported by Jain and Evans (1972). Jain and Evans (1972) carried out first-principle calculations using the Nearly-Free Electron model and reported ρ of a pure Fe core between 1.00 and 2.00 µΩm. These higher values are in agreement with direct measurements by Secco and Schloessin (1989), who used a large-volume press to measure ρ of Fe up to 7 GPa and above the melting T. The similarities in their measurements with calculations of the density of state functions at low and high P suggest ρ of an Fe solvent is probably between 1.2 and1.5 µΩm at outer core conditions.

A theory was developed by Stacey and Anderson (2001) suggesting a constant ρ along the melting boundary of pure metals such as Fe, based on a cancelling of the decreasing effects of P on ρ by the increasing effects of T on ρ. The description of their analysis, rooted mainly in thermo-elastic considerations, begins with the theory of electronic conductivity, as mentioned earlier by Elsasser (1946), while also considering the electron energy. According to the Free-Electron model and the approximation of the electron energy at the Fermi surface, the total energy varies with volume as V^−2/3. This term is multiplied by the inverse square of the Debye T in Equation 6 to calculate ρ. Stacey and Anderson (2001) then extrapolated ρ of Fe at 140 GPa (Matassov, 1977) and 2,180 K (Anderson, 1998) to core temperatures and reported values of 1.22 µΩm at CMB and 1.12 µΩm at ICB, in agreement with earlier estimates (Jain and Evans, 1972; Secco and Schloessin, 1989; Stacey and Anderson, 2001). Stacey and Loper (2007) revised the theory of constant ρ along the melting boundary and suggested that the constant behavior only applies to electronically simple metals with filled d-bands such as Cu but not Fe. They reported a revised ρ of Fe of 3.62 µΩm at the CMB and 4.65 µΩm at the ICB, higher than the values reported thus far. Experiments on several simple metals showed the ρ invariance prediction of Stacey and Loper (2007) to be over-simplified as ρ of Cu (Ezenwa et al., 2017), Ag (Littleton et al., 2018), Au (Berrada et al., 2018), all decrease on their pressure-dependent melting boundaries whereas Zn (Ezenwa and Secco, 2017a), Co (Ezenwa and Secco, 2017b), Ni (Silber et al., 2017) and Fe (Silber et al., 2018; Yong et al., 2019) all show invariant ρ along the melting boundary. Similarly, Davies (2007) revised the results of Stacey and Anderson (2001) and Bi et al. (2002) by correcting for T at the top of the core (∼4,023 K, 135 GPa), which suggested a ρ of 1.25–1.9 µΩm for Fe at CMB conditions.

First-principle calculations using the Boltzmann equation suggested ρ of 0.75 µΩm for solid ε-Fe at ICB conditions (Sha and Cohen, 2011), while using the Kubo–Greenwood equation via the Bloch–Grüneisen equation on liquid Fe suggested a ρ of ∼0.61–0.69 µΩm at core conditions (de Koker et al., 2012). These results are comparable with first-principle calculations of transport properties based on DFT on liquid Fe alloy mixtures by Pozzo et al. (2012) who reported a value of 0.64 µΩm at the ICB, and 0.73–0.74 µΩm at the CMB. Soon after this work, Pozzo et al. (2013) used first-principle simulations from DFT calculations with the Kubo-Greenwood relation to obtain k while ρ was independently calculated from σ. The appropriate Lorenz number for liquid Fe (2.47–2.51·10⁻⁸ WΩ K⁻²) was then calculated using the Wiedemann-Franz law. Their results also showed 0.64 µΩm for Fe at the ICB, and 0.747 µΩm at the CMB. First-principle calculations combined with molecular dynamic simulations on solid Fe by Pozzo et al. (2014) suggested lower values of 0.50–0.53 µΩm at ICB conditions. Pozzo and Alfè (2016a) extended the set of calculations of core ρ of ε-Fe by Pozzo et al. (2014) to lower temperatures in order to investigate the T dependence of ρ. Their results suggested that ρ increases linearly with T and eventually saturates at high T, implying ρ of Fe of ∼0.72 µΩm not far from CMB conditions (4,350 K, 97 GPa) and ∼0.54 µΩm at Earth’s center (6,350 K, 365 GPa), comparable to previous results mentioned above. This study is also in agreement with DAC experiments up to 70 GPa and 300 K by Gomi and Hirose (2015), who suggested values of 0.537 (+0.049/−0.077) µΩm and 0.431 (+0.058/−0.095) µΩm at CMB (3,750 K, 135 GPa) and ICB (4971 K, 330 GPa) conditions respectively. In contrast, extrapolations of DAC measurements from 26 to 51 GPa up to 2,880 K, assuming resistivity saturation suggested the ρ of Fe is 0.404 (+0.065/−0.097) µΩm at CMB conditions (Ohta et al., 2016). However, in the first study to measure k of Fe at CMB conditions, Konôpková et al. (2016) measured the propagation of heat pulses across Fe foils in a DAC, up to 130 GPa and 3,000 K, and then modelled the T and P dependences of ρ. They derive ρ of Fe of 3.7 ± 1.5 µΩm at the outer core. Although in agreement with the high values reported by Stacey and Loper (2007), this value is higher than the saturation resistivity of 1.43 µΩm suggested by Xu et al. (2018). Xu et al. (2018) computed the electron-phonon and electron-electron contributions to the ρ of solid ε-Fe, from first-principle calculations and molecular dynamics. They suggested values of 0.998 µΩm and 1.008 µΩm at ICB (6,000 K, 330 GPa) and CMB (4,000 K, 136 GPa) respectively. Their results also suggested that previous DAC data (Ohta et al., 2016) may have overestimated the saturation effect. Zhang et al. (2020) proposed that the saturation effect observed at high T by Ohta et al. (2016) should be considered an experimental artifact due to the incorrect positioning of the laser over the sample during heating and inaccurate geometries of the four-probe method. First, the misalignment of the laser during heating generates a large T gradient across the sample. The ρ measurements at high T are then dominated by the colder regions, leading to lower ρ values. Secondly, the measurement uncertainties are expected to be significantly larger than the reported values considering the small size of the sample compared to the location of the electrodes. The geometries of the assembly essentially result in a two-probe method. While considering these key factors, Zhang et al. (2020) used first-principle calculations to compare with their ρ measurements of ε-Fe up to ∼170 GPa and ∼3,000 K in a laser heated DAC using the Van der Pauw method. Their analysis suggested a ρ of 0.80 ± 0.05 µΩm at CMB conditions (4,000 K, 136 GPa). Values obtained from DAC measurements extrapolated based on the resistivity saturation model (Gomi and Hirose, 2015; Ohta et al., 2016) are thus expected to be almost doubled according to the results of Zhang et al. (2020). However, these results remain lower than those extrapolated from multi-anvil press measurements (Secco and Schloessin, 1989; Yong et al., 2019). For example, the reported value from Yong et al. (2019) is 1.6× higher than that from Zhang et al. (2020). While Yong et al. (2019) reported measured values of ρ of Fe on the liquid side of the melting boundary, their reported value for ρ at the CMB was linearly extrapolated to 200 GPa based on the P-dependency observed between 14–24 GPa. Zhang et al. (2020) assumed a 10% increase resistivity on melting but only extrapolated from 133 to 136 GPa. In general, the differences in values for ρ at the CMB reported from multi-anvil and DAC experimental studies may arise from uncertainties from large extrapolations, from predispositions specific to each method such as errors in sample geometries, temperature homogeneity of heated sample region, lack of sample symmetry, possible thermoelectric effects and other parasitic voltages, etc.

Silber et al. (2018) reported an invariant behavior of Fe ρ at ∼1.2 µΩm, from direct measurements in a multi-anvil press up to 12 GPa and at liquid T. A similar method was used by Yong et al. (2019), who carried out static experiments in a 3000-ton multi-anvil press from 14–24 GPa into the liquid. Their results suggested an invariant ρ of liquid Fe of 1.20 ± 0.02 µΩm along the melting boundary. However, a statistical linear regression of their measurements, in order to account for the effect of P, suggested a slight deviation from invariant behavior to 1.28 ± 0.09 µΩm along the melting boundary of Fe at 200 GPa. Wagle and Steinle-Neumann (2018) focused on the behavior of liquid Fe from first-principle calculations based on Ziman’s theory on liquid metals. Combining their ICB value of 0.58 µΩm for ε-Fe with the literature values of liquid Fe-Si/S alloys (de Koker et al., 2012; Pozzo et al., 2014), ρ of outer core is expected to be up to 36% larger than that of the inner core. In contrast, estimations of pure Fe from DFT and molecular dynamics suggested almost no increase between ICB and CMB conditions, from 0.60 ± 0.27 µΩm to 0.67 ± 0.27 respectively (Wagle et al., 2019). Recent DFT simulations by Pourovskii et al. (2020) accounted for electron-electron interactions at high T and suggested an inner core ρ of 0.637 µΩm for pure Fe, in general agreement with the lower values mentioned above. Pourovskii et al. (2020) applied DFT and DMFT to Fe and concluded that thermal disorder suppresses the non-Fermi-liquid behavior of bcc Fe which reduces electron-electron scattering at high T. The variations among pure Fe results seem to range between 0.25 µΩm (Gardiner and Stacey, 1971) and 3.7 ± 1.5 µΩm (Konôpková et al., 2016), and may not simply be attributed to the method used.

The thermal properties of Fe-Ni alloys show similar variations. Gardiner and Stacey (1971) also estimated ρ of Fe with up to 25 wt% of light element (Ni, S, Si, MgO). Their results indicate an upper bound of 2.77 µΩm at CMB conditions and 6.03 µΩm at ICB conditions. Direct measurements at 1 atm up to ∼1,373 K by Johnston and Strens (1973) show comparable results. Assuming ρ at core pressures is smaller than that at 1 atm, Johnston and Strens (1973) suggested that ρ should not exceed 2.0 µΩm for Fe-10 wt% Ni-2.6 wt% C-15 wt% S (hereinafter referred to as Fe10Ni2.6C15S) at core pressures. Stacey and Anderson (2001) predicted the addition of 23 wt% and 15 wt% Si (or Fe23Ni15Si) to increase ρ to 2.12 µΩm at CMB and 2.02 µΩm at ICB, in agreement with Johnston and Strens (1973). Davies (2007) also reported ρ in the range of 2.15–2.8 µΩm for Fe23Ni15Si at CMB conditions. In contrast, DAC experiments combined with the Bloch–Grüneisen equation suggested values of 0.675 µΩm for ε-Fe10Ni, 1.26 (+0.05/−0.17) µΩm for ε-Fe5Ni4Si and 1.77 (+0.05/−0.25) µΩm for ε-Fe5Ni8Si at CMB conditions (4,000 K, 140 GPa) (Zhang et al., 2021). Gomi and Hirose (2015) suggested similar ρ values for Fe-Ni with up to 13.4 wt% of light elements (O, Si, S, C) of 0.53–1.19 µΩm at CMB and 0.39–0.96 µΩm at ICB. Similarly, Ohta et al. (2016) combined their DAC measurements with Matthiessen’s rule and the resistivity saturation model to infer ρ of Fe11.9Ni13.4Si of 0.869 (+0.154/−0.216) µΩm at 140 GPa and 3,750 K. Gomi et al. (2016) estimated the ρ of Fe12Ni15Si (or Fe₆₅Ni₁₀Si₂₅) between 1.12 and 1.16 µΩm at 4,000–5,500 K and 156–175 GPa from the Kubo–Greenwood formula. As expected from additional impurity scattering, the previous values of Fe-alloys (Gomi and Hirose, 2015; Gomi et al., 2016) are greater than that of pure Fe (Ohta et al., 2016) using similar methods. First-principle electronic band structure calculations of Fe-alloys accounting for the saturation theory suggested values ranging from 0.58–0.74 µΩm for Fe-(5.4 to 31.6 wt%)Ni at CMB conditions (Gomi and Yoshino, 2018). In agreement with these studies, Zidane et al. (2020) also used first-principle calculations based on the Kubo-Greenwood relation and reported values of 0.62–1.22 µΩm for Fe-Ni with 2.7–37.7 wt% light elements (O, Si, S) at ICB conditions (5,500 K, 360 GPa).

The results of Gomi and Yoshino (2018) also suggested values ranging from 0.71–0.88 µΩm for Fe-(1.6 to 11.7 wt%)O at CMB conditions. Similarly, de Koker et al. (2012) reported a range of 0.67–0.82 µΩm for Fe-O alloys at core conditions, while Pozzo et al. (2012) also reported a value of ∼0.80 µΩm for Fe-O-S/Si (2.7–3.5 wt% O and wt% S/Si between 9.1 and 11.4) at the ICB and 0.90 µΩm at the CMB. Wagle et al. (2019) reported ρ values in very good agreement with de Koker et al. (2012) for the same alloys. Their results suggested that at ICB conditions, ρ is 0.65 ± 0.24 µΩm and 0.71 ± 0.27 µΩm, while at the CMB conditions ρ is 0.74 ± 0.24 µΩm and 0.81 ± 0.27 µΩm, for Fe3.9O (or Fe₇O) and Fe8.7O (or Fe₃O) respectively (Wagle et al., 2019). Similarly, Pozzo et al. (2013) reported a calculated ρ of ∼0.79 µΩm for Fe2.7O6Si (or Fe_0.82O_0.08Si_0.10) and ∼0.80 µΩm for Fe4.6O4.9Si (or Fe_0.79O_0.13Si_0.08) at the ICB, not unlike the direct calculations of resistivity for Fe-O-S/Si by Pozzo et al. (2012). They also report a Lorenz number for liquid Fe-alloys varying from 2.17 to 2.24·10⁻⁸ WΩK⁻² from the Wiedemann-Franz law (Pozzo et al., 2013).

The recent DAC experiments by Zhang et al. (2021) suggested a value of 1.00 µΩm for ε-Fe1.8Si at CMB conditions. Gomi and Yoshino (2018) considered a greater Si content and reported values ranging from 0.71–1.13 µΩm for Fe-(2.8 to 18.8 wt%)Si and 0.72–0.94 µΩm for Fe-(3.1 to 20.9 wt%)S at CMB conditions. The first-principle calculations and molecular dynamics simulations on Fe4.5Si (or Fe_0.92Si_0.08) and Fe3.9Si (or Fe_0.93Si_0.07) suggested ρ of 0.65–0.66 µΩm at the ICB (Pozzo et al., 2014). The agreement with the reported values of Fe3.9O (de Koker et al., 2012) and Fe (Keeler and Royce, 1971) suggested the contribution of Si and O to the total ρ at inner core conditions may not be significant. It has been shown though at lower pressures that increasing Si content from 2 to 17 wt% increases ρ (Berrada et al., 2020), yet Wagle et al. (2019) reported lower values than Zhang et al. (2021) for a higher Si content. At CMB and ICB conditions, ρ of Fe6.7Si (or Fe₇Si) is calculated to be 0.81 ± 0.5 µΩm and 0.73 ± 0.5 µΩm, while that of Fe14.4Si (or Fe₃Si) is 1.02 ± 0.5 µΩm and 0.92 ± 0.5 µΩm (Wagle et al., 2019). Wagle et al. (2019) also revised previous estimates by Wagle et al. (2018) of Fe7.6S (or Fe₇S) and Fe16.1S (or Fe₃S) and reported values of 0.82 ± 0.22 µΩm and 1.01 ± 0.42 µΩm at CMB conditions, and 0.75 ± 0.22 µΩm and 0.95 ± 0.42 µΩm at ICB conditions, respectively. Gomi et al. (2013) estimated that ρ of ε-Fe13.2Si (or Fe₇₈Si₂₂) is 1.02 (+0.04/−0.11) µΩm at the CMB and 0.820 (+0.054/−0.131) µΩm at the ICB. Their results are in very good agreement with Wagle et al. (2019) and were extrapolated from a combination of DAC measurements up to 100 GPa and first-principle calculations while considering the effect of ρ saturation. Silber et al. (2019) conducted direct measurements of ρ of Fe4.5Si from 3 to 9 GPa and up to liquid T and postulated that the ρ of liquid Fe alloyed with light elements remains unchanged from that of Fe at inner core conditions, but the variation in T at the CMB suggested that ρ could increase up to ∼1.50 µΩm. In only the second study to measure experimentally k of a composition in the Fe system at Earth’s core conditions, Hsieh et al. (2020) used a pulsed laser method with a DAC to measure k of Fe-Si alloys up to 144 GPa and 3,300 K. Calculations of ρ using the Wiedemann-Franz law, with the Sommerfeld value of the Lorenz number, and extrapolations to high T suggested approximately 4.6 µΩm (or 20 Wm⁻¹ K⁻¹) at ∼136 GPa and 3,750 K for ε-Fe8.7Si (or Fe_0.85Si_0.15) (Hsieh et al., 2020). Hsieh et al. (2020) note that the discrepancy with previously mentioned results may be caused by the assumptions made by studies that did not directly measure k. Both the modeled T-dependence of ρ and the use of the Sommerfeld value of the Lorenz number at high P and T lead to underestimates of k at Earth’s core conditions. Shock compression experiments by Matassov (1977) on Fe-Si alloys up to 140 GPa and 2,700 K suggested a ρ of 1.12 µΩm for an Fe33.5Si core, which is within previously reported values from shock wave measurements. As mentioned earlier, this value may be underestimated due to the shunting effect of epoxy above 50 GPa (Bi et al., 2002). The results of de Koker et al. (2012) also suggested a lower range of 0.74–1.03 µΩm for Fe-Si alloys at core conditions. Similar to the results of de Koker et al. (2012), DAC measurements up to 60 GPa and 300 K indicate ρ values for Fe9Si of 0.6–1.3 µΩm at the CMB (Seagle et al., 2013). Their measurements were extrapolated to CMB conditions using a model of ρ as a function of T, V, and Debye temperature. These results are in agreement with measurements in a cubic-anvil press up to 5 GPa and 2,200 K, indicating ρ of Fe17Si in the range of 0.90–0.94 µΩm at outer core conditions (Kiarasi, 2013). In comparison, Suehiro et al. (2017) reported CMB values of approximately 0.699 µΩm for Fe12.8S (or Fe_80.8S_19.2), 0.741 µΩm for Fe6.1Si6.7S (or Fe_79.7Si_10.3S₁₀), and 0.784 µΩm for Fe13.5Si (or Fe_77.5Si_22.5). Suehiro et al. (2017) carried out measurements in a laser-heated DAC up to 110 GPa and 300 K and used Matthiessen’s Rule and the saturation resistivity value of 1.68 µΩm, to obtain ρ of Fe-Si-S alloys at core conditions. Thus, the contribution of S to the ρ of Fe-alloys is reported to be weaker than that of Si. Gomi and Hirose (2015) proposed higher ρ values for Fe13.5Si of 1.02 (+0.04/−0.13) µΩm and 0.820 (+0.055/−0.130) µΩm at the CMB and ICB, respectively. These higher values are in agreement with Zhang et al. (2018), who applied their model of k to Fe13.5Si and reported ρ values of 0.92 µΩm at CMB conditions (4,050 K, 136 GPa). Recently, the saturation resistivity of ε-Fe-Si alloys was further investigated in an internally heated DAC up to 117 GPa and 3,120 K (Inoue et al., 2020). Results show that the saturation resistivity of ε-Fe-Si alloys is comparable to that of pure Fe at ∼100 GPa (Inoue et al., 2020). They obtained ρ values for ε-Fe12.7Si of 1.040 (+0.126/−0.212) µΩm and 0.775 (+0.150/-0.231) µΩm at ICB (3,760 K, 135 GPa) and CMB (5,120 K, 330 GPa) respectively. All values discussed above are summarized in Tables 1–4. The variations in ρ, organized in terms of composition, are visualized in Figure 2.

TABLE 1

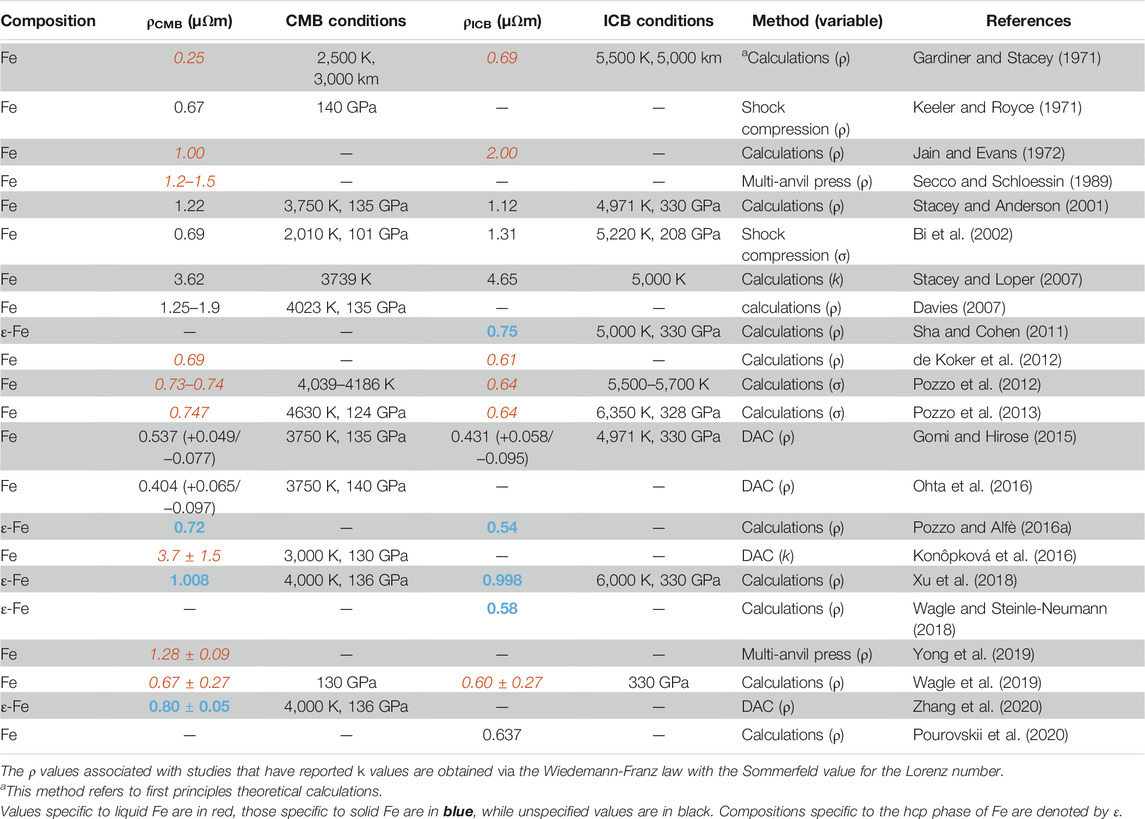
TABLE 1. Electrical resistivity values of Fe at Earth’s CMB (4,000 K, 136 GPa) and ICB (5,000 K, 330 GPa) conditions determined by different methods.

TABLE 2

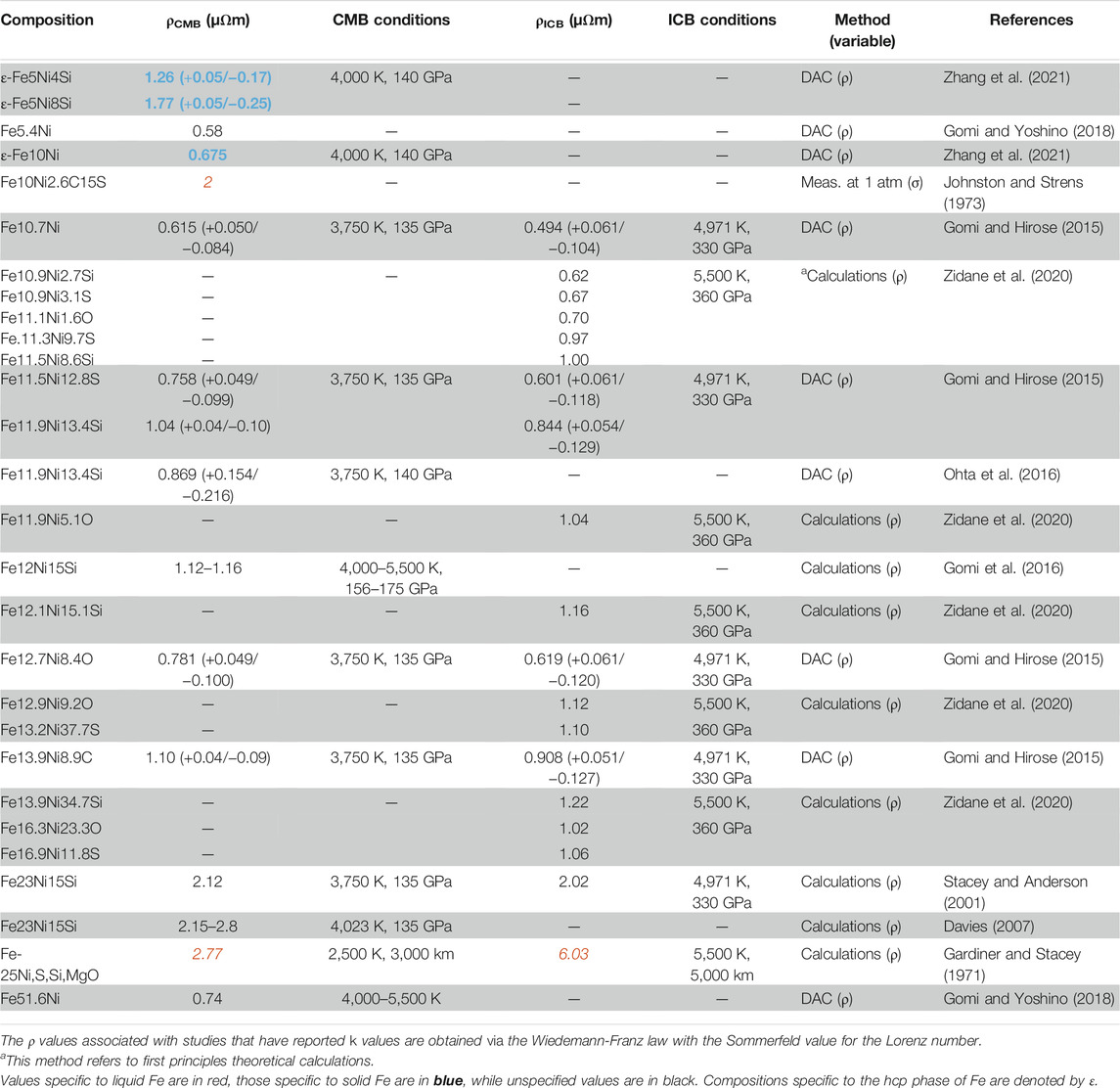
TABLE 2. Electrical resistivity values of Fe-Ni alloys at Earth’s CMB (4,000 K, 136 GPa) and ICB (5,000 K, 330 GPa) conditions determined by different methods.

TABLE 3

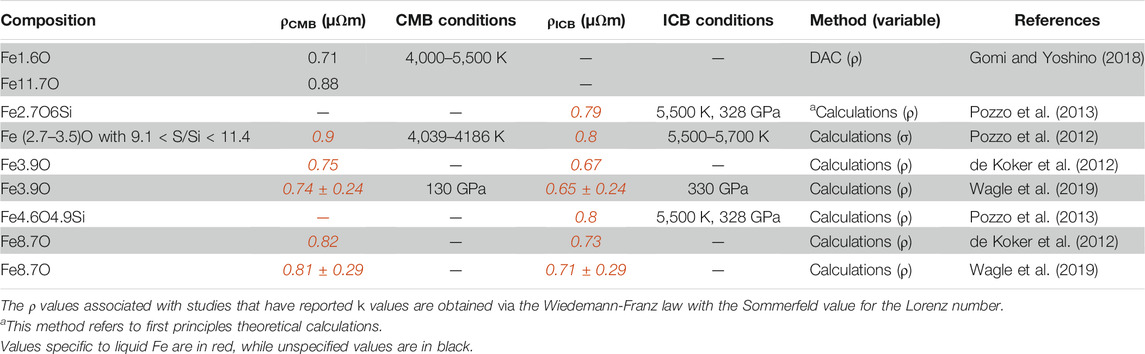
TABLE 3. Electrical resistivity values of Fe-O alloys at Earth’s CMB (4,000 K, 136 GPa) and ICB (5000 K, 330 GPa) conditions determined by different methods.

TABLE 4

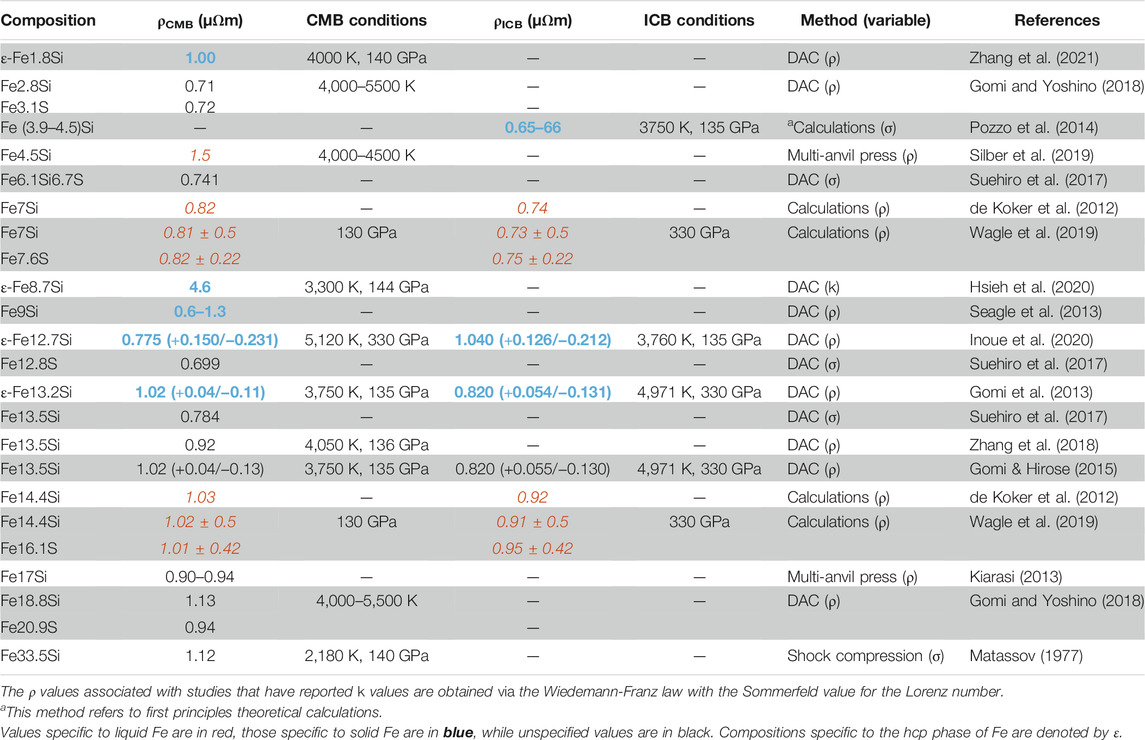
TABLE 4. Electrical resistivity values of Fe-Si/S alloys at Earth’s CMB (4000 K, 136 GPa) and ICB (5000 K, 330 GPa) conditions determined by different methods.

FIGURE 2

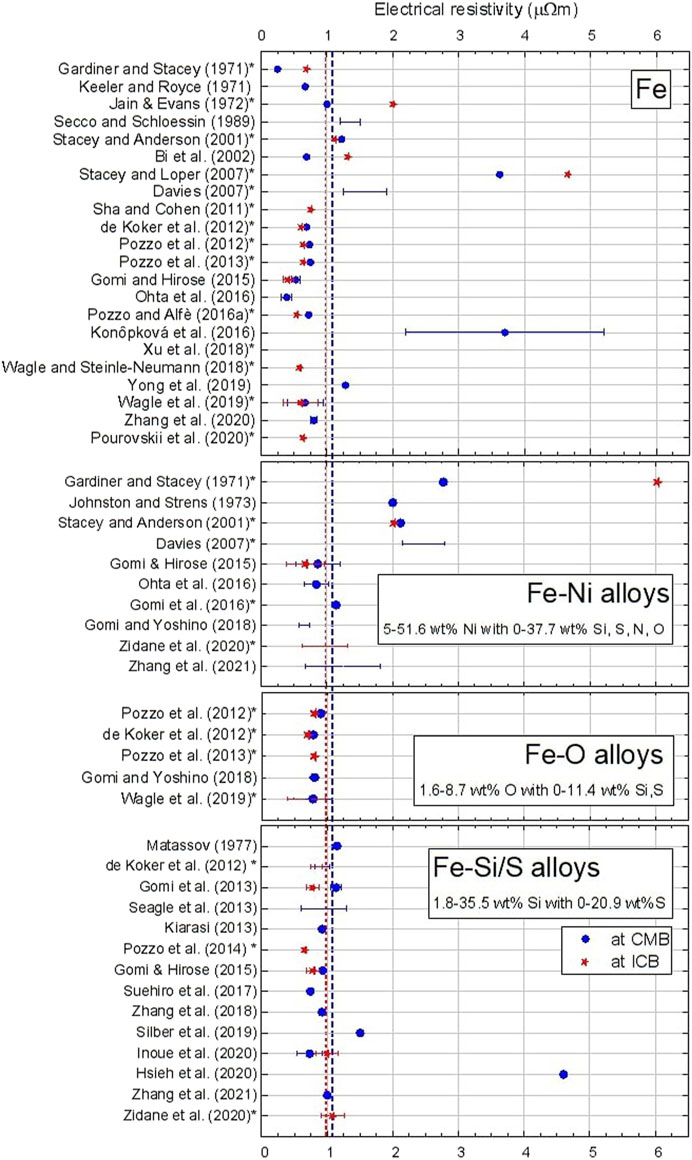
FIGURE 2. Combined values of ρ from the literature applied to Earth’s core presented in date order. The blue dashed line represents the average values (without values > 3 µΩm) at the CMB, while the red dashed line represents the average values at the ICB. The average of all reported values at CMB (4,000 K, 136 GPa) conditions is 1.07 µΩm, and that at ICB (5,000 K, 330 GPa) is 0.97 µΩm. The * denotes theoretical studies. Repeated references indicate different compositions.

A large quantity of theoretically- and experimentally-based estimates are considered for the ρ of a terrestrial core of pure Fe. In general, ρ values of Fe are centered about 1.05 and 1.08 µΩm at the CMB and ICB, respectively, without considering the high values (>3 µΩm) from Stacey and Loper (2007) and Konôpková et al. (2016). The high values reported in the theoretical work of Stacey and Loper (2007) and very challenging experimental work of Konôpková et al. (2016) can hardly be explained by the selection of P and T values since they are similar to those reported by the studies reporting lower ρ values. However, the values reported by Konôpková et al. (2016) are direct measurements of k, which include the phonon contribution. Their values are thus expected to be higher than measurements or calculations of k_e, although such a large discrepancy (3.5× higher than the average) cannot be explained by currently understood physics of the relative contributions of electron and phonon components of k in metals. The average ρ of Fe-Ni alloys is 1.35 and 1.22 µΩm at the CMB and ICB respectively, without considering the high value from Gardiner and Stacey (1971) at ICB conditions. The theoretical work of Gardiner and Stacey (1971) reported the highest values corresponding to the estimated ρ of Fe-25Ni,S,Si,MgO. The reported data on Fe-Ni alloys are scattered and a clear relationship between light element content and ρ, or even between theoretical and experimental methods, cannot be readily seen. The average ρ of Fe-O alloys is 0.80 and 0.74 µΩm at the CMB and ICB respectively. Theoretical and experimental ρ values of Fe-Si/S alloys are centered about 1.08 and 0.83 µΩm at the CMB and ICB respectively, without considering the high value from Hsieh et al. (2020) at ICB conditions. Indeed, the ρ value for Fe8.7Si (Hsieh et al., 2020) is expected to be higher than that of Fe7.6Si (Wagle et al., 2019) but lower than that of Fe9Si (Seagle et al., 2013) and higher Si content alloys. The averages of all studies reporting values for Earth are 1.07 and 0.97 µΩm at CMB and ICB conditions, respectively. Higher P and lower light element content generally result in a lower ρ for a given core composition, while high T acts to increase ρ. Yet, the consistently greater averages at CMB conditions, which consider a higher light element content and lower P, suggested that the effects of light element content and P dominate over the effects of T.

Moon

A combination of the lunar seismic profiles (Weber et al., 2011) and sound wave velocity measurements of Fe-alloys (Antonangeli et al., 2015) indicates that the Moon is currently composed of a liquid outer core and solid inner core. The exact amount and nature of light element(s) in the core is not constrained but S, C, and Ni are expected (Wieczorek et al., 2006; Steenstra and van Westrenen, 2017). The presence of Si in the lunar core is also considered possible since the lunar Si isotope composition suggests a mantle composition similar to Earth’s (Armytage et al., 2012; Nazarov et al., 2012; de Meijer et al., 2013; Zambardi et al., 2013). Szurgot (2017) reported at least 2.7 wt% Si in the lunar core when considering the uncompressed density of the Moon.

The calculated k of Fe (25–50 W m⁻¹ K⁻¹) by Anderson (1998) and Stacey and Anderson (2001) have been commonly used in thermal evolution models of the lunar dynamo (Stegman et al., 2003; Zhang et al., 2013; Evans et al., 2014; Laneuville et al., 2014; Scheinberg et al., 2015; Laneuville et al., 2018). However, the corresponding ρ via the Wiedemann-Franz law varies from study to study due to the large variations in T assigned to the lunar CMB. Direct resistivity measurements of Fe in a multi-anvil press from 3–12 GPa and into the liquid state suggested ρ of 1.23–1.31 µΩm on the core side of the CMB (1,687–1,800 K, 4.9 GPa) (Silber et al., 2018). Using a similar method, Pommier (2018) measured ρ in a multi-anvil apparatus up to 10 GPa and over a wide range of T. Their results suggested a value of 0.66 µΩm, or slightly more than half of the value measured by Silber et al. (2018). Also, Pommier (2018) reported a ρ of 2.15 µΩm for Fe5S at 4.5 GPa and 1,700 K. According to their results, the effect of S, even for such a small wt%, is not negligeable. Recently, Yin et al. (2019) reported measurements of ρ of Fe35.7P (or FeP), Fe21.7P (or Fe₂P) and Fe15.6P (or Fe₃P) in a multi-anvil press at 3.2 GPa. These authors include P as a possible light element in the lunar core considering its large solubility in liquid Fe and Fe-S alloys (Zaitsev et al., 1995; Stewart and Schmidt, 2007). Their results indicate that ρ of Fe35.7P is approximately four times that of Fe. Yin et al. (2019) conclude that ρ is expected to be lower than 1.65 µΩm for a lunar core with Fe15.6P. In addition, the direct measurements of Berrada et al. (2020) constrained the ρ of Fe-Si alloys (2, 8.5, 17 wt% Si) between 1.17–1.66 µΩm at the top of the lunar outer core (1,600 K, 5–7 GPa). These studies have all used a multi-anvil apparatus with a four-wire measurement method to measure ρ. The values discussed in this section are summarized in Table 5 and the variations in ρ are visualized in Figure 3.

TABLE 5

TABLE 5. Electrical resistivity values of Fe and Fe-alloys according to different methods, at the lunar CMB.

FIGURE 3

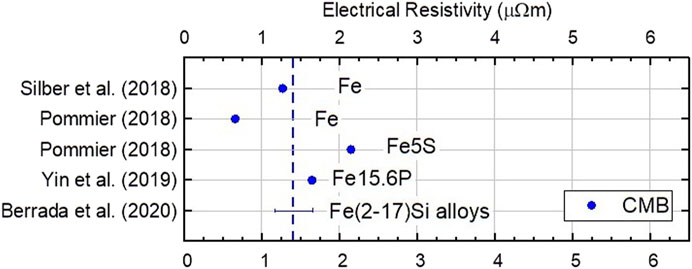
FIGURE 3. Combined values of ρ from the literature applied to the Moon’s core presented in date order. The blue dashed line represents the average values at the CMB. The average of all reported values at CMB (1,687–1,800 K, 4.5 GPa) conditions is 1.40 µΩm. Repeated references indicate different compositions.

Although the exact identity and amount of light elements in the lunar core is not constrained, to our knowledge, only few studies have reported ρ values to the relevant P and T conditions of the lunar core. At CMB conditions, the measured ρ of Fe15.6P is lower than that reported for Fe-Si alloys (up to 17 wt% Si) and Fe5S, suggesting the effect of P on the core ρ is relatively negligible. The reported Fe-alloys show greater ρ than that of Fe, as expected considering the additional scattering mechanism caused by electron-impurity interactions. The average of all studies reporting values at CMB conditions is 1.40 µΩm.

Mercury

Our understanding of the light element content of Mercury is mainly based on solar-system chemical abundances, models based on the compositions of Earth and the Moon, and data returned from the MESSENGER X-ray spectrometer (Harder and Schubert, 2001; McCubbin et al., 2012). Early estimates of the core composition of Mercury suggest ∼99 wt% is metal (Fe, Ni, Co) and ∼1 wt% is Fe36.5S (or FeS) (Morgan and Anders, 1980). Nittler et al. (2017) has argued a Si-bearing core with perhaps some small amounts of S and C, while Rivoldini et al. (2009) suggest a minimum of 5 wt% S. Various thermal evolution models consider an Fe-Si core with uncertainty on the exact Si composition (Knibbe and van Westrenen, 2017; Knibbe and van Westrenen, 2018). Estimates of Si content range between 5 and 25 wt% Si (Malavergne et al., 2010; Chabot et al., 2014), although recent studies propose that 10.5 wt% Si provides the best modelling results of the core’s elastic property and geodesy data (Terasaki et al., 2019; Steinbrügge et al., 2021).

Early models of Mercury’s core formation generally consider k of 40–43 W m⁻¹ K⁻¹, which correspond to 1.06–1.15 µΩm, at 1,880 K for a core of mainly Fe with 1–5 wt% S (Stevenson et al., 1983; Christensen, 2006; Tosi et al., 2013). Thermal evolution models by Knibbe and van Westrenen (2018) considered a range of k from 30 to 60 W m⁻¹ K⁻¹ for an Fe-Si core with T between 1,800–2,200 K, which corresponds to 0.73–1.79 µΩm via the Wiedemann-Franz law. In contrast, direct measurements of ρ of γ-Fe at 5, 7 and 15 GPa into the liquid state in a multi-anvil press suggested values of ∼0.36 µΩm and ∼0.44 µΩm at ICB (2,200–2500 K, 36 GPa) and CMB (1800–2000 K, 5–7 GPa) conditions respectively (Deng et al., 2013). The direct measurements of ρ for γ-Fe at Mercury core temperatures in a laser-heated DAC suggested values of 1.08–2.44 µΩm (or 35 ± 10 W m⁻¹ K⁻¹) at 2,200–2,500 K and ∼40 GPa (Konôpková et al., 2016). Considering the variations in the Lorenz number with T, Secco (2017) reported ρ for Fe of 1.044 µΩm at 1,823 K and 5.5 GPa. Silber et al. (2018) used direct ρ measurements of Fe from 3–12 GPa and up to liquid T and suggested a value of 0.87 ± 0.10 µΩm for Fe at CMB conditions (1,900 K, 5 GPa). Ezenwa and Secco (2019) revised previous measurements of ρ of Fe at Mercury’s CMB conditions (1,880 K, 5 GPa) to 1.18 µΩm on the solid side just before melting and 1.24 µΩm on the liquid side. Berrada et al. (2021) reported higher ρ values of Fe8.5Si between 1.40–1.44 µΩm at CMB conditions (1,600–2,100 K, 5–7 GPa) from measurements in a multi-anvil press up to 24 GPa and above the liquid T. Similarly, Pommier et al. (2019) conducted direct measurements in a multi-anvil apparatus up to 10 GPa and over a wide range of T. Their results suggested approximately 0.35 µΩm for Fe10Si, 0.49 µΩm for Fe33.5Si, and 0.33 µΩm for Fe8Si3S at CMB conditions (2,000 K, 6 GPa). In contrast, Manthilake et al. (2019) reported σ data from resistance measurements of Fe36.5S, which convert to 8.01 µΩm near CMB conditions (1,300 K, 8 GPa). This result is significantly larger that of any composition reported in the literature thus far at similar P and T conditions. The values discussed in this section are summarized in Table 6 and the variations in ρ are visualized in Figure 4.

TABLE 6

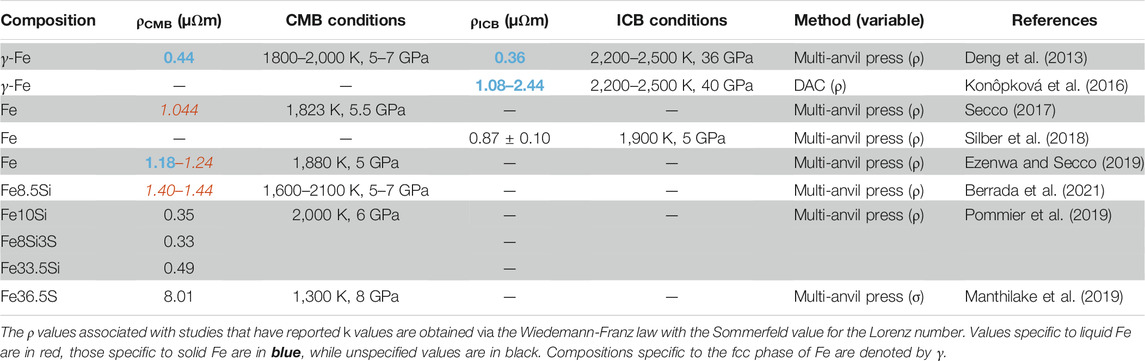
TABLE 6. Electrical resistivity values of Fe and Fe-alloys according to different methods, at Mercury’s CMB and ICB conditions.

FIGURE 4

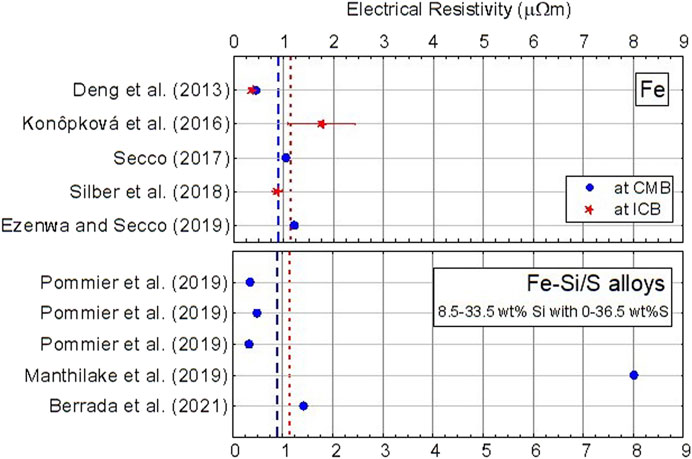
FIGURE 4. Combined values of ρ from the literature applied to Mercury’s core presented in date order. The blue dashed line represents the average values at the CMB, while the red dashed line represents the average values at the ICB. The average of all reported values at CMB (1,900 K, 5 GPa) conditions is 0.88 µΩm, and that at ICB (2,200–2,500 K, 36 GPa) is 1.12 µΩm.

Reported theoretical and experimental values of the ρ of Fe applied to Mercury’s CMB and ICB conditions show an important disagreement. Deng et al. (2013) reported lower values (∼35% less) than those reported by Konôpková et al. (2016), Secco (2017), Silber et al. (2018), and Ezenwa and Secco (2019). Such a discrepancy is not negligible when calculating q_ad at the top of the outer core. The direct k measurements by Konôpková et al. (2016) convert to similar ρ values to the direct ρ measurements by Secco (2017), Silber et al. (2018) and Ezenwa and Secco (2019). The values reported for Fe-Si/S alloys also show two distinct trends. Berrada et al. (2021) reported higher values than those by Pommier et al. (2019), although Pommier (2018) considered a higher light element content (up to 33.5 wt% Si). Indeed, the light element content is expected to increase the scattering contribution and thus the measured ρ. The values reported by Pommier (2018) are consistent with the lower ρ values for Fe reported by Deng et al. (2013) and Konôpková et al. (2016). Similarly, the values reported by Berrada et al. (2021) are consistent with the high ρ of Fe values reported by Secco (2017), Silber et al. (2018),and Ezenwa and Secco (2019). The averages of all studies reporting values for Mercury are 0.88 and 1.12 µΩm at CMB and ICB conditions, respectively, without considering the high values (>3 µΩm) from Manthilake et al. (2019). Although all the reported data at the ICB consist only of pure Fe measurements, the average ρ at ICB conditions is greater than that at CMB conditions which considers Fe-alloys. This contrast with the observations at Earth’s core conditions could be explained by the strong effect of T over the effects of light elements and P at Mercury’s core conditions, although further studies are necessary to draw reliable conclusions.

Mars

The chemical composition of the Martian core is presumed to be Fe14.2S based on analyses of Martian meteorites (Wänke et al., 1988). Laser-heated DAC experiments and in-situ X-ray diffraction confirm the phase stability of Fe36.5S at core conditions (Kavner et al., 2001). Thermal evolution models also consider a core primarily composed of Fe with 6–8 wt% Ni, and 10–17 wt% S, in addition to containing lower amounts of O, C, H and P (Rivoldini et al., 2011).

Stevenson et al. (1983) investigated core evolution models of Mars by combining theories of geomagnetism and fluid dynamics. In their model, the value of k of Fe used for Earth, Mercury, Mars and Venus is 40 W m⁻¹ K⁻¹, which corresponds to 1.15 µΩm at 1,880 K (Stevenson et al., 1983). Thermal evolution models based on measurements by Anderson (1998) suggested a range of 43–88 W m⁻¹ K⁻¹ at Martian CMB conditions (25 GPa, 1,800 K) (Nimmo and Stevenson, 2000). Using the Wiedemann-Franz law, this suggested ρ values for Fe ranging from 0.50–1.02 µΩm, which are lower than previously mentioned. In fact, Deng et al. (2013) estimated ρ of γ-Fe to be at most 0.40 µΩm at the outermost part of the Martian core (2,000 K, 24 GPa) based on their measurements at 7 GPa. Recent measurements by Silber et al. (2018) reported ρ of Fe of 1.7 µΩm at CMB conditions (1,770 K, 23 GPa), higher than previously reported. Similar experiments by Ezenwa and Yoshino (2021) in a multi-anvil apparatus from 14 to 22.5 GPa and above the liquid T, estimated ρ of 0.68 ± 0.03 µΩm at CMB conditions (2,106 K, 23 GPa). The measurements by Ezenwa and Yoshino (2021) are in agreement with first-principle calculations of pure Fe reporting values from 0.74 ± 0.29 µΩm to 0.75 ± 0.29 at the ICB and CMB respectively (Wagle et al., 2019). Wagle et al. (2019) also calculated the ρ of Fe3.9O, Fe8.7O, Fe7.6S, Fe16.1S, Fe6.7Si, and Fe14.4Si at the Martian ICB and CMB conditions, as reported in Table 7. Direct measurements of ρ up to 110 GPa at 300 K suggested values from 1.064 µΩm at the CMB to 0.952 µΩm at the center of an Fe15S (or Fe_77.7S_22.3) core (Suehiro et al., 2017). The values discussed in this section are summarized in Table 7 and the variations in ρ are visualized in Figure 5.

TABLE 7

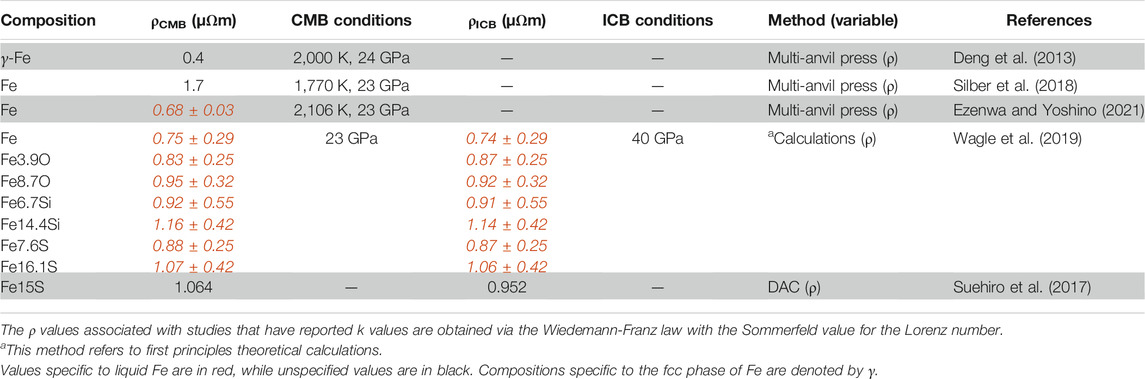
TABLE 7. Electrical resistivity values of Fe and Fe-alloys according to different methods, at the Martian CMB (1,770 K, 23 GPa) and ICB (2,000 K, 40 GPa) conditions.

FIGURE 5

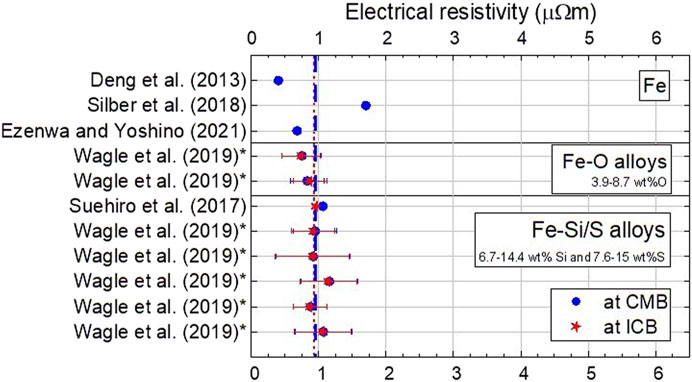
FIGURE 5. Combined values of ρ from the literature applied to Mars’ core presented in date order. The blue dashed line represents the average values at the CMB, while the red dashed line represents the average values at the ICB. The average of all reported values at CMB (1770 K, 23 GPa) conditions is 0.95 µΩm, and that at ICB (2,000 K, 40 GPa) is 0.93 µΩm. The * denotes theoretical studies. Repeated references indicate different compositions.

The literature on ρ values at Martian core conditions is insufficient to determine a reasonable value at CMB and ICB conditions. While both Deng et al. (2013) and Silber et al. (2018) reported values for solid Fe, the value reported by Deng et al. (2013) is in best agreement with the reported values of liquid Fe (Wagle et al., 2019; Ezenwa and Yoshino, 2021). However, Silber et al. (2018) considered lower T values at the CMB than Ezenwa and Yoshino (2021). Their measured ρ is therefore expected to be lower than that of Ezenwa and Yoshino (2021), although the opposite is observed. Within the results of Wagle et al. (2019), the effect of O in increasing ρ seems to be less than that of Si and S, although all alloys seems to be in agreement within uncertainty. The values for an Fe15S (Suehiro et al., 2017) are in agreement with those of Fe16.1S (Wagle et al., 2019). The average of all studies reporting values at CMB conditions is 0.95 µΩm, while that at ICB conditions is 0.93 µΩm. The greater average at CMB conditions relative to ICB conditions is comparable to that observed at Earth’s core conditions.

Ganymede

The presence of Fe36.5S in meteorites indicates that S is probably a major light element in Ganymede’s core (Krot, 2005). Hydrogen is also a light element candidate considering that a layer of H₂O in Ganymede’s interior has been proposed (Anderson et al., 1996). Although the exact composition is not constrained, the light element content is greatly dependent on the core size and oxidation state of the interior during differentiation. The CMB conditions are expected to be near 2,000 K and 7 GPa in the case of a low (1 wt%) S content, while near 1,400 K and 5 GPa in the case of a near eutectic (36.5 wt%) S content (Hauck et al., 2006; Bland et al., 2008; Kimura et al., 2009).

Silber et al. (2018) measured ρ of Fe at 1.20 µΩm at 1,500 K (Shibazaki et al., 2011) and 5.9 GPa (Hussmann et al., 2007), while a considerably lower value of 0.59 µΩm is proposed by Pommier (2018) at 1,400 K and 4.5 GPa. Similar to the measurements by Silber et al. (2018), Ezenwa and Secco (2019) estimated values of 1.17 µΩm and 1.38 µΩm on the solid and liquid sides of the ICB (2,200 K, 9 GPa) respectively. Regardless of the variation in these Fe results, adding S is expected to increase ρ, in agreement with the direct measurements of Pommier (2018). Pommier (2018) reported values of 2.23 µΩm for Fe5S at 1,880 K and 4.5 GPa, and 4.32 µΩm for Fe20S at 1,400 K and 4.5 GPa. To our knowledge, only two studies have reported measurements of Fe36.5S at the relevant P and T conditions. First, the results of Manthilake et al. (2019) applied to Ganymede’s conditions suggest 8.01 µΩm near CMB. In contrast, direct ρ measurements of Fe36.5S, from 2 to 5 GPa and up to 1,785 K in a multi-anvil press, suggested a value of 4.13 ± 0.07 µΩm at CMB conditions (1,411 K, 5 GPa) (Littleton et al., 2021). The values discussed in this section are summarized in Table 8 and the variations in ρ are visualized in Figure 6.

TABLE 8

TABLE 8. Electrical resistivity values of Fe and Fe-alloys according to different methods, at Ganymede’s CMB.

FIGURE 6

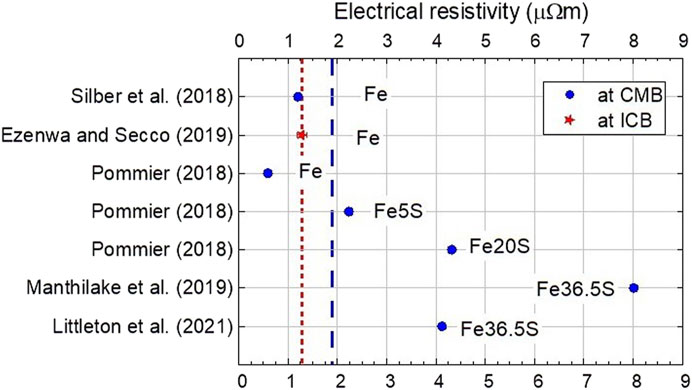
FIGURE 6. Combined values of ρ from the literature applied to Ganymede’s core presented in date order. The blue dashed line represents the average values at the CMB, while the red dashed line represents the average at the ICB. The average of all reported values at CMB (1,400–2000 K, 5–7 GPa) conditions is 1.90 µΩm, and that at the ICB (2,200 K, 9 GPa) is 1.28 µΩm. Repeated references indicate different compositions.

As with the other small planetary bodies reviewed, the available literature is scarce and insufficient to distinguish a reasonable value for ρ at core conditions. Overall, the addition of S impurity scattering increases ρ as expected. However, ρ of Fe36.5S as measured by Littleton et al. (2021) is greater than that of Fe20S (Pommier, 2018). Pressure is expected to decrease ρ, yet the ρ of Fe36.5S from Manthilake et al. (2019) at 8 GPa is almost double that from Littleton et al. (2021) at 5 GPa. Although total k measurements include the phonon contribution to conductivity, it likely does not explain the extent of the disagreement between these two studies. The average of all studies reporting values at CMB conditions is 1.90 µΩm, larger than that at the other planetary bodies reviewed, while the average at ICB conditions is 1.28 µΩm.

Contour Maps of ρ(P, T)

Figure 7 illustrates contour maps generated from the available literature on ρ for Fe, Fe-Ni alloys, Fe-O alloys and Fe-Si/S alloys, without excluding high values (>3 µΩm). The contour maps suggest ρ(P, T) is unique for each composition, and can hardly be defined by a linear function of P and T. The rich literature on Fe at Earth’s and Mercury’s CMB and ICB conditions produce an accurate contour map at the relevant P and T. Similarly, the contour map results of the ρ of Fe at the lunar and Martian CMB consist of the mean of the few reported values. However, Fe-Ni alloys were only reported at P and T conditions relevant to Earth’s core. Thus, the contour map results for Fe-Ni alloys for the Moon, Mercury, Mars, and Ganymede’s cores are unreliable extrapolations. The contour map of Fe-Ni alloys suggest ρ at low P and T is considerably higher than the values reported at high P and T. This would mean the effect of decreasing P, which acts to increase ρ, dominates over the effect of decreasing T, which acts to decrease ρ. In the same idea, ρ of Fe-O alloys was only reported at Earth’s and Mars’ core conditions, which implies the most reliable areas of the contour map are within those P and T boundaries. The contour map of Fe-Si/S alloys is in agreement with the reported data at the planetary core conditions of Earth, Moon, Mercury, Mars and Ganymede. The advantage of the contour maps is that they take into account the various P and T values used for the planetary core conditions and allow for a general estimate at a specific P and T combination. For example, the contour map of Fe-Si/S shows ρ of ∼1.70 µΩm at the lunar CMB (at 1,750 K which is the mid-T range, and 4.5 GPa), while the average of reported values is 1.66 µΩm without considering the differences in P and T conditions.

FIGURE 7

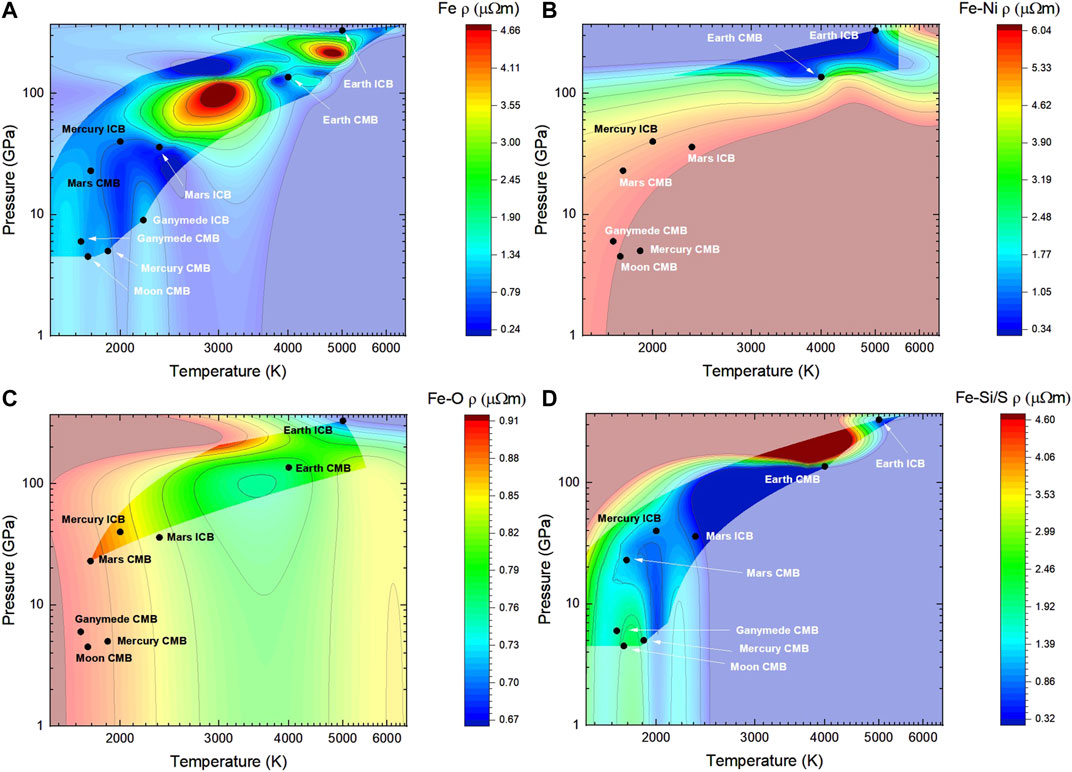
FIGURE 7. 3D visualization of the reported ρ with P and T of (A) Fe, (B) Fe-Ni alloys, (C) Fe-O alloys, and (D) Fe-Si/S alloys. Studies that did not state the exact P, T conditions for Earth’s CMB and ICB are placed at 4,000 K and 136 GPa, and 5,000 K and 330 GPa, respectively. Similarly, the lunar CMB is placed at 1,750 K (which is the mid-T range of 1,687–1,800 K) and 4.5 GPa. Mercury’s CMB and ICB are placed at 1,900 K and 5 GPa, and 2,350 K (which is the mid-T range of 2,200–2,500 K) and 36 GPa, respectively. The Martian CMB and ICB are placed at 1,770 K and 23 GPa, and 2,000 K and 40 GPa, respectively. Ganymede’s CMB is located at 1,700 K (which is the mid-T range of 1,400–2,000 K) and 6 GPa (which is the mid-P range of 5–7 GPa), while the ICB is at 2,200 K and 9 GPa. The areas encompassing the reported data are in full colour, while the faded colors are areas of extrapolations.

Discussion

The interest in determining q_ad is namely motivated by thermal evolution modelling. Direct measurements of thermal properties, and in particular k, of metals and metal-alloys at planetary core conditions are challenging and extrapolations from relatively low P and T conditions are not always consistent. Experimental progress made so far in measuring k at core conditions is very promising and future studies are needed to establish conclusively this important core property. The available literature on ρ at Earth’s core conditions is focused on pure Fe, while a few studies have considered various light elements and a range of concentrations. Results suggest that the ρ of Fe-alloys at Earth’s CMB and ICB does not significantly deviate from that of pure Fe. The scarce literature on ρ at the lunar core suggest the effect of P is negligible when compared to that of Si and S at similar wt%. On the contrary, the effect of Si and S at Mercury’s core conditions remains unclear as the literature seems to be divided into two distinct groups of ρ, with ∼35% difference. At the Martian core, the ρ of Fe-alloys are within the variations of ρ for pure Fe. In contrast, the reported ρ of Fe-S alloys at Ganymede’s CMB conditions show a great deviation from pure Fe measurements. Overall, the calculated ρ from the reported k values via the Wiedemann-Franz law, with the Sommerfeld value for L, do not significantly vary from direct measurements of ρ. Results from first-principle calculations are within the variations of those from direct measurements from multi-anvil press, DAC and shock compression experiments. Although ρ values depend on the P and T, the variations in the selection of P and T at the planetary core conditions among the literature seem to have a negligible effect on the average ρ values. The contour maps provide an interpolation of ρ as a function of P and T within the boundaries of the reported values.

Further experimental research on ρ should focus on different light element compositions, particularly in Fe with multi-light element alloys, in order to constrain reliably ρ for likely core compositions at planetary core conditions. A larger data set on measurements of k will be needed to verify both theoretically determined values of the Lorenz number at extreme conditions of P and T for pure Fe and its many alloys as well as to substantiate the use of ρ data to calculate k. Calculations that account for spin polarization and the effects of magnetism on the electron scattering have recently been developed and further progress in this area to quantify this important contribution to electrical and thermal properties at planetary core conditions is likely.

It is clear there is much to be done in the area of ρ and k property determination for application to thermal modelling of terrestrial-like planetary bodies in our Solar System. However, an even greater challenge appearing on the horizon is for similar studies to be carried out at the even greater P, T conditions of terrestrial-type exoplanets where the internal pressures are an order of magnitude higher than in Earth. Studies of those systems, which are currently in the nascent stages of characterizing equation of state and other structure-related characteristics of Fe (Smith et al., 2018) and Fe alloys (Wicks et al., 2018), will then turn to interior modelling of heat flow and core dynamics to understand dynamos in super-Earths, which will require knowledge of ρ and k behavior over much greater P, T space.

Author Contributions

MB is responsible for the formal analysis, writing and editing. RS is responsible for supervision, reviewing, editing, and funding.

Funding

This work was supported by funds to RS from the Natural Sciences and Engineering Research Council of Canada (grant number 2018-05021).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We are very grateful to Dr. Gerd Steinle-Neumann and Dr. Monica Pozzo for their insightful comments on the manuscript and to two reviewers for their constructive comments.

References

Ahrens, T. J. (2007). “Shock Wave Experiments,” in Encyclopedia of Geomagnetism and Paleomagnetism. Editors D. Gubbins, and E. Herrero-Bervera (Dordrecht: Springer Netherlands), 912–920.

Google Scholar

Alfè, D., Gillan, M. J., and Price, G. D. (2007). Temperature and Composition of the Earth's Core. Contemp. Phys. 48 (2), 63–80. doi:10.1080/00107510701529653

CrossRef Full Text | Google Scholar

Anderson, J. D., Lau, E. L., Sjogren, W. L., Schubert, G., and Moore, W. B. (1996). Gravitational Constraints on the Internal Structure of Ganymede. Nature 384 (6609), 541–543. doi:10.1038/384541a0

CrossRef Full Text | Google Scholar

Anderson, O. L. (1998). The Grüneisen Parameter for Iron at Outer Core Conditions and the Resulting Conductive Heat and Power in the Core. Phys. Earth Planet. Interiors 109 (3), 179–197. doi:10.1016/s0031-9201(98)00123-x

CrossRef Full Text | Google Scholar

Antonangeli, D., Morard, G., Schmerr, N. C., Komabayashi, T., Krisch, M., Fiquet, G., et al. (2015). Toward a mineral Physics Reference Model for the Moon’s Core. Proc. Natl. Acad. Sci. 112 (13), 3916–3919. doi:10.1073/pnas.1417490112

PubMed Abstract | CrossRef Full Text | Google Scholar

Anzellini, S., and Boccato, S. (2020). A Practical Review of the Laser-Heated Diamond Anvil Cell for University Laboratories and Synchrotron Applications. Crystals 10 (6), 459. doi:10.3390/cryst10060459

CrossRef Full Text | Google Scholar

Argaman, N., and Makov, G. (2000). Density Functional Theory: An Introduction. Am. J. Phys. 68 (1), 69–79. doi:10.1119/1.19375

CrossRef Full Text | Google Scholar

Armytage, R. M. G., Georg, R. B., Williams, H. M., and Halliday, A. N. (2012). Silicon Isotopes in Lunar Rocks: Implications for the Moon's Formation and the Early History of the Earth. Geochimica et Cosmochimica Acta 77, 504–514. doi:10.1016/j.gca.2011.10.032

CrossRef Full Text | Google Scholar

Asimow, P. D. (2015). “Dynamic Compression,” in Treatise on Geophysics. Editor G. Schubert Second Edition (Oxford: Elsevier), 393–416. doi:10.1016/b978-0-444-53802-4.00050-6

CrossRef Full Text | Google Scholar

Badro, J., Fiquet, G., Guyot, F., Gregoryanz, E., Occelli, F., Antonangeli, D., et al. (2007). Effect of Light Elements on the Sound Velocities in Solid Iron: Implications for the Composition of Earth's Core. Earth Planet. Sci. Lett. 254 (1), 233–238. doi:10.1016/j.epsl.2006.11.025

CrossRef Full Text | Google Scholar

Baum, B., Gel’d, P., and Tyagunov, G. (1967). Resistivity of Ferrosilicon Alloys in the Temperature Range 800–1700 C. The Phys. Met. Metallography 24 (181), 52–57. doi:10.1016/0016-2361(73)90012-4

CrossRef Full Text | Google Scholar

Berrada, M., Secco, R. A., and Yong, W. (2021). Adiabatic Heat Flow in Mercury's Core from Electrical Resistivity Measurements of Liquid Fe-8.5 wt%Si to 24 GPa. Earth Planet. Sci. Lett. 568, 117053. doi:10.1016/j.epsl.2021.117053

CrossRef Full Text | Google Scholar

Berrada, M., Secco, R. A., and Yong, W. (2018). Decreasing Electrical Resistivity of Gold along the Melting Boundary up to 5 GPa. High Press. Res. 38 (4), 367–376. doi:10.1080/08957959.2018.1493476

CrossRef Full Text | Google Scholar

Berrada, M., Secco, R. A., and Yong, W. (2020). Electrical Resistivity Measurements of Fe-Si with Implications for the Early Lunar Dynamo. J. Geophys. Res. Planets 125 (7), e2020JE006380. doi:10.1029/2020je006380

CrossRef Full Text | Google Scholar

Bi, Y., Tan, H., and Jing, F. (2002). Electrical Conductivity of Iron under Shock Compression up to 200 GPa. J. Phys. Condensed Matter 14 (44), 10849–10854. doi:10.1088/0953-8984/14/44/389

CrossRef Full Text | Google Scholar

Birch, F. (1961). Composition of the Earth's Mantle. Geophys. J. Int. 4 (Suppl. ment_1), 295–311. doi:10.1111/j.1365-246x.1961.tb06821.x

CrossRef Full Text | Google Scholar

Birch, F. (1964). Density and Composition of Mantle and Core. J. Geophys. Res. 69 (20), 4377–4388. 1896-1977. doi:10.1029/jz069i020p04377

CrossRef Full Text | Google Scholar

Bland, M. T., Showman, A. P., and Tobie, G. (2008). The Production of Ganymede's Magnetic Field. Icarus 198 (2), 384–399. doi:10.1016/j.icarus.2008.07.011

CrossRef Full Text | Google Scholar

Bohnenkamp, U., Sandström, R., and Grimvall, G. (2002). Electrical Resistivity of Steels and Face-Centered-Cubic Iron. J. Appl. Phys. 92 (8), 4402–4407. doi:10.1063/1.1502182

CrossRef Full Text | Google Scholar

Boltzmann, L. (1894). Zur Integration der Diffusionsgleichung bei variabeln Diffusionscoefficienten. Ann. Phys. 289 (13), 959–964. doi:10.1002/andp.18942891315

CrossRef Full Text | Google Scholar

Bridgman, P. W. (1957). Effects of pressure on binary alloys. VI. Systems for the most part of dilute Úlloys of high melting metals. Proc. Am. Acad. Arts. Sci. 84, 179–216.

Google Scholar

Chabot, N. L., Wollack, E. A., Klima, R. L., and Minitti, M. E. (2014). Experimental Constraints on Mercury's Core Composition. Earth Planet. Sci. Lett. 390, 199–208. doi:10.1016/j.epsl.2014.01.004

CrossRef Full Text | Google Scholar

Christensen, U. R. (2006). A Deep Dynamo Generating Mercury's Magnetic Field. Nature 444 (7122), 1056–1058. doi:10.1038/nature05342

PubMed Abstract | CrossRef Full Text | Google Scholar

Davies, G. F. (2007). Mantle Regulation of Core Cooling: A Geodynamo without Core Radioactivity? Phys. Earth Planet. Interiors 160 (3), 215–229. doi:10.1016/j.pepi.2006.11.001

CrossRef Full Text | Google Scholar

de Koker, N., Steinle-Neumann, G., and Vlcek, V. (2012). Electrical Resistivity and thermal Conductivity of Liquid Fe Alloys at High P and T, and Heat Flux in Earth's Core. Proc. Natl. Acad. Sci. 109 (11), 4070–4073. doi:10.1073/pnas.1111841109

PubMed Abstract | CrossRef Full Text | Google Scholar

de Meijer, R. J., Anisichkin, V. F., and van Westrenen, W. (2013). Forming the Moon from Terrestrial Silicate-Rich Material. Chem. Geology. 345, 40–49. doi:10.1016/j.chemgeo.2012.12.015

CrossRef Full Text | Google Scholar

Deng, L., Seagle, C., Fei, Y., and Shahar, A. (2013). High Pressure and Temperature Electrical Resistivity of Iron and Implications for Planetary Cores. Geophys. Res. Lett. 40 (1), 33–37. doi:10.1029/2012gl054347

CrossRef Full Text | Google Scholar

Drchal, V., Kudrnovský, J., Wagenknecht, D., and Turek, I. (2019). Alloy Disorder and Fluctuating Magnetic Moments in the Earth's Core. J. Magnetism Magn. Mater. 475, 767–771. doi:10.1016/j.jmmm.2018.11.112

CrossRef Full Text | Google Scholar

Drude, P. (1900a). Zur Elektronentheorie der Metalle. Ann. Phys. 306 (3), 566–613. doi:10.1002/andp.19003060312

CrossRef Full Text | Google Scholar

Drude, P. (1900b). Zur Elektronentheorie der Metalle; II. Teil. Galvanomagnetische und thermomagnetische Effecte. Ann. Phys. 308 (11), 369–402. doi:10.1002/andp.19003081102

CrossRef Full Text | Google Scholar

Elsasser, W. M. (1946). Induction Effects in Terrestrial Magnetism Part II. The Secular Variation. Phys. Rev. 70 (3-4), 202–212. doi:10.1103/physrev.70.202

CrossRef Full Text | Google Scholar

Evans, A. J., Zuber, M. T., Weiss, B. P., and Tikoo, S. M. (2014). A Wet, Heterogeneous Lunar interior: Lower Mantle and Core Dynamo Evolution. J. Geophys. Res. Planets 119 (5), 1061–1077. doi:10.1002/2013je004494

CrossRef Full Text | Google Scholar

Evans, R., Greenwood, D. A., and Lloyd, P. (1971). Calculations of the Transport Properties of Liquid Transition Metals. Phys. Lett. A 35 (2), 57–58. doi:10.1016/0375-9601(71)90543-3

CrossRef Full Text | Google Scholar

Ezenwa, I. C., and Secco, R. A. (2017a). Constant Electrical Resistivity of Zn along the Melting Boundary up to 5 GPa. High Press. Res. 37 (3), 319–333. doi:10.1080/08957959.2017.1340473

CrossRef Full Text | Google Scholar

Ezenwa, I. C., and Secco, R. A. (2019). Fe Melting Transition: Electrical Resistivity, Thermal Conductivity, and Heat Flow at the Inner Core Boundaries of Mercury and Ganymede. Crystals 9 (7). doi:10.3390/cryst9070359

CrossRef Full Text | Google Scholar

Ezenwa, I. C., and Secco, R. A. (2017b). Invariant Electrical Resistivity of Co along the Melting Boundary. Earth Planet. Sci. Lett. 474, 120–127. doi:10.1016/j.epsl.2017.06.032

CrossRef Full Text | Google Scholar

Ezenwa, I. C., Secco, R. A., Yong, W., Pozzo, M., and Alfè, D. (2017). Electrical Resistivity of Solid and Liquid Cu up to 5 GPa: Decrease along the Melting Boundary. J. Phys. Chem. Sol. 110, 386–393. doi:10.1016/j.jpcs.2017.06.030

CrossRef Full Text | Google Scholar

Ezenwa, I. C., and Yoshino, T. (2021). Martian Core Heat Flux: Electrical Resistivity and thermal Conductivity of Liquid Fe at Martian Core P-T Conditions. Icarus 360, 114367. doi:10.1016/j.icarus.2021.114367

CrossRef Full Text | Google Scholar

Gardiner, R. B., and Stacey, F. D. (1971). Electrical Resistivity of the Core. Phys. Earth Planet. Interiors 4 (5), 406–410. doi:10.1016/0031-9201(71)90022-7

CrossRef Full Text | Google Scholar

Gilev, S. D. (2011). Measurement of Electrical Conductivity of Condensed Substances in Shock Waves (Review). Combust Explos Shock Waves 47 (4), 375–393. doi:10.1134/s0010508211040010

CrossRef Full Text | Google Scholar

Gomi, H., Hirose, K., Akai, H., and Fei, Y. (2016). Electrical Resistivity of Substitutionally Disordered Hcp Fe-Si and Fe-Ni Alloys: Chemically-Induced Resistivity Saturation in the Earth's Core. Earth Planet. Sci. Lett. 451, 51–61. doi:10.1016/j.epsl.2016.07.011

CrossRef Full Text | Google Scholar

Gomi, H., and Hirose, K. (2015). Electrical Resistivity and thermal Conductivity of Hcp Fe-Ni Alloys under High Pressure: Implications for thermal Convection in the Earth's Core. Phys. Earth Planet. Interiors 247, 2–10. doi:10.1016/j.pepi.2015.04.003

CrossRef Full Text | Google Scholar

Gomi, H., Ohta, K., Hirose, K., Labrosse, S., Caracas, R., Verstraete, M. J., et al. (2013). The High Conductivity of Iron and thermal Evolution of the Earth's Core. Phys. Earth Planet. Interiors 224, 88–103. Article. doi:10.1016/j.pepi.2013.07.010

CrossRef Full Text | Google Scholar

Gomi, H., and Yoshino, T. (2018). Impurity Resistivity of Fcc and Hcp Fe-Based Alloys: Thermal Stratification at the Top of the Core of Super-earths. Front. Earth Sci. 6 (217). Original Research. doi:10.3389/feart.2018.00217

CrossRef Full Text | Google Scholar

Greenwood, D. A. (1958). The Boltzmann Equation in the Theory of Electrical Conduction in Metals. Proc. Phys. Soc. 71 (4), 585–596. doi:10.1088/0370-1328/71/4/306

CrossRef Full Text | Google Scholar

Gurvitch, M. (1981). Ioffe-Regel Criterion and Resistivity of Metals. Phys. Rev. B 24 (12), 7404–7407. doi:10.1103/physrevb.24.7404

CrossRef Full Text | Google Scholar

Harder, H., and Schubert, G. (2001). Sulfur in Mercury's Core? Icarus 151 (1), 118–122. doi:10.1006/icar.2001.6586

CrossRef Full Text | Google Scholar

Hauck, S. A., Aurnou, J. M., and Dombard, A. J. (2006). Sulfur's Impact on Core Evolution and Magnetic Field Generation on Ganymede. J. Geophys. Res. Planets 111 (E9). doi:10.1029/2005je002557

CrossRef Full Text | Google Scholar

Hsieh, W.-P., Goncharov, A. F., Labrosse, S., Holtgrewe, N., Lobanov, S. S., Chuvashova, I., et al. (2020). Low thermal Conductivity of Iron-Silicon Alloys at Earth's Core Conditions with Implications for the Geodynamo. Nat. Commun. 11 (1), 3332. doi:10.1038/s41467-020-17106-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Hussmann, H., Sotin, C., and Lunine, J. I. (2007). “Interiors and Evolution of Icy Satellites,” in Treatise on Geophysics. Editor G. Schubert (Amsterdam: Elsevier), 509–539. doi:10.1016/b978-044452748-6.00168-1

CrossRef Full Text | Google Scholar

Inoue, H., Suehiro, S., Ohta, K., Hirose, K., and Ohishi, Y. (2020). Resistivity Saturation of Hcp Fe-Si Alloys in an Internally Heated diamond Anvil Cell: A Key to Assessing the Earth's Core Conductivity. Earth Planet. Sci. Lett. 543, 116357. doi:10.1016/j.epsl.2020.116357

CrossRef Full Text | Google Scholar

Ito, E. (2015). “Multi-Anvil Cells and High Pressure Experimental Methods,” in Treatise on Geophysics Mineral Physics. Editors R. B.G. Schubert, and A. Dziewonski Second edition (Elsevier), 233–261. doi:10.1016/b978-0-444-53802-4.00035-x

CrossRef Full Text | Google Scholar

Jain, A., and Evans, R. (1972). Calculation of the Electrical Resistivity of Liquid Iron in the Earth's Core. Nat. Phys. Sci. 235 (61), 165–167. doi:10.1038/physci235165a0

CrossRef Full Text | Google Scholar

Jeanloz, R. (1979). Properties of Iron at High Pressures and the State of the Core. J. Geophys. Res. 84 (B11), 6059–6069. doi:10.1029/jb084ib11p06059

CrossRef Full Text | Google Scholar

Johnston, M. J. S., and Strens, R. G. J. (1973). Electrical Conductivity of Molten FeNiSC Core Mix. Phys. Earth Planet. Interiors 7 (2), 219–222. doi:10.1016/0031-9201(73)90013-7

CrossRef Full Text | Google Scholar

Kavner, A., Duffy, T. S., and Shen, G. (2001). Phase Stability and Density of FeS at High Pressures and Temperatures: Implications for the interior Structure of Mars. Earth Planet. Sci. Lett. 185 (1), 25–33. doi:10.1016/s0012-821x(00)00356-3

CrossRef Full Text | Google Scholar

Keeler, R. N., and Royce, E. B. (1971). Shock Waves in Condensed Media. Phys. High Energ. Density, 51–150.

Google Scholar

Kiarasi, S. (2013). High Pressure-Temperature Electrical Resistivity Experiments on Fe-Si Alloys Bearing on Conductive Heat Flow at the Top of the Outer Core [electronic Resource]. London, Ontario: School of Graduate and Postdoctoral Studies, University of Western Ontario.

Kiarasi, S., and Secco, R. A. (2015). Pressure-induced Electrical Resistivity Saturation of Fe17Si. Phys. Status Solidi B 252 (9), 2034–2042. doi:10.1002/pssb.201552029

CrossRef Full Text | Google Scholar

Kimura, J., Nakagawa, T., and Kurita, K. (2009). Size and Compositional Constraints of Ganymede's Metallic Core for Driving an Active Dynamo. Icarus 202 (1), 216–224. doi:10.1016/j.icarus.2009.02.026

CrossRef Full Text | Google Scholar

Kittel, C. (2005). Introduction to Solid State Physics. 8th ed. New York: J. Wiley.

Klemens, P. G., and Williams, R. K. (1986). Thermal Conductivity of Metals and Alloys. Int. Met. Rev. 31 (1), 197–215. doi:10.1179/imtr.1986.31.1.197

CrossRef Full Text | Google Scholar

Knibbe, J. S., and van Westrenen, W. (2017). Mercury's Thermal Evolution and Magnetic Field Generation with an Fe-Si Core Paper Presented at the 48th Lunar and Planetary Science Conference. The Woodlands, Texas. LPI Contribution No. 1964, id. 1094.

Knibbe, J. S., and van Westrenen, W. (2018). The thermal Evolution of Mercury's Fe-Si Core. Earth Planet. Sci. Lett. 482, 147–159. doi:10.1016/j.epsl.2017.11.006

CrossRef Full Text | Google Scholar

Konôpková, Z., McWilliams, R. S., Gómez-Pérez, N., and Goncharov, A. F. (2016). Direct Measurement of thermal Conductivity in Solid Iron at Planetary Core Conditions. Nature 534 (7605), 99–101. doi:10.1038/nature18009

PubMed Abstract | CrossRef Full Text | Google Scholar

Korell, J. A., French, M., Steinle-Neumann, G., and Redmer, R. (2019). Paramagnetic-to-Diamagnetic Transition in Dense Liquid Iron and its Influence on Electronic Transport Properties. Phys. Rev. Lett. 122 (8), 086601. doi:10.1103/PhysRevLett.122.086601

PubMed Abstract | CrossRef Full Text | Google Scholar

Krot, A. N. (2005). Classification of Meteorites. Meteorites, Comets, and Planets, 83–142. doi:10.1007/978-3-642-65863-1_2

CrossRef Full Text | Google Scholar

Kubo, R. (1957). Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 12 (6), 570–586. doi:10.1143/jpsj.12.570

CrossRef Full Text | Google Scholar

Laneuville, M., Taylor, J., and Wieczorek, M. A. (2018). Distribution of Radioactive Heat Sources and Thermal History of the Moon. J. Geophys. Res. Planets 123 (12), 3144–3166. doi:10.1029/2018je005742

CrossRef Full Text | Google Scholar

Laneuville, M., Wieczorek, M. A., Breuer, D., Aubert, J., Morard, G., and Rückriemen, T. (2014). A Long-Lived Lunar Dynamo Powered by Core Crystallization. Earth Planet. Sci. Lett. 401, 251–260. doi:10.1016/j.epsl.2014.05.057

CrossRef Full Text | Google Scholar

Li, J., and Fei, Y. (2003). “2.14 - Experimental Constraints on Core Composition,” in Treatise on Geochemistry. Editors H. D. Holland, and K. K. Turekian (Oxford: Pergamon), 1–31.

CrossRef Full Text | Google Scholar

Liebermann, R. C. (2011). Multi-anvil, High Pressure Apparatus: a Half-century of Development and Progress. High Press. Res. 31 (4), 493–532. doi:10.1080/08957959.2011.618698

CrossRef Full Text | Google Scholar

Litasov, K. D., and Shatskiy, A. F. (2016). Composition of the Earth's Core: A Review. Russ. Geology. Geophys. 57 (1), 22–46. doi:10.1016/j.rgg.2016.01.003

CrossRef Full Text | Google Scholar

Littleton, J. A. H., Secco, R. A., and Yong, W. (2018). Decreasing Electrical Resistivity of Silver along the Melting Boundary up to 5 GPa. High Press. Res. 38 (2), 99–106. doi:10.1080/08957959.2018.1435786

CrossRef Full Text | Google Scholar

Littleton, J. A. H., Secco, R. A., and Yong, W. (2021). Electrical Resistivity of FeS at High Pressures and Temperatures: Implications of Thermal Transport in the Core of Ganymede. J. Geophys. Res. Planets 126 (5), e2020JE006793. doi:10.1029/2020je006793

CrossRef Full Text | Google Scholar

Malavergne, V., Toplis, M. J., Berthet, S., and Jones, J. (2010). Highly Reducing Conditions during Core Formation on Mercury: Implications for Internal Structure and the Origin of a Magnetic Field. Icarus 206 (1), 199–209. doi:10.1016/j.icarus.2009.09.001

CrossRef Full Text | Google Scholar

Manthilake, G., Chantel, J., Monteux, J., Andrault, D., Bouhifd, M. A., Bolfan Casanova, N., et al. (2019). Thermal Conductivity of FeS and its Implications for Mercury's Long‐Sustaining Magnetic Field. J. Geophys. Res. Planets 124 (9), 2359–2368. doi:10.1029/2019je005979

CrossRef Full Text | Google Scholar

Mao, H.-K., and Mao, W. L. (2007). “Theory and Practice: Diamond-Anvil Cells and Probes for High-P-T Mineral Physics Studies,” in Treatise on Geophysics. Editor G. Schubert Second Edition (Oxford: Elsevier), 263–291. doi:10.1016/b978-0-444-53802-4.00036-1

CrossRef Full Text | Google Scholar

Mao, H. K., Wu, Y., Chen, L. C., Shu, J. F., and Jephcoat, A. P. (1990). Static Compression of Iron to 300 GPa and Fe0.8Ni0.2alloy to 260 GPa: Implications for Composition of the Core. J. Geophys. Res. 95 (B13), 21737–21742. doi:10.1029/jb095ib13p21737

CrossRef Full Text | Google Scholar

Mao, Z., Lin, J.-F., Liu, J., Alatas, A., Gao, L., Zhao, J., et al. (2012). Sound Velocities of Fe and Fe-Si alloy in the Earth's Core. Proc. Natl. Acad. Sci. 109 (26), 10239–10244. doi:10.1073/pnas.1207086109

PubMed Abstract | CrossRef Full Text | Google Scholar

Matassov, G. (1977). The Electrical Conductivity of Iron-Silicon Alloys at High Pressures and the Earth's Core. University of California.

McCubbin, F. M., Riner, M. A., Vander Kaaden, K. E., and Burkemper, L. K. (2012). Is Mercury a Volatile-Rich Planet? Geophys. Res. Lett. 39 (9), L09202. doi:10.1029/2012gl051711

CrossRef Full Text | Google Scholar

Mooij, J. H. (1973). Electrical Conduction in Concentrated Disordered Transition Metal Alloys. Phys. Stat. Sol. (A) 17 (2), 521–530. doi:10.1002/pssa.2210170217

CrossRef Full Text | Google Scholar

Morgan, J. W., and Anders, E. (1980). Chemical Composition of Earth, Venus, and Mercury. Proc. Natl. Acad. Sci. 77 (12), 6973–6977. doi:10.1073/pnas.77.12.6973

PubMed Abstract | CrossRef Full Text | Google Scholar

Mott, N. F. (1980). LIQUID AND AMORPHOUS METALS. J. Phys. Colloques 41 (C8), C1–7. doi:10.1051/jphyscol:1980801

CrossRef Full Text | Google Scholar

Mott, N. F. (1972). The Electrical Resistivity of Liquid Transition Metals. Phil. Mag. 26 (6), 1249–1261. doi:10.1080/14786437208220339

CrossRef Full Text | Google Scholar

Nazarov, M. A., Demidova, S. I., Anosova, M. O., Kostitsyn, Y. A., Ntaflos, T., and Brandstaetter, F. (2012). Native Silicon and Iron Silicides in the Dhofar 280 Lunar Meteorite. Petrology 20 (6), 506–519. doi:10.1134/s0869591112060021

CrossRef Full Text | Google Scholar

Nimmo, F., and Stevenson, D. J. (2000). Influence of Early Plate Tectonics on the thermal Evolution and Magnetic Field of Mars. J. Geophys. Res. 105 (E5), 11969–11979. doi:10.1029/1999je001216

CrossRef Full Text | Google Scholar

Nittler, L. R., Chabot, N. L., Grove, T. L., and Peplowski, P. N. (2017). “The Chemical Composition of Mercury,” in Mercury: The View after MESSENGER (Cambridge University Press).

Google Scholar

Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., and Ohishi, Y. (2016). Experimental Determination of the Electrical Resistivity of Iron at Earth's Core Conditions. Nature 534 (7605), 95–98. doi:10.1038/nature17957

PubMed Abstract | CrossRef Full Text | Google Scholar

Poirier, J.-P. (1994). Light Elements in the Earth's Outer Core: A Critical Review. Phys. Earth Planet. Interiors 85 (3), 319–337. doi:10.1016/0031-9201(94)90120-1

CrossRef Full Text | Google Scholar

Pommier, A. (2018). Influence of Sulfur on the Electrical Resistivity of a Crystallizing Core in Small Terrestrial Bodies. Earth Planet. Sci. Lett. 496, 37–46. doi:10.1016/j.epsl.2018.05.032

CrossRef Full Text | Google Scholar

Pommier, A., Leinenweber, K., and Tran, T. (2019). Mercury's thermal Evolution Controlled by an Insulating Liquid Outermost Core? Earth Planet. Sci. Lett. 517, 125–134. doi:10.1016/j.epsl.2019.04.022

CrossRef Full Text | Google Scholar

Pourovskii, L. V., Mravlje, J., Pozzo, M., and Alfè, D. (2020). Electronic Correlations and Transport in Iron at Earth's Core Conditions. Nat. Commun. 11 (1), 4105. doi:10.1038/s41467-020-18003-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Pozzo, M., and Alfè, D. (2016b). “Electrical Resistivity Saturation of Solid Iron at Earth’s Core Conditions from Density Functional Theory,” in AGU Abstract DI13A-2356 (San Francisco, CA): AGU Fall Meeting).

Google Scholar

Pozzo, M., and Alfè, D. (2016a). Saturation of Electrical Resistivity of Solid Iron at Earth's Core Conditions. SpringerPlus 5 (1), 256. doi:10.1186/s40064-016-1829-x

CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfè, D. (2012). Thermal and Electrical Conductivity of Iron at Earth's Core Conditions. Nature 485 (7398), 355–358. doi:10.1038/nature11031

PubMed Abstract | CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfè, D. (2014). Thermal and Electrical Conductivity of Solid Iron and Iron-Silicon Mixtures at Earth's Core Conditions. Earth Planet. Sci. Lett. 393, 159–164. doi:10.1016/j.epsl.2014.02.047

CrossRef Full Text | Google Scholar

Pozzo, M., Davies, C., Gubbins, D., and Alfè, D. (2013). Transport Properties for Liquid Silicon-Oxygen-Iron Mixtures at Earth's Core Conditions. Phys. Rev. B 87 (1), 014110. doi:10.1103/physrevb.87.014110

CrossRef Full Text | Google Scholar

Rivoldini, A., Van Hoolst, T., Verhoeven, O., Mocquet, A., and Dehant, V. (2011). Geodesy Constraints on the interior Structure and Composition of Mars. Icarus 213 (2), 451–472. doi:10.1016/j.icarus.2011.03.024

CrossRef Full Text | Google Scholar

Rivoldini, A., Van Hoolst, T., and Verhoeven, O. (2009). The interior Structure of Mercury and its Core Sulfur Content. Icarus 201 (1), 12–30. doi:10.1016/j.icarus.2008.12.020

CrossRef Full Text | Google Scholar

Scheinberg, A., Soderlund, K. M., and Schubert, G. (2015). Magnetic Field Generation in the Lunar Core: The Role of Inner Core Growth. Icarus 254, 62–71. doi:10.1016/j.icarus.2015.03.013

CrossRef Full Text | Google Scholar

Seagle, C. T., Cottrell, E., Fei, Y., Hummer, D. R., and Prakapenka, V. B. (2013). Electrical and thermal Transport Properties of Iron and Iron-Silicon alloy at High Pressure. Geophys. Res. Lett. 40 (20), 5377–5381. doi:10.1002/2013gl057930

CrossRef Full Text | Google Scholar

Secco, R. A., and Schloessin, H. H. (1989). The Electrical Resistivity of Solid and Liquid Fe at Pressures up to 7 GPa. J. Geophys. Res. 94 (B5), 5887–5894. doi:10.1029/jb094ib05p05887

CrossRef Full Text | Google Scholar

Secco, R. A. (2017). Thermal Conductivity and Seebeck Coefficient of Fe and Fe-Si Alloys: Implications for Variable Lorenz Number. Renew. Energ. 113, 23–34. doi:10.1016/j.pepi.2017.01.005

CrossRef Full Text | Google Scholar

Sha, X., and Cohen, R. E. (2011). First-principles Studies of Electrical Resistivity of Iron under Pressure. J. Phys. Condens. Matter 23 (7), 075401. doi:10.1088/0953-8984/23/7/075401

CrossRef Full Text | Google Scholar

Shibazaki, Y., Ohtani, E., Terasaki, H., Tateyama, R., Sakamaki, T., Tsuchiya, T., et al. (2011). Effect of Hydrogen on the Melting Temperature of FeS at High Pressure: Implications for the Core of Ganymede. Earth Planet. Sci. Lett. 301 (1), 153–158. doi:10.1016/j.epsl.2010.10.033

CrossRef Full Text | Google Scholar

Silber, R. E., Secco, R. A., and Yong, W. (2017). Constant Electrical Resistivity of Ni along the Melting Boundary up to 9 GPa. J. Geophys. Res. Solid Earth 122 (7), 5064–5081. doi:10.1002/2017jb014259

CrossRef Full Text | Google Scholar

Silber, R. E., Secco, R. A., Yong, W., and Littleton, J. A. H. (2018). Electrical Resistivity of Liquid Fe to 12 GPa: Implications for Heat Flow in Cores of Terrestrial Bodies. Sci. Rep. 8 (1), 10758. doi:10.1038/s41598-018-28921-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Silber, R. E., Secco, R. A., Yong, W., and Littleton, J. A. H. (2019). Heat Flow in Earth's Core from Invariant Electrical Resistivity of Fe‐Si on the Melting Boundary to 9 GPa: Do Light Elements Matter? J. Geophys. Res. Solid Earth 124 (6), 5521–5543. doi:10.1029/2019jb017375

CrossRef Full Text | Google Scholar

Smith, R. F., Fratanduono, D. E., Braun, D. G., Duffy, T. S., Wicks, J. K., Celliers, P. M., et al. (2018). Equation of State of Iron under Core Conditions of Large Rocky Exoplanets. Nat. Astron. 2 (6), 452–458. doi:10.1038/s41550-018-0437-9

CrossRef Full Text | Google Scholar

Sommerfeld, A. (1928). Zur Elektronentheorie der Metalle auf Grund der Fermischen Statistik. Z. für Physik 47 (1), 1–32. doi:10.1007/bf01391052

CrossRef Full Text | Google Scholar

Stacey, F. D., and Anderson, O. L. (2001). Electrical and thermal Conductivities of Fe–Ni–Si alloy under Core Conditions. Phys. Earth Planet. Interiors 124 (3), 153–162. doi:10.1016/s0031-9201(01)00186-8

CrossRef Full Text | Google Scholar

Stacey, F. D., and Loper, D. E. (2007). A Revised Estimate of the Conductivity of Iron alloy at High Pressure and Implications for the Core Energy Balance. Phys. Earth Planet. Interiors 161 (1), 13–18. doi:10.1016/j.pepi.2006.12.001

CrossRef Full Text | Google Scholar

Steenstra, E. S., and van Westrenen, W. (2017). “Sulfides in the Moon,” in Encyclopedia of Lunar Science. Editor B. Cudnik (Cham: Springer International Publishing), 1–6. doi:10.1007/978-3-319-05546-6_119-1

CrossRef Full Text | Google Scholar

Stegman, D. R., Jellinek, A. M., Zatman, S. A., Baumgardner, J. R., and Richards, M. A. (2003). An Early Lunar Core Dynamo Driven by Thermochemical Mantle Convection. Nature 421 (6919), 143–146. doi:10.1038/nature01267

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinbrügge, G., Dumberry, M., Rivoldini, A., Schubert, G., Cao, H., Schroeder, D. M., et al. (2021). Challenges on Mercury's Interior Structure Posed by the New Measurements of its Obliquity and Tides. Geophys. Res. Lett. 48 (3), e2020GL089895. doi:10.1029/2020gl089895

CrossRef Full Text | Google Scholar

Stevenson, D. J., Spohn, T., and Schubert, G. (1983). Magnetism and thermal Evolution of the Terrestrial Planets. Icarus 54 (3), 466–489. doi:10.1016/0019-1035(83)90241-5

CrossRef Full Text | Google Scholar

Stewart, A. J., and Schmidt, M. W. (2007). Sulfur and Phosphorus in the Earth's Core: The Fe-P-S System at 23 GPa. Geophys. Res. Lett. 34 (13), L13201. doi:10.1029/2007gl030138

CrossRef Full Text | Google Scholar

Stixrude, L., Wasserman, E., and Cohen, R. E. (1997). Composition and Temperature of Earth's Inner Core. J. Geophys. Res. 102 (B11), 24729–24739. doi:10.1029/97jb02125

CrossRef Full Text | Google Scholar

Suehiro, S., Ohta, K., Hirose, K., Morard, G., and Ohishi, Y. (2017). The Influence of Sulfur on the Electrical Resistivity of Hcp Iron: Implications for the Core Conductivity of Mars and Earth. Geophys. Res. Lett. 44 (16), 8254–8259. doi:10.1002/2017gl074021

CrossRef Full Text | Google Scholar

Szurgot, M. (2017). Uncompressed Density of the Moon, Lunar Mantle and Core. Budapest, Hungary: Analytical Methods Applied to Earth. Paper presented at the Workshop on Modern.

Terasaki, H., Rivoldini, A., Shimoyama, Y., Nishida, K., Urakawa, S., Maki, M., et al. (2019). Pressure and Composition Effects on Sound Velocity and Density of Core‐Forming Liquids: Implication to Core Compositions of Terrestrial Planets. J. Geophys. Res. Planets 124 (8), 2272–2293. doi:10.1029/2019je005936

CrossRef Full Text | Google Scholar

Tosi, N., Grott, M., Plesa, A.-C., and Breuer, D. (2013). Thermochemical Evolution of Mercury's interior. J. Geophys. Res. Planets 118 (12), 2474–2487. doi:10.1002/jgre.20168

CrossRef Full Text | Google Scholar

Vollhardt, D., Byczuk, K., and Kollar, M. (2012). “Dynamical Mean-Field Theory,” in Strongly Correlated Systems. Editors M. F. Avella, (Berlin, Heidelberg: Springer), 171. doi:10.1007/978-3-642-21831-6_7

CrossRef Full Text | Google Scholar

Wagle, F., Steinle-Neumann, G., and de Koker, N. (2019). Resistivity Saturation in Liquid Iron–Light-Element Alloys at Conditions of Planetary Cores from First Principles Computations. Comptes Rendus Geosci. 351 (2), 154–162. doi:10.1016/j.crte.2018.05.002

CrossRef Full Text | Google Scholar

Wagle, F., Steinle-Neumann, G., and de Koker, N. (2018). Saturation and Negative Temperature Coefficient of Electrical Resistivity in Liquid Iron-Sulfur Alloys at High Densities from First-Principles Calculations. Phys. Rev. B 97 (9), 094307. doi:10.1103/physrevb.97.094307

CrossRef Full Text | Google Scholar

Wagle, F., and Steinle-Neumann, G. (2018). Electrical Resistivity Discontinuity of Iron along the Melting Curve. Geophys. J. Int. 213 (1), 237–243. doi:10.1093/gji/ggx526

CrossRef Full Text | Google Scholar

Wänke, H., Dreibus, G., Runcorn, S. K., Turner, G., and Woolfson, M. M. (1988). Chemical Composition and Accretion History of Terrestrial Planets. Phil. Trans. R. Soc. Lond. A. 325 (1587), 545–557. doi:10.1098/rsta.1988.0067

CrossRef Full Text | Google Scholar

Weber, R. C., Lin, P.-Y., Garnero, E. J., Williams, Q., and Lognonné, P. (2011). Seismic Detection of the Lunar Core. Science 331 (6015), 309–312. doi:10.1126/science.1199375

PubMed Abstract | CrossRef Full Text | Google Scholar

Wicks, J. K., Smith, R. F., Fratanduono, D. E., Coppari, F., Kraus, R. G., Newman, M. G., et al. (2018). Crystal Structure and Equation of State of Fe-Si Alloys at Super-earth Core Conditions. Sci. Adv. 4 (4), eaao5864. doi:10.1126/sciadv.aao5864

PubMed Abstract | CrossRef Full Text | Google Scholar

Wieczorek, M. A., Jolliff, B. L., Khan, A., Pritchard, M. E., Weiss, B. P., Williams, J. G., et al. (2006). The Constitution and Structure of the Lunar Interior. Rev. Mineralogy Geochem. 60 (1), 221–364. doi:10.2138/rmg.2006.60.3

CrossRef Full Text | Google Scholar

Wiesmann, H., Gurvitch, M., Lutz, H., Ghosh, A., Schwarz, B., Strongin, M., et al. (1977). Simple Model for Characterizing the Electrical Resistivity inA−15Superconductors. Phys. Rev. Lett. 38 (14), 782–785. doi:10.1103/physrevlett.38.782

CrossRef Full Text | Google Scholar

Xu, J., Zhang, P., Haule, K., Minar, J., Wimmer, S., Ebert, H., et al. (2018). Thermal Conductivity and Electrical Resistivity of Solid Iron at Earth's Core Conditions from First Principles. Phys. Rev. Lett. 121 (9), 096601. doi:10.1103/PhysRevLett.121.096601

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, Y., Zhai, K., Zhang, B., and Zhai, S. (2019). Electrical Resistivity of Iron Phosphides at High‐Pressure and High‐Temperature Conditions with Implications for Lunar Core's Thermal Conductivity. J. Geophys. Res. Solid Earth 124 (6), 5544–5556. doi:10.1029/2018jb017157

CrossRef Full Text | Google Scholar

Yong, W., Secco, R. A., Littleton, J. A. H., and Silber, R. E. (2019). The Iron Invariance: Implications for Thermal Convection in Earth's Core. Geophys. Res. Lett. 46 (20), 11065–11070. doi:10.1029/2019gl084485

CrossRef Full Text | Google Scholar

Zaitsev, A. I., Dobrokhotova, Z. V., Litvina, A. D., and Mogutnov, B. M. (1995). Thermodynamic Properties and Phase Equilibria in the Fe-P System. J. Chem. Soc. Faraday Trans. 91 (4), 703–712. doi:10.1039/FT9959100703

CrossRef Full Text | Google Scholar

Zambardi, T., Poitrasson, F., Corgne, A., Méheut, M., Quitté, G., and Anand, M. (2013). Silicon Isotope Variations in the Inner Solar System: Implications for Planetary Formation, Differentiation and Composition. Geochimica et Cosmochimica Acta 121, 67–83. doi:10.1016/j.gca.2013.06.040

CrossRef Full Text | Google Scholar

Zhang, C., Lin, J. F., Liu, Y., Feng, S., Jin, C., Hou, M., et al. (2018). Electrical Resistivity of Fe‐C Alloy at High Pressure: Effects of Carbon as a Light Element on the Thermal Conductivity of the Earth's Core. J. Geophys. Res. Solid Earth 123 (5), 3564–3577. doi:10.1029/2017jb015260

CrossRef Full Text | Google Scholar

Zhang, N., Parmentier, E. M., and Liang, Y. (2013). A 3-D Numerical Study of the thermal Evolution of the Moon after Cumulate Mantle Overturn: The Importance of Rheology and Core Solidification. J. Geophys. Res. Planets 118 (9), 1789–1804. doi:10.1002/jgre.20121

CrossRef Full Text | Google Scholar

Zhang, Y., Hou, M., Liu, G., Zhang, C., Prakapenka, V. B., Greenberg, E., et al. (2020). Reconciliation of Experiments and Theory on Transport Properties of Iron and the Geodynamo. Phys. Rev. Lett. 125 (7), 078501. doi:10.1103/PhysRevLett.125.078501

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Hou, M., Driscoll, P., Salke, N. P., Liu, J., Greenberg, E., et al. (2021). Transport Properties of Fe-Ni-Si Alloys at Earth's Core Conditions: Insight into the Viability of thermal and Compositional Convection. Earth Planet. Sci. Lett. 553, 116614. doi:10.1016/j.epsl.2020.116614

CrossRef Full Text | Google Scholar

Zidane, M., Salmani, E. M., Majumdar, A., Ez-Zahraouy, H., Benyoussef, A., and Ahuja, R. (2020). Electrical and thermal Transport Properties of Fe-Ni Based Ternary Alloys in the Earth's Inner Core: An Ab Initio Study. Phys. Earth Planet. Interiors 301, 106465. doi:10.1016/j.pepi.2020.106465

CrossRef Full Text | Google Scholar

Ziman, J. M. (1961). A Theory of the Electrical Properties of Liquid Metals. I: The Monovalent Metals. Phil. Mag. 6 (68), 1013–1034. doi:10.1080/14786436108243361

CrossRef Full Text | Google Scholar

Ziman, J. M. (1960). Electrons and Phonons; the Theory of Transport Phenomena in Solids. Oxford: Clarendon Press.