Assessment of Future Risks of Seasonal Municipal Water Shortages Across North America

While anthropogenic climate change poses a risk to freshwater resources across the globe through increases in evapotranspiration and temperature, it is essential to quantify the risks at local scales in response to projected trends in both freshwater supply and demand. In this study, we use empirical modeling to estimate the risks of municipal water shortages across North America by assessing the effects of climate change on streamflow and urban water demand. In addition, we aim to quantify uncertainties in both supply and demand predictions. Using streamflow data from both the US and Canada, we first cluster 4,290 streamflow gauges based on hydrograph similarity and geographical location. We develop a set of multiple linear regression (MLR) models, as a simplified analog to a distributed hydrological model, with minimum input data requirements. These MLR models are calibrated to simulate streamflow for the 1993–2012 period using the ERA5 climate reanalysis data. The models are then used to predict streamflow for the 2080–2099 period in response to two climate scenarios (RCP4.5 and RCP8.5) from five global climate models. Another set of MLR models are constructed to project seasonal changes in municipal water consumption for the clustered domains. The models are calibrated against collected data on urban water use from 47 cities across the study region. For both streamflow and water use, we quantified uncertainties in our predictions using stochastic weather generators and Monte Carlo methods. Our study shows the strong predictive power of the MLR models for simulating both streamflow regimes (Kling-Gupta efficiency >0.5) and urban water use (correlation coefficient ≈0.7) in most regions. Under the RCP4.5 (RCP8.5) emissions scenario, the West Coast, the Southwest, and the Deep South (South-Central US and the Deep South) have the highest risk of municipal water shortages. Across the whole domain, the risk is the highest in the summer season when demand is high. We find that the uncertainty in projected changes to the water demand is substantially lower than the uncertainty in the projected changes to the supply. Regions with the highest risk of water shortages should begin to investigate mitigation and adaptation strategies.

Introduction

Based on current climate projections, global mean temperature is likely to increase by at least 2°C, relative to the 1850s, by the end of the century (Forster et al., 2020). This warming will lead to unprecedented consequences for life on this planet including increased wildfire risk (Goss et al., 2020), decreased snowpack (Ashfaq et al., 2013), and decreased freshwater biodiversity (Reid et al., 2019). While every location on Earth is expected to experience increases in near-surface air temperature, ranging from a 1°C increase over oceans to over 5°C in higher latitude areas, the projected changes in precipitation are less certain and less spatially uniform (Hoegh-Guldberg et al., 2018). The projections of hydrologic drought and floods are consequently uncertain, while at the same time, highly costly in terms of their impact on property damage, food shortage, loss of jobs, and loss of lives (Howitt et al., 2015; Achakulwisut et al., 2018; Tellman et al., 2020). More accurate predictions of these extreme events can lead to better mitigation and adaptation procedures, such as green infrastructure, placing restrictions on water consumption, moving water in above-ground reservoirs to below-ground aquifers, or investing in technologies that could improve water use efficiency (Tanaka et al., 2006; Mei et al., 2018; Yang and Liu, 2020).

As anthropogenic climate change progresses and populations across North America continue to grow, freshwater resources on the continent may experience more strain. The United States (US) and Canada use the most water per capita (>1,000 cubic meters per person per year) compared to other G8 countries (100–900 cubic meters per person per year) (Ritchie and Roser, 2017). Despite the use of less than 20% of their available water resources every year, freshwater resources and potential vulnerability to water shortages are non-uniformly distributed throughout the continent (Rosegrant and Cai, 2002). Such shortages will act as a vulnerability multiplier leading to socioeconomic and physical health deterioration in groups such as migrants, poor families in urban areas, and farmers (Sugg et al., 2020). The Canadian Prairies are known to have been vulnerable to historical hydrologic droughts, although few assessments of drought risk across Canada have been made to date (MacDonald et al., 2008; Bonsal et al., 2011). In the US, the regions most severely hit by recent droughts include the Central US (Basara et al., 2019), California (Howitt et al., 2015), as well as the relatively wet areas in the US South (Chen et al., 2012). Further droughts in these areas as well as more widespread droughts throughout North America may come as a result of declining summer precipitation in the latter half of the 21st century, warming Pacific and North Atlantic Oceans, and escalating climate variability (Rosegrant and Cai, 2002; MacDonald et al., 2008; Schwalm et al., 2012). Droughts, however, are not the only climate pattern of concern. Snow is crucial in the western United States for sustaining water demand, thus decreasing snowpack as a result of increasing temperatures threatens water sustainability, though uncertainties remain large (Mankin et al., 2015).

Risk of freshwater shortage is measured in a variety of ways (Rosegrant and Cai, 2002; Foti et al., 2012; Dickson and Dzombak, 2019). For example, Foti et al. (2012) defined shortage risk as the difference between water supply and demand, or more specifically, as a probability for crossing the critical threshold when water demand exceeds supply. Different types of process-based or mechanistic models (e.g., Chien and Knouft, 2013; Mahat et al., 2017) and statistical or purely data-driven models (e.g., Barbarossa et al., 2017; Mendoza et al., 2017; Brunner et al., 2020) have been used to project changes in water supply and water demand globally and in North America. Mechanistic models are efficient tools for prediction of water supply and demand in regions where a wide range of data on climatic, landscape, and socioeconomic and demographic attributes are available. Despite great progress being made on developing advanced mechanistic models (Chen et al., 2017), the application of these models in ungauged watersheds, which cover more than 90% of lands globally and across North America, is unpractical due to poor data availability required for building such models (Blöschl et al., 2013). Statistical models, on the other hand, have become known as simple and fast tools for providing general insights on the estimation and forecast of water supply and demand with minimum data requirements. For example, simple regression techniques have been used to relate physical and climate characteristics to hydrological signatures such as flow duration curves and low flow statistics (Jehn et al., 2020). While statistical models are limited in their interpretation of causality among variables and rely on assumptions that cannot be adequately tested, these simple models are widely used to provide a general picture of ungauged watersheds' responses to climate change (Besaw et al., 2010; Razavi and Coulibaly, 2013; Saadi et al., 2019), and informing water resources planning and management. Further, regression models can capture implicit relationships between runoff and explanatory variables for which there is no theoretical explanation due to the co-evolution of climate, geology, and topography (Blöschl et al., 2013).

Most assessments of water supply and demand management focused on local areas across North America and only study either supply or demand with regression or physically based models (Balling and Gober, 2007; Breyer and Chang, 2014; Shamir et al., 2015; Byun et al., 2019). Foti et al. (2012), however, provided a comprehensive risk assessment of water shortages for the contiguous US using regression and physically based models. They projected annual water supply and consumption in response to changes in temperature and precipitation from three Global Climate Models (GCMs). Areas such as Central California, Utah, Arizona, and Central US were found to be most vulnerable to water shortages. A more recent assessment of future changes in streamflow regimes across the US found that the changes are expected to be most pronounced for currently melt-dominated regimes in the Rocky Mountains (Brunner et al., 2020). While five GCMs were used in the study, very little agreement was found among the GCM projections, pointing to a relatively large uncertainty caused by the choice of GCMs. In terms of changes to water consumption across the US, negligible changes were found when the projections were based solely on population growth, income growth, and changes in water-use efficiency, i.e., without accounting for climate change (Rosegrant and Cai, 2002; Foti et al., 2012). With climate change remaining a factor, however, water consumption was projected to substantially increase, mainly due to expected increases in agricultural and landscape irrigation in response to rising potential evapotranspiration (Foti et al., 2012; Brown et al., 2013).

As the population and suburb-centered development continue to grow in North America, many municipalities in arid and semi-arid regions are acquiring water rights from agriculture in anticipation of an uptick in municipal water demand (MacDonald, 2010; Sabo et al., 2010; Maas et al., 2017). The percent of water demand used for domestic purposes is set to increase, thus the transfer of water resources from agricultural to municipal use represents an additional stressor for rural sustainability and food security (Rosegrant and Cai, 2002). Thus, changes in municipal water use in response to climatic and non-climatic factors are expected to have implications for regional water consumption as a whole. In the US, residential water use accounts for ∼60% of municipal water use (Dieter et al., 2018), with 22–65% of the residential water use coming from outdoor water use (DeOreo et al., 2016), which is shown to be highly sensitive to changes in weather and climate (Gober et al., 2016). This high sensitivity of outdoor water use to climatic drivers has triggered the use of regression models to predict the water consumption based on a combination of weather predictors, such as air temperature, wind speed, precipitation, and evapotranspiration (Wong et al., 2010; Adamowski et al., 2012; Bakker et al., 2014; Chang et al., 2014). The models have revealed a high spatial heterogeneity in the sensitivity of municipal water consumption to changes in these predictors (Opalinski et al., 2020). Maximum daily temperature was found to be the predictor with the most explanatory power across the region, with stronger predictive power in dry regions (Opalinski et al., 2020). In the same study, dry regions were found to have greater seasonality in municipal water use perhaps due to increased seasonal climate variability, with the peak use in summer when there is an increased need for irrigation of the excising green urban landscapes.

Knowledge on the risks of municipal water shortages is essential to inform science-based strategies and decision-making tools for water security (Byun et al., 2019; Dilling et al., 2019; Özerol et al., 2020). Current research has focused on forecasting the magnitude and seasonality of water supply (e.g., Chien and Knouft, 2013; Demaria et al., 2016; Mahat et al., 2017; Byun et al., 2019; Brunner et al., 2020) as well as magnitude of water demand (e.g., Ruth et al., 2007; DeOreo et al., 2016; Maas et al., 2017; Opalinski et al., 2020; Rasifaghihi et al., 2020). However, the magnitude and seasonality of water shortages, as a combined effect of water supply and water demand, are still relatively poorly characterized and forecasted in most parts of the globe including North America. Additionally, the forecast of water shortages, similar to other types of forecasts in environmental science, is prone to a wide range of uncertainties, which are generally challenging and difficult to quantify. Such uncertainties are mainly stemmed from uncertainties in time-varying climatic attributes (Katz, 2002), uncertainties associated with more static physical attributes of watersheds such as geology, land cover, and soil (Nilsson et al., 2007; Addor et al., 2017), and uncertainties corresponding to future population growth and water use (Yang et al., 2016; Hart and Halden, 2019; Keilman, 2020). Furthermore, the more complex the modelling framework is, often relying on heavily calibrated mechanistic models of water supply and demand, the more difficult it is to track and quantify its sources of uncertainties (e.g., Foti et al., 2012). On the other hand, simple statistical models with low degrees of freedom present more readily available tools for quantifying these uncertainties. Characterizing and quantifying the risks of future seasonal water shortages, and their associated uncertainties, with the use of simple statistical models were the main motivations of this study.

This study has two main goals: 1) to investigate the use of simple statistical models, based on widely available climatic data, in simulating present and future (end of the 21st century) water shortages under a changing climate across North America (US and Canada); and 2) to assess uncertainties in the projections of water shortages originating from the uncertainties in climate scenarios from the ensemble of GCMs. To address goal 1), multivariate regression models for both supply and demand are developed and calibrated with daily time series of streamflow from river stations and daily time series of municipal water consumption from cities across the region. The models are forced by state-of-the-art climate reanalysis data representing the present climate and weather attributes (e.g., temperature, precipitation, windspeed, evapotranspiration, and rainfall/snowfall characteristics), while the future climate is represented by two emission scenarios from the ensemble of five GCMs. To address goal 2), we use stochastic weather generators as it is one of the recommended methods for estimating uncertainties in climate change projections (Katz, 2002) and in hydrological forecasting (e.g., Caron et al., 2008; Breinl, 2016). By combining the projections of water supply and demand, we aim to provide a spatial pattern of seasonal municipal water shortage risks, together with estimated credibility in these risks across the whole region.

Data

Streamflow Data

Observations of daily streamflow for Canada are collected from the National Water Data Archive (Water Survey of Canada, 2019), while observations for the US are collected from the United States Geological Survey (USGS) surface-water data for the nation website (US Geological Survey, 2019). Only daily time series that have no missing data from Jan 1, 1993 to Dec 31, 2012 are considered in the analysis, which left 4,290 gauges in total, with 584 gauges in Canada and 3,706 in the US.

Climate Data

Present Climate

Surface weather data for the historical record is extracted from the ERA5 climate reanalysis (0.25 × 0.25, hourly) dataset (Copernicus Climate Change Service Climate Data Store, 2017), for the period 1993–2012. Hourly time series of total precipitation, wind speed, air temperature, dewpoint temperature, and incoming solar radiation are extracted. Dewpoint temperature and air temperature are used to estimate relative humidity with the August-Roche-Magnus approximation (Lawrence, 2005). Cubic inverse distance weighting interpolation is performed to obtain a single time series of each weather variable at each streamflow station. Interpolated precipitation totals that are below 1 mm are set to 0 mm following (Islam and Cartwright, 2020) and (Tian et al., 2009). Evapotranspiration is calculated from the Penman-Monteith equations, as outlined by (Walter et al., 2000) using maximum and minimum air temperature, maximum and minimum relative humidity, wind speed, and incoming solar radiation at the surface. Hourly time series of total precipitation, wind speed, and air temperature at the surface are also extracted at the grid square closest to each city with water consumption data.

Future Climate

Future climate scenarios are obtained from five GCMs from Coupled Model Intercomparison Project phase five [CMIP5, Table 1, (Taylor et al., 2012)], henceforward abbreviated as: GFDL-CM3, HadGEM2-ES, INM-CM4, IPSL-CM5A-MR, and CSIRO-Mk3.6.0. The data is downloaded from the Lawrence Livermore National Laboratory’s World Climate Research Programme database powered by the Earth System Grid Federation (Taylor et al., 2012; Cinquini et al., 2014). The five models are selected as they have the required variables in the desired time period and their current or earlier versions have been shown to have better performance relative to other CMIP5 models in simulating the past climate over North America (Radić and Clarke, 2011). The following variables are extracted as daily time series for each GCM: maximum and minimum air temperature, maximum and minimum relative humidity, wind speed, incoming solar radiation at surface, and total precipitation. For the projection period (2080–2099), we retrieved GCM data for two selected emission scenarios, referred to as Representative Concentration Pathways (RCPs; Moss et al., 2010): RCP4.5 and RCP8.5. The different scenarios indicate different amounts of radiative forcing by 2100, where RCP4.5 (RCP8.5) indicates 4.5 W/m² (8.5 W/m²). The RCP4.5 emissions scenario is considered a medium stabilization emissions scenario and RCP8.5 is considered a high emissions scenario (Van Vuuren et al., 2011). To obtain the continuous GCM data for 1993–2012 for bias correcting, we use GCM historical runs from 1993 to 2005 and their RCP4.5 and RCP8.5 runs from 2006 to 2012. Evapotranspiration is calculated using GCM data from the Penman-Monteith equations as done with the reanalysis data. For evapotranspiration, the bias between the present-climate GCM and ERA5 is corrected according to the quantile mismatches within the simulated cumulative distribution function (CDF) using the empirical quantile matching algorithm (Xu, 2015). This method has been shown to outperform other bias correction algorithms when the distribution of a climate variable is unknown or not gamma (Teutschbein and Seibert, 2012; Chen et al., 2013). For precipitation, the bias is corrected using the gamma quantile mismatch between ERA5 and each GCM, with a precipitation threshold of 1 mm, following the method in Xu (2015). Several studies have shown that the gamma quantile matching is one of the better methods for precipitation bias correction (Chen et al., 2013; Lafon et al., 2013).

TABLE 1

TABLE 1. Characteristics of the five GCMs used in this study for future forecasts.

Water Use and Population Data

To our knowledge, there is no database of daily municipal water use for cities across North America. To collect daily and monthly time series, we directly contacted municipalities. Each time series is at least 3 years in length from the period 1990–2018. We initially collected the data from 55 cities. The datasets from the cities that have strict water consumption laws, large population increases during summer months, or are not continuous or near continuous (missing data with valid observations for previous and subsequent entries) were removed. The gaps in the data are filled with estimates based on linear interpolation, resulting in a set of daily time series of continuous municipal water use for 38 cities and monthly time series of continuous municipal water use for nine cities for a total of 47 cities (Figure 1B). Though the data has high day-to-day variability which may cause the gap filling to be inaccurate, the gap filling causes little change in the results due to its rareness and the data smoothing applied later. Monthly datasets are converted to daily datasets by using the monthly value for each day within the month.

FIGURE 1

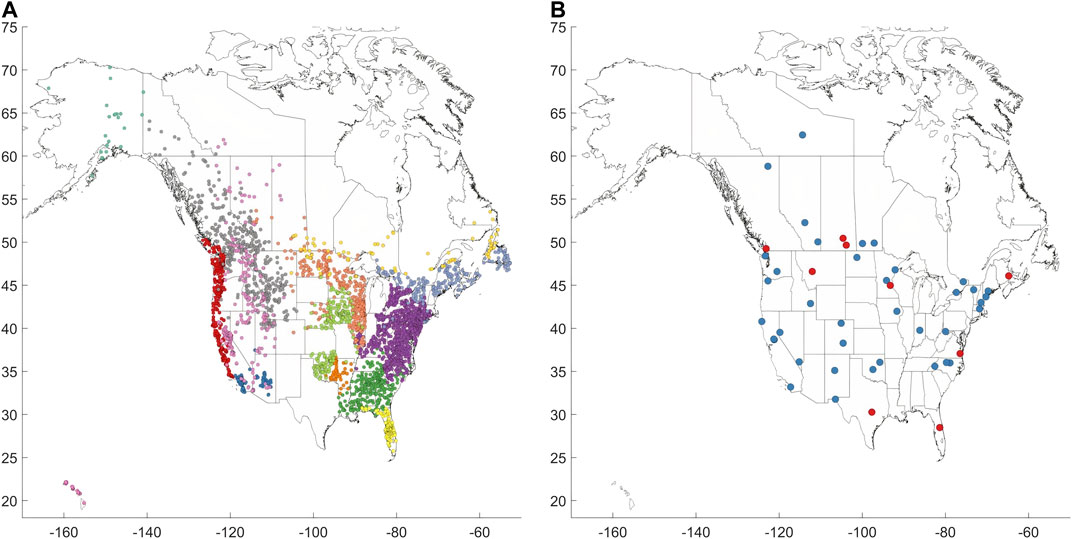
FIGURE 1. Map of localities with (A) streamflow data (4,290 gauges), and (B) water consumption data (47 cities). In (A) each station dot is colored according to the cluster it belongs to (see Clustering section). In (B) blue and red indicate daily and monthly data, respectively. Some of the city officials asked to keep their cities anonymous, so this map is meant to keep the city names anonymous while showing the spatial extent of the data.

For each city, we also downloaded its population estimates from the US (United States Census Bureau, 2019) or Canadian (Statistics Canada, 2019a) Census datasets for 1990–2018. Since the datasets provide yearly population estimates, we used a piecewise linear interpolation to derive daily population estimates. County location data is derived from Hauer (2019) and Ramey (2014) for US counties, and Statistics Canada (2019) for Canadian census divisions (Canadian county equivalent). A total of 3,425 counties or county equivalents were used, with 293 coming from Canada and 3,132 from the US.

Methods

Our overall methodology can be summarized in the following steps: first, we partition the study region into clusters based on similarity in the observed seasonal streamflow and proximity. Second, multiple linear regression (MLR) models, with climate predictors from the ERA5 reanalysis dataset, are calibrated at each river station in order to simulate its seasonal streamflow throughout the 1993–2012 period. Each MLR model is then used to predict the seasonal streamflow regime for 2080–2099 at each station. To do so, the models are forced by stochastically generated downscaled climate scenarios from an ensemble of five GCMs. Third, the same climate data (ERA5) is used to calibrate a set of MLR models to simulate the seasonality in municipal water consumption over the present climate for each of the 47 cities. The locally optimized regression coefficients from the 47 cities are then statistically upscaled to represent the coefficients for each county in the US and Canada. Future changes in seasonal municipal water consumption are then simulated for each county based on the stochastically generated GCM projections. Finally, we aggregate the changes in water supply and demand and assess the risk of water shortages for each region and each season. Seasons are separated into winter (December, January, and February—DJF), spring (March, April, and May—MAM), summer (June, July, and August - JJA), and Fall (September, October, and November—SON).

Clustering

While it is common to partition a large region into smaller domains in order to summarize the results of regional hydrological modelling, there is no consensus on how to define these subregions through clustering (Sawicz et al., 2011). The US Water Resources Council, for example, clustered regions and subregions based on topography, which is the method that has been adopted in assessments of water shortages across the US (e.g., Foti et al., 2012; Mahat et al., 2017). Another common clustering method in hydrological studies is based on climate classification (e.g., Opalinski et al., 2020), or on a combined set of climate and streamflow indices (e.g., Sawicz et al., 2011).

As the objective of our paper is to predict seasonality of water shortage and its uncertainty, we chose to partition the study region into clusters on the basis of similarity in streamflow seasonality or regime curves [similar to Brunner et al. (2020)]. For each stream gauge, we derive the average observed streamflow regime over the 20-year current period for each station. The regime curve consists of 366 days in order to account for the measurements during leap years. For non-leap years, the average value from Feb 28 and March 1 is used to fill in for Feb 29. The regime curve of each station is standardized by subtracting it by its mean and dividing it by its standard deviation such that the clustering can focus on regime curve shape similarity rather than on absolute values. We use hierarchical clustering with Ward’s algorithm (Ward, 1963), and we determine the optimal number of clusters by trial-and-error in a manner similar to (Knoben et al., 2018). The resulting clusters are then visually inspected on the map in order to further manually partition the clusters whose gauges lie in multiple distinct geographical areas. For example, streamflow regimes in the Pacific and South Atlantic regions were initially clustered together due to their similar streamflow regimes but were subsequently separated due to their distinct geographical locations. Stations that belong to a streamflow-regime cluster, but are located far outside the cluster’s perimeter, are removed as “outliers”. Similar to Ivancic and Shaw (2017), we hypothesize that these spatially isolated outliers are present due to significant human impact on the streamflow. Following the steps above, we partitioned the study region into 14 clusters or sub-regions (Figure 1A). The 4,290 original gauges are reduced to 3,852 due to the removal of outliers.

Streamflow Model

The MLR models are developed to predict the inter-annual variability of streamflow for each gauge using local weather. The MLR models are applied to the averaged streamflow and averaged climate variables (ERA5) using a 30-day moving window. In this way, the model is calibrated across the 20-year present period in order to simulate an average value for the same 30-day window (e.g., Jan 1 to Jan 30, Jan 2 to Jan 31, etc … ) in each year and for each station. For each region, we validate the model using a validation set of the last 3 years. To obtain the streamflow projections at each station, the model is forced with stochastically generated downscaled climate variables from the ensemble of five GCMs. A well-known limiting assumption of most stationary models is that the model developed over the present climate is assumed valid under future climate conditions (e.g., Ekström et al., 2015). This assumption can be considered acceptable for multiple regression models as long as the variability in present variables (e.g., temperature, precipitation, streamflow) is within the range of their variability in the future period. While the constant variance of the response would be difficult to verify due to the possible non-stationarity and the uncertainty of hydrological conditions over such timescales, we may assume each observation is independent as the observations are separated by a full year such that longer processes including snowmelt and groundwater flow will not affect adjacent years. Below, we provide details on the data smoothing procedure, calibration and validation of the model, and the simulations of future streamflow regimes (Figure 2).

FIGURE 2

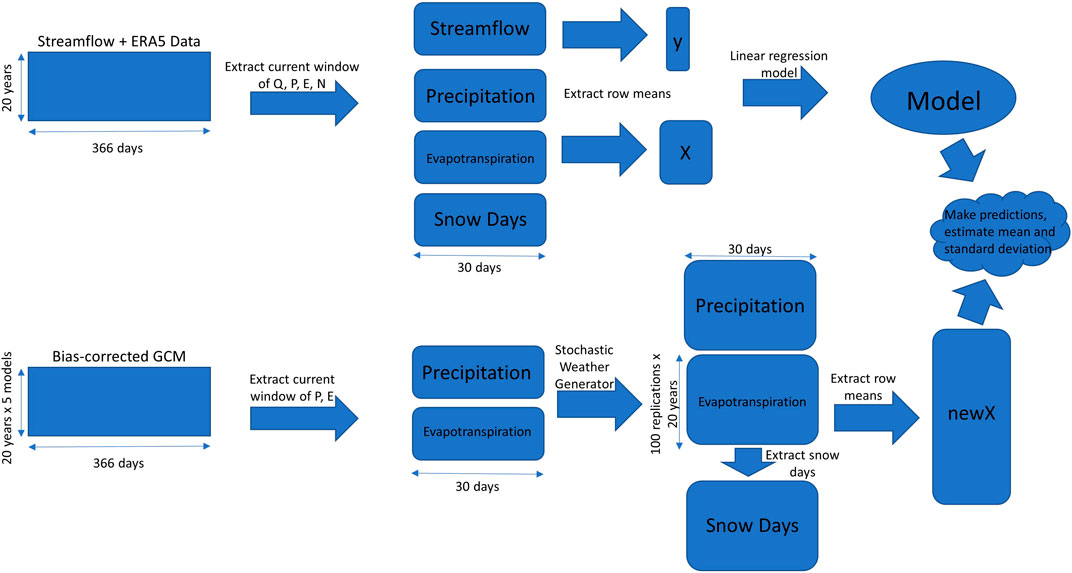
FIGURE 2. Workflow of methods for making predictions for each streamflow station and each window. Boxes indicate data matrices of streamflow (Q), precipitation (P), evapotranspiration (E), or snow days (N). Each row of data represents a single year, and each column indicates a different day.

Data Smoothing

For each station, we apply the MLR models using a selection of weather variables from ERA5 as predictors and streamflow data as the response. Prior to the model application, we apply smoothing to both predictor and response data in the following way: 30-day moving average is applied to the whole daily time series (1993–2012), where the first window spans from 1 Jan to 30 Jan, and the last window spans from 31 Dec to 29 Jan of the following year.

Calibration and Validation

The MLR models are applied for each of the 366 windows separately, so that the regression is calculated across the 20 (19) points, where each point represents the average value within the current window for the given year. The first model is applied to the first window (1 Jan) across all the years (1993–2012), the second model is applied to the second window (2 Jan) across all the years, etc. In this way, we derive 366 MLR models in total, each one with its own regression coefficients. The following variables are used as predictors: average daily precipitation (P units in mm), average daily evapotranspiration (ET, units in mm) and total number of days with snowfall (N), where P and ET are derived as the mean over the 30-day moving window, while N is calculated as the sum of days with snowfall >1 mm over the same window. We assume that when evapotranspiration is ≤0, temperature is below or equal to 0°C; consequently, a wet day when evapotranspiration is 0 indicates a snow day. For each window, the modelled streamflow (Q_i,j) (m³/s) is derived from the MLR model with optimized regression coefficients (least squares method) as:

$Q_{i,j}=a_{0,i,j}+a_{1,i,j}{P}_{i,j}+a_{2,i,j}E{T}_{i,j}+a_{3,i,j}{N}_{i,j}+{\epsilon }_{i,j}(1)$

where a_0,i,j–a_3,i,j are the regression coefficients for station i and window j.

Considering that the MLR models are built on a small sample of 20 points (20 years of data), we use the first 17 years (1993–2009) of data as a training set and 3 years (2010–2012) of data as a test set to test the predictive skill of our methods. We calibrate the model over this reduced sample and predict the streamflow regime curve for the 3 years of left-out data. Similar to Brunner et al. (2020), we then assess the model performance with the Kling-Gupta Efficiency (KGE) between the observed and modelled 3-year streamflow regime curves (Gupta et al., 2009). As the procedure is repeated for each of the streamflow stations, we summarize the model predictive skill by the first quantile, median, and third quantile of the KGEs within each region. Kling has stated that a threshold of 0.5 (0.75) can be used to differentiate poor versus intermediate (good) simulation results using the slightly modified KGE metric, thus we utilize these thresholds to interpret our results (Kling et al., 2012; Thiemig et al., 2013). KGE may be sensitive to outliers and non-normally distributed streamflow (Pool et al., 2018), however, the widespread use of the KGE metric as well as its clear interpretation makes it a strong performance metric.

Postprocessing of Global Climate Model Data

To facilitate the assessment of uncertainties stemming from the GCMs, we input the downscaled precipitation and evapotranspiration time series into a stochastic weather generator so that 2,000 time series of each variable are generated (100 for each of the 20 years). Streamflow for 2080–2099 is then simulated by the MLR models using each of the 2,000 generated time series. For each window, the final simulation is calculated through Monte-Carlo simulations by randomly sampling 1,000 observations from the 100 predicted values from each year to get a large, bootstrapped sample of possible 20-year long time series; then, the values are averaged across the 20 years. In this way, we project 1,000 values of the average seasonal streamflow regime for 2080–2099 for each station and window. Final results are then compressed by representing each day with a mean and standard deviation.

The stochastic weather generator used in this study is developed similarly to the framework illustrated by Wilks and Wilby (1999). The output is generated separately for the two RCP scenarios and for each of the 20 years in 2080–2099. The key steps are summarized as follows: First, for each 30-day window, we have a 5-GCM x 30-day block of data for both evapotranspiration and precipitation. For evapotranspiration, we assume a normal distribution conditioned on the day being wet or dry and derive its mean and standard deviation from the data points for each day type. Second, a transition matrix is calculated from the precipitation data by calculating the four transition probabilities (wet-wet, wet-dry, dry-wet, dry-dry). Then, a two-state Markov chain is created, where p < 1 mm is considered a dry day, and a wet day is assumed otherwise. One hundred 30-day time series of precipitation are generated using the Markov chain to determine wet-dry day occurrences, while the magnitude on wet days is determined by randomly sampling from the precipitation observations greater than 1 mm. The simulation of precipitation magnitude is robust, as no distribution needs to be estimated, so precipitation can be generated non-parametrically. The robust generation of evapotranspiration can be done parametrically because a large set of well-behaved daily data is available for parameter estimation (Semenov et al., 1998; Ababaei, 2014). Finally, evapotranspiration (ET) is derived by randomly generating data from either of the two normal distributions derived earlier dependent on if the Markov chain generated a wet or a dry day. This process generates 100 30-day time series of precipitation and evapotranspiration for each year in 2080–2099 for each 30-day window.

Water Use Model

Daily urban water consumption can be separated into three components that include: long-term (decadal) base water use, calendrical (weekly) water use, and seasonal water use (Wong et al., 2010). The seasonal variability in outdoor water use, which explains a relatively large fraction of variability in municipal water use (DeOreo et al., 2016), can be successfully simulated as a function of weather and climate attributes (Gober et al., 2016; Opalinski et al., 2020). Thus, our working assumption is that the seasonal component of municipal water use, represented by daily time series, needs to be decomposed into its long-term, seasonal, and short-term signal. After the signal decomposition, the model is developed for the seasonal signal only.

While the models are calibrated for selected cities, the objective is to model water use in each county. To do so, the model coefficients are upscaled from city-specific values to values representing each county. Finally, the model is forced by stochastically generated climate scenarios from the five GCMs for both the present and future periods. Below we provide details on the signal decomposition, model calibration, coefficient upscaling, and model projections.

Signal Decomposition

To focus on the seasonal signal in the municipal water use for each city, we remove the calendrical and long-term signals from the city’s original time series. Though it may slightly contribute to the violation of observation independence, it is unlikely to distort our results, and removing the calendrical signal is necessary, thus we smooth our time series with a 15-day moving median. This will remove the effects of persistence, holidays, measurement errors, and the day-of-the-week. Long-term variability is mainly driven by population and water efficiency (Wong et al., 2010). To remove the population effects, the smoothed water-use time series are divided by the daily population time series, yielding a daily time series of water efficiency.

Each city’s water efficiency time series is normalized to be between 0 and 1. A common feature of these time series is their long-term decline that best resembles an exponential decay signal (Supplementary Figure S1). It has been shown that municipal water use per capita in the US has tended to decrease due to government actions that forced manufactures to make water-efficiency improvements for the bathroom and household appliances (Donnelly and Cooley, 2015). These changes were mainly established in the 1990s, so they can be expected to have diminishing returns as time goes on (Donnelly and Cooley, 2015). Empirically, we chose to represent this long-term decline in water use with an exponential decay function that is fitted to the normalized annual water-use time series of each city (Supplementary Figure S1c). Finally, the fitted function, interpolated from annual to daily values, is subtracted from the normalized water efficiency time series (Supplementary Figure S1). The residual daily time series for each city represents the characteristic seasonal municipal water use per capita.

Calibration, Validation, and Upscaling

Each city’s remaining time series of daily water consumption per capita represents the response variable in an MLR model, while a set of weather variables from ERA5 data are used as predictors. Prior to training the MLR model, each response variable is standardized (subtracted by its mean and divided by its standard deviation) in order to facilitate the inter-comparison of regression coefficients across cities. After testing different combinations of predictors, we settled with the following list: maximum daily temperature (T, units in °C), daily mean wind speed (U, units in m/s), a binary variable for rain (R, wet/dry day for rain) and a binary variable for snow (W, wet/dry day for snow). Rain and snow days are differentiated using a maximum temperature threshold of 5°C, which is reasonable considering thresholds for mean temperatures are often between −5°C and 5°C (Rajagopal and Harpold, 2016). Standardized per-capita water consumption (C) is modeled with:

$C_k=b_{0,k}+b_{1,k}{T}_k+b_{2,k}{U}_k+b_{3,k}{R}_k+b_{4,k}{W}_k(2)$

where b_0,k-b_4,k are the regression coefficients for city k, and R(W) is the binary variable for rainfall (snowfall) which equals 1 if rainfall (snowfall) exceeds 1 mm and 0 otherwise. The model is calibrated for each city, yielding 47 sets of city-specific regression coefficients (Figure 3).

FIGURE 3

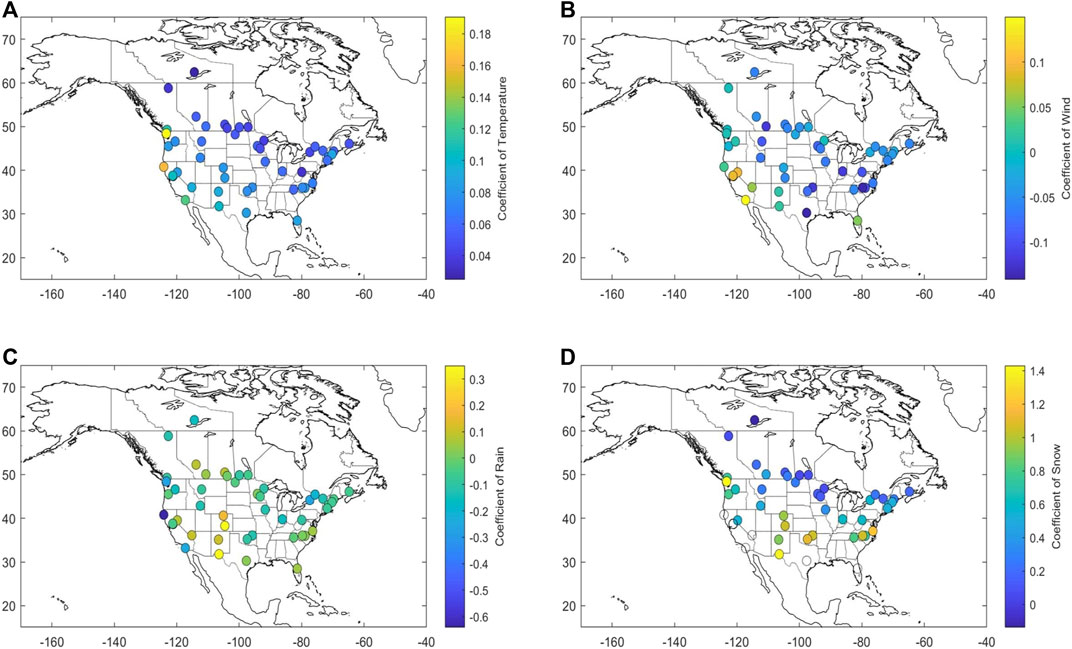
FIGURE 3. Map of regression coefficient values from 47 MLR models for municipal water consumption: (A) coefficient that multiplies maximum temperature (b₁), (B) coefficient that multiplies wind speed (b₂), (C) coefficient that multiplies the binary variable for rain (b₃), and (D) coefficient that multiplies the binary variable for snow (b₄). The model is calibrated over the available observational record (at least 3 years within 1990–2018) for each city, yielding 47 sets of city-specific regression coefficients.

Finally, the model coefficients need to be upscaled from their city-specific values to values representing each county. A study with a similar modelling approach to ours found that climatic regression coefficients are correlated in space, with nearby cities yielding more similar regression coefficients than the cities further apart (Opalinski et al., 2020). Thus, we assume that by spatially interpolating the regression coefficients from 47 cities unevenly distributed over the map to the grid of counties, we can obtain a first-order approximation for regression coefficients at each county. We choose to apply smoothed optimal inverse distance weighting with weights set as 1/(1 + d)^p, where d is the distance from the county’s geographical centre (latitude, longitude) to the city’s location, and p is the parameter that needs to be optimized.

We optimized p by maximizing the correlation between interpolated and observed C_mod using the following procedure: one out of 47 cities is left out from the sample of known regression coefficients, and its regression coefficients are instead derived from the interpolation method with each possible p. This procedure is iterated until all 47 cities are removed once from the original sample. The final value of p is the one that yields the largest mean correlation between interpolated and observed C across all the cities. The optimization yielded p = 2.1 (Supplementary Figure S2).

Post-processing of Climate Data

Time series of normalized water consumption per capita (C) for each county for both the present (1993–2012) and future (2080–2099) periods are simulated by the MLR model forced by stochastically generated climate data. Similar to the supply model, data from the five GCMs and two RCP scenarios are used as inputs to the stochastic weather generator. Present climate data is patched from the GCM historical runs from 1993 to 2005 and their RCP4.5 runs from 2006 to 2012. Because changes in the water use per county are assessed as a difference between modelled future and modelled present water use, from the same ensemble of GCMs, no bias-correcting is applied.

The predictors in the model (Equation 2) are stochastically generated in the following way: precipitation wet/dry days are derived from a two-state Markov chain where the transition probabilities are estimated from a 31-day moving window of GCM precipitation time series. For temperature, using the same 31-day moving window, we assume a normal distribution and derive its means and standard deviations conditioned on the presence of precipitation. For wind speed, a Weibull distribution is chosen following previous studies (e.g., Seguro and Lambert, 2000; Alizadeh et al., 2019), and we also assume that the wind speed is conditioned on the day being wet or dry. As a result of this assumption, two sets of two-parameter Weibull distributions are estimated using maximum likelihood estimation. The differentiation between snowfall and rainfall is determined by a maximum temperature threshold of 5°C as was done in the calibration phase.

One hundred time series of each weather variable is generated for each year (100 × 20 sets of 365-day time series). Each of the 2,000 generated sets of weather time series are then used to predict a 365-day time series of C. To obtain the uncertainty estimate for C for each day, we randomly select 1,000 outcomes from each of the 100 time series of each year. Like with the water-supply model, we take the average C across the 20 years, so a total of 1,000 20-year average time series of normalized water consumption per capita for each county are simulated. The final results are presented as the mean ± a standard deviation of C for each day in the present period, and the mean ± a standard deviation of C for each day in the future period for both RCP4.5 and RCP8.5.

Risk Scores

Defining vulnerability or risk of water shortages is difficult to do so precisely while also being implementable (Foti et al., 2012). Due to this limitation, each previous assessment of water shortage risk has developed their own risk assessment score (Hurd et al., 1999; Foti et al., 2012; Roy et al., 2012; Dickson and Dzombak, 2019). For example, Foti et al. (2012) defined vulnerability as the probability that demand will be less than supply in a region, while Dickson and Dzombak (2019) defines an overall risk index from five components of risk including 1) annual proportion of use of local water supply, 2) summer proportion of use of local water supply, 3) projected increase in demand, 4) summer proportion of use of local water demand, and 5) proportion of groundwater withdrawal to total withdrawal.

Building on previously proposed risk scores, we introduce a metric as a proxy for the risk imposed by climate change on water resources for each subregion in the study domain. The metric, defined as the risk score (RS), combines the projected changes in water supply for each station with the projected changes in water demand for each county, and congregates them by sub-region in the following way:

$RS=D+CD+S+SC,(3)$

where D is the probability of a water demand increase from 1993-2012 to 2080–2099, CD is the normalized demand, S is the probability of a supply decrease from 1993-2012 to 2080–2099, and SC is one minus the normalized supply. Each river station is already assigned a sub-region (Figure 1), while each county is assigned to the sub-region to which the closest river station belongs. The probability D is calculated by forming a new normal random variable, X, for each RCP scenario with the mean determined by the projected demand in 2080–2099 subtracted by the estimated demand in 1993–2012 and variance set as the sum of the variances of projected demand and estimated current demand. S is calculated in the same way as D, but using the projected streamflow in 2080–2099 and the streamflow regime curve from 1993–2012 to form a random variable Y. In summary, for day i, region j, county k and streamflow station l:

$D_{i,j}=mea{n}_k\left(P\left(X_{i,j,k}\ge 0\right)\right)(4)$

$S_{i,j}=mea{n}_l\left(P\left(Y_{i,j,l}\le 0\right)\right)(5)$

D and S become a 365-day x 14-region matrix with values between 0 and 1. To compute CD and SC, the demand and supply regime curves for 1993–2012 are scaled to be between 0 and 1 by subtracting by their minimums and dividing by the difference of their maximums and minimums. For each subregion, final CD is calculated as the mean CD across all stations belonging to the region, while final SC is calculated as the mean SC across all counties belonging to the region. Thus, each final CD and SC is a 365-day x 14-region matrix with values between 0 and 1. RS is thus a 365-day x 14-region matrix with values between 0 and 4, where 0 implies no risk and 4 implies maximum risk of water shortages.

Results

Regional Clusters

The clustering of streamflow data across the region yielded 14 clusters or subregions (Figure 4). Below we describe the main characteristics of the average streamflow regime and some general climatic attributes for each cluster:

1) The first cluster, which we name “the West Coast”, is characterized by high winter streamflow and minimum flows in late August. The cluster includes Vancouver Island, western half of Washington, Oregon, and California. The climate in these areas is characterized by high frequency of precipitation events in winter that are predominately rainfall rather than snowfall. Thus, relative to other clusters, the streamflow is mainly driven by rainfall.

2) The “Southwest” cluster is comprised of the desert areas of California and Arizona. Although very little precipitation is available in these areas, precipitation may occur periodically in winter months. These rainfall events are usually of high intensity, potentially causing infiltration-excess overland flow. Thus, these catchments are rainfall dominated and have relatively quick responses to precipitation input.

3) The “Deep South” cluster includes Louisiana, Mississippi, Alabama, Georgia, Tennessee, and South Carolina. These states are known to have warm and humid summers with some precipitation. Winter and spring have the highest precipitation. The landscape is covered by forests which implies overland flow is less likely compared to the Southwest cluster. With such active storage, the streams’ response to precipitation may be slower despite being a rain-dominated region with a peak in the late winter months and low flows in late-summer.

4) The “Mid-Atlantic” cluster includes North Carolina, Kentucky, Virginia, West Virginia, Ohio, Pennsylvania, Maryland, Delaware, New Jersey, southern New York, Connecticut, and Southern Ontario. Mostly covered in forest, this region is known for its hot summers and very cold winters, where winter temperatures are often at or below freezing. Precipitation is often high, with precipitation being fairly evenly distributed throughout the year. This region may be hydrologically dominated by rain-on-snow events in winter, with all snow melting by early spring. The streamflow regime curve in this region has a peak in early spring and a low in mid-summer.

5) The “South-Central US” consists of Northeast Texas, Southeastern Oklahoma, Arkansas, and northern Louisiana. These areas are covered by grass, shrubs, with some forested areas further east. Precipitation is usually highest in the spring in these areas, with little to no snowfall, leading to highest streamflow in the spring with a seasonal drought in mid-summer.

6) The “Florida” cluster is largely covered by wetlands in the southern half and forest in the north. Since Florida is subtropical and tropical in some areas, precipitation occurs throughout the year. Summers are slightly wetter and more humid than are winters. The regime curve in this region has little variance, with highs in the late summer and lows in early summer.

7) The “Hawaii” cluster is in the tropics with precipitation and warm, humid weather throughout the year. The streamflow regime curve in this region has extremely low variability, with no clear high or low.

8) The “Rockies” cluster consists of Northern Wyoming, Idaho, Montana, Eastern Washington, and parts of British Columbia and the Yukon. This region is extremely cold in winters, often with extensive snow cover. The streamflow stations are in snow-dominated catchments, so the hydrographs are characterized by low streamflow in winter when no snowmelt is present, followed by peak streamflow in late spring to early summer as snowmelt intensifies.

9) The “Alaska” cluster, similarly to the Rockies, is a snow-dominated region; however, in Alaska, the colder climate and extensive snow cover, as well as glacierized terrain, allows for the snowmelt and/or glacier runoff to last throughout the summer; thus, giving hydrographs with a wide peak throughout the summer.

10) The “Midwest” cluster contains Illinois, Wisconsin, Iowa, Minnesota, North and South Dakota, as well as Southern Alberta and Saskatchewan. This region’s land use mainly consists of agricultural areas and grasslands. This region is fairly dry; nevertheless, snow cover persists throughout much of the winter, with melt occurring in the spring leading to the peak in streamflow.

11) The “Northeast” cluster consists of New York, Vermont, New Hampshire, Maine, Southern Quebec, New Brunswick, Nova Scotia, Prince Edward Island, and Southern Newfoundland. This region is covered by forest and has very cold winters; hence, snow builds in the winter and then snowmelt generates peak streamflow in April.

12) The “West” cluster includes parts of British Columbia, Alberta, Idaho, Montana, Utah, Nevada, California, and Arizona. The hydrographs in this region peak in spring as a result of snowmelt.

13) The “Central US” cluster consists of Southern Minnesota, Iowa, Nebraska, Missouri, Kansas, and Oklahoma. The hydrographs in this region peak in spring.

14) The “Eastern Canada” cluster includes northern Newfoundland, Quebec, Ontario, and Manitoba. The hydrographs in this region peak in spring. Winters are cold and snow cover is prevalent, so runoff is driven by spring snowmelt.

FIGURE 4

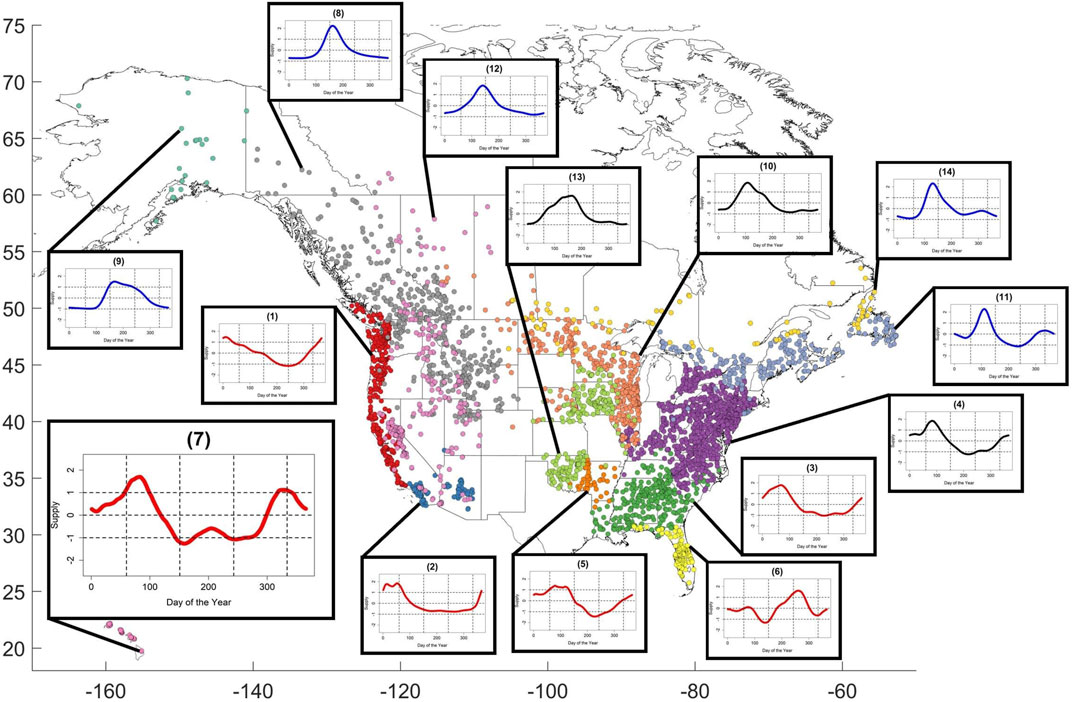
FIGURE 4. Clusters with their average normalized streamflow regime curve. The clusters are: 1) West Coast, 2) Southwest, 3) Deep South, 4) Mid-Atlantic, 5) South-Central US, 6) Florida, 7) Hawaii, 8) Rockies, 9) Alaska, 10) Midwest, 11) Northeast, 12) West, 13) Central US, 14) Eastern Canada. The colors of the regime curve indicate the regime categories where red, black, and blue indicate rain dominated, rain-on-snow dominated, and snowmelt dominated regimes respectively. Vertical dashed curves in the graphs are placed at the transition of seasons (winter, spring, summer, fall).

According to these characteristics we can group the 14 subregions into three general regime categories: rainfall dominated streamflow regime (West Coast, Southwest, Deep South, South-Central US, Florida, and Hawaii), rain-on-snow dominated regime (Mid-Atlantic, Midwest, and Central US), and snow dominated regions (Rockies, Alaska, Northeast, West, and Eastern Canada).

Simulations of Water Supply

Model Performance

The KGE is estimated for all streamflow stations within each region for the 3-year test set (Table 2). The West Coast (0.82) and Alaska (0.89) have high median KGEs. Predictions for the Southwest (0.61), Deep South (0.73), Mid-Atlantic (0.73), Rockies (0.73), South-Central US (0.65), Hawaii (0.59), Northeast (0.70), West (0.71), Midwest (0.59), and Eastern Canada (0.52) are also fairly reliable. On the other hand, our simulations perform poorly in Central US (0.46) and Florida (0.37).

TABLE 2

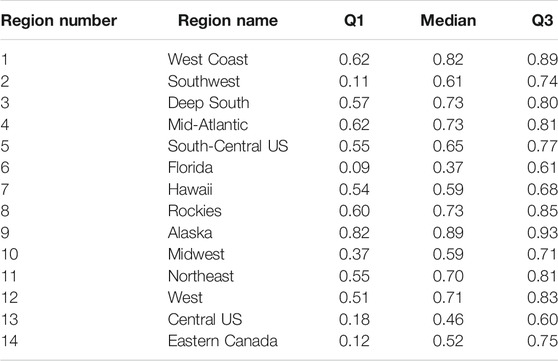
TABLE 2. The first quantile, median, and third quantile of KGE values for predicted water supply regime curves for each region.

Projections of Streamflow

An example of modelled future (2080–2099) versus present (1993–2012) streamflow regime curves are shown in Figure 5 for a streamflow station in California. The streamflow at this station is expected to substantially increase in late winter and early spring, while the streamflow will remain almost unchanged throughout the rest of the year. The uncertainty interval for both RCP scenarios is large, especially for the time window with the largest projected increase in streamflow. We estimate the water-supply components of the risk score for this station (Equation 3): on a seasonal scale, the largest CS is in the fall (median CS = 1.00) and the smallest is in the winter (CS = 0.26), while the likely decrease in streamflow is projected for the summer (S = 1.00 for RCP4.5; S = 1.00 for RCP8.5), and the least likely decrease is projected for the winter (S = 0.27 for RCP4.5; S = 0.27 for RCP8.5).

FIGURE 5

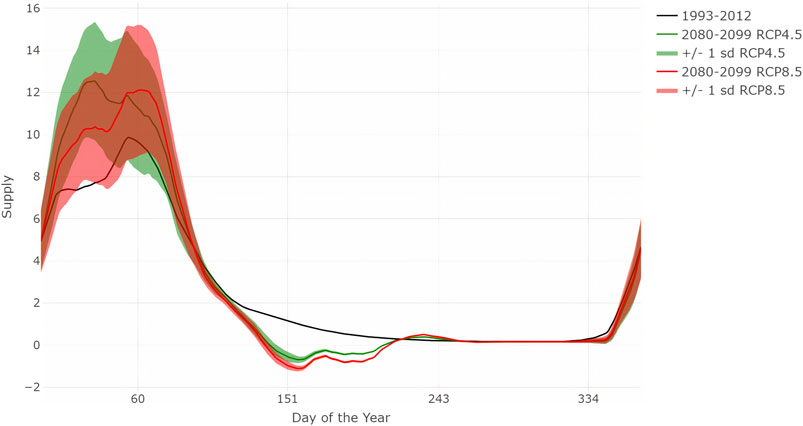
FIGURE 5. Modelled seasonal streamflow (measured in m³/sec) regime curves for 1993–2012 (black), and 2080–2099 according to RCP4.5 (green) and RCP8.5 (red) scenarios for a station in California (34.35, −119.31). The shading indicates the uncertainty (±one standard deviation).

Next, we summarize the results of regional streamflow projections for each season, with more focus on subregions where the model has higher predictive capabilities (larger KGE) relative to other subregions: Results for winter streamflow (DJF; Figure 6) reveal that the likelihood of a downward change in streamflow is linked to latitude. Specifically, for low-latitude regions (Hawaii, Southwest, Florida, Central US), streamflow is projected to decrease for one or both RCP scenarios. For these regions, the average S is 0.56 (0.68) for RCP4.5 (RCP8.5) scenario, while the average CS is 0.70. Out of these regions, only Central US and Florida have KGE <0.5 implying a low confidence in the projections. The probability of a decrease in Hawaii is certain with the interquartile range (IQR) of 0 for both RCP4.5 and RCP8.5 scenarios. The IQRs for Southwest, Florida, and Central US are much larger, ranging from 0.35 for Southwest’s RCP8.5 scenario to 0.95 for Florida’s RCP4.5 scenario. Streamflow is projected to increase in Alaska, the Rockies, the Midwest, the West Coast, and the Northeast. According the KGE values, however, we have higher confidence in the projections for the West Coast (KGE = 0.82), Alaska (KGE = 0.89) and less certain for Rockies (KGE = 0.73), Midwest (KGE = 0.59), and Northeast (KGE = 0.70).

FIGURE 6

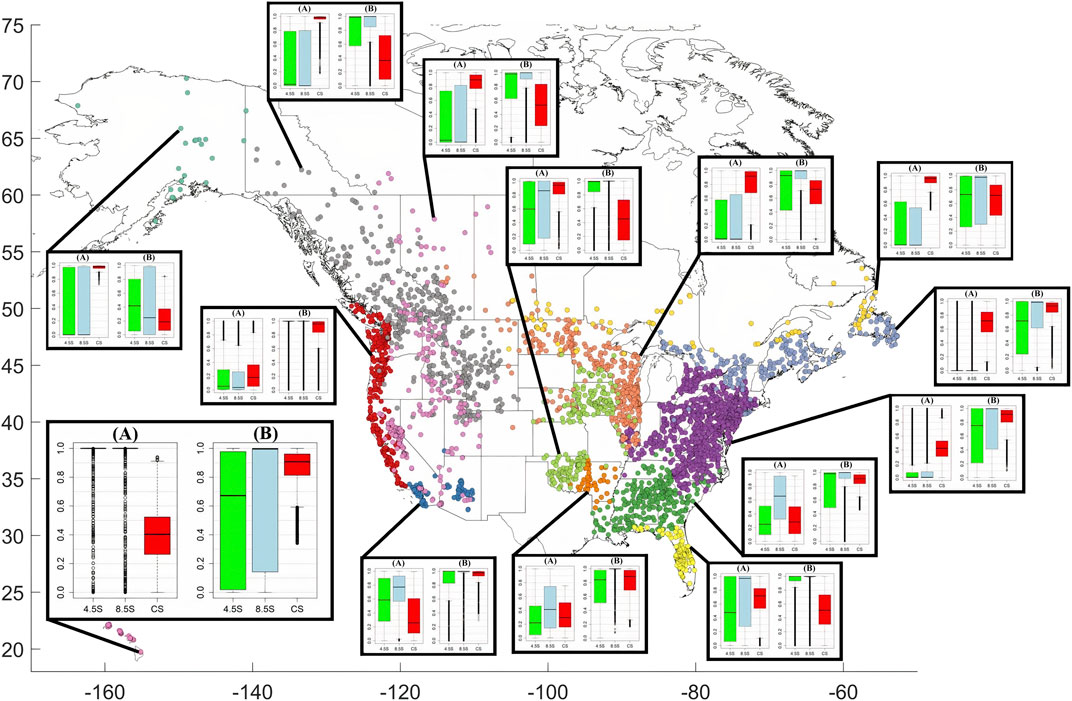
FIGURE 6. Boxplots of water-supply components of the risk score (equation 3) for each subregion in winter (A) and summer (B). The left panel for each region includes: the probability of an increase in streamflow in winter given the RCP4.5 (RCP8.5) emission scenario, and one minus the present (1993–2012) winter freshwater supply, normalized to be between 0 and 1 (CS). The right panel for each region shows the same components of the risk score, but for summer. The thick black lines of the boxplots indicate the median value while the box shows the range between the first and third quantiles. The points outside the range of the whiskers can be considered as outliers. The clusters are: 1) West Coast, 2) Southwest, 3) Deep South, 4) Mid-Atlantic, 5) South-Central US, 6) Florida, 7) Hawaii, 8) Rockies, 9) Alaska, 10) Midwest, 11) Northeast, 12) West, 13) Central US, 14) Eastern Canada.

In simulating the streamflow in spring (MAM), under the RCP4.5 scenario, Hawaii and the West Coast will experience decreases in streamflow (their average S is 0.76 and there IQRs are 0 and 0.48), whereas the Deep South, East Coast, Southern Central US, Central US, Northeast, and the Midwest will experience increases (their average S is 0.13 and their IQRs are 0.19, 0.11, 0.25, 0.17, 0.38, and 0.10 respectively). Like the RCP4.5 scenario, RCP8.5 will lead to decreases in streamflow in Hawaii, West Coast, Florida, and the Southwest (their average S is 0.75 and their IQRs are 0, 0.59, 0.12, and 0.38 respectively). These results are particularly of note for Hawaii, the Southwest, and Florida as these regions experience low present water supply in the spring relative to other seasons (their average CS is 0.64).

Projections of summer (JJA) streamflow reveal that water resources will experience strain across most of North America (Figure 6). According to the RCP4.5 scenario, the West Coast, the Southwest, South Central US, Florida, the Deep South, Central US, and the Midwest will all likely experience decreased water supply (their average S is 0.80). Following the RCP8.5 scenario, in addition to the regions affected by the RCP4.5 scenario, Hawaii, the East Coast, the Northeast, and Eastern Canada will see decreases in summer streamflow (their average S is 0.81). The IQRs of decrease probabilities are small for the West Coast (0 for RCP4.5, 0 for RCP8.5), Southwest (0.18, 0), Florida (0.08, 0), and Central US (0.18, 0).

For the projections of autumn (SON) streamflow, regardless of the RCP scenario followed, eastern regions are most likely going to be affected by decreases in their streamflow, including the Deep South, the East Coast, Southern Central US, Florida, Midwest, Northeast, and Central US (their average S is 0.73 and 0.69 for RCP4.5 and RCP8.5, respectively). The IQRs of decrease probabilities are small for the Southern Central US (0.05 for RCP4.5, 0 for RCP8.5) and the Deep South (0.20, 0.10).

Simulations of Water Demand

Model Performance

Supplementary Figure S2 shows the mean correlation (0.69) between predicted and observed daily water efficiency with optimal inverse distance weighting calculated using leave-one-out cross validation. All locations have at least 1,000 observations of daily water use efficiency, so this correlation is significant (average p-value < 0.01), and the predictions are representative of the observations.

Projections of Municipal Water Use

An example of modelled future versus present water consumption per capita is shown in Supplementary Figure S3 for a county in Alabama. As illustrated in the figure, there is a pronounced seasonal cycle in the water consumption, with the highest consumption during the summer months. The changes in water demand are projected to occur in all seasons, with the largest increases in summer, and the lowest in winter. These results are reflected in the water-use components of the risk score (Equation 3): the largest CD is in summer (CD = 0.95) and the smallest CD is winter (CD = 0.08). The likelihood that this county will experience an increase in demand is also the largest in summer (D = 0.97 for RCP4.5; D = 1.00 for RCP8.5), and the smallest in winter (D = 0.86 for RCP4.5; D = 0.98 for RCP8.5).

Projections for each subregion and each season reveal that the changes in water consumption are relatively uniform across seasons, with the main difference being between winter and summer water consumption (Figure 7). For all regions, the current water demand is the largest in summer and lowest in winter (their average CD is winter is 0.07, and their average CD in summer is 0.92). In all regions, RCP4.5 will substantially increase the annual water demand (average D = 0.93 for RCP4.5), while more increase is expected for RCP8.5 (average D = 0.99 for RCP8.5). Most of this increase is expected in the summer season (average summer D = 0.95 for RCP4.5; D = 1.00 for RCP8.5). The top three subregions with the highest projected increase in demand in summer given the RCP4.5 and RCP8.5 scenarios are Hawaii and Florida, and their average summer D is 0.99 and 1.00, respectively. The top three subregions with the highest projected increase in demand for RCP4.5 (RCP8.5) in winter are: Hawaii, Southwest, and West Coast (Hawaii, Southwest, and Eastern Canada), and their average winter D = 0.96 (1.00). During all seasons and in all regions, increases in municipal water demand are expected, regardless of the RCP scenario followed, however the increases are more certain under RCP8.5 compared to RCP4.5. The interquartile range of all regions and seasons given the RCP4.5 scenario ranges from 0 to 0.1, whereas the IQRs given RCP8.5 remain at 0.

FIGURE 7

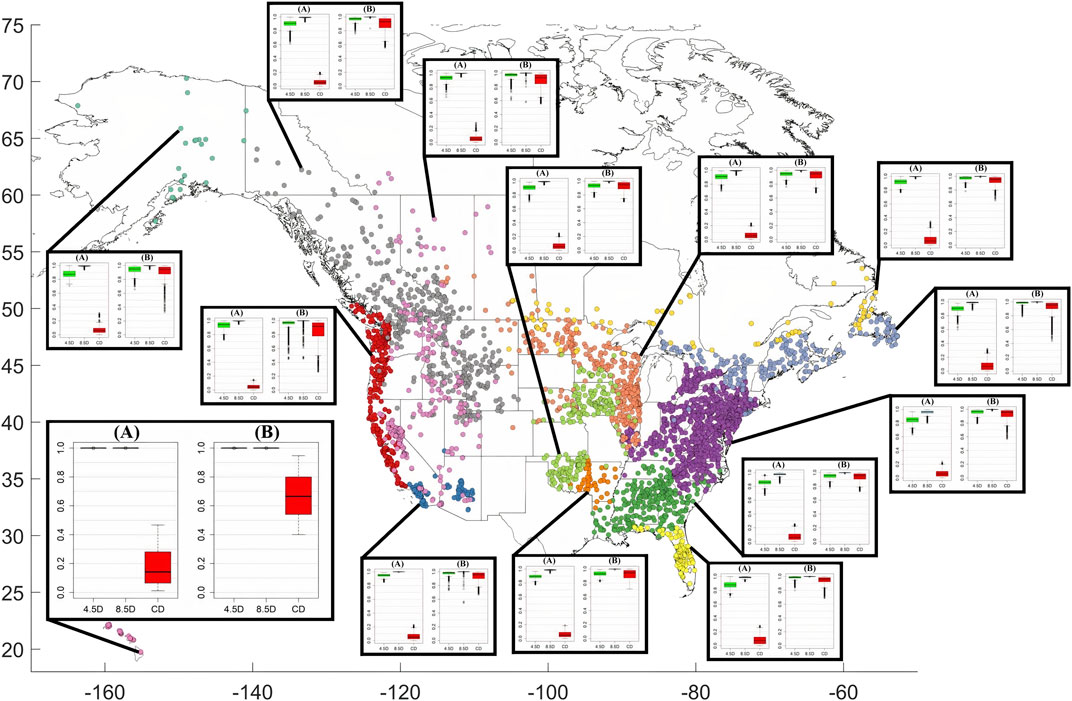
FIGURE 7. Boxplots of water-demand components of the risk score for each subregion in winter and summer. (A) for each region includes: 4.5D (8.5D)—the probability of an increase in water demand in winter given the RCP4.5 (RCP8.5) emission scenario, and CD—the present (1993–2012) freshwater demand, normalized to be between 0 and 1. (B) shows the same components (4.5D, 8.5D, and CD) but calculated for summer. The thick black lines of the boxplots indicate the median value while the box shows the range between the first and third quantiles. The points outside the range of the whiskers can be considered as outliers. Names of subregions are given in Figure 5.

Risk Assessment

Risk scores (RS) for each region and RCP scenario are quantified for each season. Because of consistently higher demand in summer (Figure 7), total risk is consistently highest in the summer, so only summer risk scores are shown (Figure 8). According to the RCP4.5 scenario, the region with the highest risk of freshwater shortage in the summer (highest median RS) is the Southwest (region 2), followed by the West Coast (region 1) and the Deep South (region 3). The West Coast and Southwest both have low uncertainty (IQRs of 0.30 and 0.10), but the Deep South has high uncertainty (IQR = 0.55) stemming from high uncertainty of streamflow projections in this region. According to the RCP8.5 scenario, the regions with the highest risk are: Southern Central United States (region 5), the Deep South (region 3), and Northeast (region 11). The IQRs of these risk scores are low for Southern Central US (0.40) and the Deep South (0.37).

FIGURE 8

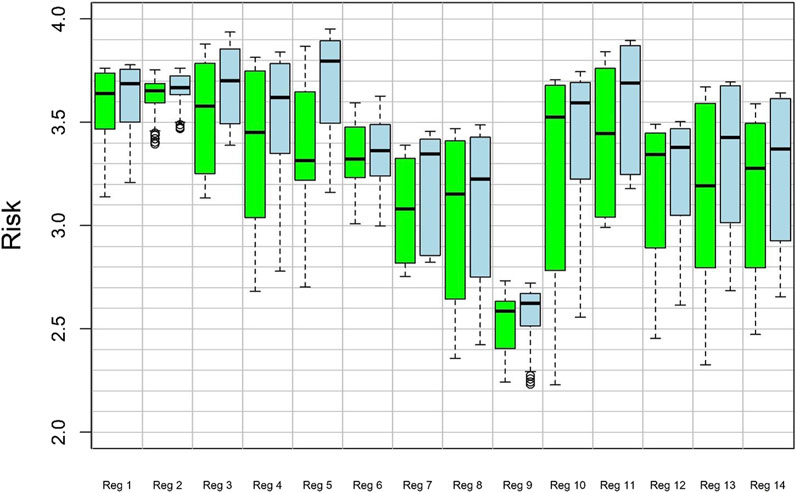
FIGURE 8. Box plot of risk scores (RS) derived for the summer for each of the 14 subregions. Green box plot is for the RCP4.5 emissions scenario, and blue is for the RCP8.5 emissions scenario. The list of regions is as follows: 1) West Coast, 2) Southwest, 3) Deep South, 4) Mid-Atlantic, 5) South-Central US, 6) Florida, 7) Hawaii, 8) Rockies, 9) Alaska, 10) Midwest, 11) Northeast, 12) West, 13) Central US, and 14) Eastern Canada. The thick black lines of the boxplots indicate the median value while the box shows the range between the first and third quantiles. The points outside the range of the whiskers can be considered as outliers.

Discussion

Summary of Results

GCMs generally agree that the entirety of North America will experience temperature increases throughout this century, while precipitation will change over time as a function of latitude, where southern areas will see decreases in precipitation, and northern areas will experience increases (Roy et al., 2012; Forster et al., 2020). This will likely lead to decreases in the fraction of precipitation falling as snow, increases in evapotranspiration, and changes in available water. But how this change in climate will alter the supply and demand of freshwater is poorly understood. Here we aimed at building a better understanding of these uncertainties while obtaining a general overview of where and when the risk of supply deficits is greatest.

We focused our paper on two objectives: First, we aimed to determine the viability of using simple regression models to capture the variability in streamflow and water consumption using globally available climate reanalysis data while assessing the risk of water shortage in multiple regions across North America. The viability of simple regression models for the use of modeling streamflow varied by region, as measured by the validation phase KGE. Florida and Central US had the lowest median KGEs. The other regions had highly acceptable KGEs, especially when the regime curves do not change much from year to year, as is the case in Alaska. Further, the correlation between simulated and observed water use was high. This result means that urban water use in a city can robustly be estimated from population data and climate data in conjunction with water use data from surrounding cities. We found that demand is consistently highest in the summer, thus making water shortage risks consistently highest in the summer. In summer, the highest risk scores are in the Southwest (Southern Central US), West Coast (Deep South), and Deep South (Northeast) given the RCP4.5 (RCP8.5) scenario.

As a second objective, we sought to quantify the uncertainties in predicting streamflow and water consumption and therefore water shortage stemming from GCM climate projections. We found that almost all of the risk score uncertainty is derived from the uncertainty of streamflow projections from GCM data, while there is little-to-no uncertainty in demand projections from GCM data. This occurs because the supply is driven by precipitation while demand is driven by maximum temperature, and GCM projections of temperature have a narrower spread of projections from the weather generator compared to precipitation.

Comparison With Previous Works

Similar to previous studies that used regression models for predicting streamflow (e.g., Barbarossa et al., 2017; Mendoza et al., 2017), we found the MLR models to be reliable in most of our 14 subregions. However, in some regions (e.g., Florida and Central US), the model performance was relatively poor. The poor performance in these regions is not limited to simple regression models. Brunner et al. (2020), using physically based models, also found that Central US was the most difficult region to reliably simulate water supply.

For the US, our projections of streamflow generally agree with the previous findings that the annual streamflow will substantially decrease in South and Western US (Hurd et al., 1999; Foti et al., 2012; Chien and Knouft, 2013; Mahat et al., 2017). Throughout the region, summer streamflow was shown to be more susceptible to decreases (Maurer and Duffy, 2005; Chien and Knouft, 2013) than streamflow in other seasons. In particular, under the RCP4.5 scenario, we projected that Florida may experience significant streamflow decreases in the summer, corroborating previous findings in (Mahat et al., 2017). Furthermore, under the RCP8.5 scenario, our results also agree with Mahat et al. (2017) that the Southwest, Southern Central US, and Florida will experience substantial drops in streamflow. These projections are relatively consistent across the climate projections stochastically generated from the five GCMs.

Our projections of water use agree with those is Foti et al. (2012), showing that climate-driven water use will increase across the United States, as well as Canada, and uncertainties around these projections will decrease as temperatures rise further. Since maximum temperature is the dominant driver of water consumption (Opalinski et al., 2020), and all CMIP5 models agree that temperatures are projected to rise across the entire United States (Mahat et al., 2017), this is in-line with expectations. The MLR modeling of municipal water demand showed that most of our city-specific regression coefficients are highly spatially dependent as previously found in (Opalinski et al., 2020). The regression coefficient that shows the contribution of the number of snowy days to water demand is negatively correlated with latitude, implying that the impacts of snowy days on water demand is greater in lower latitude areas. For example, at low latitudes, the snowfall-day coefficient is between 0.6 and 1.4, while in Canada, the coefficient drops to 0.2. The regression coefficient that shows the contribution of the maximum temperature is also spatially varying, with the highest values in western and southern areas (0.08–0.19), and the lowestin northern and eastern areas (0.03–0.08). In the West Coast, southwest US, and Florida regions, the coefficient multiplying the wind speed is normally positive (0–0.15), while in other places, the coefficient of wind is normally negative (−0.15–0), implying that warm winds could raise water demand, while colder winds could decrease demand. However, the coefficient in Texas is negative, so this hypothesis should be tested further. Rain-day coefficients seem to not be spatially dependent. We compared our spatially distributed coefficient values with those derived in Opalinski et al. (2020) and found general agreement for the coefficient multiplying the maximum temperature. In Opalinski et al. (2020), however, the link with the latitude is not as clear as in our case which is likely because we extended the assessment to Canadian cities while their study only provides the results for the contiguous US. Regarding precipitation, Opalinski et al. (2020) found that the increase in precipitation in cold regions was associated with an increase in water consumption. One interpretation for this finding is that the increased snowfall is linked to increased water use, which is also consistent with our results.

To our knowledge, there have been relatively few up-to-date assessments of water resource vulnerabilities and shortage risks due to climate change across the entire US or North America. Dickson and Dzombak (2019) as well as Foti et al. (2012) used physically based models to project streamflow, while Roy et al. (2012) calculated available precipitation (precipitation minus evaporation) instead of streamflow. Previously, urban water-demand projections have been made based on changes in population and electricity production (Roy et al., 2012; Dickson and Dzombak, 2019), or climate regression techniques combined with the effects of income, population, and efficiency (Foti et al., 2012). Our study is the first that focused on both the US and Canada, and the first to combine the use of regression models for both supply and demand projections.

Our results generally agree with those in the previous studies for the regions where the previous projections of risks have been assessed. For example, the probability of water shortage was calculated across the U.S. by Foti et al. (2012) and probabilities were highest in the same areas as our study indicated, namely the southwestern United States and the coast of California, though they showed a high risk for the central US as well. Roy et al. (2012) found that the southwest and central US as well as Florida will have the highest risk index in 2050. The latest assessment of risk showed that central California, and parts of Nevada have the highest risk of water shortage (Dickson and Dzombak, 2019). Regardless of the methods, data, or scenario chosen, all of these studies agree that California and the US Southwest have the most troubling futures, relative to other parts of North America, when it comes to the effects of climate change on water resources.

Limitations

Though we used an expansive collection of streamflow data, continuous, long-term hydrologic data is often limited to large rivers and our conclusions may not accurately extrapolate to smaller basins (Kovach et al., 2019). In a similar fashion, the water use data is mostly limited to medium-sized cities and the captured relationships between water use and weather may not extrapolate to extremely large cities or small towns. Although some hydrological extremes are included in the 20-year period of analysis used in this paper (e.g., the 2000–2004 drought in western North America), the length of time used may be seen as too modest as the full extent of climate extremes in all areas may not be present and therefore learnable in our data (Schwalm et al., 2012). Rather than developing the best possible prediction model, we aimed at exploring how well a relatively simple model (MLR) can explain interannual and seasonal variability in water consumption and streamflow. Likewise, our water shortage vulnerability framework is relatively narrow in scope. For a more complete risk assessment, one would have to consider biological and ecological sensitivity as well as adaptive capacity (Kovach et al., 2019). Though we utilized stochastic weather generators to increase the number of cases in our ensemble of future scenarios, we only included five GCMs as a baseline, so the results could be sensitive to our choice in GCMs.

Due to the number of models included for projecting streamflow, the assumptions of linear behavior and constant variance over the long period of study could not be verified. The least success in terms of MLR performance among the streamflow models is found for Central US and Florida. One of the key reasons for the poor performance is the fact that runoff could be controlled by non-linear threshold-like belowground hydrologic processes (Jones et al., 2019). In some catchments, precipitation can fall and either quickly flood the surface when the soil is saturated or recharge the groundwater system. Thus, water from similar sized precipitation events may be transferred toward the stream immediately or a few months to several decades later. The “memory” in the hydrological system, which acts on multiple time scales, is not possible to be captured by the linear regression model used in our paper. In deforested, arid, urbanized, or agricultural areas with little snowfall and little interactions between precipitation and belowground attributes, streamflow response to precipitation is relatively fast. In these regions, as well as in regions with similar year-to-year regimes, our ensemble of regression models is deemed acceptable to forecast future water shortage and its uncertainty.

With regards to our projections of water use, unlike previous studies, we did not consider water use from sectors such as agriculture or thermoelectric power which admittedly take up a large portion of water (Foti et al., 2012; Roy et al., 2012; Dickson and Dzombak, 2019). Climate successfully explained a large portion of the variability in our urban water use data, and climate change will likely explain much of the future changes in use, however, non-climatic changes can also be substantial factors. For instance, age of the population, household size, and other sociodemographic attributes can explain some water use behavior (March and Saurí, 2010). While the effects of population, income, and technological efficiency growth have been shown to negate overall, individual regions or cities may experience outsized effects of one or another (Rosegrant and Cai, 2002). City or building specific attributes related to water use such as building type, tree fraction, building age, impervious surface percentage, and population density can also change over time and should be seriously considered (Stoker and Rothfeder, 2014; Chang et al., 2017). General attitudes towards conservation and lawn upkeep are yet other examples of features that may change in tandem with water use (Hong and Chang, 2014). Further, we assumed that spatially interpolating our estimated regression coefficients from cities with data to the grid of counties gives a good enough first-order approximation of the effects of climate on water use in each county. Though the validation provides some confidence that interpolating the regression coefficients yielded optimal results for the purpose of our study, some subregions had little-to-no data (e.g., Hawaii and the Deep South), and therefore uncertainty in their results remains unaccounted for.

Conclusion

Here we presented a new method for quantifying future risks of municipal water shortages across North America in response to climate change. We applied a set of multiple regression models to project the changes in streamflow regimes (water-supply) and urban water use regimes (water-demand) in response to climate scenarios stochastically generated from an ensemble of five GCMs, for the RCP4.5 and RCP8.5 emission scenarios. The models were calibrated over the present period (1993–2012) and then used for projections over the 2080–2099 period. The results were analyzed for each of 14 identified clusters or subregions across the original domain (the US and Canada).

Results show that risk scores are considerably higher in the summer compared to the rest of the year, since urban water demand is high regardless of the location chosen. The resulting risk scores for water shortages by the end of the 21st century under the RCP4.5 emissions scenario, indicate a high risk for the West Coast, the Deep South, and the Southwestern US. Under the RCP8.5 scenario, the regions with the highest risk are Southern Central US, the Deep South, and Northeast, while the regions with the lowest risk are Alaska, Rockies, and Hawaii. The high risk scores are due to high and increasing demand concurrently happening with low and decreasing supply. Almost all uncertainty in the risk scores is rooted in the uncertainty of streamflow projections from GCM data, while there is little-to-no uncertainty in water-demand projections from GCM data. Overall, the predictive power of our streamflow model is shown to be sufficient in most subregions, while for Florida and Central US, the model yielded low predictive power. Our study reveals that simple statistical models can produce projections of water shortages that agree with those derived from more complex methods used in previous studies. Nevertheless, more work is needed to identify and implement mitigation strategies to prevent water resource shortages. In particular, the regions that we identified as those with high risk scores, should be examined in more detail so that their water resources can be analyzed at the community level. Future research should also aim to employ more complex methods, especially in those regions shown with our simple method to have high risk and relatively large uncertainty in predicted water shortages. To capture the long-term ‘memory’ and non-linear threshold-like behavior of hydrologic systems, due to snowmelt characteristics or differing geological water partitioning systems, more complex and computationally expensive methods are needed, such as Long-Short-Term Memory models (e.g., Shen, 2018), as well as diverse climatic and physical data.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: CMIP5 data is available viahttps://esgf-node.llnl.gov/search/cmip5/. ERA5 data is available viahttps://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview. Streamflow data for US and Canada can be obtained from USGS (https://waterdata.usgs.gov/nwis/sw) and the HYDAT database (https://www.canada.ca/en/environment-climate-change/services/water-overview/quantity/monitoring/survey/data-products-services/national-archive-hydat.html). The water use data for each city has been provided by individual municipalities and is not currently publicly available, however, some of the data can be shared if the corresponding author is contacted directly.

Author Contributions

JJ carried out data collection and data analysis. JJ and VR drafted the manuscript. JJ, VR, and AA designed the methods and edited the manuscript.

Funding

This research was funded by Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery grant (PI: VR) and NSF Innovations at the Nexus of Food, Energy and Water Systems (INFEWS) grant CNS-1639268 (PI: G. Characklis, UNC; co-PI: AA).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the local water mangers who kindly provided us with water usage data for their regions. We thank Sam Anderson for his contributions to methods and discussions on the earlier versions of the manuscript.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.730631/full#supplementary-material

References

Ababaei, B. (2014). Are Weather Generators Robust Tools to Study Daily Reference Evapotranspiration and Irrigation Requirement? Water Resour. Manage. 28 (4), 915–932. doi:10.1007/s11269-014-0524-3

CrossRef Full Text | Google Scholar

Achakulwisut, P., Mickley, L. J., and Anenberg, S. C. (2018). Drought-sensitivity of fine dust in the US Southwest: Implications for air quality and public health under future climate change. Environ. Res. Lett. 13 (5), 054025. doi:10.1088/1748-9326/aabf20

CrossRef Full Text | Google Scholar

Adamowski, J., Fung Chan, H., Prasher, S. O., Ozga‐Zielinski, B., and Sliusarieva, A. (2012). Comparison of multiple linear and nonlinear regression, autoregressive integrated moving average, artificial neural network, and wavelet artificial neural network methods for urban water demand forecasting in Montreal, Canada. Water Resour. Res. 48 (1), 1528. doi:10.1029/2010wr009945

CrossRef Full Text | Google Scholar

Addor, N., Newman, A. J., Mizukami, N., and Clark, M. P. (2017). The CAMELS data set: catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 21 (10), 5293–5313. doi:10.5194/hess-21-5293-2017

CrossRef Full Text | Google Scholar

Alizadeh, M. J., Kavianpour, M. R., Kamranzad, B., and Etemad-Shahidi, A. (2019). A weibull distribution based technique for downscaling of climatic wind field. Asia-pacific J. Atmos. Sci. 55 (4), 685–700. doi:10.1007/s13143-019-00106-z

CrossRef Full Text | Google Scholar

Ashfaq, M., Ghosh, S., Kao, S.-C., Bowling, L. C., Mote, P., Touma, D., et al. (2013). Near-term acceleration of hydroclimatic change in the western U.S. J. Geophys. Res. Atmos. 118 (19), 676–693. doi:10.1002/jgrd.50816

CrossRef Full Text | Google Scholar

Bakker, M., Van Duist, H., Van Schagen, K., Vreeburg, J., and Rietveld, L. (2014). Improving the performance of water demand forecasting models by using weather input. Proced. Eng. 70, 93–102. doi:10.1016/j.proeng.2014.02.012

CrossRef Full Text | Google Scholar

Balling, R. C., and Gober, P. (2007). Climate variability and residential water use in the city of Phoenix, Arizona. J. Appl. Meteorology Climatology 46 (7), 1130–1137. doi:10.1175/jam2518.1

CrossRef Full Text | Google Scholar

Barbarossa, V., Huijbregts, M. A. J., Hendriks, A. J., Beusen, A. H. W., Clavreul, J., King, H., et al. (2017). Developing and testing a global-scale regression model to quantify mean annual streamflow. J. Hydrol. 544, 479–487. doi:10.1016/j.jhydrol.2016.11.053

CrossRef Full Text | Google Scholar

Basara, J. B., Christian, J. I., Wakefield, R. A., Otkin, J. A., Hunt, E. H., and Brown, D. P. (2019). The evolution, propagation, and spread of flash drought in the Central United States during 2012. Environ. Res. Lett. 14 (8), 084025. doi:10.1088/1748-9326/ab2cc0

CrossRef Full Text | Google Scholar

Besaw, L. E., Rizzo, D. M., Bierman, P. R., and Hackett, W. R. (2010). Advances in ungauged streamflow prediction using artificial neural networks. J. Hydrol. 386 (1-4), 27–37. doi:10.1016/j.jhydrol.2010.02.037

CrossRef Full Text | Google Scholar

Blöschl, G., Bloschl, G., Sivapalan, M., Wagener, T., Savenije, H., and Viglione, A. (2013). Runoff Prediction in ungauged basins: synthesis across Processes, Places and scales. Cambridge: Cambridge University Press.

Bonsal, B. R., Wheaton, E. E., Chipanshi, A. C., Lin, C., Sauchyn, D. J., and Wen, L. (2011). Drought research in Canada: A review. Atmosphere-Ocean 49 (4), 303–319. doi:10.1080/07055900.2011.555103

CrossRef Full Text | Google Scholar

Breinl, K. (2016). Driving a lumped hydrological model with precipitation output from weather generators of different complexity. Hydrological Sci. J. 61 (8), 1395–1414. doi:10.1080/02626667.2015.1036755

CrossRef Full Text | Google Scholar

Breyer, B., and Chang, H. (2014). Urban water consumption and weather variation in the Portland, Oregon metropolitan area. Urban Clim. 9, 1–18. doi:10.1016/j.uclim.2014.05.001

CrossRef Full Text | Google Scholar

Brown, T. C., Foti, R., and Ramirez, J. A. (2013). Projected freshwater withdrawals in the United States under a changing climate. Water Resour. Res. 49 (3), 1259–1276. doi:10.1002/wrcr.20076

CrossRef Full Text | Google Scholar

Brunner, M. I., Melsen, L. A., Newman, A. J., Wood, A. W., and Clark, M. P. (2020). Future streamflow regime changes in the United States: assessment using functional classification. Hydrol. Earth Syst. Sci. 24 (8), 3951–3966. doi:10.5194/hess-24-3951-2020

CrossRef Full Text | Google Scholar

Byun, K., Chiu, C.-M., and Hamlet, A. F. (2019). Effects of 21st century climate change on seasonal flow regimes and hydrologic extremes over the Midwest and Great Lakes region of the US. Sci. Total Environ. 650, 1261–1277. doi:10.1016/j.scitotenv.2018.09.063

PubMed Abstract | CrossRef Full Text | Google Scholar

Caron, A., Leconte, R., and Brissette, F. (2008). An improved stochastic weather generator for hydrological impact studies. Can. Water Resour. J. 33 (3), 233–256. doi:10.4296/cwrj3303233

CrossRef Full Text | Google Scholar

Chang, H., Bonnette, M. R., Stoker, P., Crow-Miller, B., and Wentz, E. (2017). Determinants of single family residential water use across scales in four western US cities. Sci. Total Environ. 596-597, 451–464. doi:10.1016/j.scitotenv.2017.03.164

PubMed Abstract | CrossRef Full Text | Google Scholar

Chang, H., Praskievicz, S., and Parandvash, H. (2014). Sensitivity of urban water consumption to weather and climate variability at multiple temporal scales: The case of Portland, Oregon. Int. J. Geospatial Environ. Res. 1 (1), 7.

Google Scholar

Chen, G., Tian, H., Zhang, C., Liu, M., Ren, W., Zhu, W., et al. (2012). Drought in the Southern United States over the 20th century: variability and its impacts on terrestrial ecosystem productivity and carbon storage. Climatic change 114 (2), 379–397. doi:10.1007/s10584-012-0410-z

CrossRef Full Text | Google Scholar

Chen, J., Brissette, F. P., Chaumont, D., and Braun, M. (2013). Finding appropriate bias correction methods in downscaling precipitation for hydrologic impact studies over North America. Water Resour. Res. 49 (7), 4187–4205. doi:10.1002/wrcr.20331

CrossRef Full Text | Google Scholar

Chen, Y., Li, J., Wang, H., Qin, J., and Dong, L. (2017). Large-watershed flood forecasting with high-resolution distributed hydrological model. Hydrol. Earth Syst. Sci. 21 (2), 735–749. doi:10.5194/hess-21-735-2017

CrossRef Full Text | Google Scholar

Chien, H., and Knouft, J. (2013). Modeling future streamflow variability in the Mobile River watershed in the southeastern United States using SWAT coupled with climate change projections. AGU Fall Meet. Abstr. GC23A–0901.

Google Scholar

Cinquini, L., Crichton, D., Mattmann, C., Harney, J., Shipman, G., Wang, F., et al. (2014). The Earth System Grid Federation: An open infrastructure for access to distributed geospatial data. Future Generation Comp. Syst. 36, 400–417. doi:10.1016/j.future.2013.07.002

CrossRef Full Text | Google Scholar

Copernicus Climate Change Service Climate Data Store (2017). ERA5: Fifth generation of ECMWF atmospheric reanalyses of the global climate. United States: CDS.

Demaria, E. M. C., Palmer, R. N., and Roundy, J. K. (2016). Regional climate change projections of streamflow characteristics in the Northeast and Midwest U.S. J. Hydrol. Reg. Stud. 5, 309–323. doi:10.1016/j.ejrh.2015.11.007

CrossRef Full Text | Google Scholar

DeOreo, W. B., Mayer, P. W., Dziegielewski, B., and Kiefer, J. (2016). Residential end uses of water. United States: Water Research Foundation.

Dickson, K. E., and Dzombak, D. A. (2019). Water Supply Risk in the United States 2015-2050 Considering Projected Changes in Population and Thermoelectric Power Demand. Environ. Sci. Technol. 53 (24), 14113–14122. doi:10.1021/acs.est.9b02435

PubMed Abstract | CrossRef Full Text | Google Scholar

Dieter, C. A., Maupin, M. A., Caldwell, R. R., Harris, M. A., Ivahnenko, T. I., Lovelace, J. K., et al. (2018). Estimated use of water in the United States in 2015: U.S. Geological Survey Circular 1441. Supersedes USGS Open-File Report 2017–1131, 65. doi:10.3133/cir1441

CrossRef Full Text | Google Scholar

Dilling, L., Daly, M. E., Kenney, D. A., Klein, R., Miller, K., Ray, A. J., et al. (2019). Drought in urban water systems: Learning lessons for climate adaptive capacity. Clim. Risk Manag. 23, 32–42. doi:10.1016/j.crm.2018.11.001

CrossRef Full Text | Google Scholar

Donnelly, K., and Cooley, H. (2015). Water Use Trends. Oakland, California: Pacific Institute.

Ekström, M., Grose, M. R., and Whetton, P. H. (2015). An appraisal of downscaling methods used in climate change research. Wires Clim. Change 6 (3), 301–319. doi:10.1002/wcc.339

CrossRef Full Text | Google Scholar

Forster, P. M., Maycock, A. C., McKenna, C. M., and Smith, C. J. (2020). Latest Climate Models Confirm Need for Urgent Mitigation. Nat. Clim. Chang. 10 (1), 7–10. doi:10.1038/s41558-019-0660-0

CrossRef Full Text | Google Scholar

Foti, R., Ramirez, J. A., and Brown, T. C. (2012). Vulnerability of US water supply to shortage: a technical document supporting the Forest Service 2010 RPA Assessment. Gen. Tech. Rep. RMRS-GTR-295, 147. Fort Collins, CO: US Department of Agriculture, Forest Service, Rocky Mountain Research Station, 295.

Gober, P., Quay, R., and Larson, K. L. (2016). Outdoor Water Use as an Adaptation Problem: Insights from North American Cities. Water Resour. Manage. 30 (3), 899–912. doi:10.1007/s11269-015-1205-6

CrossRef Full Text | Google Scholar

Goss, M., Swain, D. L., Abatzoglou, J. T., Sarhadi, A., Kolden, C. A., Williams, A. P., et al. (2020). Climate Change is Increasing the Likelihood of Extreme Autumn Wildfire Conditions Across California. Environ. Res. Lett. 15 (9), 094016. doi:10.1088/1748-9326/ab83a7

CrossRef Full Text | Google Scholar

Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F. (2009). Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 377 (1-2), 80–91. doi:10.1016/j.jhydrol.2009.08.003

CrossRef Full Text | Google Scholar

Hart, O. E., and Halden, R. U. (2019). On the need to integrate uncertainty into U.S. water resource planning. Sci. Total Environ. 691, 1262–1270. doi:10.1016/j.scitotenv.2019.07.164

PubMed Abstract | CrossRef Full Text | Google Scholar

Hauer, M. E. (2019). Population projections for U.S. counties by age, sex, and race controlled to shared socioeconomic pathway. Sci. Data 6 (1), 190005–190015. doi:10.1038/sdata.2019.5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoegh-Guldberg, O., Jacob, D., Bindi, M., Brown, S., Camilloni, I., Diedhiou, A., et al. (2018). Impacts of 1.5 C global warming on natural and human systems. Global warming of 1.5 C. An IPCC Special Report. Geneva: IPCC Secretariat.

Hong, C.-y., and Chang, H. (2014). Uncovering the influence of household sociodemographic and behavioral characteristics on summer water consumption in the Portland Metropolitan Area. Int. J. Geospatial Environ. Res. 1 (2), 2.

Google Scholar

Howitt, R., MacEwan, D., Medellín-Azuara, J., Lund, J., and Sumner, D. (2015). “Economic analysis of the 2015 drought for California agriculture. UC Davis Center for Watershed Sciences,” in ERA, Economics (California: UC Agricultural Issues Center CA).

Google Scholar

Hurd, B., Leary, N., Jones, R., and Smith, J. (1999). Relative Regional Vulnerability of Water Resources to Climate Change. J. Am. Water Resour. Assoc 35 (6), 1399–1409. doi:10.1111/j.1752-1688.1999.tb04224.x

CrossRef Full Text | Google Scholar

Islam, M. A., and Cartwright, N. (2020). Evaluation of climate reanalysis and space-borne precipitation products over Bangladesh. Hydrological Sci. J. 65 (7), 1112–1128. doi:10.1080/02626667.2020.1730845

CrossRef Full Text | Google Scholar

Ivancic, T. J., and Shaw, S. B. (2017). Identifying spatial clustering in change points of streamflow across the contiguous U.S. between 1945 and 2009. Geophys. Res. Lett. 44 (5), 2445–2453. doi:10.1002/2016gl072444

CrossRef Full Text | Google Scholar

Jehn, F. U., Bestian, K., Breuer, L., Kraft, P., and Houska, T. (2020). Using hydrological and climatic catchment clusters to explore drivers of catchment behavior. Hydrol. Earth Syst. Sci. 24 (3), 1081–1100. doi:10.5194/hess-24-1081-2020

CrossRef Full Text | Google Scholar

Jones, C. N., Ameli, A., Neff, B. P., Evenson, G. R., McLaughlin, D. L., Golden, H. E., et al. (2019). Modeling Connectivity of Non‐floodplain Wetlands: Insights, Approaches, and Recommendations. J. Am. Water Resour. Assoc. 55 (3), 559–577. doi:10.1111/1752-1688.12735

CrossRef Full Text | Google Scholar

Katz, R. (2002). Techniques for estimating uncertainty in climate change scenarios and impact studies. Clim. Res. 20 (2), 167–185. doi:10.3354/cr020167

CrossRef Full Text | Google Scholar

Keilman, N. (2020). Uncertainty in population forecasts for the twenty-first century. Ann. Rev. Res. Econ. 12, 449–470.

CrossRef Full Text | Google Scholar

Kling, H., Fuchs, M., and Paulin, M. (2012). Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 424-425, 264–277. doi:10.1016/j.jhydrol.2012.01.011

CrossRef Full Text | Google Scholar

Knoben, W. J. M., Woods, R. A., and Freer, J. E. (2018). A Quantitative Hydrological Climate Classification Evaluated with Independent Streamflow Data. Water Resour. Res. 54 (7), 5088–5109. doi:10.1029/2018wr022913

CrossRef Full Text | Google Scholar

Kovach, R. P., Dunham, J. B., Al-Chokhachy, R., Snyder, C. D., Letcher, B. H., Young, J. A., et al. (2019). An integrated framework for ecological drought across riverscapes of North America. BioScience 69 (6), 418–431. doi:10.1093/biosci/biz040

CrossRef Full Text | Google Scholar

Lafon, T., Dadson, S., Buys, G., and Prudhomme, C. (2013). Bias correction of daily precipitation simulated by a regional climate model: a comparison of methods. Int. J. Climatol. 33 (6), 1367–1381. doi:10.1002/joc.3518

CrossRef Full Text | Google Scholar

Lawrence, M. G. (2005). The relationship between relative humidity and the dewpoint temperature in moist air: A simple conversion and applications. Bull. Amer. Meteorol. Soc. 86 (2), 225–234. doi:10.1175/bams-86-2-225

CrossRef Full Text | Google Scholar

Maas, A., Dozier, A., Manning, D. T., and Goemans, C. (2017). Water storage in a changing environment: The impact of allocation institutions on value. Water Resour. Res. 53 (1), 672–687. doi:10.1002/2016wr019239

CrossRef Full Text | Google Scholar

MacDonald, G. M., Stahle, D. W., Diaz, J. V., Beer, N., Busby, S. J., Cerano-Paredes, J., et al. (2008). Climate Warming and 21st-Century Drought in Southwestern North America. Eos Trans. AGU 89 (9), 82. doi:10.1029/2008eo090003

CrossRef Full Text | Google Scholar

MacDonald, G. M. (2010). Water, climate change, and sustainability in the southwest. Proc. Natl. Acad. Sci. 107 (50), 21256–21262. doi:10.1073/pnas.0909651107

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahat, V., Ramírez, J. A., and Brown, T. C. (2017). Twenty-first-century climate in CMIP5 simulations: implications for snow and water yield across the contiguous United States. J. Hydrometeorology 18 (8), 2079–2099. doi:10.1175/jhm-d-16-0098.1

CrossRef Full Text | Google Scholar

Mankin, J. S., Viviroli, D., Singh, D., Hoekstra, A. Y., and Diffenbaugh, N. S. (2015). The potential for snow to supply human water demand in the present and future. Environ. Res. Lett. 10 (11), 114016. doi:10.1088/1748-9326/10/11/114016

CrossRef Full Text | Google Scholar

March, H., and Saurí, D. (2010). The suburbanization of water scarcity in the Barcelona metropolitan region: Sociodemographic and urban changes influencing domestic water consumption. The Prof. Geographer 62 (1), 32–45. doi:10.1080/00330120903375860

CrossRef Full Text | Google Scholar

Maurer, E. P., and Duffy, P. B. (2005). Uncertainty in projections of streamflow changes due to climate change in California. Geophys. Res. Lett. 32 (3), L03704. doi:10.1029/2004gl021462

CrossRef Full Text | Google Scholar

Mei, C., Liu, J., Wang, H., Yang, Z., Ding, X., and Shao, W. (2018). Integrated assessments of green infrastructure for flood mitigation to support robust decision-making for sponge city construction in an urbanized watershed. Sci. Total Environ. 639, 1394–1407. doi:10.1016/j.scitotenv.2018.05.199

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendoza, P. A., Wood, A. W., Clark, E., Rothwell, E., Clark, M. P., Nijssen, B., et al. (2017). An intercomparison of approaches for improving operational seasonal streamflow forecasts. Hydrol. Earth Syst. Sci. 21 (7), 3915–3935. doi:10.5194/hess-21-3915-2017

CrossRef Full Text | Google Scholar

Moss, R. H., Edmonds, J. A., Hibbard, K. A., Manning, M. R., Rose, S. K., Van Vuuren, D. P., et al. (2010). The next generation of scenarios for climate change research and assessment. Nature 463 (7282), 747–756. doi:10.1038/nature08823

PubMed Abstract | CrossRef Full Text | Google Scholar

Nilsson, B., Højberg, A. L., Refsgaard, J. C., and Troldborg, L. (2007). Uncertainty in geological and hydrogeological data. Hydrol. Earth Syst. Sci. 11 (5), 1551–1561. doi:10.5194/hess-11-1551-2007

CrossRef Full Text | Google Scholar

Opalinski, N. F., Bhaskar, A. S., and Manning, D. T. (2020). Spatial and Seasonal Response of Municipal Water Use to Weather across the Contiguous U.S. J. Am. Water Resour. Assoc. 56 (1), 68–81. doi:10.1111/1752-1688.12801

CrossRef Full Text | Google Scholar

Özerol, G., Dolman, N., Bormann, H., Bressers, H., Lulofs, K., and Böge, M. (2020). Urban water management and climate change adaptation: A self-assessment study by seven midsize cities in the North Sea Region. Sust. Cities Soc. 55, 102066. doi:10.1016/j.scs.2020.102066

CrossRef Full Text | Google Scholar

Pool, S., Vis, M., and Seibert, J. (2018). Evaluating model performance: towards a non-parametric variant of the Kling-Gupta efficiency. Hydrological Sci. J. 63 (13-14), 1941–1953. doi:10.1080/02626667.2018.1552002

CrossRef Full Text | Google Scholar

Radić, V., and Clarke, G. K. (2011). Evaluation of IPCC models’ performance in simulating late-twentieth-century climatologies and weather patterns over North America. J. Clim. 24 (20), 5257–5274.

Google Scholar

Rajagopal, S., and Harpold, A. A. (2016). Testing and improving temperature thresholds for snow and rain prediction in the Western United States. J. Am. Water Resour. Assoc. 52 (5), 1142–1154. doi:10.1111/1752-1688.12443

CrossRef Full Text | Google Scholar

Ramey, J. A. (2014). noncensus: U.S. Census Regional and Demographic Data. 1 ed. Vienna: CRAN.

Rasifaghihi, N., Li, S. S., and Haghighat, F. (2020). Forecast of urban water consumption under the impact of climate change. Sust. Cities Soc. 52, 101848. doi:10.1016/j.scs.2019.101848

CrossRef Full Text | Google Scholar

Razavi, T., and Coulibaly, P. (2013). Streamflow prediction in ungauged basins: review of regionalization methods. J. Hydrol. Eng. 18 (8), 958–975. doi:10.1061/(asce)he.1943-5584.0000690

CrossRef Full Text | Google Scholar

Reid, A. J., Carlson, A. K., Creed, I. F., Eliason, E. J., Gell, P. A., Johnson, P. T. J., et al. (2019). Emerging threats and persistent conservation challenges for freshwater biodiversity. Biol. Rev. 94 (3), 849–873. doi:10.1111/brv.12480

PubMed Abstract | CrossRef Full Text | Google Scholar

Ritchie, H., and Roser, M. (2017). Water use and stress. Oxford: Our World in Data.

Rosegrant, M. W., and Cai, X. (2002). Global Water Demand and Supply Projections. Water Int. 27 (2), 170–182. doi:10.1080/02508060208686990

CrossRef Full Text | Google Scholar

Roy, S. B., Chen, L., Girvetz, E. H., Maurer, E. P., Mills, W. B., and Grieb, T. M. (2012). Projecting Water Withdrawal and Supply for Future Decades in the U.S. under Climate Change Scenarios. Environ. Sci. Technol. 46 (5), 2545–2556. doi:10.1021/es2030774

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruth, M., Bernier, C., Jollands, N., and Golubiewski, N. (2007). Adaptation of urban water supply infrastructure to impacts from climate and socioeconomic changes: the case of Hamilton, New Zealand. Water Resour. Manage. 21 (6), 1031–1045. doi:10.1007/s11269-006-9071-x

CrossRef Full Text | Google Scholar

Saadi, M., Oudin, L., and Ribstein, P. (2019). Random forest ability in regionalizing hourly hydrological model parameters. Water 11 (8), 1540. doi:10.3390/w11081540

CrossRef Full Text | Google Scholar

Sabo, J. L., Sinha, T., Bowling, L. C., Schoups, G. H. W., Wallender, W. W., Campana, M. E., et al. (2010). Reclaiming freshwater sustainability in the Cadillac Desert. Proc. Natl. Acad. Sci. 107 (50), 21263–21269. doi:10.1073/pnas.1009734108

PubMed Abstract | CrossRef Full Text | Google Scholar

Sawicz, K., Wagener, T., Sivapalan, M., Troch, P. A., and Carrillo, G. (2011). Catchment classification: empirical analysis of hydrologic similarity based on catchment function in the eastern USA. Hydrol. Earth Syst. Sci. 15 (9), 2895–2911. doi:10.5194/hess-15-2895-2011

CrossRef Full Text | Google Scholar

Schwalm, C. R., Williams, C. A., Schaefer, K., Baldocchi, D., Black, T. A., Goldstein, A. H., et al. (2012). Reduction in carbon uptake during turn of the century drought in western North America. Nat. Geosci 5 (8), 551–556. doi:10.1038/ngeo1529

CrossRef Full Text | Google Scholar

Seguro, J. V., and Lambert, T. W. (2000). Modern estimation of the parameters of the Weibull wind speed distribution for wind energy analysis. J. wind Eng. Ind. aerodynamics 85 (1), 75–84. doi:10.1016/s0167-6105(99)00122-1

CrossRef Full Text | Google Scholar

Semenov, M., Brooks, R., Barrow, E., and Richardson, C. (1998). Comparison of the WGEN and LARS-WG stochastic weather generators for diverse climates. Clim. Res. 10 (2), 95–107. doi:10.3354/cr010095

CrossRef Full Text | Google Scholar

Shamir, E., Megdal, S. B., Carrillo, C., Castro, C. L., Chang, H.-I., Chief, K., et al. (2015). Climate change and water resources management in the Upper Santa Cruz River, Arizona. J. Hydrol. 521, 18–33. doi:10.1016/j.jhydrol.2014.11.062

CrossRef Full Text | Google Scholar

Shen, C. (2018). A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 54 (11), 8558–8593. doi:10.1029/2018wr022643

CrossRef Full Text | Google Scholar

Statistics Canada (2019a). Population estimates, July 1, by census subdivision, 2016 boundaries. Available at: https://www150.statcan.gc.ca/t1/tbl1/en/tv.action?pid=1710014201.

Statistics Canada (2019b). Census division 2016. Available at: https://open.canada.ca/data/en/dataset/883964ca-be79-4d0d-ba9e-68babe59624e.

Stoker, P., and Rothfeder, R. (2014). Drivers of urban water use. Sust. Cities Soc. 12, 1–8. doi:10.1016/j.scs.2014.03.002

CrossRef Full Text | Google Scholar

Sugg, M., Runkle, J., Leeper, R., Bagli, H., Golden, A., Handwerger, L. H., et al. (2020). A scoping review of drought impacts on health and society in North America. Climatic Change, 1–19. doi:10.1007/s10584-020-02848-6

CrossRef Full Text | Google Scholar

Tanaka, S. K., Zhu, T., Lund, J. R., Howitt, R. E., Jenkins, M. W., Pulido, M. A., et al. (2006). Climate warming and water management adaptation for California. Climatic Change 76 (3), 361–387. doi:10.1007/s10584-006-9079-5

CrossRef Full Text | Google Scholar

Taylor, K. E., Stouffer, R. J., and Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93 (4), 485–498. doi:10.1175/bams-d-11-00094.1

CrossRef Full Text | Google Scholar

Tellman, B., Schank, C., Schwarz, B., Howe, P. D., and de Sherbinin, A. (2020). Using Disaster Outcomes to Validate Components of Social Vulnerability to Floods: Flood Deaths and Property Damage across the USA. Sustainability 12 (15), 6006. doi:10.3390/su12156006

CrossRef Full Text | Google Scholar

Teutschbein, C., and Seibert, J. (2012). Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 456-457, 12–29. doi:10.1016/j.jhydrol.2012.05.052

CrossRef Full Text | Google Scholar

Thiemig, V., Rojas, R., Zambrano-Bigiarini, M., and De Roo, A. (2013). Hydrological evaluation of satellite-based rainfall estimates over the Volta and Baro-Akobo Basin. J. Hydrol. 499, 324–338. doi:10.1016/j.jhydrol.2013.07.012

CrossRef Full Text | Google Scholar

Tian, Y., Peters‐Lidard, C. D., Eylander, J. B., Joyce, R. J., Huffman, G. J., Adler, R. F., et al. (2009). Component analysis of errors in satellite‐based precipitation estimates. J. Geophys. Res. Atmospheres 114 (D24), D24101. doi:10.1029/2009jd011949

CrossRef Full Text | Google Scholar

United States Census Bureau (2019). City and Town Population Totals. Available at: https://www.census.gov/data/tables/time-series/demo/popest/2010s-total-cities-and-towns.html.

US Geological Survey (2019). USGS surface water data for the nation. Available at: https://waterdata.usgs.gov/nwis/sw.

Van Vuuren, D. P., Edmonds, J., Kainuma, M., Riahi, K., Thomson, A., Hibbard, K., et al. (2011). The representative concentration pathways: an overview. Climatic change 109 (1), 5–31. doi:10.1007/s10584-011-0148-z

CrossRef Full Text | Google Scholar

Walter, I. A., Allen, R. G., Elliott, R., Jensen, M., Itenfisu, D., Mecham, B., et al. (2000). ASCE's standardized reference evapotranspiration equation. Watershed Manag. operations Manag. 2000, 1–11.

Google Scholar

Ward, J. H. (1963). Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 58 (301), 236–244. doi:10.1080/01621459.1963.10500845

CrossRef Full Text | Google Scholar

Water Survey of Canada (2019). National Water Data Archive: HYDAT. Available: https://www.canada.ca/en/environment-climate-change/services/wateroverview/quantity/monitoring/survey/data-products-services/nationalarchive-hydat.html#shr-pg0.

Wilks, D. S., and Wilby, R. L. (1999). The weather generation game: a review of stochastic weather models. Prog. Phys. Geogr. 23 (3), 329–357. doi:10.1191/030913399666525256

CrossRef Full Text | Google Scholar

Wong, J. S., Zhang, Q., and Chen, Y. D. (2010). Statistical modeling of daily urban water consumption in Hong Kong: Trend, changing patterns, and forecast. Water Resour. Res. 46 (3), W03506. doi:10.1029/2009wr008147

CrossRef Full Text | Google Scholar

Xu, Y. (2015). Hyfo: hydrology and climate forecasting R Package for data analysis and visualization. Available at: https://cran.r-project.org/web/packages/hyfo/index.html.

Yang, T.-H., and Liu, W.-C. (2020). A General overview of the risk-reduction strategies for floods and droughts. Sustainability 12 (7), 2687. doi:10.3390/su12072687

CrossRef Full Text | Google Scholar

Yang, T., Shi, P., Yu, Z., Li, Z., Wang, X., and Zhou, X. (2016). Probabilistic modeling and uncertainty estimation of urban water consumption under an incompletely informational circumstance. Stoch Environ. Res. Risk Assess. 30 (2), 725–736. doi:10.1007/s00477-015-1081-x

CrossRef Full Text | Google Scholar