
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 09 September 2021
Sec. Geochemistry
Volume 9 - 2021 | https://doi.org/10.3389/feart.2021.691699
This article is part of the Research TopicStrontium Isotope GeochemistryView all 5 articles
The δ18O values of submarine vent fluids are controlled by seawater-basalt exchange reactions, temperature of exchange, and to a lesser extent, by phase separation. These variations are translated into the δ18O values of submarine hydrothermal fluids between ca. 0 and + 4‰, a range defined by pristine seawater and equilibrium with basalt. Triple oxygen isotope systematics of submarine fluids remains underexplored. Knowing how δ17O and δ18O change simultaneously during seawater-basalt reaction has a potential to improve i) our understanding of sub-seafloor processes and ii) the rock-based reconstructions of ancient seawater. In this paper, we introduce the first combined δ17O-δ18O-87Sr/86Sr dataset measured in fluids collected from several high-temperature smoker- and anhydrite-type vent sites at the Axial Seamount volcano in the eastern Pacific Ocean. This dataset is supplemented by measurements of major, trace element concentrations and pH indicating that the fluids have reacted extensively with basalt. The salinities of these fluids range between 30 and 110% of seawater indicating that phase separation is an important process, potentially affecting their δ18O. The 87Sr/86Sr endmember values range between 0.7033 and 0.7039. The zero-Mg endmember δ18O values span from -0.9 to + 0.8‰, accompanied by the Δ′17O0.528 values ranging from around 0 to −0.04‰. However, the trajectory at individual site varies. The endmember values of fluids from focused vents exhibit moderate isotope shifts in δ′18O up to +0.8‰, and the shifts in Δ′17O are small, about −0.01‰. The diffuse anhydrite-type vent sites produce fluids that are significantly more scattered in δ′18O—Δ′17O space and cannot be explained by simple isothermal seawater-basalt reactions. To explain the observed variations and to provide constraints on more evolved fluids, we compute triple O isotope compositions of fluids using equilibrium calculations of seawater-basalt reaction, including a non-isothermal reaction that exemplifies complex alteration of oceanic crust. Using a Monte-Carlo simulation of the dual-porosity model, we show a range of possible simultaneous triple O and Sr isotope shifts experienced by seawater upon reaction with basalt. We show the possible variability of fluid values, and the causal effects that would normally be undetected with conventional δ18O measurements.
Intimately linked to generation and alteration of oceanic crust, seawater-basalt reaction at mid-ocean ridges is an essential player in partitioning of elements between the hydrosphere and silicate crust on our planet. Oxygen isotopes are traditionally used to trace the progress of seawater-basalt reaction by measuring fluids that emerge from submarine hydrothermal systems (Shanks and Seyfried, 1987; Von Damm et al., 1997; Shanks, 2001). The 18O/16O ratio in mid-ocean ridge basalts and seawater significantly differ from the equilibrium values at the temperature of hydrothermal interaction of ca. 350°C. Consequently, the exchange between seawater and basaltic rocks leads to production of vent fluids (e.g. at black smoker sites) that are 1–2‰ higher in δ18O than ambient seawater (Shanks, 2001). High-temperature altered rocks complement the shift with opposite sign. That is to say that high-temperature altered basalts are 1–2‰ lower compared to the unaltered mid-ocean ridge basalt (Alt et al., 1996). Expressed in δ18O, VSMOW altered rocks from the sheeted dike complex of ocean floor range between + 4 and + 5‰, which is low compared to ca. 6‰ of fresh basalt (Alt et al., 1996; Alt and Teagle, 2000; Eiler, 2001). Previous studies of ancient altered basalts from ophiolites (Gregory and Taylor, 1981; Schiffman and Smith, 1988; Alt and Teagle, 2000) also show a complementary shift in the δ18O values of high-temperature altered oceanic crust indicating that ancient vent fluids emerged several ‰ higher in 18O/16O ratio compared to contemporaneous seawater. These high-temperature altered rocks make up 2–3 km thick zones of oceanic crust located below the low-temperature altered pillow basalts (Alt and Teagle, 2000), and act as the most voluminous flux of exchanged oxygen in the terrestrial hydrosphere (Muehlenbachs, 1998). Meanwhile, the upper several hundred meters of pillow basalts are altered at low temperature and the accompanying δ18O values are high, between + 6 and 12‰, much higher than that of unaltered mid-ocean ridge basalt (hereinafter MORB). Together, these changes in the composition of altered oceanic crust provide a major control on the oxygen isotope composition of seawater over the geological timescale (Muehlenbachs and Clayton, 1976; Muehlenbachs, 1998).
However, for reconstructions of paleo-vent fluids, the traditionally measured δ18O in minerals sampled from ophiolites and ancient hydrothermally altered rocks cannot be uniquely translated into the δ18O of co-existing water. That is due to the apriori unknown temperature of exchange and due the unknown amount of basalt reacted with seawater. The latter is commonly expressed as water-rock ratio (W/R hereinafter). The composition of emerging vent fluid (δ18Ofluid) is modified according to the mass ratio of exchanged oxygen in the water (in this case seawater) to that of the rock (W/R). This can be expressed as (see Ohmoto and Rye, 1974):
where Δrock-water is the isotope fractionation between secondary minerals and equilibrium fluid, which varies on the order of ca. 1–3‰ at hydrothermal temperatures (250–400°C). Thus, at W/R = 1, the δ18Ofluid would be shifted about + 1.6‰ compared to initial seawater. The concept of W/R was originally explored in early studies of hydrothermal systems (Sheppard et al., 1969; Ohmoto and Rye, 1974; Taylor, 1977), yet this parameter still remains elusive and difficult to attribute to physical and chemical processes that accompany reactive fluid circulation.
Thus, the same isotope ratio of a mineral can be resulted from different combinations of variable initial fluids (e.g. Cenozoic vs modern seawater), W/R and temperature-dependent fractionation, which together result in δ18O variations on the order of ± 2‰ (Gregory and Taylor, 1981; Bowers and Taylor, 1985). Moreover, measured δ18O of vent fluids reflect space- and time-integrated exchange reactions at different temperatures. Downward traveling fluids likely undergo exchange reactions at low-temperatures at first, then at high-temperature at depth before emerging at the vent sites. Further complication is created by phase separation of vent fluids close to the seafloor interface into low-salinity vapor and high-salinity brines. The oxygen isotope fractionation between the vapor and brine can produce 0.1–2‰ changes (Shmulovich et al., 1999), a range similar to the magnitude of variations produced by seawater-basalt reactions at different W/R. Consequently, the ± 2‰ variations in the fluid values would translate into systematic errors on the order of 50–70°C for quartz-water oxygen isotope thermometer (e.g. Sharp et al., 2016) under hydrothermal conditions (∼350°C) if the fluids isotope composition treated as a fixed value. This proneness to erroneous interpretation is an eternal issue when dealing with conventual δ18O values measured in mineral species without additional constraints on the fluid composition or the temperature. Thus, it is important to resolve these processes as it would assist understanding i) how hydrothermal systems evolve over time and space and ii) how seawater δ18O might have changed on the geological scale since the hydrothermal flux of exchanged oxygen is large (Muehlenbachs, 1998).
The recent advances in measuring 17O/16O and 18O/16O with high precision (±0.01‰ or better) present a promising approach to monitor both temperature and progress of seawater-basalt reactions in hydrothermal systems (Herwartz et al., 2015; Sharp et al., 2016; Wostbrock et al., 2018; Zakharov et al., 2019). More precisely, the trajectories of seawater-basalt isotope exchange expressed in triple oxygen isotope coordinates is distinct from temperature-dependent fractionation. This distinction creates a measurable difference between minerals that precipitated in equilibrium with pure seawater and the minerals that precipitated from hydrothermal fluids (Zakharov et al., 2019; Zakharov et al., 2021b; Herwartz, 2021). The trajectory of triple oxygen isotope seawater-basalt exchange can be generally outlined based on the measurements of the fresh and altered MORBs, and from understanding of mineral-water fractionation of triple oxygen isotope ratios at high temperatures (Matsuhisa et al., 1978; Pack and Herwartz, 2014). Being close to the value of VSMOW (Vienna Standard Mean Oceanic Water) used in delta-notation, seawater δ17O, δ18O and Δ′17O values are 0‰, while the fresh unaltered MORB has δ18O of +5.6‰ and Δ′17O of around −0.05‰ (Pack et al., 2016). In this paper, we adopt the linearized δ-notation expressed as:
while Δ′17O is the δ′17O-excess from a reference line with a slope 0.528:
Thus, it was suggested that the fluids that underwent high-temperature exchange with oceanic crust are shifted positively in δ′18O and negatively in Δ′17O due to high-temperature exchange reactions (Sengupta and Pack, 2018).
Despite the promising insights carried by the relatively novel isotope system, no previous studies reported δ′18O—Δ′17O values of high-temperature submarine vent fluids to our knowledge. In this paper we explore the triple oxygen isotope ratios measured in submarine vent fluids from the Axial Seamount of the Juan de Fuca Ridge that underwent oxygen isotope exchange with MORBs. The chemical compositions of high-temperature submarine vent fluids are controlled primarily by subseafloor fluid-mineral equilibrium reactions and are also affected by phase separation. At Axial Seamount, there are two clearly distinct vent types: 1) vapor-dominated vents with relatively low dissolved metal and high gas content that form small anhydrite mounds and 2) near-seawater salinity metal-rich vents forming metal sulfide chimneys (Butterfield et al., 1990; Butterfield et al., 2004). With the roof of the Axial Seamount magma chamber at depths of 1.1 to 2.3 km below seafloor (Arnulf et al., 2014), both fluid types are produced in high-temperature reaction zones at pressures between 380 and 150 bars. Major elemental concentrations (Cl, Mg, Ca, Na, K, Si, Fe, S) were measured in the same samples to guide our interpretation of the oxygen isotope ratios. These determinations aid in tracing the effects of seawater-basalt reaction, subseafloor phase separation and the influence of locally admixed seawater. In addition, to track the progress of seawater-basalt exchange we complemented this dataset by 87Sr/86Sr measurements, an isotope ratio that is virtually insensitive to temperature-dependent fractionation.
To provide the basis for the expected isotope shifts in the δ′18O—Δ′17O space we perform a simple static seawater-basalt equilibrium reaction calculation. We calculate the triple oxygen isotope values of the fluids in equilibrium with green-schist facies mineral assemblages at 350°C and water-rock ratios close to those recorded in the natural samples. Further, we explore the changes in the δ′18O—Δ′17O values of fluids when seawater-basalt reaction proceeds under non-isothermal conditions using a model calculation at 150°C and 350°C with an intermediate fractionation step. In addition, using a statistical approach to the dual-porosity modeling, we show what can be expected in the δ′18O—Δ′17O—87Sr/86Sr coordinates. Such approach permits constraining reactive circulation models that shed light on flow parameters such as fracture spacing, reaction rates, porosity, and fluid velocity (Baumgartner and Rumble, 1988; Bickle and Baker, 1990; DePaolo, 2006).
Axial Seamount is located on the Juan De Fuca ridge in the Northeast Pacific, 250 n. mi. west of Astoria, Oregon (Figure 1). Hydrothermal fluids from the ASHES, International District, and Coquille vent fields located in the southern half of the Axial Seamount caldera were collected for this study during a single research cruise in 2017, using the Hydrothermal Fluid and Particle Sampler (HFPS, Butterfield et al., 2004) attached to the remotely operated vehicle Jason. Fluids were collected in titanium piston samplers with Teflon seals. Measured vent temperatures ranged from 173 to 341°C. Samples for oxygen isotope analysis were syringe filtered through 0.2-micron sterile filters and stored in HDPE bottles that were previously acid-cleaned, rinsed with deionized water, and air-dried. Unfiltered water was stored in acid-cleaned HDPE bottles for shore-based analysis of major, minor, and trace elements. Fluid samples collected in the field were processed and analyzed on board ship for pH, dissolved silica and total dissolved sulfide. Fluid pH was measured with a glass electrode at lab temperature (22°C) using NBS buffers for calibration. Total dissolved sulfide and dissolved silica were analyzed on board by spectrophotometry. Major, minor, and trace elements were analyzed on shore by ion chromatography, ICP-OES, and ICPMS at NOAA/PMEL and the University of Washington.
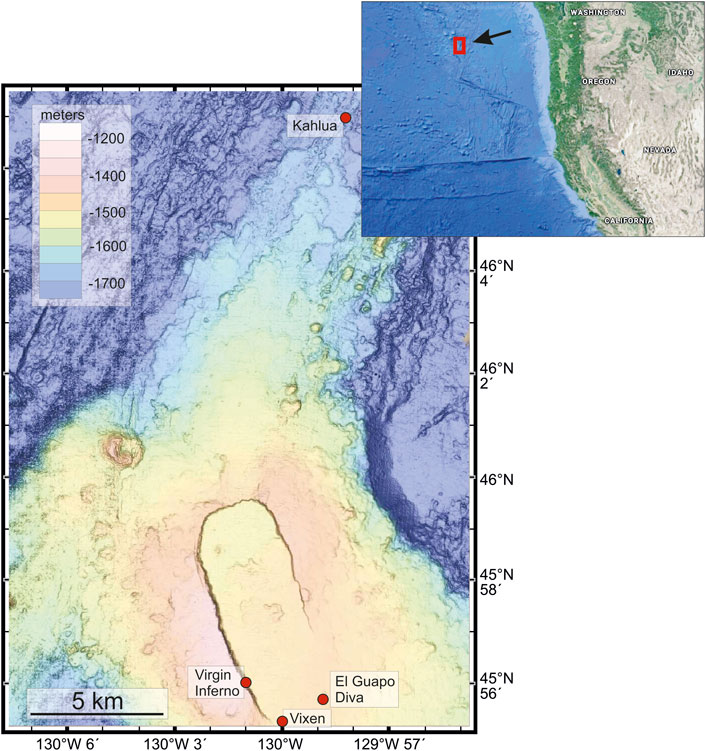
FIGURE 1. The location of the Axial Seamount volcano on the Juan de Fuca ridge of the cost of the western U.S. is shown in the inset. The bathymetry map (Wilcock et al., 2018) of the caldera is shown with the location of the vent sites used in this study. The vent fluids from sites Virgin, Inferno, Vixen, El Guapo, and Diva are presented in this paper. The Kahlua vent fluids are not presented in this study.
Triple oxygen isotope compositions of the fluids were determined at the PML, Okayama University, Japan using the fluorination line with a Ni-reactor tube. For these and Sr-isotope measurements, we used chemically untreated but filtered samples. A few microliters of fluid samples were injected into the injection port that includes a septum, cold trap, Ni-tube and two valves. The samples were introduced through the septum via a gas-tight syringe. The sample was then transferred to the Ni-tube to react with BrF5 at 250°C to liberate O2. The rest of the procedure includes several cryogenic purification steps, a fluorine trap with KBr and gas chromatography as described by Tanaka and Nakamura (2013) and (Pack et al., 2016). The resulted O2 gas was measured using the mass spectrometer MAT 253 connected to the fluorination line via a dual-inlet interface. The δ18O and δ17O of fluid samples were calibrated to the VSMOW2-SLAP2 scale using the VSMOW2 (δ′17OVSMOW2 ≡ 0 ± 0.090 and δ′18OVSMOW2 ≡ 0 ± 0.167, 2SD, N = 6) and SLAP2 (δ′17OVSMOW2 = -30.117 and δ′18OVSMOW2 = -57.097, N = 1) values measured during this study. The long-term instrumental reproducibility (2SD) defined by repeated measurements over 2 years of δ17O, δ18O and Δ′17O are 0.106, 0.197, and 0.051‰ for VSMOW2 and 0.119, 0.190, and 0.016‰ for SLAP2.
The Sr isotope composition of fluids was determined by thermal ionization mass spectrometry (TIMS) at the PML, Okayama University. The detailed procedure for chemical separation and isotope measurement of Sr are described in Yoshikawa and Nakamura (1993). A 0.25 ml sample was mixed with 30M HF, 9.2M HClO4, and 16M HNO3, then agitated for overnight. After step-wised drying procedure (Yokoyama et al., 1999), the sample was dissolved with 6M HCl and dried, and finally dissolved in 4 M HCl. To determine the optimized sample/spike ratio, semi-quantitative Sr mass fraction was measured by quadrupole ICP-MS (Thermo Scientific iCAP TQ) using 5 vol. % of the sample aliquot by the calibration curve method. The rest 95 vol. % of the aliquot was mixed with 84Sr-enriched spike, and Sr was separated using the ion chromatography. The Sr mass fraction and isotopic compositions was determined by TIMS (Thermo Fisher Scientific Triton Plus) in static multi-collection mode after (Nakamura et al., 2003). Mean value and reproducibility obtained by analyses of NIST NBS987 was 0.710253 ± 0.000012 (2σ, n = 10), and result of the reference rock standard (JB2) treated by acid digestion was 0.703680 ± 0.000009 (n = 2). Total procedural blank is about 26 pg (n = 2).
To demonstrate the triple oxygen isotope effects of seawater-basalt reaction at different W/R, we undertake a simple batch equilibrium reaction calculation. We used the program CHIM-XPT (Reed et al., 2010) to simulate simultaneous reactions during a virtual titration experiment in which a small amount of basalt is incrementally added to 1,020 g (1L) of seawater and the solution yielding equilibrium concentrations of aqueous species and minerals. The W/R ratio is expressed as the mass ratio of initial seawater to the mass of titrated basalt. A Newton-Raphson method is used to solve for a system of mass-balance and mass-action equations. The calculations were carried out for T = 350°C and P = 300 bars, similar to the conditions envisioned for high-temperature alteration in the subseafloor of the oceanic crust (Alt et al., 1996). The initial chemical composition of reactants was taken as the average MORB (Gale et al., 2013) and seawater (Berner and Berner, 1996). The W/R of this model run range from infinity (pure seawater) to 0.06. At low W/R (∼0.1) the assemblage is dominated by composition of basalt at P and T.
Another slightly different version of this calculation was performed to incorporate possible effects of low-temperature interaction between seawater and oceanic crust during the early stages of alteration. The seawater-basalt reaction was first calculated at T = 150°C and P = 300 bars for W/R ranging between infinity (pure seawater) and 1. At W/R = 1, the fluid was fractionated from the solid and the seawater-basalt reaction proceeded at lower W/R at 350°C and 300 bars. This calculation exemplifies a more realistic computation of isotope shifts experienced by fluids traveling through different sections of altered oceanic crust.
The oxygen isotope values of minerals and fluids were calculated in a fashion similar to the study of Bowers and Taylor (1985). The δ18O of the fluid was calculated from the total molar oxygen budget of the reaction, and mole abundances of oxygen bonded in each phase, including H2O:
where n is the number of moles of oxygen contained in each part of the system and 18/16α is the individual mineral-water equilibrium fractionation (e.g. chlorite-water, epidote-water, quartz-water, etc.). The fractionation factors are taken from (Zheng, 1993a; Zheng, 1993b) for most silicate minerals. For brucite and smectites (e.g. Mg-nontronite) we adapted mineral-water fractionation factors from (Savin and Lee, 1988), from (Matsuhisa et al., 1979) for albite-water, from (O’Neil et al., 1969) for calcite-water, from (Feng and Savin, 1993) for zeolites-water (wairakite, stilbite, laumontite), and from (Lloyd, 1968) for anhydrite-water fractionation. Subscript min in Eq. 4 denotes equilibrium minerals forming during the seawater-basalt reaction and H2O stands for the equilibrium amount and isotope ratio of water. The same equation (Eq. 4) can be written for 17O/16O ratios with the appropriate 17/16α fractionation factor. However, unlike the traditional fractionation factors for 18O/16O ratios, the 17/16α is far less constrained. At equilibrium, the fractionation of triple oxygen isotope ratios is expressed through the relationship (17/16αmin-H2O) = (18/16αmin-H2O)θ. Here we work under the assumption that at the temperature of interest (350°C), the value of θ is approaching its high-temperature limit (0.5305; Matsuhisa et al., 1978). For quartz-water equilibrium, the value of θ is 0.5276 (Wostbrock et al., 2018) and it is likely to be slightly higher for other minerals at high-temperature (Cao and Liu, 2011; Hayles et al., 2018; Wostbrock and Sharp, 2021). For showing the possible variability of Δ′17O depending on this parameter we provide outputs for θ = 0.526 and θ = 0.530. These values likely encompass the high-temperature triple oxygen isotope mineral-water fractionation in hydrothermal systems. The computation of isotope shift in the non-isothermal model with intermittent fractionation of the fluid was the same as for the isothermal reaction described above. The Δ′17O was again computed from θ values. The θ values were taken as 0.525 and 0.527 for the low-temperature leg of the calculation (W/R = infinity to 1), and 0.527 and 0.529 for the high-temperature leg (W/R = 1 to 0.06).
When two element isotope systems (e.g. O and Sr) are used, the exact shape of the exchange trajectories are defined by the relative concentrations each element in the reactants, and the rates of their consumption/supply. Thus, to make a proper assessment of the two elemental isotope ratio evolution paths, we adopt the dual-porosity model from previous studies (e.g. DePaolo, 2006; Brown et al., 2013; Turchyn et al., 2013). We used the steady-state formulation of the model, which is expressed as the change in isotope ratio of the fluid with distance (Eq. 27 in DePaolo 2006):
where Di is the ionic diffusivity of a species i (e.g. self-diffusion of H2O, Sr2+), ϕm is porosity in the rock matrix, vf velocity of the fracture fluid, b is fracture spacing and d is fracture width. The last term of the equation defines the reactive length of a species (L in DePaolo 2006), where ρf, ρm, Cf, Cm, and R denote fluid or rock matrix density (subscripts f and m), concertation of an element of interest and the rate of recrystallization, respectively. Instead of using fixed values for the defining parameters (e.g. fracture spacing), we computed the output of the Eq. 5 for a reactive flow of seawater along the distance of several hundred meters in a fractured medium 10,000 times with the values of b, R, vf, and ϕm uniformly varied within the realistic ranges derived from previous studies of properties of oceanic crust (Fisher, 1998; DePaolo, 2006; Kadko et al., 2007). Namely, we accepted the ranges of values b = 1–10 m, R = 0.00005–0.0002 g g−1 yr−1, vf = 1–100 m/ yr, and ϕm = 0.01–0.02. These ranges are justified because the fracture spacing likely varies on the order of several meters (1 m), while the recrystallization rates vary on the order of 0.0001 yr−1 as constrained from reactive circulation of short-lived isotopes in active hydrothermal systems (Kadko and Moore, 1988; DePaolo, 2006; Kadko et al., 2007). Further, the ground water flow convects around intrusive bodies at rates anywhere between several meters a year, up to ∼100 m/ yr (Norton, 1978; Wood and Hewett, 1982; Hayba and Ingebritsen, 1997). The porosity of the rock (ϕm) is chosen to reflect a low-porosity basaltic matrix (e.g., Tsuji and Iturrino, 2008) that hosts permeable fractures.
The major element concentrations, pH and temperature of the vent of the fluid samples from Axial Seamount are reported in Table 1. The elemental concentrations and pH are plotted against Mg concentration in Figure 2 and are color-coded by the maximum temperature measured at each vent. Magnesium concentrations range from 2 to 33 mmol/ kg. The Mg concentrations are used here for outlining the mixing paths between the ambient seawater and undiluted zero-Mg vent fluids emanating from the subseafloor (Figure 2). The salinities of the zero-Mg endmembers range between 150 and 600 mmol/ kg Cl, corresponding to the range typical for submarine fluids from the Axial Seamount (Massoth et al., 1989; Butterfield et al., 1994). The Si concentration ranges from 6 to 15 mmol/ kg, with the highest values measured at high-temperature vents Vixen, Inferno, and El Guapo. Meanwhile Ca and Sr concentrations vary within 9–45 mmol/ kg and 48–212 μmol/ kg respectively. The endmember Sr values range between 10 and 250 μmol/ kg. Samples from Diva vent have Ca and Sr values lower than that of seawater and were likely affected by anhydrite precipitation (see Figure 2). The sulfide (H2S) content ranges between 1788 and 6,479 μmol/ kg, while Fe concentrations are between 5 and 1,440 μmol/ kg, with the highest values in El Guapo vent samples. Vent fluid pH ranges between 3.7 and 4.6 at lab temperature.
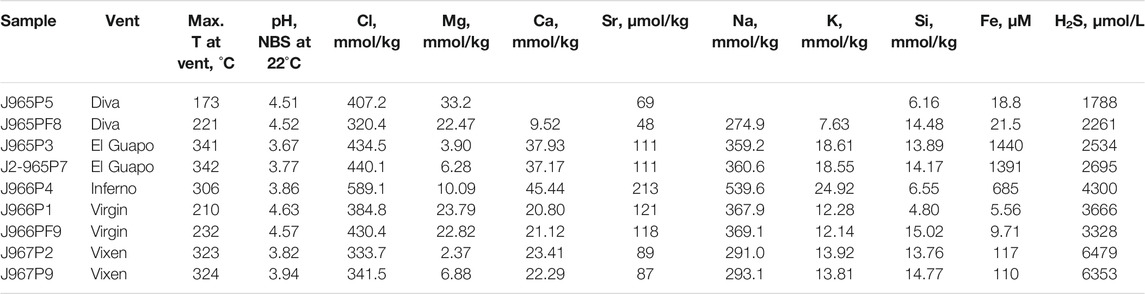
TABLE 1. Measured concentrations of chemical species in high-temperature hydrothermal fluids from the Axial Seamount.
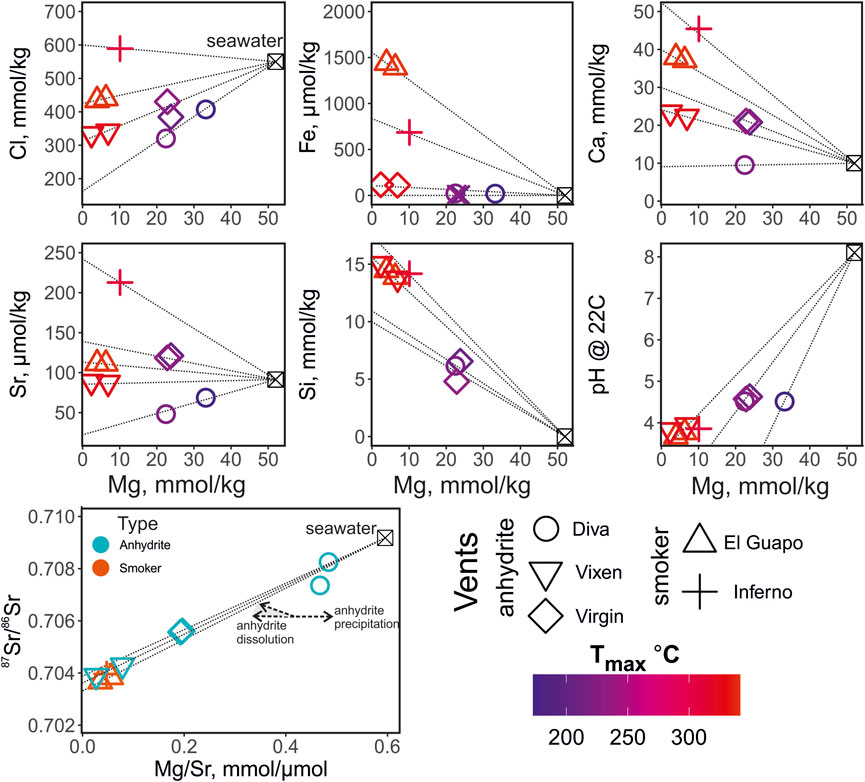
FIGURE 2. Elemental composition and pH of the vent fluids from the Axial Seamount color-coded by the maximum temperature measured at the vent (Tmax, °C). The thin dotted black lines show interpolation of the elemental concentration values from seawater (Mg = 52 mmol/ kg) to the hydrothermal fluid endmember compositions (0 mmol/ kg). The 87Sr/86Sr values are plotted against the Mg/Sr ratios to trace the zero-Mg endmember values and to distinguish anhydrite precipitation and dissolution. The anhydrite dissolution is shown with two arrows and the grey field indicating several possible trajectories due to the possible differences in 87Sr/86Sr of anhdrite. The symbols in the Mg/Sr—87Sr/86Sr plot are color coded by the type of the vent site (anhydrite- and smoker-types).
The δ′18O and Δ′17O values of the fluids are reported in Table 2. The range of δ′18O values between -0.7 and + 0.8‰ (see Figure 3). The lowest δ′18O values of ca. −0.7‰ are measured in Mg rich samples including the Diva vent fluids. The Δ′17O varies between −0.025 and + 0.018‰. The zero-Mg endmember δ′18O values are shown in Figure 3 and are reported in Table 3 along with the Cl endmember concentrations. The endmember Δ′17O values are calculated from regression of δ17O and δ18O values to zero-Mg content. The mixing arrays between seawater and endmembers in this case are linear. Moreover, the difference in δ18O and δ′18O values in our dataset is negligible, in the 4th digit after the decimal, due to the proximity of measured values to 0‰. The endmember δ′18O range between −0.9 and + 0.8‰, while the endmember Δ′17O values are mostly negative, ranging between −0.045 and + 0.007‰ (see Figure 4). The propagated uncertainties of the triple O isotope endmember values are given in Table 3. The uncertainties in zero-Mg endmember Δ′17O values were propagated using linear regression of sample uncertainties in δ17O and δ18O as shown in the Figure 3D. The estimated Δ′17O errors range between 0.01 and 0.04‰ depending on the amount of mixed seawater. The propagated δ′18O errors are substantially smaller, between 0.005 and 0.016‰ (see Table 3).
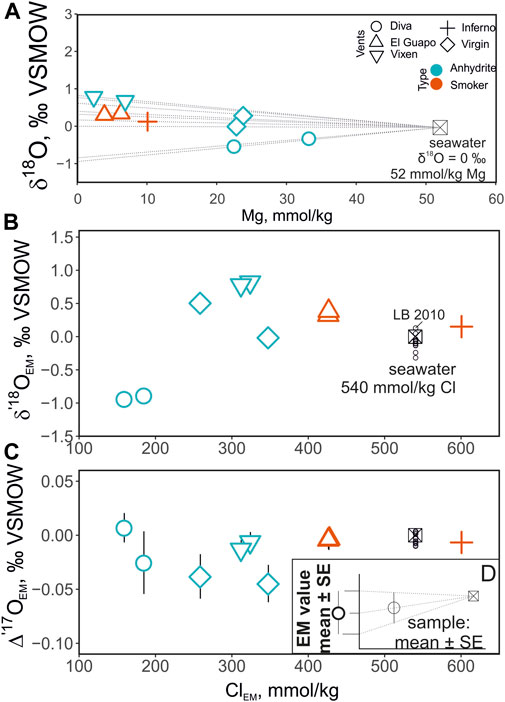
FIGURE 3. (A)—δ18O composition of the sampled fluids plotted as a function of Mg concentration. The points are color-coded by the vent type. The dashed lines show interpolation of the triple oxygen isotope values from seawater (Mg = 52 mmol/ kg) to endmember compositions (0 mmol/ kg) based on each vent site. The panels (B, C) show the zero-Mg endmember (hence subscript EM) values of vent fluids’ Cl concentrations and O isotopes. Note the change in the vertical axis scale. The small black circles labeled LB2010 are direct measurements of seawater (data from Luz and Barkan, 2010). The values are shown only for deep seawater samples (>1000 m) to eliminate the effects of surface processes (e.g. evaporation). The panel (D) shows the methodology of propagating the uncertainty in the endmember values.
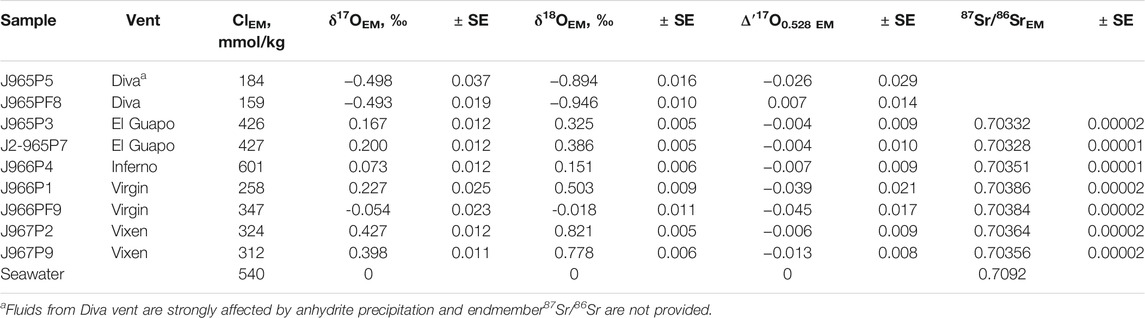
TABLE 3. Endmember (EM) Cl concentrations along with the endmember triple oxygen and strontium isotope values of hydrothermal fluids.
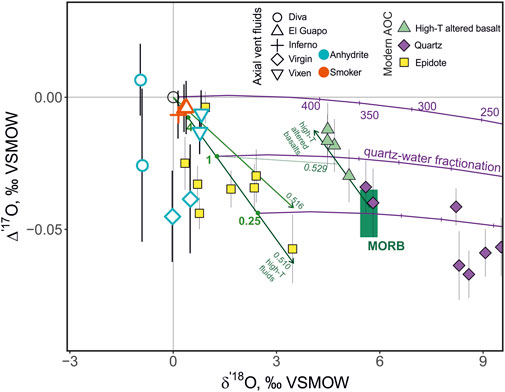
FIGURE 4. Triple oxygen isotope systematics of submarine vent fluids, oceanic quartz, epidote and high temperature altered basalts. The data is assembled from previous publications (altered basalts from Sengupta and Pack, 2018 and Zakharov and Bindeman, 2019; oceanic and quartz from Zakharov and Bindeman, 2019; Zakharov et al., 2019) and reduced for a better comparison as recently proposed in Herwartz (2021). The trajectory of high-temperature reaction between seawater and mid-ocean ridge basalt (shown as MORB) is shown with the two green arrows along the slopes of 0.510 and 0.516 for the fluids and along the slope of 0.510 for the high-temperature altered basalts (slopes are in δ′17O-δ′18O coordinates). Dots on the line correspond to W/R of 4, 1, 0.25. Equilibrium between fluids and altered basalts at W/R = 1 is shown with a dotted line with the slope of 0.529. The quartz-water equilibrium fractionation (equation after Wostbrock et al., 2018) at temperatures between 250 and 400°C is shown.
The Sr isotope ratios of fluid samples are reported in Table 2. They range between 0.703674 and 0.708253. The Mg/Sr ratios are used to reconstruct 87Sr/86Sr values of zero-Mg endmembers (see Figure 2). The samples from Diva are likely affected by anhydrite precipitation (Figure 2) and we do not provide their endmember 87Sr/86Sr value. For other samples, the zero-Mg endmember values (see Table 3) range within a relatively narrow interval between 0.70328 and 0.70386. The propagated uncertainties of the endmember 87Sr/86Sr values are low, around ± 0.00002 (Table 3). Given the modern seawater (0.7092) and average MORB (0.7025) 87Sr/86Sr values, the measured values cover 1 to 11% of the total isotope shift from the initial marine Sr towards that of unaltered rock.
The calculated total molalities of component species are shown in Figure 5 for the isothermal version of calculation at 350°C and 300bars. The moles of equilibrium minerals concentration are shown in Figure 5 panels B through D. The triple oxygen isotope shifts were calculated from the Eq. 4 are shown in Figure 5 panels E, F and G. The computed fluid values evolve along the slope of 0.516 in δ′17O—δ′18O coordinates. For the non-isothermal calculation in which temperature varied from 150°C to 350°C, the computed mineral aqueous species and triple O isotope shifts are shown in Figure 6. The computed fluid evolves along a more complex trajectory compared to the isothermal calculation. We find that applying different θ values between 0.526 and 0.530 to the calculation of oxygen isotope composition of the equilibrium H2O does not translate into resolvable differences in its Δ′17O (Figure 5). The largest difference is observed for the calculation of the low-temperature (150°C) equilibrium, where θ value was 0.525 and 0.527 (Figure 6).
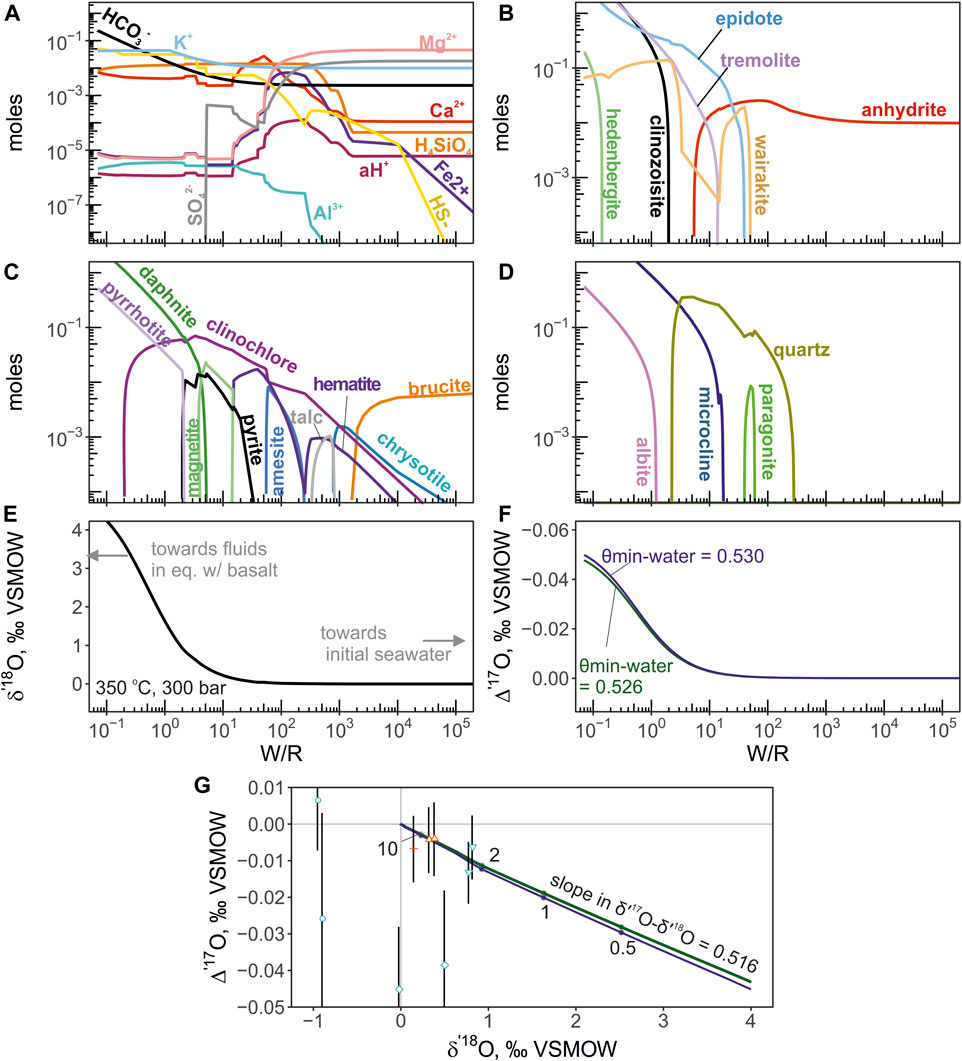
FIGURE 5. The results of mineral-aqueous equilibrium calculation of seawater-basalt reaction at 350°C and 300 bars. The progress of basalt titration into 1 L (1020 g) of seawater is shown with W/R. The triple oxygen isotope values of the equilibrium H2O are calculated from the mass balance of the reaction and the equilibrium mineral-water fractionation factors (see Methods). (A)—total molalities of aqueous species. (B)—molar abundances of Ca-bearing minerals. (C)—abundances of Fe-Mg silicates, oxides and sulfides. (D)—abundances of Al-silicates and quartz. (E, F)—the calculated triple oxygen isotope shifts experienced by the fluid. The Δ′17O is calculated using θ values of 0.526 (green line) and 0.530 (blue). Panel (G) shows the calculated trajectory of fluid evolution and the compositions of endmember values from the vents studied here in δ′18O—Δ′17O coordinates. The effect of different θ values is shown with respective colors. The slope of the trajectory is 0.516 in δ′17O—δ′18O coordinates. The W/R ratios are labeled with digits. Different vent fluid localities are denoted by symbols in the same manner as in the Figure 5.
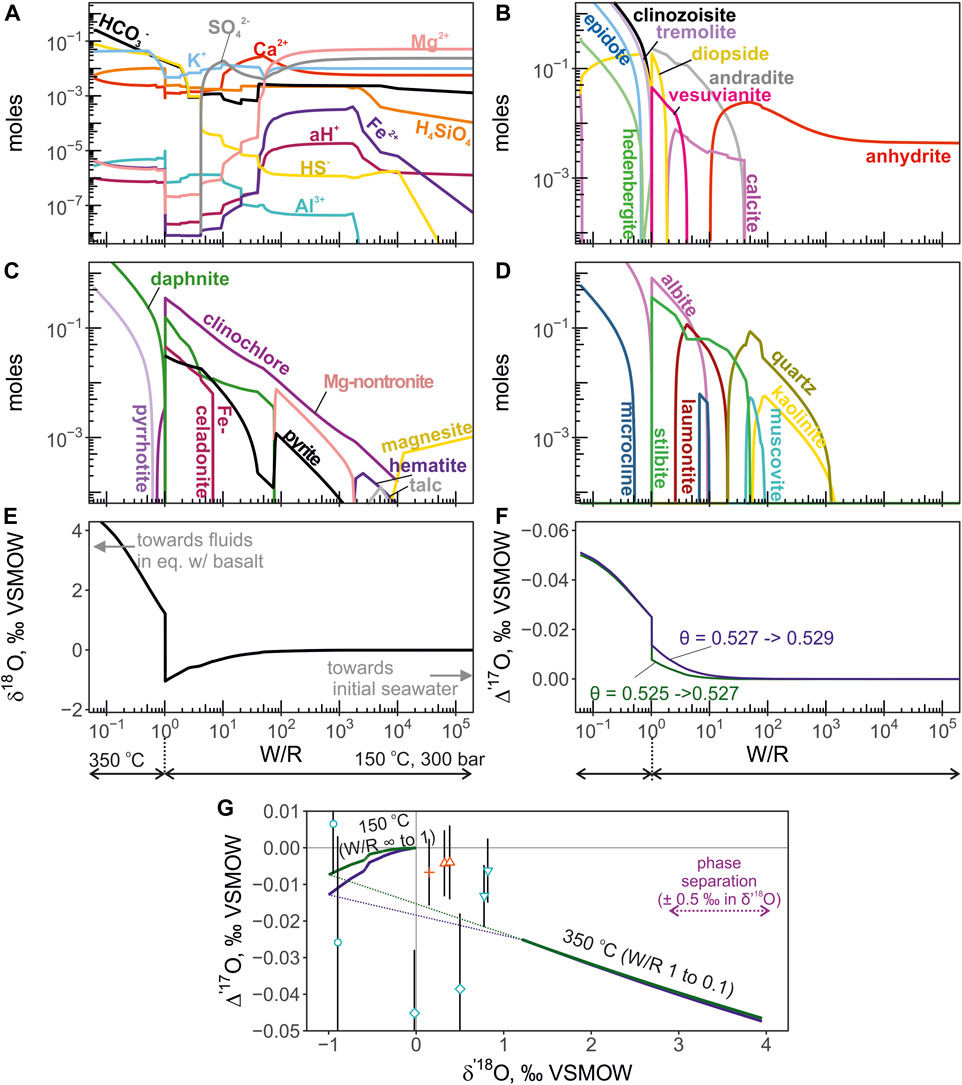
FIGURE 6. The results of mineral-aqueous equilibrium calculation simulation seawater-basalt reaction at 150°C and 350°C, at 300 bars. The low-temperature (150°C) leg of reaction is calculated for W/R between 1 and infinity (pure seawater). The high-temperature reaction proceeds at W/R between <0.1 and 1. Fluid was fractionated from the solid phases at W/R = 1. The panels are presented in the same manner is in Figure 4. In panel (F) the Δ′17O of the fluid is calculated using pairs of θ values of 0.525 and 0.527 (green curve), and 0.527 and 0.529 (blue). The first value in the pair indicates the θ for low-temperature reaction, and the second value is for the high temperature reaction. Panel (G) shows the calculated trajectory of fluid evolution and the compositions of endmember values in the δ′18O—Δ′17O coordinates. Note the negative Δ′17O shift in the low-temperature reaction that can help to explain composition of some fluids. The dotted part indicates the transition for low to high temperature accompanied by the change in fractionation factors.
These trajectories of isotope exchange in dual-porosity model are presented along with the endmember 87Sr/86Sr—δ′18O—Δ′17O values in Figure 7. The outputs of dual-porosity models are shown in two ways: a) as trajectories of two-element isotope shifts with fracture spacing of 1 and 10 m; b) as the 2D density distribution of isotope ratios computed from the Monte-Carlo simulation results. The two trajectories with different fracture spacing were calculated with constant values R = 0.0002 g g−1 yr−1, vf = 10 m/ yr, ϕm = 0.01, and d (fracture width) = 0.01 m.
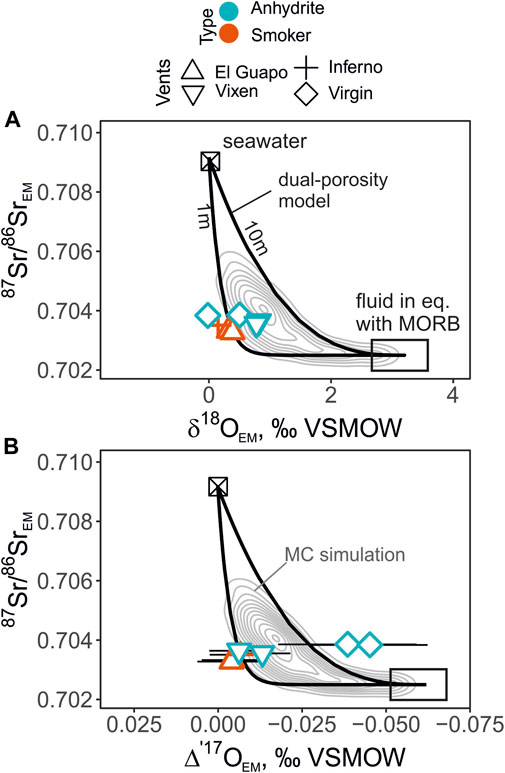
FIGURE 7. The endmember δ′18O values (A) and Δ′17O values (B) plotted against 87Sr/86Sr. The panels show the profiles of the dual-porosity model at fracture spacing of 1 and 10 m along with the Monte-Carlo simulation outputs depicted with the 2D density distribution (concentric grey lines). The individual endmember isotope values are shown except the Diva vent fluids due to the possible effect of anhydrite precipitation. The fluids from the Virgin vent have a large uncertainty in the endmember Δ′17O values due to the zero-Mg-correction, and plot outside the predicted contours. The uncertainties of the mean 87Sr/86SrEM values are smaller than the symbol sizes in these coordinates.
With the general features of the Axial Seamount hydrothermal system as background, we investigate in this paper the systematics of oxygen isotopes in relation to water-rock reaction, phase separation, and mineral precipitation Butterfield et al., 1994; Butterfield et al., 2004). High-temperature reaction of seawater with basalt results in formation of Mg-rich phases that sequester Mg into secondary silicates (e.g. serpentine, chlorites, amphiboles), release of Si through dissolution of minerals coupled with slow kinetics of silicate precipitation, exchange of seawater and basaltic Ca and Sr, coupled with precipitation of anhydrite due to heating in the recharge zone (Mottl and Holland, 1978; Seyfried and Mottl, 1982). High-temperature aqueous-mineral equilibrium reactions involving consumption/production of H+ (e.g. epidote-anorthite equilibrium) along with dissociation of OH-bearing aqueous species buffer the solutions at low pH (Reed, 1983). It is worth noting that the pH between 3.5 and 4.6 was measured here at 25°C and 1 bar and are lower than the in situ pH predicted from equilibrium at elevated temperatures (Seyfried et al., 1991). Endmember Si concentrations reach up to 15 mmol/ kg (Figure 2), and are generally controlled by quartz solubility, a function of pressure, temperature, and fluid density (Von Damm et al., 1991; Fontaine et al., 2009). Calcium and Sr are controlled by dissolution of primary basaltic plagioclase, and generally show increased concentrations in endmember fluids with seawater salinity. Mixing of upwelling endmember fluids with cold seawater and precipitation of anhydrite removes Ca and Sr from solution (Butterfield et al., 1990; Mills et al., 1998), which is reflected in their moderately increased, or even decreased concentrations relative to seawater (Diva and Virgin vents; Figure 2).
The samples collected for this study have a range of Mg concentration due to variable degrees of seawater mixing (range 4 to 63%, average 28% for nine samples) at the point of sampling. Meanwhile hydrothermal solutions have Mg concentrations close to 0 mmol/ kg due to precipitation of chlorites, serpentine and talc in the reaction zone. Diva and Virgin anhydrite vents had diffuse outflow with no well-defined orifice and were more significantly mixed as a result. Since the δ′18O values are affected by seawater mixing at the site of collection, we extrapolate the δ′18O to zero Mg to isolate the endmember properties and examine sub-seafloor processes that are evident in the data (Figure 3). Extrapolation to zero-Mg is a standard procedure that is undertaken to isolate the isotope ratios in the emanating vent fluids. In our case, the extrapolation of the triple oxygen isotope values measured at the precision ± 0.005–0.007‰ (Δ′17O’s 1SE) requires propagation of the uncertainties to the zero-Mg endmember values. The Δ′17O error substantially scales up with Mg-content of the original sampled fluids. In the sample with highest Mg concentration (33 mM) from the Diva vent, the corresponding endmember value has the uncertainty of ±0.03‰. For the rest of the fluids the Δ′17O endmember values have the errors between 0.008 and 0.021‰ (see Figures 3, 4). Previous direct measurements of deep seawater samples (data from Luz and Barkan, 2010) are shown for comparison in Figure 3. Given the uncertainties, the endmember Δ′17O values in Inferno and El Guapo are not significantly different from that of seawater but notably shifted in their δ′18O values (Figures 3, 4). The fluids from Vixen vent are shifted more notably in triple O isotope space. The vent fluids from diffuse Virgin and Diva vents exhibit more variable isotope shifts and higher uncertainty in δ′18O—Δ′17O, and are not consistent with simple seawater-basalt exchange at high temperature (Figure 4). Below we consider the possible nature of isotope shifts produced by the sub-seafloor processes.
As in major elemental concentrations, the triple oxygen isotope endmember vent fluids are affected by the extent of water-rock reactions and to a lesser extent by phase separation. However, we first start with the discussion of the possible effects of phase separation at the oceanic hydrothermal systems. The boiling point of seawater (represented by 3.2 wt% NaCl) at the seafloor pressure of Axial Seamount of 150 bars is 348°C and thus, sub-critical phase separation may occur down to 1.5 km below the seafloor, so isotopic fractionation during vapor-liquid separation is possible. With magmatic temperatures at the base of the reaction zone, halite saturation may occur, so there is a range of potential isotopic fractionation for oxygen that may accompany phase separation over a wide range of conditions between the bottom of the reaction zone and the seafloor. Fractionation factors for O isotopes for the near-seawater salinity fluid are typically, from 0.2 up to 1‰ The endmembers that we report for Axial Seamount are near or less than seawater salinity, ranging between 30 and 110% that of seawater. At 350°C, we expect that their δ18O values would be affected within 0.2–0.5‰ (Shmulovich et al., 1999). That is a significant variation compared to the total range of 1.7‰ in the endmember δ18O values and could be better resolved using hydrogen isotope δD values (see Shanks, 2001). As for their Δ′17O values, due to the high-temperature nature of phase separation we expect that at the level of analytical uncertainty (∼0.01‰) it would be difficult to resolve fractionation between vapor and liquid values. In general, this effect is controlled by the relative fractionation of 17/16α and 18/16α, commonly expressed through the relationship θ = 103ln (17/16α)/103ln (18/16α). For pure vapor-liquid equilibrium fractionation, theta has the value of 0.529 at room temperature Luz and Barkan (2010) and is likely the same or higher (up to 0.5305; Matsuhisa et al., 1978) for high-temperature boiling and phase separation. That means that even if the fluids’ δ18O values underwent fractionation due to phase separation (e.g. up to 1‰), their Δ′17O would not experience a detectable change, especially since the Δ′17O expressed in form of δ′17O-excess relative to the reference slope of 0.528 (see Eq. 3). Similar effect of near-surface boiling was shown in the geothermal systems of Iceland (Zakharov et al., 2019).
As we expect 0.2–0.5‰ variations in δ18O values due to phase separation, the entire range of endmember δ′18O values are between -0.9 and + 0.8‰. This total range of 1.7‰ is thus likely due to the variable progress of seawater-basalt reaction at each site. The most evolved endmember δ′18O values of + 0.8‰ are observed at the Vixen site, where the temperature measured at the vent are among the highest (∼322°C). Such data have been reported previously averaging at about + 1‰ compared to the δ′18O of ambient seawater (Shanks and Seyfried, 1987; Von Damm et al., 1997; Shanks, 2001; Shanks et al., 2013; James et al., 2014). The corresponding Δ′17O shift at Vixen site is −0.01‰. This trajectory is consistent with a simple seawater-basalt exchange reaction that is also characteristic for the high-temperature fluids from the El Guapo, Inferno and Vixen sites (Figures 3, 4).
The lowest endmember δ′18O values of −1‰ correspond to the low-salinity fluids from the Diva vent. Together with the slightly negative Vixen fluids, these values are a perplexing observation, since the δ′18O of bottom seawater is assumed to have 0‰ and exchange reactions at high temperature can only generate positive isotope shifts. The Δ′17O values of Diva endmember fluids are indistinguishable from that of seawater, while the Virgin fluids have the lowest Δ′17O in our dataset of −0.04‰. Possible explanations include that the initial fluids at Axial Seamount system were either: a) derived from the local bottom-water that was about −1‰ in δ′18O and/or b) underwent a complex history of interaction that includes a low-temperature seawater-basalt exchange. In addition, these fluids’ O isotope composition may have been affected by phase separation as they contain the lowest Cl concentrations in our dataset. It is unlikely that the ambient water value would deviate significantly from 0 ± 0.2‰ due to the relatively well-mixed composition of the bottom seawater (see Figure 3). Meanwhile, negative δ18O values are reported for fluids that interacted with basaltic lithologies at low temperature (Lawrence et al., 1975). Thus, these values could be a result of a potential combination of low-temperature reactions that occur within upper several hundred meters of oceanic crust that shift the δ18O of values towards negative values (Lawrence et al., 1975; Gieskes and Lawrence, 1981). The oxygen isotope of such fluids is complementary to formation of clay minerals in a low temperature environment that have high δ′18O and relatively small change in Δ′17O values compared to that of unaltered rocks (Sengupta and Pack, 2018; Bindeman et al., 2019). Due to the overall small variations in δ′18O and Δ′17O and the potential contribution of phase separation, additional measurements such as D/H ratios and measurements of ambient seawater are needed to aid the interpretation.
Despite high uncertainty in the Δ′17O values that partially encompasses that of seawater, the simultaneous change in δ18O–Δ′17O in the low-Mg fluids from the Inferno, El Guapo and Vixen is overall consistent with high-temperature reaction with basalt and the small fractionation factors between fluids and secondary minerals (Figure 4). It would be beneficial to measure more evolved low-Mg fluids that exhibit even larger, more detectable isotope shifts. In principle, the triple oxygen isotope value of fluids can be extended to the values of fluids in equilibrium with basaltic composition at temperature of ∼350°C, which represent fluids in rock-buffered conditions deeper in the oceanic crust (e.g., Schiffman and Smith, 1988; Alt and Bach, 2006), anchoring the limit of oxygen isotope exchange at δ′18O value of around + 4‰. Depending on the choice of the exact slope, between 0.5 and 0.516, the Δ′17O corresponding value of the fluid would be between −0.04 and -0.06‰ (Figure 4). Further, the exact value of the shifted fluids would depend on the initial composition of the reacting seawater and basalts as they control the endmember values. Below, we further consider the high-temperature seawater basalt exchange from a perspective of combined mineral and vent fluid data, and the isotope shifts computed from equilibrium reaction modeling.
These oxygen isotope shifts experienced by the fluids reflect the complementary isotope shift with a different sign experienced by the bulk altered oceanic crust. For further comparison, we show the previous measurements of whole rock altered basalt, epidote and quartz drilled from altered oceanic crust (Sengupta and Pack, 2018; Zakharov and Bindeman, 2019; Zakharov et al., 2019). These materials display 18O/16O fractionation, which is evident with a several ‰ offset from the seawater-basalt exchange trajectory in Figure 4, yet consistent with the overall slope. The fractionation of Δ′17O is small however, due to its expression in Eq. 3. The range of Δ′17O endmember fluid values overlaps with those of altered basalts, epidotes and quartz (Figure 4). Epidotes record minimal fractionation and, at least as a first order approximation, they could be used to directly reflect the Δ′17O of high temperature hydrothermal fluids (Zakharov et al., 2019; Herwartz, 2021). Using the present dataset, we are able to show that oceanic epidotes continue the tentative trend outlined by the high-temperature vent fluid values (Figure 4). Since the temperature-dependent fractionation of triple oxygen isotope ratios between epidote and fluids is likely small, we expect a scatter of 0–2‰ in δ′18O at 250–400°C (Zheng, 1993b; Matthews, 1994). The δ′18O of quartz is notably higher due to the well-pronounced fractionation factor (Wostbrock and Sharp, 2021). Together the mineral and fluid data outline the systematics of the seawater-basalt exchange in triple oxygen isotope space. The El Guapo, Inferno and Vixen fluids tentatively align along the same trajectory as the high temperature altered basalt but with the opposite sign. The Diva and Virgin fluids deviate from that trajectory, potentially reflect the low-temperature effects and phase separation.
These isotope shifts experienced by the fluids and altered oceanic crust during high-temperature reaction are simplistically exemplified by our mineral-aqueous equilibrium calculation, where the δ′18O and Δ′17O values of fluids are calculated as a function of W/R and equilibrium fractionation factors (see Eq. 4). The utility of these sort of calculation to dynamic systems is limited, and moreover, previous research already implemented these calculations some time ago (Reed, 1983; Bowers and Taylor, 1985). However, since we explore a new isotope parameter, namely the relationship between δ′18O—Δ′17O in fluids, we find it useful to demonstrate the trajectories calculated by static equilibrium approach. The output of our calculation shows that endmember triple oxygen isotope values at El Guapo, Inferno and Vixen vents record reactions that proceeded at W/R of around 2–10 (Figure 5), where the mineral assemblages are dominated by albite, epidote, tremolite, and chlorite, an assemblage typical for high-temperature altered oceanic crust (Alt et al., 1996). Thus, measurements of such mineral assemblages from ancient fragments of oceanic seafloor can be used to reconstruct ancient trajectories of seawater-basalt exchange. Further, at such W/R the fluids display diminishingly low Mg concentrations, and several mmol/kg Si (Figure 5), consistent with our major elemental measurements.
We show a non-isothermal reaction path as an example of combined low- and high-temperature interaction between seawater and basalt (Figure 6). In this model, seawater initially reacts with basalt at low temperature, where δ′18O fractionation is large producing high-δ′18O secondary minerals, resembling the pathway of fluids in the upper oceanic crust. The subsequent fractionation and reaction at 350°C is intended to replicate further downward pathway of fluids to the high-temperature reaction zones in the sheeted dike complex (Alt et al., 1996). The resulted combined reaction covers a much larger area in the δ′18O—Δ′17O coordinates than isothermal exchange, which would normally be undetectable with one isotope ratio δ′18O (Figure 6). The Diva and Virgin mean endmember values are partially compatible with the predicted pathways (Figure 6), perhaps reflecting a more variable set of non-isotheral reactions. Further, the combination of non-isothermal reactions and phase separation can explain the data scatter and deviations from the isothermal reactions with a static slope in δ′17O—δ′18O coordinates. We additionally acknowledge that the fraction of mixed seawater in the measurements of Diva and Virgin fluids is large, and so is the uncertainty of end-member values. Thus, it is difficult to interpret the nature of these isotope shifts with certainty.
To further explore the isotope systematics of seawater-basalt reactions, we used strontium isotope values of fluids as an additional tracer of the exchange between seawater and basalt that is not affected by temperature-dependent fractionation. Due to low Sr concentration in seawater, it is expected that the change in 87Sr/86Sr isotope values of fluid would occur much more readily compared to the δ′18O—Δ′17O values. Yet, it is difficult to precisely ‘scale’ the exchange of Sr- and O-isotopes due to fundamentally different rates and mechanisms that affect these two systems, i.e. plagioclase dissolution preferentially affects Sr, while other reactions affect O. Nonetheless, we attempted to simulate the results of the dual-porosity model using a statistical approach to show what can be expected in the triple O- and Sr-isotope coordinates. The modeled output shown as 2D-density distribution indicates that it is natural to expect some scatter of data (Figure 7). Such statistical treatment of the model helps to address the variability of the path-integrated variables that are especially difficult to measure directly. Incorporation of Δ′17O coordinates in the dual-porosity modeling should provide a more complete picture into the subseafloor hydrothermal circulation as the Δ′17O values are more affected by seawater-basalt exchange reactions at high temperature, compared to the expected effects in δ′18O caused by phase separation, or low-temperature reactions (e.g. Figure 6).
The endmember 87Sr/86Sr values of the Axial Seamount vent fluids between 0.7033 and 0.7039 indicate the extent of seawater-basalt reaction is similar to the fluids measured elsewhere in mid-ocean ridge environments (Palmer and Edmond, 1989; Bach and Humphris, 1999; James et al., 2014). These values represent Sr source dominated by basalts; most sample contain less than 10% of seawater-derived Sr. We observe that in the δ′18O—Δ′17O—87Sr/86Sr space the high-temperature vent fluids plot in a tight cluster close to the contour defined by close fracture spacing (∼1 m; Figure 7) of the dual-porosity model. The Virgin fluids plot farthest outside the modeled areas. These fluids are rich in Mg and required the largest correction for mixed seawater compared to other low-Mg samples. Since the interaction with the cold ambient seawater has occurred, precipitation of anhydrite could have affected the samples driving their Mg/Sr ratio to higher values (Figure 2). If this were the case, the actual Virgin endmember 87Sr/86Sr would be even father away from to the modeled dual-porosity output (Figure 7). On the other hand, if dissolution of anhydrite occurred in the cold water near the orifice, mixing with such fluid would result in lower in Mg/Sr (Figure 2).
In general, these results are in good agreement with the outlined areas provided by the dual-porosity model, especially for the low-Mg samples from El Guapo, Inferno and Vixen vents. This serves as a promising basis for the future studies of the samples that are affected by phase separation, where the fractionation of δ′18O is more prominent, while Δ′17O values would be primarily affected by seawater-basalt reactions. Since Δ′17Omineral-Δ′17Owater fractionation is small at high temperatures, present study also aids in interpretation of mineral data from altered oceanic crust that can point to the physical and chemical parameters of sub-seafloor fluid circulation (Brown et al., 2020; Zakharov et al., 2021a).
Our modeling and measurements indicate that upon interaction with basalt seawater acquires a negative Δ′17O signature. Further application of the combined δ′18O—Δ′17O datasets can be especially useful in reconstructing the values of ancient fluids from mineral data. Besides the utility of epidote measurements described in the Comparison With Mineral Data: Measured and Computed, we point out that many measurements of Precambrian cherts are shifted in Δ′17O negatively compared to seawater-silica equilibrium curve [i.e. towards basaltic equilibrium (Sengupta et al., 2020; Zakharov et al., 2021b; Herwartz et al., 2021; Wostbrock and Sharp, 2021)]. Apart from changes in seawater temperature and diagenetic effects, the δ′18O—Δ′17O values of such cherts may indicate influences from hydrothermal solutions contributing to abiotic silica precipitation in the Archean (de Ronde et al., 1994; De Ronde et al., 1997; Hayles et al., 2019; Liljestrand et al., 2020; Zakharov et al., 2021b). Further, there is a growing body of literature focused on the Δ′17O signature of atmospheric O2 captured by sulfate minerals (Bao et al., 2007; Crockford et al., 2016; Crockford et al., 2018; Crockford et al., 2019; Hemingway et al., 2020). The dataset presented in this study is relevant because precipitation of chert, barite and anhydrite is commonly mediated by diagenetic and hydrothermal solutions. If dissolved silica or sulfate underwent high-temperature equilibrium exchange or mixing with hydrothermal fluids, we also expect the negative Δ′17O shifts in the resulted mineral compositions. With growing precision, the small mass-dependent variations in Δ′17O (± 0.01‰) could be incorporated when interpreting the highly negative (down to Δ′17O = -1‰), yet significantly scattered, mass-independent signatures (Crockford et al., 2019). The summary of present study is outlined below.
1. Triple oxygen isotope endmember values at the Axial Seamount volcano in the eastern Pacific Ocean are used to exemplify the Δ′17O shifts experienced by seawater upon reaction with basalt at high temperature. The acidic fluids from El Guapo, Inferno and Vixen sites with Si concentrations up to 15 mmol/ kg, depict the oxygen isotope shifts from 0 to + 0.8‰ in δ′18O and from 0 to −0.01‰ in Δ17O. The fluids from Diva and Virgin vents extrapolate to δ′18O = −1 and 0‰ endmember values, while their Δ′17O endmember values are significantly scattered between + 0.01 and −0.05‰. These moderate isotope shifts overall are best explained by high-temperature interaction between seawater and basalt, with some likely contribution from phase separation. Low-temperature seawater-basalt interaction is proposed to have occurred in case of Diva and Virgin fluids that would explain their low δ′18O values (from −1 to 0‰).
2. The envisioned fully exchanged fluids with δ′18O of ca. + 4‰ would have Δ′17O values close to −0.045‰. Supporting this, we provide a mineral-aqueous equilibrium calculation showing a simple trajectory during high-temperature (T = 350°C) seawater-basalt reaction. Vent fluids from El Guapo, Inferno and Vixen sites are consistent with the expected trajectory of high-temperature seawater-basalt exchange at W/R = 2–10. Using a non-isothermal seawater-basalt reaction with intermittent fractionation, where temperature changes from 150°C to 350°C, we show that the trajectory of the fluid values in δ′18O—Δ′17O coordinates covers a much larger area compared to the isothermal reaction. Normally, the effects of non-isothermal reaction would be unnoticed using only δ′18O.
3. The 87Sr/86Sr data combined with the δ18O—Δ′17O values provide a potential to distinguish seawater-basalt exchange from other processes. We show a field of possible isotope values produced by seawater-basalt reactions in a dual-porous medium with variable reaction rates, fluid velocities, fracture spacing and porosity. During phase separation or low-temperature processes, we expect that the fluid δ18O values would be more affected than the Δ′17O values. Theoretically, the Δ′17O—87Sr/86Sr trajectories are less sensitive to these effects and they present a new way to gain insight into present and ancient seawater-basalt reactions. In our case, the vent fluid values from El Guapo, Inferno and Vixen show consistent agreement in the combined δ′18O—Δ′17O—87Sr/86Sr coordinates. The trajectories of the isotope shifts are most consistent with ∼1m fracture spacing of the sub-seafloor system.
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
DZ designed the study, wrote the original draft and conducted the calculations. RT and EN produced triple oxygen and strontium isotope data. DB provided the samples and their chemical composition. All authors contributed to editing and writing of the manuscript.
Financial support for this project was partly provided by JSPS KAKENHI grants (20K04108).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
We thank the handling editor Fang-Zhen Teng as well as two reviewers for their suggestions and constructive criticism that helped to improve the manuscript. Chie Sakaguchi and Kayo Tanaka conducted to measure the Sr isotope data. Kevin Roe analyzed vent fluids for major and minor element composition.
Alt, J. C., and Bach, W. (2006). Oxygen Isotope Composition of a Section of Lower Oceanic Crust, ODP Hole 735B: OXYGEN ISOTOPE COMPOSITION of CRUST. Geochem. Geophys. Geosystems 7, n/a. doi:10.1029/2006gc001385
Alt, J. C., and Teagle, D. A. H. (2000). “Hydrothermal Alteration and Fluid Fluxes in Ophiolites and Oceanic Crust,” in Ophiolites and Oceanic Crust: New Insights from Field Studies and the Ocean Drilling Program (Geological Society of America). doi:10.1130/0-8137-2349-3.273
Arnulf, A. F., Harding, A. J., Kent, G. M., Carbotte, S. M., Canales, J. P., and Nedimović, M. R. (2014). Anatomy of an Active Submarine Volcano. Geology 42, 655–658. doi:10.1130/g35629.1
Bach, W., and Humphris, S. E. (1999). Relationship between the Sr and O Isotope Compositions of Hydrothermal Fluids and the Spreading and Magma-Supply Rates at Oceanic Spreading Centers. Geol. 27, 1067–1070. doi:10.1130/0091-7613(1999)027
Bao, H., Rumble, D., and Lowe, D. R. (2007). The Five Stable Isotope Compositions of Fig Tree Barites: Implications on Sulfur Cycle in Ca. 3.2Ga Oceans. Geochimica et Cosmochimica Acta 71, 4868–4879. doi:10.1016/j.gca.2007.05.032
Baumgartner, L. P., and Rumble, D. (1988). Transport of Stable Isotopes: I: Development of a Kinetic Continuum Theory for Stable Isotope Transport. Contr. Mineral. Petrol. 98, 417–430. doi:10.1007/bf00372362
Berner, E. K., and Berner, R. A. (1996). Global Environment Water, Air, and Geochemical Cycles. Englewood Cliffs NewJersey: Prentice-Hall.
Bickle, M. J., and Baker, J. (1990). Advective-diffusive Transport of Isotopic Fronts: an Example from Naxos, Greece. Earth Planet. Sci. Lett. 97, 78–93. doi:10.1016/0012-821x(90)90100-c
Bindeman, I. N., Bayon, G., and Palandri, J. (2019). Triple Oxygen Isotope Investigation of fine-grained Sediments from Major World's Rivers: Insights into Weathering Processes and Global Fluxes into the Hydrosphere. Earth Planet. Sci. Lett. 528, 115851. doi:10.1016/j.epsl.2019.115851
Bowers, T. S., and Taylor, H. P. (1985). An Integrated Chemical and Stable-Isotope Model of the Origin of Midocean Ridge Hot Spring Systems. J. Geophys. Res. 90, 12583. doi:10.1029/jb090ib14p12583
Brown, S. T., Kennedy, B. M., DePaolo, D. J., Hurwitz, S., and Evans, W. C. (2013). Ca, Sr, O and D Isotope Approach to Defining the Chemical Evolution of Hydrothermal Fluids: Example from Long Valley, CA, USA. Geochimica et Cosmochimica Acta 122, 209–225. doi:10.1016/j.gca.2013.08.011
Brown, S. T., Turchyn, A. V., Bickle, M. J., Davis, A. C., Alt, J. C., Bédard, J. H., et al. (2020). High-temperature Kinetic Isotope Fractionation of Calcium in Epidosites from Modern and Ancient Seafloor Hydrothermal Systems. Earth Planet. Sci. Lett. 535, 116101. doi:10.1016/j.epsl.2020.116101
Butterfield, D. A., Massoth, G. J., McDuff, R. E., Lupton, J. E., and Lilley, M. D. (1990). Geochemistry of hydrothermal fluids from Axial Seamount hydrothermal emissions study vent field, Juan de Fuca Ridge: Subseafloor boiling and subsequent fluid-rock interaction. J. Geophys. Res. 95, 12895–12921. doi:10.1029/jb095ib08p12895
Butterfield, D. A., McDuff, R. E., Mottl, M. J., Lilley, M. D., Lupton, J. E., and Massoth, G. J. (1994). Gradients in the Composition of Hydrothermal Fluids from the Endeavour Segment Vent Field: Phase Separation and Brine Loss. J. Geophys. Res. 99, 9561–9583. doi:10.1029/93jb03132
Butterfield, D. A., Roe, K. K., Lilley, M. D., Huber, J. A., Baross, J. A., Embley, R. W., et al. (2004). Mixing, Reaction and Microbial Activity in the Sub-seafloor Revealed by Temporal and Spatial Variation in Diffuse Flow Vents at Axial Volcano. Subseafloor Biosph. -Ocean Ridges 144, 269–289. doi:10.1029/144gm17
Cao, X., and Liu, Y. (2011). Equilibrium Mass-dependent Fractionation Relationships for Triple Oxygen Isotopes. Geochimica et Cosmochimica Acta 75, 7435–7445. doi:10.1016/j.gca.2011.09.048
Crockford, P. W., Cowie, B. R., Johnston, D. T., Hoffman, P. F., Sugiyama, I., Pellerin, A., et al. (2016). Triple Oxygen and Multiple Sulfur Isotope Constraints on the Evolution of the post-Marinoan Sulfur Cycle. Earth Planet. Sci. Lett. 435, 74–83. doi:10.1016/j.epsl.2015.12.017
Crockford, P. W., Hayles, J. A., Bao, H., Planavsky, N. J., Bekker, A., Fralick, P. W., et al. (2018). Triple Oxygen Isotope Evidence for Limited Mid-proterozoic Primary Productivity. Nature 559, 613–616. doi:10.1038/s41586-018-0349-y
Crockford, P. W., Kunzmann, M., Bekker, A., Hayles, J., Bao, H., Halverson, G. P., et al. (2019). Claypool Continued: Extending the Isotopic Record of Sedimentary Sulfate. Chem. Geology 513, 200–225. doi:10.1016/j.chemgeo.2019.02.030
De Ronde, C. E. J., Channer, D. M. d., Faure, K., Bray, C. J., and Spooner, E. T. C. (1997). Fluid Chemistry of Archean Seafloor Hydrothermal Vents: Implications for the Composition of Circa 3.2 Ga Seawater. Geochimica et Cosmochimica Acta 61, 4025–4042. doi:10.1016/s0016-7037(97)00205-6
de Ronde, C. E. J., de Wit, M. J., and Spooner, E. T. C. (1994). Early Archean (>3.2 Ga) Fe-Oxide-Rich, Hydrothermal Discharge Vents in the Barberton Greenstone belt, South Africa. Geol. Soc. Am. Bull. 106, 86–104. doi:10.1130/0016-7606(1994)106
DePaolo, D. J. (2006). Isotopic Effects in Fracture-Dominated Reactive Fluid-Rock Systems. Geochimica et Cosmochimica Acta 70, 1077–1096. doi:10.1016/j.gca.2005.11.022
Eiler, J. M. (2001). 5. Oxygen Isotope Variations of Basaltic Lavas and Upper Mantle Rocks. Rev. Mineral. Geochem. 43, 319–364. doi:10.1515/9781501508745-008
Feng, X., and Savin, S. M. (1993). Oxygen Isotope Studies of Zeolites-Stilbite, Analcime, Heulandite, and Clinoptilolite: II. Kinetics and Mechanisms of Isotopic Exchange between Zeolites and Water Vapor. Geochimica et Cosmochimica Acta 57, 4219–4238. doi:10.1016/0016-7037(93)90318-q
Fisher, A. T. (1998). Permeability within Basaltic Oceanic Crust. Rev. Geophys. 36, 143–182. doi:10.1029/97rg02916
Fontaine, F. J., Wilcock, W. S. D., Foustoukos, D. E., and Butterfield, D. A. (2009). A Si-Cl Geothermobarometer for the Reaction Zone of High-Temperature, Basaltic-Hosted Mid-ocean ridge Hydrothermal Systems. Geochem. Geophys. Geosystems 10. doi:10.1029/2009gc002407
Gale, A., Dalton, C. A., Langmuir, C. H., Su, Y., and Schilling, J.-G. (2013). The Mean Composition of Ocean ridge Basalts. Geochem. Geophys. Geosyst. 14, 489–518. doi:10.1029/2012gc004334
Gieskes, J. M., and Lawrence, J. R. (1981). Alteration of Volcanic Matter in Deep Sea Sediments: Evidence from the Chemical Composition of Interstitial Waters from Deep Sea Drilling Cores. Geochimica et Cosmochimica Acta 45, 1687–1703. doi:10.1016/0016-7037(81)90004-1
Gregory, R. T., and Taylor, H. P. (1981). An Oxygen Isotope Profile in a Section of Cretaceous Oceanic Crust, Samail Ophiolite, Oman: Evidence for δ18O Buffering of the Oceans by Deep (>5 Km) Seawater-Hydrothermal Circulation at Mid-ocean Ridges. J. Geophys. Res. 86, 2737–2755. doi:10.1029/jb086ib04p02737
Hayba, D. O., and Ingebritsen, S. E. (1997). Multiphase Groundwater Flow Near Cooling Plutons. J. Geophys. Res. 102, 12235–12252. doi:10.1029/97jb00552
Hayles, J. A., Yeung, L. Y., Homann, M., Banerjee, A., Jiang, H., Shen, B., et al. (2019). Three Billion Year Secular Evolution of the Triple Oxygen Isotope Composition of Marine Chert. EarthArXiv.
Hayles, J., Gao, C., Cao, X., Liu, Y., and Bao, H. (2018). Theoretical Calibration of the Triple Oxygen Isotope Thermometer. Geochimica et Cosmochimica Acta 235, 237–245. doi:10.1016/j.gca.2018.05.032
Hemingway, J. D., Olson, H., Turchyn, A. V., Tipper, E. T., Bickle, M. J., and Johnston, D. T. (2020). Triple Oxygen Isotope Insight into Terrestrial Pyrite Oxidation. Proc. Natl. Acad. Sci. USA 117, 7650–7657. doi:10.1073/pnas.1917518117
Herwartz, D., Pack, A., Krylov, D., Xiao, Y., Muehlenbachs, K., Sengupta, S., et al. (2015). Revealing the Climate of Snowball Earth from Δ17O Systematics of Hydrothermal Rocks. Proc. Natl. Acad. Sci. USA 112, 5337–5341. doi:10.1073/pnas.1422887112
Herwartz, D., Pack, A., and Nagel, T. J. (2021). A CO2 Greenhouse Efficiently Warmed the Early Earth and Decreased Seawater 18O/16O before the Onset of Plate Tectonics. Proc. Natl. Acad. Sci. 118. doi:10.1073/pnas.2023617118
Herwartz, D. (2021). Triple Oxygen Isotope Variations in Earth's Crust. Rev. Mineral. Geochem. 86, 291–322. doi:10.2138/rmg.2021.86.09
James, R. H., Green, D. R. H., Stock, M. J., Alker, B. J., Banerjee, N. R., Cole, C., et al. (2014). Composition of Hydrothermal Fluids and Mineralogy of Associated Chimney Material on the East Scotia Ridge Back-Arc Spreading centre. Geochimica et Cosmochimica Acta 139, 47–71. doi:10.1016/j.gca.2014.04.024
Kadko, D., Gronvold, K., and Butterfield, D. (2007). Application of Radium Isotopes to Determine Crustal Residence Times of Hydrothermal Fluids from Two Sites on the Reykjanes Peninsula, Iceland. Geochimica et Cosmochimica Acta 71, 6019–6029. doi:10.1016/j.gca.2007.09.018
Kadko, D., and Moore, W. (1988). Radiochemical Constraints on the Crustal Residence Time of Submarine Hydrothermal Fluids: Endeavour Ridge. Geochimica et Cosmochimica Acta 52, 659–668. doi:10.1016/0016-7037(88)90328-6
Alt, K. H., Stokking, L. B., and Michael, P. J. (1996). Proceedings of the Ocean Drilling Program, 148 Scientific Results. (Ocean Drilling Program).
Lawrence, J. R., Gieskes, J. M., and Broecker, W. S. (1975). Oxygen Isotope and Cation Composition of DSDP Pore Waters and the Alteration of Layer II Basalts. Earth Planet. Sci. Lett. 27, 1–10. doi:10.1016/0012-821x(75)90154-5
Liljestrand, F. L., Knoll, A. H., Tosca, N. J., Cohen, P. A., Macdonald, F. A., Peng, Y., et al. (2020). The Triple Oxygen Isotope Composition of Precambrian Chert. Earth Planet. Sci. Lett. 537, 116167. doi:10.1016/j.epsl.2020.116167
Lloyd, R. M. (1968). Oxygen Isotope Behavior in the Sulfate-Water System. J. Geophys. Res. 73, 6099–6110. doi:10.1029/jb073i018p06099
Luz, B., and Barkan, E. (2010). Variations of 17O/16O and 18O/16O in Meteoric Waters. Geochimica et Cosmochimica Acta 74, 6276–6286. doi:10.1016/j.gca.2010.08.016
Massoth, G. J., Butterfield, D. A., Lupton, J. E., McDuff, R. E., Lilley, M. D., and Jonasson, I. R. (1989). Submarine venting of phase-separated hydrothermal fluids at Axial Volcano, Juan de Fuca Ridge. Nature 340, 702–705. doi:10.1038/340702a0
Matsuhisa, Y., Goldsmith, J. R., and Clayton, R. N. (1978). Mechanisms of Hydrothermal Crystallization of Quartz at 250°C and 15 Kbar. Geochimica et Cosmochimica Acta 42, 173–182. doi:10.1016/0016-7037(78)90130-8
Matsuhisa, Y., Goldsmith, J. R., and Clayton, R. N. (1979). Oxygen Isotopic Fractionation in the System Quartz-Albite-Anorthite-Water. Geochimica et Cosmochimica Acta 43, 1131–1140. doi:10.1016/0016-7037(79)90099-1
Matthews, A. (1994). Oxygen Isotope Geothermometers for Metamorphic Rocks. J. Metamorph. Geol. 12, 211–219. doi:10.1111/j.1525-1314.1994.tb00017.x
Mills, R. A., Teagle, D. A., and Tivey, M. K. (1998). “FLUID MIXING AND ANHYDRITE PRECIPITATION WITHIN THE TAG MOUND,” in Proceedings Of the Ocean Drilling Program: Scientific Results the Program, 10, 119.
Mottl, M. J., and Holland, H. D. (1978). Chemical Exchange during Hydrothermal Alteration of basalt by Seawater-I. Experimental Results for Major and Minor Components of Seawater. Geochimica et Cosmochimica Acta 42, 1103–1115. doi:10.1016/0016-7037(78)90107-2
Muehlenbachs, K., and Clayton, R. N. (1976). Oxygen Isotope Composition of the Oceanic Crust and its Bearing on Seawater. J. Geophys. Res. 81, 4365–4369. doi:10.1029/jb081i023p04365
Muehlenbachs, K. (1998). The Oxygen Isotopic Composition of the Oceans, Sediments and the Seafloor. Chem. Geology. 145, 263–273. doi:10.1016/s0009-2541(97)00147-2
Nakamura, E., Makishima, A., Moriguti, T., Kobayashi, K., Sakaguchi, C., Yokoyama, T., et al. (2003). Comprehensive Geochemical Analyses of Small Amounts (< 100 Mg) of Extraterrestrial Samples for the Analytical Competition Related to the Sample Return mission MUSES-C. Inst. Space Astronaut Sci. Rep. SP 16, 49–101.
Norton, D. (1978). Sourcelines, Sourceregions, and Pathlines for Fluids in Hydrothermal Systems Related to Cooling Plutons. Econ. Geol. 73, 21–28. doi:10.2113/gsecongeo.73.1.21
Ohmoto, H., and Rye, R. O. (1974). Hydrogen and Oxygen Isotopic Compositions of Fluid Inclusions in the Kuroko Deposits, Japan. Jpn. Econ. Geol. 69, 947–953. doi:10.2113/gsecongeo.69.6.947
O’Neil, J. R., Clayton, R. N., and Mayeda, T. K. (1969). Oxygen Isotope Fractionation in Divalent Metal Carbonates. J. Chem. Phys. 51, 5547–5558.
Pack, A., and Herwartz, D. (2014). The Triple Oxygen Isotope Composition of the Earth Mantle and Understanding ΔO17 Variations in Terrestrial Rocks and Minerals. Earth Planet. Sci. Lett. 390, 138–145. doi:10.1016/j.epsl.2014.01.017
Pack, A., Tanaka, R., Hering, M., Sengupta, S., Peters, S., and Nakamura, E. (2016). The Oxygen Isotope Composition of San Carlos Olivine on the VSMOW2-SLAP2 Scale. Rapid Commun. Mass. Spectrom. 30, 1495–1504. doi:10.1002/rcm.7582
Palmer, M. R., and Edmond, J. M. (1989). The Strontium Isotope Budget of the Modern Ocean. Earth Planet. Sci. Lett. 92, 11–26. doi:10.1016/0012-821x(89)90017-4
Reed, M. H. (1983). Seawater-basalt Reaction and the Origin of Greenstones and Related Ore Deposits. Econ. Geol. 78, 466–485. doi:10.2113/gsecongeo.78.3.466
Reed, M. H., Spycher, N. F., and Palandri, J. (2010). Users Guide for CHIM-XPT: A Program for Computing Reaction Processes in Aquous-Mineral Gas Systems and MINITAB Guide. Eugene Univ. Or.
Savin, S. M., and Lee, M. (1988). Chapter 7. ISOTOPIC STUDIES of PHYLLOSILICATES. Rev. Mineral. Geochem. 19, 189–224. doi:10.1515/9781501508998-012
Schiffman, P., and Smith, B. M. (1988). Petrology and Oxygen Isotope Geochemistry of a Fossil Seawater Hydrothermal System within the Solea Graben, Northern Troodos Ophiolite, Cyprus. J. Geophys. Res. 93, 4612–4624. doi:10.1029/jb093ib05p04612
Sengupta, S., and Pack, A. (2018). Triple Oxygen Isotope Mass Balance for the Earth's Oceans with Application to Archean Cherts. Chem. Geology 495, 18–26. doi:10.1016/j.chemgeo.2018.07.012
Sengupta, S., Peters, S. T. M., Reitner, J., Duda, J.-P., and Pack, A. (2020). Triple Oxygen Isotopes of Cherts through Time. Chem. Geology 554, 119789. doi:10.1016/j.chemgeo.2020.119789
Seyfried, W. E., Ding, K., and Berndt, M. E. (1991). Phase Equilibria Constraints on the Chemistry of Hot spring Fluids at Mid-ocean Ridges. Geochimica et Cosmochimica Acta 55, 3559–3580. doi:10.1016/0016-7037(91)90056-b
Seyfried, W. E., and Mottl, M. J. (1982). Hydrothermal Alteration of basalt by Seawater under Seawater-Dominated Conditions. Geochimica et Cosmochimica Acta 46, 985–1002. doi:10.1016/0016-7037(82)90054-0
Shanks, W. C., Böhlke, J. K., and Seal, R. R. (2013). “Stable Isotopes in Mid-ocean Ridge Hydrothermal Systems: Interactions between Fluids, Minerals, and Organisms,” in Geophysical Monograph Series. Editors S. E. Humphris, R. A. Zierenberg, L. S. Mullineaux, and R. E. Thomson (Washington, D. C.: American Geophysical Union), 194–221. doi:10.1029/gm091p0194
Shanks, W. C., and Seyfried, W. E. (1987). Stable isotope studies of vent fluids and chimney minerals, southern Juan de Fuca Ridge: Sodium metasomatism and seawater sulfate reduction. J. Geophys. Res. 92, 11387–11399. doi:10.1029/jb092ib11p11387
Shanks, W. C. (2001). Stable Isotopes in Seafloor Hydrothermal Systems: Vent Fluids, Hydrothermal Deposits, Hydrothermal Alteration, and Microbial Processes. Rev. Mineralogy Geochem. 43, 469–525. doi:10.2138/gsrmg.43.1.469
Sharp, Z. D., Gibbons, J. A., Maltsev, O., Atudorei, V., Pack, A., Sengupta, S., et al. (2016). A Calibration of the Triple Oxygen Isotope Fractionation in the SiO2-H2O System and Applications to Natural Samples. Geochimica et Cosmochimica Acta 186, 105–119. doi:10.1016/j.gca.2016.04.047
Sheppard, S. M. F., Nielsen, R. L., and Taylor, H. P. (1969). Oxygen and Hydrogen Isotope Ratios of clay Minerals from Porphyry Copper Deposits. Econ. Geol. 64, 755–777. doi:10.2113/gsecongeo.64.7.755
Shmulovich, K. I., Landwehr, D., Simon, K., and Heinrich, W. (1999). Stable Isotope Fractionation between Liquid and Vapour in Water-Salt Systems up to 600°C. Chem. Geology. 157, 343–354. doi:10.1016/s0009-2541(98)00202-2
Tanaka, R., and Nakamura, E. (2013). Determination of 17 O-Excess of Terrestrial Silicate/oxide Minerals with Respect to Vienna Standard Mean Ocean Water (VSMOW). Rapid Commun. Mass. Spectrom. 27, 285–297. doi:10.1002/rcm.6453
Taylor, H. P. (1977). Water/rock Interactions and the Origin of H2O in Granitic Batholiths. J. Geol. Soc. 133, 509–558. doi:10.1144/gsjgs.133.6.0509
Tsuji, T., and Iturrino, G. J. (2008). Velocity-porosity relationships in oceanic basalt from eastern flank of the Juan de Fuca Ridge: The effect of crack closure on seismic velocity. Exploration Geophys. 39, 41–51. doi:10.1071/eg08001
Turchyn, A. V., Alt, J. C., Brown, S. T., DePaolo, D. J., Coggon, R. M., Chi, G., et al. (2013). Reconstructing the Oxygen Isotope Composition of Late Cambrian and Cretaceous Hydrothermal Vent Fluid. Geochimica et Cosmochimica Acta 123, 440–458. doi:10.1016/j.gca.2013.08.015
Von Damm, K. L., Bischoff, J. L., and Rosenbauer, R. J. (1991). Quartz Solubility in Hydrothermal Seawater; an Experimental Study and Equation Describing Quartz Solubility for up to 0.5 M NaCl Solutions. Am. J. Sci. 291, 977–1007. doi:10.2475/ajs.291.10.977
Von Damm, K. L., Buttermore, L. G., Oosting, S. E., Bray, A. M., Fornari, D. J., Lilley, M. D., et al. (1997). Direct Observation of the Evolution of a Seafloor 'black Smoker' from Vapor to Brine. Earth Planet. Sci. Lett. 149, 101–111. doi:10.1016/s0012-821x(97)00059-9
Wilcock, W., Dziak, R., Tolstoy, M., Chadwick, W., Nooner, S., Bohnenstiel, D., et al. (2018). The Recent Volcanic History of Axial Seamount: Geophysical Insights into Past Eruption Dynamics with an Eye toward Enhanced Observations of Future Eruptions. Oceanog. 31, 114–123. doi:10.5670/oceanog.2018.117
Wood, J. R., and Hewett, T. A. (1982). Fluid Convection and Mass Transfer in Porous Sandstones-A Theoretical Model. Geochimica et Cosmochimica Acta 46, 1707–1713. doi:10.1016/0016-7037(82)90111-9
Wostbrock, J. A. G., Sharp, Z. D., Sanchez-Yanez, C., Reich, M., van den Heuvel, D. B., and Benning, L. G. (2018). Calibration and Application of Silica-Water Triple Oxygen Isotope Thermometry to Geothermal Systems in Iceland and Chile. Geochimica et Cosmochimica Acta 234, 84–97. doi:10.1016/j.gca.2018.05.007
Wostbrock, J. A. G., and Sharp, Z. D. (2021). Triple Oxygen Isotopes in Silica-Water and Carbonate-Water Systems. Rev. Mineral. Geochem. 86, 367–400. doi:10.2138/rmg.2021.86.11
Yokoyama, T., Makishima, A., and Nakamura, E. (1999). Evaluation of the Coprecipitation of Incompatible Trace Elements with Fluoride during Silicate Rock Dissolution by Acid Digestion. Chem. Geology 157, 175–187. doi:10.1016/s0009-2541(98)00206-x
Yoshikawa, M., and Nakamura, E. (1993). Precise Isotope Determination of Trace Amounts of Sr in Magnesium-Rich Samples. J. Min. Petr. Econ. Geol. 88, 548–561. doi:10.2465/ganko.88.548
Zakharov, D. O., Bindeman, I. N., Tanaka, R., Friðleifsson, G. Ó., Reed, M. H., and Hampton, R. L. (2019). Triple Oxygen Isotope Systematics as a Tracer of Fluids in the Crust: A Study from Modern Geothermal Systems of Iceland. Chem. Geology 530, 119312. doi:10.1016/j.chemgeo.2019.119312
Zakharov, D. O., and Bindeman, I. N. (2019). Triple Oxygen and Hydrogen Isotopic Study of Hydrothermally Altered Rocks from the 2.43-2.41 Ga Vetreny belt, Russia: An Insight into the Early Paleoproterozoic Seawater. Geochimica et Cosmochimica Acta 248, 185–209. doi:10.1016/j.gca.2019.01.014
Zakharov, D. O., Lundstrom, C. C., Laurent, O., Reed, M. H., and Bindeman, I. N. (2021a). Influence of High marine Ca/SO4 Ratio on Alteration of Submarine Basalts at 2.41 Ga Documented by Triple O and Sr Isotopes of Epidote. Precambrian Res. 358, 106164. doi:10.1016/j.precamres.2021.106164
Zakharov, D. O., Marin-Carbonne, J., Alleon, J., and Bindeman, I. N. (2021b). Triple Oxygen Isotope Trend Recorded by Precambrian Cherts: A Perspective from Combined Bulk and In Situ Secondary Ion Probe Measurements. Rev. Mineral. Geochem. 86, 323–365. doi:10.2138/rmg.2021.86.10
Zheng, Y.-F. (1993a). Calculation of Oxygen Isotope Fractionation in Anhydrous Silicate Minerals. Geochim. Cosmochim. Acta 57, 1079–1091. doi:10.1016/0016-7037(93)90306-h
Keywords: hydrothermal reactions, seawater-basalt interaction, triple oxygen isotopes, Axial Seamount, submarine vent fluids
Citation: Zakharov DO, Tanaka R, Butterfield DA and Nakamura E (2021) A New Insight Into Seawater-Basalt Exchange Reactions Based on Combined δ18O—Δ′17O—87Sr/86Sr Values of Hydrothermal Fluids From the Axial Seamount Volcano, Pacific Ocean. Front. Earth Sci. 9:691699. doi: 10.3389/feart.2021.691699
Received: 06 April 2021; Accepted: 10 August 2021;
Published: 09 September 2021.
Edited by:
Fang-Zhen Teng, University of Washington, United StatesReviewed by:
Xin-Yuan Zheng, University of Minnesota Twin Cities, United StatesCopyright © 2021 Zakharov, Tanaka, Butterfield and Nakamura. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: D. O. Zakharov, ZGF2aWQuemFraGFyb3ZAdW5pbC5jaA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.