Adaption of Theoretical Adsorption Model on Coal: Physical Structure

With the motivation to investigate the role of coal physical structure on the adsorption performance of coal reservoir, 18 different types of coal samples with different coal structures were collected from six coal profiles of four production mines located at China. The adsorption characteristics of CH₄ on coal samples with different coal structures were examined, and then experimental results were fitted and analyzed by the Langmuir model and the adsorption potential model (D-R and D-A). The prominent factors in terms of adsorption capacity of coal with different coal structures and its adaptability to the model were discussed. Results indicate the following: a) under the condition of a similar coal rank, the adsorption performance of coal is governed by coal rock composition and adsorption heat, the effect of structural deformation on the adsorption performance of coal is not obvious; b) the Langmuir model has a certain adaptability to coal samples with different coal structures, while the D-R model is evidently not suitable to describe coal samples with scaly coal, part of broken coal with small vitrinite content; c) the D-A model has a high adaptability to coal samples with various coal structure types, and the stronger the coal deformation is, the higher the accuracy is.

Introduction

Adsorption is a kind of surface interaction between coal solid surface and gas or liquid, and coalbed methane mainly exists in the adsorption state in coal reservoirs. All the metamorphic degree of coal, coal rock composition, moisture, temperature, reservoir pressure, and other factors have important impacts on the adsorption performance of coal. Previous studies have made many achievements in this area (Fu, 2001; Zhong et al., 2002; Zhong, 2004; Su et al., 2005; Sang et al., 2005; Zhang et al., 2006; Zhang and Sang, 2008), and the structural coal reservoir is the critical research subject for the development and prevention of coalbed methane (Zhang et al., 2007; Sang et al., 2005; Sun et al., 2019), associated deformation mechanism and structural evolution of tectonic coal have attracted extensive attention (Wang and Zhu, 1998; Jiang et al., 1998; Jiang and Ju, 2004). The coupling characteristics of different structural types of tectonic coal to gas have required due attention as well (Li, 2001; Jiang et al., 1998, Jiang and Ju, 2004; Jiang et al., 2009, Zhao et al., 2019). Moreover, the soft stratification in tectonic coal is the dangerous area of gas enrichment and outburst, which has formed a consensus in both the academy and industry. With the strengthening of structural deformation, the alteration of the occurrence state of gas inside coal takes place. And, it is worth mentioning that the evolution of coal structure leads to the change of pores and fissures, which inevitably imposes a direct impact on the adsorption behavior of coal. However, there are few reports on the related research, and current research is heavily dependent on the theoretical analysis of the Langmuir model (Ju, 2003; Zhang and Liu, 2009), while the application of the Langmuir model in the adsorption of coal with a complex pore structure remains in debate (Chen et al., 1998; Sun et al., 2020). In contrast, the volume filling model (D-R) and the optimal volume filling model (D-A), which are important models in the field of adsorption theory, both have been widely used in the study of adsorption behavior of coal (Crosdale et al., 1998; Laxminarayana and Crosdale, 1999; Dai et al., 2009). However, both D-R and D-A models have not been used in the study of adsorption behavior of coal samples with different coal structures. Therefore, adaption of different theoretical adsorption models on coal is of great significance for further understanding the influence of coal structure evolution on the adsorption performance of coal reservoir.

Sample Selection and Adsorption Experiment

In this study, 18 samples of primary structure coal, catallactic coal, granulated coal, flake coal, and mylonitic coal were collected from four production mines in China. The evolution of coal structure on the same coal rock section is continuous, which is beneficial to reduce the interference of other factors in the following comparative analysis. Concrete experimental contents include industrial analysis, vitrinite reflectance measurement, equilibrium water test, and isothermal adsorption experiment. The basic physical properties of each sample are shown in Table 1.

TABLE 1

TABLE 1. Vitrinite reflectance measurement and industrial analysis of samples.

The high-pressure isothermal adsorption instrument produced by raven ridge company of the United States is used for isothermal adsorption. The sample processing and experimental procedures are introduced in detail in our previous literature (Wu, 2010). This experiment simulates the temperature and reservoir pressure under formation conditions: the experimental temperature is 30°C and the maximum reservoir pressure is 12 MPa. The pressure adsorption capacity at seven equilibrium points is tested.

Results and Discussion

Basic Physical Characteristics

The maximum reflectance (RO, max) of vitrinite falls in the range of 0.725–0.849%, which belongs to gas coal. The metamorphic degree of the same coal section is similar.

Adsorption Characteristics of Coal Samples With Different Coal Structures

The adsorption characteristics of coal samples with different coal structures are depicted in Figure 1. It can be observed that when temperature is 30°C and the maximum pressure is 12 MPa, on the same coal rock section, with the evolution of coal structure, the adsorption characteristics of coal samples behave differently. The isothermal adsorption curves of flake coal and crushed coal are close, which have stronger adsorption capacity than deformed mylonitic coal. The adsorption capacity of three samples on the section of working face B is the largest under the maximum equilibrium pressure; it can be demonstrated that adsorption capacity increases with the increase of coal deformation strength. The adsorption capacity of mylonitic coal on the working face C is the largest. The results suggest that the adsorption capacity of one broken coal is similar to that of the mylonitic coal, while the adsorption capacity of the other broken coal is smaller than that of the primary structure coal. The adsorption curves of the two broken coal on the working face D are similar, but the adsorption capacity is different. The adsorption capacity of the primary structure coal, broken coal, broken coal, and mylonitic coal on the working face E is the largest, in which the adsorption capacity of the broken coal is the highest. Notably, the adsorption capacity of fractured coal in working face F is evidently larger than that of primary structure coal.

FIGURE 1

FIGURE 1. Distribution map of MRE to adsorption model of sheared coal.

According to the comparative analysis of adsorption curves (Figure 2) and basic physical property characteristics (Table 1), it can be concluded that the adsorption characteristics of the studied coal samples is obviously governed by coal structure, ash content, and metamorphic degree. As for the case of the same coal rock section, adsorption capacity of coal increases with the increase of structural deformation but decreases with the increase of ash content due to the weak adsorption capacity of the ash content. Among the rock sections, coal section B shares the highest metamorphic degree and the largest overall adsorption capacity.

FIGURE 2

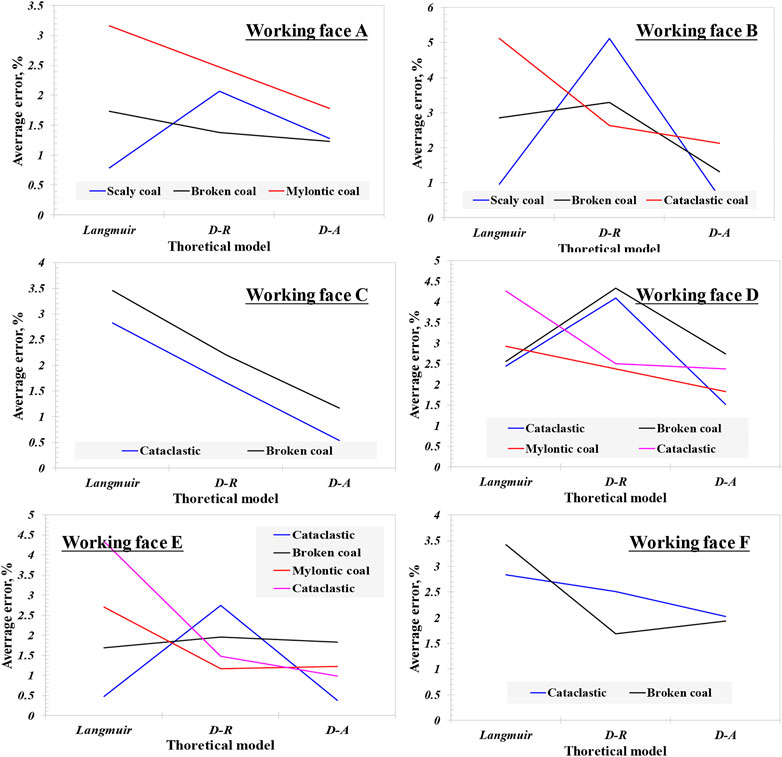
FIGURE 2. Adsorption Characteristics of coals with different structures on the same coal rock section.

Model Fitting and Evaluation

Kinetic models (Langmuir monolayer model, BET multilayer model, etc.) and Polanyi adsorption potential models (D-A model and D-R model) are commonly used to describe the coal adsorption mechanism. Different theoretical adsorption models are supported by a large number of experimental data; also each model has its own application scope. It is generally believed that Langmuir equation is mainly used to describe type-I adsorption isotherm, which is suitable for solid substances with developed pores such as activated carbon or solids with uniform surface without pores. The BET equation is mainly applied to describe porous substances with rich mesopores, while the deviation enlarges when it comes to supercritical fluids; therefore, it can be used to describe type I, II, and III adsorption isotherm and calculate specific surface area of porous substances. The D-R equation is generally suitable for adsorbents with small pore size, in which the multilayer adsorption or capillary condensation is unfavorable (Clarkson, 1997). The parameter n in D-A equation varies with the pore structure of adsorbents, which considerably expand its application scope.

Because the premise of the application of the BET model is to determine four or five points in the range of P/Po (the ratio of equilibrium gas pressure and saturated vapor pressure) = 0.05–0.35, and the monolayer adsorption volume (Vm) can be calculated, while the P/Po of the seven equilibrium points in isothermal adsorption test is mostly greater than 0.35, the calculation of BET model parameters from the data of seven equilibrium points will be seriously distorted or even have no solution. However, the Langmuir, D-R, and D-A models are not limited by the above factor, so this study uses the Langmuir, D-R, and D-A models to analyze coal samples with different coal structures.

The calculation formulas of the three models are as follows. For the Langmuir monolayer localization adsorption model:

$V=\frac{V_{L}P}{P_L+P},$

where V is the adsorption capacity, m³/g; VL is the Langmuir volume, m³/g, which represents the adsorption capacity when the surface of each gram of coal is covered with monolayer; PL is the Langmuir pressure, MPa, which represents the corresponding equilibrium pressure when the adsorption reaches half of the maximum adsorption capacity; and P is the equilibrium gas pressure, MPa.

The theoretical adsorption potential models (D-R model and D-A model) are as follows:

$V=V_0\exp \left[-D(L{n}^2\left(\frac{P_0}{P}\right)\right],\left(\text{D}-\text{R}\right),$

$V=V_0\exp \left[-D(L{n}^{\text{n}}\left(\frac{P_0}{P}\right)\right],\left(\text{D}-\text{A}\right),$

where V is the adsorption capacity, m³/g; V0 is the volume of micropore per gram (regarded as completely filled with adsorbed gas molecules), m³/g; D is the constant related to net adsorption heat in the equation; n is the parameter related to temperature and pore distribution of coal; and P is the equilibrium gas pressure, MPa.

Under the condition of 30°C, CH₄ belongs to the supercritical state. The virtual saturated vapor pressure of CH₄ can be calculated according to the formula of P0 = PC * (T/TC) 2 (PC denotes the critical pressure and TC denotes the critical temperature). After calculation, the saturated vapor pressure of CH₄ is 11.68 MPa.

Notably, SPSS17.0 software was used to fit the adsorption capacity of seven equilibrium points, and the seven parameters of the Langmuir, D-R, and D-A models, the standard deviation of each parameter, and the correlation degree of curve fitting (Table 2) were obtained. It can be observed from the table that the correlation of Langmuir model fitting parameters of 18 samples ranges from 0.980 ∼ 1, the correlation of D-R model fitting parameters was between 0.978 ∼ 0.999, and the correlation degree of D-A model fitting parameters was between 0.992 and 1. From this perspective, the fitting correlation of each model is fairly high; in other words, all the three models are favorable to describe the adsorption behavior of the coal reservoir.

TABLE 2

TABLE 2. Characteristic parameters and fitting characteristics obtained from fitting models.

The VL of the Langmuir model represents the theoretical maximum adsorption, and the VL of 18 coal samples ranges from 9.381 to 20.482 m³/g. The VL of the primary structure coal on working face F is the smallest and fragmental coal on working face B is the largest. There is no consistent rule in the variation of VL in each coal petrography section. There exist differences in the VL of the same type of fragmental coal in the same coal petrography section. However, from primary structure coal to fragmental coal, VL of scale coal is larger than that of fragmental coal, while that of mylonitic coal is the smallest on the working face A, the same as the broken coal in working face C, and larger than the broken coal in working face E, showing complex variation characteristics. PL represents the equilibrium pressure when the adsorption reaches half of the maximum adsorption capacity. The VP of 18 coal samples ranges from 1.736 to 3.689 MPa. In general, VP increases with the increase of VL, but PL of scaly coal on working face B and primary structure coal on working face F with weak deformation are larger than the VP with strong deformation, suggesting opposite characteristics.

As for the adsorption potential models (D-R and D-A), V0 is the volume of micropores per gram (regarded as completely filled with adsorbed gas molecules), D is the constant related to net adsorption heat, and n is the parameter related to temperature and pore distribution of coal. The isothermal adsorption tests of 18 coal samples are performed at 30°C; therefore, n is mainly related to the pore size distribution. When n = 2, the D-A model becomes the D-R model, and V0 in the D-R model falls in the range of 7.171–14.747 m³/g and V0 in the D-A model is in the range of 7.238–15.120 m³/g. The results show that the primary structure coal on working surface F is the smallest and the broken coal on working surface B is the largest, which is the same as the VL in the Langmuir model. The V0 in the D-R model is generally smaller than that in the D-A model, but the V0 in the D-R model of two mylonitic coal on working face A and E is larger than that in the D-A model. D in the D-R model ranges from 0.147 and 0.222, and D in the D-A model is between 0.123 and 0.337. The variation range of adsorption heat constant of the D-A model is wide. From the distribution of adsorption heat constant D in the same coal profile and coal structure of the two models, the adsorption heat parameters of the D-A model are obviously more accurate. Obviously, this is due to the introduction of pore structure parameters. n ranges from 0.143 to 2.219. The n of mylonitic coal on working face A and E are larger than 2, the smallest is scaly coal, the largest is mylonitic coal on working face A, and the corresponding adsorption heat constant is the opposite, scaly coal on working face B is the largest, the smallest is mylonitic coal on working face A, which is closely related to the pore characteristics of coal reservoir. The complexity of pore structure in turn affects the decrease of adsorption heat constant.

Adaptability of Structural Coal Adsorption Model

Although the Langmuir, D-R, and D-A models fit the adsorption equation with high correlation, they can be used to describe the adsorption behavior of tectonic coal to methane. However, the standard deviation of the ideal value and fitting value of each parameter is different, which indicates that different models describe different coal samples with different accuracy. In order to analyze the reliability of different models describing coal samples with different coal structures, this study introduces the parameter of average relative error (MRE%) to analyze. The calculation formula of MRE% is as follows:

$MRE\%=\frac{{\displaystyle {\sum }_{i=1}^N\left|\left(V^{\exp }-V^{cal}\right)/V^{\exp }\right|}}{N}\times 100,$

where Vexp is the adsorption capacity of experimental test, Vcal is the fitting value of the model, taking the pressure of each equilibrium point into the equation, cm³/g. n = 7, corresponds to the seven equilibrium points collected from the experimental test. The average relative error curve of each coal and rock profile model fitting is shown in Figure 1. It can be observed that the average relative error has two variation characteristics: a) gradually decreasing; b) small at both ends and large in the middle. Actually, the three models are almost consistent in describing the adsorption accuracy of coal samples with different coal structures. The average relative error of the Langmuir model of minced coal is the largest, then the D-R model, and that of the D-A model is the smallest. For the majority of the fractured coal and mylonitic coal, the average relative error of the Langmuir model is higher than that of the D-R and D-A models, while the average relative error of fractured coal sample on working face A is significantly higher than that of the Langmuir and D-A models. The average relative error of scaly coal ranges from the Langmuir model to the D-R to D-A models, and the average relative error manifests an inverted “V” shape. For broken coal on working face A, the average relative error is not different. On the same coal rock section, the average relative error of the Langmuir model and D-R model is complex with the aggravation of coal structure deformation, and there is no obvious rule. However, the D-A model generally shows the trend of decreasing with the aggravation of coal structure deformation.

The average relative error is a comprehensive reflection of the standard deviation of each model parameter, through which the fitting accuracy of each model can be directly reflected. From the above analysis, it can be seen that for the three models, the Langmuir model has a certain adaptability to different deformation types of tectonic coal, but the change is larger with the coal sample, while the D-R model is obviously not suitable for describing the scale coal and the D-A model has high adaptability to all kinds of coal structure types, also the stronger coal deformation will contribute to higher accuracy.

Conclusion

Under the condition of 30°C and 12 MPa maximum pressure, CH₄ adsorption isotherm experiments was carried out on 18 primary structure coal, catallactic coal, granulated coal, scaly coal, and mylonitic coal with different coal structures under the condition of equilibrium water. The results show that the isothermal adsorption capacity of coal increases with the increase of pressure and increases with the increase of structural deformation under the same pressure. However, the isothermal adsorption capacity of coal samples with strong deformation degree is not greater than that of coal samples with weak deformation degree. It is obvious that structural deformation has a significant impact on the adsorption of coal, but it is not the only factor. Key insights regarding adaptability of theoretical model on adsorption behavior of coal are summarized.

1) The Langmuir model, D-R model, and D-A model can be used to describe the CH₄ adsorption behavior of 18 coal samples. There is no consistent rule for the alteration of VL of Langmuir volume, but from primary structure coal to crushed coal, VL increases with the increase of coal structure, and the change of VL of mylonitic coal in different coal rock sections is complex. Generally speaking, the pressure VP increases with the increase of the volume VL. The variation trend of V0 in D-R and D-A is the same as that in the Langmuir model. V0 in the D-R model is generally smaller than that in the D-A model, but V0 in the D-R model is larger than that in the D-A model. The variation range of adsorption heat constant of the D-A model is larger than that of the D-R model, due to the introduction of pore structure parameters.

2) The standard deviation of the Langmuir model is generally larger than that of the D-R and D-A models, and the standard deviation of adsorption heat constant D is very small. In theory, the D-A model is more accurate than the D-R model due to the introduction of parameter n, but its parameters are less accurate. The standard deviation of D is larger than that of the D-R model.

3) According to the analysis of the average relative error of different models for 18 coals with different coal structures, it can be demonstrated that the Langmuir model has certain adaptability for different deformation types of structural coal, while the D-R model is obviously not suitable for describing flake coal and part of broken coal. The D-A model has high adaptability for all kinds of coal structure types, and the stronger coal deformation will contribute to its higher accuracy.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

GW—investigation; LP—funding acquisition and supervision; BH—investigation and supervision; JL—methodology; YZ—investigation; RZ—data analysis; ZS—manuscript drafting.

Funding

The authors would like to acknowledge the funding by Chongqing Science and Technology Bureau project (No. cstc2017jcyjBX0076) and Fundamental Research Funds for the Central Universities (No. 2019XKQYMS25).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Amankwah, K. A. G., and Schwarz, J. A. (1995). A Modified Approach for Estimating Pseudo-vapor Pressures in the Application of the Dubinin-Astakhov Equation. Carbon 33 (9), 1313–1319. doi:10.1016/0008-6223(95)00079-s

CrossRef Full Text | Google Scholar

Chen, C., Xian, X., Zhang, D., et al. (1998). Study on Adsorption Characteristics of Anthracite and Carbon for Methane by Micropore Filling Theory [J]. J. Chongqing Univ. 21 (2), 75–79.

Google Scholar

Clarkson, C. R., Bustin, R. M., and Levy, J. H. (1997). Application of the Mono/multilayer and Adsorption Potential Theories to Coal Methane Adsorption Isotherms at Elevated Temperature and Pressure. Carbon 35, 1689–1705. doi:10.1016/s0008-6223(97)00124-3

CrossRef Full Text | Google Scholar

Crosdale, P. J., Beamish, B. B., and Valix, M. (1998). Coalbed Methane Sorption Related to Coal Composition. Int. J. Coal Geology. 35, 147–158. doi:10.1016/s0166-5162(97)00015-3

CrossRef Full Text | Google Scholar

Dai, S., Zhang, B., Peng, S., et al. (2009). Discussion on the Adsorption Model of CO2 and CH4 on Late Paleozoic Coal in Kailuan Mining Area of Hebei Province [J]. Acta geologica Sinica 83 (5), 731–737.

Google Scholar

Fu, X. (2001). Physical Simulation and Numerical Simulation of Physical Properties of Coal and Rock Mass in Multiphase media [D]. Xuzhou, Jiangsu: China University of mining and technology.

Jiang, B., and Ju, Y. (2004). Structural Coal Structure and Reservoir Properties [J]. Nat. gas industry 24 (5), 27–29.

Google Scholar

Jiang, B., Qin, Y., and Jin, F. (1998). Deformation Characteristics of Coal Ultrastructure under High Temperature and High Pressure [J]. Geoscience 33 (1), 17–24.

Google Scholar

Jiang, B., Qin, Y., Ju, Y., et al. (2009). Coupling Mechanism between Chemical Structure Evolution and Gas Characteristics of Tectonic Coal [J]. Frontier of Geosciences 16 (2), 262–270.

Google Scholar

Ju, Y. (2003). Structural Evolution of Tectonic Coal, Physical Properties of Reservoir and its Working Mechanism [D]. Xuzhou: China University of mining and technology.

Laxminarayana, C., and Crosdale, P. J. (1999). Role of Coal Type and Rank on Methane Sorption Characteristics of Bowen Basin, Australia Coals. Int. J. Coal Geology. 40, 309–325. doi:10.1016/s0166-5162(99)00005-1

CrossRef Full Text | Google Scholar

Li, H. (2001). Major and Minor Structural Features of a Bedding Shear Zone along a Coal Seam and Related Gas Outburst, Pingdingshan coalfield, Northern China. Int. J. Coal Geology. 47 (2), 101–113. doi:10.1016/s0166-5162(01)00031-3

CrossRef Full Text | Google Scholar

Ozawa, S., Kusumi, S., and Ogino, Y. (1976). Physical Adsorption of Gases at High Pressure. IV. An Improvement of the Dubinin-Astakhov Adsorption Equation. J. Colloid Interf. Sci. 56, 83–91. doi:10.1016/0021-9797(76)90149-1

CrossRef Full Text | Google Scholar

Qingdao Institute of chemical technology (2002b). Data Manual of Chemical and Physical Properties (Inorganic) [M]. Beijing: Chemical Industry Press.

Qingdao Institute of chemical technology (2002a). Data Manual of Chemical and Physical Properties (Organic) [M]. Beijing: Chemical Industry Press.

Sang, S., Zhu, Y., and Zhang, J. (2005). Experimental Study on the Effect of Liquid Water on Methane Adsorption by Coal: a Case Study of Coal Reservoir in Southern Qinshui Basin [J]. Sci. Bull. 50 (Zeng 1), 70–75. doi:10.1007/bf03184087

CrossRef Full Text | Google Scholar

Shuxun, S., Hongjie, X., Liangcai, F., Guojun, L., and Huazhou, H. (2010). Stress Relief Coalbed Methane Drainage by Surface Vertical Well in China. international J. coal geology[J] 82, 196–203.

Google Scholar

Su, X., Zhang, L., and Lin, X. (2005). Effect of Coal Rank on Adsorption Capacity of Coal [J]. Nat. gas industry 25 (1), 19–21.

Google Scholar

Sun, Z., Li, X., Liu, W., Zhang, T., He, M., and Nasrabadi, H. (2020). Molecular Dynamics of Methane Flow Behavior through Realistic Organic Nanopores under Geologic Shale Condition: Pore Size and Kerogen Types. Chem. Eng. J. 398, 124341. doi:10.1016/j.cej.2020.124341

CrossRef Full Text | Google Scholar

Sun, Z., Shi, J., Wu, K., Zhang, T., Feng, D., and Li, X. (2019). Effect of Pressure-Propagation Behavior on Production Performance: Implication for Advancing Low-Permeability Coalbed-Methane Recovery. SPE J. 24 (02), 681–697. doi:10.2118/194021-pa

CrossRef Full Text | Google Scholar

Wang, G., and Zhu, Y. (1998). On Coal Seam Rheology. J. China Univ. mining Technol. (3), 16–25.

Google Scholar

Wu, G. (2010). Microstructure and Adsorption Characteristics of Tectonic Coal in Huainan Mining Area [D]. Xuzhou: Master's thesis of China University of mining and Technology.

Zhang, L., Su, X., and Zeng, R. (2006). Discussion on the Control of Coal Properties on Coal Adsorption Capacity [J]. Acta geologica Sinica 80 (6), 910–915.

CrossRef Full Text | Google Scholar

Zhang, S., and Sang, S. (2008). Effect of Liquid Water on Methane Adsorption of Different Coal Grades and its Mechanism [J]. Acta geologica Sinica 82 (10), 1350–1354.

CrossRef Full Text | Google Scholar

Zhang, X., Liu, H., et al. (2009). Adsorption Response and Control Mechanism of Coal Structure Difference [J]. Geosci. J. China Univ. Geosciences 34 (5), 848–854.

Google Scholar

Zhang, Y., Zhang, Z., and Cao, Y. (2007). Journal of Structural Coal Structure and Gas Outburst [J]. 3 (23), 281–284.

Google Scholar

Zhao, X., Huang, B., and Xu, J. (2019). Experimental Investigation on the Characteristics of Fractures Initiation and Propagation for Gas Fracturing by Using Air as Fracturing Fluid under True Triaxial Stresses. Fuel 236, 1496–1504. doi:10.1016/j.fuel.2018.09.135

CrossRef Full Text | Google Scholar

Zhao, Z., and Tang, X. (2002). Discussion on Langumir Equation of Methane Adsorption by Coal [J]. J. Jiaozuo Inst. Technol. 21 (1), 1–4.

Google Scholar

Zhong, L. (2004). Adsorption Properties of Coal and its Influencing Factors [J]. Earth Sci. J. China Univ. Geosciences 29 (3), 327–332.

Google Scholar

Zhong, L., Zhang, H., Yuan, Z., and Lei, C. (2002). Effect of Specific Surface Area and Pore Volume of Coal on Adsorption Capacity of Coal [J]. Coalfield Geology. Exploration 30 (3), 26–29.

Google Scholar

Zhou, Y., and Zhou, L. (1997). Study on Adsorption Isotherm of Supercritical Hydrogen on Activated Carbon [J]. Acta physicochemical Sinica 13 (2), 119–126.

Google Scholar