Comparing the Performance of Regional Earthquake Early Warning Algorithms in Europe

Several earthquake early warning (EEW) algorithms have been developed worldwide for rapidly estimating real-time information (i.e., location, magnitude, ground shaking, and/or potential consequences) about ongoing seismic events. This study quantitatively compares the operational performance of two popular regional EEW algorithms for European conditions of seismicity and network configurations. We specifically test PRobabilistic and Evolutionary early warning SysTem (PRESTo) and the implementation of the Virtual Seismologist magnitude component within SeisComP, VS(SC), which we use jointly with the SeisComP scanloc module for locating events. We first evaluate the timeliness and accuracy of the location and magnitude estimates computed by both algorithms in real-time simulation mode, accounting for the continuous streaming of data and effective processing times. Then, we focus on the alert-triggering (decision-making) phase of EEW and investigate both algorithms’ ability to yield accurate ground-motion predictions at the various temporal instances that provide a range of warning times at target sites. We find that the two algorithms show comparable performances in terms of source parameters. In addition, PRESTo produces better rapid estimates of ground motion (i.e., those that facilitate the largest lead times); therefore, we conclude that PRESTo may have a greater risk-mitigation potential than VS(SC) in general. However, VS(SC) is the optimal choice of EEW algorithm if shorter warning times are permissible. The findings of this study can be used to inform current and future implementations of EEW systems in Europe.

Introduction

The goal of an earthquake early warning (EEW) system is to deliver a rapid alert about impending strong shaking that provides sufficient time for protective, loss-mitigating actions to be taken by targeted end users. The process of EEW generally consists of the following steps: 1) detection of an event in the early stages of fault rupture; 2) prompt prediction of the relevant source parameters (e.g., location and magnitude) and/or the intensity of the consequent ground motion; and 3) warning issuance to end users before they experience the strong shaking that might cause damage and losses.

EEW systems may be broadly classified as “regional,” “on-site,” or “hybrid.” We specifically focus on regional systems, which are based on a dense sensor network covering a geographical area of high seismicity. When an earthquake occurs, these systems typically estimate source parameters from the early portion of signals recorded at sensors close to the rupture. Location (and resulting source-to-site distance, R) is generally computed by accounting for geometrical constraints associated with both triggered and not-yet-triggered stations; earthquake magnitude (M) is typically calculated based on empirical relationships relating the earthquake size to parameters obtained in the first 3–4 s of P- and (sometimes) S-wave signals. Figure 1 illustrates the principles of a conventional regional EEW system. For a more detailed review of various approaches to estimate location and magnitude in regional EEW systems, interested readers are referred to Cremen and Galasso (2020).

FIGURE 1

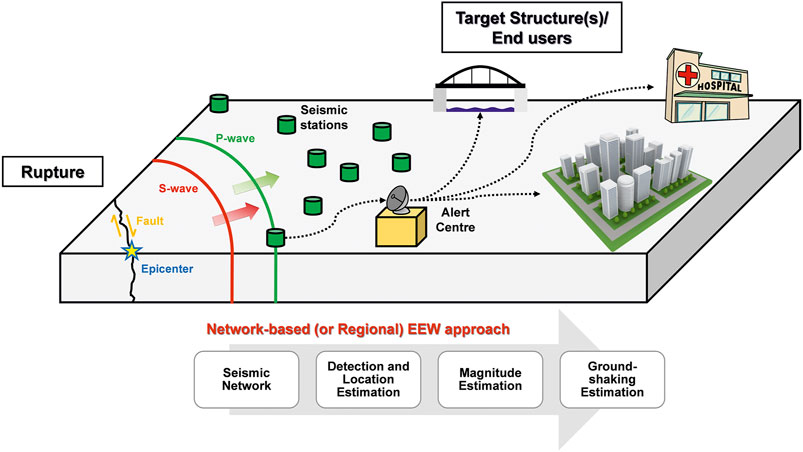
FIGURE 1. The principles of a standard regional EEW system and conceptual outline of the corresponding EEW process. Information from an EEW system sensor network is input to an EEW algorithm to detect events and compute estimates of earthquake location, magnitude, and ground-motion amplitude. An alert may then be issued to warn end users of impending shaking.

R and M estimates can be continuously updated (through Bayesian approaches or otherwise) by adding new station data as the P-wave front propagates through the regional EEW network. The real-time values are then used to predict, with quantified uncertainty, ground-motion intensity measures (IMs) at sites far away from the source (where target structures/infrastructure of interest and end users are located), by using, for example, ground-motion models (GMMs). If probabilistic distributions of M and R are available, the prediction of different IMs (e.g., Iervolino et al., 2006; Convertito et al., 2008) may be performed by analogy to the well-known Probabilistic Seismic Hazard Analysis (PSHA) framework but in real-time, as discussed in detail in Iervolino et al. (2009). Regional EEW systems typically require the arrival of P-wave signals at a number of stations to provide stable early estimates of R, M, and IM. Thus, event detection is a fundamental task for EEW. Erroneously detected or inaccurate phases, along with poor event associations, lead to inaccurate location and magnitude estimates and, ultimately, possible false or missed alerts. It is worth noting that most regional EEW algorithms assume a point-source model of the earthquake source and isotropic wave amplitude attenuation, which neglects the finite geometry of earthquake ruptures. These assumptions are generally suitable for estimating the final magnitude of events with M 6.5 7.0 (Meier et al., 2020), which are consistent with the largest seismicity that is typically observed in Europe (i.e.,the focus of our study) and the range of magnitudes we consider (5.5–6.9). We acknowledge that M > 7.0 events can occur in Europe, like the 1755 moment magnitude (M_W) 8.5 Lisbon earthquake, which is the largest listed in the SHEEC catalog (the “SHARE European Earthquake Catalog,” Grünthal et al., 2013; Stucchi et al., 2013). However, these types of events were not accounted for in this study given their very low occurrence rate.

European approaches to regional EEW have been promoted and progressed through recent EU-funded research projects (Clinton et al., 2016), such as SAFER (“Seismic early warning for Europe”) and REAKT (“Strategies and tools for real-time earthquake risk reduction”). These two projects have facilitated the development and testing of the PRESTo (Probabilistic and Evolutionary Early Warning System) and VS(SC) (Virtual Seismologist in SeisComP) regional EEW algorithms, which are the most widely applied regional EEW algorithms in Europe to date (Cremen and Galasso, 2020) and are therefore the focus of our investigations in this paper. PRESTo is currently operating in Southern Italy (Irpinia region), Turkey, Romania, and Southern Iberia (Carranza et al., 2017). It has also been tested for application at the border of Italy, Austria, and Slovenia (Picozzi et al., 2015). Instead, VS(SC) is currently operational in Switzerland and has been tested for use in Greece, Turkey, Romania, and Iceland (Behr et al., 2016).

Efforts to compare the performance of PRESTo and VS(SC) are currently underway within the Early Warning Test Center of the EPOS (“European Plate Observing System”) EU project. However, they have so far been limited to the Irpinia region of Italy. We build on the attempts of the Early Warning Test Center in this study by comparing the performance of the PRESTo and VS(SC) algorithms for multiple European conditions of seismicity and existing seismic network configurations (i.e., geometries and densities). We specifically consider five European geographic areas - Southern Italy, Pyrenees, Southwest Iceland, Western Greece, and the Vrancea region in Romania - that represent a range of hazard levels and various seismotectonic settings: collisional/subduction complex with a complicated back-arc/fore-arc/trench system (Southern Italy), continent-continent collision with the evolution of an orogenic belt (Pyrenees), oceanic crust interplate transform faulting (Southwest Iceland), interplate subduction zones (Western Greece), and intermediate-depth subcrustal seismicity (Romania).

We quantitatively assess the operational performance of the PRESTo and VS(SC) algorithms in real-time simulation mode by using playbacks of recorded seismic waveforms or those simulated through a physics-based method. EEW alerts need to be both timely and sufficiently accurate to be useful (Meier, 2017), especially in Europe, where most earthquake-prone target sites are associated with short available lead times, significant exposure, and earthquake-related vulnerability (e.g., Picozzi et al., 2015). Therefore, our performance assessment focuses on the algorithms’ capability to both quickly and correctly characterize the earthquake source (location and magnitude). We also use GMMs to investigate the impact of the source-parameter predictions on the temporal trend and quality of the resulting ground-motion amplitude estimations. Note that a further performance assessment of the two algorithms is carried out in our companion paper (Cremen et al., 2021), which focuses on the accuracy and uncertainty of the underlying methods from a theoretical perspective using similar event data.

The purpose of our comparison is to identify the best-performing regional EEW algorithms to be implemented in the TURNkey FWCR (Forecasting–Early Warning–Consequence Prediction–Response) platform, a comprehensive information system for facilitating operational earthquake forecasting, EEW, and post-earthquake rapid response actions across the continent. This platform is being developed as part of the TURNkey (“Towards more Earthquake-resilient Urban Societies through a Multi-Sensor-based Information System enabling Earthquake Forecasting, Early Warning and Rapid Response Actions”) EU Project and will rely on SeisComP (version 3-Jakarta release) for waveform acquisition. SeisComP (Helmholtz-Centre Potsdam - GFZ German Research Centre for Geosciences and gempa GmbH, 2008) is a freely available and widely distributed standard real-time earthquake monitoring platform developed by the GEOFON Program at Helmholtz Center Potsdam, GFZ German Research Centre for Geosciences and gempa GmbH (Hanka et al., 2010). It is based on a comprehensive software framework, which includes waveform acquisition (SeedLink), automated earthquake detection, source location and characterization, manual event relocation, event alerting, waveform archiving and dissemination. SeisComP follows a modular approach in which standalone programs communicate through a messaging system connected to a shared database that contains events and station metadata. This modular structure also facilitates the incorporation of seismological and EEW algorithms, which can be individually used for estimating different parameters. TURNkey will ultimately be tested for adoption across six regions with varying characteristics of seismicity in Italy, France, Iceland, Greece, Romania, and the Netherlands.

The paper is organized as follows. We first introduce the considered algorithms and the relevant input data required. We then describe the methodologies used for evaluating the performance of the algorithms. We next assess and compare the algorithms. The paper ends with a discussion of the results, which includes recommendations on the most appropriate algorithms for the TURNkey platform.

Algorithms

We specifically focus on the performance of PRESTo and VS(SC) in this study. PRESTo (Lancieri and Zollo, 2008; Satriano et al., 2008; Satriano et al., 2011) is a free and open-source software platform specifically developed for EEW, which was designed by the Ricerca in Sismologia Sperimentale e Computazionale research group (RISSC-Lab) at the University of Naples Federico II, Italy. It processes real-time waveforms that are streamed from stations using a SeisComP server via the SeedLink protocol and produces hypocentral location estimates in the form of a multivariate normal probability density function (PDF), using the RTLoc method developed by Satriano et al. (2008). According to the RTMag procedure proposed by Lancieri and Zollo (2008), a Bayesian framework is used for predicting magnitude. The RTMag regression-law coefficients that we adopt in this study are listed in Table 1.

TABLE 1

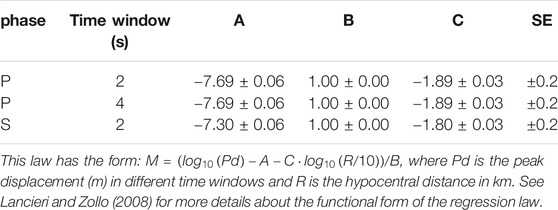
TABLE 1. Coefficients (A, B, C) and SE of the RTMag regression law used in this study for PRESTo (Festa, not published, implemented in the available release of the PRESTo platform).

PRESTo uses the picker algorithm FilterPicker initially proposed by Vassallo et al. (2012) to detect an event, which operates on continuous data-streams by applying a multiband signal processing procedure (i.e., the signal is analyzed in different predetermined frequency bandwidths). The event declaration is constrained to a predefined number of picks within a given time window. Full details of the PRESTo platform can be found in its technical manual (http://www.prestoews.org/documentation.php).

VS(SC) (Virtual Seismologist in SeisComP) (Behr et al., 2016) is the magnitude likelihood component of the Virtual Seismologist EEW algorithm (Cua, 2005; Cua and Heaton, 2007; Cua et al., 2009) that is implemented in SeisComP. It incorporates phase picks and location estimates provided by other SeisComP modules. The coefficients for magnitude estimation are hard-coded in SeisComP (scvsmag module) and provided in Cua (2005).

SeisComP allows a free configuration of recursive filters and filter chains before picking, which is performed by the scautopick module. Several types of filter can be applied, but we use the default option in this study that involves subtraction of the running mean for a given time window, a single application of a one-sided cosine taper at the beginning of new data streams, a Butterworth bandpass filter, and a Short Time Average over Long Time Average (STA/LTA) filter, i.e., the ratio of a short-time average signal amplitude to a long-time average calculated continuously in two partially overlapping time windows of different length. The STA/LTA approach is used as the basis for many triggering algorithms (Allen, 1982). A trigger is declared when the STA/LTA exceeds a certain threshold. A second-stage picker can refine the final pick of the phase. We use the Akaike Information Criterion picker for this purpose, which implements the non-AR algorithm (Maeda 1985; Zhang et al. 2003). The picker is re-initialized after a data gap.

SeisComP location estimates are typically performed using the scautoloc module, which is optimized for teleseismic phase association and requires at least 6 P-wave detections to determine a location estimate. However, we instead pair VS(SC) with the scanloc location module of SeisComP (Roessler et al., 2016; Grigoli et al., 2018) in this study, which is more appropriate for EEW purposes. scanloc can produce fast location estimates with very few P- and S- wave detections from nearby stations (i.e., 2 to define the general epicentral area and 3 to obtain a unique epicenter). It makes use of an advanced cluster search algorithm (DBSCAN) to automatically associate phase detections to potential earthquakes; when a cluster of at least a prescribed minimum number of P-wave picks is identified, all picks within configured time windows and maximum epicentral distance ranges are provisionally associated with it. It should be noted that the cluster search itself is based on P phases only; however, in a second step, more P and S phases are associated and used for locating the earthquake.

For the sake of simplicity, the suite of modules used to produce EEW estimates from SeisComP (which include scanloc and VS(SC)) are referred to as the “VS(SC) algorithm” throughout the rest of the paper. To maintain consistency in our terminology, we herein refer to the PRESTo platform as the “PRESTo algorithm.”

Input Data

Seismic Waveforms

We use observed recordings from past events and physics-based synthetic seismograms to test the two algorithms’ performance. Specifically, we consider observed recordings from Southwest Iceland, Western Greece, and Romania, while synthetic seismograms are computed for Southern Italy and the Pyrenees to compensate for the lack of empirical data from moderate-to-large events in these regions. The use of seismograms from different regions enables the performance of the considered EEW algorithms to be evaluated across a wide range of focal mechanisms, magnitudes, hypocentral depths, and seismic network densities/configurations.

We select observed seismograms from earthquakes with M_w greater than 5.5 that occurred in the last 20 years and were recorded by at least eight of the seismic stations we examined in this study, which were constrained by the availability of recordings in the consulted databases. Recordings for Greece and Romania are retrieved from the European Integrated Data Archive (EIDA, see Data Availability Statement). We consider only strong-motion and broadband sensors. We use one sensor per station, which is always the strong-motion instrument (where present); in all other cases, the broadband seismograms are clipped to prevent the use of saturated velocigrams. Strong-motion recordings from Iceland are obtained from the Internet Site for European Strong-motion Data (ISESD, see Data Availability Statement).

The synthetic seismograms for Southern Italy and the Pyrenees are computed from physics-based numerical simulations, using the broadband ground-motion simulation code described in Crempien and Archuleta (2015), which can simulate the high-frequency content of seismic waves and has already proved to be suitable for EEW feasibility studies (Zuccolo et al., 2016). We specifically generate seismograms for one scenario earthquake on each active fault in both regions. Faults parameters are retrieved from the European Database of Seismogenic Faults (ESDF; Basili et al., 2013). The magnitude of each scenario earthquake is randomly determined by assuming a uniform distribution between 5.5 and the maximum magnitude associated with the fault. The hypocentre is assumed to be located in the center of the fault plane’s horizontal projection, at the minimum fault depth plus 2/3 of the fault’s vertical width (i.e., the difference between the maximum and minimum fault depths). The focal mechanism is defined based on the average strike, dip, and rake values. Rupture fault dimensions are estimated from the Wells and Coppersmith (1994) relationships, and the position of the hypocentre on the fault plane (i.e., along the width and along the length of the fault) is established using the distributions by Causse et al. (2008). The average rupture velocity is determined by assuming a uniform distribution between 65 and 85% of the shear wave velocity on the fault plane. The corner frequency is estimated from the stress drop (Allmann and Shearer, 2009), which is assumed to be equal to 3 MPa (Caporali et al., 2011) for both regions. The seismograms are computed at the location of currently operating permanent stations according to the Incorporated Research Institutions for Seismology (IRIS) database (see Data Availability Statement), up to a maximum epicentral distance of 100 km. Finally, white noise is added to the computed seismograms to facilitate the STA/LTA algorithm’s operation. A detailed engineering validation of these physics-based simulated ground motions (e.g., Galasso et al., 2012; Galasso et al., 2013) is outside the scope of this study.

We consider 27 events in total; their locations are highlighted in Figure 2, and their main features are listed in Table 2, along with the considered seismic networks. Throughout the rest of the paper, we refer to all magnitude, longitude, latitude, and depth values listed in Table 2 as “bulletin” values (for both observed and simulated events).

FIGURE 2

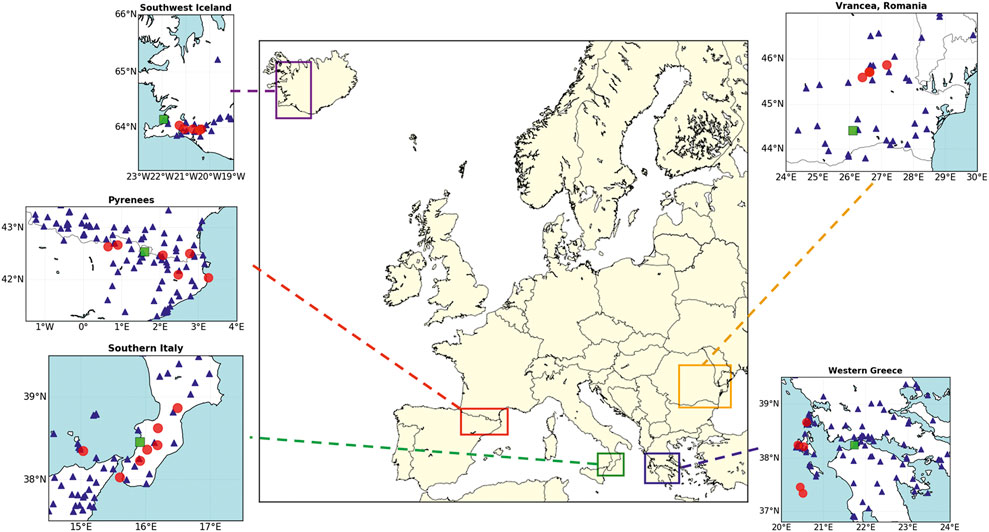
FIGURE 2. Locations of the earthquakes (red circles) and target sites (green squares) considered in this study. Blue triangles represent the considered seismic stations. The target sites are the Port of Gioia Tauro for Southern Italy, Andorra for the Pyrenees, Reykjavík for Southwest Iceland, Patras for Western Greece and Bucharest for Romania.

TABLE 2

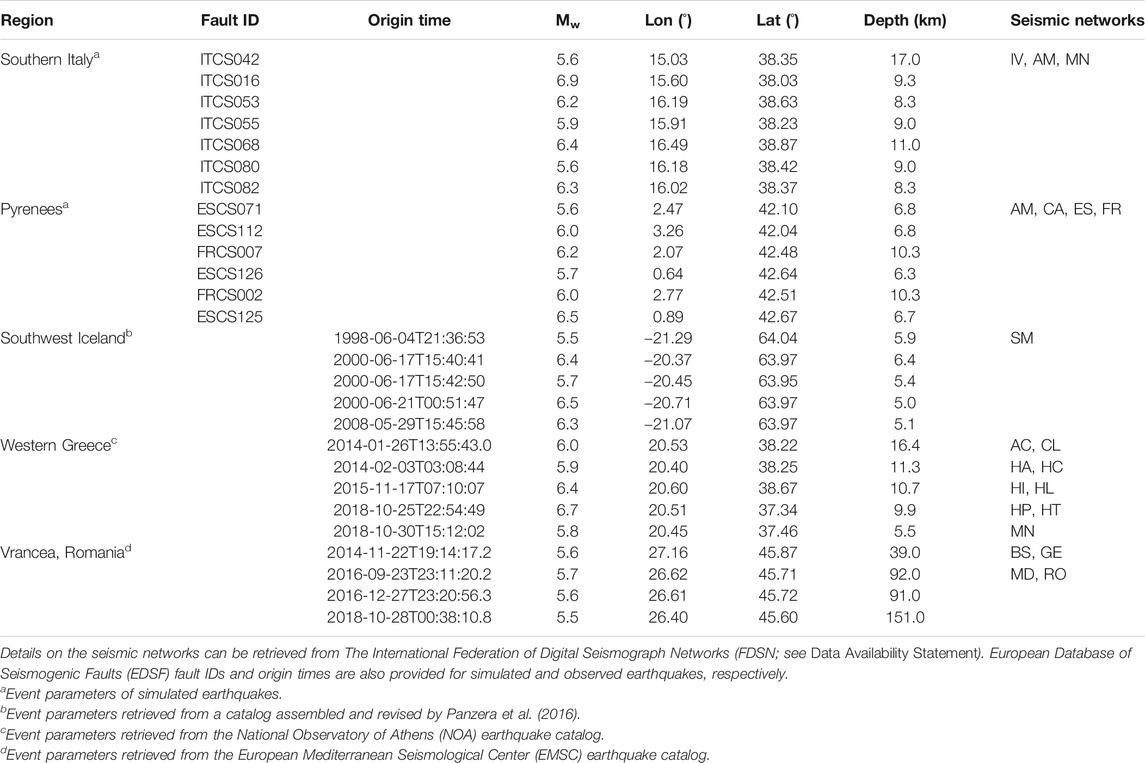
TABLE 2. Magnitude, longitude, latitude, and depth of the events considered in this study (retrieved from the seismological agencies provided in the table footnote), along with the seismic networks used in each region.

Velocity Models

We use rocky regional velocity models from the literature (see Table 3) for both location estimation and the computation of synthetic seismograms. Where not explicitly defined, P-wave velocities are converted into S-wave velocities (and vice-versa), using the Poisson solid’s approximation. Densities are converted from P-wave velocities using the Nafe-Drake relationship (Ludwig et al., 1970). The quality factors ($Q_S$ and $Q_P$), necessary for the computation of synthetic seismograms, are set as follows: $Q_S=100\times V_S$, where $V_S$ is the shear wave velocity ($km/s$), and $Q_P=9/4\times Q_S$ (Lay and Wallace, 1995).

TABLE 3

TABLE 3. Regional velocity models used in this study.

To run PRESTo, we compute 3D travel-time grids for both P- and S-waves at all stations (introduced in Seismic Waveforms), using the NonLinLoc software (Lomax et al., 2000). Grid dimensions adopted for the NonLinLoc software are defined according to the size of the considered regions (1 × 1 × 1 km for Iceland, 2 × 2 × 2 km for the remaining regions). For SeisComP, the locator is user-defined; we apply LocSAT (Bratt and Nagy, 1991) with travel-time tables prepared by replacing the shallow layers of the IASP91 model (Kennett and Engdahl, 1991) with the local velocity models of Table 3.

Ground-Motion Models

The most appropriate IM to characterize ground motion for earthquake engineering applications of EEW systems is application-specific. Since we compute ground-motion estimates only for comparison purposes in this study, we use Peak Ground Acceleration (PGA) as the selected IM in all cases, given its widespread use in the literature. The choice of GMM also has a significant impact on the estimated IM. Despite the availability of region-specific GMMs for various European regions (e.g., Zuccolo et al., 2017; Huang and Galasso 2019), we use European and global GMMs to estimate PGA, since identifying optimal GMMs for each target site is outside the scope of this paper. We specifically use the hypocentral distance version of the GMM by Akkar et al. (2014) for all earthquakes with hypocentral depth <30 km and the model of Youngs et al. (1997) for the intermediate-depth Vrancea earthquakes (Vacareanu et al., 2013). Note that we approximate the rupture distance metric of the Youngs et al. (1997) GMM using hypocentral distance, which is a valid assumption for the magnitude range of the deep events considered in this study (Cauzzi et al., 2015).

We estimate PGA values at the following target sites (Figure 2): port of Gioia Tauro (15.91 E, 38.46 N) for Southern Italy, Andorra (1.60 E, 42.54 N) for the Pyrenees, Reykjavík (21.94 W, 64.15 N) for Southwest Iceland, Patras (21.73 E, 38.25 N) for Western Greece and Bucharest (26.10 E, 44.43 N) for Romania. We assume representative rock ground conditions for all target locations, given that site class is not relevant for the comparative analyses performed in this paper.

Methodology for Comparison

We run playbacks of the seismic waveforms associated with the 27 considered events (Figure 2) through the PRESTo and VS(SC) algorithms. We evaluate and compare the performance of both algorithms in terms of their source-parameter estimates and the corresponding ground-shaking predictions at the selected target sites.

Performance in Terms of Source Parameters

The comparison of the algorithms’ performance is first assessed in terms of both the timeliness and accuracy of location and magnitude estimates. We specifically examine the most probable hypocentral estimates and the maximum likelihood magnitude estimates of each algorithm at two specific temporal instances:

a) time of the first estimate, which is the time, with respect to the actual origin time, required to produce the first joint estimate of location and magnitude;

b) time of stable estimate, which is the time at which the EEW estimates stop changing significantly, i.e., the time from which the difference between the estimated and final values is consistently less than a prefixed difference threshold. Different stable estimate times are defined with respect to the epicenter, depth, and magnitude estimates. For epicentral distance, the difference thresholds are fixed at 5 km if the final estimated depth is less than 30 km and are fixed at 10 km for larger depths. For depth and magnitude, the thresholds are fixed at 5 km and 0.2 units, respectively.

Figure 3 demonstrates the temporal evolution of the algorithms’ source-parameter performance for two sample earthquakes (i.e., the 2000-06-17 South Iceland event in the left column and the 2016-09-23 Vrancea event in the right column) that capture the range of magnitudes and depths considered in this study. These plots demonstrate the full temporal evolution of the epicentral error, the depth error, and the magnitude error. Bulletin values are assumed to be correct, such that magnitude and depth errors are computed by subtracting these values from the corresponding estimates of the algorithms, while epicentral errors are estimated as the distance between the bulletin and estimated epicenter locations. The timeline plots enable us to assess the timeliness of EEW (i.e., how quickly each algorithm can produce the first joint location-magnitude estimate and the time necessary to achieve stable source estimates, as defined above), and the accuracy of the source parameters (i.e., how much these parameter estimates deviate with respect to the bulletin values listed in Table 2).

FIGURE 3

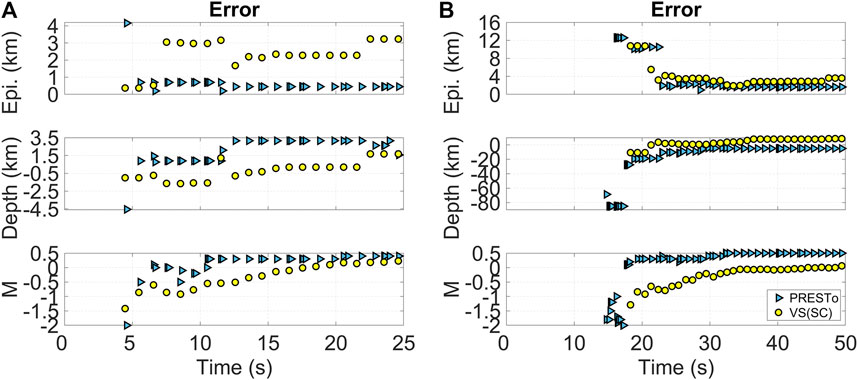
FIGURE 3. Temporal evolution (starting from the origin time) of the estimates by the PRESTo and VS(SC) algorithms for two example earthquakes: (A) the 2000-06-17 observed event in South Iceland; and (B) the 2016-09-23 observed event in Vrancea. Top: epicentral error timeline; middle: depth error timeline; and bottom: magnitude (M) error timeline. All error values are computed by subtracting the bulletin values from the corresponding estimates of the algorithms. Different symbols distinguish the two algorithms.

Performance in Terms of Ground Motion

We also explore the effect of location and magnitude estimates on the corresponding PGA predictions at the selected target sites. We compute the ground shaking for both algorithms by applying a GMM to the algorithms’ location and magnitude estimates, as described in Ground-Motion Models. We perform two analyses in terms of ground motion. The first analysis examines the temporal evolution of PGA estimates, and the second analysis investigates their accuracy.

Because of the temporal evolution of the location and magnitude estimates (Figure 3), the resulting computation of PGA also changes in time. This is an important consideration, as some EEW systems trigger an alert based on a prefixed threshold associated with the predicted ground shaking (Cremen and Galasso, 2020). For example, a warning may be issued if there is an unacceptable probability of a critical PGA value ($PG{A}_c$) being exceeded, according to Iervolino (2011):

$\mathrm{Pr}\left[PGA>PG{A}_c\right]=1-\underset{-\infty }{\overset{I{M}_c}{{\displaystyle \int }}}f\left(PGA\right)dPGA\ge P{r}_c$1

where $P{r}_c$ is a critical risk threshold related to potential damage associated with the incoming event (Cremen and Galasso, 2020), and $f\left(PGA\right)$ is the PDF of PGA, which is dependent on real-time estimates of location and magnitude at a given temporal instant.

Since location and magnitude estimates can evolve in time in a non-monotonic way, the predefined ground-motion-related threshold can be exceeded at a certain instant, but not exceeded at a subsequent instant, then exceeded again later in time, and so on (Wu et al., 2013; Wu et al., 2016). This behavior can raise questions about the integrity of an issued alarm and should be addressed when designing a decision-support system for EEW. Therefore, we perform a comparison by evaluating the number of trend inversions in the temporal evolution of the predicted PGA at the selected target sites provided in Ground-Motion Models.

In line with our companion paper (Cremen et al., 2021), ground-shaking prediction accuracy is quantified using the MD metric for sensitivity analyses (Chun et al., 2000), which has already been leveraged to examine the performance of GMMs (Cremen et al., 2020). MD measures the difference between the cumulative distribution function (CDF) of PGA produced when the bulletin source parameters are used in the GMM and the CDF obtained for a given algorithm’s source-parameter estimates at a prescribed temporal instant (considering the total standard deviation of the GMM in both cases); see Figure 4. Since the GMMs used in this study provide lognormal distributions of PGA, we calculate MD according to the following equation:

$MD=\frac{\sqrt{{\tilde{y}}_i^2\exp \left(2{\beta }_i^2\right)+{\tilde{y}}_o^2\exp \left(2{\beta }_o^2\right)-2{\tilde{y}}_i{\tilde{y}}_{o}exp\left(\frac{{\left({\beta }_i+{\beta }_o\right)}^2}{2}\right)}}{{\tilde{y}}_{o}exp\left(\frac{{\beta }_o^2}{2}\right)}$2

FIGURE 4

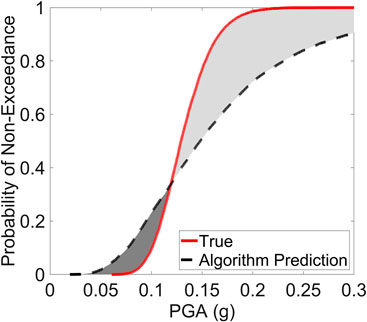
FIGURE 4. Demonstration of the GMM evaluation procedure, which measures the difference between the true and estimated GMM CDF for a given set of location and magnitude predictions. The light gray shading indicates PGA exceedance thresholds for which the predicted ground shaking is greater than the true value, which may lead to a false alert. The dark gray shading indicates exceedance thresholds for which the predicted shaking is less than the true value, which may lead to a missed alert.

The i and o subscripts respectively refer to the GMM CDF computed using the algorithmic source-parameter estimates and the GMM CDF produced by the bulletin source parameters. $\tilde{y}$ is the median predicted PGA and $\beta$ is the total logarithmic standard deviation of the PGA prediction. A lower MD value indicates a higher similarity between the GMM distributions based on estimated and bulletin source parameters. This type of comparison is useful, as discrepancies in the CDFs indicate the potential for erroneous decisions by an end user, if EEW alerts are issued based on a given probability of exceeding a prescribed value of PGA, as discussed above.

Performance Assessment: Results and Discussion

Timeliness of Location and Magnitude Estimates

The timeliness comparison of both algorithms is provided in Figure 5. Our analysis reveals that the first EEW estimates are provided slightly faster by PRESTo, with an average time-to-first-estimate ratio between PRESTo and VS(SC) of 0.94. This is partially related to the fact that VS(SC) requires 3 s of P-wave information at a single station to estimate magnitude, while RTMag uses only 2 s of P-wave signal to deliver a first magnitude estimate. VS(SC) location estimates retrieved from scanloc converge to stable values faster than those of PRESTo (the average time-to-stable-estimate ratio between PRESTo and VS(SC) is 1.3 for the epicenter and 1.5 for the depth); in contrast, VS(SC) magnitude estimates require a longer time to become stable (the average time-to-stable-estimate ratio between PRESTo and VS(SC) is 0.7), which confirms a similar observation by Chung and Allen (2019).

FIGURE 5

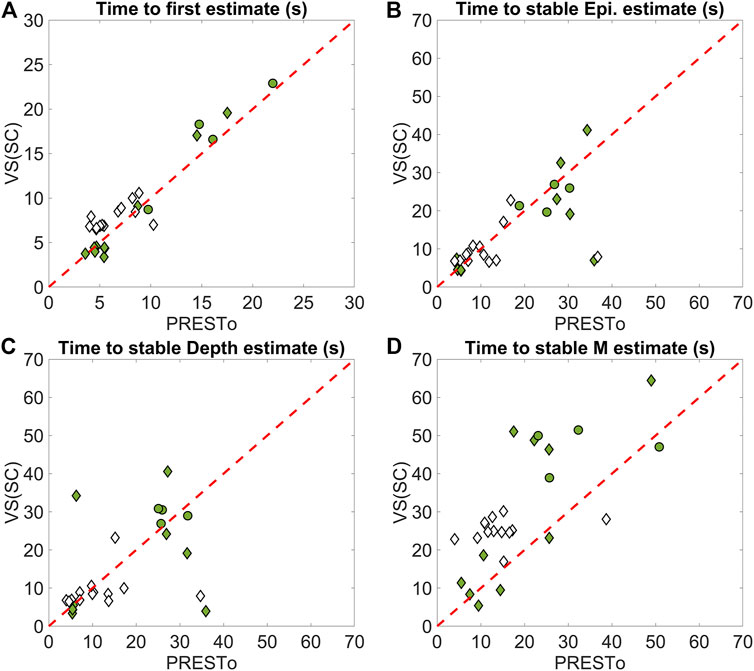
FIGURE 5. Comparison between the PRESTo and VS(SC) algorithms in terms of timeliness. The average ratio between the times of PRESTo and VS(SC) estimates is: (A) 0.94; (B) 1.3; (C) 1.5; and (D) 0.7. Note that times shown are relative to actual event times. Filled and empty markers indicate observed and simulated events, respectively. Diamond and circle markers indicate shallow and deep events, respectively.

Accuracy of Location and Magnitude Estimates

The comparison in terms of accuracy is given in Figure 6 and Table 4 for the temporal instances associated with the first and stable estimates.

FIGURE 6

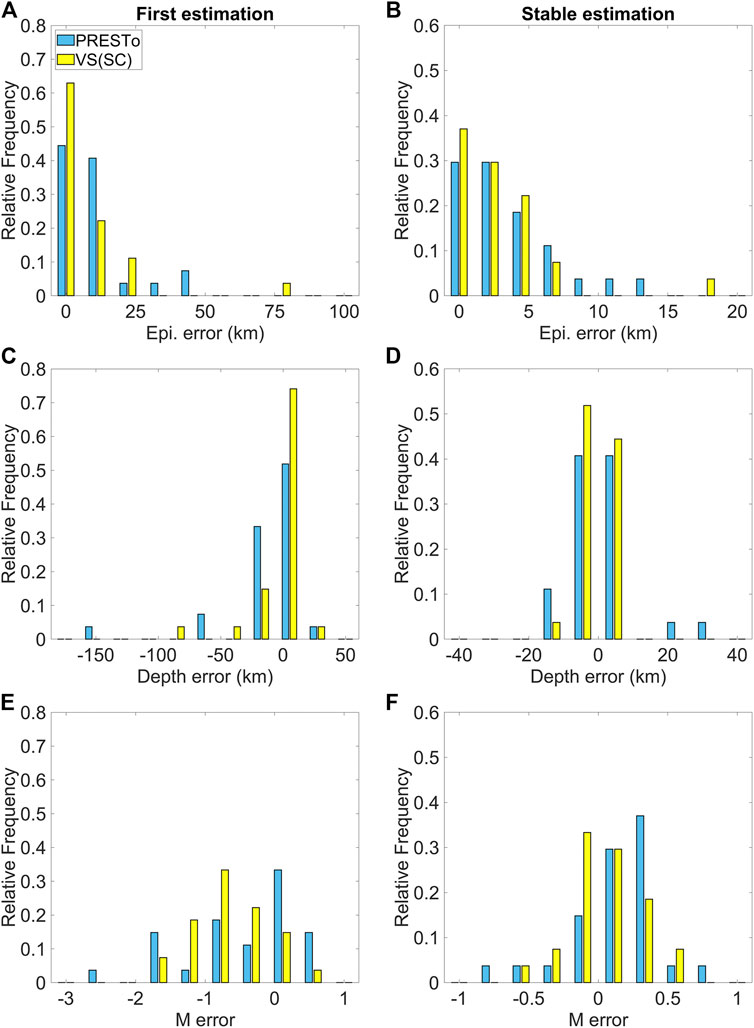
FIGURE 6. Comparison between the PRESTo and VS(SC) algorithms in terms of (A,B) epicentre; (C,D) depth; and (E,F) magnitude (M) accuracy. Each histogram contains results for all 27 considered events. The left column provides errors associated with first estimates. The right column provides errors associated with stable estimates. Magnitude and depth errors are computed by subtracting the bulletin values from the corresponding estimates of the algorithms, while epicentral errors represent the distance between the bulletin and estimated epicentre locations.

TABLE 4

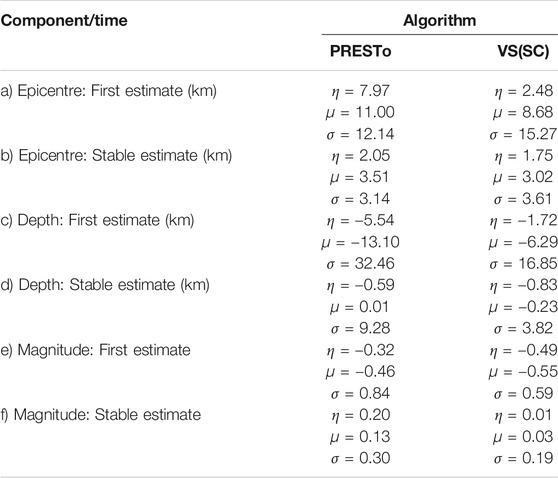
TABLE 4. Median (η), mean (μ), and standard deviation (σ) of the error distributions shown in Figure 6.

The first estimates of epicentral distance and depth by VS(SC) are more accurate than those provided by PRESTo (by approximately 5 km for the epicenter and 3 km for the depth). The location performance of both algorithms is fairly similar at the stable instant, although the dispersion of the stable depth estimate error for PRESTo (9.28) is almost 2.5 times that for VS(SC) (3.82).

The first magnitude estimate is generally underestimated with respect to the bulletin value for both algorithms due to a sparsity of recorded data. The corresponding error distributions for PRESTo and VS(SC) have respective medians of −0.32 and −0.49 and respective means of −0.46 and −0.55, which imply that the underestimation of VS(SC) is larger than that of PRESTo. However, PRESTo magnitude estimate errors are associated with a larger standard deviation (0.84) than those of VS(SC) (0.59). In contrast, the stable magnitude estimates computed by VS(SC) are more accurate than those computed by PRESTo; the corresponding error distributions for VS(SC) and PRESTo have respective medians of 0.01 and 0.20, and respective means of 0.03 and 0.13. However, accurate magnitude estimations from VS(SC) require a significantly longer time (Figure 5), which may not justify the greater amount of accuracy achieved.

It should be highlighted that the accuracy of the computed location and magnitude estimations is directly affected by the performance of each algorithm’s event-detection capability (i.e., phase picking and the seismic phase association methodology). Phase detection and association are difficult and error-prone tasks, especially during intense aftershock sequences (Meier et al., 2020). The event-detection algorithms (for both PRESTo and VS(SC)) are optimized consistently for each region of interest through an ad-hoc tuning of the relevant parameters that considers overall seismicity and the network geometry. However, discrepancies in phase picking and event association can still remain due to differences in the parameters and related procedures used in both algorithms. It should also be noted that the most appropriate tuning for a certain area could be different from that used in this study, which was calibrated using only the small sample of events analyzed.

Moreover, it should be mentioned that we do not consider an optional Bayesian prior distribution for PRESTo, to be consistent with the format of the VS(SC) magnitude calculation. Inclusion of this prior may improve PRESTo’s magnitude estimates. Finally, it should be highlighted that the empirical scaling relationships used for magnitude computation in RTMag and VS(SC) may not be appropriate/optimal for the regions considered in this study, especially for the deep events of the Vrancea region (for example, the VS(SC) relationships were calibrated for Californian events by assuming a depth of 3 km). The need for conducting region-specific recalibration of the relationship coefficients should always be investigated when implementing an EEW system in a new region (see, for example, Carranza et al., 2013). Otherwise, it may be most practical to simply evaluate and add empirically derived offsets (if any) to the magnitudes estimated for particular regions.

Trend of PGA Estimates

Figure 7 shows the number of trend inversions that occur over time for the median PGA predictions computed using the locations and magnitudes estimated by both algorithms. To eliminate insignificant changes in trend, we only consider inversions that result in at least a 20% change with respect to the previous PGA estimate. Our analysis shows that the number of inversions for VS(SC) is lower on average (1.52, compared to 3.37 for PRESTo) and has a smaller standard deviation (1.69, compared to 4.45 for PRESTo). VS(SC) has also a slightly greater number of cases with zero inversions, which correspond to situations in which there is no significant variation of the computed PGA in time (ideal case, in which the maximum possible lead time is achieved if the alert threshold is exceeded and the PGA is predicted correctly), or there is a near monotonic increase of its estimated value. Conversely, PRESTo has some cases with more than ten trend inversions, corresponding to two Greek offshore events and one event located in the central Pyrenees. They are related to erroneous PRESTo location predictions due to particular geometric network conditions that have a significantly negative effect on ground-motion estimation, thus contributing to the multiple inversion cases observed. Therefore, we conclude that the integrity of the EEW alarm issued by the VS(SC) algorithm is higher than that for PRESTo.

FIGURE 7

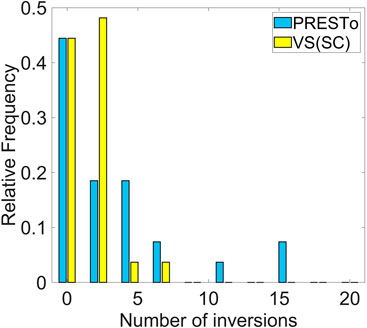
FIGURE 7. Number of trend inversions in the evolution of PGA estimates for both considered algorithms. The median (η), mean (μ) and standard deviation (σ) of the distributions are: η = 2.00, μ = 3.37, σ = 4.45 for PRESTo, and η = 1.00, μ = 1.52, σ = 1.69 for VS(SC).

Ground-Shaking Prediction Accuracy

We specifically investigate MD values for the algorithms’ source-parameter estimates at temporal instances that correspond with three different lead times at target sites: 15, 10, and 5 s. The lead time at a given target site is defined as the time difference between the S-wave arrival and the first EEW estimate; a 1 s transmission delay is also accounted for. For each lead-time analysis, only the scenario events capable of providing that lead-time at the target site of interest are considered. This means that 16 events are examined for the 15 s lead time, 19 events are examined for the 10 s lead time, and 23 events are examined for the 5 s lead time. The results of the ground-shaking prediction assessments are presented in Figure 8. It can be observed that PRESTo provides more accurate ground-motion estimates at the largest lead times considered; PRESTo average MD ($\overline{MD}$) value for 15 s lead time is 0.45, whereas the corresponding VS(SC) $\overline{MD}$ value is 0.86. However, VS(SC) produces more accurate ground-shaking predictions than PRESTo for the smallest considered lead time (5 s); in this case, the PRESTo $\overline{MD}$ value is 0.82 and the VS(SC) $\overline{MD}$ value is 0.42. The average $\overline{MD}$ values are similar for the intermediate considered lead time (10 s). Note that the temporal variations in the optimal algorithm for ground-motion accuracy reflect those observed for magnitude accuracy in Accuracy of Location and Magnitude Estimates.

FIGURE 8

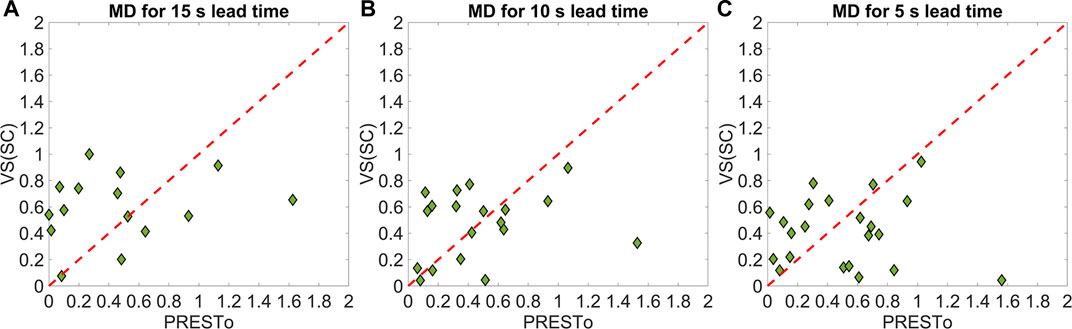
FIGURE 8. Comparing the ground-shaking prediction accuracy of both considered algorithms for three lead times: (A) 15 s, (B) 10 s, and (C) 5 s. The average MD ($\overline{MD}$) estimate is: (A)$\overline{MD}=0.45$ for PRESTo and $\overline{MD}=0.86$ for VS(SC), (B)$\overline{MD}=0.47$ for PRESTo and $\overline{MD}=0.47$ for VS(SC), (C)$\overline{MD}=0.82$ for PRESTo and $\overline{MD}=0.42$ for VS(SC).

Concluding Remarks

This study used scenario earthquakes across five European regions to quantitatively compare the performance of the PRESTo and VS(SC) (using scanloc for location) regional EEW algorithms. Our overall aim was to identify the best options for EEW location and magnitude estimation in the TURNkey platform, a multi-sensor-based information system to be implemented in Europe for earthquake forecasting, EEW, and post-earthquake rapid response actions.

We first assessed the ability of PRESTo and VS(SC) to produce rapid and accurate source (i.e., location and magnitude) estimates of events. We then evaluated the accuracy of the algorithms’ corresponding ground-shaking predictions for various lead times at prescribed target sites. We found that PRESTo may have a greater risk-mitigation potential than VS(SC) in general. This is because PRESTo produces faster and more accurate early magnitude estimates, which result in better ground-motion estimates for long lead times (15 s) that potentially enable significant earthquake preparation actions to take place, such as shutting down industrial equipment, evacuating the ground floors of buildings, and stopping surgical procedures (Goltz, 2002). Predictions by VS(SC) are eventually more accurate than those of PRESTo; however, the length of time this requires results in smaller warning windows that may only allow stakeholders to take simple automatic risk-mitigation actions like stopping traffic (i.e., turning lights red) or switching on semi-active control systems for structures (Goltz, 2002; Iervolino et al., 2008). It is also important to note that we did not use an optional Bayesian prior distribution for the RTMag magnitude algorithm of PRESTo. Its inclusion may have resulted in an even better performance of the PRESTo magnitude estimates and the associated ground-motion predictions.

We, therefore, ultimately recommend that, out of the two considered regional EEW algorithms, PRESTo is used for EEW in the TURNkey platform, which is consistent with the conclusions of our companion paper (Cremen et al., 2021). Alternatively, the PRESTo RTMag algorithm could be independently implemented within SeisComP (and, therefore, the TURNkey platform) as an additional module for EEW magnitude evaluation. This configuration would also enable scanloc to be used within the TURNkey platform, which we found to be the best algorithm for location estimation. Therefore, the combination RTMag plus scanloc may facilitate more accurate EEW ground-motion estimates than those provided by the full PRESTo algorithm.

This study’s results were obtained through playbacks of the seismic waveforms and EEW parameters associated with 27 historic/simulated earthquakes representative of different tectonic environments and regional European variation in station distributions and densities. We used actual network configurations for testbeds where synthetic seismograms were used (i.e., Southern Italy and the Pyrenees). The availability of recordings constrained the number of considered stations for all other regions examined (i.e., Greece, Romania, and Iceland). Therefore, the study’s outcome should be interpreted as an average performance of the examined algorithms across different seismicity and network geometries in Europe. A more detailed feasibility study is recommended for target- or region-specific applications of the algorithms.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, upon reasonable request. SeisComP is available at https://www.seiscomp.de, with professional software support from gempa GmbH (http://www.gempa.de). VS(SC) is available as part of the SeisComP software suite, while scanloc is a commercial software by gempa. PRESTo is available at http://www.prestoews.org/about.php. The European Integrated waveform Data Archive (EIDA, https://www.orfeus-eu.org/data/eida/) was consulted through the ORFEUS Data Center WebDC3 Web Interface (http://orfeus-eu.org/webdc3/) (doi: 10.5880/GFZ.2.4/2016.001; last accessed January 2021). The Internet Site for European Strong-motion Data (ISESD, http://www.isesd.hi.is/) was also used (last accessed January 2021). Stations metadata were retrieved from The International Federation of Digital Seismograph Networks (FDSN), accessible through http://www.fdsn.org/ (last accessed January 2021). IRIS (Incorporated Research Institutions for Seismology) station database is accessible through https://ds.iris.edu/gmap (last accessed January 2021). The European Mediterranean Seismological Center (EMSC) earthquake catalog is available at https://www.emsc-csem.org/(last accessed January 2021), while the National Observatory of Athens (NOA) earthquake catalog can be retrieved from https://bbnet.gein.noa.gr/HL (doi: https://doi.org/10.7914/SN/HL; last accessed January 2021). The European Database of Seismogenic Faults (ESDF) is available at http://diss.rm.ingv.it/share-edsf/ (doi: 10.6092/INGV.IT-SHARE-EDSF; last accessed January 2021).

Author Contributions

EZ computed synthetic seismograms, ran playbacks of the seismic waveforms, and analyzed the results. GC evaluated the ground-shaking prediction accuracy. CG and EZ prepared the figures. All authors contributed to the methodological development, the interpretation of the results and the manuscript preparation.

Funding

This paper is supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement No 821046, project TURNkey (Towards more Earthquake-resilient Urban Societies through a Multi-sensor-based Information System enabling Earthquake Forecasting, Early Warning and Rapid Response actions; https://earthquake-turnkey.eu).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Dirk Roessler (gempa GmbH, Germany) for his generous assistance with running SeisComP and his very valuable advice and feedback on this study. We would also like to express our gratitude to Nikos Melis and Stratos Liadopoulos (National Observatory of Athens, Greece), Benedikt Halldorsson and Atefe Darzi (Haskoli Islands - University of Iceland, Iceland), Stefan Balan and Alexandru Marmureanu (Institutul National de Cercetare si Dezvoltare pentru Fizica Pamantului, Romania), and Pierre Gehl (Bureau de Recherches Géologiques et Minières, France) for providing input data for the regions considered in this study. We are grateful to Bernd Weber (gempa GmbH, Germany) and the gempa team for providing the scanloc module and assistance with SeisComP. The study has also benefited from the support on PRESTo provided by Luca Elia (RISSC-Lab, University of Naples Federico II, Italy). We are additionally grateful to Alireza Azarbakht and John Douglas (University of Strathclyde, United Kingdom) for helpful feedback on parts of this study. The authors also acknowledge the insightful comments from Matteo Picozzi (RISSC-Lab University of Naples Federico II, Italy) and Elisa Buforn (Universidad Complutense de Madrid, Spain) that improved the quality of this study. Figures for this manuscript were produced using the Matplotlib Python library (Hunter, 2007) and MATLAB®.

References

Akkar, S., Sandıkkaya, M. A., and Bommer, J. J. (2014). Empirical Ground-Motion Models for point- and Extended-Source Crustal Earthquake Scenarios in Europe and the Middle East. Bull. Earthquake Eng. 12 (1), 359–387. doi:10.1007/s10518-013-9461-4

CrossRef Full Text | Google Scholar

Allen, R. (1982). Automatic Phase Pickers: Their Present Use and Future Prospects. Bull. Seismological Soc. America 72 (6B), S225–S242.

Google Scholar

Allmann, B. P., and Shearer, P. M. (2009). Global Variations of Stress Drop for Moderate to Large Earthquakes. J. Geophys. Res. Solid Earth 114 (1), 1–22. doi:10.1029/2008JB005821

CrossRef Full Text | Google Scholar

Barberi, G., Cosentino, M. T., Gervasi, A., Guerra, I., Neri, G., and Orecchio, B. (2004). Crustal Seismic Tomography in the Calabrian Arc Region, South Italy. Phys. Earth Planet. Interiors 147 (4), 297–314. doi:10.1016/j.pepi.2004.04.005

CrossRef Full Text | Google Scholar

Basili, R., Kastelic, V., Demircioglu, M. B., Garcia Moreno, D., Nemser, E. S., Petricca, P., et al. (2013). The European Database of Seismogenic Faults (EDSF) Compiled in the Framework of the Project SHARE.

Behr, Y., Clinton, J. F., Cauzzi, C., Hauksson, E., Jónsdóttir, K., Marius, C. G., et al. (2016). The Virtual Seismologist in SeisComP3: A New Implementation Strategy for Earthquake Early Warning Algorithms. Seismological Res. Lett. 87 (2A), 363–373. doi:10.1785/0220150235

CrossRef Full Text | Google Scholar

Bratt, S., and Nagy, W. (1991). The LocSAT Program. San Diego: Science Applications International Corporation.

Caporali, A., Barba, S., Carafa, M. M. C., Devoti, R., Pietrantonio, G., and Riguzzi, F. (2011). Static Stress Drop as Determined from Geodetic Strain Rates and Statistical Seismicity. J. Geophys. Res. Solid Earth 116 (2), 1–15. doi:10.1029/2010JB007671

CrossRef Full Text | Google Scholar

Carranza, M., Buforn, E., Colombelli, S., and Zollo, A. (2013). Earthquake Early Warning for Southern Iberia: A P Wave Threshold-Based Approach. Geophys. Res. Lett. 40 (17), 4588–4593. doi:10.1002/grl.50903

CrossRef Full Text | Google Scholar

Carranza, M., Buforn, E., and Zollo, A. (2017). Performance of a Network-Based Earthquake Early Warning System in the Ibero-Maghrebian Region. Seismological Res. Lett. 88 (6), 1499–1507. doi:10.1785/0220170081

CrossRef Full Text | Google Scholar

Causse, M., Cotton, F., Cornou, C., and Bard, P. Y. (2008). Calibrating Median and Uncertainty Estimates for a Practical Use of Empirical Green’s Functions Technique. Bull. Seismological Soc. America 98 (1), 344–353. doi:10.1785/0120070075

CrossRef Full Text | Google Scholar

Cauzzi, C., Faccioli, E., Vanini, M., and Bianchini, A. (2015). Updated Predictive Equations for Broadband (0.01–10 S) Horizontal Response Spectra and Peak Ground Motions, Based on a Global Dataset of Digital Acceleration Records. Bull. Earthquake Eng. 13 (6), 1587–1612. doi:10.1007/s10518-014-9685-y

CrossRef Full Text | Google Scholar

Chun, M. H., Han, S. J., and Tak, N. Il. (2000). An Uncertainty Importance Measure Using a Distance Metric for the Change in a Cumulative Distribution Function. Reliability Eng. Syst. Saf. 70 (3), 313–321. doi:10.1016/S0951-8320(00)00068-5

CrossRef Full Text | Google Scholar

Chung, A. I., and Allen, R. M. (2019). Optimizing Earthquake Early Warning Performance: ElarmS-3 ElarmS View Project Building Response Using Ambient Noise View Project. Seismological Res. Lett. 90 (2A). doi:10.1785/0220180192

CrossRef Full Text | Google Scholar

Clinton, J., Zollo, A., Marmureanu, A., Zulfikar, C., and Parolai, S. (2016). State-of-the Art and Future of Earthquake Early Warning in the European Region. Bull. Earthquake Eng. 14 (9), 2441–2458. doi:10.1007/s10518-016-9922-7

CrossRef Full Text | Google Scholar

Convertito, V., Iervolino, I., Zollo, A., and Manfredi, G. (2008). Prediction of Response Spectra via Real-Time Earthquake Measurements. Soil Dyn. Earthquake Eng. doi:10.1016/j.soildyn.2007.07.006

CrossRef Full Text | Google Scholar

Cremen, G., and Galasso, C. (2020). Earthquake Early Warning: Recent Advances and Perspectives. Earth-Science Rev. 205 (February), 103184. doi:10.1016/j.earscirev.2020.103184

CrossRef Full Text | Google Scholar

Cremen, G., Werner, M. J., and Baptie, B. (2020). A New Procedure for Evaluating Ground-Motion Models, with Application to Hydraulic-Fracture-Induced Seismicity in the United Kingdom. Bull. Seismol. Soc. Am. 110 (5), 2380–2397. doi:10.1785/0120190238

Google Scholar

Cremen, G., Zuccolo, E., and Galasso, C. (2021). Accuracy and Uncertainty Analysis of Selected Methodological Approaches to Earthquake Early Warning in Europe. Seismol. Res. Lett. doi:10.1785/0220200414

Crempien, J. G. F., and Archuleta, R. J. (2015). UCSB Method for Simulation of Broadband Ground Motion from Kinematic Earthquake Sources. Seismological Res. Lett. 86 (1), 61–67.

CrossRef Full Text | Google Scholar

Cua, G. B. (2005). Creating the Virtual Seismologist: Developments in Ground Motion Characterization and Seismic Early Warning. California. California Institute of Technology.

Cua, G., Fischer, M., Heaton, T., and Wiemer, S. (2009). Real-time Performance of the Virtual Seismologist Earthquake Early Warning Algorithm in Southern California. Seismological Res. Lett. 80 (5), 740–747. doi:10.1785/gssrl.80.5.740

CrossRef Full Text | Google Scholar

Cua, G., and Heaton, T. (2007). The Virtual Seismologist (VS) Method: a Bayesian Approach to Earthquake Early Warning by. Earthquake Early Warning Syst., 97–132.

Google Scholar

Galasso, Carmine., Zhong, Peng., Zareian, Farzin., Iervolino, Iunio., and Graves, R. W. (2013). Validation of Ground-Motion Simulations for Historical Events Using MDoF Systems. Earthquake Eng. Struct. Dyn. 42, 1395–1412. doi:10.1002/eqe

CrossRef Full Text | Google Scholar

Galasso, C., Zareian, F., Iervolino, I., and Graves, R. W. (2012). Validation of Ground-Motion Simulations for Historical Events Using SDoF Systems. Bull. Seismological Soc. America 102 (6), 2727–2740. doi:10.1785/0120120018

CrossRef Full Text | Google Scholar

Goltz, James. D. (2002). Introducing Earthquake Early Warning in California - A Summary of Social Science and Public Policy Issues. California: Pasadena.

Grigoli, F., Scarabello, L., Böse, M., Weber, B., Wiemer, S., and Clinton, J. F. (2018). Pick- and Waveform-Based Techniques for Real-Time Detection of Induced Seismicity. Geophys. J. Int. 213 (2), 868–884. doi:10.1093/gji/ggy019

CrossRef Full Text | Google Scholar

Grünthal, G., Wahlström, R., and Stromeyer, D. (2013). The SHARE European Earthquake Catalogue (SHEEC) for the Time Period 1900-2006 and its Comparison to the European-Mediterranean Earthquake Catalogue (EMEC). J. Seismology 17 (4), 1339–1344. doi:10.1007/s10950-013-9379-y

CrossRef Full Text | Google Scholar

Hanka, W., Saul, J., Weber, B., Becker, J., and Harjadi, P. (2010). Real-time Earthquake Monitoring for Tsunami Warning in the Indian Ocean and beyond. Nat. Hazards Earth Syst. Sci. 10 (12), 2611–2622. doi:10.5194/nhess-10-2611-2010

CrossRef Full Text | Google Scholar

Helmholtz-Centre Potsdam - GFZ German Research Centre for Geosciences and gempa GmbH (2008). The SeisComP Seismological Software Package. GFZ Data Services. doi:10.5880/GFZ.2.4.2020.003

CrossRef Full Text

Huang, C., and Galasso, C. (2019). Ground-motion Intensity Measure Correlations Observed in Italian strong-motion Records. Earthquake Eng. Struct. Dyn. 48 (15), 1634–1660. doi:10.1002/eqe.3216

CrossRef Full Text | Google Scholar

Hunter, J. D. (2007). Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 9 (3), 90–95. doi:10.1109/MCSE.2007.55

CrossRef Full Text | Google Scholar

Iervolino, I., Galasso, C., and Manfredi, G. (2008). Information-Dependent Lead-Time Maps for Earthquake Early Warning in the Campania Region, 14th World Conference on Earthquake Engineering, Beijing, China, October 17, 2008, 12. Available at: http://www.rissclab.unina.it.

PubMed AbstractGoogle Scholar

Iervolino, Iunio., Convertito, V., Giorgio, M., Manfredi, G., and Zollo, A. (2006). Real-time Risk Analysis for Hybrid Earthquake Early Warning Systems. J. Earthquake Eng. 10 (6), 867–885. doi:10.1142/S1363246906002955

CrossRef Full Text | Google Scholar

Iervolino, Iunio., Giorgio, M., Galasso, C., and Manfredi, G. (2009). Uncertainty in Early Warning Predictions of Engineering Ground Motion Parameters: What Really Matters?. Geophys. Res. Lett. 36 (4), L00B06. doi:10.1029/2008GL036644

CrossRef Full Text | Google Scholar

Iervolino, Iunio. (2011). Performance-based Earthquake Early Warning. Soil Dyn. Earthquake Eng. 31 (2), 209–222. doi:10.1016/j.soildyn.2010.07.010

CrossRef Full Text | Google Scholar

Kennett, B. L. N., and Engdahl, E. R. (1991). Traveltimes for Global Earthquake Location and Phase Identification. Geophys. J. Int. 105 (2), 429–465. doi:10.1111/j.1365-246X.1991.tb06724.x

CrossRef Full Text | Google Scholar

Lancieri, M., and Zollo, A. (2008). A Bayesian Approach to the Real-Time Estimation of Magnitude from the Early P and S Wave Displacement Peaks. J. Geophys. Res. Solid Earth 113 (12). doi:10.1029/2007JB005386

CrossRef Full Text | Google Scholar

Lay, T., and Wallace, T. (1995). Modern Global Seimology, Vol. 58.

Lomax, A., Virieux, J., Volant, P, and Thierry, C. B. (2000). Probabilistic Earthquake Location in 3D and Layered Models: Introduction of a Metropolis-Gibbs Method and Comparison with Linear Locations, Madison, WI: USA, 101–134.

CrossRef Full Text

Ludwig, W., Nafe, J., and Drake, C. (1970). Seismic Refraction. The Sea 4, 53–84.

Google Scholar

Maeda, N. (1985). A Method for Reading and Checking Phase Time in Auto-Processing System of Seismic Wave Data. Zisin (Journal of the Seismological Society of Japan. 2nd Ser.) 38 (3), 365–379. doi:10.4294/zisin1948.38.3_365

CrossRef Full Text | Google Scholar

Meier, M. A. (2017). How “Good” Are Real-Time Ground Motion Predictions from Earthquake Early Warning Systems?. J. Geophys. Res. Solid Earth 122 (7), 5561–5577. doi:10.1002/2017JB014025

CrossRef Full Text | Google Scholar

Meier, M., Kodera, Y., Chung, A., Hoshiba, M., Minson, S., Hauksson, E., et al. (2020). How Often Can Earthquake Early Warning Systems Alert Sites with High‐Intensity Ground Motion?. J. Geophys. Res. Solid Earth. doi:10.1029/2019JB017718

CrossRef Full Text | Google Scholar

Panzera, F., Zechar, J. D., Vogfjörd, K. S., and Eberhard, D. A. J. (2016). A Revised Earthquake Catalogue for South Iceland. Pure Appl. Geophys. 173 (1), 97–116. doi:10.1007/s00024-015-1115-9

CrossRef Full Text | Google Scholar

Picozzi, M., Elia, L., Pesaresi, D., Zollo, A., Mucciarelli, M., Gosar, A., et al. (2015). Trans-national Earthquake Early Warning (EEW) in north-eastern Italy, Slovenia and Austria: First Experience with PRESTo at the CE3RN Network. Adv. Geosciences 40, 51–61. doi:10.5194/adgeo-40-51-2015

CrossRef Full Text | Google Scholar

Picozzi, M., Zollo, A., Brondi, P., Colombelli, S., Elia, L., and Martino, C. (2015). Exploring the Feasibility of a Nationwide Earthquake Early Warning System in Italy. J. Geophys. Res. Solid Earth 120 (4), 2446–2465. doi:10.1002/2014JB011669

CrossRef Full Text | Google Scholar

Raykova, R. B., and Panza, G. F. (2006). Surface Waves Tomography and Non-linear Inversion in the Southeast Carpathians. Phys. Earth Planet. Interiors 157 (3–4), 164–180. doi:10.1016/j.pepi.2006.03.019

CrossRef Full Text | Google Scholar

Rigo, A., Lyon-Caen, H., Armijo, R., Deschamps, A., Hatzfeld, D., Makropoulos, K., et al. (1996). A Microseismic Study in the Western Part of the Gulf of Corinth (Greece): Implications for Large-Scale normal Faulting Mechanisms. Geophys. J. Int. 126 (3), 663–688. doi:10.1111/j.1365-246X.1996.tb04697.x

CrossRef Full Text | Google Scholar

Roessler, D., Becker, J., Ellguth, E., Herrnkind, S., Weber, B., Henneberger, R., et al. (2016). “Cluser-search Based Monitoring of Local Earthquakes in SeisComp3,” in Fall Meeting American Geophysical Union, San Francisco, December 12–16, 2016.

Satriano, C., Elia, L., Martino, C., Lancieri, M., Zollo, A., and Iannaccone, G. (2011). PRESTo, the Earthquake Early Warning System for Southern Italy: Concepts, Capabilities and Future Perspectives. Soil Dyn. Earthquake Eng. 31 (2), 137–153. doi:10.1016/j.soildyn.2010.06.008

CrossRef Full Text | Google Scholar

Satriano, C., Lomax, A., and Zollo, A. (2008). Real-Time Evolutionary Earthquake Location for Seismic Early Warning. Bull. Seismological Soc. America 98 (3), 1482–1494. doi:10.1785/0120060159

CrossRef Full Text | Google Scholar

Stucchi, M., Rovida, A., Gomez Capera, A. A., Alexandre, P., Camelbeeck, T., Demircioglu, M. B., et al. (2013). The SHARE European Earthquake Catalogue (SHEEC) 1000-1899. J. Seismology 17 (2), 523–544. doi:10.1007/s10950-012-9335-2

CrossRef Full Text | Google Scholar

Theunissen, T., Chevrot, S., Sylvander, M., Monteiller, V., Calvet, M., Villaseñor, A., et al. (2017). Absolute Earthquake Locations Using 3-D versus 1-D Velocity Models below a Local Seismic Network: Example from the Pyrenees. Geophys. J. Int. 212 (3), 1806–1828. doi:10.1093/gji/ggx472

CrossRef Full Text | Google Scholar

Tryggvason, A., Rögnvaldsson, S. T., and Flóvenz, Ó. G. (2002). Three-dimensional Imaging of the P- and S-Wave Velocity Structure and Earthquake Locations beneath Southwest Iceland. Geophys. J. Int. 151 (3), 848–866. doi:10.1046/j.1365-246X.2002.01812.x

CrossRef Full Text | Google Scholar

Vacareanu, R., Pavel, F., and Aldea, A. (2013). On the Selection of GMPEs for Vrancea Subcrustal Seismic Source. Bull. Earthquake Eng. 11 (6), 1867–1884. doi:10.1007/s10518-013-9515-7

CrossRef Full Text | Google Scholar

Vassallo, M., Satriano, C., and Lomax, A. (2012). Automatic Picker Developments and Optimization: A Strategy for Improving the Performances of Automatic Phase Pickers. Seismological Res. Lett. 83 (3), 541–554. doi:10.1785/gssrl.83.3.541

CrossRef Full Text | Google Scholar

Wells, D. L., and Coppersmith, K. J. (1994). New Empirical Relationships Among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement. Bull. Seismological Soc. America 84 (4), 974–1002. Available at: https://pubs.geoscienceworld.org/ssa/bssa/article-pdf/84/4/974/2707918/BSSA0840040974.pdf.

Google Scholar

Wu, S., Beck, J. L., and Heaton, T. H. (2013). ePAD: Earthquake Probability-Based Automated Decision-Making Framework for Earthquake Early Warning. Computer-Aided Civil Infrastructure Eng. 28 (10), 737–752. doi:10.1111/mice.12048

CrossRef Full Text | Google Scholar

Wu, S., Cheng, M. H., Beck, J. L., and Heaton, T. H. (2016). An Engineering Application of Earthquake Early Warning: EPAD-Based Decision Framework for Elevator Control. J. Struct. Eng. (United States) 142 (1). doi:10.1061/(ASCE)ST.1943-541X.0001356

CrossRef Full Text | Google Scholar

Youngs, R. R., Chiou, S.-J., Silva, W. J., and Humphrey, J. R. (1997). Strong Ground Motion Attenuation Relationships for Subduction Zone Earthquakes. Seismological Res. Lett. 68 (1), 58–73. doi:10.1785/gssrl.68.1.58

CrossRef Full Text | Google Scholar

Zhang, H., Thurber, C., and Rowe, C. (2003). Automatic P-Wave Arrival Detection and Picking with Multiscale Wavelet Analysis for Single-Component Recordings. Bull. Seismological Soc. America 93 (5), 1904–1912. doi:10.1785/0120020241

CrossRef Full Text | Google Scholar

Zuccolo, E., Bozzoni, F., and Lai, C. G. (2017). Regional Low-Magnitude GMPE to Estimate Spectral Accelerations for Earthquake Early Warning Applications in Southern Italy. Seismological Res. Lett. 88 (1), 61–71. doi:10.1785/0220160038

CrossRef Full Text | Google Scholar

Zuccolo, E., Gibbs, T., Lai, C. G., Latchman, J. L., Salazar, W., Di Sarno, L., et al. (2016). Earthquake Early Warning Scenarios at Critical Facilities in the Eastern Caribbean. Bull. Earthquake Eng. 14 (9), 2579–2605. doi:10.1007/s10518-016-9878-7

CrossRef Full Text | Google Scholar