- 1Department of Geological Sciences and Institute of Arctic and Alpine Research, University of Colorado, Boulder, CO, United States
- 2Helmholtz Centre Potsdam, German Research Centre for Geosciences (GFZ), Potsdam, Germany
- 3Institute of Earth Surface Dynamics, University of Lausanne, Lausanne, Switzerland
- 4Department of Geological and Environmental Sciences, Appalachian State University, Boone, NC, United States
- 5Institute of Geological Sciences, Freie Universität, Berlin, Germany
- 6Geophysical Institute, University of Alaska, Fairbanks, AK, United States
The cause of debris-covered glacier thinning remains controversial. One hypothesis asserts that melt hotspots (ice cliffs, ponds, or thin debris) increase thinning, while the other posits that declining ice flow leads to dynamic thinning under thick debris. Alaska’s Kennicott Glacier is ideal for testing these hypotheses, as ice cliffs within the debris-covered tongue are abundant and surface velocities decline rapidly downglacier. To explore the cause of patterns in melt hotspots, ice flow, and thinning, we consider their evolution over several decades. We compile a wide range of ice dynamical and mass balance datasets which we cross-correlate and analyze in a step-by-step fashion. We show that an undulating bed that deepens upglacier controls ice flow in the lower 8.5 km of Kennicott Glacier. The imposed velocity pattern strongly affects debris thickness, which in turn leads to annual melt rates that decline towards the terminus. Ice cliff abundance correlates highly with the rate of surface compression, while pond occurrence is strongly negatively correlated with driving stress. A new positive feedback is identified between ice cliffs, streams and surface topography that leads to chaotic topography. As the glacier thinned between 1991 and 2015, surface melt in the study area decreased, despite generally rising air temperatures. Four additional feedbacks relating glacier thinning to melt changes are evident: the debris feedback (negative), the ice cliff feedback (negative), the pond feedback (positive), and the relief feedback (positive). The debris and ice cliff feedbacks, which are tied to the change in surface velocity in time, likely reduced melt rates in time. We show this using a new method to invert for debris thickness change and englacial debris content (∼0.017% by volume) while also revealing that declining speeds and compressive flow led to debris thickening. The expansion of debris on the glacier surface follows changes in flow direction. Ultimately, glacier thinning upvalley from the continuously debris-covered portion of Kennicott Glacier, caused by mass balance changes, led to the reduction of flow into the study area. This caused ice emergence rates to decline rapidly leading to the occurrence of maximum, glacier-wide thinning under thick, insulating debris.
Introduction
Debris cover thicker than a few centimeters insulates the ice surface beneath it and reduces melt (Østrem, 1959; Nicholson and Benn, 2006). On debris-covered glaciers, the insulating effect of debris appears to strongly control area-averaged melt rates (Bisset et al., 2020). However, the low melt rates within debris-covered surfaces seem to conflict with the common observation that glacier-wide thinning is often highest beneath melt reducing debris (e.g., Kääb et al., 2012; Gardelle et al., 2013). This phenomenon has been referred to as the ‘debris-cover anomaly’ (Pellicciotti et al., 2015); it appears to occur globally and has been reported in High Mountain Asia, the European Alps (Mölg et al., 2019), and Alaska (Anderson et al., 2021).
We approach this topic hoping that the study of a single glacier in detail will effectively reveal the underlying processes that control the debris cover anomaly more generally. For this case study we consider Kennicott Glacier, a large, dynamic glacier in the Wrangell Mountains of Alaska (Figure 1).
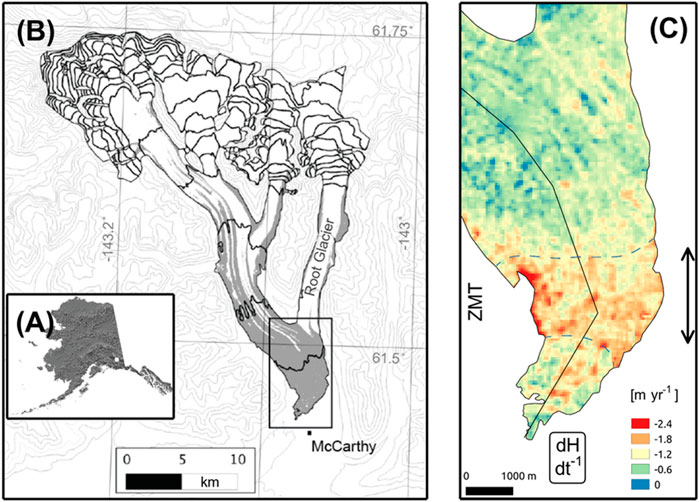
FIGURE 1. Context and thinning maps of the study area. (A) Map of Alaska showing the location of panel B as a white square. (B) Kennicott Glacier with the extent of panel C as a black rectangle. The contour interval is 200 m. The most southerly contour on the glacier represents 600 m a.s.l. (C) The study area with the rate of glacier surface elevation change (dH dt−1) between 1957 and 2004 (see Das et al., 2014). ZMT refers to the zone of maximum thinning and its extent is designated by the double headed arrow and the blue dashed lines on the glacier. The solid black line is the trace of the 1,000 m wide swath profile used to present data with distance from the terminus in later figures.
To discern the fundamental controls on debris-covered glacier evolution in response to climate change we parse the issue in two: First, we consider a modern “snapshot” of Kennicott Glacier (i.e., frozen in time) to develop our understanding of causal relationships between different parts of the system. Second, we consider the glacier’s evolution over multiple decades.
In order to study the complex interactions occurring on Kennicott Glacier, we attempt to establish causal relationships between various parts of the system, namely debris thickness, melt hotspots, and ice dynamics. Because debris thickness strongly controls melt, an understanding of the processes controlling debris thickness is essential for projecting the future evolution of debris covered glaciers (e.g., Banerjee, 2017). Processes that control the distribution of sediment on glaciers include the melt out of debris from within the glacier, the compression (or extension) of ice due to the pattern of ice velocity, the advection of typically thinner debris downglacier, and local sediment re-distribution (hillslope) processes (Moore, 2018; Huo et al., 2021). Anderson and Anderson (2018) showed that thin debris should be expected to occur where velocities are high and thick debris should occur where velocities are low. They suggested that debris melt out from the glacier to the surface should decline downglacier following the reduction of melt rates under thicker and thicker debris.
Melt hotspots like ice cliffs, streams, and ponds are scattered across debris-covered ice surfaces and locally increase melt rates (e.g., Miles et al., 2018; Buri et al., 2021). It has been previously shown that ice cliffs correlate with the degree to which surface flow is compressive (Benn et al., 2012; Kraaijenbrink et al., 2016). Streams on debris-covered glaciers tend to be larger where debris is thin and melt rates are high and smaller where debris is thick and melt rates are low (Iwata et al., 1980; Fyffe et al., 2019). Ponds on debris-covered glaciers occur preferentially where surfaces slopes are low (e.g., Reynolds, 2000).
Previous work has revealed a striking pattern in ice cliffs and debris thickness across the debris-covered tongue of Kennicott Glacier (Anderson et al., 2021). Where ice cliffs on the modern glacier are most abundant, a rapid increase in debris thickness downglacier also occurs, suggesting that there is a common control. Here we therefore first consider: What controls the patterns of ice flow, debris, and melt hotspots on the modern Kennicott Glacier (independent of significant glacier thinning)? To address this question, we produce and compile 18 different variables from the modern debris-covered tongue of Kennicott Glacier and cross-correlate them and attempt to establish causal relationships by identifying processes that connect the correlated variables.
When considering the evolution of Kennicott Glacier over several decades, our focus is on explaining how the glacier has thinned and why melt rates appear to have declined in time. The thinning of glaciers must occur either by mass loss in place or by dynamical redistribution of mass loss occurring elsewhere on the glacier surface. To show the potential for feedbacks in the debris-covered glacier system, we highlight three fundamental equations governing the evolution of debris-covered glaciers. First, the continuity equation for ice:
where H is ice thickness, t is time,
Debris thickness affects the melt rate beneath debris through Østrem’s curve, which can be described as a hyperbolic relationship [i.e., the Hyper-fit model of Anderson and Anderson (2016)]:
where
Surface debris patterns depend on ice flow and debris thickness itself. The governing equation for the evolution of debris thickness (e.g., Nakawo et al., 1986) is
where C is near-surface englacial debris concentration, φ is the porosity of the debris, ρr is the density of the rock composing the debris, and u is surface velocity in the x-direction and v is surface velocity in the y-direction. The first term on the right-hand side of Eq. 3 is the rate of debris melt out, the second and third terms represent the combined effects of surface compression (i.e., surface strain rate, ∂u/∂x+∂v/∂y) and the advection of debris in the x- and y-directions.
Feedbacks within the debris-covered glacier system are abundant and are represented by the shared terms within and between Eqs 1–3. Feedbacks occur when a ‘cause’ influences the resulting ‘effect’ and the resulting effect loops back to influence the cause. As an example, thinning, due to rising temperatures, reduces ice flow causing melt hotspot patterns to change, which in turn affects melt rates and thinning, completing the feedback loop (Supplementary Figure S1). Feedbacks are positive when the effect amplifies the cause and negative when the effect lessens the cause.
The chain of process-links from boundary conditions to observables on debris-covered glacier surfaces (like thinning or ice cliff patterns) are difficult to discern because of the sheer number of possible controls. To address and simplify this issue we consider: What processes and feedbacks control the thinning of Kennicott Glacier as it thins over multiple decades?
We quantified most terms in the first three equations as they vary in space and time. All terms of the continuity equation for ice (Eq. 1) are quantified, including annual mass balance and ice emergence. To constrain the glacier thinning pattern we difference digital elevation models (DEMs). We quantify all terms in the debris–thickness melt relationship (Eq. 2) and the continuity equation for debris (Eq. 3) excluding the debris porosity and density. The development and inversion for this range of datasets affords us a rare view into the controls of the multi-decadal-scale evolution of a large, rapidly thinning debris-covered glacier. Analyses of debris and melt hotspots as they change in time further show how essential ice dynamics are for understanding and predicting the evolution of debris-covered glaciers.
Study Glacier
Kennicott Glacier is 42 km long and broadly faces south-southeast in the Wrangell Mountains of Alaska (Figure 1; 387 km2 area). As of 2015, 20% of Kennicott Glacier was debris-covered (Anderson et al., 2021). Below the equilibrium-line altitude at about 1,500 m (Armstrong et al., 2017), nine medial moraines can be identified on the glacier surface. Debris thicknesses were measured on the glacier surface in 2011 and extrapolated across the central five medial moraines of Kennicott Glacier (Anderson et al., 2021). Debris thicknesses have also been estimated across the glacier based on remotely sensed data and modeling (Rounce et al., 2021). Above 700 m elevation debris is typically less than 5 cm thick, although, near the glacier margin debris tends to be thicker. Medial moraines coalesce 7 km from the terminus to form a debris mantle with ice cliffs, streams, and ponds scattered within an otherwise continuous debris cover. Ice cliffs are especially abundant on Kennicott Glacier (Anderson et al., 2021). The zone of maximum thinning, or the ZMT, is defined as the portion of the glacier that has thinned at a rate greater than 1.2 m yr−1 between 1957 and 2004 (Das et al., 2014; Figure 1). The ZMT has been continuously debris covered since at least 1957 and debris expanded upglacier by 1.6 km between 1957 and 2009.
Kennicott Glacier has been the focus of outburst flood research for almost two decades. Each year the ice-marginal Hidden Creek lake drains under Kennicott Glacier increasing basal water pressures leading to a 1–2 days period of enhanced basal sliding (Rickman and Rosenkrans, 1997; Anderson et al., 2005; Walder et al., 2006; Bartholomaus et al., 2008; Armstrong and Anderson, 2020). Armstrong et al. (2016) and Armstrong et al. (2017) showed that up to half of the surface displacement in the debris-covered tongue of Kennicott Glacier occurs in the summer, due to sliding at the glacier bed.
Methods
The data we produced fit into four categories: 1) glacier thinning; 2) ice dynamics; 3) mass balance (MB); and 4) surface features (melt hotspots and topography). All data sets were derived from remotely sensed data, except for the in situ measurement of the maximum height of 60 ice cliffs during the summer of 2011 (see Anderson et al., 2021).
We focus on the lower 8.5 km of Kennicott Glacier (Figure 1; Supplementary Figures S2–S4). Most of the datasets presented here are based on a 1 km wide swath profile running down the center of the glacier. Estimates of annual mass balance and ice emergence rate represent averages across the glacier surface. Our analysis of the modern glacier surface is based on datasets collected between 2011 and 2016. Although these datasets are not all from the same year, we assume that changes in the properties are negligible over this period. For temporal changes over several decades, we assemble data obtained between 1957 and 2016.
We transition between spatial scales, from ‘area-averaged’ to ‘local’ processes. We define ‘area-averaged’ mass balance, as the mean mass balance over the spatial scale for which the surface slope and ice thickness influence ice dynamics, roughly four times the local ice thickness (Kamb and Echelmeyer, 1986). We define ‘local’ as the 1–10 m spatial scale that is relevant for the control of glacier surface topography by differential ablation.
Glacier Surface Lowering From 1957 to 2016
To constrain the thinning pattern and its changes in time we differenced seven digital elevation models (DEMs) covering the period between 1957 and 2016 (Supplementary Table S1 and Supplementary Figure S5). Before differencing each pair of DEMs they were co-registered relative to one another using the pc_align routine in the Ames StereoPipeline software (Shean et al., 2016). This was accomplished using the iterative point-to-point algorithm and allowing for the translation of one raster relative to another with the glacier area masked out. Uncertainties are based on the standard deviation of elevation change within common, low-sloped areas adjacent to the glacier terminus. To minimize seasonal bias, we only differenced DEMs that 1) have acquisition years more than 9 years apart or 2) were acquired with a day-of-the-year difference of less than 3 weeks (Supplementary Table S2).
Ice Dynamics Terms
Ice Thickness
Ice thickness is a fundamental control on the flow of glaciers but can be difficult to constrain through debris cover (Pritchard et al., 2020). To estimate ice thicknesses along the centerline, we inverted the measured early spring 2013 surface velocities from Armstrong et al. (2016) for ice thickness. Ice thickness estimates from previously published, global-scale products have unrealistic step changes in the upper portion of the study area (Farinotti et al., 2019; Supplementary Figures S6–S8). It is a common glaciological practice to assume that early spring and winter surface velocities result solely from internal deformation (e.g., Armstrong et al., 2016). We acknowledge that winter sliding occurs (e.g., Raymond, 1971; Amundson et al., 2006; Armstrong et al., 2016), but its magnitude cannot be quantified without borehole observations or independent knowledge of the ice thickness distribution.
We used Glen’s flow law to estimate ice thickness H by assuming the flow law exponent n is equal to 3 and solving:
in which j is the index down the glacier centerline,
Surface Velocities
We estimated horizontal glacier surface velocity in 1991, 2005, and 2015 using Landsat 5 TM (L5) and Landsat 8 OLI (L8) imagery (available at earthexplorer.usgs.gov; Supplementary Table S3; Supplementary Figure S9). Glacier motion between images taken at different times offsets distinctive pixel “chunks”, with the offset proportional to glacier speed. We utilized Fourier-space feature tracking implemented in COSI-Corr (Leprince et al., 2007) to quantitatively estimate feature offsets across Kennicott Glacier and characterize the spatial distribution of glacier surface velocity. We produced high quality annual velocity estimates ingesting snow and cloud-free single image pairs from the same worldwide reference system (WRS) path and row, with input images spaced approximately 1 year apart. Utilizing input imagery separated by approximately 1 year minimizes seasonal effects on the velocity pattern that can arise from compositing short-term velocity estimates. Despite this long temporal baseline, the feature tracking algorithm still produced high confidence matches, indicating that the planview appearance of the glacier surface does not change substantially over this timespan.
We created our own velocity estimates rather than using existing velocity products like GO_LIVE (Fahnestock et al., 2016; Scambos et al., 2016) or ITS_LIVE (Gardner et al., 2018, Gardner et al., 2020) because site-specific tuning of processing parameters and input imagery produces higher quality results for our single site than these datasets, which are optimized for large-scale applications. The earlier L5 satellite does not have a panchromatic band, so we utilize reflectance in the green wavelengths (L5 Band 2, 0.52–0.60 μm; L8 Band 3, 0.64–0.67 μm). Reflectance in this waveband has 30 m resolution for both L5 and L8 and minimizes potential bias arising from varying spatial resolution between the missions (Dehecq et al., 2019). All feature tracking used a step between adjacent estimates of 4 pixels and a variable search window that starts as 64 × 64 pixels, then decreasing to 32 × 32 pixels. The resulting velocity estimates have a spatial resolution of 120 m (4 × 30 m). Pixels with a signal-to-noise ratio of <0.9 are removed from further analysis. Image pairs are not separated by exactly 1 year, and so displacement components are all normalized to that expected in a 1-year timespan to produce an annual velocity. We calculated apparent velocity in off-glacier pixels (Supplementary Figure S10) for each image pair to provide estimates of bias and random pixel matching error. We subtract the median off-glacier apparent velocity component from each image to remove systematic error due to image misregistration. After bias correction, we estimated random error (
To evaluate potential controls on the expansion of debris on Kennicott Glacier, we also assessed the change in surface velocity direction. We interpret aerial and satellite imagery from 1957, 1978, and 2009 (Supplementary Table S4) to constrain changes in medial moraine shape (a proxy for flow direction and surface strain).
Driving Stress, Surface Strain Rates and Accumulated Downglacier Compression
Driving stress (or the basal shear stress,
and may therefore be a control on other properties within the debris-covered glacier system.
Using the x- and y-velocities from our annual velocity fields we also calculated surface strain rate
where this term is positive debris will tend to thicken due to compressive flow and where this term is negative, debris will thin due to extensive flow (Supplementary Figure S12). Strain rates are calculated across a 200 m × 200 m grid, similar patterns resulted from calculations based on 400 × 400 m grids. We also calculated the amount of strain a debris parcel would experience as it advected downglacier using the 2015 velocity field.
Ice Emergence Rates
The reduction of ice emergence rates in time can be a strong control on debris-covered glacier thinning (e.g., Vincent et al., 2016). To estimate ice emergence rates through the study area we used a mass-continuity approach following Bisset et al. (2020). We divided the glacier surface with across-flow segments approximately 2 km apart based on glacier outlines derived from thinning maps and aerial and satellite imagery. For the 2015 ice extent we used the 2009 WorldView (WV) satellite image, and a Landsat image from 2016 (Supplementary Figure S2). For the 1991 ice extent we used a conservative extent based on a 1978 USGS aerial photo (a 2004 ice extent produces similar results; Supplementary Figures S3–S4). Ice emergence rates were estimated first by calculating the ice discharge Q:
where m represents an entire across-flow transect, i the index of the cell within each across-flow transect,
where j is the downglacier index and Area is the surface area between the across-flow transects.
We then propagated the error to produce uncertainties for ice emergence rates and mass balance estimates. For results presented in the main text we assumed that all ice motion is due to basal sliding following Bisset et al. (2020). Assuming that all motion is due to internal deformation has a small effect on the annual mass balance estimates (see next section for sensitivity tests).
(Annual) Mass Balance
Constraining annual mass balance is essential for understanding the causes of glacier thinning. We reorganize Eq. 1 to estimate the mass balance in the area between each across-flow transect:
where
We produced two estimates of annual mass balance representing the years 2015 and 1991. In both cases ice thicknesses were updated based on the thinning estimates over the intervening timespan. For the 2015 estimates we used the 2015 velocities as well as thinning data based on fall 2013 and fall 2016 DEMs. For the 1991 mass balance estimates, we used the 1991 annual surface velocity as well as the thinning data based on 1957 and 2004 DEMs. We note that this long-time interval is not ideal for estimating the mass balance in 1991, using annual velocities from 1991. We therefore provide sensitivity analyses to help reveal uncertainties.
Additional estimates of mass balance and emergence rate are provided in which we 1) assumed that all ice motion is due to internal deformation; 2) varied the tuned shapefactor; 3) assumed there is no change in thinning rate in time; 4) applied a 2004 glacier outline for the 1991 estimates; and 5) applied ITS_LIVE composite velocities (Supplementary Figures S13–S18). Note that in Figures 2, 3 surface melt rate and debris thickness estimates of Anderson et al. (2021) from the summer of 2011 are plotted for comparison.
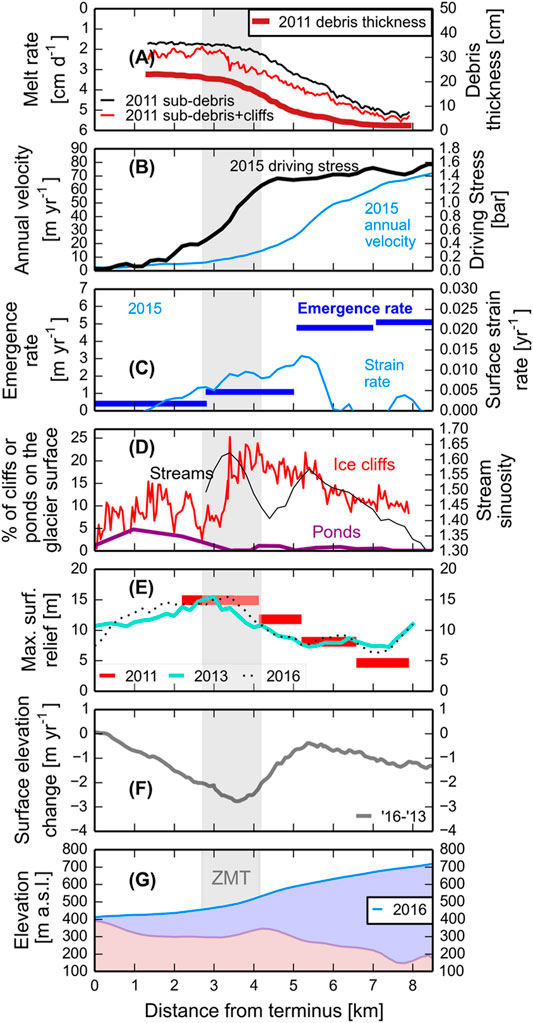
FIGURE 2. Modern snapshot comparison. The zone of maximum thinning (ZMT) is shown with grey shading. (A) Surface melt rate and debris thickness patterns from the summer of 2011 (Anderson et al., 2021). (B) 2015 annual surface velocity pattern with the driving stress based on the surface slope and ice thickness from 2016. (C) The ice emergence rate averaged over approximately 2 km intervals as well as the surface strain rate from the swath profile, smoothed with a 1 km moving window. (D) Patterns of melt hotspots, including ice cliffs and stream sinuosity from the swath profile, as well as ponds across the glacier width. (E) Maximum surface relief within the swath profile taken from 2013 (turquoise) and 2016 (black dots) DEMs. Maximum measured ice cliff relief (red) from the glacier surface in 2011 is also shown. (F) The surface elevation change pattern based on fall 2013 and fall 2016 DEMs. (G) Glacier surface elevation and bed topography from 2016 down the glacier centerline.
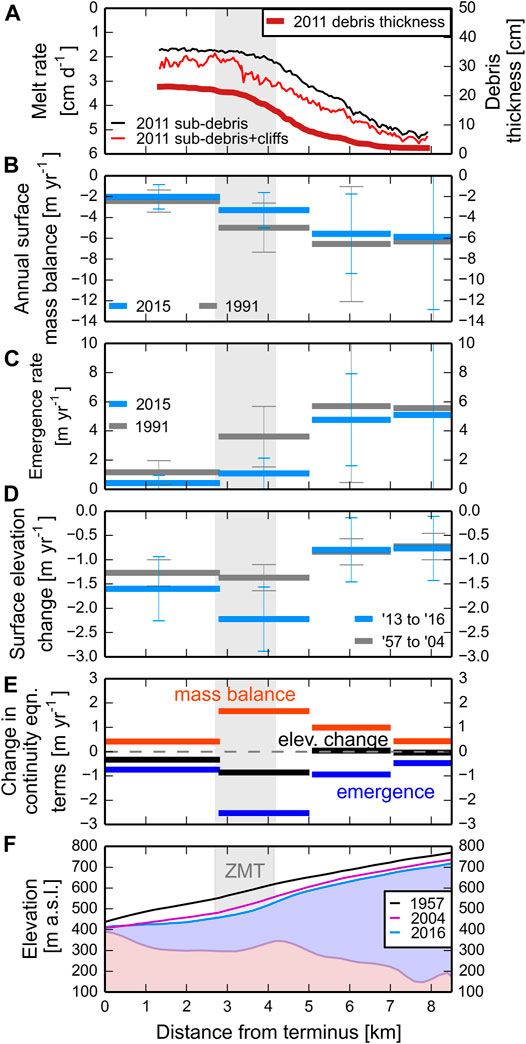
FIGURE 3. Changes in ice continuity equation terms over multiple decades. The zone of maximum thinning (ZMT) is shown with grey shading. (A) Debris thickness with distance from the terminus for the 5 central medial moraines (Anderson et al., 2021). Distributed melt rate estimates from Anderson et al. (2021). (B) Annual surface mass balance based on 2015 annual velocities and thinning between 2013 and 2016. As well as the annual surface mass balance based on 1991 annual velocities and thinning between 1957 and 2004. (C) The change in ice emergence rate in time. (D) Glacier surface elevation change from 1957 to 2004 and from 2013 to 2016. (E) The change in the terms of the continuity equation between 1991 and 2015. The bars represent the difference between the bars in each of panels B, C, and D. (F) Surface profiles through time and the bed profile of Kennicott Glacier.
Inversion to Estimate Debris Thickness Change and Englacial Debris Concentration
To aid in our understanding of the evolution of Kennicott Glacier in time we estimated debris thickness changes between 1991 and 2011 as well as the mean englacial debris concentration in the study area. To do this we inverted measured debris thickness, surface velocities, strain rates, and annual mass balance estimates from the swath profile.
The first step used a Monte Carlo approach to estimate 106 potential 1991 debris thickness patterns (e.g., Tarantola, 2005). We allow random changes in each 200 m pixel from the 2011 in situ debris thickness pattern to generate possible 1991 debris thickness patterns. Second, for each possible 1991 debris thickness pattern and englacial debris concentration we numerically solved Eq. 3 in this form starting in 1991 until an estimate of 2011 debris thickness was produced:
The first term on the right is the contribution of englacial debris melt out, the second term is the contribution of compression or extension, and the third term represents the advection of debris downglacier. The timestep, dt is set to 1 year
For the case presented in the main text we assumed that C is uniform and does not vary in time, that porosity is 0.3 (Nicholson and Benn, 2013), and that the rock density is 2,200 kg m−3 (see MacKevett, 1972; MacKevett and Smith, 1972; Miles et al., 2021). Because we have no a priori knowledge of the pattern or magnitude of C, porosity, and rock density we ran 13 additional inversions in which 1) C increases downglacier linearly through the swath profile by factors of 2, 10, 100, and 1,000; 2) C decreases linearly downglacier through the swath profile by factors of 0.5, 0.1, 0.01, and 0.001; 3) porosity varies between 0.1 and 0.4; 4) rock density varies between 2000 and 2,700 kg m−3; and 5) use the remotely sensed debris pattern of Rounce et al. (2021) instead of the in situ debris thicknesses as the 2011 evaluating dataset (Supplementary Table S5). The range of increase in near-surface C downglacier explored (up to 3 orders of magnitude) is comparable to the increase documented downglacier on Khumbu Glacier (Miles et al., 2021).
After we used Eq. 10 to calculate 2011 debris thickness patterns for each of the 1991 debris pattern guesses and value of C, we evaluated the calculated 2011 debris thickness patterns against the measured in situ debris pattern from 2011 using the RMSE. A single best 1991 debris thickness pattern and englacial debris concentration was identified for each of the 14 inversions. Because the contributions of englacial melt out and ice dynamics were also calculated while solving Eq. 10 we were also able to explore the role of each in controlling debris thickness change in time.
Melt Hotspots and Surface Relief
Melt hotspots are associated with surface features like ice cliffs, surface streams, and surface ponds which locally enhance melt and thinning. We used the delineated ice cliff extents from Anderson et al. (2021), who used an Adaptive Binary Threshold method applied to a 0.5 m resolution WV satellite image (from July 13, 2009; Supplementary Table S4).
Supraglacial Streams
Streams paths on the glacier surface were delineated using the GRASS GIS command r.stream.extract and a fall 2013 DEM with a 2 m spatial resolution (Porter et al., 2018; Supplementary Table S1). Because of the complex topography on the glacier surface, and observations of many undercut streams the filling of depressions less than 16 m2 was required to produce viable stream paths on the glacier surface. Stream sinuosity S was then calculated along individual stream paths using TopoToolbox 2 (Schwanghart and Scherler, 2014) and the equation:
where Lchannel is the length of the channel and Lstraight is the straight-line distance downstream. An S value of 1 represents a straight stream. The higher the value of S the more sinuous the stream. Each sinuosity value was calculated over a reach of 400 m. Uncertainties in surface stream sinuosity are estimated by varying the 400 m reach by ±100 m. Because sinuosity values at either end of a stream segment are biased due to the lack of a downstream reach, stream sinuosities were not plotted or analyzed for the upper and lower 200 m of each stream. Streams at the glacier margin were removed from the sinuosity calculations. In order to identify where streams are present at the glacier margin, we digitized their paths in QGIS using the 2009 WV image.
Supraglacial Ponds
Pond coverage was determined for two time periods. Pond extent was hand digitized from a United States Geological Survey (USGS) 1957 aerial photo and the 2009 WV image in QGIS. Ponds were searched for using a fixed grid to ensure complete coverage of the study area. Depressions on the glacier surface with exposed ice and/or ice-cut shorelines were digitized and assumed to be drained ponds.
Glacier Surface Relief
The topography of debris-covered glacier surfaces can vary widely over ten- to hundred-meter scales (Iwata et al., 1980). Relief is the difference in elevation between the highest and lowest point within a given area. In order to assess how finer scale topography has changed through time on Kennicott Glacier we estimated glacier surface relief at 50 m resolution using the Raster Terrain Analysis Plugin in QGIS for three DEMs. We measured maximum surface relief within each band of the swath profile for the 1957 (shown in the Supplementary Figures), as well as the fall 2013 and fall 2016 DEMs. Uncertainties in the DEMs are presented in Supplementary Table S1. Because the 1957 USGS DEM has an original resolution of 60 × 30 m we chose an intermediate resolution of 50 m over which to calculate glacier surface relief.
We also measured maximum relief of 60 ice cliffs in the summer of 2011 using a laser rangefinder (see Anderson et al., 2021 for locations). Uncertainty in these estimates arises from not targeting the actual location of lowest elevation at the base of the ice cliff. To reduce uncertainty five measurements were taken from possible lowest points at each ice cliff and the maximum value is reported. Error in these estimates is unlikely to exceed 1 m.
Correlation Between Variables
To guide the analysis relating ice dynamics, debris, and melt hotspots variables from a single snapshot in time (Figure 2), we cross-correlated 18 of the variables described above. Each variable represents the 1 km wide swath profile except for pond coverage, surface mass balance, and ice emergence which represent the full width of the glacier. The Pearson linear correlation coefficient was calculated between all variables. To explore the processes controlling the thinning pattern on Kennicott Glacier over several decades we cross-correlated each term of Eq. 1 (thinning, annual mass balance, and ice emergence) for the modern glacier and as the terms changed between 1991 between and 2015 (Figure 3). All terms from Eq. 1 represent the full width of the glacier following the discretization described in Ice Emergence Rates and (Annual) Mass Balance.
Results
Glacier Thickness Distribution and Change in Time
Our bed elevation estimates show that the glacier thickens upvalley from the terminus (Figure 2). A transverse ridge in the bed topography is predicted just upstream from the zone of maximum thinning (ZMT) under the surface topographic bulge (at ∼4 km in Figure 2G). Upglacier from the ridge, the bed is overdeepened (bed elevations are lower upglacier). The lowest bed elevation predicted within the study area is 150 m a.sl., 7.7 km upglacier from the terminus, where the glacier is estimated to be 550 m thick. A 10% change in the tuned shapefactor results in a 10% change in bed elevation.
Independent of the period examined, glacier thinning is highest in the ZMT (Figure 3D and Supplementary Figure S5). Surface lowering rates increased towards the present. Between 1957 and 2004 the surface lowering rate was −1.4 m yr−1 within the ZMT and between fall 2013 and fall 2016 the surface lowering rate was −2.2 m yr−1. Uncertainties for surface lowering rates used in the main text range from ±0.66 to 0.27 m yr−1 (Supplementary Table S2).
Ice Dynamics Terms
Surface velocities decrease downglacier and towards the glacier margin. For the 2015 (1991) surface velocities, maximum annual surface velocities of 75 (105) m yr−1 occur in the upper portion of the study area (Figure 4B and Supplementary Figure S9). The 2015 (1991) surface velocities become indistinguishable from noise 3 (1.8) km upglacier from the terminus.
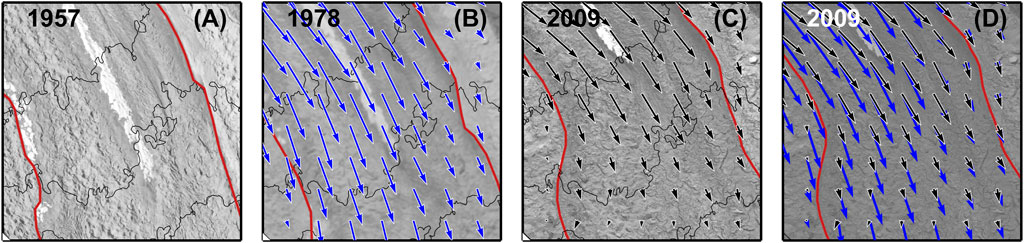
FIGURE 4. Changes in debris extent. Each panel reflects the same 3 × 3 km area on the glacier surface (see Figure 6). Red lines in each panel represent the border between the same medial moraines. Note the distinct change in medial moraine boundaries through time, especially between 1978 and 2009. (A) 1957 aerial photo. (B) 1978 aerial photo with annual surface velocity vectors from 1991. The largest vector at the top of the panel has a magnitude of 105 m yr−1. (C) 2009 WorldView image with annual surface velocity vectors from 2015. The largest vector at the top of the panel has a magnitude of 75 m yr−1. Flow is compressive where debris extent has expanded. (D) 2009 WorldView image, with darker shade, overlaid with annual surface velocity vectors from 2015, in black with white outlines, and the annual surface velocity vectors from 1991 in blue.
The terminal region of Kennicott Glacier slowed substantially over the study period, with a ∼40 m yr−1 (∼50%) velocity decrease between 1991 and 2015 (Supplementary Figure S9). Most of the velocity change occurred between 1991 and 2005, with only minor slowing occurring after this time. The fact that most of the slowing occurred between the early and middle time periods, which are both estimated using L5 imagery, indicates that this is not an artifact of intermission comparison, radiometric range, and spatial resolution of the sensors (Dehecq et al., 2019). Our use of a fixed spatial resolution for input images, restriction to snow-free acquisitions, and the study area being in a wide and low elevation location minimizes potential biases. For L5, velocity uncertainty is on the order of 10–15 m yr−1, while it is <3 m yr−1 for L8 (Supplementary Table S3).
Between 1991 and 2015 surface flow directions changed substantially in the middle of the study area (Figure 4). Between 1957 and 2009 medial moraine boundaries on the glacier surface were also deformed. The consistent change in shape of these stripes from more linear towards increasingly “S”-shaped in some cases is also reflected in the changes in velocity vectors between 1991 and 2015. Debris on the surface of Kennicott Glacier expanded between 1957 and 2009 following these changes in ice flow direction.
Surface strain rates are highest (flow is more compressive) just above the ZMT in both 1991 and 2015 and decline towards the present across the study area (Supplementary Figures S12, S19). For the ice-free error check area totaling 4.05 km2 adjacent to the terminus, where strain rates are zero, strain rate uncertainties are ±0.0017 yr−1 for the 1991 field and ±0.0006 yr−1 for the 2015 velocity field.
Averaged across the full glacier width, ice emergence rate estimates are highest at the upglacier end of the study area for both velocity fields and below 1 m yr−1 below the ZMT (Figures 2C, 3C). Ice emergence rates declined throughout the study area from 1991 to 2015, most within the ZMT (2.4 m yr−1) and within 2 km upglacier of the ZMT (1.95 m yr−1). Ice emergence rates changed least below the ZMT and at the upglacier end of the study area. Uncertainties (±3 St. dev.) scale with the magnitude of the emergence rate and range from 1 to 9 m yr−1. While there are significant uncertainties in the estimates of ice emergence rate, ice emergence rate is the dominant control on thinning in the ZMT for all sensitivity tests (Supplementary Figures S13–S18).
Annual Mass Balance
Annual surface mass balance appears to have increased from 1991 to 2015, suggesting that melt rates decreased towards the present in the study area (Figures 3B,E). The largest estimated reduction in annual melt rates occurred in the ZMT (+2.1 m yr−1) and in an area of the glacier just upglacier from the ZMT (+1.8 m yr−1). While there are significant uncertainties in the estimates of annual mass balance, the reduction in melt rate between 1991 and 2015 is present in all sensitivity tests (Supplementary Figures S13–S18).
Inversion to Estimate Debris Thickness Change and Englacial Debris Concentration
Figure 5 shows an estimate of how debris thickness changed in time in the study area assuming uniform englacial debris concentrations. Panels B and C show the change in debris thickness from 1991 to 2011. Panels B and C also show the absolute and relative roles of ice dynamics and debris melt out in changing debris thickness. In all 14 inversions, debris melt out occurs across the study area and decreases downglacier. This occurs because ice is melting across the study area and area-averaged melt rates decline downglacier. Ice dynamics thickens debris within and below the ZMT and tends to thin debris above the ZMT. This dynamical effect is present in all inversion scenarios and is the result of the measured patterns of surface velocity and strain rate.
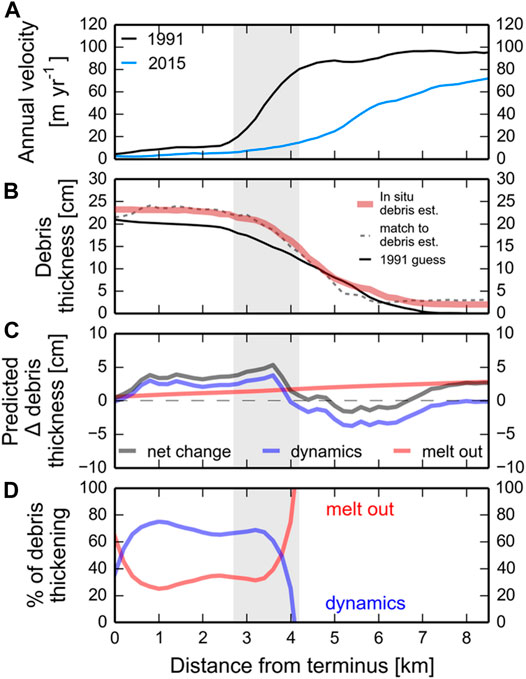
FIGURE 5. The debris feedback expressed on the surface of Kennicott Glacier. For all panels the zone of maximum thinning (ZMT) is shown in grey. (A) Annual surface velocities from 1991 to 2015 from the swath profile. (B)In situ debris thickness from 2011. The best estimate of the debris pattern in 1991 is shown as well as the simulated debris thicknesses in 2011 produced from the inversion assuming a uniform englacial debris concentration. (C) Predicted absolute change in debris thickness from 1991 to 2011 due to dynamics and debris melt out. (D) The relative role of ice dynamics and debris melt out in debris thickness change. Above the ZMT debris melt out accounts for 100% of the debris thickening because flow is high and ice dynamics tends to thin debris by advection there.
The mean of all inversions for the average englacial debris concentration across the study area was 0.017% by volume with a standard deviation of 0.0076% (Supplementary Table S5). The maximum average englacial debris concentration from a single inversion run was 0.033% and the minimum was 0.007%. The estimated mean concentrations are comparable with previous near-surface measurements from other glaciers (e.g., Bozhinskiy et al., 1986; Miles et al., 2021). All 14 inversions for surface debris thickness change between 1991 and 2011 indicated that on average debris thickened in the study area. Almost all estimates indicated that debris thickened most in and downglacier from the ZMT (Supplementary Figure S20) where both dynamics and debris melt out contribute to debris thickening.
Melt Hotspots, Surface Slope, and Surface Relief
Area-averaged surface slopes declined below the ZMT and tended to increase in the upper portion of the ZMT and 1 km above the ZMT (Supplementary Figure S21). Modern maximum glacier surface relief is highest in the ZMT, remains high downglacier towards the terminus and decreases upglacier from the ZMT (Figure 2E). The location of maximum glacier surface relief was near the toe in 1957 and shifted into the ZMT towards the present (Supplementary Figure S22). In and above the ZMT maximum relief increased from 1957 to 2016. Uncertainties in the DEMs used to calculate relief range from 15 m for the 1957 DEM to less than 3 m for the ArcticDEMs (Supplementary Table S1).
Stream paths are longer above the ZMT than below the ZMT (Figure 6C). Stream sinuosity is low in the upper portion of the study area and increases downglacier until the middle of the ZMT (Figures 2D, 6C). Streams tend to be less sinuous in the upper portion of the study area and become increasingly sinuous until the middle of the zone of maximum thinning. Field investigations in the summer of 2011 and digitization of streams on the glacier surface using the WV images suggest that streams are limited on the glacier surface below the upper portion of the ZMT (Supplementary Figure S23). At the transition between these domains in the middle of the ZMT the largest supraglacial streams descend into a series of moulins or flow off glacier (Anderson, 2014). A 10% change in the distance over which sinuosity is calculated changes the mean sinuosity across the study area by 2.2%.
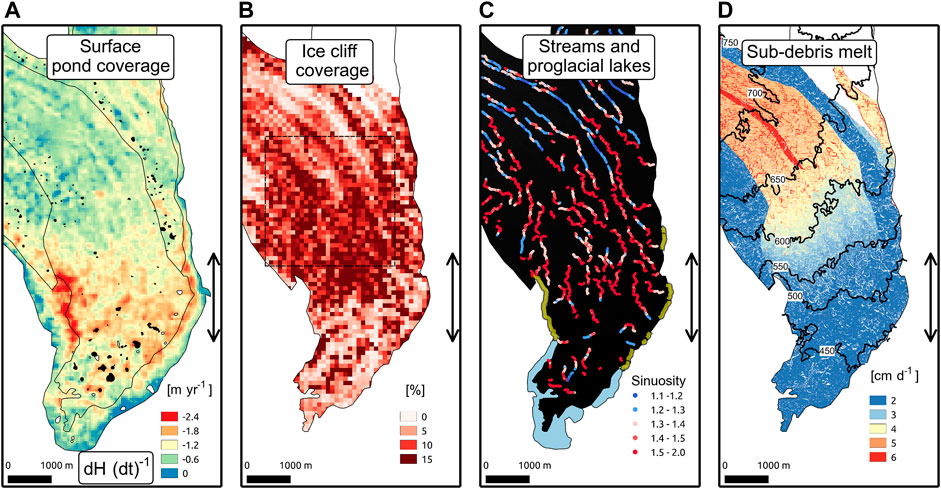
FIGURE 6. Comparison of thinning, melt hotspots, and melt in map view. The double headed arrows indicate the extent of the zone of maximum thinning (ZMT). (A) Glacier surface elevation change between 1957 and 2004 and observed surface pond extent in 1957 (white) and 2009 (black). The 1957 glacier extent is shown by the extent of the thinning map. The 2015 glacier outline is shown in black, as is the boundary between the central 5 medial moraines (compare with panel D). (B) Ice cliff coverage in fractional area
Surface pond area is largest below the ZMT (Figure 6A and Supplementary Figure S22). Based on the 2009 WV image ponds are most abundant 1 km upglacier from the terminus and occupied about 5% of the glacier surface. Uncertainty in 2009 pond area, based on digitization by an independent operator, is ±1% of the glacier surface. Digitized 1957 pond extents show that ponds were largely present near the terminus with a maximum of about 5.5% of the glacier surface near the terminus. Uncertainty in 1957 pond area, based on digitization by an independent operator, is ±2% of the glacier surface. Pond coverage increased from 1957 to 2009 (Figures 3D, 6A). Upglacier from the ZMT ponds are only abundant in medial moraines near the glacier margin, where debris tends to be thicker and ice flow slower than near the glacier center.
Correlation Between Variables
Figure 7 shows the cross-correlation matrix for the modern snapshot. Ice dynamics variables show strong correlations with one another. Surface velocity and ice thickness are highly correlated with ice emergence rate (r = 0.99 and 0.95). Variations in ice thickness are highly correlated with bed elevation (r = −0.93) and therefore bed elevation is also strongly associated with the other ice dynamics variables.
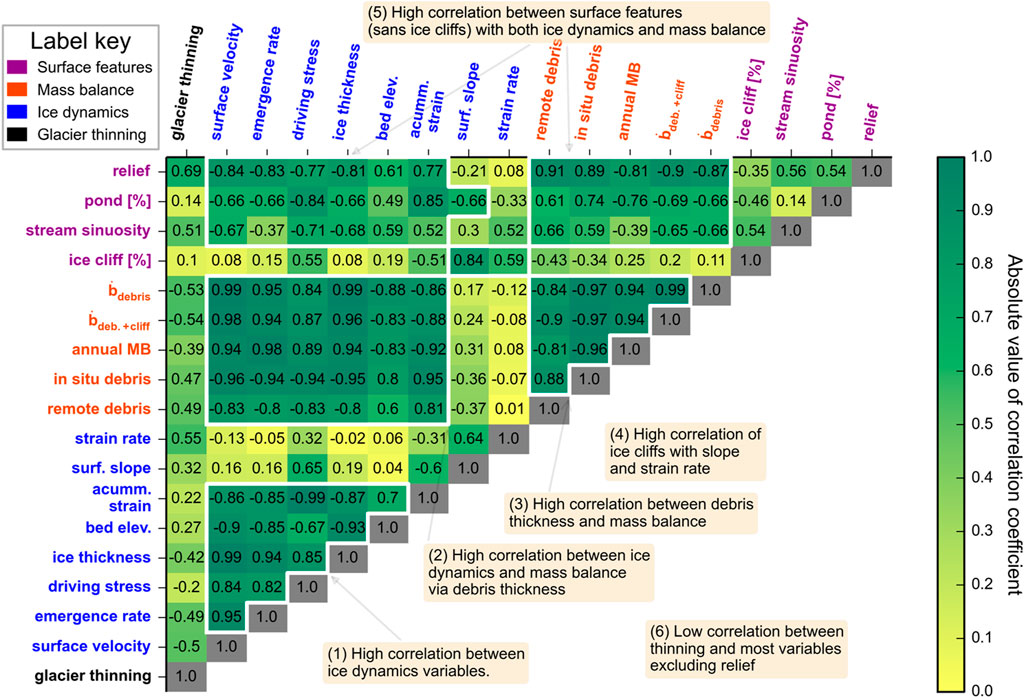
FIGURE 7. Correlations from the modern snapshot. All datasets are derived from between 2011 and 2016. Correlations between all 18 variables are contained in this matrix. The green-yellow color bar shows the magnitude of correlation. The sign of correlation can be read from the black labels in each cell. Cells with high magnitude of correlation are outlined in white and described with annotations on the figure. The numbers in the annotations follow the chain of process links presented in the discussion. Relief for example can be correlated with all other properties by starting at the upper left and looking across the row to the relief label in the upper right. Pond (%) can be correlated with all other variables by starting with the upper left label and continuing across the row until the last cell and then looking vertically to see the correlation between pond (%) and relief. Note that increased thinning is represented by positive numbers in this figure. This contrasts with Figure 8 where more negative surface elevation change is equivalent to more positive thinning.
Surface slope and strain rate are generally only weakly correlated with other dynamical terms. The surface slope plays a role in setting the ice dynamical terms through Glen’s flow law, but its role is secondary to ice thickness, especially for low sloped glaciers like the Kennicott. The strain rate is determined by the gradient in surface velocity terms and therefore does not correlate with most other ice dynamics variables, which are more closely linked to velocity at a single point.
The ice dynamical terms have high magnitudes of correlation with the annual mass balance estimates from 2015 and the independent summer 2011 melt rate estimates from Anderson et al. (2021). The magnitude of correlation between ice dynamical terms and in situ debris thickness are all higher than 0.8. The cumulative sum of compression is highly correlated with debris thickness (r = 0.95). Debris thickness patterns on Kennicott Glacier follow the inverse of surface velocity (r = −0.94). In situ debris thickness is highly correlated with all mass balance estimates (
The relief of the glacier surface is linked to in situ debris thickness and mass balance (
Figure 8 is the cross-correlation matrix for glacier change over multiple decades. See Figure 3 for the signs of individual terms in Figure 8. Glacier surface elevation change (1957–2016) and its change in time (1957–2004 minus 2013–2016) are both highly positively correlated (red) with the decline in ice emergence rate in time. In other words where thinning was highest the reduction in emergence rate was also highest and where the change in thinning was highest the decline in emergence rates in time was also highest. In contrast surface elevation change and its change in time are negatively correlated with annual mass balance and its change in time. This means that where melt is high thinning tends to be low and where thinning has increased in time melt rates have decreased in time.
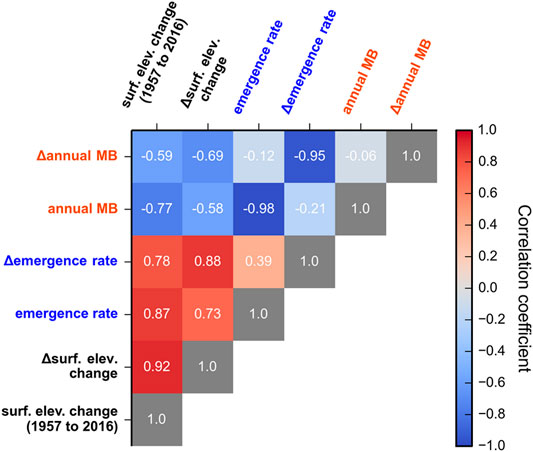
FIGURE 8. Correlations between ice continuity terms as they change over multiple decades. Correlations between all terms in the continuity equation can be read from the matrix. As an example: A high positive correlation (red) between surface elevation change and ∆emergence rate indicates that the negative surface elevation change from 1991 to 2015 is positively correlated with the negative decline in ice emergence rate in time. See Figure 3 for the patterns and signs of each term in this figure.
Discussion
In the discussion we build a chain of process links evident on the modern surface of Kennicott Glacier starting from the glacier bed. We use the correlation coefficients presented in Correlation Between Variables and Figure 7 to help identify processes links for the modern snapshot. Next, we delve into how these process links change over several decades including feedbacks related to changes in the terms of Eq. 1 in Processes Controlling Glacier Change Over Multiple Decades.
Chain of Process Links From the Modern Snapshot
Expression of the Glacier Bed in Surface Velocity
The bed pattern explains the pattern of ice dynamics apparent across the study area. Based on Glen’s flow law, glacier surface velocity varies with ice thickness to the power of 4 and surface slope to the power of 3 (Equation 4; e.g., Hooke, 1998). The topographic bulge on the glacier surface near the upglacier end of the ZMT likely exists due to a rise in the glacier bed beneath it. Because the glacier thins here, it must steepen to pass the same ice discharge coming from the thick ice upstream. Further geophysical surveys are needed to confirm this inference.
Surface Velocity Controls Debris Thickness and Mass Balance
Surface velocity is an important control on debris thickness patterns (Figure 5). Within and below the zone of maximum thinning, ice dynamics and debris melt out both tend to thicken debris. Because surface speeds are low here downglacier translation of thin debris is also low allowing debris compression to thicken debris locally. Above the ZMT ice dynamics tends to thin debris while debris melt out tends to thicken debris. High surface speeds translate debris downglacier rapidly (Figure 5). In other words, within a given pixel thin debris is translated from upglacier leading at an apparent thinning of debris. This dynamic thinning effect is compensated for by the rapid melt out of debris from within the glacier (Figure 5C).
We can expect these same general patterns on other debris covered glaciers: where velocities are high debris thicknesses will tend to be low, where velocities are low debris thickness will tend to be high. The results from Kennicott Glacier bolster the theoretical arguments laid out first by Kirkbride (2000) and later supported and expanded upon by Anderson and Anderson (2018).
The control of surface velocities on debris thickness means that area-average melt rates are also highly correlated with surface velocity and ice emergence rates. The high correlation between annual mass balance and ice emergence rate is expected because they compensate for one another via feedbacks between surface slope and ice thickness as is also the case for glaciers unperturbed by debris (e.g., Hooke, 1998). The co-evolution of ice dynamics and surface melt is a result of inevitable physical relationships (see Eq. 3) for debris-covered glaciers and should therefore be observed generally.
Thin Debris and Dynamic Thinning Control Surface Relief
Glacier surface relief correlates highly with most variables in Figure 7. Process controls on relief assuredly vary in space, depending on location relative to the ZMT and whether flow is rapid or slow. Where flow is high, surface roughness is linked to area-averaged debris thickness as differences in local melt rate help produce surface topography (e.g., Anderson, 2000; Moore, 2018). Because of the hyperbolic shape of Østrem’s curve, where area-averaged debris thicknesses are low, small differences in debris thickness produce large differences in local melt rate that rapidly increase local surface relief. The glacier surface acts like a conveyor belt, so it follows that relief cumulatively increases downglacier above the ZMT. The further down glacier the longer differential melt has acted to increase local relief. Streams are expected to increase relief production above the ZMT as discussed in Ice Cliff-Stream-Relief Feedback.
Below the ZMT, where flow is low and debris is generally thick, small differences in debris thickness do not produce significant differences in melt rate, limiting relief production. Below the ZMT, tunnel collapse has an important role in relief production (e.g., Benn et al., 2017). Interestingly, across the study area, glacier thinning is most highly correlated with surface relief. Because dynamic glacier thinning directly changes glacier surface elevations (via the decline in emergence rates in time) it follows that surface relief should correlate with thinning.
Debris Thickness and Ice Dynamics Control Melt Hotspots
Melt hotspots have distinctive patterns on the surface of Kennicott Glacier. A number of processes connect debris and ice dynamics with ice cliffs, streams, ponds, and relief which we describe below.
Ice Cliffs are Abundant Where Compression and Surface Slopes are High
Ice cliffs are most abundant where surface compression is high on Kennicott Glacier. A correlation between strain rate and ice cliffs also occurs on glaciers in the Himalaya (Benn et al., 2012; Kraaijenbrink et al., 2016; Supplementary Figure S19). But to date no clear process connecting surface compression and ice cliff coverage has been identified. One way in which surface compression could increase ice cliff abundance is if debris compression is manifested in a non-uniform fashion and localized in shear bands. This would lead to the increase of local debris thicknesses in some areas and not others, therefore allowing for differential melt, local surface slope steepening, and ice cliff formation.
An assessment of local patterns of ice emergence rate (surface uplift) is also needed to determine if dynamic steepening and ice cliff abundance correlate. Short-lived high-compression events may also play a role on Kennicott Glacier. The annual summer flood of Hidden Creek Lake produces a period of very rapid sliding (e.g., Bartholomaus et al., 2008), translating the entire ice column down glacier leading to high strain rates exactly where ice cliffs are abundant. Perhaps the shaking of the glacier surface during the summer flood encourages debris failure and cliff formation?
Ice cliffs on Kennicott Glacier are positively correlated with surface slope (Supplementary Figure S21). Where area-averaged surface slopes are high debris failure is more likely. Steep debris-covered slopes on the glacier surface, present due to differential melt, can be steepened even further as they are passively transported into areas with steep area-averaged slopes. This steepening effect would tend to encourage ice cliff formation and persistence. But on Kennicott Glacier area-averaged slopes tend to be low (<0.06) implying that this effect is minor. Ultimately the physical explanations for an area-average slope control on ice cliff abundance at Kennicott Glacier are less viable than the strain rate controls outlined in the paragraph above. For this reason, we assume that strain rate is the primary control on ice cliff abundance as it changes in time on Kennicott Glacier.
On less dynamic portions of debris-covered glaciers, with thick debris, thermal erosion from surface ponds can be the dominant control on ice cliff distribution (e.g., Röhl, 2008). This is not the case for most ice cliffs on Kennicott Glacier where ice cliffs and ponds are negatively correlated with one another. On debris-covered glaciers, the processes that control ice cliff distribution above the ZMT (e.g., compression) may in fact be different below the ZMT (e.g., tunnel collapse and ponds).
Stream Sinuosity Varies With Roughness and Surface Slope
Estimated stream sinuosity increases downglacier with glacier surface relief (Figure 2D). At the upper end of the study area troughs between medial moraines are more linear and stream sinuosity is low. As the medial moraines coalesce downglacier the troughs are occupied by increasingly chaotic topography just as streams become more sinuous. Supraglacial streams on uncovered glaciers tend to be more sinuous where slopes are steep and water discharge is high (Ferguson, 1973); observations that also appear to apply within the debris cover of Kennicott Glacier. Without further field investigations into the dynamics of supraglacial streams, it is hard to discern the degree to which rough surface topography or the physics of supraglacial stream flow itself controls stream sinuosity on debris-covered ice.
Ice Cliff-Stream-Relief Feedback
A positive feedback between ice cliffs, surface streams, and surface relief occurs on Kennicott Glacier. Streams and ice cliffs should amplify the occurrence of each other: melt from ice cliffs increases stream flow and streams maintain ice cliffs by undercutting them. Undercutting streams can create gaps between ice cliffs and the debris-covered surface below via thermal erosion (Reid and Brock, 2010; Supplementary Figure S24). This prevents ice cliff burial while still allowing debris, that trundles down the ice cliff, to accumulate across the stream.
Importantly, stream undercutting is enhanced where streams are more sinuous (Parker, 1975). As a result, the arc-shaped meander bends of streams help maintain arc-shaped ice cliffs (Supplementary Figure S24). The arc-shaped ice cliffs focus trundling debris into a smaller area, locally increasing debris thickness and increasing debris thickness variability in space. Via differential melt, local surface topography will grow in time, which can produce additional ice cliffs and increase stream sinuosity by roughening the glacier surface, therefore completing the positive feedback loop.
It is likely that this feedback will apply on other glaciers where 1) area-average debris is relatively thin (less than 20 cm), so relatively high melt rates can increase stream flow and 2) surface strain rates and slopes are high increasing ice cliff abundance. Sato et al. (2021) found a correspondence between drainage patterns and ice cliff occurrence on the more heavily debris covered Trakarding Glacier in the Nepalese Himalaya. The thicker the debris the less likely streams are to undercut ice cliffs precluding the occurrence of this feedback on heavily debris-covered portions of glaciers. Because study of the stream-ice cliff feedback is just beginning, we do not discuss it as a control on the thinning of Kennicott Glacier over multiple decades below.
Driving Stress and Ponds
On Kennicott Glacier, surface ponds are strongly negatively correlated with driving stress which is dependent on both ice thickness and surface slope (Eq. 5; Supplementary Figure 22). Ponds also occur where surface slopes are low on Kennicott Glacier, but the correlation magnitude is lower than for driving stress. A number of previous studies identified correlations between pond occurrence and low surface slopes in the Himalaya (e.g., Reynolds, 2000; Quincey et al., 2007; Sakai and Fujita, 2010; Scherler et al., 2011; Benn et al., 2012). Driving stress could be used to predict the future expansion of ponds as it eliminates false predictions where glacier surfaces are low sloped but still fast flowing.
Summary of Process Links From the Modern Snapshot
Within the debris-covered tongue of Kennicott Glacier the bed appears to be a strong control on the pattern of ice velocity, which in turn controls the pattern of debris thickness, mass balance, and ice emergence rate. Controls on surface relief are different above and below the ZMT. The pattern of dynamic thinning is an expected control on the pattern of surface relief. Ice cliff abundance appears to best follow surface strain rate. Supraglacial stream sinuosity increases with surface roughness. The interaction between ice cliffs, sinuous streams, and relief can form a positive feedback loop in which all three are amplified. Supraglacial ponds are abundant where driving stresses are low.
Processes Controlling Glacier Change Over Multiple Decades
Primary Control of Thinning: Ice Emergence Rates Declined Strongly in the ZMT
The decline in emergence rates is the primary control on the rapid thinning under thick debris at Kennicott Glacier (Figures 3E, 8). Increased mass loss upglacier of the debris cover has led to the reduction of ice flow into the debris-covered portion of the glacier reducing ice emergence rates and increasing thinning in time. Vincent et al. (2016) and Brun et al. (2018) made similar observations for the debris covered Changri Nup Glacier in Nepal. Using simple numerical glacier models and linear bed profiles, Banerjee (2017) and Ferguson and Vieli (2020) both concluded that rapid thinning under debris cover is primarily the result of the decline in ice emergence rates in time. Simulations from Crump et al. (2017) and Anderson et al. (2018) also support this conclusion. Because ice dynamics plays the primary role in controlling the location of the maximum thinning of uncovered glaciers (Nye, 1960) we should expect that it also plays a vital if not dominant role for debris-covered glaciers as well.
Melt Decreased in Time
Annual melt rates across the study area declined between 1991 and 2015 (Figure 3E). This occurred as positive degree-days at Kennicott Glacier increased by 8% specifically between the 1990–1991 and 2014–2015 image acquisition time periods (Table 1; Supplementary Figure S25). Within the ZMT, annual melt rates decreased by 51% between the years 1991 and 2015. This implies that the relationship between air temperature and area-averaged melt changed, for example by changes in debris thickness or ice cliff coverage.
We describe four additional feedbacks directly linking debris thickness, ice cliffs, ponds, and glacier surface roughness to thinning (Table 1; Figures 9, 10). These feedbacks are likely to combine to explain the decrease in melt rate across the study area between 1991 and 2015. Note that we consider the pond and relief feedbacks over a longer period (1957–2009 and 1957–2016 respectively). The two negative feedbacks (the debris and ice cliff) most likely caused the reduction in melt rates in time.
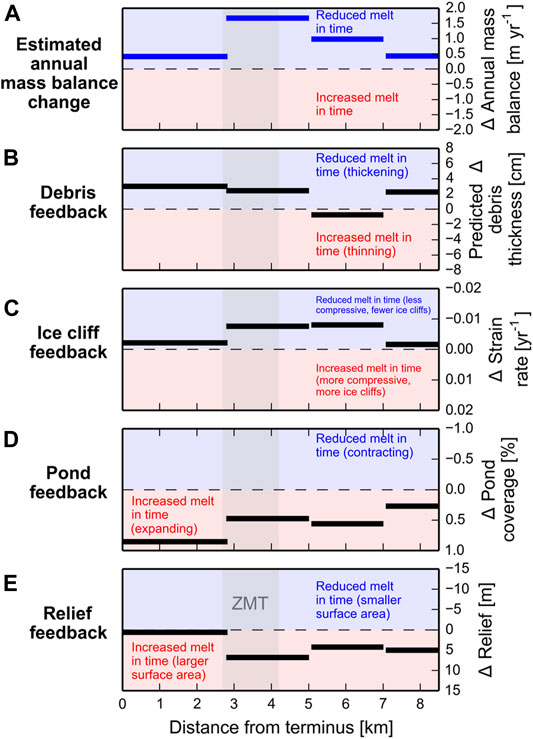
FIGURE 9. Spatial distributions of terms indicating the sign of feedbacks. The title of each panel is on the left side. In each panel blue shading indicates the area where melt will be reduced in time. Red shading indicates the portion of each panel in which melt will be increased in time. Grey shading indicates the extent of the zone of maximum thinning (ZMT). For (B–D) if the black bars are in the blue area the feedback is negative. If the black bars are in the red area the feedback is positive. (A) Observed change in annual mass balance showing a reduction of melt in time across the study area (see Figures 3B,E). (B) Representation of the negative debris feedback using predicted change in debris thickness in time as a proxy. Debris thickens due to changes in surface velocities, strain rate, and melt out leading to a reduction of melt in time. (C) Representation of the negative ice cliff feedback using change in surface compression (strain rate) as a proxy. Ice cliffs are positively correlated with strain rate, meaning areas with decreased compression tend to have fewer ice cliffs. Positive values indicate increased compression and negative values decreased compression in time. (D) Representation of the positive pond feedback using the change in pond coverage in time as a proxy. (E) Representation of the relief feedback. The steepening of local slopes on the glacier increases the total area of ice subject to surface melt within and above the ZMT.
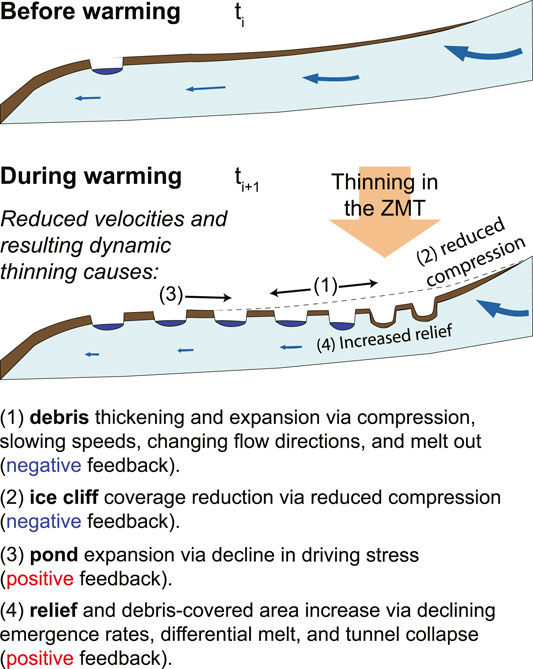
FIGURE 10. Schematic explaining the feedbacks occurring on Kennicott Glacier over multiple decades. At time ti, the glacier has not yet started to respond to warming. The blue arrows qualitatively reflect englacial flow paths. The length and width of the arrow reflects the flow velocity. At time t i+1 the glacier is responding to warming and thinning is localized in the zone of maximum thinning (ZMT). The downglacier portion of the ZMT shallows, while the upglacier portion of the ZMT steepens. Thinning across the glacier leads to reduced compression in time.
Debris Feedback (Negative Feedback)
As Kennicott Glacier thinned surface velocity declined leading to debris thickening and expansion (Surface Velocity Controls Debris Thickness and Mass Balance), feeding back to affect thinning by reducing melt rates. Debris thickening is due to the combined effects of slowing downglacier translation of debris, continued compression of debris and the melt out of debris from within the glacier (Figure 5). The reduction in surface velocity (in time) reduces the downstream translation of debris in a given pixel. Because debris is moving out of the given pixel at a slower rate, the reduction of velocity downglacier (in space), which compresses the debris, is locally able to increase debris thickness. Increases in melt rates leading to enhanced debris melt out also thicken debris on debris-covered glaciers (e.g., Deline, 2005; Kirkbride and Deline, 2013). The greatest debris thickening occurs in and below the ZMT where dynamics and melt out both thicken debris. Debris expanded in the upper portion of the study area due to changing surface velocity directions, also contributing to the decrease in melt rates.
Surface velocities typically decline as glaciers thin (e.g., Quincey et al., 2009; Neckel et al., 2017; Dehecq et al., 2019). Changes in surface velocity may be an underappreciated explanation for debris thickening and expansion on debris-covered glaciers more generally (e.g., Kirkbride, 1993; Deline, 2005; Kirkbride and Deline, 2013; Gibson et al., 2017; Azzoni et al., 2018; Stewart et al., 2021). We expect that the debris feedback generally reduces melt rates in time and is occurring on most debris-covered glaciers.
Ice Cliff Feedback (Negative Feedback)
The ice cliff feedback occurs when glacier thinning leads to reduced surface compression which reduces ice cliff occurrence and therefore area-averaged melt rates, looping back to affect the thinning pattern (Supplementary Figure S19). The negative thinning-ice cliff feedback will occur on other glaciers where strain rates are correlated with ice cliff abundance, which will most likely occur where flow is active above the ZMT on other glaciers.
Perhaps the evolution of ice cliffs, and their effect on area-averaged melt rates in time, on individual glaciers will depend on whether ice cliff abundance is controlled predominantly by changes in strain rate (more likely above the ZMT) or by the expansion of tunnel collapse-related depressions and ponds (more likely below the ZMT). Steiner et al. (2019) found no clear trend in ice cliff area over a 41-year period across five glaciers in the Nepalese Himalaya, but most of these ice cliffs are associated with depressions on the glacier surface and not surface compression.
Ferguson and Vieli (2020) used driving stress as a proxy for ice cliff change in time. This approach will be most applicable below the ZMT where debris is thick and surface depressions dominate ice cliff occurrence. Above the ZMT their approach asserts a monotonically declining abundance of ice cliffs upglacier, which is inconsistent with Watson et al. (2016)’s analysis of 14 glaciers in the Khumbu region of Nepal and Kennicott Glacier were ice cliff occurrence peaks where flow is still active and above the ZMT. Ultimately for Kennicott Glacier where most ice cliffs exist above the ZMT we expect the thinning-ice cliff feedback to have reduced melt rates in time as flow became less compressive.
Pond Feedback (Positive Feedback)
The expansion of ponds upglacier in response to thinning represents a positive feedback. Thinning leads to the decrease in surface slopes, ice thickness, and driving stress, below the ZMT, allowing for the upglacier propagation of ponds. Expanding ponds locally increase melt rates, therefore increasing thinning, completing the feedback loop. The feedback between thinning and ponds has also been documented on glaciers in High Mountain Asia (Gardelle et al., 2011; Thakuri et al., 2016; Watson et al., 2016; King et al., 2020), New Zealand (Kirkbride, 1993) and now in Alaska. The expansion of ponds upglacier as debris-covered glaciers thin is therefore likely a phenomenon occurring at the global scale. For Kennicott Glacier we expect that this feedback increased melt rates in time, but not enough to overcome the melt reducing roles of the debris and ice cliff feedbacks.
Relief Feedback (Positive Feedback)
The increase in local surface relief and debris-covered surface area in response to thinning represents a positive feedback (Figure 9E). As the glacier thins, englacial tunnel collapse (e.g., Benn et al., 2001), differential melt (e.g., Mölg et al., 2020), and the rapid decline of ice emergence rates lead to the increase in local relief. Other studies have documented the increase in surface relief on glaciers in the Himalaya (Benn et al., 2017; King et al., 2020) and Alps (Mölg et al., 2020). Increasing relief (and local slopes) in time inherently leads to an increase in the total debris-covered area susceptible to melt as a steeper surface exposes more sub-debris ice to melt than a flat surface. When averaged across a planview pixel on the glacier this effect will increase area-average melt rates and thinning, completing the feedback loop. For Kennicott Glacier we expect that this feedback increased melt rates in time, but not enough to overcome the melt-reducing effect of the debris and ice cliff feedbacks.
Implications
This case study of Kennicott Glacier highlights how important ice dynamics are for understanding and predicting debris-covered glacier behavior. It is tempting to overlook ice dynamics where ice flow appears to currently be slow (i.e., below 20 m yr−1), but neglecting it can lead to erroneous interpretations of the causes, for example, of glacier thinning or debris thickening. This is especially true considering that dynamic thinning is the dominant control on the location of maximum glacier-wide thinning for Kennicott Glacier.
The overdeepened and undulating bed under Kennicott Glacier acts as a boundary condition that strongly controls the pattern of ice flow (Expression of the Glacier Bed in Surface Velocity). This ice flow pattern in turn determines the distribution of debris thickness and surface melt which feeds back to affect ice flow (Anderson and Anderson, 2016; Anderson and Anderson, 2018), each component working in concert with the others. The basal geometry and slopes under debris-covered glaciers will certainly differ from the pattern inverted for under Kennicott Glacier. None-the-less this study reveals how important it can be to constrain basal topography when attempting to reveal cause and effect in the debris-covered glacier system.
We have highlighted some processes links between ice cliffs, ponds, streams, and local surface relief. Of special note is the potential role of streams as geomorphic and melt agents on debris-covered glaciers. We outlined how meandering, sinuous surface streams can influence ice cliff shape, debris thickness patterns, and local surface topography. Undercutting streams may also encourage the collapse of ice cliffs. Large streams may be effective at removing debris from the glacier surface via moulins and crevasses. Quantifying the role of local surface relief, ice cliffs, ponds, and streams in debris-covered glacier surface melt and evolution requires new, detailed field studies.
Out of the four thinning-ice dynamics-mass balance feedbacks discussed (debris, ice cliffs, ponds, and relief), the debris and ice cliff feedbacks appear to combine to cause in the reduction of surface melt rate in time on Kennicott Glacier as the pond and relief feedbacks work in the opposite direction and increase melt in time. Naturally these feedbacks should be quantified on other debris-covered glaciers with different geometries, rock erodibilities, and climates.
Conclusion
Kennicott Glacier is a large, thick, and dynamically active Alaskan glacier that supports striking patterns of ice dynamics and melt hotspots on its surface. We use Kennicott Glacier as a test case to reveal causality within the debris-covered glacier system in a step-by-step fashion.
Within the debris-covered tongue of Kennicott Glacier the pattern of ice flow is dominated by an overdeepened bed. This imposed pattern of ice flow in turn strongly controls patterns of both debris thickness and area-averaged melt rate. The annual mass balance gradient in the debris-covered tongue is reversed and melt rates decline towards the terminus.
Ice dynamics are an important control on debris thickness. Surface compression dominates debris thickness where velocities are low; where velocities are high downglacier advection keeps debris thin while also allowing for the efficient melt out of debris. Using an inverse modeling approach, we show that a declining, compressive flow field downglacier from the ZMT thickened debris at a rate of 0.125 cm per year between 1991 and 2011. The mean englacial debris concentration was estimated to be 0.017% by volume. Debris expansion on the glacier surface follows the change in surface velocity direction in time.
Glacier surface relief is largest where dynamic thinning is highest. Ice cliffs correlate with the rate of compression on the glacier surface. A new feedback is identified on the modern glacier surface leading to chaotic topography: ice cliffs and sinuous streams amplify each other and tend to enhance differential melt, and local surface roughness. Ponds are strongly negatively correlated with driving stress. Despite abundant ice cliffs, ponds, and streams scattered within the debris cover, melt rates averaged across the glacier width are primarily controlled by the melt-reducing effects of debris.
We also explore the consequences of glacier thinning over the last several decades. The zone of glacier-wide maximum thinning (ZMT) has been in a consistent location since at least 1957. Between 1991 and 2015, where the glacier thinned the most, melt rates appear to have contributed less to thinning over time despite generally rising air temperatures. We consider the role of four feedbacks related to decadal changes in melt and thinning: the debris feedback (negative), the ice cliff feedback (negative), the pond feedback (positive), and the relief feedback (positive). Of these four, the melt reducing debris and ice cliff feedbacks appear to cause the observed decline in melt rates in the ZMT. Maximum glacier wide thinning occurs under debris where melt rates are low and contributing less and less to thinning in time.
We provide evidence showing that rapid thinning under thick debris (i.e., the debris-cover anomaly) is predominately caused by dynamic thinning. Ultimately this occurs because increasingly negative mass balance upglacier of the continuous debris cover thins the glacier there and subsequently reduces ice flow, in a compounding fashion, downglacier. The reduced ice flux into the debris-covered tongue causes drastic reductions in ice emergence rates and maximum glacier-wide thinning despite the strong insulating effect of debris on melt rates.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation. Data used to produce the correlation figures are available at: DOI: 10.5281/zenodo.4955563.
Author Contributions
LA designed the study, composed the manuscript, and completed most analyses. WA produced the annual surface velocities and added important discussion points. RA added important discussion points and provided support throughout the effort. DS aided in the analysis of surface streams. EP added important discussion points. All authors revised the manuscript.
Funding
LA acknowledges support from a 2011 Muire Science and Learning Center Fellowship, NSF DGE-1144083 (GRFP), and funding from European Union’s Horizon 2020 research and innovation programme under grant agreement No. 851614. LA and DS were also supported by funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme under grant agreement No 759639. RA and WA acknowledge support of NSF EAR-1239281 (Boulder Creek CZO) and NSF EAR-1123855. WA acknowledges support from NSF OPP-1821002 and the University of Colorado at Boulder’s Earth Lab initiative.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Craig Anderson, Emily Longano, and Oren Leibson for field support. We thank Per Jenssen, Susan Fison, Ben Hudson, Patrick Tomco, Rommel Zulueta, the Wrangell-St. Elias Interpretive Rangers, the Wrangell Mountains Center, Indrani Das, and Ted Scambos (NSIDC) for logistical support and the gracious loan of equipment. We thank Lucy Tyrell for facilitating outreach efforts. We also thank Joshua Scott, Wrangell-St Elias National Park and the Polar Geospatial Center for access to satellite imagery. We thank Martin Truffer, Jack Holt, and Regine Hock for helpful conversations. LA thanks the organizers and participants of the 2010 Glaciological Summer School held in McCarthy, AK, who inspired this work. We appreciate helpful comments from David Rounce and Martin Kirkbride from an earlier version of the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.680995/full#supplementary-material
References
Amundson, J. M., Truffer, M., and Lüthi, M. P. (2006). Time-dependent Basal Stress Conditions beneath Black Rapids Glacier, Alaska, USA, Inferred from Measurements of Ice Deformation and Surface Motion. J. Glaciol. 52, 347–357. doi:10.3189/172756506781828593
Anderson, L. S., and Anderson, R. S. (2018). Debris Thickness Patterns on Debris-Covered Glaciers. Geomorphology 311, 1–12. doi:10.1016/j.geomorph.2018.03.014
Anderson, L. S., and Anderson, R. S. (2016). Modeling Debris-Covered Glaciers: Response to Steady Debris Deposition. Cryosphere 10, 1105–1124. doi:10.5194/tc-10-1105-2016
Anderson, L. S., Armstrong, W. H., Anderson, R. S., and Buri, P. (2021). Debris Cover and the Thinning of Kennicott Glacier, Alaska: In Situ Measurements, Automated Ice Cliff Delineation and Distributed Melt Estimates. Cryosphere 15, 265–282. doi:10.5194/tc-15-265-2021
Anderson, L. S. (2014). Glacier Response to Climate Change: Modeling the Effects of Weather and Debris-Cover. Available at: https://scholar.colorado.edu/geol_gradetds/90 (Accessed November 15, 2019).
Anderson, R. S. (2000). A Model of Ablation-Dominated Medial Moraines and the Generation of Debris-Mantled Glacier Snouts. J. Glaciol. 46, 459–469. doi:10.3189/172756500781833025
Anderson, R. S., Anderson, L. S., Armstrong, W. H., Rossi, M. W., and Crump, S. E. (2018). Glaciation of alpine Valleys: The Glacier - Debris-Covered Glacier - Rock Glacier Continuum. Geomorphology 311, 127–142. doi:10.1016/j.geomorph.2018.03.015
Anderson, R. S., Walder, J. S., Anderson, S. P., Trabant, D. C., and Fountain, A. G. (2005). The Dynamic Response of Kennicott Glacier, Alaska, USA, to the Hidden Creek Lake Outburst Flood. Ann. Glaciol. 40, 237–242. doi:10.3189/172756405781813438
Armstrong, W. H., Anderson, R. S., Allen, J., and Rajaram, H. (2016). Modeling the WorldView-Derived Seasonal Velocity Evolution of Kennicott Glacier, Alaska. J. Glaciol. 62, 763–777. doi:10.1017/jog.2016.66
Armstrong, W. H., Anderson, R. S., and Fahnestock, M. A. (2017). Spatial Patterns of Summer Speedup on South Central Alaska Glaciers. Geophys. Res. Lett. 44, 9379–9388. doi:10.1002/2017GL074370
Armstrong, W. H., and Anderson, R. S. (2020). Ice-marginal lake Hydrology and the Seasonal Dynamical Evolution of Kennicott Glacier, Alaska. J. Glaciol. 66, 699–713. doi:10.1017/jog.2020.41
Azzoni, R. S., Fugazza, D., Zerboni, A., Senese, A., D’Agata, C., Maragno, D., et al. (2018). Evaluating High-Resolution Remote Sensing Data for Reconstructing the Recent Evolution of Supra Glacial Debris. Prog. Phys. Geogr. Earth Environ. 42, 3–23. doi:10.1177/0309133317749434
Banerjee, A. (2017). Brief Communication: Thinning of Debris-Covered and Debris-free Glaciers in a Warming Climate. Cryosphere 11, 133–138. doi:10.5194/tc-11-133-2017
Bartholomaus, T. C., Anderson, R. S., and Anderson, S. P. (2008). Response of Glacier Basal Motion to Transient Water Storage. Nat. Geosci. 1, 33–37. doi:10.1038/ngeo.2007.52
Benn, D. I., Bolch, T., Hands, K., Gulley, J., Luckman, A., Nicholson, L. I., et al. (2012). Response of Debris-Covered Glaciers in the Mount Everest Region to Recent Warming, and Implications for Outburst Flood Hazards. Earth Sci. Rev. 114, 156–174. doi:10.1016/j.earscirev.2012.03.008
Benn, D. I., Thompson, S., Gulley, J., Mertes, J., Luckman, A., and Nicholson, L. (2017). Structure and Evolution of the Drainage System of a Himalayan Debris-Covered Glacier, and its Relationship with Patterns of Mass Loss. Cryosphere 11, 2247–2264. doi:10.5194/tc-11-2247-2017
Benn, D. I., Wiseman, S., and Hands, K. A. (2001). Growth and Drainage of Supraglacial Lakes on Debris-Mantled Ngozumpa Glacier, Khumbu Himal, Nepal. J. Glaciol. 47, 626–638. doi:10.3189/172756501781831729
Bisset, R. R., Dehecq, A., Goldberg, D. N., Huss, M., Bingham, R. G., and Gourmelen, N. (2020). Reversed Surface-Mass-Balance Gradients on Himalayan Debris-Covered Glaciers Inferred from Remote Sensing. Remote Sensing 12, 1563. doi:10.3390/rs12101563
Bozhinskiy, A. N., Krass, M. S., and Popovnin, V. V. (1986). Role of Debris Cover in the Thermal Physics of Glaciers. J. Glaciol. 32, 255–266. doi:10.3189/s0022143000015598
Brun, F., Wagnon, P., Berthier, E., Shea, J. M., Immerzeel, W. W., Kraaijenbrink, P. D. A., et al. (2018). Ice Cliff Contribution to the Tongue-wide Ablation of Changri Nup Glacier, Nepal, central Himalaya. Cryosphere 12, 3439–3457. doi:10.5194/tc-12-3439-2018
Buri, P., Miles, E. S., Steiner, J. F., Ragettli, S., and Pellicciotti, F. (2021). Supraglacial Ice Cliffs Can Substantially Increase the Mass Loss of Debris‐Covered Glaciers. Geophys. Res. Lett. 48, 1–11. doi:10.1029/2020GL092150
Crump, S. E., Anderson, L. S., Miller, G. H., and Anderson, R. S. (2017). Interpreting Exposure Ages from Ice-Cored Moraines: a Neoglacial Case Study on Baffin Island, Arctic Canada. J. Quat. Sci. 32, 1049–1062. doi:10.1002/jqs.2979
Cuffey, K. M., and Paterson, W. S. B. (2010). The Physics of Glaciers. 4th ed.. Oxford, UK: Academic Press.
Das, I., Hock, R., Berthier, E., and Lingle, C. S. (2014). 21st-century Increase in Glacier Mass Loss in the Wrangell Mountains, Alaska, USA, from Airborne Laser Altimetry and Satellite Stereo Imagery. J. Glaciol. 60, 283–293. doi:10.3189/2014JoG13J119
Dehecq, A., Gourmelen, N., Gardner, A. S., Brun, F., Goldberg, D., Nienow, P. W., et al. (2019). Twenty-first century Glacier Slowdown Driven by Mass Loss in High Mountain Asia. Nat. Geosci 12, 22–27. doi:10.1038/s41561-018-0271-9
Deline, P. (2005). Change in Surface Debris Cover on Mont Blanc Massif Glaciers after the'Little Ice Age' Termination. Holocene 15, 302–309. doi:10.1191/0959683605hl809rr
Fahnestock, M., Scambos, T., Moon, T., Gardner, A., Haran, T., and Klinger, M. (2016). Rapid Large-Area Mapping of Ice Flow Using Landsat 8. Remote Sensing Environ. 185, 84–94. doi:10.1016/j.rse.2015.11.023
Farinotti, D., Huss, M., Fürst, J. J., Landmann, J., Machguth, H., Maussion, F., et al. (2019). A Consensus Estimate for the Ice Thickness Distribution of All Glaciers on Earth. Nat. Geosci. 12, 168–173. doi:10.1038/s41561-019-0300-3
Ferguson, J., and Vieli, A. (2020). Modelling Steady States and the Transient Response of Debris-Covered Glaciers. Cryosphere Discuss., 1–31. doi:10.5194/tc-2020-228
Ferguson, R. I. (1973). Sinuosity of Supraglacial Streams. Geol. Soc. America Bull. 84, 251. doi:10.1130/0016-7606(1973)84<251:soss>2.0.co;2
Fyffe, C. L., Brock, B. W., Kirkbride, M. P., Mair, D. W. F., Arnold, N. S., Smiraglia, C., et al. (2019). Do debris-covered Glaciers Demonstrate Distinctive Hydrological Behaviour Compared to Clean Glaciers?. J. Hydrol. 570, 584–597. doi:10.1016/j.jhydrol.2018.12.069
Gardelle, J., Arnaud, Y., and Berthier, E. (2011). Contrasted Evolution of Glacial Lakes along the Hindu Kush Himalaya Mountain Range between 1990 and 2009. Glob. Planet. Change 75, 47–55. doi:10.1016/j.gloplacha.2010.10.003
Gardelle, J., Berthier, E., Arnaud, Y., and Kääb, A. (2013). Region-wide Glacier Mass Balances Over the Pamir-Karakoram-Himalaya During 1999-2011. The Cryosphere 7, 1885–1886. doi:10.5194/tc-7-1885-2013
Gardner, A. S., Fahnestock, M. A., and Scambos, T. A. (2020). ITS_LIVE Regional Glacier and Ice Sheet Surface Velocities. Data archived at National Snow and Ice Data Center. doi:10.5067/6II6VW8LLWJ7
Gardner, A. S., Moholdt, G., Scambos, T., Fahnstock, M., Ligtenberg, S., van den Broeke, M., et al. (2018). Increased West Antarctic and Unchanged East Antarctic Ice Discharge over the Last 7 Years. Cryosphere 12, 521–547. doi:10.5194/tc-12-521-2018
Gibson, M. J., Glasser, N. F., Quincey, D. J., Mayer, C., Rowan, A. V., and Irvine-Fynn, T. D. L. (2017). Temporal Variations in Supraglacial Debris Distribution on Baltoro Glacier, Karakoram between 2001 and 2012. Geomorphology 295, 572–585. doi:10.1016/j.geomorph.2017.08.012
Huo, D., Bishop, M. P., and Bush, A. B. (2021). Understanding Complex Debris-Covered Glaciers: Concepts, Issues and Research Directions. Front. Earth Sci. 9, 358. doi:10.3389/feart.2021.652279
Iwata, S., Watanabe, O., and Fushimi, H. (1980). Surface Morphology in the Ablation Area of the Khumbu Glacier. J. Jpn. Soc. Snow Ice 41, 9–17. doi:10.5331/seppyo.41.Special_9
Kääb, A., Berthier, E., Nuth, C., Gardelle, J., and Arnaud, Y. (2012). Contrasting Patterns of Early Twenty-First-century Glacier Mass Change in the Himalayas. Nature 488, 495–498. doi:10.1038/nature11324
Kamb, B., and Echelmeyer, K. A. (1986). Stress-gradient Coupling in Glacier Flow: Longitudinal Averaging of the Influence of Ice Thickness and Surface Slope. J. Glaciol. 32, 267. doi:10.3189/s0022143000015604
King, O., Turner, A. G. D., Quincey, D. J., and Carrivick, J. L. (2020). Morphometric Evolution of Everest Region Debris-Covered Glaciers. Geomorphology 371, 107422. doi:10.1016/j.geomorph.2020.107422
Kirkbride, M. P., and Deline, P. (2013). The Formation of Supraglacial Debris Covers by Primary Dispersal from Transverse Englacial Debris Bands. Earth Surf. Process. Landforms 38, 1779–1792. doi:10.1002/esp.3416
Kirkbride, M. P. (2000). “Ice-marginal Geomorphology and Holocene Expansion of Debris-Covered Tasman Glacier, New Zealand,” in Debris-Covered Glaciers (Seattle, Washington: IAHS Publication), 211–217.
Kirkbride, M. P. (1993). The Temporal Significance of Transitions from Melting to Calving Termini at Glaciers in the central Southern Alps of New Zealand. Holocene 3, 232–240. doi:10.1177/095968369300300305
Kraaijenbrink, P. D. A., Shea, J. M., Pellicciotti, F., Jong, S. M. d., and Immerzeel, W. W. (2016). Object-based Analysis of Unmanned Aerial Vehicle Imagery to Map and Characterise Surface Features on a Debris-Covered Glacier. Remote Sensing Environ. 186, 581–595. doi:10.1016/j.rse.2016.09.013
Leprince, S., Ayoub, F., Klinger, Y., and Avouac, J.-P. (2007). “Co-registration of Optically Sensed Images and Correlation (COSI-Corr): An Operational Methodology for Ground Deformation Measurements,” in IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July (IEEE), 1943–1946. doi:10.1109/igarss.2007.4423207
MacKevett, E. M. (1972). Geologic Map of the McCarthy C-6 Quadrangle, Alask. Geologic Quadrangle Map 979. U.S. Geological Survey.
MacKevett, E. M., and Smith, J. G. (1972). Geologic Map of the MCCarthy B-6 Quadrangle, Alaska. Geologic Quadrangle 1035. U.S. Geological Survey. doi:10.3133/gq1035
Miles, E. S., Willis, I., Buri, P., Steiner, J. F., Arnold, N. S., and Pellicciotti, F. (2018). Surface Pond Energy Absorption across Four Himalayan Glaciers Accounts for 1/8 of Total Catchment Ice Loss. Geophys. Res. Lett. 45 (10), 10,464–10,473. doi:10.1029/2018GL079678
Miles, K. E., Hubbard, B., Miles, E. S., Quincey, D. J., Rowan, A. V., Kirkbride, M., et al. (2021). Continuous Borehole Optical Televiewing Reveals Variable Englacial Debris Concentrations at Khumbu Glacier, Nepal. Commun. Earth Environ. 2, 12. doi:10.1038/s43247-020-00070-x
Mölg, N., Bolch, T., Walter, A., and Vieli, A. (2019). Unravelling the Evolution of Zmuttgletscher and its Debris Cover since the End of the Little Ice Age. Cryosphere 13, 1889, 1909. doi:10.5194/tc-13-1889-2019
Mölg, N., Ferguson, J., Bolch, T., and Vieli, A. (2020). On the Influence of Debris Cover on Glacier Morphology: How High-Relief Structures Evolve from Smooth Surfaces. Geomorphology 357, 107092. doi:10.1016/j.geomorph.2020.107092
Moore, P. L. (2018). Stability of Supraglacial Debris. Earth Surf. Process. Landforms 43, 285–297. doi:10.1002/esp.4244
Nakawo, M., Iwata, S., Watanabe, O., and Yoshida, M. (1986). Processes Which Distribute Supraglacial Debris on the Khumbu Glacier, Nepal Himalaya. A. Glaciology. 8, 129–131. doi:10.1017/s0260305500001294
Neckel, N., Loibl, D., and Rankl, M. (2017). Recent Slowdown and Thinning of Debris-Covered Glaciers in South-Eastern Tibet. Earth Planet. Sci. Lett. 464, 95–102. doi:10.1016/j.epsl.2017.02.008
Nicholson, L., and Benn, D. I. (2006). Calculating Ice Melt beneath a Debris Layer Using Meteorological Data. J. Glaciol. 52, 463–470. doi:10.3189/172756506781828584
Nicholson, L., and Benn, D. I. (2013). Properties of Natural Supraglacial Debris in Relation to Modelling Sub-debris Ice Ablation. Earth Surf. Process. Landforms 38, 490–501. doi:10.1002/esp.3299
Nye, J. F. (1960). The Response of Glaciers and Ice-Sheets to Seasonal and Climatic Changes. Proc. R. Soc. Lond. A. 256, 559–584. doi:10.1098/rspa.1960.0127
Östrem, G. (1959). Ice Melting under a Thin Layer of Moraine, and the Existence of Ice Cores in Moraine Ridges. Geografiska Annaler 41, 228–230. doi:10.1080/20014422.1959.11907953
Parker, G. (1975). Meandering of Supraglacial Melt Streams. Water Resour. Res. 11, 551–552. doi:10.1029/WR011i004p00551
Pellicciotti, F., Stephan, C., Miles, E., Herreid, S., Immerzeel, W. W., and Bolch, T. (2015). Mass-balance Changes of the Debris-Covered Glaciers in the Langtang Himal, Nepal, from 1974 to 1999. J. Glaciol. 61, 373–386. doi:10.3189/2015JoG13J237
Porter, C., Morin, P., Howat, I., Noh, M.-J., Bates, B., Peterman, K., et al. (2018). ArcticDEM. Harvard Dataverse, V1. doi:10.7910/DVN/OHHUKH
Pritchard, H. D., King, E. C., Goodger, D. J., McCarthy, M., Mayer, C., and Kayastha, R. (2020). Towards Bedmap Himalayas: Development of an Airborne Ice-Sounding Radar for Glacier Thickness Surveys in High-Mountain Asia. Ann. Glaciol. 61, 35–45. doi:10.1017/aog.2020.29
Quincey, D. J., Luckman, A., and Benn, D. (2009). Quantification of Everest Region Glacier Velocities between 1992 and 2002, Using Satellite Radar Interferometry and Feature Tracking. J. Glaciol. 55, 596–606. doi:10.3189/002214309789470987
Quincey, D. J., Richardson, S. D., Luckman, A., Lucas, R. M., Reynolds, J. M., Hambrey, M. J., et al. (2007). Early Recognition of Glacial lake Hazards in the Himalaya Using Remote Sensing Datasets. Glob. Planet. Change 56, 137–152. doi:10.1016/j.gloplacha.2006.07.013
Raymond, C. F. (1971). Flow in a Transverse Section of Athabasca Glacier, Alberta, Canada. J. Glaciol. 10, 55–84. doi:10.1017/s0022143000012995
Reid, T. D., and Brock, B. W. (2010). An Energy-Balance Model for Debris-Covered Glaciers Including Heat Conduction through the Debris Layer. J. Glaciol. 56, 903–916. doi:10.3189/002214310794457218
Reynolds, J. M. (2000). “On the Formation of Supraglacial Lakes on Debris- Covered Glaciers,” in Debris-Covered Glaciers (Seattle, Washington: IAHS Publication), 153–161.
Rickman, R. L., and Rosenkrans, D. S. (1997). Hydrologic Conditions and Hazards in the Kennicott River Basin, Wrangell-St. Elias National Park and Preserve, Alaska. Anchorage, Alaska: U.S. Geological Survey.
Röhl, K. (2008). Characteristics and Evolution of Supraglacial Ponds on Debris-Covered Tasman Glacier, New Zealand. J. Glaciol. 54, 867–880. doi:10.3189/002214308787779861
Rounce, D. R., Hock, R., McNabb, R. W., Millan, R., Sommer, C., Braun, M. H., et al. (2021). Distributed Global Debris Thickness Estimates Reveal Debris Significantly Impacts Glacier Mass Balance. Geophys. Res. Lett. 48, 1–12. doi:10.1029/2020GL091311
Sakai, A., and Fujita, K. (2010). Formation Conditions of Supraglacial Lakes on Debris-Covered Glaciers in the Himalaya. J. Glaciol. 56, 177–181. doi:10.3189/002214310791190785
Sato, Y., Fujita, K., Inoue, H., Sunako, S., Sakai, A., Tsushima, A., et al. (2021). Ice Cliff Dynamics of Debris-Covered Trakarding Glacier in the Rolwaling Region, Nepal Himalaya. Front. Earth Sci. 9, 398. doi:10.3389/feart.2021.623623
Scambos, T. A., Fahnestock, M., Moon, T., Gardner, A., and Klinger, M. (2016). Global Land Ice Velocity Extraction from Landsat 8 (GoLIVE), Version 1. (NSIDC-0710). Boulder, Colorado, USA: NSIDC: National Snow and Ice Data Center. doi:10.7265/N5ZP442BAccessed May 16, 2019)
Scherler, D., Bookhagen, B., and Strecker, M. R. (2011). Spatially Variable Response of Himalayan Glaciers to Climate Change Affected by Debris Cover. Nat. Geosci 4, 156–159. doi:10.1038/ngeo1068
Schwanghart, W., and Scherler, D. (2014). Short Communication: TopoToolbox 2 - MATLAB-Based Software for Topographic Analysis and Modeling in Earth Surface Sciences. Earth Surf. Dynam. 2, 1–7. doi:10.5194/esurf-2-1-2014
Shean, D. E., Alexandrov, O., Moratto, Z. M., Smith, B. E., Joughin, I. R., Porter, C., et al. (2016). An Automated, Open-Source Pipeline for Mass Production of Digital Elevation Models (DEMs) from Very-High-Resolution Commercial Stereo Satellite Imagery. ISPRS J. Photogram. Remote Sensing 116, 101–117. doi:10.1016/j.isprsjprs.2016.03.012
Steiner, J. F., Buri, P., Miles, E. S., Ragettli, S., and Pellicciotti, F. (2019). Supraglacial Ice Cliffs and Ponds on Debris-Covered Glaciers: Spatio-Temporal Distribution and Characteristics. J. Glaciol. 65, 617–632. doi:10.1017/jog.2019.40
Stewart, R. L., Westoby, M., Pellicciotti, F., Rowan, A., Swift, D., Brock, B., et al. (2021). Using Climate Reanalysis Data in Conjunction with Multi-Temporal Satellite thermal Imagery to Derive Supraglacial Debris Thickness Changes from Energy-Balance Modelling. J. Glaciol. 67, 366–384. doi:10.1017/jog.2020.111
Tarantola, A. (2005). Inverse Problem Theory and Methods for Model Parameter Estimation. Philadelphia, PA, USA: Society for Industrial and Applied Mathematics.
Thakuri, S., Salerno, F., Bolch, T., Guyennon, N., and Tartari, G. (2016). Factors Controlling the Accelerated Expansion of Imja Lake, Mount Everest Region, Nepal. Ann. Glaciol. 57, 245–257. doi:10.3189/2016AoG71A063
Vincent, C., Wagnon, P., Shea, J., Immerzeel, W., Kraaijenbrink, P., Shrestha, D., et al. (2016). Reduced Melt on Debris-Covered Glaciers: Investigations from Changri Nup Glacier, Nepal. Cryosphere 15, 1845–1858. doi:10.5194/tc-10-1845-2016
Walder, J. S., Trabant, D. C., Cunico, M., Fountain, A. G., Anderson, S. P., Anderson, R. S., et al. (2006). Local Response of a Glacier to Annual Filling and Drainage of an Ice-Marginal lake. J. Glaciol. 52, 440–450. doi:10.3189/172756506781828610
Keywords: ice cliff, stream, pond, feedback, velocity, expansion, bed, inversion
Citation: Anderson LS, Armstrong WH, Anderson RS, Scherler D and Petersen E (2021) The Causes of Debris-Covered Glacier Thinning: Evidence for the Importance of Ice Dynamics From Kennicott Glacier, Alaska. Front. Earth Sci. 9:680995. doi: 10.3389/feart.2021.680995
Received: 15 March 2021; Accepted: 06 August 2021;
Published: 24 August 2021.
Edited by:
Lindsey Isobel Nicholson, University of Innsbruck, AustriaReviewed by:
Takayuki Nuimura, Tokyo Denki University, JapanAndreas Vieli, University of Zurich, Switzerland
Copyright © 2021 Anderson, Armstrong, Anderson, Scherler and Petersen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Leif S. Anderson, bGVpZi5hbmRlcnNvbkB1dGFoLmVkdQ==
 Leif S. Anderson
Leif S. Anderson William H. Armstrong
William H. Armstrong Robert S. Anderson
Robert S. Anderson Dirk Scherler2,5
Dirk Scherler2,5 Eric Petersen
Eric Petersen