Changes in the Thickness of Ice Cover on Water Bodies Subject to Human Pressure (Silesian Upland, Southern Poland)

Solarski, Maksymilian; Rzetala, Mariusz

doi:10.3389/feart.2021.675216

ORIGINAL RESEARCH article

Front. Earth Sci., 20 May 2021

Sec. Hydrosphere

Volume 9 - 2021 | https://doi.org/10.3389/feart.2021.675216

Changes in the Thickness of Ice Cover on Water Bodies Subject to Human Pressure (Silesian Upland, Southern Poland)

$\r\nMaksymilian Solarski$ Maksymilian Solarski¹

Mariusz Rzetala^2*

¹Faculty of Natural Sciences, Institute of Social-Economic Geography and Spatial Management, University of Silesia in Katowice, Sosnowiec, Poland
²Faculty of Natural Sciences, Institute of Earth Sciences, University of Silesia in Katowice, Sosnowiec, Poland

The paper discusses the reasons behind the variation in the thickness of ice on 39 anthropogenic water bodies located in the Silesian Upland (southern Poland). The studies were conducted over the course of three consecutive winter seasons. The measurements and observations were scheduled every 2 days during the freezing and ablation of the ice, and every 4 days when ice cover was present. Each time the thickness of the ice cover and the snow layer covering it were measured. The results show that the 35 water bodies studied are characterized by a similar—quasi-natural—ice regime, in which ice thickness variation depends mostly on the air temperature and the thickness of the snow layer covering the ice. The ice thickness on those water bodies does not significantly differ from that observed on lakes located in northern Poland, measuring on average from circa 4 to 21 cm, and with maximum thicknesses ranging from circa 14 to 40 cm, depending on the season. Four water bodies are characterized by different ice conditions; in their case the average and maximum ice thickness was significantly lower. In the Niezdara N water body this was caused by the inflow of warmer potamic water (quasi-natural regime), whereas in Pod Borem, Sośnicka, and Somerek it was caused by discharges of warm mine water (anthropogenic regime).

Introduction

Data on the thickness of ice covering lakes and water bodies provide one of the key characteristics describing their ice regimes (Choiński, 2007b; Leppäranta, 2009, 2015; Ashton, 2011; Bengtsson, 2012a; Kirillin et al., 2012). Information on the average and maximum thickness of ice on lakes is usually juxtaposed with the dates of formation and disappearance of ice phenomena and ice layers, and how much time the ice was covering the water bodies (Skowron, 2006, 2009; Livingstone et al., 2010).

The thickness of ice covering lakes is a result of several environmental factors, out of which the most important ones include: the location of the lake, the temperature patterns during the winter season, the amount of heat accumulated in the lake water and bottom sediment, and the amount of snowfall, which translates into the thickness of the snow cover covering the ice (Richards, 1964; Leppäranta, 1983; Launiainen and Cheng, 1998; Gao and Stefan, 1999; Aihara et al., 2010; Ashton, 2011; Brown and Duguay, 2011; Bengtsson, 2012a,b; Kirillin et al., 2012). Additionally, they can be modified by anthropogenic factors, such as the inflow of thermal pollution (heated water), and the impact of the so-called urban heat island (Eloranta, 1983; Chen et al., 2000; Solarski, 2017).

The Silesian Upland is among the most man-transformed regions in Europe. The centuries-old human activity relating to the exploitation of mineral resources, the development of many branches of industry, and heavy urbanization processes are all responsible for transforming almost all the environmental components of this region. One effect of this activity is the presence of numerous anthropogenic water bodies in the landscape of this part of Poland, which result from both intentional and unintentional activity (Rzetala and Jagus, 2012; Machowski et al., 2016). Despite the fact that anthropogenic water bodies are not a natural part of the local ecosystem, they undergo the same processes as natural lakes since their very formation, and the anthropogenic modification of limnic processes, results mostly from pollution.

The phenomena and processes which take place in the water bodies located in the Silesian Upland have been the subject of many academic publications (Rzetala, 2014). The issue of the course of ice phenomena in the local water bodies has been among the leading research topics of recent years. The researchers have attempted to characterize the icing of the water bodies of this part of Poland, especially focusing on the level of modification of ice phenomena resulting from human activity (Solarski et al., 2011; Kostecki, 2013; Rzetala, 2014; Solarski, 2017; Solarski and Rzetala, 2020). Most of the studies concerning the ice phenomena in the water bodies in the Silesian Upland and its immediate vicinity tend to focus on individual water bodies or their groupings located across small areas.

The present study attempts to answer the question of the degree of variation in ice thickness on 39 water bodies located in different parts of the Silesian Upland, and the influence of human activity on this variation.

Materials and Methods

Study Lakes

The study was conducted on 39 water bodies located in the Silesian Upland (Figure 1). The selected water bodies are genetically, morphometrically, hydrologically, as well as mictically varied, and they also differ in terms of the degree of influence of human pressure.

FIGURE 1

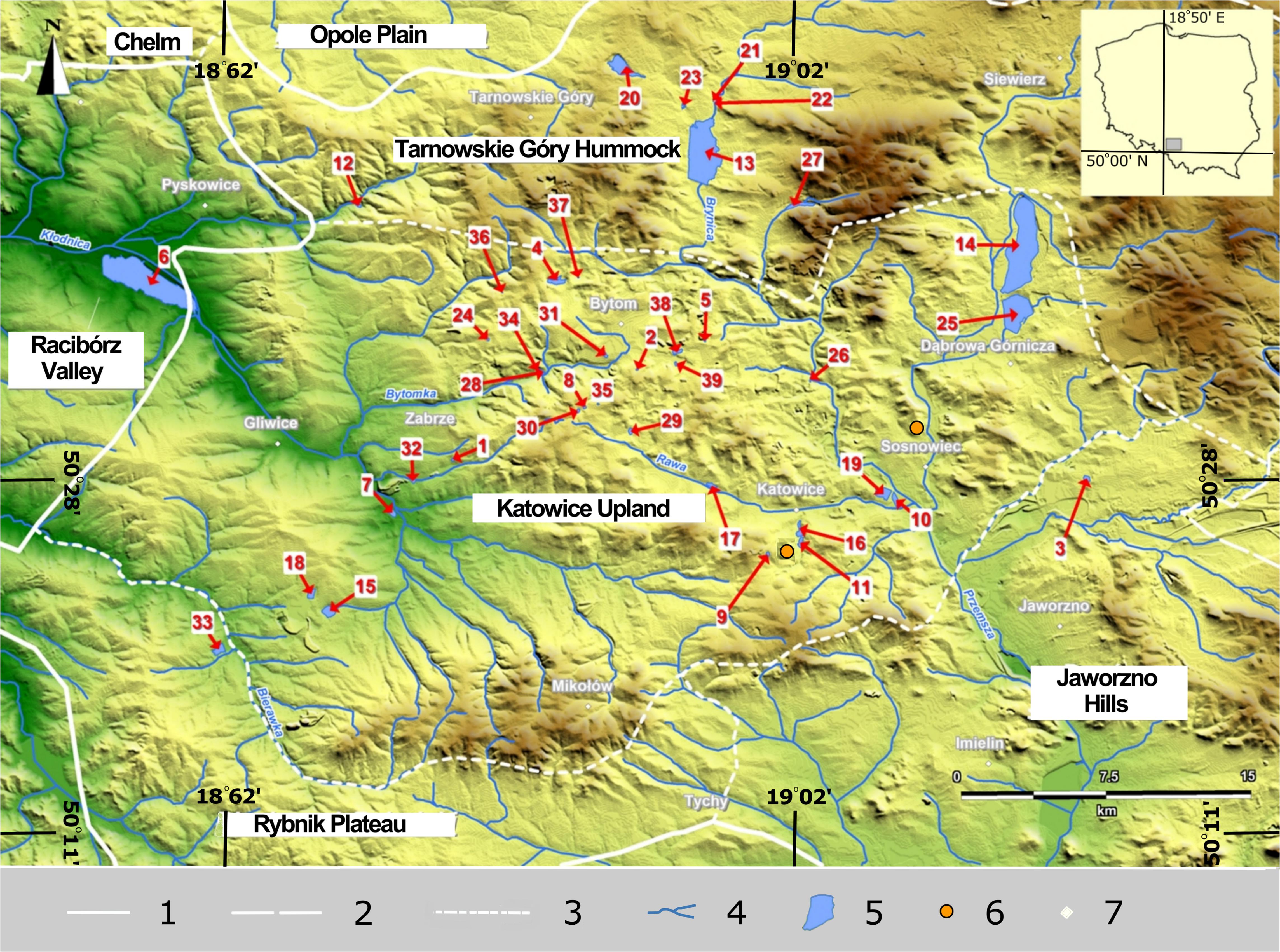
Figure 1. Location of the anthropogenic water bodies studied in the Silesian Upland: 1–province boundaries, 2–macroregion boundaries, 3–mesoregion boundaries, 4–rivers, 5–water bodies studied (numbering as in Table 1), 6–meteorological stations, and 7–major towns.

Post-mining water reservoirs which developed in former sand, clay or limestone pits constitute the biggest subgroup of water bodies studied (13); 10 were formed in subsidence basins resulting from land subsidence caused by underground mining operations; seven are water bodies of complex origin; five were created in artificially formed basins; three are dam reservoirs; and one is the result of constructing a dam across a river valley (Table 1).

TABLE 1

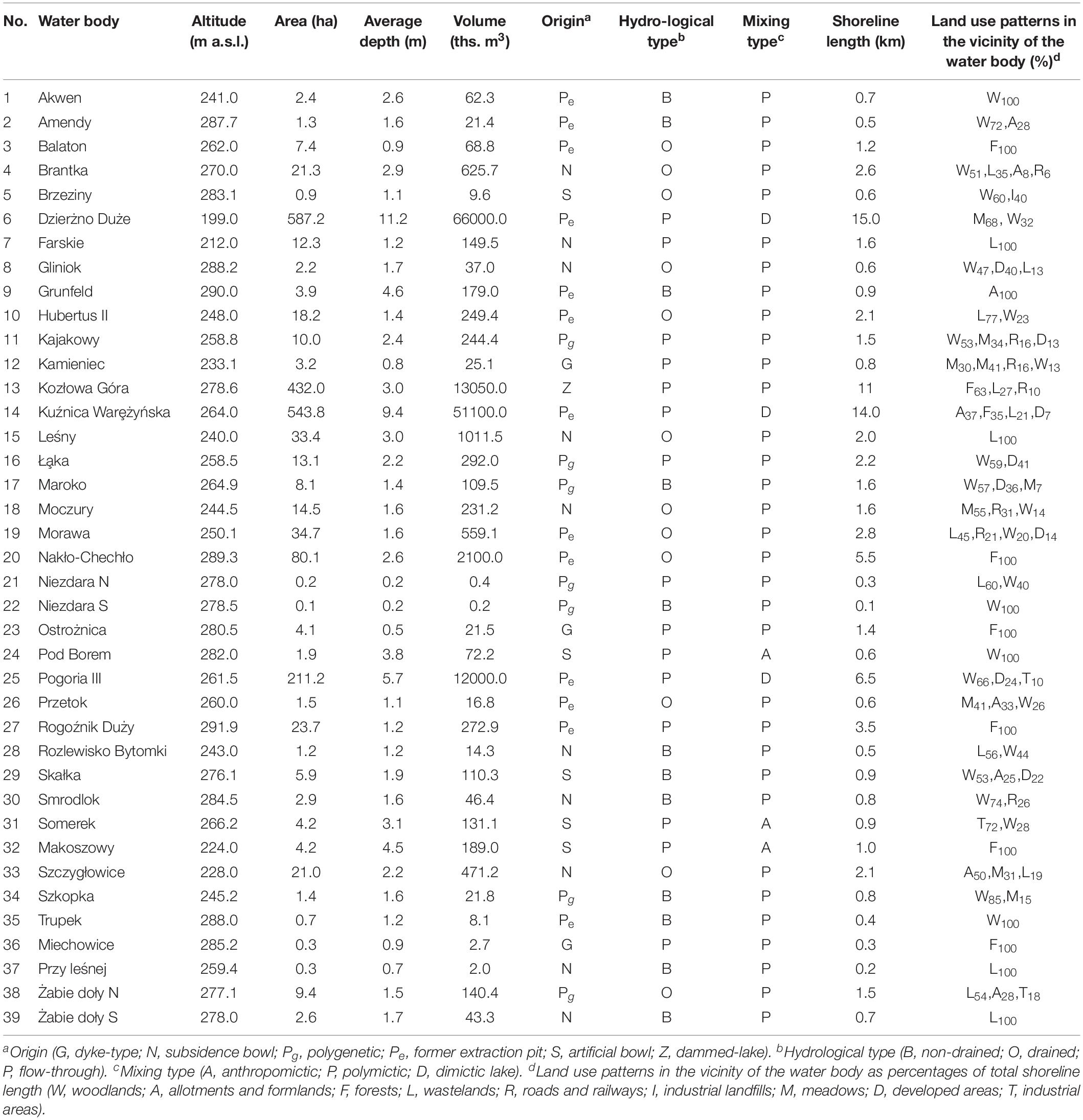
Table 1. Certain morphogenetic and hydrological parameters of the water bodies in the Silesian Upland.

Most of the water bodies studied, 61.5% (24, were no larger than several hectares. Overall 28.2% (11) of the water bodies studied measured from 10.0 to 80.1 ha. Only 10.3% (4) measured from 211.2 to 587.2 ha.

The bathymetric measurements conducted show that the vast majority of the water bodies included in the study are rather shallow (Table 1). The maximum depths were only from circa 16.0 to 23.0 m in the case of the three biggest basins which were formed in pits left after the exploitation of natural resources. The vast differences in the amount of water retained in the water bodies that were analyzed result from a significant morphometric differentiation of the basins of the water bodies. For the smallest basins, the volume measures from 0.2 to 16.8 10³ ml, and for the biggest ones from 12.0 to 66.0 10⁶ (Table 1).

In terms of hydrological type, flow-through water bodies are the biggest subgroup (15); followed by drained and non-drained water bodies (12 of each). The results of thermal-oxygen analysis show that the vast majority of the water bodies analyzed (33) are polymictic lakes, whose waters are mixed down to the lake bed (holomixis) by the wind numerous times over a 1-year period. Only the deepest pit lakes such as Dzierżno Duże, Kuźnica Warȩżyńska and Pogoria III can be classified as dimictic lakes, whose waters are mixed only twice a year, i.e., in the spring and in the fall, as a result of changes in the temperature and density of water. The mixing of water in mining waste water disposal facilities results mostly from the frequency of mine waste water discharges, hence they are classified as anthropomictic (Table 1).

Field Work

The studies and observations of ice phenomena were conducted over three consecutive winter seasons (2009/2010, 2010/2011, and 2011/2012), every other day during the freezing and ablation of the ice, and every 4 days during the occurrence of the ice cover, with the interpolation of results for the days on which measurements and observations did not take place. In this way, a database of ice thickness for each day of the period in question was obtained and used in the analysis. Only in the winter of 2011/2012 in the case of two basins (Amenda and Żabie Doły S), were the measurements and observations conducted every day from the beginning to the end of the occurrence of ice phenomena. In the case of smaller basins (34) the measurements were conducted at one measuring station, and in the case of the biggest water bodies (Dzierżno Duże, Kozłowa Góra, Kuźnica Warȩżyńska, Nakło-Chechło, Pogoria III)—at three measuring stations. Measurements were usually taken around a dozen meters from the shore, in the same part of the water body. During the measurements and observations the thickness and type of ice were analyzed. Ice thickness was measured through drillings made with an ice drill, initially with the use of a millimeter caliper, and when the ice thickness reached several centimeters—with a device specifically constructed for measuring ice thickness. A telescopic boom was also used to strike (break) thin ice and to bring thin ice floes closer to the shore in order to measure them. Measurements were taken from a pier (where one was present) or from a pontoon or small boat, which was used to break ice even where it was a few centimeters thick (also by pushing the bow onto the ice and applying pressure); in the littoral zone, thin ice was measured directly from the water using waders. Each time the presence of a snow, slush, or water layer covering the surface of the ice was noted and its thickness measured.

Statistics

The data collected during field research was processed in the course of office work and correlated with the data on air temperature obtained from a meteorological station at the Faculty of Earth Sciences at the University of Silesia in Sosnowiec. Air temperature at this weather station was almost identical to that at the Institute of Meteorology and Water Management (IMGW) weather station located in Katowice, as confirmed by the Pearson correlation coefficients calculated for the average daily air temperature at both stations. These were 0.9 (p < 0.001), 0.97 (p < 0.001), and 0.98 (p < 0.001) in the first, second and third seasons of the study, respectively (Meteorological data, 2020).

A Microsoft Excel database was compiled, including the data on the thickness of ice and the snow covering it. STATISTICA.10PL software was used to create box-whisker plots and calculate the correlations between daily temperature changes and changes in the thickness of the ice (data on the thickness of the ice were interpolated for the days on which the measurements were not taken), and the relationship between ice thickness and the thickness of the snow layer covering it. The distribution of the test covariates was determined with the use of the nonparametric Kolmogorov-Smirnov test, and dependencies were determined with the use of the Spearman correlation coefficient. The level of statistical significance for all the dependencies was p = 0.05.

A number of different models have been considered with respect to the assessment of ice thickness, such as those mentioned by Gao and Stefan (1999), Bruijn et al. (2014), and Robinson et al. (2021), but due to the limited availability of source data for calculations, a decision has been made to use one of the simplest formulas in the study of ice phenomena. In order to determine the theoretical maximum ice thickness in individual measurement seasons, the Stefan’s (1891) equation, subsequently modified by Michel (1971) and Lotsari et al. (2019) was applied:

η = α_{h} \sqrt{S}

where:

η–maximum thickness of ice cover in the season (cm),

α_h–empirical coefficient (0.014–0.017 m/°C^–1/2 day^1/2),

S–accumulated freezing degree-days (AFDD).

This model takes into account the layer of snow accumulated on the ice cover during the winter. Modeling results were compared to the actual maximum ice thickness of each of the tested water bodies.

In order to determine the similarities between the relationships between the selected morphometric features of the reservoirs, the average temperature of the water retained in them for the duration of ice phenomena occurrence (at a depth of 50 cm), the average thickness of the snow cover deposited on the ice (independent variables) and the average and maximum thickness of the ice (dependent variables) during the three winter seasons, the analysis of the discrimination function, principal components analysis (PCA) and the canonical analysis (RDA) were applied (Jolliffe, 1986; Krzanowski, 2000; Zuur et al., 2007; Topolski and Topolska, 2019; Topolski, 2019, 2020a,b). Redundancy analysis (RDA) is the canonical form of principal component analysis (PCA) and is a method for reducing the dimensionality of multivariate data by introducing a smaller number of new variables which explain the variation in the original variables with little loss of information (Misztal, 2018). To demonstrate the relationship between the groups of independent and dependent variables in the water bodies studied, principal component analysis (PCA) was used. An analysis combining PCA with RDA was applied to determine the detailed directions of the largest differences between the reservoirs and the measured parameters (Topolski, 2019). First, it was checked which dependent and independent variables are most strongly distinguished (discriminated) using discriminant function analysis. First, the characteristics were grouped using PCA. It turned out that similar PCA clusters are observed for all water bodies, therefore an exploratory model was run for all water bodies studied. Both PCA and RDA are exploratory data analysis techniques used to detect relationships between variables and to present data structure; they can be used as preliminary methods before more formal data analysis methods are applied (Misztal, 2017).

Results

Meteorological Features

During the first winter season of the research, average sub-zero temperature values were observed for 73 days, i.e., 69.6% of the duration of ice phenomena (105 days). Additionally, very low temperatures—lower than −10°C—were observed for only 10 days, i.e., less than 10% of the time when the water bodies were frozen. In the first season there were two short thaw periods: the first one took place in the third decade of December and it lasted 4 days, whereas the second one was observed at the beginning of March, and it lasted 14 days (Figure 2). The sum of negative temperatures during the first season was −411.6, and the sum of positive temperatures was 149.5.

FIGURE 2

Figure 2. Average air temperature values for the first (1), second (2), and third (3) winter seasons studied.

The second ice season was longer, but it was also milder. Average sub-zero temperature values were observed for 72 days, i.e., 63.2% of the duration of ice phenomena (114 days). Very low temperatures were only observed on 4 days, i.e., 3.5% of the duration of ice phenomena. As many as seven episodes with positive temperatures were observed for that season, out of which the shortest two lasted 2 days each (the first decade of December and the second decade of February), and the longest lasted almost 2 weeks (from 7 to 19th January). The sum of negative temperatures from the beginning to the end of the occurrence of ice phenomena was −338.74, and the sum of positive temperatures –172.7.

The third winter season studied was characterized by the longest duration of the occurrence of ice phenomena, 138 days, from the formation of ice on the first body of water until the total melting of the ice on the last one. However, average negative temperature values in that season were only observed on 48 days, i.e., 34.7% of the duration of ice phenomena. Very low temperatures were observed on 15 days, i.e., almost 11.0% of the duration of occurrence of ice phenomena. In the first part of the study period (from 11th November to 13th January), the average air temperature was around 0°C, which facilitated the formation and melting of ice on small water bodies. A significant drop in air temperature was only observed in the second half of January, and it lasted for over a month (35 days). Over the third winter season studied the sum of negative temperature values was −296.4, and the sum of positive temperature values was 316.9.

The average air temperature in the winter half-year of the three winter seasons studied was 1.8°C in the first season, 2.2°C in the second, and 2.1°C in the third. Those values do not significantly deviate from the average for the period of 1964–2012, 2.0°C (Central Statistical Office, 1964-2015).

The sums of atmospheric precipitation in the winter half-years (XI-IV) during the three study seasons were as follows: 278.4 mm (in 2009/2010), 249.1 mm (in 2010/2011), and 264.4 mm (in 2011/2012), and they did not differ significantly from the average sum of precipitation calculated for the years 1951–2012, which amounted to 266.6 mm (Central Statistical Office, 1964-2015; Meteorological data, 2020).

Snow Conditions

There was variation in the snow conditions during the three winter seasons examined (Figure 3 and Table 2). In the first winter season the average thickness of the snow covering the ice measured from 0.0 to 8.1 cm, on average 5.2 cm. Over that period the maximum thickness of snow cover was from 0.0 to 22.0 cm, on average 12.3 cm (Table 2). The thickness of snow cover grew steadily over the winter period, reaching its maximum value at the turn of the first and second decades of February, followed by a dynamic decline. Both the average and maximum thickness of the snow cover correlated with the average and maximum thickness of ice on the water bodies examined. The correlation coefficients were calculated to be 0.82 (p = 0.00) (average thickness of the snow cover vs. average and maximum thickness of the ice), 0.76 (p = 0.00) (maximum thickness of the snow vs. maximum thickness of the ice) and 0.75 (p = 0.00) (maximum thickness of the snow cover vs. average thickness of the ice).

TABLE 2

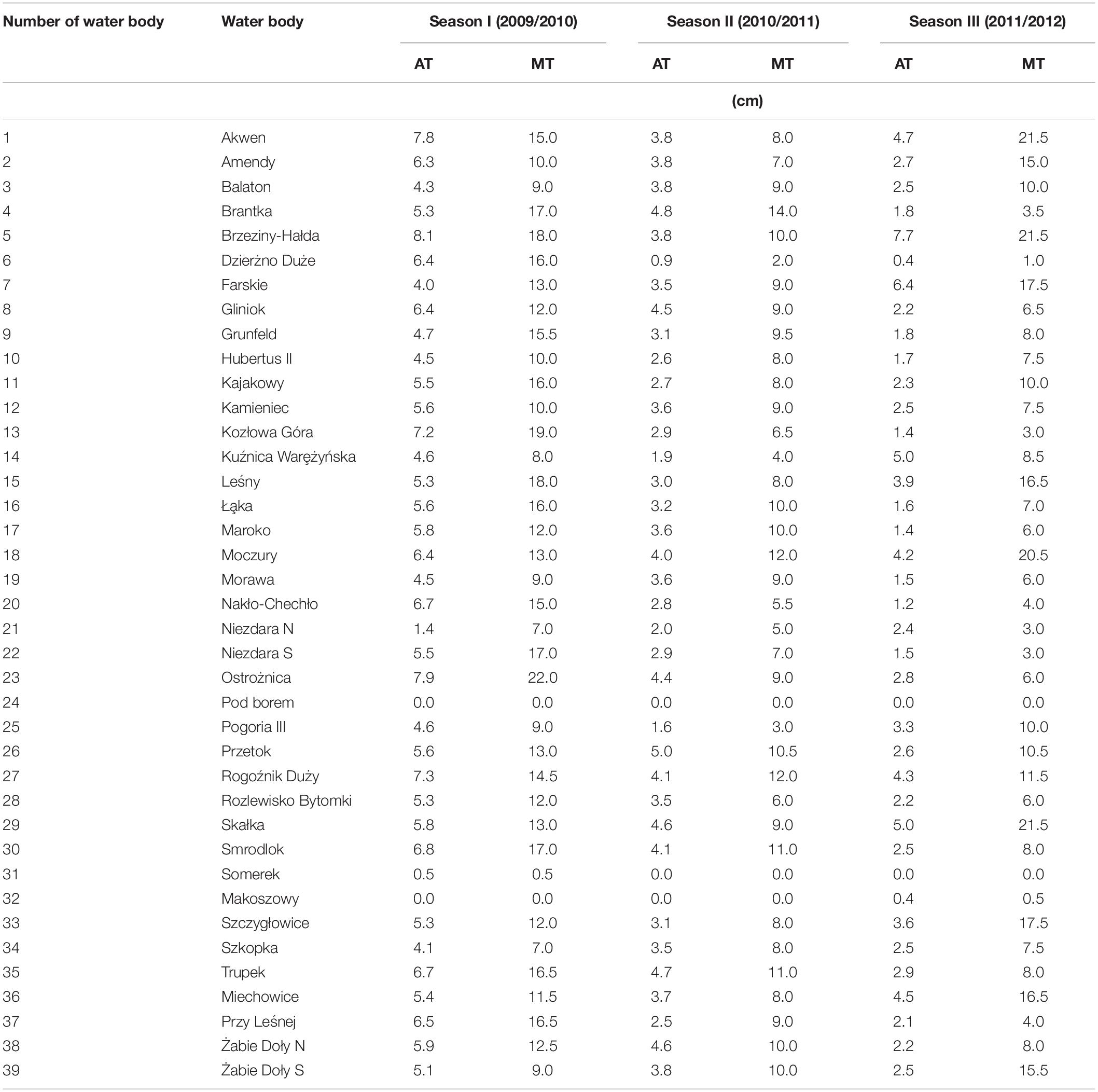
Table 2. Average (AT) and maximum (MT) values of thickness of snow cover on selected water bodies of the Silesian Upland in the winter seasons of 2009/2010–2011/2012.

FIGURE 3

Figure 3. Changes in thickness of snow cover over time on water bodies in the Silesian Upland in the (A) first, (B) second, and (C) third winter season: 1–average snow depth, 2–maximum snow depth.

In the second winter season of the study the thickness of the snow layer covering the ice on the water bodies examined was generally thinner than during the first one. The average thickness was between 0.0 and 5.0 cm; the mean value was 3.2 cm and the maximum thickness was from 0.0 to 14.0 cm, with a mean value of 7.8 cm (Table 2). During that winter season the thickest snow layer was observed in the first part of the winter (December), followed by a gradual decrease. Both the average and maximum thickness of the snow cover correlated with the average and maximum thickness of the ice on the water bodies studied. The correlation coefficients were calculated as 0.76 (p = 0.00) (average thickness of the snow cover vs. average thickness of the ice), 0.75 (p = 0.00) (average thickness of the snow cover vs. maximum thickness of the ice), 0.73 (p = 0.00) (maximum thickness of the snow cover vs. average thickness of the ice), and 0.71 (p = 0.00) (maximum thickness of the snow cover vs. maximum thickness of the ice).

In the third winter season of the study the thickness of the snow cover was from 0.0 to 7.7 cm, with an average of 2.7 cm. The maximum thickness of snow cover was from 0.0 to 21.5 cm, with an average of 9.2 cm (Table 2). A significantly thick snow cover was observed for a relatively short period of time—from the end of January until mid-February. Both average and maximum values of the thickness of the snow cover correlated poorly with the average and maximum values for the thickness of the ice on the water bodies studied. The correlation coefficients were calculated to be: 0.27 (p = 0.1) (average thickness of the snow cover vs. average thickness of the ice), 0.39 (p = 0.013) (average thickness of the snow cover vs. maximum thickness of the ice), 0.30 (p = 0.061) (maximum thickness of the snow cover vs. average thickness of the ice), and 0.40 (p = 0.012) (maximum thickness of the snow cover vs. maximum thickness of the ice).

Ice Thickness

The minimum thickness of the ice measured in the winter season of 2009/2010 was from 0.1 cm (on the majority of the water bodies in the study) to 1.4 cm (Kuźnica Warȩżyńska) (Figure 4). Ice thickness was measured in the coastal zone during the formation of shore ice at the beginning of the second decade of December. The minimum ice thickness (defined as the lowest ice thickness measured) was usually recorded on the first day of ice phenomena. Measurements were conducted in the littoral zone where shore ice was forming. The maximum ice thickness on 36 out of the 39 water bodies studied was measured in the second half of February, and measured from 13.0 (Niezdara N) to 29.5 cm (Kuźnica Warȩżyńska), on average 23.6 cm. In the case of two water bodies (Somerek, Makoszowy) the maximum thickness of the ice was measured toward the end of January, during a significant drop in average daily air temperature (see Figure 2). In both cases the thickness of the ice did not exceed 2 cm. In the first winter season investigated on only one water body, Pod Borem, were no ice phenomena observed. The median ice thickness in that season was within the range of 0.3 cm (Makoszowy) to 22.0 cm (Kuźnica Warȩżyńska), on average 14.0 cm. The average thickness of the ice in the group under investigation was slightly thinner, measuring from 0.4 cm (Makoszowy) to 19.2 cm (Kuźnica Warȩżyńska), on average 13.7 cm.

FIGURE 4

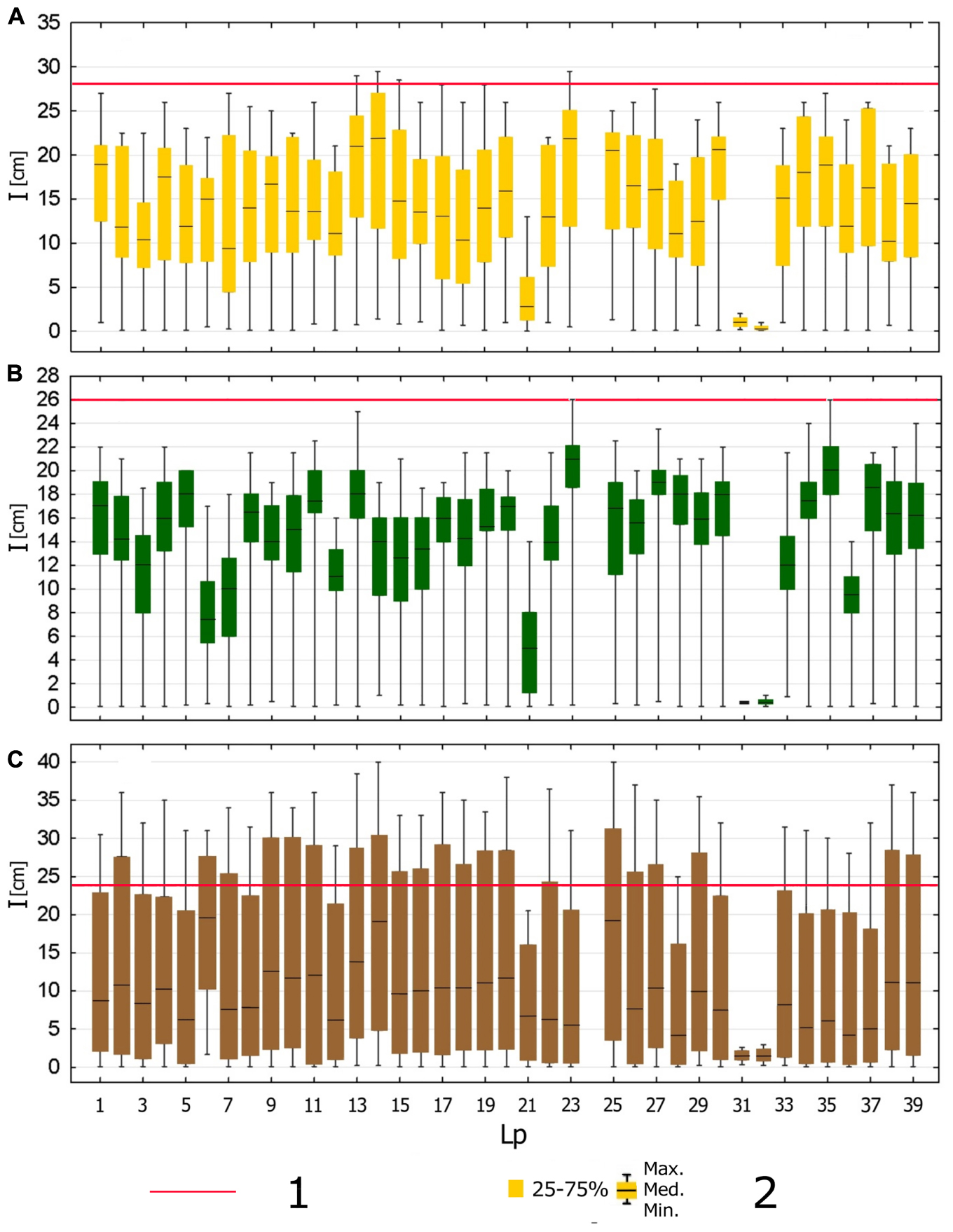
Figure 4. Ice thickness on the water bodies of the Silesian Upland in the (A) first, (B) second, and (C) third winter season: I–ice thickness, Lp–ordinal number (numbering as in Table 1). 1 - the maximum ice thickness values obtained from modelling using the Stefan’s (1891) equation, 2 - statistical parameters.

The maximum ice thickness values obtained from modeling using the Stefan’s equation were 28, 26, and 24 cm for the first, second and third measurement seasons, respectively (Figure 4).

The average difference between the measured ice thickness and the thickness obtained as a result of modeling was 5.3 cm in the first measurement season, with only four cases where the modeled value was underestimated, while in the remaining 35—the measured ice thickness values were below those obtained using the Stefan’s. (1891) equation. In four cases, the differences were significant, ranging from 15 to 28 cm.

In the second measurement season, the average difference between the modeled value and the maximum measured ice thickness was 6.8 cm. In two cases, the modeled and actual ice thickness were identical, while in the remaining 37 cases, the modeling results were higher compared to the actual values. In 30 cases, the differences were below 10 cm. Larger differences were found in five reservoirs, ranging from 12 to 26 cm.

In the third season, the differences between the modeled and measured ice thickness were the greatest. They amounted, on average, to 10.5 cm, ranging from 1.0 to 24.0 cm. In the case of 35 reservoirs, the measured maximum ice thickness values were greater than the thickness calculated using the model, in several cases the differences was as much as 16 cm. The maximum thickness of the ice covers of the four reservoirs was below the modeled value, with the differences ranging from 3.5 to 24 cm.

The correlation coefficients calculated for the relationship between the daily changes in the average air temperature and daily changes in ice thickness were from 0.0 in the case of Pod Borem waste water disposal facility to −0.77 for Kamieniec and Gliniok, with the mean of −0.59 for the whole group under investigation. Those coefficients were generally statistically significant, with statistical significance at α = 0.05 (the coefficients calculated for Pod Borem and Somerek were an exception). The lowest values for the correlation coefficient were observed in the case of waste water disposal facilities: Pod Borem (no dependencies), Somerek (−0.17; p = 0.142) and Makoszowy (−0.27; p = 0.019), and in other cases it was on average −0.61 (Table 3).

TABLE 3

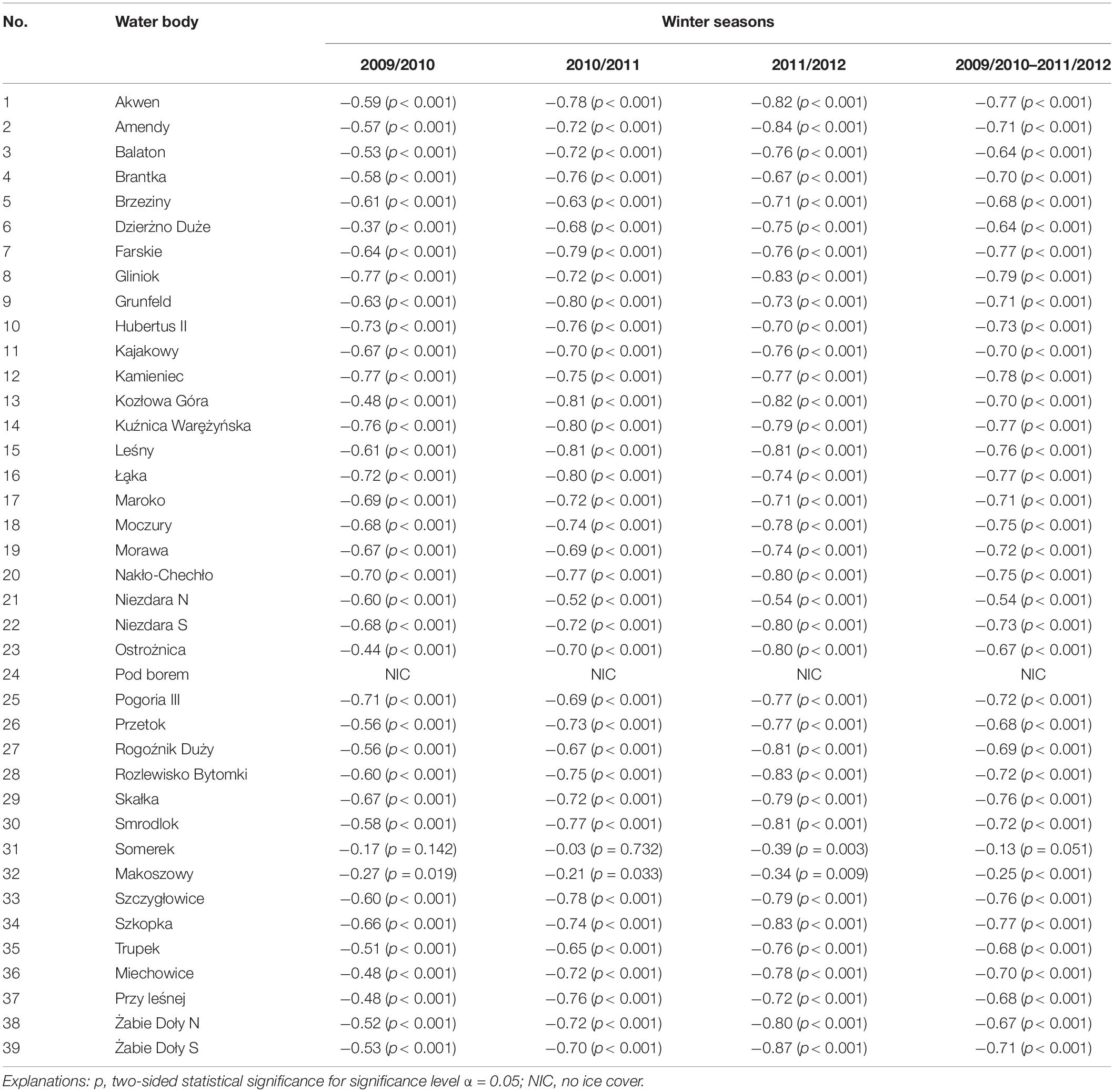
Table 3. Values of Spearman’s correlation coefficients between the daily changes in average air temperature at Sosnowiec meteorological station and daily changes in ice thickness.

In the second winter season examined the minimum ice thickness was measured at the turn of November and December during a freezing spell. The shore ice thickness on the water bodies analyzed measured from 0.1 cm (13 water bodies) to 1.0 cm (Kuźnica Warȩżyńska), on average 0.3 cm. In only one case—Pod Borem—was no ice observed in the basin. The maximum ice thickness values were from 0.5 cm (Somerek) to 26.0 cm (Trupek), on average 19.8 cm. The occurrence of the maximum thickness of the ice on a given body of water differed in time. In the case of 14 water bodies studied it was the second and third decade of December, in 12—the first decade of January, and in 3—at the turn of January and February. The median ice thickness in that winter season was within the range of 0.4 cm (Somerek) to 21.0 cm (Ostrożnica), on average 14.3 cm. The mean ice thickness in the water bodies studied was slightly thinner, measuring from 0.4 cm (Somerek) to 18.7 cm (Ostrożnica), on average 13.4 cm. The calculated correlation coefficients between the daily changes in the average air temperature and daily changes in ice thickness were 0.0 in the case of the Pod Borem waste water disposal facility, to −0.81 for Kozłowa Góra and Leśny, with the mean of −0.70 for the whole group. Those coefficients were generally statistically significant, with statistical significance at α = 0.05 (the coefficients calculated for Pod Borem and Somerek were an exception). The lowest values for the correlation coefficient were observed in the case of waste water disposal facilities: Pod Borem (no dependencies), Somerek (−0.03; p = 0.732) and Makoszowy (−0.21; p = 0.033), and in the other cases it was on average −0.73 (Table 3).

In a similar manner to the first two winter seasons in the study, the thinnest ice was measured during the formation of shore ice. That season, the freezing process took the longest due to the air temperature pattern: the temperature was 0°C at the beginning of the season, and it remained so for a long time. In such conditions shore ice had already appeared on most of the water bodies examined in the second decade of November, and its presence was observed in the third decade of January at the latest (Dzierżno Duże). The minimal ice thickness was from 0.1 cm (most of the water bodies studied) to 1.7 cm (Dzierżno Duże), on average 0.2 cm. The maximum ice thickness occurred in the second part of the winter season, measuring from 2.6 cm (Somerek) to 40.0 cm (Kuźnica Warȩżyńska, Pogoria), on average 31.8 cm. In the case of two water bodies (Somerek, Makoszowy) this was observed at the beginning of February during a significant drop in air temperature, and in 36 water bodies in the third decade of February. The median ice thickness in that season was within the range of 1.5 cm (Somerek) to 19.7 cm (Dzierżno Duże), on average 9.1 cm. That winter season the mean ice thickness in the study group of water bodies was from 1.5 cm (Somerek) to 18.6 cm (Dzierżno Duże), on average 12.6 cm (Figure 4). The correlation coefficients between the daily changes in the average air temperature and daily changes in ice thickness were calculated to be from 0.0 in the case of Pod Borem waste water disposal facility to −0.87 for Żabie Doły S, with the mean of −0.73 for the whole group. Those coefficients were generally statistically significant, with statistical significance at α = 0.05 (the coefficients calculated for Pod Borem were an exception). The lowest values for the correlation coefficient were observed in the case of waste water disposal facilities: Pod Borem (no dependencies), Somerek (−0.39; p = 0.003) and Makoszowy (−0.34; p = 0.009), and in other cases it was on average −0.75 (Table 3).

The models obtained as a result of PCA and RDA analysis for individual seasons did not differ significantly from each other (Figure 5). In the case of the four lakes (Niezdara N–21, Pod Borem–24, Somerek–30, and Sośnica-Makoszowy–32), the strongest relationships between water temperature and ice thickness are noticeable, with the relationships being inverse. The second grouping (Kozłowa Góra–13, Kuźnica Warȩżyńska–14, Ostrożnica–23, Pogoria III–25, and Smrodlok–30) was made up of lakes where large maximum and average ice thickness and significant average snow thickness were observed. In the case of the remaining lakes, correlations between their morphometric characteristics and the ice thickness are mainly visible. These mainly include the average depth and volume capacity of the reservoirs.

FIGURE 5

Figure 5. RDA biplots illustrating relations between environmental variables and selected parameters of lake ice phenology for the water reservoirs in Silesian Upland: I–winter seasons (1–winter season 2009/2010, 2–winter season 2010/2011, 3–winter season 2011/2012); II–studied lakes (numbering as in Table 1); III–correlated variables (AWT, average water temperature; AIT, average ice cover thickness; AST, average snow cover thickness; MIT, maximum ice cover thickness; LA, reservoir surface; H, average reservoir depth; V, reservoir volume capacity).

In the charts, vectors show the explanatory (LA, V, H, and ST AWT) and explained (average ice thickness—AIT and maximum ice thickness—MIT) variables; the water bodies studied are also shown, depicted as points (Figure 5). The direction of the vector corresponds to the direction of the greatest variability of the explanatory variable, and its magnitude is proportional to the significance of this variable (Misztal, 2017). The closer a point depicting the object in question is to a given variable, the more the phenomenon in question is correlated with that variable. The water bodies that were not covered by ice or were covered by very thin ice (21, 24, 31, and 32) are grouped close to the AWT variable (average water temperature during ice phenomena), which means that low ice thickness can be primarily explained by the high temperature of the water retained in those water bodies during the winter seasons studied.

In the case of some water bodies, morphometric parameters of their basins were well correlated with ice thickness, since those parameters translated into the amount of water retained, which in turn influenced, among other things, the rate of cooling of the water body and ice cover formation (e.g., 6, 8, 10,11, and 39). However, those parameters were of secondary importance (short vectors) compared to water temperature at the time when ice phenomena were present (AWT) and the average snow thickness on the ice (AST) (long vectors). For several water bodies (e.g., 13, 14, 23, 25, and 30), there are significant relationships between the thickness of snow accumulated on the ice cover and ice thickness.

Discussion

The minimum thickness of the ice covering a body of water is typically measured during the formation and disappearance phases. Those values are mostly observed by the shore, since thin ice does not guarantee safety during the measurements (Choiński, 2007b). During the three winter seasons in the study the thinnest ice was always found by the shoreline during freezing, measuring from 1 mm to several centimeters. The thinnest ice was typically found on small water bodies, for which even a small drop in air temperature below 0°C led to the formation of ice crystals (Bengtsson, 2012a). In the case of bigger water bodies, in which the process of cooling the lake water is slower, the minimum ice thickness values were typically over 1 cm, which can be explained by the fact that in order for ice to form on bigger water bodies a more significant or prolonged drop in air temperature is required, and hence in such cases the accumulation of ice is more dynamic (Solarski et al., 2011). The development of ice phenomena may also be influenced by land use patterns in the vicinity of the water bodies. Forests and woodlands whose presence results in a significant part of the surface remaining in the shade slow down the rate of ablation and as a result the ice persists the longest on such water bodies (e.g., Szkopka, Ostrożnica). It may be assumed that developed areas and roads heat up more than other forms of land use and then release heat to the air which may translate into lower ice thickness and faster ablation.

The maximum ice thickness was typically observed in the second part of the winter season (toward the end of February or the beginning of March). In the first part of the winter season gradual freezing of ice crystals took place progressively downwards toward the lake bed. This happened during significant and dynamic drops in air temperature, when there was not yet a thick layer of snow covering the ice. The snow cover makes a highly efficient insulation layer, limiting the reactions of the ice to changes in air temperature (Leppäranta, 1983; Bengtsson, 1986, 2012a,b; Ashton, 2011; Brown and Duguay, 2011; Kirillin et al., 2012; Yang et al., 2012; Solarski and Rzetala, 2020). The conditions for the development of ice change completely when it is covered by a thick snow cover, when the so-called isostasy of ice takes place (Ashton, 2011). It is responsible for an increase in the temperature of the lake ice to reach around 0°C caused by its immersion in lake waters and the water escaping above the ice, immersing the snow covering it (Adams and Shaw, 1967; Adams and Roulet, 1980; Adams, 1981; Aihara et al., 2010). The resulting layer of ice-water slush covers the ice, lying under the snow cover (Solarski, 2017). If the air temperature is negative and low enough at such times, a layer of ice crust starts to form under the snow, accumulating toward the ice cover (Ashton, 2011). Prolonged sub-zero temperatures usually lead to the merging of the two layers. Thus, snow ice develops, whose thickness depends mostly on the thickness of the snow cover. The snow cover thus plays two important roles: it inhibits the accumulation of crystal ice toward the lake bed, and when it is thick enough, it encourages the accumulation of snow ice from the top (Solarski, 2017; Solarski and Szumny, 2020). The calculated correlation between the thickness of the ice and the thickness of the snow covering it for the three winter seasons in the study confirm the above conclusions. During two winter seasons snow covered the ice almost throughout the whole winter season, and it played a key role in the increase in the thickness of the ice. On the other hand, in the third winter season the accumulation of ice proceeded without the snow (Figure 3).

During the three winter seasons in the study, in 35 out of the 39 water bodies analyzed both the maximum and average thickness of the ice did not significantly differ from each other (Figure 4). In the first season the maximum ice thickness on those water bodies was from 19.0 to 29.5 cm, on average from 9.5 to 22.0 cm. During that season the ice steadily accumulated, reaching its maximum in the third decade of February. Its accumulation was initially shaped by the freezing of crystal ice toward the lake bed, followed by gradually freezing snow ice. In the second winter season the slightly thinner ice was mostly the result of the fact that during that winter there were numerous periods with positive air temperatures, resulting in the subsequent increase and decrease in ice thickness (Figure 2). In that season the occurrence of maximum ice thickness was more varied over time. On some water bodies the thickest ice had already been observed in the first decade in January, and on some it was only seen in the beginning of March. The ice was from 26 to 14 cm thick, on average from 21 to 7.5 cm. The third winter season was significantly different from the previous two, since the temperature remained at around 0°C for a long time, and then it abruptly dropped; for the following 2 weeks it remained lower than −10°C. As a result, the thickest ice was observed in the last winter season, from 40 to 25 cm, but the average ice thickness was the lowest, from 19.7 to 4.0 cm. The lowest average values were characteristic for smaller water bodies, on which the ice layer remained 1 cm thick for a long time.

The statistical analysis of the data on ice thickness and the dynamics of changes in it in relation to the dynamics of changes in air temperature show that in most cases (35 water bodies) a drop in air temperature translated into an increase in ice thickness and vice versa. Four water bodies showed a different ice regime, one of them, Niezdara N, located in the Brynica river valley, is a backwater of the river. Niezdara N is hydraulically connected with the river, and frequent inflows of warmer potamic water result in a short duration of ice phenomena and a thin layer of ice (Figures 4, 5).

Sośnica, Somerek and Pod Borem—all mine waste water disposal facilities—constitute a different group of water bodies, on which the ice layer was no thicker than a few centimeters, even during very low temperatures, or it did not occur at all (Pod Borem). This is because the thermal regime of those water bodies depends on the frequency of mine waste water discharges, which take place from several to a dozen or so times a day (Solarski et al., 2011). In such cases their anthropothermy should be acknowledged (Figure 5; Beznosov and Suzdaleva, 2001; Chen et al.,2017).

Taking into account the fact that Stefan’s equation is mainly based on the frost degree days formula and does not take into account a number of factors which, in addition to air temperature, determine the dynamics of ice growth (e.g., the amount of heat accumulated in water and sediment, solar radiation balance, wind speed, cloud cover, relative humidity, mid-season thaw periods, thermal properties of ice and thickness of snow layer on ice), the differences between the values obtained as a result of modeling and those measured during field tests, in most of the cases, seem to be low. Only in the case of 4 lakes, they significantly exceeded 10 cm.

A better fit of the model was achieved in the first two seasons, when the ice cover was formed with a thicker layer of snow on it. In the third winter season, there was a short, rapid increase in the thickness of the ice cover during a 2-week colder period, with little snow deposited on the ice. The underestimation of modeled ice thickness in the third measurement season may result from the application of an empirical model factor that takes into account the presence of snow during its formation.

Water bodies in which there is some heated water retained are characteristic elements of industrial landscapes and those of urban-industrial sites, and they typically occur next to power plants, mines, and other industrial plants. However, those are a small part of the general number of water bodies in the Silesian Upland (Solarski et al., 2011; Machowski, 2013), where the vast majority are characterized by a natural or quasi-natural ice regime, as demonstrated by the fact that the duration of occurrence of ice phenomena, ice cover and ice thickness are not significantly different from the values observed in lakes located in other parts of Poland (Choiński, 2007a,b; Marszelewski and Skowron, 2009; Choiński and Ptak, 2012; Barańczuk et al., 2017; Barańczuk and Barańczuk, 2018; Ptak et al., 2019).

Conclusion

The research conducted on water bodies located in the Silesian Upland indicates that variation in ice thickness mostly depends on the air temperature patterns during a given winter season. In the case of the vast majority of the water bodies studied, significant drops in air temperature resulted in the formation of thick lake ice. The snow cover is an important factor influencing the variation in ice thickness between different water bodies. The differences in the thickness of snow covering the ice from the moment of its formation can translate into limiting the dynamics of accumulation of crystal ice in the initial freezing period, and into increased dynamics of accumulation of snow ice in the second part of the winter season. The ice formation processes occur in the same way as in natural lakes, and the differences in ice thickness mostly depend on environmental factors, such as topoclimatic conditions and the morphometric characteristics of a given water body (translating into the amount of heat accumulated in the water and sediment after the summer season, and consequently the pace of freezing). The performed RDA analysis shows that also the morphometric features of water bodies (mainly their average depths and the amount of retained water) translate into the thickness of the ice deposited on them during the winter.

Mine waste water disposal facilities constitute a specific, though decisively less frequent group of water bodies fed by mine water located in the Silesian Upland. In those water bodies the ice layer does not form at all, even in the case of a significant drop in air temperature (Pod Borem), or else it is very thin (Somerek, Sośnica).

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.

Author Contributions

MS and MR conceived and planned the study, conducted field work, analyzed the results, wrote the manuscript, and collaborated on manuscript editing at all stages. Both authors contributed to the article and approved the submitted version.

Funding

This research was funded by University of Silesia in Katowice (Poland)–Institute of Earth Sciences, project no. WNP/INoZ/2020_ZB25.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank the linguistic team for correcting the English language of the manuscript. We would also like to thank Mariusz Topolski and Łukasz Potempka for consulting on the statistical methods applied.

References

Adams, W. P. (1981). “Snow and ice on lakes,” in Handbook of Snow, eds D. M. Gray and D. H. Male (Toronto, ON: Pergamon Press), 437–474.