The Influence of Weathering, Water Sources, and Hydrological Cycles on Lithium Isotopic Compositions in River Water and Groundwater of the Ganges–Brahmaputra–Meghna River System in Bangladesh

The silicate weathering of continental rocks plays a vital role in determining ocean chemistry and global climate. Spatiotemporal variations in the Li isotope ratio (δ⁷Li) of terrestrial waters can be used to identify regimes of current and past weathering processes. Here we examine: 1) monthly dissolved δ⁷Li variation in the Ganges River’s lower reaches; and 2) the spatiotemporal variation of river water of the Brahmaputra, Meghna rivers, and groundwater in Bangladesh. From the beginning to maximum flood discharges of the rainy season (i.e., from June to September), Li concentrations and δ⁷Li in the Ganges River show remarkable changes, with a large influence from Himalayan sources. However, most Li discharge across the rainy season is at steady-state and strongly influenced by the secondary mineral formation in the low-altitude floodplain. Secondary mineral formation strongly influences the Meghna River’s Li isotopic composition along with fractionation lines similar to the Ganges River. A geothermal input is an additional Li source for the Brahmaputra River. For groundwater samples shallower than ∼60 m depth, both δ⁷Li and Li/Na are highly scattered regardless of the sampling region, suggesting the variable extent of fractionation. For deep groundwater (70–310 m) with a longer residence time (3,000 to 20,000 years), the lower δ⁷Li values indicate more congruent weathering. These results suggest that Li isotope fractionation in rivers and groundwater depends on the timescale of water-mineral interaction, which plays an essential role in determining the isotopic signature of terrestrial Li inputs to the ocean.

Introduction

The Ganges and Brahmaputra rivers are sourced on the Himalayan–Tibetan Plateau (Figure 1). Active physical and chemical weathering is associated with the uplift of the plateau and high-magnitude monsoonal rainfall, and the combined sediment and chemical discharges of the Ganges and Brahmaputra Rivers are among the top five major world rivers. Chemical weathering of continental rocks converts atmospheric carbon dioxide (CO₂) and silicate rocks to alkalinity and solutes on geologic timescales, and therefore essential determinants of the long-term carbon cycle (Galy and France-Lanord, 1999).

FIGURE 1

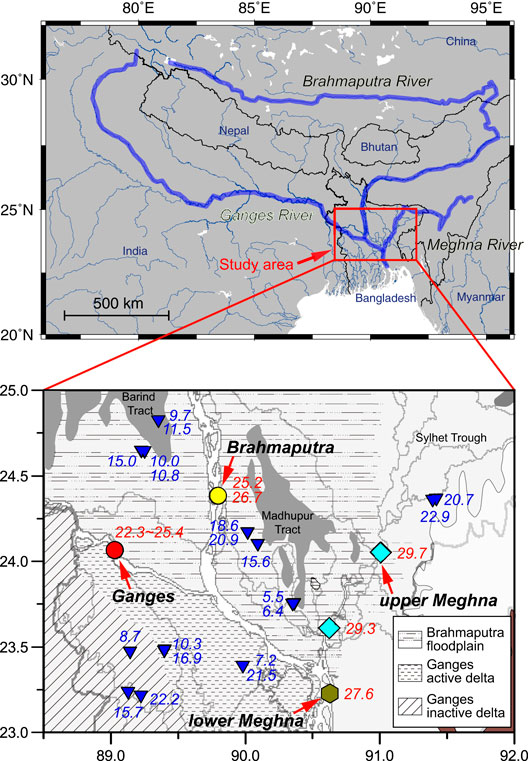
FIGURE 1. Maps of the Ganges–Brahmaputra–Meghna river system (modified after Yoshimura et al., 2021) showing geomorphologic units (Paul et al., 2010) as well as sampling locations for groundwater (blue triangles) and river water of the Ganges (red circle), Brahmaputra (yellow circle), upper Meghna (blue diamond), and lower Meghna (green hexagon) Rivers. Blue and red numbers represent δ⁷Li compositions of groundwater and river water, respectively. The light gray areas are the major Pleistocene terraces (Barind and Madhupur Tract).

Lithium isotope ratios (δ⁷Li) are a tracer of silicate weathering processes, which provide information for mass balance calculations of the ratio of primary mineral dissolution relative to the secondary mineral formation in terrestrial waters (Bagard et al., 2015; Pogge von Strandmann and Henderson, 2015; Bouchez et al., 2013). The large relative mass difference of 16% between ⁶Li and ⁷Li results in natural δ⁷Li variations of more than 60‰ (Tomascak, 2004). The δ⁷Li values of silicate rocks of the upper continental crust occupy a range of −5‰ to +5‰ (Teng et al., 2004), with an average of 0.6 ± 0.6‰ (Sauzéat et al., 2015), while the dissolved Li of rivers display a much more considerable variation, ranging from +2 to +44‰ (e.g., Tomascak, 2004; Penniston-Dorland et al., 2017). Although δ⁷Li values in the dissolved load reflect a mixture of different sources, such as contributions of atmospheric salt, and silicate sources, preferential uptake of ⁶Li by secondary minerals plays the critical role for the higher δ⁷Li values in terrestrial waters.

A higher ratio of a secondary mineral formation relative to primary mineral dissolution (i.e., medium weathering intensity, Dellinger et al., 2015) leads to more Li incorporation by clay minerals and residual waters isotopically heavier than the source material(s). If the δ⁷Li values of dissolved Li are close to those of primary silicate rocks, weathering is considered “congruent” and the delivery of cations, from the dissolution of primary minerals, to the ocean is more efficient. In contrast, high δ⁷Li values imply that more cations are retained by secondary mineral formation (“incongruent” weathering), corresponding to a medium weathering to denudation ratio (Pogge von Strandmann and Henderson, 2015; Pogge von Strandmann et al., 2020). At a very high weathering to denudation intensity regime, dissolution of pre-formed clays also causes a decrease in dissolved δ⁷Li, but this regime is characterized by lower Li flux and yields (Pogge von Strandmann et al., 2020).

Lithium inputs from the Ganges and Brahmaputra rivers are 2.60 × 10⁸ and 2.63 × 10⁸ mol/yr, respectively, accounting for approximately 10% of total input fluxes from major world rivers of 2.79 × 10⁹ mol/yr (Huh et al., 1998). Riverine Li inputs have played an important role in past changes of seawater δ⁷Li values (Hathorne and James, 2006), accounting for approximately 30% of the modern ocean’s total input fluxes with an average δ⁷Li value of 23‰ (Huh et al., 1998). Given the large discharge volume and sediment flux of the Ganges–Brahmaputra river system (Milliman and Syvitski, 1992), the chemical flux and isotopic variations of this system is important in determining the oceanic element and isotopic mass balance (Tipper et al., 2006; Bickle et al., 2018).

The δ⁷Li values in the Ganges and Brahmaputra rivers show a clear downstream trend toward higher values as the dissolved Li concentration decreases, indicating a progressive increase in preferential uptake of ⁶Li by secondary minerals (Huh et al., 1998; Kurek et al., 2005; Bagard et al., 2015; Manaka et al., 2017). More recently, Pogge von Strandmann et al. (2017) showed that dissolved δ⁷Li are low only in the Ganges headwaters, and reach a constant ∼21 ± 1.6‰ which is maintained for almost 2,000 km to the Ganges mouth. The downstream evolution of river water chemistry and the total chemical fluxes to the ocean are tightly controlled by weathering in low altitude floodplains (Frings et al., 2015; Pogge von Strandmann et al., 2017; Bickle et al., 2018).

The floodplain sediment load consists of incompletely weathered material that is delivered from high mountain areas. Continued weathering of Himalayan-derived sediment during its transport through the low-altitude plain makes a significant contribution to the total weathering fluxes (Lupker et al., 2012; Frings et al., 2015). Indeed, the retention of Li by secondary minerals has been a critical process in the long-term evolution of seawater δ⁷Li that links changes in global silicate weathering intensity (Li and West, 2014; Wanner et al., 2014; Caves Rugenstein et al., 2019). The increase in oceanic δ⁷Li during the Cenozoic (Hathorne and James, 2006; Misra and Froelich, 2012; Washington et al., 2020) could be linked to greater ⁶Li retention by clays accompanying active secondary clay formation during the uplift of the Himalayan-Tibetan Plateaus and the Andeas (Hoorn et al., 2010), accompanied by floodplain development (Pogge von Strandmann and Henderson, 2015). Chemical compositions of river waters depend on seasonal differences in relative fractions of chemical weathering inputs derived from the high mountains, floodplains, and southern tributaries (Bickle et al., 2018). There is a large seasonal difference in the Ganges River discharge, but the seasonal change in δ⁷Li is still under debate due to limited sampling. To capture a full annual variability, monthly variation is essential for evaluating the continental Li fluxes’ contribution to the ocean (Pogge von Strandmann et al., 2016; Gou et al., 2019; Hindshaw et al., 2019a, Hindshaw et al., 2019b, Hindshaw et al., 2019c).

The δ⁷Li value in groundwater is generally lower than that of rivers (Nishio et al., 2010; Millot et al., 2011; Bagard et al., 2015) and subsurface residence time and hydrological cycles have significant controls on the extent of Li incorporation into secondary minerals (Liu et al., 2015). In Bangladesh, groundwater also shows elevated Li concentration (up to 3.02 μmol/kg) with an average δ⁷Li value of 16‰; this is about 10‰ lower than the δ⁷Li composition of riverine discharge to the Bay of Bengal (Bagard et al., 2015). In the Bengal Basin, shallow groundwaters (depths down to 70–100 m below surface) are recharged regularly, resulting in residence times from tens to hundreds of years (Aggarwal et al., 2000). Deep groundwater in the Bengal Basin is isolated from shallow waters and has a residence time ranging from a few thousand to around twenty thousand years (Aggarwal et al., 2000). Previous studies showed that δ⁷Li values in the deep groundwater in the Bengal Basin are ∼4‰ lower (Manaka et al., 2017) than those at shallow depths (<50 m, Bagard et al., 2015). The lower δ⁷Li implies more congruent dissolution (less influence of secondary minerals) in the deep aquifers, where long water-rock interaction times favor the progress of mineral dissolution. Because changes in the Cenozoic seawater δ⁷Li reflect the evolution of floodplain weathering (Pogge von Strandmann and Henderson, 2015; Pogge von Strandmann et al., 2017), changes in groundwater chemistry with depth and their impact on the reaction kinetics of δ⁷Li are subject to an accurate reconstruction of weathering regimes in the geological past (Wanner et al., 2014). Although spatial variations in groundwater δ⁷Li represent a rich natural laboratory, limited studies are available for the Li isotope system in groundwater due to sampling difficulty. Our objective in sampling groundwater in the Bengal Plain in Bangladesh was to resolve whether the relative contribution of primary mineral dissolution and adsorption/desorption processes differs from shallow to deeper sediment depths.

This study investigated monthly δ⁷Li variations across large seasonal differences in both discharge amount and discharged chemical composition in the Ganges River’s lower reaches. We present new data for both the Brahmaputra and Meghna rivers in both dry and rainy seasons. Seasonal pattern contributes to the accurate estimation of continental Li isotope fluxes to the ocean. Moreover, the substantial submarine discharge of groundwater from the Bengal Plain also influences the global oceanic δ⁷Li composition (Bagard et al., 2015). The global Li flux of groundwater to the ocean is estimated to be ∼10% of the total riverine Li flux (Pogge von Strandmann et al., 2014; Mayfield et al., 2021), making it the second-largest terrestrial Li input after rivers. Because the δ⁷Li value of groundwater is still in need of further constraint, we also aimed to identify the factors responsible for the Li isotopic composition of groundwater.

Materials and Methods

Study Area and Materials

The Ganges River flows from the high Himalayas and joins with the Brahmaputra and Meghna Rivers in Bangladesh (Figure 1). The respective mean annual discharges of the Ganges River at the Hardinge Bridge station and the Brahmaputra River at the Bahadurabad station, near our sampling points, are 1.1 × 10⁴ and 2.0 × 10⁴ m³ s⁻¹ (Webster et al., 2010). Maximum flood discharges occur during the rainy season from June to September (Figure 2). During the Cenozoic, the Earth’s surface experienced large changes in global temperature in association with the Indo-Asia continental collision. The establishment of the world’s highest solute and sediment fluxes of this riverine system are linked to increased exhumation and chemical weathering in the Himalaya-Tibetan region. Since increased weathering fluxes of the High Himalayas and its low-lying floodplains have been linked to the ocean–atmosphere carbon inventory, a wide number of approaches have focused on estimates of chemical fluxes derived from silicate and carbonate weathering (e.g., Bickle et al., 2018).

FIGURE 2

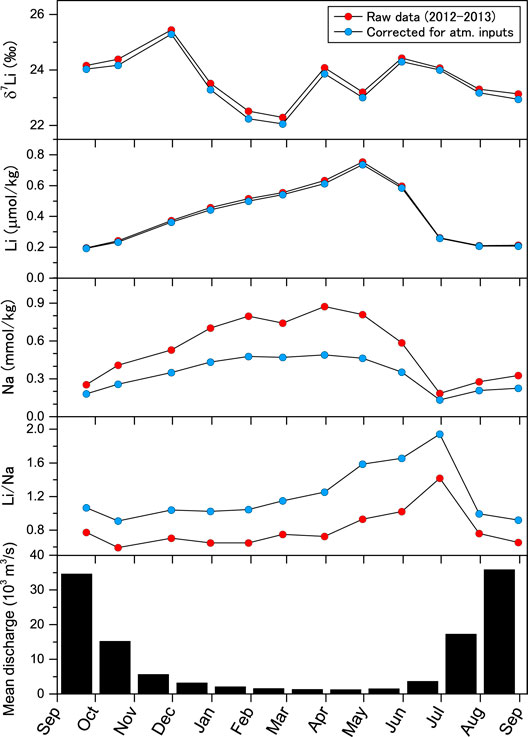
FIGURE 2. Annual variation in δ⁷Li, Li concentration, Na concentration, and the Li/Na ratio (μmol kg⁻¹/mmol kg⁻¹) of the Ganges River at the Harding Bridge, Pakshi (Figure 1) from October 2012 to August 2013. Concentration and isotopic data were corrected for atmospheric salt inputs using Li/Cl ratios. The bottom panel represents the Ganges River’s mean monthly discharge at the Harding Bridge (Mirza, 1998).

The headwaters of the Ganges and Brahmaputra rivers drain metamorphic rocks (high-grade schist, gneiss, quartzite, and carbonate rocks), felsic intrusives, and sedimentary rocks (sandstone, shale, and limestone) of Paleozoic and Mesozoic age (e.g., Heroy et al., 2003). The Brahmaputra River’s upper stream flows east across the Yarlung Tsangpo suture zone of the Tibetan Plateau, then southwest into eastern India and south to Bangladesh. The middle and lower reaches traverse widespread Pleistocene Himalayan alluvium in the middle and lower reaches. The Ganges River’s catchment is composed mainly of weathered rocks with high clay content, whereas that of the Brahmaputra River comprises less-weathered sediments (e.g., Coleman, 1969). The clay mineral assemblage in the Ganges-Brahmaputra-Meghna river system consists of illite, smectite, kaolinite, and chlorite: the Ganges sediments are more enriched in smectite formed in the lowland floodplain, and the Brahmaputra and Meghna sediments are rich in illite (Khan et al., 2019). The Meghna River drains mainly lowland deposits of Himalayan alluvium in Bangladesh. The Meghna River has the upper and lower parts divided at the confluence point with the Ganges. The upper Meghna River is small compared to the Ganges and Brahmaputra Rivers, with an average annual discharge of only 3,510 m³ s⁻¹ (Parua, 2010).

We collected river water and groundwater during dry (February 16–23) and wet (September 22–25) seasons in 2012. Mid-stream surface waters were sampled at six locations along the Ganges, Brahmaputra, and Meghna Rivers. We also collected groundwater samples from 21 wells in Bangladesh (Figure 1; Supplementary Table S1). Moreover, we conducted a monthly water sampling of the Ganges River at Pakshi from October 2012 to August 2013. Carbonate and major ion concentrations in these samples have been previously reported (Manaka et al., 2017, 2019; Yoshimura et al., 2021).

Groundwater samples were taken from 14 wells on the Bengal Plain (Figure 1; Supplementary Table S1). Based on δD, δ¹⁸O, and ³H values and ¹⁴C activity, Aggarwal et al. (2000) identified four groundwater types in Bangladesh (types I to IV with increasing depth). Their residence times range from tens of years for shallow (0–70 m) type I groundwater to several thousand years or longer for deep type III and type IV groundwater of about 3,000 and 20,000 years, respectively, (Aggarwal et al., 2000). Before groundwater sampling, each well was pumped for a while to obtain stable temperature and electrical conductivity, similar to other papers (e.g., Paul et al., 2010).

Analytical Methods

Water samples were passed through acetate membrane filters (0.45 µm pore size), then acidified with ultrapure HNO₃ (Tamapure-AA-100, Tama Chemicals, and Japan). Lithium concentrations were measured with a quadrupole inductively coupled plasma mass spectrometer (ICP-MS, iCAP Qc; Thermo Scientific, Bremen, Germany) at the Japan Agency for Marine-Earth Science and Technology. For ICP-MS analysis, water samples were diluted in polypropylene vials, then HNO₃ (0.3 M) was added to each vial. The HNO₃ used in this study was commercially supplied high-purity TAMAPURE AA-100 reagents (Tama Chemical, Japan). To control instrument drift, internal standards for Be, Sc, Y, and In were used. We measured laboratory standard solutions after every fifth sample for data correction purposes.

The water samples were evaporated to dryness in an ISO6 clean bench, and then redissolved in HNO₃. Dissolved Li in water samples was purified by ion chromatograph (Metrohm 930, Metrohm, Herisau, Switzerland) coupled to an Agilent 1,260 Infinity II (Agilent, Santa Clara, United States) with the fraction collector (IC-FC) system (Yoshimura et al., 2018; Araoka and Yoshimura, 2019). The samples were eluted through a Metrohm Metrosep C6-250/4.0 column with 8 mM ultrapure HNO₃ (TAMAPURE AA-100, Tama Chemical, and Kawasaki) at a flow rate of 0.9 ml min⁻¹. Lithium fraction was pooled in 7-ml Teflon vials (Savillex, Minnesota) and then evaporated to dryness in an ISO6 clean bench for isotope analysis. The Li isotopic composition was determined with a multiple-collector ICP-MS (NEPTUNE plus; Thermo Fisher Scientific, Waltham, United States) at the National Institute of Advanced Industrial Science and Technology, using standard sample-bracketing methods. Standards and samples were prepared as Li solutions (100 ppb) in HNO₃ (0.3 M). Sample solutions were introduced with a nebulizer (PFA MicroFlow, 100 μl min⁻¹, ESI, and Omaha) attached to a quartz dual cyclonic spray chamber operated in free aspiration mode. We performed Li isotope analysis with a standard H-skimmer cone in low-mass-resolution mode. Samples and standards were analyzed 30 times with an integration time of 4 s per cycle. Background signal intensities were determined by analyzing ultrapure HNO₃ (0.3 M) 10 times with an integration time of 4 s per cycle; baselines were subsequently subtracted from standard/sample signal intensities.

The isotopic data are calibrated using L-SVEC reference standard and reported as per mil (‰) deviations as follows:

${\delta }^7\mathrm{Li=}\left[{\left({}^{\mathrm{7}}\mathrm{L}\mathrm{i}/{}^6\mathrm{L}\mathrm{i}\right)}_{\mathrm{sample}}/{\left({}^{\mathrm{7}}\mathrm{L}\mathrm{i}/{}^6\mathrm{L}\mathrm{i}\right)}_{\mathrm{L}–\mathrm{S}\mathrm{V}\mathrm{E}\mathrm{C}}-1\right]\times 100(1)$

The analytical reproducibility was better than ±0.4‰ (2 SD) as estimated from multiple measurements of in-house standard solutions during each analytical session: 8.5 ± 0.4‰ (2 SD, n = 10) for a mono-element Li standard (Kanto Chemical Corp., Tokyo, Japan), which agrees well with the published value of 8.2 ± 0.4‰. The δ⁷Li value of the reference materials measured during the same analytical sessions was in good agreement with previously reported values for IAPSO seawater distributed by International Association for the Physical Sciences of Oceans and various rock materials distributed by the Geological Survey of Japan: andesite JA-1; basalt JB-2; granite JG-2; rhyolite JR-2 (Yoshimura et al., 2018; Araoka and Yoshimura, 2019). The δ⁷Li values of the standards measured during the same analytical sessions (JA-1 + 5.9‰; JB-2 + 4.7‰, JG-2 + 0.2‰, JR-2 + 3.9‰, and IAPSO + 31‰) agree well with the previously reported values within our analytical reproducibility of ±0.4‰ (Supplementary Table S1). To account for dilution or evaporative concentration, we normalize the Li concentration by that of Na because of its conservative behavior.

Results and Discussion

Contributions of Silicate, Carbonate, and Atmospheric Sources to Dissolved Lithium

The concentrations of Li in our river water and groundwater samples are presented in Supplementary Table S1, along with major cation and anion data reported by Manaka et al. (2017, 2019). The primary solute source is chemical weathering inputs derived from the high mountains, floodplains, and southern tributaries (Bickle et al., 2018). Additionally, solutes in the river and groundwater are derived partly from atmospheric inputs, such as rainfall and dust deposition (Millot et al., 2010a). The Li concentrations and δ⁷Li values of river water and groundwater have been corrected for the salt contribution based on the molar ratio of Li to Cl, assuming that Cl in atmospheric (rain) inputs is derived predominantly from seawater and aerosols (Li/Cl_{seawater/aerosol} = 4.7 × 10^–5, δ⁷Li = +31‰, Millot et al., 2004):

${\left[\mathrm{Li}\right]}_{\mathrm{salt}}={\left[\mathrm{Cl}\right]}_{\mathrm{river}}\times {\left[\mathrm{Li}/\mathrm{Cl}\right]}_{\mathrm{seawater}/\mathrm{aerosol}}(2)$

where [Li]_salt and [Cl]_river are dissolved Li derived from salt inputs and dissolved Cl concentrations of river water, respectively. Soil salts and evaporites (e.g., Galy et al., 1999; Galy and France-Lanord, 1999) partly affect the dissolved Li in river and groundwater, but it is challenging to estimate accurate Li concentrations and isotope ratios for these local evaporitic salts. Note that our Li/Cl correction would give maximum estimates of Li inputs from salts because Li/Cl of evaporites (∼3 × 10^–5, Dellinger et al., 2015) are generally lower than 4.7 × 10^–5. The asterisk sign for chemical compositions, such as Li/Na^* and δ⁷Li^*, denotes the Cl-corrected value (Supplementary Table S1; Figures 2, 3). The respective atmospheric contribution to Li concentrations and δ⁷Li are generally minor: <3.5% and <0.2‰ for the Ganges River, <0.5% and <0.1‰ for the Brahmaputra River, <5% and <0.4‰ for the Meghna River, and generally less than 1% and 0.2‰ for the groundwater samples (Supplementary Table S1).

FIGURE 3

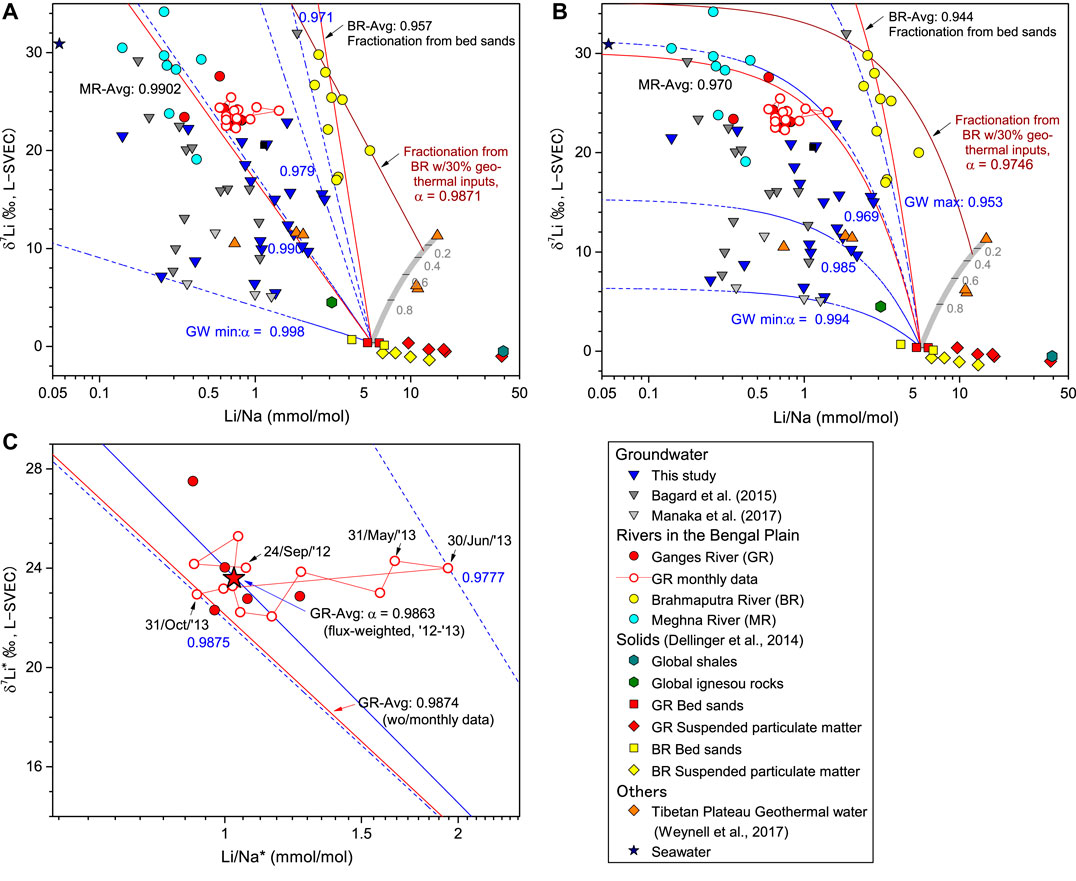
FIGURE 3. Relationships between the Li/Na ratio (μmol kg⁻¹/mmol kg⁻¹) and the δ⁷Li in the Ganges-Brahmaputra-Meghna rivers and groundwater in Bangladesh from this study and previous studies (A) Rayleigh-type and (B) batch-type fractionation from the starting composition of the average bed-sands value in the Ganges and Brahmaputra rivers (Li/Na = 5.6, δ⁷Li = 0.39‰, (Dellinger et al., 2014). Blue dashed lines are maximum, intermediate, and minimum fractionation curves for groundwaters in Bangladesh. Black solid lines are fractionation curves through the average compositions of the Brahmaputra and Meghna rivers, respectively. Gray lines represent binary mixing between silicate and geothermal sources as the starting composition of the Brahmaputra River (C) The Li concentrations and δ⁷Li values of the monthly changes in Ganges River water corrected for the atmospheric contribution. Dashed lines are the maximum and minimum Rayleigh fractionation lines for monthly change. A red line connects monthly data, and a red star is the discharge-weighted mean δ⁷Li and Li/Na compositions.

Lithium in the dissolved load is mainly sourced from silicate weathering (Ksakurek et al., 2005; Bagard et al., 2015; Manaka et al., 2017). Other weathering sources are generally estimated to contribute a minor fraction. Even in river catchments dominated by carbonate rocks, most dissolved Li in rivers is derived from silicate minerals (Kısakűrek et al., 2005). Bengal Basin sediments are mainly composed of very fine to fine siliciclastic sands with silt and clay (Aggarwal et al., 2000; Lupker et al., 2012) but contain primary and secondary carbonates. By adopting the Li/Ca ratio of 1.5 × 10^–5 of limestone (Millot et al., 2010b), the proportions of dissolved Li from carbonate weathering are estimated to be <5% of the total Li budget for the Ganges River, <2% for the Brahmaputra River, <5% for the Meghna River, and generally less than 1% for the groundwater samples (Supplementary Table S1). Although the modern marine core-top carbonates (calcite) have a narrow range with an average δ⁷Li composition of about +25% (Pogge von Strandmann et al., 2019), correction for carbonate inputs has not been adopted because sedimentary and metamorphic carbonates potentially have a wide range of δ⁷Li compositions (Hathorne and James, 2006; Misra and Froelich, 2012; Dellinger et al., 2018). Given that the proportions of carbonate inputs are similar to those from atmospheric inputs, the impact of carbonate weathering on δ⁷Li values of river and groundwater is considered to be less than the analytical reproducibility of this study (±0.4‰), however.

The Ganges and Brahmaputra rivers arise on the Himalayan–Tibetan Plateau, a region of active physical erosion, where dissolved Li is initially sourced from weathering of sedimentary (e.g., shale), igneous, and high-grade metamorphic silicate rocks (Dellinger et al., 2014). The δ⁷Li and Li/Na values of the bed-sands and suspended particulate matter were previously reported by Dellinger et al. (2014), and riverine bed-sands represent a mixture of unweathered fragments of silicate rocks. The δ⁷Li and Li/Na ratios of bed-sands in the Ganges and Brahmaputra rivers clustered in relatively uniform average values of 0.39‰ and 5.62 mmol/mol, respectively, (Figures 3A,B). Both bed-sands of these rivers plot slightly outside the range of binary mixing between the global igneous and shale sources due to the loss of Li during high-grade metamorphism of the High Himalaya Crystalline Series (Dellinger et al., 2014). The silicate Li in the Ganges and Brahmaputra Rivers have a similar δ⁷Li and Li/Na ratio. Thus, the bed-sands indicate a well-defined primary silicate Li source, rather independent of drainage area. In the following sections, we apply an approach used by Pogge von Strandmann et al. (2017) to address the sensitivity of δ⁷Li to the extent of Li uptake by secondary minerals from the Himalayan Li sources using Rayleigh fractionation (Eq. 3) and open type Batch fractionation (Eq. 4, Dellinger et al., 2015; Pogge von Strandmann et al., 2017):

${\delta }^7\mathrm{L}{\mathrm{i}}_{\mathrm{W}}={\delta }^7\mathrm{L}{\mathrm{i}}_{\mathrm{0}}+1000\left(\mathrm{\alpha -1}\right)\mathrm{In}\left({\mathrm{f}}_{\mathrm{W}}^{\mathrm{Li}}\right)(3)$

${\delta }^7\mathrm{L}{\mathrm{i}}_{\mathrm{W}}={\delta }^7\mathrm{L}{\mathrm{i}}_{\mathrm{0}}+1000\left(\mathrm{\alpha -1}\right)\left(\mathrm{1}-{\mathrm{f}}_{\mathrm{W}}^{\mathrm{Li}}\right)(4)$

where δ⁷Li_w and δ⁷Li₀ are the Li isotopic composition of river waters and their initial values; α is the fractionation factor between the dissolved Li and secondary minerals; ${\text{f}}_{\text{w}}^{\text{Li}}$ is the fraction of Li remining in the water.

A process-related fractionation of Li isotope ratios and mixing of isotopically distinct end-members could both explain the behavior of Li isotopic compositions and ${\text{f}}_{\text{w}}^{\text{Li}}$. The Rayleigh fractionation trend is shown in Figure 3A, and some main tributaries of the Amazon River basins (Dellinger et al., 2015) have also been tested by fractionation and mixing processes. Their observed data is consistent with isotope fractionation processes occurring during weathering. In the case of the Ganges River, the Li data from the headwater to 2000 km downstream of the Ganges River basically follow isotope fractionation processes, rather than mixing (Pogge von Strandmann et al., 2017). To evaluate the influence of end-member mixing for the Ganges–Brahmaputra–Meghna drainage basin within Bangladesh (Figure 3A), we used our δ⁷Li data and previously published ⁸⁷Sr/⁸⁶Sr values of the same samples (Figure 4B). The ⁸⁷Sr/⁸⁶Sr of the Meghna and more than half of the groundwater which drains only the Bengal Plain is distinctly lower than that of the Ganges and Brahmaputra Rivers. This suggests that the floodplain weathering processes exert a strong influence on inputs of solutes, and there is a small influence from redistribution and mixing of waters from the mountains. Moreover, three groundwater exhibit broadly similar ⁸⁷Sr/⁸⁶Sr values to that of the Ganges River, but have significantly lower δ⁷Li values (>10‰) compared to the Ganges River. The radiogenic ⁸⁷Sr/⁸⁶Sr are likely due to the dissolution of the Himalayan-derived sediments. Still, the low δ⁷Li values suggest that its silicate weathering process differs from the river samples and is more congruent. Overall, the mixing processes have little influence on the δ⁷Li compositions of the rivers and groundwater samples, and therefore Li isotope fractionation in Figure 3 will be discussed in the following section.

FIGURE 4

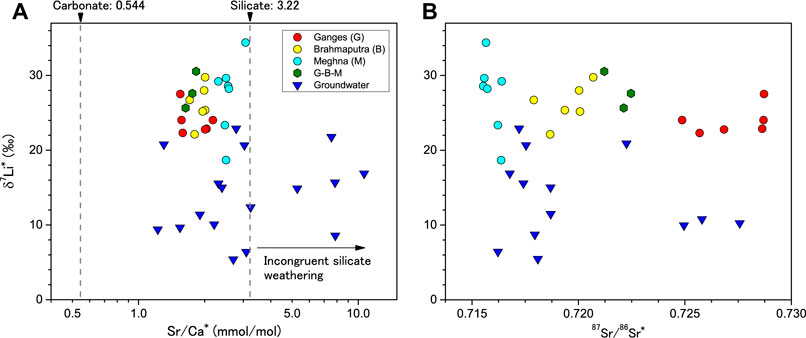
FIGURE 4. Correlations between (A) δ⁷Li and Sr/Ca and (B) δ⁷Li and ⁸⁷Sr/⁸⁶Sr of the Ganges, Brahmaputra, and Meghna rivers and groundwater in the Bengal Plain. Dashed lines represent the mean Sr/Ca values of silicate (3.22 mmol/mol) and carbonate (0.544 mmol/mol) weathering inputs in the Ganges River (Bickle et al., 2018). Incongruent dissolution and sorting effects of silicate materials results in the high Sr/Ca ratios of the silicate fractions of bedload (Yoshimura et al., 2021).

Monthly Variation in Dissolved Li in the Ganges River

The Ganges rivers show large seasonal variations in their discharge and chemical composition due to differences in relative fractions of chemical weathering inputs derived from the high mountains, floodplain, and southern tributaries (Bickle et al., 2018). An important question is whether the seasonal weathering inputs, being linked to hydrological cycles and water residence time (Liu et al., 2015), from these different sources (Henchiri et al., 2016) have a relationship with Li isotope systematics. Then the discharge-weighted mean δ⁷Li and Li/Na compositions will be calculated. The rivers and groundwater have different chemical compositions. In the ternary diagram of major cations, the water samples from the Ganges and Brahmaputra rivers, representing Himalayan weathering sources, have higher Ca and Mg concentrations than those from the upper Meghna River (Figure 5). Compared to the river water, the chemical compositions of groundwater, predominantly reflecting floodplain weathering in the Bengal Plain, vary widely, especially in the shallow groundwater. Groundwater tends to show high Na and K contents, suggesting that silicate weathering influences water chemistry more strongly than carbonate weathering (Yoshimura et al., 2021).

FIGURE 5

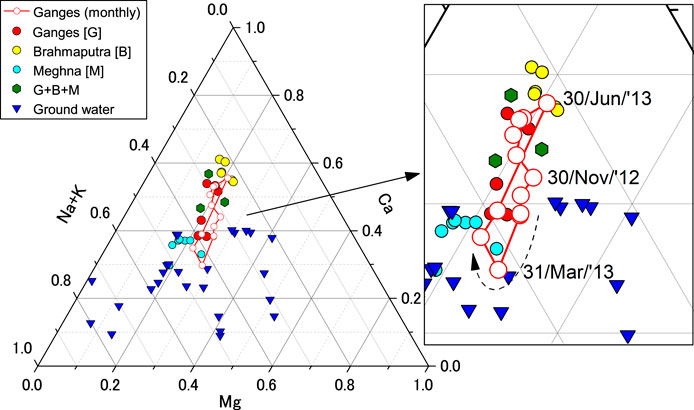
FIGURE 5. Ternary diagram showing the relative proportion of major cations for monthly river water and groundwater samples alongside previously published values (Manaka et al., 2017; Manaka et al., 2019; Yoshimura et al., 2021). A red open symbol with a line represents the Ganges River’s monthly water samples at Pakshi from October 2012 to August 2013. “G + B + M” indicates the sample from the lower Meghna River, below its confluence with the Ganges–Brahmaputra river system.

The Ganges River’s monthly samples showed that both Li and Na concentrations in the Ganges River initially increased from September 2012 to May 2013 (the end of the dry season). Both concentrations decrease rapidly from June to August 2013, accompanying a marked increase in the Li/Na ratio, from ∼0.7 to 1.4 μmol kg⁻¹/mmol, kg⁻¹ and precipitation (Figure 2). Most element concentrations were higher in the dry season (October to June) than in the wet season (June to September), simply because of the dilution by monsoon rainfall. The ternary diagram showed that the marked shift of the major cation compositions at the start of the monsoon increased the fraction of cations derived from Himalayan catchments. Conversely, the March sample (ZDB-6, Supplementary Table S1) exhibits the highest proportion of Na and K (Figure 5), indicating the maximum contribution of cations deriving from floodplain weathering. These cations are potentially derived from the dissolution of floodplain soil salts, but their inputs probably occur at the initial stage of the rainy season, accompanying higher precipitation. Regardless of the large seasonal changes in water chemistry, the temporal changes in δ⁷Li apparently did not show a clear trend, ranging from 22.3 to 25.4‰ (Figures 2, 6). The plot of δ⁷Li and Li/Na did not exhibit a linear relationship, suggesting that δ⁷Li values cannot be explained solely by binary mixing of distinct Li sources, such as the upper Ganges, southern rivers, and lowland floodplain sources. The dissolved δ⁷Li of the Congo River mouth is negatively correlated to discharge due to the mixing of waters from two contrasting continental weathering regimes (Henchiri et al., 2016). In contrast, the lack of source mixing is consistent with lower dissolved δ⁷Li values in the uppermost 500 km of the Ganges headwaters, reaching a constant steady-state value downstream 2,000 km of the Ganges mouth (Pogge von Strandmann et al., 2017).

FIGURE 6

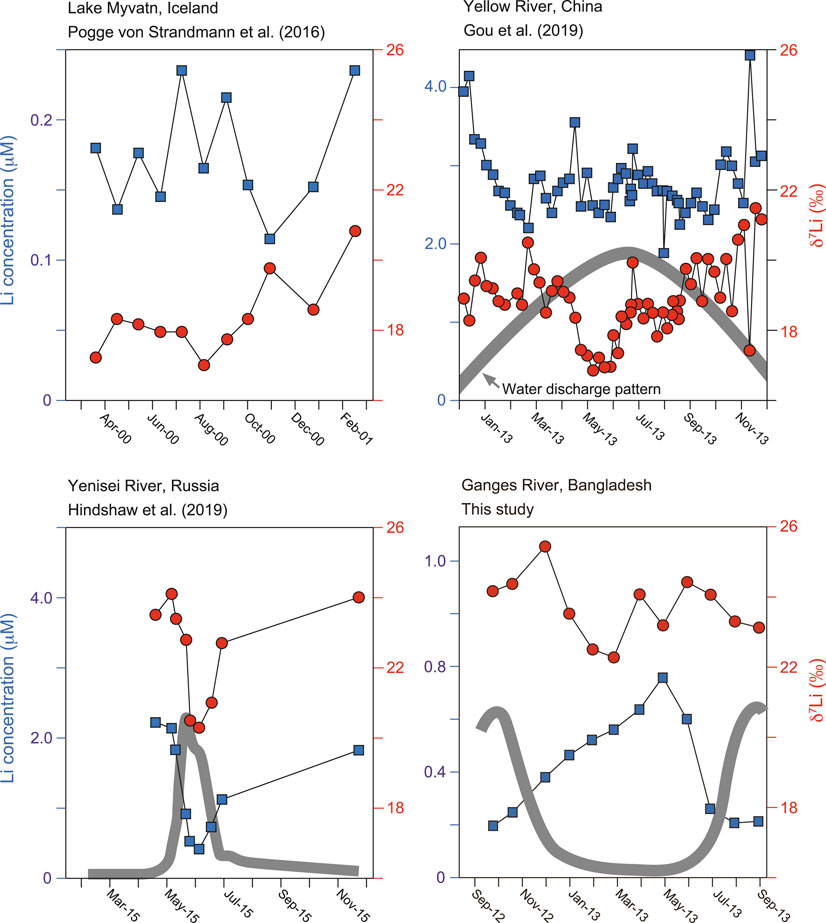
FIGURE 6. The monthly/weekly time series of dissolved Li of river water samples. Compilation of δ⁷Li values from Pogge von Strandmann et al. (2016), Gou et al. (2019), Hindshaw et al. (2019b) and this study.

Secondary mineral fractionation exerts a dominant influence over lithological controls. Preferential uptake of ⁶Li by secondary minerals has been reported to contribute to downstream δ⁷Li changes (Vigier et al., 2009; Wang et al., 2015). The δ⁷Li values for the Ganges River show an apparent, progressive increase from the upper reaches in the Himalaya-Tibetan region to the Bengal Basin (Huh et al., 1998; Kisakurek et al., 2005; Bagard et al., 2015; Manaka et al., 2017; Pogge von Strandmann et al., 2017). The downstream evolution of δ⁷Li in the Ganges River is described by Rayleigh fractionation with a fractionation factor of 0.996–0.980 (Bagard et al., 2015; Manaka et al., 2017; Pogge von Strandmann et al., 2017). The discharge-weighted mean δ⁷Li^* and Li/Na^* compositions calculated from monthly values give α values of 0.986 for Rayleigh fractionation. This value is mostly consistent with the median α value of 0.988 for previously published rain-corrected data of the Ganges samples (Pogge von Strandmann et al., 2017). The batch fractionation model results in lower α value of close to 0.97 (Figure 3B), which is lower than typical experimentally determined mineral(rock)-fluid fractionation factors for Li (Penniston-Dorland et al., 2017) and is also lower than the lowest α value of the clay structural (octahedral) site of 0.9790 ± 0.0011 (Hindshaw et al., 2019a). The Rayleigh model is largely consistent with the experimentally calculated α value for one of the abundant clay minerals in the Ganges River, smectite, at a lower temperature (0.983 for 25°C and 0.981 for 0°C, (Vigier et al., 2008)). Thus, we speculate that Li isotope systematics in this river system is best explained by the Rayleigh-type fractionation, thus dissolved Li is isolated from, and not interacting with, secondary precipitates after their precipitation. A previous study reported that the δ⁷Li values for the Ganges and Brahmaputra Rivers are lower in the rainy season than in the dry season (Manaka et al., 2017), but our monthly data demonstrate that seasonal changes in δ⁷Li, especially from the start of the rainy season to maximum discharge (May–July), would not reflect solely the fractions of ⁶Li removed to secondary minerals. Instead, this isotopic excursion in a plot of δ⁷Li^* and Li/Na^* (Figure 3C) can be best attributed to the Li source with the lowest fractionation factor α of ∼0.977 at the start of the rainy season (the sample of 30/June/’13, Figure 3C) with a corresponding increase in the relative proportion of major cations from Himalayan weathering (Figure 5). This means that different net fractionation factors expressed seasonally, because of different water/Li sources. Alternatively, assuming that SPMs partly contribute as the starting composition, the α value for 30/June/’13 tends towards lower with increasing SPMs contribution (Supplementary Figure S1) because the α value of 0.977 is quite low. The clay mineral assemblage in the Bengal Plain’s river system consists of illite, smectite, kaolinite, and chlorite, and the Ganges riverine sediments are more enriched in smectite formed in the lowland floodplain (Khan et al., 2019). Therefore, it is plausible that the different clay mineralogy being formed in the low-temperature chemical weathering of the Himalayan catchments, as well as the temperature dependence of fractionation factor (Vigier et al., 2008), links to the lower α values at around the start of the monsoon season. However, considering the monthly Li fluxes, their impact on the net Li isotope fluxes is limited. The α value of the total riverine supply of Li from the Ganges to the oceans is relatively constant at around 0.986–0.988. Therefore, floodplain weathering plays a dominant role in the downstream evolution of river water chemistry and contributes a significant fraction of the dissolved Li fluxes to the ocean. Our discharge-weighted average δ⁷Li^* value of 23.6 ± 0.1‰ is similar to the range of 21 ± 1.6‰ across the 2000 km upstream of the Ganges river mouth (Pogge von Strandmann et al., 2017). A slightly higher δ⁷Li for our samples collected at lower reaches probably reflects additional fractionated Li inputs by floodplain weathering.

Figure 6 is a compilation of the monthly/weekly variation in dissolved δ⁷Li. The ranges of seasonal fluctuations are 3.7‰ for the Lake Myvatn (Iceland, Pogge von Strandmann et al., 2016), 4.6‰ for the Yellow River (China, Gou et al., 2019), 3.8‰ for the Yenisei River (Russia, Hindshaw et al., 2019b) and 3.2‰ for the Ganges River (This study). The similar magnitude of δ⁷Li fluctuation (3.7‰) have been reported in the outlet glacier of the Greenland Ice Sheet over a sub-weekly time series during the melt season (Hindshaw et al., 2019c). Therefore, accurate estimates of average δ⁷Li and [Li⁺] compositions of rivers and lakes are better calculated from multiple samples for each important hydrological regime to cancel out any sampling bias. However, it is clear that monthly dissolved δ⁷Li and [Li⁺] are unaffected by biological productivity changes (Pogge von Strandmann et al., 2016).

The Difference Between the Ganges, Brahmaputra, and Meghna Rivers

A plot of δ⁷Li vs. Li/Na for water samples and bedload can be a good indicator to differentiate influences of primary sources and secondary minerals (Figure 3). As previously discussed, the Li source and isotopic fractionation behavior for the Ganges River are within the previous studies range. They mainly reflect the ratio of silicate dissolution, represented by the bed-sands (Dellinger et al., 2014), relative to secondary mineral formation. The values of δ⁷Li and Li/Na of the upper Meghna River, which drains only the Bengal Plain, lie on the Ganges River’s fractionation lines, but dissolved Li become more fractionated from the starting composition in both Rayleigh and Batch fractionation (Figures 3A,B). The reactive-transport modelling predicted that both Batch (equilibrium) and Rayleigh fractionation processes potentially control the riverine isotopic composition of the Amazon (Maffre et al., 2020) and Alaknanda River (the upper part of the Ganges headwaters, Bohlin and Bickle., 2019) basins. Different fractionation behavior relates to bedrock types and mountain/floodplain regions, i.e., weathering regimes, until the Li fractionation reachs the steady state values (Pogge von Strandmann et al., 2017). Weathering in floodplains contributes significantly to the total chemical fluxes (Bickle et al., 2018). Secondary mineral formation in low altitude plains makes a dominant contribution to the δ⁷Li signature of the Ganges River (Pogge von Strandmann et al., 2017). The solutes in low altitude plains are derived mainly from in-situ floodplain weathering of sediments and not from a redistribution of waters from the mountains (Bickle et al., 2018). Compared to the Ganges River, which has headwaters extending the high-denudation mountain areas, more fractionated Li in the Meghna River thus is interpreted as the lower ratio of primary mineral dissolution relative to the secondary mineral formation in the Bengal Plain. A similar observation has been reported during the incorporation of silicon into secondary solids with a greater influence on dissolved Si uptake by secondary minerals in alluvial plains rather than mountain catchments (Frings et al., 2015).

In contrast to the similarities of fractionation behavior between the Ganges and Meghna rivers, the Brahmaputra River differs in Li isotope systematics. The Brahmaputra River’s Li/Na values are significantly higher, while the δ⁷Li values were similar to the Ganges and Meghna rivers. The Ganges sediment is composed mainly of weathered sedimentary and volcanic rocks with high clay content. Contrastingly, the Brahmaputra sediment is composed of less-weathered coarser sediments (e.g., Coleman, 1969). Higher Li/Na of the Brahmaputra River is consistent with less Li uptake by secondary minerals. Because the bed-sands of the Brahmaputra River have values close to the δ⁷Li and Li/Na ratio to the Ganges River (Dellinger et al., 2014), the difference in dissolved Li cannot be attributed to the different isotope signatures of primary silicate sources. Even if Li isotopic systematics are described simply by open/closed type fractionation from bed-sands, the apparent fractionation factors will have very low values of 0.957 for Rayleigh and 0.944 for Batch fractionation (Figures 3A,B). The sedimentary constraints make it difficult to argue for these low α values by clay mineralogy: Khan et al. (2019) showed that the clay mineral assemblage in the Ganges, Brahmaputra, and Meghna rivers dominantly consists of illite, smectite, kaolinite, and chlorite; the distribution patterns of the clay mineral assemblages are similar between Brahmaputra and Meghna rivers. Moreover, the d-excess of the Brahmaputra River samples (12.9‰) fall within the range of the Nepalese rivers (Yoshimura et al., 2021), suggesting that the Brahmaputra River carries water and solutes derived predominantly from upstream precipitation and snow/glacial melts from the high-elevation mountains and is less affected by discharge from the low altitude floodplain. Therefore, it is unlikely the Li isotope composition of the Brahmaputra River is a result of secondary mineral formation, and hence isotope fractionation, occurring dominantly in low altitude floodplains.

Interestingly, some Brahmaputra River data exhibit a linear relationship in a logarithmic plot of δ⁷Li and Li/Na (Figures 3A,B), apparently attributing to a Rayleigh-type behavior with a starting composition of higher δ⁷Li and Li/Na values than bed-sands. It is, therefore, possible that an additional source is required to produce the δ⁷Li data. Previous studies have shown that the lake and stream waters in the Ganges headwaters (Bickle et al., 2005) and in the eastern Tibetan Plateau receive significant trace element inputs from geothermal waters (Weynell et al., 2017, 2021). Continental geothermal waters are highly enriched in lithium (from 0.3 to 10 ppm), and δ⁷Li values are relatively low (1.0–17.1‰, Tomascak, 2004; Araoka et al., 2014). The average δ⁷Li of the geothermal water in the northeast Tibetan Plateau is ∼11‰, in good agreement with the starting composition expected from the apparent Rayleigh-type fractionation line (Figure 3A). Assuming that the average of geothermal fluid is assigned as the end-member composition (δ⁷Li = 11.3‰, Li/Na = 14.8 mmol/mol, Weynell et al., 2017), the plausible fractionation could result from the 7:3 mixing between a congruent dissolution of bed-sands and geothermal water (δ⁷Li = 9.8‰, and Li/Na = 12.1 mmol/mol, Figures 3A,B). Liu et al. (2011) and Ma et al. (2020) reported that the Li budgets in the upper reaches of the Changjiang and Mekong rivers are significantly affected by evaporite sources. Evaporites have relatively lower Li/Na (about 2–4 mmol/mol) and δ⁷Li (about 8‰, Liu et al., 2011) compared to geothermal waters (Weynell et al., 2017) and cannot be assigned as a starting composition of the Brahmaputra River (Figure 3). This supports the importance of geothermal waters as a Li source to the Brahmaputra River, requiring a best-fit Rayleigh fractionation factor (α) of 0.987 (Figure 3A), which is well within the range of α values for the major world rivers (0.998–0.985) and for the Ganges River (0.995–0.980) which has a median α of 0.988 (Δ⁷Li = −13‰, Pogge von Strandmann et al., 2017).

The Li concentrations of geothermal waters in the eastern Tibetan region are approximately 20–110 times higher than that of the ambient stream waters (Weynell et al., 2017). The magnitude of Li enrichment is in good agreement with the typical ranges of dissolved Li concentrations for rivers (0.001 ppb to <0.023 ppm) and for continental geothermal fluids (0.3–10 ppm, Araoka et al., 2014). Hot springs and evaporite weathering provide more than 50% of all Na⁺ in some stream systems in southern Tibet. The chemical denudation rates of major cations (Na, Ca, Mg, and K) derived from hot springs in the upper Brahmaputra River is generally <2% of the total cation flux, but some streams in the middle Yarlung Tsangpo may exceed 15% (Hren et al., 2007). Therefore, the expected range of geothermal Li inputs from this cation flux is reasonably consistent with the author’s estimates of the Brahmaputra’s starting Li composition. The geothermal inputs and dissolution of silicate rocks are considered to be the primary Li sources of the Brahmaputra River. These primary sources later evolve to fractionated values by Li incorporation into secondary minerals. This additional source can be used to describe the Li budget of major rivers, and their tributaries, draining the Tibetan Plateau.

Depth Variation of δ⁷Li in Groundwater

Lithium concentrations (0.3–3.0 μmol kg⁻¹) were much higher in the groundwater, and Li/Na values in groundwater almost encompassed the entire measured range (Figure 7). The δ⁷Li values (5.5–22.9‰) were generally lower but highly variable compared to the river water (Supplementary Table S1). Four types of groundwater in Bangladesh were previously distinguished based on their distinct δD, δ¹⁸O, d-excess, ³H values, and ¹⁴C activity (Aggarwal et al., 2000; Yoshimura et al., 2021). Shallow type I and II groundwaters (depths down to 70–100 m) are recharged regularly and have residence times of tens to hundreds of years. Deep type III (70–240 m) and IV (>240 m) groundwaters are isolated from surface waters and have residence times of about 3,000 years and 20,000 years, respectively. Type II groundwater is found mainly in the nearshore area with high salinity (Aggarwal et al., 2000), and GDB12-20 only has high Na and Cl concentrations in our shallow groundwater samples. For the [Li⁺] of this sample, the salt contribution based on the Li/Cl ratio gives 70.7% (Supplementary Table S1). The δ⁷Li^* of this type II sample is −1.5‰ (rain-uncorrected value of 21.5‰), a value close to those of bed-sands (0.1–0.7‰) and suspended particulate matter (−1.4–0.3‰) of the Ganges and Brahmaputra rivers (Dellinger et al., 2014). However, a rainwater correction of groundwaters is not typical, making it difficult to evaluate the Li source for this sample.

FIGURE 7

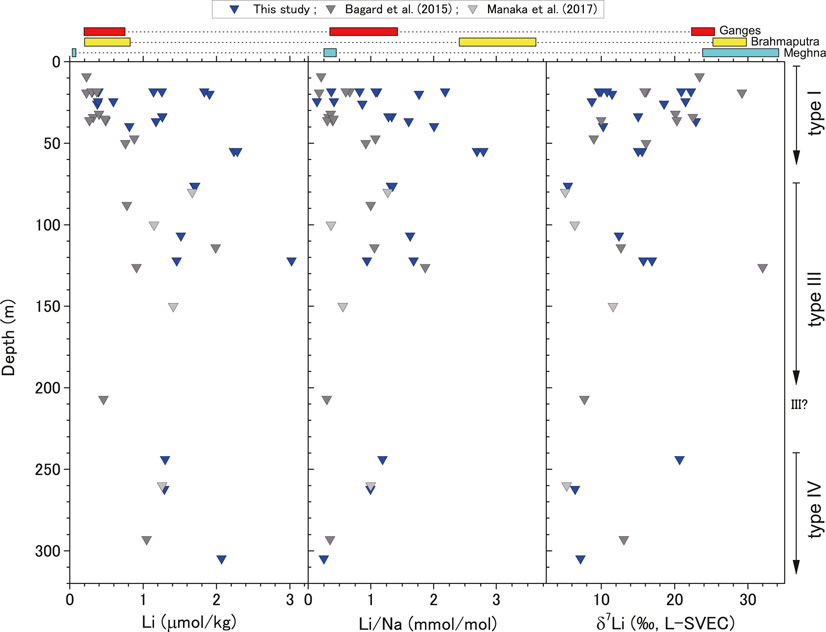
FIGURE 7. Depth profiles of Li concentration, Li/Na ratio (μmol kg⁻¹/mmol kg⁻¹), and δ⁷Li for groundwater samples. Grey triangles represent data from Bagard et al. (2015) and Manaka et al. (2017). The red, yellow, and light blue squares at the top show ranges for the Ganges, Brahmaputra, and Meghna rivers in the Bengal Plain, respectively. We only compare river data from the Bengal Plain, not from upstream sites, to groundwater.

The large scatter in d-excess, ⁸⁷Sr/⁸⁶Sr ratios, and δ⁸⁸Sr of the groundwater samples have previously been reported (Yoshimura et al., 2021). Each isotopic composition is affected by the different degrees of evapotranspiration and local-scale heterogeneity of water-sediment reactions. Considerable variability in dissolved δ⁷Li values is also observed, especially in shallow type I groundwaters of the Bengal Plain. First, it is essential to evaluate the influence of sedimentary Li sources. The Sr/Ca ratios of waters and solids provide a means to differentiate weathering and sediment heterogeneity effects of silicate materials on the river and ground waters (Jacobson et al., 2002; Bickle et al., 2018; Yoshimura et al., 2021). The Sr/Ca ratios give well-defined average compositions for the silicate (3.22 mmol/mol) and carbonate (0.544 mmol/mol) sources of the Ganges River floodplain. This contrasts with the silicate fractions of floodplain river bedloads and sediments which have much higher Sr/Ca ratios (Bickle et al., 2018; Yoshimura et al., 2021), most likely due to incongruent dissolution (e.g., a significant depletion of plagioclase) and sorting effects of silicate materials (Bickle et al., 2018; Lupker et al., 2012). The Ganges, Brahmaputra, and Meghna river waters and more than a half of groundwater samples all plot within the range of binary mixing between silicate and carbonate Sr/Ca sources (Yoshimura et al., 2021). Some groundwater samples have rain-corrected Sr/Ca ratios (Sr/Ca*) higher than the silicate value of 3.22 mmol/mol (Figure 4), suggesting that sediment heterogeneity is apparent at the local scale, implying a significant variation in the Li/Na of silicate material. The ⁸⁷Sr/⁸⁶Sr of the Bengal Plain waters are primarily controlled by three-component mixing of the floodplain weathering, the Himalayan weathering, and seawater sources (Yoshimura et al., 2021). The last seawater source, including atmospheric inputs, has already been subtracted by Cl concentrations. High ⁸⁷Sr/⁸⁶Sr values reflect radiogenic Sr in dolomite and silicate minerals such as K-feldspar and mica. However, no significant correlations of δ⁷Li^* with Sr/Ca^*, and ⁸⁷Sr/⁸⁶Sr have been identified in our groundwater samples. Therefore, preferential dissolution of certain silicate minerals and different hydrological sources, i.e., redistribution of waters from the Ganges and Brahmaputra rivers vs. in-situ floodplain weathering, are unlikely to explain the high δ⁷Li variability for the shallow groundwater.

The shallow groundwater samples displayed no spatial and depth trends that likely reflect local heterogeneities in mineral compositions and different degrees of chemical interaction between groundwater and sediment. The δ⁷Li values for shallow groundwater have been explained by Li incorporation into floodplain sediments following a Rayleigh fractionation process (Bagard et al., 2015). In the plot of δ⁷Li-Li/Na (Figure 3), the considerable variation found in shallow groundwater is also due in part to surface waters, which are regularly replenished from local rain and floodwaters at timescales of tens to hundreds of years. The chemical weathering in shallow groundwater at this time scale is caused by the local variability of kinetically limited dissolution of minerals. The weathering proceeds in a non-steady-state and weathering-limited regime.

The δ⁷Li depth profile (Figure 7) shows that deeper groundwater below 70 m exhibited the lowest values of <8‰. These values are consistent with those from previous studies: δ⁷Li values in shallow groundwater ranged from 10.0 to 29.8‰ with an average of 21.6‰ (Bagard et al., 2015). We showed a more detailed depth profile and confirmed that the δ⁷Li values converged with increasing depth to a narrow range at depths below 70 m, with deep groundwater exhibiting more negative values, i.e., 5.1–11.6‰ (Bagard et al., 2015; Manaka et al., 2017), regardless of the sampling position across the Bengal Basin (Figure 1). For deep groundwater, where water residence times are long (about 3,000 years for type III to 20,000 years for type IV), samples show lower δ⁷Li values, suggesting more congruent dissolution of silicate minerals rather than becoming progressively higher δ⁷Li with increasing time.

Similar to the rivers, we adopt the average value of bed-sands of the Ganges and Brahmaputra river (Dellinger et al., 2014) (Li/Na = 5.6 μmol kg⁻¹/mmol kg⁻¹ and δ⁷Li = 0.39‰) as the starting composition for groundwaters (Pogge von Strandmann et al., 2017). In the deep groundwater sample with the lowest δ⁷Li (Figure 7), we obtained a minimum estimate for α of 0.998 (Figure 3). The magnitude of fractionation is lower than those for the rivers in the Bengal Basin and other major world rivers (e.g., 0.991 for the Amazon River (Dellinger et al., 2015)). Previous studies have reported fractionation factors between fluid and solid phases in various primary and secondary minerals: 0.986 for gibbsite (Pistiner and Henderson, 2003); 0.997 for saprolites (Rudnick et al., 2004); and 0.999 for illite (Millot and Girard, 2007). Taking into account that alluvium sediments contain various types of secondary and clay minerals (Sarin et al., 1989; Huyghe et al., 2011), plausible explanations for low δ⁷Li values in deep groundwater include congruent isotope leaching and silicate mineral dissolution in the deep aquifer (Bagard et al., 2015). Note that Li-bearing secondary minerals contain two isotopically distinct reservoirs: 1) structural Li with fractionation factors of −14 to −24‰ and 2) exchangeable Li of 0 to −12‰ (Hindshaw et al., 2019a; Pogge von Strandmann et al., 2020), with the net isotope fractionation representing a mixture of these two reservoirs. The referenced α values correspond to the latter, which has a lower fractionation factor than clay neoformation. Therefore, clay neoformation may not play a role in controlling deep groundwater Li systematics.

Since a given secondary mineral should impose a set fractionation factor, another explanation for the low δ⁷Li values is that fractionation mechanism switches from Rayleigh to Batch-type fractionation, which imposes lower isotopic compositions (Figures 3A,B). These two fractionation types are likely competing in natural processes. Generally, high interaction times should promote chemical and isotope equilibrium between groundwater and secondary phase assemblage, which excludes the possibility of unidirectional processes. Note that the groundwater tends to have lower δ⁷Li values than the values calculated by Batch fractionation with a median α value of 0.988 (Δ⁷Li = −13‰) for the Ganges River (Pogge von Strandmann et al., 2017), indicating primary mineral dissolution exerts a strong influence on the δ⁷Li composition, especially in deeper groundwater. Alternatively, at different reaction and exchange rates, it is possible that chemical equilibrium and low net reaction rates allow for an equilibrium isotope fractionation, which might be different in magnitude than kinetic effects associated with a net forward or backward reaction (DePaolo, 2011). It can be expected that the Li exchange rates between the dissolved Li and the ambient sediments for the types III and IV groundwater are far slower than in the laboratory experiments. In this case, the apparent isotope fractionation factor for deep groundwater might be a higher value than those accessed by laboratory experiments (Fantle and DePaolo, 2007; DePaolo, 2011).

Shallow groundwater is recharged regularly and has a residence time of tens to hundreds of years (Aggarwal et al., 2000). The residence time at deep groundwater depths of 100–300 m is more than several thousand years (Aggarwal et al., 2000). Thus, the reaction period with ambient sediments is 10²–10³ times longer for deep groundwater than shallow groundwater. Elevated Na and Si concentrations were reported for deep groundwater compared with those for shallow groundwater samples (Bagard et al., 2015; Manaka et al., 2017), suggesting more substantial dissolution of silicate minerals. Similar isotopic behavior has been observed for the ⁸⁷Sr/⁸⁶Sr and δ⁸⁸Sr values of the same samples with a wide variation at shallow depths and convergence to a narrow range close to those of the carbonate fraction and the bulk silicate Earth at depths greater than 70 m (Yoshimura et al., 2021). This convergence reflects the strong chemical interactions between groundwater and ambient sediments which appear to promote more congruent weathering (Figure 7). Although δ⁸⁸Sr values would not solely reflect silicate weathering, the depth changes in both δ⁸⁸Sr and δ⁷Li suggest more congruent silicate weathering. Therefore, they are less affected by preferential uptake of ⁶Li and ⁸⁶Sr by secondary minerals. Thus, deep groundwater appears to have experienced more congruent weathering in terms of its Li isotopic signature owing to the longer residence time. Isotopic fractionation by secondary minerals does occur in shallow groundwater where it is recharged regularly, maintaining lower δ⁷Li values than the river waters.

Influence of the Ganges-Brahmaputra-Meghna Rivers System on the Oceanic Li Budget

Weathering in the low-altitude plains makes a vital contribution to the oceanic element budget via surface and submarine groundwater discharges. For example, according to the volumetric groundwater discharge and concentration-weighted Sr flux to the ocean, the global Sr flux via groundwater discharge is estimated to be a few tens of percent of the total continental Sr flux (Beck et al., 2013). This flux is the second-largest input of Sr to the ocean after riverine flux. Estimates of the global average Sr concentration of groundwater are approximately 2.4–5.8 times higher than the estimated global river discharge (Beck et al., 2013). Moreover, Georg et al. (2009) reported that the dissolved Si concentration in groundwater samples of the Bengal Basin is 2–3 times higher than in river samples taken during the dry season. The Si flux by groundwater is 40% of the total (the combined Ganges–Brahmaputra Rivers and groundwater) annual Si flux to the Bay of Bengal.

Similarly, the groundwater samples are generally enriched in Li with an average value of 1.399 mmol/kg. This is 5.5 times higher than the discharge-weighted average [Li⁺] of the Ganges River (0.255 mmol/kg). Therefore, the groundwater Li flux from the Bengal Plain may reach a few tens of percent of the riverine Li flux. A fundamental shift in weathering regimes in groundwater Li fluxes and isotopic composition may have contributed to fluctuation in the oceanic δ⁷Li evolution over geologic time. The longer residence time of groundwater corresponds to a low hydraulic gradient in low-relief early Cenozoic-type weathering conditions that are thought to enhance secondary mineral formation resulting in higher dissolved δ⁷Li values for the simulated period of 100 years (Wanner et al., 2014). Our evidence suggests that the residence time of groundwater is a critical control on Li isotope systematics in a floodplain, leading deep groundwater to more congruent weathering.

Increases in erosion driven by the Cenozoic uplift of the Himalaya-Tibetan Plateau could have enhanced denudation and silicate weathering on the continents. Another process associated with the collisional orogeny of the Himalayas is degassing and geothermal activities. Geothermal fluids exert influence on the Li isotopic signature of surface waters on the Tibetan Plateau (Hren et al., 2007; Weynell et al., 2017, 2021). If the δ⁷Li composition of the Brahmaputra River is not accompanied by geothermal inputs, the isotopic composition of dissolved Li without geothermal inputs can be calculated assuming that (1) the same amount of Li is removed into secondary minerals (${\text{f}}_{\text{w}}^{\text{Li}}$ = 0.28), i.e., same weathering intensity, and (2) the starting composition is the bed-sands’ value. Calculated δ⁷Li without geothermal inputs (16.8‰) is well below the Brahmaputra River’s modern average (26.2‰). The former assumption may be oversimplification, but Li budgets in large river systems would be in a steady-state when their flow lengths increase to a certain extent, as previously mentioned for the Ganges River (Pogge von Strandmann et al., 2017).

Mass balance calculations suggest that the approximate proportions of dissolved and particulate Li exported by Himalayan river water and sediments are 1:1 for the western Tibetan Plateau. In contrast, the proportion is 1:5 for the northeastern Tibetan plateau due to higher annual precipitation and an erosion-dominated weathering regime in this area (Weynell et al., 2021). Therefore, the Brahmaputra headwaters’ geothermal Li is also retained in clays and then delivered to the oceans as particulate matter. An increase in a flux of dissolved and particulate Li from the Brahmaputra River resulting from uplift of the Himalayan Tibetan Plateau is proposed to accompany additional geothermal δ⁷Li to the ocean with a starting composition around 9‰ higher than the silicate materials originated from volcanic, metamorphic, and sedimentary rocks (Dellinger et al., 2014). It has been proposed that enhanced secondary mineral formation with mountain uplift is responsible for the 9‰ increase in the seawater δ⁷Li from the early Cenozoic to the present (Misra and Froelich, 2012). Given that δ⁷Li flux from the Ganges River was more or less constant, once the length of the river reached more than 500 km (Pogge von Strandmann et al., 2017), it is questionable whether the observed increase in δ⁷Li directly reflects CO₂ drawdown by silicate weathering accompanying Cenozoic orogeny. In addition to previously proposed processes, such as the increased size of the floodplain (Pogge von Strandmann and Henderson, 2015) and changes in the seawater Li sinks (Li and West, 2014), the enhanced geothermal Li inputs by Himalayan uplift may have contributed partly to the change in the riverine δ⁷Li signature, and ultimately to the oceanic δ⁷Li mass balance. Given the δ⁷Li of geothermal waters (Millot et al., 2010c; Pogge von Strandmann et al., 2016), a higher geothermal input to the rivers might counteract the Cenozoic δ⁷Li rise. This suggests that the past Li cycle needs to be reconsidered to maintain δ⁷Li mass balance tightly linked to silicate weathering intensity.

Conclusions

We investigated the δ⁷Li composition of river waters and groundwater of the Ganges-Brahmaputra–Meghna river system in Bangladesh. In the Ganges River, water samples collected monthly at the same location from September 2012 to August 2013 showed that δ⁷Li values did not show a clear seasonal trend, suggesting that the relative contribution of primary mineral dissolution and secondary mineral formation is in a steady state. However, the gradual change in Li/Na and the relative proportion of major cations indicate significant influence from Himalayan weathering, especially at the start of the monsoon season. The δ⁷Li values of the Meghna River, which mainly drains the Bengal Plain, generally lie on the fractionation line of the Ganges River. For the Brahmaputra River, the δ⁷Li values indicate mixing of silicate-derived Li components with dissolved Li sourced from geothermal waters, both later fractionated by preferential uptake of ⁶Li into secondary minerals. The groundwater samples varied widely in composition, displayed no spatial trends, and generally have lower δ⁷Li values than the surface waters. Both δ⁷Li and Li/Na values of the groundwater samples shallower than 70 m depth were highly scattered, and low δ⁷Li values (<8‰) were observed mainly at depths between 70 and 310 m regardless of the sampling region. Shallow groundwater is recharged regularly and has residence times of tens to hundreds of years. In contrast, deep groundwater does not receive recharge from local rain and floodwaters, with residence time of about 3,000 to 20,000 years. The isotopic difference between groundwater depths reflects the higher magnitudes of net silicate dissolution with greater chemical interactions between groundwater and ambient sediments owing to the longer residence time of deeper groundwater. A switch from Rayleigh- to Batch-type isotope fractionation may impose the lower δ⁷Li values in deep groundwater. It can be expected that the longer residence time of groundwater in low-relief weathering conditions leads groundwater to low δ⁷Li values. The calculated δ⁷Li of the Brahmaputra River without geothermal inputs is well below the modern average, suggesting that enhanced geothermal Li inputs accompanying Himalayan uplift may be partly responsible for the changes in the seawater δ⁷Li during the Cenozoic.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

TY and DA contributed to the conception of the study. Samples were collected by TY, HK, DA, and ZH. TY and DA performed the isotopic analysis. TY wrote the first draft of the article with input from NO, and DA. All authors contributed to article revision, read, and approved the submitted version.

Funding

This study was supported by the Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research to Toshihiro Yoshimura (16H05883, 19K21908) and Daisuke Araoka (16K21682).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We express our deep appreciation for Dr. Pogge von Strandmann, Dr. Viers and reviewers’ constructive and insightful comments on an early draft and this article; Takuya Manaka and Atsushi Suzuki help in water sampling and inorganic carbon analysis; Yoshiko Yoshikawa for laboratory assistance; and to Metrohm Japan for their technical support. The suggestions of Adam D. Sproson greatly improved the language. All data used in this article are available from the corresponding author.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.668757/full#supplementary-material

References

Aggarwal, P. K., Basu, A. R., Poreda, R. J., Kulkarni, K., Froehlich, K., Tarafdar, S., et al. (2000). A Report on Isotope Hydrology of Groundwater in Bangladesh: Implications for Characterization and Mitigation of Arsenic in Groundwater. International atomic energy agency-TC project BGD/8/016, 5.

Google Scholar

Araoka, D., Kawahata, H., Takagi, T., Watanabe, Y., Nishimura, K., and Nishio, Y. (2014). Lithium and Strontium Isotopic Systematics in Playas in Nevada, USA: Constraints on the Origin of Lithium. Miner Deposita 49, 371–379. doi:10.1007/s00126-013-0495-y

CrossRef Full Text | Google Scholar

Araoka, D., and Yoshimura, T. (2019). Rapid Purification of Alkali and Alkaline-Earth Elements for Isotope Analysis (δ⁷Li, δ²⁶Mg, ⁸⁷Sr/⁸⁶Sr, and δ⁸⁸Sr) of Rock Samples Using Borate Fusion Followed by Ion Chromatography with a Fraction Collector System. Anal. Sci. 35, 751–757. doi:10.2116/analsci.18p509

PubMed Abstract | CrossRef Full Text | Google Scholar

Bagard, M.-L., West, A. J., Newman, K., and Basu, A. R. (2015). Lithium Isotope Fractionation in the Ganges-Brahmaputra Floodplain and Implications for Groundwater Impact on Seawater Isotopic Composition. Earth Planet. Sci. Lett. 432, 404–414. doi:10.1016/j.epsl.2015.08.036

CrossRef Full Text | Google Scholar

Beck, A. J., Charette, M. A., Cochran, J. K., Gonneea, M. E., and Peucker-Ehrenbrink, B. (2013). Dissolved Strontium in the Subterranean Estuary - Implications for the marine Strontium Isotope Budget. Geochim. Cosmochim. Acta 117, 33–52. doi:10.1016/j.gca.2013.03.021

CrossRef Full Text | Google Scholar

Bickle, M. J., Chapman, H. J., Bunbury, J., Harris, N. B. W., Fairchild, I. J., Ahmad, T., et al. (2005). Relative Contributions of Silicate and Carbonate Rocks to Riverine Sr Fluxes in the Headwaters of the Ganges. Geochim. Cosmochim. Acta 69, 2221–2240. doi:10.1016/j.gca.2004.11.019

CrossRef Full Text | Google Scholar

Bickle, M. J., Chapman, H. J., Tipper, E., Galy, A., De La Rocha, C. L., and Ahmad, T. (2018). Chemical Weathering Outputs from the Flood plain of the Ganga. Geochim. Cosmochim. Acta 225, 146–175. doi:10.1016/j.gca.2018.01.003

CrossRef Full Text | Google Scholar

Bohlin, M. S., and Bickle, M. J. (2019). The Reactive Transport of Li as a Monitor of Weathering Processes in Kinetically Limited Weathering Regimes. Earth Planet. Sci. Lett. 511, 233–243. doi:10.1016/j.epsl.2019.01.034

CrossRef Full Text | Google Scholar

Bouchez, J., Von Blanckenburg, F., and Schuessler, J. A. (2013). Modeling Novel Stable Isotope Ratios in the Weathering Zone. Am. J. Sci. 313, 267–308. doi:10.2475/04.2013.01

CrossRef Full Text | Google Scholar

Caves Rugenstein, J. K., Ibarra, D. E., and von Blanckenburg, F. (2019). Neogene Cooling Driven by Land Surface Reactivity rather Than Increased Weathering Fluxes. Nature 571 (7763), 99–102. doi:10.1038/s41586-019-1332-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Coleman, J. M. (1969). Brahmaputra River: Channel Processes and Sedimentation. Sediment. Geology. 3, 129–239. doi:10.1016/0037-0738(69)90010-4

CrossRef Full Text | Google Scholar

Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Galy, V., Hilton, R. G., et al. (2014). Lithium Isotopes in Large Rivers Reveal the Cannibalistic Nature of Modern continental Weathering and Erosion. Earth Planet. Sci. Lett. 401, 359–372. doi:10.1016/j.epsl.2014.05.061

CrossRef Full Text | Google Scholar

Dellinger, M., Gaillardet, J., Bouchez, J., Calmels, D., Louvat, P., Dosseto, A., et al. (2015). Riverine Li Isotope Fractionation in the Amazon River basin Controlled by the Weathering Regimes. Geochim. Cosmochim. Acta 164, 71–93. doi:10.1016/j.gca.2015.04.042

CrossRef Full Text | Google Scholar

Dellinger, M., West, A. J., Paris, G., Adkins, J. F., Pogge Von Strandmann, P. A. E., Ullmann, C. V., et al. (2018). The Li Isotope Composition of marine Biogenic Carbonates: Patterns and Mechanisms. Geochim. Cosmochim. Acta 236, 315–335. doi:10.1016/j.gca.2018.03.014

CrossRef Full Text | Google Scholar

DePaolo, D. J. (2011). Surface Kinetic Model for Isotopic and Trace Element Fractionation during Precipitation of Calcite from Aqueous Solutions. Geochim. Cosmochim. Acta 75 (4), 1039–1056. doi:10.1016/j.gca.2010.11.020

CrossRef Full Text | Google Scholar

Fantle, M. S., and DePaolo, D. J. (2007). Ca Isotopes in Carbonate Sediment and Pore Fluid from ODP Site 807A: The Ca²⁺(aq)-Calcite Equilibrium Fractionation Factor and Calcite Recrystallization Rates in Pleistocene Sediments. Geochim. Cosmochim. Acta 71, 2524–2546. doi:10.1016/j.gca.2007.03.006

CrossRef Full Text | Google Scholar

Frings, P. J., Clymans, W., Fontorbe, G., Gray, W., Chakrapani, G. J., and Conley, D. J. (2015). Silicate Weathering in the Ganges Alluvial Plain. Earth Planet. Sci. Lett. 427, 136–148.

CrossRef Full Text | Google Scholar

Galy, A., France-Lanord, C., and Derry, L. A. (1999). The Strontium Isotopic Budget of Himalayan Rivers in Nepal and Bangladesh. Geochim. Cosmochim. Acta 63, 1905–1925. doi:10.1016/s0016-7037(99)00081-2

CrossRef Full Text | Google Scholar

Galy, A., and France-Lanord, C. (1999). Weathering Processes in the Ganges-Brahmaputra basin and the Riverine Alkalinity Budget. Chem. Geol. 159, 31–60. doi:10.1016/s0009-2541(99)00033-9

CrossRef Full Text | Google Scholar

Georg, R. B., West, A. J., Basu, A. R., and Halliday, A. N. (2009). Silicon Fluxes and Isotope Composition of Direct Groundwater Discharge into the Bay of Bengal and the Effect on the Global Ocean Silicon Isotope Budget. Earth Planet. Sci. Lett. 283 (1-4), 67–74. doi:10.1016/j.epsl.2009.03.041

CrossRef Full Text | Google Scholar

Gou, L.-F., Jin, Z., Pogge von Strandmann, P. A. E., Li, G., Qu, Y.-X., Xiao, J., et al. (2019). Li Isotopes in the Middle Yellow River: Seasonal Variability, Sources and Fractionation. Geochim. Cosmochim. Acta 248, 88–108. doi:10.1016/j.gca.2019.01.007

CrossRef Full Text | Google Scholar

Hathorne, E., and James, R. (2006). Temporal Record of Lithium in Seawater: A Tracer for Silicate Weathering? Earth Planet. Sci. Lett. 246, 393–406. doi:10.1016/j.epsl.2006.04.020

CrossRef Full Text | Google Scholar

Henchiri, S., Gaillardet, J., Dellinger, M., Bouchez, J., and Spencer, R. G. (2016). Riverine dissolved lithium isotopic signatures in low-relief central Africa and their link to weathering regimes. Geophys. Res. Lett. 43, 4391–4399.

CrossRef Full Text | Google Scholar

Heroy, D. C., Kuehl, S. A., and Goodbred, S. L. (2003). Mineralogy of the Ganges and Brahmaputra Rivers: Implications for River Switching and Late Quaternary Climate Change. Sediment. Geol. 155, 343–359. doi:10.1016/s0037-0738(02)00186-0

CrossRef Full Text | Google Scholar

Hindshaw, R. S., Rickli, J., and Leuthold, J. (2019c). Mg and Li Stable Isotope Ratios of Rocks, Minerals, and Water in an Outlet Glacier of the Greenland Ice Sheet. Front. Earth Sci. 7, 316. doi:10.3389/feart.2019.00316

CrossRef Full Text | Google Scholar

Hindshaw, R. S., Teisserenc, R., Le Dantec, T., and Tananaev, N. (2019b). Seasonal Change of Geochemical Sources and Processes in the Yenisei River: A Sr, Mg and Li Isotope Study. Geochim. Cosmochim. Acta 255, 222–236. doi:10.1016/j.gca.2019.04.015

CrossRef Full Text | Google Scholar

Hindshaw, R. S., Tosca, R., Goût, T. L., Farnan, I., Tosca, N. J., and Tipper, E. T. (2019a). Experimental Constraints on Li Isotope Fractionation during clay Formation. Geochim. Cosmochim. Acta 250, 219–237. doi:10.1016/j.gca.2019.02.015

CrossRef Full Text | Google Scholar

Hoorn, C., Wesselingh, F. P., Ter Steege, H., Bermudez, M. A., Mora, A., Sevink, J., et al. (2010). Amazonia through Time: Andean Uplift, Climate Change, Landscape Evolution, and Biodiversity. Science 330, 927–931. doi:10.1126/science.1194585

PubMed Abstract | CrossRef Full Text | Google Scholar

Hren, M. T., Chamberlain, C. P., Hilley, G. E., Blisniuk, P. M., and Bookhagen, B. (2007). Major Ion Chemistry of the Yarlung Tsangpo-Brahmaputra River: Chemical Weathering, Erosion, and CO₂ Consumption in the Southern Tibetan Plateau and Eastern Syntaxis of the Himalaya. Geochim. Cosmochim. Acta 71 (12), 2907–2935. doi:10.1016/j.gca.2007.03.021

CrossRef Full Text | Google Scholar

Huh, Y., Chan, L.-H., Zhang, L., and Edmond, J. M. (1998). Lithium and its Isotopes in Major World Rivers: Implications for Weathering and the Oceanic Budget. Geochim. Cosmochim. Acta 62, 2039–2051. doi:10.1016/s0016-7037(98)00126-4

CrossRef Full Text | Google Scholar

Huyghe, P., Guilbaud, R., Bernet, M., Galy, A., and Gajurel, A. P. (2011). Significance of the clay mineral Distribution in Fluvial Sediments of the Neogene to Recent Himalayan Foreland Basin (West-central Nepal). Basin Res. 23, 332–345. doi:10.1111/j.1365-2117.2010.00485.x

CrossRef Full Text | Google Scholar

Jacobson, A. D., Blum, J. D., Chamberlain, C. P., Poage, M. A., and Sloan, V. F. (2002). Ca/Sr and Sr Isotope Systematics of a Himalayan Glacial Chronosequence: Carbonate versus Silicate Weathering Rates as a Function of Landscape Surface Age. Geochim. Cosmochim. Acta 66, 13–27. doi:10.1016/s0016-7037(01)00755-4

CrossRef Full Text | Google Scholar

Khan, M. H. R., Liu, J., Liu, S., Seddique, A. A., Cao, L., and Rahman, A. (2019). Clay mineral Compositions in Surface Sediments of the Ganges-Brahmaputra-Meghna River System of Bengal Basin, Bangladesh. Mar. Geol. 412, 27–36. doi:10.1016/j.margeo.2019.03.007

CrossRef Full Text | Google Scholar

Kısakűrek, B., James, R. H., and Harris, N. B. W. (2005). Li and δ⁷Li in Himalayan Rivers: Proxies for Silicate Weathering?. Earth Planet. Sci. Lett. 237, 387–401.

Google Scholar

Li, G., and West, A. J. (2014). Evolution of Cenozoic Seawater Lithium Isotopes: Coupling of Global Denudation Regime and Shifting Seawater Sinks. Earth Planet. Sci. Lett. 401, 284–293. doi:10.1016/j.epsl.2014.06.011

CrossRef Full Text | Google Scholar

Liu, C.-Q., Zhao, Z.-Q., Wang, Q., and Gao, B. (2011). Isotope Compositions of Dissolved Lithium in the Rivers Jinshajiang, Lancangjiang, and Nujiang: Implications for Weathering in Qinghai-Tibet Plateau. Appl. Geochem. 26, S357–S359. doi:10.1016/j.apgeochem.2011.03.059

CrossRef Full Text | Google Scholar

Liu, X.-M., Wanner, C., Rudnick, R. L., and Mcdonough, W. F. (2015). Processes Controlling δ⁷Li in Rivers Illuminated by Study of Streams and Groundwaters Draining Basalts. Earth Planet. Sci. Lett. 409, 212–224. doi:10.1016/j.epsl.2014.10.032

CrossRef Full Text | Google Scholar

Lupker, M., France-Lanord, C., Galy, V., Lavé, J., Gaillardet, J., Gajurel, A. P., et al. (2012). Predominant Floodplain over Mountain Weathering of Himalayan Sediments (Ganga basin). Geochim. Cosmochim. Acta 84, 410–432. doi:10.1016/j.gca.2012.02.001

CrossRef Full Text | Google Scholar

Ma, T., Weynell, M., Li, S.-L., Liu, Y., Chetelat, B., Zhong, J., et al. (2020). Lithium Isotope Compositions of the Yangtze River Headwaters: Weathering in High-Relief Catchments. Geochim. Cosmochim. Acta 280, 46–65. doi:10.1016/j.gca.2020.03.029

CrossRef Full Text | Google Scholar

Maffre, P., Goddéris, Y., Vigier, N., Moquet, J.-S., and Carretier, S. (2020). Modelling the Riverine δ⁷Li Variability throughout the Amazon Basin. Chem. Geol. 532, 119336. doi:10.1016/j.chemgeo.2019.119336

CrossRef Full Text | Google Scholar

Manaka, T., Araoka, D., Yoshimura, T., Hossain, H. M. Z., Nishio, Y., Suzuki, A., et al. (2017). Downstream and Seasonal Changes of Lithium Isotope Ratios in the Ganges‐Brahmaputra River System. Geochem. Geophys. Geosyst. 18, 3003–3015. doi:10.1002/2016gc006738

CrossRef Full Text | Google Scholar

Manaka, T., Hossain, H. M. Z., Yoshimura, T., Suzuki, A., and Kawahata, H. (2019). Monthly Changes in pCO₂ in the Ganges River: Implications for Carbon Release from Soil to the Atmosphere via Inland Waters. J. Agric. Meteorol. 75, 47–55. doi:10.2480/agrmet.d-18-00007

CrossRef Full Text | Google Scholar

Mayfield, K. K., Eisenhauer, A., Ramos, D. P. S., Higgins, J. A., Horner, T. J., Auro, M., et al. (2021). Groundwater discharge impacts marine isotope budgets of Li, Mg, Ca, Sr, and Ba. Nat. Commun. 12, 1–9.

PubMed Abstract | CrossRef Full Text | Google Scholar

Milliman, J. D., and Syvitski, J. P. M. (1992). Geomorphic/tectonic Control of Sediment Discharge to the Ocean: the Importance of Small Mountainous Rivers. J. Geol. 100, 525–544. doi:10.1086/629606

CrossRef Full Text | Google Scholar

Millot, R., and Girard, J. P. (2007). "Lithium Isotope Fractionation during Adsorption onto mineral Surfaces", in: International Meeting on Clays in Natural & Engineered Barriers for Radioactive Waste Confinement, 17-21 September 2007, 307–308.

Google Scholar

Millot, R., Guerrot, C., Innocent, C., Négrel, P., and Sanjuan, B. (2011). Chemical, Multi-Isotopic (Li-B-Sr-U-H-O) and thermal Characterization of Triassic Formation Waters from the Paris Basin. Chem. Geol. 283, 226–241. doi:10.1016/j.chemgeo.2011.01.020

CrossRef Full Text | Google Scholar

Millot, R., Guerrot, C., and Vigier, N. (2004). Accurate and High-Precision Measurement of Lithium Isotopes in Two Reference Materials by MC-ICP-MS. Geostand Geoanalyt Res. 28, 153–159. doi:10.1111/j.1751-908x.2004.tb01052.x

CrossRef Full Text | Google Scholar

Millot, R., Petelet-Giraud, E., Guerrot, C., and Négrel, P. (2010a). Multi-isotopic Composition (δ⁷Li-Δ¹¹B-ΔD-Δ¹⁸O) of Rainwaters in France: Origin and Spatio-Temporal Characterization. Appl. Geochem. 25, 1510–1524. doi:10.1016/j.apgeochem.2010.08.002

CrossRef Full Text | Google Scholar

Millot, R., Vigier, N., and Gaillardet, J. (2010b). Behaviour of Lithium and its Isotopes during Weathering in the Mackenzie Basin, Canada. Geochim. Cosmochim. Acta 74, 3897–3912. doi:10.1016/j.gca.2010.04.025

CrossRef Full Text | Google Scholar

Millot, R., Scaillet, B., and Sanjuan, B. (2010c). Lithium isotopes in island arc geothermal systems: Guadeloupe, Martinique (French West Indies) and experimental approach. Geochim. Cosmochim. Acta 74, 1852–1871.

CrossRef Full Text | Google Scholar

Mirza, M. M. Q. (1998). Diversion of the Ganges Water at Farakka and its Effects on Salinity in Bangladesh. Environ. Manag. 22, 711–722. doi:10.1007/s002679900141

PubMed Abstract | CrossRef Full Text | Google Scholar

Misra, S., and Froelich, P. N. (2012). Lithium Isotope History of Cenozoic Seawater: Changes in Silicate Weathering and Reverse Weathering. Science 335, 818–823. doi:10.1126/science.1214697

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishio, Y., Okamura, K., Tanimizu, M., Ishikawa, T., and Sano, Y. (2010). Lithium and Strontium Isotopic Systematics of Waters Around Ontake Volcano, Japan: Implications for Deep-Seated Fluids and Earthquake Swarms. Earth Planet. Sci. Lett. 297, 567–576. doi:10.1016/j.epsl.2010.07.008

CrossRef Full Text | Google Scholar

Parua, P. K. (2010). The Ganga: Water Use in the Indian Subcontinent. (Berlin, Germany: Springer).

Paul, M., Reisberg, L., Vigier, N., Zheng, Y., Ahmed, K. M., Charlet, L., et al. (2010). Dissolved Osmium in Bengal plain Groundwater: Implications for the marine Os Budget. Geochim. Cosmochim. Acta 74, 3432–3448. doi:10.1016/j.gca.2010.02.034

CrossRef Full Text | Google Scholar

Penniston-Dorland, S., Liu, X.-M., and Rudnick, R. L. (2017). Lithium Isotope Geochemistry. Rev. Mineral. Geochem. 82, 165–217. doi:10.2138/rmg.2017.82.6

CrossRef Full Text | Google Scholar

Pistiner, J. S., and Henderson, G. M. (2003). Lithium-isotope Fractionation during continental Weathering Processes. Earth Planet. Sci. Lett. 214, 327–339. doi:10.1016/s0012-821x(03)00348-0

CrossRef Full Text | Google Scholar

Pogge Von Strandmann, P. A. E., Burton, K. W., Opfergelt, S., Eiríksdóttir, E. S., Murphy, M. J., Einarsson, A., et al. (2016). The Effect of Hydrothermal spring Weathering Processes and Primary Productivity on Lithium Isotopes: Lake Myvatn, Iceland. Chem. Geol. 445, 4–13. doi:10.1016/j.chemgeo.2016.02.026

CrossRef Full Text | Google Scholar

Pogge Von Strandmann, P. A. E., Frings, P. J., and Murphy, M. J. (2017). Lithium Isotope Behaviour during Weathering in the Ganges Alluvial Plain. Geochim. Cosmochim. Acta 198, 17–31. doi:10.1016/j.gca.2016.11.017

CrossRef Full Text | Google Scholar

Pogge Von Strandmann, P. A. E., and Henderson, G. M. (2015). The Li Isotope Response to Mountain Uplift. Geology 43, 67–70. doi:10.1130/g36162.1

CrossRef Full Text | Google Scholar

Pogge Von Strandmann, P. A. E., Porcelli, D., James, R. H., Van Calsteren, P., Schaefer, B., Cartwright, I., et al. (2014). Chemical Weathering Processes in the Great Artesian Basin: Evidence from Lithium and Silicon Isotopes. Earth Planet. Sci. Lett. 406, 24–36. doi:10.1016/j.epsl.2014.09.014

CrossRef Full Text | Google Scholar

Pogge Von Strandmann, P. A. E., Schmidt, D. N., Planavsky, N. J., Wei, G., Todd, C. L., and Baumann, K.-H. (2019). Assessing Bulk Carbonates as Archives for Seawater Li Isotope Ratios. Chem. Geol. 530. doi:10.1016/j.chemgeo.2019.119338

CrossRef Full Text | Google Scholar

Rudnick, R. L., Tomascak, P. B., Njo, H. B., and Gardner, L. R. (2004). Extreme Lithium Isotopic Fractionation during continental Weathering Revealed in Saprolites from South Carolina. Chem. Geol. 212, 45–57. doi:10.1016/j.chemgeo.2004.08.008

CrossRef Full Text | Google Scholar

Sarin, M. M., Krishnaswami, S., Dilli, K., Somayajulu, B. L. K., and Moore, W. S. (1989). Major Ion Chemistry of the Ganga-Brahmaputra River System: Weathering Processes and Fluxes to the Bay of Bengal. Geochim. Cosmochim. Acta 53, 997–1009. doi:10.1016/0016-7037(89)90205-6

CrossRef Full Text | Google Scholar

Sauzéat, L., Rudnick, R. L., Chauvel, C., Garçon, M., and Tang, M. (2015). New Perspectives on the Li Isotopic Composition of the Upper continental Crust and its Weathering Signature. Earth Planet. Sci. Lett. 428, 181–192. doi:10.1016/j.epsl.2015.07.032

CrossRef Full Text | Google Scholar

Teng, F.-Z., Mcdonough, W. F., Rudnick, R. L., Dalpé, C., Tomascak, P. B., Chappell, B. W., et al. (2004). Lithium Isotopic Composition and Concentration of the Upper continental Crust. Geochim. Cosmochim. Acta 68, 4167–4178. doi:10.1016/j.gca.2004.03.031

CrossRef Full Text | Google Scholar

Tipper, E., Galy, A., and Bickle, M. (2006). Riverine Evidence for a Fractionated Reservoir of Ca and Mg on the Continents: Implications for the Oceanic Ca Cycle. Earth Planet. Sci. Lett. 247, 267–279. doi:10.1016/j.epsl.2006.04.033

CrossRef Full Text | Google Scholar

Tomascak, P. B. (2004). Developments in the Understanding and Application of Lithium Isotopes in the Earth and Planetary Sciences. Rev. Mineral. Geochem. 55, 153–195. doi:10.2138/gsrmg.55.1.153

CrossRef Full Text | Google Scholar

Vigier, N., Decarreau, A., Millot, R., Carignan, J., Petit, S., and France-Lanord, C. (2008). Quantifying Li Isotope Fractionation during Smectite Formation and Implications for the Li Cycle. Geochim. Cosmochim. Acta 72, 780–792. doi:10.1016/j.gca.2007.11.011

CrossRef Full Text | Google Scholar

Vigier, N., Gislason, S. R., Burton, K. W., Millot, R., and Mokadem, F. (2009). The Relationship between Riverine Lithium Isotope Composition and Silicate Weathering Rates in Iceland. Earth Planet. Sci. Lett. 287, 434–441. doi:10.1016/j.epsl.2009.08.026

CrossRef Full Text | Google Scholar

von Strandmann, P. A. E. P., Kasemann, S. A., and Wimpenny, J. B. (2020). Lithium and Lithium Isotopes in Earth's Surface Cycles. Elements 16 (4), 253–258. doi:10.2138/gselements.16.4.253

CrossRef Full Text | Google Scholar

Wang, Q.-L., Chetelat, B., Zhao, Z.-Q., Ding, H., Li, S.-L., Wang, B.-L., et al. (2015). Behavior of Lithium Isotopes in the Changjiang River System: Sources Effects and Response to Weathering and Erosion. Geochim. Cosmochim. Acta 151, 117–132. doi:10.1016/j.gca.2014.12.015

CrossRef Full Text | Google Scholar

Wanner, C., Sonnenthal, E. L., and Liu, X.-M. (2014). Seawater δ⁷Li: A Direct Proxy for Global CO₂ Consumption by Continental Silicate Weathering?. Chem. Geol. 381, 154–167. doi:10.1016/j.chemgeo.2014.05.005

CrossRef Full Text | Google Scholar

Washington, K. E., West, A. J., Kalderon-Asael, B., Katchinoff, J. A., Stevenson, E. I., and Planavsky, N. J. (2020). Lithium isotope composition of modern and fossilized Cenozoic brachiopods. Geology 48, 1058–1061.

CrossRef Full Text | Google Scholar

Webster, P. J., Jian, J., Hopson, T. M., Hoyos, C. D., Agudelo, P. A., Chang, H.-R., et al. (2010). Extended-range Probabilistic Forecasts of Ganges and Brahmaputra Floods in Bangladesh. Bull. Amer. Meteorol. Soc. 91, 1493–1514. doi:10.1175/2010bams2911.1

CrossRef Full Text | Google Scholar

Weynell, M., Wiechert, U., and Schuessler, J. A. (2021). Lithium Isotope Signatures of Weathering in the Hyper-Arid Climate of the Western Tibetan Plateau. Geochim. Cosmochim. Acta 293, 205–223. doi:10.1016/j.gca.2020.10.021

CrossRef Full Text | Google Scholar

Weynell, M., Wiechert, U., and Schuessler, J. A. (2017). Lithium Isotopes and Implications on Chemical Weathering in the Catchment of Lake Donggi Cona, Northeastern Tibetan Plateau. Geochim. Cosmochim. Acta 213, 155–177. doi:10.1016/j.gca.2017.06.026

CrossRef Full Text | Google Scholar

Yoshimura, T., Araoka, D., Tamenori, Y., Kuroda, J., Kawahata, H., and Ohkouchi, N. (2018). Lithium, Magnesium and Sulfur Purification from Seawater Using an Ion Chromatograph with a Fraction Collector System for Stable Isotope Measurements. J. Chromatogr. A 1531, 157–162. doi:10.1016/j.chroma.2017.11.052

CrossRef Full Text | Google Scholar

Yoshimura, T., Wakaki, S., Kawahata, H., Hossain, H. M. Z., Suzuki, A., Ishikawa, T., et al. (2021). Stable Strontium Isotopic Compositions of River Water, Groundwater and Sediments from the Ganges–Brahmaputra–Meghna River System in Bangladesh. Front. Earth Sci. 9, 592062. doi:10.3389/feart.2021.592062

CrossRef Full Text | Google Scholar