Calculation Model to Predict the Static Armor Layer Size Distribution After the Reconstruction of a Gravel River Bed

The size distribution of armor layer in mountain rivers is an important factor that affects the stability of the river bed. However, there are relatively few studies on the prediction of armor layer size distribution in the reconstruction process after the previous static armor layer becomes unstable. In response to the above challenges, this study considers the incipient probability of sediment particles as the starting point, and comprehensively considers the coupling relationship between the initial bed materials, bed structure, armor ratio, and flow intensity, using a simple calculation model for predicting the static armor layer size distribution after reconstruction of a gravel-river bed. This paper introduces the concept of critical incipient particle size $D_c$, and considers that sediment particles smaller than $D_c$ will incipient easily, resulting in a higher probability of being washed out, whereas the incipient probability of sediment particles larger than $D_c$ (this part of the large-particle sediment includes not only the original particles on the bed surface, but also the large sediment particles exposed by the erosion of the bed subsurface) is relatively small. At the same time, this model also uses the armor ratio to reflect the impact of the bed surface structure. This study cites data from five sets of laboratory flume experiments to verify the calculation model, and the experimental results show that the model calculation results are in good agreement with the experimentally measured data, especially in predicting the median diameter $D_{50}$ of the static armor layer. Our calculation model provides theoretical guidance for the study of mountain riverbed stability, earthquake prevention and disaster reduction.

Introduction

Natural disasters in mountain rivers profoundly affect the healthy development of rivers and, consequently, human survival. A scientific understanding of the impact of natural disasters on the evolution and development of rivers is particularly important for dealing with natural disasters in mountain rivers (Xie et al., 2018; Wang et al., 2019; Wang et al., 2021). Globally, mountainous area accounts for 30% of the total land area. Mountain water disasters have occurred frequently in the past two decades. For example, secondary disasters (such as landslides, mudslides, and collapses) caused by the 2008 Wenchuan earthquake in China have had a huge impact and profoundly changed the evolution and development of rivers Dai et al. (2011); Li et al. (2014); Fan et al. (2016), and these disasters have resulted in a huge loss of life and property in the local area. Mountain rivers are characterized by high terrain, large drops, rapid floods, and wide bed composition, and these characteristics make related scientific research challenging. For gravel-bed rivers, secondary disasters caused by the earthquake greatly affected the water and sediment supply, and the bed armor layer Hassan et al. (2006); Mao et al. (2011); Wang et al. (2020a) has been in the dynamic cyclic process of formation-destruction-reformation for a long time (Vericat et al., 2006; Orrú et al., 2016). The instability and reconstruction process of the armor layer will have an important impact on river embankment projects, water diversion and sediment prevention projects, and navigation projects.

The surface layer of a mountain river bed has a wide composition, and the particle size distribution ranges from fine sand to boulders. In addition, a gravel river bed is a morphology often present in mountain rivers, and a static armor layer is typically formed on the riverbed surface (Hassan et al., 2006; Wang et al., 2020b). Under the conditions of insufficient upstream sediment supply, the sorting effect of flow often causes fine-grained sediment to scour and move out, leaving larger particles of sediment on the river bed, which then form a static armor layer (Chin et al., 1994; Church et al., 1998; Parker and Sutherland, 1990; Wang et al., 2020a; Wang et al., 2020b). In the past, various scholars have studied the bed size distribution of the static armor layer formation process through flume experiments Little and Mayer, (1972); Shen and Lu, (1983) or field experiments Rovira and Núñez-Gonz); Gessler (1971) first developed a mixed sand and gravel size distribution that considered the coarsening process. His method only considered the pulsating effect of flow, and ignored the random distribution of the incipient drag force of sediment particles on the bed surface. He believed that the pulsation of the drag force follows the law of normal error; therefore, the probability that the sediment stays on the bed surface will not be incipient, and then the size distribution of the static armor layer can be obtained. On this basis, other scholars have begun to study the of static armor size distribution prediction model. Shen and Lu (1983) used three regression equations to calculate the surface size distribution of a river bed based on Gessler’s sediment size distribution prediction model and the research results of Einstein’s hidden coefficient Einstein, (1950); Gessler, (1971) from the perspective of its influence on the incipient heterogeneous sediment. Of course, some scholars believe that the scope of application of Shen and Lu’s model has certain limitations. For example, some scholars assert that this method has poor accuracy for beds that include fine sand Kellerhals and Church, (1977); Ettema, (1984); Odgaard (1984) discussed and analyzed the above-mentioned problems. He chose a normal curve to describe the size distribution of the static armor layer, and the results were supported by both theory and experiment. Although the method is simple in form, his conclusion is that the size distribution after the formation of the armor layer is unrelated to the initial bed materials, which does not seem to fit the actual situation very well. Garde (2006) believes that a common shortcoming of previous studies is that they are all based on the model of (Little and Mayer, 1972). Moreover, he believes that the applicability of this model depends on whether bed sampling technology is sufficiently accurate. He introduced the parameter Kramer’s M, and coupled it with the initial bed material and the flow strength to obtain a model for calculating the median particle size of the armor layer, used a wider range of laboratory flume data and channel data (median particle size range is 0.8–18.12 mm, and geometric standard deviation range is 1.5–15.76) for verification, and was able to obtain good results. He et al. (2002) believed that when the incipient probability was determined, the bed load had a maximum incipient particle size. When calculating the stable armor layer size distribution, the maximum incipient particle size of the bed surface must first be determined. Under the constraint of a certain incipient probability, sediment particles larger than this size cannot be moved. On this basis, a calculation model is proposed for the static armor layer under the condition of no upstream sediment supply. Although there are already many results that can be applied to the prediction of the bed surface size distribution of the static armor layer in the formation stage, the influencing factors that affect the static armor layer size distribution are complicated, such as exposure He et al. (2002); Bai et al. (2013); Zhang et al. (2016), riverbed structure Powell et al. (2016); Bertin and Friedrich, (2018); Wang et al. (2020b), cyclical changes in current intensity (Hassan et al., 2006; Mao, 2012). Although many achievements have been made at present, the scope of application of these results has certain limitations. For example, the results of Gessler, Shen and Liu, etc. are not suitable for a static armor layer of fine sediment, and Garde’s model (Grade et al., 2006) pays more attention to the median diameter of the armor layer. The results reported by He et al.(2002) can be used to accurately calculate the bed surface size distribution when the armor layer is formed under the condition of clear water scour, but this method is not suitable for predicting the bed surface size distribution when it forms after the previous static armor layer is broken.

To improve the relatively immature calculation model for the surface layer size distribution of the new static armor layer that forms after the previous static armor layer becomes unstable, this study proposes a new model that is based on the idea of incipient probability and the critical incipient particle size, introduces the armor ratio and other parameters, reconstructs the calculation model of the bed surface bed size distribution when the new static armor layer is formed again after the previous armor layer becomes unstable, and verifies it using laboratory flume experimental data.

Data Used for Analysis

Experiments were conducted in a 37 m long and 1 m wide flume (Figure 1A) at the State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, China. The initial bed materials comprised a unimodal gravel with a median grain size D₅₀ = 4 mm, and distribution truncated at 1 and 16 mm (Figures 1B,C). Figure 1B shows a partial picture of the initial bed materials, and Figure 1C shows the size distribution curve. During the experiment, the water level was measured using four automatic water level meters set at distances of 13, 17, 21, and 25 m from the starting point of the flume, which can measure the change in water level real time. An automatic bed load and sediment transport rate measurement system was set at a position 34 m away from the starting point; this system can continuously measure the bed load during the experiment and measure the cumulative weight of the bed load every 1 s. During the test, the topography of riverbed was measured without water during the necessary period. The topography was measured using a total station (Nikon-DTM-352c). The riverbeds at 17, 21, and 25 m were manually sampled and screened (a 20 cm × 20 cm square was sprayed with red spray paint on the target section, and colored particles were separated from the bed surface. Specifically, tweezers were used to remove the coarse-grained sediment, and then a fine-bristle brush was used to remove fine-grained sand to obtain the surface gradation information of the river bed.

FIGURE 1

FIGURE 1. Experimental flume and initial bed surface (A) Photograph of flume during experimental procedure, (B) photograph of initial bed materials (width: 20 cm), and (C) bed size distribution curve of initial bed materials.

Herein, six experiments were conducted, which contained the formation of a static armor layer and the reformation of a new static armor layer after the previous one was broken (Wang et al., 2020a). In each case, the initial bed materials and bed slopes were the same. The experiments differed in terms of discharge (flow intensity). Here, we used data from five experiments to verify our calculation model, and the hydraulic conditions of each set of laboratory flume experiments used are shown in Table 1. The entire suite of experiments has been discussed by (Wang et al., 2020a). The grain size distributions obtained through this method are weight-by-area samples, and they require conversion to weight-by-volume samples to directly compare the grain sizes using the Bunte and Abt (2001) conversion. Wang et al. (2020a) reported a study on the critical breakup condition of a static armor layer, and concluded that when the bed shear stress increases to 1.2 times that of the bed shear stress of the pre-armored bed, the previous armor layer broke. In our experiments, we used the bed shear stress $\tau$ ($\tau =\rho gRJ$, where $R$ is the hydraulic radius and $J$ is the energy slope) to express the flow intensity, in which ${\tau }_{\text{form}}$ indicates the flow intensity during the static armor layer formation phase, and $\phi =\tau /{\tau }_{\text{form}}$ indicates the relative flow intensity.

TABLE 1

TABLE 1. Hydraulic conditions of each set of laboratory flume experiments.

For natural rivers, the bed surface size distribution that determines the boundary conditions can be predicted using related models. As early as 1971, Gessler. (1971) conducted related studies on the surface size distribution of beds that determined flow conditions based on probability statistics. The calculation formula is as follows:

$F_i==\frac{{\displaystyle {\sum }_{D_{\min }}^{D_i}{q}_{D_i}{p}_{0i}}}{{\displaystyle {\sum }_{D_{\min }}^{D_{\max }}{q}_{D_i}{p}_{0i}}},(1)$

$q_{D_i}=\frac{1}{\sqrt{2\pi }\sigma }{\displaystyle {\int }_{-\infty }^{{\tau }_c/\tau }\exp \left(-\frac{x^2}{2{\sigma }^2}\right)}dx,(2)$

where, $p_{0i}$ is the sediment weight percentage of $i$-the sediment class in the bed materials, $D_i$ is the particle size of $i$-the sediment class, and $D_{\min }$ and $D_{\max }$ are the minimum and maximum particle sizes of sediment in the bed materials,respectively; $F_i$ is the sediment weight percentage of the bed materials with a particle size smaller than $D_i$; $q_{D_i}$is the probability that a particle with a size of remains immobile ; $\tau$ and ${\tau }_c$ represent the current shear stress and critical flow shear stress of $i$-the sediment class respectively, $\sigma$ is the mean square deviation of the instantaneous flow velocity; and x is the integral variable.

He et al. (2002) believed that when the incipient probability was determined, the bed load had the largest particle size $D_{c\max }$. When calculating the stable static armor layer size distribution, the maximum incipient particle size of the bed surface must first be determined. Under a certain incipient probability constraint, a sediment larger than this size cannot be moved. The bed load motion includes different forms such as sliding, rolling, and jumping, but rolling is the main form of motion, so the incipient critical shear stress ${\Theta }_c$ obtained from rolling balance is expressed as follows:

${\Theta }_c=\frac{\tau }{\left({\rho }_s-\rho \right)g{D}_i}=B\left(1+\xi \frac{D_m}{D_i}\right),(3)$

$B=\frac{4}{3}\frac{1}{\left(1+\beta {\sigma }^2\right)}\frac{1}{{\alpha }^2}\frac{L_W}{C_d{L}_d+C_L{L}_L},(4)$

where, $B$ is the comprehensive coefficient; ${\rho }_s$ and $\rho$ are the sediment and fluid densities, respectively; $g$ is the gravity acceleration; $\xi$ is the exposure factor, which can be calculated by an empirical formula Misri et al. (1984); Samaga et al. (1986); $D_m$ is the mean particle size; $\beta$ is the incipient standard; $\alpha$ is the relationship coefficient between the flow friction velocity and the average flow velocity; $L_W$ is the force arm of the gravity of the sediment particles under water; $C_d$ and $L_d$ are the drag force andarm coefficient, respectively; and $C_L$ and $L_L$ are the upward lift force and moment arm coefficient, respectively.

From Eq. 3, it can be concluded that the relative exposure coefficient $\xi \to 0$ at the time when the critical incipient shear stress and the exposure of the bed surface are maximum. According to the weak motion standard, when the bed surface sediment particles are maximally exposed, the incipient critical shear stress is 0.024. The maximum incipient particle size of the sediment particles is calculated as follows:

$D_{c\max }=\frac{\tau }{0.024g\left({\rho }_s-\rho \right)}.(5)$

Based on the above theory, He et al. (2002) obtained a calculation model for the surface size distribution of a static armor layer under no upstream sediment supply:

$p_i=\frac{D_i{p}_{0i}}{{\displaystyle \sum _{i=1}^m{D}_i{p}_{0i}+{\displaystyle \sum _{i=m+1}^n{\left(D_i{D}_{c\max }\right)}^{\frac{1}{2}}{p}_{0i}}}}\times 100\%,D_i<D_{c\max },(6)$

$p_i=\frac{{\left(D_i{D}_{c\max }\right)}^{1/2}{p}_{0i}}{{\displaystyle \sum _{i=1}^m{D}_i{p}_{0i}+{\displaystyle \sum _{i=m+1}^n{\left(D_i{D}_{c\max }\right)}^{1/2}{p}_{0i}}}}\times 100\%,D_i\ge D_{c\max },(7)$

where, $p_i$ is the percentage of particles $D_i$ in the static armor layer, $m$ is the maximum incipient particle size in the initial bed material size distribution with the number of groups corresponding to the smallest particle size being one and the number of groups corresponding to $D_{c\max }$, being $\mathrm{1}\le \mathit{m}\mathrm{<}\mathit{n}$, where $n$ is the total number of groups of the sediment size distribution.

The two models described above can provide better results for predicting the surface size distribution of the static armor layer formed by the initial bed materials. In particular, the model proposed by He et al. (2002)has the advantages of simple calculation and strong practicability. Figure 2 shows a comparison between the predicted and measured results of the bed surface size distribution after the initial static armor layer is formed in Experiments 3-0–6-0. As shown in the figure , the predicted and measured curves are in good agreement. Our data show that the relative error in predicting the median diameter $D_{50}$ of the riverbed was less than 14%.

FIGURE 2

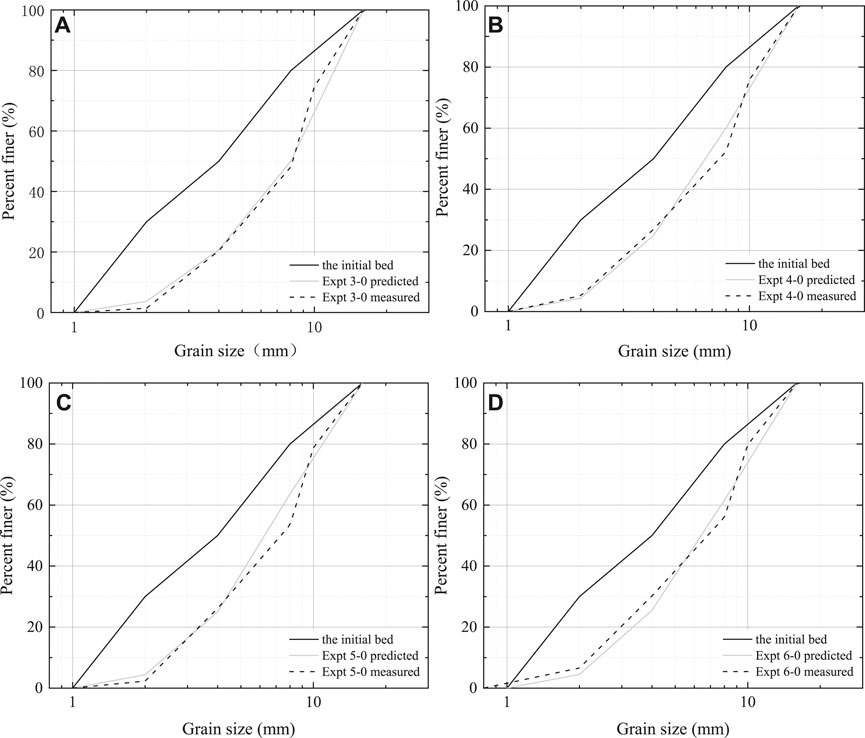
FIGURE 2. Comparison between the predicted and measured results of the bed surface size distribution after the initial static armor layer is formed in the Experiments 3-0-6-0 (A) Expt. 3-0, (B) Expt. 4-0, (C) Expt. 5-0, (D) Expt. 6-0.

As mentioned above, although Gessler (1971) pioneered a model for calculating the bed surface size distribution of the static armor layer, and the method has simple calculations, clear parameters, and good generalization, there are some obvious shortcomings. First, regardless of the strength of the flow intensity , different sediment sizes will remain on the river bed, which is not in line with the actual situation. Second, the calculation of incipient shear stress uses uniform sediment, which is inconsistent with actual rivers. Finally, the calculations of incipient shear stress and of incipient probability are nested rather than independent of each other, and thus, there is great irrationality. Although Gessler's model has the abovementioned shortcomings, it provides a very good theoretical basis for calculation of the coarsening of the bed surface size distribution. He et al. (2002) also obtained a set of methods for calculating the bed surface size distribution based on incipient probability, but these methods also have obvious defects, especially in calculating the bed surface size distribution after the previous static armor layer becomes unstable. Their theory includes the following three hypotheses: 1) The probability of particles smaller than $D_{c\max }$ on the bed changes depending on the particle size, and the probability of coarser particles on the bed is higher. Therefore, the probability of not being washed out can be expressed as ${\left(D_i/D_{c\max }\right)}^{\theta }$, where is the constant coefficient. 2) The composition of the bed surface also affects the retention of sediment particles on the riverbed. The larger the particle size, the greater the probability of staying on the bed, which is represented by ${\left(D_m/D_{c\max }\right)}^{\theta }$. 3) Particles larger than $D_{c\max }$ on the bed surface include two parts: one is particles larger than $D_{c\max }$ on the initial bed material itself, and the other is particles exposed on the subsurface layer. The above three hypotheses are very important for the prediction model of the static armor layer formation process, but for the new process of forming a new static armor layer after the previous one is destroyed, it is not sufficient to rely solely on these three hypotheses, and other influencing factors need to be considered.

Calculation Model of the Static Armor Layer Size Distribution After the Reconstruction

The current calculation method Gessler, (1971); Shen and Lu. (1983); Odgaard, (1984); He et al. (2002); Garde, 2006) for the surface size distribution of the static armor layer mostly considers the interaction between individual particles, but does not consider interactions between groups of particles, such as the stacked structure formed by different particles (a riverbed structure is used below to represent this stacked structure) Church et al. (1998); Mao et al. (2011); Powell et al. (2016); Bertin and Friedrich, (2018); therefore, the factors considered are not comprehensive enough. In particular, when a new static armor layer is formed after the previous armor layer is destroyed, the bed structure has a significant influence on the movement of the bed load (Vericat et al., 2006; Wang and Liu, 2009; Orrú et al., 2016; Wang et al., 2020a, Wang et al., 2020b). Therefore, it is necessary to fully consider the influence of the riverbed structure when calculating the riverbed surface size distribution after the static armor layer becomes unstable.

The bed surface coarsening process is not only a simple sediment particle sorting process, but also is affected by many influencing factors such as flow intensity, bed structure and texture, sediment particle shape and density, and upstream sediment supply. The bed stability of gravel-bed rivers is primarily due to bed coarsening, which is comprised two parts: 1) bed surface coarsening and 2) bed surface structure (Wilcock, 1987; Wang et al., 2020a). To study the relationship between bed structure and bed composition more intuitively, Wolcott (1989) defined the bed structure as comprising “textural structures” (including armoring and particle interlocking) and “geometric structures” (including clusters and imbrication). At present, the technology for obtaining gravel riverbed compositions is relatively mature and includes both direct sampling methods Bunte and Abt, (2001) and image processing methods (Nie et al., 2015). According to the stacking patterns between different particles, Wittenberg. (2002) described and defined the current riverbed structure and particle structure. The arrangement of sediment particles on the bed surface can reflect the performance of the riverbed structure to a certain extent. Figure 3A shows the bed morphology after the bed was roughened. After the coarsening is completed, the sediment particles on the riverbed transition from their initial free-spreading state to a large-particle sediment stacking structure. There are some significant structural characteristics in the bed, such as cluster structures (red dashed frame in Figure 3B) and linear structures (blue dashed frame in Figure 3B). These bed structures will significantly increase the stability of the bed, have a huge impact on the bed load transport rate, and then affect changes in the surface composition of the bed.

FIGURE 3

FIGURE 3. Surface morphology of the static armor layer (A) Actual image of the static armor layer, (B) Distribution of large-grained gravel (width 20 cm).

In natural rivers, when the shear stress $\tau$ of the flow exceeds the critical shear stress ${\tau }_c$, sediment transport occurs. Eq. 8 can be used to pre-calculate the bed load transport rate (Dietrich et al., 1989):

$q_b=k{\left(\tau -{\tau }_c\right)}^c,(8)$

where, $q_b$ is the bed load transport rate of single-width by weight, and $k$ and $c$ are empirical coefficients (where $c$ is approximately 1.5). Dietrich et al. (1989) obtained a dimensionless sediment transport ratio $q^{\ast }$, which is the transport rate for the coarse surface normalized by the transport rate for a surface as fine as the subsurface or load:

$q^{\ast }={\left(\frac{\tau -{\tau }_{cs}}{\tau -{\tau }_{ct}}\right)}^n={\left(\frac{\frac{\tau }{{\tau }_{ct}}-a\left(\frac{D_{50}}{D_{50t}}\right)}{\frac{\tau }{{\tau }_{ct}}-1}\right)}^n,(9)$

where, ${\tau }_{cs}$ and ${\tau }_{ct}$ are the critical boundary shear stresses of the surface and the subsurface, respectively; $a$ is gravel with a uniform specific gravity of unity; and $D_{50}$ and $D_{50l}$ are the median grain size of the bed surface and load, respectively. To estimate the influence of bed structure on the process of particle entrainment and sediment transport, Hassan and Church. (2000) established a set of methods for estimating the corresponding shear stress of the bed structure based on the total shear stress, which has been widely used. Their method quantifies the bed structure from a unique perspective, which also provides us with a comprehensive perspective for understanding the influence of the bed structure on the stability of the static armor layer. In this method, the parameter $D_{50}/D_{50t}$, which is the armor ratio, is defined as the ratio of the surface median diameter to the subsurface median diameter (Hassan et al., 2006).

Eq. 9 can be rewritten in the following form:

$\frac{{\tau }_{cs}}{{\tau }_{ct}}=q^{\ast 2/3}+\left(1-q^{\ast 2/3}\right)\frac{{\tau }_b}{{\tau }_{ct}},(10)$

where, ${\tau }_{cs}=0.045g\left({\rho }_s-\rho \right)D_{50}$, and $g$ is the acceleration due to gravity. The Shield number is close to 0.045 when dealing with a widely graded sediment mixture, so it can be approximated as ${\tau }_{cs}/{\tau }_{ct}=D_{50}/D_{50s}$. When $q^{\ast }$ = 0, there is no sediment supply upstream, which is part of the process of static armor layer formation. Figure 4 shows the loci for various $q^{\ast }$ and experimental data form the experiments (Church et al., 1998; Hassan and Church, 2000; Wang et al., 2020b). After the formation of the static armor layer, the bed load movement intensity was low, the mobilization of the river bed was small, and the river bed was in a stable state. In this analysis, our experimental data were concentrated around $q^{\ast }$ = 0.1. The degree of riverbed coarsening was positively correlated with $\tau /{\tau }_{ct}$. The higher the degree of riverbed coarsening, the stronger the stability of the riverbed, and the greater the influence of the bed structure. Especially in the pebble river channel, which had no upstream sediment supply, the “stone cells” formed on the bed surface will greatly promote the stability of the river bed (Church et al., 1998). As the current mathematical quantification method of bed structure is still difficult to apply, in the previous static armor layer size distribution calculation models, few scholars have fully considered the influence of the bed structure. Based on the above discussion, we believe that the riverbed armor ratio can be used as a reflection of the riverbed structure and, consequently, it was introduced into our model.

FIGURE 4

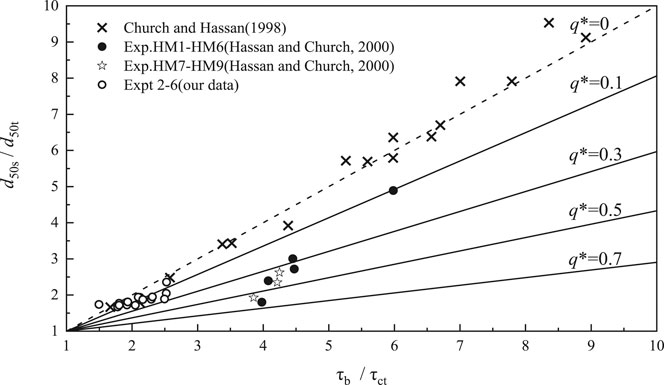
FIGURE 4. Plot of Eq. 10, showing the correlation between $D_{50}/D_{50s}$ and ${\tau }_b/{\tau }_{ct}$ for various $q^{\ast }$. The solid circles represent the data of Exp. HM1-HM6 Hassan and Church, (2000), the open five-point stars represent HM7-HM9 Hassan and Church, (2000), and the crosses represent data from (Church et al., 1998). The open circles represent values of $q^{\ast }$ computed from Eq. 10 for our data.

This study is also based on the incipient probability, by comprehensively considering the immobility probability of the large sediment particles in the riverbed and combining the influence of the bed structure on the coarsening of the gravel riverbed to establish a new calculation model. To reasonably calculate the bed surface size distribution of the static armor layer that formed afterinstability of the previous armor layer, it is necessary to determine the criterion for the large-grained sediment on the bed surface, which is like the study of He et al. (2002). However, our understanding of the critical particle size $D_c$ is different from that of He et al. (2002). They believe that sediment particles larger than the maximum incipient particle size on the river bed cannot be moved, and we believe that the sediment on the bed surface should be divided into particles that are larger and smaller than the critical size $D_c$. Out of the two particle size groups, the sediment particles larger than the critical size have a small incipient probability, while sediment particles smaller than the critical size have a higher incipient probability. Therefore, the choice of critical particle size $D_c$ has become an important factor affecting the accuracy of the model’s prediction.

The calculation of the critical incipient shear stress obtained with bed load rolling as the main form of motion is shown in Eq. 3 and Eq. 4. It can be shown that this parameter is related to the flow intensity (using shear stress $\tau$ to characterize flow strength) and the particle size on the bed surface. 0.045 or 0.047 can be used when dealing with wide-graded non-uniform Shields numbers (Andrews, 1984; Wilcock and McArdell, 1993; Hassan and Church, 2000). In this study, we continue to use this standard, and the critical dimensionless Shields number is 0.047. From this, we determined that the critical incipient particle size in the model is $D_c=\tau /\left[0.047g\left({\rho }_s-\rho \right)\right]$. Figure 5 shows the calculation results of the bed surface size distribution of the new static armor layer formed after instability of the previous armor layer with different critical particle sizes in Experiment 2. It can be seen from the figure that when the critical dimensionless Shields number ${\Theta }_c$ = 0.047, the bed size distribution obtained is closer to the measured result than ${\Theta }_c$ = 0.024, which also indicates that the value of 0.047 for this parameter is relatively accurate.

FIGURE 5

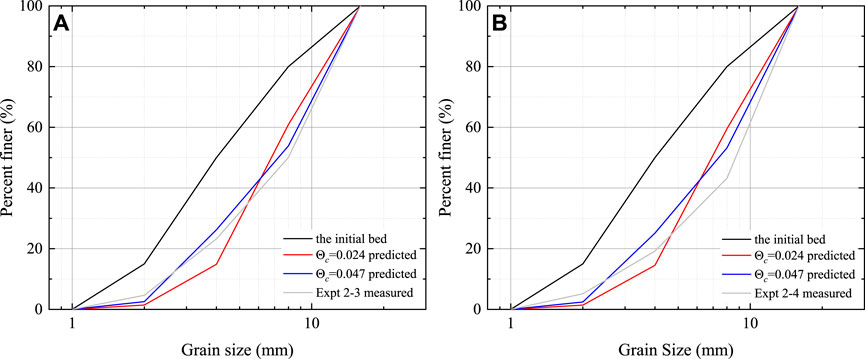
FIGURE 5. The calculation results of the bed surface size distribution of the new static armor layer formed after instability of the previous armor layer with different critical particle sizes in Experiment two.

Moreover, the value of $\theta$ in the prediction model of He et al. (2002) does not significantly consider the influence of the riverbed structure; in this model, if the linear relationship is set to 1, the non-linear relationship is set to 0.5. However, we believe that the value of this parameter will affect the prediction accuracy of the model, and we believe that the bed structure has a greater impact on the bed surface layer after the formation of the initial static armor layer. To address this, we have added a parameter known as “armor ratio” that reflects the influence of the bed structure in the model, so when considering the parameter $\theta$, its value can be increased appropriately. This is more in line with the actual situation. After increasing the coefficient $\theta$ from 0.5 to 0.6, the predicted configuration was found to be closer to the measured size distribution.

We believe that the main factors affecting the movement of sediment on a river bed include flow conditions, characteristics of the bed materials (composition of the bed surface and subsurface layers), and bed structure. The flow intensity is the main driving force affecting the sorting of the riverbed. For the same bed materials, the greater the flow intensity, the surface particles and the greater the corresponding $D_c$. Therefore, the influence of flow intensity can be determined by the value of $D_c$.The armor ratio can reflect the influence of subsurface bed materials. The bed surface sediment also affects the size distribution calculation, which can be reflected by the ratio of $D_i$ to $D_c$ and is related to thearmor ratio. After the bed materials were scoured by flow, the sediment particles formed stacked structures of different sizes, such as linear structures, triangular structures, and cluster structures (see Figure 3). The influence of these structures greatly affects the calculation of bed surface size distribution. Moreover, the influence of bed structure cannot be characterized by the characteristic particle diameter of the riverbed. However, the final result of the cluster structure formed on the surface of the river bed is to make the bed surface more stable, so we can change the value of $D_c$ and add the armor ratio to reflect the influence of the bed structure. Based on the above consideration of the factors affecting the surface sediment particles of the river bed, we propose a method for calculating the percentage of the static armor surface layer as follows:

$p_i=\frac{D_i{\left(D_{50t}/D_{50}\right)}^{0.5}{p}_{0i}}{{\displaystyle \sum _{i=1}^m{D}_i{\left(D_{50t}/D_{50}\right)}^{0.5}{p}_{0i}+{\displaystyle \sum _{i=m+1}^n{\left(\left(D_i{D}_c\right){\left(D_{50t}/D_{50}\right)}^{0.5}\right)}^{0.6}{p}_{0i}}}}\times 100\%,D_i<D_c,\text{(11)}$

$p_i=\frac{D_i{\left(D_{50t}/D_{50}\right)}^{0.5}{p}_{0i}}{{\displaystyle \sum _{i=1}^m{D}_i{\left(D_{50t}/D_{50}\right)}^{0.5}{p}_{0i}+{\displaystyle \sum _{i=m+1}^n{\left(\left(D_i{D}_c\right){\left(D_{50t}/D_{50}\right)}^{0.5}\right)}^{0.6}{p}_{0i}}}}\times 100\%,D_i>D_c.\text{(12)}$

The accuracy of Eqs 11, 12 were ascertained by comparison with the measured data form laboratory flume experiments. Figure 6 shows the comparison between the predictions of our model and the data measured by laboratory flume for the size distribution curve of the new static armor layer that formed after the previous static armor layer was broken. The results show that the values calculated by this model are consistent with the measured data.

FIGURE 6

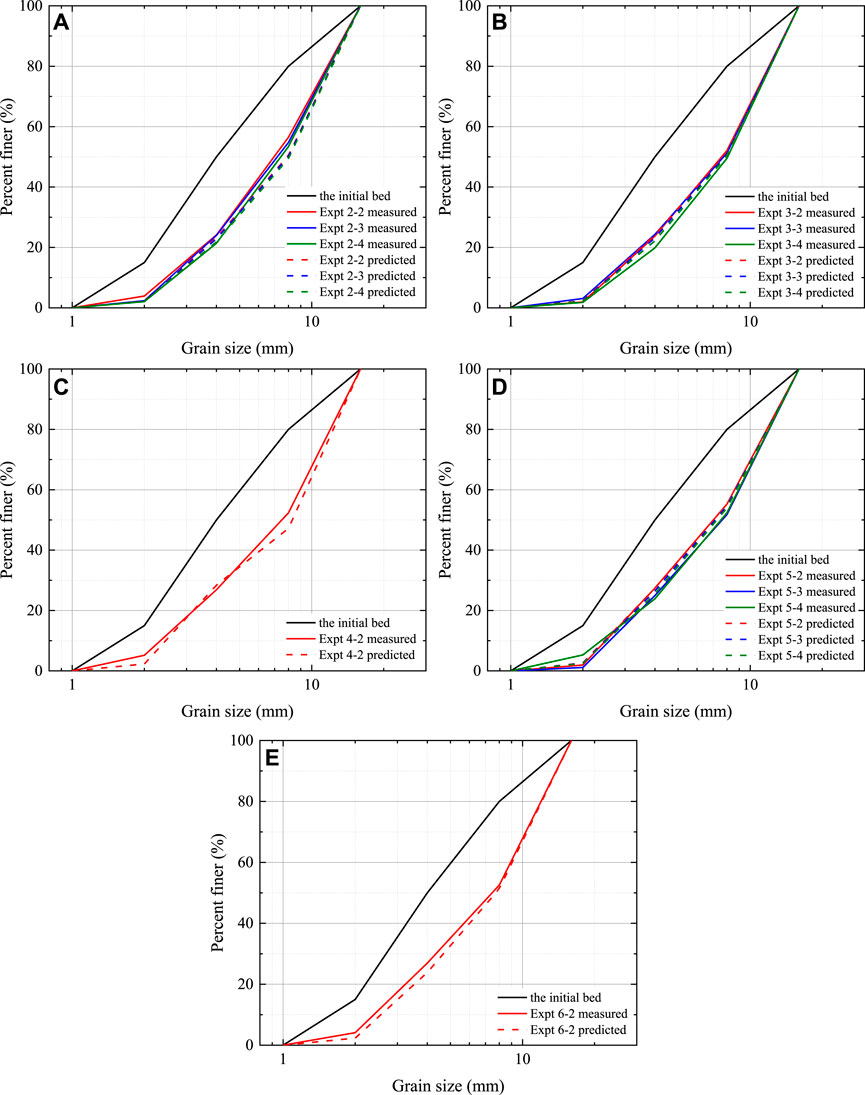
FIGURE 6. Comparison of model predicted values and actual measured values of different experiments (A) Expt. 2, (B) Expt. 3, (C) Expt. 4, (D) Expt. 5, (E) Expt. 6

Figure 7 shows a comparison between our model calculations and the actual measured static armor layer surface cumulative weight percentage. It can be seen from the figure that our predictive model still has significant deficiencies in the prediction of fine-grained sediment (the black solid squares in Figure 7, $D_i$ = 2 mm), but it has a good ability to predict the proportion of larger particles (open squares and circles in Figure 7, $D_i$ = 4 and 8 mm). The median diameter of the bed used in the static armor layer formation and breakup experiments was close to 8 mm, which means that our model is effective in calculating and grading the composition of the bed surface, especially in predicting the median diameter $D_{50}$; however, there are still some errors in the prediction of small sediment particles. We believe that this is due to the difficulty in sampling fine particles during the sampling process. Large errors will occur in the removal of fine particles from the river bed by fine brushes, which will lead to large deviations between the measured data and the calculated results.

FIGURE 7

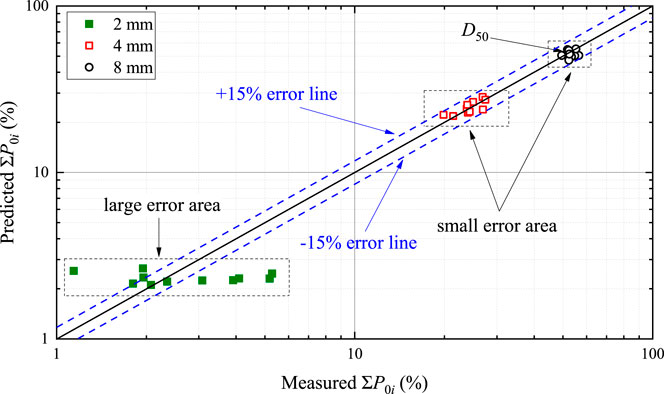
FIGURE 7. Comparison of particle diameter cumulative percentage model predictions and actual measurement values from different experiments.

Conclusion

The influence of the bed structure on the bed surface size distribution during the formation and destruction of the static armor layer was explored, and on this basis, a model that calculated the bed surface size distribution after the previous static armor layer became unstable was established and verified. The development degree of the bed structure has an impact on the formation and reconstruction of the static armor layer. After the previous static armor layer formed, the bed surface formed a structure with a different degree of particle aggregation, which increased the bed stability. The degree of influence of the bed structure on the bed stability can be initially obtained by stripping off the two factors that affect the stability of theriverbed (bed structure and the bed coarsening). The ratio of the median particle size between the bed surface and the subsurface $D_{50}/D_{50t}$ (armor ratio) was introduced to reflect the effect of the bed structure. The calculation method for the critical incipient particle size was obtained by reasonable analysis of the value of the dimensionless incipient shear stress ${\Theta }_c$. The index correction of the ratio of the fractional particle size to the critical particle size determines the influence of the initial bed materials on the formation process of the static armor layer. Combining the above theories and considering the incipient probability of sediment particles on the bed surface as the starting point, a simple prediction model for calculating the static armor layer size distribution after reconstruction of a gravel riverbed was established. The results of the calculation model are in good agreement with the results of the laboratory flume experiment data, especially for predicting the median particle size. Although our model still has certain errors in predicting small sediment particles, itstill provides information that can be used for the study of gravel riverbed stability, and provides theoretical guidance for the development and protection of mountain rivers.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

WQ and NR contributed to the conception and design of the study. LL, LX, and WY performed data analyses of the results. WQ wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Key R and D Program of China (2018YFC0407401), the National Natural Science Foundation of China (51779163, U20A20319, 42041004), the Open Research Fund of Key Laboratory of Hydro-Sediment Science and River Training, the Ministry of Water Resources, China Institute of Water Resources and Hydropower Research, Grant NO. IWHR-JH-2020-A-04.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Notation

$a$ = [−] gravel with uniform specific gravity is unity

$B$ = [−] the comprehensive coefficient

$C_d$ = [−] the drag force coefficient

$C_L$ = [−] the upward lift force coefficient

$D_{50}$ = [L] the median grain size of the bed surface load

$D_{50t}$ = [L] the median grain size of the bed load

$D_i$ = [L] the particle size of the $i$-the sediment class

$D_m$ = [L] the mean particle size

$D_{\max }$ = [L] the maximum particle size of sediment in the bed materials

$D_{\min }$ = [L] the minimum particle size of sediment in the bed materials

$F_i$ = [−] the sediment weight percentage of the bed materials with a particle size smaller than $D_i$

$g$ = [LT⁻²] gravity acceleration

$J$ = [−] energy slope

$k$ = [-] empirical coefficients

$L_d$ = [L] the arm coefficient

$L_L$ = [L] the moment arm coefficient

$L_W$ = [L] the force arm of the gravity of the sediment particles under water

$m$ = [−] the maximum incipient particle size in the initial bed materials size distribution with the number of groups corresponding to the smallest particle size being one and the number of particle groups corresponding to $D_{c\max }$, $\mathrm{1}\le \mathit{m}\mathrm{<}\mathit{n}$

$n$ = [−] the total number of groups of the sediment size distribution

$n$ = [−] empirical coefficients

$p_{0i}$ = [−] the sediment weight percentage of the $i$-the sediment class in the bed materials

$p_i$ = [−] the percentage of particle with $D_i$ in the static armor layer

$q^{\ast }$ = [−] dimensionless sediment transport ratio

$q_b$ = [M/T³] sediment transport rate per unit width by dry weight

$q_{D_i}$ = [−] the particle remains immobile probability when the particle is $D_i$

$R$ = [L] hydraulic radius

$x$ = [−] the integral variable

$\alpha$ = [−] the relationship coefficient between the flow friction velocity and the average flow velocity

$\beta$ = [−] the incipient standard

$\xi$ = [−] exposure factor

$\theta$ = [−] is the constant coefficient

$\tau$ = [ML⁻¹T⁻²] the flow shear stress

${\tau }_0$ = [ML⁻¹T⁻²] the current shear stress of group $i$-the sediment class

${\tau }_c$ = [ML⁻¹T⁻²] critical flow shear stress of group $i$-the sediment class

${\tau }_c$ = [ML⁻¹T⁻²] the critical shear stress

${\tau }_{cs}$ = [ML⁻¹T⁻²] the critical boundary shear stresses of the surface

${\tau }_{ct}$ = [ML⁻¹T⁻²] the critical boundary shear stresses of the subsurface

${\tau }_{\text{form}}$ = [ML⁻¹T⁻²] the flow shear stress during the static armor layer formation phase

$\phi$ = [−] the relative flow intensity, = $\tau /{\tau }_{\text{form}}$

References

Andrews, E. D. (1984). Bed-material Entrainment and Hydraulic Geometry of Gravel-Bed Rivers in Colorado. Geol. Soc. Am. Bull. 95 (3), 371–378. doi:10.1130/0016-7606(1984)95

CrossRef Full Text | Google Scholar

Bai, Y., Wang, X., and Cao, Y. (2013). Incipient Motion of Non-uniform Coarse Grain of Bedload Considering the Impact of Two-Way Exposure. Sci. China Technol. Sci. 56, 1896–1905. doi:10.1007/s11431-013-5264-8

CrossRef Full Text | Google Scholar

Bertin, S., and Friedrich, H. (2018). Effect of Surface Texture and Structure on the Development of Stable Fluvial Armors. Geomorphology 306, 64–79. doi:10.1016/j.geomorph.2018.01.013

CrossRef Full Text | Google Scholar

Bunte, K., and Abt, S. R. (2001). Sampling Surface and Subsurface Particle-Size Distributions in Wadable Gravel-And Cobble-Bed Streams for Analyses in Sediment Transport, Hydraulics, and Streambed Monitoring. Fort Collins, CO: US Department of Agriculture, Forest Service, Rocky Mountain Research Station. doi:10.2737/rmrs-gtr-74

CrossRef Full Text

Chin, C. O., Melville, B. W., and Raudkivi, A. J. (1994). Streambed Armoring. J. Hydraulic Eng. 120 (8), 899–918. doi:10.1061/(ASCE)0733-942910.1061/(asce)0733-9429(1994)120:8(899)

CrossRef Full Text | Google Scholar

Church, M., Hassan, M. A., and Wolcott, J. F. (1998). Stabilizing Self-Organized Structures in Gravel-Bed Stream Channels: Field and Experimental Observations. Water Resour. Res. 34 (11), 3169–3179. doi:10.1029/98WR00484

CrossRef Full Text | Google Scholar

Dai, F. C., Xu, C., Yao, X., Xu, L., Tu, X. B., and Gong, Q. M. (2011). Spatial Distribution of Landslides Triggered by the 2008 Ms 8.0 Wenchuan Earthquake, China. J. Asian Earth Sci. 40 (4), 883–895. doi:10.1016/j.jseaes.2010.04.010

CrossRef Full Text | Google Scholar

Dietrich, W. E., Kirchner, J. W., Ikeda, H., and Iseya, F. (1989). Sediment Supply and the Development of the Coarse Surface Layer in Gravel-Bedded Rivers. Nature 340 (6230), 215–217. doi:10.1038/340215a0

CrossRef Full Text | Google Scholar

Einstein, H. A. (1950). The Bed-Load Function for Sediment Transportation in Open Channel Flows (No. 1026). Washington, DC: US Government Printing Office. doi:10.5479/sil.392813.39088007099559

CrossRef Full Text

Ettema, R. (1984). Sampling Armor‐Layer Sediments. J. Hydraulic Eng. 110 (7), 992–996. doi:10.1061/(ASCE)0733-9429

CrossRef Full Text | Google Scholar

Fan, N., Nie, R., Wang, Q., and Liu, X. (2016). Dramatic Undercutting of piedmont Rivers after the 2008 Wenchuan Ms 8.0 Earthquake. Sci. Rep. 6, 37108. doi:10.1038/srep37108

PubMed Abstract | CrossRef Full Text | Google Scholar

Gessler, J. (1971). Beginning and Ceasing of Sediment Motion. River. Mech. 1 (1), 1–7. doi:10.1016/0370-2693(90)90936-Z

CrossRef Full Text | Google Scholar

Garde, R. J., Sahay, A., and Bhatnagar, S. (2006). A Simple Mathematical Model to Predict the Particle Size Distribution of the Armour Layer. J. Hydraulic Res. 44 (6), 815–821. doi:10.1080/00221686.2006.9521732

Hassan, M. A., and Church, M. (2000). Experiments on Surface Structure and Partial Sediment Transport on a Gravel Bed. Water Resour. Res. 36 (7), 1885–1895. doi:10.1029/2000WR900055

CrossRef Full Text | Google Scholar

Hassan, M. A., Egozi, R., and Parker, G. (2006). Experiments on the Effect of Hydrograph Characteristics on Vertical Grain Sorting in Gravel Bed Rivers. Water Resour. Res. 42 (9). doi:10.1029/2005WR004707

CrossRef Full Text | Google Scholar

He, W. S., Yang, J. R., Fang, D., and Cao, S. Y. (2002). Relative Exposure Degree and Equivalent Grain Size of Non-uniform Sediment. J. Hydraul. Eng. 11, 44–48. doi:10.1002/mop.10502

CrossRef Full Text | Google Scholar

Kellerhals, R., and Church, M. (1977). Discussion of “Stability of Channel Beds by Armoring,” J. Hydr. Div. 103, 826–827. doi:10.1061/jyceaj.0004802

CrossRef Full Text | Google Scholar

Li, G., West, A. J., Densmore, A. L., Jin, Z., Parker, R. N., and Hilton, R. G. (2014). Seismic Mountain Building: Landslides Associated with the 2008 Wenchuan Earthquake in the Context of a Generalized Model for Earthquake Volume Balance. Geochem. Geophys. Geosyst. 15 (4), 833–844. doi:10.1002/2013GC005067

CrossRef Full Text | Google Scholar

Little, W. C., and Mayer, P. G. (1972). The Role of Sediment Size Distribution on Channel Armoring. Atlanta, Ga: Publication No. ERC-0672, School of Civ. Engrg. and Envir. Res. Ctr., Georgia Inst. of Tech.

Mao, L., Cooper, J. R., and Frostick, L. E. (2011). Grain Size and Topographical Differences between Static and mobile armour Layers. Earth Surf. Process. Landforms 36 (10), 1321–1334. doi:10.1002/esp.2156

CrossRef Full Text | Google Scholar

Mao, L. (2012). The Effect of Hydrographs on Bed Load Transport and Bed Sediment Spatial Arrangement. J. Geophys. Res. 117 (F3), a–n. doi:10.1029/2012JF002428

CrossRef Full Text | Google Scholar

Misri, R. L., Garde, R. J., and Ranga Raju, K. G. (1984). Bed Load Transport of Coarse Nonuniform Sediment. J. Hydraulic Eng. 110, 312–328. doi:10.1061/(ASCE)0733-9429

CrossRef Full Text | Google Scholar

Nie, R., Wang, H., Yang, K., and Liu, X. (2015). Estimation of the Grain-Size Distribution Using Semisupervised Affinity Propagation. J. Hydrol. Eng. 20 (12), 04015040. doi:10.1061/(asce)he.1943-5584.0001229

CrossRef Full Text | Google Scholar

Odgaard, A. J. (1984). Grain‐Size Distribution of River‐Bed Armor Layers. J. Hydraulic Eng. 110 (10), 1479–1484. doi:10.1061/(ASCE)0733-9429

CrossRef Full Text | Google Scholar

Orrú, C., Blom, A., and Uijttewaal, W. S. J. (2016). Armor Breakup and Reformation in a Degradational Laboratory experiment. Earth Surf. Dynam. 4 (2), 461–470. doi:10.5194/esurf-4-461-2016

CrossRef Full Text | Google Scholar

Parker, G., and Sutherland, A. J. (1990). Fluvial Armor. J. Hydraulic Res. 28 (5), 529–544. doi:10.1080/00221689009499044

CrossRef Full Text | Google Scholar

Powell, D. M., Ockelford, A., Rice, S. P., Hillier, J. K., Nguyen, T., Reid, I., et al. (2016). Structural Properties of mobile Armors Formed at Different Flow Strengths in Gravel-Bed Rivers. J. Geophys. Res. Earth Surf. 121 (8), 1494–1515. doi:10.1002/2015jf003794

CrossRef Full Text | Google Scholar

Rovira, A., and Núñez-González, F. (2015). Sampling Bed Material and Bedload in a bend of the Ebro River. EGU Gen. Assembly Conf. Abstr., 8264.

Google Scholar

Samaga, B. R., Raju, K. G. R., and Garde, R. J. (1986). Bed Load Transport of Sediment Mixtures. J. Hydraulic Eng. 112, 1003–1017. doi:10.1061/(ASCE)0733-9429

CrossRef Full Text | Google Scholar

Shen, H. W., and Lu, J. Y. (1983). Development and Prediction of Bed Armoring. J. Hydraulic Eng. 109 (4), 611–629. doi:10.1061/(ASCE)0733-9429

CrossRef Full Text | Google Scholar

Vericat, D., Batalla, R. J., and Garcia, C. (2006). Breakup and Reestablishment of the armour Layer in a Large Gravel-Bed River below Dams: The Lower Ebro. Geomorphology 76 (1-2), 122–136. doi:10.1016/j.geomorph.2005.10.005

CrossRef Full Text | Google Scholar

Wang, Q., Pan, Y., Yang, K., and Nie, R. (2020b). Structural Properties of the Static Armor during Formation and Reestablishment in Gravel-Bed Rivers. Water 12 (7), 1845. doi:10.3390/w12071845

CrossRef Full Text | Google Scholar

Wang, Q., Wang, L., Wang, T., Yang, K., and Nie, R. (2020a). Experimental Study on the Critical Breakup Condition of a Static armour Layer. River. Res. Applic. 37, 484–493. doi:10.1002/rra.3759

CrossRef Full Text | Google Scholar

Wang, T., and Liu, X. (2009). “The Breakup of Armor Layer in a Gravel-Bed Stream With no Sediment Supply,” in Advances in Water Resources and Hydraulic Engineering. Berlin, Germany:Springer, 919–923.

Wang, X. K., Liu, X. N., and Zhou, J. W. (2019). Research Framework and Anticipated Results of Flash Flood Disasters under the Mutation of Sediment Supply. Adv. Eng. Sci. 51 (4), 1–10. doi:10.15961/j.jsuese.201900261

CrossRef Full Text | Google Scholar

Wang, X. K., Yang, P., Sun, T., and Xu, Z. X. (2021). Study on Division Early Warning of Flash Flood Disaster Caused by Rainstorm in Mountainous Small Watersheds. Adv. Eng. Sci. 53 (1), 29–38. doi:10.15961/j.jsuese.202000981

CrossRef Full Text | Google Scholar

Wilcock, P. R. (1987). Bed-load Transport of Mixed-Size Sediment. Doctoral dissertation. Boston (MA): Massachusetts Institute of Technology.

Wilcock, P. R., and McArdell, B. W. (1993). Surface-based Fractional Transport Rates: Mobilization Thresholds and Partial Transport of a Sand-Gravel Sediment. Water Resour. Res. 29 (4), 1297–1312. doi:10.1029/92wr02748

CrossRef Full Text | Google Scholar

Wittenberg, L. (2002). Structural Patterns in Coarse Gravelriver Beds: Typology, Survey and Assessment of the Roles of Grain Size and River Regime. Geografiska Annaler: Ser. A, Phys. Geogr. 84 (1), 25–37. doi:10.1111/j.0435-3676.2002.00159.x

CrossRef Full Text | Google Scholar

Wolcott, J. F. (1989). Flume Studies of Gravel Bed Surface Response to Flowing Water. Unpublished PhD Thesis. Vancouver (BC): University of British Columbia.

Xie, H. P., Xu, W. L., Liu, C., Yang, X. G., Xie, H. Q., Nie, R. H., et al. (2018). Water Disasters and Their Countermeasures in Mountains. Adv. Eng. Sci. 50 (03), 1–14. doi:10.15961/j.jsuese.201800345

CrossRef Full Text | Google Scholar

Zhang, G. G., Zhou, S., Xing, R., and Liang, Z. X. (2016). Incipient Velocity Formula of Non-cohesive Uniform Sediment Based on Relative Exposure Degree. J. Basic Sci. Eng. 24 (4), 688–697. doi:10.16058/j.issn.1005-0930.2016.04.005

CrossRef Full Text | Google Scholar