Acoustic Emission Reveals Multiple Slip Modes on a Frictional Fault

The spectrum of fault slip modes spans a continuum from fast ruptures to slow slip events. The nucleation of a certain slip mode is governed by the frictional heterogeneity of fault interface and the rheological fault stiffness. There is a mounting evidence that a single fault can host multiple slip modes. In laboratory experiments we study acoustic emission (AE) initiated by a sliding frictional fault and focus our attention on gouge-filled faults hosting multiple slip modes. Deformation experiments were performed on a slider model setup with a precise control of mechanical parameters and monitoring the acoustic signal in the frequency range of 20–80 kHz. We have shown that the cumulative AE energy linearly depends on block displacement. Besides that, there is a high inverse correlation (-0.94) between fault friction and b-value of frequency-amplitude distribution of AE in the performed experiments. Provided that velocity weakening is specific for the fault interface, the self-organization of a gouge-filled fault at the micro scale is the key parameter that controls the frictional behavior of fault hosting multiple slip modes. Resting on a quantitative categorization of AE waveforms, two AE subpopulations have been distinguished. One of them manifests as AEs with harsh onsets. The second one exhibits a gradual amplitude rise and tremor-like waveforms. A longer duration of the intergrain rupture is specific for the second AE subpopulation. During a laboratory seismic cycle, the first AE subpopulation retains parameters, while the second one exhibits a pronounced cyclic recurrence of b-value. The b-value of the second subpopulation gradually decreases before slip events and recovers after them. Two AE subpopulations, probably, point to the coexistence of two dynamic subsystems. The revealed precursory changes of AE subpopulations are common for the entire spectrum of slip modes. We speculate on the unity of underlying mechanisms of different slip modes.

Introduction

The blocky hierarchical structure of the Earth’s crust determines its movability and localization of deformations in interblock zones. Faults and large fractures control regularities of accumulation and relaxation of the energy of elastic deformation in a blocky massif (Scholz, 2002; Kocharyan, 2016). The dynamics of relaxation processes that are accompanied by slips along faults is determined by the ratio of the rheological stiffness of the fault to the one of the enclosing massif (Leeman et al., 2016; Kocharyan et al., 2017a). Fault slip modes observed in nature span a continuum, given the heterogeneity and complexity of natural systems (Peng and Gomberg, 2010; Burgmann, 2018). Different faults may exhibit just fast slip modes (ordinary earthquakes), or just slow slip modes (slow or low-frequency earthquakes, slow slip events), or even both fast and slow modes together (Frank et al., 2016; Veedu and Barbor, 2016; Ostapchuk et al., 2020).

The frictional instability is the most probable mechanism of ordinary and slow earthquakes (Scholz, 2002; Nielsen, 2017). During fault evolution, earthquakes are initiated when shear stresses reach the ultimate strength at a local fault segment. In the vicinity of the ultimate strength the source stays in a metastable state, so that even a slight fluctuation of stress may lead to a loss of dynamic stability. The existing models of seismic activity, describing a certain fault or a source zone, suggest that earthquake nucleation area is an integrated dynamic system which has a specific property of self-organizing criticality (Kuksenko et al., 1996; Turcotte, 1999; de Arcangelis et al., 2016). At the initial stage damage accumulates at the micro-scale. Cracks are uncorrelated and occur randomly. Further evolution of the system lifts the destruction processes to a higher hierarchical level, thus, as the stresses approach the critical value, structural changes spread wider all over the system. Systems spontaneously evolve toward critical states described by power laws in the event size distribution. A loss of dynamic stability manifests at the macro-scale as a slip event. The more accurate the earthquake detection technique is, the more distinct is the pattern of large earthquake nucleation (Trugman and Ross, 2019).

The transition of a fault to a metastable state is accompanied by a decrease of the shear stiffness of source zone (Johnson and Jia, 2005; Kocharyan and Ostapchuk, 2011). At present measuring tectonic stress and fault stiffness “in situ” is a complex problem. There are several indirect ways to estimate the state of stresses near faults (Rebetsky et al., 2016; Brodsky et al., 2020) and to trace fault behavior up to earthquake nucleation (Frank et al., 2016; Trugman and Ross, 2019). Applying the AE technique to monitoring fault dynamics assumes correlation between the AE activity and the stress-strain state of the fault (Dixon et al., 2018; Bolton et al., 2020).

The laboratory experiment is a reliable tool to verify hypotheses/assumptions or to put forward new ones (Marone, 1998; Rosenau et al., 2017). AE experiments reproduce qualitatively the main statistical laws that describe natural seismicity (Gutenberg-Richter law, Omori law, inverse Omori law) (Lei, 2003; Johnson et al., 2013; Lherminier et al., 2019; Ostapchuk et al., 2019). Nucleation of slip events in laboratory is accompanied by variations of scaling properties of AEs (Goebel et al., 2013; Riviere et al., 2018), alterations of elastic/seismic wave properties (Hedayat et al., 2014; Shreedharan et al., 2021) and seismic quiescence (Ostapchuk et al., 2016). The similarity of recurrent fast and slow earthquakes has already been demonstrated (Hulbert et al., 2019). However, a limitation of AE analysis is that results often depend on reliable detection of acoustic pulses in the background noise. This work is devoted to investigation of the AE accompanying evolution of a simulated gouge-filled fault hosting multiple slip modes. We considered in detail fault self-organization produced by frictional intergranular sliding. There is no grain crushing here. We managed to reproduce the entire spectrum of slip modes by changing filler composition and its particle size distribution. A great number of AEs were detected during laboratory seismic cycles. Their quantitative categorization led to distinguishing two distinct AE subpopulations. Analyzing their scaling characteristics, we suggested a nucleation mechanism that, as we believe, underlies the entire spectrum of fault slip modes.

Materials and Methods

Laboratory experiments were performed on a slider model. A scheme of the setup is shown in Figure 1. The model fault—a confined granular layer between two blocks—was subjected to external normal and shear stresses. The moveable granite block (1) 8 × 8 × 3 cm³ in size was put on the middle of the granite base (2) rod 2.5 m long and 10 × 10 cm² in cross section. The contact surfaces of the block and the base rod were made rough by introducing grooves 0.8–1.0 mm deep. The contact gap between the block and the base was filled with a layer of granular material 3 mm thick (3). The granular layer was prepared using a leveling frame, so that the initial thickness of the layer was the same in all the experiments. To the end of experiments the thickness of the layer usually decreased to 2–2.5 mm. Mixtures of different granular materials were used as fillers. All fillers are listed in the Supplementary Table 1. Their structural properties were responsible for reproduction of a certain slip mode (Mair et al., 2002; Anthony and Marone, 2005; Kocharyan et al., 2014). All the experiments were performed at room temperature and humidity.

FIGURE 1

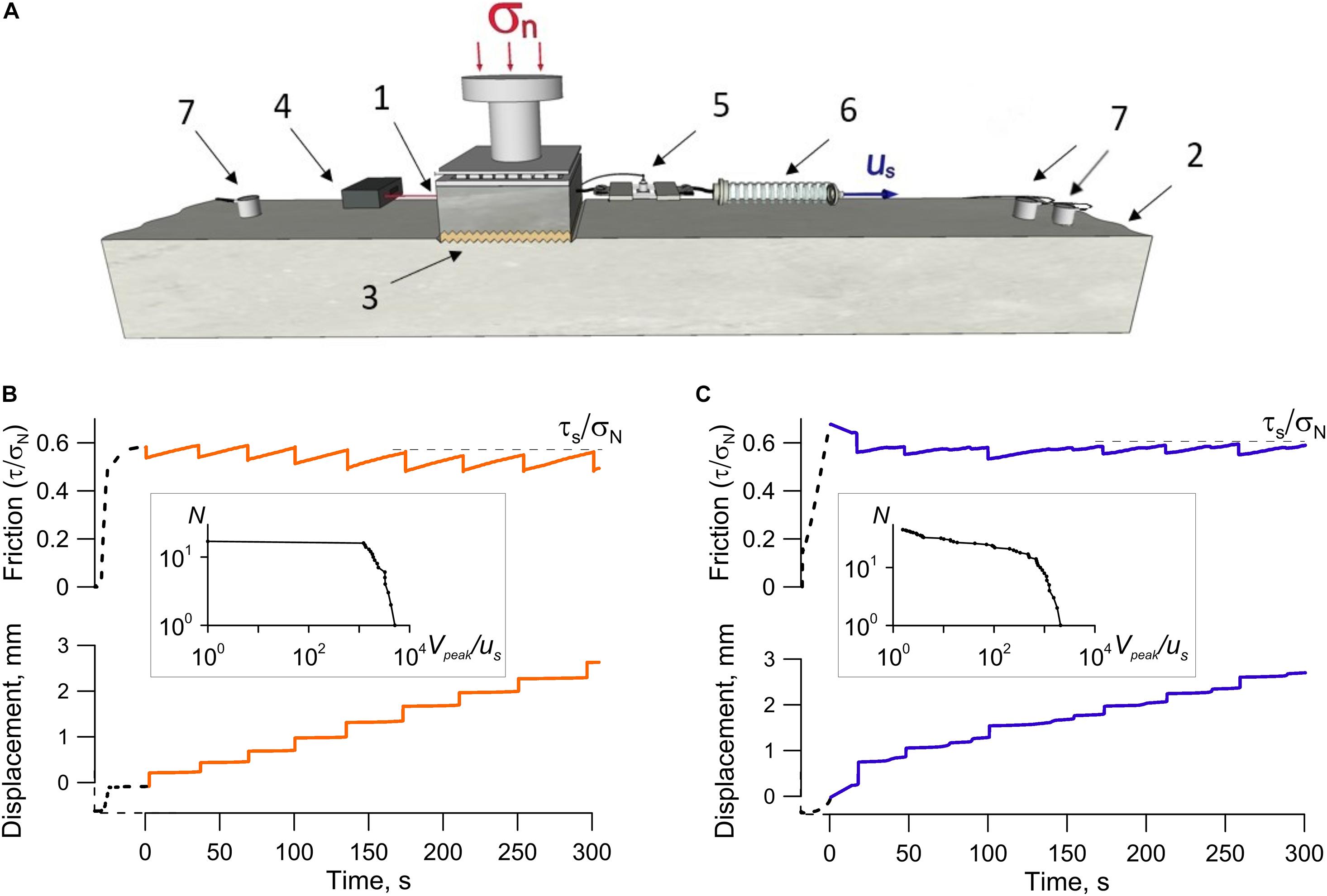
Figure 1. The slider-model performance test. Mechanical parameters (friction and displacement) and acoustic emission were measured during the experiments. (A) A scheme of the experimental setup: (1)—moveable block; (2)—base rod; (3)—gouge layer; (4)—laser sensor of displacement; (5)—force sensor; (6)—elastic element (spring); (7)—AE sensors. (B) Regular stick-slip with specific variations of friction and displacement in time (Exp. No 5). (C) Stochastic sliding regime (Exp. No 23). The point (0,0) corresponds to the moment when the ultimate strength of model fault is reached. We study the “mature” stage when friction varies in fixed range with upper limit τ_s. Insets (B,C) show the recurrence plot of slip events (number of slip events with peak velocity exceeding V_peak).

The moveable block slid along the interface under the applied normal and shear forces. The normal force was F_N = 300/400/500 N. It was applied by a set of weights. The shear force was applied to the block through an elastic element (6) with the stiffness of K = 55 kN/m. Its free end was pulled at a constant velocity of u_s = 8 μm/s. The shear force was measured with the sensor CFT/5kN (HBM, Germany) (5) accurate to 1 N. The displacement of the block relative to the base was measured with the laser sensor ILD2220-10 (Micro-Epsilon, Germany) (4) in the frequency band of 0–5 kHz, with the accuracy of 0.1 μm.

Figures 1B,C shows variations of fault friction and displacement during experiments. The fault evolution undergoes several stages (Gerasimova et al., 1995; Scuderi et al., 2017). At the initial stage the model fault reaches the ultimate shear strength. Further accumulation of shear deformation leads to the transition of the fault to a new state and a new characteristic strength τ_s is reached. Persistent cycles “loading/drop” are observed at this new stage, the frictional strength of the fault (τ_s/σ_N) remaining constant. We consider this stage in our detailed analysis. Regularities of a sliding regime are defined by structural and frictional properties of the filler. Parameters of sliding regimes are presented in Supplementary Table 1. Using, for instance, the filler composed of quartz sand with a narrow particle size distribution led to a regular stick-slip—quasi-periodically repeated fast slip events accompanied by huge drops of friction (Figure 1B). On the other hand, using the quartz sand with a wide particle size distribution resulted in a stochastic sliding regime, when the model fault hosted multiple slip modes and slip events were occasional (Figure 1C). Slip events are dynamic instabilities, during which the velocity of sliding block is higher than u_s and the relative friction decreases. The statistics of slip events for regular and stochastic sliding regimes differ.

One of the experimental outputs was the AE accompanying frictional fault evolution. Three AE sensors were mounted on the rod at the distances of 0.6 and 0.7 m at opposite sides of the moveable block using epoxy agent. The sensors were VS30-V (Vallen System, Germany). The operational frequency band was 20–80 kHz. The acoustic signal was processed by AEP5 charge amplifiers and acquired at the sample rate f_s of 1 MHz with a 14-bit analog-to-digital converter E20-10 (L-Card, Russia). The signal was provided in units of voltage.

We used a threshold algorithm to detect AEs. An AE is detected when the energy flow exceeds a fixed threshold, according to the following relation:

$$\mathrm{\pi }\left(t\right)=\frac{1}{\mathrm{△}t}\sum _t^{t+\mathrm{△}t}\frac{A{\left(t_i\right)}^2}{f_s}\ge 1.5A_{min}^2(1)$$

A(t) is the recorded signal filtered in the frequency band of 20–80 kHz, $A_{min}^2$ is the variance of the signal. The energy flow was determined in the window Δt = 0.5 ms at steps of Δt/2. $A_{min}^2$ was determined at 1 s intervals preceding the start of shear load, according to the following relation:

$$A_{min}^2=\frac{1}{f_s-1}\sum _{t_i>0}^{t_i\le 1}{\left|A\left(t_i\right)-\frac{1}{f_s}\sum _{t_i>0}^{t_i\le 1}A\left(t_i\right)\right|}^2(2)$$

Figure 2 presents the algorithm of AE detecting. The time t_s when the energy flow starts to exceed the threshold is taken to be the beginning of the AE, and the time t_e when the energy flow goes beyond the threshold—the end of the AE. The points of onset and termination were determined with the accuracy of 250 μs. We verified by visual inspection that every recorded AE was captured. Random choice of 1,000 AEs showed that only 47 multi-pulses were misidentificated as simple pulses.

FIGURE 2

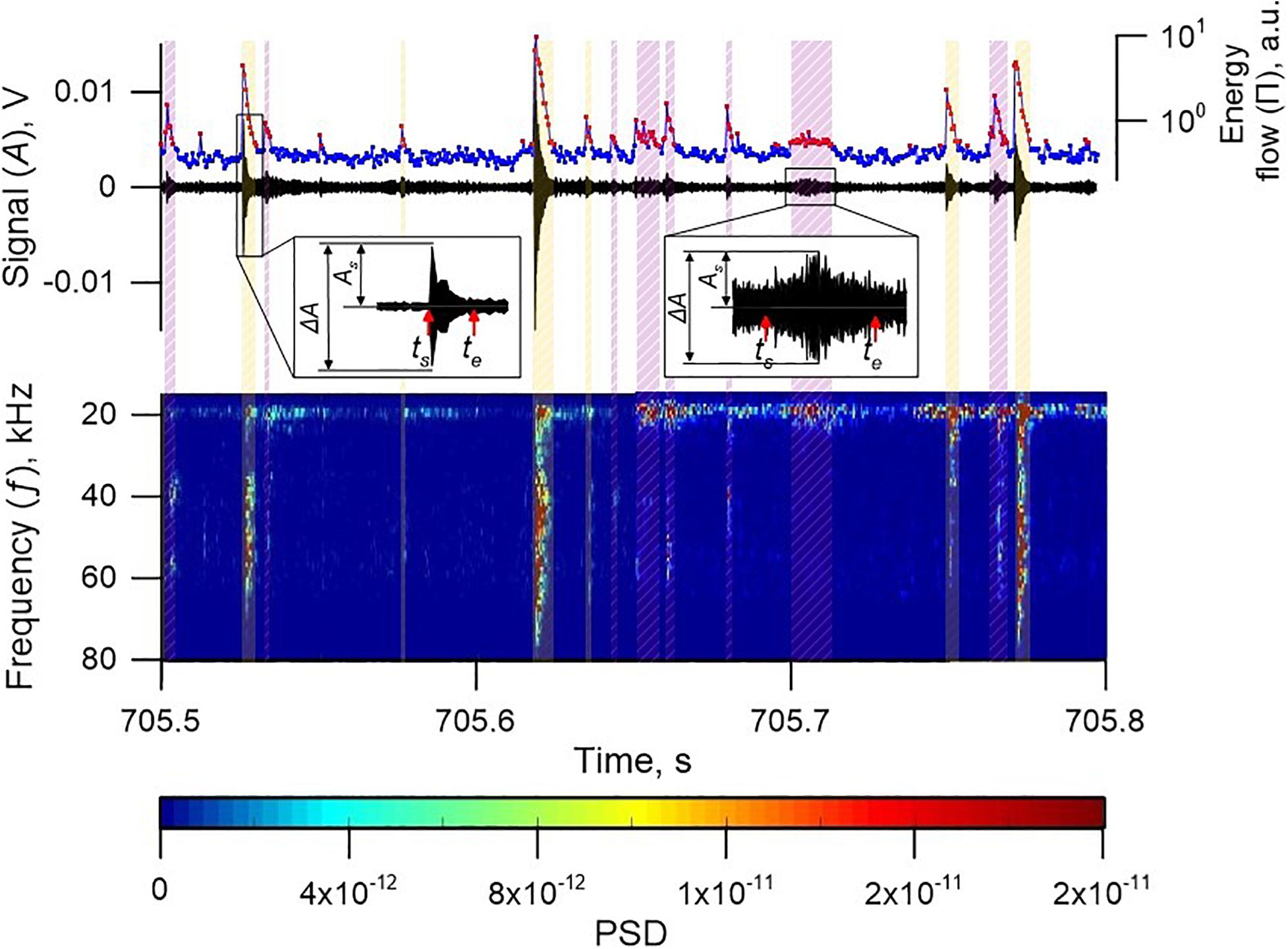
Figure 2. Algorithm of AE detection (Exp. No 5). First, the acoustic signal was filtered in the frequency band of 20–80 kHz with a Butterworth filter. Then, the energy flow (Π) was calculated (blue line). Red dots designate the excesses over a fixed experimental threshold determined by relation (1). Pulses identified as AEs are marked with dashed areas. The spectrogram of the acoustic signal clearly shows the AEs. Insets show parameters of AEs: onset (t_s), termination (t_e), amplitude (A_s) and peak-to-peak amplitude (ΔA).

The following parameters were retrieved from the detected AEs: duration (dt), amplitude (A_s), peak-to-peak amplitude (ΔA), and energy (E), which was estimated as follows:

$$E=\mathrm{△}t\sum _{t_s}^{t_e}A{\left(t_i\right)}^2(3)$$

Symbols used in the article are listed in the Table 1. We obtained amplitudes only from the digital waveforms and performed energy estimations by time integration of the signal in volts. So, these energy estimations were presented in non-physical energy units.

TABLE 1

Table 1. List of symbols.

Assuming self-similarity of the deformation process, which consequently implies a power-law distribution, we checked the AE catalog. In order to compile a homogeneous and complete AE catalog with respect to duration and amplitude, we eliminated AEs with durations less than 1.5 ms and amplitudes A_s lower than 60 dB.

It seems likely that the waveform of an AE points to the mechanism and intensity of the evolution process inside the fault (Shiotani et al., 2001; Zigone et al., 2011; Ostapchuk et al., 2016). In order to describe both the stage of AE rise and the stage of decrease, we introduced the waveform index WI (Ostapchuk and Morozova, 2020). The WI-value was calculated through the formula:

$$WI=\frac{t_{max}-t_s}{t_e-t_{max}}(4)$$

where t_max is the time when the maximum peak-to-peak amplitude was reached. WI-value is similar to the RA-value [RA = (t_max−t_s)/A_s] and a strong correlation between these two indexes is observed. The WI-value is dimensionless and allows to qualitatively evaluate AE waveform. Introduction of the WI-value is based on the assumption that various processes of self-organization take place in a stressed granular medium during formation of inhomogeneous stressed conditions in a gouge-filled fault during sliding (Hadda et al., 2015; Gao et al., 2019). More than 95% of the detected AEs had WI-value within the range of 0–1. The relative error of WI-value determination was less than 0.15. The AEs with the values of WI >> 1 were treated as double- or multi-pulses. They were not considered in our analysis.

AEs of different waveforms and amplitudes were emitted in fault sliding. Depending on the sliding regime the rate of AE varied from single “clicks” at intervals of several seconds to regularly repeating AEs at intervals of 1–2 ms. Among all the recorded AEs it was necessary to distinguish those emitted during slip events and at the stages of slip event preparation (Figure 3).

FIGURE 3

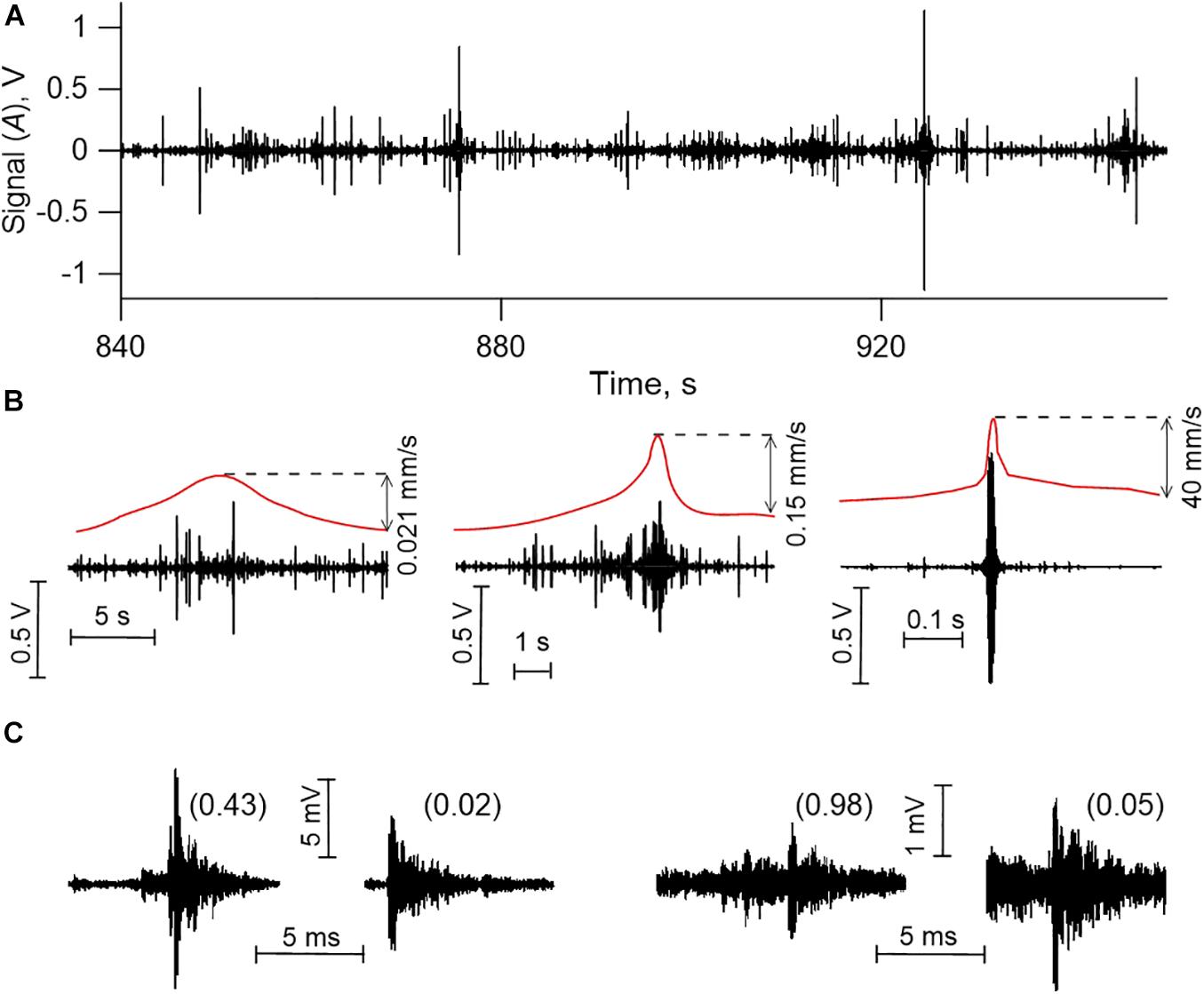
Figure 3. AE data (Exp. No 13). (A) acoustic signal recorded during fault sliding (Exp. No 13); (B) “coseismic” AEs corresponding to slip events; (C) “interseismic” AEs corresponding to slip event preparation. In (B) the red line corresponds to variations in time of the velocity at which the moveable block slides. In (C) the WI-value is indicated in parentheses.

Results

Continuum of Fault Slip Modes at the Macro Scale

Using mixtures of different materials, we managed to reproduce in laboratory the entire spectrum of slip modes. We determine slip event as a dynamic instability characterized by a decreasing friction and block sliding at a velocity exceeding u_s. The time period when block velocity exceeds u_s, corresponds to the duration of the event (T); the displacement of block for that time period is treated as the coseismic slip (ΔL). We used the record of displacement of the block relative to the base to calculate peak velocities (V_peak) during slip events. Figure 4 shows variation of parameters of slip events. They form a connected set in the space (V_peak, T, ΔL). Considering different parameters lets us to qualitatively divide the events into three modes. The first mode is the fast slip events with peak velocities higher than 8 mm/s (1,000 u_s) and durations less than 0.8 s (Figure 3B). The fastest slip events had peak velocities up to 48 mm/s (6,000 u_s) and relative values of friction drops up to 0.1 (Figure 1B). Single high-amplitude AEs with durations corresponding to the ones of slip events were emitted in fast modes. The second mode is the slow slip events. Slow slip events had peak velocities of 2–5 u_s and relative changes of friction less than 10^–2. Slow slip events were accompanied by emission of cascades of AEs (Figure 3B) that resembled low frequency earthquake bursts during slow slip events (SSE) in nature (Frank et al., 2016). Duration of laboratory slow slip events varied from 2 s to 15–20 s. It should be noted that slow slip events with durations exceeding 10 s were specific for the model fault with clay-rich gouge. The third mode is the intermediate slip events. It shows a high variety of parameters and demonstrates a diversity of slip events. The third mode fills in the gap between slow and fast slip events, indicating a continuum of slip modes.

FIGURE 4

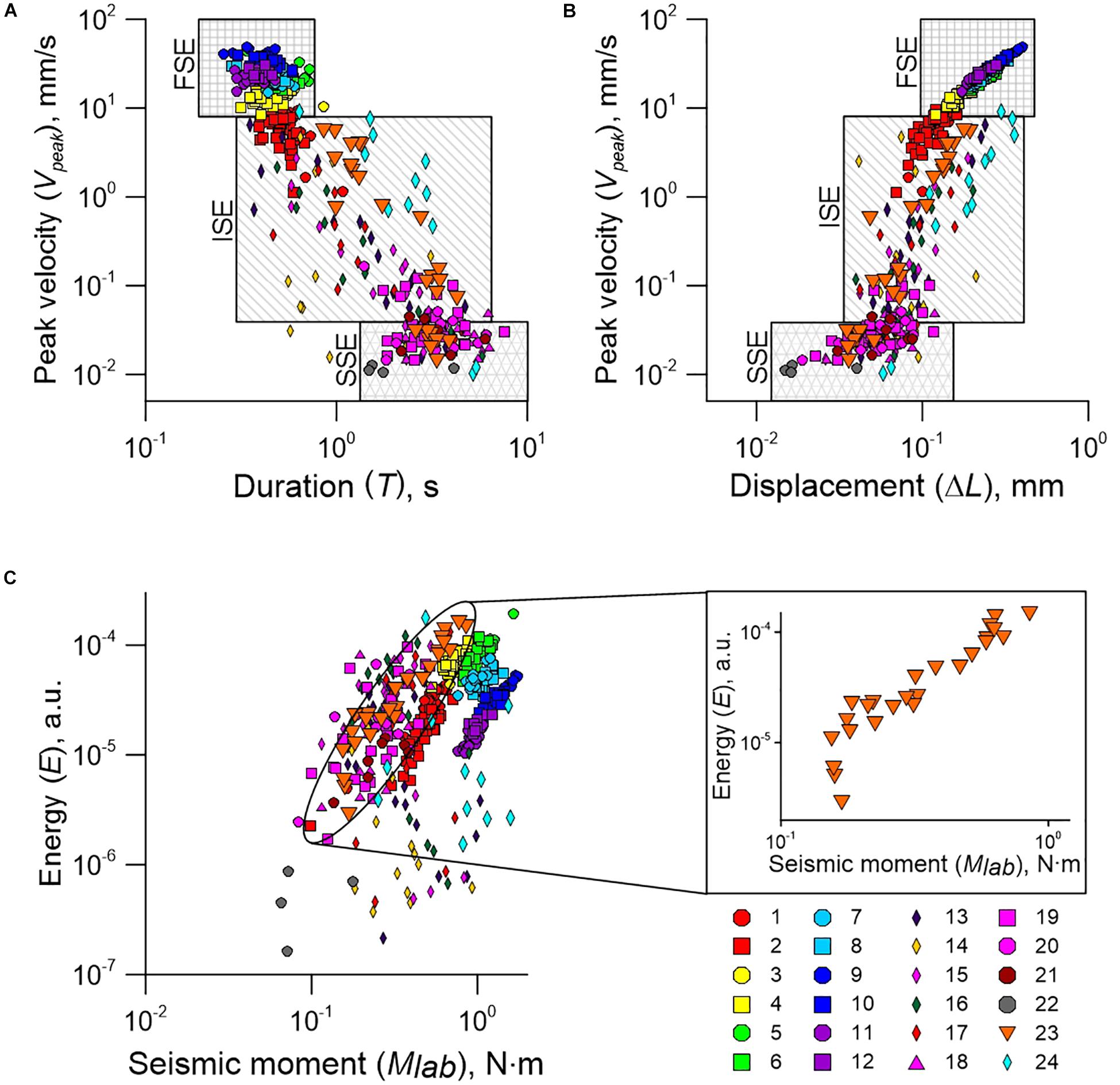
Figure 4. Variations of slip event parameters. Peak velocity dependences on slip duration (A) and on cumulative slip (B) show that the ensemble of slip events form a connected set in the space [cumulative slip (ΔL), peak velocity (V_peak), slip duration (T)]. The area in the space of parameters specific for fast slip events is marked as FSE, intermediate slip events—ISE, slow slip events—SSE. (C) The energy of “coseismic” AEs vs. the laboratory “seismic” moment. Inset shows the results of Exp. No 23. The laboratory seismic moment is M_labK⋅△L⋅s (where K and s are spring stiffness and block length, respectively) (Kocharyan et al., 2017a). The symbols 1–24 correspond to different experiments listed in the Supplementary Table 1.

The ensemble of slip events demonstrates a high spread of the emitted cumulative AE energy. The magnitude of AE energy differs by more than 2 orders of magnitude for slip events with equal laboratory “seismic moments” (Supplementary Section 1). Considering the data of a single experiment, an increase in the seismic moment is accompanied by a power-law increase in the emitted AE energy (Figure 4C, inset). Unfortunately, it is impossible to detect an analogous regularity considering the complete ensemble of slip events. The reason is the alteration of the structure of the model fault filler. The filler composition controls the radiation efficiency of slip events (Kocharyan et al., 2017a). Hence, events with equal seismic moments can show different values of emitted energy on faults with different filler.

Two AE Subpopulations at the Micro Scale

The change of stress-strain state of the model fault results in a rearrangement of grains and is accompanied by a great number of AEs. In general, the amplitude-frequency distribution of AEs is a superposition of a power-law distribution in the low-amplitude range (A_s < 0.1 V) and a peak-like distribution in the high-amplitude range (A_s > 0.1 V) (Figure 5A).

FIGURE 5

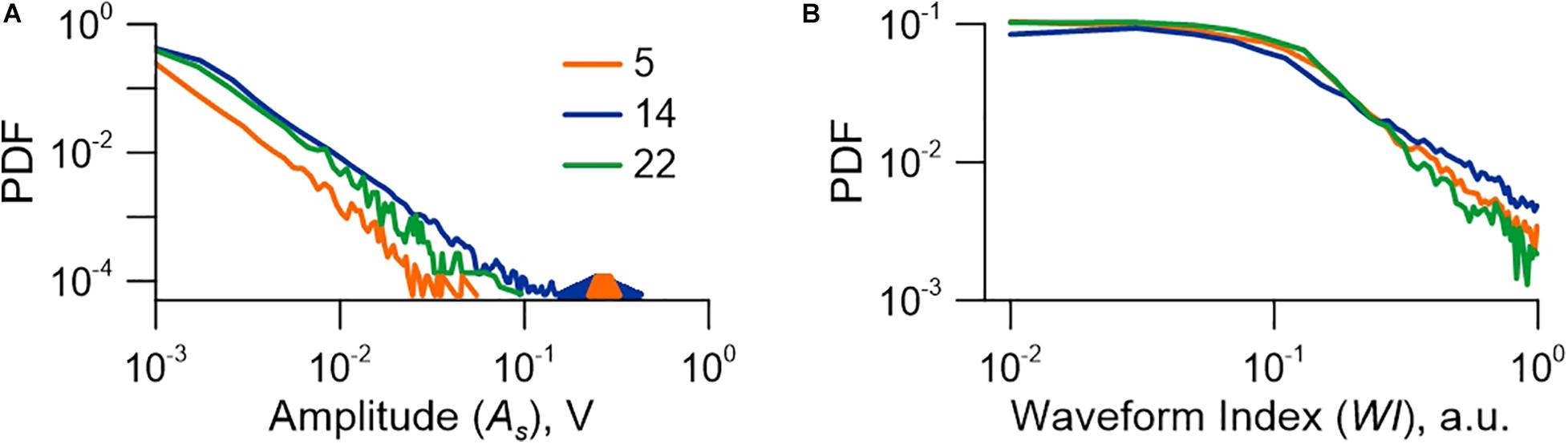
Figure 5. Probability density function (PDF) of AE. AE statistics demonstrates an essential difference between frequency-amplitude (A) and frequency-waveform (B) distributions. The “coseismic” AEs corresponding to slip events form a separate high-amplitude peak, which is marked by the filled area. The waveform index plot shows the characteristic (cut-off) value (WI = 0.1). Numbers correspond to experiments listed in Supplementary Table 1.

In the range of low A_s values the AE statistics is approximated with high accuracy by the power-law:

$$lg\left(N\right)=a-b\cdot lg\left(\frac{A_s}{A_0}\right)(5)$$

where N is the number of AEs with amplitudes of A_s. The value lg (A_s/A₀) corresponds to AE body-wave magnitude (Lei, 2003), a and b are two positive constants. The a-value is a measure of AE activity, which depends on the time window of observations. The slope of recurrence plot (b-value) is a scaling parameter, which characterizes the process of self-organization of the medium (Gutenberg and Richter, 1944; Turcotte, 1999). The power law is also typical for the AE distributions over energy (E) and duration (dt).

The distribution of AE over the WI-value shows persistence of the cut-off WI-value. WI varies from 10^–2 to 1 and can be separated into two domains: WI ≤ 10^–1 and WI > 10^–1. An even distribution is observed for low values, and a power decrease—for high values (Figure 5B). It can be written as follows:

$$N=\{\begin{array}{c}\hfill a_{WI},WI\le 0.1\hfill \\ \hfill c_{WI}\cdot W{I}^{-w},WI>0.1\hfill \end{array}(6)$$

where N is the number of AEs whose waveform parameters equal to WI, a_WI, and c_WI are positive constants, which are determined by the intensity of AE activity.

The essential difference of the AE distributions over amplitude and over waveform index points to the necessity to consider the WI-value as an independent characteristic of the process of fault evolution. The presence of a specific cut-off point in the frequency-waveform distribution motivates to conduct a quantitative categorization of the ensemble of detected AEs over the WI-value. Quantitative categorization can be considered as a sort of clustering under unsupervised machine learning. AEs with WI ≤ 0.1 will compose Type I. They are wave trains with harsh onsets. Their spectra show maxima in the range of 50–65 kHz (Figure 6). Type II will include AEs with WI > 0.1. They exhibit gradual amplitude rises and tremor-like waveforms (Figure 3). A tendency of transition of vibrations to the low-frequency area is traced for the AEs of Type II and there is an obligatory maximum at 20 kHz (Figure 6).

FIGURE 6

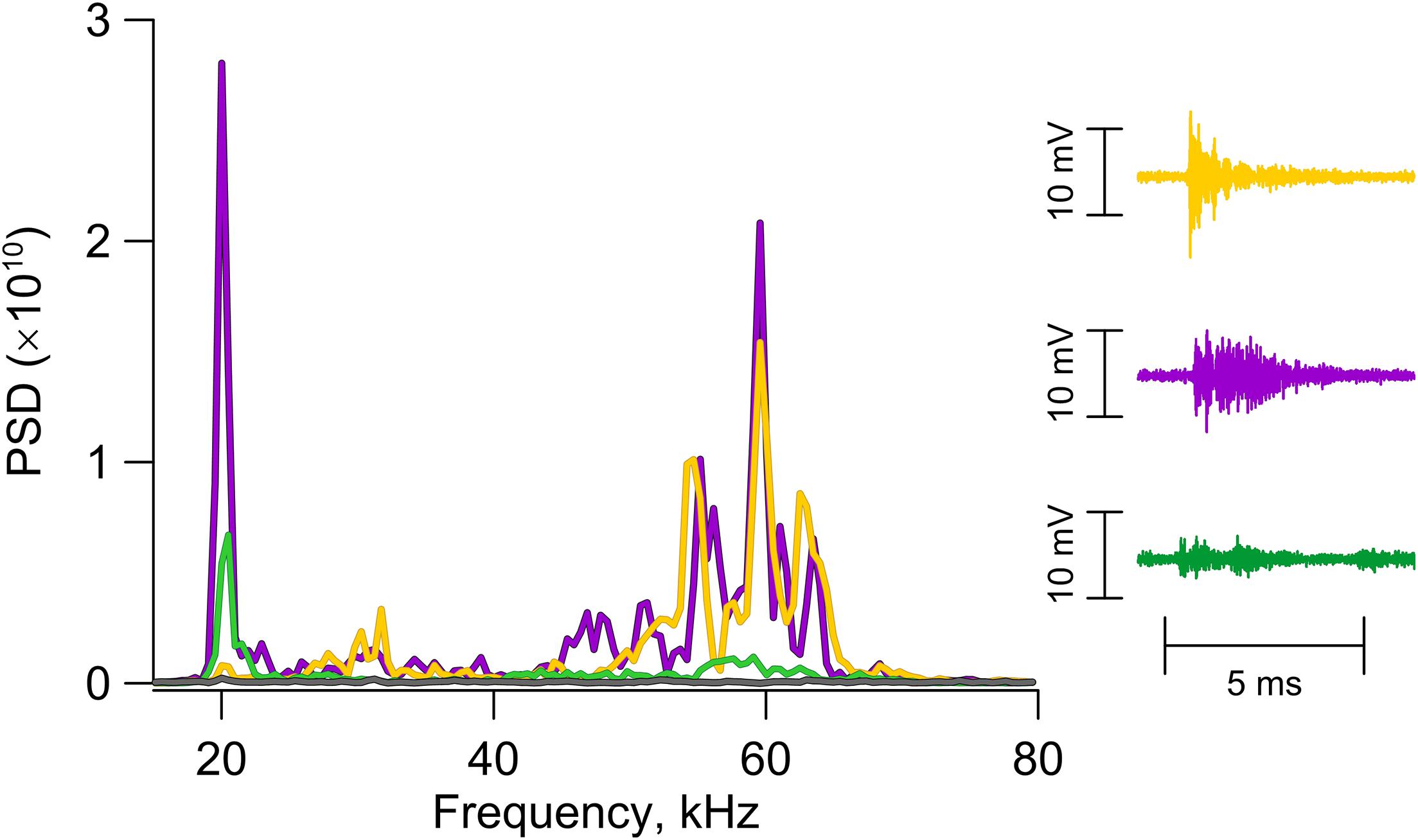
Figure 6. Power spectral density (PSD) of AE. Spectra specific for AEs with different waveforms. The AE with harsh onset shows maximum in the range of 50–65 kHz. For the AE with gradual amplitude rise two maxima emerge in the range of 18–25 and 50–65 kHz. For tremor-like AEs spectral maxima are shifted to the range of 18–25 kHz.

Figure 7 shows log-log trends between parameters of AEs of Type I and Type II. The scaling relationships provide important insights into and constraints on the dynamics of internal processes. Such a presentation gives an opportunity to qualitatively compare these trends to scaling laws for ordinary “fast” earthquakes and SSEs (Peng and Gomberg, 2010; Nishitsuji and Mori, 2014).

FIGURE 7

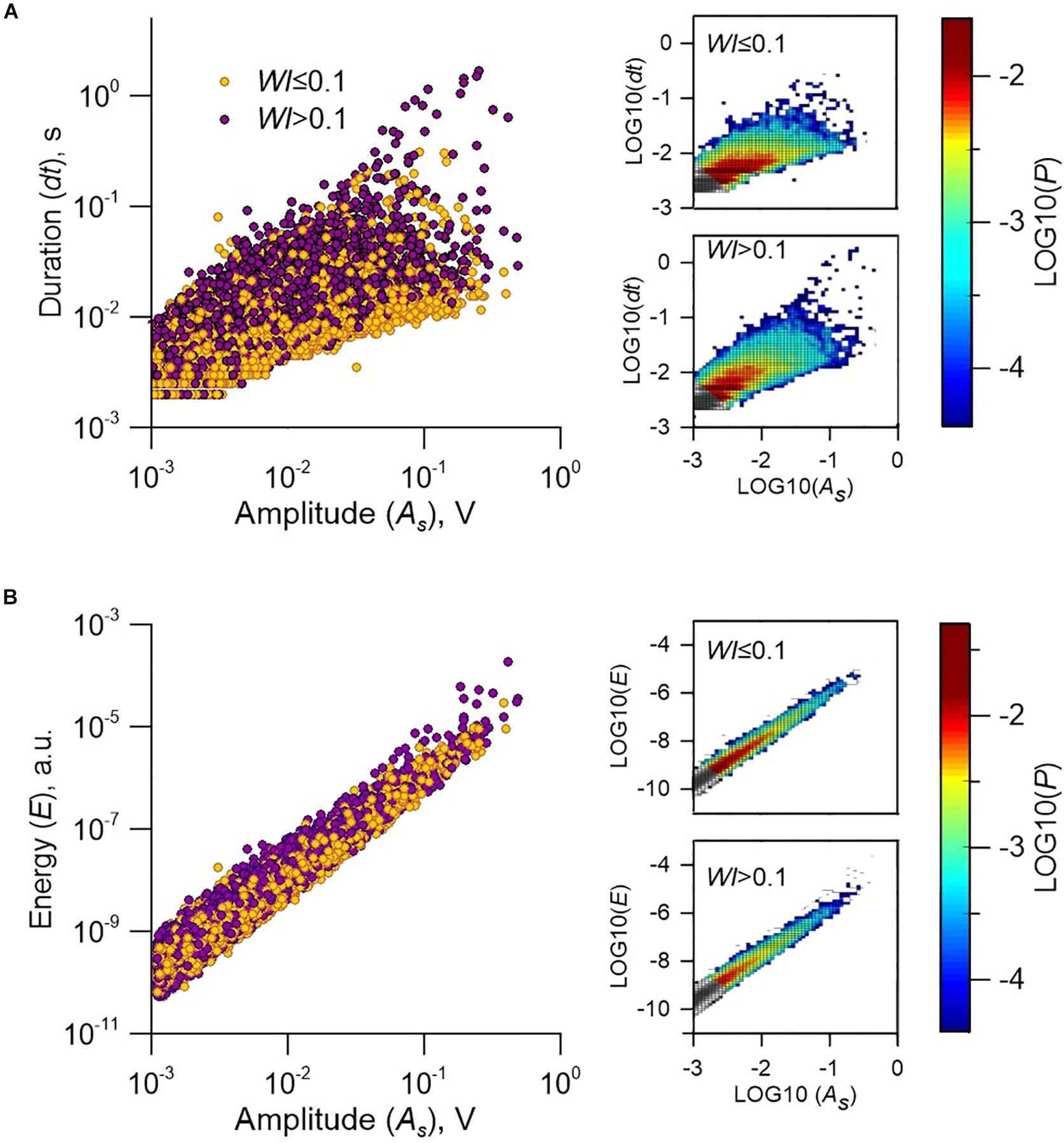
Figure 7. Scaling of two AE subpopulations in Exp. No 13. (A) AE duration vs. AE amplitude (type I—yellow, type II—purple). The complete ensemble of AEs is limited by two solid lines given by relations (7). Right plots show the two-dimensional probability density functions of AEs type I (upper) and AEs type II (lower). (B) AE energy vs. AE amplitude. The energy varies by more than an order of magnitude for AEs with one and the same amplitude. Right plots show the two-dimensional probability density functions of AEs type I (upper) and AEs type II (lower).

The AE duration scaling is viewed as a key to unraveling the rupture mechanism in nature and in lab. All the recorded AEs form a connected set, which is limited by two boundaries:

$$\begin{array}{l}d{t}_{upper}\sim A_s^{1.2\pm 0.2}\\ d{t}_{bottom}\sim A_s^{0.5\pm 0.1}(7)\end{array}$$

In nature this may correspond to the scaling between the seismic moment M₀ and the duration T_eq ranging from $T_{eq}\sim M_0^{0.8\pm 0.1}$ to $T_{eq}\sim M_0^{0.3\pm 0.1}$ (Supplementary Section 2). At the same time one can see that AEs of Type I group closer to the lower boundary, than AEs of Type II (Figure 7). It means that for AEs of equal amplitudes, Type II should have longer failure duration than Type I. At the same time, scaling of emitted energy of two types differ insignificantly, indicating that the intergranular frictional sliding is the single source of AEs.

Illumination of Frictional Behavior

A stable repeated pattern of variations of sliding velocity and AE rate is observed during a regular stick-slip (Figure 8). We distinguish three typical stages of a seismic cycle. After the dynamic failure the post-seismic stage comes with a decreasing velocity of sliding block and a lowering AE rate. The falling activity is described by the law of Omori-Utsu (Lherminier et al., 2019; Ostapchuk et al., 2019). Then approximately stable minimal values of velocity and AE rate persist at the inter-seismic stage. As the system approaches a slip event, an accelerated block sliding starts accompanied by an increase of AE rate. At the final part of inter-seismic stage leading to failure, statistics of AEs can be described by the inverse Omori’s law (Johnson et al., 2013; Ostapchuk et al., 2019). In a stochastic regime the pattern of parameter alteration is more complicated (Figure 8). It seems impossible to detect stages of a cycle through AE rate and sliding block velocity. Only small relative variations of AE rate are observed before slip events, while abrupt drops occur only after the fastest slip events.

FIGURE 8

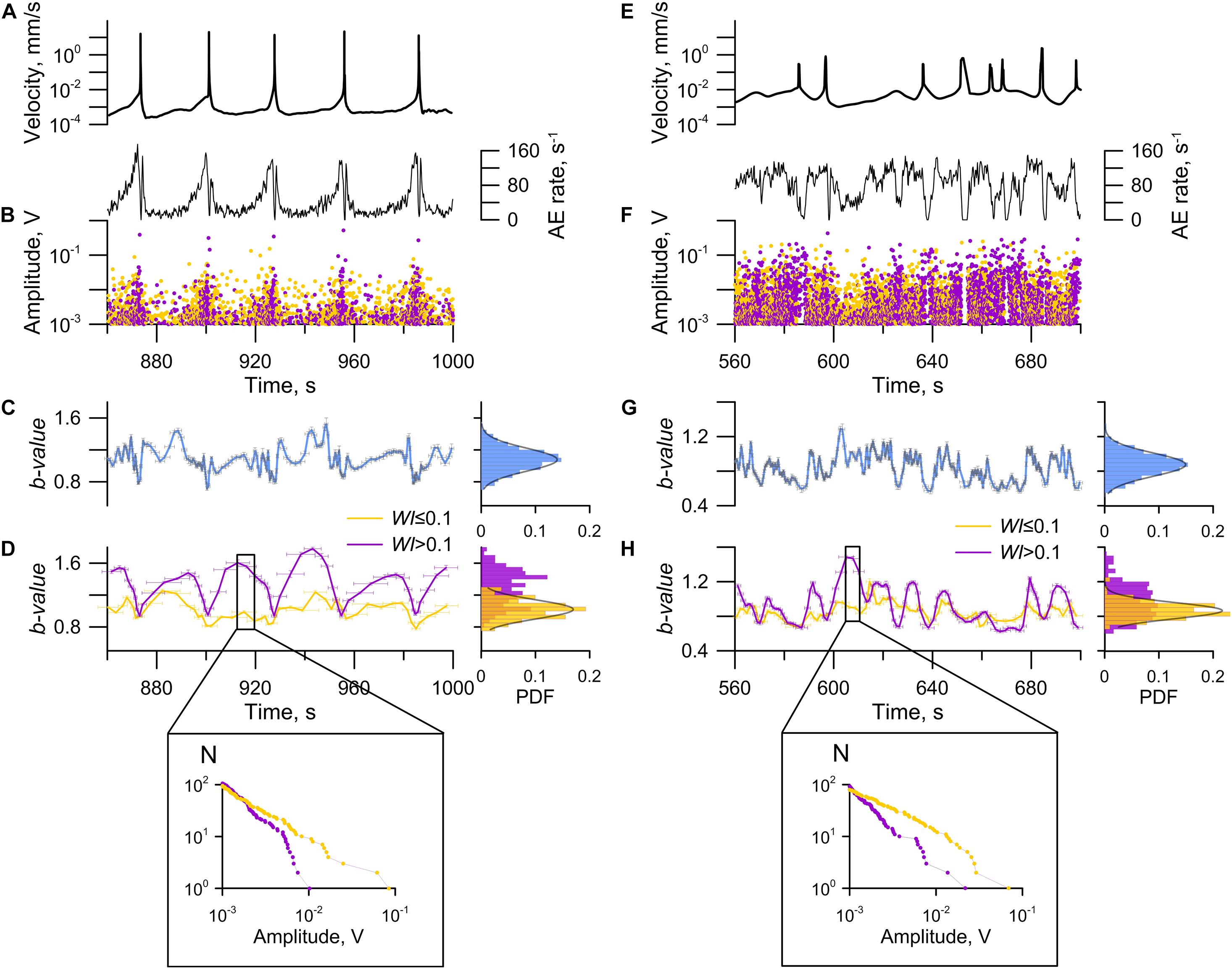
Figure 8. Evolution of model fault state. Variations of sliding velocity and AE parameters for a regular stick-slip (Exp. No 3) (A–D) and a stochastic sliding regime (Exp. No 13) (E–H). Insets (D,H) show distributions of AEs in running windows for type I (yellow) and type II (purple). Unlike the stochastic regime, the regular regime shows a high correlation between the sliding velocity and the AE rate. Occasional variations of b-value are observed for both regular and stochastic regimes for the complete ensemble of AEs. Probability density function of b-value obeys the normal distribution law. Dividing AEs into two subpopulations shows an essential difference of time variations of b-value. Occasional alterations are observed for the AEs type I (WI ≤ 0.1), while the AEs type II (WI > 0.1) show systematic variations.

Peculiarity of frictional behavior can be illuminated by the AEs. Variations of cumulative displacement (D) and cumulative AE energy (Π) have similar tendencies (Figure 9). For all the sliding regimes correlation between D and Π exceeds 0.95, and the revealed regression model is:

FIGURE 9

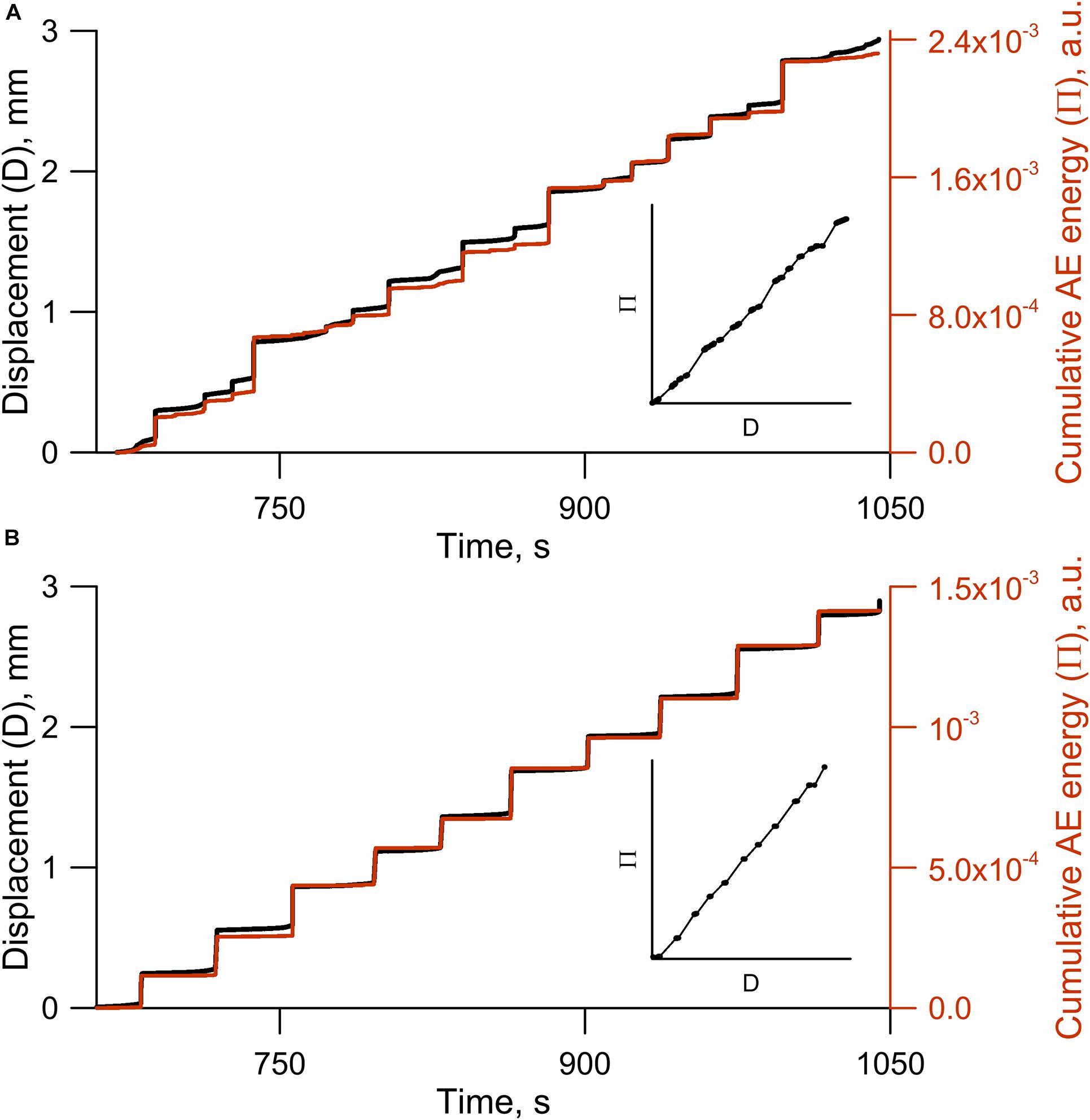
Figure 9. Variations of cumulative AE energy (Π) and block displacement (D). The inset shows the dependency Π (D). (A) Stochastic sliding regime, Exp. No 23—Π = 8.10⁻⁴⋅ D. (B) Regular sliding regime, Exp. No 5—Π = 5.10⁻⁴⋅D.

$$\mathrm{\Pi }=\mathrm{\gamma }\cdot D(8)$$

Also, we can evaluate the friction strength of model fault. In experiments with different gouge materials the friction coefficient varies significantly from 0.46 to 0.86 (Supplementary Table 1). The analysis of parameters of sliding regime have shown that the growth of friction coefficient is accompanied by a decrease in b-value, while the Pearson’s correlation is about 0.94. Besides that, the friction coefficient ranging from 0.65 to 0.83 corresponds to the b-value lower than 1.1.

Illumination of Slip Event Nucleation

Figure 8 shows variations of AE parameters for regular and stochastic sliding regimes. To investigate the temporal evolution of b-value, we calculated the b-value using the least squares regression in a running window for an equal number of AEs (nn = 100) at a running step of nn/2 (50% overlap). No clear staging of laboratory seismic cycles was observed when analyzing variations of the b-value of the complete population of AEs. The b-value distribution obeys the normal law. It should be noted that the cyclicity of b-value for the complete population of AEs in a limited range of amplitudes has been mentioned in a few works (Lei et al., 2018; Riviere et al., 2018). Clusterization of AEs into two subpopulations eliminates the ambiguity of the pattern of b-value variations.

For a regular stick-slip b-value histograms show that for AEs of type I (WI ≤ 0.1) b-value is almost constant and its changes are occasional (histogram obeys the normal distribution). At the same time the AEs of type II demonstrate certain periodic variations of b-value, and the histogram cannot be approximated by a normal distribution. If we look at the laboratory seismic cycle just after a dynamic failure at the first stage of fault recovery, we can see that a fast growth of b-value occurs. Then the stage of creep comes at a minimal velocity, and b-value remains almost constant, which in the histogram manifests as a peak of b-value around the value of 1.4 (Figure 8A). At the final stage, a monotonic decrease of b-value is observed, which means that the share of high-amplitude AEs of type II grows.

For a stochastic regime, the pattern of parameter alteration is much more complicated. But, if one performs clusterization of AEs, the duality of their population becomes apparent, and the staging of fault evolution manifests clearly (Figure 8D). The AEs of type I have only a single specific b-value during shear, and variations are random. The AEs of type II show staging of b-value alteration. The b-value decreases before each of the slip events and recovers after them.

Detecting the two subpopulations of AEs can form a new basis for revealing slip event nucleation. We have formulated a simple criterion of laboratory “alarm.” It is based on tracing specific features of AEs that reflect fault evolution in time. The alarm criterion is as follows. If for AEs type I a random variation of b-value is observed and for AEs type II for three successively estimated b-values a monotonic decrease is observed b(t_i−2) > b(t_i−1) > b(t_i), then the alarm starts at the time t_i (Figure 10). The end of the alarm is the time when the slip event starts (the “true” alarm), or the time t_n, when an increase of b-value is observed again b(t_n−1) < b(t_n) (the “false” alarm) (Figure 10, the inset).

FIGURE 10

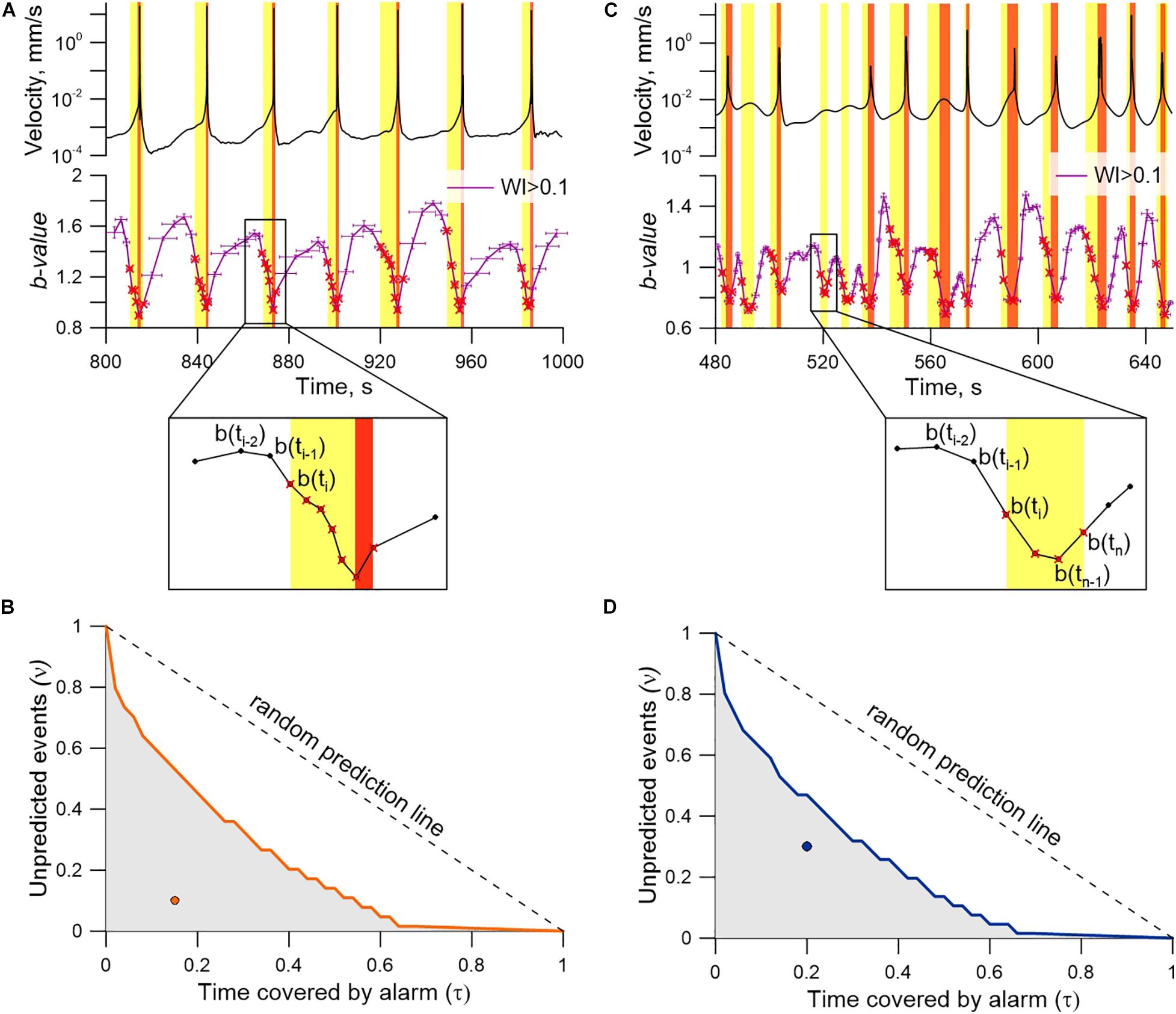
Figure 10. Transition of the model fault to a critical state. Variations of block velocity and b-value of AEs type II for a regular stick-slip in Exp. No 4 (A) and a stochastic sliding regime in Exp. No 13 (C). The yellow areas correspond to alarm intervals, the red ones—to slip events. Insets show algorithms for a “true” alarm (A) and a “false” alarm (C). We use the Molchan’s diagram to evaluate the predictive power for regular (B) and stochastic (D) sliding regimes. Shaded circles show the performance of prediction algorithm. Random binomial predictions occupy the diagonal. Random predictions with fixed alarm time (τ) fall in the gray area with the probability of α = 10^–5.

For a regular sliding regime, the alarm covers the whole pre-seismic stage of the seismic cycle. For example, in Exp. No 4 the duration of alarm was 3.9 ± 1.9 s, while the recurrent time of dynamic failures was 34.2 ± 0.8 s. At the same time, it is important to note that the critical stage (when an event can be triggered by a weak disturbance) emerges at stresses close to the critical ones at the end of the pre-seismic stage (Kocharyan et al., 2018). For a stochastic regime (Figure 10C) the pattern of b-value alteration is more complex, but the chosen alarm criterion is sensitive for such a regime too. The decrease of b-value signifies both the forthcoming fast and slow slip events, but more complex mechanisms of self-organization lead to “false alarms” (Ren et al., 2019) (Figure 10C, the inset). The Molchan’s error diagram is used to evaluate the predictive power of our prediction algorithm and its stability (Molchan, 2003, 2010). We use two interdependent measures of prediction quality: the fraction of unpredicted events ν, and the fraction of alarms τ. Each prediction corresponds to a single point in (τ, ν) space. The error diagram for our prediction of the transition of the fault to the critical state of seismic cycle is presented in Figures 10B,D. The τ-axis corresponds to the relative alarm time, the ν-axis—to the share of missed slip events. An extremely simple but easily tractable model of prediction which produces alarms independent of the target events is the random binomial prediction (Molchan, 2003; Shebalin et al., 2006). The probability for a random binomial prediction with a given value of τ to fall within the shaded area is less than or equal to 10^–5 (0.001%). The point corresponds to our prediction algorithm indicating high predictive power both for the regular and the stochastic sliding regimes. The efficiency of the precursor J_m is defined as:

$$J_m=1-\mathrm{\nu }-\mathrm{\tau }(9)$$

The value of J_m lies in the range of (0…1). The nearer the value to 1 is, the more reliable is the raise of alarm. For a regular stick-slip J_m is equal to 0.59–0.83, while for a stochastic sliding regime that includes multiple slip modes the value is J_m = 0.4 – 0.65 (Supplementary Table 1).

Discussion

Recent findings improve our understanding of the evolution of a frictional fault hosting multiple slip modes. It should be noted that laboratory experiments are by no means a sort of scale modeling since it is simply impossible to fulfill all the similarity criteria in this case (Rosenau et al., 2017). Results of laboratory experiments should be considered as insights into fundamental properties of geomaterials and their structural peculiarities which underly fault slip behavior. The similarities in the internal structures of experimental and natural faults point to similarities in the deformation mechanisms (Tchalenko, 1970). Findings should relate to the frictional instability of a model fault, just at the expense of self-organization of granular matter.

Natural faults show the evidence of localizing deformations along very narrow fault-parallel principal slip zones. These principal slip zones have undergone large cumulative deformations (Sibson, 2003). The wall rocks are separated by a layer of cataclastic rock (gouge) with self-similar structure over the range of particle diameters from 10 μm to 1 cm (Sammis et al., 1987). As a rule such faults are treated as strong faults, and their frictional strength is consistent with the Beyrlee’s rule of friction (from 0.6 to 0.85) (Collettini et al., 2019). The evolution of a laboratory gouge-filled fault is controlled by peculiarities of formation and destruction of conglomerates of loaded grains at the microscale, the so called “force chains” (Sammis et al., 1987; Mair et al., 2002; Hayman et al., 2011; Lherminier et al., 2019). The assembly of these chains has a certain spatial structure and a relatively low specific weight inside the medium (Gao et al., 2019). Thus, we may suggest that two structural subsystems emerge inside a stressed fault—a consolidated force skeleton and rather moveable relatively unloaded areas (Gao et al., 2019). Although we had no chance to visualize the inner processes of self-organization in the performed experiments, the revealed regularities of alteration of AE ensemble agree with numerical (Hadda et al., 2015; Gao et al., 2019) and laboratory (Mair et al., 2002; Hayman et al., 2011) experiments. The findings probably point to formation and evolution of two structural subsystems. When the force chains (loaded grain conglomerates with limited sizes) are destroyed, the high-frequency AEs with harsh onsets are emitted (Hadda et al., 2015; Ostapchuk et al., 2016; Gao et al., 2019). The uniformity of distribution for WI < 0.1 points to formation of stressed grain clusters of limited size which have approximately equal sizes (Hadda et al., 2015) (Figure 5B). Breaking force chain leads to increasing the volume of unloaded grain clusters, so, the size of unloaded areas varies during laboratory seismic cycle. Indeed, for AEs with WI > 0.1 the power law distribution is observed. Considering a blocky hierarchical structure of the Earth’s crust, the distribution of stresses inside separate structural forms can exhibit a partially inhomogeneous character (Sobolev and Zav’yalov, 1980; Schoenball and Davatzes, 2017). In the zones of tectonic faults stresses concentrate at asperities (Seno, 2003) or strong patches (Collettini et al., 2019), which probably correspond to laboratory force chains. It is the configuration and friction properties of asperities that determine the slip mode of the fault (Dublanchet et al., 2013; Barbot, 2019). Indeed, high temperature and stresses, specific for seismogenic depths, affect the deformation of gouge-filled faults, but under the velocity weakening it is the self-organization processes that will prevail in the evolution of fault behavior. One of the mechanisms of destruction of stressed clusters under high stresses is grain crushing. Grain crushing is accompanied by AEs with harsh onsets and low WI-values (Shiotani et al., 2001). So, grain crushing makes the structure of AE ensemble in the range of low WI-values more complex, but it is the frictional slippage that controls the rearrangement of unloaded zones. In this work we made the accent on the processes of self-organization provoked by frictional instability. Performing a quantitative categorization of AEs during grain crushing is a future prospect. We may identify qualitative similarity in the processes of self-organization of both natural and laboratory frictional faults (Mykulyak et al., 2019).

The experiments testify that the entire spectrum of slip modes results from the frictional instability of the model fault, just at the expense of friction (Figures 3, 4). Though we do not exclude other mechanisms, such as variations of fluid pore pressure, dehydration reactions, brittle-ductile transition and others (Reber et al., 2015; Saffer and Wallace, 2015; Burgmann, 2018; Cruz-Atienza et al., 2018). We demonstrate that frictional slip modes span a continuum and that the cumulative acoustic energy released during slip events varies in a wide range. From the mechanics of faults viewpoint and under velocity weakening the slip mode and the emissive efficiency of an event are determined by the ratio κ of the specific fault stiffness to the specific stiffness of the hosting rock (Leeman et al., 2016; Kocharyan et al., 2017a). When κ ∼ 1 slow slip modes prevail, when κ >> 1 fast events take place and their intensity increases as κ grows. If a fault has a spatially heterogeneous interface, reconfiguration/rearrangement of force skeleton caused by slip events may essentially change the ratio κ and different slip modes can be reproduced (Kocharyan et al., 2017b; Ostapchuk et al., 2020). In our experiments the stiffness of the hosting rock (the loading system is its analog in lab) remained constant, only the fault stiffness varied. This led to formation of a connected set in the space (V_peak, T, ΔL). Our study shows that one and the same laboratory fault can host different slip modes. Meanwhile these different slip modes are described by one and the same scaling ratio (Figure 4C, inset). Recent observations in natural field suggest that SSEs follow the same moment duration scaling as earthquakes (Michel et al., 2019; Frank and Brodsky, 2020), unlike qualitatively different scaling proposed by earlier studies (Peng and Gomberg, 2010). For example, the Cascadia slow slip events demonstrate a cubic moment-duration scaling and can produce pulse-like ruptures similar to fast slip events (Michel et al., 2019). Numerical simulations urge the same frictional origin for both earthquakes and SSEs and show that both simulated and natural SSEs have rupture velocities and stress drops that increase with earthquake magnitudes (Dal Zilio et al., 2020).

Most scholars consider the regular stick-slip, when slip events take place quasi-periodically, as the dominant fault sliding regime. Laboratory investigations of fault behavior should take into account the stochastic sliding regime too. There are very few known faults with regular periodicity of characteristic earthquakes at the human timescale (Ben-Zion, 2008); meanwhile, evidence appears systematically, that a single fault hosts both fast and slow slips (Ito et al., 2013; Meng et al., 2015; Villegas-Lanza et al., 2016).

Regularities of the model fault evolution at the micro-scale determine its characteristics at the macro-scale. It has long been recognized in soil mechanics that the apparent coefficient of friction (μ^∗), which is defined by the ratio of the shear (τ) to the normal (σ_N) stresses, is larger than the actual coefficient of friction between the particles (μ). For a 2D force chain consisting of equal size particles the apparent friction μ^∗ is as follows (Biegel and Sammis, 1989):

$${\mathrm{\mu }}^{*}=\frac{\mathrm{\mu }+tan\mathrm{\beta }}{1-\mathrm{\mu }\cdot tan\mathrm{\beta }},(10)$$

where β is the misalignment angle (the angle between the macroscopic shear plane and the interparticle slip plane). The value of β depends on particle size distribution and the packing geometry (Biegel and Sammis, 1989). Hence, changing fault structure causes a change in friction μ^∗. But changing the structure also causes a change in the b-value of the frequency-amplitude distribution (Turcotte, 1999; de Arcangelis et al., 2016). Our experiments demonstrate a high inverse correlation (-0.95) between the b-value and the fault friction (τ_s/σ_N), that is, the spatial variation of b-value may point to spatial variations of frictional/structural properties of the fault.

Improving the techniques of detecting weak and slow earthquakes and performing their statistical analysis provide important information about tectonic fault dynamics and help to trace the nucleation of a large earthquake (Gulia and Wiemer, 2019; Trugman and Ross, 2019). The performed experiments have shown that for a stochastic regime it is appropriate to supplement a classical seismic catalog containing information about time, place and magnitude with parameters that describe the dynamics of coseismic rupture. Resting on a quantitative categorization of the AE catalog, a simple, but very efficient criterion of laboratory “alarm” has been formulated. The introduced alarm algorithm indicates that the frictional fault instability is imminent, but the precise time to failure is not defined. For a stochastic regime the efficiency of the algorithm is J_m = 0.54 ± 0.14, while for a regular stick-slip it rises to J_m = 0.74 ± 0.11. For comparison, the efficiency of the ETAS forecasting model for earthquakes M > 6 in Southern California is 0.29 (Lippiello et al., 2012). Predictions based on the ultralow frequency magnetic data show the efficiency of about 0.23 (Han et al., 2017). The forecasting technique based on the effect of modulation of high frequency seismic noise in Kamchatka gives the value of about 0.5 for target earthquakes M ≥ 6 (Saltykov, 2017). Thus, the implementation of quantitative categorization of seismic data may be the next stage which can potentially mark advances in fault mechanics.

Conclusion

A unified pattern of fault slip behavior evolution is a fundamental issue. It requires linking seismic, mechanical and structural data. In the present laboratory study we have revealed two distinct subpopulations of AEs, which reflects the complexity of frictional fault evolution at the micro scale. The self-organization of a gouge-filled fault at the micro scale is the key parameter that controls the frictional behavior of a fault hosting multiple slip modes. At the macro scale a similarity of precursory changes of AEs for fast, intermediate, and slow slip modes on a frictional fault is observed. Findings point to the unity of underlying frictional mechanisms of different slip modes.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: http://dx.doi.org/10.17632/kykwmjmpgf.3.

Author Contributions

AO was responsible for the research conceptualization, design, organization of the work, and writing the first draft of the article. KM, VM, and DP performed the experiments. KM and MP performed the data analyses and prepared some figures. KM was involved in the data curation. All authors took part in editing the final version.

Funding

This work was partially supported by the Russian Science Foundation according to the Research Project No. 20-77-10087 for KM, DP, and AO. VM and MP acknowledge Program No. AAAA-A17-117112350020-9 of the Ministry of Science and Higher Education of the Russian Federation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.657487/full#supplementary-material

References

Anthony, J. L., and Marone, C. (2005). Influence of particle characteristics on granular friction. J. Geophys. Res. 110:B08409. doi: 10.1029/2004JB003399

CrossRef Full Text | Google Scholar

Barbot, S. (2019). Slow-slip, slow earthquakes, period-two cycles, full and partial ruptures, and deterministic chaos in a single asperity fault. Tectonophysics 768:228171. doi: 10.1016/j.tecto.2019.228171

CrossRef Full Text | Google Scholar

Ben-Zion, Y. (2008). Collective behavior of earthquakes and faults: continuum–discrete transitions, progressive evolutionary changes, and different dynamic regimes. Rev. Geophys. 46, 1–70. doi: 10.1029/2008RG000260

CrossRef Full Text | Google Scholar

Biegel, R. L., and Sammis, C. (1989). The frictional properties of a simulated gouge having a fractal particle distribution. J. Structural. Geol. 11, 827–846. doi: 10.1016/0191-8141(89)90101-6

CrossRef Full Text | Google Scholar

Bolton, D. C., Shreedharan, S., Rivière, J., and Marone, C. (2020). Acoustic energy release during the laboratory seismic cycle: Insights on laboratory earthquake precursors and prediction. J. Geophys. Res. 125:e2019JB018975. doi: 10.1029/2019JB018975

PubMed Abstract | CrossRef Full Text | Google Scholar

Brodsky, E. E., Mori, J. J., Anderson, L., Chester, F. M., Conin, M., Dunham, E. M., et al. (2020). The state of stress on the fault before, during, and after a major earthquake. Ann. Rev. Earth Planet. Sci. 4, 49–74.

Google Scholar

Burgmann, R. (2018). The geophysics, geology and mechanics of slow fault slip. Earth Planet. Sci. Lett. 495, 112–134. doi: 10.1016/j.epsl.2018.04.062

CrossRef Full Text | Google Scholar

Collettini, C., Tesei, T., Scuderi, M. M., Carpenter, B. M., and Viti, C. (2019). Beyond Byerlee friction, weak faults and implications for slip behavior. Earth Planet. Sci. Lett. 519, 245–263. doi: 10.1016/j.epsl.2019.05.011

CrossRef Full Text | Google Scholar

Cruz-Atienza, V. M., Villafuerte, C., and Bhat, H. S. (2018). Rapid tremor migration and pore-pressure waves in subduction zones. Nat. Commun. 9:2900. doi: 10.1038/s41467-018-05150-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Dal Zilio, L., Lapusta, N., and Avouac, J.-P. (2020). Unraveling scaling properties of slow-slip events. Geophys. Res. Lett. 47:e2020GL087477. doi: 10.1029/2020GL087477

CrossRef Full Text | Google Scholar

de Arcangelis, L., Cataldo Godano, C., Grasso, J. R., and Lippiello, E. (2016). Statistical physics approach to earthquake occurrence and forecasting. Phys. Rep. 628, 1–91. doi: 10.1016/j.physrep.2016.03.002

CrossRef Full Text | Google Scholar

Dixon, N., Smith, A., Flint, J. A., Khanna, R., Clark, B., and Andjelkovic, M. (2018). An acoustic emission landslide early warning system for communities in low-income and middle-income countries. Landslides 15, 1631–1644. doi: 10.1007/s10346-018-0977-1

CrossRef Full Text | Google Scholar

Dublanchet, P., Bernard, P., and Favreau, P. (2013). Interactions and triggering in a 3-D rate-and-state asperity model. J. Geophys. Res. Solid Earth 118, 2225–2245. doi: 10.1002/jgrb.50187

CrossRef Full Text | Google Scholar

Frank, W., Shapiro, N. M., Husker, A., Kostoglodov, V., Gusev, A. A., and Campillo, M. (2016). The evolving interaction of lowfrequency earthquakes during transient slip. Sci. Adv. 2:e1501616. doi: 10.1126/sciadv.1501616

PubMed Abstract | CrossRef Full Text | Google Scholar

Frank, W. B., and Brodsky, E. E. (2020). Daily measurement of slow slip from low-frequency earthquakes is consistent with ordinary earthquake scaling. Sci. Adv. 5:eaaw9386. doi: 10.1126/sciadv.aaw9386

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, K., Guyer, R., Rougier, E., Ren, C. X., and Johnson, P. A. (2019). From stress chains to acoustic emission. Phys. Rev. Lett. 123:048003. doi: 10.1103/PhysRevLett.123.048003

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerasimova, T. I., Kondratev, V. N., and Kocharyan, G. G. (1995). Modeling features of shear deformation of fissures containing filler. J. Mining Sci. 31, 288–295. doi: 10.1007/BF02048229

CrossRef Full Text | Google Scholar

Goebel, T. H. W., Schorlemmer, D., Becker, T. W., Dresen, G., and Sammis, C. G. (2013). Acoustic emissions document stress changes over many seismic cycles in stick-slip experiments. Geophys. Res. Lett. 40, 2049–2054. doi: 10.1002/grl.50507

CrossRef Full Text | Google Scholar

Gulia, L., and Wiemer, S. (2019). Real-time discrimination of earthquake foreshocks and aftershocks. Nature 574, 193–199. doi: 10.1038/s41586-019-1606-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutenberg, B., and Richter, C. F. (1944). Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 34, 185–188.

Google Scholar

Hadda, N., Nicot, F., Wan, R., and Darve, F. (2015). Microstructural self-organization in granular materials during failure. C. R. Mecanique 343, 143–154. doi: 10.1016/j.crme.2014.09.009

CrossRef Full Text | Google Scholar

Han, P., Hattori K., Zhuang, J., Chen, C.-H., Liu, J.-Y., and Yoshida, S. (2017). Evaluation of ULF seismo-magnetic phenomena in Kakioka, Japan by using Molchan’s error diagram. Geophys. J. Int. 208, 482–490. doi: 10.1093/gji/ggw404

CrossRef Full Text | Google Scholar

Hayman, N. W., Ducloué, L., Foco, K. L., and Daniels, K. E. (2011). Granular controls on periodicity of stick-slip events: kinematics and force-chains in an experimental fault. Pure Appl. Geophys. 168:2239. doi: 10.1007/s00024-011-0269-3

CrossRef Full Text | Google Scholar

Hedayat, A., Pyrak-Nolte, L. J., and Bobet, A. (2014). Precursors to the shear failure of rock discontinuities. Geophys. Res. Lett. 41, 5467–5475. doi: 10.1002/2014GL060848

CrossRef Full Text | Google Scholar

Hulbert, C., Rouet-Leduc, B., Johnson, P. A., Ren, C. X., Rivière, J., Bolton, D. C., et al. (2019). Similarity of fast and slow earthquakes illuminated by machine learning. Nat. Geosci. 12, 69–74. doi: 10.1038/s41561-018-0272-8

CrossRef Full Text | Google Scholar

Ito, Y., Hino, R., Kido, M., Fujimoto, H., Osada, Y., Inazu, D., et al. (2013). Episodic slow slip events in the Japan subduction zone before the 2011 Tohoku-Oki earthquake. Tectonophysics 600, 14–26. doi: 10.1016/j.tecto.2012.08.022

CrossRef Full Text | Google Scholar

Johnson, P., and Jia, X. (2005). Nonlinear dynamics, granular media and dynamic earthquake triggering. Nature 437, 871–874. doi: 10.1038/nature04015

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, P. A., Ferdowsi, B., Kaproth, B. M., Scuderi, M., Griffa, M., Carmeliet, J., et al. (2013). Acoustic emission and microslip precursors to stick-slip failure in sheared granular material. Geophys. Res. Lett. 40, 5627–5631. doi: 10.1002/2013GL057848

CrossRef Full Text | Google Scholar

Kocharyan, G. G. (2016). Geomechanics of Faults. Moscow: GEOS.

Google Scholar

Kocharyan, G. G., Markov, V. K., Ostapchuk, A. A., and Pavlov, D. V. (2014). Mesomechanics of shear resistance along a filled crack. Phys. Mesomech 17, 123–133. doi: 10.1134/S1029959914020040

CrossRef Full Text | Google Scholar

Kocharyan, G. G., Novikov, V. A., Ostapchuk, A. A., and Pavlov, D. V. (2017a). A study of different fault slip modes governed by the gouge material composition in laboratory experiments. Geophys. J. Int. 208, 521–528. doi: 10.1093/gji/ggw409

CrossRef Full Text | Google Scholar

Kocharyan, G. G., and Ostapchuk, A. A. (2011). Variations in rupture zone stiffness during a seismic cycle. Dokl. Earth Sci. 441:1591. doi: 10.1134/S1028334X11110250

CrossRef Full Text | Google Scholar

Kocharyan, G. G., Ostapchuk, A. A., Pavlov, D. V., and Markov, V. K. (2018). The effects of weak dynamic pulses on the slip dynamics of a laboratory fault. Bull. Seismol. Soc. Am. 108, 2983–2992. doi: 10.1785/0120170363

CrossRef Full Text | Google Scholar

Kocharyan, G. G., Ostapchuk, A. A., Pavlov, D. V., Ruzhich, V. V., Batukhtin, I. V., Vinogradov, E. A., et al. (2017b). Experimental study of different modes of block sliding along interface. Part 2. Field experiments and phenomenological model of the phenomenon. Phys. Mesomech. 20, 193–202. doi: 10.1134/S1029959917020096

CrossRef Full Text | Google Scholar

Kuksenko, V., Tomilin, N., Damaskinskaya, E., and Lockner, D. (1996). A two-stage model of fracture of rocks. Pageoph 146, 253–263. doi: 10.1007/BF00876492

CrossRef Full Text | Google Scholar

Leeman, J., Saffer, D., Scuderi, M., and Marone, C. (2016). Laboratory observations of slow earthquakes and the spectrum of tectonic fault slip modes. Nat. Commun. 7:11104. doi: 10.1038/ncomms11104

PubMed Abstract | CrossRef Full Text | Google Scholar

Lei, X. (2003). How does asperities fracture? An experimental study of unbroken asperities. Earth Planet. Sci. Lett. 213, 347–359. doi: 10.1016/S0012-821X(03)00328-5

CrossRef Full Text | Google Scholar

Lei, X., Li, S., and Liu, L. (2018). Seismic b-value for foreshock AE events preceding repeated stick-slips of pre-cut faults in granite. Appl. Sci. 8:2361. doi: 10.3390/app8122361

CrossRef Full Text | Google Scholar

Lherminier, S., Planet, R., Levy dit Vehel, V., Simon, G., Vanel, L., Måløy, K. J., et al. (2019). Continuously Sheared Granular Matter Reproduces in Detail Seismicity Laws. Phys. Rev. Lett. 122:218501. doi: 10.1103/PhysRevLett.122.218501

PubMed Abstract | CrossRef Full Text | Google Scholar

Lippiello, E., Marzocchi, W., de Arcangelis, L., and Godano, C. (2012). Spatial organization of foreshocks as a tool to forecast large earthquakes. Sci. Rep. 2:846. doi: 10.1038/srep00846

PubMed Abstract | CrossRef Full Text | Google Scholar

Mair, K., Frye, K. M., and Marone, C. (2002). Influence of grain characteristics on the friction of granular shear zones. J. Geophys. Res. 107:2219. doi: 10.1029/2001JB000516

CrossRef Full Text | Google Scholar

Marone, C. (1998). Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth. Planet. Sci. 26, 643–696. doi: 10.1146/annurev.earth.26.1.643

CrossRef Full Text | Google Scholar

Meng, L., Huang, H., Burgmann, R., Ampuero, J. P., and Strader, A. (2015). Dual megathrust slip behaviors of the 2014 Iquique earthquake sequence. Earth Planet. Sci. Lett. 411, 177–187. doi: 10.1016/j.epsl.2014.11.041

CrossRef Full Text | Google Scholar

Michel, S., Gualandi, A., and Avouac, J.-P. (2019). Similarity scaling laws for earthquakes and Cascadia slow-slip events. Nature 574, 522–526. doi: 10.1038/s41586-019-1673-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Molchan, G. (2010). Space–time earthquake prediction: the error diagrams. Pure Appl. Geophys. 167, 907–917. doi: 10.1007/s00024-010-0087-z

CrossRef Full Text | Google Scholar

Molchan, G. M. (2003). “Earthquake prediction strategies: a theoretical analysis,” in Nonlinear Dynamics of the Lithosphere and Earthquake Prediction. Springer Series in Synergetics, eds V. I. Keilis-Borok and A. A. Soloviev (Berlin: Springer), doi: 10.1007/978-3-662-05298-3_5

CrossRef Full Text | Google Scholar

Mykulyak, S. V., Polyakovskyi, V. O., and Skurativskyi, S. I. (2019). Statistical properties of shear deformation of granular media and analogies with natural seismic processes. Pure Appl. Geophys. 176, 4309–4319. doi: 10.1007/s00024-019-02209-0

CrossRef Full Text | Google Scholar

Nielsen, S. (2017). From slow to fast faulting: recent challenges in earthquake fault mechanics. Phil. Trans. R. Soc. A 375:20160016. doi: 10.1098/rsta.2016.0016

PubMed Abstract | CrossRef Full Text | Google Scholar

Nishitsuji, Y., and Mori, J. (2014). Source parameters and radiation efficiency for intermediate-depth earthquakes in Northeast Japan. Geophys. J. Int. 196, 1247–1259. doi: 10.1093/gji/ggt458

CrossRef Full Text | Google Scholar

Ostapchuk, A. A., and Morozova, K. G. (2020). On the mechanism of laboratory earthquake nucleation highlighted by acoustic emission. Sci. Rep. 10:7245. doi: 10.1038/s41598-020-64272-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Ostapchuk, A. A., Morozova, K. G., and Pavlov, D. V. (2019). Influence of the structure of a gouge-filled fault on the parameters of acoustic emission. Acta Acust. U. Acust. 105, 759–765. doi: 10.3813/AAA.919356

CrossRef Full Text | Google Scholar

Ostapchuk, A. A., Pavlov, D. V., Markov, V. K., and Krasheninnikov, A. V. (2016). Study of acoustic emission signals during fracture shear deformation. Acoust. Phys. 62, 505–513. doi: 10.1134/S1063771016040138

CrossRef Full Text | Google Scholar

Ostapchuk, A. A., Pavlov, D. V., Ruzhich, V. V., and Gubanova, A. E. (2020). Seismic-acoustics of a block sliding along a fault. Pure Appl. Geophys. 117, 2641–2651. doi: 10.1007/s00024-019-02375-1

CrossRef Full Text | Google Scholar

Peng, Z., and Gomberg, G. (2010). An integrated perspective of the continuum between earthquakes and slow-slip phenomena. Nat. Geosci. 3, 599–607. doi: 10.1038/ngeo940

CrossRef Full Text | Google Scholar

Reber, J., Lavier, L., and Hayman, N. (2015). Experimental demonstration of a semi-brittle origin for crustal strain transients. Nat. Geosci. 8, 712–715. doi: 10.1038/ngeo2496

CrossRef Full Text | Google Scholar

Rebetsky, Y. L., Polets, A. Y., and Zlobin, T. K. (2016). The state of stress in the Earth’s crust along the northwestern flank of the Pacific seismic focal zone before the Tohoku earthquake of 11 March 2011. Tectonophysics 685, 60–76. doi: 10.1016/j.tecto.2016.07.016

CrossRef Full Text | Google Scholar

Ren, C. X., Dorostkar, O., Rouet-Leduc, B., Hulbert, C., Strebel, D., Guyer, R. A., et al. (2019). Machine learning reveals the state of intermittent frictional dynamics in a sheared granular fault. Geophys. Res. Lett. 46, 7395–7403. doi: 10.1029/2019GL082706

CrossRef Full Text | Google Scholar

Riviere, J., Lv, Z., Johnson, P., and Marone, C. (2018). Evolution of b-value during the seismic cycle: Insights from laboratory experiments on simulated faults. Earth Planet. Sci. Lett. 482, 407–413. doi: 10.1016/j.epsl.2017.11.036

CrossRef Full Text | Google Scholar

Rosenau, M., Corbi, F., and Dominguez, S. (2017). Analogue earthquakes and seismic cycles: experimental modeling across timescales. Solid Earth 8, 597–635. doi: 10.5194/se-8-597-2017

CrossRef Full Text | Google Scholar

Saffer, D., and Wallace, L. (2015). The frictional, hydrologic, metamorphic and thermal habitat of shallow slow earthquakes. Nat. Geosci. 8, 594–600. doi: 10.1038/ngeo2490

CrossRef Full Text | Google Scholar

Saltykov, V. A. (2017). On the possibility of using the tidal modulation of seismic waves for forecasting earthquakes. Izv. Phys. Solid Earth 53, 250–261. doi: 10.1134/S1069351317010128

CrossRef Full Text | Google Scholar

Sammis, C., King, G., and Biegel, R. (1987). The kinematics of gouge deformation. PAGEOPH 125, 777–812. doi: 10.1007/BF00878033

CrossRef Full Text | Google Scholar

Schoenball, M., and Davatzes, N. C. (2017). Quantifying the heterogeneity of the tectonic stress field using borehole data. J. Geophys. Res. Solid Earth 122, 6737–6756. doi: 10.1002/2017JB014370

CrossRef Full Text | Google Scholar

Scholz, C. H. (2002). The Mechanics of Earthquakes and Faulting. Cambridge: Cambridge University Press.

Google Scholar

Scuderi, M. M., Collettini, C., Vinti, C., and Marone, C. (2017). Evolution of shear fabric in granular fault gouge from stable sliding to stick slip and implications for fault slip mode. Geology 45, 731–734. doi: 10.1130/G39033.1

CrossRef Full Text | Google Scholar

Seno, T. (2003). Fractal asperities, invasion of barriers, and interpolate earthquakes. Earth Planets Sp 55, 649–665. doi: 10.1186/BF03352472

CrossRef Full Text | Google Scholar

Shebalin, P., Keilis-Borok, V., Gabrielov, A., Zaliapin, I., and Turcotte, D. (2006). Short-term earthquake prediction by reverse analysis of lithosphere dynamics. Tectonophysics 413, 63–75. doi: 10.1016/j.tecto.2005.10.033

CrossRef Full Text | Google Scholar

Shiotani, T., Ohtsu, M., and Ikeda, K. (2001). Detection and evaluation of AE waves due to rock deformation. Constr. Build. Mater. 15, 235–246. doi: 10.1016/S0950-0618(00)00073-8

CrossRef Full Text | Google Scholar

Shreedharan, S., Bolton, D. C., Riviere, J., and Marone, C. (2021). Competition between preslip and deviatoric stress modulates precursors for laboratory earthquakes. Earth Planet. Sci. Lett. 553:116623. doi: 10.1016/j.epsl.2020.116623

CrossRef Full Text | Google Scholar

Sibson, R. H. (2003). Thickness of the seismic slip zone. Bull. Seismol. Soc. Am. 93, 1169–1178. doi: 10.1785/0120020061

CrossRef Full Text | Google Scholar

Sobolev, G. A., and Zav’yalov, A. D. (1980). About concentration criterion of seismogenic rupture. Doklady Academii Nauk USSR 252, 69–71.

Google Scholar

Tchalenko, J. S. (1970). Similarities between shear zones of different magnitudes. Geol. Soc. Am. Bull. 81, 1625–1640. doi: 10.1130/0016-7606(1970)81[1625:SBSZOD]2.0.CO;2

CrossRef Full Text | Google Scholar

Trugman, D. T., and Ross, Z. E. (2019). Pervasive foreshock activity across Southern Califirnia. Geophys. Res. Lett. 46, 8772–8781. doi: 10.1029/2019GL083725

CrossRef Full Text | Google Scholar

Turcotte, D. L. (1999). Self-organized criticality. Rep. Prog. Phys. 62:1377. doi: 10.1088/0034-4885/62/10/201

CrossRef Full Text | Google Scholar

Veedu, D. M., and Barbor, S. (2016). The Parkfield tremors reveal slow and fast ruptures on the same asperity. Nature 532, 361–365. doi: 10.1038/nature17190

PubMed Abstract | CrossRef Full Text | Google Scholar

Villegas-Lanza, J., Nocquet, J., Rolandone, F., Vallee, M., Tavera, H., Bondoux, F., et al. (2016). A mixed seismic–aseismic stress release episode in the Andean subduction zone. Nat. Geosci. 9, 150–154. doi: 10.1038/ngeo2620

CrossRef Full Text | Google Scholar

Zigone, D., Voisin, C., Larose, E., Renard, F., and Campillo, M. (2011). Slip acceleration generates seismic tremor like signals in friction experiments. Geophys. Res. Lett. 38:L01315. doi: 10.1029/2010GL045603

CrossRef Full Text | Google Scholar