Times Associated With Source-to-Sink Propagation of Environmental Signals During Landscape Transience

Sediment archives in the terrestrial and marine realm are regularly analyzed to infer changes in climate, tectonic, or anthropogenic boundary conditions of the past. However, contradictory observations have been made regarding whether short period events are faithfully preserved in stratigraphic archives; for instance, in marine sediments offshore large river systems. On the one hand, short period events are hypothesized to be non-detectable in the signature of terrestrially derived sediments due to buffering during sediment transport along large river systems. On the other hand, several studies have detected signals of short period events in marine records offshore large river systems. We propose that this apparent discrepancy is related to the lack of a differentiation between different types of signals and the lack of distinction between river response times and signal propagation times. In this review, we (1) expand the definition of the term ‘signal’ and group signals in sub-categories related to hydraulic grain size characteristics, (2) clarify the different types of ‘times’ and suggest a precise and consistent terminology for future use, and (3) compile and discuss factors influencing the times of signal transfer along sediment routing systems and how those times vary with hydraulic grain size characteristics. Unraveling different types of signals and distinctive time periods related to signal propagation addresses the discrepancies mentioned above and allows a more comprehensive exploration of event preservation in stratigraphy – a prerequisite for reliable environmental reconstructions from terrestrially derived sedimentary records.

Introduction

Sediment archives are regularly analyzed to reconstruct climatic and tectonic conditions of the past. Most terrestrial sediments are initially produced on hillslopes in mountain regions and are subsequently transported by fluvial systems to subsiding continental lowlands or to the coastal ocean, and further across the shelf and continental slope to deep marine basins (Figure 1; e.g., Schumm, 1977; Meade, 1982; Einsele et al., 1996; Hinderer and Einsele, 2001; Castelltort and Van Den Driessche, 2003). The transport pathways of sediments from a zone of production (source) through a transfer zone to an area of final deposition (sink) are generally described as sediment routing systems (SRSs) (e.g., Allen, 2008a, 2017). To reconstruct past conditions from deposited sediments, it is assumed that changes in climatic, tectonic, or anthropogenic boundary conditions generate so-called ‘environmental signals’ within the sediment. Environmental signals (signals hereafter) typically refer to measurable changes in the amount of produced, transported, and deposited sediments that can be related to changes in environmental boundary conditions (Romans et al., 2016 and references therein). Changes in environmental boundary conditions are temporary or sustained adjustments in tectonic uplift or subsidence rates, in climatic parameters, or in anthropogenic land use. However, experimental, numerical, and field studies have shown that not all signals generated in the erosion zone are faithfully transmitted to the sink, but can be delayed, buffered, modified, or even destroyed during transport along SRSs (Jerolmack and Paola, 2010; Simpson and Castelltort, 2012; Armitage et al., 2013; Blöthe and Korup, 2013; Godard et al., 2013; Forzoni et al., 2014; Braun et al., 2015; Romans et al., 2016; Straub et al., 2020). It was suggested that signals in the form of sediment flux pulses are only faithfully transmitted to the sink if the period of change in boundary conditions exceeds the response time of the river (Paola et al., 1992; Castelltort and Van Den Driessche, 2003; Li Q. et al., 2018). The river response time is the required time to achieve a new equilibrium river profile after a change in boundary conditions. Hence, for reliable reconstructions of past boundary conditions from sediment deposits it is essential to investigate the linkages between processes and times of signal transfer with processes and timescales of river adjustment.

FIGURE 1

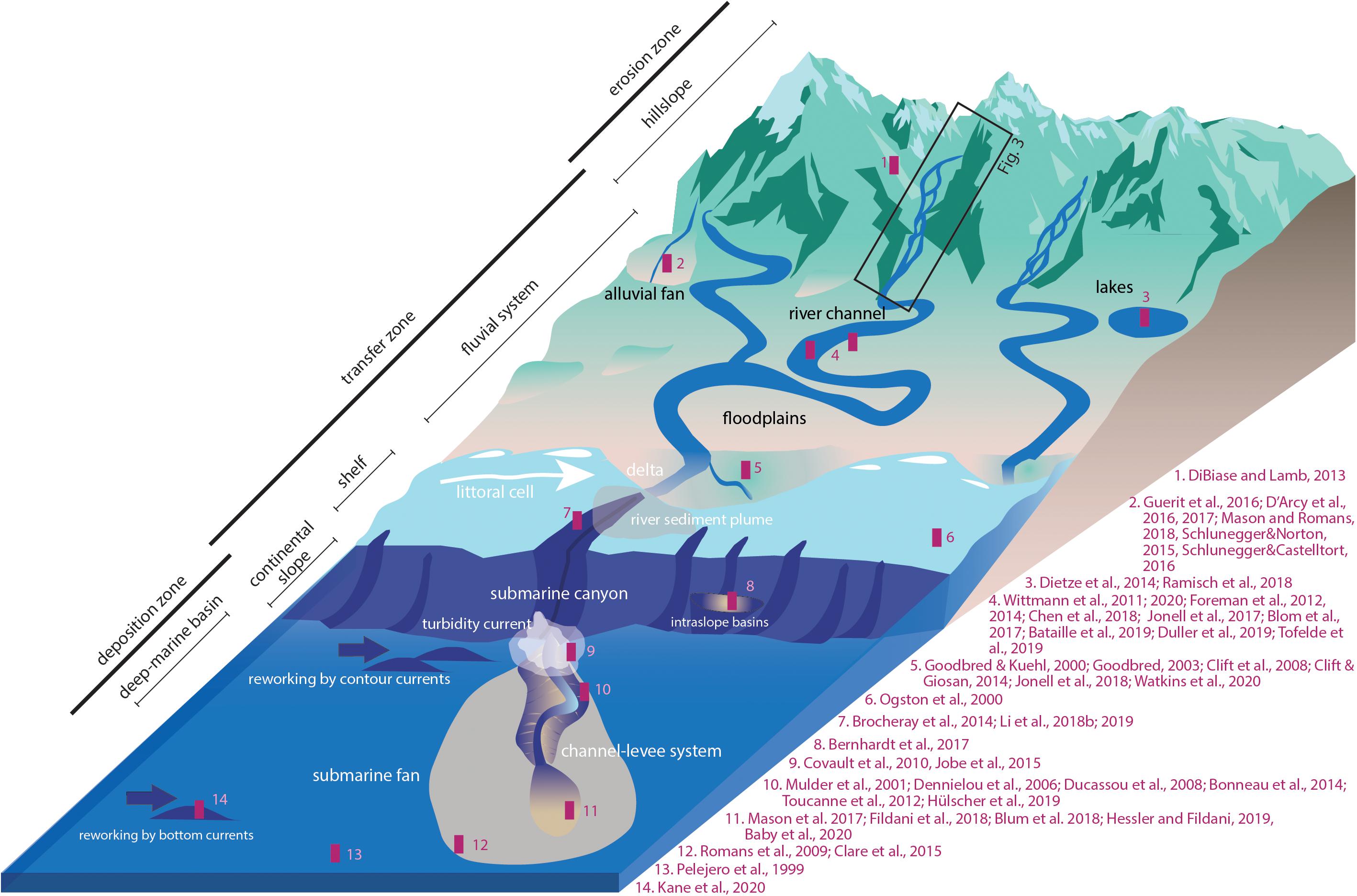
Figure 1. Schematic sketch of a continental-scale sediment routing system (SRS) from the upland source to the deep-marine sink. SRSs are typically subdivided in a zone of erosion, sediment transfer, and sediment deposition. On a continental scale, SRSs comprise five landscape segments including hillslopes, fluvial system, shelf, continental slope, and deep marine basins. Sampling sites of sediment archives discussed in the text are indicated with magenta colored symbols. The studies referred to here are not exhaustive; please see the text for additional references. Black frame marks the erosion zone as discussed in Figure 3.

Paola et al. (1992) suggested that the longitudinal profile adjustment in alluvial rivers after a change in boundary conditions can be approximated as a diffusive-like process and the according response time, T_eq [s], of a 1D river profile can be estimated as:

$$T_{eq}=L^2/K\mathit{\hspace{1em}\hspace{0.5em} }(1),$$

where L [m] is the length of the transfer system and K [m² s^–1] its coefficient of diffusivity. Hence, response times greatly depend on the size of the river basin. Allen (2008b) considered landscapes with response times, T_eq, greater than the periodicity of changes in boundary conditions as ‘buffered,’ while landscapes with response times shorter than the period of changes in boundary conditions as ‘reactive.’ Following this approach, faithful signal transmission should be limited to reactive landscapes, such that short period climate cycles should not be transmitted through large rivers systems (Paola et al., 1992; Castelltort and Van Den Driessche, 2003; Allen, 2008b; Li Q. et al., 2018; Straub et al., 2020).

A lack of signal transmission of short period climate cycles in large river systems was presented by Métivier and Gaudemer (1999). Following Eq. (1), the authors obtained river response times on the order of 10⁵ to 10⁶ year for some of Asia’s largest rivers. They found no major differences between the present-day sediment discharge and the Quaternary-averaged sediment discharge reconstructed from mass accumulation in the corresponding sedimentary basins. Hence, sediment discharge at the river’s outlet was constant, despite known climate oscillations throughout the Quaternary on the order of 10⁴ year (e.g., 20 and 40 kyr Milankovitch cycles). Métivier and Gaudemer (1999) interpreted those river systems as buffered.

However, other studies indicate that several large river systems show signal propagation occurring at an order-of-magnitude shorter timescale than their according response times. For example, Castelltort and Van Den Driessche (2003) calculated the river response times of 93 of the largest rivers worldwide using Eq. (1). The calculated response time of the Mississippi River is between 124 and 248 kyr (Castelltort and Van Den Driessche, 2003). Yet, multi-modal mixtures of detrital zircons within the Mississippi submarine fan are changing over 10 kyr (Figure 1; Mason et al., 2017; Fildani et al., 2018). Those provenance changes were interpreted by these authors to represent signals originating in the catchment, which were efficiently transferred to and preserved in the Mississippi delta and deep-sea fan. Therefore, signal transfer through the Mississippi SRS was rapid and an order-of-magnitude shorter than the theoretical response time (Mason et al., 2017; Fildani et al., 2018). Similar observations were made by Blum (2007), who also reported that signal transfer and incorporation in stratigraphy in large river systems was substantially faster than the according calculated response times. Blum (2007) explained this discrepancy by different types of perturbations. He proposed that signals related to changes in discharge (floods) can be transferred faster through SRSs compared to changes in upstream sediment supply. Similarly, the Ganges River features a T_eq of ∼99 kyr (Castelltort and Van Den Driessche, 2003). However, system-wide changes in sediment flux and aggradation and incision cycles as contemporaneous responses to multi-millennial climate changes were observed in fluvial and deltaic archives along the Ganges SRS at time scales well below 99 kyr (Figure 1, Goodbred, 2003). Within smaller SRSs along the western active margin of the Americas, offshore turbidite systems recorded late Pleistocene to Holocene climatic changes even with theoretical river response times of ∼100 kyr (Figure 1, Covault et al., 2010; Bernhardt et al., 2017).

In summary, short period climate changes seem to be recorded in marine stratigraphy offshore small and large river systems, although the calculated river response times of large river systems exceed the period of the climate changes. We propose, however, that this discrepancy is only apparent, as different concepts are compared. While each approach has its legitimacy, we believe that inconsistencies are caused by two issues:

(1) The lack of a differentiation between different types of ‘signals’ and according differences in signal propagation.

(2) The river response time is different from the time it takes for a measurable change in a sedimentary parameter to arrive in the sink.

Terrestrial and marine sedimentary archives are the result of a broad range of geomorphic processes along SRSs. Reliable environmental reconstructions from those archives therefore require interdisciplinary knowledge exchange, which relies on a common and precise terminology. To overcome any current deficiencies, we will (1) expand the definition of the term ‘signal’ and group signals in sub-categories related to hydraulic grain size characteristics (see section “Definition of Signal and Hydraulic Grain Size Fractions”), (2) clarify the different types of ‘times’ and propose a precise and consistent terminology for future use (see section “Times Related to Landscape Response and Signal Propagation”), and (3) compile and discuss factors influencing the quantification of signal transfer related times along SRSs and how those times vary with hydraulic grain size characteristics (see section “Quantification of Signal Transfer Times”).

Definition of Signal and Hydraulic Grain Size Fractions

Environmental signals are typically defined as changes in the amount of produced, transported, and deposited sediment (Q_s [m³ s^–1 or kg s^–1]) in response to a change in boundary conditions (Romans et al., 2016 and references therein). Therefore, many analog-material and numerical modeling studies investigating the effects of changing boundary conditions on signal propagation focus on changes in Q_s (e.g., Allen and Densmore, 2000; van den Berg van Saparoea and Postma, 2008; Simpson and Castelltort, 2012; Armitage et al., 2013; Coulthard and Van De Wiel, 2013; Li Q. et al., 2018; Moussirou and Bonnet, 2018; Tofelde et al., 2019). However, changes in boundary conditions do not only affect the amount of transported sediment, but can also alter the sediment grain size distribution (Armitage et al., 2011; Parsons et al., 2012; D’Arcy et al., 2016, 2017; Schlunegger and Castelltort, 2016; Roda-Boluda et al., 2018; Bataille et al., 2019), or its geochemical composition, and detrital geochronological signature (Sharman et al., 2019; Lenard et al., 2020). Therefore, we expand the definition of an environmental signal: We define an environmental signal as a measurable change in any sedimentary parameter of interest through time that can be linked to an environmental change. The change in the parameter can either be temporary or sustained.

This definition is in accordance with the broad range of sedimentary parameters that are regularly measured in terrestrial and marine sediment archives (yellow boxes in Figure 2). To summarize some commonly measured sedimentary parameters, we group them based on the sediment characteristics they are related to. We sub-divide sediment characteristics by (1) sediment amount (Q_s), (2) size distribution, density and shape of grains within a sediment package, and (3) sediment composition (blue boxes in Figure 2). Parameters investigating the change in Q_s through time include, for example, accumulation rates in one to three spatial dimensions (Covault and Graham, 2010; Guillocheau et al., 2012; Hinderer, 2012; Jobe et al., 2015; Guerit et al., 2016; Schlunegger and Castelltort, 2016; Hülscher et al., 2019; Baby et al., 2020), the frequency and thickness of flow events (Mulder et al., 2001; Ducassou et al., 2008; Romans et al., 2009; Bernhardt et al., 2017), or varve thickness, particularly in lake sediment (Zolitschka et al., 2015) (Figure 2).

FIGURE 2

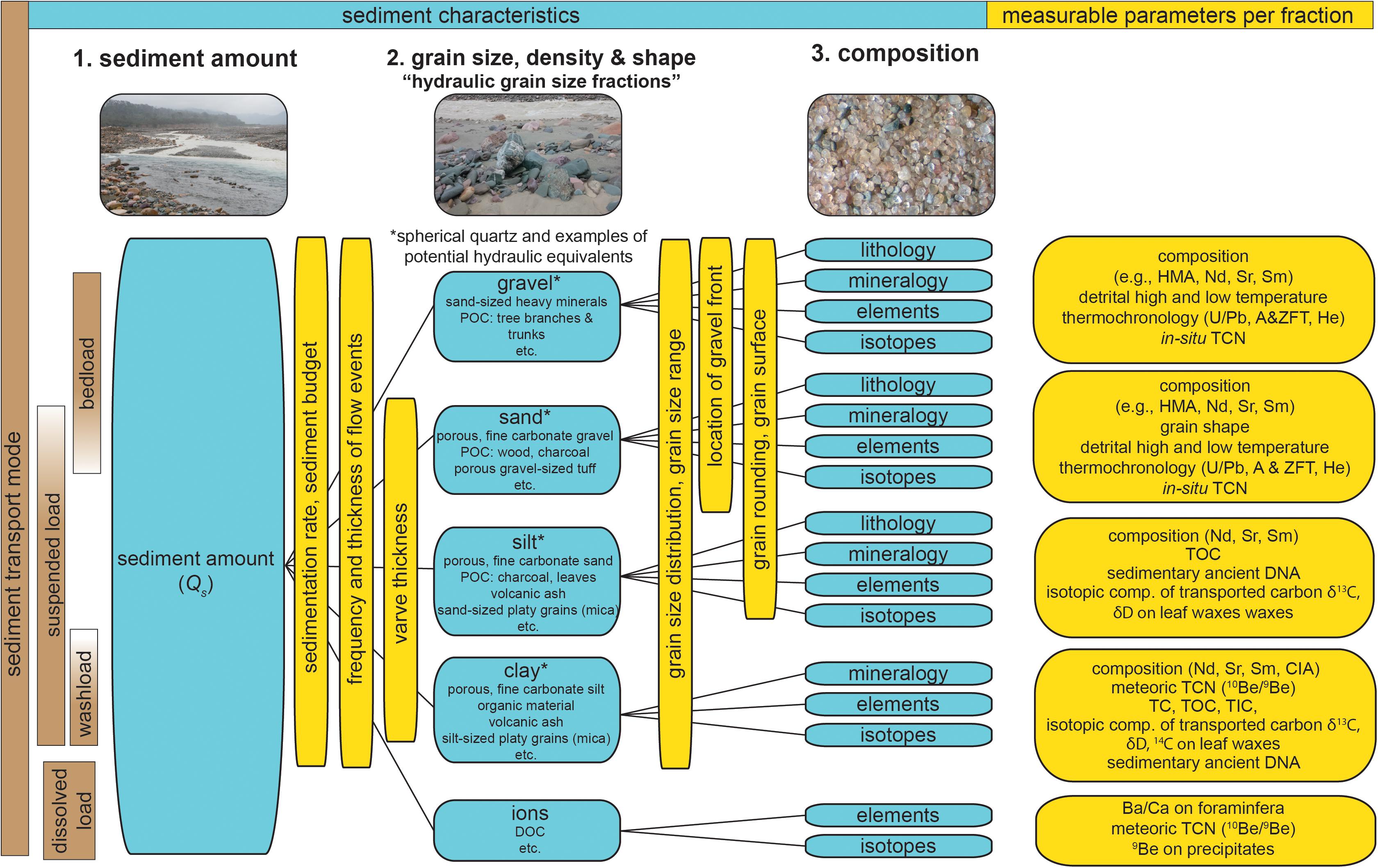
Figure 2. Subdivision of signals based on sediment characteristics. Information on boundary conditions can either be stored in the amount of sediment (or anthropogenic particles) transported per time, the grain size and shape distribution of that sediment and its changes through time, or within the changing sediment composition (blue boxes). Examples of parameters measured for environmental reconstructions (yellow boxes) can relate to any of those sediment characteristics. Individual fractions of a sediment package can differ in their primary transport mode (brown boxes) and, hence, in times required to transport the sediment to the sink. Therefore, we suggest to subdivide signals based on hydraulic grain size fraction. A hydraulic grain size fraction is defined by the size range of spherical quartz grains, but includes other grains that are transported jointly due to similar hydraulic behavior. The presented list of regularly measured sedimentary parameters (yellow boxes) is not exhaustive. TC, total carbon; TOC, total organic carbon; TIC, total inorganic carbon; POC, particulate organic carbon; DOC, dissolved organic carbon; TCN, terrestrial cosmogenic nuclides; HMA, heavy mineral analysis; A&ZFT, apatite and zircon fission track; CIA, chemical index of alteration.

FIGURE 3

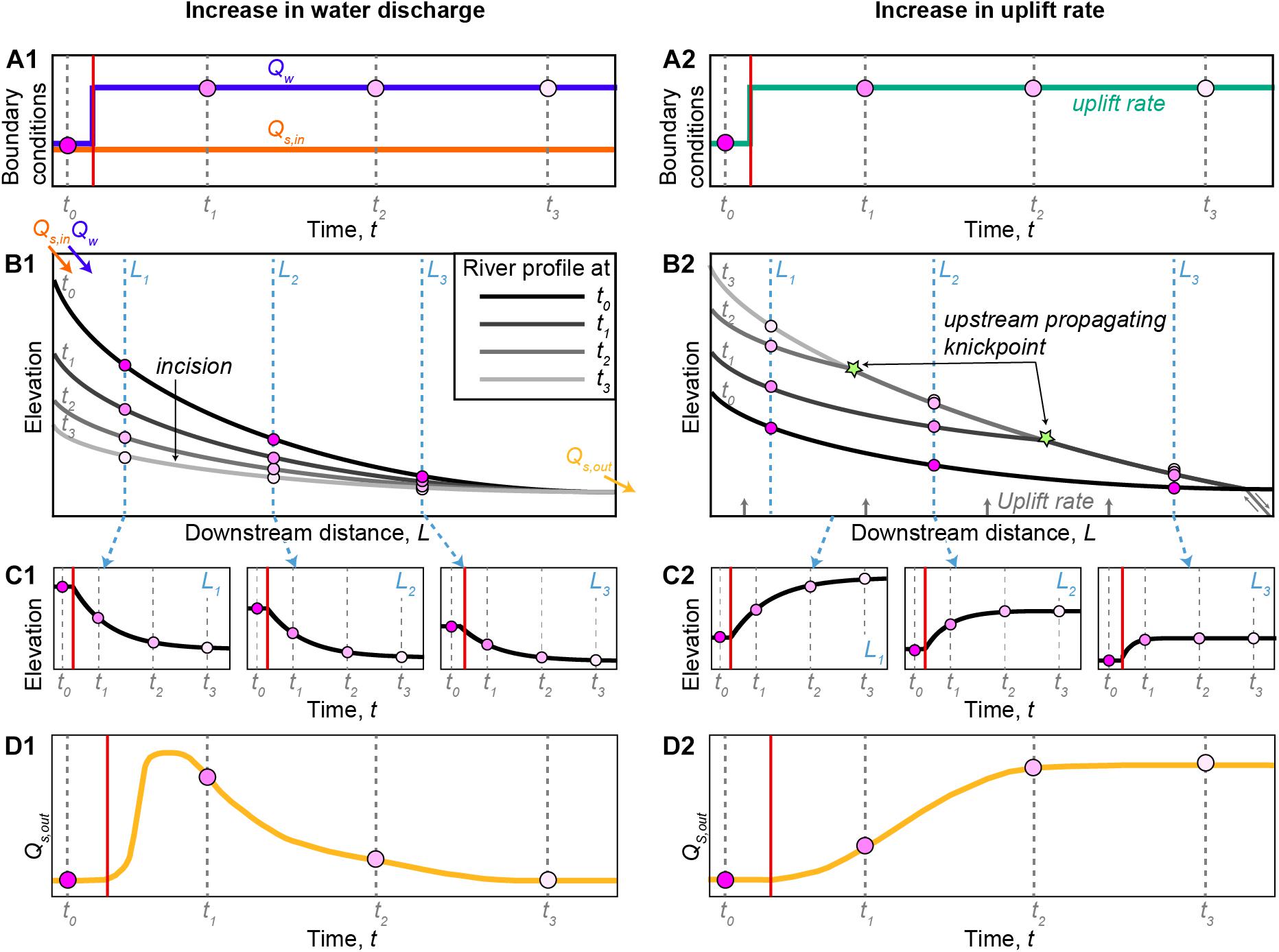
Figure 3. Conceptual response of the fluvial system to an increase in upstream water discharge, Q_w, relative to upstream sediment supply, Q_s,in (left panel) or an increase in uplift rate of the entire region relative to a fixed base level (right panel). (A) A step increase in either water discharge (A1) or uplift rate (A2) occurs between the two points in time t₀ and t₁. (B) In response, the longitudinal river profiles adjust by incision along the entire profile (B1) or by elevating the river bed combined with an upstream migrating knickpoint (B2). (C) The change in river bed elevation through time is displayed in detail for three locations along each profile L₁ to L₃. (D) In addition to the topographic response of the landscape (B,C), signals are generated; for example, in the form of changes in sediment discharge at the basin outlet, Q_s,out. An increase in upstream Q_w results in a temporary increase in Q_s,out (D1). In contrast, an increase in regional uplift rate results in a sustained increase in Q_s,out (D2). This conceptual figure represents a summary of experimental and numerical works (see text for references).

The second group of parameters focuses on differences in the characteristics of grains, such as grain size distributions (Duller et al., 2010, 2019; Whittaker et al., 2010, 2011; Foreman et al., 2012; Parsons et al., 2012; Dietze et al., 2014; Foreman, 2014; D’Arcy et al., 2017; Roda-Boluda et al., 2018), median or other characteristic grain sizes (D₅₀, D₈₄, sortable silt: McCave and Hall, 2006; Schlunegger and Norton, 2015; Chen et al., 2018; McCave and Andrews, 2019; Watkins et al., 2020), the location of the gravel-sand transition in alluvial fans and river systems (Allen et al., 2015; Dubille and Lavé, 2015; Blom et al., 2017; Dingle et al., 2017, 2020; Armitage et al., 2018a), sorting and related textural characteristics (e.g., in glacio-marine sediments: Anderson et al., 1980; D’Orsay and Van De Poll, 1985; Pudsey, 1992; Helland et al., 1997; Passchier et al., 2019), or grain shape (Stanley and De Deckker, 2002; Kalińska and Nartišs, 2014).

The third group of parameters focuses on the sediment composition. Here, we broadly consider organic and inorganic sediment composition (lithological, mineralogical, elemental, and isotopic composition) and include the geochronological and thermochronological signature of detrital minerals. While some compositional parameters can be measured on an entire sediment (bulk) package, many are bound to a specific grain size fraction (Figure 2). For example, magnetic susceptibility (Stoner et al., 1995; Da Silva et al., 2013) or XRF scanning (Weltje and Tjallingii, 2008; Kujau et al., 2010; Ramisch et al., 2018) of sediment cores measures the fraction of magnetic minerals and the elemental composition of bulk sediment, respectively. In contrast, high and low temperature detrital geo-/thermochronology is commonly analyzed on sand-sized heavy minerals, such as zircon or apatite (Weislogel et al., 2006; Heberer et al., 2011; O’Sullivan et al., 2018; Sharman et al., 2018). Paleo-denudation rates inferred from in situ cosmogenic nuclides in detrital sediments are mostly measured in sand- and silt-sized quartz grains (Schaller et al., 2004; Val et al., 2016; Lenard et al., 2020), although comparisons of the same cosmogenic nuclide in different grain size fractions at the same location have revealed great variability between grain size fractions (Puchol et al., 2014; Carretier et al., 2015, 2019; Schildgen et al., 2016; Tofelde et al., 2018; van Dongen et al., 2019). Finally, fluvially transported organic compounds, for example leaf waxes from terrestrial plants, are regularly analyzed for their hydrogen (δD) and carbon (δ¹³C) isotope composition (Galy and Eglinton, 2011; Garcin et al., 2012; Sachse et al., 2012; Schefuß et al., 2016; Diefendorf and Freimuth, 2017). Oftentimes, the organic fraction is extracted from a certain sedimentary sub-fraction only, like the suspended load (e.g., Galy et al., 2008; Ponton et al., 2014), bedload (e.g., Galy et al., 2008; Galy and Eglinton, 2011), or from flood deposits (Hoffmann et al., 2016). To investigate past biodiversity, recent efforts advanced the analyses of ancient DNA preserved in sediments (Dommain et al., 2020), which may be transported together with silt and clay. For a detailed discussion on sediment generation and composition we refer to the recent review by Caracciolo (2020).

In summary, sedimentary parameters, and hence signals, are measured on different sediment fractions. Consequently, when investigating signal transfer and modification, we suggest to group sediments in ‘hydraulic grain size fractions’ that are transported jointly (Figure 2). We define a hydraulic grain size fraction as a size range of spherical quartz grains (e.g., sand, silt, etc.) and their hydraulic equivalents (blue boxes in middle column, Figure 2). For example, a sand-sized platy mica grain might be transported in the silt-sized hydraulic grain size fraction due to lower settling velocity compared to quartz (Dietrich, 1982). Sand-sized heavy minerals, such as zircons and apatite, may be transported along with the hydraulic grain size fraction of small gravel due to the high density of zircons and apatites (4.65 and 3.2 g cm^–3, respectively) compared to quartz (2.65 g cm^–3). Similarly, particulate organic matter may be transported within the clay-sized hydraulic grain size fraction (Galy et al., 2008; Galy and Eglinton, 2011; Ponton et al., 2014). The dominant sediment transport mode (bedload, suspended load, wash load, dissolved load) varies with hydraulic grain size fraction (brown bars, Figure 2). We acknowledge that the assumption of all grains within a hydraulic grain size fraction being transported jointly is a simplification. Grains with similar characteristics can, for example, be transported as suspended load or bedload (details in section “Quantification of Signal Transfer Times”). However, we base our sub-division on grain size and not on sediment transport mode, as ancient sediments can be assigned a hydraulic grain size fraction, but not a transport mode, and because many parameters are measured on a certain grain size fraction.

The dominant transport mode of a distinct hydraulic grain size fraction exerts a major control on sediment transport times along SRSs. Sediment transport times, in turn, have direct implications for signal propagation and modification within SRSs (Chabaux et al., 2012; Carretier et al., 2019, 2020; Watkins et al., 2020). Therefore, we propose to investigate signal propagation not for bulk sediments, but for hydraulic grain size fractions individually. In order to do so, we discuss the impact of several boundary parameters on sediment transport times and whether or not the impact of those parameters varies with hydraulic grain size fraction (see section “Quantification of Signal Transfer Times”). But first, in order to overcome any discrepancies related to inconsistent terminology, we distinguish relevant times of landscape response from times related to signal propagation (see section “Times Related to Landscape Response and Signal Propagation”).

Times Related to Landscape Response and Signal Propagation

Landscapes respond to changes in boundary conditions by adjusting their topography. These adjustments are most pronounced in mountainous areas – the erosion zone (Figure 1) – and can trigger severe changes in surface erosion processes and within the hydrological regime. Also, during landscape adjustment, signals are generated and transported along SRSs to an area of final deposition. Naturally, different times are of interest when studying landscape adjustment and landscape shaping processes, compared to studies that aim to reconstruct past environmental conditions from signals preserved in sediment archives. From a landscape evolution perspective, the recovery time of a landscape after a change in boundary conditions is of major interest, while from a reconstruction perspective, the primary interest is the timescale of signal generation and signal transport to the sink (or the time lag between a change in boundary conditions and signal arrival in the archive). In this section, we first discuss timescales of landscape response with a focus on river profiles, and second timescales related to signal propagation.

Landscape Response Time

A landscape can either be in steady state or in transient state, depending on whether the landscape is adjusted to the prevailing boundary conditions or not (e.g., Mackin, 1948; Howard, 1982; Allen, 2008b). Hence, a change in boundary conditions triggers the adjustment of individual segments within a landscape. In the terrestrial realm the adjustment of river profiles exerts a major control on the state of the entire landscape, as rivers set the lower boundary for hillslopes (e.g., Hurst et al., 2012; Golly et al., 2017). Observations from several decades ago have already revealed that river longitudinal profiles are dynamic features that constantly adjust to changing boundary conditions at various temporal and spatial scales (Huntington, 1907; Fisk, 1944; Mackin, 1948; Lane, 1955; Hack, 1957; Bull, 1991). As such, the evolution of longitudinal river profiles has been extensively studied in the field (e.g., Hack, 1957; Merritts et al., 1994; Törnqvist, 1998; Whittaker et al., 2008), in analog-material experiments (e.g., Lewis, 1944; Begin et al., 1981; Gardner, 1983; van den Berg van Saparoea and Postma, 2008; Rohais et al., 2012; Grimaud et al., 2016; Baynes et al., 2018; Tofelde et al., 2019; Savi et al., 2020), and also by using numerical models (e.g., Davy and Lague, 2009; Simpson and Castelltort, 2012; Armitage et al., 2013, 2018b; Goren et al., 2014; Nie et al., 2018; Wickert and Schildgen, 2019). Following those previous studies, Figure 3 summarizes conceptually the general response of a river following a step increase in upstream water discharge (Q_w) relative to upstream sediment supply (Q_s,in) (Figure 3A1) or an increase in tectonic uplift of the entire region relative to a fixed base level (Figure 3A2). However, we would like to emphasize that rivers are generally subdivided into detachment-limited and transport-limited endmembers. In detachment-limited rivers erosion is limited by the capacity of channels to incise into their bed. In contrast, in transport-limited rivers erosion is limited by the capacity of channels to transport their sediment load. The rate of adjustment and transient geometry will differ between detachment-limited and transport-limited rivers (e.g., Davy and Lague, 2009). As such, the evolution shown in Figure 3 is only a simplified summary of several previous studies, some of which are listed above. The evolution is shown for four distinct moments in time, t [s], before (t₀) and after (t₁–t₃) the change in boundary conditions. An increase in upstream Q_w triggers river incision along the entire profile (Figure 3B1; e.g., Simpson and Castelltort, 2012; Tofelde et al., 2019). Incision is most pronounced at the upstream end, resulting in a net reduction in channel gradient. In contrast, an increase in uplift rate of the entire region relative to a fixed base level causes elevated river profiles and an upstream migrating knickpoint, eventually resulting in a steeper channel gradient (Figure 3B2; e.g., Kirby and Whipple, 2012). A knickpoint is a point along a river profile that separates an upstream and downstream reach of different steepness.

Topographic steady state is defined by no net changes in elevation, z [m], through time, t [s] (Hack, 1960; Montgomery, 2001; Willett and Brandon, 2002). Following this concept, the response time of a landscape describes the period of landscape adjustment (landscape transience) after a change in boundary condition (e.g., Howard, 1982; Whipple, 2001; Allen, 2008b; Straub et al., 2020). Depending on how response times are calculated (discussed below), it either describes the time to reach full steady state conditions (e.g., δz/δt = 0) or the time until the parameter of interest (i.e., z) has reached a fraction of its initial value. Sometimes, instead of response time, the term adjustment time (Schmid et al., 2018) is used. However, as different parts of the landscape respond to the same change in boundary conditions at different timescales (e.g., Hurst et al., 2012; Tejedor et al., 2017; Turowski, 2020), Allen (2008b) cautioned against considering response times too generally. Consequently, there have been a range of approaches of how to calculate response times for different parts within a landscape.

For signal propagation along SRSs, the response time of the river profile (river response time) is of particular importance. Following Allen (1974), Bull (1991) subdivided the river response in two components – the reaction time, which is the time lag between the onset of change in boundary conditions and the first topographic adjustment, and the relaxation time, which is the time period between the first topographic adjustment and the achievement of new steady state. In landscape evolution models, in numerical landscape evolution models the change in river elevation through space and time is most often described either by the advective stream power equation for detachment-limited rivers (e.g., Howard, 1994; Whipple and Tucker, 1999) or by a diffusion equation for transport-limited rivers (e.g., Paola et al., 1992; Wickert and Schildgen, 2019). The choice of equation to model the evolution of river elevation determines how river response times are calculated. Based on the stream-power law related equation for detachment limited rivers, Whipple and Tucker (1999) and Whipple (2001) derived equations for calculating the river response time based on the time required for the knickpoint to travel through the landscape length (equivalent to Bull’s (1991) relaxation time; Figure 3B2). The same approach can be used when channels are described as a continuum between transport- and detachment-limited behaviors (Davy and Lague, 2009; Carretier et al., 2016; Yuan et al., 2019). For transport-limited rivers, the river response time for a 1D fluvial system was suggested to scale with channel length and the diffusion coefficient and can be calculated following Eq. (1) (Howard, 1982; Paola et al., 1992; Allen et al., 2013). Paola et al. (1992) termed this the intrinsic equilibrium time. It is important to note that the response time of a diffusion equation presumes a point change, and a subsequent dispersion of this change through the system. Alternatively, Howard (1982) and Simpson and Castelltort (2012) suggested that the time to reach the new steady state elevation profile in transport-limited channels can be estimated on the basis of mass balance for the volume of sediment that needs to be deposited or removed along the channel. Densmore et al. (2007b) and Allen (2008b) named all those theory-based (diffusion or advection) river response times, which describe the time of the river longitudinal profile to attain new steady state, analytical response times.

However, a response time can also be calculated when looking at the evolution of a certain landscape parameter only through time, that is for a single point in space or an average value of a certain area (e.g., local or catchment mean elevation, channel width, sediment discharge). A single parameter normally approaches new steady conditions after a change in boundary conditions asymptotically, which can be approximated by an exponential equation (e.g., Kooi and Beaumont, 1996; Davy and Crave, 2000; Lague et al., 2003; Wickert and Schildgen, 2019). For example, while the evolution of the entire river profile through time (Figure 3B) was described either by a wave or diffusion equation, the change in elevation at a single point along this river (L₁–L₃ in Figure 3C) through time behaves exponentially. From an exponential curve, e-folding response times can be calculated (Howard, 1982; Allen and Densmore, 2000; Densmore et al., 2007a; Allen, 2008b; Wickert and Schildgen, 2019). For an exponential decay curve as in Figure 3C1, one e-folding time is equivalent to the time when the parameter of interest has decreased to 37% (≈1/e) of its initial value, or when 63% of the initial value is lost. After three e-folding times, 5% of the initial value remains (95% are lost). In case of exponential growth (Figure 3C2), one e-folding time is equivalent to the time when the parameter of interest has increased by a factor of e (∼2.718). Hence, landscape evolution studies have also calculated response times by fitting an exponential curve to a measured time series of a certain landscape parameter, for example sediment discharge at the basin outlet (Densmore et al., 2007a; Armitage et al., 2013; Wickert and Schildgen, 2019), mean catchment erosion rate and mean fan deposition rate (Allen and Densmore, 2000), or provenance changes in discharged sediment (Sharman et al., 2019). Densmore et al. (2007b) and Allen (2008b) named the response times measured by fitting an exponential curve to a parameter time-series the relaxation time (note that this relaxation time is different from the relaxation time defined by Bull (1991) and Allen (1974) as described above). However, it should be emphasized that an exponential curve asymptotically approaches a new steady state, but never reaches steady state. As analytical response times and e-folding times differ in a fundamental assumption – the first assuming the achievement of steady state and the latter not – the two concepts are incompatible.

Signal Related Times

In addition to landscape or river response times, specific signal-related times can be defined. Here, we propose times and terminology applicable to all types of signals as defined above. To illustrate this, we first discuss two endmember signal patterns (Figure 3D), and then define specific signal-related times for those patterns (Figure 4). The parameter of interest used as an example is the sediment discharge amount at the basin outlet, Q_s,out.

FIGURE 4

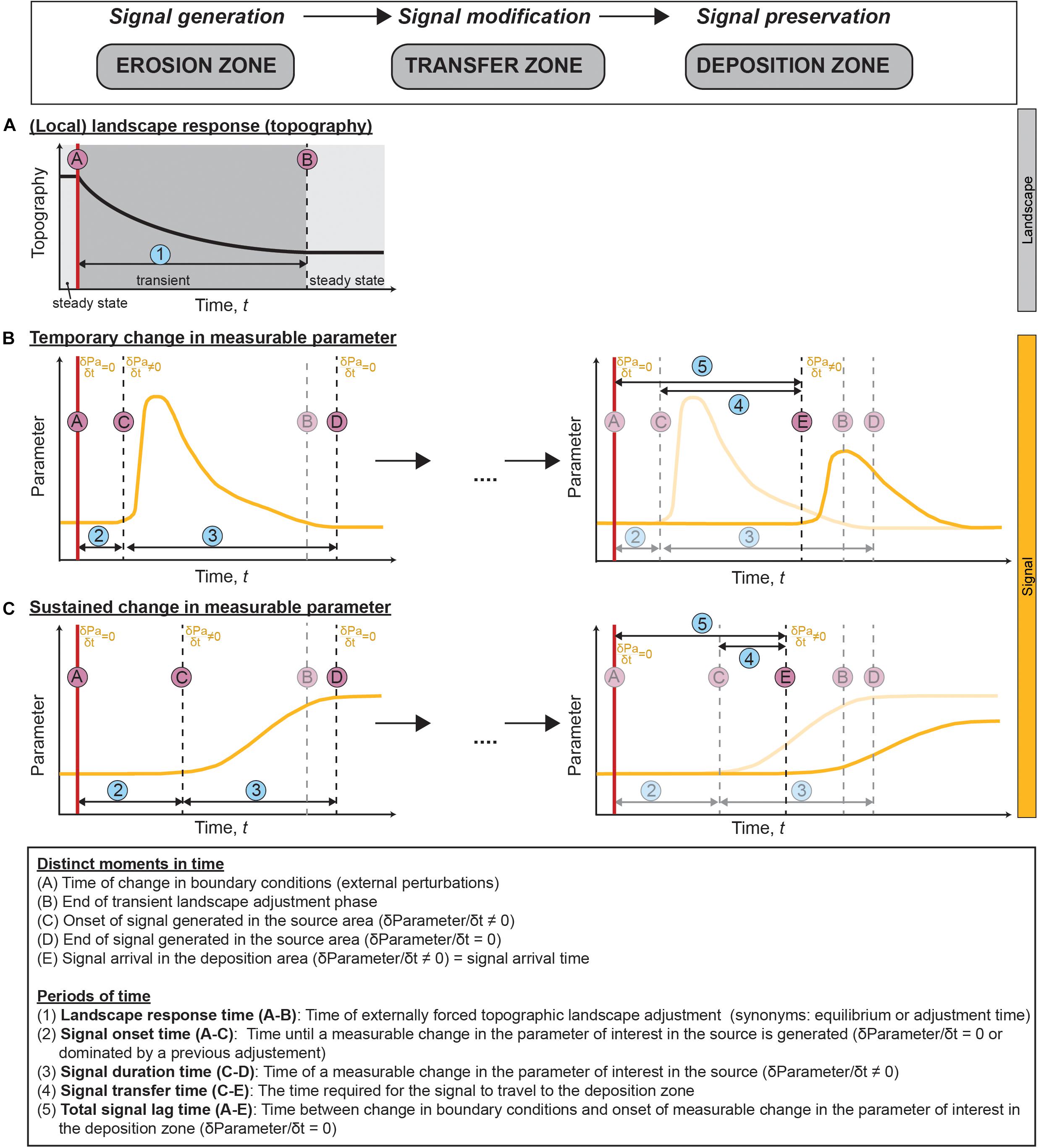
Figure 4. Conceptual diagram of landscape response times and proposed ‘times’ applicable to signals generated within and transported to different segments of SRSs. Changes in boundary conditions (vertical red line) cause a topographic response in the landscape (A) and the generation of signals (B,C). Exemplary, the proposed times are described on the two endmembers of signal shapes – temporary (B) or sustained (C) changes in the parameter of interest (e.g., Allen and Densmore, 2000; Bonnet and Crave, 2003; Armitage et al., 2011). The shape of the topographic response and signal curves is based on a range of previous studies (see text for details). We distinguish between distinct moments in time (letters) and periods of times (numbers) for both topographic and sediment parameter changes. For detailed explanations on the different types of time see main text.

Landscape adjustment after a change in boundary conditions triggers signal generation. Numerical and experimental studies have shown that a step increase in upstream Q_w (while keeping Q_s,in constant) causes a temporary peak in Q_s,out due to river incision, i.e., erosion of underlying rock or remobilization of sediment (Figure 3D1; e.g., Allen and Densmore, 2000; van den Berg van Saparoea and Postma, 2008; Armitage et al., 2011, 2013, 2018b; Tofelde et al., 2019; Zhang et al., 2020). An equivalent example in nature would be enhanced sediment discharge after a flood event. Cook et al. (2018) monitored suspended sediment discharge in the Bothe Koshi (Nepal) before, during, and after a glacial lake outburst flood. The outburst flood caused a sudden increase in sediment discharge that return to initial values over the course of ca. 2 weeks (Figure 3D1). On longer timescales glacial melt at the end of glacial phases can enhance water discharge relative to upstream sediment supply. This fast increase in discharge can trigger river incision, in particular at the upstream end (Figure 3B1). Poisson and Avouac (2004) reconstructed river longitudinal profiles preserved in terraces throughout the Holocene in the Tien Shan. They observed a continuous decrease in channel gradient due to greater incision at the upstream end compared to further downstream. In contrast, experimental and numerical work has shown that a step increase in tectonic uplift rate will cause an upstream migrating knickpoint and generate a delayed, but sustained, increase in Q_s,out (Figure 3D2; e.g., Bonnet and Crave, 2003; Armitage et al., 2011; Wickert and Schildgen, 2019; Zhang et al., 2020). For example, the Mendocino Triple Junction in northern California (United States) is characterized by a latitudinal gradient in uplift rates (Merritts and Bull, 1989). The locus of highest uplift rates is migrating though time and the transient adjustment of individual catchments to changing uplift rates is today detectable in the longitudinal river profiles (Snyder et al., 2000; Clubb et al., 2020), as well as in cosmogenic nuclide derived catchment average denudation rates (Moon et al., 2018).

Times Related to Signal Generation

Based on those two simplified endmembers of signal shapes (a temporary or a sustained change in the parameter of interest; Figure 3D) summarized from previous studies (e.g., Allen and Densmore, 2000; Bonnet and Crave, 2003; van den Berg van Saparoea and Postma, 2008; Armitage et al., 2011, 2013; Simpson and Castelltort, 2012; Tofelde et al., 2019; Wickert and Schildgen, 2019), we propose a general terminology of signal related times that can be applied to any kind of environmental signal (Figure 4). We differentiate between distinct moments in time (vertical lines and letters) and periods of time (horizontal arrows and numbers). After a change in boundary conditions (A), the landscape responds by adjusting its topography until steady state conditions are achieved again (B; Figure 4A). The required time is referred to as landscape response time (1; see section “Landscape Response Time”). Adjustments of the landscape generate signals, i.e., measurable changes in certain sediment parameters (Figures 4B,C). In the context of signal generation, we present and discuss the following two signal related time periods: the signal onset time (2) and the signal duration time (3).

We define the signal onset time (2) as the time period between the onset of a change in boundary conditions (A) and the onset of change in a sediment parameter (C). The signal onset time is equivalent to the sediment flux lag time by Li Q. et al. (2018), who investigated numerically how long expected increases or decreases in Q_s lag behind periodic step changes in uplift rates. They found that signal onset times increase the farther the landscape was from steady state prior to the change in boundary conditions (Li Q. et al., 2018), which is particularly important for cyclic climate fluctuations (e.g., Milankovitch-driven climate changes). In addition to prior landscape state, signal onset times depend on the parameter of interest. For example, an increase in uplift rates and tectonic activity might affect the grain size distribution in fluvial sediments relatively fast, while it takes longer until this change becomes detectable in samples for detrital thermochronology (e.g., Whittaker et al., 2010; Roda-Boluda et al., 2018).

Once a signal is generated, it persists until the parameter attains a stable value again (D). Hence, we define the signal duration time (3) as the time period characterized by a measurable change in a sediment parameter (δ _Parameter/δ t ≠ 0). Our definition is equivalent to the signal response time of Sharman et al. (2019) that describes the time until a sediment parameter attains a steady value within a certain percentage again. The signal duration time, as we define it, lasts at least as long as the transient landscape response phase, and potentially beyond. Consequently, during signal duration times fluvial sediments carry mixed information from parts of the landscape adjusted to prior and new conditions. A measured parameter represents current conditions within the landscape only once this parameter is fully adjusted to new steady conditions (end of signal duration, D). For example, the ¹⁰Be concentration in fluvially transported sediments are regularly applied as a proxy to estimate catchment averaged denudation rates (Balco and Stone, 2005; Charreau et al., 2011; Mandal et al., 2015; Puchol et al., 2017; Mariotti et al., 2019). A theoretical step change in a catchment averaged denudation rate causes an exponential adjustment in detrital ¹⁰Be concentrations. Hence, during the period of ¹⁰Be adjustment, the denudation rate calculated from ¹⁰Be in detrital sediments differs from true denudation rates (Willenbring et al., 2013; Garcin et al., 2017; Mudd, 2017; Mason and Romans, 2018). Thus, if boundary conditions change at a period shorter than parameter-specific signal onset (2) and signal duration times (3), the measured parameter never represents current landscape conditions. However, it does not mean that no signals are generated, nor that no information can be extracted from sedimentary signals. Signals, as we define them, are particularly generated during landscape transience, and hence can be used to identify times of environmental changes. Quantitative reconstructions of true current landscape conditions, however, are limited to times when the measured parameters are constant throughout the time period of interest or with additional knowledge on signal mixing within a landscape.

Times Related to Signal Transfer

Signals are typically generated in mountainous areas where sediment is produced (erosion zone). To be preserved in sedimentary archives, the signal-carrying sediments need to be transported along SRSs to their deposition zone, which requires time. In the context of signal transfer, we present and discuss the following two time periods: the signal transfer time (4) and the total signal lag time (5). When reconstructing past conditions from sedimentary archives, the arrival time of the first measurable change of a parameter in the deposition zone (E) (which can be continental or marine) is important. We define the signal transfer time (4) as the time between the onset of signal generation in the source (C) and the signal arrival time in the sink (E). Signal transfer times are expected to vary with the parameter of interest (due to grain size dependent differences in transport mode) and from archive to archive (due to differences in catchment size and hydraulic conditions; detailed discussion in section “Quantification of Signal Transfer Times”). Consequently, a single local change in boundary conditions can result in different times of a first detectable parameter change in the sink, as well as in differences in signal duration (e.g., Ramisch et al., 2018).

Moreover, we define the total signal lag time (5) as the total time between the change in boundary conditions (A) and the signal arrival in the sink (E). The total signal lag time is the sum of the signal onset time (2) and the signal transfer time (4). Oftentimes, studies refer to the total signal lag time simply as the lag time (Goodbred and Kuehl, 2000; Goodbred, 2003; Covault et al., 2010; Duller et al., 2019). For example, the Paleocene-Eocene boundary is characterized by a global warming event with an abrupt onset referred to as the Paleocene/Eocene Thermal Maximum (PETM), defined by an abrupt negative excursion in soil carbon isotopes, δ¹³C (McInerney and Wing, 2011). Studies from the central US (Foreman et al., 2012; Foreman, 2014) and the Spanish Pyrenees (Schmitz and Pujalte, 2003, 2007; Chen et al., 2018) have related extensive sheets of coarser fluvial sediments during the PETM to increased seasonal precipitation, despite overall drier climate conditions. Manners et al. (2013) and Duller et al. (2019) attempted to quantify the total signal lag time between the onset of the PETM and the onset of the change in depositional style both in the terrestrial and marine realm. Based on bulk organic carbon profiles, they suggested a total signal lag time of ∼16 kyr in both proximal non-marine and distal deep-marine sites separated by ∼300 km distance. However, the authors acknowledge that this is an upper estimate and a substantially shorter total signal lag time cannot be excluded (Pujalte and Schmitz, 2014).

We want to emphasize that reconstructions of past conditions from signals in sedimentary archives face further challenges in addition to the quantification of signal related times. Additional complications include (1) the modification or destruction of signals during transport along SRSs (modification indicated by transparent vs. solid yellow curves in Figure 4; Jerolmack and Paola, 2010; van de Wiel and Coulthard, 2010; Romans et al., 2016; Allen, 2017; Scheingross et al., 2020), (2) non-continuous sedimentation resulting in incomplete stratigraphic records (Sadler, 1981; Tipper, 1983; Anders et al., 1987; Strauss and Sadler, 1989; Ager, 1993; Kemp, 2012; Miall, 2015; Trampush and Hajek, 2017), (3) substantial modification of stratigraphy and signals after deposition, e.g., by bioturbation (e.g., Wetzel, 1984; Courtene-Jones et al., 2017) or chemical alteration (e.g., Lynn and Bonatti, 1965; Bouchez et al., 2010), (4) second order responses or internal feedback mechanisms within a SRS (e.g., Schumm, 1973; Steffen et al., 2010; Ramisch et al., 2018), or (5) event cascades or compound events. In an event cascade one event triggers further subsequent events, like a wildfire leading to reduced vegetation cover and eventually higher erosion rates (e.g., Moody and Martin, 2001; Kemter et al., 2021). Compound events describe a response related to the simultaneous occurrence of several forcings or drivers (e.g., Leonard et al., 2014; Zscheischler et al., 2018). Discussing all those challenges is beyond the scope of this work. But as we are particularly discussing times related to signal propagation, we point to the recent review by Straub et al. (2020), who propose the compensation timescale (T_c) to quantify timescales of geomorphic stochasticity in stratigraphy and to address the challenge of non-continuous sedimentation (Sheets et al., 2002; Wang et al., 2011; Straub et al., 2020). Here, for the purpose of discussing challenges related to the quantification of the different proposed times, we assume that signals have not been completely obscured during transport, and are preserved and measurable in the stratigraphic record.

In summary, signals are initiated during transient landscape response and can be transported through the SRS and arrive in the sink (E) even before the characteristic river response time has passed (B), such that the total signal lag time (5) can be shorter than the river response time (1) (Figure 4, Shen et al., 2012; Straub et al., 2020). These signals indicate changes in boundary conditions and are not representative of steady state conditions. It is the generation of a sediment parameter change, its transport and the archiving during this transient state that are poorly understood, but hold high potential for rapid imprint of environmental changes in the stratigraphic record.

Quantification of Signal Transfer Times

For paleo-reconstructions from sedimentary archives the total signal lag time – the time between the change in boundary condition and the arrival of the signal in the sink – is of particular importance. In sedimentary archives we can only measure signal arrival times. Hence, we need to estimate signal onset times and signal transfer times in order to relate the signal to a specific environmental change. In this section, we focus particularly on the quantification of signal transfer times. In order to calculate signal transfer times, we need to quantify sediment transport times of the hydraulic grain size fraction(s) the signal is bound to. In Section “Sediment Transport Times,” we discuss which parameters impact sediment transport times, how sediment transport times vary with hydraulic grain size fractions, and how sediment transport times can be quantified. In Section “Signal Arrival Times,” we then discuss theoretical consequences of grain size dependent sediment transport times regarding signal arrival times and the stratigraphic record. In addition, we briefly address the dependency of a parameter of interest on complete or partial sediment transfer, and the according implications on signal arrival times.

Sediment Transport Times

Signal transfer time describes the required time for a signal to travel to the deposition zone. As such, the signal transfer time greatly depends on the duration of sediment transport, the sediment transport time. Assuming a simple case in which a grain travels permanently in suspension at the same speed as water, and assuming an average travel speed of water of ∼1 m s^–1 (e.g., Schulze et al., 2005), the grain could travel ca. 90 km per day. Hence, if transported without any deposition, a single grain in suspension could theoretically reach the ocean in a 1000 km long river in less than 2 weeks. However, in reality even grains transported in suspension do not travel at the same speed as water, and transport is frequently interrupted by phases of deposition (e.g., Parsons et al., 2015). Also, signals are rarely measured on a single grain, but rather at an amalgamation of grains. Individual grains, in turn, follow different trajectories, where grain transport is interrupted by phases of no transport of variable duration. Because we cannot measure sediment transport times for each individual grain (also see section “Quantification of Sediment Transport Times”), sediment transport times of a certain sediment fraction are better represented by a probability distribution instead of a single value.

We think that sediment transport times are governed by two main factors summarized in Figure 5: (1) the fraction of time a grain is mobile vs. immobile within the active channel and (2) the fraction of time a grain is transiently stored outside the active channel. Short sediment transport times (dark colors in Figure 5) are the result of high grain mobility and short transient storage, whereas dominantly immobile grains and long storage result in long sediment transport times (light colors in Figure 5). Both, the fraction of time in motion and storage outside the active channel, depend on a range of parameters, some of which vary with hydraulic grain size fractions (blue), while others are less dependent on hydraulic grain size fractions (gray). Because individual grains follow different trajectories, we discuss how the different parameters impact the probability of storage of a single grain.

FIGURE 5

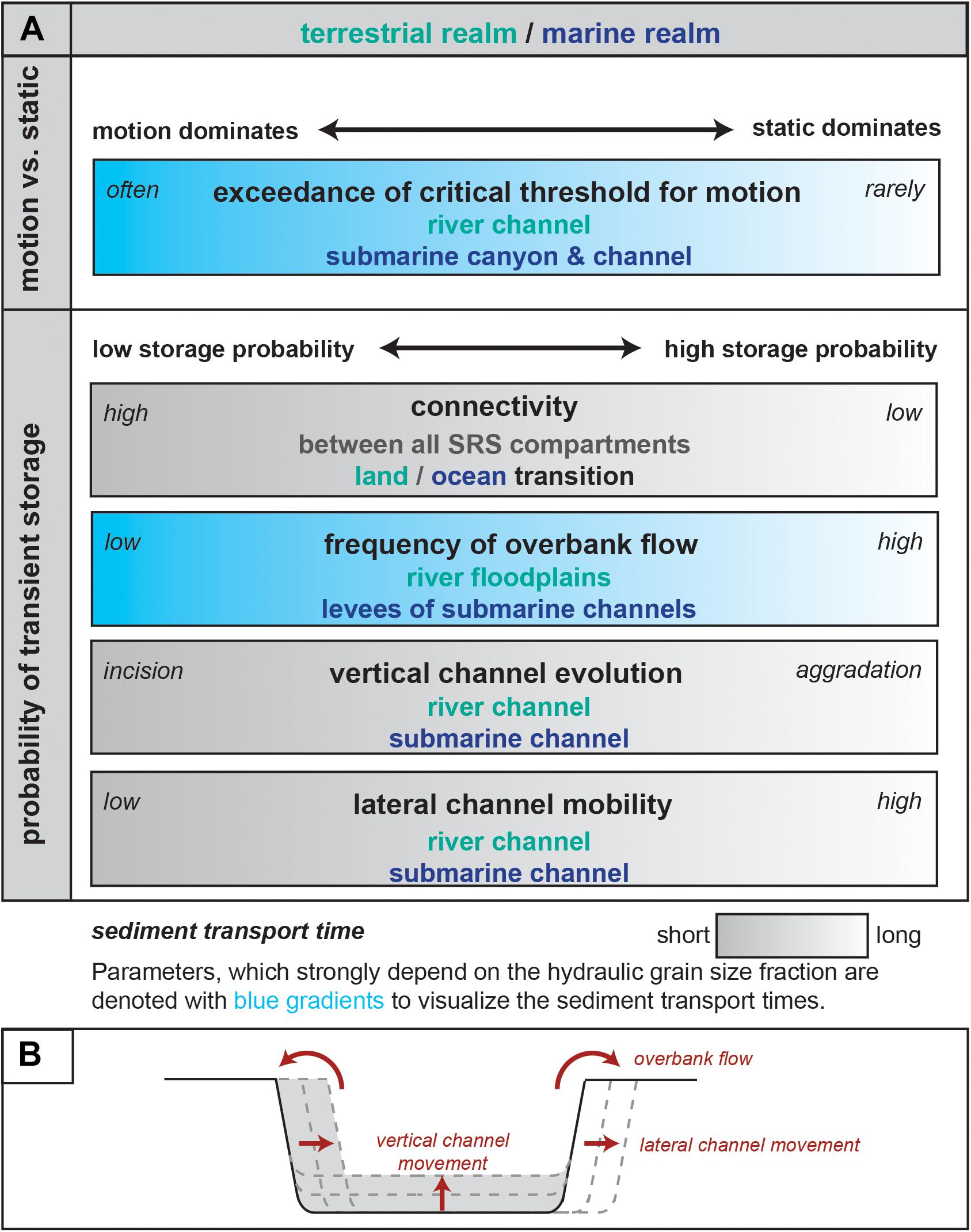
Figure 5. Schematic summary of factors influencing sediment transport times in channelized systems. (A) Sediment transport times depend on the fraction of time a grain is in motion versus immobile within the active channel, and the probability of storage outside the active channel. Both, the time in motion and probability of storage, depend on a range of factors, which themselves range between endmembers as indicated in italics. Accordingly, the sediment transport times range from short (dark colors) to long (white colors). Factors that vary greatly with hydraulic grain size fraction are marked in blue, factors that vary less between grain sizes are shown in gray. Green and blue font indicates the locations where these factors apply in the fluvial and marine realm, respectively. (B) Schematic summary of channel evolution terms.

Times of Sediment in Motion vs. Static

In the simple case of a spatially fixed, single-thread river channel with no overbank flow (no storage outside the active channel), the transport time of a certain grain is only determined by the fraction of time the grain is mobile versus sitting immobile on the river bed. Sediment particles sitting on the bed can get entrained and bedload transport persists, when the ratio of shear stress exerted by the water column on the river bed and resisting forces of the particle itself exceeds a certain threshold, the so-called critical Shields stress or ${\mathrm{\tau }}_c^{{}^{*}}$ (Figure 5A; Shields, 1936; Wiberg and Smith, 1987). The shear stress exerted by the moving water column on the river bed (= bed shear stress) increases with water depth and channel gradient (e.g., Tucker and Slingerland, 1997), and thus, varies with discharge conditions. Not only the total amount of discharge plays a role, but also the distribution of discharge through time, e.g., its seasonality or the frequency and magnitude of flooding events (Haynes and Pender, 2007; Gugliotta et al., 2016). In contrast, resisting forces of the grain increase with grain size and grain density. ${\mathrm{\tau }}_c^{{}^{*}}$ has been shown to vary little among many rivers (∼0.03 to 0.06) and is therefore often considered as constant for a given site (e.g., Meyer-Peter and Müller, 1948; Buffington and Montgomery, 1997; Wilcock and Crowe, 2003).

However, several recent studies indicate that ${\mathrm{\tau }}_c^{{}^{*}}$ cannot simply be regarded as a constant, especially not for steeper rivers (slope > 5%), but varies with channel slope (Lamb et al., 2008; Recking et al., 2009; Scheingross et al., 2013; Prancevic and Lamb, 2015), previous flow conditions (Turowski et al., 2011; Masteller et al., 2019), or sand content (Wilcock and Crowe, 2003; Curran and Wilcock, 2005; Lamb et al., 2008; Houssais and Lajeunesse, 2012), thus complicating the relationship between grain characteristics and according sediment transport times. In addition, initiation of grain motion gets even more complicated in poorly sorted sediments due to the hiding-exposure effect, as well as mixed grain shapes and densities (Parker et al., 1982; Wilcock and Crowe, 2003; Pfeiffer and Finnegan, 2018). The hiding-exposure effect describes that small grains can be protected from the initiation of motion when they hide in pockets between larger grains, thereby increasing ${\mathrm{\tau }}_c^{{}^{*}}$. In contrast, coarse grains surrounded by fine grains can protrude further from the bed into the water column than the fine grains and are exposed to increased drag, thereby decreasing ${\mathrm{\tau }}_c^{{}^{*}}$. Motion initiation on clay-sized particles may in addition be hindered by cohesion effects (e.g., Hjulstrom, 1955), as ${\mathrm{\tau }}_c^{{}^{*}}$ of cohesive sediment mixtures exceed ${\mathrm{\tau }}_c^{{}^{*}}$ of size-equivalent cohesionless sediments by a factor up to 50 (Kothyari and Jain, 2008).

In summary, small grains with low densities (cf. small hydraulic grain size fraction) are generally more frequently mobile under constant flow conditions than coarse and dense grains, as they require a lower bed shear stress to initiate motion. Consequently, their sediment transport times are shorter. However, factors like heterogenous grain size distributions (hiding-exposure effect, sand-content), channel geometry, previous flow-conditions, or cohesion effects can add complexity to this rule-of-thumb.

In channelized systems in the marine realm, grains will also be entrained when ${\mathrm{\tau }}_c^{{}^{*}}$ is exceeded (Figure 5A). However, while on land the bed shear stress acting on bed sediments is mainly exerted by the overlying water column, the bed shear stress in marine canyons and channels largely depends on the character of sediment gravity flows (such as turbidity currents) within these sediment conduits (Piper, 1970; Cossu and Wells, 2012; Talling, 2014). Turbidity currents have the ability to erode sediments from the seafloor, if they are moving fast enough so that their bed shear stress exceeds the critical value, ${\mathrm{\tau }}_c^{{}^{*}}$, of the sediment on the seafloor. Seafloor erosion causes an increase in flow density, which leads to acceleration and eventually even more erosion; a process known as self-acceleration (e.g., Heerema et al., 2020). Laboratory experiments and direct monitoring have shown that turbidity currents are highly density stratified and their basal layer is characterized by the highest sediment concentrations (Cossu and Wells, 2012 and references therein; Paull et al., 2018). The probability of initiation of grain motion will be highest, where turbidity currents occur at high frequency, carry large sediment volumes and coarse grain sizes. A setting of high confinement (synonyms: channelization or topographic roughness), such as deep submarine canyons and channels, facilitates initiation of grain motion.

Probability of Transient Storage

In addition to times of no sediment transport within a confined channel due to flow conditions not exceeding the initiation of sediment motion on the river bed or sea floor, sediment transport times can be increased due to sediment storage along the SRS outside of the active channel. The concept of SRS connectivity describes sediment transfer from all potential sources to all sinks through different geomorphic segments of the SRS and can be used to describe the continuity of mass transfer in a SRS (Hinderer, 2012; Fryirs, 2013; Bracken et al., 2015; see Najafi et al., 2021 for a recent review). A high degree of connectivity (Figure 5A) allows fast sediment transfer, while a low degree of connectivity results in sediment storage within different segments of the SRS (hillslope, fluvial system, shelf, continental slope, deep-marine basins). A first attempt to quantify the storage potential of a SRS has been proposed by Walling (1983), who defined the sediment delivery ratio as the ratio of sediment discharge at a certain point along the river relative to the amount of produced sediment upstream within a certain time. The sediment delivery ratio has been applied as a measure of connectivity, with high delivery ratios indicating low storage potential and vice versa (e.g., Walling, 1983; Hooke, 2003; Heckmann and Vericat, 2018). However, there has been further debate on whether the sediment delivery ratio is a useful measure for connectivity (for more details see e.g., Parsons et al., 2006; De Vente et al., 2007; Fryirs, 2013), resulting in the ongoing lack of agreement on how connectivity can be properly quantified (Hoffmann, 2015; Najafi et al., 2021).

On land, sediment can be stored on hillslopes due to reduced hillslope-channel connectivity (Figure 5; DiBiase and Lamb, 2013; Hoffmann, 2015; Harries et al., 2021) and within the river system. Overbank flow, as well as lateral and vertical movement of the active channel can result in long-term sediment incorporation in floodplains (Nakamura and Kikuchi, 1996; Wittmann et al., 2011, 2020; Bradley and Tucker, 2013; Coulthard and Van De Wiel, 2013), alluvial fans (Jolivet et al., 2014; D’Arcy et al., 2015, 2017; Guerit et al., 2016; Mason and Romans, 2018; Carretier et al., 2020), fluvial terraces (Blöthe and Korup, 2013; Limaye and Lamb, 2016; Schildgen et al., 2016; Malatesta et al., 2017, 2018; Tofelde et al., 2017; Quick et al., 2019), or entire valley fills (Hilley and Strecker, 2005). As storage along the fluvial system on continental scale SRSs is of major importance, we discuss storage outside the active river channel in form of (1) floodplain deposition due to overbank flow, (2) burial in the channel bed due to sediment deposition during periods of channel aggradation, and (3) deposition due to lateral channel movements (e.g., point bar accretion) (Figures 5A,B).

First, during floods causing overbank flow, sediments can be washed onto the floodplain, where they can remain for long times before remobilization (Figure 1; Wittmann et al., 2011, 2020). The likelihood of being deposited on the floodplain due to overbank flow, in turn, varies with the mode of transport. Fine particles, including sand, silt, and clay, more often travel in suspension in the water column (Shields, 1936) and are more likely to be deposited on the floodplain during overbank flow conditions. In contrast, coarse particles, such as gravel, are usually transported as bedload (Shields, 1936) and therefore remain within the channel bed even during overbank flow conditions. Consequently, gravel has a lower probability of being washed onto floodplains (Malmon et al., 2003).

Second, storage probability is increased if rivers are in a phase of aggradation and, hence, bury sediments in their beds (Figure 5B). Transport-limited rivers respond with sediment deposition along the channel to steepen their gradient, for example, following an increase in the upstream sediment-to-water discharge ratio (e.g., van den Berg van Saparoea and Postma, 2008; Armitage et al., 2013; Tofelde et al., 2019). Alternatively, base level rise (e.g., Blum and Törnqvist, 2000; Blum et al., 2013) or permanent subsidence of a terrestrial basin (e.g., Allen and Densmore, 2000; Whittaker et al., 2010) can lead to sediment deposition along the channel. In the absence of lateral channel movement, those buried sediments will only be remobilized if changes in boundary conditions trigger a switch from channel aggradation to channel incision, for example, by base level lowering or by a decrease in the upstream sediment-to-water discharge ratio (Allen and Densmore, 2000; van den Berg van Saparoea and Postma, 2008; Armitage et al., 2013; Tofelde et al., 2019).

Third, sediment gets stored due to lateral channel movement (Figure 5B). Sediments of all grain size fractions can be deposited when the active channel steps sideways either through avulsion (Slingerland and Smith, 2004; Jerolmack and Mohrig, 2007) or by gradual sideways migration and associated accretion of barforms (Einstein, 1926; Hickin and Nanson, 1984; Bufe et al., 2019). However, it should be noted that lateral channel mobility can also remobilize previously deposited sediments through erosion (e.g., Blum et al., 2013). Therefore, lateral channel mobility increases the storage probability of sediments in motion within the active channel, but decreases the storage probability of previously deposited sediment.

In the ocean, sediment can be stored proximal in deltas (e.g., Jonell et al., 2017) and on the shelf (Ogston et al., 2000; Wheatcroft and Sommerfield, 2005; Miller and Kuehl, 2010), and more distal in submarine canyons (Brocheray et al., 2014; Maier et al., 2019), in intraslope basins (Bernhardt et al., 2017), in submarine channels (Jobe et al., 2015) and their levees (Dennielou et al., 2006; Jorry et al., 2011; Toucanne et al., 2012; Bonneau et al., 2014; Hülscher et al., 2019), within lobes in submarine fans (Prélat and Hodgson, 2013; Spychala et al., 2017; Hessler and Fildani, 2019), within basin-plain turbidites (Romans et al., 2009; Clare et al., 2015), and within hemipelagic sedimentation (Pelejero et al., 1999). Whereas a high degree of connectivity between any segment of SRSs reduces sediment transport times (cf. sediment delivery ratio), the connectivity at the land-ocean transition is of particular importance. In highly connected SRSs, grains can travel unhindered from land to the ocean and are discharged directly into the submarine canyon and onto the marine basin floor (Romans et al., 2009; Covault and Graham, 2010; Bernhardt et al., 2017; Blum et al., 2018). Continental shelves have traditionally been seen as transient sedimentary sinks, however, several studies have recognized that shelves can act as fast conveyors of sediment from land to the deep ocean, if canyon heads are incised across continental shelves and tap into coast-parallel sediment transport (the ocean littoral cell) or are connected to a river mouth (Figure 1; Walsh and Nittrouer, 2003; Covault and Graham, 2010; Bernhardt et al., 2015), if terrigenous sediment supply is high enough to cause delta migration to the shelf edge (Burgess and Hovius, 1998; Carvajal and Steel, 2006), or if coast-parallel bottom currents sweep sediment off the shelf edge or into submarine canyons (Bernhardt et al., 2016). Hence, sediment transport to submarine fans is most efficient when connectivity is high, which in many (but not all) systems is enhanced during sea level lowstand, because river mouths extend to the shelf edge and discharge directly into slope canyons (Sweet and Blum, 2016; Blum et al., 2018). However, several recent studies have shown that even in times of high connectivity sediment transport processes at the shelf edge are a critical factor determining the amount and rate of sediment delivered to the continental slope and deep-sea basins (Dixon et al., 2012; Hodgson et al., 2018; Cosgrove et al., 2020). Moreover, many sediment density flows die out in the upper reaches of the marine SRS (Heerema et al., 2020), leading to intermediate storage of sediments along canyons and in channel-levee systems. Such sediments may reach the final sediment archive only after remobilization by stronger flows.

In the distal part of a marine SRSs, sediment can be buried in submarine channels by processes similar to terrestrial channels (Figure 5). Although the dynamics and frequencies of lateral (avulsion and lateral migration) and vertical (incision vs. aggradation) submarine channel movements differ from terrestrial rivers (e.g., Jobe et al., 2020), the general effect of lateral and vertical submarine channel movement on sediment transport times should be analogous to terrestrial river dynamics explained above. Different to terrestrial rivers are sediment deposition processes related to turbidity currents within submarine channels. Turbidity currents form large clouds of suspended sediment that can be several 10s of meters (Azpiroz-Zabala et al., 2017) to several 100s meter in height (Völker et al., 2008). Superelevation induces the diluted (fine-grained) upper sediment cloud of the turbidity current to spill over and deposit sediment onto the levees (overspill/flow stripping), while eroding, bypassing, and/or depositing within the channel itself (Normark et al., 1980; Piper and Normark, 1983; Fildani et al., 2006; Straub and Mohrig, 2008).

In summary, the storage and remobilization of sediments on their way to the depositional segment is a major source of complexity to unravel climatic, tectonic, or anthropogenic events within sedimentary archives. This is why accurate methods to quantify the transport time of the sediments from sources to sinks are deeply needed. Therefore, we briefly review current approaches to quantify sediment transport before discussing challenges related to signal arrival times.

Quantification of Sediment Transport Times

Quantification of sediment transport times requires the determination of the velocity of a grain at various scales: from motion within an active channel to motion at the scale of the whole SRS. In this section, we focus on methods developed to measure the total transport time of sediment.

Short-lived radionuclides (e.g., ²³⁴Th, ⁷Be, ²¹⁰Pb, ¹³⁷Cs) can be used to quantify timing of fine-grained sediment dispersal along SRSs over short timescales (10⁰–10² year) (Zapata and Nguyen, 2009; Du et al., 2012). Malmon et al. (2005) showed that the fine-grained fraction can pass through a fluvial valley of 5 km length within hours. Similarly, fine-grained fluvial flood sediments of the Eel River were dispersed widely over the shelf and continental slope to about 500 m water depth in 1 month (Sommerfield and Nittrouer, 1999). Direct tracing of gravel transport using integrated transponder tags is only applicable to the gravel grain size fraction and on short timescales (Lamarre et al., 2005). Applying this method, among others Bradley and Tucker (2012) recorded mean and maximum travel distances of ∼100 m and ∼700 m, respectively, over 3.5 year.

At longer timescales (>10³ year), periods of storage and remobilization are frequently documented. This intermittent transport considerably increases the total transport time. On small grains (<63 microns), uranium-isotope series can be used to determine a ‘comminution age,’ which refers to the time elapsed between the generation of the silt-sized sediment grain by comminution of bedrock and its deposition (DePaolo et al., 2006). The sediment transport time refers to the time difference between the comminution age and its depositional age (Chabaux et al., 2006; DePaolo et al., 2006; Li et al., 2016). Following this approach, Suresh et al. (2014) demonstrated that the small grains of the large and tectonically stable Murrumbidgee River catchment (Australia) are stored for ∼200 kyr on hillslopes before they can reach the river network and be evacuated from the catchment area. Using the same method, Li et al. (2016) quantified the transport time of the sediments deposited in the Okinawa Trough (East China Sea), which is mainly fed by the Yangtze River and by sediments coming from Taiwan. They documented transport times on the order of 100 to 200 kyr. Moreover, DePaolo et al. (2006) measured sediment transport times to a deep-marine site with depositional ages < 1 Myr. They observed transport times ranging between 10 kyr up to 400–600 kyr with uncertainties of ±40 to ±100 kyr. The duration of sediment storage outside the active river channel can also be measured from the ratio of cosmogenic meteoritic ¹⁰Be over ⁹Be within sediments (Wittmann et al., 2015). Repasch et al. (2020) tested this method along the Rio Bermejo (Andean foreland basin, northern Argentina) and observed that the suspended load travels ∼1200 km from sources to sink in 8.4 ± 2.2 kyr.

The concentration of several cosmogenic nuclides can also be used to determine periods of burial and remobilization. For example, Fülöp et al. (2020) showed successions of burial and remobilization in the modern sediments of the Murray-Darling basin (Australia) that led to a total transport time of more than 1 Myr. Similarly, Dosseto et al. (2006) showed that the suspended load issued from the Andes and traveling through the Amazon basin is temporarily stored within the foreland basin for ∼5 kyr. For the coarse-grained fraction, Sinclair et al. (2019) documented recycling of pebbles deposited 5 Myr ago based on detrital cosmogenic ²¹Ne concentrations. This is in line with the numerical work from Carretier et al. (2020), which showed that even in a steady state landscape, some pebbles can be stored for a period of time substantially longer than the average population of sediments due to the river dynamics and landscape geometry. In their specific numerical setup, most of the grains leave the piedmont after 400 year, but ∼5% are still there after 1 Myr.

Finally, Clift et al. (2008) used the Nd composition on a limited set of samples from the Indus SRS, to suggest that the clay-sized fraction travels as suspended load rapidly through the system after an increase in monsoon strength with no resolvable lag time, while the bedload fraction takes 7–14 kyr to reach the sink (Clift and Giosan, 2014). At longer-time scale, Auchter et al. (2020) used the strontium isotope signal in marine carbonate particles to show that remobilization can occur within a depositional basin at million-year timescale.

Rather than measuring the time during which the sediment has been stored, Carretier and Regard (2011) demonstrated that the concentration in terrestrial cosmogenic nuclides of boulders can be used to determine the rate of transport of a grain, when abrasion is limited. Building on this approach, Carretier et al. (2019) provide field evidence that sediment can be stored for a substantial amount of time (tens of thousands of years) on their way to the sedimentary basins simply by the way rivers transport sediments. A new tool for quantifying sediment transport times is being developed using subaqueous bleaching rates of optically stimulated luminescence (OSL) in quartz and feldspar. Observations indicate that grains progressively bleach during transport, making the degree of bleaching a potential tool for measuring sediment transport times (e.g., Gray et al., 2017; Mey et al., 2020).

Signal Arrival Times

The signal arrival time in the deposition zone marks the end of the signal transfer time and total signal lag time (Figure 4). First, we examine the consequences of grain-size related differences in sediment transport times with respect to signal arrival times in stratigraphy. Then, we briefly discuss an additional challenge related to the detection of signal onset in the stratigraphic record: how much of the signal-containing sediment fraction needs to arrive in the sink in order for the signal to be detectable (we define this as parameter sensitivity).

Hydraulic Grain Size Dependent Signal Arrival Times

As previously discussed, sediment transport times, and thus signal transfer times, vary with hydraulic grain size fractions (Figure 5). Consider a simple hypothetical scenario where hydraulic grain size fraction is directly related to signal transfer time such that fine-grained sediment transmits catchment signals quickly, whereas signals associated with coarse-grained sediment are comparably slower (Carretier et al., 2020; Watkins et al., 2020). The theoretical consequence is that the onset of the signal of interest in fine-grained parameters would be at a lower stratigraphic position (earlier signal arrival time) compared to parameters associated with coarse-grained sediment for the same change in boundary conditions (Figure 6). Thus, what might appear as a prolonged environmental change in the stratigraphic record could actually be the manifestation of different grain size-dependent signal transfer times. However, this simple scenario does not consider the additional effects related to probability of transient storage. For example, in SRSs that are characterized by significant transient storage of fine-grained sediment (e.g., in floodplains), the arrival of the signal as a function of hydraulic grain size fraction would be more complex as a consequence of segment connectivity, channel mobility, and other aspects depicted in Figure 5.

FIGURE 6

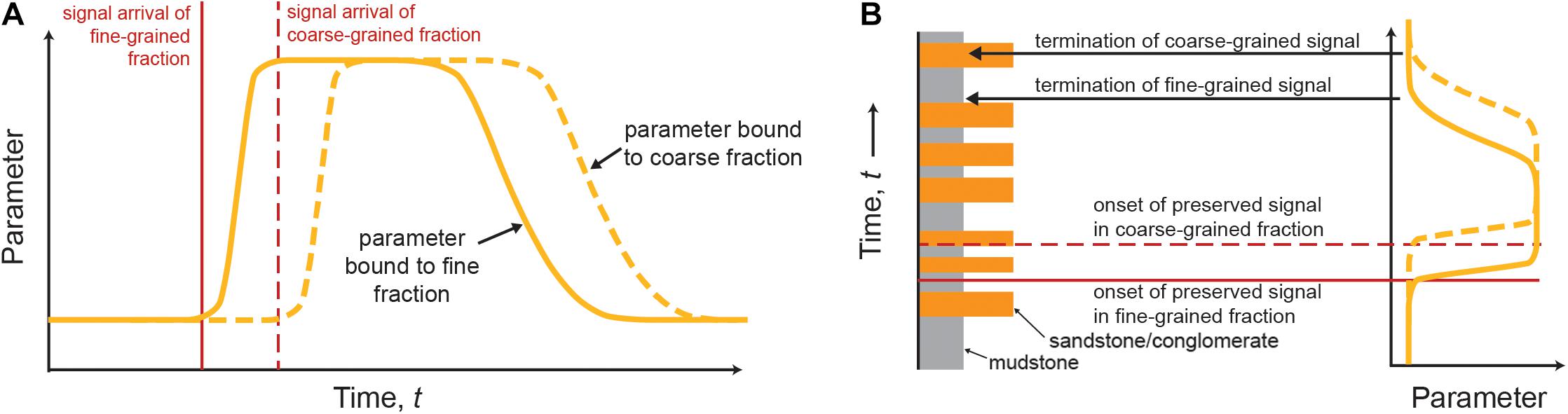
Figure 6. Hypothetical behavior of signal arrival times in the deposition area if signal transfer times vary with hydraulic grain size fractions. Time of signal arrival of two signals bound to different hydraulic grain size fractions in (A) representation of parameter expression versus time and (B) schematic expression in the stratigraphic record. This is one expression of many possible scenarios and is not meant to imply a general prediction (see text for discussion).

An analysis of the composition of the fine-grained sediment fraction (Nd and Sr isotopes of mud to fine sand) in the Indus submarine canyon by Li Y. et al. (2018) showed that modern submarine canyon sediment reflects the isotopic composition of the river sediment (Figure 1). However, the U-Pb signature of detrital zircons in the coarse silt to fine sand fraction does not mirror the river sediment composition (Li et al., 2019). Hence, in such a system, a potential signal may be transferred rapidly within the geochemical composition of the fine-grained fraction, but may be stuck in the terrestrial intermediate storage when the geochemical signal in the silt to sand-sized heavy mineral fraction is considered. Therefore, different sediment transport times of mud and zircons may result in an offset of signal arrival times in the stratigraphic record (Figure 6B). Studies characterizing parameters such as sediment geochemistry as a function of grain size (e.g., Jonell et al., 2018) suggest that bulk geochemical composition as a source-area indicator could be misleading.

Parameter Sensitivity

In order to quantify signal transfer times, it is not enough to quantify sediment transport times (see section “Sediment Transport Times”), one also needs to detect the onset of the signal in the sink. Signal transfer times in general increase during times of low connectivity between the segments of SRSs due to enhanced sediment transport times (Figure 5, see section “Probability of Transient Storage”). However, even during phases of low connectivity and enhanced sediment storage, a certain fraction of the sediment is still bypassed to the sink (e.g., Blum et al., 2013). For certain parameters of interest (Figure 2) this fraction might be sufficient to transmit the signal to the sink. Those parameters can be considered as independent or less dependent on the sediment delivery ratio (see section “Probability of Transient Storage”; Walling, 1983; Hooke, 2003; Heckmann and Vericat, 2018). If a parameter of interest is newly introduced to a SRS, its first stratigraphic occurrence does not require that its entire hydraulic grain size fraction is delivered to the sink. For example, plastic production only begun a few decades ago, but plastic particles are already widely distributed throughout the terrestrial and marine realm, including abyssal plains, submarine canyons, and deep-sea contourite drifts (e.g., Kane and Clare, 2019; Kane et al., 2020). As such, the first occurrence of plastic in a stratigraphic section has been used to characterize the onset of anthropogenic impact on our planet (Zalasiewicz et al., 2016; Matsuguma et al., 2017). Here, the signal is characterized by the first occurrence of the parameter in the record and does not require that the entire plastic fraction is transported to the sink. Another example is a drastic shift in the isotopic zinc signature detected in a sediment core from a hydroelectric reservoir in SW France, which could be related to the start-up of an industrial mine (Sivry et al., 2008). Zinc isotopes released in tailings were highly fractionated compared to naturally eroding zinc isotopes, such that even small contributions of industrial zinc caused a clearly detectable shift in the sedimentary record (Sivry et al., 2008).

In contrast, other parameters are more dependent on a high sediment delivery ratio. This is particularly true for all parameters investigating absolute changes in Q_s, for example sediment accumulation rates or varve thickness (e.g., Covault and Graham, 2010; Hinderer, 2012; Zolitschka et al., 2015; Hülscher et al., 2019). Also, grain size distribution studies require that a larger fraction of the produced sediment gets transported to the sink (e.g., Whittaker et al., 2011; Foreman et al., 2012; Parsons et al., 2012; D’Arcy et al., 2017; Duller et al., 2019). We name this dependency of a sediment parameter on the complete or partial transfer of the total sediment mass parameter sensitivity. Low parameter sensitivities, or parameters that are greatly independent of complete sediment transfer, will thus have an earlier signal arrival time and, hence, a shorter signal transfer time.

Summary and Future Perspectives

Environmental Signals

We have expanded the definition of environmental signals from changes in Q_s to changes in any sedimentary parameter of interest (e.g., Q_s, grain size distribution, geochemical or isotopic composition, and many more) related to a change in boundary conditions. Those signals are generated during transient landscape adjustment, and hence, are indicative of changes in boundary conditions. In order to preserve those signals, the signal-containing sediment needs to be transported along SRSs to a long-term sink (Figure 1). Oftentimes, the parameter of interest is bound to a certain grain size fraction only. As sediment transport times are highly variable with grain size, shape, and density, we suggest investigating signal propagation by grouping signals in hydraulic grain size fractions that are transported jointly (Figure 2). A hydraulic grain size fraction is defined by a size range of spherical quartz grains (e.g., sand or silt) and their hydraulic equivalents. However, further investigation is required, in particular regarding the transport behavior and hydraulic grain size fraction assignment of non-quartz sediment and non-mineral material (e.g., organic or anthropogenic material like pollutants or microplastic). Ideally, each sediment sample can be assigned to a hydraulic grain size fraction with a certain probability based on a combination of quantifiable characteristics, e.g., material density, weight, degree of sphericity, and others. However, the assignment to a hydraulic grain size fraction will be challenged, as some of these characterizes may evolve during transport or after deposition. For example, grain sizes get reduced during transport due to abrasion and attrition, such that a single grain can move into a smaller hydraulic grain size fraction during transport. To date, a number of studies have quantified the rate of grain size reduction during transport (Sternberg, 1875; Kuenen, 1956; Bradley, 1970; Attal and Lavé, 2006, 2009; Dingle et al., 2017), but we still lack detailed knowledge about the role of grain mineralogy, shape, or sediment sorting on the rate of size reduction. Also, assigning a hydraulic grain size fraction to sediments in ancient strata requires that the signal-containing transported sediment can be distinguished from locally produced sediments (e.g., terrestrial derived clastics versus marine carbonates). As such, more comprehensive datasets on grain size, shape, and composition, and their evolution through space (e.g., Cosgrove et al., 2019) are deeply needed. Novel methods or approaches for automatic grain characterization (e.g., Domokos et al., 2010; Ludmány and Domokos, 2018) might improve the comparison among datasets.

Times of Signal Generation and Transfer

In order to reliably reconstruct past environmental conditions from parameter measurements (signals) in sedimentary archives, the time difference between the change in environmental boundary conditions and the signal arrival time in the archive — the total signal lag time — is essential (Figure 4). The total signal lag time is the sum of the signal onset time (time between change in boundary conditions and onset of signal generation) and signal transfer time (time to transport the sediment carrying signal from the source to the sink). It is important to note that the total signal lag time is different from the landscape response time, which describes the duration of topographic landscape adjustment. Consequently, signals created due to short period climate changes can still be detectable in terrestrial and marine archives, even when transported in large river systems.

The signal onset time varies greatly with the parameter of interest and needs to be investigated for each parameter individually. Signal transfer times greatly depend on sediment transport times of the according hydraulic grain size fraction. Sediment transport times will increase when grains are immobile within the active river channel or during long-term storage outside the active channel (Figure 5). Both grain mobility and storage probability differ among hydraulic grain size fractions. To date, our knowledge on grain mobility especially beyond decadal time scales is still limited. Future research on how the amplitude and frequency of river discharge or sediment gravity flows impact grain mobility and transport distances will advance our understanding on sediment transport times. Sediment storage probability outside the active channel is a function of discharge conditions (frequency of overbank flows), and vertical and lateral channel mobility (Figure 5B). Further work investigating how prevailing tectonic and climatic boundary conditions are linked to rates of channel mobility will improve our understanding of sediment storage probability. In addition, novel tools and further development of methods to quantify sediment storage times or the degree of connectivity will help to better constrain sediment transport times.

In order to quantify the influence of individual factors on sediment transport times, tools to measure sediment transport times are key. Although methods to quantify sediment transport times have evolved, the precise measurement of the time sediment requires to move from the source to the sink is still a key challenge. Currently applied methods (see section “Quantification of Sediment Transport Times”) are oftentimes limited to a certain grain size, mineralogy, or timescale. Developing methods that can, for example, be applied to the whole range of grain sizes will allow a direct comparison of grain size related transport times and hence, uncover differences in signal transfer times. Integrating multiple methods that target a distinct hydraulic grain size fraction will reduce uncertainties of sediment transfer times estimations. If these times are to be quantified and used to interpret system-scale behavior, methods that incorporate and propagate uncertainty that originates from the chronometric tool (e.g., error bars on determined ages) must be developed.

One theoretical consequence of grain-size dependent sediment transfer times is that signal arrival times of parameters bound to different hydraulic grain size fractions might differ. If so, those signals might not be embedded in the same stratigraphic layer (Figure 6), despite being generated by the same change in boundary conditions. To date, studies investigating how a single event can be ‘smeared’ or how multiple events can lead to signal ‘spiking’ in the stratigraphic record due to hydraulic grain size fraction dependent differences in signal arrival times are rare. Further work is required, for example by comparing grain size-dependent compositional signatures among multiple SRS segments of a common age. Additional challenges arise regarding the determination of the signal arrival time in the sink. We consider the sensitivity of individual parameters regarding complete or partial sediment transfer or the degree of connectivity as one of the challenges for future research. Here, we primarily focused on signal propagation on centennial to millennial timescales. However, applying the proposed concepts (e.g., assignment of material to hydraulic grain size fractions) to anthropogenic material dispersed on decadal or even annual timescales is an area worthy of future investigation.

Approach to Holistic Reconstructions of Landscape Response

To overcome current discrepancies regarding signal propagation from source to sink, we proposed a more differentiated classification of signals based on hydraulic grain size fraction and a distinction between landscape and signal-related types of times. We recommend combining sediment parameters from different hydraulic grain size fractions to holistically reconstruct landscape response to changes in boundary conditions. For each parameter of interest, the goal should be to answer the following four questions:

(1) Which hydraulic grain size fraction is the parameter of interest bound to?

(2) What is the signal onset time of the parameter of interest?

(3) What is the signal transfer time (depending on hydraulic grain size fraction, catchment geometries, and tectonic and climatic boundary conditions) of the parameter of interest?

(4) What is the signal arrival time of the parameter of interest in the sink? How sensitive is the signal arrival time to complete sediment transfer (parameter sensitivity) and to technical or methodological choices?

The differentiated classification of signals and signal-related times helps to explain how short frequency climate events can be detected in sedimentary archives offshore large river systems. Also, when comparing several parameters within one SRS or the same parameter in different SRSs, we expect that a single event can cause signals with different signal arrival times in the sink and preservation in different stratigraphic layers. By comparing those signal-related times among various parameters of interest or under diverse changes in boundary conditions, we will systematically approach a holistic understanding of the source-to-sink propagation of environmental signals during landscape transience and of the linkage between the sedimentary record and events or changes in catchments on land.

Author Contributions

ST and AB designed the review study and led the writing of the manuscript. All authors wrote individual sections of the text, contributed to design and drafting of figures, and discussed the entirety of the manuscript.

Funding

We acknowledge the support of Deutsche Forschungsgemein- schaft (German Research Foundation) and Open Access Publication Fund of Potsdam University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Jens M. Turowski and Andrew D. Wickert, who commented on an earlier version of this manuscript. We thank Philipp Seidel (http://seidel-illustration.de/) for creating the earliest version of Figure 1. We thank Michael Blum and David Mark Hodgson for insightful and constructive comments that improved the manuscript.

Glossary

References

Ager, D. V. (1993). The Nature of the Stratigraphical Record. Hoboken, NJ: John Wiley.

Google Scholar

Allen, J. R. L. (1974). Reaction, relaxation and lag in natural sedimentary systems: general principles, examples and lessons. Earth Sci. Rev. 10, 263–342. doi: 10.1016/0012-8252(74)90109-3

CrossRef Full Text | Google Scholar

Allen, P. A. (2008a). From landscapes into geological history. Nature 451, 274–276. doi: 10.1038/nature06586

PubMed Abstract | CrossRef Full Text | Google Scholar

Allen, P. A. (2008b). Time scales of tectonic landscapes and their sediment routing systems. Geol. Soc. London Spec. Publ. 296, 7–28. doi: 10.1144/SP296.2

CrossRef Full Text | Google Scholar

Allen, P. A. (2017). Sediment Routing Systems: the Fate of Sediment from Source to Sink. Cambridge: Cambridge University Press. doi: 10.1017/9781316135754

CrossRef Full Text | Google Scholar

Allen, P. A., and Densmore, A. L. (2000). Sediment flux from an uplifting fault block. Basin Res. 12, 367–380. doi: 10.1111/j.1365-2117.2000.00135.x

CrossRef Full Text | Google Scholar

Allen, P. A., Armitage, J. J., Carter, A., Duller, R. A., and Whittaker, A. C. (2013). The Qs problem: sediment volumetric balance of proximal foreland basin systems. Sedimentology 60, 102–130. doi: 10.1111/sed.12015

CrossRef Full Text | Google Scholar

Allen, P. A., Armitage, J. J., Whittaker, A. C., Michael, N. A., Roda-Boluda, D., and D’Arcy, M. K. (2015). Fragmentation model of the grain size mix of sediment supplied to basins. J. Geol. 123, 405–427. doi: 10.1086/683113

CrossRef Full Text | Google Scholar

Anders, M. H., Krueger, S. W., and Sadler, P. M. (1987). A new look at sedimentation rates and the completeness of the stratigraphic record. J. Geol. 95, 1–14. doi: 10.1086/629103

CrossRef Full Text | Google Scholar

Anderson, J. B., Kurtz, D. D., Domack, E. W., and Balshaw, K. M. (1980). Glacial and glacial marine sediments of the Antarctic continental shelf. J. Geol. 88, 399–414. doi: 10.1086/628524

CrossRef Full Text | Google Scholar

Armitage, J. J., Burgess, P. M., Hampson, G. J., and Allen, P. A. (2018a). Deciphering the origin of cyclical gravel front and shoreline progradation and retrogradation in the stratigraphic record. Basin Res. 30, 15–35.

Google Scholar

Armitage, J. J., Duller, R. A., Whittaker, A. C., and Allen, P. A. (2011). Transformation of tectonic and climatic signals from source to sedimentary archive. Nat. Geosci. 4, 231–235. doi: 10.1038/ngeo1087

CrossRef Full Text | Google Scholar

Armitage, J. J., Dunkley Jones, T., Duller, R. A., Whittaker, A. C., and Allen, P. A. (2013). Temporal buffering of climate-driven sediment flux cycles by transient catchment response. Earth Planet. Sci. Lett. 36, 200–210. doi: 10.1111/bre.12203

CrossRef Full Text | Google Scholar

Armitage, J. J., Whittaker, A. C., Zakari, M., and Campforts, B. (2018b). Numerical modelling of landscape and sediment flux response to precipitation rate change. Earth Surf. Dyn. 6, 77–99. doi: 10.1016/j.epsl.2013.03.020

CrossRef Full Text | Google Scholar

Attal, M., and Lavé, J. (2006). Changes of bedload characteristics along the Marsyandi River (central Nepal): implications for understanding hillslope sediment supply, sediment load evolution along fluvial networks, and denudation in active orogenic belts. Tectonics Clim. Landsc. Evol. 398, 143–171. doi: 10.5194/esurf-6-77-2018

CrossRef Full Text | Google Scholar

Attal, M., and Lavé, J. (2009). Pebble abrasion during fluvial transport: experimental results and implications for the evolution of the sediment load along rivers. J. Geophys. Res. Earth Surf. 114. doi: 10.1130/2006.2398(09)

CrossRef Full Text | Google Scholar

Auchter, N. C., Romans, B. W., Hubbard, S. M., Daniels, B. G., Scher, H. D., and Buckley, W. (2020). Intrabasinal sediment recycling from detrital strontium isotope stratigraphy. Geology 48, 992–996. doi: 10.1130/g47594.1

CrossRef Full Text | Google Scholar

Azpiroz-Zabala, M., Cartigny, M. J. B., Talling, P. J., Parsons, D. R., Sumner, E. J., Clare, M. A., et al. (2017). Newly recognized turbidity current structure can explain prolonged flushing of submarine canyons. Sci. Adv. 3:e1700200. doi: 10.1126/sciadv.1700200

PubMed Abstract | CrossRef Full Text | Google Scholar

Baby, G., Guillocheau, F., Braun, J., Robin, C., and Dall’Asta, M. (2020). Solid sedimentation rates history of the Southern African continental margins: implications for the uplift history of the South African Plateau. Terra Nova 32, 53–65. doi: 10.1111/ter.12435

CrossRef Full Text | Google Scholar

Balco, G., and Stone, J. O. H. (2005). Measuring middle Pleistocene erosion rates with cosmic-ray-produced nuclides in buried alluvial sediment, Fisher valley, southeastern Utah. Earth Surf. Process. Landf. 30, 1051–1067. doi: 10.1002/esp.1262

CrossRef Full Text | Google Scholar

Bataille, C. P., Ridgway, K. D., Colliver, L., and Liu, X.-M. (2019). Early Paleogene fluvial regime shift in response to global warming: a subtropical record from the Tornillo Basin, west Texas. USA. GSA Bull. 131, 299–317. doi: 10.1130/b31872.1

CrossRef Full Text | Google Scholar

Baynes, E. R. C., Lague, D., Attal, M., Gangloff, A., Kirstein, L. A., and Dugmore, A. J. (2018). River self-organisation inhibits discharge control on waterfall migration. Sci. Rep. 8:2444. doi: 10.1038/s41598-018-20767-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Begin, Z. B., Meyer, D. F., and Schumm, S. A. (1981). Development of longitudinal profiles of alluvial channels in response to base-level lowering. Earth Surf. Process. Landf. 6, 49–68. doi: 10.1002/esp.3290060106

CrossRef Full Text | Google Scholar

Bernhardt, A., Hebbeln, D., Regenberg, M., Lückge, A., and Strecker, M. R. (2016). Shelfal sediment transport by an undercurrent forces turbidity-current activity during high sea level along the Chile continental margin. Geology 44, 295–298. doi: 10.1130/g37594.1

CrossRef Full Text | Google Scholar

Bernhardt, A., Melnick, D., Jara-Muñoz, J., Argandoña, B., González, J., and Strecker, M. R. (2015). Controls on submarine canyon activity during sea-level highstands: the Biobío canyon system offshore Chile. Geosphere 11, 1226–1255. doi: 10.1130/ges01063.1

CrossRef Full Text | Google Scholar

Bernhardt, A., Schwanghart, W., Hebbeln, D., Stuut, J.-B. W., and Strecker, M. R. (2017). Immediate propagation of deglacial environmental change to deep-marine turbidite systems along the Chile convergent margin. Earth Planet. Sci. Lett. 473, 190–204. doi: 10.1016/j.epsl.2017.05.017

CrossRef Full Text | Google Scholar

Blom, A., Chavarrías, V., Ferguson, R. I., and Viparelli, E. (2017). Advance, retreat, and halt of abrupt gravel-sand transitions in alluvial rivers. Geophys. Res. Lett. 44, 9751–9760. doi: 10.1002/2017gl074231

CrossRef Full Text | Google Scholar

Blöthe, J. H., and Korup, O. (2013). Millennial lag times in the Himalayan sediment routing system. Earth Planet. Sci. Lett. 382, 38–46. doi: 10.1016/j.epsl.2013.08.044

CrossRef Full Text | Google Scholar

Blum, M. D. (2007). “Large river systems and climate change,” in Large Rivers Geomorphology Manage, ed. A. Gupta, Hoboken, NJ: John Wiley & Sons.

Google Scholar

Blum, M. D., and Törnqvist, T. E. (2000). Fluvial responses to climate and sea-level change: a review and look forward. Sedimentology 47, 2–48. doi: 10.1046/j.1365-3091.2000.00008.x

CrossRef Full Text | Google Scholar

Blum, M., Martin, J., Milliken, K., and Garvin, M. (2013). Paleovalley systems: insights from Quaternary analogs and experiments. Earth Sci. Rev. 116, 128–169. doi: 10.1016/j.earscirev.2012.09.003

CrossRef Full Text | Google Scholar

Blum, M., Rogers, K., Gleason, J., Najman, Y., Cruz, J., and Fox, L. (2018). Allogenic and autogenic signals in the stratigraphic record of the deep-sea Bengal Fan. Sci. Rep. 8:7973.

Google Scholar

Bonneau, L., Jorry, S. J., Toucanne, S., Silva Jacinto, R., and Emmanuel, L. (2014). Millennial-scale response of a western Mediterranean river to late Quaternary climate changes: a view from the deep sea. J. Geol. 122, 687–703. doi: 10.1086/677844

CrossRef Full Text | Google Scholar

Bonnet, S., and Crave, A. (2003). Landscape response to climate change: insights from experimental modeling and implications for tectonic versus climatic uplift of topography. Geology 31, 123–126. doi: 10.1130/0091-7613(2003)031<0123:lrtcci>2.0.co;2

CrossRef Full Text | Google Scholar

Bouchez, J., Beyssac, O., Galy, V., Gaillardet, J., France-Lanord, C., Maurice, L., et al. (2010). Oxidation of petrogenic organic carbon in the Amazon floodplain as a source of atmospheric CO2. Geology 38, 255–258. doi: 10.1130/g30608.1

CrossRef Full Text | Google Scholar

Bracken, L. J., Turnbull, L., Wainwright, J., and Bogaart, P. (2015). Sediment connectivity: a framework for understanding sediment transfer at multiple scales. Earth Surf. Process. Landf. 40, 177–188. doi: 10.1002/esp.3635

CrossRef Full Text | Google Scholar

Bradley, D. N., and Tucker, G. E. (2013). The storage time, age, and erosion hazard of laterally accreted sediment on the floodplain of a simulated meandering river. J. Geophys. Res. Earth Surf. 118, 1308–1319. doi: 10.1002/jgrf.20083

CrossRef Full Text | Google Scholar

Bradley, N. D., and Tucker, G. E. (2012). Measuring gravel transport and dispersion in a mountain river using passive radio tracers. Earth Surf. Process. Landf. 37, 1034–1045. doi: 10.1002/esp.3223

CrossRef Full Text | Google Scholar

Bradley, W. C. (1970). Effect of weathering on abrasion of granitic gravel, Colorado river (Texas). Geol. Soc. Am. Bull. 81, 61–80. doi: 10.1130/0016-7606(1970)81[61:eowoao]2.0.co;2

CrossRef Full Text | Google Scholar

Braun, J., Voisin, C., Gourlan, A. T., and Chauvel, C. (2015). Erosional response of an actively uplifting mountain belt to cyclic rainfall variations. Earth Surf. Dyn. 3, 1–14. doi: 10.5194/esurf-3-1-2015

CrossRef Full Text | Google Scholar

Brocheray, S., Cremer, M., Zaragosi, S., Schmidt, S., Eynaud, F., Rossignol, L., et al. (2014). 2000 years of frequent turbidite activity in the Capbreton Canyon (Bay of Biscay). Mar. Geol. 347, 136–152. doi: 10.1016/j.margeo.2013.11.009

CrossRef Full Text | Google Scholar

Bufe, A., Turowski, J. M., Burbank, D. W., Paola, C., Wickert, A. D., and Tofelde, S. (2019). Controls on the lateral channel-migration rate of braided channel systems in coarse non-cohesive sediment. Earth Surf. Process. Landf. 44, 2823–2836. doi: 10.1002/esp.4710

CrossRef Full Text | Google Scholar

Buffington, J. M., and Montgomery, D. R. (1997). A systematic analysis of eight decades of incipient motion studies, with special reference to gravel-bedded rivers. Water Resour. Res. 33, 1993–2029. doi: 10.1029/96wr03190

CrossRef Full Text | Google Scholar

Bull, W. B. (1991). Geomorphic Responses to Climatic Change. Oxford: Oxford University Press.

Google Scholar

Burgess, P. M., and Hovius, N. (1998). Rates of delta progradation during highstands: consequences for timing of deposition in deep-marine systems. J. Geol. Soc. London 155, 217–222. doi: 10.1144/gsjgs.155.2.0217

CrossRef Full Text | Google Scholar

Caracciolo, L. (2020). Sediment generation and sediment routing systems from a quantitative provenance analysis perspective: review, application and future development. Earth Sci. Rev. 209:103226. doi: 10.1016/j.earscirev.2020.103226

CrossRef Full Text | Google Scholar

Carretier, S., and Regard, V. (2011). Is it possible to quantify pebble abrasion and velocity in rivers using terrestrial cosmogenic nuclides? J. Geophys. Res. Earth Surf. 116:F04003. doi: 10.1029/2011JF001968

CrossRef Full Text | Google Scholar

Carretier, S., Guerit, L., Harries, R., Regard, V., Maffre, P., and Bonnet, S. (2020). The distribution of sediment residence times at the foot of mountains and its implications for proxies recorded in sedimentary basins. Earth Planet. Sci. Lett. 546:116448. doi: 10.1016/j.epsl.2020.116448

CrossRef Full Text | Google Scholar

Carretier, S., Martinod, P., Reich, M., and Godderis, Y. (2016). Modelling sediment clasts transport during landscape evolution. Earth Surf. Dyn. 4, 237–251. doi: 10.5194/esurf-4-237-2016

CrossRef Full Text | Google Scholar

Carretier, S., Regard, V., Leanni, L., and Farías, M. (2019). Long-term dispersion of river gravel in a canyon in the Atacama desert, Central Andes, deduced from their 10Be concentrations. Sci. Rep. 9:17763. doi: 10.1038/s41598-019-53806-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Carretier, S., Regard, V., Vassallo, R., Aguilar, G., Martinod, J., Riquelme, R., et al. (2015). Differences in ¹⁰Be concentrations between river sand, gravel and pebbles along the western side of the Central Andes. Quat. Geochronol. 27, 33–51. doi: 10.1016/j.quageo.2014.12.002

CrossRef Full Text | Google Scholar

Carvajal, C. R., and Steel, R. J. (2006). Thick turbidite successions from supply-dominated shelves during sea-level highstand. Geology 34, 665–668. doi: 10.1130/g22505.1

CrossRef Full Text | Google Scholar

Castelltort, S., and Van Den Driessche, J. (2003). How plausible are high-frequency sediment supply-driven cycles in the stratigraphic record? Sediment. Geol. 157, 3–13. doi: 10.1016/s0037-0738(03)00066-6

CrossRef Full Text | Google Scholar

Chabaux, F., Blaes, E., Granet, M., di Chiara, Roupert, R., and Stille, P. (2012). Determination of transfer time for sediments in alluvial plains using ²³⁸U-²³⁴U-²³⁰Th disequilibria: the case of the Ganges river system. Comptes Rendus Geosci. 344, 688–703. doi: 10.1016/j.crte.2012.10.013

CrossRef Full Text | Google Scholar

Chabaux, F., Granet, M., Pelt, E., France-Lanord, C., and Galy, V. (2006). ²³⁸U–²³⁴U–²³⁰Th disequilibria and timescale of sedimentary transfers in rivers: clues from the Gangetic plain rivers. J. Geochem. Explor. 88, 373–375. doi: 10.1016/j.gexplo.2005.08.078

CrossRef Full Text | Google Scholar

Charreau, J., Blard, P. H., Puchol, N., Avouac, J. P., Lallier-Vergès, E., Bourlès, D., et al. (2011). Paleo-erosion rates in Central Asia since 9 Ma: a transient increase at the onset of Quaternary glaciations? earth planet. Sci. Lett. 304, 85–92. doi: 10.1016/j.epsl.2011.01.018

CrossRef Full Text | Google Scholar

Chen, C., Guerit, L., Foreman, B. Z., Hassenruck-Gudipati, H. J., Adatte, T., Honegger, L., et al. (2018). Estimating regional flood discharge during Palaeocene-Eocene global warming. Sci. Rep. 8:13391.

Google Scholar

Clare, M. A., Talling, P. J., and Hunt, J. E. (2015). Implications of reduced turbidity current and landslide activity for the Initial Eocene Thermal Maximum–evidence from two distal, deep-water sites. Earth Planet. Sci. Lett. 420, 102–115. doi: 10.1016/j.epsl.2015.03.022

CrossRef Full Text | Google Scholar

Clift, P. D., and Giosan, L. (2014). Sediment fluxes and buffering in the post-glacial Indus Basin. Basin Res. 26, 369–386. doi: 10.1111/bre.12038

CrossRef Full Text | Google Scholar

Clift, P. D., Giosan, L., Blusztajn, J., Campbell, I. H., Allen, C., Pringle, M., et al. (2008). Holocene erosion of the lesser Himalaya triggered by intensified summer monsoon. Geology 36, 79–82. doi: 10.1130/g24315a.1

CrossRef Full Text | Google Scholar

Clubb, F. J., Mudd, S. M., Hurst, M. D., and Grieve, S. W. D. (2020). Differences in channel and hillslope geometry record a migrating uplift wave at the Mendocino triple junction, California, USA. Geology 48, 184–188. doi: 10.1130/G46939.1

CrossRef Full Text | Google Scholar

Cook, K. L., Andermann, C., Gimbert, F., Adhikari, B. R., and Hovius, N. (2018). Glacial lake outburst floods as drivers of fluvial erosion in the Himalaya. Science 362, 53–57. doi: 10.1126/science.aat4981

PubMed Abstract | CrossRef Full Text | Google Scholar

Cosgrove, G. I. E., Hodgson, D., Mountney, N. P., and McCaffrey, W. D. (2019). Grain Character Data (Grain Size, Sorting, and Shape) From Quasi-Coeval Topset, Foreset and Bottomset Deposits of Miocene Clinothems. Berlin: Springer.

Google Scholar

Cosgrove, G. I. E., Poyatos-Moré, M., Lee, D. R., Hodgson, D. M., McCaffrey, W. D., and Mountney, N. P. (2020). Intra-clinothem variability in sedimentary texture and process regime recorded down slope profiles. Sedimentology 67, 431–456. doi: 10.1111/sed.12648

CrossRef Full Text | Google Scholar

Cossu, R., and Wells, M. G. (2012). A comparison of the shear stress distribution in the bottom boundary layer of experimental density and turbidity currents. Eur. J. Mech. 32, 70–79. doi: 10.1016/j.euromechflu.2011.09.006

CrossRef Full Text | Google Scholar

Coulthard, T. J., and Van De Wiel, M. J. (2013). Climate, tectonics or morphology: what signals can we see in drainage basin sediment yields? Earth Surf. Dyn. 1, 13–27. doi: 10.5194/esurf-1-13-2013

CrossRef Full Text | Google Scholar

Courtene-Jones, W., Quinn, B., Gary, S. F., Mogg, A. O. M., and Narayanaswamy, B. E. (2017). Microplastic pollution identified in deep-sea water and ingested by benthic invertebrates in the Rockall Trough, North Atlantic Ocean. Environ. Pollut. 231, 271–280. doi: 10.1016/j.envpol.2017.08.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Covault, J. A., and Graham, S. A. (2010). Submarine fans at all sea-level stands: tectono-morphologic and climatic controls on terrigenous sediment delivery to the deep sea. Geology 38, 939–942. doi: 10.1130/g31081.1

CrossRef Full Text | Google Scholar

Covault, J. A., Romans, B. W., Fildani, A., Mcgann, M., and Graham, S. A. (2010). Rapid climatic signal propagation from source to sink in a Southern California sediment-routing system. J. Geol. 118, 247–259. doi: 10.1086/651539

CrossRef Full Text | Google Scholar

Curran, J. C., and Wilcock, P. R. (2005). Effect of sand supply on transport rates in a gravel-bed channel. J. Hydraul. Eng. 131, 961–967. doi: 10.1061/(asce)0733-9429(2005)131:11(961)

CrossRef Full Text | Google Scholar

D’Arcy, M., Roda Boluda, D. C., Whittaker, A. C., and Carpineti, A. (2015). Dating alluvial fan surfaces in Owens Valley, California, using weathering fractures in boulders. Earth Surf. Process. Landf. 40, 487–501. doi: 10.1002/esp.3649

CrossRef Full Text | Google Scholar

D’Arcy, M., Roda-Boluda, D. C., and Whittaker, A. C. (2017). Glacial-interglacial climate changes recorded by debris flow fan deposits, Owens Valley, California. Quat. Sci. Rev. 169, 288–311. doi: 10.1016/j.quascirev.2017.06.002

CrossRef Full Text | Google Scholar

D’Arcy, M., Whittaker, A. C., and Roda-Boluda, D. C. (2016). Measuring alluvial fan sensitivity to past climate changes using a self-similarity approach to grain-size fining, Death Valley, California. Sedimentology 2, 388–424. doi: 10.1111/sed.12308

CrossRef Full Text | Google Scholar

D’Orsay, A. M., and Van De Poll, H. W. (1985). Quartz-grain surface textures: evidence for middle carboniferous glacial sediment input to the parrsboro formation of Nova Scotia. Geology 13, 285–287. doi: 10.1130/0091-7613(1985)13<285:qstefm>2.0.co;2

CrossRef Full Text | Google Scholar

Da Silva, A. C., De Vleeschouwer, D., Boulvain, F., Claeys, P., Fagel, N., Humblet, M., et al. (2013). Magnetic susceptibility as a high-resolution correlation tool and as a climatic proxy in Paleozoic rocks – merits and pitfalls: examples from the Devonian in Belgium. Mar. Pet. Geol. 46, 173–189. doi: 10.1016/j.marpetgeo.2013.06.012

CrossRef Full Text | Google Scholar

Davy, P., and Crave, A. (2000). Upscaling local-scale transport processes in large-scale relief dynamics. Phys. Chem. Earth A Solid Earth Geod. 25, 533–541. doi: 10.1016/s1464-1895(00)00082-x

CrossRef Full Text | Google Scholar

Davy, P., and Lague, D. (2009). Fluvial erosion/transport equation of landscape evolution models revisited. J. Geophys. Res. Earth Surf. 114:F03007. doi: 10.1029/2008JF001146

CrossRef Full Text | Google Scholar

De Vente, J., Poesen, J., Arabkhedri, M., and Verstraeten, G. (2007). The sediment delivery problem revisited. Prog. Phys. Geogr. 31, 155–178. doi: 10.1177/0309133307076485

CrossRef Full Text | Google Scholar

Dennielou, B., Huchon, A., Beaudouin, C., and Berné, S. (2006). Vertical grain-size variability within a turbidite levee: Autocyclicity or allocyclicity? A case study from the Rhǒne neofan, Gulf of lions, western Mediterranean. Mar. Geol. 234, 191–213. doi: 10.1016/j.margeo.2006.09.019

CrossRef Full Text | Google Scholar

Densmore, A. L., Allen, P. A., and Simpson, G. (2007a). Development and response of a coupled catchment fan system under changing tectonic and climatic forcing. J. Geophys. Res. Earth Surf. 112, 1–16. doi: 10.1029/2006JF000474

CrossRef Full Text | Google Scholar

Densmore, A. L., Gupta, S., Allen, P. A., and Dawers, N. H. (2007b). Transient landscapes at fault tips. J. Geophys. Res. Earth Surf. 112, 1–16. doi: 10.5876/9781607323693.c001

CrossRef Full Text | Google Scholar

DePaolo, D. J., Maher, K., Christensen, J. N., and McManus, J. (2006). Sediment transport time measured with U-series isotopes: results from ODP North Atlantic drift site 984. Earth Planet. Sci. Lett. 248, 394–410. doi: 10.1016/j.epsl.2006.06.004

CrossRef Full Text | Google Scholar

DiBiase, R. A., and Lamb, M. P. (2013). Vegetation and wildfire controls on sediment yield in bedrock landscapes. Geophys. Res. Lett. 40, 1093–1097. doi: 10.1002/grl.50277

CrossRef Full Text | Google Scholar

Diefendorf, A. F., and Freimuth, E. J. (2017). Extracting the most from terrestrial plant-derived n-alkyl lipids and their carbon isotopes from the sedimentary record: a review. Org. Geochem. 103, 1–21. doi: 10.1016/j.orggeochem.2016.10.016

CrossRef Full Text | Google Scholar

Dietrich, W. E. (1982). Settling velocity of natural particles. Water Resour. Res. 18, 1615–1626. doi: 10.1029/wr018i006p01615

CrossRef Full Text | Google Scholar

Dietze, E., Maussion, F., Ahlborn, M., Diekmann, B., Hartmann, K., Henkel, K., et al. (2014). Sediment transport processes across the Tibetan Plateau inferred from robust grain-size end members in lake sediments. Clim. Past 10, 91–106. doi: 10.5194/cp-10-91-2014

CrossRef Full Text | Google Scholar

Dingle, E. H., Attal, M., and Sinclair, H. D. (2017). Abrasion-set limits on Himalayan gravel flux. Nature 544, 471–474. doi: 10.1038/nature22039

PubMed Abstract | CrossRef Full Text | Google Scholar

Dingle, E. H., Sinclair, H. D., Venditti, J. G., Attal, M., Kinnaird, T. C., Creed, M., et al. (2020). Sediment dynamics across gravel-sand transitions: implications for river stability and floodplain recycling. Geology 48, 468–472. doi: 10.1130/g46909.1

CrossRef Full Text | Google Scholar

Dixon, J. F., Stee, R. J., and Olariu, C. (2012). Shelf-edge delta regime as a predictor of deep-water deposition. J. Sediment. Res. 82, 681–687. doi: 10.2110/jsr.2012.59

PubMed Abstract | CrossRef Full Text | Google Scholar

Dommain, R., Andama, M., McDonough, M. M., Prado, N. A., Goldhammer, T., Potts, R., et al. (2020). The challenges of reconstructing tropical biodiversity with sedimentary ancient DNA: a 2200-year-long metagenomic record from Bwindi impenetrable forest. Uganda. Front. Ecol. Evol. 8:218. doi: 10.3389/fevo.2020.00218

CrossRef Full Text | Google Scholar

Domokos, G., Sipos, A., Szabó, T., and Várkonyi, P. (2010). Pebbles, shapes, and Equilibria. Math. Geosci. 42, 29–47. doi: 10.1007/s11004-009-9250-4

CrossRef Full Text | Google Scholar

Dosseto, A., Bourdon, B., Gaillardet, J., Maurice-Bourgoin, L., and Allegre, C. J. (2006). Weathering and transport of sediments in the Bolivian Andes: time constraints from uranium-series isotopes. Earth Planet. Sci. Lett. 248, 759–771. doi: 10.1016/j.epsl.2006.06.027

CrossRef Full Text | Google Scholar

Du, J. Z., Zhang, J., and Baskaran, M. (2012). “Applications of short-lived radionuclides (⁷Be, ²¹⁰Pb, ²¹⁰Po, ¹³⁷Cs and ²³⁴Th) to trace the sources, transport pathways and deposition of particles/sediments in rivers, estuaries and coasts,” in Handbook of Environmental Isotope Geochemistry, ed. M. Baskaran (Berlin: Springer), 305–329. doi: 10.1007/978-3-642-10637-8_16

CrossRef Full Text | Google Scholar

Dubille, M., and Lavé, J. (2015). Rapid grain size coarsening at sandstone/conglomerate transition: similar expression in Himalayan modern rivers and Pliocene molasse deposits. Basin Res. 27, 26–42. doi: 10.1111/bre.12071

CrossRef Full Text | Google Scholar

Ducassou, E., Mulder, T., Migeon, S., Gonthier, E., Murat, A., Revel, M., et al. (2008). Nile floods recorded in deep Mediterranean sediments. Quat. Res. 70, 382–391. doi: 10.1016/j.yqres.2008.02.011

CrossRef Full Text | Google Scholar

Duller, R. A., Armitage, J. J., Manners, H. R., Grimes, S. T., Jones, T. D., and Dunkley Jones, T. (2019). Delayed sedimentary response to abrupt climate change at the Paleocene-Eocene boundary, northern Spain. Geology 47, 159–162. doi: 10.1130/g45631.1

CrossRef Full Text | Google Scholar

Duller, R. A., Whittaker, A. C., Fedele, J. J., Whitchurch, A. L., Springett, J., Smithells, R., et al. (2010). From grain size to tectonics. J. Geophys. Res. Earth Surf. 115, 1–19.

Google Scholar

Einsele, G., Ratschbacher, L., and Wetzel, A. (1996). The Himalaya-Bengal Fan denudation-accumulation system during the past 20 Ma. J. Geol. 104, 163–184. doi: 10.1086/629812

CrossRef Full Text | Google Scholar

Einstein, A. (1926). The cause of the formation of meanders in the courses of rivers and of the so-called Baer’s law. Naturwissenschaften 14, 223–224.

Google Scholar

Fildani, A., Hessler, A. M., Mason, C. C., McKay, M. P., and Stockli, D. F. (2018). Late Pleistocene glacial transitions in North America altered major river drainages, as revealed by deep-sea sediment. Sci. Rep. 8:13839.

Google Scholar

Fildani, A., Normark, W. R., Kostic, S., and Parker, G. (2006). Channel formation by flow stripping: large-scale scour features along the Monterey East channel and their relation to sediment waves. Sedimentology 53, 1265–1287. doi: 10.1111/j.1365-3091.2006.00812.x

CrossRef Full Text | Google Scholar

Fisk, H. (1944). Geological Investigation of the Alluvial Valley of the Lower Mississippi River. Vicksburg: Mississippi River Commission.

Google Scholar

Foreman, B. Z. (2014). Climate-driven generation of a fluvial sheet sand body at the Paleocene-Eocene boundary in north-west Wyoming (USA). Basin Res. 26, 225–241. doi: 10.1111/bre.12027

CrossRef Full Text | Google Scholar

Foreman, B. Z., Heller, P. L., and Clementz, M. T. (2012). Fluvial response to abrupt global warming at the Palaeocene/Eocene boundary. Nature 491, 92–95. doi: 10.1038/nature11513

PubMed Abstract | CrossRef Full Text | Google Scholar

Forzoni, A., Storms, J. E. A., Whittaker, A. C., and de Jager, G. (2014). Delayed delivery from the sediment factory: modeling the impact of catchment response time to tectonics on sediment flux and fluvio-deltaic stratigraphy. Earth Surf. Process. Landf. 39, 689–704. doi: 10.1002/esp.3538

CrossRef Full Text | Google Scholar

Fryirs, K. (2013). (Dis) Connectivity in catchment sediment cascades: a fresh look at the sediment delivery problem. Earth Surf. Process. Landf. 38, 30–46. doi: 10.1002/esp.3242

CrossRef Full Text | Google Scholar

Fülöp, R. H., Codilean, A. T., Wilcken, K. M., Cohen, T. J., Fink, D., Smith, A. M., et al. (2020). Million-year lag times in a post-orogenic sediment conveyor. Sci. Adv. 6:eaaz8845. doi: 10.1126/sciadv.aaz8845

PubMed Abstract | CrossRef Full Text | Google Scholar

Galy, V., and Eglinton, T. (2011). Protracted storage of biospheric carbon in the Ganges-Brahmaputra basin. Nat. Geosci. 4, 843–847. doi: 10.1038/ngeo1293

CrossRef Full Text | Google Scholar

Galy, V., France-Lanord, C., and Lartiges, B. (2008). Loading and fate of particulate organic carbon from the Himalaya to the Ganga-Brahmaputra delta. Geochim. Cosmochim. Acta 72, 1767–1787. doi: 10.1016/j.gca.2008.01.027

CrossRef Full Text | Google Scholar

Garcin, Y., Schildgen, T. F., Torres Acosta, V., Melnick, D., Guillemoteau, J., Willenbring, J., et al. (2017). Short-lived increase in erosion during the African Humid period: evidence from the northern kenya rift. Earth Planet. Sci. Lett. 459, 58–69. doi: 10.1016/j.epsl.2016.11.017

CrossRef Full Text | Google Scholar

Garcin, Y., Schwab, V. F., Gleixner, G., Kahmen, A., Todou, G., Séné, O., et al. (2012). Hydrogen isotope ratios of lacustrine sedimentary n-alkanes as proxies of tropical African hydrology: insights from a calibration transect across Cameroon. Geochim. Cosmochim. Acta 79, 106–126. doi: 10.1016/j.gca.2011.11.039

CrossRef Full Text | Google Scholar

Gardner, T. W. (1983). Experimental study of knickpoint and longitudinal profile evolution in cohesive, homogeneous material. Geol. Soc. Am. Bull. 94, 664–672. doi: 10.1130/0016-7606(1983)94<664:esokal>2.0.co;2

CrossRef Full Text | Google Scholar

Godard, V., Tucker, G. E., Burch Fisher, G., Burbank, D. W., and Bookhagen, B. (2013). Frequency-dependent landscape response to climatic forcing. Geophys. Res. Lett. 40, 859–863. doi: 10.1002/grl.50253

CrossRef Full Text | Google Scholar

Golly, A., Turowski, J. M., Badoux, A., and Hovius, N. (2017). Controls and feedbacks in the coupling of mountain channels and hillslopes. Geology 45, 307–310. doi: 10.1130/g38831.1

CrossRef Full Text | Google Scholar

Goodbred, S. L. (2003). Response of the Ganges dispersal system to climate change: a source-to-sink view since the last interstade. Sediment. Geol. 162, 83–104. doi: 10.1016/s0037-0738(03)00217-3

CrossRef Full Text | Google Scholar

Goodbred, S., and Kuehl, S. A. (2000). Enormous Ganges-Brahmaputra sediment discharge during strengthened early Holocene monsoon. Geology 28, 1083–1086. doi: 10.1130/0091-7613(2000)028<1083:egbsdd>2.3.co;2

CrossRef Full Text | Google Scholar

Goren, L., Willett, S. D., Herman, F., and Braun, J. (2014). Coupled numerical–analytical approach to landscape evolution modeling. Earth Surf. Process. Landf. 39, 522–545. doi: 10.1002/esp.3514

CrossRef Full Text | Google Scholar

Gray, H. J., Tucker, G. E., Mahan, S. A., McGuire, C., and Rhodes, E. J. (2017). On extracting sediment transport information from measurements of luminescence in river sediment. J. Geophys. Res. Earth Surf. 122, 654–677. doi: 10.1002/2016jf003858

CrossRef Full Text | Google Scholar

Grimaud, J. L., Paola, C., and Voller, V. (2016). Experimental migration of knickpoints: influence of style of base-level fall and bed lithology. Earth Surf. Dyn. 4, 11–23. doi: 10.5194/esurf-4-11-2016

CrossRef Full Text | Google Scholar

Guerit, L., Barrier, L., Jolivet, M., Fu, B., and Métivier, F. (2016). Denudation intensity and control in the Chinese Tian Shan: new constraints from mass balance on catchment-alluvial fan systems. Earth Surf. Process. Landf. 41, 1088–1106. doi: 10.1002/esp.3890

CrossRef Full Text | Google Scholar

Gugliotta, M., Kurcinka, C. E., Dalrymple, R. W., Flint, S. S., and Hodgson, D. M. (2016). Decoupling seasonal fluctuations in fluvial discharge from the tidal signature in ancient deltaic deposits: an example from the Neuquén Basin, Argentina. J. Geol. Soc. London 173, 94–107. doi: 10.1144/jgs2015-030

CrossRef Full Text | Google Scholar

Guillocheau, F., Rouby, D., Robin, C., Helm, C., Rolland, N., Le Carlier, et al. (2012). Quantification and causes of the terrigeneous sediment budget at the scale of a continental margin: a new method applied to the Namibia–South Africa margin. Basin Res. 24, 3–30. doi: 10.1111/j.1365-2117.2011.00511.x

CrossRef Full Text | Google Scholar

Hack, J. T. (1957). Studies of Longitudinal Stream Profiles in Virginia and Maryland. Washington, DC: Government Printing Office.

Google Scholar

Hack, J. T. (1960). Interpretation of erosional topography in humid temperate regions. Am. J. Sci. 258, 80–97.

Google Scholar

Harries, R. M., Gailleton, B., Kirstein, L. A., Attal, M., Whittaker, A. C., and Mudd, S. M. (2021). Impact of climate on landscape form, sediment transfer, and the sedimentary record. Earth Surf. Process. Landf. 1–18. doi: 10.1002/esp.5075

CrossRef Full Text | Google Scholar

Haynes, H., and Pender, G. (2007). Stress history effects on graded bed stability. J. Hydraul. Eng. 133, 343–349. doi: 10.1061/(asce)0733-9429(2007)133:4(343)

CrossRef Full Text | Google Scholar

Heberer, B., Behrmann, J. H., and Rahn, M. K. (2011). Source-to-sink relationships along the South-Central chilean margin: evidence from detrital apatite fission-track analysis. Basin Res. 23, 551–570. doi: 10.1111/j.1365-2117.2011.00504.x

CrossRef Full Text | Google Scholar

Heckmann, T., and Vericat, D. (2018). Computing spatially distributed sediment delivery ratios: inferring functional sediment connectivity from repeat high-resolution digital elevation models. Earth Surf. Process. Landf. 43, 1547–1554. doi: 10.1002/esp.4334

CrossRef Full Text | Google Scholar

Heerema, C. J., Talling, P. J., Cartigny, M. J., Paull, C. K., Bailey, L., Simmons, S. M., et al. (2020). What determines the downstream evolution of turbidity currents? Earth Planet. Sci. Lett. 532:116023. doi: 10.1016/j.epsl.2019.116023

CrossRef Full Text | Google Scholar

Helland, P. E., Huang, P. H., and Diffendal, R. F. (1997). SEM analysis of quartz sand grain surface textures indicates alluvial/colluvial origin of the quaternary “glacial” boulder clays at Huangshan (Yellow Mountain), East-Central China. Quat. Res. 48, 177–186. doi: 10.1006/qres.1997.1916

CrossRef Full Text | Google Scholar

Hessler, A. M., and Fildani, A. (2019). Deep-sea fans: tapping into Earth’s changing landscapes. J. Sediment. Res. 89, 1171–1179. doi: 10.2110/jsr.2019.64

PubMed Abstract | CrossRef Full Text | Google Scholar

Hickin, E. J., and Nanson, G. C. (1984). Lateral migration rates of river bends. J. Hydraul. Eng. 110, 1557–1567. doi: 10.1061/(asce)0733-9429(1984)110:11(1557)

CrossRef Full Text | Google Scholar

Hilley, G. E., and Strecker, M. R. (2005). Processes of oscillatory basin filling and excavation in a tectonically active orogen: quebrada del Toro Basin, NW Argentina. Bull. Geol. Soc. Am. 117, 887–901. doi: 10.1130/b25602.1

CrossRef Full Text | Google Scholar

Hinderer, M. (2012). From gullies to mountain belts: a review of sediment budgets at various scales. Sediment. Geol. 280, 21–59. doi: 10.1016/j.sedgeo.2012.03.009

CrossRef Full Text | Google Scholar

Hinderer, M., and Einsele, G. (2001). The world’s large lake basins as denudation-accumulation systems and implications for their lifetimes. J. Paleolimnol. 26, 355–372.

Google Scholar

Hjulstrom, F. (1955). Transportation of detritus by moving water. Spec. Public. SEPM 4, 15–31.

Google Scholar

Hodgson, D. M., Browning, J. V., Miller, K. G., Hesselbo, S. P., Poyatos-Moré, M., Mountain, G. S., et al. (2018). Sedimentology, stratigraphic context, and implications of Miocene intrashelf bottomset deposits, offshore New Jersey. Geosphere 14, 95–114. doi: 10.1130/ges01530.1

CrossRef Full Text | Google Scholar

Hoffmann, B., Feakins, S. J., Bookhagen, B., Olen, S. M., Adhikari, D. P., Mainali, J., et al. (2016). Climatic and geomorphic drivers of plant organic matter transport in the Arun river, E Nepal. Earth Planet. Sci. Lett. 452, 104–114. doi: 10.1016/j.epsl.2016.07.008

CrossRef Full Text | Google Scholar

Hoffmann, T. (2015). Sediment residence time and connectivity in non-equilibrium and transient geomorphic systems. Earth Sci. Rev. 150, 609–627. doi: 10.1016/j.earscirev.2015.07.008

CrossRef Full Text | Google Scholar

Hooke, J. (2003). Coarse sediment connectivity in river channel systems: a conceptual framework and methodology. Geomorphology 56, 79–94. doi: 10.1016/s0169-555x(03)00047-3

CrossRef Full Text | Google Scholar

Houssais, M., and Lajeunesse, E. (2012). Bedload transport of a bimodal sediment bed. J. Geophys. Res. 117:F04015.

Google Scholar

Howard, A. D. (1994). A detachment-limited model of drainage basin evolution. Water Resour. Res. 30, 2261–2285. doi: 10.1029/94wr00757

CrossRef Full Text | Google Scholar

Howard, A. D. A. D. (1982). Equilibrium and time scales in geomorphology: application to sand-bed alluvial streams. Earth Surf. Process. Landf. 7, 303–325. doi: 10.1002/esp.3290070403

CrossRef Full Text | Google Scholar

Hülscher, J., Fischer, G., Grunert, P., Auer, G., and Bernhardt, A. (2019). Selective recording of tectonic forcings in an Oligocene/Miocene submarine channel system: insights from new age constraints and sediment volumes from the Austrian Northern Alpine Foreland Basin. Front. Earth Sci. 7:302.

Google Scholar

Huntington, E. (1907). Some characteristics of the glacial period in non-glaciated regions. Bull. Geol. Soc. Am. 18, 351–388. doi: 10.1130/gsab-18-351

CrossRef Full Text | Google Scholar

Hurst, M. D., Mudd, S. M., Walcott, R., Attal, M., and Yoo, K. (2012). Using hilltop curvature to derive the spatial distribution of erosion rates. J. Geophys. Res. Earth Surf. 117:F002057.

Google Scholar

Jerolmack, D. J., and Mohrig, D. (2007). Conditions for branching in depositional rivers. Geology 35, 463–466. doi: 10.1130/g23308a.1

CrossRef Full Text | Google Scholar

Jerolmack, D. J., and Paola, C. (2010). Shredding of environmental signals by sediment transport. Geophys. Res. Lett. 37:L19401.

Google Scholar

Jobe, Z. R., Howes, N., Straub, K. M., Cai, D., Deng, H., Laugier, F., et al. (2020). Comparing aggradation, superelevation, and avulsion frequency of submarine and fluvial channels. Front. Earth Sci. 8:53. doi: 10.3389/feart.2020.00053

CrossRef Full Text | Google Scholar

Jobe, Z. R., Sylvester, Z., Parker, A. O., Howes, N., Slowey, N., and Pirmez, C. (2015). Rapid adjustment of submarine channel architecture to changes in sediment supply. J. Sediment. Res. 85, 729–753. doi: 10.2110/jsr.2015.30

PubMed Abstract | CrossRef Full Text | Google Scholar

Jolivet, M., Barrier, L., Dominguez, S., Guerit, L., Heilbronn, G., and Fu, B. (2014). Unbalanced sediment budgets in the catchment–alluvial fan system of the Kuitun River (northern Tian Shan, China): implications for mass-balance estimates, denudation and sedimentation rates in orogenic systems. Geomorphology 214, 168–182. doi: 10.1016/j.geomorph.2014.01.024

CrossRef Full Text | Google Scholar

Jonell, T. N., Clift, P. D., Hoang, L. V., Hoang, T., Carter, A., Wittmann, H., et al. (2017). Controls on erosion patterns and sediment transport in a monsoonal, tectonically quiescent drainage, Song Gianh, central Vietnam. Basin Res. 29, 659–683. doi: 10.1111/bre.12199

CrossRef Full Text | Google Scholar

Jonell, T. N., Li, Y., Blusztajn, J., Giosan, L., and Clift, P. D. (2018). Signal or noise? Isolating grain size effects on Nd and Sr isotope variability in Indus delta sediment provenance. Chem. Geol. 485, 56–73. doi: 10.1016/j.chemgeo.2018.03.036

CrossRef Full Text | Google Scholar

Jorry, S. J., Jégou, I., Emmanuel, L., Jacinto, R. S., and Savoye, B. (2011). Turbiditic levee deposition in response to climate changes: the Var Sedimentary Ridge (Ligurian Sea). Mar. Geol. 279, 148–161. doi: 10.1016/j.margeo.2010.10.021

CrossRef Full Text | Google Scholar

Kalińska, E., and Nartišs, M. (2014). Pleistocene and Holocene aeolian sediments of different location and geological history: a new insight from rounding and frosting of quartz grains. Quat. Int. 32, 311–322. doi: 10.1016/j.quaint.2013.08.038

CrossRef Full Text | Google Scholar

Kane, I. A., and Clare, M. A. (2019). Dispersion, accumulation, and the ultimate fate of microplastics in deep-marine environments: a review and future directions. Front. Earth Sci. 7:80.

Google Scholar

Kane, I. A., Clare, M. A., Miramontes, E., Wogelius, R., Rothwell, J. J., Garreau, P., et al. (2020). Seafloor microplastic hotspots controlled by deep-sea circulation. Science 368, 1140–1145. doi: 10.1126/science.aba5899

PubMed Abstract | CrossRef Full Text | Google Scholar

Kemp, D. B. (2012). Stochastic and deterministic controls on stratigraphic completeness and fidelity. Int. J. Earth Sci. 101, 2225–2238. doi: 10.1007/s00531-012-0784-1

CrossRef Full Text | Google Scholar

Kemter, M., Fischer, M., Luna, L. V., Schönfeldt, E., Vogel, J., Banerjee, A., et al. (2021). Cascading hazards in the aftermath of Australia’s 2019/2020 black summer wildfires. Earth’s Future 9:e2020EF001884.

Google Scholar

Kirby, E., and Whipple, K. X. (2012). Expression of active tectonics in erosional landscapes. J. Struct. Geol. 44, 54–75. doi: 10.1016/j.jsg.2012.07.009

CrossRef Full Text | Google Scholar

Kooi, H., and Beaumont, C. (1996). Large-scale geomorphology: classical concepts reconciled and integrated with contemporary ideas via a surface processes model. J. Geophys. Res. Solid Earth 101, 3361–3386. doi: 10.1029/95jb01861

CrossRef Full Text | Google Scholar

Kothyari, U. C., and Jain, R. K. (2008). Influence of cohesion on the incipient motion condition of sediment mixtures. Water Resour. Res. 44:WR006326.

Google Scholar

Kuenen, P. H. (1956). Experimental abrasion of pebbles: 2. rolling by current. J. Geol. 64, 336–368. doi: 10.1086/626370

CrossRef Full Text | Google Scholar

Kujau, A., Nürnberg, D., Zielhofer, C., Bahr, A., and Röhl, U. (2010). Mississippi River discharge over the last ~560,000 years - Indications from X-ray fluorescence core-scanning. Palaeogeogr. Palaeoclimatol. Palaeoecol. 298, 311–318. doi: 10.1016/j.palaeo.2010.10.005

CrossRef Full Text | Google Scholar

Lague, D., Crave, A., and Davy, P. (2003). Laboratory experiments simulating the geomorphic response to tectonic uplift. J. Geophys. Res. Solid Earth 108, ETG3-1–ETG3-20.

Google Scholar

Lamarre, H., MacVicar, B., and Roy, A. G. (2005). Using passive integrated transponder (PIT) tags to investigate sediment transport in gravel-bed rivers. J. Sediment. Res. 75, 736–741. doi: 10.2110/jsr.2005.059

PubMed Abstract | CrossRef Full Text | Google Scholar

Lamb, M. P., Dietrich, W. E., and Venditti, J. G. (2008). Is the critical Shields stress for incipient sediment motion dependent on channel-bed slope? J. Geophys. Res. 113, 1–20.

Google Scholar

Lane, E. W. (1955). Importance of fluvial morphology in hydraulic engineering. Proc. Am. Soc. Civil Eng. 81, 1–17.

Google Scholar

Lenard, S. J. P., Lavé, J., France-Lanord, C., Aumaître, G., Bourlès, D. L., and Keddadouche, K. (2020). Steady erosion rates in the Himalayas through late Cenozoic climatic changes. Nat. Geosci. 13, 448–452. doi: 10.1038/s41561-020-0585-2

CrossRef Full Text | Google Scholar

Leonard, M., Westra, S., Phatak, A., Lambert, M., van den Hurk, B., Mcinnes, K., et al. (2014). A compound event framework for understanding extreme impacts. Wiley Interdiscip. Rev. Clim. Chang. 5, 113–128. doi: 10.1002/wcc.252

CrossRef Full Text | Google Scholar

Lewis, W. V. (1944). Stream trough experiments and terrace formation. Geol. Mag. 81, 241–253. doi: 10.1017/s0016756800075877

CrossRef Full Text | Google Scholar

Li, C., Yang, S., Zhao, J., Dosseto, A., Bi, L., and Clark, T. R. (2016). The time scale of river sediment source-to-sink processes in East Asia. Chem. Geol. 446, 138–146. doi: 10.1016/j.chemgeo.2016.06.012

CrossRef Full Text | Google Scholar

Li, Q., Gasparini, N. M., and Straub, K. M. (2018). Some signals are not the same as they appear: how do erosional landscapes transform tectonic history into sediment flux records? Geology 46, 407–410. doi: 10.1130/g40026.1

CrossRef Full Text | Google Scholar

Li, Y., Clift, P. D., and O’Sullivan, P. (2019). Millennial and centennial variations in zircon U-Pb ages in the quaternary Indus submarine Canyon. Basin Res. 31, 155–170. doi: 10.1111/bre.12313

CrossRef Full Text | Google Scholar

Li, Y., Clift, P. D., Böning, P., Blusztajn, J., Murray, R. W., Ireland, T., et al. (2018). Continuous Holocene input of river sediment to the Indus Submarine Canyon. Mar. Geol. 406, 159–176. doi: 10.1016/j.margeo.2018.09.011

CrossRef Full Text | Google Scholar

Limaye, A. B. S., and Lamb, M. P. (2016). Numerical model predictions of autogenic fluvial terraces and comparison to climate change expectations. J. Geophys. Res. Earth Surf. 121, 512–544. doi: 10.1002/2014jf003392

CrossRef Full Text | Google Scholar

Ludmány, B., and Domokos, G. (2018). Identification of primary shape descriptors on 3D scanned particles. Period. Polytech. Electr. Eng. Comput. Sci. 62, 59–64. doi: 10.3311/ppee.12313

CrossRef Full Text | Google Scholar

Lynn, D. C. C., and Bonatti, E. (1965). Mobility of manganese in diagenesis of deep-sea sediments. Mar. Geol. 3, 457–474. doi: 10.1016/0025-3227(65)90046-0

CrossRef Full Text | Google Scholar

Mackin, J. H. (1948). Concept of the graded river. Bull. Geol. Soc. Am. 59, 463–512. doi: 10.1130/0016-7606(1948)59[463:cotgr]2.0.co;2

CrossRef Full Text | Google Scholar

Maier, K. L., Rosenberger, K. J., Paull, C. K., Gwiazda, R., Gales, J., Lorenson, T., et al. (2019). Sediment and organic carbon transport and deposition driven by internal tides along Monterey Canyon, offshore California. Deep Sea Res. Part I Oceanogr. Res. Pap. 153:103108. doi: 10.1016/j.dsr.2019.103108

CrossRef Full Text | Google Scholar

Malatesta, L. C., Prancevic, J. P., and Avouac, J. P. (2017). Autogenic entrenchment patterns and terraces due to coupling with lateral erosion in incising alluvial channels. J. Geophys. Res. Earth Surf. 122, 335–355. doi: 10.1002/2015jf003797

CrossRef Full Text | Google Scholar

Malatesta, L., Avouac, J.-P., Brown, N. D., Breitenbach, S. F. M., Pan, J., Chevalier, M.-L., et al. (2018). Lag and mixing during sediment transfer across the Tian Shan piedmont caused by climate- driven aggradation-incision cycles. Basin Res. 30, 613–635. doi: 10.1111/bre.12267

CrossRef Full Text | Google Scholar

Malmon, D. V., Dunne, T., and Reneau, S. L. (2003). Stochastic theory of particle trajectories through alluvial valley floors. J. Geol. 111, 525–542. doi: 10.1086/376764

CrossRef Full Text | Google Scholar

Malmon, D. V., Reneau, S. L., Dunne, T., Katzman, D., and Drakos, P. G. (2005). Influence of sediment storage on downstream delivery of contaminated sediment. Water Resour. Res. 41:W05008.

Google Scholar

Mandal, S. K., Lupker, M., Burg, J.-P., Valla, P. G., Haghipour, N., Christl, M., et al. (2015). Spatial variability of ¹⁰Be-derived erosion rates across the southern Peninsular Indian escarpment: a key to landscape evolution across passive margins. Earth Planet. Sci. Lett. 425, 154–167. doi: 10.1016/j.epsl.2015.05.050

CrossRef Full Text | Google Scholar

Manners, H. R., Grimes, S. T., Sutton, P. A., Domingo, L., Leng, M. J., Twitchett, R. J., et al. (2013). Magnitude and profile of organic carbon isotope records from the Paleocene-Eocene thermal maximum: evidence from northern Spain. Earth Planet. Sci. Lett. 376, 220–230. doi: 10.1016/j.epsl.2013.06.016

CrossRef Full Text | Google Scholar

Mariotti, A., Blard, P.-H., Charreau, J., Petit, C., Molliex, S., and Aster Team. (2019). Denudation systematics inferred from in situ cosmogenic ¹⁰Be concentrations in fine (50–100μm) and medium (100–250μm) sediments of the Var river basin, southern French Alps. Earth Surf. Dyn. 7, 1059–1074. doi: 10.5194/esurf-7-1059-2019

CrossRef Full Text | Google Scholar

Mason, C. C., and Romans, B. W. (2018). Climate-driven unsteady denudation and sediment flux in a high-relief unglaciated catchment–fan using ²⁶Al and ¹⁰Be: panamint Valley, California. Earth Planet. Sci. Lett. 492, 130–143. doi: 10.1016/j.epsl.2018.03.056

CrossRef Full Text | Google Scholar

Mason, C. C., Fildani, A., Gerber, T., Blum, M. D., Clark, J. D., and Dykstra, M. (2017). Climatic and anthropogenic influences on sediment mixing in the Mississippi source-to-sink system using detrital zircons: late Pleistocene to recent. Earth Planet. Sci. Lett. 466, 70–79. doi: 10.1016/j.epsl.2017.03.001

CrossRef Full Text | Google Scholar

Masteller, C. C., Finnegan, N. J., Turowski, J. M., Yager, E. M., and Rickenmann, D. (2019). History-dependent threshold for motion revealed by continuous bedload transport measurements in a steep mountain stream. Geophys. Res. Lett. 46, 2583–2591. doi: 10.1029/2018gl081325

CrossRef Full Text | Google Scholar

Matsuguma, Y., Takada, H., Kumata, H., Kanke, H., Sakurai, S., Suzuki, T., et al. (2017). Microplastics in sediment cores from Asia and Africa as indicators of temporal trends in plastic pollution. Arch. Environ. Contam. Toxicol. 73, 230–239. doi: 10.1007/s00244-017-0414-9

PubMed Abstract | CrossRef Full Text | Google Scholar

McCave, I. N., and Andrews, J. T. (2019). Distinguishing current effects in sediments delivered to the ocean by ice. I. principles, methods and examples. Quat. Sci. Rev. 212, 92–107. doi: 10.1016/j.quascirev.2019.03.031

CrossRef Full Text | Google Scholar

McCave, I. N., and Hall, I. R. (2006). Size sorting in marine muds: processes, pitfalls, and prospects for paleoflow-speed proxies. Geochem. Geophys. Geosyst. 7:Q10N05.

Google Scholar

McInerney, F. A., and Wing, S. L. (2011). The Paleocene-Eocene thermal maximum: a perturbation of carbon cycle, climate, and biosphere with implications for the future. Annu. Rev. Earth Planet. Sci. 39, 489–516. doi: 10.1146/annurev-earth-040610-133431

CrossRef Full Text | Google Scholar

Meade, R. H. (1982). Sources, sinks, and storage of river sediment in the Atlantic drainage of the United States. J. Geol. 90, 235–252. doi: 10.1086/628677

CrossRef Full Text | Google Scholar

Merritts, D. J., Vincent, K. R., and Wohl, E. E. (1994). Long river profiles, tectonism, and eustasy: a guide to interpreting fluvial terraces. J. Geophys. Res. 99, 14031–14050. doi: 10.1029/94jb00857

CrossRef Full Text | Google Scholar

Merritts, D., and Bull, W. B. (1989). Interpreting quaternary uplift rates at the Mendocino triple. Geology 17, 1020–1024. doi: 10.1130/0091-7613(1989)017<1020:iqurat>2.3.co;2

CrossRef Full Text | Google Scholar

Métivier, F., and Gaudemer, Y. (1999). Stability of output fluxes of large rivers in South and East Asia during the last 2 million years: implications on floodplain processes. Basin Res. 11, 293–303. doi: 10.1046/j.1365-2117.1999.00101.x

CrossRef Full Text | Google Scholar

Mey, J., Schwanghart, W., de Boer, A.-M., and Reimann, T. (2020). “Illuminating the speed of sand–quantifying sediment transport using optically stimulated luminescence,” in Proceedings of the EGU General Assembly Conference Abstracts, Munich.

Google Scholar

Meyer-Peter, E., and Müller, R. (1948). Formulas for Bed-Load Transport. IAHSR 2nd Meet. Stock. Append. 2. Bengaluru: IAHR.

Google Scholar

Miall, A. D. (2015). Updating uniformitarianism: stratigraphy as just a set of ‘frozen accidents’. Geol. Soc. London Spec. Publ. 404, 11–36. doi: 10.1144/sp404.4

CrossRef Full Text | Google Scholar

Miller, A. J., and Kuehl, S. A. (2010). Shelf sedimentation on a tectonically active margin: a modern sediment budget for Poverty continental shelf. New Zealand. Mar. Geol. 270, 175–187. doi: 10.1016/j.margeo.2009.10.018

CrossRef Full Text | Google Scholar

Montgomery, D. R. (2001). Slope distributions, threshold hillslopes, and steady-state topography. Am. J. Sci. 301, 432–454. doi: 10.2475/ajs.301.4-5.432

PubMed Abstract | CrossRef Full Text | Google Scholar

Moody, J. A., and Martin, D. A. (2001). Initial hydrologic and geomorphic response following a wildfire in the Colorado front range. Earth Surf. Process. Landf. 26, 1049–1070. doi: 10.1002/esp.253

CrossRef Full Text | Google Scholar

Moon, S., Merritts, D. J., Snyder, N. P., Bierman, P., Sanquini, A., Fosdick, J. C., et al. (2018). Erosion of coastal drainages in the mendocino triple junction region (MTJ), northern California. Earth Planet. Sci. Lett. 502, 156–165. doi: 10.1016/j.epsl.2018.09.006

CrossRef Full Text | Google Scholar

Moussirou, B., and Bonnet, S. (2018). Modulation of the erosion rate of an uplifting landscape by long-term climate change: an experimental investigation. Geomorphology 303, 456–466. doi: 10.1016/j.geomorph.2017.12.010

CrossRef Full Text | Google Scholar

Mudd, S. M. (2017). Detection of transience in eroding landscapes. Earth Surf. Process. Landf. 42, 24–41. doi: 10.1002/esp.3923

CrossRef Full Text | Google Scholar

Mulder, T., Migeon, S., Savoye, B., and Faugères, J.-C. (2001). Inversely graded turbidite sequences in the deep Mediterranean: a record of deposits from flood-generated turbidity currents? Geo Mar. Lett. 21, 86–93. doi: 10.1007/s003670100071

CrossRef Full Text | Google Scholar

Najafi, S., Dragovich, D., Heckmann, T., and Sadeghi, S. H. (2021). Sediment connectivity concepts and approaches. Catena 196:104880. doi: 10.1016/j.catena.2020.104880

CrossRef Full Text | Google Scholar

Nakamura, F., and Kikuchi, S. (1996). Some methodological developments in the analysis of sediment transport processes using age distribution of floodplain deposits. Geomorphology 16, 139–145. doi: 10.1016/0169-555x(95)00139-v

CrossRef Full Text | Google Scholar

Nie, J., Ruetenik, G., Gallagher, K., Hoke, G., Garzione, C. N., Wang, W., et al. (2018). Rapid incision of the Mekong river in the middle Miocene linked to monsoonal precipitation. Nat. Geosci. 11, 944–948. doi: 10.1038/s41561-018-0244-z

CrossRef Full Text | Google Scholar

Normark, W. R., Hess, G. R., Stow, D. A. V., and Bowen, A. J. (1980). Sediment waves on the monterey Fan levee: a preliminary physical interpretation. Mar. Geol. 37, 1–18. doi: 10.1016/0025-3227(80)90009-2

CrossRef Full Text | Google Scholar

O’Sullivan, G. J., Chew, D. M., Morton, A. C., Mark, C., and Henrichs, I. A. (2018). An integrated apatite geochronology and geochemistry tool for sedimentary provenance analysis. Geochem. Geophys. Geosyst. 19, 1309–1326. doi: 10.1002/2017gc007343

CrossRef Full Text | Google Scholar

Ogston, A. S., Cacchione, D. A., Sternberg, R. W., and Kineke, G. C. (2000). Observations of storm and river flood-driven sediment transport on the northern California continental shelf. Cont. Shelf Res. 20, 2141–2162. doi: 10.1016/s0278-4343(00)00065-0

CrossRef Full Text | Google Scholar

Paola, C., Heller, P., and Angevine, C. (1992). The large-scale dynamics of grain-size variation in alluvial basins, 1: theory. Basin Res. 4, 73–90. doi: 10.1111/j.1365-2117.1992.tb00145.x

CrossRef Full Text | Google Scholar

Parker, G., Klingeman, P. C., and McLean, D. G. (1982). Bedload and size distribution in paved gravel-bed streams. J. Hydraul. Div. 108, 544–571. doi: 10.1061/jyceaj.0005854

PubMed Abstract | CrossRef Full Text | Google Scholar

Parsons, A. J., Cooper, J., and Wainwright, J. (2015). What is suspended sediment? Earth Surf. Process. Landf. 40, 1417–1420. doi: 10.1002/esp.3730

CrossRef Full Text | Google Scholar

Parsons, A. J., Michael, N. A., Whittaker, A. C., Duller, R. A., and Allen, P. A. (2012). Grain-size trends reveal the late orogenic tectonic and erosional history of the south– central Pyrenees, Spain. J. Geol. Soc. 169, 111–114. doi: 10.1144/0016-76492011-087

CrossRef Full Text | Google Scholar

Parsons, A. J., Wainwright, J., Brazier, R., and Powell, M. (2006). Is sediment delivery a fallacy? Earth Surf. Process. Landf. 31, 1325–1328. doi: 10.1002/esp.1395

CrossRef Full Text | Google Scholar

Passchier, S., Ciarletta, D. J., Henao, V., and Sekkas, V. (2019). Sedimentary processes and facies on a high-latitude passive continental margin, Wilkes Land, East Antarctica. Geol. Soc. London Spec. Publ. 475, 181–201. doi: 10.1144/sp475.3

CrossRef Full Text | Google Scholar

Paull, C. K., Talling, P. J., Maier, K. L., Parsons, D., Xu, J., Caress, D. W., et al. (2018). Powerful turbidity currents driven by dense basal layers. Nat. Commun. 9:4114.

Google Scholar

Pelejero, C., Kienast, M., Wang, L., and Grimalt, J. O. (1999). The flooding of Sundaland during the last deglaciation: imprints in hemipelagic sediments from the southern South China Sea. Earth Planet. Sci. Lett. 171, 661–671. doi: 10.1016/s0012-821x(99)00178-8

CrossRef Full Text | Google Scholar

Pfeiffer, A. M., and Finnegan, N. J. (2018). Regional variation in gravel riverbed mobility, controlled by hydrologic regime and sediment supply. Geophys. Res. Lett. 45, 3097–3106. doi: 10.1002/2017gl076747

CrossRef Full Text | Google Scholar

Piper, D. J. W. (1970). Transport and deposition of Holocene sediment on La Jolla deep sea fan, California. Mar. Geol. 8, 211–227. doi: 10.1016/0025-3227(70)90044-7

CrossRef Full Text | Google Scholar

Piper, D. J. W., and Normark, W. R. (1983). Turbidite depositional patterns and flow characteristics, Navy submarine fan, California Borderland. Sedimentology 30, 681–694. doi: 10.1111/j.1365-3091.1983.tb00702.x

CrossRef Full Text | Google Scholar

Poisson, B., and Avouac, J. (2004). Holocene hydrological changes inferred from Alluvial stream entrenchment in North Tian Shan (Northwestern China). J. Geol. 112, 231–249. doi: 10.1086/381659

CrossRef Full Text | Google Scholar

Ponton, C., West, A. J., Feakins, S. J., and Galy, V. (2014). Leaf wax biomarkers in transit record river catchment composition. Geophys. Res. Lett. 41, 6420–6427. doi: 10.1002/2014gl061328

CrossRef Full Text | Google Scholar

Prancevic, J. P., and Lamb, M. P. (2015). Unraveling bed slope from relative roughness in initial sediment motion. J. Geophys. Res. Earth Surf. 120, 474–489. doi: 10.1002/2014jf003323

CrossRef Full Text | Google Scholar

Prélat, A., and Hodgson, D. M. (2013). The full range of turbidite bed thickness patterns in submarine lobes: controls and implications. J. Geol. Soc. London 170, 209–214. doi: 10.1144/jgs2012-056

CrossRef Full Text | Google Scholar

Puchol, N., Charreau, J., Blard, P.-H., Lavé, J., Dominguez, S., Pik, R., et al. (2017). Limited impact of quaternary glaciations on denudation rates in Central Asia. GSA Bull. 129, 479–499. doi: 10.1130/b31475.1

CrossRef Full Text | Google Scholar

Puchol, N., Lavé, J., Lupker, M., Blard, P., Gallo, F., France-Lanord, C., et al. (2014). Grain-size dependent concentration of cosmogenic ¹⁰Be and erosion dynamics in a landslide-dominated Himalayan watershed. Geomorphology 224, 55–68. doi: 10.1016/j.geomorph.2014.06.019

CrossRef Full Text | Google Scholar

Pudsey, C. J. (1992). Late quaternary changes in antarctic bottom water velocity inferred from sediment grain size in the northern Weddell Sea. Mar. Geol. 107, 9–33. doi: 10.1016/0025-3227(92)90066-q

CrossRef Full Text | Google Scholar

Pujalte, V., and Schmitz, B. (2014). Comment on “magnitude and profile of organic carbon isotope records from the Paleocene–Eocene thermal maximum: evidence from northern Spain” by Manners et al. [Earth Planet. Sci. Lett. 376 (2013) 220–230]. Earth Planet. Sci. Lett. 395, 291–293. doi: 10.1016/j.epsl.2014.03.054

CrossRef Full Text | Google Scholar

Quick, L., Sinclair, H. D., Attal, M., and Singh, V. (2019). Conglomerate recycling in the Himalayan foreland basin: implications for grain size and provenance. GSA Bull. 132, 1639–1656. doi: 10.1130/b35334.1

CrossRef Full Text | Google Scholar

Ramisch, A., Tjallingii, R., Hartmann, K., Diekmann, B., and Brauer, A. (2018). Echo of the younger dryas in Holocene lake sediments on the Tibetan Plateau. Geophys. Res. Lett. 45, 11154–11163.

Google Scholar

Recking, A., Frey, P., Paquier, A., and Belleudy, P. (2009). An experimental investigation of mechanisms involved in bed load sheet production and migration. J. Geophys. Res. Solid Earth 114:F03010.

Google Scholar

Repasch, M., Wittmann, H., Scheingross, J. S., Sachse, D., Szupiany, R., Orfeo, O., et al. (2020). Sediment transit time and floodplain storage dynamics in Alluvial rivers revealed by meteoric ¹⁰Be. J. Geophys. Res. Earth Surf. 125:e2019JF005419.

Google Scholar

Roda-Boluda, D. C., D’Arcy, M., McDonald, J., and Whittaker, A. C. (2018). Lithological controls on hillslope sediment supply: insights from landslide activity and grain size distributions. Earth Surf. Process. Landf. 43, 956–977. doi: 10.1002/esp.4281

CrossRef Full Text | Google Scholar

Rohais, S., Bonnet, S., and Eschard, R. (2012). Sedimentary record of tectonic and climatic erosional perturbations in an experimental coupled catchment-fan system. Basin Res. 24, 198–212. doi: 10.1111/j.1365-2117.2011.00520.x

CrossRef Full Text | Google Scholar

Romans, B. W., Castelltort, S., Covault, J. A., Fildani, A., and Walsh, J. P. (2016). Environmental signal propagation in sedimentary systems across timescales. Earth Sci. Rev. 153, 7–29. doi: 10.1016/j.earscirev.2015.07.012

CrossRef Full Text | Google Scholar

Romans, B. W., Normark, W. R., McGann, M. M., Covault, J. A., and Graham, S. A. (2009). Coarse-grained sediment delivery and distribution in the Holocene Santa Monica Basin, California: implications for evaluating source-to-sink flux at millennial time scales. Geol. Soc. Am. Bull. 121, 1394–1408. doi: 10.1130/b26393.1

CrossRef Full Text | Google Scholar

Sachse, D., Billault, I., Bowen, G. J., Chikaraishi, Y., Dawson, T. E., Feakins, S. J., et al. (2012). Molecular paleohydrology: interpreting the Hydrogen-Isotopic composition of lipid biomarkers from photosynthesizing organisms. Annu. Rev. Earth Planet. Sci. 40, 221–249. doi: 10.1146/annurev-earth-042711-105535

CrossRef Full Text | Google Scholar

Sadler, P. M. (1981). Sediment accumulation rates and the completeness of stratigraphic sections. J. Geol. 89, 569–584. doi: 10.1086/628623

CrossRef Full Text | Google Scholar

Savi, S., Tofelde, S., Wickert, A., Bufe, A., Schildgen, T., and Strecker, M. (2020). Interactions between channels and tributary alluvial fans: channel adjustments and sediment-signal propagation. Earth Surf. Dyn. 8, 303–322. doi: 10.5194/esurf-8-303-2020

CrossRef Full Text | Google Scholar

Schaller, M., von Blanckenburg, F., Hovius, N., Veldkamp, A., van den Berg, M. W., and Kubik, P. W. (2004). Paleoerosion rates from cosmogenic ¹⁰Be in a 1.3 Ma terrace sequence: response of the River Meuse to changes in climate and rock uplift. J. Geol. 112, 127–144. doi: 10.1086/381654

CrossRef Full Text | Google Scholar

Schefuß, E., Eglinton, T. I., Spencer-Jones, C. L., Rullkötter, J., De Pol-Holz, R., Talbot, H. M., et al. (2016). Hydrologic control of carbon cycling and aged carbon discharge in the Congo River basin. Nat. Geosci. 9, 687–690. doi: 10.1038/ngeo2778

CrossRef Full Text | Google Scholar

Scheingross, J. S., Limaye, A. B., McCoy, S. W., and Whittaker, A. C. (2020). The shaping of erosional landscapes by internal dynamics. Nat. Rev. Earth Environ. 1, 661–676. doi: 10.1038/s43017-020-0096-0

CrossRef Full Text | Google Scholar

Scheingross, J. S., Winchell, E. W., Lamb, M. P., and Dietrich, W. E. (2013). Influence of bed patchiness, slope, grain hiding, and form drag on gravel mobilization in very steep streams. J. Geophys. Res. Earth Surf. 118, 982–1001. doi: 10.1002/jgrf.20067

CrossRef Full Text | Google Scholar

Schildgen, T. F., Robinson, R. A. J. J., Savi, S., Phillips, W. M., Spencer, J. Q. G. G., Bookhagen, B., et al. (2016). Landscape response to late Pleistocene climate change in NW Argentina: sediment flux modulated by basin geometry and connectivity. J. Geophys. Res. Earth Surf. 121, 392–414. doi: 10.1002/2015JF003607

CrossRef Full Text | Google Scholar

Schlunegger, F., and Castelltort, S. (2016). Immediate and delayed signal of slab breakoff in Oligo/Miocene Molasse deposits from the European Alps. Sci. Rep. 6:31010.

Google Scholar

Schlunegger, F., and Norton, K. P. (2015). Climate vs. tectonics: the competing roles of late Oligocene warming and Alpine orogenesis in constructing alluvial megafan sequences in the North Alpine foreland basin. Basin Res. 27, 230–245. doi: 10.1111/bre.12070

CrossRef Full Text | Google Scholar

Schmid, M., Ehlers, T. A., Werner, C., Hickler, T., and Fuentes-Espoz, J.-P. (2018). Effect of changing vegetation and precipitation on denudation–Part 2: predicted landscape response to transient climate and vegetation cover over millennial to million-year timescales. Earth Surf. Dyn. 6, 859–881. doi: 10.5194/esurf-6-859-2018

CrossRef Full Text | Google Scholar

Schmitz, B., and Pujalte, V. (2003). Sea-level, humidity, and land-erosion records across the initial Eocene thermal maximum from a continental-marine transect in northern Spain. Geology 31, 689–692. doi: 10.1130/g19527.1

CrossRef Full Text | Google Scholar

Schmitz, B., and Pujalte, V. (2007). Abrupt increase in seasonal extreme precipitation at the Paleocene-Eocene boundary. Geology 35, 215–218. doi: 10.1130/g23261a.1

CrossRef Full Text | Google Scholar

Schulze, K., Hunger, M., and Döll, P. (2005). Simulating river flow velocity on global scale. Adv. Geosci. 5, 133–136. doi: 10.5194/adgeo-5-133-2005

CrossRef Full Text | Google Scholar

Schumm, S. A. (1973). Geomorphic thresholds and complex response. Fluv. Geomorphol. 6, 299–309.

Google Scholar

Schumm, S. A. (1977). The Fluvial System. New York: Wiley.

Google Scholar

Sharman, G. R., Hubbard, S. M., Covault, J. A., Hinsch, R., Linzer, H., and Graham, S. A. (2018). Sediment routing evolution in the North Alpine Foreland Basin, Austria: interplay of transverse and longitudinal sediment dispersal. Basin Res. 30, 426–447. doi: 10.1111/bre.12259

CrossRef Full Text | Google Scholar

Sharman, G. R., Sylvester, Z., and Covault, J. A. (2019). Conversion of tectonic and climatic forcings into records of sediment supply and provenance. Sci. Rep. 9:4115.

Google Scholar

Sheets, B. A., Hickson, T. A., and Paola, C. (2002). Assembling the stratigraphic record: depositional patterns and time-scales in an experimental alluvial basin. Basin Res. 14, 287–301. doi: 10.1046/j.1365-2117.2002.00185.x

CrossRef Full Text | Google Scholar

Shen, Z., Törnqvist, T. E., Autin, W. J., Mateo, Z. R. P., Straub, K. M., and Mauz, B. (2012). Rapid and widespread response of the lower Mississippi river to eustatic forcing during the last glacial-interglacial cycle. GSA Bull. 124, 690–704. doi: 10.1130/b30449.1

CrossRef Full Text | Google Scholar

Shields, A. (1936). Anwendung Der Aehnlichkeitsmechanik und der Turbulenzforschung Auf Die Geschiebebewegung. PhD Thesis, Tech. Univ, Berlin.

Google Scholar

Simpson, G., and Castelltort, S. (2012). Model shows that rivers transmit high-frequency climate cycles to the sedimentary record. Geology 40, 1131–1134. doi: 10.1130/g33451.1

CrossRef Full Text | Google Scholar

Sinclair, H. D., Stuart, F. M., Mudd, S. M., McCann, L., and Tao, Z. (2019). Detrital cosmogenic ²¹Ne records decoupling of source-to-sink signals by sediment storage and recycling in Miocene to present rivers of the great plains, Nebraska, USA. Geology 47, 3–6. doi: 10.1130/g45391.1

CrossRef Full Text | Google Scholar

Sivry, Y., Riotte, J., Sonke, J. E., Audry, S., Schäfer, J., Viers, J., et al. (2008). Zn isotopes as tracers of anthropogenic pollution from Zn-ore smelters The Riou Mort-Lot River system. Chem. Geol. 255, 295–304. doi: 10.1016/j.chemgeo.2008.06.038

CrossRef Full Text | Google Scholar

Slingerland, R., and Smith, N. D. (2004). River avulsions and their deposits. Annu. Rev. Earth Planet. Sci. 32, 257–285. doi: 10.1146/annurev.earth.32.101802.120201

CrossRef Full Text | Google Scholar

Snyder, N. P., Whipple, K. X., Tucker, G. E., Merritts, D. J., and College, M. (2000). Landscape response to tectonic forcing: digital elevation model analysis of stream profiles in the Mendocino triple junction region, northern California. Geol. Soc. Am. Bull. 112, 1250–1263. doi: 10.1130/0016-7606(2000)112<1250:lrttfd>2.0.co;2

CrossRef Full Text | Google Scholar

Sommerfield, C. K., and Nittrouer, C. A. (1999). Modern accumulation rates and a sediment budget for the Eel shelf: a flood-dominated depositional environment. Mar. Geol. 154, 227–241. doi: 10.1016/s0025-3227(98)00115-7

CrossRef Full Text | Google Scholar

Spychala, Y. T., Hodgson, D. M., Prélat, A., Kane, I. A., Flint, S. S., and Mountney, N. P. (2017). Frontal and lateral submarine lobe fringes: comparing sedimentary facies, architecture and flow processes. J. Sediment. Res. 87, 75–96. doi: 10.2110/jsr.2017.2

PubMed Abstract | CrossRef Full Text | Google Scholar

Stanley, S., and De Deckker, P. (2002). A Holocene record of allochthonous, aeolian mineral grains in an Australian alpine lake; implications for the history of climate change in southeastern Australia. J. Paleolimnol. 27, 207–219.

Google Scholar

Steffen, D., Schlunegger, F., and Preusser, F. (2010). Late Pleistocene fans and terraces in the Majes valley, southern Peru, and their relation to climatic variations. Int. J. Earth Sci. 99, 1975–1989. doi: 10.1007/s00531-009-0489-2

CrossRef Full Text | Google Scholar

Sternberg, H. (1875). Untersuchungen über Längen- und Querprofile geschiebeführender Flüsse. Zeitshrift fur Bauwes. 25, 483–506.

Google Scholar

Stoner, J. S., Channell, J. E. T., and Hillaire-Marcel, C. (1995). Magnetic properties of deep-sea sediments off southwest Greenland: evidence for major differences between the last two deglaciations. Geology 23, 241–244. doi: 10.1130/0091-7613(1995)023<0241:mpodss>2.3.co;2

CrossRef Full Text | Google Scholar

Straub, K. M., and Mohrig, D. (2008). Quantifying the morphology and growth of levees in aggrading submarine channels. J. Geophys. Res. Earth Surf. 113.

Google Scholar

Straub, K. M., Duller, R. A., Foreman, B. Z., and Hajek, E. A. (2020). Buffered, incomplete, and shredded: the challenges of reading an imperfect stratigraphic record. J. Geophys. Res. 93:e2019JF005079.

Google Scholar

Strauss, D., and Sadler, P. M. (1989). Stochastic models for the completeness of stratigraphic sections. Math. Geol. 21, 37–59. doi: 10.1007/bf00897239

CrossRef Full Text | Google Scholar

Suresh, P. O., Dosseto, A., Hesse, P. P., and Handley, H. K. (2014). Very long hillslope transport timescales determined from uranium-series isotopes in river sediments from a large, tectonically stable catchment. Geochim. Cosmochim. Acta 142, 442–457. doi: 10.1016/j.gca.2014.07.033

CrossRef Full Text | Google Scholar

Sweet, M. L., and Blum, M. D. (2016). Connections between fluvial to shallow marine environments and submarine canyons: implications for sediment transfer to deep water. J. Sediment. Res. 86, 1147–1162. doi: 10.2110/jsr.2016.64

PubMed Abstract | CrossRef Full Text | Google Scholar

Talling, P. J. (2014). On the triggers, resulting flow types and frequencies of subaqueous sediment density flows in different settings. Mar. Geol. 352, 155–182. doi: 10.1016/j.margeo.2014.02.006

CrossRef Full Text | Google Scholar

Tejedor, A., Singh, A., Zaliapin, I., Densmore, A. L., and Foufoula-Georgiou, E. (2017). Scale-dependent erosional patterns in steady-state and transient-state landscapes. Sci. Adv. 3:e1701683. doi: 10.1126/sciadv.1701683

PubMed Abstract | CrossRef Full Text | Google Scholar

Tipper, J. C. (1983). Rates of sedimentation, and stratigraphical completeness. Nature 302, 696–698. doi: 10.1038/302696a0

CrossRef Full Text | Google Scholar

Tofelde, S., Duesing, W., Schildgen, T. F., Wickert, A. D., Wittmann, H., Alonso, R. N., et al. (2018). Effects of deep-seated versus shallow hillslope processes on cosmogenic ¹⁰Be concentrations in fluvial sand and gravel. Earth Surf. Process. Landf. 43, 3086–3098. doi: 10.1002/esp.4471

CrossRef Full Text | Google Scholar

Tofelde, S., Savi, S., Wickert, A. D., Bufe, A., and Schildgen, T. F. (2019). Alluvial channel response to environmental perturbations: fill-terrace formation and sediment-signal disruption. Earth Surf. Dyn. 7, 609–631. doi: 10.5194/esurf-7-609-2019

CrossRef Full Text | Google Scholar

Tofelde, S., Schildgen, T. F., Savi, S., Pingel, H., Wickert, A. D., Bookhagen, B., et al. (2017). 100 kyr fluvial cut-and-fill terrace cycles since the middle pleistocene in the southern central andes, NW Argentina. Earth Planet. Sci. Lett. 473, 141–153. doi: 10.1016/j.epsl.2017.06.001

CrossRef Full Text | Google Scholar

Törnqvist, T. E. (1998). Longitudinal profile evolution of the Rhine-Meuse system during the last deglaciation: interplay of climate change and glacio-eustasy? Terra Nova 10, 11–15. doi: 10.1046/j.1365-3121.1998.00159.x

CrossRef Full Text | Google Scholar

Toucanne, S., Zaragosi, S., Bourillet, J.-F., Dennielou, B., Jorry, S. J., Jouet, G., et al. (2012). External controls on turbidite sedimentation on the glacially-influenced Armorican margin (Bay of Biscay, western European margin). Mar. Geol. 303, 137–153. doi: 10.1016/j.margeo.2012.02.008

CrossRef Full Text | Google Scholar

Trampush, S. M., and Hajek, E. A. (2017). Preserving proxy records in dynamic landscapes: modeling and examples from the Paleocene-Eocene thermal maximum. Geology 45, 967–970. doi: 10.1130/g39367.1

CrossRef Full Text | Google Scholar

Tucker, G. E., and Slingerland, R. (1997). Drainage basin responses to climate change. Water Resour. Res. 33, 2031–2047. doi: 10.1029/97wr00409

CrossRef Full Text | Google Scholar

Turowski, J. M. (2020). Mass balance, grade, and adjustment timescales in bedrock channels. Earth Surf. Dyn. 8, 103–122. doi: 10.5194/esurf-8-103-2020

CrossRef Full Text | Google Scholar

Turowski, J. M., Badoux, A., and Rickenmann, D. (2011). Start and end of bedload transport in gravel-bed streams. Geophys. Res. Lett. 38:L04401.

Google Scholar

Val, P., Hoke, G. D., Fosdick, J. C., and Wittmann, H. (2016). Reconciling tectonic shortening, sedimentation and spatial patterns of erosion from ¹⁰Be paleo-erosion rates in the Argentine Precordillera. Earth Planet. Sci. Lett. 450, 173–185. doi: 10.1016/j.epsl.2016.06.015

CrossRef Full Text | Google Scholar

van de Wiel, M. J., and Coulthard, T. J. (2010). Self-organized criticality in river basins: challenging sedimentary records of environmental change. Geology 38, 87–90. doi: 10.1130/g30490.1

CrossRef Full Text | Google Scholar

van den Berg van Saparoea, A.-P. H., and Postma, G. (2008). Control of climate change on the yield of river systems. Recent Adv. Model. Siliciclastic Shallow-Marine Stratigr. SEPM Spec. Publ. 90, 15–33. doi: 10.2110/pec.08.90.0015

PubMed Abstract | CrossRef Full Text | Google Scholar

van Dongen, R., Scherler, D., Wittmann, H., and von Blanckenburg, F. (2019). Cosmogenic ¹⁰Be in river sediment: where grain size matters and why. Earth Surf. Dyn. 7, 393–410. doi: 10.5194/esurf-7-393-2019

CrossRef Full Text | Google Scholar

Völker, D., Reichel, T., Wiedicke, M., and Heubeck, C. (2008). Turbidites deposited on southern central Chilean seamounts: evidence for energetic turbidity currents. Mar. Geol. 251, 15–31. doi: 10.1016/j.margeo.2008.01.008

CrossRef Full Text | Google Scholar

Walling, D. E. (1983). The sediment delivery problem. J. Hydrol. 65, 209–237. doi: 10.1016/0022-1694(83)90217-2

CrossRef Full Text | Google Scholar

Walsh, J. P., and Nittrouer, C. A. (2003). Contrasting styles of off-shelf sediment accumulation in New Guinea. Mar. Geol. 196, 105–125. doi: 10.1016/s0025-3227(03)00069-0

CrossRef Full Text | Google Scholar

Wang, H., Saito, Y., Zhang, Y., Bi, N., Sun, X., and Yang, Z. (2011). Recent changes of sediment flux to the western Pacific Ocean from major rivers in East and Southeast Asia. Earth Sci. Rev. 108, 80–100. doi: 10.1016/j.earscirev.2011.06.003

CrossRef Full Text | Google Scholar

Watkins, S. E., Whittaker, A. C., Bell, R. E., Brooke, S. A. S., Ganti, V., Gawthorpe, R. L., et al. (2020). Straight from the source’s mouth: controls on field-constrained sediment export across the entire active corinth rift, central Greece. Basin Res. 36, 1600–1625. doi: 10.1111/bre.12444

CrossRef Full Text | Google Scholar

Weislogel, A. L., Graham, S. A., Chang, E. Z., Wooden, J. L., Gehrels, G. E., and Yang, H. (2006). Detrital zircon provenance of the late Triassic Songpan-Ganzi complex: sedimentary record of collision of the north and south china blocks. Geology 34, 97–100. doi: 10.1130/g21929.1

CrossRef Full Text | Google Scholar

Weltje, G. J., and Tjallingii, R. (2008). Calibration of XRF core scanners for quantitative geochemical logging of sediment cores: theory and application. Earth Planet. Sci. Lett. 274, 423–438. doi: 10.1016/j.epsl.2008.07.054

CrossRef Full Text | Google Scholar

Wetzel, A. (1984). Bioturbation in deep-sea fine-grained sediments: influence of sediment texture, turbidite frequency and rates of environmental change. Geol. Soc. London Spec. Publ. 15, 595–608. doi: 10.1144/gsl.sp.1984.015.01.37

CrossRef Full Text | Google Scholar

Wheatcroft, R. A., and Sommerfield, C. K. (2005). River sediment flux and shelf sediment accumulation rates on the Pacific Northwest margin. Cont. Shelf Res. 25, 311–332. doi: 10.1016/j.csr.2004.10.001

CrossRef Full Text | Google Scholar

Whipple, K. X. (2001). Fluvial landscape response time: how plausible is steady-state denudation? Am. J. Sci. 301, 313–325. doi: 10.2475/ajs.301.4-5.313

PubMed Abstract | CrossRef Full Text | Google Scholar

Whipple, K. X., and Tucker, G. E. (1999). Dynamics of the stream-power river incision model: implications for height limits of mountain ranges, landscape response timescales, and research needs. J. Geophys. Res. Solid Earth 104, 17661–17674. doi: 10.1029/1999jb900120

CrossRef Full Text | Google Scholar

Whittaker, A. C., Attal, M., and Allen, P. A. (2010). Characterising the origin, nature and fate of sediment exported from catchments perturbed by active tectonics. Basin Res. 22, 809–828.

Google Scholar

Whittaker, A. C., Attal, M., Cowie, P. A., Tucker, G. E., and Roberts, G. (2008). Decoding temporal and spatial patterns of fault uplift using transient river long profiles. Geomorphology 100, 506–526. doi: 10.1016/j.geomorph.2008.01.018

CrossRef Full Text | Google Scholar

Whittaker, A. C., Duller, R. A., Springett, J., Smithells, R. A., Whitchurch, A. L., and Allen, P. A. (2011). Decoding downstream trends in stratigraphic grain size as a function of tectonic subsidence and sediment supply. GSA Bull. 123, 1363–1382. doi: 10.1130/b30351.1

CrossRef Full Text | Google Scholar

Wiberg, P. L., and Smith, J. D. (1987). Calculations of the critical shear stress for motion of uniform and heterogeneous sediments. Water Resour. Res. 23, 1471–1480. doi: 10.1029/wr023i008p01471

CrossRef Full Text | Google Scholar

Wickert, A. D., and Schildgen, T. F. (2019). Long-profile evolution of transport-limited gravel-bed rivers. Earth Surf. Dyn. 7, 17–43. doi: 10.5194/esurf-7-17-2019

CrossRef Full Text | Google Scholar

Wilcock, P. R., and Crowe, J. C. (2003). Surface-based transport model for mixed-size sediment. J. Hydraul. Eng. 129, 120–128. doi: 10.1061/(asce)0733-9429(2003)129:2(120)

CrossRef Full Text | Google Scholar

Willenbring, J. K., Gasparini, N. M., Crosby, B. T., and Brocard, G. (2013). What does a mean mean? The temporal evolution of detrital cosmogenic denudation rates in a transient landscape. Geology 41, 1215–1218. doi: 10.1130/g34746.1

CrossRef Full Text | Google Scholar

Willett, S. D., and Brandon, M. T. (2002). On steady states in mountain belt. Geology 30, 175–178. doi: 10.1130/0091-7613(2002)030<0175:ossimb>2.0.co;2

CrossRef Full Text | Google Scholar

Wittmann, H., Oelze, M., Gaillardet, J., Garzanti, E., and von Blanckenburg, F. (2020). A global rate of denudation from cosmogenic nuclides in the Earth’s largest rivers. Earth Sci. Rev. 204:103147. doi: 10.1016/j.earscirev.2020.103147

CrossRef Full Text | Google Scholar

Wittmann, H., von Blanckenburg, F., Dannhaus, N., Bouchez, J., Gaillardet, J., Guyot, J.-L., et al. (2015). A test of the cosmogenic ¹⁰Be (meteoric)/⁹Be proxy for simultaneously determining basin-wide erosion rates, denudation rates, and the degree of weathering in the Amazon basin. J. Geophys. Res. Earth Surf. 120, 2498–2528. doi: 10.1002/2015jf003581

CrossRef Full Text | Google Scholar

Wittmann, H., von Blanckenburg, F., Maurice, L., Guyot, J. L., and Kubik, P. W. (2011). Recycling of Amazon floodplain sediment quantified by cosmogenic ²⁶Al and ¹⁰Be. Geology 39, 467–470. doi: 10.1130/g31829.1

CrossRef Full Text | Google Scholar

Yuan, X. P., Braun, J., Guerit, L., Rouby, D., and Cordonnier, G. (2019). A new efficient method to solve the stream power law model taking into account sediment deposition. J. Geophys. Res. Earth Surf. 124, 1346–1365. doi: 10.1029/2018jf004867

CrossRef Full Text | Google Scholar

Zalasiewicz, J., Waters, C. N., do Sul, J. A. I., Corcoran, P. L., Barnosky, A. D., Cearreta, A., et al. (2016). The geological cycle of plastics and their use as a stratigraphic indicator of the Anthropocene. Anthropocene 13, 4–17. doi: 10.1016/j.ancene.2016.01.002

CrossRef Full Text | Google Scholar

Zapata, F., and Nguyen, M.-L. (2009). Soil erosion and sedimentation studies using environmental radionuclides. Radioact. Environ. 16, 295–322. doi: 10.1016/s1569-4860(09)01607-6

CrossRef Full Text | Google Scholar

Zhang, J., Sylvester, Z., and Covault, J. (2020). How do basin margins record long-term tectonic and climatic changes? Geology 48, 893–897. doi: 10.1130/g47498.1

CrossRef Full Text | Google Scholar

Zolitschka, B., Francus, P., Ojala, A. E. K., and Schimmelmann, A. (2015). Varves in lake sediments–a review. Quat. Sci. Rev. 117, 1–41. doi: 10.1016/j.quascirev.2015.03.019

CrossRef Full Text | Google Scholar

Zscheischler, J., Westra, S., Van Den Hurk, B. J. J. M., Seneviratne, S. I., Ward, P. J., and Pitman, A. (2018). Future climate risk from compound events. Nat. Clim. Chang. 8, 469–477. doi: 10.1038/s41558-018-0156-3

CrossRef Full Text | Google Scholar