- 1US Geological Survey, Earth System Processes Division, Menlo Park, CA, United States
- 2US Geological Survey, Geology, Energy, and Minerals Science Center, Reston, VA, United States
- 3US Geological Survey, Earth System Processes Division, Lakewood, CO, United States
- 4US Geological Survey, Geologic Hazards Science Center, Golden, CO, United States
The unsaturated zone (UZ) extends across the Earth’s terrestrial surface and is central to many problems related to land and water resource management. Flow of water through the UZ is typically thought to be slow and diffusive, such that it could attenuate fluxes and dampen variability between atmospheric inputs and underlying aquifer systems. This would reduce water resource vulnerability to contaminants and water-related hazards. Reducing or negating that effect, however, spatially concentrated and rapid flow and transport through the unsaturated zone is surprisingly common and becoming more so with the increasing frequency and magnitude of extreme hydroclimatic events. Arising from the wide range in the rates and complex modes of nonlinear flow processes, these effects are among the most poorly characterized hydrologic phenomena. Issues of scale present additional difficulties. Equations representing unsaturated processes have been developed and tested on the basis of field and laboratory measurements typically made at scales from pore size to plot size. In contrast, related problems of significant interest to society, including floods, aquifer recharge, landslides, and groundwater contamination, range from watershed to regional scales. The disparity between the scale of our understanding and the scale of interest for societal problems has spurred application of these model equations at increasingly coarse resolutions over larger areas than can be justified by existing measurements or theory. This mismatch in scales requires an assumption that spatially averaging slow diffusive flow and rapid preferential flow can effectively represent the influence of both processes across vast areas. Given the currently inadequate recognition and quantitative characterization of focused and rapid processes in unsaturated flow, these phenomena are critically in need of expanded attention and effort.
Introduction
Rapid hydrologic responses in the unsaturated zone (UZ), the portion of the subsurface that extends vertically from the land surface to the groundwater table, pose considerable monitoring and modeling challenges. We use the term “rapid” here to denote hydrologic responses with timescales substantially shorter than the timescale of days that is typically associated with storm/interstorm cycles (Blöschl and Sivapalan, 1995). Mounting evidence for a future in which precipitation events are both more intense (Groisman et al., 2005; Fischer and Knutti, 2016) and more frequent (Myhre et al., 2019; Papalexiou and Montanari, 2019) heightens the need for robust approaches to assess and predict consequences of major hydrologic events on water resources and hazards.
Flow within the UZ occurs in two principal modes: diffuse flow through a succession of typically microscopic pores of the bulk medium, and rapid preferential flow spatially concentrated in fractures, wormholes, and other relatively direct (i.e., preferential) paths that constitute a small volume fraction of the porous media. Rapid UZ responses can significantly influence the degree and timing of 1) runoff and infiltration, 2) stormflow response of streams, and 3) subsurface transmission of water and solutes (Ebel and Loague, 2008; Gurdak et al., 2008; Zheng et al., 2019). These processes can in turn determine the extent and severity of flooding, landslides, and contamination hazards as well as the magnitude of aquifer recharge (Luo et al., 2018). Rapid recharge occurring mainly as preferential flow can be beneficial in terms of water supply but also has the potential to carry contaminants great distances with little opportunity for the occurrence of processes that reduce contamination risk (Mirus and Nimmo, 2013). In this perspective, we describe the implications for applying small-scale UZ data and theoretical constructs to large-scale rapid-response problems, in ways we hope are useful to scientists and the broader communities of concern.
Issues of Scale
Figure 1 illustrates the mismatch between typical measurements and societal problems for the spatial scales associated with rapid UZ hydrologic response. Most measurement methods capturing rapid UZ response characterize areas at the small plot (1 m2) to hillslope (10 m2) scale. Yet most societal problems, such as aquifer recharge and landslide initiation, span from large hillslope (104 m2) to regional (1010 m2) scales. Demand for defensible approaches to managing water resources at regional scales, typically greater than 107 m2, to address integrated environmental and socioeconomic issues has grown rapidly in recent decades (National Research Council, 2000). Contamination problems do not only occur at the local source area where the pollutant is emitted but can spread regionally on the land surface and within aquifers, and also within the UZ for significant distances (Nimmo et al., 2002).
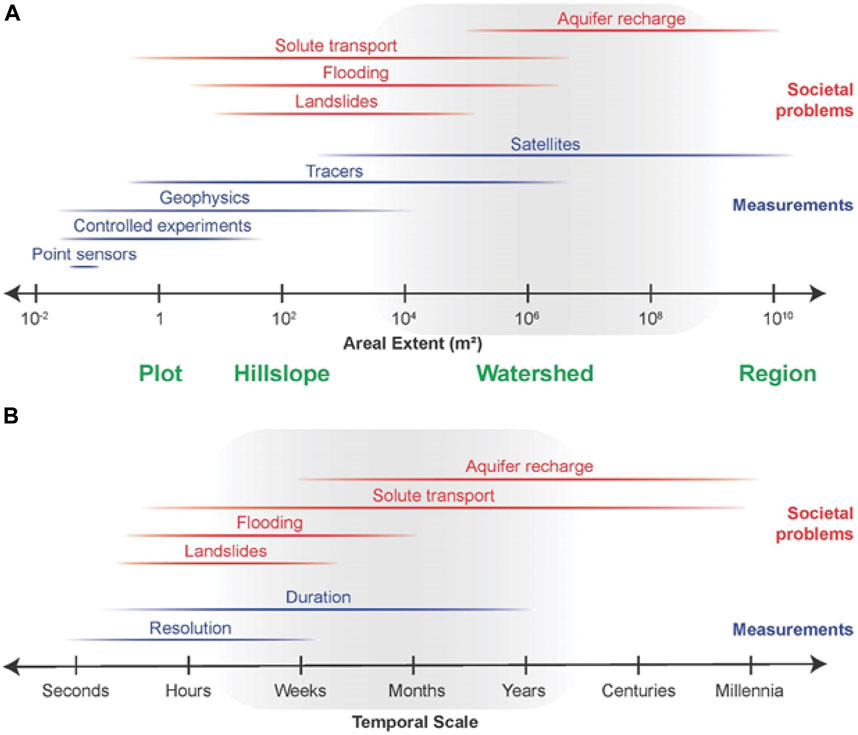
FIGURE 1. Approximate (A) areal extents and (B) temporal scales of various elements of unsaturated zone science. The gray shaded regions indicate the range of scales that are typically considered important for addressing hazards and water resource decisions. Red lines indicate the typical (A) extents and (B) durations of various problems of interest. Blue lines show the typical capabilities of various measurement technologies to provide data that are: (A) representative of a given area, and (B) collected over a given period with a given temporal resolution. Green text indicates spatial terms generally associated with corresponding areal extent.
Models that quantify rapid UZ responses are commonly applied at scales far exceeding those of the available measurements and the reliability of UZ hydrologic theory. For example, a modeling approach that effectively averages fast and slow flow paths cannot meaningfully capture the conditions that lead to initial arrival of a contaminant from a source. Likewise, a hydrologic model that uses daily time-steps cannot meaningfully capture the abrupt runoff-generation processes that lead to deadly and destructive post-fire debris flows and flash floods triggered by rapid runoff during short-duration, high-intensity rainfall (e.g., Moody and Martin, 2001; Kean et al., 2019). Early warning systems (e.g., Alias et al., 2020) would benefit from more realistic models.
Measurements and Data
Multiple difficulties arise from differences in spatial scale between measurements and societal problems. For example, they complicate the use of measurements for data-based early warning systems of flooding and landslide initiation because measurements represent only a minuscule fraction of the area at risk. While large-scale geophysical or satellite-based observations obviate the spatial coverage issue (e.g., Zhang et al., 2019), their scale of areal characterization and coarse spatial resolution is incompatible with the theory developed to understand and predict rapid UZ hydrologic response. Beyond the areal discrepancies shown in Figure 1A, the depth dimension of measurements also is typically covered inadequately by large-scale integrated measurements because it is either too shallow (e.g., for satellites, a 0.05-m surficial skin), or averaged over such a range of depths as to blur and essentially mask small-scale heterogeneities that are critical controls on rapid-response processes.
The temporal scale and resolution of UZ measurements also are commonly mismatched to those of societal problems (Figure 1B). Large-scale measurements typically lack the temporal resolution required for rapid processes. Satellite soil moisture products, for example, can provide unprecedented global coverage (https://smap.jpl.nasa.gov/), but limited temporal resolution precludes their use for capturing rapid spikes in pore-water pressure that drive landslide initiation, or even for accurately representing seasonal trends in hillslope drainage over complex terrain (Thomas et al., 2019). Small-scale measurements, such as those gathered via in-situ sensors, often have adequate resolution of an hour or less, but are seldom available over sufficient durations to characterize the range of normal system behavior and capture a spectrum of hydrometeorological drivers (Tetzlaff et al., 2017). The lack of these measurements, and the associated inadequate quantification of rapid hydrogeologic responses to extreme hydrometeorological events, stifles development of new theory and models that describe and predict rapid-response phenomena. Advances in environmental tracers show good potential in characterizing unsaturated zone travel-time distributions (e.g., Green et al., 2018). Figure 2 shows how tracer first-arrival times, which mostly fall within the very-short portion of Figure 1B time range, have demonstrated a comparable range of preferential travel speeds in rock and soil over a great range of scales. Challenges remain, however, concerning the amount and type of analyses required, and high uncertainty.
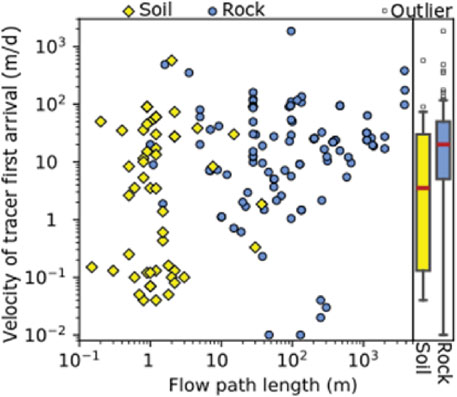
FIGURE 2. Graph of velocity of tracer first arrival in days for different flow path lengths in soil and rock and box and whiskers plots of velocity of tracer first arrival in days in soil and rock. The bottom and top of the box are the first and third quartiles, respectively. The whiskers extend 1.5 times the interquartile range beyond the first and third quartiles. The term “outliers” denotes points that extend beyond the whiskers, without implying any insignificance. Median velocity of tracer first arrival (red line in the box plots) was 3.5 m/d in soil and 20 m/d in rock. Data were harvested from the peer-reviewed literature listed in Supplementary Table S1.
Theory and Models
The dominant theory of unsaturated flow, underlying essentially all widely used predictive models of this field, is the diffusive-flow theory embodied in Richards (1931) equation, formalized in terms of surface-tension viscous-flow principles (Miller and Miller, 1956). Quantitative implementation of this theory is not simple, as unsaturated flow is characterized by severe nonlinearities and multiple-order-of-magnitude variations in properties.
Diffusive-flow models for unsaturated media were developed on the basis of measurements from experiments utilizing small samples of homogenous porous material. Richards (1931), for example, did his experiments with small (6 × 10–4 m3) samples of repacked soil. The driving motivation was problems of agricultural practice, such as evaluating irrigation needs of a field plot. Successful application was facilitated by the limited extent of plots under consideration, and frequently by artificial homogenization of the soil by tillage. This diffusive flow theory has been extended with minimal modification to hydrologic problems of large scale, tremendous heterogeneity, topographic variability, and other complexities far beyond the problems for which the theory was conceived. Despite these shortcomings, diffusive-flow approaches applied at coarse scales over large areas have revealed some important process interactions and data gaps. Regional and continental-scale modeling, for example, have shown the importance of 1) critical groundwater-atmospheric interactions through transpiration (Maxwell and Condon, 2016), 2) small-scale processes in cold regions (Hayashi, 2014; Walvoord and Kurylyk, 2016) that impact large-scale water resource assessments (Chen et al., 2020), and 3) natural soil structures that can control the global water and energy balance (Fatichi et al., 2020). While acknowledging these successes, our critique emphasizes the inadequacy of the underlying diffusive flow theory for capturing crucial rapid UZ responses.
The intrinsic heterogeneity of soil and rock poses a major problem. Strictly speaking, applying Richards’ equation must be done in terms of discrete volumes of material that can be considered internally homogeneous. The complex whole is to be treated as the set of individual volumes, each with its own set of hydraulic properties, interacting with appropriate boundary conditions. Some applications of Richards’ equation do separately represent certain separate volumes, such as soil horizons, with different property values, but never come close to representing the full heterogeneity of natural Earth materials (McDonnell et al., 2007).
A further problem with traditional approaches is that preferential flow fundamentally involves nonequilibrium processes, in that rapid flow through preferential pathways begins and usually ends long before there has been adequate time for equilibrium to be established in directions perpendicular to the direction of flow (Jarvis, 2007; Jarvis et al., 2016). Various studies, for example by Hasan et al. (2020), have demonstrated this characteristic. Thus the process is not a diffusive one in which the state of water in each individual pore is determined by conditions in the adjacent pores.
More recent alternative theoretical developments based on concepts such as films, waves, particle-tracking, or transfer functions (e.g., Jury, 1982; Dragila and Wheatcraft, 2001; Tsutsumi et al., 2005; Hincapié and Germann, 2009; Davies et al., 2013; Nimmo and Mitchell, 2013; Scaini et al., 2019), have been motivated by the incompatibility of diffusive-flow concepts with preferential flow. Many of these incorporate promising innovations, but none is yet in widespread use. Dual-domain Richards-based formulations, on the other hand, are widely used to concurrently represent both of the major flow modes, even though they cannot capture the unique and fundamentally distinct processes and characteristics of preferential flow.
The common practice of neglecting heterogeneity and misrepresenting flow processes produces results that are divorced from a physical basis in what is claimed to be the underlying theory. Diffusive flow models with grid cell volumes exceeding 106 m3, which have become somewhat common, clearly are enormous extrapolations beyond the ∼10–4 m3 scale at which the theory was originally developed. Previous studies such as Blöschl and Sivapalan (1995) and Beven (1989) have pointed out this incommensurability between measurement scales and model grid scales. Does this disconnect matter? A parameterized and calibrated model without an appropriate physical basis can fit data and generate predictions, but outcomes can be inadequate in several ways (Hsieh et al., 2001: p. 31), including:
• Wrong or misleading results are a greater possibility.
• With application to contentious issues in the public arena, results not soundly backed by scientific theory are more vulnerable to challenge.
• Perhaps most important, results are unreliable when conditions differ from those of model calibration. Increasingly, today’s predictive needs are for conditions of unprecedented climatic and land-use change, where sound physical principles are necessary to underpin results in ways that past behavior cannot.
Discussion and Conclusion
Developing theory, measurements, and models that represent regional-scale problems without losing the link to local-scale processes is a fundamental UZ challenge (Harter and Hopmans, 2004; Or, 2020). The incommensurability of measurements and models increases uncertainty in calibration and assessment of adequacy that is challenging to quantify or reduce (Hopmans, 2002). Large-scale characterizations by satellites or geophysical means do not directly measure the status of water, but rather other, indirectly related quantities such as reflectance or electrical resistivity. Before comparison with field measurements or model parameters, these large-scale measurements require interpretation or inversion for transformation into hydrologic variables of interest.
Alongside the problem of mismatched scales is the inadequacy of existing theory. Considerable efforts are being made to incrementally improve parameterization of Richards’ equation, resulting in increased complexity but without consideration of circumstances in which diffuse-flow theory cannot explain all observed phenomena. Thus, there is a danger that increasingly complex Richards-type formulations of unsaturated flow, and the associated computational challenges, are being used as a substitute for model veracity. In this situation the overparameterization in effect is tacitly and mistakenly considered to compensate for misrepresentation of process.
Neglect of process creates further difficulties. Even if there were enough data to fully support a global application of Richards’ equation, such an effort would not fully succeed because quantitative representations of rapid preferential flow processes could not be incorporated. The signals of focused, rapid UZ responses and nonequilibrium processes are overwhelmed when lumped together with diffusive processes. Brief rapid responses, often treated as insignificant outliers and either ignored or averaged out by the formulas employed, are in fact critical to many problems of societal interest. Attention to these deviations from the norm is crucial for characterizing flow responses that at first appear anomalous, in particular when considering predicted general increases in the number and severity of extreme hydroclimatic events.
We suggest multiple avenues for improving measurements, theory, and models of rapid UZ flow. Some of the simpler modeling approaches based on alternative conceptualizations of unsaturated flow (e.g., Hincapié and Germann, 2009; Nimmo and Mitchell, 2013; Orozco-López et al., 2018) may be adaptable to provide a useful path forward. Other promising options for improving large-scale modeling include machine learning and state-space modeling (e.g., Bidwell, 1998; Berendrecht et al., 2006; Kratzert et al., 2019; Orland et al., 2020), which can incorporate a variety of data streams and empirical equations to integrate fast and slow processes at scales where the direct process-based approaches have fallen short. At the same time, further efforts are needed to study small-scale rapid responses and understand how their behavior aggregates over a substantial area. Recognizing some of these scale issues and addressing them using watershed-scale networks of unsaturated zone sensors is one encouraging approach (e.g., Demand et al., 2019).
Implementations of new advances are held back by the considerable value placed on the continued use of modeling approaches that have been widely applied in the past, despite notable flaws and limitations. As a result, while land surface models are a recent and cutting-edge development in quantitative hydrology, the diffusive flow theory that underpins their soil water flow components is nearly 100 years old (i.e., Richards, 1931) and has not been updated to account for new observations or developments in understanding, even where the newer science contradicts significant elements of the old. Appropriately revised models of land-surface processes that incorporate the influence of rapid and large-scale unsaturated flow will require considerable time, effort, and iterative development. Toward that goal, near- and intermediate-term efforts could be guided by such measures as the following:
• Acknowledge the vast and fundamental differences between diffusive processes and rapid preferential flow through unsaturated soil and rock, which are best represented with different physics-based equations;
• Optimize strategies for hydrologic monitoring that not only capture how spatial patterns evolve across landscapes, but also include high-frequency point measurements to capture dynamics more accurately;
• Develop new or modified measurement techniques to better detect rapid-response signals at both large and small scales;
• Develop theory and robust models that capture extreme behavior as well as average responses;
• Promote collaboration among hydrologists working across scales to integrate theories, models, and field observations (Burt and McDonnell, 2015).
The scale of rapid UZ flow processes may be small, but the problems are too big to ignore. These processes control connections between the atmosphere, groundwater, and streamflow, and are therefore vital in addressing concerns of serious consequence to human, economic, and environmental health. Theoretical advances in UZ hydrology, however, were developed mostly several decades ago, at much smaller spatial and temporal scales than most modern applications demand. Recent development of unsaturated zone science has shortchanged important processes such as preferential flow, causing certain crucial interactions of Earth, air, and water to be inadequately understood. We need to pursue measurement techniques that can capture focused flow paths and rapid transport of solutes, and to develop new modeling approaches that can better explain observed phenomena such as non-monotonic wetting of soils, rapid pore-water pressure responses at depth, and unexpected early arrival of contaminants. These problems cannot be solved with faster computers or finer subsurface characterization—they require investment and focus on developing the scientific components that are currently lacking.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
All authors contributed to one or more sections of the manuscript. JN and MP did the final revision of coauthor comments. MP and BE created the figures with input from coauthors.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2021.613564/full#supplementary-material.
References
Alias, N. E., Salim, N. A., Taib, S. M., Mohd Yusof, M. B., Saari, R., and Ramli, A. (2020). Community responses on effective flood dissemination warnings-a case study of the December 2014 Kelantan Flood, Malaysia. J. Flood Risk Manag. 13, e12552. doi:10.1111/jfr3.12552
Berendrecht, W. L., Heemink, A. W., van Geer, F. C., and Gehrels, J. C. (2006). A non-linear state space approach to model groundwater fluctuations. Adv. Water Resour. 29, 959–973. doi:10.1016/j.advwatres.2005.08.009
Beven, K. (1989). Changing ideas in hydrology—the case of physically-based models. J. Hydrol. 105, 157–172. doi:10.1016/0022-1694(89)90101-7
Bidwell, V. J. (1998). State-space mixing cell model of unsteady solute transport in unsaturated soil. Environ. Model. Softw. 14, 161–169. doi:10.1016/s1364-8152(98)00067-x
Blöschl, G., and Sivapalan, M. (1995). Scale issues in hydrological modelling: a review. Hydrol. Process. 9 (3‐4), 251–290. doi:10.1002/hyp.3360090305
Burt, T. P., and McDonnell, J. J. (2015). Whither field hydrology? The need for discovery science and outrageous hydrological hypotheses. Water Resour. Res. 51 (8), 5919–5928. doi:10.1002/2014WR016839
Chen, J., Sudicky, E. A., Davison, J. H., Frey, S. K., Park, Y.-J., Hwang, H.-T., et al. (2020). Towards a climate-driven simulation of coupled surface-subsurface hydrology at the continental scale: a Canadian example. Can. Water Resour. J. 45 (1), 11–27. doi:10.1080/07011784.2019.1671235
Davies, J., Beven, K., Rodhe, A., Nyberg, L., and Bishop, K. (2013). Integrated modeling of flow and residence times at the catchment scale with multiple interacting pathways. Water Resour. Res. 49 (8), 4738–4750. doi:10.1002/wrcr.20377
Demand, D., Blume, T., and Weiler, M. (2019). Spatio-temporal relevance and controls of preferential flow at the landscape scale. Hydrol. Earth Syst. Sci. 23 (11), 4869–4889. doi:10.5194/hess-23-4869-2019
Dragila, M. I., and Wheatcraft, S. W. (2001). “Free-surface films,” in Conceptual models of flow and transport in the fractured vadose zone (Washington, DC: National Academy Press), pp 217–241.
Ebel, B. A., and Loague, K. (2008). Rapid simulated hydrologic response within the variably saturated near surface. Hydrol. Proc. 22 (3), 464–471.
Fatichi, S., Or, D., Walko, R., Vereecken, H., Young, M. H., Ghezzehei, T. A., et al. (2020). Soil structure is an important omission in earth system models. Nat. Commun. 11, 522. doi:10.1038/s41467-020-14411-z
Fischer, E. M., and Knutti, R. (2016). Observed heavy precipitation increase confirms theory and early models. Nat. Clim. Change 6 (11), 986–991.
Green, C. T., Liao, L., Nolan, B. T., Juckem, P. F., Shope, C. L., Tesoriero, A. J., et al. (2018). Regional variability of nitrate fluxes in the unsaturated zone and groundwater, Wisconsin, USA. Water Resour. Res. 54, 301–322. doi:10.1002/2017wr022012
Groisman, P. Y., Knight, R. W., Easterling, D. R., Karl, T. R., Hegerl, G. C., and Razuvaev, V. N. (2005). Trends in intense precipitation in the climate record. J. Clim. 18 (9), 1326–1350.
Gurdak, J. J., Walvoord, M. A., and McMahon, P. B. (2008). Susceptibility to enhanced chemical migration from depression-focused preferential flow, high plains aquifer. Vadose Zone J. 7 (4), 1218–1230. doi:10.2136/vzj2007.0145
Harter, T., and Hopmans, J. W. (2004). “Role of vadose‐zone flow processes in regional‐scale hydrology: review, opportunities, and challenges”, in Int. Symp. on unsaturated zone modelling: progress, challenges and applications, October 3-5, 2004. Editor R. A. Feddes (Dordrecht, the Netherlands: Kluwer Acad. Publ.), 179–208.
Hasan, S., Niasar, V., Karadimitriou, N. K., Godinho, J. R. A., Vo, N. T., An, S., et al. (2020). Direct characterization of solute transport in unsaturated porous media using fast X-ray synchrotron microtomography. Proc. Natl. Acad. Sci. 117 (38), 23443. doi:10.1073/pnas.2011716117
Hayashi, M. (2014). The cold vadose zone: hydrological and ecological significance of frozen‐soil processes. Vadose Zone J. 13, 1–8. doi:10.2136/vzj2013.03.0064
Hincapié, I., and Germann, P. (2009). Gravity-driven viscous flow in sand boxes assessed with neutron radiography. Vadose Zone J. 8 (4), 891–901. doi:10.2136/vzj2009.0003
Hopmans, J. W., et al. (2002). Review of vadose zone technology and solutions. Vadose Zone J. 1 (1), 199–200.
Hsieh, P. A., Bahr, J. M., Doe, T. W., Flint, A. L., Gee, G., Gelhar, L. W., et al. (2001). “Panel report,” in Conceptual models of flow and transport in the fractured vadose zone (Washington, DC: National Academy Press), pp 9–44.
Jarvis, N. J. (2007). A review of non-equilibrium water flow and solute transport in soil macropores: principles, controlling factors and consequences for water quality. Eur. J. Soil Sci. 58 (3), 523–546. doi:10.1111/j.1365-2389.2007.00915.x
Jarvis, N., Koestel, J., and Larsbo, M. (2016). Understanding preferential flow in the vadose zone: recent advances and future prospects. Vadose Zone J. 15 (12), 1–11. doi:10.2136/vzj2016.09.0075
Jury, W. A. (1982). Simulation of solute transport using a transfer function model. Water Resour. Res. 18 (2), 363–368. doi:10.1029/wr018i002p00363
Kean, J. W., Staley, D. M., Lancaster, J. T., Rengers, F. K., Swanson, B. J., Coe, J. A., et al. (2019). Debris-flow inundation and damage data from the 9 January 2018 Montecito debris-flow event. United States: Geological Survey Data Release.
Kratzert, f., Klotz, D., Herrnegger, M., Sampson, A. K., Hochreiter, S., Hochreiter, G. S., et al. (2019). Toward improved predictions in ungauged basins: exploiting the power of machine learning. Water Res. Res. 55 (12), 11344–11354.
Luo, P., Mu, D., Xue, H., Ngo-Duc, T., Dang-Dinh, K., Takara, K., et al. (2018). Flood inundation assessment for the Hanoi Central Area, Vietnam under historical and extreme rainfall conditions. Sci. Rep. 8, 12623. doi:10.1038/s41598-018-30024-5
Maxwell, R. M., and Condon, L. E. (2016). Connections between groundwater flow and transpiration partitioning. Science 353, 377–380. doi:10.1126/science.aaf7891
McDonnell, J. J., Sivapalan, M., Vaché, K., Dunn, S., Grant, G., Haggerty, R., et al. (2007). Moving beyond heterogeneity and process complexity—A new vision for watershed hydrology. Water Resour. Res. 43 (7), W07301. doi:10.1029/2006wr005467
Miller, E. E., and Miller, R. D. (1956). Physical theory for capillary flow phenomena. J. Appl. Phys. 27 (4), 324–332. doi:10.1063/1.1722370
Mirus, B. B., and Nimmo, J. R. (2013). Balancing practicality and hydrologic realism: a parsimonious approach for simulating rapid groundwater recharge via unsaturated-zone preferential flow. Water Resour. Res. 49, 1458. doi:10.1002/wrcr.20141
Moody, J. A., and Martin, D. A. (2001). Post-fire, rainfall intensity-peak discharge relations for three mountainous watersheds in the western USA. Hydrol. Process. 15, 2981–2993. doi:10.1002/hyp.386
Myhre, G., Alterskjær, K., Stjern, C. W., Hodnebrog, ∅., Marelle, L., Samset, B. H., and Stohl, A. (2019). Frequency of extreme precipitation increases extensively with event rareness under global warming. Scientific reports, 9 (1), 1–10.
National Research Council (2000). Research needs in subsurface science-U.S. Department of energy’s environmental management science program. Washington, DC: National Academy Press.
Nimmo, J. R., and Mitchell, L. (2013). Predicting vertically nonsequential wetting patterns with a source-responsive model. Vadose Zone J. 12 (4), 1–11. doi:10.2136/vzj2013.03.0054
Nimmo, J. R., Perkins, K. S., Rose, P. E., Rousseau, J. P., Orr, B. R., Twining, B. V., et al. (2002). Kilometer-scale rapid transport of naphthalene sulfonate tracer in the unsaturated zone at the Idaho national engineering and environmental laboratory. Vadose Zone J. 999, 89–101. doi:10.2113/999.999.89
Or, D. (2020). The tyranny of small scales --on representing soil processes in global land surface models. Water Res. Res. 56 (6).
Orland, E., Roering, J. J., Thomas, M. A., and Mirus, B. B. (2020). Deep learning as a tool to forecast hydrologic response for landslide‐prone hillslopes. Geophys. Res. Lett. 47 (16), e2020GL088731. doi:10.1029/2020GL088731
Orozco‐López, E., Muñoz-Carpena, R., Gao, B., and Fox, G. A. (2018). Riparian vadose zone preferential flow: review of concepts, limitations, and perspectives. Vadose Zone J. 17 (1), 1–20.
Papalexiou, M., and Montanari, A. (2019). Global and regional increase of precipitation extremes under global warming. Water Res. Res. 55 (6), 4901–4914.
Richards, L. A. (1931). Capillary conduction of liquids through porous mediums. Physics 1, 318–333. doi:10.1063/1.1745010
Scaini, A., Amvrosiadi, N., Hissler, C., Pfister, L., and Beven, K. (2019). Following tracer through the unsaturated zone using a multiple interacting pathways model: implications from laboratory experiments. Hydrol. Process. 33 (17), 2300–2313. doi:10.1002/hyp.13466
Tetzlaff, D., Carey, S. K., McNamara, J. P., Laudon, H., and Soulsby, C. (2017). The essential value of long‐term experimental data for hydrology and water management. Water Res. Res. 53 (4), 2598–2604.
Thomas, M. A., Collins, B. D., and Mirus, B. B. (2019). Assessing the feasibility of satellite‐based thresholds for hydrologically driven landsliding. Water Resour. Res. 55 (11), 9006–9023. doi:10.1029/2019WR025577
Tsutsumi, D., Sidle, R. C., and Kosugi, K. (2005). Development of a simple lateral preferential flow model with steady state application in hillslope soils. Water Resour. Res. 41 (12), W12420. doi:10.1029/2004wr003877
Walvoord, M. A., and Kurylyk, B. L. (2016). Hydrologic impacts of thawing permafrost—a review. Vadose Zone J. 15, 1–20. doi:10.2136/vzj2016.01.0010
Zhang, K., Chao, L.-j., Wang, Q.-q., Huang, Y.-c., Liu, R.-h., Hong, Y., et al. (2019). Using multi-satellite microwave remote sensing observations for retrieval of daily surface soil moisture across China. Water Sci. Eng. 12 (2), 85–97. doi:10.1016/j.wse.2019.06.001
Keywords: unsaturated zone, rapid hydrologic response, preferential flow, scaling, water resources
Citation: Nimmo JR, Perkins KS, Plampin MR, Walvoord MA, Ebel BA and Mirus BB (2021) Rapid-Response Unsaturated Zone Hydrology: Small-Scale Data, Small-Scale Theory, Big Problems. Front. Earth Sci. 9:613564. doi: 10.3389/feart.2021.613564
Received: 02 October 2020; Accepted: 11 February 2021;
Published: 26 March 2021.
Edited by:
Venkatesh Merwade, Purdue University, West Lafayette, IN, United StatesReviewed by:
Ashok K. Mishra, Clemson University, Clemson, SC, United StatesPingping Luo, Chang’an University, China
Copyright © 2021 Nimmo, Perkins, Plampin, Walvoord, Ebel and Mirus. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kim S. Perkins, a3BlcmtpbnNAdXNncy5nb3Y=
 John R. Nimmo
John R. Nimmo Kim S. Perkins
Kim S. Perkins Michelle R. Plampin
Michelle R. Plampin Michelle A. Walvoord
Michelle A. Walvoord Brian A. Ebel
Brian A. Ebel Benjamin B. Mirus
Benjamin B. Mirus