A Monte Carlo Model of Gas-Liquid-Hydrate Three-phase Coexistence Constrained by Pore Geometry in Marine Sediments

Gas hydrates form at relatively high pressures in near-surface, organic-rich marine sediments, with the base of the hydrate stability field and the onset of partial gas saturation determined by temperature increases with depth. Because of pore-scale curvature and wetting effects, the transition between gas hydrate and free gas occurrence need not take place at a distinct depth or temperature boundary, but instead can be characterized by a zone of finite thickness in which methane gas bubbles and hydrate crystals coexist with the same aqueous solution. Previous treatments have idealized pores as spheres or cylinders, but real pores between sediment grains have irregular, largely convex walls that enable the highly curved surfaces of gas bubbles and/or hydrate crystals within a given pore to change with varying conditions. In partially hydrate-saturated sediments, for example, the gas–liquid surface energy perturbs the onset of gas–liquid equilibrium by an amount proportional to bubble-surface curvature, causing a commensurate change to the equilibrium methane solubility in the liquid phase. This solubility is also constrained by the curvature of coexisting hydrate crystals and hence the volume occupied by the hydrate phase. As a result, the thickness of the three-phase zone depends not only on the pore space geometry, but also on the saturation levels of the hydrate and gaseous phases. We evaluate local geometrical constraints in a synthetic 3D packing of spherical particles resembling real granular sediments, relate the changes in the relative proportions of the phases to the three-phase equilibrium conditions, and demonstrate how the boundaries of the three-phase zone at the base of the hydrate stability field are displaced as a function of pore size, while varying with saturation level. The predicted thickness of the three-phase zone varies from tens to hundreds of meters, is inversely dependent on host sediment grain size, and increases dramatically when pores near complete saturation with hydrate and gas, requiring that interfacial curvatures become large.

1 Introduction

Natural gas hydrates are ice-like compounds that commonly form in permafrost and marine sediments from mixtures of methane and water (Sloan and Koh, 2007). As a promising source for future energy, methane hydrate has attracted much attention from the oil and gas industry, with further motivation for their study coming from the need to quantify methane migration in sediments (e.g., Nole et al., 2016), assess submarine landslide risk (e.g., Sultan et al., 2004; Handwerger et al., 2017), and understand the material cycle in benthic ecology (e.g., Suess et al., 1999). Seismic data and drilling logs from natural hydrate reservoirs have identified anomalies of high saturation level (i.e., hydrate pore volume fraction) within layers of comparatively coarse sediments, suggesting heterogeneous hydrate accumulation rates that depend not only on temperature and pressure but also on sediment properties (e.g., Borowski, 2004; Malinverno, 2010; Wang et al., 2011; Bahk et al., 2013). Experimental studies also demonstrate that pore sizes play an important role in controlling the spatial and temporal distribution of hydrate deposits (e.g., Yousif et al., 1991; Yousif and Sloan, 1991; Chong et al., 2015; Liu et al., 2015).

The formation of gas hydrate in permafrost and marine sediments is often approximated using the constraint of local bulk equilibrium between a combination of up to three methane-bearing phases: free methane gas (G), methane hydrate (H), and dissolved methane in aqueous solutions (L), in which the methane solubility is a unique function of temperature, pressure and salinity (e.g., Sloan and Koh, 2007). A more precise understanding of these systems must account for perturbations to this bulk phase behavior imposed by the surface properties and geometry of sediment particles, with the gas and hydrate acting most commonly as non-wetting phases, whereas the aqueous solution wets particle surfaces. As hydrate forms or dissociates, hydrate crystals or gas bubbles approach the pore walls, and the phase behavior is affected by the surface energy of the curved L-H or L-G interface, with high curvature causing elevated local dissolved methane concentrations. By constraining allowable interface curvatures, heterogeneously distributed sediment pores introduce deviations in the equilibrium methane concentration at in situ temperature and pressure conditions (Clennell et al., 1999; Henry et al., 1999; Daigle and Dugan, 2011; Rempel, 2011; Dai et al., 2012; Cook and Malinverno, 2013; VanderBeek and Rempel, 2018), thereby affecting both the growth of hydrate deposits and their decomposition. Existing works that approximate the role of pore geometry mostly focus on the average pore size, often simplifying the pores as circular cylinders (e.g., Millington and Quirk, 1961; Wilder et al., 2001; Denoyel and Pellenq, 2002) or spheres connected by cylindrical throats (e.g., Jang and Santamarina, 2011; Liu and Flemings, 2011). These simple pore models provide useful insight into how hydrate forms and dissociates in sediments, but they fail to capture variations in curvature as phase boundaries evolve. Rempel (2011) avoided this limitation by considering triangular pores, and a subsequent two-dimensional treatment (e.g., Rempel, 2012) examined the crevice spaces between random close-packed spheres. By treating granular porous media as packed three-dimensional spherical grains, Chen et al., (2020) used Monte Carlo sampling to effectively approximate the constraints of pore geometry on phase boundary curvatures in a two-component system within randomly packed, poly-dispersed sediments. In this work, focused on three-phase coexistence, we first outline the basic phase behavior expected within 2D triangular pores, and then extend the treatment using an averaging method to approximate the behavior in pores between spherical grains, before examining the fully 3D problem with a Monte Carlo method.

2 Equilibrium Methane Concentration Gradient in Sediments

In marine sediments that are sufficiently coarse-grained for pore-scale curvature effects to be negligible, bulk three-phase equilibrium at the base of the hydrate stability zone (BHSZ) occurs at a distinct depth that is uniquely determined by the pressure, temperature and salinity. Above the bulk BHSZ, the equilibrium methane solubility of the binary L-H system increases with depth, whereas below the BHSZ, the equilibrium is between liquid and free gas, and the methane solubility decreases with depth, driven by increases in the ambient temperature. In typical circumstances with heterogeneously distributed micron-scale pores, however, the hydrate phase, gas phase and aqueous methane solution may coexist in a zone of finite thickness where the upper and lower boundaries are shifted according to the solubility perturbations associated with confining the hydrate and gas phases in tight, and variable effective pore sizes.

The shift in methane solubility from bulk conditions in L-H and L-G two-phase equilibrium can be approximated as follows. For the L-G equilibrium,

${\text{CH}}_4\left(\text{g}\right)\rightleftharpoons {\text{CH}}_4\left(\text{aq}\right),(1)$

the thermodynamic relations for the methane solubility in molar fraction require

${\frac{\partial \ln x_{gl}}{\partial T}|}_P=\frac{{\Delta }_{\text{sol}}^{gl}{H}_m}{R{T}^2}<0,{\frac{\partial \ln x_{gl}}{\partial P}|}_T=\frac{V_m-{\overline{V}}_m}{RT}\approx \frac{1}{P}>0,(2)$

where ${\Delta }_{\text{sol}}^{gl}{H}_m$ is the molar heat of solution of methane gas (negative for this exothermic reaction), $V_m$ is molar volume of methane gas, and ${\overline{V}}_m$ is the partial molar volume of methane in water, which is negligible compared with $V_m$. Partial pressure from water vapor is also negligible because in the temperature range of interest, the saturation vapor pressure is less than 1 kPa, which is much smaller than the hydrostatic pressure. Similarly for the L-H equilibrium,

${\text{CH}}_4\left(\text{aq}\right)+{\text{nH}}_2\text{O}\rightleftharpoons {\text{CH}}_4.{\text{nH}}_2\text{O}\left(\text{s}\right),(3)$

the methane solubility follows

${\frac{\partial \ln x_{hl}}{\partial T}|}_P=\frac{{\Delta }_{\text{sol}}^{hl}{H}_m}{R{T}^2}>0,{\frac{\partial \ln x_{hl}}{\partial P}|}_T=\frac{V_h-{\overline{V}}_m-n{V}_w}{RT}<0,(4)$

where ${\Delta }_{\text{sol}}{H}_m^{hl}$ is the solution heat, and $V_h$ is the molar volume of the hydrate.

Adopting a coordinate axis with the z-direction pointing vertically downwards, the bulk BHSZ is at depth $z_3$ below the seafloor, corresponding to a three-phase equilibrium condition

$T_3=T_0+G_T{z}_3,P_3=P_0+G_P{z}_3,x_{gl}\left(z_3\right)=x_{hl}\left(z_3\right)=x_3,(5)$

where $T_0$ and $P_0$ are the temperature and pressure at the seafloor, and $G_T$ and $G_P$ are the temperature gradient and pressure gradient, respectively, in the sediment. The respective solubilities vary with depth near $z_3$ according to

$g_{gl}={\frac{\text{d}\ln x_{gl}}{\text{dz}}|}_{z_3}=\frac{{\Delta }_{\text{sol}}^{gl}{H}_m}{R{T}_3^2}{G}_T+\frac{1}{P_3}{G}_P,(6)$

$g_{hl}={\frac{\text{d}\ln x_{hl}}{\text{dz}}|}_{z_3}=\frac{{\Delta }_{\text{sol}}^{hl}{H}_m}{R{T}_3^2}{G}_T+\frac{V_h-{\overline{V}}_m-n{V}_w}{R{T}_3}{G}_p,(7)$

where the pressure dependence of L-H solubility is in fact negligible because the volume change is relatively small without the presence of a free gas phase. For illustration, we consider perturbations around the three-phase equilibrium $T_3\approx 295\text{K}$ and $P_3\approx 30\text{MPa}$, and use nominal values for $G_T$ and $G_P$ at Blake Ridge (Table 1) so that

$g_{gl}=-0.309{\text{km}}^{-1},g_{hl}=2.09{\text{km}}^{-1}.(8)$

Because $\left|g_{hl}\right|>\left|g_{sl}\right|$ (i.e., $\left|d\ln x_{hl}z\right|>\left|d\ln x_{gl}z\right|$), the gradient of the gas solubility is much gentler than that of the hydrate solubility, as depicted in Figure 1. The bulk solubilities at $z=z_3+\Delta z$ are approximately

$x_{gl}\left(z\right)=x_3\exp \left(g_{gl}\Delta z\right),x_{hl}\left(z\right)=x_3\exp \left(g_{hl}\Delta z\right).(9)$

Curved surfaces of gas bubbles and methane hydrates within the confined pore space elevate the chemical potential of the non-wetting gas and hydrate phases. At a depth z where three phases coexist, setting the radius of the methane bubble to $r_g$, and the radius of the hydrate crystal to $r_h$, the shifted solubilities are

${x^{\prime }}_{gl}\left(r_g\right)=x_{gl}\left(1+\frac{{\gamma }_{gl}}{P_3+G_P\Delta z}\frac{2}{r_g}\right),{x^{\prime }}_{hl}\left(r_h\right)=x_{hl}\exp \left[\frac{2V_h{\gamma }_{hl}}{R{r}_h\left(T_3+G_T\Delta z\right)}\right].(10)$

Equilibrium between the phases requires

${x^{\prime }}_{gl}\left(r_g\right)={x^{\prime }}_{hl}\left(r_h\right),(11)$

which is expanded to

$\frac{2V_h{\gamma }_{hl}}{r_{h}R\left(T_3+G_T\Delta z\right)}=\left(g_{gl}-g_{hl}\right)\Delta z+\ln \left(1+\frac{2{\gamma }_{gl}}{r_g}\frac{1}{P_3+G_P\Delta z}\right).(12)$

Equation 12 describes the chemical equilibrium when three phases coexist. With $r_h$ and $r_g$ constrained from the pore distribution, the offset $\Delta z$ gives the thickness of the three-phase zone. In simple porous sediment model with a single pore size so that $r_h=r_g$, the three-phase zone shrinks to one unique depth. With heterogeneously distributed effective pore sizes, however, we expect the BHSZ to be characterized by a zone of three-phase coexistence bounded by depths corresponding to equilibrium conditions for which the hydrate crystals and gas bubbles each have different interfacial curvatures (Figure 1) that are nevertheless related by the constraint that each of these non-wetting phases must also be in equilibrium with a wetting aqueous solution containing the same concentration of dissolved methane. Combined with the geometric constraints derived below, Eq. 12 enables us to determine the thickness of the three-phase zone.

TABLE 1

TABLE 1. Nominal parameter values for methane gas, methane hydrate, and water based on homogeneous three-phase equilibrium conditions $T_3=295\text{K}$ and $P_3=30\text{MPa}$ at Blake Ridge. Note that the molar dissociation heat of hydrate is ${\Delta }_{\text{dis}}{H}_m={\Delta }_{\text{sol}}^{hl}{H}_m-{\Delta }_{\text{sol}}^{gl}{H}_m\approx 54\text{kJ}/\text{mol}$, consistent with existing measurements (Anderson, 2004; Gupta et al., 2008).

FIGURE 1

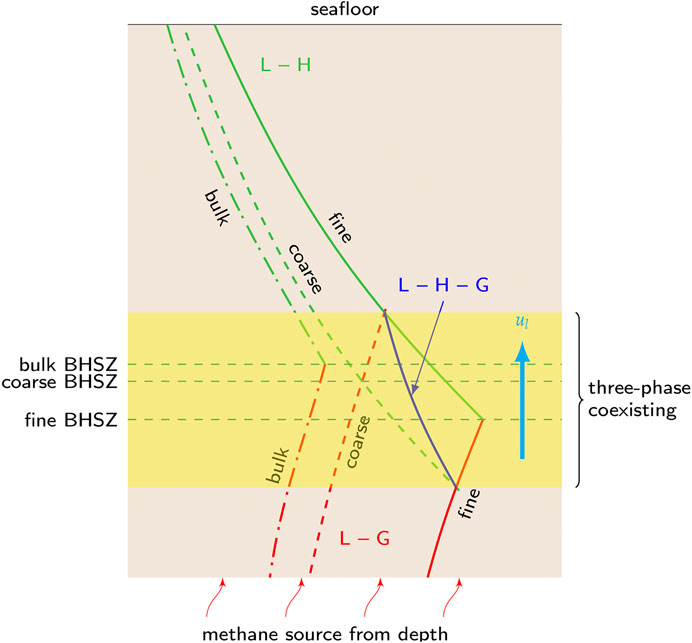
FIGURE 1. The three-phase coexisting zone near the bulk BHSZ. Above the BHSZ, no methane gas is present, and the methane solubility is determined by L-H equilibrium, increasing with depth (green curves). Below the BHSZ, hydrate dissociates so that dissolved methane is instead constrained by equilibrium with free methane gas, and the solubility decreases with depth due to increasing temperature (red curves). Bulk solubility curves correspond to the scenario where pore-scale effects can be neglected. In smaller pores, however, two-phase solubility curves shift toward higher values. The hydrate and methane gas phases can first coexist with the same aqueous solution when the emergent free gas phase at the upper boundary of the zone of three phase coexistence has the smallest possible curvature (i.e., largest radius), while the curvature that characterizes crystals of the residual hydrate phase must remain continuous with the value set by the hydrate saturation level in the two-phase L-H zone above; a parallel set of restrictions pertains at the lower boundary with the roles of gas and hydrate reversed. The dark L-H-G line labels the methane solubility such that even the smallest pores are filled with one non-wetting phase.

3 Geometric Constraints Within Pores

Models consisting of regular pores with concave interior walls, such as spheres or cylinders, permit very little variation to phase boundary curvature, as non-wetting phases fill pore centers and the wetting phase occupies thin films that coat pore walls. In natural irregular pores with predominantly convex interior walls, as the non-wetting phase grows, the phase boundary intrudes further into crevices between solid grains where the wetting phase persists in ever-shrinking convexly bounded pockets. One simplified pore model with features resembling such diminishing crevices is a 2D triangular pore; a more realistic 3D model can be constructed using a conglomerate of packed particles, idealized here as spherical grains. With changing temperatures and/or pressures, for example with increased depth below the seafloor, the hydrate phase (H) is expected to dissociate and a new non-wetting phase (G) will emerge from the wetting phase (L) so that a two-phase equilibrium (L-H) configuration gives way to a new three-phase equilibrium (G-L-H).

The zone of three-phase coexistence may have a finite thickness with varying saturation levels for the non-wetting phases, before reverting to a different two-phase equilibrium (L-G) at still greater depths. Importantly, at the onset of three-phase coexistence, surface energy considerations imply that the emergent phase (in this scenario, G at the top, H at the bottom) is bounded by the largest surface of constant curvature that can fit within the pore space (i.e., a sphere). This simplifies the geometry of the emergent phase considerably and facilitates determination of the three-phase zone thickness while avoiding the need to consider the regions of variable curvature adjacent to the extended wetting films that coat both non-wetting phases elsewhere. A second useful constraint is that the curvature of the residual phase (in this scenario, H at the top, G at the bottom) must remain continuous across the three-phase boundary.

With the two constraints, we can describe the evolution of saturation levels of the non-wetting phases when crossing the boundary from regions of two-phase equilibrium into the zone of three-phase equilibrium. For example, in the L-H region immediately above the three-phase zone, hydrate is the only non-wetting phase in pores, separated from pore walls by films of liquid phase. The hydrate crystals have a radius $r_h$ controlled by the surface energy. At low hydrate saturations, the crystals may take a spherical form, whereas at high saturation levels (with abundant methane), small spheres may coalesce, and occupy the largest pore with bumps growing into nearby crevices with the radius $r_h$. Across the three-phase boundary, a portion of hydrate dissociates, and spherical methane gas bubbles emerge with radius $r_g>r_h$ tangent to the walls of the largest pores and hydrate crystals, whereas remaining hydrate resides in smaller pores and extends into crevices with the same interfacial radius $r_h$ as the crystals in the L-H region right above. At the base of the three-phase zone, where hydrate is the emergent phase and free gas the residual phase, a parallel set of constraints applies with continuous gas radius $r_g$ and spherical hydrate crystals characterized by $r_h>r_g$. For the 2D triangular pore model, an analytical description of these geometrical constraints is available; for the 3D model, we developed an averaging method to represent a mono-dispersed scenario. We describe the geometrical constraints for these two idealized cases next, before outlining our Monte Carlo approach to addressing a more realistic synthetic sediment consisting of randomly packed spherical particles in Section 3.2.

3.1 Geometric Constraints

3.1.1 Simplified 2D Triangular Pores

In a 2D equilateral triangular pore with sides of length W, the radius of the residual non-wetting phase I near the vertices is $R_1$ (Figure 2A). The total pore area is

$A_0=\frac{\sqrt{3}}{4}{W}^2.(13)$

In the case where its boundaries are idealized as spherical, the total area of non-wetting phase I in three vertices is

$\pi R_1^2\le A_1\le 3\pi R_1^2(14)$

where the inequality means not all vertices are necessarily hosting phase I. When a new non-wetting phase II emerges, it must have lower surface energy (i.e., larger radius) so it locates near the center of the pore, with $R_2\approx 3R_1$, and

$A_2=\frac{{\left(h-d\right)}^2}{h^2}{A}_0-\left(3\sqrt{3}-\pi \right)R_2^2.(15)$

where $h=W/2\sqrt{3}$, and d is the film thickness far from vertices along pore walls. The saturations of each phase are

$S_1=\frac{A_1}{A_0},S_2=\frac{A_2}{A_0},S_w=1-S_1-S_2.(16)$

In the limit that $R_2\gg d$, the saturation of the emergent phase is

$S_2\approx 1-\frac{R_2^2}{W^2}\left(12-\frac{4\pi }{\sqrt{3}}\right).(17)$

Here, the pore geometry requires $R_2\le h=W/\left(2\sqrt{3}\right)$ so phase II has minimum saturation $S_2\approx 0.6$, and at the onset of three-phase coexistence $S_1$ may have a range of values below 0.2. However, it remains possible for the two non-wetting phases to occupy separate nearby pores as long as $R_2\approx 3R_1$, and $S_2$ remains a valid description of the saturation level of the emergent phase in equilibrium with L alone at the onset of three-phase coexistence. These geometric constraints apply only at the boundaries of the three-phase zone, and not further within the zone itself. Instead, the gas and hydrate interfacial curvatures within the interior of the three-phase zone depend on the amount of methane present, since it must be partitioned between L, H, and G. It is possible that inside the zone, pores are under-filled, i.e., neither residual phase I and emergent phase II are above a saturation level of 0.6, which we will discuss later.

FIGURE 2

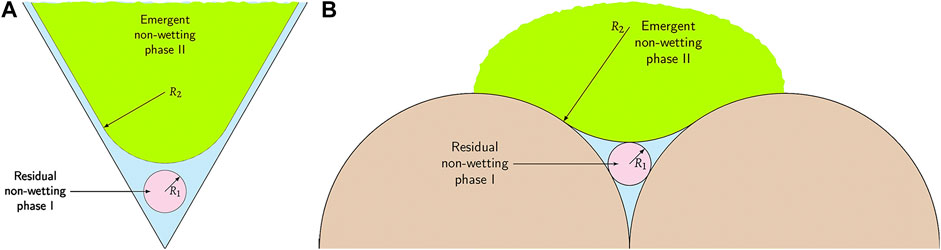
FIGURE 2. Schematic of three-phase coexistence in (A) one 2D equilateral triangular pore and (B) residual liquid reservoir inside one crevice in 3D spherical grains. As the non-wetting phase II emerges, the area or volume occupied by non-wetting phase I shrinks.

3.1.2 Mono-Dispersed 3D Pores

A similar approach combined with an averaging method can be used to obtain saturation estimates in 3D pores. In a mono-dispersed 3D sediment with particle radii R, the entire volume of each pore in a virtual triclinic cell bounded by eight grains with internal angles α, β, and γ is

$V_0=8R^3\sqrt{1+2\cos \alpha \cos \beta \cos \gamma -{\cos }^2\alpha -{\cos }^2\beta -{\cos }^2\gamma }-\frac{4\pi }{3}{R}^3.(18)$

Using the hyper-volume formula (Mackay, 1974), the radius of the largest inscribed sphere is

$r\left(\alpha ,\beta ,\gamma \right)=R\left[\left(\begin{array}{c}\frac{3-2\cos \alpha -2\cos \beta -2\cos \gamma }{1-{\cos }^2\alpha -{\cos }^2\beta -{\cos }^2\gamma +2\cos \alpha \cos \beta \cos \gamma }\\ +\frac{2\cos \alpha \cos \beta +2\cos \beta \cos \gamma +2\cos \gamma \cos \alpha }{1-{\cos }^2\alpha -{\cos }^2\beta -{\cos }^2\gamma +2\cos \alpha \cos \beta \cos \gamma }\\ -\frac{{\cos }^2\alpha +{\cos }^2\beta +{\cos }^2\gamma }{1-{\cos }^2\alpha -{\cos }^2\beta -{\cos }^2\gamma +2\cos \alpha \cos \beta \cos \gamma }\end{array}\right)\frac{1}{2}-1\right](19)$

Phase II attains equilibrium as the new non-wetting phase with radius $R_2\le r\left(\alpha ,\beta ,\gamma \right)$ given by Eq. 19. Similar to the 2D case, the emergent phase II may appear as spheres with radius $R_2\le r\left(\alpha ,\beta ,\gamma \right)$ adjacent to phase I, or as a contorted body intruding into all possible interstitial sites, with a surface characterized by small bumps of $R_2$ tangent to the bounding sediment particles to form crevices. The residual non-wetting phase I may stay inside one or more crevices, as shown in Figure 2B. Neglecting the small volumes contributed by liquid films, as before, we have

$R_1=\frac{{\left(R\cot \delta -R_2\right)}^2}{2\left(R+R\cot \delta -R_2\right)}(20)$

where $\delta =\arcsin \left[R/\left(R+R_2\right)\right]$. The wetting phase volume is well-approximated as filling a trio of minor crevices (two of which are bounded on one side by phase II while the other sides approach particle surfaces), so that the wetting volume is

$V_w=6\pi R_2^2\left(R-\delta \sqrt{R_2\left(R_2+2R\right)}\right)-V_1.(21)$

Here, the total volume $V_1$ occupied by phase I is bounded between the volume of balls of radius $R_1$ and that of three tori

$\pi R_1^3\le V_1\le 6\pi R_1^3\sqrt{1+2R/R_1},(22)$

while the volume occupied by phase II is

$V_2=V_0-6\pi R_2^2\left[R-\delta \sqrt{R_2\left(R_2+2R\right)}\right].(23)$

Finally, the saturation levels can be written as

$S_1=\frac{V_1}{V_0},S_2=\frac{V_2}{V_0},S_w=\frac{V_w}{V_0}.(24)$

For the collective values of R₁, R₂, and S₂ over numerous pores, these values are averaged over angles α, β, and γ (see Appendix 1 for details).

At the top and bottom of the three-phase coexisting zone, we recognize the emergent phase II as the gas and hydrate phases, respectively. The analyses for the 2D and 3D scenarios suggest that the saturation of the residual phase $S_1$ can vary within a range, while the saturation of the emergent phase $S_2$ is better constrained.

3.2 Monte Carlo Simulation of 3D Pores

In natural, randomly packed sediments, clearly the virtual cell of Section 3.1.2 may be heavily distorted, and the distributions of angles are affected by grain radii, so the averaging method may not work properly. We develop a Monte Carlo scheme to simulate the growth of the emergent phase as constrained by the pore geometry, as well as the requirement imposed by continuity of solubility. We test the method here using the mono-dispersed random close pack of Finney (1970), and sample the cross-section of the pack with $N=2000$ random test points. For each test point located in the pore space, we find the largest inscribed sphere containing the test point, which is recognized as emergent phase II with a radius $R_2$, and in the crevices formed between the sphere and two tangent particles, we calculate a tangent coplanar sphere as residual phase I. There may be more than one possible crevice in each pore because the phase II sphere may touch as many as four particles, and we choose the largest residual phase I sphere, with radius $R_1$. We record all pairs of phase I and II sphere radii $\left(R_1,R_2\right)$, and sort them according to the values of $R_2$. This sorting procedure enables us to approximate the saturation level of phase II with radius $R_2$ as the proportion of sampled points that are encompassed by phase II (see Chen et al., 2020, for a more detailed discussion). After scaling with particle radius, we solve for the corresponding $\Delta z$ using Eq. (12). The Monte Carlo sampling procedure results in different estimates of $\Delta z$ for estimates of the emergent-phase saturation $S_2$, and we recognize the envelope of extremal values as approximating the depth range of three-phase coexistence.

4 Model Results

We seek the upper and lower depth limits that define the zone where three-phase equilibrium may occur. At the top of this zone, free gas is the emergent phase II and hydrate is the residual phase I, whereas at the bottom these roles are reversed, with the gas constituting the residual phase I and hydrate the emergent phase II. By applying the geometric constraints derived in the 2D and 3D scenarios just described to Eq. 12, we can determine the dependence of $\Delta z$ on $S_2$. For uniform 2D triangular pores (Figure 3A), the pore geometry requires $R_2\le W/\left(2\sqrt{3}\right)$, so that the minimum $S_2\approx 0.6$. For 3D pores in mono-dispersed grains (Figure 3B), the thickness of the three-phase zone is the average over all pores, and the minimum $S_2$ is around 0.75. Because the z-direction points downwards, the figures are plotted with flipped $\Delta z$ so that shallower locations (negative $\Delta z$) are above deeper locations (positive $\Delta z$).

FIGURE 3

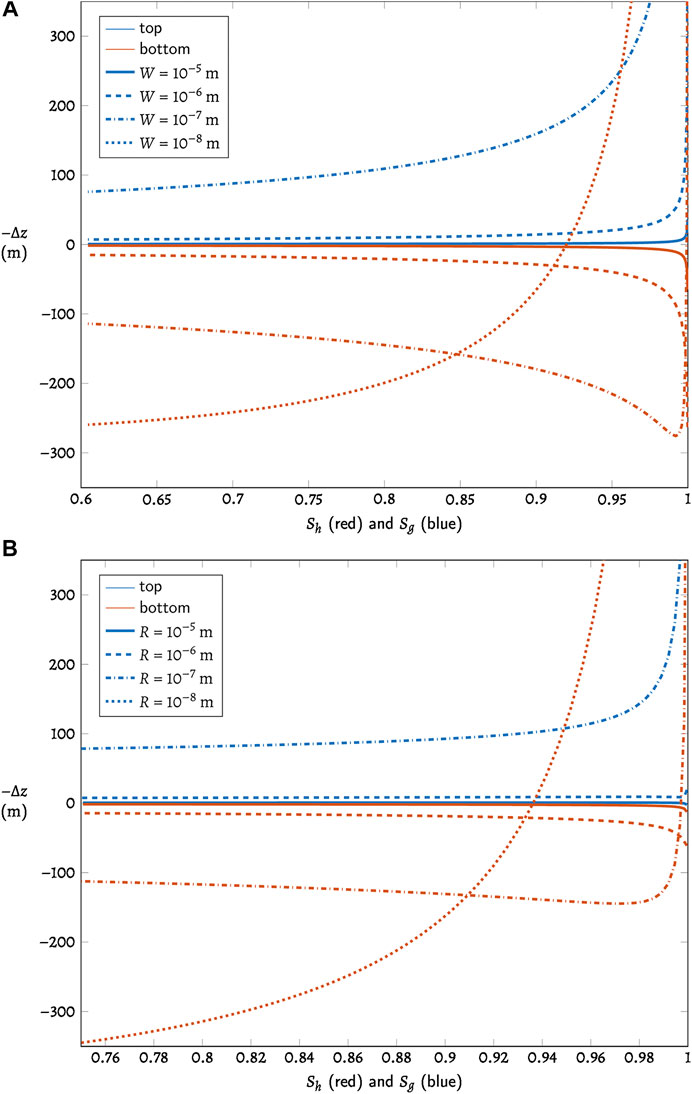
FIGURE 3. The shifted three-phase boundary $\Delta z_b$ and $\Delta z_t$ at the first appearance of the emergent phase II as a function of the saturation level $S_2$, shown for the different values of (A) pore size W and (B) grain size R noted in the legend. Note that since z is pointing downwards, we have the z-axis flipped so that shallower location stays above deeper locations.

The two scenarios behave similarly. With larger pores, the zone of three-phase coexistence is thin, but as pore size decreases (represented by the different lines in Figure 3, with sizes noted in the legends), the upper and lower boundaries of the three-phase zone deviate further from zero, corresponding to a thicker zone of three-phase coexistence. In the smaller pores of finer sediments, the hydrate phase begins to dissociate and the gas phase emerges at a depth much shallower than the bulk BHSZ, but the hydrate phase may also persist to a depth far below the bulk BHSZ. The thickness of the zone of three-phase coexistence is constrained as well by the requirement that solubility remain continuous across the boundaries with adjacent two-phase zones, leading to the dependence on $S_2$ — the saturation of emergent phase.

Figure 4 compares the 3D average result from Section 3.1.2 with the Monte Carlo simulation result from Section 3.2. The upper and lower bounds of the Monte Carlo results match well with the average curves at the beginning, but deviate further at high saturation levels. In finer sediments, boundaries marked by the Monte Carlo results begin to deviate further from the averaging result. We attribute this discrepancy to errors in the averaging procedure produced by distortions to the virtual cell.

FIGURE 4

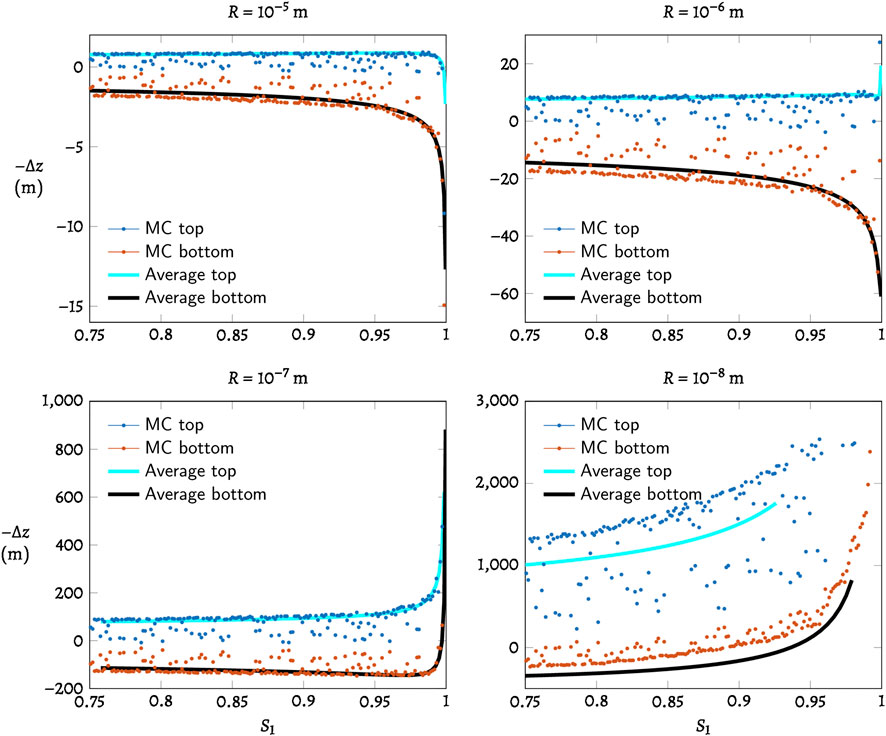
FIGURE 4. Monte Carlo simulation of shifted three-phase boundary $\Delta z_b$ and $\Delta z_t$ for residual phase I before the appearance of emergent phase II as a function of grain size R, and comparison with 3D averaging results (black and cyan solid lines). The upper and lower bounds begin to deviate when the saturation is high and R is significantly reduced.

We emphasize that it is not necessarily the case that any particular pore in the zone of three-phase coexistence can hold all three phases, and in fact such a configuration is only possible at very high methane input. Nevertheless, since the volume occupied by phase I determines its interfacial curvature and hence the methane solubility in the adjacent two-phase zone, together with the pore size constraint on the geometry available for phase II, this implies that the three-phase thickness (i.e., bounded by the first appearance of a secondary non-wetting phase) must depend on both the saturation of the primary (residual) non-wetting phase and the pore size distribution.

5 Discussion

5.1 Growth of the New Phase

The geometric constraints applied in the 2D and 3D scenarios treat the emergent phase as volumetrically dominant, limited in extent by the pore walls and residual phase. It must be noted that the radius of the emergent phase may be restricted by the presence of the residual phase; when the new phase nucleates, it is assumed to form near an interface with the residual phase, essentially replacing much of the pre-existing phase I to reach the minimum free-energy configuration while maintaining the same phase I curvature as that which pertains outside the three-phase coexisting zone.

Alternatively, the new phase could grow in the largest pores, either without being adjacent to the residual phase, or by completely replacing the residual phase that would have occupied those pores under the slightly perturbed conditions in the adjacent two-phase zone. In this situation, to satisfy the continuity of phase I curvature with that outside the three-phase zone, phase I can persist either in the form of small residual inclusions within pore crevices, or as a body filling almost all of smaller pores with bumps of small radii $R_1$. In the first case, the small radius characterizing the residual phase in the two-phase region suggests high methane solubility, which is unstable because the chemical potential can be further minimized by increasing $R_1$ and reducing methane solubility. The second case leads to unrealistically high saturation levels for the hydrate crystals or methane bubbles.

5.2 Under-Filled Region Within the Zone

In our models, both non-wetting phases are mobile in the pores as long as not limited by the pore walls and the other non-wetting phase. At the boundaries, the emergent phase spans the pore center while the residual phase stays in the crevices. If the residual phase occupies a significant fraction of the pore, emergent phase may not be able to touch the pore walls, resulting in a lower saturation ($<0.6$ for the 2D pores and $<0.75$ for 3D pores). This under-filling scenario can be intuitively investigated for the 2D model, where the residual phase has a radius $R_1>W/\left(6\sqrt{3}\right)$, or $S_1>0.2$ (Figure 5). The value of $R_2$ is smaller accordingly, and so is the value of $S_2$. Ignore d and let $R_1=\alpha W$, and we can find the corresponding $R_2$

$\frac{R_2}{W}=\frac{1}{\sqrt{3}}-\frac{2}{3}\sqrt{\sqrt{3}\alpha -2{\alpha }^2}-\frac{\alpha }{3}(25)$

where $2\sqrt{3}\le {\alpha }^{-1}\le 6\sqrt{3}$. In this configuration, $R_1$ and $R_2$ are symmetric, and it is easy to calculate that the offsets is smaller than the configuration in Figure 2A. We postulate that for the 3D pores, the under-filled configuration also gives smaller offsets. The three-phase zone is bounded by the maximum offset possible with given pore structure, pressure, and temperature, and under-filling cases are located in between the maxima. In pores located near the middle of the three-phase zone, both non-wetting phases may be under-filling, allowing the transition from L-H above the three-phase zone to L-G beneath the three-phase zone. Therefore, when seeking the boundaries of the three-phase zone, we need only consider configurations in which the emergent phase fills pore centers.

FIGURE 5

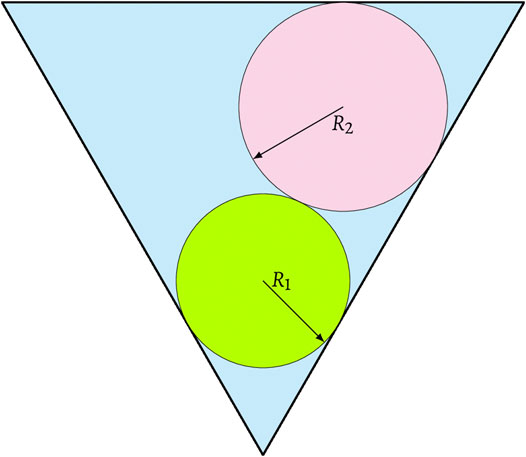
FIGURE 5. A schematic of an under-filled configuration where phase I prevents phase II to span the pore center in a triangular pore.

5.3 Shifted BHSZ and BSR

The bottom simulating reflector (BSR) is commonly interpreted as marking the BHSZ, which is the boundary separating the hydrate phase above from the free gas phase below. However, due to perturbations in salinity and the pore scale effects described here, hydrates can still be present at equilibrium below the bulk BHSZ while free gas bubbles can persist above the bulk BHSZ. Our calculations show that the resulting zone of three-phase coexistence can vary in thickness from only a few meters to many tens of meters. This may cause the temperature and pressure at the BSR to deviate from three-phase equilibrium conditions, and the observed depth of BSR may differ from the bulk BHSZ. For example, the Ocean Drilling Project Leg 164 at Blake Ridge found that the temperatures at the BSR are 0.5°–2.9 °C lower than the theoretical equilibrium temperature; this corresponds to an upwards shift of 30–100 m above the bulk BHSZ, assuming a geothermal gradient of $\sim 30\mathrm{°}\text{C}/\text{km}$ (Ruppel, 1997). Liu and Flemings (2011) showed that it is also possible to have the top of the three-phase zone below the bulk equilibrium depth, resulting in a deeper BHSZ. Such discrepancies have been attributed to shifted hydrate equilibria in porous media. In Figure 4 the simulated top positions in some cases are lower than the bulk BHSZ. Our model predicts that a zone of three-phase coexistence can be expected to span the bulk BHSZ, with its upper boundary shifted toward colder temperatures by an amount controlled both by the hydrate saturation in the L-H region above, and the largest pore sizes available to emergent gas bubbles, giving a quantitative explanation for the observed discrepancy.

5.4 Implications for Poly-Dispersed and Non-Spherical Granular Sediments

Our model deals with simplified pores in mono-dispersed spherical grains, and our averaging method is strictly valid only for pores bounded by grains in direct contact. Theoretically, crevices can occur between separated grains, but as the distance between the two grains increases, it is much more difficult for liquid connecting the grains to form a concave meniscus with positive mean curvature. Hence, at low liquid saturations, most liquid stays in crevices between contacting grains. In real sediments, grains are poly-dispersed and irregular. If the grains are silt-sized and assumed spherical and contacting, we can model a random packing using the drop-and-roll method (Chen et al., 2020) with the particle sizes following a specified distribution, and apply the Monte Carlo method similarly. When the particle sizes follow a log-normal distribution $\ln \mathcal{N}\left(\mu ,{\sigma }^2\right)$, our simulation results suggest that the shifted three-phase zone will remain mostly the same as in the mono-dispersed situation, except that the relevant grain size R should be comparable to the median radius $R_m=\exp \left(\mu \right)$ (defined by particle count rather than weight).

Constructing realistic synthetic packings that incorporate highly non-spherical grains, as expected of sediments with significant clay contents, is a more challenging numerical problem. Chen et al., (2020) pursued a simplified strategy in which two-phase saturation predictions were performed on a mono-dispersed packing with particle radii chosen so that the specific surface area matched the measured value for a silt loam (73 m²/g: 33% sand, 49% silt, 18% clay by weight; Or and Tuller, 1999). Comparisons with partial saturation measurements showed excellent agreement when the non-wetting phase occupied more than 90% of the pore space, and the agreement remained acceptable down to about 60% non-wetting phase saturation. Further exploration of these results suggests that most of the residual wetting phase under these conditions is found in the increased numbers of small crevice-like regions in the vicinity of particle contacts. In sediment with significant amounts of non-spherical grains such as clay minerals, the crevice-like regions may be smaller, which limits the size of residual phase, and possibly will cause a thicker three-phase zone.

5.5 Sensitivity of Emergent Phase Stability to Residual Phase Saturation

Because residual phase saturation has a strong influence on the thickness of the zone of three-phase coexistence, it is possible to estimate the saturation of the hydrate or gas phase from BSR observations if the median particle size is known or can be estimated. However, since both the saturation level of the residual phase and the particle size of the host sediment can vary over short distances, we may expect that in some patches there may be interleaving of two-phase and three-phase zones. This further complicates the interpretation of BSR observations, and may be responsible for discontinuities in BSR location.

6 Conclusion

By approximating porous sediments as consisting of pores with diminishing crevices, we have demonstrated that near the base of the gas hydrate stability field, the upper (cold) boundary of a three-phase region is set by the gas—liquid surface energy of the first spherical bubbles that can form in the partially hydrate-saturated sediments, while the lower (warm) boundary is controlled by the surface energy of the first hydrate crystals that can form in the partially gas-saturated sediments. Of more fundamental importance, our analysis shows that the thickness of the three-phase zone depends not only on the grain-size distribution, increasing dramatically from tens of meters in porous sediments with a median grain size of 1 µm to hundreds of meters when the median grain size is 0.1 µm, but that in a given sediment the thickness is also sensitive to the saturation levels of hydrate and gas at the boundaries with the two-phase zones above and below.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JC and AR conceived the original idea of how the residual phase must affect the thickness three-phase coexisting zone, and how it might be calculated. SM helped JC with the numerical implementation of these ideas in the Monte Carlo calculations. All authors contributed toward the writing, interpretations, and editing.

Funding

JC was supported by funding from the National Natural Science Foundation of China (Grant No. 41804085). SM was supported by Chinese Academy of Sciences (No. QYZDY-SSW-DQC029) and the National Natural Science Foundation of China (No. 41674097).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

AR appreciates the motivation and context gained during many stimulating discussions at the 2020 GRC on Natural Gas Hydrate Systems, chaired by Timothy Collett.

Appendix

1 Averaging Method in Random Packing of Mono-Dispersed Spherical Grains

Bordia (1984) provided a theoretical method to average properties in mono-dispersed random packings. The packing can be viewed as consisting of numerous virtual triclinic cells formed by eight grains (Figure A1), where $P_1$, $P_2$, $P_3$, and $P_4$ are actual grains, and the other four are virtual, with each side $2R$ and three random angles α, β, and γ.

FIGURE A1

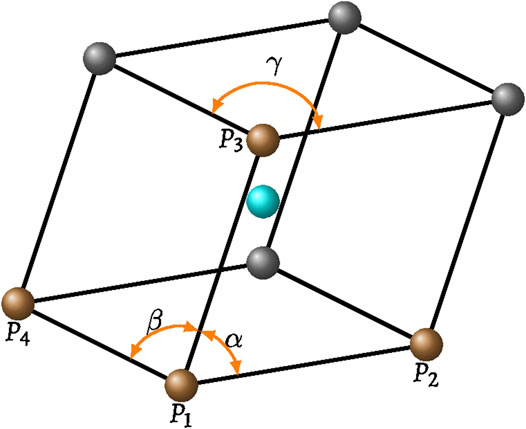
FIGURE A1. A virtual triclinic cell formed by eight grains with each side $2R$ and three random angles α, β, and γ. Bonds mean the two grains are in contact. The brown dots represent centers of actual grains, the gray dots are for virtual grains, and the cyan dot is the interstitial site.

The triclinic cells have two limits. One is the loose limit which is a simple cubic, where

$\alpha =\beta =\gamma =\frac{\pi }{2}(\mathrm{A1})$

while the tight limit is the face-centered cubic packing

$\alpha =\beta =\gamma =\frac{\pi }{3}.(\mathrm{A2})$

For an arbitrary property Y, in one arbitrary cell, its value is $Y\left(\alpha ,\beta ,\gamma \right)$, and the three independent varying angles α, β, and γ are assumed uniformly distributed in $\left[\pi /3,\pi /2\right]$, so they have the same probability density function

$\psi \left(\alpha \right)=\psi \left(\beta \right)=\psi \left(\gamma \right)=\frac{6}{\pi }(\mathrm{A3})$

and the bulk property Y can be calculated by

$\begin{array}{c}\langle Y\rangle ={\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}{\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}{\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}Y\left(\alpha ,\beta ,\gamma \right)\psi \left(\alpha \right)\psi \left(\beta \right)\psi \left(\gamma \right)d\alpha d\beta d\gamma }}}\\ ={\left(\frac{6}{\pi }\right)}^3{\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}{\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}{\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}Y\left(\alpha ,\beta ,\gamma \right)d\alpha d\beta d\gamma }}}.\end{array}(\mathrm{A4})$

For example, if Y is the packing factor F, in one cell the packing factor is

$F\left(\alpha ,\beta ,\gamma \right)=\frac{4\pi R^3}{3V\left(\alpha ,\beta ,\gamma \right)}(\mathrm{A5})$

where the volume of the cell is

$V\left(\alpha ,\beta ,\gamma \right)=8R^3\sqrt{1+2\cos \alpha \cos \beta \cos \gamma -{\cos }^2\alpha -{\cos }^2\beta -{\cos }^2\gamma }.(\mathrm{A6})$

And the mean bulk packing factor is

$\langle F\rangle ={\left(\frac{6}{\pi }\right)}^3{\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}{\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}{\displaystyle \underset{\frac{\pi }{3}}{\overset{\frac{\pi }{2}}{\int }}F\left(\alpha ,\beta ,\gamma \right)\text{d}\alpha \text{d}\beta \text{d}\gamma }}}\approx 0.599(\mathrm{A7})$

close to 0.6 for random loose packing (Dullien, 2012).

For poly-dispersed grains, the virtual cell may be heavily distorted, and the distributions of angles are affected by grain radii, so the averaging method may not work properly.

References

Anderson, G. K. (2004). Enthalpy of dissociation and hydration number of methane hydrate from the Clapeyron equation. J. Chem. Therm. 36, 1119–1127. doi:10.1016/j.jct.2004.07.005

CrossRef Full Text | Google Scholar

Bahk, J.-J., Kim, D.-H., Chun, J.-H., Son, B.-K., Kim, J.-H., Ryu, B.-J., et al. (2013). Gas hydrate occurrences and their relation to host sediment properties: results from second Ulleung basin gas hydrate drilling expedition, East Sea. Mar. Petrol. Geol. 47, 21–29. doi:10.1016/j.marpetgeo.2013.05.006

CrossRef Full Text | Google Scholar

Bordia, R. K. (1984). A theoretical analysis of random packing densities of mono-sized spheres in two and three dimensions. Scripta Metall. 18, 725–730. doi:10.1016/0036-9748(84)90328-4

CrossRef Full Text | Google Scholar

Borowski, W. S. (2004). A review of methane and gas hydrates in the dynamic, stratified system of the Blake ridge region, offshore South Eastern North America. Chem. Geol. 205, 311–346. doi:10.1016/j.chemgeo.2003.12.022

CrossRef Full Text | Google Scholar

Chen, J., Mei, S., Irizarry, J. T., and Rempel, A. W. (2020). A Monte Carlo approach to approximating the effects of pore geometry on the phase behavior of soil freezing. J. Adv. Model. Earth Syst. 12, e2020MS002117. doi:10.1029/2020ms002117

CrossRef Full Text | Google Scholar

Chong, Z. R., Yang, M., Khoo, B. C., and Linga, P. (2015). Size effect of porous media on methane hydrate formation and dissociation in an excess gas environment. Ind. Eng. Chem. Res. 55, 7981–7991. doi:10.1021/acs.iecr.5b03908

CrossRef Full Text | Google Scholar

Clennell, M. B., Hovland, M., Booth, J. S., Henry, P., and Winters, W. J. (1999). Formation of natural gas hydrates in marine sediments: 1. conceptual model of gas hydrate growth conditioned by host sediment properties. J. Geophys. Res. 104, 22985–23003. doi:10.1029/1999jb900175

CrossRef Full Text | Google Scholar

Cook, A. E., and Malinverno, A. (2013). Short migration of methane into a gas hydrate-bearing sand layer at Walker Ridge, Gulf of Mexico. Geochem. Geophys. Geosyst. 14, 283–291. doi:10.1002/ggge.20040

CrossRef Full Text | Google Scholar

Dai, S., Santamarina, J. C., Waite, W. F., and Kneafsey, T. J. (2012). Hydrate morphology: physical properties of sands with patchy hydrate saturation. J. Geophys. Res. 117, B11205. doi:10.1029/2012jb009667

CrossRef Full Text | Google Scholar

Daigle, H., and Dugan, B. (2011). Capillary controls on methane hydrate distribution and fracturing in advective systems. Geochem. Geophys. Geosyst. 12, Q01003. doi:10.1029/2010gc003392

CrossRef Full Text | Google Scholar

Denoyel, R., and Pellenq, R. J. M. (2002). Simple phenomenological models for phase transitions in a confined geometry. 1: melting and solidification in a cylindrical pore. Langmuir 18, 2710–2716. doi:10.1021/la015607n

CrossRef Full Text | Google Scholar

Duan, Z., and Mao, S. (2006). A thermodynamic model for calculating methane solubility, density and gas phase composition of methane-bearing aqueous fluids from 273 to 523K and from 1 to 2000bar. Geochem. Cosmochim. Acta 70, 3369–3386. doi:10.1016/j.gca.2006.03.018

CrossRef Full Text | Google Scholar

Dullien, F. (2012). Porous media fluid transport and pore structure. San Diego, CA: Elsevier Science.

Finney, J. L. (1970). Random packings and the structure of simple liquids. i. the geometry of random close packing. Proc. R. Soc. A 319, 479–493. doi:10.1098/rspa.1970.0189

CrossRef Full Text | Google Scholar

Gupta, A., Lachance, J., Sloan, E. D., and Koh, C. A. (2008). Measurements of methane hydrate heat of dissociation using high pressure differential scanning calorimetry. Chem. Eng. Sci. 63, 5848–5853. doi:10.1016/j.ces.2008.09.002

CrossRef Full Text | Google Scholar

Handwerger, A. L., Rempel, A. W., and Skarbek, R. M. (2017). Submarine landslides triggered by destabilization of high-saturation hydrate anomalies. Geochem. Geophys. Geosyst. 18, 2429–2445. doi:10.1002/2016gc006706

CrossRef Full Text | Google Scholar

Hardy, S. C. (1977). A grain boundary groove measurement of the surface tension between ice and water. Phil. Mag. 35, 471–484. doi:10.1080/14786437708237066

CrossRef Full Text | Google Scholar

Henry, P., Thomas, M., and Clennell, M. B. (1999). Formation of natural gas hydrates in marine sediments: 2. thermodynamic calculations of stability conditions in porous sediments. J. Geophys. Res. 104, 23005–23022. doi:10.1029/1999jb900167

CrossRef Full Text | Google Scholar

Jang, J., and Santamarina, J. C. (2011). Recoverable gas from hydrate-bearing sediments: pore network model simulation and macroscale analyses. J. Geophys. Res. 116. doi:10.1029/2010jb007841

CrossRef Full Text | Google Scholar

Liu, W., Wang, S., Yang, M., Song, Y., Wang, S., and Zhao, J. (2015). Investigation of the induction time for THF hydrate formation in porous media. J. Nat. Gas Sci. Eng. 24, 357–364. doi:10.1016/j.jngse.2015.03.030

CrossRef Full Text | Google Scholar

Liu, X., and Flemings, P. B. (2011). Capillary effects on hydrate stability in marine sediments. J. Geophys. Res. 116. doi:10.1029/2010jb008143

CrossRef Full Text | Google Scholar

Lu, W., Chou, I. M., and Burruss, R. C. (2008). Determination of methane concentrations in water in equilibrium with Si methane hydrate in the absence of a vapor phase by in situ Raman spectroscopy. Geochem. Cosmochim. Acta 72, 412–422. doi:10.1016/j.gca.2007.11.006

CrossRef Full Text | Google Scholar

Mackay, A. L. (1974). Generalized structural geometry. Acta Crystallogr. A 30, 440–447. doi:10.1107/s0567739474000945

CrossRef Full Text | Google Scholar

Malinverno, A. (2010). Marine gas hydrates in thin sand layers that soak up microbial methane. Earth Planet Sci. Lett. 292, 399–408. doi:10.1016/j.epsl.2010.02.008

CrossRef Full Text | Google Scholar

Millington, R. J., and Quirk, J. P. (1961). Permeability of porous solids. Trans. Faraday Soc. 57, 1200. doi:10.1039/tf9615701200

CrossRef Full Text | Google Scholar

Nole, M., Daigle, H., Cook, A. E., and Malinverno, A. (2016). Short-range, overpressure-driven methane migration in coarse-grained gas hydrate reservoirs. Geophys. Res. Lett. 43, 9500–9508. doi:10.1002/2016gl070096

CrossRef Full Text | Google Scholar

Or, D., and Tuller, M. (1999). Liquid retention and interfacial area in variably saturated porous media: upscaling from single-pore to sample-scale model. Water Resour. Res. 35, 3591–3605. doi:10.1029/1999wr900262

CrossRef Full Text | Google Scholar

Rempel, A. W. (2011). A model for the diffusive growth of hydrate saturation anomalies in layered sediments. J. Geophys. Res. 116, B10105. doi:10.1029/2011jb008484

CrossRef Full Text | Google Scholar

Rempel, A. W. (2012). Hydromechanical processes in freezing soils. Vadose Zone J. 11, vzj2012.0045. doi:10.2136/vzj2012.0045

CrossRef Full Text | Google Scholar

Ruppel, C. (1997). Anomalously cold temperatures observed at the base of the gas hydrate stability zone on the U.S. Atlantic passive margin. Geology 25, 699–702. doi:10.1130/0091-7613(1997)025<0699:actoat>2.3.co;2

CrossRef Full Text | Google Scholar

Sloan, E. D., and Koh, C. (2007). Clathrate hydrates of natural gases. Boca Raton, FL: CRC Press.

Suess, E., Torres, M. E., Bohrmann, G., Collier, R. W., Greinert, J., Linke, P., et al. (1999). Gas hydrate destabilization: enhanced dewatering, benthic material turnover and large methane plumes at the cascadia convergent margin. Earth Planet Sci. Lett. 170, 1–15. doi:10.1016/s0012-821x(99)00092-8

CrossRef Full Text | Google Scholar

Sultan, N., Cochonat, P., Foucher, J.-P., and Mienert, J. (2004). Effect of gas hydrates melting on seafloor slope instability. Mar. Geol. 213, 379–401. doi:10.1016/j.margeo.2004.10.015

CrossRef Full Text | Google Scholar

Sun, R., and Duan, Z. (2005). Prediction of CH₄ and CO₂ hydrate phase equilibrium and cage occupancy from ab initio intermolecular potentials. Geochem. Cosmochim. Acta 69, 4411–4424. doi:10.1016/j.gca.2005.05.012

CrossRef Full Text | Google Scholar

VanderBeek, B. P., and Rempel, A. W. (2018). On the importance of advective versus diffusive transport in controlling the distribution of methane hydrate in heterogeneous marine sediments. J. Geophys. Res. Solid Earth 123, 5394–5411. doi:10.1029/2017jb015298

CrossRef Full Text | Google Scholar

Wagner, W., and Pruss, A. (1993). International equations for the saturation properties of ordinary water substance. Revised according to the international temperature scale of 1990. Addendum to J. Phys. Chem. Ref. Data 16, 893 (1987). J. Phys. Chem. Ref. Data 22, 783–787. doi:10.1063/1.555926

CrossRef Full Text | Google Scholar

Wang, X., Hutchinson, D. R., Wu, S., Yang, S., and Guo, Y. (2011). Elevated gas hydrate saturation within silt and silty clay sediments in the Shenhu area, South China Sea. J. Geophys. Res. 116. doi:10.1029/2010jb007944

CrossRef Full Text | Google Scholar

Wilder, J. W., Seshadri, K., and Smith, D. H. (2001). Modeling hydrate formation in media with broad pore size distributions. Langmuir 17, 6729–6735. doi:10.1021/la010377y

CrossRef Full Text | Google Scholar

Yousif, M. H., Abass, H. H., Selim, M. S., and Sloan, E. D. (1991). Experimental and theoretical investigation of methane-gas-hydrate dissociation in porous media. SPE Reservoir Eng. 6, 69–76. doi:10.2118/18320-pa

CrossRef Full Text | Google Scholar

Yousif, M. H., and Sloan, E. D. (1991). Experimental investigation of hydrate formation and dissociation in consolidated porous media. SPE Reservoir Eng. 6, 452–458. doi:10.2118/20172-pa

CrossRef Full Text | Google Scholar