
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci., 16 November 2020
Sec. Hydrosphere
Volume 8 - 2020 | https://doi.org/10.3389/feart.2020.554845
This article is part of the Research TopicStochastic Modeling in HydrogeologyView all 11 articles
Surface-water divides can be delineated by analyzing digital elevation models. They might, however, significantly differ from groundwater divides because the groundwater surface does not necessarily follow the surface topography. Thus, in order to delineate a groundwater divide, hydraulic-head measurements are needed. Because installing piezometers is cost- and labor-intensive, it is vital to optimize their placement. In this work, we introduce an optimal design analysis that can identify the best spatial configuration of piezometers. The method is based on formal minimization of the expected posterior uncertainty in localizing the groundwater divide. It is based on the preposterior data impact assessor, a Bayesian framework that uses a random sample of models (here: steady-state groundwater flow models) in a fully non-linear analysis. For each realization, we compute virtual hydraulic-head measurements at all potential well installation points and delineate the groundwater divide by particle tracking. Then, for each set of virtual measurements and their possible measurement values, we assess the uncertainty of the groundwater-divide location after Bayesian updating, and finally marginalize over all possible measurement values. We test the method mimicking an aquifer in South-West Germany. Previous works in this aquifer indicated a groundwater divide that substantially differs from the surface-water divide. Our analysis shows that the uncertainty in the localization of the groundwater divide can be reduced with each additional monitoring well. In our case study, the optimal configuration of three monitoring points involves the first well being close to the topographic surface water divide, the second one on the hillslope toward the valley, and the third one in between.
Groundwater divides are curves separating different subsurface catchments. Water entering the subsurface on one side of the groundwater divide ends up in a different receptor than water infiltrating on the other side of the divide. Delineating groundwater divides is therefore important for the analysis of aquifer water budgets, for investigating contaminant fate, and other applications of groundwater management. Groundwater divides also represent attractive geometries for setting second-type boundaries of hydrogeological models, since the water flux across the divide is zero (e.g., Pöschke et al., 2018; Erdal and Cirpka, 2019; Qiu et al., 2019). Obviously, a natural stream network contains many nested surface water and groundwater divides of different order (i.e., a catchment can be subdivided into sub-catchments). That is why for the mentioned research areas, it is always important to define the scale of investigation to identify which groundwater divides are relevant and which sub-catchments can be attributed to a higher-order catchment.
A common assumption when delineating groundwater divides is that the groundwater table is a subdued representation of the surface topography (Tóth, 1963; Haitjema and Mitchell-Bruker, 2005). This simplifies the delineation to finding the surface water divides, which can be derived directly from digital elevation models using geographic information systems (Tarboton et al., 1991). However, the topography of a phreatic groundwater surface may substantially differ from the land surface so that the groundwater and surface water divides do not coincide (Haitjema and Mitchell-Bruker, 2005; Bloxom and Burbey, 2015; Han et al., 2019). In fact, Haitjema and Mitchell-Bruker (2005) reported on a whole class of aquifers naturally exhibiting such shifts between surface and subsurface water divides. They demonstrated under which conditions a groundwater table is mainly controlled by surface topography or by recharge. These authors concluded that a shifted groundwater divide may be caused by relatively high hydraulic conductivity in conjunction with a difference between the elevation of drainage points in neighboring valleys. Additional factors contributing to shifts in groundwater divides include tilted aquifer strata, spatial heterogeneity in the recharge rate, and anisotropy in hydraulic conductivity. Of course, anthropogenic influence (e.g., drinking water extraction wells) can also contribute to shifted groundwater divides.
The location of groundwater divides can be constrained by hydraulic-head measurements. Theoretically speaking, a very dense network of piezometers could be used to accurately interpolate the groundwater-table map, which could subsequently be analyzed by the same tools as used for delineating surface-water divides. In practice, this is not advisable as the number of observation wells is restricted by financial costs, labor intensity, and legal restrictions. That is, groundwater divides must be delineated with head measurements from a limited number of piezometers. A classical way of doing this is by calibrating groundwater flow-and-transport models to the head measurements, which explicitly uses all information fed into the model construction (e.g., the geometry and parameter ranges of geological units and boundary conditions) and leads to hydraulic-head fields that are consistent with conservation principles.
As only a limited number of observation wells is affordable, their placements should be specifically optimized for delineating a particular groundwater divide. Either, one wants to find the best possible piezometer configuration for a fixed number of wells, in which the optimum is defined by minimizing the uncertainty of the divide’s position, or one wants to find the well configuration requiring the least number of wells for a fixed target uncertainty of the divide’s location. In both cases, the objective is to maximize the information-to-costs ratio, which is a general problem well‐known under the name of “optimal design of experiments” (Pukelsheim, 2006; Fedorov, 1972).
In this study, we solve the described optimization problem. We provide a framework to identify the best set of points to delineate a particular groundwater divide. The “goodness” of such a point set is defined by how much the uncertainty in the divide’s location is reduced, if hydraulic-head measurements were available at these points. The best set of points might then be implemented as real-world monitoring wells, whose measurements can be used to calibrate a flow model for actually delineating the divide of interest.
Of course, during the stage of identifying promising measurement locations it is unknown which measurement values would be obtained at these locations. To circumvent this problem, we apply a specific technique of optimal experimental design, called Preposterior Data Impact Assessor (PreDIA, Leube et al., 2012). We feed it with a sample of steady-state groundwater models that is efficiently pre-selected to include only plausible subsurface flow fields (Erdal et al., 2020). By means of delineating the groundwater divide for each individual realization and virtually conducting all possible measurements, we can quantify both, the total uncertainty of the groundwater divide’s location across the domain and by how much this scalar quantity can be reduced with a specific measurement configuration.
The main contributions of the present study are the formulation of the problem and the development of a suitable objective function for delineating a groundwater divide, as well as the combination of PreDIA with the pre-selection of plausible model results.
The motivation behind our work originates from a real field site. During the investigation of a floodplain, it was discovered that the observed lateral groundwater influxes from the hillslope are too small to drain the water quantities gained by the hillslope’s expected recharge. This imbalance of in- and outfluxes has led to the conclusion that the groundwater divide underneath the hillslope is shifted in a way that the contributing area draining toward the floodplain is much smaller than expected, when considering the surface water divide as contributing boundary. The phenomenon of flow crossing surface water divides has been referred to as “interbasin groundwater flow”. It needs to be quantitatively estimated, before detailed studies focusing on the hillslope or floodplain can be conducted. The information of whether or not such interbasin flow occurs in a domain and how pronounced it is can furthermore be of utter importance, for example if contamination occurs in one basin and a sensitive receptor (e.g., a drinking water supply well) is located in the other one.
We developed our framework for cases, where the (suspected) shift of a groundwater divide is the phenomenon of interest that needs to be quantified. In reality, such a shifted divide might additionally be subject to transient processes (i.e., it might move with time). This is not covered by our methodology, but we believe our analysis might still be useful in such cases (see section 4.5). We want to emphasize that a shifted divide does not imply its movement over time. A groundwater divide can very well be at a (quasi-)steady state while being shifted due to the geological setting, which does not change significantly over time scales relevant for groundwater management.
Section 2 introduces and explains the underlying framework. Real data from a site in Southwest Germany are used in section 3 to test the method. We want to highlight that we separate our site-specific implementation details (application) from the general approach of our framework (Methods). The results of our example study are presented and discussed in section 4. Finally, we draw conclusions and give an outlook in section 5.
The optimal experimental design method we use later on (section 2.4) is based on stochastic runs of a steady-state subsurface flow model. To model saturated and unsaturated parts of the subsurface, we solve the steady-state version of the Richards equation for variably saturated flow in porous media (Richards, 1931):
in which
The relative permeability
in which
By including the Mualem/van-Genuchten parametrization, the Richards equation holds for variably saturated flow (i.e., both the saturated and unsaturated zone). In the saturated zone (
We apply the following boundary conditions:
in which
The leaky boundary condition can account for interactions between groundwater and river water. The respective exchange flux is driven by the head difference
where
A similar conductance
where A is the associated surface area (
After simulating subsurface flow, we use particle tracking to determine the groundwater divide as explained in section 2.3. Toward this end, we introduce particles at the land surface, track their advective movement according to the advective velocity
in which
The approach of delineating the groundwater divide by particle tracking obviously implies that the divide is located within the modeling domain. This is in contrast to many practical groundwater-modeling studies, where the domain is bounded by the assumed groundwater divides. Under such conditions, these groundwater divides are fixed by the model choice. Since we want to study the uncertainty of the groundwater divide, we require a model domain where the divide is in the interior so that the model has the freedom to shift it.
In order to capture the uncertainty of the divide’s location (prior to any measurements and after hypothetical measurements), our framework makes use of ensemble-modeling. This implies the repeated simulation of the same conceptual model with different numerical representations. These can be formally identical, differing only, for example, in some material property values. They could also differ in more fundamental properties, like the internal structure. We call the final group of model entities a “sample”, to avoid confusion with the term “ensemble” referring to such a group of infinite size. Each entity of the sample is termed a realization or sample member.
Formally, a sample member is defined both, by the formulation of the general model itself (common to all members) and by a member-specific set of parameters. In addition to that, the sample member also comprises its deterministic modeling results (after the model was evaluated), which can be reproduced from the general model by using the same parameter set. We denote these parameter sets
In theory, we could create a sample of sufficient size just by drawing random parameter sets from appropriate prior distributions and subsequent numerical modeling of subsurface-flow. These prior distributions could be derived from measurements (e.g., pumping tests for hydraulic conductivities), other models (e.g., recharge rates) or expert knowledge (e.g., anisotropies). Afterward, particle-tracking would obtain one groundwater divide for each realization. In practice however, we need to exclude parameter sets that lead to implausible model results (e.g., wrong signs of fluxes across boundaries; more examples in context of our application, section 3.3), because that would ignore obvious insight into the correct system behavior and thus overstretch uncertainty. Conversely, we do not want to restrict the parameter ranges too much because we want to assess the full space of plausible model parameters. Therefore, we keep the prior parameter ranges untouched, but rely on the exclusion of models with obviously unrealistic results (denoted unbehavioral or implausible).
While excluding unbehavioral realizations is a conditioning step, we would not yet consider it a model calibration, but rather a plausibility check or pre-selection (see Erdal and Cirpka, 2019; Erdal and Cirpka, 2020; Erdal et al., 2020). In a rigorous conditioning step (i.e., “stochastic calibration”) that could follow on this pre-selection, we would modify the parameters of sample members to better meet the exact measurement values. A potential method to do that would be an ensemble Kalman smoother. However, a full stochastic calibration on the existing data would be computationally expensive, but not informative about the quantity of interest, namely the position of the groundwater divide. The lack of hydraulic-head measurements that are informative about the delineation of the groundwater divide is the very reason why we perform the optimal design of experiments to begin with.
The decision about the plausibility and ultimately its acceptance or rejection of a candidate model is based on a set of criteria. Each plausibility criterion compares a scalar model outcome (e.g., the flux across a specific boundary) with a target value that must not be exceeded or fallen below. Only if a model realization fulfills all plausibility criteria, it will be included in the sample for further analysis.
A key problem of the pre-selection is that more than
(1) We create a small initial sample of
(2) We train one Gaussian process emulator per plausibility criterion with the initial sample of full model runs. A Gaussian process emulator is a kriging interpolator in parameter space (a “proxy model” or “surrogate model”) that estimates the expected value of the plausibility criterion and quantifies its estimation variance, provided that the assumptions of kriging (e.g., statistical stationarity) hold. We want to emphasize here that this is not a spatial interpolation, but an interpolation of the model response to parameter values.
(3) We then draw further random samples of
(4) For a model candidate where this product exceeds the threshold probability (a “stage-1-accepted” realization), we perform the simulation of the full subsurface-flow model. A small percentage of sample members (we use
(5) If the model candidate also meets the plausibility criteria after running the full numerical model, it is “stage-2-accepted” (i.e., included in the sample of physically plausible models), and particle-tracking simulations are performed to obtain the groundwater divide. Otherwise, it is discarded.
(6) With an increasingly large set of full model runs, the Gaussian process emulator model is regularly retrained to improve its accuracy in predicting the behavioral status of subsequent model candidates.
With this procedure, we were able to increase the overall acceptance ratio, that is, the number of stage-2-accepted full-model runs over the total number of full-model runs. In the initial small sample (full Monte Carlo), only
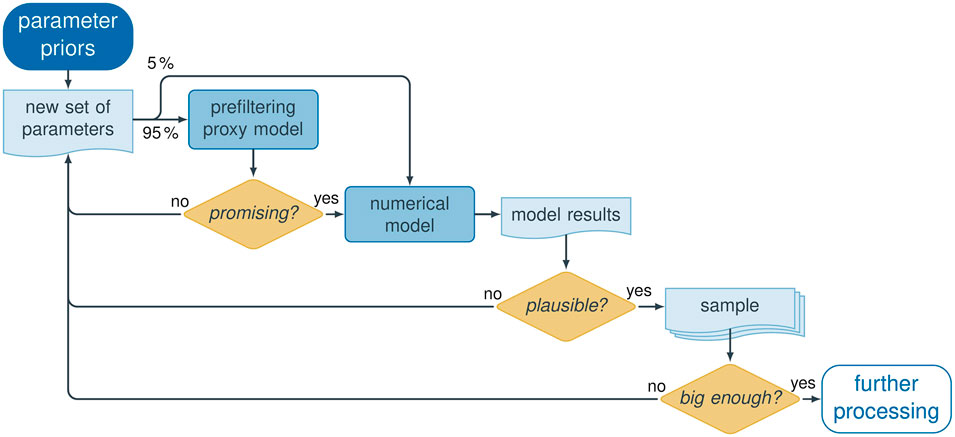
FIGURE 1. Procedure used to generate a sample of physically plausible model realizations for the optimal experimental design analysis.
For each stage-1-accepted parameter realization (see step 4 in section 2.2), we determine the scalar model outcomes of the plausibility check. Additionally, we simulate virtual measurement values of hydraulic heads at all potential measurement locations, by determining the respective elevations of the groundwater table at these locations. The number and location of such potential measurements is known prior to the analysis and part of the problem statement.
Only for the
Other approaches than particle tracking for the delineation of groundwater divides exist. They are typically based on locating the “ridge of the groundwater table”. However, they have been shown to be less reliable (Han et al., 2019).
The fate of a particle i depends on the parameter vector
in which
We can now compute the probability
This equation expresses the probability that particle i, which actually ends up in outlet A, is estimated to end up in outlet B or vice versa.
in which
As discussed in the context of Eq. 17, the probability
To find the optimal placement of piezometers in order to delineate a groundwater divide, we apply the optimal experimental design method PreDIA (the Preposterior Data Impact Assessor, Leube et al., 2012), which we briefly review in the given context.
The scientific question of optimal design is to find the combination of measurements or experiments with the largest information content regarding a target quantity, before the experiment itself is carried out. Formally, the objective is to identify the single design
A design in this notation is a vector containing information about how measurements are taken in time and space. The utility function
As previously described,
For a given realization
To answer the optimal-experimental-design question, we use the stage-2-accepted realizations to compute the
After acquiring
(1) Compute the unconditional sample mean
(2) Compute the vector of unconditional probabilities of misclassification
(3) Select a random subset of
(4) Loop over all designs
Loop over the
(1) Realization j with the virtual observations
(2) Each realization
in which
(3) Compute the mean of all prediction variables in
The
(4) Compute the conditional probability of misclassification
(5) From the vectors of conditional and unconditional probabilities of misclassification,
by using Eq. 19. Steps 4. a (1) to 4. a (5) define the inner loop, illustrated by dark blue shading in Figure 2. In the inner loop, each of the
b. Marginalize the objective function over the
in which we have assumed that all “temporary truth” realizations j are equally likely.
(5) Identify the design
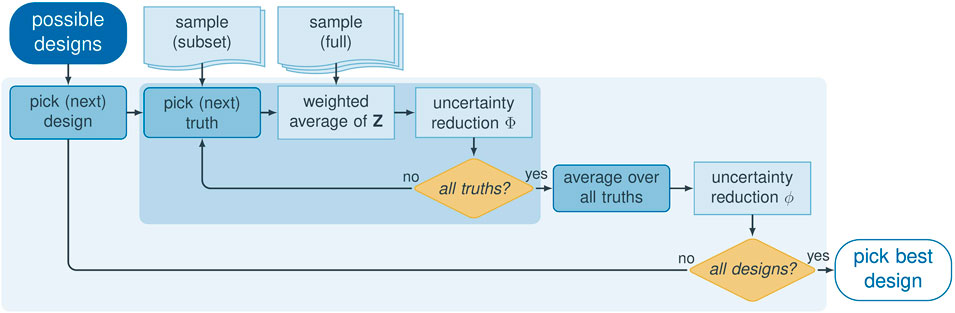
FIGURE 2. Schematic illustration of the general preposterior data impact assessor procedure. Inner loop in dark blue, outer loop in light blue.
The two loops of PreDIA require large sample sizes to make reliable statements about design performances. To estimate whether the chosen sample is large enough for the results to be meaningful, one can use the averaged effective sample size
PreDIA has fundamental advantages over other optimal-experimental-design techniques. It is applicable to inherently non-linear problems without the need of a linearization. It is also very versatile because it imposes few restrictions on the numerical model. Besides the definition and reading of some pre-run input and post-run output quantities, the actual numerical simulation code is independent of PreDIA. This independence makes it trivial to couple any numerical model with PreDIA. It can be seen as a post-processing routine for any modeling sample. PreDIA can capture all kinds of known or estimated uncertainties in boundary conditions, material properties, model structure, or any other model parameters due to its ensemble-based nature.
The disadvantage of PreDIA lies in its computational cost. The analysis requires large sample sizes (i.e., tens of thousands of model runs) and is computationally expensive itself. These difficulties, however, can be overcome with parallel computing techniques (i.e., running multiple realizations at the same time) and simplified models that are comparably quick.
Our framework does not depend on the choice of any specific software, neither for the flow simulation nor for the optimal-design analysis. In the following application, we use HydroGeoSphere to solve for three-dimensional subsurface flow using standard finite elements on triangular prisms (Therrien et al., 2010; Brunner and Simmons, 2012). Because of the Richards equation’s nonlinearity, we do not directly solve for steady-state flow. Instead, we use the transient solver of HydroGeoSphere with constant forcings over a simulation time of
The velocity field of HydroGeoSphere is transferred to Tecplot to perform advective particle tracking with Tecplot’s streamtracing routine in its command line mode (Tecplot Inc., 2019).
The stochastic engine responsible for the sampling of the parameter space and performing the plausibility check of sample members by the Gaussian process emulator-based surrogate model is written in Matlab (The MathWorks Inc., 2019) and based on the code of Erdal and Cirpka (2019). We execute the stochastic sampler on a mid-size high-performance computing cluster with 24 Intel Xeon L5530 nodes (8 cores per node;
The optimal design analysis using PreDIA is implemented as a separate Matlab code that acts on the full sample of stage-2-accepted realizations after its acquisition.
We apply the presented framework to delineate the groundwater divide between the Ammer and Neckar catchments north and south of the Wurmlingen Saddle, respectively, close to Tübingen in South-West Germany. Figure 3 shows a map of the area outlining the model domain (solid black line), the surface-water divide (dashed black line), and streams/drainage features (blue lines). The area of interest comprises a floodplain in the Ammer catchment, which is part of ongoing hydrogeologic and geophysical research (e.g., Martin et al., 2020). Previous modeling studies suggested a shift of the groundwater divide in this area toward the Ammer catchment in the north (Kortunov, 2018). This hypothesis was supported by the Neckar valley being about
In order to test the hypothesis of a shifted groundwater divide, installing up to three piezometers is planned. Due to legal and logistical reasons, all new groundwater observation points need to be placed on a transect parallel to the street from Unterjesingen to Wurmlingen (see Figure 3). We use the presented method to determine the best configuration of piezometers along this transect.
The model domain contains parts of both the Ammer and Neckar catchments, so that the groundwater divide emerges from the model instead of being set as a boundary condition. The surface elevation ranges from approximately
The model domain includes the floodplain of the Ammer river with the river itself and a network of artificial drainage channels. The drainage features running south-north on the hillslope are typically dry, unless during storm events. On the southern side, the model domain includes parts of the Neckar floodplain, but does not reach River Neckar. The only surface water on this side of the hills is a small creek (“Arbach”). However, a dense network of observation wells in the Neckar valley allowed us to define a fixed-head boundary condition along the southern boundary of the model domain.
The bedrock geology in the area is governed by sequences of sandstones and mudstones belonging to the Upper Triassic Keuper formation (Aigner and Bachmann, 1992). The regional geology has been subject to many (hydro-)geological investigations (e.g., Kekeisen, 1913; Harreß, 1973; D’Affonseca et al., 2020). The Ammer and Neckar rivers have carved small basins into the bedrock (Martin et al., 2020), which are filled with Quaternary sediments forming the floodplains. In total, we distinguish twelve hydrostratigraphic units, which we briefly characterize in the following from bottom to top:
(1) lower Erfurt formation (kuE): The kuE unit is roughly
(2) upper kuE: We divide the kuE into two subunits of similar thickness to account for its heterogeneity in hydraulic conductivity.
(3) unweathered Grabfeld formation (kmGr): The kmGr is a mudstone unit bearing gypsum, anhydrite, mudstones, and shales. It can reach thicknesses of up to
(4) weathered kmGr: Water contact has transformed anhydrite to gypsum within the kmGr. Upon further weathering, the gypsum dissolves (Ufrecht, 2017), which can increase the hydraulic conductivity by orders of magnitude (Kirchholtes and Ufrecht, 2015). Due to the strong contrast in hydraulic conductivity, we divide kmGr into the unweathered and weathered rock.
(5) mud- and sandstone formations (km2345): We lump the remaining bedrock formations Stuttgart formation (kmSt), Steigerwald/Hassberge/Mainhardt formation (kmSw/kmHb/kmMh), Löwenstein formation (kmLw), and Trossingen formation (kmTr), which are made of interbedded mudstones, silty mudrocks, dolomite layers, sandstones, and clay conglomerates, to a single unit with uniform hydraulic properties. These strata occur only at the outskirts of our model domain where they cover the kmGr.
(6) hillslope-hollow fillings: hillslope hollows on the southern hillslopes of the Ammer valley are cut into the kmGr. They are partially filled with poorly sorted sediments deposited by mudflows.
(7) Neckar-valley gravel: The floodplain material on the Neckar side mostly consists of Quaternary sandy gravel sediments of several meter thickness.
(8) Ammer-valley Quaternary: The Ammer floodplain comprises five distinct layers (Martin et al., 2020):
a. Ammer-valley gravel: The lowest floodplain unit in the Ammer valley consists of a Pleistocene clayey gravel body, acting as a local aquifer. Its thickness is in the range of
b. Ammer-valley clay: A clay unit of approximately
c. Ammer-valley tufa: This Holocene unit consists mostly of autochthonous limestone aggregates. It has a thickness of several meters. Slug tests conducted by Martin et al. (2020) identified this layer as an aquifer.
d. Ammer-valley alluvial clay: The top of the Quaternary filling of the Ammer floodplain is a several meter thick colluvium of silty and clayey fines.
e. riverbed of the Ammer river: Underneath River Ammer, a layer of recent river sediments with different grain size than the surrounding sediments can be found. This layer could have an increased hydraulic conductivity, due to consisting of coarse sediments deposited by the river. However, it is also possible that this layer has a reduced conductivity due to colmation of clayey deposits.
Figure 4 illustrates the considered hydrostratigraphic units in three-dimensional renderings.
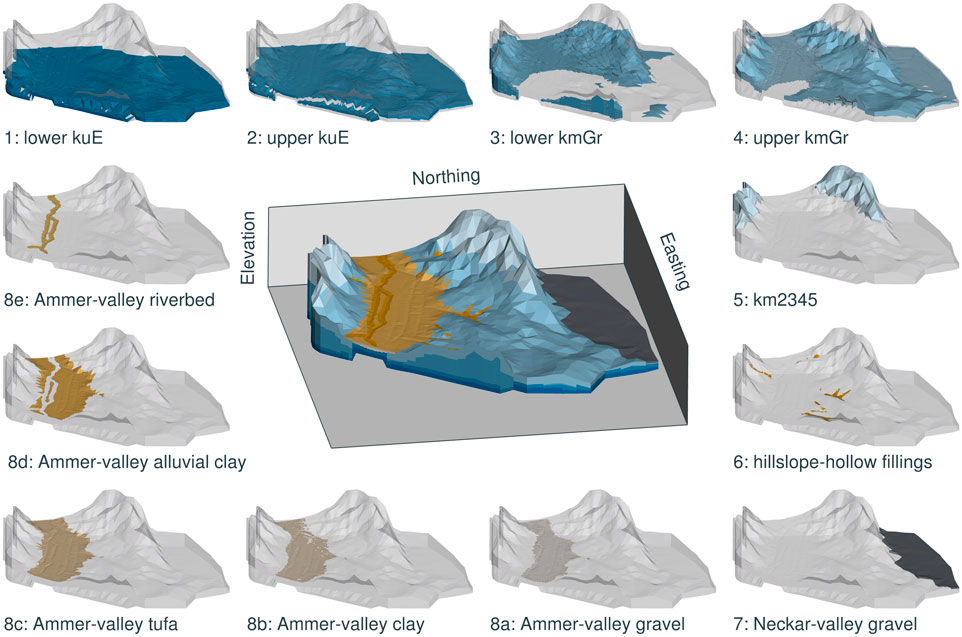
FIGURE 4. Three-dimensional overview of the subsurface-flow model. The vertical dimension is exaggerated by a factor of five to enhance distinctness.
Figure 5 shows a plan view of the model discretization and boundary conditions. The model domain covers an area of approximately
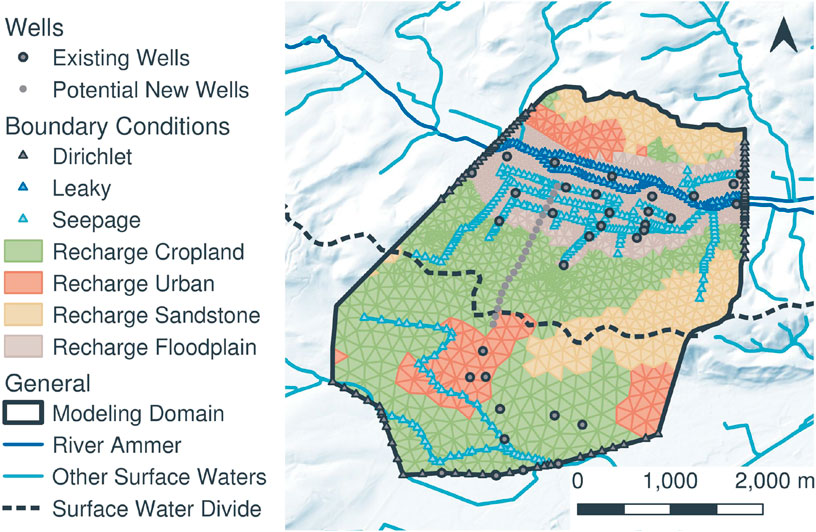
FIGURE 5. Boundary conditions and two-dimensional discretization of the underlying subsurface flow model.
Along different parts of the boundary, we apply different boundary conditions:
(1) If not specified otherwise, all outer mesh faces are assigned a no-flux (Neumann) boundary condition. These boundaries are either in formations of very low conductivity (particularly the bottom) or the boundaries are far away from the area of interest like the northern boundary, which is derived from a secondary surface water divide on the far side of the Ammer valley. The eastern and western boundaries are approximately parallel to the estimated flow field.
(2) Three fixed-head boundary sections are defined at the western, eastern, and southern sides of the domain to allow regional groundwater flow (see Figure 5). To obtain the fixed-head values, we interpolate between observation well data. In the Ammer valley, the Dirichlet boundaries extend over the Quaternary fillings, while on the Neckar side, they extend over the whole depth of the model, where the formation consists of a thin, highly conductive gravel that ends at the municipality of Wurmlingen. Because of the high hydraulic conductivity and the absence of significant vertical hydraulic gradients here, we average the interpolated head values over depth for the Dirichlet assignment.
(3) On the top surface of the domain, we apply recharge as a fixed-flux (Neumann) boundary condition across element faces. Recharge rates in different zones depend on land use (cropland, floodplain, urban areas, and km2345-covered parts). By providing recharge as a model boundary we lump the dynamic interaction of evaporation, transpiration, precipitation and soil water storage into a single stationary quantity, which is of course a simplification. However, since we are interested in the effective, long-term behavior and not the high-resolution fluctuations, we consider this simplification justified. We base our range of possible recharge rates on previous work conducted in our domain or in comparable aquifers in close proximity (Holzwarth, 1980; Wegehenkel and Selg, 2002; Selle et al., 2013).
(4) We use a leaky boundary condition to simulate the interaction between groundwater and the Ammer river.
(5) For the network of drainage ditches in the Ammer valley and the small surface water creek in the Neckar valley, we apply seepage boundaries.
(6) Drainage boundary conditions are applied to all other surface nodes, allowing water to drain whenever the groundwater table is above the ground surface. We distinguish between elements that belong to the Ammer floodplain (highlighted in light brown in Figure 5) and the remaining surface.
Note that there are no groundwater abstractions within the model domain so that we do not need to consider corresponding internal boundary conditions.
We tested different initial conditions for the flow solution (e.g., a hydraulic head field interpolated from measurements, hydraulic heads equaling the surface elevation, a constant depth to the water table). The choice of initial condition affected mostly the run time needed to reach convergence to steady-state, but influenced the steady-state flow field itself only marginally. We settled with initial hydraulic heads equal to the surface elevation. For other applications, we recommend a similar comparison procedure to identify a useful initial condition. Choices that are too far away from a realistic flow field (e.g., a completely dry domain) can lead to convergence problems due to the nonlinearity of Richards’ equation.
Each discretized spatial element (i.e., triangular prism) has a set of parameters defining the hydraulic properties of its material. All elements belonging to the same hydrostratigraphic unit share the same set of parameters, including the horizontal and vertical hydraulic conductivities
Table 1 summarizes all material properties considered random. These parameters are the first part of the parameter set
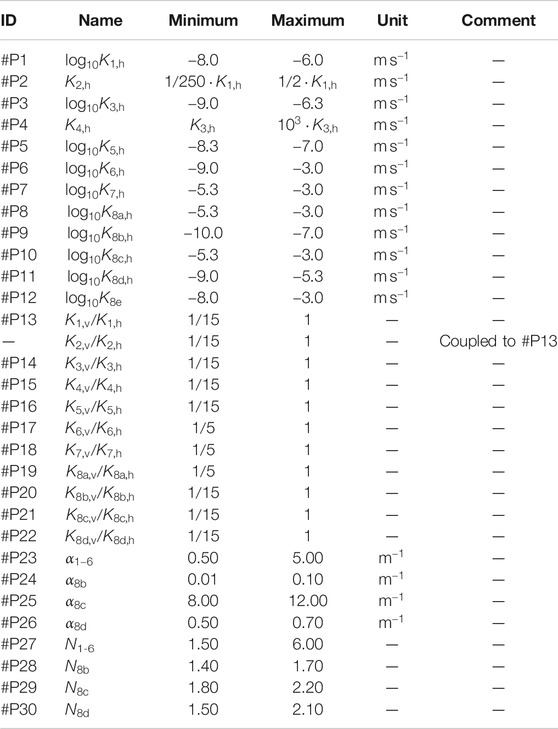
TABLE 1. Prior parameter ranges of random material properties of hydrostratigraphic units considered in the model.
The values in Table 1 are grouped by horizontal saturated hydraulic-conductivity values
We do not treat the residual water saturations as random variables. Instead, we apply the following values in all model runs:
In total, we use nine random parameters (#B1 to #B9) related to boundary conditions, listed in Table 2. We again assume uniform priors within given bounds. Parameters #B1 to #B4 regulate the groundwater recharge R [
The parameters #B5 to #B8 modify the fixed-head values at Dirichlet and river boundaries. The base values for the fixed heads used on the southern boundary in the Neckar valley (
At last, #B9 represents the uncertain thickness of the drainage boundary in Eq. 13 for all floodplain elements. The respective hydraulic conductivity is
Finally, we consider a total of five random parameters (#S1 to #S5) describing uncertain geometry of structural units. Table 3 lists the ranges of the parameters. #S1 controls the maximum depth
We define seven criteria to decide whether the flow solution of a model realization is plausible (i.e., stage-2-accepted). These criteria are listed in the following:
(1) To keep the realizations close to data observed in the field, the simulated hydraulic heads are compared to real head measurements obtained in the valleys (see section 3.4). As the model assumes steady-state flow, we time-average the available series of measured heads at 51 observation wells and compute the root mean square error (RMSE) of the corresponding simulated steady-state heads. For a model realization to be stage-2-accepted, its RMSE has to be smaller than
(2) The total groundwater flux
(3) The total groundwater flux
(4) The magnitude of the two fluxes,
This ratio can take values between
(5) The sum of all exchange fluxes between the subsurface and rivers must be negative (i.e., net groundwater discharge into rivers). Field data on the exchange fluxes are difficult to obtain because the change of river discharge due to surface-water/groundwater exchange is very small along the investigated stretch. Nonetheless we expect that the rivers are net gaining as there are no groundwater abstractions within the domain. Losing conditions might occur only locally on short stretches of the rivers and channels.
(6) A typical behavior shown in many models with randomly drawn parameters is extensive flooding of the model domain. At the real floodplain, by contrast, we do not observe permanent flooding outside of ditches. To exclude flooding of the floodplain under steady-state flow conditions, we require that the total flux across all drainage nodes is small (see section 3.2.2). As plausibility we set that the total flux leaving at the surface must be smaller than
(7) Finally, the water flux leaving at the drainage ditches should not be excessive. In the real floodplain, these ditches carry water only seasonally and in small quantities. Since the actual fluxes are unknown and hard to estimate, we require a stage-2-accepted realization to drain less than
Currently, there are 35 piezometers already installed at the field site, for which a decent-quality dataset of hydraulic head in one or multiple depths is available. Figure 5 shows the location of these observation wells by gray circular dots with black edges. Accounting for different depths in multi-level wells, hydraulic heads are measured at 51 points. However, there are no piezometers located on the hillslope between the two valleys. This lack of observation points results in high uncertainty regarding groundwater flow underneath the hillslope and in the location of the groundwater divide.
In order to fill this gap, the installation of up to three additional piezometers is planned on a transect. We identified twenty potential piezometer locations along this transect, coinciding with edges of the computational grid. These locations are marked in Figure 5 as gray circular dots without an edge. The line of points extends longer on the North than the South, because we expect the divide to be shifted toward the North. This is so, because the northern valley is at a higher elevation than the southern valley, and also the geological units dip toward the south-west. Furthermore, a preliminary study conducted by Kortunov (2018) also suggested a shift in this direction.
The optimal experimental design analysis considers designs consisting of one, two, or three new wells, each placed on one of the twenty locations. Our design space
in which
While the optimal three-well design will obviously outperform the optimal two- and one-well designs, we want to investigate which information gain (e.g., reduction in uncertainty of delineating the groundwater divide) is achieved by installing more or fewer wells. However, we do not perform a full cost-benefit analysis, as the (financial) costs are difficult to compare to the benefit of reducing the uncertainty in the groundwater-divide delineation.
Of 72,481 stage-1-accepted realizations, 20,600 needed to be rejected, because they yielded implausible results according to the given criteria. Another 1881 model runs were rejected, because they did not converge within 40 min of wall-clock time, set as limit to use the available computational resources efficiently. The remaining sample consists of
Figure 6 shows the distributions of the simulated groundwater-table measurements at the twenty proposed locations. Each profile relates to one suggested observation-well location and includes, 1) a histogram of simulated head values of all 50,000 accepted sample members, 2) the median of the simulated head (
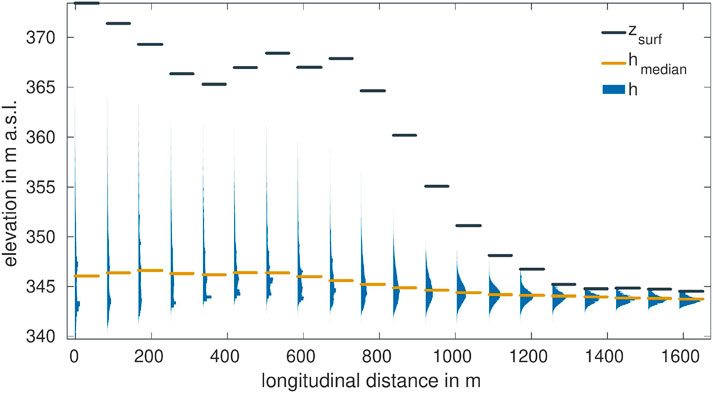
FIGURE 6. Distributions of virtual hydraulic-head observations using the sample of stage-2-accepted realizations at all twenty potential locations along the transect.
At the southern end of the transect, which is close to the surface-water divide, the statistical distributions of the groundwater table are very wide, whereas at the northern end in the Ammer floodplain they become quite narrow. This behavior can be explained with the plausibility constraints put onto the model selection. As Figure 5 shows, most existing observation wells are within the Ammer floodplain, restricting the variability of hydraulic heads by plausibility criterion 1. Also plausibility criterion 6, excluding realizations showing extended flooding, contributes to narrowing the variability of hydraulic heads within the floodplain. By contrast, there are no piezometers to constrain the models along the southern hillslope. Observation wells further away from the hydraulic-head-constraining floodplain show larger uncertainty than those close by, which reflects the uncertainty in groundwater recharge and transmissivity of the weathered part of the Grabfeld formation kmGr. The conditioning by the pre-selection procedure might also explain why the shape of the head histograms in Figure 6 transforms from near-Gaussian for the northern wells to multi-modal wide distributions toward the southern end.
As indicated by the black dashes in Figure 6, the topography along the transect is not strictly monotonic. At about one quarter along the length of the profile, a hillslope hollow oriented in the WSW-ENE direction crosses the transect. Along the transect, the median of the simulated hydraulic head follows the topography to some extent, but with a much smaller range. At the southern end, the median profile of hydraulic head drops toward the south along a distance of
To gain insights in how the head observations depend on the input parameters, we performed a global sensitivity analysis using the framework developed by Erdal et al. (2020) applying the method of active subspaces (Constantine et al., 2014; Constantine and Diaz, 2017) supported by a Gaussian process emulation of the target quantity. The active-subspace method results in activity scores, expressing the relative importance of all input parameters for a selected target variable. We performed this analysis for the simulated hydraulic-heads at the 20 potential locations for the new piezometers along the transect. At the 14 southern-most locations, which are all located along the hillslope in the weathered Grabfeld formation, the activity scores were the highest for the conductivities in the unweathered and weathered Grabfeld formation, the thickness of the weathering layer, and the recharge rate of cropland. At the six northern-most locations, located closer to/within the floodplain, we saw a shift toward conductivities of floodplain sediments and recharge in the floodplain. Similar observations on global sensitivity patterns have been made by Erdal and Cirpka (2019) in a study on a neighboring catchment with similar geology.
Figure 7 shows maps of the misclassification probability
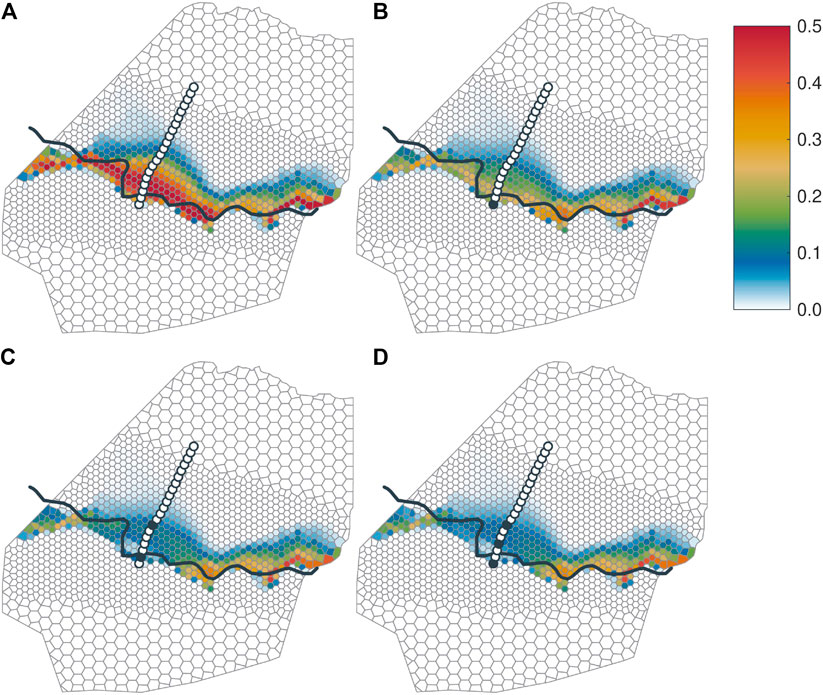
FIGURE 7. Probability maps of misclassifying the attribution to the Ammer and Neckar subsurface-catchments
Figure 7A shows the map prior to installing any new piezometers. The highest values of the misclassification probability occur close to the surface-water divide. On the Neckar (southern) side of the surface-water divide, the misclassification probability drops rapidly. Here, all model realizations agree that these points belong to the Neckar subsurface catchment. On the Ammer (northern) side of the surface-water divide, by contrast, the misclassification probability decreases gradually, overall resulting in an uncertainty belt of the groundwater divide with a width ranging between
The width of the identified uncertainty belt is comparably small at the steeper hillslopes toward the east and at the very western end, where the topmost geological layer is the low conductive km2345 (see Figure 4, layer 5). In contrast to that, the width is large on the gentle saddle in the western and middle parts of the domain, where the top subsurface-layer consists of weathered kmGr, which has a higher hydraulic conductivity. This observation agrees with the findings of Haitjema and Mitchell-Bruker (2005), stating that groundwater and surface water divides are more likely to differ in aquifers with high transmissivities (for a given recharge rate and geometry). The transect of the twenty proposed piezometer locations crosses the broadest part of the uncertainty zone perpendicular to the course of the belt. This is fortunate for the optimal experimental design, since we can acquire information just within the most uncertain parts of the system.
Figures 7B–D show the maps of the misclassification probability after performing the optimal-experimental-design analysis for one, two, and three additional piezometers, respectively. In each of these figures, the identified optimal piezometer locations are marked by circles with black filling, while the unused potential piezometer locations are depicted as white-filled circles.
Figure 7B reveals how the misclassification probability is expected to be reduced by placing a single additional piezometer. The optimal location is the southernmost point along the transect close to the surface-water divide. Unsurprisingly, the location of this piezometer coincides with the location that shows the highest uncertainty of hydraulic heads in Figure 6. A comparison between Figures 7A,B shows that the misclassification probability is not only reduced in the direct vicinity of the chosen new piezometer, but essentially over the entire width of the Wurmlingen saddle, whereas the effect at the eastern end of the model domain is negligible. This pattern reflects the smoothness of hydraulic heads, but is strongly affected by the assumption that each lithostratigraphic unit has a uniform set of hydraulic parameters (only the groundwater-recharge values are subdivided by land-use). The latter implies that conditioning the model on a single observation point in a particular unit, here the weathered kmGr, affects the model outcome at all other points within this unit. However, if we had considered internal variability within the units, individual head measurements would not have reduced the uncertainty at distant points within that unit to the same extent. Consistent to these arguments, the eastern end of the uncertainty belt (where the topmost geological unit is km2345 rather than weathered kmGr) is not affected by placing a piezometer along the transect.
Further reduction of the misclassification probability can be achieved by placing a second additional piezometer at the northern fringe of the uncertainty belt (Figure7C), whereas the uncertainty pattern does not visually change when placing a third additional piezometer between the first and second piezometers (Figure 7D).
Figure 8 summarizes the performance of all 1,350 investigated piezometer configurations (grouped by one-, two- and three-additional-piezometer designs). All plots use the design number on the abscissa. In the following discussion, we use the notation “(first piez.
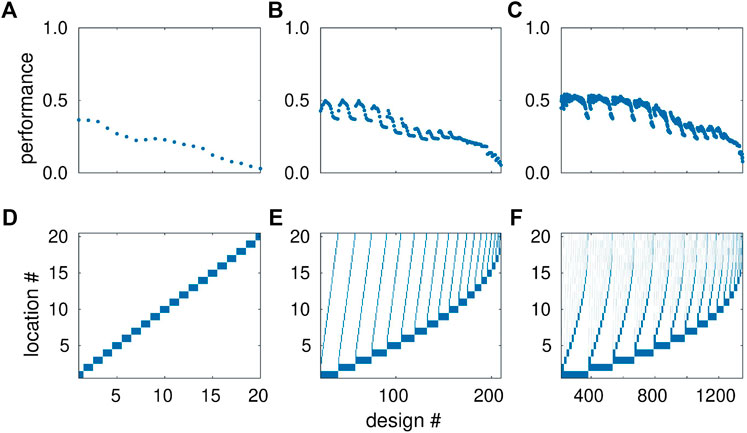
FIGURE 8. Performance of all 1,350 investigated monitoring designs. Top row (A–C): normalized utility function
The top row of Figure 8A-C shows the values of the utility function
In the single-piezometer designs (Figure 8A), the performance declines with increasing design number (placing the new piezometer further north along the transect). While the first three designs result in a similar relative uncertainty reduction of
Figure 8B shows the performances of all two-piezometer designs. Like in the one-piezometer designs, configurations including southern piezometer locations (design numbers 21 to
The optimal two-piezometer designs may be explained by the combined effects of having the highest prior uncertainty of hydraulic head at the southern end of the transect (discussed in the context of the one-piezometer designs) and the inherent spatial correlation of hydraulic head caused by the groundwater-flow equation itself: One piezometer should be located at the most informative southern end; placing two piezometers to close to each other would yield redundant information (and observing a small head difference would drown in the measurement error), while placing the second piezometer at the northern end would be of little use because here the hydraulic heads are already constrained by the plausibility criteria.
In the three-piezometer designs (Figure 8C), this pattern is maintained, with the best location of the third piezometer being in the middle of the other two new observation wells. Thus, placing the third well further north, where the head-uncertainty is low, is less beneficial than refining the spatial resolution of head measurements in the southern third of the transect. The best three-piezometer configuration is
As a quality check, we determined the average effective sample size for the three optimal designs. The values are comparably large (
Notably, all three optimal designs use very similar locations. Each larger optimal configuration basically includes the smaller ones as a subset (with the exception of switching between locations 2 and 1 in the two-location design). This means that, in the given application, one could decide whether and where to install the next observation well after installing the preceding ones, yielding essentially the same optimal designs. Such behavior is beneficial from a practical standpoint of view as, in real-world applications, the decision about extending a measurement network is often made only after realizing that the existing network is not (yet) sufficient. However, we cannot generalize that such a behavior occurs in all cases. In other applications, the optimal designs of many piezometers may not be a superset of the designs with fewer piezometers. Also, the information gained by the actual data value obtained by a first well could change the current state of knowledge, hence leading to (slightly) different later design decisions (Geiges et al., 2015). In such cases, deciding the number of observation wells would be necessary ahead of the first drilling in order to achieve optimal results.
We may compare the performance of the optimal designs with those of intuitive choices using the same number of new piezometers. When installing a single piezometer, one might place it on the middle of the transect using the design
As shown in Figure 7, installing new piezometers along the suggested transect reduces the misclassification probability
Figure 9A shows which performance ϕ can be achieved as a function of the location of the third piezometer. The maximum performance of
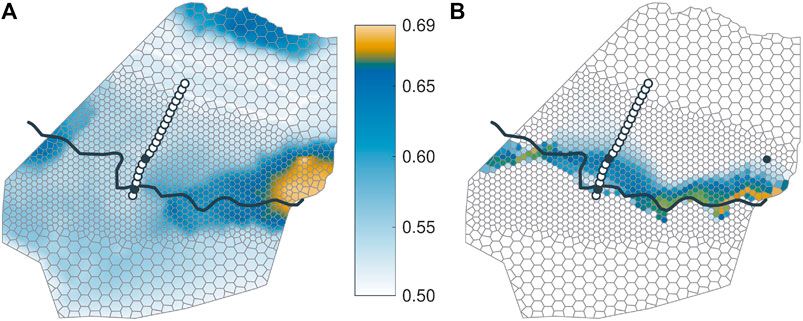
FIGURE 9. Assessment of measurement designs with the third piezometer being placed outside the transect. (A) Performance ϕ of the design as a function of where the third observation well is placed; (B) map of the misclassification probability
The average effective sample size of the optimal design in this substudy is comparably low (
Figure 9A includes an interesting and instructive artifact of the model: According to our model, hydraulic-head measurements on the northern hillslope appear to be beneficial for delineating the groundwater divide at the southern boundary of the Ammer valley. Most likely this is caused by the assumed uniformity of hydraulic parameters within each lithostratigraphic unit. In the very north of the model domain, the km2345 unit crops out, implying the same values of hydraulic conductivity and groundwater recharge as in the zone of interest at the souther boundary. Thus, a hydraulic-head measurement within this northern zone constrains model parameters of the km2345 unit, reducing the misclassification probability in the eastern part of the uncertainty belt. However, we are doubtful that this would be confirmed in a real-world application.
Our framework is easily adaptable to other cases and applications, with the underlying groundwater-flow model being trivially exchangeable. This flexibility makes it convenient to apply the presented technique to other sites. Both interfaces, from the stochastic sampler to the numerical model, and from the numerical model to the optimal experimental design analysis, require only basic input/output operations of parameter values and virtual observations. While we have implemented the stochastic sampler and PreDIA as Matlab scripts, the approach could easily be transferred to other programming environments. However, a particle tracking tool is a necessary requirement for our framework to work.
Among the most labor-intensive parts of the framework is the initial model development, which is needed in quantitative hydrogeological consultancy anyway. Computationally, the creation of the plausible sample is the most costly step, but this can largely be parallelized. To obtain reasonable uncertainty estimates, several thousand model realizations are needed. This may not be affordable by everybody who might be interested in the uncertainty of groundwater-divide delineation. These computer-time limitations may be overcome by cloud computing.
In practical applications, the costs related to elaborate modeling in the planning phase of a new observation-well needs to be compared to the other expenses. This includes filing the application for legal approval, advertising for bids, planning of the fieldwork, and the drilling and completion expenses themselves. If the presented optimal-experimental-design method is initiated at the beginning of this process, it becomes an integral part of the decision-making process of how many new piezometers to install and where to place them.
The way we use the chosen optimal-design method PreDIA, we can only rank experimental designs within a given finite set. The number of elements in this set determines the computational costs of the optimal-design part of the analysis. In our application, we confined the design space by restricting the piezometer locations to a transect, reflecting the legal constraints at the given field site. With three piezometers at twenty potential locations, we had to consider 1,350 configurations. In the additional study presented in section 4.4, we removed the constraint to stay on the transect for one piezometer, considering 2067 potential locations. Allowing all three piezometers to be placed at any of these 2067 locations, would have resulted in more than
Our application was restricted to steady-state flow. Of course, real flow systems are never fully stationary, since they are always subject to transient forcings. Depending on the investigated site, this can include climatic influences, weather, tides or anthropogenic impacts (e.g., drinking water supply wells), all of which could affect the position of groundwater divides (e.g., Rodriguez-Pretelin and Nowak, 2018). Aquifers, where the expected movement of the groundwater flow divide over time is the main research question obviously need to account for this. Characteristics of such systems might be a significant abstraction of groundwater due to pumping wells, a known imbalance of the groundwate flow field or severe temporal fluctuations in groundwater recharge (e.g., Sanz et al., 2009). An interesting extension of our framework would be a transient analysis for such systems, by using transient simulations and time-dependent observations. Consequently, the underlying objective function would need to be redefined. We provide a possible extension toward dynamic systems in the appendix (section 5.2). However, the higher uncertainties related to inherently more complex transient models would require a larger sample and would most likely deteriorate the performance of the pre-selection method. In the context of transient data and models, a worthwhile avenue would be to combine optimal experimental design techniques with data-assimilation methods, but this is beyond the scope of the present study.
For most cases, where the divide is suspected to be shifted but not dramatically moving over time, our steady-state framework is applicable, with the interpretation of the steady-state as a “most representative state”. We also want to highlight that the goal of our framework is not to derive the position of groundwater divides themselves. Instead, we want to identify those locations that are best suited to conduct measurements providing insight for this delineation. The actual delineation, for example, can then be carried out by calibrating a groundwater flow model to the obtained measurement data. This second model can be more detailed, more finely discretized and even transient, as probably fewer model runs are necessary. If not already done, a rigorous grid convercence analysis should be performed ahead of the calibration to validate the numerical accuracy of the model.
As with every model, the performance of the method depends on the validity of underlying assumptions. In particular, we have assumed that the hydraulic parameters are uniform within each lithostratigraphic unit and that groundwater recharge is spatially uniform in zones defined by the topmost geological layer and land-use. Neglecting spatial variability within these zones expands the spatial ranges over which intended measurements are informative. We may also have missed discrete features altogether, which affect the position of the groundwater divide but do not influence the existing measurements. The latter would lead to a systematic bias.
The optimal-experimental-design method chosen in this study can accommodate any kind of uncertain parameters or uncertain model choices, provided that a prior uncertainty range is given. Both identifying the sources of uncertainty and defining the related prior distributions require expert knowledge, thus questioning the objectivity of the analysis. However, as with all Bayesian methods, such choices are at least made transparent. We have made good experience by initially setting fairly wide prior parameter ranges and then constraining the parameter space to behavioral models by the Gaussian-process-emulation supported pre-selection method (Erdal et al., 2020).
In the given application, we restricted the observations to hydraulic-head measurements, but this is not a limitation of the method. It is easy to augment the virtual observation vector by other data, such as hydraulic tests to be performed using the new observation wells, borehole dilution or tracer tests. Like with the extension to transient flow, the consideration of additional data types may also require more (uncertain) parameters. Systematically analyzing which type of data is most informative for which type of question is an ongoing issue of stochastic subsurface hydrology and optimal experimental design beyond the scope of the current study.
In this work we have presented a framework to identify the best piezometer configuration from a set of possible layouts to delineate local groundwater divides. Through the combination of filtered ensemble-based modeling of steady-state subsurface flow, particle tracking, and the application of the optimal-experimental-design technique PreDIA (Leube et al., 2012), we could identify the piezometer configuration for which we expect the largest reduction in the uncertainty of the groundwater divide. We have applied the method to an appropriate case study, which revealed the following insights:
(1) Configurations involving new measurement locations that are far away from existing ones perform better, because then the variability of hydraulic head, consistent with the existing data, is higher.
(2) In our application, a medium spacing of a few hundred meters between multiple new piezometers was optimal. Closer points would have led to redundant information due to the spatial auto-correlation of hydraulic head. Larger distances would have pushed observation points into non-informative regions close to existing measurements.
(3) The designs, defined as optimal by the presented framework, perform better than intuitive equidistant piezometer placements. In fact, the identified optimal design for a single piezometer provides similar information content as the tested intuitive equidistant placing of two piezometers, implying significant savings in real-world applications.
(4) Additional information obtained by adding more piezometers leads to further reduction of uncertainty, but the additional gain of information decreases with each new piezometer.
(5) Our procedure may be used to estimate whether the additional information gain is worth the effort of installing an additional observation well or not. The actual decision depends on the case at hand and involves a tradeoff between desired certainty and available resources. In our case, sequential optimization of one piezometer location after the other led to practically the same designs as jointly optimizing multiple piezometer designs, but this observation cannot be generalized.
A worthwhile follow-up study would be the extension of the presented framework to transient flow systems.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
JA set up the numerical flow and particle-tracking model, implemented the stochastic sampler, performed the computations, created the figures, and wrote the draft manuscript. AG performed the optimal experimental design analysis and contributed to manuscript revision. DE developed the stochastic sampler and the pre-selection method. WN and OC conceived the presented idea, supervised the work, provided funding, and revised the manuscript draft; all authors read and approved the submitted version.
This research was funded by the German Research Foundation (DFG) in the framework of the Research Training Group GRK 1829 “Integrated Hydrosystem Modelling” and the Collaborative Research Centre SFB 1253 CAMPOS - Catchments as Reactors (Grant Agreements GRK 1829/2 and SFB 1253/1 2017).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer (AG) declared a past co-authorship with one of the authors (WN) to the handling editor.
We acknowledge support by the Open Access Publishing Fund of the University of Tübingen.
Generalization to Non-Binary Systems
In cases where one wants to delineate not only a particular (sub-)catchment’s boundary, but the (potentially intersecting) groundwater divides between more than two of such catchments, the formulation of our objective functon (Eq. 26) based on binary particle fate maps (Eq. 18) is insufficient. Here, the particle fates cannot be described with the binary Bernoulli distributions, where the outcome for particle i is
We denote the probability that particle i belongs to the receptor k is
All other steps of the method remain as outlined above.
Possible Generalization to Transient Systems
A potential transient implementation of our framework would require a new formulation of the objective function. In such applications both, the modeled subsurface flow-field and the observations would change over time. This means that also the particle fate maps are transient, since the fate probabilities might change throughout the simulation period. This results in dynamic maps of misclassification probability, that is
One potential way to define a metric quantifying the uncertainty of a transient groundwater divide would be to perform an additional integration/averaging over the simulation modeling duration τ.
Aigner, T., and Bachmann, G. H. (1992). Sequence-stratigraphic framework of the German Triassic. Sediment. Geol. 80, 115–135. doi:10.1016/0037-0738(92)90035-P.
Bloxom, L. F., and Burbey, T. J. (2015). Determination of the location of the groundwater divide and nature of groundwater flow paths within a region of active stream capture; the New River watershed, Virginia, USA. Environ Earth Sci. 74, 2687–2699. doi:10.1007/s12665-015-4290-1.
Brassel, K. E., and Reif, D. (1979). A procedure to generate Thiessen polygons. Geogr. Anal. 11, 289–303. doi:10.1111/j.1538-4632.1979.tb00695.x.
Brunner, P., and Simmons, C. T. (2012). HydroGeoSphere: a fully integrated, physically based hydrological model. Ground Water. 50, 170–176. doi:10.1111/j.1745-6584.2011.00882.x.
Constantine, P. G., and Diaz, P. (2017). Global sensitivity metrics from active subspaces. Reliab. Eng. Syst. Saf. 162, 1–13. doi:10.1016/j.ress.2017.01.013.
Constantine, P. G., Dow, E., and Wang, Q. (2014). Active subspace methods in theory and practice: applications to kriging surfaces. SIAM J. Sci. Comput. 36, A1500–A1524. doi:10.1137/130916138.
D’Affonseca, F. M., Finkel, M., and Cirpka, O. A. (2020). Combining implicit geological modeling, field surveys, and hydrogeological modeling to describe groundwater flow in a karst aquifer. Hydrogeol. J. [Epub ahead of print]. doi:10.1007/s10040-020-02220-z
Erdal, D., and Cirpka, O. A. (2019). Global sensitivity analysis and adaptive stochastic sampling of a subsurface-flow model using active subspaces. Hydrol. Earth Syst. Sci. 23, 3787–3805. doi:10.5194/hess-23-3787-2019.
Erdal, D., and Cirpka, O. A. (2020). Technical note: improved sampling of behavioral subsurface flow model parameters using active subspaces. Hydrol. Earth Syst. Sci. doi:10.5194/hess-2019-629.
Erdal, D., Xiao, S., Nowak, W., and Cirpka, O. A. (2020). Sampling behavioral model parameters for ensemble-based sensitivity analysis using Gaussian Process Emulation and Active Subspaces. Stoch. Environ. Res. Risk. Assess. doi:10.1007/s00477-020-01867-0
Farthing, M. W., Kees, C. E., and Miller, C. T. (2003). Mixed finite element methods and higher order temporal approximations for variably saturated groundwater flow. Adv. Water Resour. 26, 373–394. doi:10.1016/S0309-1708(02)00187-2.
Franzetti, S., and Guadagnini, A. (1996). Probabilistic estimation of well catchments in heterogeneous aquifers. J. Hydrol. 174, 149–171. doi:10.1016/0022-1694(95)02750-5.
Geiges, A., Rubin, Y., and Nowak, W. (2015). Interactive design of experiments: a priori global versus sequential optimization, revised under changing states of knowledge. Water Resour. Res. 51, 7915–7936. doi:10.1002/2015WR017193.
Haitjema, H. M., and Mitchell-Bruker, S. (2005). Are water tables a subdued replica of the topography? Ground Water. 43 (6):781–786. doi:10.1111/j.1745-6584.2005.00090.x.
Han, P.-F., Wang, X.-S., Wan, L., Jiang, X.-W., and Hu, F.-S. (2019). The exact groundwater divide on water table between two rivers: a fundamental model investigation. Water 11, 685. doi:10.3390/w11040685.
Harreß, H. M. (1973). Hydrogeologische Untersuchungen Im Oberen Gäu (Tübingen). PhD thesis. Germany: University of TübingenAvailable at: https://rds-tue.ibs-bw.de/link?kid=1073957446.
Holzwarth, W. (1980). Wasserhaushalt Und Stoffumsatz Kleiner Einzugsgebiete Im Keuper Und Jura Bei Reutlingen-Tübingen (Tübingen). Dissertation. Germany: Universität Tübingen. Available at: https://rds-tue.ibs-bw.de/link?kid=1078052956.
Hunt, R. J., Steuer, J. J., Mansor, M. T. C., and Bullen, T. D. (2001). Delineating a recharge area for a spring using numerical modeling, Monte Carlo techniques, and geochemical investigation. Ground Water. 39, 702–712. doi:10.1111/j.1745-6584.2001.tb02360.x.
Kekeisen, F. (1913). Das Ammertal – Geologische Studie (Rottenburg a. N.: Pfeffer & Hofmeister). Available at: https://rds-tue.ibs-bw.de/link?kid=1165633094.
Kirchholtes, H. J., and Ufrecht, W. (Editors) (2015). Chlorierte Kohlenwasserstoffe im Grundwasser: untersuchungsmethoden, Modelle und ein Managementplan für Stuttgart. Wiesbaden: Springer Vieweg.
Kortunov, E. (2018). Reactive transport and long-term redox evolution at the catchment scale. PhD thesis. Germany: University of Tübingen.
Leube, P. C., Geiges, A., and Nowak, W. (2012). Bayesian assessment of the expected data impact on prediction confidence in optimal sampling design. Water Resour. Res. 48, W02501. doi:10.1029/2010WR010137.
Liu, J. S. (2008). Monte Carlo strategies in scientific computing. New York, NY: Springer Science & Business Media.
Martin, S., Klingler, S., Dietrich, P., Leven, C., and Cirpka, O. A. (2020). Structural controls on the hydrogeological functioning of a floodplain. Hydrogeol. J. doi:10.1007/s10040-020-02225-8.
Mualem, Y. (1976). A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 12, 513–522. doi:10.1029/WR012i003p00513.
Pöschke, F., Nützmann, G., Engesgaard, P., and Lewandowski, J. (2018). How does the groundwater influence the water balance of a lowland lake? A field study from Lake Stechlin, north-eastern Germany. Limnologica 68, 17–25. doi:10.1016/j.limno.2017.11.005.
Qiu, H., Blaen, P., Comer‐Warner, S., Hannah, D. M., Krause, S., and Phanikumar, M. S. (2019). Evaluating a coupled phenology‐surface energy balance model to understand stream‐subsurface Temperature dynamics in a mixed‐use farmland catchment. Water Resour. Res. 55, 1675–1697. doi:10.1029/2018WR023644.
Richards, L. A. (1931). Capillary conduction of liquids through porous mediums. Physics 1, 318–333. doi:10.1063/1.1745010.
Rodriguez-Pretelin, A., and Nowak, W. (2018). Integrating transient behavior as a new dimension to WHPA delineation. Adv. Water Resour. 119, 178–187. doi:10.1016/j.advwatres.2018.07.005
Sanz, D., Gómez-Alday, J. J., Castaño, S., Moratalla, A., De las Heras, J., and Martínez-Alfaro, P. E. (2009). Hydrostratigraphic framework and hydrogeological behaviour of the mancha oriental system (SE Spain). Hydrogeol. J. 17, 1375–1391. doi:10.1007/s10040-009-0446-y.
Schmidt, M., Ohmert, W., Schreiner, A., and Villinger, E. (2005). Geologische Karte von Baden-Württemberg 1:25.000 – erläuterungen Zu Blatt 7420 Tübingen (Freiburg im Breisgau: regierungspräsidium Freiburg (Landesamt für Geologie, Rohstoffe und Bergbau)). 5th Edn.
Selle, B., Rink, K., and Kolditz, O. (2013). Recharge and discharge controls on groundwater travel times and flow paths to production wells for the Ammer catchment in southwestern Germany. Environ. Earth Sci. 69, 443–452. doi:10.1007/s12665-013-2333-z.
Suk, H., and Park, E. (2019). Numerical solution of the Kirchhoff-transformed Richards equation for simulating variably saturated flow in heterogeneous layered porous media. J. Hydrol. 579, 124213. doi:10.1016/j.jhydrol.2019.124213.
Tóth, J. (1963). A theoretical analysis of groundwater flow in small drainage basins. J. Geophys. Res. 68, 4795–4812. doi:10.1029/JZ068i016p04795.
Tarboton, D. G., Bras, R. L., and Rodriguez-Iturbe, I. (1991). On the extraction of channel networks from digital elevation data. Hydrol. Process. 5, 81–100. doi:10.1002/hyp.3360050107.
Therrien, R., McLaren, R., Sudicky, E., and Panday, S. (2010). HydroGeoSphere: a three-dimensional numerical model describing fully-integrated subsurface and surface flow and solute transport. Waterloo, ON: Groundwater Simulations Group, University of Waterloo.
Tocci, M. D., Kelley, C. T., Miller, C. T., and Kees, C. E. (1998). Inexact Newton methods and the method of lines for solving Richards’ equation in two space dimensions. Comput. Geosci. 2, 291–309. doi:10.1023/A:1011562522244.
Ufrecht, W. (2017). Zur Hydrogeologie veränderlich fester Gesteine mit Sulfatgestein, Beispiel Gipskeuper (Trias, Grabfeld-Formation). Grundwasser 22, 197–208. doi:10.1007/s00767-017-0362-3.
van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44, 892. doi:10.2136/sssaj1980.03615995004400050002x.
Keywords: gaussian process emulation, preposterior data impact assessor, bayesian analysis, uncertainty quantification, optimal design of measurements, delineation, groundwater divide
Citation: Allgeier J, González-Nicolás A, Erdal D, Nowak W and Cirpka OA (2020) A Stochastic Framework to Optimize Monitoring Strategies for Delineating Groundwater Divides. Front. Earth Sci. 8:554845. doi: 10.3389/feart.2020.554845
Received: 23 April 2020; Accepted: 08 October 2020;
Published: 16 November 2020.
Edited by:
Andrés Alcolea, Independent Researcher, Winterthur, SwitzerlandReviewed by:
Jorge Jódar, Instituto Geológico y Minero de España (IGME), SpainCopyright © 2020 Allgeier, González-Nicolás, Erdal, Nowak and Cirpka. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Olaf A. Cirpka, b2xhZi5jaXJwa2FAdW5pLXR1ZWJpbmdlbi5kZQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.