Exploratory Data Analysis and Artificial Neural Network for Prediction of Leptospirosis Occurrence in Seremban, Malaysia Based on Meteorological Data

Leptospirosis outbreaks in various parts of the world have been linked to changes in the weather. Furthermore, the effects have been shown to occur at different lags of up to 10 months, affecting the performance of simulation models that predict leptospirosis occurrence. In Malaysia, the link between different weather parameters, at different time lags, has yet to be established despite an increasing number of cases in recent years. In this study, a combination of data mining and machine learning is used to analyze, capture, and predict the relation between leptospirosis occurrence and temperature, rainfall, and relative humidity using the Seremban district in Malaysia as a case study. First, the optimal time lags for rainfall were determined using graphical exploratory data analysis (EDA) while non-graphical EDA was used for temperature. Then, an artificial neural network (ANN) model is developed to classify the combination of selected features into disease occurrence and non-occurrence using back-propagation training, optimizing the number of hidden layers and hidden nodes. The success is measured using accuracy, sensitivity, and specificity of each model. EDA has shown that leptospirosis occurrence in Seremban is highly correlated with weekly average temperature at lag 16 weeks and weekly rainfall amount at lag 12–20 weeks. Using these selected features, the ANN model achieved the highest accuracy, sensitivity, and specificity at 84.00, 86.44, and 79.33%, respectively. Overall, the EDA approach has increased the accuracy of the predictive model by 13.30–31.26% from the baseline models.

1. Introduction

1.1. Leptospirosis and Environmental Factors Influencing Transmission

Leptospirosis is a zoonotic disease caused by bacterial infection, i.e., by Leptospira with clinical symptoms, such as fever, headaches, muscle pains, and meningitis (Slack, 2010). The bacteria can be found in animals, such as rodents, dogs, pigs, and cattle (Mgode et al., 2015). More than 300 serovars have been identified worldwide and over 250 serotypes have been classified as pathogenic, which can cause diseases in people in varying severity (Levett, 2001; Lehmann et al., 2014). Human infection of leptospirosis occurs through direct contact with the product of infected animals, such as urine. Infection can also occur indirectly through contact with contaminated water or soil that contain pathogenic Leptospira species, while human to human transmission is considered rare (Chadsuthi et al., 2012).

Vector-host to human transmission is influenced by many environmental factors. Rural areas tend to present a higher risk compared to urban areas due to a larger number of animal reservoirs in agricultural and forested areas, as well as a higher level of transmission between wild and domestic animal hosts (Ellis, 2015; Mutalip et al., 2019). In contrast, urban leptospirosis is relatively easier to control by controlling the reproduction of rats due to availability of food and harborage (Grassmann et al., 2017), i.e., by proper management of dilapidated or abandoned house and public services including waste disposal. An unclean environment is always associated with the transmission of leptospirosis due to possible presence of contaminated water and soil (Schneider et al., 2013). Many studies have reported that remote rural areas with limited access to clean drinking water and sanitation to be more conducive to human infection (Maciel et al., 2008; Schneider et al., 2012, 2013). Besides, leptospirosis has been identified as an occupational disease where humans acquire infection primarily from exposure from mining, sewer maintenance, livestock farming, agricultural, and military maneuvers (Haake and Levett, 2015). In urban areas, incidence related to occupational exposure is preventable by implementation of control measures, such as by using personal protective equipment. More frequently, cases occur from participating in recreational and water-related activities, such as hiking, caving, and extreme sports (Mutalip et al., 2019).

At the same time, transmission is highly sensitive to climate and weather. Leptospira are known to thrive in warm and wet tropical and subtropical environments (Ridzlan et al., 2010). In Argentina, 76% of confirmed leptospirosis cases from 1999 to 2005 were recorded during warmer months (Vanasco et al., 2008). Leptospira were reported to survive longer, until up to 20 months when stored at 30°C, compared to 10 months at higher temperatures (Thibeaux et al., 2017). The bacteria have also been shown to survive at a low temperature, which is 4°C, and acidic environment for at least 20 months and remain harmful (Evangelista and Coburn, 2010; Andre-Fontaine et al., 2015). However, the bacteria also require high humidity and are killed by temperatures >50°C (122°F) (Manap, 2015).

Furthermore, heavy precipitation and flooding can trigger outbreaks as they can cause mobilization of the bacteria closer to human habitation (Chadsuthi et al., 2012). During flooding, the main risks arise as a result of population displacement to temporary placement that creates situations of poor sanitation, overcrowding, and contamination of food or water sources; besides, during severe disasters, populations may be forced to remain in temporary shelters for months or years, increasing exposure to contaminated water (Cook et al., 2008). Second, flooding may cause increases in outbreaks since contaminated water may be displaced over long distances (Cook et al., 2008; Lau et al., 2010). Lastly, extreme weather not only could affect the bacteria directly but also could influence human and animal behavior. For example, higher temperatures may attract humans and animals to take part in water-based activities, such as swimming and drinking. This in turn encourages human contact with the animal reservoir through sharing of water resources (Dufour et al., 2008).

1.2. Time Series Modeling and Prediction of Leptospirosis

All these factors reflecting the complexity in the transmission of leptospirosis become a major challenge for control strategies. However, an increasing number of studies have used mapping and time series modeling approaches to identify associations between different weather and environmental parameters, and allow future prediction of leptospirosis risk (Dhewantara et al., 2019).

Desvars et al. (2011) introduced the first approach to investigate the correlation between meteorological factors and seasonality of leptospirosis in the Reunion Island (Indian Ocean) using the Auto-Regressive Integrated Moving Average with eXplanatory variable (ARIMAX) time series model. The explanatory variables used were rainfall, temperature, and global solar radiation. Autocorrelation and partial autocorrelation were calculated to represent seasonal and cyclical trends in time series of leptospirosis cases as well as to optimize the ARIMAX parameters: lag order, degrees of differencing, and moving average order. The study found that at the monthly scale, leptospirosis is affected by monthly total rainfall with a lag of 2 months, and by mean temperature and solar radiation of the same month as the case. By using these three meteorological parameters, the best performing model explained 67.7% of the variance of the leptospirosis cases. The same approach was used by Chadsuthi et al. (2012) to predict the seasonal pattern of leptospirosis using historical rainfall and temperature in northern and northeastern Thailand. Using ARIMAX, they found that monthly total rainfall at lag 8 months was highly correlated with the number of leptospirosis cases in the northern region and produced the lowest root mean squared error between the prediction and observed. The RMSE is lower than that of the ARIMAX model using the combination of monthly total rainfall and mean temperature. However, in the northeastern region, the combination of monthly total rainfall at 10-months lag and temperature at 8-months lag were more associated with leptospirosis incidences. This suggests that the time lag may be different at different locations; the study further suggests consideration of other parameters, such as concentrations of oxygen and iron in water or soil and water pH (Xue et al., 2010; Parker and Walker, 2011).

A negative binomial regression model was used by Coelho and Massad to predict the daily number of leptospirosis cases in São Paulo, Brazil, also using rainfall and temperature, and additionally, minimum and maximum relative humidity (Coelho and Massad, 2012). The study found a significant correlation between the number of cases of leptospirosis and rainfall at the lag of 14–18 days. Using a similar approach, the Oceanic Nino Index and sea surface temperature used as additional variables were found to have a significant association at the 4-months lag in New Caledonia (Weinberger et al., 2014). These studies demonstrate that consideration of weather and climatic parameters beyond temperature and precipitation may be important. Compared to the findings of Chadsuthi et al. (2012), there is a large difference in the time lag of the meteorological variables. The reason is that Coelho and Massad (2012) hypothesized that the transmission of leptospirosis can be affected by rainfall in the range of 1 month prior. On the other hand, Chadsuthi et al. (2012) considered lags between 1 and 12 months. This is because a seasonal pattern was observed in Thailand, whereby higher cases were found during the rainy season across multiple years.

Joshi et al. (2017) used time series analysis to identify the lag effect of daily temperature (minimum, maximum, and mean), minimum relative humidity, cumulative rainfall, solar radiation, and total hours of sunshine prior to the initiation of leptospirosis transmission using Poisson time-series regression, among other methods. The study found the leptospirosis cases were associated with minimum temperature, rainfall, and solar radiation from 0 to 11 weeks prior. Poisson time-series regression was again used by Deshmukh et al. (2019) in Wardha district, India using temperature, rainfall, and humidity. They found relative humidity at no lag, while rainfall at 1 month lag was positively associated with leptospirosis incidence.

A recent study in Negeri Sembilan, Malaysia used similar predictors, i.e., temperature, rainfall, and relative humidity to predict weekly leptospirosis incidences using a machine learning classification algorithm (Rahmat et al., 2019). Using autocorrelation function and artificial neural network (ANN) with back-propagation, the study showed positive association of temperature, cumulative rainfall, and relative humidity at a 3-months lag, with the highest accuracy achieved of 70%. This study and the others have demonstrated the importance of time lag in the weather variables, on the predictability of leptospirosis occurrence at different locations.

In most of these studies, the optimal time lag was obtained using cross-correlation analysis, (Desvars et al., 2011; Chadsuthi et al., 2012; Weinberger et al., 2014; Rahmat et al., 2019), which is an efficient method to quantify the association between independent variables. However, the only information a correlation analysis result provides is the strength and direction of the relation. This has limited potential in feature extraction for machine learning, in contrast to exploratory data analysis (EDA, Radford et al., 1983) that instead allows analysis for patterns in the inputs, thereby allowing selection of more generalized/informative features for the machine learning model (Ho Yu, 2010).

In this study, we used EDA in place of cross-correlation to conduct feature selection for an ANN implementation of leptospirosis prediction. Several works have been reported in the literature related to the implementation of EDA in machine learning for other applications. Jones and Linder (2016) implemented EDA with a Random Forest classification algorithm to predict vote choice based on ideology. The goal of their model was to find the homogeneous partitions as well to classify the age of voters with respect to the type of political ideology. The implementation of EDA helps the Random Forest algorithm detect the interaction and non-linearity without prespecification and produce a low generalization error. Another study by Mueez et al. (2018) used EDA to help improve prediction of the success of apps released to the Google Play store. No studies have implemented EDA application in predictive model development for disease prediction, thus, the implementation in this study is a new contribution to this field.

2. Materials and Methods

2.1. Study Area

Negeri Sembilan is a state that lies on the western coast of Peninsular Malaysia. Negeri Sembilan consists of seven districts, which are Seremban, Jempol, Jelebu, Kuala Pilah, Tampin, Rembau, and Port Dickson. The state borders Selangor on the north, Pahang in the east, and Melaka and Johor to the south. Negeri Sembilan has one of the highest records of leptospirosis disease cases in the country (Tan et al., 2016), with the Seremban district having the highest number of cases between 2011 and 2017. The Seremban district is mainly urban and developing areas and the total number of population in Seremban was 606,000 in 2017 (Department of Statistics Malaysia, 2018). Between 2011 and 2017, the incidence rates were on average 13.08 per 100,000 people based on suspected cases notified to the Ministry of Health.

2.2. Data Collection

2.2.1. Human Leptospirosis Cases

The leptospirosis cases data were retrieved from the State Department of Health, Negeri Sembilan. The dataset consists of the number of cases by week between 2011 and 2017 as well as the locations of the cases within the Seremban district. The number of cases are aggregated into four analysis regions based on Euclidean distance proximity to four rainfall stations, which are at Hospital Seremban in the Seremban city (henceforth referred to as Seremban City), Sikamat, Mantin and Ladang Perentian (henceforth referred to as Perentian for brevity) stations as shown in Figure 1. The distance between each case to all four rainfall measuring stations are computed, and the case is assigned to the analysis region of the closest station. The weekly occurrences are relabeled on binary units. The binary value represents either the occurrence (1) or non-occurrence (0).

FIGURE 1

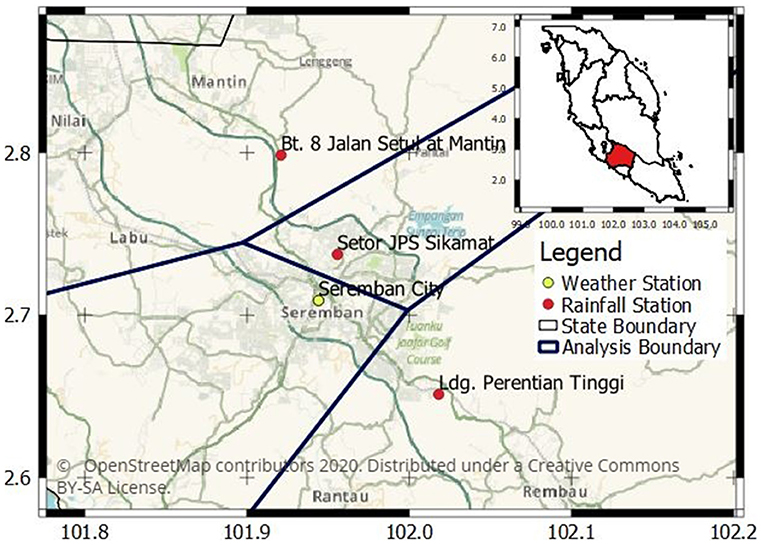
Figure 1. The location of rainfall and weather stations in Seremban, Negeri Sembilan. The weather station also provides rainfall data in addition to temperature and relative humidity. The cases falling within each analysis boundary are analyzed with respect to rainfall observations from the station within the same boundary, while the same temperature and relative humidity data from Hospital Seremban station are used in all the analysis regions.

2.2.2. Meteorological Data

Rainfall, temperature, and relative humidity data were retrieved from the Malaysia Meteorological Department weather station at Seremban City. Data from additional three rainfall stations Sikamat, Mantin, and Perentian as shown in Figure 1 were obtained from the Department of Irrigation and Drainage. Since only the Seremban City station provides temperature and relative humidity data, this study uses the same temperature and relative humidity data for all the analysis regions. The data were retrieved in daily format and aggregated from daily to weekly total for rainfall and weekly average for relative humidity. Meanwhile, temperature data were aggregated to the weekly minimum, mean, and maximum. Finally, five different lag sets were produced by lagging the meteorological variables by 4, 8, 12, 16, and 20 weeks. Each lag set contains 364 observations, representing 364 weeks.

2.3. Feature Selection: EDA

Visualization via a histogram and the probability density function (PDF) is used in the graphical approach on rainfall while k-means clustering is used in the non-graphical EDA on the temperature variables. In the preliminary analysis, temperature was also subjected to the graphical EDA; however, the dataset did not produce learnable patterns. For example, all the different lag datasets showed similar histograms, did not show normality, and/or showed many outliers resulting in high skewness. Hence, a non-graphical EDA approach was introduced. As for relative humidity, there was non-stationarity observed in the time series that did not allow generalization over the full analysis period, hence, EDA was not implemented. Instead, the lag for relative humidity was determined through test and error.

2.3.1. Analysis of Histogram and Probability Density Function

In the graphical EDA method, first, histograms were constructed to visualize the distribution of the number of leptospirosis cases per week, with respect to the weekly total rainfall as shown in Figure 4. The histogram is also used to indicate the mode value of the distribution. The PDF was also constructed from the histogram to assess the normality of the distribution. Several criteria were used in the analysis of each histogram and PDF. The first criterion is that histogram should resemble the bell-shaped curve of a normal distribution graph. The analysis of normal distribution reveals the consistency and variance in the dataset, and this consistency allows us to standardize our descriptions of data (Louangrath, 2015). To illustrate if the mean value of the weekly total rainfall to affect a high number of cases of leptospirosis is around 100 mm per week, while standard deviation is 15 mm per week, and the data are normally distributed, we are able to conclude that the number of cases will sharply decrease when the total rainfall exceeds 115 mm, i.e., the mean plus standard deviation. The second criterion is that the dataset must have a higher central tendency, which can be identified by a lower difference between mode and mean. The optimal time lag for rainfall is inferred from the lag set that meets at least one of these criteria.

2.3.2. k-Means Clustering and Centroid-Based Occurrence Likelihood

Clustering is a method that is frequently used in pattern recognition tasks (Baraldi and Blonda, 1999; Fan et al., 2018). It can help identify patterns in datasets with more than one variable. In our study, clusters of minimum, mean, and maximum temperatures will signify the different types of temperature variability in a week. k-Means clustering is used and the first step is to predefine the number of clusters, k. Second, the centroid for each cluster is initialized randomly. For every data point (minimum, mean, and maximum temperature values), the distance is computed from the centroids according to the Euclidean distance and the observation values are assigned to the closest cluster. The third step is to identify new centroids by calculating the mean of all data in each cluster. Finally, the second and third steps are repeated in multiple iterations until there is no significant change on the new centroids.

Finding the best number of clusters is necessary for better separation between data. To do so, the sum of within sums of squares resulting from different numbers (k) of clusters from 1 to 10 are calculated using all minimum, mean, and maximum temperature variables in one single analysis. The number of clusters that produce the lowest value of sum of within sum of square is selected. Based on the formula (equation 1), X_i represents the data while C_j represents the centroid for each cluster and n is the total number of data. Figure 2 shows the data clustering with k = 5.

$\begin{array}{ll}S={\displaystyle \sum _{j=1}^k{({\displaystyle \sum _{i=1}^n((}{X}_i-C_j)}^2})& (1)\end{array}$

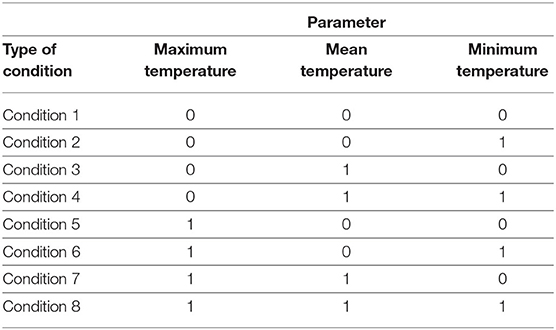
Next, the variability within each of the clustered weather condition is analyzed for probabilities of disease occurrence. Within each cluster, the centroids represent different thresholds values for mean temperature, maximum temperature, and minimum temperature, while other observation values either exceed or are below these threshold values. As there are three parameters, the observation values can be categorized into 3² possible conditions that describe whether or not each of the minimum, mean, and maximum temperatures within the cluster exceed the threshold. For each set of temperature values, there is an associated occurrence or non-occurrence of leptospirosis case, and therefore, the probability of occurrence can be calculated for each of the eight variations of weather conditions in each cluster. This is summarized in Table 1. A binary number with “0” represents the observations lower than the threshold value, whereas the binary number “1” indicates an observation exceeding the threshold value.

FIGURE 2

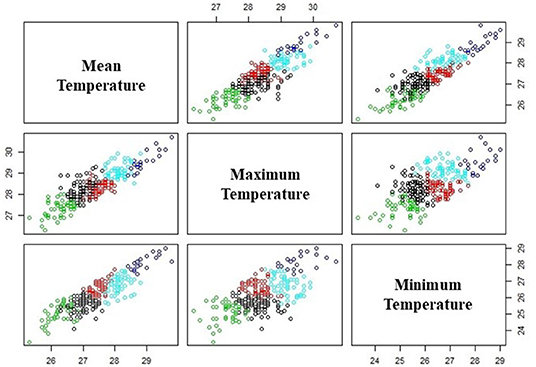
Figure 2. Clustering of temperature data by using k-mean clustering. The colors represent the five different clusters.

TABLE 1

Table 1. All temperature conditions that can be considered in each weather condition cluster.

The final step in this method is to classify across each condition into three occurrence/non-occurrence categories, which is “confirm disease occurs,” “confirm disease does not occur,” and “undefined category” based on the calculated probability, and using a predefined set of margins for each category as shown in Table 2. Then, the total number of incidences under each category can be calculated across all clusters in each lag set. The optimal time lag to be used for the predictive model is selected based on the lag set that has lowest incidences of undefined categories, indicating better separation between confirmation of disease occurring vs. not occurring.

TABLE 2

Table 2. Margins of probabilities for every exceedance/non-exceedance category.

2.4. ANN Model Development

This section discusses the development of ANN model and optimization of the model parameters, such as the types of activation function for the hidden and output neurons, normalization of the input layer, and lastly, the number of hidden neurons. Figure 3A shows an overview of the model from input to classification of the output.

FIGURE 3

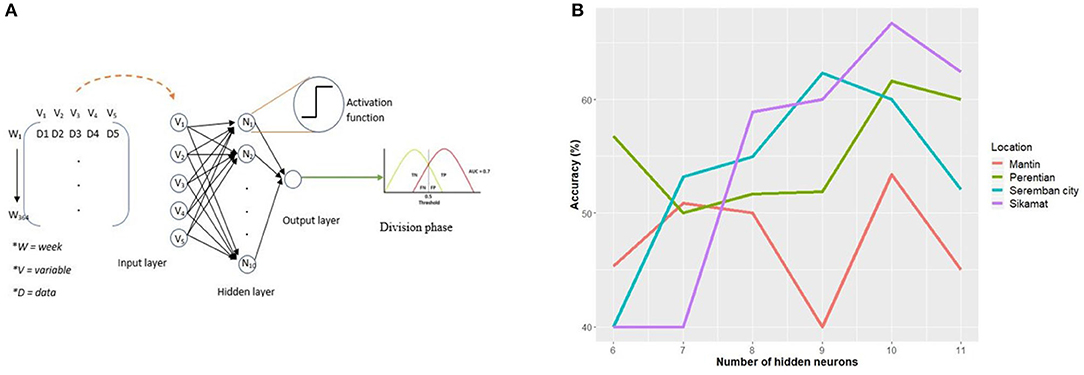
Figure 3. ANN model development. (A) The complete ANN predictive model. V1 through V5 is total rainfall per week, mean, maximum, and minimum temperature, relative humidity, respectively. (B) Performance of predictive model for each region based on the number of hidden neurons.

2.4.1. Hidden Layer: Activation Function

The first parameter selection occurred in the hidden layer, which plays an important role to train the input data supervised by the target data. The sigmoid function was selected as it is suitable for classification problems even if it has the weakness of vanishing the error gradient. To minimize this effect, a linear function is used in the output layer where the size of the error is determined. This function prevents a zero gradient, as the derivative of a linear function is always constant that is equal to 1, thus, the model will keep learning until it reaches the optimized output.

2.4.2. Normalization and Activation Function

The input data need to be normalized before being used in training. Normalization transposes the input variable into a data range appropriate for the activation function. In the function, there is a range on the x-axis that allows the model to perform aggressive learning, that is between −3 and 3. Thus, to bring input data close to this region, the input needs to be normalized. In this study, this was done by re-centering between negative values to positive values (−1 to 1). The reason for this selection is that the sigmoid function used for the activation function is not symmetrical at the origin, and the value of y axis might not have the same sign with the x axis, which can cause a slow convergence. The search for the solution to the non-convex optimization problem is using a gradient-based approach and this gradient depends on the input value times the weight. As the input data prior to normalization is in the positive range, and if the input data are normalized following the output range of sigmoid function (range from 0 to 1), a bigger change is required in the value of weights between the input and hidden layer to shift the input to the correct target of either close to 0 or 1. However, if normalization centralizes to values of the input around 0, as is done in this study, the learning becomes faster as the fluctuations in the weights in achieving convergence will become smaller.

2.4.3. Hidden Layer: Number of Hidden Neurons

There are several ways to determine the number of neurons in the hidden layer of ANN model (Panchal and Panchal, 2014; Gazzaz et al., 2015). The appropriate number of neurons can largely affect the final output, and when wrongly selected, it can lead to overfitting or underfitting. The rule of thumb of Gazzaz et al. (2015) is used as shown in Equation (2). I is the total number of inputs, H is number of hidden layers, and O is the number of outputs. The rule provides a reasonable range for the number of hidden neurons, which can increase the performance of ANN. This study considers to use only a single hidden layer with multiple hidden neurons.

$\begin{array}{ll}2(\sqrt{I})+O\le H\le 2(I)+O& (2)\end{array}$

2.4.4. Split-Validation

To prevent the model from under- or overfitting, the input and output data were divided into training, validation, and testing datasets. The validation dataset is for estimating how well the model has been trained, whereas the testing dataset is used to estimate the model properties, such as prediction or classification error, and the accuracy, specificity, and sensitivity of the model to classify the data. The Levenberg–Marquardt function was selected as the network training function, and 3,000 iterations were used as the stopping criteria. The Levenberg–Marquardt function is a fast algorithm for updating the weight of the neuron during training as was shown in previous studies (Abhishek et al., 2012; Mustafidah et al., 2014).

There are two considerations in splitting the datasets for training, validation, and testing: first, the total number of samples in data, and second, the number of parameters that needs to be selected during training (Borovicka et al., 2012). If there is a large number of samples, the split ratio should favor increasing the number of datasets for training so that the model performs adequate learning. In contrast, if the model has many parameters, the split ratio should favor increasing the size of the validation set. In this study, only one model parameter is required for tuning, which is the number of hidden neurons; therefore, emphasis is given to the training set by selecting 80% of the dataset for training, 15% for testing, and 5% for validation.

2.5. Performance Measurement

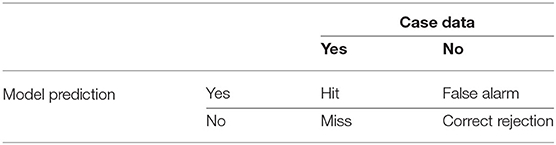
The confusion matrix or contingency table (Table 3) is used to evaluate the accuracy, sensitivity, and specificity of the model (Table 4). Accuracy is the percentage of success for the model to predict correctly whether the cases did or did not occur in a given week. Meanwhile, sensitivity measures the effectiveness of the model to predict correctly when the cases occurred (Nery et al., 2017). It also can be known as the probability of detection (POD). Lastly, specificity is the measure for successfully predicting that cases did not occur during the weeks that they did not (Lalkhen and McCluskey, 2008). All three model performance measures are equally important in producing a robust model and therefore the model development should aim to have these scores in a balance.

TABLE 3

Table 3. Definitions for model performance measures.

TABLE 4

Table 4. Definitions for model performance measures.

2.6. Robustness Test

Developing a machine learning algorithm requires regularization mechanisms to reduce overfitting and improve generalization. In other words, a model should be able to predict leptospirosis cases without only depending on the given sequence dataset. Multiple approaches can be used to test for model robustness, such as randomization or permutation test, and Jackknife and Bootstrap estimators (Walsh, 2000). These methods involve either sampling or scrambling the original data numerous times. In this work, a randomization test was implemented due to multiple input variables and their non-random pattern (Walsh, 2000). The order of data is scrambled from hundreds to thousands of times depending on the probability of observing the original datasets. The general consensus is around 1,000 samples for the test at 95% confidence interval, while 5,000 samples for test at 99% confidence interval. Commonly, 95% confidence intervals have been chosen for random sampling, unless the number of the original dataset is small (Edgington and Onghena, 2007). First, 1,000 samples were generated by scrambling the bases at random (shuffling them like a deck of cards). Then, all the random samples are tested with the four fitted models to produce new outputs. Lastly, the model outputs are analyzed for the ability of each model to generalize the input datasets by comparing the receiver operating characteristic (ROC) curves between the fitted and randomized input models. Another metric of performance considered is variance. Models with a very high variance may be overfitting the training data and not be adequately generalized for data that it has not seen before (Valentini and Dietterich, 2004).

2.7. Receiver Operating Characteristic

The ROC curve is used to determine a threshold value for separating the ANN output into 0's and 1's. The ROC is a probability curve that reflects the relationship between sensitivity (or total positive rate) and 1—specificity (or false positive rate). The area under this curve (AUC) represents the scalar measure of separability between each class. The selection of the threshold will affect sensitivity and specificity concurrently and in opposite ways. The optimal threshold is based on maximizing the AUC, as the threshold is varied between 0.3 and 0.9 at 0.01 interval.

3. Results and Discussion

This section is divided into three parts, which are discussion of the baseline models, EDA-based time lag selection for the meteorological input, and discussion on the performance of the proposed predictive model by using the selected time lagged predictors.

3.1. The Baseline Model

In selecting the best algorithm for the study, it is critical to develop a baseline of performance to compare a no-effect hypothesis model to alternatives that are more complex. Other researchers from different fields have used other terms, such as “naïve model” and “null model” (Addy et al., 2012; Schwab and Starbuck, 2013). In this work, four baseline models have been developed to represent one for each region of analysis and used as reference or control for this study with features or input parameters that are not selected through EDA. In other words, these baseline models take in meteorological data without any time lags as input.

First, the four baseline models are trained using a different number of neurons ranging from 6 neurons until 11 neurons, which are the range of values determined using Equation (2). There are trends that can be summarized from the performance of all models as the number of neurons increased as shown in Figure 3B. The predictive model in Sikamat region shows a significant increase from 40 to 66.70% when the number of neurons increases from 6 to 10. A similar trend can be observed for Seremban City, where the accuracy increases from 40 to 62.30% as the number of neurons increases to 9; however, the accuracy starts to decrease to 60.01% when the number of neurons increases to 10. In contrast, there is fluctuation in the accuracy of the model for Mantin and Perentian as the number of neurons increases toward 10.

Overall, across all four models, a higher accuracy is achieved with a higher number of neurons, demonstrating how a higher number of neurons can increase the complexity of the model and at once handle the complexity of input data. However, further addition of hidden neurons can increase the complexity to the point of negatively impacting the learning process of the network. This is evident in all models where all accuracy reduces after the 10th (ninth neuron for Seremban City). Based on this analysis, 10 neurons were selected to be used in the predictive model development for all four analysis regions.

Table 5 shows the overall results for all four models in the baseline configuration, i.e., using the input data without time lags for all meteorological variables and 10 hidden neurons. The results show that model accuracy of only around 55–67% is achieved. This shows that temperature, rainfall, and relative humidity from the same week of the disease occurrence does not allow for the best prediction. Three models have AUC values above 0.5, which are Seremban City, Mantin, and Sikamat, while the model from Perentian recorded the lowest reading, which is 0.4807. This suggests that rainfall or temperature during the same week may not completely explain human contact with contaminated water. For example, people may have the tendency to stay indoors instead of doing outdoor activities during rainy days, and therefore, could be less exposed to leptospirosis infection. Besides, the transmission of Leptospira will take at least 1 month after heavy rain (Triampo et al., 2007). In conclusion, time lag for each meteorological variable may be needed to improve the predictive model.

TABLE 5

Table 5. The performance of baseline models with no lag in input.

3.2. Exploratory Data Analysis

3.2.1. Exploratory Data Analysis on Rainfall

Figure 4 shows the histogram and PDF of rainfall data for all four analysis regions at lag 4–20 weeks, analyzed following the two criteria for the best time lag selection: a bell-shaped curve and/or the tendency to be center. The figure shows cumulative rainfall at lag 4 and 12 to have bell-shaped curves. However, the distribution of rainfall at lag 4 did not exponentially decrease after the mean, and instead increased near the tail of the distribution. The rainfall at 12-weeks lag further satisfies the second criteria with a very similar mean and mode. At all lags, the histograms show that there are higher probabilities for leptospirosis to occur when rainfall is between 100 mm until 250 mm/week. This amount of water may cause areas in the region to start ponding. Furthermore, Leptospira can survive in a time period even longer than 12 weeks (Wasiński and Dutkiewicz, 2013).

FIGURE 4

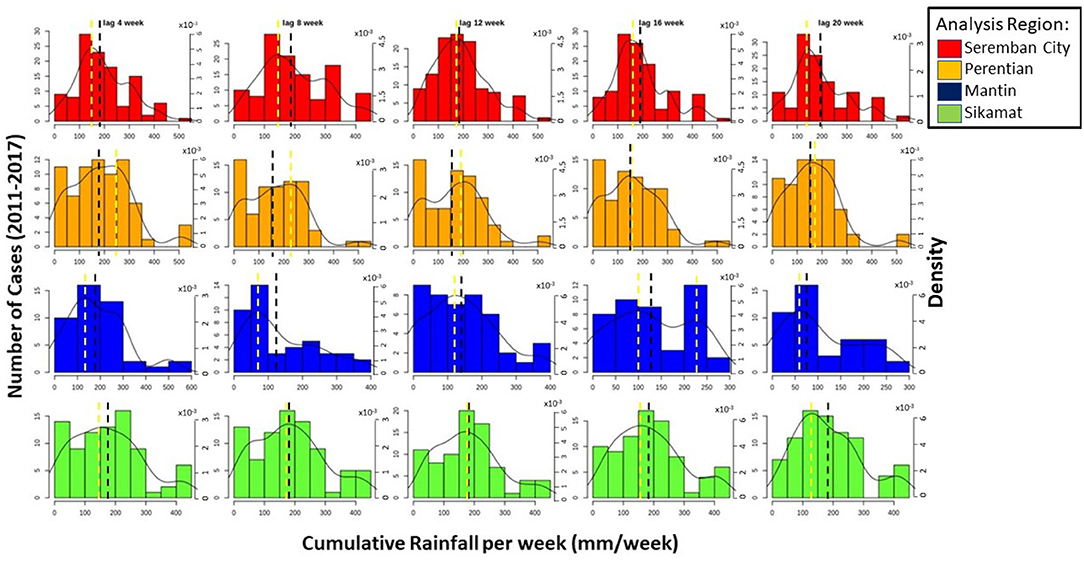
Figure 4. The distribution of the number of cases of leptospirosis against the cumulative rainfall at varying lags. The black dotted line indicates the mean, whereas the yellow dotted line represents the mode of the cumulative rainfall from 2011 until 2017. The black line indicates the probabilities distribution function graph.

In Perentian (Figure 4), the best bell-shaped curve is identified with rainfall at lag 16 weeks. Although there is also an acceptable distribution at lag 20 weeks, there is an obvious increase in probability at very high values. To avoid bias selection during training process, this dataset cannot be selected as input variable. Besides, the tendency to be center is also met by the 16 weeks lag. When comparing the lag time between Seremban City and Perentian, the difference is 4 weeks even if they are neighboring locations. However, Perentian is more industrialized, whereas Seremban City is more residential. Seremban City thus could be supported by a more efficient drainage infrastructure and have a better cleanliness level than Perentian, where the Leptospira can be contained and therefore survive for longer.

For Sikamat and Mantin regions (Figure 4), the histograms and shapes of distribution are harder to analyze. Therefore, the analysis was focused on the central tendency and the existence of outliers. The reason for this may be that the number of diseases recorded in these regions is smaller compared to those in Seremban City and Perentian, and the smaller the sample, the less accurate is the probability distribution. For the Mantin region, almost all lag sets do not show normality. Lag 8 and 16 weeks clearly shows a large distance between the mean and mode values and a bimodal distribution, respectively. Lag 12 weeks is relatively normally distributed but has increases in both tails. This leaves lags 4 and 20, and the latter is selected based on a higher tendency to be center. For the Sikamat analysis region, the data with lag 12 weeks meet the bell-curved shape distribution, despite a slight increase after 350 mm, and thus was selected.

In conclusion, the EDA results show that distribution at different time lags will take different shapes. A set of decision criteria, i.e., bell-shaped curve and central tendency allows information to be extracted from the data and consequently features to be selected for the subsequent ANN model.

3.2.2. Exploratory Data Analysis on Temperature

Each lag set was clustered based on the similarity of minimum, mean, and maximum temperature of the week. The sum of within sum of square with different number of cluster was analyzed from 1 until 10 clusters, whereby the clusters with higher values will have a greater internal variability. The results (Figure 5) show the sum of within sum of square to rapidly decline between 2 and 5 clusters and tapers off afterwards, indicating an optimal number of five clusters to classify the data.

FIGURE 5

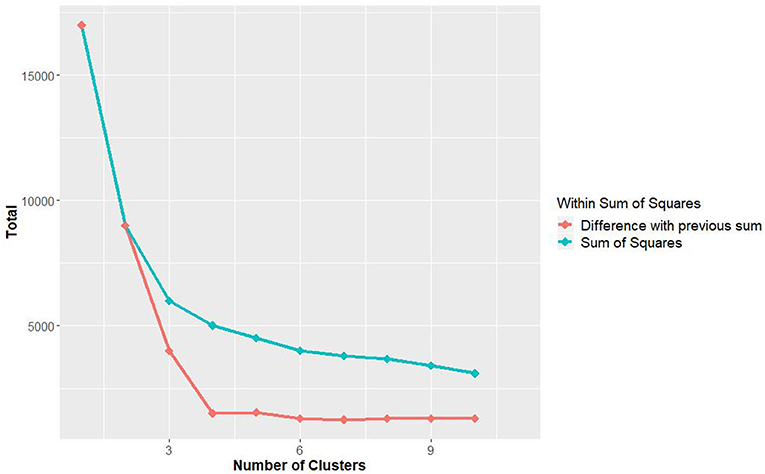
Figure 5. The sum of within sum of square with different numbers of clusters. The sums are calculated using all minimum, mean, and maximum temperatures from Hospital Seremban station.

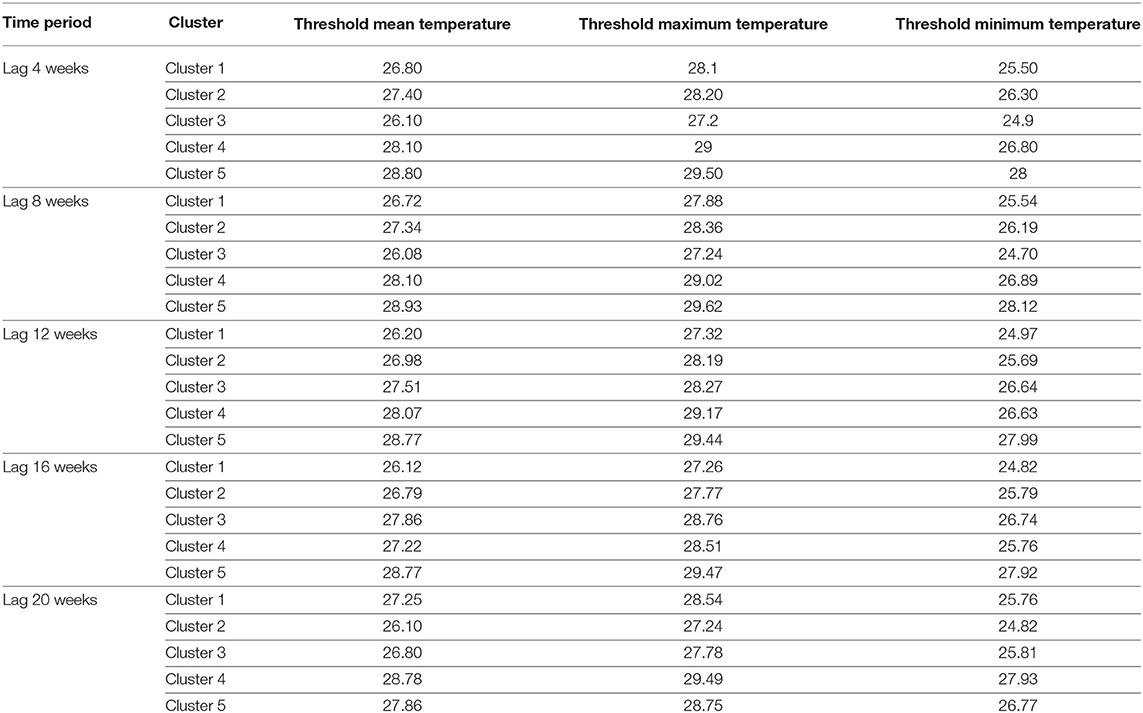
Next, each lag set was divided into five clusters and the centroids representing different threshold values for mean temperature, maximum temperature, and minimum temperature were calculated (Table 6). Within each cluster, the observations are further subdivided into eight conditions as shown in Table 1. For each condition, the number of observations (weeks) where leptospirosis occurred were converted into probability values and categorized according to the margins as shown in Table 2. This results in Table 7 that shows the number of incidences across all five clusters and eight conditions, of likely positive confirmation, likely negative confirmation, and undefined cases. Identification of the lag set with the lowest incidences of undefined cases could allow for a better prediction due to the higher classification power based on the three temperature parameters. Table 7 shows that the dataset for the 8-weeks lag consists of the highest frequency of likely cases occurring, which is nine incidences. However, it also consists of the highest frequency of undefined category with 22 incidences. Furthermore, lag 4 and 20 shows 15 incidences of likely cases do not occur, which is higher compared with the other lags. The dataset that has the lowest frequency of undefined category is lag 16 weeks with 17 incidences. Thus, this time lag was selected for temperature data including minimum, mean, and maximum temperature.

TABLE 6

Table 6. The threshold for mean, minimum, and maximum temperature datasets.

TABLE 7

Table 7. The total number for all incidences under different probability margin categories for all the lag sets.

A maximum temperature of 28.76°C was found to be the most optimal for transmission of Leptospira. This is based on the selected cluster 3 in lag 16 weeks (Table 6), in which there are more conditions (referring to Table 1) with a high possibility (more than 70%) for leptospirosis occurrence compared to the other clusters. Our finding is aligned with previous studies that have shown 28°C until 30°C to be the best temperature for Leptospira growth (Adler and de la Peña Moctezuma, 2010; DebMandal et al., 2011; Sakhaee and Gholam, 2011; Khan et al., 2012). Although a lag of 16 weeks is seemingly long, Leptospira can survive 152 days in fresh water with cellular aggregation (Wynwood et al., 2014). Besides, temperature may also correlate to the transmission of leptospirosis by affecting the human and animal behavior.

3.3. Performance of Predictive Model With Feature Selection

After selection of the best time lag for temperature and rainfall data, these features are used in the ANN model, first to identify the lag for relative humidity. Table 8 shows that almost all models produce more than 50% accuracy when using the relative humidity in the same week (no lag), with exception of Perentian at 43% accuracy. Mantin shows the highest performance, which is 69%. However, all models produce between 72 and 84% accuracy when the humidity data are between 12- and 20-weeks lags. At shorter lag times, the accuracy achieved is only from 40 to 73% at 8 weeks, and 40 to 70% at 4 weeks. The lag for humidity is similar in range with the rainfall and temperature lags, and may be due to its dependence on both parameters. Furthermore, the optimal lag time for relative humidity is similar to that found by Joshi et al. (2017) who suggested that survival of Leptospira in the environment is dependent on humid conditions, although the authors also suggested that their observed decreases in cases with increases in humidity at 0 lag could be attributed to reduced human outdoor activities. As EDA was not implemented with relative humidity data, more detailed insights could not be derived from this work.

TABLE 8

Table 8. Model accuracy at different time lags of humidity data.

The overall performance of all four models was evaluated in terms of accuracy, sensitivity, and specificity (Tables 9, 10). The range of accuracy achieved by these models is between 80 and 83.99%. Note that 178 weeks were correctly predicted by model for Seremban City, 171 week for Mantin, 185 week for Perentian, and 173 weeks for Sikamat. In terms of misses, models for Seremban City, Mantin, Perentian, and Sikamat incorrectly classified occurrences in 36, 43, 29, and 41 weeks, respectively. The analysis of the ROC identified a threshold of 0.56 for Seremban City for best classifying the output into “0” and “1,” while 0.54 for Mantin, 0.48 for Perentian, and 0.58 for Sikamat, respectively. We can summarize that these models are more likely to have the ability to predict the week where the cases are likely to occur because all specificity values are below 80%, whereas sensitivity values are always above 80%.

TABLE 9

Table 9. The performance of each model in terms of accuracy, specificity, and sensitivity.

TABLE 10

Table 10. Confusion matrix for each predictive model.

Even though models from Seremban City, Sikamat, and Mantin share similar accuracy, they slightly differ in performance in terms of sensitivity and specificity. This difference can be understood from ROC, whereby Seremban City has an AUC of 0.8706, while Sikamat has 0.8451 and Mantin only has 0.8392. Seremban City has a higher AUC because of its number of weeks when cases occur is higher than the number of weeks when cases do not occur. This may contribute to a higher true positive rate over false-positive rate by the model compared to the models for Mantin and Sikamat.

The highest sensitivity among the analyzed regions was achieved in Perentian, which is 86.44%. The model is also optimized as it scores 79.33% in specificity, which is also highest among other models. Overall, the EDA approach has increased the accuracy of the predictive model by 19.99, 24.57, 31.26, and 13.30% from the best performance by the baseline model for Seremban City, Mantin, Perentian, and Sikamat model, respectively.

Heavy rainfall is a natural cause of flooding, and we found that the weekly rainfall amounts between lag 12 and 20 weeks to be the most efficient input variable to predict the occurrence of leptospirosis. However, this time lag is seemingly long and for stagnant water to remain in the duration is improbable. However, there are other factors that can possibly explain the lag in the transmission, such as indirectly through poorer sanitation and hygiene (Victoriano et al., 2009; Schneider et al., 2013). The lower the sanitation or hygiene level, the higher it is the chance to increase the rodent population and their rates of infection. Flooding may cause poorer sanitation and hygiene levels, with flood waters carrying all types of debris, microorganisms, and drowned animals. Even though flood recession can occur within days, and especially is the case for Seremban with the smaller rivers, the unsanitary environment that results could remain depending on the rehabilitation work after floods. Besides, animal carcass can become the vector for transferring the bacteria. Another consequence of heavy rains is that the water-soaked soil can provide an advantageous environmental condition for Leptospira to live longer (Zitek and Benes, 2005).

3.4. The Robustness of the Predictive Model

Based on Figure 6, all four fitted models are robust to a randomized input as the AUC of fitted models lies within the maximum and minimum AUC of the random tests. The average AUC for 1,000 randomized runs of the model for Mantin, Seremban City, Perentian, and Sikamat, which are 0.8388, 0.8700, 0.8899, and 0.8447, respectively, are very close to the performance of the fitted models. The range of differences are 0.0004 until 0.0006. Building robust ANN models never comes without a cost (Mhamdi et al., 2017). It is clearly shown in Figure 6 that the model for Seremban City is robust as it recorded the second smallest variance, which is 6.6379e-05, even though the prediction accuracy is not as high as the model from Perentian, which has the highest AUC value. The model for Perentian achieves a variance of 6.2717e-05, which indicates less dispersion and higher consistency.

FIGURE 6

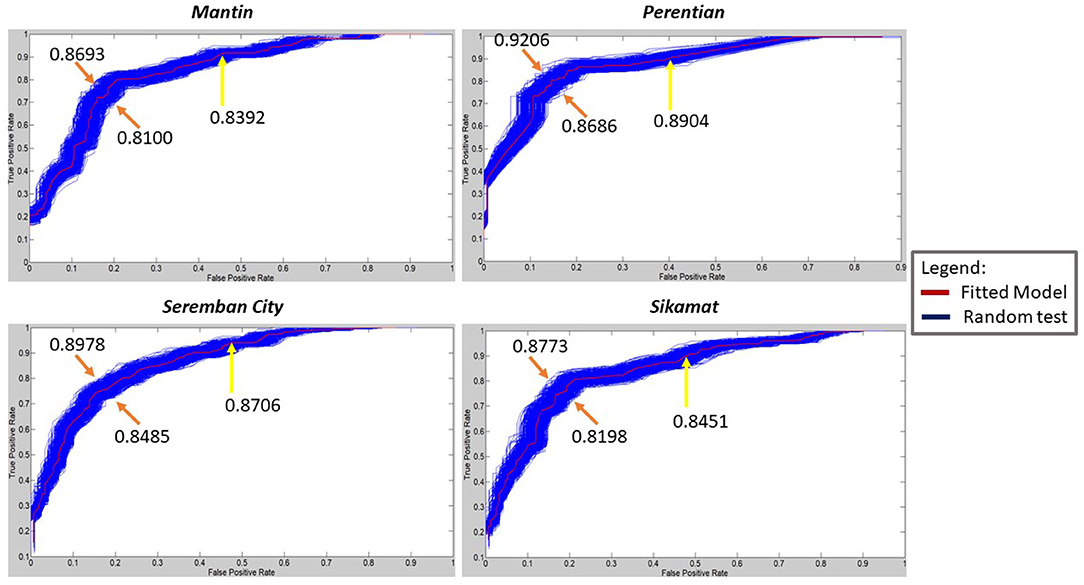
Figure 6. Receiver operating characteristic (ROC) curve and area under this curve (AUC) values for fitted models vs. randomized test.

4. Conclusion

This is the first study to implement machine learning using ANN with EDA for leptospirosis prediction. Our analysis has shown that meteorological time lags vary even in neighboring regions within a district. It is important for development of predictive models to consider and understand the relationship between input and output data, and through EDA, the accuracy of the prediction model is improved from 52.73 to 83.99% for the Perentian model, from 60.01 to 80.00% for Seremban City, 55.43 to 80.00% for Mantin, and 66.70 to 80% for Sikamat. Through our model development approach, we demonstrated that it is possible to produce highly sensitive models as an early warning before outbreaks happen, at the same highly specific models, which can help the public health in terms of preserving resources.

Our prediction of leptospirosis achieves more than 80% accuracy. However, the models with the trained ANN architecture and parameters are not able to identify which input provides a higher weight or influence on the output. This is because the ANN is a black box model, which was developed in terms of its inputs and outputs, without any knowledge of its internal workings. As a result, this could have limited the understanding to be gained on the impact of hydrometeorological variables to the transmission of leptospirosis. However, this limitation was controlled by investigating the input dataset by using EDA for discovering and selecting the most useful information. As a result, the resultant EDA-ANN can be perceived more as gray box rather than black box modeling. Besides, multiple approaches within the EDA were used to analyze and capture the patterns in input data, suggesting that a one-size-fits-all solution is not a suitable assumption for feature selection involving datasets with high complexity, such as weather variables.

Several other improvements can be done in this study to increase the understanding of the relationship between predictors and transmission of leptospirosis and increase the performance and effectiveness of the predictive model. First, this study could expand on the type of predictors, such as measures of the stage of sanitation and hygiene, the vulnerability of the target population, and the exposure of humans to the bacteria or rat population. Second, a further study can also be done to compare ANN with other predictive models either using mathematical model or machine learning, such as Auto-ARIMA, ARIMAX, Transfer Function, Support Vector Machine, Bayes Belief Network, and deep learning, to assess how the algorithm selection can affect the predictive model accuracy.

Data Availability Statement

The data analyzed in this study is subject to the following licenses/restrictions: the datasets are owned by multiple government agencies and have sharing restrictions. Requests to access these datasets should be directed to ZmFyaXFyYWhtYXQ5NCYjeDAwMDQwO2dtYWlsLmNvbQ==.

Author Contributions

FR, ZZ, and AJ conceived the research. FR processed all the data, performed the analyses, and interpreted the results. FR and ZZ wrote the manuscript with contributions from all authors.

Funding

This work was supported by a Newton Researcher Links Workshop grant from the British Council and Akademi Sains Malaysia (grant number 2016-RLWK7-10365) and a Malaysia Partnerships and Alliances in Research (MyPAIR) fund from the UK Natural Environment Council and the Ministry of Education Malaysia under the Understanding of the Impacts of Hydrometeorological Hazards programme (grant number NEWTON/1/2018/WAB05/UPM/1).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor is currently organizing a Research Topic with one of the authors ZZ.

Acknowledgments

We acknowledge the Department of Irrigation and Drainage, Ministry of Natural Resources and Environment for providing the ground-based precipitation data for free. The research was registered on the Malaysian National Medical Research Register (NMRR-19-4107-46243).

References

Abhishek, K., Kumar, A., Ranjan, R., and Kumar, S. (2012). “A rainfall prediction model using artificial neural network,” in 2012 IEEE Control and System Graduate Research Colloquium (Shah Alam: IEEE), 82–87. doi: 10.1109/ICSGRC.2012.6287140

CrossRef Full Text | Google Scholar

Addy, N., Mathieu, J. L., Kiliccote, S., and Callaway, D. S. (2012). “Understanding the effect of baseline modeling implementation choices on analysis of demand response performance,” in ASME International Mechanical Engineering Congress and Exposition, Vol. 45264 (Houston, TX: American Society of Mechanical Engineers), 133–141. doi: 10.1115/IMECE2012-86973

CrossRef Full Text | Google Scholar

Adler, B., and de la Peña Moctezuma, A. (2010). Leptospira and leptospirosis. Vet. Microbiol. 140, 287–296. doi: 10.1016/j.vetmic.2009.03.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Andre-Fontaine, G., Aviat, F., and Thorin, C. (2015). Waterborne Leptospirosis: survival and preservation of the virulence of pathogenic Leptospira spp. in fresh water. Curr. Microbiol. 71, 136–142. doi: 10.1007/s00284-015-0836-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Baraldi, A., and Blonda, P. (1999). A survey of fuzzy clustering algorithms for pattern recognition. II. IEEE Trans. Syst. Man Cybernet. B Cybernet. 29, 786–801. doi: 10.1109/3477.809033

CrossRef Full Text | Google Scholar

Borovicka, T., Jirina, M., Kordik, P., and Jiri, M. (2012). “Selecting representative data sets,” in Advances in Data Mining Knowledge Discovery and Applications, ed A. Karahoca (London: IntechOpen), 43–70. doi: 10.5772/50787

CrossRef Full Text | Google Scholar

Chadsuthi, S., Modchang, C., Lenbury, Y., Iamsirithaworn, S., and Triampo, W. (2012). Modeling seasonal leptospirosis transmission and its association with rainfall and temperature in Thailand using time-series and ARIMAX analyses. Asian Pac. J. Trop. Med. 5, 539–546. doi: 10.1016/S1995-7645(12)60095-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Coelho, M. S., and Massad, E. (2012). The impact of climate on leptospirosis in São Paulo, Brazil. Int. J. Biometeorol. 56, 233–241. doi: 10.1007/s00484-011-0419-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Cook, A., Watson, J., van Buynder, P., Robertson, A., and Weinstein, P. (2008). 10th anniversary review: Natural disasters and their long-term impacts on the health of communities. J. Environ. Monit. 10, 167–175. doi: 10.1039/b713256p

PubMed Abstract | CrossRef Full Text | Google Scholar

DebMandal, M., Mandal, S., and Pal, N. K. (2011). Is jaundice a prognosis of leptospirosis? Asian Pac. J. Trop. Dis. 1, 279–281. doi: 10.1016/S2222-1808(11)60065-0

CrossRef Full Text | Google Scholar

Department of Statistics Malaysia (2018). My Local Stats: Negeri Sembilan 2017. Technical report, Department of Statistic, Putrajaya.

Google Scholar

Deshmukh, P., Narang, R., Jain, J., Jain, M., Pote, K., Narang, P., et al. (2019). Leptospirosis in Wardha District, Central India—analysis of hospital based surveillance data. Clin. Epidemiol. Glob. Health 7, 102–106. doi: 10.1016/j.cegh.2018.02.005

CrossRef Full Text | Google Scholar

Desvars, A., Jégo, S., Chiroleu, F., Bourhy, P., Cardinale, E., and Michault, A. (2011). Seasonality of human leptospirosis in Reunion Island (Indian Ocean) and its association with meteorological data. PLoS ONE 6:e20377. doi: 10.1371/journal.pone.0020377

PubMed Abstract | CrossRef Full Text | Google Scholar

Dhewantara, P. W., Lau, C. L., Allan, K. J., Hu, W., Zhang, W., Mamun, A. A., et al. (2019). Spatial epidemiological approaches to inform leptospirosis surveillance and control: A systematic review and critical appraisal of methods. Zoonoses Public Health 66, 185–206. doi: 10.1111/zph.12549

PubMed Abstract | CrossRef Full Text | Google Scholar

Dufour, B., Moutou, F., Hattenberger, A., and Rodhain, F. (2008). Global change: impact, management, risk approach and health measures-the case of europe. Rev. Sci. Tech. 27, 529–550. doi: 10.20506/rst.27.2.1817

PubMed Abstract | CrossRef Full Text | Google Scholar

Edgington, E., and Onghena, P. (2007). Randomization Tests. London: CRC Press.

Google Scholar

Ellis, W. A. (2015). Animal Leptospirosis. Clayton: Springer. Grassmann, A. A., da Cunha, C. E. P., Bettin, E. B., and McBride, A. J. A. (2017). Overview of Leptospirosis. Cham: Springer.

Google Scholar

Evangelista, K. V., and Coburn, J. (2010). Leptospira as an emerging pathogen: a review of its biology, pathogenesis and host immune responses. Fut. Microbiol. 5, 1413–1425. doi: 10.2217/fmb.10.102

PubMed Abstract | CrossRef Full Text | Google Scholar

Fan, H., Zheng, L., Yan, C., and Yang, Y. (2018). Unsupervised person re-identification: clustering and fine-tuning. ACM Trans. Multimed. Comput. Commun. Appl. 14:83. doi: 10.1145/3243316

CrossRef Full Text | Google Scholar

Gazzaz, N. M., Yusoff, M. K., Ramli, M. F., Juahir, H., and Aris, A. Z. (2015). Artificial neural network modeling of the water quality index using land use areas as predictors. Water Environ. Res. 87, 99–112. doi: 10.2175/106143014X14062131179276

PubMed Abstract | CrossRef Full Text | Google Scholar

Grassmann, A. A., da Cunha, C. E. P., Bettin, E. B., and McBride, A. J. A. (2017). Overview of Leptospirosis.

Google Scholar

Haake, D. A., and Levett, P. N. (2015). “Leptospirosis in humans,” in Leptospira and Leptospirosis, ed B. Edler (Berlin: Springer), 65–97. doi: 10.1007/978-3-662-45059-8_5

CrossRef Full Text | Google Scholar

Ho Yu, C. (2010). Exploratory data analysis in the context of data mining and resampling. Int. J. Psychol. Res. 3:9. doi: 10.21500/20112084.819

CrossRef Full Text | Google Scholar

Jones, M. Z., and Linder, J. F. (2016). EDARF: exploratory data analysis using random forests. J. Open Source Softw. 1:92. doi: 10.21105/joss.00092

CrossRef Full Text | Google Scholar

Joshi, Y. P., Kim, E.-H., and Cheong, H.-K. (2017). The influence of climatic factors on the development of hemorrhagic fever with renal syndrome and leptospirosis during the peak season in Korea: an ecologic study. BMC Infect. Dis. 17:406. doi: 10.1186/s12879-017-2506-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, S., Dutta, P., Borah, J., Chowdhury, P., Topno, R., Baishya, M., et al. (2012). Leptospirosis presenting as acute encephalitis syndrome (AES) in Assam, India. Asian Pac. J. Trop. Dis. 2, 151–153. doi: 10.1016/S2222-1808(12)60034-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Lalkhen, A. G., and McCluskey, A. (2008). Clinical tests: sensitivity and specificity. Contin. Educa. Anaesth. Crit. Care Pain 8, 221–223. doi: 10.1093/bjaceaccp/mkn041

CrossRef Full Text | Google Scholar

Lau, C. L., Smythe, L. D., Craig, S. B., and Weinstein, P. (2010). Climate change, flooding, urbanisation and leptospirosis: fuelling the fire? Trans. R. Soc. Trop. Med. Hyg. 104, 631–638. doi: 10.1016/j.trstmh.2010.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, J. S., Matthias, M. A., Vinetz, J. M., and Fouts, D. E. (2014). Leptospiral pathogenomics. Pathogens 3, 280–308. doi: 10.3390/pathogens3020280

PubMed Abstract | CrossRef Full Text | Google Scholar

Levett, P. N. (2001). Leptospirosis. Clin. Microbiol. Rev. 14, 296–326. doi: 10.1128/CMR.14.2.296-326.2001

PubMed Abstract | CrossRef Full Text | Google Scholar

Louangrath, P. (2015). Normal Distribution and Common Tests Used to Verify Normality. Bangkok: Bangkok University.

Google Scholar

Maciel, E. A., de Carvalho, A. L. F., Nascimento, S. F., de Matos, R. B., Gouveia, E. L., Reis, M. G., et al. (2008). Household transmission of leptospira infection in urban slum communities. PLoS Negl. Trop. Dis. 2:e154. doi: 10.1371/journal.pntd.0000154

PubMed Abstract | CrossRef Full Text | Google Scholar

Manap, R. (2015). “Leptospiral infection,” in Proceeding of the 2nd International Conference on Management and Muamalah (Bangi).

Google Scholar

Mgode, G. F., Machang'u, R. S., Mhamphi, G. G., Katakweba, A., Mulungu, L. S., Durnez, L., et al. (2015). Leptospira serovars for diagnosis of leptospirosis in humans and animals in Africa: common leptospira isolates and reservoir hosts. PLoS Negl. Trop. Dis. 9:e4251. doi: 10.1371/journal.pntd.0004251

PubMed Abstract | CrossRef Full Text | Google Scholar

Mhamdi, E. M. E., Guerraoui, R., and Rouault, S. (2017). “On the robustness of a neural network,” in Proceedings of the IEEE Symposium on Reliable Distributed Systems (Hong Kong), 84–93. doi: 10.1109/SRDS.2017.21

CrossRef Full Text | Google Scholar

Mueez, A., Islam, K. A. T., and Iqbal, W. (2018). Exploratory Data Analysis and Success Prediction of Google Play Store Apps Authors. Dhaka: BRAC University.

Google Scholar

Mustafidah, H., Hartati, S., Wardoyo, R., and Harjoko, A. (2014). Selection of most appropriate backpropagation. Int. J. Comput. Trends Technol. 14, 92–95. doi: 10.14445/22312803/IJCTT-V14P120

CrossRef Full Text | Google Scholar

Mutalip, M. H. A., Mahmud, M. A. F., Yoep, N., Muhammad, E. N., Ahmad, A., Hashim, M. H., et al. (2019). Environmental risk factors of leptospirosis in urban settings: a systematic review protocol. BMJ Open 9:e023359. doi: 10.1136/bmjopen-2018-023359

PubMed Abstract | CrossRef Full Text | Google Scholar

Nery, N. R. R., Claro, D. B., and Lindow, J. C. (2017). Prediction of leptospirosis cases using classification algorithms. IET Softw. 11, 93–99. doi: 10.1049/iet-sen.2016.0193

CrossRef Full Text | Google Scholar

Panchal, F. S., and Panchal, M. (2014). Review on methods of selecting number of hidden nodes in artificial neural network. Int. J. Comput. Sci. Mobile Comput. 3, 455–464. doi: 10.1155/2013/425740

CrossRef Full Text | Google Scholar

Parker, J., and Walker, M. (2011). Survival of a pathogenic leptospira serovar in response to combined in vitro pH and temperature stresses. Vet. Microbiol. 152, 146–150. doi: 10.1016/j.vetmic.2011.04.028

PubMed Abstract | CrossRef Full Text | Google Scholar

Radford, P. J., Velleman, P. F., and Hoaglin, D. C. (1983). Applications, basics, and computing of exploratory data analysis. Biometrics 39:815. doi: 10.2307/2531118

CrossRef Full Text | Google Scholar

Rahmat, F., Ishak, A. J., Zulkafli, Z., Yahaya, H., and Masrani, A. (2019). Prediction model of Leptospirosis occurrence for Seremban (Malaysia) using meteorological data. Int. J. Integr. Eng. 11, 60–69. doi: 10.30880/ijie.2019.11.04.007

CrossRef Full Text | Google Scholar

Ridzlan, F. R., Bahaman, A. R., Khairani-Bejo, S., and Mutalib, A. R. (2010). Detection of pathogenic Leptospira from selected environment in Kelantan and Terengganu, Malaysia. Trop. Biomed. 27, 632–638.

PubMed Abstract | Google Scholar

Sakhaee, E., and Gholam, R. A. (2011). Detection of leptospiral antibodies by microscopic agglutination test in north-east of Iran. Asian Pac. J. Trop. Biomed. 1, 227–229. doi: 10.1016/S2221-1691(11)60032-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneider, M., Nájera, P., Aldighieri, S., Bacallao, J., Soto, A., Marquiño, W., et al. (2012). Leptospirosis outbreaks in nicaragua: identifying critical areas and exploring drivers for evidence-based planning. Int. J. Environ. Res Public Health 9, 3883–3910. doi: 10.3390/ijerph9113883

PubMed Abstract | CrossRef Full Text | Google Scholar

Schneider, M. C., Jancloes, M., Buss, D. F., Aldighieri, S., Bertherat, E., Najera, P., et al. (2013). Leptospirosis: a silent epidemic disease. Int. J. Environ. Res. Public Health 10, 7229–7234. doi: 10.3390/ijerph10127229

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwab, A., and Starbuck, W. H. (2013). “Why baseline modelling is better than null-hypothesis testing: examples from international business research,” in Philosophy of Science and Meta-Knowledge in International Business and Management, eds T. M. Devinney, P. Torben, and T. Laszlo (Bingley: Emerald Group Publishing), 171. doi: 10.1108/S1571-5027(2013)0000026012

CrossRef Full Text | Google Scholar

Slack, A. (2010). Leptospirosis. Aus. Fam. Phys. 39, 495–498. doi: 10.1016/j.lpm.2009.09.026

CrossRef Full Text | Google Scholar

Tan, W. L., Soelar, S. A., Suan, M. A. M., Hussin, N., Cheah, W. K., Verasahib, K., et al. (2016). Leptospirosis incidence and mortality in Malaysia. Southeast Asian J. Trop. Med. Public Health 47, 434–440.

PubMed Abstract | Google Scholar

Thibeaux, R., Geroult, S., Benezech, C., Chabaud, S., Soupé-Gilbert, M.-E., Girault, D., et al. (2017). Seeking the environmental source of Leptospirosis reveals durable bacterial viability in river soils. PLoS Negl. Trop. Dis. 11:e0005414. doi: 10.1371/journal.pntd.0005414

PubMed Abstract | CrossRef Full Text | Google Scholar

Triampo, W., Baowan, D., Tang, I. M., Nuttavut, N., and Doungchawee, G. (2007). A simple deterministic model for the spread of leptospirosis in Thailand. Int. J. Biol. Med. Sci. 2, 22–26. doi: 10.5281/zenodo.1081017

CrossRef Full Text | Google Scholar

Valentini, G., and Dietterich, T. G. (2004). Bias-variance analysis of support vector machines for the development of SVM-based ensemble methods. J. Mach. Learn. Res. 5, 725–775. doi: 10.1007/3-540-45428-4_22

CrossRef Full Text | Google Scholar

Vanasco, N. B., Schmeling, M., Lottersberger, J., Costa, F., Ko, A. I., and Tarabla, H. D. (2008). Clinical characteristics and risk factors of human leptospirosis in argentina (1999–2005). Acta Trop. 107, 255–258. doi: 10.1016/j.actatropica.2008.06.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Victoriano, A. F., Smythe, L. D., Gloriani-Barzaga, N., Cavinta, L. L., Kasai, T., Limpakarnjanarat, K., et al. (2009). Leptospirosis in the Asia Pacific region. BMC Infect. Dis. 9:147. doi: 10.1186/1471-2334-9-147

PubMed Abstract | CrossRef Full Text | Google Scholar

Walsh, B. (2000). Resampling Methods: Randomization Test, Jackknife And Bootstrap Estimators. Lecture Notes. Brussels: European Environmental Bureau.

Google Scholar

Wasiński, B., and Dutkiewicz, J. (2013). Leptospirosis–current risk factors connected with human activity and the environment. Ann. Agric. Environ. Med. 20, 239–244.

PubMed Abstract | Google Scholar

Weinberger, D., Baroux, N., Grangeon, J.-P., Ko, A. I., and Goarant, C. (2014). El Niño southern oscillation and leptospirosis outbreaks in New Caledonia. PLoS Negl. Trop. Dis. 8:e2798. doi: 10.1371/journal.pntd.0002798

PubMed Abstract | CrossRef Full Text | Google Scholar

Wynwood, S. J., Graham, G. C., Weier, S. L., Collet, T. A., McKay, D. B., and Craig, S. B. (2014). Leptospirosis from water sources. Pathog. Glob. Health 108, 334–338. doi: 10.1179/2047773214Y.0000000156

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, F., Dong, H., Wu, J., Wu, Z., Hu, W., Sun, A., et al. (2010). Transcriptional responses of leptospira interrogans to host innate immunity: significant changes in metabolism, oxygen tolerance, and outer membrane. PLoS Negl. Trop. Dis. 4:e857. doi: 10.1371/journal.pntd.0000857

PubMed Abstract | CrossRef Full Text | Google Scholar

Zitek, K., and Benes, C. (2005). Longitudinal epidemiology of leptospirosis in the Czech Republic (1963–2003). Epidemiol. Mikrobiol. Imunol. 54, 21–26.

PubMed Abstract | Google Scholar