Finite Difference Method for the One-Dimensional Non-linear Consolidation of Soft Ground Under Uniform Load

Initial stress and additional effective stress distributions in soil greatly influence the degree of ground consolidation when calculating one-dimensional soft clay ground consolidation in deep soil. The one-dimensional non-linear consolidation governing equations of soft ground under uniform load are derived and solved with the finite difference method. This method is based on the assumptions that the initial stress in soil varies with the ground depth and that the additional effective stress caused by external loads changes with both the ground depth and consolidation time and the hyperbolic model of the soil stress–strain relationship. Formulas for the degree of consolidation and the settlement of the ground are presented. A case study shows that the degree of consolidation in the ground calculated with the finite difference method agrees well with the traditional analytical solution, and the computational efficiency of the finite difference method can be effectively improved when the segmental calculation method is used throughout the consolidation process. The results of another example show that the settlement of the ground calculated with the finite difference method agrees with the in situ data. The suggested method can greatly simplify the consolidation calculation and has a high application value in engineering.

Introduction

The traditional Terzaghi one-dimensional consolidation theory assumes that external loads are applied instantaneously and does not take into account that external loads are often linear, graded, or cyclic in practical engineering. Additionally, the non-linear characteristics of the stress–strain relationship of the soil itself are not considered. Therefore, many scholars have carried out improvement studies. Schiffman (1958) first analyzed the problem of the one-dimensional consolidation of a foundation under variable loads. Later, Wilson and Elgohary (1974), Favaretti and Mazzucato (1994), Xie and Pan (1995), and Zhao and Shi (1996) conducted further research on this problem and obtained many useful conclusions. Lai and Song (2005) conducted soil consolidation and drainage tests under special stress paths, and the stress–strain relationship of soil obtained was consistent with the fitting results of the log-curve non-linear model, sinusoidal non-linear model, and traditional hyperbolic model. Yu et al. (2008) used a modified hyperbolic model to fit the quantitative relationship between the secondary consolidation coefficient and the pressure of soil under normal consolidation and proposed a modified method for calculating the secondary consolidation settlement of the normal consolidated soil. He and Jiang (2009) proposed a hyperbolic prediction model that reflects the semicubic non-linear relationship between the settlement rate and the remaining settlement. In addition, in the study of one-dimensional non-linear consolidation theory, Davis and Raymond (1965), Barden and Berry (1965), and Xie et al. (2006) considered the physical non-linear characteristics of soil based on the relation e – lgσ′. However, the value of the initial consolidation pressure is crucial to the calculation of the foundation settlement by the e – lgσ′ model. In view of this, Wei (1987) believed that, if the initial pressure and repressure could not be reasonably distinguished, then the hyperbolic model could be used to calculate the foundation settlement, and the calculation result was better than that of the e – lgσ′ model. Xu (1987) also experimentally proved that the hyperbolic model could better simulate the constitutive relationship of soft clay. On this basis, Shi et al. (2001) obtained the one-dimensional consolidation theory of the hyperbolic model at the time of instantaneous loading, and the calculated results were in good agreement with the laboratory test. Xie et al. (2010, 2016) obtained the analytical solution for the one-dimensional consolidation of clayey soils and double-layered structured soils with a threshold gradient. Lo et al. (2016) presented a one-dimensional consolidation theory in unsaturated soils under cyclic loading. Wang et al. (2017), Liu et al. (2018), Zou et al. (2018), and Zhao et al. (2020), respectively, obtained analytical solutions for the one-dimensional consolidation of clayey soils considering different load and boundary conditions. When considering time-dependent loading, Deng et al. (2019) presented closed-form solutions for one-dimensional consolidation in saturated soils, Moradi et al. (2019) analyzed the one-dimensional consolidation of a multilayered unsaturated soil under partially permeable boundary conditions, and Zhou et al. (2020) obtained an analytical solution for a classical one-dimensional thaw consolidation model.

However, due to the small sample used in the test, the applicability of this theory in the calculation of deep soft clay could not be verified. Zhang and Sun (2007) established the one-dimensional consolidation theory of foundations under variable loads based on the hyperbolic model, and Zhou et al. (2013) presented a finite difference model for a one-dimensional electro-osmotic consolidation. However, the theory assumed that the initial effective stress and the additional stress of soil remained unchanged along the depth, which was different from the actual situation. Therefore, this paper combines previous research results with the hyperbolic model of the stress and strain of soil as a starting point. This method assumes that the initial stress changes along the depth of the foundation, and at the same time, the load caused by the additional effective stress changes with time and depth. Additionally, the uniformly distributed load is derived via the control equation of the one-dimensional consolidation of soil, and the finite difference method is introduced into the degree of consolidation and settlement calculation formula.

One-Dimensional Consolidation Governing Equation

Basic Assumptions

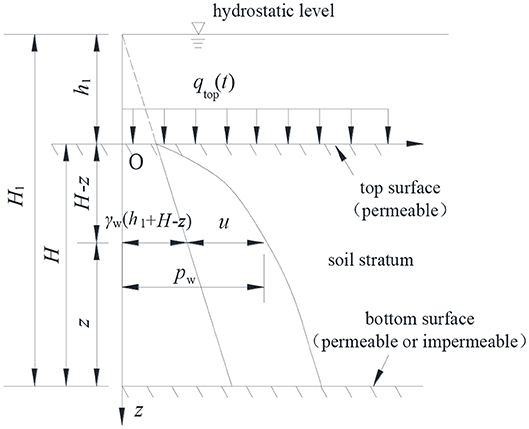
The basic assumptions are as follows: the soft soil is saturated, the thickness of the compressed soil layer is H, the surface of the soft soil is permeable, and the drainage conditions of the bottom surface can be divided into permeable and impermeable. Considering the simulation of vehicle load, the impulse load and simple harmonic load, which varies with time, can be selected. When the vehicle load is transferred to the embankment, the impulse load and simple harmonic load could be uniformed. Besides, the embankment is filled step by step, and the embankment load, which can be simulated to multiple graded loads, also varies with time. All these loads above can be simplified into the uniform load q_top(t), which varies with time.

The distribution of the water pressure in the foundation is shown in Figure 1, where γ_w(h₁ + H – z) is the hydrostatic pressure at depth z, p_w is the total water pressure, and u is the pore water pressure generated by the evenly distributed embankment load q_top(t) in the soil.

FIGURE 1

Figure 1. Schematic diagram of the one-dimensional consolidation model of the foundation.

a. The stress–strain relationship of the soil satisfies the hyperbolic model:

$\begin{array}{ll}\frac{\sigma \prime }{\epsilon }=E_0+m\sigma \prime & (1)\end{array}$

where σ′ is the effective stress, E₀ is the initial compression modulus of the soil, ε is the strain, and m is the slope of the σ′/ε ~ σ′ curve.

b. Let the permeability coefficient k be proportional to the compression coefficient a_v:

$\begin{array}{ll}\frac{k}{a_{\text{v}}}=\frac{{\gamma }_{\text{w}}{c}_{\text{v}}}{1+e_0}=\text{const}& (2)\end{array}$

where γ_w is the unit weight of water, γ_w = ρ_wg. The parameter ρ_w is the density of water, c_v is the consolidation coefficient, e₀ is the initial void ratio, and const is a constant.

c. The initial effective stress of the soil ${\sigma }_0\prime$(z) changes with depth z.

d. Considering the change in the external load with time (as shown in Figure 2A), the additional stress of the soil caused by the external load also changes with time, and the additional stress will change along the depth, so the additional stress can be expressed by q(t,z) (shown in Figure 2B).

FIGURE 2

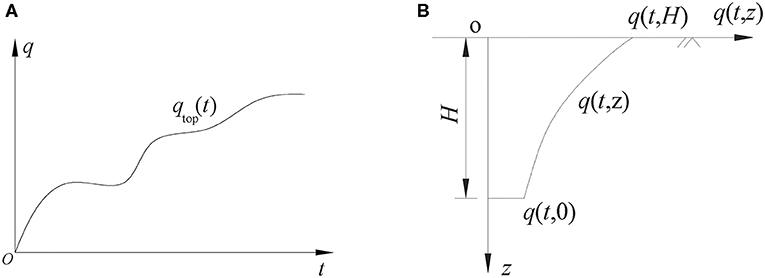
Figure 2. Distribution of the additional stress in soil when the external load increases linearly. (A) External load function curve. (B) Curve of the additional stress in the compressed soil layer.

Derivation of the Consolidation Governing Equation

Based on basic assumptions a and b, the one-dimensional consolidation governing equation can be obtained as:

$\begin{array}{l}-c_{\text{v}}{E}_0\left[\frac{1}{{(E_0+m{\sigma }^{\prime })}^2}\frac{{\text{∂}}^{2}u}{\text{∂}{z}^2}-\frac{2m}{{(E_0+m{\sigma }^{\prime })}^3}\frac{\text{∂}{\sigma }^{\prime }}{\text{∂}z}\frac{\text{∂}u}{\text{∂}z}\right]\\ =\frac{E_0}{{(E_0+m{\sigma }^{\prime })}^2}\frac{\text{∂}{\sigma }^{\prime }}{\text{∂}t}& (3)\end{array}$

According to the effective stress principle, the stress expression at depth z is

$\begin{array}{ll}{\sigma }^{\prime }(t,z)+u(t,z)=q(t,z)+{{\sigma }^{\prime }}_0(z)& (4)\end{array}$

The two sides of Equation (4) are opposite and partial derivatives, and we obtain:

$\begin{array}{ll}\frac{\text{∂}{\sigma }^{\prime }}{\text{∂}z}=\frac{\text{∂}q}{\text{∂}z}\text{+}\frac{\text{∂}{{\sigma }^{\prime }}_0}{\text{∂}z}-\frac{\text{∂}u}{\text{∂}z}& (5)\end{array}$

$\begin{array}{ll}\frac{\text{∂}{\sigma }^{\prime }}{\text{∂}t}=\frac{\text{∂}q}{\text{∂}t}-\frac{\text{∂}u}{\text{∂}t}& (6)\end{array}$

Substituting Equations (5) and (6) into Equation (3), the one-dimensional non-linear consolidation governing equation of the foundation under uniformly distributed load is

$\begin{array}{l}{c}_{\text{v}}\frac{{\text{∂}}^{2}u}{\text{∂}{z}^2}+\frac{2m{c}_{\text{v}}}{E_0+m(q+{{\sigma }^{\prime }}_0-u)}\frac{\text{∂}u}{\text{∂}z}\left(\frac{\text{∂}u}{\text{∂}z}-\frac{\text{∂}q}{\text{∂}z}-\frac{\text{∂}{{\sigma }^{\prime }}_0}{\text{∂}z}\right)\\ =\frac{\text{∂}u}{\text{∂}t}-\frac{\text{∂}q}{\text{∂}t}& (7)\end{array}$

Boundaries and Initial Conditions

a. At the initial moment, the upper load is conveyed by the pore water pressure, and its mathematical expression is

$\begin{array}{ll}u(0,z)=q(0,z)(t=0,0\le z\le H)& (8)\end{array}$

b. After loading, when the ground surface is a permeable layer, the pore water pressure on the bottom surface is zero.

$\begin{array}{ll}u(t,H)=0(t>0,z=H)& (9)\end{array}$

c. When the ground surface is an impermeable layer after loading, the surface pore water pressure is zero, and its mathematical expression is

$\begin{array}{ll}u(t,0)=0(t>0,z=0)& (10)\end{array}$

d. When the top surface of the foundation is permeable and the bottom surface is impermeable, the pore water pressure of the soil is equal to that of the underlying layer.

Differential Method for the Governing Equations

Difference Method Format

According to the basic principle of the finite difference method, with depth z as the vertical axis and time t as the horizontal axis, a calculation area for foundation consolidation analysis is established. The depth z is divided into M equal divisions, the time t is divided into N equal divisions, and a difference method calculation grid is established. As shown in Figure 3, the grid node represents the pore water pressure u, where u_{a, b} represents the value of the pore water pressure at depth b in the ground at the moment of time a.

FIGURE 3

Figure 3. Schematic diagram of meshing by the difference method.

The initial and boundary conditions in the difference equation can be expressed as

$\begin{array}{ll}\{\begin{array}{l}{u}_{0,b}=q_{\text{b}}\\ u_{a,M}=0\\ u_{a,1}=0\text{ (permeable bottom surface)}\\ u_{a,1}=u_{a,-1}\text{ (impermeable bottom surface)}\end{array}& (11)\end{array}$

For the governing Equation (7), the Crank–Nicolson format is used to discretize the following difference format:

$\begin{array}{l}\frac{u_{a+1,b}-u_{a,b}}{\Delta t}-\frac{q_{a+1,b}-q_{a,b}}{\Delta t}=c_v\left(\frac{u_{a+1,b+1}-2u_{a+1,b}+u_{a+1,b-1}}{2h^2}+\frac{u_{a,b+1}-2u_{a,b}+u_{a,b-1}}{2h^2}\right)+\\ \frac{c_{v}m}{E_0+m(q_{a,b}+{\left({{\sigma }^{\prime }}_0\right)}_b-u_{a,b})}\{\left(\frac{u_{a+1,b+1}-u_{a+1,b-1}}{2h}\right)\left(\frac{u_{a+1,b+1}-u_{a+1,b-1}}{2h}-\frac{q_{a+1,b+1}-q_{a+1,b-1}}{2h}-\frac{{\left({{\sigma }^{\prime }}_0\right)}_{b+1}-{\left({{\sigma }^{\prime }}_0\right)}_{b-1}}{2h}\right)\\ +\left(\frac{u_{a,b+1}-u_{a,b-1}}{2h}\right)\left(\frac{u_{a,b+1}-u_{a,b-1}}{2h}-\frac{q_{a,b+1}-q_{a,b-1}}{2h}-\frac{{\left({{\sigma }^{\prime }}_0\right)}_{b+1}-{\left({{\sigma }^{\prime }}_0\right)}_{b-1}}{2h}\right)\}& (12)\end{array}$

where Δt = T/N, h = H/M, T is the total consolidation time, and M and N are the number of grids of the depth and consolidation time, respectively.

To simplify the calculation, Equation (12) is linearized; then,

$\begin{array}{l}\frac{u_{a+1,b}-u_{a,b}}{\text{Δ}t}-\frac{q_{a+1,b}-q_{a,b}}{\text{Δ}t}=c_v(\frac{u_{a+1,b+1}-2u_{a+1,b}+u_{a+1,b-1}}{\text{2}{h}^2}\\ \text{+}\frac{u_{a,b+1}-2u_{a,b}+u_{a,b-1}}{\text{2}{h}^2})+\frac{c_{v}m}{E_0+m(q_{a,b}+{\left({{\sigma }^{\prime }}_0\right)}_b-u_{a,b})}\{\left(\frac{u_{a+1,b+1}-u_{a+1,b-1}}{2h}\right)\\ \left(\frac{u_{a,b+1}-u_{a,b-1}}{2h}-\frac{q_{a+1,b+1}-q_{a+1,b-1}}{2h}-\frac{{\left({{\sigma }^{\prime }}_0\right)}_{b+1}-{\left({{\sigma }^{\prime }}_0\right)}_{b-1}}{2h}\right)\\ +\left(\frac{u_{a,b+1}-u_{a,b-1}}{2h}\right)\left(\frac{u_{a,b+1}-u_{a,b-1}}{2h}-\frac{q_{a,b+1}-q_{a,b-1}}{2h}-\frac{{\left({{\sigma }^{\prime }}_0\right)}_{b+1}-{\left({{\sigma }^{\prime }}_0\right)}_{b-1}}{2h}\right)\}& (13)\end{array}$

Linearization will inevitably bring errors. To minimize the errors, the difference grid can be refined. Assume

$\begin{array}{ll}\{\begin{array}{l}\alpha (a,b)=\frac{c_{v}m}{E_0+m(q_{a,b}+{\left({{\sigma }^{\prime }}_0\right)}_b-u_{a,b})}\left(\frac{u_{a,b+1}-u_{a,b-1}}{2h}-\frac{q_{a+1,b+1}-q_{a+1,b-1}}{2h}-\frac{{\left({{\sigma }^{\prime }}_0\right)}_{b+1}-{\left({{\sigma }^{\prime }}_0\right)}_{b-1}}{2h}\right)\\ \beta (a,b)=\frac{c_{v}m}{E_0+m(q_{a,b}+{\left({{\sigma }^{\prime }}_0\right)}_b-u_{a,b})}\left(\frac{u_{a,b+1}-u_{a,b-1}}{2h}-\frac{q_{a,b+1}-q_{a,b-1}}{2h}-\frac{{\left({{\sigma }^{\prime }}_0\right)}_{b+1}-{\left({{\sigma }^{\prime }}_0\right)}_{b-1}}{2h}\right)\left(\frac{u_{a,b+1}-u_{a,b-1}}{2h}\right)\end{array}& (14)\end{array}$

Then, the formula for calculating the difference method under two boundary conditions can be written as follows:

$\begin{array}{ll}Au=B& (15)\end{array}$

When the bottom surface is permeable, A is an (M – 1) × (M – 1) order matrix, u is an (M – 1) × 1 order matrix, and B is an (M – 1) × 1 order matrix. When t = aΔt, then

$\begin{array}{ll}\left[\begin{array}{llllllllllll}\hfill A_{1,1}\hfill & \hfill A_{1,2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill A_{2,1}\hfill & \hfill A_{2,2}\hfill & \hfill A_{2,3}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill A_{b,b-1}\hfill & \hfill A_{b,b}\hfill & \hfill A_{b,b+1}\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill A_{M-2,M-3}\hfill & \hfill A_{M-2,M-2}\hfill & \hfill A_{M-2,M-1}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill A_{M-1,M-2}\hfill & \hfill A_{M-1,M-1}\hfill \end{array}\right]\left[\begin{array}{c}\hfill u_1\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill u_b\hfill \\ \hfill ⋮\hfill \\ \hfill u_{M-1}\hfill \end{array}\right]=\left[\begin{array}{c}\hfill B_1\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill B_b\hfill \\ \hfill ⋮\hfill \\ \hfill B_{M-1}\hfill \end{array}\right]& (16)\end{array}$

where $A_{b,b}=-\frac{c_v}{h^2}-\frac{1}{\text{Δ}t}$

$\begin{array}{l}{A}_{b,b+1}=\frac{c_v}{\text{2}{h}^2}+\frac{1}{2h}\alpha (a,b)(b<M-1)\hfill \\ A_{b,b-1}=\frac{c_v}{\text{2}{h}^2}-\frac{1}{2h}\alpha (a,b)(b>1)\hfill \end{array}$

$\begin{array}{l}{B}_b=-\frac{c_v}{2h^2}{u}_{a,b+1}+\left(\frac{c_v}{h^2}-\frac{1}{\text{Δ}t}\right)u_{a,b}\hfill \\ -\frac{c_v}{2h^2}{u}_{a,b-1}-\frac{1}{\text{Δ}t}(q_{a+1,b}-q_{a,b})-\beta (a,b)\hfill \end{array}$

$\begin{array}{l}{B}_{\text{1}}=-\frac{c_v}{2h^2}{u}_{a,2}+\left(\frac{c_v}{h^2}-\frac{1}{\text{Δ}t}\right)u_{a,1}\\ -\frac{1}{\text{Δ}t}(q_{a+1,1}-q_{a,1})-\beta (a,1)\end{array}$

$\begin{array}{l}{B}_{M-1}=-\frac{c_v}{2h^2}{u}_{a,M-2}+(\frac{c_v}{h^2}-\frac{1}{\text{Δ}t})u_{a,M-1}\hfill \\ -\frac{1}{\text{Δ}t}(q_{a+1,M-1}-q_{a,M-1})-\beta (a,M-1)\hfill \end{array}$

When the bottom surface is impermeable, A is an M × M order matrix, u is an M × 1 order matrix, and B is an M × 1 order matrix. When t = aΔt, then

$\begin{array}{ll}\left[\begin{array}{llllllllllll}\hfill A_{1,1}\hfill & \hfill A_{1,2}\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill A_{2,1}\hfill & \hfill A_{2,2}\hfill & \hfill A_{2,3}\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill A_{b,b-1}\hfill & \hfill A_{b,b}\hfill & \hfill A_{b,b+1}\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill ⋮\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill A_{M-1,M-2}\hfill & \hfill A_{M-1,M-1}\hfill & \hfill A_{M-1,M}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill 0\hfill & \hfill A_{M,M-1}\hfill & \hfill A_{MM}\hfill \end{array}\right]\left[\begin{array}{c}\hfill u_1\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill u_b\hfill \\ \hfill ⋮\hfill \\ \hfill u_M\hfill \end{array}\right]=\left[\begin{array}{c}\hfill B_1\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill ⋮\hfill \\ \hfill B_b\hfill \\ \hfill ⋮\hfill \\ \hfill B_M\hfill \end{array}\right]& (17)\end{array}$

where $A_{b,b}=-\frac{c_v}{h^2}-\frac{1}{\text{Δ}t}$

$\begin{array}{l}{A}_{b,b+1}=\frac{c_v}{2h^2}+\frac{1}{2h}\alpha (a,b)(b<M)\hfill \\ A_{b,b-1}=\frac{c_v}{2h^2}-\frac{1}{2h}\alpha (a,b)(1<b<M)\hfill \\ A_{M,M-1}=\frac{c_v}{h^2}-\frac{1}{h}\alpha (a,b)\hfill \end{array}$

$\begin{array}{l}{B}_b=-\frac{c_v}{2h^2}{u}_{a,b+1}+\left(\frac{c_v}{h^2}-\frac{1}{\text{Δ}t}\right)u_{a,b}\hfill \\ -\frac{c_v}{2h^2}{u}_{a,b-1}-\frac{1}{\text{Δ}t}(q_{a+1,b}-q_{a,b})-\beta (a,b)\hfill \end{array}$

$\begin{array}{l}{B}_{\text{1}}=-\frac{c_v}{2h^2}{u}_{a,2}+(\frac{c_v}{h^2}-\frac{1}{\text{Δ}t})u_{a,1}\hfill \\ -\frac{1}{\text{Δ}t}(q_{a+1,1}-q_{a,1})-\beta (a,1)\hfill \end{array}$

$\begin{array}{l}{B}_M=-\frac{c_v}{h^2}{u}_{a,M-1}+(\frac{c_v}{h^2}-\frac{1}{\text{Δ}t})u_{a,M}\hfill \\ -\frac{1}{\text{Δ}t}(q_{a+1,M}-q_{a,M})-\beta (a,M)\hfill \end{array}$

Calculation Formula of the Consolidation Degree

According to the uniaxial compression theory, the calculation formula of the ground settlement is

$\begin{array}{ll}S(t)={\displaystyle {\int }_0^H}\frac{{\sigma }^{\prime }(t)}{E_0+m{\sigma }^{\prime }(t)}dz-{\displaystyle {\int }_0^H}\frac{{{\sigma }^{\prime }}_0}{E_0+m{{\sigma }^{\prime }}_0}dz& (18)\end{array}$

The formula for calculating the average consolidation degree of a foundation defined by settlement can be written as

$\begin{array}{ll}{U}_{\text{s}}(t)=\frac{S(t)}{S_{\text{f}}}\text{=}\frac{{\int }_0^H\frac{{\sigma }^{\prime }(t)}{E_0+m{\sigma }^{\prime }(t)}dz-{\int }_0^H\frac{{{\sigma }^{\prime }}_0}{E_0+m{{\sigma }^{\prime }}_0}dz}{{\int }_0^H\frac{{{\sigma }^{\prime }}_{max}}{E_0+m{{\sigma }^{\prime }}_{max}}dz-{\int }_0^H\frac{{{\sigma }^{\prime }}_0}{E_0+m{{\sigma }^{\prime }}_0}dz}& (19)\end{array}$

In addition, the average consolidation degree of the foundation, as defined by the average pore pressure, can also be expressed as

$\begin{array}{ll}{U}_{\text{p}}=\frac{{\int }_0^H\left[q(t,z)-u\right]dz}{{\int }_0^H{q}_{max}dz}& (20)\end{array}$

Theoretical Verification

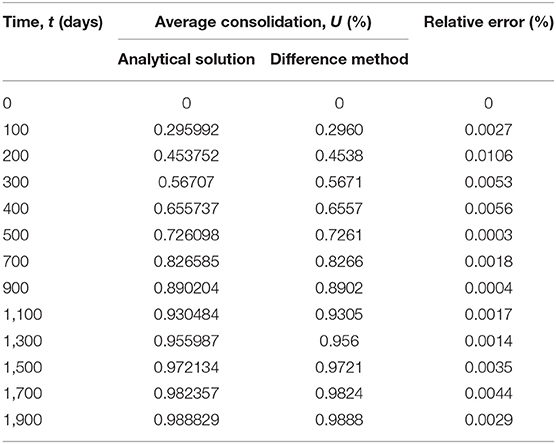
Examples are cited in the literature (Zhu and Yin, 1998) for verification. The calculation parameters are as follows: the thickness of the compressed soil layer is 5 m, and the bottom surface is a permeable layer; the load time linearly increases from q_a = 0 kPa to q_a = 300 kPa after 50 days and then remains unchanged; the consolidation coefficient of the soil is c_v = 5.7888 × 10⁻³ m²/day, and the initial compression modulus is E₀ = 1,687 kPa.

The analytical solution in Zhu and Yin (1998) assumes that the additional stress caused by the external load is linearly distributed with time and depth, and the stress–strain relationship of the soil is a linear elastic model. Corresponding to the special case of the difference method solution in this article, which is m = 0, Equation (1) can be written as

$\begin{array}{ll}\sigma \prime =E_0\epsilon & (21)\end{array}$

In the following, the finite difference method (hereinafter referred to as the method in this paper) proposed earlier is used to calculate the average consolidation degree of the foundation. To improve the calculation efficiency, the difference calculation is divided into two sections in the time dimension: the first section is 100 days in length, which is divided into 500 parts, Δt = 0.2 day; the length of the second period is the remaining 1,800 days, which is divided into 1,800 parts, Δt = 1 day. The average consolidation degree of the foundation calculated by this method and the analytical solution calculation results in Zhu and Yin (1998) are summarized in Table 1.

TABLE 1

Table 1. Average consolidation degree of the foundation.

From Table 1, it can be seen that the maximum relative error of the calculation results of the method in this paper and the analytical solution in Zhu and Yin (1998) is only 0.0106%, indicating that the method in this paper is reasonable and feasible and can meet the calculation accuracy requirements.

Illustrative Examples

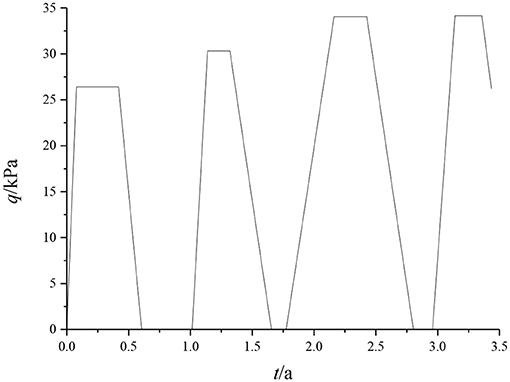
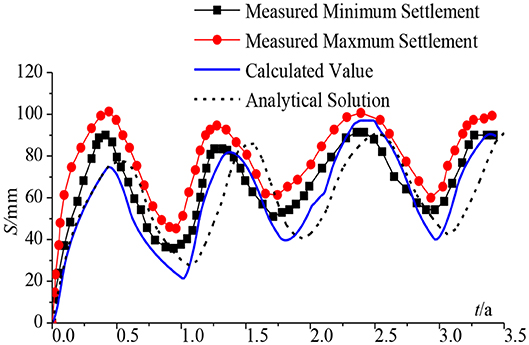
In order to verify the feasibility of the method for the calculation of the degree of consolidation of the foundation under the conditions of a variable load and one-dimensional non-linear consolidation, a calculation example in Favaretti and Mazzucato (1994) was selected for analysis. This example is a weak foundation project located under the silo of Ca'Mello. The change law of the load applied to the soft foundation with time is shown in Figure 4. Favaretti and Mazzucato (1994) carried out on-site observations of the settlement of the soft foundation and measured the consolidation coefficient of the soil (c_v = 0.1296 m²/day) and the change law of the soil stress and strain during loading by experiments. In this paper, the compression characteristics of the hyperbolic model of the soil (E₀ = 270 kPa, m = 0.9) are obtained by fitting the soil properties from on-site observations in Favaretti and Mazzucato (1994). The method in this paper is used to calculate the ground settlement, which are compared with the one calculated by an analytical solution in Rahal and Vuez (1998) and the one measured in Favaretti and Mazzucato (1994). The results are shown in Figure 5.

FIGURE 4

Figure 4. External load curve.

FIGURE 5

Figure 5. Ground settlement curve.

It can be seen from Figure 5 that the fluctuation trend of the settlement curve calculated by the method in this paper is basically consistent with the measured results, while the analytical solution settlement curve in Rahal and Vuez (1998) lags behind the measured results, indicating that the method in this paper is more reasonable and feasible.

In fact, the analytical solutions of the foundation settlement are often derived under the standard load form, which cannot flexibly deal with the problem of variable loads in actual engineering. When using the theories in Rahal and Vuez (1998) to calculate the settlement of the soft foundation, the external load needs to be simplified to a standard simple harmonic load. This simplification will inevitably lead to human error, which will cause the theoretical settlement curve to be out of sync with the measured curve. The method in this paper only needs to input the function expression of the external load into the program. Impulse loads, simple harmonic loads, or multiple graded loads can be accurately simulated, which simplifies the load form conversion step, reduces human error, and greatly simplifies the calculation process of the degree of consolidation and the settlement of the foundation. Besides, the accuracy can be improved by calculating in sections in the time dimension, which has the irreplaceable advantage than the analytical solution.

Conclusions

a. The presented method can adapt to various variable load situations, can greatly simplify the consolidation calculation process, and can effectively improve the calculation efficiency via a segmented calculation in the time dimension. The calculation results are in good agreement with the traditional analytical solution, indicating that the method is reasonable and feasible.

b. The method in this paper considers the case in which the external load is a function of time and can solve the calculation of the consolidation degree and the settlement of the foundation under the conditions of an impulse load, a simple harmonic load, or multiple step loading in actual engineering. Only the function expression of the external load is input into the program during the calculation, which avoids the steps of other theoretical calculation methods that need to convert the external load. Via this method, human error is reduced, and the calculation process for the degree of consolidation and the settlement of the foundation is greatly simplified, with good engineering application value.

c. The application condition of the presented method is the one-dimensional consolidation of a single-layered saturated soil with a permeable surface. The calculation formulas of the finite difference method should be transformed when analyzing the one-dimensional consolidation of the multilayered unsaturated soil under partially permeable boundary conditions. Besides, a multidimensional consolidation issue cannot be solved by this method.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

B-HM contributed to the study concepts and approved the final version of the manuscript. Z-YH and ZL conducted the literature research. B-HM and Z-YH provided the theoretical analysis. B-HM and ZL conducted the data analysis and interpretation. B-HM and C-BH prepared the manuscript. KC created the tables and figures. B-HM and X-CH edited the manuscript. M-HZ revised and reviewed the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China (Nos. 51778227, 51308208, and 41372303), the Provincial Natural Science Foundation of Hunan (No. 2015JJ3069), and the Youth Talent Plan Program of Hunan (No. 2016RS3032).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Barden, L., and Berry, P. (1965). “Consolidation of normally consolidated clay,” in Journal of the Soil Mechanics and Foundations Division, Vol. 91 (ASCE), Ann Arbor, Mich. 15–35.

Google Scholar

Davis, E. H., and Raymond, G. P. (1965). A non-linear theory of consolidation. Geotechnique 15, 161–173. doi: 10.1680/geot.1965.15.2.161

CrossRef Full Text | Google Scholar

Deng, J.-H., Lee, J.-W., and Lo, W.C. (2019). Closed-form solutions for one-dimensional consolidation in saturated soils under different waveforms of time-varying external loading. J. Hydrol. 573, 95–405. doi: 10.1016/j.jhydrol.2019.03.087

CrossRef Full Text | Google Scholar

Favaretti, M., and Mazzucato, A. (1994). “Settlement of a silo subjected to cyclic loading,” in Vertical and Horizontal Deformations of Foundations and Embankments (Reston, VA: ASCE; John Wiley and Son Ltd.), 775–785.

Google Scholar

He, L.-D., and Jiang, Y. (2009). Application of hyperbolic curves to prediction of embankment settlements. J. Hohai Univ. 37, 63–66. doi: 10.3876/j.issn.1000-1980.2009.02.016

CrossRef Full Text | Google Scholar

Lai, Y., and Song, X.-W, Shi, J.-Y. (2005). Experimental study on nonlinear behavior of soils at small strains. J. Hohai Univ. 33, 306–309. doi: 10.3321/j.issn:1000-1980.2005.03.016

CrossRef Full Text | Google Scholar

Liu, Q., Deng, Y. B., and Wang, T. Y. (2018). One-dimensional nonlinear consolidation theory for soft ground considering secondary consolidation and the thermal effect Comput. Geotechn. 104, 22–28. doi: 10.1680/jgere.17.00015

CrossRef Full Text | Google Scholar

Lo, W. C., Sposito, G., Lee, J. W., and Chu, H. (2016). One-dimensional consolidation in unsaturated soils under cyclic loading. Adv. Water Resour. 91, 122–137. doi: 10.1016/j.advwatres.2016.03.001

CrossRef Full Text | Google Scholar

Moradi, M., Keshavarz, A., and Fazeli, A. (2019). One dimensional consolidation of multi-layered unsaturated soil under partially permeable boundary conditions and time-dependent loading. Comput. Geotech. 107, 45–54. doi: 10.1016/j.compgeo.2018.11.020

CrossRef Full Text | Google Scholar

Rahal, M. A., and Vuez, A. R. (1998). Analysis of settlement and pore pressure induced by cyclic loading of silo. J. Geotechn. Geoenviron. Eng.124, 1208–1212. doi: 10.1061/(ASCE)1090-0241(1998)124:12(1208)

CrossRef Full Text | Google Scholar

Schiffman, R. L. (1958). “Consolidation of soil under time-dependent loading and varying permeability,” in Highway Research Board Proceedings, Washington, DC. 584–617.

Google Scholar

Shi, J.-Y., Yang, L.-A., and Zhao, W.-B. (2001). Research of one-dimensional consolidation theory considering nonlinear characteristics of soil. J. Hohai Univ. 29, 1–5. doi: 10.3321/j.issn:1000-1980.2001.01.001

CrossRef Full Text | Google Scholar

Wang, L., Sun, D.-A., Li, P. C., and Xie, Y. W. (2017). Semi-analytical solution for one-dimensional consolidation of fractional derivative viscoelastic saturated soils. Comput. Geotech. 83, 30–39. doi: 10.1016/j.compgeo.2016.10.020

CrossRef Full Text | Google Scholar

Wei, R.-L. (1987). Strength and Deformation of Soft Clay. Beijing: China Communications Press, 120–122.

Google Scholar

Wilson, N. E., and Elgohary, M. M. (1974). Consolidation of soils under cyclic loading. Can. Geotechn. J. 11, 420–423. doi: 10.1139/t74-042

CrossRef Full Text | Google Scholar

Xie, K.-H., and Pan, Q.-Y. (1995). One dimensional consolidation theory of arbitrary layers under time-dependent loading. Chinese J. Geotech. Eng. 17, 80–85.

Google Scholar

Xie, K.-H., Wang, K., Wang, Y.-L, and Li, C.-X. (2010). Analytical solution for one-dimensional consolidation of clayey soils with a threshold gradient. Comput. Geotech. 37, 487–493. doi: 10.1016/j.compgeo.2010.02.001

CrossRef Full Text | Google Scholar

Xie, K.-H., Xia, C.-Q., An, R., Hu, A.-F., and Zhang, W.-P. (2016). A study on the one-dimensional consolidation of double-layered structured soils. Comput. Geotech. 73, 189–198. doi: 10.1016/j.compgeo.2015.12.007

CrossRef Full Text | Google Scholar

Xie, K. H., Zhou, J., and Dong, Y. Q. (2006). Analytical solution for one-dimensional nonlinear consolidation of soil under cyclic loadings. Chinese J. Rock Mech. Eng. 25, 21–26. doi: 10.1631/jzus.2006.A1358

CrossRef Full Text | Google Scholar

Xu, S. (1987). The normalized curve method for the deformation of the saturated clay foundation. Chinese J. Geotech. Eng. 9, 70–77.

Google Scholar

Yu, X. J., Dong, W.-J., and Yin, Z.-Z. (2008). Relationship between loads and secondary consolidation coefficients of soft clay soils. J. Hohai Univ. 36, 63–66. doi: 10.3876/j.issn.1000-1980.2008.01.015

CrossRef Full Text | Google Scholar

Zhang, L., and Sun, S. L. (2007). One-dimensional consolidation theory based on hyperbola model under time-dependent loading for saturated soil. Chinese J. Rock Mech. Eng. 26(Suppl. 2), 4306–4310. doi: 10.7666/d.y1128451

CrossRef Full Text | Google Scholar

Zhao, W.-B., and Shi, J.-Y. (1996). Soft soil rheological theory and its application in analysis of drainage preloading reinforce. Adv. Sci. Technol. Water Res. 16, 12–17.

Google Scholar

Zhao, X.-D., Liu, Y., and Gong, W.-H. (2020). Analytical solution for one-dimensional electro-osmotic consolidation of double–layered system. Comput. Geotechn. 122:103496. doi: 10.1016/j.compgeo.2020.103496

CrossRef Full Text | Google Scholar

Zhou, Y., Zhang, L.-Y., Xu, C., Wang, T., and Zhou, G.-Q. (2020). Analytical solution for classical one-dimensional thaw consolidation model considering unfrozen water effect and time-varying load. Comput. Geotech. 122:103513. doi: 10.1016/j.compgeo.2020.103513

CrossRef Full Text | Google Scholar

Zhou, Y.-D., Deng, A., and Wang, C. (2013). Finite-difference model for one-dimensional electro-osmotic consolidation. Comput. Geotech. 54, 152–165. doi: 10.1016/j.compgeo.2013.06.003

CrossRef Full Text | Google Scholar

Zhu, G., and Yin, J. H. (1998). Consolidation of soil under depth-dependent ramp load. Can. Geotechn. J. 35, 344–350. doi: 10.1139/t97-092

CrossRef Full Text | Google Scholar

Zou, S.-F., Li, J. Z., and Xie, X. Y. (2018). A semi-analytical solution for one-dimensional elasto-viscoplastic consolidation of layered soft clay. Appl. Clay Sci. 153, 9–15. doi: 10.1016/j.clay.2017.11.042

CrossRef Full Text | Google Scholar

Nomenclature