
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Earth Sci. , 24 April 2020
Sec. Solid Earth Geophysics
Volume 8 - 2020 | https://doi.org/10.3389/feart.2020.00089
We presented a new 3D model of the geophysical properties of the crust (namely depth of the Moho and VP, VS, density, Young’s modulus, and shear modulus) of the northern tip of the Adria microplate that we called NAC (Northern Adria Crust). The horizontal dimensions of the physical properties variations are optimized at 5 × 5 km and the vertical dimension at 1 km. NAC has been built by critically choosing and integrating all available information about the depth of the main interfaces and the physical properties of the crust. We started from a VP dataset, and we converted it in VS and density by using empirical relations, tuned through the comparison with the available data from local tomographic inversion, and taking into account the lithologies of the area. Uncertainties and reliability of the model are quantified, taking into account the data quality and the interpolation procedure. NAC has two versions, different in the structure of the Moho interface: the first considers one continuous surface for the whole area, while the second implies three separate surfaces for the Adria microplate, Eurasia, and the Pannonian fragment. The differences between the two models are minimal, but the available data better sustain the solution of the fragmented crust. For its characteristics of multiparametric information and resolution, NAC can be precious for any purpose and use where a detailed knowledge of the crustal structure of this area is required. Moreover, it is easy to improve NAC, including new information on the crustal structures, when they will be available.
An accurate model of the crust is the basis for modeling in various fields as seismology, geodynamics, gravity (e.g., Zhu and Tromp, 2013; Faccenna et al., 2014; Métois et al., 2015; Root et al., 2015). Highly detailed modeling is of particular importance in areas of continental collision, i.e., the orogenic belts, still offering unanswered questions on the geometry of the boundaries, the reciprocal roles, and the relative motions of the converging plates. One of these areas is the area across North-Eastern Italy, Austria, Western Slovenia, and Croatia: namely, the transition between Eastern Alps and External Dinarides. It occupies the northernmost edge of the convergent margin between Eurasia and the Adria microplate (Figure 1), which is relatively aseismic, and encircled by active orogenic belts (Argand, 1924; McKenzie, 1972; Channell et al., 1979; Anderson and Jackson, 1987). Seismological and geodetic studies helped to establish that the Adria microplate counterclockwise rotates relatively to Eurasia around a pole of rotation located in the western Po Plain (e.g., Battaglia et al., 2003; D’Agostino et al., 2005, 2008; Serpelloni et al., 2005).
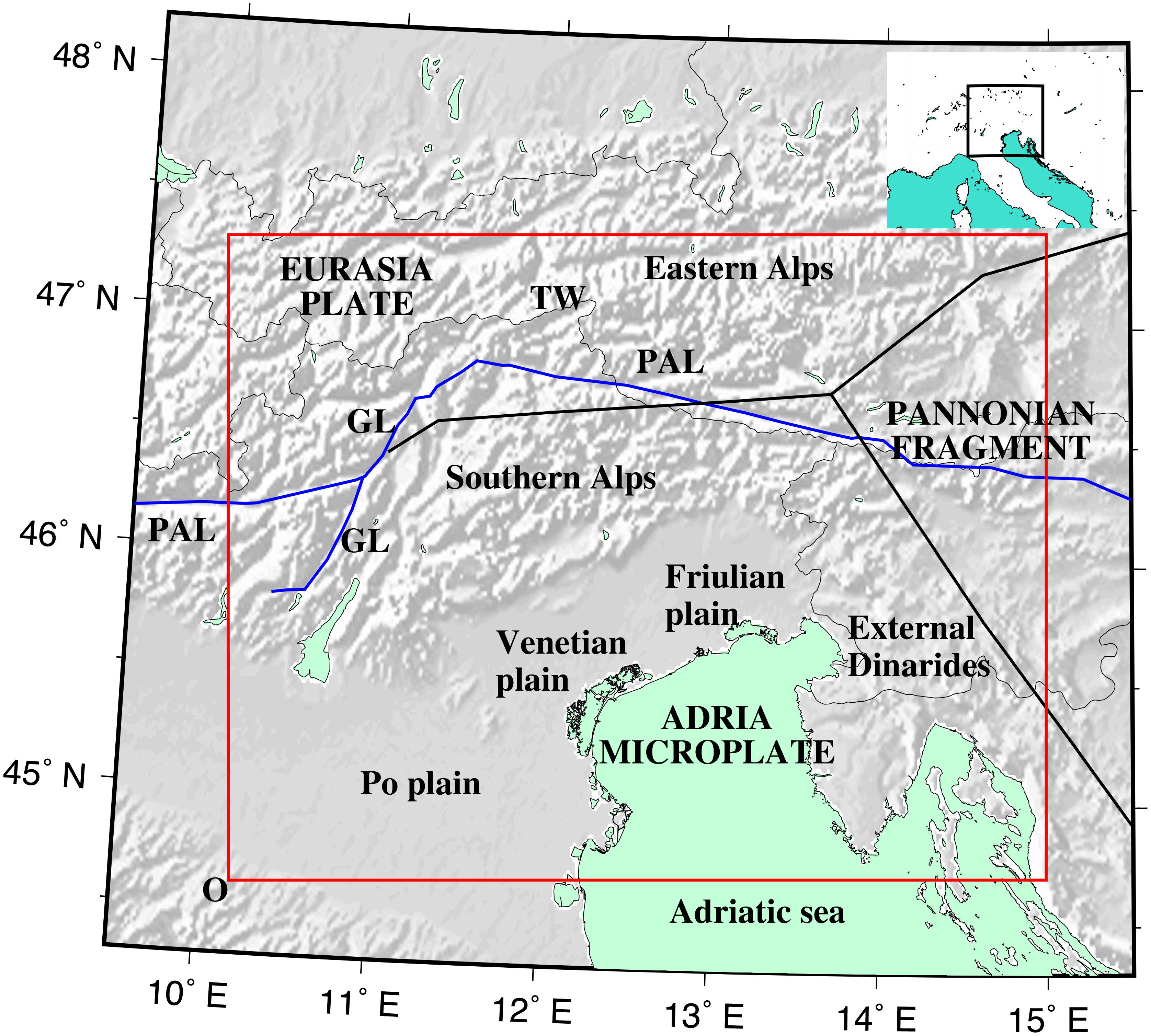
Figure 1. Map that shows the area of the model (red rectangle). The origin point of the reference system of the model (O) is located at 10.2E, 45.6N, and the model extends 380 km to the East, 300 km to the North, and from 4 km a.sl. to 60 km b.s.l in depth. TW – Tauern Window. Blue line: main tectonic lineaments: PAL – Periadriatic Lineament; GL – Giudicarie line. Black lines: boundaries between Moho fragments, according to Brückl et al. (2007).
The seismic investigations in the Eastern and Southern Alps started in the early sixties, and developed in the seventies of the last century, with Deep Seismic Soundings (DSS) profiles, later revised by Scarascia and Cassinis (1997). In the last years, new information about the crustal properties of the area became available thanks to a series of controlled-source seismic experiments: TRANSALP (TRANSALP Working Group, 2002), ALP 2002 (Brückl et al., 2007; Grad et al., 2009a; Šumanovac et al., 2009), and CROP (Finetti, 2005) experiments.
One of the main reasons for such high interest is the vivid debate about the subduction directions and the necessity of discriminating between different tectonic models. The high-resolution TRANSALP transect in the area of the Tauern Window (about 12°E) and the complementary experiments provided evidences of the subduction of the Eurasia below the Adria microplate (TRANSALP Working Group, 2002; Kummerow et al., 2004; Lüschen et al., 2004, 2006; Bleibinhaus and Gebrande, 2006; Castellarin et al., 2006). While confirming the southward subduction to the west, data from teleseismic tomography indicate a change of the subduction direction to the East (Lippitsch et al., 2003; Schmid et al., 2004; Kissling et al., 2006; Handy et al., 2015). A different perspective was offered by the CELEBRATION 2000, ALP 2002 WAR/R, and ALPASS data in the transition area between the Alps, Dinarides and Carpathians, interpreted in terms of a Moho fragmentation between Eurasia, the Adria microplate, and the Pannonian fragment (Behm et al., 2007; Brückl et al., 2007, 2010; Šumanovac et al., 2009; Mitterbauer et al., 2011; Figure 1), so that the subduction polarity of Eurasia plate would be unique in the whole Alpine region. To the south of the triple junction between the three fragments, the Adria lithosphere would underthrust below the Dinarides and the Pannonian fragment (Brückl et al., 2010; Šumanovac et al., 2016).
Recently, also ambient noise tomography was applied in the studied region (Molinari et al., 2015b; Behm et al., 2016; Guidarelli et al., 2017). Kästle et al. (2018), through the joint inversion of ambient noise and earthquake phase velocity measurements, confirmed the differences in the velocity structure of the Central and Eastern Alps, but could not give a definitive answer to the questions about the subduction direction. Kästle et al. (2020) reviewed the different slab break-off models, offering a new combined interpretation of body-wave and surface-wave tomography, to be verified by the forthcoming data. Moreover, two of the complementary experiments of the AlpArray program – EASI (AlpArray Seismic Network, 2014; Hetényi et al., 2018) and SWATH-D (Heit et al., 2017) – focus on this area. The two seismological profiles spaced 15 km apart of EASI revealed the complexity of the crustal structure (both at shallow and deep levels) while supporting the model of an Adria subduction below Eurasia, with a steep northwards dipping slab (Hetényi et al., 2018). New insights on the crustal structure, as, e.g., done by Spooner et al. (2019), are expected to add on in the next years from the SWATH-D data analysis and other AlpArray complementary experiments and continuation.
We focus on the region to the south of the PeriAdriatic Lineament (PAL in Figure 1). Here, as a result of the counterclockwise rotation of the Adria microplate, the convergence rate increases across the Alps from W to E, with a maximum N-S shortening of about 2 mm/a over ∼80 km at the easternmost part of the Southern Alps, corresponding to the Italian Friuli seismic region (D’Agostino et al., 2005; Grenerczy et al., 2005; Völksen et al., 2018). The latter is the seismically most active area of the Alps, with several destructive earthquakes in historic times, including the M = 6.4 1976 Friuli earthquake (e.g., Burrato et al., 2008; Santulin et al., 2018, and references therein). A local seismometric network monitors the region since 1977, complemented, since 2002, by a GNSS network (Bragato et al., 2013; Zuliani et al., 2018), making the region a sort of natural laboratory for the study of complex tectonic processes. The seismicity is mainly located in the upper crust (Viganò et al., 2015; Bressan et al., 2012). The stress and strain tensor inversions from the focal mechanisms reveal in the region a complex stress field with a resulting heterogeneous deformation pattern, with variations on a scale of tens of km (Bressan et al., 2018a). The inversion of fault plane solutions reveals a compression ranging from west to east from NW–SE to N–S, and NNE–SSW, in agreement with the counter-clockwise motion and interaction of the Adria microplate with the Eurasia plate, and the geodynamic frame described above (Bressan et al., 2018a). The spatial seismicity pattern is conditioned, especially in the shallowest layers (0–10 km), by the crustal heterogeneities (Bressan et al., 2012).
Recently, the increasing number and quality of GNSS data provided new insight into the kinematics of the area (Caporali et al., 2009; Métois et al., 2015; Rossi et al., 2016; Serpelloni et al., 2016). The observations confirmed the shortening of about 2 mm/a across the southern front of the Eastern Alps, and the increasing eastward rotation of velocities toward the Pannonian Basin, whereas an N–S directed extension can be related to a gravitational collapse within the Tauern Window. The sharp boundaries between the strain velocities observed are in agreement with the triple junction between Eurasia, Adria microplate, and the Pannonian fragment (Möller et al., 2011; Völksen et al., 2018).
A finite element modeling can help to relate the seismic activity with the crustal deformation observed by the GNSS measurements through the crustal geophysical properties and analyze how the forces at plate boundaries influence the intraplate stresses. The 2D finite element model presented by Bada et al. (1998), although mainly focused on the Pannonian basin, allowed to explain most of the stress patterns observed by modeling the forces acting at the plate boundaries. Rossi et al. (2005) 3D finite element model of NE Italy related the seismic focal mechanisms and the seismicity distribution to the counterclockwise rotation of the Adria microplate relative to Eurasia.
Our goal is constructing a more complex 3D model of the northern tip of the Adria microplate, based on the actual knowledge about the crust structure, and physical properties, enabling modeling also the stresses induced by density contrasts in the crust (Ranalli, 1992; Heidbach et al., 2007), horizontal gradients of gravitational potential energy (Marotta and Splendore, 2014; Métois et al., 2015), topography (Heidbach et al., 2007), and plate boundaries (Richardson, 1992) in this critical area of the Alps. Detailed knowledge of the elastic moduli (derivable from the seismic velocities and density) distribution in the crust is, hence, necessary. Moreover, mapping in detail the Moho discontinuity can help to verify its possible fragmentation while providing keys for understanding the dynamic processes causing crustal growth, accretion, delamination, and underplating (Carbonell et al., 2013, and references therein).
The physical properties (namely: seismic velocities, rock bulk density, and elastic moduli) of the upper crust of the Friuli seismic region were studied through laboratory measurements on rock samples, representative of the most common lithologies, sonic logs, local earthquake tomography, and seismo-gravimetric inversion (Faccenda et al., 2007; Bressan et al., 2012). Local earthquake tomography was also applied in other parts of the Southern Alps (Anselmi et al., 2011; Viganò et al., 2013).
The crustal models at the continental scale developed in the last 10 years include in whole or in part, the most recent data about the crustal structure. These datasets include (from old to young) EuCrust-07 (Tesauro et al., 2008), the Moho map of Grad et al. (2009b) (ESC Moho in the following), EPCrust (Molinari and Morelli, 2011), the Moho maps of Italy by Di Stefano et al. (2011) and Spada et al. (2013), and EUNAseis (Artemieva and Thybo, 2013). A density model of the Alpine lithosphere, constrained by 3D gravity modeling and based on all the recent seismic experiments is provided by Spooner et al. (2019).
EuCrust-07, EPCrust, and EUNAseis models share some critical features like a uniform parameterization that allows a simple conversion in a numerical mesh. They are an essential reference for constructing a regional model, but, because of their scale and resolution, they cannot be directly used for studies focused on the analysis of small scale features (tens of km). More detailed models, developed for seismological studies, cover only marginally the region of our interest (Vuan et al., 2011; Molinari et al., 2012, 2015a).
The present study fills this partial gap, by presenting a new 3D crustal model of the northern tip of the Adria microplate, that we call NAC (Northern Adria Crust). It has been constructed by critically collecting and integrating all available information in a 3D model (from the Moho to the topographic surface) of the crustal properties as illustrated in section Data. In section Model Construction we explain the procedure adopted to integrate the various data, interpolating them on the model grid, and evaluating the uncertainty of the interface depth and the physical properties (seismic velocities, density, Young, and shear modulus) that we retrieve. The uncertainty of the interfaces’ depth and on the various physical properties is quantified by taking into account the data quality and coverage and the effects of the interpolation procedure. In section Physical Properties of the Crust, we critically analyze the fit of different empirical relationships to convert P-wave velocity (VP) into density (ρ) and S-wave velocity (VS). We compared the results with the available information from independent measurements of VS, laboratory experiments, and borehole measurements. The uncertainty estimation, as well as the considerations on the physical properties empirical relationships can be of interest for applications in other parts of the world and tectonic frameworks. The resulting 3D crustal properties multiparameter model is described in section Main Features of the Model, and discussed in section Discussion. It is defined on a 5 × 5 km grid (∼0.05°×°0.05), enabling the modeling of the observed stress/strain variations. It can be, therefore, a useful tool for future local scale studies in the fields of gravity, geodesy, geodynamics, and seismology. Moreover, NAC’s structure is such that it will be easy to include new information and update the model.
The area here considered includes the eastern Southern Alps (to the east of the Giudicarie line and the south of the PeriAdriatic Lineament – GL and PAL, respectively in Figure 1), the southern sector of the Eastern Alps, the north-western external Dinarides, the Venetian and Friulian plains, part of the Po plain, and the northern part of the Adriatic Sea (Figure 1). We collected information about the geophysical properties (seismic velocities and bulk rock density) of the crustal layers and their geometry (Figure 2). In this section, we describe the data sources that we used in the construction of the model (Table 1).
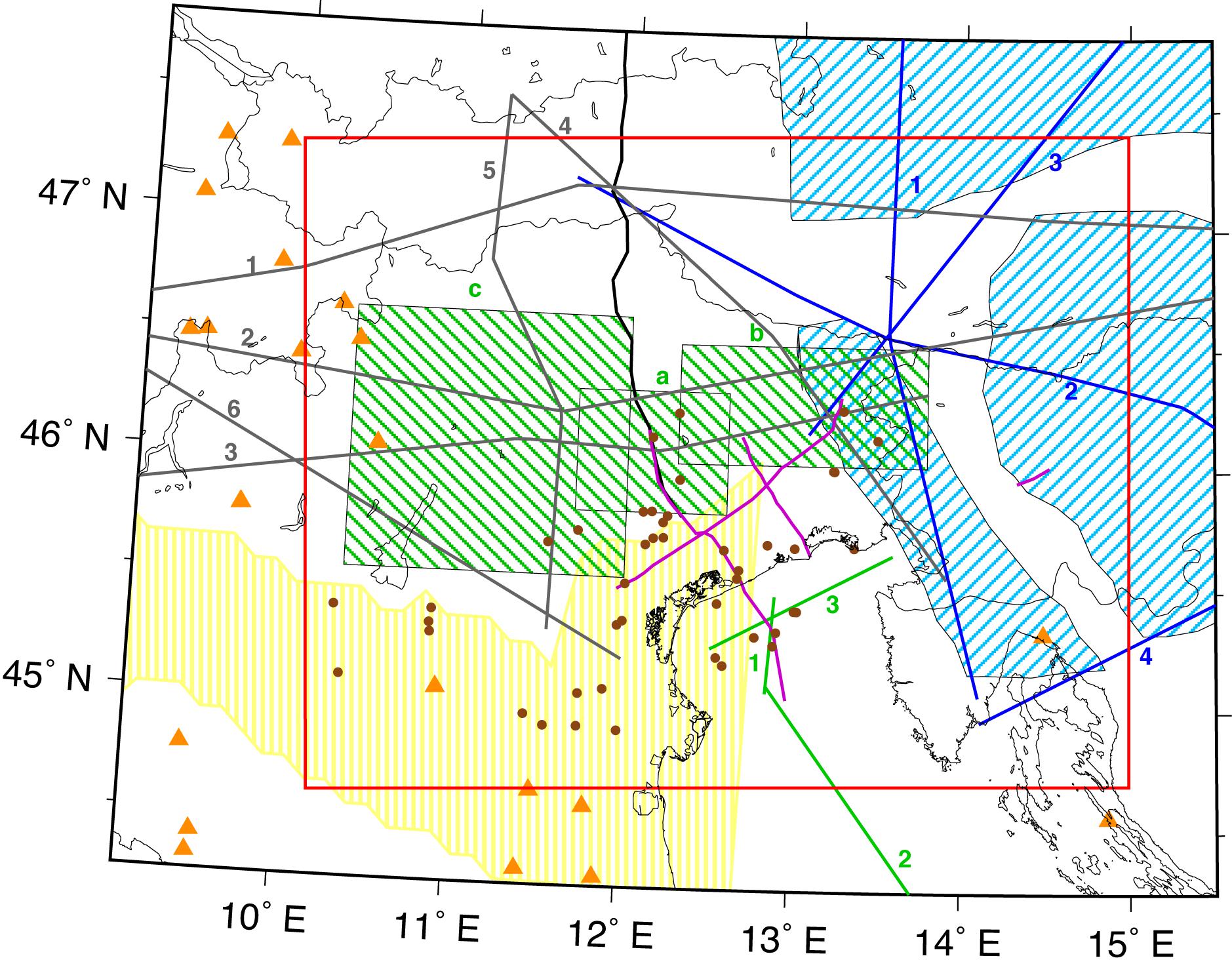
Figure 2. Location of the various data used as input within the area of the model (red rectangle). Gray lines – seismic profiles from Scarascia and Cassinis (1997) (1: Alp75; 2: Lago Bianco – Lago Lagorai – Tarvisio – east; 3: SudALP; 4: Eschenlohe – Trieste; 5: Eschenlohe – Euganei Hills; 6: Lago Bianco – Euganei Hills); black line – TRANSALP seismic profile (Castellarin et al., 2006); blue lines – ALP 2002 project profiles (1: Alp01, 2: Alp02 from Brückl et al., 2007; 3: CEL10/Alp04 from Grad et al., 2009a; 4: Alp07 from Šumanovac et al., 2009); green lines – seismic profiles from CROP (1: M-17A, 2: M-17B, and 3: M-18 from Finetti and Del Ben, 2005); purple lines – seismic lines from Fantoni et al. (2003) and Nicolich et al. (2004); area filled by light blue lines – Moho map of Behm et al. (2007) orange triangles – stations with receiver functions; area filled by yellow lines – depth of sediments from the model of Vuan et al. (2011); brown circles – position of boreholes (Nicolich et al., 2004; Cimolino et al., 2010; ViDEPI, 2015); area filled by green lines – local earthquakes tomographies (a: Anselmi et al., 2011; b: Bressan et al., 2012; c: Viganò et al., 2013).
The primary sources of information about the structure in the deepest part of the crust (from the Moho to the top of the lower crust) are the seismic profiles. The oldest data are from Scarascia and Cassinis (1997) that reinterpreted the Deep Seismic Soundings (DSS) profiles acquired in the central-eastern section of the Alps in the 1960s and 1970s. More recent seismic profiles in the Eastern and Southern Alps come from the TRANSALP (Castellarin et al., 2006), CELEBRATION 2000, and ALP 2002 (Brückl et al., 2007; Grad et al., 2009a; Šumanovac et al., 2009) experiments. For the Adriatic sea, we considered the results of the CROP project (Finetti and Del Ben, 2005). The considered seismic profiles show, in general, sharp transitions from crustal to mantle velocities. Scarascia and Cassinis (1997), however, reported a complex transition between crust and mantle for the area of thicker European crust, with low-velocity layers (7.6 km/s) below high-velocity layers (8.0 km/s).
Another data source is the Moho depth map derived from 3-D seismic wide-angle reflection and refraction data acquired during the experiments CELEBRATION 2000 and ALP 2002 (Behm et al., 2007). We used also the depth of the Moho from the teleseismic receiver functions beneath permanent or temporary seismic stations (Lombardi et al., 2008; Piana Agostinetti and Amato, 2009; Orešković et al., 2011; Stipčević et al., 2011; Miller and Piana-Agostinetti, 2012; Bianchi et al., 2015; Šumanovac et al., 2016; Hetényi et al., 2018).
The criterion adopted to choose the data to be included in the model, as well as the way of doing it, is the data uncertainty. Uncertainties of the Moho map of Behm et al. (2007) in the area of our interest are around 2 km (Behm, 2006). Brückl et al. (2007), Grad et al. (2009a), and Šumanovac et al. (2009) reported similar uncertainties of the interfaces depth: 2–3 km for mid-crustal boundaries and 1–2 km for the Moho. For the other seismic profiles, we followed the estimations of Grad et al. (2009b) that assigned an uncertainty of 6–8% to the Moho depth retrieved from old seismic profiles (i.e., about 3 km for a Moho depth of 40 km). To have a conservative estimate of the uncertainties, we used the upper bound of these ranges. We compared the various seismic profiles at the intersections (Supplementary Figure S1), and we found that the average difference between the Moho depth is about 3.6 km. The most significant difference (about 10 km) is observed between the data of the CEL10/Alp04 and the profile ALP75 (Scarascia and Cassinis, 1997), where Brückl et al. (2010) trace the boundary between Eurasia and the Pannonian fragment.
The teleseismic receiver functions have a lower resolution than the seismic profiles. Therefore, we excluded from our dataset the stations from Orešković et al. (2011); Bianchi et al. (2015), and Šumanovac et al. (2016) that cover the same areas as the seismic profiles, retaining the ones that provide information about the Moho depth in zones less covered by seismic profiles, as the South-Western part of the model (Figure 3). We used only the stations of Piana Agostinetti and Amato (2009), and of Miller and Piana-Agostinetti (2012) of quality classes 1 and 2. We also excluded the Moho depth data with a relative uncertainty >20%. When for the same station, more than one estimation of Moho depth is available, we checked if they are compatible and took the one with the lowest error. We did not include data from Hetényi et al. (2018) since they did not report a unique crust-mantle boundary, i.e., a clear Moho, and the proposed depth shows significant differences with the seismic profiles (Alp01, Alp02, and three profiles from Scarascia and Cassinis, 1997) and with other receiver function results in the same area (Bianchi et al., 2015).
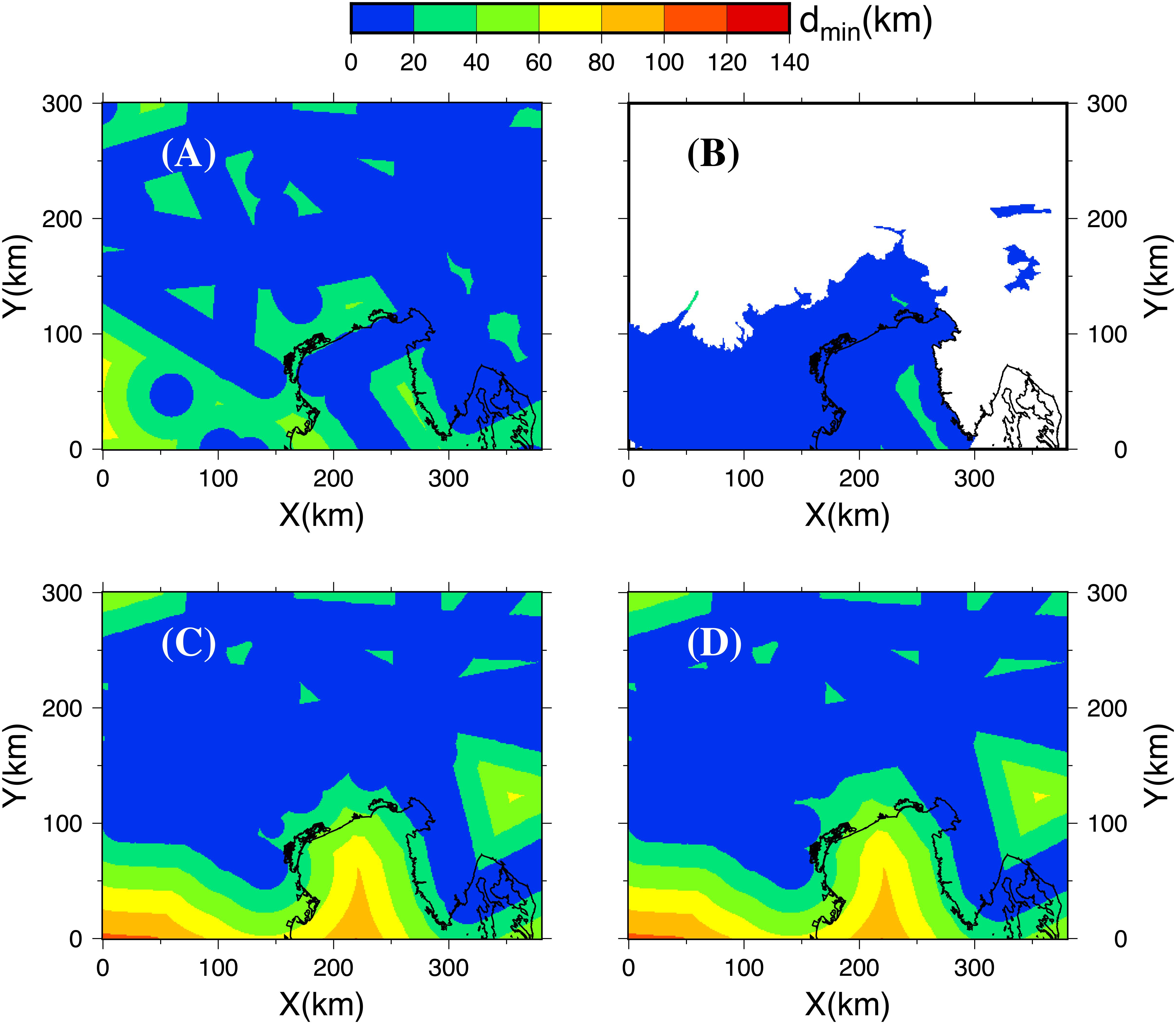
Figure 3. Minimum distance between the points of the model and the data locations (dmin). (A) MO1 interface; (B) BS interface; (C) VP at 5 km; (D) VP at 25 km.
Seismic profiles (Scarascia and Cassinis, 1997; Bleibinhaus and Gebrande, 2006; Behm et al., 2007; Brückl et al., 2007; Grad et al., 2009a; Šumanovac et al., 2009) are the principal sources of information also about seismic velocities (mainly VP). We followed Artemieva and Thybo (2013) to assign VP accuracy to the different seismic profiles. Local earthquake tomography studies provide information about VP and VS in the Southern Alps and External Dinarides (Anselmi et al., 2011; Bressan et al., 2012; Viganò et al., 2013). Gravimetric studies at regional scale provide information on the density of the crustal layers (Braitenberg et al., 1997; Cassinis et al., 1997; Dal Moro et al., 1998; Ebbing et al., 2001, 2006; Šumanovac et al., 2009; Šumanovac, 2010). The geophysical properties of the upper crust in the area between the Southern Alps and the External Dinarides were also studied by laboratory measurements (Faccenda et al., 2007) as well as through the inversion of seismic and gravimetric data (de Franco et al., 2004; Bressan et al., 2012). As explained more in detail in the following sections, the observations on ρ and VS do not enter directly in the NAC construction but are used to select the best empirical relation between VP and the other geophysical parameters and to check the results.
Data about the shallowest part of the crust are completed from other sources. A structural model of the Po and Venetian plain of Vuan et al. (2011) provides the depth of the bottom of the sedimentary layer. We also considered the stratigraphy from boreholes (Nicolich et al., 2004; Cimolino et al., 2010; ViDEPI, 2015) in the Venetian and Friulian plain, and shallow seismic profiles (Fantoni et al., 2003; Nicolich et al., 2004). We defined the uncertainty of the depth derived from the model of Vuan et al. (2011) by comparing it with independent inputs (boreholes). We included the outcropping of sedimentary rocks at the border of the plains and on the eastern side of the Adriatic Sea. We also added the thickness of the soft sediments in the Klagenfurt (Nemes et al., 1997) and Ljubljana basins (Gosar and Lenart, 2010; Gosar et al., 2010). The geophysical properties of the sediments are supplied by the seismo-gravimetric inversion of Tondi et al. (2019) for the Po Plain, the seismological model of Vuan et al. (2011) for the Venetian plain and the Po plain and by Giustiniani et al. (2008) for the Friulian plain.
NAC covers an area that extends from the origin point (at 10.2° E and 44.6° N) for 380 km to the east and 300 km to the north, hence, covers the region 10.2°E-15.0°E, 44.6°N-47.4° N. The model construction is meant to include new information quickly and to convert it in a mesh for numerical computations conveniently. To this aim, a uniform parameterization is desirable, and the procedure used in the model construction should be automatized as much as possible. The choice of the parameters of NAC, described in the following, is similar to what Kelly et al. (2007) did for the UK and Ireland. Our model comprises a first layer of sediments (S), and the crust (C), and is defined by three interfaces: the topography (T), the bottom of the sedimentary layer (BS), and the Moho. Due to the remarkable difference in depth recognized between the Eurasia and the Adria Moho surfaces (Scarascia and Cassinis, 1997; Kummerow et al., 2004; Brückl et al., 2007; Hetényi et al., 2018) the use of a unique continuous surface representing the Moho could be inappropriate and produce inaccurate results in future modeling. Hence, we consider two versions of the Moho: a unique continuous surface (MO1) and a composite Moho (MO2), consisting of three separated fragments: (i) the Adria microplate (AD); (ii) the Eurasia (EU); (iii) the Pannonian fragment (PA). Compared with other recent crustal models (EuCRUST-07; EPcrust), we adopted a single layer for the crust, in which the seismic velocities (VP, VS), the density (ρ), and the elastic parameters (Young modulus, E, and shear modulus, μ) are variable, both laterally and vertically.
The physical properties variations are sampled on a grid with cells of 5 × 5 km horizontally, and a vertical dimension of 1 km. The elastic moduli were derived from the values VP, VS, and ρ. In the absence of VS and ρ, we started from a VP dataset, and we converted it into VS and ρ by using empirical relations (section Physical Properties of the Crust). We applied to VS and ρ datasets the same interpolation procedure described in the following for VP data.
The input data is processed consistently in the whole model. The profiles described in the previous section were digitized from existing literature with a regular spacing of 6 km, similar to the estimated average horizontal resolution obtained from controlled-source seismology (CSS) methods for the Moho interface (Waldhauser et al., 1998). We took account of differences at intersections between 2-D profiles by averaging the values of Moho and velocities and, if necessary, by increasing the uncertainties assigned to the data. In the absence of an explicit interpretation of the authors, we took the Moho as the upper boundary where the VP turns to values >7.8 km/s. We extracted the well-resolved Moho depths from the Moho map of Behm et al. (2007) on their regular grid of 20 × 20 km. We defined separated datasets for the three Moho domains to define the MO2. In the eastern part of NAC, we used the plate boundaries defined by Brückl et al. (2010) through their elastic plate modeling. In the central and western parts, we considered the northern edge of the Adria Moho reported by Cassinis (2006) who compared the data from Scarascia and Cassinis (1997) with the results of the TRANSALP profile.
The 2D velocity model of each seismic section was converted into a set of 1D velocity profiles. We took the VP values from local earthquake tomography only for those nodes identified by Bressan et al. (2012) and Anselmi et al. (2011) as reliable according to a threshold of the spread function (a measure of the blurring of the tomographic image) and by Viganò et al. (2013) according to checkerboard, recovery, and synthetic data tests. The data was transformed from the geographical coordinates to a Cartesian coordinate system to obtain a regular spacing in the area and to convert the model in a mesh suitable for numerical modeling. We used the UTM (Universal Transverse Mercator) projection (zone 33N). The coordinate manipulation was done using pyproj (PROJ contributors, 2018).
As highlighted by Artemieva and Thybo (2013), the resolution of the final model depends mainly upon the input data coverage. Therefore, we analyzed the spatial distribution of the data collected on the depth of each interface and the VP at two different depths (5 and 25 km) by computing the minimum distance (horizontal for the interfaces and considering also the depth for VP) between the points inside the region (on a regular grid with step of 1 km) and the location of the data source (dmin) (Figure 3). For MO1, 70% of the surface of our region has dmin (20 km from the data points, while 90% of the surface of our region has dmin (40 km from them. The area less covered by the data is the South-Western corner. Only a little part of the Adriatic Sea has dmin > 20 km from the data points used for BS. The dmin distribution is are very similar for the two depths and gives a first approximation of the reliability of the final model in the different parts of the model.
We interpolated the data points into a regular grid (2D for interfaces and 3D for the velocity model) by kriging using the gstat package (Pebesma, 2004; Gräler et al., 2016), that was used also for the variogram analysis and cross-validation.
Kriging is a collection of generalized linear regression techniques for interpolating sparse geospatial data (Olea, 1999; Oliver and Webster, 2014). The interpolated values are estimated from a weighted sum of sample points using weights that make it unbiased and minimize the variance of the estimation error. Unbiasedness and its optimality in a minimum mean square error sense made kriging a best linear unbiased estimators (Olea, 1999). We introduce some definitions following Olea (1999). The samples are assumed to be a partial realization of a random function Z(x) of the location . An important assumption of kriging is that the spatial autocorrelation of the variable is known in the form of the semivariogram or covariance: this information is used to estimate the weights of the data points by minimizing the variance (Var) of the estimation error. Given two locations and inside the field of Z with a constant mean, the semivariogram is:
According to this definition, the semivariogram is not a single number but a continuous function of a variable , called the lag. The lag is a vector; therefore, the semivariogram depends not only on the magnitude of the separation but also on the azimuth of the line through the pairs. An assumption is that the semivariogram is independent of location and depends only on the separation of the pair of locations considered (stationarity). The lag at which the semivariogram reaches a constant value is called the range. The value of the semivariogram beyond the range is named the sill. The values of Z in two points separated by a distance larger than the range are stochastically independent. An estimate of the semivariogram is also called an experimental semivariogram. The semivariogram is considered to be isotropic when variations in the azimuth do not produce significant changes in the experimental semivariogram; otherwise, it is called anisotropic. The experimental semivariogram cannot be used directly, and, therefore, is replaced by a semivariogram model.
As explained in the following, we used both the ordinary kriging (Matheron, 1965) and the universal kriging (Matheron, 1969). The ordinary kriging can be applied if the random function has a constant (but unknown) value. The universal kriging is a generalization that does not require a constant mean. In this case, the random function has a drift: a gentle underlying fluctuation in the regionalized variable. The drift is the expected value E[:] of the random function:
A polynomial drift model is the summation
The semivariogram, γY, is defined on the residuals of the drift (Matheron, 1969). For both ordinary and universal kriging, the weights are derived from a constrained optimization that is solved through the Lagrange method of multipliers. The estimation at a site is given by:
where are sampled sites and λi are the kriging weights. The error variance of the estimation for ordinary kriging is given by:
where μl is the Lagrange multiplier resulting from the solution of the ordinary kriging system. The error variance of the estimation for ordinary kriging is given by:
where μl are the Lagrange multipliers and fl are the terms in the definition of the polynomial drift.
For each input dataset (depth of MO1, MO2, BS, and VP field), we proceeded as follows. First, we looked for any evident drift (spatial trend). This is the case for VP along the vertical direction: therefore, we defined a linear model for it. The VP residuals relative to the drift are computed through an ordinary least square estimate of the drift (Equation 2). Then, we computed the experimental semivariograms along different directions to identify the possible anisotropy (Figure 4). The directional semivariograms for the VP residuals relative to the drift have a range in the horizontal plane five times greater than in the vertical direction. Therefore, we included the anisotropy in the semivariogram model for VP. We fitted different models (Gaussian, spherical, and exponential) at each experimental semivariogram, and we chose the best one by cross-validation, comparing the mean error, the mean squared error and the mean squared deviation ratio, which is the mean of the squared errors, divided by the corresponding kriging variances (Oliver and Webster, 2014). Because in all cases we obtained similar results using the exponential and spherical models, whereas the Gaussian model provided the worst results, we used the exponential model for MO1 and each fragment of MO2 and spherical model for VP. The sill obtained for the exponential model of MO1 variogram has a value of ∼80 km, while the one for AD is ∼50 km and the ones for EU and PA are ∼20 km. The short distance variability (nugget) of AD, EU, and PA are similar and lower than the one of MO1. Because the semivariograms for EU and PA fragments are significantly different from that of AD, the stationarity assumption is violated considering a single surface (MO1).
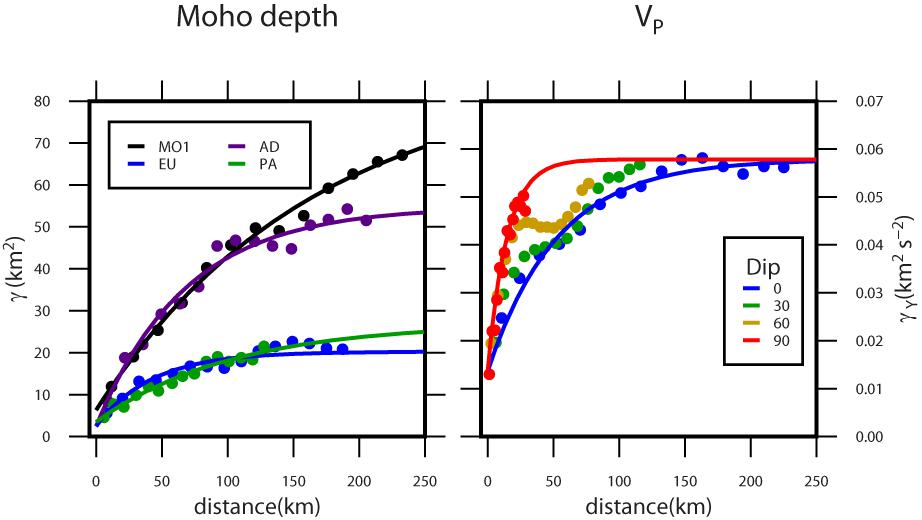
Figure 4. Experimental and model variograms (semivariance vs. distance) for (left) Moho depth data considering a unique (MO1) or three surfaces (EU, AD, PA); (right) VP for different dip directions. Details in the two legends.
The selection of the optimal grid resolution should consider the average spacing between the closest point pairs and the spatial correlation structure (a variable that is spatially auto-correlated at shorter distances would require higher resolution and vice versa) of the input dataset (Hengl, 2006). Since in the horizontal plane the average spacing between the nearest points pairs for MO1 (and MO2) and VP is about 5 km, we defined an XY grid step of 5 km, that is near to the sampling spacing used for seismic profiles. Because the range in the vertical direction is five times smaller than in the horizontal plane, we adopted a step of 1 km along the Z-axis.
To estimate the kriging weights, we also considered the inverse of the square of data uncertainties (Pebesma, 2001). We used the ordinary kriging for the depths of MO1, MO2, and BS, with stationary mean, while the universal kriging for VP data, since it shows a trend with depth. We filtered the interpolated values using a 10 km wide Gaussian filter (Wessel and Smith, 1991, 1998; Wessel et al., 2013) to remove the information not supported by the grid spacing.
To construct MO2, we independently interpolated the datasets for the three segments on three separate surfaces defined by the boundaries described before, and then we combined them in a single surface.
We interpolated the crustal VP values on the regular grid nodes of the model between the Moho and the topographic surface or (where it is present) the bottom of the sedimentary layer.
The uncertainty in the final model (σTOT) is composed of three terms: the first derives from the uncertainty in the input data (σUNC), the second from the interpolation process (σINT) and, only for the physical properties derived from VP, the dispersion of the used empirical relations (σEMP). We combined them using the law of error propagation assuming that the uncertainty associated with each term conforms to a Gaussian distribution:
We computed the first term interpolating the uncertainty of the input data with the same procedure used for the data itself. Kriging directly provided the second term of uncertainty ( or ). For the physical properties derived from VP, we propagated the uncertainties of original VP values, including also the dispersion of the used empirical relations, computing the partial derivatives of the empirical relations with respect to VP.
As described, the uppermost interface of the NAC model is constituted by the topography. Because the input data for the topography ETOPO1 (Amante and Eakins, 2009) is sampled at 1 arc-minute (about 1.3 km along longitude and 1 along latitude), we resampled them on the coarser grid of NAC, using the adjustable tension continuous-curvature surface gridding algorithm (Smith and Wessel, 1990); the resulting grids were then spatially filtered using a 5 km wide Gaussian filter (Wessel and Smith, 1991, 1998; Wessel et al., 2013).
The data about VS in the region is sparse and uneven. Hence, we chose to use empirical functions to convert VP into VS (Brocher, 2005), selected, based on the measured data in the different parts of the model.
Brocher (2005) reported two different relations between VP and VS: the “Brocher’s regression fit” (BRF) for all the lithologies except calcium-rich and mafic rocks, gabbros, and serpentinites and for 1.5 < VP < 8 km/s and the “mafic line” (ML) for calcium-rich rocks (including dolomites and anorthosites), mafic rocks, and gabbros for 5.25 < VP < 7.25. Figure 5 shows the comparison of the values so obtained with the measured data from the various authors. We considered the VP and VS computed by Faccenda et al. (2007), for four synthetic profiles from 0 to 22 km, taking into account the correction for temperature and pressure (F07 in Figure 5). We also considered the values of VP and VS from Bressan et al. (2012) (B12 in Figure 5) with a spread function <2.5, reducing the maximum depth considered to 12 km. Figure 5 shows that the seismic velocities (F07 and B12) fit well with the ones predicted by the ML. The results of the local earthquake tomography of Anselmi et al. (2011) in the Southern Alps confirm this observation. Viganò et al. (2013) results fit the ML only for depths shallower than 10 km in the eastern and south-western corners of the tomographic grid (around the Garda lake and in the eastern Southern-Alps). For greater depths and in other parts of the grid (in the Eastern Alps, and the area around GL), they better agree with the BRF.
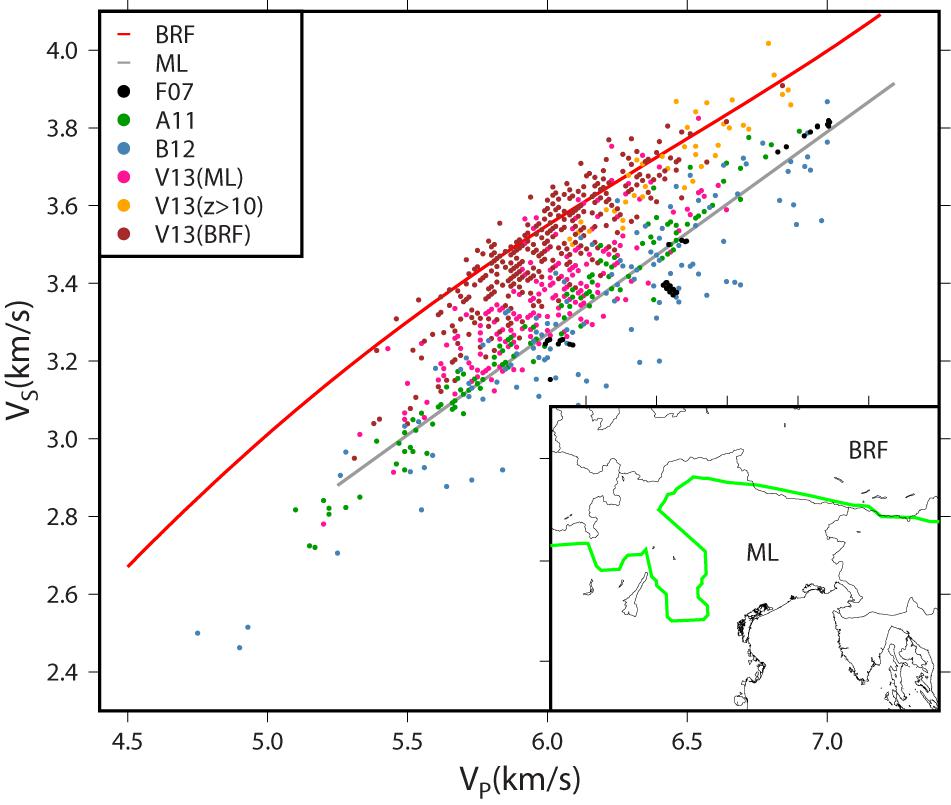
Figure 5. Comparison between the empirical relations of Brocher (2005) between VP and VS and observed VP and VS values. Red line: “Brocher’s regression fit” (BRF); gray line: “mafic line” (ML). Black dots: from the synthetic profiles of Faccenda et al. (2007) (F07); blue dots: from the seismo-gravimetric inversion of Bressan et al. (2012) (B12); green dots: from the tomography of Anselmi et al. (2011) (A11); pink dots: data from the tomography of Viganò et al. (2013) limited to the area to the south of the green line in the map shown in the inset [V13(ML)]; brown dots: data from the tomography of Viganò et al. (2013) limited to the area to the north of the green line [V13(BRF)]; yellow dots: data from the tomography of Viganò et al. (2013), with a depth >10 km [V13(>10)]. In the map in the inset, a green line represents the boundary between areas where we applied the different empirical relations (BRF and ML) to convert VP in VS.
Behm (2009) computed a 3D model of the VS of the Eastern Alps and the Bohemian Massif from the tomographic inversion of stacked active-source data used to compute the VP model (Behm et al., 2007). Based on the information about VP and VS, Behm (2009) found that the Poisson’s ratio in the Southern Alps and Dinarides between depths of 1 and 5 km is close to the values predicted by ML, while between 11 and 15 km, it is nearer to the values predicted by BRF. The Poisson’s ratio in the Tauern Window (Figure 1) is close to the BRF values between 1 and 5 km depth, while it is lower than them between 6 and 15 km. In the Eastern Alps (excluding the Tauern Window) the Poisson’s ratio values are grouped around the BRF line for the depth interval of 6–15 km, while at shallower depths the values are comprised between the BRF and ML lines. Therefore, we used the ML empirical relation in the eastern Southern Alps and the Dinarides from the topography up to 10 km of depth and the BRF law otherwise (inset in Figure 5).
For the bulk rock density, ρ, the information is also unevenly distributed. The laboratory measurements of Faccenda et al. (2007) add on the results of the gravimetric and seismo-gravimetric inversions in the area (Dal Moro et al., 1998; Ebbing et al., 2001, 2006; Šumanovac et al., 2009; Bressan et al., 2012). After converting the VP into densities using the relation of Ludwig et al. (1970) as reported by Brocher (2005), we compared the resulting distribution with the VP and density values from the various measurements (Figure 6). We can see that Ludwig et al.’s (1970) relationship plots close to an average of all the relationships that can be traced from the empirical values. The VP-density data pairs of Bressan et al. (2012) plots toward lower density values, while a fit through those of Ebbing et al. (2006) and Dal Moro et al. (1998) would tend toward higher density values, even if there is a high dispersion. The values of Šumanovac et al. (2009) best support our choice of applying the relationship of Ludwig et al. (1970).

Figure 6. Comparison between the VP and density values as calculated with the relation of Ludwig et al. (1970) (red line) and the values obtained from laboratory measurements (Faccenda et al., 2007) and from gravimetric and seismo-gravimetric inversions in the area (green dots: Dal Moro et al., 1998; brown dots: Ebbing et al., 2001, 2006; yellow dots: Šumanovac et al., 2009; blue dots: Bressan et al., 2012).
The use of empirical relations to convert VP into VS and ρ introduced an additional source of uncertainties in our model. Brocher (2005) reported the average misfit of his dataset produced by different empirical relations, but he did not quantify the dispersion around the curves. We compared ML and BRF to the values in our dataset (Anselmi et al., 2011; Bressan et al., 2012; Viganò et al., 2013) and we obtained an average model misfit of less or equal than 0.05 km/s, with a standard deviation of around 0.1 km/s for both relations.
We applied the conversion relation before the interpolation, and we analyzed the effect of this procedure. We interpolated VP from Anselmi et al. (2011), Bressan et al. (2012), and Viganò et al. (2013). Then, we computed VS with three different procedures: (i) we interpolated the tomographic results from Anselmi et al. (2011); Bressan et al. (2012), and Viganò et al. (2013) (VS0); (ii) we interpolated the VS computed from VP by empirical relation (VS1); (iii) we converted into VS the interpolated VP (VS2). We compared VS1 and VS2 with VS0: average misfits are comparable (-0.02 and 0.02 km/s), but the standard deviation of misfit of VS2 (0.12 km/s) is twice of that of VS1 (0.05 km/s), confirming greater effectiveness when empirical relationships are applied before the interpolation.
For the sediments, in the absence of laboratory measurements, we considered the properties reported by Giustiniani et al. (2008) for the Friulian plain. The values are in agreement with the measurements of the elastic moduli obtained from Vuan et al. (2011; the yellow area in Figure 2) and Tondi et al. (2019) for the Venetian and Po plains. Hence, we assigned these values to the grid points within the sedimentary layer (Table 2).
Figure 7 shows the 3D NAC multiparameter model: in this case, the VP is shown. Two vertical sections, one, in the X direction at y = 200 km (∼46.3°N), the other in the Y direction at x = 240 km, i.e., (∼13.15°E) enable to appreciate the vertical VP variations. The figure shows the Moho and an isosurface corresponding to VP = 6.4 km/s. Even if in stable continental regions commonly the lowermost part of the crust has VP greater or equal to 6.8 km/s (Mooney, 2010), in this area, the lower crust has a lower value of VP, being about 6.4 km/s at the transition between AD and EU (Bleibinhaus and Gebrande, 2006). Therefore, we interpreted the isosurface corresponding to a VP = 6.4 km/s as representative of the top of the lower crust, although NAC has not any vertical subdivision below the sedimentary layer.
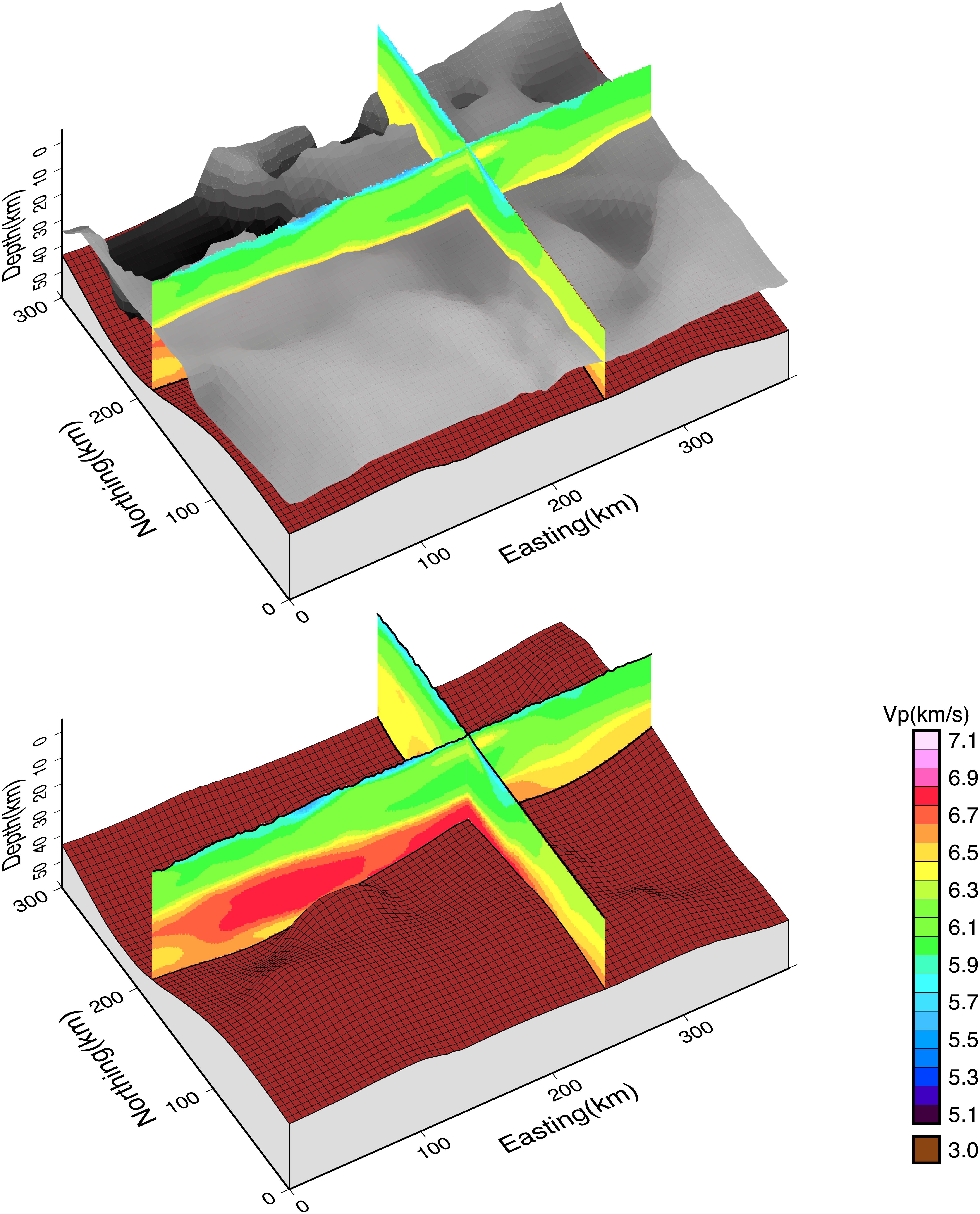
Figure 7. VP values of the 3D NAC model. Two vertical sections (one in X-direction at y = 200 km, the other in Y-direction at x = 240 km) and two surfaces (isosurface for VP = 6.4 km/s-gray scale and Moho-brown) are shown.
We compared the input data with the final depth of the interfaces and the VP values by interpolating the values from NAC in the position of the data points (Figure 8). We found that there is no systematic over- or under-estimation of the data and that the distribution of the differences is compatible with the input data uncertainties. NAC shows a high variability of the geophysical parameters (Table 2) especially in the crust at depths <10 km where VP ranges from 5.0 km/s to 6.5 km/s (with total uncertainties between 0.2 and 0.4 km/s) and estimated E has values from 50 to 100 109 Nm–2 (with total uncertainties between 5 and 20 109 Nm–2). The relative uncertainty is around 5% for VP, VS, and ρ, and between 5 and 20% for μ and E.
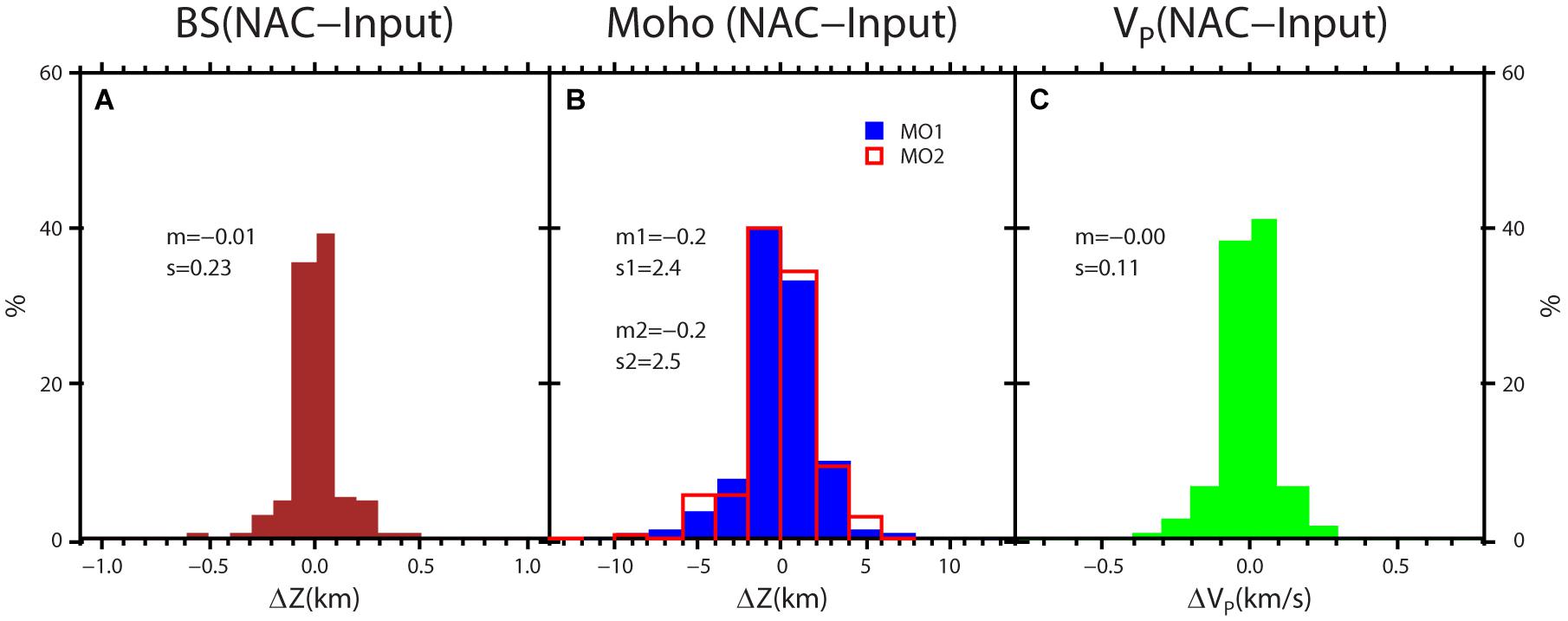
Figure 8. Histograms of the differences between NAC and input values: (A) BS interface; (B) MO1 and MO2 interfaces; (C) VP.
Figure 9 shows more in detail the depth of the interfaces of NAC. The MO1 depth (9C) ranges from a minimum of 25 km in the southern part to a maximum of 55 km in the Alps. The maximum depth is found in the Central Eastern Alps, while two minima are present: one between the Garda Lake and the Adriatic Sea, and the other in north-eastern Slovenia and Austria. The western part of NAC, where the Adria Moho reaches the shallowest depths near the boundary with Eurasia, is characterized by a steep gradient of the Moho depth. In the eastern part, the transition is more gradual, as shown by the Alp01 profile (Brückl et al., 2007; Figure 2).
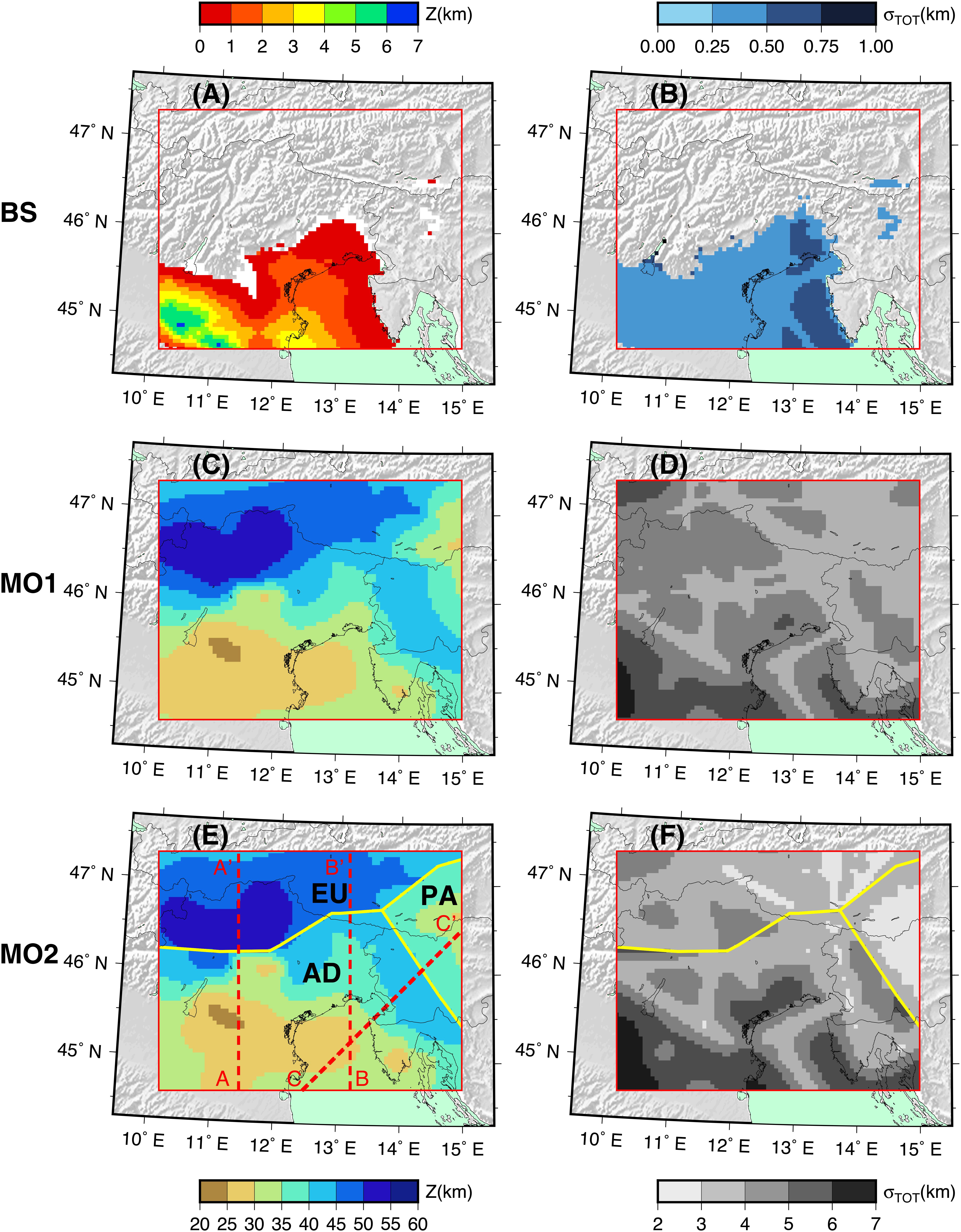
Figure 9. Maps of the depth of the interfaces and their uncertainty. (A) BS interface, (B) BS uncertainties (σTOT), (C) MO1 interface, (D) MO1 uncertainties (σTOT), (E) MO2 interface, (F) MO2 uncertainties (σTOT).
Figure 9 also shows the uncertainties of the final maps (σTOT). In general, the accuracy of the maps is variable, and it reflects the different distribution of the input data. The uncertainty due to errors in the input data (σUNC) shows low geographic variability and is comprised between 1 and 2 km.
The difference between the Moho depth of AD and EU at their boundary has its maximum value (up to 15 km) in the area close to the TRANSALP profile while it decreases from west to east, where it is comparable with the uncertainty of MO2. The differences between MO1 and MO2 are relevant only near the boundaries between the three Moho fragments, in particular in the western part of NAC between AD (MO2 shallower than MO1 up to 7 km) and EU (MO2 deeper than MO1 up to 10 km), and at the east of the triple junction, between PA and EU (differences up to 6 km) (Supplementary Figure S2).
In Figures 10A–C, two N-S profiles of the model (A-A’ and B-B’), and one NE-SW oriented (C-C’) enable the comparison of MO1 (black line), and MO2 (gray and blue lines, for EU and AD, and green for PA, respectively). Figure 10 enables to appreciate also the VP depth variations along the same profiles. The three sections show high variability both in the upper (0–20 km) and lower (z > 20 km) crust. The uncertainty (σTOT) is shown in Figures 10D–F: it is minimal for the central part of the model, with values <0.25 km/s. NAC’s southern part is less constrained, especially for the section B-B’, with uncertainty even above 0.35 km/s. As inherent in the modeling procedure, the high velocity corresponds to an increase in ρ and the elastic parameters of the multiparametric model: in particular, zones with high velocity, ρ, and rigidity are present in correspondence of the Southern Alps and the External Dinarides front. An example is shown in Figure 11, presenting the vertical sections of the profile BB’ of Figure 10 for VS (A), rho (B), μ (C), and E (D), below an exaggerated topographic profile. VS ranges between 3.0 and 4.0 km/s, with smaller values close to the front of the Southern Alps foothills. It is noteworthy, the thicker layer with VS around 3.8 km/s of Eurasia if compared with the southern part of the section. ρ shows a positive vertical gradient, with values ranging between 2.6 and 2.9 kg/m3. The elastic parameters have a pattern similar to the one of VS, showing the maximum heterogeneity and the minimum values in correspondence of the Southern Alps’ front. The value of the elastic parameters is greater in the southern part of the profile (AD) than in the northern part (EU). Figure 10 shows a similar pattern for VP, also comparing AD and PA (Figure 10C), even considering the error due to the uncertainty.
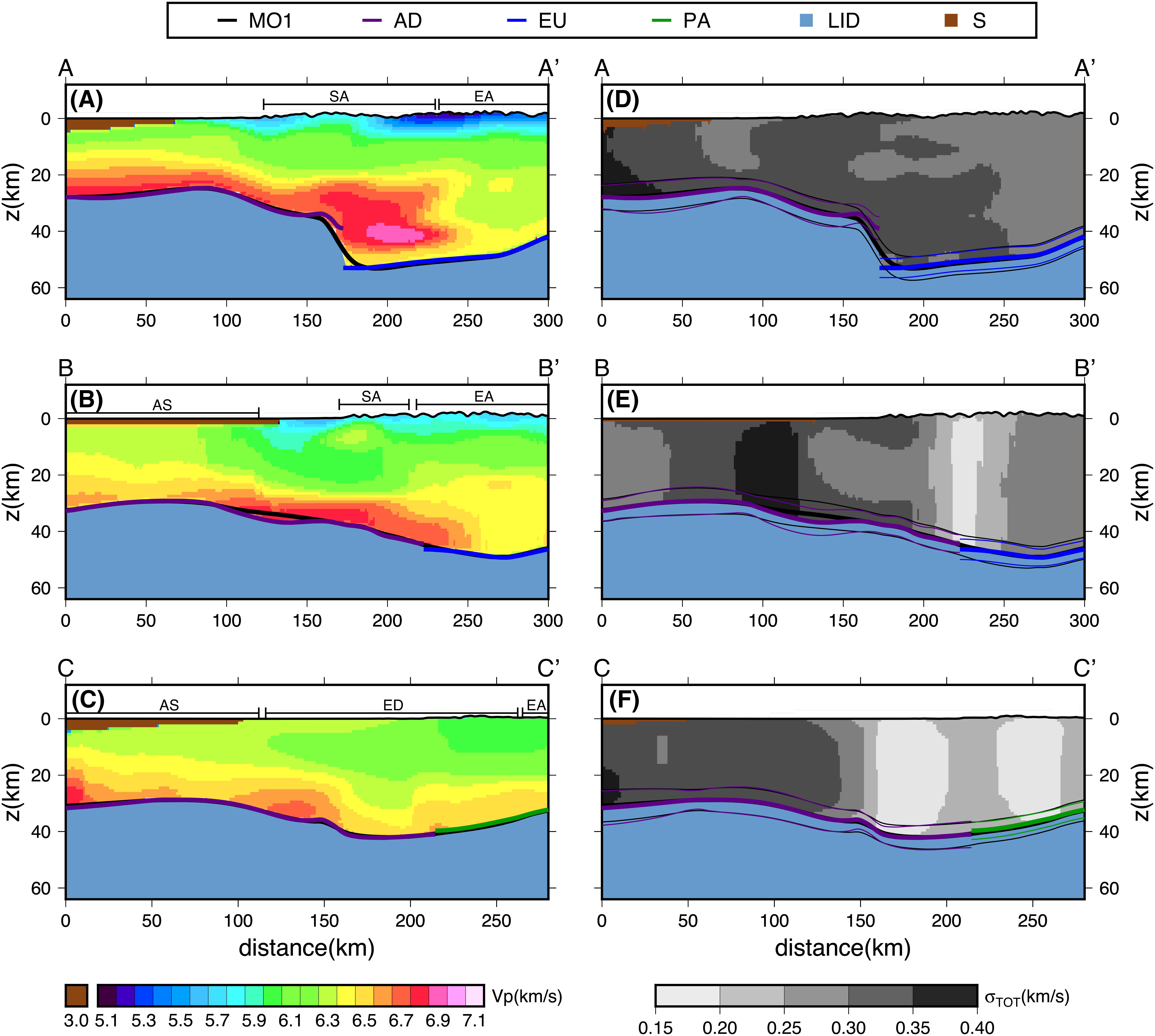
Figure 10. VP values along vertical sections for the profiles AA’, BB’, and CC’ of Figure 9E. Black line: trace of MO1; violet line: trace of Adria (AD) Moho; blue line: trace of Eurasia (EU) Moho; green line: trace of PA Moho. SA, Southern Alps; EA, Eastern Alps; AS, Adriatic Sea; ED, External Dinarides.
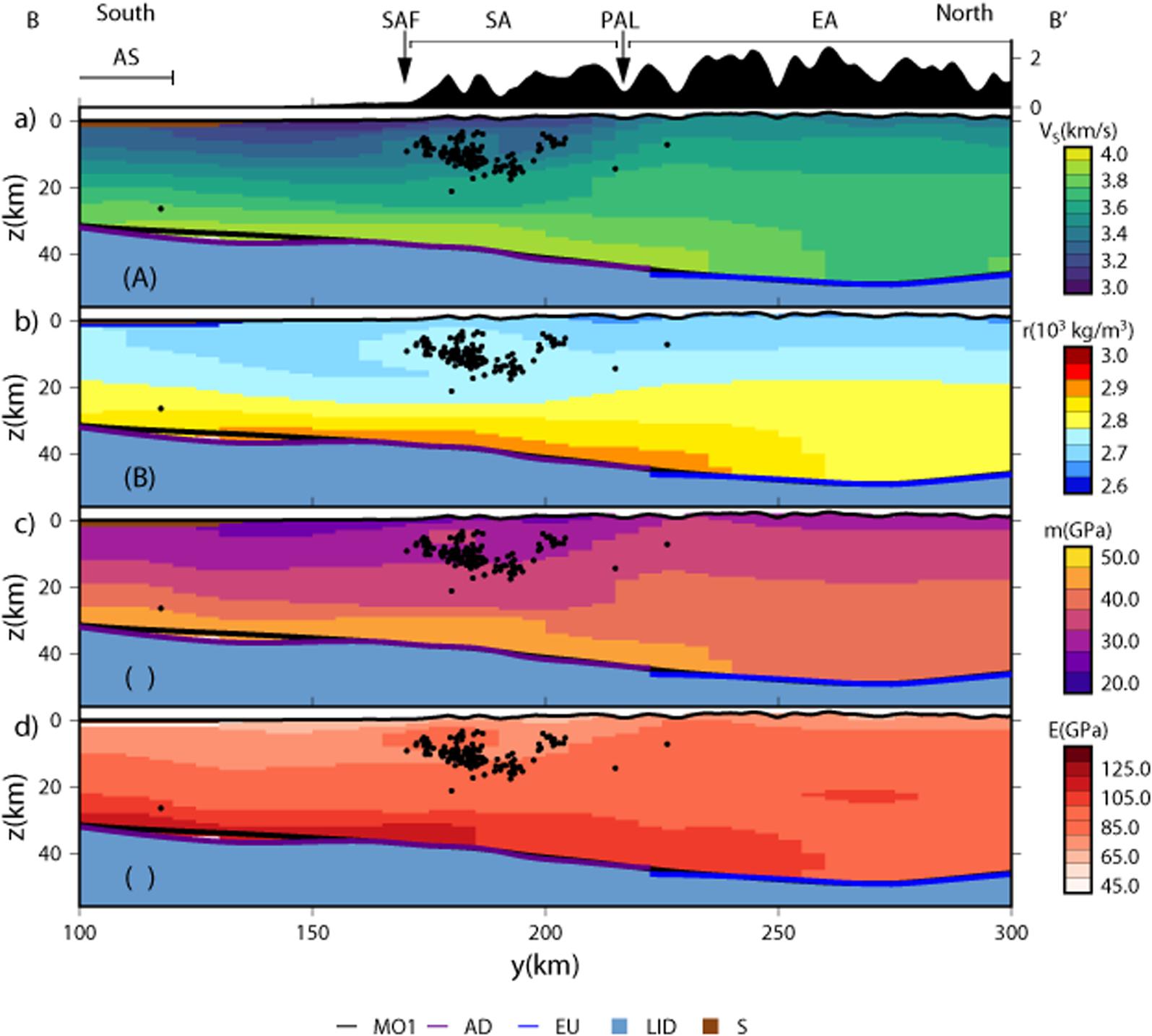
Figure 11. Vertical section for the well-defined part of profile BB’ (Figure 9E; starting from y = 100 km) with the values of (A) VS, (B) ρ; (C) μ, and (D) E. Black line: trace of MO1; violet line: trace of Adria (AD) Moho; blue line: trace of Eurasia (EU) Moho; black dots: hypocenters of earthquake with MD ≥2.0 and distance ≤10 km from profile BB’ for the 1988–2018 time span extracted from the OGS bulletins1. SA, Southern Alps; EA, Eastern Alps; AS, Adriatic Sea; SAF, Southern Alps foothills; PAL, Periadriatic Lineament.
The building of NAC was driven by the need of a detailed model of the crust and its properties at the transition from the Alps to the Dinarides, where a vivid debate is ongoing on the relative plate movements, and, hence, the structure of the deep crust and of the upper mantle (Lippitsch et al., 2003; Kissling et al., 2006; Mitterbauer et al., 2011; Handy et al., 2015; Kästle et al., 2020). The model aims at serving as a basis for modeling the stress and strain fields in this critical area and interpreting the intense seismic activity of the region.
To get new insight into the deep crustal structure, and on the processes having formed and deformed it, in the last decade several crustal models were developed at the continental scale of Europe, and in the last few years, seismic and seismological experiments are bringing new information. However, a detailed 3D model of the physical properties of the crust of the northern tip of AD is still lacking. The three most popular crustal models at European scale (EuCrust-07, EPCrust, and EUNAseis), with their uniform parameterization allowing a simple conversion in a numerical mesh, are an essential reference for constructing a regional model. Their scale and resolution yet make them unsuitable for studies in small areas, like the one we consider. EuCrust-07 has a resolution of 15’ × 15’ (or 0.25°× 0.25°), EPCrust and EUNAseis of 0.5° × 0.5°, while a higher resolution characterizes the ESC Moho: 0.1° × 0.1°. Nonetheless, the authors of the latter, to avoid aliasing effects, transformed the original data points to 10 × 10 km block averages, and low-pass filtered them, using a cut-off length of 100 km, and a passing wavelength >200 km, to highlight the features at a continental scale. More detailed models, developed for seismological studies, cover only marginally our region (Vuan et al., 2011; Molinari et al., 2012, 2015a).
NAC fills this gap: it is a 3D model of the crust from the topographic surface to the Moho discontinuity. The variations in physical properties (seismic velocities, density ρ, Young modulus E, and shear modulus μ) are sampled on a grid with cells of 5 × 5 km horizontally, and 1 km vertically (Figure 7). A highly resolved Moho structure is essential for understanding the dynamic processes at plate boundaries (e.g., Carbonell et al., 2013, and references therein). With greater detail, however, the consistency of the information from different data sets, as, e.g., from different seismic experiments (refraction/wide-angle surveys, or receiver functions) becomes crucial. In most cases, the Moho depth from these two sets of data is consistent, although not always coincident, since the Moho depths from normal incidence are generally obtained from refraction derived models (Carbonell et al., 2013). The receiver function information is increasing with the time and the multiplication of experiments, and several works adopted different weights to combine it with the controlled seismic source data in the Moho definition (e.g., Di Stefano et al., 2011).
NAC is mainly based on data from active seismic experiments that provided good coverage of most of the studied region (Figures 2, 3). We verified the consistency of their interpretation at the intersections (Supplementary Figure S1). The differences are mostly within the errors related to the original data acquisition and processing. The profiles with similar acquisition and processing characteristics (e.g., the profiles from ALP 2002 experiment), or interpreted by the same authors (e.g., the profiles from Scarascia and Cassinis, 1997) have a smaller difference between each other compared with the pairs that do not share these features (e.g., the TRANSALP and Alp02 profiles). The only way to remove such differences would be to reprocess all the profiles consistently. As observed by Brückl et al. (2007) based on the TRANSALP and Alp02 profiles, some differences in the velocity-depth functions could also be related to a degree of anisotropy in the velocity, and, therefore, are intrinsic in the different profile orientation. We integrated the dataset about the Moho depth with receiver function studies, overall for the parts of the study region not covered by the seismic profiles, like the south-western part of NAC (Figure 2).
We also considered the recent work of Hetényi et al. (2018), based on the analysis of the receiver functions along an NS transect at 13.33° E, in the framework of the EASI complementary experiment of AlpArray. They applied different methods to obtain the Moho depth from the receiver functions inversion, obtaining a good agreement to the north of the Alps but highly scattered data in correspondence of the Eastern and Southern Alps, for the greater complexity of the crustal structure and possible reverberations. Therefore, Hetényi et al. (2018) chose to focus on the migrated receiver function profiles showing a very deep Moho (up to 75 km) on the Adriatic side. The proposed depth in this area is significantly different from the seismic profiles (Alp01, Alp02, and the three profiles from Scarascia and Cassinis, 1997), and other receiver function results in the same area (Bianchi et al., 2015) and also the results obtained by Spooner et al. (2019) with gravimetric methods. Hetényi et al. (2018) analyzed in detail the data below the Eastern Alps and reported that they do not find a sharp crust-mantle boundary but a broad zone with a velocity gradient, i.e., a clear Moho. However, the most plausible velocity contrast they found using the “west profile” (35–39 km) would be in agreement with the previous data, showing an Adria Moho shallower than the European one, and a Moho maximum depth <50 km. As recognized by the authors, the Moho depth range that can be obtained by their analysis is broad (between 50 and 70 km depth), and the model reaches mantle velocities over a broad depth range (48–65 km). Because of the non uniqueness of their results and the disagreement with other models in the same area, we decided to exclude from the dataset the results of Hetényi et al. (2018), although we considered the data in some of the following tests.
We choose to weight the information from different sources and to exclude part of the data based on their uncertainties. Therefore, uncertainty estimations are critical pieces of information for the construction of NAC. Unfortunately, only in a few cases (e.g., Behm et al., 2007), a careful analysis of uncertainty was done and reported for seismic experiments so that we had to rely on considerations on the applied techniques (Grad et al., 2009b). The estimations of uncertainty in the receiver function studies considered were performed in different ways, but they are based mainly on the bootstrap technique. Lombardi et al. (2008) also considered two different contributions to the total uncertainty, namely due to uncertainty of VP and finite bandwidth. They also concluded that the natural frequency content of the data is the major contributor to the total uncertainty of their results. Piana Agostinetti and Amato (2009) provided a qualitative classification of the reliability of the results.
Hence, the different approaches used in the literature to define the uncertainty make these estimates somehow subjective. To understand how the selection of data input and the weighting of uncertainty influenced our results, we performed three tests on MO1: (a) we interpolated all the data-points (also considering the data from Hetényi et al. (2018) without weights (MO1a), (b) we removed from the datasets the data from Hetényi et al. (2018) (MO1b), (c) we considered the weights based on the uncertainty (MO1c). The differences between the results of these tests and MO1, ΔZ = MO1x−MO1, are reported in Supplementary Figure S3. We made these tests on MO1 because the definition of the boundary between Eurasia and Adria is not compatible with the results of data from Hetényi et al. (2018). The main differences between MO1a and MO1 are along the profile of Hetényi et al. (2018) with ΔZ < −20km. Removing data from Hetényi et al. (2018) from the dataset, the differences of MO1b relative to MO1 are in the range of σTOT, with the single exception of the SW corner of the NAC model, where the data coverage is poor. The inclusion of the weights due to data uncertainty further reduced the difference of MO1c relatively to MO1. As we can expect, the most unstable area coincides with the south-western corner of NAC, where the results changed appreciably in the different tests, while the eastern part of NAC is stable also changing the selection of the receiver function data.
The velocity models of the considered seismic profiles have multiple layers for the crust (with the layer number different from one model to another) and a vertical velocity gradient within the layers. Some recent crustal models (e.g., EuCRUST-07; EPcrust) used a fixed number of layers for the whole area (sediments, upper crust, and lower crust) with horizontal variations of layer thickness and the velocity. This approach is useful and justified at the continental scale, but it is too simplified to show the real complexity of the studied region. Another problem with this approach is in the arbitrariness in associating the original layers of the seismic profiles to the upper crust or the lower crust since the most evident velocity contrasts are not always associated with the same interfaces. As we already said, the division adopted in stable continental regions, where most often the lowermost part of the crust has a VP greater or equal to 6.8 km/s, is not appropriate for our area. Therefore, we chose to adopt a single layer for the crust, in which, however, the seismic velocities, ρ, and the elastic parameters are variable, both laterally and vertically. In this way, NAC includes high-velocity bodies in the upper crust and low-velocity bodies in the lower crust.
An essential step in the construction of the NAC model was the estimation of model uncertainty on the depth of the interfaces and the geophysical parameters, taking account of the uncertainty of the input data (σUNC) and the effect of the interpolation process (σINT). The total uncertainty (σTOT) of the Moho depth (both MO1 and MO2) ranges from 2.5 to 6.5 km, which means that the relative uncertainty lies between 5 and 20% (Figure 9). The variability of the uncertainty is due mainly to the distribution of the input data. The map of the Moho uncertainty (Figures 9D,F) shows values mostly >5 km where the dmin values are higher than 40 km, while the Moho uncertainty is comprised between 3.0 and 5.5 for smaller distances (see the map of dmin in Figure 3).
In the construction of NAC, we had to deal with some problems typical of the spatial-data interpolation, like the input-data selection, uncertainty and resolution evaluation, and the choice of the interpolation grid. Some of these issues could be better addressed by using a Bayesian approach where the solution is not a single best model but instead a probability distribution representing the full level of knowledge about model parameters (Bodin et al., 2012). The use of the transdimensional inversion (Sambridge et al., 2013) allows to a data-driven choice of parametrization, like the interpolation grid. A future improvement of NAC could be based on this approach.
Another peculiarity of NAC is that in its construction we performed the estimate for the Moho discontinuity, both taking into account the hypothesis of a unique (MO1) as well of a fragmented Moho (MO2), to describe at best the Moho heterogeneity.
The knowledge on the relative position of the Adria and Eurasia Moho in the western part of NAC is mainly due to the results of the TRANSALP experiment, whereas eastwards, the interpretation of the seismic profiles is more questionable. The active seismic data at disposal from Scarascia and Cassinis (1997) and the ALP 2002 experiment (Brückl et al., 2007) shows that the Adria Moho is shallower than the European one. However, as we said before, Hetényi et al. (2018) found a very deep Moho (up to 75 km) on the Adriatic side. It is worth noting that their boundary between AD and EU is further north than ours. If confirmed by other data, this would imply two oppositely dipping subduction zones (Király et al., 2018) and should lead to a re-analysis of the other datasets. The fragmentation of the Moho, leading to our MO2 model, was suggested based on the analysis of the seismic data of the CELEBRATION and ALP 2002 experiments (Behm et al., 2007) and supported by the elastic plate modeling of Brückl et al. (2010), gravimetric, geodetic, and seismicity pieces of evidence (Brückl, 2011). However, the existence of a distinct Pannonian fragment is not recognized by all the authors (e.g., Spada et al., 2013), even if the sharp boundaries between the strain velocities observed are in agreement with the triple junction between EU, AD, and PA (Völksen et al., 2018). The differences between our two Moho interfaces are small (Supplementary Figure S2) and they are more pronounced in the model areas well constrained by the data and negligible in the more controversial domains (see Figure 3). To the west, along the EU-AD plate boundary, MO2 is up to 7 km shallower than MO1 for AD, and deeper than MO1 up to 10 km for EU, whereas the differences at the east of the triple junction, between PA and EU reach a maximum of 6 km (Supplementary Figure S2). One could speculate that the choice of one or the other model is irrelevant for most of the applications. However, the analysis of the semivariograms can have a role in opting for one or the other model. The semivariograms for the different fragments are different in terms of the sill, range, and nugget; therefore, the stationarity assumption appears to be violated for MO1. AD shows a higher variability than the other fragments: the reason can be the greater heterogeneity of the used dataset or the greater complexity of Adria Moho with respect to EU and PA for the considered region. Moreover, the uncertainty σTOT has a different distribution for MO1 (Figure 9D) and MO2 (Figure 9F): it is generally lower for MO2, except that in the model eastern and southern parts, and at the fragments boundaries. These differences depend on the semivariogram models used for MO1 and MO2 and on the distribution of input datasets. The lower values of MO2 are the effect of the lowest value of the nugget for the three MO2 fragments compared with the nugget of MO1. The higher values in the region less covered by the data, on the other side, depend on the lower ranges of AD, EU, and PA relative to the one of MO1. Another reason is that at some points along the boundary of the fragments, MO2 values are produced by an extrapolation, rather than by an interpolation inside the convex hull of the input datasets.
NAC shows a high variability in the Moho depth, especially in the AD domain, as it may be appreciated in Figures 9C,E, with a depth ranging from a minimum of 25 km between the Garda lake and the Adriatic sea to a maximum of 55 km in the Central Eastern Alps. Compared with other models at a broader scale (EuCrust-07; ESC Moho; EPCrust; Moho map of Spada et al., 2013), NAC is more detailed, with more pronounced minima and maxima. Although NAC does not contradict the principle of simplicity (Kissling, 1993), it evidences the differences in depth that can be interpreted in terms of different plates or fragments. To enable a correct comparison with the other models, it is necessary to use the same grid to resample a model to the grid of the other. When the grid spacing is appreciably different (EuCrust-07; EPCrust) we decided to resample NAC at the same spacing of the model with which we want to compare it, and vice versa: in this way it is possible to appreciate both the long-wavelength variations, as well as the details of the model with the finer grid. When the grid spacing is similar (ESC Moho; Moho map of Spada et al., 2013), we used the grid of NAC. Depending on the model to be compared with, we considered MO1 or MO2, on a turn.
The long-wavelength features of the MO1 map of NAC are similar to the ESC Moho (Figure 12A). The position of the maximum depth of MO1 and ESC Moho is well constrained by the profiles of Scarascia and Cassinis (1997) and TRANSALP. Superimposed to the long-wavelength, NAC shows short-wavelength variations, as the undulations in the high-Adriatic Sea. The other most striking difference occurs in the Southern Alps, where the differences between the Eurasia and Adria are more pronounced (about 10 km greater than in ESC Moho). This is reasonable because the inputs are similar, but ESC Moho was filtered passing wavelengths larger than 200 km. The EuCRUST-07 Moho (Figure 12B) locates the maximum depth of the Moho slightly to the north of the corresponding troughs of NAC and ESC Moho. The differences are relevant also in the eastern part of NAC, which benefits of the results of the more recent ALP 2002 seismic experiment. NAC and EuCRUST-07 also disagree on the depth in the south-western corner, while being very similar in correspondence of the Northern Adriatic Sea. To construct the EPCrust model in our area, Molinari and Morelli (2011) averaged information from EuCRUST-07, ESC Moho, and other regional models (Stehly et al., 2009; Molinari et al., 2010). The main difference with NAC (Figure 12C) is, as for EuCRUST-07, the position of the maximum depth of the Moho, even if the shift is smaller than in Figure 12A. Finally, we compared MO1 with the Moho depth obtained by Spooner et al. (2019) (Figure 12D). The Moho of Spooner et al. (2019) is slightly shallower than MO1, but the two models are consistent: the only notable differences are in the south-western corner of NAC and in the central part of NAC, where MO1 shows a sharp transition between low and high depth values. The Moho of Spooner et al. (2019), aimed to fit the observed gravity in the Alpine region, was obtained trying to smooth the large vertical steps between defined plate domains, that are enhanced in models like MO2.
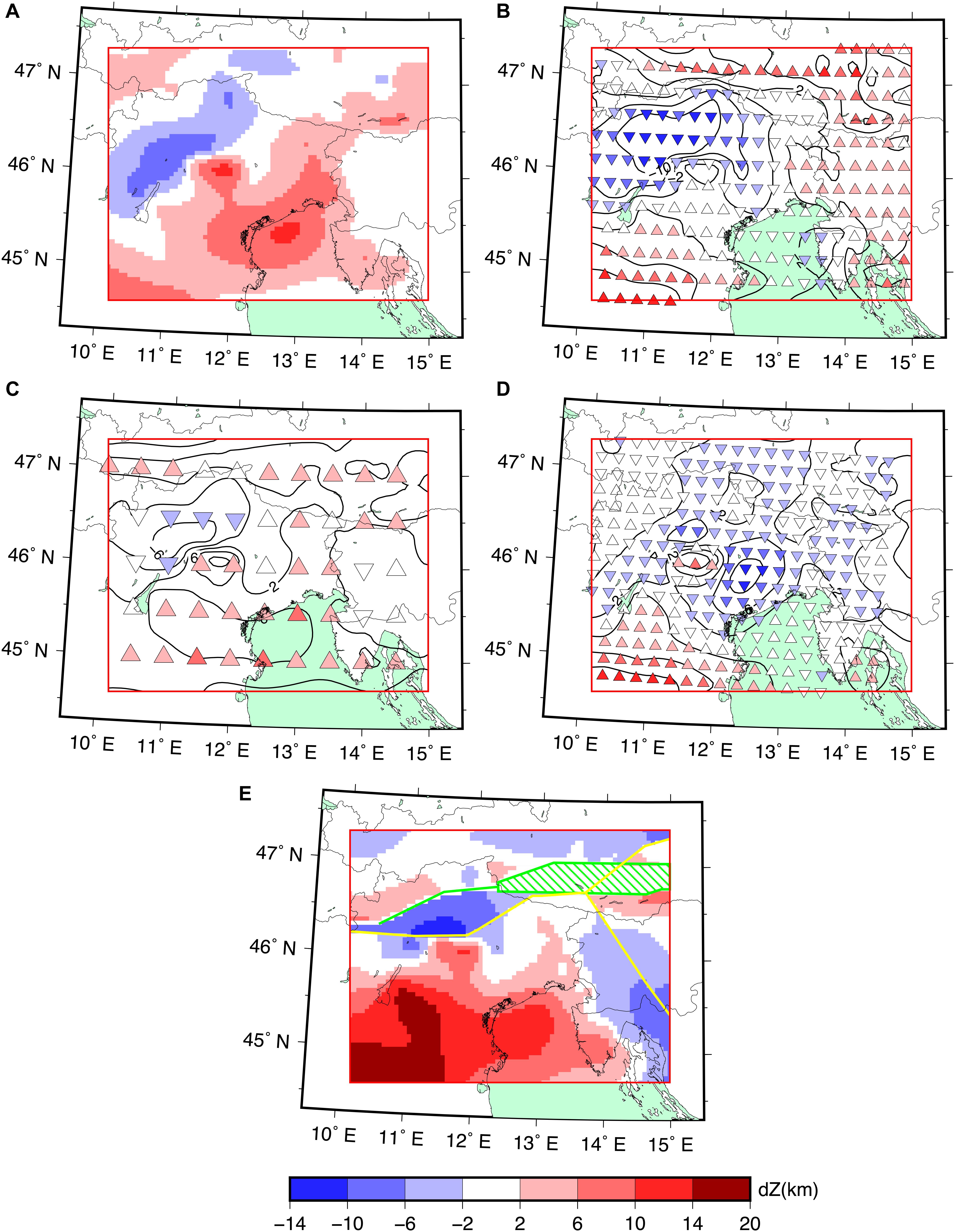
Figure 12. Differences between (A) Moho of Grad et al. (2009b) and MO1; (B) Moho of EuCRUST-07 and MO1; (C) Moho of EPCrust and MO1; (D) Moho of Spooner et al. (2019) and MO1; (E) Moho of Spada et al. (2013) and MO2. The triangles in (B–D) show the differences computed on the coarser grid and the isolines are computed from the differences on the finer grid (see text for details). The yellow lines in (E) show the boundaries between the fragments of MO2, the green lines the boundaries between the fragments of the Moho according to Spada et al. (2013) and the area filled by green lines is where Spada et al. (2013) did not define a Moho surface.
We compared our segmented Moho (MO2) with the Moho map of Spada et al. (2013) that also introduces the separation between EU and AD (Figure 12E). The differences between the depths of the EU Moho are negligible, while the two models differ in the position of the boundary between the two plates. Moreover, Spada et al. (2013) did not take into account PA as a separated Moho surface. NAC’s MO2 depth is systematically shallower than the one of Spada et al. (2013) in the AD domain (Central Southern Alps, eastern Po Plain, and Adriatic Sea), because of the constraints given by the data of Scarascia and Cassinis (1997) and of CROP experiment, not included in the other modeling.
Summarizing, except for the area less constrained by direct observations, the differences between our model and the other ones are sustained by the input dataset and are mainly related to the high resolution of NAC.
NAC allows choosing between the two models, one with a single Moho surface (MO1) and one with a fragmented Moho (MO2). The only limitation to the adoption of a fragmented Moho could be the more significant uncertainty of MO2 than MO1 in the eastern and southern part of the model (in AD) (Figure 9). However, if the chosen fragmentation is correct, the smaller uncertainty of MO1 is only apparent because we defined the Moho depth in a fragment with data from another plate. We are, therefore, in favor of MO2, although we provide also MO1, a smoother model that can be suited for, e.g., a gravimetric inversion.
NAC is a multiparametric 3D model of VP, VS, ρ, μ, and E consistent over the whole area across North-Eastern Italy and Western Slovenia. Figures 10D–F allow to appreciate how the uncertainty of VP depends on the geographic distribution of the input data: it is minimal for the central part of the model, crossed by many seismic profiles, being higher in the southern part of the model, less covered by data (see Figure 3). We verified that the interpolation procedure that we used to obtain a uniform parameterization and resolution produced an unbiased model, compatible with the uncertainties of the input data.
A uniform resolution on the whole area means that the final model cannot reproduce all the fine details of the input data, as the high VP values (up to 6.8 km/s) reported by Bressan et al. (2012) in the upper crust of the Southern Alps. Nevertheless, compared with the model of Rossi et al. (2005), it is a much more representative model of the crustal heterogeneities in the area. We computed VS, ρ, μ, and E from VP values through empirical relationships. We preferred this solution to the alternative approach of constructing independent databases of VS and ρ and interpolating them. The reason is that the distribution and the resolution of the data are different for each parameter, and, therefore, the combination of their values needed to obtain elastic moduli can produce artifacts. We propagated the uncertainty of VP to the derived quantities, taking account also of the dispersion of VS and ρ values around the empirical relations. The relative uncertainty of VS and ρ is around 5%, while it is between 5 and 20% for μ and E.
As pointed out by Diaferia et al. (2019), applying an empirical relationship can be limiting, when the crust is heterogeneous, as shown by the high point dispersion (Figure 5). We tried to overcome this problem with the “regionalization” of the data, which resulted in the definition of two main domains, characterized by lithological differences. The results confirm the better fit of the ML relationship for the Southern Alps and the outer Dinarides from topography up to 10 km of depth, in agreement with the results of Behm (2009) about the relation between VS and VP in the different regions and the dominance of limestones and dolomitic limestones in the area (Bressan et al., 2012). In the remaining of the model, where igneous and metamorphic rocks are dominant, and at greater depths, we used the BRF relationship. ML would be more appropriate for this region, if also here there is a pervasive fluid-filled cracks distribution at depth, according to the results of Diaferia et al. (2019) in the Apennines. The comparison with the available observation of VS values confirmed that we get greater effectiveness when empirical relationships to convert VP into VS, ρ, E, and μ are applied before the interpolation.
A possible drawback of this approach is that we assumed that the spatial variability of VP in the regions, where we applied the different empirical relations, provides valuable indications for the distribution of the most significant heterogeneities. Therefore, to check the validity of the procedure, we compared NAC with independent models. We compared the resulting VS of NAC with the values obtained independently by Kästle et al. (2018) through the joint inversion of ambient noise and earthquake phase velocity measurements in the whole Alpine area and by Guidarelli et al. (2017) through ambient noise tomography in an area including the central and the eastern parts of NAC (Figure 13A). We re-interpolated the VS values of NAC in the same locations, considering only the crustal part of the other models. We found that the mean difference between Kästle et al. (2018) and NAC is -0.1 km/s while between Guidarelli et al. (2017) and NAC is about -0.2 km/s. In both cases, hence, the VS of NAC is slightly faster than the other ones but, considering that σTOT of VS ranges from 0.1 to 0.25 km/s and the different methods applied, the comparison is satisfactory, especially for Kästle et al. (2018) values (Figure 13B).
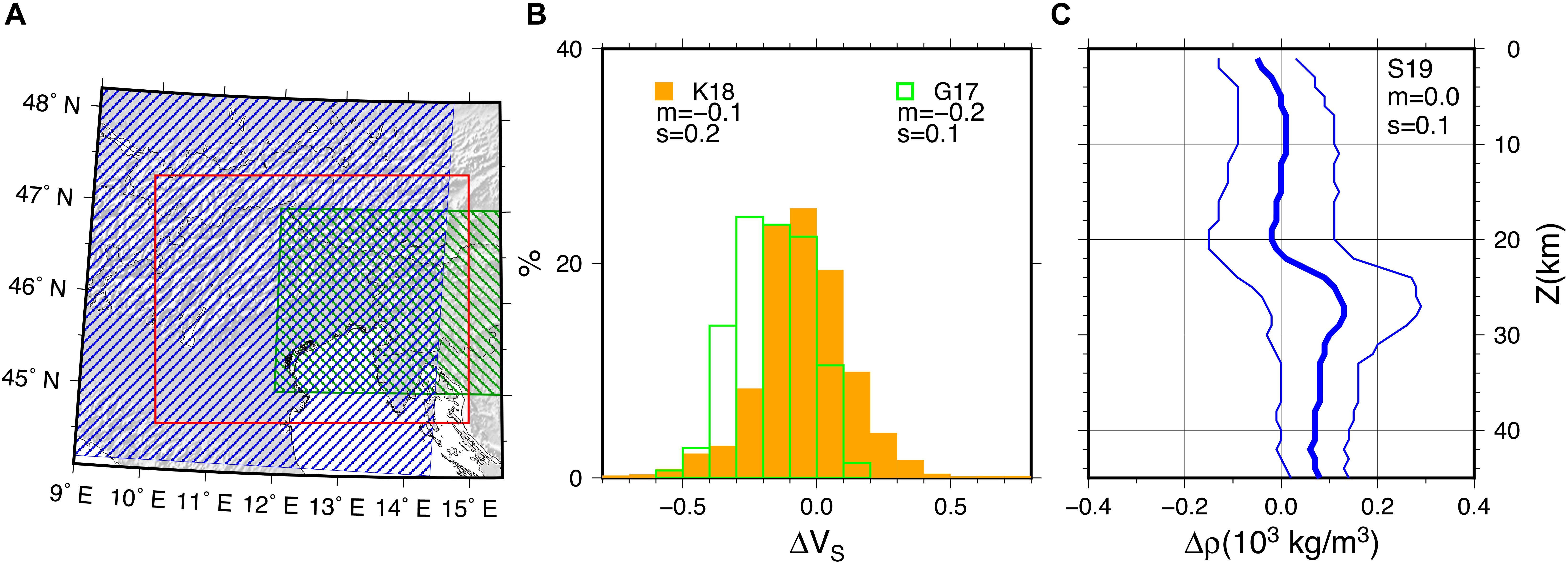
Figure 13. Comparison of NAC VS and ρ with independent models. (A) Map with area covered by NAC (red line), Spooner et al. (2019) (S19 – area filled by blue lines) and Guidarelli et al. (2017) (G17 – area filled by green lines); the model of Kästle et al. (2018) covers the whole area (K18). (B) Histograms of the differences between the VS values of K18 and G17 and the VS values of NAC. (C) The differences between the ρ values of S19 and the ρ values of NAC at different depths (thick line: average of the differences; thin lines: average plus and minus a standard deviation).
We also compared the density values of NAC with the ones from the crustal part of the model of Spooner et al. (2019). The values of NAC are systematically lower than the ones of Spooner et al. (2019) for depths >20 km (Figure 13C). These differences and the high dispersion of density values around the Ludwig et al. (1970) relationship (Figure 6) suggest that the use of different empirical relations for different depths or a relation that takes account of the depth influence on the VP-density relation (as Christensen and Mooney, 1995) could give better results for the deepest part of our model. On the contrary, for depths ≤ 20 km, the differences between NAC and the model of Spooner et al. (2019) are minimal (mean of differences lower than 0.05 103kg/m3), confirming the validity of NAC in representing the physical properties in the region in this depth interval.
NAC was built with the aim of modeling the stresses within the crust in relation to seismicity. The most seismically active region is the external front of the Southern Alps, and of the Dinarides. The seismic activity is concentrated at shallow depth (Viganò et al., 2015; Bressan et al., 2018a, b; Reiter et al., 2018). Also the Friuli, 1976 earthquake, the greatest event recorded in the instrumental period in this area, has a hypocentral depth of about 5–10 km (Slejko, 2018). Bressan et al. (2012), through the analysis of the spatial organization of seismicity in north-eastern Italy and western Slovenia, related the occurrence of seismicity in the shallowest crust to the mechanical rock heterogeneities. The interface separating media with different elastic moduli would be energetically favorable for the localization of fractures (Chatterjee and Mukhopadhyay, 2002; Bressan et al., 2018b). Spooner et al. (2019) compared the geographic distribution of large earthquakes in the Alps (M > 6) and found that their locations coincide with the upper-crustal density domain boundaries of their model, in agreement with the model of Ranalli (1992). To inquire on the relation between the seismicity pattern and the physical properties of the crust, we considered a vertical section of NAC crossing the region of the Southern Alps with the highest seismic activity and geodetic strain rate (Serpelloni et al., 2016), and well constrained by Bressan et al. (2012) (BB’ in Figures 10B, 11). The pattern displayed is particularly complex at the front of the Southern Alps, where most of the seismic events are recorded, with a sharp transition from low to high values of seismic velocities, density, rigidity, and Young’s modulus, in agreement with observations in other collisional systems (Ibarra et al., 2019). The analysis of the vertical sections AA’, BB’, and CC’ supports the model of a strong and competent AD compared to softer EU and PA (e.g., Brückl et al., 2007, 2010; Marotta and Splendore, 2014).
We presented a new 3D model of the geophysical properties of the crust in northern Adria (NAC), by critically incorporating all the information available in the literature and extrapolating to the remaining parts of the region. NAC provides information on the depth geometry of the sub-sedimentary basement and the crust-mantle-boundary (Moho), and on the spatial variations both laterally and vertically of seismic velocities (VP, VS), density (ρ), Young modulus (E), shear modulus (μ) within the sub-sedimentary crust. We quantified the uncertainties of interface depths and the physical properties by taking into account the data quality and the interpolation procedure.
NAC provides a higher resolution, especially in the Adriatic domain, than the existing crustal models at the scale of the European continent including this area. Differences in the Moho depth between NAC and the other models are sustained by the input dataset and are mainly related to the higher resolution of NAC.
We considered two different versions of the Moho surface: (i) one continuous surface (MO1) and (ii) three separate surfaces for the Adria microplate, Eurasia, and the Pannonian fragment (MO2). The differences between the two models are minimal, but, because the available data better sustain the solution of the fragmented crust MO2, we are in favor of MO2. We provide also MO1, a smoother model that can be suited for, e.g., a gravimetric inversion.
We computed VS, ρ, μ, and E from VP values by the application of empirical relations considering the regional distribution of different lithologies. We verified through a comparison with the available observation of VS values that the conversion of the original VP values should be done before interpolation. The comparison of NAC with independent models of VS and density confirms the validity of NAC in representing the physical properties in the region. At the same time, the results endorse the validity of the procedure followed, which can be applied in other contexts.
We developed NAC as a tool for a following modeling, aimed to analyze how the tectonic processes influence the intraplate stresses and the seismic activity. The model itself, however, already provides meaningful insights in this respect. The better fit obtained by the fragmented Moho, compared with the unique one, is an important reason for supporting this hypothesis. Similarly, the sharp transition from low to high values of seismic velocities, density, rigidity, and Young’s modulus in the zone of the Southern Alps, where most of the seismic events are recorded, confirms the critical role of crustal strength gradients in conditioning deformation and seismicity patterns.
The model here presented can be precious for any other purpose requiring a detailed description of the physical properties consistent over the whole area, as studies on seismic wave propagation, geodynamic modeling, tomographic inversions. Moreover, it will be easy to improve NAC, including new information, when available. We also plan to test the possibility of adopting a data-driven grid to optimize the need for details with the reliability and availability of the pieces of information.
NAC digital model is available in the publicly accessible repository zenodo.org at link https://zenodo.org/record/3666708#.XnM51i2ZM6g.
Both authors contributed to the conception and design of the study, manuscript writing, and approved the submitted version. AM collected the input dataset, and derived the final model, weighting the data and evaluating the reliability and uncertainty of the output with an original software, as well as produced the images.
This research was supported by the Direction for Civil Protection of the Regione Friuli Venezia Giulia and by the Regione Veneto of Italy.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We acknowledge G. Bressan and S. Parolai for the critical reading and constructive comments. We thank J. Bott and N. Piana Agostinetti for their accurate revision and constructive comments to our manuscript. All the figures were produced using the Generic Mapping Tool (GMT) version 5.4 (Wessel et al., 2013).
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.00089/full#supplementary-material
AlpArray Seismic Network (2014). “Eastern alpine seismic investigation (EASI) - alparray complimentary experiment,” in Proceedings of the AlpArray Working Group. Other/Seismic Network, (Vienna: EGU).
Amante, C., and Eakins, B. W. (2009). ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis. NOAA Technical Memorandum NESDIS NGDC-24. Silver Spring: NOAA.
Anderson, H., and Jackson, J. (1987). Active tectonics of the Adriatic region. Geophys. J. R. Astron. Soc. 91, 937–983. doi: 10.1111/j.1365-246X.1987.tb01675.x
Anselmi, M., Govoni, A., De Gori, P., and Chiarabba, C. (2011). Seismicity and velocity structures along the South-Alpine thrust front of the Venetian Alps (NE-Italy). Tectonophysics 513, 37–48. doi: 10.1016/j.tecto.2011.09.023
Argand, E. (1924). La tectonique de L’Asie. Paper presented at the 13th Congress Geologique International, Brussels.
Artemieva, I. M., and Thybo, H. (2013). EUNAseis: a seismic model for Moho and crustal structure in Europe, Greenland, and the North Atlantic region. Tectonophysics 609, 97–153. doi: 10.1016/j.tecto.2013.08.004
Bada, G., Cloetingh, S., Gerner, P., and Horváth, F. (1998). Sources of recent tectonic stress in the Pannonian region: inferences from finite element modelling. Geophys. J. Int. 134, 87–101. doi: 10.1046/j.1365-246x.1998.00545.x
Battaglia, M., Zuliani, D., Pascutti, D., Michelini, A., Marson, I., Murray, M. H., et al. (2003). Network assesses earthquake potential in Italy’s Southern Alps. Eos Trans. AGU 84, 262–264. doi: 10.1029/2003EO2800032003
Behm, M. (2006). Accuracy and Resolution of a 3D Seismic Model of the Eastern Alps. PhD thesis, Vienna University of Technology, Vienna.
Behm, M. (2009). 3-D modelling of the crustal S-wave velocity structure from active source data: application to the Eastern Alps and the Bohemian Massif. Geophys. J. Int. 179, 265–278. doi: 10.1111/j.1365-246X.2009.04259.x
Behm, M., Brückl, E., Chwatal, W., and Thybo, H. (2007). Application of stacking and inversion techniques to 3D wide-angle reflection and refraction seismic data of the Eastern Alps. Geophys. J. Int. 170, 275–298. doi: 10.1111/j.1365-246X.2007.03393.x
Behm, M., Nakata, N., and Bokelmann, G. (2016). Regional ambient noise tomography in the Eastern Alps of Europe. Pure Appl. Geophys. 173, 2813–2840. doi: 10.1007/s00024-016-1314-z
Bianchi, I., Behm, M., Rumpfhuber, E. M., and Bokelmann, G. (2015). A new seismic data set on the depth of the Moho in the Alps. Pure Appl. Geophys. 172, 295–308. doi: 10.1007/s00024-014-0953-1
Bleibinhaus, F., and Gebrande, H. (2006). Crustal structure of the Eastern Alps along the TRANSALP profile from wide-angle seismic tomography. Tectonophysics 414, 51–69. doi: 10.1016/j.tecto.2005.10.028
Bodin, T., Salmon, M., Kennett, B., and Sambridge, M. (2012). Probabilistic surface reconstruction from multiple data-sets - An example for the Australian Moho. J. Geophys. Res. Solid Earth 117:B0230. doi: 10.1029/2012JB009547
Bragato, P. L., Pesaresi, D., Saraò, A., Di Bartolomeo, P., and Durì, G. (2013). OGS improvements in the year 2011 in running the northeastern Italy seismic network. Adv. Geosci. 34, 5–8. doi: 10.5194/adgeo-34-5-2013
Braitenberg, C., Pettenati, F., and Zadro, M. (1997). Spectral and classical methods in the evaluation of Moho undulations from gravity data: the NE Italian Alps and isostasy. J. Geodyn. 23, 5–22. doi: 10.1016/S0264-3707(96)00024-5
Bressan, G., Barnaba, C., Bragato, P., Ponton, M., and Restivo, A. (2018a). Revised seismotectonic model of NE Italy and W Slovenia based on focal mechanism inversion. J. Seismol. 22, 1563–1578. doi: 10.1007/s10950-018-9785-2
Bressan, G., Barnaba, C., Magrin, A., and Rossi, G. (2018b). A study on off-fault aftershock pattern at N-Adria microplate. J. Seismol. 22, 863–881. doi: 10.1007/s10950-018-9737-x
Bressan, G., Gentile, G. F., Tondi, R., de Franco, R., and Urban, S. (2012). Sequential integrated inversion of tomographic images and gravity data: an application to the Friuli area (North-Eastern Italy). Boll. Geof. Teor. Appl. 53, 191–212. doi: 10.4430/bgta0059
Bressan, G., Ponton, M., Rossi, G., and Urban, S. (2012). Spatial organization of seismicity and fracture pattern in NE-Italy and W-Slovenia. J. Seismol. 20, 511–534. doi: 10.1007/s10950-015-9541-9
Brocher, T. M. (2005). Empirical relations between elastic wavespeeds and density in the Earth’s crust. Bull. Seismol. Soc. Am. 95, 2081–2092. doi: 10.1785/0120050077
Brückl, E. (2011). “Lithospheric structure and tectonics of the eastern alps – evidence from new seismic data,” in Tectonics, Intech, ed. D. Closson (London: IntechOpen Access), 39–64. doi: 10.5772/14364
Brückl, E., Behm, M., Decker, K., Grad, M., Guterch, A., Keller, G. R., et al. (2010). Crustal structure and active tectonics in the Eastern Alps. Tectonics 29. 1–17. doi: 10.1029/2009TC002491
Brückl, E., Bleibinhaus, F., Gosar, A., Grad, M., Guterch, A., Hrubcová, P., et al. (2007). Crustal structure due to collisional and escape tectonics in the Eastern Alps region based on profiles Alp01 and Alp02 from the ALP 2002 seismic experiment. J. Geophys. Res. Solid Earth 112:B06308. doi: 10.1029/2006JB004687
Burrato, P., Poli, M. E., Vannoli, P., Zanferrari, A., Basili, R., and Galadini, F. (2008). Sources of Mw 5+ earthquakes in northeastern Italy and western Slovenia: an updated view based on geological and seismological evidence. Tectonophysics 453, 157–176. doi: 10.1016/j.tecto.2007.07.009
Caporali, A., Aichhorn, C., Barlik, M., Becker, M., Fejes, I., Gerhatova, L., et al. (2009). Surface kinematics in the Alpine–Carpathian–Dinaric and Balkan region inferred from a new multi-network GPS combination solution. Tectonophysics 474, 295–321. doi: 10.1016/j.tecto.2009.04.035
Carbonell, R., Lavander, A., and Kind, R. (2013). The Mohorovičić discontinuity beneath the continental crust: an overview of seismic constraints. Tectonophysics 609, 353–376. doi: 10.1016/j.tecto.2013.08.037
Cassinis, R. (2006). Reviewing pre-TRANSALP DSS models. Tectonophysics 414, 79–86. doi: 10.1016/j.tecto.2005.10.026
Cassinis, R., Federici, F., Galmozzi, A., and Scarascia, S. (1997). A 3D gravity model of crustal structure in the Central-Eastern Alpine sector. Ann. Geophys. 40, 1095–1107. doi: 10.4401/ag-3846
Castellarin, A., Nicolich, R., Fantoni, R., Cantelli, L., Sella, M., and Selli, L. (2006). Structure of the lithosphere beneath the Eastern Alps (southern sector of the TRANSALP transect). Tectonophysics 414, 259–282. doi: 10.1016/j.tecto.2005.10.013
Channell, J. E. T., D’Argenio, B., and Horvath, F. (1979). Adria, the African promontory in Mesozoic Mediterranean paleogeography. Earth Sci. Rev. 15, 213–292. doi: 10.1016/0012-8252(79)90083-7
Chatterjee, R., and Mukhopadhyay, M. (2002). Effects of rock mechanical properties on local stress field of the Mahanadi basin, India—results from finite element modelling. Geophys. Res. Lett. 29, 28_1–28_4. doi: 10.1029/2001GL013447
Christensen, N. I., and Mooney, W. D. (1995). Seismic velocity structure and composition of the continental crust: a global view. J. Geophys. Res. 100, 9761–9788. doi: 10.1029/95JB00259
Cimolino, A., Della Vedova, B., Nicolich, R., Barison, E., and Brancatelli, G. (2010). New evidence of the outer Dinaric deformation front in the Grado area (NE-Italy). Rendiconti Lincei 21, 167–179. doi: 10.1007/s12210-010-0096-y
D’Agostino, N., Avallone, A., Cheloni, D., D’Anastasio, E., Mantenuto, S., and Selvaggi, G. (2008). Active tectonics of the Adriatic region from GPS and earthquake slip vectors. J. Geophys. Res. 113:B12413. doi: 10.1029/2008JB005860
D’Agostino, N., Cheloni, D., Mantenuto, S., Selvaggi, G., Michelini, A., and Zuliani, D. (2005). Strain accumulation in the southern Alps (NE Italy) and deformation at the northeastern boundary of Adria observed by CGPS measurements. Geophys. Res. Lett. 32:L19306. doi: 10.1029/2005GL024266
Dal Moro, G., Braitenberg, C., and Zadro, M. (1998). Geometry and mechanical crustal properties in NE Italy based on seismic and gravity data. Boll. Geof. Teor. Appl. 39, 37–46.
de Franco, R., Bressan, G., and Gentile, G. F. (2004). Elastic moduli and seismogenic aspects of the Friuli upper crust. Boll. Geof. Teor. Appl. 45, 71–87.
Di Stefano, R., Bianchi, I., Ciaccio, M. G., Carrara, G., and Kissling, E. (2011). Three-dimensional Moho topography in Italy: new constraints from receiver functions and controlled source seismology. Geochem. Geophys. Geosyst. 12:Q09006. doi: 10.1029/2011GC003649
Diaferia, G., Cammarano, F., Piana Agostinetti, N., Gao, C., Lekic, V., Molinari, I., et al. (2019). Inferring crustal temperatures beneath Italy from joint inversion of receiver functions and surface waves. J. Geophys. Res. Solid Earth 124, 8771–8785. doi: 10.1029/2019JB018340
Ebbing, J., Braitenberg, C., and Götze, H. J. (2001). Forward and inverse modelling of gravity revealing insight into crustal structures of the Eastern Alps. Tectonophysics 337, 191–208. doi: 10.1016/S0040-1951(01)00119-6
Ebbing, J., Braitenberg, C., and Götze, H.-J. (2006). The lithospheric density structure of the Eastern Alps. Tectonophysics 414, 145–155. doi: 10.1016/j.tecto.2005.10.015
Faccenda, M., Bressan, G., and Burlini, L. (2007). Seismic properties of the upper crust in the central Friuli area (northeastern Italy) based on petrophysical data. Tectonophysics 445, 210–226. doi: 10.1016/j.tecto.2007.08.004
Faccenna, C., Becker, T. W., Auer, L., Billi, A., Boschi, L., Brun, J.-P., et al. (2014). Mantle dynamics in the Mediterranean. Rev. Geophys. 52, 283–332. doi: 10.1002/2013RG000444
Fantoni, R., Della Vedova, B., Giustiniani, M., Nicolich, R., Barbieri, C., Del Ben, A., et al. (2003). Deep seismic profiles through the Venetian and Adriatic foreland (Northern Italy). Mem. Sci. Geol. 54, 131–134.
Finetti, I., and Del Ben, A. (2005). “Crustal tectono-stratigraphic setting of the Adriatic Sea from New CROP seismic data,” in CROP Project: Deep Seismic Exploration of the Central Mediterranean and Italy, Vol. 1, ed. I. R. Finetti (Amsterdam: Elsevier), 519–548.
Finetti, I. R. (ed.) (2005). CROP Project: Deep Seismic Exploration of the Central Mediterranean, and Italy, Vol. 1. Amsterdam: Elsevier.
Giustiniani, M., Accaino, F., Picotti, S., and Tinivella, U. (2008). Characterization of the shallow aquifers by high-resolution seismic data. Geophys. Prospect. 56, 655–666. doi: 10.1111/j.1365-2478.2008.00705.x
Gosar, A., and Lenart, A. (2010). Mapping the thickness of sediments in the Ljubljana Moor basin (Slovenia) using microtremors. Bull. Earthq. Eng. 8, 501–518. doi: 10.1007/s10518-009-9115-8
Gosar, A., Rošer, J., Motnikar, B. Š., and Zupančič, P. (2010). Microtremor study of site effects and soil-structure resonance in the city of Ljubljana (central Slovenia). Bull. Earthq. Eng. 8, 571–592. doi: 10.1007/s10518-009-9113-x
Grad, M., Brückl, E., Majdański, M., Behm, M., Guterch, A., and CELEBRATION 2000 and ALP 2002 Working Groups (2009a). Crustal structure of the Eastern Alps and their foreland: seismic model beneath the CEL10/Alp04 profile and tectonic implications. Geophys. J. Int. 177, 279–295. doi: 10.1111/j.1365-246X.2008.04074.x
Grad, M., Tiira, T., and ESC Working and Group (2009b). The Moho depth map of the European Plate. Geophys. J. Int. 176, 279–292. doi: 10.1111/j.1365-246X.2008.03919.x
Gräler, B., Pebesma, E., and Heuvelink, G. (2016). Spatio-Temporal Interpolation using gstat. R J. 8, 204–218.
Grenerczy, G., Sella, G., Stein, S., and Kenyeres, A. (2005). Tectonic implications of the GPS velocity field in the northern Adriatic region. Geophys. Res. Lett. 32:L16311. doi: 10.1029/2005GL022947
Guidarelli, M., Aoudia, A., and Costa, G. (2017). 3-D structure of the crust and uppermost mantle at the junction between the Southeastern Alps and External Dinarides from ambient noise tomography. Geophys. J. Int. 211, 1509–1523. doi: 10.1093/gji/ggx379
Handy, M. R., Ustaszewski, K., and Kissling, E. (2015). Reconstructing the Alps-Carpathians-Dinarides as a key to understand switches in subduction polarity, slab gaps and surface motion. Int. J. Earth Sci. 104, 1–26. doi: 10.1007/s00531-014-1060-3
Heidbach, O., Reinecker, J., Tingay, M., Müller, B., Sperner, B., Fuchs, K., et al. (2007). Plate boundary forces are not enough: second- and third-order stress patterns highlighted in the World Stress Map database. Tectonics 26:TC6014. doi: 10.1029/2007TC002133
Heit, B., Weber, M., Tilmann, F., Haberland, C., Jia, Y., and Pesaresi, D. (2017). The Swath-D seismic network in Italy and Austria. Telegrafenberg: GFZ Data Services.
Hengl, T. (2006). Finding the right pixel size. Comput. Geosci. 32, 1283–1298. doi: 10.1016/j.cageo.2005.11.008
Hetényi, G., Plomerová, J., Bianchi, I., Exnerová, H. K., Bokelmann, G., Handy, M., et al. (2018). From mountain summits to roots: crustal structure of the Eastern Alps and Bohemian Massif along longitude 13.3° E. Tectonophysics 744, 239–255. doi: 10.1016/j.tecto.2018.07.001
Ibarra, F., Liu, S., Meeßen, C., Prezzi, C. B., Bott, J., Scheck-Wenderoth, M., et al. (2019). 3D data-derived lithospheric structure of the Central Andes and its implications for deformations: insights from gravity and geodynamic modelling. Tectonophysics 766, 453–468. doi: 10.1016/j.tecto.2019.06.025
Kästle, E. D., El-Sharkawy, A., Boschi, L., Meier, T., Rosenberg, C., Bellahsen, N., et al. (2018). Surface wave tomography of the Alps using ambient-noise and earthquake phase velocity measurements. J. Geophys. Res. Solid Earth 123, 1770–1792. doi: 10.1002/2017JB014698
Kästle, E. D., Rosenberg, C., Boschi, L., Bellahsen, N., Meier, T., and El-Sharkawy, A. (2020). Slab break-offs in the Alpine subduction zone. Int. J. Earth Sci. 109, 587–603. doi: 10.1007/s00531-020-01821-z
Kelly, A., England, R. W., and Maguire, P. K. (2007). A crustal seismic velocity model for the UK, Ireland and surrounding seas. Geophys. J. Int. 171, 1172–1184. doi: 10.1111/j.1365-246X.2007.03569.x
Király, Á, Faccenna, C., and Funiciello, F. (2018). Subduction zones interaction around the Adria microplate and the origin of the Apenninic arc. Tectonics 37, 3941–3953. doi: 10.1029/2018TC005211
Kissling, E. (1993). Deep structure of the Alps–what do we really know? Phys. Earth Planet. Inter. 79, 87–112. doi: 10.1016/0031-9201(93)90144-X
Kissling, E., Schmid, S. M., Lippitsch, R., Ansorge, J., and Fügenschuh, B. (2006). “Lithosphere structure and tectonic evolution of the Alpine arc: new evidence from high- resolution teleseismic tomography,” in European Lithosphere Dynamics, 32, eds D. G. Gee and R. A. Stephenson (London: Geological Society Memoir), 29–145.
Kummerow, J., Kind, R., Oncken, O., Giese, P., Ryberg, T., Wylegalla, K., et al. (2004). A natural and controlled source seismic profile through the Eastern Alps: TRANSALP. Earth Planet. Sci. Lett. 225, 115–129. doi: 10.1016/j.epsl.2004.05.040
Lippitsch, R., Kissling, E., and Ansorge, J. (2003). Upper mantle structure beneath the Alpine orogen from high-resolution teleseismic tomography. J. Geophys. Res. Solid Earth 108, 2376. doi: 10.1029/2002JB002016 B8
Lombardi, D., Braunmiller, J., Kissling, E., and Giardini, D. (2008). Moho depth and Poisson’s ratio in the Western-Central Alps from receiver functions. Geophys. J. Int. 173, 249–264. doi: 10.1111/j.1365-246X.2007.03706.x
Ludwig, W. J., Nafe, J. E., and Drake, C. L. (1970). “Seismic refraction,” in The Sea, ed. A. E. Maxwell (New York, NY: Wiley-Interscience), 53–84.
Lüschen, E., Borrini, D., Gebrande, H., Lammerer, B., Millahn, K., Neubauer, F., et al. (2006). TRANSALP—deep crustal Vibroseis and explosive seismic profiling in the Eastern Alps. Tectonophysics 414, 9–38. doi: 10.1016/j.tecto.2005.10.014
Lüschen, E., Lammerer, B., Gebrande, H., Millahn, K., Nicolich, R., and Transalp Working Group (2004). Orogenic structure of the Eastern Alps, Europe, from TRANSALP deep seismic reflection profiling. Tectonophysics 388, 85–102. doi: 10.1016/j.tecto.2004.07.024
Marotta, A. M., and Splendore, R. (2014). 3D mechanical structure of the lithosphere below the Alps and the role of gravitational body forces in the regional present-day stress field. Tectonophysics 631, 117–129. doi: 10.1016/j.tecto.2014.04.038
Matheron, G. (1965). Les variables régionalisées et leur estimation. J. Soc. Stat. Paris 107, 263–275.
Matheron, G. (1969). Le Krigeage Universel. Cahiers du Centre de Morphologie Mathématique, 1. Fontainebleau: Ecole des Mines.
McKenzie, D. P. (1972). Active tectonics of the Mediterranean region. Geophys. J. R. Astron. Soc. 30, 109–185. doi: 10.1111/j.1365-246x.1972.tb02351.x
Métois, M., D’Agostino, N., Avallone, A., Chamot-Rooke, N., Rabaute, A., Duni, L., et al. (2015). Insights on continental collisional processes from GPS data: dynamics of the peri-adriatic belts. J. Geophys. Res. Solid Earth 120, 8701–8719. doi: 10.1002/2015JB012023
Miller, M. S., and Piana-Agostinetti, N. (2012). Insights into the evolution of the Italian lithospheric structure from S receiver function analysis. Earth Planet. Sci. Lett. 345, 49–59. doi: 10.1016/j.epsl.2012.06.02
Mitterbauer, U., Behm, M., Brückl, E., Lippitsch, R., Guterch, A., Keller, G. R., et al. (2011). Shape and origin of the East-Alpine slab constrained by the ALPASS teleseismic model. Tectonophysics 510, 195–206. doi: 10.1016/j.tecto.2011.07.001
Molinari, I., and Morelli, A. (2011). EPcrust: a reference crustal model for the European Plate. Geophys. J. Int. 185, 352–364. doi: 10.1111/j.1365-246X.2011.04940.x
Molinari, I., Argnani, A., Morelli, A., and Basini, P. (2015a). Development and testing of a 3D seismic velocity model of the Po Plain sedimentary basin, Italy. Bull. Seismol. Soc. Am. 105, 753–764. doi: 10.1785/0120140204
Molinari, I., Morelli, A., Raileanu, V., and Tataru, D. (2010). The crustal structure of South-Eastern Europe in the new European Plate reference model. Geophys. Res. Abstr. 12:8366.
Molinari, I., Raileanu, V., and Morelli, A. (2012). A crustal model for the Eastern Alps region and a new Moho map in southeastern Europe. Pure Appl. Geophys. 169, 1575–1588. doi: 10.1007/s00024-011-0431-y
Molinari, I., Verbeke, J., Boschi, L., Kissling, E., and Morelli, A. (2015b). Italian and Alpine three-dimensional crustal structure imaged by ambient-noise surface-wave dispersion. Geochem. Geophys. Geosyst. 16, 4405–4421. doi: 10.1002/2015GC006176
Möller, G., Brückl, E., and Weber, R. (2011). Active tectonic deformation at the transition from the European and Pannonian domain monitored by a local GNSS network. Vermessung Geoinform. 2, 138–148.
Mooney, W. D. (2010). “Crust and lithospheric structure–global crustal structure,” in Treatise on Geophysics, Vol. 1, eds B. Romanowicz, A. Dziewonski, and G. Schubert (Amsterdam: Elsevier), 361–417. doi: 10.1016/b978-044452748-6.00011-0
Nemes, F., Neubauer, F., Cloetingh, S., and Genser, J. (1997). The Klagenfurt Basin in the Eastern Alps: an intra-orogenic decoupled flexural basin? Tectonophysics 282, 189–203. doi: 10.1016/S0040-1951(97)00219-9
Nicolich, R., Della Vedova, B., Giustiniani, M., and Fantoni, R. (2004). Carta del Sottosuolo della pianura friulana. 4 tavole e Note Illustrative. Firenze FI: LAC-Firenze.
Olea, R. A. (1999). Geostatistics for Engineers and Earth Scientists. Cham: Springer Science & Business Media.
Oliver, M. A., and Webster, R. (2014). A tutorial guide to geostatistics: computing and modelling variograms and kriging. Catena 113, 56–69. doi: 10.1016/j.catena.2013.09.006
Orešković, J., Šumanovac, F., and Hegedûs, E. (2011). Crustal structure beneath Istra peninsula based on receiver function analysis. Geofizika 28, 247–263.
Pebesma, E. J. (2004). Multivariable geostatistics in S: the gstat package. Comput. Geosci. 30, 683–691. doi: 10.1016/j.cageo.2004.03.012
Piana Agostinetti, N., and Amato, A. (2009). Moho depth and VP/VS ratio in peninsular Italy from teleseismic receiver functions. J. Geophys. Res. Solid Earth 114:B06303. doi: 10.1029/2008JB005899
PROJ contributors (2018). PROJ Coordinate Transformation Software Library. London: Open Source Geospatial Foundation.
Ranalli, G. (1992). Average lithospheric stresses induced by thickness changes: a linear approximation. Phys. Earth Planet. Inter. 69, 263–269. doi: 10.1016/0031-9201(92)90145-L
Reiter, F., Freudenthaler, C., Hausmann, H., Ortner, H., Lenhardt, W., and Brandner, R. (2018). Active seismotectonic deformation in front of the Dolomites indenter, Eastern Alps. Tectonics 37, 4625–4654. doi: 10.1029/2017TC004867
Richardson, R. M. (1992). Ridge forces, absolute plate motions, and the intraplate stress field. J. Geophys. Res. 97, 11739–11748. doi: 10.1029/91JB00475
Root, B. C., Wal, W., Novák, P., Ebbing, J., and Vermeersen, L. L. A. (2015). Glacial isostatic adjustment in the static gravity field of Fennoscandia. J. Geophys. Res. Solid Earth 120, 503–518. doi: 10.1002/2014JB011508
Rossi, G., Ebblin, C., and Zadro, M. (2005). 3D finite-elements kinematic model of the Adria northern region: stress analysis. Boll. Geof. Teor. Appl. 46, 23–46.
Rossi, G., Zuliani, D., and Fabris, P. (2016). Long-term GNSS measurements through Northern Adria microplate reveal fault-induced fluid mobilization. Tectonophysics 690, 142–159. doi: 10.1016/j.tecto.2016.04.031
Sambridge, M., Bodin, T., Gallagher, K., and Tkalčić, H. (2013). Transdimensional inference in the geosciences. Phil. Trans. R. Soc. A. 371:20110547. doi: 10.1098/rsta.2011.0547
Santulin, M., Rebez, A., Riuscetti, M., Carulli, G. B., Grimaz, S., Cucchi, F., et al. (2018). The legacy of the 1976 Friuli earthquake. Boll. Geof. Teor. Appl. 59, 543–558. doi: 10.4430/bgta0228
Scarascia, S., and Cassinis, R. (1997). Crustal structures in the central-eastern Alpine sector: a revision of the available DSS data. Tectonophysics 271, 157–188. doi: 10.1016/S0040-1951(96)00206-5
Schmid, S. M., Fügenschuh, B., Kissling, E., and Schuster, R. (2004). Tectonic map and overall architecture of the Alpine orogen. Eclogae Geol. Helv. 97, 93–117. doi: 10.1007/s00015-004-1113-x
Serpelloni, E., Anzidei, M., Baldi, P., Casula, G., and Galvani, A. (2005). Crustal velocity and strain-rate fields in Italy and surrounding regions: new results from the analysis of permanent and non-permanent GPS networks. Geophys. J. Int. 161, 861–880. doi: 10.1111/j.1365-246X.2005.02618.x
Serpelloni, E., Vannucci, G., Anderlini, L., and Bennett, R. A. (2016). Kinematics, seismotectonics and seismic potential of the eastern sector of the European Alps from GPS and seismic deformation data. Tectonophysics 688, 157–181. doi: 10.1016/j.tecto.2016.09.026
Slejko, D. (2018). What science remains of the 1976 Friuli earthquake? Boll. Geof. Teor. Appl. 59, 327–350. doi: 10.4430/bgta0224
Smith, W. H. F., and Wessel, P. (1990). Gridding with continuous curvature splines in tension. Geophysics 55, 293–305. doi: 10.1190/1.1442837
Spada, M., Bianchi, I., Kissling, E., Piana Agostinetti, N., and Wiemer, S. (2013). Combining controlled-source seismology and receiver function information to derive 3-D Moho topography for Italy. Geophys. J. Int. 194, 1050–1068. doi: 10.1093/gji/ggt148
Spooner, C., Scheck-Wenderoth, M., Götze, H. J., Ebbing, J., and Hetényi, G. (2019). Density distribution across the Alpine lithosphere constrained by 3-D gravity modelling and relation to seismicity and deformation. Solid Earth 10, 2073–2088. doi: 10.5194/se-10-2073-2019
Stehly, L., Fry, B., Campillo, M., Shapiro, N. M., Guilbert, J., Boschi, L., et al. (2009). Tomography of the Alpine region from observations of seismic ambient noise. Geophys. J. Int. 178, 338–350. doi: 10.1111/j.1365-246X.2009.04132.x
Stipčević, J., Tkalčić, H., Herak, M., Markušić, S., and Herak, D. (2011). Crustal and uppermost mantle structure beneath the External Dinarides, Croatia, determined from teleseismic receiver functions. Geophys. J. Int. 185, 1103–1119. doi: 10.1111/j.1365-246X.2011.05004.x
Šumanovac, F. (2010). Lithosphere structure at the contact of the Adriatic microplate and the Pannonian segment based on the gravity modelling. Tectonophysics 485, 94–106. doi: 10.1016/j.tecto.2009.12.005
Šumanovac, F., Hegedűs, E., Orešković, J., Kolar, S., Kovács, A. C., Dudjak, D., et al. (2016). Passive seismic experiment and receiver functions analysis to determine crustal structure at the contact of the northern Dinarides and southwestern Pannonian Basin. Geophys. J. Int. 205, 1420–1436. doi: 10.1093/gji/ggw101
Šumanovac, F., Orešković, J., Grad, M., and ALP 2002 Working Group (2009). Crustal structure at the contact of the Dinarides and Pannonian basin based on 2-D seismic and gravity interpretation of the Alp07 profile in the ALP 2002 experiment. Geophys. J. Int. 179, 615–633. doi: 10.1111/j.1365-246X.2009.04288.x
Tesauro, M., Kaban, M. K., and Cloetingh, S. A. (2008). EuCRUST-07: a new reference model for the European crust. Geophys. Res. Lett. 35:L05313. doi: 10.1029/2007GL032244
Tondi, R., Vuan, A., Borghi, A., and Argnani, A. (2019). Integrated crustal model beneath the Po Plain (Northern Italy) from surface wave tomography and Bouguer gravity data. Tectonophysics 750, 262–279. doi: 10.1016/j.tecto.2018.10.018
TRANSALP Working Group (2002). First deep seismic reflection images of the Eastern Alps reveal giant crustal wedges and transcrustal ramps. Geophys. Res. Lett. 29, 92.1–92.4. doi: 10.1029/2002GL014911
ViDEPI (2015). Available online at: https://www.videpi.com/videpi/videpi.asp (accessed November 30, 2017).
Viganò, A., Scafidi, D., Martin, S., and Spallarossa, D. (2013). Structure and properties of the Adriatic crust in the central-eastern Southern Alps (Italy) from local earthquake tomography. Terra Nova 25, 504–512. doi: 10.1111/ter.12067
Viganò, A., Scafidi, D., Ranalli, G., Martin, S., Della Vedova, B., and Spallarossa, D. (2015). Earthquake relocations, crustal rheology, and active deformation in the central–eastern Alps (N Italy). Tectonophysics 661, 81–98. doi: 10.1016/j.tecto.2015.08.017
Völksen, C., Sokolov, A., Arenz, H., and Seitz, F. (2018). Present-day surface deformation of the Alpine region inferred from geodetic techniques. Earth Syst. Sci. Data 10, 1503–1526. doi: 10.5194/essd-10-1503-2018
Vuan, A., Klin, P., Laurenzano, G., and Priolo, E. (2011). Far-source long-period displacement response spectra in the Po and Venetian Plains (Italy) from 3D wavefield simulations. Bull. Seismol. Soc. Am. 101, 1055–1072. doi: 10.1785/0120090371
Waldhauser, F., Kissling, E., Ansorge, J., and Mueller, S. (1998). Three dimensional interface modelling with two-dimensional seismic data: the Alpine crust-mantle boundary. Geophys. J. Int. 135, 264–278. doi: 10.1046/j.1365-246X.1998.00647.x
Wessel, P., and Smith, W. H. F. (1991). Free software helps map and display data. Eos Trans. AGU 72, 445–446. doi: 10.1029/90EO00319
Wessel, P., and Smith, W. H. F. (1998). New, improved version of Generic Mapping Tools released. Eos Trans. AGU 79:579. doi: 10.1029/98EO00426
Wessel, P., Smith, W. H. F., Scharroo, R., Luis, J. F., and Wobbe, F. (2013). Generic mapping tools: improved version released. Eos Trans. AGU 94, 409–410. doi: 10.1002/2013EO450001
Zhu, H., and Tromp, J. (2013). Mapping tectonic deformation in the crust and upper mantle beneath Europe and the North Atlantic Ocean. Science 341, 871–875. doi: 10.1126/science.1241335
Keywords: crustal model, Northern Adria microplate, Moho geometry, geophysical properties, uncertainty analysis
Citation: Magrin A and Rossi G (2020) Deriving a New Crustal Model of Northern Adria: The Northern Adria Crust (NAC) Model. Front. Earth Sci. 8:89. doi: 10.3389/feart.2020.00089
Received: 28 October 2019; Accepted: 16 March 2020;
Published: 24 April 2020.
Edited by:
Pier Paolo Bruno, University of Naples Federico II, ItalyReviewed by:
Judith Bott, Helmholtz Centre Potsdam, GermanyCopyright © 2020 Magrin and Rossi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Andrea Magrin, YW1hZ3JpbkBpbm9ncy5pdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.