Mechanical Mechanism of Fault Dislocation Based on in situ Stress State

Fault dislocation occurs under certain stress conditions. Based on the mechanical relationship between the direction of crustal stress and fault occurrence, three criteria – fault dislocation trend, fault strike dislocation trend, and dip dislocation trend – are put forward. According to these three criteria, the fault slip and the type of slip can be inferred. The parameters that have great influence on the characteristics of fault slip are fault dip angle, angle between horizontal principal stress and fault strike, depth, lateral pressure coefficient, internal friction angle, and cohesion of fault plane. Fault slip is more likely to occur in the environment of high deviation stress, low friction angle, and dip angle of about 40°. Fault rupture is a point-to-surface and deep-to-shallow process. When the criterion value of the local position of the fault is greater than 0, it will lead to the slip of the nearby fault. When the slip range of the fault extends to the surface, it will cause large earthquakes with large-scale surface rupture. The theoretical calculation is basically consistent with the numerical simulation results. According to the theory in this paper, the slip instability state of Longmen Mountain Fault Zone under different stress conditions is calculated, and the results show that when the lateral pressure coefficient is greater than 2.5, dislocation occurs in the deep part of the fault.

Introduction

How did the earthquake happen? What are the physical mechanisms of fault dislocation and fracture conduction and energy release? This is one of the pressing problems in seismology (Shearer, 2009; Lu et al., 2014). People have gone through a long process of understanding earthquakes; when earthquakes occur, they are often accompanied by fault slip or other phenomena. After the San Francisco earthquake in 1906, Lawson thought that the earthquake was caused by the sudden dislocation of the fault (Lawson and Reid, 1908). The theory of elastic rebound is put forward because of the fault dislocation under the action of in-situ stress (Reid, 1910; Liu, 2014). The coupling source theory is a hypothesis of source mechanics, which provides a theoretical basis for determining the initial fault dislocation position (Nakano, 1923). The theory of plate tectonics can explain that earthquakes are caused by the dislocation of plate margin faults (Le Pichon et al., 1973). Seismic models based on fault activity have been proposed successively, such as the finite moving source model, the source model of double couple equivalent to fault dislocation (Haskell, 1964), the crack propagation model (Starr, 1928; Burridge and Knopoff, 1964), and the obstacle and convex body models (Das and Aki, 1977; Wyss et al., 1981), which describe the fault rupture process. Based on the butterfly plastic zone theory, Ma Nianjie et al. proposed a conjugate fault-seismic composite model, which partly explained the cause of earthquake (Ma et al., 2019a, b; Qiao et al., 2019).

A critical state of stress is a necessary condition for earthquake occurrence, such as the change of additional normal stress and shear stress caused by tidal action on fault plane (Li and Chen, 2018; Moncayo et al., 2019), which may lead to earthquake; the change of static Coulomb rupture stress caused by earthquake can affect the seismicity nearby (King et al., 1994; Stein, 1999; Wan et al., 2002). Coulomb stress explains the mechanical mechanism of fault dislocation to some extent, but it only pays attention to the stress increment part, ignoring the stress environment of the fault itself (Zhu and Miao, 2016). Under the continuous action of plate movement, faults will inevitably dislocate (Shi and Ma, 2018). In the Wenchuan earthquake, fault rupture propagation occurred (Chen and Li, 2018; Li et al., 2019). Experiments have suggested that earthquakes may be caused by dislocation due to overcoming fault friction under certain stress conditions (Zheng et al., 2019). According to the state of in situ stress and the occurrence of fault, the critical value of fault dislocation and the criterion value of fault dislocation type are calculated. By using the criterion of fault dislocation, whether fault dislocation occurs and the type of fault dislocation can be directly determined, and these criteria are applied to the judgment of fault dislocation of Longmenshan fault zone.

Mechanical Analysis of Fault Dislocation

We consider a planar fault surface (Figure 1). We adopt a coordinate system, and the direction of the maximum horizontal principal stress, the direction of the minimum horizontal principal stress, and the direction of the vertical stress represent the x axis, the y axis, and the z axis, respectively. The relationship between fault plane and in situ stress is shown in Figure 1.

FIGURE 1

Figure 1. Corresponding relationship between fault occurrence and principal stress direction. OA is the direction of maximum principal stress, OB is the direction of minimum principal stress, OC is the direction of vertical stress, of is the direction of resultant stress of OA and OB and OC acting on surface ABC, OO′ is the direction of normal resultant stress of three-dimensional stress acting on fault surface, O′F is the direction of tangential resultant stress of three-dimensional stress acting on fault surface, and O″F′ is the projection direction of O′F on the horizontal plane. The angle between the strike and horizontal principal stress direction of the fault slope is φ and the dip angle is θ; the maximum and minimum horizontal principal stress and vertical stress are σ_H, σ_h, and σ_v, respectively, and plane ABC is the unit plane on the fault plane.

Let the basic equation of the fault plane be:

$$\text{a}x+by+cz+d=0(1)$$

When the dip of the fault plane is θ, it is the angle between the fault plane and the horizontal plane.

The horizontal equation passing through the origin is: z = 0.

Then,

$$\cos \mathrm{\theta }=\frac{c}{\sqrt{a^2+b^2+c^2}}(2)$$

Set the strike of fault plane to ϕ, when z = 0. That is to say, the equation of the line AB on the plane is:

$$y=-\tan \mathrm{\varphi }\cdot x(3)$$

By calculating formulas (2) and (3), then formula (4):

$$\{\begin{array}{c}a=\tan \mathrm{\varphi }\hfill \\ b=1\hfill \\ c=\frac{1}{\cos \mathrm{\varphi }\cdot \tan \mathrm{\theta }}\hfill \end{array}(4)$$

The plane equation of the fault plane can be obtained as follows:

$$\tan \mathrm{\varphi }\cdot x+y+\frac{1}{\cos \mathrm{\varphi }\cdot \tan \mathrm{\theta }}\cdot z+\text{d}=0(5)$$

$$\sqrt{a^2+b^2+c^2}=\frac{1}{\sin \mathrm{\theta }\cdot \cos \mathrm{\varphi }}$$

The unit vector of line OO′ is:

$${\overrightarrow{e}}_{{\mathrm{OO}}^{\prime }}=\left[(\sin \mathrm{\theta }\cdot \sin \mathrm{\varphi })\cdot i+\sin \mathrm{\theta }\cdot \cos \mathrm{\varphi }\cdot j+\frac{1}{\cos \mathrm{\theta }}\cdot k\right](6)$$

As can be seen from Figure 1, the normal vector of surface OBC is:

$$x=0(7)$$

The normal vector of the surface OAC is:

$$y=0(8)$$

The normal vector of the plane OAB is:

$$z=0(9)$$

The angles between plane ABC and plane OBC, OAC, and OAB are a, β, and γ, respectively. According to formula (5):

$$\cos \mathrm{\alpha }=\frac{a}{\sqrt{a^2+b^2+c^2}}=\tan \mathrm{\varphi }\cdot \sin \mathrm{\theta }\cdot \cos \mathrm{\varphi }$$

$$=\sin \mathrm{\theta }\cdot \sin \mathrm{\varphi }(10)$$

$$\cos \mathrm{\beta }=\frac{b}{\sqrt{a^2+b^2+c^2}}=\sin \mathrm{\theta }\cdot \cos \mathrm{\varphi }(11)$$

$$\cos \mathrm{\gamma }=\frac{\text{c}}{\sqrt{a^2+b^2+c^2}}=\frac{\sin \mathrm{\theta }\cdot \cos \mathrm{\varphi }}{\cos \mathrm{\varphi }\cdot \tan \mathrm{\theta }}=\cos \mathrm{\theta }(12)$$

$\overrightarrow{\text{OA}}=i(13)$

$\overrightarrow{\text{OB}}=j(14)$

$\overrightarrow{\text{OC}}=k(15)$

The stress of three principal stresses acting on plane ABC is as follows:

$${\mathrm{\sigma }}_x={\mathrm{\sigma }}_{\text{H}}\cdot \cos \mathrm{\alpha }\cdot \overrightarrow{\text{OA}}={\mathrm{\sigma }}_{\text{H}}\cdot \sin \mathrm{\varphi }\cdot \sin \mathrm{\theta }\cdot i(16)$$

$${\mathrm{\sigma }}_y={\mathrm{\sigma }}_h\cdot \cos \mathrm{\beta }\cdot \overrightarrow{\text{OB}}={\mathrm{\sigma }}_h\cdot \cos \mathrm{\varphi }\cdot \sin \mathrm{\theta }\cdot j(17)$$

$${\mathrm{\sigma }}_z={\mathrm{\sigma }}_{\text{v}}\cdot \cos \mathrm{\gamma }\cdot \overrightarrow{OC}={\mathrm{\sigma }}_{\text{v}}\cdot \cos \mathrm{\theta }\cdot k(18)$$

The resultant stress is:

$${\mathrm{\sigma }}_{\text{OF}}={\mathrm{\sigma }}_{\text{H}}\cdot \sin \mathrm{\varphi }\cdot \sin \mathrm{\theta }\cdot i+{\mathrm{\sigma }}_h\cdot \cos \mathrm{\varphi }\cdot \sin \mathrm{\theta }\cdot j+{\mathrm{\sigma }}_{\text{v}}\cdot \cos \mathrm{\theta }\cdot k(19)$$

OF indicates the direction of the resultant stress, and the magnitude of the resultant stress is:

$$\left|{\mathrm{\sigma }}_{\text{OF}}\right|=\sqrt{{({\mathrm{\sigma }}_{\text{H}}\sin \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+{({\mathrm{\sigma }}_h\cos \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+{({\mathrm{\sigma }}_{\text{v}}\cos \mathrm{\theta })}^2}(20)$$

Then, the angle between σ_OF and the normal vector of surface ABC is:

$$\mathrm{\phi }=\arccos \frac{\stackrel{{\mathrm{\sigma }}_{\text{H}}\sin \mathrm{\varphi }\cdot \sin \mathrm{\theta }\cdot \tan \mathrm{\varphi }+{\mathrm{\sigma }}_h\cos \mathrm{\varphi }\cdot }{\sin \mathrm{\theta }+{\mathrm{\sigma }}_{\text{v}}\cos \mathrm{\theta }{\displaystyle \frac{1}{\cos \mathrm{\varphi }\cdot \tan \mathrm{\theta }}}}}{\sqrt{{\displaystyle \frac{1}{\cos \mathrm{\varphi }\cdot \sin \mathrm{\theta }}}}\sqrt{\stackrel{{({\mathrm{\sigma }}_H\sin \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+({\mathrm{\sigma }}_h\cos \mathrm{\varphi }\cdot }{\sin \mathrm{\theta }){}^2+({\mathrm{\sigma }}_{\text{v}}\cos \mathrm{\theta }){}^2}}}(21)$$

As shown in Figure 1, σ_OO′ and σ_O′F represent the normal stress component and tangential stress component of σ_OF in plane ABC, respectively:

$$\left|{\mathrm{\sigma }}_{{\mathrm{OO}}^{\prime }}\right|=\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi }(22)$$

$${\mathrm{\sigma }}_{{\mathrm{OO}}^{\prime }}=\left|{\mathrm{\sigma }}_{{\mathrm{OO}}^{\prime }}\right|\cdot {\overrightarrow{e}}_{{\mathrm{OO}}^{\prime }}$$

$$=\frac{\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi }}{\sin \mathrm{\varphi }\cdot \cos \mathrm{\theta }}[(\sin \mathrm{\varphi }\cdot \cos \mathrm{\theta }\cdot \tan \mathrm{\varphi })\cdot i$$

$$+\sin \mathrm{\varphi }\cdot \cos \mathrm{\theta }\cdot j+\frac{\sin \mathrm{\varphi }\cdot \cos \mathrm{\theta }}{\cos \mathrm{\varphi }\cdot \tan \mathrm{\theta }}\cdot k]$$

$$=\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi }\left(\tan \mathrm{\varphi }\cdot i+1\cdot j+\frac{1}{\cos \mathrm{\varphi }\cdot \tan \mathrm{\theta }}\cdot k\right)(23)$$

Because

$${\mathrm{\sigma }}_{\text{OF}}={\mathrm{\sigma }}_{{\mathrm{OO}}^{\prime }}+{\mathrm{\sigma }}_{{\mathrm{O}}^{\prime }\mathrm{F}}(24)$$

Then, σ_O′F can be obtained.

$${\mathrm{\sigma }}_{{\mathrm{O}}^{\prime }\mathrm{F}}={\mathrm{\sigma }}_{\text{OF}}-{\mathrm{\sigma }}_{{\mathrm{OO}}^{\prime }}$$

$$=({\mathrm{\sigma }}_{\text{H}}\cdot \sin \mathrm{\varphi }\cdot \sin \mathrm{\theta }-\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi }\cdot \tan \mathrm{\varphi })\cdot i$$

$$+({\mathrm{\sigma }}_h\cdot \cos \mathrm{\varphi }\cdot \sin \mathrm{\theta }-\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi })\cdot j$$

$$+\left({\mathrm{\sigma }}_{\text{v}}\cdot \cos \mathrm{\theta }-\frac{\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi }}{\cos \mathrm{\varphi }\cdot \tan \mathrm{\theta }}\right)\cdot k(25)$$

Simplifying Eq. 25:

$$l={\mathrm{\sigma }}_{\text{H}}\cdot \sin \mathrm{\varphi }\cdot \sin \mathrm{\theta }-\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi }\cdot \tan \mathrm{\varphi }(26)$$

$$m={\mathrm{\sigma }}_h\cdot \cos \mathrm{\varphi }\cdot \sin \mathrm{\theta }-\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi }(27)$$

$$n={\mathrm{\sigma }}_{\text{v}}\cdot \cos \mathrm{\theta }-\frac{\left|{\mathrm{\sigma }}_{\text{OF}}\right|\cdot \sin \mathrm{\phi }}{\cos \mathrm{\varphi }\cdot \tan \mathrm{\theta }}(28)$$

$${\mathrm{\sigma }}_{{\mathrm{O}}^{\prime }\mathrm{F}}=l\cdot i+m\cdot j+n\cdot k(29)$$

Whether a fault slips depends on the friction angle and cohesion of the fault plane, and the normal stress value of ABC on the fault plane is |σ_O′O|.

The tangential stress value σ_s is |σ_O′F|. The following relationships can be obtained:

$$f_1={\mathrm{\sigma }}_s-{\mathrm{\sigma }}_{\text{n}}\cdot \tan \mathrm{\phi }-C(30)$$

$$\left|{\mathrm{\sigma }}_{\text{OF}}\right|=\sqrt{{({\mathrm{\sigma }}_{\text{H}}\sin \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+{({\mathrm{\sigma }}_h\cos \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+{({\mathrm{\sigma }}_{\text{v}}\cos \mathrm{\theta })}^2}(31)$$

$\left|{\mathrm{\sigma }}_{{\mathrm{O}}^{\prime }\mathrm{O}}\right|=\sin \mathrm{\phi }\cdot \sqrt{{({\mathrm{\sigma }}_{\text{H}}\sin \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+{({\mathrm{\sigma }}_h\cos \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+{({\mathrm{\sigma }}_{\text{v}}\cos \mathrm{\theta })}^2}(32)$

$\left|{\mathrm{\sigma }}_{{\mathrm{O}}^{\prime }\mathrm{F}}\right|=\text{cos}\mathrm{\phi }\cdot \sqrt{{({\mathrm{\sigma }}_{\text{H}}\sin \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+{({\mathrm{\sigma }}_h\cos \mathrm{\varphi }\cdot \sin \mathrm{\theta })}^2+{({\mathrm{\sigma }}_{\text{v}}\cos \mathrm{\theta })}^2}(33)$

In formula (30), C is the cohesion of fault plane. When f₁ > 0, the fault slips, and when f₁ < 0, the fault does not slip, so f₁ can be used as the criterion of strike slip.

In Eq. 29, n is the vertical component of σ_O′F, and the n value is related to the fault dislocation in the vertical direction; when n > 0, the fault has a downward slip trend. When n = 0, the fault has no vertical slip trend. When n < 0, the fault has an upward slip trend. n can be used as a criterion for normal and reverse fault slip.

In order to judge the fault movement trend in horizontal direction, calculate the combined stress of σ_O^′F in the horizontal plane:

$${\mathrm{\sigma }}_{{\mathrm{O}}^{″}{\mathrm{F}}^{\prime }}=(l\cdot i+m\cdot j)(34)$$

In order to obtain the relationship between direction and fault strike, rotating σ_O″F′ counterclockwise at φ, ${\mathrm{\sigma }}_{{\mathrm{O}}^{″}\mathrm{F}}^{\prime }$.

$${\mathrm{\sigma }}_{{\mathrm{O}}^{″}{\mathrm{F}}^{\prime }}^{\prime }=\left[(l\cdot \text{cos}\mathrm{\varphi }+\text{m}\cdot \sin \mathrm{\varphi })\cdot i-(l\cdot \sin \mathrm{\varphi }-\text{m}\cdot c\text{os}\mathrm{\varphi })\cdot j\right](35)$$

At this time, the vector i is consistent with the fault strike.

$$f_2=l\cdot \text{cos}\mathrm{\varphi }+\text{m}\cdot \text{sin}\mathrm{\varphi }(36)$$

When f₂ > 0, fault sinistral slip. When f₂ = 0, the fault has no strike slip trend. When f₂ < 0, fault dextral dislocation. Therefore, f₂ can be used as the criterion of strike slip.

Then, when f₁ ≤ 0, the fault is relatively stable, and when f₁ > 0, the fault is dislocation. The dislocation trend between faults can be judged by n value and f₂ value:

(1) When n > 0, f₂ > 0, the faults tend to move downward and leftward, that is, normal faults and leftward faults.

(2) When n > 0, f₂ = 0, there is a downward dislocation trend on the wall of the fault plane, i.e., normal fault-type dislocation.

(3) When n > 0, f₂ < 0, there is a downward and leftward dislocation trend on the wall of the fault plane, that is, normal fault and dextral dislocation.

(4) When n = 0, f₂ > 0, there is a right-lateral dislocation on the wall of the fault plane, i.e., left-lateral dislocation.

(5) When n = 0, f₂ = 0, there is no dislocation trend on the wall of the fault plane.

(6) When n = 0, f₂ < 0, there is a trend of left-lateral dislocation on the wall of the fault plane, that is, right-lateral dislocation.

(7) When n < 0, f₂ > 0, the faults tend to move upward and right, i.e., reverse faults and sinistral faults.

(8) When n < 0, f₂ = 0, the fault has upward dislocation trend, i.e., reverse fault type dislocation.

(9) When n < 0, f₂ < 0, the faults tend to move upward and left, i.e., reverse faults and right-handed faults.

Influencing Factors of Fault Dislocation

There are many parameters affecting fault dislocation. As shown in Figure 2, fault dip angle, principal stress, fault strike angle, and depth are fixed parameters in a certain period of plate movement, while cohesion of fault plane has relatively little influence on fault plane slip. The influence of lateral pressure coefficient and internal friction angle is relatively large, and these two parameters are variable parameters, such as plate movement, long-range earthquake, tidal induction, and so on, which will cause minor changes in local geostress. For faults in critical state, such as f₁ value approaching 0, minor changes in geostress may prompt instantaneous slip of faults and cause earthquakes. Mining and mining activities cause a large amount of water to enter the fault, and the friction coefficient of the fault surface decreases, which leads to earthquakes.

FIGURE 2

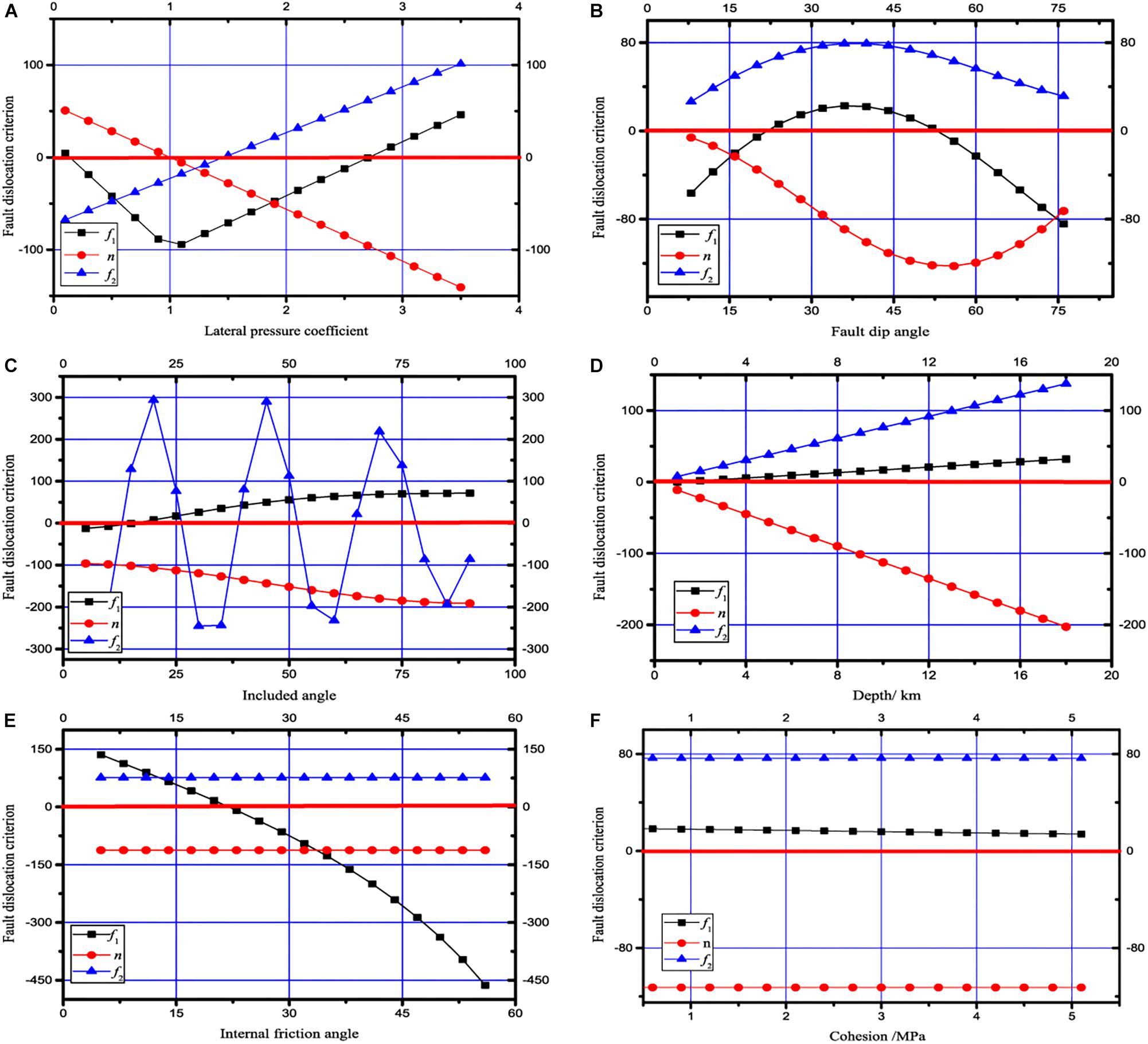
Figure 2. Numeric diagram of fault slip criterion under different parameters. Given a set of data, the dip angle of the fault is θ = 45°, the angle between the direction of principal stress σ₁ and the strike of the fault is φ = 25° degrees, the depth H = 10 km, the lateral pressure coefficient is λ = 3, the friction angle in the fault plane is φ = 20°, the cohesion force is 2 MPa, σ₃ = γH, and σ₂ = 0.5 (1 + λ) σ₃. (A) Fault dislocation criterion under different lateral pressure coefficients, (B) fault dislocation criterion under different fault dip angles, (C) fault dislocation criterion under different included angles, (D) fault dislocation criterion under different depth, (E) fault dislocation criterion under different internal friction angles, (F) fault dislocation criterion under different cohesions.

As shown in Figure 2A, when the lateral pressure coefficient is 0.1, f₁ > 0, n > 0, and f₂ < 0, indicating that normal fault and right-lateral slip can occur at this time, when the lateral pressure coefficient is 0.1; when the lateral pressure coefficient is between 0.1 and 2.8, f₁ < 0, indicating that the fault does not slip; when the lateral pressure coefficient is greater than 2.8, f₁ > 0, n < 0, and f₂ > 0, indicating that the fault can produce both normal fault and left-lateral slip, thus indicating a high deviational stress environment. Faults are more prone to slip.

As shown in Figure 2B, when the dip angle of the fault is less than 24° or more than 56°, f₁ < 0 indicates that the fault does not slip; when the dip angle of the fault is between 24° and 56°, f₁ > 0, n < 0, and f₂ > 0, indicating that the fault can produce reverse fault and dextral dislocation, which indicates that the fault is more likely to slip at the dip angle of 40°.

As shown in Figure 2C, when the angle between the maximum horizontal principal stress and the fault is greater than 15°, f₁ > 0 and the fault plane slips, of which n < 0, indicating thrusting slip of the fault, while f₂ > 0 when the angle between the maximum horizontal principal stress and the fault is 15°–26°, 38°–52°, and 64°–78°, indicating right slip of hanging wall, i.e., thrusting and left-lateral slip, when the angle is 26°–38°, 52°–64°, and 78°–90°, f₂ < 0, indicating the fault. The hanging wall slips to the left, i.e., thrust and dextral slip.

As shown in Figure 2D, when the depth is greater than 1 km, f₂ > 0, n < 0, and f₂ > 0, indicating that thrusting and sinistral slip occur in faults, but the effect of depth on f₁ value is relatively small, which indicates the dispersion of focal depth.

As shown in Figure 2E, when the friction angle of the fault plane is less than 23°, f₁ > 0, n < 0, and f₂ > 0, indicating that thrust and sinistral slip occur on the fault. When the friction angle of the fault plane is greater than 23°, f₁ < 0, indicating that no slip occurs on the fault. It shows that the friction angle of the fault plane has a great influence on the slip of the fault.

As shown in Figure 2F, cohesion between fault planes is relatively small. When cohesion varies from 0 to 5.1 MPa, the variation range of f₁, n, and f₂ is relatively small, which indicates that the value has little influence on fault slip. Therefore, for deep faults, the effect of cohesion on fault plane can be neglected (Goodman, 1989).

According to f₁, n, and f₂, we can infer whether the fault is dislocated and its type. The parameters that have great influence on the characteristics of fault slip are fault dip angle, angle between horizontal principal stress and fault strike, depth, lateral pressure coefficient, internal friction angle, and cohesion of fault plane. Faults with dislocation generally have the following characteristics: firstly, in high deviational stress environment, if the lateral pressure coefficient is less than 0.1 or more than 2.8, but there is no fault dislocation in the area where the lateral pressure coefficient approaches 1; secondly, the fault is more prone to slip at the dip angle of 40°; thirdly, the fault surface with low friction angle is more prone to slip.

Discussion

(1) Five groups of simulation schemes are designed. The occurrence and mechanical parameters of faults and the state of regional principal stress are shown in Table 1. The values of fault slip criteria f₁, n, and f₂ can be obtained by substituting the parameters into formulas (1)–(36) in turn. According to the theoretical calculation results, the faults in schemes 1 and 2 have not yet produced slip, while those in schemes 3–5 have slip, and n < 0 and f₂ > 0. It can be judged that thrusting sinistral slip occurs in faults. The simulation results are basically consistent with the theoretical calculation criteria, as shown in Figure 3, and the slip trend of schemes 3–5 is consistent with the theoretical calculation results. As shown in Figure 4, the upper wall of the fault produces upward and right displacement, indicating that the fault has thrusting left-lateral dislocation (Liu and Song, 1999; Huang et al., 2017).

TABLE 1

Table 1. Summary of simulation schemes and calculation results.

FIGURE 3

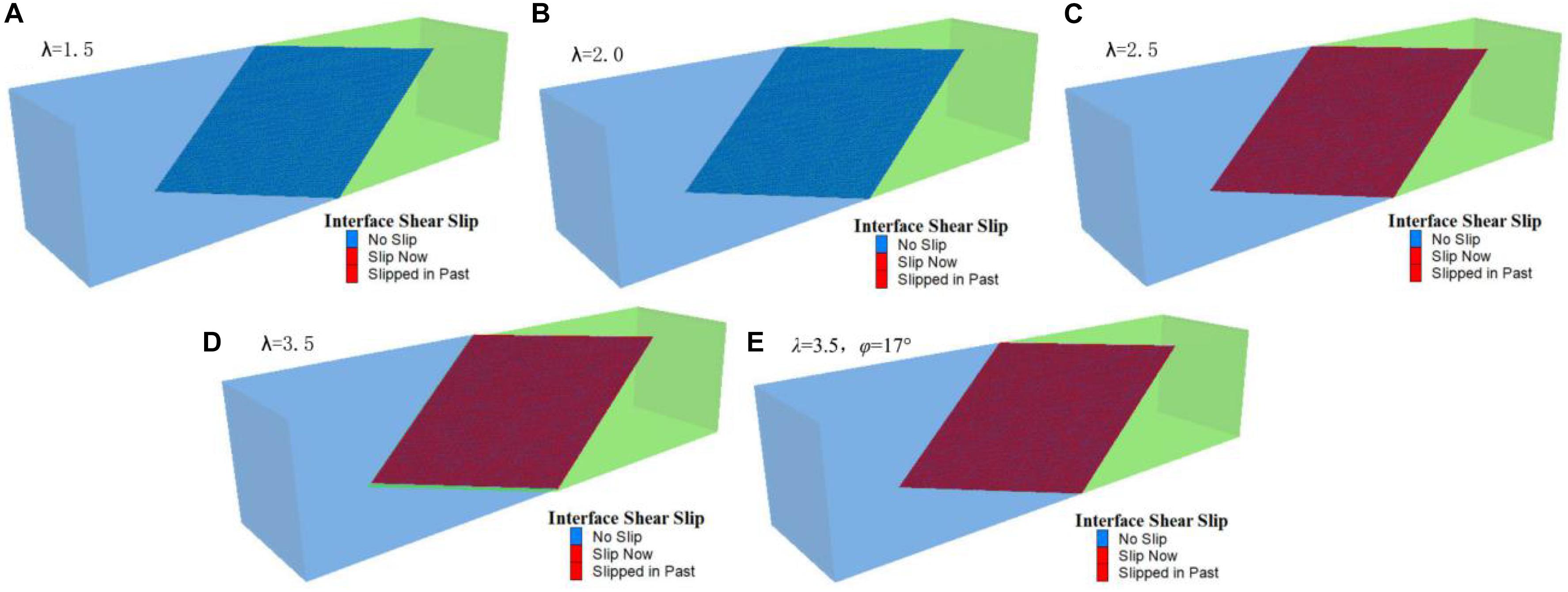
Figure 3. Fault slip simulation under different schemes. The simulation scheme is listed in Table 1, and (A) shows that the fault of simulation scheme 1 has no dislocation, (B) shows that the fault of simulation scheme 2 has no dislocation, (C) shows that the fault of simulation scheme 3 has no dislocation, (D) shows that the fault of simulation scheme 4 has dislocation, (E) shows that the fault of simulation scheme 5 has dislocation.

FIGURE 4

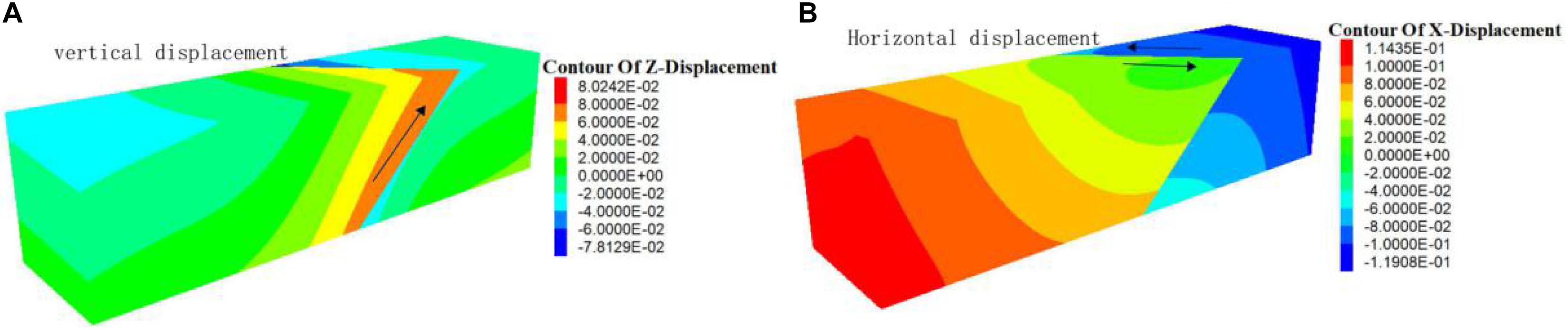
Figure 4. Thrust left-handed slip diagram of scheme 3. (A) Shows the upward slip of the hanging wall of the fault in scheme 3, (B) shows that the hanging wall of scheme 3 fault slides to the right.

(2) Taking Longmenshan fault zone as an example, the vertical stress is calculated by γH, and γ is 27 KN/m³. The in situ stress data are shown in Table 2 (Chen et al., 2012; Qin et al., 2018); the lateral pressure coefficient is 1.0–5.0, the angle between maximum horizontal principal stress and fault strike is about 80°, the cohesion of Longmenshan fault zone is 2MPa, the internal friction angle is 20°, and the Longmenshan fault zone is a typical shovel thrust fault. The relationship between dip and depth is shown in Figure 5. The slip of faults under different lateral pressure coefficients can be calculated, as shown in Figure 6, when the lateral pressure coefficient is less than 2; no slip occurs on the fault plane. When the lateral pressure coefficient is greater than 2.5, slip occurs at the depth of 12 km. With the increase of the lateral pressure coefficient, the range of slip increases, but the shallow part of the fault is still locked. At this time, the values of n and f₂ are less than 0, which indicates that when the lateral pressure coefficient is greater than 2.5, the fault will undergo thrusting and dextral slip or earthquake. Therefore, when a small stress variable is applied to a fault in the critical state, the lateral pressure coefficient will change, and the fracture range of the fault will expand accordingly. It is possible for an earthquake to be triggered by a small stress change (Shi et al., 2019). The triggering stress includes dynamic and static (Ma, 2010). For example, plate movement and other tectonic processes can cause slow and stable changes in tectonic stress. Solid tidal force, reservoir water level change, celestial tidal force, and strong earthquake stress wave can cause dynamic stress changes (Huang and Ma, 2008).

TABLE 2

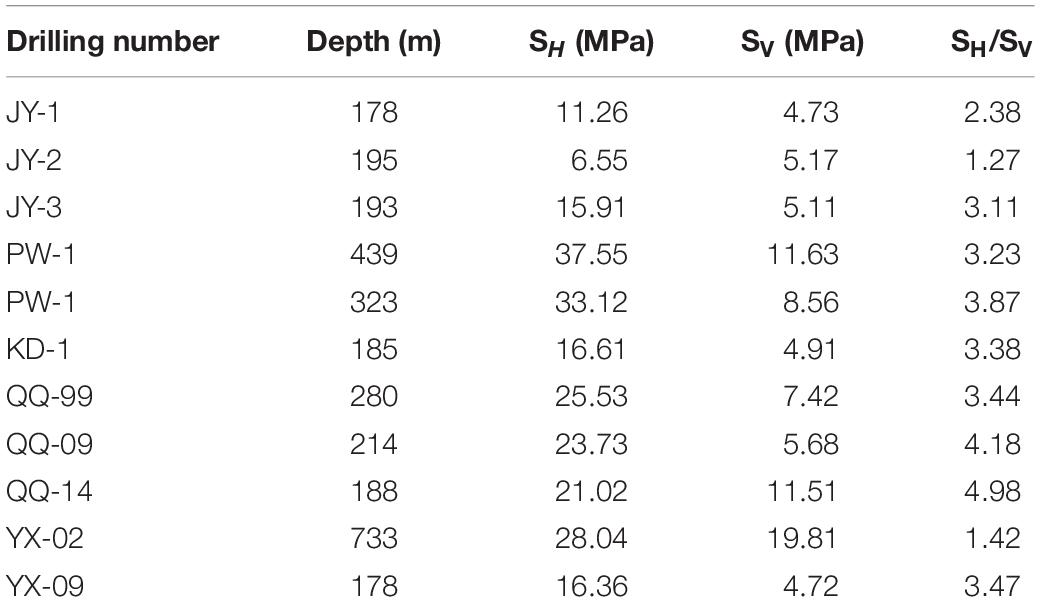
Table 2. Stress measurement values of the Longmen mountain fault zone QQ (Chen et al., 2012; Qin et al., 2018).

FIGURE 5

Figure 5. Diagram of occurrence of Longmenshan fault.

FIGURE 6

Figure 6. f₁ value of Longmenshan fault zone under different side pressure coefficients.

(3) Fault rupture is a process from point to surface, from deep to shallow. When the slip criterion f₂ of a deep point of fault is greater than 0, the point will dislocate, which will lead to the increase or decrease of tangential stress around the point, and then the fault near the point will slip. When the fault slip range is small, it can cause small earthquakes. When the fault slip range extends to the surface, it can cause large earthquakes with large-scale surface rupture (Hu and Wang, 2008; Wang et al., 2012). When a fault dislocation occurs, it will inevitably lead to volume expansion, stress reduction, and energy release of local rock mass near the fault. The strain energy released may become the energy source of the earthquake. For example, the rupture process of Wenchuan earthquake is initiated by the NW-trending Xiaoyudong fault, which triggered the Beichuan-Yingxiu fault and the Pengguan fault, and resulted in the cascade rupture of the Beichuan-Yingxiu fault in NE direction (Qian and Han, 2010).

Conclusion

Fault dislocation occurs under a certain mechanical mechanism. According to the relationship between in situ stress and fault occurrence, three criteria are put forward in this paper, i.e., fault tendency dislocation trend criterion n, strike dislocation trend criterion f₁, and fault occurrence dislocation criterion f₁. According to these criteria, the stability of fault can be evaluated directly. If f₁ approaches zero, the fault has the risk of dislocation. Fault dislocation is usually a process from deep to shallow, which is characteristic of the fault rupture process of Wenchuan earthquake. Using the mechanical model in this paper, we can calculate the dislocation criteria of different depths of major faults and evaluate the stability of faults. For unstable faults, we should further monitor the changes of in situ stress. However, our work in this measurement can be as a reference for enhancing the stress/strain monitoring network in both precision and density of observation station.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

HS responsible for the writing of the manuscript. FH provides the writing ideas of the paper and gives guidance in the writing process. ZM assists in completing the graphic processing work. YW provided geological data and JF participated in the derivation of the formula. XG assists in data sorting.

Funding

The authors are grateful to the financial support provided by the Foundation of Basic Research of Central University (3142018022) and the National Natural Science Foundation of China (41274061 and 51804118).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Thanks to the editor GM for his article organization, reviewers BZ and AP for their pertinent suggestions, and Professor Nianjie Ma of China University of Mining and Technology (Beijing) for his help in the writing process.

References

Burridge, R., and Knopoff, L. (1964). Body force equivalents for seismic dislocations. Bull. Seism. Soc. Am. 54, 1875–1888.

Google Scholar

Chen, Q. C., Feng, C. J., Meng, W., Qing, X. H., and An, Q. M. (2012). Analysis of in situ stress measurements at the northeastern section of the longmenshanfault zone after the 5.12 Wenchuan earthquake. Chinese J. Geophys. 55, 3923–3932.

Google Scholar

Chen, Q. F., and Li, L. (2018). Deep deformation of the longmenshan fault zone related to the Wenchuan earthquake. Chin. Sci. Bull. 63, 1917–1933. doi: 10.1360/n972018-00362

CrossRef Full Text | Google Scholar

Das, S., and Aki, K. (1977). Fault plane with barriers: a versatile earthquake model. J. Geophys. Res. 82, 5658–5670. doi: 10.1029/jb082i036p05658

CrossRef Full Text | Google Scholar

Goodman, R. E. (1989). Introduction to Rock Mechanics, 2nd Edn, New York, NY: Wiley.

Google Scholar

Haskell, N. A. (1964). Total energy and energy spectral density of elastic wave radiation from propagating faults. Bul.l Seism. Soc. Am. 54, 1811–1841.

Google Scholar

Hu, Y., and Wang, K. (2008). Coseismic strengthening of the shallow portion of the subduction fault and its effects on wedge taper. J. Geophys. Res. 113: B12411.

Google Scholar

Huang, F. Q., Li, M., Ma, Y. C., Han, Y. Y., Tian, L., Yan, W. (2017). Studies on earthquake precursorsin China: a review for recent 50 years. Geod. Geodyn. 8, 1–12. doi: 10.1016/j.geog.2016.12.002

CrossRef Full Text | Google Scholar

Huang, Y. M., and Ma, S. L. (2008). Discussion on mechanism of earthquake triggering by stress. Earthquake 28, 95–102.

Google Scholar

King, G. C. P., Stein, R. S., and Lin, J. (1994). Static stress ch anges and th e triggering of earth quakes. Bull. Seism. Soc. Am. 84, 935–953.

Google Scholar

Lawson, A. C., and Reid, H. F. (1908). The California Earthquake of April 18, 1906: Report of the State Earthquake Investigation Commission. Washington, DC: Carnegie institution of Washington.

Google Scholar

Le Pichon, X., Francheteau, J., and Bonnin, J. (1973). Plate Tectonics. Developments in Geotectonics. Amsterdam: Elsevier.

Google Scholar

Li, Y. E., and Chen, X. Z. (2018). Earth tidal stress as an earthquake trigger prior to the Wenchuan earthquake, Sichuan, China (in Chinese). Chin. Sci. Bull. 63, 1962–1970. doi: 10.1360/n972018-00259

CrossRef Full Text | Google Scholar

Li, C. Y., Li, X. N., and Wei, Z. Y. (2019). Fault geometries and structures associated with the rupture endpoints of the 2008 Mw 7.9 wenchuan earthquake eastern tibet plateau China. Tectonics 38, 2161–2184. doi: 10.1029/2018tc005425

CrossRef Full Text | Google Scholar

Liu, J., and Song, H. Z. (1999). Estimation of earthquake risk for northern North China by numerical modeling. Seismol. Geol. 21, 221–228.

Google Scholar

Liu, L. Q. (2014). Elastic rebound model: from the classic to the future. Seismol. Geol. 36, 825–832.

Google Scholar

Lu, K. Q., Cao, Z. X., Hou, M. Y., Jiang, Z. H., Shen, R., Wang, Q., et al. (2014). On the mechanism of earthquake. Acta Phys. Sin. 63:219101.

Google Scholar

Ma, J. (2010). Uncertainty of the earthquakes and earthquake mechanism and seismic triggering effect of instantaneous factors. Chin. J. Nat. 32, 311–313.

Google Scholar

Ma, J., Zhao, Z. Q., Shi, H. Y., Guo, X. F., Qiao, J. Y., Ma, N. J. (2019a). Sources of seismic energy based on butterfly failure theory. J. China Coal Soc. 44, 1654–1665.

Google Scholar

Ma, N. J., Ma, J., Zhao, Z. Q., Guo, X. F., Shi, H. Y., Qiao, J. Y. (2019b). Mechanical mechanism and evolution of X-shaped conjugate shear fracturesseism. J. China Coal Soc. 44, 1647–1653.

Google Scholar

Moncayo, G. A., Monsalve, G., and Zuluaga, J. I. (2019). Tidal coulomb failure stresses in the northern andean intermediate depth seismic clusters: implications for a possible correlation between tides and seismicity. Tectonophysics 762, 61–68.

Google Scholar

Nakano, H. (1923). Note on the nature of forces which give rise to the earthquake motions. Seismol. Bull. Centr. Meteorol. Obs. Tokyo 1, 92–120.

Google Scholar

Qian, Q., and Han, Z. J. (2010). Determinationoftheinitialruptureofthe2008 Wenchuan MS8.0 earthquake form analysis of faultinteraction during the main shock process. Earth Sci. Front. 17, 84–92.

Google Scholar

Qiao, J. Y., Ma, N. J., Ma, J., Zhao, Z. Q., Guo, X. F., Shi, H. Y. (2019). Conjugate shear fracture-seismic composite model based on structural stability of dynamic system. J. China Coal Soc. 44, 1637–1646.

Google Scholar

Qin, X. H., Chen, Q. C., Meng, W., Tan, C. X., Zhang, C. Y., Feng, C. J. (2018). Evaluatingmeasured insitu stress state changes associated with earthquakes and its implications: a case study in the longmenshan fault zone. J. Geomech. 24, 309–320.

Google Scholar

Reid, H. F. (1910). Mechanics of the earthquake the California Earthquake of April 18 1906. Report of the State Investigation Commission. Washington, DC: Carnegie Institution of Washington.

Google Scholar

Shearer, P. M. (2009). Introduction to Seismology, 2nd Edn, New York: Cambridge University Press.

Google Scholar

Shi, H. Y., and Ma, N. J. (2018). Geomorphic formation and crustal stress evolution mechanism in the Longmenshan fault zone and its adjacent regions. Acta Seismol. Sin. 40, 332–340.

Google Scholar

Shi, H. Y., Ma, N. J., Shi, J. J., Li, N., and Ma, J. (2019). Simulation on energy release of fault rock mass triggered by stress incrementand discussion on seismogenesis: taking longmenshan fault zone as an example. Acta Seismol. Sin. 41, 502–511.

Google Scholar

Starr, A. T. (1928). Slip in a crystal and rupture in a solid due to shear. Proc. Amb. Philso. Soc. 24, 489–500. doi: 10.1017/s0305004100014626

CrossRef Full Text | Google Scholar

Stein, R. S. (1999). The role of stress transfer in earthquake occurrence. Nature 402, 605–609. doi: 10.1038/45144

CrossRef Full Text | Google Scholar

Wan, Y. G., Wu, Z. L., Zhou, G. W., Huang, J., and Qin, L. X. (2002). Research on seismic stress triggering. Acta Seismol. Sin. 24, 533–551.

Google Scholar

Wang, K., Hu, Y., and He, J. (2012). Deformation cycles of subduction earthquakes in a viscoelastic Earth. Nature 484, 327–332. doi: 10.1038/nature11032

PubMed Abstract | CrossRef Full Text | Google Scholar

Wyss, M., Johnston, A. C., and Klein, F. W. (1981). Multiple asperity model for earthquake prediction. Nature 289, 231–234. doi: 10.1038/289231a0

CrossRef Full Text | Google Scholar

Zheng, L., Rivière, J., Yang, Q., Marpm, J., and Marone, C. (2019). On the mechanics of granular shear: the effect of normal stress and layerthickness on stick-slip properties. Tectonophysics 763, 86–99. doi: 10.1016/j.tecto.2019.04.010

CrossRef Full Text | Google Scholar

Zhu, S. B., and Miao, M. (2016). On the study of earthquake triggering: solution to paradox that Coulomb stresses increase with frictional coefficients. Chin. J. Geophys. 59, 169–173.

Google Scholar