Numerical Investigation of Heat Transfer and Phase Change Characteristics of Cold Load and Storage Functional CPB in Deep Mine

As high mine-cooling costs have become a restriction for deep mining, a new cooling method has been proposed. In the area of filling mining, the CPB (cemented paste backfill) was given the cooling function by mixing it with phase change material (PCM). In deep mines, the PCM (e.g., ice particles) absorb heat and change phases to cool the surrounding environment. A deep-mine-cooling mode based on the new CPB and upward sublevel filling method was designed, and the characteristics of the phase change were analyzed by numerical simulation. From the simulation results of the cooling period, this cooling method was effective during the whole stopes mining period. The CLS (cold load and storage) CPB mass concentration and the PCM initial proportion are the important factors controlling the cooling effect. It is concluded that the phase change duration decreased with the increasing mass concentration, while it increased with the increasing initial proportion of ice to water. Note that the thickness of CLS-functional CPB should be as small as possible to ensure the cold release rate. This study provides a theoretical foundation of heat transfer for the design and implementation of deep mine cooling by applying CLS-functional CPB.

HIGHLIGHTS

- The phase change of CLS functional CPB in deep mines was investigated numerically.

- The heat conduction model compound with hydration-porous-enthalpy model was applied.

- The phase change and heat transfer law of CLS functional CPB was investigated.

- The main influencing factors were analyzed and suggestions for engineering were presented.

Introduction

The high geothermal environment in deep mines is one of the constraints in mining and is as important as high ground pressure and high seepage pressure (Guo et al., 2017; Yang et al., 2017; Zhang et al., 2018; Lin et al., 2019a). At present, more than 150 1000 m-plus deep mines exist in the world (Xie, 2017). According to the statistics, the average geothermal gradient is 2.5∼4.0°C/100 m, even up to 7°C/100 m (Guo, 2010; Cui et al., 2018). At high geothermal temperatures, many threats stand out, such as soft rock mass, shortened equipment service life, increased accident rate and decreased labor efficiencies (Feng et al., 2017; Belle and Biffi, 2018; Wang Y. et al., 2019). These heat hazards became the obstacles for deep mining and thus cooling techniques and effects have significant meaning for deep mining (Cai and Brown, 2017; Ryan and Euler, 2017; Pretorius et al., 2019).

Many cooling techniques were applied for solving the high geothermal environment problem (Plessis et al., 2015; Feng et al., 2018; Crawford et al., 2019). These cooling techniques were basically classified into three types: ventilation, natural cooling, and manual refrigeration. Mine ventilation was used for dust control, fire, and explosion prevention and air cooling. The integrated factors limit the range of air velocity (Brune, 2019). Therefore, the cooling potential of ventilation was constrained, and it was not suitable for deep mines with high geothermal conditions (Ghoreishi-Madiseh et al., 2017). Natural cooling resources mainly referred to cold mine water (Chen et al., 2018) and seasonal stored ice (Shi et al., 2011; Bu et al., 2015). The application of natural cooling resources has good performance on energy conservation. However, it is overly reliant on environmental conditions and thus is not universal (He and Xu, 2008; He and Guo, 2013). To date, for deep mines, few natural cooling resources can be used. Manual refrigeration was the most widely used method (Van der Walt and De Kock, 1984; Wilson, 2008; du Plessis et al., 2013). However, the power consumption of mining cooling systems was up to 25% of the total mining power consumption (Plessis et al., 2015), and the cooling cost of manual refrigeration increased with the depth of the mine (Trapania et al., 2016). Considering the mining cooling cost, the upper mining depth limit is located at approximately 3000 m. The evolution of deep mine cooling requires breakthroughs in the cooling methods that differ from ordinary cooling methods and combine with the mining characteristics.

To solve the balance of the cooling effect and cost of deep mines, the concept of applying phase change materials (PCMs) and mixing it with cemented paste backfill (CPB) slurry was proposed. The mixture was named CLS (cold load and storage)-functional CPB and is suitable for cooling deep mines that practice filling mining (Wang et al., 2018). In filling mining, the backfill slurry was surveyed to gob and then the backfill was formed. The volume of the backfill was hundreds of thousands of cubic meters. Using the large CLS-functional CPB could be sufficient for cooling stopes; however, the phase change and heat transfer characteristics of the new CPB are unknown, which is the critical issue for the implementation of this technology. Relevant researches provided valuable references for this paper. The interfacial tracing method had been applied on calculating the freezing and thawing problem of rock (Shen et al., 2016) which solve the heat transfer of melting process of rock. The strength of the rock and CPB were studied by many researchers (Zhao et al., 2016; Lin et al., 2019b, c; Wu et al., 2019; Liu et al., 2020), especially, the case of CPB with ice slag (Liu et al., 2019b). From the experimental researches, the CPB with ice slag was strengthened under proper ratio which proved the feasibility from the aspect of strength. As for the rheological aspect, models were built for calculating the hydraulic pressure drop (Zhao et al., 2018, 2019). Liu studied the rheological characteristics of CPB with ice particles based on experiment and numerical calculation and the model of hydraulic characteristics of ICPB was obtained (Liu et al., 2019a).

Our previous work researched the heat transfer characteristics of the mixture of CPB slurry and PCMs in a cubic test box of 15 cm in length by numerical simulation and experimental research (Wang M. et al., 2019). An enthalpy-porosity-hydration model was verified by experiments for simulating the heat transfer of the new CPB. This is meaningful for mastering the calculation of this new mixture material. The literature (Wang et al., 2018) proposed the concept of CLS-functional CPB and indicated that it could provide cold regulation in deep mines but did not involve the calculation of the heat transfer of the cooling process. Heat transfer calculation research of this new CPB material was carried out, but it was launched in a small test box in the laboratory. Based on these two works, the deep mining environment was considered, and the CLS-functional CPB was simulated to determine the cooling process and effect of the new CPB in this study.

System Design and Cooling Process

The CLS-functional CPB cooling process relates to the mining method. In the filling mining method, a sublevel filling method is the usual approach and thus was taken as an example for simulation. Figure 1 shows the working period of CLS-functional CPB, which applies in an upward sublevel filling method. When a stope layer is mined completely, it changes to a gob layer and is filled with CPB slurry. In the filling process, the ordinary CPB slurry is filled first, and then the CLS-functional CPB is filled. The two-step filling method is better than only filling with CLS-functional CPB for two reasons. First, the heat transfer is strengthened as proved by the simulation research owing to the smaller heat transfer resistance. Second, it is flexible in supplying different cooling capacities by adjusting the ratio of CLS-functional CPB to ordinary CPB. When the two kinds of CPB slurry are filled, the stope is cooled by the cold radiation of its ground. For cold preservation, an insulating layer was considered to be set between the two kinds of CPB. With the mining progress of the stope, the cold release lasted until one layer was mined completely and changed to a new gob.

FIGURE 1

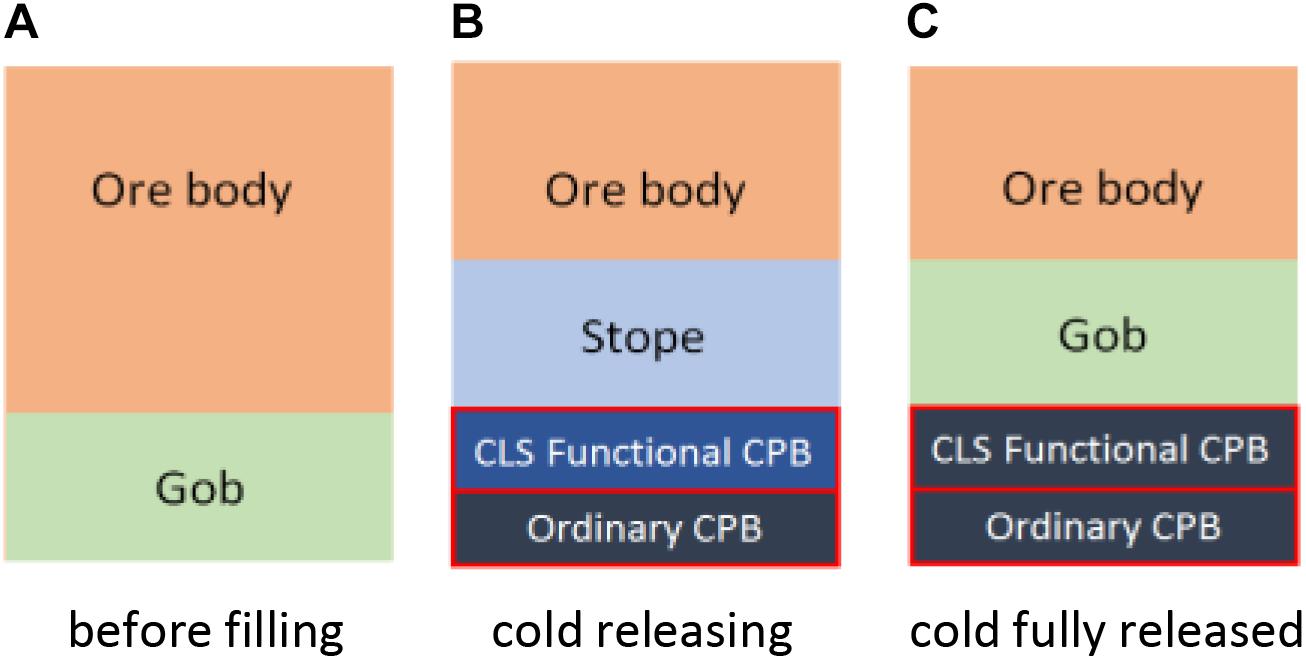
Figure 1. The working period of CLS backfill applied in upward sublevel filling method. (A) Before filling. (B) Cold releasing. (C) Cold fully released.

The thermal environment of CLS-functional CPB is shown in Figure 2. There are two kinds of cold sources and four kinds for heat sources: Q_l, PCM fusion latent cold of the CLS-functional CPB; Q_s, sensible cold of the CLS-functional CPB; Q_cond, and Q_rad, heat transferred from the ore body to CLS-functional CPB by heat conduction and radiation; Q_conv, heat transferred from the stope to CLS-functional CPB by heat convection; and Q_hyd, hydration heat produced in the CLS-functional CPB. The total thermal equilibrium equation was given as follows:

FIGURE 2

Figure 2. The total thermal equilibrium diagram of CLS functional CPB cooling.

$$Q_l+Q_s=Q_{cond}+Q_{conv}+Q_{rad}+Q_{hyd}(1)$$

As CLS-functional CPB absorbs heat from the environment, the PCM changed phase, and the temperature of the CLS-functional CPB gradually rose to match its surroundings. The heat transfer characteristics of the cooling period are critical for the stope cooling effect. Therefore, we focused on the heat transfer and phase change of CLS-functional CPB in deep mines and applied an enthalpy-porosity-hydration heat transfer model for research. Furthermore, the strength and the grouting transport characteristics should be studied (Emad et al., 2018; Qi et al., 2018) to support this research and engineering design in subsequent studies.

Physical Model

Geometry and Boundary Conditions

The CLS-functional CPB absorbs heat from the environment as Figure 2 shows. The geometry size of this 2D model of CLS-functional CPB is 20 m × 3 m. In this case, we took the half of the CLS-functional CPB as the research object because of its symmetry. The geometry model is indicated in Figure 3, and the region ABCD is the computational domain.

FIGURE 3

Figure 3. Physical model of CLS functional CPB. (A) Geometry model, (B) Boundary conditions.

The heat transfer on the boundary of CPB relates to the cooling effect and is analyzed herein. Interface AB absorbs heat from the ordinary CPB below by heat conductance. Owing to the insulating layer, the temperature influence region of upper CLS-functional CPB to lower CPB is from AB with a small thickness of δ_B downward. The equivalent thermal conductivity of this region is λ_B. The boundary temperature of this influenced region is T_B. Interface BC absorbs heat from the surrounding rock on the right side by heat conductance. The temperature influence region of CPB to rock is from BC, with a rightward thickness of δ_S. The equivalent thermal conductivity of this region is λ_S, and the boundary temperature of the influenced region is T_S. Interface CD absorbs heat from the stope above through radiation and heat convection. The temperature of air in the stope is T_G, the heat convection coefficient between the air and interface CD is h_G, and the emissivity of interface CD is ε_G. Interface DA is a symmetric interface and is treated as adiabatic. From the analysis above, the four boundary conditions are described as follows:

AB: $-{\mathrm{\lambda }}_{eff}\frac{dT}{dz}={\mathrm{\lambda }}_B\frac{T_B-T_{\text{A}B}}{{\mathrm{\delta }}_B}$

BC: ${\mathrm{\lambda }}_{eff}\frac{dT}{dx}={\mathrm{\lambda }}_S\frac{T_S-T_{BC}}{{\mathrm{\delta }}_S}$

CD: ${\mathrm{\lambda }}_{eff}\frac{dT}{dz}=h_G(T_{air}-T_{CD})+{\mathrm{\epsilon }}_G\mathrm{\sigma }(T_{air}^4-T_{CD}^4)$

AD: $\frac{dT}{dx}=0$

Governing Equations

In the computational domain, the temperature distribution variation is mainly caused by three reasons: phase change, heat conduction, and hydration reaction. For simulation, some secondary factors were neglected and the assumptions below were proposed:

1. There is no natural convection occurring in the backfill because the mass concentration of the backfill is high.

2. The seepage of the backfill is neglected.

3. The thermal physical properties of materials are isotropic.

4. The cooling regions of nearby rock and the CPB below are constant.

For the above analysis, the main governing equation is a 2-D, unsteady state heat conduction equation as follows:

$${\mathrm{\lambda }}_{eff}(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial z^2})+\frac{\partial Q_{hyd}}{\partial \mathrm{\tau }}=[\mathrm{\varphi }(\mathrm{\alpha }{\mathrm{\rho }}_l{H}_l+(1-\mathrm{\alpha }){\mathrm{\rho }}_s{H}_s)+(1-\mathrm{\varphi }){\mathrm{\rho }}_{sk}{H}_{sk}](2)$$

where, the heat conductance λ_eff is the average volume weight heat conductance value of all the CPB material. The source item $\frac{\partial Q_{hyd}}{\partial \mathrm{\tau }}$ is the heat production rate by the hydration reaction, which is relevant to curing time and temperature. The initial temperature of CPB was low, and an equation was adopted from Wang’s research for Q_hyd under low temperature conditions (T < 286 K) (Wang et al., 2015). When substantial cold released and the temperature rose, another equation was adopted from the literature (Zhu, 2012) for Q_hyd under normal temperature conditions (T ≥ 286 K). Equation (3) was concluded from the literature to calculate hydration heat. The total hydration heat of ordinary Portland cement Q₀ is 430 kJ/kg. For simulating the mixed state of CPB, a porous medium model was applied, and the parameters ϕ and α are the porosity and the liquid fraction in pores, respectively. For simulating the phase change process, the enthalpy method and VOF method were applied. This model was verified in our previous study simulating the new CPB material and experimental tests (Wang M. et al., 2019).

$$Q_{hyd}=\{\begin{array}{c}{Q}_0[1-\exp (-0.045T^{0.46}{\mathrm{\tau }}^{\prime 1.28}{(1-Q_{hyd}/Q_0)}^2),T<286K\hfill \\ Q_0[1-\exp (-m{\mathrm{\tau }}^{\prime })],T\ge 286K\hfill \end{array}(3)$$

Calculating Parameters

There are several parameters applied in the calculation, which fall into four categories: physical parameters of materials in CLS-functional CPB (shown in Table 1), proportions of main materials (shown in Table 2), physical parameters of materials surrounding materials (shown in Table 3) and thermal calculating parameters (shown in Table 4). The proportion of the CLS-functional CPB influenced the transport properties, thermal performance and the strength of CPB. Considering the factors above, the material of CPB was designed as the ratio of waste stone to tailings 6:4, the ratio of cement to solid waste 1:8, the mass concentration varying from 66.1% to 78.4%, and the ratio of ice to water varying from 3:1 to 1:3.

TABLE 1

Table 1. Physical parameter of materials in CLS functional CPB.

TABLE 2

Table 2. Proportions of main materials in CLS functional CPB.

TABLE 3

Table 3. Physical parameters of surrounding materials.

TABLE 4

Table 4. Thermal calculating parameters.

Computational Mesh

There are 30000 quad meshes in the simulation. Refined grids are utilized near the boundary. The mesh refinement factors are 1.008 in the -x direction and 1.008 in z and –z directions. The computational mesh was checked by grid independence.

Simulation Results and Discussion

Whether the stope nearby could be cooled through the whole mining period was influenced by the cooling capacity and cold release velocity. The initial proportion of ice to water, Ω, and mass concentration, C, are the two key factors relating to the cooling capacity. Numerical simulation research was studied to obtain the influence law of these two factors.

The Influence of Initial Proportion of Ice to Water

With the increase in the initial proportion of ice to water, the cooling capacity increases and the cooling period can be prolonged. Under the same mass concentration conditions (C = 72.8%), 5 group simulations with different initial proportions of ice to water were studied. From Figure 4, the temperature distributions of CLS-functional CPB showed that the cold concentrated in the lower boundary. For preserving cold capacity, the lower and right boundaries were covered with insulation layers so that the more effective cold could be transferred to the upper stope. As the insulation layer exited, heat concentrated in the upper right corner.

FIGURE 4

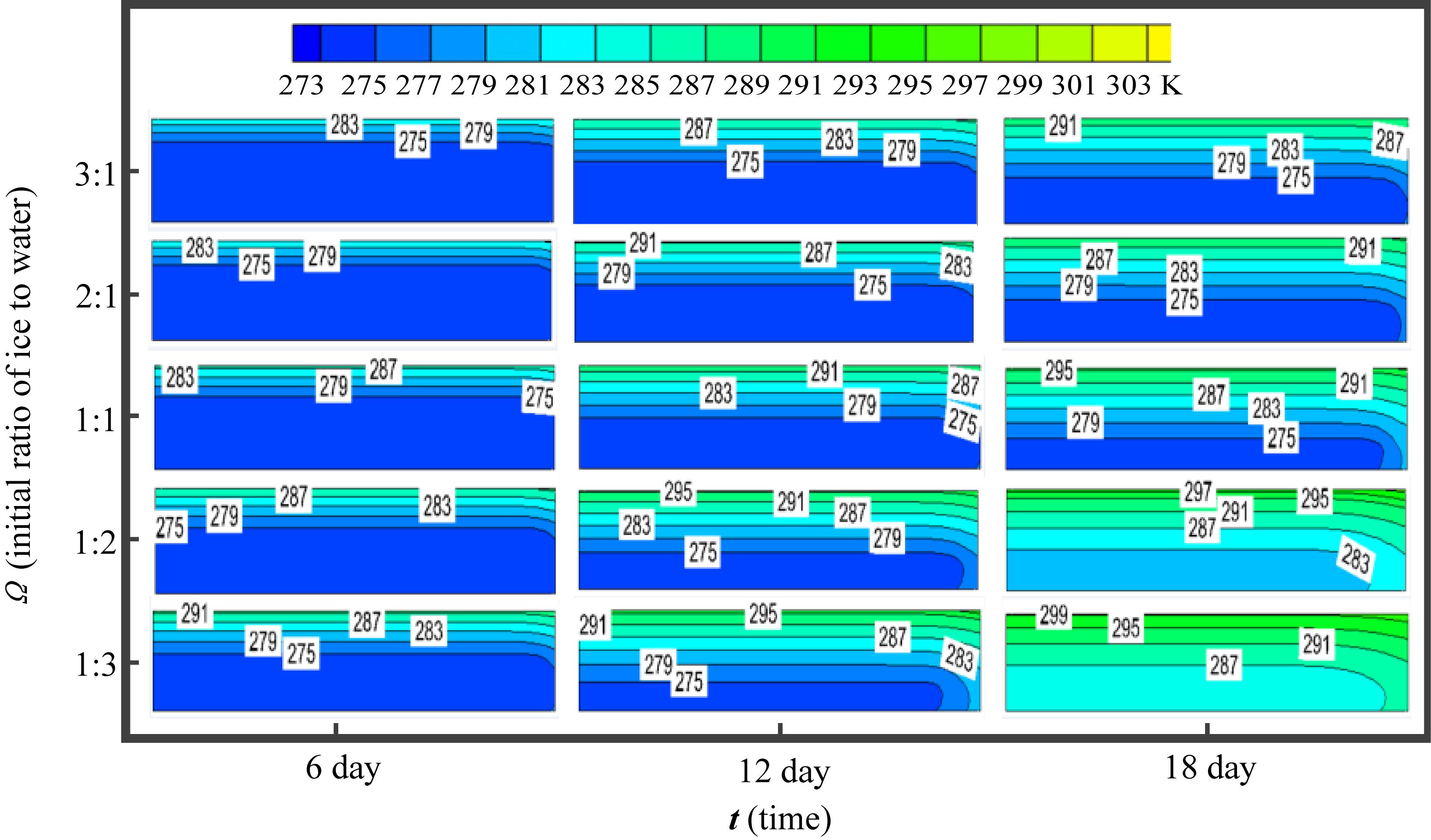
Figure 4. Temperature distributions of CLS-functional CPB under different initial proportions of ice to water.

In the CLS-functional CPB, the temperature of the upper layer first increased and the cold-release velocity from CPB to the upper stope slowed due to the increased heat resistance. This heat transfer characteristic was adverse for cold release. Considering this problem, the thickness of CLS-functional CPB should be designed as thin as possible under the cold capacity condition meeting the cold requirement of the stope, so that the heat conductance resistance would not be very high and the cold could release quickly.

Comparing the temperature distribution results under different proportions of ice to water, it was clear that the distributions varied considerably during the cold releasing process, even by the 18th day. At the 18th day, under the Ω = 3:1 condition, the surface temperature was low enough for cooling the stope, while under the Ω = 1:3 condition, the temperature difference between the environment and surface was smaller, which clearly weakens the cooling effect. This revealed that the proportion of ice to water, Ω, is a very important parameter influencing the cooling effect. According to the cold capacity and mining period of the stope, the Ω could be designed by numerical prediction in mining engineering.

The liquid ratio α is the ratio of liquid volume to total volume of liquid (water) and solid (ice). This ratio changed with the cold releasing process from the initial value to 1. At α = 1, all the ice particles melted. To study the phase change characteristics, Figure 5 was presented to show the liquid distribution in CPB. To facilitate the comparison of temperature distributions, these simulations are under the same conditions as shown in Figure 4. Figure 5 shows that the melt region developed from boundary to core. Owing to the insulating layer, the location of the ice center was at the lower part of the CPB. With smaller values of Ω, the phase changed faster. Under the Ω = 1:3 condition, most of the ice melted by the 6th day, while under the Ω = 3:1 condition, the ice still exists at the 18th day. Furthermore, the phase distribution laws were not the same under different Ω ratios. The lower the Ω is, the more homogenous the phase distribution.

FIGURE 5

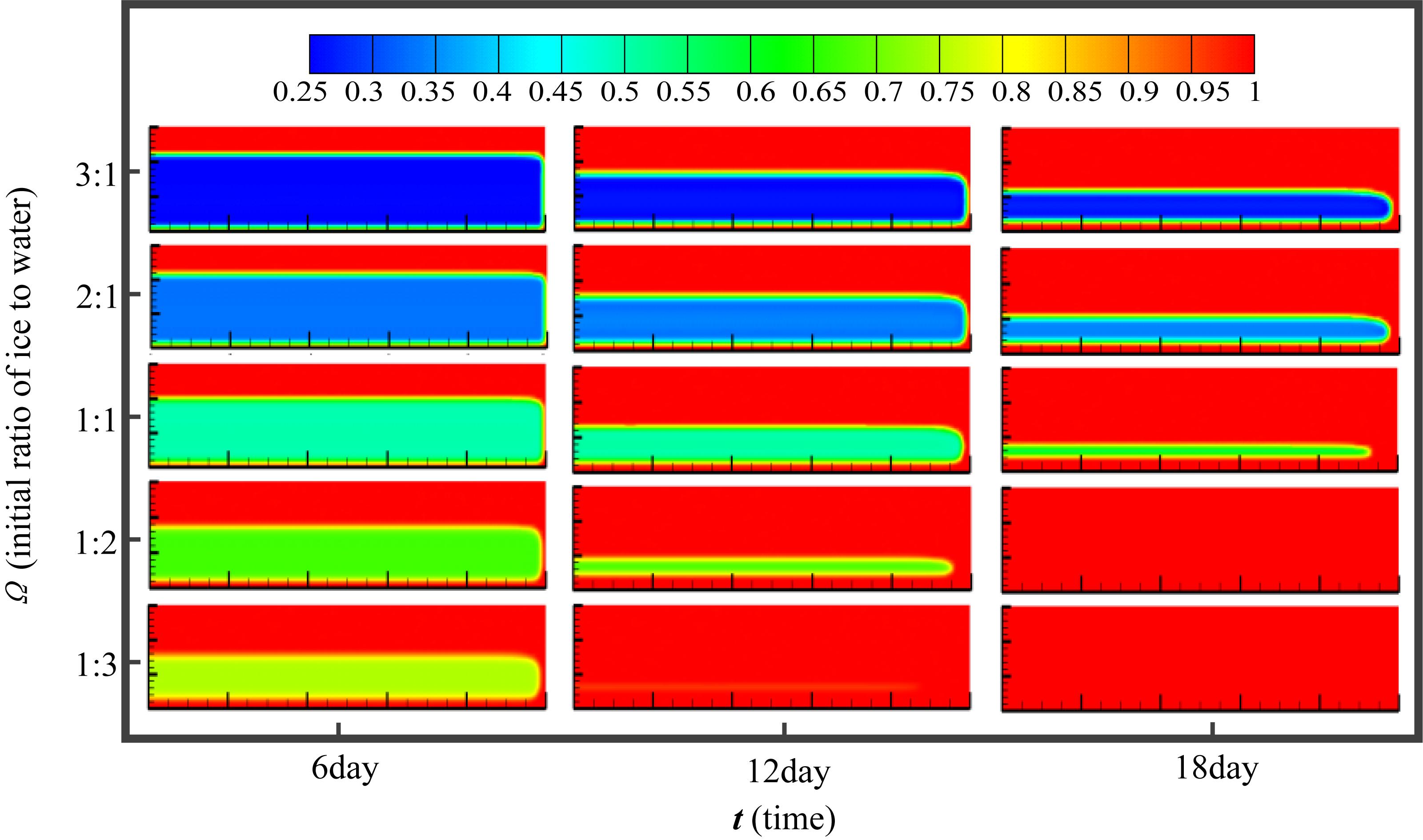
Figure 5. Liquid ratio distribution of CLS functional CPB under different initial proportion of ice to water.

Phase change processes influence heat transfer and temperature distributions. To reveal the laws of heat transfer and phase change with time, the trends of average temperature and liquid ratio were illustrated and compared in Figure 6. As the initial proportion of ice to water decreases from 3:1 to 1:3, the rate of temperature increase becomes faster. The higher the initial proportion of ice to water, Ω, the lower the overall temperature. The average temperature increase rate was different with Ω and all the cases had inflection points on the temperature vs. time curves. This could be explained by the influence of ice. Take the case of Ω = 1:1 for example, before the inflection point (the 20th day), there was ice in the CPB and the heat was transferred by both latent heat and sensible heat, thus the rate of temperature increase was slower. After the inflection point, all the ice was melted and the heat transferred only by sensible heat, so the rate of temperature increase was faster. The inflection point of the average temperature curves was in accordance with the liquid proportion curves. With the increasing initial proportion of ice to water, the durations of the phase change are longer. However, the whole liquid ratio rising trend is similar for different cases. The durations of complete phase changing are 12, 15, 20, 26, and 28 days under Ω = 1:3, 1:2, 1:1, 2:1, and 3:1 ratios, respectively. The existence of ice implies that the latent cold release endured and the cooling potential was larger. This indicated that the initial proportion of ice to water was significant for the cold releasing quantity and the cooling time. In engineering practice, the initial proportion of ice to water could be designed according to the mining period and cold quantity requirement of a stope.

FIGURE 6

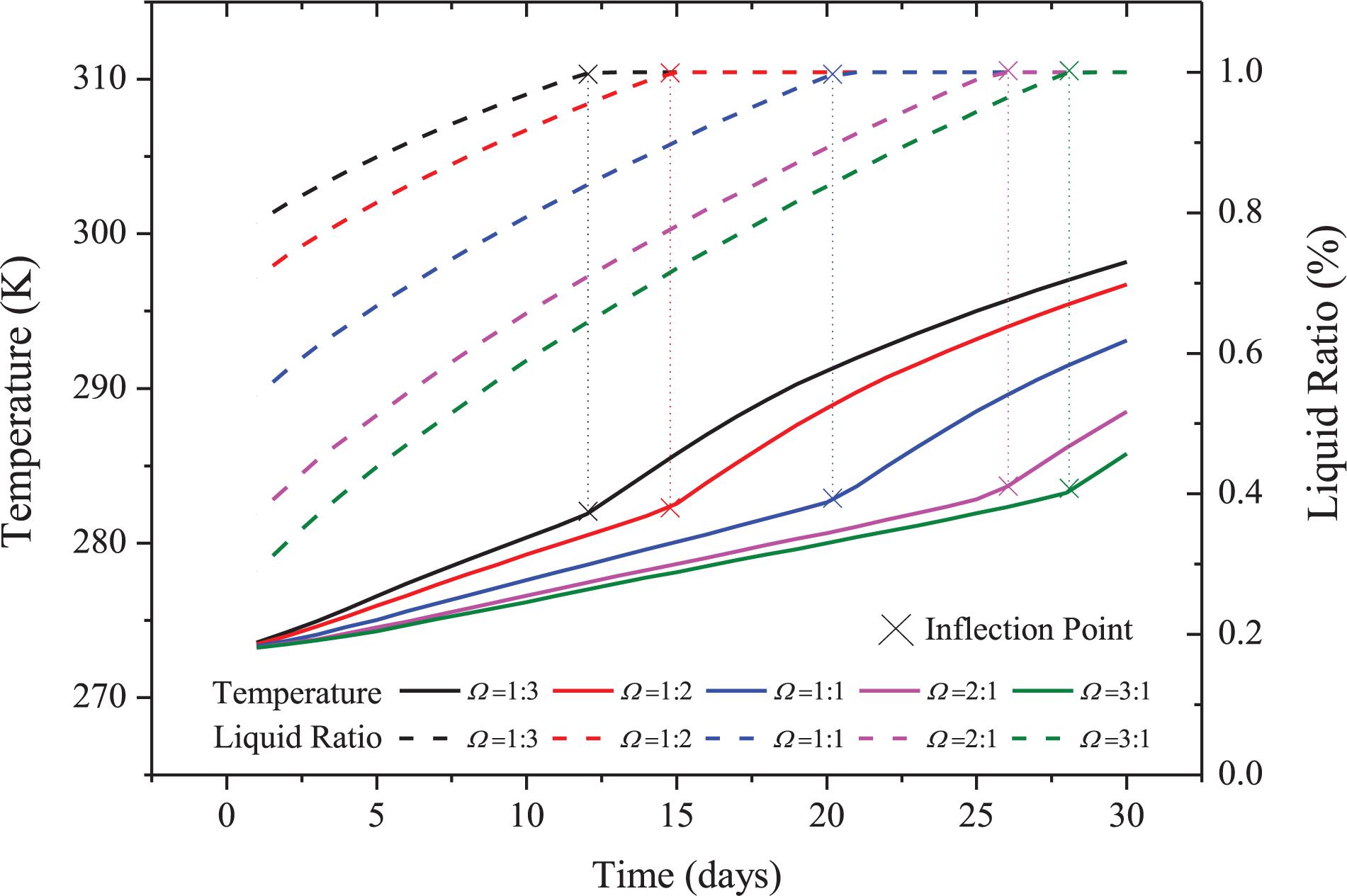
Figure 6. Average temperature and liquid ratio of CLS functional CPB under different initial proportion of ice to water.

The average temperature of the upper surface manifested the different rising law as Figure 7 shows. There was also an inflection point in the curve. However, the rate of temperature increase is faster before the inflection point. In the upper surface, the ice melted fast and the temperature rose fast because of the larger heat transfer temperature difference. Under the larger temperature difference between the CPB upper surface and the air of the stope, a larger amount of cold was released from the CPB, and the temperature rose quickly. With the temperature difference reduced, the heat transfer was weakened and the rate of temperature increase declined after the inflection point. The durations of surface temperature increase from the initial temperature to 293 K were approximately 7, 8, 11, 15, and 17 days, which implied that considerable cooling flux could be provided by CPB, and the cooling effects were satisfactory for stopes for these durations.

FIGURE 7

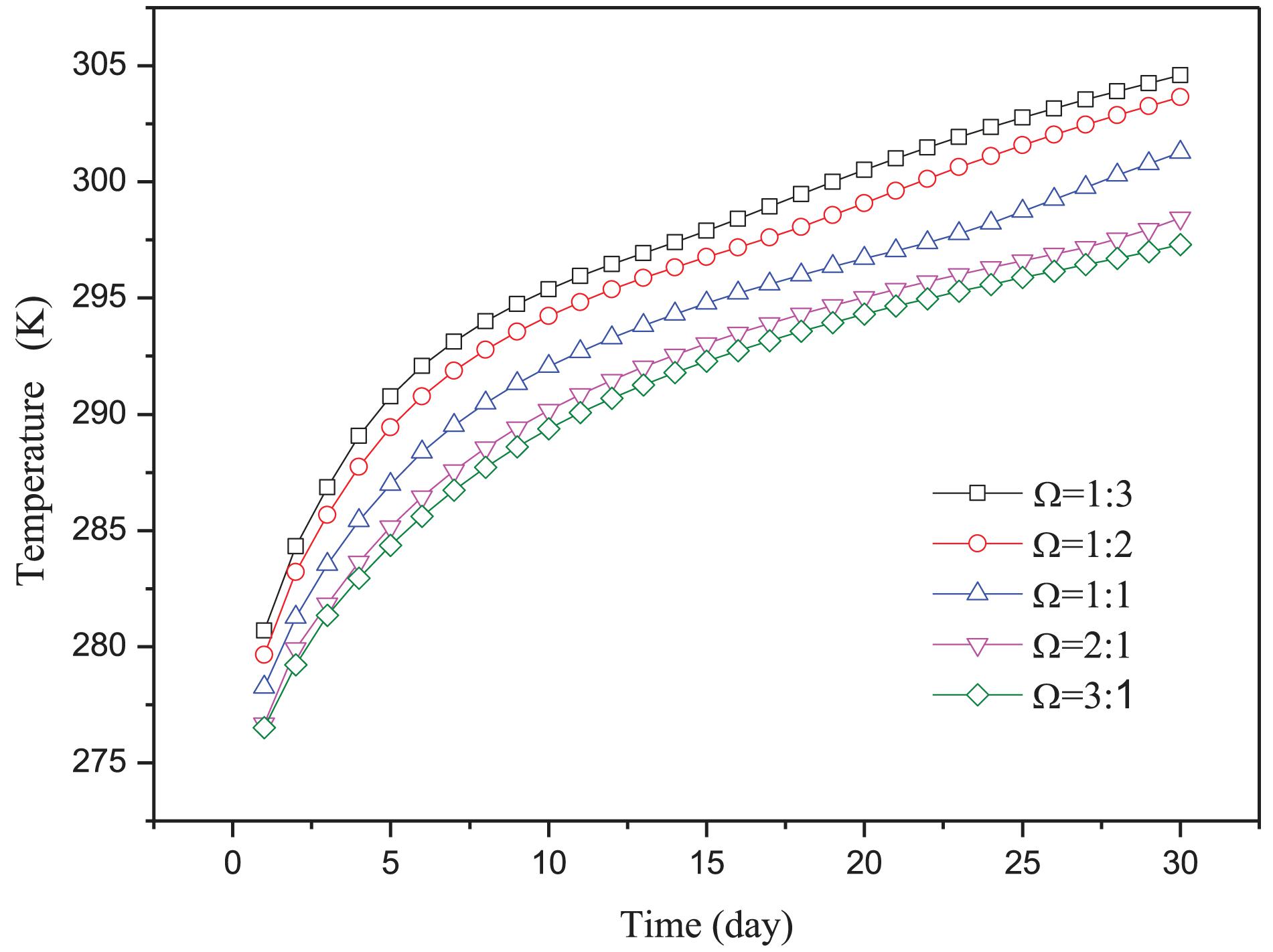
Figure 7. Average surface temperature of CLS-functional CPB under different initial proportions of ice to water.

The Influence of Mass Concentration

Mass concentration is the ratio of the total weight of waste stones, tailings and cement to the weight of CPB. Different mass concentrations lead to different water and ice quantities. Under the same initial proportion of ice to water, Ω, lower mass concentration means more total quantity of water and ice in the CPB; thus, the cold capacity is larger. Figure 8 shows the cold concentration that existed in the lower part of the CPB. As the mass concentration increase, both the temperature and liquid ratio rising rate increase as Figures 8, 9 shows, respectively. As Figures 8, 9 showed, the liquid ratio rising rate increased with the mass concentration. The higher the mass concentration was, the less the cold capacity it included was. Thus, the cold release time of higher mass concentrations was shorter than it was for lower mass concentrations resulting in the faster rate of temperature increase.

FIGURE 8

Figure 8. Temperature distribution of CLS functional CPB under different concentration.

FIGURE 9

Figure 9. Liquid ratio distribution of CLS functional CPB under different concentration.

Figure 10 shows the average temperature and liquid ratio rising laws of CLS-functional CPB. The inflection point existed as introduced in section “The Influence of Initial Proportion of Ice to Water.” The inflection points occur on the 25th, 21st, and 17th, with mass concentrations of 66.1, 72.8, and 78.5% both for temperature rising trends and liquid ratio rising trends. This accordance could also be explained by the heat transfer mechanism. Before the inflection point, ice existed and both latent and sensible heat transfer occurred. However, after the inflection point, all the ice melted and only sensible heat transfer occurred. From Figure 11, the surface temperature rising rate rank was the same as in Figure 10. Compared with the influence of the initial proportion of ice to water, the influence of mass concentration on surface temperature was smaller.

FIGURE 10

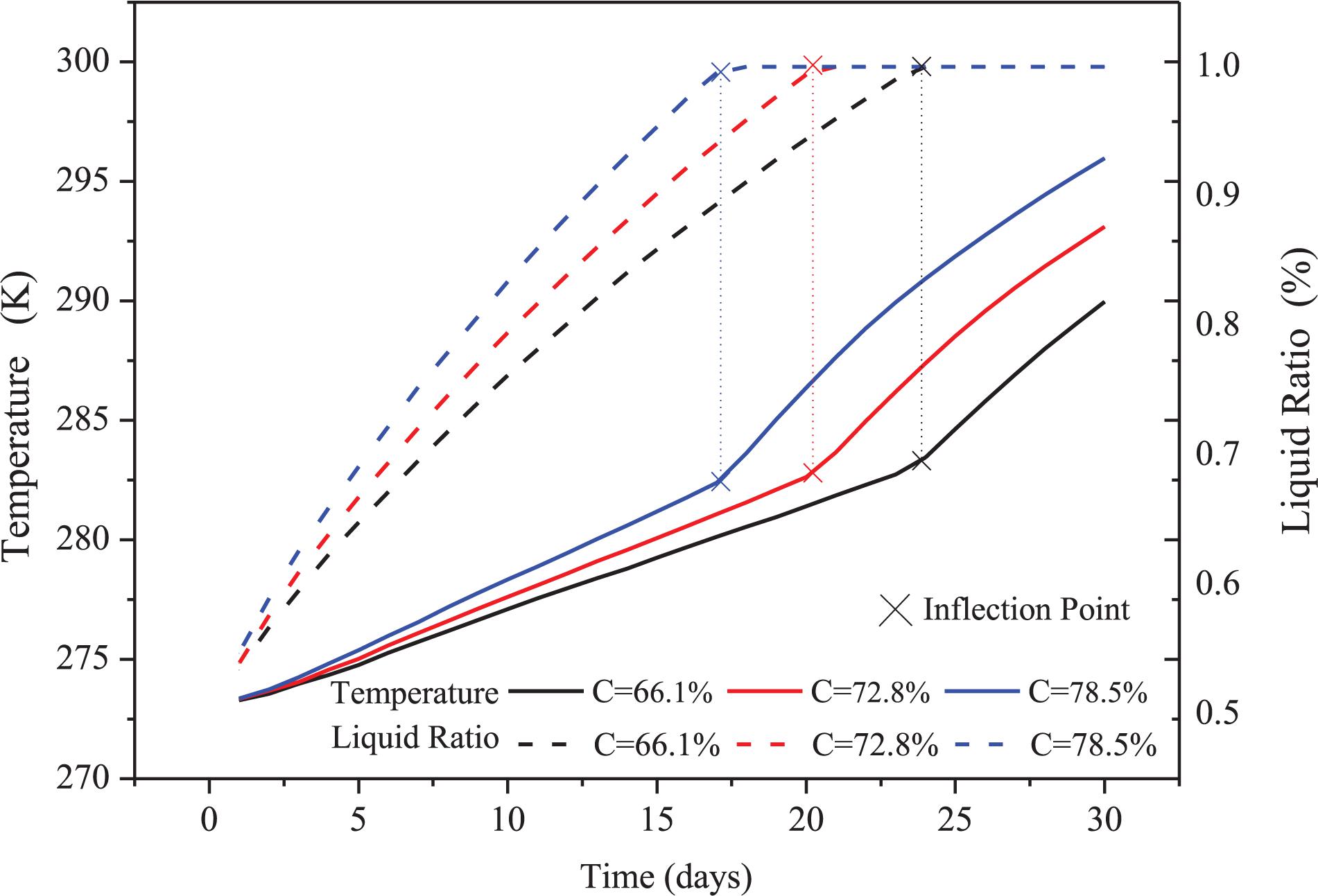
Figure 10. Average temperature and liquid ration of CLS functional CPB under different slurry concentration.

FIGURE 11

Figure 11. Average surface temperature of CLS-functional CPB under different slurry concentrations.

Conclusion

Cold load and storage-functional CPB is a new cooling method, which could be applied to deep mine cooling. A 2-D, unsteady state heat conduction model compounded with a hydration heat model, a porous media model and an enthalpy method model was applied to simulate the phase change and heat transfer process of CLS-functional CPB in deep mines. From the numerical investigation, conclusions have been drawn as follows. The cold releasing effect of different mass concentrations and initial proportions of ice to water was compared. All the average temperature curves appeared to display two-stage characteristics. The rate of temperature increase during the first stage was lower than the second. The inflection point between the two stages was according to the melt time of the liquid ratio curve. With an increasing initial proportion of ice to water, the temperature rise was slower, while with increasing mass concentration, the temperature rose faster. Compared with mass concentration, the initial proportion of ice to water had a greater influence on the temperature rise and cold capacity. With the mass concentrations increasing from 66.1% to 78.4%, the duration of the phase transition decreased 32%, while, with the PCM initial proportion of solid to liquid increasing from 1:3 to 3:1, the duration of the phase transition increased 54%. As the melting region developed from top to bottom of the CLS-functional CPB, the distance from the lowest temperature location to the upper surface increased and the heat resistance increased accordingly. In other words, if the thickness of CLS-functional CPB was smaller, it was easier to release cold and obtain a good cooling effect during the later period. It needs to be noted that this study focused on the phase change and heat transfer characteristics of the new CPB; the strength and the grouting transport characteristics of it also need to be studied for overall consideration of designing the composition of the new CPB.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

MW and LL had the idea for CLS Functional CPB, and drafted its initial concept, and wrote the initial version of the manuscript. SW and BL developed the software. BZ and XZ conducted analyses. YZ and CH edited the manuscript. All authors reviewed and finalized the manuscript.

Funding

The authors are grateful for the support provided by the National Natural Science Foundation of China (Nos. 51904224, 51674188, 51874229, 51974225, 51504182, 51904225, and 51704229), Natural Science Basic Research Plan in Shaanxi Province of China (Nos. 2018JQ5183, 2018JM5161, 2015JQ5187, and 2019JM-074), Scientific Research Program Funded by Shaanxi Provincial Education Department of China (Nos. 18JK0523, 19JK0543, and 15JK1466), Shaanxi Innovative Talents Cultivate Program-New-Star Plan of Science and Technology (No. 2018KJXX-083), China Postdoctoral Science Foundation (No. 2015M582685), Outstanding Youth Science Fund of Xi’an University of Science and Technology (No. 2018YQ2-01), Ph.D. Research Startup Foundation of Xi’an University of Science and Technology (No. 2018QDJ046), and the Scientific Research Program funded by Xi’an Science and Technology Bureau (No. 20180536YD14CG20).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors are grateful for the support provided by Energy School, Xi’an University of Science and Technology, and Key Laboratory of Western Mines and Hazards Prevention, Ministry of Education of China.

References

Belle, B., and Biffi, M. (2018). Cooling pathways for deep Australian longwall coal mines of the future. Int. J. Min. Sci. Technol. 28, 865–875. doi: 10.1016/j.ijmst.2018.02.001

CrossRef Full Text | Google Scholar

Brune, J. F. (2019). “Mine ventilation networks optimized for safety and productivity,” in Advances in Productive, Safe, And Responsible Coal Mining, ed. J. Hirschi, (Golden, CO: Colorado School of Mines), 83–99. doi: 10.1016/B978-0-08-101288-8.00005-5

CrossRef Full Text | Google Scholar

Bu, F. X., Zhang, M. G., Meng, X., Xiang-xi, M., and Qing-ren, L. (2015). Application of natural ice cold storage in mine cooling. Coal Technol. 34, 158–160.

Google Scholar

Cai, M. F., and Brown, E. T. (2017). Challenges in the mining and utilization of deep mineral resources. Engineering 3, 432–433. doi: 10.1016/J.ENG.2017.04.027

CrossRef Full Text | Google Scholar

Chen, L., Liu, L., and Zhang, B. (2018). Mechanism of backfill thermal utilization adsorption cooling system in deep mine. J. China Coal Soc. 43, 483–489. doi: 10.13225/j.cnki.jcss.2017.1365

CrossRef Full Text | Google Scholar

Crawford, J. A., Joubert, H. P. R., and Mathews, M. J. (2019). Optimised dynamic control philosophy for improved performance of mine cooling systems. Appl. Therm. Eng. 150, 50–60. doi: 10.1016/j.applthermaleng.2018.12.160

CrossRef Full Text | Google Scholar

Cui, S. G., Liu, P., Cui, E. Q., Su, J., and Huang, B. (2018). Experimental study on mechanical property and pore structure of concrete for shotcrete use in a hot-dry environment of high geothermal tunnels. Construct. Build. Mater. 173, 124–135. doi: 10.1016/j.conbuildmat.2018.03.191

CrossRef Full Text | Google Scholar

du Plessis, G. E., Mathews, E. H., and Vosloo, J. C. (2013). “A variable water flow energy efficiency strategy for mine cooling systems,” in Proceedings of the International Conference on the Industrial and Commercial Use of Energy Conference (ICUE), Cape Town.

Google Scholar

Emad, M. Z., Mitri, H., and Kelly, C. (2018). Dynamic model validation using blast vibration monitoring in mine backfill. Int. J. Rock Mech. Min. Sci. 107, 48–54. doi: 10.1016/j.ijrmms.2018.04.047

CrossRef Full Text | Google Scholar

Feng, X. P., Jia, Z. M., Liang, H., Wang, Z., Wang, B., Jiang, X., et al. (2018). A full air cooling and heating system based on mine water source. Appl. Therm. Eng. 145, 610–617. doi: 10.1016/j.applthermaleng.2018.09.047

CrossRef Full Text | Google Scholar

Feng, X. T., Liu, J. P., Chen, B. R., Xiao, Y., Feng, G., Zhang, F., et al. (2017). Monitoring, warning, and control of rockburst in deep metal mines. Engineering 3, 538–545. doi: 10.1016/j.eng.2017.04.013

CrossRef Full Text | Google Scholar

Ghoreishi-Madiseh, S. A., Sasmito, A. P., Hassani, F. P., and Amiri, L. (2017). Performance evaluation of large scale rock-pit seasonal thermal energy storage for application in underground mine ventilation. Appl. Energy 185, 1940–1947. doi: 10.1016/j.apenergy.2016.01.062

CrossRef Full Text | Google Scholar

Guo, P. Y. (2010). Characteristics of Geothermal Field Of Deep Mine and Its Heat Damage Control in China. PhD thesis, China University of Mining and Technology, Beijing.

Google Scholar

Guo, P. Y., He, M. C., Zheng, L., and Zhang, N. (2017). A geothermal recycling system for cooling and heating in deep mines. Appl. Therm. Eng. 116, 833–839. doi: 10.1016/j.applthermaleng.2017.01.116

CrossRef Full Text | Google Scholar

He, M. C., and Guo, P. Y. (2013). Deep rock mass thermodynamic effect and temperature control measures. Chin. J. Rock Mech. Eng. 32, 2377–2393.

Google Scholar

He, M. C., and Xu, M. (2008). Research and development of hems cooling system and heat-harm control in deep mine. Chin. J. Rock Mech. Eng. 27, 1353–1361.

Google Scholar

Lin, H., Ding, X., Yong, R., Xu, W., and Du, S. (2019a). Effect of non-persistent joints distribution on shear behavior. C. R. Mécan. 347, 477–489. doi: 10.1016/j.crme.2019.05.001

CrossRef Full Text | Google Scholar

Lin, H., Xie, S. J., Yong, R., Chen, Y. F., and Du, S. G. (2019b). An empirical statistical constitutive relationship for rock joint shearing considering scale effect. C. R. Mecan. 347, 561–575. doi: 10.1016/j.crme.2019.08

CrossRef Full Text | Google Scholar

Lin, H., Yang, H., Wang, Y., Zhao, Y., and Cao, R. (2019c). Determination of the stress field and crack initiation angle of an open flaw tip under uniaxial compression. Theor. Appl. Fract. Mech. 104:102358. doi: 10.1016/j.tafmec.2019.102358

CrossRef Full Text | Google Scholar

Liu, L., Fang, Z. Y., Qi, C. C., Zhang, B., Guo, L. J., and Song, K. I. (2019a). Numerical study on the pipe flow characteristics of the cemented paste backfill slurry considering hydration effects. Powder Technol. 343, 454–464. doi: 10.1016/j.powtec.2018.11.070

CrossRef Full Text | Google Scholar

Liu, L., Xin, J., Huan, C., Qi, C. C., Zhou, W. W., and Song, K. I. (2020). Pore and strength characteristics of cemented paste backfill using sulphide tailings. Construct. Build. Mater. 237:117452. doi: 10.1016/j.conbuildmat.2019.117452

CrossRef Full Text | Google Scholar

Liu, L., Zhu, C., Qi, C. C., Wang, M., Huan, C., Zhang, B., et al. (2019b). Effects of curing time and ice-to-water ratio on performance of cemented paste backfill containing ice slag. Construct. Build. Mater. 228:116639. doi: 10.1016/j.conbuildmat.2019.08.020

CrossRef Full Text | Google Scholar

Plessis, G. E., Arndt, D. C., and Mathews, E. H. (2015). The development and integrated simulation of a variable water flow energy saving strategy for deep-mine cooling systems. Sustain. Energy Technol. Assess. 10, 71–78. doi: 10.1016/j.seta.2015.03.002

CrossRef Full Text | Google Scholar

Pretorius, J. G., Mathews, M. J., Maré, P., Kleingeld, M., and van Rensburg, J. (2019). Implementing a DIKW model on a deep mine cooling system. Int. J. Min. Sci. Technol. 29, 319–326. doi: 10.1016/j.ijmst.2018.07.004

CrossRef Full Text | Google Scholar

Qi, C. C., Chen, Q. S., Fourie, A., Zhao, J., and Zhang, Q. (2018). Pressure drop in pipe flow of cemented paste backfill: experimental and modeling study. Powder Technol. 333, 9–18. doi: 10.1016/j.powtec.2018.03.070

CrossRef Full Text | Google Scholar

Ryan, A., and Euler, D. S. (2017). Heat stress management in underground mines. Int. J. Min. Sci. Technol. 27, 651–655. doi: 10.1016/j.ijmst.2017.05.020

CrossRef Full Text | Google Scholar

Shen, Y. J., Yang, G. S., Wang, M., Zhang, H. M., Jia, H., Liang, R., et al. (2016). Experimental and theoretical study on thermal conductivity of rock under cyclic freezing and thawing. Chin. J. Rock Mech. Eng. 35, 2417–2425.

Google Scholar

Shi, J. H., Xin, S., and Yu, S. J. (2011). The feasibility analysis of natural ice-making cooling technology in mine cooling. Chin. Indust. Saf. Environ. Protect. 37, 22–23.

Google Scholar

Trapania, K., Romero, A., and Millar, D. (2016). Deep mine cooling, a case for Northern Ontario. Int. J. Min. Sci. Technol. 26, 1033–1042. doi: 10.1016/j.ijmst.2016.09.011

CrossRef Full Text | Google Scholar

Van der Walt, J., and De Kock, E. M. (1984). Developments in the engineering of refrigeration installations for cooling mines. Int. J. Refrig. 7, 27–40. doi: 10.1016/0140-7007(84)90050-1

CrossRef Full Text | Google Scholar

Wang, M., Liu, L., Chen, L., Zhang, X., Zhang, B., Ji, C., et al. (2018). Cold load and storage functional backfill for cooling deep mine. Adv. Civil Eng. 2018:5435214. doi: 10.1155/2018/5435214

CrossRef Full Text | Google Scholar

Wang, M., Liu, L., Zhang, X. Y., Chen, L., Wang, S.-Q., Jia, Y.-H., et al. (2019). Experimental and numerical investigations of heat transfer and phase change characteristics of cemented paste backfill with PCM. Appl. Therm. Eng. 150, 121–131. doi: 10.1016/j.applthermaleng.2018.12.103

CrossRef Full Text | Google Scholar

Wang, Q. C., Chen, C., and Zhang, R. L. (2015). Computing model for the hydration heat of cement paste considering of the effect of sustained low temperature. Chin. J. Build. Mater. 18, 249–254.

Google Scholar

Wang, Y., Lin, H., Zhao, Y., Li, X., Guo, P., and Liu, Y. (2019). Analysis of fracturing characteristics of unconfined rock plate under edge-on impact loading. Eur. J. Environ. Civil Eng. 1–16. doi: 10.1080/19648189.2018.1509021

CrossRef Full Text | Google Scholar

Wilson, R. (2008). “Design and construction of a surface air cooling and refrigeration installation at a South African mine,” in Proceedings of the 12th US/North American Mine Ventilation Symposium, Piscataway, NJ, 191–195.

Google Scholar

Wu, Q. H., Weng, L., Zhao, Y. L., Guo, B. H., and Luo, T. (2019). On the tensile mechanical characteristics of fine-grained granite after heating/cooling treatments with different cooling rates. Eng. Geol. 253, 94–110. doi: 10.1016/j.enggeo.2019.03.014

CrossRef Full Text | Google Scholar

Xie, H. P. (2017). Research framework and anticipated results of deep rock mechanics and mining theory. Adv. Eng. Sci. 49, 1–16. doi: 10.15961/j.jsuese.201700025

CrossRef Full Text | Google Scholar

Yang, R. S., Li, Y. L., Guo, D. M., Yao, L., Yang, T., Li, T., et al. (2017). Failure mechanism and control technology of water-immersed roadway in high-stress and soft rock in a deep mine. Int. J. Min. Sci. Technol. 27, 245–252. doi: 10.1016/j.ijmst.2017.01.010

CrossRef Full Text | Google Scholar

Zhang, J., Ma, G. D., Ming, R. P., Cui, X., Li, L., Xu, I., et al. (2018). Numerical study on seepage flow in pervious concrete based on 3D CT imaging. Construct. Build. Mater. 161, 468–478. doi: 10.1016/j.conbuildmat.2017.11.149

CrossRef Full Text | Google Scholar

Zhao, Y. L., Wang, Y. X., Wang, W. J., Tang, L. M., and Liu, Q. (2019). Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses. Theor. Appl. Fract. Mech. 101, 59–66. doi: 10.1016/j.tafmec.2019.01.026

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L. Y., Wang, W. J., Pu, C. Z., Wan, W., and Tang, J. Z. (2016). Cracking and Stress–Strain Behavior of Rock-Like Material Containing Two Flaws Under Uniaxial Compressio. Rock Mech. Rock Eng. 49, 2665–2687. doi: 10.1007/s00603-016-0932-1

CrossRef Full Text | Google Scholar

Zhao, Y. L., Zhang, L. Y., Wang, W. J., Wan, W., and Ma, W. (2018). Separation of elasto-visco-plastic strains of rock and a nonlinear creep model. Int. J. Geomech. 1:04017129. doi: 10.1061/(asce)gm.1943-5622.0001033

CrossRef Full Text | Google Scholar

Zhu, B. F. (2012). Temperature Stress and Temperature Control Of Mass Concrete. Beijing: Water Power Press.

Google Scholar