Bare Earth DEM Generation for Large Floodplains Using Image Classification in High-Resolution Single-Pass InSAR

The increasing frequency and severity of flood events demand improved accuracy of hydrodynamic models to better mitigate the societal and economic consequences of these disasters. Ideally, these models derive elevation data from high-accuracy LiDAR, which often captures the subtle variations in elevation and microtopography – elements that are critical to high-resolution hydrodynamic modeling. Due largely to the cost of acquisitions, these data, however, are not widely available at high spatial resolutions for large-scale areas, i.e., floodplains and coastal regions, especially outside of the United States and Western Europe, where flood-prone communities already lack the infrastructure and resources to manage these disasters. High-resolution interferometric synthetic aperture radar (InSAR) systems may offer a viable and cost-effective alternative to LiDAR, with comparable spatial resolutions and vertical accuracies. Like any swath mapping sensor, systematic errors in calibration knowledge increase as the lever-arm increases when viewing further off vertical. InSAR-derived digital elevation models (DEMs) are often corrected using LiDAR or ground control points, although this limits the application of InSAR to those areas where these data exist. In this paper, we present a novel approach for using near-range InSAR data to correct inherent systematic bias that propagates across adjacent, overlapping swaths for the same airborne acquisition. This eliminates the need for LiDAR in generating InSAR DEMs, while maintaining a vertical error of approximately 0.26 m relative to LiDAR, at a spatial resolution of 30 m. Data was acquired using the NASA/JPL airborne, single-pass, Ka-band GLISTIN-A (Glacier and Ice Surface Topography Interferometer) InSAR over the Red River Basin (RRB), ND. The accuracy of the final DEM is evaluated using National Geodetic Survey (NGS) GPS and a high-resolution LiDAR DEM.

Introduction

GLISTIN-A (Airborne Glacier and Land Ice Surface Topography Interferometer) is a Ka-band (35.66 GHz), single-pass interferometric synthetic aperture radar (SPInSAR), inspired by the Shuttle Radar Topography Mission (SRTM) heritage (Rabus et al., 2003) and developed to provide all-weather, high-resolution swath ice surface topography (Moller et al., 2011) not available through existing spaceborne LiDAR or radar sensors. During engineering flights, GLISTIN-A also mapped parts of the Central Valley region of California and it became clear that the sensor’s capability to map land heights and water areas should be exploited. To this end, Schumann et al. (2016) undertook a feasibility study to examine this in detail. Indeed, their DEM case study over the California Central Valley confirmed for the first time that GLISTIN-A’s Ka-band technology can be used for floodplain mapping and flood studies on small to regional scales, as it generates floodplain DEMs with similar accuracies to that of state-of-the-art airborne LiDAR (mean bias of 5.6 cm, with a standard deviation of ±30 cm), therefore, furthering the international agenda of a high-accuracy, open-access global DEM (Schumann et al., 2014).

Digital elevation models (DEMs) are essential data sets for disaster risk management and humanitarian relief services, as well as many environmental process models. While in some countries, such as the United States, United Kingdom, Australia, and several others, there are available LiDAR DEMs, free global DEMs do not currently meet basic hydrodynamic requirements (Schumann and Bates, 2018). Thus, in many regions of the world, where flooding and other hazards are a major concern, we are limited in modeling and mapping primarily due to the lack of LiDAR-quality DEMs, which in turn limits our ability to unlock the full potential of these models in support of flood applications. As demonstrated by Schumann et al. (2016), however, the GLISTIN-A NASA airborne mission offers a novel single-pass InSAR technology that is cost-effective and can generate floodplain DEMs with a RMSE of approximately 0.3 m for an average spatial resolution of 30 m. While Schumann et al. (2016) study demonstrated the capability of GLISTIN-A to generate a LiDAR-quality DEM, a more targeted flood use case is required to evaluate how this DEM performs when used to condition a 2-D hydrodynamic model and simulate an actual out-of-bank flood event. In their study, Schumann et al. (2016) stated in conclusion that “in order to more fully assess the suitability of the Ka-band InSAR instrument to acquire high-accuracy land elevation data, we suggest to repeat this type of analysis over a more natural floodplain and a larger river, and for an area more prone to regular flooding.” This study addresses this type of analysis by acquiring land elevation data over the Red River of the North wide-area floodplain using the GLISTIN-A airborne SPInSAR.

Materials and Methods

Test Site

As a test location, we chose the Red River of the North (RRN) basin (Figure 1), located in North Dakota and Minnesota in the United States, and in southern Manitoba, Canada. The Red River of the North flows north through Winnipeg, Manitoba, and is a tributary of the Nelson River basin, which carries runoff into Hudson Bay from much of southern Canada, from the Great Lakes to the Continental Divide. Due to its extremely low relief, the region of the RRN depicted in Figure 1 is prone to flooding.

FIGURE 1

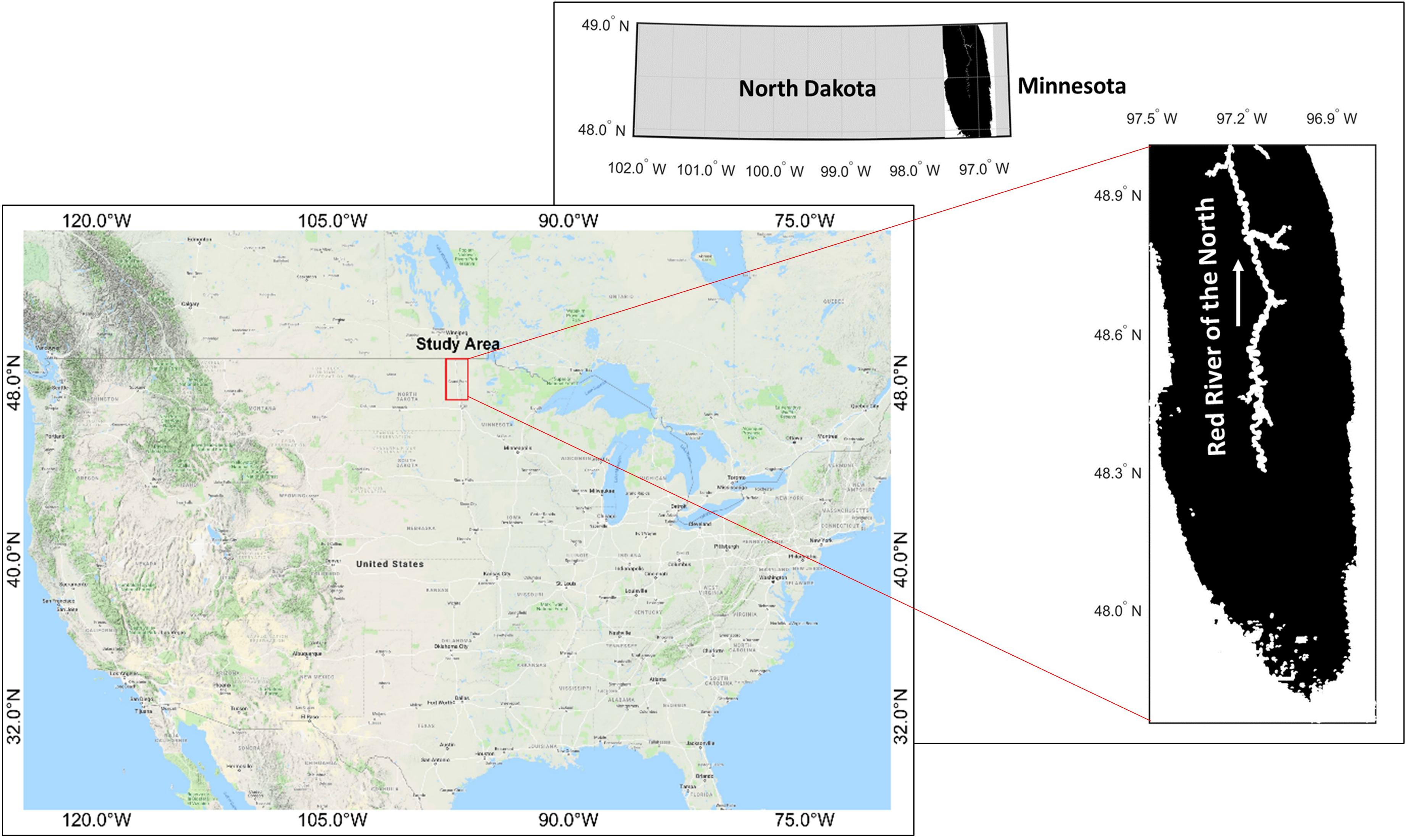
Figure 1. Map of the study area, with the Red River of the North flowing toward the United States-Canada border.

According to NOAA’s Spring Outlook released mid-March 2017, Northern North Dakota (the Souris River, Devils Lake, and the northernmost reaches of the Red River) was predicted to have the greatest risk of major flooding last spring. Snowpack was heavy in the northern plains (containing up to four inches of liquid water that could have increased with additional storms through April), and if long term warm-up had coincided with spring rains, already-saturated soils would not have been able to absorb the increased water, which may have led to increased runoff and potential flooding. Apart from the flood-prone nature of this region, the choice of this test site was also governed by the fact that (i) GLISTIN-A on its March/April 2016 Greenland mission presented a unique overpass opportunity that we leveraged in full by acquiring InSAR data over the area depicted in Figure 1 and (ii) flood hazard prediction during the snow-melt season in this region is a known challenge for the NOAA National Weather Service (NWS) North Central River Forecast Center (see e.g., Tuttle et al., 2017).

GLISTIN-A InSAR Data

InSAR is able to retrieve surface topography by displacing two antennas in the cross-track direction to view the same surface. The interferometric combination of data, received on the two antennas, allows one to resolve the path-length difference from the illuminated area to a fraction of a wavelength. From the interferometric phase, the height of the target (or phase center) can be estimated; therefore, an InSAR system such as GLISTIN-A is capable of providing not only the position of each image point in along-track and slant-range, as with a traditional SAR, but also the height of that point through the use of the interferometric phase (Rodriguez and Martin, 1992; Rosen et al., 2000).

GLISTIN-A (Table 1) is a Ka-Band (8 mm wavelength), cross-track, single-pass InSAR, developed for high-precision, high-resolution ice-surface topography mapping, with a swath-width greater than 10 km (Moller et al., 2017). Using standard processing, the imagery maintains a spatial posting of 3 m. The short-wavelength minimizes interferometric penetration of the electromagnetic wave into surface media. While airborne laser altimetry has negligible penetration into surface media, it is limited in swath width (up to 500 m) and therefore, in spatial coverage.

TABLE 1

Table 1. Summary of key GLISTIN-A operating parameters.

SAR Data Calibration

Instrument calibration and the InSAR processing was performed at the Jet Propulsion Laboratory (JPL). Range pixel location can be determined to better than a tenth of a pixel by over- sampling the slant-plane imagery. Because range measurements to the two interferometric channels may differ, a differential range correction is computed, by measuring range offsets between the two channels. Differential range measurements are accurate to better than a hundredth of a range pixel and insure proper range registration of the channels during interferogram formation. After determining the common and differential range corrections, the data are reprocessed, and strip map DEMs and orthorectified imagery are generated.

However, once the initial instrument calibration is complete, residual imperfect knowledge or instrumental drift can affect the interferometric height measurement and introduce a systematic trend in the data. Rodriguez and Martin (1992) provide a generalized summary of such error sources for a single-pass interferometer and their impact of the topographic measurement. To first order the impact of calibration uncertainty can be lumped into three categories:

1. Linear height tilt across track: Sources are geometric knowledge error (baseline angle) and residual differential phase;

2. Direct positional shift: Sources are platform position errors; and

3. Height shift and quadratic height distortion across-track: Sources are baseline knowledge error and range-timing errors.

Moller et al. (2019) predicts that quadratic height error sources (number 3 above) are negligible based on system design and measurement and this is borne out by a comprehensive validation of 2 years of GLISTIN-A data (2016 and 2017) over coastal Greenland. Validation with overlapping lidar data verify that residual systematic trends manifest as a small linear height characteristic propagating across the swath. Specifically, Moller et al. (2019) observed up to meter-scale nadir biases and evenly distributed residual slopes with a standard deviation of ∼8 millidegrees or 0.18 mm/m).

Figure 2 shows the interferometric geometry where for simplicity the baseline, B is horizontal, the platform is at altitude h_p above a reference surface, and it is imaging a point of height h₀ above that reference, located at incidence angle θ₀, and at slant range ρ. The cross-track distance of that point is therefore x₀ = ρsin(θ₀). It is well known that for (non-interferometric) SAR imagery terrain features can be displaced across-track due to layover or foreshortening, but the additional information provided using interferometry allows features to be correctly geolocated. However, any errors in the calibration knowledge will introduce an error in reconstructing the surface location of the interfered return. Figure 2 illustrates this whereby the rotated dashed triangle shows how a baseline angle error, Δθ, will introduce a positional error in both the cross-track, Δx, and height. Δh, of the reconstructed scene. With perfect system knowledge (the solid triangle):

FIGURE 2

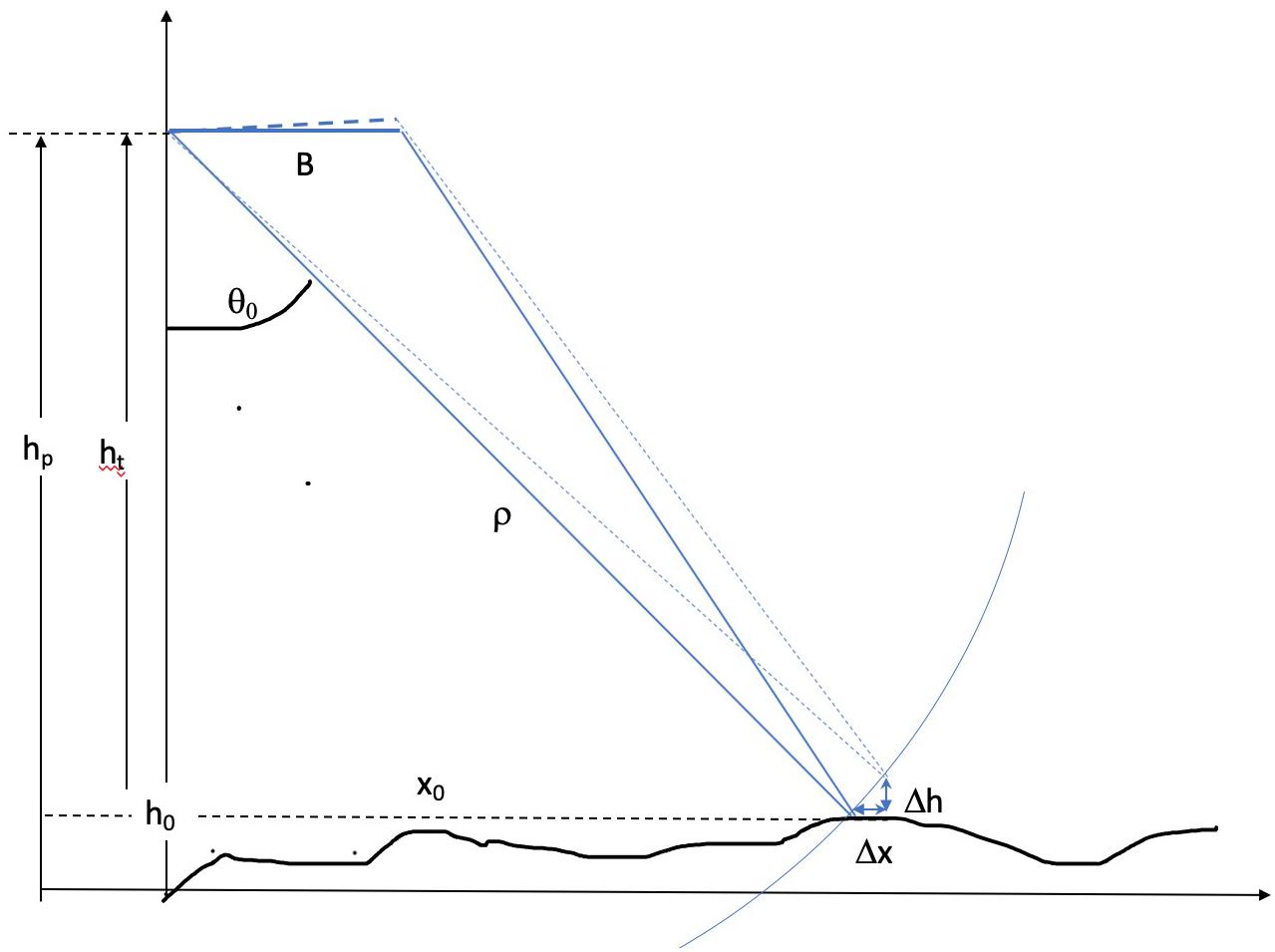
Figure 2. Interferometric geometry illustrating how a slope can be introduced in the measured surface due to imperfect geometry knowledge of the baseline angle (roll).

$$h_t=\frac{\mathrm{\rho }}{\cos ({\mathrm{\theta }}_0)}=\frac{x_0}{\tan ({\mathrm{\theta }}_0)}.$$

But with residual errors manifesting as a baseline angle error estimate, Δθ, the resulting height estimate is:

$$h_t^{{}^{\prime }}=\frac{x_0+\mathrm{\Delta }x}{\tan (\mathrm{\theta }+\mathrm{\Delta }\mathrm{\theta })}.$$

The vertical and horizontal geolocation error is a result of imperfect geometrical knowledge. This illustrates the mechanism by which a slope is introduced: that is a systematic height change that is a function of cross-track distance, x, and where the slope Δh/Δx = h_t-$h_t^{{}^{\prime }}$/Δx. For generating a DEM of large floodplain areas, the impact of Δx can be considered negligible at high incidence angles and tolerable for small incidence angles.

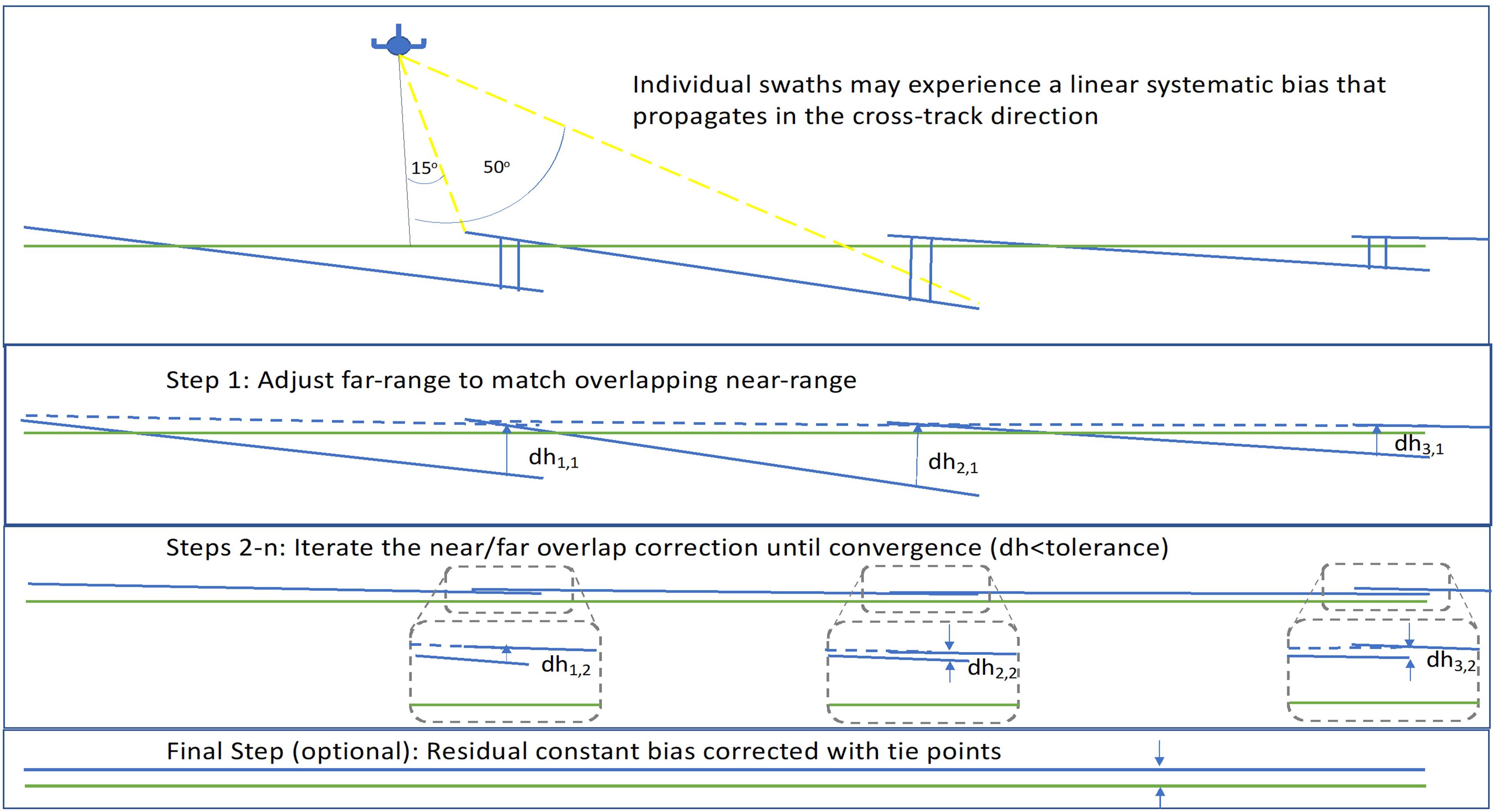
For the RRN acquisitions, the flight plan was configured to have near/far overlaps in successive passes. Figure 3 shows the iterative methodology applied to generate the area DEM. A linear trend, or an effective tilt of the swath can be characterized with two parameters: a constant offset and a slope. To enforce consistency without external control we iteratively correct for slope only by forcing the overlapping extent of the far-range of one swath to equal the near range of another. This is done by correcting the slope difference for the overlapping extent (∼2 km across track overlap) calculated as the mean for the entire line extent (>50 km). The resultant domain may have a mean vertical offset with respect to the vertical reference datum but represents a self-consistent digital surface model (DSM) with which to conduct image classification and subsequently, move toward a SAR-derived, self-consistent bare-earth DEM.

FIGURE 3

Figure 3. Schematic of InSAR data calibration and de-trending methodology.

InSAR Image Classification and DEM Generation

The accuracy of any hydrodynamic model is largely governed by the accuracy of the underlying DEM (Bates, 2004; Schumann et al., 2016). The presence of vegetation, especially in regions along river channels, may obscure or distort bank heights and microtopography, which diminishes height accuracies along the channel and in turn, the overall accuracy of the model (Baugh et al., 2013). These elements play an integral role in hydrodynamic modeling and estimates of bank overtopping. It is therefore imperative that tall features, such as trees and buildings, are successfully classified and removed from the DSM. Information available from the processed InSAR imagery include the measured surface height, the relative power (a function of the backscatter “brightness” of the scene and the radar’s illumination geometry), and the interferometric correlation, γ. The interferometric correlation, γ, is a measure of the similarity of the signal received at the two antennas. For a single-pass system, such as GLISTIN, it can be written as the product of a number of factors:

$$\mathrm{\gamma }=\mathrm{\gamma }{}_{\mathrm{\beta }}\mathrm{\gamma }{}_n\mathrm{\gamma }{}_v$$

where γ_β is the geometric decorrelation due to the cross-track separation, B, of the antennas; γ_n is the decorrelation due to thermal noise and γ_v is the decorrelation due to the interaction of the electromagnetic wave within the scattering volume. Since the wavelength of GLISTIN is just 8.4 mm, it is dominated by surface scatter for bare terrain; however, γ_v and thus γ decreases significantly with the presence of trees or vegetation. Buildings, on the other hand, are expected to exhibit a discernible height relative to the ground, while maintaining a high correlation when compared with trees. Indeed, using the same SPInSAR sensor in a snow depth study, Moller et al. (2017) show that the correlation image data alone is robust enough to successfully classify trees.

Following the reasoning above, we used the SPInSAR height image as well as the SPInSAR correlation image for developing the SPInSAR classification algorithm (see flowchart in Figure 3). Prior to conducting image classification, noise reduction was performed using an average filter, with a 7 × 7 moving window on the 3 m posted imagery. Note that analysis was conducted for imagery that is ground projected relative to the aircraft flight track (the “sch” coordinate system (Zebker et al., 2010), as opposed a geographic map projection) so that range and incidence-angle dependent behavior is reflected in the classification thresholds for robustness. Vegetated areas and buildings were classified using both height and correlation image data. Mean heights were first calculated for 300 × 300 tiles within the larger swath to both capture local variation and to minimize errors introduced by large groves of trees or buildings. A classification algorithm was initiated for any pixels that exhibited a height greater than 2σ of the mean height for a tile. While the success of this initial criteria is likely owed to the exceedingly low relief of the Red River Basin (RRB), this attribute is not unique to this area, and is often a defining characteristic of flood-prone regions.

Feature classification was performed in a 3 × 3 moving window using the coefficient of variation (CV), or relative standard deviation (RSD), to distinguish between vegetation and built structures:

$$C_v=\frac{\mathrm{\sigma }}{\mathrm{\mu }}$$

where σ is the standard deviation of correlation and μ is equal to the mean correlation value for the 3 × 3 window. If C_v > 0.01 for a 3 × 3 window, pixels are classified as trees; otherwise, they are broadly classified as buildings. High-resolution, Google Earth imagery was used to identify areas of buildings, forests and patches of trees to evaluate the relative accuracy of the proposed classifier and its parameterization in identifying these features. The classification scheme performed particularly well at identifying tall structures for near and mid-range look angles, however, delineation of trees from buildings presented a challenge (Figure 4). Here, it is important to note that the main aim of the classification procedure is not to classify tall objects in order to retrieve or count the number of trees or built structures, but rather to create a bare-earth surface, hence classification error may actually be less important. It should be noted though that the threshold value attributed to C_v for identifying and classifying features should be adjusted for areas of different topographic characteristics and for other feature types for which SAR correlation will be different. For instance, in the case presented here, uniform roofs of large farming structures (abundant in the study region) exhibit high SAR correlation values and thus have a very low coefficient of variation, the value of which was determined using a trial-and-error iterative process. In the present effort, the goal is to derive a bare-earth DEM and so the need to accurately distinguish between different land cover types is certainly less important; however, for other applications this may be the actual objective and thus a sensitivity analysis of SAR correlation statistics for various land cover types may be necessary to conduct in a region of more diverse land cover.

FIGURE 4

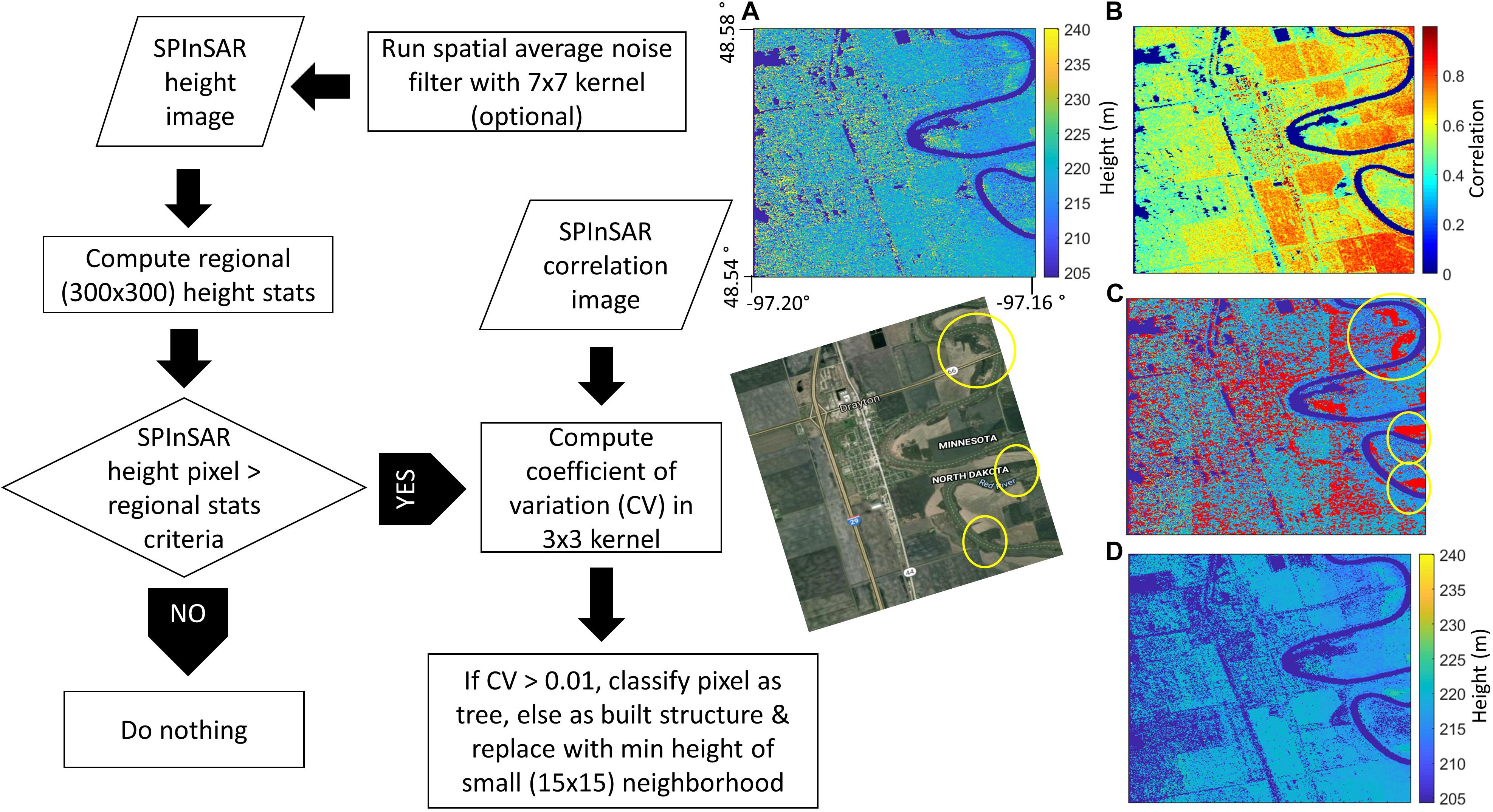
Figure 4. Flowchart and results of classifier based on informed relationships between InSAR height and correlation image data. Results: (A) Original SAR height image; (B) SAR signal correlation image; (C) SAR height image in (A) with pixels identified by the classifier in red; (D) Resulting SAR height image at 3 × 3 m before spatial aggregation to a bare-earth DEM, with tall vegetation (trees, etc.) and built structures successfully removed. The Google satellite image shown for visual comparison highlights classified groves of trees along the meandering Red River of the North. Note that shorter vegetation and the state of agricultural fields on the satellite image are not directly comparable to the SAR data that were acquired at a different time and during late winter.

Classified pixels were finally lowered to the minimum height of a 15 × 15 neighborhood. Spatial averaging may be used to further improve the height precision in the InSAR DEM, however, at the cost of resolution (Rodriguez and Martin, 1992; Schumann et al., 2016). As discussed, inundation models are highly sensitive to noise variation in topography, therefore, to improve DEM height precision for applications in flood modeling, the resulting gridded DEM was aggregated to a 30 × 30 m resolution; however, in order to get a better understanding of the influence of topographic complexity on the performance of the proposed classification scheme, a sensitivity analysis ought to be conducted, in which the size of the spatial kernel used to compute local height minima needs to be tied to the degree of topographic complexity (variation), particularly when moving into higher relief terrain. In fact, in Moller et al. (2017) a similar tree classification methodology was found to be very effective in extremely high relief terrain. The sensitivity of the classifier to the terrain relief will be a function of the window size over which height statistics are assessed and this evaluation/sensitivity study has not been done (yet). While there is a great deal of high-relief data already acquired and available, little is over populated areas.

Results

Accuracy Assessment

In order to derive a bare-earth DEM, we first removed any residual systematic cross-track tilts using the methodology discussed in see Section “GLISTIN-A InSAR Data” and illustrated by Figure 3. At a spatially aggregated DEM resolution of 30 m, this resulted in an overall negligible bias of – 2.5 cm. Convergence of this methodology validates our assumptions with respect to system stability over relevant acquisition time-frames (hours).

Next, an intelligent classifier based on informed relationships between InSAR height and correlation data was used to distinguish between bare-earth, buildings, and tall vegetation (Figure 4). Based on our evaluation of the classified SAR image using high-resolution satellite imagery, the classifier appeared to perform well at identifying tall features, however, it was not successful at distinguishing vegetation from built structures.

We derived a mosaiced, consistent, large-scale bare-earth DEM, which was collected as a series of five flight lines. When assessed at the more typical large-scale DEM resolution of 30 m, we concluded an overall negligible bias of −2.5 cm. Noted that this bias can be readily improved if required by increasing the signal-to-noise ratio of the data. Instrument customization, operational customization, and trade-offs enable this analogous-to-acquisition of LiDAR design, where point density and resolution are traded against acquisition cost. Using LiDAR terrain data and GPS ground control points from the National Geodetic Survey (NGS, Figure 5), we demonstrate suitability to a wide range of applications, particularly flood mapping, by achieving a RMSE of approximately 0.5 m (Table 2).

FIGURE 5

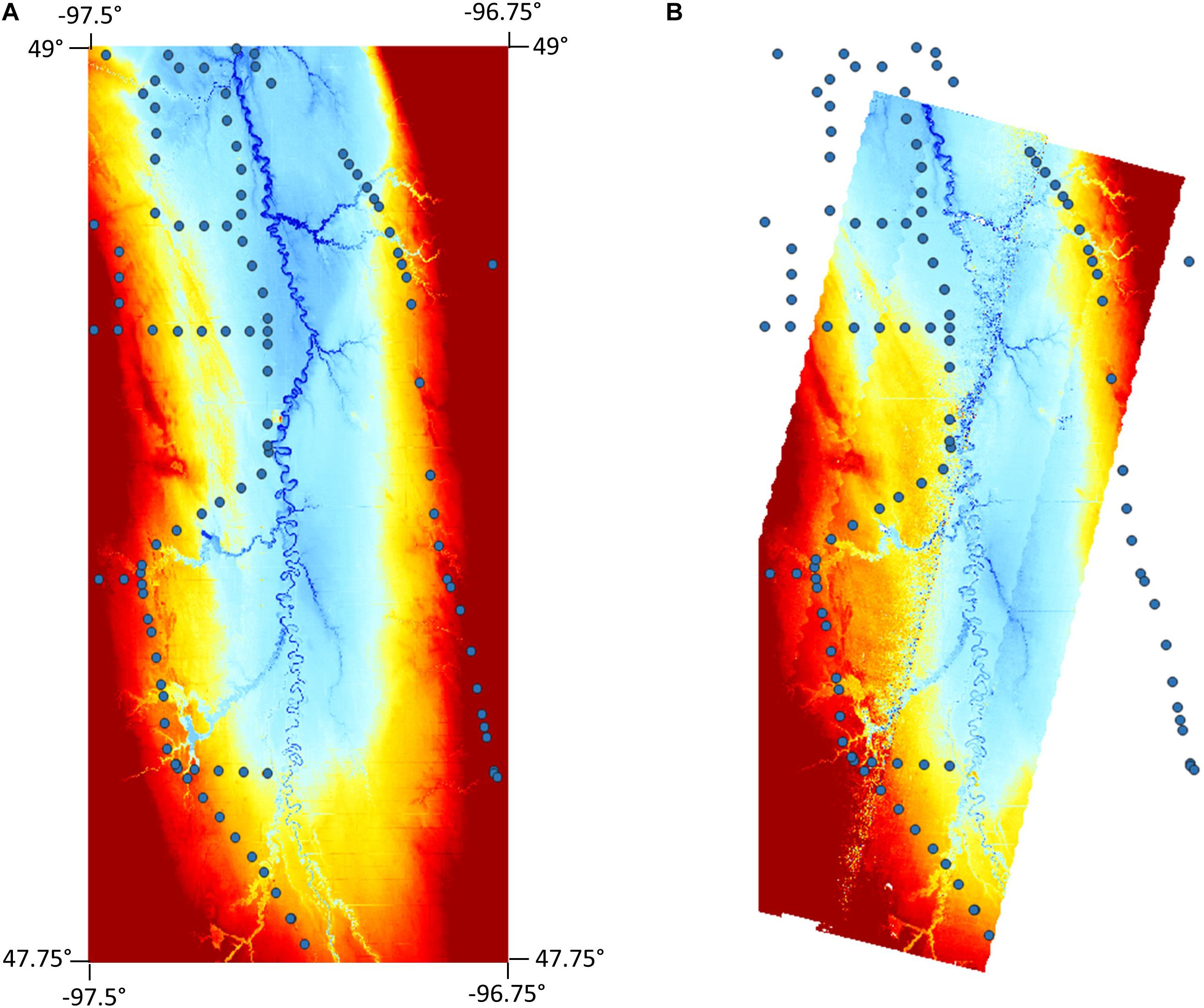
Figure 5. GPS network points overlain digital terrain models from (A) LiDAR and (B) GLISTIN-A InSAR. Height color scales for each DTM are equivalent (210–230 m).

TABLE 2

Table 2. Calculated errors for the SAR-derived DEM and LiDAR relative to GPS ground-control points, as well as SAR vs. LiDAR.

The height errors between SPInSAR and LiDAR reported in Table 2 are all computed at the location of the GPS network points, so as to avoid using LiDAR as a “truth” reference but instead as a direct comparison to the SPInSAR technology. It is, however, worth noting that in terms of overall height performance across the study region, LiDAR may be expected to perform better on average given the inherent noise level in the raw SAR data; although performance discrepancies between the two technologies may be acceptable depending, of course, on the application.

Discussion

LiDAR vs. GLISTIN-A

For obvious reasons, obtaining a high-resolution, high-accuracy LiDAR terrain (i.e., bare earth) model over floodplains and low-lying coastal areas is preferable – in particular, where such areas have very shallow gradients, such as the RRN floodplain. With a high signal pulse density per unit area and almost no random noise component, airborne LiDAR technology is capable of resolving minimal topographic variations and microtopographic features that define and control non-trivial floodplain flow pathways. In fact, LiDAR, with a typical vertical RMSE of 15–20 cm, helped shift the flood modeling community from a traditionally data-poor environment to a data-rich environment, which led to a large number of model advances and a rethinking of model design (Bates, 2004). However, as already argued by Schumann et al. (2016), over large, wide floodplains, LiDAR can quickly become prohibitively expensive due to its typically small swath width and thus, requires many overlapping flight lines to cover the total area of interest at high resolution. For large area coverage, wide-swath, single-pass airborne InSAR, therefore, presents notable advantages and has the potential to become much more cost-effective.

In this context, an airborne campaign with overpasses at different times (e.g., at different seasons) using a GLISTIN-A type sensor can be easily envisaged and becomes indeed very competitive in resource allocation and cost. A GLISTIN-A flight pass was repeated over the same study site in snow and ice conditions. This data set, coupled with the dry baseline DTM, allows identification of river ice jams as well as volumetric estimation of the floodplain snowpack. While examining the latter capability for this site is outside the scope of this study, snowpack volume estimation with GLISTIN-A has been successfully demonstrated over the Sierra Nevada (CA, United States) by Moller et al. (2017).

Flood Mapping Potential

The above-mentioned attributes make GLISTIN-A type technology highly relevant and applicable to flood mapping and modeling. It is well known that while variations of in-channel water levels (determined by local flow conditions) drive the timing and amount of river bank overtopping and subsequent flooding of adjacent low-lying land, it is variations in floodplain topography that control floodplain flow paths and the inundated area during a flood event; thus, microtopography and floodplain features, such as buildings, walls, trees, etc., become significant, particularly when interested in localized flow conditions and associated floodplain inundation at the small scale (Mason et al., 2003). Microtopographic features and variations in microtopography are only included in flood inundation (i.e., 2-D hydrodynamic) models when high-resolution, high-precision data on floodplain heights are available. In most cases, however, their effects are parameterized in models of grid resolutions that are typically orders of magnitude larger than the microtopographic controls (Dottori et al., 2013).

Within this context, Mason et al. (2003) state that the typical vertical accuracy of floodplain heights from airborne LiDAR (10 to 20 cm RMSE) provides a realistic lower limit for DEM quality as beyond this, the sensor signal becomes indistinguishable from “noise” generated by background microtopographic features. In line with this reasoning, it is fair to assume that a vertical error of 2σ of the lower limit (∼40 cm) sets an adequate upper limit target value.

In the case study presented here, the DTM generated from the GLISTIN-A InSAR data had a mean absolute error of 0.421 m and a RMSE of 0.537 compared to geodetic ground control points. This makes it suitable for flood mapping and modeling, with much better accuracy than can be obtained with conventional wide-swath, imagery-derived DTMs, such as from satellite InSAR technology or commercial multi-pair optical imagery, which typically exhibit much larger vertical errors.

Conclusion

In this study, we demonstrate the success of a new InSAR calibration technique that removes the need for ground control points and LiDAR by leveraging areas of swath overlap in the same airborne acquisition. Furthermore, we showcase the potential of InSAR image classifiers to generate floodplain DEMs with vertical accuracies suitable for high-resolution hydrodynamic modeling. Averaging to a spatial resolution of 30 m after classification, a mean error in the vertical as low as 12 cm was obtained. More research on classification algorithms is indeed required to automate the DEM-generation process and to make such classifiers readily available in commercial software. The results of this case study, however, demonstrate the potential of airborne InSAR as a cost-effective alternative to LiDAR for large-scale flood mapping, thus diminishing barriers to acquisition in the developing world and furthering the prospect of a free, global, high-resolution DEM. The InSAR DEM presented here will be examined in a follow-on study in the RRN floodplain, where its performance will be evaluated using a real-case, 2D flood model application.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

GS and DM are employed by Remote Sensing Solutions.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

DF’s time on this work was supported by the COAST internship program. The GLISTIN-A flights were funded under NASA’s Terrestrial Hydrology Program. The GLISTIN-A data are available from the JPL UAVSAR data website (https://uavsar.jpl.nasa.gov/cgi-bin/data.pl) and the DEM can be shared upon request.

Acknowledgments

The authors thank the NASA-JPL UAVSAR team for the GLISTIN-A data acquisition and calibration.

References

Bates, P. D. (2004). Invited commentary: remote sensing and flood inundation modelling. Hydrol. Process. 18, 2593–2597. doi: 10.1002/hyp.5649

CrossRef Full Text | Google Scholar

Baugh, C. A., Bates, P. D., Schumann, G., and Trigg, M. A. (2013). SRTM vegetation removal and hydrodynamic modeling accuracy. Water Resour. Res. 49, 5276–5289. doi: 10.1002/wrcr.20412

CrossRef Full Text | Google Scholar

Dottori, F., Di Baldassarre, G., and Todini, E. (2013). Detailed data is welcome, but with a pinch of salt: accuracy, precision, and uncertainty in flood inundation modeling. Water Resour. Res. 49, 6079–6085. doi: 10.1002/wrcr.20406

CrossRef Full Text | Google Scholar

Mason, D. C., Cobby, D. M., Horritt, M. S., and Bates, P. D. (2003). Floodplain friction parameterization in two-dimensional river flood models using vegetation heights derived from airborne scanning laser altimetry. Hydrol. Process. 17, 1711–1732. doi: 10.1002/hyp.1270

CrossRef Full Text | Google Scholar

Moller, D., Andreadis, K. M., Bormann, K. J., Hensley, S., and Painter, T. H. (2017). Mapping snow depth from ka-band interferometry: proof of concept and comparison with scanning lidar retrievals. IEEE Geosci. Remote Sens. Lett. 14, 886–890. doi: 10.1109/LGRS.2017.2686398

CrossRef Full Text | Google Scholar

Moller, D., Hensley, S., Mouginot, J., Willis, J., Wu, X., Larsen, C., et al. (2019). Validation of glacier topographic acquisitions from an airborne single-pass interferometer. Sensors 19:3700. doi: 10.3390/s19173700

PubMed Abstract | CrossRef Full Text | Google Scholar

Moller, D., Hensley, S., Sadowy, G. A., Fisher, C. D., Michel, T., Zawadzki, M., et al. (2011). The glacier and land ice surface topography interferometer: an airborne proof-of-concept demonstration of high-precision ka-band single-pass elevation mapping. IEEE Trans. Geosci. Remote Sens. 49, 827–842. doi: 10.1109/tgrs.2010.2057254

CrossRef Full Text | Google Scholar

Rabus, B., Eineder, M., Roth, A., and Bamler, R. (2003). The shuttle radar topography mission- a new class of digital elevation models acquired by spaceborne radar. Photogramm. Rem. Sens. 57, 241–262. doi: 10.1016/s0924-2716(02)00124-7

CrossRef Full Text | Google Scholar

Rodriguez, E., and Martin, J. M. (1992). Theory and design of interferometric synthetic-aperture radars. Proc. IEEE 139, 147–159. doi: 10.1049/ip-f-2.1992.0018

CrossRef Full Text | Google Scholar

Rosen, P. A., Hensley, S., Joughin, I. R., Li, F. K., Madsen, S. N., Rodriquez, E., et al. (2000). Synthetic aperture radar interferometry. Proc. IEEE 88, 333–382. doi: 10.1109/5.838084

CrossRef Full Text | Google Scholar

Schumann, G. J.-P., and Bates, P. D. (2018). The need for a high-accuracy, open-access global DEM. Front. Earth Sci. 6:225. doi: 10.3389/feart.2018.00225

CrossRef Full Text | Google Scholar

Schumann, G. J. P., Bates, P. D., Neal, J. C., and Andreadis, K. M. (2014). Technology: fight floods on a global scale. Nature 507:169. doi: 10.1038/507169e

PubMed Abstract | CrossRef Full Text | Google Scholar

Schumann, G. J.-P., Moller, D. K., and Mentgen, F. (2016). High-accuracy elevation data at large scales from airborne single-pass SAR interferometry. Front. Earth Sci. 3:88. doi: 10.3389/feart.2015.00088

CrossRef Full Text | Google Scholar

Tuttle, S. E., Cho, E., Restrepo, P. J., Jia, X., Vuyovich, C., Cosh, M., et al. (2017). “Remote sensing of drivers of spring snowmelt flooding in the north central U.S,” in Remote Sensing of Hydrological Extremes, ed. V. Lakshmi, (Cham: Springer), 21–45. doi: 10.1007/978-3-319-43744-6-2

CrossRef Full Text | Google Scholar

Zebker, H. A., Hensley, S., Shanker, P., and Wortham, C. (2010). Geodetically accurate InSAR data processor. IEEE Trans. Geosci. Remote Sens. 48, 4309–4321. doi: 10.1109/TGRS.2010.2051333

CrossRef Full Text | Google Scholar